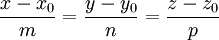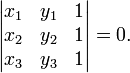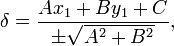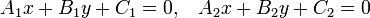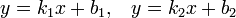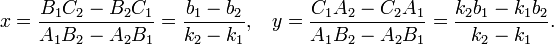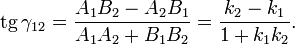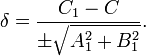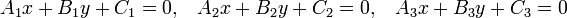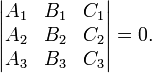Прямая на плоскости – необходимые сведения
Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.
Прямая на плоскости – понятие
Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.
Если карандашом дотронуться до стола, останется отметина, которую можно называть «точкой». Таким образом, получим представление о точке на плоскости.
Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.
Взаимное расположение прямой и точки
Имеем аксиому:
Определение 1На каждой прямой и в каждой плоскости могут быть отмечены точки.
Точки обозначают как большими, так и маленькими латинскими буквами. Например, А и D или a и d.
Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.
Чтобы обозначить, принадлежит точка плоскости или точка прямой, используют знак «∈». Если в условии дано, что точка A лежит на прямой a, тогда это имеет такую форму записи A∈a. В случае, когда точка А не принадлежит, тогда другая запись A∉a.
Справедливо суждение:
Определение 2Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.
Данное высказывание считается акисомой, поэтому не требует доказательств. Если рассмотреть это самостоятельно, видно, что при существующих двух точках имеется только один вариант их соединения. Если имеем две заданные точки А и В, то прямую, проходящую через них можно назвать данными буквами, например, прямая АВ
zaochnik.com
Прямая линия — это… Что такое Прямая линия?
Прямая — одно из основных понятий геометрии.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.
- Через любые две несовпадающие точки можно провести единственную прямую.
- Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными.
- В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
- Прямая линия — алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
Уравнения прямой на плоскости
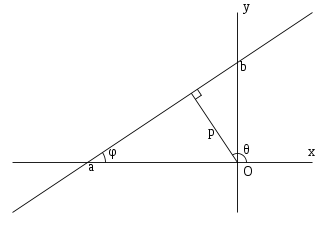 Способы задания прямой:
Способы задания прямой: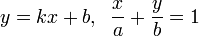 или
или 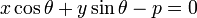
Общее уравнение прямой линии на плоскости в декартовых координатах:
где A и B одновременно не равны нулю. При C = 0 прямая проходит через начало координат.
Уравнение прямой с угловым коэффициентом. Прямая линия, пересекающая ось Oy в точке 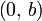 и образующая угол φ с положительным направлением оси Ox:
и образующая угол φ с положительным направлением оси Ox:
Коэффициент k называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси Oy.
Уравнение прямой в отрезках. Прямая линия, пересекающая ось Ox в точке 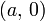
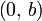 :
:В этом виде невозможно представить прямую, проходящую через начало координат.
Нормальное уравнение прямой:
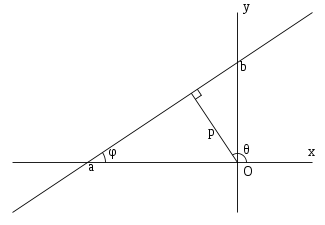
где p — длина перепендикуляра, опущенного на прямую из начала координат, а θ — угол (измеренный в положительном направлении) между положительным направлением оси Ox и направлением этого перпендикуляра. Если p = 0, то прямая проходит через начало координат, а угол 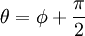
Если прямая задана общим уравнением Ax + By + C = 0, то отрезки a и b, отсекаемые ею на осях, угловой коэффициент k, расстояние прямой от начала координат p, cosθ и sinθ выражаются через коэффициенты A, B и C следующим образом:
Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие p > 0. В этом случае cosθ и sinθ являются направляющими косинусами положительной нормали прямой — перпендикуляра, опущенного из начала координат на прямую. Если C = 0, то прямая проходит через начало координат и выбор положительного напрвления произволен.
Уравнение прямой, проходящей через две заданные несовподающие точки 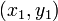 и
и 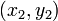
или
или в общем виде
Параметрические уравнения прямой могут быть записаны в виде:
где t — производный параметр, при этом
Уравнение прямой в полярных координатах ρ и φ:
или
Тангенциальное уравнение прямой на плоскости:
- ξx + ηy = 1
Числа ξ и η называются её тангенциальными, линейными или плюккеровыми координатами.
Уравнения прямой в пространстве
Каноническое уравнение прямой в пространстве:
- Пусть M(x0,y0,z0) — точка, лежащая на прямой, и
 — вектор, ей коллинеарный. Тогда уравнение прямой имеет вид:
— вектор, ей коллинеарный. Тогда уравнение прямой имеет вид: 
Взаимное расположение точек и прямых
Три точки 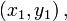
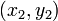 и
и 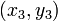 лежат на одной прямой тогда и только тогда, если выполняется условие
лежат на одной прямой тогда и только тогда, если выполняется условие
Отклонение точки 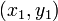 от прямой Ax + By + C = 0 может быть найдено по формуле
от прямой Ax + By + C = 0 может быть найдено по формуле
где знак перед радикалом противоположен знаку C. Отклонение по модулю равно расстоянию между точкой и прямой; оно положительно, если точка и начало координат лежат по разные стороны от прямой, и отрицательно, если по одну сторону.
Взаимное расположение нескольких прямых
Две прямые, заданные уравнениями
или
пересекаются в точке
Угол γ12 между пересекающимися прямыми определяется формулой
При этом под γ12 понимается угол, на который надо повернуть первую прямую (заданную параметрамиA1, B1, C1, k1 и b1) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.
Эти прямые параллельны, если A1B2 − A2B1 = 0 или k1 = k2, и перпендикулярны, если A1A2 + B1B2 = 0 или 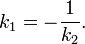
Любую прямую, паралельную A1x + B1y + C1 = 0, можно выразить уравнением A1x + B1y + C = 0. При этом расстояние между ними будет равно
Если знак перед радикалом противоположен C1, то δ будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой.
Для того, чтобы три прямые
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие
См. также
Ссылки
Wikimedia Foundation. 2010.
dal.academic.ru
Отрезок и его обозначение. Концы отрезка
Отрезок – это часть прямой линии, ограниченная двумя точками. Точки, ограничивающие отрезок, называются концами отрезка.
Проведём прямую и отметим на ней две точки A и B. Часть прямой между этими точками – это отрезок, а точки A и B – концы отрезка:

Отрезок обозначается указанием его концов. Говорят или пишут: отрезок AB
или отрезок BA
.
Часто, при обозначении отрезков на прямой линии или просто для построения отдельного отрезка, вместо точек, обозначающих концы отрезка, ставят небольшие чёрточки:

Рассмотрим как с помощью обычной линейки можно построить отрезок более длинный, чем сама линейка. Приложим к листу бумаги линейку, отметим точки A и B и какую-нибудь точку C, лежащую между точками A и B:

Затем передвинем линейку вправо так, чтобы её левый конец оказался около точки C, и отметим точку D около правого конца линейки:

И так, точки A, B, C и D лежат на одной прямой. Сначала проведём отрезок AB:

Затем проведём отрезок BD и получим в результате отрезок AD, более длинный, чем линейка:

naobumium.info
Прямая — это… Что такое Прямая?
Прямая — одно из основных понятий геометрии, то есть точного универсального определения не имеет.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.
Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить как линию, путь вдоль которой равен расстоянию между двумя точками.
Аналитически прямая задаётся уравнением (в трёхмерном пространстве — системой уравнений) первой степени.
- Через любые две несовпадающие точки можно провести единственную прямую.
- Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными.
- В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
- Прямая линия — алгебраическая линия первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
Уравнения прямой на плоскости
 Способы задания прямой:
Способы задания прямой:или .
Общее уравнение прямой
Общее уравнение прямой линии на плоскости в декартовых координатах:
где , и — произвольные постоянные, причем постоянные и не равны нулю одновременно. Вектор с координатами точки называется нормальным вектором, он перпендикулярен прямой.
При прямая проходит через начало координат. Также уравнение можно переписать в виде
Уравнение прямой с угловым коэффициентом
Уравнение прямой линии, пересекающей ось в точке и образующей угол с положительным направлением оси :
Коэффициент называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси
Получение уравнения прямой в отрезкахУравнение прямой в отрезках
Уравнение прямой линии, пересекающей ось в точке и ось в точке :
В этом виде невозможно представить прямую, проходящую через начало координат.
Нормальное уравнение прямой
где — длина перпендикуляра, опущенного на прямую из начала координат, а — угол (измеренный в положительном направлении) между положительным направлением оси и направлением этого перпендикуляра. Если , то прямая проходит через начало координат, а угол задаёт угол наклона прямой.
Вывод нормального уравнения прямой
Если прямая задана общим уравнением то отрезки и отсекаемые ею на осях, угловой коэффициент расстояние прямой от начала координат и выражаются через коэффициенты , и следующим образом:
Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие В этом случае и являются направляющими косинусами положительной нормали прямой — перпендикуляра, опущенного из начала координат на прямую. Если то прямая проходит через начало координат и выбор положительного направления произволен.
Уравнение прямой, проходящей через две заданные несовпадающие точки
Если заданы две несовпадающие точки с координатами и , то прямая, проходящая через них, задаётся уравнением
или
или в общем виде
Векторное параметрическое уравнение прямой
Векторное параметрическое уравнение прямой задается вектором конец которого лежит на прямой, и направляющим вектором прямой Параметр пробегает все действительные значения.
Параметрические уравнения прямой
Параметрические уравнения прямой могут быть записаны в виде:
где — производный параметр, — координаты и направляющего вектора прямой. При этом
Смысл параметра аналогичен параметру в векторно-параметрическом уравнении.
Каноническое уравнение прямой
Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
где — координаты и направляющего вектора прямой, и координаты точки, принадлежащей прямой.
Уравнение прямой в полярных координатах
Уравнение прямой в полярных координатах и :
или
Тангенциальное уравнение прямой
Тангенциальное уравнение прямой на плоскости:
Числа и называются её тангенциальными, линейными или плюккеровыми координатами
.Уравнения прямой в пространстве
Векторное параметрическое уравнение прямой в пространстве:
где — радиус-вектор некоторой фиксированной точки лежащей на прямой, — ненулевой вектор, коллинеарный этой прямой (называемый её направляющим вектором), — радиус-вектор произвольной точки прямой.
Параметрические уравнения прямой в пространстве:
где — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.
Каноническое уравнение прямой в пространстве:
где — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.
Общее векторное уравнение прямой[уточнить] в пространстве:
- Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:
- и
то уравнение прямой можно задать системой этих уравнений:
Векторное уравнение прямой в пространстве[1]:196-199:
- Уравнение прямой в пространстве можно записать в виде векторного произведения радиуса-вектора произвольной точки этой прямой на фиксированный направляющий вектор прямой :
где фиксированный вектор , ортогональный вектору , можно найти, подставляя в это уравнение радиус-вектор какой-нибудь одной известной точки прямой.
Взаимное расположение точек и прямых на плоскости
Три точки , и лежат на одной прямой тогда и только тогда, когда выполняется условие
Отклонение точки от прямой может быть найдено по формуле
где знак перед радикалом противоположен знаку Отклонение по модулю равно расстоянию между точкой и прямой; оно положительно, если точка и начало координат лежат по разные стороны от прямой, и отрицательно, если по одну сторону.
В пространстве расстояние от точки до прямой, заданной параметрическим уравнением
можно найти как минимальное расстояние от заданной точки до произвольной точки прямой. Коэффициент этой точки может быть найден по формуле
Взаимное расположение нескольких прямых на плоскости
Две прямые, заданные уравнениями
или
пересекаются в точке
Угол между пересекающимися прямыми определяется формулой
При этом под понимается угол, на который надо повернуть первую прямую (заданную параметрами , , , и ) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.
Эти прямые параллельны, если или , и перпендикулярны, если или .
Любую прямую, параллельную прямой с уравнением можно выразить уравнением При этом расстояние между этими прямыми будет равно
Если знак перед радикалом противоположен то будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой.
Для того, чтобы три прямые
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие
Если и , то прямые и перпендикулярны.
См. также
Примечания
Ссылки
ushakov.academic.ru
Значение слова ПРЯМОЙ. Что такое ПРЯМОЙ?
ПРЯМО́Й, —а́я, —о́е; прям, пряма́, пря́мо.
1. Ровно вытянутый в каком-л. направлении, без изгибов. Прямая линия.□ Путь наш лежал по узкой, но прямой, как линейка, проселочной дороге. Чехов, Страхи. || Идущий напрямик. Проезжей дорогой в Алешино — девять километров, а прямой тропкой — всего пять. Гайдар, Дальние страны. || Гладкий, не вьющийся (о волосах). [Андрей] был высоконький, худощавый, хорошо сложенный мальчик с рыже-русыми прямыми волосами, гладко зачесанными назад. Панова, Времена года. || Расположенный в центре, не сбоку. Расчесать волосы на прямой пробор. || Не сутулый, не согнутый. Прямой стан.□ Войнич вышла к нам все такая же прямая, хотя, как показалось мне, ступала она не так уже твердо. Б. Полевой, Встреча с легендой.
2. только полн. ф. Обеспечивающий непосредственную связь кого-, чего-л. с кем-, чем-л. Прямое сообщение. Говорить по прямому проводу.
3. только полн. ф. Непосредственный, без промежуточных ступеней. Прямые выборы. Прямые указания. Прямое обращение к массам. □ Первые успехи на переправе — — такое событие, которое он сам и не представляет без своего прямого личного участия. Емельянова, Гвардии полковник Гламазда. || Непосредственный, ближайший. Он каждое утро убирал кабинет, что было его прямой и главной обязанностью. Мамин-Сибиряк, Человек с прошлым.
4. Откровенный, правдивый. — Григорий Михайлович, вы человек прямой, вы ведь всегда говорили правду. Тургенев, Дым. Говорят, что нет никого, кто бы не боялся в бою; всякий нехвастливый и прямой человек на вопрос: страшно ли ему, ответит: страшно. Гаршин, Из воспоминаний рядового Иванова. || Выражающий откровенность, правдивость. Прямой взгляд.□ — А в этом в твоем строительстве, прости 552 старика за прямое слово, нет ни расчета, ни сообразности. Николаева, Жатва.
5. Явный, открытый. Прямой вызов. Прямой обман. Прямые улики. □ Не так он, как другие, любит, Прямой отказ его погубит, И чтоб снести его он мог, Нужны пощада и предлог. А. К. Толстой, Алхимик. Вопрос ясен и прям; его не назовешь наводящим. Ясна и цель анкеты — узнать фактическое положение, подойти к истине. Бек, Почтовая проза. || только полн. ф. Подлинный, настоящий, действительный. Дурачина ты, прямой простофиля! Выпросил, простофиля, избу! Пушкин, Сказка о рыбаке и рыбке. За лето я дважды видел панику на пароходе и оба раза она была вызвана не прямой опасностью, а страхом перед возможностью ее. М. Горький, В людях. || только полн. ф. Несомненный, безусловный, очевидный. Прямая польза. Прямой расчет сделать так. □ Хозяйственники должны понять, что от хорошей столовой помимо всего прочего прямая выгода производству. Киров, Статьи и речи 1934.
6. только полн. ф. Буквальный, не переносный. Прямое значение слова.
7. в знач. сущ. пряма́я, —о́й, ж. Мат. То же, что прямая линия . Провести прямую.
8. только полн. ф. Мат. Такой, при котором увеличение (или уменьшение) одного вызывает увеличение (или уменьшение) другого. Прямая пропорциональность.
◊
Прямой ворот — стоячий ворот, застегивающийся спереди. Прямой выстрел ( спец.) — выстрел, при котором траектория пули, снаряда приближается к прямой линии. Прямое дополнение ( грамм.) — дополнение при переходном глаголе в винительном падеже без предлога. Прямая дорога или прямой путь — непосредственный, ближайший путь к чему-л. (к успеху, славе, преступлению и т. п.). Прямая кишка ( анат.) — конечная часть кишечного канала в виде короткой прямой трубки. Прямая линия ( мат.) — линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия родства — родословная от отца к сыну, от сына к внуку. Прямая наводка ( воен.) — наводка по видимой цели. Прямые налоги ( фин.) — налоги с дохода, имущества. Прямое попадание — непосредственное поражение цели снарядом, бомбой, миной. Прямая речь ( грамм.) — чужая речь, переданная без изменений от лица говорящего. Прямой угол — угол в 90 градусов. По прямой — кратчайшим путем, напрямик. — Чтобы доехать отсюда до Москвы, надо потратить почти полмесяца!.. Десять тысяч километров по прямой! Чаковский, У нас уже утро. Я повел самолет по прямой, линия фронта была недалеко. Каверин, Два капитана.kartaslov.ru
Ответы@Mail.Ru: КАК ОБОЗНАЧАЮТ ПРЯМУЮ
Аделя <a rel=»nofollow» href=»http://gdz5.cf/30496″ target=»_blank»>»посмотри здесь, страница 172″</a>.
Аделя я вчера здесь нашел, страница 124 (!скрытая ссылка: скопируй и вставь в адресную строку браузера!) 5c2e%2ega/v
На одном конце линии поставь (.) .
Способы обозначения прямых: 1) Строчной латинской буквой: обозначение прямой «а» Прямая «a». 2) Двумя заглавными латинскими буквами в том случае, если этими буквами обозначены точки, расположенные на прямой. обозначение прямой АВ Прямая «АB».
touch.otvet.mail.ru
Таблица числовых промежутков: виды, обозначения, изображения
Среди множеств чисел имеются множества, где объектами выступают числовые промежутки. При указывании множества проще определить по промежутку. Поэтому записываем множества решений, используя числовые промежутки.
Данная статья дает ответы на вопросы о числовых промежутках, названиях, обозначениях, изображениях промежутков на координатной прямой, соответствии неравенств. В заключение будет рассмотрена таблица промежутков.
Виды числовых промежутков
Определение 1Каждый числовой промежуток характеризуется:
- названием;
- наличием обычного или двойного неравенства;
- обозначением;
- геометрическим изображением на координатой прямой.
Числовой промежуток задается при помощи любых 3 способов из выше приведенного списка. То есть при использовании неравенства, обозначения, изображения на координатной прямой. Данный способ наиболее применимый.
Произведем описание числовых промежутков с выше указанными сторонами:
Определение 2- Открытый числовой луч. Название связано с тем, что его опускают, оставляя открытым.
Этот промежуток имеет соответствующие неравенства x<a или x>a, где a является некоторым действительным числом. То есть на такое луче имеются все действительные числа, которые меньше a — (x<a) или больше a — (x>a).
Множество чисел, которые будут удовлетворять неравенству вида x<a обозначается виде промежутка (−∞, a), а для x>a, как (a, +∞).
Геометрический смыл отрытого луча рассматривает наличие числового промежутка. Между точками координатной прямой и ее числами имеется соответствие, благодаря которому прямую называем координатной. Если необходимо сравнить числа, то на координатной прямой большее число находится правее. Тогда неравенство вида x<a включает в себя точки, которые расположены левее, а для x>a – точки, которые правее. Само число не подходит для решения, поэтому на чертеже обозначают выколотой точкой. Промеж
zaochnik.com
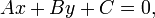
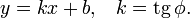
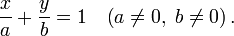
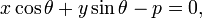
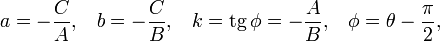
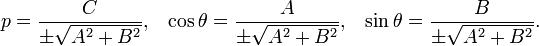
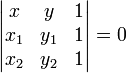
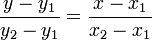
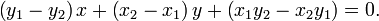
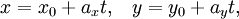
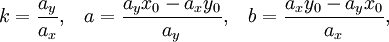
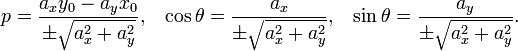
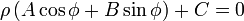
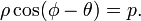
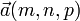 — вектор, ей коллинеарный. Тогда уравнение прямой имеет вид:
— вектор, ей коллинеарный. Тогда уравнение прямой имеет вид: