Обозначение геометрических фигур буквами / Основы геометрии / Справочник по математике для начальной школы

В математике есть правило: обозначать геометрические фигуры заглавными буквами латинского алфавита. Сегодня мы научимся этому.

Точка

Например, 

Мы читаем:

точка А, точка С, точка D, точка Е и точка F.

Задание:

Какая точка лежит на прямой?

Ответ: точка К.

---

Отрезок

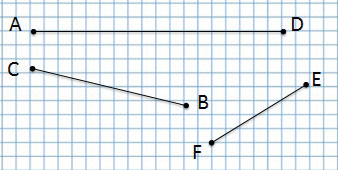
Мы читаем:

отрезок AD, отрезок СВ, отрезок FE

Задание:

Сколько всего отрезков на данном чертеже?

Ответ: 6 отрезков.

---

Ломаная линия

Мы читаем:

Ломаная линия ADCFE

А эта ломаная линия совсем по-другому, потому что соединение точек у неё другое:

Ломаная линия ACDFE

Прочитаю название следующей ломаной линии:

Ломаная линия AFDCE

---

Многоугольники

Мы читаем:

Треугольник ADE

Четырёхугольник CADB

Квадрат ABCD

Шестиугольник AKPOMN

---

Угол 

Угол обозначается тремя буквами. В середине указывается буква, которая обозначает вершину угла.

Мы читаем:

1 угол: угол BAC или CAB с вершиной А

2 угол: угол AOD  или DOA с вершиной О

3 угол: угол AED или DEA с вершиной Е

4 угол: угол BCD или DCB с вершиной С

budu5.com

Термины и определения начертательной геометрии

Содержание

1. Термины и определения;
2. Условные обозначения;
3. Способы задания плоскости на чертеже.

Термины и определения

Комплексный чертеж (эпюр Монжа) – чертеж, составленный из взаимосвязанных ортогональных проекций геометрической фигуры. Чтобы преобразовать пространственный макет в эпюр, нужно совместить плоскости проекций П₁ и П₃ с третьей плоскостью П₂, вращая П₁ вокруг оси x, а П₃ вокруг оси z.

Конкурирующие точки – точки, расположенные на одной проецирующей прямой, но при этом удаленные от плоскости проекций на разное расстояние.

Линии уровня – прямые, параллельные одной из плоскостей проекций.

• Горизонталь, h – прямая, параллельная горизонтальной плоскости;
• Фронталь, f – прямая, параллельная фронтальной плоскости;
• Профильная прямая, p – прямая, параллельная профильной плоскости.

Метрические задачи – это задачи, целью решения которых является нахождение натуральных величин отрезков, углов, расстояний.

Октант – часть пространства, ограниченная плоскостями проекций П₁, П₂, П₃. В начертательной геометрии выделяют восемь октантов, нумерация и взаимное расположение которых показаны на рисунке.

Отрезок – участок прямой, ограниченный двумя точками.

Плоскости общего положения – плоскости, которые не перпендикулярны ни одной из плоскостей проекций.

Плоскости уровня – плоскости, параллельные одной из плоскостей проекций.

Позиционные задачи – это задачи, целью решения которых является определение взаимного расположения фигур, нахождение точек и линий их пересечения.

Проецирующие плоскости – плоскости, перпендикулярные одной из плоскостей проекций.

Прямые общего положения – прямые, не параллельные ни одной из плоскостей проекций.

Проецирующие прямые – прямые, перпендикулярные одной из плоскостей проекций.

Следы плоскости – прямые, по которым данная плоскость пересекается с плоскостями проекций.

Следы прямой – точки пересечения прямой с плоскостями проекций.

Угол между прямой и плоскостью – угол между прямой и её проекцией на эту плоскость.

Условные обозначения

Оси координат:

• x – ось абсцисс;
• y – ось ординат;
• z – ось аппликат.

Проекции точек:

• A’, B’, C’ … Z’ или A₁, B₁, C₁ … Z₁ – горизонтальные;
• A», B», C» … Z» или A₂, B₂, C₂ … Z₂ – фронтальные;
• A»’, B»’, C»’ … Z»’ или A₃, B₃, C₃ … Z₃ – профильные.

Проекции прямых:

• a’, b’, c’ … z’ или a₁, b₁, c₁ … z₁ – горизонтальные;
• a», b», c» … z» или a₂, b₂, c₂ … z₂ – фронтальные;
• a»’, b»’, c»’ … z»’ или a₃, b₃, c₃ … z₃ – профильные.

Плоскости проекций:

• П₁ или H – горизонтальная;
• П₂ или V – фронтальная;
• П₃ или W – профильная.

Следы плоскости α:

• h_0α – горизонтальный;
• f_0α – фронтальный;
• p_0α – профильный.

Следы прямой l:

• H_l – горизонтальный;
• F_l – фронтальный;
• W_l – профильный.

Способы задания плоскости на комплексном чертеже

Плоскость на комплексном чертеже может быть задана шестью различными способами:

1. Тремя точками, которые не лежат на одной прямой. На рисунке это т. A, B, C.
2. Прямой и точкой, не лежащей на этой прямой.
3. Двумя пересекающимися прямыми.
4. Двумя параллельными прямыми (пересекающимися в несобственной точке).
5. Отсеком плоской фигуры Ф.
6. Следами. Этот способ удобен тем, что позволяет наглядно представить расположение плоскости в пространстве.

Дополнительные материалы:

ngeometry.ru

Угол / Начальные геометрические сведения / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Начальные геометрические сведения
5. Угол

Угол — геометрическая фигура

Мы знаем, что углом называется геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

Лучи — это сто­роны угла, а точка (их общее начало) — вершина угла

---

Изображать угол можно и так (не отмечаем точкой общее начало, считаем, что точка есть)

 

Обозначения угла

1)

На сторонах угла не отмечены точки (только обозначены большими латинскими буквами А и В)

Считается, что буква А обозначает любую точку на верхней стороне угла (по данному рисунку)

Точка В обозначает любую точку на нижней стороне угла (по данному рисунку)

Читаем: угол АОВ

Пишем: АОВ

---

2)

На сторонах угла отмечены и обозначены произвольные точки А и В 

Читаем: угол АОВ

Пишем:  АОВ

---

3)

Стороны угла (лучи) обозначены малыми латинскими буквами k и m

Читаем: угол km

Пишем:  km

---

4)

Обозначена только вершина угла

Читаем: угол О

Пишем: О

 

Развернутый угол

Построим прямую АВ и отметим на этой прямой точку О

Лучи ОА и ОВ лежат на одной прямой (являются дополнительными)

Угол АОВ называется развернутым

 

Угол на плоскости

Изобразим часть плоскости

(так как плоскость бесконечна, мы не можем изобразить ее всю, только часть ее)

Построим на этой плоскости неразвернутый угол

Этот угол делит плоскость на две части (области) — внешнюю и внутреннюю

---

Замечание

Любой

угол разделяет плоскость на две ча­сти. Названия этих частей ( внутренняя область и внешняя область) применяется для неразвернутого угла.

Если угол развёрнутый, то любую из двух частей, на которые он разделяет плоскость, мож­но считать внутренней областью угла.

---

 

Расположение точек относительно угла

По рисунку определим положение отмеченных точек A, B, C, D, K, M

Точки А и В лежат на сторонах угла

Точки D и C лежат вне угла (во внешней об­ласти угла)

Точки К и М, лежат внутри угла (во внутренней об­ласти угла)

---

При необходимости мы можем продолжить стороны угла, например, чтобы уточнить положение точки М

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Градусная мера угла

Измерение углов на местности

Смежные углы

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

Начальные геометрические сведения

Правило встречается в следующих упражнениях:

7 класс

Задание 54, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 69, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 223, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 226, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 270, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 324, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 589, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 640, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1035, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© budu5.com, 2019

Пользовательское соглашение

Copyright

budu5.com