Обратная функция. Урок алгебры в 10-м классе (профильный уровень)
Цели урока:
Образовательная:
- формировать знания по новой теме в соответствии с программным материалом;
- изучить свойство обратимости функции и научить находить функцию, обратную данной;
Развивающая:
- развивать навыки самоконтроля, предметную речь;
- овладеть понятием обратная функция и усвоить методы нахождения обратной функции;
Воспитательная: формировать коммуникативную компетентность.
Оборудование: компьютер, проектор, экран, интерактивная доска SMART Board, раздаточный материал (самостоятельная работа) для работы в группе.
Ход урока.
1. Организационный момент.
Цель – подготовка учащихся к работе на уроке:
-определение отсутствующих,
— настрой учащихся на работу, организация внимания;
— сообщение темы и цели урока.
2. Актуализация опорных знаний учащихся. Фронтальный опрос.
Цель — установить правильность и осознанность изученного теоретического материала, повторение пройденного материала.<Приложение 1>
Для учащихся на интерактивной доске демонстрируется график функции. Учителем формулируется задание – рассмотреть график функции и перечислить изученные свойства функции. Учащиеся перечисляют свойства функции в соответствии со схемой исследования. Учитель справа от графика функции маркером на интерактивной доске записывает названные свойства.
Свойства функции:
- D(f) = [-4;),E(y) = [0;),
- ни четная, ни нечетная, непериодическая, непрерывная, ограничена снизу;
- y=0, при х=0
- y>0 при на [-4;0) и на [0;)
- возрастает на [-2;-1] и на [0;)
убывает на [-4;-2] и на [-1;0] - yнаиб—
не существует
yнаим=0 при х=0 - xmax= -1 ,ymax = 2
xmin = -2, ymin = 1
xmin = 0, ymin = 0 - Выпукла вниз на [4;-1], выпукла вверх на [1;), невыпуклая на [-1;1].
По окончании исследования учитель сообщает, что сегодня на уроке они познакомятся еще с одним свойством функции – обратимостью. Для осмысленного изучения нового материала учитель предлагает ребятам познакомиться с основными вопросами, на которые учащиеся должны дать ответ по окончании урока. Вопросы записаны на обыкновенной доске и в виде раздаточного материала есть у каждого ученика (раздается до урока)
Вопросы:
- Какая функция называется обратимой?
- Любая ли функция обратима?
- Какая функция называется обратной данной?
- Как связаны область определения и множество значений функции и обратной ей функции?
- Если функция задана аналитически, как задать формулой обратную функцию?
- Если функция задана графически, как построить график обратной ей функции?
3. Объяснение нового материала.
Цель — формировать знания по новой теме в соответствии с программным материалом; изучить свойство обратимости функции и научить находить функцию, обратную данной; развивать предметную речь.
Учитель проводит изложение материала в соответствии с материалом параграфа. На интерактивной доске учитель проводит сравнение графиков двух функций, у которых области определения и множества значений одинаковы, но одна из функций монотонна, а другая нет, тем самым подводит учащихся под понятия обратимой функции.
Затем учитель формулирует определение обратимой функции и проводит доказательство теоремы об обратимой функции, используя график монотонной функции на интерактивной доске.
Определение 1: Функцию y=f(x), x X называют обратимой, если любое свое значение она принимает только в одной точке множества X.
Теорема: Если функция y=f(x) монотонна на множестве X , то она обратима.
Доказательство:
- Для определенности пусть х1<
х2.
Тогда из того, что х1 < х2 следует, что f(х1) < f(х2). - Таким образом, разным значениям аргумента соответствуют разные значения функции, т.е. функция обратима.
(По ходу доказательства теоремы учитель маркером делает все необходимые пояснения на чертеже)
Перед тем как сформулировать определение обратной функции учитель просит учащихся определить, какая из предложенных функций обратима? На интерактивной доске показаны графики функций и записаны несколько аналитически заданных функций:
А)
Б)
Г) y = 2x + 5
Д) y = -x2 + 7
Учитель вводит определение обратной функции.
Определение 2: Пусть обратимая функция y=f(x) определена на множестве Х и Е(f)=Y. Поставим в соответствие каждому y из Y то единственное значение х, при котором f(x)=y. Тогда получим функцию, которая определена на Y, а Х – область значений функции
Эту функцию обозначают x=f -1(y) и называют обратной по отношению к функции y=f(x).
Учащимся предлагается сделать вывод о связи между областью определения и множеством значений обратных функций.
Для рассмотрения вопроса о способах нахождения функции обратной данной, учитель привлек двух учащихся. Ребята накануне получили задание у учителя самостоятельно разобрать аналитический и графический способы нахождения функции обратной данной. Учитель выступил в роли консультанта при подготовке учащихся к уроку.
Сообщение первого ученика.
Замечание: монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием.
Учащийся привел примеры различных ситуаций, когда функция не монотонна, но обратима, когда функция не монотонна и не обратима, когда монотонна и обратима
Затем ученик знакомит учащихся со способом нахождения обратной функции, заданной аналитически.
Алгоритм нахождения
- Убедиться, что функция монотонна.
- Выразить переменную х через у.
- Переобозначить переменные. Вместо х=f -1(y) пишут y=f -1(x)
Затем решает два примера на нахождение функции обратной данной.
Пример 1: Показать, что для функции y=5x-3 существует обратная функция, и найти ее аналитическое выражение.
Решение. Линейная функция y=5x-3 определена на R, возрастает на R и область ее значений есть R. Значит, обратная функция существует на R. Чтобы найти ее аналитическое выражение, решим уравнение y=5x-3 относительно х; получим Это и есть искомая обратная функция. Она определена и возрастает на R.
Пример 2: Показать, что для функции y=x2, х≤0 существует обратная функция, и найти ее аналитическое выражение.
Функция непрерывна, монотонна в своей области определения, следовательно, она обратима. Проанализировав области определения и множества значений функции, делается соответствующий вывод об аналитическом выражении для обратной функции.
Ответ:
Второй ученик выступает с сообщением о графическом способе нахождения обратной функции. В ходе своего объяснения ученик использует возможности интерактивной доски .
Чтобы получить график функции y=f -1(x), обратной по отношению к функции y=f(x), надо график функции y=f(x)преобразовать симметрично относительно прямой y=x.
Во время объяснения на интерактивной доске выполняется следующее задание:
Построить в одной системе координат график функции и график обратной ей функции. Запишите аналитическое выражение обратной функции.
4. Первичное закрепление нового материала.
Цель – установить правильность и осознанность понимания изученного материала, выявить пробелы первичного осмысления материала, провести их коррекцию.
Учащиеся делятся на пары. Им раздаются листы с заданиями, в которых они и выполняют работу в парах. Время на выполнение работы ограничено (5-7 мин). Одна пара учащихся работает на компьютере, проектор на это время выключается и остальным ребятам не видно, как работают учащиеся на компьютере.
По окончании времени (предполагается, что с работой справилось большинство учащихся) на интерактивной доске (вновь включается проектор) показывается работа учащихся, где и выясняется в ходе проверки правильность выполнения задания в паре. При необходимости учителем проводится коррекционная, разъясняющая работа.
Самостоятельная работа в парах <Приложение 2
5. Итог урока. По вопросам, которые были заданы перед началом лекции. Объявление оценок за урок.
Домашнее задание §10. №№ 10.6(а,в) 10.8-10.9(б) 10.12 (б)
Алгебра и начала анализа. 10 класс В 2-х частях для общеобразовательных учреждений (профильный уровень) /А.Г.Мордкович, Л.О.Денищева, Т.А.Корешкова и др.; под ред. А.Г.Мордковича, М: Мнемозина, 2007 год
urok.1sept.ru
Обратная функция. Видеоурок. Алгебра 10 Класс
На этом уроке вы познакомитесь с понятием обратной функции. Научитесь решать прямые и обратные задачи и выясните, что для каждой монотонной функции существует обратная функция. А также узнаете, как связаны между собой графики прямой и обратной функций и разберетесь с методикой построения обратной функции и ее графика
Пусть задана функция 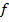 , множество
, множество 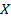 и множество
и множество 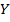 . Функция из
. Функция из 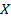 в
в 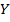 :
: 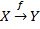 Каждому элементу из первого множества
Каждому элементу из первого множества 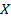 соответствует единственный элемент второго множества
соответствует единственный элемент второго множества 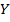 . С этой функцией связано две основные задачи:
. С этой функцией связано две основные задачи:
1 задача – прямая. Вычислить значение функции по заданному значению аргумента.
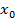 задано, необходимо вычислить
задано, необходимо вычислить 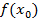 .
. 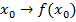
2 задача – обратная. Найти те значения аргумента, при которых функция принимает заданное значение 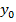 . Задаем
. Задаем 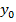 , далее необходимо решить уравнение
, далее необходимо решить уравнение 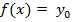 , которое может иметь одно решение, второе решение и т. д.
, которое может иметь одно решение, второе решение и т. д. 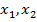 …
…
Пример обратной задачи: требуется найти время 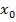 для достижения ракетой заданной высоты, самолетом скорости звука, автомобилем заданной скорости 100 км/ч. Нас будет интересовать такая обратная задача, которая имеет единственное решение.
для достижения ракетой заданной высоты, самолетом скорости звука, автомобилем заданной скорости 100 км/ч. Нас будет интересовать такая обратная задача, которая имеет единственное решение.
Пусть 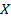 – множество слов. Слово – конечная последовательность букв, смысл здесь не важен.
– множество слов. Слово – конечная последовательность букв, смысл здесь не важен. 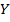 – множество слов из тех же букв, но записанных в обратном порядке.
– множество слов из тех же букв, но записанных в обратном порядке.
Например: 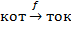 .
.
Итак, задана функция, два множества и соответствие между ними. Обратная задача для этой функции имеет единственное решение. Слову «ток» из множества 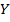 соответствует единственное слово «кот» из множества
соответствует единственное слово «кот» из множества 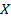 .
.
Пусть задано множество 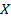 , состоящее из двух элементов
, состоящее из двух элементов 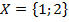 и множество
и множество 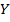 , состоящее также из двух элементов
, состоящее также из двух элементов
interneturok.ru
Презентация к уроку по алгебре (10 класс) на тему: Обратная функция
Слайд 1
Обратная функцияСлайд 2
Повторим Если каждому значению х из некоторого множества действительных чисел поставлено в соответствие по определенному правилу f число у , то, говорят, что на этом множестве задана функция . D(f) – область определения функции; х – независимая переменная или аргумент; у – зависимая переменная; множество всех значений y=f(x) , x ϵ Х называют областью значений функции и обозначают E(f) .
Слайд 3
Задача Пусть дана функция y=f(x) Найти значение функции в точке х=х 0 Например: Найти значение функции у=5х+7 в точке х=7. у(7)=5∙7+7 Ответ: у(7)=42 =35+7=42 Прямая Задача Пусть дана функция y=f(x) Найти значение аргумента в точке у=у 0 Например: Дана функция у=5х+7. Найти значе — ние аргумента при котором у=22. 22=5х+7 5х=22-7 5 x=15 х=15:5 x =3 Ответ: у(3)=22 Обратная
Слайд 4
Задача Пусть дан закон изменения скорости движения от времени Найти закон изменения времени от скорости. Решение: 0 – gt = gt = – 0 t= Обратимая функция Обратная функция к
Слайд 5
Если функция принимает каждое свое значение у только при одном значении x , то эту функцию называют обратимой . Пусть обратимая функция. Тогда каждому из множества значений функции соответствует одно определенное число из области определения, такое, что Это соответствие определяет функцию от , которую обозначим . Поменяем местами и : Функцию называют обратной к функции . Обозначают .
Слайд 6
Пример Найти функцию, обратную функции Решение: Ответ:
Слайд 7
y x 5 0 D(y)= ( ; 5) E(y )= ( ; 0) y 0 5 x D(y)= ( ; 0) E(y )= ( ; 5)
Слайд 8
Свойства обратных функций: Область определения обратной функции совпадает с множеством значений исходной функции , а множество значений обратной функции совпадает с областью определения исходной функции Монотонная функция является обратимой: а) если функция возрастает, то обратная к ней функция также возрастает; б) если функция убывает, то обратная к ней функция также убывает.
Слайд 9
Пример Показать, что для функции существует обратная функция, и найти ее аналитическое выражение. Решение: Функция возрастает на R . Значит, обратная функция существует на R . Решим уравнение относительно . Получим, Поменяв местами и получим: Это и есть искомая обратная функция.
Слайд 10
Пример Дана функция Доказать, что для нее существует обратная функция, записать аналитическое выражение обратной функции в виде и построить график обратной функции.
Слайд 11
Решение: Функция возрастает на промежутке значит, она имеет обратную функцию. Из уравнения находим: или . Промежутку принадлежат лишь значения функции .
Слайд 12
Поменяв местами и получим График этой функции получается из графика функции с помощью симметрии относительно прямой .
nsportal.ru
Обратные функции. Базовый уровень. Видеоурок. Алгебра 10 Класс
Представьте, что вы гуляете по пляжу. На песке у кромки воды остаются ваши следы, а вокруг еще множество следов (см. рис. 1).

Рис. 1. Множество следов на песке
По их форме вы с легкостью можете определить, кто здесь был до вас: другой человек, чайка или собака. Видя след мы можем установить, что за существо его оставило. И наоборот: зная, кто прошел по песку, мы можем сказать, какой след останется. Мы как бы устанавливаем соответствие между следом и существом (см. рис. 2).
Рис. 2. Соответствие между следом и существом
Однозначное ли это соответствие? Давайте подумаем. Когда человек ступает на песок, он точно знает, какой след после него останется. Тут все однозначно. Представим обратную ситуацию: Шерлок Холмс видит на песке след. Может ли он однозначно определить преступника? Он сможет лишь утверждать, что это человек, а вот какой именно – без других улик это не определить, вариантов очень много. Обратное соответствие не является однозначным.
С неоднозначностью соответствия мы сталкиваемся, даже просто глядя на часы. Такое положение стрелок (см. рис. 3) может означать как полночь, так и полдень.
Рис. 3. Заданное положение стрелок
И если бы мы были в подвале без окон, то не смогли бы однозначно определить время – у нас было бы 2 варианта. Чтобы выбрать правильный вариант, мы пользуемся дополнительной информацией: смотрим, темно или светло на улице.
Но есть и примеры, когда мы можем однозначно установить соответствие. Так, у каждого человека есть ровно один внутренний паспорт и наоборот – внутренний паспорт однозначно определяет конкретного человека. Между внутренним паспортом и человеком можно установить взаимно однозначное соответствие.
Переходя на язык математики, можно сказать, что мы устанавливаем соответствия между множествами: множеством существ и множеством следов; множеством людей и множеством паспортов. Причем в одну сторону соответствие однозначное, а в обратную не всегда.
Таких примеров неоднозначности обратной операции можно привести много. Так, если нам известны два числа, найти их сумму не составит труда, например:
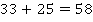
А вот зная сумму, восстановить однозначно два слагаемых не получится – вариантов будет бесконечно много:
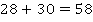
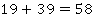
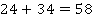
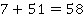

С подобными примерами соответствий мы сталкивались, говоря о числовых функциях. Так, линейная функция 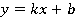 является примером взаимооднозначного соответствия (см. рис. 4). Каждому значению
является примером взаимооднозначного соответствия (см. рис. 4). Каждому значению 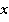 соответствует ровно одно значение
соответствует ровно одно значение 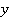 . И наоборот: каждому значению
. И наоборот: каждому значению 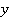 соответствует ровно одно значение
соответствует ровно одно значение 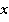 . Это похоже на соответствие паспортов и людей.
. Это похоже на соответствие паспортов и людей.
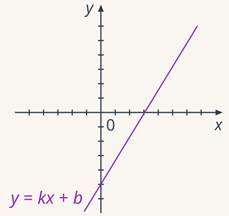
Рис. 4. График линейной функции
Ситуация с часами похожа на квадратичную функцию 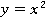 (см. рис. 5). По значению
(см. рис. 5). По значению 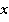 мы однозначно определим
мы однозначно определим 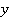 :
: 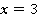 , тогда
, тогда 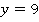 . А вот если мы знаем
. А вот если мы знаем 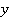 , например
, например 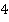 , то
, то 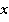 однозначно определить нельзя, хотя информации у нас много, возможно всего два варианта: или
однозначно определить нельзя, хотя информации у нас много, возможно всего два варианта: или 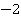 , или
, или 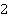 . Однозначно мы можем узнать
. Однозначно мы можем узнать 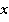 только при наличии дополнительных условий. Например, если
только при наличии дополнительных условий. Например, если 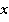 – это сторона квадрата, тогда останется лишь один вариант
– это сторона квадрата, тогда останется лишь один вариант 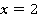 .
.
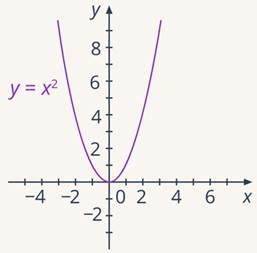
Рис. 5. График квадратичной функции
А вот многозначность, как в случае следов на песке, появляется при работе с тригонометрическими функциями (см. рис. 6). По значению аргумента 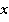 можно однозначно вычислить значение функций:
можно однозначно вычислить значение функций:
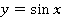
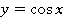
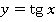
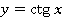
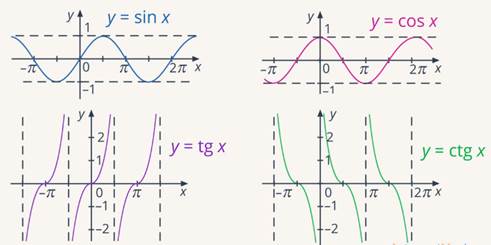
Рис. 6. Графики тригонометрических функций
Это мы уже умеем делать. А когда мы попробуем по значению 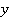 найти
найти 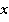 , то столкнемся с многозначностью. Например, возьмем функцию
, то столкнемся с многозначностью. Например, возьмем функцию 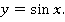 Если
Если 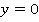 , то
, то 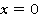 , ведь
, ведь 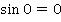 . Но
. Но 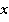 может быть равен и
может быть равен и 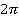 , и
, и 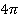 , и
, и 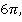 и т. д. Ведь синусы всех этих величин также равны
и т. д. Ведь синусы всех этих величин также равны 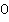 . О том, как в общем случае найти аргумент тригонометрической функции по ее значению, и пойдет речь в данном уроке.
. О том, как в общем случае найти аргумент тригонометрической функции по ее значению, и пойдет речь в данном уроке.
Для начала разберемся с терминологией. Когда мы каждому значению 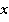 ставим в соответствие одно значение
ставим в соответствие одно значение 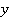 – это функция. Можно сделать и обратное: поставить каждому значению
– это функция. Можно сделать и обратное: поставить каждому значению 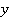 в соответствие значение
в соответствие значение 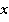 . Если мы сможем это сделать однозначно, то получим обратную функцию.
. Если мы сможем это сделать однозначно, то получим обратную функцию.
Возьмем, например, функцию 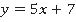 (см. рис. 7).
(см. рис. 7).
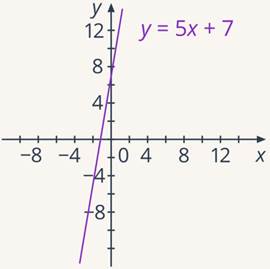
Рис. 7. График функции 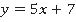
Выразив переменную 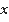 , получаем:
, получаем:
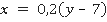
Здесь мы уже значению 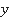 ставим в соответствие
ставим в соответствие 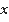 , то есть это обратная функция. Только у нее аргумент обозначен как
, то есть это обратная функция. Только у нее аргумент обозначен как 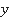 , а значение функции – как
, а значение функции – как 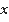 . Нам же привычнее наоборот. Поэтому переобозначим:
. Нам же привычнее наоборот. Поэтому переобозначим: 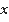 заменим на
заменим на 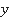 , а
, а 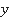 – на
– на 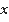 (см. рис. 8):
(см. рис. 8):

Получили, что функция  является обратной функции
является обратной функции 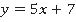 . Верно и другое: функция
. Верно и другое: функция 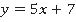 является обратной функции
является обратной функции . Поэтому подобные пары функций называют еще взаимно обратными.
. Поэтому подобные пары функций называют еще взаимно обратными.
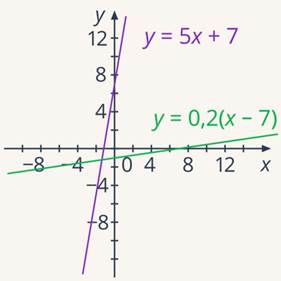
Рис. 8. Графики функций 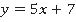 и
и 
Продолжаем разбираться с терминологией. Функцию, для которой можно найти обратную, называют обратимой функцией. Буквально – «ту, которую можно обратить». То есть функции 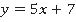 ,
,  являются обратимыми функциями. Да и в целом любая линейная функция является обратимой, ведь каждому значению
являются обратимыми функциями. Да и в целом любая линейная функция является обратимой, ведь каждому значению 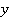 соответствует ровно одно значение
соответствует ровно одно значение 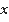 .
.
А вот функция 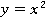 не является обратимой, ведь значению функции
не является обратимой, ведь значению функции 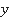 может соответствовать по два значения переменной
может соответствовать по два значения переменной 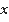 . Условие однозначности не выполнено. Чтобы сделать эту функцию обратимой, нужно добавить дополнительные условия. Так, если мы рассмотрим функцию
. Условие однозначности не выполнено. Чтобы сделать эту функцию обратимой, нужно добавить дополнительные условия. Так, если мы рассмотрим функцию 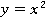 только для положительных
только для положительных 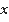 , то каждому значению
, то каждому значению 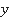 будет уже соответствовать только одно значение
будет уже соответствовать только одно значение 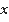 (см. рис. 9).
(см. рис. 9).
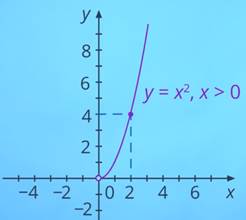
Рис. 9. График функции 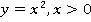
Функция 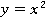 , при
, при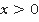 будет уже обратимой. И обратной к ней будет функция
будет уже обратимой. И обратной к ней будет функция
interneturok.ru
Обратные функции. Профильный уровень. Видеоурок. Алгебра 10 Класс
Представьте, что вы гуляете по пляжу. На песке у кромки воды остаются ваши следы, а вокруг еще множество следов (см. рис. 1).

Рис. 1. Множество следов на песке
По их форме вы с легкостью можете определить, кто здесь был до вас: другой человек, чайка или собака. Видя след мы можем установить, что за существо его оставило. И наоборот: зная, кто прошел по песку, мы можем сказать, какой след останется. Мы как бы устанавливаем соответствие между следом и существом (см. рис. 2).

Рис. 2. Соответствие между следом и существом
Однозначное ли это соответствие? Давайте подумаем. Когда человек ступает на песок, он точно знает, какой след после него останется. Тут все однозначно. Представим обратную ситуацию: Шерлок Холмс видит на песке след. Может ли он однозначно определить преступника? Он сможет лишь утверждать, что это человек, а вот какой именно – без других улик это не определить, вариантов очень много. Обратное соответствие не является однозначным.
С неоднозначностью соответствия мы сталкиваемся, даже просто глядя на часы. Такое положение стрелок (см. рис. 3) может означать как полночь, так и полдень.

Рис. 3. Заданное положение стрелок
И если бы мы были в подвале без окон, то не смогли бы однозначно определить время – у нас было бы 2 варианта. Чтобы выбрать правильный вариант, мы пользуемся дополнительной информацией: смотрим, темно или светло на улице.
Но есть и примеры, когда мы можем однозначно установить соответствие. Так, у каждого человека есть ровно один внутренний паспорт и наоборот – внутренний паспорт однозначно определяет конкретного человека. Между внутренним паспортом и человеком можно установить взаимно однозначное соответствие.
Переходя на язык математики, можно сказать, что мы устанавливаем соответствия между множествами: множеством существ и множеством следов; множеством людей и множеством паспортов. Причем в одну сторону соответствие однозначное, а в обратную не всегда.
Таких примеров неоднозначности обратной операции можно привести много. Так, если нам известны два числа, найти их сумму не составит труда, например:
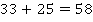
А вот зная сумму, восстановить однозначно два слагаемых не получится – вариантов будет бесконечно много:
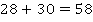
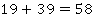
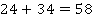
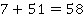

С подобными примерами соответствий мы сталкивались, говоря о числовых функциях. Так, линейная функция 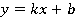 является примером взаимооднозначного соответствия (см. рис. 4). Каждому значению
является примером взаимооднозначного соответствия (см. рис. 4). Каждому значению 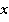 соответствует ровно одно значение
соответствует ровно одно значение 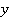 . И наоборот: каждому значению
. И наоборот: каждому значению 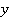 соответствует ровно одно значение
соответствует ровно одно значение
interneturok.ru
Обратная функция
Вопросы занятия:
· познакомиться с понятиями прямой и обратной функции;
· познакомиться с понятием обратимой функции;
· научиться находить обратные функции;
· рассмотреть свойство обратных функций.
Материал урока
Прежде чем приступить к изучению новой темы, давайте вспомним, что же такое функция и какие основные понятия с ней связаны.
Определение.
Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.
Область определения обозначается D(f).
x – независимая переменная или аргумент.
y – зависимая переменная.
Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).
Рассмотрим задачу.
Задача.

Рассмотрим ещё одну задачу.
Задача.

Давайте назовём первую задачу прямой, тогда вторая задача будет обратной к первой.
Давайте рассмотрим с вами ещё одну задачу.
Задача.

Назовём функцию v(t) обратимой функцией, а t(v) – обратной функцией.

Определение.
Если функция y=f(x) принимает каждое своё значение у только при одном значении x, то эту функцию называют обратимой.
Приведём примеры обратимых функций:

Рассмотрим функцию y=x2.

Определение.
Пусть y = f(x) – обратимая функция.
Тогда каждому y из множества
значений функции соответствует одно определённое число x
из области определения, такое, что f(x)
= y. Это
соответствие определяет функцию x
от
y, которую обозначим x
= g(y).
Поменяем местами x и y:
y = g(x).
Функцию
y = g(x) называют
обратной к функции y
= f(x).
Обозначают f-1(x).
Давайте разберём это определение на примере.
Пример.

Область определения исходной функции равна области значений обратной функции и наоборот, область значений исходной функции равна области определения обратной функции.

Сформулируем основные свойства обратных функций.

Решим несколько примеров.
Пример.

Пример.



videouroki.net
Взаимно обратные функции
Пусть
задана функция  ,
где каждое значение
,
где каждое значение  .
.
Понятно,
что каждому значению  соответствует
единственное значение
соответствует
единственное значение из
области значений функции. Если мы по данному значению функции
из
области значений функции. Если мы по данному значению функции  захотим
найти соответствующее значение аргумента, нам придётся решить уравнение
относительно
захотим
найти соответствующее значение аргумента, нам придётся решить уравнение
относительно ,
то есть решить уравнение
,
то есть решить уравнение  .
.
Понятно,
что такое уравнение может иметь не одно, а несколько и даже бесконечно много
решений. Решениями нашего уравнения являются абсциссы всех точек, в которых
прямая  пересекает
график функции
пересекает
график функции  .
.
Однако
существуют такие функции, для которых уравнение  имеет
единственное решение для каждого фиксированного значения
имеет
единственное решение для каждого фиксированного значения .
Такие функции называют обратимыми.
.
Такие функции называют обратимыми.
Запомните! Если
функция  принимает
каждое своё значение только при одном значении
принимает
каждое своё значение только при одном значении  ,
то эту функцию называют обратимой.
,
то эту функцию называют обратимой.
Вот,
например, рассмотрим две функции:  и
и
 .
.
Функция
 обратима,
так как каждое значение
обратима,
так как каждое значение  принимается
при единственном значении аргумента
принимается
при единственном значении аргумента  .
Чтобы найти это значение, нам нужно решить уравнение
.
Чтобы найти это значение, нам нужно решить уравнение  относительно
относительно
 .
Этим мы займёмся чуть позже.
.
Этим мы займёмся чуть позже.
Что
касается функции  ,
то она не является обратимой, так как значения
,
то она не является обратимой, так как значения  принимает
не при единственном значении аргумента
принимает
не при единственном значении аргумента .
Например, значение
.
Например, значение  функция
функция
 принимает
при
принимает
при  .
.
Итак,
пусть  —
обратимая функция. В этом случае уравнение
—
обратимая функция. В этом случае уравнение  можно
при любом
можно
при любом  однозначно
разрешить относительно
однозначно
разрешить относительно  ,
то есть каждому
,
то есть каждому  поставить
в соответствие единственное
поставить
в соответствие единственное  такое,
что
такое,
что  .
Это соответствие определяет функцию
.
Это соответствие определяет функцию  от
от
 .
Обозначим эту функцию
.
Обозначим эту функцию  .
Но мы привыкли обозначать аргумент функции буквой
.
Но мы привыкли обозначать аргумент функции буквой ,
а значения – буквой
,
а значения – буквой  .
Перейдём к привычным для нас обозначениям. Для этого поменяем в этой записи местами
.
Перейдём к привычным для нас обозначениям. Для этого поменяем в этой записи местами и
и
 .
Получим функцию
.
Получим функцию  .
.
Функцию
 называют
обратной к функции
называют
обратной к функции .
.
Давайте
найдём функцию, обратную к функции  .
.
Решение.
Решим уравнение  .
Для
этого 2 перенесём в левую часть уравнения.
.
Для
этого 2 перенесём в левую часть уравнения.

Затем разделим обе части нашего уравнения на 5. Получим

или, что то же самое,

Теперь
поменяем в нашем равенстве местами  и
и
 .
Получим
.
Получим

Итак,
функция  обратна
к функции
обратна
к функции  .
.
Сделаем
вывод. Если обратимая функция  задана
формулой, то для нахождения обратной функции нужно решить
уравнение
задана
формулой, то для нахождения обратной функции нужно решить
уравнение  относительно
относительно
 ,
а затем поменять местами
,
а затем поменять местами  и
и
 .
.
Вернёмся
к нашему примеру. Мы с вами показали, что функция  является
обратной к функции
является
обратной к функции  .
Обратите внимание: в свою очередь и функция
.
Обратите внимание: в свою очередь и функция  также
будет являться обратной к функции
также
будет являться обратной к функции  .
Такие функции называют взаимно обратными.
.
Такие функции называют взаимно обратными.
Сделаем
вывод: если  –
функция, обратная к функции
–
функция, обратная к функции ,
то и
,
то и  –
функция, обратная к
–
функция, обратная к  ,
при этом область определения обратной функции совпадает со множеством
значений исходной функции, а множество значений обратной функции
совпадает с областью определения исходной функции. Это свойство, которое
показывает, как связаны функция и обратная к ней.
,
при этом область определения обратной функции совпадает со множеством
значений исходной функции, а множество значений обратной функции
совпадает с областью определения исходной функции. Это свойство, которое
показывает, как связаны функция и обратная к ней.
Вы уже знаете, что функция называется возрастающей на некотором промежутке, если в этом промежутке большему значению аргумента соответствует большее значение функции. И функция называется убывающей в некотором промежутке, если в этом промежутке большему значению аргумента соответствует меньшее значение функции. Чаще всего возрастающие и убывающие функции называют одним словом — монотонные.
Докажем теорему. Монотонная функция является обратимой.
Доказательство.
Пусть функция  ,
например, возрастает и пусть
,
например, возрастает и пусть  —
её значение в некоторой точке
—
её значение в некоторой точке  ,
то есть
,
то есть  .
.
Тогда
если  ,
то при
,
то при  выполняется
неравенство
выполняется
неравенство  ,
в свою очередь, при
,
в свою очередь, при  выполняется
неравенство
выполняется
неравенство  .
Понятно, что значение
.
Понятно, что значение  функция
функция
 принимает
только в одной точке
принимает
только в одной точке  ,
а значит, является обратимой.
,
а значит, является обратимой.
Что и требовалось доказать.
Для убывающей функции доказательство проводится аналогично.
К
примеру, рассмотрим функцию  .
Эта функция возрастающая, значит, является обратимой. Не сложно
догадаться, что обратной к ней будет функция
.
Эта функция возрастающая, значит, является обратимой. Не сложно
догадаться, что обратной к ней будет функция  .
.
Из
теоремы вытекает следующее следствие: если функция  возрастает
(убывает), то для неё существует обратная функция, и она возрастает (убывает)
на множестве значений данной функции.
возрастает
(убывает), то для неё существует обратная функция, и она возрастает (убывает)
на множестве значений данной функции.
Другими
словами, если функция  возрастает,
то понятно, что с увеличением
возрастает,
то понятно, что с увеличением  значения
значения также
увеличиваются и, наоборот, с увеличением
также
увеличиваются и, наоборот, с увеличением  увеличиваются
увеличиваются
 .
.
Это означает, что обратная функция также возрастает.
И
аналогично с убывающей функцией: если функция  убывает,
то обратная к ней функция также убывает.
убывает,
то обратная к ней функция также убывает.
Кстати,
функция, не являющаяся монотонной, может не иметь обратной. Примером
такой функции служит функция  .
Мы
с вами уже говорили, что эта функция не имеет обратной, если
рассматривать её на всей числовой оси. Однако если мы с вами будем
рассматривать функцию
.
Мы
с вами уже говорили, что эта функция не имеет обратной, если
рассматривать её на всей числовой оси. Однако если мы с вами будем
рассматривать функцию  только
при
только
при  ,
то на промежутке
,
то на промежутке  она
возрастает и, следовательно, имеет обратную. Функция
она
возрастает и, следовательно, имеет обратную. Функция  является
обратной к функции
является
обратной к функции  при
при
 .
.
Данный
пример показывает, что некоторые функции обратной функции не
имеют, если их рассматривать на всей области определения, и имеют обратную
функцию, если область определения сузить. Часто в качестве сужения области
определения берут интервал монотонности функции .
.
А
теперь давайте докажем ещё одну теорему. Если функция имеет обратную,
то график обратной функции симметричен графику данной функции
относительно прямой  .
.
Доказательство.
Пусть некоторая точка с координатами  ,
принадлежит графику функции
,
принадлежит графику функции  ,
то есть
,
то есть  .
.
Из
существования обратной функции следует, что  .
Значит, точка с координатами
.
Значит, точка с координатами  принадлежит
графику обратной функции
принадлежит
графику обратной функции  .
Следовательно, точки с координатами
.
Следовательно, точки с координатами  и
и
 симметричны
относительно прямой
симметричны
относительно прямой  .
.
Что и требовалось доказать.
Хотелось
бы обратить внимание, что и знакомая вам степенная функция с
областью определения
с
областью определения  и
и
 обратима,
так как она монотонна. Обратной к степенной
функции
обратима,
так как она монотонна. Обратной к степенной
функции  при
при
 и
и
 является
функция
является
функция  .
.
А теперь давайте приступим к практической части нашего урока.
Задание.
Найдите обратную функцию для функции  .
.
Решение.
Решим это уравнение относительно  .
.
Имеем

Раскроем
скобки в левой части нашего уравнения. Получим, 
Затем
перенесём слагаемое  в
правую часть уравнения, а
в
правую часть уравнения, а  –
в левую. Вынесем общий множитель
–
в левую. Вынесем общий множитель  за
скобку. Заметим, что если выражение
за
скобку. Заметим, что если выражение  ,
то есть
,
то есть  ,
то последнее соотношение превращается в неверное равенство. Значит, можем
разделить обе части нашего уравнения на выражение
,
то последнее соотношение превращается в неверное равенство. Значит, можем
разделить обе части нашего уравнения на выражение  .
.
Получим
 .
Не забудем поменять
.
Не забудем поменять  и
и
 местами.
Тогда функция
местами.
Тогда функция  обратная
к функции
обратная
к функции  .
.
videouroki.net