Обратные тригонометрические функции, все формулы
Основные обратные тригонометрические функции:
1. – арксинус;
2. – арккосинус;
3. – арктангенс;
4. – арккотангенс.
Арксинус является нечетной функцией, то есть: .
Для арккосинуса справедливо следующее равенство
Арктангенс функция нечетная, поэтому для нее справедливо следующее равенство
Для функции арккотангенс справедливо следующее равенство
Для вычисления значений обратных тригонометрических функций можно пользоваться таблицей
Основные соотношения между обратными тригонометрическими функциями
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Тригонометрия
Предположим, что число a удовлетворяет неравенству 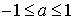 . Число x называют арксинусом числа a и обозначают x = arcsin a, если выполнены два условия:
. Число x называют арксинусом числа a и обозначают x = arcsin a, если выполнены два условия:
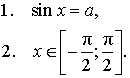
Предположим, что число a удовлетворяет неравенству 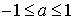 . Число x называют арккосинусом числа a и обозначают x = arccos a, если выполнены два условия:
. Число x называют арккосинусом числа a и обозначают x = arccos a, если выполнены два условия:
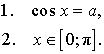
Рассмотрим произвольное число a . Число x называют арктангенсом числа a и обозначают x = arctg a, если выполнены два условия:
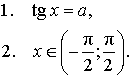
Рассмотрим произвольное число a . Число x называют арккотангенсом числа a и обозначают x = arcctg a, если выполнены два условия:
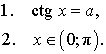
Арксинус, арккосинус, арктангенс и арккотангенс удовлетворяют, в частности, следующим соотношениям:
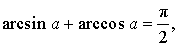 |
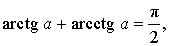 |
| arcsin (– a) = – arcsin a , |
| arccos (– a) = = π – arccos a , |
| arctg (– a) = – arctg a , |
| arcctg (– a) = = π – arcctg a . |
Обратными тригонометрическими функциями называют функции:
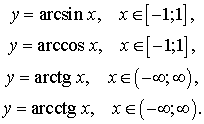
Графики этих функций изображены на рисунках 1, 2, 3, 4.
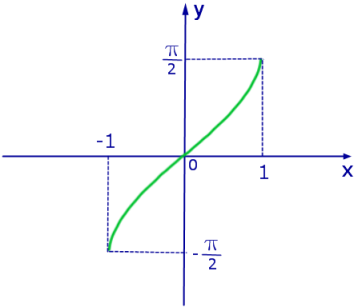
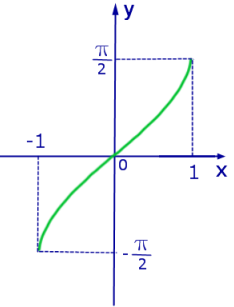
Рис. 1. График функции y = arcsin x
Таблица значений функции y = arcsin x
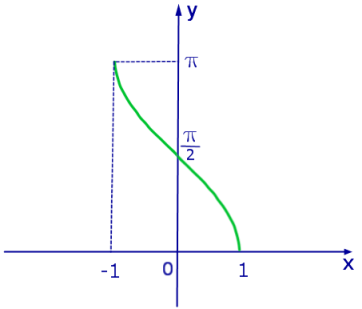
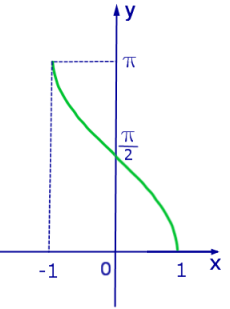
Рис. 2. График функции y = arccos x
Таблица значений функции y = arccos x
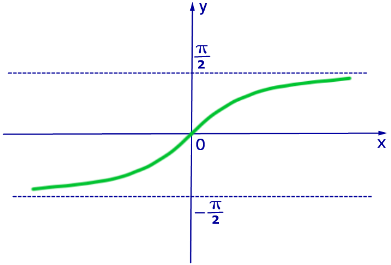
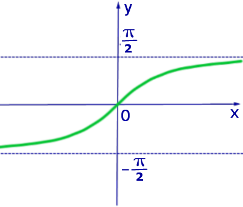
Рис. 3. График функции y = arctg x
Таблица значений функции y = arctg x
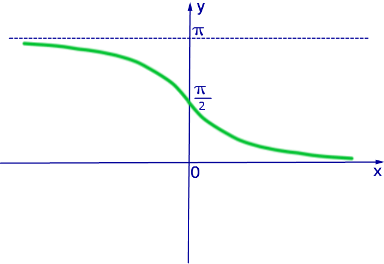
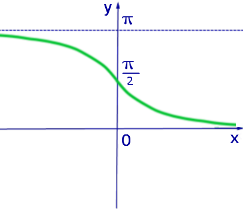
Рис. 4. График функции y = arcctg x
Таблица значений функции y = arcctg x
Пример. Решить уравнение
2 arcsin 2x = arccos 7x .
Решение. Возьмём косинус от обеих частей уравнения. Тогда в левой части уравнения получим:
cos ( 2 arcsin 2x ) = 1 – 2sin2( arcsin 2x ) = 1 – 2 ( 2x )2 = 1 – 8x2 .
cos ( 2 arcsin 2x ) =
= 1 – 2sin2( arcsin 2x ) =
= 1 – 2 ( 2x )2 = 1 – 8x2 .
В правой части уравнения получим:
cos ( arccos 7x ) = 7x.
Следовательно, возникает квадратное уравнение:
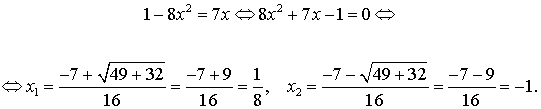
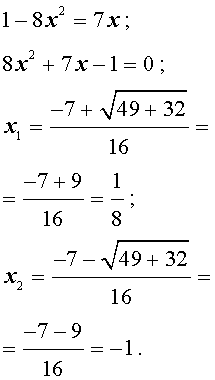
В силу того, что область определения обратных тригонометрических функций y = arcsin x и y = arccos x имеет вид: 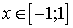 , второй корень должен быть отброшен.
, второй корень должен быть отброшен.
Ответ: 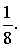

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
www.resolventa.ru
Свойства обратных тригонометрических функций
- Главная
- Справочник
- Тригонометрия
- Свойства обратных тригонометрических функций
Так как геометрически значение обратной тригонометрической функции связано с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку, то названия обратных тригонометрических функций образуются следующим образом: приставка «арк-» (от латинского arc — дуга) + соответствующие им названия тригонометрических функций.
Арксинус
Арксинусом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \sin \alpha=a,\;|a|\leqslant 1,\;\alpha\in[-\frac{\pi}{2};\frac{\pi}{2}]. \)
- Областью определения функции арксинус является отрезок \( [-1;1]. \)
- Областью значений функции арксинус является отрезок \( [-\frac{\pi}{2};\frac{\pi}{2}]. \)
- Арксинус строго возрастающая функция.
- \( \sin \left (\arcsin a \right )=a,\;|a|\leqslant 1. \)
- \( \arcsin\left (\sin \alpha \right )=\alpha,\;\alpha\in[-\frac{\pi}{2};\frac{\pi}{2}]. \)
- Арксинус является нечетной функцией: \( \arcsin(-a)=-\arcsin a,\;|a| \leqslant 1. \)
- \( \arcsin a>0,\;a\in(0;1]. \)
- \( \arcsin a=0,\;a=0. \)
- \( \arcsin a<0,\;a\in[-1;0). \)
Арккосинус
Арккосинусом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \cos \alpha=a,\;|a|\leqslant 1,\;\alpha\in[0;\pi]. \)
- Областью определения функции арккосинус является отрезок \( [-1;1]. \)
- Областью значений функции арккосинус является отрезок \( [0;\pi]. \)
- Арккосинус строго убывающая функция.
- \( \arccos\left (\cos \alpha\right )=\alpha,\;\alpha\in[0;\pi]. \)
- Арккосинус является индифферентной функцией: \( \arccos (-a)=\pi-\arccos a,\;|a|\leqslant 1. \) Функция центрально-симметрична относительно точки \( \left ( 0;\frac{\pi}{2} \right ). \)
- \( \arccos a>0,\;a\in[-1;1). \)
- \( \arccos a=0,\;a=1. \)
Арктангенс
Арктангенсом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \text{tg}\, \alpha=a,\;a\in\mathbb{R},\;\alpha\in\left (-\frac{\pi}{2};\frac{\pi}{2} \right ). \)
- Областью определения функции арктангенс является вся числовая прямая: \( \mathbb{R}. \)
- Областью значений функции арктангенс является интервал \( \left (-\frac{\pi}{2};\frac{\pi}{2} \right ). \)
- Арктангенс строго возрастающая функция.
- \( \text{tg}\left (\text{arctg}\,a \right ) =a,\;a\in\mathbb{R}. \)
- \( \text{arctg}\left (\text{tg}\,\alpha \right ) =\alpha,\;\alpha\in\left ( -\frac{\pi}{2};\frac{\pi}{2} \right ). \)
- Арктангенс является нечетной функцией: \( \text{arctg}\left (-a \right ) =-\text{arctg}\,a,\;a\in\mathbb{R}. \)
- \( \text{arctg}\,a>0,\;a\in(0;\infty ). \)
- \( \text{arctg}\,a=0,\;a=0. \)
- \( \text{arctg}\,a<0,\;a\in(-\infty;0). \)
Арккотангенс
Арккотангенсом числа \( a \) называется такое значение угла \( \alpha, \) для которого \( \text{ctg}\, \alpha=a,\;a\in\mathbb{R},\;\alpha\in\left (0;\pi \right ). \)
- Областью определения функции арккотангенс является вся числовая прямая: \( \mathbb{R}. \)
- Областью значений функции арккотангенс является интервал \( \left (0;\pi \right ). \)
- Арккотангенс строго убывающая функция.
- \( \text{ctg}\left (\text{arcctg}\,a \right ) =a,\;a\in\mathbb{R}. \)
- \( \text{arcctg}\left (\text{ctg}\,\alpha \right ) =\alpha,\;\alpha\in\left (0;\pi \right ). \)
- Арккотангенс является индифферентной функцией: \( \text{arcctg}\left (-a \right ) =\pi-\text{arcctg}\,a,\;a\in\mathbb{R}. \) Функция центрально-симметрична относительно точки \( \left ( 0;\frac{\pi}{2} \right ). \)
- \( \text{arcctg}\,a>0,\;a\in\mathbb{R}. \)
Основные соотношения
- \( \arcsin a+\arccos a=\frac{\pi}{2},\;|a|\leqslant 1. \)
- \( \text{arctg}\,a+\text{arcctg}\,a=\frac{\pi}{2},\;a\in\mathbb{R}. \)
Решение простейших тригонометрических уравнений
В общем виде
\( \sin x=a,\;|a|\leqslant 1\Rightarrow x=(-1)^k\arcsin\,a+\pi k,\;k\in\mathbb{Z} \)
или \( \left[\begin{matrix} x&=&\arcsin\,a+2\pi k,&\;k\in\mathbb{Z}\\ x&=&\pi-\arcsin\,a+2\pi l,&\;l\in\mathbb{Z} \end{matrix}\right. \)
\( \cos x=a,\;|a|\leqslant 1\Rightarrow x=\pm\arccos\,a+2\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=a,\;a\in\mathbb{R}\Rightarrow x=\text{arctg}\,a+\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=a,\;a\in\mathbb{R}\Rightarrow x=\text{arcctg}\,a+\pi k,\;k\in\mathbb{Z} \)
Частные случаи
\( \sin x=0\Rightarrow x=\pi k,\;k\in\mathbb{Z} \)
\( \cos x=0\Rightarrow x=\frac{\pi}{2}+\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=0\Rightarrow x=\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=0\Rightarrow x=\frac{\pi}{2}+\pi k,\;k\in\mathbb{Z} \)
\( \sin x=1\Rightarrow x=\frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z} \)
\( \cos x=1\Rightarrow x=2\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=1\Rightarrow x=\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=1\Rightarrow x=\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
\( \sin x=-1\Rightarrow x=-\frac{\pi}{2}+2\pi k,\;k\in\mathbb{Z} \)
\( \cos x=-1\Rightarrow x=\pi+2\pi k,\;k\in\mathbb{Z} \)
\( \text{tg}\, x=-1\Rightarrow x=-\frac{\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
\( \text{ctg}\, x=-1\Rightarrow x=\frac{3\pi}{4}+\pi k,\;k\in\mathbb{Z} \)
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
calcsbox.com
Урок 9. Обратные тригонометрические функции. Теория. Видеоурок. Алгебра 11 Класс
Подготовка к ЕГЭ по математике
Эксперимент
Урок 9. Обратные тригонометрические функции.
Теория
Конспект урока
Вспомним, когда мы встречаемся с таким понятием как обратная функция. Например, рассмотрим функцию возведения в квадрат. Пусть у нас есть квадратная комната со сторонами по 2 метра и мы хотим вычислить ее площадь. Для этого по формуле пощади квадрата возводим двойку в квадрат и в результате получаем 4 м2. Теперь представим себе обратную задачу: мы знаем площадь квадратной комнаты и хотим найти длины ее сторон. Если мы знаем, что площадь равна все тем же 4 м2, то выполним обратное действие к возведению в квадрат – извлечение арифметического квадратного корня, который нам даст значение 2 м.
Таким образом, для функции возведения числа в квадрат обратной функцией является извлечение арифметического квадратного корня.
Конкретно в указанном примере у нас не возникло проблем с вычислением стороны комнаты, т.к. мы понимаем, что это положительное число. Однако если оторваться от этого случая и рассмотреть задачу более общим образом: «Вычислить число, квадрат которого равен четырем», мы столкнемся с проблемой – таких чисел два. Это 2 и -2, т.к. 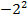 тоже равна четырем. Получается, что обратная задача в общем случае решается неоднозначно, и действие определения числа, которое в квадрате дало известное нам число? имеет два результата. Это удобно показать на графике:
тоже равна четырем. Получается, что обратная задача в общем случае решается неоднозначно, и действие определения числа, которое в квадрате дало известное нам число? имеет два результата. Это удобно показать на графике:
 |
А это значит, что такой закон соответствия чисел мы не можем назвать функцией, поскольку для функции одному значению аргумента соответствует строго одно значение функции.
Для того чтобы ввести именно обратную функцию к возведению в квадрат и было предложено понятие арифметического квадратного корня, который дает только неотрицательные значения. Т.е. для функции 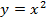 обратной функцией считается
обратной функцией считается 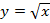 .
.
Аналогично существуют и функции, обратные к тригонометрическим, их называют обратными тригонометрическими функциями. К каждой из рассмотренных нами функций существует своя обратная, их называют: арксинус, арккосинус, арктангенс и арккотангенс.
Эти функции решают задачу вычисления углов по известному значению тригонометрической функции. Например, с использованием таблицы значений основных тригонометрических функций можно вычислить синус какого угла равен 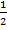 . Находим это значение в строке синусов и определяем, какому углу оно соответствует. Первое, что хочется ответить, что это угол
. Находим это значение в строке синусов и определяем, какому углу оно соответствует. Первое, что хочется ответить, что это угол 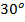 или
или  , но если у вас в распоряжении таблица значений до
, но если у вас в распоряжении таблица значений до 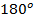 , вы тут же заметите еще одного претендента на ответ, — это угол
, вы тут же заметите еще одного претендента на ответ, — это угол 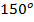
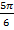 . А если мы вспомним о периоде синуса, то поймем, что углов, при которых синус равен
. А если мы вспомним о периоде синуса, то поймем, что углов, при которых синус равен 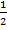 , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для косинусов, тангенсов и котангенсов, т.к. все они обладают периодичностью.
, бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для косинусов, тангенсов и котангенсов, т.к. все они обладают периодичностью.Т.е. мы сталкиваемся с той же проблемой, которая была для вычисления значения аргумента по значению функции для действия возведения в квадрат. И в данном случае для обратных тригонометрических функций было введено ограничение области значений, которые они дают при вычислении. Это свойство таких обратных функций называют
Для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно. Например, арксинус возвращает значения углов в диапазоне от 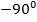 до
до 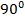 .
.
Умение работать с обратными тригонометрическими функциями нам пригодится при решении тригонометрических уравнений.
Сейчас мы укажем основные свойства каждой из обратных тригонометрических функций. Кто захочет познакомиться с ними более подробно, обратитесь к главе «Решение тригонометрических уравнений» в программе 10 класса.
Рассмотрим свойства функции арксинус и построим ее график.
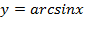
Определение.Арксинусом числа x называют такое значение угла y, для которого 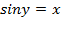 . Причем
. Причем 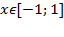 как ограничения на значения синуса, а
как ограничения на значения синуса, а 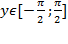 как выбранный диапазон углов.
как выбранный диапазон углов.
Основные свойства арксинуса:
1) 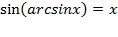 при
при 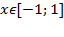
2) 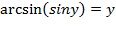 при
при 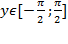 .
.
Основные свойства функции арксинус:
1) Область определения 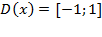 ;
;
2) Область значений 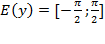 ;
;
3) Функция нечетная 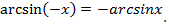 Эту формулу желательно отдельно запомнить, т.к. она полезна для преобразований. Также отметим, что из нечетности следует симметричность графика функции относительно начала координат;
Эту формулу желательно отдельно запомнить, т.к. она полезна для преобразований. Также отметим, что из нечетности следует симметричность графика функции относительно начала координат;
4) Функция монотонно возрастает.
Построим график функции 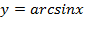 :
:
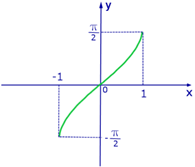
Обратим внимание, что никакой из участков графика функции не повторяется, а это означает, что арксинус не является периодической функцией, в отличие от синуса. То же самое будет относиться и ко всем остальным аркфункциям.
Рассмотрим свойства функции арккосинус и построим ее график.
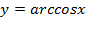
Определение.Арккосинусом числа x называют такое значение угла y, для которого 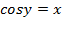
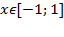 как ограничения на значения синуса, а
как ограничения на значения синуса, а 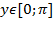 как выбранный диапазон углов.
как выбранный диапазон углов.
Основные свойства арккосинуса:
1) 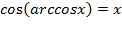 при
при 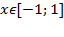 ,
,
2) 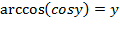 при
при 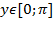 .
.
Основные свойства функции арккосинус:
1) Область определения 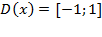 ;
;
2) Область значений 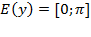 ;
;
3) Функция не является ни четной ни нечетной, т.е. общего вида 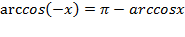 . Эту формулу тоже желательно запомнить, она пригодится нам позже;
. Эту формулу тоже желательно запомнить, она пригодится нам позже;
4) Функция монотонно убывает.
Построим график функции 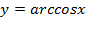 :
:
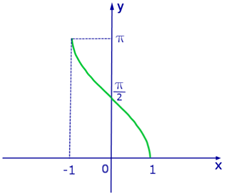
Рассмотрим свойства функции арктангенс и построим ее график.
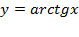
Определение.Арктангенсом числа x называют такое значение угла y, для которого 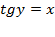 . Причем
. Причем 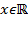 т.к. ограничений на значения тангенса нет, а
т.к. ограничений на значения тангенса нет, а 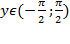 как выбранный диапазон углов.
как выбранный диапазон углов.
Основные свойства арктангенса:
1) 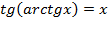 при
при 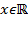 ,
,
2) 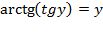 при
при 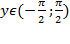 .
.
Основные свойства функции арктангенс:
1) Область определения 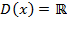 ;
;
2) Область значений 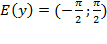 ;
;
3) Функция нечетная 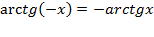 . Эта формула тоже полезна, как и аналогичные ей. Как в случае с арксинусом, из нечетности следует симметричность графика функции относительно начала координат;
. Эта формула тоже полезна, как и аналогичные ей. Как в случае с арксинусом, из нечетности следует симметричность графика функции относительно начала координат;
4) Функция монотонно возрастает.
Построим график функции 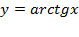 :
:
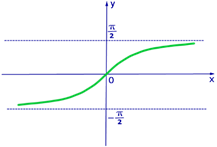
Рассмотрим свойства функции арккотангенс и построим ее график.
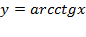
Определение.Арккотангенсом числа x называют такое значение угла y, для которого  . Причем
. Причем 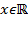 т.к. ограничений на значения котангенса нет, а
т.к. ограничений на значения котангенса нет, а 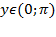 как выбранный диапазон углов.
как выбранный диапазон углов.
Основные свойства арккотангенса:
1) 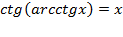 при
при 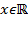 ,
,
2) 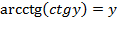 при
при 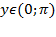 .
.
Основные свойства функции арккотангенс:
1) Область определения 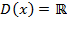 ;
;
2) Область значений 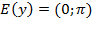 ;
;
3) Функция не является ни четной ни нечетной, т.е. общего вида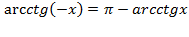 . Запомните и эту формулу, она нам тоже пригодится;
. Запомните и эту формулу, она нам тоже пригодится;
4) Функция монотонно убывает.
Построим график функции 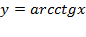 :
:
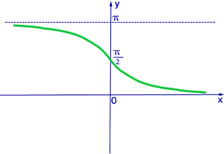
Между рассмотренными обратными тригонометрическими функциями существует два полезных соотношения, которые позволяют выражать одну функцию через другую:
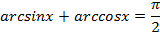
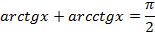
На этом уроке мы с вами рассмотрели такое понятие как обратная тригонометрическая функция, узнали их виды, свойства и построили графики.
В практической части урока мы займемся преобразованием выражений, содержащих обратные тригонометрические функции.
Полезные ссылки:
1) Алгебра 10 класс: «Арккосинус»
2) Алгебра 10 класс: «Арксинус»
3) Алгебра 10 класс: «Арктангенс и решение уравнения tg x=a»
4) Алгебра 10 класс: «Арккотангенс и решение уравнения ctg x=a»
interneturok.ru
Урок 9. Обратные тригонометрические функции. Практика. Видеоурок. Алгебра 11 Класс
Подготовка к ЕГЭ по математике
Эксперимент
Урок 9. Обратные тригонометрические функции.
Практика
Конспект урока
Главным образом умения работать с аркфункциями нам пригодятся при решении тригонометрических уравнений и неравенств.
Задания, которые мы сейчас рассмотрим, делятся на два вида: вычисление значений обратных тригонометрических функций и их преобразования с использованием основных свойств.
Начнем с вычисления значений аркфункций.
Задача №1. Вычислить 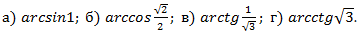
Как видим все аргументы аркфункций положительные и табличные, а это значит, что мы можем восстановить значение углов по первой части таблицы значений тригонометрических функций для углов от 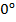 до
до 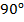 . Этот диапазон углов входит в область значений каждой из аркфункций, поэтому просто пользуемся таблицей, находим в ней значение тригонометрической функции и восстанавливаем, какому углу оно соответствует.
. Этот диапазон углов входит в область значений каждой из аркфункций, поэтому просто пользуемся таблицей, находим в ней значение тригонометрической функции и восстанавливаем, какому углу оно соответствует.
а) 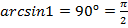
б) 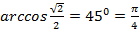
в) 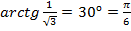
г) 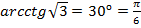
Далее будем работать с углами в радианах, т.к. это чаще используется в современной науке.
Ответ. 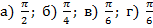 .
.
Задача №2. Вычислить 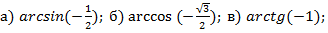
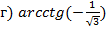 .
.
В данном примере мы уже видим отрицательные аргументы. Типичная ошибка в данном случае – это просто вынести минус из-под функции и просто свести задачу к предыдущей. Однако это делать можно не во всех случаях. Вспомним, как в теоретической части урока мы оговаривали четность всех аркфункций. Нечетными из них являются арксинус и арктангенс, т.е. из них выносится минус, а арккосинус и арккотангенс – это функции общего вида, для упрощения минуса в аргументе у них имеются специальные формулы. После расчета во избежание ошибок проверяем, чтобы результат входил в область значений.
а) 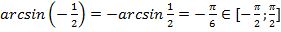
б) 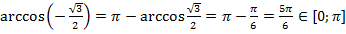
в) 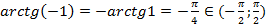
г) 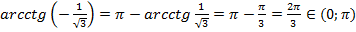
Когда аргументы функций упрощены до положительной формы, выписываем из таблицы соответствующие им значения углов.
Ответ. 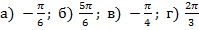 .
.
Может возникнуть вопрос, почему бы не выписывать значение угла, соответствующего, например, 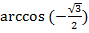 сразу из таблицы? Во-первых, потому что таблицу до
сразу из таблицы? Во-первых, потому что таблицу до 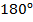 запомнить тяжелее, чем до
запомнить тяжелее, чем до 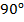 , во-вторых, потому что отрицательных значений синуса в ней нет, а отрицательные значения тангенса дадут по таблице неверный угол. Лучше иметь универсальный подход к решению, чем запутаться в множестве различных подходов.
, во-вторых, потому что отрицательных значений синуса в ней нет, а отрицательные значения тангенса дадут по таблице неверный угол. Лучше иметь универсальный подход к решению, чем запутаться в множестве различных подходов.
Задача №3. Вычислить 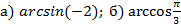 .
.
а) Типичная ошибка в данном случае – это начать выносить минус и что-то упрощать. Первое, что необходимо заметить, это то, что аргумент арксинуса не входит в область определения
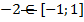 .
.
Следовательно, данная запись не имеет значения, и вычислить арксинус нельзя.
б) Стандартная ошибка в данном случае заключается в том, что путают местами значения аргумента и функции и дают ответ 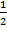 . Это неверно! Конечно, возникает мысль, что в таблице косинусу
. Это неверно! Конечно, возникает мысль, что в таблице косинусу 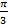 соответствует значение
соответствует значение 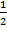 , но в таком случае перепутано то, что вычисляются аркфункции не от углов, а от значений тригонометрических функций. Т.е.
, но в таком случае перепутано то, что вычисляются аркфункции не от углов, а от значений тригонометрических функций. Т.е. 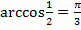 , а не
, а не 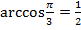 .
.
Кроме того, поскольку мы выяснили, что 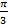 является именно аргументом арккосинуса, то необходимо проверить, чтобы он входил в область определения. Для этого вспомним, что
является именно аргументом арккосинуса, то необходимо проверить, чтобы он входил в область определения. Для этого вспомним, что 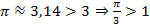 , т.е.
, т.е. 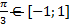 , а значит арккосинус не имеет смысла и вычислить его нельзя.
, а значит арккосинус не имеет смысла и вычислить его нельзя.
Кстати, например, выражение 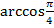 имеет смысл, т.к.
имеет смысл, т.к. 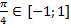 , но поскольку значение косинуса, равное
, но поскольку значение косинуса, равное 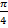 не является табличным, то и вычислить арккосинус с помощью таблицы нельзя.
не является табличным, то и вычислить арккосинус с помощью таблицы нельзя.
Ответ. Выражения не имеют смысла.
В данном примере мы не рассматриваем арктангенс и арккотангенс, т.к. у них не ограничена область определения и значения функций будут для любых аргументов.
Задача №4. Вычислить 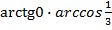 .
.
По сути дела задача сводится к самой первой, просто нам необходимо отдельно вычислить значения двух функций, а потом подставить их в исходное выражение.
Аргумент арктангенса табличный 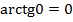 и результат принадлежит области значений.
и результат принадлежит области значений.
Аргумент арккосинуса не табличный, но нас это не должно пугать, т.к. чему бы не был равен арккосинус, его значение при умножении на ноль даст в результате ноль. Осталось одно важное замечание: необходимо проверить принадлежит ли аргумент арккосинуса области определения, поскольку если это не так, то все выражение не будет иметь смысла в независимости от того, что в нем присутствует умножение на ноль. Но 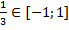 , поэтому мы можем утверждать, что
, поэтому мы можем утверждать, что 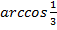 имеет смысл и в ответе получаем ноль.
имеет смысл и в ответе получаем ноль.
Ответ. 0.
Приведем еще пример, в котором необходимо уметь вычислить одну аркфункцию, зная значение другой.
Задача №5. Вычислить 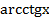 , если известно, что
, если известно, что 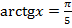 .
.
Может показаться, что необходимо из указанного уравнения вычислить сначала значение икса, а затем подставить его в искомое выражение, т.е. в арккотангенс, но этого делать не нужно.
Вспомним, по какой формуле связаны между собой указанные функции:
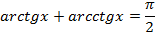
И выразим из нее то, что нам нужно:
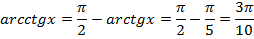
Для уверенности можете проверить, что результат лежит в области значений арккотангенса.
Ответ: 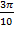 .
.
Теперь перейдем к серии заданий, в которых нам придется использовать преобразования аркфункций с использованием их основных свойств.
Задача №6. Вычислить 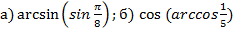 .
.
Для решения воспользуемся основными свойствами указанных аркфункций, только обязательно проверяя при этом соответствующие им ограничения.
а) 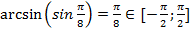
б) 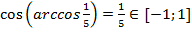 .
.
Ответ. а) 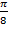 ; б)
; б) 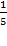 .
.
Задача №7. Вычислить  .
.
Типичная ошибка в данном случае – это сразу же написать в ответ 4. Как мы указывали в предыдущем примере, для использования основных свойств аркфункций необходимо проверить соответствующие ограничения на их аргумент. Мы имеем дело со свойством:
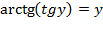 при
при 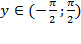
Но 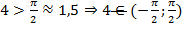 . Главное на этом этапе решения не подумать, что указанное выражение не имеет смысла и его нельзя вычислить. Ведь четверку, которая является аргументом тангенса, мы можем уменьшить при помощи вычитания периода тангенса, и это не повлияет на значение выражения. Проделав такие действия, у нас появится шанс уменьшить аргумент так, чтобы он вошел в указанный диапазон.
. Главное на этом этапе решения не подумать, что указанное выражение не имеет смысла и его нельзя вычислить. Ведь четверку, которая является аргументом тангенса, мы можем уменьшить при помощи вычитания периода тангенса, и это не повлияет на значение выражения. Проделав такие действия, у нас появится шанс уменьшить аргумент так, чтобы он вошел в указанный диапазон.
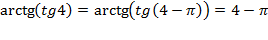 , т.к.
, т.к. 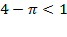 поскольку
поскольку 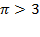 , следовательно,
, следовательно, 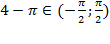 , т.к.
, т.к. 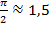 .
.
Ответ. 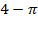 .
.
Задача №8. Вычислить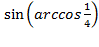 .
.
В указанном примере мы имеем дело с выражением, которое похоже на основное свойство арксинуса, но только в нем присутствуют кофункции. Его надо привести к виду синус от арксинуса или косинус от арккосинуса. Поскольку преобразовывать прямые тригонометрические функции проще, чем обратные, перейдем от синуса к косинусу с помощью формулы «тригонометрической единицы».
Как мы уже знаем:
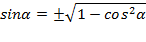
В нашем случае в роли 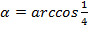 . Вычислим для удобства с
. Вычислим для удобства с
interneturok.ru
Основные тригонометрические тождества, их формулировки и вывод
В этой статье мы разберем такие важные понятия в тригонометрии, как арксинус, арккосинус, арктангенс и арккотангенс. Мы можем найти значения чисел (углов), если знаем данные тригонометрических функций; это и есть та самая задача, что приводит нас к обратным функциям.
Ниже мы не только дадим определения основных понятий и общепринятые обозначения, но и приведем расчеты, из которых будет ясно, что они из себя представляют. В конце мы попробуем связать понятия арккотангенса, арктангенса, арккосинуса и арксинуса с понятием единичной окружности.
Основные определения
Все перечисленные выше понятия — арксинус, арккосинус, арктангенс и арккотангенс – можно рассматривать как в качестве числа, так и в качестве угла. Ранее мы уже говорили о такой же двойственности восприятия прямых функций (синус, косинус и др.) Рассмотрим оба подхода отдельно.
Арксинус и другие обратные функции как угол
Допустим, у нас есть некий угол, синус которого равен 12. Обозначим его буквой альфа.
Итак, sinα=12. Такое значение синуса может быть у бесконечного числа углов: α=(−1)k·30°+180°·k (α=(−1)k·π/6+π·k), где k∈Z. Поэтому нам потребуется ввести дополнительные условия. Пусть угол альфа будет не менее -90 и не более 90 градусов (т.е. (в радианах он будет принадлежать отрезку [−π2, π2]),). В таком случае наше равенство sinα=12 позволит обозначить угол альфа более ясно: в таких условиях им будет только один угол – в 30 градусов (π6 радианов).
Исходя из указанного равенства, мы можем сделать вывод, что угол альфа определяется при условии любого числа a∈[−1, 1] и условии −90°≤α≤90° . Этот угол — и есть арксинус числа a.
Сформулируем основные определения.
Определение 1- Арксинус — это функция, обратная sin. Для некоторого числа а она представляет собой угол от -90 до 90 градусов, sin которого равен a.
- Арккосинус — функция, обратная косинусу. Для числа a — это такой угол, cos которого равен a, и который при этом находится в диапазоне от 0 до 180 градусов.
- Арктангенс -тригонометрическая функция, обратная тангенсу. Для некоторого числа a
zaochnik.com
| Техническая информация тут | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Обратные тригонометрические функции arcsix, arccos, arctg, arcctg. Свойства. Простейшие тригонометрические уравнения. Примеры значений обратных тригонометрических функций Поделиться:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dpva.ru