Касательная к окружности
Определение. Касательная к окружности — это прямая на плоскости, имеющая ровно одну общую точку с окружностью.
Вот парочка примеров:
 Окружность с центром O касается прямой l в точке A
Окружность с центром O касается прямой l в точке A Из любой точки M за пределами окружности можно провести ровно две касательных
Из любой точки M за пределами окружности можно провести ровно две касательных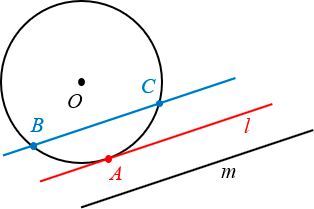 Различие между касательной l, секущей BC и прямой m, не имеющей общих точек с окружностью
Различие между касательной l, секущей BC и прямой m, не имеющей общих точек с окружностьюОсновные свойства касательных
Для того, чтобы решать любые задачи, нужно знать четыре ключевых свойства. Два из них описаны в любом справочнике / учебнике, а вот последние два — про них как-то забывают, а зря.
1. Отрезки касательных, проведённых из одной точки, равны
Чуть выше мы уже говорили про две касательных, проведённых из одной точки M. Так вот:
Отрезки касательных к окружности, проведённых из одной точки, равны.
 Отрезки AM и BM равны
Отрезки AM и BM равны2. Касательная перпендикулярна радиусу, проведённому в точку касания
Ещё раз посмотрим на картинку, представленную выше. Проведём радиусы OAи OB, после чего обнаружим, что углы OAMи OBM — прямые.
Радиус, проведённый в точку касания, перпендикулярен касательной.
Этот факт можно использовать без доказательства в любой задаче:
 Радиусы, проведённые в точку касания, перпендикулярны касательным
Радиусы, проведённые в точку касания, перпендикулярны касательнымКстати, заметьте: если провести отрезок OM, то мы получим два равных треугольника: OAM и OBM.
3. Соотношение между касательной и секущей
А вот это уже факт посерьёзнее, и большинство школьников его не знают. Рассмотрим касательную и секущую, которые проходят через одну и ту же общую точку M. Естественно, секущая даст нам два отрезка: внутри окружности (отрезок BC — его ещё называют хордой) и снаружи (его так и называют — внешняя часть MC).
Произведение всей секущей на её внешнюю часть равно квадрату отрезка касательной

4. Угол между касательной и хордой
Ещё более продвинутый факт, который часто используется для решения сложных задач. Очень рекомендую взять на вооружение.
Угол между касательной и хордой равен вписанному углу, опирающемуся на эту хорду.
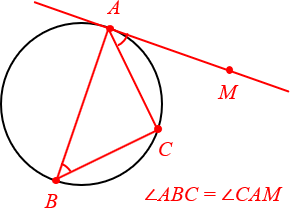
Откуда берётся точка B? В реальных задачах она обычно «всплывает» где-то в условии. Поэтому важно научиться распознавать данную конфигурацию на чертежах.
 Иногда всё-таки касается 🙂
Иногда всё-таки касается 🙂Смотрите также:
- Пробный ЕГЭ 2012. Вариант 5 (без производных)

- Формула полной вероятности

- Сводный тест по задачам B12 (2 вариант)

- Иррациональные неравенства. Часть 2

- Нестандартные задачи B2: кредит в банке

- Выделение полного квадрата

www.berdov.com
ПРОВЕДЕНИЕ ОБЩЕЙ КАСАТЕЛЬНОЙ К ГРАФИКАМ ДВУХ КВАДРАТИЧНЫХ ФУНКЦИЙ
ПРОВЕДЕНИЕ ОБЩЕЙ КАСАТЕЛЬНОЙ К ГРАФИКАМ ДВУХ КВАДРАТИЧНЫХ ФУНКЦИЙ
Мисякова Виктория
Протас Надежда
Класс 10 «Д», лицей БНТУ, Республика Беларусь, г. Минск
Лях Алла Сатуриновна
научный руководитель, преподаватель математики, лицей БНТУ, Республика Беларусь, г. Минск
 .(*)
.(*)
У данных квадратичных функций старшие коэффициенты равны 1 и -1, т. е. ветви обеих парабол направлены в разные стороны. Для определения точек пересечения графиков приравняем правые части уравнений системы ( ⃰⃰ ) и
исследуем взаимное расположение графиков заданных кривых при различных значениях их коэффициентов  и
и  .
.

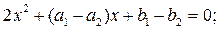

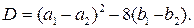
1) Если  , то параболы имеют две общие точки.
, то параболы имеют две общие точки.
2) Если 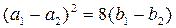 , то параболы имеют одну общую точку (касаются друг друга).
, то параболы имеют одну общую точку (касаются друг друга).
3) Если  , то параболы не имеют общих точек.
, то параболы не имеют общих точек.
Теперь проведем общие касательные к параболам:
 — уравнение касательной.
— уравнение касательной.
Пусть общая касательная касается параболы 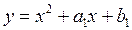 в точке
в точке  , а параболы
, а параболы  — в точке
— в точке  (рис. 1):
(рис. 1):

Рисунок 1.
Напишем уравнение касательной для кривой  :
:

Напишем уравнение касательной для кривой  :
:

Условие полного совпадения двух касательных есть равенство соответствующих коэффициентов:

Таким образом, мы имеем систему уравнений:

В результате преобразований получим уравнение:

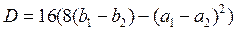 .
.
1) Если  , то параболы имеют две общие точки и в этом случае невозможно провести общую касательную.
, то параболы имеют две общие точки и в этом случае невозможно провести общую касательную.
Вывод: для парабол, у которых старшие коэффициенты равны 1 и -1 и 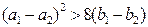 (параболы имеют две общие точки), общей касательной не существует.
(параболы имеют две общие точки), общей касательной не существует.
Пример 1:

 (рис. 2).
(рис. 2).

Рисунок 2.
2) Если  , то параболы имеют одну общую точку (касаются друг друга) и в этом случае существует единственная общая касательная, проведенная в точке касания парабол
, то параболы имеют одну общую точку (касаются друг друга) и в этом случае существует единственная общая касательная, проведенная в точке касания парабол  — точка касания.
— точка касания.
Уравнение общей касательной имеет вид:

Вывод: для парабол, у которых старшие коэффициенты равны 1 и -1 и  , (параболы будут иметь одну общую точку касания), можно провести одну общую касательную в их точке касания.
, (параболы будут иметь одну общую точку касания), можно провести одну общую касательную в их точке касания.
Пример 2:
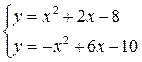
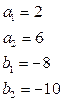 (рис. 3).
(рис. 3).

Рисунок 3.
Уравнение касательной и точка касания:

3) Если 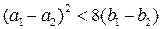 , то параболы не имеют общих точек и в этом случае можно провести две общие касательные.
, то параболы не имеют общих точек и в этом случае можно провести две общие касательные.

Обозначим А и С точки касания графиков парабол в одном случае, В и D – в другом.
Тогда:
 ;
;
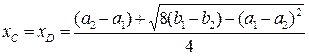 . (рис.4)
. (рис.4)
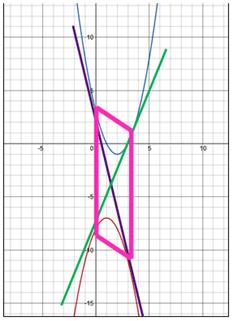
Рисунок 4.
Уравнения общих касательных имеет вид:
Для прямой AC:

Для прямой BD:
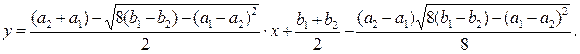
Заметим, что четыре точки касания двух общих касательных образуют четырехугольник ABCD, у которого стороны AB и CD параллельны.
Докажем, что данный четырехугольник является параллелограммом.
Пусть точка М1 — середина отрезка АС, а точка М2 — середина отрезка ВD. Тогда 

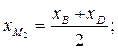

Получим 

Так как координаты точек M1 и M2 совпадают, то четырехугольник АBCD — параллелограмм.
Вывод: для парабол, у которых старшие коэффициенты равны 1 и -1 и 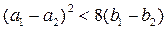 , (параболы не будут иметь общих точек), можно провести две общие касательные, и точки касания будут являться вершинами параллелограмма, две стороны которого параллельны оси ординат.
, (параболы не будут иметь общих точек), можно провести две общие касательные, и точки касания будут являться вершинами параллелограмма, две стороны которого параллельны оси ординат.
Пример 3:

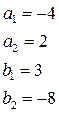 (рис. 5)
(рис. 5)

Рисунок 5.
Уравнения касательных и точки касания:
 ;
;
 ;
;
 ;
;
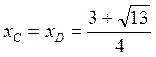 .
.
Список литературы:
1.Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия. Дополнительные главы к учебнику 9 класса М.: Вита-Пресс, 2003. — 176 с.;
2.Энциклопедический словарь юного математика. Сост. Савин А.П. М.: Педагогика, 1985. — 352 с.;
sibac.info
Свойства касательной
Относительное положение прямой и окружности
Прямая относительно окружности может находиться в следующих трех положениях:
- Расстояние от центра окружности до прямой больше радиуса. В этом случае все точки прямой лежат вне круга.
- Расстояние от центра окружности до прямой меньше радиуса. В этом случае прямая имеет точки, лежащие внутри круга и так как прямая бесконечна в обе стороны, то она пересекается сокружностью в 2 точках.
- Расстояние от центра окружности до прямой равно радиусу. Прямая — касательная.
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности.
Общая точка называется в этом случае точкой касания.
Возможность существования касательной, и притом проведенной через любую точку окружности, как точку касания, доказывается следующей теоремой.
Теорема. Если прямая перпендикулярна к радиусу в его конце, лежащем на окружности, то эта прямая — касательная.
Пусть O (рис) — центр некоторого круга и OA какой-нибудь его радиус. Через его конец A проведем MN ^ OA.
Требуется доказать, что прямая MN — касательная, т.е. что эта прямая имеет с окружностью только одну общую точку A.
Допустим противное: пусть MN имеет с окружностью еще другую общую точку, например B.
Тогда прямая OB была бы радиусом и, следовательно, равнялась бы OA.
Но этого быть не может, так как, если OA -перпендикуляр, то OB должна быть наклонной к MN, а наклонная больше перпендикуляра.
Обратная теорема. Если прямая касательна к окружности, то радиус, проведенный в точку касания, перпендикулярен к ней.
Пусть MN — касательная к окружности, A — точка касания и O — центр этой окружности.
Требуется доказать, что OA^MN.
Допустим противное, т.е. предположим, что перпендикуляром, опущенным из O на MN, будет не OA , а какая-нибудь другая прямая, например, OB.
Возьмем BС = AB и проведем OС.
Тогда OA и OС будут наклонные, одинаково удаленные от перпендикуляра OB, и следовательно, OС = OA.
Из этого следует, что окружность, учитывая наше предположение, будет иметь с прямой MN две общие точки: A и С , т.е. MN будет не касательная, а секущая, что противоречит условию.
Следствие. Через всякую данную на окружности точку можно провести касательную к этой окружности и притом только одну, так как через эту точку можно провести перпендикуляр, и притом только один, к радиусу, проведенному в нее.
Теорема. Касательная, параллельная хорде, делит в точке касания дугу, стягиваемую хордой, пополам.
Пусть прямая AB (рис.) касается окружности в точке M и параллельна хорде СD.
Требуется доказать, что ÈCM = ÈMD.
Проведя через точку касания диаметр ME, получаем: EM ^ AB, и следовательно, EM ^ СВ.
Поэтому СM=MD.
Задача. Через данную точку провести касательную к данной окружности.
Если данная точка находится на окружности, то проводят через нее радиус и через конец радиуса перпендикулярную прямую. Эта прямая будет искомой касательной.
Рассмотрим тот случай, когда точка дана вне круга.
Пусть требуется (рис.) провести к окружности с центром O касательную через точку A.
Для этого из точки A, как из центра, описываем дугу радиусом AO, а из точки O, как центра, пересекаем эту дугу в точках B и С раствором циркуля, равным диаметру данного круга.
Проведя затем хорды OB и OС, соединим точку A с точками D и E, в которых эти хорды пересекаются с данной окружностью.
Прямые AD и AE — касательные к окружности O.
Действительно, из построения видно, что тр-ки AOB и AOС равнобедренные (AO = AB =AС ) с основаниями OB и OС, равными диаметру круга O.
Так как OD и OE — радиусы, то D — середина OB, а E — середина OС, значит AD и AE — медианы, проведенные к основаниям равнобедренных тр-ков, и потому перпендикулярны к этим основаниям. Если же прямые DA и EA перпендикулярны к радиусам OD и OE, то они — касательные.
Следствие. Две касательные, проведенные из одной точки к окружности, равны и образуют равные углы с прямой, соединяющей эту точку с центром.
Так AD=AE и ÐOAD = ÐOAE (рис.), потому что прямоугольные тр-ки AOD и AOE, имеющие общую гипотенузу AO и равные катеты OD и OE (как радиусы), равны.
Заметим, что здесь под словом “касательная” подразумевается собственно “отрезок касательной” от данной точки до точки касания.
Задача. Провести касательную к данной окружности O параллельно данной прямой AB (рис.).
Опускаем на AB из центра O перпендикуляр OС и через точку D, в которой этот перпендикуляр пересекается с окружностью, проводим EF || AB.
Искомая касательная будет EF.
Действительно, так как OС ^ AB и EF || AB, то EF ^ OD, а прямая, перпендикулярная к радиусу в его конце, лежащем на окружности — касательная.
Задача. К двум окружностям O и O1 провести общую касательную (рис.).
Анализ. Предположим, что задача решена.
Пусть AB будет общая касательная, A и B — точки касания.
Очевидно, что если мы найдем одну из этих точек, например, A, то затем легко найдем и другую.
Проведем радиусы OA и O1B. Эти радиусы, будучи перпендикулярны к общей касательной, параллельны между собой.
Поэтому, если из O1 проведем O1С || BA, то тр-к OСO1 будет прямоугольный при вершине С.
Вследствие этого, если опишем из O, как центра, радиусом OС окружность, то она будет касаться прямой O1С в точке С.
Радиус этой вспомогательной окружности известен: он равен OA – СA= OA — O1B, т.е. он равен разности радиусов данных окружностей.
Построение. Из центра O описываем окружность радиусом, равным разности данных радиусов.
Из O1 проводим к этой окружности касательную O1С (способом, указанным в предыдущей задаче).
Через точку касания С проводим радиус OС и продолжаем его до встречи с данной окружностью в точке A. Наконец из A проводим AB параллельно СO1.
Совершенно таким же способом мы можем построить другую общую касательную A1B1 (рис.). Прямые AB и A1B1 называют внешними общими касательными.
Можно еще провести две внутренние касательные следующим образом:
Анализ. Предположим, что задача решена (рис.). Пусть AB — искомая касательная.
Проведем радиусы OA и O1B в точки касания A и B. Так как эти радиусы оба перпендикулярны к общей касательной, то они параллельны между собой.
Поэтому, если из O1 проведем O1С || BA и продолжим OA до точки С, то OС будет перпендикуляр к O1С.
Вследствие этого окружность, описанная радиусом OС из точки O, как центра, будет касаться прямой O1С в точке С.
Радиус этой вспомогательной окружности известен: он равен OA+AС = OA+O1B, т.е. он равен сумме радиусов данных окружностей.
Построение. Из O как центра, описываем окружность радиусом, равным сумме данных радиусов.
Из O1 проводим к этой окружности касательную O1С.
Точку касания С соединяем с O.
Наконец через точку A, в которой OС пересекается с данной окружностью, проводим AB = O1С.
Подобным же способом можем построить другую внутреннюю касательную A1B1.
Общее определение касательной
Пусть к окружности с центром (рис.) проведены через точку A касательная AT и какая-нибудь секущая AM.
Станем вращать эту секущую вокруг точки A так, чтобы другая точка пересечения B все ближе и ближе придвигалась к A.
Тогда перпендикуляр OD, опущенный из центра на секущую, будет все больше и больше приближаться к радиусу OA, и угол AOD может стать меньше всякого малого угла.
Угол MAT, образованный секущей и касательной, равен углу AOD (вследствие перпендикулярности их сторон).
Поэтому при неограниченном приближении точки B к A угол MAT также может стать как угодно мал.
Это выражают иными словами так:
касательная есть предельное положение, к которому стремится секущая, проведенная через точку касания, когда вторая точка пересечения неограниченно приближается к точке касания.
Это свойство принимают за определение касательной, когда речь идет о какой угодно кривой.
Так, касательной к кривой AB (рис.) называется предельное положение MT, к которому стремится секущая MN, когда точка пересечения P неограниченно приближается к M.
Заметим,что определяемая таким образом касательная может иметь с кривой более одной общей точки (как это видно на рис).
razdupli.ru
Окружность и касательная — урок. Геометрия, 8 класс.
В плоскости прямая и окружность могут пересекаться или не пересекаться. При пересечении могут иметь одну или две общие точки.
1. Если расстояние от центра окружности до прямой больше радиуса, то у прямой и окружности общих точек нет.

2. Если расстояние от центра окружности до прямой меньше радиуса, то у прямой и окружности две общие точки.

В этом случае прямую называют секущей окружности.
Если прямая имеет две общие точки с окружностью, то она называется секущей.
3. Если расстояние от центра окружности до прямой равно радиусу, то у прямой и окружности одна общая точка.

В этом случая прямую называют касательной к окружности.
Касательной к окружности называется прямая, имеющая с окружностью одну общую точку.
Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

Предположим, что радиус \(OA\) не перпендикулярен к прямой, но является наклонной. Тогда из точки \(O\) можно провести перпендикуляр к прямой, который будет короче радиуса. А это означает, что расстояние от центра окружности до прямой меньше радиуса, и у прямой и окружности должны быть две общие точки. Но это противоречит данной информации, наше предположение неверно.
Если из точки к окружности проведены две касательные, то
а) длины отрезков касательных от этой точки до точки касания равны,
б) прямая, проходящая через центр окружности и эту точку, делит угол между касательными пополам.

Пусть \(AB\) и \(AC\) — касательные к окружности с центром \(O\).
Требуется доказать, что \(AB = AC\) и \(OA\) является биссектрисой угла \(A\).
Треугольники \(OBA\) и \(OCA\) — прямоугольные, так как касательные перпендикулярны к радиусам в точках \(B\) и \(C\). Сторона \(OA\) — общая. Катеты \(OB\) и \(OC\) равны как радиусы одной и той же окружности. Треугольники равны по гипотенузе и катету, отсюда равны и катеты \(AB\) и \(AC\), и углы \(BAO\) и \(CAO\), то есть \(OA\) делит угол пополам.
www.yaklass.ru
Касательная прямая к окружности — Википедия
Касательная прямая к окружности в евклидовой геометрии на плоскости — прямая, которая имеет с окружностью ровно одну общую точку. Также можно определить касательную как предельное положение секущей, когда точки пересечения её с окружностью бесконечно сближаются. Касательные прямые к окружностям служат предметом рассмотрения ряда теорем и играют важную роль во многих геометрических построениях и доказательствах.
Касательные прямые к одной окружности
Касательная прямая t к окружности C пересекает окружность в единственной точке T. Для сравнения, секущие прямые пересекают окружность в двух точках, в то время как некоторые прямые могут не пересекать окружность совсем. Это свойство касательной прямой сохраняется при многих геометрических преобразованиях[en], таких как подобие, вращение, параллельный перенос, инверсия и картографическая проекция. Говоря техническим языком, эти преобразования не меняют структуру инцидентности касательных прямых и окружностей, даже если сами прямые и окружности деформируются.
Радиус окружности, проведённый через точку касания, перпендикулярен касательной прямой. И обратно, перпендикуляр к радиусу в конечной точке (на окружности) является касательной прямой. Окружность вместе с касательной прямой имеют осевую симметрию относительно радиуса (к точке касания).
По теореме о степени точки произведение длин PM•PN для любого луча PMN равно квадрату PT, длине отрезка от точки P до точки касания (отрезок показан красным цветом).Никакая касательная прямая не может проходить через точку внутри окружности, поскольку любая такая прямая должна быть секущей. В то же время для любой точки, лежащей вне круга, можно построить две проходящие через неё касательные прямые. Геометрическая фигура, состоящая из окружности и двух касательных прямых, также обладает осевой симметрией относительно прямой, соединяющей точку P с центром окружности O (см. рисунок справа). В этом случае отрезки от точки P до двух точек касания имеют одинаковую длину. По теореме о степени точки квадрат длины отрезка до точки касания равен степени точки P относительно окружности C. Эта степень равна произведению расстояний от точки P до двух точек пересечения окружности любой секущей линией, проходящей через P.
Угол θ между хордой и касательной равен половине дуги, заключённой между концами хорды.Касательная прямая t и точка касания T обладают свойством сопряжённости друг другу; это соответствие можно обобщить в идею о полюсе и поляре. Такая же взаимосвязь существует между точкой P вне окружности и секущей линией, соединяющей две точки касания.
Если точка P лежит вне окружности с центром O, и если касательные прямые из P касаются окружности в точках T и S, то углы ∠TPS и ∠TOS дают в сумме 180°.
Если хорда TM проведена из точки касания T прямой P T и ∠PTM ≤ 90°, то ∠PTM = (1/2)∠MOT.
Геометрическое построение
Построение касательной прямой к окружности (выделена красным) перпендикулярно радиусу.Относительно легко построить прямую t, касательную к окружности в точке T на окружности. Для этого следует провести прямую a через центр окружности O и точку T. Тогда прямая t является перпендикуляром к прямой a. Один из способов построения перпендикуляра следующий (см. рисунок). Проводим тем же радиусом (r) окружность с центром в точке T, получаем вторую точку G на прямой a, а точка T становится серединой отрезка OG. Проводим две окружности радиуса R>r с центрами в точках O и G. Прямая, проходящая через точки пересечения этих окружностей, будет касательной.
Построение касательной прямой к окружностиДля построения касательной прямой через точку P к окружности C можно использовать свойство угла, опирающегося на диаметр окружности. Проводится окружность с центром в точке H, середине отрезка OP, где O — центр окружности C. Пересечения T и T‘ являются точками касания прямых, проходящих через точку P, поскольку углы ∠OTP и ∠OT‘P опираются на диаметр OP окружности с центром в H.
Теорема об описанном четырёхугольнике и вписанные окружности
Описанный четырёхугольник ABCD — это замкнутая фигура с четырьмя сторонами, которые касаются окружности C. Соответственно, C — вписанная в четырёхугольник ABCD окружность. По теореме Пито суммы противоположных сторон любого такого четырёхугольника равны, то есть
- AB¯+CD¯=BC¯+DA¯.{\displaystyle {\overline {AB}}+{\overline {CD}}={\overline {BC}}+{\overline {DA}}.}
Это заключение следует из равенства отрезков касательных от вершин четырёхугольника. Обозначим точки касания как P (на отрезке AB), Q (на отрезке BC), R (на отрезке CD) и S (на отрезке DA). Симметричные отрезки до точек касания от каждой вершины четырёхугольника ABCD равны, то есть BP=BQ=b, CQ=CR=c, DR=DS=d и AS=AP=a. Но каждая сторона четырёхугольника состоит из двух таких отрезков
- AB¯+CD¯=(a+b)+(c+d)=BC¯+DA¯=(b+c)+(d+a){\displaystyle {\overline {AB}}+{\overline {CD}}=(a+b)+(c+d)={\overline {BC}}+{\overline {DA}}=(b+c)+(d+a)},
что и доказывает утверждение.
Обратное утверждение также верно — окружность можно вписать в любой выпуклый четырёхугольник, у которого суммы длин противоположных сторон равны.[1]
Эта теорема и обратная к ней имеют различные применения. Например, из теоремы немедленно следует, что ни в какой прямоугольник не может быть вписана окружность, если только это не квадрат, а также что можно вписать окружность в любой ромб, хотя в общем случае вписать в параллелограмм окружность нельзя.
Касательные прямые к двум окружностям
Внешний (сверху) и внутренний (внизу) центры гомотетии двух окружностей (выделены красным цветом), показанные зелёными точками.Для двух окружностей в общем случае имеется четыре различные прямые, касательные к обоим окружностям, если одна окружность не лежит в другой, но в вырожденных случаях может быть любое число касательных от нуля до четырёх. Эти случаи описаны ниже. Из четырёх касательных прямых две являются внешними касательными, когда окружности оказываются лежащими по одну сторону от касательной прямой. Для двух других прямых, внутренних касательных, окружности оказываются лежащими по разные стороны от касательной прямой. Внешние касательные пересекаются в центре внешней гомотетии[en], в то время как внутренние касательные пересекаются в центре внутренней гомотетии. И внутренний, и внешний центры гомотетии лежат на прямой, проходящей через центры окружностей, ближе к центру меньшей окружности. Если две окружности имеют одинаковые радиусы, остаются те же четыре касательных, но внешние касательные прямые параллельны и внешнего центра гомотетии на аффинной плоскости не существует. На проективной плоскости внешний центр гомотетии лежит в бесконечно удалённой точке, соответствующей пересечению прямых.[2]
Внешняя касательная
Построение внешних касательных.Красные прямые, соединяющие точки T1 и T3, T2 и T4, являются внешними касательными двух окружностей.
Внутренняя касательная
Внутренние касательные — это касательные, которые пересекают отрезок, соединяющий центры окружностей. Заметим, что внутренние касательные не существуют в случае пересекающихся окружностей.
Построение
Построение внутренних касательныхКасательные к двум окружностям могут быть построены с помощью нахождения центров гомотетии, как описано выше, а затем построения касательных, проходящих через эти центры. Можно также построить касательные прямые и касательные точки прямо, как описано ниже.
Элементарная геометрия
Пусть O1 и O2 — два центра двух окружностей C1 и C2 и пусть r1 и r2 — их радиусы, при этом r1 > r2. Другими словами, окружность C1 будем считать большей из двух окружностей. Два различных способа можно использовать для построения внешних и внутренних касательных прямых.
- Внешние касательные
Рисуем новую окружность C3 с радиусом r1 − r2 с центром в O1. Используя метод, описанный выше, проводим две касательные прямые из точки O2 к этой новой окружности. Эти прямые параллельны искомым касательным прямым, поскольку это соответствует уменьшению радиусов обеих окружностей C1 и C2 на одно и то же число r2, в результате чего окружность C2 превращается в точку. Через две точки касания на окружности C3 можно провести два луча из центра O1. Эти лучи пересекают C1 в искомых точках касания. Искомые касательные перпендикулярны этим радиальным лучам и могут быть построены, как показывалось выше.
- Внутренние касательные
Рисуем новую окружность C3 с радиусом r1 + r2 с центром в O1. Используя метод, описанный выше, проводим две касательные прямые из точки O2 к этой новой окружности. Эти прямые параллельны искомым касательным прямым, поскольку это соответствует уменьшению радиуса окружности C2 до нуля с одновременным увеличением радиуса C1 на ту же константу r2. Два радиальных луча можно провести из центра O1 через точки касания на C3. Эти лучи пересекают C1 в искомых точках касания. Искомые внутренние касательные перпендикулярны радиальным лучам и пересекают лучи в найденных точках, так что их можно построить вышеуказанным методом.
Фактически это то же самое построение, что и для внешних касательных, если принять, что радиус меньшей окружности отрицателен.
Аналитическая геометрия
Пусть окружности имеют центры c1 = (x1,y1) и c2 = (x2,y2) и радиусы r1 и r2 соответственно. Пусть касательная прямая имеет уравнение ax+by+c=0,{\displaystyle ax+by+c=0,} с нормализацией a2 + b2 = 1, тогда расстояние от центров окружностей до прямой вычисляется по формулам:
- ax1 + by1 + c = r1 и
- ax2 + by2 + c = r2.
Вычтем первое уравнение из второго, получим
- aΔx + bΔy = Δr
где Δx = x2 − x1, Δy = y2 − y1 и Δr = r2 − r1.
Если d=(Δx)2+(Δy)2{\displaystyle d={\sqrt {(\Delta x)^{2}+(\Delta y)^{2}}}} — расстояние от c1 до c2, мы можем нормализовать, сделав замену X = Δx/d, Y = Δy/d и R = Δr/d для упрощения уравнений, что даёт уравнения aX + bY = R и a2 + b2 = 1. Решаем их и получаем два решения (k = ±1) для двух внешних касательных линий:
- a = RX − kY√(1 − R2)
- b = RY + kX√(1 − R2)
- c = r1 − (ax1 + by1)
Геометрически это соответствует вычислению угла, образованного касательной и прямой, проведённой через центры, а затем линия центов поворачивается для получения уравнения касательной. Угол можно вычислить с помощью тригонометрии из прямоугольного треугольника, вершинами которого являются (внешний) центр гомотетии, центр окружности и точка касания. Гипотенуза лежит на прямой центров, радиус является катетом, противоположным углу, а прилегающий к углу катет лежит на касательной прямой.
(X, Y) — это единичный вектор, направленный от c1 в c2, в то время как R равен cosθ{\displaystyle \cos \theta }, где θ{\displaystyle \theta } — угол между линией центров и касательной. sinθ{\displaystyle \sin \theta } тогда равен ±1−R2{\displaystyle \pm {\sqrt {1-R^{2}}}} (в зависимости от знака θ{\displaystyle \theta }, что эквивалентно направлению вращения), и приведённые выше уравнения являются вращением (X, Y) на ±θ,{\displaystyle \pm \theta ,} с помощью матрицы вращения
- (R∓1−R2±1−R2R){\displaystyle {\begin{pmatrix}R&\mp {\sqrt {1-R^{2}}}\\\pm {\sqrt {1-R^{2}}}&R\end{pmatrix}}}
- k = 1 — это касательная прямая справа от окружностей, если смотреть из c1 в направлении c2.
- k = −1 — это касательная прямая справа от окружностей, если смотреть из c2 в направлении c1.
Все рассуждения выше предполагают, что радиусы окружностей положительны. Если r1 положителен, а r2 отрицателен, то c1 будет лежать слева от каждой прямой, а c2 — справа, и две касательные прямые пересекутся. Таким путём можно получить все четыре решения. Смена знака обоих радиусов приводит к обмену вариантов k = 1 и k = −1.
Вектора
В общем случае точки касания t1 и t2 для любой из четырёх касательных прямых к окружностям с центрами в v1 и v2 и с радиусами r1 и r2 получаются путём решения четырёх уравнений:
- (t2−v2)⋅(t2−t1)=0(t1−v1)⋅(t2−t1)=0(t1−v1)⋅(t1−v1)=r12(t2−v2)⋅(t2−v2)=r22{\displaystyle {\begin{aligned}(t_{2}-v_{2})\cdot (t_{2}-t_{1})&=0\\(t_{1}-v_{1})\cdot (t_{2}-t_{1})&=0\\(t_{1}-v_{1})\cdot (t_{1}-v_{1})&=r_{1}^{2}\\(t_{2}-v_{2})\cdot (t_{2}-v_{2})&=r_{2}^{2}\\\end{aligned}}}
Эти уравнения выражают тот факт, что касательная прямая перпендикулярна радиусам, а точки касания лежат на соответствующих окружностях.
Эти четыре квадратных уравнения с двумерными векторными переменными в общем случае дают четыре пары решений.
Вырожденные случаи
Две различные окружности могут иметь, в зависимости от взаимного расположения, от нуля до четырёх прямых, касающихся обеих окружностей. Варианты можно классифицировать по расстоянию между центрами и радиусам.
И наконец, если окружности совпадают, любая касательная прямая к одной окружности будет общей касательной.
Далее понятие общей касательной прямой можно расширить на случай окружностей отрицательного радиуса (которые образованы теми же самыми точками x2+y2=(−r)2,{\displaystyle x^{2}+y^{2}=(-r)^{2},} но «наизнанку»). В этом случае, если радиусы имеют противоположные знаки (одна окружность имеет положительный радиус, другая — отрицательный) внешний и внутренний центры гомотетии меняются местами и внешние и внутренние общие касательные меняются местами. Если же радиусы имеют один и тот же знак (оба радиуса положительны или оба отрицательны), то понятия «внешний» и «внутренний» имеют обычный смысл.
Общие касательные можно определить для окружностей с нулевым радиусом. В этом случае окружность с нулевым радиусом трактуется как двойная точка, а потому любая прямая, проходящая через эту точку, пересекает её с кратностью[en] два. Если окружность имеет радиус ноль, общая касательная прямая — это просто касательная прямая к окружности, проходящая через точку, но считается эта прямая дважды. Если обе окружности имеют нулевой радиус, то общая касательная прямая — это прямая, проходящая через две точки, и эта прямая имеет кратность четыре.
Заметим, что в этих вырожденных случаях внешний и внутренний центры гомотетии остаются (внешний центр уходит в бесконечность, если радиусы равны), за исключением случая, когда окружности совпадают (в этом случае внешний центр не определён), или когда обе окружности имеют нулевой радиус (в этом случае отсутствует внутренний центр).
Приложения
Задача о ремённой передаче
Внутренние и внешние касательные полезны при решении задачи о ремённой передаче[en], которая заключается в вычислении длины ремня, который плотно бы прилегал к колёсам передачи. Если считать ремень математической кривой с пренебрежительно малой толщиной и если колёса передачи находятся точно в одной плоскости, задача сводится к суммированию отрезков касательных с соответствующими длинами дуг. Если ремень натянут на колёса с пересечением, необходимо рассматривать внутренние касательные. Если же ремень натянут без пересечения, необходимо рассматривать внешние касательные. Последний случай иногда называется задачей шкивов.
Касательные прямые к трём окружностям: теорема Монжа
Для трёх окружностей C1, C2 и C3 существует три пары окружностей (C1C2, C2C3 и C1C3). Поскольку каждая пара окружностей имеет два центра гомотетии, всего получим шесть центров гомотетии[en]. Гаспар Монж показал в начале 19-го века, что эти шесть точек лежат на четырёх прямых, и на каждой прямой лежат три точки.
Касательные прямые и бильярд
Прицеливание удара в бильярде. Направление удара от битка (шар B) выбирается так, чтобы точка касания совпадала с точкой пересечения прямой, проходящей через центр лузы и центр прицельного шара. В этом случае прицельный шар поёдёт в сторону лузы, а биток пойдёт параллельно зелёной линии, касательной к прицельному шару (C) и воображаемому шару (M)Система касательных прямых прицеливания битка использует прямую, проходящую через середину кия, для создания двух касательных прямых от битка в направлении прицельного шара. Две касательные прямые и прямая через середину битка пересекают прямую, проходящую через середину прицельного шара и центр лузы. Необходимо направить удар так, чтобы конечное положение битка (воображаемый шар на рисунке) касалось прицельного шара в точке касания прямой, перпендикулярной направлению на лузу (на рисунке эта касательная выделена зелёным цветом).
Задача Аполлония
Много частных случаев задачи Аполлония используют нахождение окружностей, касающихся одной или нескольких прямых. В простейшем из этих случаев строится окружность, касающаяся трёх заданных прямых (задача LLL). Центр любой такой окружности должен лежать на биссектрисе угла в точке пересечения любой пары этих прямых. В каждой точке пересечения прямых есть две биссектрисы. Пересечения этих биссектрис дают центры окружностей, являющихся решением. В общем случае существует четыре таких окружностей для треугольника, образованного пересечением трёх прямых — вписанная окружность и три вневписанных.
Анимация, показывающая инверсное преобразование задачи Аполлония. Синяя и красная окружности увеличиваются, пока не коснутся, и при инверсии относительно серой окружности переходят в две параллельные прямые. Жёлтые решения получаются путём перемещения вдоль этих прямых до касания зелёной окружности.В общем случае задачу Аполлония можно свести к более простой задаче построения окружности, касающейся одной окружности и двух параллельных прямых (это сам по себе частный случай LLC). Чтобы это сделать, увеличиваем пропорционально[en] две из этих трёх заданных окружностей вплоть до их касания. Инверсия относительно окружности подходящего радиуса с центром в точке касания переводит эти две окружности в две параллельные прямые, а третью окружность — в другую окружность. Таким образом, решение может быть найдено путём перемещения окружности постоянного радиуса между двумя параллельными прямыми, пока не получим касание с преобразованной третьей окружностью. Обратная инверсия даст решения исходной задачи.
Обобщения
Понятия касательной прямой и точки касания можно обобщить до полюса Q и соответствующей ей полярной прямой q. Точки P и Q являются инверсиями друг друга относительно окружности.Понятие касательной прямой к одной и более окружностям можно обобщить несколькими путями. В первую очередь, свойство парности касательных прямых и точек касания можно обобщить до полюса и полярной прямой, когда полюс может находиться в любом месте, не обязательно на окружности. Во-вторых, объединение двух окружностей является особым (приводимым[en]) случаем плоской кривой четвёртой степени, а внешние и внутренние касательные прямые являются касательными к двум точкам[en] этой кривой. В общем случае плоская кривая четвёртой степени имеет 28 прямых, касающихся её дважды.
Третье обобщение относится скорее к касательным окружностям, а не к касательным прямым. Касательную прямую можно рассматривать как касательную окружность с бесконечным радиусом. В частности, внешние касательные прямые к двум окружностям можно рассматривать как частные случаи из семейства окружностей, касающихся с внутренней или внешней стороны обеих окружности, в то время как внутренние касательные прямые можно рассматривать как частные случаи семейства окружностей, касающихся с внутренней стороны одной окружности и с внешней стороны другой) [3].
В геометрии Мёбиуса или инверсной геометрии прямые рассматриваются как окружности с центром «в бесконечности» и для любой прямой и для любой окружности существует преобразование Мёбиуса, которое переводит одну фигуру в другую. В геометрии Мёбиуса касание прямой и окружности становится особым случаем касания двух окружностей. Эта эквивалентность развивается далее в сферической геометрии Ли[en].
Примечания
Литература
Ссылки
wikipedia.green
3.2.3 Построение касательных к двум окружностям
При вычерчивании контуров предметов сравнительно часто приходится строить общие касательные к двум дугам окружностей. Общая касательная к двум окружностям может быть внешней, если обе окружности расположены с одной стороны от нее, и внутренней, если окружности расположены с разных сторон касательной.
Построение общей внешней касательной к двум окружностям радиусами R и r (рисунок 47). Из центра окружности большего радиуса – точкиO1 описывают окружность радиусомR – r(рисунок 47, а). Находят середину отрезкаO2O1 – точкуO3и из нее проводят вспомогательную окружность радиусомO3O2 илиO3O1.Обе проведенные окружности пересекаются в точкахA иВ. ТочкиO1 иB соединяют прямой и в пересечении ее с окружностью радиусомR определяют точку касанияD (рисунок 47, б). Из точкиO2параллельно прямойO1D проводят линию до пересечения с окружностью радиусомrи получают вторую точку касанияC. ПрямаяCDявляется искомой касательной. Так же строится вторая общая внешняя касательная к этим окружностям (прямаяEF).

а б
Рисунок 47
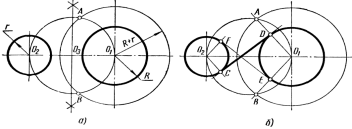
Построение общей внутренней касательной к двум окружностями радиусов R и r (рисунок 48). Из центра любой окружности, например: точкиO1, описывают окружность радиусомR +r (рисунок 48, а). Разделив отрезокO2O1 пополам, получают точкуO3. Из точкиO3как из центра описывают вторую вспомогательную окружность радиусомO3O2 = O3О1 и отмечают точки A и В пересечения вспомогательных окружностей. Соединив прямой точки A и O1 (рисунок 48, б), в пересечении ее с окружностью радиуса R получают точку касания D. Через центр окружности радиуса r проводят прямую, параллельную прямой O1D, и в пересечении ее с заданной окружностью определяют вторую точку касания С. Прямая CD – внутренняя касательная к заданным окружностям. Аналогично строится и вторая касательная EF.
а б
Рисунок 48
3.3 Сопряжения с помощью дуги окружности
3.3.1 Сопряжение двух прямых дугой окружности
Все задачи на сопряжение дугой могут быть сведены к двум видам. Сопряжение осуществляется либо заданным радиусом сопрягающей дуги, либо через точку, заданную на одной из сопрягаемых линий. В том и другом случаях необходимо построить центр сопрягающей дуги.
Сопряжение двух пересекающихся прямых дугой заданным радиусом Rc (рисунок 49, а). Так как сопрягающая дуга должна касаться заданных прямых, то центр ее должен быть удален от каждой прямой на величину равную радиусуRc. Сопряжение строят так. Проводят две прямые, параллельные заданным и удаленные от них на величину радиусаRcи в пересечении этих прямых отмечают точкуO – центр сопрягающей дуги. Из точкиОопускают перпендикуляр на каждую из заданных прямых. Основания перпендикуляров – точкиA иB – являются точками касания сопрягающей дуги. Такое построение сопряжения справедливо для двух пересекающихся прямых, составляющих любой угол. Для сопряжения сторон прямого угла можно воспользоваться также способом, указанным на рисунке 49, б.

а б
Рисунок 49
Сопряжение двух пересекающихся прямых, на одной из которых задана точка касания А сопрягающей дуги (рисунок 50). Известно, что геометрическим местом центров дуг, сопрягающих две пересекающиеся прямые, является биссектриса угла, образованного этими прямыми. Поэтому, построив биссектрису угла, из точки касанияA восстанавливают перпендикуляр к прямой до пересечения его с биссектрисой и отмечают точку O – центр сопрягающей дуги. Опустив из точки О перпендикуляр на другую прямую, получают вторую точку касания В и радиусом Rc= OA = OB осуществляют сопряжение двух прямых, на одной из которых была задана точка касания.
Сопряжение
двух параллельных прямых дугой, проходящей
через заданную точку касания А (рисунок
51). Из точкиA восставляют перпендикуляр к заданным
прямым и на пересечении его со второй
прямой отмечают точкуB.
ОтрезокAB делят
пополам и получают точкуО–
центр сопрягающей дуги радиусом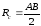 .
.
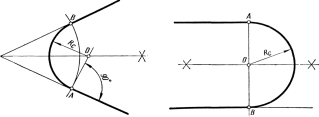
Рисунок 50 Рисунок 51
studfile.net
Касательная прямая к окружности — Википедия. Что такое Касательная прямая к окружности
Касательная прямая к окружности в евклидовой геометрии на плоскости — прямая, которая имеет с окружностью ровно одну общую точку. Также можно определить касательную как предельное положение секущей, когда точки пересечения её с окружностью бесконечно сближаются. Касательные прямые к окружностям служат предметом рассмотрения ряда теорем и играют важную роль во многих геометрических построениях и доказательствах.
Касательные прямые к одной окружности
Касательная прямая t к окружности C пересекает окружность в единственной точке T. Для сравнения, секущие прямые пересекают окружность в двух точках, в то время как некоторые прямые могут не пересекать окружность совсем. Это свойство касательной прямой сохраняется при многих геометрических преобразованиях[en], таких как подобие, вращение, параллельный перенос, инверсия и картографическая проекция. Говоря техническим языком, эти преобразования не меняют структуру инцидентности касательных прямых и окружностей, даже если сами прямые и окружности деформируются.
Радиус окружности, проведённый через точку касания, перпендикулярен касательной прямой. И обратно, перпендикуляр к радиусу в конечной точке (на окружности) является касательной прямой. Окружность вместе с касательной прямой имеют осевую симметрию относительно радиуса (к точке касания).
 По теореме о степени точки произведение длин PM•PN для любого луча PMN равно квадрату PT, длине отрезка от точки P до точки касания (отрезок показан красным цветом).
По теореме о степени точки произведение длин PM•PN для любого луча PMN равно квадрату PT, длине отрезка от точки P до точки касания (отрезок показан красным цветом).Никакая касательная прямая не может проходить через точку внутри окружности, поскольку любая такая прямая должна быть секущей. В то же время для любой точки, лежащей вне круга, можно построить две проходящие через неё касательные прямые. Геометрическая фигура, состоящая из окружности и двух касательных прямых, также обладает осевой симметрией относительно прямой, соединяющей точку P с центром окружности O (см. рисунок справа). В этом случае отрезки от точки P до двух точек касания имеют одинаковую длину. По теореме о степени точки квадрат длины отрезка до точки касания равен степени точки P относительно окружности C. Эта степень равна произведению расстояний от точки P до двух точек пересечения окружности любой секущей линией, проходящей через P.
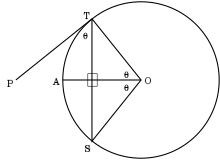 Угол θ между хордой и касательной равен половине дуги, заключённой между концами хорды.
Угол θ между хордой и касательной равен половине дуги, заключённой между концами хорды.Касательная прямая t и точка касания T обладают свойством сопряжённости друг другу; это соответствие можно обобщить в идею о полюсе и поляре. Такая же взаимосвязь существует между точкой P вне окружности и секущей линией, соединяющей две точки касания.
Если точка P лежит вне окружности с центром O, и если касательные прямые из P касаются окружности в точках T и S, то углы ∠TPS и ∠TOS дают в сумме 180°.
Если хорда TM проведена из точки касания T прямой P T и ∠PTM ≤ 90°, то ∠PTM = (1/2)∠MOT.
Геометрическое построение
 Построение касательной прямой к окружности (выделена красным) перпендикулярно радиусу.
Построение касательной прямой к окружности (выделена красным) перпендикулярно радиусу.Относительно легко построить прямую t, касательную к окружности в точке T на окружности. Для этого следует провести прямую a через центр окружности O и точку T. Тогда прямая t является перпендикуляром к прямой a. Один из способов построения перпендикуляра следующий (см. рисунок). Проводим тем же радиусом (r) окружность с центром в точке T, получаем вторую точку G на прямой a, а точка T становится серединой отрезка OG. Проводим две окружности радиуса R>r с центрами в точках O и G. Прямая, проходящая через точки пересечения этих окружностей, будет касательной.
Построение касательной прямой к окружностиДля построения касательной прямой через точку P к окружности C можно использовать свойство угла, опирающегося на диаметр окружности. Проводится окружность с центром в точке H, середине отрезка OP, где O — центр окружности C. Пересечения T и T‘ являются точками касания прямых, проходящих через точку P, поскольку углы ∠OTP и ∠OT‘P опираются на диаметр OP окружности с центром в H.
Теорема об описанном четырёхугольнике и вписанные окружности
Описанный четырёхугольник ABCD — это замкнутая фигура с четырьмя сторонами, которые касаются окружности C. Соответственно, C — вписанная в четырёхугольник ABCD окружность. По теореме Пито суммы противоположных сторон любого такого четырёхугольника равны, то есть
- AB¯+CD¯=BC¯+DA¯.{\displaystyle {\overline {AB}}+{\overline {CD}}={\overline {BC}}+{\overline {DA}}.}
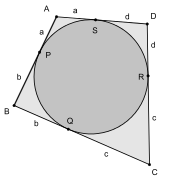 Описанный четырёхугольник
Описанный четырёхугольникЭто заключение следует из равенства отрезков касательных от вершин четырёхугольника. Обозначим точки касания как P (на отрезке AB), Q (на отрезке BC), R (на отрезке CD) и S (на отрезке DA). Симметричные отрезки до точек касания от каждой вершины четырёхугольника ABCD равны, то есть BP=BQ=b, CQ=CR=c, DR=DS=d и AS=AP=a. Но каждая сторона четырёхугольника состоит из двух таких отрезков
- AB¯+CD¯=(a+b)+(c+d)=BC¯+DA¯=(b+c)+(d+a){\displaystyle {\overline {AB}}+{\overline {CD}}=(a+b)+(c+d)={\overline {BC}}+{\overline {DA}}=(b+c)+(d+a)},
что и доказывает утверждение.
Обратное утверждение также верно — окружность можно вписать в любой выпуклый четырёхугольник, у которого суммы длин противоположных сторон равны.[1]
Эта теорема и обратная к ней имеют различные применения. Например, из теоремы немедленно следует, что ни в какой прямоугольник не может быть вписана окружность, если только это не квадрат, а также что можно вписать окружность в любой ромб, хотя в общем случае вписать в параллелограмм окружность нельзя.
Касательные прямые к двум окружностям
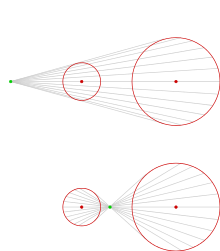 Внешний (сверху) и внутренний (внизу) центры гомотетии двух окружностей (выделены красным цветом), показанные зелёными точками.
Внешний (сверху) и внутренний (внизу) центры гомотетии двух окружностей (выделены красным цветом), показанные зелёными точками.Для двух окружностей в общем случае имеется четыре различные прямые, касательные к обоим окружностям, если одна окружность не лежит в другой, но в вырожденных случаях может быть любое число касательных от нуля до четырёх. Эти случаи описаны ниже. Из четырёх касательных прямых две являются внешними касательными, когда окружности оказываются лежащими по одну сторону от касательной прямой. Для двух других прямых, внутренних касательных, окружности оказываются лежащими по разные стороны от касательной прямой. Внешние касательные пересекаются в центре внешней гомотетии[en], в то время как внутренние касательные пересекаются в центре внутренней гомотетии. И внутренний, и внешний центры гомотетии лежат на прямой, проходящей через центры окружностей, ближе к центру меньшей окружности. Если две окружности имеют одинаковые радиусы, остаются те же четыре касательных, но внешние касательные прямые параллельны и внешнего центра гомотетии на аффинной плоскости не существует. На проективной плоскости внешний центр гомотетии лежит в бесконечно удалённой точке, соответствующей пересечению прямых.[2]
Внешняя касательная
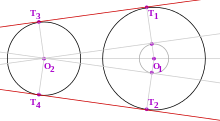 Построение внешних касательных.
Построение внешних касательных.Красные прямые, соединяющие точки T1 и T3, T2 и T4, являются внешними касательными двух окружностей.
Внутренняя касательная
Внутренние касательные — это касательные, которые пересекают отрезок, соединяющий центры окружностей. Заметим, что внутренние касательные не существуют в случае пересекающихся окружностей.
Построение
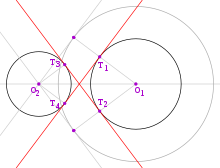 Построение внутренних касательных
Построение внутренних касательныхКасательные к двум окружностям могут быть построены с помощью нахождения центров гомотетии, как описано выше, а затем построения касательных, проходящих через эти центры. Можно также построить касательные прямые и касательные точки прямо, как описано ниже.
Элементарная геометрия
Пусть O1 и O2 — два центра двух окружностей C1 и C2 и пусть r1 и r2 — их радиусы, при этом r1 > r2. Другими словами, окружность C1 будем считать большей из двух окружностей. Два различных способа можно использовать для построения внешних и внутренних касательных прямых.
- Внешние касательные
Рисуем новую окружность C3 с радиусом r1 − r2 с центром в O1. Используя метод, описанный выше, проводим две касательные прямые из точки O2 к этой новой окружности. Эти прямые параллельны искомым касательным прямым, поскольку это соответствует уменьшению радиусов обеих окружностей C1 и C2 на одно и то же число r2, в результате чего окружность C2 превращается в точку. Через две точки касания на окружности C3 можно провести два луча из центра O1. Эти лучи пересекают C1 в искомых точках касания. Искомые касательные перпендикулярны этим радиальным лучам и могут быть построены, как показывалось выше.
- Внутренние касательные
Рисуем новую окружность C3 с радиусом r1 + r2 с центром в O1. Используя метод, описанный выше, проводим две касательные прямые из точки O2 к этой новой окружности. Эти прямые параллельны искомым касательным прямым, поскольку это соответствует уменьшению радиуса окружности C2 до нуля с одновременным увеличением радиуса C1 на ту же константу r2. Два радиальных луча можно провести из центра O1 через точки касания на C3. Эти лучи пересекают C1 в искомых точках касания. Искомые внутренние касательные перпендикулярны радиальным лучам и пересекают лучи в найденных точках, так что их можно построить вышеуказанным методом.
Фактически это то же самое построение, что и для внешних касательных, если принять, что радиус меньшей окружности отрицателен.
Аналитическая геометрия
Пусть окружности имеют центры c1 = (x1,y1) и c2 = (x2,y2) и радиусы r1 и r2 соответственно. Пусть касательная прямая имеет уравнение ax+by+c=0,{\displaystyle ax+by+c=0,} с нормализацией a2 + b2 = 1, тогда расстояние от центров окружностей до прямой вычисляется по формулам:
- ax1 + by1 + c = r1 и
- ax2 + by2 + c = r2.
Вычтем первое уравнение из второго, получим
- aΔx + bΔy = Δr
где Δx = x2 − x1, Δy = y2 − y1 и Δr = r2 − r1.
Если d=(Δx)2+(Δy)2{\displaystyle d={\sqrt {(\Delta x)^{2}+(\Delta y)^{2}}}} — расстояние от c1 до c2, мы можем нормализовать, сделав замену X = Δx/d, Y = Δy/d и R = Δr/d для упрощения уравнений, что даёт уравнения aX + bY = R и a2 + b2 = 1. Решаем их и получаем два решения (k = ±1) для двух внешних касательных линий:
- a = RX − kY√(1 − R2)
- b = RY + kX√(1 − R2)
- c = r1 − (ax1 + by1)
Геометрически это соответствует вычислению угла, образованного касательной и прямой, проведённой через центры, а затем линия центов поворачивается для получения уравнения касательной. Угол можно вычислить с помощью тригонометрии из прямоугольного треугольника, вершинами которого являются (внешний) центр гомотетии, центр окружности и точка касания. Гипотенуза лежит на прямой центров, радиус является катетом, противоположным углу, а прилегающий к углу катет лежит на касательной прямой.
(X, Y) — это единичный вектор, направленный от c1 в c2, в то время как R равен cosθ{\displaystyle \cos \theta }, где θ{\displaystyle \theta } — угол между линией центров и касательной. sinθ{\displaystyle \sin \theta } тогда равен ±1−R2{\displaystyle \pm {\sqrt {1-R^{2}}}} (в зависимости от знака θ{\displaystyle \theta }, что эквивалентно направлению вращения), и приведённые выше уравнения являются вращением (X, Y) на ±θ,{\displaystyle \pm \theta ,} с помощью матрицы вращения
- (R∓1−R2±1−R2R){\displaystyle {\begin{pmatrix}R&\mp {\sqrt {1-R^{2}}}\\\pm {\sqrt {1-R^{2}}}&R\end{pmatrix}}}
- k = 1 — это касательная прямая справа от окружностей, если смотреть из c1 в направлении c2.
- k = −1 — это касательная прямая справа от окружностей, если смотреть из c2 в направлении c1.
Все рассуждения выше предполагают, что радиусы окружностей положительны. Если r1 положителен, а r2 отрицателен, то c1 будет лежать слева от каждой прямой, а c2 — справа, и две касательные прямые пересекутся. Таким путём можно получить все четыре решения. Смена знака обоих радиусов приводит к обмену вариантов k = 1 и k = −1.
Вектора
В общем случае точки касания t1 и t2 для любой из четырёх касательных прямых к окружностям с центрами в v1 и v2 и с радиусами r1 и r2 получаются путём решения четырёх уравнений:
- (t2−v2)⋅(t2−t1)=0(t1−v1)⋅(t2−t1)=0(t1−v1)⋅(t1−v1)=r12(t2−v2)⋅(t2−v2)=r22{\displaystyle {\begin{aligned}(t_{2}-v_{2})\cdot (t_{2}-t_{1})&=0\\(t_{1}-v_{1})\cdot (t_{2}-t_{1})&=0\\(t_{1}-v_{1})\cdot (t_{1}-v_{1})&=r_{1}^{2}\\(t_{2}-v_{2})\cdot (t_{2}-v_{2})&=r_{2}^{2}\\\end{aligned}}}
Эти уравнения выражают тот факт, что касательная прямая перпендикулярна радиусам, а точки касания лежат на соответствующих окружностях.
Эти четыре квадратных уравнения с двумерными векторными переменными в общем случае дают четыре пары решений.
Вырожденные случаи
Две различные окружности могут иметь, в зависимости от взаимного расположения, от нуля до четырёх прямых, касающихся обеих окружностей. Варианты можно классифицировать по расстоянию между центрами и радиусам.
И наконец, если окружности совпадают, любая касательная прямая к одной окружности будет общей касательной.
Далее понятие общей касательной прямой можно расширить на случай окружностей отрицательного радиуса (которые образованы теми же самыми точками x2+y2=(−r)2,{\displaystyle x^{2}+y^{2}=(-r)^{2},} но «наизнанку»). В этом случае, если радиусы имеют противоположные знаки (одна окружность имеет положительный радиус, другая — отрицательный) внешний и внутренний центры гомотетии меняются местами и внешние и внутренние общие касательные меняются местами. Если же радиусы имеют один и тот же знак (оба радиуса положительны или оба отрицательны), то понятия «внешний» и «внутренний» имеют обычный смысл.
Общие касательные можно определить для окружностей с нулевым радиусом. В этом случае окружность с нулевым радиусом трактуется как двойная точка, а потому любая прямая, проходящая через эту точку, пересекает её с кратностью[en] два. Если окружность имеет радиус ноль, общая касательная прямая — это просто касательная прямая к окружности, проходящая через точку, но считается эта прямая дважды. Если обе окружности имеют нулевой радиус, то общая касательная прямая — это прямая, проходящая через две точки, и эта прямая имеет кратность четыре.
Заметим, что в этих вырожденных случаях внешний и внутренний центры гомотетии остаются (внешний центр уходит в бесконечность, если радиусы равны), за исключением случая, когда окружности совпадают (в этом случае внешний центр не определён), или когда обе окружности имеют нулевой радиус (в этом случае отсутствует внутренний центр).
Приложения
Задача о ремённой передаче
Внутренние и внешние касательные полезны при решении задачи о ремённой передаче[en], которая заключается в вычислении длины ремня, который плотно бы прилегал к колёсам передачи. Если считать ремень математической кривой с пренебрежительно малой толщиной и если колёса передачи находятся точно в одной плоскости, задача сводится к суммированию отрезков касательных с соответствующими длинами дуг. Если ремень натянут на колёса с пересечением, необходимо рассматривать внутренние касательные. Если же ремень натянут без пересечения, необходимо рассматривать внешние касательные. Последний случай иногда называется задачей шкивов.
Касательные прямые к трём окружностям: теорема Монжа
Для трёх окружностей C1, C2 и C3 существует три пары окружностей (C1C2, C2C3 и C1C3). Поскольку каждая пара окружностей имеет два центра гомотетии, всего получим шесть центров гомотетии[en]. Гаспар Монж показал в начале 19-го века, что эти шесть точек лежат на четырёх прямых, и на каждой прямой лежат три точки.
Касательные прямые и бильярд
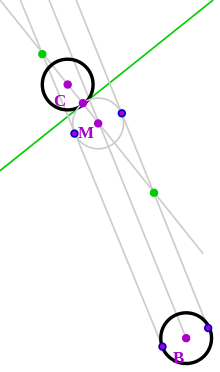 Прицеливание удара в бильярде. Направление удара от битка (шар B) выбирается так, чтобы точка касания совпадала с точкой пересечения прямой, проходящей через центр лузы и центр прицельного шара. В этом случае прицельный шар поёдёт в сторону лузы, а биток пойдёт параллельно зелёной линии, касательной к прицельному шару (C) и воображаемому шару (M)
Прицеливание удара в бильярде. Направление удара от битка (шар B) выбирается так, чтобы точка касания совпадала с точкой пересечения прямой, проходящей через центр лузы и центр прицельного шара. В этом случае прицельный шар поёдёт в сторону лузы, а биток пойдёт параллельно зелёной линии, касательной к прицельному шару (C) и воображаемому шару (M)Система касательных прямых прицеливания битка использует прямую, проходящую через середину кия, для создания двух касательных прямых от битка в направлении прицельного шара. Две касательные прямые и прямая через середину битка пересекают прямую, проходящую через середину прицельного шара и центр лузы. Необходимо направить удар так, чтобы конечное положение битка (воображаемый шар на рисунке) касалось прицельного шара в точке касания прямой, перпендикулярной направлению на лузу (на рисунке эта касательная выделена зелёным цветом).
Задача Аполлония
Много частных случаев задачи Аполлония используют нахождение окружностей, касающихся одной или нескольких прямых. В простейшем из этих случаев строится окружность, касающаяся трёх заданных прямых (задача LLL). Центр любой такой окружности должен лежать на биссектрисе угла в точке пересечения любой пары этих прямых. В каждой точке пересечения прямых есть две биссектрисы. Пересечения этих биссектрис дают центры окружностей, являющихся решением. В общем случае существует четыре таких окружностей для треугольника, образованного пересечением трёх прямых — вписанная окружность и три вневписанных.
 Анимация, показывающая инверсное преобразование задачи Аполлония. Синяя и красная окружности увеличиваются, пока не коснутся, и при инверсии относительно серой окружности переходят в две параллельные прямые. Жёлтые решения получаются путём перемещения вдоль этих прямых до касания зелёной окружности.
Анимация, показывающая инверсное преобразование задачи Аполлония. Синяя и красная окружности увеличиваются, пока не коснутся, и при инверсии относительно серой окружности переходят в две параллельные прямые. Жёлтые решения получаются путём перемещения вдоль этих прямых до касания зелёной окружности.В общем случае задачу Аполлония можно свести к более простой задаче построения окружности, касающейся одной окружности и двух параллельных прямых (это сам по себе частный случай LLC). Чтобы это сделать, увеличиваем пропорционально[en] две из этих трёх заданных окружностей вплоть до их касания. Инверсия относительно окружности подходящего радиуса с центром в точке касания переводит эти две окружности в две параллельные прямые, а третью окружность — в другую окружность. Таким образом, решение может быть найдено путём перемещения окружности постоянного радиуса между двумя параллельными прямыми, пока не получим касание с преобразованной третьей окружностью. Обратная инверсия даст решения исходной задачи.
Обобщения
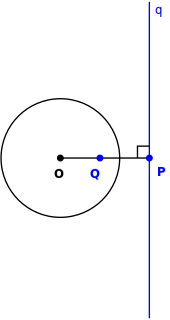 Понятия касательной прямой и точки касания можно обобщить до полюса Q и соответствующей ей полярной прямой q. Точки P и Q являются инверсиями друг друга относительно окружности.
Понятия касательной прямой и точки касания можно обобщить до полюса Q и соответствующей ей полярной прямой q. Точки P и Q являются инверсиями друг друга относительно окружности.Понятие касательной прямой к одной и более окружностям можно обобщить несколькими путями. В первую очередь, свойство парности касательных прямых и точек касания можно обобщить до полюса и полярной прямой, когда полюс может находиться в любом месте, не обязательно на окружности. Во-вторых, объединение двух окружностей является особым (приводимым[en]) случаем плоской кривой четвёртой степени, а внешние и внутренние касательные прямые являются касательными к двум точкам[en] этой кривой. В общем случае плоская кривая четвёртой степени имеет 28 прямых, касающихся её дважды.
Третье обобщение относится скорее к касательным окружностям, а не к касательным прямым. Касательную прямую можно рассматривать как касательную окружность с бесконечным радиусом. В частности, внешние касательные прямые к двум окружностям можно рассматривать как частные случаи из семейства окружностей, касающихся с внутренней или внешней стороны обеих окружности, в то время как внутренние касательные прямые можно рассматривать как частные случаи семейства окружностей, касающихся с внутренней стороны одной окружности и с внешней стороны другой) [3].
В геометрии Мёбиуса или инверсной геометрии прямые рассматриваются как окружности с центром «в бесконечности» и для любой прямой и для любой окружности существует преобразование Мёбиуса, которое переводит одну фигуру в другую. В геометрии Мёбиуса касание прямой и окружности становится особым случаем касания двух окружностей. Эта эквивалентность развивается далее в сферической геометрии Ли[en].
Примечания
Литература
Ссылки
wiki.sc

