Чем отличается окружность от круга. Чем отличается круг от шара

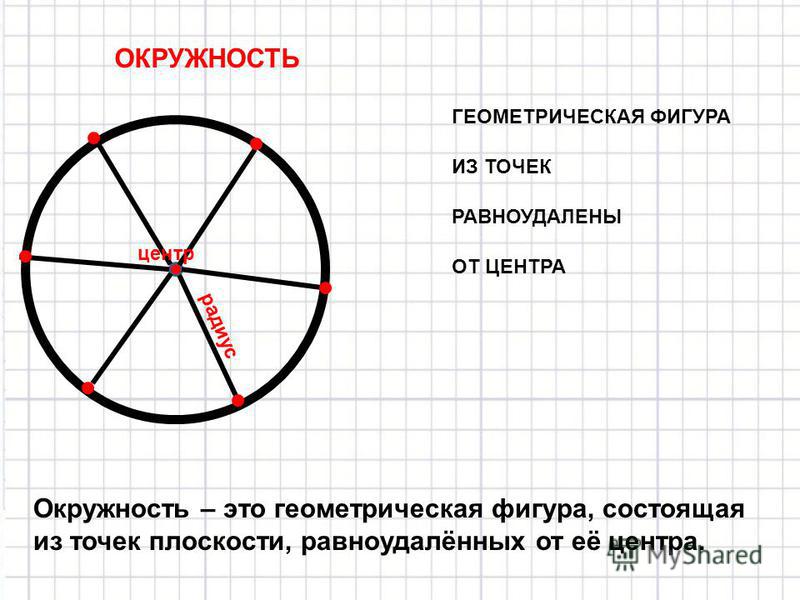
Окружность — это огромное количество точек на плоскости, равноудаленных от некой точки этой же плоскости, именуемой центром окружности. Окружность представляет собой замкнутую кривую, лежащую от центра на фиксированном расстоянии, нарываемом радиусом окружности.

Круг — это огромное количество точек плоскости, удаленных от некой точки этой же плоскости, именуемой центром круга, на расстояние, не превышающеей определенной величины, именуемой радиусом круга. Круг представляет собой сплошную фигуру, включающую окружность и все точки, лежащие в ней.

Следовательно, круг — это участок плоскости, а окружность — черта этого участка. Потому есть возможность говорить о площади круга и длине окружности, однако неправильно говорить о длине круга и площади окружности.

Так как точки окружности удалены от центра на расстояние, не превышающее радиуса, то они все принадлежат кругу. Другими словами, окружность принадлежит кругу, который она ограничивает.

В особых случаях может рассматриваться круг в отсутствие границы — огромное количество точек круга, не принадлежащих его границе (окружности).

Окружность разделяет плоскость на две части — лежащую снутри и лежащую снаружи. Попрасть из одной части в другую нереально в отсутствие скрещения окружности. Площаль внутренней части конечна, площадь наружной части нескончаема.

Центр окружности не принадлежит окружности (кроме вырожденного варианта окружности нулевого радиуса). Центр круга всегда принадлежит кругу, т.к. находится снутри ограничивающей его окружности.

openclass.ru — методическая разработка «Окружность и круг»

otvet.mail.ru — чем отличается круг от окружности?

Школьные годы для большого количества взрослых – синоним беззаботной поры детства. Вполне понятно, почему многие дети и подростки не горят желанием каждый день ходить в школу – но именно в ее стенах они получают общие знания о мире и навыки социальной жизни, которые становятся незаменимыми после получения аттестата зрелости.

Одним из таких вопросов, таких общих понятий является тема сходств и различий круга и шара. Спутать рассматриваемые понятия одновременно просто и сложно – потому что различий между кругом и шаром не так много, как кажется малоопытному ребенку.

Итак, в чем же несходства между шаром и кругом? Чем они похожи?

Что такое круг?

Начертание круга начинается с окружности. Окружность – это замкнутая черта без конца и начала , каждая точка которой находится на равном удалении от центра. Простейший пример окружности – гимнастический обруч.

Круг получится, если начертить окружность, например, на бумаге – и потом разукрасить ее. Любыми красками: желтой, синей, зеленой – какая больше нравится. Главное – заполнить чем-то пустоту. После окончания работы окружность превратится в фигуру, которую именуют кругом. Круг по сути своей – это некоторая часть двухмерной поверхности, закольцованная в окружность.

Круг обладает некоторыми важными для понимания его сущности параметрами. Кстати, часть данных параметров присуща и окружности.

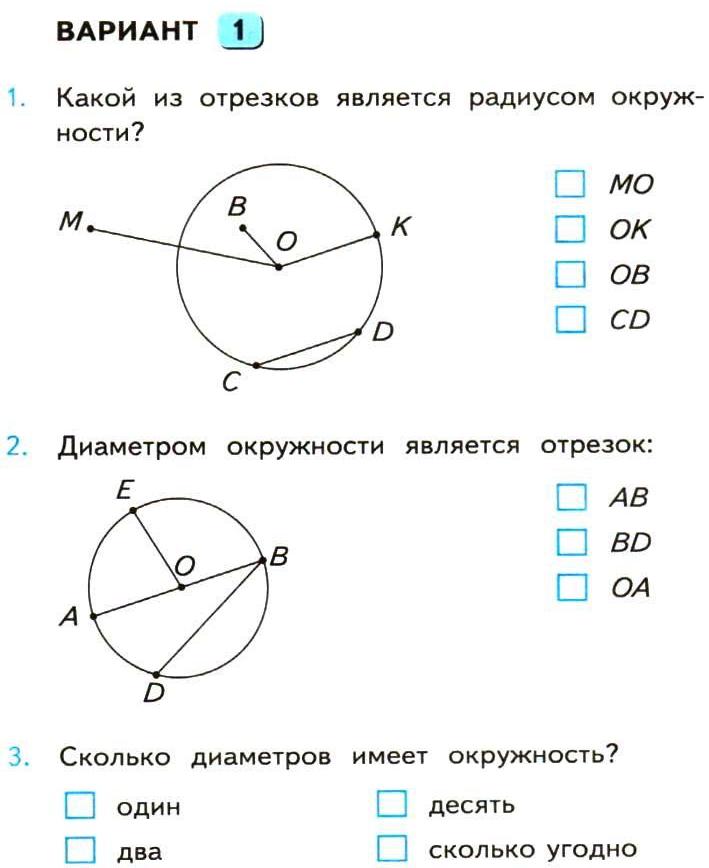
1. Радиус – расстояние от центральной точки круга или окружности до границы фигуры (линии, которая ее очерчивает).
2. Диаметр – важная характеристика, которая так часто фигурирует в школьных заданиях. Это сумма двух радиусом, то есть расстояние между двумя противоположными точками на окружности.
3. Площадь – свойство, характерное только для круга. Окружность не имеет его в силу своей структуры (потому что она пустая, а центр фигуры – воображаемая точка). В круге, напротив, несложно определить центр. Через центральную точку фигуры достаточно просто прочертить ряд линий, которые поделят круг на сектора.

Круг в реальной жизни

В реальности можно без особых усилий отыскать множество предметов, по форме тождественных кругу. К примеру, готовый образец круга – а, точнее, множество, — каждый день катается по дорогам поселков и городов. Понятно, что речь идет о колесе. Здесь стоит оговориться: круг не должен быть однотонным, это не обязательно. Он может быть украшен узорами или чем-то еще – от этого форма не изменяется.

Другой пример круга – . Да, то самое дневное светило, которое люди лицезреют каждый день. Любознательный читатель заметит, что Солнце – фигура объемная, она не может быть кругом. Это правда. Но маленькая фигура, какой предстает огненная звезда жителям Земли – по сути своей именно круг. Площадь его, конечно, высчитать не получится. Почему? Потому что этот пример приводится только для наглядности, для того, чтобы понять, что такое круг.

Сектор

Что такое круг внимательный читатель ужен разобрался. Но вот что за «зверь» этот сектор, о котором упоминалось немного выше? Сектор – это часть круга, отделенная от остальной поверхности парой начерченных радиусов. Для наглядности можно примести такой пример: все когда-нибудь видели нарезанную пиццу. Кусочки – это сектора круга, которым является все это аппетитное блюдо.

Секторы не обязательно должны быть равной величины. К примеру, если пицца разрезана пополам, обе ее половины тоже будут секторами круга.

Что такое шар?

тело, ограниченное сферической поверхностью . То есть, это не двухмерная фигура, как круг, а трехмерная. Сферическая поверхность – это геометрическое сочетание поверхности точек, расположенных на неотрицательном расстоянии от некоей центральной точки. Расстояние, на которое удалены все точки поверхности шара от его центра, называется радиусом. И оно не должно превышать некие заданные цифры. Таким образом, круг – это та же сферическая поверхность, расположенная в другом пространстве.

В этом проявляются сходства и главное различие шара и круга. Круг – это двухмерная фигура, точки которой ограничены окружностью. Шар – это фигура трехмерная, а ее точки ограничены сферической поверхностью.

Разновидности шара

В метрическом и векторном пространствах рассматриваются два понятия, имеющие связь со сферической поверхностью. Шар, который включает в себя данную сферу, именуют замкнутым . Шар, который не включает в себя сферу, называют открытым .

Характеристики шара

Шар, как и круг, имеет диаметр и радиус. Обе эти величины в шаре вычисляются по вышеописанным принципам (как для круга). Радиус шара – это отрезок между любой точкой на сферической поверхности, ограничивающей фигуру, и ее центром. Диаметр соединяет две точки на сферической поверхности шара, проходя через его центр.

Интересное дополнение: круг может быть частью шара. Точнее, шар состоит из очень большого количества кругов различного диаметра. Называются эти круги сечениями сферы. Когда сечение пролегает через центр шара, его именуют большим кругом. Все остальные сечения именуются малыми кругами. Такого рода сечений, проходящих через пару точек на поверхности шара, возможно начертить поистине бесконечное множество.

Выводы

Круг – плоская, двухмерная фигура. Шар – объемное трехмерное геометрическое тело. Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).

Чем же отличается круг от шара? Круг плоский, шар же имеет объем. Именно объемность шара позволяет ему делиться на сечения, которые по своей сути являются кругами. Круг, напротив, делится на сектора.

Школьная пора для большинства взрослых людей ассоциируется с беззаботным детством. Конечно, многие неохотно посещают школу, но только там они могут получить базовые знания, которые впоследствии пригодятся им в жизни. Одним из таких является вопрос о том, и круг. Спутать данные понятия достаточно просто, ведь слова являются однокоренными. Но разница между ними не настолько большая, как может показаться неопытному ребенку. Дети данную тему любят по причине ее простоты.

Что такое окружность?

Окружность — это замкнутая линия, каждая точка которой равно удалена от центральной. Самым ярким примером окружности является обруч, который представляет собой замкнутое тело. Собственно, и говорить особо об окружности не приходится. В вопросе о том, что такое окружность и круг, значительно интереснее вторая его часть.

Что такое круг?

Представьте, что вы решили разукрасить нарисованную выше окружность. Для этого можно выбрать любые краски: синие, желтые или зеленые — кому что ближе по душе. И вот вы начали заполнять пустоту чем-то. После того как это было закончено, у нас получилась фигура, которая называется кругом. По сути, круг — это часть поверхности, очерченная окружностью.

У круга есть несколько важных параметров, часть из которых также характерна и для окружности. Первый — это радиус. Им называется расстояние между центральной точкой круга (ну или окружности) и самой окружностью, что создает границы кругу. Вторая важная характеристика, которая неоднократно используется в школьных задачах — это диаметр (то есть расстояние между противоположными точками окружности).

Ну и наконец, третья характеристика, присущая кругу — это площадь. Данное свойство специфичное только для него, окружность не имеет площади в силу того, что у нее нет ничего внутри, а центр, в отличие от круга, скорее воображаемый, чем настоящий.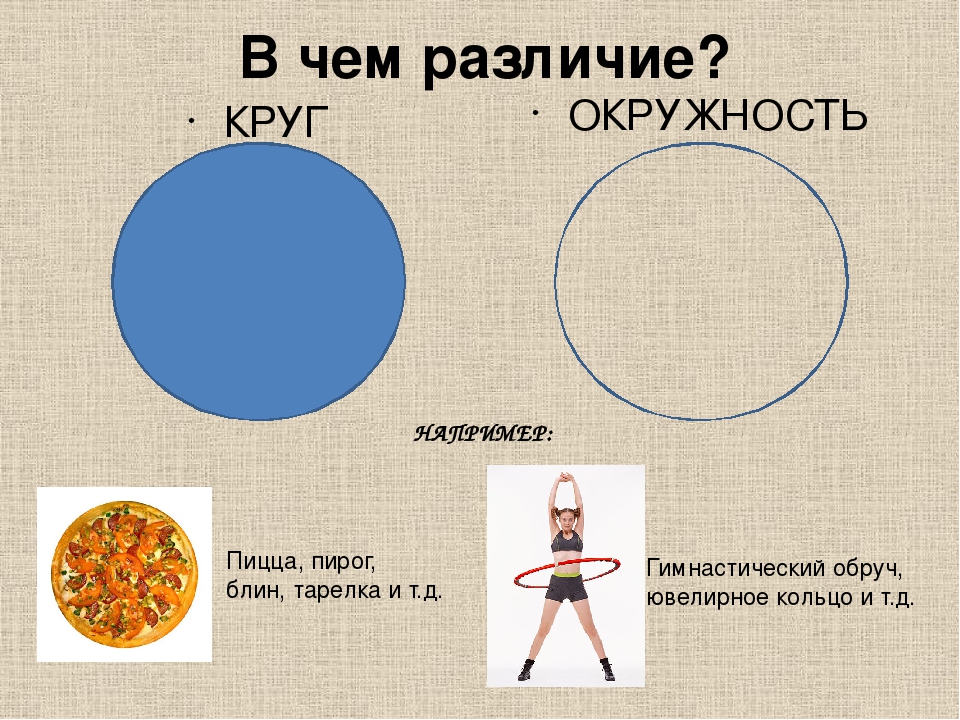

В самом же круге можно установить четкий центр, через который провести ряд линий, которые делят его на сектора.

Примеры круга в реальной жизни

На самом деле возможных предметов, которые можно назвать разновидностью круга, достаточно. Например, если посмотреть на колесо машины прямо, то вот вам пример готового круга. Да, он необязательно должен быть заполнен однотонно, вполне возможны различные узоры внутри него. Второй пример круга — это солнце. Конечно, на него посмотреть будет тяжело, но оно на небе выглядит, как маленький кружочек.

Да, сама звезда Солнце — это не круг, она имеет еще и объем. Но вот само солнце, которое мы видим над нашей головой в летнее время, является типичным кругом. Правда, площадь у него все равно высчитать не получится. Ведь сравнение его с кругом приводится только для наглядности, чтобы было проще понять, что такое окружность и круг.

Отличия окружности от круга

Значит, какой вывод мы можем сделать? Чем отличается окружность от круга, так это тем, что у последнего есть площадь, и в большинстве случаев окружность является границей круга. Хотя бывают и исключения на первый взгляд. Может показаться иногда, что нет окружности в круге, но это не так. В любом случае что-то да есть. Просто окружность может быть очень маленькой, и тогда ее не видно невооруженным глазом.

Также окружностью может быть то, что выделяет круг из фона. Например, на приведеном выше изображении синий круг находится на белом фоне. А вот та черта, по которой мы понимаем, что здесь начинается фигура, и называется в данном случае окружностью. Таким образом, окружность — круга. Вот чем отличается окружность от круга.

Что такое сектор?

Сектор — это участок круга, который образуется двумя проведенными по нему радиусами. Чтобы понять это определение, нужно просто вспомнить пиццу. Когда ее разрезают на равные кусочки, все они и являются секторами круга, который представлен в виде такого вкусного блюда. При этом совершенно необязательно секторы должны быть равны. Они могут быть разной величины. Например, если отрезать половину пиццы, то она также будет сектором этого круга.

Предмет, отображаемый этим понятием, может иметь только круг. тоже можно провести, конечно, но после этого она станет кругом) не имеет площади, поэтому и сектор выделить не получится.

Выводы

Да, тема о круге и окружности (что это такое) очень проста для понимания. Но вообще все то, что касается этих является самым сложным для изучения. Школьнику нужно быть готовым к тому, что круг — фигура капризная. Но, как говорится, тяжело в учении — легко в бою. Да, геометрия — наука сложная. Зато успешное ее освоение позволяет сделать маленький шажок в сторону успеха. Потому что старания при обучении позволяют не только пополнять багаж собственных знаний, но и получать необходимые в жизни навыки. Собственно, на это и нацелена школа. А ответ на вопрос о том, что такое окружность и круг, является вторичным, хоть и важным.

Разбираемся в том что такое окружность и круг. Формула площади круга и длины окружности.

Мы каждый день встречаем множество предметов, по форме которые образовывают круг или напротив окружность. Иногда возникает вопрос, что такое окружность и чем она отличается от круга. Конечно же, мы все проходили уроки геометрии, но иногда не помешает освежить знания весьма простыми объяснениями.

Что такое длина окружности и площадь круга: определение

Итак, окружность является замкнутой кривой линией, которая ограничивает или же напротив, образует круг. Обязательное условие окружности — у нее есть центр и все точки равноудалены от него. Проще говоря, окружность это гимнастический обруч (или как его часто называют хула-хуп) на плоской поверхности.

Длина окружности это общая длина той самой кривой, которая образует окружность. Как известно вне зависимости от размеров окружности соотношение ее диаметра и длины равно числу π = 3,141592653589793238462643.

Из этого следует, что π=L/D, где L — длина окружности, а D — диаметр окружности.

Если Вам известен диаметр, то длину можно найти по простой формуле: L= π* D

В случае если известен радиус: L=2 πR

Мы разобрались, что такое окружность и можем перейти к определению круга.

Круг — это геометрическая фигура, которая окружена окружностью. Или же, круг это фигура, рубеж которой состоит из большого количества точек равноудаленных от центра фигуры. Вся площадь, которая находится внутри окружности, включая ее центр, называется кругом.

Стоит заметить, что у окружности и круга, который находится в ней значения радиуса и диаметра одинаковые. А диаметр в свою очередь в два раза больше чем радиус.

Круг имеет площадь на плоскости, которую можно узнать при помощи простой формулы:

Где S — площадь круга, а R — радиус данного круга.

Чем круг отличается от окружности: объяснение

Основное отличие между кругом и окружностью — это то, что круг — геометрическая фигура, а окружность — замкнутая кривая. Также обратите внимание на отличия между окружностью и кругом:

• Окружность это замкнутая линия, а круг — площадь внутри этой окружности;
• Окружность это кривая линия на плоскости, а круг — пространство, сомкнутое в кольцо окружностью;
• Сходство между окружностью и кругом: радиус и диаметр;
• У круга и окружности единый центр;
• В случае если заштриховывается пространство внутри окружности, оно превращается в круг;
• У окружности есть длина, но ее нет у круга, и наоборот, у круга есть площадь, которой нет у окружности.

Круг и окружность: примеры, фото

Для наглядности предлагаем рассмотреть фото, на котором слева изображен круг, а справа окружность.

Формула длины окружности и площади круга: сравнение

Формула длины окружности L=2 πR

Формула площади круга S= πR²

Обратите внимание, что в обеих формулах присутствует радиус и число π. Данные формулы рекомендуется выучить наизусть, так как они простейшие и обязательно пригодятся в повседневной жизни и на работе.

Площадь круга по длине окружности: формула

S=π(L/2π)=L²/4π, где S — площадь круга, L — длина окружности.

Видео: Что такое круг, окружность и радиус

Альбина Сергеева
Урок математики во 2 классе. Тема «Окружность. Круг»

Тема : «Окружность . Круг »

Цель : познакомить уч-ся с новыми геометрическими фигурами : окружностью , кругом и их элементами (диаметр, радиус, центр) .

Задачи : 1) познакомить с историей возникновения математических понятий ;

2) научить уч-ся пользоваться циркулем для вычеркивания окружностей ;

3) развивать внимание, пространственное мышление, память, воображение, кругозор , словарный запас детей;

4) провести инструктаж по технике безопасности о правилах пользования циркулем;

5) воспитывать любовь к математике , трудолюбие, дисциплинированность, товарищество.

6) аккуратность и осторожность при применении циркуля.

6) воспитывать духовно-нравственные ценности. Уважение к традициям народа.

Вид урока : объяснение нового материала .

Образовательные технологии :

1. Здоровьесберегающие технологии.

3. Технология предметного проектирования.

4. Технология развивающего обучения.

5. Технология личностно-ориентированного обучения.

Место проведения урока : кабинет информатики.

Оборудование для уч-ся :

1. рабочая тетрадь

2. циркуль

3. цветные карандаши

4. линейка

Оборудование для учителя :

1. Плакат «Сиди правильно»

2. тренажёр для глаз

3. тестовая работа

4. циркуль

5. линейка

6. набор геометрических фигур

7. компьютеры

9. музыкальная шкатулка с геометрическими фигурами

10. раздаточный материал

11. таблица

12. цветные мелки

Ход урока

I. Организация класса

1. У : Прозвенел звонок для нас,

Всех ребят позвал он в класс

Чтобы дети не ленились

С удовольствием трудились,

Всем здоровья пожелаем

И урок наш начинаем

Друг на друга посмотрели

Улыбнулись друг другу

Пожелали добрым взглядом

Отличных отметок

И за парты тихо сели.

2. У : На уроке у нас присутствует много гостей – это учителя нашей школы. Давайте у них поинтересуемся для чего они к нам пришли на урок (ответ учителей) .

3. Желаю вам успехов в работе, я обязательно буду помогать, кто будет затрудняться. Наша помощница и хозяйка кабинета это Кавинская Н. А.

Девиз нашей работы : «Все помогают каждому, каждый помогает всем» . (слайд №1)

II. Проверка домашнего задания

1. Ребята, как этот девиз связан с домашним заданием? (Нужно было решить примеры, сопоставить ответ с буквой и отгадать загадку – «Возле елок из иголок, летним днём построен дом, за травой не виден он, а жильцов в нём миллион» — муравей).

2. Муравьи очень большие труженики. Они работают дружно, слажено, активно помогают друг другу. Вот так и мы должны с вами работать.

3. 6000 видов муравьев : муравьи бывают лесные, медовые, садовые, портные, листорезы и другие.

III. Актуализация знаний.

1. Посмотри внимательно на геометрические фигуры (открываю доску) .

(треугольник, квадрат, круг , пятиугольник)

2. Назови, что это за фигуры?

3. Некоторые их точки обозначены буквами. Где располагаются точки? (внутри, на границе) .

4. Посмотри внимательно на фигуры и скажи . Какая фигура лишняя?

Треугольник — одна точка на границе;

Квадрат — точка находится не в центре;

Круг — остальные многоугольники.

5. Составьте 2 слова : 1) из букв, которые находятся на границе фигуры (окружность ) ; 2) из букв, которые находятся внутри фигур (круг )

6. Сегодня на уроке мы подробно и поговорим об окружности и круге .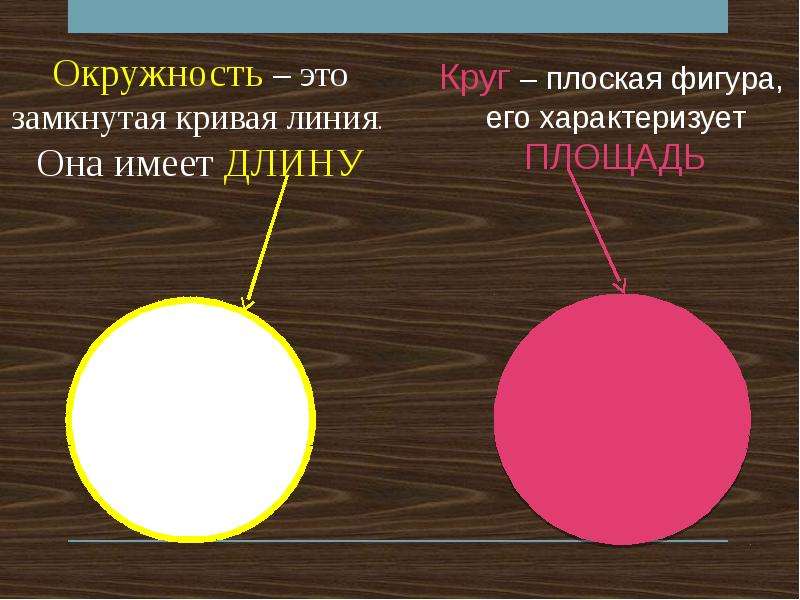

IV. Тема урока : «Окружность . Круг » (слайд №2)

1. Сейчас, ребята, вместе с вами попробуем определить цель нашего урока (если затрудняются, спросить : Что нужно для того, чтобы понять эту тему)

2. Один мудрый человек сказал : «Окружность – душа геометрии » .

(слайд №3)

3. Почему окружность называют душой геометрии нам расскажет Буйлова Алёна (Алёна выступает за кафедрой) .

«Окружность »

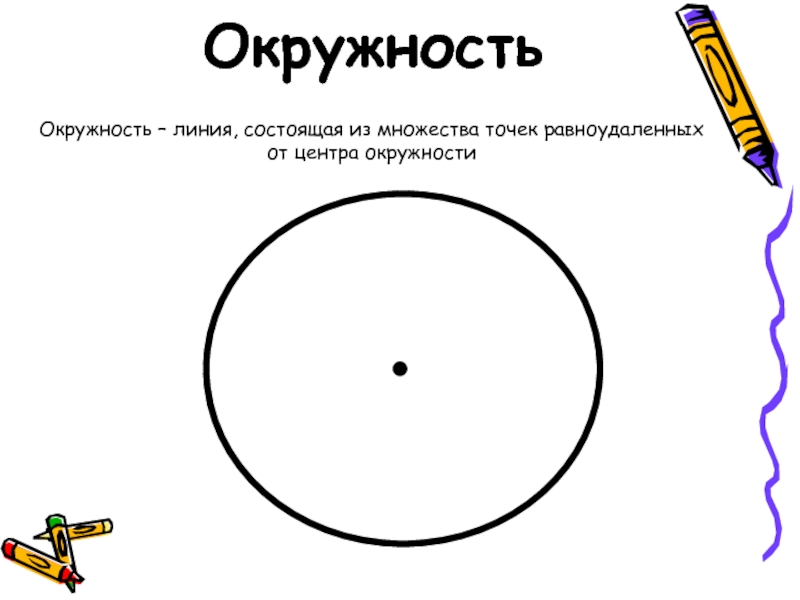
Окружность – замкнутая линия , все точки которой, равноудалены от центра.

Окружность – удивительная фигура, древние греки её считали самой совершенной. Почему не бывает треугольных колес? Представьте себе, нашелся чудак, сделал велосипед с треугольными колёсами. Только нет таких чудаков, люди давно поняли, что колёса должны быть круглыми .

Ось колеса находится в центре, спицы – радиусы, обод – окружность .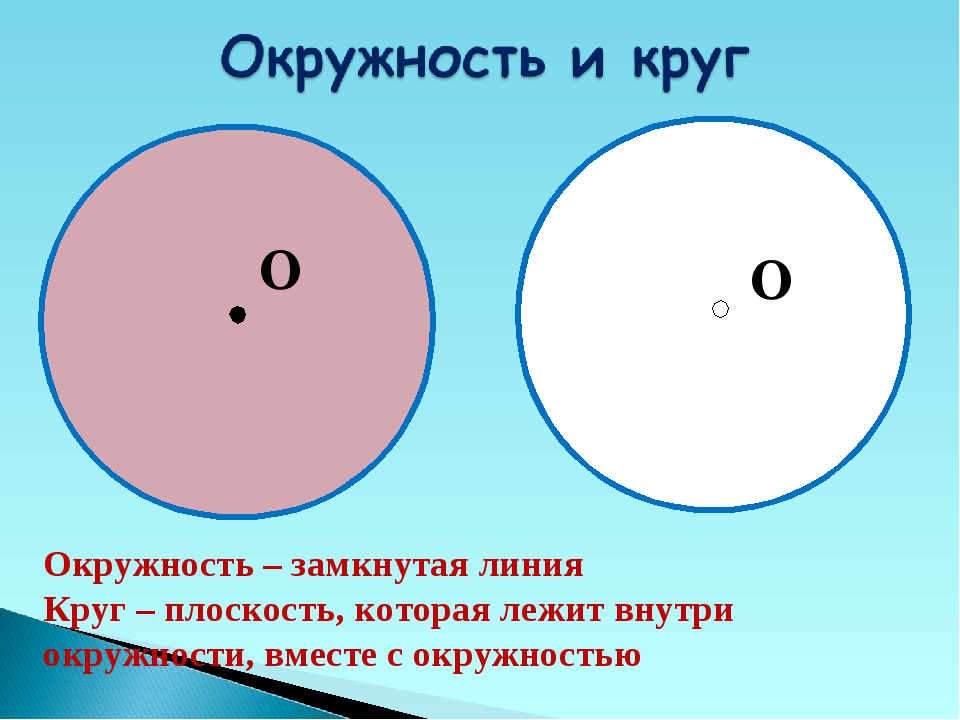

Как ни повернётся колесо, расстояние между землёй и осью остаётся одинаковое, поэтому и катится колесо плавно.

Колесо было изобретено давным – давно. С тех пор сделано много открытий и изображений, но и теперь в основе приборов и машин лежит круг .

Окружность всегда привлекала к себе внимание художников и архитекторов. Арки, полукруглые окна придают торжественность. При использовании окружности получатся очень красивые узоры.

В некоторых приборах шкалы располагаются на окружностях или её дугах .

Вот почему окружность – душа геометрии .

Окружность действительно обладает красотой и изяществом, и в этом мы с вами убедимся, когда будем чертить окружности , решать задачи. Где преобладает окружность ? (ответы детей)

V. Работа в тетрадях.

1. Открыли тетради, записали число, классная работа (опереться на плакат «Сиди правильно» ).

2. К доске попрошу выйти двух учеников.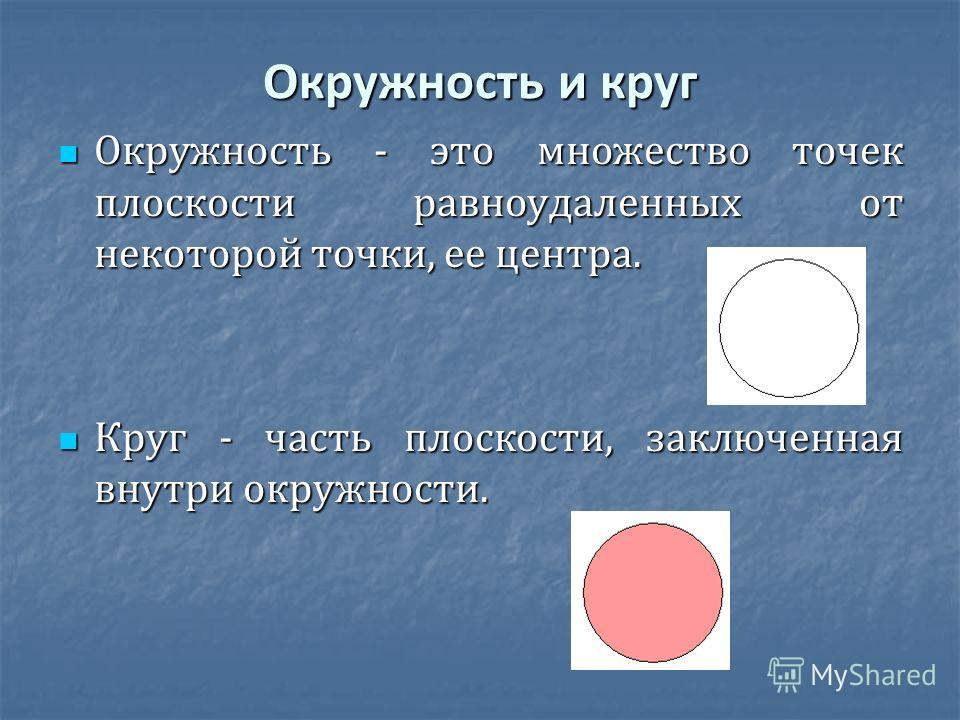 Один ученик нам нарисует окружность , другой ученик круг .

Вы ребята работаете в тетрадях : 1в. — поднимите правую руку – рисуете окружность , 2в. — поднимите левую руку – рисуете круг .

3. Были даны разные задания, а фигуры получились похожие. Чем круг отличается от окружности ? Вот эту проблему мы будем решать на уроке . (слайд №4)

4. Почему фигуры получились неточные – (не было инструмента, а от руки не проведёшь.

5. – Приготовьте циркуль. Посмотрите на него внимательно (у учителя большой циркуль) .

Из чего он состоит (2 ножки, на конце первой иголочка, на конце второй – грифель – это карандаш).

Циркуль – это чертёжный инструмент для вычеркивания окружностей . В переводе с латинского обозначает круг — циркус (если дети не ответят на вопрос, учитель помогает) .

С циркулем нужно работать очень осторожно.

6. Назовите правила как пользоваться циркулем (нельзя подносить к лицу, глазам; нельзя передавать циркуль соседу иглой вперёд; не играть; циркуль должен находиться в специальном футляре).

7. — Продемонстрируйте как нужно передавать циркуль соседу по парте (1в. передает, потом 2в., при этом сосед должен сказать волшебные слова).

Какая ножка циркуля стоит в центре окружности (с иглой) . Почему? (грифелем рисуем) .

VI. Тренировочная работа.

1. Сейчас мы с вами будем тренироваться строить окружности .

2. Любая работа выполняется по….(алгоритму) .

3. Что такое алгоритм? (порядок выполнения) .

4. Мы будем учиться строить окружность по алгоритму .

5. Внимание на экран (слайд №5)

1) — Отступите вниз 10 клеток

Отметить точку О

Поставить иглу в центр

Провели замкнутую линию

Эта замкнутая линия и называется окружность , а О – центр окружности . (кентрон – палка с заостренным концом, которым погоняли животных в упряжке). (слайд №6)

2) Расстояние между ножками циркуля – радиус, обозначается буквой r карточка r.

3) Сами попробуйте сформулировать определение радиуса (r – это отрезок, соединяет центр окружности с точкой на окружности ).

4) Провели несколько радиусов. Одинаковые ли они по длине? (да)

(слайд №7)

5) Окружность делит плоскость на 2 части. Как называется часть внутри окружности (круг ) —закрасить. (слайд №8)

6) Вывод : Чем же окружность отличается от круга ? Окружность – это граница круга . Круг – часть внутри окружности .

VII. Тренажер для глаз (физпауза) .

VIII. Практическая работа.

1) Приступаем к практической работе.

2) – Возьмите круг (слайд №9)

Сложите пополам

Нашли линию сгиба

Обведите её любым цветным карандашом

Эта линия называется диаметром и обозначается буквой d (показываю карточку)

Сами сформулируйте определение диаметра (отрезок, соединяющий две точки окружности , и проходит через центр).

IX. Работа в группах. (слайд №10)

1) Первая группа работает на компьютерах, выполняет задание.

2) Вторая группа выполняет творческое задание на местах.

3) Прошу 1 группу сесть за компьютеры, включить их и познакомиться с заданиями.

Творческое задание (2 группа)

1. Обведи окружность красным карандашом

2. Закрась внутреннюю часть фигуры

3. Проведи r

4. Проведи d

5. Из данных фигур выбери овал и раскрась его как пасхальное яйцо

4) Прочитайте внимательно задание , какие затруднения.

5) Работаем самостоятельно.

6) Работа по алгоритму

Начертите 2 окружности разных размеров

Выполни заливку

Обведи границу

Начерти диаметр

На какую фигуру похож вытянутый круг .

Попробуйте и вы оформить яйцо.

С помощью чего можно оформить его? (ластика, заливки, распылителя, карандаша) .

7) Попросим гостей посмотреть работы.

8) Информация о пасхе.

Ребята не зря мы с вами раскрашивали яйца.

Когда раскрашивают яйца?

На пасху яйца раскрашивают разными цветами, но основное место принадлежит красному цвету. Яйцо является символом жизни. В скорлупе находится скрытая жизнь, потом появляется желтый цыпленок. Мария Магдалина (святая) пришла к императору, в руке у неё было яйцо, и сказала, что Иисус Христос воскрес. Император рассмеялся и говорит : «Этого не может быть так же как белое яйцо станет вдруг красным» , не успел он это сказать, как яйцо стало красным. С тех пор это событие символизирует веру в Господа, и мы красим яйца.

X. Итог урока . (слайд №11)

1. На протяжении всего урока мы были активны , внимательны , трудились как муравьи.

2. Достигли ли мы с вами цель урока ?

3. Решили ли мы проблемные вопросы?

XI. Домашнее задание (раздаю листочки)

Составьте аппликацию из кругов разных размеров , добавляя другие геометрические фигуры.

XII. Психологическая игра (волшебный сундучок)

1. Выбрать из сундучка (я подношу сундучок, любую фигуру (треугольник, квадрат, круг ) .

2. — Хлопайте в ладоши те, кто выбрал круг .

Круг – эти люди добрые , общительные

Попрыгайте, кто выбрал треугольник.

Треугольник – это лидер, настойчивый, упорный

Выполняйте наклоны вправо, влево, кто выбрал квадрат.

Квадрат – люди спокойные, дружелюбные.

Вывод : несмотря на то, что вы все по характеру разные, но порадовали меня своей работой. Молодцы! Умнички! Спасибо за урок , а гостям спасибо за внимание. (слайд №12)

В память о нашем уроке уч-ся преподносят вербу (дарят вербу) .

Чем отличается окружность от круга правило. Разница между окружностью и кругом

На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.
Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.
Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга.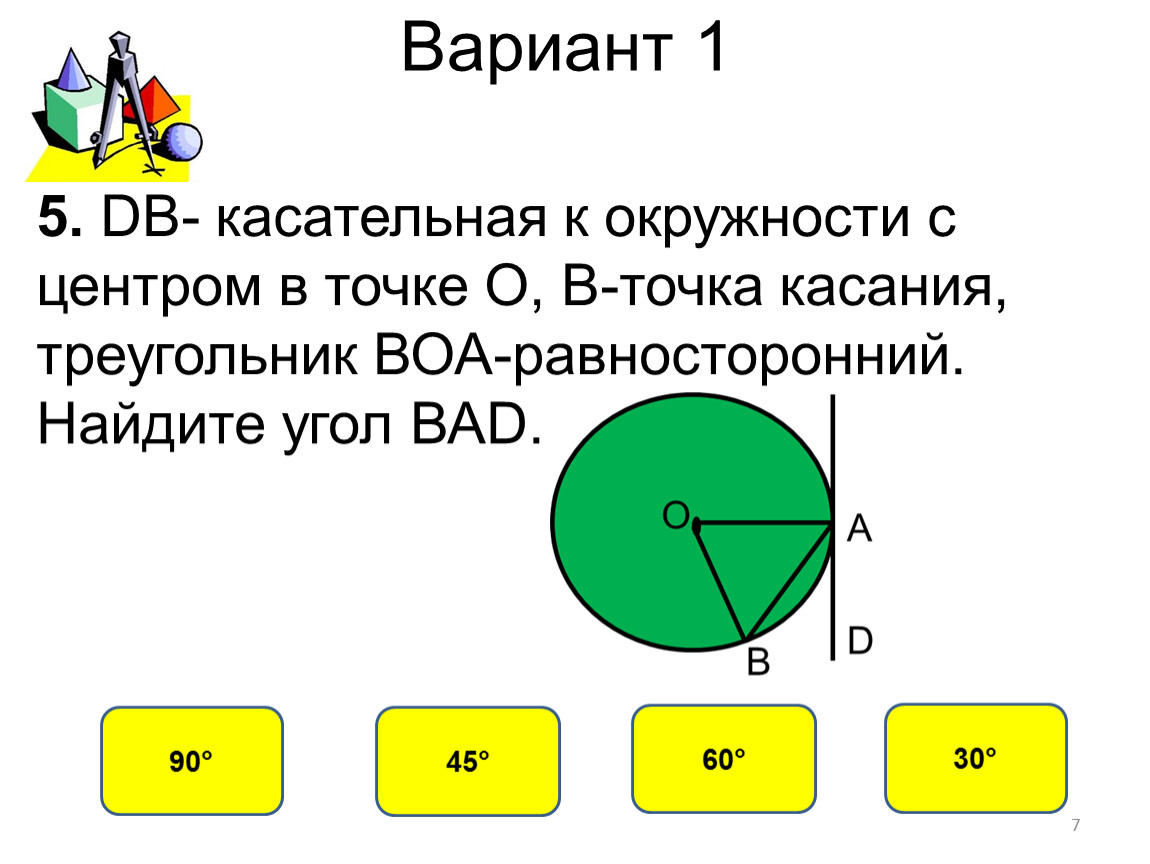 Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.

ImGist определил, что разница между кругом и окружностью заключается в следующем:

Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.

Окружность — это огромное количество точек на плоскости, равноудаленных от некой точки этой же плоскости, именуемой центром окружности. Окружность представляет собой замкнутую кривую, лежащую от центра на фиксированном расстоянии, нарываемом радиусом окружности.

Круг — это огромное количество точек плоскости, удаленных от некой точки этой же плоскости, именуемой центром круга, на расстояние, не превышающеей определенной величины, именуемой радиусом круга. Круг представляет собой сплошную фигуру, включающую окружность и все точки, лежащие в ней.

Следовательно, круг — это участок плоскости, а окружность — черта этого участка. Потому есть возможность говорить о площади круга и длине окружности, однако неправильно говорить о длине круга и площади окружности.

Так как точки окружности удалены от центра на расстояние, не превышающее радиуса, то они все принадлежат кругу. Другими словами, окружность принадлежит кругу, который она ограничивает. В особых случаях может рассматриваться круг в отсутствие границы — огромное количество точек круга, не принадлежащих его границе (окружности).

Окружность разделяет плоскость на две части — лежащую снутри и лежащую снаружи. Попрасть из одной части в другую нереально в отсутствие скрещения окружности. Площаль внутренней части конечна, площадь наружной части нескончаема.

Центр окружности не принадлежит окружности (кроме вырожденного варианта окружности нулевого радиуса). Центр круга всегда принадлежит кругу, т.к. находится снутри ограничивающей его окружности.

openclass.ru — методическая разработка «Окружность и круг»

otvet.mail.ru — чем отличается круг от окружности?

NMitra В Opera есть баг: у вложенного элемента углы не закругляются. Это можно подправить, дописав

#ball:after {
content: «»;
position: absolute;
top: 0; bottom: 0; right: 0; left: 0;
box-shadow: 0 0 0 100px #fff;
border-radius: 100%;
}

Но тогда тень в Гугл Хром «обрезанная» получается. Поскольку Опера переезжает на движок Google, то я сделала выбор в пользу его браузера. Космо Мизраил Прикольно.
Сейчас делаю дизайн как раз с планетами, но аватарки и другие изображения приходится делать плоскими, потому что img не применишь box-shadow: inset. NMitra Сделайте фоном background. Скоро благодаря поддержки трансформации CSS можно будет добавлять объём. Предвестники http://codepen.io/html5web/pen/pnbwo Космо Мизраил Мдо, вроде-бы для вебкита, а не работает х) Это будет вступать лет пять ещё, до этого надо ещё дожить 🙂

Фоны сделать не всегда получится, а вот наложить поверх изображения элемент с заданными стилями очень даже можно. Но это если известны размеры изображения.
Пример: http://jsfiddle.net/9qzm6/

Ещё нашёл скрипт, который выполняет эту работу самостоятельно:
http://www.htmldrive.net/items/demo/1156/Multiple-CSS3-Image-Styles
Здесь он сам определяет размер, если изображение загрузилось. Нужен jQuery.

Это так, на заметку 🙂 NMitra Там нужны настройки какие-то устанавливать.. Это сильно вперёд:))

Пжалст 🙂 я ваш постоянный читатель уже год как минимум 🙂 Анонимный IE 11
Все анимировано)) NMitra Молодцом IE, дотянулось. Осталась Хрому убрать -webkit-, он теперь в числе отстающих.

Что такое круг?

Начертание круга начинается с окружности. Окружность – это замкнутая черта без конца и начала , каждая точка которой находится на равном удалении от центра. Простейший пример окружности – гимнастический обруч.

Круг получится, если начертить окружность, например, на бумаге – и потом разукрасить ее. Любыми красками: желтой, синей, зеленой – какая больше нравится. Главное – заполнить чем-то пустоту. После окончания работы окружность превратится в фигуру, которую именуют кругом. Круг по сути своей – это некоторая часть двухмерной поверхности, закольцованная в окружность.

Круг обладает некоторыми важными для понимания его сущности параметрами. Кстати, часть данных параметров присуща и окружности.

1. Радиус – расстояние от центральной точки круга или окружности до границы фигуры (линии, которая ее очерчивает).
2. Диаметр – важная характеристика, которая так часто фигурирует в школьных заданиях. Это сумма двух радиусом, то есть расстояние между двумя противоположными точками на окружности.
3. Площадь – свойство, характерное только для круга. Окружность не имеет его в силу своей структуры (потому что она пустая, а центр фигуры – воображаемая точка). В круге, напротив, несложно определить центр. Через центральную точку фигуры достаточно просто прочертить ряд линий, которые поделят круг на сектора.

Круг в реальной жизни

В реальности можно без особых усилий отыскать множество предметов, по форме тождественных кругу. К примеру, готовый образец круга – а, точнее, множество, — каждый день катается по дорогам поселков и городов. Понятно, что речь идет о колесе. Здесь стоит оговориться: круг не должен быть однотонным, это не обязательно. Он может быть украшен узорами или чем-то еще – от этого форма не изменяется.

Другой пример круга – Солнце . Да, то самое дневное светило, которое люди лицезреют каждый день. Любознательный читатель заметит, что Солнце – фигура объемная, она не может быть кругом. Это правда. Но маленькая фигура, какой предстает огненная звезда жителям Земли – по сути своей именно круг. Площадь его, конечно, высчитать не получится. Почему? Потому что этот пример приводится только для наглядности, для того, чтобы понять, что такое круг.

Сектор

Что такое круг внимательный читатель ужен разобрался. Но вот что за «зверь» этот сектор, о котором упоминалось немного выше? Сектор – это часть круга, отделенная от остальной поверхности парой начерченных радиусов. Для наглядности можно примести такой пример: все когда-нибудь видели нарезанную пиццу. Кусочки – это сектора круга, которым является все это аппетитное блюдо.

Секторы не обязательно должны быть равной величины. К примеру, если пицца разрезана пополам, обе ее половины тоже будут секторами круга.

Что такое шар?

Шар – тело, ограниченное сферической поверхностью . То есть, это не двухмерная фигура, как круг, а трехмерная. Сферическая поверхность – это геометрическое сочетание поверхности точек, расположенных на неотрицательном расстоянии от некоей центральной точки. Расстояние, на которое удалены все точки поверхности шара от его центра, называется радиусом. И оно не должно превышать некие заданные цифры. Таким образом, круг – это та же сферическая поверхность, расположенная в другом пространстве.

В этом проявляются сходства и главное различие шара и круга. Круг – это двухмерная фигура, точки которой ограничены окружностью. Шар – это фигура трехмерная, а ее точки ограничены сферической поверхностью.

Разновидности шара

В метрическом и векторном пространствах рассматриваются два понятия, имеющие связь со сферической поверхностью. Шар, который включает в себя данную сферу, именуют замкнутым . Шар, который не включает в себя сферу, называют открытым .

Характеристики шара

Шар, как и круг, имеет диаметр и радиус. Обе эти величины в шаре вычисляются по вышеописанным принципам (как для круга). Радиус шара – это отрезок между любой точкой на сферической поверхности, ограничивающей фигуру, и ее центром. Диаметр соединяет две точки на сферической поверхности шара, проходя через его центр.

Интересное дополнение: круг может быть частью шара. Точнее, шар состоит из очень большого количества кругов различного диаметра. Называются эти круги сечениями сферы. Когда сечение пролегает через центр шара, его именуют большим кругом. Все остальные сечения именуются малыми кругами. Такого рода сечений, проходящих через пару точек на поверхности шара, возможно начертить поистине бесконечное множество.

Выводы

Круг – плоская, двухмерная фигура. Шар – объемное трехмерное геометрическое тело. Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).

Чем же отличается круг от шара? Круг плоский, шар же имеет объем. Именно объемность шара позволяет ему делиться на сечения, которые по своей сути являются кругами. Круг, напротив, делится на сектора.

Публикации по теме:

Детско-родительский игровой сеанс «Круг» для детей ОВЗ Игровое занятие КРУГ для детей ОВЗ Тема «Осень. Природные явления» Цели и задачи занятия КРУГ Главная цель занятия КРУГ – дать каждому ребенку.

Конкурс профессионального мастерства «Солнечный круг» (фотоотчет) С 12 по 26 октября 2015 года в нашем детском саду проходил конкурс профессионального мастерства «Воспитатель года». Цель конкурса: выявление.

Конспект НОД по ФЭМП «Знакомьтесь: круг» Конспект НОД по ФЭМП во второй младшей группе «Знакомьтесь- круг» Цель: развитие познавательных интересов детей Задачи: Познакомить.

НОД по математике «Круг и квадрат» (младшая группа) Тема: «Круг и квадрат» (младшая группа) Образовательная область: познание Цель: Продолжать учить находить один и много предметов в специально.

Поделки в технике «объемный квиллинг» Здравствуйте, коллеги! Недавно открыла для себя технику объемного квиллинга. Искусство, которое на русском языке называют «бумагокручением»,.

Проект по математическому развитию «Круг, квадрат и треугольник-фигуры важные, фигуры нужные» Номинация проекта – «Дошкольный возраст» Вид проекта: долгосрочный, фронтальный. Участники проекта: подгруппа детей средней группы, воспитатель.

«Снежинка 3-D». Объемный модуль для украшения интерьера Приближаются Новогодние праздники и перед нами, как воспитателями опять стоит вопрос «Чем же удивить детей и взрослых?». Просторы Интернета.

Совместная образовательная деятельность по ФЭМП «Круг и квадрат» Совместная образовательная деятельность взрослого и детей ФЭМП «Круг и квадрат». Цель: закреплять умение различать и называть круг и квадрат.

Весенний объемный тюльпан на открытке в подарок маме Не за горами прекрасный весенний праздник 8 Марта. И уже сейчас многие педагоги задумались над тем, что бы смастерить с детьми мамам в.

Разбираемся в том что такое окружность и круг. Формула площади круга и длины окружности.

Мы каждый день встречаем множество предметов, по форме которые образовывают круг или напротив окружность. Иногда возникает вопрос, что такое окружность и чем она отличается от круга. Конечно же, мы все проходили уроки геометрии, но иногда не помешает освежить знания весьма простыми объяснениями.

Что такое длина окружности и площадь круга: определение

Итак, окружность является замкнутой кривой линией, которая ограничивает или же напротив, образует круг. Обязательное условие окружности — у нее есть центр и все точки равноудалены от него. Проще говоря, окружность это гимнастический обруч (или как его часто называют хула-хуп) на плоской поверхности.

Длина окружности это общая длина той самой кривой, которая образует окружность. Как известно вне зависимости от размеров окружности соотношение ее диаметра и длины равно числу π = 3,141592653589793238462643.

Из этого следует, что π=L/D, где L — длина окружности, а D — диаметр окружности.

Если Вам известен диаметр, то длину можно найти по простой формуле: L= π* D

В случае если известен радиус: L=2 πR

Мы разобрались, что такое окружность и можем перейти к определению круга.

Круг — это геометрическая фигура, которая окружена окружностью. Или же, круг это фигура, рубеж которой состоит из большого количества точек равноудаленных от центра фигуры. Вся площадь, которая находится внутри окружности, включая ее центр, называется кругом.

Стоит заметить, что у окружности и круга, который находится в ней значения радиуса и диаметра одинаковые. А диаметр в свою очередь в два раза больше чем радиус.

Круг имеет площадь на плоскости, которую можно узнать при помощи простой формулы:

Где S — площадь круга, а R — радиус данного круга.

Чем круг отличается от окружности: объяснение

Основное отличие между кругом и окружностью — это то, что круг — геометрическая фигура, а окружность — замкнутая кривая. Также обратите внимание на отличия между окружностью и кругом:

• Окружность это замкнутая линия, а круг — площадь внутри этой окружности;
• Окружность это кривая линия на плоскости, а круг — пространство, сомкнутое в кольцо окружностью;
• Сходство между окружностью и кругом: радиус и диаметр;
• У круга и окружности единый центр;
• В случае если заштриховывается пространство внутри окружности, оно превращается в круг;
• У окружности есть длина, но ее нет у круга, и наоборот, у круга есть площадь, которой нет у окружности.

Круг и окружность: примеры, фото

Для наглядности предлагаем рассмотреть фото, на котором слева изображен круг, а справа окружность.

Формула длины окружности и площади круга: сравнение

Формула длины окружности L=2 πR

Формула площади круга S= πR²

Обратите внимание, что в обеих формулах присутствует радиус и число π. Данные формулы рекомендуется выучить наизусть, так как они простейшие и обязательно пригодятся в повседневной жизни и на работе.

Площадь круга по длине окружности: формула

S=π(L/2π)=L²/4π, где S — площадь круга, L — длина окружности.

Видео: Что такое круг, окружность и радиус

На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.

Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.

Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.

Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.

Выводы сайт

1. Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
2. Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.

Что это — окружность и круг, в чем их отличия и примеры данных фигур из жизни

Школьная пора для большинства взрослых людей ассоциируется с беззаботным детством. Конечно, многие неохотно посещают школу, но только там они могут получить базовые знания, которые впоследствии пригодятся им в жизни. Одним из таких является вопрос о том, что такое окружность и круг. Спутать данные понятия достаточно просто, ведь слова являются однокоренными. Но разница между ними не настолько большая, как может показаться неопытному ребенку. Дети данную тему любят по причине ее простоты.

Что такое окружность?

Окружность — это замкнутая линия, каждая точка которой равно удалена от центральной. Самым ярким примером окружности является обруч, который представляет собой замкнутое тело. Собственно, и говорить особо об окружности не приходится. В вопросе о том, что такое окружность и круг, значительно интереснее вторая его часть.

Что такое круг?

Представьте, что вы решили разукрасить нарисованную выше окружность. Для этого можно выбрать любые краски: синие, желтые или зеленые — кому что ближе по душе. И вот вы начали заполнять пустоту чем-то. После того как это было закончено, у нас получилась фигура, которая называется кругом. По сути, круг — это часть поверхности, очерченная окружностью.

У круга есть несколько важных параметров, часть из которых также характерна и для окружности. Первый — это радиус. Им называется расстояние между центральной точкой круга (ну или окружности) и самой окружностью, что создает границы кругу. Вторая важная характеристика, которая неоднократно используется в школьных задачах — это диаметр (то есть расстояние между противоположными точками окружности).

Ну и наконец, третья характеристика, присущая кругу — это площадь. Данное свойство специфичное только для него, окружность не имеет площади в силу того, что у нее нет ничего внутри, а центр, в отличие от круга, скорее воображаемый, чем настоящий. В самом же круге можно установить четкий центр, через который провести ряд линий, которые делят его на сектора.

Примеры круга в реальной жизни

На самом деле возможных предметов, которые можно назвать разновидностью круга, достаточно. Например, если посмотреть на колесо машины прямо, то вот вам пример готового круга. Да, он необязательно должен быть заполнен однотонно, вполне возможны различные узоры внутри него. Второй пример круга — это солнце. Конечно, на него посмотреть будет тяжело, но оно на небе выглядит, как маленький кружочек.

Да, сама звезда Солнце — это не круг, она имеет еще и объем. Но вот само солнце, которое мы видим над нашей головой в летнее время, является типичным кругом. Правда, площадь у него все равно высчитать не получится. Ведь сравнение его с кругом приводится только для наглядности, чтобы было проще понять, что такое окружность и круг.

Отличия окружности от круга

Значит, какой вывод мы можем сделать? Чем отличается окружность от круга, так это тем, что у последнего есть площадь, и в большинстве случаев окружность является границей круга.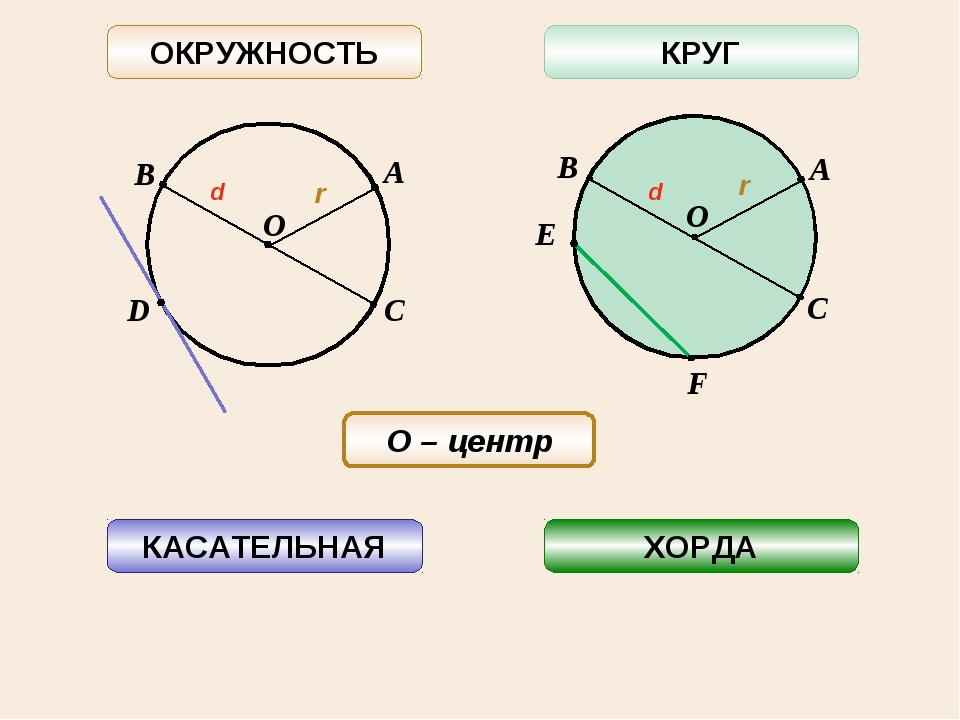 Хотя бывают и исключения на первый взгляд. Может показаться иногда, что нет окружности в круге, но это не так. В любом случае что-то да есть. Просто окружность может быть очень маленькой, и тогда ее не видно невооруженным глазом.

Также окружностью может быть то, что выделяет круг из фона. Например, на приведеном выше изображении синий круг находится на белом фоне. А вот та черта, по которой мы понимаем, что здесь начинается фигура, и называется в данном случае окружностью. Таким образом, окружность — это граница круга. Вот чем отличается окружность от круга.

Что такое сектор?

Сектор — это участок круга, который образуется двумя проведенными по нему радиусами. Чтобы понять это определение, нужно просто вспомнить пиццу. Когда ее разрезают на равные кусочки, все они и являются секторами круга, который представлен в виде такого вкусного блюда. При этом совершенно необязательно секторы должны быть равны. Они могут быть разной величины. Например, если отрезать половину пиццы, то она также будет сектором этого круга.

Предмет, отображаемый этим понятием, может иметь только круг. Окружность (радиус тоже можно провести, конечно, но после этого она станет кругом) не имеет площади, поэтому и сектор выделить не получится.

Выводы

Да, тема о круге и окружности (что это такое) очень проста для понимания. Но вообще все то, что касается этих геометрических фигур, является самым сложным для изучения. Школьнику нужно быть готовым к тому, что круг — фигура капризная. Но, как говорится, тяжело в учении — легко в бою. Да, геометрия — наука сложная. Зато успешное ее освоение позволяет сделать маленький шажок в сторону успеха. Потому что старания при обучении позволяют не только пополнять багаж собственных знаний, но и получать необходимые в жизни навыки. Собственно, на это и нацелена школа. А ответ на вопрос о том, что такое окружность и круг, является вторичным, хоть и важным.

Окружность и круг. Части окружности и круга

Многие предметы вокруг нас имеют форму, похожую на геометрические фигуры. Чтобы разобраться, что такое окружность и чем она отличается от круга, необходимо иметь чёткое представление об этих фигурах. Если поставить круглый стакан на лист бумаги и обвести его карандашом, получится линия, изображающая окружность. Если рассмотреть эту линию под микроскопом, то мы увидим толстую неровную чету. Геометрическая окружность не имеет ширины. Все её точки одинаково удалены от центра. Кольцо, обруч напоминают своей формой окружность.

Окружностью называется фигура, которая состоит из всех точек плоскости, находящихся на данном расстоянии от данной точки. Эта точка называется центром окружности и обычно обозначается О.

Расстояние от точек окружности до её центра называется радиусом окружности и обычно обозначается R. Радиусом также называется любой отрезок, соединяющий точку окружности с её центром.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр, называется диаметром.

Что же такое круг? Круг мы можем вырезать из бумаги. Арена цирка, дно стакана или тарелка имеют форму круга. Если окружность это «черта» (мы можем ниточкой выложить окружность), то круг это все, что находится внутри окружности.

Кругом называется фигура, которая состоит из всех точек плоскости, находящихся на расстоянии не большем данного, от данной точки. Эта точка называется центром круга, а данное расстояние – радиусом круга. Границей круга является окружность с теми же центром и радиусом.

Окружность и круг состоят из разнообразных частей.

Две точки, взятые на окружности, разобьют эту окружность на две части – две дуги, концами которых будут взятые точки.

Отрезок, соединяющий две точки окружности, называется хордой окружности, и хордой круга, ограниченного этой окружностью.

Хорда, проходящая через центр окружности или круга, называется диаметром окружности или круга. Диаметр делит круг на два полукруга, а окружность – на две полуокружности.

Диаметр делится центром окружности пополам, и поэтому он равен двум радиусам.

Два радиуса разбивают круг на секторы.

Хорда разбивает круг на сегменты.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Чем отличается окружность от круга. Чем отличается круг от окружности

На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.
Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.
Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.
Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.

ImGist определил, что разница между кругом и окружностью заключается в следующем:

Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.

NMitra В Opera есть баг: у вложенного элемента углы не закругляются. Это можно подправить, дописав

#ball:after {
content: «»;
position: absolute;
top: 0; bottom: 0; right: 0; left: 0;
box-shadow: 0 0 0 100px #fff;
border-radius: 100%;
}

Но тогда тень в Гугл Хром «обрезанная» получается. Поскольку Опера переезжает на движок Google, то я сделала выбор в пользу его браузера. Космо Мизраил Прикольно.
Сейчас делаю дизайн как раз с планетами, но аватарки и другие изображения приходится делать плоскими, потому что img не применишь box-shadow: inset. NMitra Сделайте фоном background. Скоро благодаря поддержки трансформации CSS можно будет добавлять объём. Предвестники http://codepen.io/html5web/pen/pnbwo Космо Мизраил Мдо, вроде-бы для вебкита, а не работает х) Это будет вступать лет пять ещё, до этого надо ещё дожить 🙂

Фоны сделать не всегда получится, а вот наложить поверх изображения элемент с заданными стилями очень даже можно. Но это если известны размеры изображения.
Пример: http://jsfiddle.net/9qzm6/

Ещё нашёл скрипт, который выполняет эту работу самостоятельно:
http://www.htmldrive.net/items/demo/1156/Multiple-CSS3-Image-Styles
Здесь он сам определяет размер, если изображение загрузилось. Нужен jQuery.

Это так, на заметку 🙂 NMitra Там нужны настройки какие-то устанавливать. . Это сильно вперёд:))

Пжалст 🙂 я ваш постоянный читатель уже год как минимум 🙂 Анонимный IE 11
Все анимировано)) NMitra Молодцом IE, дотянулось. Осталась Хрому убрать -webkit-, он теперь в числе отстающих.

Что такое круг?

Начертание круга начинается с окружности. Окружность – это замкнутая черта без конца и начала , каждая точка которой находится на равном удалении от центра. Простейший пример окружности – гимнастический обруч.

Круг получится, если начертить окружность, например, на бумаге – и потом разукрасить ее. Любыми красками: желтой, синей, зеленой – какая больше нравится. Главное – заполнить чем-то пустоту. После окончания работы окружность превратится в фигуру, которую именуют кругом. Круг по сути своей – это некоторая часть двухмерной поверхности, закольцованная в окружность.

Круг обладает некоторыми важными для понимания его сущности параметрами. Кстати, часть данных параметров присуща и окружности.

1. Радиус – расстояние от центральной точки круга или окружности до границы фигуры (линии, которая ее очерчивает).
2. Диаметр – важная характеристика, которая так часто фигурирует в школьных заданиях. Это сумма двух радиусом, то есть расстояние между двумя противоположными точками на окружности.
3. Площадь – свойство, характерное только для круга. Окружность не имеет его в силу своей структуры (потому что она пустая, а центр фигуры – воображаемая точка). В круге, напротив, несложно определить центр. Через центральную точку фигуры достаточно просто прочертить ряд линий, которые поделят круг на сектора.

Круг в реальной жизни

В реальности можно без особых усилий отыскать множество предметов, по форме тождественных кругу. К примеру, готовый образец круга – а, точнее, множество, — каждый день катается по дорогам поселков и городов. Понятно, что речь идет о колесе. Здесь стоит оговориться: круг не должен быть однотонным, это не обязательно. Он может быть украшен узорами или чем-то еще – от этого форма не изменяется.

Другой пример круга – Солнце . Да, то самое дневное светило, которое люди лицезреют каждый день. Любознательный читатель заметит, что Солнце – фигура объемная, она не может быть кругом. Это правда. Но маленькая фигура, какой предстает огненная звезда жителям Земли – по сути своей именно круг. Площадь его, конечно, высчитать не получится. Почему? Потому что этот пример приводится только для наглядности, для того, чтобы понять, что такое круг.

Сектор

Что такое круг внимательный читатель ужен разобрался. Но вот что за «зверь» этот сектор, о котором упоминалось немного выше? Сектор – это часть круга, отделенная от остальной поверхности парой начерченных радиусов. Для наглядности можно примести такой пример: все когда-нибудь видели нарезанную пиццу. Кусочки – это сектора круга, которым является все это аппетитное блюдо.

Секторы не обязательно должны быть равной величины. К примеру, если пицца разрезана пополам, обе ее половины тоже будут секторами круга.

Что такое шар?

Шар – тело, ограниченное сферической поверхностью . То есть, это не двухмерная фигура, как круг, а трехмерная. Сферическая поверхность – это геометрическое сочетание поверхности точек, расположенных на неотрицательном расстоянии от некоей центральной точки. Расстояние, на которое удалены все точки поверхности шара от его центра, называется радиусом. И оно не должно превышать некие заданные цифры. Таким образом, круг – это та же сферическая поверхность, расположенная в другом пространстве.

В этом проявляются сходства и главное различие шара и круга. Круг – это двухмерная фигура, точки которой ограничены окружностью. Шар – это фигура трехмерная, а ее точки ограничены сферической поверхностью.

Разновидности шара

В метрическом и векторном пространствах рассматриваются два понятия, имеющие связь со сферической поверхностью. Шар, который включает в себя данную сферу, именуют замкнутым . Шар, который не включает в себя сферу, называют открытым .

Характеристики шара

Шар, как и круг, имеет диаметр и радиус. Обе эти величины в шаре вычисляются по вышеописанным принципам (как для круга). Радиус шара – это отрезок между любой точкой на сферической поверхности, ограничивающей фигуру, и ее центром. Диаметр соединяет две точки на сферической поверхности шара, проходя через его центр.

Интересное дополнение: круг может быть частью шара. Точнее, шар состоит из очень большого количества кругов различного диаметра. Называются эти круги сечениями сферы. Когда сечение пролегает через центр шара, его именуют большим кругом. Все остальные сечения именуются малыми кругами. Такого рода сечений, проходящих через пару точек на поверхности шара, возможно начертить поистине бесконечное множество.

Выводы

Круг – плоская, двухмерная фигура. Шар – объемное трехмерное геометрическое тело. Тем не менее, они имеют массу сходств (наличие ограничивающей поверхности, диметра и радиуса, наполненность структуры в отличие от той же окружности, возможност вычислить площадь).

Чем же отличается круг от шара? Круг плоский, шар же имеет объем.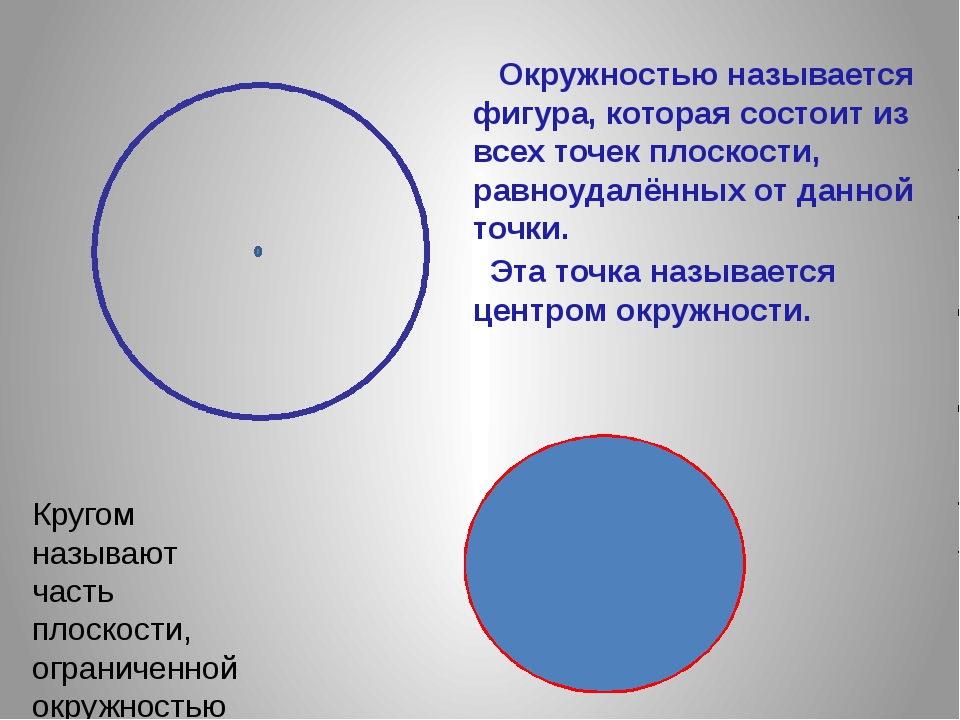 Именно объемность шара позволяет ему делиться на сечения, которые по своей сути являются кругами. Круг, напротив, делится на сектора.

Публикации по теме:

Детско-родительский игровой сеанс «Круг» для детей ОВЗ Игровое занятие КРУГ для детей ОВЗ Тема «Осень. Природные явления» Цели и задачи занятия КРУГ Главная цель занятия КРУГ – дать каждому ребенку.

Конкурс профессионального мастерства «Солнечный круг» (фотоотчет) С 12 по 26 октября 2015 года в нашем детском саду проходил конкурс профессионального мастерства «Воспитатель года». Цель конкурса: выявление.

Конспект НОД по ФЭМП «Знакомьтесь: круг» Конспект НОД по ФЭМП во второй младшей группе «Знакомьтесь- круг» Цель: развитие познавательных интересов детей Задачи: Познакомить.

НОД по математике «Круг и квадрат» (младшая группа) Тема: «Круг и квадрат» (младшая группа) Образовательная область: познание Цель: Продолжать учить находить один и много предметов в специально.

Поделки в технике «объемный квиллинг» Здравствуйте, коллеги! Недавно открыла для себя технику объемного квиллинга. Искусство, которое на русском языке называют «бумагокручением»,.

Проект по математическому развитию «Круг, квадрат и треугольник-фигуры важные, фигуры нужные» Номинация проекта – «Дошкольный возраст» Вид проекта: долгосрочный, фронтальный. Участники проекта: подгруппа детей средней группы, воспитатель.

«Снежинка 3-D». Объемный модуль для украшения интерьера Приближаются Новогодние праздники и перед нами, как воспитателями опять стоит вопрос «Чем же удивить детей и взрослых?». Просторы Интернета.

Совместная образовательная деятельность по ФЭМП «Круг и квадрат» Совместная образовательная деятельность взрослого и детей ФЭМП «Круг и квадрат». Цель: закреплять умение различать и называть круг и квадрат.

Весенний объемный тюльпан на открытке в подарок маме Не за горами прекрасный весенний праздник 8 Марта. И уже сейчас многие педагоги задумались над тем, что бы смастерить с детьми мамам в.

На уроках геометрии в школе все мы изучали свойства различных фигур и линий. Каждая из них имеет свои особенности, а порой некоторые из них взаимосвязаны друг с другом. Взять для примера хотя бы круг и окружность – между ними есть определенная связующая линия. Только вот какая? Давайте вместе разберемся в этом вопросе.

Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.

Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.

Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.

Выводы сайт

1. Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;
2. Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.

Школьная пора для большинства взрослых людей ассоциируется с беззаботным детством. Конечно, многие неохотно посещают школу, но только там они могут получить базовые знания, которые впоследствии пригодятся им в жизни. Одним из таких является вопрос о том, и круг. Спутать данные понятия достаточно просто, ведь слова являются однокоренными. Но разница между ними не настолько большая, как может показаться неопытному ребенку. Дети данную тему любят по причине ее простоты.

Что такое окружность?

Окружность — это замкнутая линия, каждая точка которой равно удалена от центральной. Самым ярким примером окружности является обруч, который представляет собой замкнутое тело. Собственно, и говорить особо об окружности не приходится. В вопросе о том, что такое окружность и круг, значительно интереснее вторая его часть.

Что такое круг?

Представьте, что вы решили разукрасить нарисованную выше окружность. Для этого можно выбрать любые краски: синие, желтые или зеленые — кому что ближе по душе. И вот вы начали заполнять пустоту чем-то. После того как это было закончено, у нас получилась фигура, которая называется кругом. По сути, круг — это часть поверхности, очерченная окружностью.

У круга есть несколько важных параметров, часть из которых также характерна и для окружности. Первый — это радиус. Им называется расстояние между центральной точкой круга (ну или окружности) и самой окружностью, что создает границы кругу. Вторая важная характеристика, которая неоднократно используется в школьных задачах — это диаметр (то есть расстояние между противоположными точками окружности).

Ну и наконец, третья характеристика, присущая кругу — это площадь. Данное свойство специфичное только для него, окружность не имеет площади в силу того, что у нее нет ничего внутри, а центр, в отличие от круга, скорее воображаемый, чем настоящий. В самом же круге можно установить четкий центр, через который провести ряд линий, которые делят его на сектора.

Примеры круга в реальной жизни

На самом деле возможных предметов, которые можно назвать разновидностью круга, достаточно. Например, если посмотреть на колесо машины прямо, то вот вам пример готового круга. Да, он необязательно должен быть заполнен однотонно, вполне возможны различные узоры внутри него. Второй пример круга — это солнце. Конечно, на него посмотреть будет тяжело, но оно на небе выглядит, как маленький кружочек.

Да, сама звезда Солнце — это не круг, она имеет еще и объем. Но вот само солнце, которое мы видим над нашей головой в летнее время, является типичным кругом. Правда, площадь у него все равно высчитать не получится. Ведь сравнение его с кругом приводится только для наглядности, чтобы было проще понять, что такое окружность и круг.

Отличия окружности от круга

Значит, какой вывод мы можем сделать? Чем отличается окружность от круга, так это тем, что у последнего есть площадь, и в большинстве случаев окружность является границей круга. Хотя бывают и исключения на первый взгляд. Может показаться иногда, что нет окружности в круге, но это не так. В любом случае что-то да есть. Просто окружность может быть очень маленькой, и тогда ее не видно невооруженным глазом.

Также окружностью может быть то, что выделяет круг из фона. Например, на приведеном выше изображении синий круг находится на белом фоне. А вот та черта, по которой мы понимаем, что здесь начинается фигура, и называется в данном случае окружностью. Таким образом, окружность — круга. Вот чем отличается окружность от круга.

Что такое сектор?

Сектор — это участок круга, который образуется двумя проведенными по нему радиусами. Чтобы понять это определение, нужно просто вспомнить пиццу. Когда ее разрезают на равные кусочки, все они и являются секторами круга, который представлен в виде такого вкусного блюда. При этом совершенно необязательно секторы должны быть равны. Они могут быть разной величины. Например, если отрезать половину пиццы, то она также будет сектором этого круга.

Предмет, отображаемый этим понятием, может иметь только круг. тоже можно провести, конечно, но после этого она станет кругом) не имеет площади, поэтому и сектор выделить не получится.

Выводы

Да, тема о круге и окружности (что это такое) очень проста для понимания. Но вообще все то, что касается этих является самым сложным для изучения. Школьнику нужно быть готовым к тому, что круг — фигура капризная. Но, как говорится, тяжело в учении — легко в бою. Да, геометрия — наука сложная. Зато успешное ее освоение позволяет сделать маленький шажок в сторону успеха. Потому что старания при обучении позволяют не только пополнять багаж собственных знаний, но и получать необходимые в жизни навыки. Собственно, на это и нацелена школа. А ответ на вопрос о том, что такое окружность и круг, является вторичным, хоть и важным.

Разница между Кругом и Эллипсом

Ключевое отличие: Круг и Эллипс имеют замкнутые изогнутые формы. В круге все точки одинаково далеки от центра, что не относится к эллипсу; в эллипсе все точки находятся на разных расстояниях от центра.

Математически круг является основной формой в области геометрии и ее определения: круг — это форма, в которой все точки находятся на одинаковом расстоянии от его центра. Он назван его центром. Некоторыми реальными примерами круга являются колеса, тарелка и (поверхность) монеты.

Слово « цирк » происходит от греческого термина « киркос », который является метатезисом греческого гомера и означает « обруч » или « кольцо ». Круг был известен еще до записи истории. Солнце и Луна являются естественными примерами круга, в то время как даже короткий стебель, дующий на ветру, образует форму круга в песке. Принцип круга был применен при формировании колес и механизмов доисторическим человеком. Сейчас, в современную эпоху, существует множество разновидностей механизмов, основанных на форме круга. Изучение круга и его развитие применимо в областях математики, геометрии, астрономии и исчисления.

В терминологии круга используются следующие термины:

Дуга : любая связанная часть круга.

Центр : точка на равном расстоянии от точек на окружности.

Радиус : отрезок, соединяющий центр круга с любой точкой на самом круге; или длина такого отрезка, равная половине диаметра.

Диаметр : отрезок, конечные точки которого лежат на окружности и который проходит через центр; или длина такого отрезка, который является наибольшим расстоянием между любыми двумя точками на окружности. Это особый случай аккорда, а именно самого длинного аккорда, и он вдвое больше радиуса.

Окружность : длина одного круга по кругу.

Аккорд : отрезок, конечные точки которого лежат на окружности.

Касательная : копланарная прямая, которая касается круга в одной точке.

Полукруглая область: область, ограниченная диаметром, и дуга, лежащая между конечными точками диаметра. Это частный случай кругового сегмента, а именно самого большого.

Круглый сектор : область, ограниченная двумя радиусами и дуга, лежащая между радиусами.

Математически эллипс является распространенной формой в области математики. Его определение гласит: изогнутая линия, образующая замкнутый контур, где сумма расстояний от двух точек (фокусов) до каждой точки на линии постоянна. Реальные примеры эллипса: обруч, стакан воды и простая тарелка для обеда, когда они наклонены, чтобы смотреть под углом.

Аполлоний Пергский в своем «Конике» дал название «эллипс», что подчеркивает связь кривой с применением областей. Это кривая на плоскости, которая окружает две точки фокусировки, так что прямая линия, проведенная из одной из точек фокусировки в любую точку кривой, а затем обратно в другую точку фокусировки, имеет одинаковую длину для каждой точки кривой.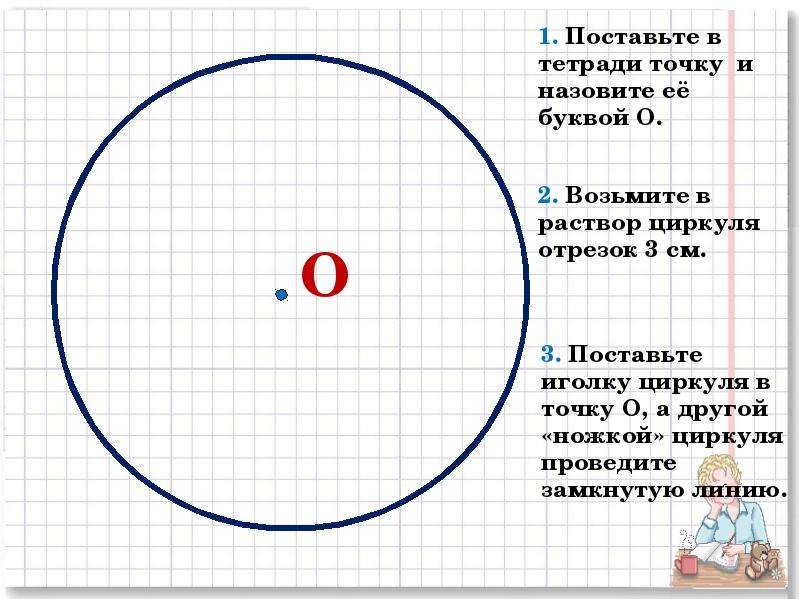 Его форма представлена ​​его эксцентриситетом, который произвольно близок к 1. Изучение эллипса и его свойств широко применимы в области физики, астрономии и техники. Орбиты планет с Солнцем в одной из фокусных точек, лун, вращающихся вокруг планет, и другие системы, имеющие два астрономических тела, являются общими примерами эллиптических траекторий. Форма планет и звезд часто хорошо описывается эллипсоидами. Эллипс также считается самой простой фигурой Лиссажу, образованной, когда горизонтальные и вертикальные движения являются синусоидами с одинаковой частотой.

Термины, используемые в основном в терминологии эллипса:

Фокус : расстояние от центра, и выражается через основные и второстепенные радиусы.

Эксцентриситет : Эксцентриситет эллипса (обычно обозначаемый как e или ε) выражается в терминах с использованием коэффициента уплощения.

Directrix : это линия, параллельная малой оси, с которой связан каждый фокус.

Latus rectum : хорды эллипса, которые перпендикулярны большой оси и проходят через один из ее фокусов, называются latus rectum эллипса.

Большая / Малая ось : самый длинный и самый короткий диаметры эллипса. Длина большой оси равна сумме двух линий генератора.

Полу мажорная / полуосновная ось : расстояние от центра до самой дальней и ближайшей точки на эллипсе. Половина большой / малой оси.

Аккорды : середины набора параллельных аккордов эллипса коллинеарны.

Окружность : она связана с длиной большой полуоси и эксцентриситетом и является неотъемлемой частью эллипса.

Сравнение между Кругом и Эллипсом:

	Круг	Эллипс
Определения	Круг — это круглая плоская фигура, граница которой (окружность) состоит из точек, равноудаленных от неподвижной точки (центра). 2 = 1
сходство	Круги — это уникальные формы, из которых происходят другие формы.	Эллипсы также возникают в виде изображений круга при параллельной проекции и ограниченных случаях перспективной проекции.

Окружность и её элементы. Знакомство с понятиями. 2-й класс

УМК: «Начальная школа XXI века».

Цели урока:

• Образовательная: создать условия для формирования представления об окружности и круге, как о геометрических фигурах и познакомить с их элементами, развивать практическое умение – пользоваться циркулем.
• Развивающая: создать условия для развития творческой деятельности, речи и мыслительных операций: обобщение, анализ, сравнение.
• Воспитательные: создать условия для воспитания трудолюбия, самостоятельности, активности, способности к познанию.

Оборудование: геометрические фигуры (квадрат, куб, шар, круг), модель круга (на каждого ученика), учебник для 2 класса В. Н. Рудницкой  «Математика» 1 часть, рабочая тетрадь, циркуль, линейка, картинка с изображением Карандаша (человечка), альбомные листы с изображением окружностей, карточки.

Ход урока

I. Организация класса

«Долгожданный дан звонок,
Начинается урок.
Тут затеи и задачи,
Игры, шутки, всё для вас!
Пожелаю всем удачи —
За работу, в добрый час!»

II. Актуализация знаний

Игра. На столе разложены различные геометрические фигуры (накрыты платком).

— Найдите на ощупь: квадрат, куб, шар, круг.

— Чем отличаются? (учитель держит в руках и показывает шар и круг).

III. Сообщение темы урока

— Сегодня на уроке, мы с вами отправимся в удивительную страну геометрию, где познакомимся с новой геометрической фигурой и её элементами.

IV. Работа по теме урока

1. Знакомство с понятием «окружность».

— Найдите на столе у каждого из вас круг. Возьмите его в руки. Обведите пальчиком границу круга так же как я.

— Может быть, кто-нибудь из вас знает, как называется граница круга? (выслушав ответы детей, учитель вывешивает карточку на доску).

— Прочитайте слово: по слогам, с ударением. Закройте глаза, представьте это слово и ещё раз проговорите его по слогам.

— Какие буквы в этом слове похожи на окружность? («О»). А что вы можете рассказать об этих буквах? (Это безударные гласные, которые нужно запомнить.)

— А теперь возьмите круг, положите его на страницу тетради и обведите шаблон по его границе.

— Уберите шаблон. Посмотрите, у вас получилась окружность. Но для того, что бы построить окружность, не обязательно каждый раз пользоваться шаблоном.

2. Построение окружности с помощью циркуля.

а) — Для построения окружности существует специальный инструмент.

— Послушайте загадку:

«Сговорились две ноги
Делать дуги и круги». Это …… (циркуль).

Учитель вывешивает карточку на доску и показывает инструмент.

— Обратите внимание на гласную, которая пишется после буквы «Ц». Кто может объяснить?

— Какое слово спряталось в слове «циркуль»? («цирк»).

— Слово «цирк» в переводе с латинского языка означает «круг».

— Как вы думаете, почему значение слова связано с кругом? Вспомните, как выглядит арена. (Она круглая,  как-будто её построили с помощью циркуля).

б) — У циркуля есть 2 ножки: одна — с остриём, другая — с грифелем.

С циркулем нужно работать очень осторожно. Назовите правила пользования циркулем (нельзя подносить к лицу и глазам, нельзя передавать циркуль соседу иглой вперёд, нельзя им играть, циркуль должен находиться в специальном футляре).

— А теперь посмотрите, как работают с этим инструментом (показ учителя): «Разведу ножки  на небольшое расстояние: ножку с остриём ставлю на бумагу, а ножка с грифелем касается бумаги. Аккуратно поворачиваем циркуль вокруг своей оси, при этом сохраняя расстояние между ножками, и получаем окружность. Если расстояние изменится — окружность не получится».

в) — Начертите окружность в тетрадях так же как я. (самостоятельная работа детей, помощь учителя), но сначала повторим порядок работы.

г) Обобщение:

— Что вы начертили? (окружность). Как вы думаете, почему её так назвали?

— Окружность — линия, которая идёт по границе круга.

— Посмотрите на свои фигуры. Чем круг отличается от окружности? (показать).

— Круг — это окружность вместе с внутренней областью, ограниченной этой окружностью; его можно погладить. Погладьте. Окружность — это только граница круга (проведите пальчиком по линии), внутри пустая. Круг и окружность как брат и сестра. Они всегда вместе! Нарисовали окружность — возник круг, вырезали круг — ножницы обозначили окружность.

Физминутка.

— А теперь отдохнём, встаньте!- Начертите окружность:

• левой рукой в воздухе;
• правой ногой на полу;
• на спине у соседа;
• носом на потолке.

—  Садитесь! Продолжаем работать дальше!

3. Работа по учебнику.

— Откройте учебник на странице 88, найдите №6.

Рассмотрите: как изображаются на плоскости круг и окружность. Сравните. В чём сходство и различие?

— А  какие предметы в учебнике на странице 87 в №1 являются окружностью? (Обруч, огненное кольцо, оправа от очков). Назовите предметы, которые имеют форму круга. (Стекло от очков, леденец, солнышко). Приведите свои примеры.

— Ребята, к нам на урок пришёл гость — весёлый Карандаш и принёс с собой замечательную песенку про круг и окружность (вывешивается картинка с изображением Карандаша).

— Послушайте её (учитель поёт):

«У круга есть одна подруга
Знакома всем её наружность.
Она идёт по краю круга
И называется ….. » (окружность).

4. Элементы окружности

— Дома вы можете сочинить свою песенку про круг и окружность.

— А сейчас Карандашик просит вас помочь ему выполнить некоторые задания:

а) — Как и любая фигура, окружность тоже имеет свой центр. Помогите найти её Карандашу.

— Как вы думаете, где она будет находиться? (Найдите у себя прокол от острой ножки циркуля — это и есть центр окружности).

— Отметьте его точкой и обозначьте латинской буквой «O».

б)  — На странице 87 учебника, на чертеже найдите центр окружности.

— А какой ещё элемент окружности вы видите на чертеже? Прочитайте!

— Карандашик просит вас помочь ему построить радиус окружности.

— Как же это сделать?

в) — Отметим на окружности точку в любом месте. Я здесь, а вы можете поставить точку в другом месте (показать), но обязательно на окружности и обозначим её латинской буквой «А». (Учитель и дети работают одновременно).

— Соедините точку «А» с центром окружности (по линейке, цветным карандашом).

— Какая получилась фигура? (отрезок ОА).

— Отрезок ОА и есть радиус.

— Радиус — это расстояние от центра окружности до любой точки, лежащей на окружности.

— А можно ещё провести радиус? Кто сможет, попробуйте? (2 ученика у доски).

— Как можно узнать длину радиуса? (с помощью линейки и циркуля).

— Как вы думаете, радиусы, которые мы построили  будут одинаковыми или разными? Докажите! (измерьте с помощью линейки или циркуля).

г) — А ведь знаете, в математике есть ещё одно определение окружности.

— Представьте себе, что вы бы отметили множество точек, которые находятся на одинаковом расстоянии  от центра, и когда их соединили между собой, то, что получилось тогда? (окружность).

— Вот вы и сами дали второе определение окружности: окружность — это множество точек, которые находятся на одинаковом расстоянии от центра окружности.

5. Рефлексия

— А теперь подведём итог урока, то есть выясним: какие же открытия вы совершили сегодня для себя на уроке? (высказываются дети).

— Ребята, а полученные знания вам в жизни пригодятся? Где?

— Итак, что такое окружность? (2 определения: Окружность — это граница круга, замкнутая кривая линия. Окружность — это множество точек, находящихся на одинаковом расстоянии от центра окружности).

— Как называется этот элемент окружности? (учитель показывает на центр окружности)

— Как называется расстояние от центра окружности до любой точки, лежащей на окружности? (радиус)

6. Творческое задание

– Вы сегодня отлично поработали на уроке, узнали много нового. Молодцы!

А теперь Карандашик предлагает вам немного отдохнуть и выполнить творческое задание.

а)  – Посмотрите, что изображено у каждого из вас на альбомном листе? (окружность)

— Проявив свою фантазию, дорисуйте окружности так, чтобы получились разные предметы. А для этого вам пригодятся знания, полученные на уроках «Окружающего мира» и «Технологии».

— А может быть, кто-нибудь из вас захочет использовать в своей работе не окружность, а круг.

— Что же тогда нужно сделать? Как превратить окружность в круг? (закрасить).

— Итак, приступаем к работе. А интересные работы вы  продемонстрируете нашему Карандашику в конце урока. (Включить музыку).

б) Просмотр интересных работ детей и учителя (эмблема олимпийского флага – на основе окружности и дорожный знак «Движение пешеходов запрещено» — на основе круга).

7. Домашнее задание

• Дома потренироваться в построении окружности с помощью циркуля и нахождении её элементов: центра и радиуса (всем учащимся обязательно).
• Сочинить песенку или стихотворение про круг и окружность (по желанию учащихся).

Разница между кругом и эллипсом

Ключевое отличие: A Круг и Эллипс имеют замкнутые изогнутые формы. В круге все точки одинаково удалены от центра, чего нельзя сказать о эллипсе; в эллипсе все точки находятся на разном расстоянии от центра.

Математически круг — это основная форма в области геометрии, и ее определение гласит: круг — это форма, все точки которой находятся на одинаковом расстоянии от ее центра.Он назван по центру. Некоторые примеры круга из реального мира — это колеса, обеденная тарелка и (поверхность) монеты.

Слово « цирк » происходит от греческого термина « kirkos », который является метатезисом гомеровского греческого языка и означает « обруч » или « кольцо ». Круг был известен прежде письменной истории. Солнце и Луна — естественные примеры круга, тогда как даже короткий стебель, развевающийся на ветру, формирует форму круга на песке.Принцип круга был применен при формировании колес и шестерен доисторическим человеком. В современную эпоху существует множество разновидностей механизмов, основанных на форме круга. Изучение круга и его развития применимо в области математики, геометрии, астрономии и исчисления.

В терминологию круга входят следующие термины:

Дуга : любая соединенная часть окружности.

Центр : точка, равноудаленная от точек на окружности.

Радиус : отрезок прямой, соединяющий центр окружности с любой точкой на самой окружности; или длина такого отрезка, составляющая половину диаметра.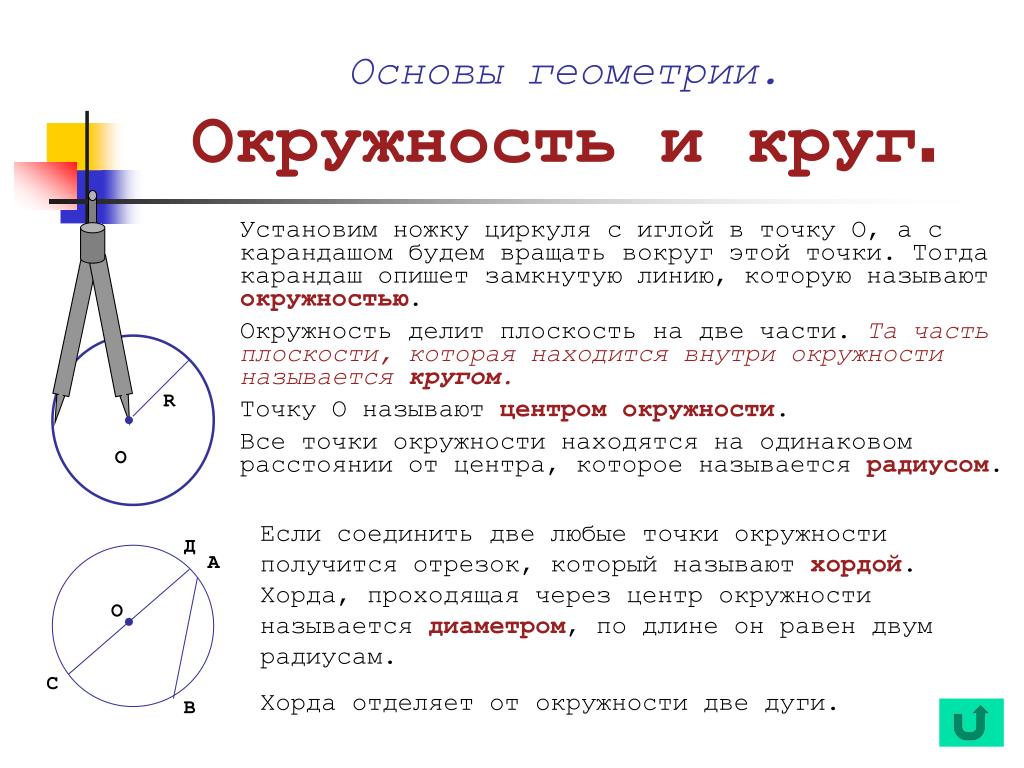

Диаметр : отрезок прямой, концы которого лежат на окружности и который проходит через центр; или длина такого отрезка прямой, которая является наибольшим расстоянием между любыми двумя точками на окружности. Это особый случай хорды, а именно самая длинная хорда, и она в два раза больше радиуса.

Circumferenc e: длина одного контура по окружности.

Хорда : отрезок прямой, концы которого лежат на окружности.

Касательная : копланарная прямая линия, которая касается окружности в одной точке.

Semicircl e: область, ограниченная диаметром и дугой, лежащей между конечными точками диаметра. Это частный случай круглого сегмента, а именно самого большого.

Круговой сектор : область, ограниченная двумя радиусами и дугой, лежащей между радиусами.

С математической точки зрения эллипс — это обычная форма в математике.Его определение гласит: изогнутая линия, образующая замкнутый контур, где сумма расстояний от двух точек (фокусов) до каждой точки на линии постоянна. Реальные примеры эллипса: хула-хуп, стакан воды и простая обеденная тарелка, которую можно наклонить для просмотра под углом.

Аполлоний из Перги дал название «эллипс» в своих «Кониках», которое подчеркивает связь кривой с нанесением площадей. Это кривая на плоскости, окружающей две фокусные точки, так что прямая линия, проведенная от одной из фокусных точек к любой точке кривой, а затем обратно к другой фокусной точке, имеет одинаковую длину для каждой точки на кривой.Его форма представлена ​​его эксцентриситетом, который произвольно близок к 1. Изучение эллипса и его свойств обычно применимо в области физики, астрономии и инженерии. Орбиты планет с Солнцем в одной из фокальных точек, луны, вращающиеся вокруг планет, и другие системы, имеющие два астрономических тела, являются общими примерами эллиптических траекторий. Форма планет и звезд часто хорошо описывается эллипсоидами. Эллипс также считается простейшей фигурой Лиссажу, образованной, когда горизонтальные и вертикальные движения представляют собой синусоиды с одинаковой частотой.

Термины, используемые в основном в терминологии эллипса:

Focus : Расстояние от центра, выражается через большой и малый радиусы.

Эксцентриситет : Эксцентриситет эллипса (обычно обозначаемый как e или ε) выражается через коэффициент сглаживания.

Directrix : это линия, параллельная малой оси, с которой связан каждый фокус.

Latus rectum : Хорды ​​эллипса, которые перпендикулярны большой оси и проходят через один из его фокусов, называются latus rectum эллипса.

Большая / Малая ось : Самый длинный и самый короткий диаметры эллипса. Длина большой оси равна сумме двух образующих.

Большая полуось / Малая полуось : расстояние от центра до самой дальней и ближайшей точки эллипса. Половина большой / малой оси.

Хорды ​​: Середины набора параллельных хорд эллипса коллинеарны.

Окружность : связана с длиной большой полуоси и эксцентриситетом и является неотъемлемой частью эллипса.

Сравнение круга и эллипса:

	Круг	Эллипс
Определения	Окружность — это круглая плоская фигура, граница (окружность) которой состоит из точек, равноудаленных от фиксированной точки (центра).	Эллипс — это правильный овал, очерченный точкой, движущейся в плоскости так, что сумма расстояний от двух других точек (фокусов) постоянна, или возникает, когда конус рассекается наклонной плоскостью, которая не пересекает основание.
Варианты	Круги не различаются по форме; они остаются той же формы даже при изменении вида.	Эллипсы различаются по форме от очень широких и плоских до почти круглых, в зависимости от того, насколько далеко друг от друга находятся фокусы.
Радиус согласованности	Имеет постоянный радиус по всей форме.	Он не имеет постоянного радиуса по всей форме. 2 = 1
Сходство	Круги — это уникальные формы, из которых происходят другие формы.	Эллипсы также возникают как изображения круга при параллельной проекции и в ограниченных случаях перспективной проекции.

Как культуры всего мира по-разному рисуют формы — Quartz

Давайте сделаем небольшое упражнение. Вы готовы? Нарисуйте круг в рамке ниже.Не думай слишком усердно!

Вы начали сверху или снизу? По часовой стрелке или против часовой стрелки? Новые данные показывают, что то, как вы рисуете круг, позволяет понять, откуда вы.

В ноябре Google выпустила онлайн-игру под названием Quick, Draw !, в которой у пользователей есть 20 секунд, чтобы нарисовать такие подсказки, как «верблюд» и «стиральная машина». Это весело, но настоящая цель игры — использовать эти наброски, чтобы научить алгоритмы рисованию людей. К маю этого года , игра собрала 50 миллионов уникальных рисунков.

Мы использовали общедоступную базу данных Quick, Draw! чтобы сравнить, как люди рисуют основные фигуры по всему миру. Наш анализ показывает, что то, как вы рисуете простой круг, связано с географией и культурным воспитанием, имеет глубокие корни в письменной речи за сотни лет и имеет важное значение для психологии развития и современных тенденций в образовании.

Круги, универсальная форма

Почитаемые древними греками, важные для исламского искусства, почитаемые в дзэн и тибетском буддизме, круги имеют универсальную форму.Независимо от того, с чего вы начнете, на самом деле есть только два способа нарисовать круг: один штрих по часовой стрелке или один штрих по часовой стрелке.

Набор данных Google содержит 119 000 уникальных кругов, нарисованных людьми из 148 стран, и включает координаты пути, пройденного пальцем (или мышью) каждого игрока. Применяя простую геометрию к данным из 66 стран, представивших более 100 кругов, мы определили направления рисования кругов, предпочитаемые разными странами.

Американцы рисуют круги против часовой стрелки.Из почти 50 000 кругов, нарисованных в США, 86% нарисованы таким образом. С другой стороны, в Японии люди рисуют круги в противоположном направлении . Из 800 кругов, нарисованных в Японии, 80% повернуты по часовой стрелке. Вот случайная выборка из 100 кругов, нарисованных людьми в каждой стране:

кругов в Великобритании, Чехии, Австралии и Финляндии нарисованы в том же направлении и с той же последовательностью, что и круги в Америке. Некоторые страны даже более регулярны — около 90% французских, немецких и филиппинских рисовальщиков представили круги, нарисованные против часовой стрелки.Во Вьетнаме так было разыграно 95%.

Похоже, что большая часть мира рисует круги против часовой стрелки, за двумя исключениями из нашего набора данных: Тайвань и Япония.

Язык для рисования

Чем объясняется разница? Одна вещь, которая отличает страны, конечно же, — это их языки. Может ли способ письма — сверху вниз, слева направо или справа налево — объяснить, почему они по-разному рисуют абстрактные формы? Американцы, западные европейцы и латиноамериканцы, конечно, сильно различаются по своим разговорным языкам, но используют схожие сценарии. Между тем в сценариях из Азии и Ближнего Востока очень разные правила написания.

Вот как сложились несколько репрезентативных языковых групп:

Скрипты на основе китайского

Начнем с японского. В японском языке используются три типа письма: хирагана, катакана и кандзи. Кандзи основано на идеограмматической системе китайских иероглифов, в то время как хирагана и катакана являются фонетическими. Хирагана, наиболее близкая к английскому алфавиту, имеет наиболее круговые штрихи, и большинство ее изогнутых букв нарисовано с кривой, идущей по часовой стрелке :

Знак あ, буква типа «а», записывается:

Оба Японские и китайские шрифты имеют строгий порядок штрихов.В целом символы рисуются из верхнего левого угла в направлении нижнего правого. Если вы рисуете горизонтальную линию, а затем вертикальную, как в «7», правило состоит в том, чтобы рассматривать эти две линии как один штрих и завершать штрих без остановки, — говорит каллиграф и профессор математики Рутгерса И-Чжи Хуанг. Таким образом, рука может иметь более естественную тенденцию двигаться по часовой стрелке, как в «了», что означает завершение действия.

В письменных языках, основанных на китайском, эти правила врезаются ученикам в головы с того момента, как они берут в руки карандаш, что является веским аргументом в пользу возможности того, что человек на Тайване и в Японии рисуют круги на основе их общей системы письма. .Хотя данных из самого Китая нет, учитывая запрет Google в стране, есть некоторые предыдущие исследования, подтверждающие это. Исследование 1985 года, посвященное китайскому рисованию кругов, показало, что 72% из 151 участника рисовали круги по часовой стрелке, возможно, из-за движений по часовой стрелке в полукурсивной китайской каллиграфии, писали исследователи.

Сходство между китайскими языками еще сильнее, если мы посмотрим на еще одну могущественную форму детства — треугольник. Полные 97% тайваньских треугольников и 90% японских и корейских треугольников, нарисованных одним штрихом, были нарисованы против часовой стрелки. Для сравнения, треугольники в США, нарисованные одним штрихом, поворачивались против часовой стрелки чуть больше чем в половине случаев.

Порядок штрихов в китайских системах требует, чтобы диагонали, как и у треугольника, рисовались справа налево, а затем слева направо. Это очевидно из общего символа 人, означающего «человек».

Написание справа налево

Есть еще один крупный кластер стран, который может помочь нам понять различия в рисовании кругов. Объединенные Арабские Эмираты, Кувейт, Алжир, Иордания, Саудовская Аравия, Израиль, Ирак и Египет теснятся на нашем участке внизу, аккуратно падая бок о бок (с Таиландом и Кореей между ними).

Арабский язык содержит множество кривых, и наряду с ивритом читается и пишется справа налево. В арабском языке изгибы букв имеют тенденцию к вращению по часовой стрелке, следуя направлению руки, и помогают соединить каждую букву с другой. Вот буквы «b» и «n»:

Скрипты с кругами

Если мы более внимательно посмотрим на рисование кругов в остальном мире, мы также сможем определить другие шаблоны. Например, корейская система письма хангыль полна кругов.Из 1500 кругов, собранных там, 72% нарисованы против часовой стрелки. Можно ожидать, что Южная Корея станет ближе к Тайваню и Японии. Но, как правило, круги в хангыле идут против часовой стрелки и , что противоположно направлению кривых в Китае или Японии. Вероятно, в результате Южная Корея стала ближе к остальному миру в этом важном вопросе.

Или возьмем Таиланд, где 64% пошли против часовой стрелки и чей сценарий состоит из кругов. Из 42 согласных почти все начинаются с «головы», крошечной петли.Головки могут вращаться по часовой стрелке или против часовой стрелки, но по часовой стрелке их примерно вдвое больше. Вот буква, обозначающая звук «м»:

(А как насчет бирманского или грузинского, двух других алфавитов, набитых кругами, можно сказать? Всего лишь 22% кругов против часовой стрелки делает Бирму похожей на Японию и Тайвань. Очень заманчиво посмотреть сюда, чтобы поддержать нашу теорию, но размер выборки из Бирмы составляет всего девять кругов. Точно так же, Грузия сообщила только о 72 кругах, поэтому мы должны воздержаться.)

Большинство против часовой стрелки

Остальные 50 стран с нечетным числом обычно рисуют свои круги против часовой стрелки. Почти все они используют латинский алфавит, который проходит слева направо и не является особенно круглым. В английском тоже есть порядок штрихов, хотя он гораздо менее жесткий: возможно, он пишет против часовой стрелки «c» и «g» снова и снова, когда дети рисуют круги таким образом.

Конечно, хотя есть много свидетельств того, что письменные языки могут влиять на то, как люди рисуют формы, эта теория не учитывает все.Вьетнам использует латинский алфавит, как и США, и нарисовал 95% кругов против часовой стрелки, в то время как Гонконг, использующий китайское письмо, нарисовал здоровенные 82% кругов против часовой стрелки.

Другое возможное объяснение заключается в доминировании рук. Возможно, дело в том, что правши обычно склонны вращаться против часовой стрелки, если их системы письма не учат их обратному. Данные из Quick, Draw! не показывает, были ли пользователи правыми или левшами, что может сильно повлиять на направление, в котором они двигались.Тем не менее, доминирование рук не сильно различается от страны к стране и, вероятно, не объясняет большого неравенства между Тайванем и Японией и остальным миром.

А что вообще нормально?

В рамках когда-то распространенного психологического упражнения для детей под названием «тест крутящего момента», разработанного в 1970-х годах в США, детям давали листок бумаги со следующим текстом:

 X X X 

Чтобы помочь исследователям выяснить, есть ли у ребенка был правшой или левшой, ребенку предлагалось нарисовать круги вокруг каждого X, а затем снова другой рукой.Если она нарисовала все круги против часовой стрелки (что считается доказательством правши), у нее, как говорят, «нет крутящего момента». Если она нарисовала хотя бы один круг по часовой стрелке (связанный с леворукостью), у нее «был крутящий момент».

В статье 1977 года Теодор Блау, тогдашний президент Американской психологической ассоциации и создатель теста крутящего момента, утверждал, что рисование кругов по часовой стрелке было признаком обучения и отклонения в поведении. Он предупредил, что дети, которые рисуют с крутящим моментом, могут быть подвержены риску шизофрении.

Позже психологи опровергли это, и некоторые из них специально сосредоточились на влиянии культуры и образования на привычки детей к рисованию фигур. В одном межкультурном исследовании 1997 года изучались американские студенты в США, японские студенты в Японии и японские студенты, живущие в США, в разном возрасте: около половины из 62 японских первоклассников, участвовавших в исследовании, рисовали по часовой стрелке, треть рисовали против часовой стрелки и пятая смешала и то, и другое. Но почти все шестиклассников рисовали свои круги по часовой стрелке, что подсказало исследователям, что по мере того, как эти дети больше знакомились с письмом, их направление рисования становилось более явным.Напротив, 64% американских детей рисовали против часовой стрелки, и этот процент лишь незначительно изменился к шестому классу.

Но это не только Япония. Межкультурное исследование 1973 года изучало, как дети из США и Израиля копировали фигуры в разном возрасте, и обнаружило, что американские дети в подавляющем большинстве рисуют круги против часовой стрелки.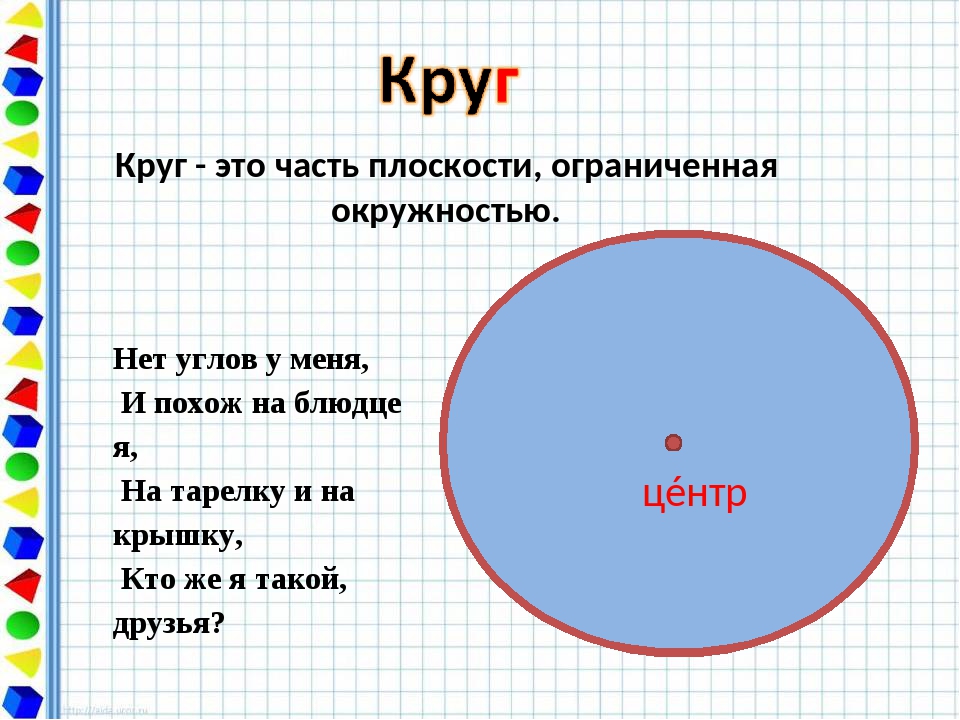 Обратное было верно в Израиле, где ближайшая к кругу буква нарисована по часовой стрелке, отметили исследователи. Со временем американцы стали более последовательными в своем направлении рисования: 100% взрослых участников рисовали круги против часовой стрелки.В Израиле 70% участников разного возраста рисовали круги в другую сторону.

Вместе эти исследования показывают не только то, что культура и почерк формируют то, как люди рисуют абстрактные формы; они также предполагают, что наши тенденции со временем усиливаются. Чем больше мы пишем, тем больше укореняются наши привычки.

Теперь, когда 90 000 кругов собраны со всего мира для той же цели, у нас есть гораздо больший и более последовательный набор данных, который может подтвердить то, что каждое из этих исследований показало в небольшом масштабе.

Правила, которые формируют привычку

Если бы английский был вашим первым языком, вы могли бы забыть свои ранние школьные годы, опасливо сжимая карандаш и неловко формируя огромные прописные и строчные буквы в рекомендуемом порядке.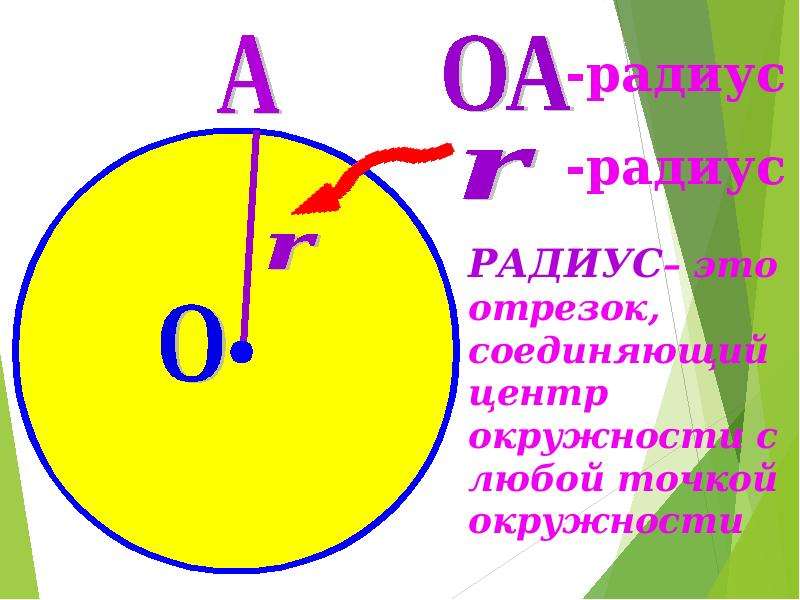 В некоторых языках эти правила не остались в прошлом, а имеют первостепенное значение для письма.

Например, в японском и китайском языках порядок штрихов является важным компонентом разборчивого письма и может даже указывать на уровень образования.

Современная китайская система приказов штрихов произошла от клерикальной письменности — системы, преобладавшей во времена династии Хань.Написание просто заняло слишком много времени, поэтому, когда люди пытались двигаться быстрее, система превратилась в канцелярский рабочий сценарий, полукурсивный стиль и, в конечном итоге, превратилась в современный сценарий. По словам Хуанга, каллиграфа, использование мягких кистей для письма могло повлиять на некоторые современные правила мазков.

Японский использует тот же порядок штрихов, что и китайский. В 1958 году министерство образования Японии установило правила страны в отношении порядка штрихов, чтобы создать последовательную систему, позволяющую избежать путаницы.(Сегодня правила смягчены. )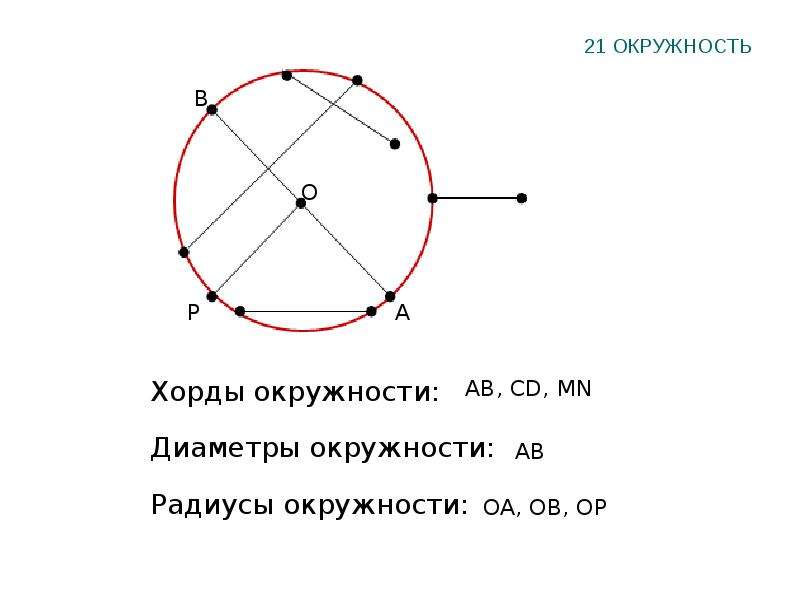

«То, как я двигаю кистью или ручкой, мне кажется, очень эффективно и приятно», — говорит Томойо Камимура, директор языкового центра Японского общества. «Некоторые взрослые пишут в совершенно неправильном порядке, но мы это презираем», — говорит Камимура. «Мы считаем этих людей необразованными».

Сегодня американские дети все чаще обучаются методу печати и курсива, который называется «Почерк без слез». Он продвигает «волшебную c» (pdf), кривую против часовой стрелки, используемую, среди прочего, в буквах c, g, q, o.Поэтому американская школа может поощрять кружки против часовой стрелки с детьми младшего возраста, чтобы помочь сформировать базовые моторные навыки, которые им понадобятся позже, чтобы написать свои первые буквы.

Очевидно, что простой процесс рисования форм — это гораздо больше, чем любой из нас может вообразить. Оказалось, что жест, который американские психологи когда-то считали естественным и правильным, может показаться носителю японского языка странным и даже грубым.

Форма того, кто мы есть

Есть бесчисленное множество способов, которыми мы тонко, бессознательно несем нашу культуру с собой: как мы рисуем, считаем на пальцах и имитируем звуки реального мира, и это лишь некоторые из них.Это радость в основе этого огромного набора данных. Чтобы проверить наши теории, мы обратились к коллегам, друзьям и родственникам, которые пишут на японском, арабском, иврите, китайском, тайском и вьетнамском языках, и, чувствуя себя немного глупо, попросили их нарисовать круги. Они с радостью прыгнули внутрь, гадая, что сделают их пальцы, и желая почувствовать себя частью чего-то большего.

Но мы еще многого не знаем. Интерес к рисованию фигур в психологии вышел из моды. За одним исключением, все исследования, которые мы обнаружили в области фигурного рисования и испытания крутящего момента, проводились до 1997 года.Люди во всем мире все чаще общаются, набирая и нажимая, но хотя искусство письма может когда-нибудь полностью исчезнуть, возможно, мы уже формируем целый новый урожай культурных различий, связанных с использованием клавиатуры.

Овал против круга — в чем разница?

Английский существительное ( en имя существительное ) Форма, похожая на яйцо или эллипс. Спортивная арена и т.п. такой формы. Примечания по использованию * Примечание: эллипс — это точная математическая форма, а овал — нет. Прилагательное ( прилагательное ) Имеет форму овала. Имеет отношение к яйцеклетке. овал концепции Производные термины * овальный * овальный * овально Примечания по использованию Прилагательные «овальный», «яйцевидный» и «яйцевидный» происходят от корней, означающих «яйцевидный». Обычно они обозначают синонимы. Значение того, что один конец больше другого (что часто верно в отношении яиц), может подразумеваться, а может и не подразумеваться. Из трех овал , скорее всего, ассоциируется с симметричным эллипсом.

Существительное ( en имя существительное ) ( lb ) Двумерная геометрическая фигура, линия, состоящая из набора всех тех точек на плоскости, которые одинаково удалены от другой точки. : набор всех точек ( x », » y ») таких, что (x-1) 2 + y 2 = r 2 представляет собой окружность с радиусом » r . около Двумерная геометрическая фигура, диск, состоящий из множества всех этих точек плоскости, находящихся на расстоянии, меньшем или равном фиксированному расстоянию от другой точки. Любой тонкий трехмерный эквивалент геометрической фигуры. : Кривая, которая более или менее образует часть или всю окружность. : Орбита. Определенная группа лиц. : * (1800–1859) *: По мере того, как его имя постепенно становилось известным, круг его знакомства расширился. * *: В этот субботний вечер в половине десятого в гостиной гостиницы «Приветствие» в Хай-Холборне находилось большинство обычных посетителей.Раньше каждая известная таверна держала такую ​​комнату для своего избранного circle , клуба или общества завсегдатаев, которые собирались каждый вечер за трубкой и веселым бокалом. * *: «Я не имею в виду всех ваших друзей — только небольшую часть, — которые, однако, соединяют ваш круг с этой смертоносной, праздной, безмозглой компанией — наглыми болтунами в опере, наеданными вдовствующими жителями, украшенных драгоценностями животных, чей моральный кодекс — кодекс скотного двора! » * 1922 , ( Марджери Уильямс ), ( Бархатный кролик ) *: Кролик не мог претендовать на то, чтобы быть моделью чего-либо, потому что он не знал, что существуют настоящие кролики; он думал, что все они были набиты опилками, как и он сам, и он понимал, что опилки сильно устарели и никогда не должны упоминаться в современных кругах . ( фунта ) Линия, состоящая из двух полукругов радиусом 30 ярдов с центром на калитках, соединенных прямыми линиями, параллельными полю, используемая для обеспечения соблюдения ограничений поля в однодневном матче. ( lb ) Ритуальный круг, который произносится трижды deosil и трижды замыкается widdershins либо в воздухе с помощью жезла, либо буквально с камнями или другими предметами, используемыми для поклонения. ( lb ) Круговая или кольцевая развязка. * 2011 , Чарльз Э.Уэбб, Падение и свобода , стр.120: *: Он прибыл на набережную и проехал по кругу , где раньше были парк развлечений и пляж, когда он был ребенком ( фунтов ) Компас; схема; корпус. * ( Уильям Шекспир ) (c.1564–1616) *: в круге этого леса ( фунтов ) Инструмент наблюдения, градуированная конечность которого состоит из полного круга. Когда он прикреплен к стене в обсерватории, он называется настенным кругом »; при установке телескопа на оси и по оси Y в плоскости меридиана, «меридиана» или «транзитного круга»; когда задействован принцип отражения, как и в секстанте, «отражающий круг»; и при непрерывном повторении угла несколько раз вдоль градуированной конечности — повторяющийся круг . Серия заканчивается там, где начинается, и повторяется. * ( Джон Драйден ) (1631-1700) *: Таким образом, в круге проходит крестьянинская боль. ( фунт ) Форма аргументации, в которой два или более недоказанных утверждения используются для доказательства друг друга; безрезультатное рассуждение. * ( Джозеф Глэнвилл ) (1636-1680) *: Эти тяжелые тела опускаются под действием силы тяжести; и, опять же, гравитация — это качество, с помощью которого опускается тяжелое тело, это неуместный круг и ничему не учит. Косвенная форма слова; болтовня. * (1579-1625) *: Он дал ложь, / В круге , или наискось, или полукругом. Территориальное деление или район. : Синонимы * ( двухмерный контур геометрической фигуры ) катушка ( не используется в математике ), кольцо ( не используется в математике ), петля ( не используется в математике ) * ( двумерная сплошная геометрическая фигура ) диск / диск ( в математическом и общем использовании, ), круглый ( не в математическом использовании; только для Великобритании и Содружества ) * ( кривая ) дуга, кривая * ( орбита ) орбита * ( определенная группа лиц ) группа, банда, группа Производные условия * Полярный круг Связанные термины * круговой * округлость * распространять * цирк Глагол ( круг ) Для передвижения по изогнутой дороге. * Александр Поуп Другие планеты вращаются вокруг других солнц. Для окружения. * Амортизатор Их головы обведены в коротком тюрбане. * Колридж Так он лежит, обведено злом. Чтобы разместить или отметить круг. Circle вакансии, на которые вы хотите подать заявку. Путешествовать по кругу. Стервятники кружили над головой . Производные условия * обвести сток

Что такое круг и его свойства? (определение, формулы, примеры)

Круг — это замкнутая форма, образованная путем отслеживания точки, которая движется в плоскости таким образом, чтобы расстояние от нее до данной точки было постоянным. Слово круг происходит от греческого слова kirkos, что означает обруч или кольцо. В этой статье мы рассмотрим важные термины, связанные с кругами, их свойствами и различными формулами кругов.

Ниже приводится краткое описание тем, которые мы рассмотрим в этой статье:

Определение круга

Когда набор всех точек , которые находятся на фиксированном расстоянии от фиксированной точки , соединяются, полученная геометрическая фигура называется окружностью.

Давайте теперь немного узнаем о терминологии, используемой в кругах.

Термины, связанные с кругами

Центр

Неподвижная точка в окружности называется центром.

• Итак, набор точек находится на фиксированном расстоянии от центра окружности.

Радиус

Радиус — это фиксированное расстояние между центром и набором точек. Обозначается цифрой «R» .

Диаметр

Диаметр — это отрезок прямой, имеющий граничные точки окружностей в качестве конечных точек и проходящий через центр.

• Итак, логически диаметр можно разбить на две части:
  • Одна часть от одной граничной точки круга до центра
  • И, другая часть от центра до другой граничной точки.
    • Следовательно, Диаметр = Двойная длина радиуса или «D = 2R»

Окружность

Это мера внешней границы круга.

Итак, длина круга или периметр круга называется окружностью.

Дуга окружности

Дуга окружности — это часть окружности.

Из любых двух точек, лежащих на границе круга, можно создать две дуги: Малую и Большую дугу.

• Малая дуга: Более короткая дуга, образованная двумя точками.
• Major Arc: Более длинная дуга, образованная двумя точками.

Сектор круга:

Сектор образуется путем соединения концов дуги с центром.

• При соединении конечных точек с центром будут получены два сектора: Minor и Major.
  • По умолчанию мы учитываем только второстепенный сектор, если не указано иное.

полукруг

Полукруг — это половина круга или,

• Полукруг получается, когда круг делится на две равные части.

Теперь, когда мы знаем всю терминологию, относящуюся к кругам, давайте узнаем о свойствах круга.

Геометрия — важная тема для асов, если вы планируете набрать 700+ на GMAT. Позвольте нам помочь вам достичь совершенства в GMAT Geometry. Начните с подписки на бесплатную пробную версию и учитесь у лучших в отрасли. В конце концов, о нас больше всего отзываются на gmatclub.

Кэрри Лоу, Гильермо, Сириш и Рагхав — это лишь некоторые из студентов, которые с помощью электронного GMAT набрали Q50 + балл в разделе GMAT Quant.

Важные свойства круга — линии

Свойства, относящиеся к линиям в окружности

аккорд

Хорда — это отрезок прямой, концы которого лежат на границе круга.

Свойства хорды

1. Перпендикуляр, опущенный из центра, делит пояс на две равные части.

Касательная

Касательная — это линия, которая касается окружности в любой точке.

Свойства касательной

1. Радиус всегда перпендикулярен касательной в точке, где он касается окружности.

Важные свойства круга, связанные с углами

Свойства, относящиеся к углам в окружности

Угол с надписью

Вписанный угол — это угол между двумя хордами, когда они встречаются на границе круга.

Свойства вписанных углов

1. Углы, образованные одной и той же дугой на окружности окружности, всегда равны.

2. Угол в полукруге всегда равен 90 °.

Центральный угол

Центральный угол — это угол, образующийся, когда две линейные сегменты встречаются таким образом, что одна из конечных точек обоих линейных сегментов находится в центре, а другая — на границе круга.

Свойство центральных углов

• Угол, образованный дугой в центре, в два раза больше, чем вписанный угол , образованный той же дугой.

Важные формулы круга: площадь и периметр

Ниже приведены некоторые математические формулы, которые помогут вам вычислить площадь и периметр / длину окружности.

Периметр:

• Периметр или окружность круга = 2 × π × R.
• Длина дуги = (Центральный угол дуги / 360 °) × 2 × π × R.

Площадь:

• Площадь круга = π × R²
• Площадь сектора = (Центральный угол, образованный сектором / 360 °) × π × R².

Обзор всех свойств круга

Вот обобщенный список всех свойств, которые мы изучили в статье до этого момента.

Важные свойства
Линии по окружности	аккорд	Перпендикуляр, опущенный из центра, делит пояс на две равные части.
	Касательная	Радиус всегда перпендикулярен касательной в точке, где он касается окружности.
Углы по окружности	Угол вписанный	1. Углы, образованные одной и той же дугой на окружности круга, всегда равны. 2. Угол в полукруге всегда равен 90.
	Центральный угол	Угол, образованный дугой в центре, в два раза больше вписанного угла, образованного той же дугой.
Важные формулы	Окружность круга	2 × π × R.
	Длина дуги	(Центральный угол, образованный дугой / 360 °) × 2 × π × R
	Площадь круга	π × R²
	Площадь сектора	(Центральный угол, образованный дугой / 360 °) × π × R²

Применение свойств в вопросах

Вопрос 1

Длина двух сторон прямоугольного треугольника, кроме гипотенузы, составляет 6 см и 8 см. Если этот прямоугольный треугольник вписан в круг, то какова площадь круга?

1. 5 π
2. 10 π
3. 15 π
4. 20 π
5. 25 π

Решение

Шаг 1: Дано

• Длина двух сторон прямоугольного треугольника, кроме гипотенузы, составляет 6 см и 8 см.
• Этот треугольник вписан в круг.

Шаг 2: найти

Шаг 3: подход и разработка

Приведем схематическое изображение.

Применяя свойство, что угол в полукруге равен 90º, мы можем сказать, что AB — это диаметр окружности.

• И, как только мы найдем длину диаметра, мы сможем найти радиус, а затем мы также сможем найти площадь круга.

Применение теоремы Пифагора в △ ABC,

• AB² = AC² + BC²
  • AB² = 6² + 8² = 36 +64 = 100
  • AB = 10 см

Поскольку AB — диаметр, AB = 2R = 10

Площадь круга = π × R² = π × 5² = 25 π.

Следовательно, правильный ответ — вариант E.

Вопрос 2

На приведенной выше диаграмме О — центр круга. Если OB = 5 см и ∠ABC = 30 ⁰ , то какова длина дуги AC?

1. 5π / 6
2. 5π / 3
3. 5π / 2
4. 5π
5. 10π

Решение

Шаг 1: Дано

Шаг 2: найти

Шаг 3: подход и разработка

• Длина дуги = (Центральный угол дуги / 360 °) × 2 × π × R.

Чтобы найти длину дуги, нам нужно значение двух переменных, центрального угла, образованного дугой, и радиуса.

• Нам уже дан радиус как OB = 5см
• Нам нужно найти ∠AOC

При визуализации диаграммы угол, вписанный дугой AC, равен ∠ABC, а центральный угол дугой AC равен AOC.

• Следовательно, мы можем применить свойство, согласно которому угол, образованный дугой в центре, вдвое превышает вписанный угол, образованный той же дугой.
• Таким образом, AOC = 2 × ∠ABC = 2 × 30 ° = 60 °

Теперь мы знаем и центральный угол, образованный дугой.

• Следовательно, длина дуги AC = (центральный угол дуги / 360 °) × 2 × π × R.
  • = (60 ° / 360 °) × 2 × π × 5.
  • = (1/6) × 2 × π × 5.
  • = (5π / 3) см

Таким образом, правильный ответ — вариант Б.

Если вам понравилась эта статья, вот еще несколько статей, связанных с геометрией:

Знать разницу между кругом и сферой

Давайте нарисуем круг и сферу на листе бумаги.Что мы находим? Обе формы одинаковы из-за их круглого формата. Таким образом, многие из нас не понимают их. Тогда в чем разница между кругом и сферой? Основное различие между сферой и кругом состоит в том, что круг является 2-мерным, а сфера — 3-мерным. Исходя из основного различия, мы можем получить еще одно отличие: можно вычислить площадь круга, но для сферы мы должны найти ее объем.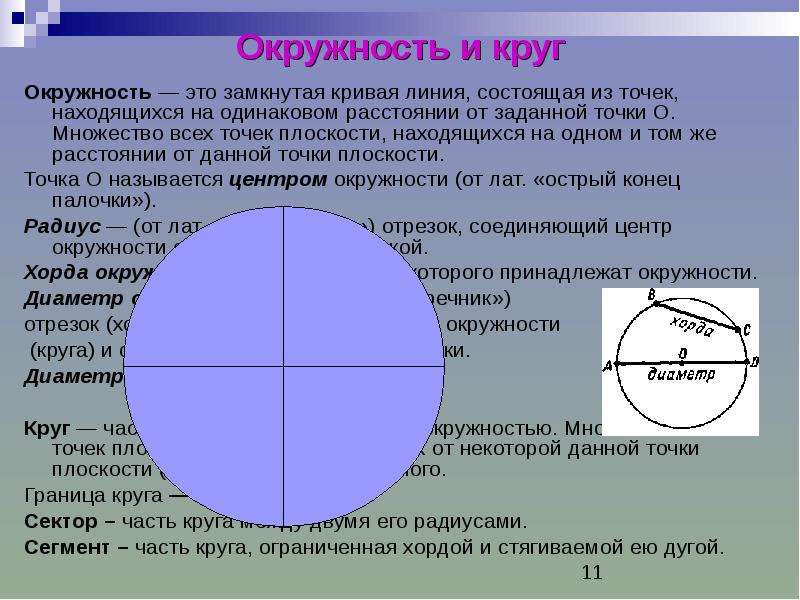

Окружность

Окружность считается разновидностью линии.Круговая линия состоит из набора точек со свойством, что все точки, присутствующие в этой линии, находятся на одинаковом расстоянии от фиксированной точки на плоскости. Он состоит из замкнутого контура, который разделяет плоскость на внутреннюю и внешнюю секции. Круги имеют различные свойства: центр, окружность, касательная и хорда. Радиус соединен с его центром линиями, а «r» обозначает длину радиуса этой конкретной круговой линии. Эллипс — это частный случай круга с набором точек с постоянной суммой расстояний между двумя фиксированными точками на плоскости.Эти две фиксированные точки называются фокусом и центром, которые в случае круга одинаковы. Во внутреннем круге можно найти три набора точек, которые не расположены в одном направлении, которое определяет края треугольника. Некоторые примеры круга: диск, часы и т. Д.

Сфера

Сфера — это своего рода линия, которая содержит различные свойства, такие как площадь поверхности, объем и радиус. Это асимметричная поверхность только с одним внешним видом. Радиус сферы связывает среднюю точку с самой внешней частью.Диаметр шара начинается от края до края, проходя через его центр. Сфера состоит из маленьких кружков и нескольких полушарий. Круг, образованный пересечением сферы и плоскости, проходящей через центр пространства, известен как самый большой круг сферы. Напротив, другие круги, образованные пересечением плоскости и копья, известны как маленькие круги этой сферы. Греческий математик Архимед сформулировал формулу шара. Примеры некоторых сфер: мрамор, футбол, капли воды и т. Д.

Есть два типа сфер

1. Твердая сфера — Твердый объект, имеющий форму сферы, известен как сплошная сфера. Твердая сфера заполнена тем же материалом, из которого она сделана.

2. Полая сфера — когда твердая сфера вырезается из середины и вынимается из нее большое твердое тело, оставляя позади сферическую оболочку, называется полой сферой.

[Изображение будет загружено в ближайшее время]

Разница между сферой и кругом

Sl.No	Properties	Circle	Sphere
1	Dimension	A circle is a 2D10 shape object 901 901 901 901 901
2	Формула площади	Площадь круга равна 4πr2	Площадь поверхности сферы по формуле 4πr2
3 9107 901 Объем Круг не имеет объема	Объем сферы составляет 4/3 πr³
4	Определение	Все точки круга находятся на одинаковом расстоянии из его центра в плоскости.	Все точки сферы равноудалены по любой оси от центра.
5	Определение	В случае круга определяется его площадь	В случае шара определяются его площадь поверхности и объем.
6	Формула диаметра	Диаметр круга 2r	Диаметр сферы 2r
0 9109 Окружность круга равна 2πr	Сфера не имеет окружности
8	Уравнение	Уравнение окружности (x — a) 2 + (y — a) 2 + (y — a) ) 2 = r2	Уравнение окружности (x — a) 2 + (y — b) 2 + (z — c) 2 = r2
9	Учет	Круг считается фигурой	Сфера рассматривается как объект

Площадь круга — формула, вывод, определение, примеры

Площадь круга — это пространство, занимаемое кругом в двухмерной плоскости. В качестве альтернативы пространство, занимаемое в пределах границы / окружности круга, называется площадью круга. Формула для вычисления площади круга: A = πr ² , где r — радиус круга. Единицей площади является квадратная единица, например, м ² , см ² , в ² и т. Д. Площадь круга = πr ² или πd ² /4 в квадратных единицах, где (Pi) π = 22/7 или 3,14. Пи (π) — это отношение длины окружности к диаметру любой окружности.Это особая математическая константа.

Формула площади круга полезна для измерения области, занимаемой круговым полем или графиком. Предположим, у вас есть круглый стол, тогда формула площади поможет нам узнать, сколько ткани нужно, чтобы покрыть его полностью. Формула площади также поможет нам узнать длину границы, то есть длину окружности круга. Есть ли у круга объем? Нет, у круга нет объема. Круг — это двухмерная форма, у нее нет объема.У круга есть только площадь и периметр / окружность. Давайте подробно узнаем о площади круга, площади поверхности и его окружности на примерах.

Круг и части круга

Круг — это набор точек, находящихся на фиксированном расстоянии от центра круга. Круг — это замкнутая геометрическая фигура. В повседневной жизни мы видим круги, такие как колесо, пицца, круглая площадка и т. Д. Мера пространства или области, заключенная внутри круга, известна как площадь круга.

Радиус : Расстояние от центра до точки на границе называется радиусом окружности. Он обозначается буквой «r» или «R». Радиус играет важную роль в формуле площади и окружности круга, которую мы узнаем позже.

Диаметр : Линия, которая проходит через центр и ее концы лежат на окружности, называется диаметром окружности. Он обозначается буквой «d» или «D».

Формула диаметра: Формула диаметра окружности равна удвоенному радиусу. Диаметр = 2 × Радиус

d = 2r или D = 2R

Если диаметр круга известен, его радиус можно рассчитать как:

r = d / 2 или R = D / 2

Окружность: Окружность круга равна длине его границы. Это означает, что периметр круга равен его длине окружности. Длина веревки, которая идеально обвивает границу круга, будет равна его длине.Приведенный ниже рисунок помогает вам представить то же самое. Окружность можно измерить по следующей формуле:

, где r — радиус круга, а π — математическая константа, значение которой приблизительно равно 3,14 или 22/7. Окружность круга может использоваться, чтобы найти площадь этого круга.

Для окружности радиуса «r» и окружности «C»:

• π = Окружность / Диаметр
• π = C / 2r = C / d
• С = 2πr

Давайте разберемся в различных частях круга на следующем примере из реальной жизни.

Рассмотрим парк круглой формы, как показано на рисунке ниже. Мы можем идентифицировать различные части круга с помощью рисунка и таблицы, приведенных ниже.

По кругу	В нашем парке	Обозначается буквой
Центр	Фонтан	F
Окружность	Граница
Хорда	Вход в игровую зону	PQ
Радиус	Расстояние от фонтана до Въездных ворот	FA
Диаметр	Прямая линия Расстояние между входными и выходными воротами через фонтан	AFB
Малый сегмент	Меньшая часть парка, обозначенная как Игровая зона
Основной сегмент	Большая территория парка, кроме игровой
Внутренняя часть круга	Зеленая зона всего парка
Внешняя часть круга	Территория за границей парка
Дуга	Любая изогнутая деталь по окружности.

Какова площадь круга?

Площадь круга — это пространство, заключенное в пределах круга. Область внутри круга — это область, занятая кругом. Его также можно назвать общим количеством квадратных единиц внутри этого круга.

Формулы площади круга

Площадь круга может быть вычислена промежуточными шагами по диаметру и длине окружности круга.По диаметру и длине окружности мы можем найти радиус, а затем площадь круга. Но эти формулы предоставляют самый короткий способ найти площадь круга. Предположим, что круг имеет радиус ‘r’, тогда площадь круга = πr ² или πd ² /4 в квадратных единицах, где π = 22/7 или 3,14, а d — диаметр.

Площадь круга, A = πr ² квадратных единиц

Окружность / Периметр = 2πr единиц

Площадь круга можно рассчитать по формулам:

• Площадь = π × r ² , где r — радиус.
• Площадь = (π / 4) × d ² , где d — диаметр.
• Площадь = C ² / 4π, где C — длина окружности.

Примеры использования формулы площади круга

Давайте рассмотрим следующие иллюстрации, основанные на формуле площади круга.

Пример1: Если длина радиуса окружности равна 4 единицам. Вычислите его площадь.

Раствор:
Радиус (r) = 4 единицы (дан)
Используя формулу площади круга,
Площадь круга = πr ²
Ставим значения,
А = π4 ²
А = π × 16
A = 16π ≈ 50.27

Ответ: Площадь круга 50,27 квадратов.

Пример 2: Длина наибольшей хорды круга составляет 12 единиц. Найдите площадь круга.

Решение:
Диаметр (d) = 12 шт. (Дано)
Используя формулу площади круга,
Площадь круга = (π / 4) × d ²
Ставим значения,
А = (π / 4) × 12 ²
А = (π / 4) × 144
A = 36π ≈ 113. 1

Ответ: Площадь круга 113,1 кв.

Площадь круга с использованием диаметра

Формула площади круга через диаметр: Площадь круга = πd ² /4. Здесь d — диаметр круга. Диаметр круга в два раза больше радиуса круга. г = 2р. Обычно, исходя из диаметра, нам нужно сначала найти радиус круга, а затем найти площадь круга. С помощью этой формулы мы можем напрямую найти площадь круга из меры диаметра круга.2} {4 \ pi} \). Есть два простых шага, чтобы найти площадь круга по заданной длине окружности. Окружность круга сначала используется, чтобы найти радиус круга. Этот радиус также помогает найти площадь круга. Но в этих формулах мы сможем напрямую найти площадь круга по его длине.

Площадь круга — расчет

Площадь круга можно удобно рассчитать по радиусу, диаметру или длине окружности.Константа, используемая при вычислении площади круга, равна пи, и имеет дробное числовое значение 22/7 или десятичное значение 3,14. Любое из значений пи может использоваться в зависимости от требований и потребностей уравнений. В таблице ниже показан список формул, если мы знаем радиус, диаметр или длину окружности.

Площадь круга с известным радиусом.	πr 2
Площадь круга с известным диаметром.	πd 2 /4
Площадь круга с известной длиной окружности.	С 2 / 4π

Определение площади круга

Почему площадь круга равна πr ² ? Чтобы понять это, давайте сначала разберемся, как выводится формула площади круга.

Внимательно обратите внимание на приведенный выше рисунок. Если мы разделим круг на более мелкие части и расположим их систематически, он образует форму параллелограмма.Когда круг делится на еще более мелкие сектора, он постепенно приобретает форму прямоугольника. Чем больше в нем секций, тем больше он имеет форму прямоугольника, как показано выше.

Площадь прямоугольника = длина × ширина

Ширина прямоугольника = радиус круга (r)

Когда мы сравниваем длину прямоугольника и окружность круга, мы видим, что длина равна ½ длины окружности круга

Площадь круга = Площадь сформированного прямоугольника = ½ (2πr) × r

Следовательно, площадь круга равна πr ² , где r — радиус круга, а значение π равно 22/7 или 3.14.

Формула площади поверхности круга

Площадь поверхности круга такая же, как площадь круга. Фактически, когда мы говорим о площади круга, мы имеем в виду не что иное, как общую площадь его поверхности. Площадь поверхности — это площадь, занимаемая поверхностью трехмерной формы. Поверхность сферы будет иметь сферическую форму, но круг — это простая плоская 2-мерная форма.

Если дана длина радиуса или диаметра, или даже длина окружности круга, то мы можем узнать площадь поверхности. Он представлен в квадратных единицах. Формула площади поверхности круга = πr ² , где r — радиус круга, а значение π составляет приблизительно 3,14 или 22/7.

Пример из реального мира на площади круга

Рон и его друзья заказали пиццу в пятницу вечером. Каждый срез имел длину 15 см.

Вычислите площадь пиццы, которую заказал Рон. Вы можете предположить, что длина ломтика пиццы равна радиусу пиццы.

Решение:

Пицца имеет круглую форму. Таким образом, мы можем использовать формулу площади круга для вычисления площади пиццы.

Радиус 15 см

Формула площади круга = πr ² = 3,14 × 15 × 15 = 706,5

Площадь пиццы = 706,5 кв. См.

Часто задаваемые вопросы о площади круга

Как рассчитать площадь круга?

Площадь круга рассчитывается по следующим формулам:

• Площадь = π × r ² , где r — радиус.
• Площадь = (π / 4) × d ² , где d — диаметр.
• Площадь = C ² / 4π, где C — длина окружности.

Что такое формула площади круга?

Формула площади круга = π × r ² . Площадь круга равна π, умноженному на квадрат радиуса. Площадь круга с заданным радиусом r равна πr ² . Площадь круга с известным диаметром d равна πd ² /4. π примерно 3.14 или 22/7. Площадь (A) также может быть найдена по формулам A = (π / 4) × d ² , где d — радиус, а A = C ² / 4π, где C — заданная длина окружности.

Что такое периметр и площадь круга?

Длина окружности равна длине ее границы. Это означает, что периметр круга равен его длине окружности. Площадь круга равна πr ² , а периметр (длина окружности) равен 2πr, когда радиус равен ‘r’ единицам, π приблизительно 3.14 или 22/7. Окружность и длина радиуса круга являются важными параметрами для определения площади этого круга. Для круга радиуса «r» и окружности «C»:

• π = Окружность ÷ Диаметр
• π = C / 2r
• Следовательно, C = 2πr

Почему площадь круга по формуле равна πr

² ?

Круг можно разделить на множество небольших секторов, которые затем можно соответствующим образом переставить в параллелограмм.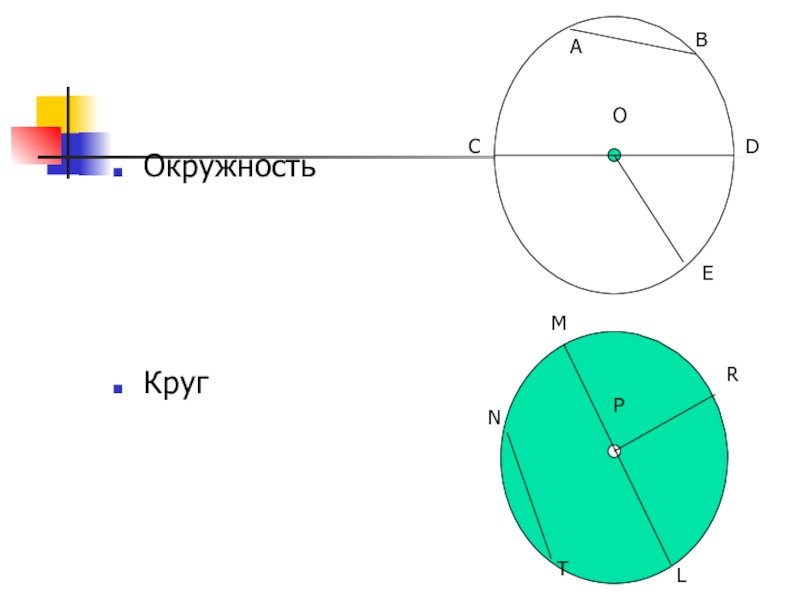 Когда круг делится на еще более мелкие сектора, он постепенно приобретает форму прямоугольника. Мы можем ясно видеть, что одна из сторон прямоугольника будет радиусом, а другая — половиной длины окружности, то есть π. Как мы знаем, площадь прямоугольника — это его длина, умноженная на ширину, которая равна π, умноженной на r. Следовательно, площадь круга равна πr ² .

Какова площадь формулы круга через π?

Значение пи (π) приблизительно равно 3.14. Пи — иррациональное число. Это означает, что его десятичная форма не заканчивается (например, 1/5 = 0,2) и не становится повторяющейся (например, 1/3 = 0,3333 …). Пи — 3,141592653589793238 … (всего с 18 знаками после запятой). Следовательно, формула площади круга в Пи задается как πr ² квадратных единиц.

Как найти окружность и площадь круга?

Площадь и окружность круга можно рассчитать по следующим формулам. Окружность = 2πr; Площадь = πr ² .Окружность круга может быть взята как π, умноженное на диаметр круга. А площадь круга в π раз больше квадрата радиуса круга.

Как рассчитать площадь круга с диаметром?

Диаметр круга в два раза больше радиуса круга. Следовательно, формула площади круга с использованием диаметра равна π / 4, умноженному на квадрат диаметра круга. Формула для вычисления площади круга с использованием диаметра круга π / 4 × диаметр ² .

Как найти площадь круга по окружности?

Площадь круга также можно найти, используя длину окружности круга. Радиус круга можно найти по длине окружности круга, и это значение можно использовать для определения площади круга. Предположим, что окружность круга равна «C». Имеем C = 2πr или r = C / 2π. Теперь применив это значение «C» в формуле площади, мы получим A = πr ² = π × (C / 2π) ² = C ² / 4π.

Какова площадь круга радиусом 3 м?

Площадь круга равна π, умноженному на квадрат радиуса. Площадь круга (A) при заданном радиусе r равна πr ² . π составляет примерно 3,14 или 22/7. Следовательно, площадь = 3,14 × 3 × 3 = 28,26 кв. М.

Окружность данного круга 16 см. Какая будет его площадь?

Окружность круга = 16 см

Мы знаем формулу длины окружности C = 2πr
Итак,
2πr = 16
или r = 16 / 2π = 8 / π
Подставляя значение r в формулу площади круга, получаем:
А = πr ²
A = π (8 / π) ² = 64 / π
На решении,
Площадь = 20.38 кв. См.

формул круга — что такое формулы круга? Примеры

Прежде чем выучить все формулы круга, давайте вспомним, что такое круг. Круг определяется как набор точек, расположенных на равном расстоянии от фиксированной точки на плоскости. Неподвижная точка называется центром круга. Радиус — это расстояние от центра круга до границы круга. Давайте разберемся во всех формулах круга на решенных примерах.

Что такое круглые формулы?

Такие параметры, как площадь, длина окружности, радиус круга, могут быть вычислены с использованием всех формул круга. Различные формулы круга для вычисления различных параметров данного круга могут быть выражены как

• Диаметр окружности D = 2 × r
• Окружность круга C = 2 × π × r
• Площадь круга A = π × r ²

Где,

• r = радиус окружности
• d = диаметр круга
• c = окружность круга

Список всех формул круга

Ниже приведен список всех формул окружности для ваших простых вычислений для окружности с радиусом ‘r’.

Параметры	Формулы круга
Формула диаметра круга	D = 2 × r
Формула окружности круга	С = 2 × π ×
Формула площади круга	A = π × r 2

Хотите находить сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. С Cuemath находите решения простым и легким способом.

Забронируйте бесплатную пробную версию Класс

Примеры круглых формул

Решим несколько интересных задач, используя формулу периметра круга.

Пример 1: Найдите площадь кругового парка, радиус которого равен 200 м.

Решение:

Найти: Площадь парка.
Дано:
Радиус парка = 200 м
Используя одну из формул для всех кругов (формула площади круга),
Площадь круга = π × r ²
= Π × 200 ²
= Π × 40000

Ответ: Площадь кругового парка 40000π м ² .

Пример 2: Используя формулу периметра окружности, найдите радиус окружности, имеющей длину окружности 100 дюймов.
Решение:

Найти: Радиус окружности

Дано: Окружность = 100 из

Используя формулу периметра круга,
Периметр круга или окружности = 2 π r

2 π г = 100

2 × 22/7 × r = 100

г = 100 × 7/44

г = 15. 909 дюймов

Ответ: Радиус окружности = 15,909 дюйма

Пример 3: Радиус окружности 8 дюймов. Используя формулу круга, вычислите длину окружности круга.

Решение:

Для штрафа: окружность
Дано: r = 8 дюймов
Формула периметра круга = 2 π r
C = 2 × (22/7) × (8)
Ответ: Окружность круга равна 50.28 дюймов.

Часто задаваемые вопросы по формуле круга

Что такое периметр по формуле полукруга?

Полукруг — это половина полного круга. Следовательно, если периметр формулы полукруга равен 1/2 (2π r) = π r единиц.

Что такое формула диаметра круга?

Формула диаметра круга определяется как двойной радиус.
Следовательно, D = 2r, где r — радиус окружности.

Что такое формула периметра круга?

Формула периметра круга задается как 2 π r, где ‘r’ — радиус, а π постоянна со значением (3.14 или 22/7).

Как рассчитать радиус по формуле круга?

Длина окружности в формуле круга равна 2 π r.