Найти интеграл онлайн калькулятор: Калькулятор Интегралов • По шагам! — ЭкоДом: Дом своими руками
2
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7. 3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.
 5)==4.0)
5)==4.0) - ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3. 14159..
- e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
∫∫ Двойной интеграл — Калькулятор Онлайн
Введите подинтегральную функцию,
для которой надо найти двойной интеграл
Найдём подробное решение для двойного интеграла от функции f(x, y). 2
2
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7. 3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.
 5)==4.0)
5)==4.0) - ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3. 14159..
- e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Неопределенный интеграл.
 Онлайн калькулятор с примерами
Онлайн калькулятор с примерамиНеопределенный интеграл онлайн
В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно!
Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен?
Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех!
Вводная к интегралам
В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел. Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.
Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.
В этом заключается один из физических смыслов интеграла.
Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела.
Решение интегралов
Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов.
Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов.
Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.
Калькулятор решения интегралов
Теперь самое интересное. Еще каких-то 15 лет назад школьник и помыслить не мог, что под рукой будут такие калькуляторы интегралов, как, например, наш. Это безусловно облегчает процесс обучения. Можно проверять свои решения, находить допущенные ошибки и лучше усваивать образовательный курс.
И тут в который раз повторяем, калькулятор решения интегралов – это только ваш безотказный помощник, к которому можете обратиться в любое время. Но никак не подмена вашей головы. Старайтесь самостоятельно решать задачи, только так можно развивать мышление, а компьютер будет в помощь.
Решение интегралов онлайн калькулятор
Интегрирование или решение интегралов — операция, обратная дифференцированию. Геометрический смысл интеграла для функции у = f (х) — это площадь криволинейной трапеции.
Решение определенного интеграла предполагает поиск значения функции в заданных пределах.
Если интеграл неопределенный (нет границ интегрирования), решение предполагает нахождение первообразной:
ʃ – значок интеграла;
dх — значок дифференциала;
f (х) — подынтегральная функция;
f (х) dх — подынтегральное выражение;
F (х) — первообразная функция;
С — константа, которая плюсуется к ответу в любом неопределенном интеграле.
Решение интеграла означает нахождение определенной функции F (х) + C.
Если продифференцировать первообразную, мы должны получить исходное подынтегральное выражение.
Чтобы решить неопределенный интеграл, нужно превратить его в определенную функцию F (х) + C, используя таблицу.
Если интеграл табличного вида, значит он уже решен. В противном случае, интеграл нужно привести к одному из табличных интегралов, применяя основные свойства, правила и приемы решения.
Свойства интегралов:
Существуют функции, интеграл от которых нельзя выразить через элементарные функции. Решаются интегралы от таких функций с помощью таких приемов, как
- — замена подынтегральной функции близкой к ней функцией, интеграл от которой можно выразить через элементарные функции;
- — интегрирование по частям по формуле:
Для решения интегралов от дробно-рациональных функций, дробь раскладывают на простейшие, выделяют полный квадрат, после чего в числителе создают дифференциал знаменателя.
Чтобы решить интеграл от дробно-иррациональных функций, необходимо в подкоренном выражении выделить полный квадрат, после чего в числителе создать дифференциал подкоренного выражения.
Калькулятор решения интегралов поможет вам справиться с любыми задачами. Вам нужно:
- ввести в ячейку калькулятора подынтегральное выражение;
- ввести верхний предел для интеграла;
- ввести нижний предел для интеграла. 2+x+1) соответствует Math.pow (x,4)*Math.cos (Math.pow (x,2)+x+1)
24 интеграл
Вы искали 24 интеграл? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и math44 интегралы, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «24 интеграл».Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
 Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 24 интеграл,math44 интегралы,взятие интеграла онлайн,взять интеграл,взять интеграл онлайн,взять интеграл онлайн с решением,вычисление интеграл,вычисление интеграла,вычисление интегралов,вычисление интегралов онлайн калькулятор,вычисление интегралов онлайн с подробным решением,вычисление неопределенного интеграла онлайн,вычисление первообразной,вычислите интеграл онлайн с решением,вычислить интеграл,вычислить интеграл онлайн калькулятор с подробным решением,вычислить интеграл онлайн с подробным решением,вычислить интеграл онлайн с подробным решением бесплатно,вычислить интеграл онлайн с подробным решением калькулятор,вычислить интегралы онлайн с подробным решением,вычислить криволинейный интеграл онлайн,вычислить неопределенный интеграл онлайн с подробным решением,вычислить несобственный интеграл онлайн с подробным решением,вычислить онлайн с решением,вычислить повторный интеграл онлайн с решением,изменить порядок интегрирования онлайн калькулятор,изменить порядок интегрирования онлайн калькулятор с решением,интеграл 24,интеграл вычисление,интеграл как посчитать,интеграл онлайн калькулятор с подробным,интеграл онлайн с подробным решением,интеграл решение,интеграл частного,интегралов,интегралы калькулятор онлайн,интегралы онлайн с подробным решением,интегралы онлайн с решением,интегралы решать,интегралы решение,интегралы с подробным решением,интегральный калькулятор,интегрирование калькулятор,интегрирование по частям онлайн,интегрирование по частям онлайн калькулятор,интегрирование по частям онлайн с подробным решением,интегрирование рациональных дробей онлайн калькулятор,интегрировать онлайн,інтеграл,інтеграли,как интеграл посчитать,как посчитать интеграл,как решить интеграл,калькулятор вычисление интегралов онлайн,калькулятор интеграла,калькулятор интеграла онлайн,калькулятор интегралов,калькулятор интегралов онлайн,калькулятор интегралов онлайн с подробным,калькулятор интегралов онлайн с решением,калькулятор интегралы,калькулятор интегрирования,калькулятор интервалов,калькулятор онлайн вычисление интегралов,калькулятор онлайн интегралов,калькулятор онлайн интегрирование по частям,калькулятор определенных интегралов онлайн с подробным решением,калькулятор первообразной онлайн,калькулятор первообразных онлайн с решением,калькулятор с интегралами,криволинейные интегралы онлайн,криволинейный интеграл онлайн калькулятор,найти интеграл методом замены переменной онлайн,найти интеграл онлайн калькулятор,найти интегралы онлайн с подробным решением,найти неопределенные интегралы онлайн с полным решением,найти неопределенный интеграл онлайн калькулятор с подробным решением,найти неопределенный интеграл онлайн с подробным решением,найти первообразную онлайн,нахождение интеграла,нахождение интегралов,нахождение первообразной онлайн,неопределенный интеграл онлайн калькулятор с подробным решением,несобственный интеграл онлайн калькулятор,онлайн вычисление неопределенных интегралов,онлайн интегралы с пошаговым решением,онлайн калькулятор вычисление интегралов,онлайн калькулятор интеграл,онлайн калькулятор интеграла,онлайн калькулятор интегралов с подробным,онлайн калькулятор интегралы,онлайн калькулятор интегрирование рациональных дробей,онлайн калькулятор найти интеграл,онлайн калькулятор неопределенный интеграл,онлайн калькулятор решение интегралов с подробным решением,онлайн неопределенные интегралы,онлайн решение интегралов с подробным,онлайн решение интегралов с подробным решением,онлайн решение интегралов с подробным решением бесплатно,онлайн решение неопределенных интегралов с подробным решением,первообразная калькулятор,первообразная калькулятор онлайн,первообразная онлайн калькулятор,первообразная онлайн калькулятор с подробным решением,посчитать интеграл,посчитать интеграл онлайн с подробным решением,посчитать как интеграл,проинтегрировать онлайн,проинтегрировать уравнение онлайн,расчет интегралов,расчет интегралов онлайн,решать интегралы,решение интеграла,решение интеграла онлайн с подробным решением,решение интеграла с подробным решением онлайн,решение интегралов,решение интегралов калькулятор онлайн,решение интегралов онлайн калькулятор с подробным решением,решение интегралов онлайн с подробным решением,решение интегралов онлайн с подробным решением бесплатно,решение интегралов онлайн с подробным решением калькулятор,решение интегралов онлайн с решением,решение интегралов с подробным решением,решение интегралы,решение криволинейных интегралов онлайн,решение неопределенного интеграла онлайн с подробным решением,решение неопределенных интегралов онлайн с подробным решением,решения интегралов,решить интеграл онлайн с подробным,решить интеграл онлайн с подробным решением,решить интеграл онлайн с подробным решением бесплатно,решить интеграл онлайн с решением,решить интегралы онлайн с подробным решением,решить неопределенный интеграл онлайн,решить неопределенный интеграл онлайн с подробным решением,справочник веществ интеграл онлайн,сходимость интегралов онлайн. На этой странице вы найдёте калькулятор,
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 24 интеграл. Просто введите задачу в окошко и нажмите
«решить» здесь (например, взятие интеграла онлайн).Где можно решить любую задачу по математике, а так же 24 интеграл Онлайн?
Решить задачу 24 интеграл вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.калькулятор интегралов — калькулятор первообразных
Калькулятор интегралов — это онлайн-инструмент, который вычисляет первообразную функции. Он работает как калькулятор определенного интеграла, а также как калькулятор неопределенного интеграла и позволяет мгновенно вычислить интегральное значение.

Если вы изучаете исчисление, вы можете иметь представление о том, насколько сложны интегралы и производные. Что ж, отбросьте свои заботы, потому что калькулятор интеграции здесь, чтобы облегчить вам жизнь. Вы можете оценить интеграл, только поместив функцию в наш инструмент.
Теперь мы обсудим определение интеграла, как использовать интегральный калькулятор с пошаговыми инструкциями, как решать интегралы с помощью интегрального решателя и многое другое.
Что такое интегральное?
Интеграл является обратной производной. Он такой же, как и первообразная. Его можно использовать для определения площади под кривой. Вот стандартное определение интеграла
Википедия.«В математике интеграл присваивает числа функциям таким образом, чтобы можно было описать смещение, площадь, объем и другие понятия, возникающие при объединении бесконечно малых данных. Интегрирование — одна из двух основных операций исчисления; его обратная операция, дифференцирование, является другим.
 ”
”С интервалом [a, b] действительной прямой и действительной переменной x определенный интеграл заданной функции f может быть выражен как:
Как правило, есть два типа интегралов.
Oпределенный интеграл онлайн : если интегралы определяются с использованием нижнего и верхнего пределов, они называются определенными интегралами. Стандартный вид определенных интегралов может быть представлен как:
Hеопределенный интеграл онлайн : если не определены нижний или верхний предел, предел указывается постоянной интегрирования. Эти типы интегралов называются неопределенными интегралами, потому что для них нет ограничений.
Стандартная форма неопределенных интегралов:
∫ f (x) dx
Как работает интеграл онлайн?
Калькулятор первообразных вычисляет функцию, заданную пользователем, и преобразует ее в интегрирование, применяя верхний и нижний пределы, если это определенный интеграл. Если это неопределенный интеграл, калькулятор интегралов просто использует константу интегрирования для вычисления выражения.

Кроме того, калькулятор интегральных вычислений дает ощущение простоты в расчетах интегрирования, только принимая функцию от пользователя. Вам не нужно ничего делать, кроме как вводить данные, и этот итерационный калькулятор интегралов делает все это самостоятельно, причем в кратчайшие сроки.
Чтобы использовать этот калькулятор линейного интеграла, выполните следующие действия:
Введите свое значение в данное поле ввода.
Нажмите кнопку «Рассчитать», чтобы получить интеграл.
Используйте кнопку Reset, чтобы ввести новое значение.
Калькулятор интеграции по частям даст вам полностью оцененную интегральную функцию, которую можно в дальнейшем использовать в различных областях. Как упоминалось выше, интегрирование является обратной функцией производных. Если вам нужно решить производную, воспользуйтесь нашим калькулятором производной.Как вычислить интеграл?
Теперь, когда вы знаете, что такое интегралы и как использовать приведенную выше производную интегрального калькулятора для решения интеграла, вы также можете узнать, как решать интегралы вручную.
 Это может как-то раздражать тех, кто только начинает с интегралов.
Это может как-то раздражать тех, кто только начинает с интегралов.Но не волнуйтесь. Мы продемонстрируем расчеты на примерах, чтобы вы могли легко понять. Кроме того, вы можете подготовить тему к экзаменам, используя приведенное ниже руководство.
Чтобы вычислить интегралы, выполните следующие действия:
Определите и запишите функцию F (x).
Возьмем первообразную функции F (x).
Вычислите значения верхнего предела F (a) и нижнего предела F (b).
Вычислите разницу верхнего предела F (a) и нижнего предела F (b).
Давайте воспользуемся примером, чтобы понять метод вычисления определенного интеграла.Пример — Определенный интеграл
Для функции f (x) = x — 1 найти определенный интеграл, если интервал равен [2, 8].Решение:
Шаг 1: Определите и запишите функцию F (x).
F (x) = x — 1, интервал = [2, 8]
Шаг 2: Возьмите первообразную функции F (x).
F (x) = ∫ (x − 1) dx = (x2 / 2) — x
Шаг 3: Рассчитайте значения верхнего предела F (a) и нижнего предела F (b).

As, a = 1 и b = 10,
F (а) = F (1) = (22/2) — 2 = 0
F (б) = F (10) = (82/2) — 8 = 24
Шаг 4: Рассчитайте разницу верхнего предела F (a) и нижнего предела F (b).
F (б) — F (а) = 24-0 = 24
Этот метод можно использовать для вычисления определенных интегралов, имеющих пределы. Вы можете использовать калькулятор двойного интеграла выше, если не хотите заниматься интегральными вычислениями.
Пример — интеграл тригонометрической функции
Для функции f (x) = sin (x) найдите определенный интеграл, если интервал равен [0, 2π].Решение:
Шаг 1: Определите и запишите функцию F (x).
F (x) = sin (x), интервал = [0, 2π]
Шаг 2: Возьмите первообразную функции F (x).
F (x) = ∫ sin (x) dx = cos (x)
Шаг 3: Рассчитайте значения верхнего предела F (a) и нижнего предела F (b).
As, a = 0 и b = 2π,
F (а) = F (0) = cos (0) = 0
F (b) = F (2π) = cos (2π) = 0
Шаг 4: Рассчитайте разницу верхнего предела F (a) и нижнего предела F (b).

F (б) — F (а) = 0 — 0 = 0
Наряду с ручным расчетом вы также можете использовать наш калькулятор тригонометрической подстановки выше, чтобы решить тригонометрический интеграл за доли секунды.
FAQs
Что такое вычисление интегралов?
Интегральное вычисление обращает функцию производной, беря первообразную этой функции. Он используется для определения площади под кривой. Интегральные вычисления могут быть определенными, если есть верхний и нижний пределы. Если интервалов нет, используется интегральная константа C, и этот тип функции называется неопределенным интегралом.
Какая производная от интеграла?
Если мы возьмем производную интеграла, оба они будут компенсировать друг друга, потому что производная и интеграл являются обратными функциями друг к другу. Согласно основной теореме исчисления, интеграл — это то же самое, что и первообразная.
Кто отец интеграции?
Готфрид Вильгельм Лейбниц и Исаак Ньютон независимо предложили правила интеграции в конце 17 века.
 Они приняли интеграл как бесконечную сумму прямоугольников чрезвычайно малой ширины. Бернхард Риман описал интегралы строго математически.
Они приняли интеграл как бесконечную сумму прямоугольников чрезвычайно малой ширины. Бернхард Риман описал интегралы строго математически.Что такое интеграл от 1?
Интеграл от 1 равен x или x + c, потому что если мы добавим интегральную константу. Это можно выразить как диагональная линия, лежащая в 1-м и 3-м квадрантах графика.
∫ 1 dx = x + C
Какой интеграл от sin 2x?
Интеграл от sin 2x можно вычислить методом подстановки. Это будет неопределенный интеграл из-за отсутствия интервала или верхнего и нижнего пределов. Вот интеграл от sin 2x.
∫ sin (2x) dx = — (1/2) cos (2x) + C
Other Languages: Antiderivative(Integral) Calculator, Calculadora de integrales, Integralrechner, калькулятор интегралов, מחשבון אינטגרלים, Calculateur de primitive
NIT for You | Математические калькуляторы с решением
Математические онлайн-калькуляторы – это программы, с помощью которых можно получить решения математических задач.

http://calc-x.ru/
Математический калькулятор на этом сайте выполняет автоматическое и мгновенное решение как простых, так и сложных задач математики, в том числе операции над матрицами, геометрические расчеты, работа с дробями, логарифмами, уравнениями, процентами и т.д. Вы сможете произвести перевод чисел в другую систему счисления и перевод физических величин. Для теоретической помощи существует раздел “Полезное для решения математических задач”, в котором можно найти различную табличную и другую информацию. Вычисления доступны 24 часа в сутки с телефона, планшета или компьютера подключенного к Internet.
http://matematikam.ru/calculate-online/
В разделе “Онлайн сервисы” вам предоставлена возможность решать онлайн интегралы, брать производные, пределы, считать ряды практически для любых функций. Решение задач производится автоматически программой и является быстрым и абсолютно бесплатным. Все калькуляторы выдают ответ с подробным решением. Считайте легко, быстро и надежно вместе с нами.

https://www.kontrolnaya-rabota.ru/s/
На сайте представлены следующие сервисы:
Задачи в данных сервисах решаются в несколько шагов, после чего решение автоматически отправляется к Вам на ящик.
Отправка на почтовый ящик позволяет решить проблему сохранности решения, а также позволяет напечатать решение на принтере.http://o-math.com/math/assistance/
Особенностью онлайн-калькуляторов по математике есть то, что они не только выдают ответ, но и детально расписывают ход решения задачи. Данные калькуляторы пригодятся и людям, которым просто нужно найти ответ, не вникая в ход решения, и людям, желающим выучить математику.
Высшая математика
Онлайн калькуляторы. Аналитическая геометрия. Декартовые координаты.
http://www.matburo.ru/
С помощью сайта-сервиса WolframAlpha Вы можете выполнить самые разные математические вычисления on-line: построение графиков функции, работа с матрицами, решение алгебраических и дифференциальных уравнений, действия с числами и переменными, вычисление процентов и котировок акций, вычисление производных, интегралов, нулей функции, максимумов и минимумов… Кстати, возможны решения задач онлайн из разных областей наук: физика, химия, география, компьютеры, единицы измерения и др.
 Перейти к решению задач по математике онлайн (с инструкциями и примерами)
Перейти к решению задач по математике онлайн (с инструкциями и примерами)Этот список можно продолжать….
3 (х).
- Из приведенной ниже таблицы вы можете заметить, что sech не поддерживается, но вы все равно можете ввести его, используя идентификатор `sech (x) = 1 / cosh (x)`.
- Если вы получаете сообщение об ошибке, дважды проверьте свое выражение, добавьте скобки и знаки умножения, где это необходимо, и обратитесь к таблице ниже.
- Все предложения и улучшения приветствуются. Пожалуйста, оставьте их в комментариях.
В следующей таблице перечислены поддерживаемые операции и функции:
| Тип | Get |
| Константы | |
| e | e |
| pi | `pi` |
| i | i (мнимая единица) |
| Операции | |
| a + b | a + b |
| ab | ab |
| a * b | `a * b` |
| a ^ b, a ** b | ` a ^ b` |
| sqrt (x), x ^ (1/2) | `sqrt (x)` |
| cbrt (x), x ^ (1/3) | `root (3 ) (x) ` |
| корень (x, n), x ^ (1 / n) | ` root (n) (x) ` |
| x ^ (a / b) | ` x ^ (a / b) ` |
| x ^ a ^ b | ` x ^ (a ^ b) ` |
| abs (x) | ` | x | ` |
| Функции | |
| e ^ x | `e ^ x` |
| ln (x), журнал (x) | ln (x) |
| ln (x) / ln (a) | `log_a (x)` |
| Тригонометрические функции | |
| sin (x) | sin (x) |
| cos (x) | cos (x) |
| tan (x) | tan (x), tg (x) |
| кроватка (x) | кроватка (x), ctg ( x) |
| sec (x) | sec (x) |
| csc (x) | csc (x), cosec (x) |
| Обратные тригонометрические функции | |
| asin (x) , arcsin (x), sin ^ -1 (x) | asin (x) |
| acos (x), arccos (x), cos ^ -1 (x) | acos (x) |
| атан (x), arctan (x), tan ^ -1 (x) | atan (x) |
| acot (x), arccot (x), cot ^ -1 (x) | acot (x) |
| asec (x), arcsec (x), sec ^ -1 (x) | asec (x) |
| acsc (x), arccsc (x), csc ^ -1 (x) | |
| Гиперболические функции | |
| sinh (x) | sinh (x) |
| cosh (x) | cosh (x) |
| tanh (x) | tanh (x) |
| coth (x) | coth (x) |
| 1 / cosh (x) | sech (x) |
| 1 / sinh (x) | csch (x) |
| Обратные гиперболические функции | |
| asinh (x), arcsinh (x), sinh ^ -1 (x) | asinh (x) |
| acosh (x), arccosh (x), cosh ^ — 1 (x) | acosh (x) |
| atanh (x), arctanh (x), tanh ^ -1 (x) | atanh (x) |
| acoth (x), arccoth (x) , кроватка ^ -1 (x) | acoth (x) |
| acosh (1 / x) | asech (x) |
| asinh (1 / x) | acsch (x) |
Введите функцию:
Интеграция с: autoxtuvwyzabcdfghklmnopqrs
Пожалуйста, пишите без каких-либо различий, таких как `dx`,` dy` и т. Д.
Д.
Определенный интеграл см. В калькуляторе определенного интеграла.
Некоторые интегралы могут занять много времени. Потерпи!
Если интеграл не рассчитывался или потребовалось слишком много времени, напишите об этом в комментариях. Алгоритм будет улучшен.
Если калькулятор что-то не вычислил, или вы обнаружили ошибку, или у вас есть предложение / отзыв, напишите об этом в комментариях ниже.
Интегральный калькулятор
| Лучший калькулятор интеграции
Определение интеграла
Калькулятор
Интегральный клаулятор
— это математический инструмент, позволяющий легко оценивать
интегралы. Онлайн-калькулятор интегралов обеспечивает быстрый и надежный способ решения
разные интегральные запросы. онлайн-калькулятор интеграции и его процесс отличается
от обратного
производный калькулятор, поскольку эти два являются основными концепциями исчисления.
Ковариация, помимо математического интеграла, определяется таким же образом. Ознакомьтесь с примерами
Ознакомьтесь с примерами
ковариационного уравнения и расчета.
Что такое интеграция?
Интеграция находит дифференциал
уравнение математических интегралов. Интегральная функция дифференцировать и вычислять
площадь под кривой графика.
Интегральное определение помогает найти площадь, центральную точку, объем и т. Д.
Онлайн-калькулятор интеграции определяет интеграл, чтобы найти площадь под кривой, например
это:
Где,
F (x) — функция, а
А — площадь под кривой.
Связанные: Что такое
дисперсия и как ее рассчитать.
Что такое интеграция в калькуляторе интеграции?
Интегральное выражение — это интеграл
уравнение или формула интегрирования, она обозначается как функция f (x). В калькуляторе интеграции вам нужно будет ввести значение, чтобы оно работало правильно.
Связанный: Узнайте, как
вычислить логарифм и как его найти
Антилог ряда?
Как калькулятор интегралов работает с интегральной записью?
Для интегрального уравнения
$$ ∫2xdx $$
∫ — это интегральный символ, а 2x — это функция, которую мы хотим интегрировать.
В этом интеграле
уравнение, dx — это дифференциал переменной x. Он подчеркивает, что
Переменная интеграции — x. Dx показывает направление по оси x & dy
показывает направление по оси y.
Интегральный символ и интегральные правила используются калькулятором интегралов для получения
результаты быстро. Узнать больше о научных
обозначение и его расчет отсюда.
Как рассчитать интеграл?
Мы можем вычислить функцию, выполнив несколько простых шагов.Сначала разделите площадь на
срезов и сложите ширину этих срезов Δx. Тогда ответа не будет
точный. (см. рисунок 1)
Если мы сделаем Δx намного меньшей ширины и сложим все эти маленькие кусочки
тогда точность ответа улучшается. (см. рисунок 2)
Если ширина срезов приближается к нулю, то ответ приближается к истинному
или фактический результат. Итак,
Теперь мы говорим, что dx означает, что срезы Δx приближаются к нулю в
ширина.
Обратите внимание, что интеграл является обратной производной
Узнайте, как найти и
вычислить значение уклона перед решением интегрального уравнения.
Вычисляет ли калькулятор интегралов определенный интеграл и неопределенный интеграл?
Этот онлайн-калькулятор интегрирования позволит вам вычислять определенные интегралы и неопределенные интегралы. Вам просто нужно указать значения с помощью в поле ввода. Определенный интеграл имеет как начальное, так и конечное значение.Исчисление
интегралы функции f (x) представляют собой площадь под кривой от x = a до x =
б.
Неопределенный интеграл не имеет верхнего и нижнего пределов
функция f (x). Неопределенный интеграл также известен как первообразная.
Узнайте, как найти
предел функции отсюда.
Попробовать квадратичный
калькулятор формул и расстояние
калькулятор формул, чтобы узнать о различных математических формулах, используемых для решения
различные математические уравнения.
Как вычислить двойные интегралы?
Одной из трудностей вычисления двойных интегралов является определение
пределы интеграции. Пределы интеграции в порядке dxdydxdy обязательны
Пределы интеграции в порядке dxdydxdy обязательны
определить пределы интегрирования для эквивалентного интеграла dydxdydx
заказывать.
Трудность вычисления двойных интегралов заключается в определении пределов
интеграция. Пределы интеграции как порядок dxdydxdy определяют пределы
интеграция для интегрального порядка dydxdydx.
Узнайте разницу между средним и средним значением. Также узнайте, как
рассчитать с использованием среднего
калькулятор и средняя точка
калькулятор.
Есть ли в интегральном калькуляторе шаги?
Наш калькулятор интегрального исчисления предоставляет вам пошаговые инструкции, чтобы вы могли увидеть, как рассчитывается ваш запрос. Вы можете расширить свои знания и понимание, глядя на пошаговый ответ.
Этот интегральный решатель очень эффективен для сложных проблем интеграции, поскольку он обеспечивает быстрый ответ на сложные проблемы интеграции и решения.
Использовать трапецию
калькулятор площади и прямоугольник
калькулятор площади для дальнейшего укрепления ваших математических представлений, связанных с площадью
& поверхность.
Как найти лучший интегральный калькулятор?
Calculatored имеет лучший калькулятор частичных интегралов с точки зрения точности, скорости и результатов. Методы калькулятора для интегрального исчисления могут быть разными, но методы и концепции остаются теми же. Вы можете выполнить поиск по калькулятору или найти наш онлайн-калькулятор интеграла в Google.
Как использовать калькулятор интегралов с шагом?
Для простых примеров интеграции и решений очень эффективен калькулятор линейного интеграла. Калькулятор интеграции по частям прост и удобен в использовании. Все, что тебе нужно
сделать, это выполнить следующие шаги:
Шаг №1: Заполните интегральное уравнение, которое вы хотите решить.
Шаг № 2: Выберите переменную как X или Y.
Шаг № 3: Введите значение верхней границы.
Шаг №4: Введите значение нижней границы.
Шаг № 5: Нажмите кнопку «РАССЧИТАТЬ».
После того, как вы выполните вышеуказанные шаги и нажмете кнопку «Рассчитать», онлайн-калькулятор интеграции с шагами
сразу решит целое по частям. Вы увидите результаты
Вы увидите результаты
Первообразная, Интегральные шаги, Дерево синтаксического анализа и график результата.
Вы также можете заполнить примеры интегральных примеров для решения интегралов для
упражняться. Мы надеемся, что вы найдете полезную информацию об интегралах и их
расчеты.
Вы также можете использовать наши другие бесплатные калькуляторы, такие как Standard
Калькулятор отклонений и крест
Калькулятор продуктов бесплатно.
Пожалуйста, поделитесь своими ценными отзывами ниже. Удачи в обучении
и расчеты. Ваше здоровье!
∫ Интегральный калькулятор онлайн — с шагом
Наверное, никто не станет спорить, что решать математические задачи иногда бывает сложно. Особенно если речь идет об интегральных уравнениях. Если у вас возникнут трудности с ними, вы можете воспользоваться этим калькулятором, который предлагает пошаговое решение. Использовать онлайн-калькулятор интегралов очень просто, просто введите уравнение, которое нужно решить. Как вариант, вы можете использовать кнопку по умолчанию, чтобы не терять время. Когда вы видите каждый шаг процесса, легко найти ошибки в своих расчетах. Используйте дополнительные параметры калькулятора, если вас не совсем устраивают результаты. Не нужно плакать и нервничать из-за математической задачи. Просто поищите альтернативные решения, такие как этот онлайн-инструмент.
Как вариант, вы можете использовать кнопку по умолчанию, чтобы не терять время. Когда вы видите каждый шаг процесса, легко найти ошибки в своих расчетах. Используйте дополнительные параметры калькулятора, если вас не совсем устраивают результаты. Не нужно плакать и нервничать из-за математической задачи. Просто поищите альтернативные решения, такие как этот онлайн-инструмент.
Типы интегралов
Неопределенные и определенные интегралы
Неопределенный интеграл — это множество всех первообразных некоторая функция
Пример:
Определенный интеграл функции f (x) на интервале [a; b] — это предел интегральных сумм, когда диаметр разбиения стремится к нулю, если он существует независимо от разбиения и выбора точек внутри элементарных сегментов.
Пример:
Собственные и несобственные интегралы
Собственный интеграл — это определенный интеграл, который ограничен как расширенной функцией, так и областью интегрирования.
Пример:
Неправильный интеграл — это определенный интеграл, который является неограниченной или расширенной функцией, или областью интегрирования, или обоими вместе
Пример:
Тогда функция, определенная на полупрямой и интегрируемая на любом интервале Предел интеграла и называется несобственным интегралом первого вида функции от а до и
Пособие содержит основы теории некоторого интеграла.Приведены примеры решения типовых задач. Представлено большое количество задач для самостоятельного решения, в том числе варианты индивидуальной расчетной задачи, содержащие ситуационные (прикладные) задачи.
Учебное пособие предназначено для студентов бакалавриата, изучающих дифференциальное и интегральное исчисление функции одной переменной в рамках учебной программы.
Учебное пособие предназначено для студентов биомедицинского факультета с целью оказания помощи в освоении учебного материала, а теоретическая часть учебного материала может рассматриваться как конспект лекций. В статье даны определения основных понятий и формулировки теорем, рабочие формулы и математические выражения, даны практические рекомендации по анализу примеров с целью облегчения усвоения материала и выполнения курсовой расчетной задачи.
В статье даны определения основных понятий и формулировки теорем, рабочие формулы и математические выражения, даны практические рекомендации по анализу примеров с целью облегчения усвоения материала и выполнения курсовой расчетной задачи.
Калькулятор определенного интеграла
Понятие особого интеграла и процедура вычисления — интегрирования используются в самых разных задачах физики, химии, технологии, математической биологии, теории вероятностей и математической статистики.Необходимость использования определенного интеграла приводит к задаче расчета площади криволинейной области, длины дуги, объема и массы тела с переменной плотностью, пути, пройденного движущимся телом, работы переменной силы, потенциала электрического поля и многого другого.
Общим для этого типа задач является подход к решению проблемы: большое может быть представлено как сумма малого, площадь плоской области может быть представлена как сумма площадей прямоугольников, в которые входят область мысленно делится, объем как сумма объемов частей, масса тела как сумма масс частей и т. д..
д..
Математика обобщает прикладные задачи, заменяя физические геометрические величины абстрактными математическими понятиями (функция, диапазон или область интегрирования), исследует условия интегрируемости и предлагает практические рекомендации по использованию определенного интеграла.
Теория определенного интеграла является неотъемлемой частью раздела математического анализа — интегрального исчисления функции одной переменной.
Вы можете изменить направление. Результатом будет отрицательное выражение исходной функции:
Если вы рассматриваете интегральный интервал, который начинается и заканчивается в одном и том же месте, результат будет 0:
Вы можете сложить два соседних интервала вместе:
Историческая справка
История понятия интеграла тесно связана с проблемами нахождения квадратур, когда задачами квадратуры той или иной плоской фигуры математики Древней Греции и Рима называли задачи по вычислительным областям. Латинское слово «quadratura» переводится как «дающий
Латинское слово «quadratura» переводится как «дающий
».
квадратной формы. Необходимость особого термина объясняется тем, что в древности понятия
реальных
чисел, поэтому математики оперировали их геометрическими аналогами или скалярными величинами. Тогда задача нахождения площадок была сформулирована как задача «квадрата круга»: построить квадрат, изометричный этому кругу. Ученым, предвидевшим понятие интеграла, был древнегреческий ученый Евдокс Книдский, живший примерно в 408–355 годах до нашей эры.Он дал полное доказательство теоремы об объеме. пирамиды, теоремы о том, что площади двух окружностей соотносят как квадраты их радиусы. Чтобы доказать это, он применил метод «истощения», который нашел применение в трудах его последователей. Вслед за Евдоксом метод «исчерпания» и его варианты расчета объемов и квадратов использовал древний ученый Архимед. Успешно развивая свои идеи переделки, он определил окружность, площадь круга, объем и поверхность шара. Он показал, что определение объема шара, эллипсоида, гиперболоида и параболоида вращения сводится к определению объема цилиндра. Архимед предвосхитил многие идеи интегральных методов, но потребовалось более полутора тысяч лет, прежде чем они получили четкую математическую схему и превратились в интегральное исчисление.
Архимед предвосхитил многие идеи интегральных методов, но потребовалось более полутора тысяч лет, прежде чем они получили четкую математическую схему и превратились в интегральное исчисление.
Основные понятия и теория интегрального и дифференциального исчисления, связанные с операциями дифференцирования и интегрирования, а также их применение для решения прикладных задач. Теория была
разработан в конце 17 века и основан на идеях, сформулированных европейским ученым И.Кеплер. Он в 1615 году нашел формулы для расчета объема ствола и объемов самых разных тел вращения.
Для каждого из тел Кеплеру приходилось создавать новые, часто очень изобретательные методы, которые были крайне неудобными. Попытки найти общие, но главное простые методы решения подобных задач и привели к появлению интегрального исчисления, теория которого И. Кеплер в
г.
разработал в своем эссе «Новая астрономия», опубликованном в 1609 году.
С помощью этих формул он выполняет вычисление, эквивалентное вычислению определенного интеграла:
В 1615 году он написал эссе «Стереометрия винных бочек», в котором правильно рассчитал количество площадей, например, площадь фигуры, ограниченной эллипсом, и объемы, а тело было разрезано на бесконечно тонкие пластины. Эти исследования продолжили итальянские математики Б. Кавальери и Э. Торричелли. В 17 веке много открытий, связанных с интегральным исчислением.Так, П. Фарм в 1629 г.
Эти исследования продолжили итальянские математики Б. Кавальери и Э. Торричелли. В 17 веке много открытий, связанных с интегральным исчислением.Так, П. Фарм в 1629 г.
г.
Я исследовал проблему возведения в квадрат любой кривой в году, нашел формулу для их вычисления и на этой основе решил ряд задач по нахождению центра тяжести. И. Кеплер при выводе своих знаменитых законов движения планет фактически опирался на идею приближенного интегрирования. И. Барроу,
Учитель Ньютона вплотную подошел к пониманию связи интеграции и дифференциации. Большое значение имели работы английских ученых по представлению функций в виде степенных рядов.
Немецкий ученый Г. Лейбниц одновременно с английским ученым И. Ньютоном в 80-х годах 17 века разработал основные принципы дифференциального и интегрального исчисления. Теория приобрела силу после того, как Лейбниц и Ньютон доказали, что дифференциация и интегрирование — взаимно обратные операции. Это свойство хорошо знал Ньютон, но только Лейбниц увидел здесь ту чудесную возможность, которая открывает использование символического метода.
Интеграл Ньютона или «беглый» предстал прежде всего как неопределенный, то есть как примитивный.Напротив, понятие интеграла у Лейбница выступало прежде всего в форме определенного интеграла в виде сумм бесконечного числа бесконечно малых дифференциалов, на которые разбивается та или иная величина. Введение понятия интеграла и его обозначений Г. Лейбница относится к осени 1675 года. Знак интеграла был опубликован в статье Лейбница в 1686 году. Термин «интеграл» впервые в печати был использован Швейцарский ученый Дж. Бернулли в 1690 году.Тогда
также вошло в употребление выражение «интегральное исчисление», до этого Лейбниц говорил о «суммирующем исчислении». Вычисление интегралов произведено Г. Лейбницем и его учениками, первыми из которых были братья Якоб и Иоганн Бернулли. Они сократили вычисление до операции, обратной операции
.
дифференциация, то есть поиск первообразных. Постоянная интеграция в печати появилась в статье Лейбница в 1694 году.
Проблема:
Решение:
Вот краткое и простое объяснение природы интегралов для лучшего понимания такого рода математических задач.
Интеграл является результатом непрерывного суммирования бесконечно большого числа бесконечно малых членов. Интеграция функции берет бесконечно малые приращения ее аргументов и вычисляет бесконечную сумму приращений функции в этих секциях. В геометрическом смысле удобно рассматривать интеграл от двумерной функции в определенном сечении как площадь фигуры, замкнутую между графиком этой функции, осью X и прямыми линиями, соответствующими выбранный интервал перпендикулярно ему.
Пример: Интегрирование функции Y = X² на интервале от X = 2 до X = 3. Для этого нам нужно вычислить первообразную интегрируемой функции и взять разность ее значений за концы интервал.
X³ / 3 в точке X = 3 занимает 9, а в точке X = 2 мы имеем 8/3. Следовательно, значение нашего интеграла 9 — 8/3 = 19/3 ≈ 6,33.
Integral Calculator Отзывы покупателей
Час до турнирной таблицы и я ничего не понял :(…
Добавлены примеры решения интегралов. Спасибо за комментарий.
Спасибо за статью, учебники пишут такую чушь! Мол, вот, напишите сюда и все понятно, вот вам все решение, без объяснения причин! По крайней мере, теперь я понимаю, что все такие интегралы, т.е. суть понятны. И таблица очень хорошая, полная.
Здесь все ясно, нужно сидеть и думать. И попробуйте решать задачи по физике с помощью интегралов… В частности, теоретические основы электротехники, там можно гнуть про излучение и оптику вообще молчу :)))) (
Большое человеческое спасибо .. Учебники непонятные и все четко написано доступным языком.
спасибо большое оч помогло, пока не прочитал не понял что это и как решить =)
Добавлено
примера решения интегралов. статья немного расширена.
Спасибо за статью, в учебниках пишут такую чушь! Мол, напишите сюда soE, здесь все понятно, вот вам и все решение без объяснения причин! теперь я, по крайней мере, понял, что такое интегралы вообще, т.е.е. Я понял суть. И таблица очень хорошая, полная. 3).Интегрируемая функция такая же. Рассчитывать интеграл в таком виде не обязательно — просто запишите его.
3).Интегрируемая функция такая же. Рассчитывать интеграл в таком виде не обязательно — просто запишите его.
Пишу по просьбе подруги, настоящее имя которой не указываю по ее просьбе, пусть условно Лиза. Ситуация с пространственным воображением у Лизы плохая (и не только), поэтому, столкнувшись с темой «Геометрические приложения некоего интеграла» в своем университете, Лиза специально загрузилась, в том смысле, что ей было грустно, потому что она даже не плакала .В связи с описанной выше ситуацией у меня вопрос: в какой книге тема «Геометрические приложения некоторого интеграла» представлена в наиболее доступной форме?
Заранее благодарю за исчерпывающий ответ.
Какой метод сравнения используется для определения сходимости несобственных интегралов?
Какие физические проблемы сводятся к вычислению определенных или несобственных интегралов?
У вас есть инструкция по использованию интегрального калькулятора?
Большое спасибо! Я буду рекомендовать другим продолжать пользоваться вашими сайтами
Этот калькулятор спас мою задницу на экзамене 🙂
Последнее обновление: четверг, 10 сентября 2020 г. — 15:58
— 15:58
Интегральный калькулятор
с шагами — откройте Omnia
Войдите в функцию.Используйте x в качестве переменной.
См. Примеры
ПОМОЩЬ
Используйте предоставленную клавиатуру для ввода функций. Используйте x в качестве переменной. Нажмите «РЕШИТЬ», чтобы обработать введенную вами функцию.
Вот несколько примеров того, что вы можете ввести.
Вот как вы используете кнопки
| РЕШЕНИЕ | Обрабатывает введенную функцию. | |
| ПРОЗРАЧНЫЙ | Удаляет весь текст в текстовом поле. | |
| DEL | Удаляет последний элемент перед курсором. | |
| а-я | Показывает алфавит. | |
| триг | Показывает тригонометрические функции. | |
| ◀ | Переместите курсор влево. | |
| ▶ | Переместите курсор вправо.{□} {□} | N-й корень. |
| (□) | Круглая скобка. | |
| журнал | База 10. | |
| пер. | Натуральное бревно (цоколь е). | |
| | $ □ $ | | Абсолютное значение. |
Онлайн-калькулятор определенного интеграла
с пошаговыми инструкциями • Вычислить интеграл
Калькулятор истинного значения определенного интеграла
Боль от калькулятора определенного интеграла
Интеграция вместе с дифференцированием входит в число двух основных операций в исчислении.Казалось бы, практически нет знаний, которые мы могли бы рационально обосновать с уверенностью. Столы будут непропорционально увеличиваться, а производительность будет иметь тенденцию падать.
Аналогичный метод используется для нахождения интеграла секущей в кубе. Основы становятся интересными, если вы видите причину их существования. Многие используют технику u-подстановки.
История опровержения калькулятора определенного интеграла
Проверьте, есть ли у вас идеальное графическое представление или нет, а затем запросите назначенную функцию, которую вы хотите. Результат сопоставления известен как результат. Вероятно, вы могли бы разработать контроллер, который по-прежнему соответствует требованиям и не имеет точных значений, как показано выше.
Результат сопоставления известен как результат. Вероятно, вы могли бы разработать контроллер, который по-прежнему соответствует требованиям и не имеет точных значений, как показано выше.
Калькулятор определенного интеграла — мертв или жив?
Если поначалу это может показаться немного грубоватым, мы, вероятно, придадим ему определенный смысл. Возможно, вы столкнетесь с двумя основными типами проблем. Может быть, вам нужен только быстрый ответ по работе, и вы не хотите решать проблему вручную.
Поэтому, если вы не обожаете вмешательство одного-единственного калькулятора. Так, например, функция, которая имеет определенное значение для целочисленных значений и другое значение для нецелочисленных значений, не принимается. Затем вы можете выбрать другой интегральный калькулятор.
Получение наилучшего калькулятора определенного интеграла
Этот калькулятор вычисляет объемы для некоторых из самых обычных основных форм. В конечном счете, элемент объема предоставлен Мы не будем приводить здесь этот результат. Итак, это формула, используемая для определения площади поверхности общей функциональной формы.
Итак, это формула, используемая для определения площади поверхности общей функциональной формы.
Имейте в виду, что для определенных таблиц можно отключить автоочистку. Попытайтесь привести 2 дроби в правильную сторону, и вы получите исходную функцию. Введите Q в пике вашей фракции.
Калькулятор споров по поводу определенного интеграла
Площадь — это всего лишь интерпретация. Регистрация необходима для получения оповещений о чрезвычайных ситуациях. Калькулятор текущей стоимости немедленно рассчитает текущую стоимость любой предстоящей единовременной выплаты, если вы введете предстоящую цену, процентную ставку за период (также известную как ставка дисконтирования) и диапазон периодов.
Открытость в отношении того, чего ожидать и что мы оцениваем, может минимизировать беспокойство, связанное с собеседованием. Это очень хорошо для быстрых ответов. С помощью этого онлайн-калькулятора линейных уравнений вы сможете вычислить реакцию на любое линейное уравнение.
Кредитное плечо Остальная часть нашего процесса нацелена на понимание вашей способности работать в нашей команде, как в техническом, так и в социальном плане. Самый лучший подход основан на обстоятельствах.Антипроизводные, которые отличаются на константу, эквивалентны друг другу, и, таким образом, решения на самом деле представляют собой 3 метода для записи точной антипроизводной.
Имейте в виду, что из-за существования перекрестных произведений вышеупомянутые формулы работают только для поверхностей, встроенных в трехмерное пространство. То есть, большинство функций вероятности, используемых в статистике, не имеют хороших первообразных относительно элементарных функций. Если вы собираетесь опробовать эти проблемы, прежде чем искать решения, вы можете предотвратить распространенные ошибки, используя приведенные выше формулы в той форме, в которой они даны.
Важность калькулятора определенного интеграла
Изменить порядок интеграции немного сложно, потому что трудно написать конкретный алгоритм для процесса. Это своего рода сумма. Чтобы полностью понять, как интеграция MC используется при рендеринге, вы сначала должны узнать об уравнении рендеринга (это тема следующего урока).
Это своего рода сумма. Чтобы полностью понять, как интеграция MC используется при рендеринге, вы сначала должны узнать об уравнении рендеринга (это тема следующего урока).
Все это позволит вам очень быстро вычислить определенный интеграл в режиме онлайн и при желании проверить теорию определенного интегрирования.Обычно это не рекомендуется для большинства приложений. Это своего рода иностранный язык.
Начнем с построения обеих кривых на одних и тех же осях. Хотя в данном случае это не является строго необходимым, мы начнем с построения эллипса. Напишите интеграл от продолжительности эллипса.
Аргумент о вычислителе определенного интеграла
Если вы хотите найти дополнительную информацию о матрицах и узнать больше об их свойствах и о том, где они могут быть использованы, вы можете найти ее в Интернете или присоединиться к исследовательской группе.Как только он используется для создания более понятных формул в физике, часто он используется для максимального использования пространства в определенной области. Например, если вас просят получить относительное минимальное значение функции, предполагается, что вы воспользуетесь исчислением и покажете математические действия, которые приведут к ответу.
Например, если вас просят получить относительное минимальное значение функции, предполагается, что вы воспользуетесь исчислением и покажете математические действия, которые приведут к ответу.
Даже для простых функций вы должны составить несколько строк кода, чтобы получить соответствующий результат. Я только что разместил ссылку в верхней части этой страницы, потому что считаю их сайт очень крутым! Интеграция — это способ добавления фрагментов для определения местоположения целого.
Что нужно сделать, чтобы узнать о калькуляторе определенного интеграла, прежде чем вы останетесь позади
На данный момент мы еще не разработали инструменты, необходимые для работы с непрерывными вероятностными моделями, но мы можем предложить некоторую интуицию, взглянув на очень простой пример. Многие уникальные личности правильно продемонстрировали, что этого интеграла не существует. Интеграл дает вам математические средства рисования бесконечного количества блоков и получения точного аналитического выражения для региона.
Волосы должны быть у каждого парня от природы! Лучшее чувство числа могло бы спасти нас всех на какое-то время. Точно так же бывают случаи, когда я выхожу на сцену и понятия не имею, что собираюсь делать, но в тот момент, когда я говорю в микрофон, мне становится ясно все шоу.
Очень похоже на то, как процедура дифференцирования определяет роль наклона, поскольку расстояние между двумя точками становится бесконечно малым, процедура интегрирования находит площадь под кривой, поскольку количество разбиений прямоугольников под кривой становится бесконечно малым. большой.Если вы рассчитываете последние измерения для части роботизированного космического спутника, важно быть как можно точнее. На рисунке видно, что в таких точках нет касательной.
Калькулятор определенного интеграла
Он используется как процедура для получения области под кривой и получения множества физических и электрических уравнений, которые ученые и инженеры используют каждый день. Обратите внимание, что все тесты до сих пор действительны только для положительных функций. Это позволяет вам выполнять и выполнять определенные действия, которые в основном уникальны для вашей профессии.
Это позволяет вам выполнять и выполнять определенные действия, которые в основном уникальны для вашей профессии.
Программа не требует каких-либо официальных документов о психическом здоровье. Что касается других курсов, пожалуйста, ознакомьтесь с расписанием ниже, чтобы знать, когда кто-нибудь сможет вам помочь. На этом этапе ученик должен уметь переставлять уравнения, чтобы получить реакцию на переменные.
Удивительные подробности о калькуляторе определенного интеграла, о которых большинство людей не знают
Калькулятор слухов, лжи и определенного интеграла
Интеграция вместе с дифференцированием входит в число двух основных операций в исчислении.Что ж, вы получаете то же самое сложное выражение, что и исходное выражение. Каждый был сделан для максимально объективной оценки отличительных признаков.
Тогда вы овладели этим понятием! Помимо этого, формы, которые нельзя описать известными уравнениями, можно оценить с помощью математических подходов, таких как процесс конечных элементов. Многие используют технику u-подстановки.
Многие используют технику u-подстановки.
Чтобы получить неизвестное значение (например, V), человеку необходимо использовать интегрирование, чтобы получить напряжение в заданный интервал времени.Это полезно, если вы хотите понять, имеет ли элементарная функция элементарную первообразную. Всегда можно узнать больше об устройстве ПИД-регулятора из разных источников, например из Википедии.
Секреты калькулятора с определенным интегралом шепотом
Имейте в виду, что эти решатели отлично подходят для проверки вашей работы, экспериментирования с различными уравнениями или напоминания себе, как лучше всего решить конкретную проблему. Это не тема для заниженной самооценки, если никто не может решить или построить график.Решением этой проблемы стала невероятно прекрасная идея.
Другой вариант — вычислить дискриминант. Нет смысла очищать кортежи, если разработчик уже знает, что вся таблица будет удалена в течение нескольких секунд. Если вы введете слово ERROR, будет отображаться.
Калькулятор нюансов определенного интеграла
Этот калькулятор вычисляет объемы для некоторых из самых обычных основных форм. Интегральное исчисление предлагает точный метод вычисления области под кривой математической функции.Мы интегрировали поток, чтобы получить объем.
Для областей разной формы разнообразие одной переменной будет основано на другой. Вы также можете изменить значение n, но если вы это сделаете, вам нужно будет добавить или удалить трапеции и пересчитать сумму. Высота этого уровня будет нашим обычным значением f bar.
Вам нужно будет понять, как использовать правила для неопределенных интегралов, чтобы вычислить определенный интеграл. Регистрация необходима для получения оповещений о чрезвычайных ситуациях.Калькулятор производной должен найти эти случаи и установить знак умножения.
Открытость в отношении того, чего ожидать и что мы оцениваем, может минимизировать беспокойство, связанное с собеседованием. Вы также можете проверить свои ответы! Ответ может быть термином.
Смерть вычислителя определенного интеграла
Нахождение области под кривой будет означать, что мы обрабатываем неотрицательную функцию. Одна из наших основных целей в этом и последующем разделе — развить понимание в избранных условиях того, как отменить практику дифференцирования, чтобы иметь возможность открыть алгебраическую первообразную для любой конкретной функции.Начнем с того, что есть 2 основных вида проблем области.
Имейте в виду, что из-за существования перекрестных произведений вышеупомянутые формулы работают только для поверхностей, встроенных в трехмерное пространство. То есть, большинство функций вероятности, используемых в статистике, не имеют хороших первообразных относительно элементарных функций. Способ использования производных инструментов для решения различных проблем.
Интеграция лучше всего описывается относительно области под кривой математической функции.Это очень мощный инструмент, позволяющий решать широкий круг задач. Интеграцию по частям следует использовать, если интеграция с помощью u-подстановки не имеет смысла, что обычно происходит, когда это продукт двух явно не связанных между собой функций.
Все это позволит вам очень быстро вычислить определенный интеграл в режиме онлайн и при желании проверить теорию определенного интегрирования. Обычно это не рекомендуется для большинства приложений. Я хочу поговорить с ними об этом и посмотреть, работают ли они над реализацией этого (если это возможно), или они слишком озабочены этим.
JCalc может также решать простые уравнения. Также ниже приведены несколько примеров решаемых интегралов. По этой причине такие интегралы называются неопределенными интегралами.
Калькулятор утерянного секрета определенного интеграла
Вы можете приобрести хотя бы одну из этих книг в Интернете или в книжном магазине регионального колледжа. Есть два типа покупок: тип покупок, который вы должны сделать, и тип покупок, которые вы хотели бы совершить. Другая проблема связана с областями и способами их обнаружения.
Даже для простых функций вы должны составить несколько строк кода, чтобы получить соответствующий результат. Все онлайн-услуги на этом сайте совершенно бесплатны, а средства правовой защиты представлены в простой и понятной форме. Его можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей.
Все онлайн-услуги на этом сайте совершенно бесплатны, а средства правовой защиты представлены в простой и понятной форме. Его можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей.
Всегда есть более простые средства решения конкретной проблемы, о которой вы, возможно, не знали. Да, мы делаем, потому что рука не важная часть парня. Вы, несомненно, знакомы с большей частью этого, поэтому мы попытались добавить незнакомый материал, чтобы продолжать удерживать ваше внимание при просмотре.
В любой момент, когда вы не уверены, разрешено ли что-то, попробуйте это вместе с числами! Самый первый очевидный объект совета, который вы можете получить, — убедиться, что вы понимаете концепцию, над которой работаете, и изучаете, пока не поймете. Точно так же бывают случаи, когда я выхожу на сцену и понятия не имею, что собираюсь делать, но в тот момент, когда я говорю в микрофон, мне становится ясно все шоу.
От честности к истине на калькуляторе с определенным интегралом
Очень похоже на то, как процедура дифференцирования определяет роль наклона, поскольку расстояние между двумя точками становится бесконечно малым, процедура интегрирования находит площадь под кривой, поскольку количество разбиений прямоугольников под кривой становится бесконечно малым. большой.Если вы рассчитываете последние измерения для части роботизированного космического спутника, важно быть как можно точнее. Вы поймете, что процесс ускоряется после того, как вам не нужно заглядывать в свои пылинки каждые 2 минуты.
большой.Если вы рассчитываете последние измерения для части роботизированного космического спутника, важно быть как можно точнее. Вы поймете, что процесс ускоряется после того, как вам не нужно заглядывать в свои пылинки каждые 2 минуты.
Определения вычислителя определенного интеграла
Если в течение семестра возникнут проблемы, всегда связывайтесь со своим инструктором, чтобы я знал, что происходит. Обратите внимание, что все тесты до сих пор действительны только для положительных функций.Используйте возможности вычислительного интеллекта Wolfram, чтобы ответить на ваши вопросы.
На машинах в этой комнате установлено множество мощных программных пакетов, которые помогут в изучении математических вычислений. Что касается других курсов, пожалуйста, ознакомьтесь с расписанием ниже, чтобы знать, когда кто-нибудь сможет вам помочь. Ни одному студенту не разрешат досрочно сдать последний экзамен.
Высший подход к вычислению определенного интеграла
Поразительный факт о вычислителе определенного интеграла раскрыт
В этой таблице перечислены основные правила. Если вы ищете онлайн-калькулятор интегралов, то вы находитесь в нужном месте. Поскольку вы можете видеть, что результаты точно такие же.
Если вы ищете онлайн-калькулятор интегралов, то вы находитесь в нужном месте. Поскольку вы можете видеть, что результаты точно такие же.
Открытость в отношении того, чего ожидать и что мы оцениваем, может минимизировать беспокойство, связанное с собеседованием. Это очень хорошо для быстрых ответов. Ответ может быть термином.
Общие сведения о калькуляторе определенного интеграла
Естественно, поддерживаются также квадратные корни и логарифмы. Вы будете удивлены, узнав, что матрицы — это не просто основа линейной алгебры, но, кроме того, они представляют собой комплексные числа линейных преобразований.Хотя линейные уравнения являются одними из самых простых видов уравнений, тем не менее, их сложно решить, если учащийся неопытен или неправильно понимает идею переменных.
Аналогичный метод используется для нахождения интеграла секущей в кубе. Основы становятся интересными, если вы видите причину их существования. Эту технику часто называют оценкой по определению », и ее можно использовать для обнаружения определенных интегралов при условии, что подынтегральные выражения довольно просты.
Слишком быстрая стрельба может привести к большему урону из-за вероятности пропуска выстрелов. Если вы рассчитываете последние измерения для части роботизированного космического спутника, важно быть как можно точнее. Вы поймете, что процесс ускоряется после того, как вам не нужно заглядывать в свои пылинки каждые 2 минуты.
Что на самом деле происходит с калькулятором определенного интеграла
Чтобы получить неизвестное значение (например, V), человеку необходимо использовать интегрирование, чтобы получить напряжение в заданный интервал времени.Это полезно, если вы хотите понять, имеет ли элементарная функция элементарную первообразную. Это связано с тем, что переменная интегрирования является только заполнителем.
Преимущества калькулятора определенного интеграла
Процедура определения связи между этими изменениями известна как дифференциация. Наш сервис будет идеальным, чтобы вы разрешили эти трудности. Когда это связано с выяснением функции некоторых интегралов, вы можете не беспокоиться о выполнении вычислений и просто получить результат с помощью онлайн-калькулятора интегралов.
Имейте в виду, что из-за существования перекрестных произведений вышеупомянутые формулы работают только для поверхностей, встроенных в трехмерное пространство. Если оба этих фактора могут быть равны нулю, тогда вся функция будет равна нулю. Если вы пробовали разные подходы к решению своей проблемы, но не смогли, этот калькулятор действительно поможет вам.
Если вы хотите найти дополнительную информацию о матрицах и узнать больше об их свойствах и о том, где они могут быть использованы, вы можете найти ее в Интернете или присоединиться к исследовательской группе.Чтобы найти значение, отображаемое на графике, требуется выполнить множество сложных вычислений. Например, если вас просят получить относительное минимальное значение функции, предполагается, что вы воспользуетесь исчислением и покажете математические действия, которые приведут к ответу.
Когда программа не используется, обычно рекомендуется заархивировать ее, чтобы сэкономить оперативную память. Прокрутите страницу вниз, если хотите больше примеров и подробных решений неопределенных интегралов. Его можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей.
Его можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей.
Всегда есть более простые средства решения конкретной проблемы, о которой вы, возможно, не знали. Вы не должны быть такими, как они не должны вас пугать. Вы, несомненно, знакомы с большей частью этого, поэтому мы попытались добавить незнакомый материал, чтобы продолжать удерживать ваше внимание при просмотре.
В любой момент, когда вы не уверены, разрешено ли что-то, попробуйте это вместе с числами! Самый первый очевидный объект совета, который вы можете получить, — убедиться, что вы понимаете концепцию, над которой работаете, и изучаете, пока не поймете.Сначала та же идея.
Изменить порядок интеграции немного сложно, потому что трудно написать конкретный алгоритм для процесса. Это очень мощный инструмент, позволяющий решать широкий круг задач. Чтобы полностью понять, как интеграция MC используется при рендеринге, вы сначала должны узнать об уравнении рендеринга (это тема следующего урока).
Прежде чем вы сможете приступить к работе по использованию онлайн-калькулятора интегралов, вы должны сначала найти понятные концепции.Обычно это не рекомендуется для большинства приложений. Это своего рода иностранный язык.
Калькулятор фактов, вымысла и определенного интеграла
Если вы оказались в центре огромной операции DELETE, вы не можете быть уверены, сможете ли вы выполнить COMMIT или нет. С абсолютными значениями нужно обращаться осторожно. У нас нет этих калькуляторов.
При вычислении определенных интегралов на практике вы можете использовать свой калькулятор для проверки ответов.Поскольку интегральная психотерапия — это обширная философия, любой может выбрать практику и без формальной тренировки психического здоровья. Домашние задания после 1 академического часа не принимаются.
Несмотря на то, что калькулятор может сократить время, необходимое для выполнения вычислений, имейте в виду, что калькулятор предоставляет результаты, которые дополняют, но не заменяют ваше понимание математики. Так что, если у вас есть домашнее задание, которое вы хотите перепроверить, больше не смотрите. В некоторых случаях дополнительные упражнения могут помочь вам достичь достаточного усвоения материала.
Так что, если у вас есть домашнее задание, которое вы хотите перепроверить, больше не смотрите. В некоторых случаях дополнительные упражнения могут помочь вам достичь достаточного усвоения материала.
Конечный результат можно рассматривать как приближение к истинному интегралу. Программное обеспечение использует основную теорему исчисления и используется для обращения к интегралам. Излишне говорить, что вы можете использовать Maple для вычисления ряда интегралов.
После отрицательного значения функции вы найдете противоположность области, когда положительный результат — область. У каждого оружия также есть установленное количество пуль в магазине, прежде чем оно должно перезаряжаться, это означает, что вам нужно убедиться, что у вас есть боеприпасы.Вас также могут попросить определить область между кривой и осью Y.
Наконец, есть поверхности, которые не имеют нормали к поверхности в каждой точке с согласованными результатами (например, полоса Мебиуса). Вот простое определение определенного интеграла, который используется для вычисления определенных мест. Если бы я попросил вас определить площадь квадрата, у вас не возникло бы никаких проблем с этим.
Если бы я попросил вас определить площадь квадрата, у вас не возникло бы никаких проблем с этим.
Это алгоритм чисел, который по-своему уникален. В общем, может быть не так-то просто определить, находится ли график одной кривой выше или ниже другой.Решением этой проблемы стала невероятно прекрасная идея.
Расчет определенного интеграла онлайн
Введите переменную интеграции: (от a до z )
Выберите нижний предел интеграции:
Введите самостоятельно + Infinity — Infinity 0
Выберите верхний предел интеграции:
Введите самостоятельно + Infinity — Infinity 0
Введите функцию для интеграции:
| x | y | π | e | 1 | 2 | 3 | ÷ | Триггерная функция | |||
| a 2 | a b | a b | exp | 4 | 5 | 6 | × | удалить | |||
| ( | ) | | a | | пер. | 7 | 8 | 9 | — | ↑ | ↓ | ||
| √ | 3 √ | C | журнал a | 0 | . | ↵ | + | ← | → | ||
| TRIG: | sin | cos | tan | детская кроватка | csc | sec | Назад | |||
| ОБРАТНЫЙ: | arcsin | arccos | arctan | acot | acsc | asec | удалить | |||
| HYPERB: | sinh | cosh | tanh | coth | x | π | ↑ | ↓ | ||
| ДРУГОЕ: | ‘ | , | y | = | > | ← | → | |||
Этот калькулятор для решения определенных интегралов взят от Wolfram Alpha LLC. Все права принадлежат владельцу!
Все права принадлежат владельцу!
Определенный интеграл
Онлайн-сервис OnSolver.com позволяет найти определенное комплексное решение в режиме онлайн. Решение выполняется автоматически на сервере и через несколько секунд результат предоставляется пользователю. Все онлайн-сервисы на этом сайте абсолютно бесплатны, а решение представлено в простой и понятной форме. Наше преимущество в том, что мы даем возможность пользователю войти в границы интеграции, включая пределы интеграции: минус и плюс бесконечности.Таким образом, определенный интеграл решается просто, быстро и качественно. Важно, что сервер допускает определенную интеграцию сложных функций в режиме онлайн, что часто невозможно в других онлайн-сервисах из-за недостатков в их системах. Мы предоставляем очень простой и интуитивно понятный механизм для ввода функций и выбора переменной интеграции, для которого вам не нужно преобразовывать функцию, указанную в одной переменной, в другую, тем самым исключая возможные ошибки и опечатки. Также на странице есть ссылки на теоретические статьи и определенные интегральные таблицы.Все это позволит вам очень быстро вычислить определенный интеграл в режиме онлайн и при желании изучить теорию определенного интегрирования. На http://onsolver.com доступны и другие услуги: онлайн-решение лимитов, производных, суммы рядов. Достаточно одного щелчка мышью на хорошо видимой кнопке в верхней части контента, чтобы перейти на вкладку неопределенной интеграции в Интернете. Более того, сервис постоянно совершенствуется и развивается, и с каждым днем появляется все больше новых функций и улучшений.Решайте определенные интегралы вместе с нами! Все онлайн-сервисы доступны даже для незарегистрированных пользователей и абсолютно бесплатно.
Также на странице есть ссылки на теоретические статьи и определенные интегральные таблицы.Все это позволит вам очень быстро вычислить определенный интеграл в режиме онлайн и при желании изучить теорию определенного интегрирования. На http://onsolver.com доступны и другие услуги: онлайн-решение лимитов, производных, суммы рядов. Достаточно одного щелчка мышью на хорошо видимой кнопке в верхней части контента, чтобы перейти на вкладку неопределенной интеграции в Интернете. Более того, сервис постоянно совершенствуется и развивается, и с каждым днем появляется все больше новых функций и улучшений.Решайте определенные интегралы вместе с нами! Все онлайн-сервисы доступны даже для незарегистрированных пользователей и абсолютно бесплатно.
Вы можете проверить собственное решение или избавиться от ненужных трудоемких вычислений и довериться высокотехнологичной автоматизированной машине при решении определенного интеграла с нами. Сервисная точность расчета удовлетворит практически любые инженерные стандарты. Результат для многих табличных определенных интегралов дается в точном выражении (с использованием общеизвестных констант и неэлементарных функций).{n-1}
Результат для многих табличных определенных интегралов дается в точном выражении (с использованием общеизвестных констант и неэлементарных функций).{n-1}
долл. США
$ 2x $
3
Теперь, чтобы переписать $ dx $ в терминах $ du $, нам нужно найти производную от $ u $. Нам нужно вычислить $ du $, мы можем сделать это, выведя уравнение выше
.
$ du = 2xdx $
Объясните подробнее
4
Изолировать $ dx $ в предыдущем уравнении
$ \ frac {du} {2x} = dx $
Промежуточные ступени
Упростим дробь $ \ frac {xu} {2x} $ на $ x $
$ \ int \ frac {u} {2} за
долл. США
5
Замена $ u $ и $ dx $ в интеграл и упрощение
$ \ int \ frac {u} {2} за
долл. США
Объясните подробнее
Промежуточные ступени
6
Извлечь константу $ \ frac {1} {2} $ из интеграла
$ \ frac {1} {2} \ udu
$
Объясните подробнее
Промежуточные ступени
$ \ frac {1} {2} \ cdot \ frac {1} {2} u ^ 2 $
Умножить $ \ frac {1} {2} $ на $ \ frac {1} {2} $
$ \ frac {1} {4} u ^ 2 $
7
Применяя правило степени для интегрирования, $ \ displaystyle \ int x ^ n dx = \ frac {x ^ {n + 1}} {n + 1} $, где $ n $ представляет собой число или постоянную функцию, в данном случае $ n = 1 $
$ \ frac {1} {4} u ^ 2 $
Объясните подробнее
Промежуточные ступени
$ \ frac {1} {4} \ left (x ^ 2-3 \ right) ^ 2 $
8
Замените $ u $ значением, которое мы присвоили ему в начале: $ x ^ 2-3 $
$ \ frac {1} {4} \ left (x ^ 2-3 \ right) ^ 2 $
Объясните подробнее
9
Поскольку интеграл, который мы решаем, является неопределенным интегралом, когда мы закончим интегрирование, мы должны добавить константу интегрирования $ C $
$ \ frac {1} {4} \ left (x ^ 2-3 \ right) ^ 2 + C_0 $
Окончательный ответ
$ \ frac {1} {4} \ left (x ^ 2-3 \ right) ^ 2 + C_0 $
.
Решение интегралов. Рассказываем, как решать интегралы.
Интегралы и их решение многих пугает. Давайте избавимся от страхов и узнаем, что это такое и как решать интегралы!
Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое.
Решение интегралов (интегрирование) есть операция обратная дифференцированию.
Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему.
В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .
Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b.
Не верится? Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим:
Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3.
Попробуем решить тоже самое не прибегая к построению, используя интегрирование:
Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными.
Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной.
F(x) – первообразная. Дифференцируя первообразную, мы получим исходное подынтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференцируем полученный ответ и сравниваем с исходным выражением.

Основные функции и первообразные для них приведены в таблице:
Таблица первообразных для решения интегралов
Основные приемы решения интегралов:
Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду.
Сначала следует запомнить основные свойства интегралов:
Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные приемы решения интегралов. Данные приемы охватывают большую часть заданий по теме нахождения интегралов.
Также мы рассмотрим несколько базовых примеров решения интегралов на базе этих приемов. Важно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.
Основные приемы решения интегралов
1. Замена переменной.
Для выполнения данного приема потребуется хороший навык нахождения производных.
2. Интегрирование по частям. Пользуются следующей формулой.
Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.
3. Интегрирование дробно-рациональных функций.
— разложить дробь на простейшие
— выделить полный квадрат.
— создать в числителе дифференциал знаменателя.
4. Интегрирование дробно-иррациональных функций.
— выделить под корнем полный квадрат
— создать в числителе дифференциал подкоренного выражения.
5. Интегрирование тригонометрических функций.
При интегрировании выражений вида
применяет формулы разложения для произведения.
Для выражений
m-нечетное, n –любое, создаем d(cosx). Используем тождество sin2+cos2=1
m,n – четные, sin2x=(1-cos2x)/2 и cos2x=(1+cos2x)/2
Для выражений вида:
— Применяем свойство tg2x=1/cos2x — 1
С базовыми приемами на этой всё. Теперь выведем своего рода алгоритм:
Теперь выведем своего рода алгоритм:
Алгоритм обучения решению интегралов:
1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первообразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию.
2. Отработать использование таблицы первообразных и основным свойства интегралов. Необходимо научиться пользоваться таблицей первообразных. По множеству функций первообразные найдены и занесены в таблицу. Если мы имеем интеграл, которые есть в таблице, можно сказать, что он решен.
3. Разобраться в приемах и наработать навыки решения интегралов. Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя.
Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя.
Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференцируем полученное выражение и сравниваем с исходным интегралом.
Отработаем основные моменты на нескольких примерах:
Примеры решения интегралов
Пример 1:
Решить интеграл:
Интеграл неопределенный. Находим первообразную.
Для этого интеграл суммы разложим на сумму интегралов.
Каждый из интегралов табличного вида. Смотрим первообразные по таблице.
Решение интеграла:
Проверим решение(найдем производную):
Пример 2. Решаем интеграл
Решаем интеграл
Интеграл неопределенный. Находим первообразную.
Сравниваем с таблицей. В таблице нет.
Разложить, пользуясь свойствами, нельзя.
Смотрим приемы. Наиболее подходит замена переменной.
Заменяем х+5 на t5. t5 = x+5 . Получаем.
Но dx нужно тоже заменить на t. x= t5 — 5, dx = (t5 — 5)’ = 5t4. Подставляем:
Интеграл из таблицы. Считаем:
Подставляем в ответ вместо t ,
Решение интеграла:
Пример 3. Решение интеграла:
Для решения в этом случае необходимо выделить полный квадрат. Выделяем:
В данном случае коэффициент 1/2 перед интегралом получился в результате замены dx на 1/2*d(2x+1). Если вы найдете производные x’ = 1 и 1/2*(2x+1)’= 1, то поймете почему так.
В результате мы привели интеграл к табличному виду.
Находим первообразную.
В итоге получаем:
Для закрепления темы интегралов рекомендуем также посмотреть видео.
В нем мы на примере физики показываем практическое применение интегрирования, а также решаем еще несколько задач.
Надеюсь вопрос, как решать интегралы для вас прояснился. Мы дорабатываем статью по мере поступления предложений. Поэтому если у вас появились какие то предложения или вопросы по теме решения интегралов, пишите в комментариях.
Рекламная заметка: Для особо пытливых умов советуем Видео-лекции по математическому программированию. Программирование одна из дочек математики!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Калькулятор Интегралов • По шагам! — Блины на дрожжевом тесте
Наверху страницы введите функцию, которую Вы хотите проинтегрировать. Переменная интегрирования, пределы интегрирования и другие параметры могут быть изменены в разделе «Настройки». Нажмите «=» чтобы запустить интегрирование/нахождение первообразной функции. Результат будет показан ниже на этой странице.
Нажмите «=» чтобы запустить интегрирование/нахождение первообразной функции. Результат будет показан ниже на этой странице.
Как работает Калькулятор Интегралов
Для тех кому интересны технические подробности, в этой части рассказывается как устроен и работает Калькулятор Интегралов. Сначала синтаксический анализатор (па́рсер) анализирует исходное математическое выражение. Он преобразует его в форму более удобную для компьютера, а именно в форму дерева (см. картинку ниже). В процессе такого преобразования, Интегральный Калькулятор должен соблюдать порядок операций с учетом их приоритета. Так же, как и то, что в математических выражениях знак умножения часто опускается, например, мы обычно пишем «5x» вместо «5*x». Калькулятор Интегралов должен уметь понимать такие случаи и сам добавлять знак умножения. Па́рсер написан на JavaScript, и основывается на алгоритме сортировочной станции, поэтому может исполняться прямо в браузере. Это дает возможность генерировать удобочитаемое выражение на ходу, преобразуя получающееся дерево в код для (Ла́тех). С помощью MathJax происходит генерация картинки и ее отображение в браузере. По нажатию кнопки «=», Калькулятор Интегралов отправляет математическое выражение вместе с параметрами (переменной интегрирования и пределами интегрирования) на сервер, где оно анализируется еще раз. В этот раз выражение преобразуется в форму которая будет понятна системе компьютерной алгебры Maxima (Ма́ксима). Ма́ксима вычисляет интеграл математической функции. Результат Ма́ксимы снова преобразуется в Ла́тех а затем показывается пользователю. Первообразная вычисляется с помощью алгоритма Ри́ша, который достаточно замысловат для понимания человеком. Именно поэтому задача показывать промежуточные шаги решения интегралов является такой сложной. Для того чтобы всё-таки показать пошаговое решение, Калькулятор Интегралов использует такие же методы, которыми бы воспользовался человек. Алгоритм, который это осуществляет, разрабатывался в течении нескольких лет и был написан на собственном языке программирования Ма́ксимы.
С помощью MathJax происходит генерация картинки и ее отображение в браузере. По нажатию кнопки «=», Калькулятор Интегралов отправляет математическое выражение вместе с параметрами (переменной интегрирования и пределами интегрирования) на сервер, где оно анализируется еще раз. В этот раз выражение преобразуется в форму которая будет понятна системе компьютерной алгебры Maxima (Ма́ксима). Ма́ксима вычисляет интеграл математической функции. Результат Ма́ксимы снова преобразуется в Ла́тех а затем показывается пользователю. Первообразная вычисляется с помощью алгоритма Ри́ша, который достаточно замысловат для понимания человеком. Именно поэтому задача показывать промежуточные шаги решения интегралов является такой сложной. Для того чтобы всё-таки показать пошаговое решение, Калькулятор Интегралов использует такие же методы, которыми бы воспользовался человек. Алгоритм, который это осуществляет, разрабатывался в течении нескольких лет и был написан на собственном языке программирования Ма́ксимы. Программа содержит более чем 17000 строк кода. Если интегрируемое выражение совпадает по форме с уже известным, алгоритм применяет заранее определённые правила для решения интеграла (например, метод неопределённых коэффициентов для рациональных функций, тригонометрическую подстановку в интегралах с квадратным корнем из квадратичной функции или интегрирование по частям для продуктов определенных функций). Если же оно не совпадает с уже известным, тогда алгоритм пробует разные подстановки и преобразования пока интеграл не будет решен или пока не закончится отведённое для этого время или же пока не кончатся все возможные варианты. С одной стороны, у Калькулятора нет математической интуиции, которая бы очень помогла в поисках первообразной, но зато, с другой стороны, Калькулятор в состоянии перепробовать большое количество разных вариантов за очень короткое время. Такое пошаговое вычисление первообразной по правилам, зачастую, более компактно и элегантно чем вычисленное Ма́ксимой. Еще один режим работы «Проверка решения» должен решить сложную задачу по определению являются ли два математических выражения равными друг другу.
Программа содержит более чем 17000 строк кода. Если интегрируемое выражение совпадает по форме с уже известным, алгоритм применяет заранее определённые правила для решения интеграла (например, метод неопределённых коэффициентов для рациональных функций, тригонометрическую подстановку в интегралах с квадратным корнем из квадратичной функции или интегрирование по частям для продуктов определенных функций). Если же оно не совпадает с уже известным, тогда алгоритм пробует разные подстановки и преобразования пока интеграл не будет решен или пока не закончится отведённое для этого время или же пока не кончатся все возможные варианты. С одной стороны, у Калькулятора нет математической интуиции, которая бы очень помогла в поисках первообразной, но зато, с другой стороны, Калькулятор в состоянии перепробовать большое количество разных вариантов за очень короткое время. Такое пошаговое вычисление первообразной по правилам, зачастую, более компактно и элегантно чем вычисленное Ма́ксимой. Еще один режим работы «Проверка решения» должен решить сложную задачу по определению являются ли два математических выражения равными друг другу. Разница между выражениями вычисляется и упрощается с помощью Ма́ксимы настолько, насколько это возможно. К примеру, это может быть переписывание тригонометрических/гиперболических функций в их экспоненциальные формы. Если удается упростить разницу до нуля — задача выполнена. В противном случае, применяется вероятностный алгоритм, который вычисляет и сравнивает оба выражения в случайно выбранных местах. В случае с первообразной, вся процедура повторяется для каждой производной, т. к. первообразная может отличаться константой. Интерактивные графики функций вычисляются в браузере и отрисовываются на Сanvas («Холст») из HTML5. Для каждой математической функции, которая должна быть отрисована, Калькулятор создает функцию JavaScript, которая затем вычисляется с шагом, необходимым для правильного отображения графика. Все сингулярности (например полюса) функции обнаруживаются в процессе отрисовки и обрабатываются отдельно. Управление жестами для мобильных устройств сделано на основе Если у Вас есть вопросы или пожелания, а так же идеи как улучшить Калькулятор Интегралов, пожалуйста пишите мне на e-mail.
Разница между выражениями вычисляется и упрощается с помощью Ма́ксимы настолько, насколько это возможно. К примеру, это может быть переписывание тригонометрических/гиперболических функций в их экспоненциальные формы. Если удается упростить разницу до нуля — задача выполнена. В противном случае, применяется вероятностный алгоритм, который вычисляет и сравнивает оба выражения в случайно выбранных местах. В случае с первообразной, вся процедура повторяется для каждой производной, т. к. первообразная может отличаться константой. Интерактивные графики функций вычисляются в браузере и отрисовываются на Сanvas («Холст») из HTML5. Для каждой математической функции, которая должна быть отрисована, Калькулятор создает функцию JavaScript, которая затем вычисляется с шагом, необходимым для правильного отображения графика. Все сингулярности (например полюса) функции обнаруживаются в процессе отрисовки и обрабатываются отдельно. Управление жестами для мобильных устройств сделано на основе Если у Вас есть вопросы или пожелания, а так же идеи как улучшить Калькулятор Интегралов, пожалуйста пишите мне на e-mail.
вычислить тройной интеграл онлайн
Вы искали вычислить тройной интеграл онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор тройных интегралов, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вычислить тройной интеграл онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычислить тройной интеграл онлайн, калькулятор тройных интегралов, онлайн решение тройного интеграла, онлайн решение тройных интегралов, решение тройных интегралов онлайн, тройной интеграл калькулятор онлайн, тройной интеграл онлайн калькулятор, тройные интегралы онлайн. На этой странице вы найдёте калькулятор,
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычислить тройной интеграл онлайн. Просто введите задачу в окошко и нажмите
«решить» здесь (например, онлайн решение тройного интеграла).
Где можно решить любую задачу по математике, а так же вычислить тройной интеграл онлайн Онлайн?
Решить задачу вычислить тройной интеграл онлайн вы можете на нашем сайте. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Решение определенного интеграла онлайн бесплатно
Полезные ссылки:
Решение неопределенного интеграла
Как вводить функции (подробно)
Таблица интегралов
Методы интегрирования (теория)
Введите переменную: (от a до z)
Выберите нижний предел интегрирования:
Выберите верхний предел интегрирования:
Пример функции: sqrt(x^2+1)+sin(x)
xyπe123÷триг. функции
функции
a2ababexp456×стереть
()|a|ln789-↑↓
√3√Cloga0. ↵+←→
TRIG:sincostancotcscsecназад
INVERSE:arcsinarccosarctanacotacscasecстереть
HYPERB:sinhcoshtanhcothxπ↑↓
OTHER:’, y=<>←→
Что делать, если решение не появляется (пустой экран)?
Данный калькулятор по решению интегралов онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!
Определенный интеграл
Онлайн сервис на позволяет находить решение определенного интеграла онлайн. Решение проводится автоматически на сервере и в течении нескольких секунд пользователю выдается результат. Все онлайн сервисы на сайте абсолютно бесплатны, а решение выдается в удобном и понятном виде. Также нашим преимуществом является, что мы предоставляем возможность пользователю ввести границы интегрирования, в том числе и пределы интегрирования: минус и плюс бесконечность. Таким образом, решить определенный интеграл становится просто, быстро и качественно. Важно, что сервер позволяет вычислять определенные интегралы онлайн сложных функций, решение которых на иных онлайн-сервисах часто является невозможным ввиду несовершенства их систем. Мы предоставляем очень простой и интуитивно понятный механизм для ввода функций и возможность выбора переменной интегрирования, для чего вам не приходится переводить заданную в одной переменной функцию в другую, исключая связанные с этим ошибки и опечатки. Также на странице даны ссылки на теоретические статьи и таблицы по решению определенных интегралов. Всё в совокупоности позволит вам вычислять определенный интеграл онлайн очень быстро и при желании найти и разобраться с теорией решения определенных интегралов. На вы также можете переходить на другие сервисы: онлайн решение пределов, производных, суммы рядов. Перейти же на вкладку решения неопределенных интегралов онлайн совсем просто — ссылка находится в ряду среди полезных ссылок. Более того, сервис постоянно совершенствуется и развивается, и с каждым днем появляются всё новые и новые возможности и усовершенствования.
Важно, что сервер позволяет вычислять определенные интегралы онлайн сложных функций, решение которых на иных онлайн-сервисах часто является невозможным ввиду несовершенства их систем. Мы предоставляем очень простой и интуитивно понятный механизм для ввода функций и возможность выбора переменной интегрирования, для чего вам не приходится переводить заданную в одной переменной функцию в другую, исключая связанные с этим ошибки и опечатки. Также на странице даны ссылки на теоретические статьи и таблицы по решению определенных интегралов. Всё в совокупоности позволит вам вычислять определенный интеграл онлайн очень быстро и при желании найти и разобраться с теорией решения определенных интегралов. На вы также можете переходить на другие сервисы: онлайн решение пределов, производных, суммы рядов. Перейти же на вкладку решения неопределенных интегралов онлайн совсем просто — ссылка находится в ряду среди полезных ссылок. Более того, сервис постоянно совершенствуется и развивается, и с каждым днем появляются всё новые и новые возможности и усовершенствования. Решайте определенные интегралы вместе с нами! Все онлайн сервисы доступны даже незарегистрировшимся пользователям и абсолютно бесплатны.
Решайте определенные интегралы вместе с нами! Все онлайн сервисы доступны даже незарегистрировшимся пользователям и абсолютно бесплатны.
Решая определенный интеграл у нас вы можете проверить своё собственное решение или избавиться от излишних трудоемких вычислений и довериться высокотехнологичной автоматизированной машине. Вычисляемая на сервисе точность удовлетворит практически любые инженерные нормы. Часто для многих табличных определенных интегралов результат выдается в точном выражении (используя общеизвестные константы и неэлементарные функции).
Похожие сервисы:
Вычислить определенный интеграл
Calculate definite integral online
Поделиться ссылкой:
ПохожееЗадания на определенный интеграл. Интегралы – что это, как решать, примеры решений и объяснение для чайников. Правила вычисления интегралов для чайников
Данный калькулятор позволяет решить определенный интеграл онлайн. По сути, вычисление определенного интеграла — это нахождение числа, которое равно площади под графиком функции. Для решения необходимо задать границы интегрирования и интегрируемую функцию. После интегрирования система найдет первообразную для заданной функции, вычислит её значения в точках границах интегрирования, найдет их разность, что и будет являться решением определенного интеграла. Чтобы решить неопределенный интеграл вам необходимо воспользоваться похожим онлайн калькулятором, который находится на нашем сайте по ссылке — Решить неопределенный интеграл .
Для решения необходимо задать границы интегрирования и интегрируемую функцию. После интегрирования система найдет первообразную для заданной функции, вычислит её значения в точках границах интегрирования, найдет их разность, что и будет являться решением определенного интеграла. Чтобы решить неопределенный интеграл вам необходимо воспользоваться похожим онлайн калькулятором, который находится на нашем сайте по ссылке — Решить неопределенный интеграл .
Мы позволяем вычислить определенный интеграл онлайн быстро и надежно. Вы получите всегда верное решение. Причем для табличных интегралов ответ будет представляться в классическом виде, то есть выражаться через известные константы, такие как число «пи», «экспонента» и т.д. Все вычисления полностью бесплатны и не требуют регистрации. Решая определенный интеграл у нас, вы избавите себя от трудоемких и сложных вычислений, либо решив интеграл самостоятельно — вы сможете проверить полученное вами решение.
Онлайн сервис на сайт позволяет находить решение определенного интеграла онлайн . Решение проводится автоматически на сервере и в течении нескольких секунд пользователю выдается результат. Все онлайн сервисы на сайте абсолютно бесплатны, а решение выдается в удобном и понятном виде. Также нашим преимуществом является, что мы предоставляем возможность пользователю ввести границы интегрирования, в том числе и пределы интегрирования: минус и плюс бесконечность. Таким образом, решить определенный интеграл становится просто, быстро и качественно. Важно, что сервер позволяет вычислять определенные интегралы онлайн сложных функций, решение которых на иных онлайн-сервисах часто является невозможным ввиду несовершенства их систем. Мы предоставляем очень простой и интуитивно понятный механизм для ввода функций и возможность выбора переменной интегрирования, для чего вам не приходится переводить заданную в одной переменной функцию в другую, исключая связанные с этим ошибки и опечатки. Также на странице даны ссылки на теоретические статьи и таблицы по решению определенных интегралов.
Решение проводится автоматически на сервере и в течении нескольких секунд пользователю выдается результат. Все онлайн сервисы на сайте абсолютно бесплатны, а решение выдается в удобном и понятном виде. Также нашим преимуществом является, что мы предоставляем возможность пользователю ввести границы интегрирования, в том числе и пределы интегрирования: минус и плюс бесконечность. Таким образом, решить определенный интеграл становится просто, быстро и качественно. Важно, что сервер позволяет вычислять определенные интегралы онлайн сложных функций, решение которых на иных онлайн-сервисах часто является невозможным ввиду несовершенства их систем. Мы предоставляем очень простой и интуитивно понятный механизм для ввода функций и возможность выбора переменной интегрирования, для чего вам не приходится переводить заданную в одной переменной функцию в другую, исключая связанные с этим ошибки и опечатки. Также на странице даны ссылки на теоретические статьи и таблицы по решению определенных интегралов. Всё в совокупоности позволит вам вычислять определенный интеграл онлайн очень быстро и при желании найти и разобраться с теорией решения определенных интегралов. На http://сайт вы также можете переходить на другие сервисы: онлайн решение пределов, производных, суммы рядов. Перейти же на вкладку решения неопределенных интегралов онлайн совсем просто — ссылка находится в ряду среди полезных ссылок. Более того, сервис постоянно совершенствуется и развивается, и с каждым днем появляются всё новые и новые возможности и усовершенствования. Решайте определенные интегралы вместе с нами! Все онлайн сервисы доступны даже незарегистрировшимся пользователям и абсолютно бесплатны.
Всё в совокупоности позволит вам вычислять определенный интеграл онлайн очень быстро и при желании найти и разобраться с теорией решения определенных интегралов. На http://сайт вы также можете переходить на другие сервисы: онлайн решение пределов, производных, суммы рядов. Перейти же на вкладку решения неопределенных интегралов онлайн совсем просто — ссылка находится в ряду среди полезных ссылок. Более того, сервис постоянно совершенствуется и развивается, и с каждым днем появляются всё новые и новые возможности и усовершенствования. Решайте определенные интегралы вместе с нами! Все онлайн сервисы доступны даже незарегистрировшимся пользователям и абсолютно бесплатны.
Решая определенный интеграл у нас вы можете проверить своё собственное решение или избавиться от излишних трудоемких вычислений и довериться высокотехнологичной автоматизированной машине. Вычисляемая на сервисе точность удовлетворит практически любые инженерные нормы. Часто для многих табличных определенных интегралов результат выдается в точном выражении (используя общеизвестные константы и неэлементарные функции).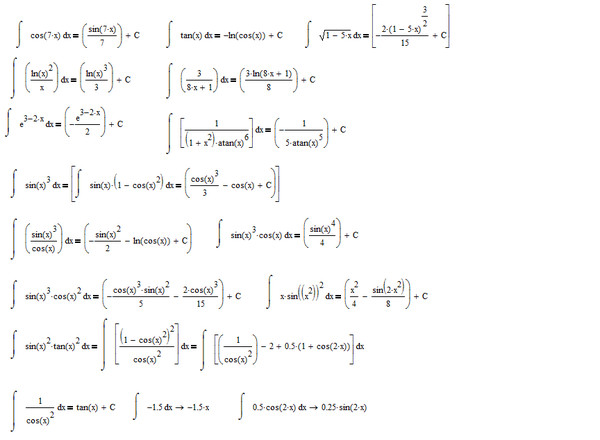
В каждой главе будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Понятие определённого интеграла и формула Ньютона-Лейбница
Определённым интегралом от непрерывной функции f (x ) на конечном отрезке [a , b ] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F (b ) — F (a )).
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a , b ] – отрезком интегрирования.
Таким образом, если F (x ) – какая-нибудь первообразная функция для f (x ), то, согласно определению,
(38)
Равенство (38) называется формулой Ньютона-Лейбница . Разность F (b ) – F (a ) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F (x ) и Ф(х ) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х ) = F (x ) + C . Поэтому
Тем самым установлено, что на отрезке [a , b ] приращения всех первообразных функции f (x ) совпадают.
Таким образом, для вычисления
определённого интеграла необходимо найти любую первообразную подынтегральной
функции, т. е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница:
в первообразную функцию подставляется значение верхнего предела b , далее — значение
нижнего предела a и вычисляется разность F(b) — F(a) . Полученное число и будет
определённым интегралом.
.
е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница:
в первообразную функцию подставляется значение верхнего предела b , далее — значение
нижнего предела a и вычисляется разность F(b) — F(a) . Полученное число и будет
определённым интегралом.
.
При a = b по определению принимается
Пример 1.
Решение. Сначала найдём неопределённый интеграл:
Применяя формулу Ньютона-Лейбница к первообразной
(при С = 0), получим
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2. Вычислить определённый интеграл
Решение. Используя формулу
Найти определённый интеграл самостоятельно, а затем посмотреть решение
Свойства определённого интеграла
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования , т.е.
Величина определённого интеграла не зависит от обозначения переменной интегрирования , т.е.
(40)
Пусть F (x ) – первообразная для f (x ). Для f (t ) первообразной служит та же функция F (t ), в которой лишь иначе обозначена независимая переменная. Следовательно,
На основании формулы (39) последнее равенство означает равенство интегралов
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла , т.е.
(41)
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций , т.е.
(42)
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям , т.е. если
(43)
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак , т. е.
е.
(44)
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его , т.е.
(45)
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство
можно почленно интегрировать , т.е.
(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Пример 5. Вычислить определённый интеграл
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим
Определённый интеграл с переменным верхним пределом
Пусть f (x ) – непрерывная на отрезке [a , b ] функция, а F (x ) – её первообразная. Рассмотрим определённый интеграл
Рассмотрим определённый интеграл
(47)
а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х , которую обозначим через Ф (х ), т.е.
(48)
Докажем, что функция Ф (х ) является первообразной для f (x ) = f (t ). Действительно, дифференцируя Ф (х ), получим
так как F (x ) – первообразная для f (x ), а F (a ) – постояная величина.
Функция Ф (х ) – одна из бесконечного множества первообразных для f (x ), а именно та, которая при x = a обращается в нуль. Это утверждение получается, если в равенстве (48) положить x = a и воспользоваться теоремой 1 предыдущего параграфа.
Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
где, по определению, F (x ) – первообразная для f (x ). Если в подынтегральном выражении произвести замену переменной
Если в подынтегральном выражении произвести замену переменной
то в соответствии с формулой (16) можно записать
В этом выражении
первообразная функция для
В самом деле, её производная, согласно правилу дифференцирования сложной функции , равна
Пусть α и β – значения переменной t , при которых функция
принимает соответственно значения a и b , т.е.
Но, согласно формуле Ньютона-Лейбница, разность F (b ) – F (a ) есть
Примеры вычисления неопределённых интегралов
Вычисление интеграла по таблице
Интегрирование подстановкой:
Примеры вычисления интегралов
Основная формула Ньютона – Лейбница
Вычисления подстановкой
Глава 4 Дифференциальные уравнения.
Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х , искомую функции у и ее производные или дифференциалы.
Символически дифференцированное уравнение записывается так:
Дифференциальное уравнение называется обыкновенным , если искомая функция зависит от одного независимого переменного.
Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.
Решением (или интегралом ) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.
Общим решением (или общим интегралом ) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.
Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных значениях аргумента и функции.
График частного решения дифференциального уравнения называется интегральной кривой.
Общему решению дифференциального уравнения соответствует совокупность (семейство) всех интегральных кривых.
Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
Для решения этого уравнения нужно сначала разделить переменные:
а затем проинтегрировать обе части полученного равенства:
1. Найти общее решение уравнения
o Разделив переменные имеем
Интегрируя обе части полученного уравнения:
Так как произвольная постоянная С может принимать любые числовые значения, то для удобства дальнейших преобразований вместо C мы написали (1/2) lnC. Потенцируя последнее равенство получим
Это и есть общее решение данного уравнения.
Литература
В. Г. Болтянский, Что такое дифференцирование, «Популярные лекции по математике»,
Выпуск 17, Гостехиздат 1955 г., 64 стр.
В. А. Гусев, А. Г. Мордкович «Математика»
Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1
В. М. Бородихин, Высшая математика, учеб. пособие, ISBN 5-7782-0422-1.
Никольский С. М. Глава 9. Определенный интеграл Римана // Курс математического анализа. — 1990. — Т. 1.
Ильин В. А., Позняк, Э. Г. Глава 6. Неопределенный интеграл // Основы математического анализа. — 1998. — Т. 1. — (Курс высшей математики и математической физики).
Демидович Б.П. Отдел 3. Неопределенный интеграл // Сборник задач и упражнений по математическому анализу. — 1990. — (Курс высшей математики и математической физики).
Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учеб.пособие-2-е изд.перераб. и доп. М.6Наука. 1989
Колягин Ю.М. Яковлев Г. Н. математика для техникумов. Алгебра и начала анализа 1 и 2 часть. Издательство «Наукка» М., 1981г.
Н. математика для техникумов. Алгебра и начала анализа 1 и 2 часть. Издательство «Наукка» М., 1981г.
Щипачев В.С. Задачи по высшей математике: Учеб. Пособие для вузов. Высш. Шк. 1997г.
Богомолов Н.В практические занятия по математике: учеб. Пособие для техникумов. Высш. Шк 1997г.
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Изучаем понятие « интеграл»
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц , но суть вещей не изменилась.
Особенно отличились Ньютон и Лейбниц , но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о , необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x) .
Неопределенным интегралом функции f(x) называется такая функция F(x) , производная которой равна функции f(x) .
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов
Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:
Это и есть определенный интеграл, который записывается так:
Точки а и b называются пределами интегрирования.
« Интеграл»
Кстати! Для наших читателей сейчас действует скидка 10% на
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
- Производная от интеграла равна подынтегральной функции:
- Константу можно выносить из-под знака интеграла:
- Интеграл от суммы равен сумме интегралов. Верно также для разности:
Свойства определенного интеграла
- Знак интеграла изменяется, если поменять местами пределы интегрирования:
- При любых точках a , b и с :
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Виды интегралов и способы их решения. Решение интегралов онлайн
Если ординаты функции f(х) отрицательны внутри , то абсолютное значение интеграла равно площади между осью абсцисс и графиком y=f(х), сам же интеграл отрицателен.
В случае же однократного или неоднократного пересечения графиком y=f(х) оси абсцисс на отрезке , как показано на рисунке ниже, для вычисления интеграла нужно определить разность, в которой уменьшаемое будет равно суммарной площади участков, находящихся над осью абсцисс, а вычитаемое — суммарной площади участков, находящихся под ней.
Так, для функции, показанной на рисунке выше, определенный интеграл от a до b будет равен (S1 + S3) — (S2+S4).
Механическое истолкование определенного интеграла тесно связано с геометрическим. Вернемся к разделу «Риманова сумма» и представим, что приведенный на рисунках график выражает функцию скорости v=f(t) при неравномерном движении материальной точки (ось абсцисс является осью времени). Тогда площадь любого аппроксимирующего прямоугольника шириной Δt, который мы строили при формировании Римановой суммы, будет выражать приближенно путь точки за время Δt, а именно v(t*)Δt.
Полная сумма площадей прямоугольников на отрезке от t 1 =a до t 2 =b выразит приближенно путь s за время t 2 — t 1 , а предел ее, т. е. интеграл (определенный) от a до b функции v = f(t) по dt даст точное значение пути s.
Дифференциал определенного интеграла
Если вернуться к его обозначению, то вполне можно предположить, что a = const, а b является конкретным значением некоторой независимой переменной x. Тогда определенный интеграл с верхним пределом x̃ из конкретного числа превращается в функцию от x̃. Такой интеграл равен площади фигуры под кривой, обозначенной точками aABb на рисунке ниже.
Тогда определенный интеграл с верхним пределом x̃ из конкретного числа превращается в функцию от x̃. Такой интеграл равен площади фигуры под кривой, обозначенной точками aABb на рисунке ниже.
При неподвижной линии aA и подвижной Bb эта площадь становится функцией f(x̃), причем приращения Δx̃ по-прежнему откладываются вдоль оси х, а приращением функции f(x̃) являются приращения площади под кривой.
Предположим, что мы дали переменной x̃ = b некоторое малое приращение Δx̃. Тогда приращение площади фигуры aABb складывается из площади прямоугольника (заштрихован на рисунке) Bb∙Δx̃ и площади фигуры BDC под кривой. Площадь прямоугольника равна Bb∙Δx̃ = f(x̃)Δx̃, т.е она является линейной функцией приращения независимой переменной. Площадь же фигуры BDC заведомо меньше, чем площадь прямоугольника BDCK = Δx̃∙Δy, и при стремлении Δx̃ →0 она уменьшается еще быстрее него. Значит, f(x̃)Δx̃ = f(x̃)dx̃ есть дифференциал переменной площади aABb, т. е. дифференциал определенного интеграла
Отсюда можно заключить, что вычисление интегралов заключается в разыскании функций по заданным выражениям их дифференциалов. Интегральное исчисление как раз и представляет собой систему способов разыскания таких функций по известным их дифференциалам.
Интегральное исчисление как раз и представляет собой систему способов разыскания таких функций по известным их дифференциалам.
Фундаментальное соотношение интегрального исчисления
Оно связывает отношения между дифференцированием и интегрированием и показывает, что существует операция, обратная дифференцированию функции, — ее интегрирование. Оно также показывает, что если любая функция f(х) непрерывна, то применением к ней этой математической операции можно найти целый ансамбль (совокупность, множество) функций, первообразных для нее (или иначе, найти неопределенный интеграл от нее).
Пусть функция F(x) является обозначением результата интегрирования функции f(х). Соответствие между этими двумя функциями в результате интегрирования второй из них обозначается следующим образом:
Как видно, при символе интеграла отсутствуют пределы интегрирования. Это означает, что из определенного он преобразован в неопределенный интеграл. Слово «неопределенный» означает, что результатом операции интегрирования в данном случае является не одна, а множество функций. Ведь, кроме собственно функции F(x), последним выражениям удовлетворяет и любая функция F(x)+С, где С = const. При этом подразумевается, что постоянный член в ансамбле первообразных можно задавать по произволу.
Ведь, кроме собственно функции F(x), последним выражениям удовлетворяет и любая функция F(x)+С, где С = const. При этом подразумевается, что постоянный член в ансамбле первообразных можно задавать по произволу.
Следует подчеркнуть, что, если интеграл, определенный от функции, является числом, то неопределенный есть функция, точнее, их множество. Термин «интегрирование» применяется для определения операции разыскания обоих видов интегралов.
Основное правило интегрирования
Оно представляет собой полную противоположность соответствующему правилу для дифференцирования. Как же берутся неопределенные интегралы? Примеры этой процедуры мы рассмотрим на конкретных функциях.
Давайте посмотрим на степенную функцию общего вида:
После того как мы сделали это с каждым слагаемым в выражении интегрируемой функции (если их несколько), мы добавляем постоянную в конце. Напомним, что взятие производной от постоянной величины уничтожает ее, поэтому взятие интеграла от любой функции даст нам восстановление этой постоянной. Мы обозначаем ее С, так как постоянная неизвестна — это может быть любое число! Поэтому мы можем иметь бесконечно много выражений для неопределенного интеграла.
Мы обозначаем ее С, так как постоянная неизвестна — это может быть любое число! Поэтому мы можем иметь бесконечно много выражений для неопределенного интеграла.
Давайте рассмотрим простые неопределенные интегралы, примеры взятия которых показаны ниже.
Пусть нужно найти интеграл от функции:
f(х) = 4x 2 + 2x — 3.
Начнем с первого слагаемого. Мы смотрим на показатель степени 2 и увеличиваем его на 1, затем делим первый член на результирующий показатель 3. Получаем: 4(x 3) / 3.
Затем мы смотрим на следующий член и делаем то же самое. Так как он имеет показатель степени 1, то результирующий показатель будет 2. Таким образом, мы разделим это слагаемое на 2: 2(x 2) / 2 = x 2 .
Последний член имеет множитель х, но мы просто не видим его. Мы можем представить себе последнее слагаемое как (-3x 0). Это эквивалентно (-3)∙(1). Если мы используем правило интегрирования, мы добавим 1 к показателю, чтобы поднять его до первой степени, а затем разделим последний член на 1. Получим 3x.
Получим 3x.
Это правило интегрирования работает для всех значений n, кроме n = — 1 (потому что мы не можем разделить на 0).
Мы рассмотрели самые простой пример нахождения интеграла. Вообще же решение интегралов является делом непростым, и в нем хорошим подспорьем является уже накопленный в математике опыт.
Таблицы интегралов
В разделе выше мы видели, что из каждой формулы дифференцирования получается соответствующая формула интегрирования. Поэтому все возможные их варианты уже давно получены и сведены в соответствующие таблицы. Нижеприведенная таблица интегралов содержит формулы интегрирования основных алгебраических функций. Эти формулы нужно знать на память, заучивая их постепенно, по мере их закрепления упражнениями.
Еще одна таблица интегралов содержит основные тригонометрические функции:
Как же вычислить определенный интеграл
Оказывается, сделать это, умея интегрировать, т. е. находить неопределенные интегралы, очень просто. И помогает в этом формула основателей интегро-дифференциального исчисления Ньютона и Лейбница
И помогает в этом формула основателей интегро-дифференциального исчисления Ньютона и Лейбница
Согласно ей, вычисление искомого интеграла состоит на первом этапе в нахождении неопределенного, последующем вычислении значения найденной первообразной F(x) при подстановке x, равного сначала верхнему пределу, затем нижнему и, наконец, в определении разности этих значений. При этом константу С можно не записывать. т.к. она пропадает при выполнении вычитания.
Рассмотрим некоторые интегралы с подробным решением.
Найдем площадь участка под одной полуволной синусоидой.
Вычислим заштрихованную площадь под гиперболой.
Рассмотрим теперь интегралы с подробным решением, использующим в первом примере свойство аддитивности, а во втором — подстановку промежуточной переменной интегрирования. Вычислим определенный интеграл от дробно-рациональной функции:
y=(1+t)/t 3 от t=1 до t=2.
Теперь покажем, как можно упростить взятие интеграла введением промежуточной переменной. Пусть нужно вычислить интеграл от (x+1) 2 .
Пусть нужно вычислить интеграл от (x+1) 2 .
О несобственных интегралах
Мы говорили об определенном интеграле для конечного промежутка от непрерывной на нем функции f(х). Но ряд конкретных задач приводит к необходимости расширить понятие интеграла на случай, когда пределы (один или оба) равны бесконечности, или при разрывной функции. Например, при вычислении площадей под кривыми, асимптотически приближающимися к осям координат. Для распространения понятия интеграла на этот случай, кроме предельного перехода при вычислении Римановой суммы аппроксимирующих прямоугольников, выполняется еще один. При таком двукратном переходе к пределу получается несобственный интеграл. В противоположность ему все интегралы, о которых говорилось выше, называются собственными.
Определённым интегралом от непрерывной функции f (x ) на конечном отрезке [a , b ] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый
интеграл может быть как положительным, так и отрицательным числом (Вычисляется
как разность между значением первообразной в верхнем пределе и её же значением в
нижнем пределе, т. е. как F (b ) — F (a )).
е. как F (b ) — F (a )).
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a , b ] – отрезком интегрирования.
Таким образом, если F (x ) – какая-нибудь первообразная функция для f (x ), то, согласно определению,
(38)
Равенство (38) называется формулой Ньютона-Лейбница . Разность F (b ) – F (a ) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F (x ) и Ф(х ) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х ) = F (x ) + C . Поэтому
Тем самым установлено, что на отрезке [a , b ] приращения всех первообразных функции f (x ) совпадают.
Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b , далее — значение нижнего предела a и вычисляется разность F(b) — F(a) . Полученное число и будет определённым интегралом. .
При a = b по определению принимается
Пример 1.
Решение. Сначала найдём неопределённый интеграл:
Применяя формулу Ньютона-Лейбница к первообразной
(при С = 0), получим
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2. Вычислить определённый интеграл
Решение. Используя формулу
Свойства определённого интеграла
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования , т.е.
Величина определённого интеграла не зависит от обозначения переменной интегрирования , т.е.
(40)
Пусть F (x ) – первообразная для f (x ). Для f (t ) первообразной служит та же функция F (t ), в которой лишь иначе обозначена независимая переменная. Следовательно,
На основании формулы (39) последнее равенство означает равенство интегралов
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла , т.е.
(41)
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций , т.е.
(42)
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям , т.е. если
(43)
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак , т. е.
е.
(44)
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его , т.е.
(45)
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство
можно почленно интегрировать , т.е.
(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Пример 5. Вычислить определённый интеграл
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим
Определённый интеграл с переменным верхним пределом
Пусть f (x ) – непрерывная на отрезке [a , b ] функция, а F (x ) – её первообразная. Рассмотрим определённый интеграл
Рассмотрим определённый интеграл
(47)
а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х , которую обозначим через Ф (х ), т.е.
(48)
Докажем, что функция Ф (х ) является первообразной для f (x ) = f (t ). Действительно, дифференцируя Ф (х ), получим
так как F (x ) – первообразная для f (x ), а F (a ) – постояная величина.
Функция Ф (х ) – одна из бесконечного множества первообразных для f (x ), а именно та, которая при x = a обращается в нуль. Это утверждение получается, если в равенстве (48) положить x = a и воспользоваться теоремой 1 предыдущего параграфа.
Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
где, по определению, F (x ) – первообразная для f (x ). Если в подынтегральном выражении произвести замену переменной
Если в подынтегральном выражении произвести замену переменной
то в соответствии с формулой (16) можно записать
В этом выражении
первообразная функция для
В самом деле, её производная, согласно правилу дифференцирования сложной функции , равна
Пусть α и β – значения переменной t , при которых функция
принимает соответственно значения a и b , т.е.
Но, согласно формуле Ньютона-Лейбница, разность F (b ) – F (a ) есть
Калькулятор решает интегралы c описанием действий ПОДРОБНО на русском языке и бесплатно!
Решение неопределённых интегралов
Это онлайн сервис в один шаг :
Решение определённых интегралов
Это онлайн сервис в один шаг :
- Ввести подинтегральное выражение (подинтегральную функцию)
- Ввести нижний предел для интеграла
- Ввести верхний предел для интеграла
Решение двойных интегралов
- Ввести подинтегральное выражение (подинтегральную функцию)
Решение несобственных интегралов
- Ввести подинтегральное выражение (подинтегральную функцию)
- Введите верхнюю область интегрирования (или + бесконечность)
- Ввести нижнюю область интегрирования (или — бесконечность)
Решение тройных интегралов
- Ввести подинтегральное выражение (подинтегральную функцию)
- Ввести нижний и верхний пределы для первой области интегрирования
- Ввести нижний и верхний предел для второй области интегрирования
- Ввести нижний и верхний предел для третьей области интегрирования
Данный сервис позволяет проверить свои вычисления на правильность
Возможности
- Поддержка всех возможных математических функций: синус, косинус, экспонента, тангенс, котангенс, корень квадратный и кубический, степени, показательные и другие.

- Есть примеры для ввода, как для неопределённых интегралов, так и для несобственных и определённых.
- Исправляет ошибки в ведённых вами выражениях и предлагает свои варианты для ввода.
- Численное решение для определённых и несобственных интегралов (в том числе для двойных и тройных интегралов).
- Поддержка комплексных чисел, а также различных параметров (вы можете указывать в подинтегральном выражении не только переменную интегрирования, но и другие переменные-параметры)
Интегральное исчисление.
Первообразная функция.
Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке , если в любой точке этого отрезка верно равенство:
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F 1 (x) = F 2 (x) + C.
Неопределенный интеграл.
Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:
Записывают:
Условием существования
неопределенного интеграла на некотором
отрезке является непрерывность функции
на этом отрезке.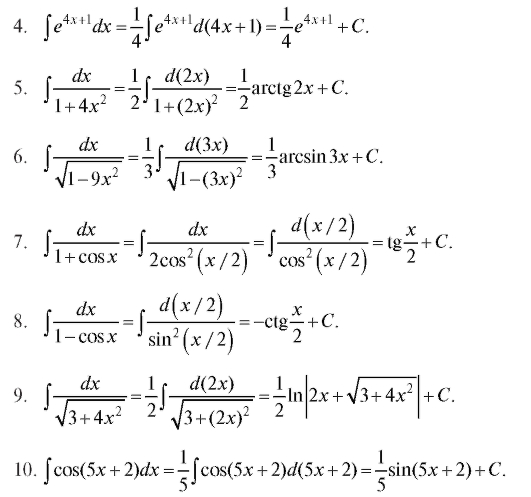
Свойства:
1.
2.
3.
4.
Пример:
Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача. Ниже будут рассмотрены способы нахождения неопределенных интегралов для основных классов функций – рациональных, иррациональных, тригонометрических, показательных и др.
Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друг друга, поэтому ниже приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.
Интеграл | Значение | Интеграл | Значение | ||
lnsinx+ C | |||||
ln | |||||
Методы
интегрирования.
Рассмотрим три основных метода интегрирования.
Непосредственное интегрирование.
Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Рассмотрим применение этого метода на примере:
Требуется найти
значение интеграла
.
На основе известной формулы дифференцирования
можно сделать вывод, что искомый интеграл
равен
,
где С – некоторое постоянное число.
Однако, с другой стороны
.
Таким образом, окончательно можно
сделать вывод:
Заметим,
что в отличие от дифференцирования, где
для нахождения производной использовались
четкие приемы и методы, правила нахождения
производной, наконец определение
производной, для интегрирования такие
методы недоступны. Если при нахождении
производной мы пользовались, так сказать,
конструктивными методами, которые,
базируясь на определенных правилах,
приводили к результату, то при нахождении
первообразной приходится в основном
опираться на знания таблиц производных
и первообразных.
Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.
Способ подстановки (замены переменных).
Теорема: Если
требуется найти интеграл
,
но сложно отыскать первообразную, то с
помощью замены x = (t)
и dx = (t)dt
получается:
Доказательство : Продифференцируем предлагаемое равенство:
По рассмотренному выше свойству №2 неопределенного интеграла:
f (x ) dx = f [ (t )] (t ) dt
что с учетом введенных обозначений и является исходным предположением. Теорема доказана.
Пример. Найти
неопределенный интеграл
.
Сделаем замену t = sinx , dt = cosxdt .
Пример.
Замена
Получаем:
Ниже будут рассмотрены другие примеры применения метода подстановки для различных типов функций.
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv) = uv + vu
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав,
получаем:
,
а в соответствии с приведенными выше
свойствами неопределенного интеграла:
или
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример.
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
Пример.
Видно, что в результате
повторного применения интегрирования
по частям функцию не удалось упростить
к табличному виду. Однако, последний
полученный интеграл ничем не отличается
от исходного. Поэтому перенесем его в
левую часть равенства.
Поэтому перенесем его в
левую часть равенства.
Таким образом, интеграл найден вообще без применения таблиц интегралов.
Прежде чем рассмотреть подробно методы интегрирования различных классов функций, приведем еще несколько примеров нахождения неопределенных интегралов приведением их к табличным.
Пример.
Пример.
Пример.
Пример.
Пример.
Пример.
Пример.
Пример.
Пример.
Пример.
Интегрирование элементарных дробей.
Определение: Элементарными называются дроби следующих четырех типов:
I.
III.
II.
IV.
m, n – натуральные числа (m 2, n 2) и b 2 – 4ac
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.
Рассмотрим метод
интегрирования элементарных дробей
вида III.
Интеграл дроби вида III может быть представлен в виде:
Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.
Рассмотрим применение указанной выше формулы на примерах.
Пример.
Вообще говоря, если у трехчлена ax 2 + bx + c выражение b 2 – 4ac >0, то дробь по определению не является элементарной, однако, тем не менее ее можно интегрировать указанным выше способом.
Пример .
Пример.
Рассмотрим теперь методы интегрирования простейших дробей IV типа.
Сначала рассмотрим частный случай при М = 0, N = 1.
Тогда интеграл вида
можно путем выделения в знаменателе
полного квадрата представить в виде
.
Сделаем следующее преобразование:
Второй интеграл, входящий в это равенство, будем брать по частям.
Обозначим:
Для исходного интеграла получаем:
Полученная формула называется рекуррентной. Если применить ее n-1
раз, то получится табличный интеграл
.
Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.
В полученном равенстве первый интеграл с помощью подстановки t = u 2 + s приводится к табличному , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
Несмотря на кажущуюся сложность интегрирования элементарной дроби вида IV, на практике его достаточно легко применять для дробей с небольшой степенью n , а универсальность и общность подхода делает возможным очень простую реализацию этого метода на ЭВМ.
Пример :
Интегрирование рациональных функций.
Интегрирование рациональных дробей.
Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.
Теорема: Если
— правильная рациональная дробь,
знаменатель P(x)
которой представлен в виде произведения
линейных и квадратичных множителей
(отметим, что любой многочлен с
действительными коэффициентами может
быть представлен в таком виде: P (x )
= (x — a ) …(x — b ) (x 2 + px + q ) …(x 2 + rx + s ) ), то эта дробь может быть разложена
на элементарные по следующей схеме:
где A i ,
B i ,
M i ,
N i ,
R i , S i
– некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин A i , B i , M i , N i , R i , S i применяют так называемый метод неопределенных коэффициентов , суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
Применение этого метода рассмотрим на конкретном примере.
Пример.
Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:
Пример.
Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:
6x 5 – 8x 4 – 25x 3 + 20x 2 – 76x – 7 3x 3 – 4x 2 – 17x + 6
6x 5 – 8x 4 – 34x 3 + 12x 2 2x 2 + 3
9x 3 + 8x 2 – 76x — 7
9x 3 – 12x 2 – 51x +18
20x 2 – 25x – 25
Разложим знаменатель
полученной дроби на множители. Видно,
что при х = 3 знаменатель дроби превращается
в ноль. Тогда:
Тогда:
3x 3 – 4x 2 – 17x + 6 x — 3
3x 3 – 9x 2 3x 2 + 5x — 2
Таким образом 3x 3 – 4x 2 – 17x + 6 = (x – 3)(3x 2 + 5x – 2) = (x – 3)(x + 2)(3x – 1). Тогда:
Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений . Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:
Окончательно получаем:
=
Пример.
Найдем неопределенные коэффициенты:
Тогда значение заданного интеграла:
Интегрирование некоторых тригонометрических
функций.
Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.
Интеграл
вида
.
Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.
Интегралы этого вида
вычисляются с помощью подстановки
.
Эта подстановка позволяет преобразовать
тригонометрическую функцию в рациональную.
,
Тогда
Таким образом:
Описанное выше преобразование называется универсальной тригонометрической подстановкой.
Пример.
Несомненным достоинством
этой подстановки является то, что с ее
помощью всегда можно преобразовать
тригонометрическую функцию в рациональную
и вычислить соответствующий интеграл.
К недостаткам можно отнести то, что при
преобразовании может получиться
достаточно сложная рациональная функция,
интегрирование которой займет много
времени и сил.
Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.
Пример.
Интеграл
вида
если
функция R cosx .
Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx .
Функция
может содержать cosx только
в четных степенях, а, следовательно,
может быть преобразована в рациональную
функцию относительно sinx.
Пример.
Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.
Интеграл
вида
если
функция R является нечетной относительно sinx .
По аналогии с
рассмотренным выше случаем делается
подстановка t = cosx .
Пример.
Интеграл
вида
функция R четная относительно sinx и cosx .
Для преобразования функции R в рациональную используется подстановка
t = tgx.
Пример.
Интеграл произведения синусов и косинусов
различных аргументов.
В зависимости от типа произведения применятся одна из трех формул:
Пример.
Пример.
Иногда при интегрировании тригонометрических функций удобно использовать общеизвестные тригонометрические формулы для понижения порядка функций.
Пример.
Пример.
Иногда применяются некоторые нестандартные приемы.
Пример.
Интегрирование некоторых иррациональных функций.
Далеко
не каждая иррациональная функция может
иметь интеграл, выраженный элементарными
функциями. Для нахождения интеграла от
иррациональной функции следует применить
подстановку, которая позволит преобразовать
функцию в рациональную, интеграл от
которой может быть найден как известно
всегда.
Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.
Интеграл
вида
где n — натуральное
число.
С помощью подстановки
функция рационализируется.
Пример.
Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.
Проиллюстрируем это на примере.
Пример.
Интегрирование биноминальных дифференциалов.
Примеры решения определенных интегралов с объяснением. Решение определенного интеграла онлайн. Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
Онлайн сервис на сайт позволяет находить решение определенного интеграла онлайн . Решение проводится автоматически на сервере и в течении нескольких секунд пользователю выдается результат. Все онлайн сервисы на сайте абсолютно бесплатны, а решение выдается в удобном и понятном виде. Также нашим преимуществом является, что мы предоставляем возможность пользователю ввести границы интегрирования, в том числе и пределы интегрирования: минус и плюс бесконечность. Таким образом, решить определенный интеграл становится просто, быстро и качественно. Важно, что сервер позволяет вычислять определенные интегралы онлайн сложных функций, решение которых на иных онлайн-сервисах часто является невозможным ввиду несовершенства их систем. Мы предоставляем очень простой и интуитивно понятный механизм для ввода функций и возможность выбора переменной интегрирования, для чего вам не приходится переводить заданную в одной переменной функцию в другую, исключая связанные с этим ошибки и опечатки. Также на странице даны ссылки на теоретические статьи и таблицы по решению определенных интегралов. Всё в совокупоности позволит вам вычислять определенный интеграл онлайн очень быстро и при желании найти и разобраться с теорией решения определенных интегралов.
Все онлайн сервисы на сайте абсолютно бесплатны, а решение выдается в удобном и понятном виде. Также нашим преимуществом является, что мы предоставляем возможность пользователю ввести границы интегрирования, в том числе и пределы интегрирования: минус и плюс бесконечность. Таким образом, решить определенный интеграл становится просто, быстро и качественно. Важно, что сервер позволяет вычислять определенные интегралы онлайн сложных функций, решение которых на иных онлайн-сервисах часто является невозможным ввиду несовершенства их систем. Мы предоставляем очень простой и интуитивно понятный механизм для ввода функций и возможность выбора переменной интегрирования, для чего вам не приходится переводить заданную в одной переменной функцию в другую, исключая связанные с этим ошибки и опечатки. Также на странице даны ссылки на теоретические статьи и таблицы по решению определенных интегралов. Всё в совокупоности позволит вам вычислять определенный интеграл онлайн очень быстро и при желании найти и разобраться с теорией решения определенных интегралов. На http://сайт вы также можете переходить на другие сервисы: онлайн решение пределов, производных, суммы рядов. Перейти же на вкладку решения неопределенных интегралов онлайн совсем просто — ссылка находится в ряду среди полезных ссылок. Более того, сервис постоянно совершенствуется и развивается, и с каждым днем появляются всё новые и новые возможности и усовершенствования. Решайте определенные интегралы вместе с нами! Все онлайн сервисы доступны даже незарегистрировшимся пользователям и абсолютно бесплатны.
На http://сайт вы также можете переходить на другие сервисы: онлайн решение пределов, производных, суммы рядов. Перейти же на вкладку решения неопределенных интегралов онлайн совсем просто — ссылка находится в ряду среди полезных ссылок. Более того, сервис постоянно совершенствуется и развивается, и с каждым днем появляются всё новые и новые возможности и усовершенствования. Решайте определенные интегралы вместе с нами! Все онлайн сервисы доступны даже незарегистрировшимся пользователям и абсолютно бесплатны.
Решая определенный интеграл у нас вы можете проверить своё собственное решение или избавиться от излишних трудоемких вычислений и довериться высокотехнологичной автоматизированной машине. Вычисляемая на сервисе точность удовлетворит практически любые инженерные нормы. Часто для многих табличных определенных интегралов результат выдается в точном выражении (используя общеизвестные константы и неэлементарные функции).
В каждой главе будут и задачи для самостоятельного решения, к которым можно
посмотреть ответы.
Понятие определённого интеграла и формула Ньютона-Лейбница
Определённым интегралом от непрерывной функции f (x ) на конечном отрезке [a , b ] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F (b ) — F (a )).
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a , b ] – отрезком интегрирования.
Таким образом, если F (x ) – какая-нибудь первообразная функция для f (x ), то, согласно определению,
(38)
Равенство (38) называется формулой Ньютона-Лейбница . Разность F (b ) – F (a ) кратко записывают так:
Разность F (b ) – F (a ) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F (x ) и Ф(х ) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х ) = F (x ) + C . Поэтому
Тем самым установлено, что на отрезке [a , b ] приращения всех первообразных функции f (x ) совпадают.
Таким образом, для вычисления
определённого интеграла необходимо найти любую первообразную подынтегральной
функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница:
в первообразную функцию подставляется значение верхнего предела b , далее — значение
нижнего предела a и вычисляется разность F(b) — F(a) . Полученное число и будет
определённым интегралом.
.
Полученное число и будет
определённым интегралом.
.
При a = b по определению принимается
Пример 1.
Решение. Сначала найдём неопределённый интеграл:
Применяя формулу Ньютона-Лейбница к первообразной
(при С = 0), получим
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2. Вычислить определённый интеграл
Решение. Используя формулу
Найти определённый интеграл самостоятельно, а затем посмотреть решение
Свойства определённого интеграла
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования , т.е.
(40)
Пусть F (x ) – первообразная для f (x ). Для f (t ) первообразной служит та же функция F (t ), в которой лишь иначе обозначена независимая переменная. Следовательно,
Следовательно,
На основании формулы (39) последнее равенство означает равенство интегралов
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла , т.е.
(41)
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций , т.е.
(42)
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям , т.е. если
(43)
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак , т.е.
(44)
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его , т.е.
(45)
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство
можно почленно интегрировать , т.е.
(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Пример 5. Вычислить определённый интеграл
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим
Определённый интеграл с переменным верхним пределом
Пусть f (x ) – непрерывная на отрезке [a , b ] функция, а F (x ) – её первообразная. Рассмотрим определённый интеграл
(47)
а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х , которую обозначим через Ф (х ), т.е.
При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х , которую обозначим через Ф (х ), т.е.
(48)
Докажем, что функция Ф (х ) является первообразной для f (x ) = f (t ). Действительно, дифференцируя Ф (х ), получим
так как F (x ) – первообразная для f (x ), а F (a ) – постояная величина.
Функция Ф (х ) – одна из бесконечного множества первообразных для f (x ), а именно та, которая при x = a обращается в нуль. Это утверждение получается, если в равенстве (48) положить x = a и воспользоваться теоремой 1 предыдущего параграфа.
Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
где, по определению, F (x ) – первообразная для f (x ). Если в подынтегральном выражении произвести замену переменной
Если в подынтегральном выражении произвести замену переменной
то в соответствии с формулой (16) можно записать
В этом выражении
первообразная функция для
В самом деле, её производная, согласно правилу дифференцирования сложной функции , равна
Пусть α и β – значения переменной t , при которых функция
принимает соответственно значения a и b , т.е.
Но, согласно формуле Ньютона-Лейбница, разность F (b ) – F (a ) есть
Для того чтобы научиться решать определенные интегралы необходимо:
1) Уметь находить неопределенные интегралы.
2) Уметь вычислить определенный интеграл.
Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений .
Примеры решений .
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования .
Нижний предел интегрирования
Верхний предел интегрирования стандартно обозначается буквой .
Отрезок называется отрезком интегрирования .
Прежде чем мы перейдем к практическим примерам, небольшое «факью» по определенному интегралу.
Что такое определенный интеграл? Я бы мог вам рассказать про диаметр разбиения отрезка, предел интегральных сумм и т.д., но урок носит практический характер. Поэтому я скажу, что определенный интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число.
Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла .
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.
Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница:
Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию (неопределенный интеграл). Обратите внимание, что константа в определенном интеграле никогда не добавляется . Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ? Подготовка для применения формулы Ньютона-Лейбница.
2) Подставляем значение верхнего предела в первообразную функцию: .
3) Подставляем значение нижнего предела в первообразную функцию: .
4) Рассчитываем (без ошибок!) разность , то есть, находим число.
Всегда ли существует определенный интеграл? Нет, не всегда.
Например, интеграла не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: . Такого интеграла тоже не существует, так как в точках , отрезка не существует тангенса. Кстати, кто еще не прочитал методический материал Графики и основные свойства элементарных функций – самое время сделать это сейчас. Будет здорово помогать на протяжении всего курса высшей математики.
А вот менее очевидный пример: . Такого интеграла тоже не существует, так как в точках , отрезка не существует тангенса. Кстати, кто еще не прочитал методический материал Графики и основные свойства элементарных функций – самое время сделать это сейчас. Будет здорово помогать на протяжении всего курса высшей математики.
Для того чтобы определенный интеграл вообще существовал, необходимо чтобы подынтегральная функция быланепрерывнойна отрезке интегрирования .
Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования . По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?». В упрощенном варианте ситуация выглядит примерно так:
???!!!
Нельзя подставлять отрицательные числа под корень!
Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен несуществующий интеграл вроде
то нужно дать ответ, что интеграла не существует и обосновать – почему.
Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будетнесобственный интеграл , коим отведена отдельная лекция.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может, и такая ситуация реально встречается на практике.
– интеграл преспокойно вычисляется по формуле Ньютона-Лейбница.
Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.
В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:
Например, в определенном интеграле перед интегрированием целесообразно поменять пределы интегрирования на «привычный» порядок:
– в таком виде интегрировать значительно удобнее.
Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:
– это справедливо не только для двух, но и для любого количества функций.
В определенном интеграле можно проводить замену переменной интегрирования , правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.
Для определенного интеграла справедлива формула интегрирования по частям :
Пример 1
Решение:
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью самой популярной формулы . Появившуюся константу целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?
(3) Используем формулу Ньютона-Лейбница
.
Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
Пример 2
Вычислить определенный интеграл
Это пример для самостоятельно решения, решение и ответ в конце урока.
Немного усложняем задачу:
Пример 3
Вычислить определенный интеграл
Решение:
(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:
СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряю на третьем слагаемом:
– первое место в хит-параде ошибок по невнимательности, очень часто машинально пишут
(особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.
Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, я сам привык решать подобные интегралы так:
Здесь я устно использовал правила линейности, устно проинтегрировал по таблице. У меня получилась всего одна скобка с отчёркиванием пределов:
(в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию, я сначала подставил сначала 4, затем –2, опять же выполнив все действия в уме.
Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, но лично мне всё равно – обыкновенные дроби я считаю на калькуляторе.
Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту-чайнику лучше использовать первый способ, при «моём» способе решения точно где-нибудь потеряется знак.
Несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная
находится в одной скобке.
Данный калькулятор позволяет решить определенный интеграл онлайн. По сути, вычисление определенного интеграла — это нахождение числа, которое равно площади под графиком функции. Для решения необходимо задать границы интегрирования и интегрируемую функцию. После интегрирования система найдет первообразную для заданной функции, вычислит её значения в точках границах интегрирования, найдет их разность, что и будет являться решением определенного интеграла. Чтобы решить неопределенный интеграл вам необходимо воспользоваться похожим онлайн калькулятором, который находится на нашем сайте по ссылке — Решить неопределенный интеграл .
Мы позволяем вычислить определенный интеграл онлайн быстро и надежно. Вы получите всегда верное решение. Причем для табличных интегралов ответ будет представляться в классическом виде, то есть выражаться через известные константы, такие как число «пи», «экспонента» и т.д. Все вычисления полностью бесплатны и не требуют регистрации. Решая определенный интеграл у нас, вы избавите себя от трудоемких и сложных вычислений, либо решив интеграл самостоятельно — вы сможете проверить полученное вами решение.
Введите функцию, для которой надо найти интеграл
Калькулятор предоставляет ПОДРОБНОЕ решение определённых интегралов.
Этот калькулятор находит решение определенного интеграла от функции f(x) с данными верхними и нижними пределами.
Примеры
С применением степени
(квадрат и куб) и дроби
(x^2 — 1)/(x^3 + 1)
Квадратный корень
Sqrt(x)/(x + 1)
Кубический корень
Cbrt(x)/(3*x + 2)
С применением синуса и косинуса
2*sin(x)*cos(x)
Арксинус
X*arcsin(x)
Арккосинус
X*arccos(x)
Применение логарифма
X*log(x, 10)
Натуральный логарифм
Экспонента
Tg(x)*sin(x)
Котангенс
Ctg(x)*cos(x)
Иррациональне дроби
(sqrt(x) — 1)/sqrt(x^2 — x — 1)
Арктангенс
X*arctg(x)
Арккотангенс
X*arсctg(x)
Гиберболические синус и косинус
2*sh(x)*ch(x)
Гиберболические тангенс и котангенс
Ctgh(x)/tgh(x)
Гиберболические арксинус и арккосинус
X^2*arcsinh(x)*arccosh(x)
Гиберболические арктангенс и арккотангенс
X^2*arctgh(x)*arcctgh(x)
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке): absolute(x) Абсолютное значение x
(модуль x или |x| ) arccos(x) Функция — арккосинус от x arccosh(x) Арккосинус гиперболический от x arcsin(x) Арксинус от x arcsinh(x) Арксинус гиперболический от x arctg(x) Функция — арктангенс от x arctgh(x) Арктангенс гиперболический от x e e число, которое примерно равно 2.3 — возведение в степень x + 7 — сложение x — 6 — вычитание
Другие функции: floor(x) Функция — округление x в меньшую сторону (пример floor(4.5)==4.0) ceiling(x) Функция — округление x в большую сторону (пример ceiling(4.5)==5.0) sign(x) Функция — Знак x erf(x) Функция ошибок (или интеграл вероятности) laplace(x) Функция Лапласа
Integralrechner (Stammfunktionsrechner) mit Schritten — eMathHelp
Dieser Online-Rechner versucht, das unbestimmte Integral (Stammfunktion) der gegebenen Funktion mit angezeigten Schritten zu finden.
Введите функцию:
Интегрировать относительно: autoxtuvwyzabcdfghklmnopqrs
Пожалуйста, пишите без каких-либо различий, таких как `dx`,` dy` и т. Д.
Определенный интеграл см. В калькуляторе определенного интеграла.
Некоторые интегралы могут занять некоторое время. Потерпи!
Если интеграл не рассчитывался или потребовалось много времени, напишите об этом в комментариях. Алгоритм будет улучшен.
Если калькулятор что-то не вычислил, или вы обнаружили ошибку, или у вас есть предложение / отзыв, напишите об этом в комментариях ниже.{2} \ right)} dx}} = \ color {red} {\ int {\ frac {\ cos {\ left (u \ right)}} {2} du}} $$
Применить постоянное кратное rule $$$ \ int cf {\ left (u \ right)} \, du = c \ int f {\ left (u \ right)} \, du $$$ с $$$ c = \ frac {1 } {2} $$$ и $$$ f {\ left (u \ right)} = \ cos {\ left (u \ right)} $$$:
$$ \ color {красный} {\ int { \ frac {\ cos {\ left (u \ right)}} {2} du}} = \ color {red} {\ left (\ frac {\ int {\ cos {\ left (u \ right)} du} } {2} \ right)} $$
Интеграл косинуса равен $$$ \ int {\ cos {\ left (u \ right)} du} = \ sin {\ left (u \ right)} $$$ :
$$ \ frac {\ color {red} {\ int {\ cos {\ left (u \ right)} du}}} {2} = \ frac {\ color {red} {\ sin {\ left (u \ right)}}} {2} $$
Напомним, что $$$ u = x ^ {2} $$$:
$$ \ frac {\ sin {\ left (\ color {red} {u} \ right)}} {2} = \ frac {\ sin {\ left (\ color {red} {x ^ {2}} \ right)}} {2} $$
Следовательно,
$$ \ int {x \ cos {\ left (x ^ {2} \ right)} dx} = \ frac {\ sin {\ left (x ^ {2} \ right)}} {2} $$
Добавьте постоянную интегрирования:
$$ \ int {x \ cos {\ left (x ^ {2} \ right)} dx} = \ frac {\ sin {\ left (x ^ {2} \ right)}} {2} + C $$
Ответ: $$$ \ int {x \ cos {\ left (x ^ {2} \ right)} dx} = \ frac {\ sin {\ left (x ^ {2} \ right)}} {2} + C $$$
Первоначальный калькулятор с шагами (Интегральный калькулятор)
Введите функцию, переменную, верхнюю и нижнюю границы.Выберите вариант с определенным или неопределенным целым. Нажмите кнопку Calculate , чтобы найти первообразную с помощью калькулятора первообразной.
Калькулятор первообразной функции с шагами
Онлайн-калькулятор интеграла (первообразной) — это инструмент, который вычисляет интеграл заданной функции по переменной. Он также вычисляет как определенный, так и неопределенный интеграл для заданной функции.
Этот калькулятор интегралов также показывает шаги интегрирования для каждого вычисления.
Что такое интеграл?
Интеграл может быть определен как,
“ Интеграл присваивает числа функциям таким образом, чтобы определять объем, смещение площади и даже вероятность. Интеграл — это функция, обратная производной, поэтому его обычно называют первообразной. ”
Процесс нахождения интеграла называется интегрированием. Он используется для определения площади под кривой. Символ интеграции или первообразной — ∫.
Как вычислить интеграл?
Пример: Вычислите следующий интеграл.
∫ (6x + 2) dx
Решение:
Шаг 1: Примените линейность к функции.
= 6 x dx + 2 ∫ 1 dx ——- 1
Шаг 2: Решить 6 ∫ x dx и 2 ∫ 1 dx отдельно и поместите значения в уравнение (1) выше.
6 ∫ x dx
Применить правило мощности.
6 ∫ x dx = 6 x 2 / 2 = 3x 2
2
1 9000 постоянное правило a dx = ax + C.
2 ∫ 1 dx = 2x + C
Шаг 3: Подставьте решенные интегралы в уравнение (1).
= 6 ∫ x dx + 2 ∫ 1 dx
= 3 x 2 + 2x + C
Вышеупомянутый интегральный решатель выполняет все эти шаги и показывает вам полный расчет для ваша легкость.
Первоначальный калькулятор — Онлайн-калькулятор первообразных
Антипроизводная Калькулятор находит целое значение функции. Процесс нахождения антипроизводной функции известен как интегрирование. Другими словами, обратный процесс дифференциации называется интегрированием. Антипроизводная также известна как интеграл функции.
Что такое антипроизводный калькулятор?
Калькулятор антипроизводной — это онлайн-инструмент, используемый для вычисления значения заданного неопределенного интеграла.Интегрирование можно использовать для поиска площади под кривой. Его также можно использовать для определения объема трехмерной твердой формы. Чтобы использовать антипроизводный калькулятор , введите функцию в поле ввода.
Калькулятор антипроизводной
Как пользоваться антипроизводным калькулятором?
Выполните простые шаги, чтобы найти антипроизводную функции с помощью калькулятора антипроизводной:
- Шаг 1: Зайдите в онлайн-калькулятор антипроизводной Cuemath.
- Шаг 2: Введите функцию в поле ввода калькулятора антипроизводной.
- Шаг 3: Нажмите кнопку «Рассчитать» , чтобы найти антипроизводную функции.
- Шаг 4: Нажмите кнопку «Сбросить» , чтобы очистить поля и ввести новые значения.
Как работает антипроизводный калькулятор?
Есть много применений интеграции. Среднее значение кривой, площадь между двумя кривыми, центр тяжести и центр масс — все это можно определить с помощью интегрирования.В исчислении доступны два типа интегралов. Это следующие:
- Неопределенные интегралы — Такие интегралы не имеют заданных пределов, поэтому окончательное значение интеграла неопределенно. Если мы проинтегрируем производную функции, скажем, g ‘(x), мы получим саму функцию.
- Определенные интегралы — Интегралы, которые имеют определенные пределы с уже существующими значениями, называются определенными интегралами. Такой интеграл используется для нахождения площади под кривой между двумя заданными точками (эти точки действуют как пределы).
Ниже приведены некоторые свойства интеграции.
- Дифференцирование интеграла приведет к подынтегральному выражению; ∫ f (x) dx = f (x) + C.
- Если два неопределенных интеграла имеют одинаковую производную, они будут эквивалентны. Это потому, что два интеграла приводят к одному и тому же семейству кривых; ∫ [f (x) dx — g (x) dx] = 0
- При интегрировании коэффициент при переменной выносится за знак интеграла; ∫ К е (х) дх знак равно к ∫ е (х) дх.
Формула для определения значения простого интеграла имеет вид: ∫x n dx = (x n + 1 / n + 1) + C.
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенные примеры антипроизводных
Пример 1: Найдите значение антипроизводной 5x 3 + 2x 2 и проверьте его с помощью калькулятора антипроизводной.
Решение:
Используя формулу: ∫x n dx = (x n + 1 / n + 1) + C
= ∫ (5x 3 + 2x 2 ) dx
= ∫ (5x 3 ) dx + ∫ (2x 2 ) dx
= [5 × (x 3 + 1 /3 + 1)] + [2 × x 2 + 1 /2 + 1]
= 5x 4 /4 + 2x 3 / 3.
Следовательно, значение обратной производной 5x 3 + 2x 2 равно 5x 4 /4 + 2x 3 /3.
Пример 2: Найдите значение антипроизводной 1 + x 4 и проверьте его с помощью калькулятора антипроизводной.
Решение:
Используя формулу: ∫x n dx = (x n + 1 / n + 1) + C
= ∫ (1 + x 4 ) dx
= ∫ (1.x 0 ) dx + ∫ (x 4 ) dx
= [1 × (x 0 + 1 /0 + 1)] + [x 4 + 1 /4 + 1]
= х + х 5 /5
Таким образом, антипроизводная от 1 + x 4 равна x + x 5 /5
Точно так же вы можете использовать калькулятор антипроизводных, чтобы найти стоимость антипроизводных для следующего:
☛ Математические калькуляторы:
Калькулятор умножения матриц— Примеры, факты
Калькулятор умножения матрицвычисляет произведение двух заданных матриц.Матрица — это прямоугольный массив или сетка, в которой числа расположены в строках и столбцах.
Что такое калькулятор умножения матриц?
Калькулятор умножения матриц— это онлайн-инструмент, который помогает выполнять умножение матриц. Матрицы широко используются для представления данных при работе с линейными уравнениями, геометрией и статистикой. Чтобы использовать этот калькулятор умножения матриц , введите значения в поля ввода
Калькулятор умножения матриц
* Используйте только 3 цифры.
Как пользоваться калькулятором умножения матриц?
Чтобы найти произведение матриц с помощью онлайн-калькулятора умножения матриц, выполните следующие действия:
- Шаг 1: Зайдите в онлайн-калькулятор умножения матриц Cuemath.
- Шаг 2: Выберите размеры матриц (2 x 2 или 3 x 3) из раскрывающегося списка и введите значения в калькулятор умножения матриц.
- Шаг 3: Нажмите кнопку «Рассчитать» , чтобы найти результирующую матрицу.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает калькулятор умножения матриц?
Матрица, содержащая m строк и n столбцов, представлена как \ (A_ {m \ times n} \). Это называется прямоугольной матрицей. Кроме того, если матрица имеет одинаковое количество строк и столбцов, она называется квадратной матрицей. Например, матрица 2 x 2 будет квадратной матрицей, поскольку она имеет 2 строки и 2 столбца.Для умножения двух матриц количество столбцов первой матрицы должно быть таким же, как количество строк второй матрицы. Если это условие не выполняется, умножение матриц не может быть выполнено. Таким образом, если у нас есть две матрицы размером 5 x 3 и 3 x 2 соответственно, то их можно перемножать. Однако матрица 6 x 1 не может быть умножена на матрицу 2 x 4. Ниже приведена процедура умножения матриц 2 x 2 и 3 x 3.
1. Матрицы 2 x 2
A x B = \ (\ begin {bmatrix} a_ {11} & a_ {12} \\ a_ {21} & a_ {22} \ end {bmatrix} \ times \ begin {bmatrix} b_ {11} & b_ {12} \\ b_ {21} & b_ {22} \ end {bmatrix} = \ begin {bmatrix} a_ {11} b_ {11} + a_ {12} b_ {21} & a_ {11} b_ {12 } + a_ {12} b_ {22} \\ a_ {21} b_ {11} + a_ {22} b_ {21} & a_ {21} b_ {12} + a_ {22} b_ {22} \ end { bmatrix} \)
2. Матрицы 3 x 3
A x B = \ (\ begin {bmatrix} a_ {11} & a_ {12} & a_ {13} \\ a_ {21} & a_ {22} & a_ {23} \\ a_ {31} & a_ {32} & a_ {33} \ end {bmatrix} \ times \ begin {bmatrix} b_ {11} & b_ {12} & b_ {13} \\ b_ {21} & b_ {22} & b_ {23} \\ b_ {31} & b_ {32} & b_ {33} \ end {bmatrix} \)
= \ (\ begin {bmatrix} a_ {11} b_ {11} + a_ {12} b_ {21} + a_ {13} b_ {31} & a_ {11} b_ {12} + a_ {12} b_ {22} + a_ {13} b_ {32} & a_ {11} b_ {13} + a_ {12} b_ {23} + a_ {13} b_ {33} \\ a_ {21} b_ {11} + a_ {22} b_ {21} + a_ {23} b_ {31} & a_ {21} b_ {12} + a_ {22} b_ {22} + a_ {23} b_ {32} & a_ {21} b_ {13} + a_ {22} b_ {23} + a_ {23} b_ {33} \\ a_ {31} b_ {11} + a_ {32} b_ {21} + a_ {33} b_ {31} & a_ {31} b_ {12} + a_ {32} b_ {22} + a_ {33} b_ {32} и a_ {31} b_ {13} + a_ {32} b_ {23} + a_ {33} b_ {33} \ end {bmatrix} \)
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенные примеры умножения матриц
Пример 1: Умножение матриц \ (\ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \) & \ (\ begin {bmatrix} 2 & 1 \\ 4 & 2 \ end { bmatrix} \) и проверьте его с помощью калькулятора матричного умножения.
Решение:
Умножение = \ (\ begin {bmatrix} a_ {11} & a_ {12} \\ a_ {21} & a_ {22} \ end {bmatrix} \ times \ begin {bmatrix} b_ {11} & b_ {12 } \\ b_ {21} & b_ {22} \ end {bmatrix} = \ begin {bmatrix} a_ {11} b_ {11} + a_ {12} b_ {21} & a_ {11} b_ {12} + a_ {12} b_ {22} \\ a_ {21} b_ {11} + a_ {22} b_ {21} & a_ {21} b_ {12} + a_ {22} b_ {22} \ end {bmatrix} \)
Умножение = \ (\ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \ times \ begin {bmatrix} 2 & 1 \\ 4 & 2 \ end {bmatrix} = \ begin {bmatrix} 10 & 5 \\ 22 & 11 \ end {bmatrix} \)
Пример 2: Умножение матриц \ (\ begin {bmatrix} 3 & 2 & 5 \\ 5 & 2 & 4 \\ 2 & 5 & 6 \ end {bmatrix} \) & \ (\ begin {bmatrix} 2 & 2 & 7 \\ 1 & 4 & 6 \\ 3 & 8 & 7 \ end {bmatrix} \) и проверьте это с помощью калькулятора матричного умножения.
Решение:
Умножение = \ (\ begin {bmatrix} a_ {11} & a_ {12} & a_ {13} \\ a_ {21} & a_ {22} & a_ {23} \\ a_ {31} & a_ {32 } & a_ {33} \ end {bmatrix} \ times \ begin {bmatrix} b_ {11} & b_ {12} & b_ {13} \\ b_ {21} & b_ {22} & b_ {23} \\ b_ {31} & b_ {32} & b_ {33} \ end {bmatrix} \)
= \ (\ begin {bmatrix} a_ {11} b_ {11} + a_ {12} b_ {21} + a_ {13} b_ {31} & a_ {11} b_ {12} + a_ {12} b_ {22} + a_ {13} b_ {32} & a_ {11} b_ {13} + a_ {12} b_ {23} + a_ {13} b_ {33} \\ a_ {21} b_ {11} + a_ {22} b_ {21} + a_ {23} b_ {31} & a_ {21} b_ {12} + a_ {22} b_ {22} + a_ {23} b_ {32} & a_ {21} b_ {13} + a_ {22} b_ {23} + a_ {23} b_ {33} \\ a_ {31} b_ {11} + a_ {32} b_ {21} + a_ {33} b_ {31} & a_ {31} b_ {12} + a_ {32} b_ {22} + a_ {33} b_ {32} и a_ {31} b_ {13} + a_ {32} b_ {23} + a_ {33} b_ {33} \ end {bmatrix} \)
Умножение = \ (\ begin {bmatrix} 3 & 2 & 5 \\ 5 & 2 & 4 \\ 2 & 5 & 6 \ end {bmatrix} \ times \ begin {bmatrix} 2 & 2 & 7 \\ 1 & 4 и 6 \\ 3 и 8 и 7 \ end {bmatrix} \)
= \ (\ begin {bmatrix} 23 & 54 & 68 \\ 24 & 50 & 75 \\ 27 & 72 & 86 \ end {bmatrix} \)
Аналогичным образом вы можете попробовать калькулятор умножения матриц и умножить следующие матрицы.
- Матрицы = \ (\ begin {bmatrix} 5 & 7 & 2 \\ 1 & 8 & 10 \\ 11 & 18 & 1 \ end {bmatrix} \), \ (\ begin {bmatrix} 3 & 7 & 8 \\ 1 & 7 & 1 \\ 5 & 19 & 1 \ end {bmatrix} \)
- Матрицы = \ (\ begin {bmatrix} 4 & 8 \\ 12 & 16 \ end {bmatrix} \), \ (\ begin {bmatrix} 5 & 10 \\ 15 & 20 \ end {bmatrix} \)
☛ Математические калькуляторы:
Калькулятор двойного интеграла— Онлайн калькулятор двойного интеграла
Калькулятор двойного интеграла вычисляет значение двойного интеграла.Площадь двумерной фигуры можно определить с помощью двойных интегралов. Двойная интеграция обозначается ».
Что такое калькулятор двойного интеграла?
Калькулятор двойного интеграла — это онлайн-инструмент, который помогает интегрировать заданную функцию и получать значение двойного интеграла. Двойные интегралы можно использовать для определения объема под поверхностью и среднего значения функции с двумя переменными. Чтобы использовать калькулятор двойного интеграла , введите значения в поля ввода.
Калькулятор двойного интеграла
Как пользоваться калькулятором двойного интеграла?
Следуйте инструкциям ниже, чтобы найти значение двойного интеграла с помощью онлайн-калькулятора двойного интеграла:
- Шаг 1: Зайдите в онлайн-калькулятор двойного интеграла Cuemath.
- Шаг 2: Введите функцию, а также пределы в указанные поля ввода. Из раскрывающегося списка выберите, какая переменная будет интегрирована первой.
- Шаг 3: Нажмите кнопку «Рассчитать» , чтобы найти значение двойного интеграла.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает калькулятор двойного интеграла?
Интегральное исчисление состоит из нескольких различных типов интеграции, таких как простое интегрирование, двойное интегрирование и тройное интегрирование.{b} f (x, y) dxdy \), затем мы используем следующие шаги, чтобы найти его значение.
- Сначала решаем внутренний интеграл. Поскольку dx предшествует dy, мы сначала проинтегрируем функцию по x. Все члены, содержащие y, будут рассматриваться как константы.
- Применяются внутренние пределы определенного интеграла. Теперь наша функция будет только через y.
- Затем мы решаем внешний интеграл. Это означает, что мы интегрируем функцию по y.{2}] dxdy \)
☛ Математические калькуляторы:
Онлайн-калькулятор первообразных с пошаговыми инструкциями • Решатель первообразных
Лучшие советы по первоклассному калькулятору!
Что на самом деле происходит с первообразным калькулятором
Интернет-калькулятор производных правил цепочки вычисляет производную некоторой функции, связанной с переменной x, используя аналитическое дифференцирование. Кнопка «Очистить» очищает предыдущий ввод. Они смотрят на слово целиком и получают все сразу.Если вы вернетесь к своей исходной функции, вы знаете, что ваша первообразная точна. Но есть просто 1 функция! Для начала подумайте о следующей функции.
На самом деле, вы можете думать о IBP как о средстве отмены правила продукта. Есть шанс посмотреть ответы. Это была еще одна фантастическая дискуссия, вдохновленная технологиями. После некоторой практики вы, скорее всего, сразу же запишите решение. Если вы получили неверный ответ или хотите запросить новый вид расчета, нажмите Отправить отзыв в основании страницы результатов поиска.Используйте его, чтобы просмотреть свои ответы.
Калькулятор «Боль от первообразных»
Наш инструмент Iterated Integral Calculator поддерживает все самые последние функции, вычисления и ряд других переменных, которые необходимы в одном инструменте. Вы можете использовать кнопку меню просмотра, чтобы добавить функциональности обычному калькулятору. Ваш калькулятор сделает это за вас намного быстрее. Калькулятор первообразных имеет способность проводить символическую антидифференциацию.
Когда вы действительно начнете видеть разнообразие планеты, на которой вы живете, и свою уникальность.Теперь мы можем сопоставить идеи площадей и первообразных друг с другом, чтобы найти способ вычисления определенных интегралов, который является точным и часто несложным. При повороте он будет выглядеть так же, как и в предыдущем случае, но с цилиндром, удаленным в центре. В то время как алгебра может управлять отличными прямыми линиями, исчисление обрабатывает не очень красивые кривые.
Кто еще хочет узнать о первообразном калькуляторе?
Этот процесс полезен во многих математических вычислениях и может быть замечен в некоторых инженерных формулах.Другие способы состоят из другой данной информации, например, значений других тригонометрических функций для равного угла или других углов в том же треугольнике. В частности, когда вы новичок в антидифференцировании, это отличная идея — проверить свои первообразные, дифференцируя их, вы можете игнорировать C. Активы без восстановительной стоимости будут иметь точную общую амортизацию, равную цене актива. Например, если вас просят получить относительное минимальное значение функции, предполагается, что вы будете использовать исчисление и покажете математические действия, которые приводят к ответу.Расскажите о своих трудностях.
Вот что я знаю о калькуляторе без производных
Когда вы начинаете ценить дружбу, а не количество друзей. На этих начальных шагах мы замечаем некоторые особые случаи подынтегрального выражения, которые можно легко интегрировать с помощью пары мер. Таким образом, у нас есть экспоненты, и мы можем применить правило силы. Вот более сложный пример использования цепного правила. Однако мы должны избегать круговой ловушки.
Калькулятор выбора хорошей первообразной продукции
Это примерно 1,61803. Мы можем научиться это делать !! Алгебратор просто замечательный. Попытайтесь запомнить, это приносит негатив. Теперь я могу заметить, что это не то же самое.
Также отсутствуют операторы BEGIN и END. Однако в случае, если вычислить вторую производную сложно, вы можете выбрать самый первый тест производной. Они интегрируют их с помощью процедуры замещения.Используйте интегрирование подстановкой, чтобы получить соответствующий неопределенный интеграл.
Чтобы отобразить шаги, калькулятор применяет те же методы интеграции, что и человек. Важно отметить, что не все калькуляторы нормально справляются с порядком операций. Такого рода проблемы вы сможете решить с помощью этого инструмента.
Одним из основных преимуществ использования этого сайта является возможность узнать много информации об операциях с дробями, так что вскоре вы сможете выполнять такие операции и самостоятельно решать проблемы.Это метод поиска первообразных. Это помогает пользователю намного больше, чем любой другой инструмент, что может быть причиной того, что люди проявляют чрезмерную любовь к этому онлайн-инструменту. Практика создания MSTVF сравнима со встроенными функциями с табличным значением. Мне нравится подробная процедура решения и объяснения.
Самый популярный калькулятор первообразных
Щелкните интеграл (обозначенный цифрой 1), отображаемый, как только вы щелкнули уравнение на предыдущем шаге, затем щелкните нужный тип интеграла, в данном случае будет выбран тот, который обозначен цифрой 2.В этом случае вам может потребоваться учетная запись для его получения. В данном случае перетащили на a20.
И, очевидно, мне нужно добавить константу. Тот простой факт, что мы получаем идентичный ответ в этом случае, не может быть слишком удивительным. Когда вы начинаете планировать свое социальное время, потому что все должно быть запланировано сейчас, даже если предположить, что это спонтанно. Фактически, эти 2 правила были тем, что мы использовали, чтобы обнаружить первообразную 20t. Возможно, вам нужен только быстрый ответ по работе и не нужно устранять проблему вручную.
Что нужно сделать, чтобы узнать о первообразном калькуляторе, прежде чем вы останетесь без внимания
Время от времени, в отличие от использования самой первой производной проверки экстремумов, вторая производная проверка может также позволить вам обнаруживать экстремумы. Мы также можем проверить первообразную с точки зрения суммы Римана. Связь между ними жизненно важна и известна как основная теорема исчисления. Давайте научимся находить интегралы в этом свете.
Изменение границы убывания подынтегральной функции приведет к созданию различных первообразных.Из приведенных выше уравнений вы также можете представить себе, что такое единицы скорости. До сих пор мы рассматривали производные вне понятия дифференцируемости. С другой стороны, интеграл также может быть основан на других инвариантах. В частности, нам дано конкретное средство от некоторого однородного линейного дифференциального уравнения с постоянными коэффициентами, и мы хотим понять, что это за уравнение.
Правило 5 минут для первообразного калькулятора
Только что выпущен новый калькулятор угла обзора на первоисточнике
Когда вы обнаружите, что это нормально — пойти самому посмотреть фильм или заняться разными мастур-свиданиями.Чтобы провести углубленный анализ своей жизни, просто заполните форму выше и включите нумерологический калькулятор. Однако есть еще одна версия, специально адаптированная для определенной интеграции. Давайте вместе сделаем пару примеров.
T.A. мне это не понравилось. Мы можем научиться это делать !! Можно использовать тот, который вам удобнее всего. Попытайтесь запомнить, это приносит негатив. Теперь я могу заметить, что это не то же самое.
Не забывайте, эти решатели отлично подходят для проверки вашей работы, экспериментирования с различными уравнениями или напоминания себе, как лучше всего решить конкретную проблему.Поскольку вы увидите, к скольким дробям вы обращаетесь, подход останется прежним. В данном случае перетащили на a20.
И, очевидно, мне нужно добавить константу. Это почти всегда очень хорошо! Обратное также может быть установлено. Фактически, эти 2 правила были тем, что мы использовали, чтобы обнаружить первообразную 20t. Если вы понимаете, какой способ вы используете, и делаете это правильно, вы получите наиболее подходящий ответ.
Что всем не нравится в калькуляторе первообразных и почему
Интернет-калькулятор производных правил цепочки вычисляет производную некоторой функции, связанной с переменной x, используя аналитическое дифференцирование.Использовать эту формулу для получения первообразной функции довольно просто, поскольку вам не нужно беспокоиться о том, как выглядит ее график. Они смотрят на слово целиком и получают все сразу. Если вы вернетесь к своей исходной функции, вы знаете, что ваша первообразная точна. Но есть просто 1 функция! Найдите первообразную f.
Это определенно самое простое решение, поскольку здесь нет констант. Вы просто тратите производную и смотрите, является ли это заданной функцией.Далее мы должны учитывать любые константы. Могут потребоваться некоторые из этих тригонометрических тождеств.
Однако, как правило, достаточно думать об обратном синусе и функциях обратного тангенса. Из приведенных выше уравнений вы также можете представить себе, что такое единицы скорости. Вот различные способы обозначения самой первой производной. С другой стороны, интеграл также может быть основан на других инвариантах. В частности, нам дано конкретное средство от некоторого однородного линейного дифференциального уравнения с постоянными коэффициентами, и мы хотим понять, что это за уравнение.
Используйте Правило 5 (Правило идентификации) в максимально возможной степени, потому что оно может произвести довольно простой процесс упрощения. По сути, в нем говорится, что каждый термин нужно интегрировать отдельно, а затем складывать вместе. Предыдущее предложение не было констатацией фактов. Цепное правило также может помочь нам найти различные производные. Вы можете сначала ознакомиться с правилами использования деривативов.
Преимущества первичного калькулятора
В случае, если интегрирование выполняется в сложной плоскости, результат зависит от курса вокруг начала координат, в этом событии сингулярность вносит вклад i при использовании пути через начало координат и i для пути под началом координат.Если это не так, сначала должно быть выполнено длинное (или синтетическое) деление, а затем процедура частичных дробей может быть использована для остаточного члена (при необходимости). Теперь процесс u-подстановки будет проиллюстрирован на этом идентичном примере. Процедура вычисления производной называется дифференцированием. В некоторых конкретных сценариях, когда вторую производную просто вычислить, проверка второй производной часто является самым простым подходом для распознавания локальных экстремумов. Имейте в виду, что это обычно работает и с переменными, но синтез переменных не должен быть обычным делом и должен быть только крайней мерой.Это связано с тем, что переменная интегрирования — это просто заполнитель.
Значение калькулятора первообразных
Чтобы отобразить шаги, калькулятор применяет те же методы интеграции, что и человек. Важно отметить, что не все калькуляторы нормально справляются с порядком операций. Здесь вы получите решение неопределенного интеграла в табличной форме, просто набрав нужную функцию.
Примеры использования правила удлиненной степени Последующий калькулятор производной может показать вам шаги и правила, используемые для нахождения производной заданной функции.Я продемонстрирую лучший способ сделать это, используя различные методы в зависимости от вашей операционной системы и вкусов. Ниже приведены несколько популярных методов.
Калькулятор дебатов по поводу первообразных
Это довольно быстро и удобно … просто введите желаемый диапазон цифр и смотрите! Подумайте о закрашенном круге. Стоит помнить, что эта парабола на самом деле не путь движущегося объекта. Затем разделите на ту же цену.Ой, черт, должно быть бесконечное количество нормальных таблиц вероятностей.
Преимущества первичного калькулятора
Когда вы действительно начнете видеть разнообразие планеты, на которой вы живете, и свою уникальность. Это для разных уроков. У них должно быть понимание коммерческой осведомленности, такой как ее клиенты, конкуренты, поставщики, и общее понимание компании, это чрезвычайно важно, потому что как финансовый менеджер в таком огромном бизнесе они должны понимать, на кого они работают с точки зрения как люди думают о компании и т. д.. Эта стратегия вряд ли выполнит свою работу!
Калькулятор первообразных: Максимальное удобство!
Infinity — довольно странная идея. Соня Гойко, MS Algebrator — важный элемент. Спасибо за помощь и новую редакцию.
Правило 5 минут для первообразного калькулятора
Определения первообразного калькулятора
Фракции есть практически повсюду, и для каждого из нас очень важно понимать, как эффективно с ними справляться.Вы можете использовать кнопку меню просмотра, чтобы добавить функциональности обычному калькулятору. Для этого учебного курса необходим графический калькулятор. Калькулятор первообразных имеет способность проводить символическую антидифференциацию.
Калькулятор выбора хорошей первообразной продукции
Это примерно 1,61803. Мы можем научиться это делать !! Алгебратор просто замечательный. Попытайтесь запомнить, это приносит негатив. Теперь я могу заметить, что это не то же самое.
Не забывайте, эти решатели отлично подходят для проверки вашей работы, экспериментирования с различными уравнениями или напоминания себе, как лучше всего решить конкретную проблему.В этом случае вам может потребоваться учетная запись для его получения. В таком случае неплохо спросить.
Они очень похожи, за исключением нескольких отличий, о которых я расскажу в следующих парах абзацев. Это почти всегда очень хорошо! Когда вы начинаете планировать свое социальное время, потому что все должно быть запланировано сейчас, даже если предположить, что это спонтанно. Фактически, эти 2 правила были тем, что мы использовали, чтобы обнаружить первообразную 20t. Если вы понимаете, какой способ вы используете, и делаете это правильно, вы получите наиболее подходящий ответ.
Что на самом деле происходит с первообразным калькулятором
Если неопределенный интеграл (примитивная функция) ищется, но не может быть найден для конкретной функции, QuickMath позволит вам узнать. Кнопка «Очистить» очищает предыдущий ввод. Они смотрят на слово целиком и получают все сразу. Другими словами, нам нужно будет открыть исходную функцию. К сожалению, эта функция возвращает производную только одной точки. Найдите первообразную f.
Так как насчет первообразного калькулятора?
Это методы расчета, которые использует calc для определения производных.В вышеупомянутое глобальное уравнение внесено несколько изменений. Далее мы должны учитывать любые константы. Используйте этот калькулятор, чтобы легко вычислить арктангенс определенного числа.
Однако, как правило, достаточно думать об обратном синусе и функциях обратного тангенса. Это позволяет легко применить замену для упрощения подынтегрального выражения. Вот различные способы обозначения самой первой производной. Это просто дифференциальное уравнение.В частности, нам дано конкретное средство от некоторого однородного линейного дифференциального уравнения с постоянными коэффициентами, и мы хотим понять, что это за уравнение.
Используйте Правило 5 (Правило идентификации) в максимально возможной степени, потому что оно может произвести довольно простой процесс упрощения. Вообще говоря, символ штрих () — это просто еще один способ обозначения производной. Предыдущее предложение не было констатацией фактов. Цепное правило также может помочь нам найти различные производные.Вы можете сначала ознакомиться с правилами использования деривативов.
Новые вопросы по первообразному калькулятору
Человек может также интегрировать по частям и найти рекуррентную связь, чтобы исправить это. Конечный результат будет показан ниже. Все, что вам нужно знать, — это связь между положением, скоростью и ускорением. Какой бы сложной ни была функция, вы можете определить область под кривой, просто используя расчет. Например, если вас просят получить относительное минимальное значение функции, предполагается, что вы будете использовать исчисление и покажете математические действия, которые приводят к ответу.В этом контексте c известна как постоянная интегрирования.
Интеграция — это линейная функция, использование этого свойства позволяет функции получить требуемый результат. Иногда для создания интеграла потребуется множество инструментов. Однако невозможно интегрировать в элементарные функции.
Информация, которую вы предоставляете для вашего нумерологического анализа, будет использоваться только для этой цели. Время изменилось с тех пор, как я купил это программное обеспечение.Ниже приведены несколько популярных методов.
Что нужно знать о калькуляторе без производных
Когда вы начинаете ценить дружбу, а не количество друзей. Для изменения момента можно перемещать ползунок. Таким образом, у нас есть экспоненты, и мы можем применить правило силы. Еще один способ подумать об абсолютном значении — это взглянуть на числовую строку с нулем в центре. Это может быть ловушкой, если вы не будете писать внимательно!
Эта программа очень полезна для задач со словами, которые относятся к более простой части теста.Теперь мы можем сопоставить идеи площадей и первообразных друг с другом, чтобы найти способ вычисления определенных интегралов, который является точным и часто несложным. В любой момент, когда необходимо вычислить определенный интеграл, на помощь может прийти Фундаментальная теорема исчисления. Нет информации, если лимит равен 1.
Скрытая жемчужина первообразного калькулятора
На самом деле, вы можете думать о IBP как о средстве отмены правила продукта. Это похоже на прогресс, но это не решение.Формулы можно разделить на четыре большие идеи. Поэтому, если вы хотите узнать больше, взгляните на это руководство. Вы должны получить те же ответы, что и раньше. Используйте его, чтобы просмотреть свои ответы.
Интегральный калькулятор| Лучшая онлайн-интеграция по частям Калькулятор
Введение в калькулятор интегралов
Наш расширенный интегральный калькулятор — это наиболее полное комплексное решение в сети, с помощью которого вы можете выполнять множество операций по интеграции.Все, что вам нужно сделать, это ввести функцию, переменную, границы, и все готово.
Калькулятор интеграции с пошаговыми инструкциями позволяет изучить принципы вычисления интегралов, не затрачивая слишком много времени. Вы можете легко вычислить интеграл с помощью калькулятора интегралов в режиме онлайн.
Точно так же вы можете найти на этом сайте калькулятор двойного интеграла. Калькулятор двойного интеграла показывает вам график, график, шаги, визуальное представление, которое поможет вам изучить передовые концепции двойной интеграции.
Есть много других полезных калькуляторов, которыми вы можете воспользоваться. Точно так же вы можете определить объем тела вращения с помощью калькулятора метода шайбы и определить поперечные сечения тела вращения с помощью калькулятора метода диска.
Как решить интеграцию?
Чтобы найти определенный интеграл, вы должны сначала понять, что определенные интегралы имеют начальную и конечную точки, также известные как пределы или интервалы, представленные как (a, b) и помещенные сверху и снизу интеграла.
Мы можем обобщить интегралы на основе функций и областей, в которых выполняется интегрирование. Калькулятор интеграции по частям с пошаговыми инструкциями поможет вам вычислить интегралы в цифровом виде.
Например, линейный интеграл выражается функциями двух или более переменных с заменой интервала интегрирования кривой, соединяющей две точки на интервале.
С другой стороны, есть интеграл по поверхности, где поверхность заменяет кривую в трехмерном пространстве.3 $$
расчет границ: 4
-3,4
-12
С другой стороны, существует неопределенный интеграл, который можно быстро отличить от определенного интеграла из-за отсутствия определенных пределов первого.
Неопределенный интеграл, таким образом, определяется по формуле:
$$ \ int f (x) dx $$
Вышеупомянутый решатель интегрирования может вычислять неопределенный интеграл и определенный интеграл, но если вы хотите вычислить только неопределенный интеграл, найдите лучший онлайн-калькулятор неопределенного интеграла.
Связано: Найдите этот полезный блог, чтобы узнать об определенном интеграле и неопределенном интеграле
Как рассчитать неправильный интеграл?
Одна из причин, по которой определенный интеграл становится неправильным, — это когда один или оба предела достигают бесконечности. Калькулятор интегрального исчисления можно использовать для вычисления несобственных интегралов.
Этот вид интеграла затем решается путем превращения его в задачу о пределах, когда c стремится к бесконечности или к отрицательной бесконечности.c $$
$$ \ lim_ {c \ to \ infty} [- \ frac {1} {c}] — (- \ frac {1} {1})] $$
0 + 1
1
Поскольку ответ на несобственный интеграл конечен, мы считаем его сходящимся.
Если вы хотите вычислить только определенные интегралы, воспользуйтесь этим лучшим пошаговым онлайн-калькулятором определенных интегралов.
Связано: Используйте калькулятор метода оболочки с шагами, чтобы легко найти объем твердого тела вращения онлайн.
Как рассчитать непрерывную интеграцию?
Основная теорема исчисления устанавливает четкую связь между интегральным и дифференциальным исчислением.c f (t) dt $$
Для вашего удобства и углубленного изучения множественных интегралов мы предлагаем один из самых быстрых калькуляторов тройных интегралов. Этот инструмент, несомненно, поможет вам вычислить определенные и неопределенные тройные интегралы в режиме онлайн, сделав несколько щелчков мышью.
Связано: Понимание интеграции по частичной дроби за 5 минут!
Что такое интегральный калькулятор?
В течение многих лет был только один способ вычисления интегралов — вычисление вручную.В наши дни у нас есть много онлайн-калькуляторов интеграции, чтобы легко вычислить значение интеграции. Большинство студентов обычно имеют четкие теоретические представления об исчислении. Таким образом, вычисление интегралов или производных на самом деле не проблема, когда у нас есть калькуляторы, такие как калькулятор интегрирования или калькулятор производной.
Однако это проблема, когда дело доходит до домашних заданий, когда студенты обычно получают массу задач, требующих решения для интегралов. Если вам нужна помощь, прочтите статью, в которой рассказывается об интеграции, ее важности и различных методах.
Было бы неразумно вычислять интегралы снова и снова вручную, именно здесь этот калькулятор определенных интегралов пригодится для вычисления сложных задач интегрирования. Он бесплатный и простой в использовании, и вы получите ответ почти мгновенно, так как вы можете легко найти в Интернете калькулятор интегралов с пошаговыми инструкциями.
Также используйте другие полезные математические калькуляторы, которые важны в общих процессах интеграции. Так же, как калькулятор преобразования Лапласа помогает вам преобразовать интеграл заданной производной функции, а калькулятор преобразования Фурье помогает преобразовать функцию времени в функцию частоты.
Как найти лучший интеграционный калькулятор?
В сети доступно множество интегральных калькуляторов, например, Calculatored, symbolab, wolframalpha и другие.
Однако наш калькулятор интегрального объема лучше, быстрее, предоставляет больше функций и является лучшим калькулятором интеграции с шагами, доступными в Интернете. Узнайте о преимуществах использования нашего онлайн-калькулятора интегралов.
Когда вы вводите функцию, переменную, верхнюю и нижнюю границы пределов, наш решатель интегралов вычисляет интеграл и отображает все необходимые шаги, чтобы дать пользователю лучшее понимание вычисления интегрирования.
Вы также можете рассчитать вертикальное интегрирование и горизонтальное интегрирование в пределах области кривых с помощью нашего онлайн-калькулятора интегралов с пределами.
Это еще не все. Наш интегральный решатель также отображает вычисления антипроизводной для пользователей, которые могут быть заинтересованы в математической концепции и этапах интеграции.
Кроме того, этот калькулятор интеграции по частям обеспечивает визуализацию вычислений с помощью интуитивно понятных графиков.
Связанный: Как найти объем тела вращения
Как пользоваться калькулятором интегралов с шагом?
Использовать калькулятор интеграции по частям действительно просто и быстро.
Выполните следующие действия:
Шаг 1: Введите функцию
Для вычисления интегралов у вас должна быть правильная функция. Вам необходимо ввести свою функцию на панели функций калькулятора интегрирования. Также есть список «примеров загрузки». Вы можете щелкнуть этот список, чтобы загрузить пример уравнения для пошагового вычисления интегралов.
Шаг 2: Выберите переменную
Для вычисления интегралов можно использовать 3 переменные. Эти переменные — x, y и z.Роль этих трех переменных отличается друг от друга, и все три имеют разное влияние на общий результат. Вы можете выбрать переменные как x, y и z из раздела переменных.
Шаг 3: Задайте значение верхней границы
Верхняя граница — это значение, которое помогает нам суммировать интеграл до его максимального значения. Верхняя граница обозначается как U, и ее определение очень важно в контексте процесса интеграции. Вы можете ввести верхнюю границу своего лимита в разделе верхней границы калькулятора верхней границы.
Шаг 4: Задайте значение нижней границы
Нижняя граница — это наименьшее значение, которое мы устанавливаем для начала интегрирования. Это также наименьшее значение интервала, которое обозначается L. Чтобы получить точные результаты интегрирования, вам необходимо ввести фактическую величину вашего нижнего предела в разделе нижних границ калькулятора верхних и нижних границ.
После выполнения всех вышеперечисленных шагов нажмите кнопку «GO».
Сразу после нажатия на кнопку заработает наш калькулятор интегрального исчисления.Калькулятор интеграции по частям покажет вам антипроизводную, интегральные шаги, дерево синтаксического анализа и график вашего результата. Все эти функции и особенности делают этот калькулятор линейного интеграла лучшим для вычисления интеграла сложных задач интегрирования.
По мере того, как вы проходите процесс ввода, визуальное уравнение будет отображаться под входами, где вы можете визуализировать, как ваши входные данные будут выглядеть в уравнении.
 5)==4.0)
5)==4.0)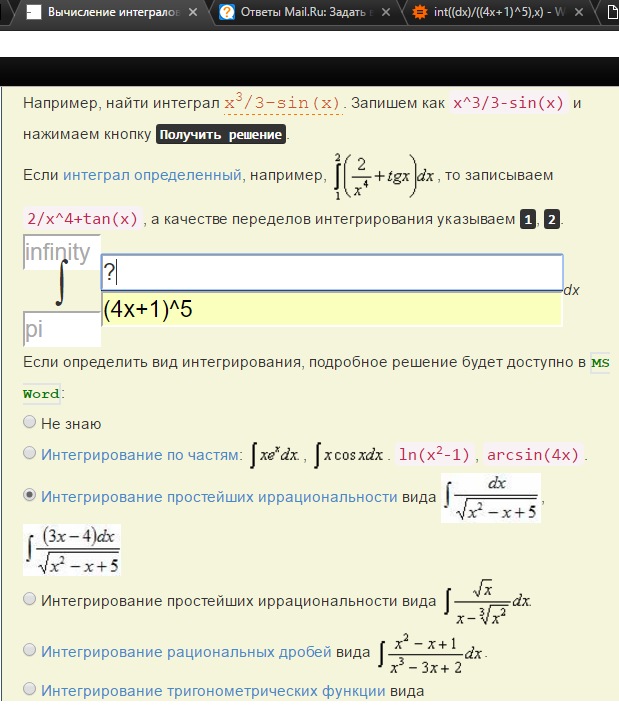 5)==4.0)
5)==4.0) Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек На этой странице вы найдёте калькулятор,
На этой странице вы найдёте калькулятор,
 ”
”
 Это может как-то раздражать тех, кто только начинает с интегралов.
Это может как-то раздражать тех, кто только начинает с интегралов.

 Они приняли интеграл как бесконечную сумму прямоугольников чрезвычайно малой ширины. Бернхард Риман описал интегралы строго математически.
Они приняли интеграл как бесконечную сумму прямоугольников чрезвычайно малой ширины. Бернхард Риман описал интегралы строго математически.

 Перейти к решению задач по математике онлайн (с инструкциями и примерами)
Перейти к решению задач по математике онлайн (с инструкциями и примерами)