Преобразования графика функции f(x)=x2 — презентация онлайн
1. Преобразования графика функции f(x)=x2
2. Перенос вдоль оси ординат
График функции y= f (x) + b при b >0можно получить параллельным
переносом вдоль оси ординат графика
функции y= f (x) на b единиц вверх.
y= x2 +2
Y
2
1
y=x2
0 1
График функции y=f(x)-b при b>0
можно получить параллельным
переносом вдоль оси ординат графика
функции y=f(x) на b единиц вниз
x
Y
1
0 1
-2
y=x2
x
y= x2 -2
3. Перенос вдоль оси ординат
График функции y= f(x)+b приb
1. построить график функции
y= f (x)
2.перенести ось абсцисс на b
единиц вверх
Y
2
На b
вверх
0
0
1
x
1
x
Y
График функции y=f(x)+b при
b>0 можно получить так:
1. построить график функции
y=f(x)
2 перенести ось абсцисс на b
единиц вниз
1
Вниз
На b
0
-2
0
x
1
x
4.
 Перенос вдоль оси абсцисс График функции y= f (x + c) можно
Перенос вдоль оси абсцисс График функции y= f (x + c) можнополучить параллельным переносом вдоль
|c| единиц влево при c >0 .
Y
y=x2
1
-2
0
1
x
y=(x+2)2
График функции y=f(x+c) можно получить
параллельным переносом вдоль оси
абсцисс графика функции y=f(x) на |c|
единиц вправо при c
y=x2
Y
y=(x-2)2
1
0
1
2
x
5. Перенос вдоль оси абсцисс
График функции y= f (x + c)при c >0 можно получить так :
1. построить график функции y=
f (x)
2.перенести ось ординат на |c|
единиц вправо
График функции y=f(x+c) при
c
можно получить так:
1. Построить график функции
y=f(x)
2. Перенести ось ординат на |c|
единиц влево
y
1
0
y
y
1
1
0
0 1
y
1
1 0
x
x
6. Сжатие ( растяжение ) графика вдоль оси ординат
График функцииy= b f (x) при b>1 можно
получить растяжением
графика функции y= f (x)
вдоль оси ординат
y=2×2
Y
1
y=x2
0 1
График функции y=bf(x)
при 0
сжатием графика
функции y=f(x) вдоль оси
ординат
x
y=0,5×2
Y
1
0 1
y=x2
x
7.
 Симметрия относительно оси абсцисс Чтобы построить график фунуции y= -f(x):
Симметрия относительно оси абсцисс Чтобы построить график фунуции y= -f(x):1. Строим график функции y=f(x)
2. Отражаем его симметрично
относительно оси абсцисс.
y=x2
0 1
x
y=-x2
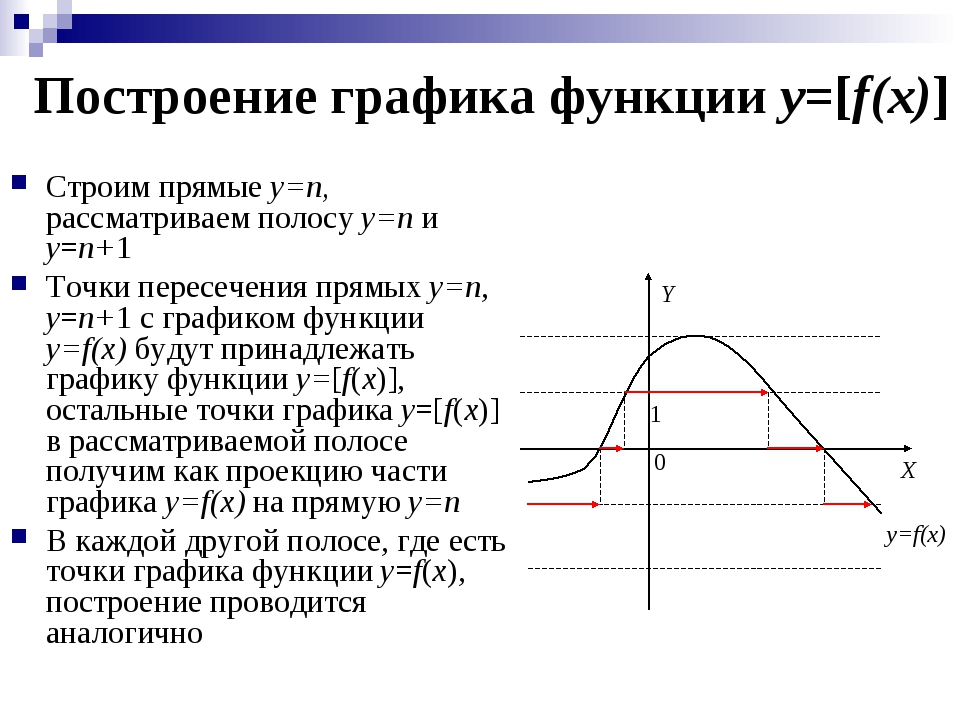
8. график функции y = f(|x|), y = |f(x)|
график функции y = f(|x|) получается из графика функции y =f(x) следующим преобразованием:
1) точки графика, имеющие неотрицательные абсциссы –
неподвижны;
2) точки графика, имеющие отрицательные абсциссы
заменяются на точки, полученные из неподвижных
отражением относительно оси y.
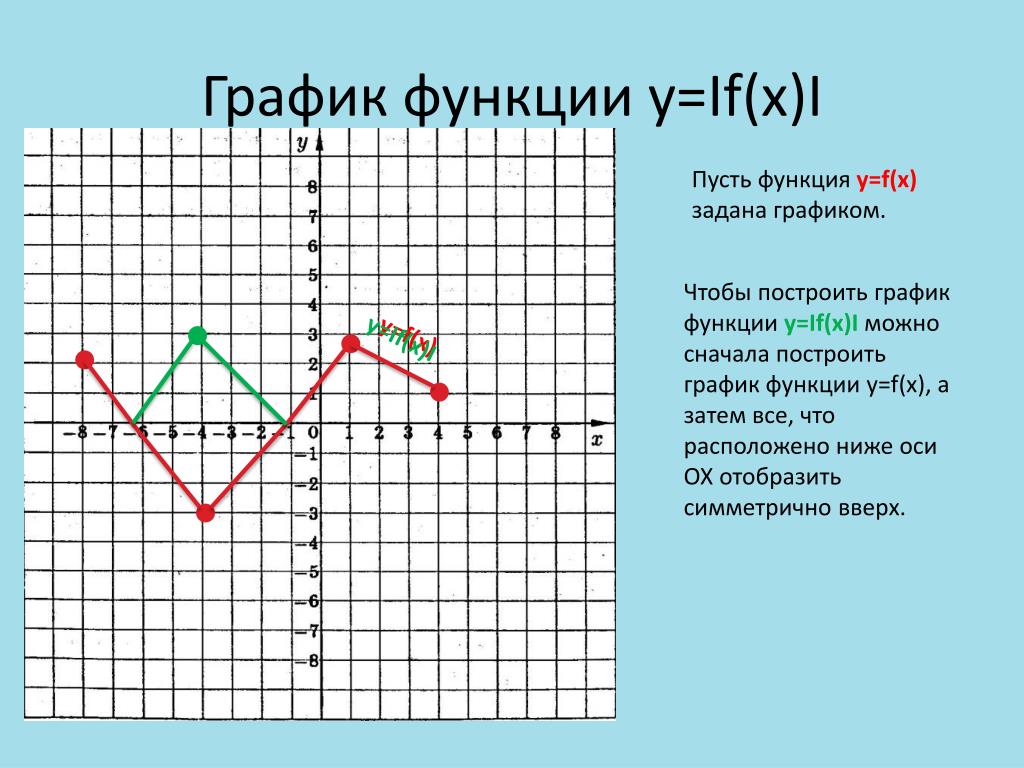
график функции y = |f(x)| получается из графика функции y =
f(x) следующим преобразованием:
1) точки графика, имеющие неотрицательные ординаты –
неподвижны;
2) точки графика, имеющие отрицательные ординаты,
отражаются относительно оси x.
9. Функция, содержащая операцию « взятие модуля»
yЧтобы построить график функции
1. Строим график функции y= f(x),
2.
 Часть графика, расположенную в
Часть графика, расположенную вверхней полуплоскости сохраняем.
3. Часть графика, расположенную в
нижней полуплоскости.
отображаем симметрично
относительно оси абсцисс в
верхнюю полуплоскость.
0
x
matematikam ru построение графиков — ComputerMaker.info
Автор admin На чтение 3 мин.
Построение графиков онлайн с помощью нашего сервиса является простой задачей. Возможность построения одновременно сразу нескольких функций, помеченных разными цветами. Укажите пределы переменной и функции — и наш сервис быстро нарисует ваш график.
Построение графиков онлайн
Построить функцию
Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos. Для ввода функций воспользуйтесь левой колонкой. Вводить можно вручную либо с помощью виртуальной клавиатуры внизу окна. Для увеличения окна с графиком можно скрыть как левую колонку, так и виртуальную клавиатуру.
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Для задания области (например, 1≤x≤7 ) используйте пределы или >= .
Трехмерные графики функции
Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3 ). 2-x/3 ).
2-x/3 ).
Чтобы построить трехмерный график в Excel , необходимо указать функцию f(x,y) , пределы по x и y и шаг сетки h .
Принципы и способы построения графика функции
Прикладное применение графика функции
Построить пирамиду ABCD по координатам можно здесь.
Введите график функции
Построим (исследуем) график функции y=f(x), для этого задайте функцию f(x)
Важно: a должно быть меньше b, иначе график не сможет построиться. Cледите за масштабом — если графика на рисунке нету, значит стоит поварьировать значения a и b
Примеры
С применением степени
(квадрат и куб) и дроби
С применением синуса и косинуса
Гиберболические синус и косинус
Гиберболические тангенс и котангенс
Гиберболические арксинус и арккосинус
Гиберболические арктангенс и арккотангенс
Исследование графика функции
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции: Да
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
Правила ввода выражений и функций
© Контрольная работа РУ — калькуляторы онлайн
Интересные факты про логотипы известных компаний
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
Построить функцию
Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos .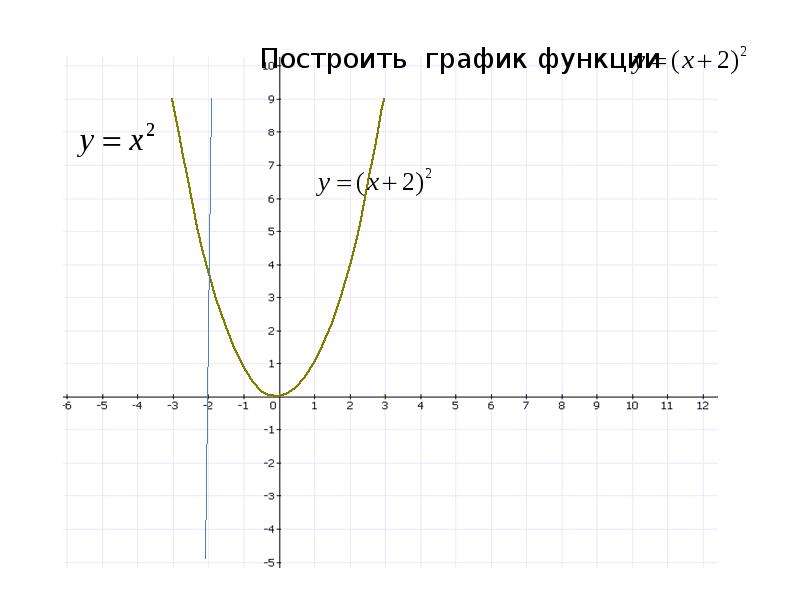 2/16=1)
2/16=1)
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т.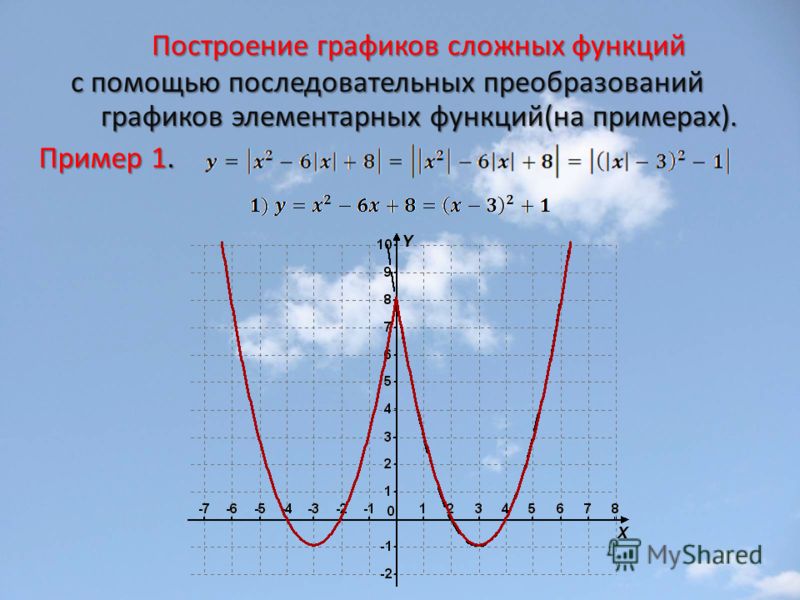 е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x
с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 наименьшее значение функция у = х 2 — 2х принимает при х = 1 .
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис.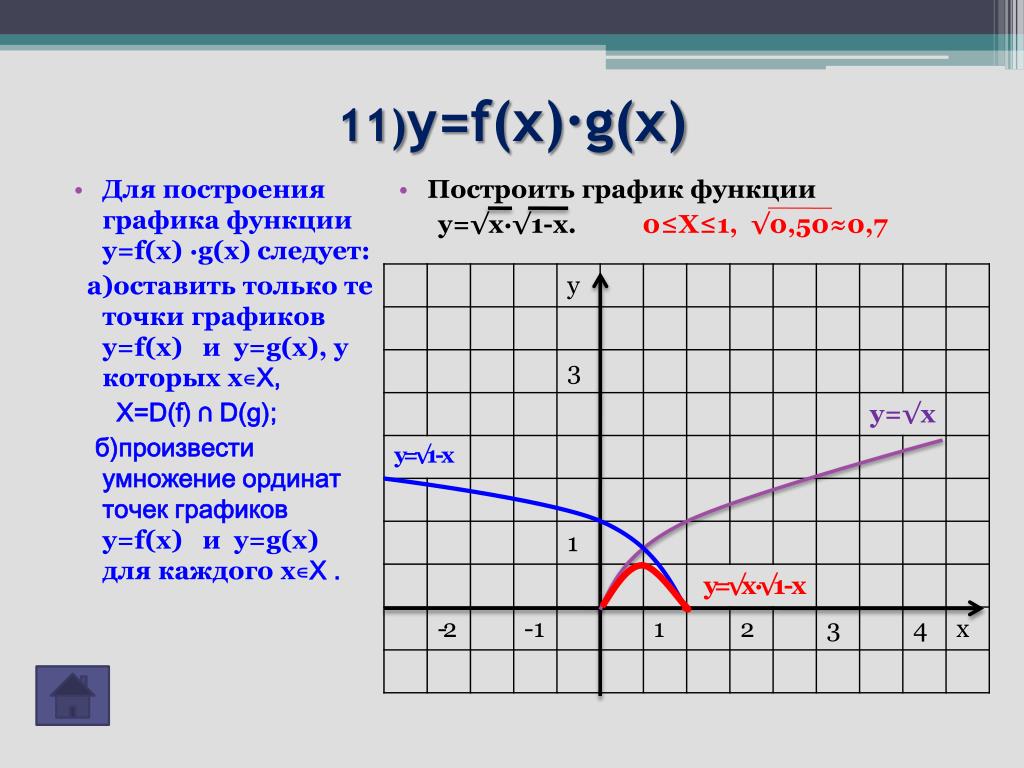 48.
48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
Построение графиков онлайн весьма полезный способ графически отобразить то, что не в силах передать словами.
Информация – это будущее электронного маркетинга, при этом правильно преподнесенные зрительные образы являются мощным инструментом для привлечения целевой аудитории.
Тут на помощь приходит инфографика, позволяющая в простой и выразительной форме преподносить различного рода информацию.
Однако построение инфографических изображений требует определенного аналитического мышления и богатства фантазии.
Спешим вас обрадовать – в интернете достаточно ресурсов, предоставляющих построение графиков онлайн.
Yotx.ru
Замечательный русскоязычный сервис, осуществляющий построение графиков онлайн по точкам (по значениям) и графиков функций (обычных и параметрических).
Этот сайт обладает интуитивно понятным интерфейсом и легок в использовании. Не требует регистрации, что существенно экономит время пользователя.
Позволяет быстро сохранять готовые графики на компьютере, а также генерирует код для размещения на блоге или сайте.
На Yotx.ru есть учебник и примеры графиков, которые были созданы пользователями.
Возможно, для людей, углубленно изучающих математику или физику, этого сервиса будет мало (например, нельзя построить график в полярных координатах, так как на сервисе нет логарифмической шкалы), но для выполнения самых простых лабораторных работ вполне достаточно.
Преимуществом сервиса является то, что он не заставляет как многие другие программы, искать полученный результат по всей двумерной плоскости.
Размер графика и интервалы по осям координат автоматически генерируются так, чтобы график оказался удобным для просматривания.
Одновременно на одной плоскости есть возможность построить несколько графиков.
Дополнительно на сайте можно использовать калькулятор матриц, с помощью которого легко производить различные действия и преобразования.
ChartGo
Англоязычный сервис для разработки многофункциональных и разноцветных гистограмм, линейных графиков, круговых диаграмм.
Для обучения пользователям представляется подробное руководство и деморолики.
ChartGo будет полезен для тех, кто нуждается в регулярно. Среди подобных ресурсов отличается простотой «Create a graph online quickly».
Построение графиков онлайн осуществляется по таблице.
В начале работы необходимо выбрать одну из разновидностей диаграмм.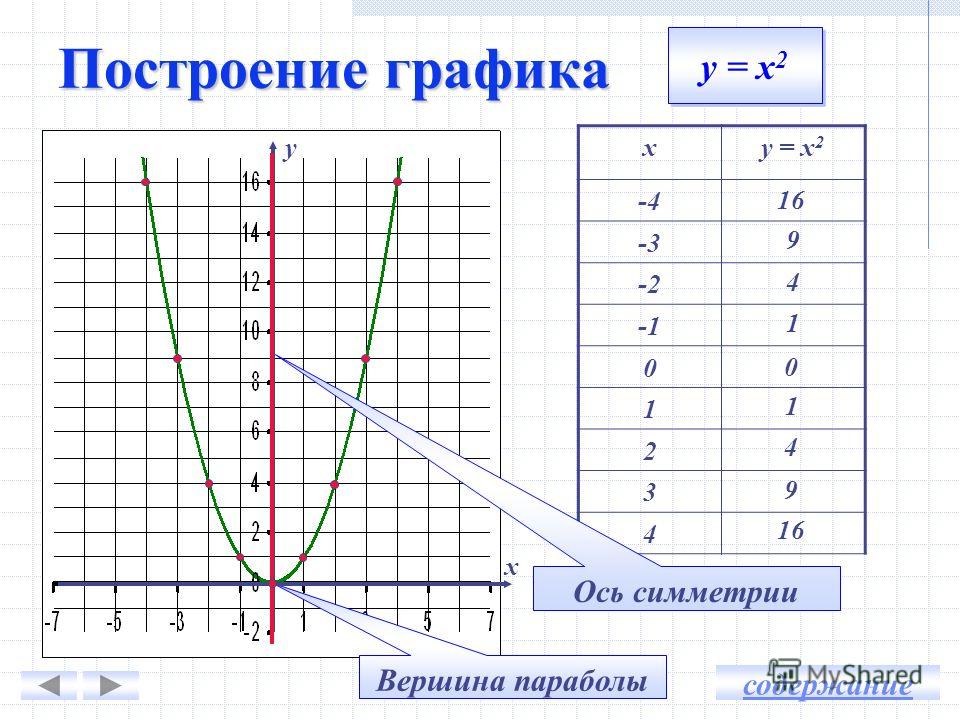
Приложение обеспечивает пользователям ряд простых вариантов настройки построения графиков различных функций в двумерных и трехмерных координатах.
Можно выбрать одну из разновидностей диаграмм и переключаться между 2D и 3D.
Настройки размера обеспечивают максимальный контроль между вертикальной и горизонтальной ориентацией.
Пользователи могут настраивать свои диаграммы с уникальным названием, а также присваивать названия для X и Y элементов.
Для построения графиков онлайн xyz в разделе «Example» доступно множество макетов, которые можно изменять на свое усмотрение.
Обратите внимание! В ChartGo в одной прямоугольной системе может быть построено множество графиков. При этом каждый график составлен с помощью точек и линий. Функции действительного переменного (аналитические) задаются пользователем в параметрическом виде.
Разработан и дополнительный функционал, который включает мониторинг и вывод координат на плоскости или в трехмерной системе, импорт и экспорт числовых данных в определенных форматах.
Программа имеет гибко настраиваемый интерфейс.
После создания диаграммы, пользователь может воспользоваться функцией печати результата и сохранения графика в виде статичного рисунка.
OnlineCharts.ru
Еще одно отличное приложение для эффектного представления информации вы можете найти на сайте OnlineCharts.ru, где можно построить график функции онлайн бесплатно.
Сервис способен работать с множеством видов диаграмм, включая линейные, пузырьковые, круговые, столбчатые и радиальные.
Система обладает очень простым и наглядным интерфейсом. Все доступные функции разделены вкладками в виде горизонтального меню.
Чтобы начать работу необходимо выбрать тип диаграммы, которую вы хотите построить.
После этого можно настроить некоторые дополнительные параметры внешнего вида, в зависимости от выбранного типа графика.
Во вкладке «Добавить данные» пользователю предлагается задать количество строк и если необходимо количество групп.
Также можно определить цвет.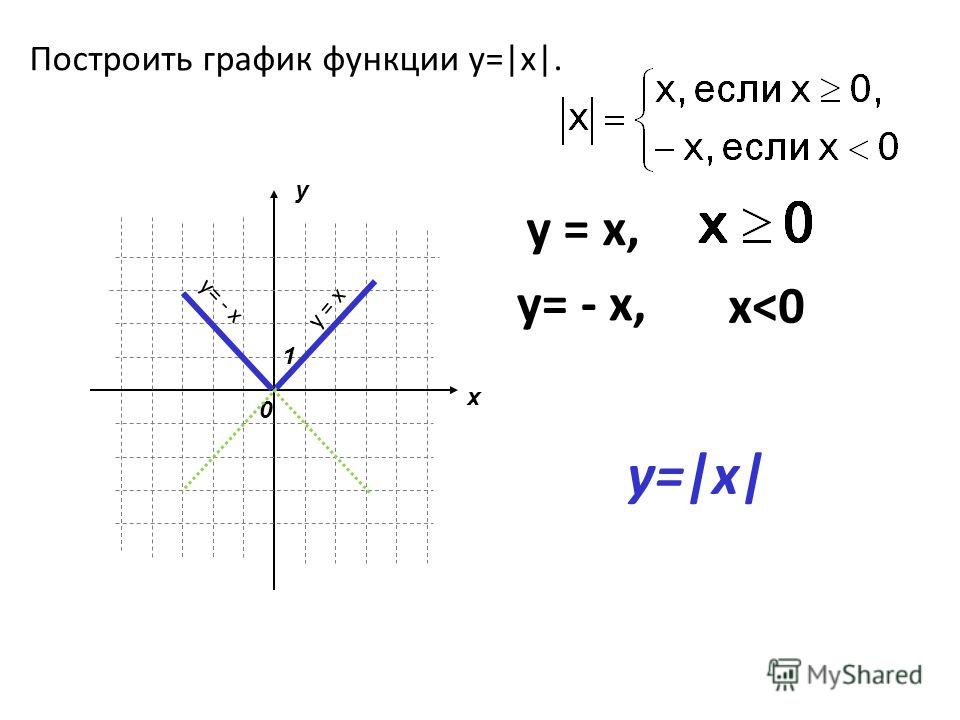
Обратите внимание! Вкладка «Подписи и шрифты» предлагает задать свойства подписей (нужно ли их выводить вообще, если да, то каким цветом и размером шрифта). Также предоставляется возможность выбора типа шрифта и его размера для основного текста диаграммы.
Все предельно просто.
Aiportal.ru
Самый простой и наименее функциональный из всех, представленных здесь онлайн-сервисов. Создать трехмерный график онлайн на этом сайте не удастся.
Он предназначен для построения графиков сложных функций в системе координат на определенном интервале значений.
Для удобства пользователей сервис предоставляет справочные данные по синтаксису различных математических операций , а также по перечню поддерживаемых функций и константных значений.
Все необходимые для составления графика данные вводятся в окно «Функции». Одновременно на одной плоскости пользователь может построить несколько графиков.
Поэтому разрешается вносить подряд несколько функций, но после каждой функции необходимо вставлять точку с запятой. Также задается и область построения.
Также задается и область построения.
Предусмотрена возможность построения графиков онлайн по таблице или без нее. Поддерживается цветовая легенда.
Несмотря на небогатый функционал, все же это онлайн-сервис, поэтому вам не придется долго искать, скачивать и устанавливать какое-либо программное обеспечение.
Для построения графика достаточно лишь иметь с любого имеющегося устройства: ПК, ноутбука, планшета или смартфона.
Построение графика функции онлайн
ТОП-4 лучших сервиса для построения графиков онлайн
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.

Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Onlinecharts.ru
Онлайн-помощник Onlinecharts.ru строит не графики, а диаграммы практически всех существующих видов. В том числе:
- Линейные.
- Столбчатые.
- Круговые.
- С областями.
- Радиальные.
- XY-графики.
- Пузырьковые.
- Точечные.
- Полярные бульки.
- Пирамиды.
- Спидометры.
- Столбчато-линейные.
Пользоваться ресурсом очень просто. Внешний вид диаграммы (цвет фона, сетки, линий, указателей, форма углов, шрифты, прозрачность, спецэффекты и т. д.) полностью определяется пользователем. Данные для построения можно ввести как вручную, так и импортировать из таблицы CSV-файла, хранимого на компьютере. Готовый результат доступен для скачивания на ПК в виде картинки, PDF-, CSV- или SVG-файлов, а также для сохранения онлайн на фотохостинге ImageShack.Us или в личном кабинете Onlinecharts.ru. Первый вариант могут использовать все, второй — только зарегистрированные.
д.) полностью определяется пользователем. Данные для построения можно ввести как вручную, так и импортировать из таблицы CSV-файла, хранимого на компьютере. Готовый результат доступен для скачивания на ПК в виде картинки, PDF-, CSV- или SVG-файлов, а также для сохранения онлайн на фотохостинге ImageShack.Us или в личном кабинете Onlinecharts.ru. Первый вариант могут использовать все, второй — только зарегистрированные.
Сложение графиков функций онлайн. Функции и графики
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 у = х 2 — 2х принимает при х = 1 .
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей.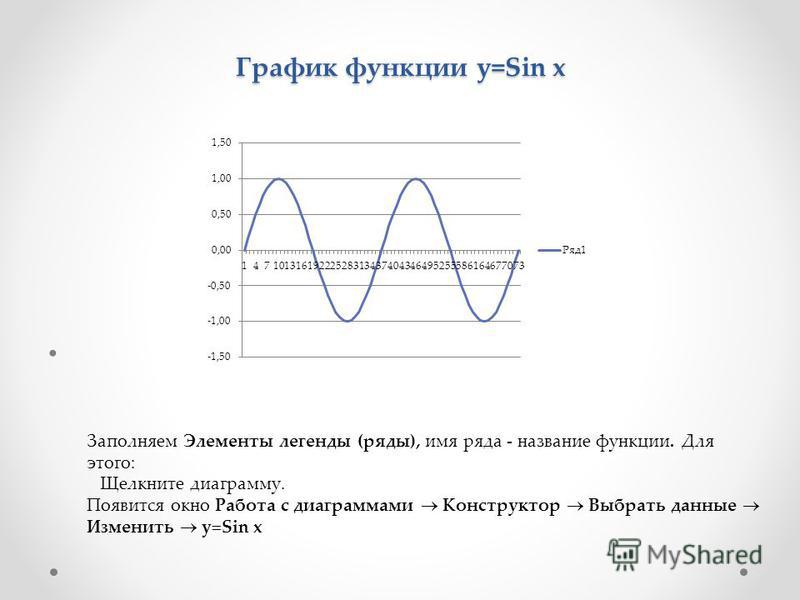 Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .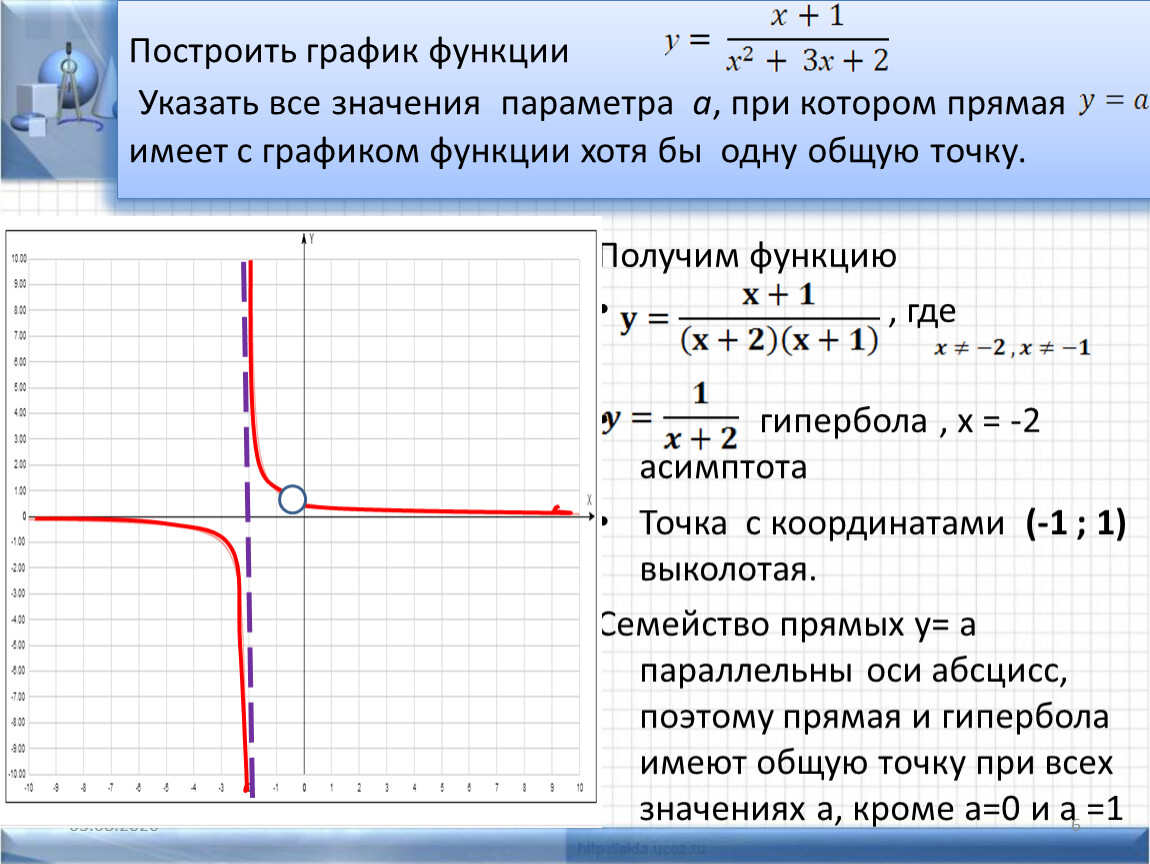
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos. com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция.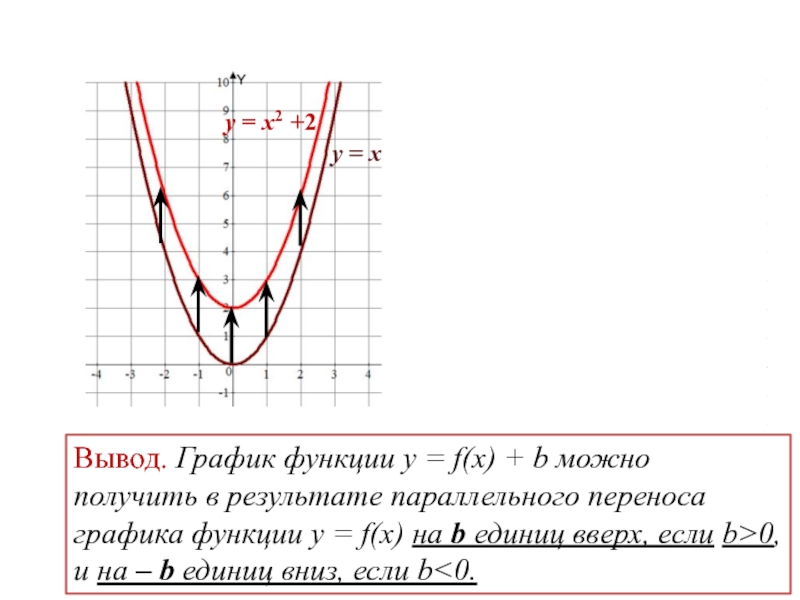 Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .

Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .

- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Построение графиков онлайн. График функции Преимущества построения графиков онлайн
Построить функцию
Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos . Для ввода функций воспользуйтесь левой колонкой. Вводить можно вручную либо с помощью виртуальной клавиатуры внизу окна. Для увеличения окна с графиком можно скрыть как левую колонку, так и виртуальную клавиатуру.
Преимущества построения графиков онлайн
- Визуальное отображение вводимых функций
- Построение очень сложных графиков
- Построение графиков, заданных неявно (например эллипс x^2/9+y^2/16=1)
- Возможность сохранять графики и получать на них ссылку, которая становится доступной для всех в интернете
- Управление масштабом, цветом линий
- Возможность построения графиков по точкам, использование констант
- Построение одновременно нескольких графиков функций
- Построение графиков в полярной системе координат (используйте r и θ(\theta))
С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.
В данном уроке мы рассмотрим методику построения эскиза графика функции, приведем разъясняющие примеры.
Тема: Повторение
Урок: Эскиз графика функции (на примере дробно-квадратичной функции)
Наша цель — построить эскиз графика дробно-квадратичной функции. Для примера возьмем уже знакомую нам функцию:
Задана дробная функция, в числителе и знаменателе которой стоят квадратичные функции.
Методика построения эскиза такова:
1. Выделим интервалы знакопостоянства и определим на каждом знак функции (рисунок 1)
Мы подробно рассматривали и выяснили, что функция, непрерывная в ОДЗ, может сменить знак только при переходе аргумента через корни и точки разрыва ОДЗ.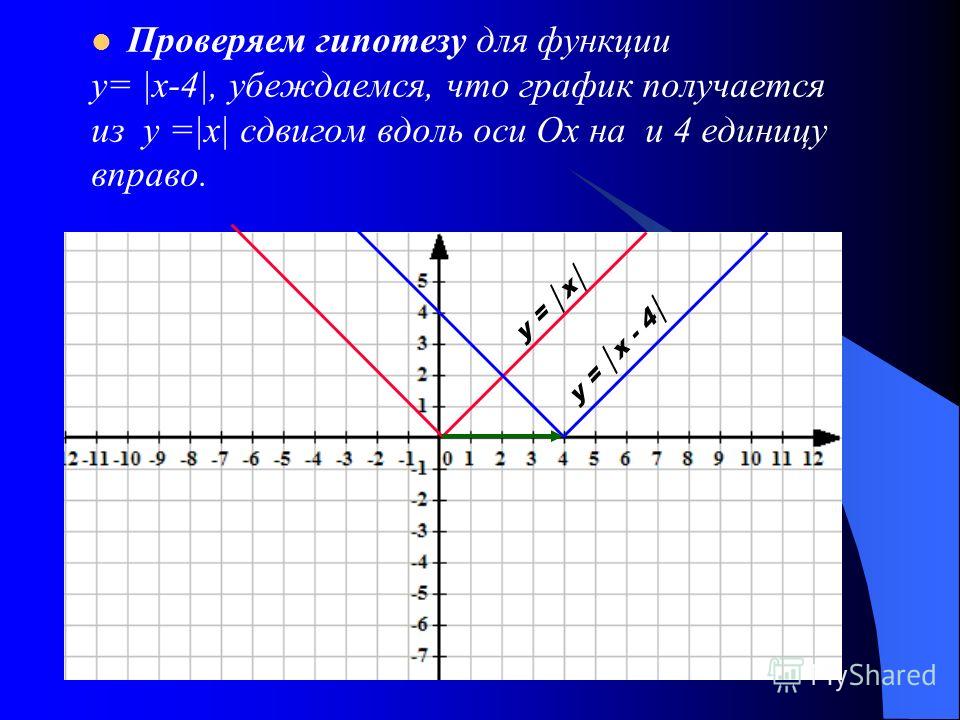
Заданная функция у непрерывна в своей ОДЗ, укажем ОДЗ:
Найдем корни:
Выделим интервалы знакопостоянства. Мы нашли корни функции и точки разрыва области определения — корни знаменателя. Важно отметить, что внутри каждого интервала функция сохраняет знак.
Рис. 1. Интервалы знакопостоянства функции
Чтобы определить знак функции на каждом интервале, можно взять любую точку, принадлежащую интервалу, подставить ее в функцию и определить ее знак. Например:
На интервале функция имеет знак плюс
На интервале функция имеет знак минус.
В этом преимущество метода интервалов: мы определяем знак в единственной пробной точке и заключаем, что функция будет иметь такой же знак на всем выбранном интервале.
Однако можно выставлять знаки автоматически, не высчитывая значений функции, для этого определить знак на крайнем интервале, а далее чередовать знаки.
1. Построим график в окрестности каждого корня. Напомним, что корни данной функции и :
Рис. 2. График в окрестностях корней
2. График в окрестностях корней
Поскольку в точке знак функции меняется с плюса на минус, то кривая сначала находится над осью, потом проходит через ноль и далее расположена под осью х. В точке наоборот.
2. Построим график в окрестности каждого разрыва ОДЗ. Напомним, что корни знаменателя данной функции и :
Рис. 3. График функции в окрестностях точек разрыва ОДЗ
Когда или знаменатель дроби практически равен нулю, значит, когда значение аргумента стремится к этим числам, значение дроби стремится к бесконечности. В данном случае, когда аргумент подходит к тройке слева функция положительна и стремится к плюс бесконечности, справа функция отрицательна и выходит из минус бесконечности. Около четверки наоборот, слева функция стремится к минус бесконечности, а справа выходит из плюс бесконечности.
Согласно построенному эскизу мы можем в некоторых промежутках угадать характер поведения функции.
Рис. 4. Эскиз графика функции
Рассмотрим следующую важную задачу — построить эскиз графика функции в окрестностях бесконечно удаленных точек, т.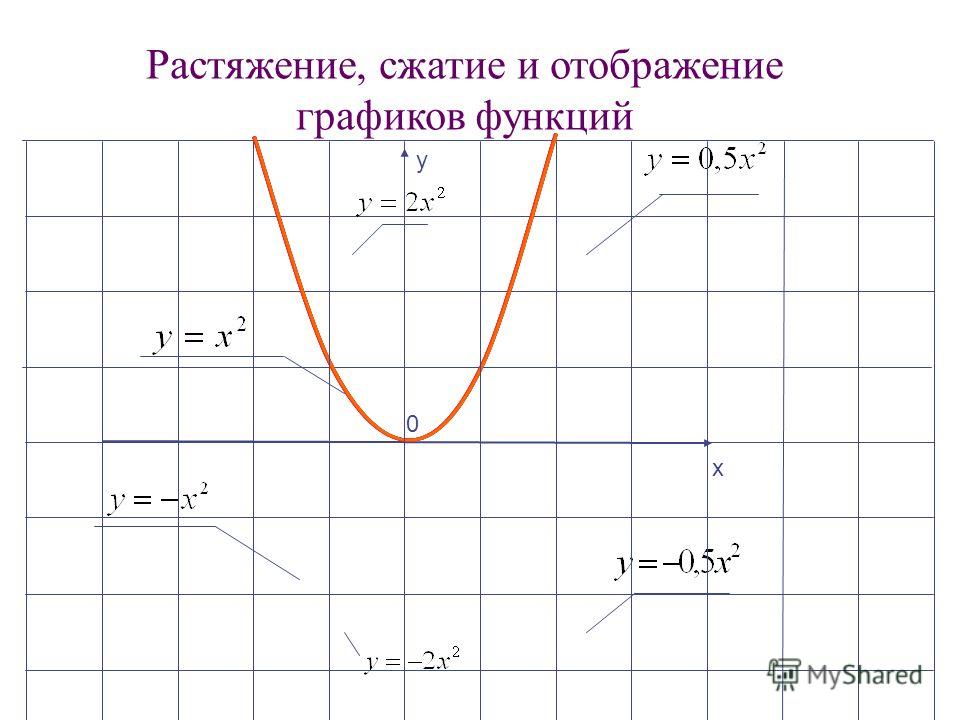 е. когда аргумент стремится к плюс или минус бесконечности. Постоянными слагаемыми при этом можно пренебречь. Имеем:
е. когда аргумент стремится к плюс или минус бесконечности. Постоянными слагаемыми при этом можно пренебречь. Имеем:
Иногда можно встретить такую запись данного факта:
Рис. 5. Эскиз графика функции в окрестностях бесконечно удаленных точек
Мы получили приблизительный характер поведения функции на всей ее области определения, далее нужно уточнять построения с применением производной.
Пример 1 — построить эскиз графика функции:
Имеем три точки, при переходе аргумента через которые функция может менять знак.
Определяем знаки функции на каждом интервале. Имеем плюс на крайнем правом интервале, далее знаки чередуются, так как все корни имеют первую степень.
Строим эскиз графика в окрестностях корней и точек разрыва ОДЗ. Имеем: поскольку в точке знак функции меняется с плюса на минус, то кривая сначала находится над осью, потом проходит через ноль и далее расположена под осью х. Когда или знаменатель дроби практически равен нулю, значит, когда значение аргумента стремится к этим числам, значение дроби стремится к бесконечности.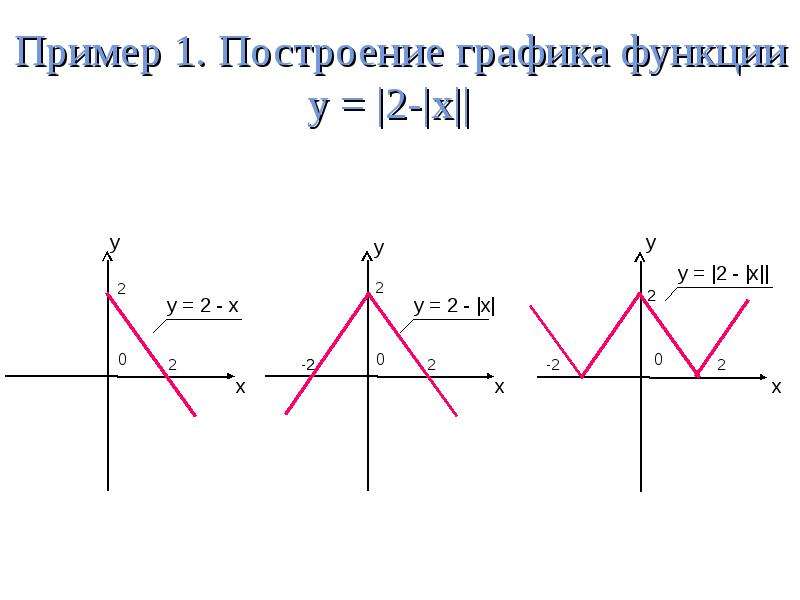 В данном случае, когда аргумент подходит к минус двум слева функция отрицательна и стремится к минус бесконечности, справа функция положительна и выходит из плюс бесконечности. Около двойки аналогично.
В данном случае, когда аргумент подходит к минус двум слева функция отрицательна и стремится к минус бесконечности, справа функция положительна и выходит из плюс бесконечности. Около двойки аналогично.
Найдем производную функции:
Очевидно, что производная всегда меньше нуля, следовательно, функция убывает на всех участках. Так, на участке от минус бесконечности до минус двух функция убывает от нуля до минус бесконечности; на участке от минус двух до нуля функция убывает от плюс бесконечности до нуля; на участке от нуля до двух функция убывает от нуля до минус бесконечности; на участке от двух до плюс бесконечности функция убывает от плюс бесконечности до нуля.
Проиллюстрируем:
Рис. 6. Эскиз графика функции к примеру 1
Пример 2 — построить эскиз графика функции:
Строим эскиз графика функции без использования производной.
Сначала исследуем заданную функцию:
Имеем единственную точку, при переходе аргумента через которую функция может менять знак.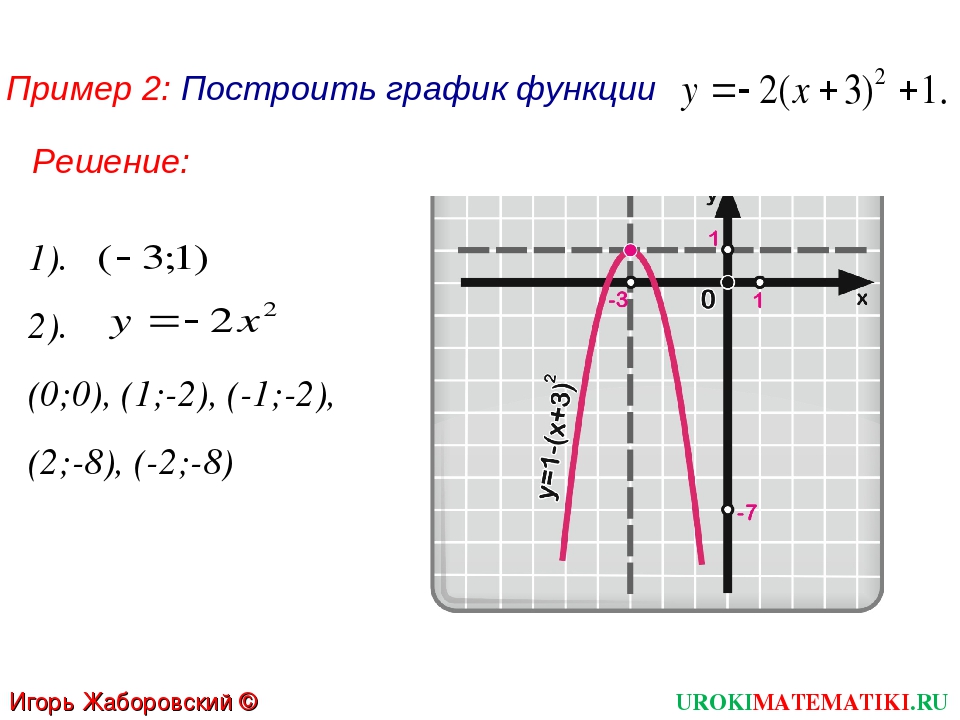
Отметим, что заданная функция нечетная.
Определяем знаки функции на каждом интервале. Имеем плюс на крайнем правом интервале, далее знак меняется, так как корень имеет первую степень.
Строим эскиз графика в окрестностях корня. Имеем: поскольку в точке знак функции меняется с минуса на плюс, то кривая сначала находится под осью, потом проходит через ноль и далее расположена над осью х.
Теперь строим эскиз графика функции в окрестностях бесконечно удаленных точек, т.е. когда аргумент стремится к плюс или минус бесконечности. Постоянными слагаемыми при этом можно пренебречь. Имеем:
После выполнения вышеперечисленных действий мы уже представляем себе график функции, но требуется уточнить его с помощью производной.
Найдем производную функции:
Выделяем интервалы знакопостоянства производной: при . ОДЗ здесь . Таким образом, имеем три интервала знакопостоянства производной и три участка монотонности исходной функции. Определим знаки производной на каждом интервале.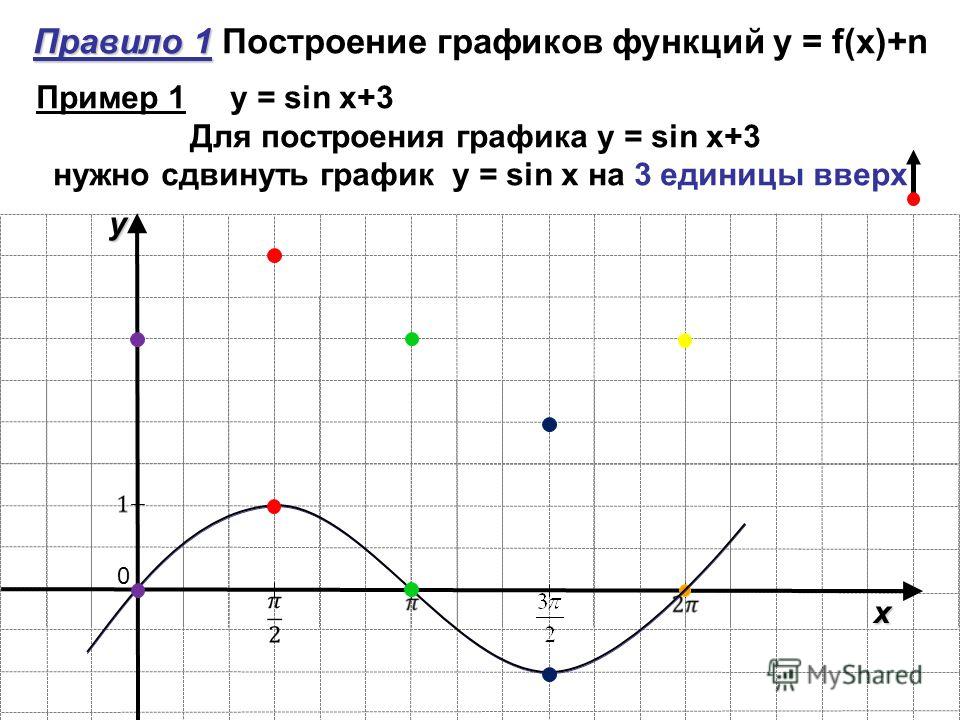 Когда производная положительна, функция возрастает; когда производная отрицательна, функция убывает. При этом — точка минимум, т.к. производная меняет знак с минуса на плюс; наоборот, точка максимума.
Когда производная положительна, функция возрастает; когда производная отрицательна, функция убывает. При этом — точка минимум, т.к. производная меняет знак с минуса на плюс; наоборот, точка максимума.
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 у = х 2 — 2х принимает при х = 1 .
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.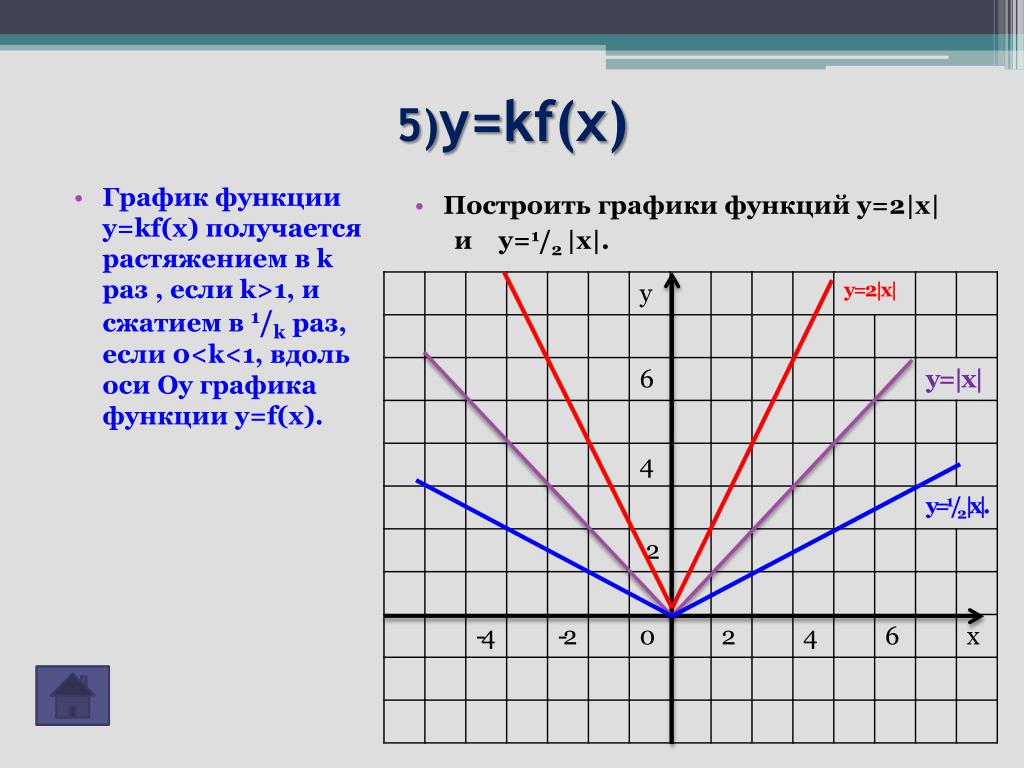
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т.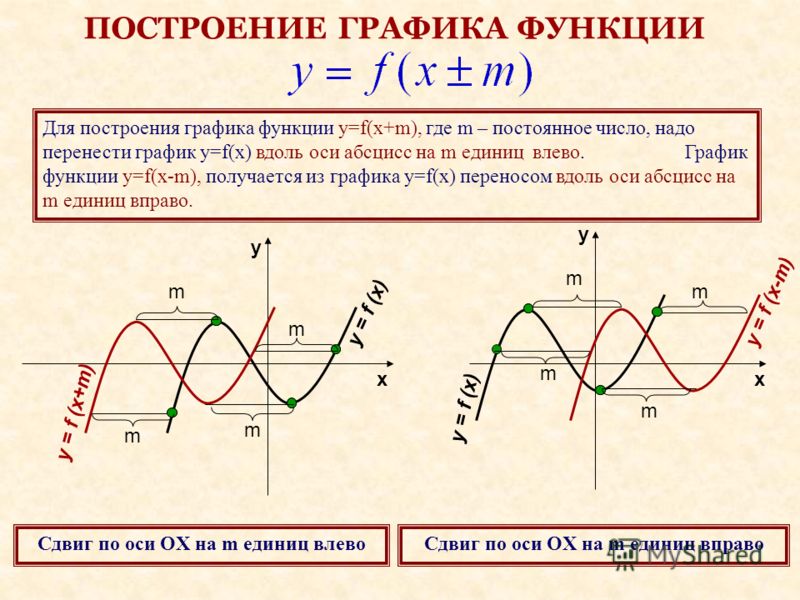 е. часть графика функции
е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x).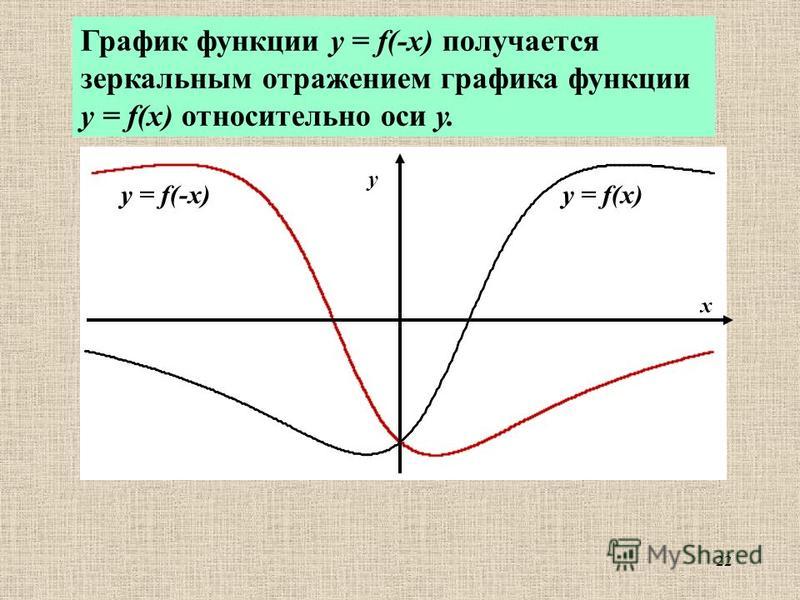 если заданы графики функций y = f(x) и y = g(x) .
если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т.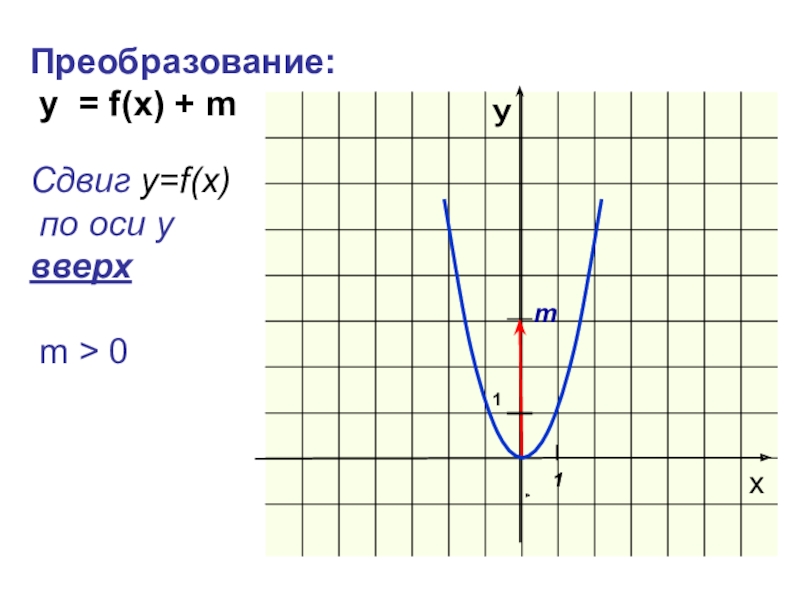 е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
Функции график построение: Построение графиков функций онлайн — ЭкоДом: Дом своими руками
Построение графиков функций
Функции и их графики — одна из самых увлекательных тем в школьной математике. Жаль только, что проходит она… мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.
Жаль только, что проходит она… мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.
Умение строить графики функций необходимо для решения задач с параметрами на ЕГЭ по математике. Это одна из первых тем курса математического анализа в вузе. Это настолько важная тема, что мы в ЕГЭ-Студии проводим по ней специальные интенсивы для старшеклассников и учителей, в Москве и онлайн. И часто участники говорят: «Жаль, что мы не знали этого раньше».
Но это не все. Именно с понятия функции и начинается настоящая, «взрослая» математика. Ведь сложение и вычитание, умножение и деление, дроби и пропорции — это все-таки арифметика. Преобразования выражений — это алгебра. А математика — наука не только о числах, но и о взаимосвязях величин. Язык функций и графиков понятен и физику, и биологу, и экономисту. И, как сказал Галилео Галилей, «Книга природы написана на языке математики».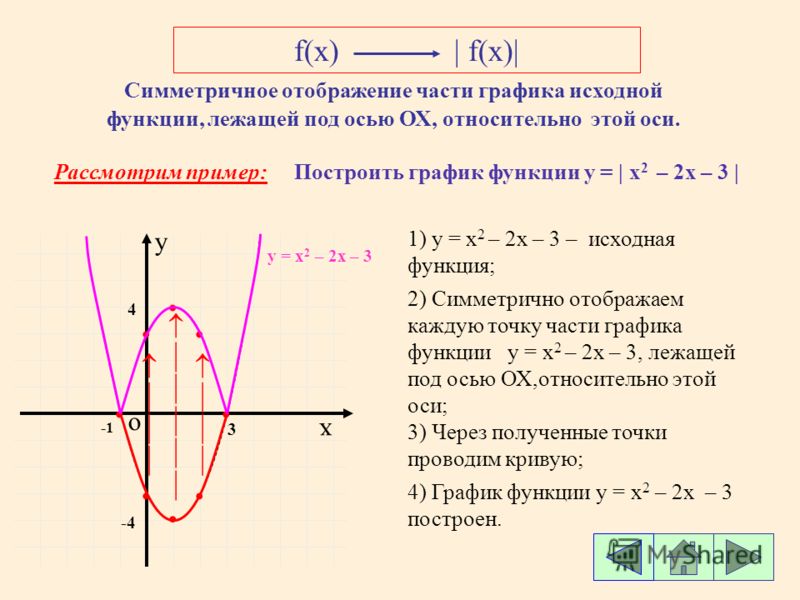
Точнее, Галилео Галилей сказал так:«Математика есть алфавит, посредством которого Господь начертал Вселенную».
Темы для повторения:
Понятие функции
Типы элементарных функций
Преобразования графиков функций
Производная функции
1. Построим график функции
Знакомая задача! Такие встречались в вариантах ОГЭ по математике. Там они считались сложными. Но сложного ничего здесь нет.
Упростим формулу функции:
при
График функции — прямая с выколотой точкой
2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, применяемый в решении неравенств, построении графиков и оценке целых величин в задачах на числа и их свойства. Он встретится вам также на первом курсе, когда придется брать интегралы.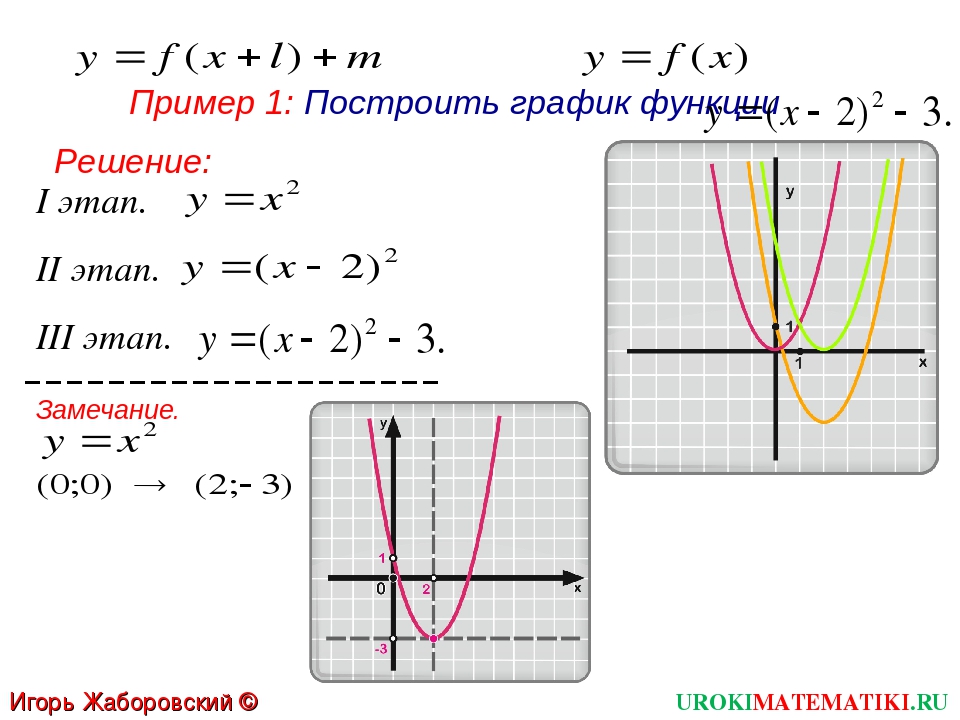
3. Построим график функции
Он получается из графика функции растяжением в 2 раза, отражением по вертикали и сдвигом на 1 вверх по вертикали
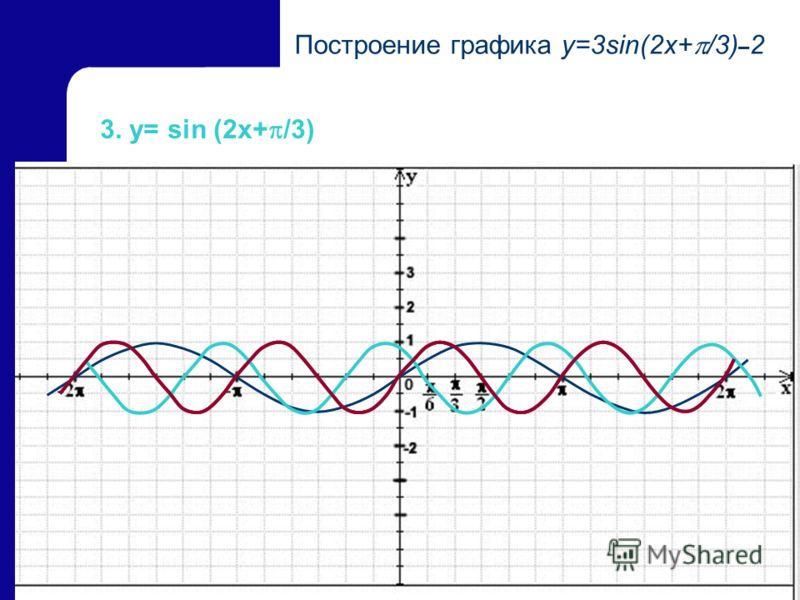
4. Построим график функции
Главное — правильная последовательность действий. Запишем формулу функции в более удобном виде:
Действуем по порядку:
1) График функции y=sinx сдвинем на влево;
2) сожмем в 2 раза по горизонтали,
3) растянем в 3 раза по вертикали,
4) сдвинем на 1 вверх
Сейчас мы построим несколько графиков дробно-рациональных функций. Чтобы лучше понять, как мы это делаем, читайте статью «Поведение функции в бесконечности. Асимптоты».
5. Построим график функции
Область определения функции:
Нули функции: и
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Прямая x = 0 (ось Y) — вертикальная асимптота функции.Асимптота — прямая, к которой бесконечно близко подходит график функции, но не пересекает ее и не сливается с ней (смотри тему «Поведение функции в бесконечности. Асимптоты»)
Асимптоты»)
Есть ли другие асимптоты у нашей функции? Чтобы выяснить это, посмотрим, как ведет себя функция, когда x стремится к бесконечности.
Раскроем скобки в формуле функции:
Если x стремится к бесконечности, то стремится к нулю. Прямая является наклонной асимптотой к графику функции.
6. Построим график функции
Это дробно-рациональная функция.
Область определения функции
Нули функции: точки — 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты:
Если x стремится к бесконечности, то у стремится к 1. Значит, — горизонтальная асимптота.
Вот эскиз графика:
Еще один интересный прием — сложение графиков.
7. Построим график функции
Если x стремится к бесконечности, то и график функции будет бесконечно близко подходить к наклонной асимптоте
Если x стремится к нулю, то функция ведет себя как Это мы и видим на графике:
Вот мы и построили график суммы функций. Теперь график произведения!
Теперь график произведения!
8. Построим график функции
Область определения этой функции — положительные числа, поскольку только для положительных x определен
Значения функции равны нулю при (когда логарифм равен нулю), а также в точках, где то есть при
При значение cos x равно единице. Значение функции в этих точках будет равно при
9. Построим график функции
Функция определена при Она четная, поскольку является произведением двух нечетных функций и График симметричен относительно оси ординат.
Нули функции — в точках, где то есть при при
Если x стремится к бесконечности, стремится к нулю. Но что же будет, если x стремится к нулю? Ведь и x, и sin x будут становиться меньше и меньше. Как же будет вести себя частное ?
Оказывается, что если x стремится к нулю, то стремится к единице. В математике это утверждение носит название «Первого замечательного предела».
А как же производная? Да, наконец-то мы до нее добрались.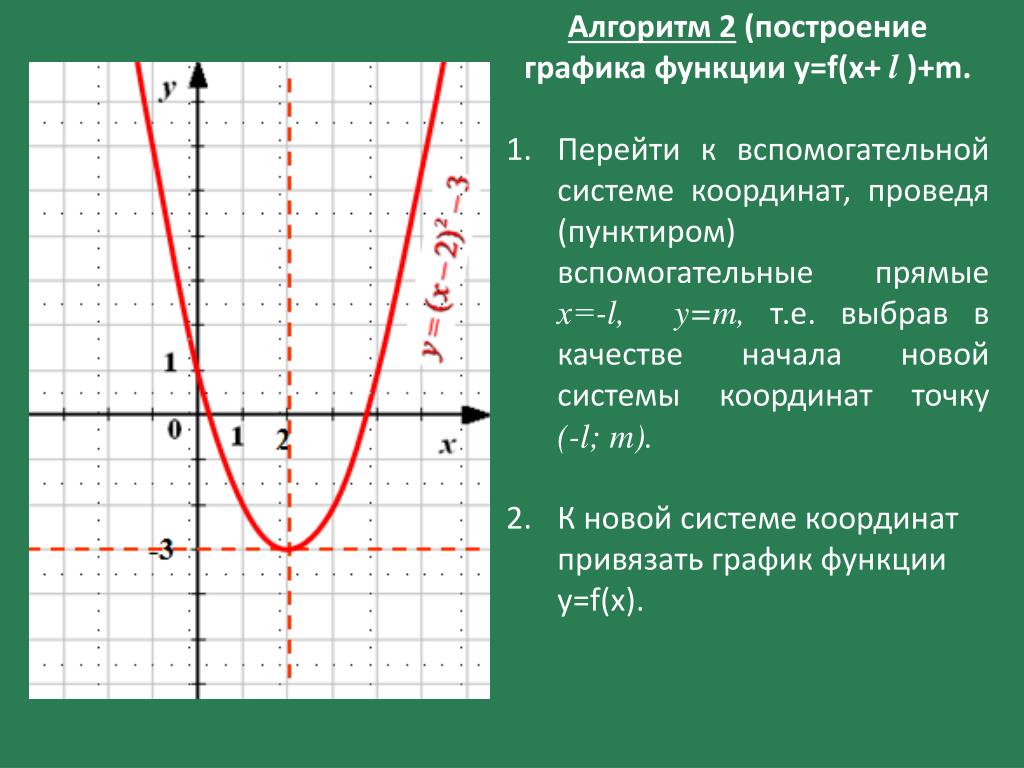 Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.
Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.
10. Построим график функции
Область определения функции — все действительные числа, поскольку
Функция нечетна. Ее график симметричен относительно начала координат.
При x=0 значение функции равно нулю. При значения функции положительны, при отрицательны.
Если x стремится к бесконечности, то стремится к нулю.
Найдем производную функции
По формуле производной частного,
если или
В точке производная меняет знак с «минуса» на «плюс», — точка минимума функции.
В точке производная меняет знак с «плюса» на «минус», — точка максимума функции.
Найдем значения функции при x=2 и при x=-2.
Графики функций удобно строить по определенному алгоритму, или схеме. Помните, вы изучали ее в школе?
Общая схема построения графика функции:
1. Область определения функции
2. Область значений функции
Область значений функции
3. Четность — нечетность (если есть)
4. Периодичность (если есть)
5. Нули функции (точки, в которых график пересекает оси координат)
6. Промежутки знакопостоянства функции (то есть промежутки, на которых она строго положительна или строго отрицательна).
7. Асимптоты (если есть).
8. Поведение функции в бесконечности
9. Производная функции
10. Промежутки возрастания и убывания. Точки максимума и минимума и значения в этих точках.
|
График функции, построение графика, урок по алгебре за 10 класс, презентация
Дата публикации: .
Ребята, мы с вами построили много графиков функций, например, параболы, гиперболы, графики тригонометрических функций и другие. Давайте вспомним, как мы это делали. Мы выбирали точки на оси абсцисс, высчитывали значения ординат нашей функций и плавно соединяли наши ординаты на координатной плоскости. То есть, мы строили график по точкам. При построении многих графиков, точки нужно выбирать обдуманно. Теперь давайте обобщим наши знания и напишем общие правила построения графиков функций.
Что же такое график функции?
График функции – это множество точек, абсциссы которых являются значениями из области определения, а ординаты — значениями функции y= f(x). График любой функций строят по точкам. Но если мы точно не знаем, какой будет вид у графика, то точки надо выбирать обдуманно. Ребята, какие важные точки есть у функций?
Давайте, вспомним их:
а) Стационарные и критические точки. Такие точки мы научились находить при вычислении экстремумов функций. Это точки, в которой производная либо равна нулю, либо не существует.
б) Точки экстремума. Точки максимума и минимума функций. Точки, возле которых определяется характер монотонности.
в) Точки пересечения графика с осью абсцисс и осью ординат. Значения, в которых функция y= f(x)= 0 – точки пересечения с осью абсцисс. А если вычислить f(0) – то эта точка пересечения с осью ординат.
г) Точки разрыва функций. Эти точки ищутся для не непрерывных функций.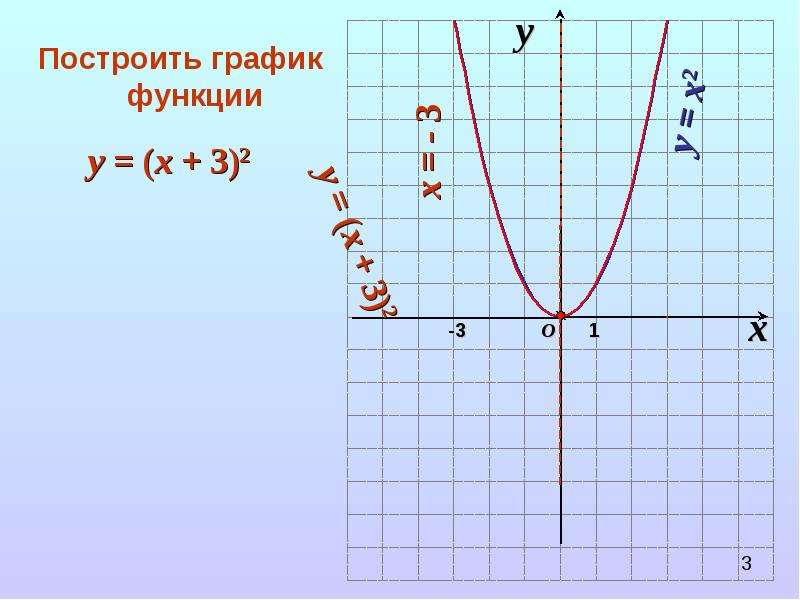
Правило построения графиков функций
Ребята, давайте запишем основные правила построения графиков функций:
- Если функция y= f(x) непрерывна на всей числовой прямой, то надо найти стационарные и критические точки, точки экстремума, промежутки монотонности, точки пересечения графика с осями координат и при необходимости выбрать еще несколько контрольных точек, в которых следует подсчитать значение нашей функции.
- Если функция y= f(x) определена не на всей числовой прямой, то начинать следует с нахождения области определения функции, с указания точек ее разрыва.
- Полезно исследовать функцию на чётность, поскольку графики четной или нечетной функций обладают симметрией (соответственно относительно оси y или относительно начала координат), и, следовательно, можно сначала построить только ветвь графика при x ≥ 0, а затем дорисовать симметричную ветвь.
- Если
то прямая y= b является горизонтальной асимптотой нашего графика функции. Асимптота — это некоторой ориентир для нашей функции. Это то, к чему стремится график функции в точке, но не достигает этого значения.
Асимптота — это некоторой ориентир для нашей функции. Это то, к чему стремится график функции в точке, но не достигает этого значения. - Если f(x)=$\frac{p(x)}{q(x)}$; и при x= a знаменатель обращается в нуль, а числитель отличен от нуля, то x= a — это вертикальная асимптота.
Несколько правил, упрощающих построение графиков функций:
а) График функции y= f(x) + a получается из графика функции y= f(x) (график y= f(x) заранее известен), путем параллельного переноса графика y= f(x) на а единиц вверх, если а > 0; и на а единиц вниз, если а
Для примера построим три графика: а) y= x2, б) y= x2 + 2, в) y= x2 — 3.
Графики наших функций получается из графика функции y=x2, путем его параллельного переноса: б) на две единицы вверх, в) на три единицы вниз.
Графики наших функций:
б) График функции y= f(x + a) получается из графика функции y= f(x) (график y= f(x) заранее известен). Используем параллельный перенос графика y= f(x) на а единиц влево, если а > 0, и на а единиц вправо, если а
Для примера построим три графика: а) y= (x — 2)2, б) y= (x + 1)2.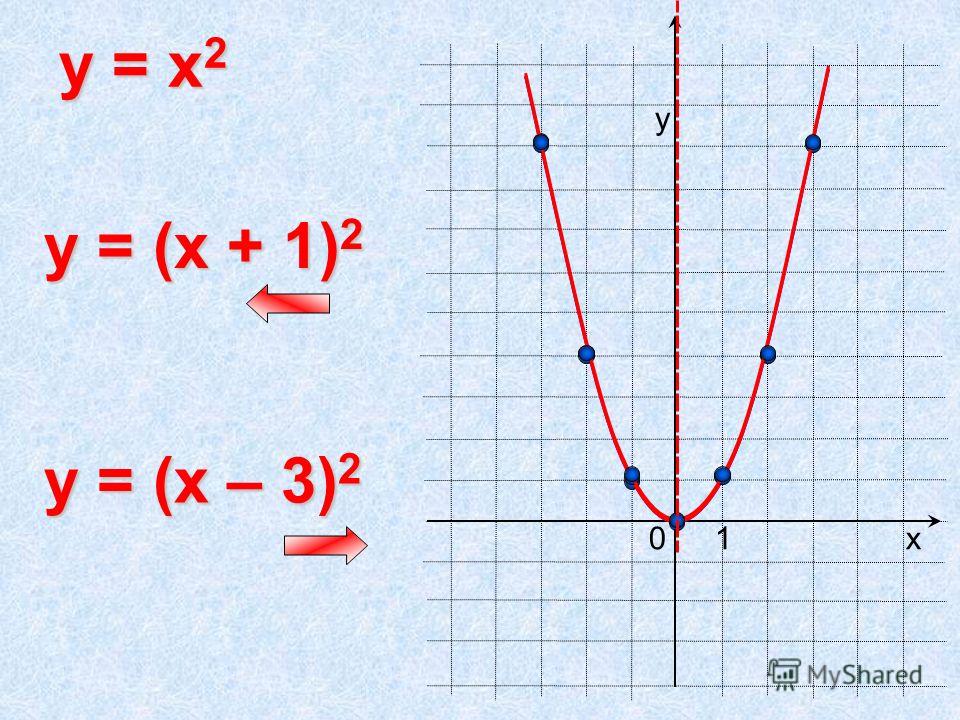
Графики наших функций получается из графика функции y= x2, путем его параллельного переноса: б) на две единицы вправо, в) на одну единицу влево.
Графики наших функций:
в) Для построения графика функции y= f(-x), следует построить график функции y= f(x) и отразить его относительно оси ординат. Полученный график является графиком функции y= f(-x).
Для примера построим два графика: a) y= x3, б) y= (-x)3.
Графики нашей функций получается из графика функции y=x3, путем отражения относительно оси ординат.
г) Для построения графика функции y= -f(x) следует построить график функции y=f(x) и отразить его относительно оси абсцисс.
Для примера построим два графика: a) y= cos(x), б) y=-cos(x). Графики нашей функций получается из графика функции y= cos(x), путем отражения относительно оси абсцисс.
Ребята, теперь давайте построим графики функций, вид которых заранее не известен. Будем использовать правила, которые мы определили в начале.
Примеры на построение
I. Построить график функции: y= 2x2 + 4x — 5.
Решение:
1) Область определения: D(y)= (-∞; +∞).
2) Найдем стационарные точки:
y’= 4x + 4,
4x + 4 = 0,
x= -1.
3) Определим вид стационарной точки и характер монотонности:
Точка x= -1 – точка минимума. Найдем значение функции в точке x= -1
y(-1)= 2(-1)2 + 4(-1) — 5= -7.
Итак, наша функция убывает на промежутке =(-∞;-1), x= -1 – точка минимума, функция возрастает на промежутке (-1; +∞).
Вычислим значения функции в паре точек:
Построим график функции:
II. Построить график функции: y= 5x3 — 3x5.
Решение:
1) Область определения: D(y)= (-∞;+∞).
2) Найдем стационарные точки:
y’= 15x2 — 15x4,
y’= 15x2(1 — x2)= 15x2(1 — x)(1 + x),
15x2(1 — x)(1 + x)= 0,
x= 0; ±1.
3) Определим вид стационарной точки и характер монотонности:
Точка x= -1 – точка минимума. 2-4}$= y(x)
2-4}$= y(x)
По определению функция четная. Значит, график функции симметричен относительно оси ординат, можно сначала построить график функции для x ≥ 0.
3) Прямая x= 2 – вертикальная асимптота, т.к. знаменатель нашей функции в этой точке обращается в нуль.
Найдем горизонтальную асимптоту:
Прямая y= 1 – горизонтальная асимптота.
4) Найдем стационарные и критические точки:
Критических точек у нашей функции нет, т.к. производная определена всюду на области определения нашей функции.
5) Определим вид стационарной точки и характер монотонности:
Точка x= 0 – точка максимума.
Итак, наша функция четная. Она возрастает на промежутке равном (-∞;0), x= 0 – точка максимума. Функция убывает на (0;+∞).
Прямая x= 2 – вертикальная асимптота. Прямая y= 1 – горизонтальная асимптота.
Вычислим значения функции в паре точек:
Т.к. функция четная построим сначала график для x ≥ 0.
Используя свойство четных функций, отразим график функции относительно оси ординат.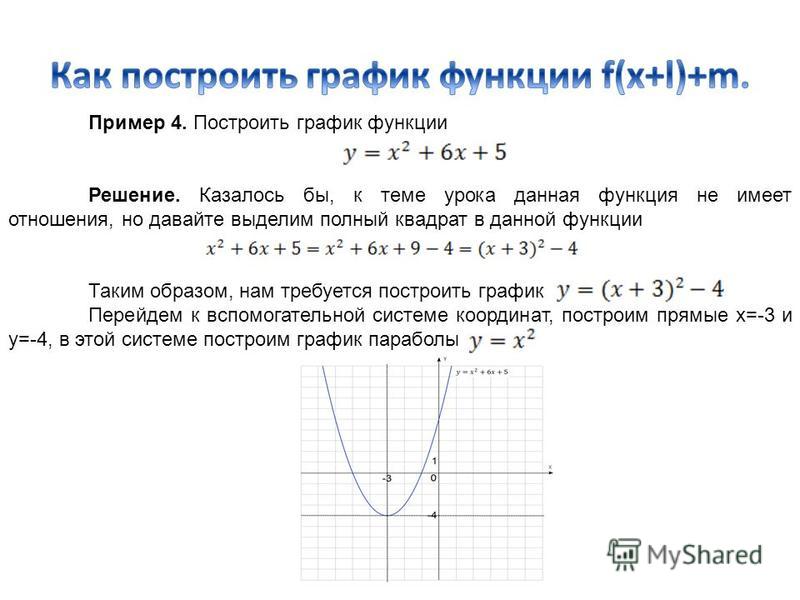 2+2)}$.
2+2)}$.
Построение графиков функций в Excel
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x2-2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5. 2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Получим:
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички
Получаем график функции y=1/x
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
на Ваш сайт.
Построение графиков — Sage Tutorial in Russian v9.3
Sage может строить двумерные и трехмерные графики.
Двумерные графики
В двумерном пространстве Sage может отрисовывать круги, линии и
многоугольники; графики функций в декартовых координатах; также графики
в полярных координатах, контурные графики и изображения векторных полей.
Некоторые примеры будут показаны ниже. Для более исчерпывающей информации
по построению графиков см. Решение дифференциальных уравнений и Maxima,
а также документацию
Sage Constructions.
Данная команда построит желтую окружность радиуса 1 с центром в начале:
sage: circle((0,0), 1, rgbcolor=(1,1,0)) Graphics object consisting of 1 graphics primitive
Также можно построить круг:
sage: circle((0,0), 1, rgbcolor=(1,1,0), fill=True) Graphics object consisting of 1 graphics primitive
Можно создавать окружность и задавать ее какой-либо переменной. 3),(x,0,2*pi),rgbcolor=hue(0.6))
3),(x,0,2*pi),rgbcolor=hue(0.6))
sage: show(p1+p2+p3, axes=false)
Хороший способ создания заполненных фигур — создание списка точек (L
в следующем примере), а затем использование команды polygon для
построения фигуры с границами, образованными заданными точками. К
примеру, создадим зеленый дельтоид:
sage: L = [[-1+cos(pi*i/100)*(1+cos(pi*i/100)), ....: 2*sin(pi*i/100)*(1-cos(pi*i/100))] for i in range(200)] sage: p = polygon(L, rgbcolor=(1/8,3/4,1/2)) sage: p Graphics object consisting of 1 graphics primitive
Напечатайте show(p, axes=false), чтобы не показывать осей на графике.
Можно добавить текст на график:
sage: L = [[6*cos(pi*i/100)+5*cos((6/2)*pi*i/100),
....: 6*sin(pi*i/100)-5*sin((6/2)*pi*i/100)] for i in range(200)]
sage: p = polygon(L, rgbcolor=(1/8,1/4,1/2))
sage: t = text("hypotrochoid", (5,4), rgbcolor=(1,0,0))
sage: show(p+t)
Учителя математики часто рисуют следующий график на доске: не одну
ветвь arcsin, а несколько, т. е. график функции \(y=\sin(x)\)
е. график функции \(y=\sin(x)\)
для \(x\) между \(-2\pi\) и \(2\pi\), перевернутый по
отношению к линии в 45 градусов. Следующая команда Sage построит
вышеуказанное:
sage: v = [(sin(x),x) for x in srange(-2*float(pi),2*float(pi),0.1)] sage: line(v) Graphics object consisting of 1 graphics primitive
Так как функция тангенса имеет больший интервал, чем синус, при
использовании той же техники для перевертывания тангенса требуется
изменить минимальное и максимальное значения координат для оси x:
sage: v = [(tan(x),x) for x in srange(-2*float(pi),2*float(pi),0.01)] sage: show(line(v), xmin=-20, xmax=20)
Sage также может строить графики в полярных координатах, контурные
построения и изображения векторных полей (для специальных видов функций).
Далее следует пример контурного чертежа:
sage: f = lambda x,y: cos(x*y) sage: contour_plot(f, (-4, 4), (-4, 4)) Graphics object consisting of 1 graphics primitive
Трехмерные графики
Sage также может быть использован для создания трехмерных графиков. 3 значит x в кубе, также можно написать xxx или x*x*x.
3 значит x в кубе, также можно написать xxx или x*x*x.
Например: root(x,3) есть корень 3й степени из x.
(с основанием е)
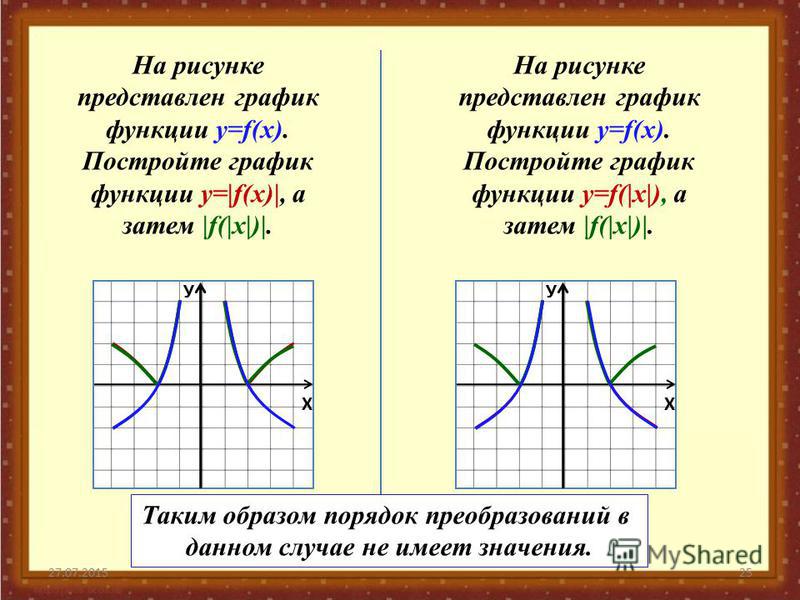 аргумент
аргумент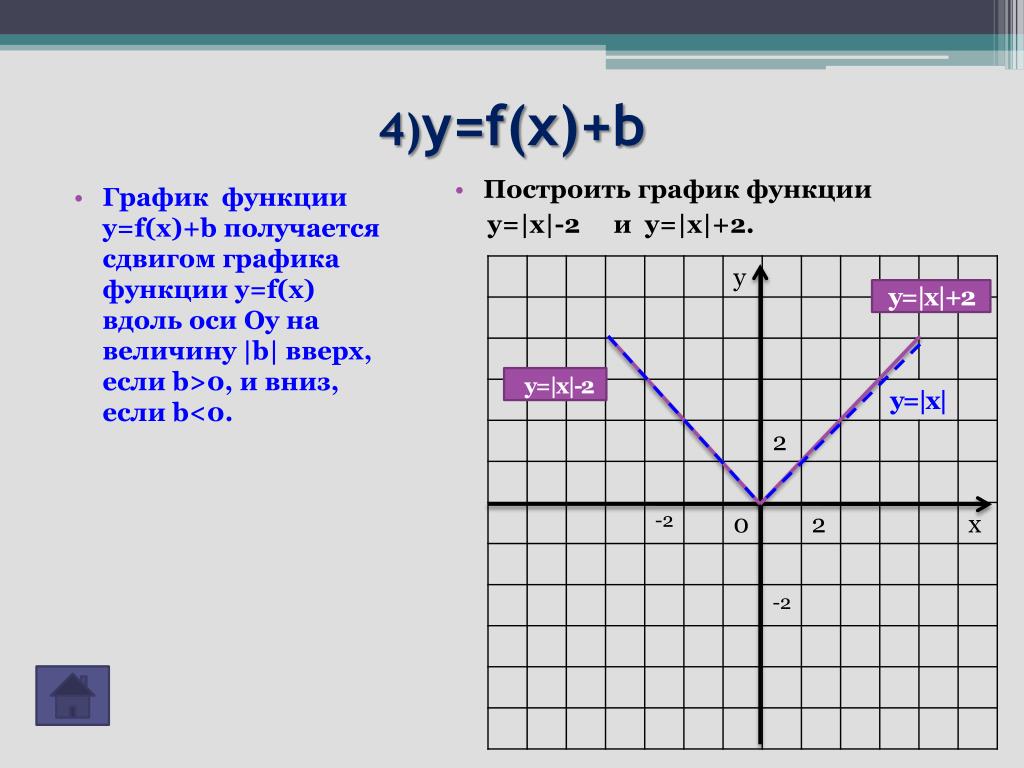 Например gaussd(x,0,1) есть нормальное стандартное расперделение со средним значением 0 и стандартным отклонением 1.
Например gaussd(x,0,1) есть нормальное стандартное расперделение со средним значением 0 и стандартным отклонением 1.| sgn(x) = | 1 for x > 0 |
| 0 for x = 0 | |
| -1 for x < 0 |
Построение графиков функций в MATLAB
Здравствуйте! В этой статье мы разберем построение графиков на MATLAB для различных математических функций, а также научимся выводить несколько графиков одновременно.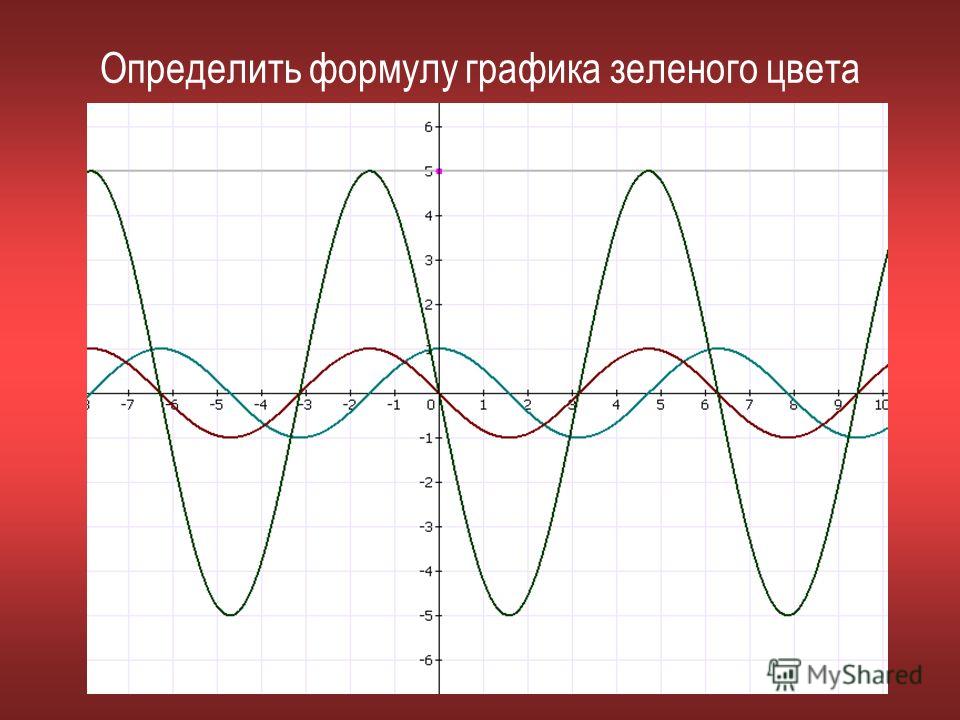 2) ‘, [-2 2])
2) ‘, [-2 2])
И последний:
Построить график функции y=tan(x/2) для интервала — π ≤ x ≤ π и -10 ≤ y ≤10.
ezplot('tan(x/2) ', [-pi pi])
axis([-pi pi -10 10])
В данном случае мы указали границы оси с помощью axis от -π до π.
Если остались вопросы по поводу построения графиков функций в MATLAB, то обязательно пишите в комментариях, ответим.
Поделиться ссылкой:
Похожее
Мобильная версия | Выходные данные и конфиденциальность | Математика / Анализ — Плоттер — Калькулятор 4.0
+ C: ConnectDottedDashed –Dashed –Заполнить заполнитьЗаполнить
+ C: ConnectDottedDashed –Dashed –Заполнить заполнитьЗаполнить
+ C: ConnectDottedDashed –Dashed –Заполнить заполнитьЗаполнить
| квадрантов: Размер: | ||||
График функций и калькулятор
Описание :: Все функции
Описание
Function Grapher — это полнофункциональная графическая утилита, которая поддерживает одновременное построение графиков до 5 функций.
Вы также можете сохранить свою работу как URL (ссылка на веб-сайт).2)
Масштабирование и повторное центрирование
Для увеличения используйте ползунок масштабирования. Влево увеличивает масштаб, вправо — уменьшает. Когда вы отпускаете ползунок, он возвращается к середине, чтобы вы могли увеличить масштаб.
Для перемещения графика можно щелкнуть и перетащить.
Если вы просто щелкнете и отпустите (не двигаясь), то место, на котором вы щелкнули, станет новым центром
Чтобы восстановить исходное масштабирование, нажмите кнопку Сбросить .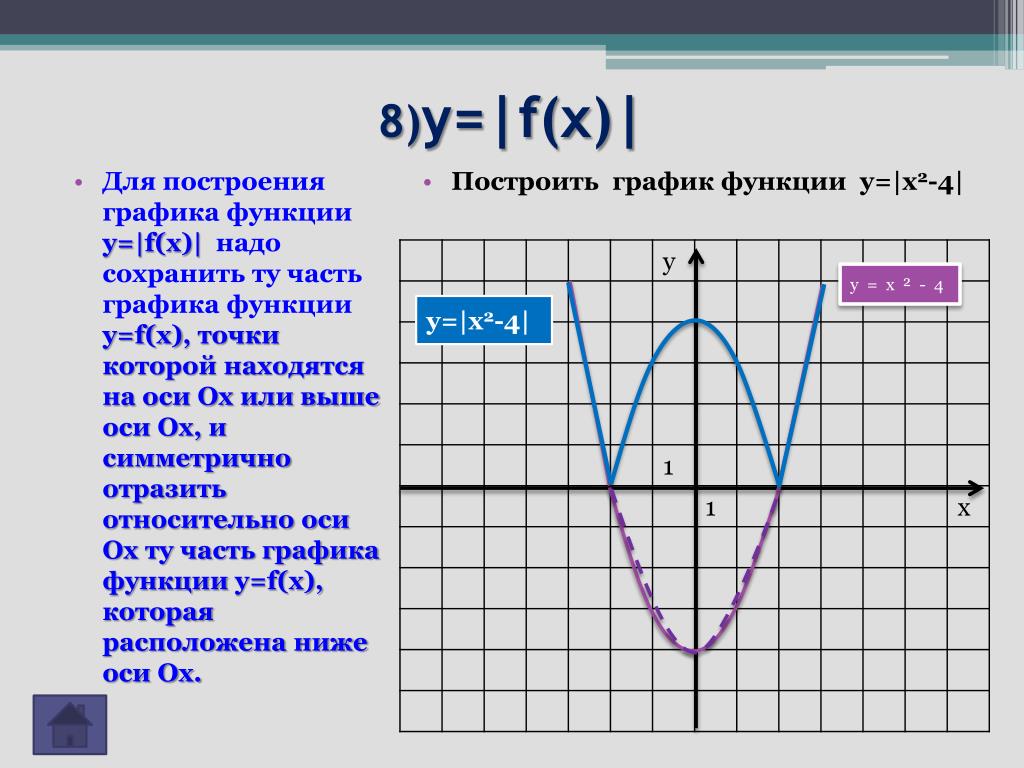
Функции
| sqrt | Квадратный корень значения или выражения. | |
|---|---|---|
| грех | синус значения или выражения | |
| cos | косинус значения или выражения | |
| желто-коричневый | тангенс значения или выражения | |
| asin | обратный синус (арксинус) значения или выражения | |
| acos | обратный косинус (arccos) значения или выражения | |
| атан | арктангенс (арктангенс) значения или выражения | |
| sh | Гиперболический синус (sinh) значения или выражения | |
| кош | Гиперболический косинус (cosh) значения или выражения | |
| танх | Гиперболический тангенс (tanh) значения или выражения | |
эксп. | e (константа Эйлера) в степени значения или выражения | |
| пер. | Натуральный логарифм значения или выражения | |
| журнал | Логарифм по основанию 10 значения или выражения | |
| этаж | Возвращает наибольшее (ближайшее к положительной бесконечности) значение, которое не больше аргумента и равно математическому целому числу. | |
| потолок | Возвращает наименьшее (ближайшее к отрицательной бесконечности) значение, которое не меньше аргумента и равно математическому целому числу. | |
| абс | Абсолютное значение (расстояние от нуля) значения или выражения | |
| знак | Знак (+1 или -1) значения или выражения | |
| факт | факториальная функция |
Константы
| пи | Константа π (3.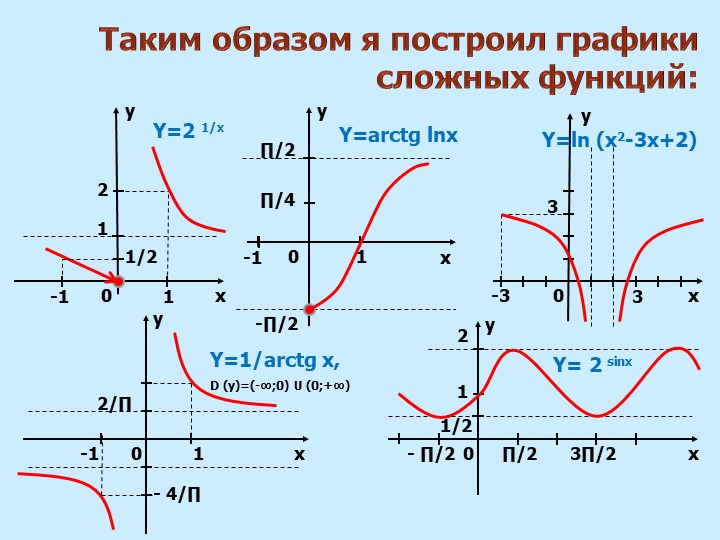 141592654 …) 141592654 …) | |
|---|---|---|
| e | Число Эйлера (2,71828 …), основание натурального логарифма |
3. Некоторые простые функции — построение графиков
3. Некоторые простые функции — построение графиков
3. Некоторые простые функции — построение графиков
Для этих примеров мы будем использовать y и x .
А.Линейные (прямые) уравнения
Это один из самых важных типов уравнений в науке,
и мы часто пытаемся свести сложные уравнения к линейному
чтобы упростить их.
Общее уравнение для линейной функции:
y ( x ) = mx + c
Значение c является константой и является точкой пересечения
y ось, так как когда x = 0, y ( x ) = c .
Значение м — это уклон или уклон
линия. Значение A + ve м означает, что уклон увеличивается
при увеличении x значение -ve означает, что оно уменьшается.
Нулевое значение м указывает горизонтальную линию, бесконечную
значение м обозначает вертикальную линию.
Примеры
а) y ( x ) = 3 x + 5
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 5 | 10 |
| y | -4 | -1 | 2 | 5 | 8 | 11 | 14 | 20 | 35 |
б) y ( x ) = 2 x — 3 (отрицательная точка пересечения)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 5 |
| y | -9 | -7 | -5 | -3 | -1 | 1 | 3 | 7 |
c) y ( x ) = -4 x + 5 (отрицательный наклон)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 10 |
| y | 17 | 13 | 9 | 5 | 1 | -3 | -7 | -11 | -15 | -35 |
г) y = 0 x + 6 (нулевой градиент)
д) y = 4 x (точка пересечения нуля)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -12 | -8 | -4 | 0 | 4 | 8 | 12 |
е) p ( n ) = 3 n — 1
| n | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| п | -10 | -7 | -4 | -1 | 2 | 5 | 8 |
г) φ (λ) = + 1
| λ | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| φ | -1 | -½ | 0 | ½ | 1 | 1½ | 2 | 2½ | 3 |
г. Квадратные уравнения
Квадратные уравнения
Это функции x 2 и
общей формы:
y ( x ) = ax 2 +
bx + c
где a , b и c — константы
Общая форма квадратичного элемента — это парабола . Ценности
of a и b определяют «резкость» параболы.Знак a определяет ориентацию (вверх или вниз)
парабола. Значение c все еще является точкой пересечения
y ось.
Примеры
Числовой пример
y ( x ) = 2 x 2 + 4 x — 6
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 10 | 0 | -6 | -8 | -6 | 0 | 10 | 24 |
Обратите внимание, что в квадратиках два значения x существуют для
каждое значение y (кроме точки поворота, см. ниже).Для такой функции мы часто хотим знать важные
ниже).Для такой функции мы часто хотим знать важные
особенности кривой: где она пересекает ось x ?
и ось y ? Где происходит минимум (или максимум)?
Каков наклон кривой при любом значении x ? Хорошо
покажите, как ответить на эти вопросы позже.
C. Высшие полиномы
Функции с x 3 , x 4 ,
x 5 , и т. Д. ., также существуют и являются
в общем посложнее.
Примеры
i) кубических уравнений
y ( x ) = ax 3 + bx 2
+ cx + d
ii) уравнения четвертой степени
y ( x ) = ax 4 + bx 3
+ cx 2 + dx + e
Д.Рациональные функции
например . y ( x ) =
Примечание: когда x = 1, функция становится неопределенной (т. е.
е.
y = бесконечность)
E. Тригонометрические функции (см. Далее)
например y ( x ) = sin x
F. Экспоненциальные и логарифмические функции (см. Ниже)
e.грамм. y ( x ) = e x , k ( T ) = A exp {- E / RT ) Arrhenius
уравнение
например y ( x ) = ln x , y ( x )
= ln (1- x 2 ).
Следующая лекция
График функций — 2-й функциональный плоттер с питанием от d3
Функциональный график — 2-й функциональный плоттер с питанием от d3
Function Plot — это библиотека построения графиков, построенная на основе D3.2 $)
В настоящее время библиотека поддерживает интерактивные линейные диаграммы и диаграммы рассеяния,
всякий раз, когда масштаб графика изменяется, функция снова оценивается с помощью
новые границы, результат: бесконечные графы!
Function Plot в отличие от других плоттеров, в которых используются $ n $ точки с равным интервалом, соединенные линейными сегментами
использует интервальную арифметику для
правильно определять участки экрана, которые необходимо построить с помощью нескольких образцов
Большинство наивных плоттеров столкнутся с проблемами при построении функций, которые колеблются слишком быстро,
например, $ f (x) = sin (e ^ x) $ быстро колеблется, когда $ x> 5 $, независимо от того, сколько раз
функция оценивается, мы никогда не сможем правильно отобразить эту функцию
График функции вместо этого будет оценивать функцию, используя математические интервалы, что означает, что когда
прямоугольник, границы которого $ x $ равны $ [x_i, x_ {i + 1}] $, появляется на экране, это гарантирует, что он
содержит все возможные $ f (\ xi) $ для $ \ xi \ in [x_i, x_ {i + 1}] $, результат: pixel perfect
представление кривых
Установка и API
npm я функция-график
import functionPlot из 'function-plot'
functionPlot ({
//. .параметры
})
.параметры
})
Старый способ:
Ознакомьтесь с документами, созданными с помощью TypeDocs API Docs
Примеры
Ознакомьтесь с дополнительными примерами в этом блокноте ObservableHQ!
А также в моем блоге!
Рецепты
Как построить график функции
Обновлено 4 декабря 2020 г.
Автор Джон Папевски
Построить график математических функций не так уж сложно, если вы знакомы с функцией, которую строите на графике.Каждый тип функции, будь то линейная, полиномиальная, тригонометрическая или какая-либо другая математическая операция, имеет свои особенности и особенности. Подробная информация об основных классах функций дает отправные точки, подсказки и общие рекомендации по их графическому отображению.
TL; DR (слишком долго; не читал)
Чтобы построить график функции, вычислите набор значений оси y на основе тщательно выбранных значений оси x , а затем постройте график полученные результаты.
Графики линейных функций
Линейные функции — одни из самых простых для построения графиков; каждый — просто прямая линия.Чтобы построить линейную функцию, вычислите и отметьте две точки на графике, а затем проведите прямую линию, проходящую через обе из них. Формы «точка-наклон» и « y -перехват» сразу дают вам одно очко; линейное уравнение с перехватом y имеет точку (0, y ), а точка наклона имеет некоторую произвольную точку ( x , y ). Чтобы найти еще одну точку, вы можете, например, установить y = 0 и найти x . Например, для построения графика функции:
y = 11x + 3
3 — пересечение y , поэтому одна точка равна (0, 3).
Установка y на ноль дает следующее уравнение:
0 = 11x + 3
Вычтем 3 с обеих сторон:
0 — 3 = 11x + 3 — 3
-3 = 11x
\ frac {-3} {11} = \ frac {11x} {11}
\ frac {-3} {11} = x
Итак, ваша вторая точка (−0,273, 0)
При использовании В общем виде вы устанавливаете y = 0 и решаете для x , а затем устанавливаете x = 0 и решаете для y , чтобы получить две точки. Чтобы построить график функции, x — y = 5, например, установка x = 0 даст вам y из -5, а установка y = 0 дает вам x из 5. Две точки: (0, −5) и (5, 0).
Чтобы построить график функции, x — y = 5, например, установка x = 0 даст вам y из -5, а установка y = 0 дает вам x из 5. Две точки: (0, −5) и (5, 0).
Графические триггерные функции
Тригонометрические функции, такие как синус, косинус и тангенс, являются циклическими, а график, построенный с помощью триггерных функций, имеет регулярно повторяющийся волнообразный узор. Например, функция
y = \ sin (x)
начинается с y = 0, когда x = 0 градусов, затем плавно увеличивается до значения 1, когда x = 90, уменьшается до 0, когда x = 180, уменьшается до -1, когда x = 270, и возвращается к 0, когда x = 360.Шаблон повторяется бесконечно. Для простых функций sin ( x ) и cos ( x ) y никогда не выходит за пределы диапазона от -1 до 1, и функции всегда повторяются каждые 360 градусов. Функции касательной, косеканса и секанса немного сложнее, хотя они тоже следуют строго повторяющимся образцам.
Функции касательной, косеканса и секанса немного сложнее, хотя они тоже следуют строго повторяющимся образцам.
Более общие триггерные функции, такие как
y = A × \ sin (Bx + C)
, предлагают свои собственные сложности, хотя с изучением и практикой вы можете определить, как эти новые термины влияют на функцию.Например, константа A изменяет максимальное и минимальное значения, поэтому она становится A и отрицательной A вместо 1 и -1. Постоянное значение B увеличивает или уменьшает частоту повторения, а постоянное значение C сдвигает начальную точку волны влево или вправо.
Построение графиков с помощью программного обеспечения
Помимо построения графиков вручную на бумаге, вы можете автоматически создавать графики функций с помощью компьютерного программного обеспечения.Например, многие программы для работы с электронными таблицами имеют встроенные возможности построения графиков. Чтобы построить график функции в электронной таблице, вы создаете один столбец со значениями x , а другой, представляющий ось y , как вычисленную функцию столбца значений x . Когда вы заполнили оба столбца, выберите их и выберите функцию точечной диаграммы программного обеспечения. Диаграмма рассеяния отображает серию дискретных точек на основе двух столбцов. При желании вы можете сохранить график как отдельные точки или соединить каждую точку, создав непрерывную линию.Перед печатью графика или сохранением электронной таблицы пометьте каждую ось соответствующим описанием и создайте основной заголовок, описывающий назначение графика.
Чтобы построить график функции в электронной таблице, вы создаете один столбец со значениями x , а другой, представляющий ось y , как вычисленную функцию столбца значений x . Когда вы заполнили оба столбца, выберите их и выберите функцию точечной диаграммы программного обеспечения. Диаграмма рассеяния отображает серию дискретных точек на основе двух столбцов. При желании вы можете сохранить график как отдельные точки или соединить каждую точку, создав непрерывную линию.Перед печатью графика или сохранением электронной таблицы пометьте каждую ось соответствующим описанием и создайте основной заголовок, описывающий назначение графика.
Рисование графиков математических функций с помощью Math Assistant в OneNote
Сначала создайте уравнение, используя рукописный ввод или текст.
На вкладке Draw напишите или введите свое уравнение. Используйте инструмент Lasso Select , чтобы нарисовать круг вокруг уравнения.Затем выберите Math . Это откроет панель Math Assistant.
Это откроет панель Math Assistant.
Из Выберите действие в раскрывающемся меню на панели Math , выберите График в 2D или График с обеих сторон в 2D .
Чтобы настроить график, созданный Math Assistant, выполните одно из следующих действий (если доступно):
Выберите (или нажмите и удерживайте), а затем перетащите график в любом направлении, чтобы переместить его положение.
Щелкайте или касайтесь кнопок лупы + и — столько раз, сколько необходимо, чтобы изменить значения параметров в вашем уравнении, увеличивая или уменьшая масштаб.
Примечание. Если вы используете OneNote на устройстве с сенсорным экраном, вы также можете настроить график пальцами. Используйте один палец, чтобы изменить положение графика, или увеличьте масштаб двумя пальцами, чтобы изменить уровень увеличения.В OneNote в Интернете вы можете использовать стрелки по бокам графика, чтобы изменить его положение.
Щелкните или коснитесь значка с двойной стрелкой Сброс , чтобы вернуть график в исходное состояние.
Когда график будет выглядеть так, как вы хотите, щелкните или коснитесь Вставить на странице , чтобы разместить его как снимок экрана на текущей странице.
Примечание. Чтобы изменить способ отображения графика (градусы, радианы, градианы), щелкните или коснитесь Настройки , когда панель «Математика» открыта.
Расширенные возможности построения графиков
Другие функции могут быть доступны в зависимости от типа вашего графика.
Считывание значений x-y: Наведите указатель мыши на точку на линии графика, чтобы увидеть значения x и y в OneNote для Windows 10. В OneNote в Интернете щелкните строку, чтобы просмотреть значения.
Управление параметрами: Если у вас есть уравнение с параметрами, например ax + b, используйте знаки плюс + и минус — под графиком, чтобы изменить значения a и b.

Ключевые особенности графика: Math Assistant вычисляет интересную информацию о графике, такую как нули, точки пересечения, минимумы, максимумы и многое другое. Используйте флажки, чтобы выбрать, какие функции вы хотите отобразить на графике.
Создавайте математические уравнения с помощью рукописного ввода или текста с помощью Math Assistant в OneNote
Решайте математические уравнения с помощью Math Assistant в OneNote
Типы задач, поддерживаемые Math Assistant
Создайте практическую викторину по математике
Типы задач, поддерживаемые Math Assistant
При использовании Math Assistant в OneNote вы заметите, что раскрывающийся список Выберите действие под уравнением изменяется в зависимости от выбранного уравнения.Вот некоторые из типов задач, которые поддерживаются в зависимости от уравнения, которое вы пытаетесь решить.
Массивы | Для списка действительных чисел поддерживаются все перечисленные ниже. |
Выражения | Для любого выражения доступны следующие действия:
|
Уравнения и неравенства | Для уравнений и неравенств доступны следующие действия:
|
Системы | Важно иметь равное количество уравнений и переменных, чтобы обеспечить доступность правильных функций.
|
Производные и интегралы | Производные могут быть записаны либо с d / dx перед функцией, либо со штрихом. Действия, доступные для производных и интегралов: |
Матрицы | Матрицы можно записывать в квадратных или круглых скобках. Для матриц поддерживаются следующие действия:
Матричные уравнения в настоящее время не поддерживаются. |
Построение графика в полярных координатах | Чтобы построить график функции в полярных координатах, необходимо выразить r как функцию от тета. |
Комплексный режим | Примечание: Выберите Настройки для переключения между действительными и комплексными числами. Для сложных выражений и чисел, содержащих мнимую единицу i, , доступны следующие действия. |
Узнать больше
Создайте математический тест в Microsoft Forms
Создайте практическую викторину по математике с помощью Math Assistant в OneNote
Решайте математические уравнения с помощью Math Assistant в OneNote
3D плоттер | Academo.org
Эта демонстрация позволяет вам ввести математическое выражение в терминах x и y. Когда вы нажмете кнопку «Рассчитать», демонстрация будет
вычислить значение выражения в предоставленных диапазонах x и y, а затем отобразить результат в виде поверхности.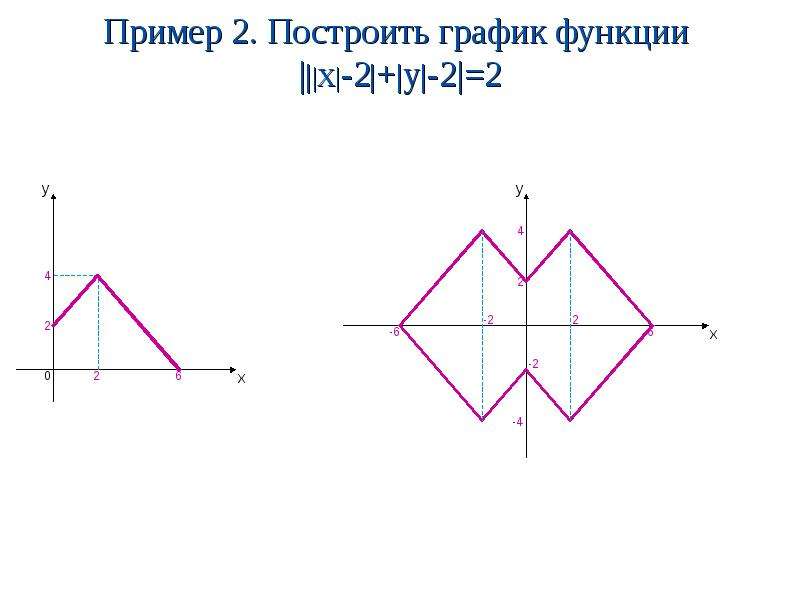
График можно увеличивать, прокручивая мышью, и вращать, перетаскивая. Щелчок по графику покажет значения x, y и z в этой конкретной точке.
В таблице ниже перечислены функции, которые можно вводить в поле выражения.
| Выражение | Описание |
|---|---|
| грех (х) | Синус x в радианах |
| cos (x) | Косинус x в радианах |
| желтовато-коричневый (x) | Тангенс x в радианах |
| asin (x), acos (x), atan (x) | Обратная из трех тригонометрических функций, перечисленных выше |
| кв. (X) | Квадратный корень из x (только для положительного x) |
| журнал (x) | Натуральный логарифм x |
| pow (x, y) | Степень от x к y |
Вы также можете применить к графику определенные ограничения / неравенства.2 \) во всех областях, где \ (x \) больше \ (y \), и \ (x \) во всех областях, где x равно , а не больше, чем y.
Ползунок разрешения можно использовать для увеличения количества точек данных, отображаемых на графике, что дает более плавный конечный результат, но поскольку для этого требуется больше вычислительной мощности, вы можете заметить небольшое снижение частоты кадров при взаимодействии с графиком.
Каждый раз, когда вы нажимаете кнопку «Рассчитать», URL-адрес обновляется с вашими текущими настройками, что означает, что вы можете поделиться ссылкой прямо на график по вашему выбору, не набирая значения в настройках.
Обратите внимание: если ваша поверхность содержит комплексные числа, будет отображена только действительная часть.
Пожалуйста, включите JavaScript, чтобы просматривать комментарии от Disqus.
.
Функции и графики — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Координаты и базовые понятия о функциях
К оглавлению…
Длина отрезка на координатной оси находится по формуле:
Длина отрезка на координатной плоскости ищется по формуле:
Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:
Функция – это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции).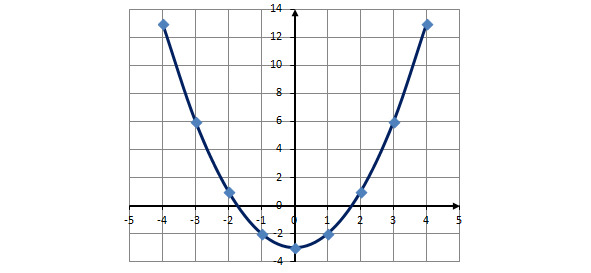 Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.
Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.
Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.
Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у).
Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.
Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.
Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.
Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.
Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:
Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны.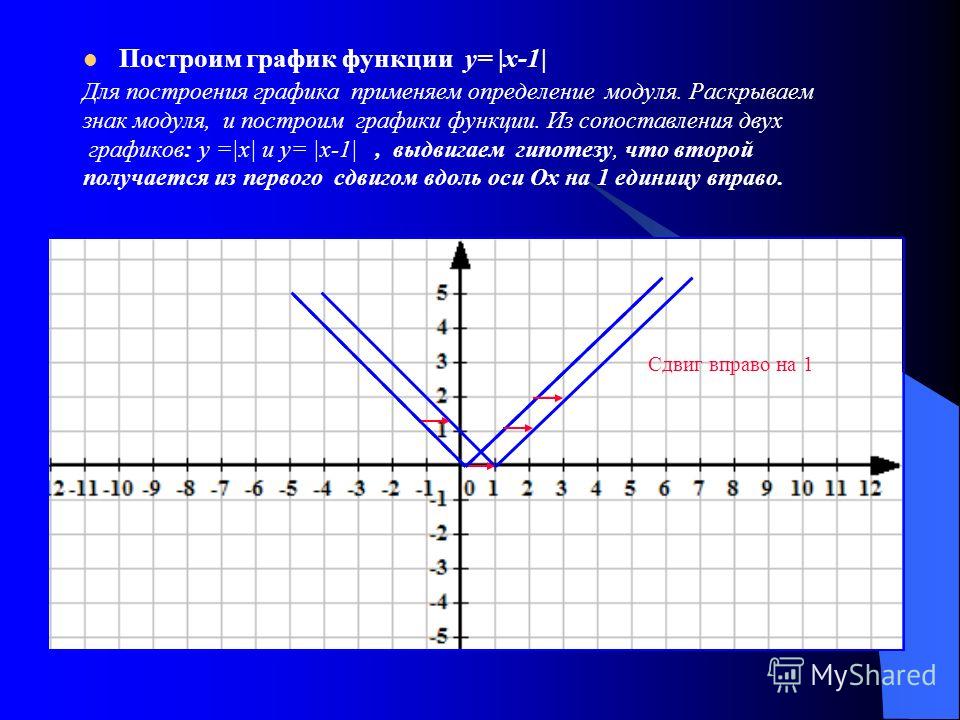 График нечётной функции всегда симметричен относительно начала координат.
График нечётной функции всегда симметричен относительно начала координат.
Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х.
Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше.
График линейной функции
К оглавлению…
Линейной функцией называют функцию, которую можно задать формулой:
График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону — слева направо):
График квадратичной функции (Парабола)
К оглавлению. ..
..
График параболы задается квадратичной функцией:
Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x1; 0) и (x2; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x0; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):
При этом:
- если коэффициент a > 0, в функции y = ax2 + bx + c, то ветви параболы направлены вверх;
- если же a < 0, то ветви параболы направлены вниз.
Координаты вершины параболы могут быть вычислены по следующим формулам.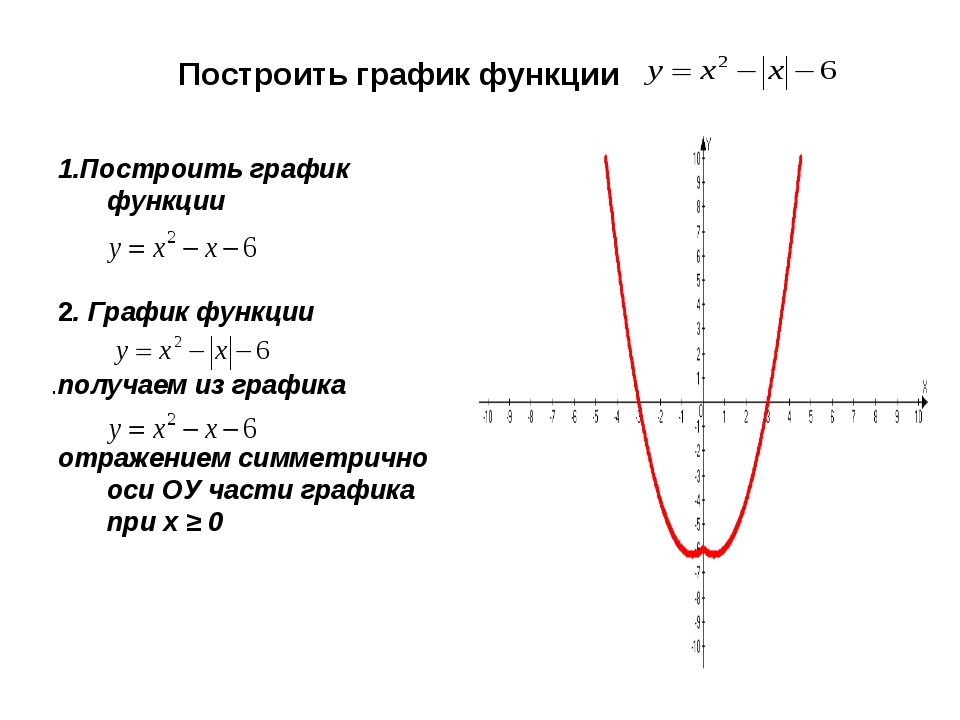 Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):
Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:
Графики других функций
К оглавлению…
Степенной функцией называют функцию, заданную формулой:
Приведем несколько примеров графиков степенных функций:
Обратно пропорциональной зависимостью называют функцию, заданную формулой:
В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:
Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает. Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.
Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.
Показательной функцией с основанием а называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):
Логарифмической функцией называют функцию, заданную формулой:
В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:
График функции y = |x| выглядит следующим образом:
Графики периодических (тригонометрических) функций
К оглавлению…
Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x).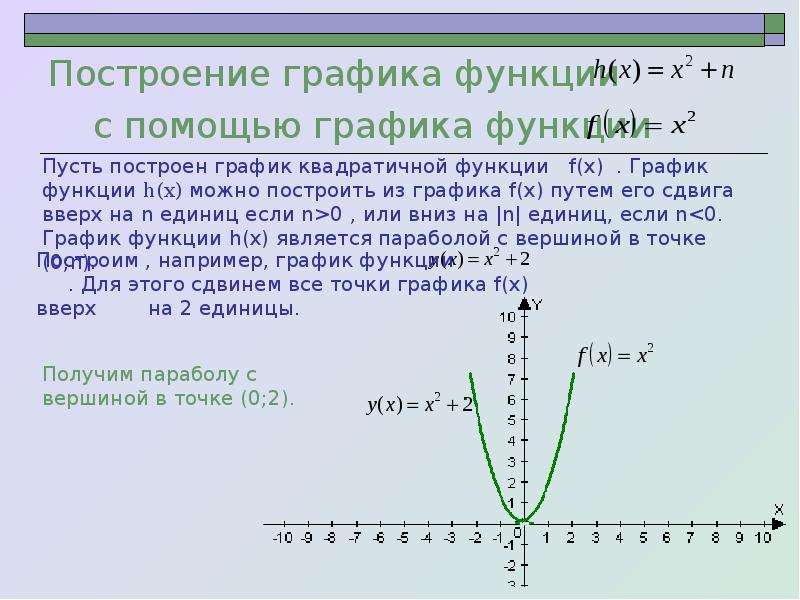 Если функция f(x) является периодической с периодом T, то функция:
Если функция f(x) является периодической с периодом T, то функция:
где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом T1, который определяется формулой:
Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой:
График функции y = cosx называется косинусоидой. Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:
График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке.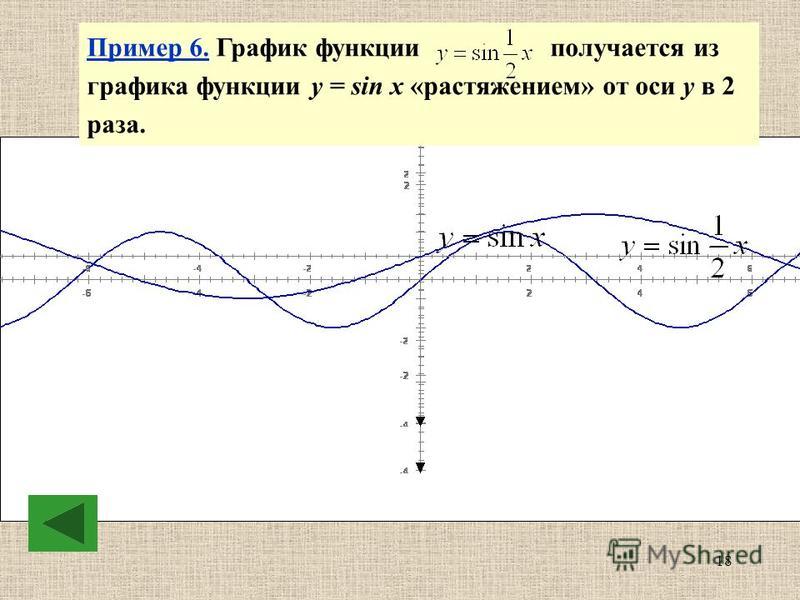 Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Ну и наконец, график функции y = ctgx называется котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.
Мобильная версия | Выходные данные и конфиденциальность
От до ConnectDottedDashed — пунктирная — заполнить заполнить Показать термин
От до ConnectDottedDashed — пунктирная — заполнить заполнить Показать термин
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
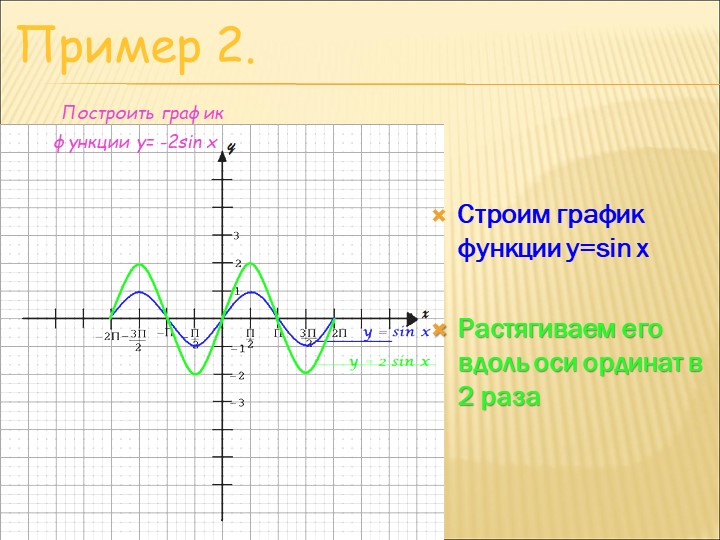



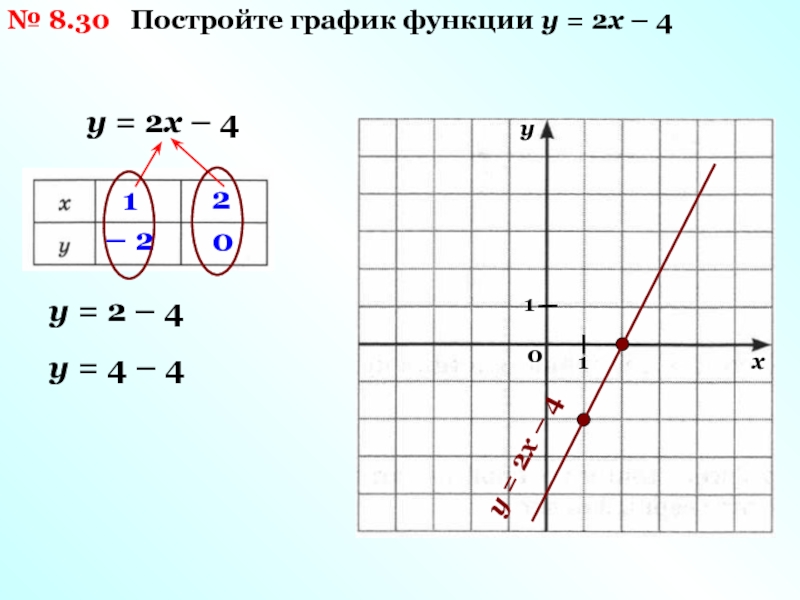 Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)
Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)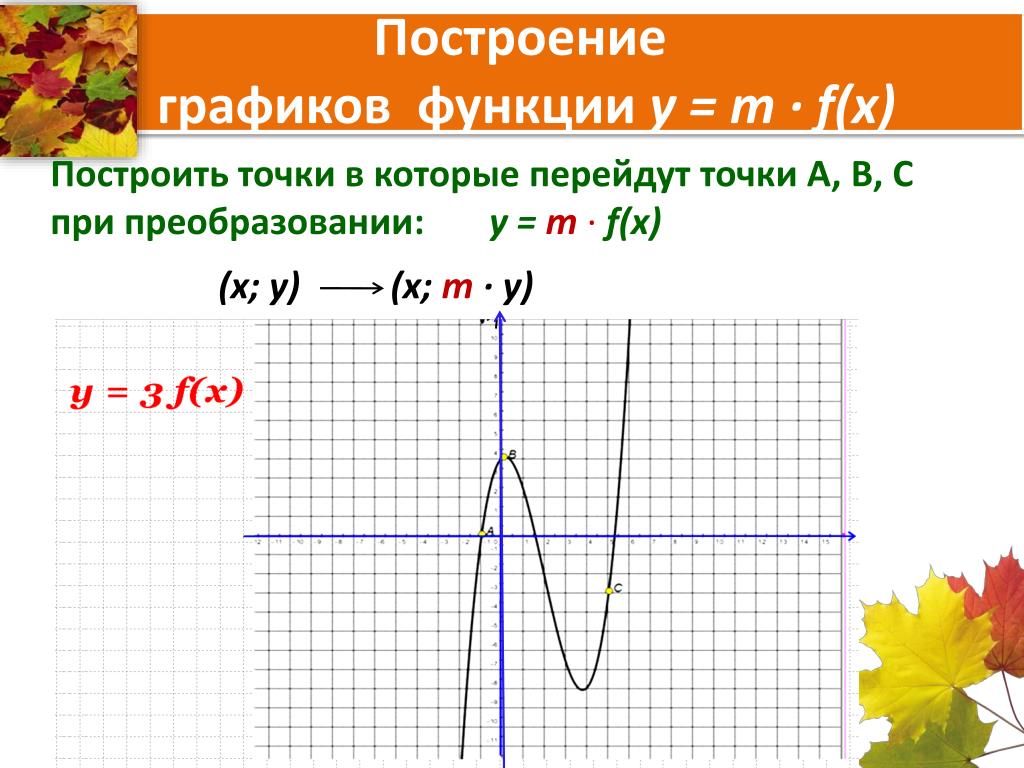
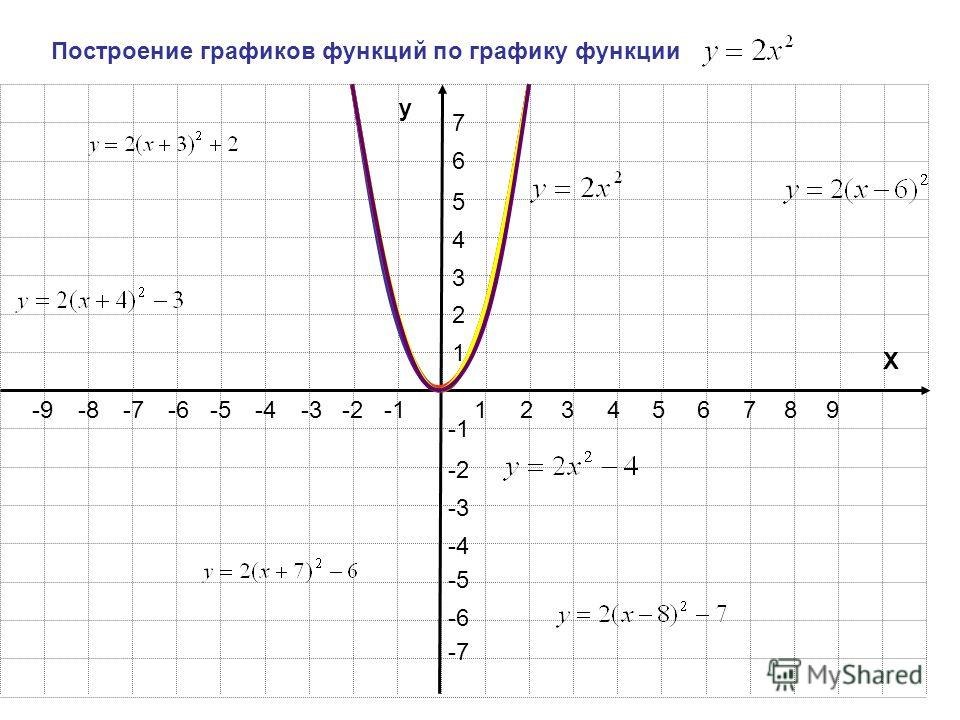 Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).
Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b). Асимптота — это некоторой ориентир для нашей функции. Это то, к чему стремится график функции в точке, но не достигает этого значения.
Асимптота — это некоторой ориентир для нашей функции. Это то, к чему стремится график функции в точке, но не достигает этого значения. масштаб x:
масштаб x: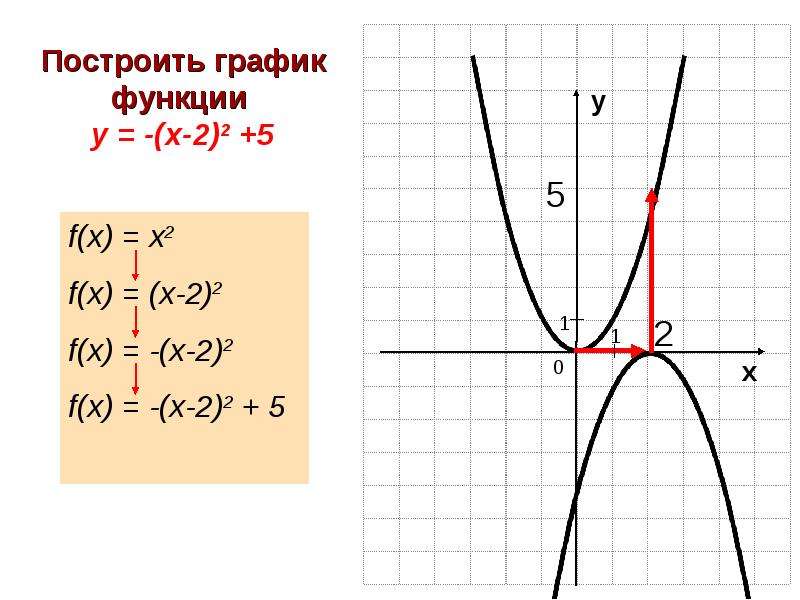 .параметры
})
.параметры
})

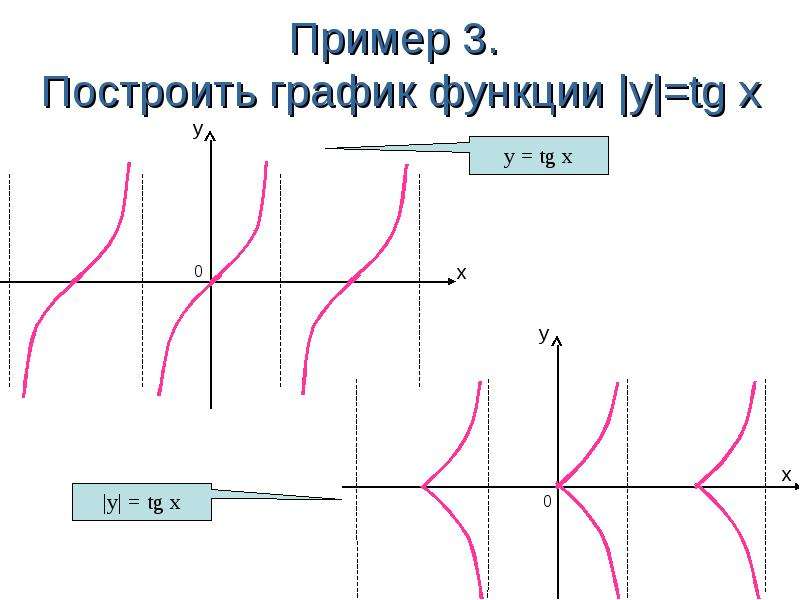
 Системы можно записать двумя разными способами:
Системы можно записать двумя разными способами:
 x) $ быстро колеблется, когда $ x> 5 $, независимо от того, сколько раз
функция оценивается, мы никогда не сможем правильно отобразить эту функцию
x) $ быстро колеблется, когда $ x> 5 $, независимо от того, сколько раз
функция оценивается, мы никогда не сможем правильно отобразить эту функцию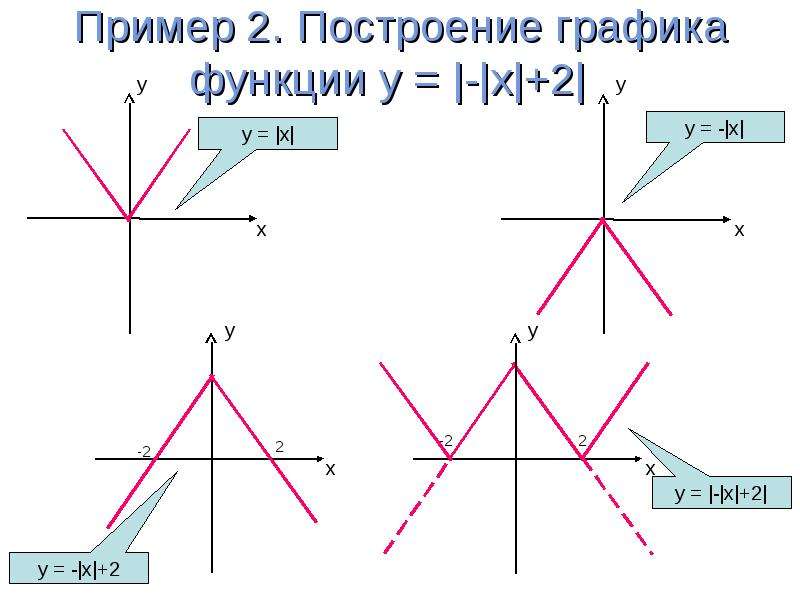 (2x) .
Вместо x «3 , конечно, вы также можете ввести xxx .
Или вместо tan (x) ‘2 вы можете ввести tan (x) tan (x) .
(2x) .
Вместо x «3 , конечно, вы также можете ввести xxx .
Или вместо tan (x) ‘2 вы можете ввести tan (x) tan (x) .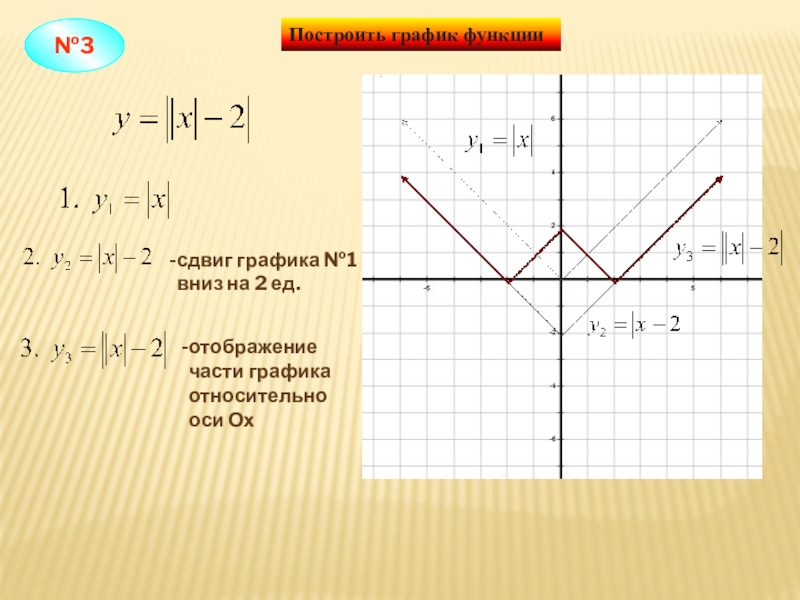 Эквивалент корня ( аргумент , 3)
Эквивалент корня ( аргумент , 3) до 1 / cos ( arg ).
до 1 / cos ( arg ).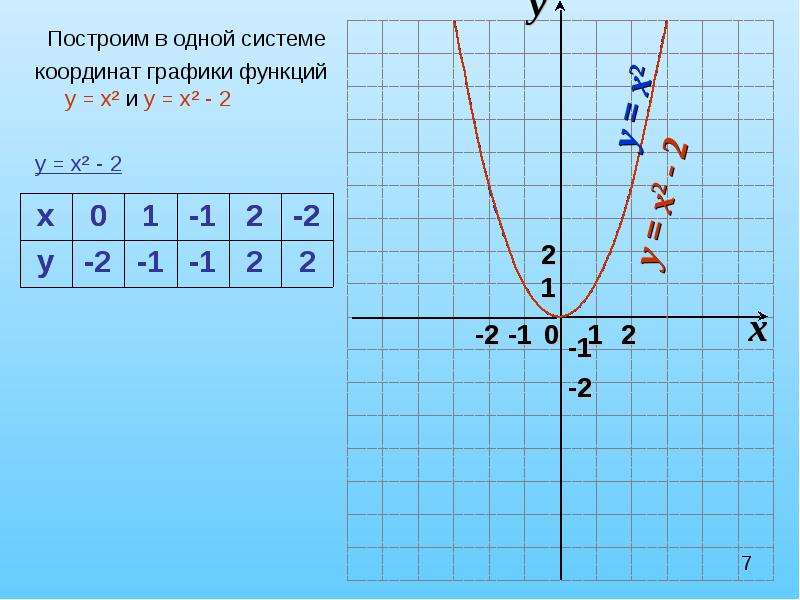



 Пример: 2abs (sin [x]) или, альтернативно, 2 | sin (x) | .
Пример: 2abs (sin [x]) или, альтернативно, 2 | sin (x) | .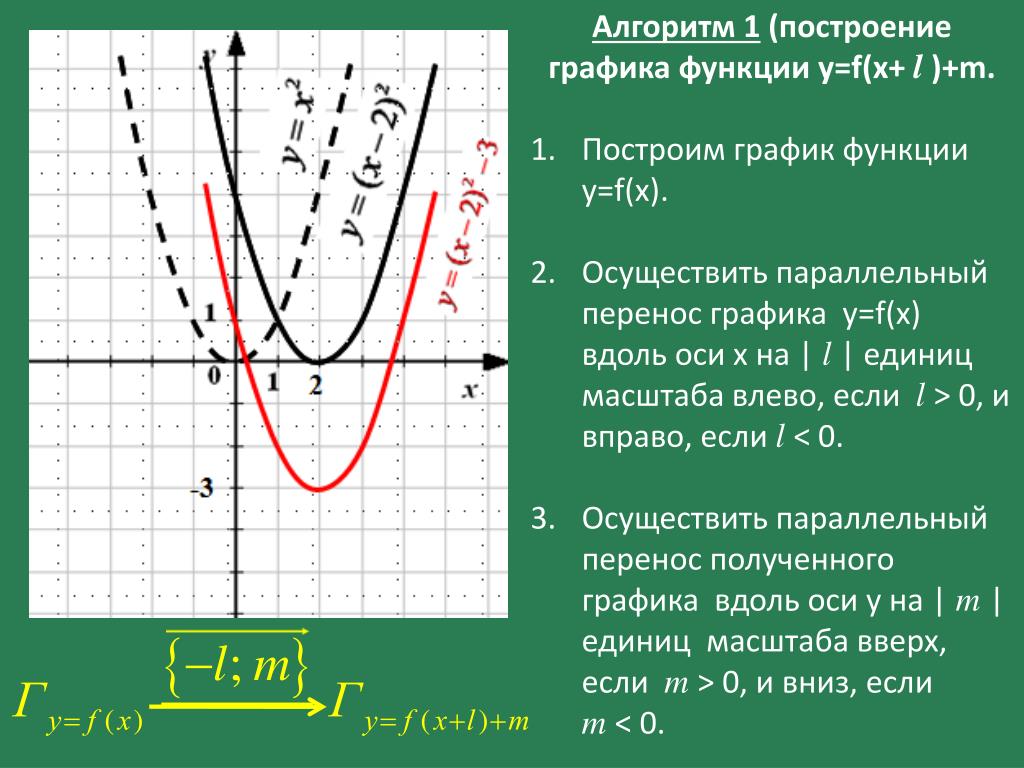 д.
Если символы группировки не используются, 2 * x-3 / x оценивается как (2 * x) — (3 / x) .
д.
Если символы группировки не используются, 2 * x-3 / x оценивается как (2 * x) — (3 / x) . 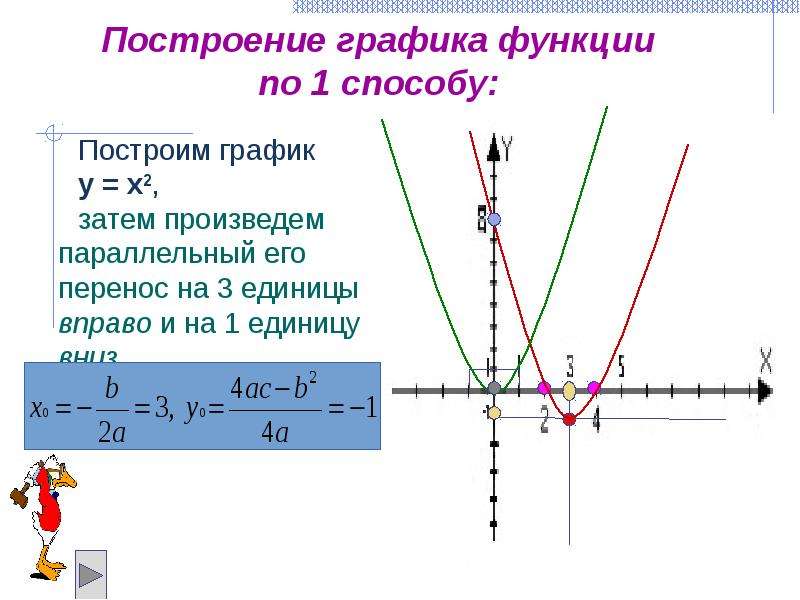
 В
значения не чувствительны к регистру. Таким образом, цветовые коды
В
значения не чувствительны к регистру. Таким образом, цветовые коды 
 Затем нарисуйте асимптоты.
Затем нарисуйте асимптоты.  Никаких пакетов или подписок, платите только за необходимое время.
Никаких пакетов или подписок, платите только за необходимое время. 09.2019
09.2019 Нажмите ОК, чтобы получить график. См. Больше [образцы функций 3D]
Нажмите ОК, чтобы получить график. См. Больше [образцы функций 3D]