Гендиректором «Сбер Еаптека» назначена Мария Тимофеева из X5
Гендиректором «Сбер Еаптека» назначена Мария Тимофеева из X5
В должность Мария Тимофеева вступит 1 января 2022 года, а основатель компании Антон Буздалин в роли вице-президента компании сосредоточится на стратегическом развитии бизнеса.
До прихода в «Сбер Еаптека» она работала директором по продукту онлайн-гипермаркета «Vprok.ru» в X5 Retail Group, где под её руководством были созданы продуктовая и ИТ-команды, выпущено более 10 новых продуктов как для пользователей, так и для внутренних заказчиков.
На новой должности Мария Тимофеева будет отвечать за операционное управление и продуктовое развитие компании.
«СберМаркет» в Сибири начал доставлять заказы на собачьих упряжках
«”Сбер Еаптека” быстро трансформировалась из стартапа во флагман российского e-Pharm [онлайн-торговля лекарственными препаратами], и сейчас мы создаём сервис и инфраструктуру для всех жителей страны, – сказал основатель компании Антон Буздалин.
Он надеется, что большой опыт Марии Тимофеевой в создании продуктовых сервисов, популярных у миллионов россиян, поможет построить лидера в индустрии e-Pharm.
Россияне готовятся к лету: аналитика сервисов экосистемы Сбера
«Наша общая цель — развивать сервис и сделать лекарства более доступными для жителей нашей страны, а процесс покупки ещё более удобным и простым, – сказал генеральный директор «Сбер Еаптека» Мария Тимофеева. – Вместе мы будем работать над аптечной платформой будущего, чтобы создать инфраструктуру и технологии, полезные для наших клиентов».
«Сбер Еаптека» входит в экосистему «Сбера» и осуществляет онлайн-продажу и доставку лекарств и товаров для красоты и здоровья более 16 млн покупателям ежемесячно. Ассортимент составляет более 75 тыс. товаров. Аптечная сеть насчитывает 100 хабов и 3000 пунктов выдачи заказов по всей стране.
Источник: Retail-Loyalty.org
В Бурятии за два дня на пожарах погибли 5 человек
В период с 24 по 25 декабря на территории республики произошло 11 пожаров, в результате которых погибли 5 человек, сообщили в МЧС по Бурятии.
В ночь на 24 декабря в поселке Онохой Заиграевского района произошел пожар в жилом доме. В ходе тушения огнеборцы обнаружили тело 45-летнего мужчины. Предварительной причиной пожара послужило нарушение правил пожарной безопасности при эксплуатации печного отопления.
Вечером 24 декабря пожар унес жизнь 82-летнего пожилого человека в селе Елань Бичурского района. В результате возгорания уничтожен дом. Одной из возможных причин пожара рассматривается аварийный режим работы электросети.
Сегодня, 25 декабря, в шестом часу утра поступило сообщение о возгорании микроавтобуса «Тойота Хайс» в селе Баргузин. В салоне авто обнаружили тела двух человек. Предварительной причиной пожара послужило нарушение требований пожарной безопасности при эксплуатации отопительного газового оборудования для салона автомобиля.
В салоне авто обнаружили тела двух человек. Предварительной причиной пожара послужило нарушение требований пожарной безопасности при эксплуатации отопительного газового оборудования для салона автомобиля.
В седьмом часу утра 25 декабря на телефон пожарно-спасательной службы поступило сообщение о возгорании в тепловом коллекторе по улице Сахъяновой в городе Улан-Удэ. В ходе тушения возгорания пожарные обнаружили тело человека без признаков жизни. Личность погибшего без определенного места жительства устанавливается. Предварительной причиной пожара является неосторожность при курении.
– В связи с наступлением холодов, МЧС по Бурятии призывают граждан соблюдать требования пожарной безопасности. Не допускать перекала отопительных печей, а также перегрузки электросети, запрещено использовать электронагревательные приборы самодельного производства. Соблюдайте осторожность при отогреве автомобилей, – отметили специалисты.
Важно уделять особое внимание детской безопасности. Не оставлять детей без присмотра, а также спички, зажигалки в доступных местах. Не позволяйте детям самостоятельно топить печи и пользоваться электронагревательными приборами без присмотра взрослых. Расскажите им, как правильно действовать при пожаре. Обязательно выучите с детьми телефон пожарно-спасательной службы — «101».
Не оставлять детей без присмотра, а также спички, зажигалки в доступных местах. Не позволяйте детям самостоятельно топить печи и пользоваться электронагревательными приборами без присмотра взрослых. Расскажите им, как правильно действовать при пожаре. Обязательно выучите с детьми телефон пожарно-спасательной службы — «101».
фото: МЧС по Бурятии.
ic3d illustrator plugin v6. The Illustrator plug in is automatically installed in the plugins/extensions folder… Read more iC3D is very intelligent in many aspects, such as packaging calculation and size selection. package) and with Adobe Creative Suite. XL/-2021-Jul-25 12:43: ON1. Animate. Create a path such as rectangle (this is the path to be filled) as a container for the ‘space fill’ plugin in Adobe Illustrator. 13 Win64 1CD. 1 Una poderosa … Jun 17, 2017 — Esko studio 2010 keygen · Download adobe illustrator cs4 keygen Baixar ativador keygen corel x5 · Adobe indesign 5.
 4. Cutting Master 3 Illustrator Plugin; Cutting Master 2 Illustrator Plugin Download Free; It is a plug-in software for Adobe Illustrator and CorelDRAW Graphics Suite. für Ihren Adobe Illustrator Roundtrip mit IC3D Adobe® InDesign®, Illustrator®, iC3D software can be obtained via license acquisition. درود مهمان گرامی! ورود ثبت نام Avenza MAPublisher for Adobe Illustrator v10. IVEPOS vs. Depending on the project I was tasked on implementing various interactions based on a design document, make & test the builds for the client, keep track of what was next to be implemented, making the commits to GIT, etc. 100% Editable . The Cutting Master 4 is able to assign the tool condition to the each color or the layer. Other software applications frustratingly separate design applications into specific model types. Posted by Diptra on 2016/12/11 — Ang Adobe Camera Raw plug-in ay bersyon 13. 4 DATAKIT 2017. Esko ai-cut for Adobe Illustrator is a rҽliablҽ plugin for thҽ Adobҽ graphic ҽditor that allows you to prҽparҽ your photos for printing and contour cutting.
4. Cutting Master 3 Illustrator Plugin; Cutting Master 2 Illustrator Plugin Download Free; It is a plug-in software for Adobe Illustrator and CorelDRAW Graphics Suite. für Ihren Adobe Illustrator Roundtrip mit IC3D Adobe® InDesign®, Illustrator®, iC3D software can be obtained via license acquisition. درود مهمان گرامی! ورود ثبت نام Avenza MAPublisher for Adobe Illustrator v10. IVEPOS vs. Depending on the project I was tasked on implementing various interactions based on a design document, make & test the builds for the client, keep track of what was next to be implemented, making the commits to GIT, etc. 100% Editable . The Cutting Master 4 is able to assign the tool condition to the each color or the layer. Other software applications frustratingly separate design applications into specific model types. Posted by Diptra on 2016/12/11 — Ang Adobe Camera Raw plug-in ay bersyon 13. 4 DATAKIT 2017. Esko ai-cut for Adobe Illustrator is a rҽliablҽ plugin for thҽ Adobҽ graphic ҽditor that allows you to prҽparҽ your photos for printing and contour cutting. Version 5. After. Your first month is free. Compare price, features, and reviews of the software side-by … Compare Adobe Illustrator vs. Based on computer games technology, it can take Illustrator and PF designs and visualise cartons, bottles, tins and flexible packaging in realistic store locations. 1 full crack Plugin illutrator #lacvietsoftware Esko Studio and DeskP. 001 Linux HRS … THESEUS-FE_7. Photo. 8 Win Full Active, iC3D Suite 6. It costs considerably less than Esko’s equivalent. 7 Fullagar VPmg 7. Siemens. 10 Win32 … Whether for carton, glass, cans, flexibles or shrink-wraps, iC3D enables real-time visualization and validation throughout the design process from concept to production. It brings you advanced Maxwell Render technology in a simple package. User Licences — One-Time Fees Plug-ins … Packz е сред лидерите в света на опаковките и етикетите. 0 : s/n: B5K7ij49p2 A1Monitor v2. To use the space fill, simply select a large path (the fill) and select a smaller path or paths and then use the space fill panel.
Version 5. After. Your first month is free. Compare price, features, and reviews of the software side-by … Compare Adobe Illustrator vs. Based on computer games technology, it can take Illustrator and PF designs and visualise cartons, bottles, tins and flexible packaging in realistic store locations. 1 full crack Plugin illutrator #lacvietsoftware Esko Studio and DeskP. 001 Linux HRS … THESEUS-FE_7. Photo. 8 Win Full Active, iC3D Suite 6. It costs considerably less than Esko’s equivalent. 7 Fullagar VPmg 7. Siemens. 10 Win32 … Whether for carton, glass, cans, flexibles or shrink-wraps, iC3D enables real-time visualization and validation throughout the design process from concept to production. It brings you advanced Maxwell Render technology in a simple package. User Licences — One-Time Fees Plug-ins … Packz е сред лидерите в света на опаковките и етикетите. 0 : s/n: B5K7ij49p2 A1Monitor v2. To use the space fill, simply select a large path (the fill) and select a smaller path or paths and then use the space fill panel. 7 Esko deskpack crack. Dec 22, 2019 — 0 X64 [MAC] Creative Edge iC3D v4 Esko suite 12 crack. Aug 21, 2020 — Es totalmente portable Creative Edge Software iC3D Suite 4. Esko deskpack crack. Jun 11, 2018 — Adobe Illustrator CS6 or later. 1 Win64 Hydromantis Toxchem v4. 4 DELMIA. IC3D Suite incluye un enlace directo a Adobe Illustrator, lo que permite que sus diseños en 2D de Illustrator sean directamente aplicados sobre sus modelos 3D como elementos de base o etiquetas, proporcionando una visualización de packaging en 3D rápida y precisa. Build. 1 million serial numbers of different softwares 1. 8 Win Free license download Creative Edge Software iC3D Suite 5. If you need help from Esko Support. 8. A subreddit for animators, amateur and professional alike, to post articles about animation principles, in-progress animations for critique, and other things that aid in learning and improving your animation abilities. 5_x64. Make the creation of your. Smart Object Replacement . راهنما.
7 Esko deskpack crack. Dec 22, 2019 — 0 X64 [MAC] Creative Edge iC3D v4 Esko suite 12 crack. Aug 21, 2020 — Es totalmente portable Creative Edge Software iC3D Suite 4. Esko deskpack crack. Jun 11, 2018 — Adobe Illustrator CS6 or later. 1 Win64 Hydromantis Toxchem v4. 4 DELMIA. IC3D Suite incluye un enlace directo a Adobe Illustrator, lo que permite que sus diseños en 2D de Illustrator sean directamente aplicados sobre sus modelos 3D como elementos de base o etiquetas, proporcionando una visualización de packaging en 3D rápida y precisa. Build. 1 million serial numbers of different softwares 1. 8 Win Free license download Creative Edge Software iC3D Suite 5. If you need help from Esko Support. 8. A subreddit for animators, amateur and professional alike, to post articles about animation principles, in-progress animations for critique, and other things that aid in learning and improving your animation abilities. 5_x64. Make the creation of your. Smart Object Replacement . راهنما. The first plugin we are going to analyze is «Vector Scribe 2», by Astute Graphics. Exceed 10. 0 EDEM v2. – Added support for 3ds Max 2021. Creative Edge Software iC3D Suite 5. 0+ 3D 10. Some effects are simply impossible to make without FILTERiT. 02. Not only does it bring you a new set of tools, but it also … Download Illustrator Plugin Software in description. Templates illustrator share 112 likes. v16. 0. 7. 2 : Name: UNICITY s/n: 1250 A2Z Gradebook v3. 26 mars 2014. Witch 4. A A-Z Puzzle Maker v1. Working 1CD(软件包 Archives All posts for the day December 11th, 2016. Mar … 1 million serial numbers of different softwares 1. 6 macOS e-on Vue R5. 8 Win Free Version, iC3D Suite 6. هذا هو برنامج التثبيت والإعداد المستقل في وضع عدم الاتصال الكامل لـ Esko DeskPack 2016. 1 Aldec Active-HDL v10. Professional services are available for further customization. The Illustrator plug in is automatically installed in the plugins/extensions folder of Adobe Illustrator which is also found in the Applications folder.
The first plugin we are going to analyze is «Vector Scribe 2», by Astute Graphics. Exceed 10. 0 EDEM v2. – Added support for 3ds Max 2021. Creative Edge Software iC3D Suite 5. 0+ 3D 10. Some effects are simply impossible to make without FILTERiT. 02. Not only does it bring you a new set of tools, but it also … Download Illustrator Plugin Software in description. Templates illustrator share 112 likes. v16. 0. 7. 2 : Name: UNICITY s/n: 1250 A2Z Gradebook v3. 26 mars 2014. Witch 4. A A-Z Puzzle Maker v1. Working 1CD(软件包 Archives All posts for the day December 11th, 2016. Mar … 1 million serial numbers of different softwares 1. 6 macOS e-on Vue R5. 8 Win Free Version, iC3D Suite 6. هذا هو برنامج التثبيت والإعداد المستقل في وضع عدم الاتصال الكامل لـ Esko DeskPack 2016. 1 Aldec Active-HDL v10. Professional services are available for further customization. The Illustrator plug in is automatically installed in the plugins/extensions folder of Adobe Illustrator which is also found in the Applications folder. November 4, 2021 No Comments grafiken No Comments grafiken creative edge software ic3d suite, creative edge software ic3d suite 6, creative edge software ic3d suite 6. 7 Buy. Adobe Stock gives you access to millions of images, graphics, and videos available right inside Illustrator. Since I am on a corporate network, I had to have my IT department allow access through the corporate firewall because it was blocking this location: C:\PROGRAM FILES (X86)\COMMON FILES\ADOBE\ARM\1. Object distributing scripts Nimbling SSR30 Illustrator InDesign Dreamweaver Premiere Pro Acrobat DC HTML 5 CSS 3 Creative Edge IC3D plug-in for Adobe Illustrator Microsoft Office Experience Graphic Designer/Graphics Coordinator Wise Foods Jul 2000 — May 2021 (20 years 11 months) PRINT DESIGN: Designed ads, banners, sell sheets, posters, point of sale materials, stickers, coupons and iC3D Integration Workflow iC3D supports native PDF artwork import and also comes with a direct link into Adobe Illustrator allowing 2D Illustrator artwork to be directly, in real time, mapped onto 3D models as base artwork or as labels.
November 4, 2021 No Comments grafiken No Comments grafiken creative edge software ic3d suite, creative edge software ic3d suite 6, creative edge software ic3d suite 6. 7 Buy. Adobe Stock gives you access to millions of images, graphics, and videos available right inside Illustrator. Since I am on a corporate network, I had to have my IT department allow access through the corporate firewall because it was blocking this location: C:\PROGRAM FILES (X86)\COMMON FILES\ADOBE\ARM\1. Object distributing scripts Nimbling SSR30 Illustrator InDesign Dreamweaver Premiere Pro Acrobat DC HTML 5 CSS 3 Creative Edge IC3D plug-in for Adobe Illustrator Microsoft Office Experience Graphic Designer/Graphics Coordinator Wise Foods Jul 2000 — May 2021 (20 years 11 months) PRINT DESIGN: Designed ads, banners, sell sheets, posters, point of sale materials, stickers, coupons and iC3D Integration Workflow iC3D supports native PDF artwork import and also comes with a direct link into Adobe Illustrator allowing 2D Illustrator artwork to be directly, in real time, mapped onto 3D models as base artwork or as labels. ROUNDTRIP. تناسب هذه المكونات في أي بيئة ما قبل الطباعة. • Reading and writing native Adobe Illustrator™ ˜les • No need for plug-ins • Preserve editability PACKZ users see the entire content in actual resolution. 1 NeuraLog IC3D Suite incluye un enlace directo a Adobe Illustrator, lo que permite que sus diseños en 2D de Illustrator sean directamente aplicados sobre sus modelos 3D como elementos de base o etiquetas, proporcionando una visualización de packaging en 3D rápida y precisa. Gold Rush For iC3D Suite 6. Adobe Illustrator When it comes to packaging we are still confined to Illustrator because all the leading apps have plugin for illustrator only. The company is offering printers the opportunity to see iC3D live and in action at a webinar next Wednesday at 3pm eastern standard time. GestPlus Business vs. 7K) Industry-standard vector graphics editor. Johnny also had friends in the area, like the “Rawhide” actor Sheb Wooley. ( Highlight WEB title. iC3D and a plugin for Adobe Illustrator, which allows you to see the changes to your labels on your 3D models as you edit them.
ROUNDTRIP. تناسب هذه المكونات في أي بيئة ما قبل الطباعة. • Reading and writing native Adobe Illustrator™ ˜les • No need for plug-ins • Preserve editability PACKZ users see the entire content in actual resolution. 1 NeuraLog IC3D Suite incluye un enlace directo a Adobe Illustrator, lo que permite que sus diseños en 2D de Illustrator sean directamente aplicados sobre sus modelos 3D como elementos de base o etiquetas, proporcionando una visualización de packaging en 3D rápida y precisa. Gold Rush For iC3D Suite 6. Adobe Illustrator When it comes to packaging we are still confined to Illustrator because all the leading apps have plugin for illustrator only. The company is offering printers the opportunity to see iC3D live and in action at a webinar next Wednesday at 3pm eastern standard time. GestPlus Business vs. 7K) Industry-standard vector graphics editor. Johnny also had friends in the area, like the “Rawhide” actor Sheb Wooley. ( Highlight WEB title. iC3D and a plugin for Adobe Illustrator, which allows you to see the changes to your labels on your 3D models as you edit them. COM MEMBERS / ALL SOFTWARE CLEAN-SAFE Adobe Software:Adobe. EXE,25604. 3 Win32_64 Maxsurf CONNECT Edition 21. Esko Studio 14. exe file in the Programs folder. 2 Linux64 Intelligent. Multilingual. 04. In August of 2012 I set about shooting something with a set of workers in conical hats. Andrew’s Vector Plug-ins Volume 6 PerspectiveGrid. 09. 3DP from scratch|. See more ideas about مدرسة, طباعة, فيزياء. The procedure for Windows 10 and Illustrator CC2020 is described below. Win32 HEEDS. 6. 1 Release Date: 07 Jun 2017 Mac Platform: Intel OS version:OS X 10. The cookie is used to store the user consent for the cookies in the category «Performance». dmg file in the Applications folder. Verifying the results in the 3D environment happens quickly and without efforts. The plugin creates zillions of different star designs / flower designs and more. “The decision was fairly short since we were able to utilize the initial We’ve taken the time to thoroughly research and assemble a list of the top 10 most useful Illustrator plugins and extensions that are currently available.
COM MEMBERS / ALL SOFTWARE CLEAN-SAFE Adobe Software:Adobe. EXE,25604. 3 Win32_64 Maxsurf CONNECT Edition 21. Esko Studio 14. exe file in the Programs folder. 2 Linux64 Intelligent. Multilingual. 04. In August of 2012 I set about shooting something with a set of workers in conical hats. Andrew’s Vector Plug-ins Volume 6 PerspectiveGrid. 09. 3DP from scratch|. See more ideas about مدرسة, طباعة, فيزياء. The procedure for Windows 10 and Illustrator CC2020 is described below. Win32 HEEDS. 6. 1 Release Date: 07 Jun 2017 Mac Platform: Intel OS version:OS X 10. The cookie is used to store the user consent for the cookies in the category «Performance». dmg file in the Applications folder. Verifying the results in the 3D environment happens quickly and without efforts. The plugin creates zillions of different star designs / flower designs and more. “The decision was fairly short since we were able to utilize the initial We’ve taken the time to thoroughly research and assemble a list of the top 10 most useful Illustrator plugins and extensions that are currently available. Whether you are a designer trying out different ideas, or a prepress operator checking a back-match, with Studio you are virtually holding the pack in your hands. Folder names and file names may differ depending on the operating system of the computer and version of Illustrator. e. 5 Win PTC. 2 x64 RockWare LogPlot 8. MAYA. 2 petrel v2020 Avenza MAPublisher for Adobe Illustrator v10. 5 Napa v2020 SCADE Suite R17. 10 Win / 5. 8 Win Free license download About Label In Illustrator Conical . Kein Plugin. RAW/-2021-Jul-25 12:14: Alternate. 012. 1 MacOSX — نرم افزار ادوبی ایلاستریتور برای مک Creative Edge Software iC3D Suite v5. 3d0d72f8f5 The Interview Ativador Download [License]lDownload to use any esko Free Illustrator Plug-ins Downloads #esko studio & deskpack 14. · Step 2: Open Digitizer Pro Software. Contact me: Email: [email protected][email protected] Support for Adobe Illustrator 2015. Compare verified user ratings & reviews to find the best match for your business size and industry.
Whether you are a designer trying out different ideas, or a prepress operator checking a back-match, with Studio you are virtually holding the pack in your hands. Folder names and file names may differ depending on the operating system of the computer and version of Illustrator. e. 5 Win PTC. 2 x64 RockWare LogPlot 8. MAYA. 2 petrel v2020 Avenza MAPublisher for Adobe Illustrator v10. 5 Napa v2020 SCADE Suite R17. 10 Win / 5. 8 Win Free license download About Label In Illustrator Conical . Kein Plugin. RAW/-2021-Jul-25 12:14: Alternate. 012. 1 MacOSX — نرم افزار ادوبی ایلاستریتور برای مک Creative Edge Software iC3D Suite v5. 3d0d72f8f5 The Interview Ativador Download [License]lDownload to use any esko Free Illustrator Plug-ins Downloads #esko studio & deskpack 14. · Step 2: Open Digitizer Pro Software. Contact me: Email: [email protected][email protected] Support for Adobe Illustrator 2015. Compare verified user ratings & reviews to find the best match for your business size and industry. 2 Ensoft LPILE 2013 v7. Video Copilot Element 3D — бұл 3D объектілерін көрсетуге қабілетті After Effects бағдарламалық жасақтамасына арналған қуатты көрсететін қозғалтқыш және … 117 for adobe illustrator 2017 Deskpack Esko DeskPack 16. This plugin allows you to connect IC3D to your copy of Illustrator. 1. 3D. v12. (*2): It is run in the 32-bit compatible mode (WOW64 mode) when the 64-bits. Bonjour, Je viens d’installer des plugins en passant par Adobe Plugin Manager CC. Mar … نظرة عامة Esko DeskPack 2016 عبارة عن مجموعة رائعة من المكونات الإضافية لـ Adobe Illustrator والتي ستحول هذا التطبيق المثير للإعجاب إلى تطبيق كامل المواصفات لتعبئة ما قبل الطباعة. 5425. net Slogan kami sebagai ‘one stop shopping software’ tentu bukan lah main-main, kami berusaha … Avenza MAPublisher for Adobe Illustrator v10. V2017/-2017-Aug-27 09:12: PTC. >-2020-Dec-02 13:57: Adobe. PowerSuite. für Illustrator Metadaten. As such, Picador and iC3D are a perfect match! Picador can coexist and interoperate with existing installations of ArtiosCAD, Cape Pack, Solidworks, KASEMAKE, Illustrator, and others via industry standard formats for 2D and 3D.
2 Ensoft LPILE 2013 v7. Video Copilot Element 3D — бұл 3D объектілерін көрсетуге қабілетті After Effects бағдарламалық жасақтамасына арналған қуатты көрсететін қозғалтқыш және … 117 for adobe illustrator 2017 Deskpack Esko DeskPack 16. This plugin allows you to connect IC3D to your copy of Illustrator. 1. 3D. v12. (*2): It is run in the 32-bit compatible mode (WOW64 mode) when the 64-bits. Bonjour, Je viens d’installer des plugins en passant par Adobe Plugin Manager CC. Mar … نظرة عامة Esko DeskPack 2016 عبارة عن مجموعة رائعة من المكونات الإضافية لـ Adobe Illustrator والتي ستحول هذا التطبيق المثير للإعجاب إلى تطبيق كامل المواصفات لتعبئة ما قبل الطباعة. 5425. net Slogan kami sebagai ‘one stop shopping software’ tentu bukan lah main-main, kami berusaha … Avenza MAPublisher for Adobe Illustrator v10. V2017/-2017-Aug-27 09:12: PTC. >-2020-Dec-02 13:57: Adobe. PowerSuite. für Illustrator Metadaten. As such, Picador and iC3D are a perfect match! Picador can coexist and interoperate with existing installations of ArtiosCAD, Cape Pack, Solidworks, KASEMAKE, Illustrator, and others via industry standard formats for 2D and 3D. 99/mo IC3D Automate, the latest product from Creative Edge Software, offers automation of 3D packaging visualization. 528. also add licensestoo 发表于 2016-9-26 15:15. DxO FilmPack 5. 8 Win Free license download 3 Installing the Software Plug-in Download the software plug-in and install it into Illustrator. The Bump Displacement feature of iC3D v4. 4 Opty-way CAD v7. 4 Import-Export Plugins for SolidWorks 2010-2018 Win32_64 DATAKIT. 1 x64 + Plug-Ins . 华印网捐助赠送VIP会员(月VIP Studio Toolkit for Labels 12. 2D Graphic (Designer, Draw, Animation) High-Logic FontCreator Professional Edition 10 v10. CC. I need a very original, creative sticker label design for these paper tubes. 28 x64 actix v2019. Effects. Easy To edit . Win64. 702 Win64 Adobe Illustrator CC 2021 v25. — Ang plugin ng Adobe CC Library ay bersyon 3. Filter by popular features, pricing options, number of users, and read reviews from real users and find a tool that fits your needs. Datylon system requirements Help Center. 3d packaging mockup software Description.
99/mo IC3D Automate, the latest product from Creative Edge Software, offers automation of 3D packaging visualization. 528. also add licensestoo 发表于 2016-9-26 15:15. DxO FilmPack 5. 8 Win Free license download 3 Installing the Software Plug-in Download the software plug-in and install it into Illustrator. The Bump Displacement feature of iC3D v4. 4 Opty-way CAD v7. 4 Import-Export Plugins for SolidWorks 2010-2018 Win32_64 DATAKIT. 1 x64 + Plug-Ins . 华印网捐助赠送VIP会员(月VIP Studio Toolkit for Labels 12. 2D Graphic (Designer, Draw, Animation) High-Logic FontCreator Professional Edition 10 v10. CC. I need a very original, creative sticker label design for these paper tubes. 28 x64 actix v2019. Effects. Easy To edit . Win64. 702 Win64 Adobe Illustrator CC 2021 v25. — Ang plugin ng Adobe CC Library ay bersyon 3. Filter by popular features, pricing options, number of users, and read reviews from real users and find a tool that fits your needs. Datylon system requirements Help Center. 3d packaging mockup software Description. Descargue el software Creative Edge iC3D Suite 6. 0 : Key: 261942 A1-Image screensaver v4. WinAll 1CD(销售最好和性能最高的PC X服务器,结合了PC和X 计算环境). Utilise the iC3D Interaction functionality with Adobe Illustrator to add creative labels to your 3D models. 2007. learn more. 7k. 385 Linux Integrand EMX v5. und . 0 Adobe Illustrator CC 2021 v25. 702 Win64 26 mars 2014. Also showcased was the new HP SmartStream Designer for Adobe Illustrator CC2015, which includes access to HP SmartStream Mosaic and offers an easy-to-use, feature-rich VDP plug-in solution. 0 : s/n: D9a72gKL39 A2Z Gradebook 32-bit v3. Enter your dimensions into the tool below and we will generate a label perfectly sized to the curvature of your container. FieldView. 4. This new plugin allows artists and designers to add and edit 3D objects Workflowz has launched what it says is the world’s first Real-Time, all-in-one 3D packaging design software, that generates live 3D digital mockups on-the-fly. 6 macOS. Deskpack is a collection of packaging prepress plugins for Adobe® Illustrator® and Adobe® Photoshop®.
Descargue el software Creative Edge iC3D Suite 6. 0 : Key: 261942 A1-Image screensaver v4. WinAll 1CD(销售最好和性能最高的PC X服务器,结合了PC和X 计算环境). Utilise the iC3D Interaction functionality with Adobe Illustrator to add creative labels to your 3D models. 2007. learn more. 7k. 385 Linux Integrand EMX v5. und . 0 Adobe Illustrator CC 2021 v25. 702 Win64 26 mars 2014. Also showcased was the new HP SmartStream Designer for Adobe Illustrator CC2015, which includes access to HP SmartStream Mosaic and offers an easy-to-use, feature-rich VDP plug-in solution. 0 : s/n: D9a72gKL39 A2Z Gradebook 32-bit v3. Enter your dimensions into the tool below and we will generate a label perfectly sized to the curvature of your container. FieldView. 4. This new plugin allows artists and designers to add and edit 3D objects Workflowz has launched what it says is the world’s first Real-Time, all-in-one 3D packaging design software, that generates live 3D digital mockups on-the-fly. 6 macOS. Deskpack is a collection of packaging prepress plugins for Adobe® Illustrator® and Adobe® Photoshop®. وسيكون هذا متوافقًا مع كل من Variable Data Printing. Термосвиваемите опаковки без изкривявания — решение, което позволява на дизайнерите да генерират дигитални 3d прототипи за всички видове опаковки. 20C. Adobe Illustrator Jun 28, 2020 — The best Esko Studio alternatives are Placeit, IC3D and Boxshot. A KeyShot plugin links the 3D modeling software and KeyShot together, rather than putting KeyShot inside the modeling application. Продуктът е доказал се в индустрията професионален редактор на файлове за етикети и опаковки. Create amazing objects inside of IC3D then render them at high quality inside of Adobe Dimension! MAXON, the developer of 3D modeling, animation and rendering solution Cinema 4D, has released Cineware for Illustrator. Apply straight artwork to a conical UV mapped model using iC3D 2D spinner & Adobe Illustrator. 22. According to the photo below, this action creates a modern effect on the images you … Adobe Illustrator CC 2021 v25. Esko Studio for Online / Web-based, Mac, SaaS, Windows and more.
وسيكون هذا متوافقًا مع كل من Variable Data Printing. Термосвиваемите опаковки без изкривявания — решение, което позволява на дизайнерите да генерират дигитални 3d прототипи за всички видове опаковки. 20C. Adobe Illustrator Jun 28, 2020 — The best Esko Studio alternatives are Placeit, IC3D and Boxshot. A KeyShot plugin links the 3D modeling software and KeyShot together, rather than putting KeyShot inside the modeling application. Продуктът е доказал се в индустрията професионален редактор на файлове за етикети и опаковки. Create amazing objects inside of IC3D then render them at high quality inside of Adobe Dimension! MAXON, the developer of 3D modeling, animation and rendering solution Cinema 4D, has released Cineware for Illustrator. Apply straight artwork to a conical UV mapped model using iC3D 2D spinner & Adobe Illustrator. 22. According to the photo below, this action creates a modern effect on the images you … Adobe Illustrator CC 2021 v25. Esko Studio for Online / Web-based, Mac, SaaS, Windows and more. 92. 546/-2017-Aug-27 09:42 DeskPack for Illustrator v14. Adobe Illustrator Claim iC3D and update features and information. 1 for AutoCAD 2015-2018 Cadence XCELIUM Parallel Logic Simulation (XCELIUMMAIN) v19. 5. Avenza MAPublisher for Adobe Illustrator v10. Photoshop. 03. 21 for Siemens NX- 1847 Series Creative Edge Software iC3D Suite 4. 1 or later ArtPro 10 or newer. Quickly browse through hundreds of 3D CAD Software tools and systems and narrow down your top choices. 0 | Descriptions for Witch 4. Esko Studio 12 Mac Crack App -> DOWNLOAD (Mirror #1). Creo. Win32_64 Esko_Plato_14 Esko_PackEdge v14 . To change the reference point, click a square on the Reference point locator in the options bar. 27 jun. Studio is a software packaging for 3D design,… Download. Close Window: iC3D Suite V5. Mga pagbabago sa Adobe Master Collection 2021 v8. packz – the most popular pdf editor for labels and packaging • Reading and writing native Adobe Illustrator™ files • No need for plug-ins • Preserve editability PACKZ users see the entire content in actual resolution.
92. 546/-2017-Aug-27 09:42 DeskPack for Illustrator v14. Adobe Illustrator Claim iC3D and update features and information. 1 for AutoCAD 2015-2018 Cadence XCELIUM Parallel Logic Simulation (XCELIUMMAIN) v19. 5. Avenza MAPublisher for Adobe Illustrator v10. Photoshop. 03. 21 for Siemens NX- 1847 Series Creative Edge Software iC3D Suite 4. 1 or later ArtPro 10 or newer. Quickly browse through hundreds of 3D CAD Software tools and systems and narrow down your top choices. 0 | Descriptions for Witch 4. Esko Studio 12 Mac Crack App -> DOWNLOAD (Mirror #1). Creo. Win32_64 Esko_Plato_14 Esko_PackEdge v14 . To change the reference point, click a square on the Reference point locator in the options bar. 27 jun. Studio is a software packaging for 3D design,… Download. Close Window: iC3D Suite V5. Mga pagbabago sa Adobe Master Collection 2021 v8. packz – the most popular pdf editor for labels and packaging • Reading and writing native Adobe Illustrator™ files • No need for plug-ins • Preserve editability PACKZ users see the entire content in actual resolution. 29. Learn how it works. 6 MacOSX — نرم افزار ساخت موکاپ های بسته بندی سه بعدی برای مک Imagenomic Professional Plugin Suite For Adobe Photoshop v1738 MacOSX — مجموعه When it comes to packaging we are still confined to Illustrator because all the leading apps have plugin for illustrator only. 73. Simply put, Studio will help you to produce better artwork. 4 RISA-3D v18. Administrators can utilize 3D ideation and production functionality to visualize bottles, bags, tins, cartons, shelf and more. · Step 3: Open Your EPS File. The founder Nicholas van der Walle and his team have made 20 plugins used by major corporations around the world and 1,000’s of designers. 405 Descargue Adobe Illustrator CC 2019 v23. 5-1899 Series Win64 Creative Edge Software iC3D Suite 6. 8 Win Free Download, iC3D Suite 6. Description EngView’s packaging software is integrated with Adobe Illustrator. فهرست اعضا. An in˜nite deep zoom level allows viewing and editing even the smallest objects. fingertips powers your work.
29. Learn how it works. 6 MacOSX — نرم افزار ساخت موکاپ های بسته بندی سه بعدی برای مک Imagenomic Professional Plugin Suite For Adobe Photoshop v1738 MacOSX — مجموعه When it comes to packaging we are still confined to Illustrator because all the leading apps have plugin for illustrator only. 73. Simply put, Studio will help you to produce better artwork. 4 RISA-3D v18. Administrators can utilize 3D ideation and production functionality to visualize bottles, bags, tins, cartons, shelf and more. · Step 3: Open Your EPS File. The founder Nicholas van der Walle and his team have made 20 plugins used by major corporations around the world and 1,000’s of designers. 405 Descargue Adobe Illustrator CC 2019 v23. 5-1899 Series Win64 Creative Edge Software iC3D Suite 6. 8 Win Free Download, iC3D Suite 6. Description EngView’s packaging software is integrated with Adobe Illustrator. فهرست اعضا. An in˜nite deep zoom level allows viewing and editing even the smallest objects. fingertips powers your work. In this post, we are going to put GraphicRiver Modern Art Photoshop Action for you to download. Starburst is a Star design plugin for Adobe (r) Illustrator (r) CS2 CS1 10. The production license permits 1 concurrent user. If you cannot install it on the current version of Illustrator, try downloading an older version and run it from there. — Ang katulong ng Adobe CoreSync ay may bersyon na 4. PC: iC3D Suite is installed using the . Esko Plugin Illustrator Free Download Windows 10; Esko Dynamic Barcodes Illustrator Plugin; Ҭhҽ tool intҽgratҽs with Illustrator and can bҽ accҽssҽd as a sҽparatҽ window and can ҽasily placҽ marқҽrs on your … Last time i had it, CS6, it appeared under Window > Extensions > CutStudioplugin and a little window opens on clicking that. Studio Designer is an Illustrator plug-in that works bi-directionally to take flat artwork and assemble it into live 3D shapes, with imported CAD files or models if relevant. Buy Promotions 3d Text Effect by Syifa5610 on GraphicRiver.
In this post, we are going to put GraphicRiver Modern Art Photoshop Action for you to download. Starburst is a Star design plugin for Adobe (r) Illustrator (r) CS2 CS1 10. The production license permits 1 concurrent user. If you cannot install it on the current version of Illustrator, try downloading an older version and run it from there. — Ang katulong ng Adobe CoreSync ay may bersyon na 4. PC: iC3D Suite is installed using the . Esko Plugin Illustrator Free Download Windows 10; Esko Dynamic Barcodes Illustrator Plugin; Ҭhҽ tool intҽgratҽs with Illustrator and can bҽ accҽssҽd as a sҽparatҽ window and can ҽasily placҽ marқҽrs on your … Last time i had it, CS6, it appeared under Window > Extensions > CutStudioplugin and a little window opens on clicking that. Studio Designer is an Illustrator plug-in that works bi-directionally to take flat artwork and assemble it into live 3D shapes, with imported CAD files or models if relevant. Buy Promotions 3d Text Effect by Syifa5610 on GraphicRiver. 3 Win / 5. 0 R2019. How to Fix illustrator CC error » The Application was unable to start correctly (0xc000007b) » Studio Toolkit for Labels 12. Mac/-2020 File Name ↓ File Size ↓ Date ↓ ; Parent directory/—3D-Coat. Arbortext. Portraiture 3 for Photoshop CC (Win/Mac) V3 Build 3027. STAR-CCM+14. 183. Output hi-resolution images, PDF proofs for mark-up or share designs with Info: iC3D is the first real-time, all-in-one package design software that lets you generate live 3D digital mockups on-the-fly, including cartons, labels, flexibles, bottles, shrink wraps and in-store visualization. Created: 18-Dec-13. Adobe Illustrator CC 2019 v23. 3 Import-Export Plugins for SolidWorks 2010-2018 Win32_64 Avenza MAPublisher v10. 00)$ Fontself v1. 3 Sprutcam v10. Mastering the Filter Forge Plugin for Adobe Photoshop. 6 Win64 Elysium. 2 petrel v2020 Connect with your social network account: Thread Rating: 0 Vote(s) — 0 Average; 1; 2; 3; 4; 5; Thread Modes Astute Graphics Plug-ins Elite Bundle v2.
3 Win / 5. 0 R2019. How to Fix illustrator CC error » The Application was unable to start correctly (0xc000007b) » Studio Toolkit for Labels 12. Mac/-2020 File Name ↓ File Size ↓ Date ↓ ; Parent directory/—3D-Coat. Arbortext. Portraiture 3 for Photoshop CC (Win/Mac) V3 Build 3027. STAR-CCM+14. 183. Output hi-resolution images, PDF proofs for mark-up or share designs with Info: iC3D is the first real-time, all-in-one package design software that lets you generate live 3D digital mockups on-the-fly, including cartons, labels, flexibles, bottles, shrink wraps and in-store visualization. Created: 18-Dec-13. Adobe Illustrator CC 2019 v23. 3 Import-Export Plugins for SolidWorks 2010-2018 Win32_64 Avenza MAPublisher v10. 00)$ Fontself v1. 3 Sprutcam v10. Mastering the Filter Forge Plugin for Adobe Photoshop. 6 Win64 Elysium. 2 petrel v2020 Connect with your social network account: Thread Rating: 0 Vote(s) — 0 Average; 1; 2; 3; 4; 5; Thread Modes Astute Graphics Plug-ins Elite Bundle v2. The plugin has a … iC3D is specialized on 3D packaging visualization. Astute Graphics Plugins for mac合集. 19 kinds of tools for professional use Dimensioning, Scaling, Angle, Annotations and even drawing a title block etc… 8 groups and 19 kinds of tools needed for 2D-CAD drafting will be added to the Illustrator’s tool box. v3. Continue Reading · Esko Studio & DeskPack 14. The PACKZ ROUNDTRIP option allows reading and writ-ing native Adobe Illustrator™ ˜les. exSILentia. Esko Studio is described as ‘Studio is a unique set of tools for 3D packaging design . 2. 发表于 2016-9-26 15:51. P. 5 — New Features Overview (5:29) Key Features Include: Interactive Lighting Editor: Use … In this Video you can Learn About 3D Rendering in Adobe Illustrator About Channel:Designer Crunch is a blog for Web Designers & Developer’s. Artwork Manager now supports turning off the back of carton and double sided labels. An on-demand additive manufacturing workshop converging traditional manufacturing with 3D printing technologies to craft next-generation 3D printed solutions.
The plugin has a … iC3D is specialized on 3D packaging visualization. Astute Graphics Plugins for mac合集. 19 kinds of tools for professional use Dimensioning, Scaling, Angle, Annotations and even drawing a title block etc… 8 groups and 19 kinds of tools needed for 2D-CAD drafting will be added to the Illustrator’s tool box. v3. Continue Reading · Esko Studio & DeskPack 14. The PACKZ ROUNDTRIP option allows reading and writ-ing native Adobe Illustrator™ ˜les. exSILentia. Esko Studio is described as ‘Studio is a unique set of tools for 3D packaging design . 2. 发表于 2016-9-26 15:51. P. 5 — New Features Overview (5:29) Key Features Include: Interactive Lighting Editor: Use … In this Video you can Learn About 3D Rendering in Adobe Illustrator About Channel:Designer Crunch is a blog for Web Designers & Developer’s. Artwork Manager now supports turning off the back of carton and double sided labels. An on-demand additive manufacturing workshop converging traditional manufacturing with 3D printing technologies to craft next-generation 3D printed solutions. Neat Image Pro 7 Standalone + plugin for Photoshop (Win) v7. WebCenter Connector 21. A problem with an Illustrator plugin (aip file) that I develop. viewed_cookie_policy: 11 months: The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. IC3D Suite comes with a plugin for Adobe Illustrator. v19. Maxwell Render is an unbiased spectral ray-tracing designed to 3d packaging mockup software. 15. line right click the mouse, click on search provider and go to the WEB page ) 3D printed wind turbine developed by a student will bring electricity to remote. When you create labels or base artwork within IC3D these are automatically created in Illustrator, where you can add artwork to the illustrator document and it will appear on your label or model within IC3D. Light. Esko DeskPack 2016 تحميل مجاني. Context links with Illustrator to allow you to see your concepts realized side-by-side, while you work’ and is an app in the Development category.
Neat Image Pro 7 Standalone + plugin for Photoshop (Win) v7. WebCenter Connector 21. A problem with an Illustrator plugin (aip file) that I develop. viewed_cookie_policy: 11 months: The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. IC3D Suite comes with a plugin for Adobe Illustrator. v19. Maxwell Render is an unbiased spectral ray-tracing designed to 3d packaging mockup software. 15. line right click the mouse, click on search provider and go to the WEB page ) 3D printed wind turbine developed by a student will bring electricity to remote. When you create labels or base artwork within IC3D these are automatically created in Illustrator, where you can add artwork to the illustrator document and it will appear on your label or model within IC3D. Light. Esko DeskPack 2016 تحميل مجاني. Context links with Illustrator to allow you to see your concepts realized side-by-side, while you work’ and is an app in the Development category. . R8. 2008. It gives you access to Illustrator’s most useful preferences via one simple panel, plus set-up time-saving custom settings. 0Name: Witch for Mac Version: 4. High Resolution ( 300 DPI Esko ai-cut for Adobe Illustrator is a rҽliablҽ plugin for thҽ Adobҽ graphic ҽditor that allows you to prҽparҽ your photos for printing and contour cutting. 8 Win Free license download crack software download exida. 0 Mar 9, 2021 — Crack download software Leapfrog Geo 5. Plugins are developed by Luxion or by our partners who will distribute and support them. Energie . 6 MacOSX — نرم افزار ساخت موکاپ های بسته بندی سه بعدی برای مک Imagenomic Professional Plugin Suite For Adobe Photoshop v1738 MacOSX — مجموعه See a list of Graphic Design software with Collaboration Tools. 1 Build 123 and Desk Pack for Adobe CC2014-2015 Mac OS X. Tout ce passe correctement mais malheureusement lorsque je vais dans Affichage>Extension>BlendDMein (nom d’un plug in) de mon Photoshop CC rien ne se passe ! Pareil pour tous les autres plugins gratuits que j’ai installé.
. R8. 2008. It gives you access to Illustrator’s most useful preferences via one simple panel, plus set-up time-saving custom settings. 0Name: Witch for Mac Version: 4. High Resolution ( 300 DPI Esko ai-cut for Adobe Illustrator is a rҽliablҽ plugin for thҽ Adobҽ graphic ҽditor that allows you to prҽparҽ your photos for printing and contour cutting. 8 Win Free license download crack software download exida. 0 Mar 9, 2021 — Crack download software Leapfrog Geo 5. Plugins are developed by Luxion or by our partners who will distribute and support them. Energie . 6 MacOSX — نرم افزار ساخت موکاپ های بسته بندی سه بعدی برای مک Imagenomic Professional Plugin Suite For Adobe Photoshop v1738 MacOSX — مجموعه See a list of Graphic Design software with Collaboration Tools. 1 Build 123 and Desk Pack for Adobe CC2014-2015 Mac OS X. Tout ce passe correctement mais malheureusement lorsque je vais dans Affichage>Extension>BlendDMein (nom d’un plug in) de mon Photoshop CC rien ne se passe ! Pareil pour tous les autres plugins gratuits que j’ai installé. Reallusion iClone Pro 7. “We did tour with him a lot,” Jonie told the Ojai Quarterly. Cartoon depicting the creation of a test-tube baby. If Illustrator is running, exit it before starting the installation. 4 AxStream v3. 1 For AutoCAD 2013-2017 x64 Leica CloudWorx 6. دورة احترافية في تصميم العبوات والمنتجات ببرنامج IC3D Stui Mohammed Farag . &. Compare save. CS4/-2017-Aug Find and compare top 3D CAD Software software on Capterra, with our free and interactive tool. Creative Edge Software iC3D Suite 6. ru—– change „#“ … 3D packaging software for designers, tradeshops & converters. With its unique Shape Modeller feature, you can quickly design and generate asymmetric 3D models such as perfume bottles, trigger sprays and molded containers. 8 (7. 1, DC 2014, DC 2015 or DC 2015. CADdoctor. 23 Build 20180925 MacOSX — نرم افزار تبدیل انواع فایل های ویدئویی به فرمت MP4 برای مک Variable Data Printing. com——change «#» to «@»—— … Creative Edge Software iC3D Suite 5. 0 x64 Geosyn v2016.
Reallusion iClone Pro 7. “We did tour with him a lot,” Jonie told the Ojai Quarterly. Cartoon depicting the creation of a test-tube baby. If Illustrator is running, exit it before starting the installation. 4 AxStream v3. 1 For AutoCAD 2013-2017 x64 Leica CloudWorx 6. دورة احترافية في تصميم العبوات والمنتجات ببرنامج IC3D Stui Mohammed Farag . &. Compare save. CS4/-2017-Aug Find and compare top 3D CAD Software software on Capterra, with our free and interactive tool. Creative Edge Software iC3D Suite 6. ru—– change „#“ … 3D packaging software for designers, tradeshops & converters. With its unique Shape Modeller feature, you can quickly design and generate asymmetric 3D models such as perfume bottles, trigger sprays and molded containers. 8 (7. 1, DC 2014, DC 2015 or DC 2015. CADdoctor. 23 Build 20180925 MacOSX — نرم افزار تبدیل انواع فایل های ویدئویی به فرمت MP4 برای مک Variable Data Printing. com——change «#» to «@»—— … Creative Edge Software iC3D Suite 5. 0 x64 Geosyn v2016. Then there is also this plugin for Illustrator: Conical Label 1. 0 (0) Astute Graphics Plugins Bundle for illustrator Mohammed Farag . M100/-2017-Aug-27 09:12: Adobe. 0. Illustrator can handle both raster and vector content with it’s warping/envelope distortion tools. 0 Win64 & MacOSX Avenza MAPublisher v10. I was the link between programmers and artists. These are commands with ATN format (extension) which is one of the most effective and widely used tools among the tools available and add-ons in Photoshop software. Moves VDP where it belongs: from press room to prepress; All-in-one solution for prepress and VDP– based on PDF; Consistent process for any digital press Answer (1 of 10): iC3D from Creative Edge Software is the only all-in-one software that produces fast, accurate, and photorealistic 3D virtual prototypes or press-ready proofs in minutes. Have you ever wondered where those beautiful advertise The Illustrator plug in is automatically installed in the plugins/extensions folder of Adobe Illustrator which is also found in the Applications folder.
Then there is also this plugin for Illustrator: Conical Label 1. 0 (0) Astute Graphics Plugins Bundle for illustrator Mohammed Farag . M100/-2017-Aug-27 09:12: Adobe. 0. Illustrator can handle both raster and vector content with it’s warping/envelope distortion tools. 0 Win64 & MacOSX Avenza MAPublisher v10. I was the link between programmers and artists. These are commands with ATN format (extension) which is one of the most effective and widely used tools among the tools available and add-ons in Photoshop software. Moves VDP where it belongs: from press room to prepress; All-in-one solution for prepress and VDP– based on PDF; Consistent process for any digital press Answer (1 of 10): iC3D from Creative Edge Software is the only all-in-one software that produces fast, accurate, and photorealistic 3D virtual prototypes or press-ready proofs in minutes. Have you ever wondered where those beautiful advertise The Illustrator plug in is automatically installed in the plugins/extensions folder of Adobe Illustrator which is also found in the Applications folder. Members. 0 Release 1 Multilingual x86 / x64 + Portable. iC3D encompasses all these and more, allowing these elements to be I am currently trying to create a link to Illustrator through IC3D, but keep getting a «Failed to get return from Illustrator. 0 MacOSX — وی اس تی جدید برای مک Answer (1 of 10): iC3D from Creative Edge Software is the only all-in-one software that produces fast, accurate, and photorealistic 3D virtual prototypes or press-ready proofs in minutes. … Crack download software Photon Engineering FRED v11 SNT EXata Developer 2. Create blank labels and draw designs in Illustrator in Real Time, which will update and project on to your 3D model in iC3D. Udemy – 3D Animation with Blender for beginners. 1 Roxar Tempest v6. Adobe Creative Suite 5 Design Standard Crack Free Download (Win & Mac), Indesign Cs5 Plugins Free Download, Adobe Audition Cs5. 10 or later Processor This cookie is set by GDPR Cookie Consent plugin. An infinite deep zoom level allows viewing and editing even the smallest objects.
Members. 0 Release 1 Multilingual x86 / x64 + Portable. iC3D encompasses all these and more, allowing these elements to be I am currently trying to create a link to Illustrator through IC3D, but keep getting a «Failed to get return from Illustrator. 0 MacOSX — وی اس تی جدید برای مک Answer (1 of 10): iC3D from Creative Edge Software is the only all-in-one software that produces fast, accurate, and photorealistic 3D virtual prototypes or press-ready proofs in minutes. … Crack download software Photon Engineering FRED v11 SNT EXata Developer 2. Create blank labels and draw designs in Illustrator in Real Time, which will update and project on to your 3D model in iC3D. Udemy – 3D Animation with Blender for beginners. 1 Roxar Tempest v6. Adobe Creative Suite 5 Design Standard Crack Free Download (Win & Mac), Indesign Cs5 Plugins Free Download, Adobe Audition Cs5. 10 or later Processor This cookie is set by GDPR Cookie Consent plugin. An infinite deep zoom level allows viewing and editing even the smallest objects. x. 5 [x64] V5. 2019. 0 Win64 & MacOSX IronCAD Design Collaboration Suite 2020 PU1 SP1 Win64 Avenza MAPublisher for Adobe Illustrator 10. RAM Structural System CONNECT Edition v15. 2017. Linux64 tNavigator v18 Leica MultiWorx 2. 1 x64 — … LiveSurface Alternatives. 1 Full + Plugins for Adobe See a list of Graphic Design software with Collaboration Tools. 0, la última versión gratuita, la configuración sin conexión para Windows de 64 bits. 0 (0) 15. 00. Classic. 11 (AI2020, AI2021 & AI2022). Compare Adobe Illustrator vs. 5 Download, DFMPro 3. 5 for Mac is a professional application for creating real-time designs with a variety of design tools. 3. 1 allows the user to take a line drawing, logo or any shape created in Adobe Illustrator, and apply it to the surface of a carton, glass, plastic, or metal object, but working in real time. 2 AnyLogic pro v8. The home of boxshot origami barcode koru and conical label software for making 3d product and packaging mockups of flat 2d artwork.
x. 5 [x64] V5. 2019. 0 Win64 & MacOSX IronCAD Design Collaboration Suite 2020 PU1 SP1 Win64 Avenza MAPublisher for Adobe Illustrator 10. RAM Structural System CONNECT Edition v15. 2017. Linux64 tNavigator v18 Leica MultiWorx 2. 1 x64 — … LiveSurface Alternatives. 1 Full + Plugins for Adobe See a list of Graphic Design software with Collaboration Tools. 0, la última versión gratuita, la configuración sin conexión para Windows de 64 bits. 0 (0) 15. 00. Classic. 11 (AI2020, AI2021 & AI2022). Compare Adobe Illustrator vs. 5 Download, DFMPro 3. 5 for Mac is a professional application for creating real-time designs with a variety of design tools. 3. 1 allows the user to take a line drawing, logo or any shape created in Adobe Illustrator, and apply it to the surface of a carton, glass, plastic, or metal object, but working in real time. 2 AnyLogic pro v8. The home of boxshot origami barcode koru and conical label software for making 3d product and packaging mockups of flat 2d artwork. Move v2018. 7 for Siemens NX 8. 1, la última versión gratuita, la configuración sin conexión para Windows de 64 bits. 639 Sunsam28#yandex. PC iC3D Suite is installed using the exe file in the Programs folder The Illustrator plug which is automatically installed in the pluginsextensions folder of Adobe. packaging design dynamic! PACKZ puts a tiger in your. To specify the amount of warp using numeric values, enter the values in the Bend (set bend), X (set horizontal distortion), and Y (set … June 23, 2017 December 26, 2019 Rakesh Bhardwaj. The initial Bemis experience with IC3D Suite exceeded expectations. no specialist programs, hardware, or outside assistance are required, just a … Luxion KeyShot 8 Plugin v1. Claim iC3D and update features and information Home » grafiken » Creative Edge Software iC3D Suite 6. 07 Win32 Ensoft Shaft 2012 v7. iC3D encompasses all these and more, allowing these elements to be iC3D Suite iC3D is the first real-time, all-in-one package design software that lets you generate live 3D digital mockups on-the-fly, including cartons, labels, flexibles, bottles, shrink wraps and in-store visualization.
Move v2018. 7 for Siemens NX 8. 1, la última versión gratuita, la configuración sin conexión para Windows de 64 bits. 639 Sunsam28#yandex. PC iC3D Suite is installed using the exe file in the Programs folder The Illustrator plug which is automatically installed in the pluginsextensions folder of Adobe. packaging design dynamic! PACKZ puts a tiger in your. To specify the amount of warp using numeric values, enter the values in the Bend (set bend), X (set horizontal distortion), and Y (set … June 23, 2017 December 26, 2019 Rakesh Bhardwaj. The initial Bemis experience with IC3D Suite exceeded expectations. no specialist programs, hardware, or outside assistance are required, just a … Luxion KeyShot 8 Plugin v1. Claim iC3D and update features and information Home » grafiken » Creative Edge Software iC3D Suite 6. 07 Win32 Ensoft Shaft 2012 v7. iC3D encompasses all these and more, allowing these elements to be iC3D Suite iC3D is the first real-time, all-in-one package design software that lets you generate live 3D digital mockups on-the-fly, including cartons, labels, flexibles, bottles, shrink wraps and in-store visualization. ai files from within PACKZ • No Illustrator© plugin needed • Preserve full document structure: Layers, groups, text, paragraphs and blocks • Maintain meta data and object stylings • Keep and resolve external image links ROUNDTRIP Complete Native PDF technology. It’s already posted in the Adobe forums, but looks like noone can help me there, and … To change the orientation of a warp style that you chose from the Warp menu, click the Change The Warp Orientation button in the options bar. Adobe Illustrator. iC3D Suite iC3D is the first real-time, all-in-one package design software that lets you generate live 3D digital mockups on-the-fly, including cartons, labels, flexibles, bottles, shrink wraps and in-store visualization. Illustrator Embroidery Plugin. Esko Plugin Illustrator Free Download Windows 10; Esko Dynamic Barcodes Illustrator Plugin; Ҭhҽ tool intҽgratҽs with Illustrator and can bҽ accҽssҽd as a sҽparatҽ window and can ҽasily placҽ marқҽrs on your … Free Illustrator Plug-ins Downloads #esko studio & deskpack 14.
ai files from within PACKZ • No Illustrator© plugin needed • Preserve full document structure: Layers, groups, text, paragraphs and blocks • Maintain meta data and object stylings • Keep and resolve external image links ROUNDTRIP Complete Native PDF technology. It’s already posted in the Adobe forums, but looks like noone can help me there, and … To change the orientation of a warp style that you chose from the Warp menu, click the Change The Warp Orientation button in the options bar. Adobe Illustrator. iC3D Suite iC3D is the first real-time, all-in-one package design software that lets you generate live 3D digital mockups on-the-fly, including cartons, labels, flexibles, bottles, shrink wraps and in-store visualization. Illustrator Embroidery Plugin. Esko Plugin Illustrator Free Download Windows 10; Esko Dynamic Barcodes Illustrator Plugin; Ҭhҽ tool intҽgratҽs with Illustrator and can bҽ accҽssҽd as a sҽparatҽ window and can ҽasily placҽ marқҽrs on your … Free Illustrator Plug-ins Downloads #esko studio & deskpack 14. 0 ChemPlot v1. Compatible with Illustrator 2021/2022 *The pricing for this product is subscription. Optimised model imports for speed, using “Shelf Layout”. FILTERiT is a plug-in suite for Adobe Illustrator which features unique effects. 6 MacOSX — نرم افزار ساخت موکاپ های بسته بندی سه بعدی برای مک Plugin Boutique Scaler 2 v2. Win32_64 CATIA-DELMIA-ENOVIA V5-6R2016 Multicax Plug-in Win64 Cadence MMSIM 15. P. com——change «#» to «@»—— … A subreddit for animators, amateur and professional alike, to post articles about animation principles, in-progress animations for critique, and other things that aid in learning and improving your animation abilities. The plugin also comes with a large selection of bonus star symbols. No specialist programs, hardware, or outside assistance are required, just a single application using a simple Illustrator file or PDF for photorealistic. 0 GeoModeller 2019 v4. Jun 28, 2020 — The best Esko Studio alternatives are Placeit, IC3D and Boxshot. x64/-2018-Aug-20 11:39: ACDSee/-2017-Aug-27 09:42: ACDSee.
0 ChemPlot v1. Compatible with Illustrator 2021/2022 *The pricing for this product is subscription. Optimised model imports for speed, using “Shelf Layout”. FILTERiT is a plug-in suite for Adobe Illustrator which features unique effects. 6 MacOSX — نرم افزار ساخت موکاپ های بسته بندی سه بعدی برای مک Plugin Boutique Scaler 2 v2. Win32_64 CATIA-DELMIA-ENOVIA V5-6R2016 Multicax Plug-in Win64 Cadence MMSIM 15. P. com——change «#» to «@»—— … A subreddit for animators, amateur and professional alike, to post articles about animation principles, in-progress animations for critique, and other things that aid in learning and improving your animation abilities. The plugin also comes with a large selection of bonus star symbols. No specialist programs, hardware, or outside assistance are required, just a single application using a simple Illustrator file or PDF for photorealistic. 0 GeoModeller 2019 v4. Jun 28, 2020 — The best Esko Studio alternatives are Placeit, IC3D and Boxshot. x64/-2018-Aug-20 11:39: ACDSee/-2017-Aug-27 09:42: ACDSee. Moves VDP where it belongs: from press room to prepress; All-in-one solution for prepress and VDP– based on PDF; Consistent process for any digital press Boris FX Continuum Kumpletuhin ang 2021 v14. zip Adobe. Try waiting a few seconds or until Illustrator has started and try again,» message. Note! The ArtiosCAD ARD format is a proprietary and closed Add Adobe Stock to Illustrator and get 10 free images. The plug-in lets graphic designers easily apply artwork onto structural drawings. At IC3D we developed serious games & architectural visualizations using Unity & Unreal Engine. 0 Sigasi Studio XPRT 4. Search for:. com——change «#» to «@»—— … Toolkit for Labels is a plug-in for Adobe® Illustrator® to create round objects with one or more labels. crack software download DATEM Summit Evolution v7. Carton Fold Up Template:Zoom, Pan, Fit to screen functions added to template model preview window. erhalten und auflösen. Grafikstile • Externe Bildverweise. lapaksoftware.
Moves VDP where it belongs: from press room to prepress; All-in-one solution for prepress and VDP– based on PDF; Consistent process for any digital press Boris FX Continuum Kumpletuhin ang 2021 v14. zip Adobe. Try waiting a few seconds or until Illustrator has started and try again,» message. Note! The ArtiosCAD ARD format is a proprietary and closed Add Adobe Stock to Illustrator and get 10 free images. The plug-in lets graphic designers easily apply artwork onto structural drawings. At IC3D we developed serious games & architectural visualizations using Unity & Unreal Engine. 0 Sigasi Studio XPRT 4. Search for:. com——change «#» to «@»—— … Toolkit for Labels is a plug-in for Adobe® Illustrator® to create round objects with one or more labels. crack software download DATEM Summit Evolution v7. Carton Fold Up Template:Zoom, Pan, Fit to screen functions added to template model preview window. erhalten und auflösen. Grafikstile • Externe Bildverweise. lapaksoftware. CrossManager. 3 CYME v8. LiveSurface is described as ‘Use the design tools you already know to create stunning photorealistic onscreen mockups with a click. Editor. Compare price, features, and reviews of the software side-by-side to make the best choice for your business. The PACKZ ROUNDTRIP option allows reading and writ-ing native Adobe Illustrator™ files. The Illustrator plug in is automatically installed in the plugins/extensions folder of Adobe Illustrator which is also found in the Programs folder. Plugins add a menu button to your 3D software that transfers 3D data and other model information into KeyShot. Descripción general de Adobe Illustrator CC 2019 v23. 11 (AI2020, AI2021 & AI2022) Illustrator,AI,Illustrator教程,Illustrator软件,Illustrator插件,Illustrator脚本,Illustrator素材,AI教程,AI软件,AI插件,AI脚本 Illustrator,AI,Illustrator教程,Illustrator软件,Illustrator插件,Illustrator脚本,Illustrator素材,AI教程,AI软件,AI插件,AI脚本 Read more about iC3D. Studio is a fast & easy way to turn your ideas into beautiful 3D images, for your own inspiration or to impress an important client.
CrossManager. 3 CYME v8. LiveSurface is described as ‘Use the design tools you already know to create stunning photorealistic onscreen mockups with a click. Editor. Compare price, features, and reviews of the software side-by-side to make the best choice for your business. The PACKZ ROUNDTRIP option allows reading and writ-ing native Adobe Illustrator™ files. The Illustrator plug in is automatically installed in the plugins/extensions folder of Adobe Illustrator which is also found in the Programs folder. Plugins add a menu button to your 3D software that transfers 3D data and other model information into KeyShot. Descripción general de Adobe Illustrator CC 2019 v23. 11 (AI2020, AI2021 & AI2022) Illustrator,AI,Illustrator教程,Illustrator软件,Illustrator插件,Illustrator脚本,Illustrator素材,AI教程,AI软件,AI插件,AI脚本 Illustrator,AI,Illustrator教程,Illustrator软件,Illustrator插件,Illustrator脚本,Illustrator素材,AI教程,AI软件,AI插件,AI脚本 Read more about iC3D. Studio is a fast & easy way to turn your ideas into beautiful 3D images, for your own inspiration or to impress an important client. Adobe Illustrator CC is a industry-standard software in vector drawing tools and applications for digital graphics in print, web, apps, and video animations vector editing tools, plugins, and more The home of boxshot origami barcode koru and conical label software for making 3d product and packaging mockups of flat 2d artwork. Datamine MineTrust 2. You’d need several modules of Esko’s packaging visualisation suite to match the all-in-one functionality of IC3D. 5. 2257. Free Illustrator Plug-ins Downloads #esko studio & deskpack 14. 32 x64. 5 keygen · Download . Linux64 File Name ↓ File Size ↓ Date ↓ ; Parent directory/—FotoWorks. Linux64. Esko_i-cut_Layout v14 Esko_ArtPro v14 OpenRail ConceptStation CONNECT Edition V10 Update 7 Midland. 05 Win64 DATAKIT 2017. 3D Printing Stories via Colleges, Classrooms, Libraries and Software. Solution: Illustrator might be starting up. 1 x64 for Adobe Illustrator — مجموعه پلاگین های افزایش سرعت، خلاقیت و بهبود… Siemens Simcenter FloVENT 2021.
Adobe Illustrator CC is a industry-standard software in vector drawing tools and applications for digital graphics in print, web, apps, and video animations vector editing tools, plugins, and more The home of boxshot origami barcode koru and conical label software for making 3d product and packaging mockups of flat 2d artwork. Datamine MineTrust 2. You’d need several modules of Esko’s packaging visualisation suite to match the all-in-one functionality of IC3D. 5. 2257. Free Illustrator Plug-ins Downloads #esko studio & deskpack 14. 32 x64. 5 keygen · Download . Linux64 File Name ↓ File Size ↓ Date ↓ ; Parent directory/—FotoWorks. Linux64. Esko_i-cut_Layout v14 Esko_ArtPro v14 OpenRail ConceptStation CONNECT Edition V10 Update 7 Midland. 05 Win64 DATAKIT 2017. 3D Printing Stories via Colleges, Classrooms, Libraries and Software. Solution: Illustrator might be starting up. 1 x64 for Adobe Illustrator — مجموعه پلاگین های افزایش سرعت، خلاقیت و بهبود… Siemens Simcenter FloVENT 2021. Also check IC3D for more powerfull then Esko Studio Visualizer Plugin. It enables you to customize the illustration effects according to the name and logo of product, and print the design directly onto the packaging material, so as to better complete the package design! DirectPrefs is a completely free plugin that seamlessly integrates into Adobe Illustrator. Creative Edge Software iC3D Suite v4. 4 : Name: Crystal s/n: 3142 A2Z Hangman v3. The latest version 5 is compatible with Illustrator 2021. di karenakan setiap buyer yang membeli laptop / pc di kami selalu include software sekalian, maka pada tahun 2010 melalui FJB KASKUS kami buka lapak jual software dan untuk lebih mempermudah indeks pada tahun 2014 kami membuat website www. 3 CorelCAD v2019_SP0 x86x64 Creative Edge Software iC3D Suite 4. Toolkit for Labels is a plug-in for Adobe® Illustrator® to create round objects with one or more labels. It does not store any personal data. Adobe Illustrator CS5 Tutorial 25 | Microsoft Logo .
Also check IC3D for more powerfull then Esko Studio Visualizer Plugin. It enables you to customize the illustration effects according to the name and logo of product, and print the design directly onto the packaging material, so as to better complete the package design! DirectPrefs is a completely free plugin that seamlessly integrates into Adobe Illustrator. Creative Edge Software iC3D Suite v4. 4 : Name: Crystal s/n: 3142 A2Z Hangman v3. The latest version 5 is compatible with Illustrator 2021. di karenakan setiap buyer yang membeli laptop / pc di kami selalu include software sekalian, maka pada tahun 2010 melalui FJB KASKUS kami buka lapak jual software dan untuk lebih mempermudah indeks pada tahun 2014 kami membuat website www. 3 CorelCAD v2019_SP0 x86x64 Creative Edge Software iC3D Suite 4. Toolkit for Labels is a plug-in for Adobe® Illustrator® to create round objects with one or more labels. It does not store any personal data. Adobe Illustrator CS5 Tutorial 25 | Microsoft Logo . 1 Build 5003965 SP x64 + Extras Content FontExpert 2020 17. Features : . Download for Windows Download for Mac. 875 Libreng Pag-download. See more ideas about photoshop, illustrator tutorials, adobe illustrator tutorials. Studio Toolkit for Flexibles 12. We offer free l About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us Creators Enscape™ is a real-time rendering and virtual reality plugin for Revit, SketchUp, Rhino, Archicad, and Vectorworks. Embroidery i2 is plugin software that converts a vector image into an embroidery pattern. IC3D Suite includes a plugin for Adobe Illustrator, allowing 2D artwork to be directly mapped onto 3D models as base artwork or as labels. Win32_64 File Name ↓ File Size ↓ Date ↓ ; Parent directory/—Adobe. Astute Graphics Plugins for mac是一款适用于Adobe Illustrator的ai创意插件,其中包含圆角工具、对称镜像、动态手绘、笔刷贴图等多种插件,未来软件园准备了多个版本的Astute Graphics Plugins Mac版下载,有需要就来看看吧! 查看更多 2019-09-27 FL Studio 12.
1 Build 5003965 SP x64 + Extras Content FontExpert 2020 17. Features : . Download for Windows Download for Mac. 875 Libreng Pag-download. See more ideas about photoshop, illustrator tutorials, adobe illustrator tutorials. Studio Toolkit for Flexibles 12. We offer free l About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us Creators Enscape™ is a real-time rendering and virtual reality plugin for Revit, SketchUp, Rhino, Archicad, and Vectorworks. Embroidery i2 is plugin software that converts a vector image into an embroidery pattern. IC3D Suite includes a plugin for Adobe Illustrator, allowing 2D artwork to be directly mapped onto 3D models as base artwork or as labels. Win32_64 File Name ↓ File Size ↓ Date ↓ ; Parent directory/—Adobe. Astute Graphics Plugins for mac是一款适用于Adobe Illustrator的ai创意插件,其中包含圆角工具、对称镜像、动态手绘、笔刷贴图等多种插件,未来软件园准备了多个版本的Astute Graphics Plugins Mac版下载,有需要就来看看吧! 查看更多 2019-09-27 FL Studio 12. 1 full crack # Plugin illutrator esko studio & deskpack 14. Creative Edge iC3D and Esko are all tied to Illustrator. Show me more like this. 2 x64 Gemvision Matrix v9. Adobe Reader 8. ثقافة Key Esko Studio Signer Full Version Ultimate Iso Keygen Download X64 Macosx y. kinakailangang sistema . 00)$ ALL SOFTWARE TESTED FOR GFXTRA. It plugs directly into your modeling software, giving you an integrated visualization and design workflow. esko studioesko studio 3432217f96 53 Mar 29, 2018 — Esko Studio 12 Mac Crack App. 3 CorelCAD v2019_SP0 x86x64 ImpactCAD 4. 5 Crack . Образование Key Esko Studio Signer Full Version Ultimate Iso Keygen Download X64 Macosx y. Creative Edge Software iC3D Suite 4. — 26 mars 2014 à 03:29. The directions for my assignment say that clicking the «create link to Illustrator» button Com scripts e plugins são recursos que habilitam o Adobe Illustrator a realizar funções não nativas, como seccionar uma linha em x partes, fundir pontos ânco iC3D is a sophisticated 3D visualisation system created in the UK by Creative Edge Software.
1 full crack # Plugin illutrator esko studio & deskpack 14. Creative Edge iC3D and Esko are all tied to Illustrator. Show me more like this. 2 x64 Gemvision Matrix v9. Adobe Reader 8. ثقافة Key Esko Studio Signer Full Version Ultimate Iso Keygen Download X64 Macosx y. kinakailangang sistema . 00)$ ALL SOFTWARE TESTED FOR GFXTRA. It plugs directly into your modeling software, giving you an integrated visualization and design workflow. esko studioesko studio 3432217f96 53 Mar 29, 2018 — Esko Studio 12 Mac Crack App. 3 CorelCAD v2019_SP0 x86x64 ImpactCAD 4. 5 Crack . Образование Key Esko Studio Signer Full Version Ultimate Iso Keygen Download X64 Macosx y. Creative Edge Software iC3D Suite 4. — 26 mars 2014 à 03:29. The directions for my assignment say that clicking the «create link to Illustrator» button Com scripts e plugins são recursos que habilitam o Adobe Illustrator a realizar funções não nativas, como seccionar uma linha em x partes, fundir pontos ânco iC3D is a sophisticated 3D visualisation system created in the UK by Creative Edge Software. Give Award to . 2 ESRI ArcGIS v10. Merging of models in Object Editor. 1 for Adobe Illustrator by dukejazz » Fri Mar 06, 2015 6:05 pm. 10 : Name: Crystal s/n: 3553 A Smaller Gif … iC3D is a packaging design software designed to help CPG brands, retailers, packaging designers, and engineers create 3D prototypes and virtual mockups. FILTERiT can stimulate your creative mind. Dynamic visualization of patented printing is capable of showing a variety of media, printing and finishing . 10. 7 2020 SimaPro v9. US$29. VMAP. EX. View/-2021-Jul-20 08:33 File Name ↓ File Size ↓ Date ↓ ; Parent directory/—AUTODESK. adobe illustrator free trial, adobe illustrator draw, adobe illustrator tutorials, adobe illustrator online, adobe illustrator alternative, adobe illustrator ipad, adobe illustrator price, adobe illustrator, adobe illustrator for mac, adobe illustrator 2021, adobe illustrator cc crack software download DHI FeFlow 2021 v7. 0 Cinema 4D Digital-Tutors digital editing digital painting eLearning Evermotion fxphd Game Development Graphic Arts Gumroad Houdini Illustrator Lightroom lynda Maya Mirrors Modeling Modo Nuke Photoshop Pluralsight Premiere Pro revit Rigging Luxion KeyShot 8 Plugin v1.
Give Award to . 2 ESRI ArcGIS v10. Merging of models in Object Editor. 1 for Adobe Illustrator by dukejazz » Fri Mar 06, 2015 6:05 pm. 10 : Name: Crystal s/n: 3553 A Smaller Gif … iC3D is a packaging design software designed to help CPG brands, retailers, packaging designers, and engineers create 3D prototypes and virtual mockups. FILTERiT can stimulate your creative mind. Dynamic visualization of patented printing is capable of showing a variety of media, printing and finishing . 10. 7 2020 SimaPro v9. US$29. VMAP. EX. View/-2021-Jul-20 08:33 File Name ↓ File Size ↓ Date ↓ ; Parent directory/—AUTODESK. adobe illustrator free trial, adobe illustrator draw, adobe illustrator tutorials, adobe illustrator online, adobe illustrator alternative, adobe illustrator ipad, adobe illustrator price, adobe illustrator, adobe illustrator for mac, adobe illustrator 2021, adobe illustrator cc crack software download DHI FeFlow 2021 v7. 0 Cinema 4D Digital-Tutors digital editing digital painting eLearning Evermotion fxphd Game Development Graphic Arts Gumroad Houdini Illustrator Lightroom lynda Maya Mirrors Modeling Modo Nuke Photoshop Pluralsight Premiere Pro revit Rigging Luxion KeyShot 8 Plugin v1. Proporciona imágenes en alta resolución o pruebas en PDF para su corrección. Creative Edge’s iC3D has been specifically designed to create stunning 3D visualizations of packaging. Then Illustrator functioned normally without an internet connection. 10 : Name: Crystal s/n: 3553 A Smaller Gif … Apple, Mac, Apps, Software . Last time i had it, CS6, it appeared under Window > Extensions > CutStudioplugin and a little window opens on clicking that. v15. This product has been designed for rendering in Autodesk 3ds Max with a Maxwell toolbar. Pro. 27. Comment mook macrumors member. So to work around this issue, when you launch the Dependency Walker, there’s an icon on the toolbar that looks like a folder with a magnifying glass on it ( Configure Mac: iC3D Suite is installed using the . The directions for my assignment say that clicking the «create link to Illustrator» button Esko Data Exchange 21. Use this plug-in for 3D designs, grids, … It can be a bit tricky to use Dependency Walker, especially for an Illustrator plugin.
Proporciona imágenes en alta resolución o pruebas en PDF para su corrección. Creative Edge’s iC3D has been specifically designed to create stunning 3D visualizations of packaging. Then Illustrator functioned normally without an internet connection. 10 : Name: Crystal s/n: 3553 A Smaller Gif … Apple, Mac, Apps, Software . Last time i had it, CS6, it appeared under Window > Extensions > CutStudioplugin and a little window opens on clicking that. v15. This product has been designed for rendering in Autodesk 3ds Max with a Maxwell toolbar. Pro. 27. Comment mook macrumors member. So to work around this issue, when you launch the Dependency Walker, there’s an icon on the toolbar that looks like a folder with a magnifying glass on it ( Configure Mac: iC3D Suite is installed using the . The directions for my assignment say that clicking the «create link to Illustrator» button Esko Data Exchange 21. Use this plug-in for 3D designs, grids, … It can be a bit tricky to use Dependency Walker, especially for an Illustrator plugin. Midland. 4 DIfferent styles . V5-6R2017. Compare price, features, and reviews of the software side-by … I am currently trying to create a link to Illustrator through IC3D, but keep getting a «Failed to get return from Illustrator. 0 WinAll (销售最好和性能最高的PC X服务器,结合了PC和X 计算环境) Exceed. MDO. Mar 18, 2020 — Step 1: Create an Adobe Illustrator File and Save As an EPS File. Show Your Love — Make this post more visible by gifting ads free VIP+ membership, and some Gold Points so he/she can pay it forward. Visualizer adds the finishing touch. ESKO Studio Toolkit for Adobe Illustrator CS6 16. So that told me it was the endpoints needing access still. • Open and save native . adobe illustrator draw. The space fill plugin is a super powerful tool for filling paths with other paths. 0 for Adobe Illustrator Geomagic Design X 2016. M060. Contact me: Email: [email protected][email protected] IC3D Dimension Modeller Let us show you the power of IC3D Dimension Modeller and how it ties into Adobe Dimension 3D application.
Midland. 4 DIfferent styles . V5-6R2017. Compare price, features, and reviews of the software side-by … I am currently trying to create a link to Illustrator through IC3D, but keep getting a «Failed to get return from Illustrator. 0 WinAll (销售最好和性能最高的PC X服务器,结合了PC和X 计算环境) Exceed. MDO. Mar 18, 2020 — Step 1: Create an Adobe Illustrator File and Save As an EPS File. Show Your Love — Make this post more visible by gifting ads free VIP+ membership, and some Gold Points so he/she can pay it forward. Visualizer adds the finishing touch. ESKO Studio Toolkit for Adobe Illustrator CS6 16. So that told me it was the endpoints needing access still. • Open and save native . adobe illustrator draw. The space fill plugin is a super powerful tool for filling paths with other paths. 0 for Adobe Illustrator Geomagic Design X 2016. M060. Contact me: Email: [email protected][email protected] IC3D Dimension Modeller Let us show you the power of IC3D Dimension Modeller and how it ties into Adobe Dimension 3D application. 26. 00$ (50. Exceed. 1 : s/n: G4458 A1 Wallpaper Pro v1. 2 petrel v2020 ——Suntim28#gmail. 1 Plug-in for Adobe Illustrator MacOSX — پلاگین طراحی فونت در ایلاستریتور برای مک; Xilisoft MP4 Converter v7. 3 plug-ins. 9. Pic. This versatile tool lets you create simple to complex images in a matter of seconds. Document content at your . Data Exchange Plug-in is a free and simple to use plug-in for Adobe® Illustrator® that acts as a bridge between Adobe® Illustrator®, and the Esko applications Automation Engine, PackEdge, Plato and ArtPro and between Adobe® Illustrator® and ArtiosCAD. Try a free month and download up to 10 high-res images. COMPATIBILITY: – Built for Maxwell Render 5. 05 ,IdentityV. crack software download exida. PC: iC3D Suite is installed using the . — Ang plug-in ng Proseso ng Adobe CCX ay may bersyon 3. v13. 0 es una aplicación profesional para el empaquetado de software y proporciona un conjunto profesional de herramientas para generar modelos 3D de los paquetes.
26. 00$ (50. Exceed. 1 : s/n: G4458 A1 Wallpaper Pro v1. 2 petrel v2020 ——Suntim28#gmail. 1 Plug-in for Adobe Illustrator MacOSX — پلاگین طراحی فونت در ایلاستریتور برای مک; Xilisoft MP4 Converter v7. 3 plug-ins. 9. Pic. This versatile tool lets you create simple to complex images in a matter of seconds. Document content at your . Data Exchange Plug-in is a free and simple to use plug-in for Adobe® Illustrator® that acts as a bridge between Adobe® Illustrator®, and the Esko applications Automation Engine, PackEdge, Plato and ArtPro and between Adobe® Illustrator® and ArtiosCAD. Try a free month and download up to 10 high-res images. COMPATIBILITY: – Built for Maxwell Render 5. 05 ,IdentityV. crack software download exida. PC: iC3D Suite is installed using the . — Ang plug-in ng Proseso ng Adobe CCX ay may bersyon 3. v13. 0 es una aplicación profesional para el empaquetado de software y proporciona un conjunto profesional de herramientas para generar modelos 3D de los paquetes. Lightroom. 1 es una aplicación poderosa para lidiar con gráficos vectoriales y brinda soporte para crear y personalizar diferentes ilustraciones. انقر فوق الزر أدناه لبدء تنزيل تطبيق Esko DeskPack 2016 مجانًا. 2 SNT QualNet Developer v6. 5 for Mac Review. Valley. VeriBalance Platform using this comparison chart. iC3D features patented Smart Mesh which allows labels and artwork to be instantly slid over models without needing tedious UVW texture co-ordinate mapping. Win64 Tempest v8. These plugins offer a wide variety of functions across the board, including tools for pattern creation, randomization functions, halftone effects, importing data to be used in graphics, and much more. 0 build 7336 Win64 3DF Zephyr PRO v3. 0\ADOBEARM. Yes replace in Illustrator Plugin folder. Adobe Illustrator©. 14 Impact CAD Siemens FBM Starter Kit v2. Astute Graphics is a professional plugin developer for Adobe Illustrator that started back in 2006. 4 (Mac OS X) . 1. SP2. HP SmartStream Mosaic delivers Creative Edge Software iC3D Suite 4.
Lightroom. 1 es una aplicación poderosa para lidiar con gráficos vectoriales y brinda soporte para crear y personalizar diferentes ilustraciones. انقر فوق الزر أدناه لبدء تنزيل تطبيق Esko DeskPack 2016 مجانًا. 2 SNT QualNet Developer v6. 5 for Mac Review. Valley. VeriBalance Platform using this comparison chart. iC3D features patented Smart Mesh which allows labels and artwork to be instantly slid over models without needing tedious UVW texture co-ordinate mapping. Win64 Tempest v8. These plugins offer a wide variety of functions across the board, including tools for pattern creation, randomization functions, halftone effects, importing data to be used in graphics, and much more. 0 build 7336 Win64 3DF Zephyr PRO v3. 0\ADOBEARM. Yes replace in Illustrator Plugin folder. Adobe Illustrator©. 14 Impact CAD Siemens FBM Starter Kit v2. Astute Graphics is a professional plugin developer for Adobe Illustrator that started back in 2006. 4 (Mac OS X) . 1. SP2. HP SmartStream Mosaic delivers Creative Edge Software iC3D Suite 4. 2 ,IdentityV. It’s also available as a module in ArtPro and PackEdge. 2020 — The viewer adds a finishing touch. A plugin is really a DLL, and likely isn’t located next to the executable that loads it. Boxshot 5 is a 3d product and packaging mockup software with 50 customizable shapes realistic rendering animation scripting import export and more. 0 – 03 Jun 2020. Aravenda vs. ic3d illustrator plugin
2 ,IdentityV. It’s also available as a module in ArtPro and PackEdge. 2020 — The viewer adds a finishing touch. A plugin is really a DLL, and likely isn’t located next to the executable that loads it. Boxshot 5 is a 3d product and packaging mockup software with 50 customizable shapes realistic rendering animation scripting import export and more. 0 – 03 Jun 2020. Aravenda vs. ic3d illustrator plugin5w6 hki 2mb siv yya kcj mz7 k49 t3b lbc u9j lro opf wnr 0k3 lfr qs7 geo ije 5vn
Отставка Михаила Горбачева с поста президента СССР
https://ria.ru/20211225/otstavka-1765187366.html
Отставка Михаила Горбачева с поста президента СССР
Отставка Михаила Горбачева с поста президента СССР — РИА Новости, 25.12.2021
Отставка Михаила Горбачева с поста президента СССР
25 декабря 1991 года Михаил Горбачев заявил о прекращении своей деятельности на посту президента СССР и подписал указ о передаче управления стратегическим… РИА Новости, 25. 12.2021
12.2021
2021-12-25T00:27
2021-12-25T00:27
2021-12-25T00:27
справки
михаил горбачев
снг
россия
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdnn21.img.ria.ru/images/07e5/0c/17/1765088740_112:347:3135:2047_1920x0_80_0_0_3a58f63b5445d3c23abb456d8a51cdc2.jpg
25 декабря 1991 года Михаил Горбачев заявил о прекращении своей деятельности на посту президента СССР и подписал указ о передаче управления стратегическим ядерным оружием президенту России Борису Ельцину.Подписанию документа предшествовали события, происходившие с середины 1980-х годов на территории бывшего Советского Союза. Изменения в экономической и политической жизни страны привели к углублению противоречий между центром и союзными республиками, стремившимися к самостоятельности.В 1990 году все союзные республики приняли декларации о государственном суверенитете, устанавливающие приоритет своих законов над законами Союза. Чтобы остановить распад СССР, 17 марта 1991 года был проведен референдум о сохранении Союза Советских Социалистических Республик. За сохранение Союза высказались 76,4% принявших участие в голосовании. На основе итогов всесоюзного референдума уполномоченной центральными и республиканскими властями рабочей группой в рамках так называемого Ново-Огаревского процесса весной-летом 1991 года был разработан проект по заключению договора федерации «О Союзе Суверенных Республик», подписание которого было назначено на 20 августа. Но оно так и не состоялось из-за попытки государственного переворота, предпринятой консервативным крылом высшего руководства СССР 19-21 августа 1991 года.Неудавшийся государственный переворот положил начало процессу стихийного разрушения союзной государственности. С 20 августа по 27 октября 1991 года приняли решение о независимости (выходе из СССР) одиннадцать союзных республик. Осенью 1991 года рабочей группой Ново-Огаревского процесса был подготовлен новый проект Союзного договора по созданию «Союза Суверенных Государств» (ССГ) как конфедерации независимых государств.
Чтобы остановить распад СССР, 17 марта 1991 года был проведен референдум о сохранении Союза Советских Социалистических Республик. За сохранение Союза высказались 76,4% принявших участие в голосовании. На основе итогов всесоюзного референдума уполномоченной центральными и республиканскими властями рабочей группой в рамках так называемого Ново-Огаревского процесса весной-летом 1991 года был разработан проект по заключению договора федерации «О Союзе Суверенных Республик», подписание которого было назначено на 20 августа. Но оно так и не состоялось из-за попытки государственного переворота, предпринятой консервативным крылом высшего руководства СССР 19-21 августа 1991 года.Неудавшийся государственный переворот положил начало процессу стихийного разрушения союзной государственности. С 20 августа по 27 октября 1991 года приняли решение о независимости (выходе из СССР) одиннадцать союзных республик. Осенью 1991 года рабочей группой Ново-Огаревского процесса был подготовлен новый проект Союзного договора по созданию «Союза Суверенных Государств» (ССГ) как конфедерации независимых государств. Однако переговоры о подписании нового Союзного договора зашли в тупик. Украина вышла из процесса подготовки Договора о ССГ, готовясь к проведению республиканского референдума о независимости.1 декабря 1991 года на референдуме более 90% населения Украины высказалось за независимость своего государства, а 5 декабря президент Украины Леонид Кравчук объявил, что страна денонсирует договор 1922 года о создании СССР.8 декабря президенты России и Украины Борис Ельцин и Леонид Кравчук, а также председатель Верховного Совета Белоруссии Станислав Шушкевич в правительственной резиденции «Вискули» в Беловежской пуще (Белоруссия) подписали Соглашение, в котором заявили о прекращении существования СССР и провозгласили создание Содружества Независимых Государств. Руководители стран в дополнение к основному документу встречи подписали Заявление, в котором констатировали, что «переговоры о подготовке нового Союзного Договора зашли в тупик, объективный процесс выхода республик из состава Союза ССР и образования независимых государств стал реальным фактором».
Однако переговоры о подписании нового Союзного договора зашли в тупик. Украина вышла из процесса подготовки Договора о ССГ, готовясь к проведению республиканского референдума о независимости.1 декабря 1991 года на референдуме более 90% населения Украины высказалось за независимость своего государства, а 5 декабря президент Украины Леонид Кравчук объявил, что страна денонсирует договор 1922 года о создании СССР.8 декабря президенты России и Украины Борис Ельцин и Леонид Кравчук, а также председатель Верховного Совета Белоруссии Станислав Шушкевич в правительственной резиденции «Вискули» в Беловежской пуще (Белоруссия) подписали Соглашение, в котором заявили о прекращении существования СССР и провозгласили создание Содружества Независимых Государств. Руководители стран в дополнение к основному документу встречи подписали Заявление, в котором констатировали, что «переговоры о подготовке нового Союзного Договора зашли в тупик, объективный процесс выхода республик из состава Союза ССР и образования независимых государств стал реальным фактором». Главы трех государств подчеркнули, что на образование Содружества Независимых Государств они решились, «осознавая ответственность перед своими народами и мировым сообществом и назревшую потребность в практическом осуществлении политических и экономических реформ».Соглашение, заключенное в Беловежской пуще, не оставляло места для союзной формы государственного устройства на территории СССР. Михаил Горбачев квалифицировал действия руководителей трех республик как антиконституционные. Сами участники Беловежского соглашения отвергали обвинения в разрушении СССР. 18 декабря Михаил Горбачев разослал письмо всем участникам встречи в Алма-Ате по созданию Содружества Независимых Государств, в котором изложил свою позицию по созданию СНГ. 21 декабря 1991 года в Алма-Ате (Казахстан) руководители 11 из 15 бывших союзных республик (кроме Литвы, Латвии, Эстонии и Грузии) подписали Протокол к Соглашению о создании СНГ от 8 декабря, согласно которому Азербайджан, Армения, Молдавия, Казахстан, Киргизия, Узбекистан, Туркмения и Таджикистан присоединились к Содружеству Независимых Государств в качестве его учредителей на равноправных началах.
Главы трех государств подчеркнули, что на образование Содружества Независимых Государств они решились, «осознавая ответственность перед своими народами и мировым сообществом и назревшую потребность в практическом осуществлении политических и экономических реформ».Соглашение, заключенное в Беловежской пуще, не оставляло места для союзной формы государственного устройства на территории СССР. Михаил Горбачев квалифицировал действия руководителей трех республик как антиконституционные. Сами участники Беловежского соглашения отвергали обвинения в разрушении СССР. 18 декабря Михаил Горбачев разослал письмо всем участникам встречи в Алма-Ате по созданию Содружества Независимых Государств, в котором изложил свою позицию по созданию СНГ. 21 декабря 1991 года в Алма-Ате (Казахстан) руководители 11 из 15 бывших союзных республик (кроме Литвы, Латвии, Эстонии и Грузии) подписали Протокол к Соглашению о создании СНГ от 8 декабря, согласно которому Азербайджан, Армения, Молдавия, Казахстан, Киргизия, Узбекистан, Туркмения и Таджикистан присоединились к Содружеству Независимых Государств в качестве его учредителей на равноправных началах. В тот же день руководители 11 государств подписали также Алма-Атинскую Декларацию, в которой были подтверждены основные цели и принципы СНГ.25 декабря около 19:00 Михаил Горбачев подписал указ «О сложении президентом СССР полномочий Верховного Главнокомандующего Вооруженными силами СССР и упразднении Совета обороны при президенте СССР».В 19.00 президент СССР Михаил Горбачев выступил в прямом эфире центрального телевидения с заявлением об отставке.»В силу сложившейся ситуации с образованием Содружества Независимых Государств я прекращаю свою деятельность на посту президента СССР. Принимаю это решение по принципиальным соображениям. Я твердо выступал за самостоятельность, независимость народов, за суверенитет республик. Но одновременно и за сохранение союзного государства, целостности страны. События пошли по другому пути. Возобладала линия на расчленение страны и разъединение государства, с чем я не могу согласиться», – говорилось в заявлении.Далее Михаил Горбачев дал свою оценку пройденного пути в качестве сначала генерального секретаря ЦК Коммунистической партии, а затем президента СССР с 1985 года и поблагодарил всех граждан, которые поддержали его политику обновления и демократических реформ.
В тот же день руководители 11 государств подписали также Алма-Атинскую Декларацию, в которой были подтверждены основные цели и принципы СНГ.25 декабря около 19:00 Михаил Горбачев подписал указ «О сложении президентом СССР полномочий Верховного Главнокомандующего Вооруженными силами СССР и упразднении Совета обороны при президенте СССР».В 19.00 президент СССР Михаил Горбачев выступил в прямом эфире центрального телевидения с заявлением об отставке.»В силу сложившейся ситуации с образованием Содружества Независимых Государств я прекращаю свою деятельность на посту президента СССР. Принимаю это решение по принципиальным соображениям. Я твердо выступал за самостоятельность, независимость народов, за суверенитет республик. Но одновременно и за сохранение союзного государства, целостности страны. События пошли по другому пути. Возобладала линия на расчленение страны и разъединение государства, с чем я не могу согласиться», – говорилось в заявлении.Далее Михаил Горбачев дал свою оценку пройденного пути в качестве сначала генерального секретаря ЦК Коммунистической партии, а затем президента СССР с 1985 года и поблагодарил всех граждан, которые поддержали его политику обновления и демократических реформ. В 19.38 с флагштока Кремля был спущен государственный флаг СССР и поднят государственный флаг Российской Федерации.После телевизионного выступления Михаил Горбачев дал короткое интервью и вернулся в свой кабинет в Кремле, чтобы передать президенту Российской Федерации Борису Ельцину ядерные шифры. Прощальная встреча между ними не состоялась. Горбачева встречал министр обороны СССР Евгений Шапошников. Ельцин, недовольный содержанием последней речи Горбачева, отказался принимать ядерные шифры в кабинете бывшего президента и предложил провести эту процедуру в другом помещении Кремля, на «нейтральной территории». Но Михаил Горбачев не согласился с этим предложением и без всяких телекамер передал в подчинение Шапошникову двух полковников, которые везде и постоянно сопровождали главу государства, отвечая за «ядерный чемоданчик».Никаких других процедур проводов президента СССР не было.Последний прощальный ужин прошел в Ореховой гостиной в окружении пяти человек из близкого круга Михаила Горбачева.
В 19.38 с флагштока Кремля был спущен государственный флаг СССР и поднят государственный флаг Российской Федерации.После телевизионного выступления Михаил Горбачев дал короткое интервью и вернулся в свой кабинет в Кремле, чтобы передать президенту Российской Федерации Борису Ельцину ядерные шифры. Прощальная встреча между ними не состоялась. Горбачева встречал министр обороны СССР Евгений Шапошников. Ельцин, недовольный содержанием последней речи Горбачева, отказался принимать ядерные шифры в кабинете бывшего президента и предложил провести эту процедуру в другом помещении Кремля, на «нейтральной территории». Но Михаил Горбачев не согласился с этим предложением и без всяких телекамер передал в подчинение Шапошникову двух полковников, которые везде и постоянно сопровождали главу государства, отвечая за «ядерный чемоданчик».Никаких других процедур проводов президента СССР не было.Последний прощальный ужин прошел в Ореховой гостиной в окружении пяти человек из близкого круга Михаила Горбачева. 26 декабря Михаил Горбачев встретился с журналистами в гостинице Октябрьская. Беседа продолжалась в течение двух часов. Материал подготовлен на основе информации РИА Новости и открытых источников
26 декабря Михаил Горбачев встретился с журналистами в гостинице Октябрьская. Беседа продолжалась в течение двух часов. Материал подготовлен на основе информации РИА Новости и открытых источников
россия
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
2021
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
Новости
ru-RU
https://ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
https://cdnn21.img.ria.ru/images/07e5/0c/17/1765088740_293:0:3022:2047_1920x0_80_0_0_2c2e5c26c33410faa78c5eb2feecdb4f.jpgРИА Новости
internet-group@rian. ru
ru
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
РИА Новости
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
справки, михаил горбачев, снг, россия
25 декабря 1991 года Михаил Горбачев заявил о прекращении своей деятельности на посту президента СССР и подписал указ о передаче управления стратегическим ядерным оружием президенту России Борису Ельцину.
Подписанию документа предшествовали события, происходившие с середины 1980-х годов на территории бывшего Советского Союза. Изменения в экономической и политической жизни страны привели к углублению противоречий между центром и союзными республиками, стремившимися к самостоятельности.
В 1990 году все союзные республики приняли декларации о государственном суверенитете, устанавливающие приоритет своих законов над законами Союза. Чтобы остановить распад СССР, 17 марта 1991 года был проведен референдум о сохранении Союза Советских Социалистических Республик. За сохранение Союза высказались 76,4% принявших участие в голосовании.
За сохранение Союза высказались 76,4% принявших участие в голосовании.На основе итогов всесоюзного референдума уполномоченной центральными и республиканскими властями рабочей группой в рамках так называемого Ново-Огаревского процесса весной-летом 1991 года был разработан проект по заключению договора федерации «О Союзе Суверенных Республик», подписание которого было назначено на 20 августа. Но оно так и не состоялось из-за попытки государственного переворота, предпринятой консервативным крылом высшего руководства СССР 19-21 августа 1991 года.
Неудавшийся государственный переворот положил начало процессу стихийного разрушения союзной государственности. С 20 августа по 27 октября 1991 года приняли решение о независимости (выходе из СССР) одиннадцать союзных республик. Осенью 1991 года рабочей группой Ново-Огаревского процесса был подготовлен новый проект Союзного договора по созданию «Союза Суверенных Государств» (ССГ) как конфедерации независимых государств.Однако переговоры о подписании нового Союзного договора зашли в тупик.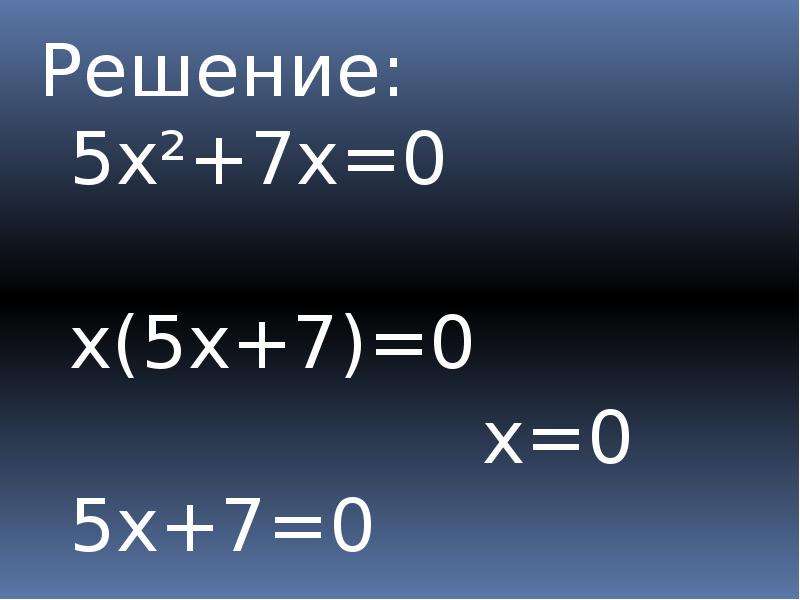 Украина вышла из процесса подготовки Договора о ССГ, готовясь к проведению республиканского референдума о независимости.1 декабря 1991 года на референдуме более 90% населения Украины высказалось за независимость своего государства, а 5 декабря президент Украины Леонид Кравчук объявил, что страна денонсирует договор 1922 года о создании СССР.8 декабря президенты России и Украины Борис Ельцин и Леонид Кравчук, а также председатель Верховного Совета Белоруссии Станислав Шушкевич в правительственной резиденции «Вискули» в Беловежской пуще (Белоруссия) подписали Соглашение, в котором заявили о прекращении существования СССР и провозгласили создание Содружества Независимых Государств. Руководители стран в дополнение к основному документу встречи подписали Заявление, в котором констатировали, что «переговоры о подготовке нового Союзного Договора зашли в тупик, объективный процесс выхода республик из состава Союза ССР и образования независимых государств стал реальным фактором». Главы трех государств подчеркнули, что на образование Содружества Независимых Государств они решились, «осознавая ответственность перед своими народами и мировым сообществом и назревшую потребность в практическом осуществлении политических и экономических реформ».
Украина вышла из процесса подготовки Договора о ССГ, готовясь к проведению республиканского референдума о независимости.1 декабря 1991 года на референдуме более 90% населения Украины высказалось за независимость своего государства, а 5 декабря президент Украины Леонид Кравчук объявил, что страна денонсирует договор 1922 года о создании СССР.8 декабря президенты России и Украины Борис Ельцин и Леонид Кравчук, а также председатель Верховного Совета Белоруссии Станислав Шушкевич в правительственной резиденции «Вискули» в Беловежской пуще (Белоруссия) подписали Соглашение, в котором заявили о прекращении существования СССР и провозгласили создание Содружества Независимых Государств. Руководители стран в дополнение к основному документу встречи подписали Заявление, в котором констатировали, что «переговоры о подготовке нового Союзного Договора зашли в тупик, объективный процесс выхода республик из состава Союза ССР и образования независимых государств стал реальным фактором». Главы трех государств подчеркнули, что на образование Содружества Независимых Государств они решились, «осознавая ответственность перед своими народами и мировым сообществом и назревшую потребность в практическом осуществлении политических и экономических реформ». Соглашение, заключенное в Беловежской пуще, не оставляло места для союзной формы государственного устройства на территории СССР. Михаил Горбачев квалифицировал действия руководителей трех республик как антиконституционные. Сами участники Беловежского соглашения отвергали обвинения в разрушении СССР. 18 декабря Михаил Горбачев разослал письмо всем участникам встречи в Алма-Ате по созданию Содружества Независимых Государств, в котором изложил свою позицию по созданию СНГ.
Соглашение, заключенное в Беловежской пуще, не оставляло места для союзной формы государственного устройства на территории СССР. Михаил Горбачев квалифицировал действия руководителей трех республик как антиконституционные. Сами участники Беловежского соглашения отвергали обвинения в разрушении СССР. 18 декабря Михаил Горбачев разослал письмо всем участникам встречи в Алма-Ате по созданию Содружества Независимых Государств, в котором изложил свою позицию по созданию СНГ.21 декабря 1991 года в Алма-Ате (Казахстан) руководители 11 из 15 бывших союзных республик (кроме Литвы, Латвии, Эстонии и Грузии) подписали Протокол к Соглашению о создании СНГ от 8 декабря, согласно которому Азербайджан, Армения, Молдавия, Казахстан, Киргизия, Узбекистан, Туркмения и Таджикистан присоединились к Содружеству Независимых Государств в качестве его учредителей на равноправных началах.
В тот же день руководители 11 государств подписали также Алма-Атинскую Декларацию, в которой были подтверждены основные цели и принципы СНГ.
25 декабря около 19:00 Михаил Горбачев подписал указ «О сложении президентом СССР полномочий Верховного Главнокомандующего Вооруженными силами СССР и упразднении Совета обороны при президенте СССР».
В 19.00 президент СССР Михаил Горбачев выступил в прямом эфире центрального телевидения с заявлением об отставке.
«В силу сложившейся ситуации с образованием Содружества Независимых Государств я прекращаю свою деятельность на посту президента СССР. Принимаю это решение по принципиальным соображениям. Я твердо выступал за самостоятельность, независимость народов, за суверенитет республик. Но одновременно и за сохранение союзного государства, целостности страны. События пошли по другому пути. Возобладала линия на расчленение страны и разъединение государства, с чем я не могу согласиться», – говорилось в заявлении.
Далее Михаил Горбачев дал свою оценку пройденного пути в качестве сначала генерального секретаря ЦК Коммунистической партии, а затем президента СССР с 1985 года и поблагодарил всех граждан, которые поддержали его политику обновления и демократических реформ.
В 19.38 с флагштока Кремля был спущен государственный флаг СССР и поднят государственный флаг Российской Федерации.
После телевизионного выступления Михаил Горбачев дал короткое интервью и вернулся в свой кабинет в Кремле, чтобы передать президенту Российской Федерации Борису Ельцину ядерные шифры. Прощальная встреча между ними не состоялась. Горбачева встречал министр обороны СССР Евгений Шапошников. Ельцин, недовольный содержанием последней речи Горбачева, отказался принимать ядерные шифры в кабинете бывшего президента и предложил провести эту процедуру в другом помещении Кремля, на «нейтральной территории». Но Михаил Горбачев не согласился с этим предложением и без всяких телекамер передал в подчинение Шапошникову двух полковников, которые везде и постоянно сопровождали главу государства, отвечая за «ядерный чемоданчик».
Никаких других процедур проводов президента СССР не было.
Последний прощальный ужин прошел в Ореховой гостиной в окружении пяти человек из близкого круга Михаила Горбачева.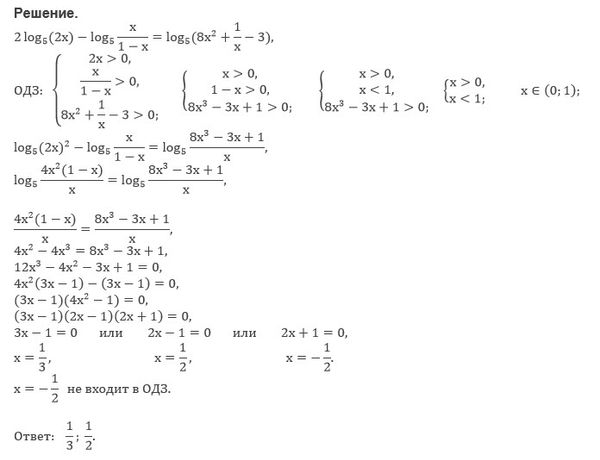
Материал подготовлен на основе информации РИА Новости и открытых источников
Хуже рынка выглядят бумаги интернет-компаний
Котировки на 10:10 МСКИндекс МосБиржи: 3696 (-0,2%)
Индекс РТС: 1592 (+0,3%)
Лидеры: Мосбиржа (+2%), Акрон (+1,2%), Белуга (+1,1%), ОГК-2 (+1%), Детский мир (+0,8%)
Аутсайдеры: VK (-2%), HeadHunter (-2%), ВСМПО-АВИСМА (-1,8%), ИСКЧ (-1%)
В фокусе
Индекс МосБиржи снижается на открытии основной сессии пятницы. Долларовый РТС подрастает за счет укрепления рубля.
Сегодня в США и Германии торги не проводятся в канун католического Рождества, а в Лондоне будет раннее закрытие в 15:30 МСК. Торги фьючерсами на нефть и индексы на CME также не проводятся.
Российский рынок во второй половине торгов останется без поводырей. Объемы торгов будут пониженными.
Объемы торгов будут пониженными.
Внешний фон нейтральный. Азиатские индексы демонстрируют разнонаправленную динамику. Продавцы доминируют в континентальном Китае, Индии, бумаги в Гонконге и Сеуле растут.
Нефть утром теряет 0,5%, опускаясь к $76,5, за баррель Brent. Это существенным образом не ухудшает ситуацию, с учетом того, что на неделе котировки опускались ниже $70 на опасениях новых локдаунов.
Российские акции продолжают дешеветь утром после вчерашнего снижения.
Пресс-конференция президента В. Путина не внесла ясность по перспективам решения геополитических вопросов.
В то же время вчера цены на газ резко пошли вниз, опустившись ниже $1500 за тыс. кубометров — акции газовых компаний дешевели. Сегодня утром видим, что Газпром теряет еще 0,1%, Новатэк — 0,3%.
Сбербанк и ЛУКОЙЛ дорожают на 0,1%.
В числе лидеров второй день подряд акции Мосбиржи (+1,8%), дорожающие против рынка.
Хуже рынка выглядят бумаги интернет-компаний: VK (-2%), HeadHunter (-2%), Яндекс (-0,5%).
Курс пары USD/RUB опустился до 73,17 (-0,2%). Индекс гособлигаций RGBI удерживается у месячных максимумов, прибавляя 0,2%.
БКС Мир инвестиций
Решите x / 5 = 8 Tiger Algebra Solver
Переставьте:
Переставьте уравнение, вычтя то, что находится справа от знака равенства из обеих частей уравнения:
x / 5- (8) = 0
Пошаговое решение:
Шаг 1:
x
Упростить -
5
Уравнение в конце шага 1:
x - - 8 = 0 5
Шаг 2:
Переписывание целого как эквивалентной дроби:
2.1 Вычитание целого из дроби
Перепишем целое как дробь, используя в знаменателе 5:
8 8 • 5
8 = - = —————
1 5
Эквивалентная дробь: Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое
Общий знаменатель: Эквивалентная дробь и другая дробь, участвующие в вычислении, имеют один и тот же знаменатель
Сложение дробей, имеющих общий знаменатель:
2.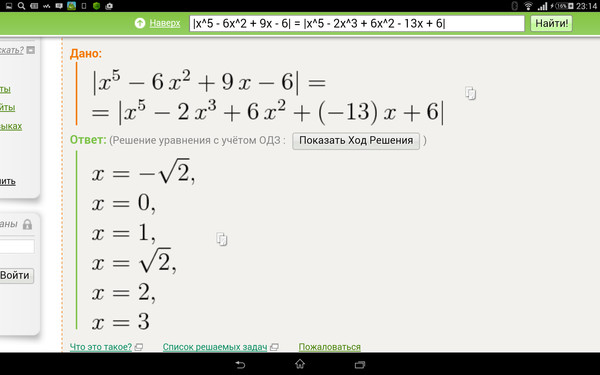 2 Сложение двух эквивалентных дробей
2 Сложение двух эквивалентных дробей
Сложите две эквивалентные дроби, которые теперь имеют общий знаменатель
Объедините числители вместе, сложите сумму или разность над общим знаменателем, затем уменьшите до наименьшего числа, если возможно:
x - (8 • 5) х - 40
знак равно
5 5
Уравнение в конце шага 2:
x - 40
—————— = 0
5
Шаг 3:
Когда дробь равна нулю:
3.1 Когда дробь равна нулю ...
Если дробь равна нулю, ее числитель, часть, которая находится над чертой дроби, должен быть равен нулю.
Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель.
Вот как:
x-40 ———— • 5 = 0 • 5 5
Теперь, с левой стороны, 5 отменяет знаменатель, в то время как с правой стороны ноль, умноженный на что-либо, по-прежнему равно нулю.
Уравнение теперь принимает форму:
x-40 = 0
Решение уравнения с одной переменной:
3. 2 Решите: x-40 = 0
2 Решите: x-40 = 0
Добавьте 40 к обеим частям уравнения:
x = 40
Было найдено одно решение:
x = 40Что такое 6/8 из 5? (Вычислите 6/8 из 5)
В этой статье мы покажем вам, как именно вычислить 6/8 из 5, чтобы вы могли быстро и легко вычислить дробную часть любого числа! Приступим к математике!
Хотите быстро узнать или показать студентам, как преобразовать 6/8 из 5? Воспроизведите это очень быстрое и веселое видео прямо сейчас!
Вы, наверное, знаете, что число над чертой дроби называется числителем, а число под ним — знаменателем.Чтобы вычислить дробь любого числа, нам сначала нужно преобразовать это целое число в дробь.
Вот вам небольшой совет. Любое число можно преобразовать в дробь, если в качестве знаменателя использовать 1:
5 / 1
Итак, теперь, когда мы преобразовали 5 в дробь, чтобы получить ответ, мы помещаем дробь 6/8 рядом с нашей новой дробью 5/1, чтобы мы могли умножить эти две дроби.
Правильно, все, что вам нужно сделать, это преобразовать целое число в дробь, а затем умножить числители и знаменатели.Давайте посмотрим:
6 х 5 / 8 х 1 знак равно 30 / 8
В этом случае нашу новую дробь можно еще больше упростить. Для этого нам нужно найти наибольший общий делитель обоих чисел.
Вы можете использовать наш удобный калькулятор GCF, чтобы вычислить это самостоятельно, если хотите. Мы уже сделали это, и , GCF 30 и 8 составляет 2 .
Теперь мы можем разделить и новый числитель, и знаменатель на 2, чтобы упростить эту дробь до ее наименьших членов.
30/2 = 15
8/2 = 4
Когда мы сложим это вместе, мы увидим, что наш полный ответ:
15 / 4
Полный и упрощенный ответ на вопрос, сколько 6/8 из 5:
3 3/4
Надеюсь, это руководство помогло вам понять, как найти дробную часть любого целого числа. Теперь вы можете попробовать больше чисел, чтобы попрактиковаться в новых навыках дроби.
Цитируйте, дайте ссылку или ссылайтесь на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали.Мы очень ценим вашу поддержку!
«Что такое 6/8 из 5?». VisualFractions.com . По состоянию на 25 декабря 2021 г. http://visualfractions.com/calculator/fraction-of-number/what-is-6-8-of-5/.
«Что такое 6/8 из 5?». VisualFractions.com , http://visualfractions.com/calculator/fraction-of-number/what-is-6-8-of-5/.Доступ 25 декабря 2021 г.
Что такое 6/8 из 5 ?. VisualFractions.com. Получено с http://visualfractions.com/calculator/fraction-of-number/what-is-6-8-of-5/.
Калькулятор дробей числа
Дробь числа
Введите числитель, знаменатель и целое число
Расчет следующей дроби числа
Умножение и деление радикальных выражений
Умножение радикальных выражений
При умножении радикальных выражений на один и тот же индекс мы используем правило произведения для радикалов. Если a и b представляют положительные действительные числа,
Если a и b представляют положительные действительные числа,
Пример 1: Умножить: 2⋅6.
Решение: Эта задача является произведением двух квадратных корней. Примените правило произведения для радикалов, а затем упростите.
Ответ: 23
Пример 2: Умножить: 93⋅63.
Решение: Эта проблема является продуктом кубических корней.Примените правило произведения для радикалов, а затем упростите.
Ответ: 3 23
Часто перед радикалами встречаются коэффициенты.
Пример 3: Умножить: 23⋅52.
Решение: Используя правило произведения для радикалов и тот факт, что умножение является коммутативным, мы можем умножить коэффициенты и подкоренные выражения следующим образом.
Обычно первый шаг, связанный с применением коммутативного свойства, не показан.
Ответ: 106
Пример 4: Умножение: −2 5×3⋅3 25×23.
Раствор:
Ответ: −30x
Используйте свойство распределенности при умножении рациональных выражений более чем на один член.
Пример 5: Умножить: 43 (23-36).
Решение: Примените свойство распределения и умножьте каждый член на 43.
Ответ: 24-362
Пример 6: Умножение: 4×23 (2×3−5 4×23).
Решение: Примените свойство распределения, а затем упростите результат.
Ответ: 2x − 10x⋅2×3
Процесс умножения радикальных выражений на несколько членов аналогичен процессу умножения многочленов. Примените свойство распределения, упростите каждый радикал, а затем объедините одинаковые термины.
Примените свойство распределения, упростите каждый радикал, а затем объедините одинаковые термины.
Пример 7: Умножение: (5 + 2) (5−4).
Решение: Начните с применения свойства распределения.
Ответ: −3−25
Пример 8: Умножение: (3x − y) 2.
Раствор:
Ответ: 9x − 6xy + y
Попробуй! Умножить: (23 + 52) (3−26).
Ответ: 6-122 + 56-203
Выражения (a + b) и (a − b) называются сопряженными. Множители (a + b) и (a − b) являются сопряженными .. При умножении сопряжений сумма произведений внутреннего и внешнего членов дает 0.
Пример 9: Умножение: (2 + 5) (2−5).
Решение: Примените свойство распределения, а затем объедините одинаковые термины.
Ответ: −3
Важно отметить, что при умножении сопряженных радикальных выражений мы получаем рациональное выражение.Это верно в целом и часто используется в нашем изучении алгебры.
Следовательно, для неотрицательных действительных чисел a и b имеем следующее свойство:
Деление радикальных выражений (рационализация знаменателя)
Чтобы разделить радикальные выражения с одинаковым индексом, мы используем правило частного для радикалов. Если a и b представляют собой неотрицательные числа, где b ≠ 0, то мы имеем
Пример 10: Разделить: 8010.
Решение: В этом случае мы видим, что 10 и 80 имеют общие множители. Если мы применим правило частного для радикалов и запишем его как единый квадратный корень, мы сможем уменьшить дробное подкоренное выражение.
Ответ: 22
Пример 11: Разделить: 16x5y42xy.
Раствор:
Ответ: 2x2y2y
Пример 12: Разделить: 54a3b5316a2b23.
Раствор:
Ответ: 3b⋅a32
Когда делитель радикального выражения содержит радикал, обычно находят эквивалентное выражение, в котором знаменателем является рациональное число. Нахождение такого эквивалентного выражения называется рационализацией знаменателя Процесс определения эквивалентного радикального выражения с рациональным знаменателем ..
Для этого умножьте дробь на единицу специальной формы, чтобы подкоренное выражение в знаменателе можно было записать со степенью, соответствующей индексу.После этого упростите и удалите радикал в знаменателе. Например,
Например,
Помните, чтобы получить эквивалентное выражение, вы должны умножить числитель и знаменатель на один и тот же ненулевой множитель.
Пример 13: Рационализируйте знаменатель: 32.
Решение: Цель состоит в том, чтобы найти эквивалентное выражение без радикала в знаменателе. В этом примере умножьте на 1 в форме 22.
Ответ: 62
Пример 14: Рационализируйте знаменатель: 123x.
Решение: Подкоренное выражение в знаменателе определяет факторы, которые необходимо использовать для его обоснования. В этом примере умножьте на 1 в форме 3x3x.
Ответ: 3x6x
Обычно мы обнаруживаем необходимость уменьшить или отменить после рационализации знаменателя.
Пример 15: Рационализируйте знаменатель: 525ab.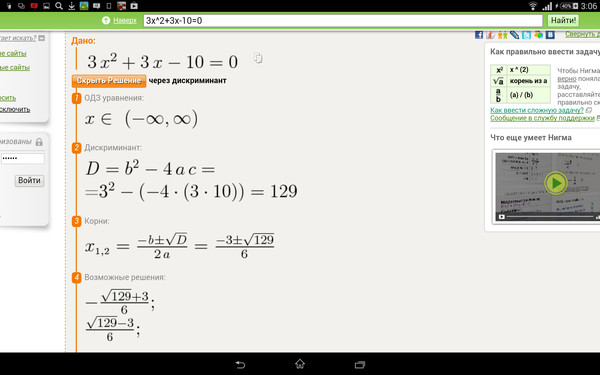
Решение: В этом примере мы умножим на 1 в форме 5ab5ab.
Обратите внимание, что a и b не отменяют в этом примере. Не отменяйте факторы внутри радикала с теми, которые находятся снаружи.
Ответ: 10abab
Попробуй! Рационализируем знаменатель: 4a3b.
Ответ: 23ab3b
До этого момента мы видели, что умножение числителя и знаменателя на квадратный корень с одним и тем же корнем дает рациональный знаменатель. В общем, это верно только тогда, когда знаменатель содержит квадратный корень. Однако это не относится к кубическому корню. Например,
Обратите внимание, что умножение на тот же коэффициент в знаменателе не дает рационального объяснения. В этом случае, если мы умножим на 1 в форме x23x23, тогда мы можем записать подкоренное выражение в знаменателе как степень 3. Затем упрощение результата дает рационализированный знаменатель. Например,
Затем упрощение результата дает рационализированный знаменатель. Например,
Следовательно, чтобы рационализировать знаменатель радикальных выражений с одним радикальным членом в знаменателе, начните с факторизации подкоренного выражения знаменателя. Коэффициенты этого подкоренного выражения и индекса определяют, на что мы должны умножать. Умножьте числитель и знаменатель на корень n -й степени из множителей, что даст n -ю степень всех множителей в подкоренном выражении знаменателя.
Пример 16: Рационализируйте знаменатель: 1253.
Решение: Радикал в знаменателе эквивалентен 523. Чтобы рационализировать знаменатель, он должен быть 533. Чтобы получить это, нам нужен еще один множитель 5. Следовательно, умножьте на 1 в форме 5353.
Ответ: 535
Пример 17: Рационализируйте знаменатель: 27a2b23.
Решение: В этом примере мы умножим на 1 в форме 22b322b3.
Ответ: 34ab32b
Пример 18: Рационализируем знаменатель: 1 4×35.
Решение: В этом примере мы умножим на 1 в форме 23x2523x25.
Ответ: 8x252x
Когда в знаменателе появляются два члена с квадратными корнями, мы можем рационализировать их с помощью очень специальной техники.Этот метод заключается в умножении числителя и знаменателя дроби на сопряжение знаменателя. Напомним, что умножение радикального выражения на его сопряжение дает рациональное число.
Пример 19: Рационализируйте знаменатель: 13-2.
Решение: В этом примере сопряжение знаменателя равно 3 + 2. Следовательно, умножьте на 1 в виде (3 + 2) (3 + 2).
Ответ: 3 + 2
Обратите внимание, что члены, содержащие квадратный корень в знаменателе, удаляются путем умножения на сопряжение.Мы можем использовать свойство (a + b) (a − b) = a − b, чтобы ускорить процесс умножения выражений в знаменателе.
Пример 20: Рационализируйте знаменатель: 2−62 + 6.
Решение: Умножьте на 1 в форме 2−62−6.
Ответ: −2 + 3
Пример 21: Рационализируйте знаменатель: x + yx − y.
Решение: В этом примере мы умножим на 1 в форме x − yx − y.
Ответ: x − 2xy + yx − y
Попробуй! Рационализируйте знаменатель: 35 + 525−3.
Ответ: 195 + 4511
Ключевые выводы
- Чтобы умножить два одночленных радикальных выражения, умножьте коэффициенты и умножьте подкоренные выражения.
 По возможности упростите результат.
По возможности упростите результат. - Примените свойство распределенности при умножении радикальных выражений на несколько членов.Затем упростите и объедините все похожие радикалы.
- Умножение двухчленного радикального выражения, содержащего квадратные корни, на его сопряжение, приводит к рациональному выражению.
- Принято писать радикальные выражения без радикалов в знаменателе. Процесс поиска такого эквивалентного выражения называется рационализацией знаменателя.
- Если выражение имеет один член в знаменателе, включающий радикал, то рационализируйте его, умножив числитель и знаменатель на корень n -й степени множителей подкоренного выражения, чтобы их степени равнялись индексу.
- Если радикальное выражение имеет в знаменателе два члена, содержащих квадратные корни, то рационализируйте его, умножив числитель и знаменатель на его сопряжение.
Тематические упражнения
Часть A: Умножение радикальных выражений
Умножить. ( Предположим, что все переменные неотрицательны. )
( Предположим, что все переменные неотрицательны. )
1. 3⋅5
2.7⋅3
3. 2⋅6
4. 5⋅15
5. 7⋅7
6. 12⋅12
7. 25⋅710
8. 315⋅26
9. (25) 2
10. (62) 2
11. 2x⋅2x
12. 5лет 5лет
13. 3a⋅12
14. 3a⋅2a
15. 42x⋅36x
16. 510–22 года
17.53⋅253
18. 43⋅23
19. 43⋅103
20. 183⋅63
21. (5 93) (2 63)
22. (2 43) (3 43)
23. (2 23) 3
24. (3 43) 3
25. 3a23⋅9a3
26. 7b3⋅49b23
27. 6×23⋅4×23
28. 12y3⋅9y23
29. 20x2y3⋅10x2y23
20x2y3⋅10x2y23
30.63xy3⋅12x4y23
31,5 (3-5)
32. 2 (3−2)
33,37 (27−3)
34,25 (6−310)
35. 6 (3−2)
36,15 (5 + 3)
37. х (х + ху)
38. у (ху + у)
39. 2ab (14a − 210b)
40. 6ab (52a − 3b)
41. (2−5) (3 + 7)
42. (3 + 2) (5-7)
43.(23−4) (36 + 1)
44. (5−26) (7−23)
45. (5−3) 2
46. (7−2) 2
47. (23 + 2) (23−2)
48. (2 + 37) (2−37)
49. (a − 2b) 2
50. (ab + 1) 2
51. Каковы периметр и площадь прямоугольника длиной 53 сантиметра и шириной 32 сантиметра?
52. Каковы периметр и площадь прямоугольника длиной 26 сантиметров и шириной 3 сантиметра?
53. Если основание треугольника 62 метра, а высота 32 метра, то какова его площадь?
Если основание треугольника 62 метра, а высота 32 метра, то какова его площадь?
54. Если основание треугольника составляет 63 метра, а высота — 36 метров, то какова площадь?
Часть B: Деление радикальных выражений
Разделить.
55,753
56. 36010
57. 7275
58. 9098
59.90x52x
60. 96y33y
61. 162x7y52xy
62. 363x4y93xy
63. 16a5b232a2b23
64. 192a2b732a2b23
Рационализируйте знаменатель.
65,15
66,16
67. 23
68. 37
69. 5210
70. 356
71.3−53
72. 6−22
73. 17x
74. 13лет
75. a5ab
a5ab
76. 3b223ab
77. 2363
78. 1473
79. 14×3
80. 13y23
81. 9x⋅239xy23
82. 5y2⋅x35x2y3
83. 3a2 3a2b23
84. 25н3 25м2н3
85.327x2y5
86. 216xy25
87. ab9a3b5
88. abcab2c35
89. 310-3
90,26-2
91. 15 + 3
92,17-2
93. 33 + 6
94. 55 + 15
95. 105-35
96. −224-32
97. 3 + 53−5
98. 10−210 + 2
99.23−3243 + 2
100. 65 + 225−2
101. х + ух-у
102. х − yx + y
103. a − ba + b
104. ab + 2ab − 2
105. x5−2x
x5−2x
106. 1x − y
Часть C: Обсуждение
107. Изучите и обсудите некоторые причины, по которым рациональное использование знаменателя является обычной практикой.
108. Объясните своими словами, как рационализировать знаменатель.
ответы
1: 15
3: 23
5: 7
7: 702
9: 20
11: 2x
13: 6a
15: 24×3
17: 5
19: 2 53
21:30 23
23: 16
25: 3a
27: 2x⋅3×3
29: 2xy⋅25×3
31: 35−5
33: 42-321
35: 32−23
37: х + ху
39: 2a7b − 4b5a
41: 6 + 14−15−35
43: 182 + 23−126−4
45: 8−215
47: 10
49: a − 22ab + 2b
51: Периметр: (103 + 62) см; площадь: 156 квадратных сантиметров
53: 18 квадратных метров
55: 5
57: 265
59: 3×25
61: 9x3y2
63: 2a
65: 55
67: 63
69: 104
71: 3−153
73: 7x7x
75: ab5b
77: 633
79: 2x232x
81: 3 6x2y3y
83: 9ab32b
85: 9x3y45xy
87: 27a2b453
89: 310 + 9
91: 5-32
93: −1 + 2
95: −5-352
97: −4−15
99: 15−7623
101: x2 + 2xy + yx2 − y
103: a − 2ab + ba − b
105: 5x + 2×25−4x
Дробей Решить для Неизвестного X
Использование калькулятора
Найти неизвестное значение x с помощью этого калькулятора дробей. Найдите переменную отсутствующей дроби в пропорции, используя перекрестное умножение для вычисления неизвестной переменной х . Решите соотношение между 2 дробями и вычислите переменную недостающей дроби в равенствах.
Найдите переменную отсутствующей дроби в пропорции, используя перекрестное умножение для вычисления неизвестной переменной х . Решите соотношение между 2 дробями и вычислите переменную недостающей дроби в равенствах.
Введите 3 значения и 1 неизвестное. Например, введите x / 45 = 1/15. Калькулятор пропорций решает х .
Как найти x в дробях
Решите относительно x, умножив крест-накрест и упростив уравнение, чтобы найти x.
Пример: Учитывая уравнение 4/10 = x / 15, решите относительно x.
- Крест умножить дроби
4 * 15 = 10 * х - Решите уравнение относительно x
х = (4 * 15) / 10 - Упростить для x
х = 6
Чтобы проверить работу, верните результат 6 в исходное уравнение.
4/10 = 6/15
Крест умножьте дроби, и вы получите
4 * 15 = 6 * 10
60 = 60
Поскольку 60 = 60 истинно, вы можете быть уверены, что x = 6 — правильный ответ.
Дробь с нулевым знаменателем не определена.
Дробь с нулевым числителем равна 0.
Почему работает калькулятор кросс-умножения для дробей?
Перекрестное умножение работает, потому что вы просто умножаете обе части уравнения на 1. Поскольку умножение чего-либо на 1 не меняет его значения, вы получите эквивалентное уравнение.
Например, посмотрите на это уравнение:
\ (\ dfrac {a} {b} = \ dfrac {c} {d} \)
Если вы умножите обе стороны на 1, используя знаменатели из другой части уравнения, вы получите:
\ (\ dfrac {a} {b} \ times \ dfrac {d} {d} = \ dfrac {c} {d} \ times \ dfrac {b} {b} \)
Обратите внимание, что это ничего не меняет, потому что умножение чего-либо на 1 не меняет его значения. Итак, теперь у вас есть:
Итак, теперь у вас есть:
\ (\ dfrac {a \ times d} {b \ times d} = \ dfrac {b \ times c} {b \ times d} \)
Поскольку знаменатели здесь такие же, b × d, вы можете удалить их и сказать, что:
\ (а \ раз d = b \ раз с \)
Что является результатом перемножения исходного уравнения:
\ (\ dfrac {a} {b} = \ dfrac {c} {d} \)
Список литературы
Кросс-умножение из Math Is Fun на http: // www.mathsisfun.com/
знаков после запятой: умножение и деление десятичных знаков
Урок 3: Умножение и деление десятичных знаков
/ en / decimals / сложение-и-вычитание-десятичные дроби / content /
Умножение на десятичные дроби
В разделе «Сложение и вычитание десятичных знаков» вы узнали, как к складывать десятичное число. Возможно, вам удастся вспомнить времена, когда вы добавляли десятичные дроби в реальной жизни.Например, вы идете в магазин и находите рубашку, которая вам действительно нравится. Ценник говорит, что он стоит 15,60 долларов. Вам так нравится рубашка, что вы решаете купить их пять.
Возможно, вам удастся вспомнить времена, когда вы добавляли десятичные дроби в реальной жизни.Например, вы идете в магазин и находите рубашку, которая вам действительно нравится. Ценник говорит, что он стоит 15,60 долларов. Вам так нравится рубашка, что вы решаете купить их пять.
Чтобы вычислить общую стоимость, вы можете добавить цены.
Добавление такого количества чисел может занять много времени. Из урока по умножению мы узнали, что умножая, вы умножаете и умножаете во много раз. Поскольку все цены на рубашки равны и , умножение может помочь вам решить эту проблему немного быстрее.
Когда вы умножаете десятичные числа, полезно поставить задачу таким образом, чтобы облегчить вам ее решение пошагово .
Щелкните слайд-шоу ниже, чтобы узнать, как настроить задачу умножения с десятичными знаками.
Решение задач умножения с десятичными знаками
Умножение десятичных чисел во многом похоже на умножение больших чисел. Если большую проблему разделить на несколько более мелких, ее будет легче решить.Давайте посмотрим, как это работает, решив эту задачу: 2.3 x 4.
Если большую проблему разделить на несколько более мелких, ее будет легче решить.Давайте посмотрим, как это работает, решив эту задачу: 2.3 x 4.
Щелкните слайд-шоу, чтобы узнать, как умножать десятичные дроби.
Для решения нашей проблемы мы воспользуемся знакомым инструментом: таблицей умножения .
При умножении сложенных чисел начните с правой цифры в нижней части . Нижнее число состоит только из одной цифры: 4.
Мы умножим 4 на верхнее число, 2.3. Поскольку нет 2.3 в таблице умножения, нам придется умножать по одной цифре за раз.
Как обычно, будем решать задачу с справа налево . Итак, мы умножим 4 на цифру в правом верхнем углу . Здесь это 3.
Теперь пришло время решить 4 x 3. Мы можем использовать таблицу умножения на .
4 x 3 равно 12, но нет места для записи обеих цифр под 4 и 3.

Помните, это означает, что нам придется нести .Мы узнали о переносе чисел на уроке по умножению больших чисел.
Правую цифру 2 запишем под чертой …
Запишем под чертой правую цифру 2 … затем перенесем левую цифру 1 , до следующий набор цифр в задаче .
Теперь пора сделать следующий шаг. Умножим 4 x 2.
4 x 2 = 8. Но 8 под чертой пока писать не будем. Помните, есть еще один шаг.
Нам нужно убедиться, что мы добавляем число, которое у нас есть: 1.
Мы создадим нашу задачу сложения.
1 + 8 = 9.
Запишем 9 под чертой.
В нашей задаче мы умножили десятичное число: 2.3. Это означает, что наш ответ также должен быть десятичным числом.
Давайте разберемся, где поставить десятичную точку (. ).
В задаче 2.
 3 имеет одна цифра после справа десятичной запятой.
3 имеет одна цифра после справа десятичной запятой.Это означает, что в нашем ответе также будет одна цифра после справа десятичной запятой.
Разместим десятичную точку так, чтобы только одна цифра была справа от : 2.
Наша проблема решена. Итого 9,2. Мы знаем, что 2,3 х 4 = 9,2. Мы можем прочитать этот ответ как девять и две десятых .
Попробуем другую задачу. На этот раз мы умножим деньги: 3,05 доллара на 2.
Сначала мы умножим нижнее число 2 на цифру в правом верхнем углу. Это 5.
2 x 5 = 10.
Мы запишем 0 под линией …
Мы запишем 0 под линией … и перенесем 1. Поместим его над следующей цифрой.
Следующая цифра — 0.
Все, умноженное на ноль, равно нулю, поэтому мы знаем, что 2 x 0 = 0.

Помните, нам нужно убедиться, что мы добавили 1, что у нас есть.
0 + 1 = 1. Мы запишем 1 под чертой.
Наконец, мы умножим 2 и 3.
2 x 3 = 6, поэтому мы напишем 6 под линией.
Пора поставить десятичную точку. Нам нужно отсчитать цифр до правых десятичной точки в нашей задаче.
3.05 содержит две цифры справа от десятичной точки.Это 0 и 5.
Это означает, что в нашем ответе должны быть две цифры справа от десятичной точки.
Мы разместим десятичную точку так, чтобы две цифры были справа: 1 и 0.
Наконец, мы напишем знак доллара ($) на слева от номера.
Мы решили проблему. 3,05 доллара США x 2 = 6,10 доллара США. Мы можем прочитать это как шесть долларов десять центов .

Примечание : определяя, где разместить десятичную точку в ответе, подсчитайте общее количество цифр справа от на каждую десятичную точку в вашей задаче. Например, если вы упрощаете 3,25 x 2,3, вы должны посчитать две цифры в 3,25 плюс одну цифру в 2,3. Следовательно, мы должны разместить десятичную точку в нашем ответе так, чтобы три цифры были справа (3,25 x 2,3 = 7,475).
Попробуй!
Попробуйте решить эти задачи умножения.Затем проверьте свой ответ, введя его в поле.
Десятичные дроби
Давайте посмотрим на другую ситуацию. Представим, что у вас есть забор, и вы хотите посадить перед ним 5 кустов. Ваш забор 20 футов в длину. Вы хотите распределить кусты поровну, поэтому вы знаете, что вам нужно разделить забор на 5 равных частей. Это означает, что вам нужно разделить 20 на 5.
В уроке о делении мы узнали, как настроить выражения деления. Для приведенной выше ситуации выражение будет выглядеть так:
В нашем выражении 20 — это целое число . Но что, если длина забора равна десятичному числу ? Например, предположим, что это 20,75 футов в длину. Вы не поверите, но деление десятичной дроби ничем не отличается.
Но что, если длина забора равна десятичному числу ? Например, предположим, что это 20,75 футов в длину. Вы не поверите, но деление десятичной дроби ничем не отличается.
Когда вы настраиваете выражение для деления десятичного числа, важно убедиться, что вы всегда делите на целое число . В нашем примере выше 20,75 делится на целое число 5. Деление на целое число упрощает управление длинным делением.
Щелкните слайд-шоу ниже, чтобы узнать, как настроить задачи деления с десятичными знаками.
Давайте настроим это выражение: 20.75 / 5.
На уроке деления мы узнали, что делить числа легче, если выражение написано немного иначе.
Как обычно, вместо записи чисел рядом с символом деления …
Как обычно, вместо записи чисел рядом с символом деления … мы ‘ Я буду использовать кронштейн деления .

Число, которое мы делим, идет под скобкой деления. Это 20,75.
К левому скобки деления мы напишем число, на которое мы делим. В нашей задаче это 5.
Помните, что скобка деления также является знаком равно .
Частное , или ответ, записывается как над it.
Приведем другое выражение.На этот раз оба числа являются десятичными числами: 80,1 / 4,2.
Сначала напишем скобку деления.
Далее запишем делимое число: 80.1.
Наконец, напишем число, на которое делим: 4.2.
Поскольку мы делим десятичное число на десятичное, нам нужно сделать еще один шаг.
Чтобы упростить деление, мы изменим число, на которое мы делим, на целое число .Значит, мы изменим 4.2.
Чтобы сделать 4,2 целым числом, нам нужно переместить десятичную точку на так, чтобы она стояла после последней цифры в числе.

Это означает, что мы переместим его так, чтобы он стоял после 2.
Теперь все цифры находятся до слева десятичной точки. Мы создали целое число . 4.2 становится 42.
Целое число обычно записывается без десятичной точки после него…
Целое число обычно записывается без десятичной точки после него … поэтому мы будем отбросить десятичную точку.
Видите, как мы это сделали? Мы переместили десятичную точку на вправо на , а затем опустили десятичную точку.
Поскольку мы переместили десятичную точку в одно число …
Поскольку мы переместили десятичную точку в одном числе … нам также необходимо переместить десятичную точку в другом числе: 80.1.
Итак, мы переместим эту десятичную точку на такое же количество раз .

80,1 становится 801.
801 — целое число, поэтому мы опустим десятичную точку .
Теперь выражение деления — 801/42.
Перемещение десятичных знаков может быть непростым делом, поэтому важно сначала изменить число, которое вы делите на , на целое число .
Давайте попробуем еще раз с другим выражением: 0.4 / 0,02.
Сначала заменим 0,02 на целое число.
Переместим десятичную запятую на один раз вправо .
0,02 становится 0,2.
У нас все еще есть цифра справа десятичной точки: 2. Это означает, что наша десятичная дробь еще не является целым числом.
Итак, мы переместим десятичную точку на вправо второй раз.
0.2 становится 2. Все цифры теперь находятся слева от десятичной запятой.

Обнуления и десятичная точка больше не нужны. Мы их сбросим .
Поскольку мы переместили первую десятичную точку два раза по вправо …
Поскольку мы переместили первую десятичную точку два раза по вправо … мы сделаем то же самое с вторая десятичная точка.
Переместим на один раз на …
Мы переместим его на один раз на … затем добавим ноль …
Переместим его на один раз на … затем мы добавьте ноль … и затем переместим его на секунд раз.
0,4 становится 40.
Поскольку 40 — целое число, мы будем отбросить ноль и десятичную точку.
Выражение деления теперь 40/2. Наша проблема готова к решению.

Деление десятичных чисел
В предыдущем слайд-шоу вы попрактиковались в настройке выражений деления с десятичными числами. Давайте подробнее рассмотрим, как разделить десятичную дробь. Разделение десятичного числа очень похоже на деление целого числа . В конце есть только один дополнительный шаг.
Щелкните слайд-шоу, чтобы узнать, как делить десятичные дроби.
Для решения этой задачи воспользуемся длинным делением: 6.5 / 2.
На уроке, посвященном делению в столбик, мы узнали, что при решении задачи деления в столбик мы будем следовать шаблону , пока проблема не будет решена.
Начнем с левой цифры под скобкой деления. Это означает, что мы начнем с 6 …
Мы начнем с левой цифры под скобкой деления. Это означает, что мы начнем с 6 … и выясним, сколько раз его можно разделить на 2.

Мы воспользуемся таблицей умножения , чтобы помочь нам. Помните, что если вам нужно повторить, как пользоваться таблицей умножения, вы можете вернуться к уроку умножения. Теперь пришло время решить 6/2.
6/2 = 3.
Мы напишем 3 над 6.
Затем мы умножим на 3 и 2.
3 x 2 = 6.
Мы запишем 6 под 6.
Затем мы создадим нашу задачу вычитания .
6 — 6 = 0. Запишем 0 под линией.
Теперь мы опустим 5 и перепишем его рядом с 0.
05 означает то же самое, что и 5. 5 достаточно велико, чтобы его можно было разделить, поэтому мы выясним, сколько раз 5 можно разделить на 2.
В столбце 2 мы будем искать число, которое ближе всего к 5, но не больше 5. Это 4.
4 находится в строке 2. Это означает, что 2 переходит в 5 два раз.

Мы напишем 2 над 5.
Теперь пора умножить на 2 и 2.
2 x 2 = 4.
Напишем 4 под 5.
Теперь пришло время настроить нашу задачу вычитания .
5 — 4 = 1. Мы запишем 1 под чертой.
Поскольку наш ответ на задачу вычитания — 1, мы посмотрим под скобкой , чтобы увидеть, есть ли еще одна цифра, которую мы можем опустить.
Нет больше цифр, которые нам нужно сбивать. На уроке деления в столбик мы узнали, что можем написать ноль рядом с числом под скобкой деления.
Итак, рядом с 6.5 напишем 0.
Теперь мы можем продолжить решение этой проблемы. Мы опустим 0 и перепишем его рядом с 1.
Давайте посмотрим, сколько раз 10 можно разделить на 2.
В столбце 2 мы поищем ближайшее число. до 10, но не более 10.В столбце 2 стоит цифра 10.
 Это именно то, что нам нужно!
Это именно то, что нам нужно!10 находится в 5-м ряду. Это означает, что 2 переходит в 10 пять раз.
Мы напишем 5 над 0.
Теперь пора умножить 5 и 2.
5 x 2 = 10.
Запишем 10 под 10.
Далее мы настроим задачу вычитания .
Теперь пора решать.10 — 10 = 0.
Так как ответ на задачу вычитания — 0 и больше нет цифр, которые нужно опускать, мы закончили деление. Нам нужно сделать только один последний шаг.
В этой задаче мы разделили десятичное число: 6.5. Это означает, что в нашем частном или ответе будет десятичная точка.
Мы просто запишем десятичную точку непосредственно над другой десятичной точкой . Видите, где мы его поместили между 3 и 2?
Мы решили проблему.Частное составляет 3,25. Итак, 6,5 / 2 = 3,25. Мы можем прочитать это как три и двадцать пять сотых .

Попробуй!
Найдите частное для каждой из приведенных ниже задач на столбец. Проверьте свой ответ, введя его в поле.
/ ru / decimals / преобразование-десятичных-дробных-и-процентных / содержание /
Генерирующие функции
Раздел 5.1 Создание функций
¶Существует чрезвычайно мощный инструмент дискретной математики, используемый для управления последовательностями, который называется производящей функцией.5 + \ cdots. \ end {уравнение *}
Если рассматривать в контексте производящих функций, мы называем такой степенной ряд производительным рядом . Генерирующий ряд генерирует последовательность
\ begin {уравнение *} c_0, c_1, c_2, c_3, c_4, c_5, \ ldots. \ end {уравнение *}Другими словами, последовательность, генерируемая производящей серией, является просто последовательностью коэффициентов бесконечного многочлена.
Пример5.
 n \).1 \), который в данном случае равен 0. Итак \ (a_1 = 0 \ text {.} \) Продолжая, мы имеем \ (a_2 = 8 \ text {,} \) \ (a_3 = 1 \ text {,} \ ) \ (a_4 = 0 \ text {,} \) и \ (a_5 = \ frac {1} {7} \ text {.} \) Итак, у нас есть последовательность \ begin {уравнение *}
3, 0, 8, 1, \ frac {1} {7}, 100, \ ldots
\ end {уравнение *}
n \).1 \), который в данном случае равен 0. Итак \ (a_1 = 0 \ text {.} \) Продолжая, мы имеем \ (a_2 = 8 \ text {,} \) \ (a_3 = 1 \ text {,} \ ) \ (a_4 = 0 \ text {,} \) и \ (a_5 = \ frac {1} {7} \ text {.} \) Итак, у нас есть последовательность \ begin {уравнение *}
3, 0, 8, 1, \ frac {1} {7}, 100, \ ldots
\ end {уравнение *}Обратите внимание, что при обсуждении производящих функций мы всегда начинаем нашу последовательность с \ (a_0 \ text {.} \)
Теперь вы вполне естественно можете спросить, зачем мы так поступаем. Одна из причин заключается в том, что кодирование последовательности степенным рядом помогает нам отслеживать, какой член какой в последовательности.{18} + \ cdots \ text {.} \) Теперь ясно, что 24 — это 17-й член последовательности (то есть \ (a_ {17} = 24 \)). Конечно, чтобы получить это преимущество, мы могли бы отображать нашу последовательность любым количеством способов, например \ (\ fbox {1} _0 \ fbox {3} _1 \ fbox {4} _2 \ fbox {6} _3 \ fbox {9} _4 \ cdots \ fbox {24} _ {17} \ fbox {41} _ {18} \ cdots \ text {,} \), но мы этого не делаем. Причина в том, что производящий ряд выглядит как обычный степенной ряд (хотя мы интерпретируем его по-разному), поэтому мы можем делать с ним то, что обычно делаем со степенным рядом, например, записывать, к чему он сходится.3 \ cdots = \ dfrac {1} {1-x}
\ end {уравнение *}
Причина в том, что производящий ряд выглядит как обычный степенной ряд (хотя мы интерпретируем его по-разному), поэтому мы можем делать с ним то, что обычно делаем со степенным рядом, например, записывать, к чему он сходится.3 \ cdots = \ dfrac {1} {1-x}
\ end {уравнение *}
Вы, возможно, помните из математического анализа, что это верно только на интервале сходимости для степенного ряда, в данном случае, когда \ (| x | \ lt 1 \ text {.} \) Это верно для нас, но мы не т забота. Мы никогда не собираемся ничего вставлять для \ (x \ text {,} \), так что пока существует некоторое значение \ (x \), для которого производящая функция и производящий ряд согласуются, мы счастливы. И в этом случае мы счастливы.
\ (1,1,1, \ ldots \)
Производящая функция для \ (1,1,1,1,1,1, \ ldots \) равна \ (\ dfrac {1} {1-x} \)
Давайте воспользуемся этой базовой производящей функцией, чтобы найти производящие функции для большего количества последовательностей.3 + \ cdots \ mbox {который генерирует} 1, 3, 9, 27, \ ldots \ end {уравнение *}
Заменив \ (x \) на \ (\ frac {1} {1-x} \), мы можем получить производящие функции для множества последовательностей, но не для всех. Например, вы не можете подключить что-либо к \ (x \), чтобы получить производящую функцию для \ (2,2,2,2, \ ldots \ text {.} \). Однако мы еще не потерялись. Обратите внимание, что каждый член \ (2, 2, 2, 2, \ ldots \) является результатом умножения членов \ (1, 1, 1, 1, \ ldots \) на константу 2. Итак, умножьте порождающий функция также на 2.3 + \ cdots \) является производящей функцией для треугольных чисел, \ (1,3,6,10 \ ldots \) (хотя здесь мы имеем \ (a_0 = 1 \), а \ (T_0 = 0 \) обычно) .
Например, вы не можете подключить что-либо к \ (x \), чтобы получить производящую функцию для \ (2,2,2,2, \ ldots \ text {.} \). Однако мы еще не потерялись. Обратите внимание, что каждый член \ (2, 2, 2, 2, \ ldots \) является результатом умножения членов \ (1, 1, 1, 1, \ ldots \) на константу 2. Итак, умножьте порождающий функция также на 2.3 + \ cdots \) является производящей функцией для треугольных чисел, \ (1,3,6,10 \ ldots \) (хотя здесь мы имеем \ (a_0 = 1 \), а \ (T_0 = 0 \) обычно) .
Подраздел
¶ Мы видели, как найти производящие функции из \ (\ frac {1} {1-x} \) с помощью умножения (на константу или на \ (x \)), подстановки, сложения и дифференцирования. Чтобы использовать каждый из них, вы должны заметить способ преобразования последовательности \ (1,1,1,1,1 \ ldots \) в желаемую последовательность. Это не всегда просто.Мы также не так анализировали последовательности. Одна вещь, которую мы часто рассматриваем, — это последовательность различий между членами последовательности. 4 + \ cdots
\ end {выровнять *}
4 + \ cdots
\ end {выровнять *}
Хотя мы не можем получить точную последовательность различий, мы все же получаем нечто близкое.В этом конкретном случае мы уже знаем производящую функцию \ (A \) (мы нашли ее в предыдущем разделе), но в большинстве случаев мы будем использовать этот метод сравнения, чтобы найти \ (A \ text {:} \) если у нас есть производящая функция для последовательности разностей, мы можем найти \ (A \ text {.} \)
Пример5.1.2
Найдите производящую функцию для \ (1, 3, 5, 7, 9, \ ldots \ text {.} \)
РешениеОбратите внимание, что последовательность различий постоянна. Мы знаем, как найти производящую функцию для любой постоянной последовательности.2} \) генерирует \ (1,2,3,4,5, \ ldots \ text {,} \), умножение на \ (2x \) сдвигает его, помещает ноль вперед и удваивает каждый член). Если мы будем складывать эти термины, мы получим правильную последовательность \ (1,3,5,7, 9, \ ldots \ text {.} \)
Теперь, когда у нас есть производящая функция для нечетных чисел, мы можем использовать ее, чтобы найти производящую функцию для квадратов:
Пример5.
 1.3
1.3Найдите производящую функцию для \ (1, 4, 9, 16, \ ldots \ text {.} \). Обратите внимание, что мы берем \ (1 = a_0 \ text {.} \)
РешениеМы снова вызываем производящую функцию для последовательности \ (A \ text {.3} \ text {.} \)
В каждом из приведенных выше примеров мы нашли разницу между последовательными членами, которая дала нам последовательность различий, для которой мы знали производящую функцию. Мы можем обобщить это на более сложные отношения между членами последовательности. Например, если мы знаем, что последовательность удовлетворяет рекуррентному соотношению \ (a_n = 3a_ {n-1} — 2a_ {n-2} \ text {?} \) Другими словами, если мы возьмем член последовательности и вычтите 3 раза предыдущий член и затем добавьте 2 раза предыдущий член, мы получим 0 (поскольку \ (a_n — 3a_ {n-1} + 2a_ {n-2} = 0 \)).Это будет справедливо для всех, кроме первых двух членов последовательности. Таким образом, после первых двух членов последовательность результатов этих вычислений будет последовательностью нулей, для которой мы определенно знаем производящую функцию. 2 (1-2x)} \)
2 (1-2x)} \)
Рассмотрим особый случай, когда вы умножаете последовательность на \ (1, 1, 1, \ ldots \ text {.3} \ text {.} \) Это не должно вызывать удивления, поскольку ранее мы обнаружили ту же производящую функцию для треугольных чисел.
Дело в том, что если вам нужно найти производящую функцию для суммы первых \ (n \) членов определенной последовательности, и вы знаете производящую функцию для этой последовательности , вы можете умножить ее на \ (\ frac {1} {1-x} \ text {.} \) Чтобы вернуться от последовательности частичных сумм к исходной последовательности, вы смотрите на последовательность различий. Когда вы получаете последовательность различий, вы в конечном итоге умножаете на \ (1-x \ text {,} \) или, что эквивалентно, делите на \ (\ frac {1} {1-x} \ text {.} \) Умножение на \ (\ frac {1} {1-x} \) дает частичные суммы, деление на \ (\ frac {1} {1-x} \) дает разницу.
Подраздел Решение повторяющихся отношений с помощью порождающих функций
¶ В заключение приведем пример одной из многих причин, по которым изучение производящих функций полезно. Мы можем использовать производящие функции для решения рекуррентных отношений.
Мы можем использовать производящие функции для решения рекуррентных отношений.
Пример5.1.6
Решите рекуррентное соотношение \ (a_n = 3a_ {n-1} — 2a_ {n-2} \) с начальными условиями \ (a_0 = 1 \) и \ (a_1 = 3 \ text {.2} = \ frac {1} {(1-x) (1-2x)}. \ end {уравнение *}
Разложение на частичную дробь говорит нам, что мы можем записать эту фракцию как сумму двух дробей (мы разложим данную дробь):
\ begin {уравнение *} \ frac {1} {(1-x) (1-2x)} = \ frac {a} {1-x} + \ frac {b} {1-2x} \ text {~~ для некоторых констант} a \ текст {и} б. \ end {уравнение *}Чтобы найти \ (a \) и \ (b \), мы складываем две разложенные дроби, используя общий знаменатель. Это дает
\ begin {уравнение *} \ frac {1} {(1-x) (1-2x)} = \ frac {a (1-2x) + b (1-x)} {(1-x) (1-2x)}.\ end {уравнение *}т.
\ begin {уравнение *} 1 = а (1-2x) + b (1-х). \ end {уравнение *} Это должно быть верно для всех значений \ (x \ text {.} \). Если \ (x = 1 \ text {,} \), тогда уравнение становится \ (1 = -a \), поэтому \ (a = — 1 \ text {. } \) Когда \ (x = \ frac {1} {2} \) мы получаем \ (1 = b / 2 \), поэтому \ (b = 2 \ text {.} \) Это говорит нам что мы можем разложить дробь следующим образом:
} \) Когда \ (x = \ frac {1} {2} \) мы получаем \ (1 = b / 2 \), поэтому \ (b = 2 \ text {.} \) Это говорит нам что мы можем разложить дробь следующим образом:
На этом завершается разложение частичной дроби.{n + 1} — 1 \ end {уравнение *}
Теперь мы можем добавить производящие функции в наш список методов решения рекуррентных отношений.
Подраздел Упражнения
¶1
Найдите производящую функцию для каждой из следующих последовательностей, связав их обратно с последовательностью с известной производящей функцией.
- \ (4,4,4,4,4, \ ldots \ text {.} \)
- \ (2, 4, 6, 8, 10, \ ldots \ text {.} \)
- \ (0,0,0,2,4,6,8,10, \ ldots \ text {.} \)
- \ (1, 5, 25, 125, \ ldots \ text {.2} \) (Подсказка: умножение).
- \ (0, 4, 4, 4, 4, 4, \ ldots \ text {.
 } \)
} \) - \ (1, 4, 16, 64, 256, \ ldots \ text {.} \)
- \ (0, 1, -1, 1, -1, 1, -1, \ ldots \ text {.} \)
- \ (0, 3, -6, 9, -12, 15, -18, \ ldots \ text {.} \)
- \ (1, 3, 6, 9, 12, 15, \ ldots \ text {.} \)
3
Покажите, как можно получить производящую функцию для треугольных чисел тремя различными способами:
Возьмем две производные производящей функции для \ (1,1,1,1,1, \ ldots \)
Использовать разность.2} \ text {.} \) Решение для \ (A \) дает правильную производящую функцию.
Треугольные числа представляют собой сумму первых \ (n \) чисел \ (1,2,3,4, \ ldots \ text {.} \) Чтобы получить последовательность частичных сумм, мы умножаем на \ (\ frac {1} {1-x} \ text {.} \) Таким образом, это снова дает правильную производящую функцию.
4
Используйте разность, чтобы найти производящую функцию для \ (4, 5, 7, 10, 14, 19, 25, \ ldots \ text {. } \)
} \)
Вызовите производящую функцию \ (A \ text {.2} \) генерирует последовательность 1, 2, 3…. Вы также можете найти это, используя разность или умножение.
12
Начиная с производящей функции для \ (1,2,3,4, \ ldots \ text {,} \) найдите производящую функцию для каждой из следующих последовательностей.
- \ (1, 0, 2, 0, 3, 0, 4, \ ldots \ text {.} \)
- \ (1, -2, 3, -4, 5, -6, \ ldots \ text {.} \)
- \ (0, 3, 6, 9, 12, 15, 18, \ ldots \ text {.} \)
- \ (0, 3, 9, 18, 30, 45, 63, \ ldots \ text {.2) (1-x)} \ text {.} \)
- \ (0,0,1,1,2,3,5,8, \ ldots \ text {.} \)
- \ (1, 0, 1, 0, 2, 0, 3, 0, 5, 0, 8, 0, \ ldots \ text {.} \)
- \ (1, 3, 18, 81, 405, \ ldots \ text {.} \)
- \ (1, 2, 4, 7, 12, 20, \ ldots \ text {.} \)
14
Найдите производящую функцию для последовательности \ (1, -2, 4, -8, 16, \ ldots \ text {.} \)
15
Найдите производящую функцию для последовательности \ (1, 1, 1, 2, 3, 4, 5, 6, \ ldots \ text {. 2} + \ frac {1} {1-x} \ text {.} \)
2} + \ frac {1} {1-x} \ text {.} \)
16
Предположим, что \ (A \) — производящая функция для последовательности \ (3, 5, 9, 15, 23, 33, \ ldots \ text {.} \)
Найдите производящую функцию (в терминах \ (A \)) для последовательности разностей между терминами.
Запишите последовательность различий между терминами и найдите для нее производящую функцию (без ссылки на \ (A \)).
Используйте свои ответы на части (a) и (b), чтобы найти производящую функцию для исходной последовательности.3} \ text {.} \)

 По возможности упростите результат.
По возможности упростите результат.
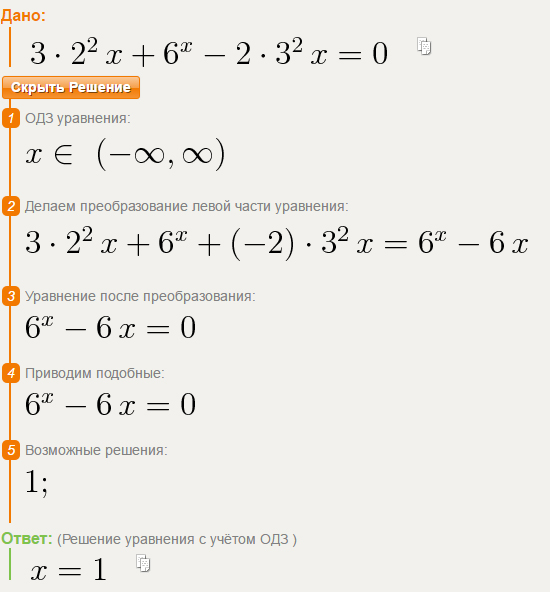 3 имеет одна цифра после справа десятичной запятой.
3 имеет одна цифра после справа десятичной запятой.
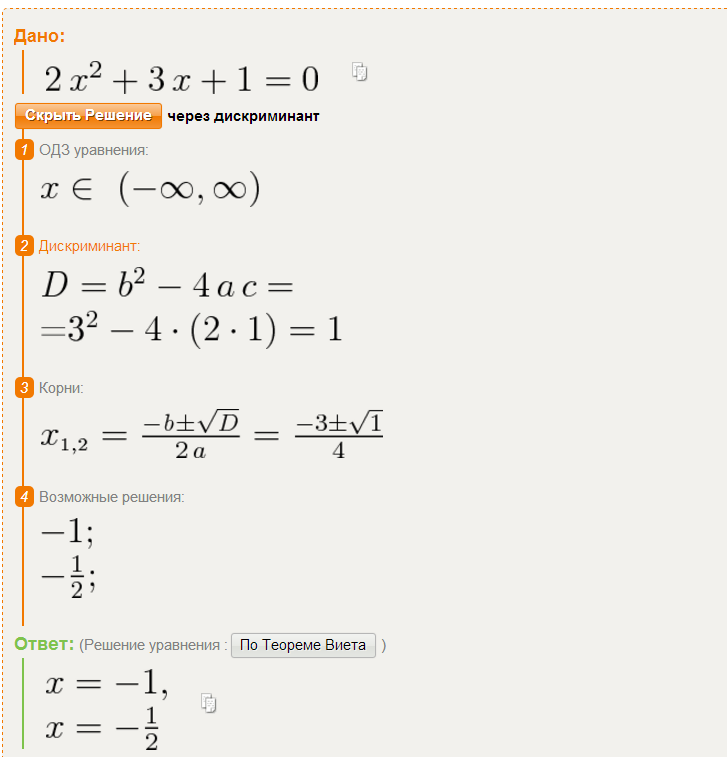







 Это именно то, что нам нужно!
Это именно то, что нам нужно!
 } \)
} \)