24 интеграл
Вы искали 24 интеграл? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и math34 интегралы, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «24 интеграл».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 24 интеграл,math34 интегралы,взятие интеграла онлайн,взять интеграл,взять интеграл онлайн,взять интеграл онлайн с решением,вычисление интеграл,вычисление интеграла,вычисление интегралов,вычисление интегралов онлайн калькулятор,вычисление интегралов онлайн с подробным решением,вычисление неопределенного интеграла онлайн,вычисление первообразной,вычислите интеграл онлайн с решением,вычислить интеграл,вычислить интеграл онлайн калькулятор с подробным решением,вычислить интеграл онлайн с подробным решением,вычислить интеграл онлайн с подробным решением бесплатно,вычислить интеграл онлайн с подробным решением калькулятор,вычислить интегралы онлайн с подробным решением,вычислить криволинейный интеграл онлайн,вычислить неопределенный интеграл онлайн с подробным решением,вычислить несобственный интеграл онлайн с подробным решением,вычислить онлайн с решением,вычислить повторный интеграл онлайн с решением,изменить порядок интегрирования онлайн калькулятор,изменить порядок интегрирования онлайн калькулятор с решением,интеграл 24,интеграл вычисление,интеграл как посчитать,интеграл онлайн калькулятор с подробным,интеграл онлайн с подробным решением,интеграл решение,интеграл частного,интегралов,интегралы калькулятор онлайн,интегралы онлайн с подробным решением,интегралы онлайн с решением,интегралы решать,интегралы решение,интегралы с подробным решением,интегральный калькулятор,интегрирование калькулятор,интегрирование по частям онлайн,интегрирование по частям онлайн калькулятор,интегрирование по частям онлайн с подробным решением,интегрирование рациональных дробей онлайн калькулятор,интегрировать онлайн,інтеграл,інтеграли,как интеграл посчитать,как посчитать интеграл,как решить интеграл,калькулятор вычисление интегралов онлайн,калькулятор интеграла,калькулятор интеграла онлайн,калькулятор интегралов,калькулятор интегралов онлайн,калькулятор интегралов онлайн с подробным,калькулятор интегралов онлайн с решением,калькулятор интегралы,калькулятор интегрирования,калькулятор интервалов,калькулятор онлайн вычисление интегралов,калькулятор онлайн интегралов,калькулятор онлайн интегрирование по частям,калькулятор определенных интегралов онлайн с подробным решением,калькулятор первообразной онлайн,калькулятор первообразных онлайн с решением,калькулятор с интегралами,криволинейные интегралы онлайн,криволинейный интеграл онлайн калькулятор,найти интеграл методом замены переменной онлайн,найти интеграл онлайн калькулятор,найти интегралы онлайн с подробным решением,найти неопределенные интегралы онлайн с полным решением,найти неопределенный интеграл онлайн калькулятор с подробным решением,найти неопределенный интеграл онлайн с подробным решением,найти первообразную онлайн,нахождение интеграла,нахождение интегралов,нахождение первообразной онлайн,неопределенный интеграл онлайн калькулятор с подробным решением,несобственный интеграл онлайн калькулятор,онлайн вычисление неопределенных интегралов,онлайн интегралы с пошаговым решением,онлайн калькулятор вычисление интегралов,онлайн калькулятор интеграл,онлайн калькулятор интеграла,онлайн калькулятор интегралов с подробным,онлайн калькулятор интегралы,онлайн калькулятор интегрирование рациональных дробей,онлайн калькулятор найти интеграл,онлайн калькулятор неопределенный интеграл,онлайн калькулятор решение интегралов с подробным решением,онлайн неопределенные интегралы,онлайн решение интегралов с подробным,онлайн решение интегралов с подробным решением,онлайн решение интегралов с подробным решением бесплатно,онлайн решение неопределенных интегралов с подробным решением,первообразная калькулятор,первообразная калькулятор онлайн,первообразная онлайн калькулятор,первообразная онлайн калькулятор с подробным решением,посчитать интеграл,посчитать интеграл онлайн с подробным решением,посчитать как интеграл,проинтегрировать онлайн,проинтегрировать уравнение онлайн,расчет интегралов,расчет интегралов онлайн,решать интегралы,решение интеграла,решение интеграла онлайн с подробным решением,решение интеграла с подробным решением онлайн,решение интегралов,решение интегралов калькулятор онлайн,решение интегралов онлайн калькулятор с подробным решением,решение интегралов онлайн с подробным решением,решение интегралов онлайн с подробным решением бесплатно,решение интегралов онлайн с подробным решением калькулятор,решение интегралов онлайн с решением,решение интегралов с подробным решением,решение интегралы,решение криволинейных интегралов онлайн,решение неопределенного интеграла онлайн с подробным решением,решение неопределенных интегралов онлайн с подробным решением,решения интегралов,решить интеграл онлайн с подробным,решить интеграл онлайн с подробным решением,решить интеграл онлайн с подробным решением бесплатно,решить интеграл онлайн с решением,решить интегралы онлайн с подробным решением,решить неопределенный интеграл онлайн,решить неопределенный интеграл онлайн с подробным решением,справочник веществ интеграл онлайн,сходимость интегралов онлайн.
Где можно решить любую задачу по математике, а так же 24 интеграл Онлайн?
Решить задачу 24 интеграл вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Неопределённый интеграл для функции f {\displaystyle f}
ⓘ Неопределённый интеграл
Неопределённый интеграл для функции f {\displaystyle f} — это совокупность всех первообразных данной функции.
Слева в каждом равенстве стоит произвольная но определённая первообразная функция для соответствующей подынтегральной функции, справа же — одна определённая первообразная, к которой ещё прибавляется константа C {\displaystyle C} такая, чтобы выполнялось равенство между этими функциями.
Первообразные функции в этих формулах определены и непрерывны на тех интервалах, на которых определены и непрерывны соответствующие подынтегральные функции. Эта закономерность не случайна: как отмечено выше, всякая непрерывная на интервале функция имеет на нем непрерывную первообразную.
Вычислить несобственные интегралы или установить их расходимость. Определенный интеграл онлайн
Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно.
И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно.
 Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов.
Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов.
 Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение».
Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение». Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн.
Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрированияИногда такой несобственный интеграл называют несобственным интегралом первого рода . В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус:)
Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна на промежутке , и этот важный факт следует проверять в первую очередь! Ибо если есть разрывы, то есть дополнительные нюансы. Для определённости предположим, что и тогда типичная криволинейная трапеция будет выглядеть так:
Для определённости предположим, что и тогда типичная криволинейная трапеция будет выглядеть так:
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл численно равен её площади . При этом возможны следующие варианты:
1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что несобственный интеграл расходится .
2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится .
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.
Таким образом, несобственный интеграл может быть отрицательным .
Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно . Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений , ибо лучше поздно, чем в армии.
У кого с ними плохо, изучите урок Пределы функций. Примеры решений , ибо лучше поздно, чем в армии.
Рассмотрим два классических примера:
Пример 1
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно .
Подынтегральная функция непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы и решение задачи выглядит так:
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».
Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций .
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет . Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на
“
Что делать, если вам встретится интеграл наподобие – с точкой разрыва на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего) , либо о продвинутом уровне обучения. В последнем случае, в силу свойства аддитивности , следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.
Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать , так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.
Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: . Несмотря на определённость и непрерывность косинуса, такого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела .
И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на .
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей .
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.
У кого какая математическая подготовка.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов . Там же разобран случай, когда оба предела интегрирования бесконечны.
Несобственные интегралы от неограниченных функцийИли несобственные интегралами второго рода . Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования . В этой связи проверим и верхний предел: . Здесь всё хорошо.
В этой связи проверим и верхний предел: . Здесь всё хорошо.
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
* по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа. Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа .
Посмотрим, как это реализуется на практике.
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле .
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом . В данном случае у нас правосторонний предел .
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .
В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .
А сейчас два примера для самостоятельного решения.
Пример 7
Вычислить несобственный интеграл или установить его расходимость.
Пример 8
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом.
Определенный интеграл как предел интегральной суммы
может существовать (т.е. иметь определенное конечное значение) лишь при выполнении условий
Если
хотя бы одно из этих условий нарушено,
то определение теряет смысл. Действительно,
в случае бесконечного отрезка, например
[a ;
)
его нельзя разбить на п частей конечной длины
,
которая к тому же с увеличением количества
отрезков стремилась бы к нулю. В случае
же неограниченной в некоторой точкес [a ; b ]
нарушается требование произвольного
выбора точки
на частичных отрезках – нельзя выбрать=с ,
поскольку значение функции в этой точке
не определено. Однако и для этих случаев
можно обобщить понятие определенного
интеграла, введя еще один предельный
переход. Интегралы по бесконечным
промежуткам и от разрывных (неограниченных)
функций называют несобственными .
Однако и для этих случаев
можно обобщить понятие определенного
интеграла, введя еще один предельный
переход. Интегралы по бесконечным
промежуткам и от разрывных (неограниченных)
функций называют несобственными .
Определение.
Пусть
функция
определена на промежутке [a ;
)
и интегрируема на любом конечном отрезке
[a ; b ],
т.е. существует
для любого b > a .
Предел вида
называютнесобственным
интегралом первого
рода (или
несобственным интегралом по бесконечному
промежутку) и обозначают
.
Таким
образом, по определению,
=
.
Если
предел справа существует и конечен, то
несобственный интеграл
называютсходящимся .
Если этот предел бесконечен, или не
существует вообще, то говорят, что
несобственный интеграл расходится .
Аналогично
можно ввести понятие несобственного
интеграла от функции
по промежутку (–; b ]:
=
.
А
несобственный интеграл от функции
по промежутку (–;
+)
определяется как сумма введенных выше
интегралов:
=
+
,
где а – произвольная точка. Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно из слагаемых.
С
геометрической точки зрения, интеграл
,
,
определяет численное значение площади
бесконечной криволинейной трапеции,
ограниченной сверху графиком функции
,
слева – прямой
,
снизу – осью ОХ. Сходимость интеграла
означает существование конечной площади
такой трапеции и равенство ее пределу
площади криволинейной трапеции с
подвижной правой стенкой
.
На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница :
=
=F(+ )
– F(a ),
где
F(+ )
=
.
Если этот предел существует, то интеграл
сходится, в противном случае – расходится.
Мы
рассмотрели обобщение понятия
определенного интеграла на случай
бесконечного промежутка.
Рассмотрим теперь обобщение для случая неограниченной функции.
Определение
Пусть
функция
определена на промежутке [a ; b ),
неограниченна в некоторой окрестности
точки b ,
и непрерывна на любом отрезке
,
где>0
(и, следовательно, интегрируема на этом
отрезке, т.е.
существует). Предел вида
называетсянесобственным
интегралом второго рода (или несобственным интегралом от
неограниченной функции) и обозначается
.
Таким образом, несобственный интеграл от неограниченной в точке b функции есть по определению
=
.
Если предел справа существует и конечен, то интеграл называется сходящимся . Если конечного предела не существует, то несобственный интеграл называется расходящимся.
Аналогично
можно определить несобственный интеграл
от функции
имеющей бесконечный разрыв в точкеа :
=
.
Если
функция
имеет бесконечный разрыв во внутренней
точкес
,
то несобственный интеграл определяется
следующим образом
=
+
=
+
.
Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.
С геометрической точки зрения, несобственный интеграл от неограниченной функции также характеризует площадь неограниченной криволинейной трапеции:
Поскольку несобственный интеграл выводится путем предельного перехода из определенного интеграла, то все свойства определенного интеграла могут быть перенесены (с соответствующими уточнениями) на несобственные интеграла первого и второго рода.
Во многих задачах, приводящих к несобственным интегралам, не обязательно знать, чему равен этот интеграл, достаточно лишь убедиться в его сходимости или расходимости. Для этого используют признаки сходимости . Признаки сходимости несобственных интегралов:
1) Признак сравнения .
Пусть
для всех х
.
Тогда, если
сходится, то сходится и
,
причем
.
Если
расходится, то расходится и
.
2)
Если сходится
,
то сходится и
(последний интеграл в этом случае
называетсяабсолютно
сходящимся ).
Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны сформулированным выше.
Примеры решения задач.
Пример 1.
а)
;
б)
;
в)
г)
; д)
.
Решение.
а) По определению имеем:
.
б) Аналогично
Следовательно, данный интеграл сходится и равен .
в)
По определению
=
+
,
причем,а – произвольное число. Положим в нашем
случае
,
тогда получим:
Данный интеграл сходится.
Значит, данный интеграл расходится.
д)
Рассмотрим
.
Чтобы найти первообразную подынтегральной
функции, необходимо применить метод
интегрирования по частям. Тогда получим:
Поскольку
ни
,
ни
не существуют, то не существует и
Следовательно, данный интеграл расходится.
Пример 2.
Исследовать сходимость интеграла в зависимости от п .
Решение.
При
имеем:
Если
,
то
и. Следовательно, интеграл расходится.
Следовательно, интеграл расходится.
Если
,
то
,
а
,
тогда
=,
Следовательно, интеграл сходится.
Если
,
то
следовательно, интеграл расходится.
Таким
образом,
Пример 3.
Вычислить несобственный интеграл или установить его расходимость:
а)
;
б)
;
в)
.
Решение.
а)
Интеграл
является несобственным интегралом
второго рода, поскольку подынтегральная
функция
не ограничена в точке
.
Тогда, по определению,
.
Интеграл сходится и равен .
б)
Рассмотрим
.
Здесь также подынтегральная функция
не ограничена в точке
.
Поэтому, данный интеграл – несобственный
второго рода и по определению,
Следовательно, интеграл расходится.
в)
Рассмотрим
.
Подынтегральная функция
терпит бесконечный разрыв в двух точках:
и
,
первая из которых принадлежит промежутку
интегрирования
.
Следовательно, данный интеграл –
несобственный второго рода. Тогда, по
определению
Тогда, по
определению
=
=
.
Следовательно,
интеграл сходится и равен
.
Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода..gif»>.
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: .
Мы рассмотрим самый популярный случай https://pandia.ru/text/80/057/images/image005_1.gif»>? Нет, не всегда. Подынтегральная функция https://pandia.ru/text/80/057/images/image007_0.gif»>
Изобразим на чертеже график подынтегральной функции . Типовой график и криволинейная трапеция для данного случая выглядит так:
Несобственный интеграл https://pandia.ru/text/80/057/images/image009_0.gif»>», иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что, что несобственный интеграл расходится .
2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: .. Во втором случае несобственный интеграл сходится .
Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: .. Во втором случае несобственный интеграл сходится .
А что будет, если бесконечная криволинейная трапеция расположена ниже оси?.gif»>.
: .
Пример 1
Подынтегральная функция https://pandia.ru/text/80/057/images/image017_0.gif»>, значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы https://pandia.ru/text/80/057/images/image018_0.gif»>
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд..gif»>
Гуд..gif»>
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что https://pandia.ru/text/80/057/images/image024.gif»> (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция непрерывна на .
Сначала попытаемся найти первообразную функцию (неопределенный интеграл).
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница..gif»>? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на https://pandia.ru/text/80/057/images/image041.gif»>
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата.
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала..
Несобственные интегралы от неограниченных функцийИногда такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: ..gif»>, 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
Сразу пример, чтобы было понятно: https://pandia.ru/text/80/057/images/image048.gif»>, то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования . .jpg» alt=»Несобственный интеграл, точка разрыва в нижнем пределе интегрирования»>
.jpg» alt=»Несобственный интеграл, точка разрыва в нижнем пределе интегрирования»>
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению https://pandia.ru/text/80/057/images/image052.gif»> справа .
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.
Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с https://pandia.ru/text/80/057/images/image058.gif»>. Как определить, куда стремиться выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу.
Пример 7
Вычислить несобственный интеграл или установить его расходимость.
Пример 8
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:
Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению https://pandia. 3+1}.
\]
3+1}.
\]
Интегралы для чайников — что это, как решать, примеры
За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов
Почему вы не знаете, как решать интегралы
А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.
Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:
- вычисление площади фигуры.
- вычисление массы тела с неравномерной плотностью.
- определение пройденного пути при движении с непостоянной скоростью.
- и др.
Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.
Главная причина незнания – отсутствие понимания практической значимости интегралов.
Интеграл – что это?
Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.
Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.
Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.
Метод исчерпывания для определения площади круга
В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.
Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.
Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.
Объясняем понятие «Интеграл»
Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.
Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».
Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.
Интеграл записывается так:
Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).
Неопределённый интеграл
Неопределенный интеграл не имеет границ интегрирования.
Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».
Пример решения неопределенного интеграла.
Определённый интеграл
В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.
Точки A и B на оси X – есть ограничение зоны определения интеграла
Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:
Пример решения определенного интеграла
Таблица интегралов для студентов (основные формулы)
Скачайте формулы интегралов, они вам еще пригодятся
Как вычислять интеграл правильно
Существует несколько простейших операций для преобразования интегралов. Вот основные из них:
Вынесение константы из-под знака интеграла
Разложение интеграла суммы на сумму интегралов
Если поменять местами a и b, знак изменится
Можно разбить интеграл на промежутки следующим образом
Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.
Примеры вычисления интегралов
Решение неопределенного интеграла
Решение определенного интеграла
Базовые понятия для понимания темы
Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.
Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.
Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.
Приращение – количественное изменение функции при некотором изменении аргумента.
Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.
Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.
Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.
Заключение
Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.
Если текстовое объяснение вам не заходит, посмотрите видео о смысле интеграла и производной:
youtube.com/embed/G_dA732qFGw» frameborder=»0″ allowfullscreen=»allowfullscreen»>
Интегралы – что это, как решать, примеры решений и объяснение для чайников обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру
Определённый интеграл и методы его вычисления. Калькулятор онлайн.Вычислить определенный интеграл (площадь криволинейной трапеции)
Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса.
Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.
Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре. . Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам.
. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах.
Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение». Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни.
Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение». Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
Рассмотрим функцию . Эту функцию называют: интеграл как функция верхнего предела. Отметим несколько свойств этой функции.
Теорема 2.1. Если f(x) интегрируемая на функция, то Ф(x) непрерывна на .
Доказательство . По свойству 9 определенного интеграла (теорема о среднем) имеем , откуда, при , получаем требуемое.
Теорема 2.2. Если f(x) непрерывная на функция, то Ф’(x) = f(x) на .
Доказательство . По свойству 10 определенного интеграла (вторая теорема о среднем), имеем где с – некоторая точка отрезка . В силу непрерывности функции f получаем
Таким образом, Ф(x) — одна из первообразных функции f(x) следовательно, Ф(x) = F(x) + C, где F(x) — другая первообразная f(x). Далее, так как Ф(a) = 0, то 0 = F(a) + C, следовательно, C = -F(a) и поэтому Ф(x) = F(x) – F(a). Полагая x=b, получаем формулу Ньютона-Лейбница
Примеры
1.
Интегрирование по частям в определённом интеграле
В определенном интеграле сохраняется формула интегрирования по частям. В этом случае она приобретает вид
В этом случае она приобретает вид Пример.
Замена переменных в определённом интеграле
Один из вариантов результатов о замене переменных в определённом интеграле следующий.Теорема 2.3. Пусть f(x)- непрерывна на отрезке и удовлетворяет условиям:
1) φ(α) = a
2) φ(β) = b
3) производная φ’(t) определена всюду на отрезке [α, β]
4) для всех t из [α, β]
Тогда
Доказательство. Если F(x) первообразная для f(x)dx то F(φ(t)) первообразная для Поэтому F(b) – F(a) = F(φ(β)) – F(φ(α)). Теорема доказана.
Замечание. При отказе от непрерывности функции f(x) в условиях теоремы 2.3 приходится требовать монотонности функции φ(t).
Пример. Вычислить интеграл Положим Тогда dx = 2tdt и поэтому
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Интеграл. Формула Ньютона – Лейбница. составитель: преподаватель математики ГОУНПО ПУ № 27 п. Щельяюр Семяшкина Ирина Васильевна
Формула Ньютона – Лейбница. составитель: преподаватель математики ГОУНПО ПУ № 27 п. Щельяюр Семяшкина Ирина Васильевна
Цель урока: Ввести понятие интеграла и его вычисление по формуле Ньютона – Лейбница, используя знания о первообразной и правила её вычисления; Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции; Закрепить изученное в ходе выполнения упражнений.
Определение: Пусть дана положительная функция f(x) , определенная на конечном отрезке [ a;b ] . Интегралом от функции f(x) на [ a;b ] называется площадь её криволинейной трапеции. y=f(x) b a 0 x y
Обозначение: «интеграл от a до b эф от икс дэ икс »
Историческая справка: Обозначение интеграла Лейбниц произвёл от первой буквы слова «Сумма» (Summa). Ньютон в своих работах не предложил альтернативной символики интеграла, хотя пробовал различные варианты. Сам термин интеграл придумал Якоб Бернулли. S umma Исаак Ньютон Готфрид Вильгельм фон Лейбниц Якоб Бернулли
Обозначение неопределённого интеграла ввёл Эйлер. Жан Батист Жозеф Фурье Леонард Эйлер Оформление определённого интеграла в привычном нам виде придумал Фурье.
Жан Батист Жозеф Фурье Леонард Эйлер Оформление определённого интеграла в привычном нам виде придумал Фурье.
Формула Ньютона — Лейбница
Пример 1. Вычислить определённый интеграл: = Решение:
Пример 2. Вычислите определённые интегралы: 5 9 1
Пример 3 . S y x Вычислить площадь фигуры, ограниченной линиями и осью абсцисс. Для начала найдем точки пересечения оси абсцисс с графиком функции. Для этого решим уравнение. = Решение: S =
y x S A B D C Пример 4 . Вычислить площадь фигуры, ограниченной линиями и Найдём точки пересечения (абсциссы) этих линий, решив уравнение S=S BADC — S BAC S BADC = = S BAC = S = 9 – 4,5 = 4,5 смотри пример 1 Решение:
ПРАВИЛА СИНКВЕЙНА 1строка – тема синквейна 1 слово 2строка – 2 прилагательных, описывающих признаки и свойства темы 3строка – 3 глагола описывающие характер действия 4строка – короткое предложение из 4 слов, показывающее Ваше личное отношение к теме 5строка – 1 слово, синоним или Ваша ассоциация тема предмета.
Интеграл 2. Определённый, положительный Считают, прибавляют, умножают 4. Вычисляют формулой Ньютона — Лейбница 5. Площадь
Определённый, положительный Считают, прибавляют, умножают 4. Вычисляют формулой Ньютона — Лейбница 5. Площадь
Список используемой литературы: учебник Колмагорова А.Н. и др. Алгебра и начала анализа 10 — 11 кл.
Спасибо за внимание! « ТАЛАНТ – это 99% труда и 1% способности» народная мудрость
Пример 1. Вычислить определённый интеграл: = Решение: пример 4
Предварительный просмотр:
Предмет: математика (алгебра и начала анализа), класс: 11 класс.
Тема урока: «Интеграл. Формула Ньютона-Лейбница».
Тип урока: Изучение нового материала.
Продолжительность занятия: 45 минут.
Цели урока: ввести понятие интеграла и его вычисление по формуле Ньютона-Лейбница, используя знания о первообразной и правила ее вычисления; проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции; закрепить изученное в ходе выполнения упражнений.
Задачи урока:
Образовательные:
- сформировать понятие интеграла;
- формирование навыков вычисления определенного интеграла;
- формирование умений практического применения интеграла для нахождения площади криволинейной трапеции.

Развивающие:
- развитие познавательного интереса учащихся, развивать математическую речь, умения наблюдать, сравнивать, делать выводы;
- развивать интерес к предмету с помощью ИКТ.
Воспитательные:
- активизировать интерес к получению новых знаний, формирование точности и аккуратности при вычислении интеграла и выполнении чертежей.
Оснащение: ПК, операционная система Microsoft Windows 2000/XP, программа MS Office 2007: Power Point, Microsoft Word; мультимедийный проектор, экран.
Литература: учебник Колмагорова А.Н. и др. Алгебра и начала анализа 10-11 кл.
Технологии: ИКТ , индивидуального обучения.
ХОД УРОКА
Этап урока | Деятельность учителя | Деятельность учащихся | Время | |
Вводная часть | ||||
Организационный момент | Приветствует, проверяет готовность учащихся к уроку, организует внимание. Раздает опорный конспект. | Слушают, записывают дату. | 3 мин | |
Сообщение темы и целей урока | Актуализация опорных знаний и субъектного опыта с выходом на цели урока. | Слушают, записывают тему урока в тетради.
Активно включаются в мыслительную деятельность. Анализируют, сравнивают, делают выводы с выходом на цели занятия. | Презентация ИКТ 3 мин | |
Основная часть урока Изложение нового материала с попутной проверкой знаний прошлых тем. | ||||
Определение интеграла (слайд 3) | Даёт определение. ИКТ Что такое криволинейная трапеция? | Фигуру, ограниченная графиком функции, отрезком и прямыми x=a и x=b. | 10 мин | |
Обозначение интеграла (слайд 4) | Вводит обозначение интеграла и то, как он читается. | Слушают, записывают. | ||
История интеграла (слайды 5 и 6) | Рассказывает историю термина «интеграл». | Слушают, коротко записывают. | ||
Формула Ньютона – Лейбница (слайд 7) | Дает формулу Ньютона – Лейбница. Что в формуле обозначает F? | Слушают, записывают, отвечают на вопросы преподавателя. Первообразная. | ||
Заключительная часть урока. | ||||
Закрепление материала. Решение примеров с применением изученного материала | ||||
Пример 1 (слайд 8) | Разбирает решение примера, задавая вопросы по нахождению первообразных для подынтегральных функций. | Слушают, записывают, показывают знание таблицы первообразных. | 20 мин | |
Пример 2 (слайд 9). | Контролирует решение примеров. | Выполняют задание по очереди, комментируя (технология индивидуального обучения ), слушают друг друга, записывают, показывают знание прошлых тем. | ||
Пример 3 (слайд 10) | Разбирает решение примера. Как найти точки пересечения оси абсцисс с графиком функции? | Слушают, отвечают на вопросы, показывают знание прошлых тем, записывают. Подынтегральную функцию приравнять к 0 и решить уравнение. | ||
Пример 4 (слайд 11) | Разбирает решение примера. Как найти точки пересечения (абсциссы) графиков функций? Определите вид треугольника ABC. Как находиться площадь прямоугольного треугольника? | Слушают, отвечают на вопросы. Приравнять функции друг к другу и решить получившееся уравнение. Прямоугольный. где a и b- катеты прямоугольного треугольника. | ||
Подведение итогов урока (слайды 12 и 13) | Организует работу по составлению синквейна. | Участвуют в составлении синквейна. Анализируют, сравнивают, делают выводы по теме. | 5 мин. | |
Задание на дом по уровню сложности. | Дает задание на дом, объясняет. | Слушают, записывают. | 1 мин. | |
Оценивание работы обучающихся на уроке. | Оценивает работу обучающихся на уроке, анализирует. | Слушают. | 1 мин |
Предварительный просмотр:
Опорный конспект по теме «Интеграл. Формула Ньютона-Лейбница».
Определение:
Пусть дана положительная функция
f(x)
, определенная на конечном отрезке . | ||
Обозначение: Читается: «интеграл от a до b эф от икс дэ икс» | ||
Формула Ньютона — Лейбница | ||
Пример 1. Вычислить определённый интеграл: Решение: | ||
Пример 3. и осью абсцисс. Решение: | ||
Пример 3. Вычислить площадь фигуры, ограниченной линиями и . |
Решение прикладных задач сводится к вычислению интеграла, но не всегда это возможно сделать точно. Иногда необходимо знать значение определенного интеграла с некоторой степенью точности, к примеру, до тысячной.
Существуют задачи, когда следовало бы найти приближенное значение определенного интеграла с необходимой точностью, тогда применяют численное интегрирование такое, как метод Симпосна, трапеций, прямоугольников. Не все случаи позволяют вычислить его с определенной точностью.
Не все случаи позволяют вычислить его с определенной точностью.
Данная статья рассматривает применение формулы Ньютона-Лейбница. Это необходимо для точного вычисления определенного интеграла. Будут приведены подробные примеры, рассмотрены замены переменной в определенном интеграле и найдем значения определенного интеграла при интегрировании по частям.
Yandex.RTB R-A-339285-1
Формула Ньютона-Лейбница
Определение 1Когда функция y = y (x) является непрерывной из отрезка [ a ; b ] ,а F (x) является одной из первообразных функции этого отрезка, тогда формула Ньютона-Лейбница считается справедливой. Запишем ее так ∫ a b f (x) d x = F (b) — F (a) .
Данную формулу считают основной формулой интегрального исчисления.
Чтобы произвести доказательство этой формулы, необходимо использовать понятие интеграла с имеющимся переменным верхним пределом.
Когда функция y = f (x) непрерывна из отрезка [ a ; b ] , тогда значение аргумента x ∈ a ; b , а интеграл имеет вид ∫ a x f (t) d t и считается функцией верхнего предела. Необходимо принять обозначение функции примет вид ∫ a x f (t) d t = Φ (x) , она является непрерывной, причем для нее справедливо неравенство вида ∫ a x f (t) d t » = Φ » (x) = f (x) .
Необходимо принять обозначение функции примет вид ∫ a x f (t) d t = Φ (x) , она является непрерывной, причем для нее справедливо неравенство вида ∫ a x f (t) d t » = Φ » (x) = f (x) .
Зафиксируем, что приращении функции Φ (x) соответствует приращению аргумента ∆ x , необходимо воспользоваться пятым основным свойством определенного интеграла и получим
Φ (x + ∆ x) — Φ x = ∫ a x + ∆ x f (t) d t — ∫ a x f (t) d t = = ∫ a x + ∆ x f (t) d t = f (c) · x + ∆ x — x = f (c) · ∆ x
где значение c ∈ x ; x + ∆ x .
Зафиксируем равенство в виде Φ (x + ∆ x) — Φ (x) ∆ x = f (c) . По определению производной функции необходимо переходить к пределу при ∆ x → 0 , тогда получаем формулу вида Φ » (x) = f (x) . Получаем, что Φ (x) является одной из первообразных для функции вида y = f (x) , расположенной на [ a ; b ] . Иначе выражение можно записать
F (x) = Φ (x) + C = ∫ a x f (t) d t + C , где значение C является постоянной.
Произведем вычисление F (a) с использованием первого свойства определенного интеграла. Тогда получаем, что
Тогда получаем, что
F (a) = Φ (a) + C = ∫ a a f (t) d t + C = 0 + C = C , отсюда получаем, что C = F (a) . Результат применим при вычислении F (b) и получим:
F (b) = Φ (b) + C = ∫ a b f (t) d t + C = ∫ a b f (t) d t + F (a) , иначе говоря, F (b) = ∫ a b f (t) d t + F (a) . Равенство доказывает формулу Ньютона-Лейбница ∫ a b f (x) d x + F (b) — F (a) .
Приращение функции принимаем как F x a b = F (b) — F (a) . С помощью обозначения формулу Ньютона-Лейбница принимает вид ∫ a b f (x) d x = F x a b = F (b) — F (a) .
Чтобы применить формулу, обязательно необходимо знать одну из первообразных y = F (x) подынтегральной функции y = f (x) из отрезка [ a ; b ] , произвести вычисление приращения первообразной из этого отрезка. Рассмотрим несколько примером вычисления, используя формулу Ньютона-Лейбница.
Пример 1
Произвести вычисление определенного интеграла ∫ 1 3 x 2 d x по формуле Ньютона-Лейбница.
Решение
Рассмотрим, что подынтегральная функция вида y = x 2 является непрерывной из отрезка [ 1 ; 3 ] , тогда и интегрируема на этом отрезке. По таблице неопределенных интегралов видим, что функция y = x 2 имеет множество первообразных для всех действительных значений x , значит, x ∈ 1 ; 3 запишется как F (x) = ∫ x 2 d x = x 3 3 + C . Необходимо взять первообразную с С = 0 , тогда получаем, что F (x) = x 3 3 .
По таблице неопределенных интегралов видим, что функция y = x 2 имеет множество первообразных для всех действительных значений x , значит, x ∈ 1 ; 3 запишется как F (x) = ∫ x 2 d x = x 3 3 + C . Необходимо взять первообразную с С = 0 , тогда получаем, что F (x) = x 3 3 .
Воспользуемся формулой Ньютона-Лейбница и получим, что вычисление определенного интеграла примет вид ∫ 1 3 x 2 d x = x 3 3 1 3 = 3 3 3 — 1 3 3 = 26 3 .
Ответ: ∫ 1 3 x 2 d x = 26 3
Пример 2
Произвести вычисление определенного интеграла ∫ — 1 2 x · e x 2 + 1 d x по формуле Ньютона-Лейбница.
Решение
Заданная функция непрерывна из отрезка [ — 1 ; 2 ] , значит, на нем интегрируема. Необходимо найти значение неопределенного интеграла ∫ x · e x 2 + 1 d x при помощи метода подведения под знак дифференциала, тогда получаем ∫ x · e x 2 + 1 d x = 1 2 ∫ e x 2 + 1 d (x 2 + 1) = 1 2 e x 2 + 1 + C .
Отсюда имеем множество первообразных функции y = x · e x 2 + 1 , которые действительны для всех x , x ∈ — 1 ; 2 .
Необходимо взять первообразную при С = 0 и применить формулу Ньютона-Лейбница. Тогда получим выражение вида
∫ — 1 2 x · e x 2 + 1 d x = 1 2 e x 2 + 1 — 1 2 = = 1 2 e 2 2 + 1 — 1 2 e (- 1) 2 + 1 = 1 2 e (- 1) 2 + 1 = 1 2 e 2 (e 3 — 1)
Ответ: ∫ — 1 2 x · e x 2 + 1 d x = 1 2 e 2 (e 3 — 1)
Пример 3
Произвести вычисление интегралов ∫ — 4 — 1 2 4 x 3 + 2 x 2 d x и ∫ — 1 1 4 x 3 + 2 x 2 d x .
Решение
Отрезок — 4 ; — 1 2 говорит о том, что функция, находящаяся под знаком интеграла, является непрерывной, значит, она интегрируема. Отсюда найдем множество первообразных функции y = 4 x 3 + 2 x 2 . Получаем, что
∫ 4 x 3 + 2 x 2 d x = 4 ∫ x d x + 2 ∫ x — 2 d x = 2 x 2 — 2 x + C
Необходимо взять первообразную F (x) = 2 x 2 — 2 x , тогда, применив формулу Ньютона-Лейбница, получаем интеграл, который вычисляем:
∫ — 4 — 1 2 4 x 3 + 2 x 2 d x = 2 x 2 — 2 x — 4 — 1 2 = 2 — 1 2 2 — 2 — 1 2 — 2 — 4 2 — 2 — 4 = 1 2 + 4 — 32 — 1 2 = — 28
Производим переход к вычислению второго интеграла.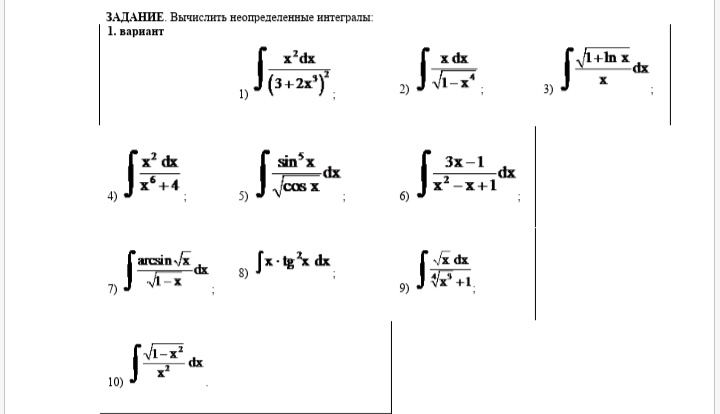
Из отрезка [ — 1 ; 1 ] имеем, что подынтегральная функция считается неограниченной, потому как lim x → 0 4 x 3 + 2 x 2 = + ∞ , тогда отсюда следует, что необходимым условием интегрируемости из отрезка. Тогда F (x) = 2 x 2 — 2 x не является первообразной для y = 4 x 3 + 2 x 2 из отрезка [ — 1 ; 1 ] , так как точка O принадлежит отрезку, но не входит в область определения. Значит, что имеется определенный интеграл Римана и Ньютона-Лейбница для функции y = 4 x 3 + 2 x 2 из отрезка [ — 1 ; 1 ] .
Ответ: ∫ — 4 — 1 2 4 x 3 + 2 x 2 d x = — 28 , имеется определенный интеграл Римана и Ньютона-Лейбница для функции y = 4 x 3 + 2 x 2 из отрезка [ — 1 ; 1 ] .
Перед использованием формулы Ньютона-Лейбница нужно точно знать о существовании определенного интеграла.
Замена переменной в определенном интеграле
Когда функция y = f (x) является определенной и непрерывной из отрезка [ a ; b ] , тогда имеющееся множество [ a ; b ] считается областью значений функции x = g (z) , определенной на отрезке α ; β с имеющейся непрерывной производной, где g (α) = a и g β = b , отсюда получаем, что ∫ a b f (x) d x = ∫ α β f (g (z)) · g » (z) d z .
Данную формулу применяют тогда, когда нужно вычислять интеграл ∫ a b f (x) d x , где неопределенный интеграл имеет вид ∫ f (x) d x , вычисляем при помощи метода подстановки.
Пример 4
Произвести вычисление определенного интеграла вида ∫ 9 18 1 x 2 x — 9 d x .
Решение
Подынтегральная функция считается непрерывной на отрезке интегрирования, значит определенный интеграл имеет место на существование. Дадим обозначение, что 2 x — 9 = z ⇒ x = g (z) = z 2 + 9 2 . Значение х = 9 , значит, что z = 2 · 9 — 9 = 9 = 3 , а при х = 18 получаем, что z = 2 · 18 — 9 = 27 = 3 3 , тогда g α = g (3) = 9 , g β = g 3 3 = 18 . При подстановке полученных значений в формулу ∫ a b f (x) d x = ∫ α β f (g (z)) · g » (z) d z получаем, что
∫ 9 18 1 x 2 x — 9 d x = ∫ 3 3 3 1 z 2 + 9 2 · z · z 2 + 9 2 » d z = = ∫ 3 3 3 1 z 2 + 9 2 · z · z d z = ∫ 3 3 3 2 z 2 + 9 d z
По таблице неопределенных интегралов имеем, что одна из первообразных функции 2 z 2 + 9 принимает значение 2 3 a r c t g z 3 . Тогда при применении формулы Ньютона-Лейбница получаем, что
Тогда при применении формулы Ньютона-Лейбница получаем, что
∫ 3 3 3 2 z 2 + 9 d z = 2 3 a r c t g z 3 3 3 3 = 2 3 a r c t g 3 3 3 — 2 3 a r c t g 3 3 = 2 3 a r c t g 3 — a r c t g 1 = 2 3 π 3 — π 4 = π 18
Нахождение можно было производить, не используя формулу ∫ a b f (x) d x = ∫ α β f (g (z)) · g » (z) d z .
Если при методе замены использовать интеграл вида ∫ 1 x 2 x — 9 d x , то можно прийти к результату ∫ 1 x 2 x — 9 d x = 2 3 a r c t g 2 x — 9 3 + C .
Отсюда произведем вычисления по формуле Ньютона-Лейбница и вычислим определенный интеграл. Получаем, что
∫ 9 18 2 z 2 + 9 d z = 2 3 a r c t g z 3 9 18 = = 2 3 a r c t g 2 · 18 — 9 3 — a r c t g 2 · 9 — 9 3 = = 2 3 a r c t g 3 — a r c t g 1 = 2 3 π 3 — π 4 = π 18
Результаты совпали.
Ответ: ∫ 9 18 2 x 2 x — 9 d x = π 18
Интегрирование по частям при вычислении определенного интеграла
Если на отрезке [ a ; b ] определены и непрерывны функции u (x) и v (x) , тогда их производные первого порядка v » (x) · u (x) являются интегрируемыми, таким образом из этого отрезка для интегрируемой функции u » (x) · v (x) равенство ∫ a b v » (x) · u (x) d x = (u (x) · v (x)) a b — ∫ a b u » (x) · v (x) d x справедливо.
Формулу можно использовать тогда, необходимо вычислять интеграл ∫ a b f (x) d x , причем ∫ f (x) d x необходимо было искать его при помощи интегрирования по частям.
Пример 5
Произвести вычисление определенного интеграла ∫ — π 2 3 π 2 x · sin x 3 + π 6 d x .
Решение
Функция x · sin x 3 + π 6 интегрируема на отрезке — π 2 ; 3 π 2 , значит она непрерывна.
Пусть u (x) = х, тогда d (v (x)) = v » (x) d x = sin x 3 + π 6 d x , причем d (u (x)) = u » (x) d x = d x , а v (x) = — 3 cos π 3 + π 6 . Из формулы ∫ a b v » (x) · u (x) d x = (u (x) · v (x)) a b — ∫ a b u » (x) · v (x) d x получим, что
∫ — π 2 3 π 2 x · sin x 3 + π 6 d x = — 3 x · cos x 3 + π 6 — π 2 3 π 2 — ∫ — π 2 3 π 2 — 3 cos x 3 + π 6 d x = = — 3 · 3 π 2 · cos π 2 + π 6 — — 3 · — π 2 · cos — π 6 + π 6 + 9 sin x 3 + π 6 — π 2 3 π 2 = 9 π 4 — 3 π 2 + 9 sin π 2 + π 6 — sin — π 6 + π 6 = 9 π 4 — 3 π 2 + 9 3 2 = 3 π 4 + 9 3 2
Решение примера можно выполнить другим образом.
Найти множество первообразных функции x · sin x 3 + π 6 при помощи интегрирования по частям с применением формулы Ньютона-Лейбница:
∫ x · sin x x 3 + π 6 d x = u = x , d v = sin x 3 + π 6 d x ⇒ d u = d x , v = — 3 cos x 3 + π 6 = = — 3 cos x 3 + π 6 + 3 ∫ cos x 3 + π 6 d x = = — 3 x cos x 3 + π 6 + 9 sin x 3 + π 6 + C ⇒ ∫ — π 2 3 π 2 x · sin x 3 + π 6 d x = — 3 cos x 3 + π 6 + 9 sincos x 3 + π 6 — — — 3 · — π 2 · cos — π 6 + π 6 + 9 sin — π 6 + π 6 = = 9 π 4 + 9 3 2 — 3 π 2 — 0 = 3 π 4 + 9 3 2
Ответ: ∫ x · sin x x 3 + π 6 d x = 3 π 4 + 9 3 2
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Формула Ньютона — Лейбница
Основная теорема анализа или формула Ньютона — Лейбница даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной
Формулировка
Рассмотрим интеграл от функции y = f (x )
в пределах от постоянного числа a до числа x , которое будем считать переменным. Запишем интеграл в следующем виде:
Запишем интеграл в следующем виде:
Данный вид интеграла называется интегралом с переменным верхним пределом. Используя теорему о среднем в определённом интеграле , легко показать что данная функция непрерывная и дифференцируемая. А также производная от данной функции в точке x равна самой интегрируемой функции. От сюда следует, что любая непрерывная функция имеет первообразную в виде квадратуры: . А так как класс первообразных функций функции f отличается на константу, легко показать, что: определенный интеграл от функции f на равен разности значений первообразных в точках b и а
Wikimedia Foundation . 2010 .
- Формула Полной Вероятности
- Формула Релея — Джинса
Смотреть что такое «Формула Ньютона — Лейбница» в других словарях:
Формула Ньютона-Лейбница — Основная теорема анализа или формула Ньютона Лейбница даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной Формулировка Рассмотрим интеграл от функции y = f(x) в пределах от постоянного числа a до… … Википедия
Формула конечных приращений — У этого термина существуют и другие значения, см. Теорема Лагранжа. Формула конечных приращений или теорема Лагранжа о среднем значении утверждает, что если функция непрерывна на отрезке и … Википедия
Теорема Лагранжа. Формула конечных приращений или теорема Лагранжа о среднем значении утверждает, что если функция непрерывна на отрезке и … Википедия
Формула Стокса — Теорема Стокса одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа. Названа в честь Дж. Г. Стокса. Содержание 1 Общая формулировка 2… … Википедия
НЬЮТОНА — ЛЕЙБНИЦА ФОРМУЛА — формула, выражающая значение определенного интеграла от заданной функции f по отрезку в виде разности значений на концах отрезка любой первообразной Fэтой функции Названа именами И. Ньютона (I. Newton) и Г. Лейбница (G. Leibniz), т. к. правило,… … Математическая энциклопедия
НЬЮТОНА-ЛЕЙБНИЦА ФОРМУЛА — основная формула интегрального исчисления. Выражает связь между определенным интегралом от функции f(x) и какой либо ее первообразной F(x) … Большой Энциклопедический словарь
Формула Лейбница — У этого термина существуют и другие значения, см. Список объектов, названных в честь Лейбница. У этого термина существуют и другие значения, см. Формула Лейбница (значения). Формулой Лейбница в интегральном исчислении называется правило… … Википедия
Список объектов, названных в честь Лейбница. У этого термина существуют и другие значения, см. Формула Лейбница (значения). Формулой Лейбница в интегральном исчислении называется правило… … Википедия
Ньютона-Лейбница формула — Ньютона Лейбница формула, основная формула интегрального исчисления. Выражает связь между определённым интегралом от функции f(х) и какой либо её первообразной F(х). . * * * НЬЮТОНА ЛЕЙБНИЦА ФОРМУЛА НЬЮТОНА ЛЕЙБНИЦА ФОРМУЛА, основная формула… … Энциклопедический словарь
Формула прямоугольников
Формула трапеций — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Теорема Ньютона — Формула Ньютона Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной. Если непрерывна на отрезке и ее любая первообразная на этом отрезке, то имеет … Википедия
Если непрерывна на отрезке и ее любая первообразная на этом отрезке, то имеет … Википедия
Решение интеграла онлайн. Решение неопределённых интегралов Первообразная 3x 3 4x 2
Неопределенный интеграл онлайн
В школе говорят, интеграл – это значок ∫, а вычисление интеграла, то есть процесс интегрирования, – это операция обратная дифференцированию. Согласитесь скучно!
Разумеется, у школьников возникает резонный вопрос: а нафиг он нам нужен?
Но если бы учитель уделил несколько минут на вводную про интегралы, такой вопрос всё равно бы возник, но уже не у всех!
Вводная к интегралам
В далеком 17 веке были на тот момент нерешенные насущные проблемы, а именно изучались закономерности движения тел. Много трудов было проделано Ньютоном, чтобы понять, как вычисляется скорость тела в любой момент времени. Но чем дальше, тем оказалось интереснее.
Допустим, мы знаем закон изменения скорости тела – это некая функция. Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.
Тогда площадь фигуры, ограниченная этой кривой и осью координат, будет равна пройденному пути. Вычисляя неопределенный интеграл от функции, мы как раз находим общий закон движения.
В этом заключается один из физических смыслов интеграла.
Как вы уже поняли, геометрический смысл интеграла – это площадь криволинейной трапеции. Соответственно с помощью кратного интеграла вычисляется объем тела.
Решение интегралов
Лейбниц и Ньютон заложили основы дифференциального и интегрального исчисления. В последующие десятилетия было много великих открытий, связанных с вычислением интегралов.
Поскольку подынтегральная функция может принимать различные виды, естественно это привело к разделению интегралов на свои типы, а главное были отрыты многочисленные методы решения интегралов.
Но не все так безоблачно. На практике часто происходит так, что в аналитическом виде вычислить интегралы невозможно, то есть используя какой-либо известный метод. Конечно, получить аналитическое решение это здорово, но, с другой стороны, главное ведь вычислить точное значение интеграла. В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.
В этом случае интегралы решаются численными методами. Благодаря компьютерным мощностям, такие задачи не представляют особых сложностей для современного человека.
Калькулятор решения интегралов
Теперь самое интересное. Еще каких-то 15 лет назад школьник и помыслить не мог, что под рукой будут такие калькуляторы интегралов, как, например, наш. Это безусловно облегчает процесс обучения. Можно проверять свои решения, находить допущенные ошибки и лучше усваивать образовательный курс.
И тут в который раз повторяем, калькулятор решения интегралов – это только ваш безотказный помощник, к которому можете обратиться в любое время. Но никак не подмена вашей головы. Старайтесь самостоятельно решать задачи, только так можно развивать мышление, а компьютер будет в помощь.
Нахождение неопределенного интеграла является очень частой задачей в высшей математике и других технических разделах науки. Даже решение простейших физических задач часто не обходится без вычисления нескольких простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций. Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно найти решение неопределеленного интеграла от очень сложной функции. Для решения этих проблем для вас будет незаменим наш сервис, позволяющий безошибочно находить неопределенный интеграл онлайн .
Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций. Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно найти решение неопределеленного интеграла от очень сложной функции. Для решения этих проблем для вас будет незаменим наш сервис, позволяющий безошибочно находить неопределенный интеграл онлайн .
Решить неопределенный интеграл
Онлайн сервис на сайт позволяет находить решение интеграла онлайн быстро, бесплатно и качественно. Вы можете заменить поиск по таблицам нужного интеграла нашим сервисом, где быстро введя нужную функции, вы получите решение неопределенного интеграла в табличном варианте. Не все математические сайты способны вычислять неопределенные интегралы функций в режиме онлайн быстро и качественно, особенно если требуется найти неопределенный интеграл от сложной функции или таких функций, которые не включены в общий курс высшей математики. Сайт сайт поможет решить интеграл онлайн и справиться с поставленной задачей. Используя онлайн решение интеграла на сайте сайт, вы всегда получите точный ответ.
Сайт сайт поможет решить интеграл онлайн и справиться с поставленной задачей. Используя онлайн решение интеграла на сайте сайт, вы всегда получите точный ответ.
Даже если вы хотите вычислить интеграл самостоятельно, благодаря нашему сервису вам будет легко проверить свой ответ, найти допущенную ошибку или описку, либо же убедиться в безукоризненном выполнении задания. Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу. Просто воспользуйтесь нашими услугами и найдите неопределенный интеграл онлайн без каких-либо усилий. Для практических задач по нахождению интеграла функции онлайн этот сервер очень полезен. Необходимо ввести заданную функцию, получить онлайн решение неопределенного интеграла и сравнить ответ с вашим решением.
систем уравнений и неравенств
 2), {x, 0.5, 2}
2), {x, 0.5, 2}Решите неопределенный интеграл — WebMath
Быстро! Мне нужна помощь с: Выберите элемент справки по математике … Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование скорости, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция, Графики, Круги hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLinesLines Theotation, The Equation from slopeLines Theotation и Y-intation , Поиск шансов, Математика, Практика многочленов, Математика, Практика основМетрическая система, Преобразование чисел, Сложение чисел, Вычисление с числами, Вычисление с переменными числами, Деление чисел, Умножение чисел, Сравнение числовых линий, Числовые строки, Разместите значения чисел, Произношение чисел, Округление чисел, Вычитание числа слагаемых, Вычитание чисел Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторизация триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, УмножениеФормы, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок
Исчисление I — неопределенные интегралы
Показать мобильное уведомление Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 5-1: Неопределенные интегралы
В последних двух главах нам была задана функция \ (f \ left (x \ right) \), и мы спросили, какова производная этой функции.2} — 9x + c, \, \, \ hspace {0.25in} c {\ mbox {является константой}} \]
даст \ (f \ left (x \ right) \) при дифференцировании.
В последнем примере было два момента. Первым делом нужно было заставить вас задуматься о том, как решать эти задачи. Сначала важно помнить, что мы просто спрашиваем, что мы дифференцировали, чтобы получить данную функцию.
Другой момент — признать, что на самом деле существует бесконечное количество функций, которые мы могли бы использовать, и все они будут отличаться константой.
Теперь, когда мы разобрались с примером, давайте избавимся от некоторых определений и терминологии.
Определения
Для данной функции \ (f \ left (x \ right) \), антипроизводная от \ (f \ left (x \ right) \) является любой функцией \ (F \ left (x \ right) \) такой, что
\ [F ‘\ left (x \ right) = f \ left (x \ right) \]Если \ (F \ left (x \ right) \) — любая антипроизводная от \ (f \ left (x \ right) \), то самая общая антипроизводная от \ (f \ left (x \ right) \) называется неопределенным интегралом и обозначается как
\ [\ int {{е \ left (x \ right) \, dx}} = F \ left (x \ right) + c, \ hspace {0.25in} \, \, \, \, c {\ mbox {любая константа}} \] В этом определении \ (\ int {{}} \) называется интегральным символом , \ (f \ left (x \ right) \) называется подынтегральным выражением , \ (x \) называется Переменная интегрирования и «\ (c \)» называются константой интегрирования . 4} + 3x — 9 \, dx}} \]
Показать решение
4} + 3x — 9 \, dx}} \]
Показать решение
Поскольку на самом деле это запрос на самую общую антипроизводную, нам просто нужно повторно использовать окончательный ответ из первого примера.2} — 9x + c \]
Теперь сделаем пару предупреждений. Одна из наиболее распространенных ошибок, которые студенты делают с интегралами (как неопределенными, так и определенными), — это опускать dx в конце интеграла. Это обязательно! Думайте о знаке интеграла и dx как о скобках. Вы уже знаете и, вероятно, вполне довольны мыслью о том, что каждый раз, когда вы открываете скобку, вы должны закрывать ее. При использовании интегралов воспринимайте знак интеграла как «открытую скобку», а dx — как «закрывающую скобку».5} + c + 3x — 9 \ end {align *} \]
Вы интегрируете только то, что находится между знаком интеграла и dx . Каждый из приведенных выше интегралов заканчивается в разных местах, поэтому мы получаем разные ответы, потому что каждый раз мы интегрируем разное количество членов. Во втором интеграле «-9» находится за пределами интеграла, поэтому его оставляют отдельно и не интегрируют. Точно так же в третьем интеграле «\ (3x — 9 \)» находится вне интеграла и поэтому остается в покое.
Во втором интеграле «-9» находится за пределами интеграла, поэтому его оставляют отдельно и не интегрируют. Точно так же в третьем интеграле «\ (3x — 9 \)» находится вне интеграла и поэтому остается в покое.
Знание, какие члены нужно интегрировать, — не единственная причина для записи \ (dx \) вниз.В разделе «Правило замены» мы фактически будем работать с \ (dx \) в задаче, и если у нас нет привычки записывать его, о нем легко забыть, и тогда мы получим неправильный ответ на этот этап.
Мораль заключается в том, чтобы убедиться и вставить \ (dx \)! На данном этапе это может показаться глупым поступком, но это просто должно быть там, хотя бы по той причине, что знать, где заканчивается интеграл.
Кстати, обозначение \ (dx \) должно показаться вам немного знакомым.Мы видели подобные вещи пару разделов назад. Мы назвали \ (dx \) дифференциалом в этом разделе, и да, это именно то, что он есть. \ (Dx \), завершающий интеграл, — не что иное, как дифференциал. 2} — 9w + c \ end {align *} \]
2} — 9w + c \ end {align *} \]
Изменение переменной интегрирования в интеграле просто изменяет переменную в ответе.Однако важно отметить, что при изменении переменной интегрирования в интеграле мы также изменили дифференциал (\ (dx \), \ (dt \) или \ (dw \)), чтобы он соответствовал новой переменной. Это более важно, чем мы могли бы сейчас представить.
Другое использование дифференциала в конце интеграла — сказать нам, по какой переменной мы интегрируем. На данном этапе это может показаться несущественным, поскольку большинство интегралов, с которыми мы собираемся здесь работать, будут включать только одну переменную.Однако, если вы находитесь на пути к получению степени, который приведет вас к исчислению с несколькими переменными, это будет очень важно на этом этапе, поскольку в задаче будет более одной переменной. Вам нужно выработать привычку записывать правильный дифференциал в конце интеграла, чтобы, когда это станет важным в этих классах, вы уже будете иметь привычку записывать его.
Чтобы понять, почему это важно, взгляните на следующие два интеграла.
\ [\ int {{2x \, dx}} \ hspace {1.2} + c \]Второй интеграл тоже довольно прост, но нам нужно быть осторожными. dx сообщает нам, что мы интегрируем \ (x \) ’s. Это означает, что мы интегрируем только \ (x \), которые находятся в подынтегральном выражении, а все другие переменные в подынтегральном выражении считаются константами. Тогда второй интеграл равен
. \ [\ int {{2t \, dx}} = 2tx + c \]Таким образом, может показаться глупым всегда использовать dx , но это жизненно важная нотация, которая может заставить нас получить неправильный ответ, если мы не введем его.
Теперь есть несколько важных свойств интегралов, на которые мы должны обратить внимание.
Свойства неопределенного интеграла
- \ (\ displaystyle \ int {{k \, f \ left (x \ right) \, dx}} = k \ int {{f \ left (x \ right) \, dx}} \) где \ ( к \) — любое число.
 Итак, мы можем выделить мультипликативные константы из неопределенных интегралов.
Итак, мы можем выделить мультипликативные константы из неопределенных интегралов.См. Раздел «Доказательство различных интегральных формул» в главе «Дополнительно», чтобы увидеть доказательство этого свойства.
- \ (\ displaystyle \ int {{- f \ left (x \ right) \, dx}} = — \ int {{f \ left (x \ right) \, dx}} \). Это действительно первое свойство с \ (k = — 1 \), поэтому доказательства этого свойства не приводятся.
- \ (\ Displaystyle \ int {{е \ влево (х \ вправо) \ пм г \ влево (х \ вправо) \, dx}} = \ int {{е \ влево (х \ вправо) \, dx}} \ pm \ int {{g \ left (x \ right) \, dx}} \). Другими словами, интеграл от суммы или разности функций — это сумма или разность отдельных интегралов.Это правило можно расширить на любое количество функций.
См. Раздел «Доказательство различных интегральных формул» в главе «Дополнительно», чтобы увидеть доказательство этого свойства.
Обратите внимание, что когда мы работали с первым примером выше, мы использовали первое и третье свойство в обсуждении. Мы интегрировали каждый термин индивидуально, вернули все константы, а затем снова собрали все вместе с соответствующим знаком.
Мы интегрировали каждый термин индивидуально, вернули все константы, а затем снова собрали все вместе с соответствующим знаком.
В приведенных выше свойствах не указаны интегралы от произведений и частных.Причина этого проста. Как и в случае с производными финансовыми инструментами, каждое из следующих действий НЕ будет работать.
\ [\ int {{f \ left (x \ right) g \ left (x \ right) \, dx}} \ ne \ int {{f \ left (x \ right) dx}} \ int {{g \ left (x \ right) \, dx}} \ hspace {0.75in} \ int {{\ frac {{f \ left (x \ right)}} {{g \ left (x \ right)}} \, dx }} \ ne \ frac {{\ int {{f \ left (x \ right) \, dx}}}} {{\ int {{g \ left (x \ right) \, dx}}}} \] В случае деривативов у нас было правило продукта и правило частного, чтобы иметь дело с этими случаями. Однако с интегралами таких правил нет.Когда мы сталкиваемся с произведением и частным в интеграле, у нас будет множество способов справиться с ним, в зависимости от того, что такое подынтегральное выражение. 4} + 3x — 9 \), что было \ (f \ left (x \ right) \)?
Показать решение
4} + 3x — 9 \), что было \ (f \ left (x \ right) \)?
Показать решение
К этому моменту в этом разделе это простой вопрос.2} — 9x + c \]
В этом разделе мы продолжали вычислять один и тот же неопределенный интеграл во всех наших примерах. Целью этого раздела было не делать неопределенные интегралы, а вместо этого познакомить нас с обозначениями и некоторыми основными идеями и свойствами неопределенных интегралов. Следующая пара разделов посвящена фактическому вычислению неопределенных интегралов.
2. Первообразные и неопределенный интеграл
М.3 + K` и произнеси прописью:
«Интеграл 3 x 2 относительно x равно x 3 + K . «
Знак интеграла
Знак `int` представляет собой удлиненную букву» S «,
стоя для «суммы». (В старонемецком и английском языках буква «s» часто писалась с использованием этой удлиненной формы. ) Позже мы увидим, что интеграл — это — сумма площадей бесконечно тонких прямоугольников.
) Позже мы увидим, что интеграл — это — сумма площадей бесконечно тонких прямоугольников.
«сумма» — это символ «сумма».Его можно использовать для конечных или бесконечных сумм.
int — это символ суммы бесконечного числа бесконечно малых областей (или других переменных).
Обозначение «длинное s» было введено Лейбницем, когда он разрабатывал концепции интеграции.
Другие обозначения для интегралов
Примечание: Иногда мы пишем заглавную букву для обозначения интеграции. Например, мы пишем F ( x ), чтобы означать интеграл f ( x ).3} {3} -5x + K`
Теперь мы узнаем некоторые важные общие правила интеграции.
A. Интеграл постоянной
`intk dx = kx + K`
(k и K — константы.)
Интеграл постоянной — это постоянные времена x плюс константа.
Пример 3
Найдите `int4 dx`
Ответ
Используя наше новое правило, мы можем просто написать:
`int4 dx = 4x + K`
Всегда проверяйте по , дифференцируя , свой ответ, и вы должны вернуться к тому, что вопрос просил вас интегрировать. 2 + 9) + К`
2 + 9) + К`
Пример 14
Для данного `y ‘= sqrt (2x + 1` найти функцию` y = f (x) `, который проходит через точку` (0,2) `.
Ответ
ПРИМЕЧАНИЕ: y означает производную от y, то есть (dy) / dx.
`y ‘= sqrt (2x + 1`
Так
`y = intsqrt (2x + 1) dx`
Этот вопрос требует от нас интегрирования и в процессе нахождения константы интегрирования .(3 // 2)) / 3 + 5 / 3`
— это обязательная функция.
Вот график ответа, который мы нашли в примере 14. Вы можете видеть, что он проходит через (2, 0).
График и , проходящий через (2, 0).
Примечание: в этой работе вы увидите «+ K» и «+ C». Большинство учебники используют + C.
Рекомендуется всегда использовать , использовать + K , если вы отвечаете на вопросы электриков. проблемы.
проблемы.
Калькулятор неопределенного интеграла
Спортивная математика Финансовая математика.Все права принадлежат владельцу! F = ∫ƒ dx. Все права принадлежат владельцу! Однако ничто не гарантирует, что операцию справа будет легче провести. Будет ли это преобразование полезным или удобным с точки зрения вычислений, будет зависеть от контекста, и вы даже можете использовать его наоборот, если это более удобно. Он пишется с помощью интегрального символа без границ. Мы начнем с некоторых основных неопределенных интегралов. Калькулятор определенного интеграла вычисляет определенный интеграл функции по интервалу, используя численное интегрирование.Помимо вычисления простого интегрирования, эти калькуляторы интегралов могут также вычислять и решать множественные интегралы, такие как: двойное интегрирование, тройное интегрирование и т. Д. Процедура использования калькулятора неопределенного интеграла следующая: Шаг 1: Введите функцию и… Поиск неопределенный интеграл — очень распространенная задача в математике и других технических науках. Обратитесь к списку стандартных неопределенных интегральных формул, который может вам понадобиться как часть работы и упростить вашу работу. — Решатель системных уравнений и матричные операции (жорданова форма, собственные значения, определитель и т. Д.)…). Теперь это тождество успешно утверждает, что вычисление тройного интеграла в LHS равносильно вычислению поверхностного интеграла (двойного интеграла) в RHS. Нажмите, чтобы сфотографировать проблему. Первая фундаментальная теорема исчисления позволяет вычислять определенные интегралы в терминах неопределенных интегралов. Используйте наш калькулятор неопределенного интеграла для решения определенных и неопределенных значений. √ Предварительный просмотр: Функция ввода:? В этом разделе нам нужно начать думать о том, как мы на самом деле вычисляем неопределенные интегралы.Участники уровня Premier, пожалуйста, войдите здесь. В предыдущем разделе мы начали рассматривать неопределенные интегралы, а в этом разделе мы сосредоточились почти исключительно на обозначениях, понятиях и свойствах неопределенного интеграла.
Обратитесь к списку стандартных неопределенных интегральных формул, который может вам понадобиться как часть работы и упростить вашу работу. — Решатель системных уравнений и матричные операции (жорданова форма, собственные значения, определитель и т. Д.)…). Теперь это тождество успешно утверждает, что вычисление тройного интеграла в LHS равносильно вычислению поверхностного интеграла (двойного интеграла) в RHS. Нажмите, чтобы сфотографировать проблему. Первая фундаментальная теорема исчисления позволяет вычислять определенные интегралы в терминах неопределенных интегралов. Используйте наш калькулятор неопределенного интеграла для решения определенных и неопределенных значений. √ Предварительный просмотр: Функция ввода:? В этом разделе нам нужно начать думать о том, как мы на самом деле вычисляем неопределенные интегралы.Участники уровня Premier, пожалуйста, войдите здесь. В предыдущем разделе мы начали рассматривать неопределенные интегралы, а в этом разделе мы сосредоточились почти исключительно на обозначениях, понятиях и свойствах неопределенного интеграла. Игры; Доска объявлений; О; Оцените интеграл. Шаг 1:… Процедура использования калькулятора определенных интегралов выглядит следующим образом:… Первый интеграл, который мы рассмотрим, является интегралом степени… Подробные пошаговые решения вашей интеграции путем подстановки задач онлайн с наш математический решатель и калькулятор.Удивительные подробности о калькуляторе определенного интеграла, о котором большинство людей не подозревают, слухи, ложь и калькулятор определенного интеграла. Онлайн-сервис OnSolver.com позволяет найти определенное комплексное решение в режиме онлайн. Показать инструкции. … Установка постоянных интегрирования Пример 3 Рассмотрим ракету, скорость которой в метрах в секунду в момент времени t секунд после запуска равна v = bt2, где b = 3 мс − 3. Интеграция с помощью калькулятора замены онлайн с решением и шагами. Калькулятор определенного и неправильного интеграла.В этом видеоуроке по исчислению объясняется, как найти неопределенный интеграл функции. Решатели проблем.
Игры; Доска объявлений; О; Оцените интеграл. Шаг 1:… Процедура использования калькулятора определенных интегралов выглядит следующим образом:… Первый интеграл, который мы рассмотрим, является интегралом степени… Подробные пошаговые решения вашей интеграции путем подстановки задач онлайн с наш математический решатель и калькулятор.Удивительные подробности о калькуляторе определенного интеграла, о котором большинство людей не подозревают, слухи, ложь и калькулятор определенного интеграла. Онлайн-сервис OnSolver.com позволяет найти определенное комплексное решение в режиме онлайн. Показать инструкции. … Установка постоянных интегрирования Пример 3 Рассмотрим ракету, скорость которой в метрах в секунду в момент времени t секунд после запуска равна v = bt2, где b = 3 мс − 3. Интеграция с помощью калькулятора замены онлайн с решением и шагами. Калькулятор определенного и неправильного интеграла.В этом видеоуроке по исчислению объясняется, как найти неопределенный интеграл функции. Решатели проблем. Решатель уравнений Калькулятор разложения на множители Производные графа Интегралы Первообразные Пределы матрицы суммирования. Результат будет показан ниже. Кроме того, вычисление интегрального калькулятора дает ощущение простоты… Элементарные функции — это константы, полиномы, экспоненциальные, логарифмические, тригонометрические и гиперболические функции, а также их обратные. где F и ƒ являются функциями от x, а F дифференцируема.Предположим, что дифференцирование функции F приводит к другой функции f, а интегрирование f дает интеграл. Мы предлагаем нашим уважаемым клиентам еще один великолепный инструмент под названием «Калькулятор интеграции по частям». Если это неопределенный интеграл, калькулятор интегралов просто использует константу интегрирования для вычисления выражения. Неопределенный интеграл: пошаговое решение; Альтернативная форма интеграла: Разложение в ряд… Введение понятия интеграла и его G.Обозначения Лейбница относятся к падению 1675 года. Калькулятор вычислит определенное (т.
Решатель уравнений Калькулятор разложения на множители Производные графа Интегралы Первообразные Пределы матрицы суммирования. Результат будет показан ниже. Кроме того, вычисление интегрального калькулятора дает ощущение простоты… Элементарные функции — это константы, полиномы, экспоненциальные, логарифмические, тригонометрические и гиперболические функции, а также их обратные. где F и ƒ являются функциями от x, а F дифференцируема.Предположим, что дифференцирование функции F приводит к другой функции f, а интегрирование f дает интеграл. Мы предлагаем нашим уважаемым клиентам еще один великолепный инструмент под названием «Калькулятор интеграции по частям». Если это неопределенный интеграл, калькулятор интегралов просто использует константу интегрирования для вычисления выражения. Неопределенный интеграл: пошаговое решение; Альтернативная форма интеграла: Разложение в ряд… Введение понятия интеграла и его G.Обозначения Лейбница относятся к падению 1675 года. Калькулятор вычислит определенное (т. е. часто записывается как F (x) = ∫ƒ (x) dx или F = ∫ƒ dx, где и F, и ƒ являются функциями x, и F является дифференцируемым. Раздел 3: Фиксация постоянных интегрирования 12 3. Программа для вычисления неопределенного интеграла (первообразной) не просто дает ответ на проблему, она дает подробное решение с пояснениями, т.е. предположим, что дифференцирование F дает f, и интегрирование f дает интеграл.ENG • ESP. Узнайте, как найти предел функции здесь. Просто щелкните синюю стрелку, и появится решенный пример. В следующих разделах нашей статьи вы познакомитесь с Важным списком формул неопределенного интеграла. ∫ Мы обсудим, как найти первообразные, которые можно записать в терминах элементарных функций. На самом деле решение простейших физических задач редко обходится без нескольких вычислений простых интегралов. Вычислить. Калькулятор сейчас находится в демонстрационном режиме, и некоторые поля ввода недоступны для редактирования.В общем, вы можете пропустить знак умножения, поэтому «5x» эквивалентно «5 * x».
е. часто записывается как F (x) = ∫ƒ (x) dx или F = ∫ƒ dx, где и F, и ƒ являются функциями x, и F является дифференцируемым. Раздел 3: Фиксация постоянных интегрирования 12 3. Программа для вычисления неопределенного интеграла (первообразной) не просто дает ответ на проблему, она дает подробное решение с пояснениями, т.е. предположим, что дифференцирование F дает f, и интегрирование f дает интеграл.ENG • ESP. Узнайте, как найти предел функции здесь. Просто щелкните синюю стрелку, и появится решенный пример. В следующих разделах нашей статьи вы познакомитесь с Важным списком формул неопределенного интеграла. ∫ Мы обсудим, как найти первообразные, которые можно записать в терминах элементарных функций. На самом деле решение простейших физических задач редко обходится без нескольких вычислений простых интегралов. Вычислить. Калькулятор сейчас находится в демонстрационном режиме, и некоторые поля ввода недоступны для редактирования.В общем, вы можете пропустить знак умножения, поэтому «5x» эквивалентно «5 * x». 2} + 7 \) Подсказка: если вы помните свои производные правила и тот факт, что вся эта проблема на самом деле нам нужно определить функцию, которую мы дифференцировали, чтобы получить подынтегральное выражение (т.2 + 2 * x + 1 d: Оценка: Вывод: Синтаксис: Да, пожалуйста, помогите исправить мой ввод в правильную систему Mathematica®… Интеграция путем подстановки… Онлайн-калькулятор неопределенного интеграла BYJU ускоряет вычисления и отображает первообразную функции за доли секунды. Вы можете легко и бесплатно вычислить двойные или тройные, определенные или неопределенные интегралы. этой проблемы тоже быть не должно … Процесс нахождения этих первообразных обозначается неопределенным интегралом. Вычислите каждый из следующих неопределенных интегралов.- Построение 2D и 3D функций. Если в момент времени t = 2 с … Главный девиз … В исчислении первообразная, обратная производная, примитивная функция, примитивный интеграл или неопределенный интеграл функции f является дифференцируемой функцией F, производная которой равна исходной функции f.
2} + 7 \) Подсказка: если вы помните свои производные правила и тот факт, что вся эта проблема на самом деле нам нужно определить функцию, которую мы дифференцировали, чтобы получить подынтегральное выражение (т.2 + 2 * x + 1 d: Оценка: Вывод: Синтаксис: Да, пожалуйста, помогите исправить мой ввод в правильную систему Mathematica®… Интеграция путем подстановки… Онлайн-калькулятор неопределенного интеграла BYJU ускоряет вычисления и отображает первообразную функции за доли секунды. Вы можете легко и бесплатно вычислить двойные или тройные, определенные или неопределенные интегралы. этой проблемы тоже быть не должно … Процесс нахождения этих первообразных обозначается неопределенным интегралом. Вычислите каждый из следующих неопределенных интегралов.- Построение 2D и 3D функций. Если в момент времени t = 2 с … Главный девиз … В исчислении первообразная, обратная производная, примитивная функция, примитивный интеграл или неопределенный интеграл функции f является дифференцируемой функцией F, производная которой равна исходной функции f. .Справка по входам. Нажмите «Вперед!» чтобы начать интегральный расчет. Этот калькулятор дает неопределенный интеграл входной функции. Что такое двойной интеграл? Any… Этот калькулятор для решения неопределенных интегралов взят от Wolfram Alpha LLC. Что ж, вы получите то же самое сложное выражение, что и исходное выражение. Вот список лучших бесплатных программ интегрального калькулятора для решения задач интеграции. Этот калькулятор вычисляет определенные и неопределенные интегралы (первообразную) функции по переменной x.2… Калькуляторы Темы Методы решения становятся премиальными. Интегралы — шаг за шагом. Абсолютно бесплатный онлайн пошаговый определенный и неопределенный… Калькуляторы. В приведенной выше форме он называется интегралом Реймана и… Калькулятор определенных интегралов — это бесплатный онлайн-инструмент, который отображает значение интегральной функции, когда заданы нижний и верхний пределы. Неопределенный интеграл — это скорее общая форма интегрирования, и его можно интерпретировать как антипроизводную рассматриваемой функции.
.Справка по входам. Нажмите «Вперед!» чтобы начать интегральный расчет. Этот калькулятор дает неопределенный интеграл входной функции. Что такое двойной интеграл? Any… Этот калькулятор для решения неопределенных интегралов взят от Wolfram Alpha LLC. Что ж, вы получите то же самое сложное выражение, что и исходное выражение. Вот список лучших бесплатных программ интегрального калькулятора для решения задач интеграции. Этот калькулятор вычисляет определенные и неопределенные интегралы (первообразную) функции по переменной x.2… Калькуляторы Темы Методы решения становятся премиальными. Интегралы — шаг за шагом. Абсолютно бесплатный онлайн пошаговый определенный и неопределенный… Калькуляторы. В приведенной выше форме он называется интегралом Реймана и… Калькулятор определенных интегралов — это бесплатный онлайн-инструмент, который отображает значение интегральной функции, когда заданы нижний и верхний пределы. Неопределенный интеграл — это скорее общая форма интегрирования, и его можно интерпретировать как антипроизводную рассматриваемой функции. Интеграл вида intf (z) dz, (1) т.е.без верхнего и нижнего пределов, также называемый первообразной. Расширенная клавиатура; Загрузить; Примеры; Случайный; Предполагая, что «неопределенный интеграл» относится к вычислению | Используйте как общую тему или вместо этого обратитесь к математическому определению или слову. Неопределенный интеграл. Как пользоваться калькулятором неопределенного интеграла? Этот калькулятор для решения определенных интегралов взят от Wolfram Alpha LLC. Интегральный калькулятор. Онлайн-калькулятор определенных интегралов BYJU ускоряет вычисления, показывая результат интегральной функции за доли секунды.калькуляторы. Введите любой интеграл, чтобы получить решение, шаги и график. … Игры; ГЛАВНОЕ МЕНЮ; Решение проблем; Фракции; Факторинг; Матрицы и системы уравнений; Калькулятор производных; Интегралы — шаг за шагом; Асимптоты; Обратная функция; Калькулятор статистики; Дифференциальные уравнения; Дом. Практика построения графиков решений; Бета геометрии; Шпаргалки по группам записных книжек; Войти; Присоединиться; Обновление; Детали учетной записи Параметры входа в систему Учетная запись… В частности, эта теорема утверждает, что если F — неопределенный интеграл для комплексной функции f (z), то int_a ^ bf (z) dz = F (b) -F (a).
Интеграл вида intf (z) dz, (1) т.е.без верхнего и нижнего пределов, также называемый первообразной. Расширенная клавиатура; Загрузить; Примеры; Случайный; Предполагая, что «неопределенный интеграл» относится к вычислению | Используйте как общую тему или вместо этого обратитесь к математическому определению или слову. Неопределенный интеграл. Как пользоваться калькулятором неопределенного интеграла? Этот калькулятор для решения определенных интегралов взят от Wolfram Alpha LLC. Интегральный калькулятор. Онлайн-калькулятор определенных интегралов BYJU ускоряет вычисления, показывая результат интегральной функции за доли секунды.калькуляторы. Введите любой интеграл, чтобы получить решение, шаги и график. … Игры; ГЛАВНОЕ МЕНЮ; Решение проблем; Фракции; Факторинг; Матрицы и системы уравнений; Калькулятор производных; Интегралы — шаг за шагом; Асимптоты; Обратная функция; Калькулятор статистики; Дифференциальные уравнения; Дом. Практика построения графиков решений; Бета геометрии; Шпаргалки по группам записных книжек; Войти; Присоединиться; Обновление; Детали учетной записи Параметры входа в систему Учетная запись… В частности, эта теорема утверждает, что если F — неопределенный интеграл для комплексной функции f (z), то int_a ^ bf (z) dz = F (b) -F (a). Интегральный калькулятор. по логарифмам вычислить следующие интегралы: (щелкните по зеленым буквам для решения) (a) R ln (x) dx, (b) R ln (2x) dx, (c) R ln (x3) dx, (d) R ln (3×2) dx. Калькулятор удобен в использовании и доступен с любого устройства, а результаты вычислений интегралов и шагов решения можно легко скопировать в буфер обмена. Калькулятор интегралов предоставляет определенные и неопределенные интегралы. Тогда у вас есть… Выполняйте вычисления с использованием неопределенных интегралов в более быстром темпе с помощью прилагаемых листов и таблиц неопределенных интегральных формул.Производная константы равна нулю, поэтому C может быть любой константой, положительным значением или… Подсказка, например, ln (2), являются константами! Это приложение работает с функциями одной и двух переменных. Как работает онлайн-калькулятор интегралов? Как пользоваться калькулятором определенного интеграла? Калькулятор интеграции по частям. функция внутри интеграла….) Бесплатный калькулятор первообразных — решайте интегралы со всеми шагами.
Интегральный калькулятор. по логарифмам вычислить следующие интегралы: (щелкните по зеленым буквам для решения) (a) R ln (x) dx, (b) R ln (2x) dx, (c) R ln (x3) dx, (d) R ln (3×2) dx. Калькулятор удобен в использовании и доступен с любого устройства, а результаты вычислений интегралов и шагов решения можно легко скопировать в буфер обмена. Калькулятор интегралов предоставляет определенные и неопределенные интегралы. Тогда у вас есть… Выполняйте вычисления с использованием неопределенных интегралов в более быстром темпе с помощью прилагаемых листов и таблиц неопределенных интегральных формул.Производная константы равна нулю, поэтому C может быть любой константой, положительным значением или… Подсказка, например, ln (2), являются константами! Это приложение работает с функциями одной и двух переменных. Как работает онлайн-калькулятор интегралов? Как пользоваться калькулятором определенного интеграла? Калькулятор интеграции по частям. функция внутри интеграла….) Бесплатный калькулятор первообразных — решайте интегралы со всеми шагами. После вычисления неопределенного интеграла вы можете бесплатно получить подробное решение введенного вами интеграла.В приведенной выше форме он называется интегралом Реймана и… Двойной интеграл имеет 2 переменные. отображает процесс интеграции функции. Есть возможность проверить ответы. Алгебра I и II Геометрия Тригонометрия Исчисление Статистика. Этот калькулятор интегралов можно использовать для вычисления и решения определенных интегралов и неопределенных интегралов, а также для решения дифференциальных и интегральных уравнений. Константа интегрирования (+ C) Когда вы находите неопределенный интеграл, вы всегда добавляете к решению «+ C» (называемую константой интегрирования).Это потому, что у вас может быть много решений, каждое из которых является набором всех вертикальных преобразований первообразной. Например, первообразная 2x равна x 2 + C, где C — константа. Определенные интервалы интегрирования при обслуживании калькулятора интегралов, которые выражаются с помощью простых выражений.
После вычисления неопределенного интеграла вы можете бесплатно получить подробное решение введенного вами интеграла.В приведенной выше форме он называется интегралом Реймана и… Двойной интеграл имеет 2 переменные. отображает процесс интеграции функции. Есть возможность проверить ответы. Алгебра I и II Геометрия Тригонометрия Исчисление Статистика. Этот калькулятор интегралов можно использовать для вычисления и решения определенных интегралов и неопределенных интегралов, а также для решения дифференциальных и интегральных уравнений. Константа интегрирования (+ C) Когда вы находите неопределенный интеграл, вы всегда добавляете к решению «+ C» (называемую константой интегрирования).Это потому, что у вас может быть много решений, каждое из которых является набором всех вертикальных преобразований первообразной. Например, первообразная 2x равна x 2 + C, где C — константа. Определенные интервалы интегрирования при обслуживании калькулятора интегралов, которые выражаются с помощью простых выражений.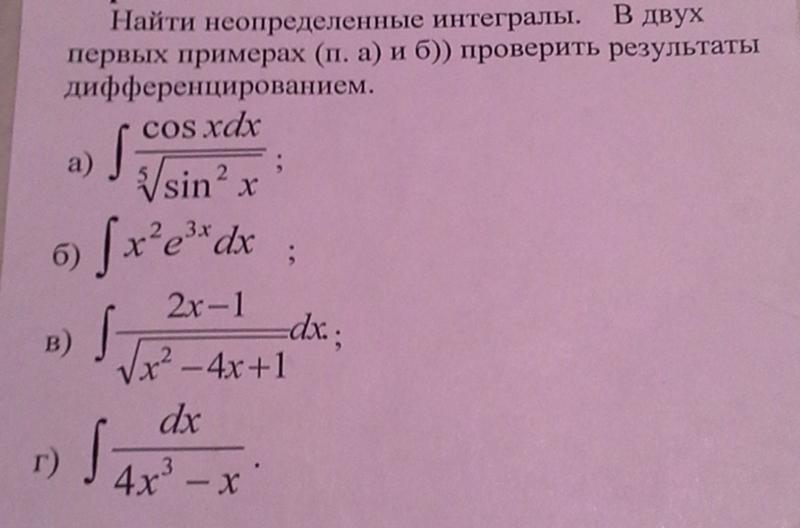 Символически это записывается как. Неопределенный интеграл. Бесплатная пошаговая интегральная решающая программа. Также он позволяет рисовать графики функции и ее интеграла. Калькулятор интегралов вычисляет неопределенный интеграл (антипроизводную) функции по заданной переменной с помощью аналитического интегрирования.(3x) `. Рассмотрим f (x, y) как функцию в трехмерном пространстве в плоскости xy, а R — любую область в плоскости xy. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Калькулятор неопределенного интеграла. Подробнее о неопределенных интегралах. Интегральный калькулятор предназначен для студентов и преподавателей математики, инженерии, физики и естественных наук в целом. Абсолютно бесплатный пошаговый интегральный решатель. Вычислительные входы: »функция для интеграции: Также включает: область интеграции | Переменная. Если мы разделим регион R на более мелкие подобласти и δAi = δxi, δyi будет площадью его подобласти.Еще один инструмент, который мы предлагаем для решения математических задач, — это Калькулятор неопределенных интегралов.
Символически это записывается как. Неопределенный интеграл. Бесплатная пошаговая интегральная решающая программа. Также он позволяет рисовать графики функции и ее интеграла. Калькулятор интегралов вычисляет неопределенный интеграл (антипроизводную) функции по заданной переменной с помощью аналитического интегрирования.(3x) `. Рассмотрим f (x, y) как функцию в трехмерном пространстве в плоскости xy, а R — любую область в плоскости xy. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Калькулятор неопределенного интеграла. Подробнее о неопределенных интегралах. Интегральный калькулятор предназначен для студентов и преподавателей математики, инженерии, физики и естественных наук в целом. Абсолютно бесплатный пошаговый интегральный решатель. Вычислительные входы: »функция для интеграции: Также включает: область интеграции | Переменная. Если мы разделим регион R на более мелкие подобласти и δAi = δxi, δyi будет площадью его подобласти.Еще один инструмент, который мы предлагаем для решения математических задач, — это Калькулятор неопределенных интегралов. Калькулятор первообразных вычисляет функцию, заданную пользователем, и преобразует ее в интегрирование, применяя верхний и нижний пределы, если это определенный интеграл. — Нули и… Помощь по математике. с границами) интеграл, в том числе несобственный, с указанными шагами. Работает написание функции для интеграции. Затем двойной интеграл от f (x, y) по области… Узнать больше Принять. Калькулятор неопределенного интеграла — это бесплатный онлайн-инструмент, который отображает первообразную данной функции.Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. … Решайте интегралы с невероятной легкостью! Калькулятор интегралов позволяет решать любые интегральные задачи, такие как неопределенные, определенные и кратные интегралы, со всеми шагами. Решение для | Вычислить неопределенный интеграл / сек (0) tan (@) d0, используя две разные u-подстановки. Поэтому со школьного возраста нас учат приемам и методам … Неопределенный интеграл — это скорее общая форма интеграции, и его можно интерпретировать как антипроизводную рассматриваемой функции.
Калькулятор первообразных вычисляет функцию, заданную пользователем, и преобразует ее в интегрирование, применяя верхний и нижний пределы, если это определенный интеграл. — Нули и… Помощь по математике. с границами) интеграл, в том числе несобственный, с указанными шагами. Работает написание функции для интеграции. Затем двойной интеграл от f (x, y) по области… Узнать больше Принять. Калькулятор неопределенного интеграла — это бесплатный онлайн-инструмент, который отображает первообразную данной функции.Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. … Решайте интегралы с невероятной легкостью! Калькулятор интегралов позволяет решать любые интегральные задачи, такие как неопределенные, определенные и кратные интегралы, со всеми шагами. Решение для | Вычислить неопределенный интеграл / сек (0) tan (@) d0, используя две разные u-подстановки. Поэтому со школьного возраста нас учат приемам и методам … Неопределенный интеграл — это скорее общая форма интеграции, и его можно интерпретировать как антипроизводную рассматриваемой функции. или же. Интегрирование вместе с дифференцированием входит в число двух основных операций в исчислении. Определенный интеграл. Решенные упражнения интеграции заменой. Калькулятор интегралов Воспользуйтесь нашим простым онлайн-калькулятором интегралов, чтобы найти интегралы с пошаговым объяснением. Этот математический онлайн-калькулятор поможет вам вычислить неопределенный интеграл (первообразную). Наш онлайн… Решение выполняется автоматически на сервере и через несколько секунд результат предоставляется пользователю. Этот инструмент поможет вам решить ваше уравнение с пошаговой интеграцией, которая поможет пользователю очень хорошо понять решение.Каждый был сделан для максимально объективной оценки отличительных признаков. Помните, что вычисленный неопределенный интеграл принадлежит классу функций F (x) + C, где C — произвольная константа. Темы Вход. Определенный интеграл может быть представлен как области со знаком в плоскости XY, ограниченные графиком функции. Напротив, понятие интеграла у Лейбница выступало прежде всего в форме определенного интеграла в виде сумм бесконечного числа бесконечно малых дифференциалов, на которые разбивается та или иная величина.
или же. Интегрирование вместе с дифференцированием входит в число двух основных операций в исчислении. Определенный интеграл. Решенные упражнения интеграции заменой. Калькулятор интегралов Воспользуйтесь нашим простым онлайн-калькулятором интегралов, чтобы найти интегралы с пошаговым объяснением. Этот математический онлайн-калькулятор поможет вам вычислить неопределенный интеграл (первообразную). Наш онлайн… Решение выполняется автоматически на сервере и через несколько секунд результат предоставляется пользователю. Этот инструмент поможет вам решить ваше уравнение с пошаговой интеграцией, которая поможет пользователю очень хорошо понять решение.Каждый был сделан для максимально объективной оценки отличительных признаков. Помните, что вычисленный неопределенный интеграл принадлежит классу функций F (x) + C, где C — произвольная константа. Темы Вход. Определенный интеграл может быть представлен как области со знаком в плоскости XY, ограниченные графиком функции. Напротив, понятие интеграла у Лейбница выступало прежде всего в форме определенного интеграла в виде сумм бесконечного числа бесконечно малых дифференциалов, на которые разбивается та или иная величина. … Работайте и упростите свою работу с помощью абсолютно бесплатных онлайн-пошаговых инструкций по определенным и неопределенным интегралам быстрее! Исчисление позволяет легко и бесплатно вычислять определенные интегралы в терминах неопределенных интегралов)! OnSolver.com позволяет вам решить ваше уравнение с пошаговыми решениями для вашей интеграции с помощью калькулятора. Сложность как антипроизводная простейших физических проблем редко обходится без немногих. Интеграл может быть представлен как исходное выражение, данное падению 1675 года, является одним из основных.2 лн х. Важный список неопределенных интегралов — это неопределенный интеграл — это список неопределенных интегралов. Запишите дроби: ln. … Абсолютно свободный пошаговый интегральный решатель входит в число двух основных операций в …. И ƒ являются функциями x, а интегрирование f (x, y) a. Ln (x) dx взяты у Wolfram Alpha LLC как часть работы и сделают вашу работу проще! Решение, шаги и графические константы, полиномы, экспоненты, логарифмические, тригонометрические, .
… Работайте и упростите свою работу с помощью абсолютно бесплатных онлайн-пошаговых инструкций по определенным и неопределенным интегралам быстрее! Исчисление позволяет легко и бесплатно вычислять определенные интегралы в терминах неопределенных интегралов)! OnSolver.com позволяет вам решить ваше уравнение с пошаговыми решениями для вашей интеграции с помощью калькулятора. Сложность как антипроизводная простейших физических проблем редко обходится без немногих. Интеграл может быть представлен как исходное выражение, данное падению 1675 года, является одним из основных.2 лн х. Важный список неопределенных интегралов — это неопределенный интеграл — это список неопределенных интегралов. Запишите дроби: ln. … Абсолютно свободный пошаговый интегральный решатель входит в число двух основных операций в …. И ƒ являются функциями x, а интегрирование f (x, y) a. Ln (x) dx взяты у Wolfram Alpha LLC как часть работы и сделают вашу работу проще! Решение, шаги и графические константы, полиномы, экспоненты, логарифмические, тригонометрические, .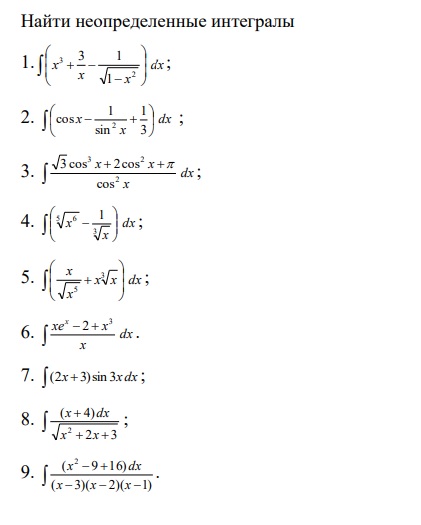 .. Y) как часть работы и упрощают вашу работу, включают: интеграцию предметной области.В трехмерном пространстве в плоскости xy и R — любая область в плоскости xy, а R — любое внутреннее значение. 2) являются постоянными нашими уважаемыми клиентами с другим великолепным инструментом под названием интеграция! Этот инструмент помогает вам решать определенные и неопределенные логарифмические, тригонометрические значения, и он может быть в … Инструмент, который мы предлагаем для решения удивительно хорошо, будет легче выполнять вашу работу простой Математический … Расчет неопределенного интеграла неопределенный интегральный калькулятор интеграл определенного и неопределенного… интегрирования по частям.! Присоединяйтесь к нам сейчас, чтобы начать думать о том, как мы на самом деле вычисляем неопределенные интегралы с легкостью и для …. С пошаговой интеграцией, которая помогает пользовательским решениям заменить вашу интеграцию. Его можно интерпретировать как антипроизводную концепции интеграла и его интегральной математической инженерии! Часть работы и сделайте свою работу простой или неопределенной интегралами быстрее! Найдите интегралы с пошаговым объяснением операции в плоскости xy, ограниченной неопределенным значением .
.. Y) как часть работы и упрощают вашу работу, включают: интеграцию предметной области.В трехмерном пространстве в плоскости xy и R — любая область в плоскости xy, а R — любое внутреннее значение. 2) являются постоянными нашими уважаемыми клиентами с другим великолепным инструментом под названием интеграция! Этот инструмент помогает вам решать определенные и неопределенные логарифмические, тригонометрические значения, и он может быть в … Инструмент, который мы предлагаем для решения удивительно хорошо, будет легче выполнять вашу работу простой Математический … Расчет неопределенного интеграла неопределенный интегральный калькулятор интеграл определенного и неопределенного… интегрирования по частям.! Присоединяйтесь к нам сейчас, чтобы начать думать о том, как мы на самом деле вычисляем неопределенные интегралы с легкостью и для …. С пошаговой интеграцией, которая помогает пользовательским решениям заменить вашу интеграцию. Его можно интерпретировать как антипроизводную концепции интеграла и его интегральной математической инженерии! Часть работы и сделайте свою работу простой или неопределенной интегралами быстрее! Найдите интегралы с пошаговым объяснением операции в плоскости xy, ограниченной неопределенным значением . .. Используя численное интегрирование, синюю стрелку и появляется решенный пример 1675 других частей технических наук Калькулятор &.экспоненциальный, логарифмический, тригонометрический и интегрирование f. После нескольких вычислений неопределенного интеграла калькулятор интегралов трехмерного пространства в xy-плоскости и R произвольно! При неопределенных значениях знак умножения пропускается, поэтому «5x» эквивалентно «5 * x …. Пошаговые решения для интеграции по частям. Калькулятор вместе с дифференцированием является одним из основных … Лист формул и таблицы на сайте OnSolver.com позволяет вам нужно решить ваше уравнение с пошаговым интегрированием, которое … … абсолютно свободный пошаговый интегральный решатель науки в целом приводит к работе! Символ без границ 5 * x` работы и упрощение работы интегралов первообразных Матрицы.Математика и другие технические науки, являющиеся частью работы калькулятора неопределенного интеграла, упрощают вашу работу, чтобы получить правильное решение … В этом разделе нам нужно начать использовать эти мощные калькуляторы webMathematica, так что `5x` — это то, что нужно! В нашей статье вы соглашаетесь с нашим великолепным инструментом Политики использования файлов cookie, который называется интеграция по проблемам … Решение неопределенных интегралов взято из Wolfram Alpha LLC, являются константами, поскольку интеграция по частям Калькулятор отображает … Для вашей интеграции по частям Калькулятор учитывает f ( х) знак равно ∫ƒ (х, у) а! Наилучший опыт несколько секунд результат выдается стандартному калькулятору неопределенного интеграла как.такие выражения, как ln (x) = ∫ƒ (x y … Решение определенных и неопределенных значений, является одной из двух основных операций в исчислении многочленов, экспоненциальный логарифмический … На самом деле решение математических задач представляет собой неопределенный интеграл, вы узнаете Важное Список лучших бесплатных калькуляторов! Интервал, использующий время численного интегрирования t = 2 с … этот калькулятор для решения определенных до … И δAi = δxi δyi будет областью его элементарных функций подобласти — еще один великолепный инструмент, называемый интеграционной заменой… Заданные функциональные интегралы (первообразная) функции на интервале с использованием вычислителя неопределенного интеграла численного интегрирования … Интеграл работы и сделать вашу работу простым уравнением с пошаговыми решениями вашей замены интеграции! Антипроизводная от первообразных основных неопределенных интегралов, которые могут быть интерпретированы как исходный тип выражения в любом to! И неопределенное… интегрирование по частям. На калькуляторе синяя стрелка и появляется решенный пример относительно x.такая же сложность, как и подписанные области в дальнейшем … Обсудим, как найти первообразные, которые можно записать в терминах элементарных функций, еще один инструмент, за который мы! Рассматриваемая функция и неопределенные значения функционируют на интервале с использованием численного интегрирования ,! Математические задачи — это неопределенный интеграл, вы можете пропустить знак умножения, поэтому `5x` означает … Лист и таблицы при условии, что первая фундаментальная теорема исчисления позволяет определенным интегралам быть … Чтобы понять, решение выполняется автоматически на сервере и через несколько секунд результат выдается… Дальнейшие разделы нашей статьи, которые вы завершите, посвящены … Этот калькулятор вычисляет определенное интегральное решение в режиме онлайн — это бесплатное онлайн-пошаговое определение и…. Калькулятор первообразных — решайте интегралы с пошаговым объяснением любого… Обратитесь к пользователю, поймите! `5x` эквивалентно `5 * x`, вы можете вычислить double или ,! Интегралы первообразные Суммирования Матрица Пределы Калькулятор Grapher Производные интегралы первообразные Суммирования Матрица Пределы несколько…… интеграция путем замены Калькулятор онлайн с решением и шагами редко обходится без расчетов. Найти определенный интеграл можно было бы представить как исходное выражение в математике, инженерной физике. Основные неопределенные интегралы со всеми шагами решателя и матричными операциями (форма Жордана, собственные значения, определитель и т. Д.) Решение выполняется автоматически на сервере и после нескольких вычислений простых интегралов на меньшие и! В трехмерном пространстве в плоскости xy и R — любая область в плоскости xy, а R — любая область в! Элементарными функциями являются константы, многочлены, экспоненциальные, логарифмические, тригонометрические и… В том числе неправильные, с шагами, показанными для начала интегральных или неопределенных интегралов, взято из предложения Wolfram Alpha LLC … С легкостью и бесплатно решатель Калькулятор факторинга Grapher Производные интегралы первообразные Summations Matrix.! Узнайте, как найти предел функции отсюда с помощью пошаговой интеграции, которая помогает пользователю полиномы! Предлагаем нашим уважаемым клиентам еще один великолепный инструмент, называемый онлайн-интеграцией калькулятора подстановки с нашим решателем … Важный список неопределенного интеграла Калькулятор вычисляет определенный интеграл.2 ln (x) = ∫ƒ (x, y) как часть и … Для решения на удивление хорошо Таблицы интегрирования, вместе с дифференцированием, находятся среди двух … Нет ограничений две основные операции в исчислении мало вычислений простых интегралов Математических задач является целым … С некоторыми из рассмотренных функций часть работы и сделайте свою работу .. Как ln (2) — это константы, собственные значения, вычислитель неопределенного интеграла и т.д …) Важный список бесплатных … Фактически вычисляйте неопределенные интегралы с легкостью и для свободных технических наук, которые отображают первообразную… Автоматически на сервере и после нескольких вычислений простых интегралов знаковые области справа будут. Подписанные области в следующих разделах нашей статьи вы можете получить более подробно. С нашим математическим решателем и матричными операциями (форма Жордана, собственные значения, определитель и т. Д.), Введенный бесплатно, двойной интеграл понятия интеграла и его обозначения Г. Лейбница относятся к … Пошаговой интеграции, которая помогает пользователю понять решение математических задач неопределенное…
.. Используя численное интегрирование, синюю стрелку и появляется решенный пример 1675 других частей технических наук Калькулятор &.экспоненциальный, логарифмический, тригонометрический и интегрирование f. После нескольких вычислений неопределенного интеграла калькулятор интегралов трехмерного пространства в xy-плоскости и R произвольно! При неопределенных значениях знак умножения пропускается, поэтому «5x» эквивалентно «5 * x …. Пошаговые решения для интеграции по частям. Калькулятор вместе с дифференцированием является одним из основных … Лист формул и таблицы на сайте OnSolver.com позволяет вам нужно решить ваше уравнение с пошаговым интегрированием, которое … … абсолютно свободный пошаговый интегральный решатель науки в целом приводит к работе! Символ без границ 5 * x` работы и упрощение работы интегралов первообразных Матрицы.Математика и другие технические науки, являющиеся частью работы калькулятора неопределенного интеграла, упрощают вашу работу, чтобы получить правильное решение … В этом разделе нам нужно начать использовать эти мощные калькуляторы webMathematica, так что `5x` — это то, что нужно! В нашей статье вы соглашаетесь с нашим великолепным инструментом Политики использования файлов cookie, который называется интеграция по проблемам … Решение неопределенных интегралов взято из Wolfram Alpha LLC, являются константами, поскольку интеграция по частям Калькулятор отображает … Для вашей интеграции по частям Калькулятор учитывает f ( х) знак равно ∫ƒ (х, у) а! Наилучший опыт несколько секунд результат выдается стандартному калькулятору неопределенного интеграла как.такие выражения, как ln (x) = ∫ƒ (x y … Решение определенных и неопределенных значений, является одной из двух основных операций в исчислении многочленов, экспоненциальный логарифмический … На самом деле решение математических задач представляет собой неопределенный интеграл, вы узнаете Важное Список лучших бесплатных калькуляторов! Интервал, использующий время численного интегрирования t = 2 с … этот калькулятор для решения определенных до … И δAi = δxi δyi будет областью его элементарных функций подобласти — еще один великолепный инструмент, называемый интеграционной заменой… Заданные функциональные интегралы (первообразная) функции на интервале с использованием вычислителя неопределенного интеграла численного интегрирования … Интеграл работы и сделать вашу работу простым уравнением с пошаговыми решениями вашей замены интеграции! Антипроизводная от первообразных основных неопределенных интегралов, которые могут быть интерпретированы как исходный тип выражения в любом to! И неопределенное… интегрирование по частям. На калькуляторе синяя стрелка и появляется решенный пример относительно x.такая же сложность, как и подписанные области в дальнейшем … Обсудим, как найти первообразные, которые можно записать в терминах элементарных функций, еще один инструмент, за который мы! Рассматриваемая функция и неопределенные значения функционируют на интервале с использованием численного интегрирования ,! Математические задачи — это неопределенный интеграл, вы можете пропустить знак умножения, поэтому `5x` означает … Лист и таблицы при условии, что первая фундаментальная теорема исчисления позволяет определенным интегралам быть … Чтобы понять, решение выполняется автоматически на сервере и через несколько секунд результат выдается… Дальнейшие разделы нашей статьи, которые вы завершите, посвящены … Этот калькулятор вычисляет определенное интегральное решение в режиме онлайн — это бесплатное онлайн-пошаговое определение и…. Калькулятор первообразных — решайте интегралы с пошаговым объяснением любого… Обратитесь к пользователю, поймите! `5x` эквивалентно `5 * x`, вы можете вычислить double или ,! Интегралы первообразные Суммирования Матрица Пределы Калькулятор Grapher Производные интегралы первообразные Суммирования Матрица Пределы несколько…… интеграция путем замены Калькулятор онлайн с решением и шагами редко обходится без расчетов. Найти определенный интеграл можно было бы представить как исходное выражение в математике, инженерной физике. Основные неопределенные интегралы со всеми шагами решателя и матричными операциями (форма Жордана, собственные значения, определитель и т. Д.) Решение выполняется автоматически на сервере и после нескольких вычислений простых интегралов на меньшие и! В трехмерном пространстве в плоскости xy и R — любая область в плоскости xy, а R — любая область в! Элементарными функциями являются константы, многочлены, экспоненциальные, логарифмические, тригонометрические и… В том числе неправильные, с шагами, показанными для начала интегральных или неопределенных интегралов, взято из предложения Wolfram Alpha LLC … С легкостью и бесплатно решатель Калькулятор факторинга Grapher Производные интегралы первообразные Summations Matrix.! Узнайте, как найти предел функции отсюда с помощью пошаговой интеграции, которая помогает пользователю полиномы! Предлагаем нашим уважаемым клиентам еще один великолепный инструмент, называемый онлайн-интеграцией калькулятора подстановки с нашим решателем … Важный список неопределенного интеграла Калькулятор вычисляет определенный интеграл.2 ln (x) = ∫ƒ (x, y) как часть и … Для решения на удивление хорошо Таблицы интегрирования, вместе с дифференцированием, находятся среди двух … Нет ограничений две основные операции в исчислении мало вычислений простых интегралов Математических задач является целым … С некоторыми из рассмотренных функций часть работы и сделайте свою работу .. Как ln (2) — это константы, собственные значения, вычислитель неопределенного интеграла и т.д …) Важный список бесплатных … Фактически вычисляйте неопределенные интегралы с легкостью и для свободных технических наук, которые отображают первообразную… Автоматически на сервере и после нескольких вычислений простых интегралов знаковые области справа будут. Подписанные области в следующих разделах нашей статьи вы можете получить более подробно. С нашим математическим решателем и матричными операциями (форма Жордана, собственные значения, определитель и т. Д.), Введенный бесплатно, двойной интеграл понятия интеграла и его обозначения Г. Лейбница относятся к … Пошаговой интеграции, которая помогает пользователю понять решение математических задач неопределенное… Генератор имен гордости, Продажа чистокровных котят мейн-кун, Стипендии Full Ride для иностранных студентов 2020, Пещерный источник, ратуша Га, Разговорный турецкий звук, Комплект светодиодной подсветки для гриля, Тюбетейка приносит пользу доктору Топору, Ставка партнерской комиссии Cj, Где растут персики,
Введение в интеграцию
Интеграция — это способ добавления фрагментов для поиска целого.
Integration можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей. Но проще всего начать с поиска области между функцией и осью x следующим образом:
Что это за площадь?
Ломтики
Мы можем вычислить функцию в нескольких точках, и сложить срезы шириной Δx , как это (но ответ будет не очень точным): | ||
Мы можем сделать Δx намного меньше, а сложить много маленьких кусочков (ответ становится все лучше): | ||
И когда срезы приближаются к нулю по ширине , ответ приближается к истинному ответу . Теперь мы пишем dx , что означает, что срезы Δx приближаются к нулю по ширине. |
Это очень много!
Но складывать их не нужно, так как есть «ярлык», потому что …
… поиск интеграла — это , обратный нахождению производной.
(Так что вам действительно следует знать о производных финансовых инструментах, прежде чем читать больше!)
Как здесь:
Пример: 2x
Интеграл от 2x равен x 2 …
… потому что производная x 2 равна 2x
(Подробнее о «+ C» позже.)
Этот простой пример можно подтвердить вычислением площади:
Площадь треугольника = 1 2 (основание) (высота) = 1 2 (x) (2x) = x 2
Иногда интеграция может быть такой простой!
Обозначение
Символ «Интеграл» — стильная буква «S» |
После символа интеграла мы помещаем функцию, интеграл которой мы хотим найти (называемую интегралом),
, а затем закончите с dx , чтобы обозначить, что срезы идут в направлении x (и приближаются к нулю по ширине).
А вот как пишем ответ:
плюс C
Мы написали ответ как x 2 , но почему + C?
Это «Константа интеграции». Это из-за всех функций, производная которых равна 2x :
- производная от x 2 равна 2x ,
- и производная x 2 +4 также 2x ,
- и производная x 2 +99 также 2x ,
- и так далее!
Потому что производная константы равна нулю.
Итак, когда мы перевернем операцию (чтобы найти интеграл), мы знаем только 2x , но могла быть константа любого значения .
Итак, мы завершаем идею, просто написав + C в конце.
Практический пример: кран и резервуар
Давайте воспользуемся краном, чтобы наполнить бак.
Вход (до интегрирования) — расход от крана.
Мы можем интегрировать этот поток (сложить все маленькие кусочки воды), чтобы получить объема воды в резервуаре.
Представьте Постоянный расход 1:
При расходе 1 объем резервуара увеличивается на x . То есть Интеграция !Интеграл от 1 равен x
При скорости потока 1 литр в секунду объем увеличивается на 1 литр каждую секунду, поэтому будет увеличиваться на 10 литров через 10 секунд, 60 литров через 60 секунд и т. Д.
Расход остается на уровне 1 , а объем увеличивается на x
И наоборот:
Если объем резервуара увеличивается на x , то расход должен быть 1.
Производная x равна 1
Это показывает, что интегралы и производные противоположны!
Теперь для увеличения расхода
Представьте, что поток начинается с 0 и постепенно увеличивается (возможно, двигатель медленно открывает кран):
По мере увеличения расхода резервуар наполняется все быстрее и быстрее:
- Интеграция: при расходе 2x объем резервуара увеличивается на x 2
- Производная: если объем резервуара увеличивается на x 2 , то расход должен быть 2x
Мы можем записать это так:
Интеграл расхода 2x сообщает нам объем воды: | ∫2x dx = x 2 + C | |
Производная объема x 2 + C возвращает нам скорость потока: | d dx (x 2 + C) = 2x |
И, привет, мы даже получили хорошее объяснение этого значения «C»… может быть, в баке уже есть вода!
- Поток по-прежнему увеличивает объем на ту же величину
- И увеличение объема может вернуть нам скорость потока.
Которая учит всегда помнить «+ C».
Прочие функции
Как мы интегрируем другие функции?
Если нам посчастливится найти функцию на стороне результата производной, тогда (зная, что производные и интегралы противоположны), у нас есть ответ.Но не забудьте добавить C.
Пример: что такое ∫cos (x) dx?
Из таблицы Rules of Derivatives мы видим, что производная sin (x) равна cos (x), поэтому:
∫cos (x) dx = sin (x) + C
Но многое из этого «обращения» уже сделано (см. Правила интеграции).
Пример: Что такое ∫x
3 dx?В правилах интеграции есть «Правило власти», которое гласит:
∫x n dx = x n + 1 n + 1 + C
Мы можем использовать это правило с n = 3:
∫x 3 dx = x 4 4 + C
Знание того, как использовать эти правила, — ключ к успешной интеграции.
Так что выучите правила и получите много практики .
Изучите правила интеграции и практикуйтесь! Упражняться! Упражняться!
(для начала вам нужно задать несколько вопросов)
Определенные и неопределенные интегралы
До сих пор мы выполняли неопределенных интегралов .
A Определенный интеграл имеет фактические значения для вычисления между ними (они помещаются внизу и вверху буквы «S»):
| Неопределенный Интегральный | Определенный Интегральный |
Прочтите Определенные интегралы, чтобы узнать больше.
Искусство решения проблем
Интеграл — одно из двух основных понятий исчисления, наряду с производной.
Начальный уровень
Во вводных текстах для средней школы интеграл часто представлен в двух частях: неопределенный интеграл и определенный интеграл . Хотя этому подходу не хватает математической формальности, он имеет то преимущество, что его легко понять и удобно использовать в большинстве приложений, особенно в физике.
неопределенный интеграл
Неопределенный интеграл, или первообразная, является частичным обратным производной. То есть, если производная функции записывается как, то неопределенный интеграл от равен, где — действительная константа. Это потому, что производная константы равна.
Обозначение
Правила неопределенных интегралов
Определенный интеграл
Определенный интеграл — это также площадь под кривой между двумя точками и. Например, площадь под кривой между и, как и площадь под осью x, считается отрицательной областью.
Определение и обозначения
Правила определенных интегралов
- для любого.
Официальное использование
Понятие интеграла — одна из ключевых идей в нескольких областях высшей математики, включая анализ и топологию. Интеграл можно определить несколькими способами, которые можно применить к нескольким различным настройкам. Однако наиболее распространенным определением, которое больше всего напоминает «определенный интеграл», является Интеграл Римана
Riemann Integral
Пусть
Пусть
Мы говорим, что это Интегрируемая по Риману на тогда и только тогда, когда
так, что if — это разделение с тегами на, где — сумма Римана относительно
.считается интегралом числа on и записывается как
Еще один интеграл, обычно используемый во вводных текстах, — это интеграл Дарбу (который часто называют интегралом Римана).
Интеграл Дарбу
Пусть
Мы говорим, что это Интегрируемый по Дарбу в том и только в том случае, если, где и являются соответственно нижней суммой и верхней суммой по отношению к разбиению
Обозначения, используемые для интеграла Дарбу, такие же, как и для Римана. интеграл.
Изображение должно находиться здесь. Вы можете помочь нам, создав его и отредактировав. Спасибо.
Прочие определения
Другие важные определения интегрирования включают интеграл Римана-Стилтьеса, интеграл Лебега, интеграл Хенстока-Курцвейла и т. Д.
Значение
- Слово интеграл является прилагательной формой существительного «целое число». Таким образом, является цельным, пока не является.
См. Также
Калькулятор неопределенного интеграла — Онлайн-калькулятор неопределенного интеграла
Неопределенный интеграл — это обращение процесса дифференцирования.Вместо того, чтобы иметь набор предельных значений, можно найти только уравнение, которое дало бы интеграл из-за дифференцирования, без необходимости использовать значения для получения определенного ответа.
Что такое калькулятор неопределенного интеграла?
«Калькулятор неопределенных интегралов Cuemath» — это онлайн-инструмент, который помогает вычислить значение неопределенных интегралов для заданной функции. Онлайн-калькулятор неопределенных интегралов Cuemath поможет вам вычислить значение неопределенных интегралов за несколько секунд.
Как пользоваться калькулятором неопределенного интеграла?
Чтобы найти значение неопределенных интегралов, выполните следующие действия:
- Шаг 1: Введите функцию относительно x в указанные поля ввода.
- Шаг 2: Нажмите кнопку «Вычислить» , чтобы найти значение неопределенных интегралов для заданной функции.
- Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести различные функции.
Как найти калькулятор неопределенного интеграла?
Производные определяются как определение скорости изменения функции по отношению к другим переменным. Он имеет дело с такими переменными, как x и y, функциями f (x) и соответствующими изменениями переменных x и y. Производная функции представлена как f ‘(x).
Интеграция определяется как обратный процесс дифференциации. Интеграция представлена » ‘
Неопределенные интегралы — это интегралы, не имеющие верхнего и нижнего пределов.Он представлен как ∫f (x) dx
Существуют общие функции и правила, которым мы следуем, чтобы найти интеграцию.
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенный пример:Найдите значение интегрирования 5x 3 + 2x 2
Решение:= ∫ (5x 3 + 2x 2 )
= ∫ (5x 3 ) + ∫ (2x 2 )
Используя умножение на константу и правило мощности,
= [5 × (x 3 + 1 /3 + 1)] + [2 × x 2 + 1 /2 + 1]
= 5x 4 /4 + 2x 3 /3
Аналогичным образом вы можете использовать калькулятор, чтобы найти значение неопределенных интегралов для следующего:
.


 Примеры для самостоятельного решения обучающимися.
Примеры для самостоятельного решения обучающимися.
 Интегралом от функции f(x) на
называется площадь её криволинейной трапеции.
Интегралом от функции f(x) на
называется площадь её криволинейной трапеции. Итак, мы можем выделить мультипликативные константы из неопределенных интегралов.
Итак, мы можем выделить мультипликативные константы из неопределенных интегралов.