Основные свойства функций.

• 1) Область определения функции и область значений функции.

• Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена. Область значений функции — это множество всех действительных значений y, которые принимает функция.

• В элементарной математике изучаются функции только на множестве действительных чисел.

• 2) Нули функции.

• Нуль функции – такое значение аргумента, при котором значение функции равно нулю.

• 3) Промежутки знакопостоянства функции.

• Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.

• 4) Монотонность функции.

• Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.

• Убывающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.

• 5) Четность (нечетность) функции.

• Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.

• Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого 

  х из области определения справедливо равенство f(-x) = — f(x). График нечетной функции симметричен относительно начала координат.

• 6) Ограниченная и неограниченная функции.

• Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.

• 7) Периодическость функции.

• Функция f(x) — периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).

• 19. Основные элементарные функции, их свойства и графики. Применение функ-ций в экономике.

Основные элементарные функции. Их свойства и графики

1. Линейная функция.

Линейной функцией называется функция вида 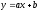, где х — переменная, а и b — действительные числа.

Число а называют угловым коэффициентом прямой, он равен тангенсу угла наклона этой прямой к положительному направлению оси абсцисс. Графиком линейной функции является прямая линия. Она определяется двумя точками.

Свойства линейной функции

1. Область определения — множество всех действительных чисел: Д(y)=R

2. Множество значений — множество всех действительных чисел: Е(у)=R

3. Функция принимает нулевое значение при или.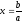

4. Функция возрастает (убывает) на всей области определения.

5. Линейная функция непрерывная на всей области определения, дифференцируемая и .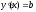

2. Квадратичная функция.

Функция вида 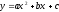, где х — переменная, коэффициенты а, b, с — действительные числа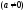, называетсяквадратичной.

Коэффициенты а, b, с определяют расположение графика на координатной плоскости

Коэффициент а определяет направление ветвей. График квадратичной функции — парабола. Координаты вершины параболы находятся по формулам:

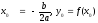
Свойства функции:

1. D(у)=R.

2. Множество значений одного из промежутков: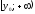

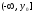или.

3. Функция принимает нулевые значения при 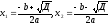, где дискриминант вычисляется по формуле:.

4. Функция непрерывна на всей области определения и производная функции равна .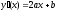

studfile.net

Основные элементарные функции и их графики.

Определение 2. Основными элементарными функциями принято называть степенную, показательную, логарифмическую, тригонометрические и обратные тригонометрические функции. Ниже приведены графики этих функций, которые наглядно характеризуют их основные свойства.

1) Показательная функция y = α^x, a>0, a 1;

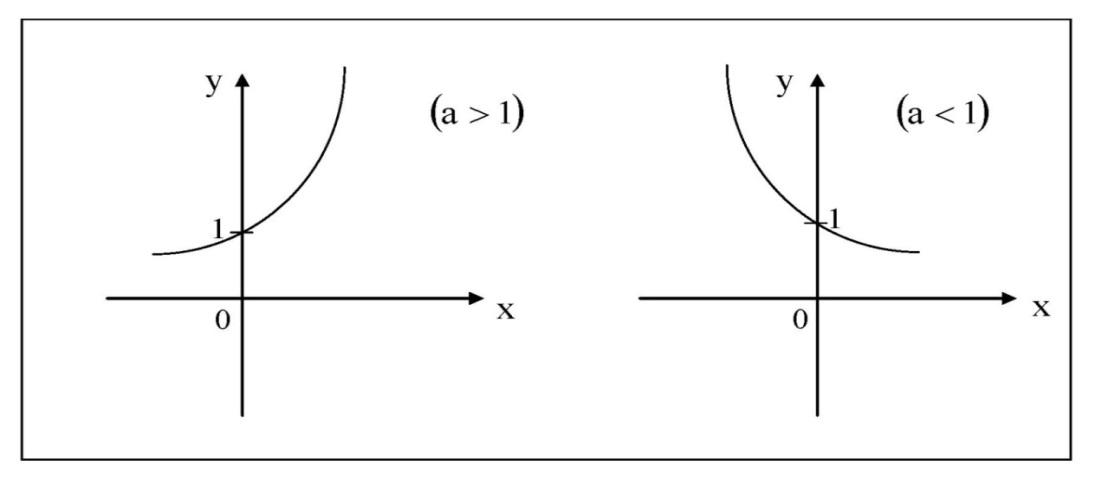
Рис. 1

2) Степенная функция y = x ^α , α ∈ R .

Графики степенных функций, соответствующих различным показателям степени, представлены на рис. 2

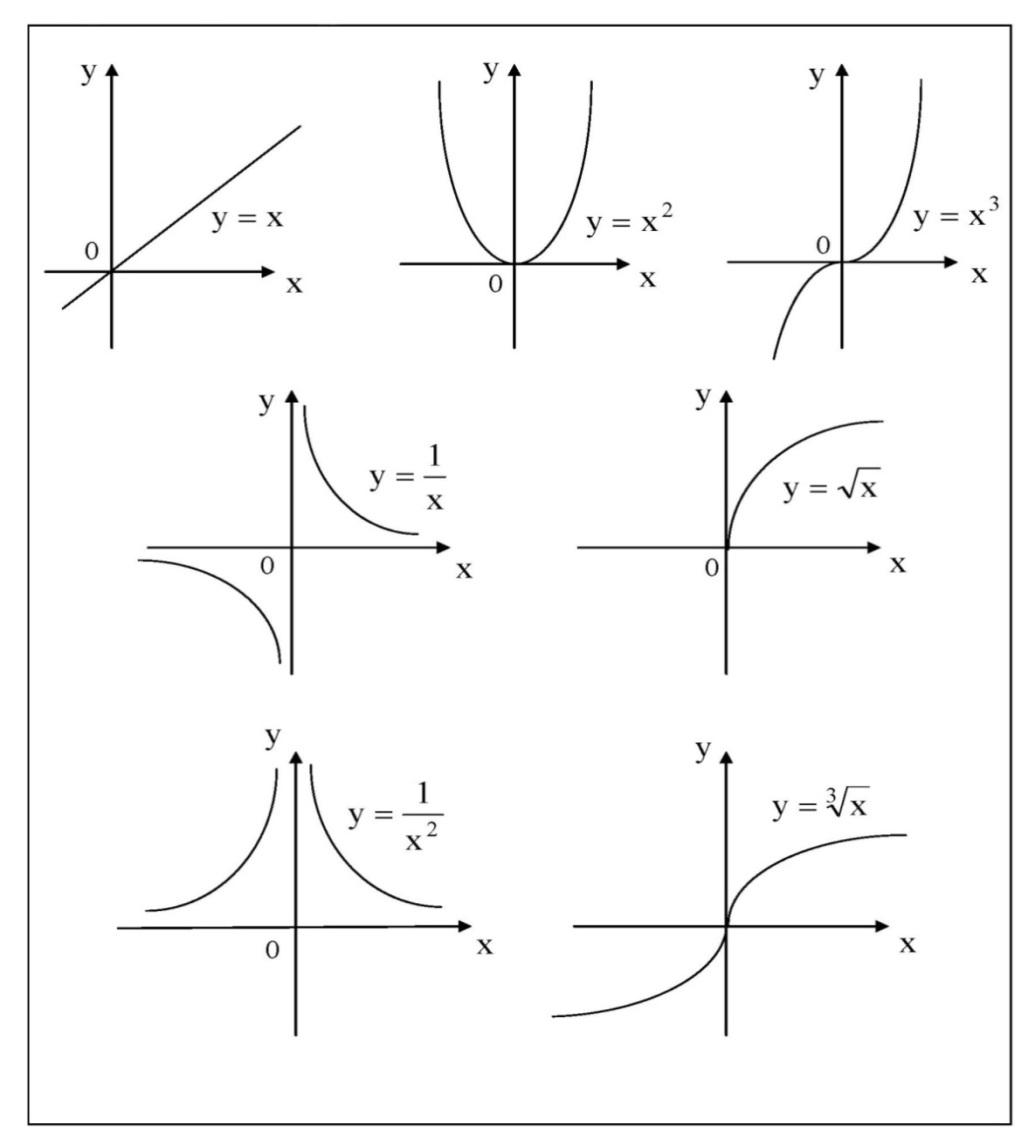
Рис. 2

3) Логарифмическая функция y = log_ax, a> 0, a

 1;

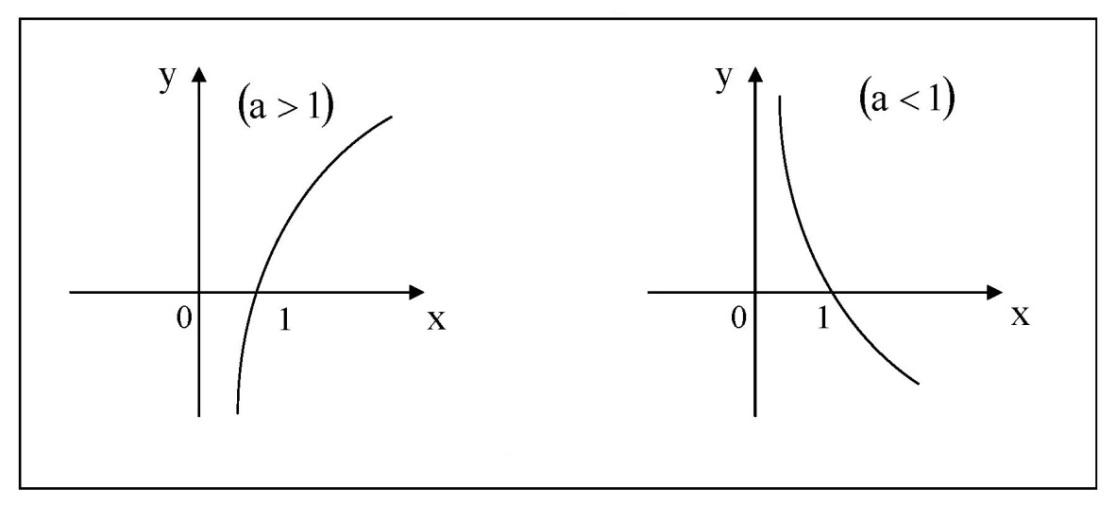
Рис. 3

4) Тригонометрические функцииy = sinx, y = cosx,

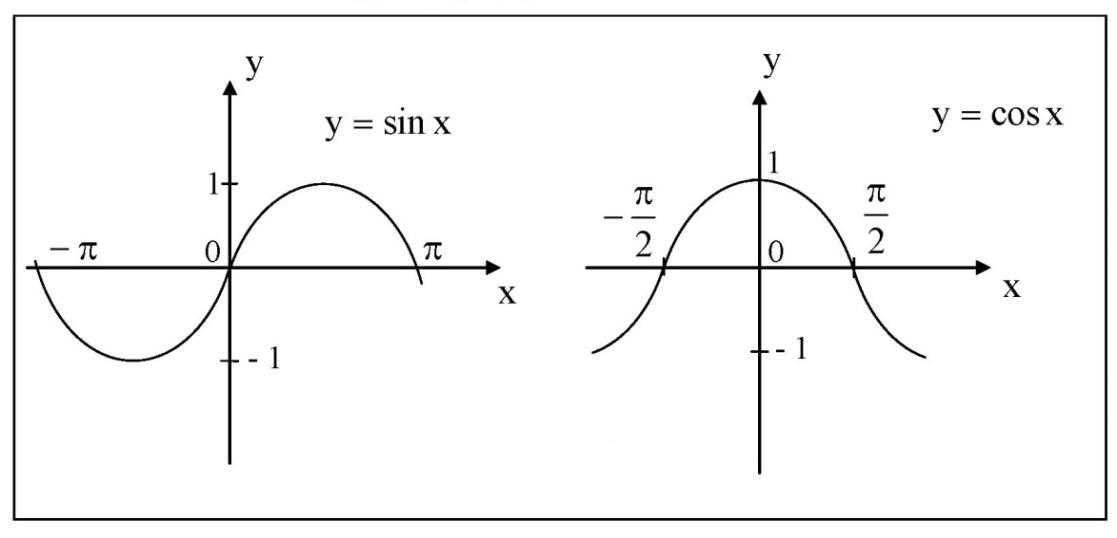
Рис. 4

y = tgx, y = ctgx

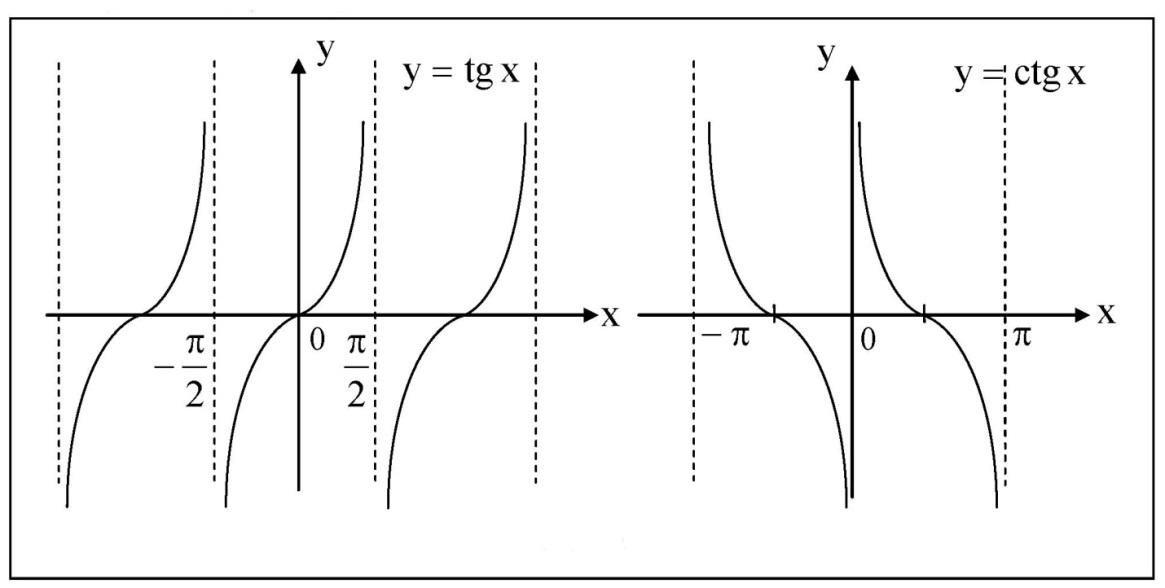
Рис. 5

5) Обратные тригонометрические функции

y = arcsinx, D (f) = [-1; 1], E (f) =;

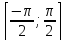y = arccos x, D (f ) = [- 1; l], E (f) =

;

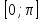
y = arctg x, D (f) = R, E (f) =;

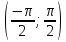y = arcctg x, D (f) = R, E (f) =

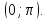
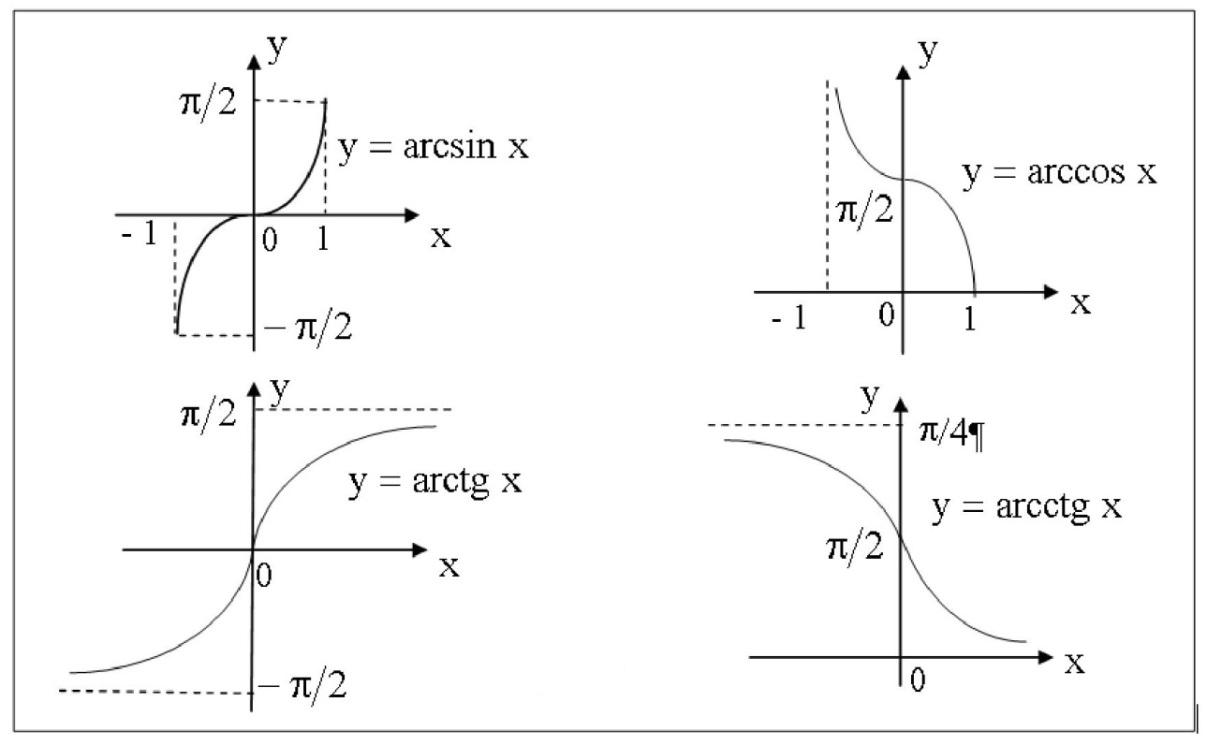
Рис. 6

Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных величин с помощью конечного числа арифметических операций сложения, вычитания, умножения, деления и операций взятия функции от функции, называется элементарной функцией.

Примерами элементарных функций являются:

у = ax + b–линейная функция a,b∈ R;

у = ax + bx +

c– квадратичная функция a, b, с ∈ R;

у =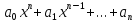– целая рациональная функция или многочлен степениn,;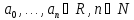

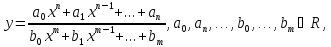
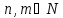–дробно‒рациональная функция; частным случаем дробно‒рациональной функции является дробно‒линейная функция ,.

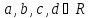Примерами неэлементарных функций могут служить

у =sinx =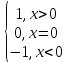

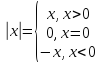
, у =

Лекция 3.Предел последовательности Числовые последовательности. Пределчисловойпоследовательности.

Пусть каждому натуральному числу nпоставлено в соответствие действительное число x_п. Тогда говорят, что задана последовательность чисел x₁, x₂, x₃, …, x_n, … .

Числа x₁, x₂, x₃, …, x_n, будем называть элементами (или членами)последовательности, x_n–общимчленомпоследовательности. Сокращенно последовательность обозначается .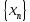

Например:

1) 1, 3, 5, …, 2n – 1 – арифметическая прогрессия.

d = 2;x_n= 2n – 1; x₁₀₀ = 2 ·100 – 1 = 199.

d =x₂ – x_{1 =} x₃– x₂ = … – разность прогрессии.

2)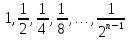– геометрическая прогрессия.

q= 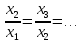– знаменатель прогрессии.

x₅=;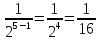

3)

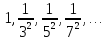
x_n= ;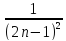

Определение 1. Последова­тельность {x_n} называется ограниченной, если она ограничена и сверху и снизу, то есть существуют числа mиMтакие, что любой элемент этой последовательности удовлетворяет неравенствам:

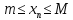
Пример:

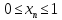
В противном случаи последова­тельность {x_n} называется неограниченной.

Пример:

1, 2, 3, …, n – неограниченная последовательность.

Определение 2. Числоa называется пределом числовой последовательности {x_n}, если для любого сколь угодно малого ε> 0найдетсячисло N (номер), зависящее от ε, такое, что для всех натуральных чисел n>Nвыполняется неравенство:

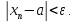
Тогда последовательность {x_n} называется сходя­щейся,и в этом случае пишут:

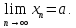
Пример:

Для любого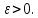

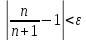
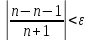
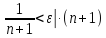
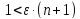
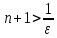
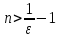
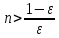
Так как , то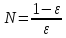

Пусть 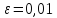, тогда .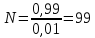

Следовательно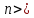99.

Например:

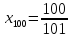, тогда .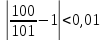

studfile.net

Построение графиков функций

Функции и их графики — одна из самых увлекательных тем в школьной математике. Жаль только, что проходит она… мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.

Умение строить графики функций необходимо для решения задач с параметрами на ЕГЭ по математике. Это одна из первых тем курса математического анализа в вузе. Это настолько важная тема, что мы в ЕГЭ-Студии проводим по ней специальные интенсивы для старшеклассников и учителей, в Москве и онлайн. И часто участники говорят: «Жаль, что мы не знали этого раньше».

Но это не все. Именно с понятия функции и начинается настоящая, «взрослая» математика. Ведь сложение и вычитание, умножение и деление, дроби и пропорции — это все-таки арифметика. Преобразования выражений — это алгебра. А математика — наука не только о числах, но и о взаимосвязях величин. Язык функций и графиков понятен и физику, и биологу, и экономисту. И, как сказал Галилео Галилей, «Книга природы написана на языке математики».

Точнее, Галилео Галилей сказал так:«Математика есть алфавит, посредством которого Господь начертал Вселенную».

Темы для повторения:

Понятие функции

Типы элементарных функций

Преобразования графиков функций

Производная функции

1. Построим график функции

Знакомая задача! Такие встречались в вариантах ОГЭ по математике. Там они считались сложными. Но сложного ничего здесь нет.

Упростим формулу функции:

при

График функции — прямая с выколотой точкой

2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, применяемый в решении неравенств, построении графиков и оценке целых величин в задачах на числа и их свойства. Он встретится вам также на первом курсе, когда придется брать интегралы.

3. Построим график функции

Он получается из графика функции растяжением в 2 раза, отражением по вертикали и сдвигом на 1 вверх по вертикали

4. Построим график функции

Главное — правильная последовательность действий. Запишем формулу функции в более удобном виде:

Действуем по порядку:

1) График функции y=sinx сдвинем на влево;

2) сожмем в 2 раза по горизонтали,

3) растянем в 3 раза по вертикали,

4) сдвинем на 1 вверх

Сейчас мы построим несколько графиков дробно-рациональных функций. Чтобы лучше понять, как мы это делаем, читайте статью «Поведение функции в бесконечности. Асимптоты».

5. Построим график функции

Область определения функции:

Нули функции: и

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Прямая x = 0 (ось Y) — вертикальная асимптота функции. Асимптота — прямая, к которой бесконечно близко подходит график функции, но не пересекает ее и не сливается с ней (смотри тему «Поведение функции в бесконечности. Асимптоты»)

Есть ли другие асимптоты у нашей функции? Чтобы выяснить это, посмотрим, как ведет себя функция, когда x стремится к бесконечности.

Раскроем скобки в формуле функции:

Если x стремится к бесконечности, то стремится к нулю. Прямая является наклонной асимптотой к графику функции.

6. Построим график функции

Это дробно-рациональная функция.

Область определения функции

Нули функции: точки — 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты:

Если x стремится к бесконечности, то у стремится к 1. Значит, — горизонтальная асимптота.

Вот эскиз графика:

Еще один интересный прием — сложение графиков.

7. Построим график функции

Если x стремится к бесконечности, то и график функции будет бесконечно близко подходить к наклонной асимптоте

Если x стремится к нулю, то функция ведет себя как Это мы и видим на графике:

Вот мы и построили график суммы функций. Теперь график произведения!

8. Построим график функции

Область определения этой функции — положительные числа, поскольку только для положительных x определен

Значения функции равны нулю при (когда логарифм равен нулю), а также в точках, где то есть при

При , значение {cos x} равно единице. Значение функции в этих точках будет равно

9. Построим график функции

Функция определена при Она четная, поскольку является произведением двух нечетных функций и График симметричен относительно оси ординат.

Нули функции — в точках, где то есть при

Если x стремится к бесконечности, стремится к нулю. Но что же будет, если x стремится к нулю? Ведь и x, и sin x будут становиться меньше и меньше. Как же будет вести себя частное ?

Оказывается, что если x стремится к нулю, то стремится к единице. В математике это утверждение носит название «Первого замечательного предела».

А как же производная? Да, наконец-то мы до нее добрались. Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.

10. Построим график функции

Область определения функции — все действительные числа, поскольку

Функция нечетна. Ее график симметричен относительно начала координат.

При x=0 значение функции равно нулю. При значения функции положительны, при отрицательны.

Если x стремится к бесконечности, то стремится к нулю.

Найдем производную функции
По формуле производной частного,

если или

В точке производная меняет знак с «минуса» на «плюс», — точка минимума функции.

В точке производная меняет знак с «плюса» на «минус», — точка максимума функции.

Найдем значения функции при x=2 и при x=-2.

Графики функций удобно строить по определенному алгоритму, или схеме. Помните, вы изучали ее в школе?

Общая схема построения графика функции: 

1. Область определения функции

2. Область значений функции

3. Четность — нечетность (если есть)

4. Периодичность (если есть)

5. Нули функции (точки, в которых график пересекает оси координат)

6. Промежутки знакопостоянства функции (то есть промежутки, на которых она строго положительна или строго отрицательна).

7. Асимптоты (если есть).

8. Поведение функции в бесконечности

9. Производная функции

10. Промежутки возрастания и убывания. Точки максимума и минимума и значения в этих точках.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

« Основные свойства функции. » – Яндекс.Знатоки

К основным свойствам функции относятся:

1. Четность и нечетность функции

Функция называется четной, если
      – область определения функции симметрична относительно нуля
      – для любого х из области определения f(-x) = f(x)

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image003.gif

График четной функции симметричен относительно оси 0y

Функция называется нечетной, если
      – область определения функции симметрична относительно нуля
      – для любого х из области определения f(-x) = –f(x)

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image004.gif

График нечетной функции симметричен относительно начала координат.

2.Периодичность

Функция f(x) называется периодической с периодом !https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image005.gif, если для любого х из области определения f(x) = f(x+Т) = f(x-Т).

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image006.gif

График периодической функции состоит из неограниченно повторяющихся одинаковых фрагментов.

3. Монотонность (возрастание, убывание)

Функция f(x) возрастает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1)< f(x2).

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image011.gif

Функция f(x) убывает на множестве Р , если для любых x1 и x2 из этого множества, таких, что x1 < x2 выполнено неравенство f(x1) > f(x2).

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image013.gif

4. Экстремумы

Точка Хmax называется точкой максимума функции f(x) , если для всех х из некоторой окрестности Хmax , выполнено неравенство f(х)!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image014.gif f(Xmax).

Значение Ymax=f(Xmax) называется максимумом этой функции.

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image015.gif

Хmax – точка максимума
Уmax – максимум

Точка Хmin называется точкой минимума функции f(x) , если для всех х из некоторой окрестности Хmin , выполнено неравенство f(х)!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image016.gif f(Xmin).

Значение Ymin=f(Xmin) называется минимумом этой функции.

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image017.gif

Xmin – точка минимума
Ymin – минимум

Xmin, Хmax – точки экстремума
Ymin, Уmax – экстремумы.

5. Нули функции

Нулем функции y = f(x) называется такое значение аргумента х , при котором функция обращается в нуль: f(x) = 0.

!https://ykl-shk.azureedge.net//goods/ymk/algebra/work3/theory/5/image018.gif

Х1,Х2,Х3 – нули функции y = f(x).

yandex.ru

Свойства функции

В этой статье мы коротко суммируем сведения, которые касаются такого важного математического понятия, как функция. Мы поговорим о том, что такое  числовая функция и какие свойства функции необходимо знать и уметь исследовать.

Что такое  числовая функция? Пусть у нас есть два числовых множества: Х и Y, и  между этими множествами есть определенная зависимость. То есть каждому элементу х из множества Х по определенному правилу ставится в соответствие  единственный элемент  y из множества Y.

Важно, что каждому элементу х из множества Х соответствует один и только один элемент y из множества Y.

Правило, с помощью которого каждому элементу из множества Х мы ставим в соответствие единственный элемент из множества Y, называется числовой функцией. 

Множество Х называется областью определения функции.

Множество Y называется множеством значений значений функции.

Равенство   называется уравнением функции. В этом уравнении    — независимая переменная, или аргумент функции.   — зависимая переменная.

Если мы возьмем все пары и поставим им в соответствие соответствующие точки координатной плоскости, то  получим график функции. График функции — это графической изображение зависимости между множествами Х и Y.

Свойства функции мы можем определить, глядя на график функции, и, наоборот, исследуя свойства функции мы можем построить ее график.

Основные свойства функций. 

1. Область определения функции.

Область определения функции D(y)-это множество всех допустимых значений аргумента x ( независимой переменной x), при которых выражение, стоящее в правой части уравнения функции   имеет смысл. Другими словами, это область допустимых значений выражения .

Чтобы по графику функции найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.

2. Множество значений функции.

Множество значений функции  Е(y)— это множество всех значений, которые может принимать  зависимая переменная y.

Чтобы по графику функции  найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.

3.  Нули функции.

Нули функции — это те значения аргумента х, при которых значение функции (y) равно нулю.

Чтобы найти нули функции , нужно решить уравнение  . Корни этого уравнения и будут нулями функции .

Чтобы найти нули функции по ее графику, нужно найти точки пересечения графика с осью ОХ. Абсциссы точек пересечения и будут нулями функции  .

4. Промежутки знакопостоянства функции. 

Промежутки знакопостоянства функции — это такие промежутки значений аргумента, на которых функция сохраняет свой знак, то есть  или .

Чтобы найти промежутки знакопостоянства функции , нужно решить неравенства и  .

Чтобы найти  промежутки знакопостоянства функции  по ее графику, нужно

• найти промежутки значений аргумента х, при которых график функции расположен выше оси ОХ — при этих значениях аргумента , 
• найти промежутки значений аргумента х, при которых график функции расположен ниже оси ОХ — при этих значениях аргумента  .

5. Промежутки монотонности функции.

Промежутки монотонности функции — это такие промежутки значений  аргумента х, при которых функция возрастает или убывает.

Говорят, что функция   возрастает на промежутке I, если для любых двух значений аргумента  , принадлежащих промежутку I таких, что   выполняется соотношение:.

Другими словами, функция   возрастает на промежутке I, если большему значению аргумента из этого промежутка соответствует большее значение функции.

Чтобы по графику функции определить промежутки возрастания функции, нужно, двигаясь  слева направо по линии графика функции, выделить промежутки значений аргумента х, на которых график идет вверх.

Говорят, что функция   убывает на промежутке I, если для любых двух значений аргумента  , принадлежащих промежутку I таких, что   выполняется соотношение: .

Другими словами, функция   убывает на промежутке I, если большему значению аргумента из этого промежутка соответствует меньшее значение функции. 

Чтобы по графику функции определить промежутки убывания функции, нужно, двигаясь  слева направо вдоль линии графика функции, выделить промежутки значений аргумента х, на которых график идет вниз.

6. Точки максимума и минимума функции.

Точка называется точкой максимума функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:

.

Графически это означает что точка с абсциссой  x_0 лежит выше других точек из окрестности I графика функции y=f(x).

Точка называется точкой минимума  функции , если существует такая окрестность I точки , что для любой точки х из этой окрестности выполняется соотношение:

Графически это означает что точка с абсциссой  лежит ниже других точек  из окрестности I графика функции .

Обычно мы находим точки максимума и минимума функции, проводя исследование функции с помощью производной.

 7. Четность (нечетность) функции.

Функция  называется четной, если выполняются два условия:

а) Для любого значения аргумента , принадлежащего области определения функции,   также принадлежит области определения функции.

Другими словами, область определения  четной функции симметрична относительно начала координат.

б)  Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .

Функция называется нечетной, если выполняются два условия:

а) Для любого значения аргумента , принадлежащего области определения функции, также принадлежит области определения функции.

Другими словами, область определения нечетной функции симметрична относительно начала координат.

б)  Для любого значения аргумента х, принадлежащего области определения функции, выполняется соотношение .

Все функции делятся на четные, нечетные, и те, которые не являются четными и не являются нечетными. Они называются функциями общего вида.

Чтобы определить четность функции, нужно:

а). Найти область определения функции , и определить, является ли она симметричным множеством.

Если, например,  число х=2 входит в область определения функции, а число х=-2 не входит, то D(y) не является симметричным множеством, и функция — функция общего вида.

Если область определения  функции — симметричное множество, то проверяем п. б)

б). В уравнение функции  нужно вместо х подставить -х, упростить полученное выражение, и постараться привести его к виду  или .

Если , то функция четная.

Если , то функция нечетная.

Если не удалось привести ни к тому ни к другому, то наша функция — общего вида.

График четной функции симметричен относительно оси ординат ( прямой OY ).

График нечетной функции симметричен относительно начала координат ( точки (0,0) ).

8. Периодичность функции.

Функция называется периодической, если существует такое положительное число Т, что

• для любого значения х из области определения функции, х+Т также принадлежит D(x)
• 

В программе средней школы из числа периодических функций изучают только тригонометрические функции.

Предлагаю вам посмотреть  ВИДЕОУРОК, в котором  я рассказываю, как определить свойства функции по ее графику.

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Графики функций. Построение графиков функций

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны отношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

Следовательно, график функции – это множество точек (x; y), где x – это аргумент, а y – значение функции, соответствующее данному аргументу. Координаты каждой точки можно ещё изобразить так:

(x; f(x))   или   (x; y(x))

Для примера возьмём самую простую функцию, где аргумент равен значению функции:

y = x

В этом случае нам не придётся для каждого аргумента вычислять значение функции, так как они равны, значит, и у всех точек нашего графика абсцисса будет равна ординате. Отметим три точки на координатной плоскости, например: L(-2; -2), M(0; 0) и N(1; 1):

Если мы последовательно (от наименьшего значения аргумента к большему) соединим отмеченные точки, то у нас получится прямая линия, значит, графиком функции y = x является прямая:

Надпись на чертеже y = x – это уравнение графика. На многих чертежах с графиками можно увидеть надпись с уравнением, к которому относится данный график.

Обратите внимание, что прямая линия бесконечна в обе стороны, поэтому, хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика. Поэтому большинство чертежей изображает только часть графика, обычно расположенную около начала координат.

naobumium.info

Линейная функция, график — прямая. Нули, промежутки возрастания, убывания, знакопостоянства, пересечения, свойства. Тесты

Тестирование онлайн

• Линейная функция

Определение. График

Линейной функцией называется функция вида

где k, b — некоторые числа.

Функция вида называется прямой пропорциональностью, является частным случаем линейной зависимости.

Графиком линейной функции является прямая линия.

Для построения графика достаточно знать координаты двух точек.

Свойства линейной функции

1) Область определения функции — множество всех действительных чисел

2) Множеством значений функции является множество всех действительных чисел

3) Функция не имеет ни наибольшего, ни наименьшего значений.

4) Функция не является ни четной, ни нечетной (кроме особых случаев).

5) Функция непериодическая.

6) График функции пересекает ось Ох в точке , а ось Оу — в точке (0; b).

7) — является нулем функции.

8) Функция монотонно возрастает на области определения при k>0, монотонно убывает при k.

9) При k>0: функция принимает отрицательные значения на промежутке и положительные значения на промежутке

При k: функция принимает отрицательные значения на промежутке и положительные значения на промежутке

10) Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом. Если k>0, то этот угол острый, если k — тупой, если k=0, то прямая совпадает с осью Ох.

Для построения графика функции — прямой линии, очевидно, достаточно двух точек.

Особые случаи

1) Если b=0, получим уравнение y=kx. Функция такого вида называется прямой пропорциональностью. Графиком является прямая, проходящая через начало координат.

2) Если k=0, получим уравнение y=b. Графиком является прямая, параллельная оси Ох, проходящая через точку (0; b).

fizmat.by