Градусная мера угла / Начальные геометрические сведения / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Начальные геометрические сведения
5. Градусная мера угла

Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения. Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения —  с  градусом.

---

Градус — это угол, который равен 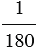части развернутого угла,обозначается знаком

часть градуса называется минутой, обозначается знаком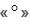

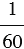
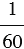часть минуты называется секундой, обозначается знаком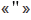

Пример: 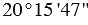(двадцать градусов пятнадцать минут сорок семь секунд)

Градусная мера угла — это положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.

Пример:

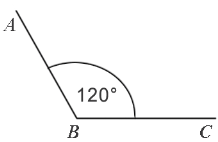
Градусная мера угла ABC

равна 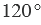. Говорят: «Угол ABC равен 120 градусам». Пишут: .

---

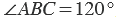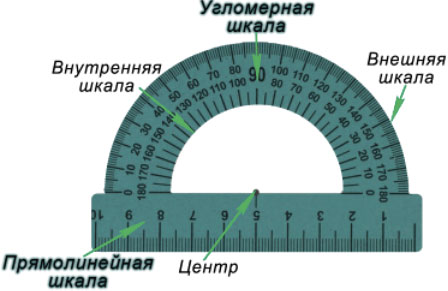
Транспортир — это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .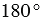

Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через

нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.

Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).

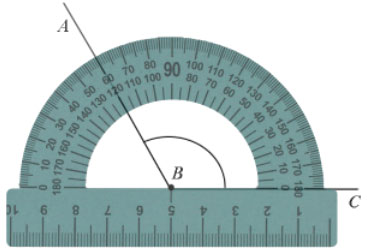
Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .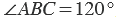

---

Свойства:

• Равные углы имеют равные градусные меры.
• Меньший угол имеет меньшую градусную меру.
• Развернутый угол равен .
• Неразвернутый угол меньше .
• Если луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.

---

Основные типы углов:

1. Острый угол — угол, градусная мера которого меньше 90°.

2. Прямой угол — угол, градусная мера которого равна 90°.

3. Тупой угол — угол, градусная мера которого больше 90°, но меньше 180°.

4. Развернутый угол — угол, градусная мера которого равна 180°.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Угол

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Измерение углов на местности

Смежные углы

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

Начальные геометрические сведения

Правило встречается в следующих упражнениях:

7 класс

Задание 41, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 54, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 14, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 300, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 345, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 14, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 465, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 663, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 704, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© budu5.com, 2019

Пользовательское соглашение

Copyright

budu5.com

Градусная мера угла. Определение

Основные понятия

В рамках вопроса измерения углов, в данном разделе рассмотрим несколько понятий, относящихся к начальным геометрическим сведениям:

• угол;
• развёрнутый и неразвёрнутый угол;
• градус, минута и секунда;
• градусная мера угла;
• прямой, острый и тупой углы.

Углом называют такую геометрическую фигуру, которая представляет собой точку (вершину) и исходящие из неё два луча (стороны). Угол называют развёрнутым, если оба луча лежат на одной прямой.

Рисунок 1. Угол. Автор24 — интернет-биржа студенческих работ

Благодаря градусной мере угла можно произвести измерение углов. Измерение углов проводится аналогично измерению отрезков. Так же, как и при измерении отрезков, при измерении углов используется специальная единица измерения. Чаще всего это градус.

Определение 1

Градус — это единица измерения. В геометрии он представляет собой угол, с которым сравнивают другие углы. Градус равен $\frac{1}{180}$ от развёрнутого угла.

Теперь можно дать определение градусной мере угла.

Определение 2

Градусная мера угла — это такое положительное число, которое обозначает, сколько раз градус помещается в данном угле.

Для измерения углов используют транспортир.

Рисунок 2. Транспортир. Автор24 — интернет-биржа студенческих работ

Пример записи градусной меры: $\angle ABC = 150^{\circ}$. На рисунке эта запись означает следующее:

Рисунок 3. Градусная мера. Автор24 — интернет-биржа студенческих работ

В устной форме говорят так: «Угол АВС равен 150 градусам».

Некоторые части градуса имеют свои специальные названия. Минутой называют $\frac{1}{60}$ часть градуса, для обозначения используется знак $’$. Секундой называют $\frac{1}{60}$ часть минуты, для обозначения используют $»$. Пример записи угла в 75 градусов, 45 минут и 28 секунд: $75^{\circ}45’28»$.

Равными называют те углы, у которых градусные меры равны. Соответственно, углы можно сравнивать, говоря, что один угол меньше другого или один угол больше другого.

Выше было дано определение развернутому углу. Владея понятием градусной меры, мы можем описать разницу между развернутым и неразвернутым углом. Развернутый угол всегда равен $180^{\circ}$. Неразвернутый угол — это любой угол меньше $180^{\circ}$.

Различают прямой, острый и тупой углы. Прямой угол равен $90^{\circ}$, острый — меньше $90^{\circ}$, тупой — больше $90^{\circ}$ и меньше $180^{\circ}$.

Рисунок 4. Прямой, острый и тупой углы. Автор24 — интернет-биржа студенческих работ

В повседневной жизни есть примеры необходимости и важности умения измерять углы и понимать градусную меру. Измерение углов необходимо в различных исследованиях, в том числе в астрономии при определении положения небесных тел.

Для практики, попробуйте начертить хотя бы три неразвёрнутых угла и один развёрнутый разными способами, измерьте с помощью транспортира углы и запишите эти результаты. Можно задать случайные числа и попрактиковаться в точности черчения углов с помощью транспортира, деления их с помощью биссектрисы (биссектриса — это луч, исходящий из вершины данного угла и делящий угол пополам).

Примеры задач

Пример 1

Задача. Есть рисунок:

Рисунок 5. Задача. Автор24 — интернет-биржа студенческих работ

Лучи $DE$ и $DF$ — биссектрисы соответствующих углов $ADB$ и $BDC$. Требуется найти угол $ADC$, если $\angle EDF = 75^{\circ}$.

Решение. Так как угол $EDF$ содержит по половинке от каждого угла $ADB$ и $BDC$, то можем сделать вывод, что $EDF$ — это ровно половина самого угла $ADC$. Получаем простые вычисления: $\angle ADC=75\cdot 2=150^{\circ}$.

Ответ: $150^{\circ}$.

Приведём ещё один интересный пример.

Пример 2

Задача. Дан рисунок.

Рисунок 6. Задача. Автор24 — интернет-биржа студенческих работ

Угол $ABC$ прямой. Углы $ABE$, $EBD$ и $DBC$ равны. Требуется найти угол, образованный биссектрисами $ABE$ и $DBC$.

Решение. Так как $ABC$ — прямой угол, то, значит, он равен $90^{\circ}$. Угол $\angle EBD=90/3=30^{\circ}$. Так как углы $ABE$, $EBD$ и $DBC$ равны, то любой из них будет равен $30^{\circ}$. Биссектриса любого из этих углов поделит любой из этих углов на два угла, равных $15^{\circ}$. Так как две половины углов $ABE$ и $DBC$ принадлежат искомому углу, то мы можем утверждать, что искомый угол равен $30+15+15=60^{\circ}$.

Ответ. $60^{\circ}$

В данной статье мы раскрыли полностью вопрос о градусной мере угла и как измерять углы.

spravochnick.ru

Что такое градусная мера угла? Свойства углов. Как узнать меру угла

Математика, геометрия – многим эти науки, как, впрочем, и большинство других точных, даются крайне тяжело. Людям трудно разобраться в формулах и странной терминологии. Что скрывается под этим странным понятием?

Определение

Для начала, нужно рассмотреть просто меру угла. В этом поможет изображение луча и прямой линии. Сначала нужно провести, например, горизонтальную прямую линию. Затем от её первой точки проводится луч, не параллельный прямой. Таким образом, между прямой и лучом появляется некоторое расстояние, небольшой угол. Мера угла – это размер этого самого поворота луча.

Это понятие обозначает определенное цифровое значение, которое будет больше нуля. Оно выражается в градусах, а также его составных частях, то есть минутах и секундах. То количество градусов, которое поместится в угол между лучом и прямой, и будет градусной мерой.

Свойства углов

• Абсолютно каждый угол будет иметь определённую градусную меру.
• Если он полностью развернут, то число будет равняться 180 градусам.
• Для нахождения градусной меры рассматривается сумма всех углов, которые разбил луч.
• С помощью любого луча можно создать полуплоскость, в которой реально сделать угол. Он будет иметь градусную меру, величина которой будет менее 180, и такой угол может быть лишь один.

Как узнать меру угла?

Как правило, минимальной градусной мерой является 1 градус, который составит 1/180 от развернутого угла. Однако иногда нельзя получить настолько четкую цифру. В этих случаях применяют секунды и минуты.

При их нахождении значение можно перевести в градусы, таким образом получится доля градуса. Иногда применяют дробные числа, вроде 80,7 градуса.

Также важно запомнить ключевые величины. Прямой угол всегда будет равняться 90 градусам. Если мера больше, то он будет считаться тупым, а если меньше, то острым.

topkin.ru

Центральный угол. Градусная мера дуги окружности. Видеоурок. Геометрия 8 Класс

На этом уроке мы познакомимся с понятиями центрального угла и градусной меры дуги окружности.

Напомним определение окружности. Сейчас мы дадим определение с ошибкой, задача – найти эту ошибку.

Определение:

Окружностью с центром в точке О и радиусом R называют множество точек плоскости, удаленных от одной точки – центра окружности О – на расстояние R.

Очевидно, что ошибка – пропущенное важное слово всех, то есть окружность – множество всех точек, равноудаленных от ее центра.

Например, вершины A, B, C, D квадрата – это множество точек, равноудаленных от центра квадрата, но это не есть окружность (рис. 1).

Рис. 1. Квадрат

Вспомним важные элементы окружности:

Дуга ;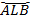

Угол  – центральный угол;

Точка О – центр окружности.

Имеем дугу и соответствующий центральный угол (рис. 2).

Рис. 2. Элементы окружности

Рассмотрим понятие градусной меры дуги.

Задана окружность с центром О. Дуга ALB не больше полуокружности; дуга AМB больше полуокружности.

Градусной мерой дуги ALB называется градусная мера соответствующего центрального угла – .

Для дуги, большей полуокружности, градусной мерой будет следующая разность:

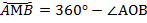 (рис. 3).

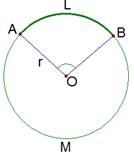
Рис. 3. Градусная мера дуги

Две дуг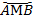и  и  вместе составляют целую окружность, запишем это:

Таким образом, градусная мера окружности – это .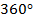

Задана окружность с центром О, диаметром АВ, радиусом, перпендикулярным диаметру, ОС, радиусом ОМ, который составляет с ОС угол .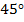

Дуга 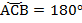 – пол-окружности;

Дуга 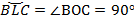 – четверть окружности, угол  прямой;

Дуга ;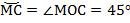

Дуга 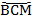 состоит из двух дуг, ее градусная мера равна сумме градусных мер двух дуг: ;

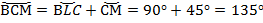Дуга 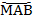 больше полуокружности, значит, ее градусная мера – это разность: .

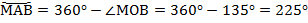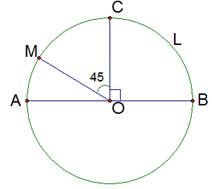
Рис. 4. Иллюстрация к примерам

Каждая дуга стягивается своей хордой, во многих задачах требуется найти длину этой хорды.

Пример:

Радиус окружности с центром О – 16 см. Найдите хорду АВ, если:

а)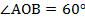

б)

в)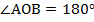

Решение:

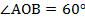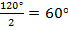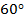Итак, в случае а . Треугольник  равнобедренный, стороны ОА и ОВ равны как радиусы окружности. Углы при основании равны и сумма их равна , значит, на каждый из углов приходится , таким образом, в треугольнике  все углы составляют , а значит, этот треугольник равносторонний и сторона АВ равна также радиусу окружности, то есть 16 см (рис. 5).

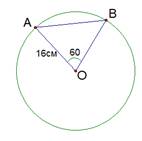
Рис. 5. Иллюстрация к случаю а

В случае б центральный угол  составляет 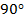. Рассмотрим прямоугольный равнобедренный треугольник  и применим теорему Пифагора, чтобы найти его гипотенузу: . Нашли

 см (рис. 6).

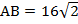
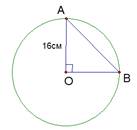
Рис. 6. Иллюстрация к случаю б

В случае в 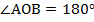, значит, в данном случае АВ является диаметром окружности. Мы знаем, что диаметр равен двум радиусам, радиус нам известен. Таким образом,  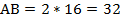см (рис. 7).

Рис. 7. Иллюстрация к случаю в

Итак, мы узнали, что такое центральный угол, познакомились с понятием градусной меры дуги окружности. На следующем уроке мы изучим вписанный угол и теорему о нем.

 

Список литературы

1. Александров А.Д. и др. Геометрия 8 класс. – М.: Просвещение, 2006.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия 8. – М.: Просвещение, 2011.
3. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Uztest.ru (Источник).
2. Raal100.narod.ru (Источник).
3. Uztest.ru (Источник).

 

Домашнее задание

1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др., Геометрия 7–9, № 649, № 651, № 652, с. 73.

interneturok.ru

определение угла, измерение углов, обозначения и примеры

Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.

Определение угла

Определение 1

Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.

Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.

Определение 2

Дана прямая a на плоскости. На ней обозначим некоторую точку O. Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.

Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O.

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.

Перейдем к понятию определения угла.

Определение 3

Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.

Имеет место случай, когда стороны угла могут выступать в роли прямой линии.

Определение 4

Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.

На рисунке ниже изображен развернутый угол.

Точка на прямой

zaochnik.com

Радианная мера угла

Цель урока «Радианная мера угла»  9 класс:

Усвоить определение угла в один радиан, запомнить  формулы  перехода от градусной меры угла к радианной и от радианной к градусной.

Научиться использовать полученные знания при выполнении упражнений

Наравне с  градусной мерой угла используется  радианная.

Возьмем на координатной плоскости окружность с центром в точке О и радиусом R. Отметим на ней дугу РМ, длина которой равна R и угол РОМ.

Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан.

Градусная мера угла в 1 радиан равна:

Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е.

И наоборот

Так как π = 3,14, то 1 рад = 57,3°

Если угол содержит a радиан, то его градусная мера равна

И наоборот

Обычно при обозначении меры угла в радианах наименование «рад» опускают.

Например, 360° = 2π рад, пишут 360° = 2π

В таблице указаны наиболее часто встречающиеся углы в градусной и радианной мере.

Градусы	0	15	30	45	60	75	90	120	135	150	180	270	360
Радианы	0	π/12	π/6	π/4	π/3	5π/12	π/2	2π/3	3π/4	5π/6	π	3π/2	2π

Пример 1.

Найти радианную меру угла равного а) 40° ,  б)120° ,  в)105°

Решение

а) 40° = 40·π / 180 = 2π/9

б) 120° = 120·π/180 = 2π/3

в) 105° = 105·π/180 = 7π/12

Пример 2.

Найти градусную меру угла выраженного в радианах а) π/6 ,  б) π/9,  в) 2·π/3

Решение

а) π/6 = 180°/6 = 30°

б) π/9 = 180°/9 = 20°

в) 2π/3 = 2·180°/6 = 120°

mirurokov.ru