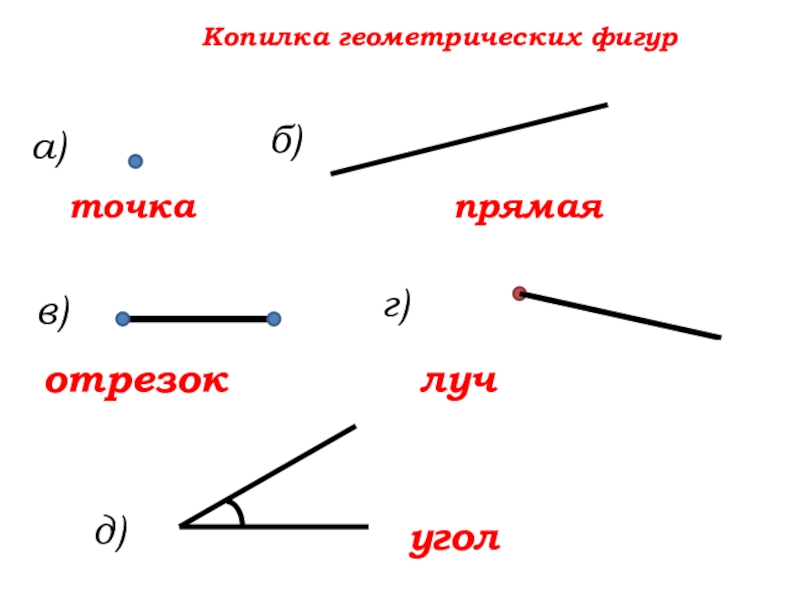
Правило что такое луч. Точка, линия, прямая, луч, отрезок, ломанная
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
A B Cточка 1, точка 2, точка 3
1 2 3Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А». Но как понять через какие? A A A
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
a b cЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
B AПрямые могут быть
- пересекающимися, если имеют общую точку.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
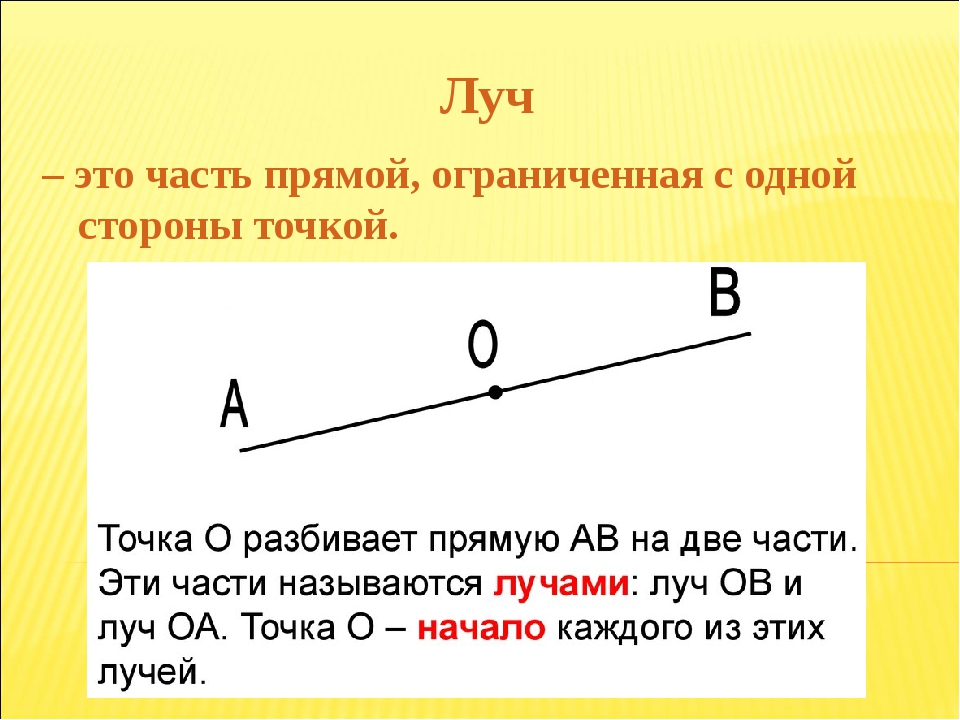
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
B AЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C B AОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.
 Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точкамиЧерез одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B Aпрямая линия AB
B AОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ B A ✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
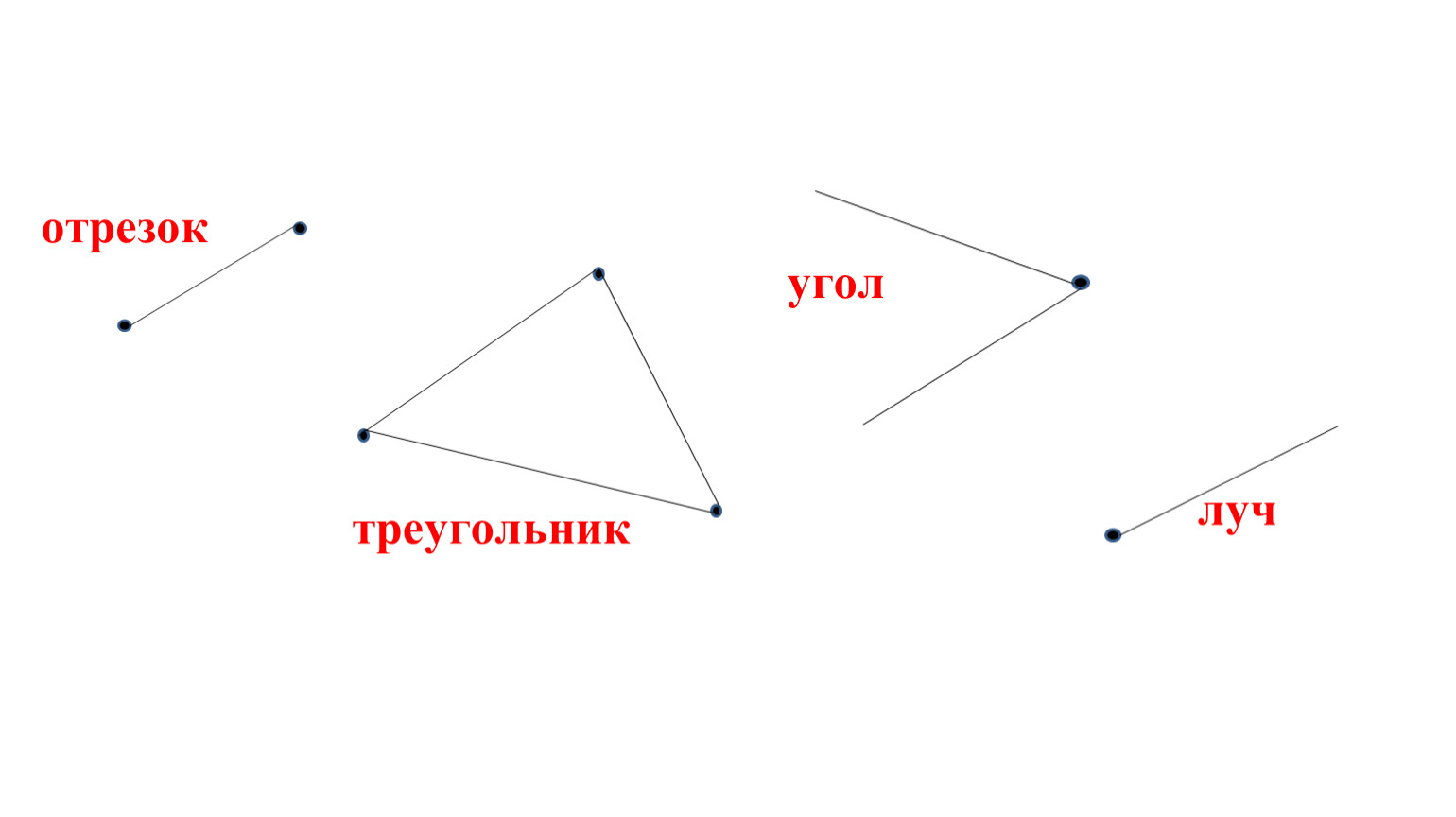
B AЗадача: где прямая , луч , отрезок , кривая ?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
A B C D E 64 62 127 52Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее
, а у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A B C D E F 120 60 58 122 98 141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
д.
Луч и прямая относятся к числу основных геометрических элементов. Сведения о них даются уже на первом этапе изучения соответствующего раздела математики. Чем отличается луч от прямой? Информация об этом изложена ниже.
Определение
Луч – это полупрямая, с одной стороны исходящая из конкретной точки, с другой – ничем не ограниченная.
Прямая – это бесконечная с обеих сторон линия, проходящая через две любые точки и не меняющая свое направление (в отличие от кривой или ломаной).
Прямая
Сравнение
Из определений видно, что кардинальное отличие луча от прямой заключается в том, ограниченны ли они в пространстве. Так, луч обязательно имеет начало и продолжается только с одной стороны. У прямой, в свою очередь, нет предела ни с того, ни с другого края. В связи с этим начертить можно лишь ее часть, что, впрочем, относится и к лучу.
Если взять на прямой произвольную точку, то отходящая от нее бесконечная линия будет являться лучом. В этом смысле луч можно назвать частью прямой. Справедливо и то, что избранная точка будет служить в качестве исходной сразу для двух противоположно направленных лучей.
В этом смысле луч можно назвать частью прямой. Справедливо и то, что избранная точка будет служить в качестве исходной сразу для двух противоположно направленных лучей.
Сравнивая луч и прямую, следует сказать о способах их обозначения. Каждый из геометрических объектов может называться латинской строчной буквой: луч a (с, d, t) или прямая b (a, h, c). Также в том и другом случае используется обозначение двумя заглавными буквами: луч NK или прямая OD.
Однако в последнем пункте имеются отличия. Буквы в названии прямой, помечающие точки, через которые она проведена, при чтении и записи можно менять местами. Между тем относительно луча первым указывается строго его начало, а затем точка, расположенная на определенном расстоянии от исходной.
Кроме того, луч имеет собственный вариант обозначения. В этом случае после заглавного символа, называющего начальную точку, с помощью строчной буквы указывается прямая, на которой расположен луч. Таким образом, обозначение Bo трактуется так: луч с началом в точке B принадлежит прямой o.
В чем разница между лучом и прямой, кроме сказанного? В том, что лучи могут образовывать угол. Для этого они должны исходить из одной точки. Прямые углов не образуют.
Цели:
- Познакомить учащихся с понятием луча как бесконечной фигуры;
- Учить показывать луч с помощью указки;
- Продолжить формирование вычислительных навыков;
- Совершенствовать умение решать задачи;
- Развивать умение анализировать и обобщать.
Ход урока
I . Организационный момент.
Ребята, вы готовы к уроку? (Да . )
На вас надеюсь я, друзья!
Вы хороший дружный класс.
Всё получится у вас!
II . Мотивация учебной деятельности.
Я очень хочу, чтобы урок получился интересным, познавательным, чтобы мы вместе повторили и закрепили то, что мы уже знаем и постарались открыть для себя что-то новое.
III. Актуализация знаний.
- Прочитайте числа и назовите «лишнее» число в каждом ряду:
а) 90, 30, 40, 51,60;
б) 88, 64,55,11, 77, 33;
с) 47, 27, 87, 74, 97, 17; - Назовите числа по порядку:
а) от 20 до 30;
б) от 46 до 57;
в) от 75 до 84; - Как вы думаете, будут ли эти тексты задачами?
Измените вопрос второго текста так, чтобы он стал задачей.
Измените условие так, чтобы текст стал задачей.
Решите полученные задачи.
IV . Первичное усвоение новых знаний.
Начертите такую линию.
Как она называется?
Начертите такую линию.
Как она называется? Чем отличается отрезок от прямой?
Начертите такую линию.
Кто знает, как она называется?
Посмотрите на картинку, вы видите похожие линии, что это?
Вот и эта линия называется луч. Чем он отличается от прямой и отрезка?
Это очень интересная фигура: у неё есть начало и нет конца.
А изображают её так. (Работа на доске и в тетрадях. ) Отметим на точку, приложим к ней линейку и по линейке проведём линию.
) Отметим на точку, приложим к ней линейку и по линейке проведём линию.
Какой бы длинной ни была линейка, весь луч мы всё равно не сможем начертить. На рисунке мы изобразили лишь часть луча, которая показывает направление луча.
Луч можно начертить в любом направлении:
Начертите три разных луча у себя в тетради.
Чтобы отличать один луч от другого, договоримся обозначать луч двумя буквами латинского алфавита так, как мы обозначали с вами отрезки. Писать буквы нужно в строго определённом порядке: первой пишется та буква, которая обозначает начало луча, вторая пишется над или под лучом.
Посмотрите на рисунок в учебнике. Луч красного цвета обозначен двумя буквами. Какой буквой обозначено начало луча?
Прочитаем все вместе запись: «Луч АВ»
Теперь прочитайте следующие записи: луч ВС, луч МК, луч ВА, луч ОХ.
Важно научиться правильно показывать луч. Мы будем делать это концом указки. (Показ учителем. )
Теперь посмотрите на плакат. (Подготавливается заранее, на нём 3 луча .) На нём изображены 3 луча. Прочитайте название каждого из них. Называя луч, показывайте его указкой.
(Подготавливается заранее, на нём 3 луча .) На нём изображены 3 луча. Прочитайте название каждого из них. Называя луч, показывайте его указкой.
Физминутка
1, 2, 3, 4, 5
Все умеем мы считать.
Отдыхать умеем тоже:
Руки за спину положим,
Голову поднимем выше
И легко-легко подышим.
Раз, два – выше голова,
Три, четыре – ноги шире,
Пять, шесть – тихо сеть.
Раз – подняться, потянуться.
Два – согнуться, разогнуться.
Три – в ладоши три хлопка,
Головою три кивка.
На четыре – руки шире.
Пять – руками помахать.
Шесть – за парту тихо сесть.
V. Первичная проверка понимания.
1) Работа с учебником.
Можно ли нарисовать весь луч?
В каком направлении можно начертить луч?
Учащиеся называют каждый луч, сначала читая букву, соответствующую началу луча.
Учащиеся чертят в тетради луч, обозначают его буквами.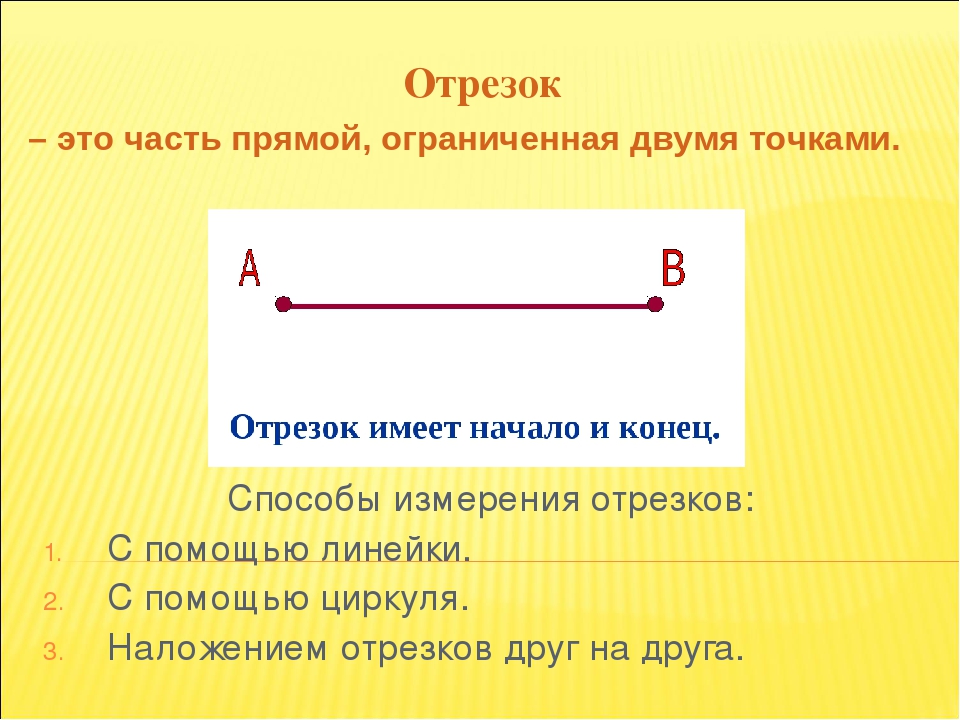
Поставьте в тетради точку О. Проведите через неё прямую линию. Сколько получилось лучей?
Проведите ещё одну прямую линию через эту точку. Сколько теперь лучей?
VI . Организация усвоения способов деятельности.
1) Работа в тетради на печатной основе.
Дифференцированное задание.
1-я группа — № 19
2-я группа — № 20
3-я группа — № 21
2) Физминутка – офтальмотренажёр.
3) Работа по учебнику
Прочитайте, какие способы сложения придумал Знайка?
Найдите результаты сложения такими же способами.
Что известно в задаче?
Что надо узнать?
Короче – это больше или меньше?
Как узнать длину карандаша?
Запишите ответ.
VII . Рефлексия.
Что нового узнали на уроке?
Что такое луч?
Как начертить луч?
Сколько лучей можно провести через одну точку?
Сегодня на уроке мне помогали…. .
.
VIII . Домашнее задание.
Все мы когда-то изучали в школе геометрию, но далеко не каждый из нас вспомнит, что представляет собой отрезок. А уж тем более мало кто сможет объяснить понятие лучей, и как они обозначаются. Давайте постараемся в этой статье напомнить себе данные определения и рассмотрим их в математике. Также определим, что такое луч, и чем он отличается от светового. Если вникнуть, то понять будет несложно.
Определение понятий
Для начала давайте вспомним, что называется геометрией. Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства. К ним относятся треугольник, квадрат, прямоугольник, параллелепипед, круг, овал, ромб, цилиндр и т. п. Простейшая фигура — это прямая. Она является бесконечной и не имеет начала. Две прямые пересекутся только в одной единственной точке. Через одну точку можно проводить бессчетное количество прямых линий. Каждая точка на линии делит ее на два .
Он состоит из точек, расположенных по одну сторону.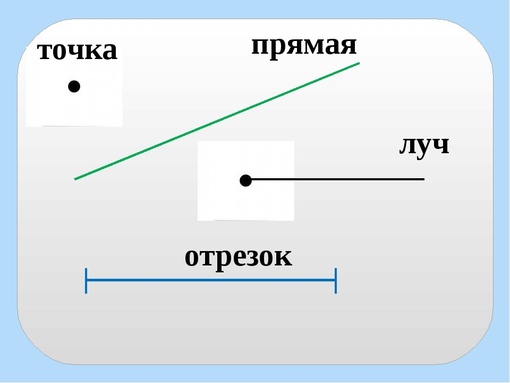 Все понятия данных подмножеств можно именовать таким образом. Луч обозначают одной строчной латинской буквой или двумя заглавными, когда одна точка — начало (например, О), а вторая лежит на нем (например, F, К и Е) .
Все понятия данных подмножеств можно именовать таким образом. Луч обозначают одной строчной латинской буквой или двумя заглавными, когда одна точка — начало (например, О), а вторая лежит на нем (например, F, К и Е) .
В основе геометрической фигуры, имеющей углы, лежат полупрямые. Они начинаются в точке, где пересекаются, но второй стороной направлены в бесконечность. Начало делит прямую на 2 части. На письме его обычно именуют двумя заглавными (OF) или одной буквой латиницы (а, в, с). Если дана прямая, то записывается ОВ в закругленных скобках: (ОВ). Если же это отрезок — в квадратных скобках.
Таким образом, луч — это часть прямой. Через любую точку можно провести множество прямых, но через 2 несовпадающие — только одну. Последние могут быть взаимодействовать только в трех вариантах: пересекаться, скрещиваться, быть параллельными друг другу. Существуют линейные уравнения, которые задают прямую на плоскости.
Обозначения в геометрии
Вариантов для обозначения несколько:
Нужно знать: Что такое и горизонтальное положение?
Отличие световых лучей от геометрических
В геометрии таковые понятия очень схожи. Луч — это линия, но она является энергией света . Другими словами — это небольшой пучок света. В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток света очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
Луч — это линия, но она является энергией света . Другими словами — это небольшой пучок света. В оптике данное понятие, как и понятие прямой, в геометрии — базовое. У световых нет сконцентрированного направления, происходит дифракция. Но когда поток света очень сильный, расходимостью пренебрегают, и можно выделять четкое направление.
Из курса школьной геометрии мало у кого остались точные сведения о том, что представляет собой отрезок, как он обозначается, что такое ломаная линия, прямая, точка и как обозначаются лучи. Если вы не можете вспомнить начальный курс геометрии, достаточно ознакомиться с этой статьей.
Что такое геометрия? Это математический раздел, в котором школьник знакомится с геометрическими фигурами и их свойствами. Информации много, иногда недостаточно времени для того, чтобы все охватить и запомнить. Некоторые знания необходимо освежить спустя несколько месяцев и даже лет. Например, вспомнить, что такое лучи и как они обозначаются.
Что такое луч в геометрии
Луч – это прямая, с одной стороны ограниченная точкой, а с другой стороны – свободная, то есть не имеющая ограничений. Чтобы быстрее запомнить, как обозначаются лучи и как они выглядят, можно привести простой пример: мы ведь можем направить лучик света из фонарика в небо? С одной стороны луч ограничен – с того места, откуда он выходит, то есть – из фонарика. С другой стороны – он не имеет ограничений. Получается, что крайняя точка начала луча только одна, она и называется «начало». Второй точки не существует, потому что луч уходит в бесконечность.
Чтобы быстрее запомнить, как обозначаются лучи и как они выглядят, можно привести простой пример: мы ведь можем направить лучик света из фонарика в небо? С одной стороны луч ограничен – с того места, откуда он выходит, то есть – из фонарика. С другой стороны – он не имеет ограничений. Получается, что крайняя точка начала луча только одна, она и называется «начало». Второй точки не существует, потому что луч уходит в бесконечность.
Чтобы понимать, как обозначить луч на листке бумаги, нужно начертить прямую линию. Например, пусть это будет отрезок, равный 10 см. С правой стороны поставим ограничение – точку, это начало луча. Второй точки на конце отрезка не будет.
Как обозначаются лучи
Продолжим вспоминать, что представляет собой луч и как его обозначить.
Вариантов обозначения несколько:
- Начертим в тетрадке прямую, обозначим точку начала луча. И присвоим ей имя. Например, пусть это будет луч «С». Первая точка – это начало луча, второй точки, как вы уже вспомнили, не существует.
 Это классическая схема обозначения лучей.
Это классическая схема обозначения лучей. - Второй вариант поинтереснее: луч можно обозначить несколькими буквами. Например, на одном луче может быть 2 буквы. Первая – это начало луча, пусть это будет буква А, а вторая может располагаться с определенным шагом. Допустим, на отрезке длиной 10 см начало луча обозначено буквой А, а на расстоянии 4 см от начала луча имеется вторая точка, точка В. Тогда луч нужно обозначить, как луч «АВ». Чтобы было понятнее, читать можно так: вторая точка В – это точка, через которую проходит луч.
- Лучи еще можно обозначить и третьим способом, когда начальная точка будет находиться не в начале луча, а с небольшим отступлением. Например, чертим прямую длиной 10 см, отступаем от левого края 1 см, ставим точку – это будет начало луча. Обозначаем, например, буквой О. Посередине луча точку не ставим, но обозначаем эту часть луча буквой К. В данном случае буква О, будет началом этого луча, он исходит из этой точки. Читается луч так: «ОК», он является полупрямым.

Как обозначается луч в тетрадке
Обозначение на письме луча нужно один раз запомнить: записываются лучи латинскими заглавными буквами. Если это прямая, то записать луч нужно АВ в круглых скобочках: (АВ). Если перед вами отрезок, то он записывается только в квадратных скобках.
Рекомендуем также
Отрезок, угол, луч — геометрия и искусство
Из истории. Единицы измерения углов.
Градусное измерение углов возникло в Древнем Вавилоне задолго до новой эры. Жрецы считали, что свой дневной путь Солнце совершает за 180 «шагов», и, значит, один «шаг» равен 1/180 развернутого угла.
В Вавилоне была принята шестидесятиричная система счисления, т. е. фактически числа записывались в виде суммы степеней числа 60, а не 10, как это принято в нашей десятеричной системе. Естественно поэтому, что для введения более мелких единиц измерения углов один «шаг» последовательно делился на 60 частей.
Вавилонская система измерения углов оказалась достаточно удобной, и ее сохранили математики Греции и Рима.
Термины, которыми мы пользуемся для названия угловых величин, имеют латинские корни. Слово «градус» происходит от латинского gradus (шаг, ступень). В переводе с латинского minutus означает «уменьшенный». Наконец, secunda переводится как «вторая». Имеется в виду следующее: деление градуса на 60 частей, т. е. минуты,— это первое деление; деление минуты на 60 секунд — второе деление градуса. Малоупотребительное название 1/60 секунды — терцина, латинское tercina означает «третье» (деление градуса).
Принятая сейчас система обозначения величин углов получила широкое распространение на рубеже XVI и XVII вв.; ею уже пользовались такие известные астрономы, как Н. Коперник и Т. Браге. Но еще К. Птолемей (II в. н. э.) количество градусов обозначал кружком, число минут — штрихом, а секунд — двумя штрихами.
Другая единица измерения углов — радиан — введена совсем недавно. Первое издание (это были экзаменационные билеты), содержащее термин «радиан», появилось в 1873 г. в Англии. Сначала в обозначениях указывалось, что имеется в виду радианная мера , но вскоре инадекс R (или г) стали опускать. Сам термин «радиан» происходит от латинского radius (спица, луч).
Первое издание (это были экзаменационные билеты), содержащее термин «радиан», появилось в 1873 г. в Англии. Сначала в обозначениях указывалось, что имеется в виду радианная мера , но вскоре инадекс R (или г) стали опускать. Сам термин «радиан» происходит от латинского radius (спица, луч).
Если вспомнить определение угла в один радиан (центральный угол, длина дуги которого равна радиусу окружности), то выбор корня «рад» для названия такого угла представляется совершенно естественным.
Понятия точка прямая отрезок луч угол. Точка, линия, прямая, луч, отрезок, ломанная
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки ,,,, и , а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т. к. у них общее начало.
к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
Точка и прямая являются основными геометрическими фигурами на плоскости.
Древнегреческий учёный Евклид говорил: «точка» – это то, что не имеет частей». Слово «точка» в переводе с латинского языка означает результат мгновенного касания, укол. Точка является основой для построения любой геометрической фигуры.
Прямая линия или просто прямая – это линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия бесконечна, и изобразить всю прямую и измерить её невозможно.
Точки обозначают заглавными латинскими буквами А, В, С, D, Е и др., а прямые теми же буквами, но строчными а, b, c, d, e и др. Прямую можно обозначить и двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую a можно обозначить АВ.
Можно сказать, что точки АВ лежат на прямой а или принадлежат прямой а. А можно сказать, что прямая а проходит через точки А и В.
Простейшие геометрические фигуры на плоскости – это отрезок, луч, ломаная линия.
Отрезок – это часть прямой, которая состоит из всех точек этой прямой, ограниченных двумя выбранными точками. Эти точки – концы отрезка. Отрезок обозначается указанием его концов.
Луч или полупрямая – это часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой или началом луча. Луч имеет точку начала, но не имеет конца.
Полупрямые или лучи обозначаются двумя строчными латинскими буквами: начальной и любой другой буквой, соответствующей точке, принадлежащей полупрямой. При этом начальная точка ставится на первом месте.
Получается, что прямая бесконечна: у неё нет ни начала, ни конца; у луча есть только начало, но нет конца, а отрезок имеет начало и конец. Поэтому только отрезок мы можем измерить.
Поэтому только отрезок мы можем измерить.
Несколько отрезков, которые последовательно соединены между собой так, что имеющие одну общуюточкуотрезки (соседние) располагаются не на одной прямой, представляют собой ломаную линию.
Ломаная линия может быть замкнутой и незамкнутой. Если конец последнего отрезка совпадает с началом первого, перед нами замкнутая ломаная линия, если же нет – незамкнутая.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
В этой статье мы подробно остановимся на одном из первичных понятий геометрии – на понятии прямой линии на плоскости. Сначала определимся с основными терминами и обозначениями. Далее обсудим взаимное расположение прямой и точки, а также двух прямых на плоскости, приведем необходимые аксиомы. В заключении, рассмотрим способы задания прямой на плоскости и приведем графические иллюстрации.
Навигация по странице.
Прямая на плоскости — понятие.
Прежде чем дать понятие прямой на плоскости, следует четко представлять себе что же представляет собой плоскость. Представление о плоскости позволяет получить, к примеру, ровная поверхность стола или стены дома. Следует, однако, иметь в виду, что размеры стола ограничены, а плоскость простирается и за пределы этих границ в бесконечность (как будто у нас сколь угодно большой стол).
Представление о плоскости позволяет получить, к примеру, ровная поверхность стола или стены дома. Следует, однако, иметь в виду, что размеры стола ограничены, а плоскость простирается и за пределы этих границ в бесконечность (как будто у нас сколь угодно большой стол).
Если взять хорошо заточенный карандаш и дотронуться его стержнем до поверхности «стола», то мы получим изображение точки. Так мы получаем представление о точке на плоскости .
Теперь можно переходить и к понятию прямой линии на плоскости .
Положим на поверхность стола (на плоскость) лист чистой бумаги. Для того чтобы изобразить прямую линию, нам необходимо взять линейку и провести карандашом линию на сколько это позволяют сделать размеры используемой линейки и листа бумаги. Следует отметить, что таким способом мы получим лишь часть прямой. Прямую линию целиком, простирающуюся в бесконечность, мы можем только вообразить.
Взаимное расположение прямой и точки.
Начать следует с аксиомы: на каждой прямой и в каждой плоскости имеются точки.
Точки принято обозначать большими латинскими буквами, например, точки А и F . В свою очередь прямые линии обозначают малыми латинскими буквами, к примеру, прямые a и d .
Возможны два варианта взаимного расположения прямой и точки на плоскости : либо точка лежит на прямой (в этом случае также говорят, что прямая проходит через точку), либо точка не лежит на прямой (также говорят, что точка не принадлежит прямой или прямая не проходит через точку).
Для обозначения принадлежности точки некоторой прямой используют символ «». К примеру, если точка А лежит на прямой а , то можно записать . Если точка А не принадлежит прямой а , то записывают .
Справедливо следующее утверждение: через любые две точки проходит единственная прямая.
Это утверждение является аксиомой и его следует принять как факт. К тому же, это достаточно очевидно: отмечаем две точки на бумаге, прикладываем к ним линейку и проводим прямую линию. Прямую, проходящую через две заданные точки (например, через точки А
и В
), можно обозначать двумя этими буквами (в нашем случае прямая АВ
или ВА
).
Следует понимать, что на прямой, заданной на плоскости, лежит бесконечно много различных точек, причем все эти точки лежат в одной плоскости. Это утверждение устанавливается аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Множество всех точек, расположенных между двумя заданными на прямой точками, вместе с этими точками называют отрезком прямой или просто отрезком . Точки, ограничивающие отрезок, называются концами отрезка. Отрезок обозначают двумя буквами, соответствующими точкам концов отрезка. К примеру, пусть точки А и В являются концами отрезка, тогда этот отрезок можно обозначить АВ или ВА . Обратите внимание, что такое обозначение отрезка совпадает с обозначением прямой. Чтобы избежать путаницы, рекомендуем к обозначению добавлять слово «отрезок» или «прямая».
Для краткой записи принадлежности и не принадлежности некоторой точки некоторому отрезку используют все те же символы и . Чтобы показать, что некоторый отрезок лежит или не лежит на прямой пользуются символами и соответственно. К примеру, если отрезок АВ
принадлежит прямой а
, можно кратко записать .
Чтобы показать, что некоторый отрезок лежит или не лежит на прямой пользуются символами и соответственно. К примеру, если отрезок АВ
принадлежит прямой а
, можно кратко записать .
Следует также остановиться на случае, когда три различных точки принадлежат одной прямой. В этом случае одна, и только одна точка, лежит между двумя другими. Это утверждение является очередной аксиомой. Пусть точки А , В и С лежат на одной прямой, причем точка В лежит между точками А и С . Тогда можно говорить, что точки А и С находятся по разные стороны от точки В . Также можно сказать, что точки В и С лежат по одну сторону то точки А , а точки А и В лежат по одну сторону от точки С .
Для полноты картины заметим, что любая точка прямой делит эту прямую на две части – два луча . Для этого случая дается аксиома: произвольная точка О
, принадлежащая прямой, делит эту прямую на два луча, причем две любые точки одного луча лежат по одну сторону от точки О
, а две любые точки разных лучей – по разные стороны от точки О
.
Взаимное расположение прямых на плоскости.
Сейчас ответим на вопрос: «Как могут располагаться две прямые на плоскости относительно друг друга»?
Во-первых, две прямые на плоскости могут совпадать .
Это возможно в том случае, когда прямые имеют по крайней мере две общие точки. Действительно, в силу аксиомы, озвученной в предыдущем пункте, через две точки проходит единственная прямая. Иными словами, если через две заданные точки проходят две прямые, то они совпадают.
Во-вторых, две прямые на плоскости могут пересекаться .
В этом случае прямые имеют одну общую точку, которую называют точкой пересечения прямых. Пересечение прямых обозначают символом «», к примеру, запись означает, что прямые а
и b
пересекаются в точке М
. Пересекающиеся прямые приводят нас к понятию угла между пересекающимися прямыми . Отдельно стоит рассмотреть расположение прямых на плоскости, когда угол между ними равен девяноста градусам. В этом случае прямые называются перпендикулярными (рекомендуем статью перпендикулярные прямые, перпендикулярность прямых).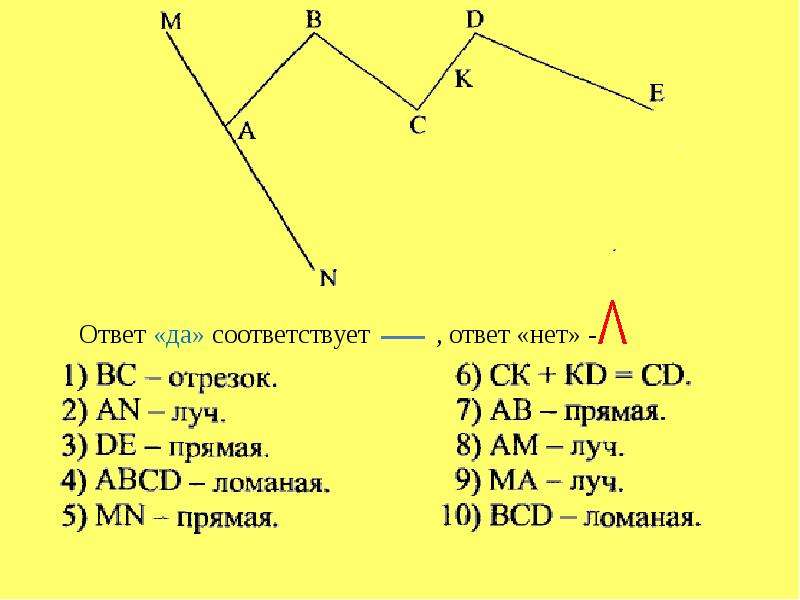 Если прямая a
перпендикулярна прямой b
, то можно использовать краткую запись .
Если прямая a
перпендикулярна прямой b
, то можно использовать краткую запись .
В-третьих, две прямые на плоскости могут быть параллельными.
Прямую линию на плоскости с практической точки зрения удобно рассматривать вместе с векторами. Особое значение имеют ненулевые векторы, лежащие на данной прямой или на любой из параллельных прямых, их называют направляющими векторами прямой . В статье направляющий вектор прямой на плоскости даны примеры направляющих векторов и показаны варианты их использования при решении задач.
Также следует обратить внимание на ненулевые векторы, лежащие на любой из прямых, перпендикулярных данной. Такие векторы называют нормальными векторами прямой . О применении нормальных векторов прямой рассказано в статье нормальный вектор прямой на плоскости .
Когда на плоскости даны три и более прямых линии, то возникает множество различных вариантов их взаимного расположения. Все прямые могут быть параллельными, в противном случае некоторые или все из них пересекаются. При этом все прямые могут пересекаться в единственной точке (смотрите статью пучок прямых), а могут иметь различные точки пересечения.
При этом все прямые могут пересекаться в единственной точке (смотрите статью пучок прямых), а могут иметь различные точки пересечения.
Не будем подробно останавливаться на этом, а приведем без доказательства несколько примечательных и очень часто используемых фактов:
- если две прямые параллельны третьей прямой, то они параллельны между собой;
- если две прямые перпендикулярны третьей прямой, то они параллельны между собой;
- если на плоскости некоторая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую прямую.
Способы задания прямой на плоскости.
Сейчас мы перечислим основные способы, которыми можно задать конкретную прямую на плоскости. Это знание очень полезно с практической точки зрения, так как на нем основывается решение очень многих примеров и задач.
Во-первых, прямую можно задать, указав две точки на плоскости.
Действительно, из аксиомы, рассмотренной в первом пункте этой статьи, мы знаем, что через две точки проходит прямая, и притом только одна.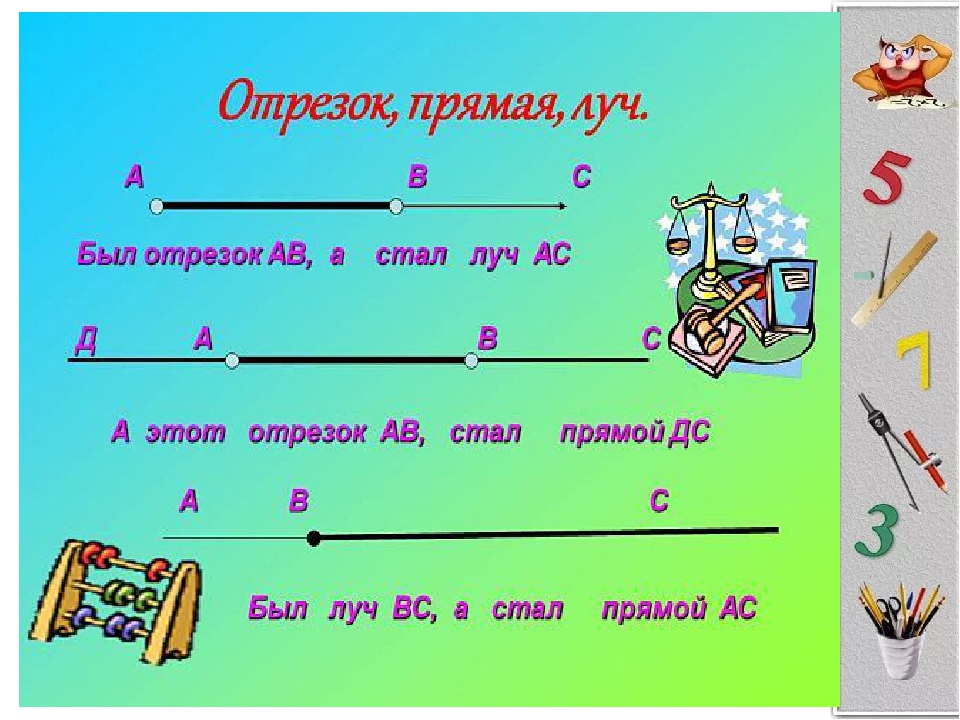
Если в прямоугольной системе координат на плоскости указаны координаты двух несовпадающих точек, то есть возможность записать уравнение прямой, проходящей через две заданные точки .
Во-вторых, прямую можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна. Этот способ справедлив, так как через данную точку плоскости проходит единственная прямая, параллельная заданной прямой. Доказательство этого факта проводилось на уроках геометрии в средней школе.
Если прямую на плоскости задать таким способом относительно введенной прямоугольной декартовой системы координат, то есть возможность составить ее уравнение. Об этом написано в статье уравнение прямой, проходящей через заданную точку параллельно заданной прямой .
В-третьих, прямую можно задать, если указать точку, через которую она проходит, и ее направляющий вектор.
Если прямая линия задана в прямоугольной системе координат таким способом, то легко составить ее каноническое уравнение прямой на плоскости и параметрические уравнения прямой на плоскости .
Четвертый способ задания прямой заключается в том, что следует указать точку, через которую она проходит, и прямую, которой она перпендикулярна. Действительно, через заданную точку плоскости проходит единственная прямая, перпендикулярная данной прямой. Оставим этот факт без доказательства.
Наконец, прямую на плоскости можно задать, указав точку, через которую она проходит, и нормальный вектор прямой.
Если известны координаты точки, лежащей на заданной прямой, и координаты нормального вектора прямой, то есть возможность записать общее уравнение прямой .
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.

- Ильин В.А., Позняк Э.Г. Аналитическая геометрия.
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Точка и прямая являются основными геометрическими фигурами на плоскости.
Древнегреческий учёный Евклид говорил: «точка» – это то, что не имеет частей». Слово «точка» в переводе с латинского языка означает результат мгновенного касания, укол. Точка является основой для построения любой геометрической фигуры.
Прямая линия или просто прямая – это линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия бесконечна, и изобразить всю прямую и измерить её невозможно.
Точки обозначают заглавными латинскими буквами А, В, С, D, Е и др., а прямые теми же буквами, но строчными а, b, c, d, e и др.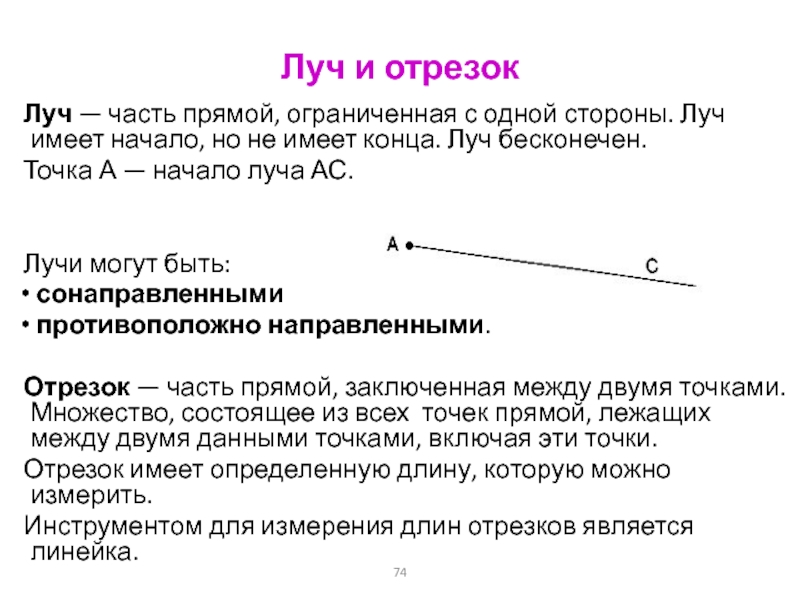 Прямую можно обозначить и двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую a можно обозначить АВ.
Прямую можно обозначить и двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую a можно обозначить АВ.
Можно сказать, что точки АВ лежат на прямой а или принадлежат прямой а. А можно сказать, что прямая а проходит через точки А и В.
Простейшие геометрические фигуры на плоскости – это отрезок, луч, ломаная линия.
Отрезок – это часть прямой, которая состоит из всех точек этой прямой, ограниченных двумя выбранными точками. Эти точки – концы отрезка. Отрезок обозначается указанием его концов.
Луч или полупрямая – это часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой или началом луча. Луч имеет точку начала, но не имеет конца.
Полупрямые или лучи обозначаются двумя строчными латинскими буквами: начальной и любой другой буквой, соответствующей точке, принадлежащей полупрямой. При этом начальная точка ставится на первом месте.
Получается, что прямая бесконечна: у неё нет ни начала, ни конца; у луча есть только начало, но нет конца, а отрезок имеет начало и конец.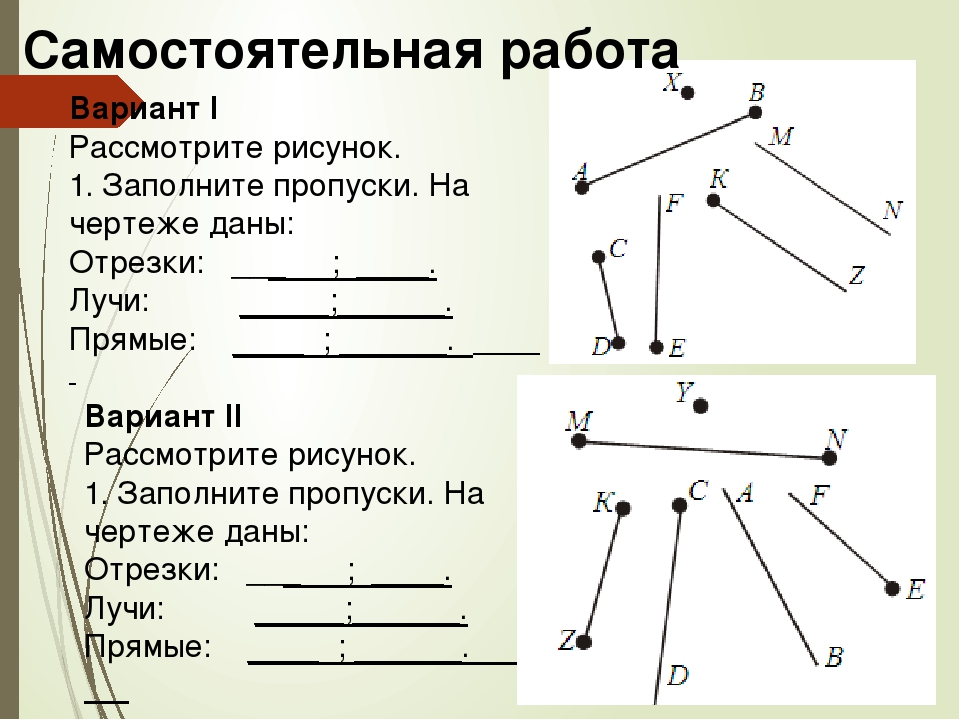 Поэтому только отрезок мы можем измерить.
Поэтому только отрезок мы можем измерить.
Несколько отрезков, которые последовательно соединены между собой так, что имеющие одну общуюточкуотрезки (соседние) располагаются не на одной прямой, представляют собой ломаную линию.
Ломаная линия может быть замкнутой и незамкнутой. Если конец последнего отрезка совпадает с началом первого, перед нами замкнутая ломаная линия, если же нет – незамкнутая.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Презентация и конспект урока по теме «Прямая, луч, отрезок»
План-конспект урока математики № 45
Класс: 5-АДата: 12.11.2019
Учитель: Коротаева Н.А.
Тема:
Прямая, луч, отрезок
Тип урока:
Урок усвоения новых знаний, умений и навыков
Место урока в разделе:
Первый урок в теме «Измерение величин»
Оборудование:
Мультимедийный комплекс
Формы работы на уроке
Фронтальная, групповая, индивидуальная
Цели:
обучающие
(ориентированные на достижение предметных результатов обучения)
Ввести понятия «плоскость», «луч», «прямая», «отрезок»; установить свойства изучаемых объектов; научить строить и распознавать данные фигуры.
развивающие (ориентированные на достижение метапредметных результатов обучения)
Развивать внимание, память, образное мышление; формировать самостоятельность и коммуникативность; создавать условия для проявления познавательной активности.
воспитательные (ориентированные на достижение личностных результатов обучения)
Воспитывать умение слушать, вступать в диалог, участвовать в коллективном обсуждении проблем;
УУД:
познавательные
Поиск и выделение необходимой информации;
анализ объектов с целью выделения признаков; выделение и формулирование познавательной цели, рефлексия способов и условий действий.
регулятивные
Прогнозирование своей деятельности; планирование своей деятельности для решения поставленной задачи.
коммуникативные
Умение слушать и вступать в диалог; умение с достаточной полнотой и точностью выражать свои мысли.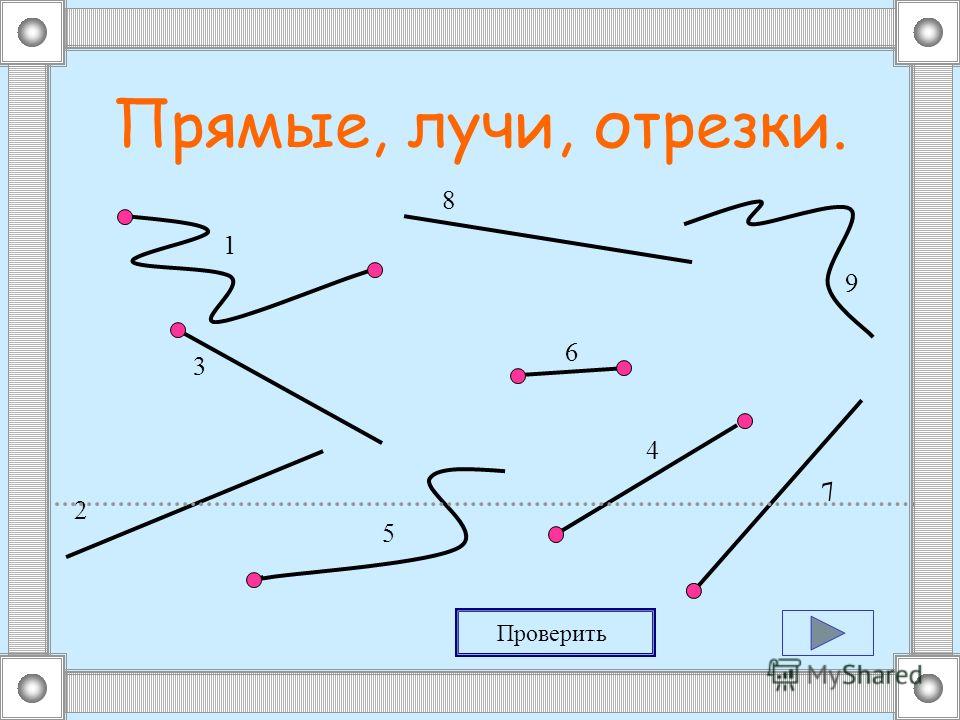
личностные
Установление связи между целью деятельности и ее мотивом; проявление внимания и терпения; проявление доброжелательности в дискуссии, доверия к собеседнику.
Прямая, луч, отрезок
Цели: Ввести понятия «плоскость», «луч», «прямая», «отрезок»; установить свойства изучаемых объектов; научить строить и распознавать данные фигуры.
Развивать внимание, память, образное мышление; формировать самостоятельность и коммуникативность; создавать условия для проявления познавательной активности.
Воспитывать умение слушать, вступать в диалог, участвовать в коллективном обсуждении проблем; поиск и выделение необходимой информации; проявление доброжелательности в дискуссии, доверия к собеседнику
Ход урока
I.Организационный момент
Приветствие учителя, проверка готовности учащихся к уроку.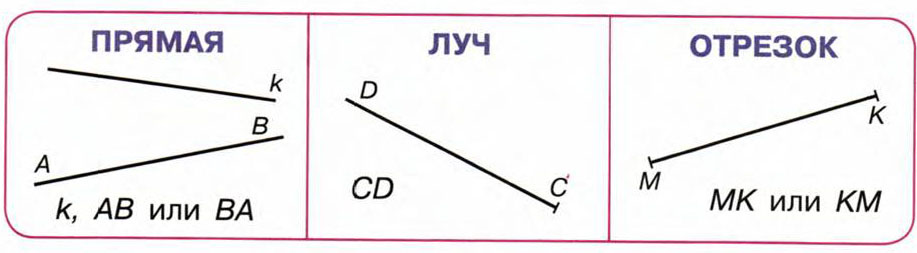
II. Мотивация учебной деятельности
1. Сообщение темы (устный счет).
Решив все примеры и расположив ответы в порядке возрастания, вы сможете прочитать три слова, которые являются темой нашего урока (прямая, луч, отрезок).
15х0= (П)
44+150= (Р)
120:2= (Л)
32:32= (Р)
16-14= (Я)
25х4= (Ч)
160-80= (У)
90:10= (М)
11х10= (О)
920-800= (Т)
12+18= (А)
1000х15= (К)
1000:2= (О)
90-35= (Я)
50х4= (Е)
450-150= (З)
2. Формулирование цели урока.
3. Актуализация опорных знаний, полученных в начальной школе.
(Вспомнить понятия точки, прямой, отрезка)
III. Восприятие и первичное осознание нового материала
1. Определение плоскости.
Поверхность стола, стена, классная доска, оконное стекло могут служить примером части плоскости. Всю плоскость невозможно изобразить потому, что она бесконечна, но ее можно представить себе (привести примеры части плоскости).
2. Определение и обозначение прямой.
— прямая не имеет ни начала, ни конца – она бесконечна;
— прямую обозначают одной строчной латинской буквой или двумя заглавными;
— через любые две точки можно провести только одну прямую;
— две прямые на плоскости могут пересекаться или быть параллельными.
3. Определение луча.
Точка А, лежащая на прямой, делит ее на две части. Каждую их этих частей называют лучом с началом в точке А, обозначают луч двумя заглавными буквами.
4. Определение отрезка.
— определение отрезка;
— обозначение отрезка;
— определение равных отрезков.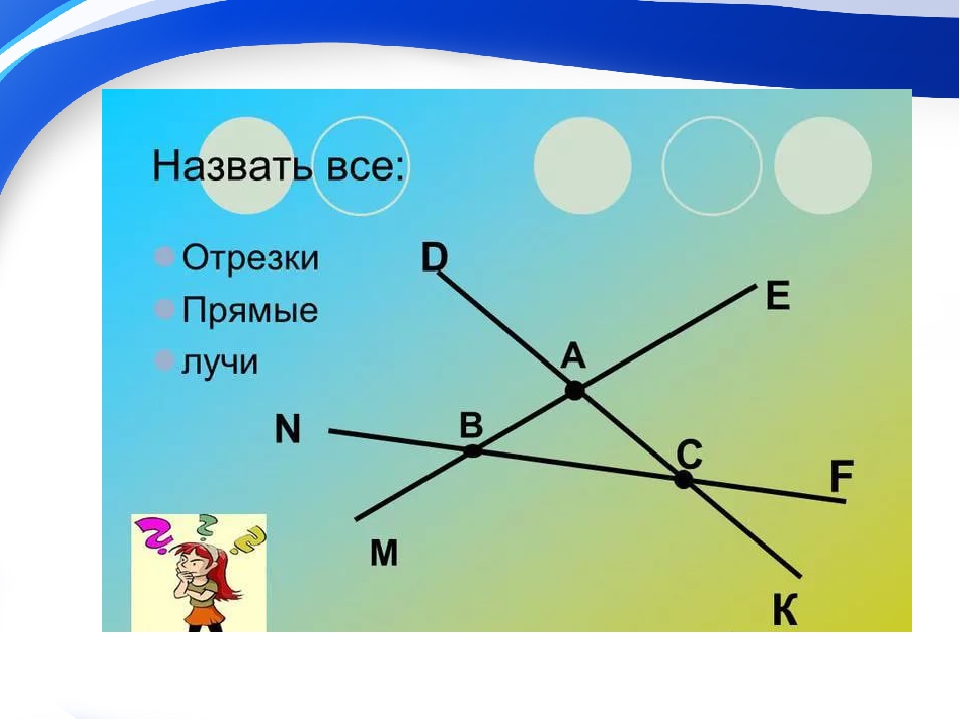
IV. Первичное применение новых знаний
Решение упражнений №356, 359.
V. Физминутка
VI. Применение знаний в стандартных условиях с целью усвоения навыков
1. Фронтальный опрос (1 группа):
— Какие точки лежат на прямой l ?
— Какие точки не лежат на прямой l ?
— Назовите все лучи с вершиной в точках M, N, S?
— Какие точки не лежат на луче MS?
— Перечислите все отрезки, изображенные на рисунке.
2. Индивидуальная работа по карточкам (2 группа):
Тест (Приложение 1).
Начало формы
Конец формы
VII. Итог урока.
Сообщение домашнего задания:
Прочитать п.2.1. стр. 77-79, выполнить №355, РТ 2 часть – № 170, №171.
Рефлексия:
— Сегодня на уроке я научился…
— Мне было интересно…
— Мне было трудно…
— Я понял, что…
— Больше всего мне понравилось…
— Своей работой на уроке я доволен (не совсем, не доволен), потому что…
ТЕСТ
Как правильно записать обозначение луча?
А) АМ
Б) МА
Сколько лучей на рисунке?
А) один
Б) два
В) три
Г) четыре
Какие из обозначенных точек не лежат на луче АС?
А) К, D, В
Б) D, К
В) О, В
Г) К, О
Какая из фигур, изображенных на рисунке, является прямой?
А) ВА
Б) АС
В) ВС
Г) ВМ
Укажите пару пересекающихся фигур.

А) отрезок ОА и прямая СD
Б) луч КР и прямая ВМ
В) прямые СD и ВМ
Г) луч КР и отрезок ОА
Что является общей частью лучей АС и ВС?
А) отрезок АВ
Б) луч ВС
В) точка А
Г) точка В
Пересекаются ли прямые CD и АВ?
А) да
Б) нет
Пересекаются ли лучи АВ и СD?
А) да
Б) нет
Приложение 2
Технологическая карта урока
Деятельность учителяДеятельность ученика
Время
(в мин.)
Формируемые УУД
Познавательные
Регулятивные
Коммуникативные
Личностные
1
2
3
4
5
6
7
8
9
1
Организационный момент
Приветствие; проверка готовности класса к уроку; организация внимания.
2
Осознанное и произвольное построение речевого высказывания
Прогнозирование своей деятельности
Умение слушать и вступать в диалог
Умение выделять нравственный аспект поведения
2
Мотивация учебной деятельности
Вместе с учениками определяет тему урока (Слайд 2-3).
Вспомнить понятия точки, прямой, отрезка, полученные ранее.
Задает учащимся наводящие вопросы
(Слайд 4-5)
Выполняют задание, решая примеры.
Записывают тему урока в тетрадь.
Участвуют в определении цели урока.
Участвуют в работе по повторению, в беседе с учителем, отвечают на поставленные вопросы.
7
Поиск и выделение необходимой информации.
Анализ объектов с целью выделения признаков.
Выдвижение гипотез.
Постановка цели.
Выделение и осознание того, что уже пройдено.
Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог
Установление связи между целью деятельности и ее мотивом
3
Восприятие и первичное осознание нового материала
Знакомит учащихся с определением плоскости, прямой, луча, отрезка.
Задает вопросы, подводящие к определению понятий (Слайды 6-10)
Слушают, задают вопросы.
8
Анализ объектов с целью выделения признаков.
Умение слушать и вступать в диалог
Проявление внимания и терпения
4
Первичное применение новых знаний
Решают упражнения из учебника №342, 354, 355, 356, 359.
Выполняют задания, отвечая на вопросы
проверяют правильность выполнения.
10
Поиск и выделение необходимой информации.
Структурирование знаний.
Подведение под понятие
Планирование своей деятельности для решения поставленной задачи
Умение слушать и вступать в диалог.
Коллективное обсуждение проблем (при необходимости)
Проявление
терпения и аккуратности при построении чертежей
5
Физминутка
Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.
Учащиеся сменили вид деятельности (отдохнули) и готовы продолжать работу.
3
Осознание ценности здоровья
6
Применение знаний в стандартных условиях с целью усвоения навыков
Комментирует, направляет работу учащихся.
Постановка проблемного вопроса.
1 группа работает с учителем, выполняя задания у доски (Слайд 11-12).
2 группа работает индивидуально с тестовыми заданиями на карточках с последующей самопроверкой (Слайд 13)
10
Выделение и формулирование познавательной цели, рефлексия способов и условий действия
Анализ объектов и синтез
Контроль изученного материала
Умение с достаточной полнотой и точностью выражать свои мысли
Проявление доброжелательности в дискуссии, доверия к собеседнику
7
Подведение итогов
Сообщает домашнее задание. Подводит итог урока
Дает возможность самим ученикам оценить себя, затем оценивает учащихся с комментированием.
Рефлексия.
Записывают домашнее задание в дневник
Подводят итог урока, оценивают себя своих товарищей.
5
Осознанное и произвольное построение речевого высказывания
Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог
Ориентация в межличностных отношениях
Точка, линия, прямая, луч, отрезок, ломанная. Точка
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки ,,,, и , а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
Цели:
- Познакомить учащихся с понятием луча как бесконечной фигуры;
- Учить показывать луч с помощью указки;
- Продолжить формирование вычислительных навыков;
- Совершенствовать умение решать задачи;
- Развивать умение анализировать и обобщать.

Ход урока
I . Организационный момент.
Ребята, вы готовы к уроку? (Да . )
На вас надеюсь я, друзья!
Вы хороший дружный класс.
Всё получится у вас!
II . Мотивация учебной деятельности.
Я очень хочу, чтобы урок получился интересным, познавательным, чтобы мы вместе повторили и закрепили то, что мы уже знаем и постарались открыть для себя что-то новое.
III. Актуализация знаний.
- Прочитайте числа и назовите «лишнее» число в каждом ряду:
а) 90, 30, 40, 51,60;
б) 88, 64,55,11, 77, 33;
с) 47, 27, 87, 74, 97, 17; - Назовите числа по порядку:
а) от 20 до 30;
б) от 46 до 57;
в) от 75 до 84; - Как вы думаете, будут ли эти тексты задачами?
Измените вопрос второго текста так, чтобы он стал задачей.
Измените условие так, чтобы текст стал задачей.
Решите полученные задачи.
IV . Первичное усвоение новых знаний.
Первичное усвоение новых знаний.
Начертите такую линию.
Как она называется?
Начертите такую линию.
Как она называется? Чем отличается отрезок от прямой?
Начертите такую линию.
Кто знает, как она называется?
Посмотрите на картинку, вы видите похожие линии, что это?
Вот и эта линия называется луч. Чем он отличается от прямой и отрезка?
Это очень интересная фигура: у неё есть начало и нет конца.
А изображают её так. (Работа на доске и в тетрадях. ) Отметим на точку, приложим к ней линейку и по линейке проведём линию.
Какой бы длинной ни была линейка, весь луч мы всё равно не сможем начертить. На рисунке мы изобразили лишь часть луча, которая показывает направление луча.
Луч можно начертить в любом направлении:
Начертите три разных луча у себя в тетради.
Чтобы отличать один луч от другого, договоримся обозначать луч двумя буквами латинского алфавита так, как мы обозначали с вами отрезки. Писать буквы нужно в строго определённом порядке: первой пишется та буква, которая обозначает начало луча, вторая пишется над или под лучом.
Писать буквы нужно в строго определённом порядке: первой пишется та буква, которая обозначает начало луча, вторая пишется над или под лучом.
Посмотрите на рисунок в учебнике. Луч красного цвета обозначен двумя буквами. Какой буквой обозначено начало луча?
Прочитаем все вместе запись: «Луч АВ»
Теперь прочитайте следующие записи: луч ВС, луч МК, луч ВА, луч ОХ.
Важно научиться правильно показывать луч. Мы будем делать это концом указки. (Показ учителем. )
Теперь посмотрите на плакат. (Подготавливается заранее, на нём 3 луча .) На нём изображены 3 луча. Прочитайте название каждого из них. Называя луч, показывайте его указкой.
Физминутка
1, 2, 3, 4, 5
Все умеем мы считать.
Отдыхать умеем тоже:
Руки за спину положим,
Голову поднимем выше
И легко-легко подышим.
Раз, два – выше голова,
Три, четыре – ноги шире,
Пять, шесть – тихо сеть.
Раз – подняться, потянуться.
Два – согнуться, разогнуться.
Три – в ладоши три хлопка,
Головою три кивка.
На четыре – руки шире.
Пять – руками помахать.
Шесть – за парту тихо сесть.
V. Первичная проверка понимания.
1) Работа с учебником.
Можно ли нарисовать весь луч?
В каком направлении можно начертить луч?
Учащиеся называют каждый луч, сначала читая букву, соответствующую началу луча.
Учащиеся чертят в тетради луч, обозначают его буквами.
Поставьте в тетради точку О. Проведите через неё прямую линию. Сколько получилось лучей?
Проведите ещё одну прямую линию через эту точку. Сколько теперь лучей?
VI . Организация усвоения способов деятельности.
1) Работа в тетради на печатной основе.
Дифференцированное задание.
1-я группа — № 19
2-я группа — № 20
3-я группа — № 21
2) Физминутка – офтальмотренажёр.
3) Работа по учебнику
Прочитайте, какие способы сложения придумал Знайка?
Найдите результаты сложения такими же способами.
Что известно в задаче?
Что надо узнать?
Короче – это больше или меньше?
Как узнать длину карандаша?
Запишите ответ.
VII . Рефлексия.
Что нового узнали на уроке?
Что такое луч?
Как начертить луч?
Сколько лучей можно провести через одну точку?
Сегодня на уроке мне помогали…..
VIII . Домашнее задание.
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
A B Cточка 1, точка 2, точка 3
1 2 3Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А». Но как понять через какие?
A
A
A
Но как понять через какие?
A
A
A
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
a b cЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой.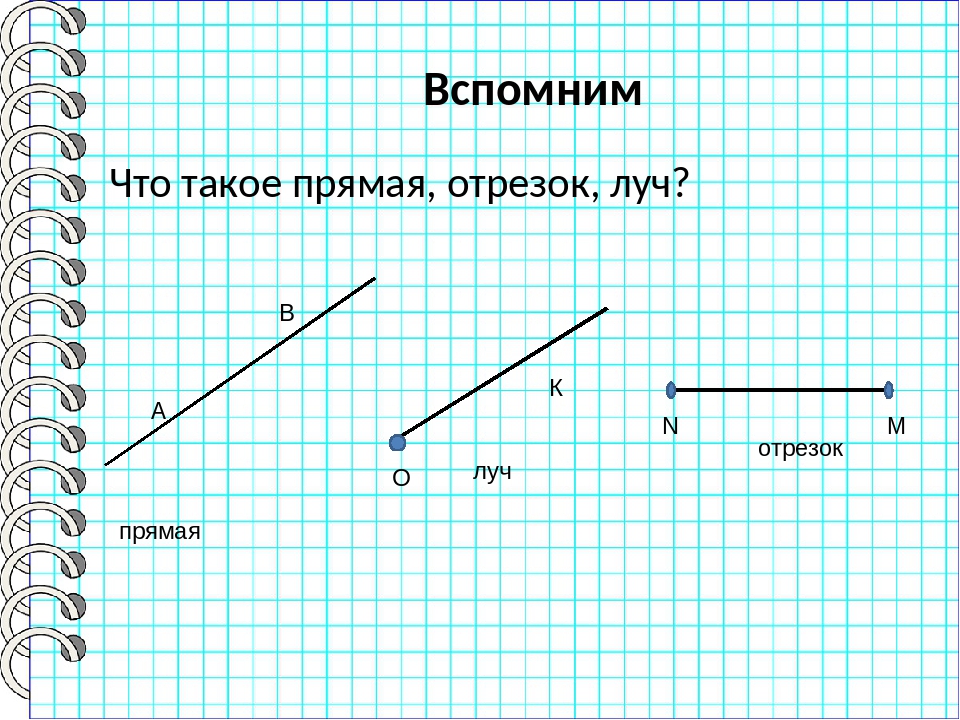 Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
B AПрямые могут быть
- пересекающимися, если имеют общую точку. Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
B AЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C B AОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.
 Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точкамиЧерез одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B Aпрямая линия AB
B AОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ B A ✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
B AЗадача: где прямая , луч , отрезок , кривая ?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
A B C D E 64 62 127 52Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее
, а у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A B C D E F 120 60 58 122 98 141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.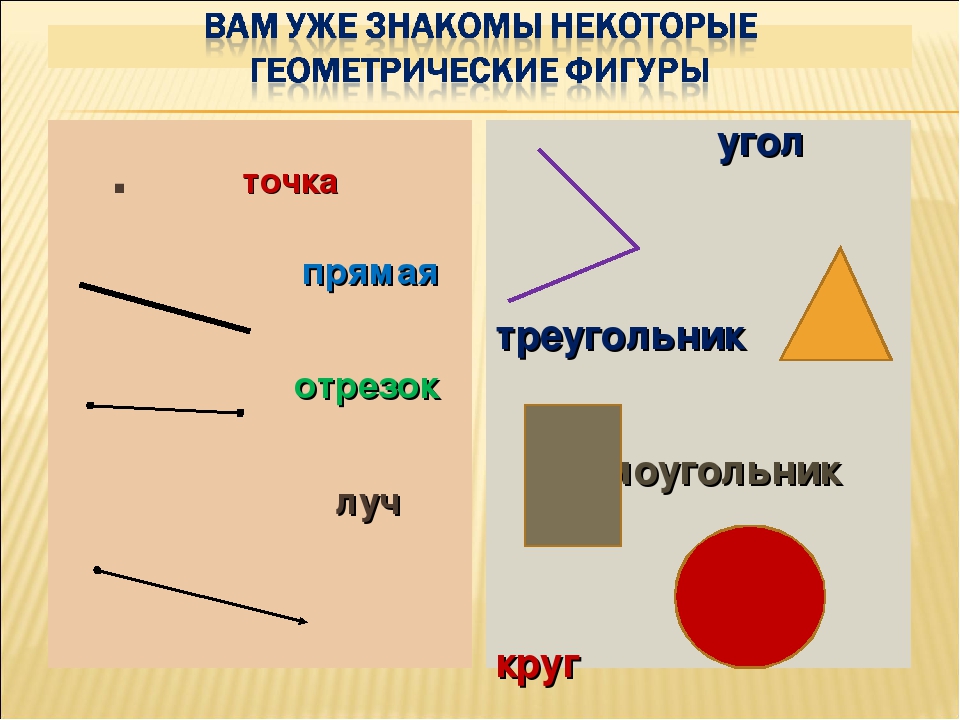 д.
д.
Многие воспринимают Солнце не только как объект изучение астрономии, источник жизни на Земле в самом прагматичном смысле, но и как символ добра, радости, искренности. Не зря ведь хороших, добрых людей часто ласково называют «солнышком». Сейчас мы рассмотрим несколько вариантов того, как нарисовать солнце.
Солнышко с веселой мордашкой
Вначале изобразим милую, мультипликационную версию солнышка с улыбающимся личиком. Конечно, этот вариант больше подходит для деток — он отлично научит малыша тому, как нарисовать солнце красиво. Но взрослому такое солнышко тоже непременно подарит заряд позитива.
Сначала наметим основную фигуру — круг.
Потом изобразим детали личика — большие блестящие глазки, улыбку, маленькие бровки и румянец на щеках.
И, конечно же, надо нарисовать лучи. Они будут образовывать единую фигуру, похожую на корону.
Теперь раскрасим наш шедевр — кружок будет желтым, лучи — оранжевыми, а глаза — нежно-голубыми.
На этом все, солнышко нарисовано.
Солнце с большими бровями
Продолжим тему мультипликационных солнышек. На этот раз у нашего небесного тела будут не только большие глаза и ослепительная улыбка, но и густые темные брови. А еще — веснушки. Это очень забавный пример того, как нарисовать солнце поэтапно.
Как и в прошлый раз, начнем с круга. Это будет самая основная фигура.
Потом наметим угловатые лучики разного размера. Так они будут выглядеть естественнее.
После этого начнем изображать лицо: глаза будут вытянутыми и темными, рот — большим, а брови, как мы и договаривались, густыми и темными. И не забудьте про веснушки!
Солнце с маленькими глазками
Время опробовать еще один стиль — хотя в этом случае черты «лица» у солнышка будут очень маленькими, выглядеть оно будет невероятно симпатичным. В этом вы сможете убедиться сами, если попробуете научиться тому, как нарисовать солнце карандашом.
Начало по традиции будет заключаться в изображении окружности. Постарайтесь сделать фигуру максимально ровной, правильной. Не переживайте, если с первого раза это не удастся: прелесть карандашной техники заключается в том, что все недостатки можно быстро скорректировать.
Постарайтесь сделать фигуру максимально ровной, правильной. Не переживайте, если с первого раза это не удастся: прелесть карандашной техники заключается в том, что все недостатки можно быстро скорректировать.
Теперь лучики. Здесь они будут ровными, треугольными, фигурными.
Время заняться мордашкой. Маленькие глазки-точечки, стеснительная улыбка, кружочки румянца — разве не прелесть?
На этой ноте мы закончим — рисунок готов.
Широко улыбающееся солнышко — заряжаемся позитивом
Что может быть позитивнее, чем буквально лучащееся радостью солнце? Такое может развеселить даже в самый хмурый и напряженный день. Так что если вы хотите всегда сохранять приподнятый настрой, стоит научиться тому, как нарисовать солнце с улыбкой. Правду говорила детская песенка — от нее и впрямь становится светлей.
Как и во всех остальных случаях, наше солнце будет круглым. Кружок должен быть ровным, красивым.
Теперь — овальные глаза с бликами и широкая улыбка.
После этого изобразим лучи. Они будут очень своеобразные, изогнутые, будто языки пламени. Притом короткие лучи будут чередоваться с длинными.
А сейчас хорошенько наведем все контуры. Лучше всего сделать это фломастером или маркером.
Теперь все готово — улыбнитесь своему солнышку. И никакой дождь теперь не страшен!
Солнцу дождик ни по чем — рисуем солнышко с зонтиком
Осенью небо часто затягивается тучками. Многим это не по вкусу, ведь серая, дождливая погода вызывает уныние и грусть. Но наше солнышко не боится ни туч, ни дождя, ведь у него для таких случаев есть замечательный зонтик. Изобразим его — заодно научимся тому, как нарисовать солнце красками.
Первым делом нарисуем тучку, мягкую и пушистую на вид.
Теперь круглое солнце с открытым в улыбке ртом, смешным носиком-пуговкой и милыми глазами. Правда, пока что оно будет будет чем-то похоже на Колобка.
А сейчас изобразим наше главное оружие в борьбе с тучками — сложенный зонтик. К слову, на руках у нашего сияющего персонажа будут перчатки.
К слову, на руках у нашего сияющего персонажа будут перчатки.
Время нарисовать лучи — извивающиеся, неровные, практически живые. А на зонтике сделаем горошек.
Время заняться красками. «Тельце» сделаем желтым, лучи и нос — красными, зонтик — розовым, а тучку — синей. Краски можно взять любые — акварель, гуашь, акрил или даже масло.
Теперь наш яркий рисунок окончен.
1 класс, прямая, отрезок, точка, урок и презентация по математике луч, ломанная
Дата публикации: .
Урок и презентация на тему:
«Точка, прямая и кривая линии, отрезок, луч, ломаная»
Точка
Дорогие ребята, сегодня вместе с нашими героями мы будем изучать простейшие геометрические фигуры.
Начнем с точки. В математике точка обозначается буквой алфавита, например, буквой А. В тетради это выглядит так.
Если у вас на рисунке есть несколько точек, то их необходимо называть разными буквами, чтобы не путаться.

Линии
Вжик нарисовал линию. В математике линию принято обозначать строчными латинскими буквами, например, буквой b.
Если на рисунке несколько линий, то разные линии нужно обозначать разными буквами.
Прямая линия
Линия называется прямой, если она нигде не искривляется.
Вжик нарисовал несколько прямых линий разного цвета.
В математике прямая линия бесконечная, а это значит, что у неё нет ни начала, ни конца.
Кривая линия
Чип нарисовал несколько кривых линий. Каждый может их нарисовать от руки.
Отрезок
Если отрезать от прямой линии некоторую часть, то получится отрезок с началом и концом, что мы попробуем сделать. Получится отрезок AB. У данного отрезка есть длина, и обозначается она так, АB = 4 см.
На этом рисунке нарисовано 2 отрезка: АВ и СЕ.
Луч
Луч – часть прямой, которая имеет начало, но не имеет конца. Обозначается, как показано на рисунке.
Ломаная линия
Ломаная линия – это фигура, которая состоит из отрезков, последовательно соединенных своими концами.
Ломаная на рисунке обозначается $A_1A_2A_3A_4A_5A_6$.
Ребята, определите, какие фигуры изображены на рисунке? Назовите каждую фигуру.
Методические указания по теме:
По программе ученики начальных классов знакомят¬ся с плоскостными фигурами, именуемыми вообще многоугольниками; в частности с различного вида треугольниками, прямоугольниками и другими видами четырех-угольников, фигурами с большим числом сторон: пяти-угольниками, шестиугольниками, которые легко можно разбить на треугольники и четырехугольники.При ознакомлении с указанными фигурами необходимо с самых первых шагов (когда дети пользуются различными фигурами как дидактическим материалом) дать практически понятие детям о том, что треугольник, четырехугольник, прямоугольник, квадрат и вообще многоугольник— это часть плоскости (поверхность бумаги, картона, фанеры, ткани), ограниченная сторонами — от-резками прямых линий, как в прямоугольнике или тре-угольнике, или кривой линией, как в круге, или кривой и прямой, как в полукруге.
 Надо избегать обычной, повторяющейся и в пособиях, и в учебниках ошибки, заключающейся в том, что вместо понятия о треугольнике, четырехугольнике и вообще о всяком многоугольнике детям внедряется понятие о контуре этой фигуры. Например, ученика спрашивают, сколько нужно взять палочек, что-бы сложить квадрат (вместо того чтобы спросить, сколь-ко надо взять палочек, чтобы составить контур, границы квадрата). После таких вопросов ученик начинает думать, что квадрат, треугольник, прямоугольник можно сделать из палочек.
Надо избегать обычной, повторяющейся и в пособиях, и в учебниках ошибки, заключающейся в том, что вместо понятия о треугольнике, четырехугольнике и вообще о всяком многоугольнике детям внедряется понятие о контуре этой фигуры. Например, ученика спрашивают, сколько нужно взять палочек, что-бы сложить квадрат (вместо того чтобы спросить, сколь-ко надо взять палочек, чтобы составить контур, границы квадрата). После таких вопросов ученик начинает думать, что квадрат, треугольник, прямоугольник можно сделать из палочек.Чтобы избежать этих ошибок, мы предлагаем знакомство с треугольником, прямоугольником и любым многоугольником начинать путем вырезывания этой фигу¬ры из бумаги (контур фигуры очерчивается по линейке карандашом, а затем по начерченному контуру ножницами или ножичком вырезывается фигура). Вторым этапом ознакомления с такими фигурами являются чертежи на бумаге с обязательной затушевкой. Пусть ученик знает, что когда он начертил только стороны треугольника или квадрата, то это только контур (границы) фигуры, а когда он сделает затушевку, то будет видеть всю фигуру.

Если же учитель желает провести с учениками практическую работу с палочками, то им можно предложить примерно такие вопросы:
1) Сколько надо взять палочек и каких, чтобы из них сложить все стороны (или границы) квадрата? треугольника с равными сторонами?
2) Какая получится линия из сторон квадрата, если убрать одну сторону квадрата, т. е. одну палочку? (По-лучится ломаная линия из трех равных отрезков.) И т. п.
При изучении сотни ученики I класса знакомятся с мерами длины — сантиметром, дециметром и метром, а также с мерой массы — килограммом и с мерой емкости— литром. С мерой длины сантиметром желательно познакомить детей раньше, лучше в самом начале за¬нятий, так как знакомство с этой мерой даст возможность разнообразить занятия различными задачами практического характера.
Практика:
52. Начертите три прямые линии: одну —слева на-право (по строке), другую — снизу вверх, третью — на-искось. Подумайте и скажите, можно ли каждую из этих линий продолжить в обе стороны.
 Чертите хорошо отто-ченным карандашом по линейке слева направо. Линейку придерживайте левой рукой, а карандаш — наклонно.
Чертите хорошо отто-ченным карандашом по линейке слева направо. Линейку придерживайте левой рукой, а карандаш — наклонно.Указание. Надо показать, как правильно проводить пря¬мую линию. Для этого можно листок клетчатой бумаги при¬крепить кнопками к доске и по¬казать, как держать линейку и вести карандаш. После этого не-обходимо проследить, как каждый из учеников выполняет это задание, и тем, кто делает неправильно, показать в тетради, как надо держать линейку и карандаш. Если этого не сделать вначале, то потом уйдет больше времени на поправки и указания.
53. Отметьте в тетради точку и проведите через нее две прямые линии. Подумайте, можно ли через эту же точку провести еще прямые линии. Проведите еще две прямые через эту точку и скажите, сколько еще можно провести прямых линий через ту же точку.
Указание. Дети должны сделать вывод, что через одну точку можно провести сколько угодно прямых.
54. Отметьте две точки и проведите через них пря-мую линию. Можно ли через эти две точки провести еще прямую линию, чтобы она не слилась с первой? Теперь попробуйте провести кривую линию, чтобы она про¬шла через те же две точки.
 Можно ли еще через те же две точки провести кривую линию? А сколько кривых линий можно провести через две точки?
Можно ли еще через те же две точки провести кривую линию? А сколько кривых линий можно провести через две точки?Конспект урока по теме `Прямая луч отрезок`, УМК С. М. Никольский_5 класс
Тема урока: Прямая. Луч. Отрезок. Дата: 15.11.19г
Цели урока:
- Формировать понятия «плоскость», «прямая», «луч», «отрезок»,
- Формировать умения и навыки построения и обозначения прямой, луча, отрезка, построения точек, принадлежащих и не принадлежащих прямой; формировать умения учащихся воспроизводить мысли устной и письменной речью; развивать УУД: анализировать, сравнивать, обобщать и делать выводы, выступать перед аудиторией.
- Воспитывать способность к самоуправлению, сознательную дисциплину, трудолюбие, усидчивость.
Ход урока.
I. Организационный момент.
подготовить учащихся к работе
(Приветствие учащихся; проверка их готовности к уроку, организация внимания детей)
Организация проверки наличия домашнего
задания. §2.1 №353, №357 №358
§2.1 №353, №357 №358
Постановка целей и задач урока.
Ставят перед собой цель: «Что я хочу получить сегодня от урока»
Уметь с достаточной полнотой и точностью выражать свои мысли.
Формулируют тему и ставят цель урока вместе с учителем и записывают тему урока в тетради.
Планируют учебное сотрудничество с учителем и одноклассниками
II. Актуализация опорных знаний.
На прошлом уроке мы познакомились с понятиями «плоскость», «прямая», «луч», «отрезок». Давайте проверим, как вы усвоили тему.
Фронтальный опрос и работа у доски.
1. Сформулируйте определение понятия «плоскость» (дети отвечают – точного определения нет, можно лишь привести примеры, которые дают представление о плоскости, приводят примеры)
2. Дайте определение понятию «прямая». (дети отвечают – точного определения нет, можно лишь привести примеры, которые дают представление о прямой, можно сказать, что прямая – бесконечна, она не имеет ни начала, ни конца, приводят примеры)
3. Как обозначается
прямая? (либо одной строчечной латинской буквой, либо двумя заглавными
латинскими буквами)
Как обозначается
прямая? (либо одной строчечной латинской буквой, либо двумя заглавными
латинскими буквами)
4. Пойти к доске, построить прямую, обозначить её двумя способами и записать. (один ученик у доски)
5. Сколько прямых можно провести через две разные точки? (одну)
6. Как могут располагаться две прямые на плоскости? (могут совпадать, могут пересекаться, могут не пересекаться, т.е. быть параллельными)
7. Сколько общих точек имеют две пересекающиеся прямые? (одну)
8. Какие прямые называются параллельными? (Две различные прямые на плоскости, которые никогда не пересекутся)
9. Пойти к доске построить две параллельные прямые, с помощью линейки и угольника и записать, что эти прямые параллельны. (ученик у доски объясняет как строить параллельные прямые)
10. Что называют лучом? (луч – это часть прямой, у которой есть начало, но нет конца)
11. Как
обозначается луч? (двумя заглавными латинскими буквами, на первом месте
ставиться буква, обозначающая начало луча, а на втором – буква, обозначающая
какую-либо другую его точку)
Как
обозначается луч? (двумя заглавными латинскими буквами, на первом месте
ставиться буква, обозначающая начало луча, а на втором – буква, обозначающая
какую-либо другую его точку)
12. Пойти к доске, построить луч, обозначить его и записать. (один ученик у доски)
13. Что называют отрезком? (отрезок – это часть прямой, ограниченная двумя точками, точки – это концы отрезка)
14. Как обозначается отрезок? (двумя заглавными латинскими буквами, причем в любом порядке)
15. Пойти к доске, построить отрезок, обозначить его и записать. (один ученик у доски)
16. Какие отрезки называются равными? (два отрезка называются равными, если они совмещаются при наложении)
III. Физкультминутка
IV. Закрепление изученного материала.
Работа с учебником. Выполнить номера: №349, № 352, №359, № 360
№ 349: Даны четыре точки так, что никакие
три из них не лежат на одной прямой. Через каждые две точки проведена прямая.
Сколько прямых проведено? (выполняем вместе, рассуждая, делая выводы)
Через каждые две точки проведена прямая.
Сколько прямых проведено? (выполняем вместе, рассуждая, делая выводы)
№ 359: На прямой отметили четыре точки. Образовалось 6 отрезков с концами в этих точках. Проверьте. (выполняем вместе, называем все полученные отрезки)
Работа по рядам: первый ряд выполняет задание № 352, второй ряд — № 353, третий ряд — № 360. Ребята работают самостоятельно, затем вместе проверяем решение задач по слайдам.
№ 352: На сколько частей можно разделить плоскость тремя прямыми.
№ 360: перечертите рисунок 49 в тетрадь. Обозначьте все точки пересечения прямых, продолжив их, если нужно. На сколько частей разделилась плоскость?
V. Домашнее задание.
п. 2.1., стр. 77 — 79, определения выучить,
стр. 80 № 355(устно), № 348(в тетрадях)
VI. Итог урока.
Подвести
итог урока. Оценить работу класса. Выставить оценки учащимся.
Оценить работу класса. Выставить оценки учащимся.
ü Сегодня мы выяснили, что прямые делят плоскость на несколько частей, в зависимости от их расположения на плоскости.
ü Ещё раз убедились, что через две различные точки можно провести только одну прямую.
ü Проверили, что от одной точки можно отложить множество лучей, а значит верно и то, что через одну точку можно провести сколько угодно прямых.
Умарова П.С
Скачано с www.znanio.ru
ЧАСТЬ ТРЕТЬЯ
ИЗГИБ БАЛОК С НЕСИММЕТРИЧНЫМ ПОПЕРЕЧНЫМ СЕЧЕНИЕМ
Большинство элементов конструкции самолета состоят из балок с несимметричным поперечным сечением.
сечение, действующее на изгиб. По этой причине необходимо вывести выражение, позволяющее определить напряжения, вызванные изгибающими моментами в таких сечениях.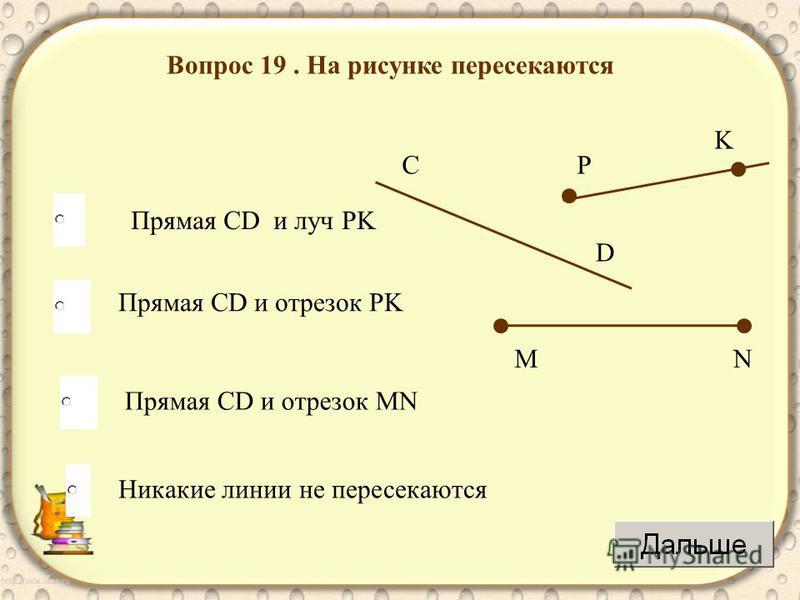
УСЛОВИЯ ЗНАКОВ И ОБОЗНАЧЕНИЯ
Посмотрите на систему координат Oxyz с произвольным лучом, параллельным оси Z:
Рис. 8 : Обозначения и знаки для положительных сил, моментов и перемещений. |
Где:
Т = Крутящий момент
М = изгибающий момент
S = сила сдвига
w
= распределенная нагрузкаP = осевая или прямая нагрузка
u,v,w = Осевые смещения
Все эти внешние нагрузки являются положительными в направлении, указанном на рисунке. Внутренний момент и силы, приложенные к грани А, имеют то же направление и направление, что и внешние. нагрузки.Однако на грани B положительные внутренние моменты и силы действуют в противоположном направлении.
РАЗРЕШЕНИЕ ИЗГИБАЮЩИХ МОМЕНТОВ Изгибающий момент M, приложенный в любой плоскости, параллельной оси z, может быть разложен на составляющие M x и M y по правилам нормального вектора.
Сделав это визуально, будет легче увидеть:
Рис. 9: Разрешенный изгибающий момент относительно осей x и y. |
Из рисунка 9 можно получить следующие соотношения:
M x = M sin θ
M y = M cos θ
и что эти моменты могут иметь разный знак в зависимости от значения θ. Например, если θ > π/2, M x является положительным, а M y отрицательным.
РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ (ETB-NonSym)
Рассмотрим балку произвольного несимметричного поперечного сечения, которая воспринимает изгибающие моменты Mx и My, изгибаясь вокруг некоторой оси в поперечном сечении.Это плоскость отсутствия напряжения изгиба, называемая нейтральной осью (N.A.).
Рис. |
Пусть начало оси совпадает с центром тяжести G поперечного сечения, а нейтральная ось находится на расстоянии p от G.
Прямое напряжение s z на элементе d A в точке (x,y) и на расстоянии x от нейтральной оси составляет:
Посмотрите на луч в плоскости, параллельной нейтральной оси, с двумя сегментами ij и kl , которые имеют одинаковую длину, когда луч не отклонен:
Рисунок 11: Вид сбоку неотклоненной балки с маркировкой сегментов ij и kl . |
После отклонения луча этот участок будет выглядеть так:
| Рис. |
где:
R = радиус кривизны
dq = угол между плоскостями ik и jl
Деформация в плоскости kl может быть определена как:
с
и
дающий
При подстановке обратно в уравнение напряжения получается:
(3.2)
Теперь, когда получено уравнение напряжения, необходимо обеспечить как вращательное, так и линейное равновесие на концах балки. То есть сумма сил по глубине балки равна «0», а сумма моментов по глубине балки равна приложенным моментам Mx и My.
Поскольку балка выдерживает только изгиб, результирующая нагрузка на концевую секцию должна быть равна нулю. Отсюда
Подставляя уравнение 3. 2 дает:
2 дает:
Это уравнение определяет положение центра тяжести сечения, из него следует, что нейтральная ось должна проходить через центр тяжести.
Вместо того, чтобы использовать это уравнение для определения положения центроида, намного проще определить местонахождение центроида относительно оси xy, используя уравнение 3.3.
Чтобы получить равновесие моментов, необходимо перерисовать рис. 10, но с осью, проходящей через центр тяжести.| Рис. 13: Сечение балки с нейтральной осью, проходящей через центр тяжести. |
Чтобы увидеть это более подробно, на Рисунке 14 показан крупный план оси и области dA .
| Рисунок 14: Фрагмент области дА в поперечном сечении балки. |
Если наклон нейтральной оси (N.A.) находится под углом к оси x, то:
х
= х sin α + y cos α (3,4)и подстановка в 3.2 дает:
(3,5)
Результирующие моменты имеют тот же смысл, что и приложенные моменты, следовательно:
, (3,6)
и подставив уравнение 3.4 в уравнения 3.5 дает:
и
Члены sin α и cos α не являются функцией dA, поэтому их можно исключить из интегрирования. Остаются члены, которые имеют отношение только к характеристикам формы поперечного сечения балки, и это всего лишь 2 и моменты площади балки.
Секунды площади вокруг осей xy:
что дает:
решение одновременно дает,
Подстановка в уравнение (3.5) дает:
Путем определения терминов Эффективный изгибающий момент , как:
и
Уравнение 3. 8 можно переписать следующим образом:
8 можно переписать следующим образом:
, а оси x и y являются главными осями .
ПОЛОЖЕНИЕ НЕЙТРАЛЬНОЙ ОСИ
Положение нейтральной оси было определено уравнением (3.3) .
Для балки с симметричным поперечным сечением центроидом является точка, определяемая уравнением 3.3, а нейтральная ось параллельна осям x и y. Для несимметричного поперечного сечения однако нейтральная ось проходит под некоторым углом a по отношению к оси x. Что нужно сделать определить угол нейтральной оси.
В N.A. нормальные напряжения изгиба равны s z = 0, что дает:
где:
x Н.A. и y N.A. являются координатами точек вдоль нейтральной оси, что дает:
Взяв обратный тангенс угла «а», можно найти угол нейтральной оси по отношению к оси x, определяемый уравнением 3.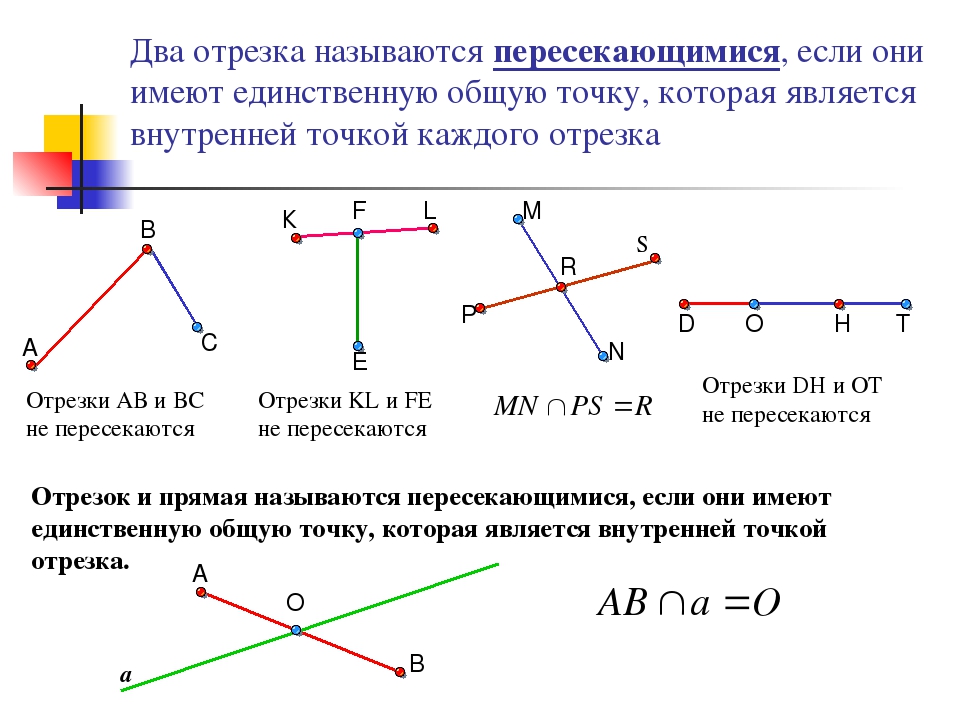 12.
12.
Пример 1: На показанную балку действует изгибающий момент 150 Нм вокруг оси x. Рассчитайте максимальное прямое напряжение из-за изгиба, указав, где оно действует.
Рис. 15: Поперечное сечение балки с приложенным изгибающим моментом. |
b) Сдвиг оси к центроиду
Рис. 16: Поперечное сечение балки со смещенной осью в центроид. |
c) Определить другие свойства сечения
d) Рассчитать эффективные изгибающие моменты
Поскольку M x = 1500 и M y = 0, подстановка этих значений в уравнения (3.9) и (3.10) дает:
e) Определить уравнение напряжения изгиба и напряжения поперечного сечения
Подставьте рассчитанные выше значения в уравнение (3.11) .
Подстановка координат всех угловых точек с рисунка 16 дает следующее:
| Точка | х (мм) | г (мм) | с z (МПа) |
|---|---|---|---|
| 1 | 72 | 21,6 | 0,436 |
| 2 | -48 | 21. 6 6 | 5.1 |
| 3 | -48 | 13,6 | 3,9 |
| 4 | -16 | 13,6 | 2,66 |
| 5 | -16 | -66,4 | -9,32 |
| 6 | -8 | -66,4 | -9,63 |
| 7 | -8 | 13.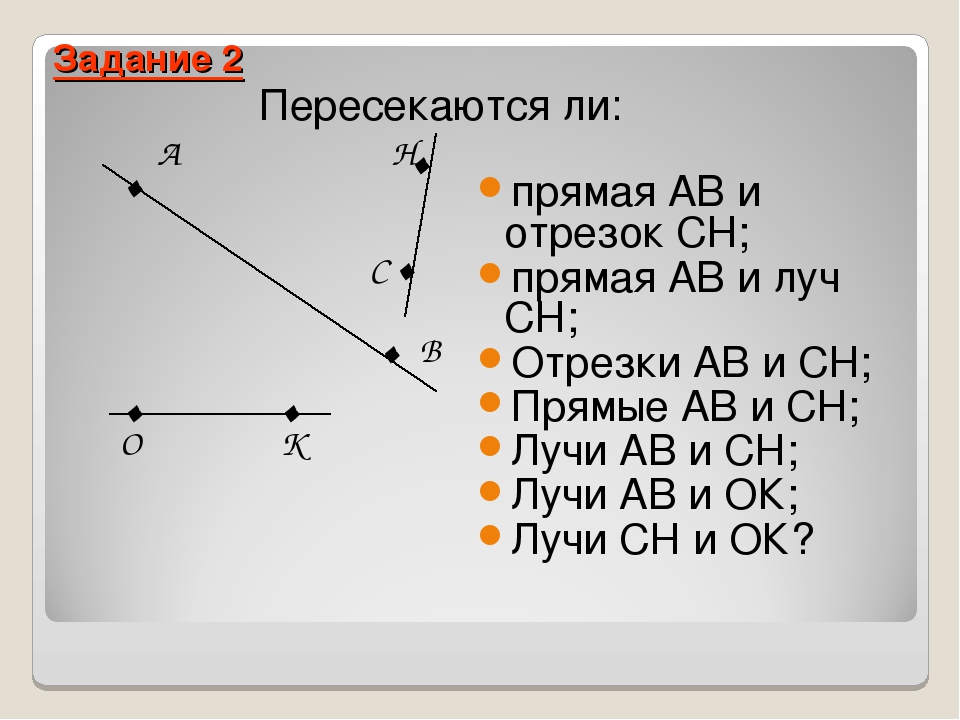 6 6 | 2,34 |
| 8 | 72 | 13,6 | -0,76 |
Вы можете использовать этот метод для определения напряжений из-за изгиба в любом типе балки с любым типом поперечного сечения.
ПРИБЛИЖЕНИЕ ДЛЯ ТОНКОСТЕННЫХ СЕКЦИЙ
Из-за тонкости конструкции самолета можно сделать предположение, что напряжения постоянны по всей толщине t обшивки.Говоря это, квадратом и более высокими степенями «t» можно пренебречь при вычислении свойств сечения.
Чтобы увидеть это, посмотрите на раздел канала:
Рис. 17: Тонкостенный участок канала. |
Это указывает на то, что свойства сечения могут быть рассчитаны так, как если бы сечение было представлено тонкой линией, как показано на рисунке 18, без учета любых условий t 2 или выше.
Рисунок 18: Примерное сечение канала. |
Для этого дискретного тонкостенного сечения свойства сечения будут найдены следующим образом:
1) Определить положение центроида
2) Смещение оси к центроиду
Рис. 19: Ось в центре тяжести |
3) Определение моментов инерции
Эти результаты точно такие же, как и для разреза с учетом толщины материала обшивки, а затем без учета всех членов t 2 и выше.
Поскольку не все участки кожи будут располагаться параллельно оси x или оси y, локальные моменты или площади участка кожи, расположенного под углом q по отношению к оси x, определяются следующими уравнениями.
Рисунок 20: Срез тонкой кожи, наклоненный под углом θ относительно оси x |
ОБЩИЕ ВЗАИМООТНОШЕНИЯ НАГРУЗКИ
Рассмотрим элемент длины dz из балки с несимметричным поперечным сечением со всеми видами нагрузок, приложенных в плоскости y-z, рисунок 21.
| Рисунок 21: Равновесие балочного элемента с общей нагрузкой в плоскости zy. |

| Рисунок 22: Уравновешивание крутящего момента секции балки длиной dz. |

…В начало
Элементы балочной конструкции — документация 3DEC 7.0
Механическое поведение
Каждый элемент конструкции балки определяется своими геометрическими свойствами и свойствами материала. Предполагается, что элемент балки представляет собой прямолинейный отрезок с однородными бисимметричными свойствами поперечного сечения, лежащий между двумя узловыми точками. Конструктивную балку произвольной кривизны можно смоделировать как криволинейную конструкцию, состоящую из набора элементов балки. По умолчанию каждый элемент балки ведет себя как изотропный линейно-упругий материал без предела разрушения; однако можно указать ограничивающий пластический момент или ввести положение пластического шарнира (в котором может возникнуть разрыв при вращении) между балочными элементами (см. Формирование пластического шарнира в балочной конструкции).Общие свойства конечного элемента, используемого каждым элементом балки, описаны в разделе Конечный элемент балки. Балочные элементы пригодны для моделирования конструкционных балок, в которых можно пренебречь перемещениями, вызванными деформациями поперечного сдвига и неплоскостным (продольным) короблением поперечного сечения.
Балочные элементы пригодны для моделирования конструкционных балок, в которых можно пренебречь перемещениями, вызванными деформациями поперечного сдвига и неплоскостным (продольным) короблением поперечного сечения.
Как и все структурные элементы (и в отличие от зон), отдельные элементы идентифицируются по их идентификационным номерам компонентов. Группы лучей идентифицируются идентификационными номерами. Отдельные структурные узлы и звенья также идентифицируются по идентификационным номерам компонентов.Узлы и ссылки также можно выбирать по идентификатору элементов, к которым они прикреплены.
Каждый элемент балки имеет собственную локальную систему координат, показанную на рис. 1. Эта система используется для задания моментов инерции поперечного сечения и приложенной распределенной нагрузки, а также для определения правил знаков для распределения сил и моментов по элементам балки, которые составляют единый пучок (см. рис. 2). Система координат балочного элемента определяется расположением двух его узловых точек (обозначенных цифрами 1 и 2 на рисунке 1) и вектором \(\bf Y\). Система координат элемента балки определяется таким образом, что
Система координат элемента балки определяется таким образом, что
- центральная ось совпадает с осью \(х\),
- ось \(x\) направлена от узла-1 к узлу-2, а
- ось \(y\) совмещена с проекцией \(\bf Y\) на плоскость поперечного сечения (т. е. плоскость, нормаль которой направлена вдоль оси \(x\)).
Рис. 1: Система координат элемента балки и 12 активных степеней свободы конечного элемента балки
Рисунок 2: Правила знаков для сил и моментов на концах балочного элемента (оси показывают систему координат балочного элемента, концы 1 и 2 соответствуют порядку в списке узловых соединений, и все величины нарисованы в положительном смысле.)
Систему координат элемента балки можно изменить с помощью команды свойство балки конструкции направление-y . (Если \(\bf Y\) не указан или параллелен локальной оси \(x\), то \(\bf Y\) по умолчанию соответствует глобальной \(y\)- или \(x\ )-направление, в зависимости от того, что не параллельно локальной оси \(x\). ) Систему координат элемента балки можно просмотреть с помощью элемента графика Балка и распечатать с помощью команды
) Систему координат элемента балки можно просмотреть с помощью элемента графика Балка и распечатать с помощью команды Structure Beam List system-local . Узловое соединение можно распечатать с помощью команды Информация о списке балок конструкции .
12 активных степеней свободы конечного элемента балки показаны на рисунке 1. Каждому обобщенному перемещению (перемещению и вращению), показанному на рисунке, соответствует соответствующая обобщенная сила (сила и момент). Матрица жесткости конечного элемента балки включает все шесть степеней свободы в каждом узле для представления осевого, сдвигового и изгибающего действия внутри балочной конструкции.
Количество ответов
Реакции балки включают векторы силы и момента, действующие на конце каждого элемента балки.Эти величины могут быть выражены в глобальной системе или в системе координат элемента балки. Доступ к откликам луча можно получить через FISH и
.- напечатано с помощью команды
список структурных балокс использованием последующих ключевых слов force-node или force-end, - , отслеживаемый с помощью команды
истории балки конструкции, и - визуализируется с помощью элемента графика Beam.

Знаки на рис. 2 обеспечивают непрерывное описание распределения сил и моментов по элементам балки, из которых состоит одна балка.Предполагается, что набор элементов балки, составляющих балку, ориентирован согласованно, так что их локальные системы координат образуют непрерывное описание ориентации балки. Так будет в случае, если балка создается с помощью команды «Структурная балка создать ». Узлы каждого элемента балки, созданного таким образом, будут упорядочены таким образом, чтобы общее направление балки шло от первой точки ко второй заданной точке. Узловое соединение можно распечатать с помощью команды Информация о списке балок конструкции .P\) считается бесконечным) [F\(\cdot\)L]
Поведение материала описывается свойствами 1-5, а геометрия поперечного сечения описывается свойствами 6-10. 2 \, дА
\конец{разделить}\конец{разделить}\]
2 \, дА
\конец{разделить}\конец{разделить}\]
, в котором две главные оси поперечного сечения определяются осями элемента балки \(y\) и \(z\).
Рисунок 3: Общее поперечное сечение элемента балки в плоскости yz элемента
Свойства балки легко рассчитать или взять из справочников. Например, типичные значения для конструкционной стали составляют 200 ГПа для модуля Юнга и 0,3 для коэффициента Пуассона. Для бетона типичные значения составляют от 25 до 35 ГПа для модуля Юнга от 0,15 до 0.2 для коэффициента Пуассона и от 2100 до 2400 кг/м 3 для массовой плотности. Композитные системы, например железобетонные, должны опираться на преобразованное сечение.
Если указан пластический момент, значение можно рассчитать следующим образом. Рассмотрим изгибаемый элемент шириной \(b\) и высотой \(h\). Если элемент состоит из материала, который ведет себя упруго-идеально пластично, можно рассчитать упругий и пластический моменты сопротивления. Момент, необходимый для создания предела текучести \(\sigma_y\) во внешних волокнах, определяется как момент упругости \(M^E\) и рассчитывается как
\[M^E\ =\ \sigma_y\ {bh^2 \over{6}}\]
Чтобы текучесть происходила по всему сечению, предел текучести должен действовать на все сечение, а расположение равнодействующей силы на половине сечения должно быть \(h/4\) от нейтральной поверхности. П\). Способность к пластическому моменту ограничивает внутренний момент, воспринимаемый каждым элементом балки.
П\). Способность к пластическому моменту ограничивает внутренний момент, воспринимаемый каждым элементом балки.
Для ограничения момента, передаваемого между элементами балки, необходимо также ограничить допустимый момент в узлах. Состояние нарастающей деформации с предельным моментом сопротивления, приводящее к прерывности вращательного движения, называется пластическим шарниром. Потенциальные местоположения пластиковых шарниров можно определить, создав двойные узлы в каждом месте шарнира, добавив связь между узлами между этими узлами, а затем указав соответствующие условия прикрепления ссылки.Если в элементе балки, соединенном таким двухузловым пластическим шарниром, будет достигнут предельный момент, то во вращательном движении возникнет разрыв. См. Формирование пластиковых шарниров в балочной конструкции для примера применения пластиковых шарниров, смоделированных как с одинарными, так и с двойными узлами.
Предыдущее обсуждение предполагает сечение, симметричное относительно нейтральной оси. Однако, если сечение несимметрично (например, Т-образное сечение) или если соотношения между напряжениями и деформациями при растяжении и сжатии существенно различаются (например, железобетон), нейтральная ось смещается в сторону от волокон, которые поддаются деформации первыми. , и необходимо переместить нейтральную ось, прежде чем можно будет оценить момент сопротивления.Нейтральную ось можно найти, интегрируя профиль напряжения по сечению и находя положение оси, на которой напряжение равно нулю. В некоторых случаях интеграл можно выразить через одно неизвестное (в этом случае решение может быть несложным). Однако, если соотношение между напряжением и деформацией для материала не похоже на идеальную упруго-пластическую диаграмму, решение может потребовать ряда испытаний. Почти все тексты по железобетонному или стальному проектированию содержат процедуры и примеры расчета пластических моментов.Е\) невелик. Однако для железобетона пластический момент может быть на порядок больше упругого момента.
Однако, если сечение несимметрично (например, Т-образное сечение) или если соотношения между напряжениями и деформациями при растяжении и сжатии существенно различаются (например, железобетон), нейтральная ось смещается в сторону от волокон, которые поддаются деформации первыми. , и необходимо переместить нейтральную ось, прежде чем можно будет оценить момент сопротивления.Нейтральную ось можно найти, интегрируя профиль напряжения по сечению и находя положение оси, на которой напряжение равно нулю. В некоторых случаях интеграл можно выразить через одно неизвестное (в этом случае решение может быть несложным). Однако, если соотношение между напряжением и деформацией для материала не похоже на идеальную упруго-пластическую диаграмму, решение может потребовать ряда испытаний. Почти все тексты по железобетонному или стальному проектированию содержат процедуры и примеры расчета пластических моментов.Е\) невелик. Однако для железобетона пластический момент может быть на порядок больше упругого момента.
Заявка на патент США НА ПЕРЕДНЮЮ БАЛКУ РАМЫ ТРАНСПОРТНОГО СРЕДСТВА И СПОСОБ ФОРМИРОВАНИЯ ЕЕ Заявка на патент (заявка № 20150115666 от 30 апреля 2015 г.)
ОБЛАСТЬ ИЗОБРЕТЕНИЯНастоящее изобретение в целом относится к балке головного убора транспортного средства и, более конкретно, относится к полой балке верхнего сегмента, которая образована из удлиненной экструдированной балки.
УРОВЕНЬ ТЕХНИКИ ИЗОБРЕТЕНИЯ Общеизвестно, что рамы транспортных средств включают балку, которая проходит между передними стойками рамы транспортного средства и поддерживает крышу транспортного средства и ветровое стекло. Чтобы обеспечить постоянную кривизну балки перемычки для крепления ветрового стекла, балки перемычки обычно формируются с помощью процесса штамповки, что может привести к образованию значительного количества брака. Кроме того, перемычки часто имеют несколько элементов крепления по длине перемычки, которые могут привести к снижению структурной целостности балок, что затрудняет использование легкого прессованного металла на перемычках. Поскольку становится все более желательным, чтобы автомобили изготавливались из более легких материалов, которые также соответствуют более высоким стандартам безопасности, все более желательно использовать компоненты, изготовленные из экструдированного металла и с меньшим количеством структурных разрывов, при сохранении или снижении стоимости компонентов.
Поскольку становится все более желательным, чтобы автомобили изготавливались из более легких материалов, которые также соответствуют более высоким стандартам безопасности, все более желательно использовать компоненты, изготовленные из экструдированного металла и с меньшим количеством структурных разрывов, при сохранении или снижении стоимости компонентов.
В соответствии с одним аспектом настоящего изобретения экструдированная балка головного убора транспортного средства включает удлиненный элемент, имеющий внутреннюю полость, проходящую по длине балки между ее противоположными концами.Передние и задние ножки непрерывно проходят внутри полого внутреннего пространства между противоположными концами. Между передними и задними ножками определена центральная область, имеющая отверстия для зацепления, разнесенные по длине. Передние и задние ножки образуют непрерывные коробчатые секции за пределами центральной области.
В соответствии с другим аспектом настоящего изобретения экструдированная перемычка для рамы транспортного средства включает удлиненный элемент, имеющий внутреннюю полость, проходящую между его противоположными концами. Передние и задние ножки непрерывно проходят внутри полого внутреннего пространства между противоположными концами.В центральной части между передней и задней опорами имеются отверстия для соединения с рамой автомобиля. Передняя и задняя непрерывные коробчатые секции выходят за пределы центральной области и определяются удлиненным элементом и передней и задней ножками соответственно.
Передние и задние ножки непрерывно проходят внутри полого внутреннего пространства между противоположными концами.В центральной части между передней и задней опорами имеются отверстия для соединения с рамой автомобиля. Передняя и задняя непрерывные коробчатые секции выходят за пределы центральной области и определяются удлиненным элементом и передней и задней ножками соответственно.
В соответствии с еще одним аспектом настоящего изобретения рама транспортного средства включает в себя передние стойки и экструдированную верхнюю балку, проходящую между передними стойками. Штампованная поперечная балка включает удлиненный элемент, имеющий верхнюю, нижнюю, переднюю и заднюю стенки, образующие полую внутреннюю часть, проходящую между противоположными концами ведущей балки.Передняя и задняя ножки проходят между верхней и нижней стенками непрерывно внутри полого внутреннего пространства, образуя переднюю и заднюю секции коробки. Крепления проходят через нижнюю стенку между передними и задними стойками и крепятся противоположными концами к передним стойкам. Передняя и задняя коробчатые секции несут непрерывные пути нагрузки между передними стойками.
Передняя и задняя коробчатые секции несут непрерывные пути нагрузки между передними стойками.
Эти и другие аспекты, цели и признаки настоящего изобретения станут понятны и оценены специалистами в данной области техники после изучения следующего описания, формулы изобретения и прилагаемых чертежей.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙНа чертежах:
РИС. 1 представляет собой вид сверху в перспективе транспортного средства, имеющего поперечную балку, в соответствии с одним вариантом осуществления настоящего изобретения;
РИС. 2 представляет собой вид сверху в перспективе балки заголовка, прикрепленной к соответствующей паре передних стоек и проходящей между ними, в соответствии с одним вариантом осуществления;
РИС. 3 представляет собой вид сверху на верхнюю балку, показывающий части одного варианта выполнения панели крыши, покрывающей верхнюю балку;
РИС.4 — вид снизу на балку верхнего лонжерона;
РИС. 5 представляет собой вид сверху в перспективе с торца, показывающий полую внутреннюю часть траверсы;
5 представляет собой вид сверху в перспективе с торца, показывающий полую внутреннюю часть траверсы;
РИС. 5А представляет собой вид с торца ведущей балки, как показано на ФИГ. 5;
РИС. 6 представляет собой вид сверху в перспективе поперечного сечения ведущей балки, показывающий внутреннюю полость вблизи центральной части ведущей балки;
РИС. 6А представляет собой вид с торца в поперечном сечении ведущей балки, как показано на ФИГ. 6;
РИС. 7 представляет собой вид сверху на поперечную балку, показывающий переднюю и заднюю опоры, показанные пунктирными линиями, проходящие внутри полого внутреннего пространства по длине ведущей балки;
РИС.8 представляет собой блок-схему, показывающую способ формирования луча заголовка вместе с иллюстрациями луча заголовка на каждом этапе способа согласно одному варианту осуществления настоящего изобретения; и
РИС. 9 представляет собой блок-схему, показывающую способ формирования головного луча согласно дополнительному варианту осуществления настоящего изобретения.
Для целей описания здесь термины «верхний», «нижний», «правый», «левый», «задний», «передний», «вертикальный», «горизонтальный», и их производные должны относиться к изобретению, как показано на фиг.1. Однако следует понимать, что изобретение может иметь различные альтернативные ориентации, если прямо не указано иное. Также следует понимать, что конкретные устройства и процессы, проиллюстрированные на прилагаемых чертежах и описанные в следующем описании, являются просто примерными вариантами осуществления идей изобретения, определенных в прилагаемой формуле изобретения. Следовательно, конкретные размеры и другие физические характеристики, относящиеся к раскрытым здесь вариантам осуществления, не должны рассматриваться как ограничивающие, если в формуле изобретения прямо не указано иное.
Ссылаясь на ФИГ. 1-9 ссылочным номером 10 обычно обозначена балка лонжерона для рамы 12 кузова 14 транспортного средства.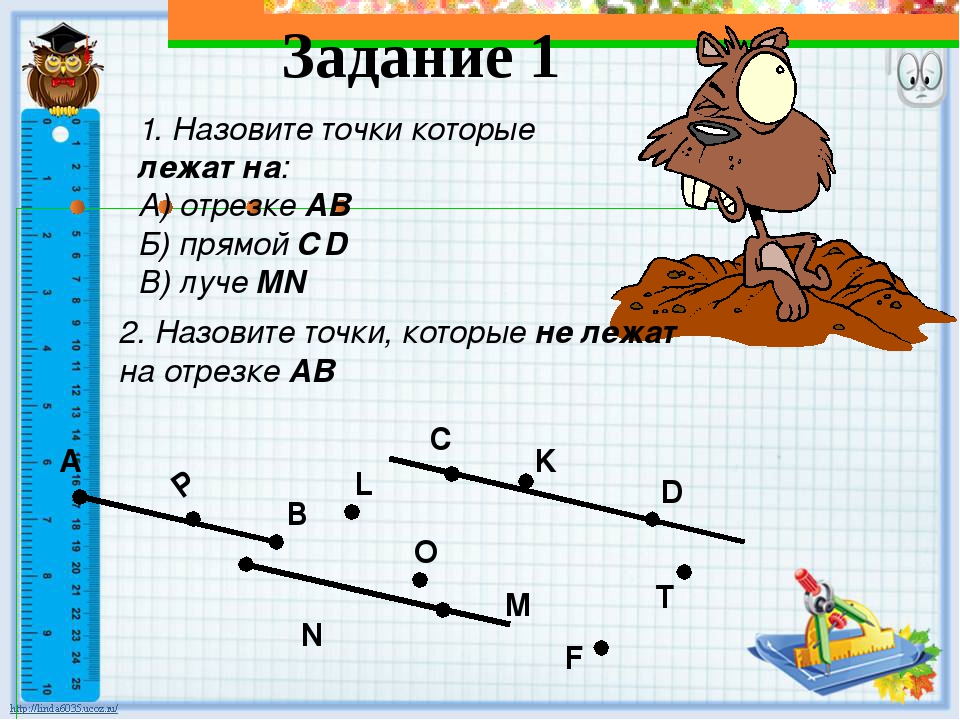 Кузов автомобиля 14 включает панель крыши 16 и пару передних стоек 18 , каждая из которых имеет верхний конец 20 с верхней поверхностью 22 . Полая балка 10 включает изогнутую центральную часть 24 длиной 26 балки 10 , которая имеет кривизну 28 , выступающую вперед, чтобы соответствовать ветровому стеклу 30 .Концевые части 32 длины 26 верхней балки 10 ближайшие противоположные концы 34 центральной части 24 пара с верхней поверхностью 22 пара стоек А 90 иметь в целом прямолинейную ориентацию относительно кривизны 28 центральной части 24 . Передний фланец 36 проходит вперед по длине 26 балки 10 и имеет кромку, параллельную изгибу 28 вблизи концевых частей 32 для зацепления с ветровым стеклом 30 Передний фланец 36 также имеет центральную область 38 , выступающую вперед, которая включает в себя ряд пазов 40 , расположенных вдоль центральной области 38 для соединения с панелью крыши 16 .
Кузов автомобиля 14 включает панель крыши 16 и пару передних стоек 18 , каждая из которых имеет верхний конец 20 с верхней поверхностью 22 . Полая балка 10 включает изогнутую центральную часть 24 длиной 26 балки 10 , которая имеет кривизну 28 , выступающую вперед, чтобы соответствовать ветровому стеклу 30 .Концевые части 32 длины 26 верхней балки 10 ближайшие противоположные концы 34 центральной части 24 пара с верхней поверхностью 22 пара стоек А 90 иметь в целом прямолинейную ориентацию относительно кривизны 28 центральной части 24 . Передний фланец 36 проходит вперед по длине 26 балки 10 и имеет кромку, параллельную изгибу 28 вблизи концевых частей 32 для зацепления с ветровым стеклом 30 Передний фланец 36 также имеет центральную область 38 , выступающую вперед, которая включает в себя ряд пазов 40 , расположенных вдоль центральной области 38 для соединения с панелью крыши 16 .
Обратимся теперь к фиг. 1 показано транспортное средство 42 , имеющее один вариант осуществления ведущей балки 10 настоящего изобретения. Как обычно понимается в данной области техники, рама 12 транспортного средства 42 включает ряд стоек, которые проходят вверх вокруг салона транспортного средства 42 для поддержки панели 16 крыши или ее частей.Стойки в показанном варианте осуществления включают передние стойки 18 , средние стойки 44 и задние стойки 46 . Однако возможно, что транспортное средство 42 может представлять собой другой вариант осуществления или тип транспортного средства, например легковой автомобиль или фургон, который может включать большее или меньшее количество стоек для вертикальной поддержки панели крыши 16 или балки 10 или иным образом ограничивать внутреннюю часть салона транспортного средства 42 . Кроме того, предполагается, что панель 16 крыши и перемычка 10 могут быть альтернативно сконфигурированы с узлом люка в крыше, узлом складного верха или другой альтернативной конфигурацией крыши, как это обычно понятно специалистам в данной области. искусство.
Кроме того, предполагается, что панель 16 крыши и перемычка 10 могут быть альтернативно сконфигурированы с узлом люка в крыше, узлом складного верха или другой альтернативной конфигурацией крыши, как это обычно понятно специалистам в данной области. искусство.
Как показано на РИС. 2, передние стойки 18 , каждая из которых соединена с передним концом 48 продольной балки крыши 50 , которая проходит назад от верхней балки 10 для поддержки боковых сторон панели крыши 16, и поддерживают ее вертикально. и любые дополнительные поперечины, которые могут пересекать транспортное средство 42 в поперечном направлении, как правило, параллельно главной балке 10 . Продольные рейлинги на крыше 50 соединяются как одно целое с верхними концами 20 передних стоек 18 , образуя угловое соединение, в результате чего передние стойки 18 проходят вниз и вперед, образуя наклонную конструкцию ветрового стекла . 30 (РИС.1). Перемычка 10 обычно проходит между угловыми соединениями между передними стойками 18 и продольными рейлингами 50 крыши. Предполагается, что передние стойки 18 и продольные рейлинги 50 крыши могут представлять собой единое целое с другими стойками или поперечинами рамы автомобиля 12 или могут быть отдельными частями, которые соединяются непосредственно друг с другом или отделяются друг от друга. другими структурными элементами. Кроме того, следует понимать, что в показанном варианте передние стойки 18 и продольные рейлинги 50 крыши вместе с другими частями автомобиля 42 , которые имеют соответствующие детали на противоположных боковых сторонах автомобиля 42 , являются по существу зеркальными отображениями друг друга, так что иллюстрация и описание одного могут быть выведены из другого, если не указано иное.
30 (РИС.1). Перемычка 10 обычно проходит между угловыми соединениями между передними стойками 18 и продольными рейлингами 50 крыши. Предполагается, что передние стойки 18 и продольные рейлинги 50 крыши могут представлять собой единое целое с другими стойками или поперечинами рамы автомобиля 12 или могут быть отдельными частями, которые соединяются непосредственно друг с другом или отделяются друг от друга. другими структурными элементами. Кроме того, следует понимать, что в показанном варианте передние стойки 18 и продольные рейлинги 50 крыши вместе с другими частями автомобиля 42 , которые имеют соответствующие детали на противоположных боковых сторонах автомобиля 42 , являются по существу зеркальными отображениями друг друга, так что иллюстрация и описание одного могут быть выведены из другого, если не указано иное.
С дополнительной ссылкой на фиг. 2, верхние концы 20 передних стоек 18 имеют выступающие внутрь элементы крепления 52 , которые определяют верхнюю поверхность 22 передних стоек 18 для соединения с балкой 05 . Крепежные элементы , 52, имеют форму, которая соответствует концевым частям , 32, балки 10 для прикрепления к ним. В частности, балка 10 имеет полую часть 54 корпуса с задним фланцем 58 и передним фланцем 36 на противоположных сторонах части 54 корпуса вблизи концевых частей 32 верхняя балка 10 , которая соединяется с приподнятыми участками крепежного элемента 52 .Соответственно, полость 64 на крепежных элементах 52 соединяется с нижней поверхностью 56 основной части 54 балки 10 и приподнятой верхней частью 60 и приподнятой нижней частью 62 на противоположных сторонах полости 64 зацепите задний фланец 58 и передний фланец 36 балки 10 , соответственно.
Как также показано на РИС.2, соединение между крепежными элементами 52 и поперечиной 10 осуществляется рядом самонарезающих заклепок 63 , которые проходят через корпусную часть 54 поперечины 10 вблизи конца части 32 и прикрепить к полости 64 соединительного элемента 52 . В других вариантах осуществления предполагается, что соединение между крепежными элементами 52 и балкой 10 может быть выполнено с помощью дополнительных или альтернативных средств, включая сварку, крепление и другие общепризнанные способы крепления, специалистом, имеющим обычные навыки. в искусстве.Также предполагается, что крепежные элементы 52 могут быть отдельными компонентами от передних стоек 18 , которые крепятся либо к передней балке 10 , либо к передним стойкам 18 до того, как верхняя балка 10 будет крепится к передним стойкам 18 . Крепежные элементы 52 в других возможных вариантах осуществления также могут выступать внутрь больше или меньше, чем в проиллюстрированном варианте осуществления, или полностью охватывать ширину передних стоек 18 .
Крепежные элементы 52 в других возможных вариантах осуществления также могут выступать внутрь больше или меньше, чем в проиллюстрированном варианте осуществления, или полностью охватывать ширину передних стоек 18 .
Как показано на РИС. 3, центральная часть 24 передней балки 10 проходит между концевыми частями 32 , которые крепятся к передним стойкам 18 (РИС. 2) и проходит вперед по изгибу 28 (РИС. 4), соответствующий кривизне лобового стекла 30 (фиг. 1). Панель крыши 16 крепится к балке 10 и соответствует переднему краю 66 (РИС. 4) балки 10 .Передний фланец 36 ведущей балки 10 обычно выступает горизонтально из части 54 корпуса и проходит по длине 26 ведущей балки 10 .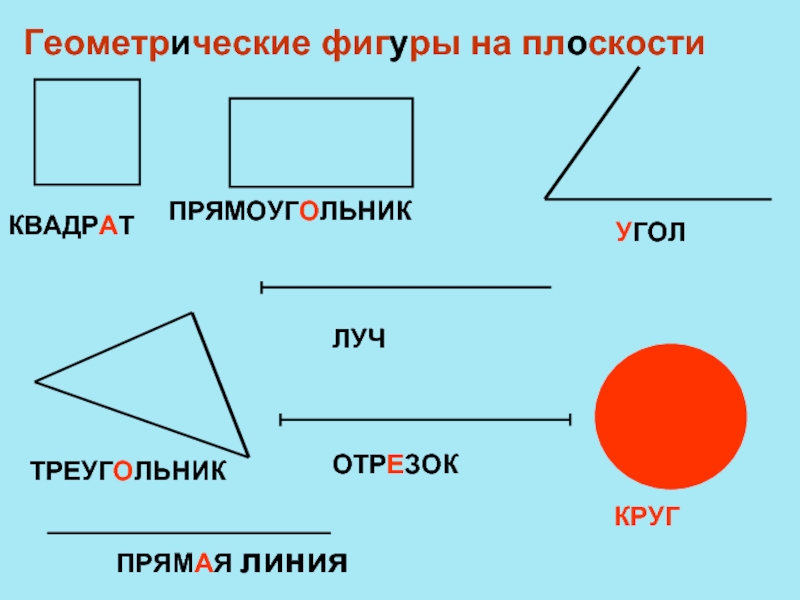 Передний фланец 36 сформирован так, чтобы выступать вблизи центральной области 38 , определяя язычковую часть, которая выступает вперед на большее расстояние, чем передний фланец 36 вблизи концевых частей 32 . Соответственно, центральная область 38 передней полки 36 имеет глубину, позволяющую разместить серию пазов 40 вдоль передней кромки 66 для обеспечения точек крепления между передней кромкой 17 панели крыши. 16 и передний край 66 балки 10 .Передняя кромка 66 передней полки 36 также сформирована вблизи концевых частей 32 , чтобы быть параллельной кривизне 28 основной части 54 балки 10 24 . Соответственно, передний фланец 36 , расположенный рядом с концевыми частями 32 , выполнен с возможностью соединения с кривизной ветрового стекла 30 (фиг.
Передний фланец 36 сформирован так, чтобы выступать вблизи центральной области 38 , определяя язычковую часть, которая выступает вперед на большее расстояние, чем передний фланец 36 вблизи концевых частей 32 . Соответственно, центральная область 38 передней полки 36 имеет глубину, позволяющую разместить серию пазов 40 вдоль передней кромки 66 для обеспечения точек крепления между передней кромкой 17 панели крыши. 16 и передний край 66 балки 10 .Передняя кромка 66 передней полки 36 также сформирована вблизи концевых частей 32 , чтобы быть параллельной кривизне 28 основной части 54 балки 10 24 . Соответственно, передний фланец 36 , расположенный рядом с концевыми частями 32 , выполнен с возможностью соединения с кривизной ветрового стекла 30 (фиг. 1). Предполагается, что язычковая часть может отсутствовать или иметь альтернативную форму, так что передний край , 66, может быть параллелен кривизне , 28, (фиг.4) основной части 54 вблизи центральной области 38 и, таким образом, обеспечивает постоянную кривизну передней кромки 66 по длине 26 балки 10 жатки.
1). Предполагается, что язычковая часть может отсутствовать или иметь альтернативную форму, так что передний край , 66, может быть параллелен кривизне , 28, (фиг.4) основной части 54 вблизи центральной области 38 и, таким образом, обеспечивает постоянную кривизну передней кромки 66 по длине 26 балки 10 жатки.
Также, как показано на РИС. 3, на верхней поверхности 70 корпусной части 54 сформирован ряд отверстий 68 , расположенных вблизи центральной области 38 переднего фланца 36 , которые проходят во внутреннюю полость 72 (ИНЖИР.5) балки перемычки 10 . Отверстия 68 облегчают доступ к полой внутренней части 72 для поддержки нижней стенки 88 при деформации нижней стенки 88 для штамповки или иного создания внутренних углублений 104 , как более подробно поясняется ниже. 10 . Обратимся теперь к фиг. 4 показана задняя балка 10 , имеющая внутренние соединительные отверстия 83 , образованные на нижней поверхности 56 основной части 54 вблизи концевых частей 32 верхней балки 10 .Внутренние соединительные отверстия 83 включают внешнюю прямоугольную часть и внутреннюю круглую часть, которые в совокупности образуют форму внутренних соединительных отверстий 83 . Как также показано на РИС. 4 кривизна 28 центральной части 24 ведущей балки 10 выделена показанными пунктирными линиями, проходящими за пределы центральной части 24 и пересекающимися с концевыми частями 32 , тем самым показывая прерывистую форму. по общей длине 26 балки перемычки 10 . Аналогичным образом, в целом прямая ориентация 33 корпуса 54 концевых частей 32 показана пунктирными линиями, выходящими за пределы длины 26 ведущей балки 10 , чтобы аналогичным образом проиллюстрировать отклонение от кривизны. 28 центральной части 24 балки 10 .Кроме того, показана передняя кромка 66 передней полки 36 , выступающая за пределы длины 26 балки 10 , параллельная кривизне 28 центральной части 24 , тем самым расходясь. Корпусная часть 54 ведущей балки 10 , как показано на ФИГ. 5-5 А, является полым и, таким образом, граничит с верхней стенкой 86 , нижней стенкой 88 , передней стенкой 90 и задней стенкой 92 , образуя полую внутреннюю часть 72 . . В частности, отверстия 68 включают в себя центральное отверстие 74 , имеющее в целом прямоугольную форму, и задний выступ, продолжающийся вперед и придающий прямоугольную форму примерно в средней точке ведущей балки 10 .Задний выступ можно использовать для крепления части конструкции крыши и, таким образом, для поддержки панели крыши 16 . Отверстия 68 также включают пару боковых отверстий 76 , которые расположены на равном расстоянии друг от друга на противоположных сторонах центрального отверстия 74 и также имеют в целом прямоугольную форму. Несколько отверстий 78 для доступа и крепления также образованы через верхнюю поверхность 70 вблизи концевых частей 32 балки 10 перемычки.Эти отверстия 78 включают два дистальных отверстия 80 на каждой концевой части 32 и группу из четырех круглых отверстий 82 немного внутрь от двух дистальных отверстий 80 и концевых частей 32
. В частности, отверстия 68 включают в себя центральное отверстие 74 , имеющее в целом прямоугольную форму, и задний выступ, продолжающийся вперед и придающий прямоугольную форму примерно в средней точке ведущей балки 10 .Задний выступ можно использовать для крепления части конструкции крыши и, таким образом, для поддержки панели крыши 16 . Отверстия 68 также включают пару боковых отверстий 76 , которые расположены на равном расстоянии друг от друга на противоположных сторонах центрального отверстия 74 и также имеют в целом прямоугольную форму. Несколько отверстий 78 для доступа и крепления также образованы через верхнюю поверхность 70 вблизи концевых частей 32 балки 10 перемычки.Эти отверстия 78 включают два дистальных отверстия 80 на каждой концевой части 32 и группу из четырех круглых отверстий 82 немного внутрь от двух дистальных отверстий 80 и концевых частей 32 Эти отверстия 78 используются для вставки и соединения самонарезающих заклепок 63 (РИС. 2) или других возможных крепежных элементов через балку 10 и в элементы крепления 52 на передних стойках. 18 .Однако также предполагается, что их можно использовать для крепления частей панели крыши 16 или для вставки сварочных инструментов для формирования сварных швов между балкой 10 балки и передними стойками 18 .
Эти отверстия 78 используются для вставки и соединения самонарезающих заклепок 63 (РИС. 2) или других возможных крепежных элементов через балку 10 и в элементы крепления 52 на передних стойках. 18 .Однако также предполагается, что их можно использовать для крепления частей панели крыши 16 или для вставки сварочных инструментов для формирования сварных швов между балкой 10 балки и передними стойками 18 . Каждое из соединительных отверстий используется для крепления узла солнцезащитного козырька к балке 10 лонжерона, а также может использоваться для сопряжения и выравнивания балки 10 лонжерона с крепежными элементами 52 . В нижней поверхности 56 корпуса 54 также выполнен ряд небольших установочных и зазорных отверстий 84 , например, фрезерованием или сверлением.Установочные и зазорные отверстия 84 расположены в основном симметрично по длине 26 (РИС. 3) верхней балки 10 между внутренними соединительными отверстиями 83 для выравнивания и позиционирования верхней балки 10 на автомобиле 42 (РИС. 1). Предполагается, что отверстия , 84, можно использовать для соединения с элементами внутренней отделки или другими компонентами автомобиля. Также понятно, что размер и форма отверстий, проемов и проемов на верхней и нижней поверхностях 70 , 56 могут быть изменены в дополнительных вариантах осуществления для размещения различных потенциальных точек крепления между балкой 10 и панель крыши 16 , передние стойки 18 и другие возможные компоненты автомобиля.
Каждое из соединительных отверстий используется для крепления узла солнцезащитного козырька к балке 10 лонжерона, а также может использоваться для сопряжения и выравнивания балки 10 лонжерона с крепежными элементами 52 . В нижней поверхности 56 корпуса 54 также выполнен ряд небольших установочных и зазорных отверстий 84 , например, фрезерованием или сверлением.Установочные и зазорные отверстия 84 расположены в основном симметрично по длине 26 (РИС. 3) верхней балки 10 между внутренними соединительными отверстиями 83 для выравнивания и позиционирования верхней балки 10 на автомобиле 42 (РИС. 1). Предполагается, что отверстия , 84, можно использовать для соединения с элементами внутренней отделки или другими компонентами автомобиля. Также понятно, что размер и форма отверстий, проемов и проемов на верхней и нижней поверхностях 70 , 56 могут быть изменены в дополнительных вариантах осуществления для размещения различных потенциальных точек крепления между балкой 10 и панель крыши 16 , передние стойки 18 и другие возможные компоненты автомобиля.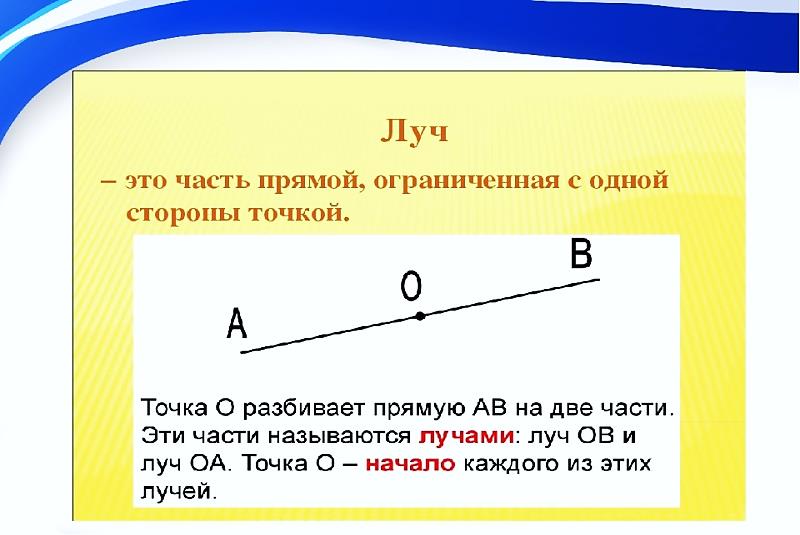
 от прямой ориентации 33 корпуса 54 концевых частей 32 . В проиллюстрированном варианте осуществления кривизна 28 центральной части 24 представляет собой по существу непрерывную дугу вдоль окружности, хотя понятно, что кривизна 28 в дополнительных вариантах реализации может не совпадать вдоль центральной части 24 . , такие как более выпуклые вблизи концевых частей 32 и более прямые в центре или более или менее выпуклые в других различных местах вдоль центральной части 24 .Однако концевые части , 32, останутся по существу прямыми.
от прямой ориентации 33 корпуса 54 концевых частей 32 . В проиллюстрированном варианте осуществления кривизна 28 центральной части 24 представляет собой по существу непрерывную дугу вдоль окружности, хотя понятно, что кривизна 28 в дополнительных вариантах реализации может не совпадать вдоль центральной части 24 . , такие как более выпуклые вблизи концевых частей 32 и более прямые в центре или более или менее выпуклые в других различных местах вдоль центральной части 24 .Однако концевые части , 32, останутся по существу прямыми. Передний фланец 36 проходит вперед от средней области передней стенки 90 , и аналогичным образом задний фланец 58 проходит назад от средней области задней стенки 92 .Передняя стойка 94 и задняя стойка 96 проходят линейно между верхней стенкой 86 и нижней стенкой 88 и проходят непрерывно внутри полой внутренней части 72 по длине 26 балки
Передний фланец 36 проходит вперед от средней области передней стенки 90 , и аналогичным образом задний фланец 58 проходит назад от средней области задней стенки 92 .Передняя стойка 94 и задняя стойка 96 проходят линейно между верхней стенкой 86 и нижней стенкой 88 и проходят непрерывно внутри полой внутренней части 72 по длине 26 балки  Таким образом, в показанном варианте осуществления передняя и задняя ножки 94 , 96 расположены под углом друг к другу, поскольку они проходят вниз от верхней стенки 86 к нижней стенке 88 , прикрепляясь к нижней стенке . 88 у передней и задней стенок 90 , 92 соответственно. Таким образом, полость 72 разделена передними и задними стойками 94 , 96 на центральную зону 98 , переднюю зону 100 и заднюю зону 102 , причем участки 100 , 102 имеют одинаковые размеры и образуют непрерывные коробчатые секции, не имеющие отверстий для крепления или других прерываний.Понятно, что в дополнительных вариантах осуществления может быть выполнено большее или меньшее количество ножек, которые проходят вертикально внутри полой внутренней части 72 , чтобы альтернативно поддерживать верхнюю стенку 86 на расстоянии от нижней стенки 88 .
Таким образом, в показанном варианте осуществления передняя и задняя ножки 94 , 96 расположены под углом друг к другу, поскольку они проходят вниз от верхней стенки 86 к нижней стенке 88 , прикрепляясь к нижней стенке . 88 у передней и задней стенок 90 , 92 соответственно. Таким образом, полость 72 разделена передними и задними стойками 94 , 96 на центральную зону 98 , переднюю зону 100 и заднюю зону 102 , причем участки 100 , 102 имеют одинаковые размеры и образуют непрерывные коробчатые секции, не имеющие отверстий для крепления или других прерываний.Понятно, что в дополнительных вариантах осуществления может быть выполнено большее или меньшее количество ножек, которые проходят вертикально внутри полой внутренней части 72 , чтобы альтернативно поддерживать верхнюю стенку 86 на расстоянии от нижней стенки 88 .
Как показано на РИС. 6-6A, центральная часть 98 полой внутренней части 72 имеет внутреннее углубление 104 , которое выступает в центральную область 98 и образует вставную поверхность на нижней поверхности 56 для сопряжения компонентов автомобиль 42 (РИС.1), что может потребовать альтернативного угла крепления окружающих частей нижней поверхности 56 . Внутреннее углубление 104 включает в себя первую поверхность 106 , которая наклонена внутрь вблизи передней ноги 94 , и вторую поверхность 108 , которая наклонена внутрь вблизи задней ноги 96 . Первая и вторая поверхности , 106, , , 108, внутреннего углубления , 104, , как правило, плоские и сходятся под углом, наиболее удаленным от внутреннего пространства , 72, . В проиллюстрированном варианте осуществления внутренняя выемка 104 и соответствующая вставная поверхность проходят непрерывно вдоль сечения центральной части 24 (фиг. 4) ведущей балки 10 . Однако следует понимать, что внутреннее углубление 104 может быть сегментировано в различных точках вдоль балки 10 ведущей балки, иметь альтернативную форму или может иным образом не включаться, если сопряженные компоненты транспортного средства 42 (фиг. 1) ) не требуют поверхности с альтернативным углом крепления.
В проиллюстрированном варианте осуществления внутренняя выемка 104 и соответствующая вставная поверхность проходят непрерывно вдоль сечения центральной части 24 (фиг. 4) ведущей балки 10 . Однако следует понимать, что внутреннее углубление 104 может быть сегментировано в различных точках вдоль балки 10 ведущей балки, иметь альтернативную форму или может иным образом не включаться, если сопряженные компоненты транспортного средства 42 (фиг. 1) ) не требуют поверхности с альтернативным углом крепления.
Как дополнительно показано на РИС. 7, передняя и задняя опоры 94 , 96 непрерывно проходят внутри полой внутренней части 72 по длине 26 балки 10 жатки. Соответствующие передняя и задняя области 100 , 102 полой внутренней части 72 соответственно проходят по длине 26 балки 10 и определяют непрерывные и непрерывные коробчатые сечения 109 90 90 трубчатой формы и проходят вдоль переднего и заднего краев корпусной части 54 . Непрерывные коробчатые секции 109 не содержат отверстий, проемов или других неровностей по длине 26 ведущей балки 10 для обеспечения непрерывного распределения нагрузки по длине 26 ведущей балки 10 и для обеспечения постоянной структурной поддержки между передними стойками 18 и вдоль передней части панели крыши 16 . Таким образом, непрерывные коробчатые секции 109 предназначены для поглощения ударных нагрузок и восприятия нагрузок, приложенных к балке 10 при нормальных условиях эксплуатации транспортного средства 42 .Центральная зона 98 между непрерывными коробчатыми секциями 109 прикрепляет непрерывные коробчатые секции 109 друг к другу, чтобы предотвратить скручивание или скручивание между непрерывными коробчатыми секциями 109 .
Непрерывные коробчатые секции 109 не содержат отверстий, проемов или других неровностей по длине 26 ведущей балки 10 для обеспечения непрерывного распределения нагрузки по длине 26 ведущей балки 10 и для обеспечения постоянной структурной поддержки между передними стойками 18 и вдоль передней части панели крыши 16 . Таким образом, непрерывные коробчатые секции 109 предназначены для поглощения ударных нагрузок и восприятия нагрузок, приложенных к балке 10 при нормальных условиях эксплуатации транспортного средства 42 .Центральная зона 98 между непрерывными коробчатыми секциями 109 прикрепляет непрерывные коробчатые секции 109 друг к другу, чтобы предотвратить скручивание или скручивание между непрерывными коробчатыми секциями 109 . Также за счет непрерывных коробчатых профилей 109 , несущих основные нагрузки на балку 10 , проемов 78 , отверстий 68 , 84 , (рис. 4) и других элементов, образованных на вершине и нижние стенки 86 , 88 конструктивно не нарушают перемычки 10 .
Также за счет непрерывных коробчатых профилей 109 , несущих основные нагрузки на балку 10 , проемов 78 , отверстий 68 , 84 , (рис. 4) и других элементов, образованных на вершине и нижние стенки 86 , 88 конструктивно не нарушают перемычки 10 .
Обратимся теперь к фиг. 8 блок-схема иллюстрирует один вариант осуществления способа формирования ведущего луча 10 . На этапе 110 непрерывная балка 112 выдавливается из экструзионной головки 114 , чтобы получить полую внутреннюю часть 72 (фиг. 5) с передними и задними ножками 94 , 96 96 05 5A), продолжающийся непрерывно внутри полой внутренней части 72 , чтобы определить центральную, переднюю и заднюю области 98 , 100 , 102 (ФИГ. 5А). Непрерывная балка 112 разрезается на режущей станции 116 для формирования сегмента балки 118 с концами, в целом перпендикулярными длине 26 сегмента балки 118 . Сегменты балки 118 затем складываются в штабели для транспортировки. Непрерывная балка 112 и, следовательно, образующаяся в результате верхняя балка 10 иллюстрируемого варианта осуществления выдавлены в основном из алюминия, хотя понятно, что для формирования верхней балки 10 могут использоваться дополнительные и альтернативные материалы.Также предполагается, что перемычка 10 или ее части могут быть изготовлены из альтернативных металлов и могут быть альтернативно прокатаны, гидроформованы или альтернативно соединены, например, с помощью лазерной или дуговой сварки.
5А). Непрерывная балка 112 разрезается на режущей станции 116 для формирования сегмента балки 118 с концами, в целом перпендикулярными длине 26 сегмента балки 118 . Сегменты балки 118 затем складываются в штабели для транспортировки. Непрерывная балка 112 и, следовательно, образующаяся в результате верхняя балка 10 иллюстрируемого варианта осуществления выдавлены в основном из алюминия, хотя понятно, что для формирования верхней балки 10 могут использоваться дополнительные и альтернативные материалы.Также предполагается, что перемычка 10 или ее части могут быть изготовлены из альтернативных металлов и могут быть альтернативно прокатаны, гидроформованы или альтернативно соединены, например, с помощью лазерной или дуговой сварки.
Сегменты 118 луча, как показано на этапе 120 на фиг.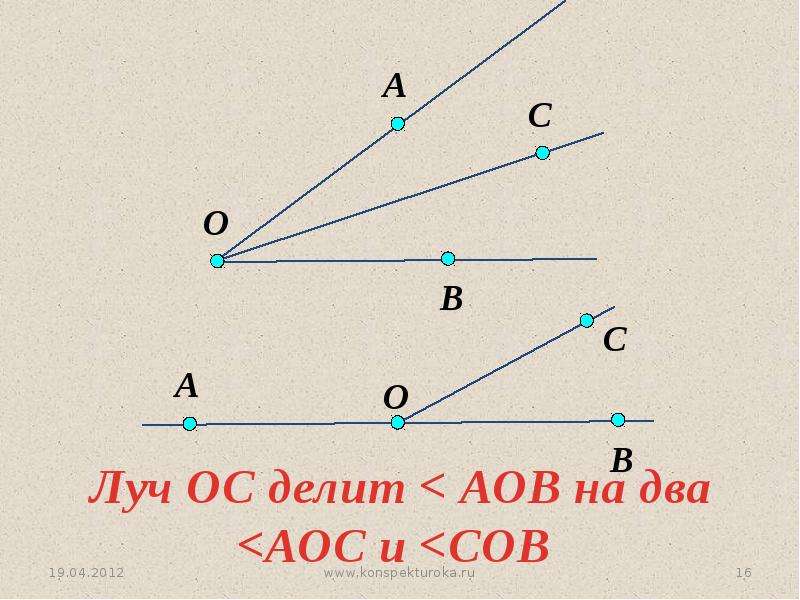 8, раскладываются, измеряются и центрируются на конвейере. Конвейер подает сегменты балки на станцию обрезки 121 , где обрезается задний фланец 58 , который непрерывно проходит по длине сегмента балки 118 .Более конкретно, задний фланец 58 обрезан для образования удлиненного выреза 59 , который определяет выступы заднего фланца 58 вблизи концевых частей 32 . Предполагается, что задний фланец 58 можно альтернативно ударить или иным образом разрезать для удаления удлиненной части заднего фланца 58 , которая образует удлиненный вырез 59 .
8, раскладываются, измеряются и центрируются на конвейере. Конвейер подает сегменты балки на станцию обрезки 121 , где обрезается задний фланец 58 , который непрерывно проходит по длине сегмента балки 118 .Более конкретно, задний фланец 58 обрезан для образования удлиненного выреза 59 , который определяет выступы заднего фланца 58 вблизи концевых частей 32 . Предполагается, что задний фланец 58 можно альтернативно ударить или иным образом разрезать для удаления удлиненной части заднего фланца 58 , которая образует удлиненный вырез 59 .
Как также показано на РИС. 8, на шаге 122 , концевые части 32 сегмента балки 118 зажимаются с помощью гибочного устройства 124 , которое надежно крепится к концевым частям 32 сегмента балки 118 9Гибочное устройство 124 в показанном варианте осуществления имеет два зажимных узла 126 , которые одинаково зажимают концевые части 32 для центрирования сегмента балки 118 между двумя зажимными узлами 126 .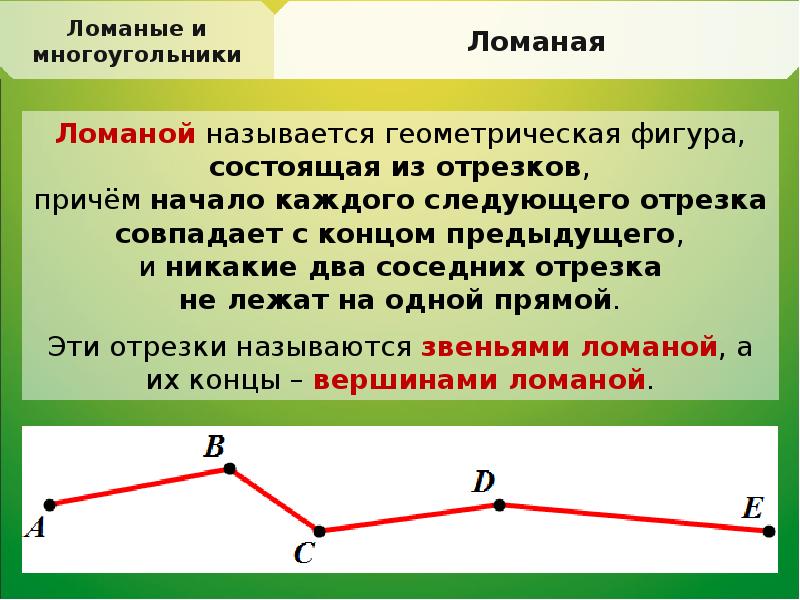 На этапе 128 гибочное устройство 124 перемещает зажимные узлы 126 в основном в противоположных направлениях для растягивания и изгиба центральной части 24 сегмента 118 балки в форме, которая соответствует в целом постоянной кривизне 20004 22 по центральной части 24 сегмента балки 118 .Более конкретно, гибочное устройство 124 растягивает сегмент балки 118 в трех измерениях, так что задняя полка 58 и задняя стенка 92 и нижняя стенка 88 (фиг. 5А) часть корпуса 54 подвергается некоторому сжатию в процессе гибки с растяжением. Однако удлиненный вырез 59 в заднем фланце 58 значительно уменьшает сжатие в заднем фланце 58 , чтобы предотвратить коробление или нежелательное искривление в процессе гибки растяжением.Понятно, что в дополнительных вариантах осуществления изгибающее устройство 124 может иметь один зажимной узел 126 , который перемещается относительно стационарного зажимного узла 126 для растяжения и изгиба сегмента балки 118 до кривизны 28 . Зажимные узлы 126 освобождаются от сегмента балки 118 на этапе 130 , и концевые части сегмента балки остаются в основном прямыми, как описано выше.
На этапе 128 гибочное устройство 124 перемещает зажимные узлы 126 в основном в противоположных направлениях для растягивания и изгиба центральной части 24 сегмента 118 балки в форме, которая соответствует в целом постоянной кривизне 20004 22 по центральной части 24 сегмента балки 118 .Более конкретно, гибочное устройство 124 растягивает сегмент балки 118 в трех измерениях, так что задняя полка 58 и задняя стенка 92 и нижняя стенка 88 (фиг. 5А) часть корпуса 54 подвергается некоторому сжатию в процессе гибки с растяжением. Однако удлиненный вырез 59 в заднем фланце 58 значительно уменьшает сжатие в заднем фланце 58 , чтобы предотвратить коробление или нежелательное искривление в процессе гибки растяжением.Понятно, что в дополнительных вариантах осуществления изгибающее устройство 124 может иметь один зажимной узел 126 , который перемещается относительно стационарного зажимного узла 126 для растяжения и изгиба сегмента балки 118 до кривизны 28 . Зажимные узлы 126 освобождаются от сегмента балки 118 на этапе 130 , и концевые части сегмента балки остаются в основном прямыми, как описано выше.
Все еще ссылаясь на РИС.8, на шаге 132 , пресс с режущей матрицей 133 ударяет по передней полке 36 сегмента балки 118 по схеме, обеспечивающей в целом однородность передних кромок 66 передней полки 36 при производстве нескольких сегментов балки 118 . Более конкретно, передний фланец 36 штампуется для образования передней кромки 66 , которая параллельна кривизне 28 вблизи концевых частей 32 балки для зацепления с ветровым стеклом 30 .Режущая матрица 133 также формирует серию пазов 40 в центральной области 38 передней полки 36 для уменьшения напряжения в передней полке 36 , вызванного процессом гибки растяжением, и для обеспечения точек соединение передней кромки 17 панели крыши 16 . Выемки 40 соприкасаются с панелью крыши 16 , а также обеспечивают зону для удаления скопившейся жидкости между передним фланцем 36 и панелью крыши 16 (РИС.3), например, в процессе покраски кузова автомобиля. Кроме того, вырезание пазов 40 в передней полке 36 также обеспечивает снижение веса в центральной области 38 передней полки 36 , что увеличивает несущую способность балки 10 и уменьшает общий вес траверсы 10 .
На этапах 134 и 136 , как показано на фиг. 8, верхняя и нижняя поверхности 70 , 56 корпуса 54 сегмента балки 118 обработаны и гидроформованы для создания проемов 78 , проемов 68 ,0 , и другие элементы на корпусной части 54 , как описано ранее.В дополнительных вариантах осуществления несколько этапов, включая этапы , 134, и 136, , могут выполняться одновременно, в виде дополнительных отдельных этапов или могут выполняться в любой комбинации этапов. Кроме того, механическая обработка и гидроформовка могут быть полностью или частично заменены для формирования любого элемента альтернативными формовочными средствами, такими как сверление, штамповка, различные формы резки или другие формовочные средства, как это обычно понимают специалисты в данной области техники. .
Дополнительная блок-схема показана на РИС.9, иллюстрирующий другой вариант осуществления способа формирования головного луча 10 , имеющего несколько этапов, показанных на ФИГ. 8. Как показано, в проиллюстрированном варианте осуществления один станок с ЧПУ выполняет шаги 128 и 132 наряду с проверкой соответствующего изгиба по кривизне 28 и проверкой соответствующего ориентирования переднего фланца 36 ближайшего концевые части 32 и центральная область 38 . После проверки обработки переднего фланца 36 второй станок с ЧПУ выполняет этапы 134 и 136 в дополнение к подкраске удлиненного выреза 59 в заднем фланце 58 и обрезке торцов для изготовления передний фланец 36 и проточенные отверстия, симметричные относительно середины балки 10 , а также любую другую доработку, чтобы балка 10 находилась в пределах производственных допусков.Последний этап 138 проиллюстрированного варианта осуществления включает чистовую обработку ведущей балки 10 , включая удаление заусенцев, сдувание любого мусора с ведущей балки 10 , лазерное травление идентификационного номера и/или кода и нагрев. обработка траверсы 10 . Предполагается, что головная балка 10 может быть подвергнута тепловой обработке или другим средствам изменения твердости балки в любой точке процесса формования, как это обычно понимает специалист в данной области техники.Кроме того, после формирования сегмента балки 118 в головную балку 10 концевые части 32 сегмента балки 118 прикрепляются к передним стойкам 18 автомобиля 42 9005 (FI). 2), панель крыши 16 крепится к ряду пазов 40 и другим элементам крепления на переднем крае 66 или других частях балки 10 (РИС. 3) и лобового стекла . 30 крепится к переднему краю 66 (РИС.1), как показано и описано выше.
Специалисту в данной области техники будет понятно, что конструкция описанного изобретения и другие компоненты не ограничиваются каким-либо конкретным материалом. Другие иллюстративные варианты осуществления изобретения, раскрытые здесь, могут быть образованы из самых разных материалов, если здесь не указано иное.
Для целей настоящего раскрытия термин «связанный» (во всех его формах, пара, соединение, соединение и т. д.) обычно означает соединение двух компонентов (электрических или механических) прямо или косвенно друг с другом.Такое соединение может быть неподвижным или подвижным. Такое соединение может быть достигнуто с двумя компонентами (электрическими или механическими) и любыми дополнительными промежуточными элементами, образующими единое целое друг с другом или с двумя компонентами. Такое соединение может быть постоянным по своей природе или может быть съемным или разъединяемым по своей природе, если не указано иное.
Также важно отметить, что конструкция и расположение элементов изобретения, как показано в примерных вариантах осуществления, являются только иллюстративными.Хотя в этом раскрытии подробно описано лишь несколько вариантов осуществления настоящих инноваций, специалисты в данной области техники, просматривающие это раскрытие, без труда поймут, что возможны многие модификации (например, изменения в размерах, размерах, структурах, формах и пропорциях различные элементы, значения параметров, способы монтажа, использование материалов, цветов, ориентаций и т. д.) без существенного отклонения от новых учений и преимуществ изложенного предмета.Например, элементы, показанные как выполненные как единое целое, могут быть сконструированы из нескольких частей, или элементы, показанные как несколько частей, могут быть выполнены как единое целое, работа интерфейсов может быть изменена на противоположную или иным образом изменена, длина или ширина конструкций и/или элементов или соединителя или другие элементы системы могут быть изменены, характер или количество регулировочных позиций, предусмотренных между элементами, могут быть изменены. Следует отметить, что элементы и/или узлы системы могут быть изготовлены из любого из большого разнообразия материалов, обеспечивающих достаточную прочность или долговечность, в любом из большого разнообразия цветов, текстур и комбинаций.Соответственно, предполагается, что все такие модификации включены в объем настоящих нововведений. Другие замены, модификации, изменения и упущения могут быть сделаны в конструкции, рабочих условиях и компоновке желаемых и других примерных вариантов осуществления без отхода от сущности настоящих нововведений.
Следует понимать, что любые описанные процессы или этапы в рамках описанных процессов могут быть объединены с другими раскрытыми процессами или этапами для формирования структур в пределах объема настоящего изобретения.Типичные структуры и процессы, раскрытые в данном документе, предназначены для иллюстративных целей и не должны рассматриваться как ограничивающие.
Также следует понимать, что в вышеупомянутую структуру могут быть внесены изменения и модификации без отступления от идей настоящего изобретения, и, кроме того, следует понимать, что такие концепции охватываются следующей формулой изобретения, если только они не утверждения их языком прямо говорят об обратном.
| Получение Знакомство | ||||||||||||||
| Расчет изгиба балок был
освященный веками центральный элемент в раннем обучении «техническому
механика», то, что должен был пройти каждый подающий надежды инженер и ученый.
через своего рода обряд посвящения.Многие не успели. Мастеринг
изгиб луча просто не делается на обратной стороне конверта, в то время как
пиво или два. Вам действительно нужно применить себя, чтобы сдать эти экзамены. Давайте сначала посмотрим на грандиозность задачи, а затем разберем ее на части, которые мы может справиться. На рисунке ниже показано, о чем идет речь, при довольно простом обстоятельства. У нас есть то, что иллюминаты называют «лучом». фиксируется на одном конце. С таким же успехом это мог быть меч, увиденный лезвием.Некоторые силы воздействовать на наш луч; в результате изгибается. Давайте рассмотрим основные моменты, связанные к этому по одному: | ||||||||||||||
| ||||||||||||||
| Сначала , давайте уточним, что я имею в виду
со словом « балка «.»Балка» должно быть общим названием для любого длинного объекта с некоторыми
поперечное сечение одинаковое по всей длине l .
Кроме того, длина l должна быть значительно больше длины
размеры поперечного сечения. Поскольку поперечное сечение большинства мечей зависит от длины, эти мечи являются 90 158 не 90 161 правильными лучами, а в лучшем случае 90 158 приблизительными 90 161 лучами. | ||||||||||||||
| Второй , давайте определить « изгиб «.если ты сгибая что-либо, в частности балку, вы ее механически деформируете. Насколько здесь речь идет о слове изгибе , мы ограничиваем себя к чисто упругим деформациям в любом месте луча. Снимите силы, действующие на балку сверху, и она должна снова быть совершенно прямым. | ||||||||||||||
| Третий , мы
посмотрите на силы которые могут согнуть
луч. Мы допускаем все виды сил, действующих в любом месте на балке — до тех пор, пока
они действуют только в направлении z .В противном случае у нас есть две проблемы с изгибом балки — изгиб в з — направление и в y — направление, перпендикулярное плоскости чертежа. Применение сил
в x -направлении будет означать испытание на растяжение (или сжатие), поэтому
мы тоже не разрешаем. Конечно, силы, действующие на реальные балки или
мечи не заботятся об этих ограничениях, но я смотрю на простой луч
сгибаясь здесь. Силы могли быть точек силы, как у силу испытывает ваш меч, когда по нему ударяют лезвием другого меча, или распределили сил, как вы их получите, когда вы кладете, например, груз на балку, как показано выше. Наша балка должна изгибаться, но не двигаться иначе. Он не будет вращаться и никуда не денется, а значит, сумма всех сил и моментов должен быть равен нулю по определению. на картинке явно не то выше.Ну и забыли: | ||||||||||||||
| Четвертый г. граничные условия .
На картинке выше балка прочно закреплена в какой-то стене. Математически
что означает прогиб z ( x ) , величина изгиба по координате x или просто линия изгиба, равна нулю для x =0 . Выражаясь математически, мы имеем в качестве граничного условия: z ( x =0)=0 , и по понятным причинам d z /d x ( x =0)=0 . Для математически сложных: производная d z /d x дает наклон кривой изгиба z ( x ) , который должен быть ноль (т.е. он параллелен оси x ) рядом со стеной Эти граничные условия могут быть выполнены только в том случае, если на балку действуют силы и моменты. при x =0 , которые точно компенсируют силы и моменты внешние силы.Это довольно мило, потому что это означает, что нам не нужно беспокоиться об этом. Проще говоря, если вы каким-то образом обездвижите одно острие своего меча (поместив его в тиски) он не может двигаться или вращаться по определению, независимо от того, силы действуют на него где-то в другом месте. | ||||||||||||||
| Пятый и
чтобы не забыть, луч может иметь произвольное сечение , в т.ч.
полые. Три показанных примера уже довольно особенные, поскольку они очень симметричный.Это не требуется, тем не менее мы будем рассматривать только сечения с некоторой симметрией от а теперь, чтобы не заморачиваться слишком сильно. | ||||||||||||||
| Теперь давайте рассмотрим поставленную задачу.
Мы хотим вычислить z ( x ) кривую, которая
описывает форму изогнутой балки. Мы допускаем любую длину l и
формы поперечного сечения балки и всевозможные силы, сила
распределения и всевозможные (разумные) граничные условия. Даже если вы настолько сложны в математике, что вам пришлось заняться банковским делом, вы поймете, что это не может быть легкой задачей. Как вы выражаете сечение № 2 выше (меч с долом) в уравнениях? Что бы граничные условия будут, если вы попытаетесь удерживать меч в фиксированном положении своим руками, а не в тиски? Если его ударит другой меч, ты никак не может сохранить положение руки и меча полностью неизменным — в отличие от (очень сильный) порок. | ||||||||||||||
| Ну задача конечно не из легких — но тоже не так сложно, как может показаться. Давайте сделаем в два шага и модули. Во-первых, в этом модуле я даю довольно простое описание специального ситуацию, которую я затем буду использовать, чтобы вывести несколько общих правил о сгибании лучи. Во втором модуле я дам более общее лечение. | ||||||||||||||
| Угадай Специальное решение | ||||||||||||||
| Хорошая новость в том, что я не математик.Если бы я был одним из них, я бы не смог нарисовать картинку выше потому что он уже содержит своего рода решение проблемы, поскольку он показывает (путем угадывания), как изгибается балка. Математики только решают задачи без какого-либо предварительного представления о результате, а это значит, без милого маленького фотографий. Вот почему они часто на самом деле не решают реальных проблем, а только подробно обсудите, может ли проблема иметь решение, много решений — или, возможно, ни одного. | ||||||||||||||
| Все мы
нематематики же, только знают что
балка изгибается примерно так, как показано выше для данной ситуации.Мы знаем даже
более. Мы знаем, что если мы посмотрим на небольшую часть луча, то сможем, по крайней мере,
В качестве хорошего приближения предположим, что изгиб можно локально описать как круговой. Верхнюю и нижнюю поверхность балки затем можно нарисовать циркулем, используя два радиуса, отличающиеся толщиной d . По сравнению с длиной недеформированной балки верхняя часть теперь немного длиннее, нижняя часть немного короче. Мы рассмотрели это до и там можно не сомневаться, что у нас всегда есть нейтраль ось внутри балки, длина которой не изменилась.В нашем простой пример, у нас на самом деле есть нейтраль поверхность , но для более сложных сечений, примыкающих к нейтральной оси (иногда также называемая нейтральной линией или центроидом ) лучше, поскольку она более общая. Этот нейтральная ось (а здесь и вся нейтральная поверхность), несомненно, тоже будет в середине прямоугольной балки, как показано ниже. | ||||||||||||||
| ||||||||||||||
| Теперь, в процессе мысли, мы
«вырезаем» желтую часть изгиба балки. Чтобы держать его в форме
он имел, когда он еще был составной частью балки, мы должны приложить усилия.
Очевидно, что следует отметить, что только распределение сил, изображенное на рис.
синий на правой стороне и то же самое на другом конце (не
показано) может вызвать деформацию, как показано на рисунке.Мы всегда можем заменить дистрибутив на синего цвета.
двухточечных сил F каким-то умным усреднением, и в результате получится то, что показано на
коричневый на левом конце нашей части луча. Теперь мы видим, что суммарное действие сил должно вызвать крутящий момент. или крутящий момент T с угадал величину T =½ Fd так как расстояние между парой сил при предположим, что равно d /2 или половине толщина балки как на чертеже.Если вы на самом деле вычислить все это, расстояние будет 2d /3 . | ||||||||||||||
| Пока я просто описываю
рисунок, генерируя первые уравнения, как я продвигаюсь вперед. Если вы продолжите смотреть на рисунок, вы поймете, что есть еще что увидеть которые можно описать простыми уравнениями. В частности, максимальное напряжение справа вверху e t max = d /2 r ; это растяжение .Максимальное напряжение прямо на дно e b max =– d /2 r ; он сжимающий. | ||||||||||||||
| Почему? На картинке все показано. То
длина крайней части l 0 +
D л = л 0 + ½ d · sina= l 0 + ( d ·
л 0 )/2р) . Отсюда получаем e max = [ l 0 + ( d · л 0 /2р) – л 0 ]/ л 0 = д /2 г .Вуаля! В равной степени, конечно, деформация уменьшается линейно от максимального значения на снаружи до нуля в нейтральной плоскости при движении внутри луча. | ||||||||||||||
| Включено средний , мы предполагаем, что верхняя или нижняя часть таким образом испытывает средний штамм e av =± d /4 r . | ||||||||||||||
| Пока мы рассматриваем только упругие деформации, деформация e и напряжение s являются связанные: s= Y · e ; где Y = модуль Юнга. | ||||||||||||||
| Среднее напряжение при нашей средней деформации представляет собой среднюю силу F , деленную на половину
площадь поперечного сечения бод . Другими словами: с = ( F ) / (½ bd ) = 2 F / bd = Y · e av = Y · д / 4 р . Это дает нам силу F =( Y · d / 4 r ) · бд / 2= б · д 2 · Y / 8 р | ||||||||||||||
| Теперь легко понять, что в конец это крутящий момент T = F · d /2 , что вызывает изгиб. Итак, давайте свяжем крутящий момент T на радиус кривизны r .С уравнением выше мы получаем как окончательный результат : | ||||||||||||||
| ||||||||||||||
| Вывод Немного предметов первой необходимости | ||||||||||||||
| У нас есть красивое и простое уравнение.Мы сделали много предположений, поэтому мы не можем ожидать, что это уравнение абсолютно верно.
правильный. Тем не менее, мы не сделали ничего возмутительно неправильного, так что это не должно быть
совершенно неправильно, но наполовину приличное приближение. Но что делает
уравнение означает? Во-первых, я собираюсь сказать вам, что это определенно означает, несмотря на догадки. Затем я собираюсь обсудить недостатки этого простого подхода и то, как мы может исправить это.. | ||||||||||||||
Основные выводы, которые мы можем сделать:
| ||||||||||||||
| ||||||||||||||
| На рисунке показан ряд
вещи.Прежде всего, становится ясно, что для показанной точечной силы локальная
изгиб сильнее вокруг зажима балки, потому что там у вас есть
наибольший крутящий момент и, следовательно, наименьший радиус кривизны. Радиус кривизны
таким образом плавно изменяется по длине луча до места расположения
сила. Вправо от силы изгиба в этом случае вообще нет
(имеется в виду бесконечный радиус кривизны). Заметьте, что мы еще не рассчитали кривую прогиба, а только видели, как она
результат местных искривлений. Не иллюстрируя это напрямую, мы также можем вывести несколько других точек: | ||||||||||||||
| Если бы у нас не было точка сила, но какая-то распределенная сила , мы все еще можем рассчитать крутящий момент
в любой точке путем суммирования или интегрирования по распределению сил. Как это
сделано, не важно на данный момент, все, что нам нужно знать, это то, что это может быть
Выполнено. Если бы мы приложили силу 90 158 секунд в 90 161 точечной где-то правее показанного выше, мы просто суммируем моменты силы. | ||||||||||||||
| Удивительно, как много можно делать выводы о сложной проблеме, фактически не решая ее «с первого принципов»? Прежде чем я перейду к дальновидным предположениям, давайте взглянем на проблемы, упущения и недостатки моего «угадывающего» подхода. | ||||||||||||||
| Первое замечание состоит в том, что маленькие кубики внутри нашего
изгиб балки опыт только одноосный нормальный
стрессы.Любой
маленький куб
внутри луч становится немного длиннее в x -направлении;
это показано
здесь немного в другом контексте. Деформация увеличивается линейно с
расстояние до нейтральной поверхности. Это приближение. Реальные лучи испытали бы боковой сужение в верхней половине и соответствующее расширение в нижней. Форма поперечного сечения изменится с прямоугольной на трапециевидную. Кроме того, внешние силы также вызывают некоторые компоненты сдвига в напряжении, которыми мы пренебрегали.Понятно, что разобраться в этом будет непросто, так что позвольте мне сразу сообщить вам хорошие новости: Нам не нужно этого делать. При обработке изгиба балки с помощью только одноосные нормальные напряжения, конечно, не совсем верно, этого достаточно для почти всех практических случаев. | ||||||||||||||
| Вторая точка более серьезна и откроет большую
банка червей. В нашем подходе к угадыванию мы приняли прямоугольную форму.
поперечное сечение, определяемое толщиной d , умноженной на ширину или
«широта» б .Мы догадались, что нейтральный самолет
находится прямо посередине. Если мы перепишем окончательное уравнение для радиуса
кривизну, как указано выше, мы можем выразить ее как r =( b d 3 / 16) ·
( Y / T ) и множитель ( бд 3 /
16) содержит всю информацию о
геометрия поперечного сечения, предположение о нейтральной плоскости (и, таким образом,
направление изгиба), плюс процедуры усреднения.Другими словами,
он содержит все возможные ошибки и
недостатки угадывающего подхода. Таким образом, не должно быть большим сюрпризом, что правильное значение этого фактора в результате правильных расчетов на самом деле: ( б д 3 /12) . Ну, это очень плохо. Тем не менее, метод угадывания был не таким уж плохо и конечно стоит делать для простого прямоугольного сечения. | ||||||||||||||
| Настоящая проблема в том, что для произвольных сечений, угадывание
подход не работает вообще больше для
вывод значения коэффициента перед Y / T который заботится о геометрии луча. Хотя можно было бы сделать хорошее предположение
о положении нейтральной поверхности для
сечения, приведенные выше, вы
пришлось бы нелегко, т.е.г., треугольного сечения и многие другие. Хуже того, вы не могли легко угадать средние значения по очевидным причинам. Так вы видите проблему: | ||||||||||||||
| ||||||||||||||
| Что ж, результат нашего предположения дает
явный намек: мы можем сохранить общее соотношение r µ ( Y / T ) .Все, что меняется, это то, что
константа пропорциональности ( b d 3 /16) в нашем
догадки) необходимо рассчитывать по реальному поперечному сечению балки. Это на самом деле не
очень трудно сделать (при условии, что вы знаете немного об интеграции в два
Габаритные размеры). В результате получается просто число , т.е. называется моментом инерции площади I А .Если когда-либо было неправильное название, то это оно. То площадь момент инерции ничего не значит никакого отношения к тому, что называется « моментом инерция » по уважительным причинам, когда вы вычисляете, как вращаются тела вокруг некоторой оси. Единственная связь между ними заключается в том, что если вы запишете интегралы для вычисления этих моментов, математические выражения похожий. | ||||||||||||||
| Так что все нам нужно сделать, это вычислить момент инерции площади I для используемое поперечное сечение и переписать наш основное уравнение как | ||||||||||||||
| ||||||||||||||
| Это требует расчета положение нейтральной оси или центроид первый.Затем он определит систему координат, так как мы центрируем ее на нейтральной оси. | ||||||||||||||
| Посмотрите на прямоугольный поперечное сечение на картинке ниже, чтобы получить это: Красный кружок обозначает положение нейтральной оси (она проходит перпендикулярно картинной плоскости в x — направления, конечно). С тех пор, как он наклонился z -ось (путем приложения силы в y -направлении) дают результаты различной формы изгиба вокруг оси y (по приложив силу в z -направлении), нам нужно вычислить два момента инерции площади, I y и I y , с учетом тот. | ||||||||||||||
| Как центроид и
Моменты площади I A определяются и как они определяются
рассчитывается, является предметом другого модуля. Все, что нам нужно знать, это то, что
если кто-то рассчитал это в прошлом, нам не нужно делать это самим. Мы
просто может использовать сгенерированные числа. Вот несколько примеров; положение центроида показано красной точкой. | ||||||||||||||
| Красная точка обозначает нейтральную линию.Для тот же модуль Юнга Y , моменты площади теперь дают сопротивление Чтобы изгибаться в Y — или — или Z — Направление ( I Z или 1 или I Y , соответственно. Inde обозначает ось, вокруг которой происходит изгиб). Что можно оценить сразу заключается в том, что легкая трубка с несколько больший радиус, чем у тяжелого сплошного круглого сечения стержень может иметь такой же момент инерции площади и, следовательно, сопротивление изгибу.Вот почему у вас всегда есть полые балки (или и двойной фигурные) в любой структурная конструкция. | ||||||||||||||
| Поперечное сечение меча, как правило, больше сложнее, чем приведенные выше, но с эллиптическим мы могли бы по крайней мере сделать обоснованное предположение для мечей. Это позволяет оценить деформацию в самых внешних слоях в зависимости от изгиба, и это дает нам последний важная информация: | ||||||||||||||
| Как только эта деформация e (или напряжение, связанное соотношением s/e= Y ) достигает предел либо для пластической деформации, либо для разрушения, все кончено.Поскольку мы должны предположить, что где-то вдоль лезвия может быть «слабое» место, все кончается несколько раньше, чем мы рассчитывали. | ||||||||||||||
| Наконец, я просто скажу вам, что мы узнали здесь, также могут быть перенесены на «изгибание бемаса» проблема, или эффект, что ваш меч может сгибаться, когда вы пытаетесь пронзить прямо во что-то. Это будет рассмотрено в специальном модуле | .||||||||||||||
ИЗГИБ, ИЗГИБ И ИЗГИБ В КОНСТРУКЦИОННЫХ СТАЛЬНЫХ БАЛКАХ
ИЗГИБ, ИЗГИБ И ПРОЛЕТ СТАЛЬНЫХ БАЛОК
Должны ли при проектировании конструкционной стали быть все прямые участки, углы и соединения? К счастью, нет. Одним из многих достоинств конструкционной стали является ее пластичность — способность подвергаться растяжению и сжатию, оставаясь при этом такой же прочной, как и прежде. Поэтому ничто не мешает стальной балке изогнуться.
Многие приложения из конструкционной стали могут потребовать индивидуального изгиба фрезерованных балок. Изогнутая стальная балка может обеспечить большую устойчивость к тяжелым вертикальным нагрузкам; кривые и изгибы могут привнести в архитектурный дизайн приятные для глаз декоративные элементы.
В чем разница между изгибами, кривыми и закруглениями?
КАМЕРА
Изгиб стальной балки – это изгиб по ее вертикальной оси. Представьте себе макароны длиной десять дюймов в форме двутавровой балки, приготовленные и лежащие на прилавке.Если вы установите его на узкие края его фланцев со стенкой, параллельной столешнице, а затем надавите на секцию пальцем или двумя, вы введете изгиб. Подъем появляется на прямолинейном участке «луча» на его вертикальной оси.
На первый взгляд разница между изгибом и изгибом может показаться довольно тонкой. Оба они связаны с кривизной, но кривая изгиба обычно включает не всю балку. Когда концы балки оставлены прямыми или имеют другой радиус, кривая представляет собой параболическую арку, а не сегмент круга.
Изогнутые стальные балки позволяют выдерживать большие нагрузки, поскольку их арочная форма препятствует провисанию под весом.
КРИВАЯ
Используя нашу аналогию с макаронами, если вы нажимаете на нее в форме диска — например, на крышке кастрюли — до тех пор, пока она полностью не приспосабливается к ней, вы создаете однородную часть круга, а не параболическую арку. Макаронные изделия могут лежать на краях или поверхностях фланцев. В любом случае, у вас есть кривая.
Вы часто видите изгибы опор мостов и бочкообразных крыш.Равномерная дуга от конца до конца балок предлагает огромное усиление конструкции в элегантной физической операции.
РАЗМЕТКА
Если вы толкаете пасту, когда она лежит на широкой стороне фланца, пальцем или диском, вы создаете завихрение. Развертка означает изгиб стальной балки по горизонтальной оси. Он может образовывать дугу, круг или принимать змеевидный профиль.
Кривыепредлагают простой способ изменить направление моста, если это необходимо, или создать необычные архитектурные элементы в здании, среди прочего.
МЕХАНИКА СОЗДАНИЯ ИЗГИБОВ В КОНСТРУКЦИОННЫХ СТАЛЬНЫХ БАЛКАХ
Производители стали могут изгибать балки, используя ряд методов. Наиболее распространенные включают:
- Тепло
- Профилировочный станок, также известный как профилегибочный станок
- Изгиб для балок, также известный как угловой ролик
ТЕПЛО
Применение тепла к сгибаемой секции при приложении давления требует определенных навыков и может не дать однородных результатов, если только это не выполняется на специальном станке.
СТАНОК ДЛЯ РАЗГИМА
В профилегибочном станке используются гидравлические домкраты, очень похожие на листогибочные прессы. Они надавливают на изогнутую секцию, в то время как концы балки удерживаются на месте. Этот метод может дать более точные результаты, чем нагрев.
БАЛОЧНОГИБОЧНЫЙ СТАНОК
Устройство для гибки балок пропускает балку через ряд роликов и создает очень точные кривые и более узкие радиусы. Эти угловые катки предлагают большую гибкость, когда речь идет о развале и стреловидности.
ЗАЧЕМ ИСПОЛЬЗОВАТЬ ИЗГОТОВИТЕЛЬ?
Хотя вы можете заказать нестандартные изогнутые балки прямо с завода, дополнительные транспортные расходы могут достигать обескураживающих высот.Длинные изогнутые балки создают проблемы с погрузкой и могут потребовать нескольких дополнительных грузов при транспортировке.
Однако, когда вы покупаете криволинейные балки у местного производителя, близость к месту проведения работ работает в вашу пользу и значительно снижает затраты.
Если для проектирования металлоконструкций Colorado Front Range требуются изогнутые балки, вам нужен производитель стали с большим опытом гибки балок. В Barton Supply у нас есть не только машины для гибки конструкционной стали, но и наши сотрудники понимают особые условия.Мы можем оценить, детализировать, согнуть и доставить на вашу рабочую площадку в соответствии с вашими требованиями. Чтобы узнать больше, позвоните нам сегодня.
Простой и эффективный трехузловой криволинейный балочный элемент для внеплоскостного сдвига, изгиба и кручения на основе концепции связанной интерполяции
%PDF-1.6 % 103 0 объект > эндообъект 98 0 объект > эндообъект 102 0 объект >поток 2021-09-27T10:37:48+02:002021-09-27T10:23:01+02:002021-09-27T10:37:48+02:00PScript5.dll Версия 5.2.2application/pdf
}Ǹazвязь#a(k!Gtww}_UW R7{$RuTi!cd!KźNeYQL/Ǘ2*82*ʺ’XD>Nԝ P /VPP 6ZCWt `^& ]_| njPbϗf»0^`CR;4NBE4xO|Kvd0@ PG:/?)oPk XZbh*\C|q4ͦ!{h?B>Z5NVNa\Snj´lh_H»5\%xwim][kۓWKx%gT{J];n ^=cfBLJ$G~[GQ9gLճ~%
16.Изогнутые балки — Механика твердых тел, 2-е издание — Dev Guis
ГЛАВА 16
Изогнутые балки
16.1 Введение
Существует несколько практических элементов машин и конструкций, которые изгибаются до приложения к ним изгибающей нагрузки. К таким элементам относятся крюки, звенья цепи, зажимы, рамы машин и т. д. Их изогнутая форма становится очевидной, поскольку размеры поперечного сечения совпадают с радиусом кривизны в порядке. При анализе балки на напряжение в главе 8 предполагалось, что после изгиба длины верхних и нижних волокон между двумя близко выбранными поперечными сечениями были равными.В криволинейной или изогнутой балке это не так, но длины волокон могут значительно различаться. В последующем анализе окажется, что эта разница заметно повлияет на распределение напряжений.
Предмет криволинейных балок будет рассматриваться отдельно в двух аспектах напряжения и прогиба.
16.2 Напряжения в криволинейных балках
На рис. 16.1 показана резко изогнутая балка. На балку действует изгибающий момент M . Для получения выражения для ударения целесообразно изложить допущения, сделанные для решения такой задачи.Эти допущения почти такие же, как уже заявлено в случае прямой балки в разделе 8.2. Предположения:
- Предел упругости не превышен, напряжение пропорционально деформации.
- Плоские поперечные сечения остаются гладкими после изгиба, а центральная линия, проходящая через центры тяжести всех поперечных сечений, полностью лежит в одной плоскости до и после изгиба.
- Поперечное (радиальное) сечение имеет по крайней мере одну ось симметрии и что приложенный изгибающий момент лежит в плоскости этих осей симметрии.
Здесь указывается, что предположение (ii) не является строго точным, но практические измерения не сильно отличаются от тех, которые рассчитаны на основе приведенных выше предположений.
Для начала выберите две радиальные секции ab и cd , как показано на рис. 16.1. Изгиб заставляет секцию cd поворачиваться относительно секции ab в положение c’d’ . Если два волокна 1 и 2 выбрать на равном расстоянии от нейтральной поверхности (поверхности, не меняющей своей длины в результате применения M ), то волокна будут иметь равные деформации, т.е.е.
Если длины волокон 1 и 2 равны l 1 и l 2 соответственно, то
Рис. 16.1 Криволинейная балка под действием изгибающего момента
, где σ 1 — напряжение в волокне 1, σ 2 — напряжение в волокне 2, а E — модуль упругости материала криволинейной балки.Сочетание (i) и (ii)
Из рис. 16.1 видно, что l 1 > l 2 , что дает
Поскольку волокна 1 и 2 равноудалены от нейтральной поверхности, изменение напряжения между 1 и 2 нелинейно. Также понятно, что в то время как волокно 1 растянулось, волокно 2 сжалось, что привело к растяжению σ 1 и сжатию σ 2 .Распределение напряжения можно предположить, как показано на рис. 16.1 (b), следовательно, если нейтральная поверхность проходит через центр тяжести сечений, не может быть баланса между растягивающей и сжимающей силой, действующей выше и ниже нейтральной поверхности. Следовательно, нейтральная поверхность смещается в сторону нижнего волокна или площадь, на которую действует сжимающее напряжение, меньше, чем площадь, на которую действует растягивающее напряжение.
Необходимо определить смещение нейтральной поверхности от центроидальной плоскости.Как и в случае прямой балки, линию пересечения поперечного сечения криволинейной балки и нейтральной плоскости будем называть нейтральной осью поперечного сечения криволинейной балки. Расстояние между центральной осью сечения и нейтральной осью, как показано на рис. 16.2, должно быть определено.
Рис. 16.2 Сечение изогнутой балки различных размеров
Поперечное сечение криволинейной балки показано на рис. 16.2 справа от элемента криволинейной балки между радиальными сечениями ab и cd .Центральная ось проходит через центроид C , а нейтральная ось (обозначенная NA ) находится на расстоянии e ниже центральной оси. Все расстояния можно измерить от центра кривизны балки O . Таким образом, R является радиусом центральной поверхности и, следовательно, центральная ось находится на расстоянии R от центра, O . Нейтральная ось NA находится на расстоянии R – e от центра.Выберите небольшой элемент площадью dA на участке на расстоянии y от NA .
Пусть элемент abdc образует угол d в центре O , а угол, на который cd поворачивается на c ‘ d ‘, равен d 9047 ‘
Элемент площади находится на конце волокна fg .
Длина волокна fg = ( R – e + y ) d
Удлинение в фг = гх = ярда θ
Применение закона Гука, напряжение на элементе дА
Нагружение балки только моментами (чистый изгиб) требует, чтобы результирующая сила на поперечном сечении (нормальная сила) обращалась в нуль.
Существование d θ и d является основным условием задачи (т.е. изогнутой или криволинейной балки и ее изгиба). Поэтому
(vii) теперь можно использовать для определения и .
Пусть R – e + y = v
, так что y = v – ( R – e )
Следовательно, (vii) можно переписать как
Если напряжение на малом элементе dA равно σ , то сила на этом элементе равна σ dA , а его момент относительно нейтральной оси равен y σ dA 9Следовательно, приложенный момент M равен
.
В (vii) было показано, что второй член равен нулю. Первый член — это момент площади около NA , который равен A . эл.
Используйте (ix) в (v) и получите
Таким образом, задача определения напряжения в изогнутой балке требует двух шагов. На первом этапе определяется положение NA или звездная величина e , а на втором этапе вычисляется σ .Решение будет зависеть от типа сечения и относительных размеров, в основном R и положения NA .
Напряжение изгиба в прямой балке описывалось уравнением. (8.13) и его максимальное значение равно
, где I — второй момент инерции сечения около NA через центр тяжести. Эта формула даст неправильный результат для изогнутой балки, потому что NA больше не будет центроидальным.Однако Уилсон и Кверин предложили применить поправочный коэффициент к ( x ), и они дополнительно рассчитали значения поправочного коэффициента для нескольких соотношений R / y max . Следует помнить, что y max могут быть по обе стороны от NA и могут не совпадать с двух сторон, потому что все секции не симметричны относительно NA . (Вначале предполагалось, что сечение балки по существу будет иметь одну ось симметрии и будет лежать в плоскости приложения момента.Итак, согласно Уилсону и Кереану
где K — поправочный коэффициент, зависящий от R / y max .
Для примера возьмем круглое сечение диаметром d для которого . Следовательно, из ( x ) для прямого луча
Если балка изогнута до радиуса (в нейтральной плоскости) 10 d , то напряжение на внутренней стороне изогнутой балки при таком же изгибающем моменте будет равно
1.03 и 0,97 — соответствующие поправочные коэффициенты. Эти поправочные коэффициенты становятся соответственно 1,08 и 0,93, если R = 5 d , и соответственно 1,62 и 0,7, если R = d . Из вышеприведенных рисунков можно судить и решить, что по мере того, как R становится сравнимым с размером сечения, теория изгиба применительно к прямым балкам может быть неприменима к криволинейным балкам и формулам уравнений. необходимо использовать (16.1) и (16.2).
Выведенные до сих пор уравнения относятся только к чистому изгибу.Однако сила, действующая параллельно сечению, вызовет касательное напряжение, а действующая перпендикулярно сечению, вызовет прямое напряжение. Напряжение изгиба и прямое напряжение могут быть наложены друг на друга, в то время как касательное напряжение учитывается путем расчета главных напряжений и максимальных касательных напряжений в любой интересующей точке изогнутой балки.
16.3 Определение эксцентриситета
Для решения задачи о криволинейной балке необходимо определить эксцентриситет или расстояние между центральной осью и нейтральной осью.уравнение (16.1) дает выражение для e , и количество подлежит определению. Нужно понимать, что v — это расстояние любого элемента от центра кривизны, откуда отсчитываются все расстояния.
Обычно криволинейная балка может иметь любое поперечное сечение, но обычно представляют интерес прямоугольные трапециевидные, круглые и треугольные.
1. Прямоугольное сечение На рис. 16.3 показано прямоугольное сечение шириной b и глубиной h (в радиальном направлении).Радиус центроидальной плоскости равен R , а NA находится на расстоянии e ниже центральной оси.
Выберем элемент полосы на расстоянии v от центра и пусть d v будет глубиной элемента полосы так, что
, где v 1 — расстояние нижнего волокна, а v 2 — расстояние верхнего волокна секции от центра.
Рис. 16.3 Прямоугольное сечение криволинейной балки
Помните, что y измеряется от NA , а v измеряется от центра.
2. Трапецеидальное сечение Ссылка делается на рис. 16.4, где показано трапециевидное сечение со всеми его размерами.
Рис.16.4 Трапециевидное сечение криволинейной балки
При высоте h ширина уменьшается на B – b .
Если h 1 — расстояние от центра тяжести до B , ширина сечения через центр тяжести.
Элемент полосы глубиной d v выбран на радиальном расстоянии v от центра и b 1 ширина этой полосы так, что
дА = b 1 d v
Пределы интеграции V 1 = R — H 1 и V 2 = R — H 1 + ч
Отсюда из уравнения.(16.1),
Напряжение может быть рассчитано по уравнению. (16.3).
Если на каждом этапе используются числовые значения, нет необходимости использовать сложную формулу. Приведенный выше вывод был сделан специально для того, чтобы показать детали процедуры. Нет никакого намерения использовать уравнение. (16.7). Для начала расчета следует начать с первых принципов, используя уравнение (16.1).
3. Циркулярная секция Процедура была подробно разъяснена для двух вышеуказанных секций.Круговое сечение представляет собой пример интегрирования, которое сильно усложняется. На рис. 16.5 показано круглое сечение, центр тяжести и центр которого совпадают. Элементарная полоса в этом случае также выбрана на расстоянии y от центральной оси, в то время как NA находится на y ниже центральной оси. Полоса расположена под углом θ от центральной оси. θ имеет два пределы — π /2 и π /2 совпадают с V 1 = R — R и V 2 = R + R где радиус круглого сечения.
Ширина элементарной полосы = b = 2 r cos θ
Рис. 16.5 Круговое сечение криволинейной балки.
Можно отметить, что уравнения, полученные для расстояния между центральной осью и нейтральной осью, т.е. e , должны быть дополнительно решены, чтобы получить фактическое значение e .Это будет удобно после подстановки числовых значений.
Уравнение. (16.1) было получено путем принятия радиуса центральной поверхности как R и измерения расстояния элементарной полосы от нейтральной оси. В некоторых текстах радиус нейтральной поверхности определяется из уравнения, аналогичного формуле (16.1). Однако настоящий способ очень удобен.
Пример 16.1 Поперечное сечение крюка представляет собой треугольник с основанием 50 мм и высотой 75 мм. Если радиус кривизны 50 мм на внутренней поверхности хвостовика, какова допустимая безопасная нагрузка на крюк, если безопасное растяжение 105 МПа и безопасное сжатие 84 МПа. Грузовая линия находится на расстоянии 75 мм от края хвостовика .
Раствор
В качестве первого шага определите e .
См. рис. 16.6. Показан крюк и его треугольное поперечное сечение. Центр тяжести сечения находится в точке G , а центральная ось проходит через G . C — центр кривизны изогнутых поверхностей крюка с основанием треугольника к центру. Нейтральная ось NA сечения направлена к C на расстоянии e от G . На расстоянии v от C выбран полосовой элемент шириной d v . Ширина полосы рассчитывается из подобных треугольников.
Рис. 16.6
v варьируется от v 1 = 50 мм до v 2 = 50 + 75 = 125 мм
Из уравнения.(16.1)
R = радиус центральной поверхности или расстояние от центральной оси до центра кривизны.
Используйте уравнение (16.3) для напряжения изгиба
По нагрузке и геометрии крюка видно, что растяжение происходит внутри, а сжатие снаружи.
(Чек y t + y c = 75 мм)
Используя значения M , A , e и в (iii) и σ = 105 Н/мм 2
Дополнительно имеется прямое растягивающее напряжение
Использование допустимого растягивающего напряжения
Использование допустимого напряжения сжатия
Из (v) и (vi) будет выбрано меньшее значение i.е.
[ Отв. ]
Пример 16.2 Круглое звено, показанное на рис. 16.7, имеет прямоугольное сечение шириной 100 мм и толщиной 50 мм . Рассчитайте напряжение в точках A и B при сжимающей нагрузке 50 кН.
Решение Значение e для прямоугольного сечения было определено и приведено в уравнении.(16.5).
Рис. 16.7
По-видимому, это сжимающее напряжение на A и растягивающее напряжение на B из-за изгиба. Кроме того, будет сжимающее напряжение из-за прямой нагрузки.
Нейтральная ось смещена внутрь на расстояние e .
Напряжение изгиба рассчитывается по формуле.(16.3)
[ Отв. ]
Пример 16.3 Высота и поперечное сечение сегмента рамы штамповочного пресса из серого чугуна показаны на рис. 16.8. Определить максимальные растягивающие и сжимающие напряжения. На сегмент действует чистый изгибающий момент M = 57 × 10 6 Н-мм.
Рис.16,8
Решение Для определения e расстояние между центральной осью, проходящей через центроид G , и нейтральной осью NA будет определено из уравнения. (16.1). Сечение состоит из двух прямоугольников, поэтому интегрирование будет выполняться для двух прямоугольников отдельно.
Также v 1 = 380 мм, v 2 = 380 + 76 = 456 мм, v 3 = 456 + 305 = 761 мм
Определяется расстояние G от нижней стороны T -секции.Назовите это расстояние.
Из уравнения. (16.1)
Максимальное растягивающее напряжение возникает внутри кривизны, а максимальное сжатие — снаружи.
Напряжение изгиба из уравнения. (16.3)
[ Отв. ]
Пример 16.4 Основное сечение крюка представляет собой симметричную трапецию глубиной 75 мм с внутренней шириной крюка 75 мм и внешней шириной 25 мм. Центр кривизны как внутри, так и снаружи крюка на сечении находится в плоскости сечения и 68,75 мм с внутренней стороны его, а грузовая линия проходит 56,25 мм с внутренней стороны сечения. Рассчитайте безопасную нагрузку на крюк так, чтобы наибольшее растягивающее напряжение не превышало 110 МПа.
Решение Крюк и его основная часть AB показаны на рис. 16.9.
Рис.16,9
Положение центроида G . Г. находится на линии симметрии на расстоянии от большей стороны.
На расстоянии v от центра кривизны ширина сечения b 1 . На расстоянии v 2 – v 1 = 75 мм ширина уменьшается на 75 – 25 = 50 мм.
Следовательно, на расстоянии v – v 1 ширина уменьшается на
Из уравнения.(16.1)
Растягивающее напряжение возникает внутри, где
Использование уравнения. (16.3) для изгибающего напряжения для записи выражения для полного растягивающего напряжения в главном сечении AB в точке B
и значение A , e , y t / v 1 в уравнении для σ
σ не должен превышать 110 МПа или Н/мм 2
[ Отв. ]
Пример 16.5 Пруток круглого сечения диаметром 100 мм и диаметром был согнут, чтобы сформировать крюк, как показано на рис. 16.10. Внутренняя сторона представляет собой окружность радиусом 50 мм , тогда как линия нагрузки проходит через прямую часть на расстоянии 50 мм вправо от центра кривизны. Если максимально допустимое растягивающее напряжение в материале составляет 120 МПа, найти безопасную нагрузку Вт и каково будет напряжение в точке В затем ?
Решение Рис.16.10 показано круглое сечение крюка, а также показана геометрия, используемая для получения выражения для и . Вывод длинный и был сделан в разделе 16.4. уравнение (16.8) описывает e .
Рис. 16.10
Напряжение изгиба дается уравнением. (16.3). Таким образом, общее напряжение в точке A записывается как
.
Напряжение не должно превышать 120 МПа
Для напряжения при B y c = 50 + e = 50 + 6.7 = 56,7 мм
[ Отв. ]
16.4 Кольца под нагрузкой
Кольцевые элементыиспользуются для нескольких целей, наиболее распространенным примером являются звенья цепи. Обоймы подшипников качения также рассматриваются как кольца, но контактные напряжения в них становятся гораздо более важными, чем напряжения изгиба. Кольцо обычно нагружено в диаметральной плоскости, как показано на рис. 16.11, и одиночная диаметральная нагрузка может вызвать прямые, изгибающие и касательные напряжения в различных сечениях.Нетрудно представить, что в точке a будет изгибающее напряжение растяжения, а в точке b изгибающее напряжение будет сжимающим. Кроме того, в поперечном сечении ab будет действовать прямое растягивающее напряжение. Очевидно, будет происходить удлинение кольца вдоль направления приложения нагрузки, сопровождающееся сжатием в плоскости ab .
Задача такого рода, изображенная на рис. 16.11, является неопределенной в том смысле, что из уравнений равновесия нельзя определить силы и моменты, действующие в различных сечениях.С другой стороны, если кольцо расколото или разрезано в каком-либо сечении (см. рис. 16.7), задача является детерминированной , так что момент, действующий в любом сечении, можно найти из условий равновесия.
Рис. 16.11
При решении задач кольцевых конструкций, показанных на рис. 16.11, на первом этапе определяются моменты и силы, действующие в различных сечениях, рассматривая кольцо как прямую балку.Это не приведет к большой ошибке, поскольку кривизна учитывается при расчете напряжений.
Рассмотрим свободное тело правой половины кольца, предполагая, что полукольцо будет нести половинную нагрузку Вт /2. Из-за соединения кольца в сечениях А и С будут существовать внутренние моменты М А и М С . Показано, что их направления удовлетворяют условиям равновесия Σ F = 0 и Σ M = 0.
Если сечение 1, 2 выбрано вдоль радиального направления, составляющего угол θ с вертикалью по часовой стрелке, то момент на этом сечении, обозначаемом M θ , можно записать следующим образом.
, где R — средний радиус кольца.
На данном этапе можно сделать одно важное замечание, что сечения А, и С, в свободном теле, показанные справа на рис.16.11, не повернуты относительно друг друга. Они остаются в вертикальной плоскости после деформации под действием нагрузки W . Это означает, что между участками A и C нет чистого изменения уклона или, другими словами,
.
Ссылаясь на уравнение. (10.1) или в разделах 9.2 и 9.3 можно написать, что
В приведенном выше уравнении di — уклон между участками 1, 2 и 3, 4, y — смещение в радиальном направлении, ds — длина между участками 1, 2 и 3, 4; M θ – момент на участке 1, 2. I и E соответственно — момент инерции сечения и модуль упругости материала кольца.
Обратите внимание, что по сравнению с прямой балкой из главы 9 или 10 длина представлена как σ , а не как x .
Если (iii) интегрирован из раздела A в раздел C IE от θ = 0 до θ = π , то di приведет к I A — I С я.е.
Обратите внимание еще на один момент в деформации кольца. Секция B останется в горизонтальной плоскости, а секции A и C останутся в вертикальной плоскости. Это означает, что после деформации нет чистого вращения между секциями А и В . Отсюда
Преследовать (v), получается следующее
и если ds это длина 1, 4 или 2, 3, то
Использовать M θ из (i) и (iv)
Обратите внимание, что если (iv) проинтегрировать, заменив M θ , получится тот же результат.Если в уравнении (16.9)
В сечении B будет прямое напряжение и напряжение изгиба σ b , где A площадь поперечного сечения и σ b 9004 , где Z — модуль сечения кольца при B и K — поправка на кривизну, как описано в уравнении.(16.4). Однако σ b 1 также можно рассчитать по уравнению (16.3). (viii) будет использоваться, если поперечный размер мал по сравнению с радиусом кольца. Если поперечный размер и радиус кольца сравнимы, то будет использоваться (ix). Отклонение кольца увеличивает диаметр по линии W — W или по вертикали и уменьшает поперечный или горизонтальный диаметр. Если U обозначить энергию деформации кольца, нагруженного диаметральной нагрузкой Вт , то по теореме Кастильяно прогиб вдоль Вт — Вт или перемещение точки приложения нагрузки Вт , Энергия деформации элемента длины ds Энергия деформации полукольца Используйте уравнение (16.9) в (i) Нахождение смещения точки A или точки приложения W /2, U частично дифференцируется по отношению к W /2.(Следует помнить, что энергия деформации всего кольца равна 2 U , а прогиб будет частным дифференциалом 2 U относительно Вт ) Рассмотрим разрез полукольца по поперечному диаметру, как показано на рис. 16.12. Моменты M B и M D на сечениях B и D складываются как внутреннее сопротивление несущей нагрузке W θ измеряется от горизонтального или поперечного диаметра по часовой стрелке. Рис. 16.12 Из (iii) гл. 16.4.1?, так как в силу симметрии – M D = M B Когда секция D открыта, для удержания свободного тела в равновесии W /2 будет действовать нормально к каждой из секций D и B .Будут моменты в D и B , заданные (i). Теперь пусть две силы θ , противоположные друг другу, приложены соответственно к точкам B и D кольца. Когда кольцо разрезано посередине, сила, действующая на половину свободного тела, будет θ /2. Условия равновесия сил, по-видимому, выполняются. Выбран радиальный разрез 1, 2 под углом θ , как показано на рис. 16.12. Изгибающий момент на участке 1, 2, Энергия деформации небольшого элемента, стягивающего угол d θ в центре (рис.16.12) это Если δ t — поперечный прогиб, то Для интегрирования можно выбрать пределы от 0 до π /2, определяющие четверть кольца. Поскольку кольцо симметрично, энергия кольца будет в четыре раза больше энергии четверти. и для Q = 0 Можно отметить, что деформация в поперечном направлении меньше, чем вдоль нагрузки.Отношение Приведенная процедура указывает на метод. Изогнутый стержень не всегда может быть полным кольцом, но этот метод также применим к полным кольцам, трем четвертям, полукольцам и четвертям колец. Каждая секция кольца будет подвергаться (i) прямому напряжению, (ii) напряжению сдвига и (iii) прямому напряжению изгиба. (i) и (iii) имеют одинаковую природу, но их распределение по разрезу различно. В то время как прямое напряжение распределено равномерно, напряжение изгиба изменяется от отрицательного или сжимающего максимума до положительного или растягивающего максимума, обращаясь в нуль на нейтральной оси сечения.Следует с осторожностью отметить, что изгибающий момент, M θ , как указано в уравнении. (16.9) меняется по окружности как по величине, так и по характеру. В то время как на участке, где действует W , изгибающий момент имеет тенденцию к уменьшению радиуса кривизны, он стремится увеличить радиус кривизны по бокам. На рис. 16.13 (б) показана вариация Б.М. Таким образом, очевидно, что в сечении A изгибающее напряжение внутри будет сжимающим, а снаружи — растягивающим.В секции B состояние будет обратным. На чистое распределение будет влиять прямое напряжение, которое распределяется равномерно. Прямое напряжение в любом сечении под углом θ от линии действия силы W равно P n / A где A площадь поперечного сечения кольца Точно так же напряжение сдвига составляет P t / A . Касательное напряжение также распределено равномерно.[Рисунок 16.13(а)] По-видимому, P n исчезает на участке A и, следовательно, не имеет прямого ударения. P n максимум на секции B . P t ведет себя как раз наоборот. Поэтому распределение касательных и прямых напряжений будет таким, как показано на рис. 16.13 (в). Например, рассчитайте напряжения в сечениях A и B диаметрально нагруженного кольца, как показано на рис.16.13 (а). Рис. 16.13 Секция A: Без прямого напряжения, σ 0 = 0 Результирующее прямое напряжение будет σ = σ 0 + σ b . Звено цепи показано на рис. 16.14. Две полукруглые части соединены двумя прямыми частями одинакового диаметра.Нормальная ситуация с нагрузкой по длине, но иногда также применяются поперечные нагрузки. Оба кольца и эти звенья используются для образования цепей, и отношение радиуса сечения к радиусу кривизны зависит от грузоподъемности. Как правило, для более высокой грузоподъемности это соотношение велико. Рис. 16.14 Испытательное кольцо — это устройство, обычно используемое для калибровки испытательных машин. В круглом поверочном кольце, изготовленном из прямоугольного сечения, применяют диаметральное сжатие и уменьшение диаметра, измеряемое с помощью стрелочного индикатора.Иногда используются контрольные устройства звенного типа, в которых растягивающая нагрузка может быть приложена к прямому участку и измеряется деформация в перпендикулярном направлении. Это дает преимущество более высокой деформации по длине. Напряжения и прогиб в звене цепи рассчитываются так же, как и для колец. Процедура будет продемонстрирована на решенном примере. Прогиб изогнутой балки удобно вычислять с помощью теоремы Кастильяно , сформулированной в гл.16.6.1 по уравнению (16.10). Возможно, стоит упомянуть, что теорема Кастильяно широко применима ко всем балкам и конструкциям. Его можно использовать для расчета вращения из-за момента путем частичного дифференцирования энергии деформации по моменту. Пример 16.6 Испытательное кольцо 254 мм со средним радиусом, шириной 38,1 мм и толщиной 26 мм требуется для восприятия поперечной растягивающей нагрузки. Если максимально допустимое напряжение равно 560 Н/мм 2 , , найдите нагрузку.При какой нагрузке диаметр груза увеличится на 6,26 мм? Решение См. кольцо, показанное на Рис. 16.11 или Рис. 16.13 (a) и M B = 0,182 WR из того же уравнения, θ = π /2 Поскольку средний радиус примерно в пять раз превышает глубину сечения, не рекомендуется рассчитывать напряжение изгиба по формуле прямой балки. Для прямоугольного сечения глубиной d и средним радиусом R , из уравнения. (16,5) Секция А (рис. 16.11) Главные напряжения Максимальное напряжение сдвига Секция Б (рис. 16.11) Максимальное напряжение (растягивающее и сжимающее) возникает в сечении A .Напряжение сжатия больше по величине. Прогиб по диаметру груза определяется уравнением (16.11) Нагрузка 28,72 кН вызовет напряжение 560 МПа, а нагрузка 30,04 кН вызовет прогиб 6,26 мм. [ Отв. ] Пример 16.7 Кольцо со средним радиусом 30 мм подвергается натяжению силой 1 кН так, что натяжение проходит через его центр.Найдите (i) увеличение и уменьшение диаметра кольца и (ii) максимальное напряжение в точке нагрузки. E = 200 × 10 3 МПа. Предположим, что кольцо наименьшее в звене цепи и что каждое звено цепи сделано из проволоки одинакового диаметра. Решение Первым шагом будет определение диаметра поперечного сечения кольца. Для этого используется условие наименьшего звена.Обращаясь к рис. 16.15, видно, что в кольцо должны входить провода двух диаметров. Тогда средний диаметр будет равен трем диаметрам проволоки, из которой сделаны звенья. Рис. 16.15 . . . 3 d = средний диаметр кольца = 60 мм . . . d = 20 мм Из уравнения. (16.11) увеличение диаметра нагрузки Из уравнения.(16.13) где δ t — уменьшение поперечного диаметра Для расчета напряжения в секции A найдите e . Из уравнения. (16.8) Напряжение изгиба рассчитывается по формуле. (16.3) Для напряжения растяжения снаружи сечения A на рис.16.15. Для напряжения сжатия внутри кольца используйте 16,2 МПа – более высокое напряжение. Однако существует касательное напряжение Максимальное сжимающее напряжение, которое является минимальным главным напряжением, равно Также максимальное растягивающее напряжение снаружи и максимальное основное напряжение там Таким образом, максимальное растягивающее напряжение снаружи секции A равно 10.6 МПа, тогда как максимальное сжимающее напряжение внутри секции A составляет 16,8 МПа. [ Отв. ] Пример 16.8 Стальная труба с наружным диаметром 50 мм и внутренним диаметром 37,5 мм изогнута в квадранте радиусом 1,8 м . Один конец жестко прикреплен к горизонтальной опорной плите так, что касательная к квадранту в фиксированной точке перпендикулярна горизонтали. К свободному концу приложена нагрузка 450 Н .Определить вертикальное и горизонтальное отклонение свободного конца . E = 210 × 10 3 МПа. Решение Прогиб в любом случае можно рассчитать, применяя теорему Кастильяно. В котором говорится, что Рис. 16.16 , где δ З — отклонение в направлении З в точке, где действует З .Он прямой, если требуется отклонение в вертикальном направлении. Для горизонтального прогиба под W принимается фиктивная нагрузка θ , вычисляется U путем дифференцирования по θ и затем присваивается θ = 0. Этот метод использовался в разд. 16.5.2. См. рис. 16.16. В сечении по радиусу, составляющему угол θ с вертикалью, действует изгибающий момент М = WR sin θ Если малая длина ds = Rd θ считается содержащей рассматриваемый участок, то . . . Отклонение точки нагрузки в вертикальном направлении С фиктивной нагрузкой θ вместе с W на свободном конце [ Отв. ] Пример 16.9 На рис. 16.16 показан стальной стержень диаметром 25 мм , один конец которого закреплен, а другой конец ограничен горизонтально и может свободно перемещаться только в вертикальном направлении.Если нагрузка 4,50 Н действует на другой конец, как показано, найти вертикальное отклонение и горизонтальную реакцию , θ . R = 150 мм, E = 210 × 10 3 МПа. Рис. 16.17 Решение Выбор малого элемента длиной ds = Rd θ под углом θ от вертикального радиуса (рис.16.17), изгибающий момент на дс , M = QR (1 – cos θ ) + WR sin θ Энергия деформации в элементе ds равна dU Пусть δ h и d v обозначают горизонтальное и вертикальное отклонения точки нагрузки соответственно. Но точка нагрузки ограничена для перемещения в горизонтальном направлении Знак минус указывает, что направление реакции Q противоположно принятому на рис.16.17. Использование (iii) в (ii) [ Отв. ] Пример 16.10 Звено состоит из двух полукругов и двух прямых частей. Две равные и противоположные силы действуют в крайних точках A и B вдоль продольной оси, как показано на рис. 16.17 . Предполагая, что размеры поперечного сечения малы по сравнению с радиусом R , определить максимальный изгибающий момент . Решение Рассмотрим только одну четверть связи, как показано на рис. 16.18. Свободное тело четверти звена должно удовлетворять условию равновесия и, следовательно, на прямолинейном участке через B будет действовать сила W /2 . Момент M B также будет действовать на открытое сечение свободного тела в точке B , а момент M A будет действовать в точке A . Из-за симметрии секции А и В не поворачиваются относительно друг друга, а значит Рис.16.18 M θ обозначает момент как на прямых, так и на изогнутых участках между A и B . , где dl — элемент длины на прямом участке, а ds — элемент длины на изогнутом участке. С правильными ограничениями и использованием di = 0 , где M ′ θ — изгибающий момент в криволинейной области, а ds = Rd θ . м ‘ м ‘ θ становится м A AT 16.4.1 Прогиб колец в направлении нагрузки
16.4.2 Прогиб кольца под поперечной нагрузкой
16.5 Напряжения в кольцах
Звено цепи 16,6
Использование вышеуказанного в (i)
Следовательно, максимальный изгибающий момент возникает в нагруженном сечении.
[ Отв. ]
Пример 16.11 Звенья цепи изготовлены из круглой стали диаметром 12,5 мм и имеют полукруглые концы, средний радиус которых 37,5 мм. Концы соединены прямыми отрезками длиной 37,5 мм . Оценить интенсивности растягивающих и сжимающих напряжений в различных точках звена при нагрузке ·10 кН.
Решение На рис. 16.19 показано соединение и его различные размеры. Из геометрии видно, что:
Рис.16.19 Звено цепи
В секции A растягивающее изгибающее напряжение возникает в точке 1, а сжимающее изгибающее напряжение возникает в точке 2. В секции B растягивающее изгибающее напряжение возникает в точке 3, а сжимающее изгибающее напряжение возникает в точке 4. Кроме того, на сечение A будет действовать равномерно распределенное касательное напряжение, а на сечение B — равномерно распределенное растягивающее напряжение.
Напряжения будут обнаружены в точках 1, 2, 3 и 4. Может быть интересно изучить напряжения в сечении C , где встречаются круглая и прямая части.
Изгибающие моменты в сечениях A и B были получены в последнем примере. Результат
Можно отметить, что на участке C изгибающий момент будет таким же, как на участке B , т.е. М С = М Б .
Напряжения в сечении B Поскольку B является прямым участком, напряжение изгиба будет рассчитываться по формуле балки.
Равномерное прямое растягивающее напряжение
Напряжения на участке C Особое внимание следует уделить этому участку, который соединяет прямые и криволинейные участки.Из-за кривизны напряжения изгиба будут определяться по формулам криволинейной балки.
Напряжения в сечении A Используемая формула напряжения криволинейной балки.
На участке A присутствует равномерно распределенное напряжение сдвига.
Максимальное основное напряжение в точке 1 сечения А
Минимальное основное напряжение в точке 2 будет самым высоким сжимающим напряжением
Определены напряжения в сечениях А , В и С .
[ Отв. ]
16.1 Стальной стержень должен быть согнут в виде крюка для подъема груза в 8 кН таким образом, чтобы максимальное напряжение не превышало 140 МПа. Отношение радиуса кривизны центроидальной плоскости к радиусу стержня должно быть равно 4, а нагрузка действует через центр кривизны. Определить диаметр стержня.
[ Ответ . d = 39,12 мм]
16.2 Криволинейная балка прямоугольного сечения изогнута со средним радиусом 120 мм. Сечение балки имеет глубину 114,5 мм в радиальном направлении и ширину 76 мм. К искривленной балке приложен момент для увеличения кривизны. Если растягивающее напряжение не должно превышать 64,8 МПа, какова величина приложенного момента. Какова тогда величина максимального напряжения сжатия?
[ Ответ. M = 9,1 кН-м, σ C = 100 МПа]
16.3 Крюк круглого сечения имеет диаметр главного сечения 75 мм. Самая внешняя точка главного сечения находится на расстоянии 75 мм от центра кривизны, который находится в той же плоскости. Груз массой 17,86 кН должен быть поднят крюком через его центр кривизны. Определить максимальное растягивающее и сжимающее напряжение.
[ Ответ . 121 МПа (растяжение) и 61,85 МПа (сжатие)]
16,4 Основное сечение крюка представляет собой симметричную трапецию 41.Ширина 3 мм по направлению к кривизне и глубина 95,25 мм в радиальной плоскости. Внешняя ширина поперечного сечения составляет 16 мм. Центр кривизны как внутри, так и снаружи крюка находится в плоскости этого сечения и на расстоянии 31,75 мм от внутренней стороны. Определить напряжения внутри и снаружи главного сечения, когда нагрузка 20 кН проходит крюком через центр кривизны.
[ Ответ . 65,8 и 25 МПа]
16,5 Двутавр из гнутого стержня глубиной 90 мм с полкой и стенкой шириной по 20 мм.Фланцы неодинаковой длины, но сумма их длин равна 150 мм. Более длинный фланец находится на внутренней стороне кривизны с радиусом 80 мм. Если максимальные растягивающие и сжимающие напряжения равны по величине, определяют длину полки.
[ Ответ. Внутренний фланец 13,06 мм, внешний фланец 46,4 мм]
16,6 В экспериментальной установке кольца в три четверти на рис. 16.20 латунный скользящий блок, в центре которого кольцо соединено штифтом, трется о обработанную стальную поверхность.Кольцо изготовлено из тонкой стальной полосы толщиной 2 мм и шириной 10 мм. Кольцо имеет средний радиус кривизны 100 мм. Груз массой 100 г помещается в поддон весом 23 г, подвешенный к латунному скользящему блоку, и на нониусной шкале фиксируется отклонение 2,15 мм. Вычислите коэффициент трения.
[ Ответ . мк = 0,1]
Рис. 16.20
16.7 В стальное кольцо прямоугольного сечения (ширина 31,75 мм × радиальная глубина 12,7 мм) и средним радиусом 76,2 мм по диаметру вставлен жесткий стержень. Натяжение прикладывается к кольцу по диаметру, перпендикулярному стержню. Допустимое напряжение в материале кольца 126 МПа. Определите максимальное усилие, которое может выдержать кольцо.
[ Ответ. 5,9 кН]
16,8 Стальное кольцо со средним диаметром 250 мм изготовлено из круглого стального прутка диаметром 50 мм.Если максимальная интенсивность напряжения ограничена 140 МПа, а максимальное изменение диаметра ограничено 0,25 мм, найти допустимую нагрузку.
[ Ответ. 4,75 кН]
16,9 Звенья цепи изготовлены из круглой стальной проволоки диаметром 25 мм и имеют полукруглые концы со средним радиусом 31,75 мм. Концы соединяют прямыми отрезками длиной 25 мм каждый. Рассчитайте максимальные растягивающие и сжимающие напряжения, когда натяжение цепи равно 13.4 кН.
[ Ответ. 47,8 МПа и 87 МПа]
16.10 Звено цепи состоит из стальной полосы шириной 25 мм и толщиной 12,7 мм. Полукруглые концы имеют средний радиус 31,75 мм и соединены прямыми участками длиной 25 мм. Звено несет нагрузку 13,4 кН вдоль продольной оси симметрии. Определить напряжения в сечении, несущем нагрузку, и в сечении стыка круглого и прямого участков.
[ Ответ. На участке нагрузки 88,5 МПа (тенс) и 152,5 МПа (сж.), на участке соединения. 108,5 МПа (Тен) и 31,2 МПа (сост.)]
16.11 Стержень диаметром 60 мм согнут так, чтобы получился квадрант радиусом 1 м и прямой участок длиной 1,5 м. Он прочно встроен в горизонтальную плоскость в конце прямого участка, а свободный конец квадранта нагружен 0,8 кН. Рассчитайте вертикальное отклонение свободного конца. E = 210 × 10 МПа.
[ Ответ. д v = 13,7]
16.1 Нейтральная плоскость в прямой балке и криволинейной балке означает одно и то же, что вдоль нее не действуют напряжения. Для балок одинакового сечения
- нейтральные плоскости в прямых и криволинейных балках проходят через центральные оси всех сечений.
- нейтральная плоскость в криволинейной балке смещается к центру кривизны
- нейтральная плоскость в криволинейной балке смещается от центра кривизны
- нейтральная плоскость в криволинейной балке может смещаться к центру кривизны или от него в зависимости от соотношения глубины сечения и радиуса балки.
16,2 Напряжение изгиба в любой точке на расстоянии y от нейтральной оси в криволинейной балке, нейтральная плоскость которой изогнута до радиуса R до нагрузки, а нейтральная плоскость находится на e ниже центральной плоскости, определяется как
16,3 Распределение напряжения изгиба по сечению криволинейной балки
- логарифмический
- линейный
- параболический
- экспоненциальный
16.4 Кольцо сечением А и радиусом R сжимается силой W по вертикальной оси. Если сечение выбрано так, что оно находится под углом θ от вертикальной силовой линии, изгибающий момент в этом сечении равен
16,5 Крючок имеет круглое основное сечение диаметром 75 мм. Внутренняя поверхность представляет собой круг радиусом 75 мм слева от центра. Осевая линия хвостовика находится на расстоянии 50 мм вправо от сечения.Нагрузка 10 кН. Чему равен изгибающий момент в главном сечении?
- 2000 Н·м
- 1625 Н·м
- 1250 Н·м
- 500 Н·м
16,6 Крюк круглого сечения выдерживает нагрузку 50 кН. Диаметр главного сечения 55 мм. Напряжение изгиба при сжатии рассчитывается как 50 Н/мм 2 . Чему равно результирующее сжимающее напряжение?
- 71 Н/мм 2
- 55,26 Н/мм 2
- 44.74 Н/мм 2
- 29 Н/мм 2
16,7 Кольцо прямоугольного сечения имеет радиус R , что в 2 раза больше глубины сечения. Кольцо нагружено силой Вт по вертикали диам. Площадь сечения A и модуль сечения Z . Напряжение на внешней поверхности кольца в горизонтальном сечении
16,8 Кольцо, радиус которого больше глубины сечения, нагружено силой по горизонтальному диам.Создание отклонения δ H по своей собственной линии и по своей линии и Δ V вдоль вертикальной линии, соотношение δ V / δ H —
- 1,092
- 1.000
- 0,915
- 0,900
16,9 Четверть кольца прочно закреплена одним концом в горизонтальной плоскости, а другой конец свободен и над опорой. Радиус кольца намного больше размеров поперечного сечения кольца.К свободному концу приложена вертикальная сила. Отношение горизонтальной составляющей прогиба к вертикальной составляющей прогиба составляет
.16.10 Звено цепи состоит из двух полукругов и двух прямых частей. Звено натягивается приложением сил, которые проходят от центров полуокружностей и между прямыми участками. M A — момент, действующий в средней части полукруга, а M B — момент в средней части прямого участка.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке. Это классическая схема обозначения лучей.
Это классическая схема обозначения лучей.


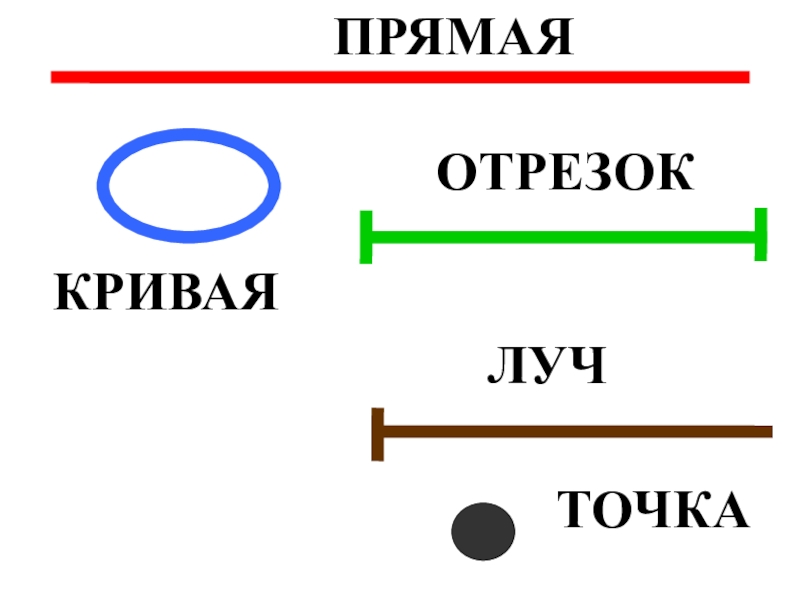
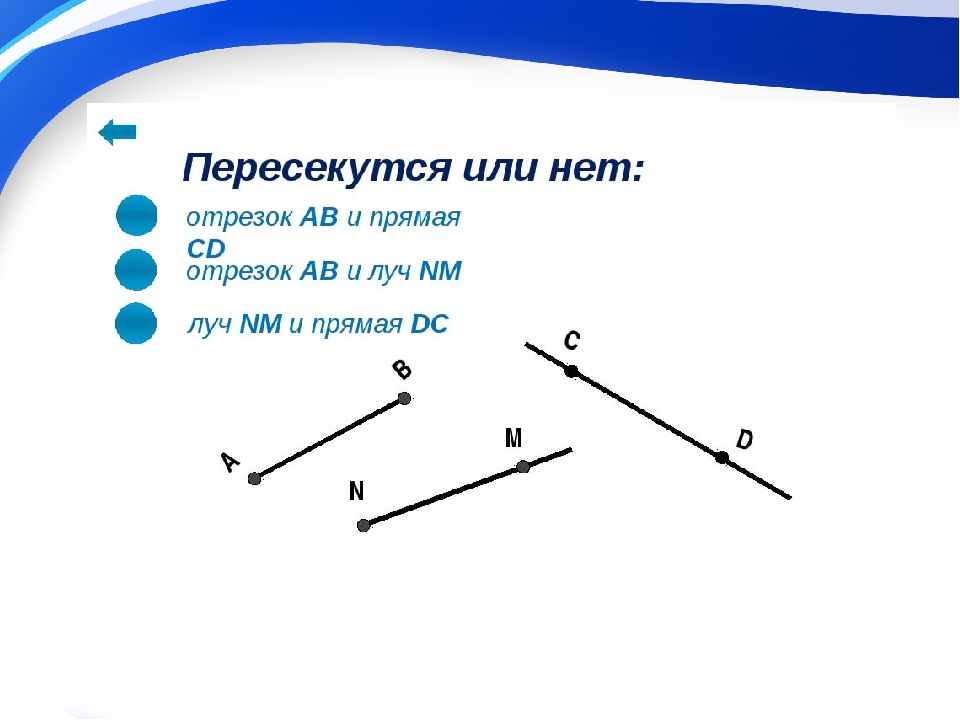
 10: Определение положения нейтральной оси.
10: Определение положения нейтральной оси. 12:
12: