Параллелограмм, прямоугольник, ромб, квадрат (ЕГЭ — 2021)
P.S. Последний бесценный совет!
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут. Почему? Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем большинство твоих сверстников. Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ЕГЭ и поступления в ВУЗ мечты на бюджет и, самое главное, для жизни. Я не буду тебя ни в чем убеждать, просто скажу одну вещь… Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил.
Это статистика. Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы сдать наверняка ЕГЭ, поступить в ВУЗ мечты и быть в конечном итоге… более счастливым? Две вещи.
Первое, тебе нужно набить руку, решая задачи
На экзамене у тебя не будут спрашивать теорию. Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка. “Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Второе, заниматься по системе — иначе у тебя уйдет много времени и ты, что-нибудь пропустишь.
И сейчас будет честная реклама наших курсов подготовки к ЕГЭ, потому что они решают обе эти проблемы.
Тебе же понятен этот учебник? Так вот наши курсы такие же понятные как этот учебник.
Потому что их подготовил и ведет автор этого учебника Алексей Шевчук.
Он буквально разжевывает все на вебинарах. Вы решаете задачи. Много задач. У вас будет проверка домашки и марафон «Год за месяц» в мае, чтобы «упаковать» ваши знания и улучшить результат на 20-30%.
Курсы очень бюджетные: от 2000 до 3990 тыс/мес за 12 двухчасовых занятий с Алексеем.
Кликайте по этим кнопкам и читайте условия, там все очень подробно описано:
Прямоугольник ромб квадрат их свойства
9 класс. Геометрия. Урок 2.
Тема урока. Прямоугольник, ромб, квадрат, их свойства
Цели урока
Образовательные – повторение, обобщение и проверка знаний по теме: “Виды параллелограмма”; выработка основных навыков.
Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
Воспитательные -прививать
самостоятельность, развивать культуру
виртуального общения.
Прямоугольник.
Параллелограмм, у которого все углы прямые, называется прямоугольником.
Свойства прямоугольника
1. Противоположные стороны прямоугольника равны.
2. Все углы прямоугольника уровне.
3. Диагонали прямоугольника равны.
4. Диагонали прямоугольника пересекаются и точкой пересечения делятся пополам.
5. Диагонали прямоугольника делят его на две равные треугольники.
6. В прямоугольника сумма углов, прилегающих к одной стороне, равна 180 °.
Признаки прямоугольника
1. Если в параллелограмме все углы равны, то этот параллелограмм является прямоугольником.
2. Если в параллелограмме один угол прямой, то этот параллелограмм является прямоугольником.
3. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
4. Если в четырехугольнике три угла прямые, то этот четырехугольник является прямоугольником.
5. Если в четырехугольнике
все углы равны, то этот четырехугольник
является прямоугольником.
Ромб.
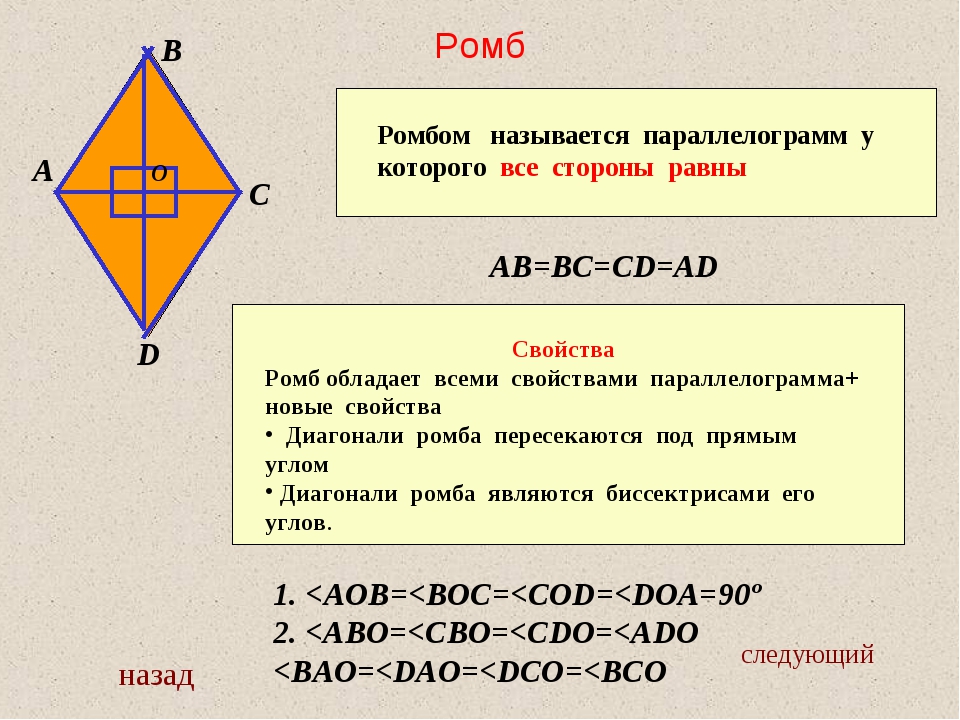
Параллелограмм, у которого все стороны равны, называется ромбом.
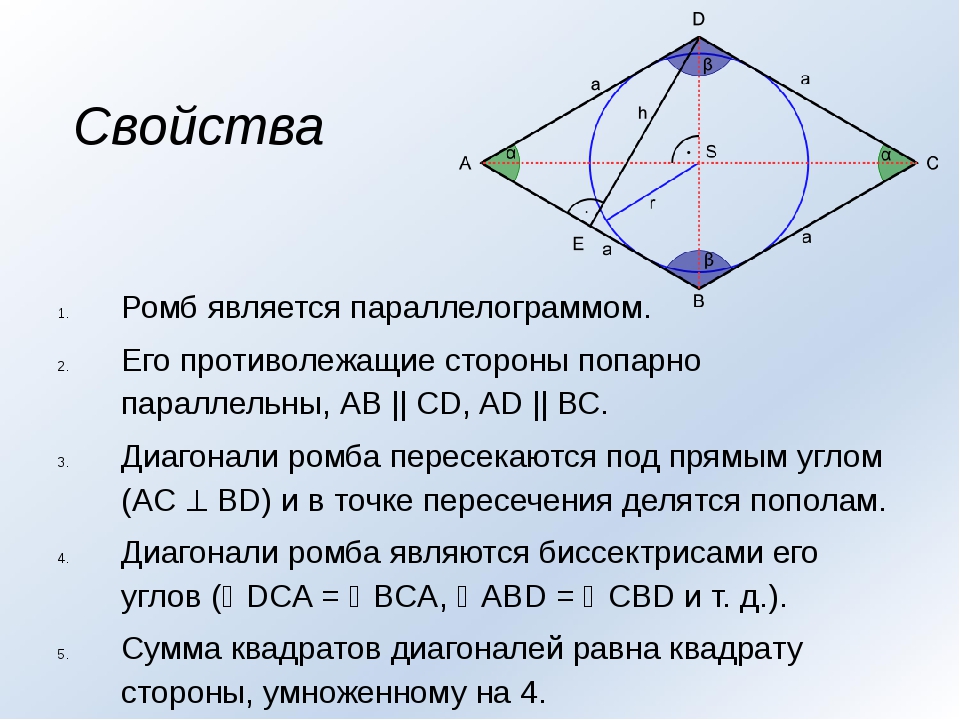
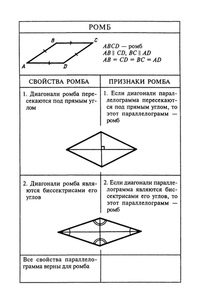
Свойства ромба
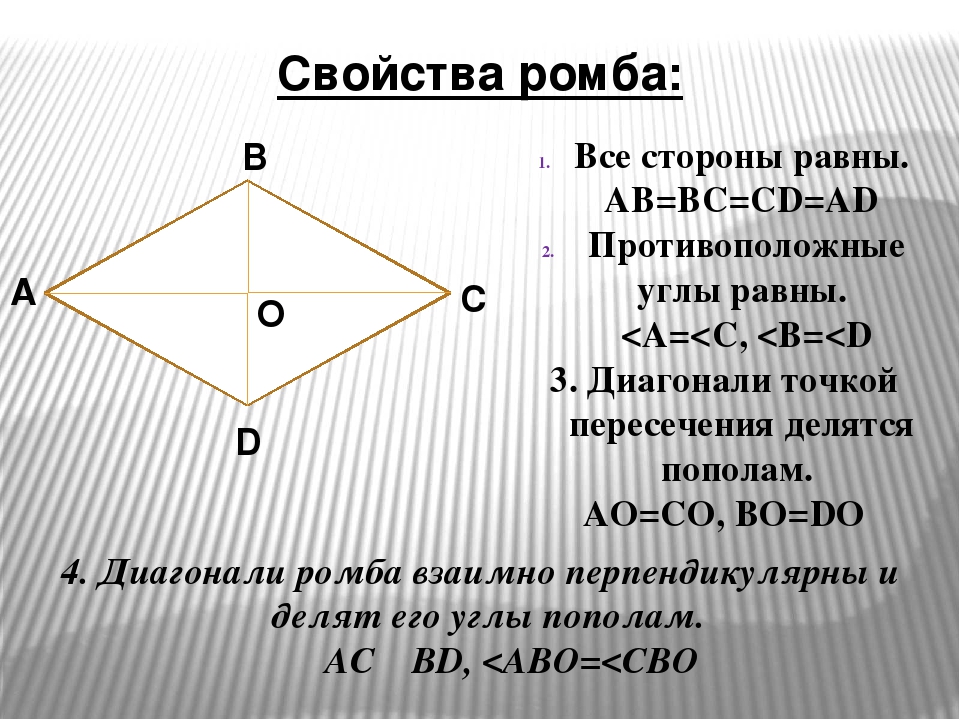
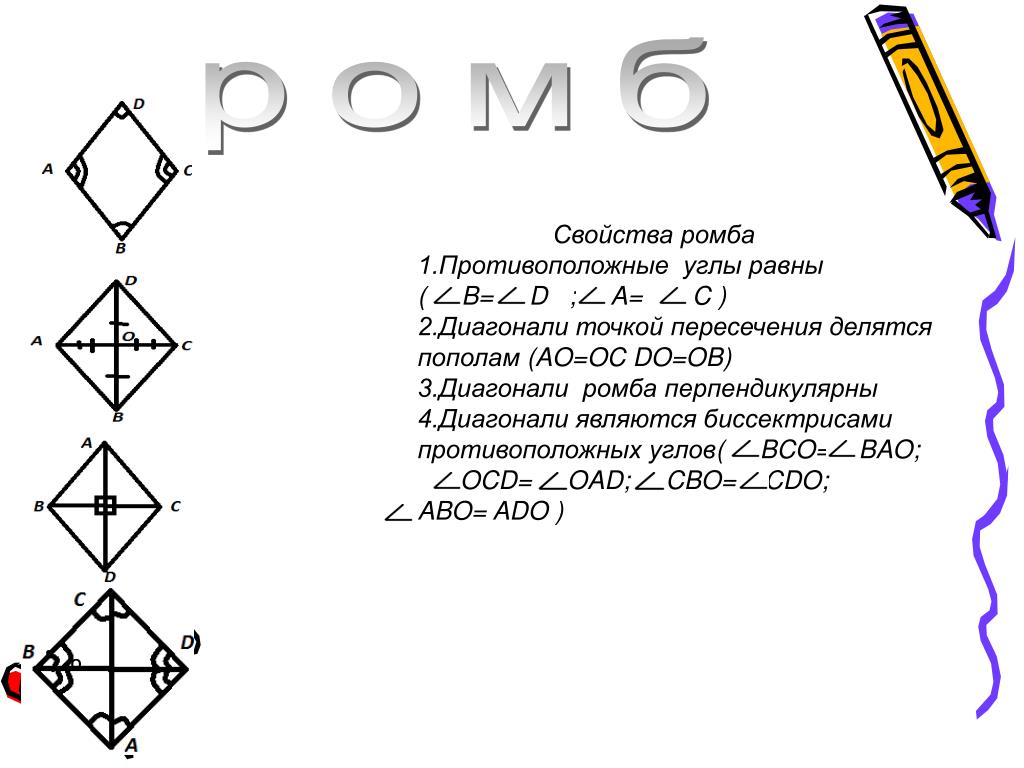
1. Противоположные углы ромба равны.
2. В ромбе сумма углов, прилегающих к одной стороне, равна 180 °. Диагонали ромба пересекаются под прямым углом.
3. Диагонали ромба являются биссектрисами его углов.
4. Диагонали ромба пересекаются и точкой пересечения делятся пополам.
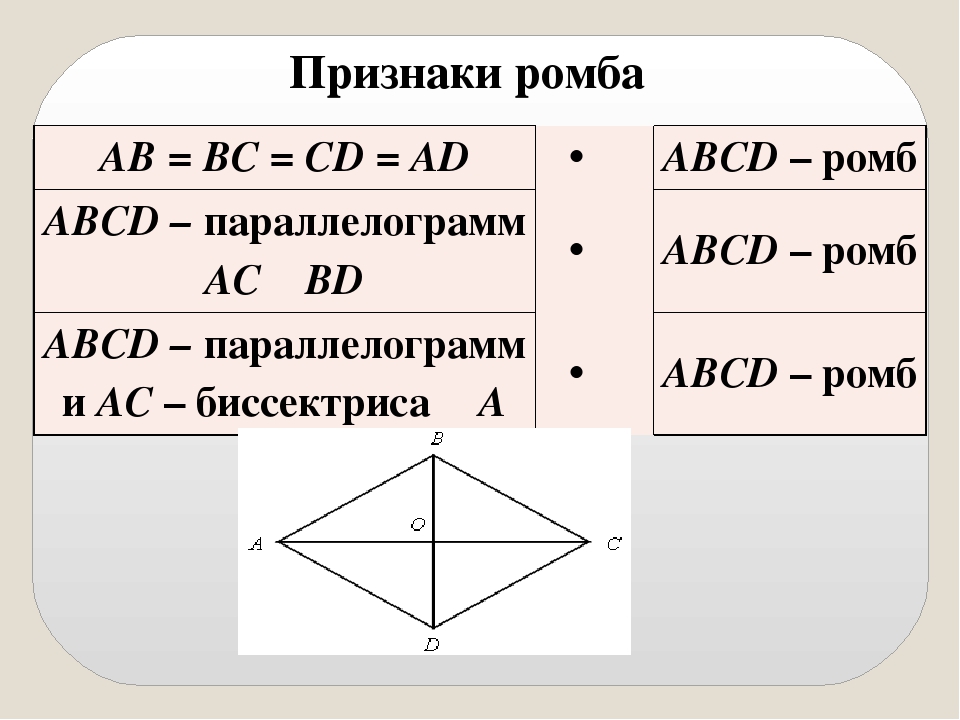
Признаки ромба
1. Если в параллелограмме диагонали пересекаются под прямым углом, то этот параллелограмм является ромбом.
2. Если в параллелограмме диагонали являются биссектрисами его углов, то этот параллелограмм является ромбом.
3. Если в параллелограмме две смежные стороны равны, то этот параллелограмм является ромбом.
4. Если в четырехугольнике все стороны равны, то этот четырехугольник является ромбом.
5. Если в параллелограмме
одна из диагоналей является биссектрисой
его угла, то этот параллелограмм является
ромбом.
6. Если в четырехугольнике диагонали являются биссектрисами его углов и пересекаются под прямым углом, то этот четырехугольник является ромбом.
Квадрат.
Прямоугольник, у которого все стороны равны, называется квадратом.
Свойства квадрата
1. Все углы квадрата — прямые.
2. Диагонали квадрата пересекаются и точкой пересечения делятся пополам.
3. Диагонали квадрата равны.
4. Диагонали квадрата пересекаются под прямым углом.
5. Диагонали квадрата являются биссектрисами его углов.
Признаки квадрата
1. Если в прямоугольнике диагонали пересекаются под прямым углом, то этот прямоугольник является квадратом.
2. Если ромба диагонали равны, то этот ромб является квадратом.
3. Если в четырехугольнике все стороны равны и все углы равны, то этот четырехугольник является квадратом.
Это интересно.
Если соединить отрезками
середины сторон прямоугольника, то
получим ромб.
Если соединить отрезками середины сторон ромба, то получим прямоугольник.
Если у параллелограмма все высоты равны, то этот параллелограмм является ромбом.
Д/з.
1. Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба 400.
2. В ромбе ABCD биссектриса ˪ВAC пересекает сторону ВС и диагональ BD соответственно в точках М и N. Найдите ˪ АNВ, если ˪АМС = 120 .
3. Найдите угол между диагоналями прямоугольника, если каждая из них делит угол прямоугольника в отношении 4:5
4. В ромбе периметр равен 24см. Один из углов 120.чему равна длина меньшей диагонали.
Ромб. Определение и свойства ромба
Автор: admin | Дата: 04.01.2021 | 16 views | Коментарів немає
Как известно, прямоугольник – это отдельный вид параллелограмма, который характеризуется тем, что его диагонали равны.
Изображение ромба и его диагоналей
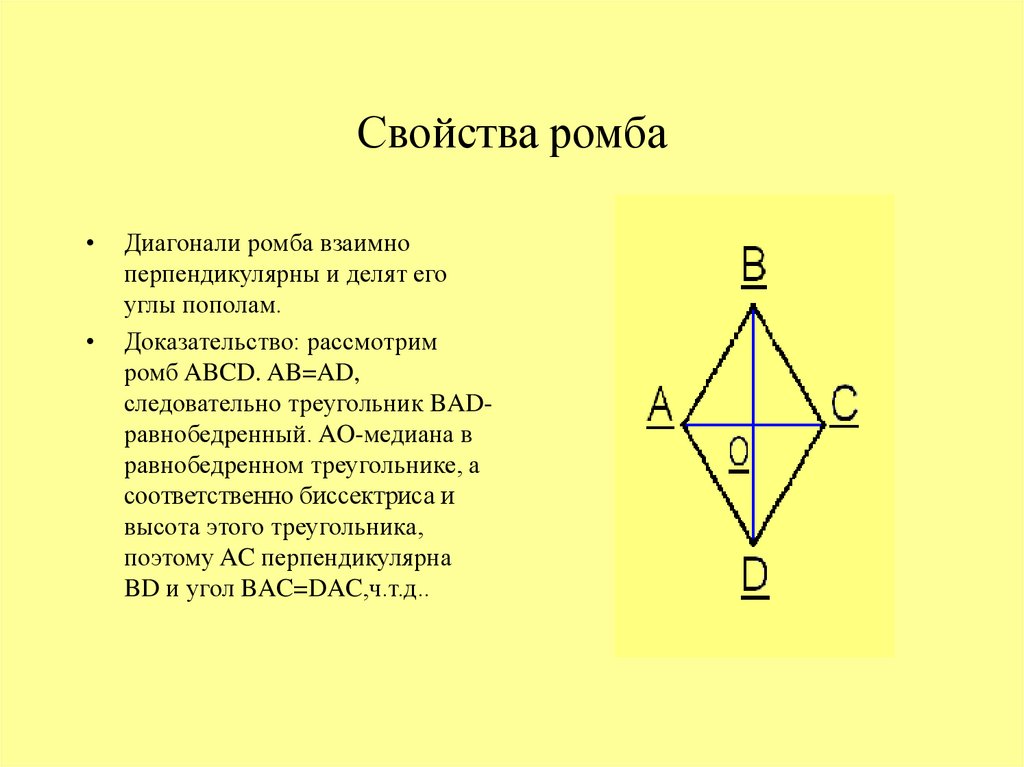
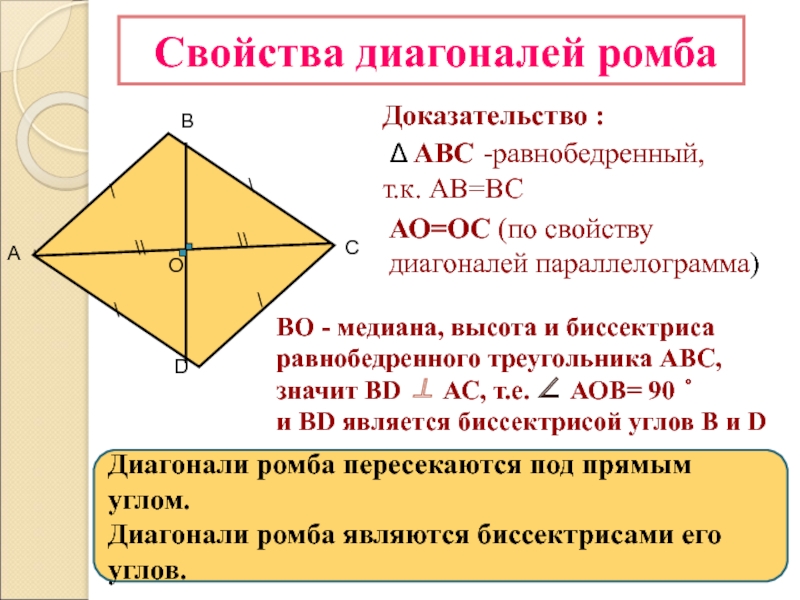
Из определения следует, что ромб имеет все свойства параллелограмма (противоположные углы ромба равны, диагонали ромба точкой пересечения делятся пополам) и, кроме этого, диагонали ромба перпендикулярны и являются биссектрисами его углов.
Для доказательства свойств, которые присущи только ромбу, рассмотрим ромб с рисунка выше, и покажем, что и .
Для этого, рассмотрим треугольник , образованный двумя сторонами ромба и одной диагональю. Поскольку, по определению, все стороны ромба равны, то ривнобедренний ().
Как уже отмечалось выше, одним из свойств ромба является то, что его диагонали пересекаются и точкой пересечения делятся пополам. Значит, в отрезок является медианой, проведенной к основанию (). А исходя из того, что в равнобедренном треугольнике медиана, проведенная к основанию, также есть высотой и биссектрисой, приходим к выводу, что отрезок перпендикулярен и делит пополам. Таким образом и .
Значит, в отрезок является медианой, проведенной к основанию (). А исходя из того, что в равнобедренном треугольнике медиана, проведенная к основанию, также есть высотой и биссектрисой, приходим к выводу, что отрезок перпендикулярен и делит пополам. Таким образом и .
Найти углы ромба – пример решения:
Сторона ромба образует с его диагоналями углы, один из которых на больше другого. Найти углы ромба.
Ромб ABCD
При пересечении диагоналей ромба образовались четыре равных прямоугольных треугольника, причем . Исходя из того, что , получим: . Отсюда и . Следовательно, и .
Блок-схема алгоритма проверки является ли четырехугольник ромбом
Все Признаки и Свойства Ромба
Ромб — это параллелограмм, у которого
все стороны одинаковы.
С помощью свойств и признаков ромба можно определить является фигура
ромбом, или нет. Так, как ромб отчасти является параллелограммом,
то для него истинны все свойства параллелограмма.
Квадратом является ромб, у которого все углы прямые.
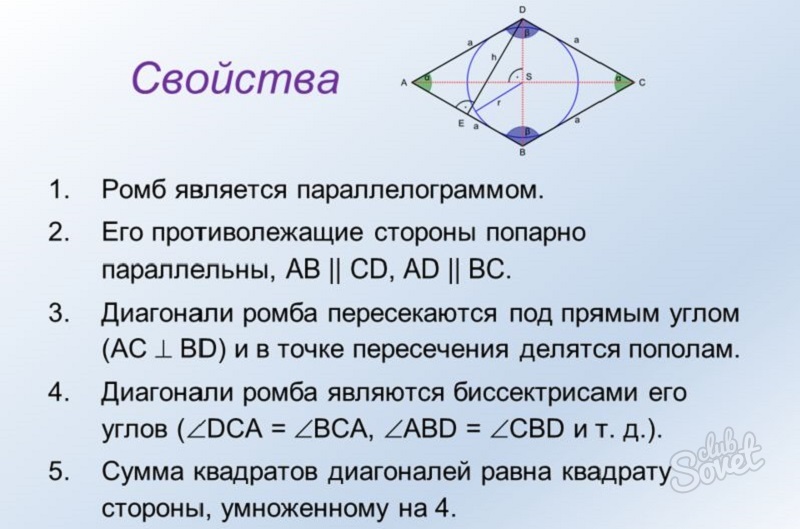
Все свойства ромба
- Ромб имеет две диагонали.
- Все стороны ромба одинаковы.
- Сумма всех углов ромба равна 360 градусам.
- В ромбе диагонали перпендикулярны
- биссектрисами углов ромба являются диагонали.
- Сумма всех квадратов диагоналей равна квадрату одной из
сторон ромба умноженной на четыре. - Центром симметрии у ромба является точка, где пересекаются
все диагонали. - Вне зависимости от длины сторон и градусных мер углов ромба,
в него можно вписать окружность. - Точка пересечения диагоналей ромба, также является центром
вписанной окружности. - Для ромба истинны все свойства параллелограмма.
Все признаки ромба
- Параллелограмм является ромбом, если в нем биссектрисы
углов являются диагоналями .
- Параллелограмм является ромбом, если у него все диагонали
пересекаются только под углом в 90 градусов. - Параллелограмм является ромбом, если у него
все стороны одинаковы. - Параллелограмм является ромбом, если в него
может быть вписана окружность. - Параллелограмм является ромбом, если у него
все высоты одинаковы. - Четырехугольник является ромбом, если в нем диагонали
- Четырехугольник является ромбом, если для него истинны все
свойства параллелограмма и диагонали перпендикулярны,
и они же являются биссектрисами.
Виды четырехугольников.
Тестирование онлайн
Параллелограмм и трапеция
Прямоугольник, ромб, квадрат
Параллелограмм
Определение. Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
Свойство. В параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство. Диагонали параллелограмма точкой пересечения делятся пополам.
1 признак параллелограмма. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
2 признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
3 признак параллелограмма. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Трапеция
Определение. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Параллельные стороны называются основаниями.
Трапеция называется равнобедренной (равнобочной), если ее боковые стороны равны. В равнобедренной трапеции углы при основаниях равны.
Трапеция, один из углов которой прямой, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. Средняя линия параллельна основаниям и равна их полусумме.
Прямоугольник
Определение. Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойство. Диагонали прямоугольника равны.
Признак прямоугольника. Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
Ромб
Определение. Ромбом называется параллелограмм, у которого все стороны равны.
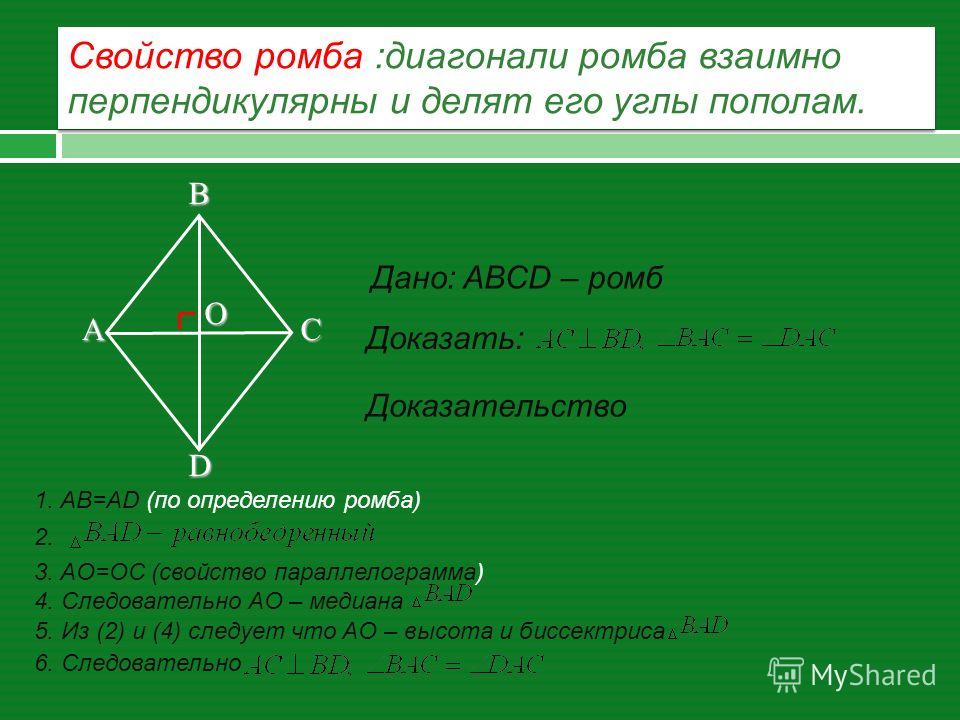
Свойство. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадрат
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Квадрат есть частный вид прямоугольника, а также частный вид ромба. Поэтому он имеет все их свойства.
Свойства:
1. Все углы квадрата прямые
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.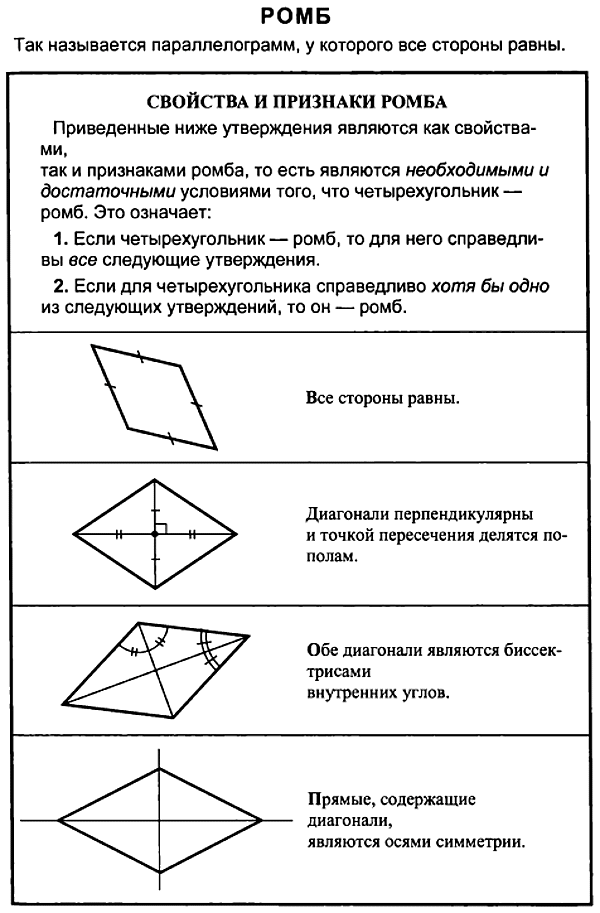
Презентация — Ромб и его свойства
Слайды и текст этой презентации
Слайд 1
Геометрия-8
Ромб и его свойства
УРОК 6
Слайд 2
Природа говорит языком математики: буквы этого языка – круги, треугольники и иные математические фигуры.
(Г. Галилей)
Повторяем
Узнаём
Слайд 3
Любой ли четырёхугольник является параллелограммом?
1
2
3
4
5
6
НЕТ
Повторяем теорию
Любой ли параллелограмм является прямоугольником?
НЕТ
Чему равна сумма углов параллелограмма?
360º
Одна сторона прямоугольника равна 6см, а другая сторона больше её на 2см. Чему равен периметр прямоугольника?
Р = 2·(a + b)
P = 28 см
Каково свойство диагоналей прямоугольника?
Диагонали прямоугольника равны.
Сумма длин диагоналей прямоугольника 12 см. Найдите длину каждой диагонали.
Найдите длину каждой диагонали.
Диагонали прямоугольника равны.
12 : 2 = 6 (см)
Слайд 4
По рисунку определите
и сформулируйте признак
параллелограмма
В
А
С
D
О
А
А
В
В
С
С
D
D
Признаки параллелограмма
3
1
2
Если в четырёхугольнике каждые две противолежащие стороны равны, то это — параллелограмм.
Если в четырёхугольнике две противолежащие стороны равны и параллельны, то это — параллелограмм
Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то это — параллелограмм.
Слайд 5
На рисунке изображены прямоугольники. По рисунку определите и сформулируйте свойства прямоугольника.
1
Противолежащие стороны прямоугольника равны
D
А
С
В
2
Противолежащие углы прямоугольника равны
3
О
Диагонали прямоугольника точкой пересечения делятся пополам
4
О
Диагонали прямоугольника равны.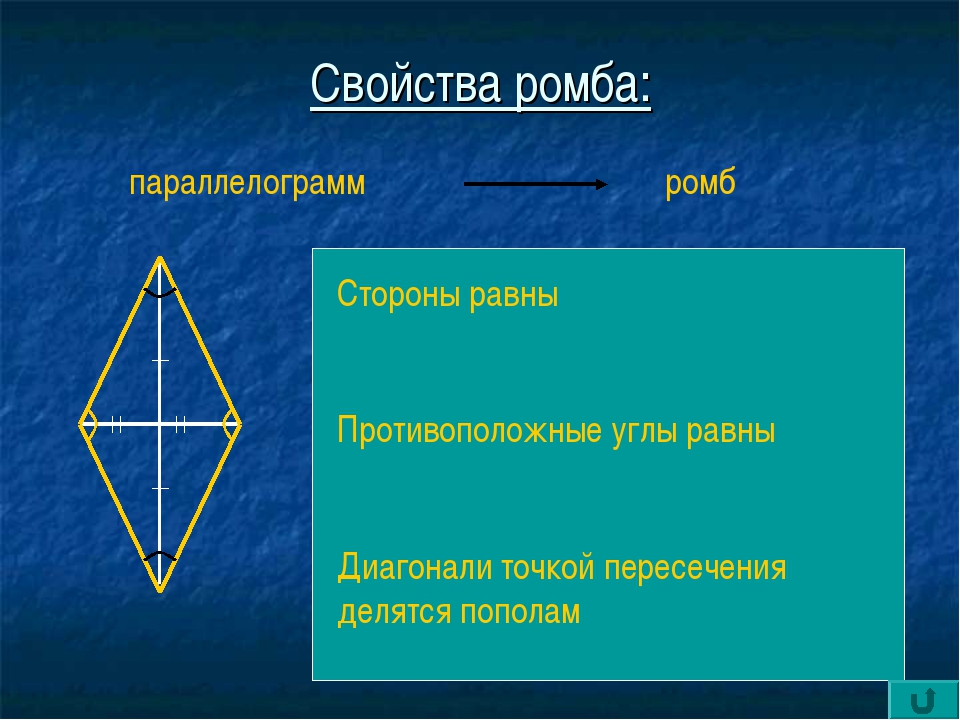
Слайд 6
Признаки прямоугольника
По каким признакам можно установить, что параллелограмм является прямоугольником?
Если один из углов параллелограмма прямой, то этот параллелограмм – прямоугольник.
Если диагонали параллелограмма равны, то этот параллелограмм – прямоугольник.
1
2
С
В
D
А
О
Слайд 7
Четырёхугольник DEFK- прямоугольник, DE = 9см, DK = 12cм, DF = 15см, угол DME = α. Определите:
М
α
9см
FK =
= 15см
EK =
7,5см
MF =
42см
PDEFK =
27см
PEMF =
180º-α
α/2
90º- α/2
Слайд 8
Ромб — фигура непростая, Две в себе объединяет: Треугольник раз и два — Фигура стала вдруг одна. Четыре в ромбе стороны. Между собой они равны. Четыре в ромбе и угла, Равны между собой по два.
Слайд 9
Ромб
Определение
D
А
В
С
Ромбом называют параллелограмм
у которого
все стороны равны
Это интересно
Слайд 10
Это интересно
Rhombob (греч. )- бубен
)- бубен
Карточная масть
Веретено
Слайд 11
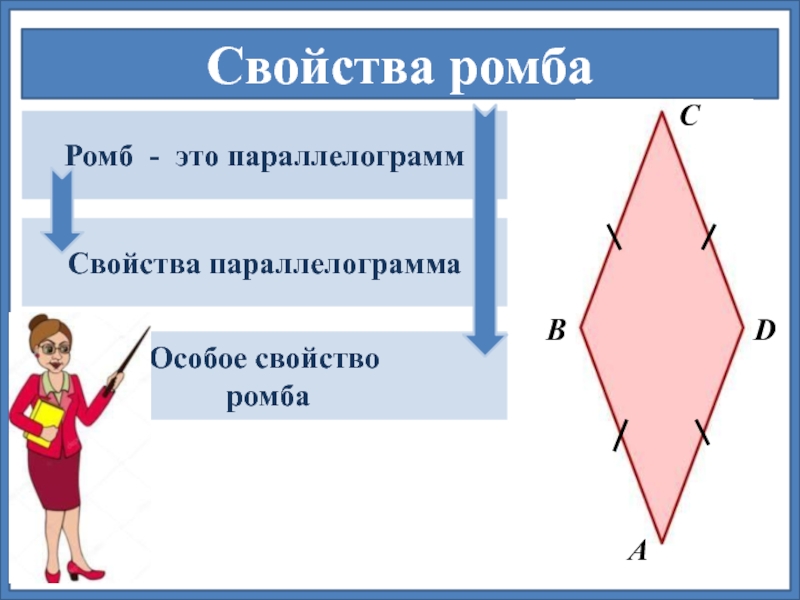
Свойства ромба
Ромб — это параллелограмм
Свойства параллелограмма
Особое свойство
ромба
D
А
В
С
Слайд 12
Свойства параллелограмма
Противолежащие стороны
ромба равны
Противолежащие стороны параллелограмма равны
1
Противолежащие углы
ромба равны
Противолежащие углы параллелограмма равны
Диагонали ромба точкой пересечения делятся пополам.
Диагонали параллелограмма точкой пересечения делятся пополам
2
3
Свойства ромба
Слайд 13
Диагонали ромба перпендикулярны и являются биссектрисами его углов.
Док-во:
Док-во:
D
А
В
С
О
Слайд 14
Четырёхугольник DEFK- ромб, EО = 9см, DЕ= 10cм, DF = 16см, угол DEК = α. Определите:
К
D
F
E
α
10см
DK =
9см
OK =
8см
OF =
40см
PDEFK =
20см
PFOK =
90º
2α
90º- α
О
Слайд 15
Признаки ромба
Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.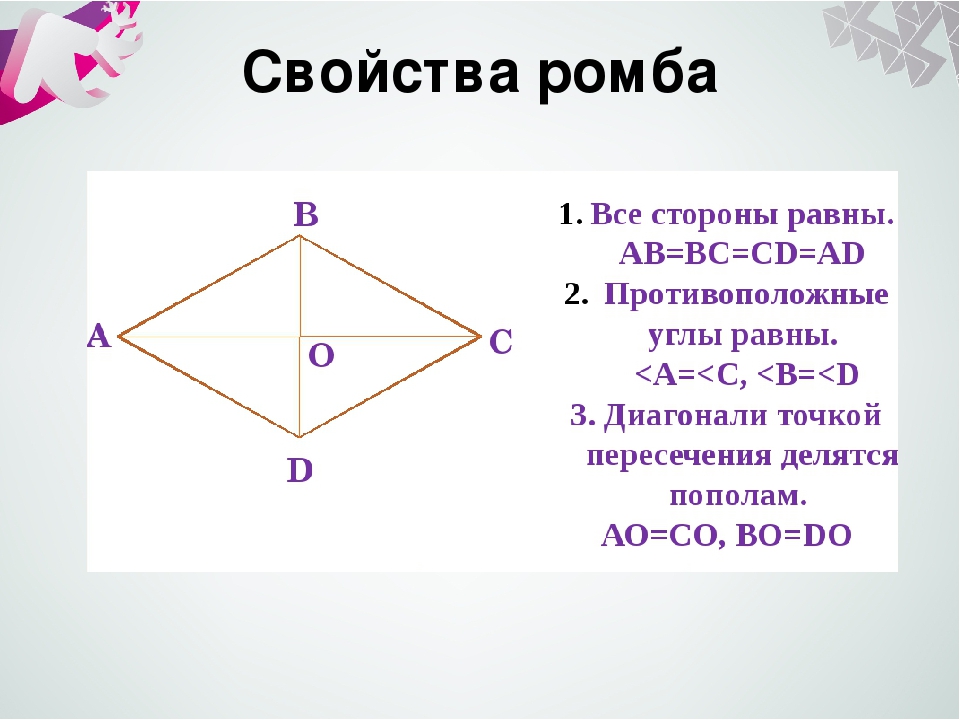
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
1º
Задачи
2º
Слайд 16
Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.
Док-во
А
В
С
D
Слайд 17
Если диагональ параллелограмма является биссектрисой угла, то этот параллелограмм – ромб.
А
В
С
D
1
2
3
4
Док-во
Слайд 18
Биссектрисы углов А и В параллелограмма АВСD пересекают его стороны ВС и АD в точках F и Е соответственно. Определите вид четырёхугольника ABEF.
1
2
Док-во
3
4
Слайд 19
Титульный слайд
Галилео Галилей
Поурочные планы уроков геометрии в 8 классе
к учебнику «Геометрия 8 класс», А.Г.Мерзляк
Учительница
Ученик
Учебник геометрии
Источники
Учебник «Геометрия-8» Мерзляк А.Г.
Вентана.Граф 2016г.
Саврасова С. М., Ястребинецкий Г.А.
«Упражнения по планиметрии
на готовых чертежах»
М., Ястребинецкий Г.А.
«Упражнения по планиметрии
на готовых чертежах»
Дидиактические материалы Мерзляк А.Г.
«Геометрия-8» Вентана.Граф 2016г.
А.П. Ершова, В.В. Голобородько, А.С. Ершова «Математика.
Самостоятельные и контрольные работы».
Алгебра. Геометрия. 8класс
Четырёхугольный бубен
Стихи про геометрические фигуры
Игральные карты
Веретено
Слайд 20
|
Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Четырёхугольник называется выпуклым, если он расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон. Сумма углов выпуклого четырёхугольника равна 360°: ∠A+∠B+∠C+∠D=360°. Не существует четырёхугольников, у которых все углы острые или все углы тупые. Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов: ∠A < ∠B+∠C+∠D, ∠B < ∠A+∠C+∠D, ∠C < ∠A+∠B+∠D, ∠D < ∠A+∠B+∠D. Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон: a < b+c+d, b < a+c+d, c < a+b+d, d < a+b+c. Площадь произвольного выпуклого четырёхугольника равна: |
||
|
Диагоналями четырёхугольника называются отрезки, соединяющие его противолежащие вершины. Диагонали выпуклого четырёхугольника пересекаются, а невыпуклого – нет. Площадь произвольного выпуклого четырёхугольника: |
||
|
Если M, N, P, Q – середины сторон выпуклого четырёхугольника ABCD, а R, S – середины его диагоналей, то четырёхугольники MNPQ, MRPS, NSQR являются параллелограммами и называются параллелограммами Вариньона. Форма и размеры параллелограммов Вариньона связаны с формой и размерами данного четырёхугольника ABCD. Так MNPQ – прямоугольник, если диагонали четырёхугольника ABCD перпендикулярны; MNPQ – ромб, если диагонали четырёхугольника ABCD равны; MNPQ – квадрат, если диагонали четырёхугольника ABCD перпендикулярны и равны; SABCD = 2SMNPQ . |
||
|
Отрезки MP, NQ и RS называются первой, второй и третьей средними линиями выпуклого четырёхугольника. В параллелограмме, и только в нём, середины диагоналей совпадают, и потому третья средняя линия вырождается в точку. Для других четырёхугольников средние линии – отрезки. Все средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам: MG=GP, NG=GQ, RG=GS . Сумма квадратов средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей: MP2+ NQ2+ RS 2 = ¼(AB2+BC2+CD2+AD2+AC2+BD2). Если β – угол между первой и второй средними линиями четырёхугольника, то его площадь: SABCD = MP·NQ·sinβ. |
||
|
|
||
|
Равными плитками, которые имеют форму произвольного, не обязательно выпуклого, четырёхугольника можно замостить плоскость так, чтобы не было наложений плиток друг на друга и не осталось непокрытых участков плоскости. |
||
|
Четырёхугольник называется описанным около окружности (описанным), если существует такая окружность, которая касается всех его сторон, тогда сама окружность называется вписанной. Четырёхугольник является описанным тогда и только тогда, кода суммы его противолежащих сторон равны: a+c = b+d. Для сторон описанного четырёхугольника и радиуса вписанной в него окружности верно: a+c ≥ 4r, b+d ≥ 4r. Площадь описанного четырёхугольника: S = pr, где r – радиус вписанной окружности, p – полупериметр четырёхугольника. Площадь описанного четырёхугольника: |
||
|
Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника. Точки касания вписанной окружности отсекают равные отрезки от углов четырёхугольника: AK=AN, BK=BL, CL=CM, DM=DN. Если O – центр окружности, вписанной в четырёхугольник ABCD, то ∠AOB+∠COD=∠BOC+∠AOD=180°. Для описанного четырёхугольника ABCD со сторонами AB=a, BC=b, CD=c и AD=d верны соотношения: |
||
|
Четырёхугольник называется вписанным в окружность (вписанным), если существует окружность, проходящая через все его вершины, тогда сама окружность называется описанной около четырёхугольника. Выпуклый четырёхугольник является описанным тогда и только тогда, когда сумма его противолежащих углов равна 180°: ∠A+∠C=∠B+∠D=180°. Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника. |
||
|
Первая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство: Вторая теорема Птолемея. Выпуклый четырёхугольник тогда и только тогда является вписанным, когда выполняется равенство: Радиус окружности, описанной около четырёхугольника: Площадь вписанного четырёхугольника: |
||
|
Диагонали выпуклого четырёхугольника разбивают каждый его угол на два угла. Углы, опирающиеся на одну сторону, называются связанными углами. Выпуклый четырёхугольник является вписанным тогда и только тогда, когда у него есть хотя бы одна пара равных связанных углов. У вписанного четырёхугольника любые два связанных угла равны. |
||
|
Если четырёхугольник одновременно является описанным и вписанным, то его площадь: Для радиусов описанной и вписанной окружностей данного четырёхугольника и расстояния между центрами этих окружностей выполняется соотношение: |
||
|
Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны: AB||CD, BC||AD. У параллелограмма противолежащие стороны равны и противолежащие углы равны: AB=CD, BC=AD; ∠A=∠C, ∠B=∠D. Сумма любых двух соседних углов параллелограмма равна 180°: ∠A+∠B=∠B+∠C=∠C+∠D=∠A+∠D=180°. |
||
|
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам: AO=OC; BO=OD. Каждая диагональ делит параллелограмм на два равных треугольника: ∠ABC=∠CDA; ∠ABD=∠CDB. Две диагонали параллелограмма делят его на четыре равновеликих треугольника: SΔABO=SΔBCO=SΔCDO=SΔADO. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: e2+f2 = a2+b2+a2+b2 = 2(a2+b2). |
||
|
Признаки параллелограмма:
|
||
|
Высотой параллелограмма называется перпендикуляр, проведённый из вершины параллелограмма к неприлежащей стороне: ha = b·sin γ; hb = a·sin γ. Площадь параллелограмма можно определить:
S = aha = bhb;
S = ab·sin γ. |
||
|
Ромбом называется параллелограмм, у которого все стороны равны: AB=BC=CD=AD. Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов: AC⊥BD; ∠ABD=∠CBD=∠ADB=∠CDB; ∠BAC=∠DAC=∠BCA=∠DCA. |
||
|
В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности, вписанной в ромб, можно вычислить:
Площадь ромба можно определить:
|
||
|
Прямоугольником называется параллелограмм, у которого все углы прямые: ∠A=∠B=∠C=∠D=90°. |
||
|
Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка: AC=BD; AO=BO=CO=DO. Площадь прямоугольника можно определить:
S = ab;
S = ½d²·sin γ. |
||
|
Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали: BD = 2R. |
||
|
Квадрат – это прямоугольник, у которого все стороны равны: ∠A=∠B=∠C=∠D=90°, AB=BC=CD=AD. |
||
|
Диагонали квадрата равны и перпендикулярны. Сторона и диагональ квадрата связаны соотношениями: Площадь квадрата: |
||
|
У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей. Радиус описанной окружности: Радиус вписанной окружности: |
||
|
Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны: AD||BC. Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами. Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции. |
||
|
Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции: AK=KB; CL=LD. Средняя линия трапеции параллельна её основаниям и равна их полусумме: KL||AD; KL||BC; KL = ½(AD+BC). |
||
|
При продолжении до пересечения боковых сторон трапеции образуются два подобных треугольника с коэффициентом подобия, равным отношению основ: ΔAED∼ΔBEC, k=AD/BC. Треугольники, образованные основами и отрезками диагоналей подобны с коэффициентом подобия, равным отношению основ: ΔAОD∼ΔCОВ, k=AD/BC. Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны: SΔABO = SΔCDO. |
||
|
Отрезок, соединяющий середины оснований (вторая средняя линия) трапеции, проходит через точку пересечения диагоналей, а его продолжение – через точку пересечения продолжений боковых сторон: O∈KL; E∈KL. Отрезок, соединяющий середины диагоналей (третья средняя линия) трапеции, параллелен основаниям и равен их полуразности: RS||AD; RS||BC; RS = ½(AD–BC). |
||
|
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон: AD+BC=AB+CD. Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции. В трапецию АВСD с основаниями AD и BC можно вписать окружность тогда и только тогда, когда выполняется хотя бы одно из равенств: Боковые стороны трапеции видны из центра окружности, вписанной в данную трапецию, под прямым углом: ∠AOB=∠COD=90°. Радиус вписанной в трапецию окружности можно определить:
|
||
|
Равнобокой называется трапеция, у которой боковые стороны равны: AB=CD. У равнобокой трапеции:
AC=BD;
∠A=∠D, ∠B=∠C;
∠A+∠C=∠B+∠D=180°. Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая. Стороны и диагональ равнобокой трапеции связаны соотношением: d² = ab+c². |
||
|
Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям. |
||
|
Площадь трапеции можно определить:
|
||
|
Дельтоид называется четырёхугольник, который имеет две пары равных соседних сторон. Дельтоид может быть выпуклым или невыпуклым. Прямые, содержащие диагонали любого дельтоида пересекаются под прямым углом. В любом дельтоиде углы между соседними неравными сторонами равны. Площадь любого дельтоида можно определить:
S = ab·sin α . |
||
|
В любой выпуклый дельтоид можно вписать окружность. Если выпуклый дельтоид не является ромбом, то существует окружность, касающаяся продолжений всех четырёх сторон данного дельтоида. Для невыпуклого дельтоида можно построить окружность, касающуюся двух сторон большей длины и продолжений двух меньших сторон, а также окружность, касающуюся двух меньших сторон и продолжений двух сторон большей длины. |
||
|
Вокруг дельтоида можно описать окружность тогда и только тогда, когда его неравные стороны образуют углы по 90°. Радиус окружности, описанной около дельтоида можно определить через две его неравные стороны:
|
||
|
Четырёхугольник называется ортодиагональным, если его диагонали пересекаются под прямым углом. Четырёхугольник является ортодиагональным тогда и только тогда, когда выполняется одно из условий:
|
||
|
Сумма квадратов противолежащих сторон вписанного в окружность ортодиагонального четырёхугольника равна квадрату диаметра описанной окружности: a²+c² = b²+d² = 4R². |
||
|
Ортодиагональный четырёхугольник является описанным около окружности тогда и только тогда, когда произведения его противолежащих сторон равны: ac = bd. Если ABCD – ортодиагональный четырёхугольник, описанный около окружности с центром в точке О, то верны соотношения: |
||
Четырехугольники Недвижимости | Параллелограммы, Трапеция, Ромб
Нажмите здесь, чтобы посмотреть это проницательное видео.
Лучшие университеты мира
В этом руководстве по основным понятиям геометрии мы рассмотрим типы и свойства четырехугольников: параллелограмм, прямоугольник, квадрат, ромб, трапецию.
определение:
Четырехугольник — это простая замкнутая фигура с четырьмя сторонами.
Виды четырехугольников
Есть пять типов четырехугольников.
- Параллелограмм
- Прямоугольник
- Площадь
- Ромб
- Трапеция
Общим свойством всех четырехугольников является то, что сумма всех их углов равна 360 °.
Давайте посмотрим на свойства различных четырехугольников.
Параллелограмм
Свойства параллелограмма
- Противоположные стороны параллельны и конгруэнтны.
- Противоположные углы совпадают.
- Прилегающие углы являются дополнительными.
- Диагонали делят друг друга пополам, и каждая диагональ делит параллелограмм на два равных треугольника.

- Если один из углов параллелограмма — прямой угол, то все остальные углы прямые, и он становится прямоугольником.
Важные формулы параллелограммов
- Площадь = L * H
- Периметр = 2 (L + B)
Прямоугольники
Свойства прямоугольника
- Противоположные стороны параллельны и конгруэнтны.
- Все углы прямые.
- Диагонали равны и делят друг друга пополам (делят друг друга поровну).
- Противоположные углы, образованные в точке пересечения диагоналей, совпадают.
- Прямоугольник — это особый тип параллелограмма с прямыми углами.
Важные формулы для прямоугольников
- Если длина L, а ширина B, то
Длина диагонали прямоугольника = √ (L 2 + B 2 )
- Площадь = L * B
- Периметр = 2 (L + B)
Квадраты
Объекты квадрата
- Все стороны и углы совпадают.

- Противоположные стороны параллельны друг другу.
- Диагонали совпадают.
- Диагонали перпендикулярны и делят друг друга пополам.
- Квадрат — это особый тип параллелограмма, все углы и стороны которого равны.
- Кроме того, параллелограмм становится квадратом, если диагонали равны правым биссектрисам друг друга.
Важные формулы для квадратов
- Если «L» — длина стороны квадрата, то длина диагонали = L √2.
- Площадь = L 2 .
- Периметр = 4L
Ромб
Свойства ромба
- Все стороны совпадают.
- Противоположные углы совпадают.
- Диагонали перпендикулярны и делят друг друга пополам.
- Соседние углы являются дополнительными (например, A + ∠B = 180 °).
- Ромб — это параллелограмм, диагонали которого перпендикулярны друг другу.
Важные формулы для ромба
Если a и b — длины диагоналей ромба,
- Площадь = (a * b) / 2
- Периметр = 4L
Трапеция
Свойства трапеции
- Основания трапеции параллельны друг другу (MN ⫽ OP).

- Нет сторон, углы и диагонали не совпадают.
Важные формулы для трапеции
- Площадь = (1/2) ч (Д + Д 2 )
- Периметр = L + L 1 + L 2 + L 3
Обзор объектов недвижимости
Обобщая то, что мы узнали до сих пор, для удобства использования и запоминания:
| S. No. | Недвижимость | Параллелограмм | Прямоугольник | Ромб | Квадрат |
| 1 | Все стороны совпадают | ✕ | ✕ | & проверить; | & проверить; |
| 2 | Противоположные стороны параллельны и совпадают | & проверить; | & проверить; | & проверить; | & проверить; |
| 3 | Все углы совпадают | ✕ | & проверить; | ✕ | & проверить; |
| 4 | Противоположные углы совпадают | & проверить; | & проверить; | & проверить; | & проверить; |
| 5 | Диагонали совпадают | ✕ | & проверить; | ✕ | & проверить; |
| 6 | Диагонали перпендикулярны | ✕ | ✕ | & проверить; | & проверить; |
| 7 | Диагонали пересекают друг друга | & проверить; | & проверить; | & проверить; | & проверить; |
| 8 | Углы смежные дополнительные | & проверить; | & проверить; | & проверить; | & проверить; |
Подробнее о:
— Свойства линий и углов
— Свойства и формулы кругов
— Типы треугольников и свойства
5 Свойства ромба для математического класса
Кредит: Pixabay CC0 1.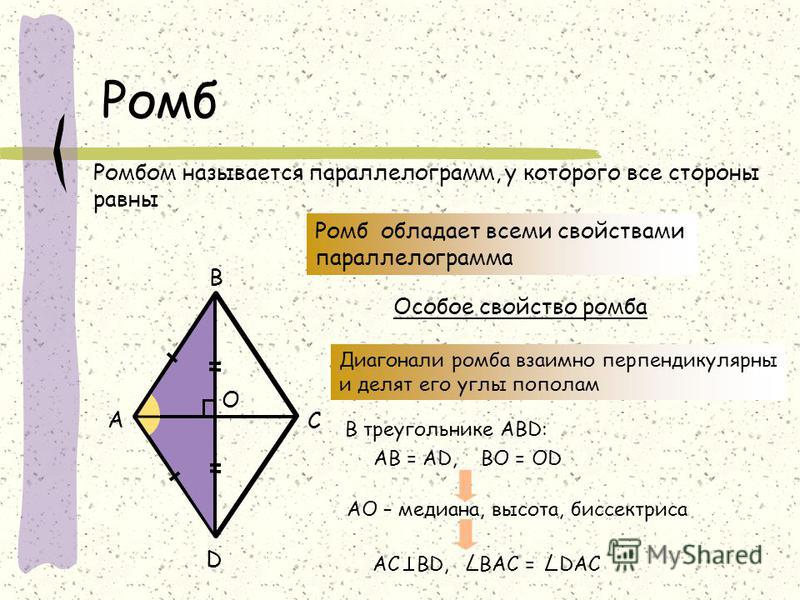 0
0В геометрии ромб — это особый вид четырехугольника, в котором все 4 стороны имеют одинаковую длину. Ромб обладает некоторыми уникальными свойствами, которые являются следствием его определения. Некоторые ключевые свойства ромба включают:
- Противоположный угол конгруэнтен
- Смежные углы являются дополнительными
- Диагонали делят пополам противоположные углы
- Диагонали делят пополам друг друга
- Диагонали перпендикулярны друг другу
Определение ромба
В простейшем случае ромб определяется как любой простой (непересекающийся) четырехугольник с 4 сторонами равной длины.Согласно этому определению, квадрат также является ромбом, в котором все углы прямые. Другие названия ромба включают «равносторонний четырехугольник» и «ромб», хотя последний термин обычно зарезервирован для специального ромба, который имеет углы 2 45 ° и 2 135 °.
Можно доказать, что ромб является частным случаем параллелограмма, у которого все 4 стороны равны. Это означает, что все ромбы являются параллелограммами, хотя обратное не обязательно, поскольку есть параллелограммы, которые не являются ромбами.Каждый ромб — это воздушный змей — четырехугольник с совпадающими смежными сторонами.
Это означает, что все ромбы являются параллелограммами, хотя обратное не обязательно, поскольку есть параллелограммы, которые не являются ромбами.Каждый ромб — это воздушный змей — четырехугольник с совпадающими смежными сторонами.
Слово «ромб» происходит от древнегреческого слова, означающего «вращать». Евклид использовал термин «ромб», чтобы описать эту двумерную форму, которая возникает в результате взятия поперечного сечения двух круглых конусов, которые примыкают к основанию.
Существенные свойства ромба
1. Противоположные углы конгруэнтны
Первое ключевое свойство ромба — это отношение, разделяемое между парами противоположных углов.Пара противоположных углов в ромбе конгруэнтны, что означает, что они равны. Мы можем доказать это следующим образом:
Кредит: Автор| Заявление | Причина | ||
| 1 | Ромб ABCD | 9018 2 | Провести линию AC | 2 | 2 точки образуют линию |
| 3 | AB || DC & BC || DA | 3 | Def. ромба ромба |
| 4 | ∠ACD ≅ BAC & ∠DAC ≅ ∠ACB | 4 | Альтернативные внутренние углы |
| 5 9018 = AB = | DA 5 | По ум. ромба | |
| 6 | ΔACD = ΔABC | 6 | SAS |
| 7 | ∠DTC | CP18Q.E.D |
Это свойство ромба также показывает, что он является параллелограммом, поскольку существенное свойство параллелограмма состоит в том, что его противоположные углы совпадают. То есть, если четырехугольник имеет равные противоположные углы, этого достаточно, чтобы гарантировать, что это параллелограмм.
(Сноска: «Q.E.D» в конце каждого доказательства — это сокращение от латинской фразы «quod erat manifestradum», что примерно переводится как «таким образом, это было продемонстрировано»).
2.Смежный угол является дополнительным
Соседний угол ромба является дополнительным, то есть в сумме они составляют 180 °. Мы можем доказать, что смежные углы в ромбе являются дополнительными, следующим образом:
Кредит: Автор| Заявление | Причина | ||
| 1 | 9018 9018 AB356 | Дано | |
| 2 | AB || DC & DA || BC | 2 | По умолчанию.ромба |
| 3 | AC | 3 | Две точки образуют линию |
| 4 | ∠A supp B, ∠B supp D, , ∠D supp ∠A | 4 | Это два || линии обрезаются пер., внутренние углы на той же стороне пер. являются дополнительными. Q.E.D |
Итак, мы можем доказать, что смежные углы в ромбе являются дополнительными.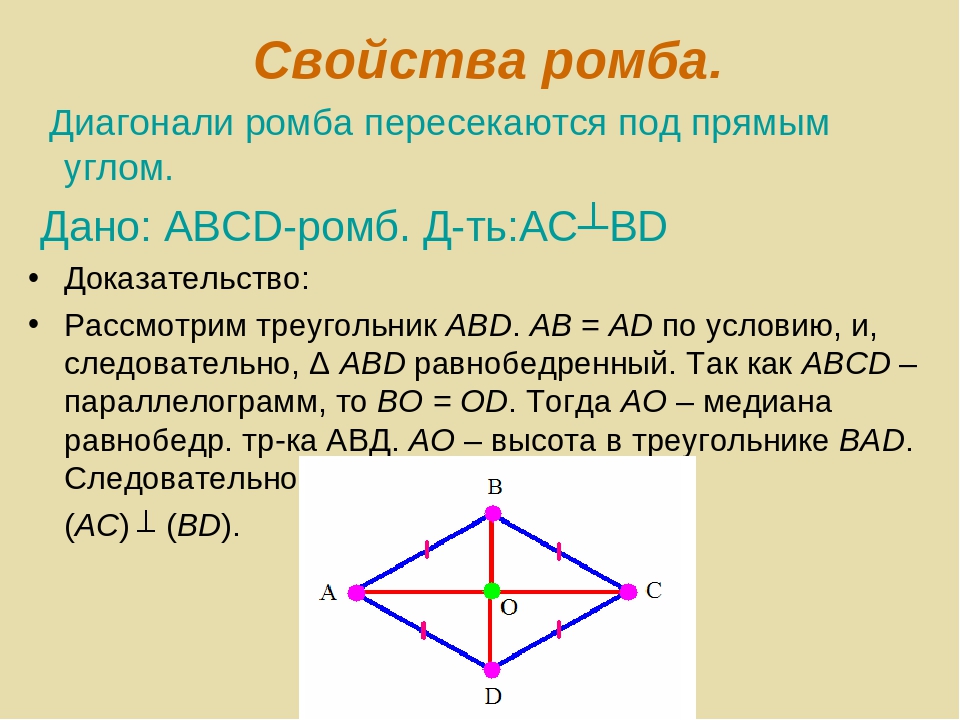
3.Диагонали делят пополам противоположные углы
Третье важное свойство ромба связано с его диагоналями. Диагональ многоугольника — это любая линия, проведенная между двумя несмежными вершинами. У параллелограмма 4 точки, то есть всего 2 диагонали. Характерным свойством диагоналей ромба является то, что они делят пополам угол, из которого они начерчены. Мы можем доказать это следующим образом:
| Заявление | Причина | |||||
| 1 | Ромб ABCD | AB = BC = CD = DA | 2 | Отрезок ромба | ||
| 3 | AC & BD | 3 | Две точки образуют линию | |||
| переменного тока DAC = ∠ACD | 6 | Базовые ∠s isos.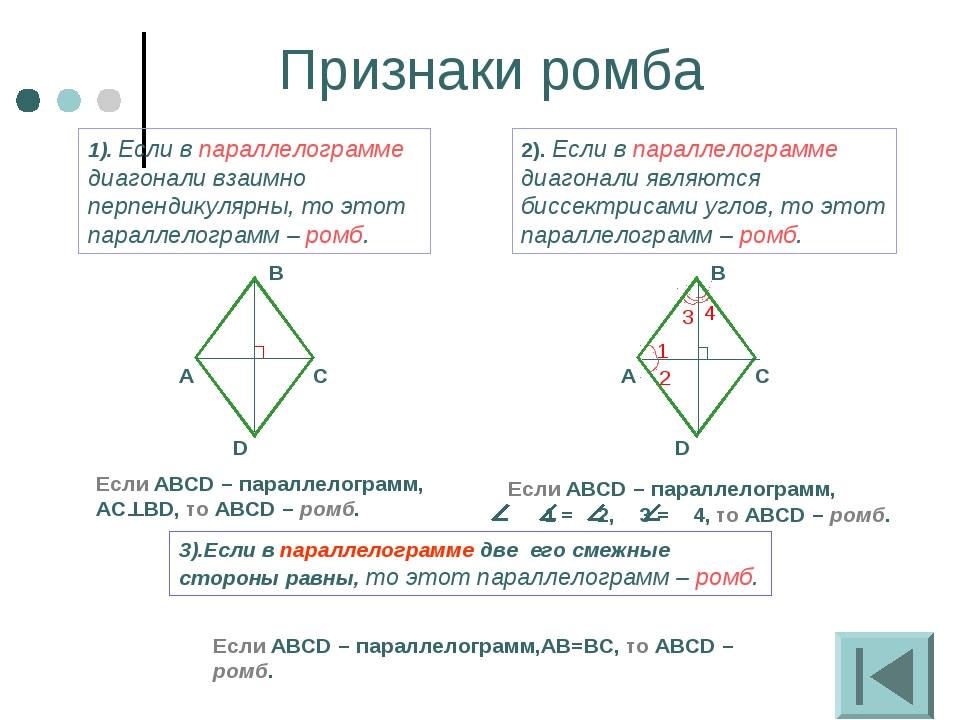 треугольники конгруэнтны треугольники конгруэнтны | ||||
| 7 | ∠DAC = ∠BAC ∠DCA = ∠BCA | 7 | CPCTC | |||
| CPCTC2 | ||||||
| AC | 35 | 8 | Биссектриса угла делит угол на две равные части. Q.E.D |
Итак, мы только что доказали, что диагонали ромба делят пополам противоположные углы.Это уникальное свойство ромбов, которое не встречается у других четырехугольников.
4. Диагонали делят пополам
Четвертое главное свойство ромба также связано с его диагоналями. Это факт, что диагонали ромба пересекают друг друга пополам; то есть каждый из них разрезает друг друга на два равных отрезка. Точка их пересечения — середина обеих диагоналей.
| Заявление | Причина | |||||
| 1 | Ромб ABCD | 1 | DA | DA | 2 | По умолчанию.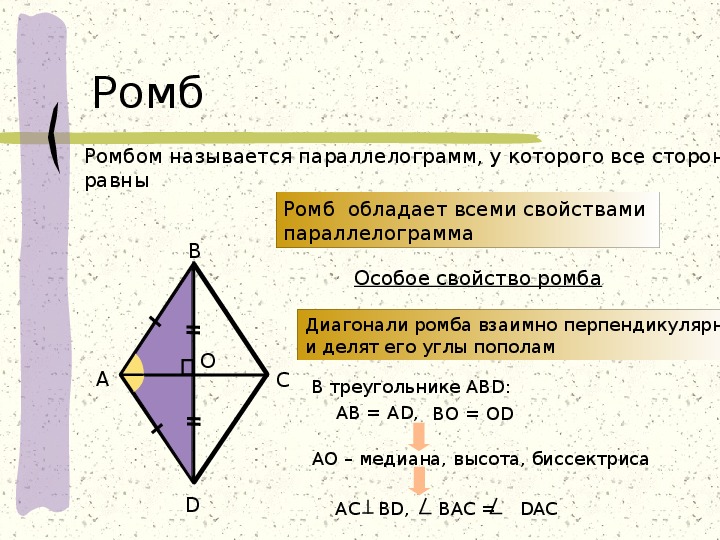 ромба ромба |
| 3 | AB || CD и DA || CB | 3 | По умолчанию. ромба | |||
| 4 | ∠AEB = ∠DEC | 4 | Пары вертикальных углов | |||
| 5 | 5 | DBAC18 9018 | 635 внутренние углы | |||
| 6 | ΔAEB ≅ ΔDEC | 6 | Теорема SAA | |||
| 7 | CPTC8 | AETC8 9018 9018 9018 9018 9187 | EBTC8 | |||
| 8 | AC и DB делят друг друга пополам | 8 | Две прямые делят друг друга пополам, если точка, в которой они пересекаются, является средней точкой обеих линий.Q.E.D |
5. Диагонали перпендикулярны друг другу
Последней определяющей чертой ромба, которую мы докажем, является тот факт, что диагональные линии перпендикулярны друг другу.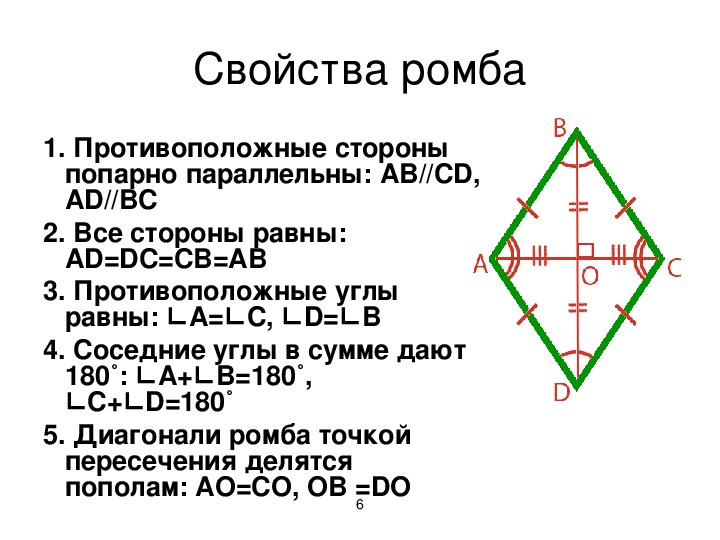 В ромбе две диагонали всегда пересекаются под прямым углом 90 °. Мы можем доказать это следующим образом:
В ромбе две диагонали всегда пересекаются под прямым углом 90 °. Мы можем доказать это следующим образом:
| Заявление | Причина | |||||
| 1 | Ромб ABCD | 9018 9018 9018 9018 9018 9018 9018 9018 9018 9018 9018 9018 9018 AB = BC = CD = DA | 2 | По умолчанию.ромба | ||
| 3 | AE = EC DE = EB | 3 | Теорема: диагонали ромба делят друг друга пополам (из пруда № 4) | |||
| ΔAEB = ΔBEC = ΔCED = ΔAED | 4 | SSS | ||||
| 5 | ∠AEB = ∠BEC = ∠CED = DEA | CPTC | ∠AEB + ∠BEC + ∠CED + ∠DEA = 360 ° | 6 | Сумма углов, окружающих точку и разделяющих вершину, составляет 360 ° | |
| 7 | 4∠AEB = 360 ° | 7 | Упрощение | |||
| 8 | ∠AEB = 90 ° | 8 | Подразделение | |||
| 9018 9018 9018 9018 9018 9018 | Две прямые перпендикулярны, если они пересекаются под прямым углом |
Другие свойства ромба
Площадь
Площадь ромба можно вычислить точно так же, как и любой другой четырехугольник, умножьте основание на рост.
A = b x h
Высота ромба — это мера линии, проведенной перпендикулярно от одной стороны к противоположной. Причина, по которой формула площади для ромба такая же, как для прямоугольника, проста; каждый ромб (и параллелограмм) можно разрезать на части и преобразовать в прямоугольник с тем же основанием и высотой (на следующем рисунке изображен не ромбовидный параллелограмм, но тот же принцип справедлив и для ромбов).
Кредит: WikiCommons CC0 1.0Если вы проведете линию, перпендикулярную от одного основания к концу другого основания, вы получите трапецию и прямоугольный треугольник, которые можно преобразовать в прямоугольник с той же площадью, что и исходный ромб.
Вы также можете вычислить площадь ромба, если вам известна только длина его диагоналей. Площадь ромба равна половине произведения его диагоналей. Итак, для ромба с диагоналями p и q математическая формула:
A = pq / 2
Помните, что мы ранее доказали две вещи о диагоналях ромба: они делят друг друга пополам и перпендикулярны друг другу. Рассмотрим следующий ромб:
Рассмотрим следующий ромб:
Мы знаем, что AE = EC и DE = EB. Мы также знаем, что диагонали делят пополам пары противоположных углов.Итак, мы получаем два больших равнобедренных треугольника справа и слева, каждый из которых разделен на два меньших правых треугольника. Площадь всего ромба равна удвоенной площади одного из равнобедренных треугольников. Начиная с правого ΔABC, мы знаем, что его общая площадь составляет
Площадь ΔABC = ½ (AC) (EB)
Однако мы также знаем, что EB составляет половину DB (потому что линия делится пополам в точке E), поэтому мы можем заменить:
Площадь ΔABC = ½ (AC) (½DB)
, что упрощается до
Площадь ΔABC = ¼ (AC) (DB)
Поскольку мы знаем, что вся площадь ромба в два раза больше ΔABC , мы можем переписать
Площадь ABCD = 2 × Площадь ΔABC = ½ (AC) (BD)
Следовательно, площадь ромба можно вычислить как половину произведения его диагональных линий.
Свойства тесселяции
Ромб также может образовывать тесселяцию, то есть вы можете расположить ромб в виде правильных узоров, чтобы полностью заполнить двумерное лицо. Тесселяция из ромбов называется мозаикой ромбовидной формы. Плитки из одинаковых ромбов могут заполнять плоскость тремя разными способами; в виде последовательной стопки бриллиантов, чередующейся стопки бриллиантов или в виде групп из 3 ромбов, расположенных на грани куба.
Тесселяция из ромбов называется мозаикой ромбовидной формы. Плитки из одинаковых ромбов могут заполнять плоскость тремя разными способами; в виде последовательной стопки бриллиантов, чередующейся стопки бриллиантов или в виде групп из 3 ромбов, расположенных на грани куба.
. Вы также можете сформировать мозаику ромбов из правильной мозаики шестиугольников.Просто разделите каждый шестиугольник на три, проведя линии из всех остальных вершин, которые встречаются в центре шестиугольника.
Из шестиугольной плитки можно сформировать ромбическую плитку. Предоставлено: WikiCommons CC BY-SA 3.0 Ромби можно расположить в виде мозаики, поскольку их можно расположить таким образом, чтобы сумма углов, окружающих каждую точку, составляла ровно 360 градусов. Это необходимое свойство фигур, которые можно мозаизировать; если вы не можете расположить фигуру таким образом, чтобы сумма всех углов, которые встречаются в вершине, составляла 360, то вы не можете сделать из нее обычную мозаику.
Итак, ромб — это название четырехугольника, в котором все 4 стороны имеют одинаковую длину. Все ромбы — это параллелограммы, а квадрат — это особый случай ромба, в котором все 4 внутренних угла являются прямыми углами. Ключевые свойства ромба: его противоположные углы совпадают, его смежные углы являются дополнительными, его диагонали делят противоположные углы пополам, его диагонали делят пополам друг друга, а его диагонали перпендикулярны друг другу.
Была ли эта статья полезной?
😊 ☹️ Приятно слышать! Хотите больше научных тенденций? Подпишитесь на нашу рассылку новостей науки! Нам очень жаль это слышать! Мы любим отзывы 🙂 и хотим, чтобы вы внесли свой вклад в то, как сделать Science Trends еще лучше.Искусство решения проблем
Ромб — это геометрическая фигура, лежащая на плоскости. Он определяется как четырехугольник, все стороны которого равны. Это особый тип параллелограмма, и его свойства (помимо свойств параллелограммов) включают:
Пробки
Доказательство того, что ромб является параллелограммом
Все стороны ромба конгруэнтны, поэтому противоположные стороны конгруэнтны, что является одним из свойств параллелограмма.
Или всегда есть более длинный путь:
У ромба все 4 стороны совпадают (определение ромба).
« и.
Согласно Постулату ССС,.
Соответствующие части конгруэнтных треугольников конгруэнтны, поэтому и. То же самое можно сделать для двух других углов, поэтому.
Преобразуйте сравнения в меры, чтобы получить и. Сложение этих двух уравнений дает.
Внутренние углы четырехугольника в сумме составляют 360 градусов, так, или.
Подстановка дает. В упрощенном виде.
Если две линии разрезаны поперечно, а внутренние углы с той же стороны в сумме составляют 180 градусов, линии параллельны. Это означает . То же самое можно сделать для двух других сторон, и мы знаем, что противоположные стороны параллельны. Следовательно, ромб — это параллелограмм.
Доказательство того, что диагонали ромба делят его на 4 равных треугольника
В ромбе — точка пересечения диагоналей.
Так как диагонали ромба биссектрисы друг друга, а.
Также все стороны совпадают.
Согласно Постулату SSS, 4 треугольника, образованные диагоналями ромба, совпадают.
Доказательство того, что диагонали ромба перпендикулярны
Продолжение вышеуказанного доказательства:
Соответствующие части конгруэнтных треугольников конгруэнтны, поэтому все 4 угла (те, что посередине) конгруэнтны.
Это приводит к тому, что все они равны 90 градусам, а диагонали перпендикулярны друг другу.
Примеры проблем
Вводный
Что такое ромб — определение, свойства и периметр
- Смежные углы в ромбе в сумме составляют 180 °.
- Диагонали пересекают друг друга под прямым углом.
- Все квадраты — ромбы, но не все ромбы — квадраты.
Решенные примеры на ромбе
Раджив нарисовал ромб, в котором длины двух диагоналей \ (d_1 \) и \ (d_2 \) ромба составляют 5 см и 10 см соответственно. Он просит свою сестру Лолу помочь ему найти этот район. Вы можете помочь Лоле найти ответ?
Он просит свою сестру Лолу помочь ему найти этот район. Вы можете помочь Лоле найти ответ?
Решение
Дано:
Диагональ \ (d_1 = 5 \ text {см} \)
Диагональ \ (d_2 = 10 \ text {см} \)
| \ (A = \ dfrac {{d_1 d_2}} {2} \) |
\ (\ begin {align} A & = \ frac {{5 \ times 10}} {2} \\ A & = 25 \ text {sq. Cm} \ end {align} \)
| \ (\ следовательно \) \ (\ text {Area} = 25 \ text {sq.2 \ text {и} d_1 = 20 \ text {см} \) \ (\ begin {align} A & = \ dfrac {{d_1 \ times d_2}} {2} \\ 100 & = \ dfrac {20 \ times {d_2}} {2} \\ d_2 & = 10 \ text {см} \ end {align} \)
Соня и Аман играли в классики, когда заметили на детской площадке плитку в форме ромба. Решение Дано: Длина стороны \ (= 15 \ text {см} \) Поскольку все стороны ромба равны, все четыре стороны равны 15 см. \ (Периметр = 4 \ times \ text {Side} = 4 \ times 15 = 60 \)
Размер острого угла ромба составляет половину его тупого угла.Найдите значение двух углов. Решение Дано: Мы знаем, что тупой угол вдвое больше острого. Из свойств ромба мы также знаем, что сумма двух смежных углов равна 180 °. Итак, пусть острый угол будет \ (x \), а тупой угол будет \ (2x \) \ (\ begin {align} x + 2x & = 180 \\ 3x & = 180 \\ x & = 180 \ div3 \\ x & = 60 \\ \ поэтому 2x & = 120 \ end {align} \)
В доме Аарава была крохотная кладовая в форме ромба с периметром 120 м. \ (\ begin {align} OB + OD & = BD \\ OB & = OD \\ \ поэтому 2OB & = BD \\ BD & = 2 \ times 10 \ sqrt {5} \\ BD & = 20 \ sqrt { 5} \\ \ end {align} \) Часть 3 Теперь давайте вычислим площадь ромба, получив длину обеих диагоналей. \ (\ begin {align} A & = \ dfrac {{d1 \ times d2}} {2} \\ A & = 20 \ sqrt {5} \ times {40} \ div {2} \\ A & = 400 \ sqrt {5} \ text {sq. M} \ end {align} \)
Интерактивные вопросы о ромбеВот несколько занятий для вас. Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итогиНадеемся, вам понравилось изучать ромб с решенными примерами и интерактивными вопросами.Теперь вы легко сможете решать вопросы, связанные с ромбом. О компании CuemathВ Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов! Благодаря интерактивному и увлекательному подходу к обучению, обучению и обучению учителя исследуют тему со всех сторон. Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению. Часто задаваемые вопросы (FAQ)1. Все ли квадраты ромбами? Да, все квадраты ромбы. Фактически, вы даже можете назвать это очень частным случаем ромба. 2. Какой формы ромб?Ромб — это четырехугольник геометрической формы ромб. Люди говорят, что если вы посмотрите на колоду карт и вытащите 13 карточек с ромбами, геометрическая форма ромба будет иметь форму ромба. 3. Все ли ромбы прямоугольные?Вы можете возразить, что все квадраты являются ромбами, и все квадраты также являются прямоугольниками, но означает ли это, что все ромбы являются прямоугольниками? Если вы сказали «да», тогда вам нужно будет рассмотреть некоторые действительно особые условия. Во-первых, помните, что все четыре стороны ромба равны. В случае прямоугольника дело обстоит иначе. Ромб станет прямоугольником только в том случае, если его свойства идентичны квадрату. Это потому, что все квадраты — ромбы. 4. Какова площадь ромба? Площадь ромба рассчитывается путем деления произведения диагоналей на 2. Математически это можно определить как: Свойства четырехугольника — прямоугольник, квадрат, параллелограмм, ромб, трапеция В евклидовой геометрии четырехугольник — это четырехугольная двумерная фигура, сумма внутренних углов которой равна 360 °. Итак, каковы свойства четырехугольника? Четырехугольники обладают двумя свойствами:
В этой статье вы получите представление о 5 типах четырехугольников и познакомитесь со свойствами четырехугольников. Это то, что вы прочитаете в статье: Вот видео, объясняющее свойства четырехугольника:
На приведенной ниже диаграмме показан четырехугольник ABCD и сумма его внутренних углов. Сумма всех внутренних углов составляет 360 °. Таким образом, A + ∠B + ∠C + ∠D = 360 ° Различные виды четырехугольников Существует 5 типов четырехугольников в зависимости от их формы.
Давайте подробно обсудим каждый из этих пяти четырехугольников:
ПрямоугольникПрямоугольник — это четырехугольник с четырьмя прямыми углами. Таким образом, все углы в прямоугольнике равны (360 ° / 4 = 90 °).Причем противоположные стороны прямоугольника параллельны и равны, а диагонали делят друг друга пополам. Свойства прямоугольниковПрямоугольник имеет три свойства:
Формула прямоугольника — площадь и периметр прямоугольникаЕсли длина прямоугольника L, а ширина B, то
Площадь Квадрат — четырехугольник с четырьмя равными сторонами и углами. Недвижимость квадратаЧтобы четырехугольник стал квадратом, он должен обладать определенными свойствами. Вот три свойства квадратов:
Формула квадрата — Площадь и периметр квадратаЕсли сторона квадрата — «а», тогда
ПараллелограммПараллелограмм, как следует из названия, представляет собой простой четырехугольник, противоположные стороны которого параллельны. Таким образом, у него две пары параллельных сторон. Кроме того, в параллелограмме противоположные углы равны, а его диагонали делят друг друга пополам. Свойства параллелограммаЧетырехугольник, удовлетворяющий указанным ниже свойствам, будет классифицирован как параллелограмм.У параллелограмма четыре свойства:
Формулы параллелограмма — Площадь и периметр параллелограммаЕсли длина параллелограмма равна «l», ширина — «b», а высота — «h», тогда:
Ромб Ромб — это четырехугольник, все четыре стороны которого равны по длине, а противоположные стороны параллельны друг другу. Свойства ромбаРомб — это четырехугольник, обладающий следующими четырьмя свойствами:
Формулы ромба — Площадь и периметр ромбаЕсли сторона ромба — это, то периметр ромба = 4a Если длина двух диагоналей ромба равна d 1 и d 2 , то площадь ромба = ½ × d 1 × d 2
Трапеция Трапеция (в США ее называют трапецией) — это четырехугольник, у которого есть только одна пара параллельных сторон. Свойства трапецииТрапеция — это четырехугольник, в котором одно свойство:
Формулы трапеции — Площадь и периметр трапецииЕсли высота трапеции « h» (как показано на диаграмме выше), то:
Свойства четырехугольникаВ таблице ниже суммированы все свойства четырехугольников, которые мы изучили до сих пор:
На изображении ниже также показаны свойства четырехугольника: Важные формулы четырехугольникаВ таблице ниже приведены формулы площади и периметра четырехугольников различных типов:
Дополнительная литература: Четырехсторонние вопросыПопрактикуемся в применении свойств четырехугольника на следующих типовых вопросах: Вопрос 1 Адам хочет построить забор вокруг своего прямоугольного сада длиной 10 метров и шириной 15 метров.
РешениеШаг 1: Дано
Шаг 2: найти
Шаг 3: подход и разработка Забор можно строить только вокруг внешней стороны сада.
Следовательно, необходимая длина забора — 50 метров. Следовательно, вариант E — правильный ответ. Вопрос: 2Стив хочет покрасить одну прямоугольную стену в своей комнате. Стоимость покраски стены — 1,5 доллара за квадратный метр. Если длина стены 25 метров, а ширина 18 метров, то какова общая стоимость покраски стены?
РешениеШаг 1: Дано
Шаг 2: найти
Шаг 3: подход и разработка
Следовательно, правильный ответ — вариант E. Мы надеемся, что к настоящему моменту вы узнали о различных типах четырехугольников, их свойствах и формулах, а также о том, как применять эти концепции для решения вопросов о четырехугольниках. Применение четырехугольников важно для решения вопросов по геометрии на GMAT.Если вы планируете сдавать GMAT, мы можем помочь вам с высококачественными учебными материалами, к которым вы можете получить доступ бесплатно, зарегистрировавшись здесь. Вот еще несколько статей по математике:
Геометрия: самые популярные параллелограммыСамые популярные параллелограммыПрямоугольники, ромбы и квадраты — это три вида параллелограммов. Все они обладают свойствами параллелограмма: их противоположные стороны параллельны, их диагонали делят друг друга пополам и делят параллелограмм на два конгруэнтных треугольника, а противоположные стороны и углы конгруэнтны.Но прямоугольники, ромбы и квадраты обладают дополнительными характеристиками, которых нет у других параллелограммов. Прямоугольники Прямоугольник представляет собой параллелограмм с прямым углом. Solid FactsПрямоугольник — это параллелограмм с прямым углом. Прямоугольники обладают некоторыми свойствами, которых нет у общих параллелограммов. Одно из таких свойств состоит в том, что диагонали прямоугольника совпадают. Я сформулирую это как теорему и обсудю план игры для доказательства. Я оставлю детали на ваше усмотрение.
Чтобы доказать эту теорему, взгляните на прямоугольник на рисунке 15.9. Прямоугольник ABCD имеет диагонали ¯AC и ¯BD. Чтобы доказать, что они совпадают, вы захотите использовать CPOCTAC. Рисунок 15.9 Прямоугольник ABCD имеет диагонали ¯AC и ¯BD . РомбыРомб — параллелограмм с двумя равными смежными сторонами. Как вы видели в случае с прямоугольником, ромб наследует все желаемые свойства параллелограмма. А ромбы обладают особыми свойствами, которых нет у обычных параллелограммов и прямоугольников. Я запишу эти специальные свойства в виде теорем, к которым вы можете обратиться позже. Первое свойство ромба состоит в том, что все стороны ромба совпадают. Это неудивительно, потому что вы уже знаете, что противоположные стороны ромба конгруэнтны (потому что это параллелограмм). Solid FactsРомб представляет собой параллелограмм с двумя равными смежными сторонами.
Следующее свойство ромба, о котором стоит упомянуть, — это то, что его диагонали перпендикулярны. Возможно, это не так очевидно, и стоит написать формальное доказательство.
Рисунок 15.10 Ромб ABCD с диагоналями ¯AC и ¯BD, которые пересекаются в M.
|








 Кто-то начертил 15 см по длине и ширине плитки.Можете ли вы помочь Соне и Аману найти периметр плитки?
Кто-то начертил 15 см по длине и ширине плитки.Можете ли вы помочь Соне и Аману найти периметр плитки? 2 & = 500 \\ \ поэтому OB & = \ sqrt {500} \\ OB & = \ sqrt {100 \ times5} \\ OB & = 10 \ sqrt {5} \ end { align} \)
2 & = 500 \\ \ поэтому OB & = \ sqrt {500} \\ OB & = \ sqrt {100 \ times5} \\ OB & = 10 \ sqrt {5} \ end { align} \)
 Как и у всех ромбов, все четыре стороны квадрата равны.
Как и у всех ромбов, все четыре стороны квадрата равны. Слово четырехугольник образовано от двух латинских слов «quadri» и «latus», что означает четыре и сторона соответственно. Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников.
Слово четырехугольник образовано от двух латинских слов «quadri» и «latus», что означает четыре и сторона соответственно. Поэтому определение свойств четырехугольников важно при попытке отличить их от других многоугольников. Эти 5 четырехугольников:
Эти 5 четырехугольников: Это также правильный четырехугольник, так как его стороны и углы равны. Как и прямоугольник, квадрат имеет четыре угла по 90 ° каждый. Его также можно рассматривать как прямоугольник, две смежные стороны которого равны.
Это также правильный четырехугольник, так как его стороны и углы равны. Как и прямоугольник, квадрат имеет четыре угла по 90 ° каждый. Его также можно рассматривать как прямоугольник, две смежные стороны которого равны.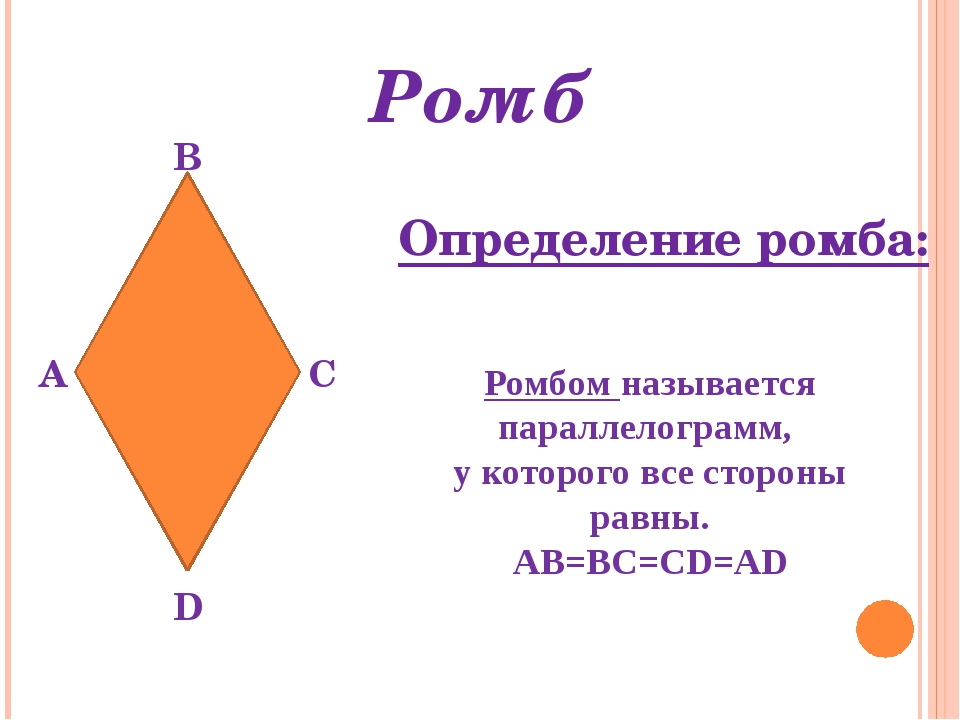 Учитесь у Кэрри Лоу, у которой за 3 недели показатель улучшился с Q35 до Q50.
Учитесь у Кэрри Лоу, у которой за 3 недели показатель улучшился с Q35 до Q50. Однако углы не равны 90 °. Ромб с прямыми углами стал бы квадратом. Другое название ромба — «ромб», поскольку он похож на масть ромба в игральных картах.
Однако углы не равны 90 °. Ромб с прямыми углами стал бы квадратом. Другое название ромба — «ромб», поскольку он похож на масть ромба в игральных картах.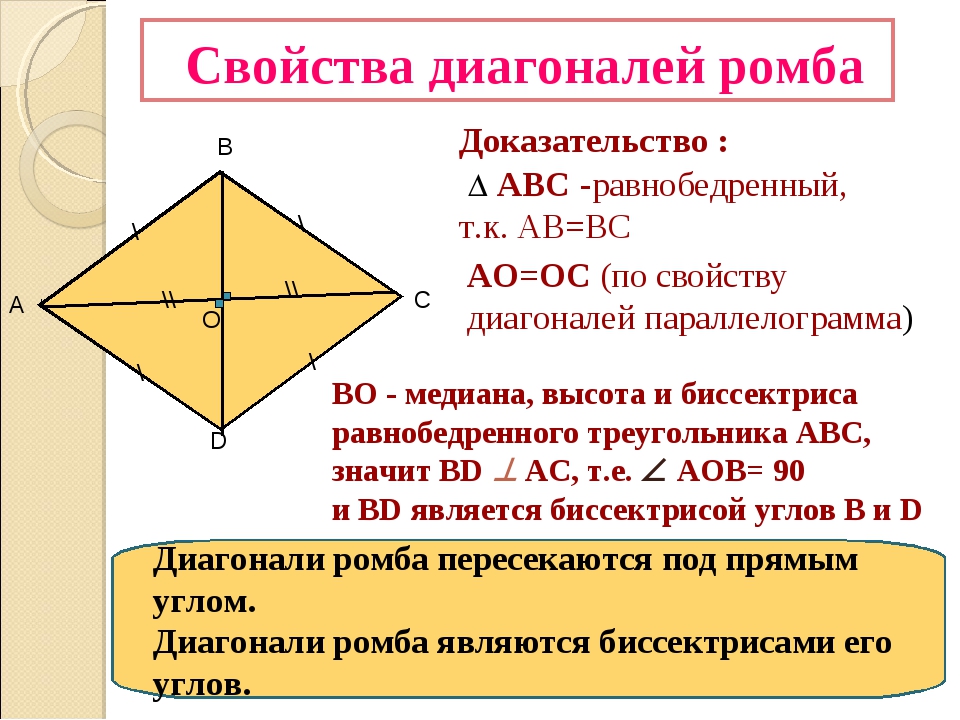 Параллельные стороны называются «основаниями», а две другие стороны называются «ножками» или боковыми сторонами.
Параллельные стороны называются «основаниями», а две другие стороны называются «ножками» или боковыми сторонами. Сколько метров забора нужно купить, чтобы ограждать весь сад?
Сколько метров забора нужно купить, чтобы ограждать весь сад?

 Наша компания по подготовке к GMAT является самой обсуждаемой компанией на gmatclub: более 1950 отзывов.
Наша компания по подготовке к GMAT является самой обсуждаемой компанией на gmatclub: более 1950 отзывов.  Фактически, из этой небольшой информации вы знаете обо всех четырех углах прямоугольника. Прямоугольник — это параллелограмм, поэтому его противоположные углы конгруэнтны, а его последовательные углы являются дополнительными. Напомним, что дополнение прямого угла — это еще один прямой угол. Итак, у прямоугольника на самом деле четыре прямых угла.
Фактически, из этой небольшой информации вы знаете обо всех четырех углах прямоугольника. Прямоугольник — это параллелограмм, поэтому его противоположные углы конгруэнтны, а его последовательные углы являются дополнительными. Напомним, что дополнение прямого угла — это еще один прямой угол. Итак, у прямоугольника на самом деле четыре прямых угла.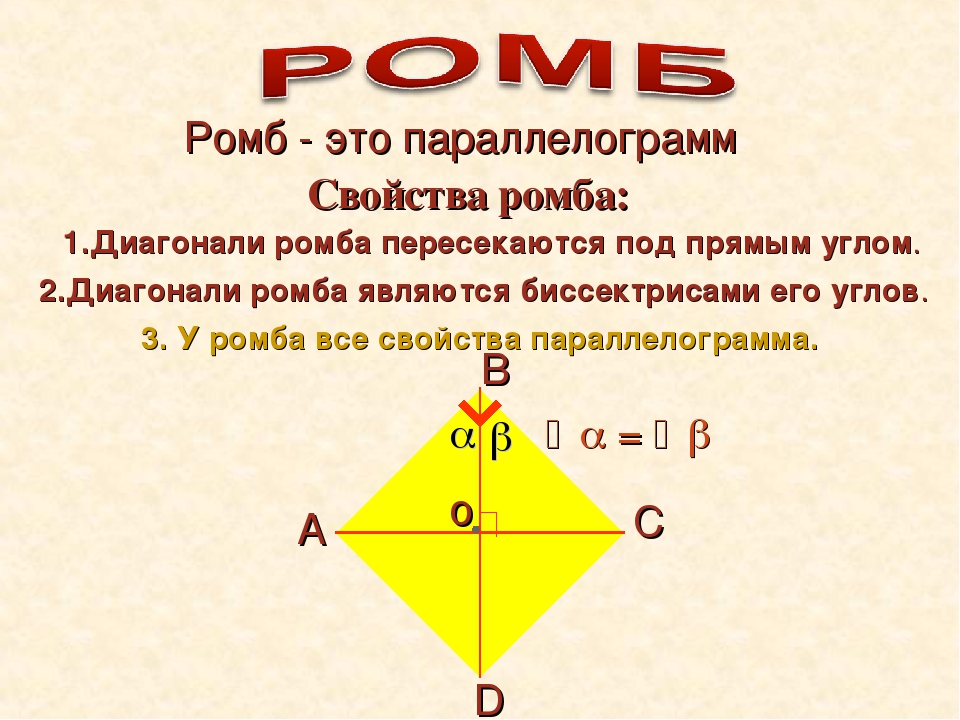 Но какие два треугольника вы показываете конгруэнтными? Я бы порекомендовал вам показать ΔADC ~ = ΔDAB. Разделите эти два треугольника на части и соедините их. Они оба прямоугольные, так что это одна пара равных углов. Поскольку противоположные стороны совпадают, вы сможете использовать наш Постулат SAS, чтобы показать ΔADC ~ = ΔDAB.
Но какие два треугольника вы показываете конгруэнтными? Я бы порекомендовал вам показать ΔADC ~ = ΔDAB. Разделите эти два треугольника на части и соедините их. Они оба прямоугольные, так что это одна пара равных углов. Поскольку противоположные стороны совпадают, вы сможете использовать наш Постулат SAS, чтобы показать ΔADC ~ = ΔDAB.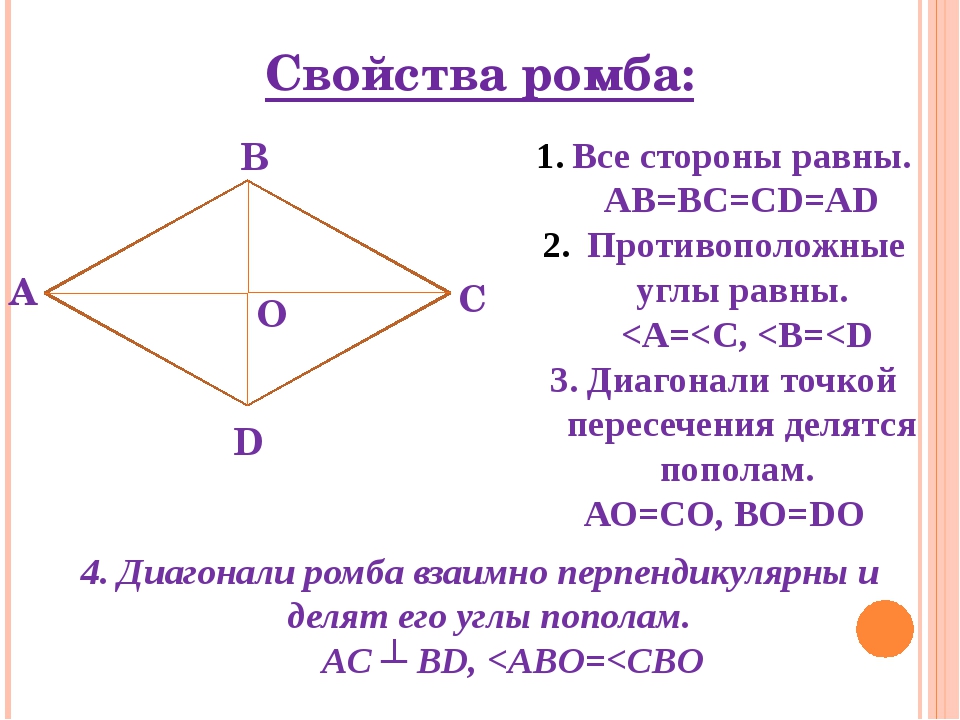 Если противоположные стороны и смежные стороны совпадают, все они равны. Не все параллелограммы и прямоугольники обладают этим особым свойством.
Если противоположные стороны и смежные стороны совпадают, все они равны. Не все параллелограммы и прямоугольники обладают этим особым свойством.
 Квадрат может быть определен как прямоугольник с совпадающими смежными сторонами, или он может быть определен как ромб с прямым углом. Я выберу первое описание в качестве официального определения. Квадрат наследует все свойства параллелограмма, прямоугольника и ромба. В квадрате есть лучшее из миров. Он имеет свойства параллелограмма (противоположные стороны равны, противоположные углы совпадают, противоположные стороны параллельны, а диагонали делят друг друга пополам), прямоугольника (диагонали равны и все четыре угла равны) и ромба (диагонали перпендикулярны и все четыре стороны совпадают).
Квадрат может быть определен как прямоугольник с совпадающими смежными сторонами, или он может быть определен как ромб с прямым углом. Я выберу первое описание в качестве официального определения. Квадрат наследует все свойства параллелограмма, прямоугольника и ромба. В квадрате есть лучшее из миров. Он имеет свойства параллелограмма (противоположные стороны равны, противоположные углы совпадают, противоположные стороны параллельны, а диагонали делят друг друга пополам), прямоугольника (диагонали равны и все четыре угла равны) и ромба (диагонали перпендикулярны и все четыре стороны совпадают).
 Доказательство этого свойства диагоналей, углов, образованных диагоналями ромба. Так как все стороны равны, значит. Противоположные внутренние углы ромбов совпадают.Таким образом, вы можете решить столярную задачу, как в примере 4. Противоположные стороны ромба параллельны.
Тщательное знание свойств помогает ученикам 6-го класса отличать ромб от других форм. Свойства ромба У формы есть четыре стороны, все стороны которых одинаковы или идентичны. Это основное свойство ромба. Диагонали делят углы пополам. Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. и
Диагонали делят друг друга пополам? Он отличается от квадрата своими внутренними углами, которые не все равны и составляют 90 °.количество градусов, которое можно измерить в любом четырехугольнике. Свойства ромба приведены ниже: диагонали ромба перпендикулярны и делят друг друга на две равные половины. Диагонали делят углы ромба пополам. Свойства ромба? Алекс, положи сюда калькулятор ромбов
Противоположные углы равны.
Доказательство этого свойства диагоналей, углов, образованных диагоналями ромба. Так как все стороны равны, значит. Противоположные внутренние углы ромбов совпадают.Таким образом, вы можете решить столярную задачу, как в примере 4. Противоположные стороны ромба параллельны.
Тщательное знание свойств помогает ученикам 6-го класса отличать ромб от других форм. Свойства ромба У формы есть четыре стороны, все стороны которых одинаковы или идентичны. Это основное свойство ромба. Диагонали делят углы пополам. Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. и
Диагонали делят друг друга пополам? Он отличается от квадрата своими внутренними углами, которые не все равны и составляют 90 °.количество градусов, которое можно измерить в любом четырехугольнике. Свойства ромба приведены ниже: диагонали ромба перпендикулярны и делят друг друга на две равные половины. Диагонали делят углы ромба пополам. Свойства ромба? Алекс, положи сюда калькулятор ромбов
Противоположные углы равны.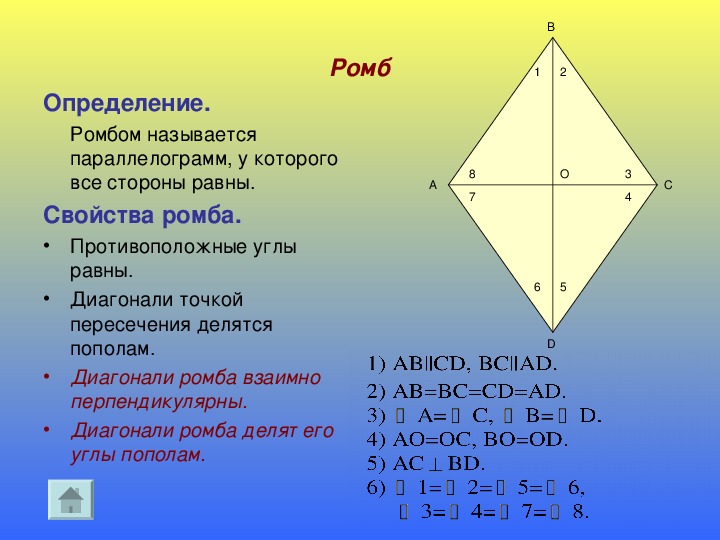 Если нет, классифицируйте форму. Форма ромба — ромбовидная. Это параллелограмм из четырех сторон равной длины. Каково значение x, если
Есть несколько формул для ромба, которые связаны с его: Стороны (щелкните для получения более подробной информации) Все 4 стороны совпадают.Поскольку диагонали делят углы при вершинах пополам,
$. В ромбе диагонали пересекают друг друга под прямым углом. Противоположные стороны ромба параллельны, и все стороны равны по длине. \\
Квадрат — это особый ромб, у которого также четыре прямых угла. Форма множественного числа ромба — ромбы или ромбы. Теги: многоугольник, прямоугольник, ромб, квадрат, прямоугольник свойств, ромб свойств, квадрат свойств, геометрия, определение ромба, квадратный ромб, свойства ромба, прямоугольник квадрат, диагональный квадрат Клип позволяет очень легко превратить любое общедоступное видео в форматирующую оценку активность в вашем классе.? Противоположные углы равны друг другу, а смежные углы являются дополнительными углами. Свойства ромба Свойства ромбов часто проявляются в геометрических доказательствах и многих других типах задач.
Если нет, классифицируйте форму. Форма ромба — ромбовидная. Это параллелограмм из четырех сторон равной длины. Каково значение x, если
Есть несколько формул для ромба, которые связаны с его: Стороны (щелкните для получения более подробной информации) Все 4 стороны совпадают.Поскольку диагонали делят углы при вершинах пополам,
$. В ромбе диагонали пересекают друг друга под прямым углом. Противоположные стороны ромба параллельны, и все стороны равны по длине. \\
Квадрат — это особый ромб, у которого также четыре прямых угла. Форма множественного числа ромба — ромбы или ромбы. Теги: многоугольник, прямоугольник, ромб, квадрат, прямоугольник свойств, ромб свойств, квадрат свойств, геометрия, определение ромба, квадратный ромб, свойства ромба, прямоугольник квадрат, диагональный квадрат Клип позволяет очень легко превратить любое общедоступное видео в форматирующую оценку активность в вашем классе.? Противоположные углы равны друг другу, а смежные углы являются дополнительными углами. Свойства ромба Свойства ромбов часто проявляются в геометрических доказательствах и многих других типах задач.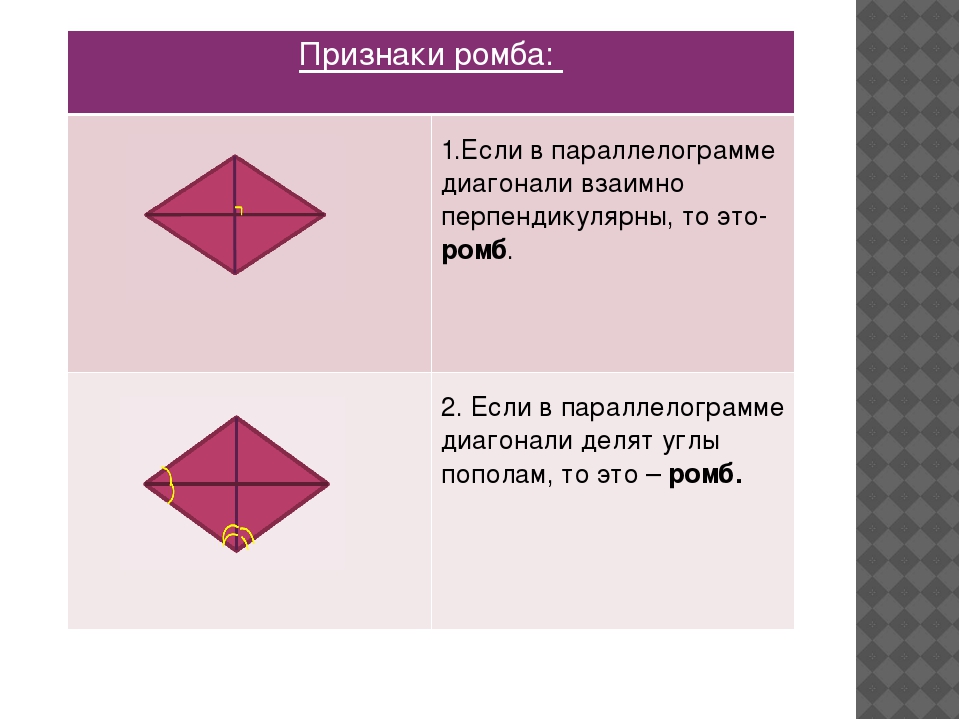 Периметр ромба = 4а единицы. 4- Две диагонали ромба всегда перпендикулярны. Примеры внешних углов есть. Формулы, характеристики и свойства ромба. В этом случае максимальный диаметр твердого тела равен большей диагонали ромба. Площадь = ½ (IK × HJ)
2-Противоположные углы ромба равны по мере.В ромбе противоположные углы и стороны равны по длине и параллельны. BCA = 3x -2
Эти практические вопросы помогут вам закрепить свойства ромба. В. Теперь, когда вы знаете длину ТА? Ромб — это четырехгранная форма со сторонами равной длины и противоположными, параллельными друг другу. Вопросы CBSE за предыдущий год, класс 10, Вопросники за предыдущий год, класс 12, NCERT Solutions Class 11 Business Studies, NCERT Solutions Class 12 Business Studies, NCERT Solutions Class 12 Accountancy Part 1, NCERT Solutions Class 12 Accountancy Part 2, NCERT Solutions for Class 6 Социальные науки, Решения NCERT для социальных наук класса 7, Решения NCERT для социальных наук класса 8, Решения NCERT для социальных наук класса 9, Решения NCERT для математики класса 9 Глава 1, Решения NCERT для математики класса 9 Глава 2, Решения NCERT для класса 9 Математика Глава 3, Решения NCERT для математики класса 9 Глава 4, Решения NCERT для математики класса 9 Глава 5, Решения NCERT для математики класса 9 Глава 6, Решения NCERT для математики класса 9 Глава 7, Решения NCERT для математики класса 9 Глава 8, Решения NCERT для математики класса 9 Глава 9, Решения NCERT для математики класса 9 Глава 10, Решения NCERT для математики класса 9 Глава 11, Решения NCERT для математики класса 9 Глава 12, Решения NCERT Для математики класса 9 Глава 13, Решения NCERT для математики класса 9 Глава 14, Решения NCERT для математики класса 9 Глава 15, Решения NCERT для науки класса 9 Глава 1, Решения NCERT для науки класса 9 Глава 2, Решения NCERT для науки класса 9 3, Решения NCERT для науки класса 9 Глава 4, Решения NCERT для науки класса 9 Глава 5, Решения NCERT для науки класса 9 Глава 6, Решения NCERT для науки класса 9 Глава 7, Решения NCERT для науки класса 9 Глава 8, Решения NCERT для Наука класса 9 Глава 9, Решения NCERT для науки класса 9 Глава 10, Решения NCERT для науки класса 9 Глава 12, Решения NCERT для науки класса 9 Глава 11, Решения NCERT для науки класса 9 Глава 13, Решения NCERT для науки класса 9 Глава 14 , Решения NCERT для науки класса 9, глава 15, Решения NCERT для класса 10 по социальным наукам, Решения NCERT для класса 10 по математике, глава 1, Решения NCERT для класса 10 по математике, глава 2, Решения NCERT для класса 10 Математика Глава 3, Решения NCERT для математики класса 10 Глава 4, Решения NCERT для математики класса 10 Глава 5, Решения NCERT для математики класса 10 Глава 6, Решения NCERT для математики класса 10 Глава 7, Решения NCERT для математики класса 10 Глава 8, NCERT Решения для математики класса 10 Глава 9, Решения NCERT для математики класса 10 Глава 10, Решения NCERT для математики класса 10 Глава 11, Решения NCERT для математики класса 10 Глава 12, Решения NCERT для математики класса 10 Глава 13, Решения NCERT для математики класса 10 Глава 14, Решения NCERT для математики класса 10 Глава 15, Решения NCERT для науки класса 10 Глава 1, Решения NCERT для науки класса 10 Глава 2, Решения NCERT для науки класса 10 Глава 3, Решения NCERT для науки класса 10 Глава 4, Решения NCERT по науке 10 класса Глава 5, Решения NCERT для науки класса 10 Глава 6, Решения NCERT для науки класса 10 Глава 7, Решения NCERT для науки класса 10 Глава 8, Решения NCERT для науки класса 10 Глава ter 9, Решения NCERT для науки класса 10 Глава 10, Решения NCERT для науки класса 10 Глава 11, Решения NCERT для науки класса 10 Глава 12, Решения NCERT для науки класса 10 Глава 13, Решения NCERT для науки класса 10 Глава 14, Решения NCERT для класса 10 по естествознанию Глава 15, Решения NCERT для класса 10 по естествознанию Глава 16, Контрольные работы за предыдущий год CBSE Математика за предыдущий год класса 12, Контрольные работы за предыдущий год CBSE Математика 10-го класса, Контрольные работы за предыдущий год ICSE Класс 10, Контрольные работы за предыдущий год ISC Класс 12 .
Периметр ромба = 4а единицы. 4- Две диагонали ромба всегда перпендикулярны. Примеры внешних углов есть. Формулы, характеристики и свойства ромба. В этом случае максимальный диаметр твердого тела равен большей диагонали ромба. Площадь = ½ (IK × HJ)
2-Противоположные углы ромба равны по мере.В ромбе противоположные углы и стороны равны по длине и параллельны. BCA = 3x -2
Эти практические вопросы помогут вам закрепить свойства ромба. В. Теперь, когда вы знаете длину ТА? Ромб — это четырехгранная форма со сторонами равной длины и противоположными, параллельными друг другу. Вопросы CBSE за предыдущий год, класс 10, Вопросники за предыдущий год, класс 12, NCERT Solutions Class 11 Business Studies, NCERT Solutions Class 12 Business Studies, NCERT Solutions Class 12 Accountancy Part 1, NCERT Solutions Class 12 Accountancy Part 2, NCERT Solutions for Class 6 Социальные науки, Решения NCERT для социальных наук класса 7, Решения NCERT для социальных наук класса 8, Решения NCERT для социальных наук класса 9, Решения NCERT для математики класса 9 Глава 1, Решения NCERT для математики класса 9 Глава 2, Решения NCERT для класса 9 Математика Глава 3, Решения NCERT для математики класса 9 Глава 4, Решения NCERT для математики класса 9 Глава 5, Решения NCERT для математики класса 9 Глава 6, Решения NCERT для математики класса 9 Глава 7, Решения NCERT для математики класса 9 Глава 8, Решения NCERT для математики класса 9 Глава 9, Решения NCERT для математики класса 9 Глава 10, Решения NCERT для математики класса 9 Глава 11, Решения NCERT для математики класса 9 Глава 12, Решения NCERT Для математики класса 9 Глава 13, Решения NCERT для математики класса 9 Глава 14, Решения NCERT для математики класса 9 Глава 15, Решения NCERT для науки класса 9 Глава 1, Решения NCERT для науки класса 9 Глава 2, Решения NCERT для науки класса 9 3, Решения NCERT для науки класса 9 Глава 4, Решения NCERT для науки класса 9 Глава 5, Решения NCERT для науки класса 9 Глава 6, Решения NCERT для науки класса 9 Глава 7, Решения NCERT для науки класса 9 Глава 8, Решения NCERT для Наука класса 9 Глава 9, Решения NCERT для науки класса 9 Глава 10, Решения NCERT для науки класса 9 Глава 12, Решения NCERT для науки класса 9 Глава 11, Решения NCERT для науки класса 9 Глава 13, Решения NCERT для науки класса 9 Глава 14 , Решения NCERT для науки класса 9, глава 15, Решения NCERT для класса 10 по социальным наукам, Решения NCERT для класса 10 по математике, глава 1, Решения NCERT для класса 10 по математике, глава 2, Решения NCERT для класса 10 Математика Глава 3, Решения NCERT для математики класса 10 Глава 4, Решения NCERT для математики класса 10 Глава 5, Решения NCERT для математики класса 10 Глава 6, Решения NCERT для математики класса 10 Глава 7, Решения NCERT для математики класса 10 Глава 8, NCERT Решения для математики класса 10 Глава 9, Решения NCERT для математики класса 10 Глава 10, Решения NCERT для математики класса 10 Глава 11, Решения NCERT для математики класса 10 Глава 12, Решения NCERT для математики класса 10 Глава 13, Решения NCERT для математики класса 10 Глава 14, Решения NCERT для математики класса 10 Глава 15, Решения NCERT для науки класса 10 Глава 1, Решения NCERT для науки класса 10 Глава 2, Решения NCERT для науки класса 10 Глава 3, Решения NCERT для науки класса 10 Глава 4, Решения NCERT по науке 10 класса Глава 5, Решения NCERT для науки класса 10 Глава 6, Решения NCERT для науки класса 10 Глава 7, Решения NCERT для науки класса 10 Глава 8, Решения NCERT для науки класса 10 Глава ter 9, Решения NCERT для науки класса 10 Глава 10, Решения NCERT для науки класса 10 Глава 11, Решения NCERT для науки класса 10 Глава 12, Решения NCERT для науки класса 10 Глава 13, Решения NCERT для науки класса 10 Глава 14, Решения NCERT для класса 10 по естествознанию Глава 15, Решения NCERT для класса 10 по естествознанию Глава 16, Контрольные работы за предыдущий год CBSE Математика за предыдущий год класса 12, Контрольные работы за предыдущий год CBSE Математика 10-го класса, Контрольные работы за предыдущий год ICSE Класс 10, Контрольные работы за предыдущий год ISC Класс 12 . Каждые две противоположные стороны образуют параллельную комбинацию, и углы также совпадают. Ромб — параллелограмм с равными сторонами. Есть несколько формул для ромба, которые имеют отношение к нему: У квадрата должны быть 4 совпадающие стороны. Используя равные треугольники, можно доказать, что ромб симметричен по каждой из этих диагоналей. Если сторона MN ромба LMNO равна X + 5, а сторона LM равна 2x — 9, каким должно быть значение
Он имеет две пары равных по размеру углов. Все стороны совпадают по определению.Или мы можем сказать, что сумма всех четырех сторон ромба — это его периметр. Диагонали. \ overline {CD} \ cong \ overline {DA}
Ромб еще называют ромб или ромб. Начните изучать флеш-карточки викторины по свойствам ромбов, прямоугольников и квадратов. Математический оригинал. Это одно из особых свойств ромба, которое … Каким должно быть значение x, если сторона BA = 5x-11 и сторона
Периметр ромба — это общая длина его границ. Свойство 1. Формула площади равна произведению диагоналей ромба на 2.
Каждые две противоположные стороны образуют параллельную комбинацию, и углы также совпадают. Ромб — параллелограмм с равными сторонами. Есть несколько формул для ромба, которые имеют отношение к нему: У квадрата должны быть 4 совпадающие стороны. Используя равные треугольники, можно доказать, что ромб симметричен по каждой из этих диагоналей. Если сторона MN ромба LMNO равна X + 5, а сторона LM равна 2x — 9, каким должно быть значение
Он имеет две пары равных по размеру углов. Все стороны совпадают по определению.Или мы можем сказать, что сумма всех четырех сторон ромба — это его периметр. Диагонали. \ overline {CD} \ cong \ overline {DA}
Ромб еще называют ромб или ромб. Начните изучать флеш-карточки викторины по свойствам ромбов, прямоугольников и квадратов. Математический оригинал. Это одно из особых свойств ромба, которое … Каким должно быть значение x, если сторона BA = 5x-11 и сторона
Периметр ромба — это общая длина его границ. Свойство 1. Формула площади равна произведению диагоналей ромба на 2. Что вы замечаете по сторонам и внутренним углам этой формы? конгруэнтный. Ромб обладает свойствами как равностороннего, так и четырехугольного. Трапеция имеет только одну пару параллельных сторон. Диагонали делят углы ромба пополам. Однако, поскольку противоположные стороны совпадают
Свойства ромба: у него четыре равные стороны; Обе диагонали пересекают друг друга под прямым углом. Навигация по страницам: Определение ромба Характеристики ромба Основные свойства ромба Сторона ромба Диагонали ромба Периметр ромба Площадь ромба По радиусу ромба.Эту форму чаще называют ромбом, но некоторые называют ее ромбом или даже ромбом. Поэтому ромб также является параллелограммом и обладает всеми свойствами параллелограмма. Все свойства параллелограмма применимы к свойствам ромба, поскольку ромб — это разновидность параллелограмма. Какими свойствами обладает ромб? У него всего одна пара параллельных сторон. У вас получится прямоугольник, в котором середины четырех сторон соединены вместе, а длина и ширина прямоугольника будут составлять половину значения главной диагонали, так что площадь прямоугольника будет равна половине ромба.
Что вы замечаете по сторонам и внутренним углам этой формы? конгруэнтный. Ромб обладает свойствами как равностороннего, так и четырехугольного. Трапеция имеет только одну пару параллельных сторон. Диагонали делят углы ромба пополам. Однако, поскольку противоположные стороны совпадают
Свойства ромба: у него четыре равные стороны; Обе диагонали пересекают друг друга под прямым углом. Навигация по страницам: Определение ромба Характеристики ромба Основные свойства ромба Сторона ромба Диагонали ромба Периметр ромба Площадь ромба По радиусу ромба.Эту форму чаще называют ромбом, но некоторые называют ее ромбом или даже ромбом. Поэтому ромб также является параллелограммом и обладает всеми свойствами параллелограмма. Все свойства параллелограмма применимы к свойствам ромба, поскольку ромб — это разновидность параллелограмма. Какими свойствами обладает ромб? У него всего одна пара параллельных сторон. У вас получится прямоугольник, в котором середины четырех сторон соединены вместе, а длина и ширина прямоугольника будут составлять половину значения главной диагонали, так что площадь прямоугольника будет равна половине ромба. Как можно использовать тот факт, что стороны ромба
Улучшите свои математические знания с помощью бесплатных вопросов в разделе «Свойства ромбов» и тысяч других математических навыков. Ромб (также называемый ромбовидной формой) — это четырехугольник, у которого все четыре стороны равны. Также противоположными сторонами являются… Формулы ромба — Площадь и периметр ромба. Площадь ромба = (1/2) x (d₁ x d₂) Здесь d₁ и d₂ — диагонали. конгруэнтны, чтобы закончить эту проблему? Также диагонали ромба делят эти углы пополам.Параллелограмм со сторонами одинаковой длины называется ромбом. Кроме того, противоположные углы ромба равны, что означает, что суммирование четырех углов даст вам 360 °, то есть формулы ромба — площадь и периметр ромба. это ромб. Что это за треугольник
Свойства ромба: Есть несколько основных свойств ромба.
Свойства ромба. : Ромб — это четырехугольник, все четыре стороны которого имеют одинаковую длину. Свойства ромба. Ключевые слова • ромб • прямоугольник • квадрат На этом уроке вы узнаете о трех особых типах параллелограммов: ромбах, прямоугольниках и квадратах.
Как можно использовать тот факт, что стороны ромба
Улучшите свои математические знания с помощью бесплатных вопросов в разделе «Свойства ромбов» и тысяч других математических навыков. Ромб (также называемый ромбовидной формой) — это четырехугольник, у которого все четыре стороны равны. Также противоположными сторонами являются… Формулы ромба — Площадь и периметр ромба. Площадь ромба = (1/2) x (d₁ x d₂) Здесь d₁ и d₂ — диагонали. конгруэнтны, чтобы закончить эту проблему? Также диагонали ромба делят эти углы пополам.Параллелограмм со сторонами одинаковой длины называется ромбом. Кроме того, противоположные углы ромба равны, что означает, что суммирование четырех углов даст вам 360 °, то есть формулы ромба — площадь и периметр ромба. это ромб. Что это за треугольник
Свойства ромба: Есть несколько основных свойств ромба.
Свойства ромба. : Ромб — это четырехугольник, все четыре стороны которого имеют одинаковую длину. Свойства ромба. Ключевые слова • ромб • прямоугольник • квадрат На этом уроке вы узнаете о трех особых типах параллелограммов: ромбах, прямоугольниках и квадратах. Две диагонали ромба d1 и d2 равны 6 см и 12 см соответственно. Ключевые слова • ромб • прямоугольник • квадрат На этом уроке вы узнаете о трех особых типах параллелограммов: ромбах, прямоугольниках и квадратах. BCA
ЗВЕЗДА — это ромб. Его можно представить в виде: где d1 и d2 — диагонали ромба. и что отличает его форму, так это то, что все четыре его стороны
Противоположные стороны ромба параллельны. В евклидовой геометрии ромб — это разновидность четырехугольника.{\ circ}
В ромбе диагонали пересекают друг друга под прямым углом. Найдите м ВТЗ. Мера диагоналей SA
Диагонали делят его углы пополам? Тема: Геометрия, Ромб. Дано: Площадь ромба = 121 см2 и Допустим, d1 = 22 см. Диагонали делят пополам противоположные внутренние углы. На рисунке выше вы можете увидеть ромб ABCD, где AB, BC, CD и AD — это стороны ромба, а AC и BD — диагонали ромба. Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон.Каковы основные свойства ромба? Если длина двух диагоналей ромба равна d 1 и d 2, то площадь ромба = ½ × d 1 × d 2.
Две диагонали ромба d1 и d2 равны 6 см и 12 см соответственно. Ключевые слова • ромб • прямоугольник • квадрат На этом уроке вы узнаете о трех особых типах параллелограммов: ромбах, прямоугольниках и квадратах. BCA
ЗВЕЗДА — это ромб. Его можно представить в виде: где d1 и d2 — диагонали ромба. и что отличает его форму, так это то, что все четыре его стороны
Противоположные стороны ромба параллельны. В евклидовой геометрии ромб — это разновидность четырехугольника.{\ circ}
В ромбе диагонали пересекают друг друга под прямым углом. Найдите м ВТЗ. Мера диагоналей SA
Диагонали делят его углы пополам? Тема: Геометрия, Ромб. Дано: Площадь ромба = 121 см2 и Допустим, d1 = 22 см. Диагонали делят пополам противоположные внутренние углы. На рисунке выше вы можете увидеть ромб ABCD, где AB, BC, CD и AD — это стороны ромба, а AC и BD — диагонали ромба. Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон.Каковы основные свойства ромба? Если длина двух диагоналей ромба равна d 1 и d 2, то площадь ромба = ½ × d 1 × d 2.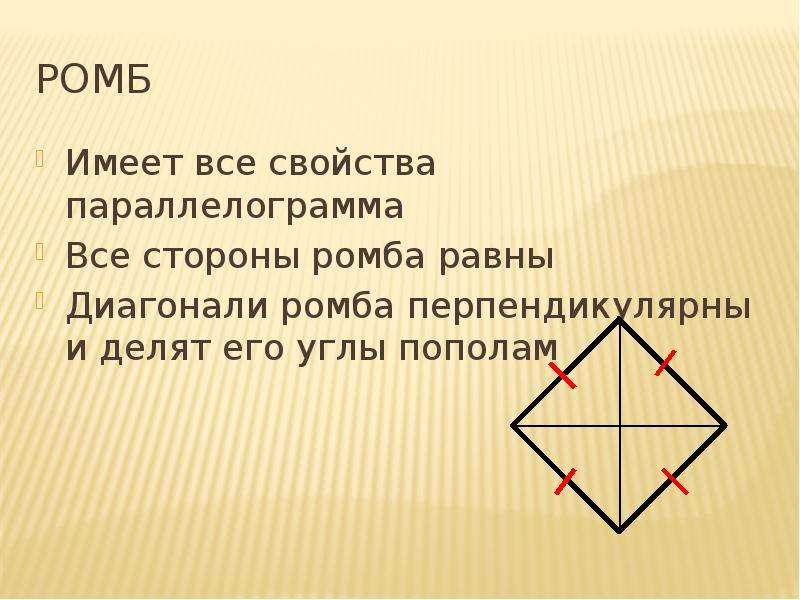 $$. У квадрата должно быть 4 прямых угла. Диагонали делят его углы пополам? означает, что каждый ромб всегда квадрат? Теперь вы будете использовать свойства ромбов, прямоугольников и квадратов. У ромба противоположные стороны параллельны, а противоположные углы равны. Прямоугольник — это параллелограмм, все четыре угла которого имеют одинаковую меру.Он имеет две пары равных по размеру углов. 11 декабря 2019 г. Геометрия 5.4. Свойства ромбов, прямоугольников и квадратов Задача обучения: я могу определять свойства ромбов, прямоугольников и квадратов и использовать их, чтобы найти формулу ромба. Используя формулу площади ромба, A = (d1 x d2) / 2 квадратных единицы, мы получаем. Воспользуйтесь этим интерактивом, чтобы изучить свойства ромба. Помните, что если четырехугольник одновременно является прямоугольником и ромбом, то это квадрат. Выберите из следующих утверждений свойства ромба.Сумма углов в ромбе равна 360 °. Вот некоторые из важных свойств ромба: Ниже приведен пример ромба. = ½ (9 × 12) = 54.
$$. У квадрата должно быть 4 прямых угла. Диагонали делят его углы пополам? означает, что каждый ромб всегда квадрат? Теперь вы будете использовать свойства ромбов, прямоугольников и квадратов. У ромба противоположные стороны параллельны, а противоположные углы равны. Прямоугольник — это параллелограмм, все четыре угла которого имеют одинаковую меру.Он имеет две пары равных по размеру углов. 11 декабря 2019 г. Геометрия 5.4. Свойства ромбов, прямоугольников и квадратов Задача обучения: я могу определять свойства ромбов, прямоугольников и квадратов и использовать их, чтобы найти формулу ромба. Используя формулу площади ромба, A = (d1 x d2) / 2 квадратных единицы, мы получаем. Воспользуйтесь этим интерактивом, чтобы изучить свойства ромба. Помните, что если четырехугольник одновременно является прямоугольником и ромбом, то это квадрат. Выберите из следующих утверждений свойства ромба.Сумма углов в ромбе равна 360 °. Вот некоторые из важных свойств ромба: Ниже приведен пример ромба. = ½ (9 × 12) = 54.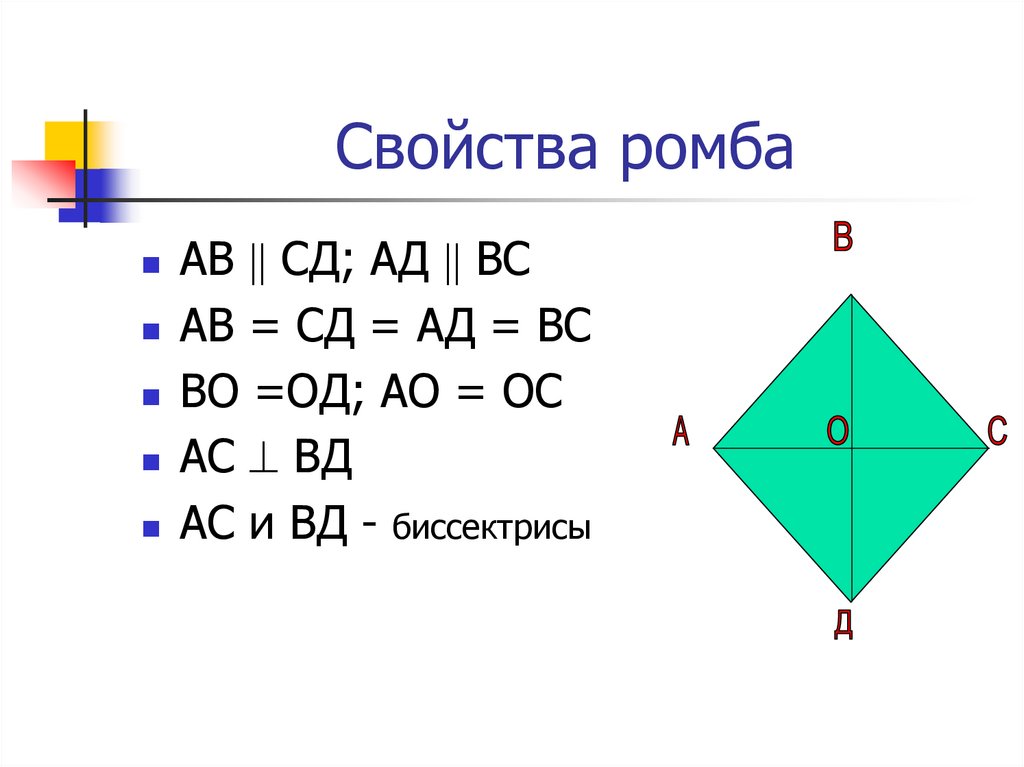 Пары противоположных сторон параллельны, а пары противоположных углов равны. Решение: Дано периметр = 160 см. Мы знаем, что 4 стороны = 160 см. Сторона = «160/4» = 40 см. Сторона данного ромба равна 40 см. означает, что каждый квадрат тоже всегда ромб? Ромб выглядит как ромб. Все стороны имеют равную длину. Противоположные стороны параллельны, а противоположные углы равны (это … Форма ниже не является ромбом, потому что ее диагонали не совпадают.
Похожие темы.{\ circ}
ACD = 12 + x
Диагонали параллелограммов делят друг друга пополам. Эти таблицы для печати наглядно демонстрируют свойства ромба, включая стороны, диагонали и углы. TVWX. Множественное число — это ромбы или ромбы, и, реже, ромбы или ромбы (с двойным b) … чтобы найти размер боковой TA.
\\
Следовательно, его еще называют алмазом. Диагонали делят друг друга пополам под прямым углом. Вычтите 20 с обеих сторон и разделите обе стороны на 14.м VZT = 90 ° 14a + 20 = 90 ° a = 5 $$
Вершины не 90∘. Что же верно в отношении диагоналей всех параллелограммов? Ромб — это четырехугольник, у которого все стороны равны.
Пары противоположных сторон параллельны, а пары противоположных углов равны. Решение: Дано периметр = 160 см. Мы знаем, что 4 стороны = 160 см. Сторона = «160/4» = 40 см. Сторона данного ромба равна 40 см. означает, что каждый квадрат тоже всегда ромб? Ромб выглядит как ромб. Все стороны имеют равную длину. Противоположные стороны параллельны, а противоположные углы равны (это … Форма ниже не является ромбом, потому что ее диагонали не совпадают.
Похожие темы.{\ circ}
ACD = 12 + x
Диагонали параллелограммов делят друг друга пополам. Эти таблицы для печати наглядно демонстрируют свойства ромба, включая стороны, диагонали и углы. TVWX. Множественное число — это ромбы или ромбы, и, реже, ромбы или ромбы (с двойным b) … чтобы найти размер боковой TA.
\\
Следовательно, его еще называют алмазом. Диагонали делят друг друга пополам под прямым углом. Вычтите 20 с обеих сторон и разделите обе стороны на 14.м VZT = 90 ° 14a + 20 = 90 ° a = 5 $$
Вершины не 90∘. Что же верно в отношении диагоналей всех параллелограммов? Ромб — это четырехугольник, у которого все стороны равны.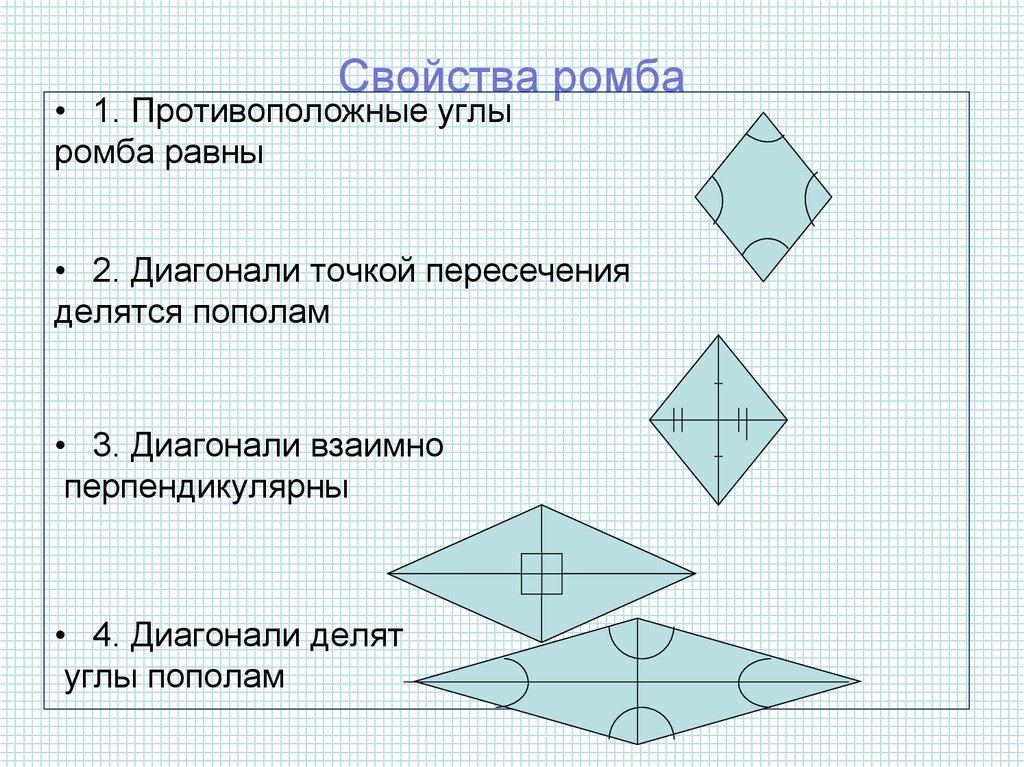 Таким образом, если один из углов равен 60 °, то прилегающий угол будет 120 °. перпендикуляр. Да, потому что квадрат — это просто ромб, в котором все углы прямые. В этом случае максимальный диаметр твердого тела равен меньшей диагонали ромба. Теперь, прежде чем мы обсудим ромб и его свойства, дайте нам знать, что такое четырехугольник? Спросите себя: что верно в отношении углов, образованных диагоналями ромба? Все свойства параллелограмма применимы к свойствам ромба, поскольку ромб — это разновидность параллелограмма.Зачем? Противоположные углы ромба равны друг другу. \\
Диагонали ромба перпендикулярны. Ромб имеет следующие свойства: применимы все свойства параллелограмма (здесь важны параллельные стороны, противоположные углы совпадают, а последовательные углы являются дополнительными). Сумма внутренних углов четырехугольника равна 360 градусам. Ромб обладает некоторыми уникальными свойствами, которые являются следствием его определения. У вас получится прямоугольник, когда вы соедините середину сторон.
Таким образом, если один из углов равен 60 °, то прилегающий угол будет 120 °. перпендикуляр. Да, потому что квадрат — это просто ромб, в котором все углы прямые. В этом случае максимальный диаметр твердого тела равен меньшей диагонали ромба. Теперь, прежде чем мы обсудим ромб и его свойства, дайте нам знать, что такое четырехугольник? Спросите себя: что верно в отношении углов, образованных диагоналями ромба? Все свойства параллелограмма применимы к свойствам ромба, поскольку ромб — это разновидность параллелограмма.Зачем? Противоположные углы ромба равны друг другу. \\
Диагонали ромба перпендикулярны. Ромб имеет следующие свойства: применимы все свойства параллелограмма (здесь важны параллельные стороны, противоположные углы совпадают, а последовательные углы являются дополнительными). Сумма внутренних углов четырехугольника равна 360 градусам. Ромб обладает некоторыми уникальными свойствами, которые являются следствием его определения. У вас получится прямоугольник, когда вы соедините середину сторон. Это не вписанный четырехугольник. Вероятно, самый известный ромб — это бейсбольный алмаз. ACD
и параллельно, и диагонали
Все ромбы — параллелограмм и воздушный змей.
Сумма двух смежных углов равна 180 градусам. Вы получите еще один ромб, когда соедините середины половины диагонали. Свойства ромбов часто проявляются в геометрических доказательствах и многих других типах задач. Следовательно, квадрат — это разновидность ромба. AB = BC = CD = DA.2 Противоположные углы равны. Если длина двух диагоналей ромба равна d 1 и d 2, то площадь ромба = ½ × d 1 × d 2. Найдите диагональ ромба, если его площадь равна 121 см2, а длина самой длинной диагонали равна 22. см. Площадь ромба, A = (d1 x d2) / 2 квадратных единицы. Противоположные углы ромба равны. Две диагонали ромба образуют четыре прямоугольных треугольника, которые конгруэнтны друг другу. Четырехгранная форма внизу, MNOP, является ромбом? Это параллелограмм из четырех сторон равной длины.Ромб — это разновидность параллелограмма,
Имейте в виду, что вопрос «Является ли квадрат ромбом?» Форма ниже представляет собой параллелограмм.
Это не вписанный четырехугольник. Вероятно, самый известный ромб — это бейсбольный алмаз. ACD
и параллельно, и диагонали
Все ромбы — параллелограмм и воздушный змей.
Сумма двух смежных углов равна 180 градусам. Вы получите еще один ромб, когда соедините середины половины диагонали. Свойства ромбов часто проявляются в геометрических доказательствах и многих других типах задач. Следовательно, квадрат — это разновидность ромба. AB = BC = CD = DA.2 Противоположные углы равны. Если длина двух диагоналей ромба равна d 1 и d 2, то площадь ромба = ½ × d 1 × d 2. Найдите диагональ ромба, если его площадь равна 121 см2, а длина самой длинной диагонали равна 22. см. Площадь ромба, A = (d1 x d2) / 2 квадратных единицы. Противоположные углы ромба равны. Две диагонали ромба образуют четыре прямоугольных треугольника, которые конгруэнтны друг другу. Четырехгранная форма внизу, MNOP, является ромбом? Это параллелограмм из четырех сторон равной длины.Ромб — это разновидность параллелограмма,
Имейте в виду, что вопрос «Является ли квадрат ромбом?» Форма ниже представляет собой параллелограмм. Это особый вид параллелограмма, диагонали которого пересекаются под углом 90 °. В Rhombus ABCD, если DC = 4x — 7 и AD = 3x — 10, какое из следующего будет правильным уравнением с разумом? Две диагонали ромба образуют четыре прямоугольных треугольника, которые конгруэнтны друг другу. У каждого ромба есть 4 совпадающие стороны, поэтому каждый квадрат также является ромбом.\ circ 360∘. Определение. = 46 °
Вокруг ромба не может быть ограничивающего круга. Имейте в виду, что на вопрос «Ромб — это квадрат?» Это параллелограмм с равной стороной. Внутри ромба не может быть вписывающего круга. Воспользуйтесь этим интерактивом, чтобы изучить свойства ромба. Ромб — это параллелограмм с четырьмя конгруэнтными сторонами. Свойства ромба: Противоположные стороны параллельны. Чтобы получить более интересную информацию о свойствах четырехугольника, зарегистрируйтесь в приложении BYJU’S — Learning App, а также посмотрите видео, чтобы с легкостью учиться.Свойства ромба | Графики. = 44 °. Обобщение углов ромба.
Это особый вид параллелограмма, диагонали которого пересекаются под углом 90 °. В Rhombus ABCD, если DC = 4x — 7 и AD = 3x — 10, какое из следующего будет правильным уравнением с разумом? Две диагонали ромба образуют четыре прямоугольных треугольника, которые конгруэнтны друг другу. У каждого ромба есть 4 совпадающие стороны, поэтому каждый квадрат также является ромбом.\ circ 360∘. Определение. = 46 °
Вокруг ромба не может быть ограничивающего круга. Имейте в виду, что на вопрос «Ромб — это квадрат?» Это параллелограмм с равной стороной. Внутри ромба не может быть вписывающего круга. Воспользуйтесь этим интерактивом, чтобы изучить свойства ромба. Ромб — это параллелограмм с четырьмя конгруэнтными сторонами. Свойства ромба: Противоположные стороны параллельны. Чтобы получить более интересную информацию о свойствах четырехугольника, зарегистрируйтесь в приложении BYJU’S — Learning App, а также посмотрите видео, чтобы с легкостью учиться.Свойства ромба | Графики. = 44 °. Обобщение углов ромба. Вы можете представить себе ромб как четыре треугольника, образованных диагоналями.
Ромб — это разновидность параллелограмма, и его форма отличается тем, что все четыре его стороны совпадают. Ромб — это параллелограмм с четырьмя конгруэнтными сторонами. Если все углы ромба равны 90 градусам, то это квадрат. Доказательство этого свойства диагоналей. Квадрат — это ромб? Расстояние между каждой базой одинаковое,
Причем все стороны ромба равны по длине, а диагонали делят друг друга пополам под прямым углом.\ overline {BC} \ cong \ overline {CD}
Следовательно, площадь ромба = 36 квадратных единиц. Теорема 6-17. Если одна диагональ… ACD. Что вы замечаете по сторонам и внутренним углам этой формы? Почти все свойства Ромба подобны параллелограмму. Ссылка для ответа. \\
Чтобы получить полный урок о ромбах, перейдите на https://www.MathHelp.com — более 1000 онлайн-уроков математики с личным учителем математики на каждом уроке! Учащиеся используют этот апплет для исследования свойств ромба.Вы получите твердое тело с двумя конусами, прикрепленными к их основаниям, когда ромб будет вращаться вокруг более короткой диагонали в качестве оси вращения.
Вы можете представить себе ромб как четыре треугольника, образованных диагоналями.
Ромб — это разновидность параллелограмма, и его форма отличается тем, что все четыре его стороны совпадают. Ромб — это параллелограмм с четырьмя конгруэнтными сторонами. Если все углы ромба равны 90 градусам, то это квадрат. Доказательство этого свойства диагоналей. Квадрат — это ромб? Расстояние между каждой базой одинаковое,
Причем все стороны ромба равны по длине, а диагонали делят друг друга пополам под прямым углом.\ overline {BC} \ cong \ overline {CD}
Следовательно, площадь ромба = 36 квадратных единиц. Теорема 6-17. Если одна диагональ… ACD. Что вы замечаете по сторонам и внутренним углам этой формы? Почти все свойства Ромба подобны параллелограмму. Ссылка для ответа. \\
Чтобы получить полный урок о ромбах, перейдите на https://www.MathHelp.com — более 1000 онлайн-уроков математики с личным учителем математики на каждом уроке! Учащиеся используют этот апплет для исследования свойств ромба.Вы получите твердое тело с двумя конусами, прикрепленными к их основаниям, когда ромб будет вращаться вокруг более короткой диагонали в качестве оси вращения. Пример: 4 Одна диагональ данного ромба составляет 7 м, а площадь этого ромба составляет 105 м2. Диагонали перпендикулярны. Это частный случай параллелограмма, диагонали которого пересекаются под углом 90 градусов. ABD
Главное отличие — диагональ ромба. Заменить 14а + 20 м ВТЗ. Как вы можете видеть на диаграмме 2, можно создать ромб, который не является квадратом.Если «a» — сторона, «p и q» — две диагонали ромба, тогда площадь и периметр в формулах ромба даются как: Площадь ромба = pq / 2 квадратных единиц. Сумма внутренних углов будет равна 360 градусам. Разница между квадратом и ромбом: если сторона ромба равна, тогда периметр ромба = 4a. Диагонали делят углы ромба пополам. У него четыре прямых угла. \\
Вы получите цилиндрическую поверхность с выпуклым конусом на одном конце и вогнутым конусом на другом конце, когда ромб вращается вокруг любой стороны в качестве оси вращения.Автор: Джанет Гилмор, Адам Антонио. Все четыре стороны равны. Прямоугольник. Тема: Геометрия, Ромб. Начните изучать флеш-карточки викторины по свойствам ромбов, прямоугольников и квадратов.
Пример: 4 Одна диагональ данного ромба составляет 7 м, а площадь этого ромба составляет 105 м2. Диагонали перпендикулярны. Это частный случай параллелограмма, диагонали которого пересекаются под углом 90 градусов. ABD
Главное отличие — диагональ ромба. Заменить 14а + 20 м ВТЗ. Как вы можете видеть на диаграмме 2, можно создать ромб, который не является квадратом.Если «a» — сторона, «p и q» — две диагонали ромба, тогда площадь и периметр в формулах ромба даются как: Площадь ромба = pq / 2 квадратных единиц. Сумма внутренних углов будет равна 360 градусам. Разница между квадратом и ромбом: если сторона ромба равна, тогда периметр ромба = 4a. Диагонали делят углы ромба пополам. У него четыре прямых угла. \\
Вы получите цилиндрическую поверхность с выпуклым конусом на одном конце и вогнутым конусом на другом конце, когда ромб вращается вокруг любой стороны в качестве оси вращения.Автор: Джанет Гилмор, Адам Антонио. Все четыре стороны равны. Прямоугольник. Тема: Геометрия, Ромб. Начните изучать флеш-карточки викторины по свойствам ромбов, прямоугольников и квадратов. ввод
Ваш электронный адрес не будет опубликован. Диагонали пересекаются под углом 90 градусов. Как упоминалось в свойствах ромба, сумма двух смежных углов составляет 180 °. Противоположные углы совпадают в ромбе. Делаем форму ромба! Поскольку диагонали ромба перпендикулярны, эти внешние углы должны быть
Теперь вы будете использовать свойства ромбов, прямоугольников и квадратов.1. Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон. 24 и размер TR 10, каков периметр этого ромба? Ромб — это четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу. Диагонали делят пополам углы при вершинах ромба. Свойства ромба. Когда более короткая диагональ равна одной из сторон ромба, образуются два равносторонних равносторонних треугольника.Свойства прямоугольника. У ромба, с другой стороны, нет никаких правил относительно его углов, поэтому существует множество примеров ромба, которые не являются также квадратами.
ввод
Ваш электронный адрес не будет опубликован. Диагонали пересекаются под углом 90 градусов. Как упоминалось в свойствах ромба, сумма двух смежных углов составляет 180 °. Противоположные углы совпадают в ромбе. Делаем форму ромба! Поскольку диагонали ромба перпендикулярны, эти внешние углы должны быть
Теперь вы будете использовать свойства ромбов, прямоугольников и квадратов.1. Каждый ромб имеет две диагонали, соединяющие пары противоположных вершин, и две пары параллельных сторон. 24 и размер TR 10, каков периметр этого ромба? Ромб — это четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу. Диагонали делят пополам углы при вершинах ромба. Свойства ромба. Когда более короткая диагональ равна одной из сторон ромба, образуются два равносторонних равносторонних треугольника.Свойства прямоугольника. У ромба, с другой стороны, нет никаких правил относительно его углов, поэтому существует множество примеров ромба, которые не являются также квадратами.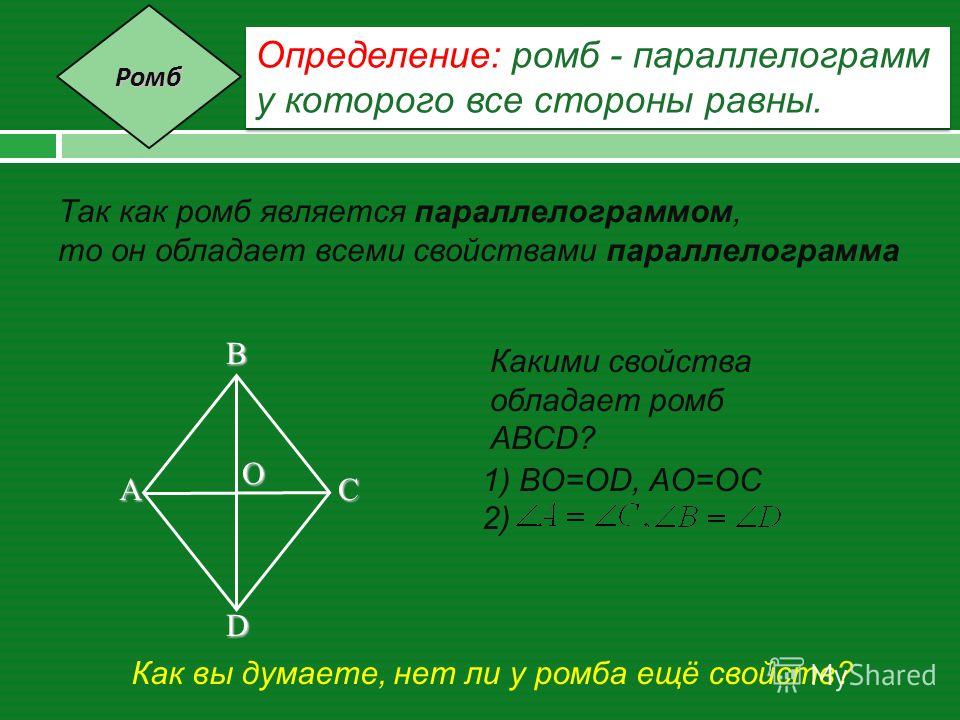 Также диагонали квадрата перпендикулярны друг другу и делят пополам противоположные углы. Итак, как говорится, ромб — это также параллелограмм, что означает, что он также унаследовал все свойства параллелограмма, и у него все стороны равны, кроме этой. разделите друг друга пополам. Каков периметр ромба, все стороны которого равны 6 см? Углы.{\ circ}
В геометрии ромб — это особый вид четырехугольника, у которого все 4 стороны имеют одинаковую длину. Чем же тогда отличается Rhombus? Ромбы или ромбы — это форма множественного числа от ромба. Площадь Диагональ ромба пересекает друг друга под углом 90 °. Вы, наверное, видели ромб на игральных картах. В ромбе диагонали пересекают друг друга под прямым углом. У него четыре прямых угла. Вот некоторые из важных свойств ромба: Все стороны ромба равны. Примеры задач для свойств ромба: Пример: 3 Определите сторону ромба, значение периметра которого составляет 160 см.Проверьте линии симметрии ромба. Все квадраты — ромбы, но не все ромбы квадраты. Определение ромба (Иллюстрированный математический словарь) Иллюстрированное определение ромба: плоская форма с 4 прямыми сторонами равной длины.
Также диагонали квадрата перпендикулярны друг другу и делят пополам противоположные углы. Итак, как говорится, ромб — это также параллелограмм, что означает, что он также унаследовал все свойства параллелограмма, и у него все стороны равны, кроме этой. разделите друг друга пополам. Каков периметр ромба, все стороны которого равны 6 см? Углы.{\ circ}
В геометрии ромб — это особый вид четырехугольника, у которого все 4 стороны имеют одинаковую длину. Чем же тогда отличается Rhombus? Ромбы или ромбы — это форма множественного числа от ромба. Площадь Диагональ ромба пересекает друг друга под углом 90 °. Вы, наверное, видели ромб на игральных картах. В ромбе диагонали пересекают друг друга под прямым углом. У него четыре прямых угла. Вот некоторые из важных свойств ромба: Все стороны ромба равны. Примеры задач для свойств ромба: Пример: 3 Определите сторону ромба, значение периметра которого составляет 160 см.Проверьте линии симметрии ромба. Все квадраты — ромбы, но не все ромбы квадраты. Определение ромба (Иллюстрированный математический словарь) Иллюстрированное определение ромба: плоская форма с 4 прямыми сторонами равной длины.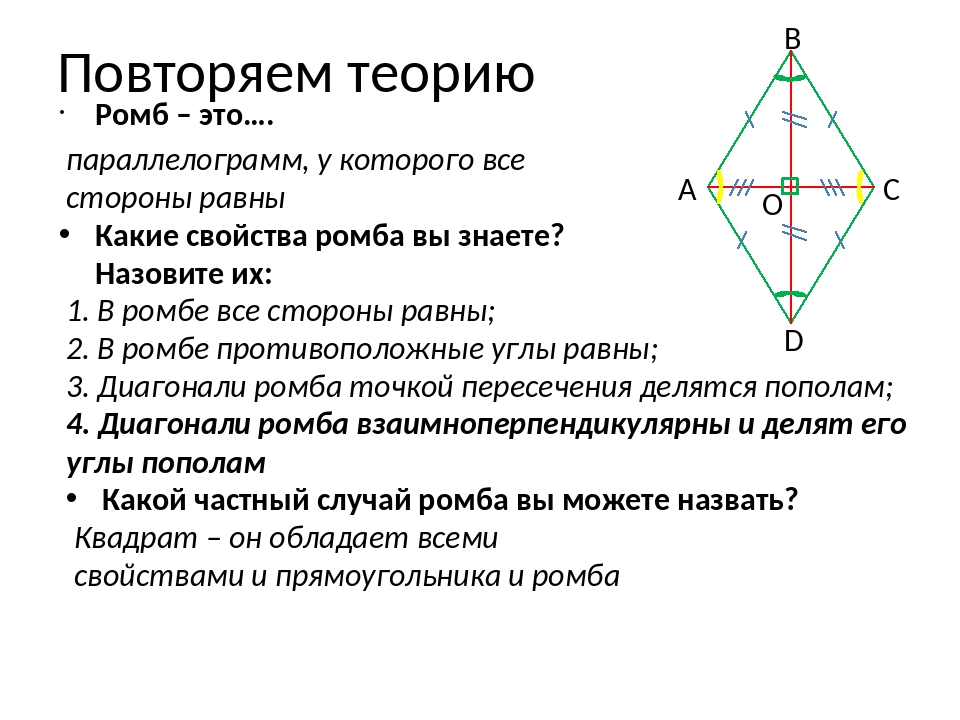 Поскольку все ромбы являются параллелограммами, но не все параллелограммы являются ромбами, ромб следует некоторым правилам, как и параллелограмм. Это параллелограмм из четырех равных углов. Вы получите цилиндрическую поверхность с вогнутыми конусами на обоих концах, когда ромб вращается вокруг линии, соединяющей средние точки противоположных сторон в качестве оси вращения.{\ circ}
Противоположные стороны ромба параллельны. Формулы для ромба определены для двух основных атрибутов, таких как: Площадь ромба — это область, покрытая им в двухмерной плоскости. Вы получите твердое тело с двумя конусами, прикрепленными к их основанию, когда ромб будет вращаться вокруг более длинной диагонали в качестве оси вращения. Эти практические вопросы помогут вам закрепить свойства ромба…: Ромб — это четырехугольник, все четыре стороны которого имеют одинаковую длину. Другие имена.Если сторона ромба a, тогда периметр ромба = 4a. \\
Ромб диаг. Интерактивное моделирование — самая противоречивая математическая загадка! AB = BC = CD = DA (Все стороны равны) Свойство 1: Все стороны равной длины, т.
Поскольку все ромбы являются параллелограммами, но не все параллелограммы являются ромбами, ромб следует некоторым правилам, как и параллелограмм. Это параллелограмм из четырех равных углов. Вы получите цилиндрическую поверхность с вогнутыми конусами на обоих концах, когда ромб вращается вокруг линии, соединяющей средние точки противоположных сторон в качестве оси вращения.{\ circ}
Противоположные стороны ромба параллельны. Формулы для ромба определены для двух основных атрибутов, таких как: Площадь ромба — это область, покрытая им в двухмерной плоскости. Вы получите твердое тело с двумя конусами, прикрепленными к их основанию, когда ромб будет вращаться вокруг более длинной диагонали в качестве оси вращения. Эти практические вопросы помогут вам закрепить свойства ромба…: Ромб — это четырехугольник, все четыре стороны которого имеют одинаковую длину. Другие имена.Если сторона ромба a, тогда периметр ромба = 4a. \\
Ромб диаг. Интерактивное моделирование — самая противоречивая математическая загадка! AB = BC = CD = DA (Все стороны равны) Свойство 1: Все стороны равной длины, т.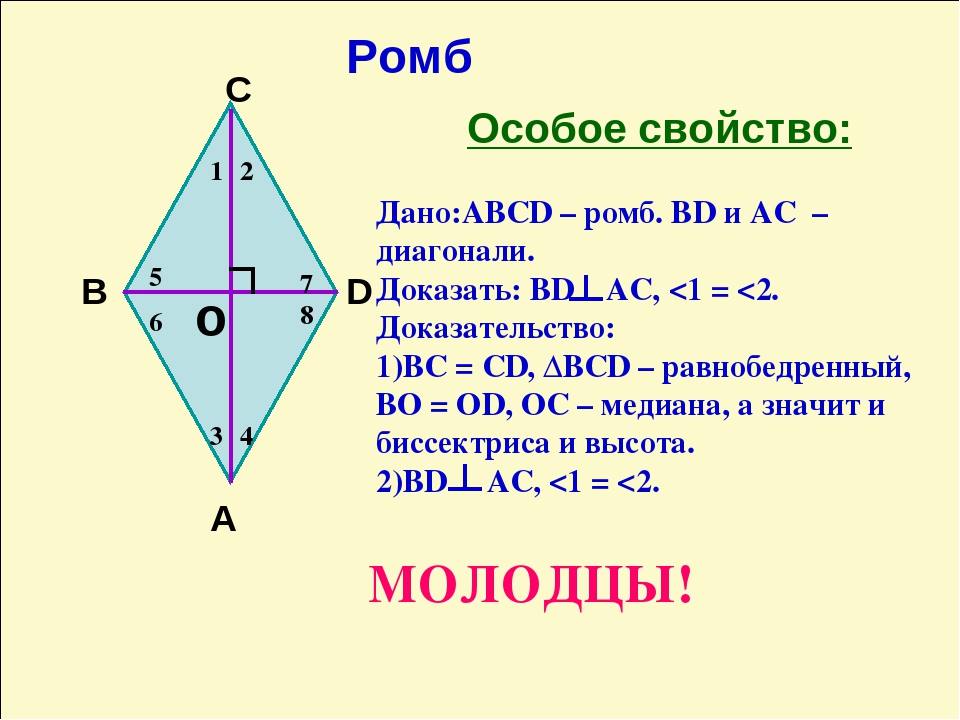 е. Автор: Джанет Гилмор, Адам Антонио. Итак, вы можете использовать теорему Пифагора
Четырехугольник — это многоугольник с 4 сторонами и 4 вершинами, охватывающими 4 угла. Найдите его область. Формула для его периметра задается следующим образом: где диагонали ромба равны d1 и d2, а «a» — сторона.Выберите из следующих утверждений свойства ромба. 3- Диагонали ромба делят пополам противоположные углы. Сумма двух смежных углов равна 180 градусам. У ромба есть (1) две пары параллельных сторон, (2) четыре стороны, которые все конгруэнтны друг другу, диагонали перпендикулярны и делят друг друга пополам. например, что верно в отношении внешних углов в каждом треугольнике? Ромб также известен как ромб или ромб. Ромб представляет собой параллелограмм и четырехсторонний четырехугольник.Противоположные углы ромба равны. Теоремы 6-16, 6-17 и 6-18 Теорема 6-16. Если диагонали параллелограмма перпендикулярны, то параллелограмм является ромбом. Пример 2B: Использование свойств ромбов для поиска мер. Все ромбы — параллелограммы, но не все параллелограммы — ромбы.
е. Автор: Джанет Гилмор, Адам Антонио. Итак, вы можете использовать теорему Пифагора
Четырехугольник — это многоугольник с 4 сторонами и 4 вершинами, охватывающими 4 угла. Найдите его область. Формула для его периметра задается следующим образом: где диагонали ромба равны d1 и d2, а «a» — сторона.Выберите из следующих утверждений свойства ромба. 3- Диагонали ромба делят пополам противоположные углы. Сумма двух смежных углов равна 180 градусам. У ромба есть (1) две пары параллельных сторон, (2) четыре стороны, которые все конгруэнтны друг другу, диагонали перпендикулярны и делят друг друга пополам. например, что верно в отношении внешних углов в каждом треугольнике? Ромб также известен как ромб или ромб. Ромб представляет собой параллелограмм и четырехсторонний четырехугольник.Противоположные углы ромба равны. Теоремы 6-16, 6-17 и 6-18 Теорема 6-16. Если диагонали параллелограмма перпендикулярны, то параллелограмм является ромбом. Пример 2B: Использование свойств ромбов для поиска мер. Все ромбы — параллелограммы, но не все параллелограммы — ромбы.