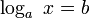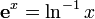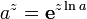1.1.7 Свойства степени с действительным показателем
Видеоурок 1: Степень с рациональным и действительным показателями. Часть 1
Видеоурок 2: Степень с рациональным и действительным показателями. Часть 2
Лекция: Свойства степени с действительным показателем
Действительные числа — это все числа огромного множества, которые окружают нас вокруг.
При рассмотрении степеней с действительным показателем в показателе может быть абсолютно любое значение, а, значит, при работе с такими степенями следует использовать следующие свойства.
 Свойства степени с действительным показателем
Свойства степени с действительным показателем
Если в основании степени лежит положительное число, а в качестве показателя используются действительные числа, то можно пользоваться следующими формулами:
1. Так как в основании степени используется положительное число, то, несмотря на знак показателя степени, результат всегда будет числом положительным.

2. Если показатель степени является отрицательным числом, то его можно заменить на равный по модулю положительный показатель, а основание дроби перевернуть.

3. При умножении чисел с одинаковыми основаниями, действительные показатели степени следует сложить.

4. При делении чисел с одинаковыми основаниями, действительные показатели степени вычитаются:

5. При возведении числа в степени в дополнительную степень показатели умножаются.

6. При возведении произведения некоторых чисел в действительную степень можно возвести каждое число по отдельности в данную степень и только после этого перемножить.

7. При возведении частного некоторых чисел в действительную степень можно возвести каждое число по отдельности в данную дробь и только после этого разделить.

cknow.ru
7.1.1. Степень с целым показателем математика-повторение
I. Определение. (- n)-й степенью (n – натуральное) числа
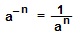
Примеры. Вычислить:

Решение.

II. Следующая формула позволяет заменить обыкновенную дробь с отрицательным показателем на обратную ей дробь с положительным показателем:
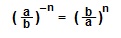
Примеры. Вычислить:

Решение.

Свойства степени с натуральным показателем справедливы и для степеней с любым показателем.
Свойства степени с натуральным показателем с примерами смотрите в предыдущем уроке здесь.
Примеры на все свойства степени.
Упростить:

Решение.
 При решении 7) примера I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями: am∙an=am+n и am:an=am-n. При решении II способом мы использовали понятие степени с отрицательным показателем:
При решении 7) примера I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями: am∙an=am+n и am:an=am-n. При решении II способом мы использовали понятие степени с отрицательным показателем:  и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .
и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .
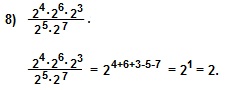
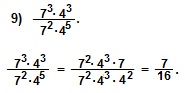
В примере 9) представим 73как 72∙7, а степень 45как 43∙42, а затем сократим дробь на (72∙43).
В 10) примере применим формулу степени произведения: (ab)n=an∙bn, а затем сократим дробь на (26∙35).

www.mathematics-repetition.com
Показатель степени — это… Что такое Показатель степени?
- Показатель степени
Число ab называется степенью с основанием a и показателем b.
Число с называется n-ной степенью числа а, если
 .
.Свойства:


- anam = an + m
 , n>m.
, n>m.
Существует алгоритм быстрого возведения в степень, выполняющий возведение в степень за меньшее, чем в определении, число умножений.

 не определён
не определёнПо определению,
![a^{p\over q} = \sqrt[q]{a^p}, \quad p \in \mathbb{Z}\ , q \in \mathbb{N}\](//xn--90abjbtjdof1b8dvb.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
См. корень степени q
Пусть
 .
.В школе действительную функцию вводят, используя тот факт, что между любыми двумя рациональными числами существует иррациональное, а между любыми двумя иррациональными — рациональное. Тогда
 , где p < q, | p − q | < ε, где ε — погрешность вычисления. Таким образом, для любого иррационального числа r подбираются два рациональных p и q с необходимой степенью точности и любое число между ap и aq принимается за ответ.
, где p < q, | p − q | < ε, где ε — погрешность вычисления. Таким образом, для любого иррационального числа r подбираются два рациональных p и q с необходимой степенью точности и любое число между ap и aq принимается за ответ.Другой подход основан на теории рядов и логарифмов. (см. определение комплексной степени)
Потенцирование
Потенцирование — это нахождение числа по известному значению его логарифма, то есть решение уравнения:
Из определения логарифма вытекает, что x = ab. Таким образом, потенцирование означает возведение основания логарифма в степень, равную значению логарифма. Например, если десятичный логарифм числа равен L, то искомое число равно 10L.
Определим некоторые функции:
теперь для вычисления az можно использовать свойства степеней и логарифмов:
Степень как функция
Поскольку в выражении xy принимает участие две переменных, то его можно рассматривать как:
См. также
Ссылки
- А. Б. Будак, Б. М. Щедрин «Элементарная математика» — Подготовка к вступительным экзаменам в МГУ
Wikimedia Foundation. 2010.
- Показатель удобочитаемости
- Показательное распределение
Смотреть что такое «Показатель степени» в других словарях:
Показатель степени — по техн. правилам набора должен набираться шрифтом, кегль которого в два раза меньше кегля шрифта символов и цифр, но без ущерба для удобочитаемости: Кегль символа или цифры Показатель степени 1 го порядка 2 го порядка 12 6 4 или 6 10 5 или 6 4… … Издательский словарь-справочник
показатель степени — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN power exponentsuperscript … Справочник технического переводчика
показатель степени — laipsnio rodiklis statusas T sritis fizika atitikmenys: angl. potenz vok. Exponent, m; Potenz, f rus. показатель степени, m pranc. exposant, m … Fizikos terminų žodynas
показатель степени — Syn: степень … Тезаурус русской деловой лексики
показатель степени сосредоточенности источников информации в сети — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN locality … Справочник технического переводчика
показатель степени числа — порядок числа — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы порядок числа EN number exponent … Справочник технического переводчика
показатель степени опасности компонента отхода — 3.1.9 показатель степени опасности компонента отхода: Интегральный показатель, характеризующий степень опасности компонента отхода при воздействии его на окружающую природную среду; Источник: СТО Газпром 12 2005: Каталог отходов производства и… … Словарь-справочник терминов нормативно-технической документации
ПОКАЗАТЕЛЬ СТЕПЕНИ СЖАТИЯ ГРУНТА — величина, характеризующая уменьшение объема породы по отношению к начальному объему осадки. Определяется по формуле где еf коэффициент пористости грунта при верхнем пределе пластичности; е коэффициент пористости при естественной влажности и… … Словарь по гидрогеологии и инженерной геологии
ЭКСПОНЕНТА, ПОКАЗАТЕЛЬ СТЕПЕНИ — (exponent) Одно из названий показателя степени; если у = хn, n является экспонентой. Экспонента не обязательно должна быть целым числом; если z – натуральный логарифм х, т. е., х = еz, мы получаем у = хn = (еz)n = ezn, значение которого может… … Экономический словарь
дробный показатель степени — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN fractional exponent … Справочник технического переводчика
dic.academic.ru
Урок по теме «Степень с действительным показателем» в 11-м классе
Тема урока: Степень с действительным показателем.
Задачи:
- Образовательные:
- обобщить понятие степени;
- отработать умение находить значение степени с действительным показателем;
- закрепить умения использовать свойства степени при упрощении выражений;
- выработать навык использования свойств степени при вычислениях.
- Развивающие:
- интеллектуальное, эмоциональное, личностное развитие ученика;
- развивать умение обобщать, систематизировать на основе сравнения, делать вывод;
- активизировать самостоятельную деятельность;
- развивать познавательный интерес.
- Воспитательные:
- воспитание коммуникативной и информационной культуры обучающихся;
- эстетическое воспитание осуществляется через формирование умения рационально, аккуратно оформлять задание на доске и в тетради.
Учащиеся должны знать: определение и свойства степени с действительным показателем.
Учащиеся должны уметь:
- определять имеет ли смысл выражение со степенью;
- использовать свойства степени при вычислениях и упрощении выражений;
- решать примеры, содержащие степень;
- сравнивать, находить сходства и отличия.
Форма урока: семинар – практикум, с элементами исследования. Компьютерная поддержка.
Форма организации обучения: индивидуальная, групповая.
Тип урока: урок исследовательской и практической работы.
ХОД УРОКА
Организационный момент
Притча:
«Однажды царь решил выбрать из своих
придворных первого помощника. Он подвёл всех к
огромному замку. «Кто первым откроет, тот и будет
первым помощником». Никто даже не притронулся к
замку. Лишь один визирь подошёл и толкнул замок,
который открылся. Он не был закрыт на ключ.
Тогда царь сказал: «Ты получишь эту должность,
потому что полагаешься не только на то, что
видишь и слышишь, а надеешься на собственные силы
и не боишься сделать попытку».
И мы сегодня будем пытаться, пробовать, чтобы
прийти к правильному решению.
1. С каким математическим понятием связаны слова:
Основание
Показатель (Степень)
Какими словами можно объединить слова:
Рациональное число
Целое число
Натуральное число
Иррациональное число (Действительное
число)
Сформулируйте тему урока. (Степень с
действительным показателем)
2. Какая наша стратегическая
цель? (ЕГЭ)
Какие цели нашего урока?
– Обобщить понятие степени.
Задачи:
– повторить свойства степени
– рассмотреть применение свойств степени при
вычислениях и упрощениях выражений
– отработка вычислительных навыков.
3. Итак, ар, где р – число
действительное.
Приведите примеры (выберете из выражений 5–2,
, 43, ) степени
– с натуральным показателем
– с целым показателем
– с рациональным показателем
– с иррациональным показателем
4. При каких значениях а имеет смысл выражение
аn, где n (а
– любое)
аm, где m (а 0) Как от степени с
отрицательным показателем перейти к степени с
положительным показателем?
, где (а0)
5. Из данных выражений выберете те,
которые смысла не имеют:
( –3)2, , , 0–3, , ( –3)–1, .
6. Вычислите. Ответы в каждом столбике
обладают одним общим свойством. Укажите лишний
ответ (этим свойством не обладающий)
=
2
=
=
=
6
= (неправ.
др.)
= (нельзя записать дес. др.)
= (дробь)
= =
7. Какие действия (математические операции) можно выполнять со степенями?
Установите соответствие:
| При умножении степеней с равными основаниями | Основания умножаются, а показатель остаётся прежним |
| При делении степеней с равными основаниями | Основания делятся, а показатель остаётся прежним |
| При возведении степени в степень | Основание остаётся прежним, а показатели умножаются |
| При умножении степеней с равными показателями | Основание остаётся прежним, а показатели вычитаются |
| При делении степеней с равными показателями | Основание остаётся прежним, а показатели складываются |
Один ученик записывает формулы (свойства) в общем виде.
8. Дополнить степени из п.3 так, чтобы к полученному примеру можно было применить свойства степени.
(Один человек работает у доски, остальные в тетрадях. Для проверки обменяться тетрадями, а ещё один выполняет действия на доске)
9. На доске (работает ученик):
Вычислите : =
Самостоятельно (с проверкой на листах)
=
=
Какой из ответов не может получиться в части «В» на ЕГЭ? Если в ответе получилось , то как записать такой ответ в части «В»?
10. Самостоятельное выполнение задания (с проверкой у доски – несколько человек)
Задание с выбором ответа
1 |
2 |
3 |
4 |
||
| 1 | 25 – |
19 |
|||
| 2 | : | –7 |
–9 |
||
| 3 | 0,3 | 9,1 |
2,9 |
89,9 |
8,9 |
| 4 | 1 |
0 |
2,5 |
4 |
11. Задание с кратким ответом (решение у доски):
+ + (60)5 2 – 3–4 27 =
Самостоятельно с проверкой на скрытой доске:
– – 322– 4 + (30)4 4 =
12. Сократите дробь (на доске):
=
В это время один человек решает на доске самостоятельно: = (класс проверяет)
13. Самостоятельное решение (на проверку)
На отметку «3»: Тест с выбором ответа:
1. Укажите выражение, равное степени
| 1. | 2. | 3. | 4. |
2. Представьте в виде степени произведение:
| 1. | 2. | 3. | 4. |
3. Упростите выражение : и найдите его значение при х = 2
| 1. | 2. 8 | 3. | 4. – 8 |
4. Чему равно значение выражения при а =
| 1. – 9 | 2. | 3. | 4. 9 |
5. Вычислите
| 1. | 2. | 3. 16 | 4. – 16 |
На отметку «4»: № 439 (1, 2, 4, 5, 6)
На отметку «5»:
1.
2. Упростите выражение
14. Дополнительно (индивидуально) тем, кто быстрее справится с заданиями:
Сравните числа и
15. Дома: №438, придумать по 2 примера на свойства степени.
В заключение урока:
«Музыка может возвышать или умиротворять душу,
Живопись – радовать глаз,
Поэзия – пробуждать чувства,
Философия – удовлетворять потребности разума,
Инженерное дело – совершенствовать
материальную сторону жизни людей,
А математика способна достичь всех этих целей»
– Так сказал американский математик Морис
Клайн.
– Спасибо за урок!
urok.1sept.ru
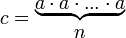 .
.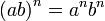
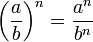
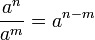 , n>m.
, n>m.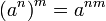

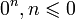 не определён
не определён![a^{p\over q} = \sqrt[q]{a^p}, \quad p \in \mathbb{Z}\ , q \in \mathbb{N}\](/800/600/https/dic.academic.ru/pictures/wiki/files/98/ba5ef381235aee96027fbe5e876d0d3e.png)
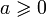 .
.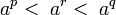 , где p < q, | p − q | < ε, где ε — погрешность вычисления. Таким образом, для любого иррационального числа r подбираются два рациональных p и q с необходимой степенью точности и любое число между ap и aq принимается за ответ.
, где p < q, | p − q | < ε, где ε — погрешность вычисления. Таким образом, для любого иррационального числа r подбираются два рациональных p и q с необходимой степенью точности и любое число между ap и aq принимается за ответ.