Броуновское движение — Википедия
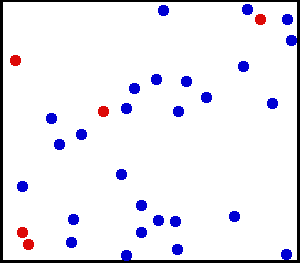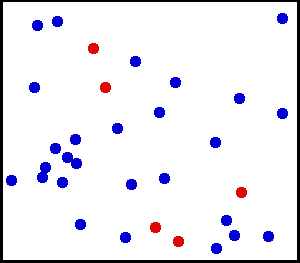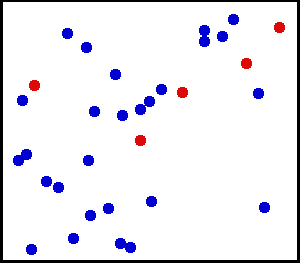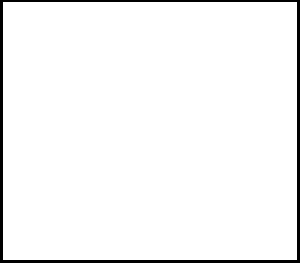 Тепловое движение частиц вещества, таких как атомы и молекулы — причина броуновского движения
Тепловое движение частиц вещества, таких как атомы и молекулы — причина броуновского движенияБро́уновское движе́ние (бра́уновское движе́ние) — беспорядочное движение микроскопических видимых взвешенных в жидкости или газе частиц твёрдого вещества, вызываемое тепловым движением частиц жидкости или газа. Было открыто в 1827 году Робертом Броуном (правильнее Брауном)[1]. Броуновское движение никогда не прекращается. Оно связано с тепловым движением, но не следует смешивать эти понятия. Броуновское движение является следствием и свидетельством существования теплового движения.
Броуновское движение является наглядным экспериментальным подтверждением хаотического теплового движения атомов и молекул, являющегося фундаментальным положением молекулярно-кинетической теории. Если промежуток наблюдения гораздо больше, чем характерное время изменения силы, действующей на частицу со стороны молекул среды, и прочие внешние силы отсутствуют, то
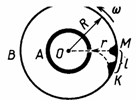
Кроме поступательного броуновского движения, существует также вращательное броуновское движение — беспорядочное вращение броуновской частицы под влиянием ударов молекул среды. Для вращательного броуновского движения среднее квадратичное угловое смещение частицы пропорционально времени наблюдения.
Броуновское движение происходит из-за того, что все жидкости и газы состоят из атомов или молекул — мельчайших частиц, которые находятся в постоянном хаотическом тепловом движении, и потому непрерывно толкают броуновскую частицу с разных сторон. Было установлено, что крупные частицы с размерами более 5 мкм в броуновском движении практически не участвуют (они неподвижны или седиментируют), более мелкие частицы (менее 3 мкм) двигаются поступательно по весьма сложным траекториям или вращаются.
Когда в среду погружено крупное тело, то толчки, происходящие в огромном количестве, усредняются и формируют постоянное давление. Если крупное тело окружено средой со всех сторон, то давление практически уравновешивается, остаётся только подъёмная сила Архимеда — такое тело плавно всплывает или тонет.
Если же тело мелкое, как броуновская частица, то становятся заметны флуктуации давления, которые создают заметную случайно изменяющуюся силу, приводящую к колебаниям частицы. Броуновские частицы обычно не тонут и не всплывают, а находятся в среде во взвешенном состоянии.
Философская поэма римского поэта Лукреция «О природе вещей» (60 до н. э.) имеет описание броуновского движения пылевых частиц в стихах 113—140 из книги II. Он использует это как доказательство существования атомов:
«Посмотрите, что происходит, когда солнечные лучи проникают в здание и проливают свет на его темные места. Вы увидите множество крошечных частиц, смешивающихся множеством способов… их танец является фактическим указанием на скрытые от нашего взгляда движения материи… Они возникают из атомов, которые движутся сами по себе (то есть спонтанно). Затем те небольшие составные тела, которые меньше всего удалены от импульса атомов, приводятся в движение воздействием их невидимых ударов и, в свою очередь, приводят к движению немного больших тел. Таким образом, движение поднимается от атомов и постепенно выходит на уровень наших чувств, так что те тела в движении, которые мы видим в солнечных лучах, движутся ударами, которые остаются невидимыми.»
Хотя смешивающееся движение пылевых частиц вызвано в основном воздушными потоками, прерывистое, кувыркающееся движение мелких пылевых частиц действительно вызвано в основном истинной броуновской динамикой.
Примерно в 1785 году, Ян Ингенхауз систематически изучал броуновское движение частиц угольной пыли на поверхности спирта. В 1827 году Роберт Броун (Браун) переоткрыл броуновское движение наблюдая пыльцевые зёрна в жидкости.
Наиболее точные исследования броуновского движения в XIX веке провёл французский физик Луи Жорж Гуи. Он установил, что интенсивность броуновского движения возрастает с уменьшением внутреннего трения жидкости, никак не зависит от интенсивности освещения и внешнего электромагнитного поля. Он также пришёл к выводу, что броуновское движение вызвано влиянием теплового движения молекул. Л. Ж. Гуи оценил скорость броуновских частиц, она оказалась равной приблизительно одной стомиллионной молекулярной скорости[2].
Математическое изучение броуновского движения было начато А. Эйнштейном[3], П. Леви[4][5] и Н. Винером[6][7][8][9][10].
Построение классической теории[править | править код]
В 1905 году Альбертом Эйнштейном была создана молекулярно-кинетическая теория для количественного описания броуновского движения[11]. В частности, он вывел формулу для коэффициента диффузии сферических броуновских частиц
- D=RT6NAπaξ,{\displaystyle D={\frac {RT}{6N_{A}\pi a\xi }},}
где D{\displaystyle D} — коэффициент диффузии, R{\displaystyle R} — универсальная газовая постоянная, T{\displaystyle T} — абсолютная температура, NA{\displaystyle N_{A}} — постоянная Авогадро, a{\displaystyle a} — радиус частиц, ξ{\displaystyle \xi } — динамическая вязкость.
При выводе закона Эйнштейна предполагается, что смещения частицы в любом направлении равновероятны и что можно пренебречь инерцией броуновской частицы по сравнению с влиянием сил трения (это допустимо для достаточно больших времён). Формула для коэффициента D основана на применении закона Стокса для гидродинамического сопротивления движению сферы радиусом a в вязкой жидкости.
Коэффициент диффузии броуновской частицы связывает средний квадрат её смещения x (в проекции на произвольную фиксированную ось) и время наблюдения τ:
- ⟨x2⟩=2Dτ.{\displaystyle \langle x^{2}\rangle =2D\tau .}
Среднеквадратичный угол поворота броуновской частицы φ (относительно произвольной фиксированной оси) также пропорционален времени наблюдения:
- ⟨φ2⟩=2Drτ.{\displaystyle \langle \varphi ^{2}\rangle =2D_{r}\tau .}
Здесь Dr — вращательный коэффициент диффузии, который для сферической броуновской частицы равен
- Dr=RT8NAπa3ξ.{\displaystyle D_{r}={\frac {RT}{8N_{A}\pi a^{3}\xi }}.}
Экспериментальное подтверждение[править | править код]
 Воспроизведение рисунка из книги Перрена Les Atomes, показывающего движение трёх коллоидальных частиц радиусом 0,53 мкм, наблюдавшееся под микроскопом. Последовательные положения частицы отмечены через каждые 30 секунд, шаг сетки 3,2 мкм[13]
Воспроизведение рисунка из книги Перрена Les Atomes, показывающего движение трёх коллоидальных частиц радиусом 0,53 мкм, наблюдавшееся под микроскопом. Последовательные положения частицы отмечены через каждые 30 секунд, шаг сетки 3,2 мкм[13]Формула Эйнштейна была подтверждена опытами Жана Перрена[11] и его студентов в 1908—1909 гг., а также T. Сведберга[14]. Для проверки статистической теории Эйнштейна-Смолуховского и закона распределения Л. Больцмана Ж. Б. Перрен использовал следующее оборудование: предметное стекло с цилиндрическим углублением, покровное стекло, микроскоп с малой глубиной изображения. В качестве броуновских частиц Перрен использовал зёрнышки смолы мастикового дерева и гуммигута — густого млечного сока деревьев рода гарциния[15]. Для наблюдений Перрен использовал изобретенный в 1902 г. ультрамикроскоп. Микроскоп этой конструкции позволял видеть мельчайшие частицы благодаря рассеянию на них света от мощного бокового осветителя. Справедливость формулы была установлена для различных размеров частиц — от 0,212 мкм до 5,5 мкм, для различных растворов (раствор сахара, глицерин), в которых двигались частицы[16].
Большого труда потребовала от экспериментатора подготовка эмульсии с частичками гуммигута. Смолу Перрен растер в воде. Под микроскопом было видно, что в подкрашенной воде находится огромное число желтых шариков. Эти шарики отличались по величине, они представляли собой твердые образования, которые не слипались друг с другом при соударениях. Чтобы распределить шарики по размеру, Перрен помещал пробирки с эмульсией в центробежную машину. Машина приводилась во вращение. За несколько месяцев кропотливой работы Перрену удалось наконец получить порции эмульсии с одинаковыми по размеру зернами гуммигута r ~ 10-5 см). В воду было добавлено большое количество глицерина. Фактически крошечные шарики почти сферической формы были взвешены в глицерине, содержащем лишь 11 % воды. Повышенная вязкость жидкости препятствовала появлению в ней внутренних потоков, которые бы привели к искажению истинной картины броуновского движения.
По предположению Перрена одинаковые по размеру зернышки раствора должны были расположиться в соответствии с законом распределения числа частиц с высотой. Именно для исследования распределения частиц по высоте экспериментатор сделал в предметном стекле цилиндрическое углубление. Это углубление он заполнил эмульсией, затем закрыл сверху покровным стеклом. Для наблюдения эффекта Ж. Б. Перрен использовал микроскоп с малой глубиной изображения .
Свои исследования Перрен начал с проверки основной гипотезы статистической теории Эйнштейна. Вооружившись микроскопом и секундомером, он наблюдал и фиксировал в освещенной камере положения одной и той же частицы эмульсии через одинаковые промежутки времени.
Наблюдения показали, что беспорядочное движение броуновских частиц приводило к тому, что они перемещались в пространстве очень медленно. Частицы совершали многочисленные возвратные движения. В итоге сумма отрезков между первым и последним положениями частицы была намного больше прямого смещения частицы от первой точки до последней.
Перрен отмечал и потом зарисовывал в масштабе на разграфленном листе бумаги положение частиц через равные временные интервалы. Наблюдения проводились через каждые 30 с. Соединяя полученные точки прямыми, он получал замысловатые ломаные траектории.
Далее Перрен определил число частиц в разных по глубине расположения слоях эмульсии. Для этого он последовательно фокусировал микроскоп на отдельные слои взвеси. Выделение каждого последующего слоя осуществлялось через каждые 30 микрон. Таким образом, Перрен мог наблюдать число частиц, находящихся в очень тонком слое эмульсии. Частицы других слоев при этом не попадали в фокус микроскопа. Используя этот метод, ученый мог количественно определить изменение числа броуновских частиц с высотой.
Опираясь на результаты этого эксперимента, Перрен смог определить значение постоянной Авогадро NА.
Способ расчета постоянной Больцмана k базировался на следующих рассуждениях.
Броуновские частицы, как и молекулы, находятся в беспорядочном движении. Соответственно, они подчиняются всем газовым законам. Из общих соображений можно показать, что средняя кинетическая энергия Ek¯{\displaystyle {\overline {E_{k}}}} одной броуновской частицы равна средней кинетической энергии молекул при данной температуре T{\displaystyle T}, то есть:
- Ek¯=32kT=32(RNA)T.{\displaystyle {\displaystyle {\overline {E_{k}}}}={\frac {3}{2}}kT={\frac {3}{2}}\left({\frac {R}{N_{A}}}\right)T.}
Из этой формулы можно выразить число Авогадро NA{\displaystyle N_{A}}:
- NA=32REk¯T.{\displaystyle N_{A}={\frac {3}{2}}{\frac {R}{\displaystyle {\overline {E_{k}}}}}T.}
Определив среднюю кинетическую энергию Ek¯{\displaystyle {\overline {E_{k}}}} броуновской частицы при данной температуре, можно найти значение NA{\displaystyle N_{A}}. Однако Перрен не смог вычислить среднюю кинетическую энергию броуновской частицы Ek¯=mv22{\displaystyle {\displaystyle {\overline {E_{k}}}}={\frac {mv^{2}}{2}}} по массе частицы m{\displaystyle m} и среднему квадрату скорости v2{\displaystyle v^{2}}. Это было связано с тем, что очень трудно в эксперименте определить среднее значение квадрата скорости частицы, движущейся хаотически. Поэтому Ж. Перрен нашел среднюю кинетическую энергию другим способом (из закона распределения частиц с высотой). Действительно, в формулу распределения броуновских частиц с высотой можно вместо температуры подставить её выражение через Ek¯{\displaystyle {\overline {E_{k}}}} , тогда формула Больцмана приобретет вид:
- nh=n0exp(−3mgh3Ek¯).{\displaystyle n_{h}=n_{0}\exp \left(-{\frac {3mgh}{2{\displaystyle {\overline {E_{k}}}}}}\right).}
Зная массу частиц m{\displaystyle m}, их число в слоях, находящихся на различных высотах, можно найти Ek¯{\displaystyle {\overline {E_{k}}}} а затем и число Авогадро.
Очевидно, что для определения числа Авогадро необходимо найти массу шариков гуммигута. С той целью Перрен выпаривал каплю раствора гуммигута. Взвесив сухой остаток, он сосчитал количество зернышек, затем определил размеры и массу каждого из них.[17]
Соотношения для вращательного броуновского движения были также подтверждены опытами Перрена, хотя этот эффект гораздо труднее наблюдать, чем поступательное броуновское движение.
Броуновское движение как немарковский случайный процесс[править | править код]
Хорошо разработанная за последнее столетие теория броуновского движения является приближенной. Хотя в большинстве практически важных случаев существующая теория даёт удовлетворительные результаты, в некоторых случаях она может потребовать уточнения. Так, экспериментальные работы, проведённые в начале XXI века в Политехническом университете Лозанны, Университете Техаса и Европейской молекулярно-биологической лаборатории в Гейдельберге (под руководством С. Дженей) показали отличие поведения броуновской частицы от теоретически предсказываемого теорией Эйнштейна — Смолуховского, что было особенно заметным при увеличении размеров частиц. Исследования затрагивали также анализ движения окружающих частиц среды и показали существенное взаимное влияние движения броуновской частицы и вызываемое ею движение частиц среды друг на друга, то есть наличие «памяти» у броуновской частицы, или, другими словами, зависимость её статистических характеристик в будущем от всей предыстории её поведения в прошлом. Данный факт не учитывался в теории Эйнштейна — Смолуховского.
Процесс броуновского движения частицы в вязкой среде, вообще говоря, относится к классу немарковских процессов, и для более точного его описания необходимо использование интегральных стохастических уравнений.
- ↑ Броуновское движение / В. П. Павлов // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- ↑ Опыт Перрена: броуновское движение (неопр.) (недоступная ссылка). Дата обращения 26 сентября 2015. Архивировано 9 сентября 2015 года.
- ↑ Эйнштейн А. К теории броуновского движения // Эйнштейн А. Собр. соч., — М., Наука, 1966. —т. 3, — с. 118-127
- ↑ Леви П. Конкретные проблемы функционального анализа. — М., Наука, 1967
- ↑ Леви П. Стохастические процессы и броуновское движение. — М., Наука, 1972
- ↑ Wiener N. Differential space. — J. Math. and Phys., 1923, v.2, p. 131-174
- ↑ Wiener N. Hermitian polynomials and Fourier analysis. — J. Math. and Phys., 1928-29, v.8, p. 70-73
- ↑ Wiener N. The homogeneous chaos. — Amer. J. Math., 1938, v.60, p. 897-936
- ↑ Винер Н. Кибернетика, или Управление и связь в животном и машине. — М., Советское радио, 1958
- ↑ Винер Н. Нелинейные задачи в теории случайных процессов. — М., ИЛ, 1961
- ↑ 1 2 Б. Б. Буховцев, Ю. Л. Климонтович, Г. Я. Мякишев. Физика. Учебник для 9 класса средней школы. — 3 изд., переработанное. — М.: Просвещение, 1986. — С. 13. — 3 210 000 экз.
- ↑ Einstein, Albert. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen (нем.) // Annalen der Physik : magazin. — 1905. — Mai (Bd. 322, Nr. 8). — S. 549—560. — doi:10.1002/andp.19053220806.
Перевод на русский: Эйнштейн, А. О движении взвешенных в покоящейся жидкости частиц, требуемом молекулярно-кинетической теорией теплоты. - ↑ Perrin, Jean. Atoms (неопр.). — 1914. — С. 115.
- ↑ И Сведберг, и Перрен получили в 1926 году Нобелевские премии за исследования взвесей, но первый по химии, а второй — по физике.
- ↑ Гуммигут — статья из Большой советской энциклопедии.
- ↑ Perrin, J. Atoms. — London: Constable & Company, 1916. — P. 109—133.
Один из самых ранних переводов на русский: Перрен, Ж. Атомы. — М.: Госиздат, 1921. — 254 с. — (Современные проблемы естествознания). - ↑ Опыт Перрена: броуновское движение (неопр.). school-collection.lyceum62.ru. Дата обращения 19 декабря 2017.
Урок 19. температура. энергия теплового движения молекул — Физика — 10 класс
Физика, 10 класс
Урок №19. Температура. Энергия теплового движения молекул
На уроке рассматриваются понятия: температура и тепловое равновесие; шкалы Цельсия и Кельвина; абсолютная температура как мера средней кинетической энергии теплового движения частиц вещества, зависимость давления от концентрации молекул и температуры.
Глоссарий по теме:
Макроскопические параметры — величины объём V, давление p и температура t, характеризующие состояние макроскопических тел без учёта их молекулярного строения.
Температура характеризует степень нагретости тела (холодное, тёплое, горячее).
Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.
Тепловым равновесием называют – такое состояние тел, при котором температура во всех точках системы одинакова.
Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.
Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.
Абсолютная температура Т прямо пропорциональна температуре Θ (тета), выражаемой в энергетических единицах (Дж).
Абсолютный нуль — предельная температура, при которой давление идеального газа обращается в нуль при фиксированном объёме или объём идеального газа стремится к нулю при неизменном давлении.
Абсолютный нуль – температура, при которой прекращается тепловое движение молекул.
Абсолютная шкала температур (Шкала Кельвина) –
Кельвин — единица абсолютной температуры в Международной системе измерений (СИ).
Постоянная Больцмана – коэффициент , связывает температуру Θ энергетических единицах (Дж) с абсолютной температурой Т (К).
, связывает температуру Θ энергетических единицах (Дж) с абсолютной температурой Т (К).
Абсолютная температура есть мера средней кинетической энергии молекул.
Давление газа прямо пропорционально концентрации его молекул и абсолютной температуре Т.
Закон Авогадро – в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул
Обязательная литература:
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 195 – 203.
Дополнительная литература:
- Смородинский Я.А. Температура. — 3-е издание. — М.: Бюро Квантум, 2007. (Библиотечка «Квант». Вып. 103. Приложение к журналу «Квант» № 5/2007.) С. 5— 25.
- Кирик Л.А., Генденштейн Л.Э., Гельфгат И.М.. Задачи по физике. 10-11 классы для профильной школы. – М.: Илекса, 2010. – С. 111-115.
- Рымкевич А.П. Физика. Задачник. 10-11 классы. – М.: Дрофа, 2013. — С. 65 – 67.
- Орлов В.А., Сауров Ю.А. Практика решения физических задач. 10-11классы. – М.: Вентана-Граф, 2014. – С. 98-99.
- http://kvant.mccme.ru/1991/09/idealnyj_gaz_-_universalnaya_f.htm
Теоретический материал для самостоятельного изучения
Измеряя расположение звёзд на небе, расстояния на земле, время, люди знали, для чего они это делают и изобретали, телескопы, часы, прототипы современных линеек. О температуре такого же сказать было нельзя. О том, что такое тепловое равновесие и что означает степень нагрева тела (температура), существовали разные мнения. Но человек с незапамятных времен точно знал, что, когда два тела плотно соприкасаются, между ними устанавливается, выражаясь современным языком, тепловое равновесие.
Любое макроскопическое тело или группа макроскопических тел при неизменных внешних условиях самопроизвольно переходят в состояние теплового равновесия.
Тепловым равновесием называют такое состояние тел, при котором температура во всех точках системы одинакова.
Температура (от лат. temperatura — надлежащее смешение, соразмерность, нормальное состояние) — физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы.
К числу характеристик состояния макроскопических тел (твёрдых тел, жидкостей, газов) и процессов изменения их состояний, относят объём, давление и температуру. Эти величины описывают в целом тела, состоящие из большого числа молекул, а не отдельные молекулы. При этом микроскопические процессы внутри тела не прекращаются при тепловом равновесии: расположения молекул всё время меняются и меняются их скорости при столкновениях.
Величины объём, давление и температуру, характеризующие состояние макроскопических тел без учёта их молекулярного строения, называют макроскопическими параметрами.
Тепловым или термодинамическим равновесием, изолированной системы тел, называют состояние, при котором все макроскопические параметры в системе остаются неизменными.
Для точной характеристики нагретости тела, необходим прибор, способный измерить температуры тел и дать возможности их сравнения.
Термометр — это прибор для измерения температуры путём контакта с исследуемым телом. Различают жидкостные, газовые термометры, термопары, термометры сопротивления.
В 1597 году Галилей создал термоскоп, в собственных сочинениях учёного нет описания этого прибора, но его ученики засвидетельствовали этот факт. Аппарат представлял собой устройство для поднятия воды при помощи нагревания.
Изобретение термометра, данные которого не зависели бы от перепадов атмосферного давления, произошли благодаря экспериментам физика Э. Торричелли, ученика Галилея.
Во всех приборах, изобретённых в XVIII веке, измерение температуры было относительно расширению столбика воды, спирта или ртути и произвольности выбора начала отсчёта, т.е. нулевой температуры. Наполняющие их вещества замерзали или кипели и этими термометрами нельзя было измерять очень низкие или очень высокие температуры. Необходимо было изобрести такую шкалу, чтобы избавиться от зависимости выбранного вещества, на основе которого формировалось градуирование.
Шкала, предложенная шведским учёным Андерсом Цельсием в 1742 г., точно устанавливала положение двух точек: 0 и 100 градусов. По шкале Цельсия температура обозначается буквой t, измеряется в градусах Цельсия (ºС).
На территории Англии и США используется шкала Фаренгейта. Такая шкала была предложена немецким учёным Даниелем Габриелем Фаренгейтом в 1724 г.: 0 °F — температура смеси снега с нашатырём или поваренною солью, 96 °F —температура здорового человеческого тела, во рту или под мышкой.
Рене Антуан де Реомюр не одобрял применения ртути в термометрах вследствие малого коэффициента расширения ртути. В 1730 году изобрёл водно-спиртовой термометр и предложил шкалу от 0 до 80°.
Шкала Реомюра очень долго использовалась на родине учёного во Франции вплоть до настоящего времени.
Различные жидкости при нагревании расширяются не одинаково. Поэтому расстояния на шкале между нулевой отметкой 0 °C и 100 °C будут разными.
Однако существует способ создать тело, которое приближенно обладает нужными качествами. Это идеальный газ. Было замечено, что в отличие от жидкостей все разряжённые газы – водород, гелий, кислород – расширяются при нагревании одинаково и одинаково меняют своё давление при изменении температуры. Это свойство газов позволяет избавиться в термометрах от одного существенного недостатка шкалы Цельсия – произвольности выбора начала отсчёта, то есть нулевой температуры.
При тепловом равновесии, если давление и объём газа массой m постоянны, то средняя кинетическая энергия молекул газа должна иметь строго определённое значение, как и температура.
Практически такую проверку произвести непосредственно невозможно, но с помощью основного уравнения молекулярно-кинетической теории её можно выразить через макроскопические параметры:

 ;
;  ;
;  ;
;  ;
; 

Если кинетическая энергия действительно одинакова для всех газов в состоянии теплового равновесия, то и значение давления р должно быть тоже одинаково для всех газов при постоянном значении отношения объёма к числу молекул. Подтвердить или опровергнуть данное предположение может только опыт.

Возьмём несколько сосудов, заполненных различными газами, например, водородом, гелием и кислородом. Сосуды имеют определённые объёмы и снабжены манометрами, для измерения давления газов в сосудах. Массы газов известны, тем самым известно число молекул в каждом сосуде. Приведём газы в состояние теплового равновесия. Для этого поместим их в тающий лёд и подождём, пока не установится тепловое равновесие и давление газов перестанет меняться.
Здесь устанавливается тепловое равновесие и все газы имеют одинаковую температуру 0 °С. При этом показания манометра показывают разное давление р, объёмы сосудов V изначально были разными и число молекул N различно, так как газы, закаченные в баллоны разные. Найдём отношение для водорода всех параметров для одного моля вещества:

Такое значение отношения произведения давления газа на его объём к числу молекул получается для всех газов при температуре тающего льда. Обозначим это отношение через Θ0 (тета нулевое):

Таким образом, предположение, что средняя кинетическая энергия, а также давление р в состоянии теплового равновесия одинаковы для всех газов, если их объёмы и количества вещества одинаковы или если отношение

Если же сосуды с газами поместить в кипящую воду при нормальном атмосферном давлении, то согласно эксперименту, отношение макроскопических параметров будет также одинаковым для всех газов, но значение будет больше предыдущего

Отсюда следует, что величина Θ растёт с повышением температуры и не зависит от других параметром, кроме температуры. Этот опытный факт позволяет рассматривать величину Θ тета как естественную меру температуры и измерять в энергетических единицах — джоулях.
А теперь вместо энергетической температуры введём температуру, которая будет измеряться в градусах. Будем считать величину тета Θ прямо пропорциональной температуре Т, где k- коэффициент пропорциональности

Так как  , то тогда
, то тогда 
По этой формуле вводится температура, которая даже теоретически не может быть отрицательной, так как все величины левой части этого равенства больше или равны нулю. Следовательно, наименьшим значением этой температуры является нуль, при любом другом параметре p, V, N равным нулю.
Предельную температуру, при которой давление идеального газа обращается в нуль при фиксированном объёме или при которой объём идеального газа стремится к нулю при неизменном давлении, называют абсолютным нулём температуры.
Тепловое движение молекул непрерывно и бесконечно, а при абсолютном нуле молекулы поступательно не двигаются. Следовательно, абсолютный нуль температур при наличии молекул вещества не может быть достигнут. Абсолютный нуль температур — это самая низкая температурная граница, верхней не существует, та «наибольшая или последняя степень холода», существование которой предсказывал М.В. Ломоносов.
В 1848 г. английскому физику Вильяму Томсону (лорд Кельвин) удалось построить абсолютную температурную шкалу (её в настоящее время называют шкалой Кельвина), которая имеет две основные точки 0 К (или абсолютный нуль) и 273К, точка в которой вода существует в трёх состояниях (в твёрдом, жидком и газообразном).
Абсолютная температурная шкала — шкала температур, в которой за начало отсчёта принят абсолютный нуль. Температура здесь обозначается буквой T и измеряется в кельвинах (К).
На шкале Цельсия, есть две основные точки: 0°С (точка, в которой тает лёд) и 100°С (кипение воды). Температура, которую определяют по шкале Цельсия, обозначается t. Шкала Цельсия имеет как положительные, так и отрицательные значения.
Из опыта мы определили значения величины Θ (тета) при 0 °С и 100 °С. Обозначим абсолютную температуру при 0 °С через Т1, а при 100 °С через Т2. Тогда согласно формуле:



Отсюда можно вычислить коэффициент k, который связывает температуру в Θ энергетических единицах (Дж) с абсолютной температурой Т (К)
k = 1,38 • 10-23 Дж/К — постоянная Больцмана.
Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдём сначала значение абсолютной температуры, соответствующее 0°С:

 значение абсолютной температуры.
значение абсолютной температуры.
Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры t по Цельсию:


Теперь выведем ещё одну зависимость температуры от средней кинетической энергии молекул. Из основного уравнения молекулярно-кинетической теории и уравнения для определения абсолютной температуры


Здесь видно, что левые части этих уравнений равны, значит правые равны тоже.

Средняя кинетическая энергия хаотического поступательного движения молекул газа пропорциональна абсолютной температуре.
Абсолютная температура есть мера средней кинетической энергии движения молекул.
Из выведенных формул мы можем получить выражение, которое показывает зависимость давления газа от концентрации молекул и температуры



Из этой зависимости вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же. Отсюда следует закон Авогадро, известный нам из курса химии.
Закон Авогадро: в равных объёмах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Рассмотрим задачи тренировочного блока урока.
1. При температуре _______ (370C; 2830C; 270C) средняя кинетическая энергия поступательного движения молекул равна 6,21·10-21Дж.
Дано:

k = 1,38 • 10-23 Дж/К — постоянная Больцмана
t -?
Решение:
Запишем значение средней кинетической энергии хаотического поступательного движения молекул с зависимостью от абсолютной температуры:

Отсюда выразим Т:


Соотношение между абсолютной температурой и температурой в градусах Цельсия:

Подставим значение абсолютной температуры:

Правильный вариант ответа:
2. При температуре 290 К и давлении 0,8 МПа, средняя кинетическая энергия молекул равна __________ Дж, а концентрация составляет молекул ___________ м-3.
Дано:
Т = 290К
р = 0,8 МПа =0,8·106 Па
k = 1,38 • 10-23 Дж/К — постоянная Больцмана
Ек -? n — ?
Решение:
Значение средней кинетической энергии хаотического поступательного движения молекул:

Подставив значение абсолютной температуры, найдём ответ:

Определим концентрацию газа из соотношения:



Правильный вариант ответа: 6·10-21; 2·1026 м-3.
| Основные положения МКТ | ||
Левкипп и Демокрит — 400 лет до н.э. М. В. Ломоносов — XVIII в. «0 причине теплоты и холода», «О коловратном движении корпускул». 1. Все вещества состоят из мельчайших частиц (молекул и атомов). Молекулы разделены промежутками. 2. Молекулы находятся в беспрерывном хаотическом движении. 3. Между молекулами существуют силы взаимодействия (притяжение и отталкивание). | ||
АТОМ — наименьшая частица химического элемента, которая является носителем его химических свойств. А. состоит из положительно заряженного ядра и отрицательно заряженных электронов, движущихся в кулоновском поле ядра по законам квантовой механики. Размеры А. порядка 10-10 м. | ||
МОЛЕКУЛА — наименьшая устойчивая частица вещества, обладающая всеми химическими свойствами и состоящая из одинаковых (простое вещество) или разных (сложное вещество) атомов, объединенных химическими связями. | ||
Опытные обоснования МКТ | ||
Существование молекул |
|
|
Наличие промежутков |
|
|
Хаотическое движение молекул |
|
|
Силы взаимодействия |
|
|
Диффузия. Броуновское движение. | ||
Диффузия — явление проникновения частиц одного вещества в промежутки между частицами другого. Скорость диффузии зависит от температуры и состояния вещества (быстрее в газах). | Фильм «Диффузия« | |
Броуновское движение — беспорядочное движение мелких частиц, взвешенных в жидкости или газе, происходящее под влиянием теплового движения молекул. Р. Броун (1827) наблюдал. Создание теории — А. Эйнштейн и М. Смолуховский (1905). Ж.Б. Перрен (1908—1911) — опыты. Движение не прекращается | ||
Роль в природе, технике
| ||
Скорость теплового движения молекул МКТ газов основана на том, что газы состоят из беспорядочно движущихся молекул. Понятие температуры связано со скоростью хаотического движения молекул формулой где — Так как NА.k=const=R, то
При t0=0°С средние скорости для азота – 500 м/с, для водорода – 1800 м/с. | ||
Экспериментальное определение скорости движения молекул Сущность опыта О. Штерна (1920)
|
| |
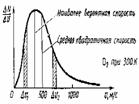
Распределение молекул по скоростям График распределения молекул по скоростям. Английский физик Дж. Максвелл и австрийский физик Л. Больцман. Кривая распределения Максвелла соответствует результатам, полученным в опыте Штерна. Количество частиц, имеющих скорости в интервале ΔV1, равно ΔN, V — одна из скоростей этого интервала. Из графика видно, что количество частиц, имеющих скорости в равных интервалах ΔV1 и Δv2, различно. Скорость, около которой расположены наиболее «населенные» интервалы,— наиболее вероятная скорость теплового движения молекул. |
| |
Основные выводы
|
| |
Тепловая скорость — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 октября 2019; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 октября 2019; проверки требуют 2 правки.Теплова́я скорость — значение среднеквадратичной скорости теплового движения частиц.
Если распределение частиц по скоростям задано некоторой функцией f(v){\displaystyle f(v)}, то тепловая скорость определяется как
- vT=[∫0∞v2f(v)dv]1/2.{\displaystyle v_{T}=\left[\int \limits _{0}^{\infty }v^{2}f(v)\,dv\right]^{1/2}.}
В случае максвелловского распределения по скоростям, определяемого температурой T, тепловая скорость равна
- vT=3kTm,{\displaystyle v_{T}={\sqrt {\frac {3kT}{m}}},}
где k — постоянная Больцмана, m — масса частиц. Таким образом, тепловая скорость частиц и температура вещества однозначно связаны между собой.
Тепловая скорость характеризует среднюю кинетическую энергию частиц вещества:
- ⟨Ek⟩=mvT22.{\displaystyle \langle E_{k}\rangle ={\frac {mv_{T}^{2}}{2}}.}
Таким образом, тепловая скорость также характеризует и внутреннюю энергию вещества, связанную с поступательным движением составляющих его частиц.
- Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика. — С. 193—196.
Основные положения МКТ
Определение 1Молекулярно-кинетическая теория – это учение о строении и свойствах вещества, основанное на представлении о существовании атомов и молекул, как наименьших частиц химических веществ.
Основные положения молекулярно кинетической теории строения вещества
Основные положения молекулярно-кинетической теории молекулы:
- Все вещества могут быть в жидком, твердом и газообразном состоянии. Они образуются из частиц, которые состоят из атомов. Элементарные молекулы могут иметь сложное строение, то есть иметь в своем составе несколько атомов. Молекулы и атомы – электрически нейтральные частицы, которые в определенных условиях приобретают дополнительный электрический заряд и переходят в положительные или отрицательные ионы.
- Атомы и молекулы движутся непрерывно.
- Частицы с электрической природой силы взаимодействуют друг с другом.
Основные положения мкт и их примеры были перечислены выше. Между частицами имеется малое гравитационное воздействие.

Рисунок 3.1.1. Траектория Броуновской частицы.
Определение 2Броуновское движение молекул и атомов подтверждает существование основных положений молекулярно кинетической теории и опытно обосновывает его. Данное тепловое движение частиц происходит с взвешенными в жидкости или газе молекулами.
Опытное обоснование основных положений молекулярно кинетической теории
В 1827 году Р. Броун открыл это движение, которое было обусловлено беспорядочными ударами и перемещениями молекул. Так как процесс происходил хаотично, то удары не могли уравновесить друг друга. Отсюда вывод, что скорость броуновской частицы не может быть постоянной, она постоянно меняется, а движение направления изображается в виде зигзага, показанное на рисунке 3.1.1.
О броуновском движении говорил еще А. Эйнштейн в 1905 году. Его теория нашла подтверждение в опытах Ж. Перрена 1908-1911 гг.
Определение 3Следствие из теории Эйнштейна: квадрат смещения <r2> броуновской частицы относительно начального положения, усредненное по многим броуновским частицам, пропорционален времени наблюдения t.
Выражение <r2>=Dt объясняет диффузионный закон. По теории имеем, что D монотонно возрастает с увеличением температуры. Беспорядочное движение проглядывается при наличии диффузии.


 ,
,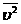 среднее значение квадрата скорости. Следовательно
среднее значение квадрата скорости. Следовательно