Определённый интеграл — Википедия
Материал из Википедии — свободной энциклопедии
Определённый интеграл — одно из основных понятий математического анализа, один из видов интеграла. Определённый интеграл является числом, равным пределу сумм особого вида (интегральных сумм)[⇨]. Геометрически определённый интеграл выражает площадь «криволинейной трапеции», ограниченной графиком функции[⇨].[1] В терминах функционального анализа, определённый интеграл — аддитивный монотонный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала)[2].
Что такое определённый интеграл, анимация (нажмите для воспроизведения)Пусть функция f(x){\displaystyle f(x)} определена на отрезке [a;b]{\displaystyle [a;b]}. Разобьём [a;b]{\displaystyle [a;b]} на части несколькими произвольными точками: a=x0<x1<x2<…<xn=b{\displaystyle a=x_{0}<x_{1}<x_{2}<\ldots <x_{n}=b}. Тогда говорят, что произведено разбиение R{\displaystyle R} отрезка [a;b].{\displaystyle [a;b].} Далее, для каждого i{\displaystyle i} от 0{\displaystyle 0} до n−1{\displaystyle n-1} выберем произвольную точку ξi∈[xi;xi+1]{\displaystyle \xi _{i}\in [x_{i};x_{i+1}]}.
Определённым интегралом от функции f(x){\displaystyle f(x)} на отрезке [a;b]{\displaystyle [a;b]} называется предел интегральных сумм при стремлении ранга разбиения к нулю λR→0{\displaystyle \lambda _{R}\rightarrow 0}, если он существует независимо от разбиения R{\displaystyle R} и выбора точек ξi{\displaystyle \xi _{i}}, то есть
- ∫abf(x)dx=limΔx→0∑i=0n−1f(ξi)Δxi{\displaystyle \int \limits _{a}^{b}f(x)dx=\lim \limits _{\Delta x\rightarrow 0}\sum \limits _{i=0}^{n-1}f(\xi _{i})\Delta x_{i}}
Если существует указанный предел, то функция f(x){\displaystyle f(x)} называется интегрируемой на [a;b]{\displaystyle [a;b]} по Риману.
Обозначения[править | править код]
![[a;b]](/800/600/https/upload.wikimedia.org/wikipedia/commons/thumb/f/f2/Integral_as_region_under_curve.svg/125px-Integral_as_region_under_curve.svg.png) Определённый интеграл как площадь фигуры
Определённый интеграл как площадь фигурыОпределённый интеграл от неотрицательной функции ∫abf(x)dx{\displaystyle \int \limits _{a}^{b}f(x)\,dx} численно равен площади фигуры, ограниченной осью абсцисс, прямыми x=a{\displaystyle x=a} и x=b{\displaystyle x=b} и графиком функции f(x){\displaystyle f(x)}.[1]
- Если функция f(x){\displaystyle f(x)} интегрируема по Риману на [a;b]{\displaystyle [a;b]}, то она ограничена на нем.
Далее приведены примеры расчёта определенных интегралов с помощью формулы Ньютона — Лейбница.
- ∫89x2dx=x33|89=7293−5123=2173=72,(3)≈72,3{\displaystyle \int \limits _{8}^{9}x^{2}\,dx={\frac {x^{3}}{3}}{\Big |}_{8}^{9}={\frac {729}{3}}-{\frac {512}{3}}={\frac {217}{3}}=72{,}(3)\approx 72{,}3}
- ∫1bdxx=lnx|1b=lnb{\displaystyle \int \limits _{1}^{b}{\frac {dx}{x}}=\ln x{\Big |}_{1}^{b}=\ln b}
- ∫142dxx=2lnx|14≈2,8{\displaystyle \int \limits _{1}^{4}{\frac {2dx}{x}}=2\ln x{\Big |}_{1}^{4}\approx 2{,}8}
Формулы и уравнения определенных интегралов
Формулы и уравнения определенных интегралов- Формула Ньютона-Лейбница:
, где - Формула интегрирования по частям в определенном интеграле:
- Замена переменной в определенном интеграле:
Если функция f(x) непрерывна на отрезке [a;b], а функция x=ϕ(t) непрерывно дифференцируема на отрезке [α;β], где a=ϕ(α), b=ϕ(β), то - Интегралы с бесконечными пределами:
- Признаки сходимости интегралов с бесконечными пределами (признаки сравнения):
1. Если a≤x≤+∞, 0≤f(x)≤g(x), то из сходимости
сходимость
≤
из расходимости расходимость
2. Если при a≤x≤+∞, f(x)>0, g(x)>0 и существует конечный предел ≠0, то интегралы сходятся или расходятся одновременно.
Эталоном сравнения служит интеграл:
он сходится при p>1 и расходится при p≤1. - Интегралы от неограниченных функций:
Если функция f(x) непрерывна при a≤x<b и
, то
. - Признаки сходимости несобственных интегралов от неограниченных функций:
Аналогичны признакам сходимости интегралов с бесконечными пределами. Эталоном сравнения служит интеграл он сходится при 0<p<1 и расходится при p>1.
- Приложения определенного интеграла
- Площадь плоской фигуры
1.1. Фигура ограничена графиком функции y=f(x)(f(x)≥0), прямыми x=a, x=b и осью Ox:
.
1.2. Фигура ограничена графиками функций y=f1(x) и y=f2(x), f1(x)≤2f2(x), и прямыми x=a, x=b:
.
1.3. Фигура ограничена кривой, имеющей параметрические уравнения x=x(t), y=y(t), прямыми x=a, x=b и осью Ox:
, где f=x(t1), b=x(t2), y(t)≥0 на отрезке [t1; t2].
1.4. Площадь криволинейного сектора, ограниченного графиком непрерывной функции ρ=ρ(ϕ), лучами ϕ=α, ϕ=β, где ϕ и ρ — полярные координаты:
. - Длина дуги кривой
2.1. Гладкая кривая задана явно, y=f(x), a≤x≤b:
.
2.2. Кривая задана параметрически, x=x(t), y=y(t), z=z(t), t1≤t≤t2:
(для плоской кривой z(t)≡0).
2.3. Кривая задана в полярных координатах, ρ=ρ(ϕ), α≤ϕ≤β:
. - Площадь поверхности вращения, образованной вращением вокруг оси Ox дуги кривой
3.1. Дуга задана явно, y=f(x), a≤x≤b:
.
3.2. Дуга задана параметрически, x=x(t), y=y(t), t1≤t≤t2:
.
3.3. Дуга задана в полярных координатах, ρ=ρ(ϕ), α≤ϕ≤β:
. - Объем тела
4.1. Тело заключено между плоскостями x=a и x=b, площадь сечения тела плоскостью, перпендикулярной оси Ox – известная функция S=f(x), непрерывная на отрезке [a; b], f(x)≥0:
.
4.2. Криволинейная трапеция, ограниченная кривой y=f(x), a≤x≤b вращается вокруг оси Ox:
.
4.3. Криволинейная трапеция, ограниченная кривой x=g(y), c≤y≤d вращается вокруг оси Oy:
.
Формулы, уравнения, теоремы, примеры решения задач
Понятие определённого интеграла, формула Ньютона-Лейбница
На данном уроке мы познакомимся с определенным интегралом, рассмотрим формулу Ньютона-Лейбница.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Производная и интеграл»
Напомним три задачи, рассмотренные на прошлом уроке, которые сводятся к нахождению одной и той же площади криволинейной трапеции.

Рис. 1. Нахождение площади криволинейной трапеции
О площади 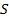 под кривой
под кривой 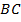
Дано: 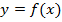 .
.
Найти: 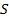 .
.
О массе стержня 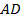
Дано: 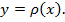
Найти: 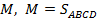
О перемещении точки по прямой
Дано: 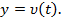
Найти: 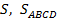 .
.
Таким образом, если мы сумеем найти площадь под кривой, площадь криволинейной трапеции, мы решим эти три, а также многие другие задачи.

Рис. 2. Метод решения
Напомним метод решения. Он заключается в следующем:
Разбить отрезок 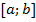
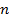 равных частей:
равных частей: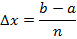
Сосчитать 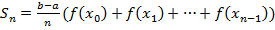 , то есть площадь подступенчатой ломаной.
, то есть площадь подступенчатой ломаной.
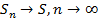
Найти:
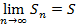
Прежде чем найти указанный предел, примем важное определение и переобозначение.
Рассмотрим интегральную сумму:
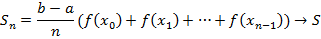
Площадь криволинейной трапеции записывается следующим образом:
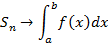
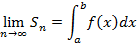
Определение: Определенный интеграл от функции 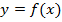 по отрезку
по отрезку 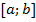 – это предел интегральных сумм
– это предел интегральных сумм 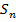 при
при 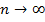
Обсудим каждый элемент введенного определения:
a, b – пределы интегрирования.
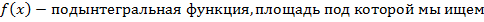
 площадь криволинейной трапеции подынтегральной функции
площадь криволинейной трапеции подынтегральной функции 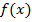 в пределах от
в пределах от 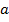 до
до  .
.
Выпишем решение трех задач через определенный интеграл.
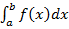
Масса неоднородного стержня ,
, 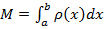 .
.
Перемещение точки вдоль прямой, если известна скорость, 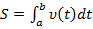 (геометрический и физический смысл определенного интеграла).
(геометрический и физический смысл определенного интеграла).
Для того чтобы вычислить определенный интеграл, а с ней и площадь криволинейной трапеции, для начала рассмотрим теорему.
Теорема: Если 
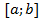 функция, а
функция, а 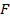 – ее первообразная на этом отрезке, то площадь
– ее первообразная на этом отрезке, то площадь 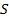 соответствующей криволинейной трапеции равна приращению первообразной на отрезке
соответствующей криволинейной трапеции равна приращению первообразной на отрезке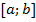 , то есть:
, то есть: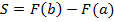
Обсудим полученную формулу (рис. 3).

Рис. 3. Иллюстрация к теореме
Доказательство: На отрезке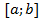 зафиксируем
зафиксируем 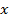 и найдем площадь под кривой на отрезке
и найдем площадь под кривой на отрезке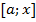 , то есть каждому
, то есть каждому 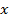 ставится в соответствие
ставится в соответствие 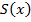 , введена новая функция.
, введена новая функция.
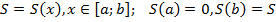
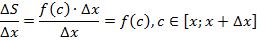

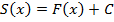
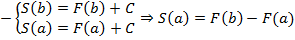
Отсюда площадь криволинейной трапеции равняется приращению любой первообразной на отрезке 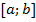 .
.
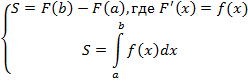
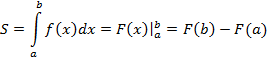
 – непрерывная на отрезке
– непрерывная на отрезке  .
.

Рис. 4. Непрерывная функция
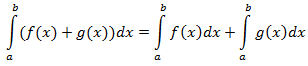
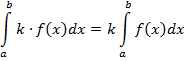

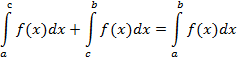
Пример:
Вычислить: 
Решение:
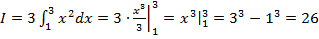 .
.
Пояснение: 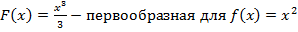
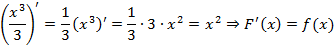
Геометрическая интерпретация:

Рис. 5. Площадь криволинейной трапеции
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Mathprofi.ru (Источник).
- Energy.bmstu.ru (Источник).
- Math34.ru (Источник).
Домашнее задание
- Докажите, что равенство верно:
 .
. - Вычислите интеграл:

- Вычислите интеграл:

- Алгебра и начала анализа, Мордкович А.Г.: № 1021–1025
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Определенный интеграл как площадь криволинейной трапеции
Рассмотрим на плоскости прямоугольную систему координат Oty , ось абсцисс которой в данном разделе будем обозначать Ot , а не Ox (рис. 1).

Рис.1
Пусть y = f (t) – непрерывная на отрезке [a, b] функция, принимающая только положительные значения.
Определение 1. Фигуру, ограниченную графиком функции y = f (t) сверху, отрезком [a, b] снизу, а справа и слева отрезками прямых t = a и t = b (рис. 2), называют криволинейной трапецией.
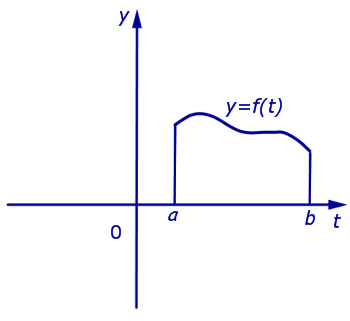
Рис.2
Определение 2. Число, равное площади криволинейной трапеции, изображенной на рисунке 2, называют определенным интегралом от функции f (t) в пределах от a до b и обозначают
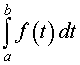 | (1) |
Формула (1) читается так: «Интеграл от a до b от функции f (t) по dt»
Определение 3. В формуле (1) функцию f (t) называют подынтегральной функцией, переменную t называют переменной интегрирования, отрезок [a, b] называют отрезком интегрирования, число b называют верхним пределом интегрирования, а число a – нижним пределом интегрирования.
Производная от определенного интеграла по верхнему пределу
Если обозначить S (x) площадь криволинейной трапеции, ограниченной с боков отрезками прямых t = a и t = x (рис. 3),

Рис.3
то будет справедлива формула
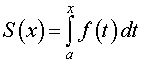 | (2) |
Теорема 1. Производная от определенного интеграла по верхнему пределу интегрирования равна значению подынтегральной функции в верхнем пределе интегрирования.
Другими словами, справедлива формула
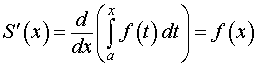
Доказательство. Из формулы (2) следует, что
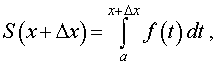 | (3) |
где через Δx обозначено приращение аргумента x (рис. 4)

Рис.4
Из формул (3) и (2) получаем, что
 | (4) |
где через ΔS обозначено приращение функции S (x), соответствующее приращению аргумента Δx (рис. 5)

Рис.5
Если ввести обозначения


(см. раздел «Наибольшее и наименьшее значение функции на отрезке»), то можно заметить, что выполнено неравенство
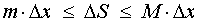 | (5) |
смысл которого заключается в том, что площадь криволинейной трапеции, изображенной на рисунке 5, не может быть меньше, чем площадь прямоугольника с основанием Δx и высотой m, и не может быть больше, чем площадь прямоугольника с основанием Δx и высотой M.
Из неравенства (5) следует, что


откуда, переходя к пределу при Δx → 0, получаем


В силу непрерывности функции y = f (t) выполнено равенство


По определению производной функции S (x) имеем
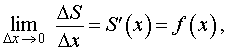 | (6) |
что и завершает доказательство теоремы 1.
Следствие 1. Функция S (x) является первообразной подынтегральной функции f (x) .
Теорема Ньютона — Лейбница
Теорема Ньютона-Лейбница. Если F (x) – любая первообразная функции f (x), то справедливо равенство
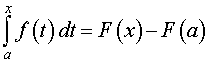 | (7) |
Доказательство. Поскольку S (x) и F (x) – две первообразных функции f (x), то существует такое число c, что выполнено равенство
Воспользовавшись равенством (8), из формулы (2) получаем, что
 | (9) |
Подставив в формулу (9) значение x = a, получаем равенство
 | (10) |
Заметим, что
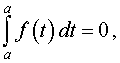 | (11) |
поскольку площадь криволинейной трапеции, «схлопнувшейся» в отрезок, лежащий на прямой t = a, равна 0 .
Из формул (10) и (11) следует, что
c = – F (a) ,
и формула (9) принимает вид
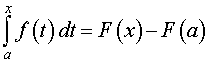 ,
,
что и завершает доказательство теоремы Ньютона-Лейбница.
Замечание 1. Формулу (7) часто записывают в виде
 | (12) |
и называют формулой Ньютона-Лейбница.
Замечание 2. Для правой части формулы Ньютона-Лейбница часто используют обозначение
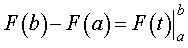
Замечание 3. Формулу Ньютона-Лейбница (12) можно записывать, как с переменной интегрирования t , так и с любой другой переменной интегрирования, например, x :
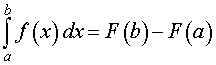
Замечание 4.Все определения и теоремы остаются справедливыми не только в случае положительных непрерывных функций f (x), но и для гораздо более широкого класса функций, имеющих произвольные знаки и интегрируемых по Риману, однако этот материал уже выходит за рамки школьного курса математики.
Примеры решения задач
Задача 1. Найти площадь фигуры, ограниченной линиями
y = e – x, y = 0, x = 0, x = ln 3.
Решение. Рассматриваемая фигура является криволинейной трапеции (рис. 6)
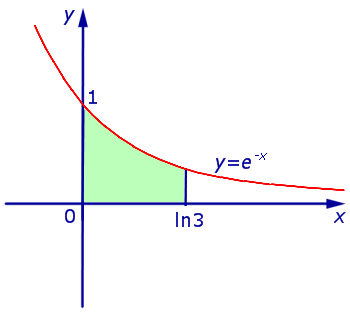
Рис.6
Найдем площадь этой криволинейной трапеции:


Ответ.
Задача 2. График функции y = f (x) изображен на рисунке 7.
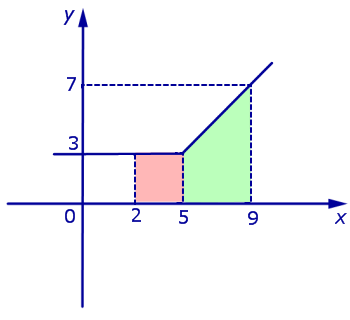
Рис.7
Вычислить интеграл
 | (13) |
Решение. Интеграл (13) равен площади криволинейной трапеции, ограниченной сверху графиком функции y = f (x), ограниченной снизу осью абсцисс Ox и ограниченной с боков отрезками прямых x = 2 и x = 9. Криволинейная трапеция состоит из квадрата, раскрашенного на рисунке 7 розовым цветом, и трапеции, раскрашенной на рисунке 7 зеленым цветом. Площадь квадрата равна 9, а площадь трапеции равна 20. Таким образом, интеграл (13) равен 29.
Ответ. 29.
Задача 3. Вычислить определенный интеграл
 | (14) |
Решение. Поскольку одной из первообразных подынтегральной функции интеграла (14) является функция
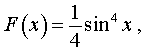
то в соответствии с формулой Ньютона-Лейбница получаем


Ответ.

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
11. Формула ньютона-лейбница (основная формула интегрального исчисления (!) )
Если f(x) непрерывна на отрезке [a;b], и F(x) — некоторая первообразная функции f(x), То:
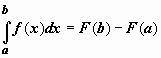
Формулу Ньютона-Лейбница обычно записывают так:
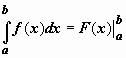
12. Методы интегрирования определенного интеграла
1) Метод замены переменной. Пусть функция x=φ(t) имеет производную во всех точках отрезка [α;β] и отображает этот отрезок на отрезке [a,b] таким образом, что a= φ(α) и b=φ(β). Тогда
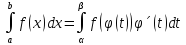
2) Интегрирование по частям
Пусть функции u(x) и v(x) имеют производные во всех точках отрезка [a,b]. Тогда:
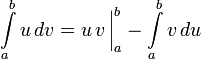
3) Метод непосредственного интегрирования. С помощью тождественных преобразований подынтегральной функции интеграл сводится к интегралу, к которому применимы основные правила интегрирования и возможно использование таблицы основных интегралов.
4) Интегрирование дробей. Элементарными дробями называются дроби следующих 4-ёх типов:
1) 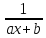 ;
2)
;
2)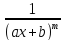 ;
3)
;
3)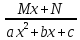 ; 4)
; 4) , гдеm,
n–натуральные
числа (m≥2,
n≥2,
b2-4ac<0)
, гдеm,
n–натуральные
числа (m≥2,
n≥2,
b2-4ac<0)
Дробь  — правильная, если степень числителя
меньше степени знаменателя, в противном
случае дробь называется неправильной.
— правильная, если степень числителя
меньше степени знаменателя, в противном
случае дробь называется неправильной.
Если 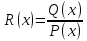 – правильная рациональная дробь,
знаменательP(x)
которой представлен в виде линейных и
квадратичных множителей P(x)=
– правильная рациональная дробь,
знаменательP(x)
которой представлен в виде линейных и
квадратичных множителей P(x)= ,
то эта дробь может быть разложена на
элементарные дроби по схеме:
,
то эта дробь может быть разложена на
элементарные дроби по схеме:
 =
=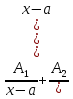 +…
+…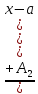 +…+
+…+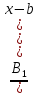 +
+ +…+
+…+ +
+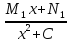 +
+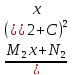 +…+
+…+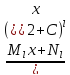 ,где
A1…Ak,
B1
… Bp,
M1…Me,
N1…Nl
– некоторые
действительные числа. Коэффициенты Аi,
Bi,
Mi,
Ni находят методом неопределенных
коэффициентов или методом частных
значений. Для этого необходимо привести
равенства к общему знаменателю, приравнять
коэффициенты при одинаковых степенях
x
в левой и правой частях полученного
тождества и решить систему линейных
уравнений относительно искомых
коэффициентов. Можно определить
коэффициент и другим способом, придавая
в полученном тождестве переменной х
произвольное числовое значение.
,где
A1…Ak,
B1
… Bp,
M1…Me,
N1…Nl
– некоторые
действительные числа. Коэффициенты Аi,
Bi,
Mi,
Ni находят методом неопределенных
коэффициентов или методом частных
значений. Для этого необходимо привести
равенства к общему знаменателю, приравнять
коэффициенты при одинаковых степенях
x
в левой и правой частях полученного
тождества и решить систему линейных
уравнений относительно искомых
коэффициентов. Можно определить
коэффициент и другим способом, придавая
в полученном тождестве переменной х
произвольное числовое значение.
5)Интегрирование тригонометрических функций: универсальная тригонометрическая подстановка.
Интеграла вида 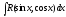 ,
гдеR
– рациональная функция, приводятся к
интегралам от рациональных функций с
помощью универсальной
тригонометрической подстановки:
tg
,
гдеR
– рациональная функция, приводятся к
интегралам от рациональных функций с
помощью универсальной
тригонометрической подстановки:
tg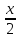 =t
=t
В результате
подстановки: sinx=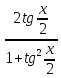 =
= cosx=
cosx=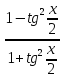 =
=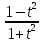 x=2arctg(t)
dx=
x=2arctg(t)
dx=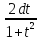
Интегралы вида 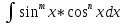
1) Один из показателей m или n – нечетное положительное число.
Если n — нечетное положительное число, то подстановка sin x=t
Если m — нечетное положительное число, то подстановка cos x=t
2) Оба показателя степени m и n – четные положительные числа. Надо преобразовать подынтегральную функцию с помощью формул:
sinx*cosx=½sin(2x) 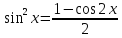
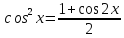
Интегралы вида 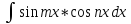 ,
, ,
, .
Подынтегральную функцию преобразовываем
с помощью тригонометрических формул:
.
Подынтегральную функцию преобразовываем
с помощью тригонометрических формул:
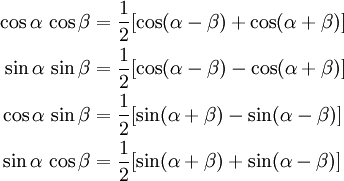
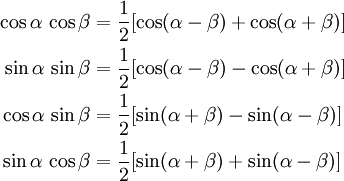
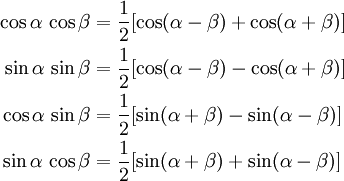
13) Геометрические приложения определенного интеграла
а) Пусть f(x) положительна и непрерывна на [a;b]. Тогда площадь криволинейной трапеции, ограниченной сверху кривой y=f(x) выражается определенным интегралом: (выше оси Ox)
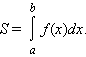
б) Пусть функция y=f(x) отрицательна и непрерывна на [a;b], т.е. кривая y=f(x) и криволинейная трапеция лежат под осью Ох. Тогда:


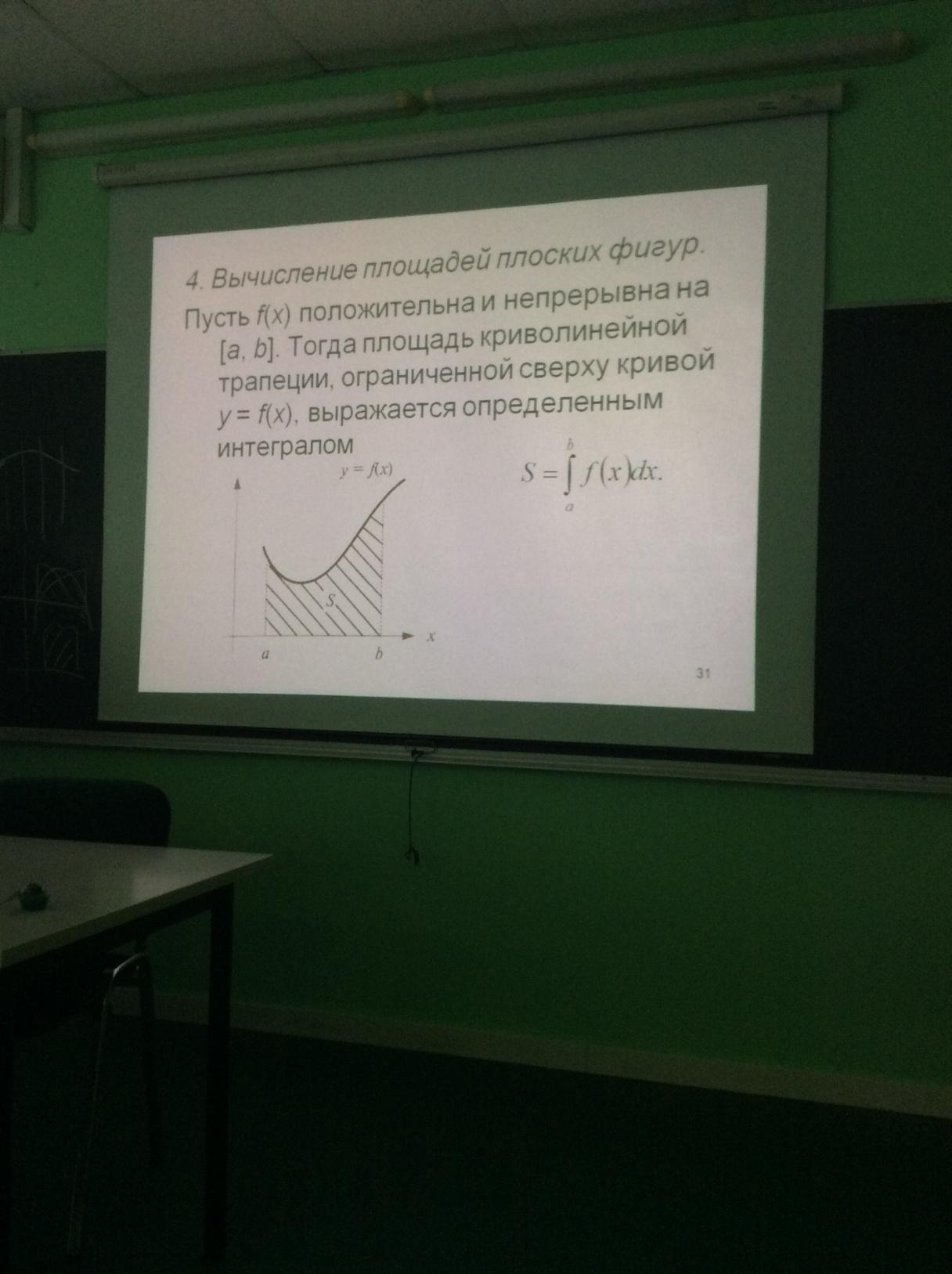
в) Общий случай, когда некоторые части кривой лежат над осью Ох, а другие – под осью Ох. Площадь криволинейной трапеции — алгебраическая сумма площадей тех частей фигуры, которые расположены над Ох, и тех ее частей, которые под Ох, причем первые входят в сумму с «+», а вторые – с «-».
Тогда:
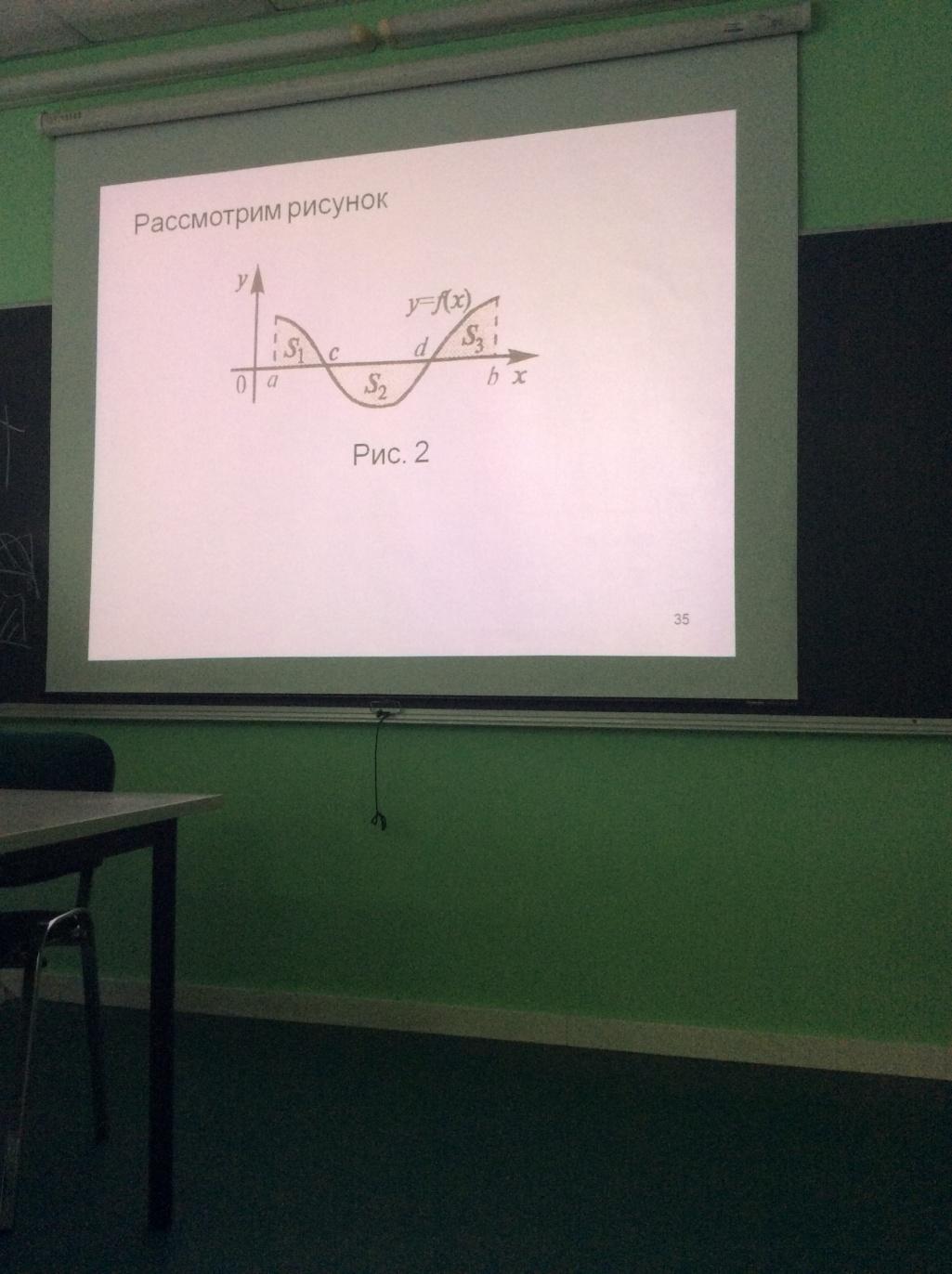
г) Пусть фигура ограничена сверху и снизу кривыми y1=f1(x), y2=f2(x) и f1(x)≤f2(x), a≤x≥b, где f1(x), f2(x) – непрерывные функции. Тогда:
 f1(x),
f2(x)
– отрицательные значения
f1(x),
f2(x)
– отрицательные значения
Объем тела вращения:
y=f(x), f(x) – непрерывна на [a;b]. Если соответственно ей криволинейную трапецию вращать вокруг оси Ох, то получим тело вращения. Каждое сечение тела плоскостью х=const – это круг радиуса R=│y(x)│
Vx=π

Если криволинейную трапецию вращать вокруг оси Оy, то объем тела вращения по формуле:
Vy=π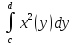

 .
.
