Определить отношения между понятиями, изобразить их с помощью кругов Эйлера:
Федеральное Государственное Бюджетное Образовательное Учреждение
Высшего Профессионального Образования
Башкирский Государственный Университет
Кафедра этики, эстетики и культурологии
по дисциплине:
«Логика»
Вариант 3
Выполнил:
Студент 1 курса СФО з/о гр.1
Проверила:
Иткулова Л.А.
Уфа 2012
а) Виновность. Невиновность.
Понятия «Виновность» и «Невиновность» находятся в отношении противоречия (контрадикторности), одно из которых содержит признаки, а другое эти же понятия исключает. Из схемы видно что понятие А противоречит понятию Не-А, и исчерпывает весь объем понятия «Виновность». Между противоречиями не может быть никакого третьего понятия, в круговых схемах это отношение выглядит так:


А Не-А
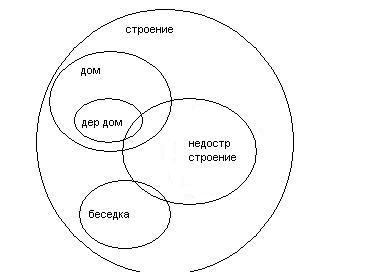
б) Строение, дом, деревянный дом, беседка, недостроенное строение.
Самое крупное понятия- «Строение».Это может быть и недостроенное строение и беседка, и дом, и деревянный дом. Понятие «Дом» включает в себя «Деревянный дом». Понятие «Недостроенное здание» пересекается с «Домом», «Деревянным домом» и «Беседкой», так как они тоже могут быть недостроенным строением.
в) Кража. Мошенничество. Разбой. Преступление против собственности. Разбой.

Понятия «Кража», «Мошенничество», «Разбой», «Преступление против собственности», «Разбой» имеют отношение подчинения (субординации), объем одного полностью входит в объем другого, составляя его часть, в круговых схемах это отношение выглядит так где:
А – «Кража», В – «Мошенничество», С –«Разбой», D – «Преступление против собственности», Е – «Разбой».
D
A B CЕ
г) Студент. Уфимец. Отец. Рыбак.
Понятия «Студент», «Уфимец», «Отец», «Рыбак», находятся в равнообъемности, в которых мыслится один и тот же предмет. Объемы этих понятии полностью совпадают (хотя содержание различно). Так отношение между понятиями «Студент», «Уфимец», «Отец», «Рыбак», изображено в виде четырех полностью совпадающих кругов А, В, С и D, где: А – «Студент», В – «Уфимец», С – «Отец», D – «Рыбак».
 А В С D
А В С D
д) Старый человек. Молодой человек.
Понятия «Старый человек», «Молодой человек» — противоположности (контарности) одно из которых содержит некоторые признаки, а другое — признаки не совместимые с ним.
Объемы двух противоположных понятий составляют в своей сумме лишь часть объема общего для них родового понятия, видами которого они являются и которому они соподчинены. Из схемы видно что понятие В, содержит признаки, не совместимые с признаками понятия А, и исчерпывает весь объем понятия «Старый человек». Пунктиром изображено родовое понятие «человек». Между противоречиями не может быть никакого третьего понятия, в круговых схемах это отношение выглядит так где: А – «Старый человек», В – «Молодой человек».
| |
А В
Отношение между понятиями. Круги Эйлера.
Понятие – это форма мысли, отображающая предметы в их наиболее общих и существенных признаках.
Понятие – это форма мысли, а не форма слова, так как слово лишь метка, которой мы помечаем ту или иную мысль.
ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ. КРУГИ ЭЙЛЕРА.
По содержанию между понятиями могут быть два основных вида отношений: сравнимость и несравнимость.
Понятия, имеющие в своих содержаниях общие признаки, называются СРАВНИМЫМИ («адвокат» и «депутат»; «студент» и «спортсмен»).
В противном случае, понятия считаются НЕСРАВНИМЫМИ («крокодил» и «блокнот»; «человек» и «пароход»).
Если кроме общих признаков понятия имеют и общие элементы объёма, то они называются СОВМЕСТИМЫМИ.
Существует шесть видов отношений между сравнимыми понятиями. Отношения между объёмами понятий удобно обозначать с помощью кругов Эйлера (круговые схемы, где каждый круг обозначает объём понятия).
ВИД ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ | ИЗОБРАЖЕНИЕ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА |
РАВНОЗНАЧНОСТЬ (ТОЖДЕСТВЕННОСТЬ) Объёмы понятий полностью совпадают. Т.е. это понятия, которые различаются по содержанию, но в них мыслятся одни и те же элементы объёма. |
|
ПОДЧИНЕНИЕ (СУБОРДИНАЦИЯ) Объём одного понятия полностью входит в объём другого, но не исчерпывает его. | 1) А – человек В – студент 2) А – животное В – слон |
ПЕРЕСЕЧЕНИЕ (ПЕРЕКРЕЩИВАНИЕ) Объёмы двух понятий частично совпадают. То есть понятия содержат общие элементы, но и включают элементы, принадлежащие только одному из них. |
|
СОПОДЧИНЕНИЕ (КООРДИНАЦИЯ) Понятия, не имеющие общих элементов, полностью входят в объём третьего, более широкого понятия. |
|
ПРОТИВОПОЛОЖНОСТЬ (КОНТРАРНОСТЬ) Понятия А и В не просто включены в объём третьего понятия, а как бы находятся на его противоположных полюсах. То есть, понятие А имеет в своём содержании такой признак, которых в понятии В заменён на противополжный. |
|
ПРОТИВОРЕЧИЕ (КОНТРАДИКТОРНОСТЬ) Отношение между понятиями, одно из которых выражает наличие каких-либо признаков, а другое – их отсутствие, то есть просто отрицает эти признаки, не заменяя их никакими другими. |
|
§ 2. Отношения между понятиями
Предметы мира находятся друг с другом во взаимосвязи и взаимообусловленности. Поэтому и понятия, отражающие эти предметы, также находятся в определенных отношениях. Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются несравнимыми например, «поэма» и «колодец»; «невоспитанность» и «радуга»), остальные понятия называются
Сравнимые понятия делятся по объему на совместимые (объемы этих понятий совпадают полностью или частично) и несовместимые (их объемы не \ имеют общих элементов)
Типы совместимости: равнозначность (тождество), перекрещивание, подчинение (отношение рода и вида)
Отношения между понятиями изображают с помощью круговых схем {кругов Эйлера)1, где каждый круг обозначает объем понятия. Кругом изображается и единичное понятие.
Равнозначными, или тождественными, называются понятия, которые, различаясь содержанием, имеют равные объемы, В них мыслится или одноэлементный класс, или один и тот же класс предметов, состоящий более чем из одного элемента. Примеры равнозначных понятий: 1) «река Нил» и «самая длинная река в мире»; 2) «автор романа «Красное и черное», «автор романа «Пармская обитель»; 3) «равносторонний прямоугольник»: «квадрат»; «равноугольный ромб». Объемы тождественных понятий изображаются кругами, полностью совпадающими.
Понятия, объемы которых совпадают частично, т.е. содержат общие элементы, находятся в отношении перекрещивания. Примерами их являются следующие пары: «горожанин» и «садовод»; «студент» и «нумизмат»; «спортсмен» и «учащийся педагогического колледжа». Они изображаются пересекающимися кругами (рис. 3). 13 заштрихованной части двух кругов мыслятся учащиеся педагогического колледжа, являющиеся спортсменами, или (что одно и то же) спортсмены, являющиеся учащимися педагоги чес ко: го колледжа, в левой части круга А мыслятся учащиеся педагогического колледжа, не являющиеся спортсменами. В правой части круга В мыслятся спортсмены, которые не являются учащимися педагогического колледжа.
Отношение подчинения (субординации) характеризуется тем, что объем одного понятия целиком включается (входит) в объем другого понятия, но не исчерпывает его. Это отношение вида и рода;
Типы несовместимости: соподчинение, противоположность, противоречие
Соподчинение (координация) — это отношение между объемами двух или нескольких понятий, исключающих друг друга, но принадлежащих некоторому более общему (родовому) понятию (например, «пианино», «скрипка», «виолончель» принадлежат объему понятия «музыкальный инструмент»). Они изображаются отдельными неперекрещивающимися кругами внутри более обширного круга (рис. 3). Это виды одного итого же рода.
Сравнимые понятия

Несовместимые |
Равнозначные (тождествен-ные) |
Перекрещи-вающиеся |
Подчиняющие и подчиненные |
Соподчинен-ные |
Противоположные |
Противоре-чащие |






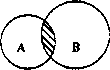
 А
А


 — «русский писатель
М.Ю.Лермонтов»
— «русский писатель
М.Ю.Лермонтов»
В — «автор романа «Герой нашего времени»
А — «учащийся педагогического колледжа»
В — «спортсмен»
А — «цветок»
В- «чайная роза»
А- «пианино»
В — «скрипка»
С — «виолончель»
Д — «музыкальный инструмент» (А, В и С соподчинены Д)
А — «глубокое озеро»
В — «мелкое озеро»
А —«Громкая речка»
В—«негромкая речка»
В отношении противоположности (контрарности) находятся объемы таких двух понятий, которые являются видами одного и того же рода, и притом одно из них содержит какие-то признаки, а другое эти признаки не только отрицает, но и заменяет их другими, исключающими (т.е. противоположными признаками). Слова, выражающие противоположные понятия, яатаются антонимами. Антонимы широко используются в обучении. Примеры противоположных понятий: «великан» — «карлик»; «белые туфли» — «черные туфли». Объемы последних двух понятий разделены объемом некоторого третьего понятия, куда, например, входит понятие «коричневые туфли».
В отношении противоречия (контрадикторности) находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя их никакими другими признаками. Если одно понятие обозначить А (например, «глубокое озеро»), то другое понятие, находящееся с ним в отношении противоречия, следует обозначить не-А (т.е. «неглубокое озеро»). Круг Эйлера, выражающий объем таких понятий, делится на две части (А и не-А), и между ними не существует третьего понятия. Например, товар может быть либо дорогой, либо недорогой; комната бывает светлой или несветлой; животное — позвоночным или беспозвоночным и т.д. Понятие А является положительным, а понятие не-А — отрицательным. Понятия А и не-А также являются антонимами.
Задачи. Определить отношения между данными понятиями и изобразить эти отношения кругами Эйлера.
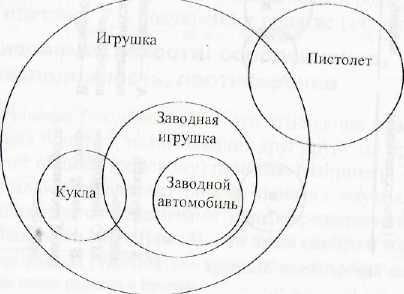
Игрушка, заводная игрушка, кукла, заводной автомобиль, пистолет
Стихийное бедствие, землетрясение, явление природы, наводнение, гроза
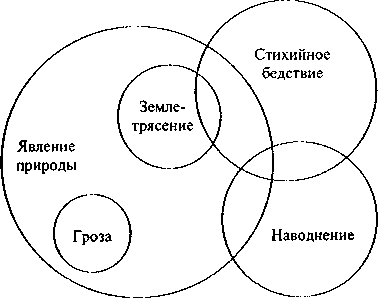
Рис. 5.
1. Определить отношения между понятиями, изобразить их с помощью кругов Эйлера:
ВАРИАНТ №4
а) Правонарушение. Административное правонарушение. Дисциплинарное правонарушение.
Данные понятия находятся в отношения соподчинения. Понятие «Правонарушение» является родовым понятием для его видовых понятий «Административное правонарушение» и «Дисциплинарное правонарушение». Понятия «Административное правонарушение» и «Дисциплинарное правонарушение» являются подвидами видового понятия «Правонарушение».
Обозначим понятия латинскими буквами: А, В, С, а их объем – круговыми схемами (круги Эйлера):
А – «Правонарушение»
В – «Административное правонарушение»
С – «Дисциплинарное правонарушение»
А
С
В
б) Честь. Бесчестье.
Понятия «Честь» и «Бесчестье» находятся между собой в отношении противоречия. Понятие «Честь» выражает наличие признака, а «Бесчестье» — его отсутствие (отсутствие чести). Данные понятия исключают друг друга по содержанию, в рамках родового понятия они по объему полностью исчерпывают объем.
Обозначим понятия латинскими буквами: А, В, а их объем круговыми схемами (круги Эйлера):
А В
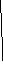
A – «Честь»
В – «Бесчестье»
в) Художественная литература. Английская литература. Трагедия У.Шекспира. «Ромео и Джульетта».
Понятия «Художественная литература», «Английская литература», «Трагедия У. Шекспира «Ромео и Джульетта»», находятся в отношении подчинения: объем одного понятия входит в объем другого, но не исчерпывает его.
Обозначим понятия латинскими буквами: А, В, С, а их объем – круговыми схемами (круги Эйлера):
А – «Художественная литература»
В – «Английская литература»
С – «Трагедия У. Шекспира «Ромео и Джульетта»»
А
В
С
г) Пистолет. Финский нож. Оружие. Огнестрельное оружие;
Понятие «Оружие» является родовым понятием для его видового понятий «Огнестрельное оружие». Понятие «Оружие» является подвидом понятия «Огнестрельное оружие». Понятие «Пистолет» является подвидом понятия «Огнестрельное оружие». Понятие «Финский нож» входит в родовое для него понятие «Оружие». (Понятие «Финский нож» является подвидом понятия «Холодное оружие»)
Обозначим понятия латинскими буквами: А, В, С, D, а их объем – круговыми схемами (круги Эйлера):
А – «Пистолет»
С
В – «Финский нож»
В
С – «Оружие»
D – «Огнестрельное оружие»
D
А
д) Тайное хищение чужого имущества. Кража. Хищение. Разбой.
Понятие «Хищение» является родовым понятием для его видовых понятий «Кража», «Разбой». Понятие «Тайное хищение чужого имущества» является определением понятия «Кража» (ч. 1 ст. 158 УК РФ). Следовательно, они являются равнозначными понятиями.
Обозначим понятия латинскими буквами: А, В, С, D, а их объем – круговыми схемами (круги Эйлера):
А – «Тайное хищение чужого имущества»
В – «Кража»
С
С – «Хищение»
D – «Разбой»
D
А, В
2. Установить правильность следующих определений; в неправильных определениях – укажите и исправьте ошибку:
а) Мошенник – человек, занимающийся мошенничеством.
Данное определение неверно. Нарушено правило «запрета круга». Нельзя определять понятие через само себя или определять через такое другое понятие, которое в свою очередь определяется через него.
б) Адвокат – юрист, оказывающий юридическую помощь гражданам и организациям.
Данное определение неверно. Нарушено правило о том, что определение должно быть ясным. Понятие «юрист» само требует соответствующего определения.
в) Правовые нормы – это правила поведения. Данное определение ошибочное. Объем определяющего больше объема определяемого. Имеет место ошибка слишком широкого определения.
23.Приведите пример совместимых понятий и изобразите отношения между ними с помощью кругов Эйлера.
Пример. Понятия (А) «студент» и (В) «школьник» соподчинены понятию (С) «учащийся», потому что «студент» подчиняется понятию «учащийся», «школьник» подчиняется тому же понятию, но существуют еще учащиеся, например, аспиранты, которые не являются ни школьниками, ни студентами.
Противоречащими называются понятия А и В, если существует третье понятие С, такое, что А подчиняется С и В подчиняется С и не существует такого элемента объема понятия С, который бы не был элементом объема понятия А или элементом объема понятия В.
24. Объясните на примере отношение равнообъемности понятий.
Совместимые понятия.
Понятия, объемы которых полностью или частично совпадают, называются совместимыми. В содержании этих понятий нет признаков, исключающих совпадение их объемов. Существуют три вида отношений совместимости: 1) равнообъемность, 2) пересечение (перекрещивание) и 3) подчинение (субординация).
В отношении равнообъемности находятся понятия, в которых мыслится один и тот же предмет. Объемы этих понятий полностью совпадают. Эти понятия отражают один предмет мысли: равноугольный (равносторонний) треугольник, их объемы полностью совпадают, однако содержание различно, поскольку каждое из них содержит разные признаки треугольника.
Отношение между понятиями принято изображать с помощью круговых схем (кругом Эйлера), где каждый круг обозначает объем понятия, а каждая его точка — предмет, мыслимый в его объеме.
25. Объясните на примере отношение пересечения понятий.
В отношении пересечения (перекрещивания) находятся понятия, объем одного из которых частично входит в объем другого. Содержание этих понятий различно.
Понятия находятся в отношении пересечения тогда, когда их объемы совпадают только частично. Например, пересекающимися будут понятия «школьник» и «спортсмен»: есть такие школьники, которые являются спортсменами, и есть такие спортсмены, которые являются школьниками; но в то же время школьник может не быть спортсменом, так же, как и спортсмен может не быть школьником. На схеме Эйлера отношение пересечения изображается двумя пересекающимися кругами
26. Объясните на примере отношение подчинения понятий.
Понятия находятся в отношении подчинения в том случае, когда объем одного из них обязательно больше объема другого и полностью его в себя включает (один объем как бы подчиняется другому). Например, в отношении подчинения находятся понятия «карась» и «рыба», т.к. все караси — это обязательно рыбы, но рыбами являются не только караси, есть и другие виды рыб. Таким образом, объем понятия «карась» является меньшим по отношению к объему понятия «рыба» и полностью в него включается (подчиняется ему). В отношении подчинения понятия с меньшим объемом называются видовыми, а с большим — родовыми. На схеме Эйлера отношение подчинения изображается двумя кругами, один из которых располагается внутри другого
1.6. Круговые схемы Эйлера. Логика. Учебное пособие
1.6. Круговые схемы Эйлера
Как мы уже знаем, в логике выделяется шесть вариантов отношений между понятиями. Два любых сравнимых понятия обязательно находятся в одном из этих отношений. Например, понятия писатель и россиянин находятся в отношении пересечения, писатель и человек – подчинения, Москва и столица России – равнозначности, Москва и Петербург – соподчинения, мокрая дорога и сухая дорога – противоположности, Антарктида и материк – подчинения, Антарктида и Африка – соподчинения и т. д. и т. п.
Надо обратить внимание на то, что если два понятия обозначают часть и целое, например месяц и год, то они находятся в отношении соподчинения, хотя может показаться, что между ними отношение подчинения, ведь месяц входит в год. Однако, если бы понятия месяц и год были подчиненными, то тогда надо было бы утверждать, что месяц – это обязательно год, а год – это не обязательно месяц (вспомним отношение подчинения на примере понятий карась и рыба: карась – это обязательно рыба, но рыба – это не обязательно карась). Месяц – это не год, а год – это не месяц, но и то, и другое – отрезок времени, следовательно, понятия месяц и год, так же, как и понятия книга и страница книги, автомобиль и колесо автомобиля, молекула и атом и т. п., находятся в отношении соподчинения, т. к. часть и целое – не то же самое, что вид и род.
В начале говорилось о том, что понятия бывают сравнимыми и несравнимыми. Считается, что рассмотренные шесть вариантов отношений применимы только к сравнимым понятиям. Однако возможно утверждать, что все несравнимые понятия находятся между собой в отношении соподчинения. Например, такие несравнимые понятия, как пингвин и небесное тело возможно рассматривать как соподчиненные, ведь пингвин – это не небесное тело и наоборот, но в то же время объемы понятий пингвин и небесное тело входят в более широкий объем третьего понятия, родового по отношению к ним: это может быть понятие объект окружающего мира или форма материи (ведь и пингвин и небесное тело – это различные объекты окружающего мира или различные формы материи). Если же одно понятие обозначает что-то материальное, а другое – нематериальное (например, дерево и мысль), то родовым для этих (как возможно утверждать) соподчиненных понятий является понятие форма бытия, т. к. и дерево, и мысль, и что угодно еще – это различные формы бытия.
Как нам уже известно, отношения между понятиями изображаются круговыми схемами Эйлера. Причем до сих пор мы изображали схематично отношения между двумя понятиями, а это можно сделать и с большим количеством понятий. Например, отношения между понятиями боксер, негр и человек изображаются следующей схемой:

Взаимное расположение кругов показывает, что понятия боксер и негр находятся в отношении пересечения (боксер может быть негром и может им не быть, а также негр может быть боксером и может им не быть), а понятия боксер и человек, так же как и понятия негр и человек находятся в отношении подчинения (ведь любой боксер и любой негр – это обязательно человек, но человек может не быть ни боксером, ни негром).
Рассмотрим отношения между понятиями дедушка, отец, мужчина, человек с помощью круговой схемы:

Как видим, указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; и, наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина. Отношения между понятиями хищник, рыба, акула, пиранья, щука, живое существо изображаются следующей схемой:

Попробуйте самостоятельно прокомментировать эту схему, установив все имеющиеся на ней виды отношений между понятиями.
Подытоживая сказанное, отметим, что отношения между понятиями – это отношения между их объемами. Значит, для того, чтобы было возможно установить отношения между понятиями, их объем должен быть резким, а содержание, соответственно, ясным, т. е. эти понятия должны быть определенными. Что касается неопределенных понятий, о которых шла речь выше, то установить точные отношения между ними достаточно сложно, фактически невозможно, ведь из-за неясности их содержания и нерезкости объема два каких-нибудь неопределенных понятия можно будет характеризовать как равнозначные или как пересекающиеся, или как подчиняющиеся и т. д. Например, возможно ли установить отношения между неопределенными понятиями неаккуратность и небрежность? То ли это будет равнозначность, то ли подчинение – точно сказать невозможно. Таким образом, отношения между неопределенными понятиями являются так же неопределенными. Понятно поэтому, что в тех ситуациях интеллектуально-речевой практики, где требуется точность и однозначность в определении отношений между понятиями, использование неопределенных понятий является нежелательным.
Поделитесь на страничкеСледующая глава >
Учебное пособие для юридических вузов
§ 5. Логические отношения между понятиями
Так как все предметы находятся во взаимодействии и взаимообусловленности, то и понятия, отражающие данные предметы, также находятся в определенных отношениях. Конкретные виды отношений устанавливаются в зависимости от содержания и объема понятий, которые сравниваются.
Если понятия не имеют общих признаков, далеки друг от друга по своему содержанию, то они называются несравнимыми. Например, «симфоническая музыка» и «кассационная жалоба», «процессуальные акты предварительного расследования» и «общая тетрадь».
Сравнимыми называются понятия, отражающие некоторые общие существенные признаки предмета или класса однородных предметов. Например, «юрист» и «адвокат», «взятка» и «кража».
В логических отношениях могут находиться только сравнимые понятия. В зависимости от того, как соотносятся их объемы, понятия делятся на две группы: совместимые и несовместимые.
Совместимые — это такие понятия, объемы которых совпадают полностью или частично. Несовместимые — это понятия, объемы которых не совпадают ни в одном элементе, но которые могут быть включены частично или полностью в объем общего для них понятия. На представленной схеме показаны виды совместимых и несовместимых понятий.

Отношения между понятиями принято иллюстрировать при помощи кругов Эйлера (круговых схем), названных так в честь Леонардо Эйлера (1707-1783) — одного из крупнейших математиков XVIII века, родившегося в Швейцарии, но весь свой талант отдавшего России. Каждый круг обозначает объем понятия, а любая точка внутри круга — предмет, входящий в его объем. Круговые схемы позволяют наглядно представить отношения между различными понятиями, лучше осмыслить и усвоить эти отношения.
Рассмотрим совместимые понятия.
В отношениях равнозначности находятся совместимые понятия, объемы которых полностью совпадают. В таких понятиях мыслится один и тот же предмет или класс однородных предметов. Однако содержание этих понятий различно, так как каждое из них отражает только определенную сторону (существенный признак) данного предмета или класса однородных предметов.
Например, объемы понятий А — «сын» и В — «внук» совпадают (каждый сын есть чей-то внук и каждый внук — чей-то сын), но содержания их различны.

Необходимо отличать равнозначные понятия от равнозначных слов-синонимов. У равнозначных понятий одинаковый объем, но разное содержание. А слова-синонимы выражают понятия с одинаковым объемом и содержанием. Замена в любом осмысленном высказывании слов-синонимов друг с другом не влияет на смысл высказывания. Замена же слов, выражающих равнозначные понятия, может привести к существенному искажению смысла. Например, в высказывании «В 1980 году Москва была столицей игр XXII Олимпиады» нельзя заменить понятие «столица игр XXII Олимпиады» равнозначным ему понятием «центр Московской области». Таким образом, слова или словосочетания, выражающие равнозначные понятия, сами по себе не являются равнозначными.
В отношении пересечения находятся совместимые понятия, у которых объемы частично совпадают. Частично совпадает и содержание данных понятий.

Например, пересекающимися понятиями являются А -«спортсмен» и В — «юрист»: часть спортсменов являются юристами, a часть юристов — спортсменами. В совместившейся части кругов мыслятся те спортсмены, которые являются юристами, а также те юристы, которые являются спортсменами.
В отношении подчинения находятся совместимые понятия, объем одного из которых полностью входит в объем другого, составляя его часть.
В таком отношении, например, находятся понятия А -«кража» и В — «кража личного имущества граждан».

Объем первого понятия шире объема второго понятия: кроме кражи личного имущества граждан в него входит также кража государственного, кооперативного имущества.
Из двух понятий, находящихся в отношении подчинения, понятие с большим объемом (подчиняющее) является родовым, или родом по отношению к понятию с меньшим объемом (подчиненному), а последнее по отношению к первому называется видовым, или видом. Родовидовые отношения лежат в основе логических операций ограничения и обобщения понятий, деления объема понятий и некоторых видов определения.
Перейдем к рассмотрению несовместимых понятий.
При иллюстрации отношений между несовместимыми понятиями возникает потребность во введении более широкого по объему понятия, которое включало бы объемы несовместимых понятий.
В отношении соподчинения находятся два или более непересекающихся понятий, принадлежащих общему родовому понятию.
Соподчиненные понятия В и С — это виды одного рода А, у них общий родовой признак, но видовые признаки различны. Например, В — «должностное преступление» и С — «хозяйственное преступление», где А — «преступление».


В отношении противоположности находятся понятия, которые являются видами одного и того же рода, и при этом одно из них содержит какие-то признаки, а другое эти признаки отрицает и заменяет противоположными признаками.
Например, А — «тяжкое телесное повреждение» и В — «легкое телесное повреждение», где родовое понятие — «телесное повреждение». Объемы противоположных понятий составляют лишь часть объема общего для них родового понятия.
Слова, выражающие противоположные понятия, называются антонимами. Например: осудить — оправдать, обвинение — защита, алиби — улики, мягкое наказание — строгое наказание и др. Неудачное использование антонимов приводит к неясности мысли: «Потерпевший делал все возможное, силясь побороть свою слабость или «Гудов участвовал в преступных действиях в силу слабости своего характера».

В отношении противоречия находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя их никакими другими признаками.
Например, А — «виновный» и не-А — «невиновный», где родовое понятие — «человек». Объемы двух противоречащих понятий составляют весь объем рода, видами которого они являются.
Таким образом, уяснение логической структуры понятий, определение их видов и отношений между сравнимыми понятиями дает возможность перейти к рассмотрению логических действий, или операций над понятиями.
Поделитесь на страничкеСледующая глава >

 1)
А – Аристотель В – основатель логики
2) А – квадрат В – равносторонний
прямоугольник
1)
А – Аристотель В – основатель логики
2) А – квадрат В – равносторонний
прямоугольник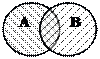 1)
А – юрист В – депутат 2) А – студент
В – спортсмен
1)
А – юрист В – депутат 2) А – студент
В – спортсмен 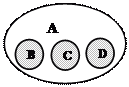 1)
А – животное В – кот; С – собака; D –
мышь 2) А – драгоценный металл В –
золото; С – серебро; D — платина
1)
А – животное В – кот; С – собака; D –
мышь 2) А – драгоценный металл В –
золото; С – серебро; D — платина  1)
А – белый кот; В – рыжий кот (коты
бывают и чёрными и серыми) 2) А –
горячий чай; холодный чай (чай может
быть и тёплым) Т.е. понятия А и В не
исчерпывают всего объёма понятия, в
которое они входят.
1)
А – белый кот; В – рыжий кот (коты
бывают и чёрными и серыми) 2) А –
горячий чай; холодный чай (чай может
быть и тёплым) Т.е. понятия А и В не
исчерпывают всего объёма понятия, в
которое они входят.  1)
А – высокий дом В – невысокий дом
2) А – выигрышный билет В – невыигрышный
билет Т.е. понятия А и не-А исчерпывают
весь объём понятия, в которое они
входят, так как между ними нельзя
поставить никакое дополнительное
понятие.
1)
А – высокий дом В – невысокий дом
2) А – выигрышный билет В – невыигрышный
билет Т.е. понятия А и не-А исчерпывают
весь объём понятия, в которое они
входят, так как между ними нельзя
поставить никакое дополнительное
понятие. 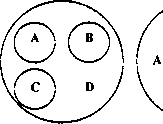 А
А

 — «русский писатель
М.Ю.Лермонтов»
— «русский писатель
М.Ю.Лермонтов»