Задачи ЕГЭ на относительность движения
Задачи на относительность движения – пожалуй, самые сложные из задач кинематики. Здесь надо очень хорошо представлять себе, как будет выглядеть картина движения, если ты находишься на этом самом корабле и ощущаешь ветер на своем лице, или ты едешь на конце движущегося стержня и можешь видеть второй его конец. То есть нужно уметь поставить себя на место другого, и вообразить, что он ощущает или видит – это всегда сложно, и в задаче, и в жизни.
Задача 1. Один корабль идет по морю на север с постоянной скоростью 20 узлов, а другой – навстречу ему, на юг, с такой же скоростью. Корабли проходят на малом расстоянии друг от друга. Шлейф дыма от первого корабля вытянулся в направлении на запад, а от второго – на северо-запад. Определите модуль  скорости ветра. 1 узел – 1 морская миля в час, 1 морская миля – 1852 м. Ответ выразить в км/ч и округлить до целых.
скорости ветра. 1 узел – 1 морская миля в час, 1 морская миля – 1852 м. Ответ выразить в км/ч и округлить до целых.
Для начала переведем скорость судов в км/ч:  узлов/ час
узлов/ час  км/ч
км/ч км/ч.
км/ч.

К задаче 1. Корабли и ветер
Пусть ветер дует под углом 
![Rendered by QuickLaTeX.com \[\upsilon_k=\upsilon \cos{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-eeb393512dcf885ba9883867db9fd33c_l3.png)
Скорость второго корабля, наоборот, накладывается на скорость ветра, на его борту «ветер сильнее». Результатом сложения скоростей ветра и корабля является направление сноса дыма. Чтобы найти скорость ветра в неподвижной системе, нужно из скорости дыма вычесть скорость корабля, который здесь – подвижная система отсчета. Тогда:
![Rendered by QuickLaTeX.com \[\vec{\upsilon}=\vec{\upsilon_k}+\vec{\upsilon_d}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ce8035c3c2345d946e9bd473b2e2e0c9_l3.png)

Вектора дымов и кораблей
Проекция скорости ветра на северное направление тогда равна
![Rendered by QuickLaTeX.com \[\upsilon_k+\upsilon \cos{\alpha}=2\upsilon \cos{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-981e17598c00dea866b0019726ddcd54_l3.png)
Проекция скорости ветра на западное направление равна  , и, следовательно,
, и, следовательно,
![Rendered by QuickLaTeX.com \[\upsilon \cos{\alpha}+\upsilon_k=\upsilon \sin{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4c78ea41a4fc6077daca530e7838dfd8_l3.png)
![Rendered by QuickLaTeX.com \[2\upsilon \cos{\alpha}=\upsilon \sin{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ab98d1cd5e210dfc0ea86f1bd1447910_l3.png)
![Rendered by QuickLaTeX.com \[\operatorname{tg}{\alpha}=2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6e9dddac37497321ad7300be4ba4a927_l3.png)
![Rendered by QuickLaTeX.com \[\alpha=\operatorname{arctg} 2=63^{\circ}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-63a0b8b1726a85c00b1ffb1a8e65167b_l3.png)
Тогда скорость ветра равна:
![Rendered by QuickLaTeX.com \[\upsilon=\frac{\upsilon_k }{\cos{\alpha}}=\frac{37,04}{\cos{63^{\circ}}}=\frac{37,04}{0,45}=82,7\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-494ff0efe0148079b193aae5b5d70cf7_l3.png)
Ответ: 83 км/ч
Задача 2. Стержень скользит по инерции по гладкому горизонтальному столу. В некоторый момент времени в неподвижной системе отсчета скорости концов стержня составляют с направлением стержня углы  и
и  . Какой угол
. Какой угол  образует со стержнем в этот момент скорость его центра?
образует со стержнем в этот момент скорость его центра?
Пусть скорость одного конца стержня равна  , а второго
, а второго  . Стержень участвует в двух движениях: в поступательном и вращательном. Если спроецировать скорости концов на направление стержня, то можно определить скорость поступательного движения, а проекции скорости, перпендикулярные направлению стержня, дадут возможность найти мгновенный центр вращения.
. Стержень участвует в двух движениях: в поступательном и вращательном. Если спроецировать скорости концов на направление стержня, то можно определить скорость поступательного движения, а проекции скорости, перпендикулярные направлению стержня, дадут возможность найти мгновенный центр вращения.

К задаче 2. Стержень
Проекции скорости на направление стержня обязаны быть равными, так как стержень не претерпевает растяжения:
![Rendered by QuickLaTeX.com \[\upsilon_1 \cos{\alpha}=\upsilon_2 \cos{\beta}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b80a6b967d6d1d19d55e236fc553c651_l3.png)
Проекции скоростей на перпендикулярное стержню направление относятся так же, как расстояния концов стержня до мгновенного центра вращения:
![Rendered by QuickLaTeX.com \[\frac{\upsilon_1 \sin{\alpha}}{c}=\frac{l+x}{x}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f70fce9b5de9e6d3a9d710afb1e23337_l3.png)
Отсюда
![Rendered by QuickLaTeX.com \[x=\frac{\upsilon_1 \sin{\alpha} l}{\upsilon_2 \sin{\beta}-\upsilon_1 \sin{\alpha}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3af626ad87be30a72c754efdddc36e7a_l3.png)
Теперь можем найти скорость середины стержня, и угол, под которым она направлена к стержню. Проекция скорости центра на направление стержня такая же, как и у концов:  . Найдем перпендикулярную составляющую. Для этого составим пропорцию:
. Найдем перпендикулярную составляющую. Для этого составим пропорцию:
![Rendered by QuickLaTeX.com \[\frac{\upsilon_3 \sin{\gamma}}{\upsilon_1 \sin{\alpha}}=\frac{\frac {l}{2} +x}{x}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-82bc84476f44554c26198c823e1516c8_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_3 \sin{\gamma}=\frac{(\frac {l}{2} +x)\upsilon_1 \sin{\alpha}}{x}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e2131902cf228e012fb028ed6dfc286d_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_3 \sin{\gamma}=\frac{\upsilon_1 \sin{\alpha}+\upsilon_2 \sin{\beta}}{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5db500df908c519c95267b0914a039d5_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_3 \sin{\gamma}=\frac{\upsilon_1 \sin{\alpha}+\upsilon_1 \frac{\cos{\alpha}}{\cos{\beta}}\sin{\beta}}{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ea5ab08ee92e482917eb014ba1107f78_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_3 \sin{\gamma}=\upsilon_1 \frac{\sin{\alpha}+ \cos{\alpha} \operatorname{tg}{\beta}}{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2617c519dd88f4abde75da41519906eb_l3.png)
Проекция скорости центра стержня на направление стержня такая же, как у концов:
![Rendered by QuickLaTeX.com \[\upsilon_3\cos{\gamma}=\upsilon_1 \cos{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2f74221bc080cdcc18d5cff18c415697_l3.png)
Сам угол равен
![Rendered by QuickLaTeX.com \[\gamma=\operatorname{arctg}\frac{\upsilon_1 \frac{\sin{\alpha}+ \cos{\alpha} \operatorname{tg}{\beta}}{2}}{\upsilon_1 \cos{\alpha}}=\operatorname{arctg} \left(\frac{\operatorname{tg}{\alpha}}{2}+\operatorname{tg}{\beta}}{2}\right)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3be0d60ecdf34b6dc42703546055e0a3_l3.png)
![Rendered by QuickLaTeX.com \[\gamma=\operatorname{arctg} \left(\frac{\operatorname{tg}{30^{\circ}}}{2}+\frac{\operatorname{tg}{60^{\circ}}}{2}\right)= \operatorname{arctg} 1,15= 49,1^{\circ}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e87cc5c73f249b05d77d5ffdef4ce914_l3.png)
Ответ:  .
.
Решение задач на относительность движения
Горбанева Лариса ВалерьевнаРешение задач на относительность движения
Движение любого тела можно рассматривать по отношению к любым другим телам. По отношению к разным телам данное тело будет совершать различные движения: чемодан, лежащий на полке в вагоне идущего поезда, относительно вагона покоится, но относительно Земли движется. Воздушный шар, уносимый ветром, относительно Земли движется, но относительно воздуха покоится. Самолет, летящий в строю эскадрильи, относительно других самолетов строя покоится, но относительно Земли он движется с большой скоростью, например 800 км в час, а относительно такого же встречного самолета он движется со скоростью 1600 км в час.
Всякое движение, а также покой тела (как частный случай движения) относительны. Отвечая на вопрос, покоится тело или движется и как именно движется, необходимо указать, относительно каких тел рассматривается движение данного тела. Иначе никакое высказывание о его движении не может иметь смысла.
В ряде задач приходится рассматривать движение одного и того же тела относительно разных систем отсчета, причем эти системы могут двигаться относительно друг друга.
Тела, относительно которых рассматривается данное движение, называют системой отсчета. Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными.
Выбор системы отсчета при изучении данного движения делают в зависимости от условий задачи. При изучении движений на поверхности Земли обычно принимают за систему отсчета Землю (хотя можно выбрать за систему отсчета и поезд, и самолет, и любое другое тело). Изучая движение Земли в целом или движение планет, принимают за систему отсчета Солнце и звезды.
Рассмотрим движение одного и того же тела относительно двух разных систем отсчета, движущихся одна относительно другой прямолинейно и равномерно. Одну из них мы будем условно считать неподвижной. Другая движется относительно нее прямолинейно и равномерно. Вот простой пример. Лодка пересекает реку перпендикулярно течению, двигаясь с некоторой скоростью относительно воды. Вода в реке движется относительно берега со скоростью течения реки.
Представим себе, что за движением лодки следят два наблюдателя: один неподвижный, расположился на берегу в точке О (рис. 1), другой – на плоту, плывущем по течению (со скоростью течения реки).
Оба наблюдателя измеряют перемещение лодки и время, затраченное на него. Относительно воды плот неподвижен, а по отношению к берегу, он движется со скоростью течения реки.
Проведем мысленно через точку О систему координат XOY. Ось X направим вдоль берега, ось Y – перпендикулярно течению реки. Это неподвижная система координат.
Другую систему координат X’O’Y’ свяжем с плотом. Оси X` и У` параллельны осям X и Y. Это – подвижная система координат.
Рассмотрим движение лодки относительно этих двух систем.
Наблюдатель на плоту, двигаясь вместе со «своей» системой координат по течению, видит, что лодка удаляется от него к противоположному берегу все время перпендикулярно течению. Он видит это и в точке А, и в точке В, и в любой другой точке. А когда через некоторое время плот окажется в точке С, лодка достигнет противоположного берега в точке С. Относительно подвижной системы координат (плота) лодка совершила перемещение S1 = СС’. Разделив его на t, подвижный наблюдатель получит скорость лодки V1 относительно плота:
Совсем другим представится движение лодки неподвижному наблюдателю на берегу. Относительно «его» системы координат лодка за то же время t совершила перемещение . За это же время подвижная система отсчета вместе с плотом совершила перемещение S2 (лодку, как говорят, «отнесло» вниз по течению). Схематически перемещения лодки показаны на рисунке 2.
Формула сложения перемещений.
Из рисунков 1 и 2 видно, что перемещение S лодки относительно неподвижной системы координат связано с перемещениями S1 и S2 формулой:
Формула сложения скоростей.
Скорость V лодки относительно неподвижной системы координат можно получить, разделив перемещение S на время t:
или
,
где – скорость плота относительно берега (скорость течения).
Скорость тела относительно неподвижной системы координат равна геометрической сумме скорости тела относительно подвижной системы координат и скорости подвижной системы относительно неподвижной.
Из вышесказанного видно, что и перемещение и скорость тела относительно разных систем отсчета различна. Различны и траектории движения (СС` – относительно подвижной системы и ОС` – относительно неподвижной).
В этом и состоит относительность движения.
В данном примере за неподвижную систему координат был выбран берег. Но можно было условиться считать неподвижной систему координат, связанную с плотом. Тогда подвижным оказался бы берег и связанная с ним система координат, и тогда рассматривали бы движение берега относительно плота и лодки. Формулы сложения перемещений и скоростей остались бы такими же. Это еще раз показывает, что относительно не только движение, относителен и покой.
При решении задач предлагаем использовать следующий алгоритм.
Анализ условия задачи, выделение движущихся тел. Краткая запись условия задачи. Определение неподвижной и подвижной системы отсчета (НСО и ПСО), движущегося тела.
Записать закон сложения скоростей или перемещений в векторной форме.
Записать закон сложения скоростей (перемещений) в проекциях на оси координат, объединив их в систему (или найти геометрическую сумму путем сложения векторов).
Решить полученную систему уравнений. Подставить в решение общего вида значения величин и произвести вычисления.
На примерах решения типовых задач на относительность движения покажем применение данного способа решения.
Задача № 1. Два поезда движутся равномерно друг за другом. Скорость первого 80 км/ч, а второго 60 км/ч. Какова скорость второго поезда относительно первого?
Первый и второй поезда движутся относительно Земли с некоторыми скоростями. Скорость первого поезда , скорость второго .
Решение:
За НСО примем Землю, за ПСО – первый поезд.
Скорость ПСО относительно НСО – V.
Движущимся телом является второй поезд.
Скорость движущегося тела относительно НСО – V2.
Неизвестная скорость второго поезда относительно первого (ПСО) – V1.
Закон сложения скоростей . Скорость второго поезда относительно НСО равна геометрической сумме скорости второго поезда относительно ПСО и скорости ПСО относительно НСО.
Через t=1час положение ПСО (первого поезда) изменится на расстояние, равное 80 км, а второго поезда, относительно НСО окажется на расстоянии 60 км.
5. Соотнесем график и формулу закона сложения скоростей Убеждаемся в том, что обе формы отражения закона совпадают.
6. Для вычисления скорости второго поезда относительно первого найдем проекции и запишем:
V1 = 80 км/ч – 60 км/ч = 20 км/ч
Ответ: скорость второго относительно первого поезда равна 20 км/ч.
Задача № 2. Скорость течения реки V= 1,5м/с. Каков модуль скорости V1 катера относительно воды, если катер движется перпендикулярно к берегу со скоростью V2 = 2 м/с относительно него.
Решение. За НСО примем берег реки, за ПСО – реку (скорость течения реки V), движущееся тело – катер.
Закон сложения скоростей . Скорость катера относительно НСО (берега реки) равна геометрической сумме скорости катера относительно ПСО (течения реки) и скорости течения реки.
Так как полученный треугольник прямоугольный, то .
Задача № 3. Два поезда движутся навстречу друг другу со скоростями 72 и 54 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 14 с. Какова длина второго поезда?
Решение. Так как движение поездов можно считать равномерным, то длину второго поезда можно найти по формуле , где V21 – скорость второго поезда относительно первого поезда. Значит, для определения l необходимо найти V21.
Примем за НСО Землю, а за ПСО – первый поезд, движущееся тело – второй поезд.
V2 – скорость второго поезда относительно НСО. Скорость ПСО – V1.
Закон сложения скоростей . Скорость второго поезда относительно НСО равна геометрической сумме скорости второго поезда относительно ПСО (первого поезда) и скорости ПСО (первого поезда).
. направлены в одну сторону, а . в противоположную, тогда закон сложения скоростей можно записать – V2 = V1 – V21
Или V21 = V1 + V2
Тогда l = (V1 + V2) t
l = (20 м/с + 15 м/с) 14 с = 490 м.
Ответ: длина второго поезда 490 м.
Задача №4. Катер, двигаясь против течения реки, проплывает около стоящего на якоре буя и встречает там плот. Через 12 минут после встречи катер повернул обратно и догнал плот на расстоянии 800м ниже буя. Найти скорость течения реки.
НСО свяжем с буем, ПСО – плот (движущийся со скоростью течения реки V0), движущееся тело – катер.
Скорость катера относительно НСО – V, а относительно ПСО – V1.
Закон сложения скоростей для катера, движущегося по течению и против течения реки, в геометрической форме совпадает: . Скорость катера относительно НСО равна геометрической сумме скорости ПСО (течения реки) и скорости катера относительно ПСО.
Тогда – V = V0 – V1 или V = V1 – V0
Аналогично найдем скорость катера, двигающегося по течению реки
V = V0 + V1
Запишем уравнения движения плота и катера:
где S1 – расстояние, пройденное катером по течению, S2 – расстояние, пройденное катером против течения.
Расстояние, пройденное катером от буя до того места, где катер догнал плот, равно расстоянию пройденному плотом, то есть Sпл = Sк, тогда
V0 t = – ( V1 – V0 ) t1 + (V0 + V1) (t – t1)
V0 t = – V1 t1 + V0 t1 + V0 t + V1 t – V0 t1 – V1 t1
V1 t = 2 V1 t1
t = 2 t1
.
Задача № 5. В лобовой щит танка, движущегося со скоростью Vт=54км/ч, ударяется пуля, летящая со скоростью V0 = 1800 км/ч под углом φ= 60° к направлению движения танка, и упруго отскакивает от него (рис. 3). С какой скоростью V полетит отскочившая пуля?
Решение. Задачу удобно сначала решить в системе отсчета, связанной с танком, а затем перейти в неподвижную систему отсчета.
Относительно танка скорость пули до удара равна (рис. 4). После упругого удара модуль скорости пули остается прежним, а угол «отражения» β´ будет равен углу «падения» φ´.
Запишем закон сложения скоростей .
Модуль и направление этой скорости найдем из рисунка 4:
.
Задачи для самостоятельного решения
Ф.10.1. Пловец переплывает реку шириной H. Под каким углом α к течению он должен плыть, чтобы переправиться на противоположный берег в кратчайшее время? Где он в этом случае окажется, переплыв реку, и какой путь S он проплывает, если скорость течения равна V1, скорость пловца относительно воды V2?
Ф.10.2. Корабль идет на запад со скоростью V. Известно, что ветер дует с юго-запада. Скорость ветра, измеренная на палубе корабля, равна V1. Найти скорость ветра относительно земли.
Ф.10.3. С подводной лодки, погружающейся равномерно, испускаются звуковые импульсы длительностью 30,1с. Длительность импульса, принятого на лодке после его отражения от дна, равна 29,9с. Определите скорость погружения лодки. Скорость звука в воде 1500м/с.
Ф.10.4. Спортсмены бегут колонной длиной 20м с одинаковой скоростью 3м/с. Навстречу бежит тренер со скоростью 1м/с. Каждый спортсмен, поравнявшись с тренером, бежит назад с прежней скоростью. Какова будет длина колоны, когда все спортсмены развернутся?
Ф.10.5. В безветренную погоду самолет затрачивает на перелет между городами 6ч. На сколько минут увеличится время полета, если будет дуть боковой ветер со скоростью 20м/с перпендикулярно линии полета? Скорость самолета относительно воздуха равна 328км/ч.
Ф.10.6. Два велосипедиста одновременно выехали из пунктов А и В навстречу друг другу и встретились через 1 час. После встречи они продолжили свое движение в прежнем направлении. Доехав до пунктов В и А соответственно, они сразу развернулись и поехали обратно. Через какое время, после первой встречи, они опять поравняются друг с другом.
Ф.10.7. Расстояние S=90км между двумя пристанями, расположенными на реке, теплоход проходит без остановки в одном направлении (по течению) за t1=3ч и в обратном направлении (против течения) за t2=5ч. Определить скорость течения реки и собственную скорость теплохода.
Ф.10.8. От одного берега реки к другому плывет лодка, держа курс перпендикулярно к берегам. Ширина реки 800 м; лодка достигает противоположного берега через 12 мин после начала переправы. За это время лодку сносит вниз по течению на расстояние 600 м. Определить скорость течения реки; собственную скорость лодки; скорость лодки относительно берегов. Скорость течения у берегов и на середине реки считать одинаковой.
Ф.10.9. Трассы двух воздушных лайнеров пересекаются над поселком А. Первый лайнер летит точно на север, второй лайнер – на юго-восток. Скорости V1 и V2 обоих лайнеров численно равны (V1=V2=V). Определить, чему равна и как направлена в этот момент скорость второго лайнера относительно первого.
Ф.10.10. Два снаряда выпущены горизонтально вперед один вслед за другим с интервалом времени t со скоростью U из орудия, находящегося на самолете, который летит горизонтально со скоростью υ. Пренебрегая сопротивлением воздуха, найдите: 1) уравнение траектории первого снаряда относительно земли; 2) уравнение траектории первого снаряда относительно самолета; 3) как изменяется положение первого снаряда относительно второго (после обоих выстрелов).
Ф.10.11. Горизонтальный диск вращается вокруг своей оси, делая n=5об/мин. Человек идет вдоль радиуса диска с постоянной скоростью U=1,5м/с относительно диска. Как меняется модуль скорости человека относительно земли в зависимости от расстояния r от оси диска? Чему равен модуль этой скорости на расстоянии R= 3м от оси диска?
Ф.10.12. Автоколонна длиной 2 км движется со скоростью 40 км/ч. Мотоциклист выехал из хвоста колонны со скоростью 60 км/ч. За какое время он достигнет головной машины? Какой путь за это время пройдет мотоциклист относительно Земли?
Конспект «Относительность движения» — УчительPRO
Механическое движение. Относительность движения
Код ОГЭ 1.1. Механическое движение. Относительность движения. Траектория. Путь. Перемещение. Равномерное и неравномерное движение. Средняя скорость. Формула для вычисления средней скорости.
Внимание! Это конспект для 9 класса! Чтобы прочитать конспект «Механическое движение» для 7 класса перейдите по ссылке.Механическим движением называется изменение положения тела в пространстве относительно других тел с течением времени.
Материальной точкой считается тело, размеры которого малы по сравнению с другими характерными размерами, встречающимися при решении поставленной задачи.
Траектория – воображаемая линия, вдоль которой движется тело.
Относительность механического движения:
- Механическое движение можно наблюдать только относительно других тел. Тело, относительно которого рассматривается механическое движение, называется телом отсчёта.
- В различных системах отсчёта скорость и перемещение, характеризующие движение одного и того же тела, могут иметь разные модули и направления.
- Координаты тела, траектория движения, путь зависят от выбора системы отсчёта, то есть для одного и того же тела могут быть разными.
Основные физические величины, характеризующие механическое движение
- Путь
 – длина траектории. Внимание! Путь не может быть отрицательным!
– длина траектории. Внимание! Путь не может быть отрицательным!
- Перемещение
 – направленный отрезок прямой (вектор), соединяющий начальное положение тела с его последующим положением.
– направленный отрезок прямой (вектор), соединяющий начальное положение тела с его последующим положением.
Проекция вектора перемещения на координатную ось sx = x – x0 , где х0 – начальная координата тела, х – конечная координата тела.
Модуль вектора перемещения может не совпадать по числовому значению с длиной пути. Его можно рассчитать с помощью проекций вектора перемещения на координатные оси 
- Средняя путевая скорость
 равна отношению всего пути, пройденного телом, к промежутку времени, в течение которого этот путь пройден: ʋср = l/t. Внимание! Не является векторной величиной!
равна отношению всего пути, пройденного телом, к промежутку времени, в течение которого этот путь пройден: ʋср = l/t. Внимание! Не является векторной величиной!
- Вектор средней скорости
 равен отношению вектора перемещения к промежутку времени, в течение которого это перемещение произошло:
равен отношению вектора перемещения к промежутку времени, в течение которого это перемещение произошло:  . В проекциях на координатную ось 0х
. В проекциях на координатную ось 0х  . Внимание! Вектор средней скорости сонаправлен с вектором перемещения.
. Внимание! Вектор средней скорости сонаправлен с вектором перемещения.
- Мгновенная скорость
 – скорость тела в данной точке пространства в данный момент времени.
– скорость тела в данной точке пространства в данный момент времени.
Внимание! 1). Вектор мгновенной скорости направлен по касательной к траектории движения в каждой её точке. 2). Проекция перемещения на соответствующую координатную ось численно равна площади под графиком зависимости проекции скорости на эту ось от времени.
- Ускорение
 – векторная физическая величина, характеризующая изменение скорости с течением времени. Для равноускоренного движения вектор ускорения равен отношению вектора изменения скорости к тому промежутку времени, в течение которого это изменение произошло:
– векторная физическая величина, характеризующая изменение скорости с течением времени. Для равноускоренного движения вектор ускорения равен отношению вектора изменения скорости к тому промежутку времени, в течение которого это изменение произошло:  . В проекциях на координатную ось
. В проекциях на координатную ось  . Физический смысл: численно равно изменению скорости за 1 с.
. Физический смысл: численно равно изменению скорости за 1 с.


Конспект урока в 9 классе «Механическое движение. Относительность движения».
Дополнительные материалы (конспекты 7 класса): 1) Механическое движение. Траектория и путь. 2) Прямолинейное движение 3) Неравномерное движение. Средняя скорость. 4) ЗАДАЧИ на движение с решениями.
Следующая тема для 9 класса: «Равномерное прямолинейное движение» (код ОГЭ 1,2).
Урок 2. равномерное прямолинейное движение материальной точки — Физика — 10 класс
Физика, 10 класс
Урок 2. Равномерное прямолинейное движение материальной точки
Перечень вопросов, рассматриваемых в теме: 1) основная задача механики; 2) относительность механического движения; 3) система отсчёта, материальная точка, перемещение, траектория, скорость; 4) кинематическое уравнение.
Глоссарий по теме:
Раздел механики, в котором изучается движение тел без выяснения причин, вызывающих данное движение, называют кинематикой.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени.
Материальной точкой называют тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь. Тело, относительно которого рассматривается движение, называется телом отсчета. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Траектория — линия, по которой движется точка в пространстве.
Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путем, пройденным за этот промежуток времени.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения.
Скорость равномерного прямолинейного движения точки – величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.
Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016.– С.10-30.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.
Открытые электронные ресурсы по теме урока:
http://kvant.mccme.ru/1974/12/byvaet_li_ravnomernoe_dvizheni.htm.
Теоретический материал для самостоятельного изучения
Основная задача классической механики — определить положение тела в пространстве в любой момент времени. По характеру решаемых задач классическую механику делят на кинематику, динамику и статику. В кинематике описывают движение тел без выяснения причин, вызывающих данное движение. Раздел механики, в котором изучаются причины движения, называют динамикой. Статика — раздел механики, в котором изучаются условия равновесия абсолютно твердых тел. Законы сохранения импульса и энергии являются следствиями законов Ньютонов.
Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени. Сформулируем закон относительности движения: характер движения тела зависит от того, относительно каких тел мы рассматриваем движение. Нет абсолютно неподвижных тел.
Рассмотрим самое простое движение – прямолинейное равномерное движение. Описать движение тела – это значит, указать способ определения его положения в пространстве в любой момент времени.
Для описания движения нужно ввести некоторые понятия: материальная точка, траектория, путь, перемещение, координата, момент времени, промежуток времени, скорость. Материальной точкой называют тело, размерами которого в условиях рассматриваемой задачи можно пренебречь. Это первая физическая модель реальных тел. Практически всякое тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела, очень велики по сравнению с его размерами. Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные её суточным вращением, не влияют на величины, описывающие годовое движение. Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода солнца в разных местах поверхности земного шара), считать планету материальной точкой нельзя, так как результат задачи зависит от размеров этой планеты и скорости движения точек её поверхности.
Тело, движущееся поступательно, можно принимать за материальную точку даже в том случае, если его размеры соизмеримы с проходимыми им расстояниями. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе.
Что нужно знать для того, чтобы в любой момент времени указать положение тела? Надо, во-первых, знать, где оно было в начальный момент времени; во-вторых, каков вектор перемещения в любой момент времени. Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение рассматривается. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.
Рассмотрим два наиболее часто применяемых способа описания движения тел: координатный и векторный. В координатном способе положение тела в пространстве задается координатами, которые с течением времени меняются.
Рассмотрим движение материальной точки М с координатами (х, y, z) в момент времени t.
Математически это принято записывать в виде:

Количество координат зависит от условия задачи: на прямой – одна, в плоскости – две, в пространстве – три.
В векторном способе используется радиус-вектор. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку. Закон (или уравнение) движения в векторной форме — зависимость радиуса-вектора от времени:

Итак, для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех трех ее координат от времени, либо зависимость от времени радиус-вектора этой точки.
Три скалярных уравнения или эквивалентное им одно векторное уравнение называются кинематическими уравнениями движения материальной точки.
Двигаясь, материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом она «описывает» в пространстве какую-то линию. Линия, по которой движется точка в пространстве, называется траекторией. По форме траектории все движения делятся на прямолинейные и криволинейные. Траектория движения указывает все положения, которые занимала точка, но, зная траекторию, ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки траектории. Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путём, пройденным за этот промежуток времени, его обозначают буквой S. Путь – скалярная величина.
Для описания движения тела нужно указать, как меняется положение точек с течением времени. Если участки криволинейные, то изменение координат тела описывают с помощью такого понятия как перемещение. Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением. Обозначается на чертежах как направленный отрезок, соединяющий начальное и конечное положение тела в пространстве:

Путь и модуль перемещения могут совпадать по значению, только в том случае, если тело движется вдоль одной прямой в одном направлении.
Важной величиной, характеризующей движение тела, является его скорость. Скорость – векторная величина. Она считается заданной, если известен ее модуль и направление. Скорость равномерного прямолинейного движения точки – векторная величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло. Пусть радиус-вектор  задает положение точки в начальный момент времени t0, а радиус-вектор
задает положение точки в начальный момент времени t0, а радиус-вектор — в момент времени t. Тогда промежуток времени:
— в момент времени t. Тогда промежуток времени:
 ,
,
и перемещение:
 .
.
Подставляя  выражение для скорости, получим:
выражение для скорости, получим:

Если начальный момент времени t0 принять равным нулю, то скорость равна:

Выразим отсюда радиус-вектор  :
:

Это и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени. В проекциях на ось ОХ уравнение можно записать в виде:
х=х0+vхt.
Это уравнение есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х0.
Путь S, пройденный точкой при движении вдоль оси ОХ, равен модулю изменения ее координаты:

Его можно найти, зная модуль скорости

Строго говоря, равномерного прямолинейного движения не существует. Но приближенно на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.
Полученные результаты можно изобразить наглядно с помощью графиков. Для прямолинейного равномерного движения график зависимости проекции скорости от времени очень прост. Это прямая, параллельная оси времени.
Как мы уже знаем, зависимость координаты тела от времени описывается формулой х=х0+𝞾хt. График движения представляет собой прямую линию:


Из второго рисунка видим, что углы наклона прямых разные. Угол наклона второй прямой  больше угол наклона первой прямой
больше угол наклона первой прямой  , т.е за одно и тоже время тело, движущееся со скоростью
, т.е за одно и тоже время тело, движущееся со скоростью  , проходит большее расстояние, чем при движении со скоростью
, проходит большее расстояние, чем при движении со скоростью  А значит
А значит  А что же в случае 3, когда угол α < 0? В случае 3 тело движется в сторону, противоположную оси ОХ. Проекция скорости в случае 3 имеет отрицательное значение и график проходит ниже оси ОХ. Проекция скорости
А что же в случае 3, когда угол α < 0? В случае 3 тело движется в сторону, противоположную оси ОХ. Проекция скорости в случае 3 имеет отрицательное значение и график проходит ниже оси ОХ. Проекция скорости  определяет угол наклона прямой х(t) к оси t и численно равна тангенсу угла
определяет угол наклона прямой х(t) к оси t и численно равна тангенсу угла 

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта. В рамках классической механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.
Примеры и разбор решения заданий
1. Тело движется равномерно и прямолинейно в положительном направлении оси ОХ. Координата тела в начальный момент времени равна xо = -10м. Найдите координату тела через 5с, если модуль её скорости равен ʋ=2 м/с. Какой путь проделало тело за это время?
Дано: xо = — 10 м, t = 5 c, ʋ = 2 м/с. Найти s, х.
Решение: координату точки найдем по формуле:
х = х0 + 𝞾х t
Так как направление вектора скорости совпадает с направлением оси координат, проекция вектора скорости положительна и равна ʋx=ʋ; тогда вычисляем:
х = — 10 + 2· 5 = 0 (м).
Пройденный путь найдем s = ʋ t; s = 2·5 = 10 м.
2. Равномерно друг за другом движутся два поезда. Скорость первого равна 72 км/ч, а скорость второго — 54 км/ч. Определите скорость первого поезда относительно второго.
Дано:


Найти  .
.
Решение: Из условия задачи ясно, что векторы скоростей поездов направлены в одну сторону. По закону сложения скоростей запишем:
 ,
,
где  — искомая величина.
— искомая величина.

Находим проекцию скоростей на ось ОХ и записываем, чему равен модуль искомой величины



Ответ:  .
.
Задача на относительность движения
В данной статье репетитор по математике и физике рассказывает о простом способе решения достаточно сложной задачи на относительность движения, которому вас не научат в школе. Материал разобран на примере задачи о движущихся подводных лодках. Дочитайте эту статью до конца. Знания, которые вы получите, могут очень пригодиться на экзамене или олимпиаде по физике.
Подводная лодка-разведчик и подводная лодка-обнаружитель движутся на одной глубине по взаимно перпендикулярным траекториям. Лодка-разведчик — с запада на восток со скоростью 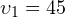 км/ч, лодка-обнаружитель — с юга на север со скоростью км/ч, лодка-обнаружитель — с юга на север со скоростью 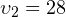 км/ч. Известно, что в 12:00 лодка-разведчик находилась прямо по курсу относительно лодки-обнаружителя, и расстояние между ними составляло км/ч. Известно, что в 12:00 лодка-разведчик находилась прямо по курсу относительно лодки-обнаружителя, и расстояние между ними составляло 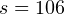 км. Обнаружит ли в процессе движения лодка-обнаружитель присутствие лодки-разведчика, радиус обнаружения которой при текущих погодных условиях составляет км. Обнаружит ли в процессе движения лодка-обнаружитель присутствие лодки-разведчика, радиус обнаружения которой при текущих погодных условиях составляет 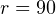 км? Если да, то в какой момент времени это произойдёт? км? Если да, то в какой момент времени это произойдёт? |
Решение задачи на относительность движения
Для наглядности изобразим рисунок к задаче. Зона обнаружения лодки-разведчика обведём на рисунке красной пунктирной окружностью:

Постараемся определить сперва минимальное расстояние, которое будет между подводными лодками в процессе их движения. Если решать задачу в системе отсчёта, связанной с землёй, то для нахождения минимального расстояния между подводными лодками потребуется очень много времени и сил. Нужно будет найти зависимость расстояния между субмаринами от времени и исследовать получившуюся функцию на минимум с помощью производной. Всё это долго и сложно.
Разберём гораздо более простой способ. Для решения этой задачи используем принцип относительности движения. В чём он заключается? В том, что характер движения любого тела зависит от выбора системы отсчёта, относительно которой это движение рассматривается. Говорят, что Эйнштейн в своё время любил задавать вопрос: «В каком часу станция отходит от поезда?» Потому что с точки зрения кинематики для описания движения мы можем взять любую систему отсчёта, важно лишь правильно записать в ней кинематическое уравнение движения.
Вот и в этой задаче, гораздо проще связать систему отсчёта с положением лодки-обнаружителя. Тогда в этой системе отсчёта лодка-обнаружитель будет покоится, а лодка-разведчик станет двигаться вдоль по прямой ON, изображённой на рисунке:
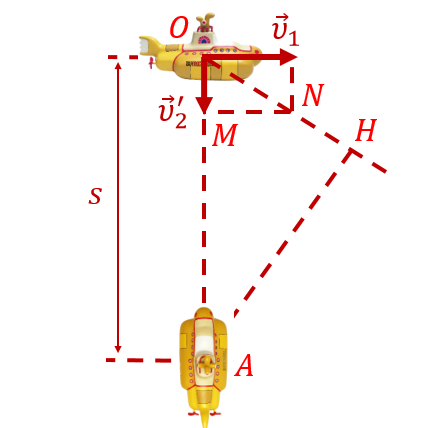
Эта прямая задаётся вектором скорости движения лодки-разведчика в системе отсчёта, связанной с лодкой-обнаружителем. Этот вектор получен вычитанием вектора скорости лодки-обнаружителя относительно земли из вектора скорости лодки-разведчика относительно земли, в полном соответствии с принципом относительности движения.
Теперь, если посмотреть внимательно на получившийся рисунок, станет понятно, что искомое минимальное расстояние между лодками в процессе их движения будет равно длине перпендикуляра, проведённого из точки, в которой находится лодка-обнаружитель (точки A), к прямой, изображающей траекторию движения лодки-разведчика в системе отсчёта, связанной с лодкой-обнаружителем. То есть длине перпендикуляра AH. Осталось найти длину этого перпендикуляра, и задача будет решена. Довольно просто, не правда ли?
Видно, что треугольник OMN подобен треугольнику AOH (они оба прямоугольные, и у них есть общий угол O). Тогда спарведливо соотношение 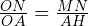 . По теореме Пифагора находим численное значение длины ON, оно равно
. По теореме Пифагора находим численное значение длины ON, оно равно 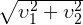 . Численные значения длин отрезков OA и MN равны
. Численные значения длин отрезков OA и MN равны  и
и 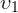 , соответственно. Тогда получаем, что
, соответственно. Тогда получаем, что
![Rendered by QuickLaTeX.com \[ AH = s_{min} = \frac{s\upsilon_1}{\sqrt{\upsilon_1^2+\upsilon_2^2}}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-204ff8e2cbb39e335563510c424a1f30_l3.png)
Расчёты дают результат 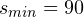 км.
км.
Итак, минимальное расстояние между подводными лодками в процессе их движения в точности равно радиусу обнаружения лодки-разведчика, поэтому она будет обнаружена. Но в какой момент это произойдет?
Через столько времени с 12:00, сколько потребуется лодке-разведчику, чтобы в системе отсчёта, связанной с лодкой-обнаружителем, двигаясь со скоростью  м/с, дойти до точки H. То есть пройти расстояние OH. Длину OH ищем по теореме Пифагора из прямоугольного треугольника OAH:
м/с, дойти до точки H. То есть пройти расстояние OH. Длину OH ищем по теореме Пифагора из прямоугольного треугольника OAH: 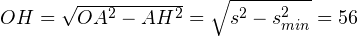 км. Тогда искомое время равно
км. Тогда искомое время равно 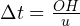 . Расчёты дают следующий результат:
. Расчёты дают следующий результат: 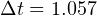 ч
ч  ч.
ч.  мин.
мин.  c. То есть момент обнаружения наступит примерно в 13:03:24.
c. То есть момент обнаружения наступит примерно в 13:03:24.
Вот такое простое решение достаточно сложной задачи на относительность движения. Советую вам запомнить его и использовать при решении подобных задач на различных экзаменах и олимпиадах по физике.
Материал подготовлен репетитором по физике в Москве, Сергеем Валерьевичем
Смотрите также:
О методике решения задач на относительность
О методике решения задач на относительность движения при изучении основ кинематики в 9 классе общеобразовательной школы
Антощук Л.Г.
Одним из сложных и недостаточно разработанных вопросов методики физики является методика решения задач на относительность движения. Анализ специальной литературы и имеющийся практический опыт убеждают в том, что учащиеся школы и студенты не умеют решать задачи на относительность движения. В методических пособиях предлагается преимущественно логические приемы решения, иллюстрируемые иногда рисунками.
Я предлагааю способ решения задач на относительность движения, который позволяет конкретизировать представления учащихся о законе сложения скоростей и перемещений, о понятии неподвижной системы отсчета (НСО) и подвижной системы отсчета (ПСО). Учит определять скорости, перемещения тел относительно различных систем отсчета (СО) и другие величины, убеждает в относительности скорости и перемещения тел.
Сущность предлагаемого способа решения задач сводится к следующему алгоритму:
Анализ условия задачи, выделение движущихся тел. Краткая запись условия задачи. Определение неподвижной и подвижной системы отсчета (НСО и ПСО), движущегося тела.
Записать закон сложения скоростей или перемещений в векторной форме.
Изобразить графически параметры заданных движений, при этом выбрать начальный момент времени и совместить начало НСО и ПСО.
Отобразить на графике, который строится под первоначальным, изменение величин, описанных в задаче со временем.
Сравнение закона сложения скоростей (перемещений) и графика.
Записать закон сложения скоростей (перемещений) в проекциях на оси координат, объединив их в систему (или найти геометрическую сумму путем сложения векторов).
Решить полученную систему уравнений. Подставить в решение общего вида значения величин и произвести вычисления.
На примерах решения типовых задач на относительность движения покажем применение данного способа решения.
Задача № 1.
Два поезда движутся равномерно друг за другом. Скорость первого 80 км/ч, а второго 60 км/ч. Какова скорость второго поезда относительно первого ?
1. Первый и второй поезда движутся относительно Земли с некоторыми скоростями. Скорость первого поезда V, скорость второго V2 (жирным шрифтом обозначены векторные величины).
Дано: Решение:
V = 80 км/ч За НСО примем Землю, за ПСО – первый поезд.
V2 = 60 км/ч Скорость ПСО относительно НСО – V.
V1 — ? Движущимся телом является второй поезд.
Скорость движущегося тела относительно НСО – V2.
Неизвестная скорость второго поезда относительно первого (ПСО) – V1.
2
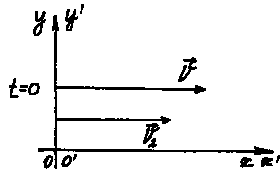 рис.1
рис.1
. Закон сложения скоростей V2 = V + V1. Скорость второго поезда относительно НСО равна геометрической сумме скорости второго поезда относительно ПСО и скорости ПСО относительно НСО.
3. Систему координат XY свяжем с Землей (НСО).
Систему координат X Y параллельную XY свяжем с первым поездом (ПСО)
В начальный момент времени (t = 0) совместим НСО и ПСО.
4. Через t = 1 час положение ПСО (первого поезда) изменится на расстояние, равное 80 км, а второго поезда, относительно НСО окажется на расстоянии 60 км.

рис. 2
5. Соотнесем график и формулу закона сложения скоростей V2 = V + V1. Убеждаемся в том, что обе формы отражения закона совпадают.
6. Для вычисления скорости второго поезда относительно первого найдем проекции и запишем:
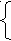 V2x = Vx + V1x
V2x = Vx + V1x
V2y = Vy + V1y
V2 = V — V1
-V1 = V2 – V
V1 = V – V2
V1 = 80 км/ч — 60 км/ч = 20 км/ч
Ответ: скорость второго относительно первого поезда равна 20 км/ч.
Задача №2
Скорость течения реки V= 1,5 м/с. Каков модуль скорости V1 катера относительно воды, если катер движется перпендикулярно к берегу со скоростью V2 = 2 м/с относительно него.
1. Дано:
 V= 1,5 м/с За НСО примем берег реки,
V= 1,5 м/с За НСО примем берег реки,
V2 = 2 м/с за ПСО – реку (скорость течения реки V),
V
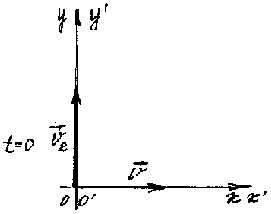 рис. 3
рис. 3
— ? движущееся тело – катер.
2. Закон сложения скоростей V2 = V + V1. Скорость катера относительно НСО (берега реки) равна геометрической сумме скорости катера относительно ПСО (течения реки) и скорости течения реки.
3. Свяжем НСО с системой координат XY, а ПСО с системой координат X`Y`. Ось OX направим вдоль берега, а ось OY поперек реки (O`X` и O`Y` соответственно).
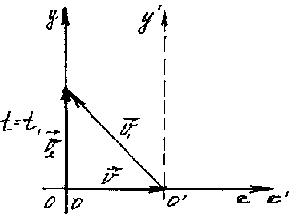
рис. 4
4.5. Сравним закон сложения скоростей и графика. Для простоты решения найдем геометрическую сумму векторов скорости.
6. Так как полученный треугольник прямоугольный, то
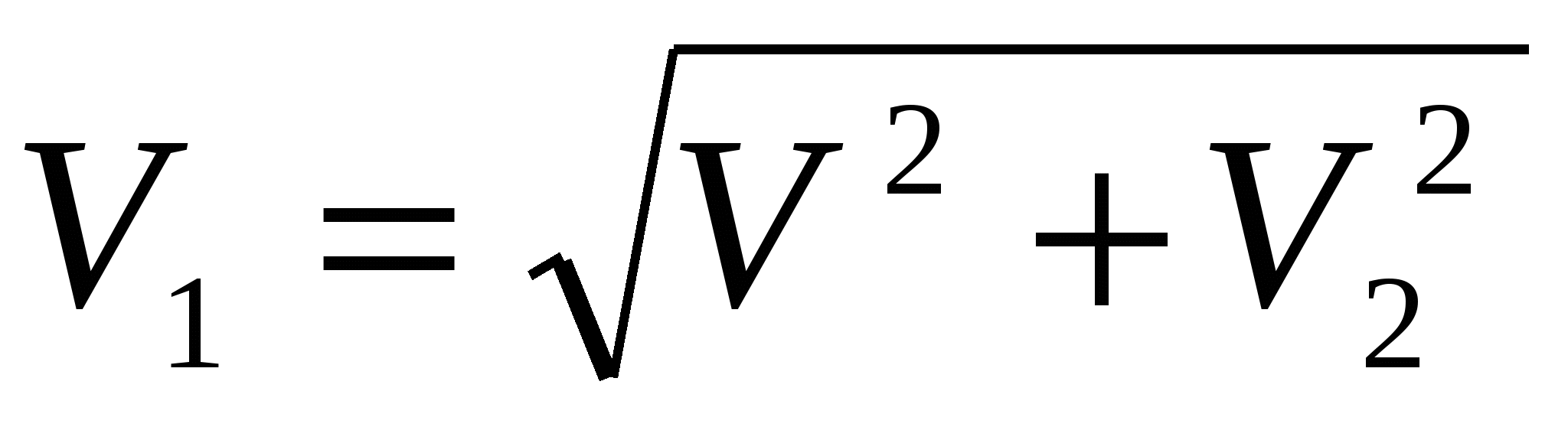
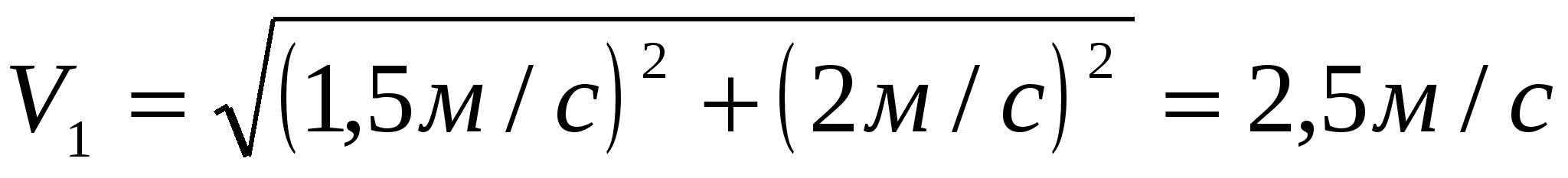
Ответ: модуль скорости катера относительно реки 2,5 м/с.
Задача № 3
Два поезда движутся навстречу друг другу со скоростями 72 и 54 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 14 с. Какова длина второго поезда ?
1 . Дано:
. Дано:
V1 =72 км/ч =20 м/с Так как движение поездов можно считать равномерным,
V2 = 54 км/ч = 15 м/с то длину второго поезда можно найти по формуле
l — ? l = V21 t, где V21 – скорость второго поезда относительно первого поезда. Значит, для определения l необходимо найти V21.
Примем за НСО Землю, а за ПСО – первый поезд, движущееся тело – второй поезд. V2 скорость второго поезда относительно НСО. Скорость ПСО — V1.
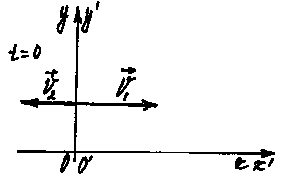
рис. 5
2. Закон сложения скоростей V2 = V2 1 + V1. Скорость второго поезда относительно НСО равна геометрической сумме скорости второго поезда относительно ПСО (первого поезда) и скорости ПСО (первого поезда).3. 4.
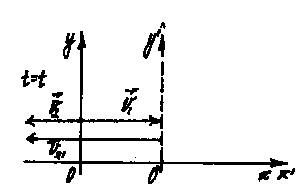 рис.6
рис.6
5. На графике V2 и V2 1 направлены в одну сторону, а V1 в противоположную,
тогда -V2 = V1 — V21
6 V2 1 = V1 + V2
l
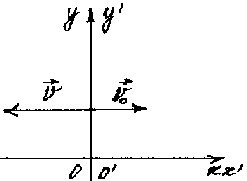
рис.7
= (V1 + V2) t
l = (20 м/с + 15 м/с) 14 с = 490 м.
Ответ: длина второго поезда 490 м.
Задача № 4
Катер, двигаясь против течения реки, проплывает около стоящего на якоре буя и встречает там плот. Через 12 минут после встречи катер повернул обратно и догнал плот на расстоянии 800м ниже буя. Найти скорость течения реки.
 Дано:
Дано:
t = 12 мин = 720с НСО свяжем с буем, ПСО – плот (движущийся со скоростью
S = 800 м течения реки V0), движущееся тело – катер.
V0 — ? Скорость катера относительно НСО – V,
а относительно ПСО – V1.
Закон сложения скоростей для катера, движущегося по течению и против течения реки, в геометрической форме совпадает: V = V0 + V1. Скорость катера относительно НСО равна геометрической сумме скорости ПСО (течения реки) и скорости катера относительно ПСО.
Найдем скорость катера, двигающегося против течения реки
V = V0 + V1
— V = V0 — V1
V = V1 — V0
Аналогично найдем скорость катера, двигающегося по течению реки
V = V0 + V1
V = V0 + V1
Запишем уравнения движения плота и катера:
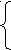 Sпл. = V0 t
Sпл. = V0 t
Sк= S1 — S2 , где S1 – расстояние, пройденное катером по течению,
S2 – расстояние, пройденное катером против течения.
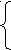 Sпл. = V0t
Sпл. = V0t
Sк = -( V1 — V0 ) t1 + (V0 + V1) (t – t1)
Расстояние, пройденное катером от буя до того места, где катер догнал плот, равно расстоянию пройденному плотом, то есть Sпл = Sк, то
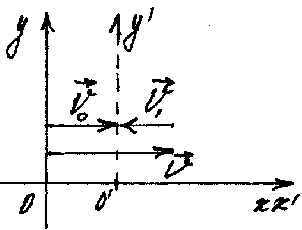
рис. 10
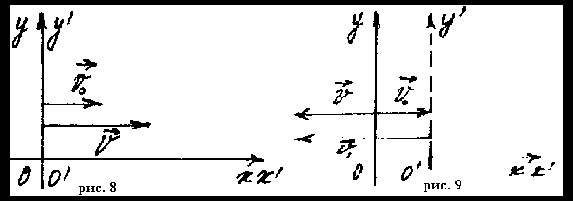
V0 t = — V1 t1 + V0 t1 + V0 t + V1 t – V0 t1 — V1 t1
V1 t = 2 V1 t1
t = 2 t1
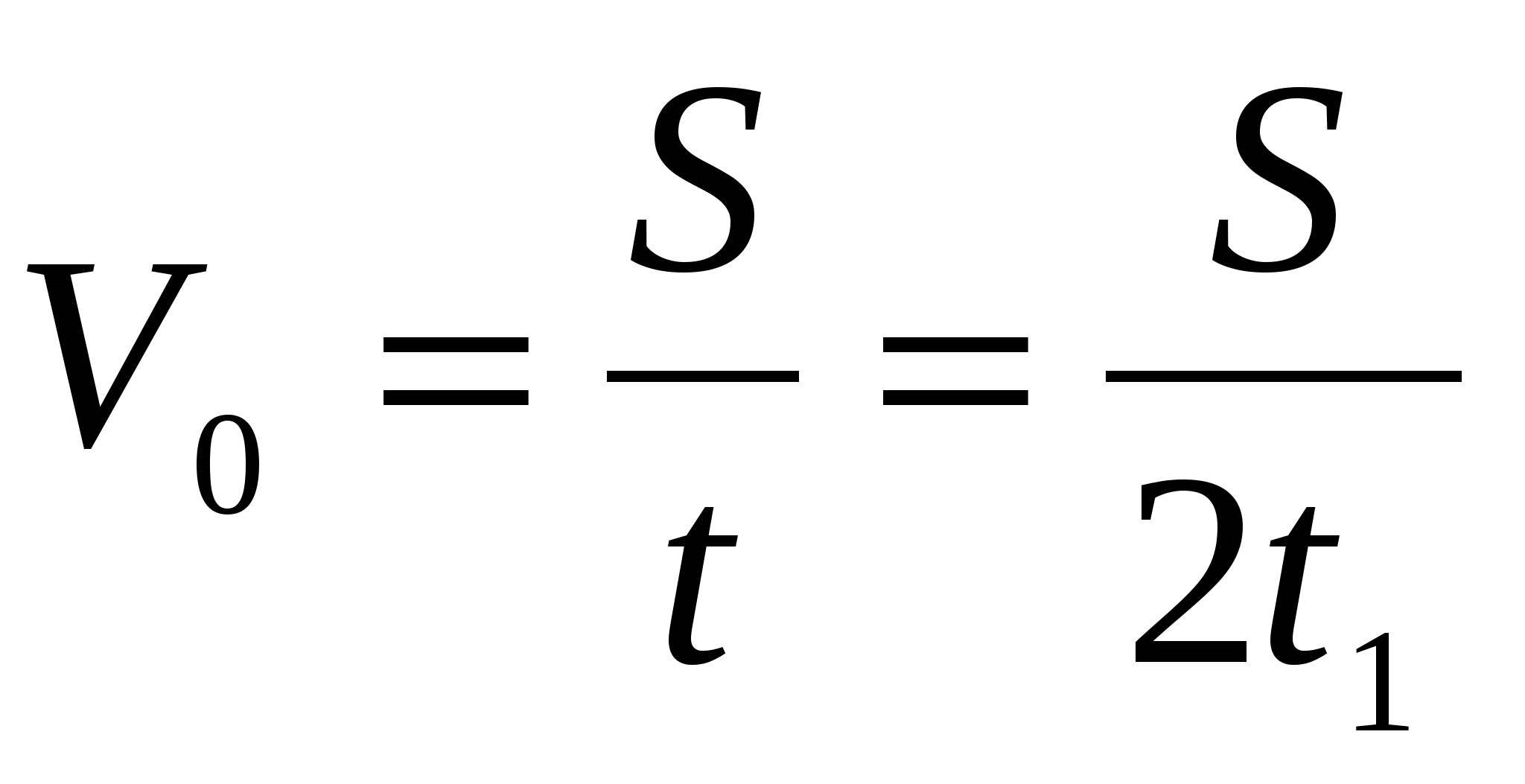
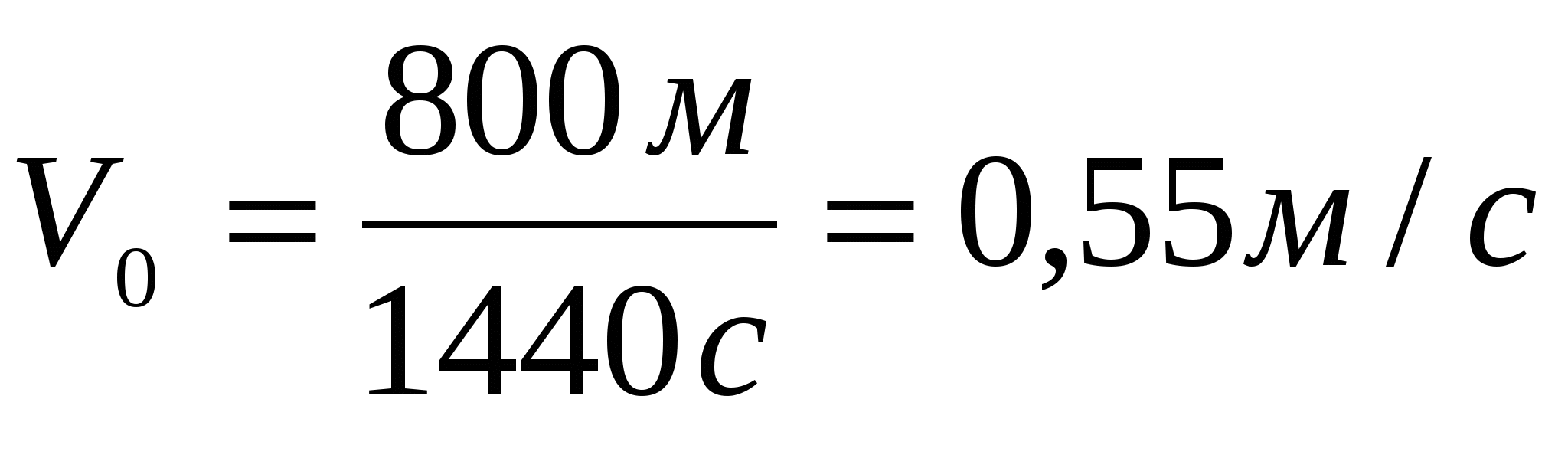
Ответ: скорость течения реки 0,55 м/с.
Задача № 5
Автоколонна длиной 2 км движется со скоростью 40 км/ч. Мотоциклист выехал из хвоста колонны со скоростью 60 км/ч. За какое время он достигнет головной машины ? Какой путь за это время пройдет мотоциклист относительно Земли ?
Д ано:
ано:
l = 2 км. Примем за НСО землю,
V1 = 40км/ч за ПСО – колонну, движущееся тело – мотоциклиста.
V2 = 60 км/ч Время, за которое мотоциклист догонит головную
t` — ? Sм.з. — ? машину 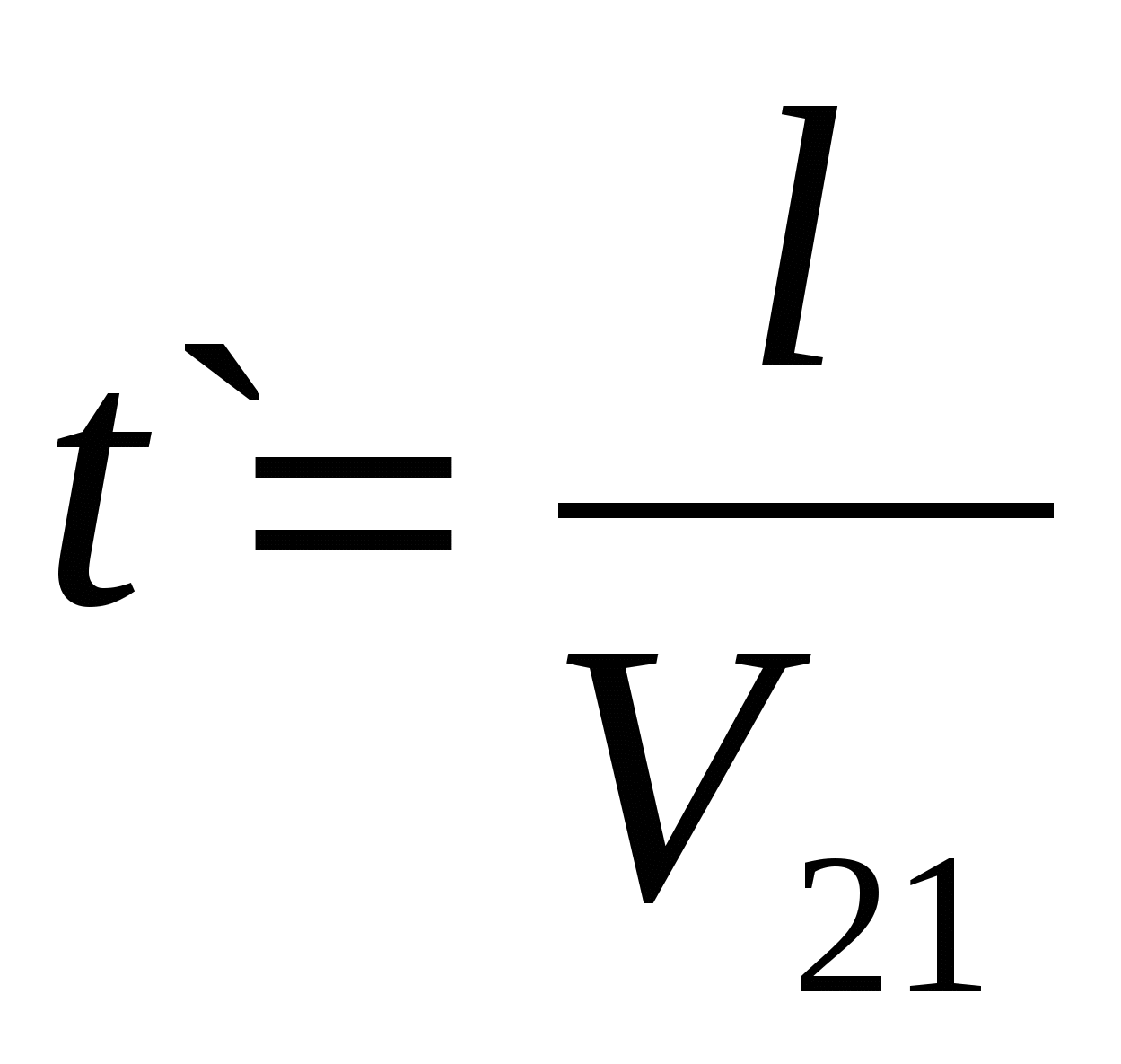 , где V2 1 – скорость мотоциклиста
, где V2 1 – скорость мотоциклиста
относительно ПСО (колонны)..
2. Закон сложения скоростей для данной задачи запишем в виде: V2 = V1 + V2 1. Скорость мотоциклиста относительно НСО равна геометрической сумме скорости колонны и скорости мотоциклиста относительно колонны.
3
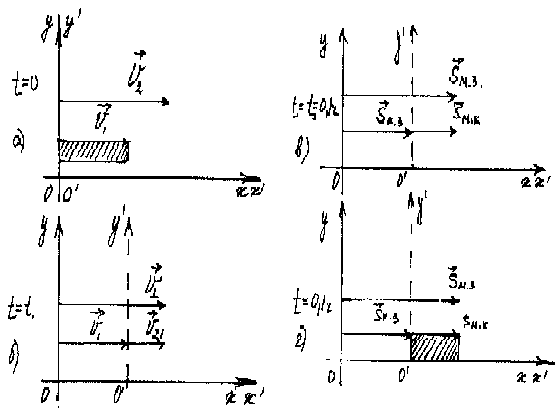 рис. 11
рис. 11
. Отразим на рисунке – чертеже процесс, описанный в условии задачи.
Обозначим колонну прямоугольником, и совместим её конец (начало ПСО) с началом НСО в начальный момент времени (t = 0).
Укажем скорости V1 и V2 (рис. а).
4. Отразим геометрически закон сложения скоростей, выяснив, что произойдет через 1 час.
5. Сравним чертеж и формулу закона. Убедимся, что V2 = V1 + V2 1 соответствует геометрическому чертежу (рис. б).
6. Найдем проекции скоростей и вычислим время t` .
V2 = V1 + V2 1
V2 1 = V2 — V 1
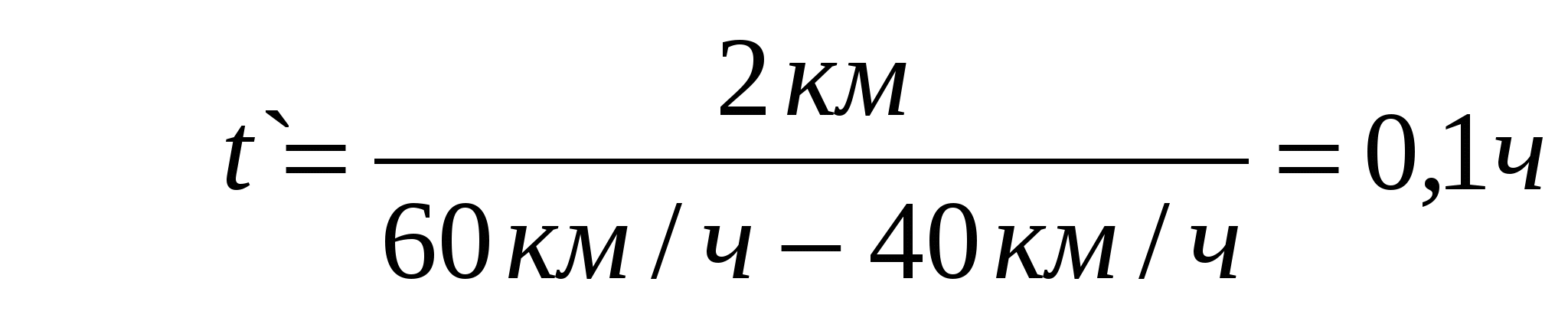
Определить путь можно алгебраически по известной формуле ( S.=V t) и проиллюстрировать чертежом (рис. в, г ) при t = t1=0,1 ч.
По закону сложения перемещений Sм.з = Sк.з. + Sм.к
где Sм.з – перемещение мотоциклиста за 0,1 часа относительно Земли
Sм.к. — перемещение мотоциклиста за 0,1 часа относительно колонны,
Sк.з. – перемещение колонны за 0,1 часа относительно Земли.
Произведя вычисления Sм.з = 6 км.
Ответ: через 0,1 часа мотоциклист достигнет головной машины колонны, при этом пройдет путь 6 км.
Задача № 6
Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 1 мин. По неподвижному эскалатору пассажир поднимается за 3 мин. Сколько времени будет подниматься идущий вверх пассажир по движущемуся эскалатору ?
Д ано:
ано:
tэ.з. = 1 мин. =60 с. Примем за НСО – Землю, за ПСО – эскалатор,
tч.э. = 3 мин. = 180 с движущееся тело – человек.
tч.з. – ? tэ.з. – время движения эскалатора относительно НСО,
tч.э. – время движения пассажира относительно ПСО,
tч.з. – время движения пассажира относительно НСО.
2. Запишем закон сложения скоростей Vч.з. = Vэ.з.. + Vч.э.. Скорость человека относительно НСО (идущего вверх по движущемуся эскалатору) равна геометрической сумме скорости эскалатора относительно НСО и скорости человека относительно ПСО ( неподвижному эскалатору).
3
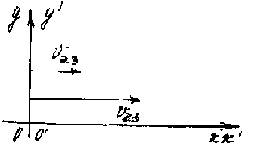 рис. 12
рис. 12
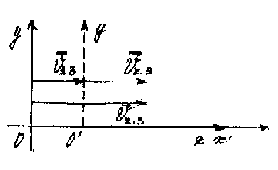 рис. 13
рис. 13
.
4.
5. Vч.з. = Vэ.з.. + Vч.э.
Vч.з. = Vэ.з.. + Vч.э.
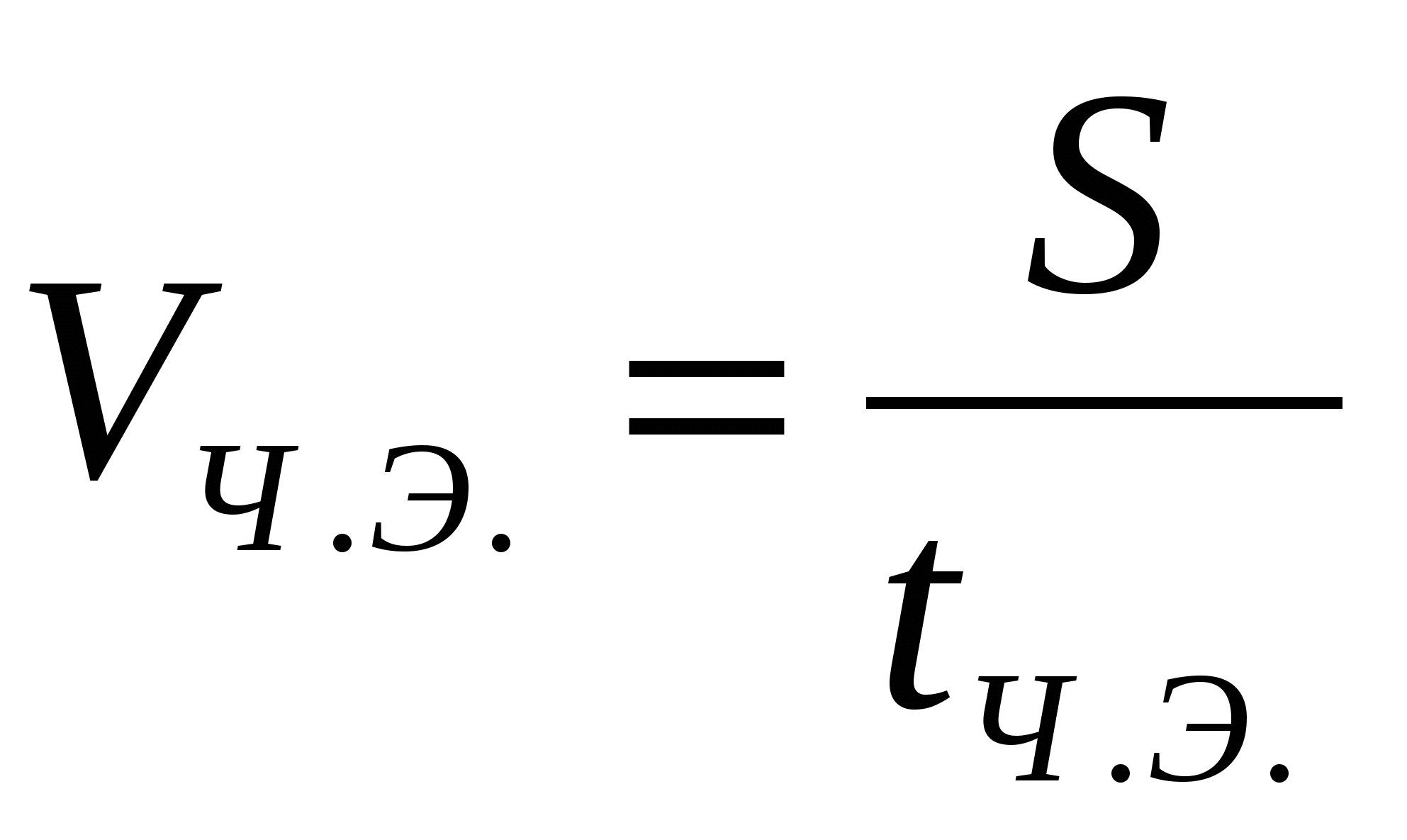 — скорость движения человека относительно эскалатора,
— скорость движения человека относительно эскалатора, 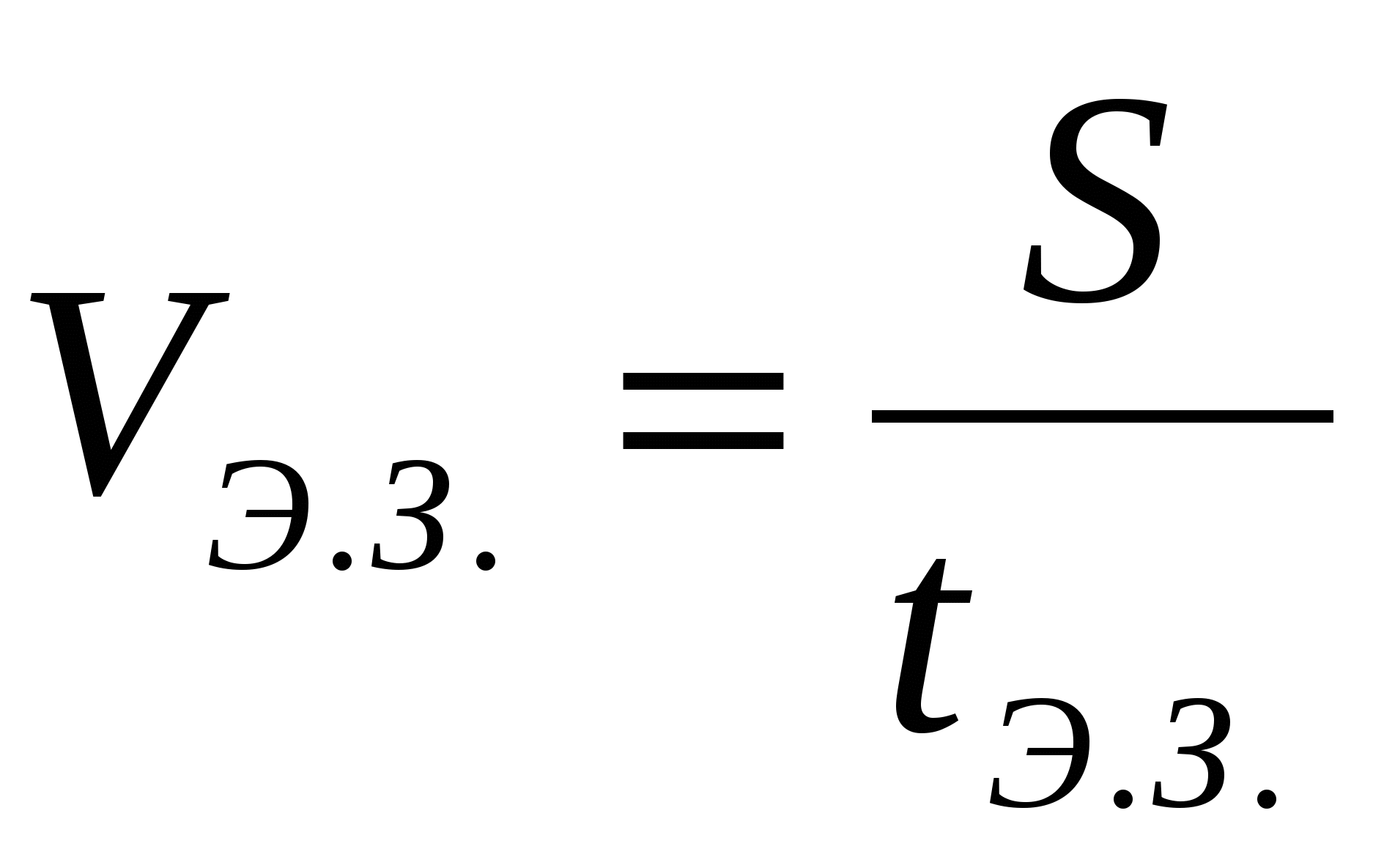 — скорость движения эскалатора относительно Земли,
— скорость движения эскалатора относительно Земли, 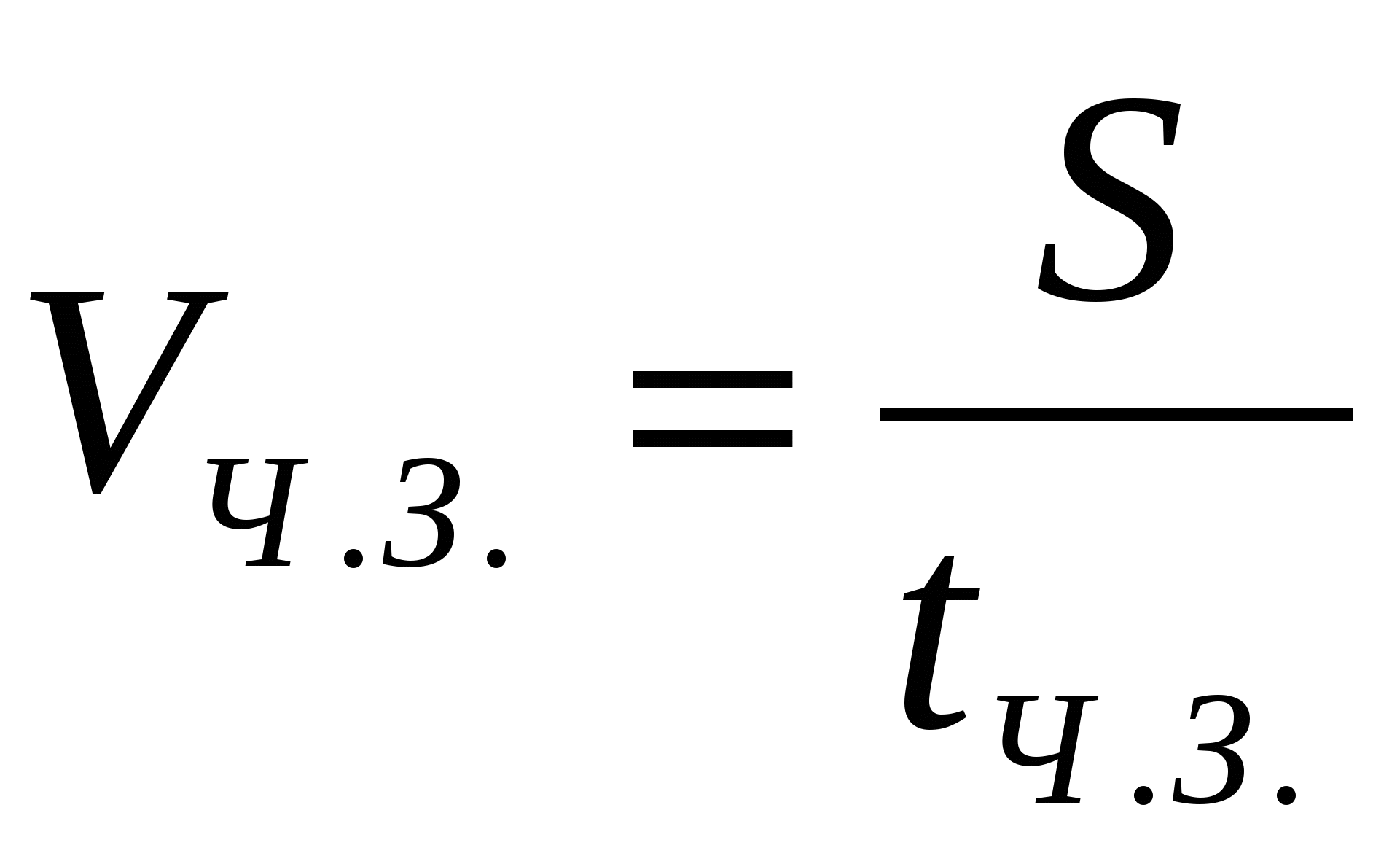 — скорость движения человека относительно Земли. Подставив в полученную формулу, получим:
— скорость движения человека относительно Земли. Подставив в полученную формулу, получим:
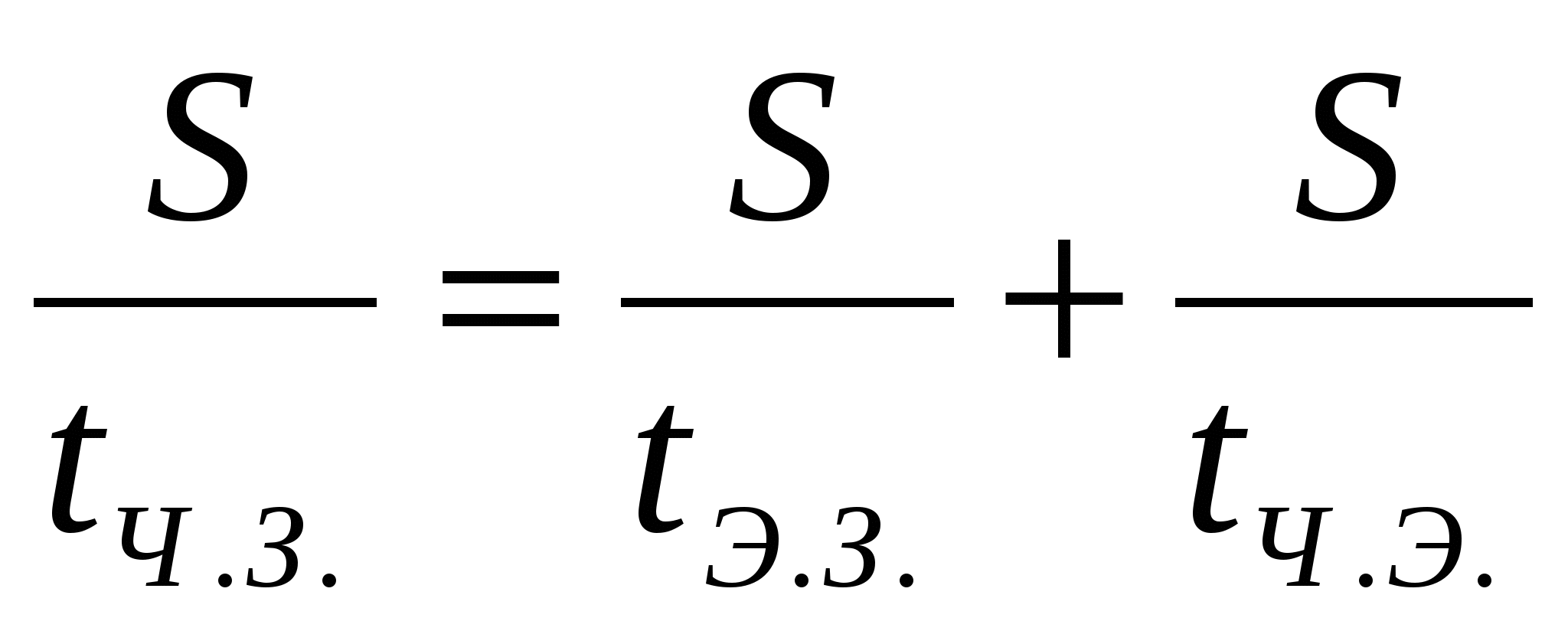
Так как путь, пройденный человеком один и тот же, то
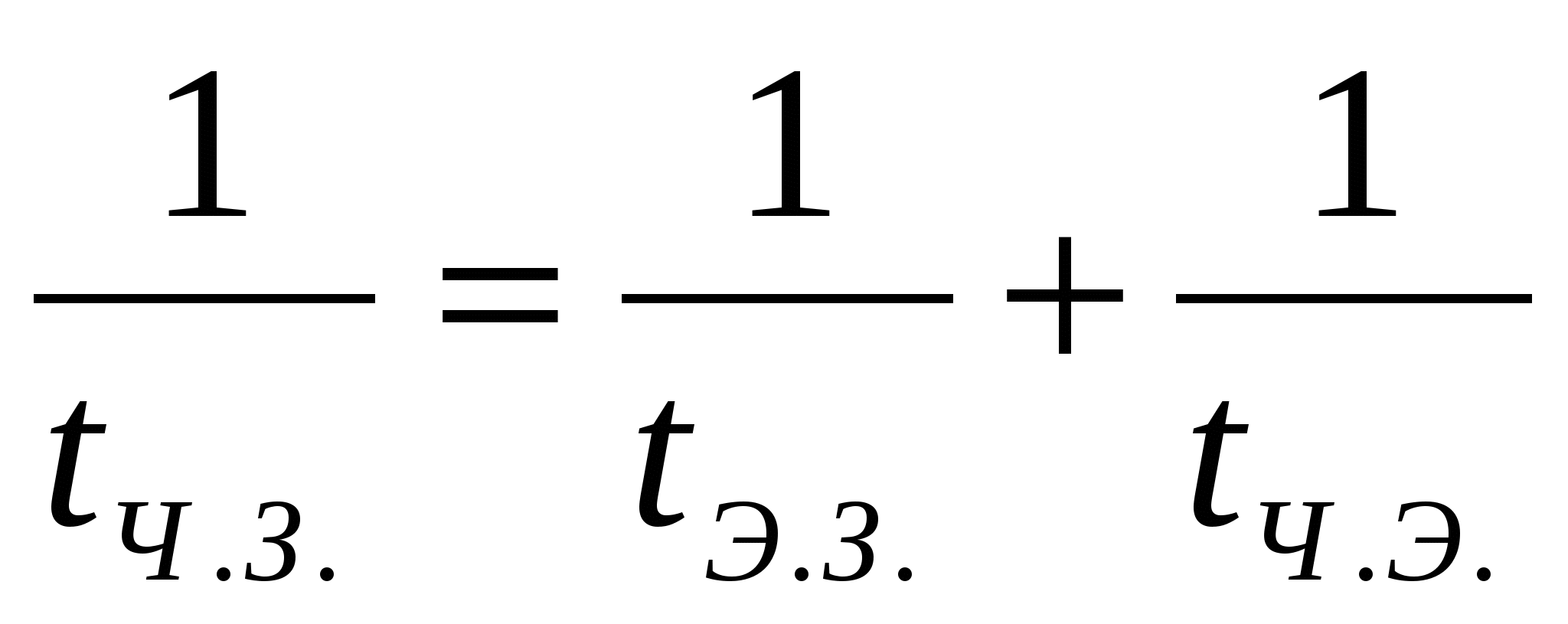 ,
, 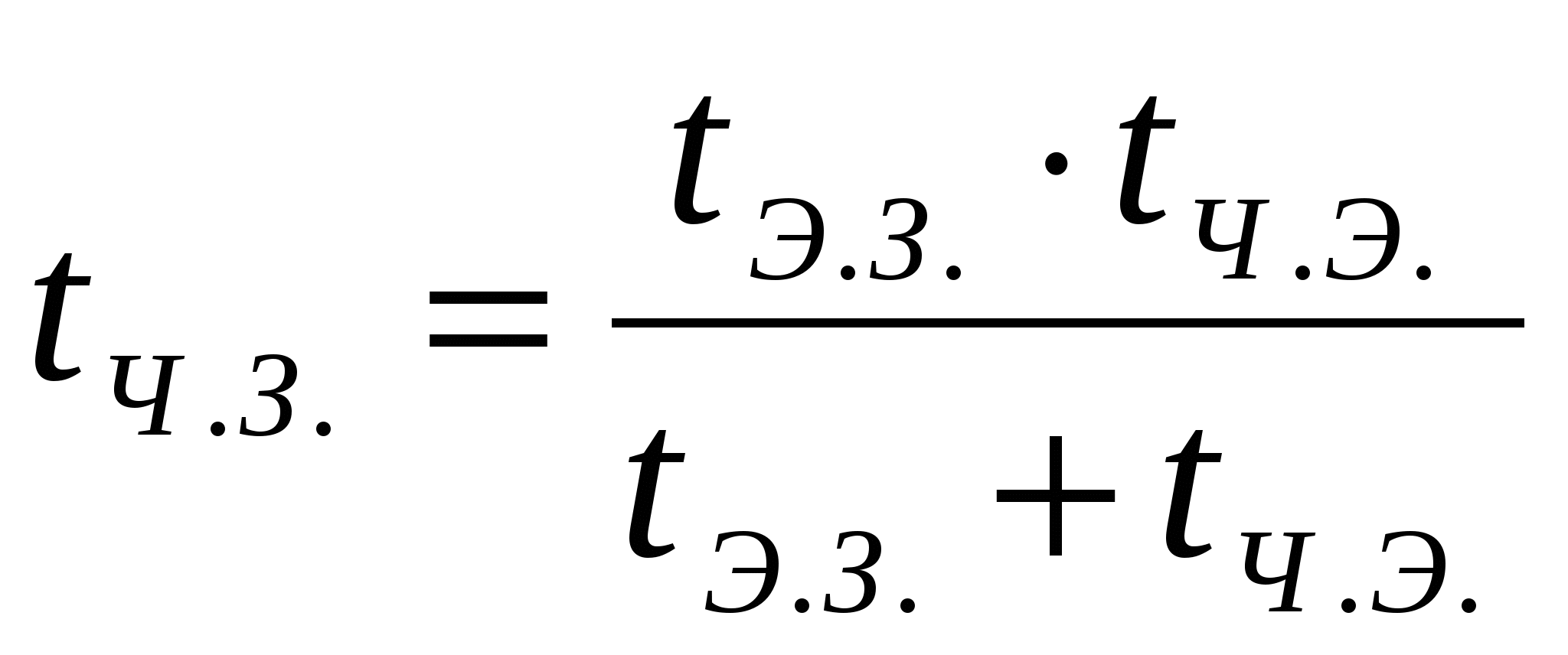 ,
, 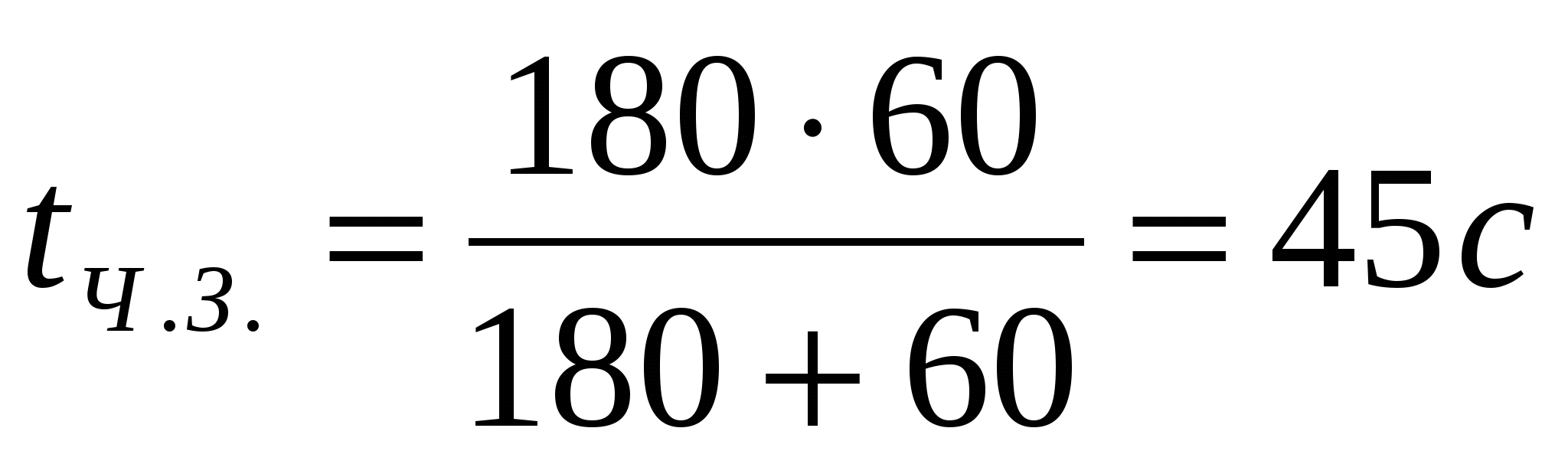
Ответ: пассажир идущий вверх по движущемуся эскалатору поднимется за 45 с.
Примерные вопросы к учащимся (студентам) по анализу и решению задач на относительность можно сформулировать следующим образом.
Движение каких тел рассматривается в задаче ?
Что известно о движущихся телах ?
С какими телами можно связать подвижную и неподвижную системы отсчета ?
Какой момент времени можно принять за начальный ?
Как на чертеже отразить начальные условия состояния тел ?
Как записать закон сложения скоростей (или перемещений) для данной задачи ?
В какой точке чертежа (графика) будет находится начало отсчета подвижной системы относительно неподвижной через единицу времени (если речь идет о скоростях движения) ?
Как это отразить на чертеже ?
В какой точке чертежа будет находится движущееся тело относительно НСО и ПСО ?
Как геометрически отразить процесс перемещения тел за единицу времени?
Сравните геометрический чертеж с законом сложения скоростей ? Сделайте вывод.
Найдите проекции скоростей, проведите вычисления искомой величины.
При необходимости можно напомнить основные формулы перемещения и координатный метод решения задач.
Данная статья является исходным моментом для разработки методики решения задач на относительность движения. Дальнейшее её развитие возможно на пути рассмотрения движения тел относительно разных систем отсчета.
Материал статьи может быть использован студентами физмат факультетов и учителями физики базовой школы.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.khspu.ru
119. Человек начинает подниматься по движущемуся вверх эскалатору метро с ускорением 0,2 м/с2. добежав до середины эскалатора, он поворачивает и начинает спускаться вниз с тем же ускорением. Сколько времени человек находился на эскалаторе, если длина эскалатора 105 м, скорость движения эскалатора 2 м/с.
При подъеме по эскалатору модуль перемещения человека равен
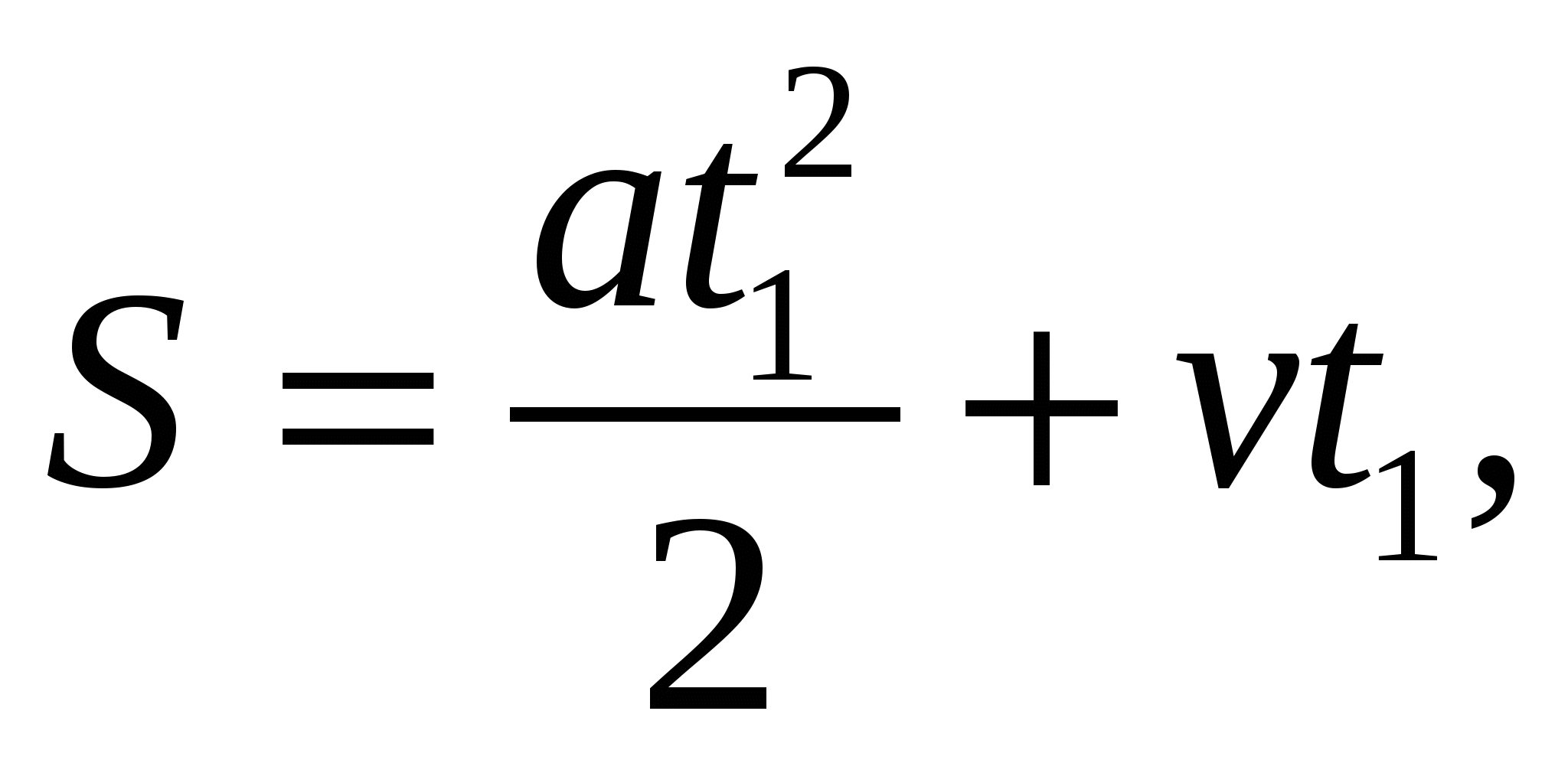
а при спуске
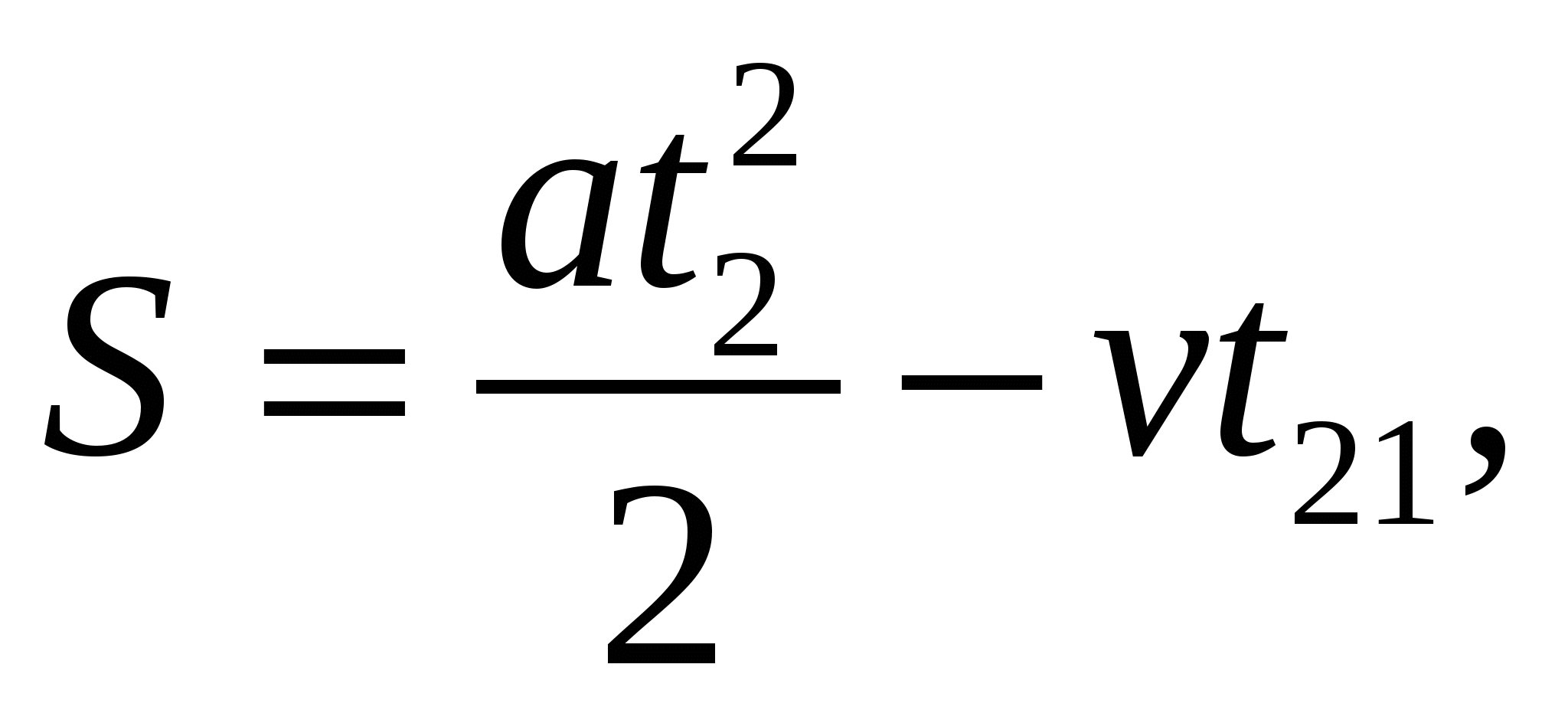
где t1 и t2 – время подъема и спуска соответственно.
Эти выражения приводят к двум квадратным уравнениям
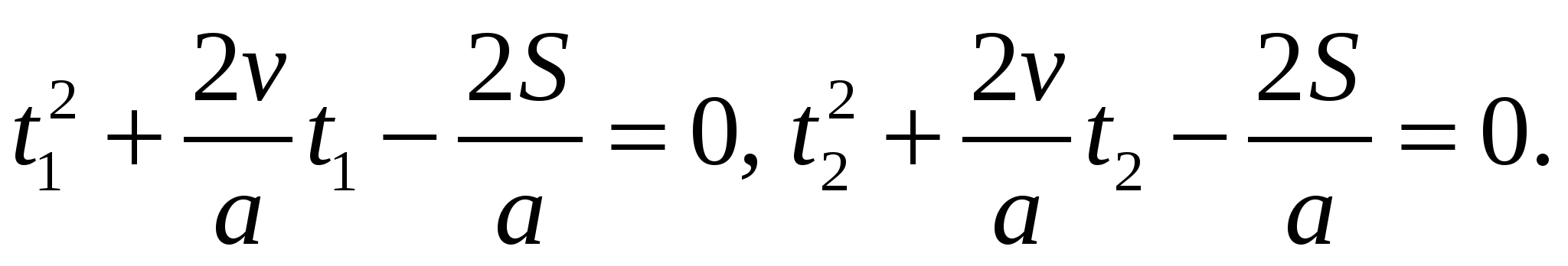
Решая эти уравнения, находим:
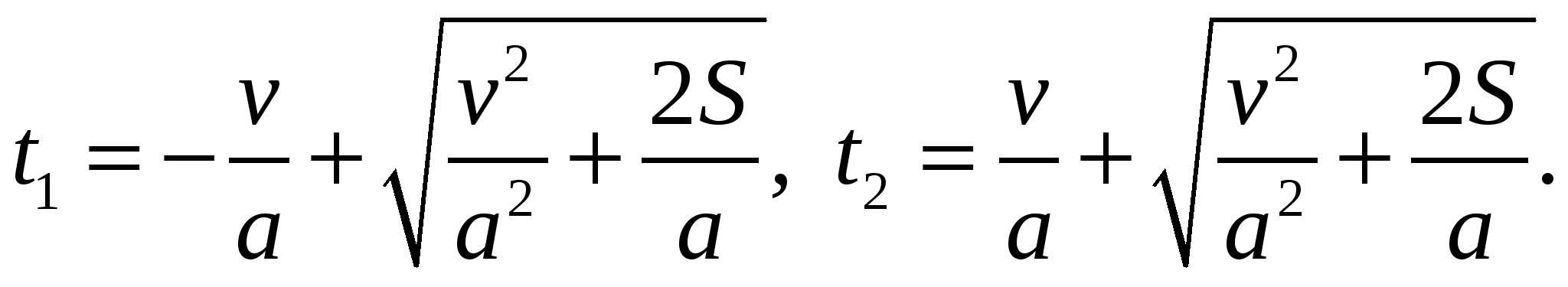
Время нахождения человека на эскалаторе t = t1 + t2, поэтому
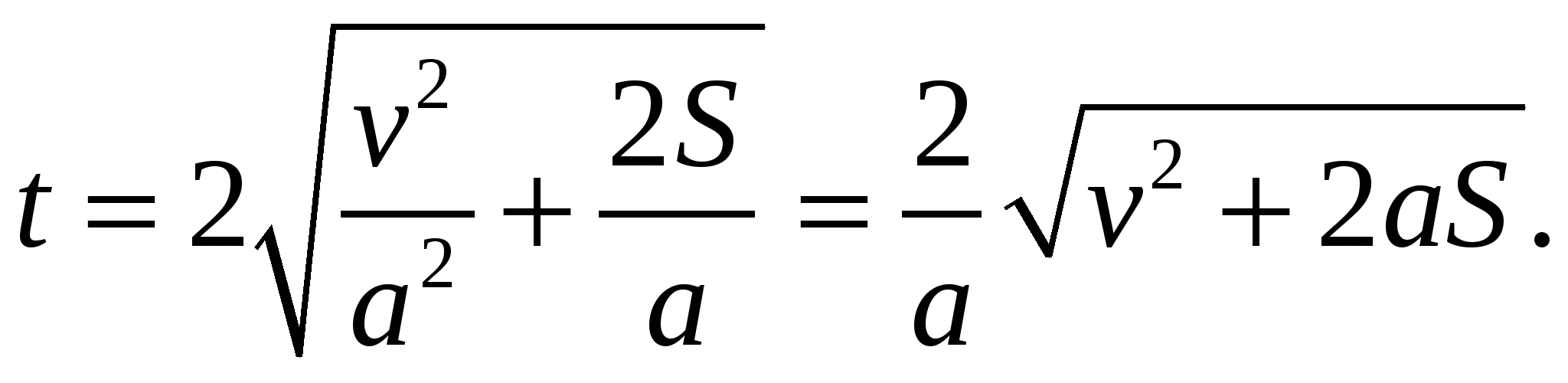
Подставляя числовые значения, найдем
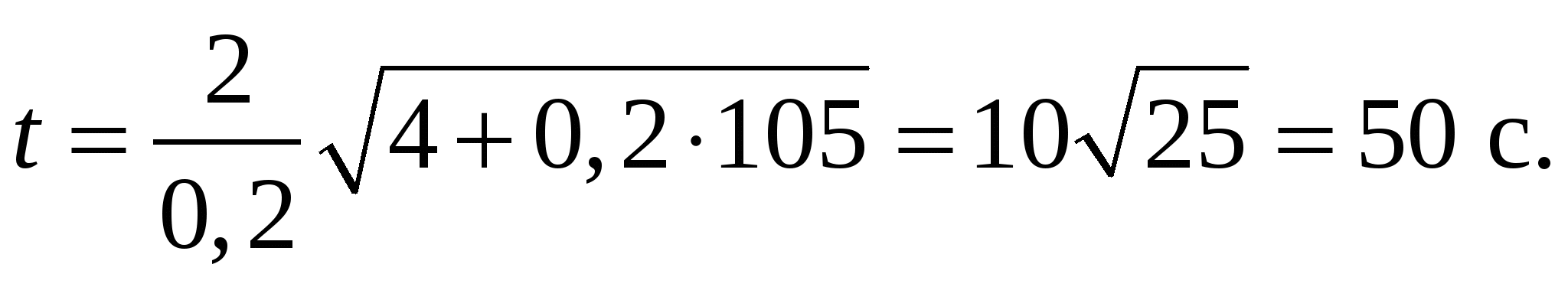
10 класс. Урок 2. Механическое движение и его виды. Относительность механического движения.
Урок 2
Тема урока: Механическое движение и его виды. Относительность механического движения.
Цели урока:
познакомить учащихся с основной задачей механики и понятиями: материальная точка, система отчета, траектория, путь и перемещение;
Оборудование:
Ход урока
Организационный момент.
Изучение нового материала.
Учитель: Давайте вспомним основные разделы физики:
Механика.
Термодинамика.
Электродинамика.
Мы начинаем изучение с механики, так как относящиеся сюда явления более просты, а также потому, что знание законов механики окажет нам существенную помощь при изучении других разделов. На уроках физики в 7 классе вам уже встречалось понятие механическое движение.
Примеры механического движения: движение звезд и планет, самолетов и автомобилей, артиллерийских снарядов и ракет.
Двигаетесь ли вы, находясь в классе? (Вы находитесь в классе в покое относительно Земли, но движетесь вместе с ним вокруг Солнца. Например, автомобиль движется относительно деревьев, зданий, но пассажиры, находящиеся в нем, находятся в покое относительно автомобиля.)
Механическое движение часто является составной частью более сложных немеханических процессов, например тепловых. Поэтому изучение физики целесообразно начать с механического движения. Этим вопросом занимается раздел физики, называемый механикой.
Изучить движение тела — значит определить, как изменяется его положение в пространстве с течением времени. Если это известно, можно узнать положение тела в любой момент времени. С учетом этого можно сформулировать основную задачу механики:
Основная задача механики состоит в том, чтобы определить положение тела в пространстве в любой момент времени, если известны положение и скорость тела в начальный момент.
Система отсчета.
Тело отсчета «присутствует» в любой задаче о движении тел — даже тогда, когда оно явно не упоминается. Очень часто в качестве тела отсчета подразумевается Земля.
С телом отсчета связывают систему координат.
Какие системы координат вы знаете, приведите примеры. (Одномерные, двухмерные, трехмерные.)
Положение точки в пространстве задается тремя числами, которые называются координатами точки и обозначаются буквами х, у, z. Часто удается выбрать систему координат так, чтобы одна или две координаты тела оставались неизменными во время всего движения. Тогда описать движение тела можно с помощью только одной или двух координат.
Связанная с телом отсчета система координат и выбранный способ измерения времени образуют систему отсчета.
Таким образом, система отсчета состоит из:
Материальная точка. При определении положения тела в
пространстве возникают затруднения, связанные с тем, что тело
имеет размеры. Тем не менее, при решении многих задач размерами тела можно пренебречь, рассматривая его как одну точку. При
этом описание движения тела намного упрощается.
Тело, размерами которого в данной задаче можно пренебречь, называется материальной точкой.
Можно или нельзя считать тело материальной точкой зависит не от размеров тела («большое» оно или «маленькое»), а от поставленной задачи: один и тот же самолет можно рассматривать как материальную точку, если надо найти время его перелета из одного города в другой, но нельзя, если самолет выполняет фигуры высшего пилотажа.
Можно не учитывать размеры и в том случае, когда перемещения всех точек одинаковы. Такое движение тела называется поступательным.
Траектория, путь и перемещение. В процессе движения материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом движущаяся точка «описывает» в пространстве какую-то линию. Иногда эта линия видна, — например, высоко летящий самолет может оставлять за собойслед в небе. Более знакомый пример — след куска мела на доске.
Очень часто траектория — невидимая линия. Траектория движущейся точки может быть прямой или кривой линией. Соответственно форме траектории движение бывает прямолинейным и криволинейным.
Путь является скалярной величиной и обозначается буквой l. Путь увеличивается, если тело движется, и остается неизменным, если тело покоится. Таким образом, путь не может уменьшаться с течением времени.
Перемещением тела называется направленный отрезок, проведенный из начального положения тела в его положение в данный момент времени.
Перемещение является векторной величиной и обозначается обычно s; модуль перемещения обозначается s.
Чем же отличается путь от перемещения? Эти два понятия часто смешивают, хотя на самом деле они очень сильно отличаются друг от друга. Рассмотрим эти отличия:
Путь — скалярная величина и характеризуется только числовым значением.
Перемещение — векторная величина и характеризуется как числовым значением (модулем), так и направлением.
При движении тела путь может только увеличиваться, а модуль перемещения может как увеличиваться, так и уменьшаться.
Если тело вернулось в начальную точку, его перемещение равно нулю, а путь нулю не равен.
Механику можно разделить на:
Раздел механики, в котором движения изучаются без исследования причин, называют кинематикой.
Закрепление изученного материала.
Упражнение 1. Какую систему координат следует выбрать (одномерную, двухмерную или трехмерную) для определения положения следующих тел:
Трактор в поле.
Вертолет.
Поезд.
Люстра в комнате.
Лифт.
Подводная лодка.
Шахматная фигура.
Самолет на взлетной полосе.
Упражнение 2.
Задание 1. В рабочей тетради нарисуйте дорогу, на которой изобразите велосипедиста, мост, автомобиль, дерево, идущего пешехода, светофор.
Проведите в тетради координатную ось параллельно дороге. Примите дерево за тело отсчета.
Выберите масштаб (1 деление — 100 м).
Определите координаты моста, дерева и светофора.
Определите начальные координаты пешехода, велосипедиста и автомобиля.
Покажите вектор перемещения для каждого из этих тел, его проекцию на ось Y и найдите модуль вектора перемещения, а также пройденный путь в следующих случаях:
автомобиль доехал до светофора;
пешеход дошел до дерева;
велосипедист доехал до светофора и вернулся к дереву.
Задание 2. Выполните те же упражнения, что и в задании 1, но за тело отсчета выберите мост.
Сравните пути и перемещения каждого из тел (полученные при выполнении заданий 1 и 2).
В чем состоит основная задача механики?
Зачем введено понятие материальной точки? Когда тело можно считать материальной точкой?
Что такое система отсчета (СО)? Для чего вводится?
Какие виды систем координат (СК) вы знаете?
Что такое траектория?
В чем отличие пути от перемещения?
1. Наука о неживой природе. 2. Тысячная доля метра. 3. Прибор для измерения объема жидкостей. 4. Что означает греческое слово цэушы [физис], от которого произошло слово «физика»? 5. Механические, тепловые, электрические, световые явления – это явления… 6. Все, что есть во Вселенной. 7. Древнегреческий ученный. 8. «Отец» русской авиации. 9. Город, в котором в 1954 г. была построена первая в мире атомная электростанция. 10. Величина, характеризующая степень нагретости тела. 11. Русский ученый, усовершенствовавший лампы дневного света. 12. Свертывающаяся в круг металлическая или матерчатая измерительная лампа с делениями. 13. Название транспортного отечественного самолета, грузоподъемностью 150 т, построенного в 1985 году. 14. Единица длины, равная 0,1 м. 15. Русский ученый и организатор, с именем которого связано развитие отечественной автономной энергетики. 16. Физическая величина, характеризующая расстояние. 17. «Он создал первый русский университет. Он, лучше сказать, сам был первым нашим университетом» (А. С. Пушкин). 18. Критерий истины.
И
З
И
Ч
Е
Ф 1








Е
И
К
С
4


3


2



7


6


5





8




9

12

11
10

14

13


16
15


18
17





Е
В



И
Ч
И
Л



Ы
Н

























































Ответы: 1. Физика. 2. Миллиметр. 3. Мензурка. 4. Природа. 5.… физические. 6. Материя. 7. Аристотель. 8. Жуковский. 9. Обнинск. 10. Температура. 11. Вавилова. 12. Рулетка. 13. Руслан. 14. Дециметр. 15. Курчатов. 16. Длина. 17. Ломоносов. 18. Опыт.
Подведение итогов урока.
Домашнее задание.
Устно: §§ 1, 2.
Самостоятельное изучение: приложение 1 (стр. 255 – 257).

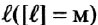 – длина траектории. Внимание! Путь не может быть отрицательным!
– длина траектории. Внимание! Путь не может быть отрицательным!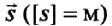 – направленный отрезок прямой (вектор), соединяющий начальное положение тела с его последующим положением.
– направленный отрезок прямой (вектор), соединяющий начальное положение тела с его последующим положением. равна отношению всего пути, пройденного телом, к промежутку времени, в течение которого этот путь пройден: ʋср = l/t. Внимание! Не является векторной величиной!
равна отношению всего пути, пройденного телом, к промежутку времени, в течение которого этот путь пройден: ʋср = l/t. Внимание! Не является векторной величиной!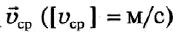 равен отношению вектора перемещения к промежутку времени, в течение которого это перемещение произошло:
равен отношению вектора перемещения к промежутку времени, в течение которого это перемещение произошло: 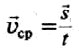 . В проекциях на координатную ось 0х
. В проекциях на координатную ось 0х 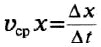 . Внимание! Вектор средней скорости сонаправлен с вектором перемещения.
. Внимание! Вектор средней скорости сонаправлен с вектором перемещения. – скорость тела в данной точке пространства в данный момент времени.
– скорость тела в данной точке пространства в данный момент времени.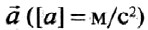 – векторная физическая величина, характеризующая изменение скорости с течением времени. Для равноускоренного движения вектор ускорения равен отношению вектора изменения скорости к тому промежутку времени, в течение которого это изменение произошло:
– векторная физическая величина, характеризующая изменение скорости с течением времени. Для равноускоренного движения вектор ускорения равен отношению вектора изменения скорости к тому промежутку времени, в течение которого это изменение произошло:  . В проекциях на координатную ось
. В проекциях на координатную ось  . Физический смысл: численно равно изменению скорости за 1 с.
. Физический смысл: численно равно изменению скорости за 1 с.