Относительность движения Примеры решения задач
1.Мимо пристани проходит плот. В этот момент в поселок, находящийся на расстоянииs1 = 15 км от пристани, вниз по реке отправляетсямоторная лодка. Она дошла до поселка за времяt= 3/4 ч и, повернув обратно, встретила плот на расстоянииs2 = 9 км от поселка. Каковы скорость течения рекиVи скорость лодки относительно водыv’?
Решение.Выберем систему отсчета, связанную с плотом (с водой). В этой системе отсчета плот покоится, а лодка движется вверх и вниз по реке с одинаковой по величине скоростью. Следовательно, время удаления лодки от плота равно времени приближения к нему. Поэтому время движения плота до встречи с лодкой равно 2tи его скорость (скорость течения) равна

По закону сложения скоростей скорость лодки при ее движении вниз по реке относительно берега равна
v = v’ + V.
С другой стороны

Cледовательно,

2.Скорость лодки в стоячей водеv’ меньше скорости течения рекиVвn= 2 раза. Под каким угломк берегу нужно держать корпус лодки во время переправы, чтобы снос лодки был минимальным?
Р ешение.Если лодку направить по течению реки,
то, очевидно, снос будет бесконечно
большим (лодка никогда не переправится
на противоположный берег).
ешение.Если лодку направить по течению реки,
то, очевидно, снос будет бесконечно
большим (лодка никогда не переправится
на противоположный берег).
Такой же результат получается в случае,
если направить лодку вверх по течению
реки. Значит, существует некоторое
направление, при котором снос лодки
минимален. Если  — скорость лодки в стоячей воде, а
— скорость лодки в стоячей воде, а —
скорость течения реки, то скорость лодки
относительно берега определится
законом сложения скоростей:
—
скорость течения реки, то скорость лодки
относительно берега определится
законом сложения скоростей:
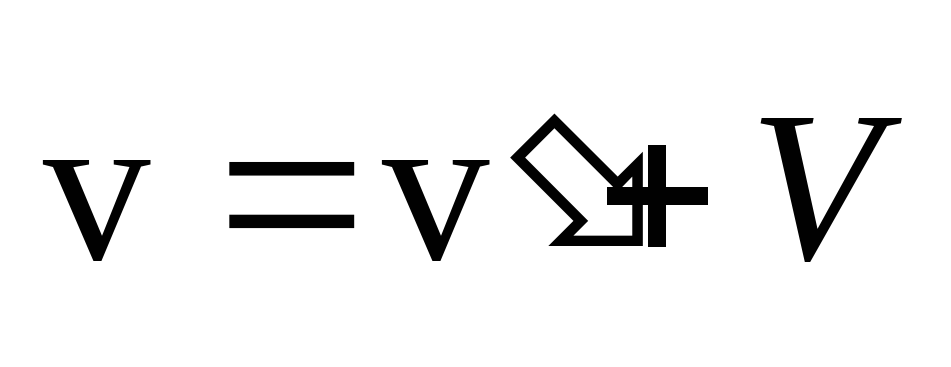 .
.
Векторное сложение скоростей,
соответствующее этому закону, показано
на рисунке. Там же показаны система
отсчета x0y,
связанная с берегом, и угол,
определяющий направление вектора .
Очевидно, что величина сноса лодки равна
.
Очевидно, что величина сноса лодки равна
s = vх t, 
где vx = V – vcos
— проекция скорости  на осьx,
на осьx,  — время переправы. Здесьd — ширина реки, vy — проекция скорости
— время переправы. Здесьd — ширина реки, vy — проекция скорости  на осьy.
на осьy.
Запишем выражение для величины сноса в явном виде:
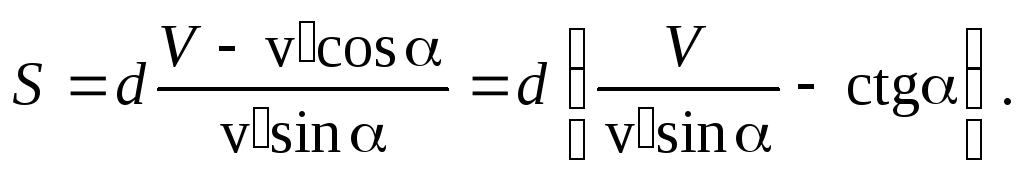
Минимум сноса соответствует минимуму выражения в скобках. Найдем угол , при котором достигается этот минимум из условия, что производная поот этого выражения должна равняться нулю в точке минимума. Дифференцирование дает:

Отсюда следует:


3. Приборы, установленные на корабле, идущем на север со скоростью V = 10 м/с, показывают скорость ветра v’ = 5 м/с, а его направление — восточное. Что покажут аналогичные приборы, установленные на берегу?
Р ешение.По закону сложения скоростей скорость
ветра относительно берега равна
ешение.По закону сложения скоростей скорость
ветра относительно берега равна

Найдем эту скорость построением (см. рис.). Из рисунка следует:

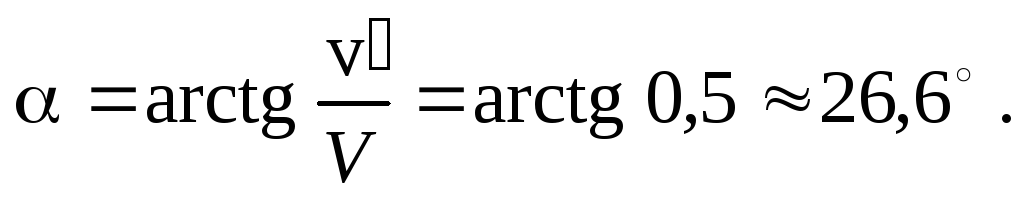
4.Два корабля движутся перпендикулярными курсами с постоянными скоростямиv1= 15 км/ч иv2= 20 км/ч. В некоторый момент времени они находятся на расстоянииS = 10 км друг от друга, а вектор скорости первого корабля составляет с линией, соединяющие корабли, угол= 30. На какое минимальное расстояниеdкорабли сблизятся при своем движении?
Р

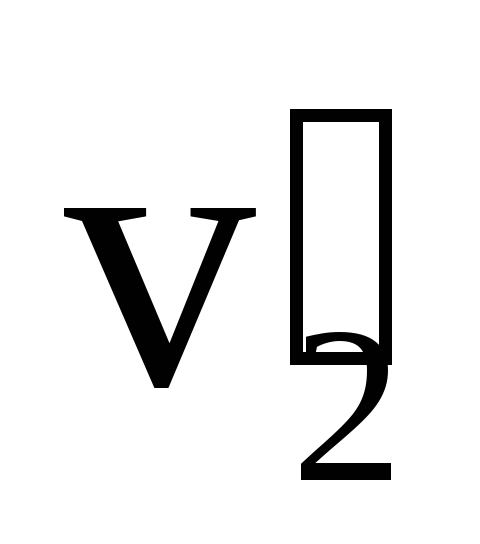 ,
определяемой из закона сложения
скоростей:
,
определяемой из закона сложения
скоростей: 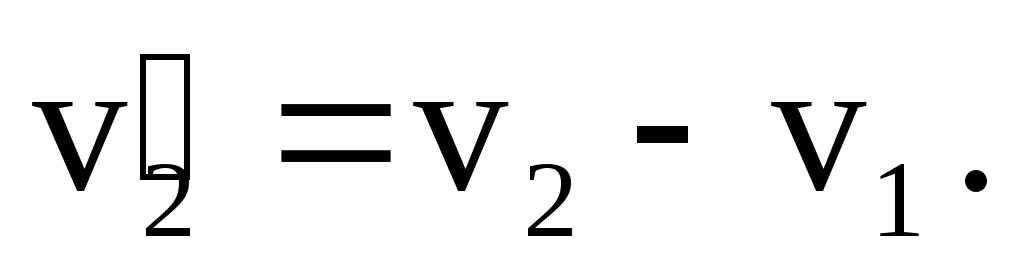
И



Следовательно,

5.Скорость лодки в стоячей воде ,
скорость течения рекиv= 4 м/с,
а ширина рекиL= 360 м.
Под каким угломк
берегу нужно держать нос лодки, чтобы
переправиться на противоположный берег
в кратчайшее время? Чему равно это времяTmin?
Какой путьSпроплывет
за это время лодка?
,
скорость течения рекиv= 4 м/с,
а ширина рекиL= 360 м.
Под каким угломк
берегу нужно держать нос лодки, чтобы
переправиться на противоположный берег
в кратчайшее время? Чему равно это времяTmin?
Какой путьSпроплывет
за это время лодка?
Решение.По закону сложения
скоростей скорость лодки относительно берега равна
относительно берега равна

Движение лодки можно
рассматривать как наложение двух
движений, одно из которых происходит
перпендикулярно берегу, а другое —
по течению реки. Первое происходит со
скоростью 
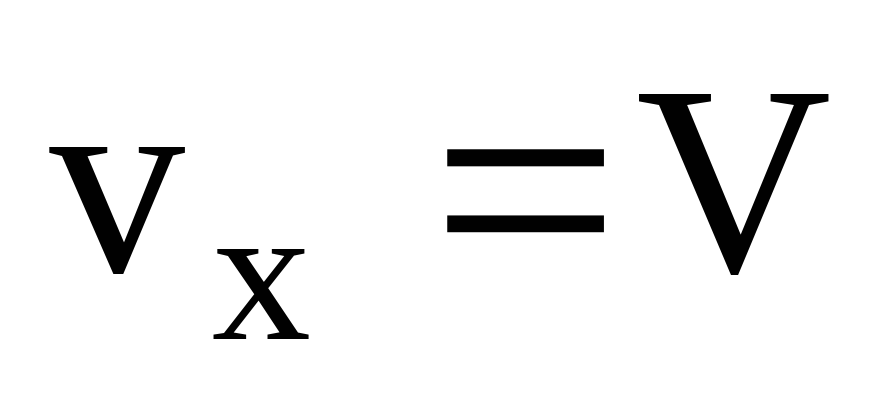 .
Тогда времяT переправы на противоположный берег
.
Тогда времяT переправы на противоположный берег 
Это время будет минимально в том случае,
когда проекция скорости на ось y,
перпендикулярную к берегу, максимальна,
т.е. равна .
В этом случае скорость
.
В этом случае скорость перпендикулярна берегу, т.е.= 90,
а
перпендикулярна берегу, т.е.= 90,
а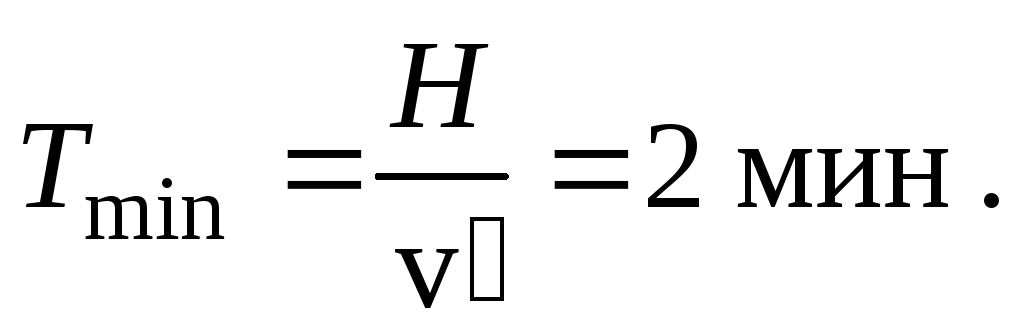
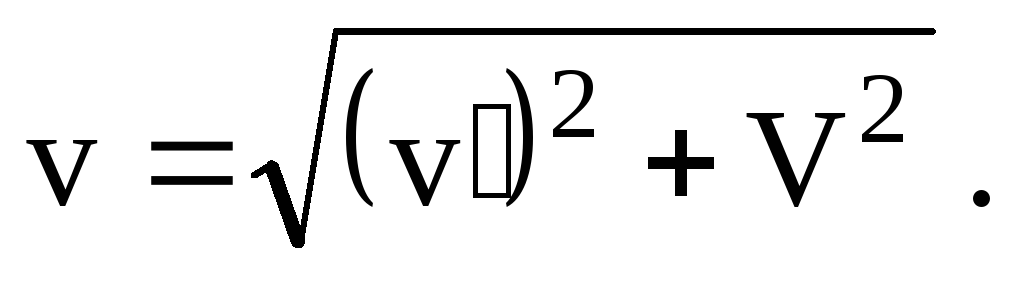 Следовательно, за времяTminлодка пройдет путь
Следовательно, за времяTminлодка пройдет путь 
6 .Два
пешехода движутся к перекрёстку по
дорогам, пересекающимися под прямым
углом. Найти их относительную скорость
.Два
пешехода движутся к перекрёстку по
дорогам, пересекающимися под прямым
углом. Найти их относительную скорость ,
если скорость первого пешехода
,
если скорость первого пешехода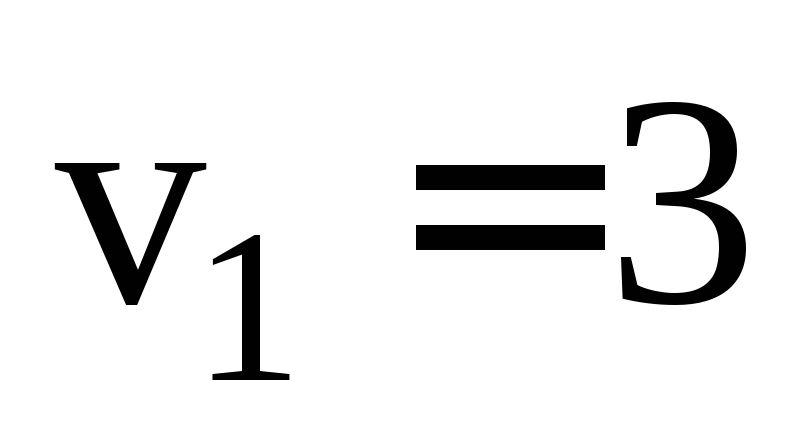 км/ч,
а скорость второго —
км/ч,
а скорость второго — км/ч.
км/ч.
Решение.Изобразим на рисунке скорости пешеходов. По определению скорость первого пешехода относительно второго равна:
 .
.
Найдем построением эту скорость (см. рис.).
И з
рисунка видно, что
з
рисунка видно, что
 км/ч.
км/ч.
Задачи на тему Относительность движения (механика, кинематика)
Нашли ошибку? Сообщите в комментариях (внизу страницы)
Какова траектория движения точки обода велосипедного колеса при равномерном и прямолинейном движении велосипедиста в системах отсчета, жестко связанных: а) с вращающимся колесом; б) с рамой велосипеда; в) с землей?РЕШЕНИЕ
Может ли человек, находясь на движущемся эскалаторе метро, быть в покое в системе отсчета, связанной с землей
РЕШЕНИЕ
На рисунке 11 помещен кадр из диафильма по сказке Г.-Х. Андерсена Дюймовочка . Объяснить физическую несостоятельность текста под кадром
РЕШЕНИЕ
Скорость штормового ветра равна 30 м/с, а скорость автомобиля Жигули достигает 150 км/ч. Может ли автомобиль двигаться так, чтобы быть в покое относительно воздуха
РЕШЕНИЕ
Скорость велосипедиста 36 км/ч, а скорость ветра 4 м/с. Какова скорость ветра в системе отсчета, связанной с велосипедистом, при: а) встречном ветре; б) попутном ветре
РЕШЕНИЕ
Гусеничный трактор Т-150 движется с максимальной скоростью 18 км/ч. Найти проекции векторов скоростей верхней и нижней части гусеницы на оси X и X1 Ось X связана с землей, ось X1 — с трактором. Обе оси направлены по ходу движения трактора
РЕШЕНИЕ
Эскалатор метро движется со скоростью 0,75 м/с. Найти время, за которое пассажир переместится на 20 м относительно земли, если он сам идет в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчета, связанной с эскалатором
РЕШЕНИЕ
Два поезда движутся навстречу друг другу со скоростями 72 и 54 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 14 с. Какова длина второго поезда
РЕШЕНИЕ
Скорость движения лодки относительно воды в n раз больше скорости течения реки. Во сколько раз больше времени занимает поездка на лодке между двумя пунктами против течения, чем по течению? Решить задачу для значений n = 2 и n = 11
РЕШЕНИЕ
Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 1 мин. По неподвижному эскалатору пассажир поднимается за 3 мин. Сколько времени будет подниматься идущий вверх пассажир по движущемуся эскалатору
РЕШЕНИЕ
Легковой автомобиль движется со скоростью 20 м/с за грузовым, скорость которого 16,5 м/с. В момент начала обгона водитель легкового автомобиля увидел встречный междугородный автобус, движущийся со скоростью 25 м/с. При каком наименьшем расстоянии до автобуса можно начинать обгон, если в начале обгона легковая машина была в 15 м от грузовой, а к концу обгона она должна быть впереди грузовой на 20 м
РЕШЕНИЕ
Рыболов, двигаясь на лодке против течения реки, уронил удочку. Через 1 мин он заметил потерю и сразу же повернул обратно. Через какой промежуток времени после потери он догонит удочку? Скорость течения реки и скорость лодки относительно воды постоянны. На каком расстоянии от места потери он догонит удочку, если скорость течения воды равна 2 м/с
РЕШЕНИЕ
На рисунке приведены графики движения велосипедиста I и движения мотоциклиста II в системе отсчета, связанной с землей. Написать уравнение движения велосипедиста в системе отсчета, связанной с мотоциклистом, и построить график его движения в этой системе
РЕШЕНИЕ
На рисунке 13 изображен график движения второго автомобиля в системе отсчета, связанной с первым автомобилем. Написать уравнения движений и построить графики в системе отсчета, связанной с землей (начало координат расположить в месте нахождения первого автомобиля в начальный момент времени), если скорость первого автомобиля относительно земли: а) направлена по оси X и равна 2 м/с; б) направлена по оси X и равна 6 м/с; в) направлена в сторону, противоположную оси xy и равна 2 м/с. Описать картину движения в каждом случае
РЕШЕНИЕ
Скорость продольной подачи резца токарного станка 12 см/мин, а поперечной подачи 5 см/мин. Какова скорость резца в системе отсчета, связанной с корпусом станка
РЕШЕНИЕ
Вертолет летел на север со скоростью 20 м/с. С какой скоростью и под каким углом к меридиану будет лететь вертолет, если подует западный ветер со скоростью 10 м/с
РЕШЕНИЕ
Катер, переправляясь через реку, движется перпендикулярно течению реки со скоростью 4 м/с в системе отсчета, связанной с водой. На сколько метров будет снесен катер течением, если ширина реки 800 м, а скорость течения 1 м/с
РЕШЕНИЕ
На токарном станке вытачивают деталь в форме усеченного конуса (рис. 14). Какова должна быть скорость поперечной подачи резца, если скорость продольной подачи 25 см/мин? Размеры детали (в миллиметрах) указаны на рисунке
РЕШЕНИЕ
В безветренную погоду вертолет двигался со скоростью 90 км/ч точно на север. Найти скорость и курс вертолета, если подул северо-западный ветер под углом 45° к меридиану. Скорость ветра 10 м/с
РЕШЕНИЕ
В системе отсчета, связанной с землей, трамвай движется со скоростью v = 2,4 м/с (рис. 15), а три пешехода — с одинаковыми по модулю скоростями v1= v2 = v3=1 м/с. Найти: а) модули скоростей пешеходов в системе отсчета, связанной с трамваем; б) проекции векторов скоростей пешеходов на оси координат в этой системе отсчета
РЕШЕНИЕ
Относительность движения: задачи посложнее
Всякое тело одновременно и движется, и покоится. Смотря откуда на него посмотреть. Например, дерево нам кажется неподвижным, а если представить, с какой скоростью оно несется в космическом пространстве? Поэтому важно, какое тело принять за точку наблюдения, то есть относительно какого тела мы измеряем скорость. Это тело называется системой отсчета или телом отсчета. Системы отсчета могут быть неподвижными (опять же, откуда посмотреть) и подвижными. Чтобы определить скорость тела, пользуются правилом сложения классических скоростей. Классических -потому что не релятивистских, там все немного по-другому.
Правило сложения: скорость тела относительно неподвижной системы отсчета  равна сумме скорости тела относительно подвижной системы отсчета
равна сумме скорости тела относительно подвижной системы отсчета  и скорости самой подвижной
и скорости самой подвижной  системы относительно неподвижной:
системы относительно неподвижной:
![Rendered by QuickLaTeX.com \[\vec{\upsilon}=\vec{\upsilon_1}+\vec{\upsilon_0}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4e33067d5a13f159d9170ec841b0f41d_l3.png)
Пример: поезд двигается по рельсам, а в вагоне поезда упало со стола и покатилось по направлению движения поезда яблоко. Тогда относительно поезда скорость яблока равна  (поезд – подвижная система отсчета). Скорость поезда относительно земли –
(поезд – подвижная система отсчета). Скорость поезда относительно земли –  , а скорость яблока относительно земли будет равна
, а скорость яблока относительно земли будет равна  . Не забываем, что скорости – вектора, и в последнем выражении мы сняли стрелочки над скоростями только потому, что яблоко и поезд двигались в одну сторону! Если бы яблоко покатилось против направления движения поезда, то его скорость тоже складывалась бы со скоростью поезда, но направлена-то она в противоположную сторону! И по правилу сложения векторов мы бы складывали так:
. Не забываем, что скорости – вектора, и в последнем выражении мы сняли стрелочки над скоростями только потому, что яблоко и поезд двигались в одну сторону! Если бы яблоко покатилось против направления движения поезда, то его скорость тоже складывалась бы со скоростью поезда, но направлена-то она в противоположную сторону! И по правилу сложения векторов мы бы складывали так:

Правило сложения векторов
То есть  – теперь уже без знаков векторов.
– теперь уже без знаков векторов.
Еще хорошо бывает пользоваться такой подсказкой: чтобы принять за начало (или систему) отсчета движущийся объект, надо вычесть его скорость из скорости объектов, находящихся в неподвижной системе отсчета.
Попробуем потренировать эти правила.
Задача 1. Танк движется со скоростью  км/ч. С какими скоростями относительно земли движутся: нижняя часть гусеницы –
км/ч. С какими скоростями относительно земли движутся: нижняя часть гусеницы –  ; верхняя часть гусеницы –
; верхняя часть гусеницы –  , часть гусеницы, которая в данный момент вертикальна по отношению к земле –
, часть гусеницы, которая в данный момент вертикальна по отношению к земле –  ?
?
Внимательно посмотрев видео, мы заметим, что нижняя часть гусеницы относительно земли неподвижна. Тогда  . Поскольку эта точка является центром вращения, то можно определить линейную скорость точек обода колеса, если знать угловую. Угловая скорость центра колеса относительно нижней точки – мгновенного центра вращения – равна:
. Поскольку эта точка является центром вращения, то можно определить линейную скорость точек обода колеса, если знать угловую. Угловая скорость центра колеса относительно нижней точки – мгновенного центра вращения – равна:
![Rendered by QuickLaTeX.com \[\omega=\frac{\upsilon}{R}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7d395b16c56d110f7f7ac11288b18bc0_l3.png)
Тогда верхний край колеса (или верхняя часть гусеницы) будет вращаться со скоростью
![Rendered by QuickLaTeX.com \[\upsilon_v=\omega \cdot 2R=2\upsilon=144\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-dae67f9e573a9a6520f81e04a96de425_l3.png)

Задача 1
Теперь попробуем найти скорость самой правой точки – точки, линейная скорость вращения которой направлена вертикально по отношению к земле. Не забываем, что скорости – величины векторные, и складывать их необходимо по правилам сложения векторов. Данная точка принимает участие в двух движениях: во-первых, она движется вперед со скоростью танка (скорость поступательного движения направлена горизонтально и равна скорости танка, скорость танка – скорость подвижной системы), во-вторых, она вращается вокруг центра колеса, и линейная скорость вращения как раз и направлена вертикально вниз (и тоже равна скорости танка:  , это скорость в подвижной системе отсчета). Поэтому складывать будем два перпендикулярных вектора, а следовательно, модуль результата сложения может быть найден по теореме Пифагора:
, это скорость в подвижной системе отсчета). Поэтому складывать будем два перпендикулярных вектора, а следовательно, модуль результата сложения может быть найден по теореме Пифагора:
![Rendered by QuickLaTeX.com \[\upsilon_1=\sqrt{\upsilon^2+\upsilon^2}=\upsilon \sqrt{2}=101,52\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c66209b555365e82ec61ef584ce8e30c_l3.png)
Ответ: нижняя точка гусеницы неподвижна:  , верхняя двигается с удвоенной скоростью:
, верхняя двигается с удвоенной скоростью:  км/ч, скорость крайней правой точки гусеницы (и крайней левой) равна
км/ч, скорость крайней правой точки гусеницы (и крайней левой) равна  км/ч.
км/ч.
Задача 2. Капли дождя на окнах неподвижного трамвая оставляют полосы, наклоненные под углом  к вертикали. При движении трамвая со скоростью
к вертикали. При движении трамвая со скоростью  полосы от дождя вертикальны. Оценить скорость капель дождя в безветренную погоду.
полосы от дождя вертикальны. Оценить скорость капель дождя в безветренную погоду.

Задача 2
Итак, раз капли падают наклонно, то имеют горизонтальную и вертикальную составляющие скорости. Причем при движении скорость трамвая компенсирует горизонтальную составляющую, сводя ее к нулю:
![Rendered by QuickLaTeX.com \[u \cdot \sin{\alpha}= \upsilon\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-24565b2a02a740967bf5ab8f83f148d9_l3.png)
![Rendered by QuickLaTeX.com \[u=\frac{\upsilon}{\sin{\alpha}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a6562787752947be65ba69ce577899e7_l3.png)
А при безветренной погоде у капель останется только вертикальная составляющая скорости:  , которая, следовательно, будет равна:
, которая, следовательно, будет равна:
![Rendered by QuickLaTeX.com \[u\cos{\alpha}=\frac{\upsilon}{\sin{\alpha}}\cos{\alpha}=\upsilon \operatorname{ctg}{\alpha}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3e2d764c1f2e75487dbe44228a4b9214_l3.png)
Ответ: в безветренную погоду скорость капель  .
.
Здесь  – скорость капель в неподвижной системе отсчета «земля»,
– скорость капель в неподвижной системе отсчета «земля»,  – скорость подвижной системы отсчета «трамвай». Поэтому скорость капель в подвижной системе отсчета будет равна векторной разности
– скорость подвижной системы отсчета «трамвай». Поэтому скорость капель в подвижной системе отсчета будет равна векторной разности  и
и  .
.
Задача 3. Поезд движется на север со скоростью  м/с. Пассажиру вертолета, пролетающего над поездом, кажется, что поезд движется на запад со скоростью
м/с. Пассажиру вертолета, пролетающего над поездом, кажется, что поезд движется на запад со скоростью  м/с. Найти скорость вертолета и направление его полета.
м/с. Найти скорость вертолета и направление его полета.
В этой задаче подвижная система отсчета – вертолет. Поезд двигается в неподвижной системе отсчета – земля. Поэтому реальная скорость поезда будет результатом сложения скорости вертолета и того, что кажется его пассажиру.

Задача 3
Следовательно, скорость вертолета в неподвижной системе отсчета – это векторная разность скорости поезда в неподвижной системе и скорости поезда в подвижной системе отсчета – того, что кажется пассажиру. Тогда
![Rendered by QuickLaTeX.com \[\upsilon_v=\sqrt{\upsilon^2+u^2}=\sqrt{20^2+20^2}=20\sqrt{2}=28,2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8651e108ee12a2e5404295b1885b886f_l3.png)
Угол, под которым направлена скорость вертолета относительно земли найдем из отношения катетов в этом прямоугольном треугольнике:
![Rendered by QuickLaTeX.com \[\alpha=\operatorname{arctg}\frac{u}{\upsilon}=\operatorname{arctg} 1=45^{\circ}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4a4ba3ce7e9c87d061b2fbf2011a5694_l3.png)
Таким образом, скорость вертолета равна  м/с, а направление скорости – на северо-восток.
м/с, а направление скорости – на северо-восток.
Задача 4. Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится в 3 км от перекрестка. Через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние?
Введем систему координат. Пусть первый велосипедист движется вниз по оси  , а второй – влево по оси
, а второй – влево по оси  . Тогда уравнение движения первого будет:
. Тогда уравнение движения первого будет:
![Rendered by QuickLaTeX.com \[y=y_0-\upsilon_y t\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-092b03d950f66ba2b07aeefb714519a0_l3.png)
А уравнение движения второго –
![Rendered by QuickLaTeX.com \[x=x_0-\upsilon_x t\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ebf276461cbcecf4431230fe11fa35d5_l3.png)
Так как наши велосипедисты движутся по катетам треугольника, то расстояние между ними – его гипотенуза. Следовательно, нам надо найти минимум длины этой гипотенузы. Запишем ее уравнение:
![Rendered by QuickLaTeX.com \[l^2=x^2+y^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b3e8ab6509883dc49f7870880b5fbbae_l3.png)
![Rendered by QuickLaTeX.com \[l^2=(x_0-\upsilon_x t )^2 +(y_0-\upsilon_y t )^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3da4f2a422b7776840e6518a48f03921_l3.png)
Раскроем скобки:
![Rendered by QuickLaTeX.com \[l^2=x_0^2-2x_0\upsilon_x t +\upsilon_x^2 t^2 + y_0^2-2y_0\upsilon_y t +\upsilon_y^2 t^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-42d156349e9b3464c52091a2540436e2_l3.png)
Объединим подобные относительно  слагаемые:
слагаемые:
![Rendered by QuickLaTeX.com \[l^2=(\upsilon_x^2+ \upsilon_y^2)t^2 -t(2x_0\upsilon_x + 2y_0\upsilon_y )+ y_0^2 + x_0^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2884bc6d74cea874dc4ee877fe6b4b0e_l3.png)
Видно, что в правой части равенства имеем квадратичную зависимость относительно  , причем парабола расположена ветвями вверх и минимум будет достигнут в вершине, поэтому найдем вершинку этой параболы:
, причем парабола расположена ветвями вверх и минимум будет достигнут в вершине, поэтому найдем вершинку этой параболы:
![Rendered by QuickLaTeX.com \[t_{min}=\frac{-b}{2a}=\frac{2x_0\upsilon_x + 2y_0\upsilon_y }{2(\upsilon_x^2+ \upsilon_y^2)}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-34ce262a6a278d534c80d702667cc755_l3.png)
Также, чтобы найти это время, можно было бы воспользоваться и производной – если, конечно, вы учитесь в старших классах и вам уже знакомо это понятие:

![Rendered by QuickLaTeX.com \[t_{min}=\frac{2x_0\upsilon_x + 2y_0\upsilon_y }{2(\upsilon_x^2+ \upsilon_y^2)}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e0f7f76a8060de26db44ecec11f3dbba_l3.png)
Определив время, сможем найти и минимальное расстояние:
![Rendered by QuickLaTeX.com \[t_{min}=\frac{2\cdot3\cdot30 + 2\cdot5\cdot40}{2(30^2+40^2)}=\frac{180+400}{5000}=\frac{29}{250}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a66ddeae198a986b9ef7a0d549d1e1ee_l3.png)
Мы получили время в часах. В задаче нужно найти время в минутах, поэтому просто умножим это время на 60:  минут.
минут.
Теперь определим минимальное расстояние:
![Rendered by QuickLaTeX.com \[l=\sqrt{(\upsilon_x^2+ \upsilon_y^2)t^2 -t(2x_0\upsilon_x t+ 2y_0\upsilon_y t)+ y_0^2 + x_0^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3a3b9e8d79ed5c3656f7db437b9f0274_l3.png)
![Rendered by QuickLaTeX.com \[l=\sqrt{2500\cdot \left(\frac{29}{250}\right)^2 -\frac{29}{250}\cdot 180 +25+9}=\sqrt{\frac{225}{625}}=\frac{15}{25}=0,6\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9f879ad9e2b3b1d11e8239da9015649e_l3.png)
Ответ: минимальное расстояние – 0,6 км, велосипедисты максимально сблизятся через 6,96 минут.
Задача 5. Два лодочника должны переплыть реку из пункта А в пункт В. Один из них направляет лодку по прямой АВ и, достигнув противоположного берега, оказывается в точке С. Для того, чтобы попасть в пункт В, он движется против течения от пункта С к пункту В. Второй лодочник направляет лодку так, что сразу, достигнув противоположного берега, оказывается в пункте В. Кто из них попадет в пункт В быстрее и во сколько раз? Скорость лодки относительно воды в обоих случаях одинакова и равна  м/с, скорость течения воды
м/с, скорость течения воды  м/с.
м/с.

Задача 5
Первого лодочника сносит течением. Следовательно, пока он преодолевает расстояние  со скоростью
со скоростью  , следовательно, тратит на это время
, следовательно, тратит на это время  , течение сносит его со скоростью
, течение сносит его со скоростью  и снесет на расстояние
и снесет на расстояние  . Это расстояние ему придется преодолевать против течения, следовательно, со скоростью
. Это расстояние ему придется преодолевать против течения, следовательно, со скоростью  , и он потратит на это время, равное
, и он потратит на это время, равное  ,
,
![Rendered by QuickLaTeX.com \[t_1=\frac{AB\cdot u}{\upsilon(\upsilon-u)}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d0c0d3dd0cf93c15c6054a6247cf5473_l3.png)
А общее время переправы первого лодочника составит
![Rendered by QuickLaTeX.com \[t+t_1=\frac{AB}{\upsilon}\left(1+\frac{u}{\upsilon-u }\right)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8c674a52fcc79e137819b82b84d76366_l3.png)
Теперь второй лодочник. Он правит так, чтобы попасть в точку  сразу, следовательно, он направляет нос лодки под определенным углом против скорости течения, и итоговая его скорость равна векторной сумме его скорости относительно реки (подвижной системы отсчета) и скорости самой реки. По теореме Пифагора его скорость равна
сразу, следовательно, он направляет нос лодки под определенным углом против скорости течения, и итоговая его скорость равна векторной сумме его скорости относительно реки (подвижной системы отсчета) и скорости самой реки. По теореме Пифагора его скорость равна
![Rendered by QuickLaTeX.com \[\upsilon_2=\sqrt{\upsilon^2-u^2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-995804dad33fffd69eff25e320c1114e_l3.png)
Тогда время, которое он потратит на переправу,
![Rendered by QuickLaTeX.com \[t_2=\frac{AB}{\upsilon_2}=\frac{AB}{\sqrt{\upsilon^2-u^2}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e9ed09ee9b330e77d237efc57497ed83_l3.png)
Видимо, время  меньше, чем
меньше, чем  . В задаче спрашивают, во сколько раз, следовательно, надо найти отношение:
. В задаче спрашивают, во сколько раз, следовательно, надо найти отношение:
![Rendered by QuickLaTeX.com \[\frac{t+t_1}{t_2}=\frac{\sqrt{\upsilon^2-u^2}}{\upsilon}\left(1+\frac{u}{\upsilon-u }\right)=\frac{\sqrt{\upsilon^2-u^2}}{\upsilon}\cdot\frac{\upsilon}{\upsilon-u }=\sqrt{\frac{\upsilon+u}{\upsilon-u}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-db5a4b71f0ef047da4bdd153cb75fce9_l3.png)
![Rendered by QuickLaTeX.com \[\frac{t+t_1}{t_2}=\sqrt\frac{5,2+1,2}{5,2-1,2}=1,26\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5793c3a9a83f0ed155701ba342150b9b_l3.png)
Ответ: второй лодочник прибудет в 1,26 раза быстрее первого.
Задачи на относительность механического движения.
Задачи на относительность механического движения.
Вопрос 1. Найти скорость относительно берега реки лодки, идущей против течения. Скорость течения реки 1 м/с, скорость лодки относительно воды 2 м/с.
Вопрос 2. Скорость мотоциклиста 54 км/ч, скорость встречного ветра 3 м/с. Какова скорость ветра (в м/с) в системе отсчета связанной с мотоциклистом?
Вопрос 3. Автоколонна длиной 600 м движется со скоростью 10 м/с. Мотоциклист выехал из конца колонны по направлению к ее началу со скоростью 20 м/с. Достигнув головной машины, мотоциклист повернул обратно к концу автоколонны. За какое время (в с) он совершит весь свой путь?
Вопрос 4. Определите скорость течения в (км/ч), если скорость лодки вниз по реке 27 км/ч, а вверх 15 км/ч.
Вопрос 5. Скорость лодки относительно воды равна 4 м/с и направлена перпендикулярно берегу, а скорость течения реки – 3 м/с. Найдите скорость лодки относительно берега ( в м/с).
Вопрос 6. Самолет летит относительно воздуха со скоростью 800 км/ч. Ветер дует с запада на восток со скоростью 15 м/с. С какой скоростью (в км/ч) самолет будет двигаться относительно земли, чтобы перемещение было на север?
Вопрос 7. Пассажир поезда, движущегося равномерно со скоростью 54 км/ч, видит в течение 60 с другой поезд длиной 300 м, который движется по соседнему пути в том же направлении с большей скоростью. Найдите скорость (в км/ч) второго поезда.
Вопрос 8. Автомобиль, двигаясь со скоростью 45 км/ч, в течение 10 с прошел такой же путь, какой автобус, двигающийся в том же направлении с постоянной скоростью, прошел за 15 с. Найдите величину их относительной скорости (в км/ч).
Вопрос 9. Эскалатор метрополитена, двигаясь равномерно, поднимает неподвижно стоящего на нем пассажира в течение одной минуты. По неподвижному эскалатору пассажир, двигаясь равномерно, поднимается за 3 минуты. Сколько секунд будет подниматься пассажир по движущемуся вверх эскалатору?
Вопрос 10. Два автомобиля находятся на расстоянии 2,5 км друг от друга и движутся навстречу один другому со скоростями 20 м/с и 15 м/с соответственно. Какое расстояние (в км) будет между автомобилями через 5 мин?
Вопрос 11. Из двух пунктов, расстояние между которыми 100 м, одновременно навстречу друг другу начали двигаться два тела. Скорость одного из них 20 м/с. Какова скорость второго тела (в м/с), если они встретились через 4с?
Вопрос 12.
Методика решения задач на относительность механического движения
Библиографическое описание:
Маманова А. К. Методика решения задач на относительность механического движения // Молодой ученый. 2017. №13. С. 576-577. URL https://moluch.ru/archive/147/41287/ (дата обращения: 10.01.2020).
Свойство относительности механического движения заключается в различии его характеристик по отношению к тем или иным объектам. Из практического опыта преподавания физики нами установлено, что трудности, возникающие у школьников, чаще всего связаны с применением закона сложения скоростей. Для их преодоления и успешного усвоения учащимися материала нами разработано содержание урока, на котором ребята многократно применяют изученный закон в конкретных ситуациях. Для усвоения закона сложения скоростей большинством учащихся класса перед непосредственным решением подобных задач школьникам предлагается составить программу своих действий по нахождению скорости тела относительно разных систем отсчета. Каждый ученик во время урока выполняет эту систему действий многократно (не менее 8 раз) в различных ситуациях. Покажем возможности обучения учащихся методу решения задач на относительность механического движения на следующем примере урока.
Тема урока: Решение задач по теме: «Относительность механического движения».
Цель урока: учащиеся должны выделить метод решения задач на относительность движения и научиться применять его в конкретных ситуациях.
Ход урока
Актуализация знаний и умений по теме «Относительность механического движения»
Учитель. Мы с вами выяснили, что понятие относительности движения, закон сложения скоростей и перемещений являются очень важными и имеют очень важное практическое применение. Например, для правильной стыковки космического корабля с орбитальной станцией необходимо правильно рассчитать скорости обоих тел, относительно Земли и относительно друг друга. Необходимо это и для противовоздушной обороны, для уничтожения ракеты противника противоракетой. Мы, конечно, такие глобальные задачи решать не будем, будем учиться на более простых задачах. Они перед вами. Начнём с первой.
Задача 1. Эскалатор метро движется со скоростью 0,75 м/с. Найдите время, за которое пассажир переместится на 20 м относительно земли, если он сам идет в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчета, связанной с эскалатором.
Для того чтобы решить эту задачу, и не только эту, а многие другие подобные ей нам надо выработать программу наших действий. Для этого нужно разделиться на группы. Итак, каждая группа работает над созданием программы, у вас 5 минут.
После групповой работы, результаты обсуждаются и в ходе обсуждения вырабатывается программа — каждое её действие отображается на слайде
Метод решения задач на относительность движения
- Записать данные в определенной системе отсчета
- Изобразить графическую модель ситуации задачи, выбрав подвижную и неподвижную систему координат.
- Записать классический закон сложения скоростей или перемещений в векторном виде.
- Выбрать систему отсчета.
- Записать классический закон сложения скоростей или перемещений в скалярном виде.
- Найти искомую величину.
Учитель. Эта программа, ребята, называется методом решения задач на относительность движения, с его помощью можно решить любую задачу по данной теме.
Итак, давайте применим его для решения первой задачи.
Учитель. Следующую задачу разбираем самостоятельно, следуя методу (по ходу работы учитель контролирует ход решения вопросами, учащиеся чётко проговаривают каждое действие при ответе).
Учитель. А теперь работаем в парах «учитель-ученик», сначала решаем задачу 3а, затем меняемся ролями и решаем задачу 3б, чётко проговариваем действия метода.
Задача 3. На рисунке даны направления движения трех автомобилей, движущихся равномерно по трассе. Модули их скоростей относительно неподвижного наблюдателя соответственно равны: υ1 = 10 м/с, υ2 = 8 м/с, υ3 = 5 м/с. Применяя закон сложения скоростей, определите скорости движения автомобилей относительно: а) первого автомобиля; б) третьего автомобиля.
Учитель. Задачу № 4 решаем полностью самостоятельно, действия метода проговариваем про себя. Меня интересует конечный результат.
 Задача 4. Пассажир, сидящий у окна поезда, идущего со скоростью 72 км/ч, видит в течение 10 с встречный поезд. Длина встречного поезда 290 м. Определите его скорость.
Задача 4. Пассажир, сидящий у окна поезда, идущего со скоростью 72 км/ч, видит в течение 10 с встречный поезд. Длина встречного поезда 290 м. Определите его скорость.
Учитель. Также решаем задачи № 5, 6.
Задача 5. Велосипедист и мотоциклист одновременно выезжают на шоссе и движутся в одну сторону. Скорость первого 12 м/с, второго — 54 км/ч. Каким будет расстояние между ними через 5 мин?
Задача 6. Два поезда идут навстречу друг другу по двум параллельным путям со скоростью 36 и 54 км/ч. Длины поездов 125 и 150 м. Чему будет равно время, в течение которого поезда проходят мимо друг друга?
Учитель. Задачи 7 и 8 решаем по вариантам и на отдельных листочках.
Задача 7. По двум параллельным путям в одном направлении идут товарный поезд длиной L1 = 560 м со скоростью v1= 68,4 км/ч и электропоезд длиной L2 = 440 м со скоростью v2 = 104,4 км/ч. За какое время электропоезд обгонит товарный состав?
Задача 8. Автоколонна длиной 1,2 км движется со скоростью 36 км/ч. Мотоциклист выезжает из головы колонны, доезжает до ее хвоста и возвращается обратно. Определите время, за которое мотоциклист преодолеет данное расстояние, если его скорость равна 72 км/ч.
Учитель. Внимание, листочки сдаём.
Итак, чему сегодня мы научились на уроке?
Ученик.Мы научились решать задачи на закон сложения скоростей.
Учитель. Урок окончен. Всем спасибо.
Литература:
- Талызина Н. Ф. Управление процессом усвоения знаний. — М.: Изд-во Москов. гос. ун-та, 1985.
- Анофрикова С. В., Стефанова Г. П. Применение задач в процессе обучения физике. Учебное пособие для студентов физических факультетов педагогических институтов. — М.: Прометей, 1991.
- Джалмухамбетов А. У., Фисенко М. А. Роль инерциальных систем отсчета в описании движения и взаимодействия тел в механике // Материалы 5-й Межрегиональной научной конференции «Проблемы научного обеспечения изучения философии и истории естествознания в современных условиях».‑ Армавир, 2010. С.37–40.
- Рымкевич А. П., Рымкевич П. А. Сборник задач по физике для 8–10 классов средней школы (9-е издание).– М.: Издательство «Просвещение», 1984.– 192 с.
Основные термины (генерируются автоматически): сложение скоростей, задача, скорость, система отсчета, относительность движения, метод решения задач, механическое движение, учитель, встречный поезд, действие метода.
Относительность движения. 9 класс.
Задачи на относительность движения часто кажутся ребятам сложными и многие их “боятся”. Давайте разберем несколько и почувствуем себя увереннее!
Задача 1. На пути движения автомобиля расположены два звуковых датчика, один впереди, другой позади. Когда движущийся автомобиль оказался ровно посередине между датчиками, то водитель подал звуковой сигнал. Первый датчик регистрировал звуковой сигнал автомобиля в течение  с, второй
с, второй — в течение
— в течение  с. С какой скоростью двигался автомобиль? Скорость звука в воздухе примерно равна
с. С какой скоростью двигался автомобиль? Скорость звука в воздухе примерно равна  м/с? Ответ дать в м/с, округлив до целых.
м/с? Ответ дать в м/с, округлив до целых.
Решение.
До датчика, находящегося впереди автомобиля, сигнал будет идти в течение времени  , а до датчика, находящегося позади автомобиля, в течение времени
, а до датчика, находящегося позади автомобиля, в течение времени  .
.
Отношение времен регистрации сигналов
![Rendered by QuickLaTeX.com \[\frac{t_1}{t_2}=\frac{ c-\upsilon }{ c+\upsilon}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-40aecbacda830cd46291cb55d04c81a0_l3.png)
позволит найти скорость автомобиля
![Rendered by QuickLaTeX.com \[\upsilon=\frac{(t_1+t_2)\cdot c}{t_1-t_2}=33.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a266bf61435db163f56e9e3b6a0b872d_l3.png)
Ответ: 33 м/с
Задача 2. Мальчик, который может плавать со скоростью  км/ч, хочет переплыть эту реку так, чтобы его не снесло течением. За какое время он достигнет другого берега, если ширина реки
км/ч, хочет переплыть эту реку так, чтобы его не снесло течением. За какое время он достигнет другого берега, если ширина реки  м? Скорость течения
м? Скорость течения  км/ч. Ответ дать в секундах, округлив до целых.
км/ч. Ответ дать в секундах, округлив до целых.
Решение.
Если мальчик хочет переплыть реку перпендикулярно берегу, то он должен держать курс несколько против течения. Скорость мальчика относительно реки  , скорость реки относительно берега
, скорость реки относительно берега  . Тогда по закону сложения скоростей можно найти абсолютную скорость мальчика относительно берега (см. рис.)
. Тогда по закону сложения скоростей можно найти абсолютную скорость мальчика относительно берега (см. рис.)

Задача 2
Она будет равна
![Rendered by QuickLaTeX.com \[w=\sqrt{\upsilon^2-u^2}=4.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5b27bf545caea5b9bf04f2899da99016_l3.png)
Время, которое мальчик затратит на переправу, составит
![Rendered by QuickLaTeX.com \[t=\frac{L}{w}=\frac{L}{\sqrt{\upsilon^2-u^2}}=180 c.\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-906ecd751bdba1fe8cb25f419a4581e2_l3.png)
Ответ: 180 с.
Задача 3. Имеется пучок одинаковых ядер, движущихся со скоростью  м/с. Ядра в пучке самопроизвольно делятся на пары одинаковых осколков. Скорость осколков, движущихся в направлении пучка, равна
м/с. Ядра в пучке самопроизвольно делятся на пары одинаковых осколков. Скорость осколков, движущихся в направлении пучка, равна  . Найдите скорость осколков, движущихся в направлении, перпендикулярном пучку (в
. Найдите скорость осколков, движущихся в направлении, перпендикулярном пучку (в СО наблюдателя). Ответ дать в
СО наблюдателя). Ответ дать в м/с. Округлить до целых.
м/с. Округлить до целых.
Решение.
В системе отсчета, связанной с ядрами, все осколки разлетаются во все стороны с одинаковыми скоростями. Так как осколки, летящие вперед в земной СО имеют скорость  , то в системе отсчета ядер их скорость
, то в системе отсчета ядер их скорость  .
.
Тогда

Но мы выяснили, что

Следовательно,
![Rendered by QuickLaTeX.com \[u_{perp}^2+\upsilon^2=4\upsilon^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-be05fdc1a4cb0e0f209a369f54c990b9_l3.png)
![Rendered by QuickLaTeX.com \[u_{perp}^2=3\upsilon^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4fd7ddecfafff2b6a3dbd15fd766dd8b_l3.png)
![Rendered by QuickLaTeX.com \[u_{perp}=\sqrt{3}\upsilon=\sqrt{3}\cdot 173=300\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-df1e78dcd31b5f825fd1b1851c642051_l3.png)
Ответ: 300 м/с.
Задача 4. Стальной шарик, движущийся горизонтально со скоростью  м/с, упруго ударяется о массивную стальную вертикальную стенку, движущуюся в ту же сторону со скоростью
м/с, упруго ударяется о массивную стальную вертикальную стенку, движущуюся в ту же сторону со скоростью  м/с. Определите скорость шарика после отскока. Ответ дать в
м/с. Определите скорость шарика после отскока. Ответ дать в м/с, округлив до целых.
м/с, округлив до целых.
Решение.
Так как при упругом ударе скорость после отскока равна скорости до удара лишь в том случае, если массивная стенка неподвижна, то перейдём в СО стенки. Тогда шарик налетает со скоростью  м/с. Затем опять перейдем в земную систему отсчета и к полученной скорости добавим переносную скорость системы отсчета стенки. Окончательно получим, что скорость отскочившего шарика
м/с. Затем опять перейдем в земную систему отсчета и к полученной скорости добавим переносную скорость системы отсчета стенки. Окончательно получим, что скорость отскочившего шарика  м/с.
м/с.
Ответ: 6 м/с.
Задача 5. Пассажир катера, идущего по течению, уронил в воду спасательный круг. После чего катер еще  мин продолжал движение, затем развернулся и вновь встретил круг. На каком расстоянии от точки бросания они встретились, если скорость течения реки
мин продолжал движение, затем развернулся и вновь встретил круг. На каком расстоянии от точки бросания они встретились, если скорость течения реки  м/с? Ответ дать в метрах.
м/с? Ответ дать в метрах.
Решение.
В системе отсчета воды катер движется с постоянной скоростью, как в озере. Следовательно, время удаления от круга и время возвращения будут одинаковыми, т.е.  . Это же время круг плыл по течению относительно берега. Новая встреча произойдет на расстоянии
. Это же время круг плыл по течению относительно берега. Новая встреча произойдет на расстоянии 
Ответ: 1800 м.
Задачи на тему Относительность движения
Какова траектория движения точки обода велосипедного колеса при равномерном и прямолинейном движении велосипедиста в системах отсчета, жестко связанных: а) с вращающимся колесом; б) с рамой велосипеда; в) с землей?РЕШЕНИЕ
Может ли человек, находясь на движущемся эскалаторе метро, быть в покое в системе отсчета, связанной с землей
РЕШЕНИЕ
На рисунке 11 помещен кадр из диафильма по сказке Г.-Х. Андерсена Дюймовочка . Объяснить физическую несостоятельность текста под кадром
РЕШЕНИЕ
Скорость штормового ветра равна 30 м/с, а скорость автомобиля Жигули достигает 150 км/ч. Может ли автомобиль двигаться так, чтобы быть в покое относительно воздуха
РЕШЕНИЕ
Скорость велосипедиста 36 км/ч, а скорость ветра 4 м/с. Какова скорость ветра в системе отсчета, связанной с велосипедистом, при: а) встречном ветре; б) попутном ветре
РЕШЕНИЕ
Гусеничный трактор Т-150 движется с максимальной скоростью 18 км/ч. Найти проекции векторов скоростей верхней и нижней части гусеницы на оси X и X1 Ось X связана с землей, ось X1 с трактором. Обе оси направлены по ходу движения трактора
РЕШЕНИЕ
Эскалатор метро движется со скоростью 0,75 м/с. Найти время, за которое пассажир переместится на 20 м относительно земли, если он сам идет в направлении движения эскалатора со скоростью 0,25 м/с в системе отсчета, связанной с эскалатором
РЕШЕНИЕ
Два поезда движутся навстречу друг другу со скоростями 72 и 54 км/ч. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 14 с. Какова длина второго поезда
РЕШЕНИЕ
Скорость движения лодки относительно воды в n раз больше скорости течения реки. Во сколько раз больше времени занимает поездка на лодке между двумя пунктами против течения, чем по течению? Решить задачу для значений n = 2 и n = 11
РЕШЕНИЕ
Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 1 мин. По неподвижному эскалатору пассажир поднимается за 3 мин. Сколько времени будет подниматься идущий вверх пассажир по движущемуся эскалатору
РЕШЕНИЕ
Легковой автомобиль движется со скоростью 20 м/с за грузовым, скорость которого 16,5 м/с. В момент начала обгона водитель легкового автомобиля увидел встречный междугородный автобус, движущийся со скоростью 25 м/с. При каком наименьшем расстоянии до автобуса можно начинать обгон, если в начале обгона легковая машина была в 15 м от грузовой, а к концу обгона она должна быть впереди грузовой на 20 м
РЕШЕНИЕ
Рыболов, двигаясь на лодке против течения реки, уронил удочку. Через 1 мин он заметил потерю и сразу же повернул обратно. Через какой промежуток времени после потери он догонит удочку? Скорость течения реки и скорость лодки относительно воды постоянны. На каком расстоянии от места потери он догонит удочку, если скорость течения воды равна 2 м/с
РЕШЕНИЕ
На рисунке приведены графики движения велосипедиста I и движения мотоциклиста II в системе отсчета, связанной с землей. Написать уравнение движения велосипедиста в системе отсчета, связанной с мотоциклистом, и построить график его движения в этой системе
РЕШЕНИЕ
На рисунке 13 изображен график движения второго автомобиля в системе отсчета, связанной с первым автомобилем. Написать уравнения движений и построить графики в системе отсчета, связанной с землей (начало координат расположить в месте нахождения первого автомобиля в начальный момент времени), если скорость первого автомобиля относительно земли: а) направлена по оси X и равна 2 м/с; б) направлена по оси X и равна 6 м/с; в) направлена в сторону, противоположную оси xy и равна 2 м/с. Описать картину движения в каждом случае
РЕШЕНИЕ
Скорость продольной подачи резца токарного станка 12 см/мин, а поперечной подачи 5 см/мин. Какова скорость резца в системе отсчета, связанной с корпусом станка
РЕШЕНИЕ
Вертолет летел на север со скоростью 20 м/с. С какой скоростью и под каким углом к меридиану будет лететь вертолет, если подует западный ветер со скоростью 10 м/с
РЕШЕНИЕ
Катер, переправляясь через реку, движется перпендикулярно течению реки со скоростью 4 м/с в системе отсчета, связанной с водой. На сколько метров будет снесен катер течением, если ширина реки 800 м, а скорость течения 1 м/с
РЕШЕНИЕ
На токарном станке вытачивают деталь в форме усеченного конуса (рис. 14). Какова должна быть скорость поперечной подачи резца, если скорость продольной подачи 25 см/мин? Размеры детали (в миллиметрах) указаны на рисунке
РЕШЕНИЕ
В безветренную погоду вертолет двигался со скоростью 90 км/ч точно на север. Найти скорость и курс вертолета, если подул северо-западный ветер под углом 45° к меридиану. Скорость ветра 10 м/с
РЕШЕНИЕ
В системе отсчета, связанной с землей, трамвай движется со скоростью v = 2,4 м/с (рис. 15), а три пешехода с одинаковыми по модулю скоростями v1= v2 = v3=1 м/с. Найти: а) модули скоростей пешеходов в системе отсчета, связанной с трамваем; б) проекции векторов скоростей пешеходов на оси координат в этой системе отсчета
РЕШЕНИЕ