Отрезок — Википедия с видео // WIKI 2

Эта статья — о понятии в геометрии и математическом анализе. О насильно отрезанных от крестьянских наделов землях см. Отрезки (земля).

Отрезок AB (выделен красным)

Отре́зком называются два близких понятия: в геометрии и математическом анализе.

Энциклопедичный YouTube

• 1/3

  Просмотров:

  8 748

  7 106

  2 810

• ✪ Точка, луч, прямая, отрезок и ломаная. Математика 1 класс

• ✪ Отрезок. Длина отрезка. Треугольник. Математика 5 класс. Часть 3(1)

• ✪ Что такое кривая, прямая линии, луч отрезок ,Что такое ломанная, звено, вершина, замкнутые и не замк

Содержание

Отрезок в геометрии

Отрезок прямой

 — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки A {\displaystyle \;A} и B {\displaystyle \;B} , обозначается символом A B {\displaystyle AB} . Расстояние между концами отрезка называют его длиной и обозначают A B {\displaystyle AB} или | A B | {\displaystyle |AB|} .

Направленный отрезок

Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки A B {\displaystyle AB} и B A {\displaystyle BA} представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, направленные отрезки A B {\displaystyle AB} и B A {\displaystyle BA} не совпадают. Отдельного обозначения для направленных отрезков нет — то, что у отрезка важно его направление, обычно указывается особо.

Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.

Отрезок числовой прямой

Отрезок числовой (координатной) прямой (иначе числовой отрезок, сегмент) — множество вещественных чисел { x } {\displaystyle \{x\}} , удовлетворяющих неравенству a ≤ x ≤ b {\displaystyle a\leq x\leq b} , где заранее заданные вещественные числа a {\displaystyle a} и b {\displaystyle b} ( a < b ) {\displaystyle (a<b)} называются концами (граничными точками) отрезка. В противоположность им, остальные числа x {\displaystyle x} , удовлетворяющие неравенству a < x < b {\displaystyle a<x<b} , называются внутренними точками отрезка^[1].

Отрезок обычно обозначается [ a , b ] {\displaystyle [a,b]} :

[ a , b ] = { x ∈ R ∣ a ≤ x ≤ b } {\displaystyle [a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}} .

Любой отрезок, по определению, заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.

Число b − a {\displaystyle b-a} называется длиной числового отрезка [ a , b ] {\displaystyle [a,b]} .

Стягивающаяся система сегментов

Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой { [ a , b ] | a , b ∈ R ∧ a < b } {\displaystyle \{[a,b]|a,b\in \mathbb {R} \land a<b\}} .

Система сегментов обозначается { [ a n , b n ] } n = 1 ∞ {\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} . Подразумевается, что каждому натуральному числу n {\displaystyle n} поставлен в соответствие отрезок [ a n , b n ] {\displaystyle [a_{n},b_{n}]} .

Система сегментов { [ a n , b n ] } n = 1 ∞ {\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} называется стягивающейся, если^[2]

• каждый следующий отрезок содержится в предыдущем;

  ∀ n ∈ N : [ a n + 1 , b n + 1 ] ⊆ [ a n , b n ] {\displaystyle \forall n\in \mathbb {N} \colon [a_{n+1},b_{n+1}]\subseteq [a_{n},b_{n}]}

• соответствующая последовательность длин отрезков бесконечно мала.

  lim n → ∞ ( b n − a n ) = 0 {\displaystyle \lim _{n\to \infty }(b_{n}-a_{n})=0}

У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.

∀ { [ a n , b n ] } n = 1 ∞   ∃ ! c ∈ R   ∀ n ∈ N : c ∈ [ a n , b n ] {\displaystyle \forall \{[a_{n},b_{n}]\}_{n=1}^{\infty }~\exists !c\in \mathbb {R} ~\forall n\in N\colon c\in [a_{n},b_{n}]}

Этот факт следует из свойств монотонной последовательности.

См. также

Примечания

Эта страница в последний раз была отредактирована 25 апреля 2019 в 20:18.

Урок 21. прямая, луч, отрезок — Математика — 5 класс

Математика

5 класс

Урок №21

Прямая, луч, отрезок

Перечень рассматриваемых вопросов:

— понятия «прямая», «луч», «отрезок»;

— отличия прямой, луча, отрезка;

— прямая, луч, отрезок на чертежах, рисунках и моделях.

Тезаурус

Отрезок – часть прямой, ограниченный двумя точками.

Концы отрезка – точки, ограничивающие отрезок.

Обязательная литература

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.

Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).

Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.

Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.

Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.

Через любые две точки можно провести только одну прямую.

Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.

Провести через точки А и В другую прямую, отличную от прямой b, нельзя.

Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.

Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.

Каждую из этих частей называют лучом, исходящим из точки А.

Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.

Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.

Переставлять буквы в названии луча нельзя. 

Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.

Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.

В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.

Заметим, что два отрезка называются равными, если они совмещаются при наложении.

Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.

Это интересно

Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.

• Космические лучи – это элементарные частицы и ядра атомов, движущиеся с высокими энергиями в космическом пространстве.
• Противосумеречные лучи (англ. anticrepuscular rays) – расходящиеся веером лучи, наблюдающиеся на закате дня со стороны, противоположной Солнцу (то есть, на востоке).
• Белохохлый солнечный луч (лат. Aglaeactis castelnaudii) – вид птиц из семейства колибри (Trochilidae).
• Луч света в темном царстве – крылатое выражение, вошедшее в речь после публикации в 1860 году статьи публициста-демократа Николая Александровича Добролюбова, посвящённой драме А. Н. Островского «Гроза».

Разбор решения заданий тренировочного модуля

№ 1. Тип задания: добавление подписей к изображениям.

Разместите нужные подписи к изображениям.

Для выполнения задания обратитесь к теоретическому материалу урока.

Правильные ответы:

1) а – это прямая.

2) АВ – это отрезок.

3) А – это луч.

№ 2. Тип задания: подстановка элементов в пропуски в тексте.

Вставьте в текст нужные слова.

Через__________ две____________ можно провести только одну _________.

Слова: любые; точки; прямую; ломаную.

Правильный ответ: через любые две точки можно провести только одну прямую.

Отрезок — это… Что такое отрезок?

Всякий отрезок, который при построении на нем квадрата дает площадь, выраженную равносторонним числом, мы назвали длиной, а всякий отрезок, который дает разностороннее продолговатое число, мы назвали [несоизмеримой с единицей] стороной квадрата, потому что такие отрезки соизмеримы первым не по длине, а лишь по площадям, которые они образуют.

Проведем на полу мелом отрезок прямой длиною в метр и, если мы не упремся в стенку, из его конца под прямым углом проведем еще такой же

отрезок.

Системы вооружения стены отдельными участками придерживались две большие рабочие армии – Восточная и Западная; и на каждом отрезке происходило это так, что были созданы группы рабочих по двадцать человек, каждой поручалось построить отрезок стены примерно в пятьсот метров, а соседняя группа строила встречный отрезок такой же длины.

примером может служить фигура (рис.), получаемая следующим образом: из вершин равностороннего треугольника со стороной а проводят шесть дуг окружностей, радиус трёх из них — произвольный отрезок с, радиус трёх других — отрезок, равный а + с.   В алгебраической геометрии О.

В этот отрезок португальской истории (отрезок? – а для нации – растянувшаяся на столетия переходная эпоха, а для поколений – мучительная чреда тщетных ожиданий и надежд, а для отдельного человека – вечность…) вместилось многое.

Сажали в камеру белую мышь, фиксировали ее там на определенный отрезок времени, а через сутки восстанавливали в камере этот отрезок, умерщвляли ее, возвращались в свое время — а она жива-живехонька.

Он оглянулся на некий пройденный им длинный отрезок, на весь свой брак, и отрезок этот показался ему длинной, утомительной, пустынной дорогой, по которой тащится в пыли одинокий путник с тяжелой кладью.

Вполне резонно именно на этот отрезок дистанции сохранить запас сил, именно этот отрезок станет решающим.

Считая, что в большой

отрезок точка попадает с вероятностью один, получаем, что вероятность попадания точки в черный отрезок равна отношению длин черного и белого отрезков.

рис. 1.7).На рис. 1.8 приведены примеры иллюзий, возникающих при восприятии группы объектов.1. Иллюзия стрелок Мюллера-Лиера (слева – отрезок разделен на две равные части; справа – правая часть отрезка короче левой на 25 %).2. Иллюзия сходящихся и расходящихся линий (слева – горизонтальные части ломаных линий равны; в центре – в обеих трапециях длины верхних оснований равны; справа – нижний горизонтальный отрезок равен верхнему).3. Иллюзия разной кривизны: радиус кривизны всех дуг одинаков.4. Иллюзия изменения размера объекта: внутренние окружности в обоих случаях одинаковы.5. Иллюзия непараллельности параллельных линий: параллельные прямые, пересеченные короткими отрезками, кажутся непараллельными.6. Иллюзия волнистой линии.

отрезок — это… Что такое отрезок?

ОТРЕЗОК — ОТРЕЗОК, отрезка, муж. 1. Небольшой отрезанный кусок. Отрезки ткани. 2. чаще мн. Земельные участки, захваченные помещиками у крестьян после отмены крепостного права в 1861 г. (ист.). Существование отрезков являлось одним из источников… …   Толковый словарь Ушакова

отрезок — См. часть… Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. отрезок кусок, часть; сегмент, хорда, медиана, отрезочек, составная часть, этап Словарь русских синонимов …   Словарь синонимов

ОТРЕЗОК — (сегмент) в математике множество чисел или точек на прямой между двумя числами или точками a и b, включая сами точки a и b; обозначается ОТРЕПЬЕВ Григорий Богданович по утверждению правительства Бориса Годунова, беглый дьякон московского Чудова… …   Большой Энциклопедический словарь

ОТРЕЗОК — ОТРЕЗОК, зка, муж. 1. Небольшой отрезанный кусок чего н. 2. Часть чего н., измеряемого в пространстве или во времени. О. пути. О. прямой (в математике: часть прямой, лежащая между двумя её точками). О. времени (промежуток времени). Толковый… …   Толковый словарь Ожегова

отрезок — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN spline …   Справочник технического переводчика

ОТРЕЗОК — часть прямой, заключённая между двумя её точками и включающая обе эти точки …   Большая политехническая энциклопедия

Отрезок — Отрезком может называться одно из двух близких понятий в геометрии и математическом анализе. Отрезок  множество точек, к …   Википедия

отрезок — зка; м. 1. Часть чего л. измеряемого в пространстве или во времени. О. линии. О. времени. О. пути. О. прямой (часть прямой, лежащая между двумя её точками). 2. только мн.: отрезки, ов. Ист. = Отрезные земли. ◁ Отрезочек, чка; м. Разг. Уменьш. * * …   Энциклопедический словарь

отрезок — ▲ фрагмент ↑ линия отрезок кусок линии; часть последовательности между двумя точками, включая и эти точки; конечная последовательность; внутренняя часть плюс оконечности. на отрезке. тире (сине зеленый. юго восток. 10 22 штук). двоеточие (1:7).… …   Идеографический словарь русского языка

отрезок — tarpsnis statusas T sritis Kūno kultūra ir sportas apibrėžtis Periodas, nuotolio dalis, tarpas. atitikmenys: angl. period; phase vok. Abschnitt, m; Periode, f rus. отрезок; период …   Sporto terminų žodynas

Количество сегментов между точками

Наша цель в этом уроке — вывести формулу для количества сегментов между n точками. Чтобы вывести формулу, наша стратегия будет заключаться в том, чтобы увидеть, сколько сегментов можно сформировать с 2, 3, 4 или 5 точками

Затем мы попытаемся определить шаблон, который может помочь нам вывести формулу

Сколько сегментов может быть образоваться с 2 точками?

Это простой вопрос. Можем получить один сегмент

Сколько сегментов можно сформировать из 3 точек?

Я рекомендую не ставить 3 точки на одной линии.Будет легче отслеживать и считать сегменты

Отметьте точки на листе бумаги, как показано ниже:

По-прежнему легко видеть, что мы можем сделать 3 сегмента с 3 точками. Сколько сегментов можно образовать с 4 точками? Опять же, не ставьте точки на одной линии Осторожно: Обычно люди без труда показывают 4 сегмента синим цветом.Однако многие люди забывают два отрезка красного цвета

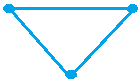Итак, можно нарисовать 6 отрезков с помощью 4 точек

Сколько сегментов можно сформировать из 5 точек?

Здесь все становится немного сложнее. Я покажу вам способ подсчета, чтобы вы не пропустили и не пропустили ни один сегмент

Имейте в виду, что то, как я расставляю точки, — это то, как я считаю, облегчит подсчет, особенно когда вы начинаете считать количество сегментов вы можете получить 5, 6 или 7 баллов

Во-первых, вы можете сделать эти 5 быстрых сегментов, которые показаны синим цветом. Затем из каждой вершины нарисуйте все возможные диагонали

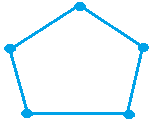. Я использую другой цвет и систему нумерации, чтобы вы могли четко видеть

. Вы можете получить еще два из вершины № 1, показанной красным, еще две из вершины № 2, показанной на зеленый, и еще 1 от вершины № 3 показано черным

Таким образом, можно нарисовать 10 сегментов с 5 точками

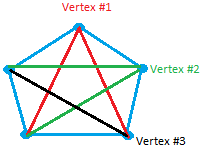Давайте систематизируем наши выводы.Таблица ниже покажет вам, что у нас есть на данный момент, и математические расчеты

2 балла	1 сегмент = 2 × 1 / 2
3 балла	3 сегмента = 3 × 2 / 2
4 балла	6 сегментов = 4 × 3 / 2
5 баллов	10 сегментов = 5 × 4 / 2
n баллов	п × (п -1) / 2 сегменты

Пояснения:

Знаменатель всегда равен 2, поэтому знаменателем в общей формуле будет 2.

В числителе два числа.Число в правой части умножения всегда на 1 меньше, чем слева

Вот почему, если число слева равно n, то справа будет n — 1

Что означает n? Посмотрите внимательно, и вы увидите, что он представляет собой количество точек

Теперь, когда у вас есть формула, вы даже можете рассчитать количество сегментов, которые вы можете получить с 25 баллами, если вам нравится

25 × 24 / 2

= 300 сегментов

Очень полезно получить формулу, чтобы получить количество сегментов с большим количеством точек, например 25

Если вы попытаетесь нарисовать рисунок выше, все станет очень беспорядочно

Новые уроки математики

Ваша электронная почта в безопасности.Мы будем использовать его только для информирования вас о новых уроках математики.

.

Постулат добавления сегмента

Постулат сложения сегментов утверждает следующее для трех коллинеарных точек.

Рассмотрим сегмент справа.

Если 3 точки A, B и C коллинеарны и B находится между A и C, то

AB + BC = AC

Использование постулата сложения сегментов для решения проблемы.

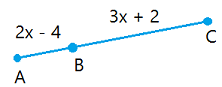
Предположим, AC = 48, найдите значение x.Затем найдите длину AB и длину BC.

AB + BC = AC

(2x — 4) + (3x + 2) = 48

2x + 3x — 4 + 2 = 48

5x — 4 + 2 = 48

Добавьте 4 к обеим сторонам уравнения.

5x — 4 + 4 + 2 = 48 + 4

5x + 2 = 52

Вычтем 2 с обеих сторон.

5x + 2-2 = 52-2

5x = 50

Разделим обе стороны на 5

5x / 5 = 50/5

x = 10

Теперь, когда у нас есть значение x, мы можем найти длину AB и длину BC.

AB = 2x — 4

AB = 2 × 10 — 4

AB = 20 — 4 = 16

Длина AB равна 16

BC = 3x + 2

BC = 3 × 10 + 2

BC = 30 + 2 = 32

Длина BC 32.

Постулат сложения сегментов и средняя точка

Предположим, что XA = 3x и AY = 4x — 6. Если A является средней точкой XY, какова длина XY?

3x 4x — 6
_________________________________
X A Y

Уловка в этой задаче состоит в том, чтобы увидеть, что если A — средняя точка, то XA = AY.

Поскольку XA = AY, 3x = 4x — 6

Вычтем 3x с обеих сторон.

3x — 3x = 4x — 3x — 6

0 = x — 6

Добавьте 6 к обеим сторонам уравнения.

0 + 6 = x — 6 + 6

6 = x

Для вычисления XA вы можете использовать 3x или 4x — 6

Используя 3x, мы получаем XA = AY = 3 × 6 = 16

Используя 4x — 6, получаем XA = AY = 3 × 6-6 = 18-6 = 12

XY = XA + AY = 16 + 16 = 32

Длина XY равна 32.

Новые уроки математики

Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.

.

Как разделить отрезок линии на несколько частей

2. Образование
3. Математика
4. Тригонометрия
5. Как разделить отрезок линии на несколько частей

Мэри Джейн Стерлинг

Если вы можете найти середину отрезка, вы можете разделить его на две равные части. Определение середины каждой из двух равных частей позволяет вам найти точки, необходимые для разделения всего сегмента на четыре равные части.Если найти середину каждого из этих сегментов, получится восемь равных частей и так далее.

Например, чтобы разделить сегмент с конечными точками (–15,10) и (9,2) на восемь равных частей, найдите различные средние точки следующим образом:

• Середина главного сегмента от (–15,10) до (9,2) — (–3,6).

• Средняя точка половины основного сегмента, от (–15,10) до (–3,6), равна (–9,8), а средняя точка другой половины основного сегмента, от (–3, 6) — (9,2), равно (3,4).

• Середины четырех определенных выше сегментов: (–12,9), (–6,7), (0,5) и (6,3).

На рисунке показаны координаты точек, которые делят этот отрезок прямой на восемь равных частей.

Использование метода средней точки — это нормально, если вы просто хотите разделить сегмент на четное количество равных сегментов. Но ваша работа не всегда бывает легкой. Например, вам может потребоваться разделить сегмент на три равные части, пять равных частей или какое-то другое нечетное количество равных частей.

Чтобы найти точку, которая не равноудалена от конечных точек сегмента, просто используйте эту формулу:

В этой формуле ( x ₁ , y ₁ ) — это конечная точка, с которой вы начинаете, ( x ₂ , y ₂ ) — другая конечная точка, и k — это дробная часть нужного сегмента.

Итак, чтобы найти координаты, разделяющие отрезок с конечными точками (–4,1) и (8,7) на три равные части, сначала найдите точку, которая составляет одну треть расстояния от (–4,1) до другую конечную точку, а затем найдите точку, которая составляет две трети расстояния от (–4,1) до другой конечной точки.Следующие шаги покажут вам, как это сделать.

Чтобы найти точку, которая составляет одну треть расстояния от (–4,1) до другой конечной точки, (8,7):

1. Заменить x ₁ на –4, x ₂ на 8, y ₁ на 1, y ₂ на 7 и k на 1/3.

2. Вычтите значения во внутренних круглых скобках.

3. Произведите умножение, а затем сложите результаты, чтобы получить координаты.

   = (- 4 + 4,1 + 2) = (0,3)

Чтобы найти точку, которая составляет две трети расстояния от (–4,1) до другой конечной точки, (8,7):

1. Заменить x ₁ на –4, x ₂ на 8, y ₁ на 1, y ₂ на 7 и k на 2/3.

2. Вычтите значения во внутренних круглых скобках.

3. Произведите умножение, а затем сложите результаты, чтобы получить координаты.

   = (- 4 + 8,1 + 4) = (4,5)

На следующем рисунке показан график этого линейного сегмента и точек, которые делят его на три равные части.

Об авторе книги

Мэри Джейн Стерлинг — автор книги Алгебра I для чайников и многих других книг Для чайников . Она преподавала математику в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет и любила работать с будущими руководителями бизнеса, физиотерапевтами, учителями и многими другими.

.Алгоритм

— (ACM) Как использовать дерево сегментов, чтобы подсчитать, сколько элементов в [a, b] меньше заданной константы?

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. Вакансии Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. Реклама Обратитесь к разработчикам и технологам со всего мира
6. О компании

Загрузка…

2. Авторизоваться Зарегистрироваться

.