Отрезок — что это такое

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Одним из понятий геометрии, с которым знакомятся еще в начальной школе, является отрезок. Уйма задач по математике и геометрии строится на понятиях отрезка и прямой.

Понимание, что такое отрезок, поможет решать всевозможные задачи и примеры на уроках математики как в школе, так и в высших учебных заведениях.

Отрезок — это геометрическая фигура

Согласно определению в словаре, отрезком называют часть прямой, ограниченную двумя точками, находящимися на ней. Именно по обозначениям этих точек и дается название отрезка.

На рисунке, изображенном ниже, показан отрезок AB. Точки A и B являются концами отрезка. Длиной отрезка называют расстояние между его концами.

В математике принято обозначать точки, и соответственно отрезки, большими буквами латинского алфавита. Если нужно нарисовать отрезок, чаще всего его изображают без прямой, а лишь от одного конца до другого.

Также можно сказать, что отрезок — это совокупность всех точек, которые лежат на одной прямой и находятся между двумя заданными точками, которые являются концами данного отрезка.

Если на отрезке между его концами отметить еще одну точку, она разделит данный отрезок на два. Длину отрезка АВ можно посчитать, просуммировав длины отрезков АС и СВ.

Разница между отрезком, лучом и прямой

Школьники иногда путают понятия прямой, луча и отрезка. И вправду, эти понятия очень схожи между собой, однако имеют принципиальное различие:

1. Прямой называется линия, которая не искривляется, а также не имеет начала и конца.
2. Луч — это часть прямой, ограниченная одной точкой. Он имеет начало и не имеет конца.
3. Отрезок ограничивается двумя точками. Он имеет и начало, и конец.

Точка, находящаяся на прямой, делит ее на два луча. Количество же отрезков на одной прямой может быть бесконечным.

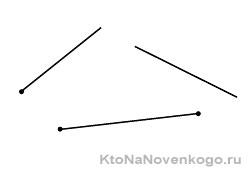
Чтобы различать эти фигуры на рисунке, в начале и конце рисуемой линии ставятся или не ставятся точки. Рисуя луч, точка ставится в одном конце, а изображая отрезок — в обоих концах. Прямая не имеет концов, поэтому точки в конце линии не ставятся.

Направленный отрезок — это вектор

Отрезки бывают двух видов:

1. Ненаправленные.
2. Направленные.

Для ненаправленных отрезков, АВ и ВА — одинаковые отрезки, так как направление не имеет значения.

Если же говорить о направленных отрезках, порядок перечисления его концов имеет решающее значение. В таком случае, АВ^➜ и ВА^➜ — разные отрезки, так как они противоположно направленные.

Направленные отрезки называются векторами. Векторы могут обозначаться как двумя заглавными буквами латинского алфавита со стрелочкой над ними, так и одной маленькой буквой со стрелочкой.

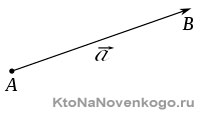
Модулем вектора называется длина направленного отрезка. Обозначается как АВ^➜. Модули векторов АВ^➜ и ВА^➜ равны.

Векторы часто рассматривают в системе координат. Модуль вектора равен квадратному корню суммы квадратов координат концов вектора.

Коллинеарными векторами называются те, что лежат на одной или на параллельных прямых.

Ломаная линия — это множество соединенных отрезков

Ломаная линия состоит из множества отрезков, которые называются ее звеньями. Эти отрезки соединены друг с другом своими концами и не расположены под углом 180°.

Вершинами ломаной являются следующие точки:

1. Точка, с которой началась ломаная.
2. Точка, которой ломаная закончилась.
3. Точки, в которых соединяются смежные звенья (отрезки ломаной).

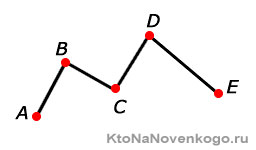
Число вершин ломаной всегда на один больше, чем количество ее звеньев. Обозначается ломаная перечислением всех ее вершин начиная с одного конца и заканчивая другим.

Например, ломаная ABCDEF состоит из отрезков AB, BC, CD, DE и EF и вершин A, B, C, D, E и F. Звенья AB и BC являются смежными, так как имеют общий конец — точку В. Длина ломаной вычисляется как сумма длин всех ее звеньев.

Любая замкнутая ломаная является геометрической фигурой — многоугольником.

Сумма углов многоугольника кратна 180° и вычисляется по следующей формуле 180*(n-2), где n — количество углов или отрезков, составляющих данную фигуру.

Отрезок времени

Интересно, что слово отрезок применимо не только к геометрическим понятиям, но и как временной термин.

Отрезком времени называют период между двумя событиями, датами. Он может измеряться как секундами или минутами, так и годами или даже десятилетиями.

Время в целом в таком случае определяется как временная прямая.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Использую для заработка

Рубрика: ЧАстые ВОпросы

Отрезок — Википедия

Материал из Википедии — свободной энциклопедии

Эта статья — о понятии в геометрии и математическом анализе. О насильно отрезанных от крестьянских наделов землях см. Отрезки (земля). Отрезок AB (выделен красным)

Отре́зком называются два близких понятия: в геометрии и математическом анализе.

Отрезок в геометрии

Отрезок прямой — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки A {\displaystyle \;A} и B {\displaystyle \;B} , обозначается символом A B {\displaystyle AB} . Расстояние между концами отрезка называют его

длиной и обозначают A B {\displaystyle AB} или | A B | {\displaystyle |AB|} .

Направленный отрезок

Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки A B {\displaystyle AB} и B A {\displaystyle BA} представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, направленные отрезки A B {\displaystyle AB} и B A {\displaystyle BA} не совпадают. Отдельного обозначения для направленных отрезков нет — то, что у отрезка важно его направление, обычно указывается особо.

Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.

Отрезок числовой прямой

Отрезок числовой (координатной) прямой (иначе числовой отрезок, сегмент) — множество вещественных чисел { x } {\displaystyle \{x\}} , удовлетворяющих неравенству a ≤ x ≤ b {\displaystyle a\leq x\leq b} , где заранее заданные вещественные числа a {\displaystyle a} и b {\displaystyle b} ( a < b ) {\displaystyle (a<b)} называются концами (граничными точками) отрезка. В противоположность им, остальные числа x {\displaystyle x} , удовлетворяющие неравенству a < x < b {\displaystyle a<x<b} , называются

внутренними точками отрезка^[1].

Отрезок обычно обозначается [ a , b ] {\displaystyle [a,b]} :

[ a , b ] = { x ∈ R ∣ a ≤ x ≤ b } {\displaystyle [a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}} .

Любой отрезок, по определению, заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.

Число b − a {\displaystyle b-a} называется длиной числового отрезка [ a , b ] {\displaystyle [a,b]} .

Стягивающаяся система сегментов

Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой { [ a , b ] | a , b ∈ R ∧ a < b } {\displaystyle \{[a,b]|a,b\in \mathbb {R} \land a<b\}} .

Система сегментов обозначается { [ a n , b n ] } n = 1 ∞ {\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} . Подразумевается, что каждому натуральному числу n {\displaystyle n} поставлен в соответствие отрезок [ a n , b n ] {\displaystyle [a_{n},b_{n}]} .

Система сегментов { [ a n , b n ] } n = 1 ∞ {\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} называется стягивающейся, если^[2]

• каждый следующий отрезок содержится в предыдущем;

  ∀ n ∈ N : [ a n + 1 , b n + 1 ] ⊆ [ a n , b n ] {\displaystyle \forall n\in \mathbb {N} \colon [a_{n+1},b_{n+1}]\subseteq [a_{n},b_{n}]}

• соответствующая последовательность длин отрезков бесконечно мала.

  lim n → ∞ ( b n − a n ) = 0 {\displaystyle \lim _{n\to \infty }(b_{n}-a_{n})=0}

У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.

∀ { [ a n , b n ] } n = 1 ∞   ∃ ! c ∈ R   ∀ n ∈ N : c ∈ [ a n , b n ] {\displaystyle \forall \{[a_{n},b_{n}]\}_{n=1}^{\infty }~\exists !c\in \mathbb {R} ~\forall n\in N\colon c\in [a_{n},b_{n}]}

Этот факт следует из свойств монотонной последовательности.

См. также

Примечания

Отрезок — Википедия. Что такое Отрезок

Эта статья — о понятии в геометрии и математическом анализе. О насильно отрезанных от крестьянских наделов землях см. Отрезки (земля). Отрезок AB (выделен красным)

Отре́зком называются два близких понятия: в геометрии и математическом анализе.

Отрезок в геометрии

Отрезок прямой — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки A {\displaystyle \;A} и B {\displaystyle \;B} , обозначается символом A B {\displaystyle AB} . Расстояние между концами отрезка называют его длиной и обозначают A B {\displaystyle AB} или | A B | {\displaystyle |AB|} .

Направленный отрезок

Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки A B {\displaystyle AB} и B A {\displaystyle BA} представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, направленные отрезки A B {\displaystyle AB} и B A {\displaystyle BA} не совпадают. Отдельного обозначения для направленных отрезков нет — то, что у отрезка важно его направление, обычно указывается особо.

Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.

Отрезок числовой прямой

Отрезок числовой (координатной) прямой (иначе числовой отрезок, сегмент) — множество вещественных чисел { x } {\displaystyle \{x\}} , удовлетворяющих неравенству a ≤ x ≤ b {\displaystyle a\leq x\leq b} , где заранее заданные вещественные числа a {\displaystyle a} и b {\displaystyle b} ( a < b ) {\displaystyle (a<b)} называются концами (граничными точками) отрезка. В противоположность им, остальные числа x {\displaystyle x} , удовлетворяющие неравенству a < x < b {\displaystyle a<x<b} , называются внутренними точками отрезка^[1].

Отрезок обычно обозначается [ a , b ] {\displaystyle [a,b]} :

[ a , b ] = { x ∈ R ∣ a ≤ x ≤ b } {\displaystyle [a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}} .

Любой отрезок, по определению, заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.

Число b − a {\displaystyle b-a} называется длиной числового отрезка [ a , b ] {\displaystyle [a,b]} .

Стягивающаяся система сегментов

Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой { [ a , b ] | a , b ∈ R ∧ a < b } {\displaystyle \{[a,b]|a,b\in \mathbb {R} \land a<b\}} .

Система сегментов обозначается { [ a n , b n ] } n = 1 ∞ {\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} . Подразумевается, что каждому натуральному числу n {\displaystyle n} поставлен в соответствие отрезок [ a n , b n ] {\displaystyle [a_{n},b_{n}]} .

Система сегментов { [ a n , b n ] } n = 1 ∞ {\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} называется стягивающейся, если^[2]

• каждый следующий отрезок содержится в предыдущем;

  ∀ n ∈ N : [ a n + 1 , b n + 1 ] ⊆ [ a n , b n ] {\displaystyle \forall n\in \mathbb {N} \colon [a_{n+1},b_{n+1}]\subseteq [a_{n},b_{n}]}

• соответствующая последовательность длин отрезков бесконечно мала.

  lim n → ∞ ( b n − a n ) = 0 {\displaystyle \lim _{n\to \infty }(b_{n}-a_{n})=0}

У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.

∀ { [ a n , b n ] } n = 1 ∞   ∃ ! c ∈ R   ∀ n ∈ N : c ∈ [ a n , b n ] {\displaystyle \forall \{[a_{n},b_{n}]\}_{n=1}^{\infty }~\exists !c\in \mathbb {R} ~\forall n\in N\colon c\in [a_{n},b_{n}]}

Этот факт следует из свойств монотонной последовательности.

См. также

Примечания

Что такое отрезок в математике? (тема математики, 5 класс)

Отрезок – это часть прямой. В математике тема отрезков имеет большое значение: из них составляют фигуры, с помощью отрезков чертятся рисунки к задачам и сравниваются числа. Поговорим о отрезках и способах их использования в математике 5 класса.

Определение

Отрезок – это часть прямой, ограниченный двумя точками. Это значит, что в отличие от прямой или луча, отрезок конечен и не имеет направления. Числовой отрезок на числовом луче или числовой прямой означает конкретное число. С помощью числовых отрезков можно выполнять сравнение чисел.

Рис. 1. Отрезок, прямая и луч.

Числовой луч обычно принимается для сравнения положительных чисел. Если среди ряда чисел, которые необходимо сравнить, есть отрицательные значения – правильнее будет воспользоваться числовой прямой.

Отрезок всегда имеет определенное значение. Прямую или луч нельзя определить конечным числом в метрах или сантиметрах, поэтому во всех современных подсчетах, как теоретических, так и практических, используются отрезки.

Задача на построение

Построим треугольник со сторонами 3, 5 и 4. Каждая из сторон это отрезок заданной величины. Это еще одно из свойств отрезков. По трем отрезкам заданной величины всегда можно построить треугольник.

Для начала проведем отрезок АВ=3. Можно выбрать и любую другую величину из заданных.

Конкретно в этой задаче такой подбор чисел выполнен для возможности дальнейшей проверки.

Примем точку А за центр окружности с радиусом 4 и проведем ее. Затем примем точку В за центр окружности с радиусом 5. В точке пересечения двух окружностей мы получим точку С – третью точку треугольника.

Треугольник со сторонами 3, 4 и 5 – это классический прямоугольный треугольник. Соответственно с катетами 3, 4 и гипотенузой 5. Эти пропорции были выведены еще в Древней Греции и сегодня очень часто применяются в простых задачах на решение прямоугольных треугольников.

Рис. 2. Построение треугольника.

Конкретно в нашем случае это означает, что получившийся треугольник должен быть прямоугольным по теореме, обратной теореме Пифагора.

Проверим:

$$5^2=3^2+4^2$$

$$25=9+16$$

25=25 – все верно, условие выполняется. И на рисунке визуально понятно, что треугольник построен правильно. В случае построения произвольного треугольника по трем заданным отрезкам, убедитесь заранее, что выполняются условия неравенства в треугольнике: сторона всегда меньше суммы двух других сторон.

Задача с числовым лучом

Необходимо сравнить пять чисел: ${5over6}; {7over15}; {18over4}; {25over7}$

Нанесем значения на числовой луч. Каждой дроби будет соответствовать свое значение.

$${5over6}$$ обозначим отрезком ОА. Он будет меньше единичного отрезка

$${7over15}$$ обозначим отрезком ОВ. Он так же меньше единичного отрезка

$${18over4}$$ обозначим отрезком ОС. Он будет больше значения 4, нанесенного на числовом луче.

$${25over7}$$ обозначим отрезком ОD, который будет расположен между 3 и 4.

Значит, вместо сравнения 4 дробей, нам необходимо сравнить только две: ${5over6}$ и ${7over15}$.

Разложим 6 и 15 на простые числа и найдем НОК.

$$6=2*3$$

$$15=5*3$$

$$НОК=2*3*5=30$$

$${5over6}={{5*5}over{6*5}}={25over30}$$

$${7over15}={{7*2}over{15*2}}={14over30}$$

$${25over30}>{14over30}$$

Значит:

${5over6}>{7over15}$ – теперь можно обозначить точное положение этих чисел. Сравнение выполнено, задача решена.

Рис. 3. Числовой луч.

Что мы узнали?

Мы разобрались, что такое отрезок в математике, выделили отличие от луча и прямой. Определили возможность применения его в геометрии для построения треугольников по значениям сторон и в математике для сравнения ряда дробей.

Предыдущая

МатематикаЧисловые и буквенные выражения – формулы (5 класс, математика)

Следующая

МатематикаВершина треугольника – определение

Отрезок — Википедия. Что такое Отрезок

Эта статья — о понятии в геометрии и математическом анализе. О насильно отрезанных от крестьянских наделов землях см. Отрезки (земля). Отрезок AB (выделен красным)

Отре́зком называются два близких понятия: в геометрии и математическом анализе.

Отрезок в геометрии

Отрезок прямой — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки A {\displaystyle \;A} и B {\displaystyle \;B} , обозначается символом A B {\displaystyle AB} . Расстояние между концами отрезка называют его длиной и обозначают A B {\displaystyle AB} или | A B | {\displaystyle |AB|} .

Направленный отрезок

Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки A B {\displaystyle AB} и B A {\displaystyle BA} представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, направленные отрезки A B {\displaystyle AB} и B A {\displaystyle BA} не совпадают. Отдельного обозначения для направленных отрезков нет — то, что у отрезка важно его направление, обычно указывается особо.

Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.

Отрезок числовой прямой

Отрезок числовой (координатной) прямой (иначе числовой отрезок, сегмент) — множество вещественных чисел { x } {\displaystyle \{x\}} , удовлетворяющих неравенству a ≤ x ≤ b {\displaystyle a\leq x\leq b} , где заранее заданные вещественные числа a {\displaystyle a} и b {\displaystyle b} ( a < b ) {\displaystyle (a<b)} называются

концами (граничными точками) отрезка. В противоположность им, остальные числа x {\displaystyle x} , удовлетворяющие неравенству a < x < b {\displaystyle a<x<b} , называются внутренними точками отрезка^[1].

Отрезок обычно обозначается [ a , b ] {\displaystyle [a,b]} :

[ a , b ] = { x ∈ R ∣ a ≤ x ≤ b } {\displaystyle [a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}} .

Любой отрезок, по определению, заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.

Число b − a {\displaystyle b-a} называется длиной числового отрезка [ a , b ] {\displaystyle [a,b]} .

Стягивающаяся система сегментов

Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой { [ a , b ] | a , b ∈ R ∧ a < b } {\displaystyle \{[a,b]|a,b\in \mathbb {R} \land a<b\}} .

Система сегментов обозначается { [ a n , b n ] } n = 1 ∞ {\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} . Подразумевается, что каждому натуральному числу n {\displaystyle n} поставлен в соответствие отрезок [ a n , b n ] {\displaystyle [a_{n},b_{n}]} .

Система сегментов { [ a n , b n ] } n = 1 ∞ {\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} называется стягивающейся, если^[2]

• каждый следующий отрезок содержится в предыдущем;

  ∀ n ∈ N : [ a n + 1 , b n + 1 ] ⊆ [ a n , b n ] {\displaystyle \forall n\in \mathbb {N} \colon [a_{n+1},b_{n+1}]\subseteq [a_{n},b_{n}]}

• соответствующая последовательность длин отрезков бесконечно мала.

  lim n → ∞ ( b n − a n ) = 0 {\displaystyle \lim _{n\to \infty }(b_{n}-a_{n})=0}

У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.

∀ { [ a n , b n ] } n = 1 ∞   ∃ ! c ∈ R   ∀ n ∈ N : c ∈ [ a n , b n ] {\displaystyle \forall \{[a_{n},b_{n}]\}_{n=1}^{\infty }~\exists !c\in \mathbb {R} ~\forall n\in N\colon c\in [a_{n},b_{n}]}

Этот факт следует из свойств монотонной последовательности.

См. также

Примечания

определение сегмента по The Free Dictionary

Форма хребта представляла собой сегмент круга, с более высокими точками в глубь материка на запад. (18) Этот и следующий фрагмент предназначены для совместного чтения. Эти буквы, обозначенные этими буквами, представляют собой сходство с вершинами трех Анд. ; от одного пламени; башня на другом; на третьем кукарекает петух; в то время как над всем изгибался сегмент разделенного зодиака, все знаки отмечены своей обычной каббалистикой, а замковое солнце входит в точку равноденствия в Весах.Даже если бы я смог оторвать прутья, это не помогло бы мне, так как отверстие образовывало сегмент круга, длина хорды которого составляла всего несколько дюймов. Если вы возьмете свою Encyclopaedia Britannica, Volume III, AUS to BIS, вы обнаружите, что пчелы — это « большое и естественное семейство зоологического отряда перепончатокрылых, характеризующееся перистой формой многих волосков, большим размером базального сегмента стопы … Круг из нескольких Было нарисовано сто футов в окружности, и каждый из отряда взял себе долю.Ричард появился в воздухе, описывая отрезок круга, радиусом которого были поводья, и приземлился на расстоянии примерно пятнадцати футов в тот сугроб, которого боялись лошади, правым концом вверх. посреди этой торжественной тишины минуты улетали прочь, и пока они мчались, полная луна все глубже и глубже уходила в тень земли, а чернильный сегмент ее круга с ужасающей величественностью скользил по лунным кратерам. Это вулкан. конус выступил из глубокого моря, с проломленным сегментом стены кратера.Это немного пойманный звездной пылью, сегмент радуги, который я схватил. Итак, должник был совсем другим человеком, чем доктор, но он уже начал путешествовать по своей противоположной части круга к В переднем фронтоне, под нависающим бровом второго этажа, рядом с улицей, была дверь магазина, разделенная посередине горизонтально, с окном в верхней части, что часто можно увидеть на жилища несколько древнего возраста. .

определение сегмента (математика) и синонимов сегмента (математика) (английский)

сегмент (математика): определение сегмента (математика) и синонимы сегмента (математика) (английский)

арабский болгарский китайский язык хорватский Чешский Датский нидерландский язык английский эстонский Финский французский язык Немецкий Греческий иврит хинди венгерский язык исландский индонезийский Итальянский японский язык корейский язык Латышский Литовский Малагасийский Норвежский Персидский Польский португальский румынский русский сербский словацкий словенский испанский Шведский Тайский турецкий вьетнамский

арабский болгарский китайский язык хорватский Чешский Датский нидерландский язык английский эстонский Финский французский язык Немецкий Греческий иврит хинди венгерский язык исландский индонезийский Итальянский японский язык корейский язык Латышский Литовский Малагасийский Норвежский Персидский Польский португальский румынский русский сербский словацкий словенский испанский Шведский Тайский турецкий вьетнамский

содержание сенсагента

• определения
• синонимы
• антонимы
• энциклопедия

Решение для веб-мастеров

Александрия

Всплывающее окно с информацией (полное содержание Sensagent), вызываемое двойным щелчком по любому слову на вашей веб-странице.Предоставьте контекстные объяснения и перевод с вашего сайта !

Попробуйте здесь или получите код

SensagentBox

С помощью SensagentBox посетители вашего сайта могут получить доступ к надежной информации на более чем 5 миллионах страниц, предоставленных Sensagent.com. Выберите дизайн, который подходит вашему сайту.

Бизнес-решение

Улучшите содержание своего сайта

Добавьте новый контент на свой сайт из Sensagent by XML.

Сканирует продукты или добавляет

Получите доступ к XML для поиска лучших продуктов.

Индексирование изображений и определение метаданных

Получите доступ к XML, чтобы исправить значение ваших метаданных.

Напишите нам, чтобы описать вашу идею.

Lettris

Lettris — любопытная игра-клон-тетрис, в которой все кубики имеют одинаковую квадратную форму, но разное содержание. На каждом квадрате есть буква. Чтобы квадраты исчезли и сэкономили место для других квадратов, вам нужно собрать английские слова (left, right, up, down) из падающих квадратов.

болт

Boggle дает вам 3 минуты, чтобы найти как можно больше слов (3 буквы и более) в сетке из 16 букв. Вы также можете попробовать сетку из 16 букв. Буквы должны располагаться рядом, и более длинные слова оцениваются лучше. Посмотрите, сможете ли вы попасть в Зал славы сетки!

Английский словарь
Основные ссылки

WordNet предоставляет большинство определений на английском языке.
Английский тезаурус в основном получен из The Integral Dictionary (TID).
English Encyclopedia лицензирована Википедией (GNU).

Перевод

Измените целевой язык, чтобы найти перевод.
Советы: просмотрите семантические поля (см. От идей к словам) на двух языках, чтобы узнать больше.

2910 онлайн посетителей

вычислено за 0,032 с

.

определение сегмента_ (математика) и синонимов сегмента_ (математика) (английский)

сегмент_ (математика): определение сегмента_ (математика) и синонимы сегмента_ (математика) (английский)

арабский болгарский китайский язык хорватский Чешский Датский нидерландский язык английский эстонский Финский французский язык Немецкий Греческий иврит хинди венгерский язык исландский индонезийский Итальянский японский язык корейский язык Латышский Литовский Малагасийский Норвежский Персидский Польский португальский румынский русский сербский словацкий словенский испанский Шведский Тайский турецкий вьетнамский

арабский болгарский китайский язык хорватский Чешский Датский нидерландский язык английский эстонский Финский французский язык Немецкий Греческий иврит хинди венгерский язык исландский индонезийский Итальянский японский язык корейский язык Латышский Литовский Малагасийский Норвежский Персидский Польский португальский румынский русский сербский словацкий словенский испанский Шведский Тайский турецкий вьетнамский

содержание сенсагента

• определения
• синонимы
• антонимы
• энциклопедия

Решение для веб-мастеров

Александрия

Всплывающее окно с информацией (полное содержание Sensagent), вызываемое двойным щелчком по любому слову на вашей веб-странице.Предоставьте контекстные объяснения и перевод с вашего сайта !

Попробуйте здесь или получите код

SensagentBox

С помощью SensagentBox посетители вашего сайта могут получить доступ к надежной информации на более чем 5 миллионах страниц, предоставленных Sensagent.com. Выберите дизайн, который подходит вашему сайту.

Бизнес-решение

Улучшите содержание своего сайта

Добавьте новый контент на свой сайт из Sensagent by XML.

Сканирует продукты или добавляет

Получите доступ к XML для поиска лучших продуктов.

Индексирование изображений и определение метаданных

Получите доступ к XML, чтобы исправить значение ваших метаданных.

Напишите нам, чтобы описать вашу идею.

Lettris

Lettris — любопытная игра-клон-тетрис, в которой все кубики имеют одинаковую квадратную форму, но разное содержание. На каждом квадрате есть буква. Чтобы квадраты исчезли и сэкономили место для других квадратов, вам нужно собрать английские слова (left, right, up, down) из падающих квадратов.

болт

Boggle дает вам 3 минуты, чтобы найти как можно больше слов (3 буквы и более) в сетке из 16 букв. Вы также можете попробовать сетку из 16 букв. Буквы должны располагаться рядом, и более длинные слова оцениваются лучше. Посмотрите, сможете ли вы попасть в Зал славы сетки!

Английский словарь
Основные ссылки

WordNet предоставляет большинство определений на английском языке.
Английский тезаурус в основном получен из The Integral Dictionary (TID).
English Encyclopedia лицензирована Википедией (GNU).

Перевод

Измените целевой язык, чтобы найти перевод.
Советы: просмотрите семантические поля (см. От идей к словам) на двух языках, чтобы узнать больше.

2910 онлайн посетителей

вычислено за 0,032 с

.Сеть

— Определение сетевых единиц: фрагмент, сегмент, пакет, кадр, дейтаграмма

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. Вакансии Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. Реклама Обратитесь к разработчикам и технологам со всего мира
6. О компании

Загрузка…

.