Квадратичная функция одной переменной — Википедия

Материал из Википедии — свободной энциклопедии

График функции f(x)=x2−x−2{\displaystyle f(x)=x^{2}-x-2} Эта статья — о числовой функции одной переменной. О функции второй степени с несколькими переменными см. Квадратичная форма; о геометрическом месте точек см. Парабола.

Квадратичная функция — целая рациональная функция второй степени вида f(x)=ax2+bx+c{\displaystyle f(x)=ax^{2}+bx+c}, где a≠0{\displaystyle a\neq 0} и a,b,c∈R{\displaystyle a,b,c\in \mathbb {R} }. Уравнение квадратичной функции содержит квадратный трёхчлен. Графиком квадратичной функции является парабола. Многие свойства графика квадратичной функции так или иначе связаны с вершиной параболы, которая во многом определяет положение и внешний вид графика.

Многие свойства квадратичной функции f(x)=ax2+bx+c{\displaystyle f(x)=ax^{2}+bx+c} зависят от значения коэффициента a{\displaystyle a}. В следующей таблице приводится обзор основных свойств квадратичной функции^[1]. Их доказательство рассматривается в статье в соответствующих разделах.

Свойство	a>0{\displaystyle a>0}	a<0{\displaystyle a<0}
Область определения функции	D(f)=R{\displaystyle D(f)=\mathbb {R} }
Множество значений функции	E(f)=[−b2−4ac4a;+∞){\displaystyle E(f)=\left[-{\frac {b^{2}-4ac}{4a}};+\infty \right)}	E(f)=(−∞;−b2−4ac4a]{\displaystyle E(f)=\left(-\infty ;-{\frac {b^{2}-4ac}{4a}}\right]}
Чётность функции	Чётная функция при b=0{\displaystyle b=0}; ни чётная, ни нечётная при b≠0{\displaystyle b\neq 0}
Периодичность функции	Непериодическая функция
Непрерывность функции	Всюду непрерывная функция, точек разрыва нет
Нули функции	x1,2=−b±D2a{\displaystyle x_{1,2}={\frac {-b\pm {\sqrt {D}}}{2a}}}, если D=b2−4ac≥0{\displaystyle D=b^{2}-4ac\geq 0} нет действительных нулей, если D=b2−4ac<0{\displaystyle D=b^{2}-4ac<0}
Предел функции при x→±∞{\displaystyle x\to \pm \infty }	f(x)→+∞{\displaystyle f(x)\to +\infty } при x→±∞{\displaystyle x\to \pm \infty }	f(x)→−∞{\displaystyle f(x)\to -\infty } при x→±∞{\displaystyle x\to \pm \infty }
Дифференцируемость функции	Всюду многократно дифференцируема: f′(x)=2ax+b,f″(x)=2a,f‴(x)=0{\displaystyle f'(x)=2ax+b,f»(x)=2a,f»'(x)=0}
Точки экстремума (абсолютный экстремум)	xmin=−b2a{\displaystyle x_{min}={\frac {-b}{2a}}} (минимум)	xmax=−b2a{\displaystyle x_{max}={\frac {-b}{2a}}} (максимум)
Интервалы строгой монотонности	убывает на (−∞;b2a]{\displaystyle \left(-\infty ;{\frac {b}{2a}}\right]} возрастает на [−b2a;+∞){\displaystyle \left[-{\frac {b}{2a}};+\infty \right)}	возрастает на (−∞;b2a]{\displaystyle \left(-\infty ;{\frac {b}{2a}}\right]} убывает на [−b2a;+∞){\displaystyle \left[-{\frac {b}{2a}};+\infty \right)}
Выпуклость функции	Всюду выпуклая вниз функция	Всюду выпуклая вверх функция
Точки перегиба	Точки перегиба отсутствуют
Ограниченность функции	Ограничена снизу	Ограничена сверху
Наибольшее значение функции	Отсутствует (неограничена сверху)	ymax=−b2−4ac4a{\displaystyle y_{max}=-{\frac {b^{2}-4ac}{4a}}}
Наименьшее значение функции	ymin=−b2−4ac4a{\displaystyle y_{min}=-{\frac {b^{2}-4ac}{4a}}}	Отсутствует (неограничена снизу)
Положительные значения функции	(−∞;x1)∪(x2;+∞){\displaystyle (-\infty ;x_{1})\cup (x_{2};+\infty )}	(x1;x2){\displaystyle (x_{1};x_{2})}
Отрицательные значения функции	(x1;x2){\displaystyle (x_{1};x_{2})}	(−∞;x1)∪(x2;+∞){\displaystyle (-\infty ;x_{1})\cup (x_{2};+\infty )}

Влияние коэффициентов на трансформацию графика[править | править код]

Стандартная запись уравнения квадратичной функции[править | править код]

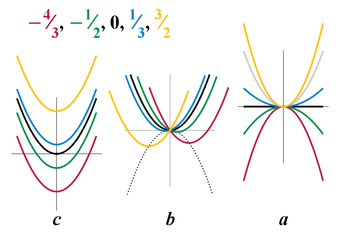Влияние коэффициентов a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c} на параболу

Действительные числа a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c} в общей записи квадратичной функции называются её коэффициентами. При этом коэффициент a{\displaystyle a} принято называть старшим, а коэффициент c{\displaystyle c} — свободным. Изменение каждого из коэффициентов приводит к определённым трансформациям параболы.

По значению коэффициента a{\displaystyle a} можно судить о том, в какую сторону направлены её ветви (вверх или вниз) и оценить степень её растяжения или сжатия относительно оси ординат:

• Если a>0{\displaystyle a>0}, то ветви параболы направлены вверх, то есть её вершина расположена снизу.
• Если a<0{\displaystyle a<0}, то ветви параболы направлены вниз, то есть её вершина расположена сверху.
• Если |a|<1{\displaystyle |a|<1}, то парабола сжата по оси ординат, то есть кажется более широкой и плоской.
• Если |a|>1{\displaystyle |a|>1}, то парабола растянута по оси ординат, то есть кажется более узкой и крутой.

Влияние значения коэффициента a{\displaystyle a} наиболее просто позволяет проиллюстрировать квадратичная функция вида f(x)=ax2{\displaystyle f(x)=ax^{2}}, то есть в случае b=0{\displaystyle b=0} и c=0{\displaystyle c=0}. В случае a=0{\displaystyle a=0} квадратичная функция превращается в линейную.

Изменение коэффициента b{\displaystyle b} повлечёт за собой сдвиг параболы как относительно оси абсцисс, так и относительно оси ординат. При увеличении значения b{\displaystyle b} на 1 произойдёт сдвиг параболы на 1/2a{\displaystyle 1/2a} влево и одновременно на (2b+1)/4a{\displaystyle (2b+1)/4a} вниз. При уменьшении b{\displaystyle b} на 1 произойдёт сдвиг параболы на 1/2a{\displaystyle 1/2a} вправо и одновременно на (2b−1)/4a{\displaystyle (2b-1)/4a} вверх. Такие трансформации объясняются тем, что коэффициент b{\displaystyle b} характеризует угловой коэффициент касательной к параболе в точке пересечения с осью ординат (то есть при x=0{\displaystyle x=0}).

Коэффициент c{\displaystyle c} характеризует параллельный перенос параболы относительно оси ординат (то есть вверх или вниз). При увеличении значения этого коэффициента на 1, парабола переместится на 1 вверх. Соответственно, если уменьшить коэффициент c{\displaystyle c} на 1, то и парабола сместится на 1 вниз. Так как коэффициент b{\displaystyle b} также влияет на положение вершины параболы, то по одному лишь значению коэффициента c{\displaystyle c} нельзя судить о том, расположена ли вершина выше оси абсцисс или ниже неё.

Запись квадратичной функции через координаты вершины параболы[править | править код]

Любая квадратичная функция f(x)=ax2+bx+c{\displaystyle f(x)=ax^{2}+bx+c} может быть получена с помощью растяжения/сжатия и параллельного переноса простейшей квадратичной функции f(x)=x2{\displaystyle f(x)=x^{2}}. Так, график функции вида f(x)=a(x−x0)2+y0{\displaystyle f(x)=a(x-x_{0})^{2}+y_{0}} получается путём сжатия (при a<0{\displaystyle a<0}) или растяжения (при a>0{\displaystyle a>0}) графика функции f(x)=x2{\displaystyle f(x)=x^{2}} в a{\displaystyle a} раз с последующем его параллельным переносом на x0{\displaystyle x_{0}} единиц вправо и y0{\displaystyle y_{0}} единиц вверх (если эти значения являются отрицательными числами тогда, соответственно, влево и вниз). Очевидно, что при проделанной трансформации вершина параболы функции f(x)=x2{\displaystyle f(x)=x^{2}} переместится из точки (0;0){\displaystyle (0;0)} в точку (x0;y0){\displaystyle (x_{0};y_{0})}. Этот факт даёт ещё один способ вычисления координат вершины параболы произвольной квадратичной функции путём приведения её уравнения к виду f(x)=a(x−x0)2+y0{\displaystyle f(x)=a(x-x_{0})^{2}+y_{0}}, позволяющему сразу увидеть координаты вершины параболы — (x0;y0){\displaystyle (x_{0};y_{0})}.

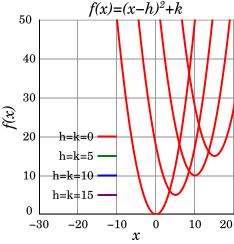Влияние коэффициентов в записи вида f(x)=a(x−x0)2+y0{\displaystyle f(x)=a(x-x_{0})^{2}+y_{0}} на параболу

Преобразовать произвольную квадратичную функцию вида f(x)=ax2+bx+c{\displaystyle f(x)=ax^{2}+bx+c} к форме f(x)=a(x−x0)2+y0{\displaystyle f(x)=a(x-x_{0})^{2}+y_{0}} позволяет метод выделения полного квадрата, использующий формулы сокращённого умножения биномов:

f(x)=ax2+bx+c{\displaystyle f(x)=ax^{2}+bx+c}

=a⋅(x2+ba⋅x)+c{\displaystyle =a\cdot \left(x^{2}+{\frac {b}{a}}\cdot x\right)+c}

=a⋅(x2+ba⋅x+b24a2−b24a2)+c{\displaystyle =a\cdot \left(x^{2}+{\frac {b}{a}}\cdot x+{\frac {b^{2}}{4a^{2}}}-{\frac {b^{2}}{4a^{2}}}\right)+c}

=a⋅(x2+2⋅x⋅b2a+b24a2)−b24a+c{\displaystyle =a\cdot \left(x^{2}+2\cdot x\cdot {\frac {b}{2a}}+{\frac {b^{2}}{4a^{2}}}\right)-{\frac {b^{2}}{4a}}+c}

=a⋅(x+b2a)2+−b24a+4ac4a{\displaystyle =a\cdot \left(x+{\frac {b}{2a}}\right)^{2}+{\frac {-b^{2}}{4a}}+{\frac {4ac}{4a}}}

=a⋅(x−−b2a)2+−b2+4ac4a{\displaystyle =a\cdot \left(x-{\frac {-b}{2a}}\right)^{2}+{\frac {-b^{2}+4ac}{4a}}}

=a⋅(x−x0)2+y0{\displaystyle =a\cdot \left(x-x_{0}\right)^{2}+y_{0}}, где x0=−b2a{\displaystyle x_{0}={\frac {-b}{2a}}} и y0=−b2+4ac4a{\displaystyle y_{0}={\frac {-b^{2}+4ac}{4a}}}

Сравнивая значения для x0{\displaystyle x_{0}} и y0{\displaystyle y_{0}}, вычисленные дифференциальным методом (см. соответствующий раздел статьи), можно также убедиться, что они являются координатами вершины параболы. В конкретных случаях вовсе не требуется запоминать приведённые громоздкие формулы, удобней всякий раз выполнять преобразования многочлена к желаему виду непосредственно. На конкретном примере этот метод выглядит так:

f(x)=2×2+8x+5=2⋅(x2+4⋅x)+5{\displaystyle f(x)=2x^{2}+8x+5=2\cdot \left(x^{2}+4\cdot x\right)+5}

=2⋅(x2+4⋅x+4−4)+5{\displaystyle =2\cdot \left(x^{2}+4\cdot x+4-4\right)+5}

=2⋅((x+2)2−4)+5{\displaystyle =2\cdot \left(\left(x+2\right)^{2}-4\right)+5}

=2⋅(x+2)2−8+5{\displaystyle =2\cdot \left(x+2\right)^{2}-8+5}

=2⋅(x+2)2−3⇒S(−2;−3){\displaystyle =2\cdot \left(x+2\right)^{2}-3\Rightarrow S(-2;-3)}

Недостатком данного метода является его громоздкость, особенно в случае, когда в результате вынесения за скобки приходится работать с дробями. Также он требует определённого навыка в обращении с формулами сокращённого умножения.

Однако, рассмотренное выше доказательство в общем виде приводит к более простому способу вычисления координат вершины параболы с помощью формул x0=−b2a{\displaystyle x_{0}={\frac {-b}{2a}}} и y0=f(x0){\displaystyle y_{0}=f(x_{0})}. Например, для той же функции f(x)=2×2+8x+5{\displaystyle f(x)=2x^{2}+8x+5} имеем:

x0=−b2a=−82⋅2=−2{\displaystyle x_{0}={\frac {-b}{2a}}={\frac {-8}{2\cdot 2}}=-2}

y0=f(−2)=2⋅(−2)2+8⋅(−2)+5=−3⇒S(−2;−3){\displaystyle y_{0}=f(-2)=2\cdot (-2)^{2}+8\cdot (-2)+5=-3\Rightarrow S(-2;-3)}.

Таким образом, f(x)=2×2+8x+5=2⋅(x+2)2−3{\displaystyle f(x)=2x^{2}+8x+5=2\cdot \left(x+2\right)^{2}-3}

ru.wikipedia.org

Парабола — Википедия

Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

Изображение конического сечения, являющегося параболой Построение параболы как конического сечения Конические сечения

Точка параболы, ближайшая к её директрисе, называется вершиной этой параболы. Вершина является серединой перпендикуляра, опущенного из фокуса на директрису.

Каноническое уравнение параболы в прямоугольной системе координат:

y2=2px,p>0{\displaystyle \textstyle y^{2}=2px,p>0} (или x2=2py{\displaystyle \textstyle x^{2}=2py}, если поменять местами оси).

Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы^[1]. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии p2{\displaystyle {\frac {p}{2}}} от обоих.

Парабола, заданная квадратичной функцией[править | править код]

Квадратичная функция y=ax2+bx+c{\displaystyle y=ax^{2}+bx+c} при a≠0{\displaystyle a\neq 0} также является уравнением параболы и графически изображается той же параболой, что и y=ax2,{\displaystyle y=ax^{2},} но в отличие от последней имеет вершину не в начале координат, а в некоторой точке A, координаты которой вычисляются по формулам:

xA=−b2a,yA=−D4a,{\displaystyle x_{\textrm {A}}=-{\frac {b}{2a}},\;y_{\textrm {A}}=-{\frac {D}{4a}},} где D=b2−4ac{\displaystyle D=b^{2}-4ac} — дискриминант квадратного трёхчлена.

Ось симметрии параболы, заданной квадратичной функцией, проходит через вершину параллельно оси ординат. При a > 0 (a < 0) фокус лежит на этой оси над (под) вершиной на расстоянии 1/4a, а директриса — под (над) вершиной на таком же расстоянии и параллельна оси абсцисс. Уравнение y=ax2+bx+c{\displaystyle y=ax^{2}+bx+c} может быть представлено в виде y=a(x−xA)2+yA,{\displaystyle y=a(x-x_{\textrm {A}})^{2}+y_{\textrm {A}},} а в случае переноса начала координат в точку A уравнение параболы превращается в каноническое. Таким образом, для каждой квадратичной функции можно найти систему координат такую, что в этой системе уравнение соответствующей параболы представляется каноническим. При этом p=1|2a|.{\displaystyle p={\frac {1}{|2a|}}.}

Общее уравнение параболы[править | править код]

В общем случае парабола не обязана иметь ось симметрии, параллельную одной из координатных осей. Однако, как и любое другое коническое сечение, парабола является кривой второго порядка и, следовательно, её уравнение на плоскости в декартовой системе координат может быть записано в виде квадратного многочлена:

Ax2+Bxy+Cy2+Dx+Ey+F=0.{\displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0.}

Если кривая второго порядка, заданная в таком виде, является параболой, то составленный из коэффициентов при старших членах дискриминант B2−4AC{\displaystyle B^{2}-4AC} равен нулю.

Уравнение в полярной системе[править | править код]

Парабола в полярной системе координат (ρ,ϑ){\displaystyle (\rho ,\vartheta )} с центром в фокусе и нулевым направлением вдоль оси параболы (от фокуса к вершине) может быть представлена уравнением

ρ(1+cos⁡ϑ)=p,{\displaystyle \rho (1+\cos \vartheta )=p,}

где p — фокальный параметр (расстояние от фокуса до директрисы или удвоенное расстояние от фокуса до вершины)

Расчёт коэффициентов квадратичной функции[править | править код]

Если для уравнения параболы с осью, параллельной оси ординат, y=ax2+bx+c{\displaystyle y=ax^{2}+bx+c} известны координаты трёх различных точек параболы (x1;y1),(x2;y2),(x3;y3),{\displaystyle (x_{1};y_{1}),\;(x_{2};y_{2}),\;(x_{3};y_{3}),} то его коэффициенты могут быть найдены так:

a=y3−x3(y2−y1)+x2y1−x1y2x2−x1x3(x3−x1−x2)+x1x2,  b=y2−y1x2−x1−a(x1+x2),  c=x2y1−x1y2x2−x1+ax1x2.{\displaystyle a={\frac {y_{3}-{\tfrac {x_{3}(y_{2}-y_{1})+x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}}{x_{3}(x_{3}-x_{1}-x_{2})+x_{1}x_{2}}},\ \ b={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}-a(x_{1}+x_{2}),\ \ c={\frac {x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}+ax_{1}x_{2}.}

Если же заданы вершина (x0;y0){\displaystyle (x_{0};y_{0})} и старший коэффициент a{\displaystyle a}, то остальные коэффициенты и корни вычисляются по формулам:

b=−2ax0{\displaystyle b=-2ax_{0}}

c=ax02+y0{\displaystyle c=ax_{0}^{2}+y_{0}}

x1=x0+−y0a{\displaystyle x_{1}=x_{0}+{\sqrt {-{\frac {y_{0}}{a}}}}}

x2=x0−−y0a{\displaystyle x_{2}=x_{0}-{\sqrt {-{\frac {y_{0}}{a}}}}}

Отражательное свойство параболы (оптика) 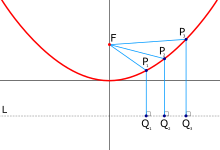Расстояние от P_n до фокуса F такое же, как и от P_n до Q_n (на директрисе L) 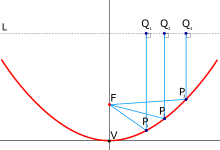Длина линий FP_nQ_n одинакова. Можно сказать, что, в отличие от эллипса, второй фокус у параболы — в бесконечности (см. также Шары Данделена)

• Парабола — кривая второго порядка.
• Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.
• Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.
• Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
• Отрезок, соединяющий середину произвольной хорды параболы и точку пересечения касательных к ней в концах этой хорды, перпендикулярен директрисе, а его середина лежит на параболе.
• Парабола является антиподерой прямой.
• Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
• Траектория фокуса параболы, катящейся по прямой, есть Цепная линия
  [2].

Парабола есть Синусоидальная спираль при n=−12{\displaystyle \textstyle n=-{\frac {1}{2}}};

Параболический компас Леонардо да Винчи

Траектории некоторых космических тел (комет, астероидов и других), проходящих вблизи звезды или другого массивного объекта (звезды или планеты) на достаточно большой скорости, имеют форму параболы (или гиперболы). Эти тела, вследствие своей большой скорости, не захватываются гравитационным полем звезды и продолжают свободный полёт. Это явление используется для гравитационных манёвров космических кораблей (в частности, аппаратов Вояджер).

Для создания невесомости в земных условиях проводятся полёты самолётов по параболической траектории, так называемой параболе Кеплера.

При отсутствии сопротивления воздуха траектория полёта тела в приближении однородного гравитационного поля представляет собой параболу.

Также параболические зеркала используются в любительских переносных телескопах систем Кассергена, Шмидта — Кассергена, Ньютона, а в фокусе параболы устанавливают вспомогательные зеркала, подающие изображение на окуляр.

При вращении сосуда с жидкостью вокруг вертикальной оси поверхность жидкости в сосуде и вертикальная плоскость пересекаются по параболе.

Свойство параболы фокусировать пучок лучей, параллельных оси параболы, используется в конструкциях прожекторов, фонарей, фар, а также телескопов-рефлекторов (оптических, инфракрасных, радио- …), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанций и в других областях.

Форма параболы иногда используется в архитектуре для строительства крыш и куполов.

1. ↑ Александров П.С. Парабола // Курс аналитической геометрии и линейной алгебры. — М.: Наука, 1979. — С. 69—72. — 512 с.
2. ↑ Савелов А. А. Плоские кривые. Систематика, свойства, применения (Справочное руководство)/ Под ред. А. П. Нордена. М.: Физматлит, 1960. С. 250.

ru.wikipedia.org

График квадратичной функции | Формулы с примерами

Графики квадратичной функции 9 класс

Правило
Любую квадратичную функцию можно представить в виде , где

Примеры, свойства, правила

Правила
1)  y = 2x² — 4x + 3.

   I способ

— выделение полного квадрата:

y = 2x² — 4x + 3 = 2(x² — 2x) + 3 =

= 2(x² — 2 • x • 1 + 1²) — 2 • 1² + 3 = 2(x — 1)² + 1;

   II способ — по формулам:

x₀ =    -4   2 • 2 = 1,    y₀ = y(1) = 2 • 1² — 4 • 1 + 3 = 1, значит y = 2(x — 1)² + 1.

2)  y = 2 — 3x² + x = 2 — 3(x² — 13x) =

= 2 — 3(x² — 2 • 16 • x + (16)² + 3 • (16)²) = -3 (x — 16)² + 2 1 12.

График квадратичной функции, рисунок

Правило
График функции — y = a(x — x₀)² + y₀ — парабола, которую можно получить из параболы y = ax² с помощью двух параллельных переносов (сдвигов:

1)  вдоль оси OX на X₀

вправо, если x₀ > 0,
или на |x₀| влево, если x₀

2)  вдоль оси OY на y₀ вверх, если y₀ > 0,
или на |y₀| вниз, если y₀

Порядок выполнения сдвигов — любой.

Правило
Вершина параболы y = a(x — x₀)² + y₀— точка O₁(x₀,y₀).

Ось симметрии — прямая x = x₀.

Область значений — интервал [y₀, +?), если a > 0, или (-?, y₀], если a

Пример 1
1)  y = 2x² — 4x + 3 y = 2(x -1)² + 1

Пример 2
2)  y = 1 — 12x² — 2x y = -(x + 2)² + 3

Формулы по алфавиту:

© 2020 Все права защищены
При использовании материалов данного сайта обязательно указывать ссылку на источник

formula-xyz.ru