определение, неравенства и их системы
Статья раскрывает тему неравенств, разбираются определения систем и их решения. Будут рассмотрены часто встречающиеся примеры решения систем уравнений в школе на алгебре.
Определение системы неравенств
Системы неравенств определяют по определениям систем уравнений, значит, что особое внимание уделяется записям и смыслу самого уравнения.
Определение 1Системой неравенств называют запись уравнений, объединенных фигурной скобкой с множеством решений одновременно для всех неравенств, входящих в систему.
Ниже приведены примеры неравенств. Даны два неравенства 2·x−3>0 и 5−x≥4·x−11. Необходимо записать одно уравнение под другим, после чего объединим при помощи фигурной скобки:
2·x-3>0,5-x≥4·x-11
Таким же образом определение систем неравенств представлены в школьных учебниках как для использования одной переменной, так и двух.
Основные виды системы неравенств
Имеет место составление бесконечного множества систем неравенств. Их классифицируют по группам, отличающихся по определенным признакам. Неравенства подразделяют по критериям:
- количество неравенств системы;
- количество переменных записи;
- вид неравенств.
Количество входящих неравенств может насчитывать от двух и более. В предыдущем пункте рассматривался пример решения системы с двумя неравенствами.
2·x-3>0,5-x≥4·x-11
Рассмотрим решение системы с четырьмя неравенствами.
x≥-2,y≤5,x+y+z≥3,z≤1-x2-4·y2
Решение неравенства отдельно не говорит о решение системы в целом. Для решения системы необходимо задействовать все имеющиеся неравенства.
Такие системы неравенств могут иметь одну, две, три и более переменных. В последней изображенной системе это отчетливо видно, там имеем три переменные: x, y, z. Уравнения могут содержать по одной переменной, как в примере, либо по несколько. Исходя из примеров, неравенство x+0·y+0·z≥−2 и 0·x+y+0·z≤5 не считают равнозначными. Школьным программам уделяют внимание решению неравенств с одной переменной.
При записи системы могут быть задействованы уравнения разных видов и с разным количеством переменных. Чаще всего встречаются целые неравенства разных степеней. При подготовке к экзаменам могут встретиться системы с иррациональными, логарифмическими, показательными уравнениями вида:
zaochnik.com
Линейные неравенства. Системы и совокупности неравенств
Мы часто сравниваем те или иные объекты по их числовым характеристикам: товары по их ценам, людей по их росту или возрасту, смартфоны по их диагонали или результаты команд по количеству забитых мячей в матче.
Соотношения вида 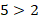 или
или  называют неравенствами
называют неравенствами
Чтобы сравнивать натуральные числа в десятичной записи, мы упорядочили цифры:  , а дальше чаще всего использовали преимущества десятичной записи: начинали сравнивать цифры чисел с крайних левых разрядов до первого несоответствия.
, а дальше чаще всего использовали преимущества десятичной записи: начинали сравнивать цифры чисел с крайних левых разрядов до первого несоответствия.
Но этот способ не всегда удобен.
Проще всего сравнивать положительные числа, т.к. они обозначают количества. Действительно, если число  можно эквивалентно представить в виде суммы числа
можно эквивалентно представить в виде суммы числа 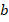 с каким-то другим числом
с каким-то другим числом 
 больше
больше 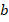 :
:  .
.Эквивалентная запись:  .
.
Это определение можно расширить не только на положительные числа, но и на любые два числа:  .
.
Число  больше числа
больше числа
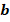 (записывается как
(записывается как  или
или  ), если число
), если число 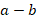 является положительным. Соответственно, если число
является положительным. Соответственно, если число 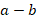 отрицательно, то
отрицательно, то  .
.Например, сравним две дроби: 
 . Сразу так и не скажешь, какая из них больше. Поэтому обратимся к определению и рассмотрим разность
. Сразу так и не скажешь, какая из них больше. Поэтому обратимся к определению и рассмотрим разность 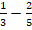 :
:
Получили отрицательное число, значит, 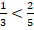 .
.
На числовой оси большее число всегда будет располагаться правее, меньшее – левее (Рис. 1).

Рис. 1. На числовой оси большее число располагается правее, меньшее – левее
Зачем нужны такие формальные определения? Одно дело – наше понимание, а другое – техника. Если сформулировать строгий алгоритм сравнения чисел, то его можно поручить компьютеру. В этом есть плюс – такой подход избавляет нас от выполнения рутинных операций. Но есть и минус – компьютер точно следует заданному алгоритму. Если компьютеру поставлена задача: поезд должен отправиться со станции в  , то, даже если вы окажетесь на платформе в
, то, даже если вы окажетесь на платформе в 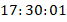 , на этот поезд вы уже не успеете. Поэтому алгоритмы, которые мы задаём компьютеру для выполнения различных вычислений или решения задач, должны быть очень точными и максимально формализованными.
, на этот поезд вы уже не успеете. Поэтому алгоритмы, которые мы задаём компьютеру для выполнения различных вычислений или решения задач, должны быть очень точными и максимально формализованными.
Как и в случае равенств, с неравенствами можно совершать некоторые действия и получать эквивалентные неравенства.
Рассмотрим некоторые из них.
1. Если 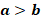 , то
, то  для любого числа
для любого числа  . Т.е. можно прибавлять или вычитать одно и то же число к обеим частям неравенства.
. Т.е. можно прибавлять или вычитать одно и то же число к обеим частям неравенства.
У нас уже есть хороший образ – весы. Если одна из чашек весов перевешивала, то, сколько бы мы ни добавляли (или не забирали) к обеим чашам, эта ситуация не изменится (Рис. 2).

Рис. 2. Если чаши весов не уравновешены, то после добавления (убавления) к ним одинакового количества гирь они останутся в таком же неуравновешенном положении
Это действие можно сформулировать по-другому: можно переносить слагаемые из одной части неравенства в другую, изменяя их знак на противоположный:  .
.
2.Если 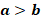 , то
, то 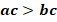 и
и  для любого положительного
для любого положительного 
Для понимания этого свойства можно опять воспользоваться аналогией с весами: если, к примеру, левая чаша перевешивала, то, если возьмём две левые чаши и две правые, перевес точно сохранится. Та же ситуация для 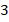 ,
,  чаш и т.д. Даже если возьмём половины каждой из чаш, ситуация тоже не изменится (Рис. 3).
чаш и т.д. Даже если возьмём половины каждой из чаш, ситуация тоже не изменится (Рис. 3).

Рис. 3. Если чаши весов не уравновешены, то, после того как забрать половину каждой из них, они останутся в таком же неуравновешенном положении
Если же умножить или разделить обе части неравенства на отрицательное число, то знак неравенства изменится на противоположный. С аналогией для этой операции чуть сложнее – отрицательных количеств нет. Здесь поможет тот факт, что у отрицательных чисел всё наоборот (чем больше модуль числа, тем меньше само число): 
Для чисел разных знаков ещё легче:  . Т.е., умножая на
. Т.е., умножая на  , мы должны изменить знак неравенства на противоположный.
, мы должны изменить знак неравенства на противоположный.
Что касается умножения на отрицательное число 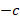 , то можно выполнить эквивалентную операцию из двух частей: сначала умножить на противоположное положительное число
, то можно выполнить эквивалентную операцию из двух частей: сначала умножить на противоположное положительное число  – как мы уже знаем, знак неравенства не изменится:
– как мы уже знаем, знак неравенства не изменится: 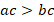 .
.
А дальше умножить полученное неравенство на  :
: 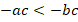 .
.
Подробнее о сложении и умножении
В первом свойстве мы записали:  , но при этом сказали, что можно не только прибавлять, но и вычитать. Почему? Потому что вычитание числа – это то же самое, что и прибавление противоположного числа:
, но при этом сказали, что можно не только прибавлять, но и вычитать. Почему? Потому что вычитание числа – это то же самое, что и прибавление противоположного числа:  . Именно поэтому мы говорим не только о сложении, но и о вычитании.
. Именно поэтому мы говорим не только о сложении, но и о вычитании.
Аналогично и со вторым свойством: деление – это умножение на обратное число: 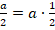 . Поэтому во втором свойстве мы говорим не только об умножении на число, но и о делении.
. Поэтому во втором свойстве мы говорим не только об умножении на число, но и о делении.
3. Для положительных чисел  и
и 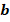 , если
, если 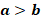 , то
, то  .
.
Это свойство мы хорошо знаем: если мы торт делим на 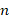 человек, то, чем больше
человек, то, чем больше 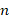 , тем меньше достанется каждому. Например:
, тем меньше достанется каждому. Например:  , поэтому
, поэтому 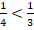 (действительно, четвёртая часть торта явно меньше третьей части того же торта) (Рис. 4).
(действительно, четвёртая часть торта явно меньше третьей части того же торта) (Рис. 4).
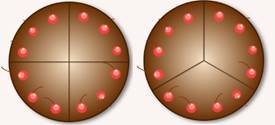
Рис. 4. Четвёртая часть торта меньше третьей части того же торта
4.Если 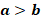 и
и  , то
, то  .
.
Продолжая аналогию с весами: если на одних весах левая чаша перевешивает правую и на других – такая же ситуация, то, ссыпав отдельно содержимое левых и отдельно содержимое правых чаш, снова получим, что левая чаша перевешивает (Рис. 5).
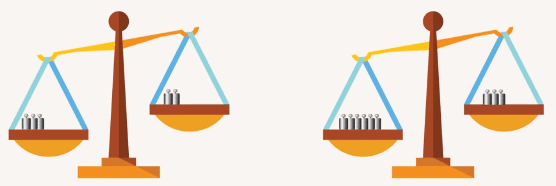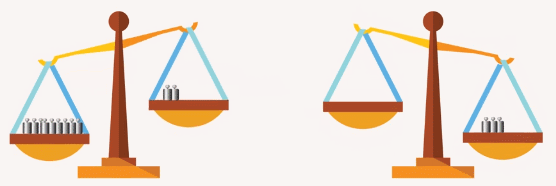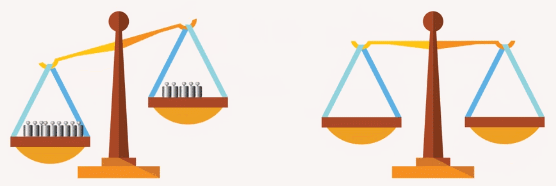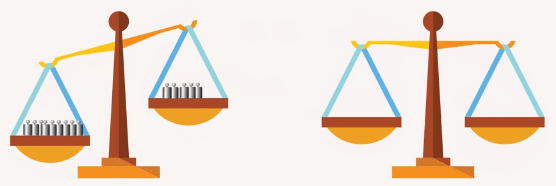
Рис. 5. Если левые чаши двух весов перевешивают правые, то, ссыпав отдельно содержимое левых и отдельно содержимое правых чаш, получится, что левая чаша перевешивает
5. Для положительных  , если
, если 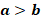 и
и  , то
, то  .
.
Здесь аналогия чуть более сложная, но тоже ясная: если левая чаша тяжелее правой и мы возьмём больше левых чаш, чем правых, то точно получим более массивную чашу (Рис. 6).

Рис. 6. Если левая чаша тяжелее правой, то если взять больше левых чаш, чем правых, то получится более массивная чаша
Последние два свойства интуитивно понятны: сложив или умножив числа побольше, мы в результате получим большее число.
Большинство из этих свойств можно строго доказать, используя различные алгебраические аксиомы и определения, но мы не будем этого делать. Для нас процесс доказательства представляет не такой интерес, как непосредственно полученный результат, который мы будем использовать на практике.
До сих пор мы говорили о неравенствах как о способе записи результата сравнения двух чисел:  или
или 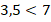 . Но неравенства можно использовать и для записи различной информации об ограничениях для того или иного объекта. В жизни мы часто используем такие ограничения для описания, например: Россия – это миллионы людей от Калининграда до Владивостока; в лифте можно перевозить не больше
. Но неравенства можно использовать и для записи различной информации об ограничениях для того или иного объекта. В жизни мы часто используем такие ограничения для описания, например: Россия – это миллионы людей от Калининграда до Владивостока; в лифте можно перевозить не больше 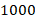 кг, а в пакет – класть не больше
кг, а в пакет – класть не больше  кг. Ограничения могут быть использованы и для классификации объектов. Например, в зависимости от возраста выделяют различные категории населения – дети, подростки, молодёжь и т.д.
кг. Ограничения могут быть использованы и для классификации объектов. Например, в зависимости от возраста выделяют различные категории населения – дети, подростки, молодёжь и т.д.
Во всех рассмотренных примерах можно выделить общую идею: некоторая величина ограничена сверху или снизу (или с обеих сторон сразу). Если  – грузоподъёмность лифта, а
– грузоподъёмность лифта, а  – допустимая масса товаров, которые можно класть в пакет, то описанную выше информацию можно записать так:
– допустимая масса товаров, которые можно класть в пакет, то описанную выше информацию можно записать так:  ,
,  и т.д.
и т.д.
В рассмотренных примерах мы были немного неточны. Формулировка «не больше» подразумевает, что в лифте можно перевозить ровно 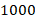 кг, а в пакет можно положить ровно
кг, а в пакет можно положить ровно  кг. Поэтому правильнее было записать так:
кг. Поэтому правильнее было записать так: 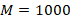 или
или  . Естественно, так писать неудобно, поэтому придумали специальный знак:
. Естественно, так писать неудобно, поэтому придумали специальный знак:  , который читается как «меньше или равно». Такие неравенства называются нестрогими (соответственно, неравенства со знаками
, который читается как «меньше или равно». Такие неравенства называются нестрогими (соответственно, неравенства со знаками  – строгими). Их используют тогда, когда переменная может быть не только строго больше или меньше, но может и равняться граничному значению.
– строгими). Их используют тогда, когда переменная может быть не только строго больше или меньше, но может и равняться граничному значению.
Решением неравенства называются все такие значения переменной, при подстановке которых полученное числовое неравенство будет верным. Рассмотрим, например, неравенство:  . Числа
. Числа 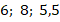 – решения этого неравенства, т.к. неравенства
– решения этого неравенства, т.к. неравенства  являются верными. А вот числа
являются верными. А вот числа  и
и 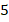 не являются решениями, поскольку числовые неравенства
не являются решениями, поскольку числовые неравенства  и
и 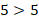 не являются верными. Решить неравенство, значит, найти все значения переменных, при которых неравенство будет верным.
не являются верными. Решить неравенство, значит, найти все значения переменных, при которых неравенство будет верным.
Вернемся к неравенству  . Его решения можно эквивалентно описать так: все действительные числа, которые больше
. Его решения можно эквивалентно описать так: все действительные числа, которые больше 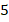 . Понятно, что таких чисел бесконечное множество, как же в таком случае записать ответ? Обратимся к числовой оси: все числа, большие
. Понятно, что таких чисел бесконечное множество, как же в таком случае записать ответ? Обратимся к числовой оси: все числа, большие 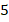 , расположены справа от
, расположены справа от 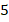 . Заштрихуем эту область, тем самым показывая, что это и будет ответ к нашему неравенству. Чтобы показать, что число
. Заштрихуем эту область, тем самым показывая, что это и будет ответ к нашему неравенству. Чтобы показать, что число 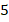 не является решением, его заключают в пустой круг, или, по-другому, выкалывают точку (Рис. 7).
не является решением, его заключают в пустой круг, или, по-другому, выкалывают точку (Рис. 7).

Рис. 7. На числовой оси показано, что число 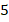 не является решением (выколотая точка)
не является решением (выколотая точка)
Если же неравенство нестрогое и выбранная точка является решением, то её заключают в закрашенный круг.
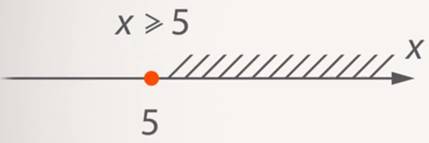
Рис. 8. На числовой оси показано, что число 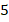 является решением (закрашенная точка)
является решением (закрашенная точка)
Итоговый ответ удобно записывать с помощью промежутков. Промежуток записывается по следующим правилам:
- Записываются левая и правая границы промежутка.
- Если граница включена в промежуток, т.е. неравенство нестрогое, ставят квадратные скобки
 ; если неравенство строгое и граница не включена, то скобки круглые
; если неравенство строгое и граница не включена, то скобки круглые  .
. - Если у промежутка нет правой границы, то её записывают как
 или
или  , если нет левой границы, то как
, если нет левой границы, то как  .
.
Знак 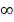 обозначает бесконечность, т.е. показывает, что число может принимать сколь угодно большое (
обозначает бесконечность, т.е. показывает, что число может принимать сколь угодно большое ( ) или сколь угодно малое значение (
) или сколь угодно малое значение ( ).
).
Ответ к неравенству  мы можем записать так:
мы можем записать так: 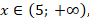 или просто:
или просто: 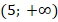 . Это означает, что неизвестная
. Это означает, что неизвестная 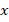 принадлежит указанному промежутку, т.е. может принимать любые значения из этого промежутка.
принадлежит указанному промежутку, т.е. может принимать любые значения из этого промежутка.
Если обе скобки промежутка круглые, как в нашем примере, то такой промежуток ещё называют интервалом.
Обычно решением неравенства является промежуток, но возможны и другие варианты, например, решением может быть множество, состоящее из одного или несколько чисел. Например, неравенство  имеет только одно решение
имеет только одно решение 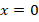 . Ведь при любых других значениях выражение
. Ведь при любых других значениях выражение  будет положительным, а значит, соответствующее числовое неравенство выполняться не будет.
будет положительным, а значит, соответствующее числовое неравенство выполняться не будет.
Неравенство может и не иметь решений. В этом случае ответ записывают как 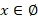 («Переменная
(«Переменная 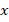 принадлежит пустому множеству»). В том, что решением неравенства может быть пустое множество, нет ничего необычного. Ведь в реальной жизни ограничения также могут привести к тому, что не найдется ни одного элемента, удовлетворяющего требованиям. Например, людей с ростом выше
принадлежит пустому множеству»). В том, что решением неравенства может быть пустое множество, нет ничего необычного. Ведь в реальной жизни ограничения также могут привести к тому, что не найдется ни одного элемента, удовлетворяющего требованиям. Например, людей с ростом выше  метров и при этом весом до
метров и при этом весом до  кг – точно нет. Множество таких людей не содержит ни одного элемента, или, как говорят, это пустое множество.
кг – точно нет. Множество таких людей не содержит ни одного элемента, или, как говорят, это пустое множество.
Неравенства могут использоваться не только для записи известной информации, но и, как математические модели, для решения различных задач.
interneturok.ru
Математика по полочкам: 13. Системы неравенств
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Если ставится задача найти множество общих решений двух или более неравенств, то говорят, что надо решить систему неравенств.Неравенства, входящие в систему, объединяются фигурной скобкой. Иногда системы неравенств записывают в виде двойного неравенства:
-5<x<12 илиРешением системы неравенств называется число, которое при его подстановке в систему обращает каждое неравенство в верное числовое неравенство.
Решить систему неравенств – значит найти решения для всей системы, либо доказать, что у данной системы решений нет.
Чтобы решить систему неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти пересечение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это пересечение и является множеством решений системы неравенств.
Пример:Решить систему неравенств:
Решим каждое неравенство в отдельности
1) 5x-x2≥0,
5x-x2=0,
x(5-x)=0,
x=0 или 5-x=0,
-x=-5,
x=5.
Находим решение с помощью метода интервалов:
2) 6-2x<-2,
-2x<-2-6,
-2x<-8,
x>-8:(-2),
x>4.
Объединим оба решения:
Ответ: (4; 5].Говорят, что несколько неравенств с одной переменной образуют совокупность, если необходимо найти все такие значения переменной, каждое из которых является решением хотя бы одного из данных неравенств. Совокупность неравенств обозначается квадратной скобкой.
Решением совокупности неравенств называют такие значения переменной, которые являются верными хотя бы для одного из этих неравенств.
Чтобы решить совокупность неравенств с одной переменной, надо:
1) отдельно решить каждое неравенство;
2) найти объединение найденных решений, отметив решение каждого неравенства на числовой прямой.
Это объединение и является решением совокупности неравенств.
Пример:
Решить совокупность неравенств:
Решим каждое неравенство в отдельности
1) 5х+6≤1,
5х≤ -5,
х≤ -1.
2) 2х+1≥3,
2х≥2,
х≥1.
Объединим оба решения:
Ответ: (-∞; -1]U[1;+∞).
УПРАЖНЕНИЯ
1. Решите систему неравенств:Решение:
а)
Ответ: (5; 7]
2. Решите систему неравенств:
Решение:
Ответ: (1; 10].
3. Найдите целые решения системы неравенств:
Решение:
а)
Ответом являются все целые числа, которые принадлежат промежутку (-15; 5).
Ответ: -14; -13; -12; -11; -10; -9; -8; -7; -6.
4. Решите систему неравенств:
Решение:
Ответ: (-1; 3).
5. Решите систему неравенств:
Решение:
Ответ: (-1;2).
6. Решите систему неравенств:
Решение:
Ответ: нет решений.
7. Решите систему неравенств:
Решение:
Ответ: (0; +∞).
8. Решите неравенство:
а) -2<3x+5≤10; б) 2<4x+6≤12.
Решение:Ответ: (-2 1/3; 1 2/3].
9. Решите систему неравенств:
Решение:
Ответ: [0,4; 0,5).
10. Решите систему неравенств (№ 3.4.52 [7]):
Решение:
Ответ: (-1; 2).
11. Решите систему неравенств:
Решение:
Ответ: [-9; 3)U(3; 9].
12. Решите систему неравенств:
Решение:
Ответ: (-7; -6)U(1;7).
13. Решите систему неравенств:
Решение:
Ответ: (2; 4).
14. Решите систему неравенств:
Решение:
Ответ: (-7; -2)U(0; 2).ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Решите систему неравенств:
2. Решите систему неравенств:
3. Решите систему неравенств:
4. Решите систему неравенств:
5. Решите систему неравенств:
6. Решите систему неравенств:
7. Решите систему неравенств:
8. Решите систему неравенств:
9. Решите систему неравенств:
10. Решите систему неравенств:
Проверь себя
mathembs.blogspot.com
Системы и совокупности неравенств. Видеоурок. Алгебра 11 Класс
В данном уроке мы рассмотрим системы и совокупности различных неравенств, приведем соответствующие примеры.
Тема: Уравнения и неравенства. Системы уравнений и неравенств
Урок: Системы и совокупности неравенств
Рассмотрим систему неравенств:

Мы знаем, как решить каждое из этих неравенств. Найти решение каждого неравенства – значит найти множество всех х, при которых неравенство обращается в верное числовое соотношение. Предположим, мы нашли такое множество для каждого из заданных уравнений системы:
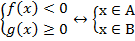
Решить систему – означает найти все х, удовлетворяющие одновременно и первому, и второму неравенству, то есть принадлежащие и множеству А, и множеству В.
Пример 1 – решить систему неравенств:

Покажем решение системы графически:

Рис. 1. Иллюстрация к примеру
Очевиден ответ: 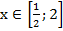
Комментарий: только значения х, находящиеся на выбранном отрезке, удовлетворяют одновременно первому и второму неравенству.
Рассмотрим совокупность двух неравенств:
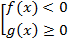
Предположим, мы нашли решения обоих неравенств:
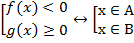
Решить совокупность – означает найти все х, которые удовлетворяют хотя бы одному неравенству, то есть входят хотя бы в одно из множеств А или В.
Например:
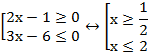
Полученные интервалы проиллюстрированы на рисунке 10.1. Очевиден ответ: 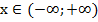
Теперь можем дать строгие определения.
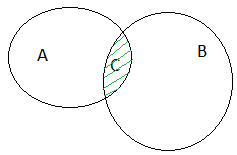
Рис. 2. Пересечение двух множеств
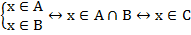
Определение:
Пересечением двух множеств А и В называют такое множество С, которое состоит из всех элементов, входящих одновременно и в множество А, и в множество В.
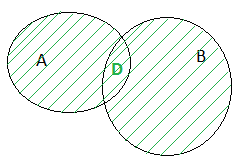
Рис. 3. Объединение двух множеств
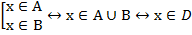
Определение:
Объединением двух множеств А и В называют такое множество D, которое состоит из всех элементов, входящи
interneturok.ru
Системы неравенств. Как решить систему неравенств?
Системой неравенств называют несколько неравенств, которые должны выполняться одновременно.
Например:
\(\begin{cases}5x+2≥0\\x<2x+1\\x-4>2\end{cases}\)
\(\begin{cases}x^2-55x+250<(x-14)^2\\x^2-55x+250≥0\\x-14>0\end{cases}\)
\(\begin{cases}(x^2+1)(x^2+3)(x^2-1)≥0\\x<3\end{cases}\)
Решение системы неравенств
Чтобы решить систему неравенств нужно найти значения иксов, которые подойдут всем неравенствам в системе – это и значит, что они выполняются одновременно.
Пример. Решим систему \(\begin{cases}x>4\\x\leq7\end{cases}\)
Решение: Первое неравенство становится верным, если икс больше \(4\). То есть, решения первого неравенства – все значения иксов из интервала \((4;\infty)\), или на числовой оси:
Второму неравенству подойдут значения иксов меньшие чем 7, включая саму семерку, то есть любой икс из интервала \((-\infty;7]\) или на числовой оси:
А какие значения подойдут обоим неравенствам? Те, которые принадлежат обоим промежуткам, то есть где промежутки пересекаются.
Ответ: \((4;7]\)
Как вы могли заметить для пересечения решений неравенств в системе удобно использовать числовые оси.
Общий принцип решения систем неравенств: нужно найти решение каждого неравенства, а потом пересечь эти решения с помощью числовой прямой.
Пример: (Задание из ОГЭ) Решить систему \(\begin{cases} 7(3x+2)-3(7x+2)>2x\\(x-5)(x+8)<0\end{cases}\)
Решение:
|
\(\begin{cases} 7(3x+2)-3(7x+2)>2x\\(x-5)(x+8)<0\end{cases}\) |
Давайте каждое неравенство решим отдельно от другого. |
|
1) \(7(3x+2)-3(7x+2)>2x\) |
Раскроем скобки. |
|
\(21x+14-21x-6>2x\) |
Приведем подобные слагаемые. |
|
\(8>2x\) |
Перевернем получившееся неравенство. |
|
\(2x<8\) |
Поделим все неравенство на \(2\). |
|
\(x<4\) |
Отметим решение на числовой прямой. |
|
Запишем ответ для первого неравенства. |
|
|
\(x∈(-∞;4)\) |
Теперь решим второе неравенство. |
|
2) \((x-5)(x+8)<0\) |
Неравенство уже в идеальном виде для применения метода интервалов.
|
|
Запишем ответ для второго неравенства. |
|
|
\(x∈(-8;5)\) |
Объединим оба решения с помощью числовых осей. |
|
Выпишем в ответ промежуток, на котором есть решение обоих неравенств — и первого, и второго. |
Ответ: \((-8;4)\)
Пример: (Задание из ОГЭ) Решить систему \(\begin{cases} \frac{10-2x}{3+(5-2x)^2}≥0\\ 2-7x≤14-3x \end{cases}\)
Решение:
|
\(\begin{cases} \frac{10-2x}{3+(5-2x)^2}≥0\\ 2-7x≤14-3x \end{cases}\) |
Снова будем решать неравенства по отдельности. |
|
1)\(\frac{10-2x}{3+(5-2x)^2}\)\(≥0\) |
Если вас испугал знаменатель – не бойтесь, сейчас мы его уберем. |
|
\(10-2x≥0\) |
Перед нами обычное линейное неравенство – выразим \(x\). Для этого перенесем \(10\) в правую часть. |
|
\(-2x≥-10\) |
Поделим неравенство на \(-2\). Так как число отрицательное меняем знак неравенства. |
|
\(x≤5\) |
Отметим решение на числовой прямой. |
|
Запишем ответ к первому неравенству. |
|
|
\(x∈(-∞;5]\) |
На данном этапе главное не забыть, что есть второе неравенство. |
|
2) \(2-7x≤14-3x\) |
Опять линейное неравенство – опять выражаем \(x\). |
|
\(-7x+3x≤14-2\) |
Приводим подобные слагаемые. |
|
\(-4x≤12\) |
Делим все неравенство на \(-4\), перевернув при этом знак. |
|
\(x≥-3\) |
Изобразим решение на числовой оси и выпишем ответ для этого неравенства. |
| \(x∈[-3;∞)\) |
А теперь объединим решения. |
|
Запишем ответ. |
Ответ: \([-3;5]\)
Пример: Решить систему \(\begin{cases}x^2-55x+250<(x-14)^2\\x^2-55x+250≥0\\x-14>0\end{cases}\)
Решение:
|
\(\begin{cases}x^2-55x+250<(x-14)^2\\x^2-55x+250≥0\\x-14>0\end{cases}\) |
В первом неравенстве раскроем скобку, во втором — разложим квадратный трехчлен на множители, а в третьем — перенесем 14 в правую |
|
\(\begin{cases}x^2-55x+250<x^2-28x+196\\(x-5)(x-50)≥0\\x>14\end{cases}\) |
В первом перенесем все слагаемые в левую часть. И приведем подобные слагаемые. |
|
\(\begin{cases}-27x+54<0\\(x-5)(x-50)≥0\\x>14\end{cases}\) |
Теперь в нем же перенесем \(54\) в левую сторону и поделим обе части на \((-27)\), не забыв при этом перевернуть знак сравнения. |
|
\(\begin{cases}x>2\\(x-5)(x-50)≥0\\x>14\end{cases}\) |
Отметим решения неравенств на числовых прямых. |
|
Решения подходящие всем неравенствам системы находятся от \(50\) и дальше. Запишем ответ. |
Ответ: \([50;+∞)\)
Смотрите также:
Системы линейных неравенств
Совокупности неравенств
cos-cos.ru
что это такое, как решить
Тема совокупностей уравнений и др. систем, как правило, в рамках школьного курса представлена скупо. В 10-11 классе она изучается совсем недолго. Мы считаем, что это неверный подход, поскольку совокупности — прекрасный способ оформления привычных решений при работе с неравенствами и уравнениями, поэтому в рамках статьи мы раскроем этот вопрос.
В данной статье мы сформулируем общее понятие совокупностей неравенств, уравнений и их систем, а также их комбинации. Кроме определений здесь, как обычно, есть решения задач, наглядно поясняющие тот или иной фрагмент текста.
Понятие совокупности
Для того, чтобы хорошо понимать, что такое совокупность уравнений, нужно вспомнить еще одно понятие из школьного курса алгебры — система уравнений (аналогично неравенствам). Тогда определения совокупности покажутся вам знакомыми и легко усвоятся.
Проанализировав несколько учебников, выберем наиболее удачное определение:
Определение 1Совокупность уравнений представляет собой несколько уравнений, записанных друг под другом и объединенных квадратной скобкой. Значение этой записи таково: совокупность объединяет такие значения переменных, при которых хотя бы одно из входящих в нее уравнений превращается в верное равенство.
Сравним между собой понятие совокупности и понятие системы:
- Запись совокупности, как мы уже говорили выше, осуществляется с помощью квадратной скобки, а системы записываются с фигурной.
- Совокупность включает в себя множество решений, которые относятся хотя бы одному из уравнений, входящих в ее состав. Система объединяет решения, которые подходят для каждого уравнения.
Вот примеры совокупности уравнений:
x+1=0,x2-1=-8 x+y2+z4=0,x·y·z=0,z=5
Иногда при записи совокупности можно обойтись и без квадратной скобки: так часто делают в школе. В таком случае уравнения можно просто указать через запятую. Для примера выше это может быть запись вида x+y2+z4=0, x·y·z=0, z=5.
Понятие совокупности неравенств формулируется схожим образом.
Определение 2Совокупность неравенств представляет собой несколько неравенств, записанных друг под другом и объединенных квадратной скобкой. Она включает в себя решения, которые подходят хотя бы для о
zaochnik.com
Равносильные системы неравенств, преобразование систем, определение
Продолжаем обсуждать термин «равносильные системы». Мы уже обсудили, что он означает применительно к уравнениям. В этой статье мы попробуем разобрать его применительно к неравенствам. План материала выглядит следующим образом: сначала мы введем основные определения, потом преобразуем их возможными способами, а в конце докажем, что получившаяся в итоге преобразований система равносильна той, что была взята первоначально.
Определение равносильной системы неравенств
Понятие равносильной системы неравенств в учебниках алгебры встречается нечасто. Почему-то применительно к уравнениям это термин более употребим. При этом мы можем встретить, что решения систем неравенств записываются следующим образом:
2·x-1>6,5-3·x>-13,2·x>7,-3·x>-18,x>3,5,x<6.
Аналогично определению системы равносильных уравнений мы можем сформулировать схожее и для неравенств. При этом изначальные системы неравенств можно заменить на равносильные, но более простые для понимания. Итак, определение:
Определение 1Равносильные системы неравенств — это такие системы, у которых одни и те же решения (или эти решения одинаково отсутствуют).
Как понять, равносильны ли данные системы неравенств?
Если мы знаем все решения систем, то можно сразу дать ответ — да или нет, исходя из указанного выше определения.
Пример 1Допустим, мы знаем, что:
2·x>2,x4≤-2 — решений не имеет.
Для системы x>5,x<-1- аналогично.
Если обе системы не имеют решения, то они равносильны.
А если мы не знаем решений? Логично вычислить их и определить это. Но есть способ обойтись и без предварительных расчетов. Для этого нам надо будет провести так называемые равносильные преобразования. Давайте разберем подробнее, что же это такое.
Что такое равносильные преобразования систем неравенств
Для уравнений существует довольно много преобразований, которые могут быть полезны на практике, но для неравенств же их заметно меньше. Разберем два основных способа, которые применяются для решения задач чаще всего:
- перестановка компонентов системы неравенств;
- замена одного из неравенств системы на равносильное ему.
Также указанные выше понятия можно называть свой
zaochnik.com
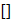 ; если неравенство строгое и граница не включена, то скобки круглые
; если неравенство строгое и граница не включена, то скобки круглые 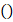 .
.