Параллелограмм — Википедия

Материал из Википедии — свободной энциклопедии

Параллелограмм

Параллелогра́мм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Противоположные стороны параллелограмма равны, а диагонали в точке пересечения делятся пополам. Противоположные углы параллелограмма равны, а сумма соседних равна 180°.

• Противолежащие стороны параллелограмма равны.
• Противолежащие углы параллелограмма равны.
• Сумма углов, прилежащих к одной стороне, равна 180° (по свойству параллельных прямых).
• Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам:

  |AO|=|OC|,|BO|=|OD|{\displaystyle \left|AO\right|=\left|OC\right|,\left|BO\right|=\left|OD\right|}.

• Точка пересечения диагоналей является центром симметрии параллелограмма.
• Параллелограмм диагональю делится на два равных треугольника.
• Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
• Тождество параллелограмма: сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть а — длина стороны AB, b — длина стороны BC, d1{\displaystyle d_{1}} и d2{\displaystyle d_{2}} — длины диагоналей; тогда

  d12+d22=2(a2+b2).{\displaystyle d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2}).}

Тождество параллелограмма есть простое следствие формулы Эйлера для произвольного четырехугольника: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумма квадратов его диагоналей. У параллелограмма противоположные стороны равны, а расстояние между серединами диагоналей равно нулю.

• Аффинное преобразование всегда переводит параллелограмм в параллелограмм. Для любого параллелограмма существует аффинное преобразование, которое отображает его в квадрат.

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий (в этом случае выполняются и все остальные):

1. У четырёхугольника без самопересечений две противоположные стороны одновременно равны и параллельны: AB=CD,AB∥CD{\displaystyle AB=CD,AB\parallel CD}.
2. Все противоположные углы попарно равны: ∠A=∠C,∠B=∠D{\displaystyle \angle A=\angle C,\angle B=\angle D}.
3. У четырёхугольника без самопересечений все противоположные стороны попарно равны: AB=CD,BC=DA{\displaystyle AB=CD,BC=DA}.
4. Все противоположные стороны попарно параллельны: AB∥CD,BC∥DA{\displaystyle AB\parallel CD,BC\parallel DA}.
5. Диагонали делятся в точке их пересечения пополам: AO=OC,BO=OD{\displaystyle AO=OC,BO=OD}.
6. Сумма соседних углов равна 180 градусов: ∠A+∠B=180∘,∠B+∠C=180∘,∠C+∠D=180∘,∠D+∠A=180∘{\displaystyle \angle A+\angle B=180^{\circ },\angle B+\angle C=180^{\circ },\angle C+\angle D=180^{\circ },\angle D+\angle A=180^{\circ }}.
7. Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру.
8. Сумма квадратов диагоналей равна сумме квадратов сторон выпуклого четырёхугольника: AC2+BD2=AB2+BC2+CD2+DA2{\displaystyle AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}}.

Здесь приведены формулы, свойственные именно параллелограмму. См. также формулы для площади произвольных четырёхугольников.

Площадь параллелограмма равна произведению его основания на высоту:

S=ah{\displaystyle S=ah} , где a{\displaystyle a} — сторона, h{\displaystyle h} — высота, проведенная к этой стороне.

Площадь параллелограмма равна произведению его сторон на синус угла между ними:

S=absin⁡α,{\displaystyle S=ab\sin \alpha ,}

где a{\displaystyle a} и b{\displaystyle b} — стороны, а α{\displaystyle \alpha } — угол между сторонами a{\displaystyle a} и b{\displaystyle b}.

Также площадь параллелограмма может быть выражена через стороны a, b{\displaystyle a,\ b} и длину любой из диагоналей d{\displaystyle d} по формуле Герона как сумма площадей двух равных примыкающих треугольников:

S=2⋅p(p−a)(p−b)(p−d){\displaystyle S=2\cdot {\sqrt {p(p-a)(p-b)(p-d)}}}

где p=(a+b+d)/2.{\displaystyle p=(a+b+d)/2.}

Ромб и Параллелограмма 2020

Ромб против Параллелограммы

Параллелограмм представляет собой четырехстороннюю или четырехстороннюю фигуру, в которой противоположные стороны параллельны. А потому, что противоположные линии параллельны, следовательно, противоположные углы также равны.

Ромб, с другой стороны, может быть определен как равносторонний параллелограмм. Это четырехсторонняя фигура, которая имеет все четыре стороны равными. Это свойство ромба похоже на квадрат. Отличительная характеристика между ними состоит в том, что квадрат имеет все углы, равные 90 градусам, но в ромбе равны только противоположные углы. Тем не менее, есть отличительная особенность, что в прямоугольнике противоположный угол равен 90 градусам, но в случае ромба углы не равны 90 градусам. Они являются дополнительными углами. Таким образом, мы можем сказать, что каждый ромб является параллелограммом, но обратное неверно.

Ромб также называют алмазом или лепешкой.

Мы рассмотрим приведенный выше рисунок, чтобы обсудить параллелограмм и ромб один за другим.

Ромб В ромбе: Стороны AB = BC = CD = AD. Угол 伪 = угол 尾 и угол 未 = угол 纬. Но угол 伪 = угол 尾 не равен углу 未 = угол 纬. Диагонали AC и BD пересекаются друг с другом, делая правый угол (правый угол — угол 90 градусов) или параллельны друг другу. Диагонали делят пополам противоположные углы. Окружность или периметр ромба может быть рассчитана как:

Окружность = 4 x сторона.

Параллелограмм В параллелограмме: Противоположные стороны равны, т. Е. AB = CD и BC = AD. Угол 伪 = угол 尾 и угол 未 = угол 纬 Угол может быть равен 90 градусам. (Это случай прямоугольника.) Каждая из диагоналей образует треугольник, который является конгруэнтным между собой. Диагонали делят пополам противоположные углы.

Окружность или периметр параллелограмма могут быть рассчитаны как:

Окружность = 2 (AB + BC).

Резюме: В параллелограмме противоположные стороны равны, тогда как в ромбе все четыре стороны равны. В параллелограмме диагонали делят друг друга пополам, тогда как в ромбе они не делят друг друга пополам. В ромбе диагонали пересекаются друг с другом под прямым углом и, следовательно, перпендикулярны друг другу. Это не так в случае параллелограмма. В параллелограмме углы могут быть равны 90 градусам, но в случае ромба никогда не может быть 90 градусов. Ромб можно рассматривать как подмножество параллелограмма.

Параллелограмм / ромб — примеры решений

Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 18, а одна из диагоналей равна 72. Найдите углы ромба.

#726

Высота АН ромба ABCD делит сторону CD на отрезки DH=15 и CH=2. Найдите высоту ромба.

#671

В ромбе ABCD угол АВС равен 156°. Найдите угол ACD. Ответ дайте в градусах.

#598

Биссектриса угла М параллелограмма МРКС пересекает сторону РК в точке В. Найдите периметр параллелограмма, если МР = 14, ВК = 15 см.

#593

Диагонали ромба относятся как 2 : 5. Периметр ромба равен 116. Найдите высоту ромба.

#575

Угол А параллелограмма в 4 раза больше угла D. Найдите угол С. Ответ дайте в градусах.

#574

Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К. а) Докажите, что треугольник BKA равнобедренный. б) Найдите периметр параллелограмма, если ВК=4, СК=19.

#560

В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник.

#514

В ромбе ABCD угол АВС равен 84°. Найдите угол ACD. Ответ дайте в градусах.

#484

Сторона ромба равна 12, а расстояние от точки пересечения диагоналей ромба до нее равно 1. Найдите площадь этого ромба.

#481

Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.

#479

Найдите величину острого угла параллелограмма ABCD, если биссектриса угла А образует со стороной ВС угол, равный 21°. Ответ дайте в градусах.

#478

Найдите площадь ромба, если его диагонали равны 32 и 4.

#474

Найдите площадь параллелограмма, изображенного на рисунке.

#468

Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найдите его высоты. В ответе укажите бо́льшую высоту.

#356

5.1.2 Параллелограмм, прямоугольник, ромб, квадрат

Видеоурок 1: Прямоугольник, ромб и квадрат. Часть 1

Видеоурок 2: Прямоугольник, ромб и квадрат. Часть 2

Лекция: Параллелограмм, прямоугольник, ромб, квадрат

Четырехугольники

Один подраздел многоугольников мы изучили в прошлом вопросе, сейчас же перейдем к изучению четырехугольников – это многоугольники, у которых 4 стороны, 4 вершины, 4 угла.

В школьном курсе геометрии изучают несколько основных типов четырехугольников – это параллелограмм, прямоугольник, ромб, квадрат и трапецию. В этом же вопросы мы рассмотрим все, кроме трапеции, поскольку все первые 4 типа многоугольников имеют некоторые похожие черты – у них противолежащая пара сторон параллельна.

Отличительная особенность всех четырехугольников – это то, что сумма всех углом равна 360 градусов.

Ну давайте начнем характеризовать все четырехугольники, имеющиеся в теме.

Параллелограмм

Исходя из названия, можно судить, что у данного четырехугольника что-то параллельное. Это совершенно верно, параллелограмм – это четырехугольник, у которого противолежащие стороны параллельны.

Все четырехугольники характеризуются своими свойствами, поэтому давайте ознакомимся со свойствами параллелограмма:

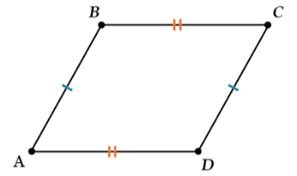
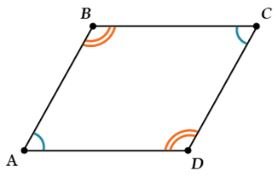
Если у четырехугольника присутствуют перечисленные свойства, то он является параллелограммом:

• Какой — то Один признак выполнен
• Все свойства параллелограмма можно использовать

Для любого параллелограмма справедлива следующая формула, по которой ясно, что сумма квадратов сторон диагоналей равна сумме квадратов всех сторон:

Данное свойство вытекает из теоремы Пифагора для двух прямоугольных треугольников.

Любую сторону можно найти по известным величинам диагоналей и углов между ними:

Найти стороны параллелограмма можно не только через диагонали, но и через высоты и площади:

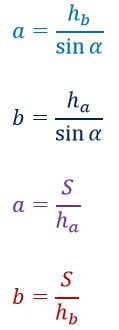
Одними из наиболее важных формул являются формулы для нахождения диагоналей найти их можно по известным сторонам и углу между ними:

Но на самом деле самыми важными формулами являются формулы для нахождения площадей:

Квадрат

Правильный четырехугольник – это квадрат. Как известно, у всех правильных фигур равны стороны и равны углы. Квадрат можно назвать частным случаем параллелограмма, поскольку все свойства и признаки параллелограмма видны и у квадрата.

Свойства квадрата:

• Все стороны равны.
• Все углы равны 90 градусам.
• Диагонали квадрата равны и пересекаются под прямым углом, а точка их пересечения делит их пополам.

Отличительной особенностью диагонали квадрата является то, что она есть гипотенузой прямоугольного треугольника с катетами, равными сторонам квадрата, а гипотенузой равной диагонали. Именно поэтому из теоремы Пифагора диагональ квадрата всегда в раз больше его стороны.

Так как у квадрата все стороны равны, то найти периметр и площадь этой фигуры не составляет ни малейшего труда:

Прямоугольник

Эта фигура характеризуется тем, что все её углы прямые, то есть по 90 градусов.

Свойства прямоугольника:

• У прямоугольника все противолежащие стороны параллельны и равны между собой.

• Все углы прямые.

• Точка пересечения диагоналей делит их на равные части.

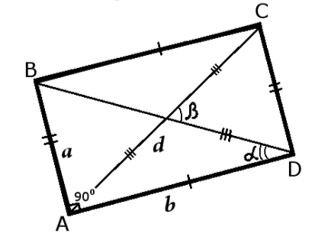
Квадрат диагонали прямоугольника равен сумме квадратов его сторон:

Как можно было понять, данная формула была выведена из теоремы Пифагора, поскольку в основе прямоугольника лежат 2 прямоугольных треугольника.

Формулы нахождения сторон по известным величинам диагоналей, а также площадей:

Формулы сторон прямоугольника

Формулы периметра прямоугольника

Формулы площадей

Ромб

И наконец-то мы подошли к последнему из параллелограммов, который называется ромбом.

У ромба, как и у квадрата, все стороны равно, но, как и у любого параллелограмма, его стороны попарно параллельны.

Отличительной особенностью ромба считается то, что его диагонали, пересекаясь под прямым углом, делятся пополам.

Не имеет смысла перечислять все свойства ромба, поскольку они аналогичны свойствам параллелограмма, а так же квадрата.

У ромба так же существует связь между длинами диагоналей и его сторон. Поскольку в основании ромба лежат 4 прямоугольных треугольника, то можно было вывести формулу связи диагоналей и сторон через теорему Пифагора:

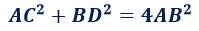
Формулы для сторон ромба

Формулы площадей ромба