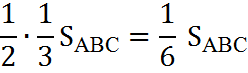Теорема Менелая
— Что общего между теоремой Менелая и наркотиками?
— О них все знают, но никто не говорит.
© Типичный разговор с учеником
Это прикольная теорема, которая поможет вам в тот момент, когда кажется, что уже ничего не поможет. В уроке мы сформулируем саму теорему, рассмотрим несколько вариантов её использования, а в качестве десерта вас ждёт суровое домашнее задание. Поехали!
Для начала — формулировка. Возможно, я дам не самую «красивую» версию теорему, но зато самую понятную и удобную.
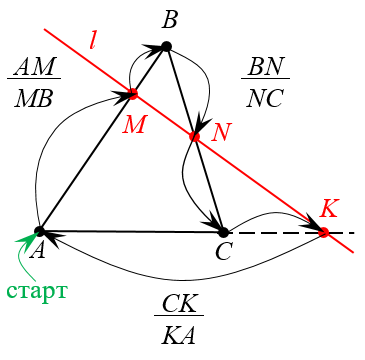
Теорема Менелая. Рассмотрим произвольный треугольник $ABC$ и некую прямую $l$, которая пересекает две стороны нашего треугольника внутренним образом и одну — на продолжении. Обозначим точки пересечения $M$, $N$ и $K$:
Треугольник $ABC$ и секущая $l$ Тогда верно следующее соотношение:
\[\frac{AM}{MB}\cdot \frac{BN}{NC}\cdot \frac{CK}{KA}=1\]
Хочу отметить: не надо зубрить расположение букв в этой злобной формуле! Сейчас я расскажу вам алгоритм, по которому вы всегда сможете восстановить все три дроби буквально на лету. Даже на экзамене в состоянии стресса. Даже если вы сидите за геометрией в 3 часа ночи и вообще уже ничего не понимаете.:)
Схема простая:
- Чертим треугольник и секущую. Например, так, как показано в теореме. Обозначаем вершины и точки какими-нибудь буквами. Это может быть произвольны треугольник $ABC$ и прямая с точками $M$, $N$, $K$, либо какая-нибудь другая — суть не в этом.
- Ставим ручку (карандаш, маркер, гусиное перо) в любую вершину треугольника и начинаем обход сторон этого треугольника с обязательным заходом в точки пересечения с прямой . Например, если сначала пойти из точки $A$ в точку $B$, то получим отрезки: $AM$ и $MB$, затем $BN$ и $NC$, а затем (внимание!) $CK$ и $KA$. Поскольку точка $K$ лежит на продолжении стороны $AC$, то при движении из $C$ в $A$ придётся временно свалить из треугольника.
- А теперь просто делим соседние отрезки друг на друга ровно в том порядке, в котором мы получили их при обходе: $AM/MB$, $BN/NC$, $CK/KA$ — получим три дроби, произведение которых и даст нам единицу.
На чертеже это будет выглядеть вот так:
 Простая схема, позволяющая восстановить формулу из т. Менелая
Простая схема, позволяющая восстановить формулу из т. МенелаяИ сразу пара замечаний. Точнее, это даже не замечания, а ответы на типичные вопросы:
- Что будет, если прямая $l$ пройдёт через вершину треугольника? Ответ: ничего. Теорема Менелая в этом случае не работает.
- Что будет, если выбрать другую вершину для старта или пойти в другую сторону? Ответ: будет то же самое. Просто изменится последовательность дробей.
Думаю, с формулировкой разобрались. Давайте посмотрим, как вся эта дичь применяется для решения сложных геометрических задач.
Зачем всё это нужно?
Предупреждение. Чрезмерное применение теоремы Менелая для решения планиметрических задач может нанести непоправимый вред вашей психике, поскольку данная теорема значительно ускоряет вычисления и заставляет вспоминать другие важные факты из школьного курса геометрии.
Доказательство
Я не буду её доказывать.:)
Ладно, докажу:
- Дополнительное построение: прямая $CT\parallel AB$, причём $T$ — точка пересечения $CT$ с исходной прямой $l$.
Дополнительное построение: прямая $CT$
- Заметим, что $\Delta AMK\sim \Delta CTK$ по двум углам (угол $CKT$ — общий, а $\angle KAB=\angle KCT$ как соответственные при параллельных прямых $AB$ и $CT$ и секущей $AK$). Следовательно: \[\frac{AM}{CT}=\frac{MK}{TK}=\frac{AK}{CK}\]
Откуда легко видеть, что $CT=\frac{AM\cdot CK}{AK}$.
- С другой стороны, $\Delta BMN\sim \Delta CTN$ — опять же по двум углам ($\angle MNB=\angle TNC$ как вертикальные, а $\angle MBN=\angle CTN$ как внутренние накрест лежащие при параллельных прямых $AB$ и $CT$ и секущей $BC$). Следовательно:
\[\frac{BM}{CT}=\frac{MN}{TN}=\frac{BN}{CN}\]
В частности, опять же $CT=\frac{BM\cdot CN}{BN}$.
Теперь осталось сравнить два полученных значения для отрезка $CT$:
\[CT=\frac{AM\cdot CK}{AK}=\frac{BM\cdot CN}{BN};\]
\[AM\cdot BN\cdot CK=BM\cdot CN\cdot AK;\]
\[\frac{AM\cdot BN\cdot CK}{BM\cdot CN\cdot AK}=1;\]
\[\frac{AM}{BM}\cdot \frac{BN}{CN}\cdot \frac{CK}{AK}=1;\]
Ну вот и всё. Осталось только «причесать» эту формулу, правильно расставив буквы внутри отрезков — и формула готова.:)
Смотрите также:
- Как применяется теорема косинусов и подобие треугольников для решения широкого класса задач в планиметрии.

- Что такое теорема косинусов и как она помогает решать геометрические задачи

- Пробный ЕГЭ 2012. Вариант 5 (без производных)

- Специфика работы с логарифмами в задаче B15

- Учимся расщеплять ответы в тригонометрических уравнениях

- Что такое обход точек

www.berdov.com
Применение теорем Менелая и Чевы для решения задач. 9-й класс
Цели урока:
- обобщить, расширить и систематизировать знания и умения учащихся; научить использовать знания при решении сложных задач;
- способствовать развитию навыков самостоятельного применения знаний при решении задач;
- развивать логическое мышление и математическую речь учащихся, умение анализировать, сравнивать и обобщать;
- воспитывать у учащихся уверенность в себе, трудолюбие; умение работать в коллективе.
Задачи урока:
- Образовательная: повторить теоремы Менелая и Чевы; применить их при решении задач.
- Развивающая: учить выдвигать гипотезу и умело доказательно отстаивать свое мнение; проверить умение обобщать и систематизировать свои знания.
- Воспитательная: повысить интерес к предмету и подготовить к решению более сложных задач.
Тип урока: урок обобщения и систематизации знаний.
Оборудование: карточки для коллективной работы на уроке по данной теме, индивидуальные карточки для самостоятельной работы, компьютер, мультимедийный проектор, экран.
Ход урока
I этап. Организационный момент (1 мин.)
Учитель сообщает тему и цель урока.
II этап. Актуализация опорных знаний и умений (10 мин.)
Учитель: На уроке вспомним теоремы Менелая и Чевы для того, чтобы успешно перейти к решению задач. Давайте вместе с вами посмотрим на экран, где представлен. Для какой теоремы дан этот рисунок? (теорема Менелая). Постарайтесь четко сформулировать теорему.
Рисунок 1
Пусть точка A1 лежит на стороне BC треугольника АВС, точка C1 – на стороне AB, точка B1 – на продолжении стороны АС за точку С. Точки A1, B1и C1 лежат на одной прямой тогда и только тогда, когда выполняется равенство
Учитель: Давайте вместе рассмотрим следующий рисунок. Сформулируйте теорему для этого рисунка.
Рисунок 2
Прямая AD пересекает две стороны и продолжение третьей стороны треугольника ВМС.
По теореме Менелая
Прямая МВ пересекает две стороны и продолжение третьей стороны треугольника АDС.
По теореме Менелая
Учитель: Какой теореме соответствует рисунок? (теорема Чевы). Сформулируйте теорему.
Рисунок 3
Пусть в треугольнике АВС точка A1лежит на стороне ВС, точка B1 – на стороне АС, точка C1 – на стороне АВ. Отрезки AA1, BB1и CC1 пересекаются в одной точке тогда и только тогда, когда выполняется равенство
III этап. Решение задач. (22 мин.)
Класс разбивается на 3 команды, каждая получает карточку с двумя различными задачами. Дается время на решение, затем на экране появляются <Рисунки 4-9>. По готовым чертежам к задачам представители команд поочередно объясняют свое решение. После каждого объяснения следует обсуждение, ответы на вопросы и проверка правильности решения на экране. В обсуждении принимают участие все члены команд. Чем активнее команда, тем выше она оценивается при подведении итогов.
Карточка 1.
1. В треугольнике АВС на стороне ВС взята точка N так, что NC = 3BN; на продолжении стороны АС за точку А взята точка М так, что МА = АС. Прямая MN пересекает сторону АВ в точке F. Найдите отношение
2. Докажите, что медианы треугольника пересекаются в одной точке.
Решение 1
Рисунок 4
По условию задачи МА = АС, NC = 3BN. ПустьMA = AC =b, BN = k, NC = 3k. Прямая MNпересекает две стороны треугольника АВС и продолжение третьей.
По теореме Менелая
Ответ:
Доказательство 2
Рисунок 5
Пусть AM1, BM2, СM3 – медианы треугольника АВС. Чтобы доказать, что эти отрезки пересекаются в одной точке, достаточно показать, что
Тогда по теореме Чевы (обратной) отрезки AM1, BM2 и СM3 пересекаются в одной точке.
Имеем:
Итак, доказано, что медианы треугольника пересекаются в одной точке.
Карточка 2.
1. На стороне PQтреугольника PQR взята точка N, а на стороне PR – точка L, причем NQ = LR. Точка пересечения отрезков QL и NR делит QL в отношении m:n, считая от точки Q. Найдите
2. Докажите, что биссектрисы треугольника пересекаются в одной точке.
Решение 1
Рисунок 6
По условию NQ = LR, ПустьNA = LR =a, QF = km, LF = kn. Прямая NR пересекает две стороны треугольника PQL и продолжение третьей.
По теореме Менелая
Ответ:
Доказательство 2
Рисунок 7
Покажем, что
Тогда по теореме Чевы (обратной) AL1, BL2, CL3 пересекаются в одной точке. По свойству биссектрис треугольника
Перемножая почленно полученные равенства, получаем
Для биссектрис треугольника равенство Чевы выполняется, следовательно, они пересекаются в одной точке.
Карточка 3.
1. В треугольнике АВС AD – медиана, точка O – середина медианы. Прямая ВО пересекает сторону АС в точке К. В каком отношении точка К делит АС, считая от точки А?
2. Докажите, если в треугольник вписана окружность, то отрезки, соединяющие вершины треугольника с точками касания противоположных сторон, пересекаются в одной точке.
Решение 1
Рисунок 8
Пусть BD = DC = a, AO = OD = m. Прямая ВК пересекает две стороны и продолжение третьей стороны треугольника ADC.
По теореме Менелая
Ответ:
Доказательство 2
Рисунок 9
Пусть A1, B1и C1 – точки касания вписанной окружности треугольника АВС. Для того чтобы доказать, что отрезки AA1, BB1и CC1 пересекаются в одной точке, достаточно показать, что выполняется равенство Чевы:
Используя свойство касательных, проведенных к окружности из одной точки, введем обозначения: C1B = BA1 = x, AC1 = CB1 = y, BA1 = AC1 = z.
Равенство Чевы выполняется, значит, биссектрисы треугольника пересекаются в одной точке.
IV этап. Решение задач (самостоятельная работа) (8 мин.)
Учитель: Работа команд закончена и сейчас приступим к самостоятельной работе по индивидуальным карточкам для 2-х вариантов.
Материалы к уроку для самостоятельной работы учащихся
Вариант 1. В треугольнике АВС, площадь которого равна 6, на стороне AB взята точка К, делящая эту сторону в отношении АК:BK = 2:3, а на стороне АС – точка L, делящая АС в отношении AL:LC = 5:3. Точка Qпересечения прямых СК и BL удалена от прямой AB на расстоянии . Найдите длину стороны АВ. (Ответ: 4.)
Вариант 2. На стороне АС в треугольнике АВС взята точка К. АК = 1, КС = 3. На стороне АВ взята точка L. AL:LВ = 2:3, Q – точка пересечения прямых ВК и СL. Найдите длину высоты треугольника АВС, опущенной из вершины В. (Ответ: 1,5.)
Работы сдаются учителю для проверки.
V этап. Итог урока (2 мин.)
Анализируются допущенные ошибки, отмечаются оригинальные ответы и замечания. Подводятся итоги работы каждой команды и выставляются оценки.
VI этап. Домашнее задание (1 мин.)
Домашнее задание составлено из задач №11, 12 стр. 289-290, №10 стр. 301 [1].
Заключительное слово учителя (1 мин).
Сегодня вы услышали со стороны математическую речь друг друга и оценили свои возможности. В дальнейшем, будем применять такие обсуждения для большего понимания предмета. Аргументы на уроке дружили с фактами, а теория с практикой. Вам всем спасибо.
Литература:
- Ткачук В.В. Математика абитуриенту. – М.: МЦНМО, 2005.
urok.1sept.ru
Применение теорем Чевы и Менелая при решении задач ЕГЭ
 Выпускная работа
Выпускная работа
Тема: «Применение теорем Чевы и Менелая
при решении геометрических задач ЕГЭ»
Содержание
Теоретические факты:
Применение теорем Чевы и Менелая при подготовке к ЕГЭ
Теоретические факты
Решение задач с помощью теорем Чевы и Менелая более рационально, чем их решение другими способами, требующими дополнительных действий и построений, которые не всегда оказываются очевидными.
Теорема Чевы.
С
Если на сторонах AB, BC и CA треугольника ABC взяты соответственно точки C1, A1 и B1 (рис.1), то отрезки AA1, BB1 и CC1 пересекаются в одной точке тогда и только тогда, когда выполнено равенство

Теорема Менелая.
Если на сторонах ВС, АВ и продолжении стороны АС треугольника АВС за точку С отмечены соответственно точки А´, С´,В´, лежащие на одной прямой, то 
Применение теорем Чевы и Менелая при подготовке к ЕГЭ
Хочу вам предложить два способа решения одной интересной задачи из ЕГЭ. Первый способ довольно длинный, но его нужно знать, поскольку прием, который в нем используется, применяется довольно часто при решении задач, в которых дано отношение отрезков.
Второй способ позволяет решить задачу в одно действие, но в нем используется Теорема Менелая.
Итак задача №1:
На сторонах AB и BC треугольника ABC взяты соответственно точки M и N так, что AM:MB=2:3, BN:NC=2:1. Отрезки AN и CM пересекаются в точке O. Найти отношение CO:OM.
Вот наш треугольник:
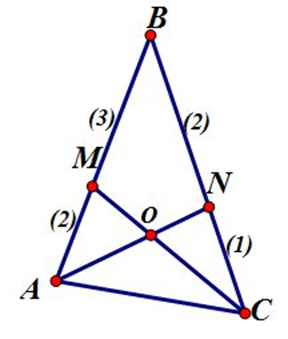
Проведем через точку В прямую параллельно отрезку AB, затем продолжим отрезок AN до пересечения с этой прямой и поставим там точку К:

Рассмотрим треугольники ANC и BNK. Эти треугольники подобны, так как AC||BK. Стороны треугольника BNK относятся к сторонам треугольника ANC как 2:1.
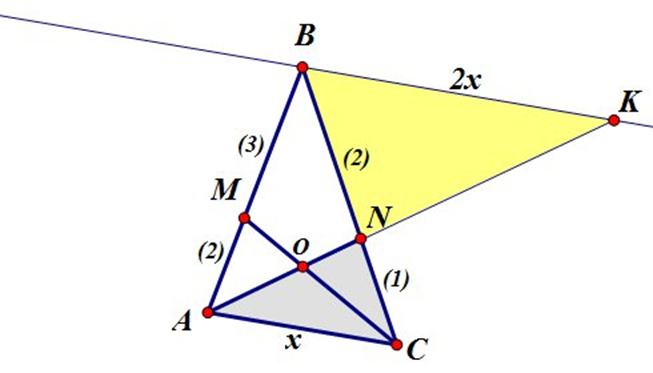
Пусть AC=x, BK=2x.
Теперь продолжим отрезок MC до пересечения с прямой BK. Поставим там точку L.

Мы получили подобные треугольники LMB и AMC, сходственные стороны которых относятся как 3:2. Так как AC=x, то LB=1,5x.
Пусть LM=3n, MC=2n. Тогда LC=5n.
Теперь рассмотрим подобные треугольники LOK и AOC.

 , следовательно,
, следовательно, 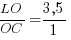 . Пусть LO=3,5z, OC=z. Тогда LO+OC=LC=4,5z.
. Пусть LO=3,5z, OC=z. Тогда LO+OC=LC=4,5z.
Получили, что 5n=4,5z. Тогда MC=2n= z. Отсюда MO=MC-CO=
z. Отсюда MO=MC-CO= z-z=
z-z= z
z
Отсюда CO:OM=z: z=5:4=1,25.
z=5:4=1,25.
Ответ: 1,25
Применим теорему Менелая к нашей задаче. Рассмотрим треугольник MBC и прямую AN:

Запишем теорему Менелая для этого треугольника:
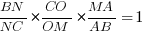
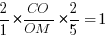
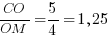
Ответ: 1,25
Задача №2.
Точки В´ и С´ лежат на сторонах соответственно АС и АВ ∆АВС, причем АВ´:В´С=АС´:С´В. Прямые ВВ´ и СС´ пересекаются в точке О.
а) Доказать, что прямая АО делит пополам сторону ВС.
б) Найти отношение площади четырехугольника АВ´ОС´ к площади ∆АВС, если АВ´:В´С=АС´:С´=1:2.
а)Доказать, что прямая АО делит пополам сторону ВС.
Докажем, что ВК=КС. Используем теорему Чевы. 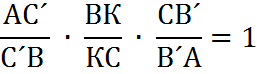
т.к. 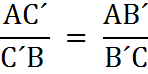 , то ВК=КС
, то ВК=КС
б) Найти отношение площади четырехугольника АВ´ОС´ к площади ∆АВС, если АВ´:В´С=АС´:С´В=1:2.
Т.к. АВ´:АС= 1:3, то

По теореме Менелая найдем 
Для ∆АВВ´ и секущей СС´:
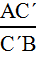


 ,
, 
Значит 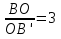
 , значит
, значит 
 =
= 
Найдем  .
.
Ответ: 
Используемая литература
Учебник «Геометрия»10-11кл.: Л.С. Атанасян, В.Ф. Бутузов и др.-М.: Просвещение, 2011.
Атанасян Л.С., Бутузов В.Ф., Кадомцев С. Б., Шестаков С.А., Юдина И.И. Геометрия. Доп. главы к учебнику 8 кл.: Учеб. пособие для учащихся школ и классов с углубл. изуч. математики / Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др.-М.: Вита-пресс, 2008.
Математика. ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под ред. А.Л.Семенова, И.В.Ященко. 2013г.
Математика. ЕГЭ-2014. Под ред. А.Л.Семенова, И.В.Ященко. 2014г.
Математика. ЕГЭ-2014. Под ред. А.Л.Семенова, И.В.Ященко. 2015г.
Математика. Подготовка к ЕГЭ. Под ред.Ф.Ф.Лысенко. 2014г
Математика. Подготовка к ЕГЭ. Под ред.Ф.Ф.Лысенко. 2015г.
Математика. Подготовка к ЕГЭ. Под ред.Ф.Ф.Лысенко. 2016г.
Журнал математика в школе. М.: 2014
Пособие по геометрии. Часть І. Планиметрия, векторы. В помощь учащимся 10-11-х кл.О.В.Нагорнов, А.В.Баскаков и др.М.:НИЯУ МИФИ,2009.
Пособие по геометрии. Часть І. Планиметрия, векторы. В помощь учащимся 10-11-х кл.О.В.Нагорнов, А.В.Баскаков и др.М.:НИЯУ МИФИ,2009.
http://hijos.ru/2011/03/16/teorema-chevy/
http://www.resolventa.ru/demo/inform/demoinform.htm
http://fipi.ru/
http://alexlarin.net/
infourok.ru
Применение теоремы Чевы и Менелая при решении геометрических задач
Применение теоремы Чевы и Менелая при решении геометрических задач
Расмухамбетов А.А. 11МБОУ «Адамовская СОШ №1 им М.И.Шеменева»
Дильжанов А.Л. 11МБОУ «Адамовская СОШ №1 им М.И.Шеменева»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
«Прежде, чем думать о решении будущих задач, научитесь справляться с сегодняшними за наименьшее время и с большей эффективностью.»
Друкер П.
При решении мы сталкиваемся не только с проблемами поиска решений, но и выборе наиболее рационального способа решения задач.
В школьном учебнике геометрии Л.С. Атанасяна для 7-9 классов теорем Чевы и Менелая не изучаются. Однако применение теорем Чевы и Менелая помогает нам решать задачи повышенного уровня сложности более рационально, чем метод подобия и применения дополнительных построений.
Эти теоремы просты, интересны и лаконичны. Их можно применять как при решении задач профильного уровня, так и простых задач.
При подготовке к основному государственному экзамену и олимпиадам школьников по математике я встретился с задачами по геометрии, связанными с нахождением отношений длин отрезков и площадей в треугольнике, которые я не смог решить.
Проблема: Можно ли решить задачи, связанные с отношениями длин отрезков и площадей в треугольнике, без дополнительного построения?
Актуальность темы: данная тема является дополнением и углублением изученных в курсе геометрии свойств треугольника. Изучение данной темы является основательной и более глубокой подготовкой к Государственной Итоговой Аттестации и к олимпиадам. При решении задач с применением теорем Чевы и Менелая развивается уровень пространственного воображения и уровень логической культуры.
Объект исследования: решение геометрических задач, связанных с нахождением отношений длин отрезков и площадей в треугольнике.
Предмет исследования: теоремы Чевы и Менелая.
Цель исследования: ознакомление с теоремами Чевы и Менелая, применение теорем при решении геометрических задач, подготовка к Основному Государственному Экзамену и олимпиадам, проверить целесообразность применения теорем при решении задач
Задачи:
Выявить теоретические положения для доказательства теорем;
«Открыть» и систематизировать теоретический материал для доказательства теорем Чевы и Менелая;
Изучить состояние проблемы в школьной программе геометрии;
Проверить эффективность применения теорем при решении задач по сравнению с другими теоремами;
Сравнить способы решения задач традиционным способом и с использованием теорем Чевы и Менелая;
Собрать банк ключевых задач.
Научная новизна исследования состоит в том, чтобы доказать теоремы Чевы и Менелая разными способами.
Гипотеза: Знание теорем Чевы и Менелая один из способов простого и изящного решения сложных планиметрических задач.
Методы исследования:
Теоретический;
Общенаучный.
Историческая справка
Джованни Чева (рис.1)родился 7 декабря в 1647 году в Италии. Он окончил иезуитский колледж в Милане, после чего стал студентом Университета в Пизе , где позже и стал работать профессором математики. С 1686 года Чева работал в университете в Мантуе, оставаясь на этом посту до самого конца своей жизни. Большую часть жизни Чева изучал геометрию, стараясь возродить греческую геометрию; кроме того, сегодня его помнят и по изысканиям в области механики.
В 1678-м Чева опубликовал свою, ставшую знаменитой, теорему «О взаимно пересекающихся прямых» о синтетической геометрии треугольника; теорема эта впоследствии получила его имя — теорема Чевы. Теорема эта сегодня является классической теоремой геометрии треугольника. Кстати, отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется чевианой — также по имени Джованни Чевы. Можно сказать, что эта теорема служит фундаментом всей геометрии треугольника. Джованни Чева умер 15 июня 1734 года, в возрасте 85 лет; смерть его последовала во время осады Мантуи франко-сардинской армией.
Менела́й Александри́йский (рис.2) (ок. 100 н. э.) — древнегреческий математик и астроном. Время его жизни и деятельности определяется приведёнными в «Алмагесте» Птолемея двумя астрономическими наблюдениями, которые Менелай произвёл в Риме в первом году царствования Траяна, то есть в 98 году н. э..
Менелаем были написаны не дошедшие до нас сочинения «О вычислении хорд» в 6 книгах, «Начала геометрии» в 3 книгах, «Книга о треугольнике», «Книга о заходах знаков зодиака».
Менелай изучал кривые высших порядков. Особенным его вниманием, по словам Паппа, пользовалась одна кривая, которая была названа им «необыкновенной линией». Какая это была кривая, из слов Паппа, однако же, определить нельзя. По мнению Поля Таннери, она представляла собой кривую, образующуюся при пересечении сферы и кругового цилиндра, радиус которого вдвое меньше радиуса сферы, а образующая проходит через центр. Эта кривая возникает в решении задачи об удвоении куба, принадлежащем Архиту Тарентскому, а из трактата братьев Бану Муса известно, что Менелай занимался этим решением.
Доказательства теоремы Чевы
Т еорема Чевы. Пусть точки А1 , В1, С1 лежат на сторонах ВС, АС и АВ треугольника АВС соответственно. Пусть отрезки АА1, ВВ1 и СС1 пересекаются в одной точке. Тогда
Доказательство. Пусть отрезки АА1, ВВ1 и
СС1 пересекаются в однойточке O. Проведем
через вершину B треугольника прямую a║AC
Пусть прямые АА1 и ВВ1 пересекают прямую a в точках M и N соответственно. Тогда из подобия треугольников АА1С и МА1В1 по двум углам ( как накрест лежащие и как вертикальные ) имеем:
А налогично из подобия треугольников АС1С и ВС1N по двум углам
( и – как пары накрест лежащих):
Наконец, из подобия треугольников OAC и OMN по двум углам
( и ) получаем
Перемножив соответственно правые и левые части выписанных равенств, получим необходимое равенство.
Достаточность. Пусть выполнено равенство. Покажем, что отрезки AA1, BB1 и CC1 проходят через одну точку.
Пусть O – точка пересечения отрезков AA1 и CC1 а C’ – точка пересечения отрезка AB с лучом CO. Тогда из только что доказанного следует, что
С равнивая с условием теоремы, получим Следовательно, точки C’ и C1 совпадают.
П редложим еще один способ доказательства теоремы Чевы, использующий понятие площади.
Доказательство. Пусть O – точка пересечения
AA1, BB1 и CC1. Опустим из вершин A и C
перпендикуляры на прямую BB1.
L и K – основания перпендикуляров.(рис.4)
Теорема доказана.
Вот еще один способ доказательства теоремы Чевы:
Доказательство.
Пусть точки A1, B1, C1 принадлежат одной прямой a.
Опустим из вершин треугольника ABC
перпендикуляры AA’, BB’, CC’ на эту прямую
( рис. 5). Треугольники AC1A’ и BC1B’ подобны и,
следовательно,
Аналогичным образом показывается, что и
Перемножая эти три равенства, будем иметь требуемое равенство.
Доказательства теоремы Менелая
Теорема Менелая. Пусть прямая пересекает треугольник ABC, причём C1 – точка пересечения со стороной AB, A1 – со стороной BC, B1 – с продолжением стороны AC.
Тогда выполняется равенство:
Д оказательство. Проведём через точку
C прямую CK параллельно AB
(K – точка пересечения с C1B1)
Теорема доказана.
Решение задач с помощью теоремы Чевы
Задача 1. Точки C1 и A1 делят стороны AB и BC треугольника ABC в отношении 1:2. Прямые CC1 и AA1 пересекаются в точке O. Найдите
З адача 2. Докажите, что прямые, проходящие через вершины треугольника и точки касания вписанной окружности пересекаются в одной точке, называемой точкой Жергона.
З адача 3. Докажите, что прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей пересекаются в одной точке, называемой точкой Нагеля.
Решение задач с помощью теоремы Менелая
Задача 1. Точки В´ и С´ лежат на сторонах соответственно АС и АВ ∆АВС, причем АВ´:В´С=АС´:С´В. Прямые ВВ´ и СС´ пересекаются в точке О.
а) Доказать, что прямая АО делит пополам сторону ВС.
б) Найти отношение площади четырехугольника АВ´ОС´ к площади ∆АВС, если АВ´:В´С=АС´:С´=1:2.
Задача 2. На сторонах AB и BC треугольника ABC взяты соответственно точки M и N так, что AM:MB=2:3, BN:NC=2:1. Отрезки AN и CM пересекаются в точке O. Найти отношение CO:OM.
Сравнение решения задач с помощью теорем и другими способами
Задача 1. Доказать, что точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2:1, считая от вершины.
З адача 2. Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая, пересекающая сторону ВС в точке Р. Наудите отношение площади треугольника АВК к площади четырехугольника КРСМ.
Банк задач
Точка С1 и А1 делят стороны АВ и ВС треугольника АВС в отношении 1:2. Прямые СС1 и АА1 пересекаются в точке О. Найдите отношение, в котором прямая ВО делит сторону АС.
Точка А1 и В1 делят стороны ВС и АС треугольника АВС в отношениях 2:1 и 1:2. Прямые АА1 и ВВ1пересекаются в точке О. Площадь треугольника АВС равна 1. Найдите площадь треугольника. ОВС.
В треугольнике АВС точки D и К лежат соответственно на сторонах АВ и АС, отрезки ВК и CD пересекаются в точке О, при этом ВО : ОК = 3:2 и CO:OD =2:1. Найти в каком отношении точка К делит сторону АС, т.е. АК : КС.
Точка D и F лежат на сторонах ВС и АС треугольника АВС, отрезки AD и BF пересекаются в точке О. Известно, что AF:FC =3:2 и ВО = OF. Чему равно отношение BD:DC?
Площадь треугольника ABC равна 80. Биссектриса AD пересекает медиану BK в точке E, при этом BD:CD=1:3. Найдите площадь четырехугольника EDCK.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK : KM = 4 : 1. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 9:7. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
В треугольнике АВС точка D на стороне ВС и точка F на стороне АС расположены так, что ВD:DC=3:2, AF:FC=3:4. Отрезки AD и BF пересекаются в точке Р. Найдите отношение АР:PD.
Заключение
Теоремы Чевы и Менелая казались сложными и непонятными на первый взгляд, но они оказались простыми и интересными.
Теоремы Чевы и Менелая находят применение в задачах, в которых присутствуют секущие прямые. Они не изучаются в курсе 7-9 классов. Но решение с помощью теорем Чевы и Менелая более рационально, чем решение другими способами.
Я считаю, что теоремы Чевы и Менелая должны быть включены в курс 7-9 классов, потому что они расширяют кругозор ученика, дают возможность решать задачи просто и легко.
Я думаю, что исследование, проведенное мной, поможет мне хорошо сдать экзамены.
Литература и ссылки
Смирнова, И.М. Материалы курса «Геометрия на профильном уровне обучения» : лекции 1-4/И.М. Смирнова, В.А. Смирнов.-Москва: Педагогический университет «Первое сентября», 2006.-76 с.
http://biozvezd.ru/dzhovanni-cheva
https://ru.wikipedia.org/wiki/Менелай_Александрийский
https://mathematics.ru/courses/planimetry/content/chapter14/section/paragraph2/theory.html
https://studopedia.ru/7_132766_okruzhnost-apolloniya.html
https://studopedia.ru/7_132764_teorema-menelaya-pryamaya-i-obratnaya.html
https://infourok.ru/primenenie-teorem-chevi-i-menelaya-pri-reshenii-zadach-ege-621402.html
http://www.geometry2006.narod.ru/Lessons/Lessons7-9.htm
Приложение
Рис. 1 Джованни Чева
Рис. 2 Менелай Александрийский
Анкетирование учащихся 9-ых классов.
Заключение анкетирования: На основе опроса учащихся 9-ых классов можно сделать вывод, что 63% учеников не знают теорему Менелая, 83% теорему Чевы. 29% Учащихся использовали теоремы Менелая и Чевы. Приблизительно половина учеников считают, что данные теоремы должны быть включены в школьный курс. Также после опроса было выявлено, что 71% учащихся решают задачи # 26 ОГЭ, связанные с отношением длин отрезков и площадей. Можно сказать, что ученики в основном не используют данные теоремы, так как не знают об их существовании.
Просмотров работы: 200
school-science.ru
Теорема Менелая и ее применение при решении задач (подготовка к ЕГЭ)

Теорема Менелая и ее применение при решении задач (подготовка к ЕГЭ)
Методическая разработка
Рудаковой Татьяны Викторовны
Учителя математики МБОУ «Гимназия № 2»
г. Курчатова Курской области

Содержание
- Теоретические факты:
а) пропорциональные отрезки в треугольниках
б) отношение площадей треугольников.
- Теорема Менелая.
- Применение теоремы для решения задач.

Теоретические факты
Теоремы об отношении площадей треугольников
Теорема Фалеса
1. Если угол одного треугольника равен углу другого треугольника, то отношение площадей этих треугольников равно отношению произведений сторон, содержащих эти углы
Параллельные прямые пересекая стороны угла, отсекают на них пропорциональные отрезки.
С´
В´
В
А´
О
С
В
А
К
С
А
М

Теоремы об отношении площадей треугольников
3.Отношение площадей треугольников,
2. Пусть ∆АВС и ∆АВD имеют общую сторону АВ. Тогда отношение их площадей равно отношению высот, проведенных из вершин С и D.
имеющих равные высоты равно
отношению оснований:
S(∆АВС) : S(АВD) = СР:DQ.
S(∆АВС) : S(АВD) =AC:АD.
В
С
D
D
С
P
А
Q
А
В
P

Задача.(Р.К.Гордин.Математика.ЕГЭ-2014.ЗадачаС4.№6.3) На стороне ВС треугольника АВС и на продолжении стороны АВ за вершину В расположены точки М и К соответственно, причем ВМ:МС = 4:5 и ВК:АВ=1:5. Прямая КМ пересекает сторону АС в точке N. Найти отношение СN: АN.
Решение
- Проведем ВР параллельно КМ.
- По теореме Фалеса для угла NАК:
- По теореме Фалеса для угла ВСР:
4. Итак, z=4d , тогда АN= 6z=24d , значит СN:АN=5:24.
Ответ: 5:24
С
N
5d
N
5х
z
4d
Р
М
5z
4х
К
4x
у
В
5у
А

Предложенный вариант решения задачи – один из традиционных, без применения теоремы Менелая.
Рассмотрим другой (более рациональный) способ решения, применяя указанную теорему
Теорема Менелая
Пусть на сторонах AB, BC и на продолжении стороны AC ∆ABC взяты соответственно точки С´, А´ и В´, не совпадающие с вершинами ∆ABC. Точки лежат на одной прямой тогда и только тогда, когда выполняется равенство
Для дальнейшего решения задач воспользуемся необходимым условием данной теоремы.

Теорема Менелая
Если на сторонах ВС, АВ и продолжении стороны АС треугольника АВС за точку С отмечены соответственно точки А´, С´,В´, лежащие на одной прямой, то
В
С´
А´
В´
С
А
3

Доказательство
- Проведем СК //АВ, тогда ∆СКВ´ ~ ∆ АС´В´ , поэтому
СК =
2. ∆ СКА´ ~ ∆ВС´А´ , поэтому
3. Подставляя СК из п.1, имеем
В
С´
А´
К
С
В´
А

Задача. (Р.К.Гордин.Математика.ЕГЭ-2014.ЗадачаС4.№6.3) На стороне ВС треугольника АВС и на продолжении стороны АВ за вершину В расположены точки М и К соответственно, причем ВМ:МС = 4:5 и ВК:АВ=1:5. Прямая КМ пересекает сторону АС в точке N. Найти отношение СN: АN.
Стрелки на рисунке (от точки А) показывают, как легко запомнить последовательность отрезков в пропорции .
Найдем
Ответ:
С
5х
N
M
у
K
4х
В
А
5у

Задача . (Р.К.Гордин. Математика. ЕГЭ-2014. ЗадачаС4. №6.10) В треугольнике АВС АВ=с, ВС=а, АС=в. В каком отношении центр вписанной окружности треугольника делит биссектрису СD?
Решение:
- Для треугольника ВСD и секущей АК:
ДА =
Найти:
Ответ:
3. Найдем :
С
К
О
В
D
А

Задача . (Р. К. Гордин. Математика. ЕГЭ-2014. Задача С4. №6.14) В ∆ АВС, площадь которого равна 6, на стороне АВ взята т.К, делящая эту сторону в отношении АК:ВК=2:3, а на стороне АС взята т. L, делящая АС в отношенииAL:LС=5:3. Точка Q пересечения прямых СК и ВL отстоит от прямой АВ на расстояние 1,5. Найти сторону АВ.
Решение:
- Для тр. АСК и секущей ВL найдем отношение CQ:QK.
2. Проведем высоту СР. СР// QH.
3. По теореме Фалеса Н – середина РК, тогда QH-средняя линия СРК, значит СР=3.
4. S (АВС) =0,5 АВ•СР, тогда АВ=2S(АВС) :СР=4.
Ответ: АВ = 4.
С
3y
L
Q
5y
Р
В
К
3x
H
2x
А

Задача.( Математика ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под редакцией А.Л.Семенова, И.В.Ященко. Трениров.работа 28. С4) На сторонах АВ, ВС и АС ∆АВС взяты соответственно точки К, L и М, причем АК:КВ=2:3, ВL:LС=1:2, СМ:МА=3:1. В каком отношении отрезок КL делит отрезок ВМ?
Решение:
- Для ∆АВС и секущей КL:
2. АР = РС = АС = 4 z = 2 z, значит
=
Найти
3. Для ∆АВМ и секущей КL:
Ответ:
В
у
L
3х
О
2у
К
2х
С
А
Р
М
z
2z
3z

Задача. (Сайт А.А.Ларина. Тренировочный вариант №67. от 09.03.2014. С4) В ∆АВС на сторонах АВ, ВС, и СА отложены соответственно отрезки АD =⅓ АВ, ВЕ = ⅓ ВС, СF = ⅓ CА. а) доказать, что , где М = АЕ ∩ СD, К = СD ∩ ВF, N = АЕ∩ВF. б) найти, какую часть от площади ∆АВС составляет площадь ∆MNK.
- Для ∆АВF и секущей DC:
а) докажем, что
2. Для ∆АЕС и секущей FВ:
3. Для ∆DBC и секущей ЕА аналогично
В
у
Е
2 х
N
2у
D
М
К
х
С
А
F
z
2z

Задача. (Сайт А.А.Ларина. Тренировочный вариант №67. от 09.03.2014. С4) В ∆АВС на сторонах АВ, ВС, и СА отложены соответственно отрезки АD =⅓ АВ, ВЕ = ⅓ ВС, СF = ⅓ CА. б) найти, какую часть от площади ∆АВС составляет площадь ∆MNK.
б) Итак,
Тогда
Ответ:
В
E
N
М
М
D
K
К
С
А
F

Заключение Решение задач с помощью теоремы Менелая более рационально, чем их решение другими способами, требующими дополнительных действий и построений, которые не всегда оказываются очевидными. Теорема Менелая помогает быстро и оригинально решить задачи повышенной сложности, в том числе и задачи уровня С единого государственного экзамена.
Используемая литература
- ЕГЭ 2014.Математика. Задача С4. Гордин Р.К. Под ред. Семенова А.Л.2013г.
- Математика. ЕГЭ-2014. Типовые тестовые задания. 30 вариантов. Под ред. А.Л.Семенова, И.В.Ященко. 2014г.
- http://alexlarin.net/ege/2014/trvar67.html
kopilkaurokov.ru
Простой способ решения непростых геометрических задач
Слайд 1
Исследовательская работа на тему: «Простой способ решения непростых геометрических задач» Выполнила: ученица 8 класса «А» Каратецкая Мария Руководитель: учитель математики Колина Наталья Константиновна «Правильный взгляд на математику открывает не только истину, но и безупречную красоту…» Бертран РасселСлайд 2
Задача . На стороне AB треугольника ABC отмечена точка K . Отрезок CK пересекает медиану AM треугольника в точке P , причем AK =АР. Найти отношение BK : PM . Теорема Фалеса Подобие треугольников Дополнительное построение! Проблема
Слайд 3
Гипотеза: существуют более простые способы решения задач, связанных с отрезками в треугольнике. Актуальность темы: решения задач на отношение длин обычными методами получаются достаточно объёмными и сложными. Алгебраический метод с помощью теорем Менелая и Чевы – наиболее рациональный способ решения подобных задач.
Слайд 4
Цели: «открыть» разные способы решения задач, связанных с нахождением отношений длин отрезков и площадей в треугольниках и четырехугольниках; найти наиболее простой способ решения такого типа задач
Слайд 5
найти, изучить и проанализировать литературу по теме исследования; использовать разные способы для решения задач, связанных с отношениями длин отрезков и площадей в треугольнике; «открыть» теоремы Менелая и Чевы и показать их приложения; повысить уровень культуры решения геометрических задач; научиться решать интересные, сложные геометрические задачи алгебраическим способом. развивать навыки исследовательской работы . Задачи:
Слайд 6
Пусть на сторонах AB, BC и на продолжении стороны AC ∆ABC взяты соответственно точки C 1 ,A 1 и B 1 , не совпадающие с вершинами ∆ABC . Точки A 1 , B 1 , C 1 лежат на одной прямой тогда и только тогда, когда выполняется равенство Теорема Менелая
Слайд 7
Пусть в ∆ ABC на сторонах BC,AC,AB или их продолжениях взяты соответственно точки A 1 , B 1 и C 1 ,не совпадающие с вершинами треугольника. Прямые A A 1 , BB 1 и CC 1 пересекаются в одной точке или параллельны тогда и только тогда, когда выполняется равенство Теорема Чевы
Слайд 8
Задача1. Доказать, что биссектрисы в треугольнике пересекаются в одной точке. Задача2. Доказать, что медианы в треугольнике пересекаются в одной точке. Задача3. Доказать с помощью теоремы Чевы, что высоты в треугольнике пересекаются в одной точке. Применение теорем Менелая и Чевы в решении геометрических задач
Слайд 9
Задача 4. На сторонах АВ и ВС треугольника АВС взяты соответственно точки М и N так, что АМ:МВ=2:3, BN : NC =2:1. Отрезки AN и C М пересекаются в точке О. Найдите отношение СО : ОМ. Задача 5 . В АВС точки А ,В ,С лежат соответственно на сторонах ВС, АС,АВ ,причем отрезки АА ,ВВ ,СС пересекаются в точке О. АС:СВ=1:3; ВА :АС=3:2.Найдите отношение АВ :В С. В каком отношении точка О делит отрезок АА ? Какую часть площади АВС составляет площадь АВВ ? Применение теорем Менелая и Чевы в решении геометрических задач
Слайд 10
Задача 6 . На сторонах AC и BC треугольника ABC отмечены точки N и K так, что AN : NC = m : n , AK BN = Q , BQ : QN = p : q . Найти отношение площадей треугольников AKC и ABK . Задача7. Через вершину B проведена прямая, параллельная биссектрисе С и пересекающая продолжение стороны АС в точке D . Пусть Е – середина отрезка В D . Определить, в каком отношении прямая АЕ делит площадь , если известно, что АС=5, ВС=10. Применение теорем Менелая и Чевы в решении геометрических задач
Слайд 11
Историческая справка Менелай Александрийский- древнегреческий математик и астроном. Автор работ по сферической тригонометрии. Также упоминается как автор книги по гидростатике.
Слайд 12
Джованни Чева — итальянский математик и инженер, доказавший теорем Чевы о геометрии треугольника, положил начало новой синтетической геометрии. Историческая справка
Слайд 13
Итак, я изучала одни из самых интересных теорем: теоремы Менелая и Чевы; научилась с их помощью решать разнообразные задачи, тем самым сокращая и упрощая их решения. Я считаю, что эти теоремы очень полезны для учащихся, особенно тем, кто серьезно занимается математикой и участвует в олимпиадах по предмету. В дальнейшем я хочу ознакомиться с еще одним способом решения задач на отношение длин отрезков — методом геометрии масс, сравнить этот способ с рассмотренным мной в работе. Заключение
Слайд 14
Литература Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.Геометрия: Учебник для 7-9 классов средней школы / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2014. Атанасян Л.С., Бутузов В.Ф., Кадомцев С. Б., Шестаков С.А., Юдина И.И. Геометрия. Доп. главы к учебнику 8 кл.: Учеб. пособие для учащихся школ и классов с углубл. изуч. математики / Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др.-М.: Вита-пресс, 2006. Качалкина Е.Применение теорем Чевы и Менелая/Математика. Издательский дом «Первое сентября», 2004, — №13,№14 Колина Н.К. Теорема Менелая и теорема Чевы в школьном курсе математики. Учебно-методическое пособие.-Н.Новгород,2007г. Шарыгин И.Ф. Геометрия 7-9 кл.: Учеб. для общеобразоват. учеб.завед.-М.,Дрофа,2012г Шестаков С.А. Сборник задач для подготовки и проведения письменного экзамена по алгебре за курс основной школы: 9-й кл.–М: АСТ:Астрель,2006
Слайд 15
Используемые сайты Математика, которая мне нравится.(Математика для школьников и студентов) http :// hijos . ru /2011/04/20/ teorema — menelaya / https :// ru . wikipedia . org / wiki /% D 0% A 7% D 0% B 5% D 0% B 2% D 0% B 0 http :// dic . academic . ru / dic . nsf / enc _ mathematics /6165/% D 0% A 7% D 0%95% D 0%92% D 0% AB http :// hijos . ru /2011/03/16/ teorema — chevy / http://festival.1september.ru/articles/591871/ Сайт Российской академии наук. http://ranip.ru/matem/298-menelaj-konets-1-vne.html
nsportal.ru
Теорема Менелая | Математика, которая мне нравится
Менелай Александрийский (, I в.) – древнегреческий математик и астроном. Автор работ по сферической тригонометрии: написал 6 книг о вычислении хорд и 3 книги “Сферики’’, сохранившиеся в арабском переводе. Для получения формул сферической тригонометрии использовал теорему, известную сегодня как теорема Менелая.
Теорема Менелая. Пусть прямая пересекает треугольник , причем — точка ее пересечения со стороной , — точка ее пересечения со стороной , и — точка ее пересечения с продолжением стороны . Тогда
Доказательство. Проведем через точку прямую, параллельную . Обозначим через ее точку пересечения с прямой .
Треугольники и подобны (). Следовательно,
Треугольники и также подобны (). Значит,
Из каждого равенства выразим :
откуда
что и требовалось доказать.
Теорема (обратная теорема Менелая). Пусть дан треугольник . Пусть точка лежит на стороне , точка — на стороне , а точка — на продолжении стороны , причем выполняется соотношение
Тогда точки и лежат на одной прямой.
Доказательство. Заметим для начала, что , поскольку, по условию, это выражение равно . Следовательно, прямые и не параллельны.
Проведем прямую через точки и . Она пересечет прямую в некоторой точке . Для точек и справедлива теорема Менелая, так что
Отсюда следует, что
Из этого равенства следует, что обе точки и лежат на продолжении отрезка за одну и ту же точку, ибо правее данное отношение меньше , а левее оно строго больше . Пусть . Тогда, учитывая, что и , перепишем полученное равенство в виде
Из равенства следует, что , и доказано, что точка , совпадающая с , лежит на прямой .
Замечание. Теоремы Менелая (прямая и обратная) верны также и в том случае, когда все три точки лежат на продолжениях сторон треугольника . То есть справедлива следующая
Теорема. Пусть дан треугольник . Точки лежат на продолжениях сторон и соответственно. Три точки и лежат на одной прямой тогда и только тогда, когда выполняется равенство
Доказательство этой теоремы точно такое же, как и доказательство, приведенное выше.
Источники: В.В. Ткачук, “Математика абитуриенту”, М.: Изд-во МЦНМО, 2004.
Я.П. Понарин, “Элементарная геометрия. Т.1. Планиметрия, преобразования плоскости”, М.: Изд-во МЦНМО, 2004.
hijos.ru

 Дополнительное построение: прямая $CT$
Дополнительное построение: прямая $CT$


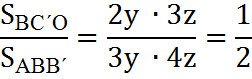 , значит
, значит 
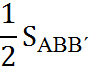 =
=