Парамагнетики Общее описание 1 Парамагнетики вещества которые

Парамагнетики

Общее описание 1)Парамагнетики — вещества, которые намагничиваются во внешнем магнитном поле в направлении внешнего магнитного поля и имеют положительную магнитн ую восприимчивость. Парамагнетики относятся к слабомагнитным веществам, магнитная проницаемость незначит ельно отличается от единицы .

Общее описание Магнитная проницаемость для парамагнетиков: 2)Магнитная проницаемость безразмерная физическая скалярная величина, характеризующая изменение магнитной индукции В среды под воздействием магнитного поля напряженностью Н. Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды (подразумевая ее состав, состояние, температуру и т. д. ). В случае однородной изотропной среды магнитная проницаемость m: m = В/(mo. Н), где mo — магнитная постоянная, температуру и т. д. ). 3)Обычно магнитную проницаемость веществ сравнивают с магнитной проницаемостью пустоты (вакуума) ц0, проницаемость которой принимают за единицу. Если магнитная проницаемость вещества больше единицы, то вещество называют парамагнитным.

Магнитный момент парамагнетиков 1)Магнитный момент— основная величина, характеризующая магнитные свойства вещества (источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро и микро токи; элементарным источником магнетизма считают замкнутый ток). Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитный момент элементарных частиц (электронов, протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента — спина. 2)Магнитный момент измеряется в А⋅м 2 или Дж/Тл (СИ), либо эрг/Гс (СГС), 1 эрг/Гс = 10 3 Дж/Тл. Специфической единицей элементарного магнитного момента является магнетон Бора.

Магнитный момент парамагнетиков Формула для вычисления магнитного момента: В случае плоского контура с электрическим током магнитный момент вычисляется как m=ISn. Где I — сила тока в контуре, S — площадь контура, n — единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.

Опыты Отто Штрена и Вальтера Герлаха Вальтер Герлах Отто Штрен

Опыты Отто Штрена и Вальтера Герлаха Опыт Штерна — Герлаха — опыт немецких физиков Отто Штерна и Вальтера Герлаха, осуществлённый в 1922 году. Опыт подтвердил наличие у атомов спина (изначально в эксперименте участвовали атомы серебра, а потом и других металлов) и факт пространственного квантования направления их магнитных моментов. Опыт состоял в следующем: пучок атомов серебра пропускали через сильно неоднородное магнитное поле, создаваемое мощным постоянным магнитом. При прохождении атомов через это поле, в силу обладания ими магнитных моментов, на них действовала зависящая от проекции спина на направление магнитного поля сила, отклонявшая летящие между магнитами атомы от их первоначального направления движения. Причём, если предположить, что магнитные моменты атомов ориентированы хаотично (непрерывно), то тогда на расположенной далее по направлению движения атомов пластинке должна была проявиться размытая полоса. Однако вместо этого на пластинке образовались две достаточно чёткие узкие полосы, что свидетельствовало в пользу того, что магнитные моменты атомов вдоль выделенного направления принимали лишь два определённых значения, что подтверждало предположение квантово механической теории о квантовании магнитного момента атомов.

Опыты Отто Штрена и Вальтера Герлаха Позднее с аналогичными результатами были проделаны опыты для пучков атомов других металлов, а также пучков протонов и электронов. Эти опыты доказали существование магнитного момента у рассмотренных частиц и показали их квантовую природу, явив собой доказательство постулатов квантовой теории.

Зависимости парамагнетиков

Применение парамагнетиков 1) Охлаждение адиабатическим размагничиванием Парамагнетизм имеет одно весьма интересное применение. При очень низкой температуре и в сильном магнитном поле атомные магнитики выстраиваются. При этом с помощью про цесса, называемого диабатическим а размагничиванием, можно получить самые низкие температуры. Возьмем какую то пара магнитную соль, содержащую некоторое число редкоземель ных атомов (например, аммиачный нитрат празеодима), и начнем охлаждать ее жидким гелием до 1— 2° К в сильном магнитном поле. Большинство спинов направлено вверх, и намагни ченность почти достигает насыщения.

Применение парамагнетиков 2. Ядерный магнитный и электронный парамагнитный резонанс Метод ЯМР широко применяется для исследования структуры органических соединений наряду с методами оптической спектроскопии. Поглощение энергии радиочастотного излучения, которое используется в этом методе, связано с магнитными свойствами ядер. Для получения спектров ЯМР образец помещают в сильное однородное магнитное поле и действуют на него радиочастотным излучением. Изменяя частоту генератора, возбуждающего магнитое поле, перпендикулярное к постоянному полю магнита, достигают условия резонансного поглощения энергии. Резонансная частота зависит от напряженности постоянного магнитного поля и значения магнитного момента ядер. Наиболее широко в исследованиях органических соединений, в том числе нефти, применяется протонный магнитный резонанс (ПМР).

present5.com

Парамагнетики и парамагнетизм

Парамагнетики представляют собой вещества или тела, которые способны намагничиваться при воздействии на них внешних магнитных полей. При этом они, в противоположность диамагнетикам, намагничиваются не против, а по направлению к полю, которое вызвало этот эффект. Другими словами, магнитные моменты парамагнетиков направляются в ту же сторону, что и силовые линии магнитного поля.

Примечательно, что парамагнетики обладают собственным магнитным полем – магнитные моменты не компенсируют друг друга. Правда, это поле очень слабое, поэтому такие вещества называют слабомагнитными.

Парамагнетизм – это явление увеличение магнитной индукции внешнего поля внутри парамагнетика за счет наличия у него собственного поля.

К парамагнетикам относятся: газы (азот, воздух и кислород), эбонит,  вольфрам, алюминий, платина и другие редкоземельные металлы.

Интересно

Парамагнетизм широко используется не только в науке и технике. Ученые и инженеры создали специальную парамагнитную краску, которая под воздействием слабого электрического тока способна практически мгновенно менять цвет.

Перед покраской машины на ее кузов наносится окись железа, являющаяся парамагнитным веществом. Затем автомобиль покрывается специальной краской. Под воздействием электричества частицы окисижелеза меняют свою способность отражать свет, то есть выступают своеобразным световым фильтром, который каждый раз меняет свои настройки. Такое парамагнитное покрытие способно воспроизвести практически любой цвет.

< Предыдущая		Следующая >

scsiexplorer.com.ua

3.4. Парамагнетизм. Парамагнетики и их свойства

Парамагнетизм — это свойство веществ, помещенных во внешнее магнитное поле, намагничиваться (приобретать магнитный момент) в направлении, совпадающем с направлением этого поля. Под общим названием парамагнетизм подразумевается совокупность всех магнитных свойств указанных материалов. Вещества, обладающие таким свойством, называют парамагнетиками.

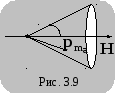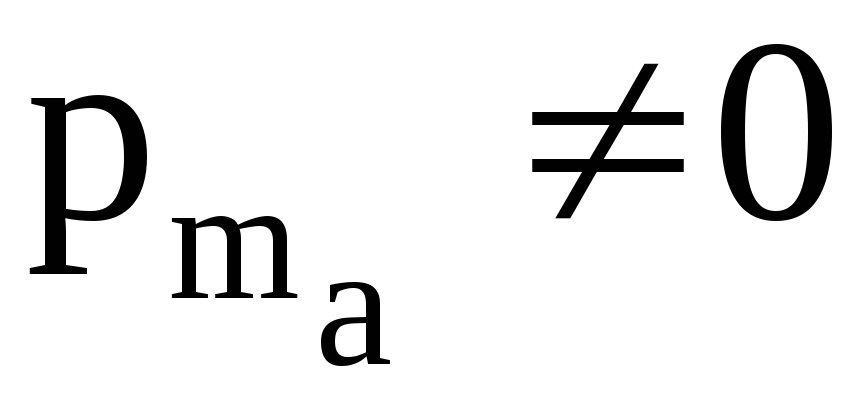Парамагнетизм характерен для веществ, частицы которых (атомы, молекулы, ионы, атомные ядра) обладают собственным магнитным моментом. В отсутствие внешнего магнитного поля атомы парамагнетика представляют собой молекулярные магнитные диполи, следовательно, магнитный момент атома парамагнетика не скомпенсирован, т.е. . Однако в отсутствие внешнего поля эти моменты ориентированы хаотически, так что в целом намагниченность вещества J = 0.

Таким образом, при помещении парамагнитного вещества во внешнее магнитное поле молекулярные магнитные диполи стремятся ориентироваться вдоль направления вектора 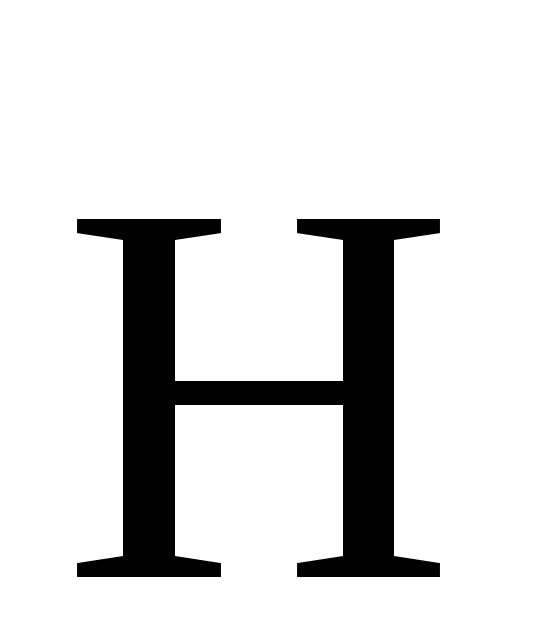(рис. 3.9), (3.10). Ориентированию магнитных диполей препятствует тепловое движение атомов.

У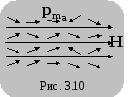парамагнетиков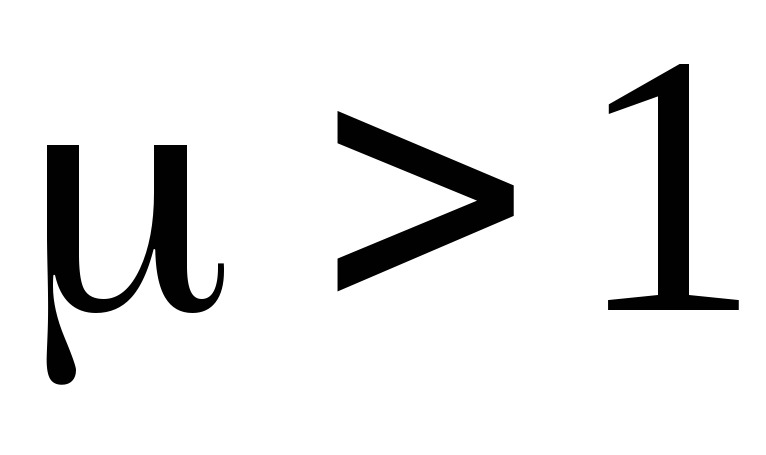,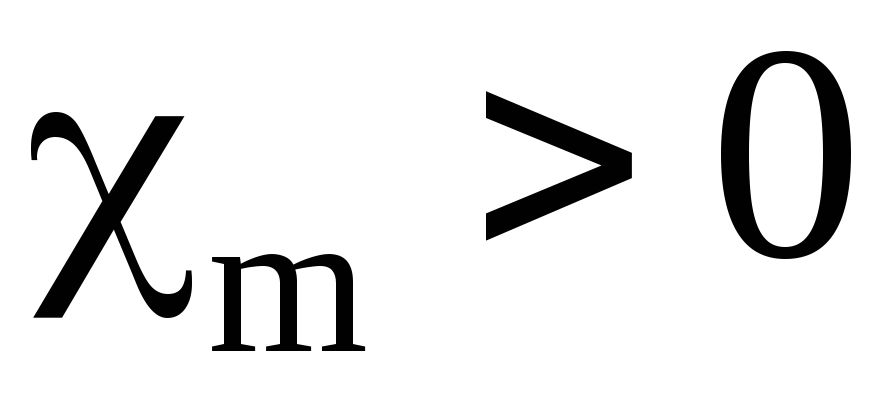. В не слишком больших магнитных полях уравнение магнитного состояния парамагнетиков является линейным:

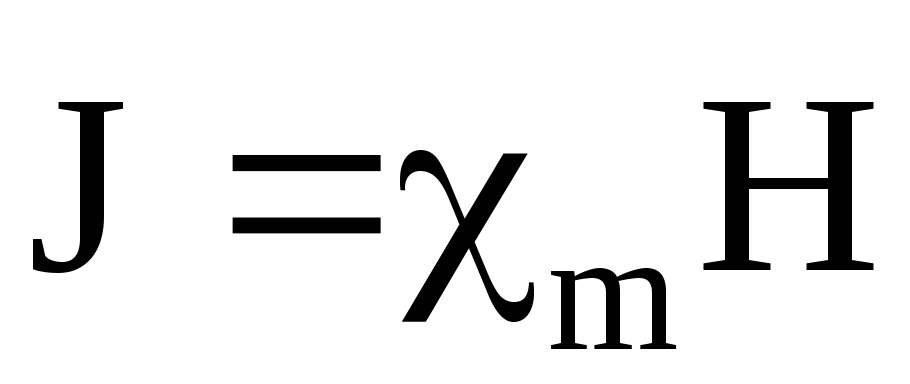. (3.29)

Для доказательства данного утверждения предположим, что число частиц, магнитные моменты которых лежат в пределах телесного угла (рис. 3.9) может быть определено с использованием распределения Больцмана:

.

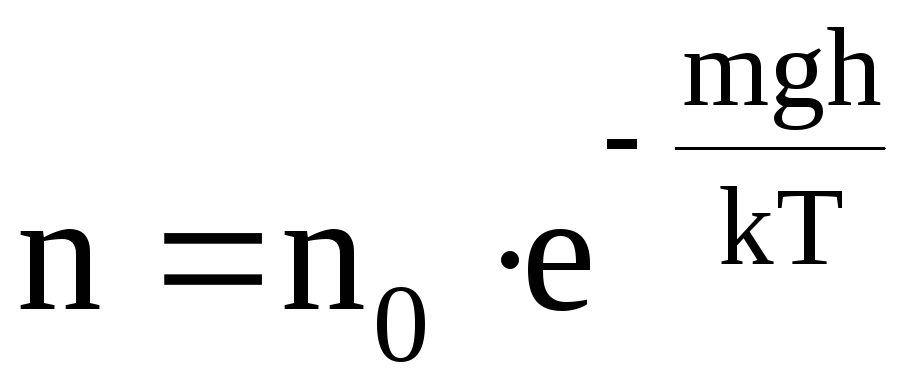В рассматриваемом случае

,

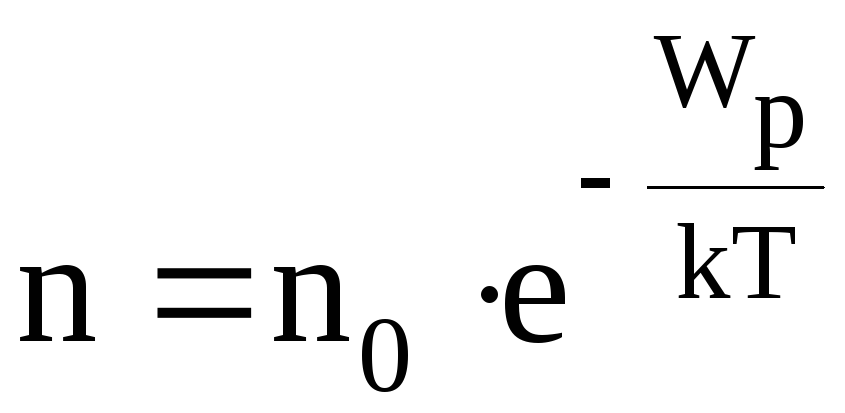где W_p — потенциальная энергия магнитного диполя в магнитном поле.

Потенциальная энергия магнитного диполя в магнитном поле определяется соотношением

.

Воспользовавшись разложением функции 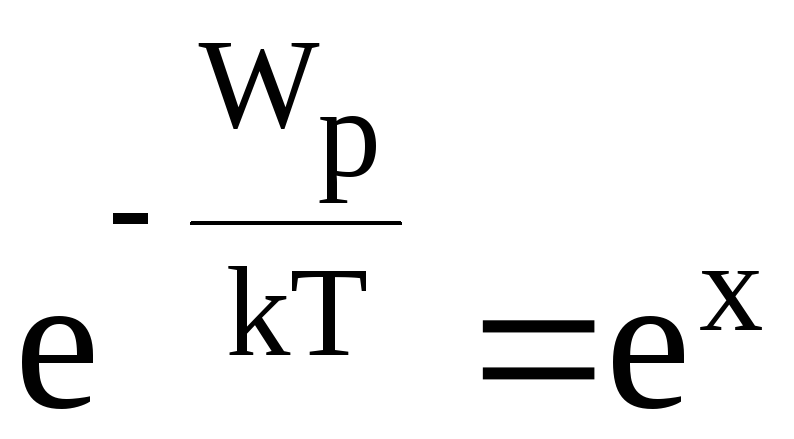в степенной ряд:

,

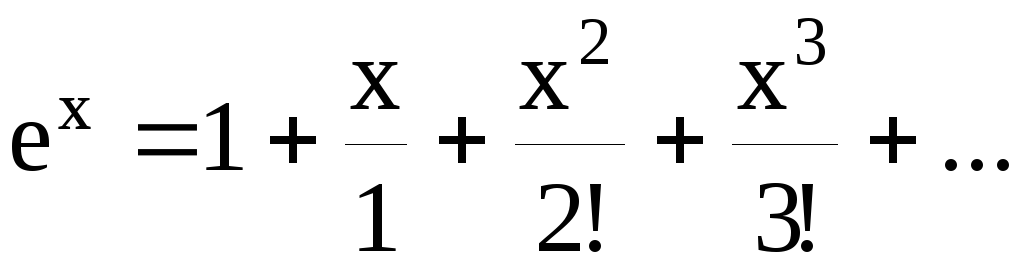где 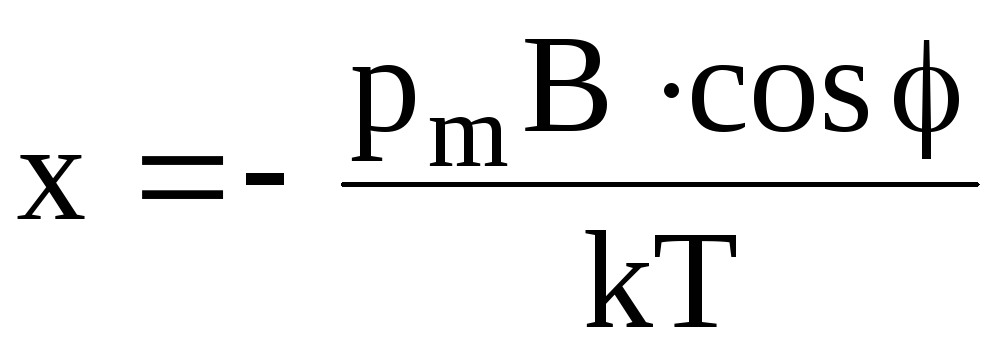, ограничившись двумя первыми членами разложения, с учетом того, что в случае малых магнитных полей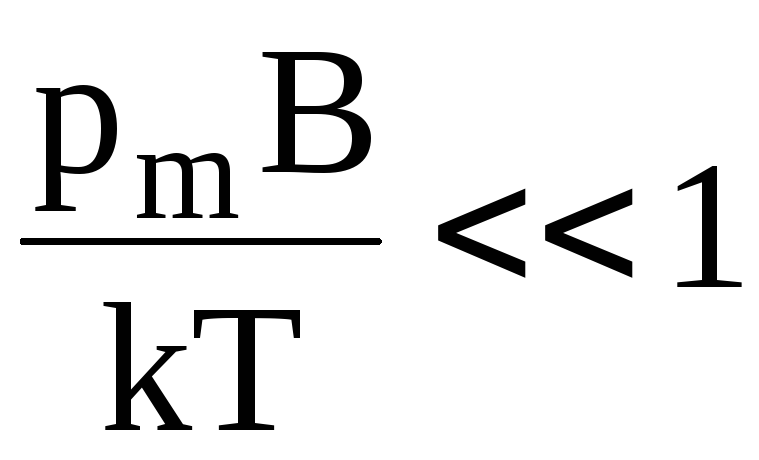, будем иметь

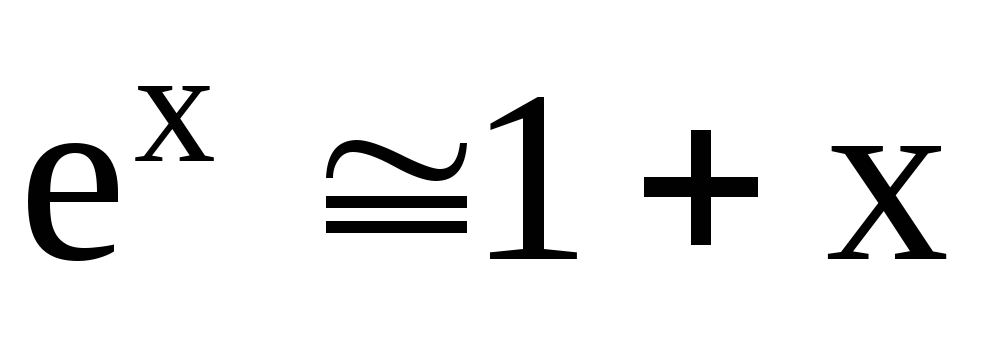или .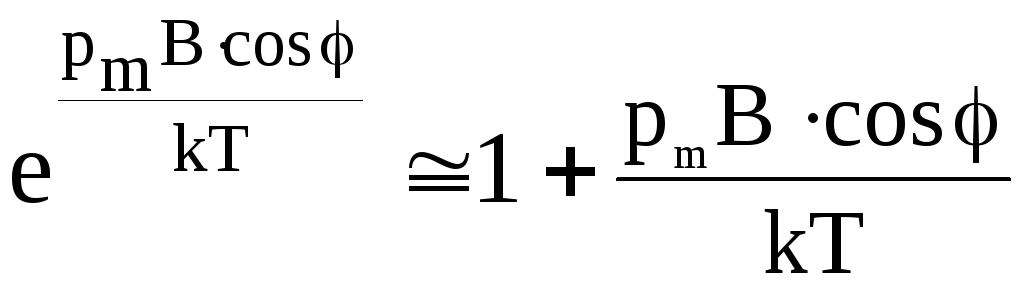

Тогда число частиц, магнитные моменты которых заключены в телесном угле ,

,

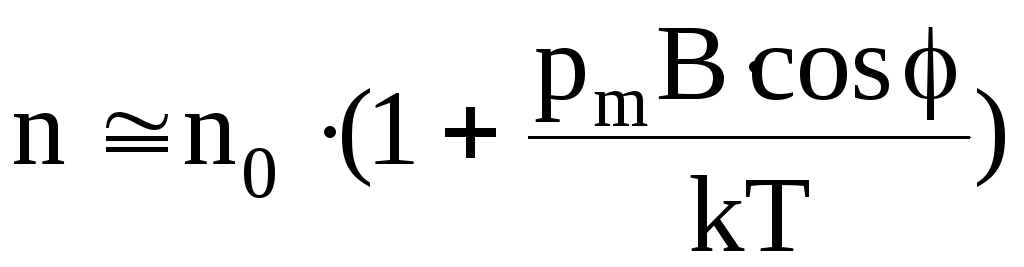где 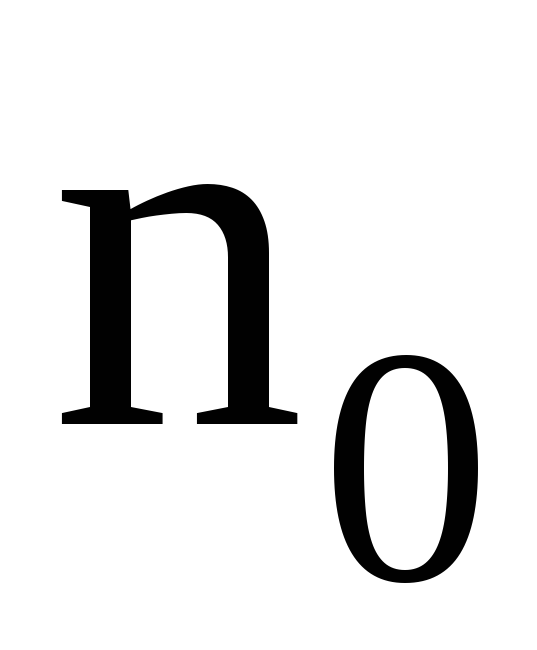— число частиц, заключенных в телесном углепри В = 0.

Отсюда превышение числа частиц с ориентированными моментами будет равно

.

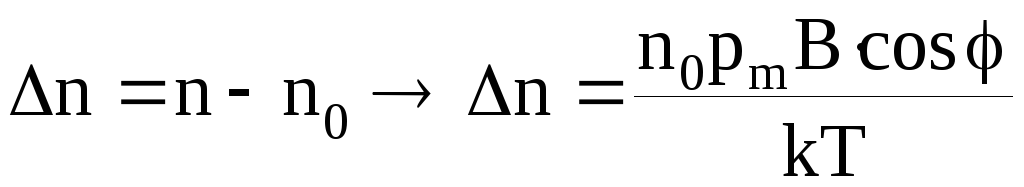Соответственно в направлении поля

.

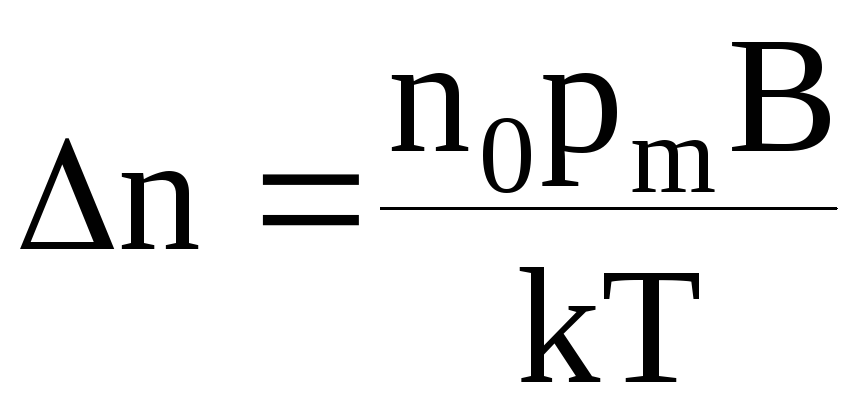Намагниченность вещества, согласно определению,

.

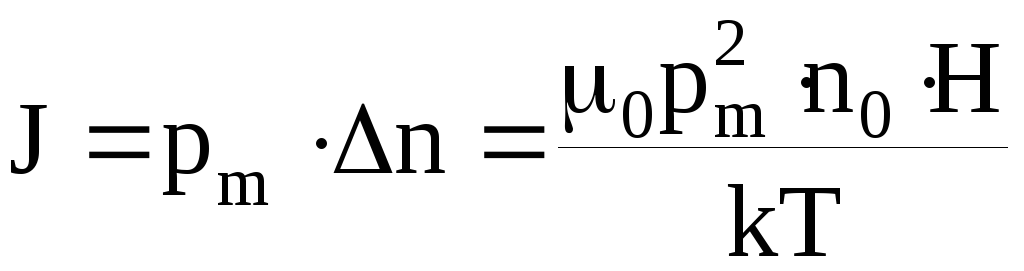Строгая теория парамагнетизма, созданная французским физиком Ланжевеном в 1905 г., приводит к выражению

. (3.30).

Следовательно, магнитная восприимчивость парамагнетиков действительно не зависит от напряженности магнитного поля:

.

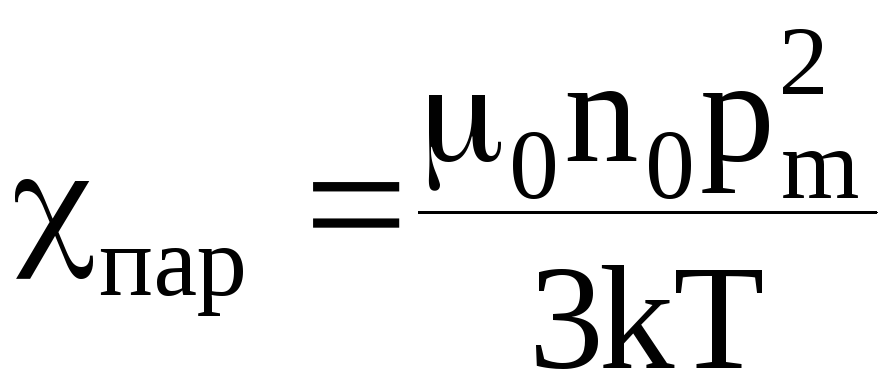О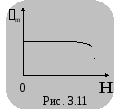днако на практике в области достаточно больших напряженностей магнитных полей наблюдается некоторая зависимость магнитной восприимчивости парамагнетиков от напряженности внешнего магнитного поля (по мере выстраивания магнитных моментов вдоль направления векторавнешнего магнитного поля) (рис. 3.11).

Из формулы (3.30) следует, что на намагниченность парамагнетика влияют магнитные свойства вещества (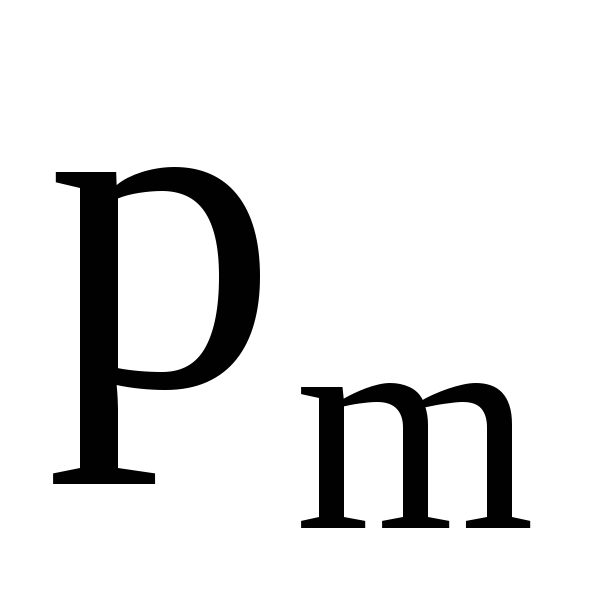,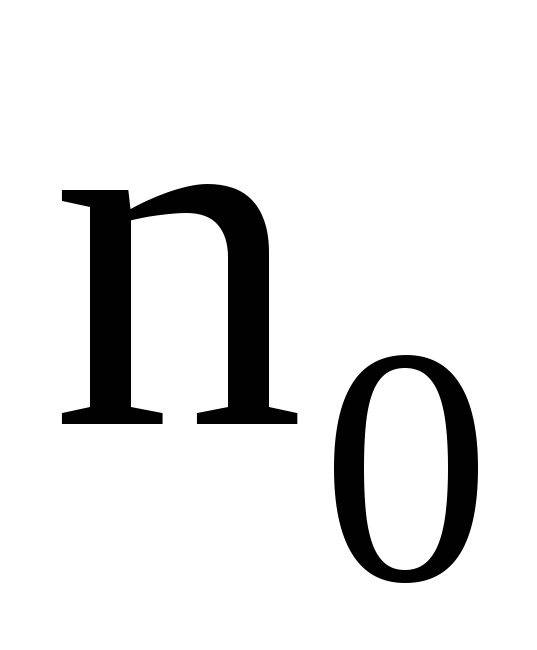), напряженность внешнего магнитного поляН и температура.

Причем два первых фактора и последний фактор оказывают на намагниченность J противоположное воздействие.

П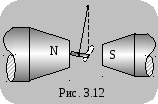оскольку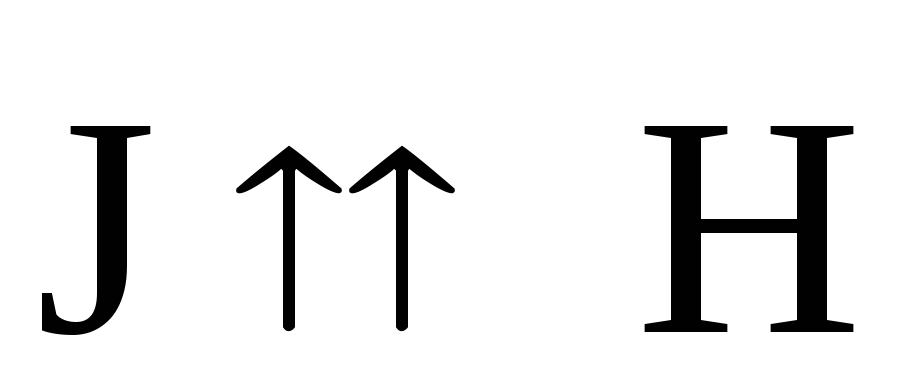, то парамагнетики втягиваются в область максимального магнитного поля (хотя и очень слабо).Парамагнитные тела притягиваются к полюсам магнита (диамагнитные — отталкиваются). На рис. 3.12 представлено поведение ампулы с парамагнитным раствором хлористого железа в неоднородном магнитном поле.

Для парамагнетиков _m~10^-710^-4 и всегда положительна. Если поле велико, то все магнитные моменты парамагнитных частиц будут ориентированы строго по полю (магнитное насыщение).

В парамагнитных веществах намагниченность, обусловленная упорядоченным расположением электронов, атомов и т.д. (элементарных магнитов), значительно превосходит диамагнитный эффект.

В слабых полях и при низких температурах удельная магнитная восприимчивость парамагнитных веществ обратно пропорциональна температуре (закон Кюри):

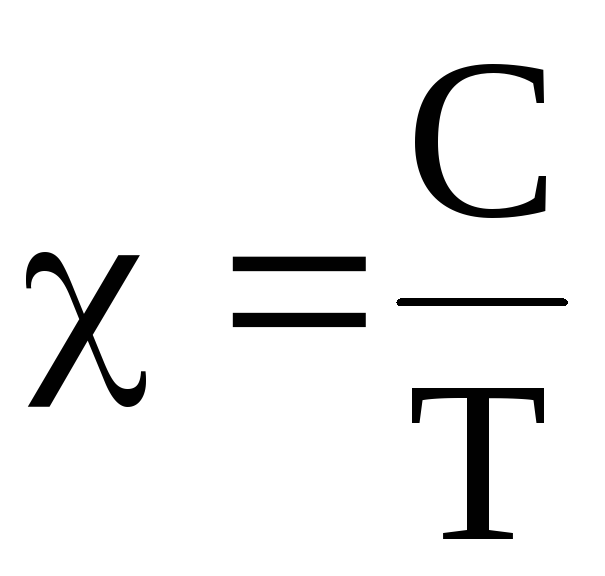, (3.31)

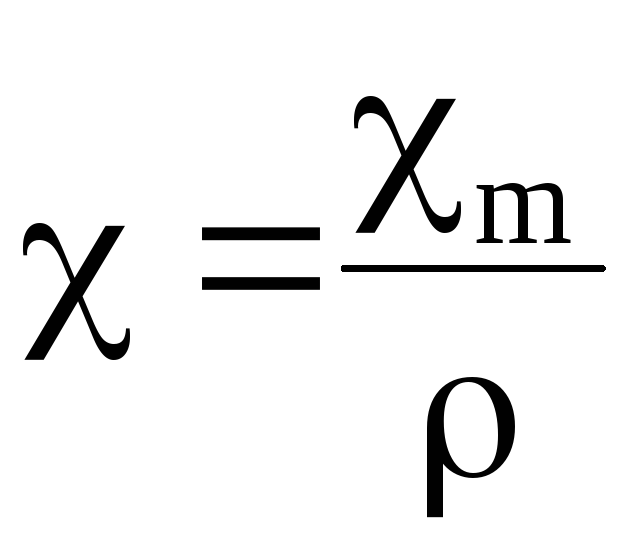где — удельная (массовая) магнитная восприимчивость;

_m — магнитная восприимчивость единицы объема вещества;

 — плотность вещества;

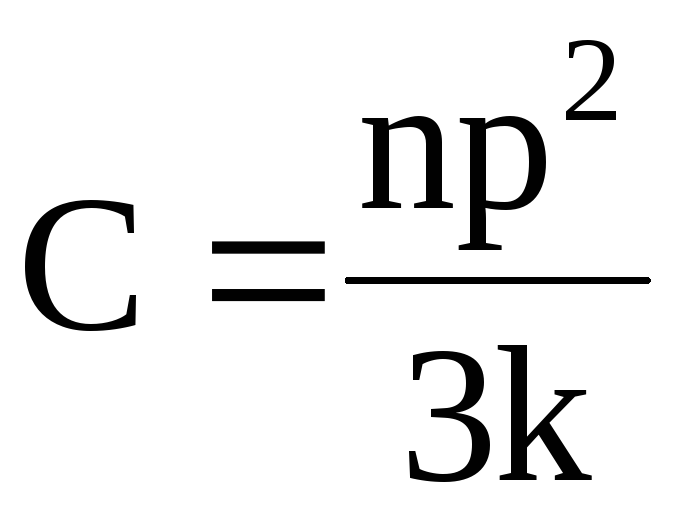— постоянная Кюри;

n — число молекул в единице объема;

k -постоянная Больцмана;

T — абсолютная температура.

Закону Кюри подчиняются газы (O₂, NO), пары щелочных металлов, разбавленные жидкие растворы парамагнитных солей редкоземельных элементов и некоторые парамагнитные соли в кристаллическом состоянии (у таких солей между ионами — носителями магнитного момента p_m расположены препятствующие их взаимодействию группы атомов, лишенные магнитного момента, например молекулы аммиака). Классическая теория закона Кюри основана на статистическом рассмотрении свойств системы слабо взаимодействующих атомов, молекул или ионов, имеющих дипольный магнитный момент («газа»).

В сильных магнитных полях, при низких температурах (когда тепловое движение не нарушает ориентацию магнитных моментов H/T) J^‘pN (при насыщении все атомные моменты ориентированы одинаково), закон Кюри не выполняется.

studfile.net

3.4. Парамагнетизм. Парамагнетики и их свойства

Парамагнетизм — это свойство веществ, помещенных во внешнее магнитное поле, намагничиваться (приобретать магнитный момент) в направлении, совпадающем с направлением этого поля. Под общим названием парамагнетизм подразумевается совокупность всех магнитных свойств указанных материалов. Вещества, обладающие таким свойством, называют парамагнетиками.

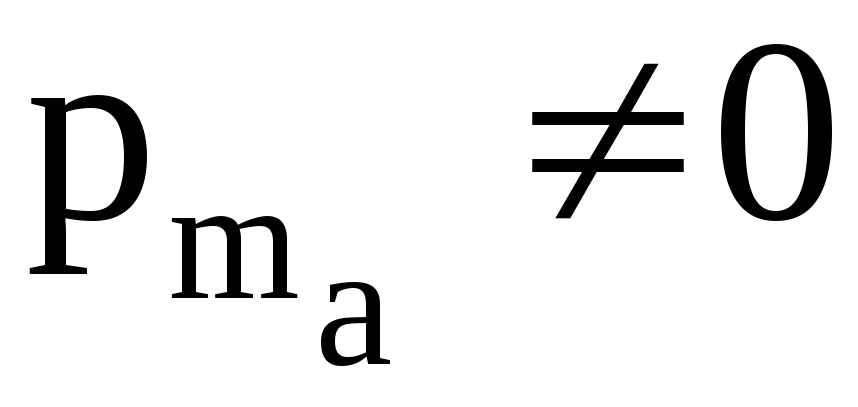Парамагнетизм характерен для веществ, частицы которых (атомы, молекулы, ионы, атомные ядра) обладают собственным магнитным моментом. В отсутствие внешнего магнитного поля атомы парамагнетика представляют собой молекулярные магнитные диполи, следовательно, магнитный момент атома парамагнетика не скомпенсирован, т.е. . Однако в отсутствие внешнего поля эти моменты ориентированы хаотически, так что в целом намагниченность вещества J = 0.

Таким образом, при помещении парамагнитного вещества во внешнее магнитное поле молекулярные магнитные диполи стремятся ориентироваться вдоль направления вектора (рис. 3.9), (3.10). Ориентированию магнитных диполей препятствует тепловое движение атомов.

У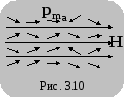парамагнетиков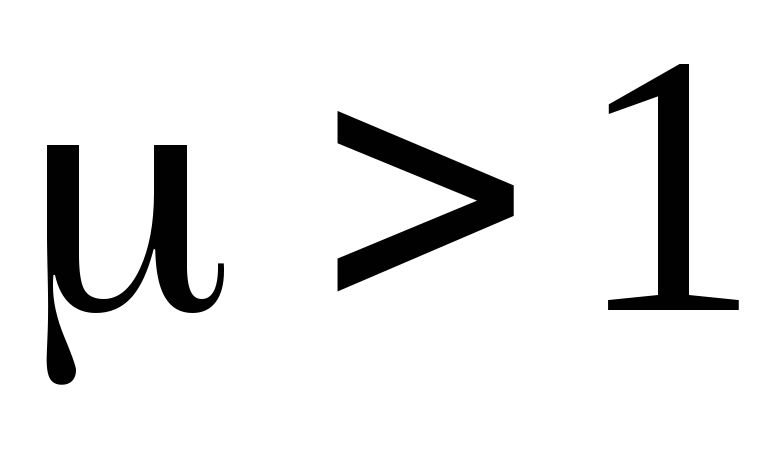,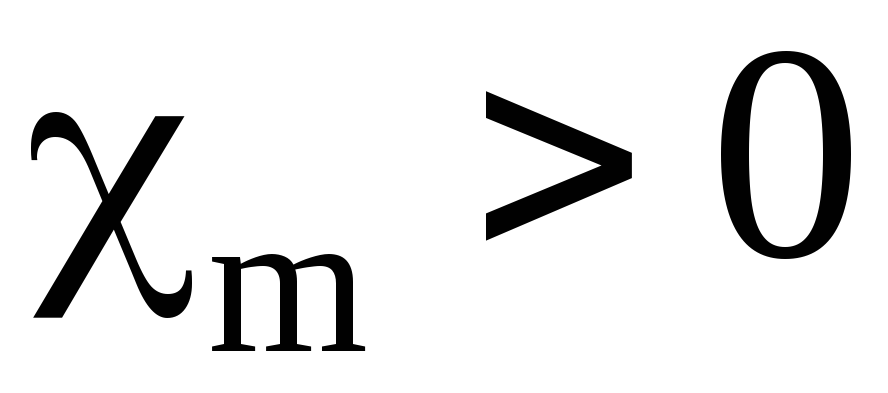. В не слишком больших магнитных полях уравнение магнитного состояния парамагнетиков является линейным:

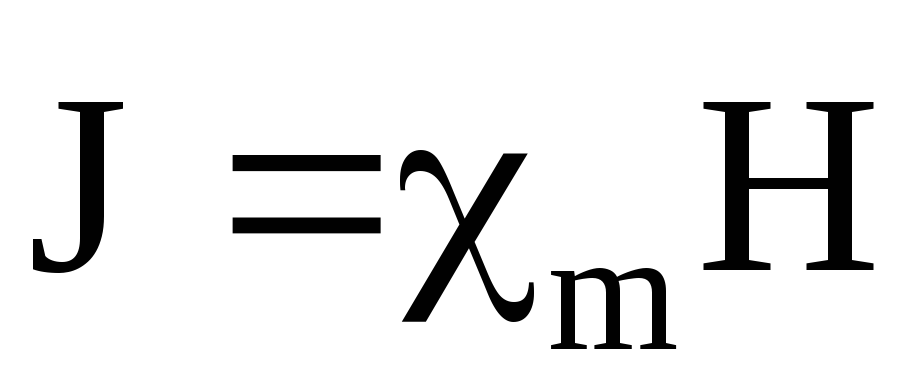. (3.29)

Для доказательства данного утверждения предположим, что число частиц, магнитные моменты которых лежат в пределах телесного угла (рис. 3.9) может быть определено с использованием распределения Больцмана:

.

В рассматриваемом случае

,

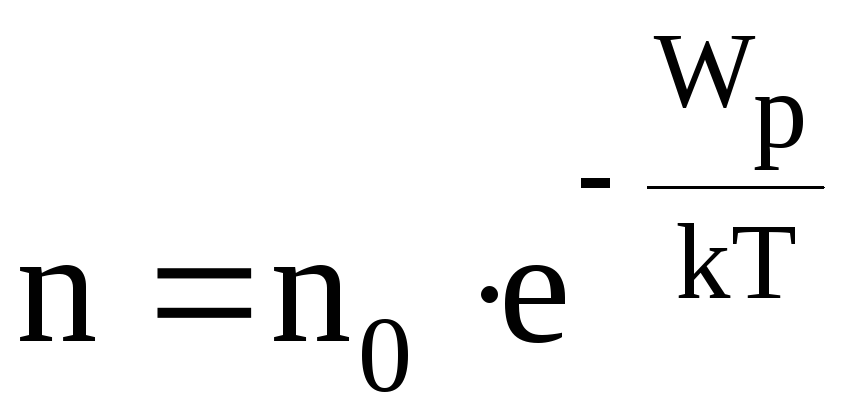где W_p — потенциальная энергия магнитного диполя в магнитном поле.

Потенциальная энергия магнитного диполя в магнитном поле определяется соотношением

.

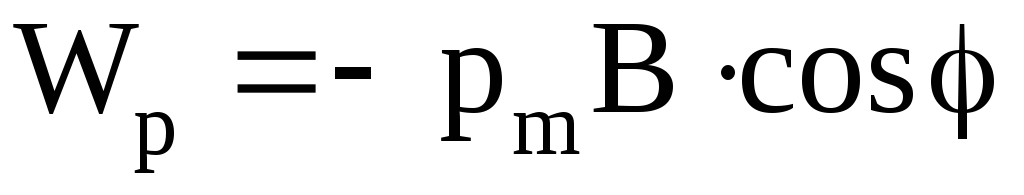Воспользовавшись разложением функции 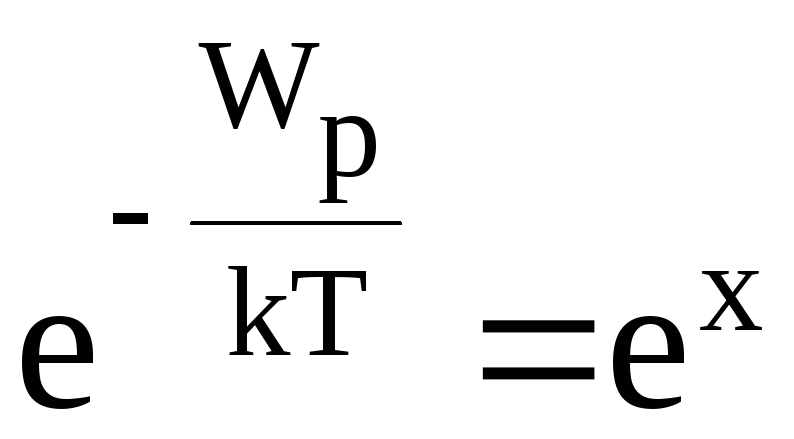в степенной ряд:

,

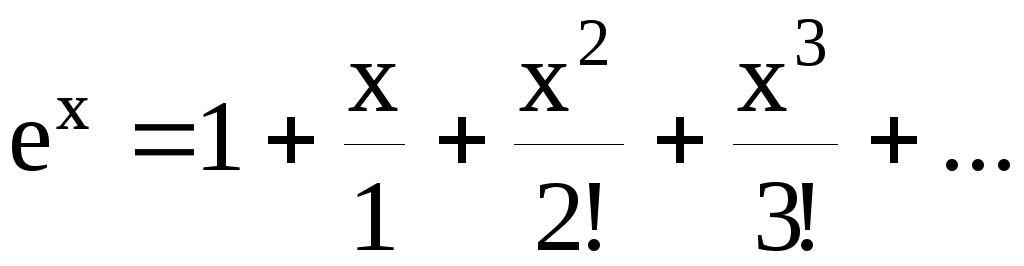где 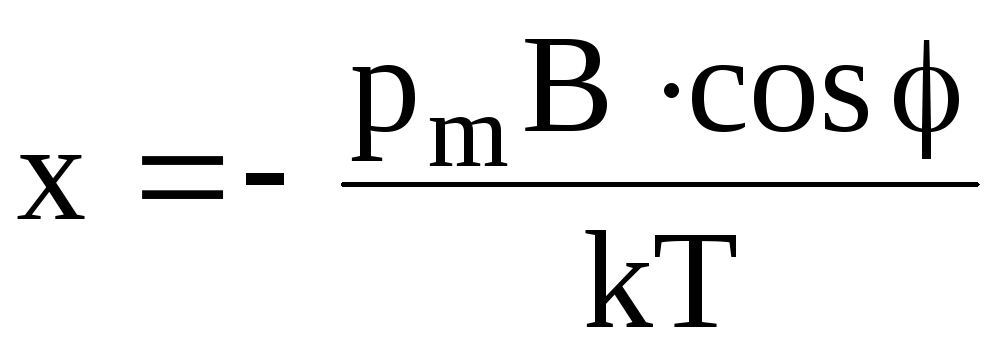, ограничившись двумя первыми членами разложения, с учетом того, что в случае малых магнитных полей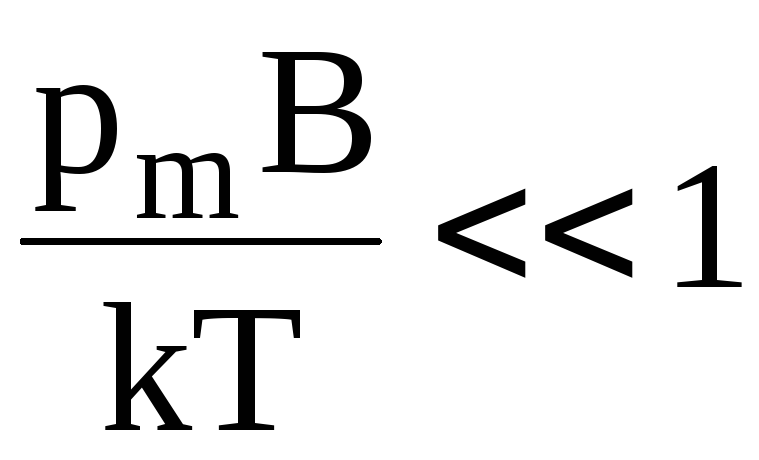, будем иметь

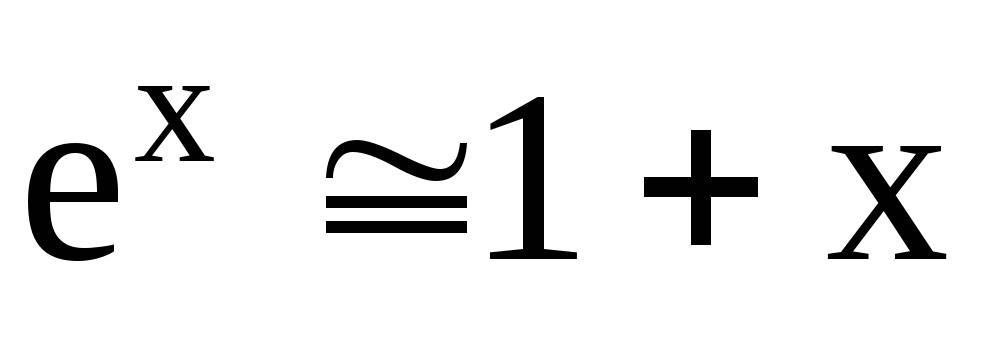или .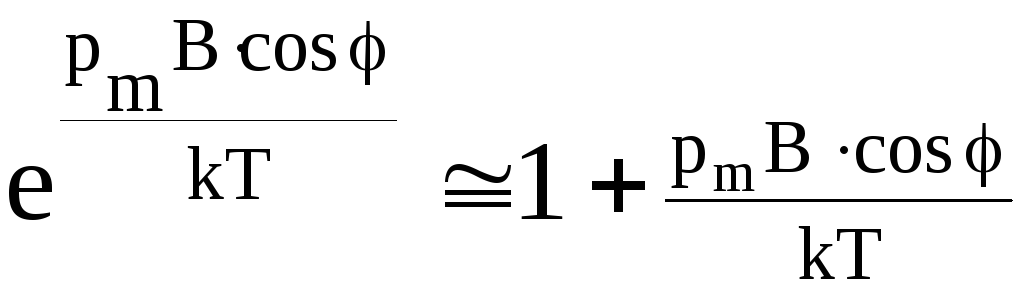

Тогда число частиц, магнитные моменты которых заключены в телесном угле ,

,

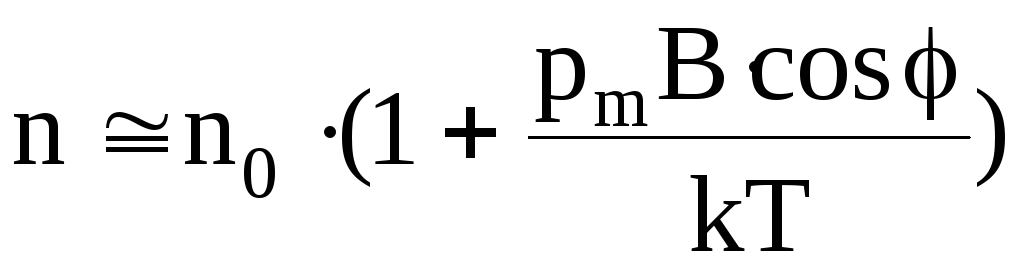где 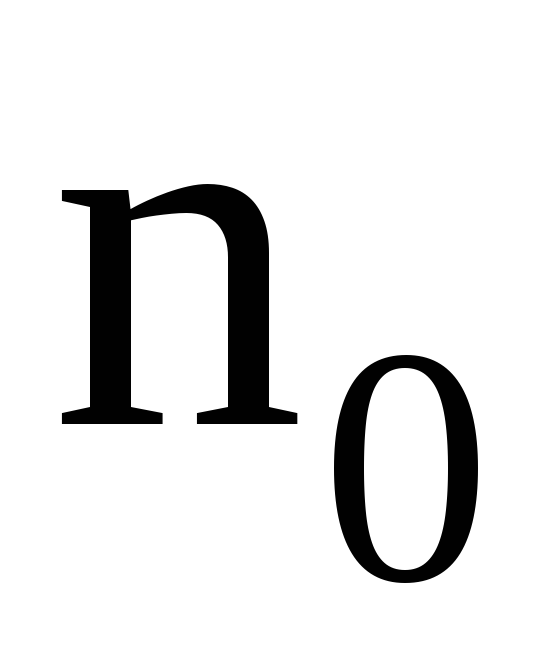— число частиц, заключенных в телесном углепри В = 0.

Отсюда превышение числа частиц с ориентированными моментами будет равно

.

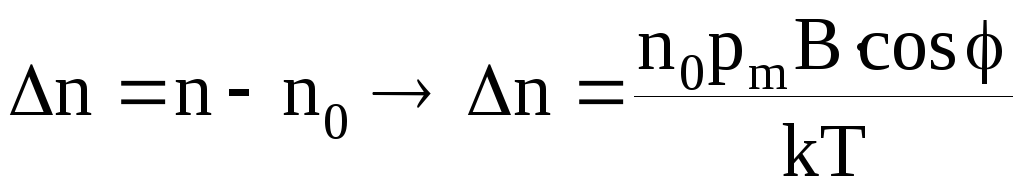Соответственно в направлении поля

.

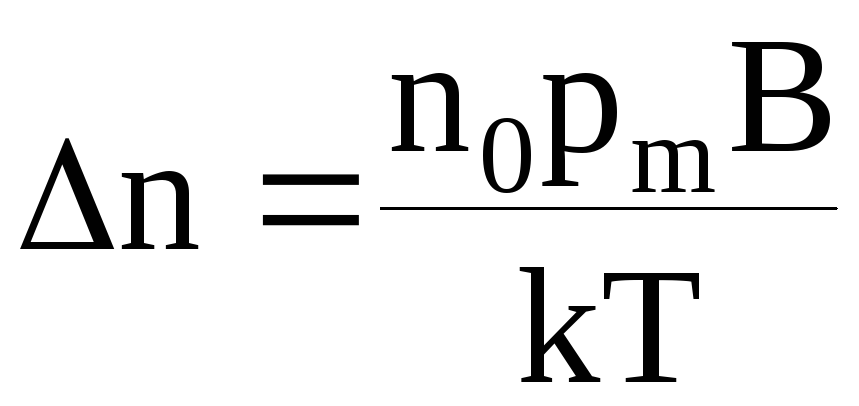Намагниченность вещества, согласно определению,

.

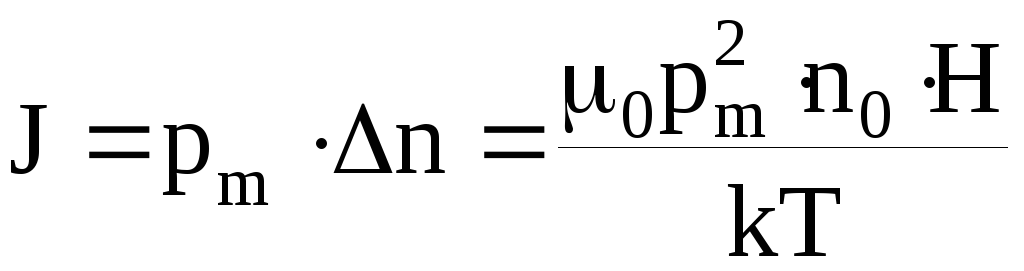Строгая теория парамагнетизма, созданная французским физиком Ланжевеном в 1905 г., приводит к выражению

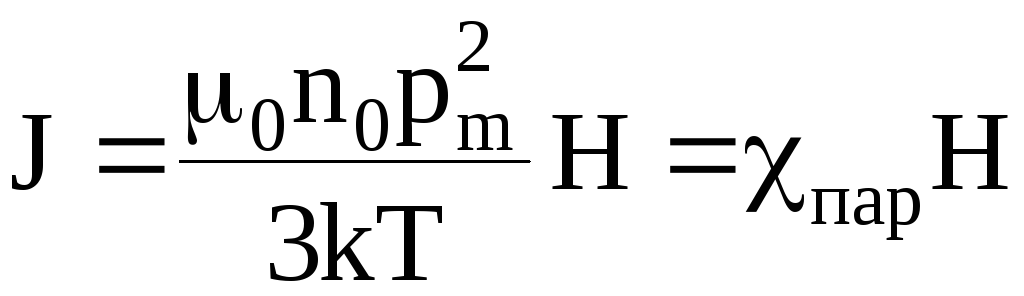. (3.30).

Следовательно, магнитная восприимчивость парамагнетиков действительно не зависит от напряженности магнитного поля:

.

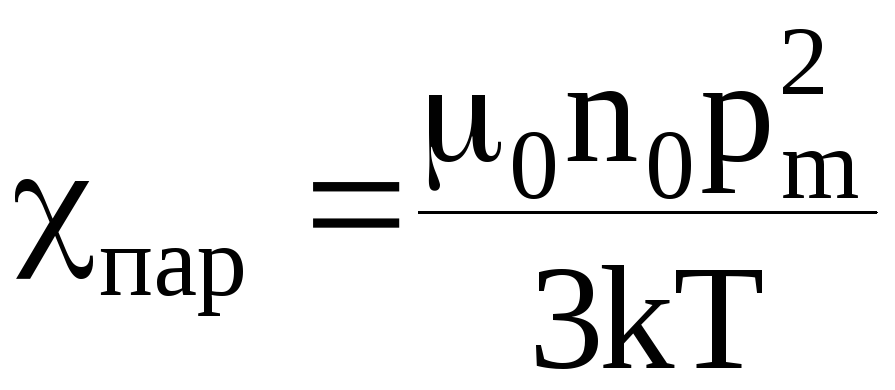О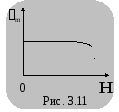днако на практике в области достаточно больших напряженностей магнитных полей наблюдается некоторая зависимость магнитной восприимчивости парамагнетиков от напряженности внешнего магнитного поля (по мере выстраивания магнитных моментов вдоль направления векторавнешнего магнитного поля) (рис. 3.11).

Из формулы (3.30) следует, что на намагниченность парамагнетика влияют магнитные свойства вещества (,), напряженность внешнего магнитного поляН и температура.

Причем два первых фактора и последний фактор оказывают на намагниченность J противоположное воздействие.

Поскольку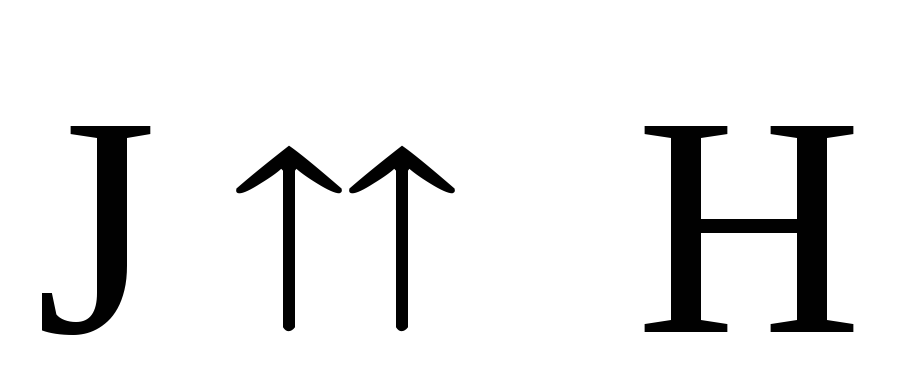, то парамагнетики втягиваются в область максимального магнитного поля (хотя и очень слабо).Парамагнитные тела притягиваются к полюсам магнита (диамагнитные — отталкиваются). На рис. 3.12 представлено поведение ампулы с парамагнитным раствором хлористого железа в неоднородном магнитном поле.

Для парамагнетиков _m~10^-710^-4 и всегда положительна. Если поле велико, то все магнитные моменты парамагнитных частиц будут ориентированы строго по полю (магнитное насыщение).

В парамагнитных веществах намагниченность, обусловленная упорядоченным расположением электронов, атомов и т.д. (элементарных магнитов), значительно превосходит диамагнитный эффект.

В слабых полях и при низких температурах удельная магнитная восприимчивость парамагнитных веществ обратно пропорциональна температуре (закон Кюри):

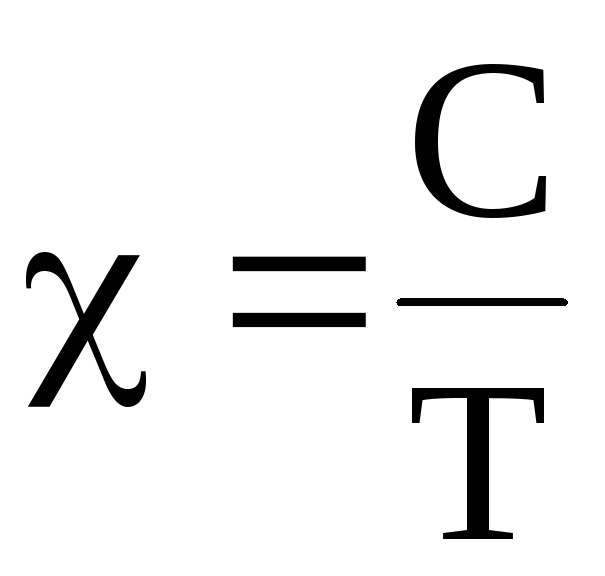, (3.31)

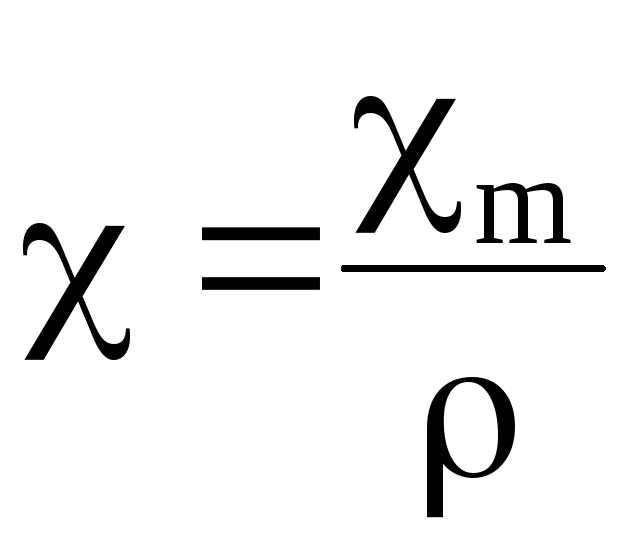где — удельная (массовая) магнитная восприимчивость;

_m — магнитная восприимчивость единицы объема вещества;

 — плотность вещества;

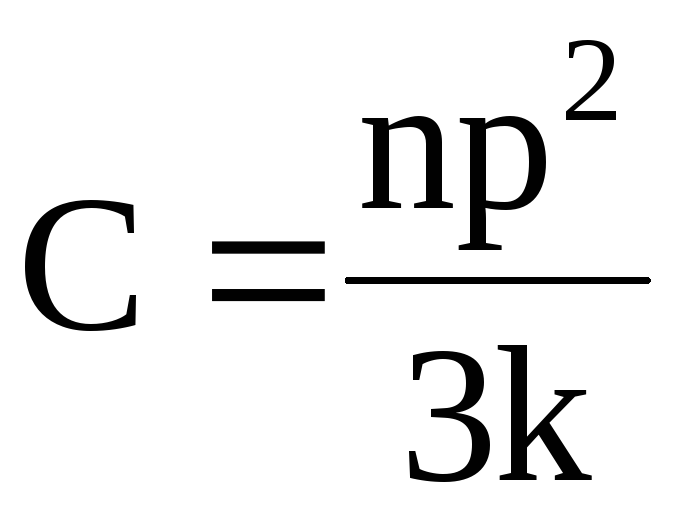— постоянная Кюри;

n — число молекул в единице объема;

k -постоянная Больцмана;

T — абсолютная температура.

Закону Кюри подчиняются газы (O₂, NO), пары щелочных металлов, разбавленные жидкие растворы парамагнитных солей редкоземельных элементов и некоторые парамагнитные соли в кристаллическом состоянии (у таких солей между ионами — носителями магнитного момента p_m расположены препятствующие их взаимодействию группы атомов, лишенные магнитного момента, например молекулы аммиака). Классическая теория закона Кюри основана на статистическом рассмотрении свойств системы слабо взаимодействующих атомов, молекул или ионов, имеющих дипольный магнитный момент («газа»).

В сильных магнитных полях, при низких температурах (когда тепловое движение не нарушает ориентацию магнитных моментов H/T) J^‘pN (при насыщении все атомные моменты ориентированы одинаково), закон Кюри не выполняется.

studfile.net

Парамагнетизм. Парамагнетики и их свойства — Мегаобучалка

Парамагнетизм — это свойство веществ, помещенных во внешнее магнитное поле, намагничиваться (приобретать магнитный момент) в направлении, совпадающем с направлением этого поля. Под общим названием парамагнетизм подразумевается совокупность всех магнитных свойств указанных материалов. Вещества, обладающие таким свойством, называют парамагнетиками.

Парамагнетизм характерен для веществ, частицы которых (атомы, молекулы, ионы, атомные ядра) обладают собственным магнитным моментом. В отсутствие внешнего магнитного поля атомы парамагнетика представляют собой молекулярные магнитные диполи, следовательно, магнитный момент атома парамагнетика не скомпенсирован, т.е. . Однако в отсутствие внешнего поля эти моменты ориентированы хаотически, так что в целомнамагниченность вещества J = 0.

Таким образом, при помещении парамагнитного вещества во внешнее магнитное поле молекулярные магнитные диполи стремятся ориентироваться вдоль направления вектора (рис. 3.9), (3.10). Ориентированию магнитных диполей препятствует тепловое движение атомов.

У парамагнетиков , . В не слишком больших магнитных полях уравнение магнитного состояния парамагнетиков является линейным:

. (3.29)

(СМ. функция ЛАНЖЕВЕНА) .

Поскольку , то парамагнетики втягиваются в область максимального магнитного поля (хотя и очень слабо). Парамагнитные тела притягиваются к полюсам магнита (диамагнитные — отталкиваются). На рис. 3.12 представлено поведение ампулы с парамагнитным раствором хлористого железа в неоднородном магнитном поле.

Для парамагнетиков c_m~10^-7¸10^-4 и всегда положительна. В парамагнитных веществах намагниченность, обусловленная упорядоченным расположением электронов, атомов и т.д. (элементарных магнитов), значительно превосходит диамагнитный эффект.

В слабых полях и при низких температурах удельная магнитная восприимчивость парамагнитных веществ обратно пропорциональна температуре (закон Кюри):

, (3.31)

где — удельная (массовая) магнитная восприимчивость;

c_m — магнитная восприимчивость единицы объема вещества;

r — плотность вещества;

— постоянная Кюри;

n — число молекул в единице объема;

k -постоянная Больцмана;

T — абсолютная температура.

Закону Кюри подчиняются газы (O₂, NO), пары щелочных металлов, разбавленные жидкие растворы парамагнитных солей редкоземельных элементов и некоторые парамагнитные соли в кристаллическом состоянии (у таких солей между ионами — носителями магнитного момента p_m расположены препятствующие их взаимодействию группы атомов, лишенные магнитного момента, например молекулы аммиака).

В сильных магнитных полях, при низких температурах (когда тепловое движение не нарушает ориентацию магнитных моментов H/T®¥) J^‘®pN (при насыщении все атомные моменты ориентированы одинаково), закон Кюри не выполняется.

 

Ферромагнетики

В отсутствие внешнего магнитного поля ферромагнетик можно представить состоящим из областей однородной намагниченности – доменов, образований, содержащих в себе большое количество молекулярных магнитных диполей, ориентированных параллельно друг другу (рис. 3.16). Эти образования достигают размеров 10^-3 – 10^{-5 мм. Уединенные домены могут достигать в диаметре 5-10 нм. Домены называют еще областями спонтанного (самопроизвольного) намагничивания.}

Образование доменов — результат конкуренции двух типов взаимодействия: обменного и магнитного (диполь-дипольного взаимодействия магнитных моментов). Первое взаимодействие близкодействующее, оно стремится установить магнитные моменты параллельно и ответственно за однородную намагниченность в домене. Второе взаимодействие, дальнодействующее, ориентирует антипараллельно векторы намагниченности соседних доменов. Теория ферромагнетизма качественно удовлетворительно объясняет размеры и форму доменов. Между доменами существуют переходные слои конечной толщины, в которыхМ_s непрерывно меняет свое направление. При некоторых критически малых размерах ферромагнитных образцов образование в них нескольких доменов может стать энергетически невыгодным, и тогда такие мелкие ферромагнитные частицы оказываются при T<q однородно намагниченными.

При решении многих технических вопросов можно считать, что отдельно взятый домен представляет собой вещество, намагниченное до насыщения. Параллельность магнитных моментов молекулярных диполей внутри домена имеет квантово – механическую природу и обусловлена так называемым обменным взаимодействием между атомами. При определенных условиях внутри кристаллической решетки расстояния между соседними атомами должны обеспечить необходимую величину перекрытия электронных оболочек. Становится энергетически выгодным состояние с параллельной ориентацией спиновых магнитных моментов соседних атомов в решетке.

Изолированные кластеры в зависимости от атомного состава и размеров обладают различными по интенсивности и характеру магнитными свойствами. Так, единичные атомы железа, обладающие магнитным моментом и включенные с низкой концентрацией в немагнитную, например, полимерную матрицу, обладают парамагнитными свойствами при всех температурах. Несколько атомов железа в кластере уже обладают обменным взаимодействием, но это не приводит к самопроизвольной намагниченности из-за тепловых флуктуаций и быстрой спин-спиновой релаксации. Число магнитных моментов , и, соответственно, размер кластера, должно быть таковым, чтобы суммарная обменная энергия превосходила энергию тепловых флуктуаций – кТ. Вычислив суммарную энергию обменного взаимодействия, можно сравнить ее с энергией тепловых флуктуаций и определить критический размер кластера, менее которого он потеряет спонтанную намагниченность. Однако помимо механизма обменных взаимодействий и, следовательно, на критический размер кластера будут влиять и другие причины, например, химическое состояние его поверхности, межкластерное взаимодействие, форма кластера. Поэтому точное вычисление такого критического размсера представляет собой весьма сложную задачу.

Если принять, что ΔpΔx=Δpd_cr»ћ, где d_cr – критических размер (диаметр) кластера, то Δp=ћ/d_cr и тогда неопределенность энергии электрона, обменного взаимодействия за счет квантового ограничения будет Δε»(Δp)²/(2m)»ћ²/(2md_cr²). Теперь, если эту энергию приравнять энергии обменного взаимодействия, которая, главным образом, ответственна за возникновение магнитного упорядочения, т.е. Δε»kT_С, где T_С – температура Кюри массивного материала, то величина критического размера будет определяться, например, простой оценкой

d_cr (м) ~ 2∙10^-8 T_С^-1/2. (16.23)

Петлей гистерезиса называется кривая изменения магнитной индукции В ферромагнитного тела (рис. 3.19) или намагниченности М (рис. 3.20) при изменении напряженности внешнего магнитного поля от до и обратно, где — напряженность магнитного поля, соответствующая насыщению. При этом достигается предельное значение намагниченности вещества . Если довести намагничивание до насыщения и затем уменьшать напряженность магнитного поля, то индукция В (намагниченность М) изменяется не по первоначальной кривой 0 -1, а в соответствии с кривой 1-2. В результате, когда напряженность внешнего поля станет равной 0, намагниченность , а — остаточная индукция ( — остаточная намагниченность). Существование остаточной намагниченности является основой создания постоянных магнитов, записи и длительного хранения различного рода информации — магнитной памяти.

Напряженность магнитного поля обратного направления , при которой магнитная индукция (намагниченность) становится равной 0, называется коэрцитивной силой.

Однодоменные частицы можно считать намагниченными до насыщения. Намагниченность насыщения M_so зависит от размера частиц и падает при его уменьшении; при типичных для магнитных коллоидов размеров частиц M_so составляет ~50% от соответствующей величины многодоменного материала. Уменьшение M_so связывается с дефицитом соседей по обменному взаимодействию в поверхностном слое или химическими изменениями поверхностного слоя частиц.

Численные значения магнитной восприимчивости в МЖ при ком­натной температуре в тысячи раз превышает восприимчивость обычных жидкостей. Намагниченность насыщения концентрированных МЖ M_s может достигать ~120 кА/м в магнитных полях ~100 кА/м, при этом их вязкость близка к вязкости жидкости-носителя и почти не зависит от напряженности магнитного поля. Магнитный момент частицы выражается через намагниченность насыщения ферромагнетика:

m_*=M_SO·V_f,

где V_f – объем магнитной части частицы. Если «магнитное ядро» имеет форму шара диаметра d, то

Для частицы магнетита при M_SO= 477,7 кА/м, d=10 нм m_*=2,5·10^-19 А·м².

Наложение внешнего магнитного поля приводит к быстрому насыщению намагниченности МЖ в слабых и средних магнитных полях M~100 кА/м, поскольку магнитный момент однодоменной частицы во много раз превосходит магнитные моменты отдельных атомов, что дополнительно подчеркивает уместность в отношении этих сред термина «суперпарамагнетик».

Процесс намагничивания МЖ определяется в основном двумя механизмами ориентации магнитных моментов ФЧ вдоль магнитного поля. Один механизм связан с броуновским вращательным движением частиц в жидкой матрице, другой обусловлен тепловыми флуктуациями момента внутри самой частицы (неелевский механизм), характеризуемые определенным временем протекания τ_B и τ_N соответственно. Механизм, обусловленный тепловыми флуктуациями магнитного момента внутри самой частицы, свойственен малым однодоменным частицам. С уменьшением размеров однодоменных частиц до нескольких нанометров характеризующая их коэрцитивная сила резко падает до нуля. Ансамбль малых твердых частиц ведет себя подобно парамагнитным атомам с большим магнитным моментом. В одноосной магнитной частице при отсутствии магнитного поля магнитный момент повернут в ту или иную сторону вдоль оси легкого намагничивания. Чтобы направление магнитного момента изменилось на противоположное, магнитный момент должен преодолеть потенциальный барьер, высота которого определяется энергией кристаллографической магнитной анизотропии К_аV_f, где К_а – константа анизотропии, V_f – объем магнитного ядра. Время неелевской релаксации τ_N ~ τ₀ехрs_*, где s_* = K_аV_f/k₀T — безразмерный параметр, равный отношению энергии анизотропии к энергии тепловых флуктуаций, τ₀— время релаксации магнитного момента у определенного направления двухсто­ронней оси легкого намагничения (время ларморовской прецессии магнитного момента частицы). Характерное значение для τ₀ ≈ 10^‑9 с, поэтому для многих гидродинамических процессов усредненный магнитный момент можно считать установившимся возле определенного направления оси магнит­ной анизотропии частицы. Неелевское время τ_Nэкспоненциально растет с уве­личением s_*и может изменяться в широких пределах. При значениях диаметра частицы магнетита, диспергированного в керосине, 8, 10 и 12,5 нм при Т = 25⁰С t_N принимает значения соответственно 10^-18, 10^-9 и 1 с, между тем время τ_B принимает значение 3,8∙10^-7, 7,6∙10^-7 и 1,5∙10^-6 с, т.е. изменяется незначительно. Поэтому динамические свойства МЖ могут существенно зависеть от характера протекания неелевской релаксации в частицах, применяемых при ее изготовлении. Реальные МЖ представляют собой смесь частиц различного размера, причем распределение их по размерам не всегда известно. Из двух механизмов релаксации намагниченности важен тот, который характеризуется меньшим временем вращательной диффузии. В случае t_N>> τ_B установление равновесной ориентации магнитных моментов обеспечивается в основном броуновским вращением частиц.

Особенности магнитных свойств наночастиц связаны с дискретностью их электронных и фононных состояний. Ферромагнитные материалы имеют доменную структуру, которая возникает благодаря минимизации суммарной энергии. Эта энергия включает: энергию обменного взаимодействия, минимальную при параллельном расположении спинов электронов; энергию кристаллографической магнитной анизотропии, обусловленную наличием в кристалле осей легкого и трудного намагничивания; магнитострикционную энергию, связанную с изменением равновесных состояний между узлами решетки и длины доменов; магнитостатическую энергию, связанную с существованием магнитных полюсов как внутри кристаллов, так и на его поверхности. Замыкание магнитных потоков доменов снижает магнитостатическую энергию. Нарушения однородности ферромагнетиков (границы раздела) увеличивают внутреннюю энергию.

При уменьшении размеров ферромагнетика замыкание магнитных потоков внутри него становится все менее энергетически выгодным. По мере приближения размеров ферромагнитных частиц к однодоменному состоянию основным механизмом перемагничивания становится когерентное вращение большинства магнитных моментов отдельных атомов. Этому препятствует анизотропия формы частицы, кристаллографическая и магнитная анизотропия. При достижении некоторого критического размера феррочастицы становятся однодоменными, что сопровождается увеличением коэрцитивной силы Н_с до максимального значения:

,

где К – константа анизотропии, M_S — намагниченность насыщения.

Согласно литературным данным наибольший размер однодоменных частиц Fe и Ni составляет 20 и 60 нм соответственно. Дальнейшее уменьшение размера частиц приводит к резкому падению коэрцитивной силы до нуля вследствие перехода в суперпарамагнитное состояние.

Основной вклад вносят размерные эффекты, влияние поверхности, межчастичные взаимодействия или взаимодействие частиц с матрицей, внутричастичная и межчастичная (кластерная) организация. Однако, домен, как квантовый объект, имеет также нижний критический размер d_cr, при d<d_cr частицы будут находиться в магнитонеупорядоченном состоянии. Теоретическая оценка критического (минимального) размера однодоменной частицы d_cr основана на использовании соотношения неопределенности [253]: Δp·d_cr»ћ. Неопределенность энергии обменного взаимодействия электрона за счет квантового ограничения записывается в виде Δε»ћ²/(2md_cr²). Приравнивая эту энергию энергии обменного взаимодействия, которая, главным образом, ответственна за возникновение магнитного упорядочения, т.е. Δε»k₀T_k, где T_k– температура Кюри массивного материала, получают формулу для оценки критического размера:

d_cr ≈ 2∙10^-8T_k^-1/2.

Для магнетита с температурой Кюри 586К переход в парамагнитное состояние происходит, когда размер домена составляет ~1 нм.

Число магнитных моментов в частице должно быть достаточным, чтобы суммарная энергия обменного взаимодействия превосходила энергию тепловых колебаний k₀T. На интенсивность обменных взаимодействий влияют различные факторы химического или геометрического характера, поэтому точное вычисление d_cr представляет собой сложную задачу.

Одна из особенностей физического состояния наночастицы заключается в воздействии на нее значительного давления поверхностного натяжения p_σ=2σ/R. Так, при σ=1 Дж/м², R=2 нм, p_σ=10⁹ Па.

И.П. Суздалев, основываясь на результатах термодинамической модели магнитных фазовых переходов, приводит соотношение [253]:

Т_k0=Т₀(1-ß_*λ_*p_σ),

где Т_{k0 –} температура Кюри наночастицы; Т₀ – температура Кюри вещества с кристаллической решеткой, не подвергнутой сжатию; ß_* – объемная сжимаемость; λ_* – константа магнитострикции вещества. Таким образом, Т_k0 за счет давления p_σ уменьшается по сравнению с Т₀.

Возрастание внешнего давления на магнитную наночастицу от p₀ до p₀+Δp приводит к изменению температуры магнитного перехода на величину ΔT_k0= –T_kb_* λ_*Δp.

Тогда

.

Отношение ΔТ_k0/Т_k0 пропорционалено Δp. При этом коэффициент пропорциональности сильно зависит от разности (2σ/R–1/(b_*λ_*))^-1.

Пондеромоторная сила.

При движении магнитной суспензии в неоднородном магнитном поле на каждую частицу с магнитным моментом действует сила

. (2.49)

Движение непроводящей МЖ изменяется под действием объемной магнитной силы:

, (2.50)

которая получена из (1) путем суммирования: — намагниченность системы частиц. Поскольку при не слишком высоких частотах , то вместо (2) можно записать [4]:

. (2.51)

Силы, действующие на магнетик со стороны неоднородного магнитного поля, называют пондеромоторными силами. Применительно к неэлектропроводным намагничивающимся вязким жидким средам можно принять, что электропроводность , и, если роль токов смещения невелика, то . В результате этого, а также в силу того, что , уравнение движения принимает вид:

. (2.52)

Для несжимаемой жидкости уравнение движения записывается следующим образом:

. (2.53).

В ряде случаев, например, в акустике, вторым членом в квадратных скобках пренебрегают:

. (2.54)

Напряженность магнитного поля определяется уравнениями магнитостатики: ; .

При наличии системы с неоднородно намагниченной жидкости (смесь МЖ различной концентрации, неравномерное распределение пузырьков воздуха по объему, неравномерное распределение температуры по МЖ) в магнитной жидкости существует градиент намагниченности . Наименьшее значение намагниченность магнитной жидкости принимает там, где ее температура максимальна, то есть на границе с теплообменной поверхностью. Пондеромоторная сила, обусловленная градиентом намагниченности , в однородном магнитном поле будет определяться выражением:

. (2.55)

В систему уравнений магнитогидродинамики входит также уравнение переноса тепла, которое в представлении украинского ученого И.Е. Тарапова (1973 г.) имеет вид:

.

где S– энтропия единицы массы вещества; – коэффициент теплопроводности; τ_ik – тензор вязких напряжений. s– удельная электропроводность среды. Остальные обозначения имеют прежний смысл. Принято , причем M║H, а уравнение состояния среды задано в форме

.

Применительно к неэлектропроводным МЖ можно принять . Если роль токов смещения невелика, то , и уравнение переноса тепла принимает вид:

; (2.56)

Уравнение (2.56) отличается от соответствующего уравнения для «обычных» ненамагничивающихся жидких сред вторым слагаемым в круглых скобках левой части, представляющим собой источник тепла магнитокалорической природы. Магнитокалорический эффект при нормальных условиях вдали от точки Кюри дисперсного магнетика очень слаб, поэтому указанным членом в уравнении (2.56) можно пренебречь.

megaobuchalka.ru

ПАРАМАГНЕТИЗМ • Большая российская энциклопедия

ПАРАМАГНЕТИ́ЗМ (от па­ра… и маг­не­тизм), свой­ст­во ве­ществ, по­ме­щён­ных во внеш­нее маг­нит­ное по­ле, при­об­ре­тать на­маг­ни­чен­ность, на­прав­лен­ную вдоль век­то­ра на­пря­жён­но­сти $\boldsymbol H$ маг­нит­но­го по­ля. П. впер­вые опи­сан М. Фа­ра­де­ем в 1847. В не­од­но­род­ном внеш­нем маг­нит­ном по­ле па­ра­маг­нит­ные те­ла (пара­маг­не­ти­ки) втя­ги­ва­ют­ся в об­ласть с бо́ль­шим зна­че­ни­ем $\boldsymbol H$. П. про­ти­во­по­став­ля­ет­ся диа­маг­не­тиз­му, при ко­то­ром при­об­ре­тае­мая ве­ще­ст­вом на­маг­ни­чен­ность про­ти­во­по­лож­на по на­прав­ле­нию внеш­не­му маг­нит­но­му по­лю. Для П. ха­рак­тер­на воз­мож­ность пре­неб­речь по тем или иным при­чи­нам ори­ен­ти­рую­щим взаи­мо­дей­ст­ви­ем ме­ж­ду ло­каль­ны­ми маг­нит­ны­ми мо­мен­та­ми ато­мов или мо­ле­кул ве­ще­ст­ва, на­ли­чие ко­то­ро­го ха­рак­тер­но для фер­ро­маг­не­тиз­ма и ан­ти­фер­ро­маг­не­тиз­ма, по­это­му П. про­ти­во­пос­тав­ля­ет­ся фер­ро- и ан­ти­фер­ро­маг­не­тиз­му, так же как и лю­бо­му др. маг­ни­то­упо­ря­до­чен­но­му со­стоя­нию (см. Маг­не­тизм).

В мик­ро­ско­пич. тео­рии П. счи­та­ет­ся, что ато­мы, ио­ны или мо­ле­ку­лы па­ра­маг­не­ти­ка об­ла­да­ют от­лич­ны­ми от ну­ля сред­ни­ми ло­каль­ны­ми маг­нит­ны­ми мо­мен­та­ми, взаи­мо­дей­ст­вие ме­ж­ду ко­то­ры­ми дос­та­точ­но мало́, и им мож­но пре­неб­речь. В от­сут­ст­вие внеш­не­го маг­нит­но­го по­ля эти мо­мен­ты слу­чай­ным об­ра­зом ори­ен­ти­ро­ва­ны в про­стран­ст­ве и не­за­ви­си­мы друг от дру­га. Из-за те­п­ло­во­го воз­бу­ж­де­ния сред­ние зна­че­ния про­ек­ций ло­каль­ных маг­нит­ных мо­мен­тов па­ра­маг­не­ти­ков на лю­бое на­прав­ле­ние в про­стран­ст­ве рав­ны ну­лю (в от­ли­чие от спи­но­вых стё­кол) и сум­мар­ная спон­тан­ная на­маг­ни­чен­ность ве­ще­ст­ва рав­на ну­лю (в от­ли­чие от фер­ро- и ан­ти­фер­ро­маг­не­ти­ков). Внут­ри па­ра­маг­не­ти­ка, по­ме­щён­но­го во внеш­нее маг­нит­ное по­ле $\boldsymbol H$, на маг­нит­ные мо­мен­ты те­ла дей­ст­ву­ет не толь­ко внеш­нее по­ле, но и воз­ни­каю­щая в об­раз­це на­маг­ни­чен­ность $\boldsymbol М$, по­это­му те­ло на­маг­ни­чи­ва­ет­ся в на­прав­ле­нии, при­мер­но сов­па­даю­щем с на­прав­ле­ни­ем внеш­не­го по­ля, и на­маг­ни­чен­ность в об­щем слу­чае яв­ля­ет­ся тен­зо­ром, а не ска­ляр­ной ве­ли­чи­ной. При ма­лых зна­че­ни­ях $\boldsymbol H$ на­маг­ни­чен­ность $\boldsymbol М$ па­ра­маг­не­ти­ков ли­ней­но за­ви­сит от $\boldsymbol H \! : \boldsymbol M=\hat χ \boldsymbol H$, где $\hat χ$ – тен­зор маг­нит­ной вос­при­им­чи­во­сти, ком­по­нен­ты ко­то­ро­го не за­ви­сят от $\boldsymbol H$. При уве­ли­че­нии $\boldsymbol H$ до зна­че­ний, пре­вос­хо­дя­щих т. н. по­ле на­сы­ще­ния $H_s$, воз­мож­но яв­ле­ние маг­нит­но­го на­сы­ще­ния, при ко­то­ром $M$ стре­мит­ся к на­маг­ни­чен­но­сти на­сы­ще­ния $M_s$.

Ориентационный парамагнетизм

Ес­ли ори­ен­та­ция ло­каль­ных маг­нит­ных мо­мен­тов час­тиц ве­ще­ст­ва во внеш­нем маг­нит­ном по­ле не свя­за­на с дви­же­ни­ем этих час­тиц в про­стран­ст­ве, то го­во­рят об ори­ен­та­ци­он­ном П. (П. Лан­же­вен, 1905). В этом слу­чае П. оп­ре­де­ля­ет­ся не­за­ви­си­мой ори­ен­та­ци­ей маг­нит­ных мо­мен­тов во внеш­нем по­ле $\boldsymbol H$ и опи­сы­вает­ся на ос­но­ве рас­пре­де­ле­ния Гиб­бса для про­ек­ций ло­каль­ных маг­нит­ных мо­мен­тов на на­прав­ле­ние по­ля. При клас­сич. рас­смот­ре­нии для на­маг­ни­чен­но­сти $M$ спра­вед­ли­ва фор­му­ла $M=Nμ_0μL(μH/kT)$, где $μ_0$ – маг­нит­ная по­сто­ян­ная, $μ$ – маг­нит­ный мо­мент ато­ма, $N$ – чис­ло ато­мов в еди­ни­це объ­ё­ма ве­ще­ст­ва, $k$ – по­сто­ян­ная Больц­ма­на, $L(x)= \text {cth}\,x-1/x$ – функ­ция Лан­же­ве­на, $T$ – темп-ра. В слу­чае сла­бых по­лей или вы­со­ких тем­пе­ра­тур (при $μH/kT≪1$) ори­ен­та­ци­он­ная па­ра­маг­нит­ная вос­при­им­чи­вость $χ_{пм}=Nμ_0μ^2/3kT$, т. е. вы­пол­ня­ет­ся Кю­ри за­кон: $χ_{пм}=C/T$, где $C=Nμ_0μ^2/3k$ – кон­стан­та Кю­ри.

Про­ек­ция $m_z=g_Jμ_БJ_z$ ло­каль­но­го маг­нит­но­го мо­мен­та на ось $Oz$ (вдоль ко­торой на­прав­ле­но по­ле $\boldsymbol H$) при­ни­ма­ет $2J+1$ зна­че­ний (здесь $g_J$ – фак­тор Лан­де, $μ_Б$ – маг­не­тон Бо­ра, $J$ – кван­то­вое чис­ло, оп­ре­де­ляю­щее пол­ный мо­мент ко­ли­че­ст­ва дви­же­ния ато­ма). В этом слу­чае на­маг­ни­чен­ность сис­те­мы, со­стоя­щей из $N$ ато­мов, име­ет вид $$M=Nμ_0g_JJμ_БB_J(g_JJμ_БH/kT)$$ и оп­ре­де­ля­ет­ся функ­ци­ей Брил­лю­эна $$B_J(x)=((2J+1)/2J)\text{cth}((2J+1)/2J)x-(1/2J)\text{cth}(1/2J)x.$$ При $J→∞$ это вы­ра­же­ние пе­ре­хо­дит в клас­сич. фор­му­лу с функ­ци­ей Лан­же­ве­на. В слу­чае $μH/kT≪1$ из вы­ра­же­ния для на­маг­ни­чен­но­сти по­лу­ча­ет­ся фор­му­ла для маг­нит­ной вос­при­им­чи­во­сти: $χ_{пм}=Nμ_0μ_Б^2g_J^2J(J+1)/3kT$, т. е. вы­пол­ня­ет­ся за­кон Кю­ри: $χ_{пм}=C/T$, где $C=N[μ_0μ_Б^2g_J^2J(J+1)]/3k$. Т. о., оп­ре­де­лив из экс­пе­ри­мен­та $C$ и зная $N$, $k$ и $μ_Б$, мож­но рас­счи­тать эф­фек­тив­ное чис­ло маг­не­то­нов Бо­ра $p_{эфф}$, при­хо­дя­щих­ся на 1 атом па­ра­маг­не­ти­ка: $p_{эфф}=g_J\sqrt{J(J+1)}$.

Поляризационный парамагнетизм

При по­сле­до­ва­тель­ном кван­то­во­ме­ха­нич. рас­смот­ре­нии ока­за­лось, что, кро­ме ори­ен­та­ци­он­ной вос­при­им­чи­во­сти сис­те­мы ато­мов или ио­нов, су­ще­ст­ву­ет ещё т. н. по­ля­ри­за­ци­он­ный вклад в вос­при­им­чи­вость (Дж. Ван Флек, 1927). По­ля­ри­за­ци­он­ный П. име­ет чис­то кван­то­вую при­ро­ду и свя­зан с тем, что за счёт тем­пе­ра­тур­ных флук­туа­ций к осн. со­стоя­нию ато­мов или мо­ле­кул при­ме­ши­ва­ют­ся воз­бу­ж­дён­ные со­стоя­ния (см. Ван­фле­ков­ский па­ра­маг­не­тизм). При боль­ших зна­че­ни­ях раз­но­сти энер­гий ос­нов­но­го и воз­бу­ж­дён­но­го со­стоя­ний ато­мов или мо­ле­кул по­ля­ри­за­ци­он­ный вклад в сум­мар­ную вос­при­им­чи­вость мал и для вос­при­им­чи­во­сти вы­пол­ня­ет­ся за­кон Кю­ри; при не­боль­ших зна­че­ни­ях этой раз­но­сти по­ля­ри­за­ци­он­ный вклад ста­но­вит­ся оп­ре­де­ляю­щим и реа­ли­зу­ет­ся П., не за­ви­ся­щий от тем­пе­ра­ту­ры.

Я. Г. Дорф­ман (1924) и Ф. Хунд (1925) пред­по­ло­жи­ли, что в си­лу осо­бен­но­стей строе­ния элек­трон­ной обо­лоч­ки РЗЭ не­ко­то­рые их со­ли пред­став­ля­ют со­бой под­хо­дя­щий объ­ект для срав­не­ния с тео­ри­ей маг­нит­ной вос­при­им­чи­во­сти иде­аль­но­го га­за маг­нит­ных мо­мен­тов, напр. со­еди­не­ние $\ce{Pr2(SO4)3·8h3O}$, маг­нит­ные свой­ст­ва ко­то­ро­го оп­ре­де­ля­ют­ся маг­нит­ным мо­мен­том ио­нов $\ce{Pr^{3+}}$. Маг­нит­ные мо­мен­ты $4f$-обо­лоч­ки хо­ро­шо эк­ра­ни­ро­ва­ны от воз­дей­ст­вия со­сед­них ато­мов за­пол­нен­ны­ми внеш­ни­ми $5s-$ и $5p$-обо­лоч­ка­ми ио­нов ред­ко­зе­мель­но­го ме­тал­ла; с др. сто­ро­ны, взаи­мо­дей­ст­ви­ем маг­нит­ных ио­нов мож­но пре­неб­речь, по­сколь­ку они на­хо­дят­ся на боль­ших рас­стоя­ни­ях друг от дру­га. Т. о., маг­нит­ные свой­ст­ва со­лей ред­ко­зе­мель­ных ме­тал­лов по­доб­ны маг­нит­ным свой­ст­вам па­ров ме­тал­лов. При их тео­ре­тич. опи­са­нии не­об­хо­ди­мо учи­ты­вать кван­то­вую при­ро­ду маг­нит­ных мо­мен­тов ато­мов ред­ко­зе­мель­ных ме­тал­лов; по­ля­ри­за­ци­он­ный вклад в вос­при­им­чи­вость в та­ких па­ра­маг­не­ти­ках дос­та­точ­но ве­лик.

На­ли­чие взаи­мо­дей­ст­вия ме­ж­ду маг­нит­ны­ми мо­мен­та­ми ато­мов наи­бо­лее су­ще­ст­вен­но в кон­ден­си­ров. сре­дах и при­во­дит к от­кло­не­нию за­ви­си­мо­сти $χ_{пм}(T)$ от за­ко­на Кю­ри и вы­пол­не­нию Кю­ри – Вей­са за­ко­на $χ_{пм}(T)=C/(T-θ_{пм})$, где $θ_{пм}$ – па­ра­маг­нит­ная темп-ра Кю­ри, ко­то­рая мо­жет быть по­ло­жи­тель­ной или от­ри­ца­тель­ной в за­ви­си­мо­сти от осо­бен­но­стей маг­нит­ной струк­ту­ры ве­ще­ст­ва. Энер­ге­тич. па­ра­метр $∣kθ_{пм}∣$ по по­ряд­ку ве­ли­чи­ны со­от­вет­ст­ву­ет энер­гии взаи­мо­дей­ст­вия маг­нит­ных мо­мен­тов. Тем­пе­ра­тур­ная за­ви­си­мость маг­нит­ной вос­при­им­чи­во­сти та­ких маг­не­ти­ков име­ет слож­ный вид и тре­бу­ет ин­ди­ви­ду­аль­но­го рас­смот­ре­ния.

Парамагнетизм металлов и полупроводников

На­ли­чие в ме­тал­лах элек­тро­нов про­во­ди­мо­сти, об­ла­даю­щих спи­ном $s=1/2$ и спи­но­вым маг­нит­ным мо­мен­том $μ_Б$, да­ёт до­пол­нит. вклад в П. ме­тал­лов. Сис­те­ма элек­тро­нов про­во­ди­мо­сти пред­став­ля­ет со­бой вы­ро­ж­ден­ный фер­ми-газ, в ко­то­ром по­яв­ле­ние на­маг­ни­чен­но­сти, т. е. не­ра­вен­ст­во чис­ла фер­мио­нов с разл. зна­че­ния­ми про­ек­ции спи­на, в си­лу прин­ци­па Пау­ли, при­во­дит к уве­ли­че­нию ср. ки­не­тич. энер­гии га­за. Во внеш­нем маг­нит­ном по­ле про­ис­хо­дит ори­ен­ти­ро­ва­ние маг­нит­ных мо­мен­тов вдоль на­прав­ле­ния внеш­не­го по­ля. Со­от­вет­ст­вую­щая вос­при­им­чи­вость прак­ти­че­ски не за­ви­сит от темп-ры (см. Пау­ли па­ра­маг­не­тизм).

П. элек­тро­нов и ды­рок в по­лу­про­водни­ках оп­ре­де­ля­ет­ся их кон­цен­тра­ци­ей и ве­ли­чи­ной эф­фек­тив­ных маг­нит­ных мо­мен­тов, за­ви­ся­щих от зон­ной струк­ту­ры по­лу­про­вод­ни­ка. Кон­цен­тра­ция но­си­те­лей за­ря­да силь­но за­ви­сит от темп-ры, по­это­му су­ще­ст­ву­ет за­ви­си­мость па­ра­маг­нит­ной вос­при­им­чи­во­сти па­ра­маг­нит­ных по­лу­про­вод­ни­ков от $T$. В про­стей­шем слу­чае мож­но по­ла­гать, что $χ_{пм}(T)=AT^{1/2}\exp(–ΔE/2kT)$, где $A$ – па­ра­метр ве­ще­ст­ва, $ΔE$ – ши­ри­на за­пре­щён­ной зо­ны по­лу­про­вод­ни­ка. Элек­трон­ный П. в по­лу­про­вод­ни­ках час­то пе­ре­кры­ва­ет­ся диа- и па­ра­маг­не­тиз­мом ио­нов кри­стал­лич. ре­шёт­ки, по­это­му на­блю­дать чис­тый П. элек­тро­нов в по­лу­про­вод­ни­ках за­труд­ни­тель­но. Осо­бен­но­сти зон­ной струк­ту­ры при­во­дят к ис­ка­же­ни­ям про­сто­го вы­ра­же­ния для $χ_{пм}$.

Суперпарамагнетизм

На­блю­да­ет­ся в ан­самб­ле сла­бо­взаи­мо­дей­ст­вую­щих од­но­до­мен­ных фер­ро­маг­нит­ных час­тиц ма­ло­го объ­ё­ма, об­ла­даю­щих боль­шим маг­нит­ным мо­мен­том. Пе­ре­маг­ни­чи­ва­ние внут­ри та­ких час­тиц про­ис­хо­дит пу­тём ко­ге­рент­но­го вра­ще­ния всех маг­нит­ных мо­мен­тов ио­нов внут­ри час­ти­цы, по­это­му су­пер­па­ра­маг­не­тик во внеш­нем маг­нит­ном по­ле ве­дёт се­бя как па­ра­маг­не­тик (см. Су­пер­па­ра­маг­не­тизм).

Ядер­ный па­ра­маг­не­тизм. Обу­слов­лен маг­нит­ны­ми мо­мен­та­ми ядер. Ес­ли взаи­мо­дей­ст­вие ме­ж­ду ни­ми и маг­нит­ны­ми мо­мен­та­ми элек­трон­ных обо­ло­чек до­ста­точ­но малo, то ядер­ная па­ра­маг­нит­ная вос­при­им­чи­вость под­чи­ня­ет­ся за­ко­ну Кю­ри: $χ_я=Nμ_0μ_{я\,эфф}^2/3kT$, где $μ_{я\,эфф}$ – эф­фек­тив­ный маг­нит­ный мо­мент яд­ра, ко­то­рый при­мер­но в 1000 раз мень­ше $μ_Б$ (см. Маг­не­тизм мик­ро­час­тиц), по­это­му ядер­ная па­ра­маг­нит­ная вос­при­им­чи­вость при­мер­но в 10⁶ раз мень­ше па­ра­маг­нит­ной вос­при­им­чи­во­сти ио­нов (см. Ядер­ный па­ра­маг­не­тизм).

bigenc.ru

Большая Энциклопедия Нефти и Газа, статья, страница 2

Парамагнетики

Cтраница 2

Диамагнетики и парамагнетики имеют относительную магнитную проницаемость, близкую к единице.  [16]

Диамагнетики и парамагнетики имеют магнитную проницаемость, близкую к единице.  [17]

Диамагнетики и парамагнетики имеют магнитную проницаемость, близкую к единице, и по магнитным свойствам нашли себе ограниченное применение в технике.  [18]

Диамагнетики и парамагнетики имеют магнитную проницаемость, близкую к единице, и по магнитным свойствам нашли себе ограниченное применение в технике.  [19]

Ферромагнетиками называются парамагнетики, у которых относительная магнитная проницаемость при температуре, меньшей точки Кюри, ц1 и зависит от напряженности внешнего магнитного поля.  [20]

Ферромагнетиками называются парамагнетики с самопроизвольной намагниченностью, у которых относительная магнитная проницаемость при температуре, меньшей точки Кюри, ( I 1 и зависит от напряженности внешнего магнитного поля.  [22]

Диамагнетики и парамагнетики иногда объединяют под названием слабомагнитных веществ, не обладающих атомным магнитным порядком, а ферромагнетики и ферримагнетики — под названием сильномагнитных веществ, обладающих атомным магнитным порядком; для антиферромагнетиков характерен атомный магнитный порядок, но количественно этот эффект весьма мал.  [23]

Итак, парамагнетики и диамагнетики в магнитном поле намагничиваются по-разному. Поэтому их поведение в магнитном поле должно быть различным.  [24]

Парамагнитные вещества ( парамагнетики) состоят из атомов, у которых орбитальные магнитные моменты электронов не компенсируют друг друга. Парамагнитные атомы обладают магнитным моментом и создают в окружающем пространстве магнитное поле. В отсутствие внешнего магнитного поля в парамагнетике магнитные моменты атомов ориентированы хаотично и вследствие теплового движения их ориентация непрерывно изменяется.  [25]

Сравнивая диамагнетики и парамагнетики, мы легко обнаруживаем, чем они отличаются: парамагнетики состоят из атомов или молекул, имеющих магнитные моменты, а диамагнетики — из атомов или молекул, магнитные моменты которых равны нулю. Теперь мы покажем, что наше наблюдение зафиксировало существенное обстоятельство: тела, состоящие из атомов ( молекул), имеющих магнитный момент, должны быть парамагнетиками, а тела, состоящие из атомов ( молекул) с нулевым моментом, — диамагнетиками.  [26]

Заметим, что парамагнетики намагничиваются очень слабо даже и в сильных внешних полях. Из рис. 25.21 видно, что парамагнетик должен втягиваться во внешнее магнитное поле, поскольку разноименные полюсы магнитов притягиваются.  [28]

Диа — и парамагнетики обычно относят к слабомагнитным, а остальные — к сильномагнитным веществам.  [30]

Страницы:      1    2    3    4

www.ngpedia.ru