Все формулы диагонали параллелограмма
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.

a, b — стороны параллелограмма
D — большая диагональ
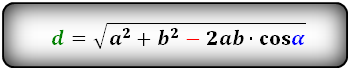
d — меньшая диагональ
α, β — углы параллелограмма
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
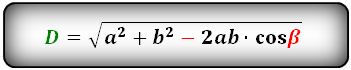


Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
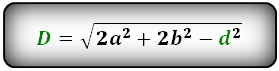
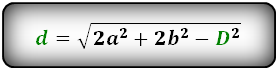
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.
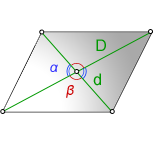
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
S — площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
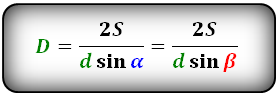
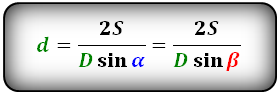
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Формулы диагонали параллелограмма
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β
— углы параллелограмма
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
S — площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Периметр и площадь параллелограмма
Параллелограммом называют четырехугольник у которого противоположные стороны параллельны между собой. Основные задачи в школе по данной теме заключаются в вычислении площади параллелограмма, его периметра, высоты, диагоналей. Указанные величины и формулы для их вычисления будут приведены ниже.
Свойства параллелограмма
Противоположные стороны параллелограмма как и противоположные углы равны между собой:
AB=CD, BC=AD,
Диагонали параллелограмма в точке пересечения делятся на две равные части:
АО=OC, OB=OD.
Углы прилегающие к любой стороне (соседние углы) в сумме равны 180 градусов.
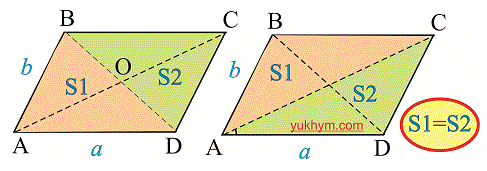
Каждая из диагоналей параллелограмма делит его на два одинаковые по площади и геометрическими размерами треугольники.
Еще одно замечательное свойство которое часто применяют при решении задач состоит в том, что сумма квадратов диагоналей в параллелограмме равна сумме квадратов всех сторон:
AC^2+BD^2=2*(AB^2+BC^2).
Основные признаки параллелограммов:
1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
2. Четырехугольник с равными противоположными сторонами является параллелограммом.
3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом.
4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.
5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом
Биссектрисы параллелограмма
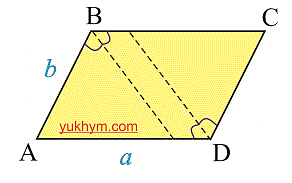
Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.
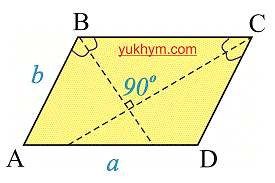
Биссектрисы соседних углов ( прилегающие к одной стороне ) пересекаются под прямым углом (перпендикулярные).
Высота параллелограмма
Высота параллелограмма — это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.
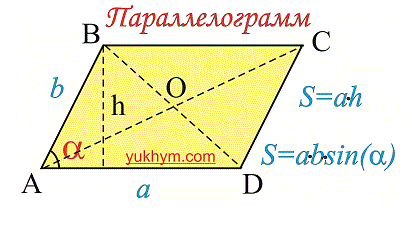
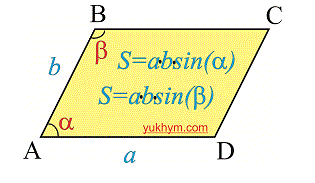
Формула площади параллелограмма
Площадь параллелограмма равна произведению стороны на высоту проведенную к ней. Формула площади следующая
Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.
Периметр параллелограмма
Формула для вычисления периметру параллелограмма имеет вид
то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.
Посмотреть материалы:
Периметр параллелограмма
Параллелограмм это геометрическая фигура имеющая четыре параллельные стороны, противоположных друг другу. В школьной программе все задания по решению параллелограмма, направлены на нахождение высоты, площади, диагонали и периметра. О них и пойдет речь.
Параллелограмм обладает свойствами, такими как:
В параллелограмме и углы и стороны, которые противоположны между собой одинаковы: АВ = CD, BC =AD. Так же как углы АВС = ADC и ВАD = BCD.
Диагонали проведенные из углов параллелограмма в месте пересечения разделятся на две одинаковые части. АО = ОС, ОВ = OD.
Сумма двух углов, одной стороны всегда 180 градусов.
углы: А + В = 1800, В + С = 1800, С + D =1800, A + D = 1800 .
Любая диагональ разделяет параллелограмм на две одинаковые фигуры (треугольник) как по площади так и по размеру.
Зачастую встречается такое интересное свойство как, сума диагоналей в квадрате одинакова с суммой сторон в квадрате.
АС2 + BD2 = (AB2 + BC2). AC2 + BD2 = 2 * (AB2 + BC2)
У параллелограмма есть несколько основных признаков.
— Четырехугольная фигура с противоположными сторонами параллельными друг другу и есть параллелограмм.
— Четырехугольная фигура имеющая одинаковые противоположные стороны, есть параллелограмм.
— Четырехугольная фигура имеющая одинаковые параллельные и противоположные стороны, есть параллелограмм.
— Когда встречающиеся диагонали четырехугольной фигуры в месте пересечения разделяются на равные части. Данная фигура является параллелограммом.
— Четырехугольная фигура в которой противоположные углы одинаковы называется параллелограммом.
Периметр параллелограмма находится по формуле
Р = 2 (а+b)
что означает что периметр равняется двойной сумме сторон.
Биссектриса параллелограмма
Из школьной программы помню определение которое засело в памяти на всю жизнь — Биссектриса это крыса, что ходит по углам и делит угол пополам. Если же говорить научным языком, то:
Биссектрисы углов находящихся на одной стороне встречаются в точке пересечения под углом в 90 градусов.
Так же они могут совпадать и быть параллельны друг другу.
Так же в параллелограмме можно найти высоту, она обозначается в виде отрезка исходящего из угла к основанию, следовательно, от каждого угла их можно провести две.
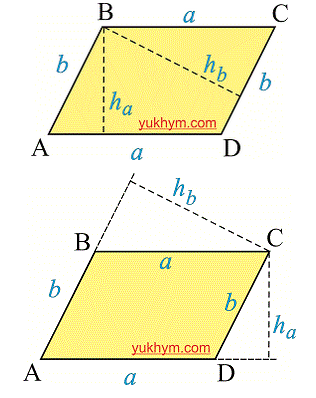
Площадь параллелограмма это произведение стороны и высоты приведенную к ней. Находится по формуле.
S = a * ha = b * hb
Есть еще один способ вычисления, но им не так часто пользуются в расчетах. Она звучит как площадь параллелограмма это произведение рядом лежащих сторон умноженный на синус угла находящегося между ними.
S = a * b * sin(?) = a * b * sin(?)
Все приведенные в данной статье формулы помогут Вам в решении различных задач по нахождению величин параллелограмма, это не сложно но очень интересно.
Заметка: если Вы находитесь в поиске персонала. Империя кадров поможет вам в этом вопросе. Просто перейдите по ссылке персонал временный (http://www.imperia.ru/client/temp_staff/) и узнайте подробнее.
Если материал был полезен, вы можете
Как найти стороны параллелограмма
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Формулы длины сторон через диагонали и угол между ними.

a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), ( a, b):




Формулы сторон параллелограмма через диагонали и сторону, (a, b):


Формулы сторон параллелограмма , (a, b):


2. Формулы длины сторон параллелограмма через высоту.

a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
α, β — углы параллелограмма
Формулы сторон параллелограмма через высоту, (a, b):


3. Дополнительные, интересные формулы параллелограмма:

a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α — острый угол между диагоналями
Формула суммы квадратов диагоналей:

Формула разности квадратов сторон:

Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Периметр параллелограмма: онлайн калькулятор, формулы, примеры решений
Параллелограмм — четырехугольник, стороны которого являются попарно параллельными отрезками. Параллелограмм представляет собой фигуру, частными случаями которой являются ромб, прямоугольник и квадрат — четырехугольники, знакомые нам с самого детства.
Геометрия параллелограмма
Четырехугольник считается параллелограммом, если соблюдается хотя бы одно из нижеперечисленных условий:
- противоположные стороны параллельны друг другу;
- противоположные стороны равны друг другу;
- пересекающиеся диагонали в точке пересечения делятся пополам.
Параллелограмм и его частные случаи — наиболее встречающаяся в реальной жизни фигура. В трехмерном пространстве параллелограмм превращается в четырехугольную призму, форму которой имеет большинство рукотворных объектов: кирпичи, системные блоки компьютеров, стены, книги или коробки. Косоугольные фигуры встречаются реже, однако форму таких параллелограммов имеют грани резцов металлообрабатывающих станков или элементы дизайна и декора, такие как ковры или геометрические узоры на стенных покрытиях.
Параллелограмм также можно увидеть прямо на улице. Прямоугольные или косоугольные окна — это параллелограммы. Кроме того, прямо под ногами вы можете увидеть один из наиболее банальных воплощений ромба в реальности — тротуарную плитку. Столь широкое распространение данной фигуры в повседневной жизни делает вопрос определения площади и периметра параллелограмма актуальной задачей.
Периметр параллелограмма
Периметр представляет собой количественную оценку общей длины сторон любой фигуры. Параллелограмм имеет четыре стороны, которые попарно равны и параллельны друг другу. Исходя из этого, периметр геометрической фигуры выражается простой формулой:
P = 2 (a + b)
Путем подстановок мы можем найти стороны геометрической фигуры при помощи диагоналей и одной из ее высот. Наш онлайн-калькулятор позволяет определить периметр параллелограмма, зная три переменных: две диагонали и высоту четырехугольника.
Естественно, что вы можете воспользоваться и самой простой формулой для подсчета периметра, однако программный код калькулятора требует введения 3 переменных, поэтому для его корректной работы помимо длин сторон введите значение высоты, равное ha = b или hb = a. К примеру, если a = 3, b = 4, то укажите, что hb = 3 или ha = 4. Такая подстановка превратит параллелограмм в квадрат, однако при известных сторонах периметр не зависит от величины углов геометрической фигуры, что позволит нам корректно рассчитать требуемый параметр. Рассмотрим пару примеров.
Примеры из жизни
Пример №1
Давайте определим периметр четырехугольника, зная, что его диагонали равны 3 и 5 см, а высота фигуры составляет 2 см. Свойства четырехугольника подсказывают нам, что высота численно не может быть больше длин диагоналей, поэтому параметр h всегда меньше и d1, и d2. Введем эти данные в форму калькулятора и получим мгновенный ответ:
P = 11,45 см
Зная эти переменные, мы можем определить периметр любого параллелограмма.
Пример №2
Определить периметр абстрактного параллелограмма можно и по стандартной, самой простой формуле. Если стороны четырехугольника равны a = 3 и b = 4, то нам понадобится ввести эти данные в калькулятор, а также указать, что ha = 4. Мы получим ответ в виде:
P = 14,
что полностью соответствует расчетам по классической формуле P = 2 (a + b).
Заключение
Параллелограмм и его частные случаи занимают в деятельности человека важное место. В реальной жизни вам понадобится определять периметры и площади прямоугольников, квадратов, ромбов или параллелограммов, которые являются гранями соответствующих призм или полноценными фигурами на плоскости. Используйте наши калькуляторы для выполнения расчетов при решении повседневных, школьных или профессиональных задач.
Диагонали параллелограмма | Онлайн калькулятор
Параллелограмм — это четырехугольник, у которого по определению противоположные стороны параллельны и равны. Как следствие, противоположные углы параллелограмма также будут между собой равны, а так как сумма всех углов в четырехугольнике равна 360 градусам, то можно сделать вывод, что сумма двух последовательных углов будет равна 180 градусам. Данное свойство будет играть существенную роль для нахождения диагоналей параллелограмма, с учетом того, что они разной длины.
Так как каждая диагональ параллелограмма делит его на два равновеликих треугольника, именно их свойства и будут использованы для выведения формулы диагонали параллелограмма.
В любом треугольнике угол и сторона, лежащие напротив, пропорциональны друг другу. Для параллелограмма это будет значить, что более длинная диагональ будет лежать напротив тупого угла, а более короткая диагональ — напротив острого.С учетом того, что стороны треугольников, полученных в результате проведения диагоналей, одинаковы — это стороны параллелограмма, значение градусной меры угла между данными сторонами определяет чему будет равна длина диагонали,вычисленной по формуле. Другими словами, если в формулудиагонали подставить значение острого угла параллелограмма, то калькулятор вычислит длину короткой диагонали, а если подставить значение тупого угла — то длинной.
Для того чтобы перейти от одного угла к другому, используется разность 180 градусов и заданного угла, таким образом калькулятор одновременно может вычислить обе диагонали.
α=180°-β
Чтобы вывести формулу диагонали параллелограмма, используется теорема косинусов в треугольнике, который диагональ образует со сторонами. В любом из подобных треугольников, диагональ является стороной, противолежащей углу параллелограмма и, соответственно, ее квадрат равен сумме квадратов двух других сторон треугольника (сторон параллелограмма, в данном случае) за вычетом удвоенного произведения тех же сторон на косинус приведенного угла. Чтобы найти длину диагонали параллелограмма, калькулятор вычисляет квадратный корень из данного выражения.
