«Производная. Первообразная и интеграл», ФГОС
Контрольная работа по теме:
«Производная. Первообразная и интеграл»
Раздел. Начала математического анализа. | |||
Тема. Производная. Первообразная и интеграл | Знание свойств производной и умение находить производную функции | 2 | К.р.№5(1,2,3) |
Умение находить угловой коэффициент касательной к графику функции. Знание формулы углового коэффициента касательной к графику функции | 2 | К.р.№5(3) | |
Умение находить критические точки | 2 | К. | |
Умение находить промежутки монотонности | 2 | К.р.№5(2) | |
Знание алгоритма нахождения наибольшего и наименьшего значений функции на отрезке. Умение его применить | 2 | К.р.№5(2) | |
Умение находить все первообразные функции. Знание свойств первообразной функции | 2 | К.р.№5(4,5) | |
Умение находить абсциссу точки графика функции. Знание формулы углового коэффициента касательной к графику функции | 2 | К.р.№5(3) | |
Умение находить площадь фигуры через производную. Знание формулы Ньютона-Лейбница | 2 | К. | |
Контрольная работа по теме:
«Производная. Первообразная и интеграл»
Вариант № 1
Найдите критические (стационарные) точки функции f(x)=2×3-9×2-60x+127.
Найдите наибольшее и наименьшее значение функции y=2×3-3×2-12x+24 на отрезке [-2;1].
Составьте уравнение касательной к графику функции f(x)=2×2-5x+1, в точке графика с абсциссой x0=2.
Найдите площадь криволинейной трапеции, ограниченной графиком функции f(x)=x2+3x и прямыми x=0, x=1.
Первообразная функции f(x)=3×2+2x при x=1 принимает значение 81. Найдите ее значение при x=-1.
Контрольная работа по теме:
«Производная. Первообразная и интеграл»
Вариант № 2
Найдите критические (стационарные) точки функции f(x)=2×3+3×2-72x-213.
Найдите наибольшее и наименьшее значение функции y=x3-9×2+24x-15 на отрезке [1;3].
Составьте уравнение касательной к графику функции f(x)=3×2-4x-2, в точке графика с абсциссой x0=-1.
Найдите площадь криволинейной трапеции, ограниченной графиком функции f(x)=2×2+x и прямыми x=0, x=1.
Первообразная функции f(x)=4×3+2x при x=1 принимает значение 25. Найдите ее значение при x=2.
Эталоны ответов
Вариант № 1
f(x)=2×3-9×2-60x+127
Решение:
f’(x)=6×2-18x-60
f’(x)=0 => 6×2-18x-60=0
x2-3x-10=0
По теореме, обратной теореме Виета:
x1+x2=3
x1*x2=-10
x1=-2, x2=5
Ответ: x1=-2, x2=5
y=2×3-3×2-12x+24, [-2;1]
Решение:
y’=6×2-6x-12
y’=0 => 6×2-6x-12=0
x2-x-2=0
По теореме, обратной теореме Виета:
x1+x2=1
x1*x2=-2
x1=-1, x2=2
Отрезку [-2;1] принадлежит только точка x1=-1.
y(-2)=-16-12+24+24=20
y(-1)=-2-3+12+24=31
y(1)=2-3-12+24=11
Ответ: yнаиб=31 при x=-1, yнаим=11 при x=1
f(x)=2×2-5x+1, в точке графика с абсциссой x0=2
Решение:
f’(x)=4x-5
f(2)=8-10+1=-1, f’(2)=8-5=3
y=f(x0)+f’(x0)(x-x0)
y=-1+3(x-2)
y=3x-7
Ответ: y=3x-7
f(x)=x2+3x, x=0, x=1
Решение:
Ответ:
f(x)=3×2+2x, F(1)=81. F(-1)=?
Решение:
F(x)=x3+x2+C
F(1)=1+1+C, F(1)=81 => C=79
F(-1)=-1+1+79=79
Ответ: F(-1)=79
Вариант № 2
f(x)=2×3+3×2-72x-213
Решение:
f’(x)=6×2+6x-72
f’(x)=0 => 6×2+6x-72=0
x2+x-12=0
По теореме, обратной теореме Виета:
x1+x2=-1
x1*x2=-12
x1=-4, x2=3
Ответ: x1=-4, x2=3
y=x3-9×2+24x-15, [1;3]
Решение:
y’=3×2-18x+24
y’=0 => 3×2-18x+24=0
x2-6x+8=0
По теореме, обратной теореме Виета:
x1+x2=6
x1*x2=8
x1=2, x2=4
Отрезку [1;3] принадлежит точка x1=2.
y(1)=1-9+24-15=1
y(2)=8-36+48-15=5
y(3)=27-81+72-15=3
Ответ: yнаиб=5 при x=2, yнаим=1 при x=1
f(x)=3×2-4x-2, в точке графика с абсциссой x0=-1
Решение:
f’(x)=6x-4
f(-1)=3+4-2=5, f’(-1)=-6-4=-10
y=f(x0)+f’(x0)(x-x0)
y=5-10(x+1)
y=-10x-5
Ответ: y=-10x-5
f(x)=2×2+x, x=0, x=1
Решение:
Ответ:
f(x)=4×3+2x, F(1)=25. F(2)=?
Решение:
F(x)=x4+x2+C
F(1)=1+1+C, F(1)=25 => C=23
F(2)=16+4+25=45
Ответ: F(2)=45
Таблица первообразных и правила их нахождения
На этой странице вы найдёте:
1. Собственно, таблицу первообразных — её можно скачать в формате PDF и распечатать;
2. Видео, посвящённое тому, как этой таблицей пользоваться;
3. Кучу примеров вычисления первообразной из различных учебников и контрольных работ.
Кучу примеров вычисления первообразной из различных учебников и контрольных работ.
В самом видео мы разберём множество задач, где требуется посчитать первообразные функций, зачастую довольно сложных, но главное — не являющихся степенными. Все функции, сведённые в таблицу, предложенную выше, необходимо знать наизусть, подобно производным. Без них невозможно дальнейшее изучение интегралов и их применение для решения практических задач.
Сегодня мы продолжаем заниматься первообразными и переходим у чуть более сложной теме. Если в прошлый раз мы рассматривали первообразные только от степенных функций и чуть более сложных конструкций, то сегодня мы разберем тригонометрию и многое другое.
Как я говорил на прошлом занятии, первообразные в отличие от производных, никогда не решаются «напролом» с помощью каких-либо стандартных правил. Более того, плохая новость состоит в том, что в отличие от производной, первообразная вообще может не считаться. {2}}}}\]
{2}}}}\]
\[M=\left( \frac{1}{2};\text{ }\!\!\pi\!\!\text{ } \right)\]
Здесь также речь идет о тригонометрических функциях. Если мы посмотрим в таблицу, то, действительно, так и получится:
\[F\left( x \right)=\arcsin x+C\]
Нам нужно среди всего множества первообразных найти ту, которая проходит через указанную точку:
\[\text{ }\!\!\pi\!\!\text{ }=\arcsin \frac{1}{2}+C\]
\[\text{ }\!\!\pi\!\!\text{ }=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}+C\]\[C=\text{ }\!\!\pi\!\!\text{ }-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}=\frac{6\text{ }\!\!\pi\!\!\text{ }-\text{ }\!\!\pi\!\!\text{ }}{6}=\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}\]
Давайте окончательно запишем:
\[F\left( x \right)=\arcsin x+\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}\]
Вот так все просто. Единственная проблема состоит в том, для того чтобы считать первообразные простых функций, нужно выучить таблицу первообразных. Однако после изучения таблицы производных для вас, я думаю, это не будет проблемой. {2}}+1}\]
{2}}+1}\]
Теперь найдем то, что искали:
\[F\left( x \right)=x-\text{arctg}x+C\]
Вот и все вычисления. Несмотря на кажущуюся большую сложность, чем в предыдущей задаче, объем вычислений получился даже меньшим.
Нюансы решения
И вот в этом кроется основная сложность работы с табличными первообразными, особенно это заметно на второй задаче. Дело в том, что для того чтобы выделить какие-то элементы, которые легко считаются через таблицу, нам нужно знать, что конкретно мы ищем, и именно в поиске этих элементов и состоит все вычисление первообразных.
Другими словами, недостаточно просто зазубрить таблицу первообразных — нужно уметь видеть что-то, чего пока еще нет, но что подразумевал автор и составитель этой задачи. Именно поэтому многие математики, учителя и профессора постоянно спорят: «А что такое взятие первообразных или интегрирование — это просто инструмент либо это настоящее искусство?» На самом деле, лично на мой взгляд, интегрирование — это никакое не искусство — в нем нет ничего возвышенного, это просто практика и еще раз практика.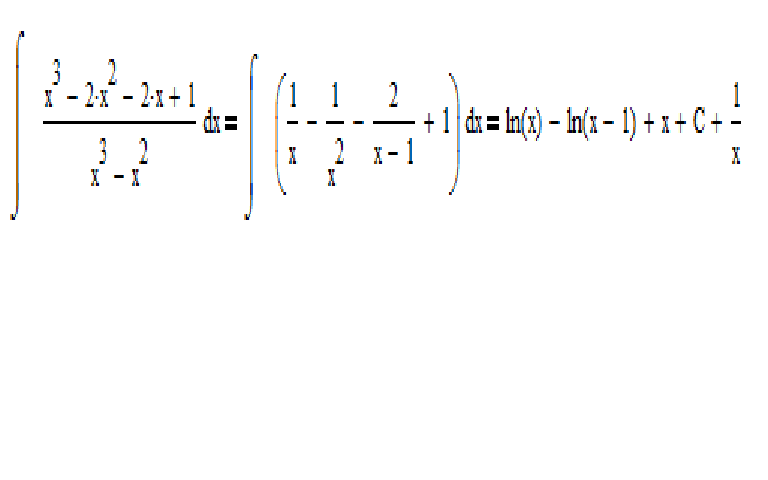 {x}}}{\ln \frac{3}{2}}+C\]
{x}}}{\ln \frac{3}{2}}+C\]
Несмотря на кажущуюся большую сложность показательных функций по сравнению со степенными, общий объем вычислений и выкладок получился гораздо проще.
Конечно, для знающих учеников то, что мы только что разобрали (особенно на фоне того, что мы разобрали до этого), может показаться элементарными выражениями. Однако выбирая именно две эти задачи для сегодняшнего видеоурока, я не ставил себе цель рассказать вам еще один сложный и навороченный прием — все, что я хотел вам показать, так это то, что не стоит бояться использовать стандартные приемы алгебры для преобразования исходных функций.
Использование «секретного» приема
В заключение хотелось бы разобрать еще один интересный прием, который, с одной стороны выходит за рамки того, что мы сегодня в основном разбирали, но, с другой стороны, он, во-первых, отнюдь не сложный, т.е. его могут освоить даже начинающие ученики, а, во-вторых, он довольно часто встречается на всевозможных контрольных и самостоятельных работах, т. {n}}\]
{n}}\]
Это то самое выражение, которое изначально и было. Таким образом, эта формула тоже верна, и ею можно дополнить таблицу первообразных, а лучше просто запомнить всю таблицу.
Выводы из «секретного: приема:
- Обе функции, которые мы только что рассмотрели, на самом деле, могут быть сведены к первообразным, указанным в таблице, путем раскрытия степеней, но если с четвертой степенью мы еще более-менее как-то справимся, то вот девятую степень я бы вообще не рискнул раскрывать.
- Если бы мы раскрыли степени, то мы бы получили такой объем вычислений, что простая задача заняла бы у нас неадекватно большое количество времени.
- Именно поэтому такие задачи, внутри которых стоят линейные выражения, не нужно решать «напролом». Как только вы встречаете первообразную, которая отличается от той, что в таблице, лишь наличием выражения $kx+b$ внутри, сразу вспоминайте написанную выше формулу, подставляйте ее в вашу табличную первообразную, и все у вас получится намного быстрее и проще.

Естественно, в силу сложности и серьезности этого приема мы еще неоднократно вернемся к его рассмотрению в будущих видеоуроках, но на сегодня у меня все. Надеюсь, этот урок действительно поможет тем ученикам, которые хотят разобраться в первообразных и в интегрировании.
До новых встреч!
Смотрите также:
- Первообразная функции
- Интегрирование по частям
- Решение задач B12: №448—455
- Что такое ЕГЭ по математике 2011 и как его сдавать
- Материалы для подготовки к ЕГЭ по математике
- Нестандартная задача B2: студенты, гонорары и налоги
Алгебра – 11 класс. Первообразная функция
Дата публикации: .
Урок и презентация на тему: «Первообразная функция. График функции»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Ребята, обратите внимание: наша задача имеет бесконечное множество решений!
Если в задаче не задано начальное или какое-то другое условие, не забывайте прибавлять константу к решению. Например, в нашей задаче может быть задано положение нашего тела в самом начале движения. Тогда вычислить константу не трудно, подставив ноль в полученное уравнение, получим значение константы.
Как называется такая операция?
Операция обратная дифференцированию называется – интегрированием.
Нахождение функции по заданной производной – интегрирование.
Сама функция будет называться первообразной, то есть образ, то из чего была получена производная функции.
Первообразную принято записывать большой буквой $y=F'(x)=f(x)$.
Определение. Функцию $y=F(x)$ называется первообразной функции $у=f(x)$ на промежутке Х, если для любого $хϵХ$ выполняется равенство $F’(x)=f(x)$.
Давайте составим таблицу первообразных для различных функции. Ее надо распечатать в качестве памятки и выучить. 2
2
2.3+K` и сказать прописью:
«Интеграл от 3 x 2 относительно х равно х 3 + К .»
Интегральный знак
Знак `int` представляет собой удлиненную букву «S», означает «сумма». (В старонемецком и английском языках буква «s» часто писалась с использованием этой вытянутой формы.) Позже мы увидим, что интеграл — это суммируют площадей бесконечно малых прямоугольников.
«сумма» — это символ «сумма».Его можно использовать для конечных или бесконечных сумм.
`int` — это символ суммы бесконечного числа бесконечно малых областей (или других переменных).
Это обозначение «длинное s» было введено Лейбницем при разработке концепции интегрирования.
Другие обозначения для интегралов
Примечание: Иногда мы пишем заглавную букву, чтобы обозначить интеграцию. Например, мы пишем F ( x ) для обозначения
интеграл от f ( x ).3}{3}-5x+K`
Например, мы пишем F ( x ) для обозначения
интеграл от f ( x ).3}{3}-5x+K`
Теперь мы изучим некоторые важные общие правила интегрирования.
A. Интеграл от постоянной
`интк дх=кх+К`
(‘k’ и ‘K’ являются константами.)
Интеграл константы состоит в том, что постоянное время x плюс константа.
Пример 3
Найти `int4 dx`
Ответить
Используя наше новое правило, мы можем просто написать:
`int4 dx=4x+K`
Всегда проверяйте , дифференцируя свой ответ, и вы должны вернуться к тому, что вопрос просил вас интегрировать.2+9)+К`
Пример 14
Учитывая `y’=sqrt(2x+1`, найдите функцию `y = f(x)`, которая проходит через точку `(0,2)`.
Ответить
ПРИМЕЧАНИЕ: `y’` означает производную от `y`, то есть `(dy)/dx`.
`y’=sqrt(2x+1`
Так
`y=intsqrt(2x+1) dx`
Этот вопрос требует от нас интегрирования и в процессе нахождения константы интегрирования . (3//2))/3+5/3`
(3//2))/3+5/3`
— необходимая функция.
Вот график ответа, который мы нашли в примере 14. Вы можете видеть, что он проходит через (2, 0).
График и , проходящий через (2, 0).
Примечание. В этой работе вы увидите «+K» и «+C». Большинство использование учебников + с.
Рекомендуется всегда звонить по номеру
Интеграция функции с пошаговым решением математических задач
Этот учебник начинается с обсуждения первообразных, математических объектов
которые тесно связаны с производными.После введения интеграла через
показано, что задача площадей, интеграл и первообразная связаны соотношением
удивительная теорема, называемая основной теоремой исчисления. После
устанавливая некоторые методы вычисления интегралов, мы обнаруживаем важные
интерпретация интеграла как предела некоторой суммы и
разнообразие приложений интеграла к задачам в бизнесе и экономике,
геометрия и наука.
Антипроизводные
Три примера типа проблемы, которая возникает в различных контекстах:
следующее: найти функцию издержек C(x), если известны предельные издержки C'(x); найти
население P (t) биологической колонии, если скорость P ‘(r), с которой
изменение населения известно; найти перемещение s(t) тела в
момент времени t, если известна скорость v (t) = s ‘(r).
Обратите внимание, что все эти задачи имеют один и тот же базовый формат: найти f(x), зная
ф'(х). Все такие проблемы решает антидифференциация. элементарный
Примером из бизнеса является случай производителя, который определяет, что над
начальный период производства. предельные издержки производства растут линейно
и определяется как C ‘(x) = 2x. Попытаемся найти соответствующую функцию стоимости
С(х), для которого С'(х) = 2х. Хотя у нас нет аналитических процедур для
найдя такое C(x), должно быть ясно, что функция стоимости C(x) = x 2 даст нам известные предельные издержки C ‘(x) = 2x.Но другие функции затрат будут
работать также. Например,
Например,
и фактически для любого числа a ,
Таким образом, любая функция стоимости вида C (x) = x 2 + a даст
желаемый предельный доход C ‘(x) = 2x; требуется дополнительная информация для определения
конкретное значение а. Мы вернемся к этому через мгновение. Процесс, который мы
сейчас рассмотрение называется антидифференциацией. В общем случае может быть
формулируется следующим образом:
Определение
Для заданной функции f(x) функция g такая, что
, называется первообразной функции f.Процесс нахождения такой функции g таков:
называется антидифференцировкой. Некоторые математики предпочитают называть этот процесс
бессрочная интеграция или просто интеграция по причинам, которые станут
очевидно в более поздних разделах.
В нашем вводном примере каждая из функций затрат x 2 , x 2 + 1, а x 2 + 10 — первообразная f(x) = 2x; кроме того, C(x) =
x 2 + a является первообразной f(x) = 2x для любого выбора a. В
вообще говоря, всякий раз, когда g (x) является первообразной f (x), то g (x) + a для любого
номер а, с
В
вообще говоря, всякий раз, когда g (x) является первообразной f (x), то g (x) + a для любого
номер а, с
Можно доказать следующий еще более сильный результат:
Если g — любая первообразная f, то любая другая первообразная off должна иметь
форма g(x) + a для некоторого числа a.
Таким образом, мы можем думать о g(x) + a как о наиболее общей первообразной функции f.
Следовательно, наиболее общая первообразная функции f — это не одна функция, а
скорее класс функций g (x) + a, зависящих от a.
Немецкий математик Готфрид Вильгельм Лейбниц (1646-1716) ввел обозначение
(читается как «первообразная от f» или «неопределенный интеграл от f») до
представляют собой наиболее общую первообразную f. Таким образом, если g — любая первообразная
f, то для любого числа a.
Вкратце:
Пример 1
Пример 2
Пример 3
постоянной. » (По причинам, которые станут очевидными позже, это также называется
«постоянная интегрирования».) В наших примерах мы использовали букву a для
обозначают эту константу, но на практике обычно используется c.(Мы использовали букву a вместо c для нашей первоначальной иллюстрации, включающей стоимость, поскольку c
использовался для обозначения стоимости.) Следующий пример дает нам представление о
значение этой произвольной константы.
» (По причинам, которые станут очевидными позже, это также называется
«постоянная интегрирования».) В наших примерах мы использовали букву a для
обозначают эту константу, но на практике обычно используется c.(Мы использовали букву a вместо c для нашей первоначальной иллюстрации, включающей стоимость, поскольку c
использовался для обозначения стоимости.) Следующий пример дает нам представление о
значение этой произвольной константы.
Пример 4
Предположим, что на начальных этапах производства предельные издержки произвести товар C ‘(x) = 2x долларов за единицу. На этот раз, предположим, Производитель также знает, что постоянные издержки производства C(0) составляют 500 долларов.Находить соответствующую функцию стоимости C(x).
Мы уже видели, что любая функция затрат для этих предельных затрат должна иметь вид форма C(x) = x 2 + a для некоторой константы a. С
годаС (0) = 500 = 0 2 + а = а,
имеем a = 500. Таким образом, функция стоимости задается выражением C(x) = x 2 +
500
Таким образом, функция стоимости задается выражением C(x) = x 2 +
500
Из этого примера мы видим, что произвольная константа c представляет собой фиксированную стоимость производство. Знание только предельных издержек не может сказать нам, каковы будут эти постоянные издержки. является; фиксированная стоимость является дополнительной информацией.Каждая из функций затрат соответствующий предельным издержкам C'(x) = 2x, будет иметь вид
C(x) = x 2 + (постоянная стоимость).
Следующие два результата очень полезны при оценке первообразных. Здесь n обозначает действительное число, а c — константа интегрирования.
Обратите внимание, что правило (2) выполняется для n != — 1, а правило (3) охватывает случай, когда n = -1. Для проверки правила (2) воспользуемся определением (1) следующим образом:
Чтобы проверить Правило (3), вспомним, что
Пример 5 Используйте правило (2) для вычисления каждой первообразной производной:
Решения:
Деловой расчет
У нас не так много правил интеграции. Для довольно многих проблем, которые мы видим, правила не будут применяться напрямую; сначала нам придется проделать некоторые алгебраические манипуляции. На практике гораздо сложнее записать первообразную функции, чем найти производную. (На самом деле очень легко написать функцию, не имеющую первообразной, которую можно найти с помощью алгебры, хотя доказать , что у нее нет первообразной, гораздо сложнее.)
Для довольно многих проблем, которые мы видим, правила не будут применяться напрямую; сначала нам придется проделать некоторые алгебраические манипуляции. На практике гораздо сложнее записать первообразную функции, чем найти производную. (На самом деле очень легко написать функцию, не имеющую первообразной, которую можно найти с помощью алгебры, хотя доказать , что у нее нет первообразной, гораздо сложнее.)
Метод подстановки (также называемый \(u\)-подстановкой) — это один из способов алгебраического манипулирования подынтегральным выражением, чтобы применялись правила.Это способ раскрутить или отменить Цепное правило для деривативов. Когда вы находите производную функции с помощью цепного правила, вы получаете произведение чего-то вроде исходной функции умножить на производную. Мы можем обратить это, чтобы написать интеграл: \[ \frac{d}{dx} f\left(g(x) \right) = f’\left(g(x) \right)g'(x) \] поэтому \[f\left(g(x)\right) =\int f’\left(g(x) \right)g'(x)\, dx\]
С подстановкой мы заменим \( u=g(x) \) (отсюда и название \( u \)-подстановка
). Это означает \( \frac{du}{dx}=g'(x)\), поэтому \( du=g'(x)dx \). Делая эти замены, \( \int f’\left( g(x) \right)g'(x)\, dx \) становится \( \int f'(u)\, du \), что, вероятно, будет легче интегрировать.
Это означает \( \frac{du}{dx}=g'(x)\), поэтому \( du=g'(x)dx \). Делая эти замены, \( \int f’\left( g(x) \right)g'(x)\, dx \) становится \( \int f'(u)\, du \), что, вероятно, будет легче интегрировать.
Попробуйте \( u \)-подстановку, когда вы видите произведение в своем интеграле, особенно если вы распознаете один множитель как производную некоторой части другого множителя.
Для просмотра этого видео включите JavaScript и рассмотрите возможность обновления до веб-браузера, поддерживающего видео HTML5
Метод \(u\)-замены для первообразных
Цель состоит в том, чтобы превратить \( \int f\left( g(x) \right)\, dx \) в \( \int f(u)\, du \), где \(f(u)\) гораздо менее запутан, чем \(f\left(g(x)\right)\).
- Пусть \(u\) — некоторая часть подынтегральной функции. Хорошим первым выбором будет
, один шаг внутрь самого запутанного бита.
- Вычислить \( du=\frac{du}{dx}dx \).
- Переведите все ваши \(x\) в \(u\) везде в интеграле, включая \(dx\).
 Когда вы закончите, у вас должен быть новый интеграл, который полностью находится в \(u\). Если у вас остались какие-либо \(x\), то это указывает на то, что замена не сработала или не завершена; возможно, вам придется вернуться к шагу 1 и попробовать другой вариант для \(u\).2-\frac{5}{x}+C.
\end{выравнивание*} \]
Когда вы закончите, у вас должен быть новый интеграл, который полностью находится в \(u\). Если у вас остались какие-либо \(x\), то это указывает на то, что замена не сработала или не завершена; возможно, вам придется вернуться к шагу 1 и попробовать другой вариант для \(u\).2-\frac{5}{x}+C.
\end{выравнивание*} \]
Подстановка и определенные интегралы
Когда вы используете подстановку, чтобы помочь вычислить определенный интеграл, у вас есть выбор, как обращаться с пределами интегрирования. Вы можете сделать любой из них, в зависимости от того, что кажется вам лучше. Важно помнить, что исходными пределами интегрирования были значения исходной переменной (скажем, \(x\)), а не значения новой переменной (скажем, \(u\)).
Вы можете решить первообразную как побочную задачу, переведя обратно в \(x\), а затем использовать первообразную с исходными пределами интегрирования.
Или…
Вы можете подставить пределы интегрирования одновременно с подстановкой всего внутри интеграла, а затем пропустить шаг преобразования
обратно в \(x\)
. {u=g(b)} \text{(новое подынтегральное выражение)}\, du.3 +\sin x — \sqrt{5}
\end{массив}$$ все согласуются с $f(x)$ и, следовательно, все являются первообразными $f(x)$.
{u=g(b)} \text{(новое подынтегральное выражение)}\, du.3 +\sin x — \sqrt{5}
\end{массив}$$ все согласуются с $f(x)$ и, следовательно, все являются первообразными $f(x)$.Приведенные выше примеры предполагают, что мы можем найти дополнительные первообразные для данной функции, если у нас есть один из них, просто добавив константу в конце. Можно задаться вопросом, существуют ли какие-либо функции, которые отличаются более чем на константу и имеют одну и ту же производную. Чтобы ответить на этот вопрос, рассмотрим разницу между функциями $F_1(x)$ и $F_2(x)$, которые являются первообразными некоторой функции $f(x)$.Более конкретно, рассмотрим производную этой разности: $$\frac{d}{dx}[F_1(x) — F_2(x)] = F_1′(x) — F_2′(x) = f(x) — f(x) = 0$$ Значит, производная этой разности равна нулю.
$$\frac{d}{dx}[F_1(x) — F_2(x)] = 0$$Напомним, ранее мы доказали (с помощью теоремы о среднем значении), что функции с нулевой производной должны быть постоянными функциями.
Таким образом, должно быть так, что для некоторой константы $c$ $$F_1(x) — F_2(x) = c$$ Или эквивалентно $$F_2(x) = F_1(x) + c$$ Таким образом, если мы сможем получить одну первообразную $F(x)$ заданной функции $f(x)$, мы сможем описать весь набор первообразных $f(x)$.
 Это множество содержит все функции вида
$$F(x)+c$$
где $c$ — константа.
Это множество содержит все функции вида
$$F(x)+c$$
где $c$ — константа.По причинам, которые станут ясны после понимания основной теоремы исчисления, мы будем обозначать множество всех первообразных $f(x)$, также называемое неопределенным интегралом $f(x)$, через $$\int f(x) \, dx$$
Действие нахождения неопределенного интеграла известно как интегрирование , а символ $\int$ известен как знак интеграла .
Учитывая приведенный выше анализ, когда мы знаем одну первообразную $F(x)$ функции $f(x)$, мы можем написать: $$\int f(x) \, dx = F(x) + C$$ где $C$ следует рассматривать как любую константу .
Нетрудно заметить, что многие базовые правила дифференцирования можно «переработать в обратном порядке», чтобы получить некоторые базовые правила интегрирования. Например, можно быстро установить:
$ \ displaystyle {\ int \, dx = x + C} $
$ \ displaystyle {\ int k f (x) \, dx = k \ int f (x) dx} $
$\displaystyle{\int [f(x)\pm g(x)] \, dx = \int f(x) \, dx \pm \int g(x) \, dx}$
$\displaystyle{\int x^n \, dx = \frac{x^{n+1}}{n+1} + C}$, когда $n \neq 1$
$\displaystyle{\int \frac{1}{x} \, dx = \ln |x| + С}$
 х + С}$
х + С}$
Можно заметить, что ни одно из приведенных выше основных правил интеграции не является обращением правил произведения, частного или цепочки.
К сожалению, несмотря на то, что имеется результат, связанный с обращением правила произведения для производных, который поможет нам найти интегралы некоторых произведений, а также существуют средства для работы с интегралами от частных, эти методы интегрирования потребуют дальнейшего развития. . Таким образом, мы сохраняем их для будущей темы обсуждения.2}.\]
Следовательно, если \(F\left( x \right)\) является первообразной \(f\left( x \right)\) на отрезке \(I,\), то наиболее общая первообразная \(f \left( x \right)\) на \(I\) равно
\[{F\влево( х \вправо) + C,}\]
, где \(С\) — произвольная константа.
Проблемы с начальным значением
Нахождение первообразной \(f\left( x \right)\) эквивалентно решению дифференциального уравнения
\[\frac{{dy}}{{dx}} = f\left( x \right)\;\;\text{or}\;\;y^\prime\left( x \right) = f \влево( х \вправо). \]
\]
Дифференциальное уравнение с начальным условием \(y\left( {{x_0}} \right) = {y_0}\) называется начальной задачей.
Наиболее общая первообразная \(F\left( x \right) + C\) функции \(f\left( x \right)\) дает общее решение дифференциального уравнения \(\frac{{dy} }{{dx}} = f\left( x \right).\)
Частным решением начальной задачи является функция, удовлетворяющая как дифференциальному уравнению, так и начальному условию.2} + \frac{1}{x} + 3.\]
Дополнительные проблемы см. на стр. 2.
.
 р.№5(1,2)
р.№5(1,2) р.№5(4)
р.№5(4)
 Когда вы закончите, у вас должен быть новый интеграл, который полностью находится в \(u\). Если у вас остались какие-либо \(x\), то это указывает на то, что замена не сработала или не завершена; возможно, вам придется вернуться к шагу 1 и попробовать другой вариант для \(u\).2-\frac{5}{x}+C.
\end{выравнивание*} \]
Когда вы закончите, у вас должен быть новый интеграл, который полностью находится в \(u\). Если у вас остались какие-либо \(x\), то это указывает на то, что замена не сработала или не завершена; возможно, вам придется вернуться к шагу 1 и попробовать другой вариант для \(u\).2-\frac{5}{x}+C.
\end{выравнивание*} \] {u=g(b)} \text{(новое подынтегральное выражение)}\, du.3 +\sin x — \sqrt{5}
\end{массив}$$ все согласуются с $f(x)$ и, следовательно, все являются первообразными $f(x)$.
{u=g(b)} \text{(новое подынтегральное выражение)}\, du.3 +\sin x — \sqrt{5}
\end{массив}$$ все согласуются с $f(x)$ и, следовательно, все являются первообразными $f(x)$. Это множество содержит все функции вида
$$F(x)+c$$
где $c$ — константа.
Это множество содержит все функции вида
$$F(x)+c$$
где $c$ — константа. х + С}$
х + С}$