Экзаменационные вопросы по математике / 10. Первообразная функции. Свойства первообразной. Теорема об общем виде первообразной

10. Первообразная функции. Свойства первообразной. Теорема об общем виде первообразной.

Если на некотором промежутке задана функция f(x), а функция F(x) на этом же промежутке дифференцируема и в каждой точке F’(x)=f(x), то функция F(x) называется первообразной для функции f(x) на этом промежутке.

Пример: Предположим, имеется функция:

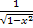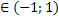f(x)=, x . Найти F(x). F(x)=arcsinx.

Свойства первообразных:

1. Если F(x) есть первообразная для f(x) на промежутке, тогда F(x)+C тоже первообразная для f(x), где C – произвольная постоянная.

Доказательство:

(F(x)+C)’=F(x)’+C’=F’(x)=f(x).

2. Если F(x) – первообразная для f(x) на промежутке, то для функции f(kx+b) (k,b const) первообразной будет функция (1/k)F(kx+b).

Доказательство:

((1/k)F(kx+b))’=(1/k)F’(kx+b)=(1/k)f(kx+b)(kx+b)’=(1/k)f(kx+b)k=f(kx+b).

Свойство линейной замены переменных:

Пусть f(x)=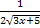 , k=3

Найдем первообразную для функции 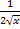, тогда F(x)=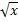, тогда F=1/3

f(x)=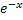, k=-1/x, F=

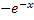
3. Основное свойство первообразной

Две различные первообразные одной и той же функции могут отличаться только на постоянное значение.

Лемма Ла-Гранжа:

Если производная некоторой функции тождественно равна нулю на некотором промежутке, то функция тождественно равна постоянной на этом промежутке.

Доказательство:

Пусть 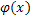во всех точках некоторого промежутка имеет производную.

Докажем то, что 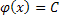на этом промежутке. Т.к. 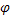имеет производную, то x

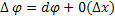
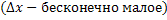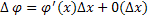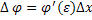. , . Т.к.

Теорема:

Докажем, что первообразная отличается только на const. F1(x)-F2(x)=C.

F’1(x)=f(x)

F’2(x)=f(x)

Рассмотрим функцию 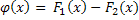. Вычислим производную этой функции:

по лемме следует, что 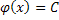, F1(x)-F2(x)=C, ч.т.д.

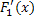+C=f(x) – общий вид.

7.1. Первообразные.

1. Понятия первообразной и неопределенного интеграла. Существование первообразных, структура множества первообразных для функции. Свойства неопределенного интеграла. (7.1, 7.2)

Определение. Функция F(x) называется первообразной для функции f(x) на интервале (a, b), если x(a, b):.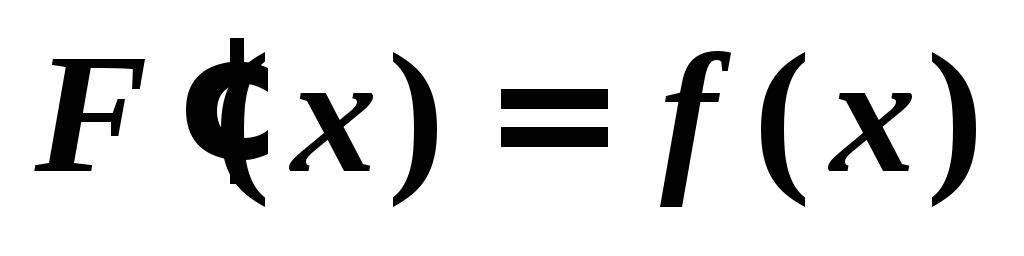

Возникают вопросы:

• когда

   первообразная для f(x),

• сколько первообразных у f(x) и чем они различаются,

• как находить первообразные.

Ответ на первый вопрос. Докажем позднее, что у непрерывных функций существуют первообразные.

Ответ на второй вопрос.

Теорема 1. Если функция f(x) имеет на (a, b) первообразную, то она имеет на (a, b) бесконечно много первообразных.

Доказательство. F(x) – первообразная для f(x) сR F(x) + c – тоже первообразная для f(x), так как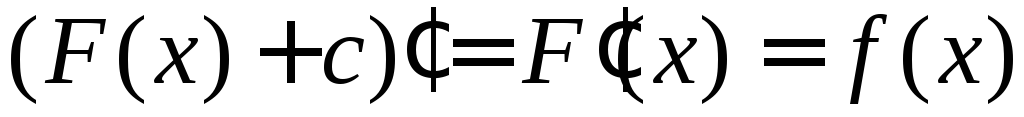

.

Теорема 2. Пусть 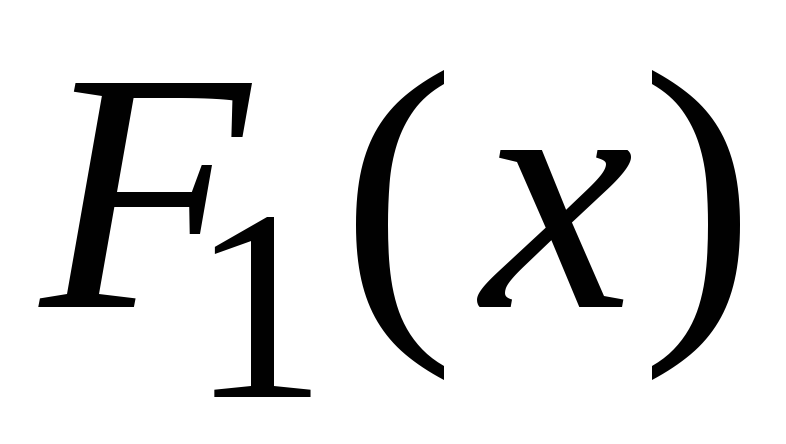и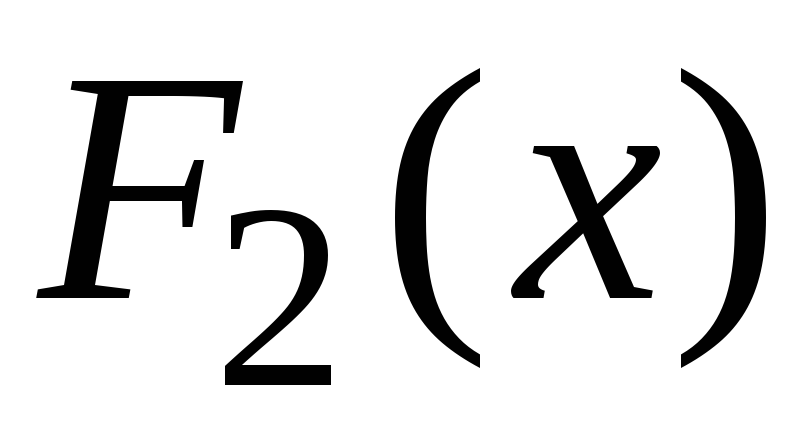– две первообразные для одной и той же функцииf(x) на (a, b), тогда.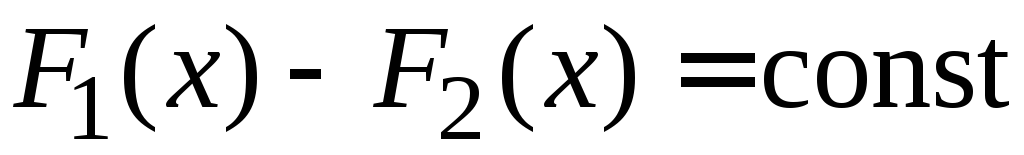

Доказательство.

, 

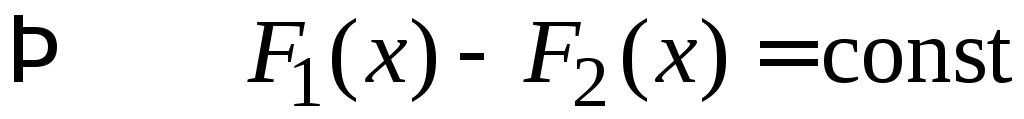(по следствию теоремы Лагранжа, п. 4.1.4).

Замечание. Если первообразные определять не на интервале, теорема 2 будет не верна, что показывает следующий пример.

Пример. 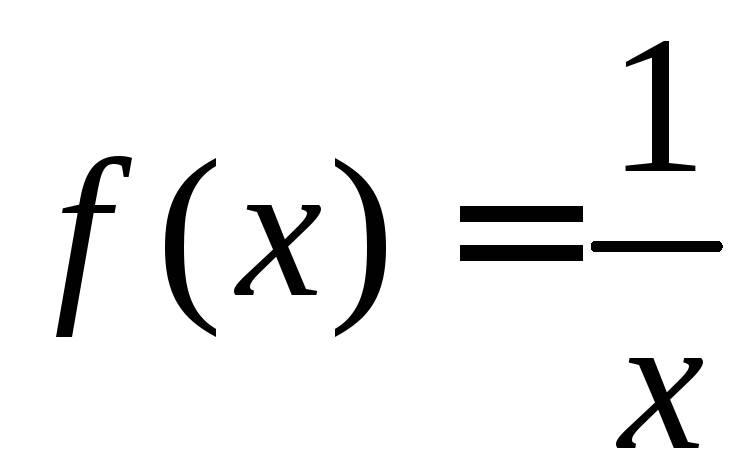на (–, 0)(0, +). Покажем, что F(x) = ln |x| – первообразная для f(x).

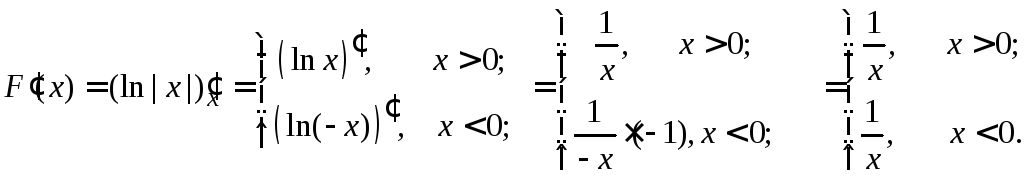
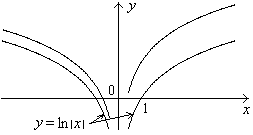сR функция ln |x| + c – тоже первообразная для

на (–, 0)(0, +), но первообразными будут и функции вида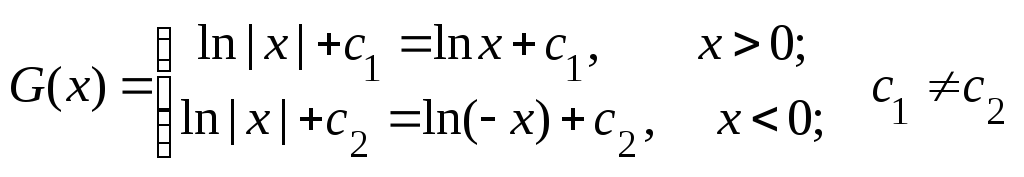

7.2. Неопределенный интеграл.

Определение. Неопределённым интегралом от функции f(x) на интервале (a, b) называется

совокупность всех её первообразных на (a, b).

Обозначение: ,

f(x) – подынтегральная функция,

х – переменная интегрирования.

Из теорем пункта 7.1:,

F(x) – одна из первообразных для f(x) на (a, b), сR.

Замечание 1. Из определения следует:.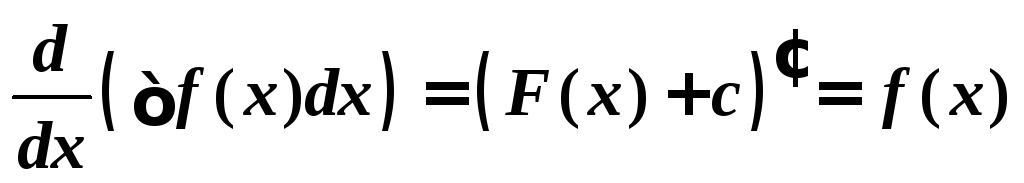

Замечание 2.Под интегралом пишетсядифференциал первообразной:

f(x)dx = F (x)dx = dF(x).

Пример.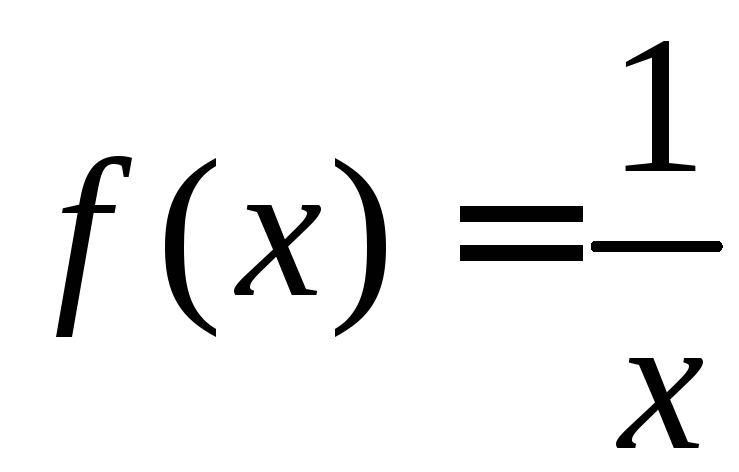

_.

На (0, +) ,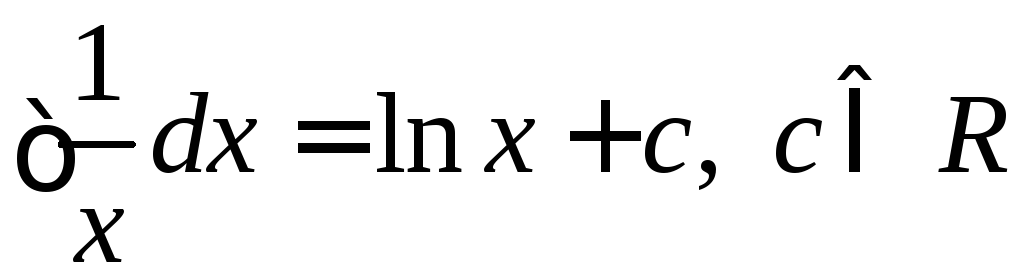

на (–, 0) .

Сокращенная запись: .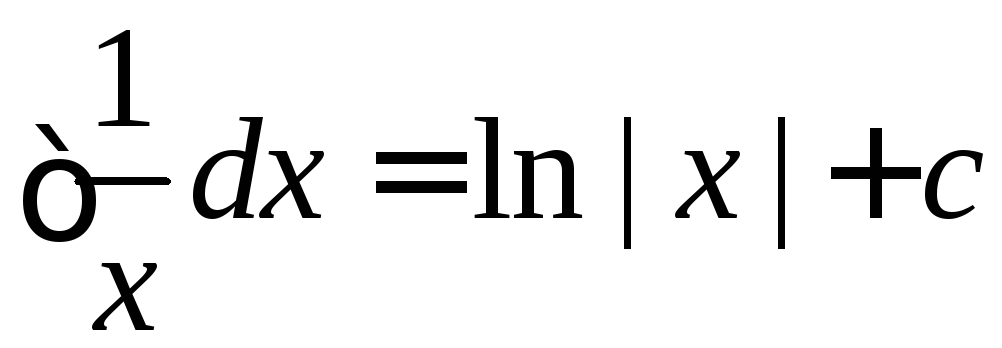

Теорема. Основные свойства неопределённого интеграла.

1. Линейность. .

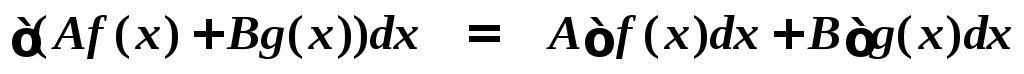Доказательство. В левой части равенства бесконечно много функций, отличающихся на константу, в правой части – тоже.

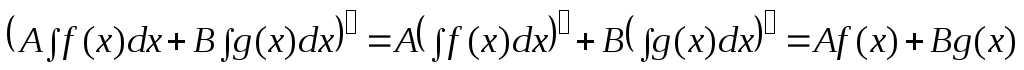
 Это множества первообразных для одной и той же функции.

2. Взаимная обратность операций дифференцирования и неопределенного интегрирования.

;

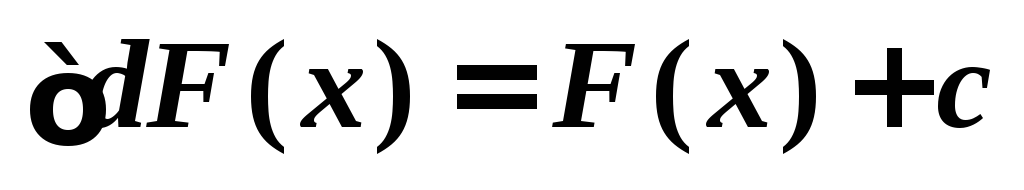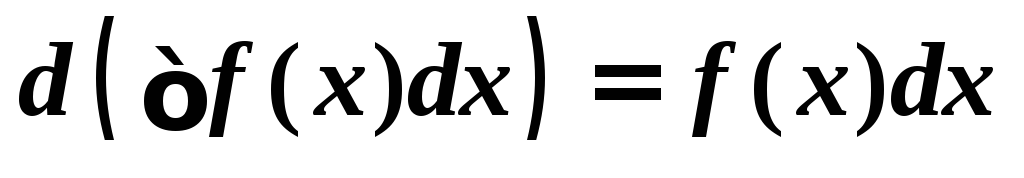
Пример. ,.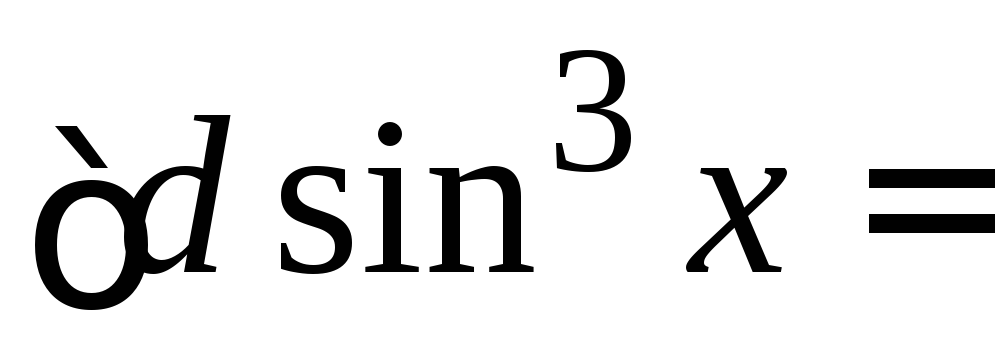

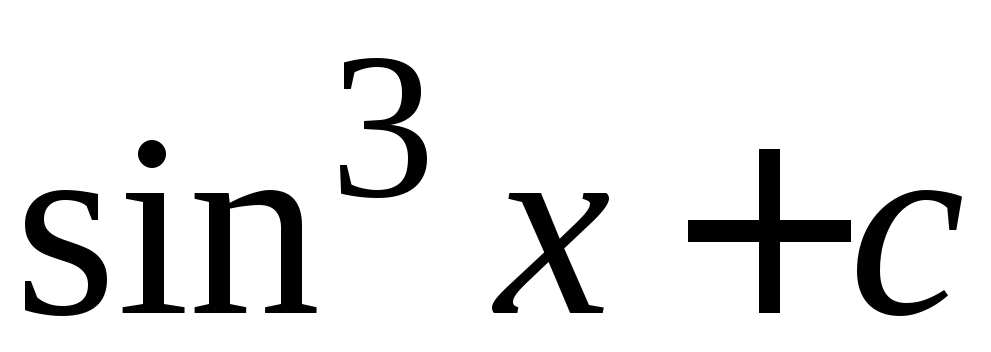3. Инвариантность интегральных формул.



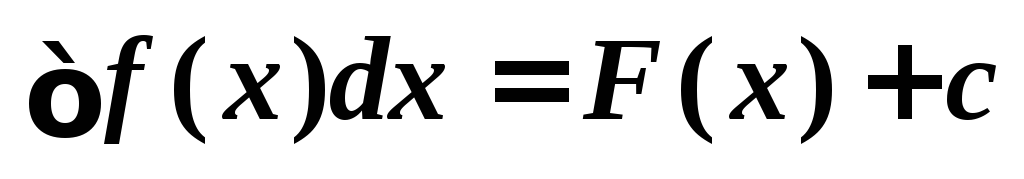
(x = x(t) – функция, имеющая непрерывную производную).

Доказательство. f(x)dx = dF(x)

 (по инвариантности формы дифференциала) f(x(t))dx(t) = dF(x(t))

.

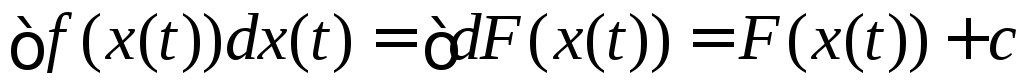Пример..(подчеркнем, что ).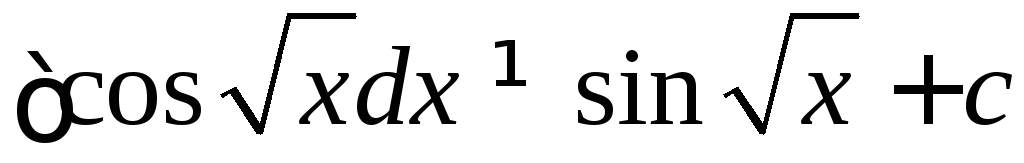

Замечание. Не для всех элементарных функций первообразные являются элементарными функциями. Примеры «не берущихся» интегралов:

, ,,,,.

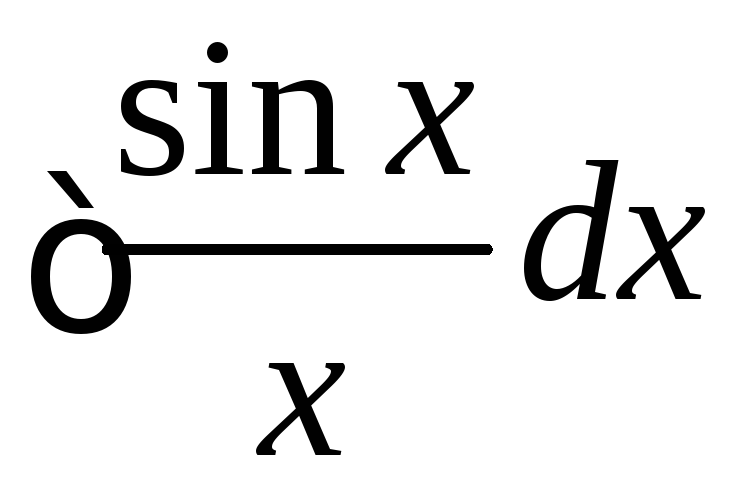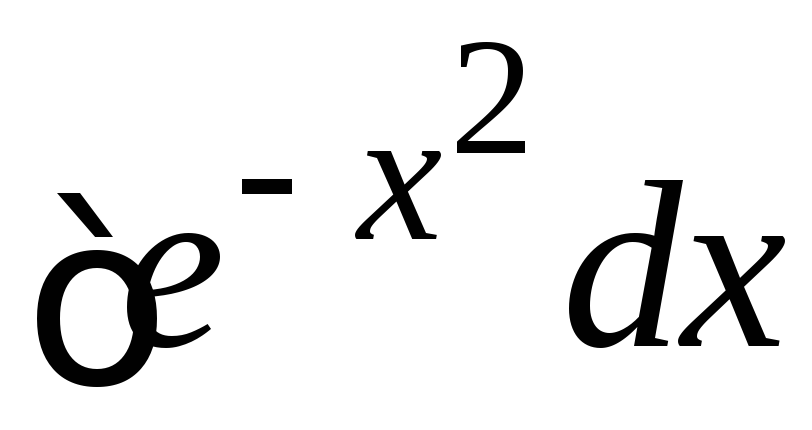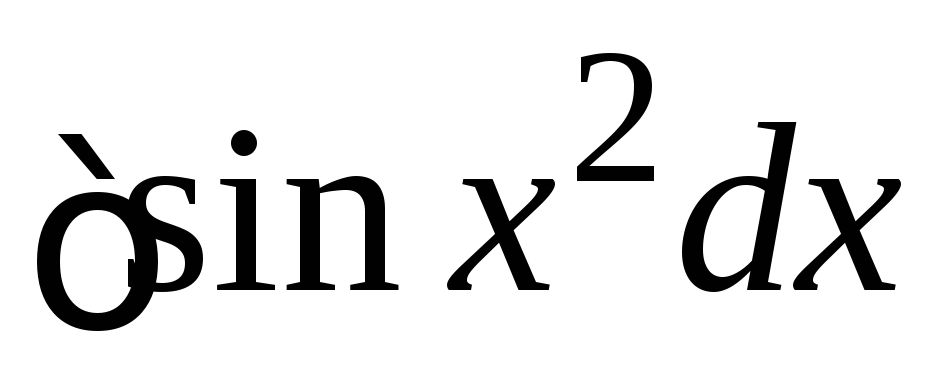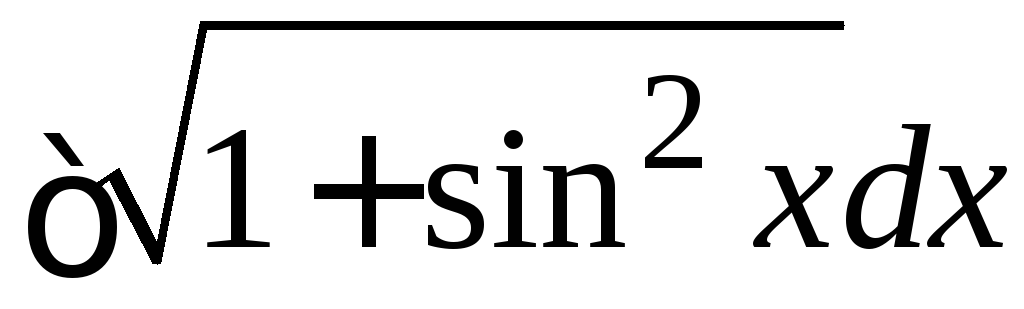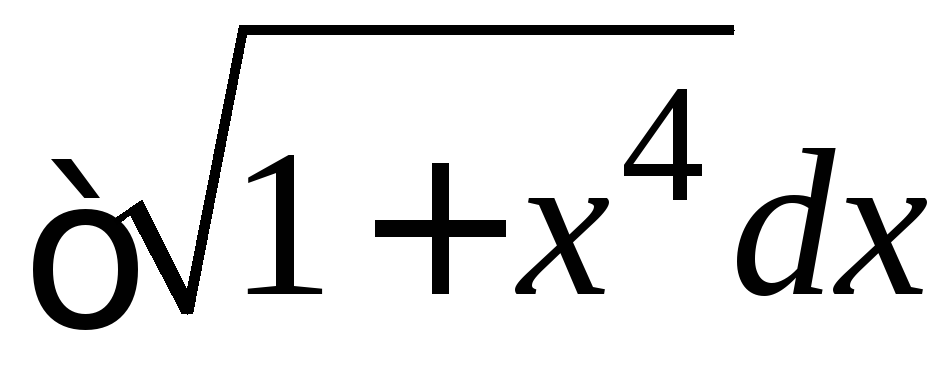2. Основные методы нахождения неопределенного интеграла. (7.4.1-7.4.3)

7.4.1. Разложение интеграла в сумму более простых интегралов (использование свойства линейности).

Примеры.

1.

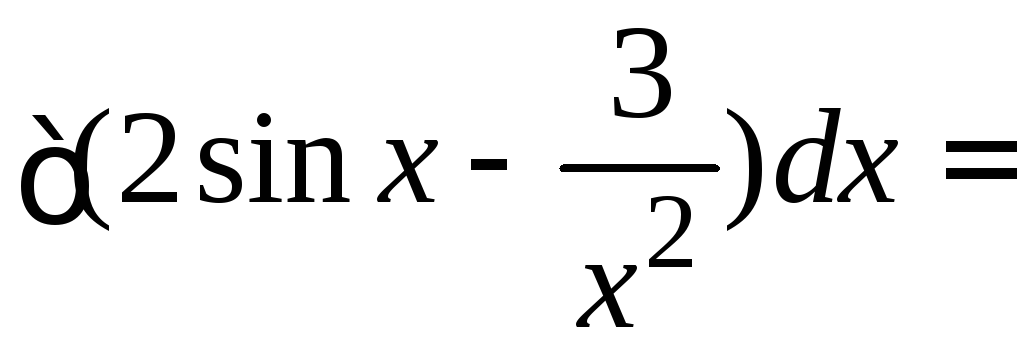
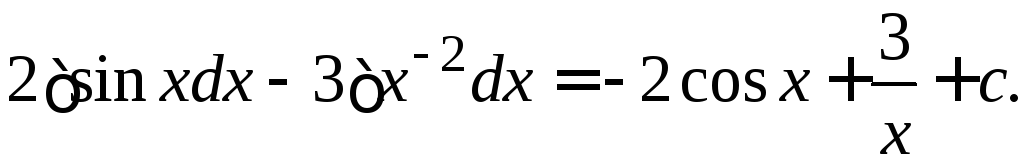
2. ===

=.

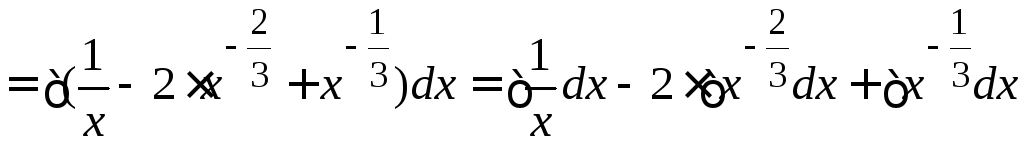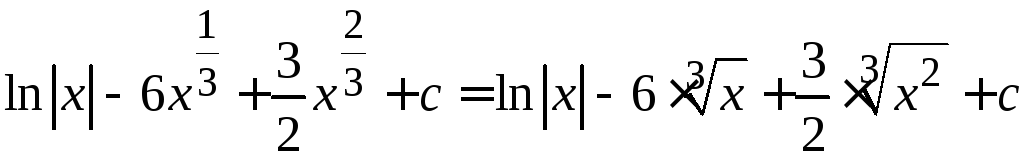3. .

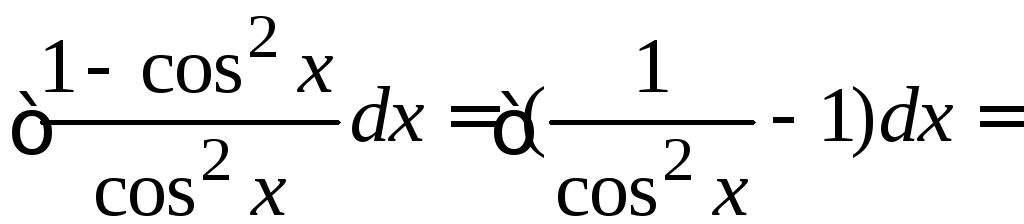
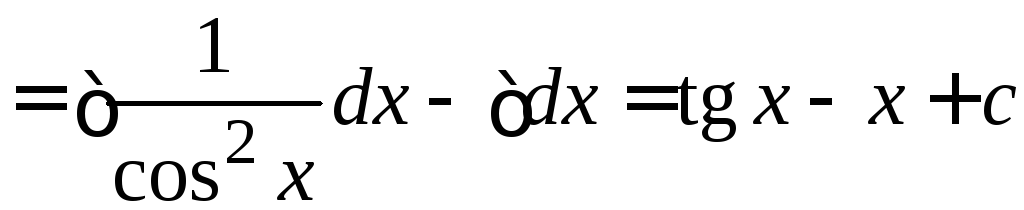7.4.2. Замена переменной в неопределенном интеграле (использование свойства инвариантности интегральных формул). Рассмотрим две разновидности этого метода

Если интеграл имеет вид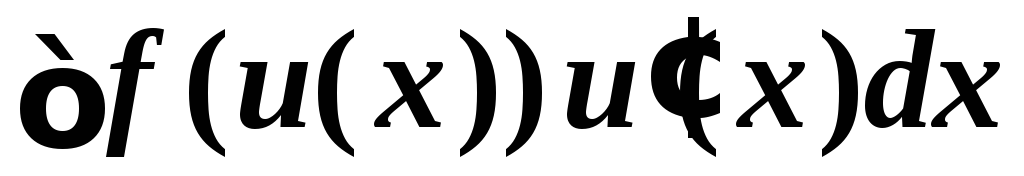,то запишем его так: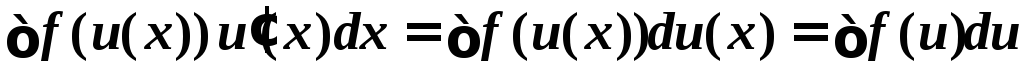и будем интегрировать по переменнойu.

Если найдем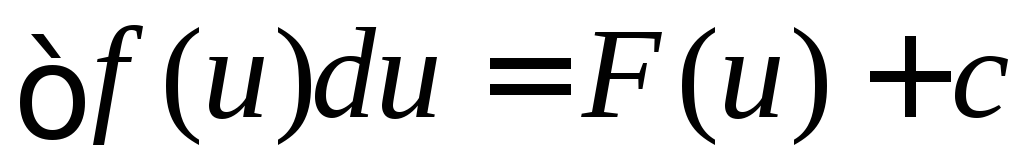,то сделаем подстановкуu = u(x).

Примеры.

1. =

.

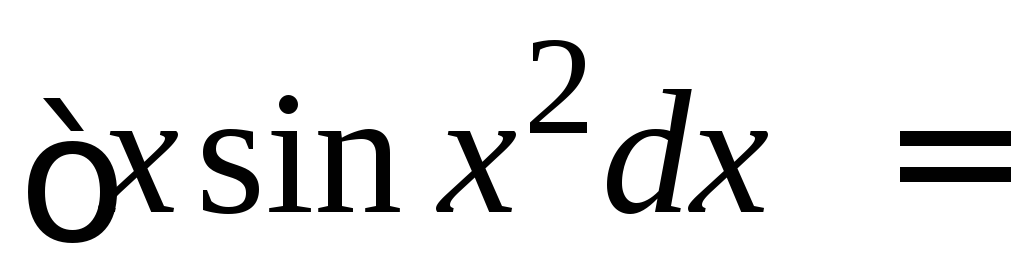
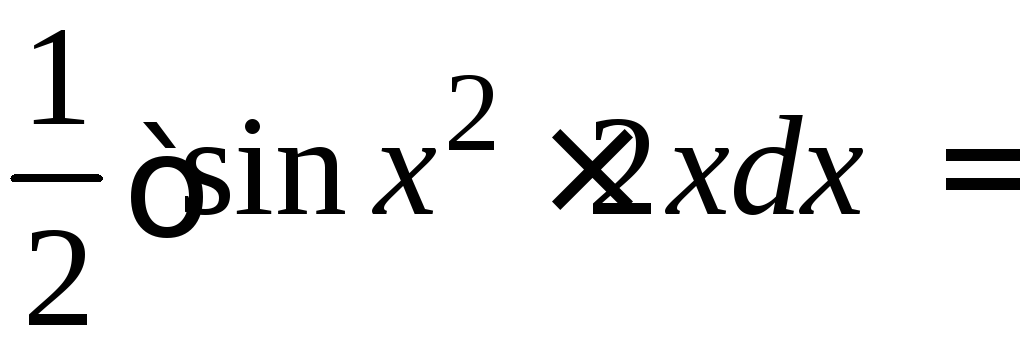
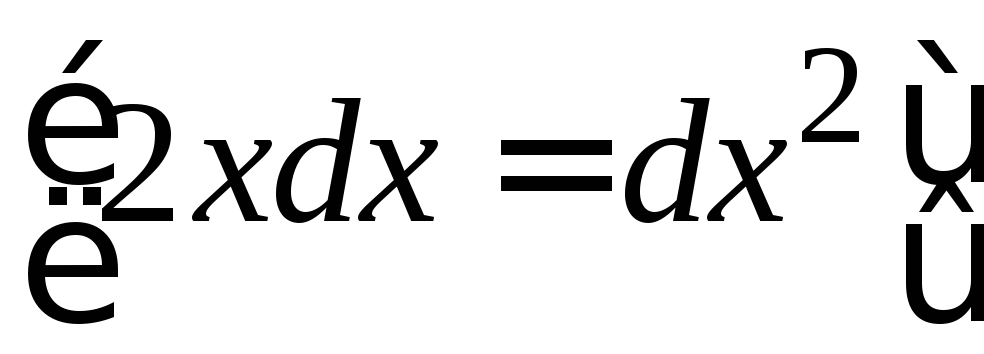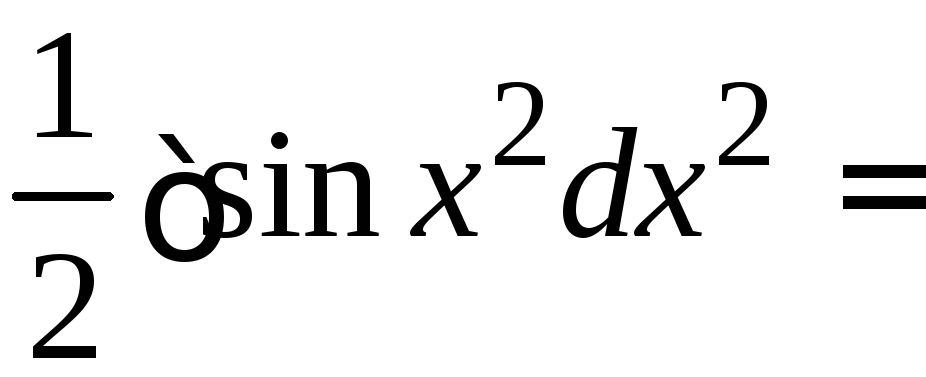
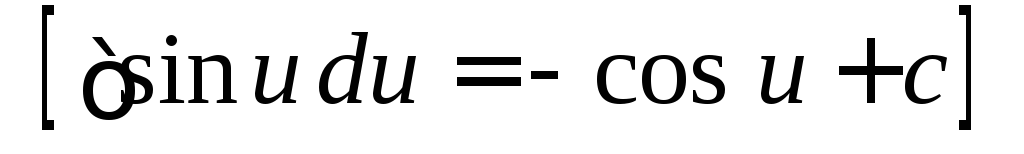
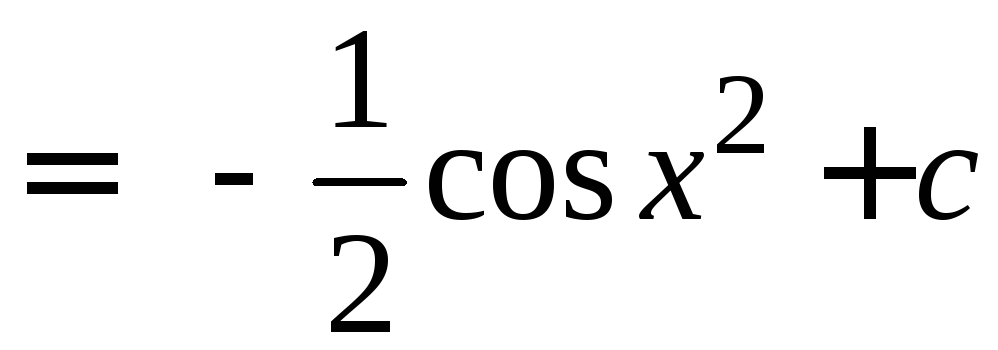2. =

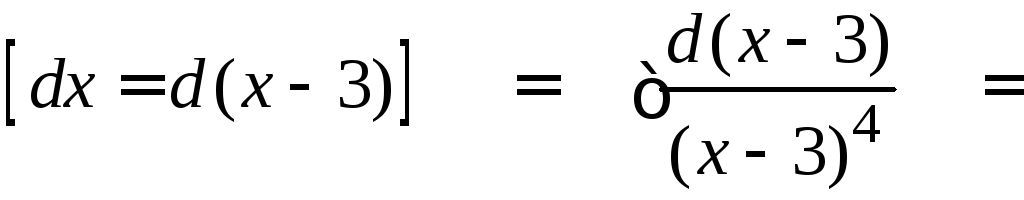
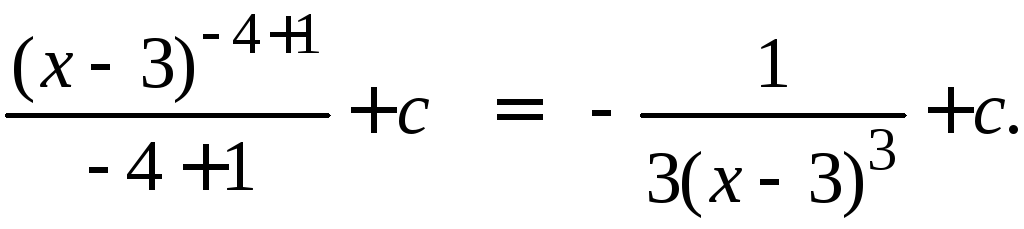
3.

4. .

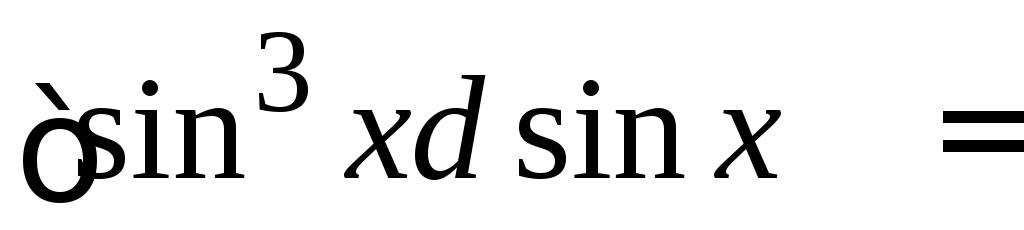
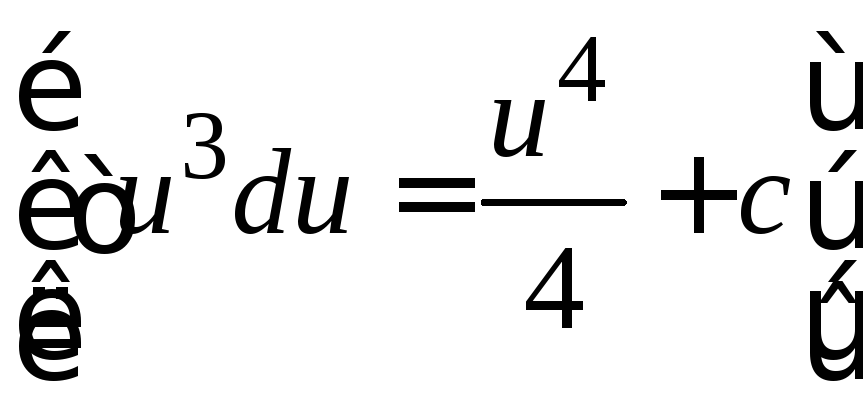5. =.

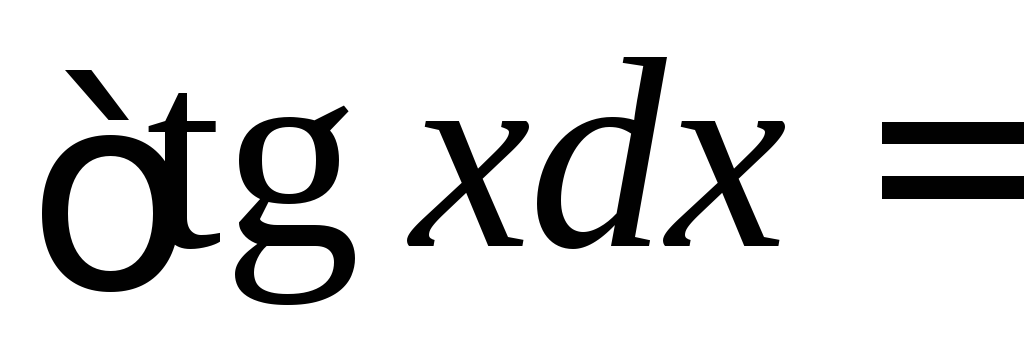
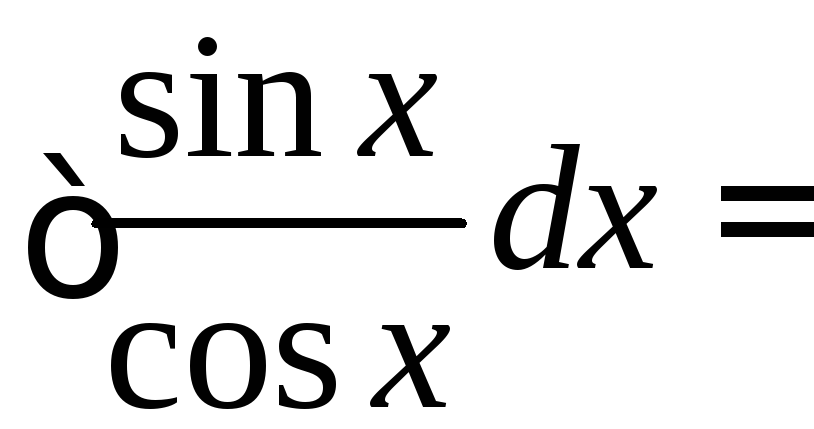
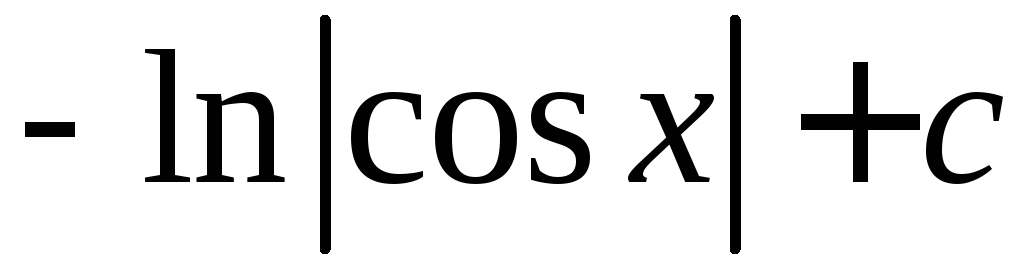6.

.

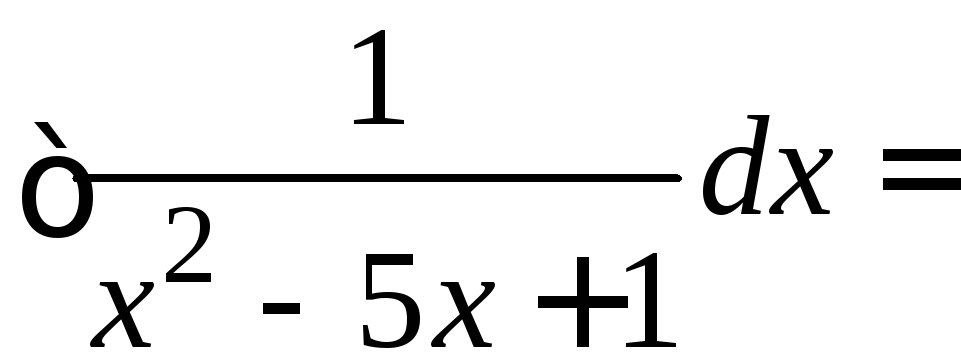
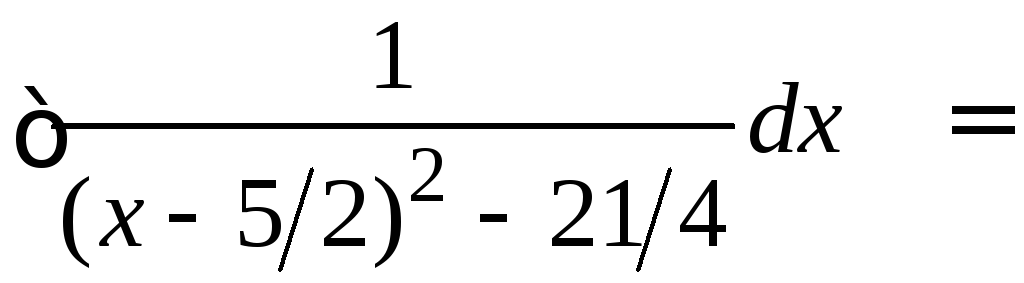
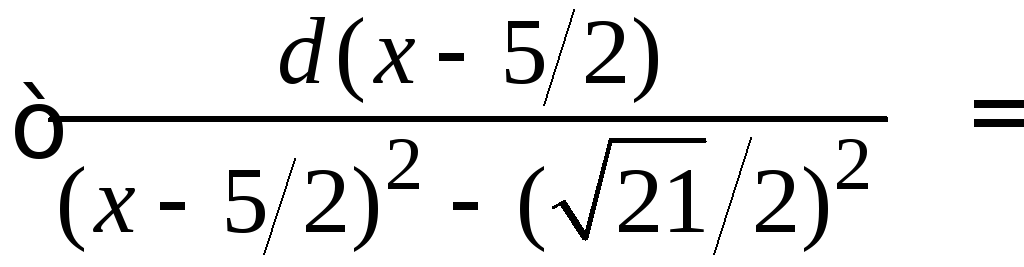
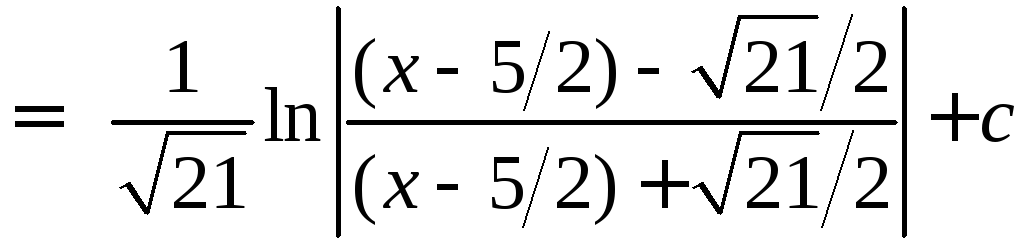7.

=

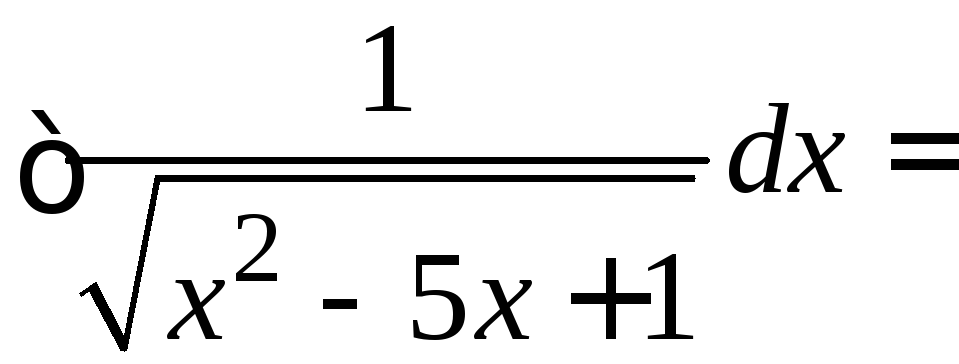
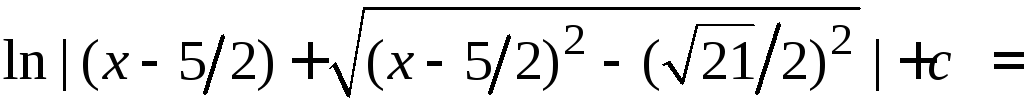
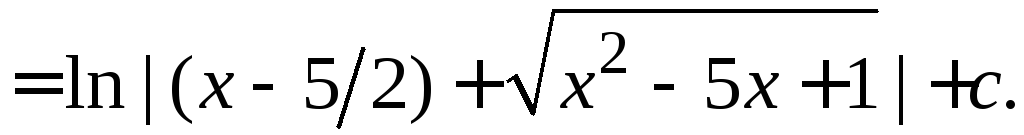
б) Подстановка вместо переменной интегрирования монотонной непрерывно дифференцируемой функции другого аргумента и переход к интегрированию по новой переменной. .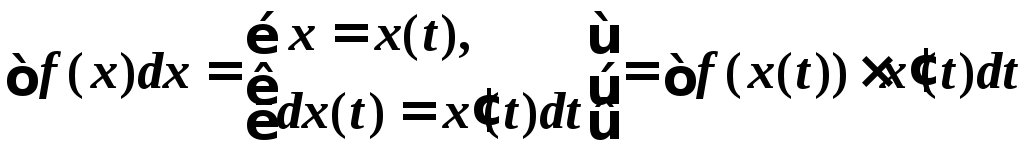

Примеры.1. .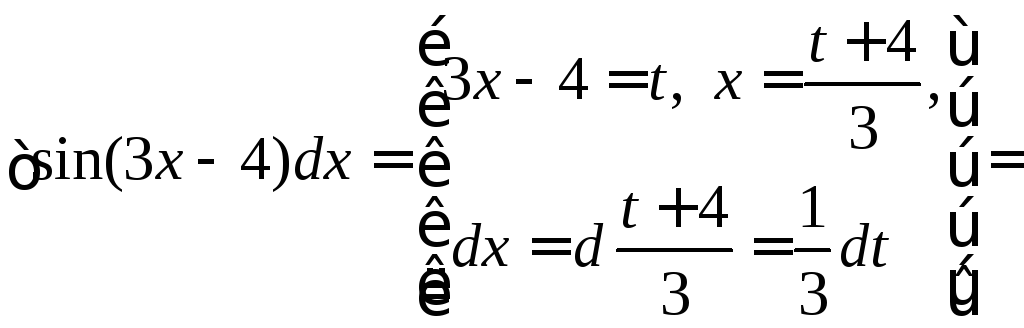

2. .

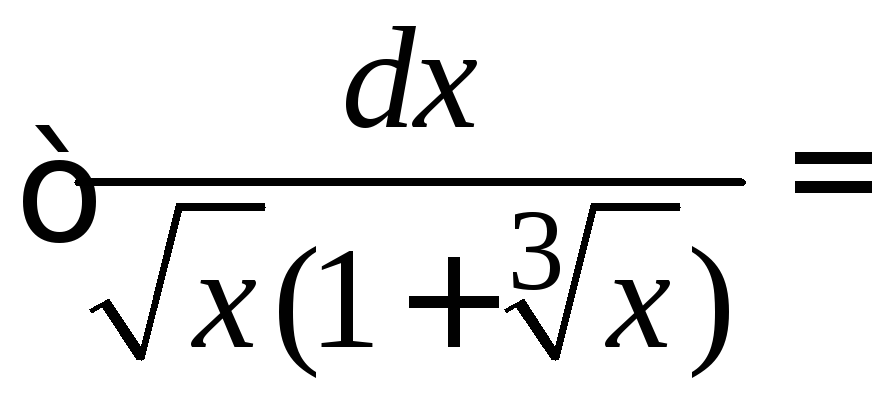
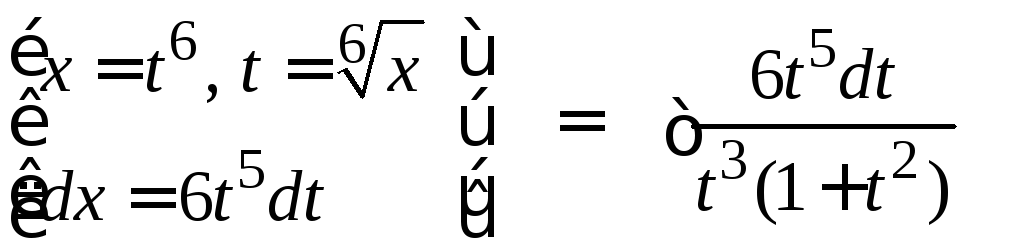
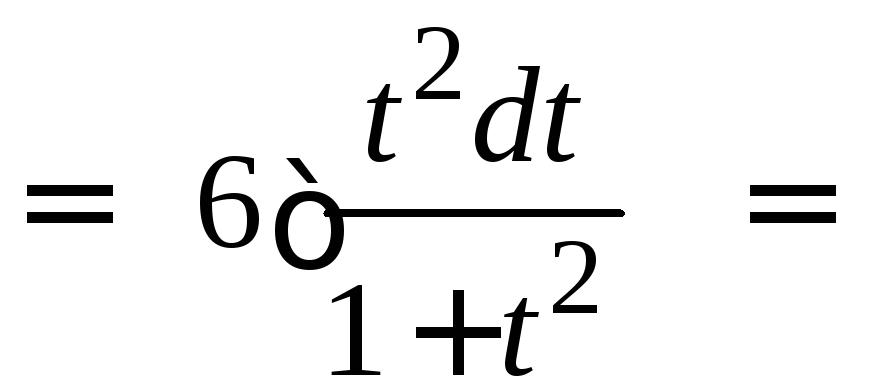
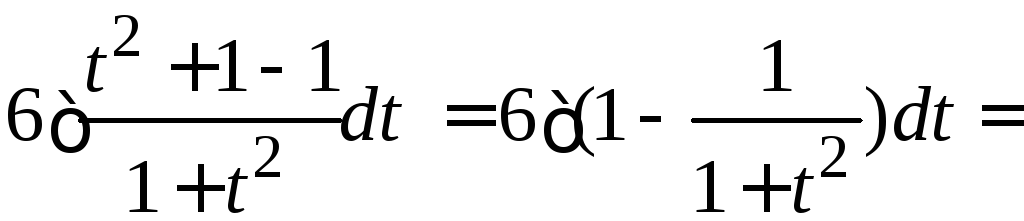
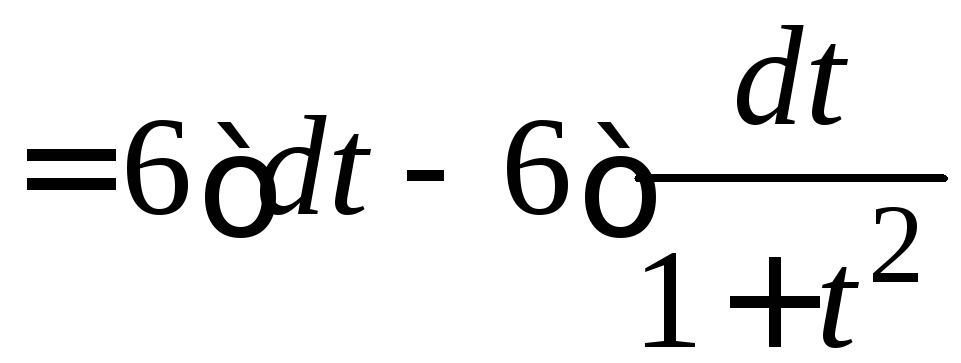
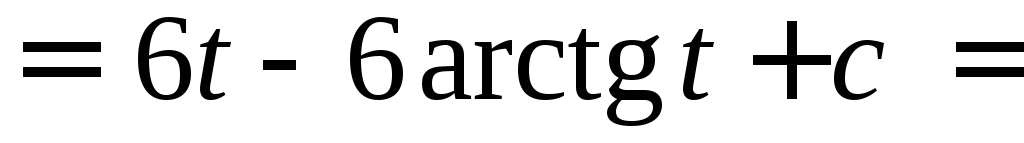
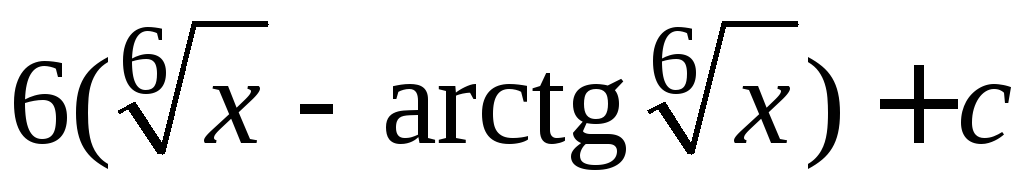3.

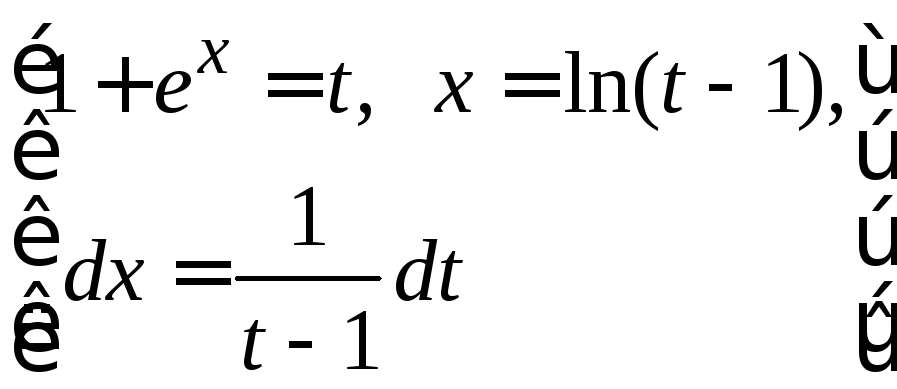
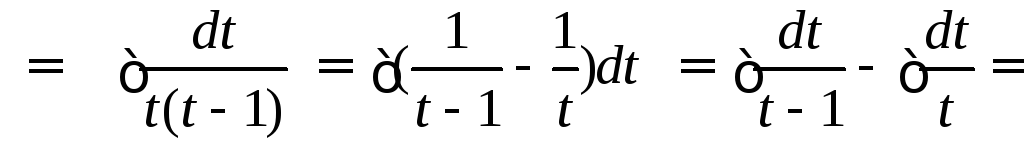
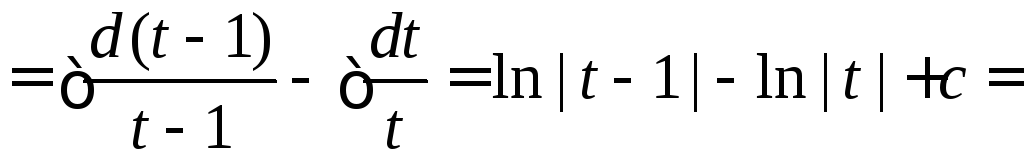
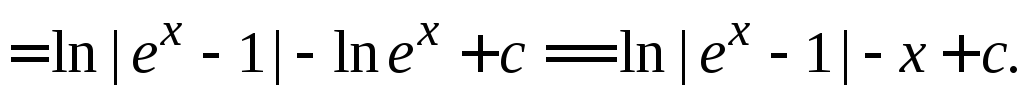
7.4.3. Интегрирование по частям (основывается на формуле производной произведения).

Пусть u(x) иv(x) имеют непрерывные производные. Тогда.\

Доказательство..

Интегрируем:,,.

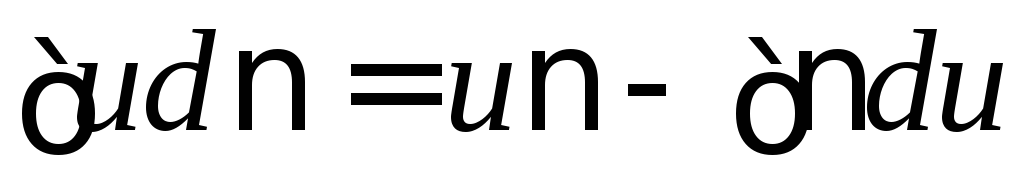Чтобы лучше понять возможности метода, перепишем формулу в виде .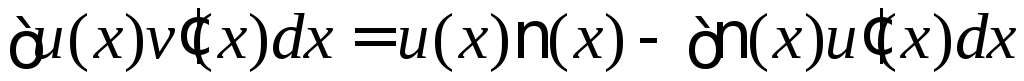

Один из множителей подынтегрального выраженияв новом интеграле заменен своей производной, а второй заменен своей первообразной.

Примеры.

1. _.

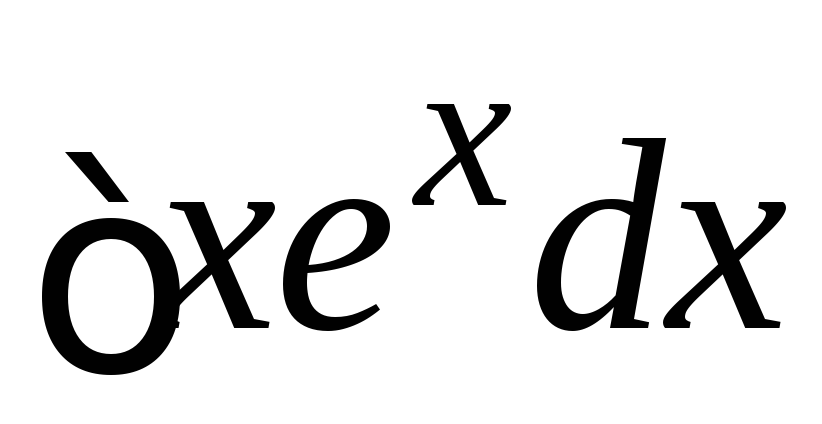Функцию x можно уничтожить дифференцированием.

==.

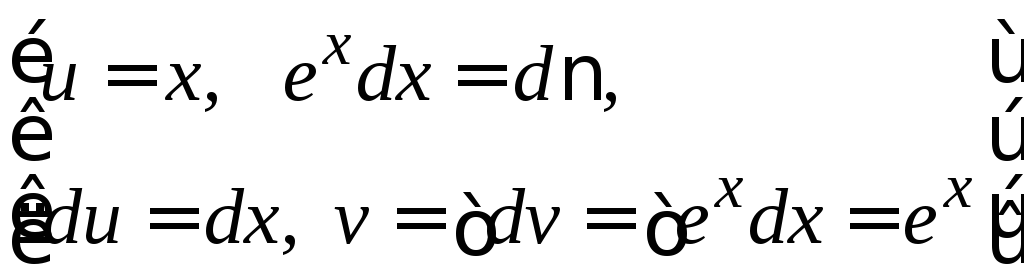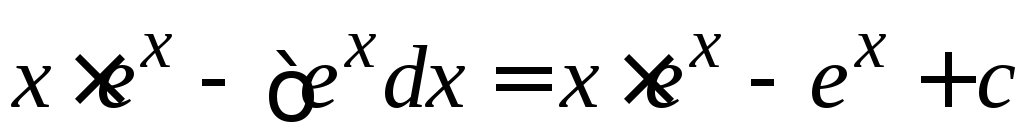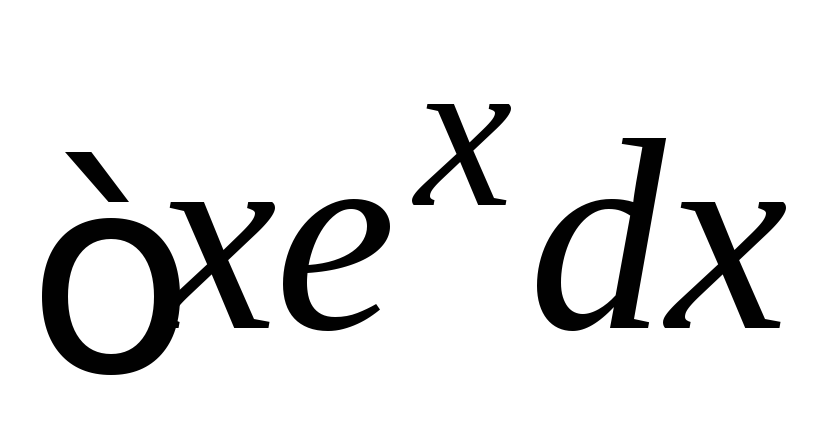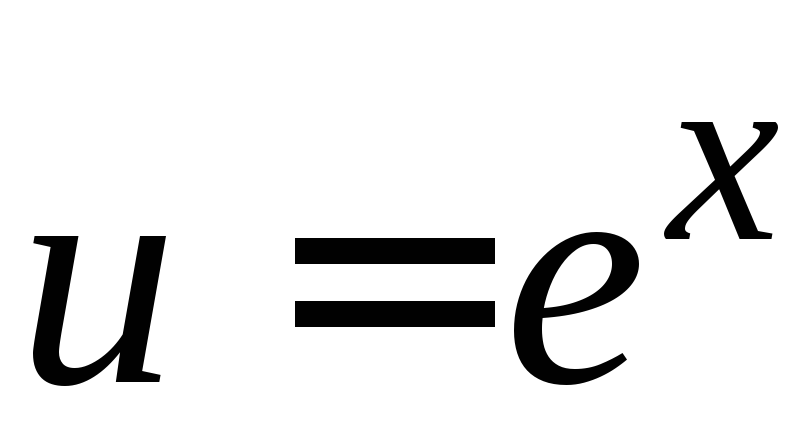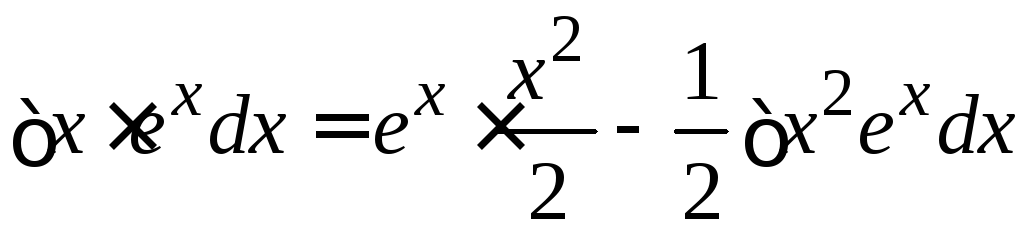Замечание. Неверный выбор u и dv может завести в тупик. Например, если в взять(тогда), придем к равенству,говорящему о бессмысленности выполненных действий.

2. (=

= .

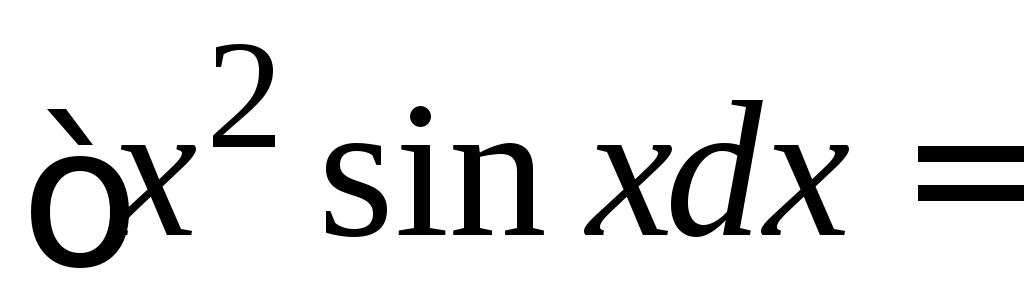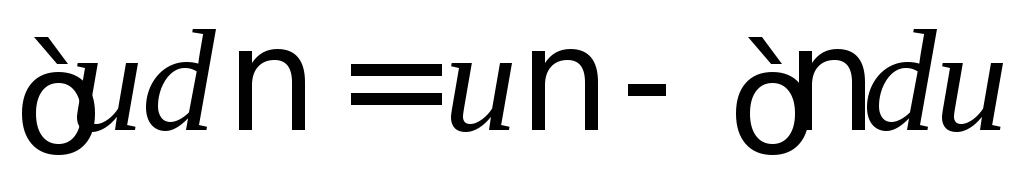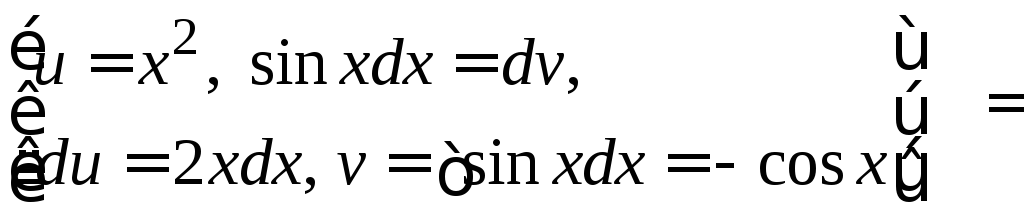
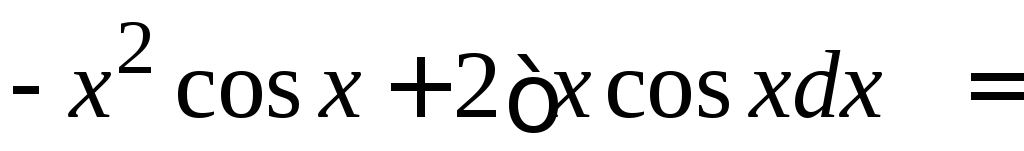
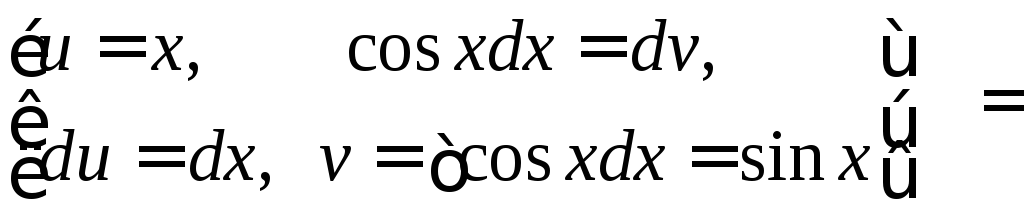
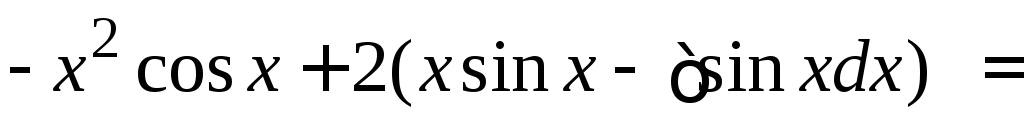
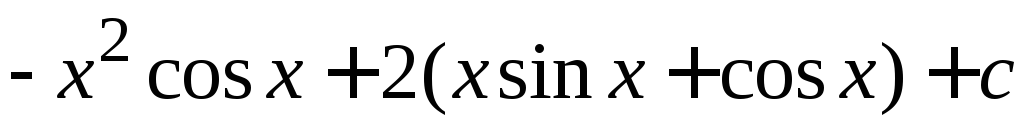3.

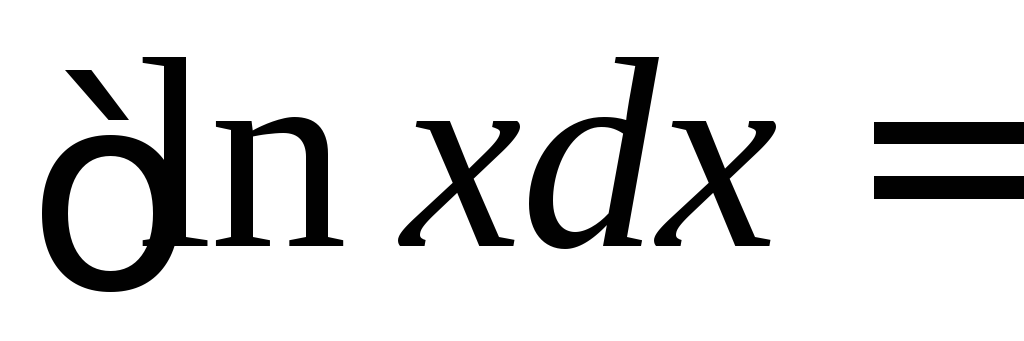
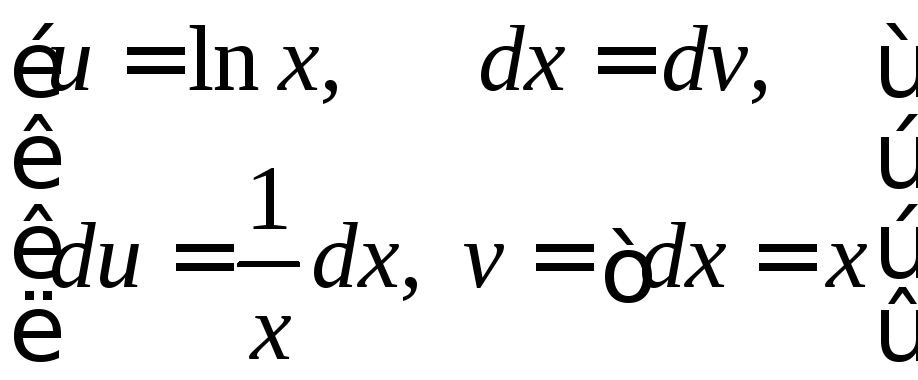
4. =

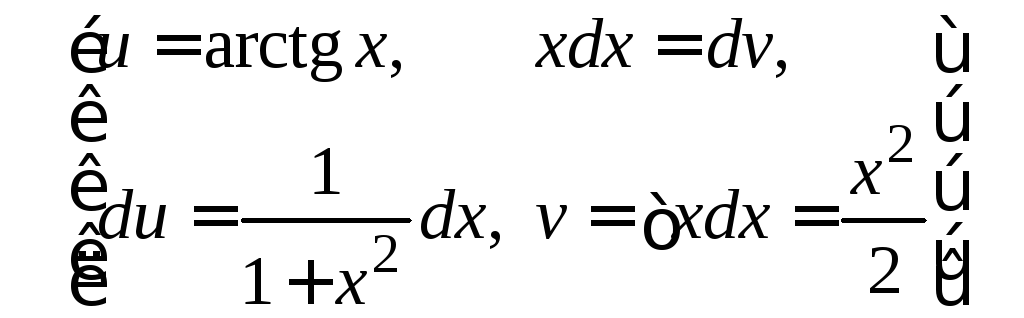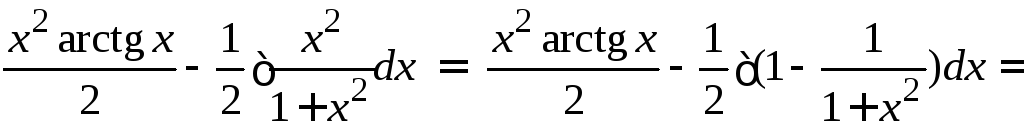
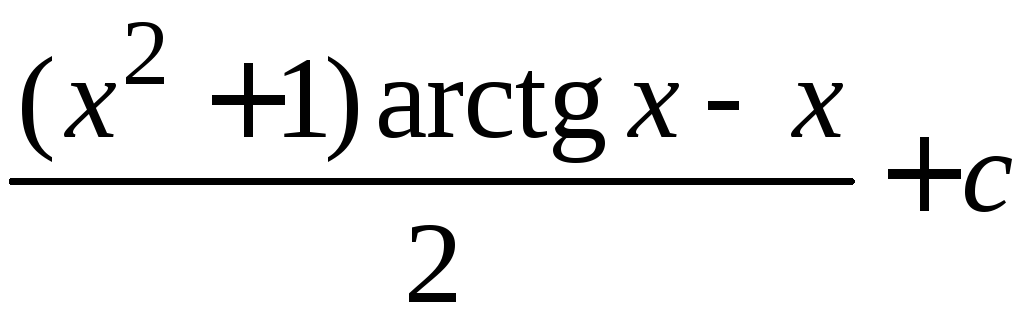
5. Пример «циклического» интеграла: после двух применений формулы метода интегрирования по частям интеграл находится решением полученного уравнения.

=

.

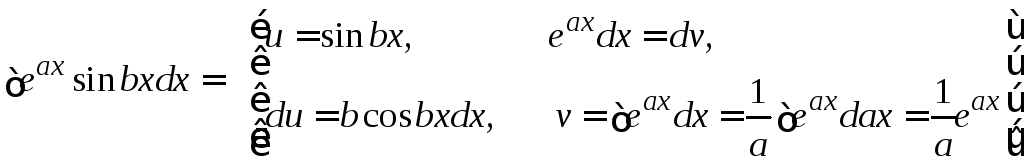
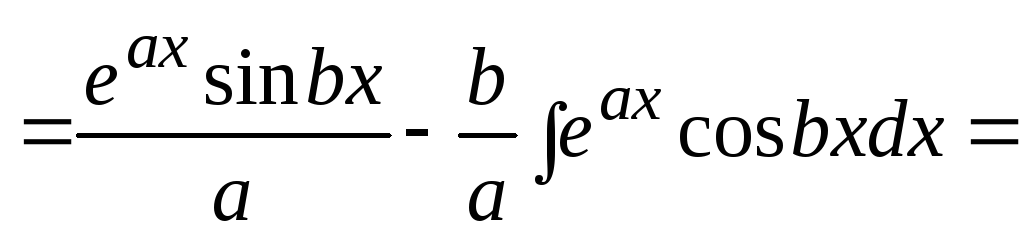
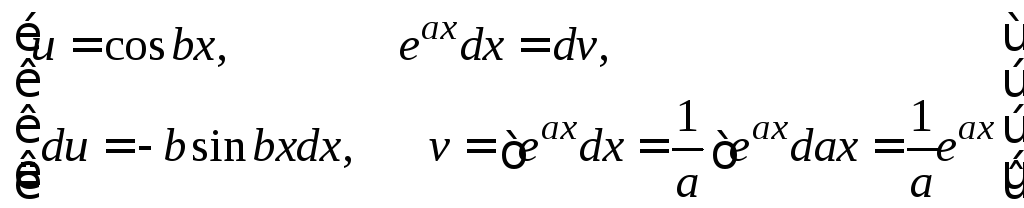
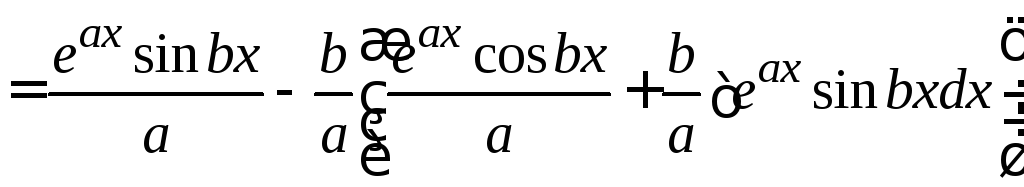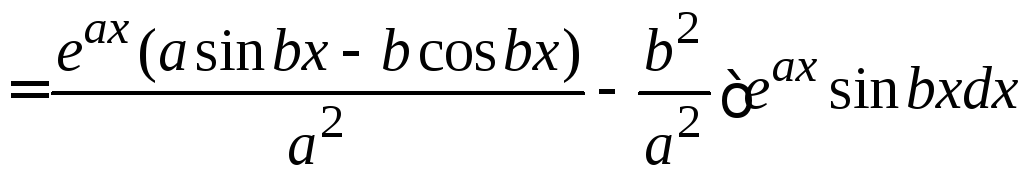Получено уравнение, содержащее искомый интеграл:

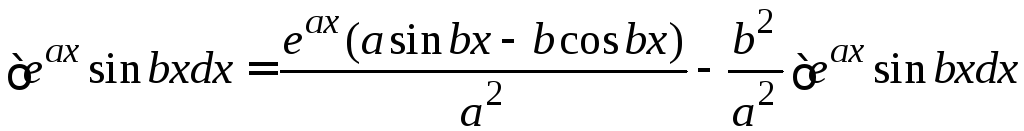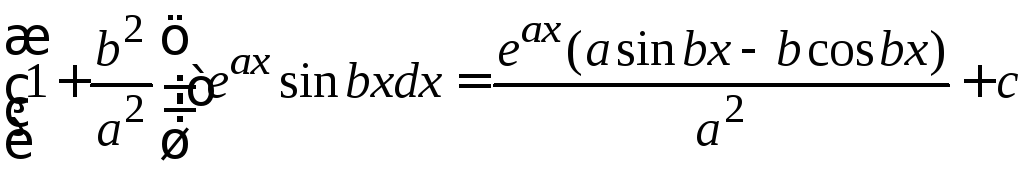..Окончательно,.

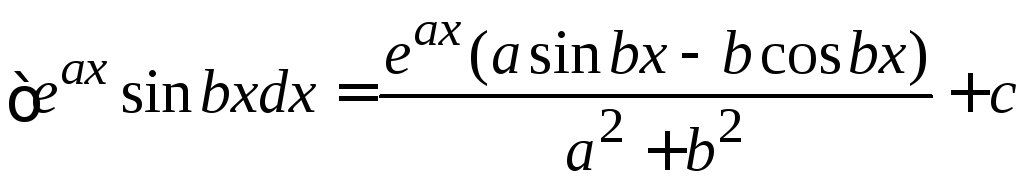Аналогично.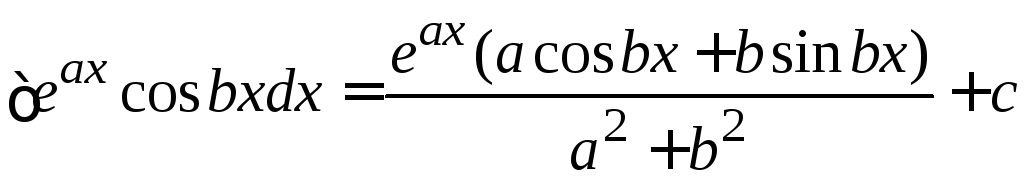

3. Интегрирование рациональных функций. (7.5.1)

Понятие и свойства неопределённого интеграла, таблица интегралов

Неопределённый интеграл: 8 фактов, которые надо знать студенту

Факт 1. Интегрирование — действие, обратное дифференцированию, а именно, восстановление функции по известной производной этой функции. Восстановленная таким образом функция F(x) называется первообразной для функции f(x).

Определение 1. Функция F(x) называется первообразной для функции f(x) на некотором промежутке X, если для всех значений x из этого промежутка выполняется равенство F ‘(x)=f(x), то есть данная функция f(x) является производной от первообразной функции F(x)..

Например, функция F(x) = sin x является первообразной для функции f(x) = cos x на всей числовой прямой, так как при любом значении икса (sin x)’ = (cos x).

Определение 2. Неопределённым интегралом функции f(x) называется совокупность всех её первообразных. При этом употребляется запись

∫ 

f(x)dx

,

где знак ∫  называется знаком интеграла, функция f(x) – подынтегральной функцией, а f(x)dx – подынтегральным выражением.

Таким образом, если F(x) – какая-нибудь первообразная для f(x) , то

∫ 

f(x)dx = F(x) +C

,                 (1)

где C — произвольная постоянная (константа).

Для понимания смысла множества первообразных функции как неопределённого интеграла уместна следующая аналогия. Пусть есть дверь (традиционная деревянная дверь). Её функция — «быть дверью». А из чего сделана дверь? Из дерева. Значит, множеством первообразных подынтегральной функции «быть дверью», то есть её неопределённым интегралом, является функция «быть деревом + С», где С — константа, которая в данном контексте может обозначать, например, породу дерева. Подобно тому, как дверь сделана из дерева при помощи некоторых инструментов, производная функции «сделана» из первообразной функции при помощи формулы, которую мы узнали, изучая производную.

Тогда таблица функций распространённых предметов и соответствующих им первообразных («быть дверью» — «быть деревом», «быть ложкой» — «быть металлом» и др.) аналогична таблице основных неопределённых интегралов, которая будет приведена чуть ниже. В таблице неопределённых интегралов перечисляются распространённые функции с указанием первообразных, из которых «сделаны» эти функции. В части задач на нахождение неопределённого интеграла даны такие подынтегральные функции, которые без особых услилий могут быть проинтегрированы непосредственно, то есть по таблице неопределённых интегралов. В задачах посложнее подынтегральную функцию нужно предварительно преобразовать так, чтобы можно было использовать табличные интегралы.

Факт 2. Восстанавливая функцию как первообразную, мы должны учитывать произвольную постоянную (константу) C, а чтобы не писать список первообразной с различными константами от 1 до бесконечности, нужно записывать множество первообразных с произвольной константой C, например, так: 5x³+С. Итак, произвольная постоянная (константа) входит в выражение первообразной, поскольку первообразная может быть функцией, например, 5x³+4 или 5x³+3 и при дифференцировании 4 или 3, или любая другая константа обращаются в нуль.

Поставим задачу интегрирования: для данной функции f(x) найти такую функцию F(x), производная которой равна f(x).

Пример 1.Найти множество первообразных функции

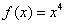
Решение. Для данной функции первообразной является функция

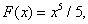
так как

Функция F(x) называется первообразной для функции f(x), если производная F(x) равна f(x), или, что одно и то же, дифференциал F(x) равен f(x) dx, т.е.

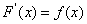
или

                     (2)

Следовательно, функция — первообразная для функции . Однако она не является единственной первообразной для . Ими служат также функции

и вообще

где С – произвольная постоянная. В этом можно убедиться дифференцированием.

Таким образом, если для функции существует одна первообразная, то для неё существует бесконечное множество первообразных, отличающихся на постоянное слагаемое. Все первообразные для функции 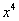записываются в приведённом выше виде. Это вытекает из следующей теоремы.

---

Теорема (формальное изложение факта 2). Если F(x) – первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x) + C , где С – произвольная постоянная.

---

В следующем примере уже обращаемся к таблице интегралов, которая будет дана в параграфе 3, после свойств неопределённого интеграла. Делаем это до ознакомления со всей таблицей, чтобы была понятна суть вышеизложенного. А после таблицы и свойств будем пользоваться ими при интегрировании во всей полносте.

Пример 2.  Найти множества первообразных функций:

1)   

2)

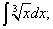
3)

Решение. Находим множества первообразных функций, из которых «сделаны» данные функции. При упоминании формул из таблицы интегралов пока просто примите, что там есть такие формулы, а полностью саму таблицу неопределённых интегралов мы изучим чуть дальше.

1) Применяя формулу (7) из таблицы интегралов при n = 3, получим

2) Используя формулу (10) из таблицы интегралов при n = 1/3,  имеем

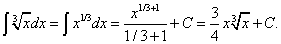
3) Так как

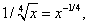
то по формуле (7) при n = -1/4 найдём

Под знаком интеграла пишут не саму функцию f, а её произведение на дифференциал dx. Это делается прежде всего для того, чтобы указать, по какой переменной ищется первообразная. Например,

, ;

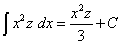здесь в обоих случаях подынтегральная функция равна , но её неопределённые интегралы в рассмотренных случаях оказываются различными. В первом случае эта функция рассматривается как функция от переменной x, а во втором — как функция от z.

Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции.

Пусть требуется найти кривую y=F(x) и мы уже знаем,что тангенс угла наклона касательной в каждой её точке есть заданная функция f(x) абсциссы этой точки.

Согласно геометрическому смыслу производной, тангенс угла наклона касательной в данной точке кривой y=F(x) равен значению производной F'(x). Значит, нужно найти такую функцию F(x), для которой F'(x)=f(x). Требуемая в задаче функция F(x) является первообразной от f(x). Условию задачи удовлетворяет не одна кривая, а семейство кривых. y=F(x) — одна из таких кривых, а всякая другая кривая может быть получена из неё параллельным переносом вдоль оси Oy.

Назовём график первообразной функции от f(x) интегральной кривой. Если F'(x)=f(x), то график функции y=F(x) есть интегральная кривая.

Факт 3. Неопределённый интеграл геометрически представлен семеством всех интегральных кривых, как на рисунке ниже. Удалённость каждой кривой от начала координат определяется произвольной постоянной (константой) интегрирования C.

Факт 4. Теорема 1. Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.

---

Факт 5. Теорема 2. Неопределённый интеграл от дифференциала функции f(x) равен функции f(x) с точностью до постоянного слагаемого, т.е.

                  (3)

Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями.

---

Факт 6. Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.

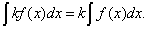  (4)

---

Факт 7. Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.

  (5)

---

Факт 8. Пользусь таблицей неопределённых интегралов, свойствами неопределённого интеграла и методами интегрирования, можно отыскать неопределённый интеграл любой функции.

Из определения неопределённого интеграла вытекают следующие формулы, которые в дальнейшем будем называть табличными интегралами:

(6)

(7)

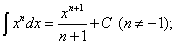
(8)

(9)

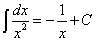
(10)

(11)

(12)

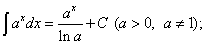
(13)

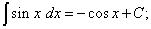
(14)

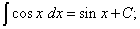
(15)

(16)

(17)

(18)

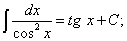
(19)

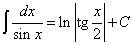
(20)

(21)

(22)

(23)

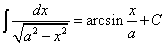
(24)

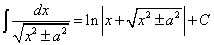
(25)

 

Продолжение темы «Интеграл»

Поделиться с друзьями

Первообразная — это… Что такое Первообразная?

Первообра́зной^[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Так, например, функция является первообразной . Так как производная константы равна нулю, будет иметь бесконечное количество первообразных, таких как или … и т. д.; таким образом семейство первообразных функции можно обозначить как , где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.

Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:

Это соотношение называется формулой Ньютона — Лейбница.

Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:

Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.

Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:

Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, с не непрерывна при , но имеет первообразную с .

Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:

Более развёрнутое изложение этих фактов см. в дифференциальной теории Галуа.

Свойства первообразной

• Первообразная суммы равна сумме первообразных
• Первообразная произведения константы и функции равна произведению константы и первообразной функции
• Достаточным условием существования первообразной у заданной на отрезке функции является непрерывность на этом отрезке
• Необходимыми условиями существования являются принадлежность функции первому классу Бэра и выполнение для неё свойства Дарбу
• У заданной на отрезке функции любые две первообразные отличаются на постоянную.

Техника интегрирования

Нахождение первообразных значительно сложнее, чем нахождение производных. Для этого имеется несколько методов:

• линейность интегрирования позволяет разбивать сложные интегралы на части,
• интегрирование через подстановку, часто применяемое вместе с тригонометрическими тождествами или натуральным логарифмом,
• интегрирование по частям для операций с произведениями функций,
• метод обратной цепочки, особый случай интегрирования по частям,
• метод интегрирования рациональных дробей позволяет интегрировать любые рациональные функции (дроби с полиномами в числителе и знаменателе),
• алгоритм Риша (en:Risch algorithm),
• некоторые интегралы можно найти в таблице интегралов,
• при многократном интегрировании можно использовать дополнительную технику, для примера см. двойной интеграл и полярные координаты, Якобиан и теорема Стокса,
• Системы компьютерной алгебры помогают автоматизировать некоторые вышеприведённые символические операции, что очень удобно, когда алгебраические вычисления становятся слишком громоздкими,
• если функция не имеет элементарной первообразной (как, например, ), её интеграл может быть вычислен приближённо с помощью численного интегрирования.

Другие определения

Это определение является наиболее распространенным, но встречаются и другие, в которых ослаблены требования существования всюду конечной и выполнения всюду равенства , иногда в определении используют обобщения производной.

Примечания

Ссылки

См. также

Первообразная — это… Что такое Первообразная?

Первообра́зной^[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Так, например, функция является первообразной . Так как производная константы равна нулю, будет иметь бесконечное количество первообразных, таких как или … и т. д.; таким образом семейство первообразных функции можно обозначить как , где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.

Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:

Это соотношение называется формулой Ньютона — Лейбница.

Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:

Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.

Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:

Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, с не непрерывна при , но имеет первообразную с .

Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:

Более развёрнутое изложение этих фактов см. в дифференциальной теории Галуа.

Свойства первообразной

• Первообразная суммы равна сумме первообразных
• Первообразная произведения константы и функции равна произведению константы и первообразной функции
• Достаточным условием существования первообразной у заданной на отрезке функции является непрерывность на этом отрезке
• Необходимыми условиями существования являются принадлежность функции первому классу Бэра и выполнение для неё свойства Дарбу
• У заданной на отрезке функции любые две первообразные отличаются на постоянную.

Техника интегрирования

Нахождение первообразных значительно сложнее, чем нахождение производных. Для этого имеется несколько методов:

• линейность интегрирования позволяет разбивать сложные интегралы на части,
• интегрирование через подстановку, часто применяемое вместе с тригонометрическими тождествами или натуральным логарифмом,
• интегрирование по частям для операций с произведениями функций,
• метод обратной цепочки, особый случай интегрирования по частям,
• метод интегрирования рациональных дробей позволяет интегрировать любые рациональные функции (дроби с полиномами в числителе и знаменателе),
• алгоритм Риша (en:Risch algorithm),
• некоторые интегралы можно найти в таблице интегралов,
• при многократном интегрировании можно использовать дополнительную технику, для примера см. двойной интеграл и полярные координаты, Якобиан и теорема Стокса,
• Системы компьютерной алгебры помогают автоматизировать некоторые вышеприведённые символические операции, что очень удобно, когда алгебраические вычисления становятся слишком громоздкими,
• если функция не имеет элементарной первообразной (как, например, ), её интеграл может быть вычислен приближённо с помощью численного интегрирования.

Другие определения

Это определение является наиболее распространенным, но встречаются и другие, в которых ослаблены требования существования всюду конечной и выполнения всюду равенства , иногда в определении используют обобщения производной.

Примечания

Ссылки

См. также

Первообразная — это… Что такое Первообразная?

Первообра́зной^[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Так, например, функция является первообразной . Так как производная константы равна нулю, будет иметь бесконечное количество первообразных, таких как или … и т. д.; таким образом семейство первообразных функции можно обозначить как , где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.

Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:

Это соотношение называется формулой Ньютона — Лейбница.

Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:

Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.

Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:

Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, с не непрерывна при , но имеет первообразную с .

Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:

Более развёрнутое изложение этих фактов см. в дифференциальной теории Галуа.

Свойства первообразной

• Первообразная суммы равна сумме первообразных
• Первообразная произведения константы и функции равна произведению константы и первообразной функции
• Достаточным условием существования первообразной у заданной на отрезке функции является непрерывность на этом отрезке
• Необходимыми условиями существования являются принадлежность функции первому классу Бэра и выполнение для неё свойства Дарбу
• У заданной на отрезке функции любые две первообразные отличаются на постоянную.

Техника интегрирования

Нахождение первообразных значительно сложнее, чем нахождение производных. Для этого имеется несколько методов:

• линейность интегрирования позволяет разбивать сложные интегралы на части,
• интегрирование через подстановку, часто применяемое вместе с тригонометрическими тождествами или натуральным логарифмом,
• интегрирование по частям для операций с произведениями функций,
• метод обратной цепочки, особый случай интегрирования по частям,
• метод интегрирования рациональных дробей позволяет интегрировать любые рациональные функции (дроби с полиномами в числителе и знаменателе),
• алгоритм Риша (en:Risch algorithm),
• некоторые интегралы можно найти в таблице интегралов,
• при многократном интегрировании можно использовать дополнительную технику, для примера см. двойной интеграл и полярные координаты, Якобиан и теорема Стокса,
• Системы компьютерной алгебры помогают автоматизировать некоторые вышеприведённые символические операции, что очень удобно, когда алгебраические вычисления становятся слишком громоздкими,
• если функция не имеет элементарной первообразной (как, например, ), её интеграл может быть вычислен приближённо с помощью численного интегрирования.

Другие определения

Это определение является наиболее распространенным, но встречаются и другие, в которых ослаблены требования существования всюду конечной и выполнения всюду равенства , иногда в определении используют обобщения производной.

Примечания

Ссылки

См. также

Первообразная и неопределенный интеграл

Константа интегрирования

Доказательство. Так как – первообразная функции , то по определению имеем, что

   

Рассмотрим функцию и покажем, что она также является первообразной для функции . Найдем производную:

   

То есть , а это означает, что и функция является первообразной для функции .

Что и требовалось доказать.

Правила нахождения первообразных

1. Если – первообразная для функции , а – первообразная функции , то – первообразная функции .
2. Если – первообразная для функции , а – некоторое число, то является первообразной для функции .
3. Если является первообразной функции , а и – некоторые числа, то функция – первообразная для функции .

Понравился сайт? Расскажи друзьям!