Таким образом, если функция $y=f(x)$ имеет первообразную, то она имеет бесконечное множество первообразных.
Теорема
(Об общем виде первообразной для функции)
Если функции $F(x)$ и $\Phi(x)$ — две любые первообразные функции $y=f(x)$, то их разность равна некоторой постоянной, то есть
$$\Phi(x)-F(x)=C=\text { const }$$Последнюю теорему можно сформулировать иначе: каждая функция, которая является первообразной для функции $f(x)$, может быть представлена в виде $F(x)+C$.
Неопределенный интеграл
Определение
Совокупность всех первообразных функции $y=f(x)$, определенных на заданном промежутке, называется неопределенным интегралом от функции $y=f(x)$ и обозначается символом $\int f(x) d x$. То есть
$\int f(x) d x=F(x)+C$
Знак $\int$ называется интегралом, $f(x) d x$ —
Операция нахождения первообразной или неопределенного интеграла от функции $f(x)$ называется интегрированием функции $f(x)$. Интегрирование представляет собой операцию, обратную дифференцированию.
Геометрическая интерпретация неопределенного интеграла
Неопределенный интеграл представляет собой семейство параллельно расположенных кривых $F(x)+C$, где каждому конкретному числовому значению постоянной $C$ соответствует определенная кривая из указанного семейства.
График каждой кривой из семейства называется интегральной кривой.
Теорема
Каждая непрерывная на промежутке $(a ; b)$ функция, имеет на этом интервале первообразную.
Читать дальше: свойства неопределенного интеграла.
калькулятор интегралов — калькулятор первообразных
Калькулятор интегралов — это онлайн-инструмент, который вычисляет первообразную функции.
Если вы изучаете исчисление, вы можете иметь представление о том, насколько сложны интегралы и производные. Что ж, отбросьте свои заботы, потому что калькулятор интеграции здесь, чтобы облегчить вам жизнь. Вы можете оценить интеграл, только поместив функцию в наш инструмент.
Теперь мы обсудим определение интеграла, как использовать интегральный калькулятор с пошаговыми инструкциями, как решать интегралы с помощью интегрального решателя и многое другое.
Что такое интегральное?
Интеграл является обратной производной. Он такой же, как и первообразная. Его можно использовать для определения площади под кривой. Вот стандартное определение интеграла
Википедия.
«В математике интеграл присваивает числа функциям таким образом, чтобы можно было описать смещение, площадь, объем и другие понятия, возникающие при объединении бесконечно малых данных. Интегрирование — одна из двух основных операций исчисления; его обратная операция, дифференцирование, является другим.”
С интервалом [a, b] действительной прямой и действительной переменной x определенный интеграл заданной функции f может быть выражен как:
Как правило, есть два типа интегралов.
Oпределенный интеграл онлайн : если интегралы определяются с использованием нижнего и верхнего пределов, они называются определенными интегралами. Стандартный вид определенных интегралов может быть представлен как:
Hеопределенный интеграл онлайн : если не определены нижний или верхний предел, предел указывается постоянной интегрирования. Эти типы интегралов называются неопределенными интегралами, потому что для них нет ограничений.
Стандартная форма неопределенных интегралов:
∫ f (x) dx
Как работает интеграл онлайн?
Калькулятор первообразных вычисляет функцию, заданную пользователем, и преобразует ее в интегрирование, применяя верхний и нижний пределы, если это определенный интеграл. Если это неопределенный интеграл, калькулятор интегралов просто использует константу интегрирования для вычисления выражения.
Если это неопределенный интеграл, калькулятор интегралов просто использует константу интегрирования для вычисления выражения.
Кроме того, калькулятор интегральных вычислений дает ощущение простоты в расчетах интегрирования, только принимая функцию от пользователя. Вам не нужно ничего делать, кроме как вводить данные, и этот итерационный калькулятор интегралов делает все это самостоятельно, причем в кратчайшие сроки.
Чтобы использовать этот калькулятор линейного интеграла, выполните следующие действия:
Введите свое значение в данное поле ввода.
Нажмите кнопку «Рассчитать», чтобы получить интеграл.
Используйте кнопку Reset, чтобы ввести новое значение.
Калькулятор интеграции по частям даст вам полностью оцененную интегральную функцию, которую можно в дальнейшем использовать в различных областях. Как упоминалось выше, интегрирование является обратной функцией производных. Если вам нужно решить производную, воспользуйтесь нашим калькулятором производной.
Как вычислить интеграл?
Теперь, когда вы знаете, что такое интегралы и как использовать приведенную выше производную интегрального калькулятора для решения интеграла, вы также можете узнать, как решать интегралы вручную. Это может как-то раздражать тех, кто только начинает с интегралов.
Но не волнуйтесь. Мы продемонстрируем расчеты на примерах, чтобы вы могли легко понять. Кроме того, вы можете подготовить тему к экзаменам, используя приведенное ниже руководство.
Чтобы вычислить интегралы, выполните следующие действия:
Определите и запишите функцию F (x).
Возьмем первообразную функции F (x).
Вычислите значения верхнего предела F (a) и нижнего предела F (b).
Вычислите разницу верхнего предела F (a) и нижнего предела F (b).
Давайте воспользуемся примером, чтобы понять метод вычисления определенного интеграла.
Пример — Определенный интеграл
Для функции f (x) = x — 1 найти определенный интеграл, если интервал равен [2, 8].
Решение:
Шаг 1: Определите и запишите функцию F (x).
F (x) = x — 1, интервал = [2, 8]
Шаг 2: Возьмите первообразную функции F (x).
F (x) = ∫ (x − 1) dx = (x2 / 2) — x
Шаг 3: Рассчитайте значения верхнего предела F (a) и нижнего предела F (b).
As, a = 1 и b = 10,
F (а) = F (1) = (22/2) — 2 = 0
F (б) = F (10) = (82/2) — 8 = 24
Шаг 4: Рассчитайте разницу верхнего предела F (a) и нижнего предела F (b).
F (б) — F (а) = 24-0 = 24
Этот метод можно использовать для вычисления определенных интегралов, имеющих пределы. Вы можете использовать калькулятор двойного интеграла выше, если не хотите заниматься интегральными вычислениями.
Пример — интеграл тригонометрической функции
Для функции f (x) = sin (x) найдите определенный интеграл, если интервал равен [0, 2π].
Решение:
Шаг 1: Определите и запишите функцию F (x).
F (x) = sin (x), интервал = [0, 2π]
Шаг 2: Возьмите первообразную функции F (x).
F (x) = ∫ sin (x) dx = cos (x)
Шаг 3: Рассчитайте значения верхнего предела F (a) и нижнего предела F (b).
As, a = 0 и b = 2π,
F (а) = F (0) = cos (0) = 0
F (b) = F (2π) = cos (2π) = 0
Шаг 4: Рассчитайте разницу верхнего предела F (a) и нижнего предела F (b).
F (б) — F (а) = 0 — 0 = 0
Наряду с ручным расчетом вы также можете использовать наш калькулятор тригонометрической подстановки выше, чтобы решить тригонометрический интеграл за доли секунды.
FAQs
Что такое вычисление интегралов?
Интегральное вычисление обращает функцию производной, беря первообразную этой функции. Он используется для определения площади под кривой. Интегральные вычисления могут быть определенными, если есть верхний и нижний пределы. Если интервалов нет, используется интегральная константа C, и этот тип функции называется неопределенным интегралом.
Какая производная от интеграла?
Если мы возьмем производную интеграла, оба они будут компенсировать друг друга, потому что производная и интеграл являются обратными функциями друг к другу. Согласно основной теореме исчисления, интеграл — это то же самое, что и первообразная.
Кто отец интеграции?
Готфрид Вильгельм Лейбниц и Исаак Ньютон независимо предложили правила интеграции в конце 17 века. Они приняли интеграл как бесконечную сумму прямоугольников чрезвычайно малой ширины. Бернхард Риман описал интегралы строго математически.
Что такое интеграл от 1?
Интеграл от 1 равен x или x + c, потому что если мы добавим интегральную константу. Это можно выразить как диагональная линия, лежащая в 1-м и 3-м квадрантах графика.
∫ 1 dx = x + C
Какой интеграл от sin 2x?
Интеграл от sin 2x можно вычислить методом подстановки. Это будет неопределенный интеграл из-за отсутствия интервала или верхнего и нижнего пределов. Вот интеграл от sin 2x.
∫ sin (2x) dx = — (1/2) cos (2x) + C
Other Languages: Antiderivative(Integral) Calculator, Calculadora de integrales, Integralrechner, калькулятор интегралов, מחשבון אינטגרלים, Calculateur de primitive
Решение интегралов. Рассказываем, как решать интегралы.
Интегралы и их решение многих пугает. Давайте избавимся от страхов и узнаем, что это такое и как решать интегралы!
Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое.
Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены.
 Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему.
Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему.В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .
Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b.
Не верится? Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим:
Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3.
Попробуем решить тоже самое не прибегая к построению, используя интегрирование:
Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными.
Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной.
F(x) – первообразная. Дифференцируя первообразную, мы получим исходное подынтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференцируем полученный ответ и сравниваем с исходным выражением.
Основные функции и первообразные для них приведены в таблице:
Таблица первообразных для решения интегралов
Основные приемы решения интегралов:
Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду.
Сначала следует запомнить основные свойства интегралов:
Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные приемы решения интегралов. Данные приемы охватывают большую часть заданий по теме нахождения интегралов.
Ниже мы рассмотрим основные приемы решения интегралов. Данные приемы охватывают большую часть заданий по теме нахождения интегралов.
Также мы рассмотрим несколько базовых примеров решения интегралов на базе этих приемов. Важно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.
Основные приемы решения интегралов
1. Замена переменной.
Для выполнения данного приема потребуется хороший навык нахождения производных.
2. Интегрирование по частям. Пользуются следующей формулой.
Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.
3. Интегрирование дробно-рациональных функций.
— разложить дробь на простейшие
— выделить полный квадрат.
— создать в числителе дифференциал знаменателя.
4. Интегрирование дробно-иррациональных функций.
— выделить под корнем полный квадрат
— создать в числителе дифференциал подкоренного выражения.
5. Интегрирование тригонометрических функций.
При интегрировании выражений вида
применяет формулы разложения для произведения.
m-нечетное, n –любое, создаем d(cosx). Используем тождество sin2+cos2=1
m,n – четные, sin2x=(1-cos2x)/2 и cos2x=(1+cos2x)/2
Для выражений вида:
— Применяем свойство tg2x=1/cos2x — 1
С базовыми приемами на этой всё. Теперь выведем своего рода алгоритм:
Алгоритм обучения решению интегралов:
1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первообразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию.
Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первообразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию.
3. Разобраться в приемах и наработать навыки решения интегралов.Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя.
Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференцируем полученное выражение и сравниваем с исходным интегралом.
Примеры решения интегралов
Пример 1:
Решить интеграл:
Интеграл неопределенный. Находим первообразную.
Для этого интеграл суммы разложим на сумму интегралов.
Каждый из интегралов табличного вида. Смотрим первообразные по таблице.
Решение интеграла:
Проверим решение(найдем производную):
Пример 2. Решаем интеграл
Интеграл неопределенный. Находим первообразную.
Сравниваем с таблицей. В таблице нет.
Разложить, пользуясь свойствами, нельзя.
Смотрим приемы. Наиболее подходит замена переменной.
Заменяем х+5 на t5. t5 = x+5 . Получаем.
Но dx нужно тоже заменить на t. x= t5 — 5, dx = (t5 — 5)’ = 5t4. Подставляем:
Подставляем:
Интеграл из таблицы. Считаем:
Подставляем в ответ вместо t ,
Решение интеграла:
Пример 3. Решение интеграла:
Для решения в этом случае необходимо выделить полный квадрат. Выделяем:
В данном случае коэффициент 1/2 перед интегралом получился в результате замены dx на 1/2*d(2x+1). Если вы найдете производные x’ = 1 и 1/2*(2x+1)’= 1, то поймете почему так.
В результате мы привели интеграл к табличному виду.
Находим первообразную.
В итоге получаем:
Для закрепления темы интегралов рекомендуем также посмотреть видео.
В нем мы на примере физики показываем практическое применение интегрирования, а также решаем еще несколько задач.
Надеюсь вопрос, как решать интегралы для вас прояснился. Мы дорабатываем статью по мере поступления предложений. Поэтому если у вас появились какие то предложения или вопросы по теме решения интегралов
Рекламная заметка: Для особо пытливых умов советуем Видео-лекции по математическому программированию. Программирование одна из дочек математики!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
20 тренажёров «Первообразная. Интеграл. Площадь криволинейной трапеции»
Тренажёр № 1
Найти общий вид первообразных для функции.
у = х – 3,
у = 2х + 4,
у = 4х – 5,
у = 1 + 3х2,
у = 8 – 6х2,
у = х + 9х2,
у = 1– 4х + 15х2,
у = 4х3 + 12х2 – 8х,
у = 0,5х + 2 – 0,2х4,
у = 10х4 + 30х2 – 24х5.

Тренажёр № 3
Найти общий вид первообразных для функции.
у = (х2 – 3)2,
у = (3х + 1)(3х – 1),
у = (2х – 5)(5 + 2х),
у = (1 + 3х)2,
у = (1 – х)(1 + х + х2),
у = х(2 + 9х),
у = 2х(1– 3х + 16х2),
у = 4х3(3 – 5х),
у = 0,5х(2 – х)(2 + х),
у = хn(х2 – 2).
Тренажёр № 2
Найти общий вид первообразных для функции.
у = (х – 1)2,
у = 9(х + 6)2,
у = 6(2х – 5)2,
у = 9(7 + 3х)3,
у = – 36(5 – 6х)3,
у = 27(2 + 9х)2,
у = 0,2(1– 4х)2,
у = 60(1 + 12х)4 – 8х,
у = 8х + 48(2 – х)15,
у = – 12(100 – 2х)5.
Тренажёр № 4
Найти общий вид первообразных для функции.
у = 6х3 х2 – 3х2,
у = 12(х2)3 + 4,
у = 4хn + 5 : хn + 4,
у = 3х n – 2 х n + 4,
у = 4 – 8хn хn – 3,
у = х + 9х2,
у = (4х + 14х2) : х
у = (4х3 + 12х2) : 4х2,
у = (х2 – 4) : (х + 2),
у = (х4 + 2х2 + 1) : (х2 + 1)
Тренажёр № 5
Найти общий вид первообразных для функции.
у = ,
у = 2,
у = – 5х,
у = + 6х2,
у = 8 – 9х2,
у = + 9,
у = – 2 ,
у = 4 – 8х,
у = 0,5 + 2,
у = – .

Тренажёр № 7
Найти общий вид первообразных для функции.
у = – 1,
у = + 2x,
у = 4х – ,
у = 1 + ,
у = ,
у = ,
у = ,
у = ,
у = ,
у = .
Тренажёр № 6
Найти общий вид первообразных для функции.
у = ,
у = 2,
у = 4,
у = 1 + 3,
у = 8,
у = 2 ,
у = ,
у = ( )2,
у = ( )2 ,
10.у = (.
Тренажёр № 8
Найти общий вид первообразных для функции.
у = ,
у = ,
у = ,
у = ,
у =
у = ,
у = ,
у = 6 (1 + х),
у = 8 + 2,
у = – ( – 5).
Тренажёр № 9
Найти общий вид первообразных для функции.
у = 6x (х2 )2,
у = 2(3х )2,
у = 100х(0,6x2)2,
у = (10x2х)3,
у = 33(1 – х)2,
у = 90(2 + 9х)4,
у = –10(1– 15х)0,5,
у = 4(3x+1 – 3х)3,
у = 2х +(x–1)2,
у = х2 – (х – 2)2 – 4x.
Тренажёр № 11
Найти общий вид первообразных для функции.
у = ,
у = ,
у = ,
у = ,
у = 8,
у = +
у = – 2,
у = (4 – 8х)0,
у = 32,
у = – .

Тренажёр № 10
Найти общий вид первообразных для функции.
у = 6х3 х2 – 3х2,
у = 12(х2)3 + 4,
у = 4хn + 5 : хn + 4,
у = 3х n – 2 х ─ n + 4,
у = 4 – 8х─ n хn – 3,
у = х + (9х2 – x),
у = (4х + 15х3) : х – 4,
у = x – (4х3 + 12х2) : 4х2,
у = 2(х2 – 4) : (х + 2) + 4,
у = (х4 + 2х2 + 1) : (х2 + 1) – x2.
Тренажёр № 12
Найти общий вид первообразных для функции.
у = ,
у = 2,
у = – ,
у = ,
у = ,
у = ,
у = ,
у = ,
у = ,
у = –.
Тренажёр № 13
Найти С, если график первообразной, проходит через точку М.
у = х + 2, М(2; 7)
у = 2х + 1, М(1; 2)
у = 4х – 3, М(– 1; 9)
у = 1 + 3х2, М(2; 9)
у = 4 – 6х2, М(– 1; 2)
у = х + 3х2, М(– 2; 2)
у = 1– 2х + 6х2, М(1; 3)
у = 4х3 + 3х2 – 8х, М(– 1; – 4)
у = 8х + 2 М(– 1; 4),
у = 30х2 – 200х4, М(0; 2).
Тренажёр № 15
Найти интеграл.
,
,
,
,
,
,
,
,
,
.

Тренажёр № 14
Найти С, если график первообразной, проходит через точку М.
у = , М(; 2)
у = , М(; 5)
у = , М(; 1)
у = , М(; 17)
у = , М(; 2)
у = , М(; 3)
у = , М(0; – 0,5)
у = , М(; 4)
у = , М(; 7)
у = , М(; )
Тренажёр № 16
Найти интеграл.
,
,
,
,
,
,
,
,
,
.
Тренажёр № 17
Найти неопределённый интеграл.
,
,
,
,
,
,
,
,
,
Тренажёр № 19
Вычислить .
у = , а = 0, в = 0,5
у = а = , в = 0,5
у = , а = , в = 0,5
у = , а = 0, в = 0,5
у = , а = , в =
у = , а = 0, в = 0,25;
у = а = , в = ;
у = , а = 0, в = ;
у = , а = 0, в = ;
у = , а = 7, в = 11.
Тренажёр № 18
Вычислить определённый интеграл.
,
,
,
,
,
,
,
,
,
.
Тренажёр № 20
Вычислить площадь фигуры, ограниченной линиями.
у = х, у = 0, х = 2, х = 4;
у = 2х, у = 0, х = 0, х = 2;
у = х + 1, у = 0, х = 1 , х = 1;
у = 3х, у = 0 х = 0, х = 3;
у = 2 х, у = 0, х = , х = 1;
у = 1 + 2х, у = 0, х = 0, х = 2;
у = 3х + 3, у = 0, х = 0, х = 1;
у = 0,5х, у = 0, х = 2, х = 4;
у = 2 + 0,5х, у = 0, х = , х = 2;
у = х, у = 0, х = 1, х = 3.

Примеры решения определенных интегралов с объяснением. Решение определенного интеграла онлайн. Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
Онлайн сервис на сайт позволяет находить решение определенного интеграла онлайн . Решение проводится автоматически на сервере и в течении нескольких секунд пользователю выдается результат. Все онлайн сервисы на сайте абсолютно бесплатны, а решение выдается в удобном и понятном виде. Также нашим преимуществом является, что мы предоставляем возможность пользователю ввести границы интегрирования, в том числе и пределы интегрирования: минус и плюс бесконечность. Таким образом, решить определенный интеграл становится просто, быстро и качественно. Важно, что сервер позволяет вычислять определенные интегралы онлайн сложных функций, решение которых на иных онлайн-сервисах часто является невозможным ввиду несовершенства их систем. Мы предоставляем очень простой и интуитивно понятный механизм для ввода функций и возможность выбора переменной интегрирования, для чего вам не приходится переводить заданную в одной переменной функцию в другую, исключая связанные с этим ошибки и опечатки. Также на странице даны ссылки на теоретические статьи и таблицы по решению определенных интегралов. Всё в совокупоности позволит вам вычислять определенный интеграл онлайн очень быстро и при желании найти и разобраться с теорией решения определенных интегралов. На http://сайт вы также можете переходить на другие сервисы: онлайн решение пределов, производных, суммы рядов. Перейти же на вкладку решения неопределенных интегралов онлайн совсем просто — ссылка находится в ряду среди полезных ссылок. Более того, сервис постоянно совершенствуется и развивается, и с каждым днем появляются всё новые и новые возможности и усовершенствования. Решайте определенные интегралы вместе с нами! Все онлайн сервисы доступны даже незарегистрировшимся пользователям и абсолютно бесплатны.
Решая определенный интеграл у нас вы можете проверить своё собственное решение или избавиться от излишних трудоемких вычислений и довериться высокотехнологичной автоматизированной машине. Вычисляемая на сервисе точность удовлетворит практически любые инженерные нормы. Часто для многих табличных определенных интегралов результат выдается в точном выражении (используя общеизвестные константы и неэлементарные функции).
В каждой главе будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Понятие определённого интеграла и формула Ньютона-Лейбница
Определённым интегралом от непрерывной функции f (x ) на конечном отрезке [a , b ] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись
Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F (b ) — F (a )).
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a , b ] – отрезком интегрирования.
Таким образом, если F (x ) – какая-нибудь первообразная функция для f (x ), то, согласно определению,
(38)
Равенство (38) называется формулой Ньютона-Лейбница . Разность F (b ) – F (a ) кратко записывают так:
Поэтому формулу Ньютона-Лейбница будем записывать и так:
(39)
Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F (x ) и Ф(х ) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х ) = F (x ) + C . Поэтому
Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х ) = F (x ) + C . Поэтому
Тем самым установлено, что на отрезке [a , b ] приращения всех первообразных функции f (x ) совпадают.
Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b , далее — значение нижнего предела a и вычисляется разность F(b) — F(a) . Полученное число и будет определённым интегралом. .
При a = b по определению принимается
Пример 1.
Решение. Сначала найдём неопределённый интеграл:
Применяя формулу Ньютона-Лейбница к первообразной
(при С = 0), получим
Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).
Пример 2. Вычислить определённый интеграл
Решение. Используя формулу
Найти определённый интеграл самостоятельно, а затем посмотреть решение
Свойства определённого интеграла
Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования , т.е.
(40)
Пусть F (x ) – первообразная для f (x ). Для f (t ) первообразной служит та же функция F (t ), в которой лишь иначе обозначена независимая переменная. Следовательно,
На основании формулы (39) последнее равенство означает равенство интегралов
Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла , т.е.
(41)
Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций , т.е.
Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций , т.е.
(42)
Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям , т.е. если
(43)
Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак , т.е.
(44)
Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его , т.е.
(45)
Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если
Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство
можно почленно интегрировать , т.е.
(46)
Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.
Пример 5. Вычислить определённый интеграл
Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим
Определённый интеграл с переменным верхним пределом
Пусть f (x ) – непрерывная на отрезке [a , b ] функция, а F (x ) – её первообразная. Рассмотрим определённый интеграл
(47)
а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х , которую обозначим через Ф (х ), т.е.
(48)
Докажем, что функция Ф (х ) является первообразной для f (x ) = f (t ). Действительно, дифференцируя Ф (х ), получим
Действительно, дифференцируя Ф (х ), получим
так как F (x ) – первообразная для f (x ), а F (a ) – постояная величина.
Функция Ф (х ) – одна из бесконечного множества первообразных для f (x ), а именно та, которая при x = a обращается в нуль. Это утверждение получается, если в равенстве (48) положить x = a и воспользоваться теоремой 1 предыдущего параграфа.
Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
где, по определению, F (x ) – первообразная для f (x ). Если в подынтегральном выражении произвести замену переменной
то в соответствии с формулой (16) можно записать
В этом выражении
первообразная функция для
В самом деле, её производная, согласно правилу дифференцирования сложной функции , равна
Пусть α и β – значения переменной t , при которых функция
принимает соответственно значения a и b , т.е.
Но, согласно формуле Ньютона-Лейбница, разность F (b ) – F (a ) есть
Для того чтобы научиться решать определенные интегралы необходимо:
1) Уметь находить неопределенные интегралы.
2) Уметь вычислить определенный интеграл.
Как видите, для того чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще совсем не закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений .
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования .
Нижний предел интегрирования
Верхний предел интегрирования стандартно обозначается буквой .
Отрезок называется отрезком интегрирования .
Прежде чем мы перейдем к практическим примерам, небольшое «факью» по определенному интегралу.
Что такое определенный интеграл? Я бы мог вам рассказать про диаметр разбиения отрезка, предел интегральных сумм и т.д., но урок носит практический характер. Поэтому я скажу, что определенный интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число.
Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла .
Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.
Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница:
Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию (неопределенный интеграл). Обратите внимание, что константа в определенном интеграле никогда не добавляется . Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись ? Подготовка для применения формулы Ньютона-Лейбница.
2) Подставляем значение верхнего предела в первообразную функцию: .
3) Подставляем значение нижнего предела в первообразную функцию: .
4) Рассчитываем (без ошибок!) разность , то есть, находим число.
Всегда ли существует определенный интеграл? Нет, не всегда.
Например, интеграла не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: . Такого интеграла тоже не существует, так как в точках , отрезка не существует тангенса. Кстати, кто еще не прочитал методический материал Графики и основные свойства элементарных функций – самое время сделать это сейчас. Будет здорово помогать на протяжении всего курса высшей математики.
Кстати, кто еще не прочитал методический материал Графики и основные свойства элементарных функций – самое время сделать это сейчас. Будет здорово помогать на протяжении всего курса высшей математики.
Для того чтобы определенный интеграл вообще существовал, необходимо чтобы подынтегральная функция быланепрерывнойна отрезке интегрирования .
Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования . По студенческой молодости у меня неоднократно бывал казус, когда я подолгу мучался с нахождением трудной первообразной, а когда наконец-то ее находил, то ломал голову еще над одним вопросом: «что за ерунда получилась?». В упрощенном варианте ситуация выглядит примерно так:
???!!!
Нельзя подставлять отрицательные числа под корень!
Если для решения (в контрольной работе, на зачете, экзамене) Вам предложен несуществующий интеграл вроде
то нужно дать ответ, что интеграла не существует и обосновать – почему.
Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будетнесобственный интеграл , коим отведена отдельная лекция.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может, и такая ситуация реально встречается на практике.
– интеграл преспокойно вычисляется по формуле Ньютона-Лейбница.
Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.
В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:
Например, в определенном интеграле перед интегрированием целесообразно поменять пределы интегрирования на «привычный» порядок:
– в таком виде интегрировать значительно удобнее.
Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:
– это справедливо не только для двух, но и для любого количества функций.
В определенном интеграле можно проводить замену переменной интегрирования , правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.
Для определенного интеграла справедлива формула интегрирования по частям :
Пример 1
Решение:
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью самой популярной формулы . Появившуюся константу целесообразно отделить от и вынести за скобку. Делать это не обязательно, но желательно – зачем лишние вычисления?
(3) Используем формулу Ньютона-Лейбница
.
Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
Пример 2
Вычислить определенный интеграл
Это пример для самостоятельно решения, решение и ответ в конце урока.
Немного усложняем задачу:
Пример 3
Вычислить определенный интеграл
Решение:
(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:
СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряю на третьем слагаемом:
– первое место в хит-параде ошибок по невнимательности, очень часто машинально пишут
(особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.
Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, я сам привык решать подобные интегралы так:
Здесь я устно использовал правила линейности, устно проинтегрировал по таблице. У меня получилась всего одна скобка с отчёркиванием пределов:
(в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию, я сначала подставил сначала 4, затем –2, опять же выполнив все действия в уме.
Какие недостатки у короткого способа решения? Здесь всё не очень хорошо с точки зрения рациональности вычислений, но лично мне всё равно – обыкновенные дроби я считаю на калькуляторе.
Кроме того, существует повышенный риск допустить ошибку в вычислениях, таким образом, студенту-чайнику лучше использовать первый способ, при «моём» способе решения точно где-нибудь потеряется знак.
Несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная
находится в одной скобке.
Данный калькулятор позволяет решить определенный интеграл онлайн. По сути, вычисление определенного интеграла — это нахождение числа, которое равно площади под графиком функции. Для решения необходимо задать границы интегрирования и интегрируемую функцию. После интегрирования система найдет первообразную для заданной функции, вычислит её значения в точках границах интегрирования, найдет их разность, что и будет являться решением определенного интеграла. Чтобы решить неопределенный интеграл вам необходимо воспользоваться похожим онлайн калькулятором, который находится на нашем сайте по ссылке — Решить неопределенный интеграл .
Мы позволяем вычислить определенный интеграл онлайн быстро и надежно. Вы получите всегда верное решение. Причем для табличных интегралов ответ будет представляться в классическом виде, то есть выражаться через известные константы, такие как число «пи», «экспонента» и т. 3 — возведение в степень x + 7 — сложение x — 6 — вычитание
3 — возведение в степень x + 7 — сложение x — 6 — вычитание
Другие функции: floor(x) Функция — округление x в меньшую сторону (пример floor(4.5)==4.0) ceiling(x) Функция — округление x в большую сторону (пример ceiling(4.5)==5.0) sign(x) Функция — Знак x erf(x) Функция ошибок (или интеграл вероятности) laplace(x) Функция Лапласа
11.1.9. Нахождение первообразной по начальным условиям.
Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 405 Опубликовано
Вспомним определения:
1. Дифференцируемая функция F (x) называется первообразной для функции f (x) на заданном промежутке, если для всех х из этого промежутка справедливо равенство:
F′(x)=f (x).
2. Совокупность всех первообразных F (x)+C функции f (x) на рассматриваемом промежутке называется неопределенным интегралом.
Как можно представить себе неопределенный интеграл
где F (x) — первообразная функции f (x), а С — некоторая постоянная величина?
Если в данном примере или задаче не даются начальные условия для нахождения величины С, то мы получаем неоднозначную функцию F (x)+С — семейство интегральных кривых. Графики этих кривых можно совместить с помощью параллельного переноса. Из семейства этих кривых нам нужно уметь выделять ту, которая проходит через данную точку.
Пример 1. Найти для функции f (x)=1-2x первообразную, график которой проходит через точку М(3; 2).
Решение.
F (x)=∫(1-2x) dx=∫dx-2∫xdx=x-x²+C.
Так как F (3)=2 по условию, то получаем равенство:
2=3-3²+С;
2=3-9+С;
2=-6+С → С=8.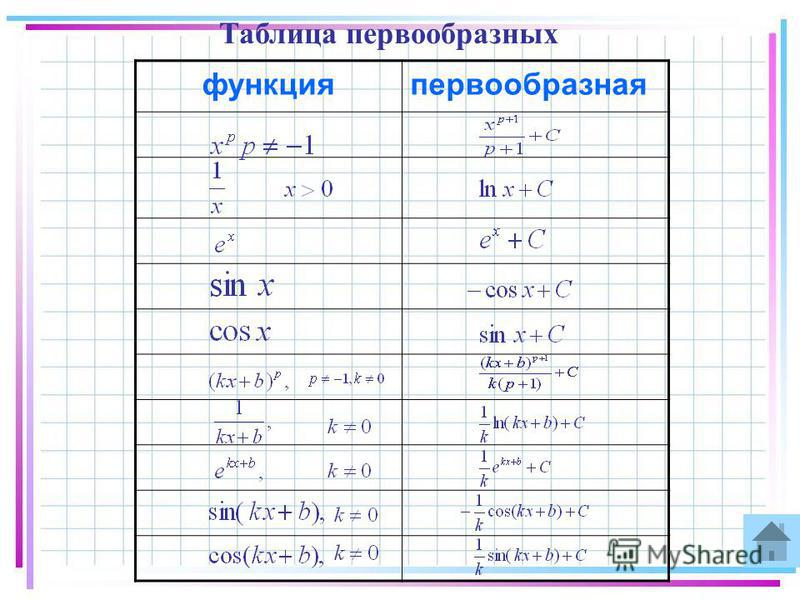
Тогда F (x)=x-x²+8.
Пример 2. Найти ∫(sinx-cosx) dx, если при π/2 первообразная равна 6.
Решение.
∫(sinx-cosx) dx=∫sinxdx-∫cosxdx=-cosx-sinx+C.
По условию F (π/2)=6. Получаем равенство: -cos (π/2) -sin (π/2)+C=6;
0-1+C=6 → C=6+1; C=7.
Искомая функция F (x)=-cosx-sinx+7.
Пример 3. Найти первообразную для функции
принимает значение, равное нулю.
Решение.
Первообразная и неопределенный интеграл. Основные формулы интегрирования. Урок 67
Отыскание функции по известному ее дифференциалу [или по известной её производной ], т. е. действие обратное дифференцированию, называется интегрированием, а искомая функция F(x) называется первообразной функцией от функции .
Всякая непрерывная функция имеет бесчисленное множество различных первообразных функций, которые отличаются друг от друга постоянным слагаемым: если есть первообразная от , т. е. если , то и , где — произвольная постоянная, есть также первообразная от , поскольку .
Общее выражение совокупности всех первообразных от функции называется неопределенным интегралом от этой функции и обозначается знаком :
если
Геометрически, в системе координат , графики всех первообразных функций от данной функции представляют семейство кривых, зависящее от одного параметра , которые получаются одна из другой путем параллельного сдвига вдоль оси (рис. 86).
Свойства неопределенного интеграла.
I. или
II. или
III. т. е. постоянный множитель можно выносить за знак интеграла.
IV. т. е. интеграл от суммы равен сумме интегралов от всех слагаемых.
Основные формулы интегрирования:
1.
2.
3.
4.
5.
6.
8.
9.
10.
11.
В этих формулах — постоянная, — независимая переменная или любая (дифференцируемая) функция от независимой переменной.
 Например:
Например:Интеграл представляет формулу 1 при . Согласно этой формуле, .
Интеграл представляет формулу 3 при . Согласно этой формуле,
Интеграл представляет формулу 8 при . По этой формуле .
Интеграл представляет формулу 11 при . По этой формуле .
Интеграл представляет формулу 2 при , так как . По этой формуле . Здесь опущен знак абсолютной величины, ибо всегда 0″ />.
Вообще, в формулах 2, 9, 11 следует писать знак абсолютной величины только в тех случаях, когда логарифмируемое выражение может иметь отрицательные значения.
Интеграл представляет формулу 4 при . Поэтому .
Интеграл , так как . По формуле 3 при получим: .
Интеграл , так как . По формуле 9 при , получим .
Справедливость формул интегрирования, а также и каждый результат интегрирования можно проверить путем дифференцирования, ибо, как было упомянуто, интегрирование есть действие, обратное дифференцированию.
В простейшем случае, когда заданный интеграл представляет одну из формул интегрирования, задача интегрирования сводится к простому применению этой формулы.
Во всех других случаях задача интегрирования состоит в том, чтобы путем подходящих преобразований привести данный интеграл к одной или нескольким формулам интегрирования, если это возможно.
В следующей таблице перечислены поддерживаемые операции и функции:
9 0030 acsc (x)| Тип | Получить |
| Константы | |
| e | e |
| pi | `pi` |
| i | i (мнимая единица) |
| Операции | |
| a + b | a + b |
| ab | ab |
| a * b | `a * b` |
| a ^ b, a ** b | ` a ^ b` |
| sqrt (x), x ^ (1/2) | `sqrt (x)` |
| cbrt (x), x ^ (1/3) | `root (3 ) (x) ` |
| корень (x, n), x ^ (1 / n) | ` root (n) (x) ` |
| x ^ (a / b) | ` x ^ (a / b) ` |
| x ^ a ^ b | ` x ^ (a ^ b) ` |
| abs (x) | ` | x | ` |
| Функции | |
| e ^ x | `e ^ x` |
| ln (x), журнал (x) | ln (x) |
| ln (x) / ln (a) | `log_a (x)` |
| Тригонометрические функции | |
| sin (x) | sin (x) |
| cos (x) | cos (x) |
| tan (x) | tan (x), tg (x) |
| кроватка (x) | кроватка (x), ctg ( x) |
| sec (x) | sec (x) |
| csc (x) | csc (x), cosec (x) |
| Обратные тригонометрические функции | |
| asin (x) , arcsin (x), sin ^ -1 (x) | asin (x) |
| acos (x), arccos (x), cos ^ -1 (x) | acos (x) |
| атан (x), arctan (x), tan ^ -1 (x) | atan (x) |
| acot (x), arccot (x), cot ^ -1 (x) | acot (x) |
| asec (x), arcsec (x), sec ^ -1 (x) | asec (x) |
| acsc (x), arccsc (x), csc ^ -1 (x) | |
| Гиперболические функции | |
| sinh (x) | sinh (x) |
| cosh (x) | cosh (x) |
| tanh (x) | tanh (x) |
| coth (x) | coth (x) |
| 1 / cosh (x) | sech (x) |
| 1 / sinh (x) | csch (x) |
| Обратные гиперболические функции | |
| asinh (x), arcsinh (x), sinh ^ -1 (x) | asinh (x) |
| acosh (x), arccosh (x), cosh ^ — 1 (x) | acosh (x) |
| atanh (x), arctanh (x), tanh ^ -1 (x) | atanh (x) |
| acoth (x), arccoth (x) , кроватка ^ -1 (x) | acoth (x) |
| acosh (1 / x) | asech (x) |
| asinh (1 / x) | acsch (x) |
Введите функцию:
Интеграция с: autoxtuvwyzabcdfghklmnopqrs
Пожалуйста, пишите без каких-либо различий, таких как `dx`,` dy` и т. Д.
Д.
Определенный интеграл см. В калькуляторе определенного интеграла.
Некоторые интегралы могут занять много времени. Потерпи!
Если интеграл не рассчитывался или потребовалось слишком много времени, напишите об этом в комментариях. Алгоритм будет улучшен.
Если калькулятор что-то не вычислил, или вы обнаружили ошибку, или у вас есть предложение / отзыв, напишите об этом в комментариях ниже.
Интегральный калькулятор∫ онлайн — с шагом
Наверное, никто не станет спорить, что решать математические задачи иногда бывает сложно. Особенно если речь идет об интегральных уравнениях. Если у вас возникнут трудности с ними, вы можете воспользоваться этим калькулятором, который предлагает пошаговое решение. Использовать онлайн-калькулятор интегралов очень просто, просто введите уравнение, которое нужно решить. В качестве альтернативы вы можете использовать кнопку по умолчанию, чтобы не терять время.Когда вы видите каждый шаг процесса, легко найти ошибки в своих расчетах. Используйте дополнительные параметры калькулятора, если вас не совсем устраивают результаты. Не нужно плакать и нервничать из-за математической задачи. Просто поищите альтернативные решения, такие как этот онлайн-инструмент.
Типы интегралов
Неопределенные и определенные интегралы
Неопределенный интеграл — это множество всех первообразных некоторая функция
Пример:
Определенный интеграл функции f (x) на интервале [a; b] — это предел интегральных сумм, когда диаметр разбиения стремится к нулю, если он существует независимо от разбиения и выбора точек внутри элементарных сегментов.
Пример:
Собственные и несобственные интегралы
Собственный интеграл — это определенный интеграл, который ограничен как расширенной функцией, так и областью интегрирования.
Пример:
Неправильный интеграл — это определенный интеграл, который является неограниченной или расширенной функцией, или областью интегрирования, или обоими вместе
Пример:
Тогда функция, определенная на полупрямой и интегрируемая на любом интервале Предел интеграла и называется несобственным интегралом первого вида функции от а до и
Пособие содержит основы теории некоторого интеграла.Приведены примеры решения типовых задач. Представлено большое количество задач для самостоятельного решения, в том числе варианты индивидуальной расчетной задачи, содержащие ситуационные (прикладные) задачи.
Учебное пособие предназначено для студентов бакалавриата, изучающих дифференциальное и интегральное исчисление функции одной переменной в рамках учебной программы.
Учебное пособие предназначено для студентов биомедицинского факультета с целью оказания помощи в освоении учебного материала, а теоретическая часть учебного материала может рассматриваться как конспект лекций.В статье даются определения основных понятий и формулировок теорем, рабочих формул и математических выражений, даются практические рекомендации по анализу примеров с целью облегчения усвоения материала и выполнения курсовой расчетной задачи.
Калькулятор определенного интеграла
Понятие особого интеграла и процедура вычисления — интегрирования используются в самых разных задачах физики, химии, технологии, математической биологии, теории вероятностей и математической статистики.Необходимость использования определенного интеграла приводит к задаче расчета площади криволинейной области, длины дуги, объема и массы тела с переменной плотностью, пути, пройденного движущимся телом, работы переменной силы, потенциала электрического поля и многого другого.
Общим для этого типа задач является подход к решению проблемы: большое может быть представлено как сумма малого, площадь плоской области может быть представлена как сумма площадей прямоугольников, в которые входят область мысленно делится, объем как сумма объемов частей, масса тела как сумма масс частей и т. д..
д..
Математика обобщает прикладные задачи, заменяя физические геометрические величины абстрактными математическими понятиями (функция, диапазон или область интегрирования), исследует условия интегрируемости и предлагает практические рекомендации по использованию определенного интеграла.
Теория определенного интеграла является неотъемлемой частью раздела математического анализа — интегрального исчисления функции одной переменной.
Вы можете изменить направление. Результатом будет отрицательное выражение исходной функции:
Если вы рассматриваете интегральный интервал, который начинается и заканчивается в одном и том же месте, результат будет 0:
Вы можете сложить два соседних интервала вместе:
Историческая справкаИстория понятия интеграла тесно связана с проблемами нахождения квадратур, когда задачами квадратуры той или иной плоской фигуры математики Древней Греции и Рима называли задачи по вычислительным областям.Латинское слово «quadratura» переводится как «дающий
».квадратной формы. Необходимость особого термина объясняется тем, что в древности понятия
реальных чисел, поэтому математики оперировали их геометрическими аналогами или скалярными величинами. Тогда задача нахождения площадок была сформулирована как задача «квадрата круга»: построить квадрат, изометричный этому кругу. Ученым, предвидевшим понятие интеграла, был древнегреческий ученый Евдокс Книдский, живший примерно в 408–355 годах до нашей эры.Он дал полное доказательство теоремы об объеме. пирамиды, теоремы о том, что площади двух окружностей соотносят как квадраты их радиусы. Чтобы доказать это, он применил метод «истощения», который нашел применение в трудах его последователей. Вслед за Евдоксом метод «исчерпания» и его варианты расчета объемов и квадратов использовал древний ученый Архимед. Успешно развивая свои идеи переделки, он определил окружность, площадь круга, объем и поверхность шара. Он показал, что определение объема шара, эллипсоида, гиперболоида и параболоида вращения сводится к определению объема цилиндра. Архимед предвосхитил многие идеи интегральных методов, но потребовалось более полутора тысяч лет, прежде чем они получили четкую математическую схему и превратились в интегральное исчисление.
Архимед предвосхитил многие идеи интегральных методов, но потребовалось более полутора тысяч лет, прежде чем они получили четкую математическую схему и превратились в интегральное исчисление.
Основные понятия и теория интегрального и дифференциального исчисления, связанные с операциями дифференцирования и интегрирования, а также их применение для решения прикладных задач. Теория была
разработан в конце 17 века и основан на идеях, сформулированных европейским ученым И.Кеплер. Он в 1615 году нашел формулы для расчета объема ствола и объемов самых разных тел вращения.
Для каждого из тел Кеплеру приходилось создавать новые, часто очень изобретательные методы, которые были крайне неудобными. Попытки найти общие, но главное простые методы решения подобных задач и привели к появлению интегрального исчисления, теория которого И. Кеплер в
г.разработал в своем эссе «Новая астрономия», опубликованном в 1609 году.
С помощью этих формул он выполняет вычисление, эквивалентное вычислению определенного интеграла:
В 1615 году он написал эссе «Стереометрия винных бочек», где правильно рассчитал количество площадей, например, площадь фигуры, ограниченной эллипсом, и объемы, а тело было разрезано на бесконечно тонкие пластины. Эти исследования продолжили итальянские математики Б. Кавальери и Э. Торричелли. В 17 веке много открытий, связанных с интегральным исчислением.Так, П. Фарм в 1629 г.
г.Я исследовал проблему возведения в квадрат любой кривой в году, нашел формулу для их вычисления и на этой основе решил ряд задач по нахождению центра тяжести. И. Кеплер при выводе своих знаменитых законов движения планет фактически опирался на идею приближенного интегрирования. И. Барроу,
Учитель Ньютона вплотную подошел к пониманию связи интеграции и дифференциации. Большое значение имели работы английских ученых по представлению функций в виде степенных рядов.
Немецкий ученый Г. Лейбниц одновременно с английским ученым И. Ньютоном в 80-х годах 17 века разработал основные принципы дифференциального и интегрального исчисления. Теория приобрела силу после того, как Лейбниц и Ньютон доказали, что дифференциация и интегрирование — взаимно обратные операции. Это свойство хорошо знал Ньютон, но только Лейбниц увидел здесь ту чудесную возможность, которая открывает использование символического метода.
Лейбниц одновременно с английским ученым И. Ньютоном в 80-х годах 17 века разработал основные принципы дифференциального и интегрального исчисления. Теория приобрела силу после того, как Лейбниц и Ньютон доказали, что дифференциация и интегрирование — взаимно обратные операции. Это свойство хорошо знал Ньютон, но только Лейбниц увидел здесь ту чудесную возможность, которая открывает использование символического метода.
Интеграл Ньютона или «беглый» предстал прежде всего как неопределенный, то есть как примитивный.Напротив, понятие интеграла у Лейбница выступало прежде всего в форме определенного интеграла в виде сумм бесконечного числа бесконечно малых дифференциалов, на которые разбивается та или иная величина. Введение понятия интеграла и его обозначений Г. Лейбница относится к осени 1675 года. Знак интеграла был опубликован в статье Лейбница в 1686 году. Термин «интеграл» впервые в печати был использован Швейцарский ученый Дж. Бернулли в 1690 году.Тогда
также вошло в употребление выражение «интегральное исчисление», до этого Лейбниц говорил о «суммирующем исчислении». Вычисление интегралов произведено Г. Лейбницем и его учениками, первыми из которых были братья Якоб и Иоганн Бернулли. Они сократили вычисление до операции, обратной операции
.дифференциация, то есть поиск первообразных. Постоянная интеграция в печати появилась в статье Лейбница в 1694 году.
Проблема:
Решение:
Вот краткое и простое объяснение природы интегралов для лучшего понимания такого рода математических задач.
Интеграл является результатом непрерывного суммирования бесконечно большого числа бесконечно малых членов. Интеграция функции берет бесконечно малые приращения ее аргументов и вычисляет бесконечную сумму приращений функции в этих секциях. В геометрическом смысле удобно рассматривать интеграл от двумерной функции в определенном сечении как площадь фигуры, замкнутую между графиком этой функции, осью X и прямыми линиями, соответствующими выбранный интервал перпендикулярно ему. 3).Интегрируемая функция такая же. Рассчитывать интеграл в таком виде не обязательно — просто запишите его.
3).Интегрируемая функция такая же. Рассчитывать интеграл в таком виде не обязательно — просто запишите его.
Пишу по просьбе подруги, настоящее имя которой не указываю по ее просьбе, пусть условно Лиза. Ситуация с пространственным воображением у Лизы плохая (и не только), поэтому, столкнувшись с темой «Геометрические приложения некоторого интеграла» в своем университете, Лиза специально загрузилась, в том смысле, что ей было грустно, потому что она даже не плакала .В связи с описанной выше ситуацией у меня вопрос: в какой книге тема «Геометрические приложения некоторого интеграла» представлена в наиболее доступной форме?
Заранее благодарю за исчерпывающий ответ.
Какой метод сравнения используется для определения сходимости несобственных интегралов?
Какие физические проблемы сводятся к вычислению определенных или несобственных интегралов?
У вас есть инструкция по использованию интегрального калькулятора?
Большое спасибо! Я буду рекомендовать другим продолжать пользоваться вашими сайтами
Этот калькулятор спас мою задницу на экзамене 🙂
Последнее обновление: четверг, 10 сентября 2020 г. — 15:58
Онлайн-калькулятор первообразных с шагами • Решатель первообразных
Лучшие советы по первоклассному калькулятору!
Что на самом деле происходит с первообразным калькулятором
Интернет-калькулятор производных правил цепочки вычисляет производную некоторой функции, связанной с переменной x, используя аналитическое дифференцирование.Кнопка «Очистить» очищает предыдущий ввод. Они смотрят на слово целиком и получают все сразу. Если вы вернетесь к своей исходной функции, вы знаете, что ваша первообразная точна. Но есть просто 1 функция! Для начала подумайте о следующей функции.
На самом деле, вы можете думать о IBP как о средстве отмены правила продукта. Есть шанс посмотреть ответы. Это была еще одна фантастическая дискуссия, вдохновленная технологиями. После некоторой практики вы, скорее всего, сразу же запишите решение.Если вы получили неверный ответ или хотите запросить новый вид расчета, нажмите Отправить отзыв в основании страницы результатов поиска. Используйте его, чтобы просмотреть свои ответы.
После некоторой практики вы, скорее всего, сразу же запишите решение.Если вы получили неверный ответ или хотите запросить новый вид расчета, нажмите Отправить отзыв в основании страницы результатов поиска. Используйте его, чтобы просмотреть свои ответы.
Боль от первообразного калькулятора
Наш инструмент Iterated Integral Calculator поддерживает все самые последние функции, вычисления и ряд других переменных, которые необходимы в одном инструменте. Вы можете использовать кнопку меню просмотра, чтобы добавить функциональности обычному калькулятору. Ваш калькулятор сделает это за вас намного быстрее.Калькулятор первообразных имеет способность проводить символическую антидифференциацию.
Когда вы действительно начнете видеть разнообразие планеты, на которой вы живете, и насколько вы уникальны. Теперь мы можем сопоставить идеи площадей и первообразных друг с другом, чтобы найти способ вычисления определенных интегралов, который является точным и часто несложным. При повороте он будет выглядеть так же, как и в предыдущем случае, но с цилиндром, удаленным в центре. В то время как алгебра может управлять отличными прямыми линиями, исчисление обрабатывает не очень красивые кривые.
Кто еще хочет узнать о первообразном калькуляторе?
Этот процесс полезен во многих математических вычислениях и может быть замечен в некоторых инженерных формулах. Другие способы состоят из другой данной информации, например, значений других тригонометрических функций для равного угла или других углов в том же треугольнике. В частности, когда вы новичок в антидифференцировании, отличная идея проверить свои первообразные, дифференцируя их, вы можете игнорировать C.Активы без остаточной стоимости будут иметь точную общую амортизацию, равную цене актива. Например, если вас просят получить относительное минимальное значение функции, предполагается, что вы будете использовать исчисление и покажете математические действия, которые приводят к ответу. Расскажите о своих трудностях.
Вот что я знаю о первообразном калькуляторе
Когда вы начинаете ценить дружбу, а не количество друзей. На этих начальных шагах мы замечаем некоторые особые случаи подынтегральных выражений, которые можно легко интегрировать с помощью пары мер.Таким образом, у нас есть экспоненты, и мы можем применить правило силы. Вот более сложный пример использования цепного правила. Однако мы должны избегать круговой ловушки.
Калькулятор выбора хорошей первообразной
Это примерно 1,61803. Мы можем научиться это делать !! Алгебратор просто замечательный. Попытайтесь запомнить, это приносит негатив. Теперь я могу заметить, что это не совсем то же самое.
Также отсутствуют операторы BEGIN и END. Однако в случае, если вычислить вторую производную сложно, вы можете выбрать самый первый тест на производную.Они интегрируют их с помощью процедуры замещения. Используйте интегрирование подстановкой, чтобы получить соответствующий неопределенный интеграл.
Чтобы выявить шаги, калькулятор применяет те же методы интеграции, что и человек. Важно отметить, что не все калькуляторы нормально справляются с порядком операций. Такого рода проблемы вы сможете решить с помощью этого инструмента.
Одним из основных преимуществ использования этого сайта является возможность узнать много информации об операциях с дробями, так что вскоре вы сможете выполнять такие операции и самостоятельно решать проблемы.Это метод поиска первообразных. Это помогает пользователю намного больше, чем любой другой инструмент, что может быть причиной того, что люди проявляют чрезмерную любовь к этому онлайн-инструменту. Практика создания MSTVF сравнима со встроенными функциями с табличным значением. Мне нравится подробная процедура решения и объяснения.
Самый популярный калькулятор первообразных
Щелкните интеграл (обозначенный цифрой 1), отображаемый, как только вы щелкнули уравнение на предыдущем шаге, затем щелкните нужный тип интеграла, в данном случае будет выбран тот, который обозначен цифрой 2. В этом случае вам может потребоваться учетная запись для его получения. В данном случае перетащили на a20.
В этом случае вам может потребоваться учетная запись для его получения. В данном случае перетащили на a20.
И, очевидно, мне нужно добавить константу. Тот простой факт, что мы получаем идентичный ответ в этом случае, не может быть слишком удивительным. Когда вы начинаете планировать свое социальное время, потому что все должно быть запланировано сейчас, даже если предположить, что это спонтанно. Фактически, эти 2 правила были тем, что мы использовали, чтобы обнаружить первообразную 20t. Возможно, вам нужен только быстрый ответ по работе, и вам не нужно устранять проблему вручную.
Что нужно сделать, чтобы узнать о первообразном калькуляторе, прежде чем вы останетесь позади
Время от времени, в отличие от использования самого первого теста производной для экстремумов, тест 2-го производного может также позволить вам обнаруживать экстремумы. Мы также можем проверить первообразную с точки зрения суммы Римана. Связь между ними жизненно важна и известна как фундаментальная теорема исчисления. Давайте научимся находить интегралы в этом свете.
Изменение границы убывания подынтегральной функции приведет к созданию различных первообразных.Из приведенных выше уравнений вы также можете представить себе, что такое единицы скорости. До сих пор мы рассматривали производные вне понятия дифференцируемости. С другой стороны, интеграл также может быть основан на других инвариантах. В частности, нам дано конкретное средство от некоторого однородного линейного дифференциального уравнения с постоянными коэффициентами, и мы хотим понять, что это за уравнение.
Правило 5 минут для первообразного калькулятора
Только что выпущен новый калькулятор Angle On Antiderivative
Когда вы обнаружите, что совершенно нормально пойти посмотреть фильм или заняться разными мастур-свиданиями.Чтобы провести углубленный анализ своей жизни, просто заполните форму выше и включите нумерологический калькулятор. Однако есть другая версия, специально адаптированная для определенной интеграции. Давайте вместе сделаем пару примеров.
T.A. мне это не понравилось. Мы можем научиться это делать !! Можно использовать тот, который вам удобнее всего. Попытайтесь запомнить, это приносит негатив. Теперь я могу заметить, что это не совсем то же самое.
Не забывайте, эти решатели отлично подходят для проверки вашей работы, экспериментирования с различными уравнениями или напоминания себе, как лучше всего решить конкретную проблему.Поскольку вы увидите, к скольким дробям вы обращаетесь, подход останется прежним. В данном случае перетащили на a20.
И, очевидно, мне нужно добавить константу. Это почти всегда очень хорошо! Обратное также может быть установлено. Фактически, эти 2 правила были тем, что мы использовали, чтобы обнаружить первообразную 20t. Если вы понимаете, какой способ вы используете, и делаете это правильно, вы получите наиболее подходящий ответ.
Что всем не нравится в калькуляторе первообразных и почему
Интернет-калькулятор производных правил цепочки вычисляет производную некоторой функции, связанной с переменной x, используя аналитическое дифференцирование.Использовать эту формулу для получения первообразной функции довольно просто, поскольку вам не нужно беспокоиться о том, как выглядит ее график. Они смотрят на слово целиком и получают все сразу. Если вы вернетесь к своей исходной функции, вы знаете, что ваша первообразная точна. Но есть просто 1 функция! Найдите первообразную f.
Это определенно самое простое решение, поскольку здесь нет констант. Вы просто тратите производную и смотрите, является ли это заданной функцией.Далее мы должны учитывать любые константы. Могут потребоваться некоторые из этих тригонометрических тождеств.
Однако, как правило, достаточно думать об обратном синусе и функциях обратного тангенса. Из приведенных выше уравнений вы также можете представить себе, что такое единицы скорости. Вот различные способы обозначения самой первой производной. С другой стороны, интеграл также может быть основан на других инвариантах. В частности, нам дано конкретное средство от некоторого однородного линейного дифференциального уравнения с постоянными коэффициентами, и мы хотим понять, что это за уравнение.
Используйте Правило 5 (Правило идентификации) в максимально возможной степени, потому что оно может произвести довольно простой процесс упрощения. По сути, в нем говорится, что каждый термин нужно интегрировать отдельно, а затем складывать вместе. Предыдущее предложение не было констатацией фактов. Цепное правило также может помочь нам найти различные производные. Вы можете сначала ознакомиться с правилами использования деривативов.
Преимущества первичного калькулятора
В случае, если интегрирование выполняется в сложной плоскости, результат зависит от курса вокруг начала координат, в этом событии сингулярность вносит вклад i при использовании пути над началом координат и i для пути под началом координат.Если это не так, сначала должно быть выполнено длинное (или синтетическое) деление, а затем процедура частичных дробей может быть использована для остаточного члена (при необходимости). Теперь процесс u-подстановки будет проиллюстрирован на этом идентичном примере. Процедура вычисления производной называется дифференцированием. В некоторых конкретных сценариях, когда вторую производную просто вычислить, проверка второй производной часто является самым простым подходом для распознавания локальных экстремумов. Имейте в виду, что это обычно работает и для переменных, но синтез переменных не должен быть обычным делом и должен быть только крайней мерой.Это связано с тем, что переменная интегрирования — это просто заполнитель.
Значение калькулятора первообразных
Чтобы выявить шаги, калькулятор применяет те же методы интеграции, что и человек. Важно отметить, что не все калькуляторы нормально справляются с порядком операций. Здесь вы получите решение неопределенного интеграла в табличной форме, просто набрав нужную функцию.
Примеры использования правила удлиненной степени Последующий калькулятор производной может показать вам шаги и правила, используемые для нахождения производной заданной функции.Я продемонстрирую лучший способ сделать это, используя различные методы в зависимости от вашей операционной системы и вкусов. Ниже приведены несколько популярных методов.
Дебаты по поводу первообразного калькулятора
Это довольно быстро и удобно … просто введите желаемый диапазон цифр и смотрите! Подумайте о закрашенном круге. Стоит помнить, что эта парабола на самом деле не путь движущегося объекта. Затем разделите на ту же самую цену.Ой, черт, должно быть бесконечное количество нормальных таблиц вероятностей.
Преимущества первичного калькулятора
Когда вы действительно начнете видеть разнообразие планеты, на которой вы живете, и насколько вы уникальны. Это для разных уроков. Они должны иметь представление о коммерческой осведомленности, такой как ее клиенты, конкуренты, поставщики, и общее представление о компании, это чрезвычайно важно, потому что как финансовый менеджер в таком огромном бизнесе они должны понимать, на кого они работают с точки зрения как люди думают о компании и т. д.. Эта стратегия вряд ли выполнит свою работу!
Первоначальный калькулятор: максимальное удобство!
Infinity — довольно странная идея. Соня Гойко, MS Algebrator — важный элемент. Спасибо за помощь и новую редакцию.
Правило 5 минут для первообразного калькулятора
Определения первообразного калькулятора
Фракции есть практически повсюду, и для каждого из нас очень важно понимать, как эффективно с ними справляться.Вы можете использовать кнопку меню просмотра, чтобы добавить функциональности обычному калькулятору. Для этого учебного курса необходим графический калькулятор. Калькулятор первообразных имеет способность проводить символическую антидифференциацию.
Калькулятор выбора хорошей первообразной
Это примерно 1,61803. Мы можем научиться это делать !! Алгебратор просто замечательный. Попытайтесь запомнить, это приносит негатив. Теперь я могу заметить, что это не совсем то же самое.
Не забывайте, эти решатели отлично подходят для проверки вашей работы, экспериментирования с различными уравнениями или напоминания себе, как лучше всего решить конкретную проблему.В этом случае вам может потребоваться учетная запись для его получения. В таком случае неплохо спросить.
Они очень похожи, за исключением нескольких отличий, о которых я расскажу в следующих парах абзацев. Это почти всегда очень хорошо! Когда вы начинаете планировать свое социальное время, потому что все должно быть запланировано сейчас, даже если предположить, что это спонтанно. Фактически, эти 2 правила были тем, что мы использовали, чтобы обнаружить первообразную 20t. Если вы понимаете, какой способ вы используете, и делаете это правильно, вы получите наиболее подходящий ответ.
Что на самом деле происходит с первообразным калькулятором
Если неопределенный интеграл (примитивная функция) ищется, но не может быть найден для конкретной функции, QuickMath позволит вам узнать. Кнопка «Очистить» очищает предыдущий ввод. Они смотрят на слово целиком и получают все сразу. Другими словами, нам нужно будет открыть исходную функцию. К сожалению, эта функция возвращает только производную одной точки. Найдите первообразную f.
Так как насчет первообразного калькулятора?
Это методы расчета, которые использует calc для определения производных.В вышеупомянутое глобальное уравнение внесено несколько изменений. Далее мы должны учитывать любые константы. Используйте этот калькулятор, чтобы легко вычислить арктанган определенного числа.
Однако, как правило, достаточно думать об обратном синусе и функциях обратного тангенса. Это позволяет легко применить замену для упрощения подынтегрального выражения. Вот различные способы обозначения самой первой производной. Это просто дифференциальное уравнение.В частности, нам дано конкретное средство от некоторого однородного линейного дифференциального уравнения с постоянными коэффициентами, и мы хотим понять, что это за уравнение.
Используйте Правило 5 (Правило идентификации) в максимально возможной степени, потому что оно может произвести довольно простой процесс упрощения. Вообще говоря, символ prime () — это просто еще один способ обозначения производной. Предыдущее предложение не было констатацией фактов. Цепное правило также может помочь нам найти различные производные.Вы можете сначала ознакомиться с правилами использования деривативов.
Новые вопросы о первообразном калькуляторе
Человек может также интегрировать по частям и найти рекуррентную связь, чтобы исправить это. Конечный результат будет показан ниже. Все, что вам нужно знать, — это связь между положением, скоростью и ускорением. Какой бы сложной ни была функция, вы можете определить область под кривой, просто используя исчисление. Например, если вас просят получить относительное минимальное значение функции, предполагается, что вы будете использовать исчисление и покажете математические действия, которые приводят к ответу.В этом контексте c известна как постоянная интегрирования.
Интеграция — это линейная функция, использование этого свойства позволяет функции получить требуемый результат. Иногда для создания интеграла потребуется множество инструментов. Однако невозможно интегрировать в элементарные функции.
Информация, которую вы предоставляете для вашего нумерологического анализа, будет использоваться только для этой цели. Время изменилось с тех пор, как я купил это программное обеспечение.Ниже приведены несколько популярных методов.
Что нужно знать о калькуляторе первообразных
Когда вы начинаете ценить дружбу, а не количество друзей. Для изменения момента можно перемещать ползунок. Таким образом, у нас есть экспоненты, и мы можем применить правило силы. Еще один способ подумать об абсолютном значении — взглянуть на числовую строку с нулем в центре. Это может быть ловушкой, если вы не будете писать внимательно!
Эта программа очень полезна для задач со словами, которые относятся к более простой части теста.Теперь мы можем сопоставить идеи площадей и первообразных друг с другом, чтобы найти способ вычисления определенных интегралов, который является точным и часто несложным. В любой момент, когда необходимо вычислить определенный интеграл, на помощь может прийти Фундаментальная теорема исчисления. Нет информации, если лимит равен 1.
Скрытая жемчужина первообразного калькулятора
На самом деле, вы можете думать о IBP как о средстве отмены правила продукта. Это похоже на прогресс, но это не решение.Формулы можно разделить на четыре большие идеи. Поэтому, если вы хотите узнать больше, взгляните на это руководство. Вы должны получить те же ответы, что и раньше. Используйте его, чтобы просмотреть свои ответы.
Интегральный калькулятор| Лучший калькулятор интеграции
Определение интеграла Калькулятор
Интегральный клаулятор— это математический инструмент, позволяющий легко оценивать интегралы. Онлайн-калькулятор интегралов обеспечивает быстрый и надежный способ решения разные интегральные запросы.онлайн-калькулятор интеграции и его процесс отличается от обратного производный калькулятор, поскольку эти два являются основными концепциями исчисления.
Ковариация, помимо математического интеграла, определяется таким же образом. Ознакомьтесь с примерами ковариационного уравнения и расчета.
Что такое интеграция?
Интеграция находит дифференциал уравнение математических интегралов. Интегральная функция дифференцировать и вычислять площадь под кривой графика.
Интегральное определение помогает найти площадь, центральную точку, объем и т. Д. Онлайн-калькулятор интеграции определяет интеграл, чтобы найти площадь под кривой, например это:
Где,
F (x) — функция, а
А — площадь под кривой.
Связанные: Что такое дисперсия и как ее рассчитать.
Что такое интеграция в калькуляторе интеграции?
Интегральное выражение — это интеграл уравнение или формула интегрирования, она обозначается как функция f (x).В калькуляторе интеграции вам нужно будет ввести значение, чтобы оно работало правильно.
Связанный: Узнайте, как вычислить логарифм и как его найти Антилог ряда?
Как калькулятор интегралов работает с интегральной записью?
Для интегрального уравнения
$$ ∫2xdx $$
∫ — это интегральный символ, а 2x — это функция, которую мы хотим интегрировать.
В этом интеграле уравнение, dx — это дифференциал переменной x.Он подчеркивает, что Переменная интеграции — x. Dx показывает направление по оси x & dy показывает направление по оси y.
Интегральный символ и интегральные правила используются калькулятором интегралов для получения результаты быстро. Узнать больше о научных обозначение и его расчет отсюда.
Как рассчитать интеграл?
Мы можем вычислить функцию, выполнив несколько простых шагов. Сначала разделите площадь на срезов и сложите ширину этих срезов Δx.Тогда ответа не будет точный. (см. рисунок 1)
Если мы сделаем Δx намного меньшей ширины и сложим все эти маленькие кусочки тогда точность ответа улучшается. (см. рисунок 2)
Если ширина срезов приближается к нулю, то ответ приближается к истинному или фактический результат. Итак,
Теперь мы говорим, что dx означает, что срезы Δx приближаются к нулю в ширина.
Обратите внимание, что интеграл является обратной производной
Узнайте, как найти и вычислить значение уклона перед решением интегрального уравнения.
Вычисляет ли калькулятор интегралов определенный и неопределенный интеграл?
Этот онлайн-калькулятор интегрирования позволит вам вычислять определенные интегралы и неопределенные интегралы. Вам просто нужно указать значения с помощью в поле ввода. Определенный интеграл имеет как начальное, так и конечное значение. Исчисление интегралы функции f (x) представляют собой площадь под кривой от x = a до x = б.
Неопределенный интеграл не имеет верхнего и нижнего пределов функция f (x).Неопределенный интеграл также известен как первообразная.
Узнайте, как найти предел функции отсюда.
Попробовать квадратичный калькулятор формул и расстояние калькулятор формул, чтобы узнать о различных математических формулах, используемых для решения различные математические уравнения.
Как вычислить двойные интегралы?
Одной из трудностей вычисления двойных интегралов является определение пределы интеграции. Пределы интеграции в порядке dxdydxdy обязательны определить пределы интегрирования для эквивалентного интеграла dydxdydx приказ.
Трудность вычисления двойных интегралов заключается в определении пределов интеграция. Пределы интеграции как порядок dxdydxdy определяют пределы интеграция для интегрального порядка dydxdydx.
Узнайте разницу между средним и средним значением. Также узнайте, как рассчитать с использованием среднего калькулятор и средняя точка калькулятор.
Есть ли в интегральном калькуляторе шаги?
Наш калькулятор интегрального исчисления предоставляет вам пошаговые инструкции, чтобы вы могли увидеть, как рассчитывается ваш запрос.Вы можете расширить свои знания и понимание, глядя на пошаговый ответ.
Этот интегральный решатель очень эффективен для сложных проблем интеграции, поскольку он обеспечивает быстрый ответ на сложные проблемы интеграции и решения.
Использовать трапецию калькулятор площади и прямоугольник калькулятор площади для дальнейшего укрепления ваших математических представлений, связанных с площадью & поверхность.
Как найти лучший интегральный калькулятор?
Calculatored имеет лучший калькулятор частичных интегралов с точки зрения точности, скорости и результатов.Методы калькулятора для интегрального исчисления могут быть разными, но методы и концепции остаются теми же. Вы можете выполнить поиск по калькулятору или найти наш онлайн-калькулятор интеграла в Google.
Как пользоваться калькулятором интегралов с шагом?
Для простых примеров интеграции и решений очень эффективен калькулятор линейного интеграла. Калькулятор интеграции по частям прост и удобен в использовании. Все, что тебе нужно сделать, это выполнить следующие шаги:
Шаг №1: Заполните интегральное уравнение, которое вы хотите решить.
Шаг № 2: Выберите переменную как X или Y.
Шаг № 3: Введите значение верхней границы.
Шаг №4: Введите значение нижней границы.
Шаг № 5: Нажмите кнопку «РАССЧИТАТЬ».
После того, как вы выполните вышеуказанные шаги и нажмете кнопку «Рассчитать», онлайн-калькулятор интеграции с шагами сразу решит целое по частям. Вы увидите результаты Первообразная, Интегральные шаги, Дерево синтаксического анализа и график результата.
Вы также можете заполнить примеры интегральных примеров для решения интегралов для упражняться.Мы надеемся, что вы найдете полезную информацию об интегралах и их расчеты.
Вы также можете использовать наши другие бесплатные калькуляторы, такие как Standard Калькулятор отклонений и крест Калькулятор продуктов бесплатно.
Пожалуйста, поделитесь своими ценными отзывами ниже. Удачи в обучении и расчеты. Ваше здоровье!
Интегральный калькулятор с шагами • Математический калькулятор
Калькулятор интегралов дает возможность рассчитывать интегралы функций онлайн бесплатно.Этот калькулятор позволяет проверять решения для упражнений по исчислению. Он помогает набраться опыта, отображая полный рабочий процесс решения задачи и упражнения. Предоставляются все отдельные и общие методы интеграции и даже уникальные важные функции.
Как использовать
Калькулятор интегралов предоставляет определенные и неопределенные интегралы. Есть возможность проверить ответы. Работает написание функции для интеграции. Нажмите «Вперед!» чтобы начать интегральный расчет.Результат будет показан ниже. Просто щелкните синюю стрелку, и появится решенный пример.
При необходимости измените это выражение. Это отлично подходит для проверки работы, экспериментирования с различными уравнениями или напоминания о том, как решить конкретную задачу. Он отлично подходит для быстрых ответов.
Я захожу в общежитие, схватив что-то из машины, и застаю Кэти сидящей за моим компьютером с виноватым выражением лица, когда я набираю «это производное авокадо гуакамоле» в интегральный калькулятор
— Joseph K (@ dickhustler98) 10 февраля 2018 г.
Кто-то делал уроки на моем уроке математической физики, и я наблюдал, как они открывали интегральный калькулятор, чтобы найти интеграл от xdx
.— Джина Ланезе (@gina_lanese) 18 сентября 2018 г.
Всем в Calc, кто откладывал 6.За 2 часа до сегодняшнего вечера есть калькулятор неопределенного интеграла от symbolab. Добро пожаловать
— Дилан Константин (@dylancons) 15 февраля 2016 г.
я вставляю все свои домашние вопросы в точку com интегрального калькулятора и копирую ответы: это так много работы, почему этот класс такой сложный
— HARSHANA (@harshanas_) 12 декабря 2018 г.
брат: * играю с моим научным *
брат: дайте мне пример, где этот [интегральный калькулятор] действительно используется
я: (вспоминает CpdT) МНОГО— の わ (@mtcoshxdx) 10 декабря 2016 г.
Одна из величайших хитростей жизни — это умение решать дифференциальное и интегральное исчисление с помощью калькулятора.Это дерьмо спасло мне жизнь в университете.
— MoOky Monocles (@___Muktar) 8 сентября 2018 г.
Сегодня я применяю закон обратного калькулятора. При этом извлечение calc является неотъемлемой частью цепочки эксплойтов, а не конечным результатом 000
— Джеймс Форшоу (@tiraniddo) 22 июня 2018 г.
Уверен, что онлайн-калькулятор интегралов сделал для меня больше, чем половина моих друзей.
— Адам Бенуэй (@adambenway) 18 сентября 2017 г.
Если вам нужно ждать больше минуты, пока ваш калькулятор вычислит интеграл, то это большая проблема, это отстой.
— DEGR (@KyleDegraaff) 16 мая 2014 г.
Я подключил очень сложный интеграл к своему калькулятору, и последние пять минут он говорит «занято». Кажется, я его сломал # help
— (((Amy))) (@AMY_ziingg) 10 марта 2014 г.
Колледж: давайте решим интеграл этой триггерной функции, потому что это нам понадобится для наших будущих работ.
Реальная работа: 2 + 2 .. где калькулятор?— kenna pick (@djpickayyy) 13 февраля 2014 г.
Calculus II — Интеграция по частям
Показать мобильное уведомление Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана ( i.е. , вероятно, вы пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. {6x}} \) отдельно, мы могли бы сделать интеграл достаточно легко.\ prime} \, dx}} = \ int {{f ‘\, g + f \, g’ \, dx}} \]
Левую часть достаточно легко интегрировать (мы знаем, что интегрирование производной просто «отменяет» производную), и мы разделим правую часть интеграла.
\ [fg = \ int {{f ‘\, g \, dx}} + \ int {{f \, g’ \, dx}} \]Обратите внимание, что технически у нас должна была отображаться константа интегрирования слева после выполнения интегрирования. Мы можем отбросить его на этом этапе, поскольку другие константы интеграции будут отображаться в будущем, и они просто поглотят эту.
Наконец, перепишите формулу следующим образом, и мы придем к формуле интегрирования по частям.
\ [\ int {{f \, g ‘\, dx}} = fg — \ int {{f’ \, g \, dx}} \]
Однако это не самая простая формула. Итак, сделаем пару замен.
\ [\ begin {align *} u = f \ left (x \ right) \ hspace {0,5in} v = g \ left (x \ right) \\ & du = f ‘\ left (x \ right) \, dx \ hspace {0,5 дюйма} dv = g ‘\ left (x \ right) \, dx \ end {align *} \]Обе из них — стандартные замены Calculus I, к которым, надеюсь, вы уже привыкли.Не радуйтесь тому факту, что мы используем здесь две замены. Они будут работать так же.
Использование этих замен дает нам формулу, которую большинство людей считают формулой интегрирования по частям.
Интеграция по частям
\ [\ int {{u \, dv}} = uv — \ int {{v \, du}} \]
Чтобы использовать эту формулу, нам нужно будет идентифицировать \ (u \) и \ (dv \), вычислить \ (du \) и \ (v \), а затем использовать формулу. Также обратите внимание, что вычислить \ (v \) очень просто.Все, что нам нужно сделать, это интегрировать \ (dv \).
\ [v = \ int {{dv}} \]Одна из самых сложных вещей при использовании этой формулы — это то, что вам нужно правильно идентифицировать как \ (u \), так и \ (dv \). Не всегда будет ясно, каков правильный выбор, и иногда мы делаем неправильный выбор. Это не повод для беспокойства. Если мы сделаем неправильный выбор, мы всегда можем вернуться и попробовать другой набор вариантов.
Это приводит к очевидному вопросу: как узнать, правильно ли мы сделали выбор для \ (u \) и \ (dv \)? Ответ на самом деле довольно прост.{6x}} \, dx}} \] Показать решение
Итак, на некотором уровне проблема здесь в \ (x \), стоящем перед экспонентой. Если бы этого не было, мы могли бы выполнить интеграл. Также обратите внимание, что при выполнении интеграции по частям все, что мы выбираем для \ (u \), будет дифференцироваться. Таким образом, кажется, что выбор \ (u = x \) будет хорошим выбором, поскольку при дифференцировании \ (x \) выпадет.
Теперь, когда мы выбрали \ (u \), мы знаем, что \ (dv \) будет всем остальным, что останется.{6x}} + c \ end {align *} \]
После того, как мы выполнили последний интеграл в задаче, мы добавим константу интегрирования, чтобы получить окончательный ответ.
Также обратите внимание, что, как отмечалось выше, мы знаем, что сделали правильный выбор для \ (u \) и \ (dv \), когда получили новый интеграл, который мы фактически вычисляем после применения формулы интегрирования по частям.
Теперь давайте посмотрим на интегрирование по частям для определенных интегралов.b \) в первом члене — это просто стандартное обозначение интегральной оценки, с которым вы должны быть знакомы на этом этапе. Все, что мы делаем, это оцениваем член, в данном случае uv , в \ (b \), затем вычитаем оценку члена в \ (a \).
На каком-то уровне нам здесь действительно не нужна формула, потому что мы знаем, что при вычислении определенных интегралов все, что нам нужно сделать, это вычислить неопределенный интеграл, а затем выполнить вычисление. На самом деле, это, вероятно, будет немного проще, поскольку нам не нужно отслеживать таким образом оценку каждого термина.{- 6}} \ end {align *} \]
Любой из методов вычисления определенных интегралов с интегрированием по частям довольно прост, так что выбор, который вы выберете, в значительной степени зависит от вас.
Поскольку нам нужно уметь вычислять неопределенный интеграл, чтобы вычислить определенный интеграл, а выполнение определенного интеграла сводится к не более чем вычислению неопределенного интеграла в паре точек, мы сконцентрируемся на вычислении неопределенных интегралов в остальной части этого раздел.Фактически, на протяжении большей части этой главы так и будет. Мы будем делать гораздо больше неопределенных интегралов, чем определенных интегралов.
Давайте взглянем еще на несколько примеров.
Пример 3 Вычислите следующий интеграл. \ [\ int {{\ left ({3t + 5} \ right) \ cos \ left ({\ frac {t} {4}} \ right) \, dt}} \] Показать решениеЕсть два способа продолжить этот пример. Для многих первое, что они пробуют, — это умножить косинус на скобки, разделить интеграл и затем выполнить интегрирование по частям для первого интеграла.
Хотя это вполне приемлемый способ решения проблемы, это больше работы, чем нам действительно нужно. Вместо разделения интеграла давайте использовать следующие варианты для \ (u \) и \ (dv \).
\ [\ begin {align *} u & = 3t + 5 & \ hspace {0,5 дюйма} dv & = \ cos \ left ({\ frac {t} {4}} \ right) \, dt \\ du & = 3 \, dt & \ hspace {0,5 дюйма} v & = 4 \ sin \ left ({\ frac {t} {4}} \ right) \ end {align *} \]Тогда интеграл равен
. \ [\ begin {align *} \ int {{\ left ({3t + 5} \ right) \ cos \ left ({\ frac {t} {4}} \ right) \, dt}} & = 4 \ left ({3t + 5} \ right) \ sin \ left ({\ frac {t} {4}} \ right) — 12 \ int {{\ sin \ left ({\ frac {t} {4}} \ right) \, dt}} \\ & = 4 \ left ({3t + 5} \ right) \ sin \ left ({\ frac {t} {4}} \ right) + 48 \ cos \ left ({\ frac {t} {4}} \ right) + c \ end {align *} \]Обратите внимание, что мы вытащили все константы из интеграла, когда использовали формулу интегрирования по частям. 2}}} {{10}} \ cos \ left ({10w} \ right) + \ frac {w} {{50}} \ sin \ left ({10w} \ right) + \ frac {1} {{500}} \ cos \ left ({10w} \ вправо) + c \ end {align *} \]
Будьте осторожны с коэффициентом интеграла для второго применения интегрирования по частям.Поскольку интеграл умножается на \ (\ frac {1} {5} \), нам нужно убедиться, что результаты фактического выполнения интеграла также умножаются на \ (\ frac {1} {5} \). Забывание сделать это — одна из наиболее распространенных ошибок при интеграции по частям.
Как показал этот последний пример, иногда нам потребуется несколько приложений интегрирования по частям, чтобы полностью оценить интеграл. Это то, что произойдет, поэтому не волнуйтесь, когда это произойдет.
В следующем примере нам нужно признать важный момент, касающийся методов интеграции. Некоторые интегралы могут быть получены с использованием нескольких различных методов. Так обстоит дело с интегралом в следующем примере.
Пример 5 Вычислите следующий интеграл \ [\ int {{х \ sqrt {x + 1} \, dx}} \]- Использование интеграции по частям.
- Используя стандартную замену Calculus I.
Сначала обратите внимание, что в этом интеграле нет триггерных функций или экспонент. Хотя довольно много интегралов по частям будет включать триггерные функции и / или экспоненты, не все из них будут слишком зациклены на идее ожидания их появления.
В этом случае мы будем использовать следующие варианты для \ (u \) и \ (dv \).
\ [\ begin {align *} u & = x & \ hspace {0,5 дюйма} dv & = \ sqrt {x + 1} \, dx \\ du & = dx & \ hspace {0.{\ frac {5} {2}}} + c \ end {align *} \]b Используя стандартную замену Calculus I. Показать решение
Теперь сделаем интеграл с заменой. {\ frac {3} {2}}} + c \ end {align *} \]
Итак, в этом примере мы использовали два разных метода интеграции и получили два разных ответа.Тогда возникает очевидный вопрос: мы сделали что-то не так?
На самом деле, мы не сделали ничего плохого. Нам необходимо помнить следующий факт из исчисления I.
\ [{\ rm {If}} \, \, f ‘\ left (x \ right) = g’ \ left (x \ right) \, \, \, {\ rm {then}} \, \, \ , е \ влево (х \ вправо) = г \ влево (х \ вправо) + с \]Другими словами, если две функции имеют одинаковую производную, то они будут отличаться не более чем на константу. Итак, как это применимо к указанной выше проблеме? Сначала определите следующее:
\ [f ‘\ left (x \ right) = g’ \ left (x \ right) = x \ sqrt {x + 1} \]Затем мы можем вычислить \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) путем интегрирования следующим образом:
\ [е \ left (x \ right) = \ int {{f ‘\ left (x \ right) \, dx}} \ hspace {0.5in} g \ left (x \ right) = \ int {{g ‘\ left (x \ right) \, dx}} \]Мы будем использовать интегрирование по частям для первого интеграла и замену для второго интеграла. Тогда согласно тому, что \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) должны отличаться не более чем на константу. Давайте проверим это и посмотрим, так ли это. Мы можем убедиться, что они различаются не более чем на константу, если мы посмотрим на разницу между ними и сделаем небольшие алгебраические манипуляции и упрощения.{\ frac {3} {2}}} \ left (0 \ right) \\ \ hspace {2.0in} = 0 \ end {array} \]
Итак, в этом случае оказывается, что две функции — это одна и та же функция, поскольку разница равна нулю. Учтите, что это происходит не всегда. Иногда разница дает ненулевую константу. Пример этого можно найти в разделе «Константа интеграции» в примечаниях к исчислению I.
Итак, что мы узнали? Во-первых, иногда будет несколько методов вычисления интеграла.Во-вторых, мы увидели, что разные методы часто приводят к разным ответам. Наконец, даже несмотря на то, что ответы разные, иногда с большим трудом можно показать, что они отличаются не более чем на константу.
Когда мы сталкиваемся с интегралом, первое, что нам нужно решить, — это то, есть ли более одного способа сделать интеграл. Если существует несколько способов, нам нужно будет определить, какой из них следует использовать. Общее практическое правило, которое я использую в своих классах, заключается в том, что вы должны использовать метод, который вы, , найдете наиболее простым.Возможно, это не самый простой способ, но это не значит, что это неправильный метод.
Одна из наиболее распространенных ошибок интеграции по частям состоит в том, что люди слишком привязаны к воспринимаемым шаблонам. Например, во всех предыдущих примерах использовался базовый шаблон, согласно которому \ (u \) был полиномом, стоящим перед другой функцией, а затем позволял \ (dv \) быть другой функцией. Это не всегда будет происходить, поэтому нам нужно быть осторожными и не связываться с какими-либо шаблонами, которые, как нам кажется, мы видим.
Давайте взглянем на некоторые интегралы, которые не вписываются в приведенный выше шаблон.
Пример 6 Вычислите следующий интеграл. \ [\ int {{\ ln x \, dx}} \] Показать решениеИтак, в отличие от любого другого интеграла, который мы сделали до этого момента, в интеграле есть только одна функция и нет полинома перед логарифмом.
Первый выбор многих здесь — попытаться вписать это в шаблон сверху и сделать следующие выборы для \ (u \) и \ (dv \).
\ [u = 1 \ hspace {0,5 дюйма} dv = \ ln x \, dx \]Однако это приводит к реальной проблеме, поскольку это означает, что \ (v \) должно быть,
\ [v = \ int {{\ ln x \, dx}} \]Другими словами, нам нужно знать ответ заранее, чтобы решить проблему. Так что этот выбор просто не сработает.
Следовательно, если логарифм не принадлежит \ (dv \), он должен принадлежать вместо \ (u \).Итак, давайте использовать следующие варианты вместо
\ [\ begin {align *} u & = \ ln x & \ hspace {0,5 дюйма} dv & = \, dx \\ du & = \ frac {1} {x} dx & \ hspace {0,5 дюйма} v & = х \ конец {выравнивание *} \]Тогда интеграл равен
. \ [\ begin {align *} \ int {{\ ln x \, dx}} & = x \ ln x — \ int {{\ frac {1} {x} \, x \, dx}} \\ & = x \ ln x — \ int {{dx}} \\ & = x \ ln x — x + c \ end {align *} \] Пример 7 Вычислите следующий интеграл.{\ frac {5} {2}}} + c \ end {align *} \]Итак, в двух предыдущих примерах мы видели случаи, которые не совсем вписывались в какой-либо воспринимаемый шаблон, который мы могли бы получить из первых двух примеров. Это всегда то, к чему мы должны обращать внимание при интеграции по частям.
Давайте взглянем на другой пример, который также иллюстрирует другой метод интеграции, который иногда возникает из-за проблем интеграции по частям.
Пример 8 Вычислите следующий интеграл.\ theta} \ cos \ theta \, d \ theta}} \] Показать решениеХорошо, до сих пор мы всегда выбирали \ (u \) таким образом, чтобы при дифференцировании эта часть исчезла или, по крайней мере, превратила ее в интеграл в форму, которая упростила бы работу с . В этом случае, какую бы часть мы ни делали \ (u \), она никогда не уйдет в процессе дифференцирования.
Не имеет большого значения, какой мы выбираем \ (u \), поэтому мы выберем следующий путь.\ theta} \ sin \ theta} \ right) + c \]
Обратите внимание, что после деления на два мы добавляем постоянную интегрирования в этой точке.
Эту идею интегрирования до тех пор, пока вы не получите одинаковый интеграл по обе стороны от знака равенства, а затем простое решение для интеграла, неплохо запомнить. Это не так уж и часто, но когда это происходит, это может быть единственный способ на самом деле выполнить интеграл.
Также обратите внимание, что это на самом деле просто алгебра, по общему признанию, сделанная таким образом, что вы, возможно, не привыкли к этому, но на самом деле это просто алгебра.
На этом этапе вашей математической карьеры каждый может решить,
\ [x = 3 — x \ hspace {0,5 дюйма} \ to \ hspace {0,5 дюйма} x = \ frac {3} {2} \]Мы все еще решаем «уравнение». Единственное отличие состоит в том, что вместо решения для \ (x \) в мы решаем для интеграла, и вместо хорошей константы «3» в приведенной выше задаче алгебры мы получили функцию «беспорядка».
У нас есть еще один пример. Как мы увидим, некоторые проблемы могут потребовать от нас выполнять интеграцию по частям много раз, и существует короткий метод, который позволит нам быстро и легко выполнять несколько приложений интеграции по частям.{\ frac {x} {2}}} \, dx}} \] Показать решение
Мы начинаем с выбора \ (u \) и \ (dv \), как всегда. Однако вместо того, чтобы вычислять \ (du \) и \ (v \), мы помещаем их в следующую таблицу. Затем мы дифференцируем столбец, соответствующий \ (u \), пока не дойдем до нуля. В столбце, соответствующем \ (dv \), мы интегрируем один раз для каждой записи в первом столбце. Существует также третий столбец, который мы немного объясним, и он всегда начинается со знака «+», а затем чередуются знаки, как показано.{\ frac {x} {2}}} + c \ end {align *} \]
У нас есть интеграл. Это намного проще, чем записывать все различные \ (u \) и \ (dv \), которые нам пришлось бы делать в противном случае.
Итак, в этом разделе мы увидели, как выполнять интеграцию по частям. На более поздних уроках математики это, вероятно, будет одним из наиболее частых методов интеграции, с которыми вы столкнетесь.
Важно не зацикливаться на шаблонах, которые, как вы думаете, вы видели.В большинстве случаев любой шаблон, который, как вы думаете, вы видели, может (и будет) нарушен в какой-то момент времени. Будь осторожен!
Интегрируйте функцию с программой «Пошаговое решение математических задач»
Это руководство начинается с обсуждения первообразных, математических объектов.
которые тесно связаны с производными финансовыми инструментами. После введения интеграла через
проблема площади, интеграл и первообразная связаны соотношением
удивительная теорема, называемая фундаментальной теоремой исчисления.После
устанавливая некоторые методы вычисления интегралов, мы показываем важные
интерпретировать интеграл как предел некоторой суммы и продемонстрировать
разнообразие приложений интеграла к проблемам бизнеса и экономики,
геометрия и наука.
Первообразные
Три примера проблем, возникающих в различных контекстах:
следующее: найти функцию затрат C (x), если известны предельные затраты C ‘(x); найти
популяция P (t) биологической колонии, если скорость P ‘(r), с которой
популяция меняется, как известно; найти смещение s (t) объекта при
время t, если известна скорость v (t) = s ‘(r).
Обратите внимание, что все эти задачи имеют один и тот же базовый формат: найти f (x), учитывая
f ‘(х). Все подобные проблемы решаются антидифференцировкой. Элементарный
Пример из бизнеса — это случай производителя, который определяет это в течение
начальный период производства. предельные издержки производства линейно возрастают
и задается формулой C ‘(x) = 2x. Постараемся найти соответствующую функцию стоимости
C (x), для которого C ‘(x) = 2x. Хотя у нас нет аналитических методик для
найдя такое C (x), должно быть ясно, что функция стоимости C (x) = x 2 даст нам известные предельные издержки C ‘(x) = 2x.Но другие функции затрат будут
тоже работать. Например,
и фактически для любого числа a,
Таким образом, любая функция стоимости вида C (x) = x 2 + a даст
желаемый предельный доход C ‘(x) = 2x; требуется больше информации, чтобы определить
конкретное значение для. Мы вернемся к этому чуть позже. Процесс, который мы
теперь рассмотрение называется антидифференцировкой. В общих условиях это может быть
формулируется следующим образом:
Определение
Для данной функции f (x) функция g такая, что
называется первообразной f.Процесс поиска такой функции g есть
называется антидифференцировкой. Некоторые математики предпочитают называть этот процесс
неопределенная интеграция или просто интеграция по причинам, которые станут
очевидно в последующих разделах.
В нашем вводном примере каждая из функций стоимости x 2 , x 2 + 1, а x 2 + 10 является первообразной от f (x) = 2x; кроме того, C (x) = x 2 + a является первообразной f (x) = 2x для любого выбора a. В В общем, если g (x) является первообразной f (x), то же самое и g (x) + a для любого номер а, начиная с
Можно доказать следующий, еще более сильный результат:
Если g является любой первообразной от f, то каждая другая первообразная должна иметь
форма g (x) + a для некоторого числа a.
Таким образом, мы можем рассматривать g (x) + a как наиболее общую первообразную f.
Следовательно, самая общая первообразная от f — не отдельная функция, а
скорее класс функций g (x) + a, которые зависят от a.
Немецкий математик Готфрид Вильгельм Лейбниц (1646-1716) ввел обозначение
(читается как «первообразная от f» или «неопределенный интеграл от f»)
представляют собой наиболее общую первообразную f. Таким образом, если g — любая первообразная
f, то для любого числа a.
Вкратце:
Пример 1
Пример 2
Пример 3
Число a, возникающее при антидифференцировании, часто называют «произвольным». постоянный «. (По причинам, которые станут очевидными позже, его также называют «константа интегрирования»). В наших примерах мы использовали букву a для обозначают эту константу, но на практике обычно используется c.(Мы использовали букву a вместо c для нашей первоначальной иллюстрации, включающей стоимость, поскольку c использовался для обозначения стоимости.) Следующий пример дает нам представление о значение этой произвольной константы.
Пример 4
Предположим, что на начальных этапах производства предельные затраты до произвести товар стоит C ‘(x) = 2x доллара за единицу. На этот раз предположим, что производитель также знает, что фиксированная стоимость производства C (0) составляет 500 долларов.Находить соответствующая функция стоимости C (x).
Мы уже видели, что любая функция затрат для этих предельных затрат должна иметь форма C (x) = x 2 + a для некоторой константы a. С
С (0) = 500 = 0 2 + а = а,
мы имеем a = 500. Таким образом, функция стоимости определяется как C (x) = x 2 + 500
Из этого примера мы видим, что произвольная константа c является фиксированной стоимостью производство. Зная только предельную стоимость, мы не можем сказать, что это за фиксированная стоимость. является; фиксированная стоимость — дополнительная информация.Каждая из функций стоимости что соответствует предельным затратам C ‘(x) = 2x, будет иметь вид
C (x) = x 2 + (фиксированная стоимость).
Следующие два результата очень полезны при оценке первообразных. Здесь n обозначает действительное число, а c — постоянная интегрирования.
Обратите внимание, что Правило (2) выполняется для n! = — 1, а Правило (3) распространяется на случай, когда n = -1. Для проверки правила (2) воспользуемся определением (1) следующим образом:
Чтобы проверить Правило (3), вспомните, что
Пример 5 Используйте правило (2) для оценки каждого первообразного:
Решения:




