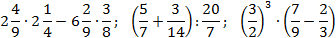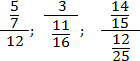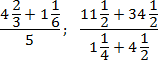Сложение и вычитание дробей с разными знаменателями. Сравнение дробей
Вспомним, что мы уже знаем об обыкновенных дробях.
1. Любая дробь обозначает количество, часть от какого-то числа. Эту часть мы умеем находить. Например,  от
от 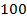 это
это 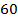 :
: 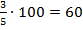 .
.
2. Одно и то же количество, одну и ту же часть можно выразить разными дробями. Такие дроби называются эквивалентными (Рис. 1).
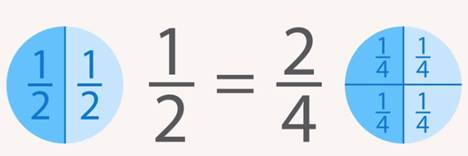
Рис. 1. Пример эквивалентных дробей
3. При сложении/вычитании дробей с одинаковыми знаменателями складываем/вычитаем числители.
4. При сравнении двух дробей с одинаковыми знаменателями большей является та, у которой числитель больше (Рис. 2).
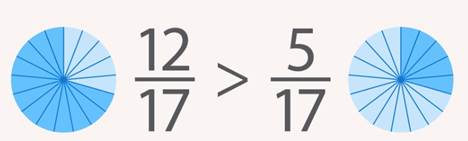
Рис. 2. Пример сравнения дробей с одинаковым знаменателем
Теперь перейдем к вопросу о том, что делать, если у дробей будут разные знаменатели. Например, как нам сложить  и
и 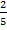 (Рис. 3)?
(Рис. 3)?
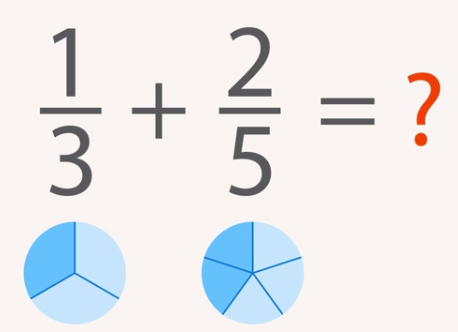
Рис. 3. Иллюстрация к примеру
Если мы заменим одну из дробей на эквивалентную (равную ей), то сумма, очевидно, не изменится.
Для дроби  существует бесконечное множество дробей, которые ей эквивалентны. Чтобы их получить, нужно одновременно умножать и числитель, и знаменатель на одно и то же число (
существует бесконечное множество дробей, которые ей эквивалентны. Чтобы их получить, нужно одновременно умножать и числитель, и знаменатель на одно и то же число (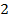 ,
, 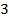 ,
, 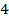 и т.д.). Тем самым мы получим цепочку эквивалентных дробей:
и т.д.). Тем самым мы получим цепочку эквивалентных дробей:
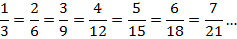
Аналогично поступим и со второй дробью: 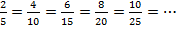
Мы можем заменить исходные дроби эквивалентными. Но выбирать нужно так, чтобы новые дроби имели одинаковые знаменатели, ведь мы уже умеем их складывать. Одинаковый знаменатель у дробей 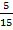 и
и 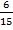 , заменим исходные дроби на них:
, заменим исходные дроби на них:
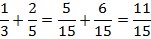
То есть идея оказался очень простой. Если нам нужно сложить две дроби, то смотрим на их знаменатели.
1) Если знаменатели одинаковые, то складываем сразу.
2) Если знаменатели разные, то заменяем исходные дроби эквивалентными, чтобы новые дроби имели одинаковые знаменатели. И складываем эти новые дроби.
Выполните вычисление:
1)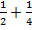 2)
2) 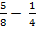 3)
3) 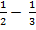 4)
4)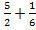 5)
5) 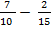
Решение:
1) Несложно заметить, что дробь 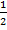
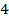 . Для этого нам нужно домножить ее числитель и знаменатель на
. Для этого нам нужно домножить ее числитель и знаменатель на 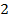 :
: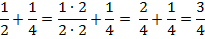
2) Несложно увидеть, что мы вторую дробь можем превратить в дробь со знаменателем 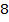 , для этого умножим ее числитель и знаменатель на
, для этого умножим ее числитель и знаменатель на 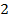
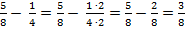 .
.3) Обе дроби мы можем заменить эквивалентными дробями со знаменателем 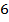 . Числитель и знаменатель первой дроби домножим на
. Числитель и знаменатель первой дроби домножим на 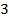 , а второй – на
, а второй – на 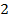 :
:
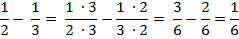
Таким образом, если знаменатели разные, то нужно заменить исходные дроби равными так, чтобы у новых дробей были одинаковые знаменатели. Такое преобразование называют приведением дробей к одному знаменателю (или к общему знаменателю).
4) Приведем дроби к общему знаменателю. Видно, что первую дробь можно привести к знаменателю 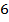 . А у второй дроби он уже
. А у второй дроби он уже 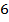 . Общий знаменатель
. Общий знаменатель 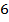 .
.
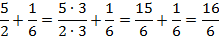
5) Общим знаменателем для этих дробей является число 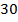
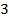 , а второй – на
, а второй – на 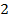 :
: 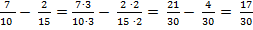 .
.Ответим теперь сами себе на следующий вопрос: Все ли мы умеем, чтобы сложить две дроби?
Если у них одинаковые знаменатели, то да, несомненно.
Если у них разные знаменатели, то мы начнем заменять дроби равными им, чтобы у новых дробей были одинаковые знаменатели. Иными словами, будем приводить их к общему знаменателю. Всегда ли это легко сделать? Нет, не всегда.
Пример 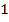
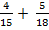 .
.Решение. Очевидно, что в знаменателе будет такое число, которое получается и из 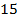 домножением на что-то, и из 18 домножением на что-то. Но такое число найти нетрудно.
домножением на что-то, и из 18 домножением на что-то. Но такое число найти нетрудно.
Это 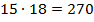 .
.
Числитель и знаменатель первой дроби умножим на 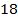 . Числитель и знаменатель второй дроби умножим на
. Числитель и знаменатель второй дроби умножим на 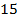 . Дроби, конечно, стали более громоздкими, но зато теперь у них одинаковый знаменатель:
. Дроби, конечно, стали более громоздкими, но зато теперь у них одинаковый знаменатель: 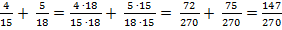
Теперь мы можем решить задачу и на сравнение этих дробей: 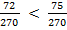 .
.
Следовательно, первое слагаемое меньше второго: 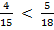 .
.
Пример 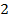 . Сравните две дроби
. Сравните две дроби 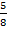 и
и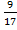
Решение. Чтобы сравнить две эти дроби, приведем их к общему знаменателю. Общий знаменатель найдем как произведение 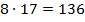 .
.
Чтобы в первой дроби получить знаменатель 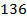 , умножим ее числитель и знаменатель на
, умножим ее числитель и знаменатель на 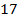 :
: 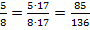 .
.
Чтобы у второй дроби получить знаменатель 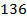 , умножим ее числитель и знаменатель на
, умножим ее числитель и знаменатель на 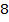 :
: 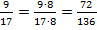 .
.
Итак, мы видим, что первая дробь больше: 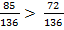 . Значит,
. Значит, 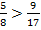 .
.
Вычтем из большей дроби меньшую: 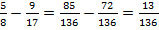 .
.
На этом уроке мы научились складывать, вычитать, сравнивать дроби с разными знаменателями. Существуют способы упрощения сложения громоздких дробей. Не всегда общий знаменатель ищут как произведение имеющихся знаменателей. Для этого в шестом классе вы будете изучать такое понятие, как наименьшее общее кратное.
Список рекомендованной литературы
1) Виленкин Н.Я. Математика. 6 класс: учеб. для учащихся общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013. – 288 с. : ил.
2) Зубарева И.И., Мордкович А.Г. Математика. 6 класс. – М.: Мнемозина.
3) Истомина И.Б. Математика, 6 класс. – М.: Ассоциация ХХI век.
Рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-портал Ru.onlinemschool.com (Источник).
2. Интернет-портал Cleverstudents.ru (Источник).
3. Интернет-портал Calc.ru (Источник).
Домашнее задание
1) Виленкин Н.Я. Математика. 6 класс: учеб. для учащихся общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013., ст. 49-50 чит., ст. 50 № 308, 310.
2) Сложите дроби:
а) 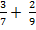 б)
б) 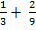
3) Укажите разность:
а) 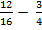 б)
б) 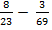
4) * Сравните дроби и из большей вычтите меньшую:
а) 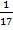 и
и 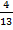 б)
б) 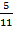 и
и  в)
в) 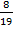 и
и 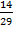
interneturok.ru
Сложение и вычитание алгебраических дробей с разными знаменателями (более сложные случаи)
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Сложение и вычитание алгебраических дробей с разными знаменателями (более сложные случаи)
На уроке мы продолжим тему предыдущего урока и будем рассматривать задачу сложения и вычитания алгебраических дробей с разными знаменателями, т.е. упрощение выражений вида: 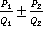 , где
, где 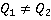 . В основном, задача сводится к нахождению наименьшего общего знаменателя дробей, а это делается, как мы уже знаем, по аналогии с обыкновенными дробями. Рассмотрим примеры.
. В основном, задача сводится к нахождению наименьшего общего знаменателя дробей, а это делается, как мы уже знаем, по аналогии с обыкновенными дробями. Рассмотрим примеры.
Пример 1. Выполнить действие 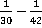 .
.
Решение. Для нахождения наименьшего общего знаменателя дробей воспользуемся основной теоремой арифметики и разложим знаменатели на простые множители.
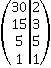 и
и 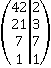 . Следовательно,
. Следовательно, 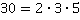 и
и 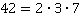 .
.
Вспомним, что наименьший общий знаменатель должен содержать множители всех знаменателей, причем так, чтобы множителей было минимально возможное количество. В нашем случае необходимы множители 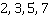 . Следовательно, общий знаменатель
. Следовательно, общий знаменатель 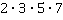 , а дополнительные множители: к первой дроби
, а дополнительные множители: к первой дроби 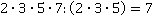 , ко второй дроби
, ко второй дроби 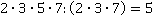 .
.
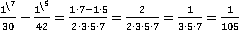 .
.
Как видно из решения, удобно даже не перемножать простые множители в знаменателе до получения числителя общей дроби, чтобы потом было легче сокращать дробь.
Ответ.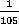 .
.
Теперь рассмотрим аналогичные операции с алгебраическими дробями. Не сложно догадаться, что самой трудоемкой частью сложения или вычитания дробей с разными знаменателями является нахождение наименьшего общего знаменателя. Если в случае обыкновенных дробей можно было пользоваться разложением чисел на множители, то в алгебраических дробях на множители необходимо будет раскладывать многочлены. Для этого существует несколько известных нам методов: вынесение общего множителя, применение формул сокращенного умножения и метода группировки слагаемых. Рассмотрим более подробно их применение для решения сложных задач на сложение и вычитание алгебраических дробей с разными знаменателями.
Пример 2. Выполнить действия 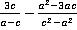 .
.
Решение. Для нахождения наименьшего общего знаменателя и дополнительных множителей разложим знаменатели на множители. Первый знаменатель уже представляет собой простое выражение, а второй раскладывается по формуле разности квадратов:
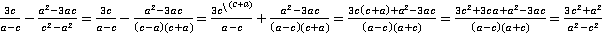 . Как видно по ходу решения, в качестве наименьшего общего знаменателя выбран знаменатель второй дроби, который делится и на первый знаменатель и сам на себя. Дополнительный множитель в таком случае пригодился только для первой дроби. Во втором переходе можно обратить внимание на внесение минуса перед дробью в один из множителей знаменателя для того, чтобы сделать знаменатели дробей максимально похожими друга на друга; такой прием нам уже знаком из темы «сложение алгебраических дробей с одинаковыми знаменателями (более сложные случаи)» (урок №5).
. Как видно по ходу решения, в качестве наименьшего общего знаменателя выбран знаменатель второй дроби, который делится и на первый знаменатель и сам на себя. Дополнительный множитель в таком случае пригодился только для первой дроби. Во втором переходе можно обратить внимание на внесение минуса перед дробью в один из множителей знаменателя для того, чтобы сделать знаменатели дробей максимально похожими друга на друга; такой прием нам уже знаком из темы «сложение алгебраических дробей с одинаковыми знаменателями (более сложные случаи)» (урок №5).
Ответ.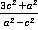 .
.
Пример 3. Выполнить действия 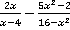 .
.
Решение. Поступим аналогично с предыдущим примером и разложим по ходу решения знаменатель второй дроби на множители по формуле разности квадратов, перед этим внесем минус перед дробью в знаменатель для того, чтобы он получил более удобный вид:
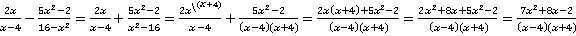 .
.
Ответ.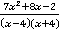 .
.
Рассмотрим теперь более сложные примеры на сложение/вычитание трех дробей.
Пример 4. Выполнить действия 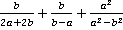 .
.
Решение. Как и ранее, разложим на множители каждый знаменатель, найдем наименьший общий знаменатель и дополнительные множители.
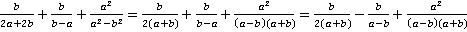 .
.
Как и ранее, для приведения выражения к удобному виду, вынесем минус из знаменателя второй дроби. Поскольку в выражении присутствует три дроби, чтобы не запутаться, выпишем наименьший общий знаменатель отдельно, составив его из множителей, входящих во все знаменатели: 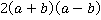 . Исходя из него, укажем и дополнительные множители для каждой из дробей, как те множители, которых не хватает знаменателю, чтобы стать общим.
. Исходя из него, укажем и дополнительные множители для каждой из дробей, как те множители, которых не хватает знаменателю, чтобы стать общим.
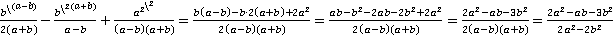 .
.
Последний переход (раскрывание скобок) не принципиален, и можно было указать в ответ выражение, записанное предпоследним.
Ответ.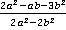 .
.
Пример 5. Выполнить действия 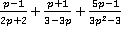 .
.
Решение. Поступаем уже известным для нас образом: раскрываем знаменатели на множители, при необходимости меняем знаки в знаменателях дробей, находим наименьший общий знаменатель и дополнительные множители.
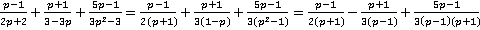 .
.
Наименьший общий знаменатель: 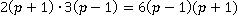 .
.
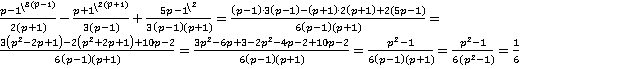 .
.
Можно заметить, что выражение в числителе 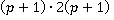 представимо в виде
представимо в виде 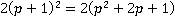 по формуле квадрата суммы, аналогично выражение
по формуле квадрата суммы, аналогично выражение 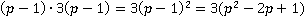 .
.
В конце проведено сокращение на 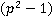 , значит необходимо обязательно записать область недопустимых значений переменной, связанную с этим сокращением:
, значит необходимо обязательно записать область недопустимых значений переменной, связанную с этим сокращением: 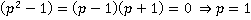 и
и 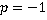 являются недопустимыми значениями переменных. Во всех остальных случаях выражение равно
являются недопустимыми значениями переменных. Во всех остальных случаях выражение равно  .
.
Ответ. .
.
На следующем уроке мы подробно остановимся на технике разложения на множители знаменателей дробей для их последующего сложения и вычитания. Эта техника чрезвычайно важна, т.к. мы видим, что она активно используется во всех рассмотренных ранее операциях с дробями.
Список рекомендованной литературы
1. Башмаков М.И. Алгебра 8 класс. М.: Просвещение. 2004 г.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. М.: Просвещение. 2010 г.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
1. ЕГЭ оп математике (Источник).
2. Так то ЕНТ. Методическая копилка (Источник).
3. Презентации для школьников (Источник).
Рекомендованное домашнее задание
1. № 55, 56, 63, 66, 68. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. М.: Просвещение. 2010 г.
2. Выполнить действия 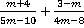 .
.
3. Выполнить действия 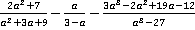 .
.
4. Доказать тождество: 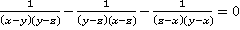 .
.
interneturok.ru
Сложные выражения с дробями. Порядок действий
Теперь, когда мы научились складывать и умножать отдельные дроби, можно рассматривать более сложные конструкции. Например, что, если в одной задаче встречается и сложение, и вычитание, и умножение дробей?
В первую очередь, надо перевести все дроби в неправильные. Затем последовательно выполняем требуемые действия — в том же порядке, как и для обычных чисел. А именно:
- Сначала выполняется возведение в степень — избавьтесь от всех выражений, содержащих показатели;
- Затем — деление и умножение;
- Последним шагом выполняется сложение и вычитание.
Разумеется, если в выражении присутствуют скобки, порядок действий изменяется — все, что стоит внутри скобок, надо считать в первую очередь. И помните о неправильных дробях: выделять целую часть надо лишь тогда, когда все остальные действия уже выполнены.
Задача. Найдите значения выражений:
Переведем все дроби из первого выражения в неправильные, а затем выполним действия:
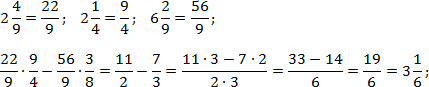
Теперь найдем значение второго выражения. Тут дробей с целой частью нет, но есть скобки, поэтому сначала выполняем сложение, и лишь затем — деление. Заметим, что 14 = 7 · 2. Тогда:
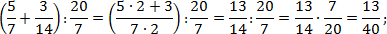
Наконец, считаем третий пример. Здесь есть скобки и степень — их лучше считать отдельно. Учитывая, что 9 = 3 · 3, имеем:
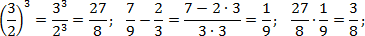
Обратите внимание на последний пример. Чтобы возвести дробь в степень, надо отдельно возвести в эту степень числитель, и отдельно — знаменатель.
Можно решать по-другому. Если вспомнить определение степени, задача сведется к обычному умножению дробей:
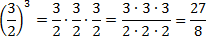
Многоэтажные дроби
До сих пор мы рассматривали лишь «чистые» дроби, когда числитель и знаменатель представляют собой обыкновенные числа. Это вполне соответствует определению числовой дроби, данному в самом первом уроке.
Но что, если в числителе или знаменателе разместить более сложный объект? Например, другую числовую дробь? Такие конструкции возникают довольно часто, особенно при работе с длинными выражениями. Вот пара примеров:
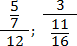
Здесь и далее мы будем называть эти дроби многоэтажными. Однако имейте в виду, что общепризнанного названия у них нет, и в разных учебниках могут встречаться другие определения.
Правило работы с многоэтажными дробями всего одно: от них надо немедленно избавляться. Удалить «лишние» этажи довольно просто, если вспомнить, что дробная черта означает стандартную операцию деления. Поэтому любую дробь можно переписать следующим образом:
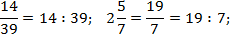
Пользуясь этим фактом и соблюдая порядок действий, мы легко сведем любую многоэтажную дробь к обычной. Взгляните на примеры:
Задача. Переведите многоэтажные дроби в обычные:
В каждом случае перепишем основную дробь, заменив разделительную черту знаком деления. Также вспомним, что любое целое число представимо в виде дроби со знаменателем 1. Т.е. 12 = 12/1; 3 = 3/1. Получаем:
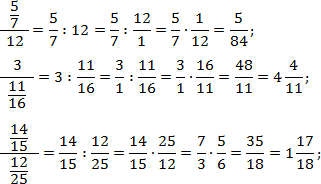
В последнем примере перед окончательным умножением дроби были сокращены.
Специфика работы с многоэтажными дробями
В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:
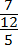
Это выражение можно прочитать по-разному:
- В числителе стоит отдельное число 7, а в знаменателе — дробь 12/5;
- В числителе стоит дробь 7/12, а в знаменателе — отдельное число 5.
Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:
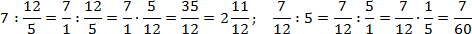
Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно — в несколько раз.
Если следовать этому правилу, то приведенные выше дроби надо записать так:
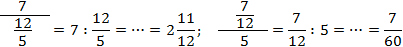
Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок — пара примеров, где действительно возникают многоэтажные дроби:
Задача. Найдите значения выражений:
Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:
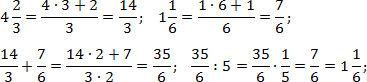
Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:
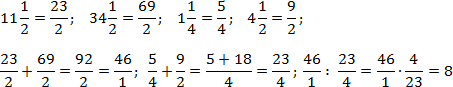
Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили число 46/1 в форме дроби, чтобы выполнить деление.
Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем — частное.
Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.
Смотрите также:
- Умножение и деление дробей

- Тест к уроку «Сложные выражения с дробями» (легкий)

- Тест к уроку «Округление с избытком и недостатком» (1 вариант)

- Что такое ЕГЭ по математике 2011 и как его сдавать

- Периодические десятичные дроби

- Задача B5: метод узлов

www.berdov.com
Сложение и вычитание обыкновенных дробей. Приведение дробей к одному знаменателю. Понятие о НОК
- Сложение и вычитание дробей с одинаковыми знаменателями
- Сложение и вычитание дробей с разными знаменателями
- Понятие о НОК
- Приведение дробей к одному знаменателю
- Как сложить целое число и дробь
1Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,
Пример 1:
Пример 2:
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
2Сложение и вычитание дробей с разными знаменателями.
Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи. Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
3Наименьшее общее кратное (НОК)
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
- Перемножить все числа в произведении, это и будет НОК.
Например, найдем НОК чисел 28 и 21:
4Приведение дробей к одному знаменателю
Вернемся к сложению дробей с разными знаменателями.
Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители. Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.
5Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например:
Если мы складываем целое число и смешанную дробь, мы прибавляем это число к целой части дроби, например:
Тренажер 1
Сложение и вычитание дробей с одинаковыми знаменателями.
Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Информация
В этом тесте проверяется умение складывать дроби с одинаковыми знаменателями. При этом нужно соблюдать два правила:
- Если в результате получается неправильная дробь, нужно перевести ее в смешанное число.
- Если дробь можно сократить, обязательно сократите ее, иначе будет засчитан неправильный ответ.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- С ответом
- С отметкой о просмотре
Тренажер 2
Сложение и вычитание дробей с разными знаменателями.
Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Информация
Тест поможет проверить, как вы умеете складывать дроби с разными знаменателями. Перед тем, как сложить дроби, необходимо привести их к одинаковому знаменателю. Записывая результат, соблюдаем два правила:
- Если в результате сложения получается неправильная дробь, нужно перевести ее в смешанное число.
- Если дробь можно сократить, обязательно сократите ее, иначе будет засчитан неправильный ответ.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- С ответом
- С отметкой о просмотре
kid-mama.ru
Отрицательные дроби. Действия с отрицательными дробями
Отрицательные дроби – это дроби, числитель или знаменатель которых является отрицательным числом.
Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:
-2 : 7 и 2 : (-7)
каждое из них равно отрицательному числу
Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:
| -2 : 7 | = | -2 | и | 2 : (-7) | = | 2 |
| 7 | -7 |
Следовательно, при записи отрицательных дробей знак минус
можно ставить перед дробью, перед числителем или перед знаменателем:
Сложение и вычитание
Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.
Пример:
Приведём дроби к общему знаменателю:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 |
| 5 | 4 | 20 | 20 |
Теперь сложим числители дробей по правилам сложения рациональных чисел:
| -8 | + | -5 | = | -8 + (-5) | = | -13 | = | — | 13 |
| 20 | 20 | 20 | 20 | 20 |
Таким образом:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | = | -8 + (-5) | = | -13 | = | — | 13 |
| 5 | 4 | 20 | 20 | 20 | 20 | 20 |
Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.
Пример:
| — | 5 | — (- | 11 | ) = | — | 5 | + (+ | 11 | ) = | — | 5 | + | 11 | = | -5 + 11 | = | 6 |
| 12 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.
Умножение и деление
Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.
Пример:
| — | 2 | · (- | 4 | ) = | -2 | · | -4 | = | -2 · (-4) | = | 8 |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить, сразу отбросив оба минуса:
| — | 2 | · (- | 4 | ) = | 2 | · | 4 | = | 2 · 4 | = | 8 |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
При умножении отрицательной дроби на положительную результат будет отрицательным.
Пример:
| — | 2 | · | 4 | = | — | 2 · 4 | = | — | 8 |
| 3 | 5 | 3 · 5 | 15 |
К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:
| 4 | · (- | 2 | ) = | — | 4 · 2 | = | — | 8 |
| 5 | 3 | 5 · 3 | 15 |
То есть при умножении положительной дроби на отрицательную результат будет отрицательным.
Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.
Пример:
| — | 2 | : (- | 4 | ) = | -2 | : | -4 | = | -2 · 5 | = | -10 | = | 10 |
| 3 | 5 | 3 | 5 | 3 · (-4) | -12 | 12 |
Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.
naobumium.info
Вычитание дробей. Вычитание дробей с разными знаменателями
Следующее действие, которое можно выполнять с обычными дробями это вычитание. Вычитание дробей выполняется по нескольким правилам. Рассмотрим эти правила подробнее. Вычитание смешанных дробей с разными знаменателями можно посмотреть нажав на ссылку.
Вычитание дробей с одинаковым знаменателем.
Рассмотрим, пока примеры в которых уменьшаемое больше вычитаемого.
\(\frac{7}{13}-\frac{3}{13} = \frac{7-3}{13} = \frac{4}{13}\)Чтобы выполнить вычитание дробей с одинаковыми знаменателями, нужно посчитать разность числителя уменьшаемого и вычитаемого, а знаменатель оставить без изменения.
\(\frac{a}{b}-\frac{c}{b} = \frac{a-c}{b}\)Вычитание дробей с разными знаменателями.
Чтобы выполнить вычитание дробей с разными знаменателями, нужно привести дроби к общему знаменателю, а потом применить правило вычитания дробей с одинаковыми знаменателями.
Рассмотрим пример:
Выполните вычитание дробей \(\frac{5}{6}\) и \(\frac{1}{2}\).
Общий знаменатель этих двух дробей latex]\frac{5}{6}[/latex] и \(\frac{1}{2}\) равен 6. Умножим вторую дробь \(\frac{1}{2}\) на дополнительный множитель 3.
\(\frac{5}{6}-\frac{1}{2} = \frac{5}{6}-\frac{1 \times \color{red} {3}}{2 \times \color{red} {3}} = \frac{5}{6}-\frac{3}{6} = \frac{2}{6} = \frac{1}{3}\)Дробь \(\frac{2}{6}\) сократили и получили \(\frac{1}{3}\).
Буквенная формула вычитания дробей с разными знаменателями.
\(\bf \frac{a}{b}-\frac{c}{d} = \frac{a \times d-c \times b}{b \times d}\)Вопросы по теме:
Как вычитать дроби с разными знаменателями?
Ответе: нужно найти общий знаменатель и далее по правилу выполнить вычитание дробей с одинаковыми знаменателями.
Как выполнить вычитание дробей с одинаковыми знаменателями?
Ответ: у числителей посчитать разность, а знаменатель оставить тот же.
Как правильно сделать проверку вычитания двух дробей?
Ответ: для проверки правильности вычитания дробей, нужно выполнить сложение вычитаемого и разности, результат их суммы будет равен вычитаемому.
Проверка:
\(\frac{4}{8} + \frac{3}{8} = \frac{4 + 3}{8} = \frac{7}{8}\)Пример №1:
Выполните вычитание дробей: а) \(\frac{1}{2}-\frac{1}{2}\) б) \(\frac{10}{19}-\frac{7}{19}\)
Решение:
а) \(\frac{1}{2}-\frac{1}{2} = \frac{1-1}{2} = \frac{0}{2} = 0\)
При вычитание двух одинаковых дробей получаем нуль.
б) \(\frac{10}{19}-\frac{7}{19} = \frac{10-7}{19} = \frac{3}{19}\)
Пример №2:
Выполните вычитание и проверьте сложением: а) \(\frac{13}{21}-\frac{3}{7}\) б) \(\frac{2}{3}-\frac{1}{5}\)
Решение:
а)Найдем общий знаменатель дробей \(\frac{13}{21}\) и \(\frac{3}{7}\), он будет равен 21. Умножим вторую дробь \(\frac{3}{7}\) на 3.
\(\frac{13}{21}-\frac{3}{7} = \frac{13}{21}-\frac{3 \times \color{red} {3}}{7 \times \color{red} {3}} = \frac{13}{21}-\frac{9}{21} = \frac{13-9}{21} = \frac{4}{21}\)Выполним проверку вычитания:
\(\frac{4}{21} + \frac{3}{7} = \frac{4}{21} + \frac{3 \times \color{red} {3}}{7 \times \color{red} {3}} = \frac{4}{21} + \frac{9}{21} = \frac{4 + 9}{21} = \frac{13}{21}\)б) Найдем общий знаменатель дробей \(\frac{2}{3}\) и \(\frac{1}{5}\), он будет равен 15. Умножим первую дробь \(\frac{2}{3}\) на дополнительный множитель 5, вторую дробь \(\frac{1}{5}\) на 3.
\(\frac{2}{3}-\frac{1}{5} = \frac{2 \times \color{red} {5}}{3 \times \color{red} {5}}-\frac{1 \times \color{red} {3}}{5 \times \color{red} {3}} = \frac{10}{15}-\frac{3}{15} = \frac{10-3}{15} = \frac{7}{15}\)Выполним проверку вычитания:
\(\frac{7}{15} + \frac{1}{5} = \frac{7}{15} + \frac{1 \times \color{red} {3}}{5 \times \color{red} {3}} = \frac{7}{15} + \frac{3}{15} = \frac{7 + 3}{15} = \frac{10}{15} = \frac{2}{3}\)tutomath.ru