Сокровище геометрии

Наталья Карпушина
«Наука и жизнь» №9, 2016

Римский архитектор Витрувий особо выделял теорему Пифагора «из многочисленных открытий, оказавших услуги развитию человеческой жизни», и призывал относиться к ней с величайшим почтением. Было это ещё в I веке до н. э. На рубеже XVI–XVII веков знаменитый немецкий астроном Иоганн Кеплер назвал её одним из сокровищ геометрии, сравнимым с мерой золота. Вряд ли во всей математике найдётся более весомое и значимое утверждение, ведь по числу научных и практических приложений теореме Пифагора нет равных.

Пифагоровы штаны

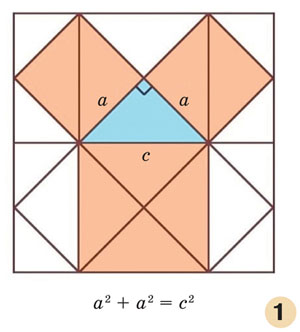
Теорема Пифагора едва ли не самая узнаваемая и, несомненно, самая знаменитая в истории математики. В геометрии она применяется буквально на каждом шагу. Несмотря на простоту формулировки, эта теорема отнюдь не очевидна: глядя на прямоугольный треугольник со сторонами

a < b < c, усмотреть соотношение a² + b² = c² невозможно. Однажды известный американский логик и популяризатор науки Рэймонд Смаллиан, желая подвести учеников к открытию теоремы Пифагора, начертил на доске прямоугольный треугольник и по квадрату на каждой его стороне и сказал: «Представьте, что эти квадраты сделаны из кованого золота и вам предлагают взять себе либо один большой квадрат, либо два маленьких. Что вы выберете?» Мнения разделились пополам, возникла оживлённая дискуссия. Каково же было удивление учеников, когда учитель объяснил им, что никакой разницы нет! Но стоит только потребовать, чтобы катеты были равны, — и утверждение теоремы станет явным (рис. 1). И кто после этого усомнится, что «пифагоровы штаны» во все стороны равны? А вот те же самые «штаны», только в «сложенном» виде (рис. 2). Такой чертёж использовал герой одного из диалогов Платона под названием «Менон», знаменитый философ Сократ, разбирая с мальчиком-рабом задачу на построение квадрата, площадь которого в два раза больше площади данного квадрата. Его рассуждения, по сути, сводились к доказательству теоремы Пифагора, пусть и для конкретного треугольника.

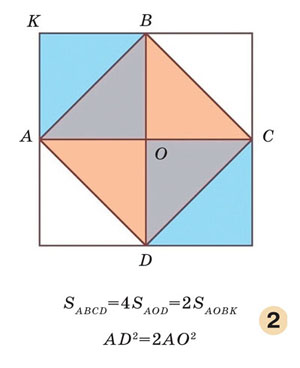
Фигуры, изображённые на рис. 1 и 2, напоминают простейший орнамент из квадратов и их равных частей — геометрический рисунок, известный с незапамятных времён. Им можно сплошь покрыть плоскость. Математик назвал бы такое покрытие плоскости многоугольниками паркетом, или замощением^*. При чём тут Пифагор? Оказывается, он первым решил задачу о правильных паркетах, с которой началось изучение замощений различных поверхностей. Так вот, Пифагор показал, что плоскость вокруг точки могут покрыть без пробелов равные правильные многоугольники только трёх видов: шесть треугольников, четыре квадрата и три шестиугольника.

4000 лет спустя

История теоремы Пифагора уходит в глубокую древность. Упоминания о ней содержатся ещё в вавилонских клинописных текстах времён царя Хаммурапи (XVIII век до н. э.), то есть за 1200 лет до рождения Пифагора. Теорема применялась как готовое правило во многих задачах, самая простая из которых — нахождение диагонали квадрата по его стороне. Не исключено, что соотношение a² + b² = c² для произвольного прямоугольного треугольника вавилоняне получили, попросту «обобщив» равенство a² + a² = c². Но им это простительно — для практической геометрии древних, сводившейся к измерениям и вычислениям, строгих обоснований не требовалось.

Теперь, почти 4000 лет спустя, мы имеем дело с теоремой-рекордсменом по количеству всевозможных доказательств. Между прочим, их коллекционирование — давняя традиция. Пик интереса к теореме Пифагора пришёлся на вторую половину XIX — начало XX столетия. И если первые коллекции содержали не более двух-трёх десятков доказательств, то к концу XIX века их число приблизилось к 100, а ещё через полвека превысило 360, и это только тех, что удалось собрать по разным источникам. Кто только не брался за решение этой нестареющей задачи — от именитых учёных и популяризаторов науки до конгрессменов и школьников. И что примечательно, в оригинальности и простоте решения иные любители не уступали профессионалам!

Самым древним из дошедших до нас доказательствам теоремы Пифагора около 2300 лет. Одно из них — строгое аксиоматическое — принадлежит древнегреческому математику Евклиду, жившему в IV–III веках до н. э. В I книге «Начал» теорема Пифагора значится как «Предложение 47». Самые наглядные и красивые доказательства построены на перекраивании «пифагоровых штанов». Они выглядят как хитроумная головоломка на разрезание квадратов. Но заставьте фигуры правильно двигаться — и они откроют вам секрет знаменитой теоремы.

Вот какое изящное доказательство получается на основе чертежа из одного древнекитайского трактата (рис. 3), и сразу проясняется его связь с задачей об удвоении площади квадрата.

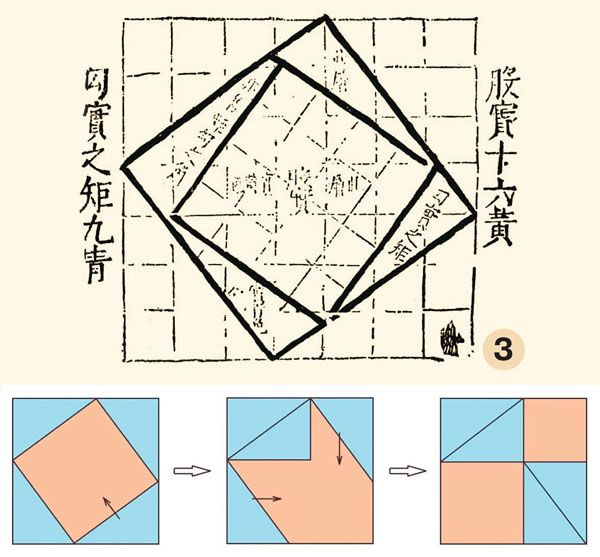
Именно такое доказательство пытался объяснить своему младшему другу семилетний Гвидо, не по годам смышлёный герой новеллы английского писателя Олдоса Хаксли «Маленький Архимед». Любопытно, что рассказчик, наблюдавший эту картину, отметил простоту и убедительность доказательства, поэтому приписал его… самому Пифагору. А вот главный герой фантастической повести Евгения Велтистова «Электроник — мальчик из чемодана» знал 25 доказательств теоремы Пифагора, в том числе данное Евклидом; правда, ошибочно назвал его простейшим, хотя на самом деле в современном издании «Начал» оно занимает полторы страницы!

Первый математик

Пифагора Самосского (570–495 годы до н. э.), чьё имя давно и неразрывно связано с замечательной теоремой, в известном смысле можно назвать первым математиком. Именно с него математика начинается как точная наука, где всякое новое знание — результат не наглядных представлений и вынесенных из опыта правил, а итог логических рассуждений и выводов. Лишь так можно раз и навсегда установить истинность любого математического предложения. До Пифагора дедуктивный метод применял только древнегреческий философ и учёный Фалес Милетский, живший на рубеже VII–VI веков до н. э. Он высказал саму идею доказательства, но применял его не систематически, избирательно, как правило, к очевидным геометрическим утверждениям типа «диаметр делит круг пополам». Пифагор продвинулся гораздо дальше. Считается, что он ввёл первые определения, аксиомы и методы доказательства, а также создал первый курс геометрии, известный древним грекам под названием «Предание Пифагора». А ещё он стоял у истоков теории чисел и стереометрии.

Другая важная заслуга Пифагора — основание славной школы математиков, которая более столетия определяла развитие этой науки в Древней Греции. С его именем связывают и сам термин «математика» (от греческого слова μαθημa — учение, наука), объединивший четыре родственные дисциплины созданной Пифагором и его приверженцами — пифагорейцами — системы знаний: геометрию, арифметику, астрономию и гармонику.

Отделить достижения Пифагора от достижений его учеников невозможно: следуя обычаю, они приписывали собственные идеи и открытия своему Учителю. Никаких сочинений ранние пифагорейцы не оставили, все сведения они передавали друг другу устно. Так что 2500 лет спустя историкам не остаётся ничего иного, кроме как реконструировать утраченные знания по переложениям других, более поздних авторов. Отдадим должное грекам: они хоть и окружали имя Пифагора множеством легенд, однако не приписывали ему ничего такого, чего он не мог бы открыть или развить в теорию. И носящая его имя теорема не исключение.

Такое простое доказательство

Неизвестно, Пифагор сам обнаружил соотношение между длинами сторон в прямоугольном треугольнике или позаимствовал это знание. Античные авторы утверждали, что сам, и любили пересказывать легенду о том, как в честь своего открытия Пифагор принёс в жертву быка. Современные историки склонны считать, что он узнал о теореме, познакомившись с математикой вавилонян. Не знаем мы и о том, в каком виде Пифагор формулировал теорему: арифметически, как принято сегодня, — квадрат гипотенузы равен сумме квадратов катетов, или геометрически, в духе древних, — квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.

Считается, что именно Пифагор дал первое доказательство теоремы, носящей его имя. Оно, конечно, не сохранилось. По одной из версий, Пифагор мог воспользоваться разработанным в его школе учением о пропорциях. На нём основывалась, в частности, теория подобия, на которую опираются рассуждения. Проведём в прямоугольном треугольнике с катетами a и b высоту к гипотенузе c. Получим три подобных треугольника, включая исходный. Их соответствующие стороны пропорциональны, a : с = m : a и b : c = n : b, откуда a² = c · m и b² = c · n. Тогда a² + b² = c · (m + n) = c² (рис. 4).

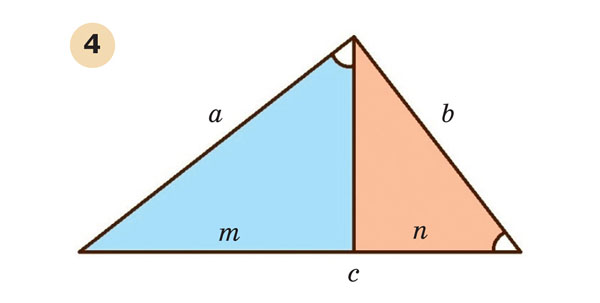Это всего лишь реконструкция, предложенная одним из историков науки, но доказательство, согласитесь, совсем простое: занимает всего-то несколько строк, не нужно ничего достраивать, перекраивать, вычислять… Неудивительно, что его не раз переоткрывали. Оно содержится, например, в «Практике геометрии» Леонардо Пизанского (1220), и его до сих пор приводят в учебниках.

Такое доказательство не противоречило представлениям пифагорейцев о соизмеримости: изначально они считали, что отношение длин любых двух отрезков, а значит, и площадей прямолинейных фигур, можно выразить с помощью натуральных чисел. Никакие другие числа они не рассматривали, не допускали даже дробей, заменив их отношениями 1 : 2, 2 : 3 и т. д. Однако, по иронии судьбы, именно теорема Пифагора привела пифагорейцев к открытию несоизмеримости диагонали квадрата и его стороны. Все попытки численно представить длину этой диагонали — у единичного квадрата она равна √2 — ни к чему не привели. Проще оказалось доказать, что задача неразрешима. На такой случай у математиков есть проверенный метод — доказательство от противного. Кстати, и его приписывают Пифагору.

Существование отношения, не выражаемого натуральными числами, положило конец многим представлениям пифагорейцев. Стало ясно, что известных им чисел недостаточно для решения даже несложных задач, что уж говорить обо всей геометрии! Это открытие стало поворотным моментом в развитии греческой математики, её центральной проблемой. Сначала оно привело к разработке учения о несоизмеримых величинах — иррациональностях, а затем — и к расширению понятия числа. Иными словами, с него началась многовековая история исследования множества действительных чисел.

---

^* Паркет, или замощение, — разбиение плоскости многоугольниками (или пространства многогранниками) без пробелов и перекрытий.

Пифагор: учение, теория о числе

Используя данные различных авторов, А.О. Маковельский  излагает гипотезу о математических достижениях пифагорейцев:  

«Прежде всего мы назовем Пифагора великим математиком. Вера в религиозно-катартическое действие науки дала ему силу положить основание чистой математики. В арифметике пифагорейцев основным (и, может быть, первоначальным) следует считать прежде всего деление чисел на чётные, нечётные и чётно-нечётное первичное число (единица).

Этому тройному делению составляют параллель три вида чисел, открытых пифагорейцами: так называемые квадратные, прямоугольные и треугольные числа.

Квадратные числа получаются через сложение нечётных: 1+3=4=22; 1+3+5=9; 1+3+5+7=16 и т. д.  Прямоугольные числа получаются через сложение чётных: 2+4=6; 2+4+6=12 и т. д.

Треугольные числа получаются через сложение по порядку четных и нечетных чисел: 1 + 2 + 3 + … + N =   .

В пифагорейской школе рано было открыто также взаимоотношение квадратов чисел (учение о сумме квадратов чисел). Далее у них мы находим учение о средних величинах, т. е. о пропорциях и отношениях величин. Средними величинами в древности назывались группы таких трёх величин, средняя из которых есть функция двух крайних. Насчитывали всего десять видов «средних величин». Из них три вида: так наз. арифметическое, геометрическое и гармоническое среднее вошли в современную математику под названием непрерывных пропорций (арифметическая непрерывная пропорция а – c = c — b, геометрическая а : с = с : b, и гармоническая (а — b) : (b — с) = а : с  […]

Из пифагорейской же школы вышла Пифагорова таблица умножения, вписанная в четырехугольник.

Размышления над основами математического счета привели Пифагорейцев к поклонению священной декаде. Все остальные числа суть для них простые повторения первых десяти. Декаду они отождествляли с четвёркой, так как сумма первых четырёх цифр равна 10.

Священными числами считались по преимуществу единица, как первоначало чисел, троица, так как истинное единство представлялось им триединством, четверица, как заключающая в себе тайну декады, и, наконец, сама десятка. Впоследствии мистика чисел у пифагорейцев сильно развилась. Переходя к пифагорейской геометрии, прежде всего, отметим применение ими числа к пространству.

Элементы пространства и геометрические фигуры они сводят к числам. Так, точка есть пространственная единица, линия — пространственное 2, поверхность 3, тело 4. К пифагорейским открытиям в геометрии принадлежит прежде всего так наз. Пифагорова теорема (в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов). Другая теорема, открытая Пифагором, говорит о сумме углов в треугольнике […]

Вообще содержание двух первых книг «Начал Эвклида» — собственность пифагорейской школы. Сам Пифагор открыл несоизмеримость диагонали квадрата с его стороной.

В стереометрии пифагорейцы первые открыли 5 правильных геометрических тел: куб, тетраэдр, октаэдр, икосаэдр и додекаэдр.

По Эвдему, Пифагор первый сделал геометрию подлинной наукой. И мы полагаем, что именно его, а не Фалеса, следует считать основателем дедуктивной геометрии. Впервые у Пифагора математика из практического искусства становится чистой наукой.  

Наконец, Пифагор полагает начало математическому естествознанию. Он создает математическую акустику (а именно, тот отдел её, который назывался каноникой или гармоникой, т. е. учение о музыкальных интервалах) и теоретическую астрономию (сферику, т. е. начала небесной механики). Он открывает математическую закономерность, с одной стороны, в музыке, с другой, в обращении небесных светил и, исходя отсюда, постулирует существование такой же математической закономерности во всех явлениях. И не только физические и метафизические, но также социальные, этические и теологически понятия получают математическую окраску.

«Всё есть число» становится основоположением пифагорейского мировоззрения и универсальным методом их научных построении. Но так как поставленная ими задача — выразить в форме математических законов не только всю действительность, но и содержание своих мифологических и теологических верований, а равным образом этических и социальных идеалов — была неразрешимой, то они прибегли к произвольной аналогии и игре числами и таким образом создали фантастическую числовую символику.  

Древнейшая форма пифагорейской космологии, восходящая, вероятно, к самому Пифагору, примыкает самым тесным образом к учению — Анаксимена. Последний учил, что мир дышит, что в мир постоянно втекает воздушная масса из бесконечного пространства за миром. Беспредельный воздух Анаксимена тождествен для Пифагора с геометрическим пространством, но для создания мира, по его мнению, недостаточно этого единого «неограниченного» принципа, необходимо еще другое, «ограничивающее» начало. Таковым является огонь. Жизнь мира заключается в том, что он вдыхает, втягивает в себя воздушную пустоту. Таким образом, пифагорейцы первые выдвинули понятие пустоты, и у них же впервые признается первоэлементом огонь (последнее — Аристотель приписывает пифагорейцу Гиппасу).

Мировоззрение пифагорейцев было дуалистическим: основную противоположность образовывали предел и беспредельное, или огонь и воздух (или свет и тьма). Высшим принципом являлось у них не безразличие противоположностей, как у Анаксимандра, но примирение противоположностей, т. е. гармония, или мера.

Жизнь вселенной есть постоянное ограничивание неограниченного и познание есть определение неопределенного. Единство первичных противоположностей (границы и безграничного) есть гармония. Гармония не есть нечто субъективное, человеческое, напротив, это объективная сущность, высший мировой закон.  Таковы основы пифагорейской космологии.

Сверх того, следует упомянуть, что пифагорейцы признавали множественность миров и бесконечную повторяемость всех явлений. Всё возвращается бесконечное число раз: все наши поступки и все обстоятельства нашей жизни до мельчайших подробностей повторятся в будущем бесчисленное число раз подобно тому, как и в прошлом они уже совершались бесконечное число раз. Из астрономических взглядов Пифагорейцев отметим учение о шарообразности земли и связанную с этим теорию климатических поясов, учение о движении земли вокруг центрального мирового огня, учение о движении светил в шарообразных сферах, которые при движении издают звуки — «гармонию сфер», различение движения планет с запада на восток от их суточного движения с востока на запад. Все эти учения, вероятно, восходят к самому Пифагору».

Маковельский А.О., Досократики: доэлеатовский и элеатовский периоды, Минск, «Харвест», 1999 г., с.142-145. 

Доклад на тему Теорема Пифагора сообщение (описание для детей)

Теорема Пифагора представляет собой один из наиболее фундаментальных постулатов геометрии. Именно эта теорема используется довольно активно в самых разных областях. Не удивительно, ведь теорема Пифагора располагается в основе самых разнообразных вычислений, которые могут применяться и для строительства зданий и для того чтобы передавать сигнал на космический корабль.

Суть этой теоремы заключается в пропорциях отношений сторон прямоугольного треугольника. Как гласит эта теорема, сумма квадратов сторон (катетов) прямоугольного треугольника равна квадрату длины гипотенузы, то есть стороны противоположной прямому углу.

На самом деле Пифагор, который открыл данную теорему в 6 веке до новой эры, фактически не являлся первооткрывателем в этом направлении. Как не трудно понять, до него люди тоже пользовались этими соотношениями. Ведь людям требовалось использовать различные пропорции в строительстве и архитектуре.

К примеру, известен способ с веревкой из Древнего Египта, где строители использовали веревку с 12 узлами через равные дистанции. Эта веревка позволяла сделать прямоугольный треугольник со сторонами 3,4,5. Таким образом и формировался прямоугольные треугольник с нужным соотношением сторон, который позволял проводить различные измерения, к примеру, строить пирамиды.

Также за пару веков до Пифагора в Индии описывали теорему, согласно которой, диагональ квадрата может стать стороной квадрата, который вдвое больше начального. По сути, речь идет о теореме Пифагора. Только в немного другом описании.

Существует огромное количество способов доказательства теоремы Пифагора. В частности Эвклид предложил использовать вариант с пропорциями треугольников:

• прямоугольный треугольник делят биссектрисой, которая идет от угла между катетами;
• в итоге появляется два прямоугольных треугольника в пространстве одного большого;
• соотношения сторон между этими прямоугольниками равны;
• идентичным образом соотносятся стороны маленьких треугольников и большого;
• этот факт доказывает универсальность теоремы.

Помимо этого теорема может доказываться через соотношения сторон квадратов, которые прилегают к сторонам любого прямоугольного треугольника, суммарные площади этих квадратов всегда равны.

Сообщение 2

Каждый из нас ещё в школьные годы слышал о теореме Пифагора.

Теорема древнегреческого математика занимает одну из основных позиций в геометрии и немало поспособствовала становлению математики.

Разносторонний и талантливый учёный М. Ломоносов восхищался теоремой Пифагора, говорил, что современники не в состоянии были осознать и оценить учёного, как не способны это сделать и современники. Намекая на то что «масса» не может понять интеллекта и порой делает земное существование интеллектуала не выносимым.

Многие историки и математики считали что её создал Пифагор, однако это не так. Он лишь привёт её доказательства. Споры продолжаются.

Однако можно увидеть, что каким мощным интеллектом обладали мыслители Древней Греции. Пифагор Самосский или как его называли некоторые «вещатель», был не только мыслителем и математиком, но и философом. Он создал свою собственную философскую школу.

Философская школа пифогорианцев (6-4 вв. до н. э.), пытались постичь природу, узнать и понять законы мироздания и т. д. Именно там и тогда Пифагор начал работать над своей знаменитой теорией.

Жизнь Пифагора полна легенд и сказок поэтому трудно понять где вымысел, где правда. Он очень интересовался магией и спиритизмом, не смотря на математический склад ума, он верил в такие вещи. Свою философскую позицию Пифагор формировал на основе информации о видимом и невидимом мире, о единении сил духовных и природных, он был сторонник теории о бессмертии человеческой души. Мировоззрение Пифагора оказало влияние на эзотерику и теософию, которую использовали масоны в формировании своей идеологии. В натуре Пифагора уживались, скептик и фантазёр. Он был разносторонней личностью с высоким IQ (айкью).

Пифагор в свой время являлся оппозиционером, в Вавилоне, где он проживал определённое время, был вынужден бежать так как вступил в конфликт с властью.

Суть Теоремы Пифагора: она устанавливает параллели между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы. Современная математическая литература даёт более 400 доказательств Теореме Пифагора. Эта положение Пифагора о треугольниках и стала тем фундаментом, на котором возвели такой предмет как геометрия.

Древнеиндийские математики говорили об этой теории, и о Пифагоре: «Как сообщают, занятие данной отраслью знания (геометрией) Пифагор превратил в настоящую науку». Теорема имела успех в древние времена, имеет и поныне. Её изучают в школах, институтах. Она написана во всех учебниках математики. Каждый слышал об этой теореме.

Картинка к сообщению Теорема Пифагора

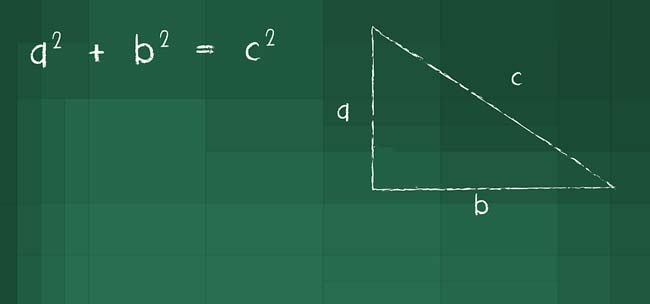
Популярные сегодня темы

• Почему нельзя загрязнять воду?

  Изначальные запреты загрязнять воду носят религиозный характер и связаны с пониманием священности стихий, тем не менее, там есть и сугубо практическое зерно, которое актуально и для всех совр

• Лицейские друзья Пушкина

  Период обучения в Царскосельском лицее представляет собой основу для развития поэтического дарования Пушкина под влиянием не только талантливых педагогов, но и одаренных, умных и верный друзе

• Почему надо беречь водоемы и реки

  Вся планета представляет собой многообразие живых существ, различных организмов, материалов, природных элементов, стихий. Целостность этой структуры представляет собой глобальную экосистему,

• Евразия

  Евразия представляет собой крупнейший материк на планете, он располагается практически полностью в Северном и Восточном полушариях. Он является крупнейшим и занимает треть

• Хищные растения

  Среди представителей флоры встречаются поистине удивительные и необычные. Например, в болотистой местности или на других скудных почвах растениям с автотрофным питанием может быть недостаточн

• Божья коровка

  Божья коровка – представитель семейства КОКЦИНЕЛЛИДЫ, относится к отряду жесткокрылых типа членистоногих. Это насекомое знает любой ребенок. Размер составляет от четырех до десяти миллиметров

Проект по математике «Теорема Пифагора»

МБОУ ДОД Дворец творчества детей и молодежи г Ростова — на- Дону

Донская академия наук юных исследователей им. Ю. А. Жданова

Математика/ Общая математика

Тема: « Теорема Пифагора»

Автор работы:

Казачкова Виктория, 9 кл.,

МБОУ СОШ УИОП

г Зерноград, Ростовская область

Руководитель

Афанасьева Светлана Владиславовна

учитель математики МБОУ СОШ УИОП

г Зерноград, Ростовская область

г Ростов – на — Дону

2016 год

Оглавление.

1. Введение 3

2. Биография Пифагора.

3. Доказательство Вольдхейма.

4. Доказательство теоремы Пифагора с

помощью домино.

5. Выводы.

6. Литература.

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Строго говоря, хоть теорема и называется «теоремой Пифагора», сам Пифагор ее не открывал. Прямоугольный треугольник и его особенные свойства изучались задолго до него. Есть две полярных точки зрения на этот вопрос. По одной версии Пифагор первым нашел полноценное доказательство теоремы. По другой доказательство не принадлежит авторству Пифагора.

В средние века теорема Пифагора, magister mathe- seos, определяла границу если не наибольших возможных, то по крайней мере хороших математических знаний. Характерный чертеж теоремы Пифагора, который ныне иногда превращается школьниками, например, в облеченного в мантию профессора или в человечка в цилиндре, в те времена всеобщей страсти к символам нередко употреблялся как символ математики. Теорема Пифагора занимала умы математиков с древнейших времен. Из нее выводится или так или иначе с нею связано большинство теорем геометрии.

Теорему Пифагора доказывали через подобные треугольники, методом площадей и даже через дифференциальные уравнения – это сделал английский математик начала двадцатого века Годфри Харди. Известны доказательства теоремы Пифагора, предложенные Евклидом и Леонардо Да Винчи. А Электроник – мальчик из чемоданчика в книге Евгения Велтистова знал целых двенадцать способов, а среди них «метод укладки паркета» и «стул невесты». 

Существуют различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков. У Евклида эта теорема гласит (дословный перевод):»В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямойугол». Латинский перевод арабского текста Аннаирици (около 900 г. до н. э. ), сделанный Герхардом Клемонским (начало 12 в.), в переводе на русский гласит:»Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол». В Geometria Culmonensis (около 1400 г.) в переводе теорема читается так «Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу». В первом русском переводе евклидовых «Начал», сделано Ф.И.Петрушевским, теорема Пифагора изложена так: «В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол».

Интересный материал был найден в книге «Теорема Пифагора» Перевод с немецкого В. С. Бермана под редакцией И. М. Яглома. В ходе работы вызвала интерес и биография Пифагора. Основным методом работы была систематизация и обработка информации по теме.

1. 1. Биография Пифагора.

Пифагор Самосский ( 570—490 гг. до н. э.) — древнегреческий философ, математик и мистик, создатель религиозно-философской школы пифагорейцев. Великая теорема Пифагора! Уже благодаря ей Пифагор Самосский стал бессмертным. Вплоть да настоящего времени его считают загадкой. А в эпоху его жизни, о нём отзывались, как о манне и мудреце, а Пифагор – это не имя. Его прозвали так потому, что она был великим оратором, обладающим даром убеждения. Слово “пифагор” в переводе с греческого значит “убеждающий речью”. Своей первой публичной лекцией он сделал последователями две тысячи человек.
Историю жизни Пифагора трудно отделить от легенд, представляющих его в качестве совершенного мудреца и великого посвящённого во все таинства греков и варваров. Ещё Геродот называл его «величайшим эллинским мудрецом»
Родителями Пифагора были Мнесарх и Партенида с острова Самос. Мнесарх был камнерезом; по словам же Порфирия он был богатым купцом из Тира, получившим самосское гражданство за раздачу хлеба в неурожайный год. Первая версия предпочтительнее, так как Павсаний приводит генеалогию Пифагора по мужской линии от Гиппаса из пелопоннесского Флиунта, бежавшего на Самос и ставшего прадедом Пифагора. Партенида, позднее переименованная мужем в Пифаиду, происходила из знатного рода Анкея, основателя греческой колонии на Самосе.
В юном возрасте Пифагор отправился в Египет, чтобы набраться мудрости и тайных знаний у египетских жрецов. Диоген и Порфирий пишут, что самосский тиран Поликрат снабдил Пифагора рекомендательным письмом к фараону Амасису, благодаря чему он был допущен к обучению и посвящён не только в египетские достижения медицины и математики, но и в таинства, запретные для прочих чужеземцев. В Египта, где пробыл 22 года, пока его не увёл в Вавилон в числе пленников персидский царь Камбиз, завоевавший Египет в 525 до н. э. В Вавилоне Пифагор пробыл ещё 12 лет, общаясь с магами, пока наконец не смог вернуться на Самос в 56-летнем возрасте, где соотечественники признали его мудрым человеком. По словам античных авторов, Пифагор встретился чуть ли не со всеми известными мудрецами той эпохи, греками, персами, халдеями, египтянами, впитал в себя всё накопленное человечеством знание.

В современном мире Пифагор считается великим математиком и космологом древности, однако ранние свидетельства до III в. до н. э. не упоминают о таких его заслугах. Как пишет Ямвлих про пифагорейцев: «У них также был замечательный обычай приписывать всё Пифагору и нисколько не присваивать себе славы первооткрывателей, кроме, может быть, нескольких случаев.»

Античные авторы нашей эры отдают Пифагору авторство известной теоремы: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Такое мнение основывается на сведениях Аполлодора-исчислителя (личность не идентифицирована) и на стихотворных строках (источник стихов не известен):

“В день, когда Пифагор открыл свой чертёж знаменитый, славную он за него жертву быками воздвиг”

Современные историки предполагают, что Пифагор не доказывал теорему, но мог передать грекам это знание известное в Вавилоне за 1000 лет до Пифагора (согласно вавилонским глиняным табличкам с записями математических уравнений). Хотя сомнение в авторстве Пифагора существует, но весомых аргументов, чтобы это оспорить, нет.

1.2. Доказательство теоремы Пифагора методом разложения.

Существует целый ряд доказательств теоремы Пифагора, в которых квадраты, построенные на катетах и на гипотенузе, разрезаются так, что каждой части квадрата, построенного на гипотенузе, соответствует часть одного из двух квадратов, построенных на катетах. Во всех этих случаях для понимания доказательства достаточно одного взгляда на чертеж; рассуждение здесь может быть ограничено единственным словом: «смотри!», как это делалось в сочинениях древних индусских математиков.

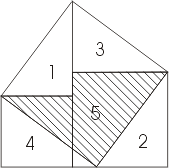
1.3. Доказательство теоремы Пифагора « Стул невесты.»

На рисунке квадраты, построенные на катетах, размещены ступенями один рядом с другим. Эту фигуру, которая встречается в доказательствах, датируемых не позднее, чем 9 столетием н. э., индусы называли «стулом невесты». Способ построения квадрата со стороной, равной гипотенузе, ясен из чертежа. Общая часть двух квадратов, построенных на катетах, и квадрата, построенного на гипотенузе, — неправильный заштрихованный пятиугольник 5. Присоединив к нему треугольники 1 и 2, получим оба квадрата, построенные на катетах; если же заменить треугольники 1 и 2 равными им треугольниками 3 и 4, то получим квадрат, построенный на гипотенузе.

1.4. Доказательство Вольдхейма.

Это доказательство имеет вычислительный характер. Для того чтобы доказать теорему пользуясь рисунком достаточно только выразить площадь трапеции двумя путями.

Sтрапеции=(a+b)²/2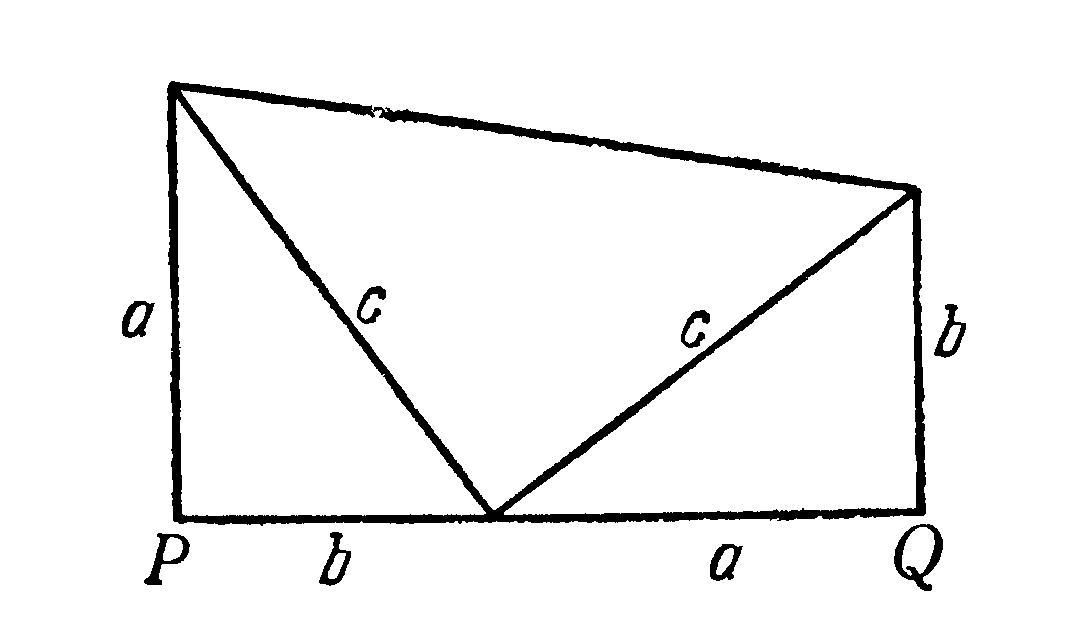

Sтрапеции=a²b²+c²/2

Приравнивая правые части получим:

a²+b²=c²

Теорема доказана.

Теорема.
В прямоугольном треугольнике квадрат гипотенузы
равен сумме квадратов катетов

Простейшее доказательство

Треугольник АВС — равнобедренный

Квадрат, построенный на гипотенузе АB, содержит 4 исходных треугольника, а квадраты, построенные на катетах,- по два.

1.5. Доказательство теоремы Пифагора с помощью домино.

ВЫВОДЫ:

• Теорема Пифагора по праву считается самой важной в

курсе геометрии. Пифагор превратил математику в

дедуктивную науку: ввел доказательство.

• Она является основой решения множества геометрических

задачи и является основой для вывода многих формул

геометрии. На её основе возникла целая наука

тригонометрия. Эта наука применяется в космонавтике.

• Теоремой Пифагора и пифагорейской школой восхищается

человечество на протяжении всей истории, им посвящают

стихи, песни, рисунки, картины.

• Работа над этим проектом нам позволила расширить свои

знания в области в геометрии.

Знания теоремы и его приложений позволят нам применить

их при решении геометрических задач.

ОТКРЫТИЯ ДРЕВНЕГРЕЧЕСКОГО ФИЛОСОФА ПИФАГОРА

ОТКРЫТИЯ ПИФАГОРА

Пифагор Самосский, древнегреческий философ, великий посвященный Земли, политический и религиозный деятель, математик, основатель пифагореизма. Его главное жизненное понятие — «Все есть Число». Так обычно указывается в энциклопедиях и его жизнеописаниях.

Но то, кем был, кто есть ныне и кем будет Пифагор в будущем, остается космической Тайной…

Он – гениальнейший ученый, великий посвященный философ, мудрец, основатель прославленной школы пифагорейцев и духовный учитель целого ряда выдающихся философов с мировым именем. Пифагор стал родоначальником учений о Числах, Музыке небесных сфер и Космосе, создал основу монадологии и квантовой теории строения материи. Он сделал открытия огромной важности в области таких наук, как математика, музыка, оптика, геометрия, астрономия, теория чисел, теория суперструн (Земного монохорда), психология, педагогика, этика.

Свою философию Пифагор развивал на основе знаний законов взаимосвязей видимого и невидимого мира, единства духа и материи, на понятии бессмертия души и ее постепенного очищения через переселение (теория инкарнации). Множество легенд связано с именем Пифагора, а его ученики смогли завоевать себе славу и стали выдающимися людьми, благодаря трудам которых нам стали известны основы учения Пифагора, его высказывания, практические и этические советы, а также теоретические постулаты и духовные сказки Пифагора.

Возможно, не каждый из нас сможет вспомнить теорему Пифагора, но присказку «Пифагоровы штаны на все стороны равны» знают все. Пифагор, кроме всего прочего, был довольно хитрым человеком. Всех своих учеников — пифагорейцев, великий ученый научил простой тактике, которая была очень выгодна для него: сделал открытия – припиши их своему учителю. Может быть, это довольно спорное суждение, но именно благодаря своим ученикам за Пифагором числится действительно невероятное количество открытий:

— В геометрии: знаменитая и любимая всеми теорема Пифагора, а также построение отдельных многогранников и многоугольников.

— В географии и астрономии: одним из первых выразил гипотезу, что Земля круглая, а также считал, что мы не одиноки во Вселенной.

— В музыке: определил, что звук зависит от длины флейты или струны.

— В нумерологии: в наше время нумерология стала известной и довольно популярной, но именно Пифагор совместил числа с прогнозами на будущее.

Пифагор учил, что как начало, так и конец всего существующего заключается в определенной абстрактной величине, так называемой Монадой. Она представляет собой непознаваемую абсолютную пустоту, хаос, прародину всех богов и вместе с тем вмещает в себя полноту бытия в форме божественного Света. Монада, как эфир, пронизывает все вещи, однако не находится в какой-то одной из них. Это – сумма всех чисел, которая рассматривается всегда как неделимое целое, как единица.

Пифагорейцы изображали Монаду фигурой, которая состоит из десяти точек – так называемых узлов. Все эти десять узлов, названных пифагорейцами тетрактисом, между собой создают девять равносторонних треугольников, которые олицетворяют всю полноту всеобщей пустоты и Крест Животворящий.

Считается также, что Пифагор создал основы планиметрии, ввел широкое и обязательное использование доказательств в геометрии, создал учение о подобии.

Все эти открытия Пифагор сделал более двух с половиной тысячелетий назад! Открытия Пифагора, как и его верных учеников, живут и будут жить в будущем.

История теоремы Пифагора

Великие открытия Пифагора-математика нашли свое применение в разные времена и по всему миру. В наибольшей степени это касается теоремы Пифагора.

Например, в Китае особое внимание в этом плане следует обратить на математическую книгу Чу-пей, в которой так сказано об известном пифагоровом треугольнике, имеющем стороны 3, 4, 5: «Если разложить прямой угол на составные части, тогда соединяющая концы всех его сторон линия, будет 5, тогда как основание будет 3 и высота 4». Эта же книга демонстрирует рисунок, который аналогичен одному из чертежей в индусской геометрии Басхары.

Выдающийся немецкий исследователь истории математики Кантор считает, что равенство Пифагора 3?+4?=5? знали уже в Египте приблизительно в 2300 годах до н. э., в период правления царя Аменемхета I (в соответствии с папирусом 6619 Берлинского музея). Как считает Кантор, гарпедонапты, или так называемые «натягиватели веревок», прямые углы строили с помощью прямоугольных треугольников, стороны которых были — 3, 4, 5. Их способ построения довольно легко воспроизводится. Если взять кусок веревки длиной 12 м, привязать к нему цветные полоски – одну на трехметровом расстоянии от одного конца, а другую в 4 метрах от другого, то прямой угол будет заключен между двумя сторонами — 3 и 4 метра. Можно возразить гарпедонаптам, что такой способ построения будет лишним, если взять, к примеру, деревянный треугольник, которым пользуются все плотники. Действительно существуют египетские рисунки, например, с изображением столярной мастерской, на которых встречается такой инструмент. Но тем не менее, факт остается фактом и пифагоров треугольник использовался еще в древнем Египте.

Немногим больше сведений есть о теореме Пифагора, применяемой у вавилонян. В найденном тексте, который относят к временам Хаммураби, а это 2000 год до н. э., есть приблизительное определение гипотенузы прямоугольного треугольника. Следовательно, это подтверждает, что в Двуречье уже производили вычисления со сторонами прямоугольных треугольников, хотя бы в некоторых случаях. Математик Ван-дер-Варден из Голландии, с одной стороны, используя сегодняшний уровень знаний о вавилонской и египетской математике, и с другой, основываясь на тщательном изучении греческих источников, пришел к таким выводам: «Заслуга первых греческих математиков: Фалеса, Пифагора и пифагорейцев – не открытие математики, а ее обоснование и систематизация. Основанные на расплывчатых представлениях вычислительные рецепты они смогли превратить в точную науку».

У индусов, наряду с вавилонянами и египтянами, геометрия тесно связывалась с культом. Вполне возможно, что теорема Пифагора в Индии была известна уже в 18 веке до н. э.

«Перечень математиков», который предположительно составил Евдем, говорит о Пифагоре так: «Как сообщают, занятие данной отраслью знания (геометрией) Пифагор превратил в настоящую науку, проанализировав ее основы с высочайшей точки зрения и исследовав ее теории более умственным и менее материальным образом».

Дерево Пифагора

Дерево Пифагора — один из видов фрактала, который основан на фигуре, известной под именем «Пифагоровы штаны».

Доказывая свою знаменитую теорему, Пифагор построил фигуру, в которой на каждой стороне прямоугольного треугольника были расположены квадраты. Спустя время эта фигура Пифагора превратилась в целое дерево. Первым дерево Пифагора построил в период второй мировой войны А. Босман, пользуясь обычной чертежной линейкой.

Одним из основных свойств дерева Пифагора считается то, что когда площадь первого квадрата составляет единицу, то на каждом из уровней сумма площадей квадратов также будет равна единице. Классическое дерево Пифагора имеет угол, равный 45 градусам, но также можно построить обобщённое дерево Пифагора, используя другие углы. Такое дерево называют обдуваемым ветром деревом Пифагора. Если изобразить только отрезки, которые соединяют каким-либо образом определенные «центры» треугольников, тогда получится обнаженное дерево Пифагора.

Дерево Пифагора — это фрактал, сгенерированный следующим образом:

• Начните с единичного квадрата. Затем, выбрав одну из его сторон, как основание (в анимации нижняя сторона является основанием):

• Постройте прямоугольный треугольник на противоположной основанию стороне с гипотенузой, совпадающей с этой стороной, и отношением сторон 3:4:5. Заметьте, что меньший катет должен быть справа относительно основания (см. анимацию).

• На каждом катете прямоугольного треугольника постройте квадрат со стороной, совпадающей с этим катетом.

• Повторите это процедуру для обоих квадратов, считая за основания их стороны, касающиеся треугольника.

• Фигура, получившаяся после бесконечного числа итераций, является деревом Пифагора.

Презентация к уроку по геометрии (8 класс) на тему: Теорема Пифагора

Слайд 1

ТЕОРЕМА ПИФАГОРА Автор урока: Гапонова Марина Александровна, учитель математики МОУ «Средняя школа №9» г.Петрозаводск. Республика Карелия -2015-

Слайд 2

«Геометрия обладает двумя великими сокровищами. Первое – это теорема Пифагора…»

Слайд 3

НЕОБХОДИМО ВЫЯСНИТЬ: кто такой Пифагор; в чём заключается теорема Пифагора; доказать теорему; показать практическое применение; показать задачи, используемые в экзамене по данной теме.

Слайд 4

ЦЕЛИ: овладение необходимыми знаниями и умениями по теме урока; воспитание серьёзного отношения к геометрии, понимание значимости предмета ; развитие умения использовать разнообразные источники информации; воспитание познавательного интереса в изучении геометрии; развитие логического мышления.

Слайд 5

ЗАДАЧИ: познакомиться с теоремой Пифагора, её доказательством, историей её создания, биографией Пифагора; показать применение теоремы в ходе решения задач; расширить круг задач, используемых на уроках геометрии; отработать умение делать выводы; формировать учебно-познавательные действия; развивать умение работать в коллективе, парами и самостоятельно.

Слайд 6

ПОРЯДОК РАБОТЫ: цели, задачи; разделение на команды для соревнования; история Пифагора и его теоремы; формулировка теоремы; разные способы её доказательства; применение теоремы в задачах; рефлексия; домашнее задание.

Слайд 7

КОМАНДЫ: 1 ряд 2 ряд 3 ряд «Историки» «Теоретики» «Практики»

Слайд 8

ИСТОРИЯ О ПИФАГОРЕ: Пифагор родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море, поэтому его называют Пифагором Самосским. Его отец был резчиком по камню. Ещё в детстве Пифагор проявлял незаурядные способности, и когда подрос, воображению юноши стало тесно на маленьком острове.

Слайд 9

Пифагор перебрался в г. Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет. Когда Пифагор постиг науку египетских жрецов, то отправился домой, чтобы там создать свою школу. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками.

Слайд 10

ИСТОРИЯ ТЕОРЕМЫ: Изучение вавилонских клинописных таблиц и древних китайских рукописей показало, что это утверждение было известно задолго до Пифагора. Заслуга же Пифагора состояла в том, что он открыл доказательство этой теоремы. Согласно одной из легенд, знаменитую теорему Пифагор добыл как выигрыш с неизвестным математиком. Тот отдал свиток с теоремой Пифагору и сказал, что человек, который владеет этим свитком, будет известным не одно тысячелетие…

Слайд 11

Теорему называли «мостом ослов», так как слабые ученики, заучивающие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста .

Слайд 12

ПОВТОРЕНИЕ: 1)Определите вид треугольника. 2)Назовите катеты и гипотенузу данного треугольника. 3)Как найти площадь Δ АВС? 4)Как найти площадь квадрата? С А В

Слайд 13

ПРАКТИЧЕСКАЯ РАБОТА: Постройте прямоугольный треугольник, катеты которого выражаются целыми числами; Измерьте катеты и гипотенузу, результаты запишите в тетрадь; Возведите все величины в квадрат и запишите: a 2 ; b 2 ; c 2 ; Сложите квадраты катетов а 2 + b 2 Получилось ли, что a 2 + b 2 = c 2 ?

Слайд 14

ТЕОРЕМА ПИФАГОРА В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. с 2 = а 2 + b 2

Слайд 15

ДОКАЗАТЕЛЬСТВО: 1)Достроим прямоугольник до квадрата со стороной a + b. 2)Площадь квадрата равна ( а + b )² 3)С другой стороны квадрат составлен из четырёх равных прямоугольных треугольников с площадью ½ а b и квадрата, площади с² 4) S= 4 *1/2 ab + с 2 = 2bc + с 2 . (а+ b) 2 =2 ab + с 2 . с 2 = а 2 + b 2 .

Слайд 16

Пифагоровы штаны во все стороны равны

Слайд 17

ТЕОРЕМА, ОБРАТНАЯ К ТЕОРЕМЕ ПИФАГОРА: позволяет проверить, является ли тот или иной треугольник прямоугольным. Этим пользовались землемеры и строители Древнего Египта: они размечали прямые углы с помощью веревки, разделенной узлами на 12 равных кусков; прямоугольный треугольник со сторонами 3, 4, 5 называется «египетским», а тройки ( a, b, c ) натуральных чисел, удовлетворяющие уравнению c 2 = a 2 + b 2 , т. е. служащие длинами сторон прямоугольных треугольников, Пифагоровыми.

Слайд 18

НЕКОТОРЫЕ ПИФАГОРОВЫ ТРОЙКИ: (3,4,5), (6,8,10), (5,12,13), (9,12,15), (8,15,17), (12,16,20), (15,20,25), (7,24,25), (10,24,26), (20,21,29), (18,24,30),(10,30,34), (21,28,35), (12,35,37), (15,36,39), (24,32,40), (9,40,41), (27,35,45), (14,48,50), (30,40,50)…

Слайд 19

ЕЩЁ ОДНА ФОРМУЛИРОВКА ТЕОРЕМЫ: Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

Слайд 20

АЛГЕБРАИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО: 1) Проведем высоту CD из вершины прямого угла С. 2) По определению косинуса угла соsА=AD/AC=AC/AB, отсюда следует AB*AD=AC 2 . 3) Аналогично соsВ=BD/BC=BC/AB, значит AB*BD=BC 2 . 4) Сложив полученные равенства почленно, получим: AC 2 +BC 2 = АВ *(AD + DB) AB 2 =AC 2 +BC 2 . С А В Д

Слайд 21

ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО: 1) Построим отрезок CD равный отрезку AB на продолжении катета AC прямоугольного треугольника ABC . Затем опустим перпендикуляр ED к отрезку AD , равный отрезку AC , соединим точки B и E . 2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников: SABED=2*AB*AC/2+BC2/2 3) Фигура ABED является трапецией, значит, её площадь равна: SABED= (DE+AB)*AD/2. 4) Если приравнять левые части найденных выражений, то получим: AB*AC+BC2/2=(DE+AB)(CD+AC)/2 AB*AC+BC2/2= (AC+AB)2/2 AB*AC+BC2/2= AC2/2+AB2/2+AB*AC BC2=AB2+AC2. Это доказательство было опубликовано в 1882 году Гэрфилдом.

Слайд 22

ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе.

Слайд 23

МОБИЛЬНАЯ СВЯЗЬ Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.) Решение: Пусть AB= x , BC=R=200 км , OC= r =6380 км. OB=OA+AB OB=r + x. Используя теорему Пифагора, получим ответ: 2,3 км.

Слайд 24

ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА Теорему Пифагора широко применяют и в строительстве, при вычислении размеров крыши, построении окон, используется в большинстве архитектурных сооружений. В астрономии используют для вычисления расстояний.

Слайд 25

ИНТЕРЕСНОЕ О ПИФАГОРЕ: Пифагор – это на самом деле прозвище, а не имя (Пифагор — «убеждающий речью»). Увлекался спортом, побеждал в кулачном бою на Олимпийских играх. Придумал специальную кружку, которая заставляла пить только в ограниченных количествах. Сегодня она продается на Родосе, Самосе и Крите как сувенир. Пифагор считал, что нельзя употреблять пищу животного происхождения. Он верил, что в животных переселяются души людей.

Слайд 26

ВАЖНЫЕ ОТКРЫТИЯ, СВЯЗАННЫЕ С ИМЕНЕМ ПИФАГОРА: в географии и астрономии – представление о том, что Земля – шар и что существуют другие, похожие на неё миры; в музыке – зависимость между длиной струны арфы и звуком, который она издаёт; в геометрии – построение правильных многоугольников (один из них пятиконечная звезда – стал символом пифагорейцев).

Слайд 27

Если дан нам треугольник И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдём: Катеты в квадрат возводим, Сумму степеней находим – И таким простым путём К результату мы придём.

Слайд 28

Не знаю, чем кончу поэму, И как мне печаль избыть: Древнейшую теорему Никак я не в силах забыть. Стоит треугольник как ментор, И угол прямой в нём есть, И всем его элементам Повсюду слава и честь! Вебер

Слайд 29

ИТОГОВЫЙ КОНТРОЛЬ Выбрать задачу и решить её Задачи для проверки Задачи из открытого банка заданий к экзамену

Слайд 30

РЕФЛЕКСИЯ: На ваших карточках дорисуйте снеговика: Я пришёл на урок с таким настроением Я присутствовал на уроке с таким настроением Я ухожу с урока с таким настроением

Слайд 31

ДОМАШНЕЕ ЗАДАНИЕ НА ВЫБОР: найти другой способ доказательства теоремы Пифагора; найти пифагоровы тройки; придумать свою задачу на применение теоремы Пифагора; найти задачи из базы задач по геометрии с сайта fipi .

Слайд 32

«Не гоняйся за счастьем: оно всегда находится в тебе самом». Пифагор.

Слайд 33

ЛИТЕРАТУРА: Л.С. Атанасян учебник «Геометрия 7-9» Москва «Просвещение» 2009 г. Е.М. Рабинович «Задачи и упражнения на готовых чертежах». Волошинов А.В. «Математика и искусство». — М.: «Просвещение» 2000. Волошинов А.В. «Пифагор». — М.: «Просвещение» 2001. Литцман В. «Теорема Пифагора». — М.: «Государственное издательство физико-математической литературы» 2000. Глейзер И. «История математики в школе». Чистяков В.Д. «Старинные задачи по элементарной математике»

Слайд 34

РЕСУРСЫ ИНТЕРНЕТ http://encyklopedia.narod.ru/bios/nauka/pifagor/pifagor.html http://fevt.ru/load/prezentacii_powerpoint/teorema_pifagora_prezentacija/110-1-0-967 http://volna.org/geometrija/tieoriema_pifaghora.html http://prezentacii.com/matematike/9566-teorema-pifagora-i-ee-primenenie.html http://video.promail.kz/video/226022 http://moypifagor.narod.ru/media.htm

Методическая разработка по геометрии (8 класс) по теме: Учебный проект по теме «Теорема Пифагора», геометрия 8 класс

Визитная карточка проекта

Тема проекта:          Теорема Пифагора

Творческое название:  «Для тех, кому интересно»

Основополагающий вопрос: Справедливо ли некоторые правила и законы названы именами учёных?

Проблемный вопрос: Почему теорема Пифагора        называется          теоремой Пифагора?

© Автор:          Варганова Любовь Юрьевна

Типология проекта:    информационный, предметный,  внутришкольный, групповой, средней продолжительности с открытой координацией.

Категория учащихся:          Участвуют учащиеся 8-х классов.

 

Предметная область:            математика

Аннотация:        «И ныне теорема Пифагора

                                  Верна, как и в его далёкий век.»

                                                        Шамиссо

                Закон Архимеда, теорема Пифагора… Почему некоторые правила называют именами учёных? Справедливы ли такие названия? Почему теорему Пифагора назвали теоремой Пифагора?

                Пифагор – едва ли не самый популярный учёный за всю историю человечества. Трудно найти человека, который бы не знал теорему Пифагора. Теорема Пифагора – одна из важнейших теорем геометрии, она имеет богатую историю. Но познакомится с историей теоремы, фактами из жизни Пифагора, другими доказательствами теоремы  на уроках нет возможности из-за недостатка времени, а материал этот интересен учащимся. Поэтому я предлагаю им поучаствовать в этом проекте.

В результате реализации проекта учащиеся получат следующие приращения:

1. Познакомятся с биографией Пифагора;
2. Узнают историю развития теоремы Пифагора;
3. Получат представление о различных доказательствах теоремы Пифагора и сферах её применения;
4. Научатся представлять результаты своей работы с помощью компьютера.

Ребята узнают некоторые тайны истории, и найдут ответ на вопрос «Почему теорема Пифагора называется теоремой Пифагора?»

Участники проекта:                 учащиеся 8-х классов.

Проект реализуется в ходе изучения темы «Теорема Пифагора».      (ноябрь, 24 – декабрь, 10)

Образовательные цели:

ознакомление учащихся с историей развития теоремы Пифагора и фактами из жизни Пифагора; ознакомление с методикой построения отрезков, имеющих длину, выраженную иррациональным числом

Развивающие цели:

развитие познавательного интереса учащихся; развитие умения работать с информационными ресурсами; развитие самостоятельности в работе с литературой, в подборе материала по данной теме.

Воспитательные цели:

развитие умения преодолевать трудности; развитие коммуникативных и презентационных умений и навыков; развитие умения взаимодействовать в группе.

Учебные вопросы темы:

1. Кто такой Пифагор?
2. Можно ли доказать теорему Пифагора другими способами (в отличие от учебника)?
3. Зачем нужна теорема Пифагора?

Темы исследований учащихся

1. Жизнь Пифагора

2. История теоремы Пифагора.

3. Применение теоремы Пифагора.

Этапы проведения проекта

Подготовительный	24.11.04	1-й урок по теме «Теорема Пифагора»
Основной	24.11- 3.12	Во внеурочное время ( в качестве дом. задания)
Презентация	10.12	Обобщающий урок по теме «Теорема Пифагора»
Оценивание	10.12	«4», «5»; благодарности