Площадь трапеции: онлайн калькулятор, формулы, примеры решений
Трапеция — специфический вид четырехугольника, две стороны которого параллельны друг другу, а две другие — нет. Несмотря на свой оригинальный вид, трапеция находит широкое распространение в реальности, поэтому расчет площади фигуры становится актуальной задачей не только в школьных упражнениях, но и в повседневности.
Геометрия трапеции
Трапеция и трапеза — однокоренные слова, ведь название фигуры произошло от греческого слова «трапезион», которое в переводе означает «стол». В геометрическом определении трапеция — четырехугольник, у которого две стороны лежат на параллельных прямых (основания фигуры), а две другие — на непараллельных (боковые стороны). Так как у данной фигуры есть две параллельных стороны, прямоугольник и параллелограмм можно считать частными случаями трапеции. Существует несколько видов трапеций:
- разносторонняя — «классическая» трапеция с двумя непараллельными сторонами;
- равнобокая (равнобедренная) — фигура, у которой боковые стороны равны, следовательно, равны и углы основания;
- прямоугольная — четырехугольник, одна боковая сторона которого образует с основанием прямой угол.

Грубо говоря, трапецию можно представить как усеченный треугольник, вершина которого отсечена прямой, параллельной основанию. Именно поэтому разнообразие трапеций напоминает разнообразие треугольников.
Трапеция в реальности
Данная фигура встречается не только в геометрии, но и в реальности. Форму трапеции принимают такие реальные объекты, как автомобильные и обычные окна, скаты крыш, столешницы, паруса и даже юбки. Кроме того, название «трапеция» носят спортивный и цирковой снаряды, широкая мышца на спине, упражнение в конном спорте и многое другое. Такое распространение четырехугольника в реальности делает вопрос определения его площади актуальной задачей.
Площадь трапеции
Площадь геометрической фигуры — это числовая характеристика, показывающая, какая часть плоскости ограничена сторонами четырехугольника. Площадь трапеции определяется по простой формуле:
S = 0,5 (a + b) × h,
где a и b – основания фигуры, h – ее высота.
Площадь трапеции можно определить пятью способами разной степени сложности, однако в нашем онлайн-калькуляторе используется только два из них, которые оперируют:
- двумя основаниями и высотой;
- четырьмя сторонами трапеции и высотой.

Вы можете использовать любой способ в зависимости от того, какую форму имеет трапеция. Для равнобедренной вам понадобится замерить только основания и высоту, а для разносторонней или прямоугольной — все сторону и высоту. Таким образом, для определения площади фигуры вам понадобится измерить 3 или 5 параметров. Рассмотрим пару примеров.
Примеры из реальной жизни
Автомобильное окно
Сегодня в автопроме правят бал обтекаемые формы, однако в советских автомобилях в почете были строгие геометрические фигуры. Дверные окна «Жигулей» имели форму прямоугольной трапеции, поэтому инженеры вычисляли площадь стекла по стандартной формуле. Давайте определим, сколько материала понадобилось бы для застекления одного дверного окна. Стандартное окно имеет приблизительно такие размеры: a = 90 см, b = 40 см, c = 60 см, а d = 50 см. Высота окна при этом составляетh = 50 см. Введем эти данные в форму и получим результат в виде:
S = 3 250
Таким образом, приблизительная площадь дверного окна «Жигулей» составляет 3 250 квадратных сантиметров или 0,325 квадратных метров.
Лисель
Лисель — это дополнительный парус в форме трапеции, который ставится с внешней стороны прямого паруса. Несмотря на то, что на современных судах лиселя уже не устанавливаются, мы можем подсчитать размер ткани, который понадобится нам для изготовления такого паруса. Допустим, размеры лиселя составляют a = 120 см, b = 100 см, h = 80 см. Используем эта данные для расчетов и получим
S = 8 800
Следовательно, площадь лиселя составляет 8 800 квадратных сантиметров или 0,880 квадратных метров.
Заключение
Трапеция — специфический четырехугольник, тем не менее, он широко распространен в повседневной жизни. Чаще всего с трапециями имеют дело инженеры и проектировщики, которые рассчитывают площади трапециевидных фигур при создании тех или иных изделий. Используйте наш сборник онлайн-калькуляторов для вычисления параметров любых плоских фигур или объемных тел.
Трапеция
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях.
 Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен. Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие;
— прямоугольные
.Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.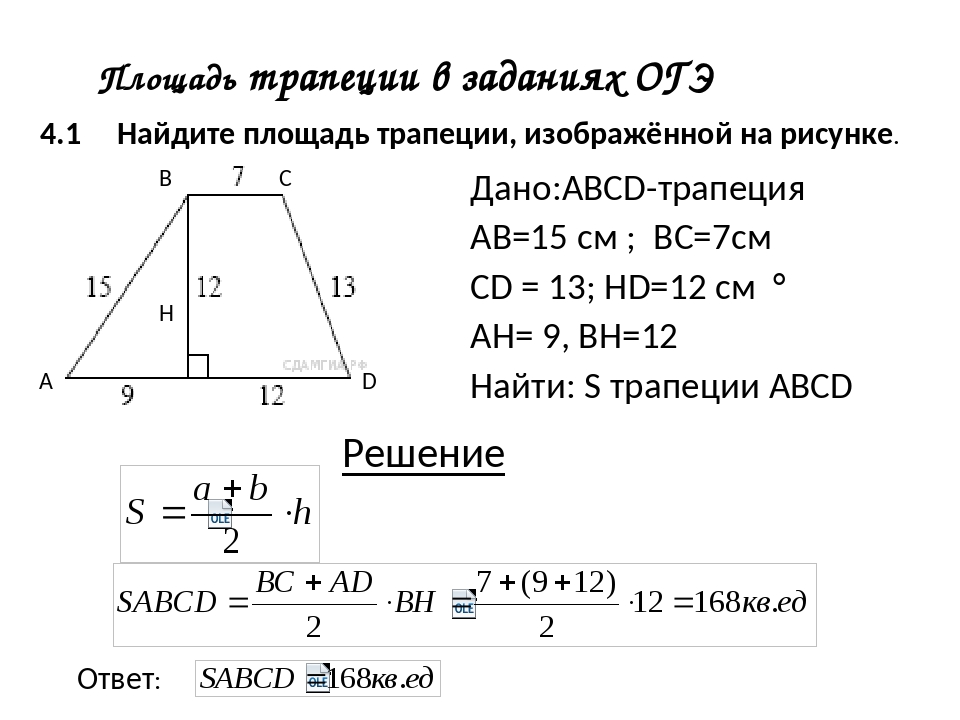
У равнобокой трапеции боковые стороны равны, а основания параллельны.
У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей, равен половине разности оснований и лежит на средней линии. Его длина
- Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными.
 Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции - Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
- Отрезок, параллельный основаниям
Углы трапеции
Углы трапеции бывают острые, прямые и тупые.Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые, а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник, у которого линия сечения параллельна основанию треугольника.
Важно. Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h1h2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Площадь трапеции
где
a и b — параллельные основания трапеции
c и d — боковые стороны трапеции
m — средняя линия трапеции
r — радиус вписанной в трапецию окружности
S — площадь трапеции Содержание главы:
Ромб | Описание курса | Площадь трапеции
Как найти площадь трапеции если известны.
 Как найти площадь трапеции
Как найти площадь трапецииМноголикая трапеция… Она может быть произвольной, равнобедренной или прямоугольной. И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.
Несколько слов о трапеции и ее элементах
Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями. Большее из них — нижнее, а другое — верхнее.
Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.
Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.
Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.
Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:
- высота, то есть отрезок, перпендикулярный обоим основаниям;
- средняя линия, которая имеет своими концами середины боковых сторон.

По какой формуле вычислить площадь, если известны основания и высота?
Это выражение дается основным, потому что чаще всего можно узнать эти величины, даже когда они не даны явно. Итак, чтобы понять, как найти площадь трапеции, потребуется сложить оба основания и разделить их на два. Получившееся значение потом еще умножить на значение высоты.
Если обозначить основания буквами а 1 и а 2 , высоту — н, то формула для площади будет выглядеть так:
S = ((а 1 + а 2)/2)*н.
Формула, по которой вычисляется площадь, если даны ее высота и средняя линия
Если посмотреть внимательно на предыдущую формулу, то легко заметить, что в ней явно присутствует значение средней линии. А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:
S = l * н.
Возможность найти площадь по диагоналям
Этот способ поможет, если известен угол, образованный ими. Предположим, что диагонали обозначены буквами д 1 и д 2 , а углы между ними — α и β. Тогда формула того, как найти площадь трапеции, будет записана следующим образом:
Тогда формула того, как найти площадь трапеции, будет записана следующим образом:
S = ((д 1 * д 2)/2) * sin α.
В этом выражении можно легко заменить α на β. Результат не изменится.
Как узнать площадь, если известны все стороны фигуры?
Бывают и такие ситуации, когда в этой фигуре известны именно стороны. Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в 1 и в 2 , основание а 1 больше, чем а 2 . Тогда формула площади примет такой вид:
S = ((а 1 + а 2) / 2) * √ {в 1 2 — [(а 1 — а 2) 2 + в 1 2 — в 2 2) / (2 * (а 1 — а 2))] 2 }.
Способы вычисления площади равнобедренной трапеции
Первый связан с тем, что в нее можно вписать окружность. И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:
S = (4 * r 2) / sin γ.
Последняя общая формула, которая основана на знании всех сторон фигуры, существенно упростится за счет того, что боковые стороны имеют одинаковое значение:
S = ((а 1 + а 2) / 2) * √ {в 2 — [(а 1 — а 2) 2 / (2 * (а 1 — а 2))] 2 }.
Методы вычисления площади прямоугольной трапеции
Понятно, что подойдет любой из перечисленных для произвольной фигуры. Но иногда полезно знать об одной особенности такой трапеции. Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.
Часто формулы для трапеции забываются, в то время как выражения для площадей прямоугольника и треугольника помнятся. Тогда можно применить простой способ. Разделить трапецию на две фигуры, если она прямоугольная, или три. Одна точно будет прямоугольником, а вторая, или две оставшиеся, треугольниками. После вычисления площадей этих фигур останется их только сложить.
Это достаточно простой способ того, как найти площадь прямоугольной трапеции.
Как быть, если известны координаты вершин трапеции?
В этом случае потребуется воспользоваться выражением, которое позволяет определить расстояние между точками. Его можно применить три раза: для того, чтобы узнать оба основания и одну высоту. А потом просто применить первую формулу, которая описана немного выше.
А потом просто применить первую формулу, которая описана немного выше.
Для иллюстрации такого метода можно привести такой пример. Даны вершины с координатами А(5; 7), В(8; 7), С(10; 1), Д(1; 1). Нужно узнать площадь фигуры.
До того как найти площадь трапеции, по координатам нужно вычислить длины оснований. Потребуется такая формула:
длина отрезка = √{(разность первых координат точек) 2 + (разность вторых координат точек) 2 }.
Верхнее основание обозначено АВ, значит, его длина будет равна √{(8-5) 2 + (7-7) 2 } = √9 = 3. Нижнее — СД = √ {(10-1) 2 + (1-1) 2 } = √81 = 9.
Теперь нужно провести высоту из вершины на основание. Пусть ее начало будет в точке А. Конец отрезка окажется на нижнем основании в точке с координатами (5; 1), пусть это будет точка Н. Длина отрезка АН получится равной √{(5-5) 2 + (7-1) 2 } = √36 = 6.
Осталось только подставить получавшиеся значения в формулу площади трапеции:
S = ((3 + 9) / 2) * 6 = 36.
Задача решена без единиц измерения, потому что не указан масштаб координатной сетки.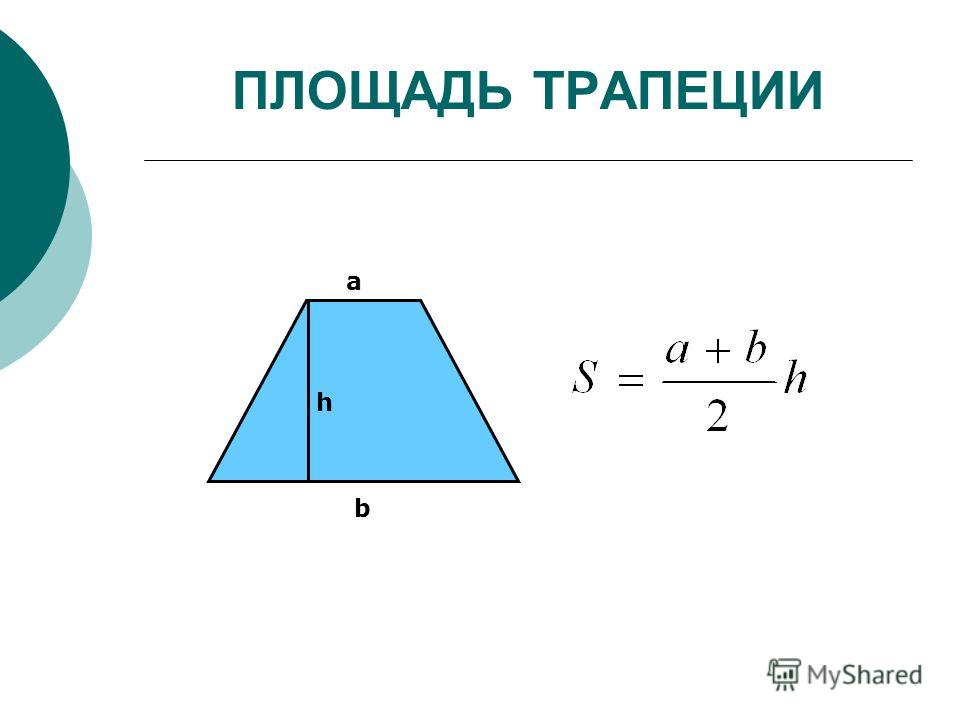 Он может быть как миллиметр, так и метр.
Он может быть как миллиметр, так и метр.
Примеры задач
№ 1. Условие. Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.
Решение. Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).
Теперь нужно воспользоваться подходящей формулой для площади:
S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (дм 2). Задача решена.
Ответ: площадь трапеции равна 4,5 дм 2 .
№ 2. Условие. В трапеции АВСД основаниями являются отрезки АД и ВС. Точка Е — середина стороны СД. Из нее проведен перпендикуляр к прямой АВ, конец этого отрезка обозначен буквой Н. Известно, что длины АВ и ЕН равны соответственно 5 и 4 см. Нужно вычислить площадь трапеции.
Решение. Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх.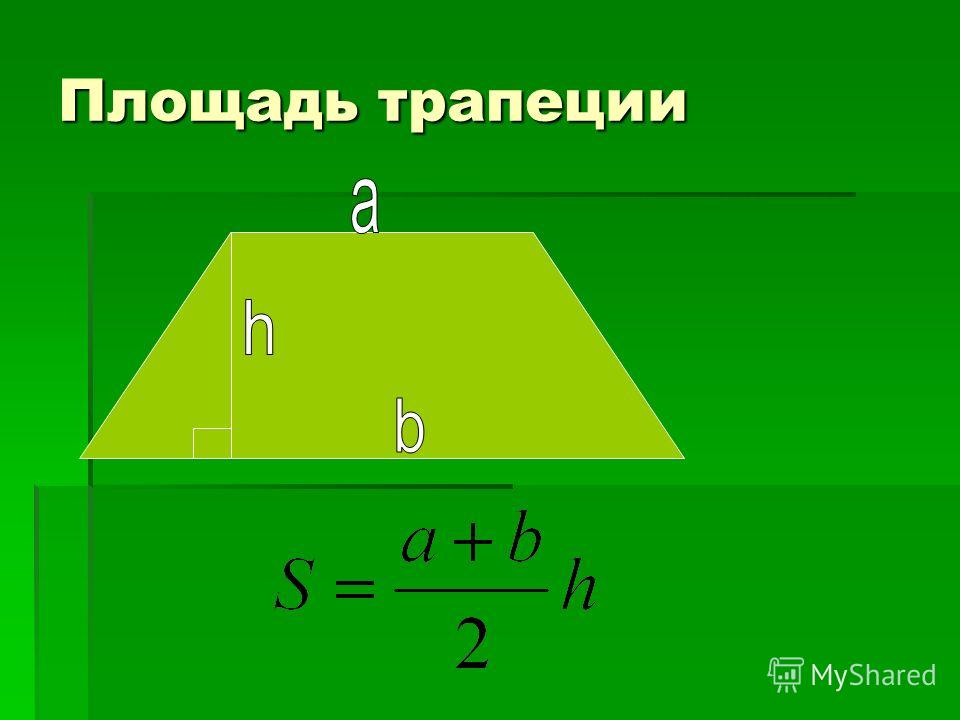
Чтобы отчетливо увидеть ход решения задачи, потребуется выполнить дополнительное построение. А именно, провести прямую, которая будет параллельна стороне АВ. Точки пересечения этой прямой с АД — Р, а с продолжением ВС — Х. Получившаяся фигура ВХРА — параллелограмм. Причем его площадь равна искомой. Это связано с тем, что треугольники, которые получились при дополнительном построении, равны. Это следует из равенства стороны и двух прилежащих к ней углов, один — вертикальный, другой — накрест лежащий.
Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.
Таким образом, площадь трапеции равна 5 * 4 = 20 см 2 .
Ответ: S = 20 см 2 .
№ 3. Условие. Элементы равнобедренной трапеции имеют такие значения: нижнее основание — 14 см, верхнее — 4 см, острый угол — 45º. Нужно вычислить ее площадь.
Решение. Пусть меньшее основание имеет обозначение ВС.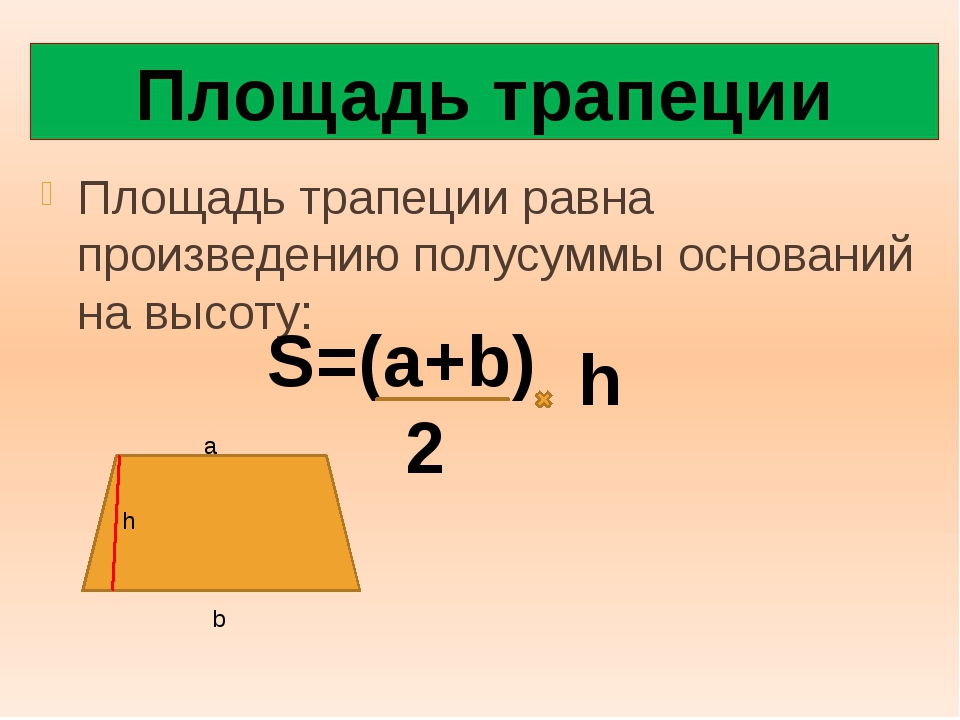 Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Высота, проведенная из точки В, будет называться ВН. Поскольку угол 45º, то треугольник АВН получится прямоугольный и равнобедренный. Значит, АН=ВН. Причем АН очень легко найти. Она равна половине разности оснований. То есть (14 — 4) / 2 = 10 / 2 = 5 (см).
Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2).
Ответ: Искомая площадь равна 45 см 2 .
№ 4. Условие. Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.
Решение. Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т; вторую через Е и точкой пересечения с АД будет М.
Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н 1 , большей АОЕД — н 2 .
Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:
(х + а 2) * н 1 = 1/5 (х + а 1) * н 2
н 1 /н 2 = (х + а 1) / (5(х + а 2)).
Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:
н 1 /н 2 = (х — а 2) / (а 1 — х).
В двух последних записях в левой части стоят равные величины, значит, можно написать, что (х + а 1) / (5(х + а 2)) равно (х — а 2) / (а 1 — х).
Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.
В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь квадратный корень.
Ответ : х = √ {(а 1 2 + 5 а 2 2) / 6}.
Что такое равнобедренная трапеция? Это геометрическая фигура, противолежащие не параллельные стороны которой равны. Существует несколько различных формул для нахождения площади трапеции с различными условиями, которые даны в задачах.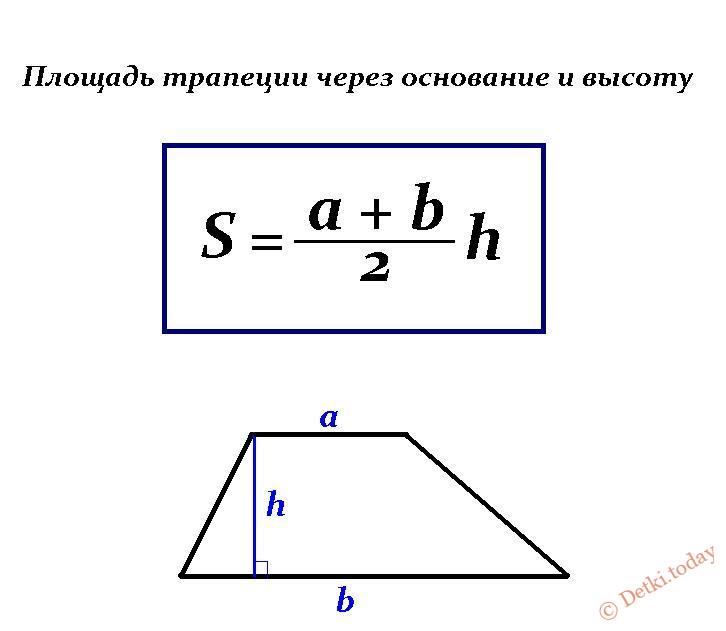 То есть площадь найти можно, если дана высота, стороны, углы, диагонали и т.д. Также нельзя не упомянуть, что для равнобедренных трапеций существует некоторые “исключение”, благодаря которым поиск площади и сама формула значительно упрощается. Ниже описаны подробные решения каждого случая с примерами.
То есть площадь найти можно, если дана высота, стороны, углы, диагонали и т.д. Также нельзя не упомянуть, что для равнобедренных трапеций существует некоторые “исключение”, благодаря которым поиск площади и сама формула значительно упрощается. Ниже описаны подробные решения каждого случая с примерами.
Необходимые свойства для нахождения площади равнобедренной трапеции
Мы уже выяснили, что геометрическая фигура, имеющая противолежащие не параллельные, но равные стороны – это трапеция, причем, равнобедренная. Существуют специальные случаи, когда трапеция считается равнобедренной.
- Это условия равенства углов. Итак, обязательный пункт: углы при основании (возьмем рисунок ниже) должны быть равны. В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD
- Второе важное правило – в подобной трапеции диагонали должны быть равны. Следовательно, АС = ВD.
- Третий аспект: противоположные углы трапеции в сумме должны давать 180 градусов. Это значит, что угол ABC + угол CDA = 180 градусов.
 С углами BCD и BAD аналогично.
С углами BCD и BAD аналогично. - В-четвертых, если трапеция допускает описание вокруг нее окружности – то она равнобедренная.
Как найти площадь равнобедренной трапеции – формулы и их описание
- S = (a+b)h/2 – это самая распространенная формула для нахождения площади, где а – нижнее основание, b – верхнее основание, а h – это высота.
- Если высота неизвестна, то искать ее можно по подобной формуле: h = с*sin(x), где с это либо AB, либо CD. sin(x) – это синус угла при любом основании, то есть угол DAB = угол CDA = x. В конечном итоге формула принимает вот такой вид: S = (a+b)*с*sin(x)/2.
- Высота также может находиться по этой формуле:
- Итоговая формула имеет такой вид:
- Площадь равнобедренной трапеции можно найти и через среднюю линию и высоту. Формула такова: S = mh .
Рассмотрим условие, когда в трапецию будет вписана окружность.
В случае, изображенном на картинке,
QN = D = H – диаметр окружности и одновременно высота трапеции;
LO, ON, OQ = R – радиусы окружности;
DC = a – верхнее основание;
AB = b – нижнее основание;
DAB, ABC, BCD, CDA – альфа, бета – углы оснований трапеции.
Подобный случай допускает нахождение площади по таким формулам:
- Теперь попробуем найти площадь через диагонали и углы между ними.
На рисунке обозначим AC, DB – диагонали – d. Углы COB, DOB – альфа; DOC, AOB – бета. Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ) такова:
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.
Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие ;
— прямоугольные
.Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У боковые стороны равны, а основания параллельны.
У основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей , равен половине разности оснований и лежит на средней линии.
 Его длина
Его длина - Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции , точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
- Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность , если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые .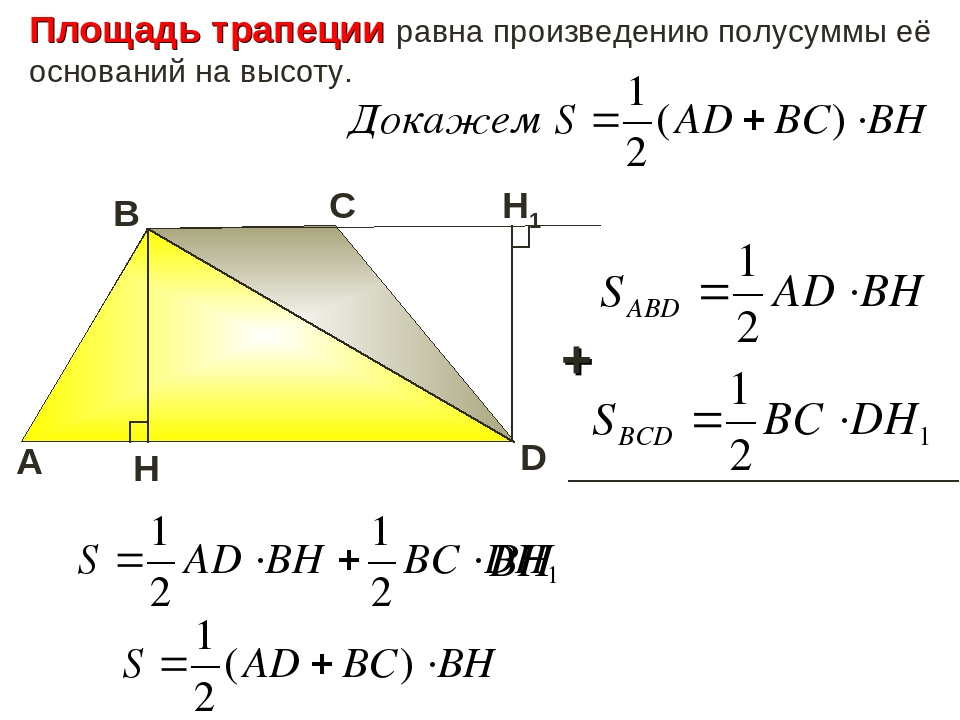
Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые , а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник , у которого линия сечения параллельна основанию треугольника.
Важно . Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h 1 h 2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.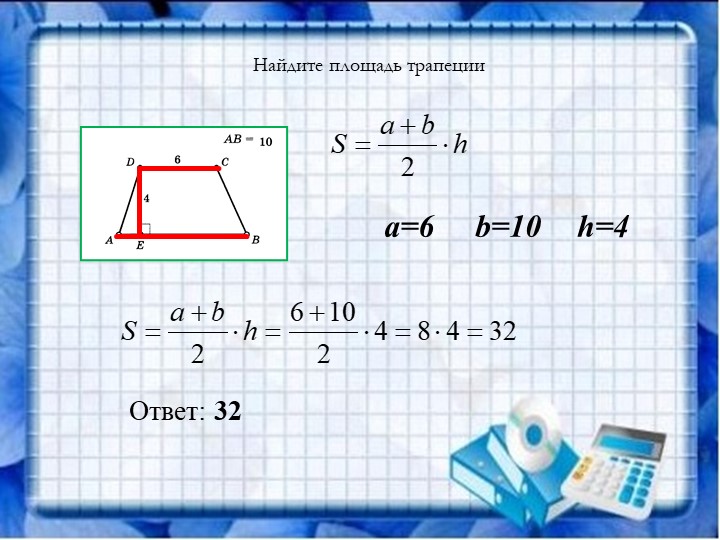
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:
найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.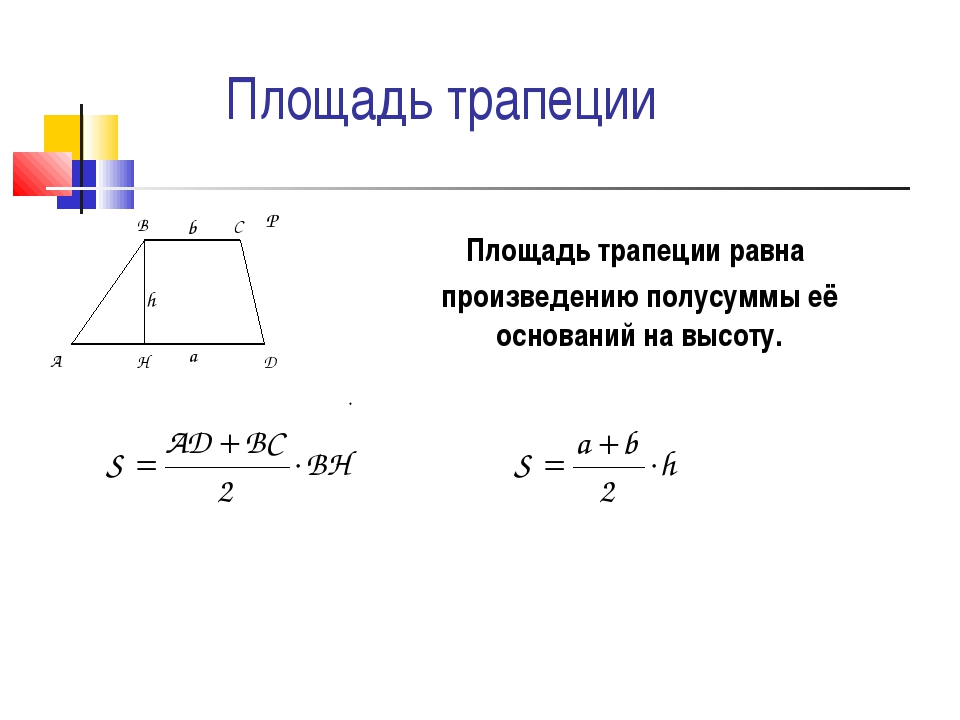
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон.
Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что треугольника равна половине параллельного ей основания, то есть:
Хорошо, разобрались. Теперь о площади трапеции.
Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
С уважением, Александр.
Как вычислить площадь трапеции по четырем сторонам. Калькулятор периметра трапеции
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого.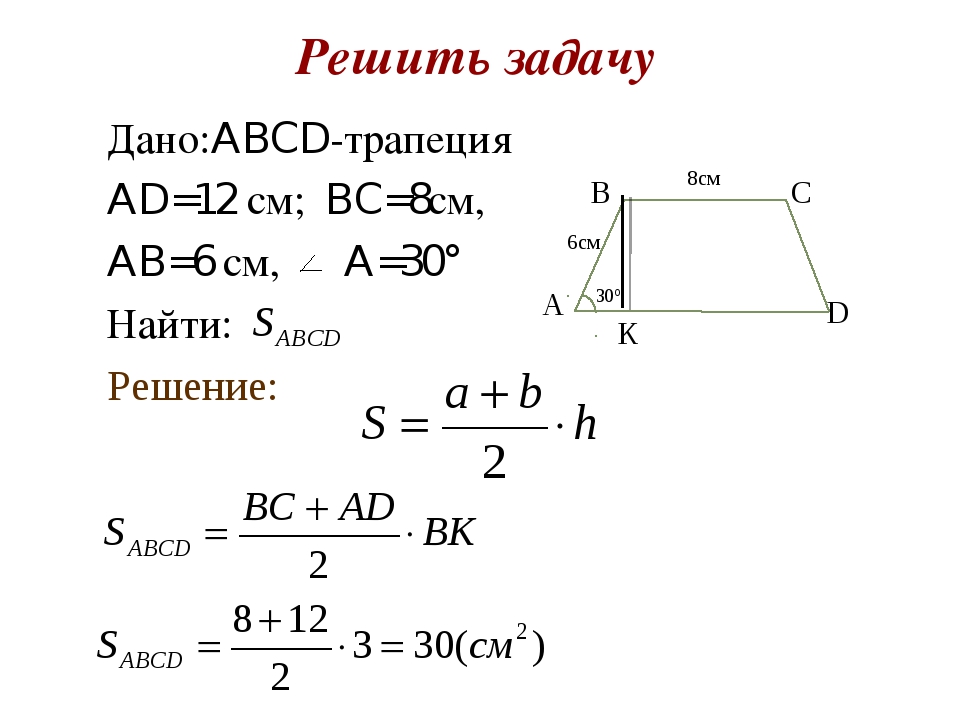 Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .
Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα . Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
Пускай хороших оценок за ЕГЭ и ГИА будет больше!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Этот калькулятор рассчитал 2192 задачи на тему «Площадь трапеции»
ПЛОЩАДЬ ТРАПЕЦИИ
Выберете формулу вычисления площади трапеции, которую Вы планируете применить для решения поставленной перед Вами задачи:
Общая теория для вычисления площади трапеции.
Трапеция — это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.
Точки называются вершинами трапеции и обозначаются заглавными латинскими буквами.
Отрезки называются сторонами трапеции и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.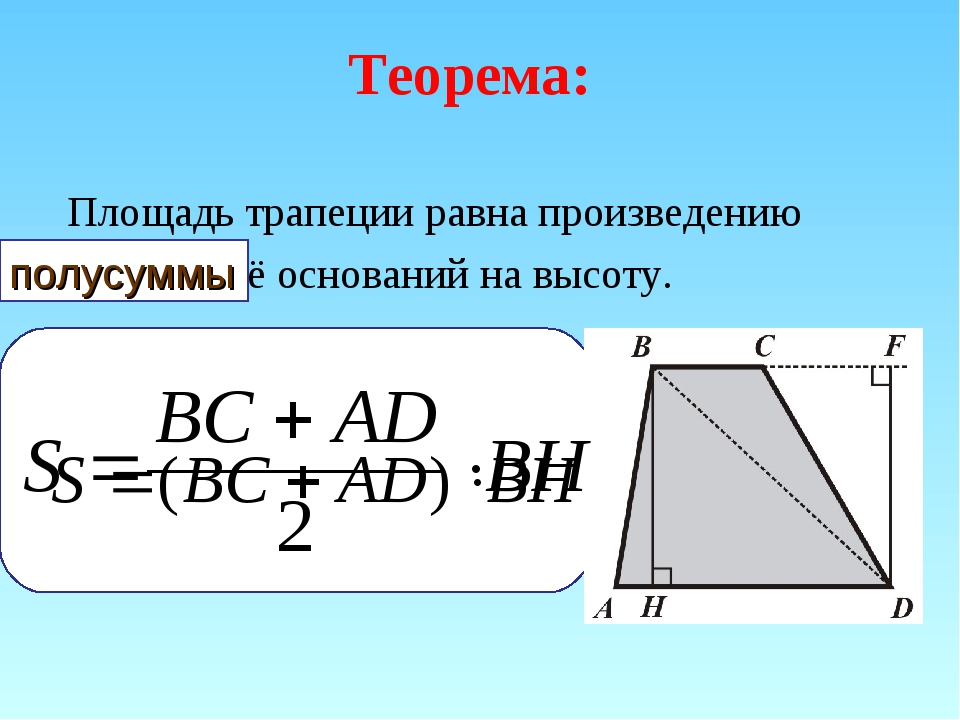
Две параллельные стороны трапеции называются основаниями трапеции .
Две не параллельные стороны трапеции называются боковыми сторонами трапеции .
Рисунок №1: Трапеция ABCD
На рисунке №1 представлена трапеция ABCD с вершинами A,B ,C, D и сторонами AB, BC, CD, DA.
AB ǁ DC — основания трапеции ABCD.
AD, BC — боковые стороны трапеции ABCD.
Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.
Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.
Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.
Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.
Рисунок №2: Трапеция ABCD
На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. То есть,.
Рисунок №3: Равнобедренная трапеция ABCD
На Рисунке №3, AD=BC.
Трапеция называется равнобедренной (равнобокой) , если ее боковые стороны равны.
Рисунок №4: Прямоугольная трапеция ABCD
На Рисунке №4 угол D — прямой (равен 90 о).
Трапеция называется прямоугольной, если угол при боковой стороне прямой.
Площадью S плоской фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.
Площадь обладает несколькими свойствами:
1. Она не может быть отрицательной.
2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.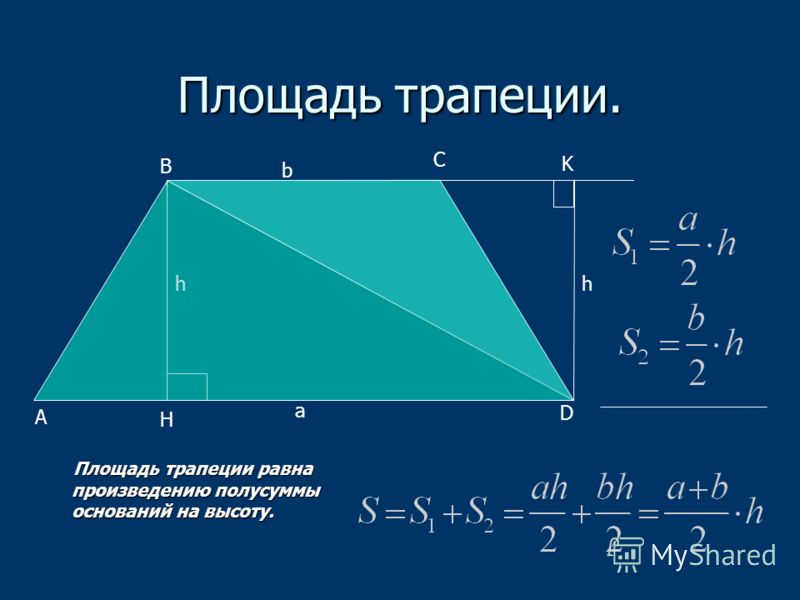
3. Если две фигуры равны, то и площади их равны.
4. Площадь квадрата, который построен на единичном отрезке, равна единице.
За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
При решении задач часто используются следующие формулы вычисления площади трапеции:
1. Площадь трапеции равна полусумме ее оснований умноженной на высоту:
2. Площадь трапеции равна произведению ее средней линии на высоту:
3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле:
4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:
Пример 1: Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.
Решение:
Ответ:
Пример 2: Найти сторону основания трапеции с площадью S=35 см 2 , высотой h=7см и вторым основанием b = 2 см.
Решение:
Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:
Выразим из данной формулы сторону основания трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 3: Найти высоту трапеции с площадью S=17 см 2 и основаниями a=30 см, b = 4 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 4: Вычислить площадь трапеции с высотой h=24 и средней линией m=5.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 5: Найти высоту трапеции с площадью S = 48 см 2 и средней линией m=6 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы высоту трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 6: Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.
Решение:
Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы среднюю линию трапеции:
Таким образом, имеем следующее.
И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.
- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.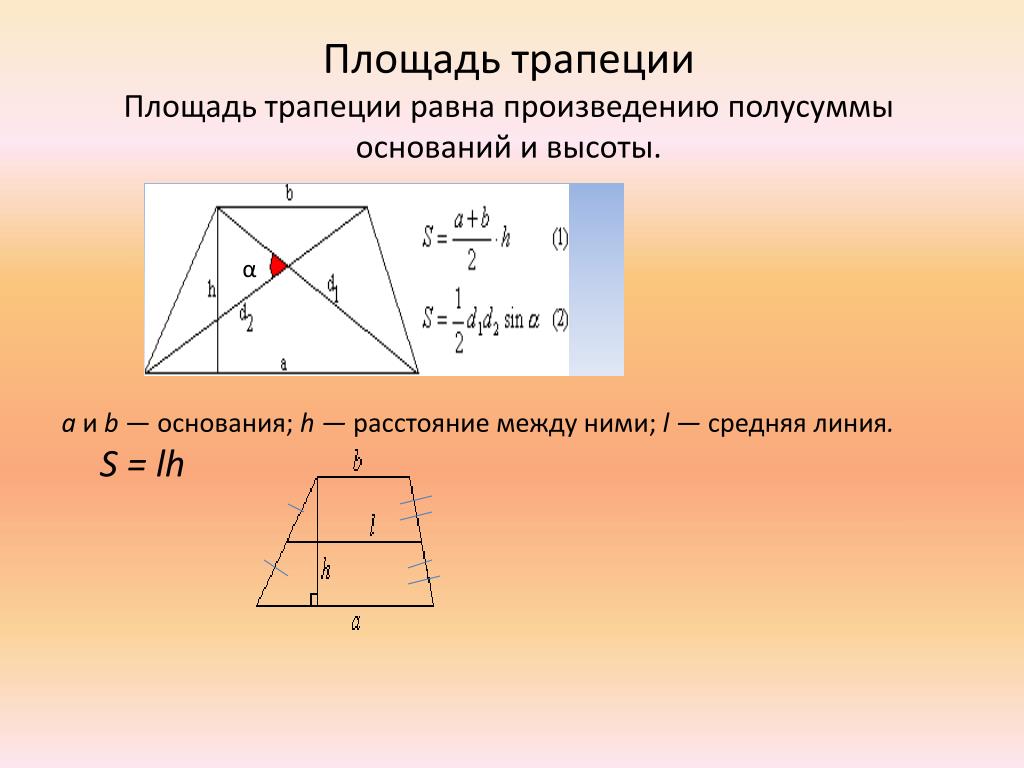
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними.
 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям.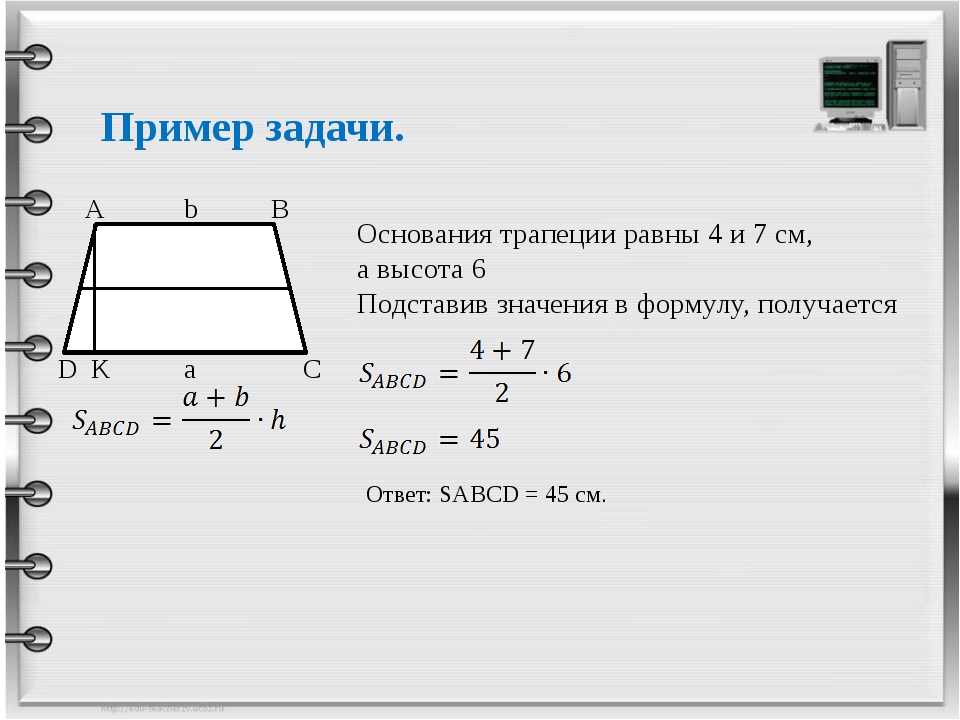 В этом случае боковая сторона по длине совпадает с высотой трапеции.
В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — отрезок, соединяющий середины боковых сторон.
Данная геометрическая фигура широко распространена в реальной жизни.
Трапеция в реальности
В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
- дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
- ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, основания зданий;
- производство — различные изделия и детали.
При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
P = a + b + c + d,
где a и c – основания фигуры, b и d – ее боковые стороны.
Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.
Примеры из реальной жизни
Платок
Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.
Откосы
К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.
Заключение
Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
Формула площади трапеции через четыре стороны. Все варианты того, как найти площадь трапеции
И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.

- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Трапеция — это особый вид четырехугольника, у которого две противолежащие стороны параллельны друг другу, а две другие — нет. Трапецеидальную форму имеют различные реальные объекты, поэтому вам может понадобиться рассчитать периметр такой геометрической фигуры для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греч. «трапезион» — стол) — это фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет. Параллельные отрезки носят название оснований трапеции, а непараллельные — боковых сторон фигуры. Боковые стороны и их углы наклона определяют вид трапеции, которая может быть разносторонней, равнобедренной или прямоугольной. Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
Помимо оснований и боковых сторон, трапеция имеет еще два элемента:
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — отрезок, соединяющий середины боковых сторон.
Данная геометрическая фигура широко распространена в реальной жизни.
Трапеция в реальности
В повседневной жизни трапецеидальную форму принимают многие реальные предметы. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
- дизайн интерьеров и декор — диваны, столешницы, стены, ковры, подвесные потолки;
- ландшафтный дизайн — границы газонов и искусственных водоемов, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, основания зданий;
- производство — различные изделия и детали.
При столь широком использовании трапеций специалистам часто приходится вычислять периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, которая рассчитывается как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
Трапеция — это четырехугольник и в общем случае все его стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
P = a + b + c + d,
где a и c – основания фигуры, b и d – ее боковые стороны.
Несмотря на то, что при вычислении периметра трапеции нам нет нужды узнавать высоту, программный код калькулятора требует ввода этой переменной. Так как высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты, которое больше нуля. Рассмотрим пару примеров.
Примеры из реальной жизни
Платок
Допустим, у вас есть платок в форме трапеции, и вы хотите отделать его бахромой. Вам понадобится узнать периметр платка, чтобы не купить лишнего материала или не ходить в магазин два раза. Пусть ваш равнобедренный платок имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Таким образом, периметр платка составляет 340 см, и именно такой длины должна быть тесьма бахромы для его отделки.
Откосы
К примеру, вы решили сделать откосы для нестандартных металлопластиковых окон, которые имеют трапецеидальную форму. Такие окна широко используются при дизайне зданий, создавая композицию из нескольких створок. Чаще всего такие окна выполняются в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для выполнения откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Используем эти данные и получим результат в виде
Следовательно, периметр трапециевидного окна составляет 390 см, и именно столько вам понадобится купить пластиковых панелей для формирования откосов.
Заключение
Трапеция — популярная в повседневности фигура, определение параметров которой может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам выполнить расчеты для любых геометрических фигур и тел.
Этот калькулятор рассчитал 2192 задачи на тему «Площадь трапеции»
ПЛОЩАДЬ ТРАПЕЦИИ
Выберете формулу вычисления площади трапеции, которую Вы планируете применить для решения поставленной перед Вами задачи:
Общая теория для вычисления площади трапеции.
Трапеция — это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.
Точки называются вершинами трапеции и обозначаются заглавными латинскими буквами.
Отрезки называются сторонами трапеции и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.
Две параллельные стороны трапеции называются основаниями трапеции .
Две не параллельные стороны трапеции называются боковыми сторонами трапеции .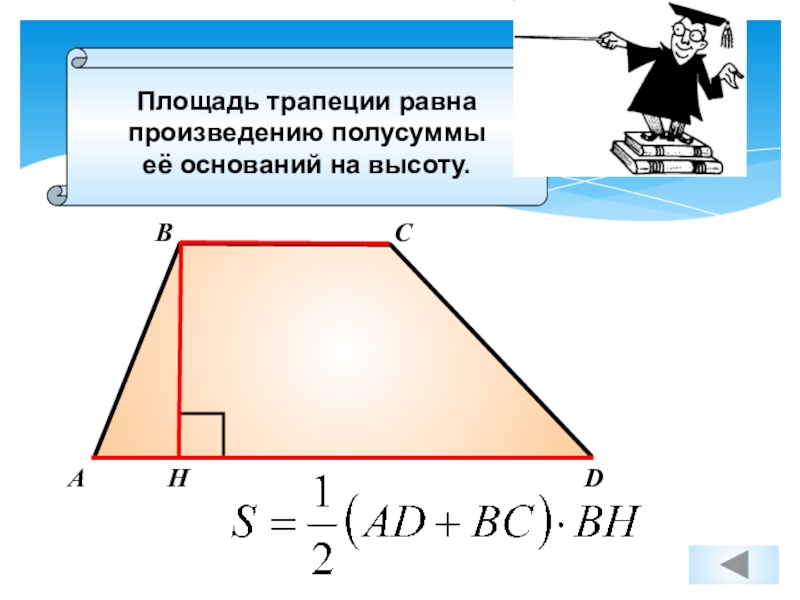
Рисунок №1: Трапеция ABCD
На рисунке №1 представлена трапеция ABCD с вершинами A,B ,C, D и сторонами AB, BC, CD, DA.
AB ǁ DC — основания трапеции ABCD.
AD, BC — боковые стороны трапеции ABCD.
Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.
Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.
Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.
Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.
Рисунок №2: Трапеция ABCD
На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. То есть,.
Рисунок №3: Равнобедренная трапеция ABCD
На Рисунке №3, AD=BC.
Трапеция называется равнобедренной (равнобокой) , если ее боковые стороны равны.
Рисунок №4: Прямоугольная трапеция ABCD
На Рисунке №4 угол D — прямой (равен 90 о).
Трапеция называется прямоугольной, если угол при боковой стороне прямой.
Площадью S плоской фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.
Площадь обладает несколькими свойствами:
1. Она не может быть отрицательной.
2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.
3. Если две фигуры равны, то и площади их равны.
4. Площадь квадрата, который построен на единичном отрезке, равна единице.
За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
При решении задач часто используются следующие формулы вычисления площади трапеции:
1. Площадь трапеции равна полусумме ее оснований умноженной на высоту:
2. Площадь трапеции равна произведению ее средней линии на высоту:
3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле:
4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:
Пример 1: Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.
Решение:
Ответ:
Пример 2: Найти сторону основания трапеции с площадью S=35 см 2 , высотой h=7см и вторым основанием b = 2 см.
Решение:
Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:
Выразим из данной формулы сторону основания трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 3: Найти высоту трапеции с площадью S=17 см 2 и основаниями a=30 см, b = 4 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 4: Вычислить площадь трапеции с высотой h=24 и средней линией m=5.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 5: Найти высоту трапеции с площадью S = 48 см 2 и средней линией m=6 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы высоту трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 6: Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.
Решение:
Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы среднюю линию трапеции:
Таким образом, имеем следующее.
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:
найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
Определяем трапецию
Что это за фигура в целом? Трапецией называют многоугольник из четырех углов с двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под различными углами. Ее параллельные стороны называют основаниями, а для непараллельных сторон применяют наименование «боковые стороны» или «бедра». Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других. Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.
Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.
Свойства трапеции
Остановимся коротко на свойствах этой фигуры. Сумма углов, прилегающих к любой боковой стороне, всегда равняется 180°. Надо заметить, что все углы трапеции в сумме составляют 360°. У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком — это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:
Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!
У трапеции всегда можно опустить высоту на основание. Высота — это перпендикуляр, часто обозначаемый символом h, который проведен из любой точки одного основания на другое основание или его продолжение. Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Самые простые формулы площади трапеции
Разберем две самые популярные и простые формулы, с помощью которых находят площадь трапеции. Достаточно умножить высоту на полусумму оснований, чтобы легко найти искомое:
S = h*(a + b)/2.
В этой формуле a, b обозначают основания трапеции, h — высоту. Для удобства восприятия в этой статье знаки умножения отмечены символом (*) в формулах, хотя в официальных справочниках знак умножения обычно опускают.
Рассмотрим пример.
Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?
Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2 = 12. Итак, полусумма равняется 12 см. Теперь полусумму умножаем на высоту: 12*7 = 84. Искомое найдено. Ответ: площадь трапеции равна 84 кв.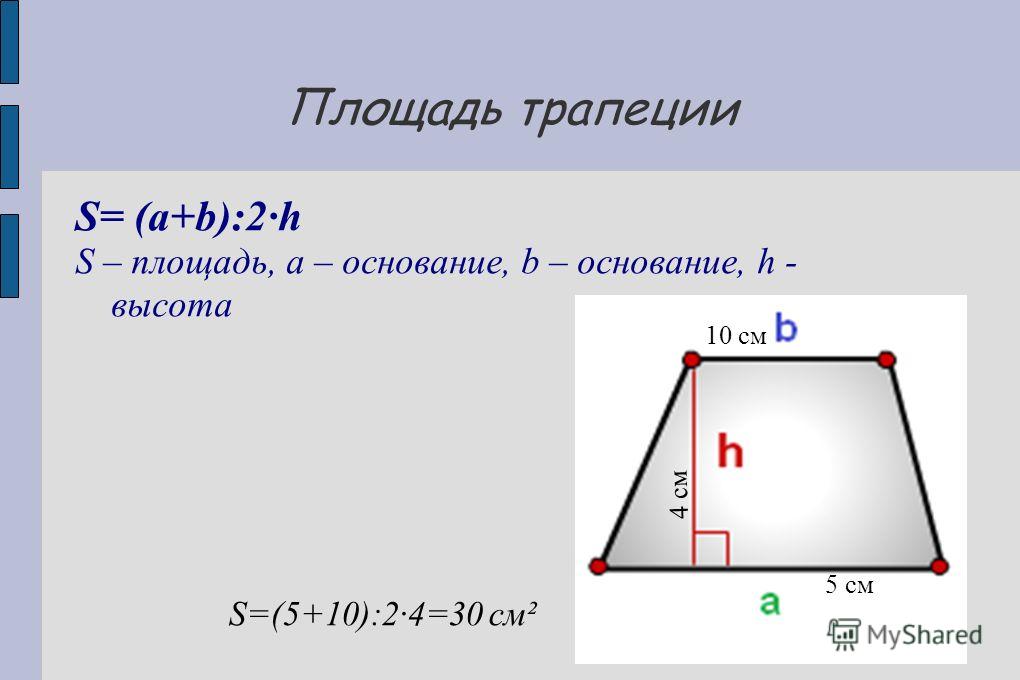 см.
см.
Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически вытекает из предшествующего понятия средней линии: S=m*h.
Использование диагоналей для вычислений
Другой способ нахождения площади трапеции на самом деле не так уж сложен. Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d 1 d 2) на синус угла между ними:
S = ½ d 1 d 2 sina.
Рассмотрим задачу, которая показывает применение этого способа. Дано: трапеция с длиной диагоналей равной соответственно 8 и 13 см. Угол a между диагоналями равняется 30°. Найти площадь трапеции.
Решение. Используя вышеприведенную формулу, легко вычислить требуемое. Как известно, sin 30° составляет 0,5. Следовательно, S = 8*13*0,5=52. Ответ: площадь равна 52 кв. см.
Ищем площадь равнобокой трапеции
Трапеция может быть равнобокой (равнобедренной). Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок. Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Какие же есть методики вычисления площади такой фигуры? Нижеприведенный способ потребует больших вычислений. Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор. Вот эта формула:
S = c *sin a *(a — c *cos a ),
где с — боковое бедро, a — угол при нижнем основании.
Равнобокая трапеция обладает диагоналями одинаковой длины. Верно и обратное утверждение: если у трапеции диагонали равны, то она является равнобедренной. Отсюда следующая формула, помогающая найти площадь трапеции — полупроизведение квадрата диагоналей на синус угла между ними: S = ½ d 2 sina.
Находим площадь прямоугольной трапеции
Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Применяем смекалку
Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.
Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.
Требуется вычислить площадь фигуры.
Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Используем формулу Пика
Напоследок приведем еще одну оригинальную формулу, помогающую искать площадь трапеции. Она называется формулой Пика. Ею удобно пользоваться, когда трапеция нарисована на клетчатой бумаге. Подобные задачи часто встречаются в материалах ГИА. Выглядит она следующим образом:
S = M/2 + N — 1,
в этой формуле M — количество узлов, т.е. пересечений линий фигуры с линиями клетки на границах трапеции (оранжевые точки на рисунке), N — количество узлов внутри фигуры (синие точки). Удобнее всего пользоваться ею при нахождении площади неправильного многоугольника. Тем не менее, чем больше арсенал используемых методик, тем меньше ошибок и лучше результаты.
Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.
Формула по нахождению площади трапеции. Как найти площадь равнобедренной трапеции
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.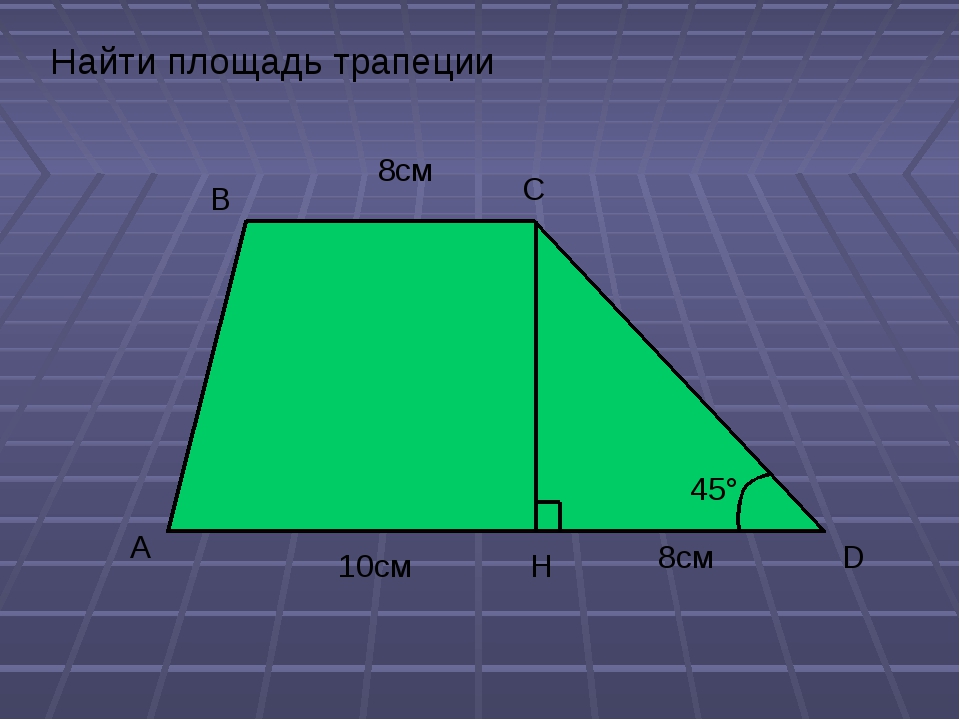
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что треугольника равна половине параллельного ей основания, то есть:
Хорошо, разобрались. Теперь о площади трапеции.
Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
С уважением, Александр.
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см. найдем площадь фигуры:
найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие ;
— прямоугольные
.Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У боковые стороны равны, а основания параллельны.
У основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей , равен половине разности оснований и лежит на средней линии. Его длина
- Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции , точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
- Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность , если сумма длин оснований трапеции равна сумме длин её боковых сторон.
 Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований) - Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые .Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые , а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник , у которого линия сечения параллельна основанию треугольника.
Важно . Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h 1 h 2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b).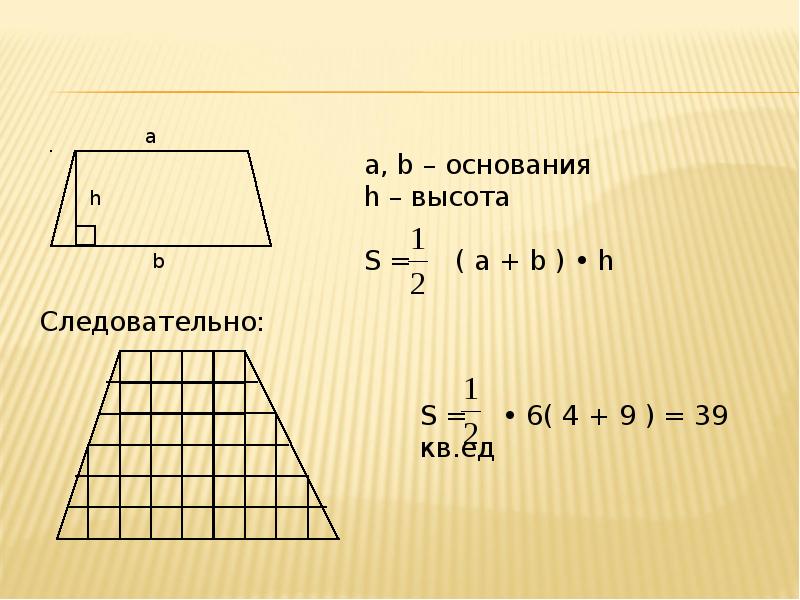 Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.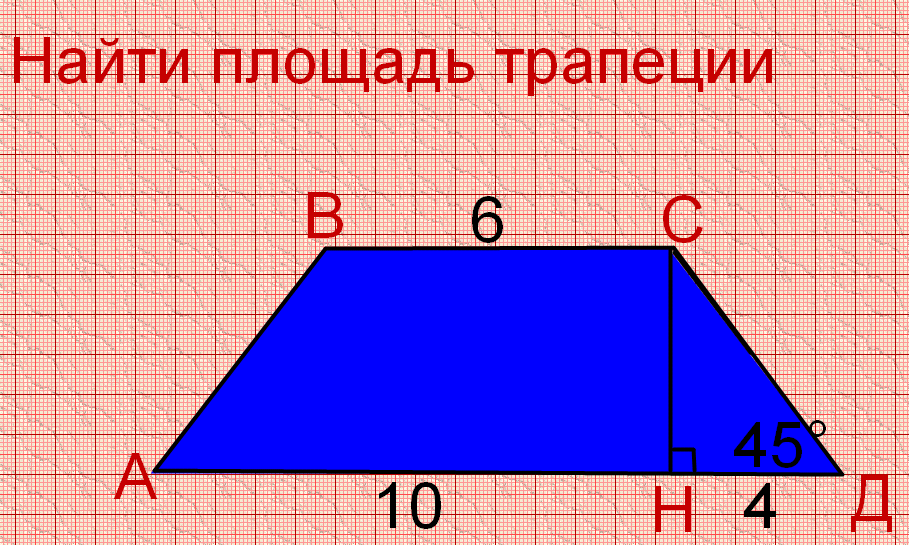
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα . Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b).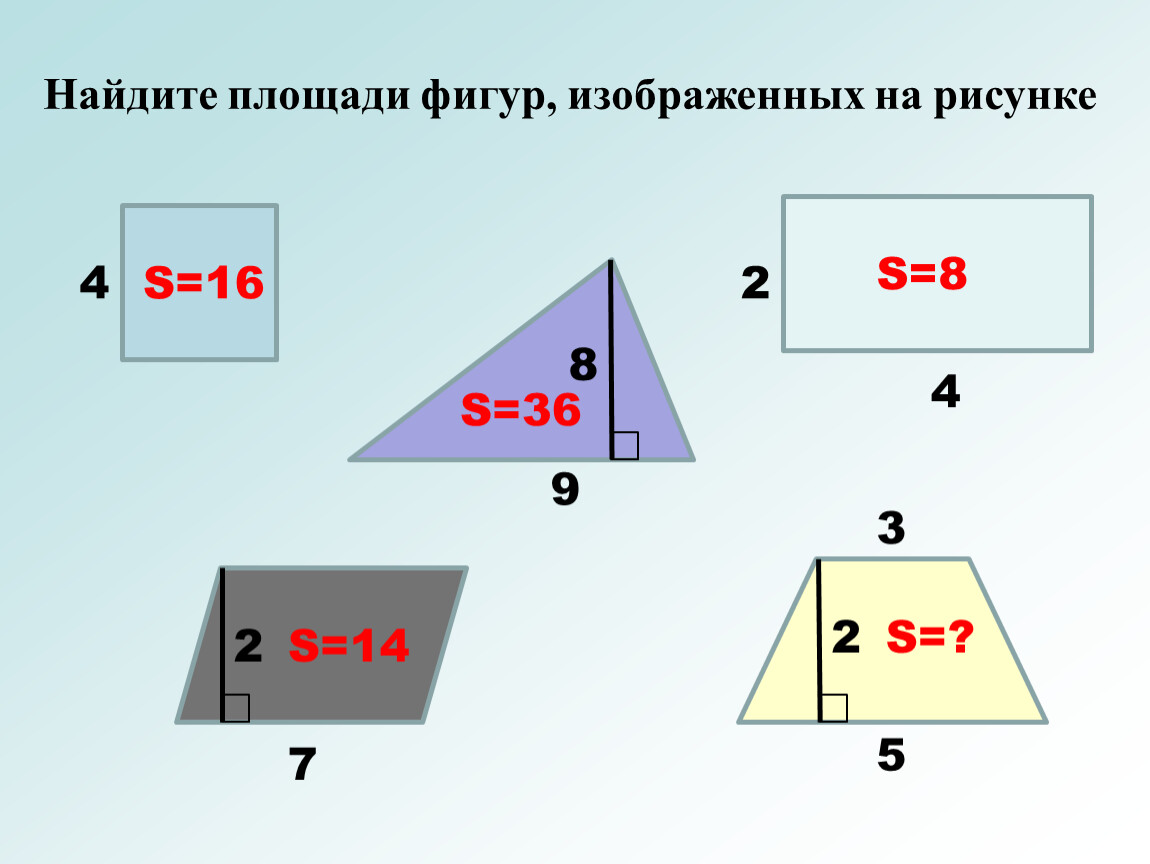 Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции.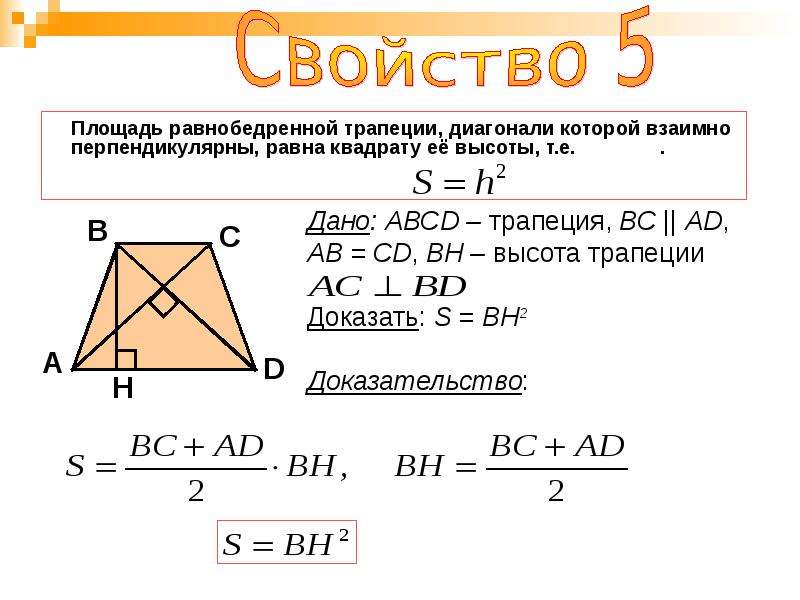 Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
blog.сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.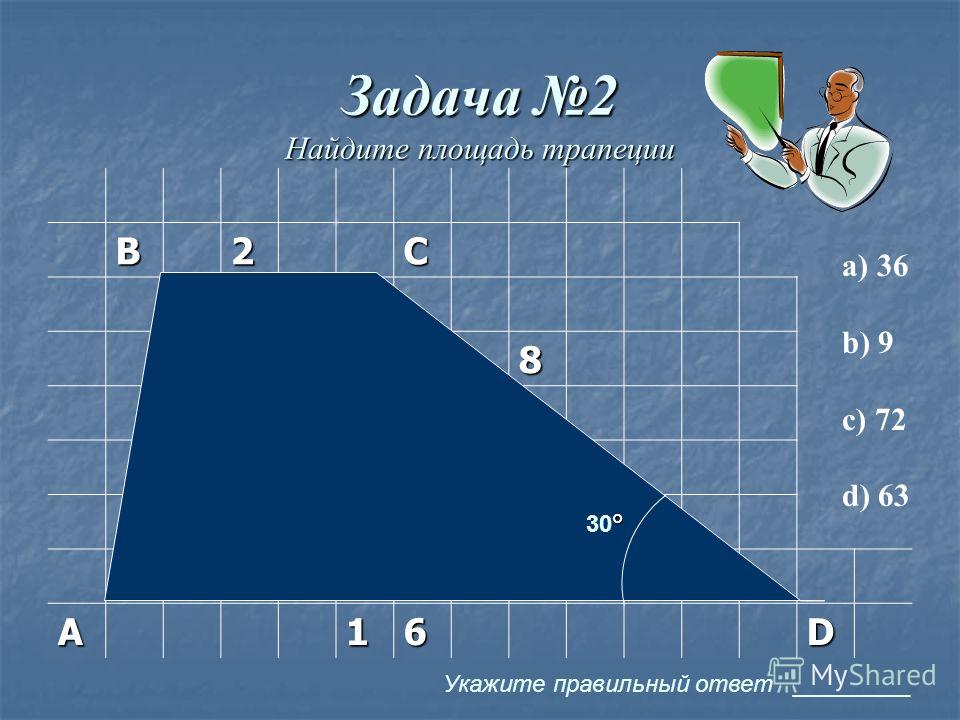
Как найти площадь трапеции формула 8. Как найти площадь трапеции: формулы и примеры
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие ;
— прямоугольные
.Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У боковые стороны равны, а основания параллельны.
У основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей , равен половине разности оснований и лежит на средней линии. Его длина
- Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции , точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
- Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность , если сумма длин оснований трапеции равна сумме длин её боковых сторон.
 Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований) - Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые .Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые , а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник , у которого линия сечения параллельна основанию треугольника.
Важно . Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.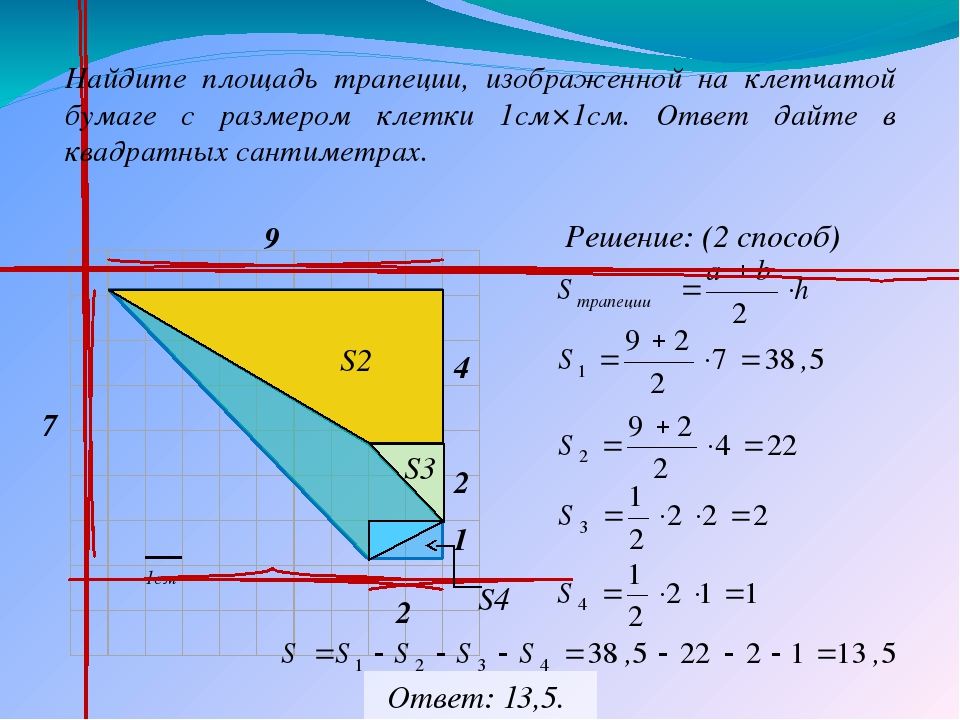
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h 1 h 2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Что такое равнобедренная трапеция? Это геометрическая фигура, противолежащие не параллельные стороны которой равны. Существует несколько различных формул для нахождения площади трапеции с различными условиями, которые даны в задачах. То есть площадь найти можно, если дана высота, стороны, углы, диагонали и т.д. Также нельзя не упомянуть, что для равнобедренных трапеций существует некоторые “исключение”, благодаря которым поиск площади и сама формула значительно упрощается. Ниже описаны подробные решения каждого случая с примерами.
Необходимые свойства для нахождения площади равнобедренной трапеции
Мы уже выяснили, что геометрическая фигура, имеющая противолежащие не параллельные, но равные стороны – это трапеция, причем, равнобедренная. Существуют специальные случаи, когда трапеция считается равнобедренной.
- Это условия равенства углов. Итак, обязательный пункт: углы при основании (возьмем рисунок ниже) должны быть равны. В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD
- Второе важное правило – в подобной трапеции диагонали должны быть равны. Следовательно, АС = ВD.
- Третий аспект: противоположные углы трапеции в сумме должны давать 180 градусов. Это значит, что угол ABC + угол CDA = 180 градусов. С углами BCD и BAD аналогично.
- В-четвертых, если трапеция допускает описание вокруг нее окружности – то она равнобедренная.
Как найти площадь равнобедренной трапеции – формулы и их описание
- S = (a+b)h/2 – это самая распространенная формула для нахождения площади, где а – нижнее основание, b – верхнее основание, а h – это высота.

- Если высота неизвестна, то искать ее можно по подобной формуле: h = с*sin(x), где с это либо AB, либо CD. sin(x) – это синус угла при любом основании, то есть угол DAB = угол CDA = x. В конечном итоге формула принимает вот такой вид: S = (a+b)*с*sin(x)/2.
- Высота также может находиться по этой формуле:
- Итоговая формула имеет такой вид:
- Площадь равнобедренной трапеции можно найти и через среднюю линию и высоту. Формула такова: S = mh .
Рассмотрим условие, когда в трапецию будет вписана окружность.
В случае, изображенном на картинке,
QN = D = H – диаметр окружности и одновременно высота трапеции;
LO, ON, OQ = R – радиусы окружности;
DC = a – верхнее основание;
AB = b – нижнее основание;
DAB, ABC, BCD, CDA – альфа, бета – углы оснований трапеции.
Подобный случай допускает нахождение площади по таким формулам:
- Теперь попробуем найти площадь через диагонали и углы между ними.

На рисунке обозначим AC, DB – диагонали – d. Углы COB, DOB – альфа; DOC, AOB – бета. Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ) такова:
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что треугольника равна половине параллельного ей основания, то есть:
Хорошо, разобрались. Теперь о площади трапеции.
Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.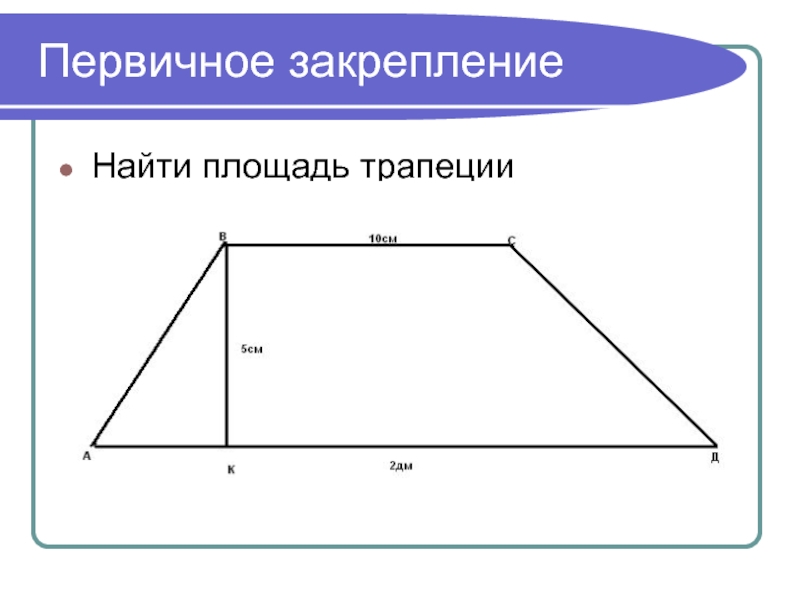
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
С уважением, Александр.
Прежде чем найти площадь трапеции, необходимо определится с известными элементами трапеции. Трапеция – это геометрический объект, а именно: четырёхугольник, который имеет две параллельные стороны (два основания). Другие две стороны – боковые. Если же параллельны будут и эти две стороны четырёхугольника, то это уже будет не трапеция, а параллелограмм.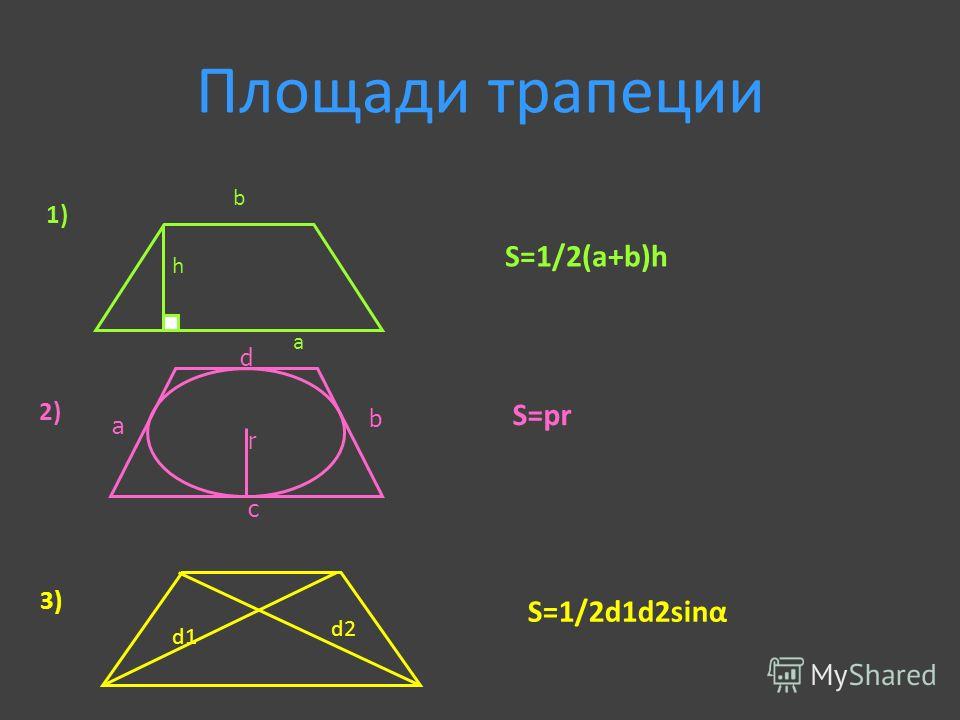 d2) – это синус угла, между диагоналями трапеции.
d2) – это синус угла, между диагоналями трапеции.
Существуют также различные формулы, выведенные из основных, а также формула для расчёта площади трапеции, когда известны все её стороны. Однако эта формула достаточно громоздкая и используется редко, ведь, зная все стороны трапеции можно просто определить высоту или её среднюю линию. Также в равнобедренную трапецию можно вписать окружность. В этом случае площадь трапеции будет высчитываться по формуле: 8*радиус окружности в квадрате.
Как найти площадь прямоугольной трапеции
Как и говорилось ранее, прямоугольной называется та трапеция, у которой хотя бы один угол прямой. Найти площадь такой трапеции очень просто. В основном, для поиска площади прямоугольной трапеции используются те же формулы, что и для обычной трапеции. Однако стоит помнить, что одна из боковых сторон такой трапеции и будет являться высотой. Также часто решение задач поиска площади прямоугольной трапеции сводится к поиску площади прямоугольника и треугольника, образованных опущенной высотой. Такие задачи достаточно просты.
Такие задачи достаточно просты.
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними. В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Свойства трапеций | Номер
Стенограмма видеозаписи
Ребята, мы здесь сегодня, чтобы поговорить о дополнительных боковых стволах Quadra, и мы сосредоточимся конкретно на словах Трампа, так что вы, возможно, слышали это слово раньше. Это какое-то забавное слово. Ловушка избегает, но, по сути, трапеция — это четырехугольник, поэтому у нее четыре стороны с ровно одной парой параллельных противоположных сторон. Так, например, это главы, в которых эта пара противоположных сторон параллельна.Вот еще один пример трапеции, у которой две противоположные стороны параллельны. Итак, трапеция — это четырехугольник с ключевым словом. Вот ровно одна пара противоположных параллельных сторон. Важно указать ровно одну пару противоположных параллельных сайтов. В некоторых учебниках параллелограмм считается особым случаем, потому что параллелограмм состоит из одной пары. Ну, технически у них есть две пары, мм, противоположных параллельных сторон. Но многие математики, когда они ссылаются на пустоты ловушек, я имею в виду, что это ровно одна пара противоположных параллельных сайтов.Так что есть несколько черт, которые привлекают его первое слово. Как мы уже говорили, у него есть одна пара противоположных параллельных сайтов. Помимо этого, у трапеции не так много особенностей. Хм, одна особенность Трэвиса Вуда — это если вы посмотрите на углы, идущие последовательно между параллельными сторонами. Так, например, я называю этот угол одним, и я называю этот угол, мм, углом один плюс угол, равным одному е. Итак, по сути, последовательные углы, последовательные углы, то есть углы, расположенные спиной к спине между параллельными линиями.Они будут дополнительными, так что это не просто любые два последовательных угла. Так, например, они будут считаться последовательными, расположенными спиной к спине вокруг четырехугольника. Но я имею в виду углы, идущие последовательно между параллельными линиями, то есть один и два или дополнительные.
Но многие математики, когда они ссылаются на пустоты ловушек, я имею в виду, что это ровно одна пара противоположных параллельных сайтов.Так что есть несколько черт, которые привлекают его первое слово. Как мы уже говорили, у него есть одна пара противоположных параллельных сайтов. Помимо этого, у трапеции не так много особенностей. Хм, одна особенность Трэвиса Вуда — это если вы посмотрите на углы, идущие последовательно между параллельными сторонами. Так, например, я называю этот угол одним, и я называю этот угол, мм, углом один плюс угол, равным одному е. Итак, по сути, последовательные углы, последовательные углы, то есть углы, расположенные спиной к спине между параллельными линиями.Они будут дополнительными, так что это не просто любые два последовательных угла. Так, например, они будут считаться последовательными, расположенными спиной к спине вокруг четырехугольника. Но я имею в виду углы, идущие последовательно между параллельными линиями, то есть один и два или дополнительные. И если бы вы обозначили эти три и четыре, тогда также углы три плюс четыре равнялись бы 1 80. Точно так же я мог бы сказать, что угол пять и угол 61 80, а угол семь и восемь равны 80. Но это действительно неудивительно, учитывая, если вы есть две параллельные линии и пересекающая их транс-мурсаль, затем угол Альфа и угол немного более приятный угол Альфа и Угол бета.Находясь на одной стороне с транс-универсалом, они будут равняться 1 80, так что то же самое происходит и над единственной супер особенной вещью, если бы даже равнобедренная трапеция, а я видел трапецию Селеш. Это все еще четырехугольник. Очевидно, это все же ровно одна пара противоположных параллельных сторон, кроме ног. Мы называем это ногами. Теперь, если две ноги воздушно-конгруэнтны, то у вас есть то, что мы называем в соусе трапеции Элизы. По сути, это трапеция с двумя конгруэнтными ножками. Здесь происходят две вещи, во-первых, ну, помимо двух вещей, которые у нас все еще есть: эти особые последовательные углы, которые находятся между двумя параллельными линиями, они все еще являются дополнительными.
И если бы вы обозначили эти три и четыре, тогда также углы три плюс четыре равнялись бы 1 80. Точно так же я мог бы сказать, что угол пять и угол 61 80, а угол семь и восемь равны 80. Но это действительно неудивительно, учитывая, если вы есть две параллельные линии и пересекающая их транс-мурсаль, затем угол Альфа и угол немного более приятный угол Альфа и Угол бета.Находясь на одной стороне с транс-универсалом, они будут равняться 1 80, так что то же самое происходит и над единственной супер особенной вещью, если бы даже равнобедренная трапеция, а я видел трапецию Селеш. Это все еще четырехугольник. Очевидно, это все же ровно одна пара противоположных параллельных сторон, кроме ног. Мы называем это ногами. Теперь, если две ноги воздушно-конгруэнтны, то у вас есть то, что мы называем в соусе трапеции Элизы. По сути, это трапеция с двумя конгруэнтными ножками. Здесь происходят две вещи, во-первых, ну, помимо двух вещей, которые у нас все еще есть: эти особые последовательные углы, которые находятся между двумя параллельными линиями, они все еще являются дополнительными. Они по-прежнему равны 1 80, поэтому угол один плюс угол к этому глупому равен 1 80. Однако у нас есть две дополнительные особенности. То, что мы называем базовыми углами. Они равны. Итак, эти два нижних угла равны. Точно так же две вершины расположены под двумя верхними углами. Они тоже в равной мере. Итак, в равнобедренной трапеции два угла выше, которые мы называем вершинными углами, совпадают, и два низких угла также приветствуются. Еще одна особенность в том, что в красивой колбасной трапеции, опять же характерной для красивого дома в форме трапеции, диагонали навсегда.Они не делят друг друга пополам, но они конгруэнтны, и вы можете доказать это с помощью конгруэнтных треугольников, но в итоге — на равнобедренном треугольнике. Вот ваша. Я видел трапецию Seles, я мог бы сказать «Треугольник» в той поездке. Эти две стороны равны, углы основания равны, углы вершины равны и диагонали равны. Таковы особенности равнобедренной трапеции. В противном случае, если вы просто обычная трапеция, ни одна из этих функций не имеет отношения к ней.
Они по-прежнему равны 1 80, поэтому угол один плюс угол к этому глупому равен 1 80. Однако у нас есть две дополнительные особенности. То, что мы называем базовыми углами. Они равны. Итак, эти два нижних угла равны. Точно так же две вершины расположены под двумя верхними углами. Они тоже в равной мере. Итак, в равнобедренной трапеции два угла выше, которые мы называем вершинными углами, совпадают, и два низких угла также приветствуются. Еще одна особенность в том, что в красивой колбасной трапеции, опять же характерной для красивого дома в форме трапеции, диагонали навсегда.Они не делят друг друга пополам, но они конгруэнтны, и вы можете доказать это с помощью конгруэнтных треугольников, но в итоге — на равнобедренном треугольнике. Вот ваша. Я видел трапецию Seles, я мог бы сказать «Треугольник» в той поездке. Эти две стороны равны, углы основания равны, углы вершины равны и диагонали равны. Таковы особенности равнобедренной трапеции. В противном случае, если вы просто обычная трапеция, ни одна из этих функций не имеет отношения к ней. За исключением двух последовательных углов между двумя параллельными альянсами.Дополнительный. В противном случае это вроде того. Когда дело доходит до ловушек, избегает.
За исключением двух последовательных углов между двумя параллельными альянсами.Дополнительный. В противном случае это вроде того. Когда дело доходит до ловушек, избегает.
Как рассчитать площадь трапеции с четырех сторон. Калькулятор периметра трапеции
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают трудности у многих школьников. С ними легко справишься, если все запомнить. требуемые формулы и практика решения задач.
В этой статье вы увидите формулы для нахождения площади трапеции, а также примеры задач с решениями.Вы можете найти такие же в KIM на сертификационных экзаменах или на олимпиадах. Поэтому относитесь к ним осторожно.
Что нужно знать о трапеции?
Во-первых, давайте вспомним, что трапеция называется четырехугольником, у которого две противоположные стороны, их еще называют основаниями, параллельны, а два других нет.
Высота также может быть уменьшена в трапеции (перпендикулярно основанию).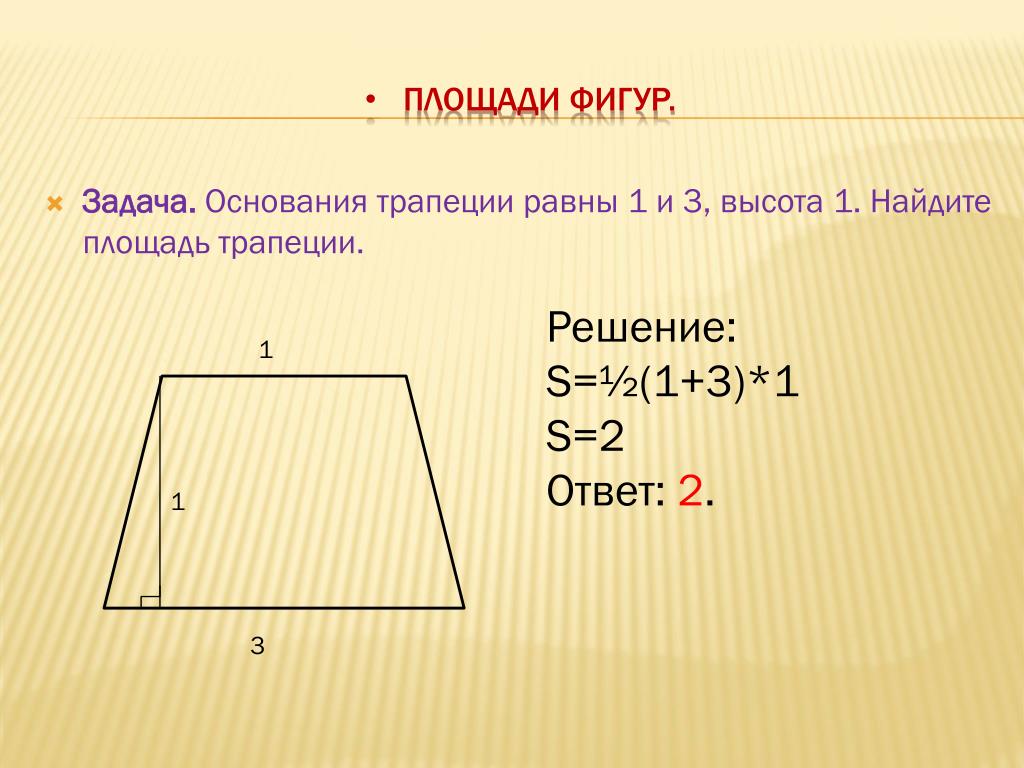 Проведена средняя линия — это прямая линия, параллельная основаниям и равная половине их суммы.А также диагонали, которые могут пересекаться, образуя острые и тупые углы … Или, в отдельных случаях, под прямыми углами. Кроме того, если трапеция равнобедренная, в нее можно вписать круг. И опишите круг вокруг него.
Проведена средняя линия — это прямая линия, параллельная основаниям и равная половине их суммы.А также диагонали, которые могут пересекаться, образуя острые и тупые углы … Или, в отдельных случаях, под прямыми углами. Кроме того, если трапеция равнобедренная, в нее можно вписать круг. И опишите круг вокруг него.
Формулы площади трапеции
Сначала рассмотрим стандартные формулы для определения площади трапеции. Способы расчета площади равнобедренных и криволинейных трапеций мы рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, у которой высота h понижена до большего основания.Вычислить площадь фигуры в этом случае проще простого. Вам просто нужно разделить на два сумму длин оснований и умножить полученное на высоту: S = 1/2 (a + b) * h .
Возьмем другой случай: предположим, что в трапеции, помимо высоты, проведена средняя линия m. Нам известна формула определения длины средней линии: m = 1/2 (a + b). Поэтому формулу площади трапеции с полным правом можно упростить до следующего вида: S = m * h . .. Другими словами, чтобы найти площадь трапеции, нужно умножить среднюю линию на высоту.
.. Другими словами, чтобы найти площадь трапеции, нужно умножить среднюю линию на высоту.
Рассмотрим другой вариант: в трапеции нарисованы диагонали d 1 и d 2, которые не пересекаются под прямым углом α. Чтобы вычислить площадь такой трапеции, нужно произведение диагоналей разделить на два и результат умножить на sin угла между ними: S = 1 / 2d 1 d 2 * sinα .
Теперь рассмотрим формулу для определения площади трапеции, если о ней ничего не известно, кроме длин всех ее сторон: a, b, c и d.Это громоздкая и сложная формула, но вам будет полезно ее запомнить на всякий случай: S = 1/2 (a + b) * √c 2 — ((1/2 (b — a)) * ((б — а) 2 + в 2 — г 2)) 2 .
Кстати, приведенные выше примеры верны и для случая, когда вам нужна формула площади прямоугольная трапеция … Это трапеция, сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность радиуса r, а боковая сторона и большее основание образуют острый угол α. В трапецию можно вписать круг при условии, что сумма длин его оснований равна сумме длин сторон.
Площадь равнобедренной трапеции рассчитывается следующим образом: умножьте квадрат радиуса вписанной окружности на четыре и разделите все на sinα: S = 4r 2 / sinα … Другая формула площади является частным случаем, когда угол между большим основанием и стороной равен 30 0: S = 8r 2 .
Второй вариант: на этот раз берем равнобедренную трапецию, на которой дополнительно нарисованы диагонали d 1 и d 2, а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота равна половине суммы оснований: h = 1/2 (a + b). Зная это, легко преобразовать уже знакомую формулу для площади трапеции в следующий вид: S = h 2 .
Формула площади криволинейной трапеции
Давайте начнем с изучения того, что такое изогнутая трапеция. Представьте себе координатную ось и график непрерывной неотрицательной функции f, которая не меняет знак в пределах данного сегмента на оси x. Криволинейная трапеция образована графиком функции y = f (x) — вверху, ось x — внизу (отрезок), а по бокам — прямыми линиями, проведенными между точками a и b и точкой график функции.
Рассчитать площадь такой нестандартной формы описанными выше методами невозможно.Здесь нужно применить математический анализ и воспользоваться интегралом. А именно: формула Ньютона-Лейбница — S = ∫ baf (x) dx = F (x) │ ba = F (b) — F (a) … В этой формуле F является первообразной нашей функции на выбранный сегмент. А область изогнутой трапеции соответствует приращению первообразной на данном отрезке.
Примеры задач
Чтобы все эти формулы лучше закрепились в вашей голове, вот несколько примеров задач по нахождению площади трапеции. Будет лучше, если вы сначала попробуете решить проблемы самостоятельно, а уже потом сверить полученный ответ с готовым решением.
Будет лучше, если вы сначала попробуете решить проблемы самостоятельно, а уже потом сверить полученный ответ с готовым решением.
Задача № 1: Дана трапеция. Его большее основание — 11 см, меньшее — 4 см. В трапеции начерчены диагонали, длина одной 12 см, длина другой 9 см.
Решение: построить трапецию AMRS. Проведите прямую PX через вершину P так, чтобы она оказалась параллельной диагонали MC и пересекала прямую AC в точке X. У вас получится треугольник ARX.
Рассмотрим две фигуры, полученные в результате этих манипуляций: треугольник ARX и параллелограмм CMRX.
Благодаря параллелограмму мы узнаем, что PX = MC = 12 см и CX = MR = 4 см. Где можно рассчитать сторону AX треугольника ARX: AX = AC + CX = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник ARX прямоугольный (для этого применим теорему Пифагора — AX 2 = AR 2 + PX 2). И вычислите его площадь: S APX = 1/2 (AP * PX) = 1/2 (9 * 12) = 54 см 2.
Далее нужно доказать, что треугольники AMP и PCX равны. Основанием будет равенство сторон МР и СХ (уже доказано выше). А также высота, которую вы опускаете с этих сторон — они равны высоте трапеции AMRS.
Основанием будет равенство сторон МР и СХ (уже доказано выше). А также высота, которую вы опускаете с этих сторон — они равны высоте трапеции AMRS.
Все это позволит утверждать, что S AMPC = S APX = 54 см 2.
Задача № 2: Дана трапеция KRMS. Точки O и E расположены на его боковых сторонах, а точки OE и KC параллельны. Также известно, что площади трапеций ORME и OCE находятся в соотношении 1: 5.PM = a и KC = b. Требуется найти OE.
Решение: Проведите прямую линию через точку M, параллельную RC, и обозначьте точку ее пересечения с OE буквой T. A — точку пересечения прямой линии, проведенной через точку E, параллельную RC, с основанием. КС.
Введем еще одно обозначение — OE = x. А также высоту h 1 для треугольника TME и высоту h 2 для треугольника AEC (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b> a. Площади трапеций ORME и OKSE соотносятся как 1: 5, что дает нам право составить следующее уравнение: (x + a) * h 1 = 1/5 (b + x) * h 2. Преобразуем и получаем: h 1 / h 2 = 1/5 * ((b + x) / (x + a)).
Преобразуем и получаем: h 1 / h 2 = 1/5 * ((b + x) / (x + a)).
Поскольку треугольники TME и AEC подобны, имеем h 1 / h 2 = (x — a) / (b — x). Объедините обе записи и получите: (x — a) / (b — x) = 1/5 * ((b + x) / (x + a)) ↔ 5 (x — a) (x + a) = (b + x) (b — x) ↔ 5 (x 2 — a 2) = (b 2 — x 2) ↔ 6x 2 = b 2 + 5a 2 ↔ x = √ (5a 2 + b 2) / 6.
Таким образом, OE = x = √ (5a 2 + b 2) / 6.
Заключение
Геометрия — не самая легкая наука, но с заданиями на экзамене вы точно справитесь. Достаточно проявить немного настойчивости в подготовке. И, конечно же, запомнить все необходимые формулы.
Мы постарались собрать в одном месте все формулы расчета площади трапеции, чтобы вы могли использовать их при подготовке к экзаменам и просмотре материала.
Обязательно расскажите об этой статье одноклассникам и друзьям.соцсети … Пусть идут хорошие оценки на ЕГЭ и ГИА будет больше!
блог. сайт, при полном или частичном копировании материала ссылка на источник обязательна.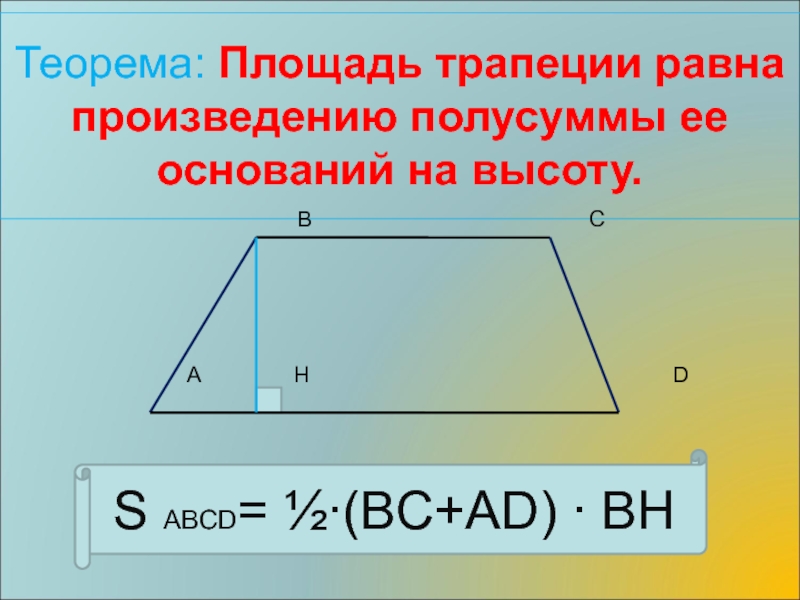
Калькулятор рассчитал 2192 задач по теме «Площадь трапеции»
КВАДРАТНАЯ ТРАПЕЦИЯ
Выберите формулу для расчета площади трапеции, которую вы планируете использовать для решения поставленной перед вами задачи:
Общая теория расчета площади трапеции.
Трапеция — это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих эти четыре точки попарно, причем две противоположные стороны параллельны (лежат на параллельных линиях), и два других не параллельны.
Точки называются вершины трапеции и обозначаются заглавными латинскими буквами.
Отрезки называются стороны трапеции и обозначаются парой заглавных латинских букв, соответствующих вершинам, которые соединяют сегменты.
Две параллельные стороны трапеции называются основания трапеции .
Две непараллельные стороны трапеции называются боковыми сторонами трапеции .
Рисунок №1: Трапеция ABCD
На рисунке 1 изображена трапеция ABCD с вершинами A, B, C, D и сторонами AB, BC, CD, DA.
AB ǁ DC — основания трапеции ABCD.
AD, BC — боковые стороны трапеции ABCD.
Угол, образованный лучами AB и AD, называется углом при вершине A. Он обозначается как ÐA или ÐBAD, или ÐDAB.
Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB, или ÐABC, или ÐCBA.
Угол, образованный лучами CB и CD, называется углом при вершине C. Он обозначается как ÐC или ÐDCB, или ÐBCD.
Угол, образованный лучами AD и CD, называется углом при вершине D. Он обозначается как ÐD или ÐADC, или ÐCDA.
Рисунок № 2: Трапеция ABCD
На рисунке 2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. Это, .
Рисунок № 3: Равнобедренная трапеция ABCD
На рисунке 3 AD = BC.
Трапеция называется равнобедренная (равнобедренная) , если ее стороны равны.
Рисунок №4: Прямоугольная трапеция ABCD
На рисунке 4 угол D представляет собой прямую линию (равную 90 °).
Трапеция называется прямоугольной, , если угол сбоку прямой.
Квадрат S плоских фигур, к которым относится трапеция, называют ограниченным замкнутым пространством на плоскости. Площадь плоской фигуры показывает размер этой фигуры.
На участке расположено несколько объектов недвижимости:
1. Не может быть отрицательным.
2. Если дана некоторая замкнутая область на плоскости, состоящая из нескольких фигур, не пересекающихся друг с другом (то есть фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой площади равна сумме площадей составляющих ее фигур . ..
..
3. Если две фигуры равны, то их площади равны.
4. Площадь квадрата, построенного на единичной прямой, равна единице.
На единицу измерений квадратов занимает площадь квадрата, сторона которого равна единицам измерений сегментов.
При решении задач часто используются следующие формулы расчета площади трапеции:
1. Площадь трапеции равна полусумме ее оснований, умноженной на высоту:
2. Площадь трапеции равна произведению ее средней линии на высоту:
3.При известной длине оснований и сторон трапеции ее площадь можно рассчитать по формуле:
4. Можно рассчитать площадь равнобедренной трапеции с известной длиной радиуса круга, вписанного в трапецию, и известным значением угла при основании по следующей формуле:
Пример 1: Вычислите площадь трапеции с основаниями a = 7, b = 3 и высотой h = 15.
Решение:
Ответ:
Пример 2: Найдите сторону основания трапеции с площадью S = 35 см 2, высотой h = 7 см и вторым основанием b = 2 см.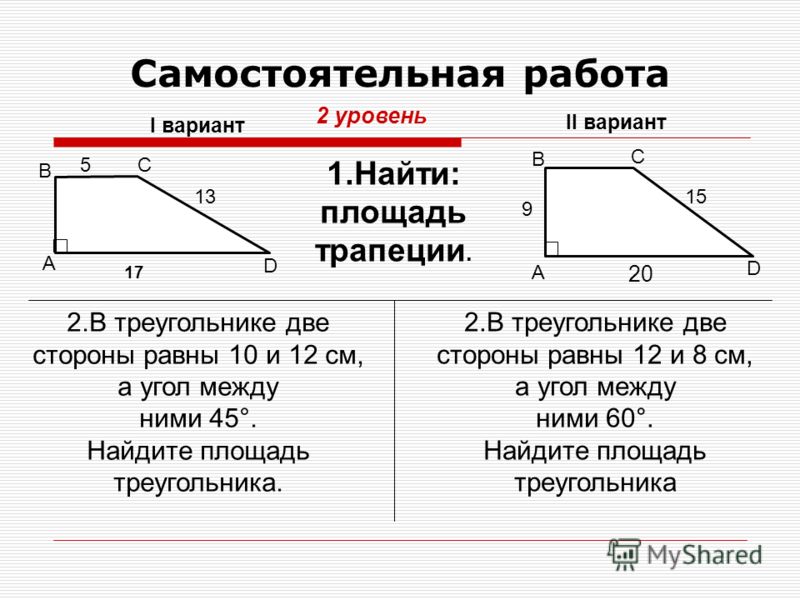
Решение:
Чтобы найти сторону основания трапеции, воспользуемся формулой расчета площади:
Выразим из этой формулы сторону основания трапеции:
Таким образом, имеем:
Ответ:
Пример 3: Найдите высоту трапеции с площадью S = 17 см 2 и основаниями a = 30 см, b = 4 см.
Решение:
Чтобы найти высоту трапеции, используйте формулу для расчета площади:
Таким образом, имеем:
Ответ:
Пример 4: Вычислить площадь трапеции с высотой h = 24 и средней линией m = 5.
Решение:
Чтобы найти площадь трапеции, мы используем следующую формулу для расчета площади:
Таким образом, имеем:
Ответ:
Пример 5: Найдите высоту трапеции с площадью S = 48 см 2 и средней линией m = 6 см.
Решение:
Чтобы найти высоту трапеции, воспользуемся формулой расчета площади трапеции:
Выразим высоту трапеции по этой формуле:
Таким образом, имеем:
Ответ:
Пример 6: Найдите среднюю линию трапеции с площадью S = 56 и высотой h = 4.
Решение:
Чтобы найти среднюю линию трапеции, используйте формулу для расчета площади трапеции:
Выразим из этой формулы среднюю линию трапеции:
Таким образом, имеем следующее.
И. Теперь вы можете начать думать, как найти площадь трапеции. Эта задача в повседневной жизни встречается очень редко, но иногда оказывается необходимым, например, найти площадь комнаты в виде трапеции, которые все чаще используются при строительстве современных квартир или в дизайне. проекты под ремонт.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками прямых, два из которых параллельны друг другу и называются основаниями трапеции.Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем будет полезно еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок линии, соединяющий середины сторон и высоту трапеции, равную расстоянию между основаниями.
Подобно треугольникам, трапеция имеет особые виды в виде равнобедренной (равнобедренной) трапеции, у которой длины сторон одинаковы, и прямоугольной трапеции, у которой одна из сторон образует прямой угол с основанием.
Трапеции обладают интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.
- У равнобедренных трапеций стороны и углы, которые они образуют с основаниями, равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции на любом из ее оснований равняется 90, то длина отрезка, соединяющего середины оснований, равна их половинной разности.
- Равнобедренную трапецию можно описать кружком. И наоборот. Если трапеция вписывается в круг, то она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции, будет перпендикулярен ее основаниям и представляет собой ось симметрии.
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
В виде формулы это записывается в виде выражения:
где S — площадь трапеции, a, b — длина каждого из оснований трапеции, h — высота трапеции.
Вы можете понять и запомнить эту формулу следующим образом. Как следует из рисунка ниже, трапецию с помощью средней линии можно трансформировать в прямоугольник, длина которого будет равна полусумме оснований.
Вы также можете расширить любую трапецию до более простых форм: прямоугольника и одного или двух треугольников, и, если вам так удобнее, найдите площадь трапеции как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для расчета его площади. Согласно ему, площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается как: S = m * h, где S — площадь, m — длина средней линии, h — высота трапеции. Эта формула больше подходит для задач по математике, чем для повседневных задач, так как в реальных условиях вы не узнаете длину средней линии без предварительных расчетов … А вы будете знать только длины оснований и сторон.
В этом случае площадь трапеции можно найти по формуле:
S = ((a + b) / 2) * √c 2 — ((b-a) 2 + c 2 -d 2/2 (b-a)) 2
где S — площадь, a, b — основания, c, d — стороны трапеции.
Есть еще несколько способов найти площадь трапеции. Но они примерно так же неудобны, как и последняя формула, а значит, нет смысла на них останавливаться. Поэтому мы рекомендуем вам использовать первую формулу из статьи, и мы хотим всегда получать точные результаты.
В математике известно несколько типов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них трапеция — разновидность выпуклого четырехугольника, у которого две стороны параллельны, а две другие — нет. Параллельные противоположные стороны называются основаниями, а две другие — сторонами трапеции. Отрезок, соединяющий середины сторон, называется средней линией. Есть несколько видов трапеций: равнобедренные, прямоугольные, изогнутые. Для каждого типа трапеции есть формулы нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину и высоту ее оснований. Высота трапеции — это отрезок прямой, перпендикулярный основаниям. Пусть верхнее основание будет a, нижним основанием b, а высота h. Тогда можно рассчитать площадь S по формуле:
S = ½ * (a + b) * h
тех. возьмите полусумму оснований, умноженную на высоту.
Также можно будет вычислить площадь трапеции, если вы знаете значение высоты и средней линии.Обозначим среднюю линию — m. Тогда
Решим более сложную задачу: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь будет найдена по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется следующим образом:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В этой формуле для вычисления дан синус угла.
При известных базовых длинах a и b и двух углах у нижнего основания площадь рассчитывается следующим образом:
S = ½ * (b2 — a2) * (sin α * sin β / sin (α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это трапеция особого случая.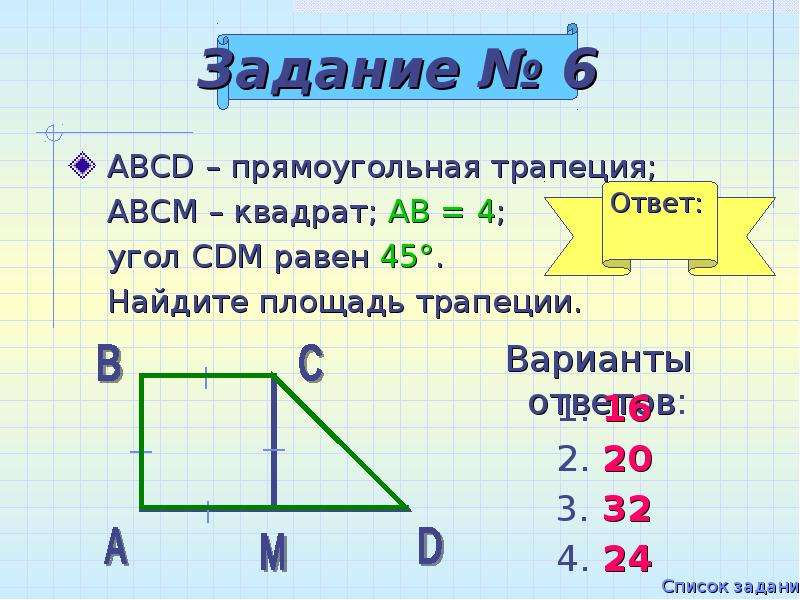 Его отличие в том, что такая трапеция представляет собой выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон … Его стороны равны.
Его отличие в том, что такая трапеция представляет собой выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон … Его стороны равны.
Есть несколько способов найти площадь равнобедренной трапеции.
- По длине с трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому они обозначаются одинаковым значением — c, а a и b — длины оснований:
- Если вы знаете длину верхнего основания, стороны и угол у нижнего основания, то площадь рассчитывается следующим образом:
S = c * sin α * (a + c * cos α)
где a — верхнее основание, c — сторона.
- Если вместо верхнего основания известна длина нижнего, b, то площадь рассчитывается по формуле:
S = c * sin α * (b — c * cos α)
- Если известны два основания и угол у нижнего основания, площадь вычисляется через тангенс угла:
S = ½ * (b2 — a2) * tan α
- Также площадь рассчитывается по диагоналям и углу между ними.
 В этом случае диагонали равны по длине, поэтому каждая обозначается буквой d без индексов:
В этом случае диагонали равны по длине, поэтому каждая обозначается буквой d без индексов:
S = ½ * d2 * sin α
- Рассчитываем площадь трапеции, зная длину стороны, среднюю линию и угол у нижнего основания.
Пусть боковая сторона будет c, средняя линия m, угол a, тогда:
S = m * c * sin α
Иногда круг можно вписать в равностороннюю трапецию, радиус которой будет равен r .
Известно, что круг можно вписать в любую трапецию, если сумма длин оснований равна сумме длин его боковых сторон. Затем площадь находится через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
То же самое вычисление проводится через диаметр D вписанной окружности (кстати, совпадает с высотой трапеции):
Зная основание и угол, площадь равнобедренной трапеции рассчитывается следующим образом:
S = a * b / sin α
(эта и следующие формулы действительны только для трапеций с вписанной окружностью).
Площадь определяется по основаниям и радиусу круга следующим образом:
Если известны только основания, площадь рассчитывается по формуле:
По основаниям и боковой линии площадь трапеции с вписанной окружностью через основания и среднюю линию — м рассчитывается следующим образом:
Площадь прямоугольной трапеции
Называется прямоугольная трапеция, у которой одна из боковых сторон является перпендикулярно основаниям.В этом случае длина стороны совпадает с высотой трапеции.
Прямоугольная трапеция — это квадрат и треугольник. Найдя площадь каждой формы, сложите результаты и получите цифры общей площади.
Также для расчета площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если длина оснований и высота (или перпендикулярная сторона) известны, то площадь рассчитывается по формуле:
S = (a + b) * h / 2
h (высота) может быть стороной c.Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ вычисления площади — умножение длины средней линии на высоту:
или по длине боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синуса угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, формула упрощается до:
S = ½ * d1 * d2
- Другой способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна по причинам. Если взять длины сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписан круг, то площадь рассчитывается аналогично:
где м — длина средней линии.
Область криволинейной трапеции
Криволинейная трапеция — это плоская фигура, ограниченная графиком неотрицательной непрерывной функции y = f (x), заданной на отрезке, осью абсцисс и прямыми линиями x = a, x = б.Фактически, две его стороны параллельны друг другу (основаниям), третья сторона перпендикулярна основаниям, а четвертая — кривая, соответствующая графику функции.
Площадь криволинейной трапеции ищется через интеграл по формуле Ньютона-Лейбница:
Так рассчитываются площади трапеций разных типов. Но, помимо свойств сторон, трапеции обладают такими же свойствами углов. Как и во всех существующих четырехугольниках, сумма внутренних углов трапеции составляет 360 градусов. А сумма углов, примыкающих к стороне, равна 180 градусам.
А сумма углов, примыкающих к стороне, равна 180 градусам.
Трапеция — это особый вид четырехугольника, в котором две противоположные стороны параллельны друг другу, а две другие — нет. Различные объекты из реальной жизни имеют трапециевидную форму, поэтому вам может понадобиться рассчитать периметр такой геометрической формы для решения повседневных или школьных задач.
Геометрия трапеции
Трапеция (от греческого «трапеция» — стол) — фигура на плоскости, ограниченная четырьмя отрезками, два из которых параллельны, а два — нет.Параллельные отрезки называются основаниями трапеции, а непараллельные — боковыми сторонами фигуры. Стороны и их углы наклона определяют тип трапеции, которая может быть универсальной, равнобедренной или прямоугольной. Помимо оснований и бортов у трапеции есть еще два элемента:
- высота — расстояние между параллельными основаниями фигуры;
- средняя линия — это отрезок, соединяющий середины сторон.
Эта геометрическая форма широко распространена в жизни.
Трапеция в реальности
V Повседневная жизнь Многие реальные объекты принимают трапециевидную форму. Вы легко найдете трапеции в следующих сферах человеческой деятельности:
- дизайн и декор интерьеров — диваны, столешницы, стены, ковры, натяжные потолки;
- ландшафтный дизайн — бордюры газонов и искусственные водоемы, формы декоративных элементов;
- мода — форма одежды, обуви и аксессуаров;
- архитектура — окна, стены, фундаменты зданий;
- продукция — различные изделия и детали.
При таком широком использовании трапеций специалистам часто приходится рассчитывать периметр геометрической фигуры.
Периметр трапеции
Периметр фигуры — это числовая характеристика, вычисляемая как сумма длин всех сторон n-угольника. Трапеция — это четырехугольник, и, как правило, все ее стороны имеют разную длину, поэтому периметр рассчитывается по формуле:
п = а + б + с + г,
, где a и c — основания фигуры, b и d — ее стороны.
Несмотря на то, что при расчете периметра трапеции нам не нужно знать высоту, программный код калькулятора требует ввода этой переменной. Поскольку высота никак не влияет на вычисления, при использовании нашего онлайн-калькулятора вы можете ввести любое значение высоты больше нуля. Давайте посмотрим на пару примеров.
Примеры из жизни
Платок
Допустим, у вас есть шаль трапециевидной формы и вы хотите отделать ее бахромой.Вам нужно будет знать периметр шарфа, чтобы не покупать лишний материал и не ходить в магазин дважды. Пусть ваша равнобедренная шаль имеет следующие параметры: a = 120 см, b = 60 см, c = 100 см, d = 60 см. Вбиваем эти данные в онлайн-форму и получаем ответ в виде:
Таким образом, периметр шарфа равен 340 см, а это как раз длина тесьмы с бахромой для его обрезки.
Склоны
Например, вы решили сделать откосы для нестандартных металлопластиковых окон трапециевидной формы.Такие окна широко используются при оформлении построек, создавая композицию из нескольких створок. Чаще всего такие окна делают в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для изготовления откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Мы используем эти данные и получаем результат в виде
Чаще всего такие окна делают в виде прямоугольной трапеции. Давайте выясним, сколько материала потребуется для изготовления откосов такого окна. Стандартное окно имеет следующие параметры a = 140 см, b = 20 см, c = 180 см, d = 50 см. Мы используем эти данные и получаем результат в виде
Следовательно, периметр трапециевидного окна составляет 390 см, на столько нужно покупать пластиковые панели для формирования откосов.
Заключение
Трапеция — популярный в быту рисунок, определение параметров которого может понадобиться в самых неожиданных ситуациях. Расчет периметров трапецией необходим многим профессионалам: от инженеров и архитекторов до дизайнеров и механиков. Наш каталог онлайн-калькуляторов позволит вам производить расчеты для любых геометрических фигур и тел.
Анатомия, спина, трапеция — StatPearls
Введение
Трапециевидная мышца — это большая поверхностная мышца спины, напоминающая трапецию.Он простирается от наружного выступа затылочной кости до нижних грудных позвонков и латерально до ости лопатки.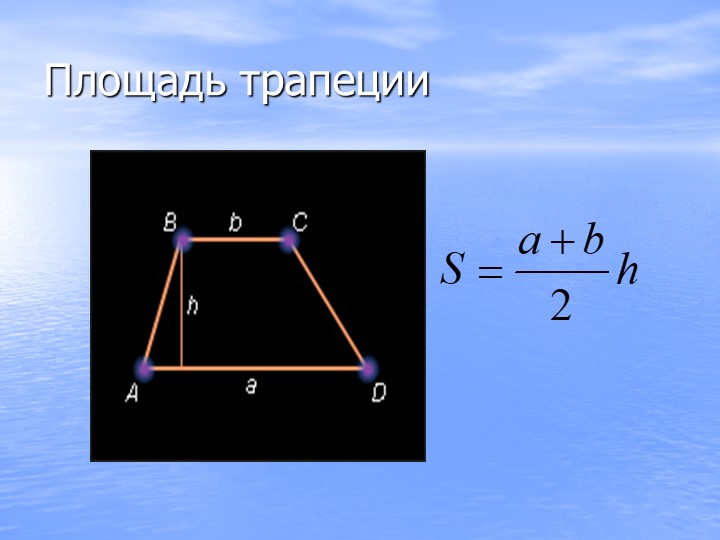 Трапеция имеет верхнюю, среднюю и нижнюю группы волокон.
Трапеция имеет верхнюю, среднюю и нижнюю группы волокон.
Брюшные ветви C3, C4 иннервируют сенсорную функцию трапеции. Черепной нерв XI иннервирует двигательную функцию трапециевидной мышцы.
Функция трапеции — стабилизация и перемещение лопатки. Верхние волокна могут поднимать и вращать вверх лопатку и расширять шею.Средние волокна приводят (втягивают) лопатку. Нижние волокна вдавливают и помогают верхним волокнам вращать лопатку вверх. Эти движения позволяют лопатке вращаться относительно поднимающей лопатки и ромбовидных мышц. Это вращение важно в сочетании с дельтовидной мышцей при метании предметов.
Неравномерное развитие трех трапециевидных волокон вызывает мышечный дисбаланс и нарушение осанки. Повреждение XI черепного нерва может привести к денервации и последующей потере двигательной функции трапециевидной мышцы, что приведет к истощению мышц.Черепный нерв XI можно исследовать во время клинического обследования, попросив пациента пассивно пожать плечами, а затем активно, преодолевая сопротивление исследователя.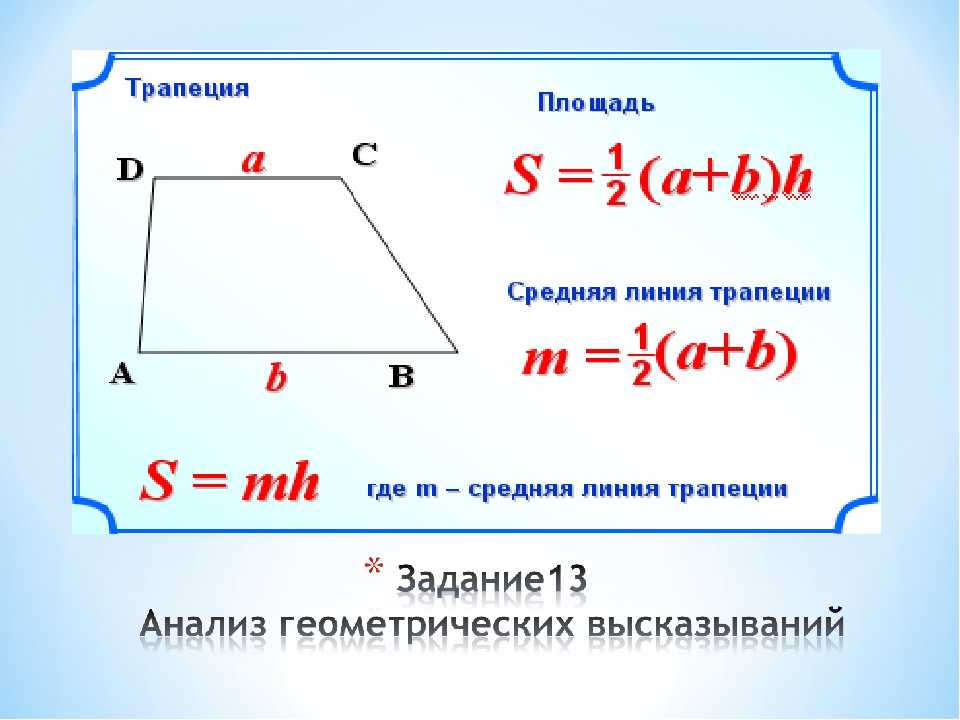
Структура и функции
Трапеция — это мышца, состоящая из особенно длинных мышечных волокон, охватывающих большую ширину верхней части спины. Функционально это позволяет трапеции в основном поддерживать осанку, позволяя и поддерживая позвоночник оставаться в вертикальном положении, когда человек стоит. Трапеция — одна из самых широких и поверхностных (ближайших к коже) мышц верхней части спины и туловища, то есть при вскрытии трупа она часто используется в качестве ориентира, поскольку встречается первой.Эта мышца треугольной формы, широкая и тонкая, покрывает верхнюю часть плеч и шею сзади. Его точки прикрепления состоят из остистого отростка C7-T12 позвоночника, выйной связки, лопаток, ключиц и ребер. Трапециевидная мышца в основном является постуральной, но также используется для активных движений, таких как наклоны в стороны и поворот головы, подъем и опускание плеч и внутреннее вращение руки. Трапеция поднимает, вдавливает и втягивает лопатку. Нисходящие мышечные волокна трапециевидной мышцы вращают руки внутрь. Поперечные мышечные волокна втягивают лопатки, а восходящие мышечные волокна кнутри вращают лопатки.
Поперечные мышечные волокна втягивают лопатки, а восходящие мышечные волокна кнутри вращают лопатки.
Эмбриология
Вся мускулатура человеческого тела, как поперечно-полосатая, так и гладкая, возникает из мезодермы. Несколько исключений возникают из-за эктодермы. Трапециевидная и грудинно-ключично-сосцевидная мышца берут начало в латеральной затылочной области и первоначально формируются как единое образование. В этот очень ранний период он иннервируется дополнительным нервом (CN XI у взрослой формы), и по мере того, как мышечная масса перемещается в свое взрослое положение, она расширяется и движется каудально, неся с собой нерв.Трапециевидная и грудинно-ключично-сосцевидная мышца возникают из единого образования и затем разделяются примерно на 20-й неделе развития. Нет ничего необычного в том, что мышца получает вторичные новые нервы, сохраняя при этом свой исходный нерв CN XI, а затем получая ответвления от шейного сплетения. [1]
Кровоснабжение и лимфатика
Два основных варианта кровоснабжения трапециевидной мышцы развиваются из трех общих источников.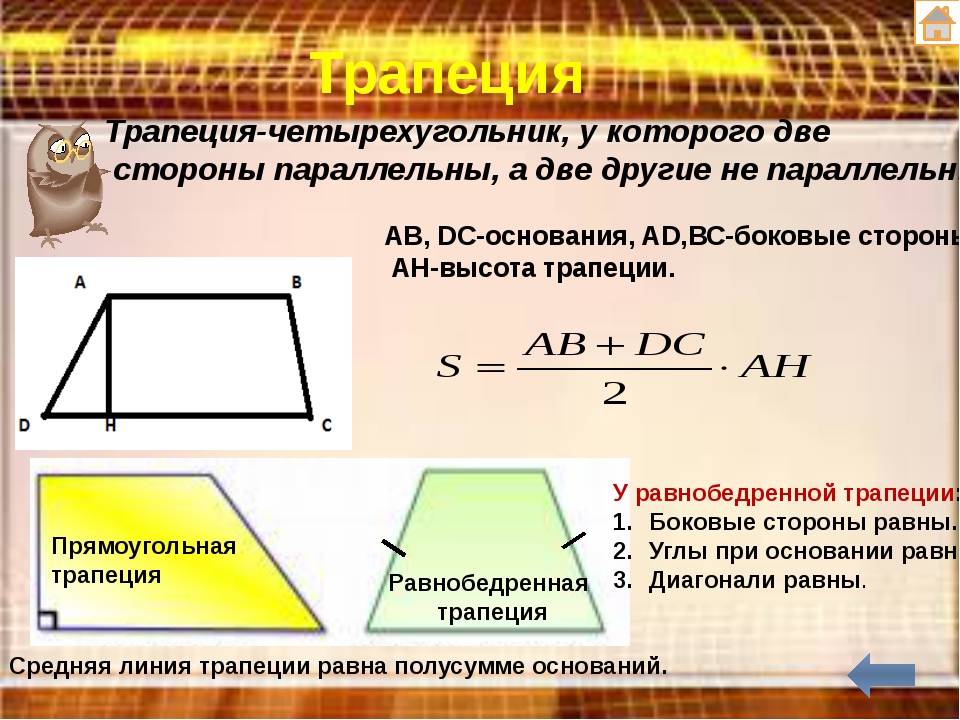 Наиболее распространенный вариант включает основной приток крови из поперечной шейной артерии с коллатеральным кровоснабжением из дорсальной лопаточной артерии для верхней части и ветвей задней межреберной артерии из глубоких частей.Второй, менее распространенный вариант, имеет большее кровоснабжение от дорсальной лопаточной артерии. [2]
Наиболее распространенный вариант включает основной приток крови из поперечной шейной артерии с коллатеральным кровоснабжением из дорсальной лопаточной артерии для верхней части и ветвей задней межреберной артерии из глубоких частей.Второй, менее распространенный вариант, имеет большее кровоснабжение от дорсальной лопаточной артерии. [2]
Нервы
Двигатель, обеспечивающий работу трапециевидной мышцы, происходит от добавочного нерва, также известного как CN XI. Диапазон движений плеч (ROM) с движением плеч в головной части, «пожимание плечами» — это обычный маневр физического осмотра для проверки CN XI. [3] Ощущение трапециевидных мышц, включая боль и проприоцепцию или ощущение положения в пространстве, происходит через вентральные ветви третьего (C3) и четвертого (C4) шейных нервов.Можно подумать, что, поскольку трапециевидная мышца находится на спине, она будет иннервируется спинными ветвями; однако трапеция — это мышца верхней конечности, которая иннервируется брюшными ветвями.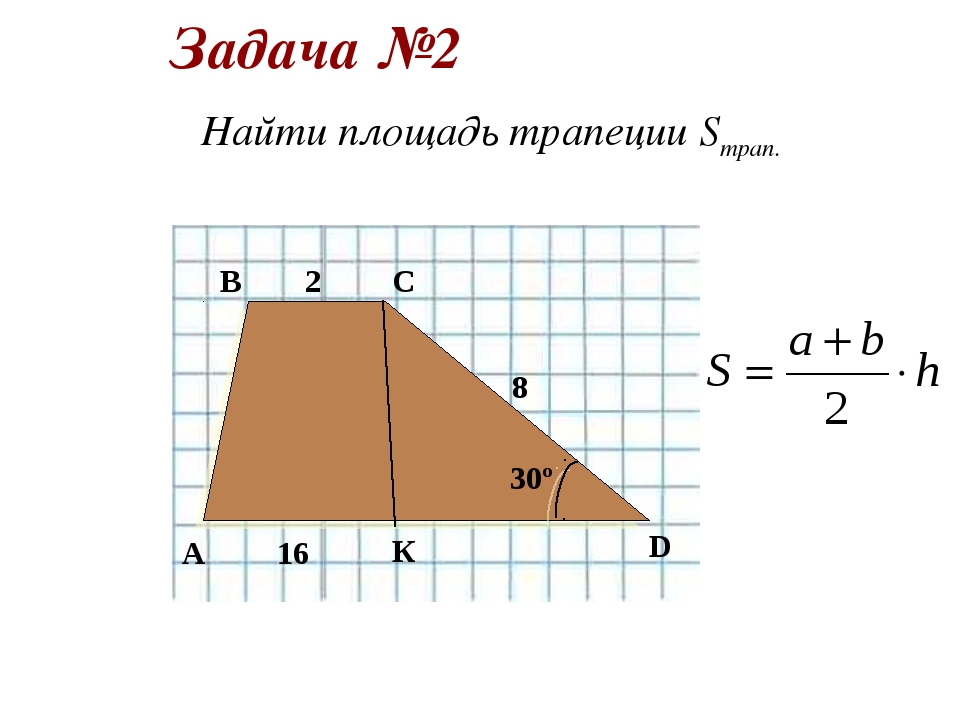
Мышцы
Дополнительные мышцы, которые поддерживают трапециевидные мышцы или им помогают, включают широчайшую мышцу спины, ромбовидные кости и поднимающую лопатку. Трапециевидная и полуостистная мышцы головы образуют основную массу мышц в затылочной области у основания черепа.
Физиологические варианты
Анатомические варианты трапециевидной мышцы, хотя статистически редки, заслуживают внимания и разнообразны.Многие из этих вариантов связаны с развитием и связаны с агенезом трапециевидной мышцы, будь то односторонний или двусторонний, что приводит к гипоплазии или добавочным долям мышцы. [4] В одном зарегистрированном случае наследственного отсутствия трапециевидной мышцы у дочери двух родителей с отсутствующей трапециевидной мышцей также было отсутствие трапеции. Другим феноменом может быть дисфункция или отсутствие добавочного нерва (CN XI), вызывающая гипоплазию, а не фактическое отсутствие трапециевидной мышцы.
Хирургическое вмешательство
Хирургическое вмешательство ограничено из-за устойчивости качества жизни, если трапециевидная мышца повреждена. Если происходит расслоение добавочного нерва, предпринимались попытки восстановить его, но процент успеха находится в среднем подростковом возрасте в процентиле. Из-за плохих результатов от этой процедуры часто отказываются. Одно из наиболее распространенных хирургических вмешательств, затрагивающих трапециевидную область, включает использование трапециевидного лоскута для тех пациентов, которые перенесли или имеют латеральные черепно-лицевые или боковые базилярные дефекты черепа. Лоскуты трапеции также используются при дефектах полости рта или глотки. [5]
Если происходит расслоение добавочного нерва, предпринимались попытки восстановить его, но процент успеха находится в среднем подростковом возрасте в процентиле. Из-за плохих результатов от этой процедуры часто отказываются. Одно из наиболее распространенных хирургических вмешательств, затрагивающих трапециевидную область, включает использование трапециевидного лоскута для тех пациентов, которые перенесли или имеют латеральные черепно-лицевые или боковые базилярные дефекты черепа. Лоскуты трапеции также используются при дефектах полости рта или глотки. [5]
Клиническая значимость
Трапециевидный гипертонус и спазм являются частой причиной головных болей напряжения среди населения в целом.Из-за прохождения добавочного и затылочного нервов они могут защемиться, вызывая классическую головную боль напряжения, вызывающую распространение головной боли из-за бараньего рога. Эта головная боль двусторонняя, пульсирующая, распространяется из затылочной области и распространяется на верхнюю часть головы и область лба. Стресс, осанка и недостаточная растяжка перед физической нагрузкой могут усугубить эти симптомы. Продромальных или нейросенсорных обострений, связанных со светом или звуком, нет. Головные боли напряжения часто лечат с помощью субзатылочного расслабления, растяжения, снятия стресса / тревоги и НПВП.[6]
Рисунок
Мышцы, соединяющие верхнюю конечность с позвоночником, затылочную кость, верхнюю затылочную линию, грудинно-ключично-сосцевидную мышцу, заднюю связку, шейную спинку шеи, леватор лопатки, большое и малое ромбовидное мышечное кольцо, трапециевидную мышцу лопатки, лопатку , (подробнее …)
Рисунок
Поверхностная анатомия спины, трапеции, позвоночника лопатки, большого Rhomboideus, большой круглой мышцы, дельтовидной мышцы, нижнего угла лопатки, крестцово-подвздошной мышцы, гребня подвздошной кости, широчайшей мышцы спины, Glutaeus Medius и максимальной.Предоставлено Gray’s Anatomy Plates
Ссылки
- 1.
- Бадура М., Грзонковска М., Баумгарт М., Шпинда М. Количественная анатомия трапециевидной мышцы у плода человека. Adv Clin Exp Med. 2016 июль-август; 25 (4): 605-9. [PubMed: 27629832]
- 2.
- Netterville JL, Wood DE. Нижний трапециевидный лоскут. Анатомия сосудов и хирургическая техника. Arch Otolaryngol Head Neck Surg. 1991 Янв; 117 (1): 73-6. [PubMed: 1986765]
- 3.
- Бэ Дж. Х., Ли Дж. С., Чой Д. Ю., Сук Дж., Ким СТ.Распределение добавочного нерва для эстетических инъекций ботулотоксина в верхнюю трапециевидную мышцу: анатомическое исследование и клиническое испытание: воспроизводимые места инъекции BoNT в верхнюю трапециевидную мышцу. Хирург Радиол Анат. 2018 ноя; 40 (11): 1253-1259. [PubMed: 29946827]
- 4.
- Ранаде А.В., Рай Р., Рай А.Р., Дасс П.М., Пай М.М., Вадгаонкар Р. Варианты широчайшей мышцы спины с точки зрения операции по пересадке сухожилий: анатомическое исследование. J Shoulder Elbow Surg. 2018 Янв; 27 (1): 167-171. [PubMed: 28939333]
- 5.
- Frobert P, Bekara F, Bertheuil N, Delay E, Herlin C, Chaput B. Трапециевидный перфораторный лоскут: универсальность для локорегиональной реконструкции. Анн Чир Пласт Эстет. 2019 Февраль; 64 (1): 61-67. [PubMed: 29937362]
- 6.
- Rodríguez-Huguet M, Gil-Salú JL, Rodríguez-Huguet P, Cabrera-Afonso JR, Lomas-Vega R. Влияние миофасциального высвобождения на пороги болевого давления у пациентов с болью в шее: Единичное слепое рандомизированное контролируемое исследование. Am J Phys Med Rehabil. 2018 Янв; 97 (1): 16-22.[PubMed: 28678033]
Что такое трапециевидный ребристый профиль крыши?
Трапециевидный профиль крыши имеет ребристый трапециевидный рисунок поперек панели. Это означает, что это четырехугольник (или четырехугольник — см. Рисунок 1), который имеет только одну пару параллельных сторон. Иногда трапециевидные крыши ошибочно называют профнастилом . Это неправильное название, поскольку гофрированный профиль имеет повторяющийся волнистый узор по всей поверхности. Крыши с трапециевидными ребрами популярны у производителей, поскольку форма делает их очень экономичными (высокое соотношение прочности и веса).
Это делает профиль очень экономичным. Тени трапециевидных форм создают четкие линии независимо от того, установлены ли они вертикально, диагонально или горизонтально. Они также обладают хорошими конструктивными характеристиками и хорошо выдерживают расчетные нагрузки (например, снеговые и ветровые подъемы). Однако он не считается таким премиальным профилем, как стоячий шов, из-за способа крепления.
Как правило, трапециевидные крыши крепятся лицевым или сквозным креплением (иначе говоря, открытыми креплениями) — это означает, что панели удерживаются на месте крепежными элементами, которые проникают сквозь материал с помощью винтов с шайбой, закрепленных в конструкции.Расстояние между ребрами варьируется от 6 до 12 дюймов, и между ними могут быть крошечные «второстепенные ребра», которые помогают придать панели жесткость. Хотя на первый взгляд они могут выглядеть одинаково, их точные размеры и углы варьируются от одного производителя к другому. Популярные во всем мире трапециевидные кровли с ребрами жесткости дешевле, чем обычные кровельные профили со стоячим фальцем. На самом деле существуют профили со стоячим швом, которые также обладают преимуществами трапециевидной формы. Фактически, они являются отраслевыми стандартами для больших зданий из-за рентабельности трапециевидной геометрии ребер.
Рисунок 1
Это сработало для египтян…Для объяснения хороших структурных характеристик трапециевидного ребристого профиля крыши можно использовать отличную аналогию. Рассмотрим древние пирамиды. Форма пирамиды — это всего лишь трапеция с обрезанной вершиной. Пирамиды буквально выдержали испытание временем — за тысячи лет. Прочная конструкция пирамид доказывает, что форма способствует распределению нагрузки, создавая более стабильную опорную конструкцию.
Word De-Construction Слово недели: трапециевидный
ПРОИЗВОДСТВО: \ ˈtra-pə-ˌzȯid-al
ЧАСТЬ РЕЧИ: Прилагательное
ПРЕДЛОЖЕНИЕ: // Трапециевидная конструкция крыши в сочетании с RibBracket ™ I-IV обеспечивает достаточно места для прокладки проводов во время установки солнечной фотоэлектрической батареи.
СИНОНИМЫ И Родственные слова: R-панель, трапециевидное ребро
ДЕЛАЕТ С-5! ПРЕДЛАГАЕТЕ КРОНШТЕЙНЫ ДЛЯ МОНТАЖА К ТРАПЕЦОИДАЛЬНОМУ НЕРЖАЛУ КРЫШИ ?: Мы уверены!
THE RIBBRACKET ™ I-IV: S-5! предлагает первоклассное солнечное решение для подавляющего большинства трапециевидных крыш.RibBracket поставляется с четырьмя вариантами ширины, позволяющими регулировать трапециевидную ширину. («Ножки» также сгибаются, чтобы соответствовать разным размерам и углам). Посетите S-5! , веб-сайт , чтобы узнать больше о конкретных профилях шва, подходящих для каждого кронштейна.
Ниже представлены габаритные чертежи С-5! RibBracket. Более высокий профиль нашего кронштейна также обеспечивает достаточное расстояние между крышей и солнечными модулями. Четыре точки крепления увеличивают его удерживающую способность.В то время как другие продукты крепятся прямо к верхней части трапециевидного профиля, RibBracket крепится к боковым стенкам, обеспечивая гораздо большую удерживающую способность для приложений прямого крепления. А верхний слот предназначен для «подгонки» выравнивания модулей при установке.
С-5! RibBracket I | С-5! RibBracket II |
С-5! RibBracket III | С-5! RibBracket IV |
Подробнее о RibBracket ™ I-IV
ПРОСТО ДЛЯ ПРЯМОГО ПРИСОЕДИНЕНИЯ СОЛНЦА: S-5! RibBracket разработан для наиболее распространенных трапециевидных профилей с открытым креплением в Северной Америке.Нет необходимости в грязных герметиках. Кронштейн имеет двойное уплотнение с резиновым уплотнением EPDM уже в основании кронштейна и защищено от УФ-излучения. Специальные винты с шайбой из EPDM, поставляемые с RibBracket, завершают сборку с двойным уплотнением.
Подробнее о RibBracket ™
Трапециевидный профиль крыши с RibBracket ™ и PVKIT ™ 2.0
SolarFoot ™ и ProteaBracket ™
С-5! также предлагает два других продукта, которые являются основными решениями для крепления солнечных панелей: SolarFoot ™ и ProteaBracket ™ .Используйте SolarFoot для монтажа солнечных панелей на рейке. Он совместим с любой «L-Foot». Хотите продукт, который может все? Полностью регулируемый S-5! ProteaBracket может использоваться как для прямого крепления с PVKIT ™, так и для монтажа на боковой и нижней направляющих. L-Foot никогда не требуется — в комплект ProteaBracket входит полностью универсальная стопа. И все С-5! продукты полностью протестированы под нагрузкой для инженерных приложений. Просто проконсультируйтесь с нашим сайтом или спросите одного из наших дружелюбных технических специалистов!
С-5! SolarFoot ™
С-5! ProteaBracket ™
ЧТО НАСчет ТРАПЕЦОИДАЛЬНЫХ КРОВЕЛЬНЫХ ПРОФИЛЕЙ С ПОСТОЯННЫМ ФВОВОМ? Рассмотрим зажим S-5-V .Этот зажим предназначен для соединения с двойным сложением или трапециевидным замком с защелкой (вертикальным) в стоячих швах. S-5-U и S-5-V Mini — два других универсальных зажима, которые мы предлагаем для этого типа кровельного профиля. Этот зажим подходит как для вертикальных, так и для горизонтальных швов. Кроме того, S-5-H , H-90 и S-5-U , а также их соответствующие мини-версии подходят для различных вариантов трапециевидного профиля ребер.
Вот два примера разновидностей стоячих швов: профили с трапециевидной двойной складкой и трапециевидные профили с защелкиванием (рис. 2 и 3, соответственно).
|
С-5! Зажимы SSR непроникающие
https://www.s-5.com/products/clamps-brackets/clamps/
Почему С-5! Зажимы — это правильный путь ™ для Крепление практически чего угодно к трапециевидной крыше: С-5! Совместимый с трапециевидным профилем ребра
RibBracket ™
RibBracket I-IV ™
S-5-U Хомуты
S-5-V Хомуты
S-5-H Зажимы
S-5-H-90 Зажимы
ProteaBracket ™
SolarFoot ™
С-5! PVKIT ™ Solar Solutions
Лучшие практики 2019 для крыш с солнечными батареями и металлических крыш с открытыми крепежными элементами
Что такое гофрированная металлическая кровельная панель?
Quick Ожидается возврат инвестиций от проекта установки солнечных батарей McElroy
Слово недели: что входит в список UL?
Слово недели: что такое фотоэлектрическая солнечная технология?
Простая и универсальная микрофлюидика для 3D-печати с использованием плавленых волокон
Abstract
Освоение микрофлюидики более широким научным сообществом было ограничено производственным барьером, создаваемым навыками и оборудованием, необходимыми для производства традиционных микрофлюидных устройств.Здесь мы представляем простые микрожидкостные устройства, напечатанные на 3D-принтере, с использованием недорогого и легкодоступного принтера с коммерчески доступными материалами для принтера. Мы демонстрируем, что ранее заявленные ограничения прозрачности и точности были преодолены, в то время как устройства, способные работать при давлениях, превышающих 2000 кПа, показывают, что проблемы утечки также были решены. Полезность микрожидкостных устройств, напечатанных на 3D-принтере, иллюстрируется заключением стволовых клеток пульпы зуба в капельки альгината; Анализы жизнеспособности клеток показывают, что подавляющее большинство клеток остаются живыми, а прозрачность устройства достаточна для визуализации отдельных клеток.Доступность этих устройств дополнительно повышается за счет изготовления интегрированных портов и внедрения модульной системы, подобной Lego ® , которая облегчает быстрое создание прототипов, предлагая новичкам возможность создавать микрофлюидные системы из базы данных микрожидкостных компонентов.
Образец цитирования: Морган А.Дж., Идальго Сан-Хосе Л., Джеймисон В.Д., Ваймант Дж. М., Сонг Б., Стивенс П. и др. (2016) Простая и универсальная микрофлюидика с 3D-печатью с использованием изготовления плавленых волокон.PLoS ONE 11 (4): e0152023. https://doi.org/10.1371/journal.pone.0152023
Редактор: Мин-Сянь Ву, Университет Чанг Гун, Тайвань
Поступила: 17 декабря 2015 г .; Одобрена: 8 марта 2016 г .; Опубликовано: 6 апреля 2016 г.
Авторские права: © 2016 Morgan et al. Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Доступность данных: Все соответствующие данные находятся в документе и его файлах с вспомогательной информацией.
Финансирование: Это исследование финансировалось synbiCITE (synbicite.com) через Инициативу по синтетической биологии Кардиффского университета, AJLM и Европейский исследовательский совет, грант StG 243261, LHSJ. Финансирующие организации не играли никакой роли в дизайне исследования, сборе и анализе данных, принятии решения о публикации или подготовке рукописи.
Конкурирующие интересы: Авторы заявили, что никаких конкурирующих интересов не существует.
Введение
В течение многих лет микрофлюидика считалась областью, которая может изменить методы проведения исследований в биологическом и химическом сообществах [1–3]. Microfluidics обеспечивает точное манипулирование жидкостями в небольших масштабах, позволяя использовать небольшие объемы образцов, снижая затраты, увеличивая пропускную способность, а также параллельную и последовательную обработку, легко поддающуюся автоматизации и переносимости в масштабах, превышающих те, которые достигаются ручными или традиционными роботизированными манипуляциями [ 4].Microfluidics использует уникальное поведение жидкостей в микромасштабе, где поверхностные и вязкие силы преобладают над силой тяжести и инерции, вызывая ламинарный поток в однофазных системах и воспроизводимый и программируемый поток капель в многофазных системах [5]. Эта полезная гидродинамика использовалась в различных областях, включая инкапсуляцию клеток [6], анализ ДНК [7, 8], прототипирование лекарств [9], высокопроизводительный скрининг [10, 11], сортировку и разделение клеток и капель [12]. –15], химический синтез [16], химическое разделение [17], производство радиофармпрепаратов [18], протеомика [19] и диагностические технологии [20] среди прочего.
Несмотря на эти уникальные свойства и разнообразные области применения, микрофлюидика в значительной степени оставалась в некоторой степени специализированной областью исследований с ограниченным вниманием тех, кто мог бы извлечь наибольшую пользу из этой технологии. Два ключевых фактора ограничили использование более широких дисциплин; производство и универсальность. Во-первых, традиционные методы микрожидкостного производства, такие как мягкая литография, требуют навыков и оборудования, которые часто недоступны в типичных биологических, химических или фармацевтических лабораториях [21, 22].Во-вторых, фиксированный характер изготовленных устройств ограничивает итеративную оптимизацию процесса или гибкость применения.
Преодоление производственного барьера
Барьеры на пути к более широкому внедрению очевидны, если использовать только один пример технологии изготовления мягкой литографии с полидиметилсилоксаном (ПДМС). Несмотря на преимущества этого метода изготовления, создание устройства PDMS требует знания и доступа к оборудованию для фотолитографии и плазменной сварки.Аналогичные требования к ноу-хау и оборудованию справедливы и для других распространенных технологий производства, таких как изготовление с помощью лазера, микроперерезания, ионного травления и фотолитографического производства. Бертье и др. резюмируют проблему, заявляя, что «принятие микромасштабных технологий биологами зависит от… успешного сотрудничества между инженерами и биологами… и создания стандартных платформ, которые… широко доступны и доступны биологическому сообществу в целом» [23]. Здесь мы представляем микрожидкостную платформу, способную решить эту проблему, перенося универсальную микрофлюидику в лаборатории более широкого научного сообщества по низкой цене и без необходимости в специализированном оборудовании или опыте.
В последнее время 3D-печать на основе экструзии (производство плавленых нитей (FFF)) превратилась в легкодоступную потребительскую технологию. По мере того как простота использования и разрешения улучшились, а цены упали, возможность быстро и легко создавать нестандартные объекты стала доступной для всех, что привело к смене парадигмы в мелкомасштабном производстве. Легкость и дешевизна создания нестандартных объектов и устройств демократизирует ранее специализированные области производства, значительно расширяя возможности неспециалистов и позволяя дешевое и быстрое прототипирование и производство.
До недавнего времени возможности 3D-печати были ограничены разрешением или стоимостью принтеров [24, 25]. Однако недавние достижения означают, что микротехнология теперь возможна в готовом виде, без сложных производственных центров [26], и прогресс продолжается быстрыми темпами, что означает, что возможности, вероятно, еще больше увеличатся. 3D-печать применялась к микро- и миллифлюидикам в сочетании с другими методами [27] или как самостоятельный процесс изготовления [22, 24, 26, 28–31]. Стереолитографическая (SL) печать, которая чаще используется в микрофлюидике, включает в себя послойное фотоотверждение полимерной смолы, что позволяет изготавливать трехмерные объекты из резервуара с жидкой смолой.Более распространенная и доступная технология печати, изготовление плавленых волокон (FFF), часто не принималась во внимание при производстве микрофлюидных устройств [22]. От этого типа печати часто отказываются из-за утечки между экструдированными слоями, а также из-за отсутствия прозрачности и кажущегося отсутствия разрешения и точности [32]. FFF-печать (также известная как моделирование методом наплавленного осаждения (FDM) или экструзионная печать) — это аддитивный производственный процесс, при котором экструзия расплавленного полимера слой за слоем позволяет создавать трехмерные объекты.С помощью этого метода проверенные концепции микрофлюидные каналы диаметром 800 мкм были изготовлены из полипропилена [24]. Хотя SL-печать может обеспечить большее разрешение канала, чем FFF, она редко демонстрировалась с размерами канала ниже 500 мкм. Примечательно, что возросшая сложность и стоимость процесса SL-печати означает, что изготовление таких устройств часто передается специалистам [22, 29, 33, 34], что создает сопоставимые препятствия для внедрения, как при использовании традиционных методов производства.Поскольку в настоящее время принтеры доступны по цене ниже 1000 фунтов стерлингов, FFF предлагает гораздо более высокий уровень доступности, а это означает, что большинство лабораторий должны иметь возможность изготавливать свои собственные устройства на месте, облегчая дешевое производство и быстрое прототипирование для широкого спектра приложений.
Концепция дизайна
Представленные здесь устройства для 3D-печати были разработаны для обеспечения простой интеграции с традиционными системами обработки жидкостей. Таким образом, резьбовые порты на впускных и выпускных отверстиях позволяют использовать простые фитинги из ПЭЭК с фиксацией вручную для подсоединения устройств к трубкам и насосам.Пример конструкции показан на рис. 1. Для большей доступности были также спроектированы соединяемые жидкостные модули. Гидравлические модули были основаны на блоках Lego ® , которые известны во всем мире и могут быть просто соединены вместе, создавая без утечек реконфигурируемые микрожидкостные системы.
Рис. 1. Схематическое изображение узла фокусировки потока, показывающее включение отверстий, затягиваемых вручную.
После создания этой модели с помощью SOLIDWORKS или аналогичного программного обеспечения для проектирования устройство можно создать на 3D-принтере простым нажатием кнопки.
https://doi.org/10.1371/journal.pone.0152023.g001
Экспериментальный
Производство устройств
Устройства были произведены путем изготовления плавленых волокон на принтере Ultimaker 2. Устройства печатали со скоростью 30 мм / с при температуре сопла 215 ° C. Модули были напечатаны со 100% плотностью заполнения на рабочей пластине, нагретой до 70 ° C. Схемы устройств были разработаны в Solidworks 2013 перед преобразованием в образец печати с помощью Simplify3D 2.2.2 программное обеспечение. Были напечатаны чередующиеся слои толщиной 50 мкм, так что узор шел перпендикулярно, а затем параллельно длине устройства, что позволяло печатать герметичные и прозрачные устройства с использованием прозрачной полимолочной кислоты (PLA). Микрожидкостные устройства, напечатанные на 3D-принтере, также были изготовлены стереолитографически с использованием принтера Miicraft со слоями 100 мкм и временем отверждения 25 с. Полные настройки печати можно найти в таблице S1.
Испытание под давлением
Для характеристики жидкостного интерфейса и соединений между модулями было измерено максимальное давление, которое соединения могли выдержать до утечки.Это было достигнуто путем блокировки выхода одного модуля при закачке воды на вход подключенного модуля с постоянной скоростью потока 12 мл / ч (Rheos 2000, Flux Instruments). Давление, необходимое для подачи воды, контролировалось на протяжении всего эксперимента. Утечки были обнаружены при визуальном осмотре. Данные по давлению регистрировались с помощью программного обеспечения для управления насосом (Janeiro II 2.6).
Материалы и устройства
Первоначальные испытания были проведены для изучения пригодности ряда имеющихся в продаже нитей для принтеров.Устройства с Т-образным соединением для генерации капель были созданы с каналами диаметром 1 мм, и выход устройства был изучен. Подсолнечное масло и вода (содержащая краситель Red Silverspoon) подавали с помощью шприцевых насосов (Legato 210, KD Scientific) для создания эмульсий воды в каплях масла. Устройства были изготовлены с использованием нити PLA (Ultimaker PLA 2,85 мм), прозрачной нити из полиэтилентерефталата (PET) (Taulman t-glase 3 мм), прозрачной нити модифицированного акрилонитрилбутадиенстирола (ABS) (Bendlay 3 мм) и прозрачной PLA (Faberdashery, Crystal Прозрачный 3мм).Печатные устройства SL были изготовлены с использованием прозрачной смолы DETAX Luxaprint.
Переходы с фокусировкой потока были испытаны с использованием минерального масла (Sigma-Aldrich), окрашенного Oil Blue N (Sigma-Aldrich). В дальнейших тестах использовался раствор альгината, который содержал 2% альгината в дистиллированной воде с 7,5 мг / мл карбоната кальция, CaCO 3 , (Sigma-Aldrich) (с красным пищевым красителем SilverSpoon для визуализации). Раствор перемешивали с помощью магнитной мешалки в течение 1 часа при 50 ° C для растворения альгината. Для создания эмульсий масло в воде использовали 10 мМ водный раствор олеиновой кислоты (Sigma-Aldrich) с pH 23 с регулированием pH, достигаемым с помощью гидроксида натрия (Sigma-Aldrich) в деионизированной воде (4 г / л).Затем раствор обрабатывали ультразвуком в течение 1 минуты после добавления олеиновой кислоты, чтобы убедиться, что раствор был однофазным. Измерения капель, образовавшихся на стыках фокусировки потока, проводились с помощью высокоскоростной камеры (Megaspeed) в сочетании с NIS Elements 3.2.
Измерения верности
Для оценки качества и точности 3D-печати была напечатана серия каналов диаметром от 400 мкм до 1,5 мм с шагом 100 мкм. Затем размеры каналов были измерены с помощью микроскопа Nikon AZ100 с NIS Elements 3.2 программное обеспечение. Каналы были напечатаны с использованием как печати FFF, так и печати SL. Печатные каналы FFF были напечатаны как в горизонтальной, так и в вертикальной ориентации. Горизонтально напечатанные каналы измеряли в двух направлениях, чтобы оценить ширину и высоту каналов. Оценивались отпечатки с толщиной слоя 25 мкм, 50 мкм и 100 мкм. Измеренные размеры каналов сравнивались с исходными размерами, указанными в моделях, созданных в Solidworks.
Инкапсуляция стволовых клеток
Стволовые клетки пульпы зуба человека (hDPSC) инкапсулировали в альгинатные капсулы (1 × 10 9 10 27 6 9 10 28 клеток / мл).Клетки были получены от третьих моляров (доноры в возрасте 17–20 лет) с информированного письменного согласия всех пациентов в соответствии с Законом об исследованиях и тканях человека 2004 г. Этическое одобрение было предоставлено Комитетом по этике исследований Юго-Восточного Уэльса Национальной службы этики исследований (разрешение номер: 07 / WESE04 / 84. Этическую документацию можно найти на рис. S1 – S3) и культивировать в минимально необходимой среде α-модификации (αMEM), содержащей 2 мМ глутамина, рибонуклеозиды и дезоксирибонуклеозиды (Life Technologies, Великобритания).В среду добавляли 1% (об. / Об.) Пенициллин / стрептомицин, 10% (об. / Об.) Термоинактивированной фетальной бычьей сывороткой (FBS) (Life Technologies, UK) и 100 мкМ 2-фосфата 1-аскорбиновой кислоты (Sigma- Олдрич, Великобритания). Среду меняли каждые 2–3 дня, пока клетки не достигли 80–90% слияния. По достижении слияния культуральную среду удаляли путем аспирации и клетки промывали фосфатно-солевым буфером (PBS) (Sigma-Aldrich, UK). Клетки диссоциировали, добавляя 0,25% трипсин-ЭДТА (об. / Об.) (Sigma-Aldrich, UK), и возвращали в инкубатор на 3-5 минут, пока они не стали округлыми и не отделились.Трипсин нейтрализовали добавлением питательной среды. Затем среду и клеточный раствор переносили в 15 мл пробирки Falcon и центрифугировали при 1500 об / мин в течение 5 минут. После удаления супернатанта осадки ресуспендировали в среде и подсчет клеток выполняли с помощью гемоцитометра. Наконец, клетки снова центрифугировали и ресуспендировали при плотности 1 миллион клеток на мл альгината в 2% растворе альгината с низкой вязкостью (AO682, Sigma Aldrich, UK). Раствор альгината создавали добавлением 5 мг / мл карбоната кальция (Sigma-Aldrich) к αMEM с добавлением 1% (об. / Об.) Пенициллина / стрептомицина перед добавлением 20 мг / мл альгината и перемешиванием в течение 2 часов при 50 ° C.Монодисперсные альгинатные капли, содержащие стволовые клетки, были созданы на устройствах для 3D-печати в непрерывной фазе подсолнечного масла. Капли альгината превращались в гель в течение приблизительно 10 минут на выходе из чипа в растворе подсолнечного масла для ванны, содержащем ледяную уксусную кислоту (0,3% об. / Об.). После гелеобразования капсулы промывали культуральной средой и после различных периодов времени в культуре оценивали жизнеспособность с использованием набора для анализа жизнеспособности / цитотоксичности LIVE / DEAD ® для клеток млекопитающих (Invitrogen) с кальцеином-AM (зеленый), указывающим внутриклеточный активность эстеразы в живых клетках и флуоресценция гомодимера этидия-1 (красная), указывающая на потерю целостности плазматической мембраны в мертвых клетках.Конфокальную визуализацию инкапсулированных клеток с помощью лазерного сканирования проводили с использованием конфокального микроскопа Leica SP5 и программного обеспечения для визуализации LAS AF (Leica Microsystems, Германия). Изображения инкапсулированных клеток были получены с помощью конфокального Z-сканирования на глубине 600 мкм.
Мечение стволовых клеток на плазматической мембране
Клетки центрифугировали при 400 g в течение 5 мин. Супернатант отбрасывали, и клетки ресуспендировали в 1 мл стерильного PBS, содержащего CellMask Orange (C10045, Molecular Probes) в концентрации 5 нг / мл.Клетки инкубировали с этим мембранным красителем в течение 10 минут при комнатной температуре, а затем центрифугировали при 900 g в течение 2 минут. Супернатант удаляли, а осадок клеток промывали ресуспендированием в стерильном PBS и инкубацией при комнатной температуре в течение 1 мин. Затем клетки повторно центрифугировали (900 g, 2 мин) и еще раз ресуспендировали в 1 мл PBS для последующего анализа. Капли, содержащие сульфородамин b (250 нМ и 25 нМ) и водную суспензию стволовых клеток, меченных CellMask Orange, были визуализированы в условиях потока в прозрачном устройстве PLA, эквивалентном тем, которые использовались в тестах на прозрачность устройства.Визуализацию проводили при 4-кратном или 10-кратном увеличении с освещением 532 нм через оптоволоконную пару TIRF, соединенную в эпифлуоресцентном режиме на инвертированном микроскопе Nikon Eclipse Ti-U. Эмиссионный флуоресцентный фильтр 590/50 нм (Chroma, США) отфильтровывал излучаемый свет перед визуализацией на камере Andor iXon при времени кадра сбора данных 18 мс.
Результаты и обсуждение
Чтобы продемонстрировать возможности микрожидкостных устройств с печатью FFF, были созданы фокусирующие поток соединения для контролируемого образования капель (рис. 2).Легко образуются капли воды в масле. Кроме того, были продемонстрированы капли альгината в масле и капли масла в непрерывной фазе воды и олеиновой кислоты, что демонстрирует возможность последовательного образования капель в микрожидкостных устройствах, напечатанных на 3D-принтере. Важно отметить, что на рис. 2 также показано, что можно наблюдать поток жидкости в устройствах из PLA, напечатанных на 3D-принтере, либо за счет использования встроенного стеклянного смотрового окна для микроскопических приложений (рис. 2A), либо за счет использования полупрозрачного PLA с достаточной тонкие стенки (рис. 2B и 2C).
Рис. 2. Экструзионные 3D-печатные фокусирующие переходы.
A) Вода в каплях масла, образованных в модуле PLA, в который встроено стеклянное смотровое окно. Б) Капли раствора альгината в подсолнечном масле, полученные в полупрозрачном модуле PLA. Скорость потока масла: 3 мл / час, скорость потока альгината: 1 мл / час C) Капли минерального масла в воде и 10 мМ фазе носителя олеиновой кислоты. Создан на полупрозрачном PLA-устройстве. Расход воды: 4 мл / час, расход масла: 1,5 мл / час. Разъемы A и C имеют ширину впускного канала 1 мм с 1.Выход шириной 4 мм. В разветвлении B имеются каналы шириной 600 мкм и выходным отверстием шириной 900 мкм.
https://doi.org/10.1371/journal.pone.0152023.g002
Узел фокусировки потока PLA со стеклянным окном наблюдения (рис. 2A) использовался для оценки воспроизводимости и контроля содержания воды в образовании капель нефти (рис. 3). ). Размер капель можно контролировать, изменяя соотношение расходов воды и масла с более высоким расходом масла по сравнению со скоростью потока воды, что приводит к меньшему размеру капель.Геометрия канала и свойства жидкости определяют минимальный размер капель. Частоту образования капель исследовали путем увеличения общего расхода при фиксированном соотношении потоков масло: вода. Это приводит к увеличению частоты капель без изменения диаметра. На протяжении всего частотного теста образовывались капли постоянного диаметра 504 мкм (± 18 мкм), поскольку частота образования капель увеличивалась с 1 до 10,4 Гц. Изменение частоты было очень небольшим, о чем свидетельствует небольшой диапазон колебаний 0.2–1,2% (95% доверительный интервал), что свидетельствует о высокой стабильности работы. Однако при самой низкой скорости потока (1,5 мл / час) было измерено 13% отклонение в производственной частоте, это связано с тем, что эти данные собираются с более низкой частотой кадров с использованием другой камеры, чем другие точки данных. Поведение этого 3D-печатного узла фокусировки потока согласуется с предыдущими исследованиями переходов фокусировки потока [35].
Рис. 3. Данные о каплях с 3D-печати на стыке фокусировки потока (рис. 2А).В минеральном масле образуются капли воды.A) Диаметр капель при увеличении скорости потока в каждое впускное отверстие для масла. Расход нефти был увеличен кратно расходу воды. Кривая добавлена, чтобы проиллюстрировать тенденцию. Ошибка находилась в диапазоне 1,3–3,3% при уровне достоверности 95%. B) Частота капель при увеличении расхода масла и воды на каждом входе (фиксированное соотношение расхода масла: воды 2: 1). Например, в точке данных 10 мл / час оба впускных отверстия для масла установлены на 10 мл / час, в то время как впускное отверстие для воды установлено на 5 мл / час. Ошибка ошибка для файла 1.Точка данных 5 мл / час составила 13% из-за сбора данных с использованием альтернативной камеры с более низкой частотой кадров, ошибка для всех других точек данных находилась в диапазоне 0,2–1,2% при 95% достоверности. Как в A), так и в B) для каждой точки данных было измерено по 10 капель (n = 10). Планки погрешностей не отображаются, поскольку они закрыты точками данных.
https://doi.org/10.1371/journal.pone.0152023.g003
Тесты на верность
Критика печати FFF заключалась в отсутствии точности между напечатанными размерами и исходной моделью САПР [32].Здесь мы исследуем корреляцию между измеренным круглым поперечным сечением напечатанных каналов по сравнению с первоначально разработанной геометрией в различных условиях печати (слои толщиной 50 мкм показаны на рис. 4). Дальнейший анализ качества печати можно найти на рис. S4, где показаны различные толщины слоев. и сравнение с SL-печатью.). Высокая точность возможна при правильных параметрах печати (в данном случае высота слоя 50 мкм) при высоте и ширине канала в среднем в пределах 2,5% от проектных размеров канала.Рис. 4 иллюстрирует постоянство размеров во всех направлениях, хотя есть некоторая неизбежная шероховатость, возникающая из-за послойной природы FFF-печати, как это видно на Фиг. 4C. Хотя шероховатость поверхности не рассматривалась для оптимизации в этой работе, типичная шероховатость поверхности была охарактеризована интерферометрическим измерением (S5 Рис.) Покрытых золотым напылением устройств, изготовленных при 1200 мм мин. -1 , с нанесением слоя 50 мкм, как используется в прозрачности. тесты. Более 1.Было обнаружено, что поверхности материалов с площадью 4 x 1,4 мм имеют размах размаха 16,81 мкм. Характер метода осаждения приводит к появлению пиков на границе раздела между двумя экструдированными «полосами». Дальнейшая оптимизация шероховатости поверхности может быть достигнута либо за счет дальнейшей оптимизации параметров печати, либо за счет обработки растворителем после изготовления, но это считалось выходящим за рамки этого. учеба и ненужность с учетом успешной функциональности печатных устройств. По мере улучшения разрешения печати и уменьшения производственных габаритов оптимизация шероховатости поверхности может приобретать все большее значение.
Рис. 4. Измерения точности 3D-принтера.
a и b) Сравнение измеренных и желаемых размеров круглых каналов, напечатанных на 3D-принтере. Пунктирная линия указывает на идеальное соответствие между CAD-моделью и напечатанным каналом. a) Измеренная ширина горизонтально напечатанного канала с использованием печати FFF со слоями 50 мкм. б) Измеренная глубина горизонтально напечатанного канала с использованием печати FFF со слоями 50 мкм. c) Изображение каналов диаметром 1,4 мм, изготовленных с помощью экструзионной 3D-печати. Для каждой точки данных было выполнено 3 измерения.Планки погрешностей показывают уровень достоверности 95%.
https://doi.org/10.1371/journal.pone.0152023.g004
Измерения точности показывают, что минимально достижимый размер канала составляет 500 мкм. Несмотря на то, что он относительно большой, он подходит для многих микрофлюидных приложений. В настоящее время это определяется размером текущих сопел принтера. Однако с учетом недавно выпущенных сопел меньшего размера и ожидаемых достижений в технологии печати этот предел должен снизиться, что приведет к дальнейшему расширению областей применения микрожидкостных материалов с экструзионной печатью по мере уменьшения размеров каналов.
Прозрачность устройства
Хотя это и не является необходимым для работы, часто желательно производить прозрачные микрофлюидные устройства для наблюдений или аналитических целей. Ранее опубликованные микрожидкостные устройства с печатью FFF были в основном непрозрачными, хотя полупрозрачные устройства также были недавно созданы за счет использования очень тонких боковых стенок [36]. Пример этой проблемы можно увидеть на рис. 5A (Т-образный переход PLA). Невозможность визуализировать архитектуру канала или флюид внутри затрудняет разработку и эксплуатацию устройства.Ряд имеющихся в наличии волокон был исследован вместе с оптимизацией условий печати с целью улучшения прозрачности сверх того, что было достигнуто с помощью полупрозрачного PLA (рис. 2B и 2C).
Рис 5. Преодоление барьера прозрачности.
A) Т-образный переходник из PLA с использованием обычного цветного PLA. Кажется, что устройство работает эффективно, но можно наблюдать только жидкости, входящие и выходящие из устройства. Сегментированный поток создается с помощью воды (красный) и масла (прозрачный).Б) Устройство, созданное с использованием ПЭТ-нити. Прозрачность достигается за счет использования достаточно тонких стенок, однако смачивающие свойства материала приводят к ненадежному образованию капель. Эта проблема также была очевидна с C) модифицированным ABS (T-glase), вероятно, из-за проникновения водной фазы в основной материал устройства, о чем свидетельствует легкий розовый оттенок устройства на изображении C. D) Полностью прозрачный микрожидкостный устройства были получены с использованием прозрачного PLA с оптимизацией параметров печати.Печатный текст на бумаге, помещенной под устройство, легко читается на отпечатанном материале во время работы устройства. E) Схема устройства, показанного на изображении D. F) Фотография устройства, используемого на изображении D.
https://doi.org/10.1371/journal.pone.0152023.g005
Было обнаружено, что нити ПЭТ (рис. 5В) и АБС (рис. 5С) обеспечивают разумную прозрачность за счет использования тонких стенок каналов, позволяющих легко визуализировать. Однако характеристики смачивания материала оказались неидеальными для надежного образования капель (см. S6 рис.).Используя прозрачный PLA вместе с оптимизацией параметров печати, таких как толщина слоя, скорость печати и узор заполнения, стало возможным достичь беспрецедентного уровня прозрачности устройства, исключив необходимость наблюдения с одной конкретной стороны и необходимость использования очень тонких стенок. Достаточная прозрачность печати была достигнута для быстрой визуализации печатного текста через устройство (рис. 5D) и для динамической флуоресцентной визуализации отдельных клеток в условиях потока внутри каналов (рис. 6B).Насколько нам известно, это первое действительно прозрачное микрожидкостное устройство FFF, напечатанное на 3D-принтере.
Рис. 6. Оптическая передача 3D-печатных устройств при различной скорости печати и высоте слоя.
A) Коэффициент пропускания изготовленного устройства в процентах от исходного материала на длине волны 550 нм. Сравнение слоев 25 мкм со слоями 50 мкм, а также сравнение с настройками Cura по умолчанию (только процент заполнения изменен на 100%) Вставка: микрожидкостное устройство, напечатанное на 3D-принтере, напечатанное со скоростью 1200 мм / мин со слоями 25 мкм, текст, напечатанный на бумаге под устройством Подробная информация об условиях производства четко видна на всем устройстве.Канал диаметром 1 мм проходит через центр устройства. B) отдельные стволовые клетки, помеченные мембранным красителем (CellMask Orange), отображаемые в условиях потока в трехмерном напечатанном прозрачном микрофлюидном устройстве, напечатанном со скоростью 1200 мм / мин со слоями 25 мкм. Толщина устройства 3 мм с каналом, заделанным на глубину 1,5 мм. Видео этих клеток в движении можно найти в Интернете в видеороликах S1 – S3).
https://doi.org/10.1371/journal.pone.0152023.g006
Была исследована оптимизация параметров печати для достижения прозрачности, и прозрачность количественно оценивалась по пропусканию видимого света через печатное устройство по сравнению с чистым полимером эквивалентной длины пути передачи ( Рис 6).Было обнаружено, что как высота производственного слоя, так и скорость печати оказывают сильное влияние на прозрачность, при этом более низкие скорости и более тонкие слои улучшают передачу (данные о полной передаче в видимом спектре света можно найти на S7 Рис.). Кажется, существует верхний порог, выше которого снижение скорости не улучшает передачу. Этот предел ниже, чем у непечатных, но формованных листов PLA той же толщины. Это может объясняться рассеянием на более шероховатой печатной поверхности. Свойства пропускания материала нити PLA определяют предел прозрачности.Дальнейшее развитие печатных материалов могло бы еще больше улучшить это. Хотя в настоящее время прозрачность ограничена примерно 63% от прозрачности необработанного полимера, из рисунков 5D, 5F и 6B очевидно, что оптическое наблюдение в этих устройствах с 3D-печатью легко достижимо. Капли, содержащие 25 нМ сульфородамина b, и отдельные стволовые клетки, окрашенные оранжевым красителем плазматической мембраны CellMask, легко визуализируются с помощью флуоресцентной микроскопии в каналах устройства. Это представляет собой значительное улучшение в микрофлюидике, напечатанной на 3D-принтере FFF.Для приложений, где желательны более высокие уровни оптической прозрачности, мы продемонстрировали возможность использования стеклянного смотрового окна, как показано на рис. 2A.
Предыдущая работа была предпринята попытка улучшить прозрачность за счет использования тонких стенок, уменьшив количество слоев между каналом и внешней средой [36]. Однако наши результаты показывают, что ключом к достижению прозрачности в устройствах для 3D-печати на самом деле является отсутствие недоэкструзии.Действительно, было обнаружено, что устройства со слоем 25 мкм обеспечивают лучшую передачу, чем устройства со слоем 50 мкм, несмотря на то, что в них вдвое больше слоев и интерфейсов печати. Точно так же более низкие скорости печати также могут дать аналогичные улучшения, поскольку обе конфигурации позволяют экструдировать один и тот же объем материала в течение более длительного периода времени. Недостаточная экструзия приводит к образованию полостей между слоями печатного материала, что приводит к увеличению светорассеяния и, как следствие, снижению прозрачности. Предотвращение недостаточной экструзии также значительно улучшает герметичность микрожидкостных каналов за счет исключения возможности межслоевых зазоров, через которые могут протекать жидкости; проблема, ранее определенная Walbaur и др. [37] как возможное ограничение микрожидкостных устройств для 3D-печати.Хотя слои 25 мкм, по-видимому, обеспечивают улучшенную прозрачность, улучшенная точность воспроизведения (рис. 4), обеспечиваемая слоями 50 мкм, делает их, вероятно, более подходящими для производства микрофлюидных устройств, где важен точный контроль геометрии каналов. Следует отметить, что можно было наблюдать прохождение жидкостей через устройство даже при наименее прозрачной конфигурации печати в этом эксперименте (слои 50 мкм при 2400 мм / мин), хотя это было сильно ограничено настройками слайсера по умолчанию.
Инкапсуляция стволовых клеток
Чтобы продемонстрировать практическую полезность 3D-печатной микрофлюидики FFF для био- и химических применений, мы создали устройство для производства монодисперсных альгинатных микросфер для инкапсуляции живых стволовых клеток.Такие системы инкапсуляции клеток в гидрогеле позволяют производить трехмерное культивирование клеток и легко манипулировать ими [38]. Кроме того, инкапсуляция клеток может обеспечить средства для пролонгированного биотерапевтического высвобождения in vivo [39]. Физический барьер, обеспечиваемый инкапсулирующей микросферой, означает, что системы инкапсулированных стволовых клеток вызывают большой интерес с точки зрения их потенциального применения в терапии тканевой инженерии и регенеративной медицины [40–42]. Монодисперсные стволовые клетки, содержащие капли альгината и карбонат кальция, были созданы на устройствах для 3D-печати в непрерывной фазе подсолнечного масла.Капли альгината (диаметром 800 мкм) превращались в гель при входе в камеру для подкисленного масла. Разделение кислоты вызывает снижение pH в альгинате и высвобождение Ca 2+ из карбоната кальция, вызывая последующее гелеобразование альгината. После гелеобразования капсулы очищали в культуральной среде, а затем оценивали жизнеспособность клеток, используя анализ жизнеспособности живых / мертвых клеток, при этом кальцеин-AM (зеленый) указывает на внутриклеточную активность эстеразы в живых клетках, а флуоресценция гомодимера этидия-1 (красная) указывает на потерю целостность плазматической мембраны в мертвых клетках.Конфокальная визуализация показала, что подавляющее большинство инкапсулированных клеток остались живыми (рис. 7C).
Рис. 7. Живые стволовые клетки пульпы зуба, заключенные в капельки альгината, созданные на устройстве для 3D-печати.
A) Монодисперсные альгинатные капсулы, выходящие из микрофлюидного устройства. B) Изображение альгинатной капсулы, содержащей стволовые клетки. C) Конфокальная z-проекция, показывающая живые инкапсулированные стволовые клетки, окрашенные зеленым, и мертвые клетки, окрашенные в красный цвет. На изображении показан край капсулы.
https: // doi.org / 10.1371 / journal.pone.0152023.g007
Модульная система
Доступность и практичность устройств для 3D-печати можно еще больше повысить за счет использования модульной системы, которая позволяет пользователям распечатывать модульные компоненты и соединять их вместе для создания реконфигурируемых микрожидкостных систем. С этой целью была разработана модульная система, основанная на взаимосвязи блоков Lego ® . Использование закругленных шпилек, выступающих из верхней поверхности блоков, и обратной полости на нижней стороне, обеспечивает взаимную блокировку модулей и гидравлическое соединение.Герметичные уплотнения могут быть выполнены быстро и многократно между различными модулями (рис. 8A и 8B). Уплотнительное кольцо внутри соединительного порта охватывающего модуля обеспечивает герметичное уплотнение. Чтобы продемонстрировать возможности модульной системы, был создан ряд модулей, которые демонстрируют многие из типичных компонентов микрофлюидных систем, таких как Т-образные переходы, каналы смешения и переходы фокусировки потока. Схемы этих компонентов можно найти в таблице S2. Соединение без утечек стало возможным при диаметрах каналов до 600 мкм (по высоте и ширине).Семикомпонентную модульную систему, состоящую из камеры наблюдения, 4 независимых входов жидкости, а также последовательных геометрических форм Т-образного соединения и фокусирования потока для получения капель жидкости с переменным составом можно увидеть на рис. 8D.
Рис. 8. Lego ® как модули, напечатанные на 3D-принтере.
A) Изображение профиля входного / выходного модулей с внутренней (верхней) и охватываемой (нижней) части, когда они не соединены друг с другом, показывает внутреннюю структуру модулей с каналом, проходящим через оба модуля через резьбовое соединение с затяжкой вручную.Б) Фотография двух модулей, соединенных вместе. Модули соединяются простым сдвигом их вместе, блокируя закругленные шпильки на охватываемом блоке в выемке на охватывающих блоках. Никакой формы склеивания не требуется. Модули на этом изображении были созданы на стереолитографическом принтере для повышения прозрачности. C) Предел давления модульной системы, подобной Lego ® , как определено экспериментально. Планки погрешностей представляют собой уровень достоверности 95%. Предел давления сравнивается с ранее сообщенными допусками по давлению для альтернативных методов: максимальное давление плазменных устройств PDMS-PDMS и PDMS-Glass [43]; Печатные модули стереолитографии, подключенные к микрожидкостному «макету» [33]; Модули PDMS, прикрепленные к стеклу с помощью неотвержденного PDMS с блоками, соединенными вместе с помощью УФ-отверждаемого клея [44]; Самоцентрирующиеся модули лобзика PDMS, прикрепленные к стеклу с помощью неотвержденного PDMS [45].D) Модульная система, созданная с использованием 7 различных модулей, соединенных вместе без использования клея. Эта система включает 4 входных / выходных модуля, Т-образное соединение, соединение для фокусировки потока и модуль сборного сосуда.
https://doi.org/10.1371/journal.pone.0152023.g008
Испытания под давлением были выполнены для исследования целостности уплотнения между печатными модулями PLA, а также портами, напечатанными на 3D-принтере (рис. 8C). Давления, которые устройства смогли выдержать (~ 2000 кПа +), намного превышают давления, которые требуются для большинства микрофлюидных приложений.Допуск по давлению соединенных модулей выгодно отличается от заявленных допусков к давлению для устройств, изготовленных традиционным способом изготовления полидиметилсилоксана (PDMS) [43], а также ранее описанных модульных систем, изготовленных более традиционными методами изготовления [44, 45] (рис. 8C). Следует отметить, что в двух испытаниях под давлением отказ произошел на соединении с насосом, а не между модулями. Когда давление превысило ~ 2900 кПа, трубки, соединяющие модули с насосом, отсоединились от затяжки вручную в насосе, при этом утечки внутри модулей или в местах соединения между ними не наблюдалось.
Выводы
Были продемонстрированы простые, легко производимые микрожидкостные устройства, напечатанные на 3D-принтере. Несмотря на предыдущие опасения, можно достичь высокой точности геометрических форм жидкости, чтобы точно отразить предполагаемый дизайн, создать прозрачные устройства для наблюдения и использовать уплотнения высокого давления в микрофлюидных устройствах, напечатанных с использованием дешевых «готовых» FFF-принтеров. Эти устройства подходят для применения многими исследователями в области наук о жизни, которым может пригодиться микрофлюидная технология.Эта полезность демонстрируется здесь путем инкапсуляции живых стволовых клеток в альгинатные микросферы в таких печатных устройствах. Мы также показали, что многокомпонентные жидкостные системы могут быть легко созданы, просто соединяя вместе модульные блокирующие блоки. Эта система, подобная Lego ® , также обеспечивает самовыравнивание модулей, что означает, что герметичные, реконфигурируемые микрофлюидные системы могут быть быстро собраны и использованы в лаборатории. Использование печати FFF обеспечивает большую доступность для производства микро- и миллижидкостей, поскольку снижение стоимости и повышение разрешения этих принтеров делают их доступными для большинства лабораторий.Как технология демократизации, дизайны 3D-печати легко распространяются между исследователями по электронной почте или в онлайн-хранилищах. Это имеет потенциал для дальнейшего расширения доступности за счет устранения конструктивного барьера в дополнение к производственному барьеру, в значительной степени ограничивающему доступ к микрожидкостным технологиям в настоящее время. Насколько известно автору, полностью прозрачные микрофлюидные устройства ранее не реализовывались методом FFF-печати, а функциональная геометрия фокусировки потока не была продемонстрирована для капельных микрожидкостных приложений.Кроме того, простота изготовления даже сложных жидкостных путей делает 3D-печать очень привлекательной, позволяя людям с ограниченным опытом в этой области получить доступ ко многим преимуществам микрофлюидных технологий. Соединения между модулями продемонстрировали способность выдерживать давление более 2000 кПа; давление выше, чем у многих альтернативных методов производства, и больше, чем требуется для многих микрофлюидных приложений.
Предполагается, что в будущем при разработке микрожидкостных устройств, напечатанных на 3D-принтере, можно будет использовать еще одно ключевое преимущество 3D-печати; возможность создавать действительно трехмерные конструкции.Традиционные методы изготовления обычно ограничиваются плоскими путями 2,5D для жидкости, но 3D-печать дает возможность использовать z-размер, как никогда раньше.
Дополнительная информация
S4 Рис. Измерения точности 3D-принтера.
a-h) Сравнение измеренных и желаемых размеров круглых каналов, напечатанных на 3D-принтере. Пунктирная линия указывает на идеальное соответствие между CAD-моделью и напечатанным каналом. Уравнения и значение R 2 предназначены для линейной аппроксимации измеренных данных.a) Измеренная ширина горизонтально напечатанного канала с использованием печати FFF со слоями 50 мкм. б) Измеренная глубина горизонтально напечатанного канала с использованием печати FFF со слоями 50 мкм. c) Измеренная ширина горизонтально напечатанного канала с использованием печати FFF со слоями 100 мкм. г) Измеренная глубина горизонтально напечатанного канала с использованием печати FFF со слоями 100 мкм. e) Измеренная ширина горизонтально напечатанного канала с использованием печати FFF со слоями 25 мкм. е) Измеренная глубина горизонтально напечатанного канала с использованием печати FFF со слоями 25 мкм.g) Измеренный диаметр вертикально напечатанного канала с использованием печати FFF. з) Измеренный диаметр вертикально напечатанного канала с использованием SL печати. i-k) Изображения каналов диаметром 1,4 мм, изготовленные с помощью 3D-печати: i) Горизонтально напечатанные с использованием FFF со слоями 50 мкм. j) Горизонтальная печать с использованием FFF со слоями 100 мкм. k) Вертикальная печать с использованием SL.
https://doi.org/10.1371/journal.pone.0152023.s004
(DOCX)
S5 Рис. Сканирование поверхности 3D-печати интерферометром.
Образец для испытаний со слоями 50 мкм со слоем 1200 мм / мин, использованный в тестах на прозрачность, был покрыт золотом и затем сканирован с помощью интерферометра Veeco. Средняя шероховатость составила 2,28 мкм, а шероховатость от пика до пика — 1,81 мкм. Природа 3D-печати на основе экструзии создает повторяющийся узор из пиков и впадин, причем пики создаются на границе раздела между двумя «полосами» экструдированного материала.
https://doi.org/10.1371/journal.pone.0152023.s005
(DOCX)
S6 Фиг.Проблемы смачивания наблюдаются при использовании нити t-glase.
И A, и B показывают одно и то же Т-образное соединение, создающее сегменты воды в масле, однако B снимается примерно через 5 минут после A, показывая, что разрыв сегмента переместился вниз по каналу.
https://doi.org/10.1371/journal.pone.0152023.s006
(DOCX)
S7 Рис. Оптическая передача 3D-печатных устройств при различной скорости печати и высоте слоя.
Максимальное пропускание — это прозрачный PLA, который плавится в печи так, чтобы его толщина была такой же, как у печатных устройств.
https://doi.org/10.1371/journal.pone.0152023.s007
(DOCX)
S2 Таблица. Библиотека микрожидкостных модулей на основе Lego
® , которые были разработаны и напечатаны.Каждый модуль назван (слева), показан в форме 3D CAD (в центре) и, наконец, показаны внутренние структуры (справа). Внутренние границы обозначены синей пунктирной линией.
https://doi.org/10.1371/journal.pone.0152023.s009
(DOCX)
Благодарности
Эта работа была частично профинансирована Cardiff Synthetic Biology Initiative, частью программы SynbiCITE.Эта работа также была частично поддержана грантом StG 243261 Европейского исследовательского совета.
Стволовые клетки пульпы зубов были предоставлены профессором Аластером Слоаном из стоматологической школы Кардиффского университета.
Окрашивание клеток было с благодарностью получено от профессора Арвина Джонса, Школа фармацевтики и фармацевтических наук, Кардиффский университет. J. Wymant поддерживается организацией Cancer Research Wales. Оливер К. Кастелл — научный сотрудник SBP Кардиффского университета.
Вклад авторов
Задумал и спроектировал эксперименты: AJLM OKC DAB LHSJ JMW.Проведены эксперименты: AJLM LHSJ JMW WDJ. Проанализированы данные: AJLM. Предоставленные реагенты / материалы / инструменты для анализа: DAB BS PS JMW. Написал статью: AJLM OKC DAB.
Ссылки
- 1. Мао X, Хуан Т.Дж. Микрожидкостная диагностика для развивающихся стран. Лаборатория на чипе. 2012. 12 (8): 1412–6. pmid: 22406768
- 2. Kim P, Kwon KW, Park MC, Lee SH, Kim SM, Suh KY. Мягкая литография для микрофлюидики: обзор. 2008.
- 3. Уэллс WA.Следующая революция на базе микросхем. Химия и биология. 1998; 5 (5): R115 – R6.
- 4. Вирт Т. Микрореакторы в органической химии и катализе: Wiley; 2013.
- 5. Сакманн Э.К., Фултон А.Л., Биби ди-джей. Настоящая и будущая роль микрофлюидики в биомедицинских исследованиях. Природа. 2014; 507 (7491): 181–9. pmid: 24622198
- 6. Koster S, Angile FE, Duan H, Agresti JJ, Wintner A, Schmitz C и др. Микрожидкостные устройства на капельной основе для инкапсуляции отдельных клеток.Лаборатория на чипе. 2008. 8 (7): 1110–5. pmid: 18584086
- 7. Хандурина Дж., Макнайт Т. Э., Джейкобсон СК, Уотерс ЛК, Фут Р.С., Рэмси Дж. М.. Интегрированная система для быстрого анализа ДНК на основе ПЦР в микрофлюидных устройствах. Аналитическая химия. 2000. 72 (13): 2995–3000. pmid: 10
- 0
- 8. Хосокава К., Сато К., Итикава Н., Маэда М. Энергосберегающие микрофлюидные устройства на основе поли (диметилсилоксана) для анализа ДНК на основе наночастиц золота. Лаборатория на чипе. 2004. 4 (3): 181–5. pmid: 15159775
- 9.Weigl BH, Bardell RL, Cabrera CR. Лаборатория на чипе для разработки лекарств. Расширенные обзоры доставки лекарств. 2003. 55 (3): 349–77. pmid: 12628321
- 10. Guo MT, Rotem A, Heyman JA, Weitz DA. Капельная микрофлюидика для высокопроизводительных биологических анализов. Лаборатория на чипе. 2012. 12 (12): 2146–55. pmid: 22318506
- 11. Agresti JJ, Antipov E, Abate AR, Ahn K, Rowat AC, Baret JC, et al. Сверхвысокопроизводительный скрининг в капельной микрофлюидике для направленной эволюции.Труды Национальной академии наук. 2010. 107 (9): 4004–9.
- 12. Baret JC, Miller OJ, Taly V, Ryckelynck M, El-Harrak A, Frenz L, et al. Сортировка капель с активацией флуоресценции (FADS): эффективная микрофлюидная сортировка клеток на основе ферментативной активности. Лаборатория на чипе. 2009. 9 (13): 1850–8. pmid: 19532959
- 13. Autebert J, Coudert B, Bidard F-C, Pierga J-Y, Descroix S, Malaquin L и др. Microfluidic: инновационный инструмент для эффективной сортировки клеток.Методы. 2012. 57 (3): 297–307. pmid: 22796377
- 14. Чой С., Сонг С., Цой С., Пак Дж.К. Непрерывное разделение клеток крови путем гидрофоретической фильтрации. Лаборатория на чипе. 2007. 7 (11): 1532–8. pmid: 17960282
- 15. Ву Л., Гуань Г., Хоу Х.В., Бхагат А.А., Хан Дж. Отделение лейкоцитов от крови с использованием спирального канала с трапециевидным поперечным сечением. Аналитическая химия. 2012. 84 (21): 9324–31. pmid: 23025404
- 16. Гюнтер А., Дженсен К.Ф. Многофазная микрофлюидика: от характеристик текучести до химического синтеза и синтеза материалов.Лаборатория на чипе. 2006. 6 (12): 1487–503. pmid: 17203152
- 17. Барроу Д.А., Кастелл О.К., Сайкс Н., Майерс П., Ричи Х. Микро-графитовая углеродная колонка для высокоэффективной жидкостной хроматографии. Журнал хроматографии А. 2011; 1218 (15): 1983–7. pmid: 21241990
- 18. Gillies JM, Prenant C, Chimon GN, Smethurst GJ, Dekker BA, Zweit J. Микрожидкостная технология для радиохимии ПЭТ. Прикладное излучение и изотопы. 2006. 64 (3): 333–6. pmid: 162
- 19.Lion N, Rohner TC, Dayon L, Arnaud IL, Damoc E, Youhnovski N, et al. Микрожидкостные системы в протеомике. ЭЛЕКТРОФОРЕЗ. 2003. 24 (21): 3533–62. pmid: 14613180
- 20. Ягер П., Эдвардс Т., Фу Э, Хелтон К., Нельсон К., Там М.Р. и др. Микрожидкостные диагностические технологии для глобального общественного здравоохранения. Природа. 2006. 442 (7101): 412–8. pmid: 16871209
- 21. Ценг П., Мюррей С., Ким Д., Ди Карло Д. Основные моменты исследования: печать будущего микротехнологии. Лаборатория на чипе.2014. 14 (9): 1491–5. pmid: 24671475
- 22. Au AK, Ли В., Фолч А. Микрофлюидика по почте: оценка стереолитографии для производства микрофлюидных устройств. Лаборатория на чипе. 2014. 14 (7): 1294–301. pmid: 24510161
- 23. Бертье Э., Янг EWK, Биби Д. Инженеры из PDMS-land, биологи из Полистирении. Лаборатория на чипе. 2012; 12 (7): 1224–37. pmid: 22318426
- 24. Китсон П.Дж., Роснес М.Х., Санс В., Драгон В., Кронин Л. Настраиваемая миллижидкостная и микрофлюидная «лаборатория» на 3D-принтере на устройствах с реакционным ПО.Лаборатория на чипе. 2012; 12 (18): 3267–71. pmid: 22875258
- 25. Кейпел А.Дж., Эдмондсон С., Кристи СДР, Гудридж Р.Д., Бибб Р.Дж., Терстанс М. Разработка и производство добавок для проточной химии. Лаборатория на чипе. 2013. 13 (23): 4583–90. pmid: 24100659
- 26. Мэтисон Дж. С., Роснес М. Х., Санс В., Китсон П. Дж., Кронин Л. Непрерывный параллельный ESI-MS-анализ реакций, проводимых на изготовленном на заказ устройстве для 3D-печати. Журнал нанотехнологий Бейльштейна. 2013; 4 (1): 285–91.
- 27.Мартино С., Бергер С., Вуттон RCR, де Мелло А.Дж. Напечатанный на 3D-принтере микрокапиллярный узел для простого создания двойной эмульсии. Лаборатория на чипе. 2014. 14 (21): 4178–82. pmid: 25202859
- 28.
Therriault D, White SR, Lewis JA. Хаотическое перемешивание в трехмерных микрососудистых сетях, созданных сборкой прямой записи. Материалы природы. 2003. 2 (4): 265–71. pmid: 126
- 29. Бхаргава К.С., Томпсон Б., Мальмштадт Н. Дискретные элементы для трехмерной микрофлюидики.Труды Национальной академии наук. 2014. 111 (42): 15013–8.
- 30. Эркал Дж. Л., Селимович А., Гросс BC, Локвуд С. Ю., Уолтон Е. Л., Макнамара С. и др. Микрожидкостные устройства, напечатанные на 3D-принтере, со встроенными универсальными и многоразовыми электродами. Лаборатория на чипе. 2014. 14 (12): 2023–2032. pmid: 24763966
- 31. Шаллан А.И., Смейкал П., Корбан М., Гийт Р.М., Бредмор М.С. Экономичная трехмерная печать прозрачных микрочипов за считанные минуты. Аналитическая химия.2014; 86 (6): 3124–30. pmid: 24512498
- 32. Хо CMB, Нг Ш, Ли ХХ, Юн Й-Дж. Микрофлюидика, напечатанная на 3D-принтере, для биологических приложений. Лаборатория на чипе. 2015.
- 33. Юэнь ПК. SmartBuild — модульная микрофлюидная система, работающая по принципу plug-n-play. Лаборатория на чипе. 2008. 8 (8): 1374–8. pmid: 18651081
- 34. Ли В., Квон Д., Чанг Б., Юнг Дж., Ау А, Фолч А. и др. Сверхбыстрое обнаружение патогенных бактерий с помощью иммуномагнитного анализа потока 3D. Аналитическая химия.2014. 86 (13): 6683–8. pmid: 24856003
- 35. Йобас Л., Мартенс С., Онг В. Л., Ранганатан Н. Высокоэффективная геометрия фокусировки потока для спонтанного образования монодисперсных капель. Лаборатория на чипе. 2006; 6 (8): 1073–9. pmid: 16874381
- 36.
Бишоп Г.В., Саттервайт Дж.Э., Бхакта С., Кадимисетти К., Джиллетт К.М., Чен Э. и др. Напечатанные на 3D-принтере жидкостные устройства для приготовления наночастиц и проточно-инжекционной амперометрии с использованием интегрированных электродов, модифицированных наночастицами берлинского синего цвета.Аналитическая химия. 2015; 87 (10): 5437–43. pmid: 25
0
- 37. Вальдбаур А, Рапп Х, Ланге К., Рапп БЭ. Пусть будет стремление к быстрому прототипированию микрофлюидных устройств: одноэтапные производственные процессы. Аналитические методы. 2011; 3 (12): 2681–716.
- 38. Ли Дж., Каддихи М.Дж., Котов Н.А. Трехмерные матрицы клеточных культур: современное состояние. Тканевая инженерия, часть B: обзоры. 2008. 14 (1): 61–86.
- 39. Махлуф М., Орсола А., Атала А.Контролируемое высвобождение терапевтических агентов: медленная доставка и инкапсуляция клеток. Всемирный журнал урологии. 2000. 18 (1): 80–3. pmid: 10766049
- 40. Кревенстен Дж., Уолш А. Дж., Анантакришнан Д., Пейдж П., Вахба Г. М., Лотц Дж. К. и др. Клеточная терапия межпозвонкового диска для регенерации: имплантация мезенхимальных стволовых клеток в межпозвонковые диски крыс. Летопись биомедицинской инженерии. 2004. 32 (3): 430–4. pmid: 15095817
- 41. Каплан А.И. Обзор: мезенхимальные стволовые клетки: клеточная реконструктивная терапия в ортопедии.Тканевая инженерия. 2005. 11 (7–8): 1198–211. pmid: 16144456
- 42. Табар В., Студер Л. Плюрипотентные стволовые клетки в регенеративной медицине: проблемы и недавний прогресс. Nat Rev Genet. 2014; 15 (2): 82–92. pmid: 24434846
- 43. Бхаттачарья С., Датта А., Берг Дж. М., Гангопадхай С. Исследования смачиваемости поверхности поли (диметил) силоксана (ПДМС) и стекла при кислородно-плазменной обработке и корреляция с прочностью связи. Микроэлектромеханические системы, Журнал. 2005. 14 (3): 590–7.
- 44. Ри М., Бернс М.А. Микрожидкостные монтажные блоки. Лаборатория на чипе. 2008. 8 (8): 1365–73. pmid: 18651080
- 45. Langelier SM, Livak-Dahl E, Manzo AJ, Johnson BN, Walter NG, Burns MA. Гибкое литье модульных самовыравнивающихся микрожидкостных монтажных блоков. Лаборатория на чипе. 2011; 11 (9): 1679–87. pmid: 21412522
Листовой металл с трапециевидной формой | garden-lawn-edging.co.uk
Trapezibleche используются для покрытия крыш, а также стен.Они чрезвычайно устойчивы и надежны. В сочетании с относительно низкой ценой это делает его очень популярным строительным материалом, который часто используется в коммерческой сфере, а также подходит для частных строительных проектов.
Поэтому, конечно, неудивительно, что трапециевидные листы давно стали обычным явлением во многих малых и больших городах на зданиях.
Лист трапециевидной формы имеет множество преимуществ
Листс трапециевидной формой имеет целый ряд преимуществ, которые могут быть оценены по сравнению с другими строительными материалами и которые делают его хорошим выбором для различных строительных проектов.
Использование трапециевидных листов говорит о следующих преимуществах:
низкие производственные затраты обеспечивают соответственно низкую стоимость.
Из-за небольшого веса трапециевидные листы сравнительно легки в обращении.
Компоненты можно хранить и транспортировать без особых усилий.
Высококачественные материалы обеспечивают хорошую атмосферостойкость и долгий срок службы.
Установка трапециевидных листов несложна и обычно легко выполняется с небольшим мастерством.
крупногабаритные компоненты подходящих размеров обеспечивают крепление листов для особенно быстрого продвижения.
Лист трапециевидной формы имеет высокую устойчивость
По краям трапециевидные листы особенно устойчивы. Поэтому даже при относительно небольшой толщине материала они обладают сравнительно высокой грузоподъемностью.Это обстоятельство делает их хорошим выбором, особенно когда требуется прочная и устойчивая конструкция.
Листы трапециевидной формы как строительный материал в коммерческой сфере
Трапеции используются в разных сферах. Их можно использовать как для покрытия крыш, так и для облицовки стен и потолков. Особенно при строительстве промышленных зданий и складов очень часто устанавливается на трапециевидные листы, где часто используется в сочетании со стальным каркасом.
Благодаря своей высокой стабильности и быстрой сборке, они особенно популярны для крупногабаритных стен и крыш. По крайней мере, для промышленных зданий трапециевидные листы даже являются одним из наиболее часто используемых материалов для кровельного покрытия, независимо от размера крыши.
Плиты трапециевидные для частного строительства
В частном секторе трапециевидный лист среди прочего пользуется большой популярностью как недорогой, устойчивый к атмосферным воздействиям и простой в использовании строительный материал для крыш садовых домиков и навесов для автомобилей.
Использование трапециевидных листов в качестве кровли жилых домов также возможно. Однако по сравнению с коммерческой недвижимостью, несмотря на связанные с этим преимущества, по крайней мере, в настоящее время все еще явно реже, поскольку обычно все еще используется для классического покрытия кирпичом.
Как предотвратить появление пота с помощью трапециевидных листов
Долгое время трапециевидные листы были довольно непопулярны в качестве строительного материала, так как образование конденсата на них считалось недостатком.Эта точка зрения широко распространена и сегодня. Предполагаемая проблема с конденсацией может быть легко решена путем использования так называемых антиконденсаторов.
Флис прикреплен к нижней части трапециевидного полотна и способен впитывать определенное количество пота. Если соответствующая вентиляция соответствующего здания обеспечивается, влага, поглощаемая флисом, может легко испаряться, и, таким образом, можно предотвратить нежелательное образование конденсата на трапециевидных листах.
Противососудистые покрытия в качестве звукоизоляции на трапециевидном листе
Между прочим, Antikondensenvlies не только помогает предотвратить образование пота на простынях. Кроме того, нетканый материал также обладает звукопоглощающим эффектом и, таким образом, обеспечивает заметное снижение шума, например, во время дождя.Таким образом, его использование оплачивается одинаково в нескольких терминах. Потому что, предотвращая чрезмерный шум, флис помогает лишить другого возможного аргумента, который часто называют недостатком при использовании трапециевидных листов в качестве строительного материала.
При использовании конденсаторов в связи с назначением соответствующего здания в центре внимания особенно эффективное подавление шума, в идеале оно используется,
Конечно, флис высочайшего качества из возможных.
Листы трапециевидной формы Винт водонепроницаемый
Конечно, он также должен быть соединен с винтами, с помощью которых отдельные трапециевидные листы соединяются и прикрепляются к основанию, вода не может проникнуть через крышу или стены.
Поэтому рекомендуется использовать высококачественные кровельные саморезы с подходящими уплотнениями из EPDM. С их помощью можно надежно избежать утечек на фитингах трапециевидных листов, что обязательно приведет к проблемам из-за выпадения осадка на короткое или длительное время.
Из какого металла изготавливаются трапециевидные листы?
Термин трапециевидный лист дает информацию только о форме листов. Выводы по материалу, из которого они сделаны, затягивать нельзя.Потому что трапециевидные листы изготавливаются как из алюминия, так и из нержавеющей стали.
Обе породы металла имеют свои достоинства и недостатки. Алюминий, например, может быть отмечен, в частности, своим известным относительно низким весом. Соответственно, алюминиевые трапециевидные листы, конечно, легче стальных листов того же размера и толщины.
Однако это не обязательно означает, что алюминий — лучший металл. Поскольку даже трапециевидные стальные листы обладают различными свойствами, они могут быть хорошим выбором для различных строительных проектов. Например, сталь очень устойчива, и ее можно перекрыть листами достаточной толщины, особенно на больших расстояниях между двумя планками или балками опорной конструкции. Кроме того, трапециевидные стальные листы меньше расширяются. И последнее, но не менее важное: это может быть заметно с точки зрения шума.Листы трапециевидной формы разных цветов
Конечно, трапециевидные листы, конечно, доступны не только в цвете металла, из которого они существуют.Кроме того, есть еще множество других цветов, таких как темно-зеленый, антрацитовый или кирпично-красный.
Таким образом, как правило, легко найти трапециевидные листы, соответствующие вашему вкусу и подходящие, соответственно, к остальной части оставшегося здания.
Если, например, навес для машины или садовый коттедж накрыт крышей из трапециевидных листов, часто можно схватить цвет кирпича на жилом здании и, таким образом, обеспечить особенно целостную общую картину.
На что следует обращать внимание при покупке трапеций?
Конечно, при покупке трапеции очень важно обращать внимание на некоторые моменты. Только так можно быть уверенным, что листы подходят для запланированного проекта и нет лишних проблем во время или после сборки.
При выборе подходящих листов для соответствующего строительного проекта решающую роль играет особенно так называемый пролет.Это дает информацию о том, какое расстояние можно преодолеть с помощью трапециевидного листа без необходимости обеспечения достаточной устойчивости дополнительной опорой.
Конечно, даже сильный ветер и возможный снегопад являются возможной дополнительной нагрузкой на трапециевидный лист. Поэтому при использовании на открытом воздухе необходимо соблюдать различные ветровые и бесснежные зоны.
Несущая способность трапециевидного листа определяется следующими факторами:
Материал (сталь более упругая, чем алюминий.)
толщина листа (чем толще лист, тем он обычно прочнее)
глубина профиля (чем глубже профиль, тем устойчивее трапециевидный лист)
Качественные трапециевидные листы купить недорого в интернет-магазине
Если вы ищете трапеции для своего строительного объекта, вы точно с нами. Ведь в нашем магазине вы найдете качественные трапециевидные листы, которые легко заказать и доставить онлайн.
Безусловно, при покупке вы можете рассчитывать на отличное качество продукции по разумным ценам и отличное обслуживание клиентов. Мы уверены, что вы останетесь полностью довольны покупкой трапеций в нашем магазине.
13 альтернативных диванов Nugget для родителей, которые хотят их сейчас
Если у вас нет молниеносных рефлексов, чтобы взять кушетку Nugget Comfort, вы можете заполучить одну из этих забавных альтернатив.
Если у вас есть дети в доме и вы любите Instagram, вы, вероятно, слышали о неуловимом игровом диване Nugget , единороге в мире детской мебели.Универсальный модульный диван позволяет малышам проявлять творческий подход, строя замысловатые крепости, и дает им удобное место для отдыха в вечерние киносеансы. Когда разразится пандемия, вы, вероятно, даже подумали о попытке заполучить Самородок — только для того, чтобы обнаружить, что обеспечение его безопасности зависит от выигрыша в лотерею, а конкуренция составляет . Но знаете что? Доступны и другие версии, которые так же увлекательны и гораздо менее напряжены ( виртуальных школ нам достаточно для на один год, TYVM).Ознакомьтесь с нашими любимыми альтернативами Nugget ниже:
Кокос
Фотография: Go Coconut
Этот игровой диван от Go Coconut разработан и изготовлен на 100% в Канаде, а это значит, что вам не нужно беспокоиться об уплате пошлин при его отправке. Кроме того, они также предлагают возможность получить полукокосового ореха , если у вас нет места в игровой комнате для полного набора. 489 долл. США, indigo.ca
Детский диван из пеноматериала Whatsit
Фото: Wayfair
Пусть ваши дети проявят творческий подход с этим модульным диваном, и когда они закончат играть, они могут сконфигурировать его в свои собственные стулья для тихого времени.Кроме того, чехлы можно стирать в стиральной машине!
$ 520, wayfair.ca
Кушетка My Puffin Play
Фото: My Puffin
Этот игровой диван долговечен с прочными тканевыми чехлами, которые предназначены для того, чтобы выдерживать жесткие удары во время игры. Кроме того, прочные молнии покрыты тканью, чтобы дети не поранились во время игр.
499 долл. США, mypuffin.ca
Джоуи
Фото: Chew Chew Baby Roo
Подушка-полумесяц, которая идет в комплекте с этим набором, является идеальным подлокотником, и если вы хотите дать детям еще больше возможностей, Chew Chew Baby Roo предлагает дополнительные наборы подушек различной формы, такие как полукруглые качалки, трапеции и треугольные клинья.
300 $, chewchewbabyroo.com
Гнездо
Фото: Стилизованное гнездо
Этот роскошный игровой диван на 100% произведен в Канаде и оснащен двумя очень большими радужными валиками, которые универсальны. Вы можете использовать их с подушками для штабелирования для всех типов конструкций, но они так же хороши сами по себе, как сиденье, подставка для ног или супер-веселый рокер!
$ 598, stylizednest.com
Мой диван
Фото: My Couchy Couch
Подушки My Couchy имеют форму трапеции с плоским верхом, а не полные треугольники, что обеспечивает дополнительный комфорт и универсальность!
349 $, mycouchy.com
Мягкий диван
Фото: Cushy Couch
Доступный в восьми шикарных цветах, Cushy Couch идеально сочетается с любым декором. Они также предлагают комплект расширения для еще более приятного развлечения!
399 долл. США, cushycouch.ca
Фигги
Фото: предоставлено Мелиссой де Мата
Подушки этого игрового дивана легко соединяются на липучке для создания любых конфигураций. Кроме того, наволочки имеют встроенные водонепроницаемые подкладки для беспроблемной игры.Следите за тем, чтобы доставка в Канаду стала доступной в конце этого года.
От 309 долларов США, figgyplay.com
Jaxx Zipline Playscape
Фотография: Jaxx
Прекрасное дополнение к любой игровой комнате, Zipline Playscape доступен в восьми ярких цветах, которые разыграют детское воображение!
295 долларов США, jaxxbeanbags.com
IGLU Soft Play Shapes Activity Toys
Фото: Amazon
. Эти противоскользящие блоки так же легко чистить, поскольку они могут поднять творческий потенциал ваших малышей, которые могут лазить, строить или просто бездельничать.
$ 290, amazon.ca
Альпинист SoftScape
Фото: Wayfair
Какой ребенок не любит ползать по туннелю? Этот игровой набор — идеальный способ для маленьких альпинистов получить заряд энергии в мягкой и безопасной обстановке.
$ 422, wayfair.ca
Пенный складной матрас Milliard Tri-Fold
Фото: Amazon
. Доступный в четырех размерах матраса, этот продуманный дизайн складывается для создания дивана с подушкой для спины.Дети могут использовать его как игровой коврик или диван, а когда гости появятся, большие размеры удваиваются как кровать.
63–206 долларов, amazon.ca
IKEA SLÄKT складной матрас
Фото: Ikea
.Этот удобный в хранении матрас идеально подходит для просмотра фильмов и может использоваться в качестве матраса для ночевки.


 Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
 С углами BCD и BAD аналогично.
С углами BCD и BAD аналогично. Его длина
Его длина Средняя линия параллельна основаниям трапеции и равна их полусумме.
Средняя линия параллельна основаниям трапеции и равна их полусумме.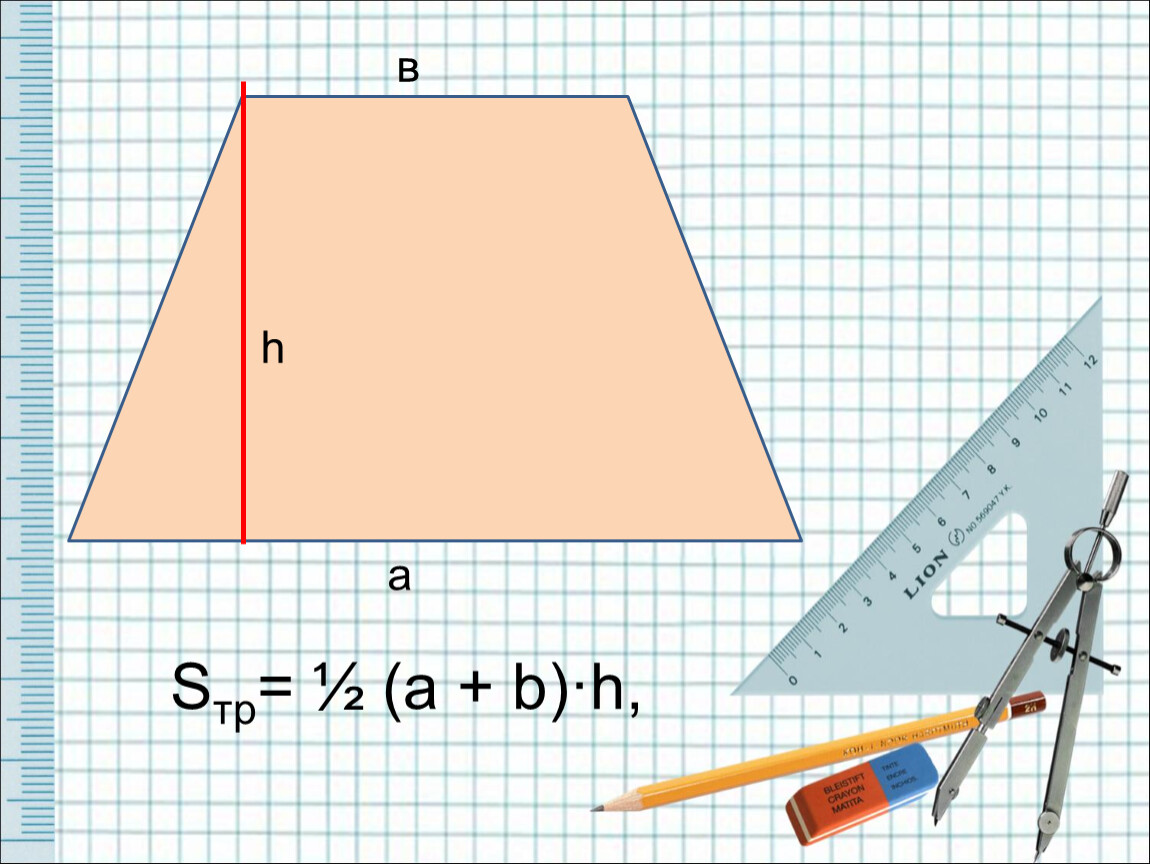 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:

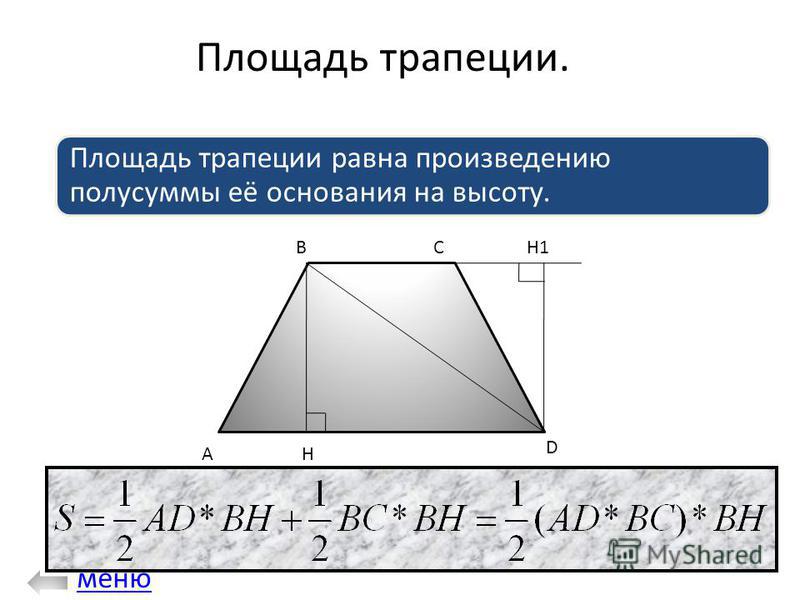 Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований) Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
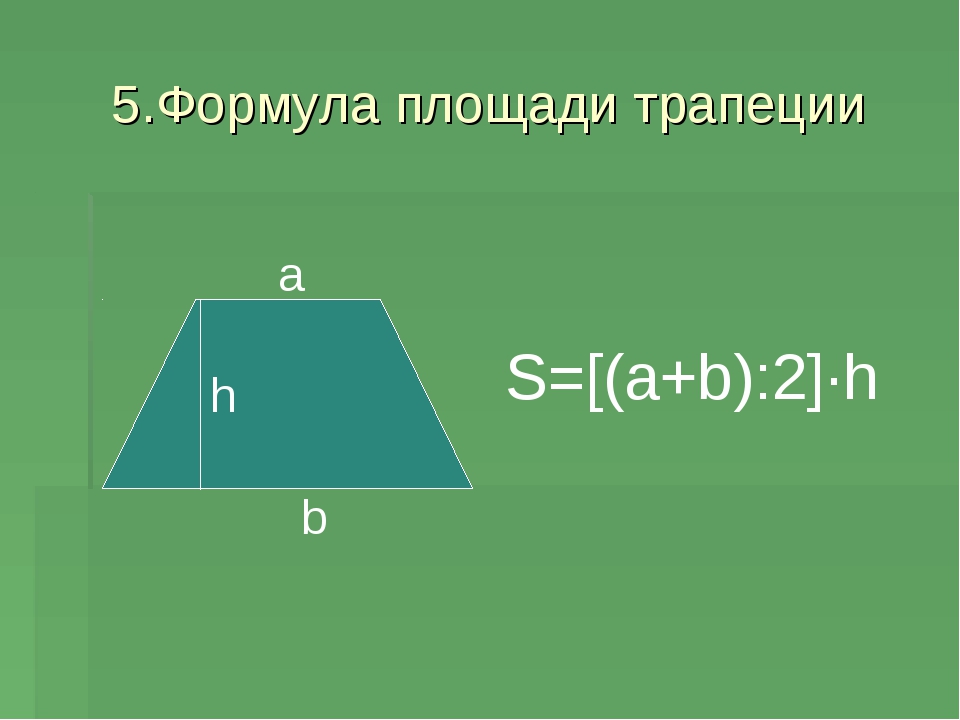

 В этом случае диагонали равны по длине, поэтому каждая обозначается буквой d без индексов:
В этом случае диагонали равны по длине, поэтому каждая обозначается буквой d без индексов: