Вычитание отрицательных чисел — Kid-mama
Сейчас мы рассмотрим на примерах вычитание отрицательных чисел, и вы убедитесь, что это очень легко. Нужно просто помнить правило : два минуса, стоящие рядом, дают плюс.
Пример 1. Вычитание отрицательного числа из положительного числа
56 – (–34) = 56 + 34 = 90
Как видим, чтобы вычесть из положительного числа отрицательное число, нужно просто сложить их модули.
Пример 2. Вычитание отрицательного числа из отрицательного числа
– 60 – (– 25) = – 60 + 25 = – 35
– 15 – (– 30) = – 15 + 30 = 15
Таким образом, при вычитании отрицательного числа из отрицательного мы действуем по правилу сложения чисел с разными знаками, и у нас может получиться как положительное, так и отрицательное число.
Существует единое правило, определяющее вычитание любых чисел: как отрицательных, так и положительных, и звучит оно так:
Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому. a — b = a + (-b) |
Для того, чтобы избавиться от лишних скобок при вычитании отрицательных чисел, мы можем воспользоваться правилом знаков. Это правило гласит:
| Если перед скобками стоит знак «+» , то при раскрытии скобок знак числа не изменяется. Если перед скобками стоит знак «-», то при раскрытии скобок знак числа меняется на противоположный. |
Например:
| 5 + (-7) = 5-7 | 9-(-5) = 9 + 5 | |
| -10 + (-6) = -10-6 | -4- (-6) = -4 + 6 |
Правило знаков действует также, если в скобках стоит несколько чисел. При этом,если перед скобками стоит минус, изменяются знаки у всех чисел:
Примеры:
a+(b-c-d)=a+b-c-da-(b-c-d)=a-b+c+d
a+(-b+c-d)=a-b+c-d
a-(-b+c-d)=a+b-c+d
Это правило обычно запоминают так:
| Минус на минус дает плюс, Плюс на минус дает минус |
А теперь пройдите тест и проверьте себя!
Сложение и вычитание отрицательных чисел
Лимит времени: 0
0 из 20 заданий окончено
Вопросы:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Информация
Выполните сложение или вычитание и введите ответ. Минус вводите при помощи дефиса (кнопка между «0» и «=» на клавиатуре). Ответ вводите без пробела (например: -3,4)
Минус вводите при помощи дефиса (кнопка между «0» и «=» на клавиатуре). Ответ вводите без пробела (например: -3,4)
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- 1
- 2
- 3
- 4
- 5
- 6
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- С ответом
- С отметкой о просмотре
Минус на минус даёт плюс.
 А почему?
А почему?Минус на минус даёт плюс – это правило, которые мы выучили в школе и применяем всю жизнь. А кто из нас интересовался почему? Конечно, проще без лишних вопросов запомнить данное утверждение и глубоко не вникать в суть вопроса. Сейчас и без того достаточно информации, которую необходимо «переварить». Но для тех, кого всё же заинтересует этот вопрос, постараемся дать объяснение этому математическому явлению.
С древних времён люди пользуются положительными натуральными числами: 1, 2, 3, 4, 5,… С помощью чисел считали скот, урожай, врагов и т.д. При сложении и умножении двух положительных чисел получали всегда положительное число, при делении одних величин на другие не всегда получали натуральные числа – так появились дробные числа. Что же с вычитанием? С детских лет мы знаем, что лучше к большему прибавить меньшее и из большего вычесть меньшее, при этом мы опять же не используем отрицательные числа. Получается, если у меня есть 10 яблок, я могу отдать кому-то только меньше 10 или 10.
Только с VII века н.э. отрицательные числа использовались в некоторых счётных системах, как вспомогательные величины, которые позволяли получить положительное число в ответе.
Рассмотрим пример, 6х – 30 = 3х – 9. Чтобы найти ответ, необходимо члены с неизвестными оставить в левой части, а остальные — в правую: 6х – 3х = 30 – 9, 3х = 21, х = 7. При решении этого уравнения нам даже не встретились отрицательные числа. Мы могли бы члены с неизвестными перенести в правую часть, а без неизвестных — в левую: 9 – 30 = 3х – 6х, (-21) = (-3х). При деление отрицательного числа на отрицательное получаем положительный ответ: х = 7.
Что мы видим?
Действия с использованием отрицательных чисел должны привести нас к такому же ответу, что и действия только с положительными числами. Мы можем больше не думать о практической непригодности и осмысленности действий – они помогают нам решить задачу гораздо быстрее, не приводя уравнение к виду только с положительными числами. В нашем примере мы не использовали сложных вычислений, но при большом количестве слагаемых вычисления с отрицательными числами могут облегчить нам работу.
В нашем примере мы не использовали сложных вычислений, но при большом количестве слагаемых вычисления с отрицательными числами могут облегчить нам работу.
Со временем, после проведения длительных опытов и вычислений удалось выявить правила, которым подчиняются все числа и действия над ними (в математике они называются аксиомами). Отсюда и появилась аксиома, которая утверждает, что при умножении двух отрицательных чисел получаем положительное.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
какие так называют, что такое в математике, чем отличаются
Какие числа называются положительными и отрицательными
Отрицательными числами в алгебре являются числа со знаком минус (-). Например, к таким числам относят -1, -2, -3. Прочитать запись можно, как минус один, минус два, минус три.
Отрицательное число — это какое-либо число меньше нуля, перед которым ставится знак минус.
Положительные числа — числа, состоящее в множестве положительных чисел, являются числами без знака минус в обозначении и не являются нулем.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В системе отрицательных чисел так же, как и среди положительных есть дроби: обыкновенные и десятичные, целые числа, корни и так далее. Почти все подвиды чисел, которые встречаются среди положительных чисел, есть и среди отрицательных. Стоит отметить, что, согласно понятию, число 0 не является ни положительным, ни отрицательным числом.
Положительные числа — это числа, соответствующие точкам в той части координатной прямой, которая лежит с правой стороны относительно начала отсчета.
Отрицательные числа — являются числами, соотносящимися с точками в части координатной прямой, которая расположена с левой стороны относительно начала отсчета (нуля).
Наглядным примером использования отрицательных чисел является термометр. Прибор демонстрирует температуру тела, воздуха, почвы, воды. Зимой при холодной погоде температура воздуха снижается до отрицательных значений. К примеру, -10 градусов мороза:
Обычные числа, в том числе, 1, 2, 3 называют положительными. Данные числа имеют знак (+). Обычно, его не записывают.
Координатная прямая — является прямой линией, на которой размещены все числа, включая отрицательные и положительные.
Координатная прямая имеет следующий вид:
В данном случае отмечены только числа от −5 до 5. В действительности координатная прямая бесконечна. На изображении можно увидеть только фрагмент этой прямой. Для того чтобы отметить на координатной прямой числа, использую точки. Началом отсчета является нуль. С левой стороны от нуля отмечают отрицательные числа, а с правой — положительные.
Координатная прямая продолжается бесконечно по обе стороны. Бесконечность в математике обозначается символом \(\infty\). Отрицательное направление будет обозначаться символом −\(\infty\), а положительное — символом +\(\infty\). Таким образом, координатная прямая содержит все числа от минус бесконечности до плюс бесконечности:
Бесконечность в математике обозначается символом \(\infty\). Отрицательное направление будет обозначаться символом −\(\infty\), а положительное — символом +\(\infty\). Таким образом, координатная прямая содержит все числа от минус бесконечности до плюс бесконечности:
\((−\infty; +\infty)\)
Каждая точка на координатной прямой обладает определенным именем и координатой. Именем является какая-либо латинская буква. Координата представляет собой число, указывающее на положение точки на прямой. Таким образом, координатой является то число, которое требуется отметить на координатной прямой. К примеру, точка А(2) читается, как «точка А с координатой 2» и обозначается на координатной прямой таким образом:
При рассмотрении изображения координатной прямой можно заметить, что отрицательные числа лежат левее относительно начала отсчета, а положительные числа — правее. С каждым шагом в левую сторону число будет уменьшаться в меньшую сторону. При каждом шаге в правом направлении число будет увеличиваться.
Сравнение положительных и отрицательных чисел
Положительные числа, то есть те, которые больше 0, можно рассматривать в качестве прибыли, прибавки, увеличения количества чего-либо. Отрицательные числа можно представить, как недостаток, убыток, расход, долг. Предположим, что имеется 55 неких предметов, например, яблок. Цифра 55 является положительной. В том случае, когда требуется отдать кому-то 5 яблок, данной действие можно обозначить, как -5. На градуснике рост температуры на 4,5 значений можно описать как +4,5, а снижение, в свою очередь, как −4,5. В приборах, которые используют для измерений, часто применяют положительные и отрицательные числа. Это объясняется удобством отображения изменения величин.
Любое отрицательное число меньше, чем любое положительное число. К примеру, если сравнить -5 и 3, то минус пять меньше трех. Это объясняется тем, что -5 представляет собой отрицательное число, а 3 является положительным числом. С помощью координатной прямой достаточно просто определить положение данных чисел.
На прямой -5 расположено левее относительно числа 3. Согласно правилу, любое отрицательное число меньше любого положительного числа. Отсюда следует, что:
−5 < 3
Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. К примеру, при сравнении чисел -4 и -1 можно сделать вывод, что минус четыре меньше, чем минус единица. Причина заключается в том, что на координатной прямой -4 располагается левее, чем -1.
Видно, что -4 лежит левее, а -1 правее. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. Таким образом:
-4 < -1
Ноль больше, чем любое отрицательное число. К примеру, при сравнении 0 и -3 можно сделать вывод, что ноль больше, чем минус три. Это объясняется тем, что на координатной прямой 0 располагается правее, чем -3.
При рассмотрении координатной прямой можно заметить, что 0 лежит правее, а -3 левее. Согласно правилу, нуль больше любого отрицательного числа. Таким образом:
Таким образом:
0 > -3
Нуль меньше любого положительного числа. К примеру, можно сравнить 0 и 4. Ноль меньше, чем 4.
На координатной прямой 0 располагается левее, а 4 правее. Исходя из правила, ноль меньше, чем какое-либо положительное число. Таким образом:
0 < 4
Правила действий с отрицательными и положительными числами
Существуют следующие правила знаков при умножении и делении отрицательных чисел:
- Умножение или деление отрицательного числа на отрицательное приводит в результате к получению положительного числа.
- При умножении или делении положительного числа на отрицательное число результатом является отрицательное число.
- Если требуется умножить или разделить отрицательное число на положительное, то получится отрицательное число.
В процессе сложения отрицательных чисел следует руководствоваться аналогичными правилами знаков в несколько ином виде. По общей формулировке правило знаков звучит так: «Плюс на минус дает минус, минус на минус дает плюс и плюс на плюс дает плюс». В таком случае, при сложении отрицательного числа с другим, получится:
По общей формулировке правило знаков звучит так: «Плюс на минус дает минус, минус на минус дает плюс и плюс на плюс дает плюс». В таком случае, при сложении отрицательного числа с другим, получится:
-а+(-в)=-а-в — то есть из отрицательного числа вычитается положительное.
Аналогичное правило применимо для примеров с вычитанием отрицательных чисел:
-а-(-в)=-а+в — к отрицательному числу в итоге прибавляется положительное.
В том случае, когда требуется сложить два отрицательных числа, следует сложить два числа и поставить знак минус. К примеру:
(−2)+(−3)=−5(−2)+(−3)=−5
Если первое число положительное, а второе отрицательное, требуется определить, какое число по модулю больше. Далее нужно отнять от большего меньшее число и поставим знак большего числа. Например:
(−8)+4=4−8=−4
9+(−4)=9−4=5
Каждое число, за исключением 0, соответствует противоположному элементу. В сумме с ним число дает 0. Например:
−9+9=0
7,1+(−7,1)=0
При вычитании двух отрицательных чисел следует руководствоваться правилом: минус на минус дает плюс. Таким образом, когда стоят рядом два минуса, в сумме получается плюс. К примеру:
Таким образом, когда стоят рядом два минуса, в сумме получается плюс. К примеру:
(−7)−(−6)=(−7)+6=(−1)
В том случае, когда первое число положительное, а второе число является отрицательным, вычитание выполняют по тому же принципу, что и сложение. Нужно определить, какое число по модулю больше. Далее следует отнять от большего меньшее число и поставить знак большего числа.
7−9=−2
так как 9>7
Одним из ключевых свойств является то, что минус на минус дает плюс:
7−(−9)=7+9=16
Примеры задач с решением
Задача 1
ЗадачаНужно решить: (+3) + (+4)
Решение:
(+3) + (+4) = +7
Ответ: 7
Задача 2
ЗадачаТребуется решить: (-4) + (-3)
Решение:
(-4) + (-3) = -7
Ответ: -7
Задача 3
ЗадачаНеобходимо выполнить сложение: (+15) + (-7)
Решение:
(+15) + (-7) = 15 — 7 = 8
Ответ: 8
Задача 4
ЗадачаНужно выполнить вычитание: (+7) — (+4)
Решение:
(+7) — (+4) = +3
Ответ: 3
Задача 5
ЗадачаТребуется найти разность чисел: -17 — (-14)
Решение:
-17 — (-14) = -17 + 14 = -3
Ответ: -3
Задача 6
ЗадачаНеобходимо решить пример: (+5) ⋅ (-8)
Решение:
(+5) ⋅ (-8) = -40
Ответ: -40
Задача 7
ЗадачаНужно найти произведение двух чисел: -9 ⋅ (-9)
Решение:
-9 ⋅ (-9) = 81
Ответ: 81
Задача 8
ЗадачаТребуется решить пример: -6 ⋅ 5
Решение:
-6 ⋅ 5 = -30
Ответ: -30
Задача 9
ЗадачаНужно выполнить деление двух чисел: 40 : (-8)
Решение:
40 : (-8) = -5
Ответ: -5
Задача 10
ЗадачаТребуется найти разность: (-6) — (+6) — (-8)
Решение:
(-6) — (+6) — (-8) = -12 — (-8) = -12 + 8 = -4
Ответ: -4
Задача 11
ЗадачаНеобходимо решить пример: (-5) ⋅ (-4) + (+3) ⋅ (-2)
Решение:
(-5) ⋅ (-4) + (+3) ⋅ (-2) = 20 + (-6) = 14
Ответ: 14
Задача 12
ЗадачаНужно найти ответ: (-15) ⋅ [-3 + (-15)] : (+5)
Решение:
(-15) ⋅ [-3 + (-15)] : (+5) = -15 ⋅ (-18) : 5 = (-15 : 5) ⋅ (-18) = -3 ⋅ (-18) = 54
Ответ: 54
Задача 13
ЗадачаТребуется выполнить деление: -18 : [-20 — (30 — 56)]
Решение:
-18 : [-20 — (30 — 56)] = -18 : [-20 — (-26)] = -18 : (-20 + 26) = -18 : 6 = -3
Ответ: -3
Задача 14
ЗадачаНужно найти значение выражения:
(−1)−(−512)⋅(+411)=(−1)−(−521)⋅(+114)
Решение:
(−1)−(−512)⋅411=−1−(−112)⋅411=(−1)−(−521)⋅114=−1−(−211)⋅114=−1−(−2)=−1+2=1−1−(−2)=−1+2=1
Ответ: 1
Задача 15
ЗадачаНеобходимо вычислить:
Вычислить |a| — |b| + |c|
при a = -8, b = -5, c = 1
Решение:
|-8| — |-5| + |1| = 8 — 5 + 1 = 4
Ответ: 4
Задача 16
ЗадачаТребуется решить пример:
[2,4−(0,3−0,21)⋅2+0,44:(−2)]:45=[2,4−(0,3−0,21)⋅2+0,44:(−2)]:54
Решение:
[2,4−(0,3−0,21)⋅2+0,44:(−2)]:45=[2,4−(0,3−0,21)⋅2+0,44:(−2)]:54=
[2,4−0,09⋅2+(−0,22)]:45=[2,4−0,09⋅2+(−0,22)]:54= (2,4−0,18−0,22):25=
2:45=52=2,5(2,4−0,18−0,22):52=2:54=25=2,5
Ответ: 2,5
Сложение и вычитание целых чисел
В данном уроке мы изýчим сложение и вычитание целых чисел.
Напомним, что целые числа — это все положительные и отрицательные числа, а также число 0. Например, следующие числа являются целыми:
−3, −2, −1, 0, 1, 2, 3
Положительные числа легко складываются и вычитаются, умножаются и делятся. К сожалению, этого нельзя сказать об отрицательных числах, которые смущают многих новичков своими минусами перед каждой цифрой.
Примеры сложения и вычитания целых чисел
Первое чему следует научиться это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа и где положительные.
Рассмотрим следующее простейшее выражение
1 + 3
Значение данного выражения равно 4
1 + 3 = 4
Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:
На рисунке можно увидеть, как это происходит:
Знак плюса в выражении 1 + 3 указывает нам, что нужно двигаться вправо в сторону увеличения чисел.
Пример 2. Найдём значение выражения 1 − 3
Значение данного выражения равно −2
1 − 3 = −2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −2. На рисунке можно увидеть, как это происходит:
Знак минуса в выражении 1 − 3 указывает нам, что нужно двигаться влево в сторону уменьшения чисел.
Вообще, если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.
Пример 3. Найти значение выражения −2 + 4
Значение данного выражения равно 2
−2 + 4 = 2
Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2
Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на четыре шага, и оказались в точке, где располагается положительное число 2.
Пример 4. Найти значение выражения −1 − 3
Значение данного выражения равно −4
−1 − 3 = −4
Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4
Видно, что мы сдвинулись из точки где располагается отрицательное число −1 в левую сторону на три шага, и оказались в точке, где располагается отрицательное число −4.
Пример 5. Найти значение выражения −2 + 2
Значение данного выражения равно 0
−2 + 2 = 0
Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0
Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на два шага и оказались в точке, где располагается число 0.
Правила сложения и вычитания целых чисел
Чтобы сложить или вычесть целые числа, вовсе необязательно каждый раз воображать координатную прямую, и тем более рисовать её. Можно воспользоваться готовыми правилами.
Применяя правила, нужно обращать внимания на знак операции и знаки чисел, которые нужно сложить или вычесть. От этого будет зависеть какое правило применять.
Пример 1. Найти значение выражения −2 + 5
Здесь к отрицательному числу прибавляется положительное число. Другими словами, осуществляется сложение чисел с разными знаками, потому что −2 это отрицательное число, а 5 — положительное. Для таких случаев применяется следующее правило:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Итак, посмотрим какой модуль больше:
Модуль числа 5 больше, чем модуль числа −2. Правило требует из большего модуля вычесть меньший. Поэтому мы должны из 5 вычесть 2, и перед полученным ответом поставить знак того числа, модуль которого больше.
У числа 5 модуль больше, поэтому знак этого числа и будет в ответе. То есть ответ будет положительным:
−2 + 5 = 5 − 2 = 3
Обычно записывают покороче: −2 + 5 = 3
Пример 2. Найти значение выражения 3 + (−2)
Здесь как и в предыдущем примере, осуществляется сложение чисел с разными знаками. 3 это положительное число, а −2 — отрицательное. Обратите внимание, что число −2 заключено в скобки, чтобы сделать выражение понятнее. Это выражение намного проще для восприятия, чем выражение 3 + −2.
Итак, применим правило сложения чисел с разными знаками. Как и в прошлом примере, из большего модуля вычитаем меньший модуль и перед ответом ставим знак того числа, модуль которого больше:
3 + (−2) = |3| − |−2| = 3 − 2 = 1
Модуль числа 3 больше, чем модуль числа −2, поэтому мы из 3 вычли 2, и перед полученным ответом поставили знак того числа, модуль которого больше. У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть ответ положительный.
У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть ответ положительный.
Обычно записывают покороче 3 + (−2) = 1
Пример 3. Найти значение выражения 3 − 7
В этом выражении из меньшего числа вычитается большее. Для такого случая применяется следующее правило:
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее, и перед полученным ответом поставить минус.
3 − 7 = 7 − 3 = −4
В этом выражении есть небольшая загвоздка. Вспомним, что знак равенства (=) ставится между величинами и выражениями тогда, когда они равны между собой.
Значение выражения 3 − 7 как мы узнали равно −4. Это означает, что любые преобразования которые мы будем совершать в данном выражении, должны быть равны −4
Но мы видим, что на втором этапе располагается выражение 7 − 3, которое не равно −4.
Чтобы исправить эту ситуацию, выражение 7 − 3 нужно взять в скобки и перед этой скобкой поставить минус:
3 − 7 = − (7 − 3) = − (4) = −4
В этом случае равенство будет соблюдаться на каждом этапе:
После того, как выражение вычислено, скобки можно убрать, что мы и сделали.
Поэтому, чтобы быть более точным, решение должно выглядеть так:
3 − 7 = − (7 − 3) = − (4) = − 4
Данное правило можно записать с помощью переменных. Выглядеть оно будет следующим образом:
a − b = − (b − a)
Большое количество скобок и знаков операций могут усложнять решение, казалось бы совсем простой задачи, поэтому целесообразнее научиться записывать такие примеры коротко, например 3 − 7 = − 4.
На самом деле сложение и вычитание целых чисел сводится только к сложению. Это означает, что если требуется осуществить вычитание чисел, эту операцию можно заменить сложением.
Итак, знакомимся с новым правилом:
Вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Например, рассмотрим простейшее выражение 5 − 3. На начальных этапах изучения математики мы ставили знак равенства и записывали ответ:
5 − 3 = 2
Но сейчас мы прогрессируем в изучении, поэтому надо приспосабливаться к новым правилам. Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.
На примере выражения 5 − 3 попробуем понять это правило. Уменьшаемое в данном выражении это 5, а вычитаемое это 3. Правило говорит, что для того, чтобы из 5 вычесть 3 , нужно к 5 прибавить такое число, которое будет противоположно 3. Противоположное для числа 3 это число −3. Записываем новое выражение:
5 + (−3)
А как находить значения для таких выражений мы уже знаем. Это сложение чисел с разными знаками, которое мы рассмотрели ранее. Чтобы сложить числа с разными знаками, мы из большего модуля вычитаем меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше:
5 + (−3) = |5| − |−3| = 5 − 3 = 2
Модуль числа 5 больше, чем модуль числа −3. Поэтому мы из 5 вычли 3 и получили 2. У числа 5 модуль больше, поэтому знак этого числа и поставили в ответе. То есть ответ положителен.
Поначалу быстро заменять вычитание сложением удаётся не всем. Это связано с тем, что положительные числа записываются без знака плюс.
Это связано с тем, что положительные числа записываются без знака плюс.
Например, в выражении 3 − 1 знак минуса, указывающий на вычитание, является знаком операции и не относится к единице. Единица в данном случае является положительным числом, и у неё есть свой знак плюса, но мы его не видим, поскольку плюс перед положительными числами не записывают.
А стало быть, для наглядности данное выражение можно записать следующим образом:
(+3) − (+1)
Для удобства числа со своим знаками заключают в скобки. В таком случае заменить вычитание сложением намного проще.
В выражении (+3) − (+1) вычитаемое это число (+1), а противоположное ему число это (−1).
Заменим вычитание сложением и вместо вычитаемого (+1) записываем противоположное ему число (−1)
(+3) − (+1) = (+3) + (−1)
Дальнейшее вычисление не составит особого труда.
(+3) − (+1) = (+3) + (−1) = |3| − |−1| = 3 − 1 = 2
На первый взгляд покажется, какой смысл в этих лишних телодвижениях, если можно старым добрым методом поставить знак равенства и сразу записать ответ 2. На самом деле это правило ещё не раз нас выручит.
На самом деле это правило ещё не раз нас выручит.
Решим предыдущий пример 3 − 7, используя правило вычитания. Сначала приведём выражение к понятному виду, расставив каждому числу свои знаки.
У тройки знак плюса, поскольку она является положительным числом. Минус, указывающий на вычитание не относится к семёрке. У семёрки знак плюса, поскольку она является положительным числом:
(+3) − (+7)
Заменим вычитание сложением:
(+3) − (+7) = (+3) + (−7)
Дальнейшее вычисление не составляет труда:
(+3) − (−7) = (+3) + (-7) = −(|−7| − |+3|) = −(7 − 3) = −(4) = −4
Пример 7. Найти значение выражения −4 − 5
Приведём выражение к понятному виду:
(−4) − (+5)
Перед нами снова операция вычитания. Эту операцию нужно заменить сложением. К уменьшаемому (−4) прибавим число, противоположное вычитаемому (+5). Противоположное число для вычитаемого (+5) это число (−5).
(−4) − (+5) = (−4) + (−5)
Мы пришли к ситуации, где нужно сложить отрицательные числа. Для таких случаев применяется следующее правило:
Для таких случаев применяется следующее правило:
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Итак, сложим модули чисел, как от нас требует правило, и поставим перед полученным ответом минус:
(−4) − (+5) = (−4) + (−5) = |−4| + |−5| = 4 + 5 = −9
Запись с модулями необходимо заключить в скобки и перед этими скобками поставить минус. Так мы обеспечим минус, который должен стоять перед ответом:
(−4) − (+5) = (−4) + (−5) = −(|−4| + |−5|) = −(4 + 5) = −(9) = −9
Решение для данного примера можно записать покороче:
−4 − 5 = −(4 + 5) = −9
или ещё короче:
−4 − 5 = −9
Пример 8. Найти значение выражения −3 − 5 − 7 − 9
Приведём выражение к понятному виду. Здесь все числа, кроме числа −3 являются положительными, поэтому у них будут знаки плюса:
(−3) − (+5) − (+7) − (+9)
Заменим вычитания сложениями. Все минусы, кроме минуса, стоящего перед тройкой, поменяются на плюсы, и все положительные числа поменяются на противоположные:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9)
Теперь применим правило сложения отрицательных чисел. Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:
(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9) =
= −( |−3| + |−5| + |−7| + |−9| ) = −(3 + 5 + 7 + 9) = −(24) = −24
Решение данного примера можно записать покороче:
−3 − 5 − 7 − 9 = −(3 + 5 + 7 + 9) = −24
или ещё короче:
−3 − 5 − 7 − 9 = −24
Пример 9. Найти значение выражения −10 + 6 − 15 + 11 − 7
Приведём выражение к понятному виду:
(−10) + (+6) − (+15) + (+11) − (+7)
Здесь сразу две операции: сложение и вычитание. Сложение оставляем без изменения, а вычитание заменяем сложением:
(−10) + (+6) − (+15) + (+11) − (+7) = (−10) + (+6) + (−15) + (+11) + (−7)
Соблюдая порядок действий, выполним поочерёдно каждое действие, опираясь на ранее изученные правила. Записи с модулями можно пропустить:
Первое действие:
(−10) + (+6) = − (10 − 6) = − (4) = − 4
Второе действие:
(−4) + (−15) = − (4 + 15) = − (19) = − 19
Третье действие:
(−19) + (+11) = − (19 − 11) = − (8) = −8
Четвёртое действие:
(−8) + (−7) = − (8 + 7) = − (15) = − 15
Таким образом, значение выражения −10 + 6 − 15 + 11 − 7 равно −15
Примечание. Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.
Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила:
Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.
Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить минус.
Вычесть одно число из другого означает, прибавить к уменьшаемому такое число, которое противоположно вычитаемому.
Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:
−50 + 40
Решение
−50 + 40 = −10
Задание 2. Найдите значение выражения:
Найдите значение выражения:
25 + (−5)
Решение
25 + (−5) = 20
Задание 3. Найдите значение выражения:
−20 + 60
Решение
−20 + 60 = 40
Задание 4. Найдите значение выражения:
20 + (−8)
Решение
20 + (−8) = 12
Задание 5. Найдите значение выражения:
30 + (−50)
Решение
30 + (−50) = −20
Задание 6. Найдите значение выражения:
27 + (−19)
Решение
27 + (−19) = 8
Задание 7. Найдите значение выражения:
−17 + (−12) + (−8)
Решение
Задание 8. Найдите значение выражения:
−6 − 4
Решение
−6 − 4 = −6 + (−4) = −10
Задание 9. Найдите значение выражения:
−6 − (−4)
Решение
−6 − (−4) = −6 + 4 = −2
Задание 10. Найдите значение выражения:
−15 − (−15)
Решение
−15 − (−15) = −15 + 15 = 0
Задание 11. Найдите значение выражения:
−11 − (−14)
Решение
−11 − (−14) = −11 + 14 = 3
Задание 12. Найдите значение выражения:
Найдите значение выражения:
−3 + 2 − (−1)
Решение
Задание 13. Найдите значение выражения:
−5 − 6 − 3
Решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Обзор формул
Если вы еще не Excel в Интернете, скоро вы увидите, что это не просто сетка для ввода чисел в столбцах или строках. Да, с помощью Excel в Интернете можно найти итоги для столбца или строки чисел, но вы также можете вычислять платежи по ипотеке, решать математические или инженерные задачи или находить лучшие сценарии в зависимости от переменных чисел, которые вы подключали.
Excel в Интернете делает это с помощью формул в ячейках. Формула выполняет вычисления или другие действия с данными на листе. Формула всегда начинается со знака равенства (=), за которым могут следовать числа, математические операторы (например, знак «плюс» или «минус») и функции, которые значительно расширяют возможности формулы.
Формула всегда начинается со знака равенства (=), за которым могут следовать числа, математические операторы (например, знак «плюс» или «минус») и функции, которые значительно расширяют возможности формулы.
Ниже приведен пример формулы, умножающей 2 на 3 и прибавляющей к результату 5, чтобы получить 11.
=2*3+5
Следующая формула использует функцию ПЛТ для вычисления платежа по ипотеке (1 073,64 долларов США) с 5% ставкой (5% разделить на 12 месяцев равняется ежемесячному проценту) на период в 30 лет (360 месяцев) с займом на сумму 200 000 долларов:
=ПЛТ(0,05/12;360;200000)
Ниже приведены примеры формул, которые можно использовать на листах.
-
=A1+A2+A3 Вычисляет сумму значений в ячейках A1, A2 и A3.
-
=КОРЕНЬ(A1) Использует функцию КОРЕНЬ для возврата значения квадратного корня числа в ячейке A1.
 («крышка») применяется для возведения числа в степень, а оператор * («звездочка») — для умножения.
(«крышка») применяется для возведения числа в степень, а оператор * («звездочка») — для умножения.Использование констант в формулах
Константа представляет собой готовое (не вычисляемое) значение, которое всегда остается неизменным. Например, дата 09.10.2008, число 210 и текст «Прибыль за квартал» являются константами. выражение или его значение константами не являются. Если формула в ячейке содержит константы, но не ссылки на другие ячейки (например, имеет вид =30+70+110), значение в такой ячейке изменяется только после изменения формулы.
Использование операторов в формулах
Операторы определяют операции, которые необходимо выполнить над элементами формулы. Вычисления выполняются в стандартном порядке (соответствующем основным правилам арифметики), однако его можно изменить с помощью скобок.
Типы операторов
Приложение Microsoft Excel поддерживает четыре типа операторов: арифметические, текстовые, операторы сравнения и операторы ссылок.

Арифметические операторы
Арифметические операторы служат для выполнения базовых арифметических операций, таких как сложение, вычитание, умножение, деление или объединение чисел. Результатом операций являются числа. Арифметические операторы приведены ниже.
Арифметический оператор
Значение
Пример
+ (знак «плюс»)
Сложение
3+3
– (знак «минус»)
Вычитание
Отрицание3–1
–1* (звездочка)
Умножение
3*3
/ (косая черта)
Деление
3/3
% (знак процента)
Доля
20%
^ (крышка)
Возведение в степень
3^2
Операторы сравнения
Операторы сравнения используются для сравнения двух значений.
 Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.
Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.Оператор сравнения
Значение
Пример
= (знак равенства)
Равно
A1=B1
> (знак «больше»)
Больше
A1>B1
< (знак «меньше»)
Меньше
A1<B1
>= (знак «больше или равно»)
Больше или равно
A1>=B1
<= (знак «меньше или равно»)
Меньше или равно
A1<=B1
<> (знак «не равно»)
Не равно
A1<>B1
Текстовый оператор конкатенации
Амперсанд (&) используется для объединения (соединения) одной или нескольких текстовых строк в одну.

Текстовый оператор
Значение
Пример
& (амперсанд)
Соединение или объединение последовательностей знаков в одну последовательность
Выражение «Северный»&«ветер» дает результат «Северный ветер».

Операторы ссылок
Для определения ссылок на диапазоны ячеек можно использовать операторы, указанные ниже.
Оператор ссылки
Значение
Пример
: (двоеточие)
Оператор диапазона, который образует одну ссылку на все ячейки, находящиеся между первой и последней ячейками диапазона, включая эти ячейки.

B5:B15
; (точка с запятой)
Оператор объединения. Объединяет несколько ссылок в одну ссылку.
СУММ(B5:B15,D5:D15)
(пробел)
Оператор пересечения множеств, используется для ссылки на общие ячейки двух диапазонов.
B7:D7 C6:C8
Порядок выполнения Excel в Интернете формулах
В некоторых случаях порядок вычисления может повлиять на возвращаемое формулой значение, поэтому для получения нужных результатов важно понимать стандартный порядок вычислений и знать, как можно его изменить.

Порядок вычислений
Формулы вычисляют значения в определенном порядке. Формула всегда начинается со знака равно(=).Excel в Интернете интерпретирует знаки после знака равно как формулу. После знака равно вычисляются элементы (операнды), такие как константы или ссылки на ячейки. Они разделены операторами вычислений. Excel в Интернете вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.
Приоритет операторов
Если в одной формуле несколько операторов, Excel в Интернете выполняет операции в том порядке, который показан в таблице ниже. Если формула содержит операторы с одинаковым приоритетом, например операторы деления и умножения, Excel в Интернете эти операторы оцениваются слева направо.
Оператор
Описание
: (двоеточие)
(один пробел)
, (запятая)
Операторы ссылок
–
Знак «минус»
%
Процент
^
Возведение в степень
* и /
Умножение и деление
+ и —
Сложение и вычитание
&
Объединение двух текстовых строк в одну
=
< >
<=
>=
<>Сравнение
Использование круглых скобок
Чтобы изменить порядок вычисления формулы, заключите ее часть, которая должна быть выполнена первой, в скобки.
 Например, следующая формула дает результат 11, так как Excel в Интернете умножение выполняется перед с добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.
Например, следующая формула дает результат 11, так как Excel в Интернете умножение выполняется перед с добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.=5+2*3
Если же изменить синтаксис с помощью скобок, Excel в Интернете сбавляет 5 и 2, а затем умножает результат на 3, чтобы получить 21.
=(5+2)*3
В следующем примере скобки, в которые заключена первая часть формулы, принудительно Excel в Интернете сначала вычислить ячейки B4+25, а затем разделить результат на сумму значений в ячейках D5, E5 и F5.
=(B4+25)/СУММ(D5:F5)
Использование функций и вложенных функций в формулах
Функции — это заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке.
 Эти функции позволяют выполнять как простые, так и сложные вычисления.
Эти функции позволяют выполнять как простые, так и сложные вычисления.Синтаксис функций
Приведенный ниже пример функции ОКРУГЛ, округляющей число в ячейке A10, демонстрирует синтаксис функции.
1. Структура. Структура функции начинается со знака равно (=), за которым следуют имя функции, открывая скобка, аргументы функции, разделенные запятой, и закрывая скобка.
2. Имя функции. Чтобы отобразить список доступных функций, щелкните любую ячейку и нажмите клавиши SHIFT+F3.
3. Аргументы. Существуют различные типы аргументов: числа, текст, логические значения (ИСТИНА и ЛОЖЬ), массивы, значения ошибок (например #Н/Д) или ссылки на ячейки. Используемый аргумент должен возвращать значение, допустимое для данного аргумента. В качестве аргументов также используются константы, формулы и другие функции.
4.
 Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.Ввод функций
Диалоговое окно Вставить функцию упрощает ввод функций при создании формул, в которых они содержатся. При вводе функции в формулу в диалоговом окне Вставить функцию отображаются имя функции, все ее аргументы, описание функции и каждого из аргументов, текущий результат функции и всей формулы.
Чтобы упростить создание и редактирование формул и свести к минимуму количество опечаток и синтаксических ошибок, пользуйтесь автозавершением формул. После того как вы введите знак «= » (знак равно) и начинательные буквы или триггер отображения Excel в Интернете под ячейкой будет отображаться динамический список действительных функций, аргументов и имен, которые соответствуют этим буквам или триггеру.
 После этого элемент из раскрывающегося списка можно вставить в формулу.
После этого элемент из раскрывающегося списка можно вставить в формулу.Вложенные функции
В некоторых случаях может потребоваться использовать функцию в качестве одного из аргументов другой функции. Например, в приведенной ниже формуле для сравнения результата со значением 50 используется вложенная функция СРЗНАЧ.
1. Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.
Допустимые типы вычисляемых значений Вложенная функция, используемая в качестве аргумента, должна возвращать соответствующий ему тип данных. Например, если аргумент должен быть логическим, т. е. Если эта функция не работает, Excel в Интернете отобразит #VALUE! В противном случае TE102825393 выдаст ошибку «#ЗНАЧ!».
<c0>Предельное количество уровней вложенности функций</c0>.
 В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, в приведенном выше примере функции СРЗНАЧ и СУММ являются функциями второго уровня, поскольку обе они являются аргументами функции ЕСЛИ. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.
В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, в приведенном выше примере функции СРЗНАЧ и СУММ являются функциями второго уровня, поскольку обе они являются аргументами функции ЕСЛИ. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.Использование ссылок в формулах
Ссылка указывает на ячейку или диапазон ячеек на сайте и сообщает Excel в Интернете, где искать значения или данные, которые вы хотите использовать в формуле. С помощью ссылок в одной формуле можно использовать данные, которые находятся в разных частях листа, а также значение одной ячейки в нескольких формулах. Вы также можете задавать ссылки на ячейки разных листов одной книги либо на ячейки из других книг. Ссылки на ячейки других книг называются связями или внешними ссылками.

Стиль ссылок A1
Стиль ссылок по умолчанию По умолчанию в Excel в Интернете используется стиль ссылок A1, который ссылается на столбцы буквами (от A до XFD, всего 16 384 столбца) и ссылается на строки с числами (от 1 до 1 048 576). Эти буквы и номера называются заголовками строк и столбцов. Для ссылки на ячейку введите букву столбца, и затем — номер строки. Например, ссылка B2 указывает на ячейку, расположенную на пересечении столбца B и строки 2.
Ячейка или диапазон
Использование
Ячейка на пересечении столбца A и строки 10
A10
Диапазон ячеек: столбец А, строки 10-20.

A10:A20
Диапазон ячеек: строка 15, столбцы B-E
B15:E15
Все ячейки в строке 5
5:5
Все ячейки в строках с 5 по 10
5:10
Все ячейки в столбце H
H:H
Все ячейки в столбцах с H по J
H:J
Диапазон ячеек: столбцы А-E, строки 10-20
A10:E20
<c0>Ссылка на другой лист</c0>.
 В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.
В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.1. Ссылка на лист «Маркетинг».
2. Ссылка на диапазон ячеек с B1 по B10 включительно.
3. Ссылка на лист, отделенная от ссылки на диапазон значений.
Различия между абсолютными, относительными и смешанными ссылками
<c0>Относительные ссылки</c0>. Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейки, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании или заполнении формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании или заполнении относительной ссылки из ячейки B2 в ячейку B3 она автоматически изменяется с =A1 на =A2.

<c0>Абсолютные ссылки</c0>. Абсолютная ссылка на ячейку в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам и столбцам абсолютная ссылка не корректируется. По умолчанию в новых формулах используются относительные ссылки, а для использования абсолютных ссылок надо активировать соответствующий параметр. Например, при копировании или заполнении абсолютной ссылки из ячейки B2 в ячейку B3 она остается прежней в обеих ячейках: =$A$1.
Смешанные ссылки Смешанная ссылка имеет абсолютный столбец и относительную строку либо абсолютную строку и относительный столбец. Абсолютная ссылка на столбец принимает форму $A 1, $B 1 и так далее. Абсолютная ссылка на строку имеет форму A$1, B$1 и так далее. При изменении позиции ячейки, содержаной формулу, изменяется относительная ссылка, а абсолютная ссылка не изменяется.
 При копировании или заполнении формулы по строкам или вниз по столбцам относительная ссылка автоматически корректируется, а абсолютная ссылка не корректируется. Например, при копировании или заполнении смешанной ссылки из ячейки A2 в B3 она будет меняться с =A$1 на =B$1.
При копировании или заполнении формулы по строкам или вниз по столбцам относительная ссылка автоматически корректируется, а абсолютная ссылка не корректируется. Например, при копировании или заполнении смешанной ссылки из ячейки A2 в B3 она будет меняться с =A$1 на =B$1.Стиль трехмерных ссылок
Удобный способ для ссылки на несколько листов Трехмерные ссылки используются для анализа данных из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка содержит ссылку на ячейку или диапазон, перед которой указываются имена листов. Excel в Интернете использует все таблицы, которые хранятся между начальным и конечним именами ссылки. Например, формула =СУММ(Лист2:Лист13!B5) суммирует все значения, содержащиеся в ячейке B5 на всех листах в диапазоне от листа 2 до листа 13 включительно.
-
При помощи трехмерных ссылок можно создавать ссылки на ячейки на других листах, определять имена и создавать формулы с использованием следующих функций: СУММ, СРЗНАЧ, СРЗНАЧА, СЧЁТ, СЧЁТЗ, МАКС, МАКСА, МИН, МИНА, ПРОИЗВЕД, СТАНДОТКЛОН.
 Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.
Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА. -
Трехмерные ссылки нельзя использовать в формулах массива.
-
Трехмерные ссылки нельзя использовать вместе с оператор пересечения (один пробел), а также в формулах с неявное пересечение.
<c0>Что происходит при перемещении, копировании, вставке или удалении листов</c0>. Нижеследующие примеры поясняют, какие изменения происходят в трехмерных ссылках при перемещении, копировании, вставке и удалении листов, на которые такие ссылки указывают. В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для суммирования значений в ячейках с A2 по A5 на листах со второго по шестой.
-
Вставка или копирование Если вставить листы между листами 2 и 6, Excel в Интернете будет включать в расчет все значения из ячеек с A2 по A5 на добавленных листах.

-
Удалить Если удалить листы между листами 2 и 6, Excel в Интернете вы вычислите их значения.
-
Переместить Если переместить листы между листами 2 и 6 в место за пределами диапазона, на который имеется ссылка, Excel в Интернете удалит их значения из вычислений.
-
Перемещение конечного листа Если переместить лист 2 или 6 в другое место книги, Excel в Интернете скорректирует сумму с учетом изменения диапазона листов.
-
Удаление конечного листа Если удалить лист 2 или 6, Excel в Интернете скорректирует сумму с учетом изменения диапазона листов между ними.
Стиль ссылок R1C1
Можно использовать такой стиль ссылок, при котором нумеруются и строки, и столбцы.
 Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает на расположение ячейки с помощью R, за которым следует номер строки, и C, за которым следует номер столбца.
Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает на расположение ячейки с помощью R, за которым следует номер строки, и C, за которым следует номер столбца.Ссылка
Значение
R[-2]C
относительная ссылка на ячейку, расположенную на две строки выше в том же столбце
R[2]C[2]
Относительная ссылка на ячейку, расположенную на две строки ниже и на два столбца правее
R2C2
Абсолютная ссылка на ячейку, расположенную во второй строке второго столбца
R[-1]
Относительная ссылка на строку, расположенную выше текущей ячейки
R
Абсолютная ссылка на текущую строку
При записи макроса Excel в Интернете некоторые команды с помощью стиля ссылок R1C1.
 Например, если записать команду (например, нажать кнопку «Автоумма»), чтобы вставить формулу, в которую добавляется диапазон ячеек, Excel в Интернете записи формулы со ссылками с помощью стиля R1C1, а не A1.
Например, если записать команду (например, нажать кнопку «Автоумма»), чтобы вставить формулу, в которую добавляется диапазон ячеек, Excel в Интернете записи формулы со ссылками с помощью стиля R1C1, а не A1.Использование имен в формулах
Можно создавать определенные имена для представления ячеек, диапазонов ячеек, формул, констант и Excel в Интернете таблиц. Имя — это значимое краткое обозначение, поясняющее предназначение ссылки на ячейку, константы, формулы или таблицы, так как понять их суть с первого взгляда бывает непросто. Ниже приведены примеры имен и показано, как их использование упрощает понимание формул.
Тип примера
Пример использования диапазонов вместо имен
Пример с использованием имен
Ссылка
=СУММ(A16:A20)
=СУММ(Продажи)
Константа
=ПРОИЗВЕД(A12,9.
 5%)
5%)=ПРОИЗВЕД(Цена,НСП)
Формула
=ТЕКСТ(ВПР(MAX(A16,A20),A16:B20,2,FALSE),»дд.мм.гггг»)
=ТЕКСТ(ВПР(МАКС(Продажи),ИнформацияОПродажах,2,ЛОЖЬ),»дд.мм.гггг»)
Таблица
A22:B25
=ПРОИЗВЕД(Price,Table1[@Tax Rate])
Типы имен
Существует несколько типов имен, которые можно создавать и использовать.

Определенное имя Имя, используемое для представления ячейки, диапазона ячеек, формулы или константы. Вы можете создавать собственные определенные имена. Кроме Excel в Интернете иногда задайте определенное имя, например при создании области печати.
Имя таблицы Имя таблицы Excel в Интернете, которая является набором данных по определенной теме, которые хранятся в записях (строках) и полях (столбцах). Excel в Интернете создает таблицу Excel в Интернете имя таблицы «Таблица1», «Таблица2» и так далее, каждый раз при вставке таблицы Excel в Интернете, но эти имена можно изменить, чтобы сделать их более осмысленными.
Создание и ввод имен
Имя создается с помощью «Создать имя из выделения». Можно удобно создавать имена из существующих имен строк и столбцов с помощью фрагмента, выделенного на листе.

Примечание: По умолчанию в именах используются абсолютные ссылки на ячейки.
Имя можно ввести указанными ниже способами.
-
Ввод с клавиатуры Введите имя, например, в качестве аргумента формулы.
-
<c0>Автозавершение формул</c0>. Используйте раскрывающийся список автозавершения формул, в котором автоматически выводятся допустимые имена.
Использование формул массива и констант массива
Excel в Интернете не поддерживает создание формул массива. Вы можете просматривать результаты формул массива, созданных в классическом приложении Excel, но не сможете изменить или пересчитать их. Если на вашем компьютере установлено классическое приложение Excel, нажмите кнопку Открыть в Excel, чтобы перейти к работе с массивами.

В примере формулы массива ниже вычисляется итоговое значение цен на акции; строки ячеек не используются при вычислении и отображении отдельных значений для каждой акции.
При вводе формулы «={СУММ(B2:D2*B3:D3)}» в качестве формулы массива сначала вычисляется значение «Акции» и «Цена» для каждой биржи, а затем — сумма всех результатов.
<c0>Вычисление нескольких значений</c0>. Некоторые функции возвращают массивы значений или требуют массив значений в качестве аргумента. Для вычисления нескольких значений с помощью формулы массива необходимо ввести массив в диапазон ячеек, состоящий из того же числа строк или столбцов, что и аргументы массива.
Например, по заданному ряду из трех значений продаж (в столбце B) для трех месяцев (в столбце A) функция ТЕНДЕНЦИЯ определяет продолжение линейного ряда объемов продаж. Чтобы можно было отобразить все результаты формулы, она вводится в три ячейки столбца C (C1:C3).

Формула «=ТЕНДЕНЦИЯ(B1:B3;A1:A3)», введенная как формула массива, возвращает три значения (22 196, 17 079 и 11 962), вычисленные по трем объемам продаж за три месяца.
Использование констант массива
В обычную формулу можно ввести ссылку на ячейку со значением или на само значение, также называемое константой. Подобным образом в формулу массива можно ввести ссылку на массив либо массив значений, содержащихся в ячейках (его иногда называют константой массива). Формулы массива принимают константы так же, как и другие формулы, однако константы массива необходимо вводить в определенном формате.
Константы массива могут содержать числа, текст, логические значения, например ИСТИНА или ЛОЖЬ, либо значения ошибок, такие как «#Н/Д». В одной константе массива могут присутствовать значения различных типов, например {1,3,4;ИСТИНА,ЛОЖЬ,ИСТИНА}. Числа в константах массива могут быть целыми, десятичными или иметь экспоненциальный формат.
 Текст должен быть заключен в двойные кавычки, например «Вторник».
Текст должен быть заключен в двойные кавычки, например «Вторник».Константы массива не могут содержать ссылки на ячейку, столбцы или строки разной длины, формулы и специальные знаки: $ (знак доллара), круглые скобки или % (знак процента).
При форматировании констант массива убедитесь, что выполняются указанные ниже требования.
-
Константы заключены в фигурные скобки ( { } ).
-
Столбцы разделены запятыми (,). Например, чтобы представить значения 10, 20, 30 и 40, введите {10,20,30,40}. Эта константа массива является матрицей размерности 1 на 4 и соответствует ссылке на одну строку и четыре столбца.
-
Значения ячеек из разных строк разделены точками с запятой (;). Например, чтобы представить значения 10, 20, 30, 40 и 50, 60, 70, 80, находящиеся в расположенных друг под другом ячейках, можно создать константу массива с размерностью 2 на 4: {10,20,30,40;50,60,70,80}.

Сложение и вычитание отрицательных чисел
Действия с отрицательными числами — совсем не сложная для понимания тема. И сложение, и вычитание производятся элементарно и легко подтверждаются проверкой на координатной прямой. Однако рисовать ее для каждого выражения было бы неудобно, кроме того, обилие знаков отвлекает внимание.
Чтобы не путаться, будет проще запомнить несколько простых правил. Приведем их с краткими пояснениями.
Сложение отрицательных чисел
Главное, что нужно запомнить — при сложении чисел со знаком «минус» их сумма также будет отрицательной. Сделать нужно следующее:
- Взять модули обоих отрицательных чисел, или их абсолютные величины. Это очень просто, поскольку для любого числа со знаком «минус» модулем будет само же это число, но со знаком «плюс».
- Сложить модули между собой.

- Поставить «минус» перед числом, получившимся в ответе.
В числовом виде это выражается следующим образом: (-a) + (-c), то берем и складываем |a| и |с|, а затем ставим «минус» в ответе. Иными словами, (-а) + (-с) = — (а + с).
Вычитание отрицательных чисел
Правило вычитания выглядит немного сложнее, чем предыдущее — но все равно остается очень легким. Чтобы выполнить действие по вычитанию, необходимо прибавить к уменьшаемому вычитаемое со знаком, измененным на противоположный. В числовой записи это выглядит так: а – с = а + (-с). Можно записать правило и немного иначе: (-а) – (-с) = -а + с.
Приведем пару образцов.
- Для начала сложим между собой два произвольно взятых отрицательных числа. Например, — 5 + (- 10) = — (5 + 10) = — 15. Правило, приведенное выше, полностью подтверждается.
- Теперь попробуем вычесть – 7 из – 20. Согласно рассмотренному правилу, -20 – (-7) = -20 + 7 = — 13.
 Решение снова получается верным, правило подтверждается.
Решение снова получается верным, правило подтверждается.
Перечисленные правила для сложения и для вычитания одинаковым образом работают для всех отрицательных чисел — вне зависимости от того, идет ли речь о целых, о дробях или о смешанных числах. В последних двух случаях числа нужно просто привести в наиболее удобный для действий с ними вид — а затем применять указанные правила.
Кстати, вычитание из отрицательного числа того же самого отрицательного числа всегда дает нуль в ответе. Здесь нужно помнить о противоположных числах — ведь согласно правилу, выражение вида (-а) – (-а) в итоге приобретет вид – а + а. В таких случаях подробных действий над выражением можно не производить и сразу уверенно ставить в ответе 0.
Похожие статьи
Сложение и вычитание в прямом, обратном и дополнительном кодах. Деление двоичных чисел в прямом, обратном и дополнительном кодах
Похожие главы из других работ:
Арифметические операции с BCD числами
2.
 4. Вычитание.
4. Вычитание.SUB приемник, источник ВЫЧИТАНИЕ БАЙТОВ ИЛИ СЛОВ Содержимое источника вычитается из содержимого приемника, и результат помещается на место приемника. Операнды могут быть байтами или словами и содержать двоичные числа со знаком или без него (см…
Выполнение операций алгебраического сложения и сдвига в ЭВМ
1.1.2 Сложение в прямом коде
Правила сложения чисел в прямом коде не отличаются от обычных правил сложения, т.е. если оба слагаемых имеют одинаковые знаки, то их числовые разряды складываются, а сумме присваивается знак одного из них. Если слагаемые имеют разные знаки…
Выполнение операций алгебраического сложения и сдвига в ЭВМ
1.1.4 Алгебраическое сложение в дополнительном коде
В дополнительном коде операция вычитания заменяется операцией алгебраического сложения. При этом знаковый разряд и цифровая часть числа рассматриваются как единое целое…
Выполнение операций алгебраического сложения и сдвига в ЭВМ
1.
 1.6 Сложение в обратном коде
1.6 Сложение в обратном кодеВ обратном коде, как и в дополнительном, операция вычитания заменяется операцией сложения. При этом знаковый разряд и цифровая часть числа рассматриваются как единое целое…
Выполнение операций алгебраического сложения и сдвига в ЭВМ
3.1 Округление чисел в прямом коде
Если предположить, что исходная информация не содержит никаких ошибок и все вычислительные процессы выполняются абсолютно точно, то всегда существует третий тип ошибок — ошибки округления…
Деление двоичных чисел в прямом, обратном и дополнительном кодах
Деление в прямом, обратном и дополнительном кодах
Деление в вычислительной машине обычно сводится к выполнению последовательности вычитаний делителя сначала из делимого, а затем из образующихся в процессе деления частичных остатков и сдвига частичных остатков на один разряд влево…
Конвертирование величин из одной системы исчисления в другую при помощи ЭВМ
4.
 1.1 Операция сложения положительных чисел, представленных в прямом коде
1.1 Операция сложения положительных чисел, представленных в прямом кодеПрямой код числа «5»: 0 000 0101 Прямой код числа «7»: 0 000 0111 Два исходных числа сравниваются. В разряд знака результата записывается знак большего исходного числа. Если числа имеют разные знаки…
Конвертирование величин из одной системы исчисления в другую при помощи ЭВМ
5. Сложение и вычитание чисел с плавающей запятой
Спецификой представления числа с плавающей запятой является разделение его на две компоненты: ax — порядок числа;fx — мантисса, значащая часть (представляется в дробном виде). Пример: 55,71 = 5,571*10-1, где 5,571 — мантисса, 10-1 — порядок…
Основы реляционной алгебры
1.3 Вычитание
реляционный алгебра оператор синтаксис Вычитанием двух совместимых по типу отношений и называется отношение с тем же заголовком, что и у отношений и , и телом, состоящим из кортежей, принадлежащих отношению и не принадлежащих отношению.
 ..
..Программная реализация модуля PlagiatSearch поиска плагиата методами сравнения произвольных текстов
2 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПОИСКА ПЛАГИАТА В ИСХОДНЫХ КОДАХ ПРОГРАММ
…
Разработка калькуляторов. Комплексные числа в алгебраической, тригонометрической и экспоненциальной формах
Сложение, вычитание, умножение, деление, возведение в целую степень, извлечение квадратного корня (по формуле Муавра), преобразование из одной формы в другую
…
Розробка програми-емулятора мовою Турбо Паскаль
2. Програмування в кодах навчальної ЕОМ
…
Русское народное умножение
5.1 Сложение и вычитание
Схема для сложения такова: складываем цифры слева направо (цифры хранятся в обратном порядке). Если зафиксировано переполнение (т.е. при сложении получена цифра, большая максимально возможной в данной системе счисления)…
Цифровой автомат деления двоичных чисел
1.
 4 Представление чисел в дополнительном коде
4 Представление чисел в дополнительном кодеДополнительный код — наиболее распространённый способ представления отрицательных целых чисел в компьютерах…
Числовая и нечисловая обработка информации
Сложение и вычитание в дополнительном коде
При выполнении сложения чисел с одинаковыми знаками результат может оказаться таким, что не вмешается в используемую разрядную сетку, т.е. получается число, которое выходит за диапазон представления…
Сложение и вычитание положительных и отрицательных чисел
Числа могут быть положительными или отрицательными
Это числовая строка:
Отрицательные числа (-) Положительные числа (+) «-» — отрицательный знак. «+» — положительный знак Отсутствие знака означает положительный результат
Если число имеет без знака , это обычно означает, что это положительное число .

Играй с этим!
На числовой прямой положительное значение идет вправо, а отрицательное — влево.
Попробуйте использовать ползунки ниже и посмотрите, что получится:
числа / изображения / номер-строка-add.js? sub = n
Воздушные шары и гиря
Давайте подумаем о числах как о воздушных шарах (положительных) и весах (отрицательных):
В этой корзине привязаны воздушные шары и гирьки:
- Воздушные шары подтягиваются ( положительный )
- И грузики тянутся вниз ( минус )
Добавление положительного числа
Сложение положительных чисел — это просто сложение.
Мы можем добавить шары (мы добавляем положительное значение )
корзина тянется вверх (положительно)
Пример: 2 + 3 = 5
действительно говорит
«Положительное 2 плюс Положительное 3 равно Положительное 5»
Мы могли бы записать это как (+2) + (+3) = (+5)
Вычитание положительного числа
Вычитание положительных чисел — это просто вычитание.

Воздушные шары можно забрать ( вычитаем положительное значение )
корзина тянется вниз (минус)
Пример: 6 — 3 = 3
действительно говорит
«Положительных 6 минус Положительных 3 равно Положительных 3»
Мы могли бы записать это как (+6) — (+3) = (+3)
Добавление отрицательного числа
Теперь посмотрим, как выглядит сложение и вычитание отрицательных чисел :
Мы можем добавлять веса (мы добавляем отрицательные значения )
корзина тянется вниз (минус)
Пример: 6 + (−3) = 3
действительно говорит
«Положительных 6 плюс отрицательных 3 равно положительных 3»
Мы могли бы записать это как (+6) + (−3) = (+3)
Последние два примера показали нам, что удаление воздушных шаров (вычитание положительного значения) или прибавление веса (добавление отрицательного числа) заставляют корзину опускаться.

Значит, результат тот же :
- (+6) — (+3) = (+3)
- (+6) + (−3) = (+3)
Другими словами, вычитание положительного аналогично добавлению отрицательного .
Вычитание отрицательного числа
Наконец, мы можем убрать веса (мы вычитаем отрицательных значений )
корзина тянется вверх (положительно)
Пример: Что такое 6 — (−3)?
6 — (- 3) = 6 + 3 = 9
Да, действительно! Вычесть отрицание — это то же самое, что добавить!
Два отрицания дают положительный результат
Что мы нашли?
Добавление положительного числа — это простое сложение…
Добавление положительного значения Добавление
Положительное и отрицательное вместе …
Вычитание положительного
или
Добавление отрицательного
равно
ВычитаниеПример: Что такое 6 — (+3)?
6 — (+ 3) = 6 — 3 = 3
Пример: Что такое 5 + (−7)?
5 + (- 7) = 5 — 7 = −2
Вычитание негатива.
 ..
..Вычитание отрицательного аналогично Добавление
Пример: Что такое 14 — (−4)?
14 — (- 4) = 14 + 4 = 18
Правила:
Все это можно поместить в два правила :
Правило Пример + (+) Два одинаковых знака превращаются в знак плюс 3 + (+ 2) = 3 + 2 = 5 — (-) 6 — (- 3) = 6 + 3 = 9 + (-) Два непохожих знака превращаются в знак минуса 7 + (- 2) = 7 — 2 = 5 — (+) 8 — (+ 2) = 8 — 2 = 6 Они «как знаки», когда они похожи друг на друга (другими словами: одинаковые).

Итак, все, что вам нужно запомнить, это:
Два знака , похожие на , становятся положительным знаком
Два знака , отличных от , становятся отрицательным знаком
Пример: Что такое 5 + (- 2)?
+ (-) — это в отличие от знаков (они не совпадают), поэтому они становятся отрицательным знаком .
5 + (- 2) = 5 — 2 = 3
Пример: Что такое 25 — (- 4)?
— (-) — это , как знак , поэтому они становятся положительным знаком .
25 — (- 4) = 25 + 4 = 29
Начальный отрицательный
Что, если мы начнем с отрицательного числа?
Может помочь числовая линия:
Пример: Что такое −3 + (+ 2)?
+ (+) — это , как знак , поэтому они становятся положительным знаком .
−3 + (+ 2) = −3 + 2
Начните с −3 на числовой прямой,
двигайтесь вперед 2, и вы получите −1−3 + (+ 2) = −3 + 2 = −1
Пример: Что такое −3 + (- 2)?
+ (-) — это в отличие от знаков , поэтому они становятся отрицательным знаком .

−3 + (- 2) = −3 — 2
Начните с −3 на числовой прямой,
вернитесь на 2, и вы получите −5−3 + (- 2) = −3 — 2 = −5
А теперь поиграйте с ним!
Попробуйте сыграть в Casey Runner, вам нужно знать правила положительного и отрицательного, чтобы добиться успеха! Объяснение здравого смысла
И есть объяснение «здравого смысла»:
Если я скажу «Ешь!» Я призываю вас поесть (положительный результат)
Если я скажу «Не ешьте!» Я говорю об обратном (отрицательном).
Теперь, если я говорю « НЕ, не ешьте!», Я говорю, что не хочу, чтобы вы умерли с голоду, поэтому я снова говорю: «Ешь!» (положительный).
Итак, два отрицания дают положительный результат, и если это вас устраивает, тогда вы сделали!
Другое объяснение здравого смысла
Друг +, враг —
+ + ⇒ + .
друг друга мой друг + — ⇒ — друг врага — мой враг — + ⇒ — враг друга — мой враг — — ⇒ + .враг врага мой друг Пример банка
Пример. В прошлом году банк по ошибке снял с вашего счета 10 долларов, и они хотят это исправить.
Значит, банк должен забрать отрицательные 10 долларов.
Допустим, ваш текущий баланс составляет 80 долларов США, тогда у вас будет:
80 долларов — (- 10 долларов) = 80 долларов + 10 долларов = 90
долларовИтак, вы получаете на свой счет $, еще 10 .
Длинный пример, который вам может понравиться
Очки союзника
Элли может быть непослушным или милым. Так родители Элли сказали
«Если вы будете любезны, мы добавим 3 балла (+3).

Если непослушный, снимаем 3 балла (−3).
Когда вы набираете 30 очков, вы получаете игрушку ».Союзник начинает день с 9 очками: 9 Мама Элли обнаруживает пролитое молоко: 9 — 3 = 6 Тогда папа признается, что пролил молоко и пишет «отменить».
Как «отменить» минус 3?
Мы добавляем 3 снова!Итак, мама считает: 6 — (−3) = 6 + 3 = 9 Итак, когда мы вычитаем отрицательное, мы получаем
баллов (т. е.е. так же, как добавление очков).
е.е. так же, как добавление очков).Таким образом, вычитание отрицательного числа аналогично добавлению
Несколько дней спустя. У Элли 12 очков. Мама добавляет 3 очка, потому что комната Элли чистая. 12 + 3 = 15 Папа говорит: «Я убрал эту комнату» и пишет «отменить» на диаграмме.Мама считает: 15 — (+3) = 12 Папа видит, как Элли чистит собаку.  Пишет на графике «+3». Мама считает:
Пишет на графике «+3». Мама считает:12 + (+3) = 15 Элли бросает камень в окно.Папа пишет на диаграмме «−3». Мама считает: 15 + (−3) = 12 См .: как « 15 — (+3) », так и « 15 + (−3) » дают 12.
Итак:
Неважно, вычтете ли вы положительные
баллов или добавите отрицательные,
вы все равно потеряете баллы.Таким образом, вычитание положительного
или
Добавление отрицательного
равно
ВычитаниеПопробуйте эти упражнения…
Теперь попробуйте этот лист и посмотрите, как у вас дела.

А еще попробуйте эти вопросы:
11715, 11716, 11717, 11718, 11719, 11720, 11721, 3445, 3446
Сложение и вычитание с минусами
Добавление любого числа к его противоположный — также называемый аддитивным обратным — всегда дает нулевой результат. Например:
— 999 + 999 знак равно 0 2.5 + ( — 2,5 ) знак равно 0 1 + ( — 1 ) знак равно 0
Как только вы это узнаете, есть несколько способов подумать о сложении.
Метод алгебраической плитки
Пусть желтые плитки представляют положительные числа, а красные плитки — отрицательные числа.
Пример 1:
Проблема сложения 5 + ( — 2 ) можно представить как
Сгруппируйте две отрицательные плитки с двумя положительными плитками.

С 2 + ( — 2 ) знак равно 0 , эти плитки исчезнут.Мы остались с 3 положительная плитка.
Так 5 + ( — 2 ) знак равно 3 .
Когда оба числа отрицательны , у нас только отрицательные плитки, поэтому ответ тоже отрицательный.
Пример 2:
Проблема сложения — 3 + ( — 4 ) можно представить как
Результат просто 7 негативы плитки.
Так — 3 + ( — 4 ) знак равно — 7 .

Метод числовой линии
Когда ты добавить положительный номер, вы переходите к правильно в числовой строке.
Когда ты добавить отрицательный номер, вы переходите к левый в числовой строке.
Пример 3:
Добавлять 6 + ( — 8 ) используя числовую строку.
Начать с 6 , и двигаться 8 единиц слева.
6 + ( — 8 ) знак равно — 2
Вычитание числа равносильно сложению его противоположности.
Так, вычитание положительного число похоже на добавление минуса; вы переходите к левый в числовой строке.

Вычитание отрицательного число похоже на добавление плюса; вы переходите к правильно в числовой строке.
Пример 4:
Вычесть — 4 — ( — 7 ) .
Начать с — 4 , и двигаться 7 единиц вправо.
— 4 — ( — 7 ) знак равно 3 .
Сложение и вычитание отрицательных чисел
Purplemath
Как вы справляетесь с сложением и вычитанием минусов? Процесс работает аналогично сложению и вычитанию положительных чисел.
 Когда вы добавляли положительное число, вы перемещались вправо в числовой строке. Когда вы вычитали положительное число, вы двигались влево.
Когда вы добавляли положительное число, вы перемещались вправо в числовой строке. Когда вы вычитали положительное число, вы двигались влево.Теперь, если вы добавляете отрицательный результат, вы можете рассматривать это почти так же, как когда вы вычитали положительное, если вы рассматриваете «добавление отрицательного» как добавление к левому . То есть, добавляя минус, вы добавляете в обратном направлении. Точно так же, если вы вычитаете отрицательное значение (то есть вычитаете минус), вы вычитаете в другом направлении; то есть вы будете вычитать, перемещая вправо на .
Например:
MathHelp.com
Вернемся к первому примеру с предыдущей страницы: «9 — 5» можно также записать как «9 + (–5)».
 Графически это будет выглядеть как «стрелка от нуля до девяти, а затем« отрицательная »стрелка длиной пять единиц»:
Графически это будет выглядеть как «стрелка от нуля до девяти, а затем« отрицательная »стрелка длиной пять единиц»:← проведите по экрану , чтобы просмотреть изображение полностью →
… и вы получите «9 + (–5) = 4».
Теперь взгляните на то вычитание, которое вы не смогли сделать: 5 — 9. Поскольку теперь у вас есть отрицательные числа слева от нуля, у вас также теперь есть «пробел» для завершения этого вычитания.Рассматривайте вычитание как добавление отрицательного числа 9; то есть нарисуйте стрелку от нуля до пяти, а затем «отрицательную» стрелку длиной девять единиц:
← проведите по экрану , чтобы просмотреть изображение полностью →
… или, что то же самое:
← проведите по экрану , чтобы просмотреть изображение полностью →
Тогда 5 — 9 = 5 + (–9) = –4.

Конечно, этот метод отсчета вашего ответа в числовой строке не будет работать так хорошо, если вы имеете дело с большими числами. Например, подумайте о том, чтобы сделать «465 — 739». Вы, конечно, не хотите использовать для этого числовую линию. Однако, поскольку 739 больше 465, вы знаете, что ответ на «465–739» должен быть отрицательным, потому что «минус 739» приведет вас куда-нибудь слева от нуля. Но как определить , какое отрицательное число является ответом?
Посмотрите еще раз на «5 — 9».Теперь вы знаете, что ответ будет отрицательным, потому что вы вычитаете большее число, чем вы начали (девять больше пяти). Самый простой способ справиться с этим — выполнить вычитание «как обычно» (меньшее число вычитается из большего числа), а затем поставить знак «минус» в ответ: 9-5 = 4, поэтому 5-9 = –4. Это работает так же для больших чисел (и намного проще, чем пытаться нарисовать картинку): так как 739 — 465 = 274, то 465 — 739 = –274.

Сложить два отрицательных числа просто: вы просто добавляете две «отрицательные» стрелки, так что это похоже на «обычное» сложение, но в противоположном направлении. Например, 4 + 6 = 10 и –4 — 6 = –4 + (–6) = –10. Но что делать, если у вас много как положительных, так и отрицательных чисел?
Упростить 18 — (–16) — 3 — (–5) + 2
Наверное, самое простое — это преобразовать все в сложение, сгруппировать положительные и отрицательные стороны, объединить и упростить.Выглядит это так:
18 — (–16) — 3 — (–5) + 2
= 18 + 16 — 3 + 5 + 2
= 18 + 16 + (–3) + 5 + 2
= 18 + 16 + 5 + 2 + (–3)
= 41 + (–3)
= 41 — 3
= 38
«Стоп! Погодите!» Я слышу, как вы говорите.
 «Как перейти от« — (–16) »к« +16 »на первом этапе? Как« минус минус 16 »превратился в« плюс 16 »?»
«Как перейти от« — (–16) »к« +16 »на первом этапе? Как« минус минус 16 »превратился в« плюс 16 »?»На самом деле это довольно важная концепция, и, если вы спрашиваете, я предполагаю, что объяснение вашего учителя не имело для вас особого смысла. Поэтому я не буду давать вам «правильного» математического объяснения этого правила «минус минус — плюс». Вместо этого вот мысленная картина, с которой я столкнулся много лет назад в группе новостей по алгебре:
Представьте, что вы готовите тушеное мясо в большой кастрюле, но не на плите.Вместо этого вы контролируете температуру рагу с помощью волшебных кубиков. Эти кубики бывают двух типов: горячие и холодные.
Если вы добавите в кастрюлю горячий кубик (добавьте положительное число), температура тушеного мяса повысится. Если добавить холодный кубик (добавить отрицательное число), температура понизится.
 Если убрать горячий куб (вычесть положительное число), температура снизится. А если убрать холодный куб (вычесть отрицательное число), температура поднимется! То есть вычитание отрицательного значения равносильно добавлению положительного.
Если убрать горячий куб (вычесть положительное число), температура снизится. А если убрать холодный куб (вычесть отрицательное число), температура поднимется! То есть вычитание отрицательного значения равносильно добавлению положительного.Теперь предположим, что у вас есть двойные и тройные кубики. Если вы добавите три кубика двойного обжига (добавьте два кубика с плюсом), температура повысится на шесть. И если вы удалите два кубика с тройным охлаждением (вычтите дважды отрицательные три), вы получите тот же результат. То есть –2 (–3) = + 6.
Вот еще одна аналогия, которую я видел. Допустим, что «хороший» будет «позитивным», а «плохой» будет «негативным», вы можете сказать:
хорошего, что происходит с хорошими людьми: хорошее дело
хорошие вещи случаются с плохими людьми: плохие вещи
плохих вещей происходит с хорошими людьми: плохие вещи
плохих вещей происходит с плохими людьми: хорошо
Для конкретного примера:
семья из четырех человек в минивэне возвращается домой в целости и сохранности: хорошее дело
пьяный водитель в угнанной машине, свернувший на всю дорогу, не пойман и не остановлен: плохо
семья из четырех человек убита пьяным водителем, в то время как пьяный без единой царапины убегает с места происшествия: плохо
пьяный водитель пойман и заперт, прежде чем он кого-нибудь обидит: хорошо
Приведенные выше аналогии не являются техническими объяснениями или доказательствами, но я надеюсь, что они делают правила «минус минус — плюс» и «минус, умноженный на минус — плюс», кажутся немного более разумными.

По какой-то причине кажется полезным использовать термины «плюс» и «минус» вместо «сложить», «вычесть», «положительный» и «отрицательный». Так, например, вместо слов «вычитание отрицательного» «, вы бы сказали» минус-минус «. Я понятия не имею, почему это так полезно, но я знаю, что эта словесная техника помогла негативу» щелкнуть «и со мной.
Партнер
Давайте рассмотрим еще несколько примеров:
Упростить –43 — (–19) — 21 + 25.
–43 — (–19) — 21 + 25
= –43 + 19 — 21 + 25
= (–43) + 19 + (–21) + 25 *
= (–43) + (–21) + 19 + 25 *
= (–64) + 44
= 44 + (–64)
Технически, я могу перемещать числа так, как я это делал, между двумя отмеченными звездочкой шагами выше только после , я преобразовал все в сложение.
 Я не могу отменить вычитание, я могу только отменить сложение; только сложение коммутативно. На практике это означает, что я могу перемещать числа вокруг , только если я также перемещаю их знаки вместе с ними . Если я буду перемещать только числа, а не их знаки, я изменю значения и получу неправильный ответ. Продолжая …
Я не могу отменить вычитание, я могу только отменить сложение; только сложение коммутативно. На практике это означает, что я могу перемещать числа вокруг , только если я также перемещаю их знаки вместе с ними . Если я буду перемещать только числа, а не их знаки, я изменю значения и получу неправильный ответ. Продолжая …Поскольку 64 — 44 = 20, тогда 44 — 64 = –20.
Упростить 84 + (–99) + 44 — (–18) — 43.
84 + (–99) + 44 — (–18) — 43
= 84 + (–99) + 44 + 18 + (–43)
= 84 + 44 + 18 + (–99) + (–43)
= 146 + (–142)
= 146–142
= 4
URL: https: // www.
 purplemath.com/modules/negative2.htm
purplemath.com/modules/negative2.htmДобавление положительных и отрицательных чисел
Сложить положительные числа, такие как 2 + 2, очень просто.
Когда мы добавляем отрицательное число к положительному или к двум отрицательным числам, это иногда может показаться сложным. Однако есть несколько простых правил, которым нужно следовать, и мы их здесь вводим.
Правило 1. Добавление положительных чисел к положительным — это обычное сложение.
Например: это то, что вы усвоили с самого начала. 3 + 2 — два положительных числа. Вы можете вычислить эти задачи так же, как и всегда: 3 + 2 = 5.
Правило 2. Добавление положительных чисел к отрицательным — считайте добавляемую сумму вперед.
Здесь становится немного сложнее. Обратите особое внимание на то, где в проблеме находятся отрицательные знаки.

Например: -6 + 3. Это будет «минус шесть плюс три». Лучший способ подумать об этой проблеме — использовать числовую строку, которая продолжается до отрицательных чисел.
Вы начинаете с отрицательного числа -6.
И вы добавляете три к этому числу, что означает, что вы перемещаете три точки вправо.
class = «green-text»> Ответ -3. -6 + 3 = -3.
Правило 3. Добавление отрицательных чисел к положительным — считайте в обратном порядке, как если бы вы вычитали.
Теперь давайте посмотрим на обратное уравнение. Когда вы добавляете отрицательное число к положительному, вы фактически вычитаете второе число из первого.
Например, возьмите 4 + (-2). Как это выглядит в строке чисел?Вы начинаете с 4.
И затем вы добавляете отрицательное число, что означает, что вы движетесь влево — в отрицательном направлении. Обычно вы вычитаете 2,
.Ответ — 2.
 4 + (-2) = 2.
4 + (-2) = 2.Правило 4: Добавление отрицательных чисел к отрицательным числам — относитесь к проблеме как к вычитанию (обратный счет).
Когда вы добавляете отрицательное число к отрицательному, это становится вычитанием, когда вы начинаете с отрицательной точки в строке чисел и перемещаетесь влево.
Например, -3 + (-2). Это читается как «три отрицательных плюс два отрицательных». Вам нужно игнорировать знак плюса и понимать, что второй минус означает, что вы вычитаете это число.
Мы начинаем с -3.
Затем вычитаем 2.
Ответ -5. -3 + (-2) = -5.
Что есть минус плюс минус
Что такое минус плюс минус
Что такое отрицательный плюс отрицательный?
Если два положительных числа умножаются или делятся, ответ — да. Если два отрицательных числа умножить или разделить, ответ будет положительным.Если положительное число и отрицательное число умножаются или делятся, ответ будет отрицательным.

Точно так же, что такое отрицательный плюс отрицательный?
Когда вы добавляете отрицательное число к отрицательному, это становится вычитанием, которое начинается с отрицательной точки на числовой строке и перемещается влево. Это минус три плюс минус 2. Вам нужно игнорировать знак плюса и понимать, что другой знак минус означает, что вы вычитаете это число.
Что означает отрицательный плюс положительный?
Резюме: сумма двух положительных целых чисел всегда дает положительную сумму, а два отрицательных целых числа всегда дает отрицательную сумму.Чтобы найти сумму положительного и отрицательного целого числа, возьмите абсолютное значение каждого целого числа и вычтите эти значения. Сумма целого числа и наоборот равна нулю.
Так почему же отрицательный плюс отрицательный равен положительному?
Если вы умножите отрицательное значение на отрицательное, вы получите положительный результат, потому что оба отрицательных знака удалены.

Какое правило сложения и вычитания положительных и отрицательных чисел?
Правил:
Пример правила+ (+) Два знака равенства становятся положительным знаком 3 + (+ 2) = 3 + 2 = 5 — (-) 6 — (- 3) = 6 + 3 = 9 + (-) Два разных символа становятся отрицательным знаком 7+ (- 2) = 7-2 = 5 — (+) 8 — ( +2) = 8 — 2 = 6 Хорошо ли добавить 2 негатива?
Если у вас два отрицательных знака, переверните один, и они сложатся, чтобы получить положительный знак.Если у вас есть положительный и отрицательный результат, оставляется прочерк и ответ отрицательный.
Что эквивалентно отрицательному и отрицательному?
Мы можем представить движения отрицательным числом и найти ответ умножением. 12 * 700 = 8 400. Это иллюстрация умножения отрицательного числа на отрицательное, в результате чего получается положительное.
 Если вы думаете об умножении как о группировке, мы создали положительную группу, удалив отрицательное число 12 раз.
Если вы думаете об умножении как о группировке, мы создали положительную группу, удалив отрицательное число 12 раз.Как вычитаете отрицательные целые числа?
Чтобы вычесть целые числа, измените знак целого числа, которое вы хотите вычесть. Если оба знака положительные, ответ положительный. Если оба знака отрицательные, ответ отрицательный. Если символы разные, вычтите наименьшее абсолютное значение из наибольшего абсолютного значения.
Что вы получите, если сложите отрицательное и отрицательное?
Не обращайте внимания на знак плюса в начале и поймите, что второе отрицательное число означает, что вы вычитаете это число.Итак, вы видите эту проблему как минус четыре минус два. Начните с 4, а затем сосчитайте (откатите) еще 2. Итак, ваш ответ 6.
Какие четыре математических правила?
Почему отрицательное квадратное число отрицательно?
Да, отрицательное число можно возвести в квадрат. Потому что возведение числа в квадрат означает просто умножение его на себя.
 Например, (2) в квадрате (2) (2) = 4. Обратите внимание, что это положительный результат, потому что если вы умножите два отрицательных числа, вы получите положительный результат.
Например, (2) в квадрате (2) (2) = 4. Обратите внимание, что это положительный результат, потому что если вы умножите два отрицательных числа, вы получите положительный результат.Зачем нужно вычитать положительный отрицательный?
Если добавить холодную матрицу (добавить отрицательное число) температура упадет.Если вынуть горячий орех (вычесть положительное число), температура упадет. А если убрать холодный куб (вычесть отрицательное число), температура повысится! Другими словами, вычитание отрицательного — это то же самое, что добавление положительного.
Является ли отрицательное время положительным и отрицательным?
Комбинация положительного и отрицательного числа, независимо от порядка их ввода, означает, что ваш ответ отрицательный. Правило 3. Отрицательное число, умноженное на отрицательное, дает положительное число.
Почему две отрицательные и положительные вещи?
Каждое число связано с аддитивным обратным (своего рода противоположным числом), которое, добавленное к исходному числу, равно нулю.
 Тот факт, что произведение двух отрицательных чисел является положительным, связан с тем, что обратное значение, обратное положительному числу, является положительным возвращаемым числом.
Тот факт, что произведение двух отрицательных чисел является положительным, связан с тем, что обратное значение, обратное положительному числу, является положительным возвращаемым числом.Какие целые числа от 1 до 10?
Что такое номер 1?
1 (единица, также называемая единицей и единицей) — это число и число, которые используются для представления этого числа в числах.Представляет одну единицу, количество или единицу измерения. Например, линейный сегмент единичной длины — это линейный сегмент длины 1. 1 — наименьшее положительное целое число.
Что произойдет, если умножить отрицательное на положительное?
Следует помнить два простых правила: если вы умножите отрицательное число на положительное, произведение всегда будет отрицательным. Если вы умножите два отрицательных числа или два положительных числа, произведение всегда будет положительным.
Каковы правила для отрицательных чисел?
Отрицательное число — это число меньше нуля, а положительное число — это число больше нуля.
 Ноль не является ни положительным, ни отрицательным. Вы можете складывать, вычитать, умножать и делить положительные и отрицательные числа, комбинируя отрицательные, положительные или их комбинацию.
Ноль не является ни положительным, ни отрицательным. Вы можете складывать, вычитать, умножать и делить положительные и отрицательные числа, комбинируя отрицательные, положительные или их комбинацию.Как составлять числа плюс и минус?
, является ли целое число положительным или отрицательным. является ли операция сложением или вычитанием. Правила сложения и вычитания положительных и отрицательных целых чисел.
Что такое формула плюс-минус?
Каковы три правила сложения и вычитания целых чисел?
Чтобы сложить целые числа с одинаковым знаком, сохраните тот же знак и добавьте абсолютное значение каждого числа.Чтобы сложить целые числа с разными знаками, сохраните знак числа с наибольшим абсолютным значением и вычтите наименьшее абсолютное значение из наибольшего. Вычтите целое число, добавив противоположное.
Каковы правила сложения, вычитания, умножения и деления отрицательных чисел?
Что такое минус плюс минусСложение и вычитание чисел с помощью числовой строки
Добавление чисел в числовую строку — отличный способ увидеть, как добавляются числа с помощью визуальной интерпретации.

I. Действия по сложению чисел в числовой строке
Как показано на схеме ниже:
- Добавление положительного числа означает, что мы перемещаем точку вправо от числовой строки.
- Точно так же добавление отрицательного числа означает, что мы перемещаем точку влево от числовой строки.
Примеры сложения чисел в числовой строке
Пример 1 : Упростите, добавив числа, 2 + 4 .
Первый шаг — найти первое число, которое составляет два (2) в числовой строке.
Добавление четырех (4) означает, что мы должны переместить точку, четыре (4) единицы вправо .
После этого мы получаем 6. Следовательно, 2 + 4 = 6 .
Пример 2 : Упростите, добавив числа, 3 + (–5) .
Найдите первую точку 3 на числовой прямой.

Теперь мы собираемся к добавить отрицательную пятерку (-5) , которая говорит нам переместить точку на 5 единиц влево на .
Мы приходим к −2. Поэтому 3 + (–5) = — 2 .
Пример 3 : Упростите, добавив числа, –6 + 5 .
Найдите первое число −6 в числовой строке. К добавьте пять (5) , исходная точка будет перемещена на пять (5) единиц вправо на числовой строки.
Это дает нам –6 + 5 = –1 .
Пример 4 : Упростите, добавив числа, –1 + (–6) .
На этот раз мы складываем два отрицательных числа. Для начала найдите первое число — -1 . Затем добавляет к нему отрицательное число 6 , что означает перемещение существующей точки на 6 единиц влево на числовой прямой.

Следовательно, имеем –1 + (–6) = –7 .
II. Шаги по вычитанию чисел путем преобразования в сложение в числовой строке
Процесс вычитания чисел очень похож на сложение чисел с очень небольшим «поворотом». Уловка состоит в том, чтобы изменить операцию с вычитания на сложение, а затем поменять знак числа, которое следует за ним.
Другими словами, «вычесть» означает « сложить противоположное ».
Примеры вычитания чисел в числовой прямой
Пример 5 : Упростите, вычитая числа, 5 — (+6) .
Как упоминалось ранее, вычитание — это просто сложение. После изменения операции с вычитания на сложение мы должны принять противоположный знак числа, следующего за ним. Это означает, что мы можем переписать задачу как
5 — (+6) → 5 + (–6)
Поскольку мы уже знаем, как добавлять, эта проблема должна быть легкой! Мы находим первое число, которое составляет 5 , а затем перемещаем его на 6 единиц влево на .

Это дает нам ответ 5 — (+6) = 5 + (–6) = –1 .
Пример 6 : Упростите, вычитая числа, –4 — (–7) .
Это пример вычитания двух отрицательных чисел. Давайте превратим это вычитание в задачу сложения. Помните, всегда добавляйте к противоположному.
–4 — (–7) → –4 + (+7)
Начните с поиска первого числа, −4 , а затем переместите его на 7 единиц вправо на числовой строки.
Мы приходим к 3.Поэтому –4 — (–7) = –4 + (+7) = 3 .
Тем по алгебре: Отрицательные числа
Урок 3: Отрицательные числа
/ ru / algebra-themes / exponents / content /
Что такое отрицательные числа?
Отрицательное число — любое число меньше нуля.
 Например, -7 — это число, которое на семь меньше , чем 0.
Например, -7 — это число, которое на семь меньше , чем 0.-7
Может показаться немного странным, если будет сказано, что число меньше , чем 0.В конце концов, мы часто думаем, что ноль означает ничто . Например, если в вашей конфетной чаше осталось 0 кусочков шоколада, у вас останется или конфет. Осталось , ничего не осталось . В этом случае сложно представить, что у вас будет меньше, чем ничего.
Однако в реальной жизни бывают случаи, когда вы используете числа меньше нуля. Например, бывали ли вы когда-нибудь на улице в очень холодный зимний день, когда температура была ниже нуля? Любая температура ниже нуля — отрицательное число.Например, температура на этом градуснике -20 , или двадцать градусов ниже нуля.
Вы также можете использовать отрицательные числа для более абстрактных идей.
 Например, в финансах отрицательные числа можно использовать для отображения долга . Если я переоцениваю свой счет (вытаскиваю больше денег, чем у меня есть на самом деле), мой новый банковский баланс будет отрицательным числом . У меня не только не будет денег в банке — на самом деле у меня будет меньше , чем ничего, потому что я должен банку денег.
Например, в финансах отрицательные числа можно использовать для отображения долга . Если я переоцениваю свой счет (вытаскиваю больше денег, чем у меня есть на самом деле), мой новый банковский баланс будет отрицательным числом . У меня не только не будет денег в банке — на самом деле у меня будет меньше , чем ничего, потому что я должен банку денег.Посмотрите видео ниже, чтобы узнать больше об отрицательных числах.
Любое число без знака минус перед ним считается положительным числом , то есть числом, которое на больше нуля . Таким образом, в то время как -7 — это отрицательная семерка , 7 — это положительная семерка или просто семь .
Что такое отрицательные числа
Как вы могли заметить, отрицательные числа пишутся с помощью того же символа, что и при вычитании: знака минус (-).
 Знак минус не означает, что вы должны думать о числе типа -4 как о и вычесть четыре . В конце концов, как бы это вычесть?
Знак минус не означает, что вы должны думать о числе типа -4 как о и вычесть четыре . В конце концов, как бы это вычесть?-4
Вы не могли — потому что вычесть это не из чего. Мы можем написать -4 само по себе именно потому, что не означает, что означает вычитание 4 . То есть напротив из четырех.
Посмотрите на 4 и -4 в числовой строке:
Вы можете представить себе числовую прямую как состоящую из трех частей: положительное направление , отрицательное направление и нулевое .Все, что находится справа от нуля, — это положительное значение , а все, что находится слева от нуля, — это отрицательное значение . Мы думаем, что положительные и отрицательные числа — это противоположность , потому что они находятся на противоположных сторонам числовой прямой.

Еще одна важная вещь, которую нужно знать об отрицательных числах, заключается в том, что они становятся на меньше, чем , чем дальше они уходят от 0. В этой числовой строке чем дальше слева от число, тем оно меньше. Таким образом, 1 меньше, чем 3 .-2 меньше 1 , а -7 меньше -2 .
Абсолютное значение
Когда мы говорим об абсолютном значении числа , мы говорим о расстоянии этого числа от 0 на числовой прямой. Помните, как мы сказали, что 4 и -4 были на одном и том же расстоянии от 0? Это означает, что 4 и -4 имеют одинаковое абсолютное значение. Представим взятие абсолютного значения числа двумя прямыми вертикальными линиями | | .Например, | -3 | = 3. Это читается как «абсолютное значение отрицательных трех равно трем».
Важно запомнить: хотя отрицательные числа уменьшаются на на по мере удаления от 0, их абсолютное значение увеличивается на на .
 Например, -10 меньше -6. Однако | -10 | больше чем | -6 | потому что -10 имеет большее расстояние от 0, чем -6.
Например, -10 меньше -6. Однако | -10 | больше чем | -6 | потому что -10 имеет большее расстояние от 0, чем -6.Вычисление с отрицательными числами
Использовать отрицательные числа в арифметике довольно просто.Следует помнить лишь о нескольких особых правилах.
Сложение и вычитание отрицательных чисел
Когда вы складываете и вычитаете отрицательные числа, полезно подумать о числовой прямой, по крайней мере, сначала. Давайте посмотрим на эту проблему: 6-7 . Даже если 7 больше 6, вы можете вычесть его точно так же, как любое другое число, если вы понимаете, что есть числа , меньшие , чем 0.
6-7 = -1
Хотя числовая прямая позволяет легко представить себе эту проблему, есть также уловка, которую вы могли бы использовать для ее решения.
Во-первых, на мгновение игнорируйте отрицательные знаки. Просто найдите разницу в между двумя числами. В данном случае это означает решение для 7 — 6 , что составляет 1.
 Затем посмотрите на свою исходную проблему. Какое число имеет наибольшее абсолютное значение ? В данном случае это -7. Поскольку -7 — отрицательное число, наш ответ тоже будет единичным: -1. Поскольку абсолютное значение -7 больше, чем расстояние между 6 и 0 , наш ответ оказывается на меньше 0 .
Затем посмотрите на свою исходную проблему. Какое число имеет наибольшее абсолютное значение ? В данном случае это -7. Поскольку -7 — отрицательное число, наш ответ тоже будет единичным: -1. Поскольку абсолютное значение -7 больше, чем расстояние между 6 и 0 , наш ответ оказывается на меньше 0 .Добавление отрицательных чисел
Как бы вы решили эту проблему?
6 + -7
Вы не поверите, но это точно та же проблема, которую мы только что решили!
Это потому, что знак «плюс» просто указывает на то, что вы объединяете два числа. Когда вы объединяете отрицательное число с положительным, сумма будет на минус , чем исходное число, так что вы также можете получить при вычитании . Итак, 6 + -7 — то же самое, что 6-7 , и оба они равны -1.
6 + -7 = -1
Всякий раз, когда вы видите положительный и отрицательный знак рядом друг с другом, вы должны читать его как отрицательный .
 Так же, как 6 + -7 это то же самое, что 6-7:
Так же, как 6 + -7 это то же самое, что 6-7:- 10 + -11 равно 10-11.
- 3 + -2 равно 3-2.
- 50 + -100 равно 50-100.
Это верно всякий раз, когда вы добавляете отрицательное число. Добавление отрицательного числа всегда аналогично вычитанию абсолютного значения этого числа.
Вычитание отрицательных чисел
Если сложение отрицательного числа на самом деле равно вычитанию, как вы из вычитаете отрицательное число? Например, как решить эту проблему?
6 — — 3
Если вы догадались, что вы прибавите их , то вы правы. И вот почему: помните, как мы говорили, что отрицательное число противоположно положительному? Мы сравнили их с вами и вашим зеркальным отображением. Ваше зеркальное отражение — ваша противоположность, а это значит, что противоположность вашего зеркального отражения — , вы .Другими словами, противоположность вашей противоположности — вы .

Таким же образом вы можете упростить эти два знака минус, прочитав их как два отрицания. Первый знак минус отрицает — или делает отрицательным — второе. Поскольку отрицательное или противоположное отрицательное значение является положительным, вы можете заменить оба знака минус знаком плюс. Это означает, что вы должны решить это:
6 + 3
Это намного проще решить, верно? Если это кажется запутанным, вы можете просто запомнить этот простой трюк: Когда вы видите два знака минус подряд , замените их знаком плюс .
Итак, 6 минус отрицательное 3 равно 6 плюс 3. Это равно 9. Другими словами, 6 — -3 равно 9.
Может быть сложно запомнить все правила сложения и вычитания чисел. Посмотрите видео ниже, чтобы узнать, как вам помочь.
Умножение и деление отрицательных чисел
Есть два правила умножения и деления чисел:
- Если вы умножаете или делите два положительных или отрицательных числа, результатом будет положительный результат .

- Если вы умножаете или делите положительное и отрицательное число, результатом будет отрицательное число .
Вот и все! Вы умножаете или делите как обычно, а затем пользуетесь этими правилами, чтобы определить положительный или отрицательный ответ. Например, возьмем эту задачу: -3 ⋅ -4 . 3 ⋅ 4 равно 12. Поскольку оба умноженных числа были отрицательными, ответ будет положительным : 12.
-3 ⋅ -4 = 12
С другой стороны, если бы мы умножили 3 ⋅ -4 на , мы получили бы другой ответ:
3 ⋅ -4 = -12
Опять же, 3 ⋅ 4 равно 12.Но поскольку один из наших кратных равен отрицательный , а другой — положительный , наш ответ также должен быть отрицательным : -12.
То же самое и с делением. -40 / -10 равно 4, потому что — 40 и -10 оба являются отрицательными .

-
 («крышка») применяется для возведения числа в степень, а оператор * («звездочка») — для умножения.
(«крышка») применяется для возведения числа в степень, а оператор * («звездочка») — для умножения.
 Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.
Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.



 Например, следующая формула дает результат 11, так как Excel в Интернете умножение выполняется перед с добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.
Например, следующая формула дает результат 11, так как Excel в Интернете умножение выполняется перед с добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5. Эти функции позволяют выполнять как простые, так и сложные вычисления.
Эти функции позволяют выполнять как простые, так и сложные вычисления. Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций. После этого элемент из раскрывающегося списка можно вставить в формулу.
После этого элемент из раскрывающегося списка можно вставить в формулу. В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, в приведенном выше примере функции СРЗНАЧ и СУММ являются функциями второго уровня, поскольку обе они являются аргументами функции ЕСЛИ. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.
В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, в приведенном выше примере функции СРЗНАЧ и СУММ являются функциями второго уровня, поскольку обе они являются аргументами функции ЕСЛИ. Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.

 В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.
В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.
 При копировании или заполнении формулы по строкам или вниз по столбцам относительная ссылка автоматически корректируется, а абсолютная ссылка не корректируется. Например, при копировании или заполнении смешанной ссылки из ячейки A2 в B3 она будет меняться с =A$1 на =B$1.
При копировании или заполнении формулы по строкам или вниз по столбцам относительная ссылка автоматически корректируется, а абсолютная ссылка не корректируется. Например, при копировании или заполнении смешанной ссылки из ячейки A2 в B3 она будет меняться с =A$1 на =B$1. Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.
Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.
 Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает на расположение ячейки с помощью R, за которым следует номер строки, и C, за которым следует номер столбца.
Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает на расположение ячейки с помощью R, за которым следует номер строки, и C, за которым следует номер столбца. Например, если записать команду (например, нажать кнопку «Автоумма»), чтобы вставить формулу, в которую добавляется диапазон ячеек, Excel в Интернете записи формулы со ссылками с помощью стиля R1C1, а не A1.
Например, если записать команду (например, нажать кнопку «Автоумма»), чтобы вставить формулу, в которую добавляется диапазон ячеек, Excel в Интернете записи формулы со ссылками с помощью стиля R1C1, а не A1. 5%)
5%)


 Текст должен быть заключен в двойные кавычки, например «Вторник».
Текст должен быть заключен в двойные кавычки, например «Вторник».

 Решение снова получается верным, правило подтверждается.
Решение снова получается верным, правило подтверждается.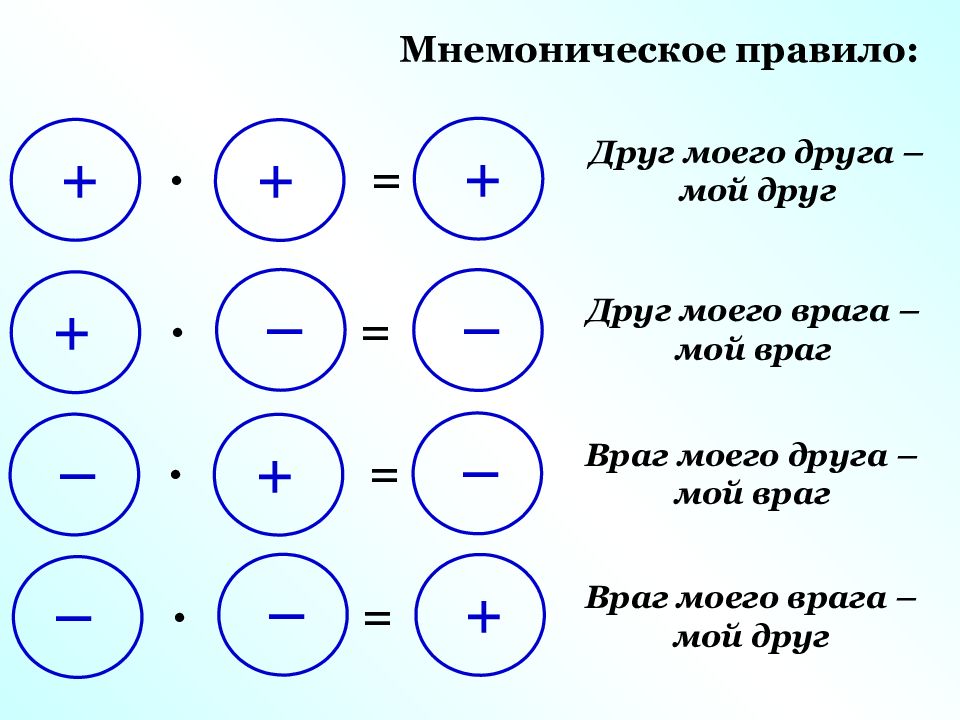 4. Вычитание.
4. Вычитание. 1.6 Сложение в обратном коде
1.6 Сложение в обратном коде 1.1 Операция сложения положительных чисел, представленных в прямом коде
1.1 Операция сложения положительных чисел, представленных в прямом коде ..
.. 4 Представление чисел в дополнительном коде
4 Представление чисел в дополнительном коде


 ..
..
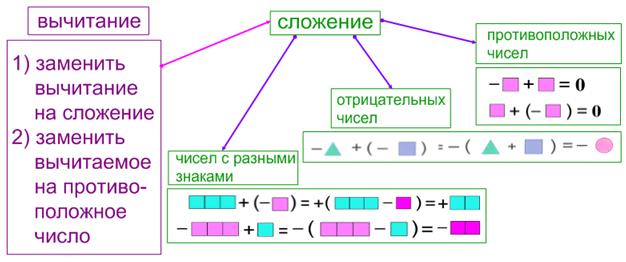


 е.е. так же, как добавление очков).
е.е. так же, как добавление очков). Пишет на графике «+3». Мама считает:
Пишет на графике «+3». Мама считает:



 Когда вы добавляли положительное число, вы перемещались вправо в числовой строке. Когда вы вычитали положительное число, вы двигались влево.
Когда вы добавляли положительное число, вы перемещались вправо в числовой строке. Когда вы вычитали положительное число, вы двигались влево. Графически это будет выглядеть как «стрелка от нуля до девяти, а затем« отрицательная »стрелка длиной пять единиц»:
Графически это будет выглядеть как «стрелка от нуля до девяти, а затем« отрицательная »стрелка длиной пять единиц»:

 «Как перейти от« — (–16) »к« +16 »на первом этапе? Как« минус минус 16 »превратился в« плюс 16 »?»
«Как перейти от« — (–16) »к« +16 »на первом этапе? Как« минус минус 16 »превратился в« плюс 16 »?» Если убрать горячий куб (вычесть положительное число), температура снизится. А если убрать холодный куб (вычесть отрицательное число), температура поднимется! То есть вычитание отрицательного значения равносильно добавлению положительного.
Если убрать горячий куб (вычесть положительное число), температура снизится. А если убрать холодный куб (вычесть отрицательное число), температура поднимется! То есть вычитание отрицательного значения равносильно добавлению положительного.
 Я не могу отменить вычитание, я могу только отменить сложение; только сложение коммутативно. На практике это означает, что я могу перемещать числа вокруг , только если я также перемещаю их знаки вместе с ними . Если я буду перемещать только числа, а не их знаки, я изменю значения и получу неправильный ответ. Продолжая …
Я не могу отменить вычитание, я могу только отменить сложение; только сложение коммутативно. На практике это означает, что я могу перемещать числа вокруг , только если я также перемещаю их знаки вместе с ними . Если я буду перемещать только числа, а не их знаки, я изменю значения и получу неправильный ответ. Продолжая … purplemath.com/modules/negative2.htm
purplemath.com/modules/negative2.htm
 4 + (-2) = 2.
4 + (-2) = 2.

 Если вы думаете об умножении как о группировке, мы создали положительную группу, удалив отрицательное число 12 раз.
Если вы думаете об умножении как о группировке, мы создали положительную группу, удалив отрицательное число 12 раз. Например, (2) в квадрате (2) (2) = 4. Обратите внимание, что это положительный результат, потому что если вы умножите два отрицательных числа, вы получите положительный результат.
Например, (2) в квадрате (2) (2) = 4. Обратите внимание, что это положительный результат, потому что если вы умножите два отрицательных числа, вы получите положительный результат. Тот факт, что произведение двух отрицательных чисел является положительным, связан с тем, что обратное значение, обратное положительному числу, является положительным возвращаемым числом.
Тот факт, что произведение двух отрицательных чисел является положительным, связан с тем, что обратное значение, обратное положительному числу, является положительным возвращаемым числом. Ноль не является ни положительным, ни отрицательным. Вы можете складывать, вычитать, умножать и делить положительные и отрицательные числа, комбинируя отрицательные, положительные или их комбинацию.
Ноль не является ни положительным, ни отрицательным. Вы можете складывать, вычитать, умножать и делить положительные и отрицательные числа, комбинируя отрицательные, положительные или их комбинацию.
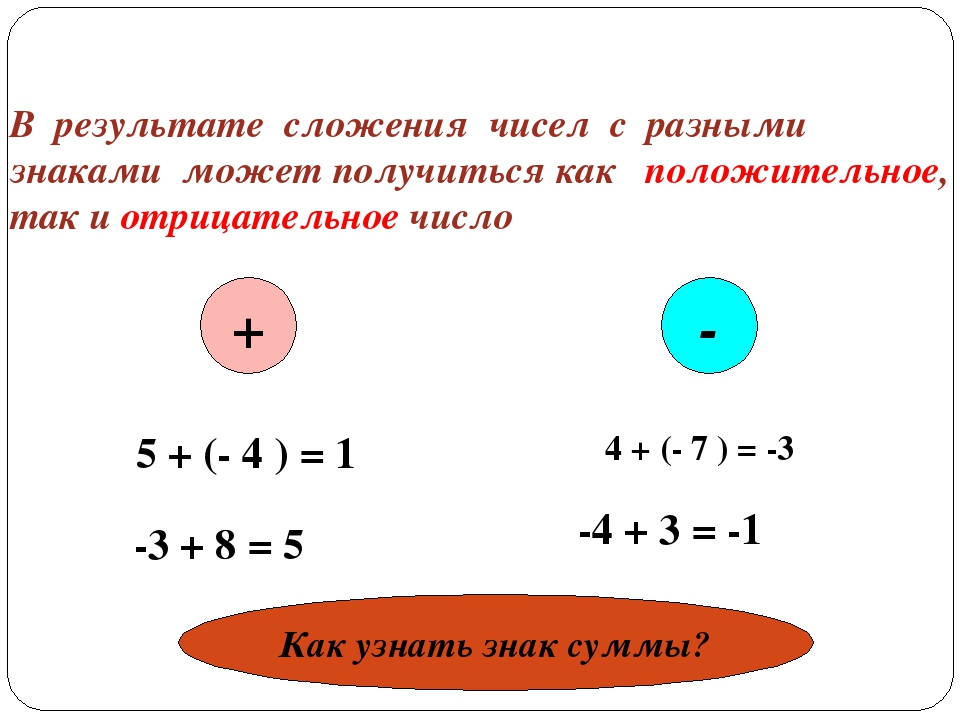


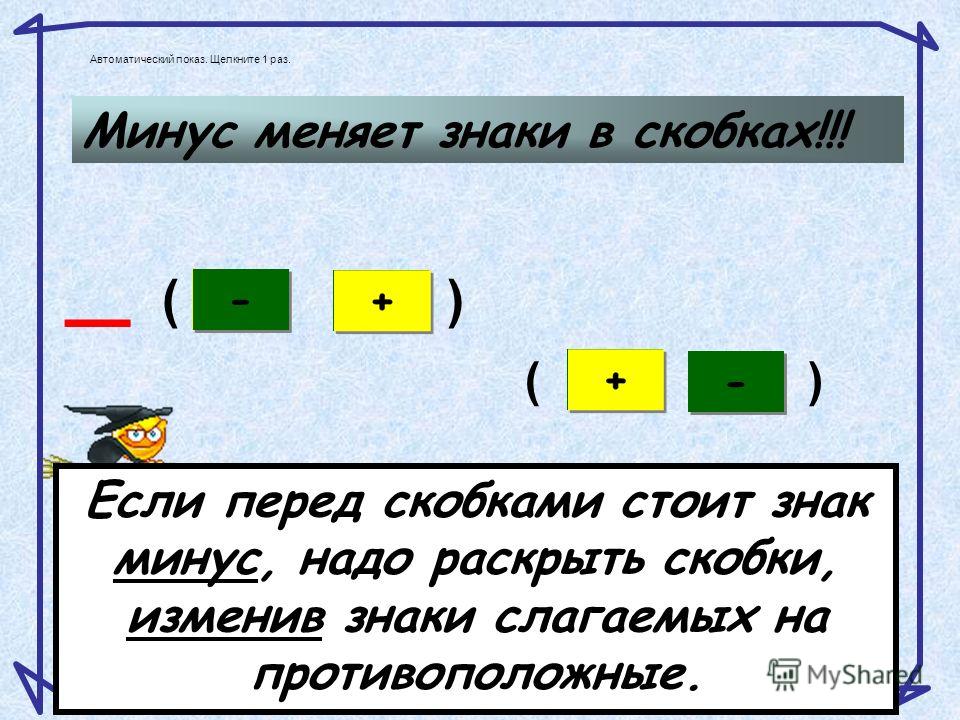 Например, -7 — это число, которое на семь меньше , чем 0.
Например, -7 — это число, которое на семь меньше , чем 0. Например, в финансах отрицательные числа можно использовать для отображения долга . Если я переоцениваю свой счет (вытаскиваю больше денег, чем у меня есть на самом деле), мой новый банковский баланс будет отрицательным числом . У меня не только не будет денег в банке — на самом деле у меня будет меньше , чем ничего, потому что я должен банку денег.
Например, в финансах отрицательные числа можно использовать для отображения долга . Если я переоцениваю свой счет (вытаскиваю больше денег, чем у меня есть на самом деле), мой новый банковский баланс будет отрицательным числом . У меня не только не будет денег в банке — на самом деле у меня будет меньше , чем ничего, потому что я должен банку денег. Знак минус не означает, что вы должны думать о числе типа -4 как о и вычесть четыре . В конце концов, как бы это вычесть?
Знак минус не означает, что вы должны думать о числе типа -4 как о и вычесть четыре . В конце концов, как бы это вычесть?
 Например, -10 меньше -6. Однако | -10 | больше чем | -6 | потому что -10 имеет большее расстояние от 0, чем -6.
Например, -10 меньше -6. Однако | -10 | больше чем | -6 | потому что -10 имеет большее расстояние от 0, чем -6. Затем посмотрите на свою исходную проблему. Какое число имеет наибольшее абсолютное значение ? В данном случае это -7. Поскольку -7 — отрицательное число, наш ответ тоже будет единичным: -1. Поскольку абсолютное значение -7 больше, чем расстояние между 6 и 0 , наш ответ оказывается на меньше 0 .
Затем посмотрите на свою исходную проблему. Какое число имеет наибольшее абсолютное значение ? В данном случае это -7. Поскольку -7 — отрицательное число, наш ответ тоже будет единичным: -1. Поскольку абсолютное значение -7 больше, чем расстояние между 6 и 0 , наш ответ оказывается на меньше 0 . Так же, как 6 + -7 это то же самое, что 6-7:
Так же, как 6 + -7 это то же самое, что 6-7:

