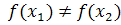|
Мы получили два эквивалентных определения определителя третьего порядка (формулы (4) и (5)). С помощью (4) определитель 3-го порядка вводится с помощью определителей второго порядка (разложение по столбцу). При этом легко проверяется, что все столбцы равноправны. Аналогично рекуррентным образом можно определить определитель n-го порядка (определитель квадратной матрицы n-го порядка), т. е. = = (7) Но в этом случае уже не так просто, как для определителя третьего порядка, проверить, что разложения по остальным столбцам или строкам дают тот же самый результат. Поэтому чаще всего используют в качестве исходного другой подход к определению определителя n-го порядка. Но при этом используются в качестве вспомогательного материала перестановки и подстановки. Пусть дан упорядоченный набор из N элементов. Элементы этого набора занумеруем числами 1, 2, 3, … , n. Очевидно, вместо того, чтобы говорить об элементах, можно говорить об их номерах. Определение 5. Перестановкой Из N Чисел (или N символов) называется расположение этих чисел (или символов) в любом определённом порядке (без повторений). Теорема 1. Число перестановок из N Символов равно n! Доказательство. Составляя перестановку, в качестве первого её элемента можно выбрать точно n символов. Если первый элемент выбран, то в качестве второго элемента можно выбрать любой из оставшихся (n – 1) символов. Следовательно, первые два места можно заполнить n×(n – 1 ) способами. Если два места в перестановке уже заполнены, то на третье место можно поставить любой из оставшихся (n – 2) символов. Следовательно, первые три места можно заполнить n×(n – 1)×(n – 2 ) способами. Продолжая этот процесс, получим, что все n мест в перестановке можно заполнить n×(n – 1)×(n – 2)×…×3×2×1 = n! способами. Говорят, что числа К и Р образуют в перестановке (… К…р…) Инверсию, если К > Р, Но в перестановке К стоит раньше Р. Перестановка называется Чётной, если она содержит чётное число инверсий. Перестановка называется Нечётной, если она содержит нечётное число инверсий. Пример. 1) Перестановка (9, 7, 1, 3, 4, 8, 5, 2, 6) чётная. В ней число 9 образует инверсии со всеми стоящими за ней числами, их 8. Число 7 образует новые инверсии со всеми стоящими за ней числами, кроме числа 8, их 6. Число 1 не образует ни одной новой инверсии. Числа 3 и 4 образуют по одной новой инверсии с числом 2. Число 8 образует ещё инверсии с 5, 2 и 6, их 3. Число 5 образует инверсию с числом 2. Итак, получается 8 + 6 + 1 + 1 + 3 + 1 = 20 инверсий. 2) Перестановка ( 2, 1, 3, 5, 4, 6, 9, 8, 7) нечётная. В ней инверсии образуют пары чисел 2 и 1, 5 и 4, 9 и 8, 9 и 7, 8 и 7. Получилось 5 инверсий. Если в перестановке два символа поменять местами, а все остальные символы оставить на старых местах, то получим новую перестановку. Это преобразование перестановки называется Теорема 2. Всякая транспозиция меняет чётность перестановки. Доказательство. Пусть в перестановке символы К и Р меняются местами. При этом возможны два случая. 1) Символы К и Р В данной перестановке стоят рядом, т. е. (…К, Р …). После транспозиции получится перестановка (….Р, к …). Если К и Р Составляли инверсию в данной перестановке, то после инверсии они уже не будут составлять инверсию и наоборот. Число инверсий, которые К и Р Составляли в данной перестановке с остальными символами, не изменится. Следовательно, число инверсий изменится на 1, т. е. чётность перестановки изменится. 2) Символы К и Р В данной перестановке стоят не рядом, т. е. (….К,…,р…). После транспозиции получится перестановка (… Р,…,к…). Число инверсий, которые К и Р Составляли в данной перестановке с символами, стоящими перед К И после Р, не изменится. Если между К и Р Стоят M символов, то переставить К и Р можно следующим образом: переставить К последовательно с каждым из этих M Символов, затем переставить К и Р, затем в обратном порядке переставить Р с каждым из этих M символов. Получим 2m + 1 транспозиций соседних символов. По доказанному каждая из них меняет чётность перестановки. Итак, чётность перестановки изменилась. Следствие. При n > 1 число чётных перестановок равно числе нечётных перестановок и равно 0,5×n!. Определение 6. Подстановкой из N символов ( или Подстановкой N-ой степени) называется любое взаимнооднозначное отображение множества этих символов на себя. Элементы данного множества будем обозначать 1, 2, …, n А = = . Запись подстановки А = будем называть стандартной. Всякую подстановку можно записать в стандартном виде. Верхнюю и нижнюю строки подстановки можно рассматривать как перестановки. Подстановка А называется чётной, если её верхняя и нижняя строки есть перестановки одинаковой чётности, т. е. общее число инверсий в них – чётное. В противном случае А Называется Нечётной. Так как перестановка столбцов равносильна транспозиции как в верхней так и в нижней строке, то при перестановке столбцов чётность подстановки не изменится, поэтому чётность подстановки можно вычислять по её стандартному виду и в этом случае она совпадает с чётностью нижней строки. Подстановка Е = называется Тождественной Или Единичной. Произведением двух подстановок одного и того же порядка называется результат последовательного выполнения тех отображений, которые задают эти подстановки. Например, если А = , В = , то А×В = . Действительно, первая подстановка переводит 1 в 5, вторая переводит 5 в 4, следовательно, окончательно 1 перейдёт в 4. Аналогично, , , следовательно, ; , , следовательно, ; , , следовательно, ; , , следовательно, ; , , следовательно, . Аналогично получаем, что В×А = . Отсюда следует, что умножение подстановок не подчиняется коммутативному закону. Но можно проверить, что (А×В)×С = А×(В×С) для любых подстановок А, В, С Одного и того же порядка. Очевидно, А×Е = Е×А для любой подстановки
|
Перестановка — Википедия
 6 перестановок трёх шаров
6 перестановок трёх шаровВ комбинаторике перестано́вка — это упорядоченный набор без повторений чисел 1,2,…,n,{\displaystyle 1,2,\ldots ,n,} обычно трактуемый как биекция на множестве {1,2,…,n}{\displaystyle \{1,2,\ldots ,n\}}, которая числу i ставит в соответствие i-й элемент из набора. Число n при этом называется длиной перестановки[1].
В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово подстановка. (Другие авторы подстановкой называют наглядный способ записи перестановки.)
Термин перестановка возник потому, что сначала брались объекты, каким-то образом расставленные, а другие способы упорядочения требовали переставить эти объекты. [2].
- Pn=Ann=n!(n−n)!=n!0!=n!=1⋅2⋅⋯⋅n.{\displaystyle P_{n}=A_{n}^{n}={\frac {n!}{(n-n)!}}={\frac {n!}{0!}}=n!=1\cdot 2\cdot \dots \cdot n.}
Специальные типы перестановок[править | править код]
- Тождественная перестановка — перестановка e,{\displaystyle e,} которая каждый элемент x∈X{\displaystyle x\in X} отображает в себя: e(x)=x.{\displaystyle e(x)=x.}
- Инволюция — перестановка τ,{\displaystyle \tau ,} которая является обратной самой себе, то есть τ⋅τ=e.{\displaystyle \tau \cdot \tau =e.}
- Беспорядок — перестановка без неподвижных точек.
- Циклом длины ℓ{\displaystyle \ell } называется такая подстановка π,{\displaystyle \pi ,} которая тождественна на всём множестве X,{\displaystyle X,} кроме подмножества {x1,x2,…,xℓ}⊂X{\displaystyle \{x_{1},x_{2},\dots ,x_{\ell }\}\subset X} и π(xℓ)=x1,π(xi)=xi+1.{\displaystyle \pi (x_{\ell })=x_{1},\pi (x_{i})=x_{i+1}.} Обозначается (x1,x2,…,xℓ).{\displaystyle (x_{1},x_{2},\dots ,x_{\ell }).}.
- Транспозиция — перестановка элементов множества X{\displaystyle X}, которая меняет местами два элемента. Транспозиция является циклом длины 2.
Подстановка[править | править код]
Перестановка π{\displaystyle \pi } множества X{\displaystyle X} может быть записана в виде подстановки, например:
- (x1x2x3…xny1y2y3…yn),{\displaystyle {\begin{pmatrix}x_{1}&x_{2}&x_{3}&\dots &x_{n}\\y_{1}&y_{2}&y_{3}&\dots &y_{n}\end{pmatrix}},}
где {x1,…,xn}={y1,…,yn}=X{\displaystyle \{x_{1},\dots ,x_{n}\}=\{y_{1},\dots ,y_{n}\}=X} и π(xi)=yi.{\displaystyle \pi (x_{i})=y_{i}.}
Произведения циклов и знак перестановки[править | править код]
Любая перестановка π{\displaystyle \pi } может быть разложена в произведение (композицию) непересекающихся циклов длины ℓ⩾2{\displaystyle \ell \geqslant 2}, причём единственным образом с точностью до порядка следования циклов в произведении. Например:
- (123456516423)=(1,5,2)(3,6).{\displaystyle {\begin{pmatrix}1&2&3&4&5&6\\5&1&6&4&2&3\end{pmatrix}}=(1,5,2)(3,6).}
Часто также считают, что неподвижные точки перестановки представляют собой самостоятельные циклы длины 1, и дополняют ими цикловое разложение перестановки. Для приведенного выше примера таким дополненным разложением будет (1,5,2)(3,6)(4){\displaystyle (1,5,2)(3,6)(4)}. Количество циклов разной длины, а именно набор чисел (c1,c2,…){\displaystyle (c_{1},c_{2},\dots )}, где cℓ{\displaystyle c_{\ell }} — это количество циклов длины ℓ{\displaystyle \ell }, определяет цикловую структуру перестановки. При этом величина 1⋅c1+2⋅c2+…{\displaystyle 1\cdot c_{1}+2\cdot c_{2}+\dots } равна длине перестановки, а величина c1+c2+…{\displaystyle c_{1}+c_{2}+\dots } равна общему количеству циклов. Количество перестановок из n элементов с k циклами даётся числом Стирлинга первого рода без знака [nk]{\displaystyle {\begin{bmatrix}n\\k\end{bmatrix}}}.
Любой цикл может быть разложен в произведение (не обязательно непересекающихся) транспозиций. При этом цикл длины 1 (являющийся по сути тождественной перестановкой e) можно представить как пустое произведение (англ.) транспозиций или, например, как квадрат любой транспозиции: (1,2)(1,2)=(2,3)(2,3)=e.{\displaystyle (1,2)(1,2)=(2,3)(2,3)=e.} Цикл длины ℓ⩾2{\displaystyle \ell \geqslant 2} можно разложить в произведение ℓ−1{\displaystyle \ell -1} транспозиций следующим образом:
- (x1,…,xl)=(x1,xℓ)(x1,xℓ−1)…(x1,x2).{\displaystyle (x_{1},\dots ,x_{l})=(x_{1},x_{\ell })(x_{1},x_{\ell -1})\dots (x_{1},x_{2}).}
Следует заметить, что разложение циклов на произведение транспозиций не является единственным:
- (1,2,3)=(1,3)(1,2)=(2,3)(1,3)=(1,3)(2,4)(2,4)(1,2).{\displaystyle (1,2,3)=(1,3)(1,2)=(2,3)(1,3)=(1,3)(2,4)(2,4)(1,2).}
Таким образом, любая перестановка может быть разложена в произведение транспозиций. Хотя это можно сделать многими способами, чётность количества транспозиций во всех таких разложениях одинакова. Это позволяет определить знак перестановки (чётностью перестановки или сигнатурой перестановки) π{\displaystyle \pi } как
- επ=(−1)t,{\displaystyle \varepsilon _{\pi }=(-1)^{t},}
где t{\displaystyle t} — количество транспозиций в каком-то разложении π{\displaystyle \pi }. При этом π{\displaystyle \pi } называют чётной перестановкой, если επ=1,{\displaystyle \varepsilon _{\pi }=1,} и нечётной перестановкой, если επ=−1.{\displaystyle \varepsilon _{\pi }=-1.}
Эквивалентно, знак перестановки определяется её цикловой структурой: знак перестановки π{\displaystyle \pi } из n{\displaystyle n} элементов, состоящий из k{\displaystyle k} циклов, равен
- επ=(−1)n−k.{\displaystyle \varepsilon _{\pi }=(-1)^{n-k}.}
Знак перестановки π{\displaystyle \pi } также может быть определен через количество инверсий N(π){\displaystyle N(\pi )} в π{\displaystyle \pi }:
- επ=(−1)N(π).{\displaystyle \varepsilon _{\pi }=(-1)^{N(\pi )}.}
Рассмотрим n элементов m различных типов, причем в каждом типе все элементы одинаковы. Тогда перестановки из всех этих элементов с точностью до порядка следования однотипных элементов называются перестановками с повторением. Если ki — количество элементов i-го типа, то k1+k2+⋯+km=n{\displaystyle k_{1}+k_{2}+\dots +k_{m}=n} и количество всевозможных перестановок с повторениями равно мультиномиальному коэффициенту (nk1, k2, …, km)=n!k1!k2!…km!.{\displaystyle \textstyle {\binom {n}{k_{1},\ k_{2},\ \dots ,\ k_{m}}}={\frac {n!}{k_{1}!k_{2}!\dots k_{m}!}}.}
Перестановку с повторениями можно также рассматривать как перестановку мультимножества {1k1,2k2,…,mkm}{\displaystyle \{1^{k_{1}},2^{k_{2}},\dots ,m^{k_{m}}\}} мощности k1+k2+⋯+km=n{\displaystyle k_{1}+k_{2}+\dots +k_{m}=n}.
Случайной перестановкой называется случайный вектор ξ=(ξ1,…,ξn),{\displaystyle \xi =(\xi _{1},\ldots ,\xi _{n}),} все элементы которого принимают натуральные значения от 1 до n,{\displaystyle n,} и при этом вероятность совпадения любых двух элементов равна 0.
Независимой случайной перестановкой называется такая случайная перестановка ξ{\displaystyle \xi }, для которой
- P{ξ=σ}=p1σ(1)…pnσ(n)∑π∈Snp1π(1)…pnπ(n){\displaystyle P\{\xi =\sigma \}={\frac {p_{1\sigma (1)}\ldots p_{n\sigma (n)}}{\sum \limits _{\pi \in S_{n}}p_{1\pi (1)}\ldots p_{n\pi (n)}}}}
для некоторых pij,{\displaystyle p_{ij},} таких, что
- ∀i(1⩽i⩽n):pi1+…+pin=1{\displaystyle \forall i(1\leqslant i\leqslant n):p_{i1}+\ldots +p_{in}=1}
- ∑π∈Snp1π(1)…pnπ(n)>0.{\displaystyle \sum \limits _{\pi \in S_{n}}p_{1\pi (1)}\ldots p_{n\pi (n)}>0.}
Если при этом pij{\displaystyle p_{ij}} не зависят от i{\displaystyle i}, то перестановку ξ{\displaystyle \xi } называют одинаково распределённой. Если же нет зависимости от j{\displaystyle j}, то есть ∀i,j(1≤i,j≤n):pij=1/n,{\displaystyle \scriptstyle \forall i,j(1\leq i,j\leq n):p_{ij}=1/n,} то ξ{\displaystyle \xi } называют однородной.
§ 4. Перестановки и подстановки
Вычисление определителей 4-го и более высоких порядков не может быть представлено достаточно простой «геометрической схемой», как это сделано для определителей 2-го и 3-го порядков.
Для определения и изучения определителей n-го порядка используются понятия, относящиеся к конечным множествам некоторых элементов.
4.1. Перестановки.
Рассмотрим множество М целых чисел: 1, 2, … , n. Элементы множества М можно расположить разными способами.
Определение: всякое расположение чисел 1, 2, … , n в некотором порядке называется пе-рестановкой из n чисел. Общий вид записи перестановки из n элементов:
i1 , i2 , … , in , (42)
где каждое is есть одно из чисел 1, 2, … , n, причем ни одно из этих чисел не встречается дважды и не пропущено.
В качестве i1 можно выбрать любое из чисел 1, 2, … , n. Это дает n различных возможностей. Если i1 уже выбрано, то в качестве i2 можно выбрать лишь одно из оставшихся (n-1) чисел, т.е. различных способов выбрать числа (символы) i1 и i2 равно произведению n∙(n-1) и т.д. Число перестановок из n символов равно произведению:
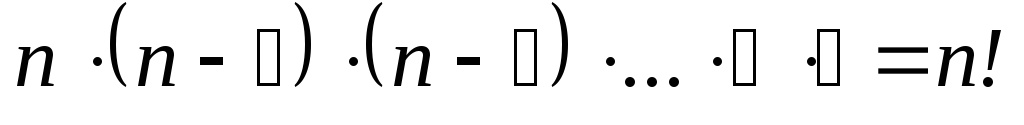
Если в некоторой перестановке поменяем местами какие-либо два символа (не обязательно стоящие рядом), а все остальные оставим на месте, то получим новую перестановку. Такое преобразование перестановки называется транспозицией.
Теорема 1. Все перестановки из n символов можно расположить в таком порядке, что каждая следующая перестановка получается из предыдущей одной транспозицией, причем начинать можно с любой перестановки.
► При n=2 утверждение справедливо: 1, 2 → 2, 1;
2, 1 → 1, 2.
Рассмотрим
все перестановки из n элементов, у которых на первом месте
стоит символ i1.
Таких перестановок 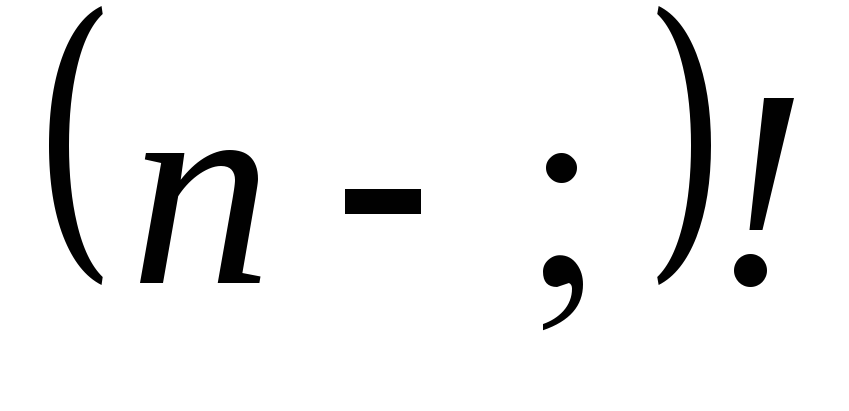 и
их можно упорядочить в соответствии с
требованиями теоремы для (n-1)
символов. Пусть последняя из таких
перестановок (с учетом того, что символ i1 был все время неперемещаем) имеет вид:
и
их можно упорядочить в соответствии с
требованиями теоремы для (n-1)
символов. Пусть последняя из таких
перестановок (с учетом того, что символ i1 был все время неперемещаем) имеет вид:
i1 , i2 , … , in (43)
В перестановке (43), содержащей n символов, совершим транспозицию символа i1 с любым другим (например, с символом i2) и вновь упорядочим все перестановки из (n-1) символов при фиксированном на первом месте i2 и т.д. Так можно перебрать все перестановки из n символов. ◄
Следствие: от любой перестановки из n символов можно перейти к любой другой перестановке из тех же символов при помощи нескольких транспозицией.
Если
в перестановке символ i1 стоит раньше, чем символ i2,
но 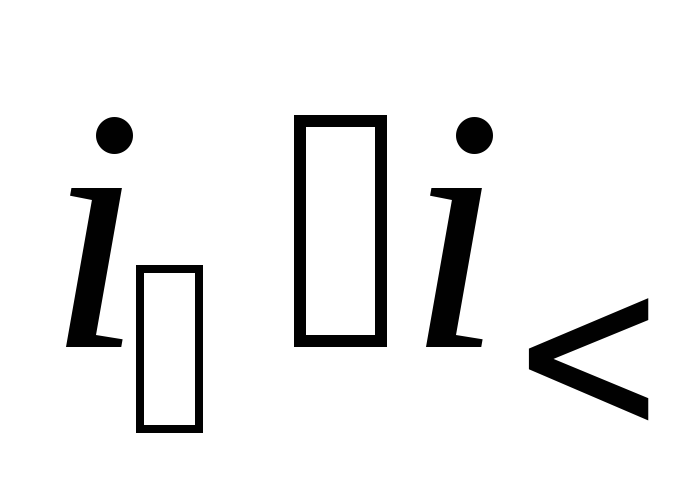 ,
то говорят, символы i1 и i2 составляют инверсию (нарушение порядка), иначе указанные
символы составляют порядок.
Перестановка называется четной,
если ее символы составляют четное число
инверсий, и нечетной – в противном случае.
,
то говорят, символы i1 и i2 составляют инверсию (нарушение порядка), иначе указанные
символы составляют порядок.
Перестановка называется четной,
если ее символы составляют четное число
инверсий, и нечетной – в противном случае.
Замечание: 1) всякая транспозиция меняет четность перестановки.
2)
сумма порядков и инверсий постоянна и
равна 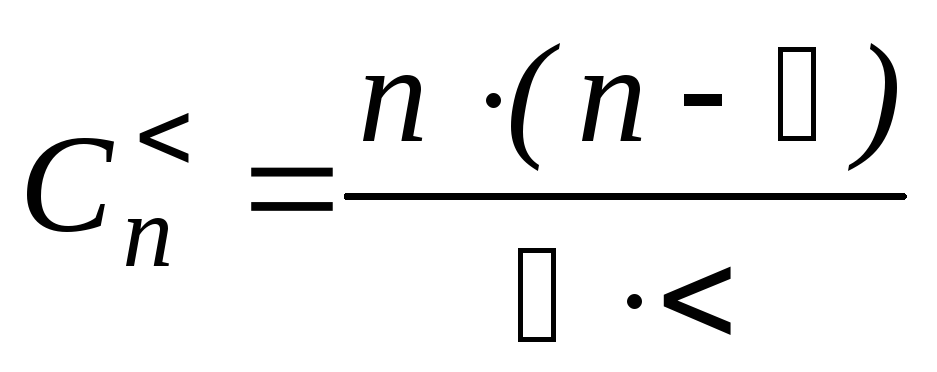
☺ Пример 31. Определим четность перестановки 1, 2, … , n.
Решение: Заданная перестановка четная, т.к. в ней нет инверсий (нарушений порядка).
Ответ: Четная.
Пример 32. Определите четность перестановки 4 5 1 3 6 2.
Решение: Для подсчета числа инверсий воспользуемся таблицей 1, в которой указаны инверсии выделяемых элементов со всеми последующими (учет нарушений порядка).
4 | 5 | 1 | 3 | 6 | 2 | |||
╙ | ☼ | ☼ | ☼ | =3 | ||||
╙ | ☼ | ☼ | ☼ | =3 | ||||
╙ | =0 | |||||||
╙ | ☼ | =1 | ||||||
╙ | ☼ | =1 | ||||||
—————————————————— | ||||||||
Число инверсий : | =8 | |||||||
Ответ: Четная.
☻Решите примеры:
Пример 33. Укажите число инверсий в перестановке: 1, 9, 6, 3, 2, 5, 4, 7, 8.
Пример 34. В какой перестановке чисел 1, 2, 3, …, 99 число инверсий наибольшее и чему оно равно?
Пример 35. Сколько инверсий образует число 99, стоящее на 50 месте в перестановке 1, 2, …, 99.
Вопросы для самопроверки
Перестановка – это матрица?
Что такое «транспозиция» двух элементов перестановки?
Что такое «инверсия» для двух выделенных элементов перестановки?
Что такое «порядок» для двух выделенных элементов перестановки?
Чему равна сумма числа инверсий и числа порядков в любой перестановке чисел 1, 2, … , 99.
4.2. Подстановки.
Определение:
Запишем одну перестановку под другой: 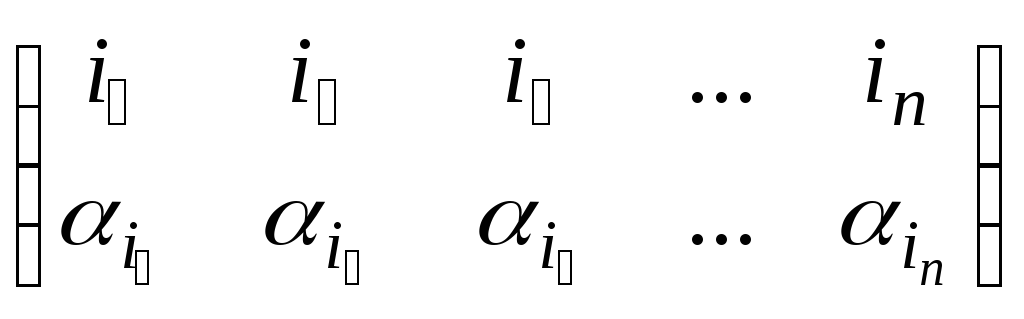 .
Эту запись
.
Эту запись
называют подстановкой,
понимая под этим отображение (соответствие) множества символов,
состоящего из первых n
чисел: 1, 2, …, n,
на себя: 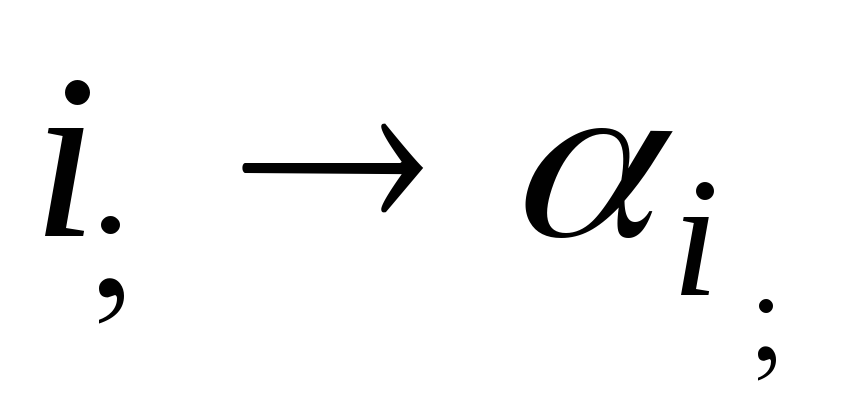
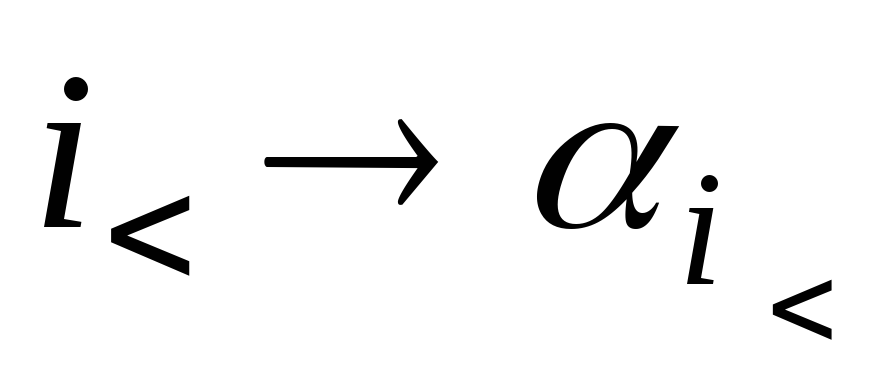 ,
, 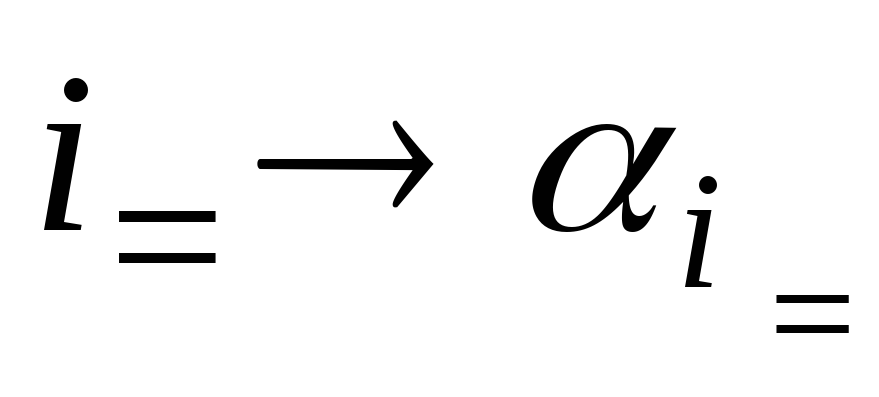 ,
…,
,
…, 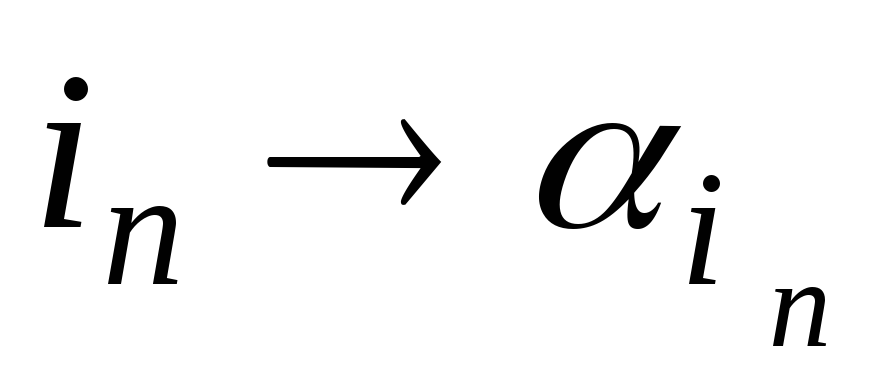
Если учесть, что подстановка как отображение множества чисел 1, 2, … , n не меняется при транспозиции столбцов, выберем для нее простейшее выражение:
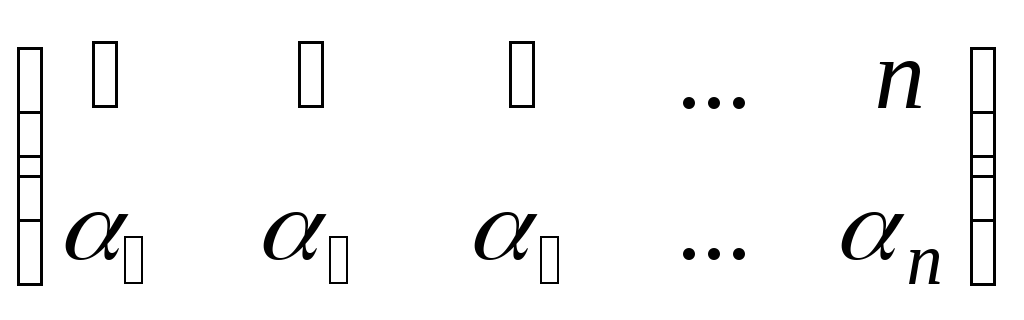 , (44)
, (44)
где αi – число, в которое переходит число i.
В
выражении (44) подстановки порядка n различаются только перестановками в
нижней строке записи, т.е. подстановку однозначно
определяет перестановка,
записан-ная в ее нижней строке. Это
значит, что всего подстановок порядка n столько же, сколь-ко и перестановок,
т.е. 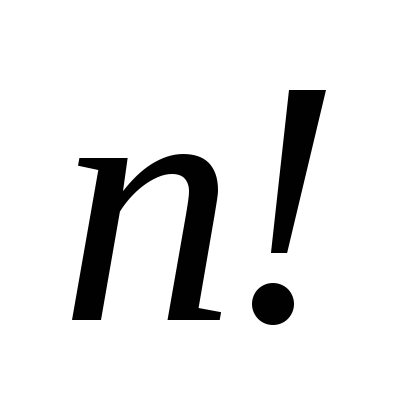
Определим понятие четности для подстановок:
А. Исходя из общего определения подстановки:
подстановка четная, если четности верхней и нижней перестановок совпадают;
подстановка нечетная, если четности верхней и нижней перестановок противоположны.
Б. Учитывая частную запись подстановки (44):
подстановка четная, если ее определяет четная перестановок;
подстановка нечетная, если ее определяет нечетная перестановка.
Кроме подсчета числа инверсий в перестановках для определения четности подстановок применяют также разложение их в циклы. Воспользуемся этим приемом (не обосновывая его, примем на веру), рассмотрев конкретный пример.
☺ Пример 36. Определим
четность подстановки  .
.
Решение: Для определения четности подстановки разложим ее в произведение циклов:
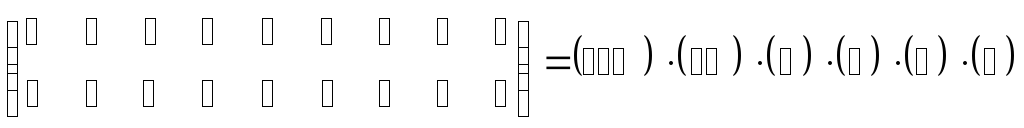 ,
,
где скобки после знака “=” отражают циклы: (1→6→3→1), (2→5→2), (4→4), (7→7), (8→8), (9→9) отображения символов 1,2,…,9 по определению подстановки (в циклах учтены также символы «остающиеся на месте»). Имея разложение подстановки в циклы, определим число декремент: d = n – s, где n – порядок подстановки, s – число циклов в разложении подстановки. В рассматриваемом примере: d = 9 – 6 = 3 – нечетное число → подстановка нечетная.
Ответ: Четная.
Пример 37. Для определения четности подстановки разложим ее в произведение циклов:
 ,
,
где скобки после знака “=” отражают циклы: (1→5→1), (2→8→6→4→2),(3→9→7→3) отображения символов 1,2,…,9 по определению подстановки. Вычислим декремент для рассматриваемой подстановки: d = 9 – 3 = 6 – четное число → подстановка четная.
☻Решите примеры:
Пример 38. Укажите число инверсий в перестановке: 1, 9, 6, 3, 2, 5, 4, 7, 8.
Пример 39. В какой перестановке чисел 1, 2, 3, …, 99 число инверсий наибольшее и чему оно равно?
Пример 40. Сколько инверсий образует число 99, стоящее на 50 месте в перестановке 1, 2, …, 99.
Вопросы для самопроверки:
Подстановка – это матрица?
Что такое «транспозиция» столбцов подстановки?
Что такое «инверсия» в подстановке?
Что такое «порядок» в подстановке?
Чему равна сумма числа инверсий и числа порядков в любой подстановке чисел 1, 2, … , 99.
Лекция№ 3-4 Подстановки
Определение. Всякое взаимно однозначное отображение множества А первых n натуральных чисел на себя называется подстановкой n-й степени, причем, очевидно, всякая подстановка А может быть записана при помощи двух перестановок, подписанных одна под другой
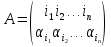 (1)
(1)
Через αi здесь обозначается то число, в которое при подстановке А переходит число i , i = 1, 2, …, n.
Запишем одну под другой две перестановки из n символов, беря полученные две строки в скобки; например, n=5:
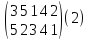
Мы скажем, что число 3 переходит в число 5, число 5 переходит в 2, число 1 переходит в 3, число 4 переходит в 4(или остаётся на месте), и, наконец, число 2 переходит в 1. Таким образом, две перестановки, записанные друг под другом в виде (2), определяют некоторое взаимно однозначное отображение множества из первых пяти натуральных чисел на себя, т. е. отображение, которое каждому из натуральных чисел 1, 2, 3, 4, 5 ставит в соответствие одно из этих же натуральных чисел, причем разным числам ставятся в соответствие различные же числа.
Ясно, что то взаимно однозначное отображение множества их первых пяти натуральных чисел, которые мы получили при помощи (2), можно было получить, записывая одну под другой и некоторые другие пары перестановок из пяти символов. Эти записи получаются из (2) путем нескольких транспозиций (перестановок) столбиков; таковы, например,
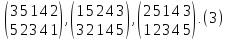
Во всех этих записях 3 переходит в 5, 5 в 2 и т. д.
Подстановка А обладает многими различными записями вида (1). Так, (2) и (3) являются различными записями одной и той же подстановки 5-й степени.
Канонический вид подстановки
В частности, всякая подстановка n-й степени А может быть записана в каноническом виде
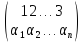 (4)
(4)
т. е. с натуральным расположением чисел в верхней строке. При такой записи различные подстановки отличаются друг от друга перестановками, стоящими в нижней строке.
Примером подстановки n-й степени служит тождественная подстановка
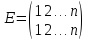 ,
,
при котором на месте остаются все символы.
Замечание. Следует заметить, что верхняя и нижняя строки в записи (1) подстановки А играют разные роли и, переставив их, мы, вообще говоря, получаем другую подстановку.
Цикловая структура подстановки
Подстановка вида
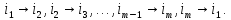
(При этом все числа i1, i2, …, im — различны)
называется циклом длины m.
Для циклов вводят специальное обозначение:
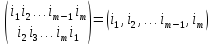
Пример 1.
Цикл (2 3 4 1) действует следующим образом
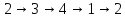
Циклы, не содержащие общих элементов называются независимыми(непересекающимися).
Теорема. Каждую подстановку можно разложить в произведение независимых циклов. Это разложение единственно с точностью до порядка циклов.
Алгоритм составления цикла:
1.Берем подстановку, смотрим, во что переходит первый элемент.
2.Полученный элемент пишем за первым элементом и находим его образ под действием подстановки.
3. Как только образ совпадает с элементом, с которого началось построение цикла, закрываем цикл.
4. Дальше берем любой элемент, не входящий в уже выписанные циклы и начинаем построение нового цикла.
Пример 2.
Разложить подстановку
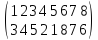
в произведение независимых циклов.
Решение.
Так
как 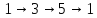 ,
то получаем цикл (135). Цепочка 2→4→2
дает транспозицию (24). Так же 6→8→6
дает транспозицию (68). 7 остается на
месте.
,
то получаем цикл (135). Цепочка 2→4→2
дает транспозицию (24). Так же 6→8→6
дает транспозицию (68). 7 остается на
месте.
Ответ: 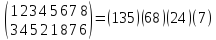
Раздел 5. Отображения. Подстановки.
Тема 5.1 Отображения и их свойства.
Пусть XY – произвольные множества, если каждому элементу x из множества X (x ∈ X) ставится в соответствие элемент y ∈ Y, то говорят, что на множестве X задано отображение со значениями во множестве Y.
Пусть: X→Y либо f(x) = y.
Множество X – называется областью определения.
Множество Y – область прибытия.
Областью значений отображения f: X→Y называется множество f(X), состоящее из y ∈ Y, такого что y= f(x) для x ∈ X
f(X)={y| y ∈ Y, y= f(x), для x ∈ X }
Область значения всегда является подмножеством Y, но не всегда совпадает с ним f(X)≤Y
Существуют следующие способы задания отображений:
аналитический, то есть когда отображение задается в виде формулы;
словесный – описанием с помощью слов;
табличный
графический (график , диаграмма)
Свойства:
Отображение f: X→Y называется сюръекцией, если область прибытия совпадает с областью значений, то есть f(X)=Y или если для любого y ∈ Y J x ∈ X, такой что f(x)=y
X Y
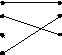
Отображенное f: X→Y называется инъекцией, если для любых
 ,
таких что
,
таких что  выполняется что значения соответствовать
этим аргументам не будут совпадать
выполняется что значения соответствовать
этим аргументам не будут совпадать
А
если для 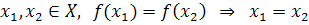
X Y X Y
 не
является инъекцией
не
является инъекцией
Отображение f=X→Y называется биекцией, если оно является сюръекцией и инъекцией, или для любого элемента y ∈ Y существует и притом единственный x ∈ X, такой, что f(x)=y.
X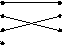 Y
Y
Биекция также называется взаимно-однозначным отображением.
Самостоятельная работа №11.
Тема 5.2 Композиция отображений и обратное отображение.
Пусть f: X→Y а g:Y→Z, тогда композицией (произведением) отображений f и g называется новое отображение обозначается
g  f: X→Z,
при этом выполняется
(g
f: X→Z,
при этом выполняется
(g  f)(x)=g(f(x))
f)(x)=g(f(x))
Свойства:
1. 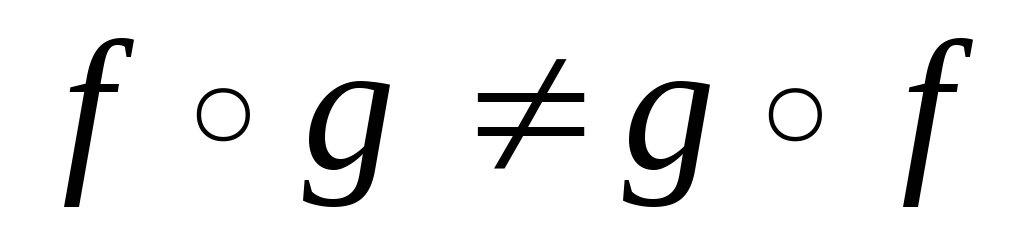 композиция
отображений не коммутативно.
композиция
отображений не коммутативно.
Пусть 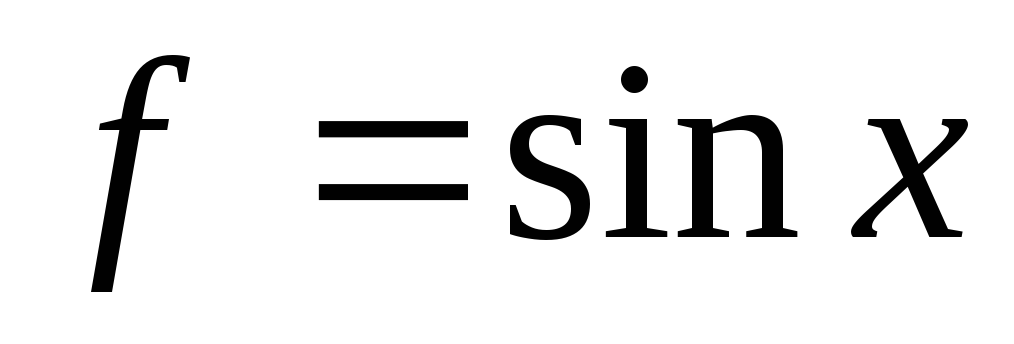 ,
,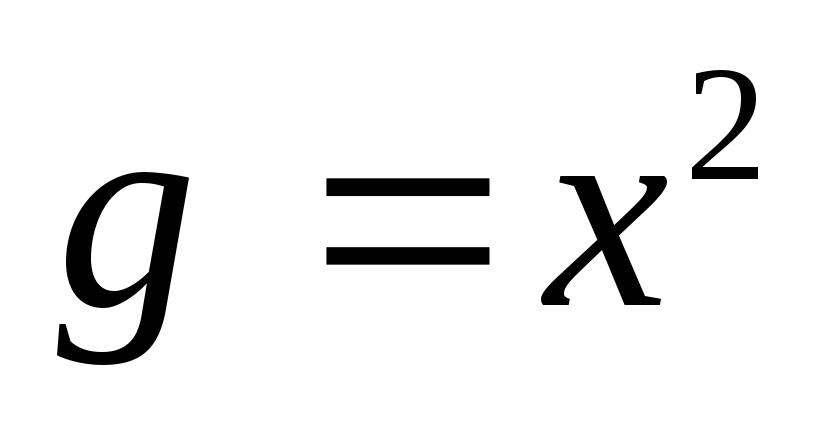
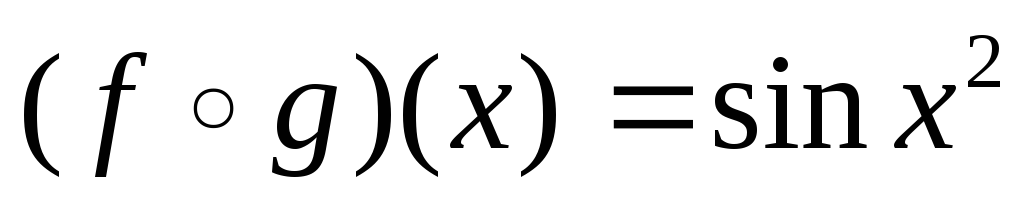
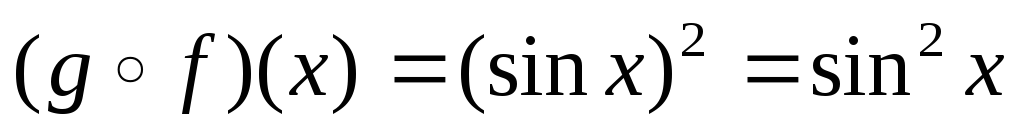
2. 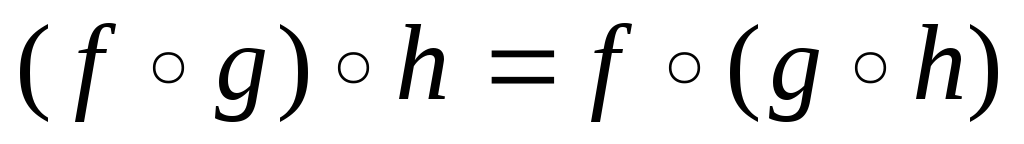 — ассоциативность.
— ассоциативность.
Отображение f: X→Y
является биекцией тогда обратным
отображением, когда 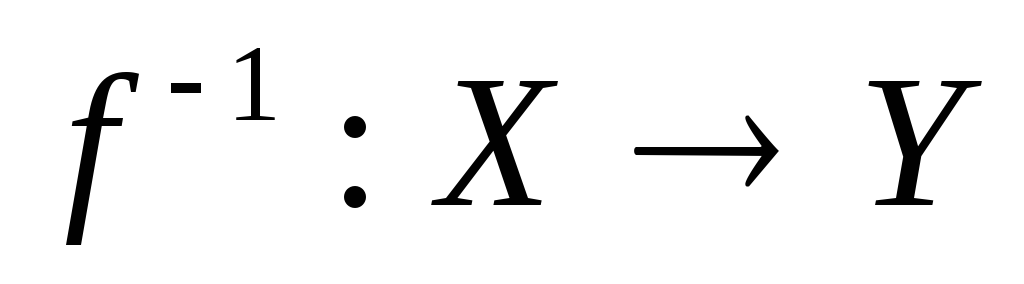 такое что
такое что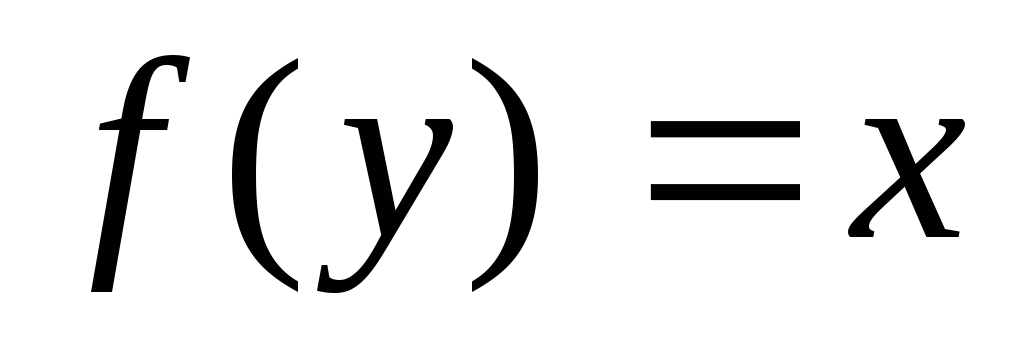
Тема 5.3 Подстановки. Обратные подстановки. Формула количества подстановок.
Взаимооднозначное отображение множества {1,2,3, …,n} на само себя называется подстановкой n чисел, где n – степень подстановки.
Обычно подстановку записывают в виде двух строк, заключенных в скобки. При этом в первой строке аргументы (первые координаты), а во второй строке в соответствующие им образы (вторые координаты).
Общая формула количества подстановок:
Если степень подстановки =n – то количество подстановок: n!
Из всех подстановок выделяют так называемую тождественную подстановку.

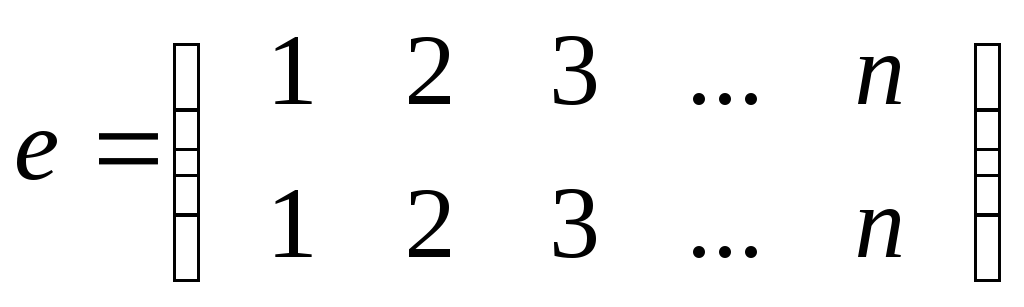
Если
подстановка  имеет
вид
имеет
вид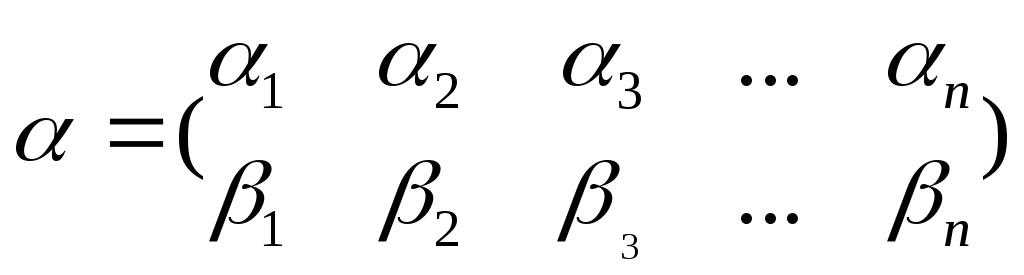 ,
то симметричная ей подстановка
,
то симметричная ей подстановка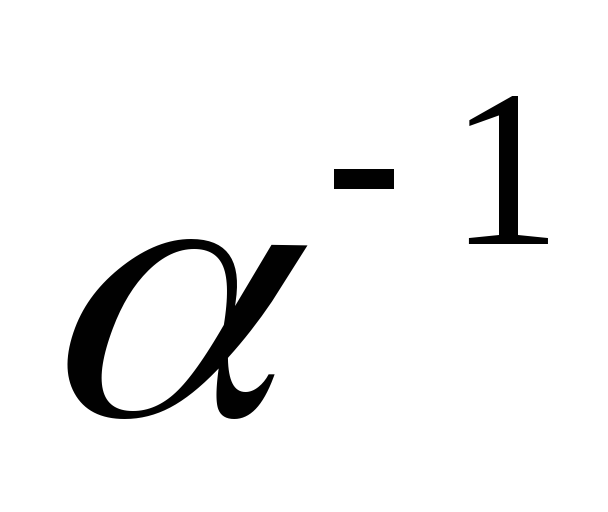 получается если поменять местами строки
подстановки
получается если поменять местами строки
подстановки
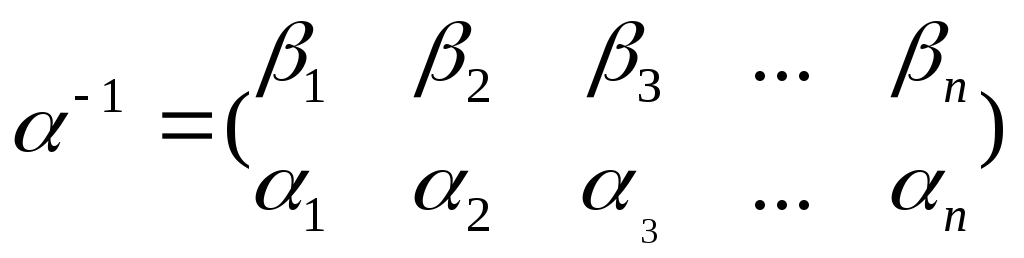
Произведением
подстановок  и
и называется новая подстановка
называется новая подстановка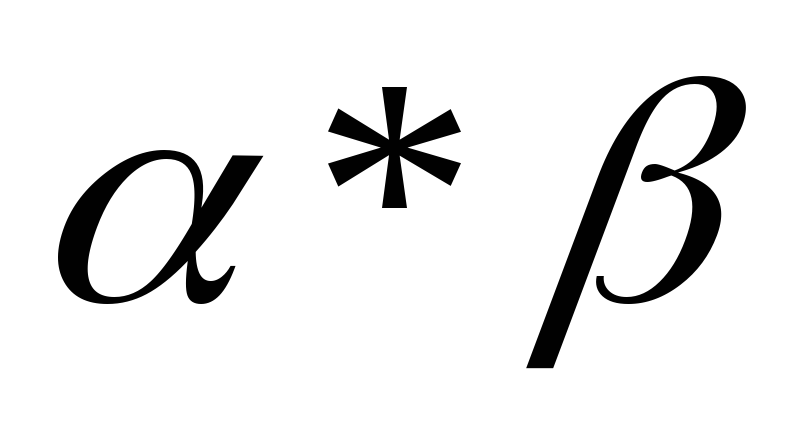 ,
полученная путем применения сначала
подстановки
,
полученная путем применения сначала
подстановки ,
затем подстановки
,
затем подстановки .
.
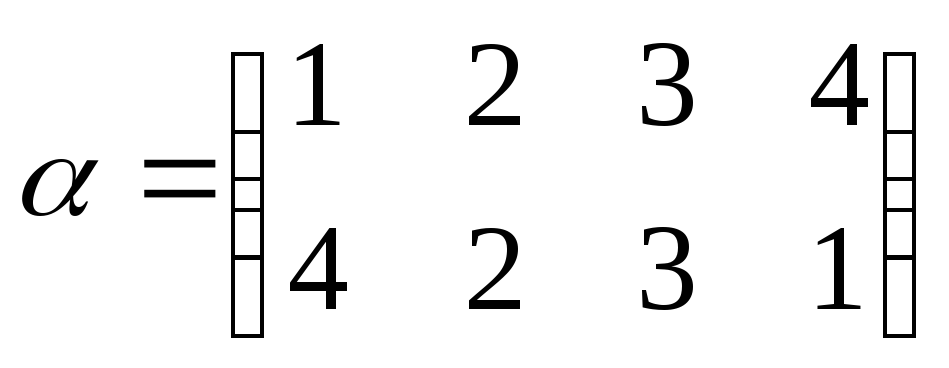
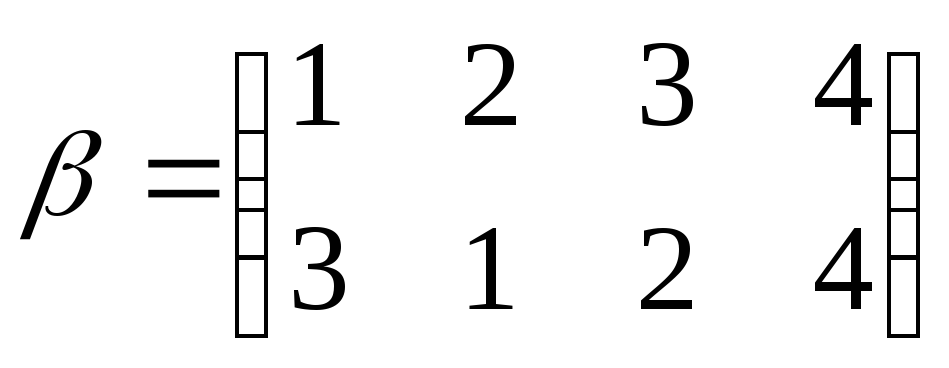
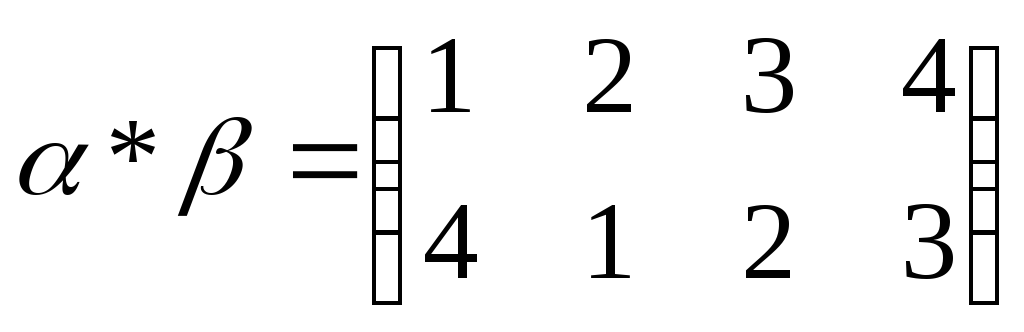
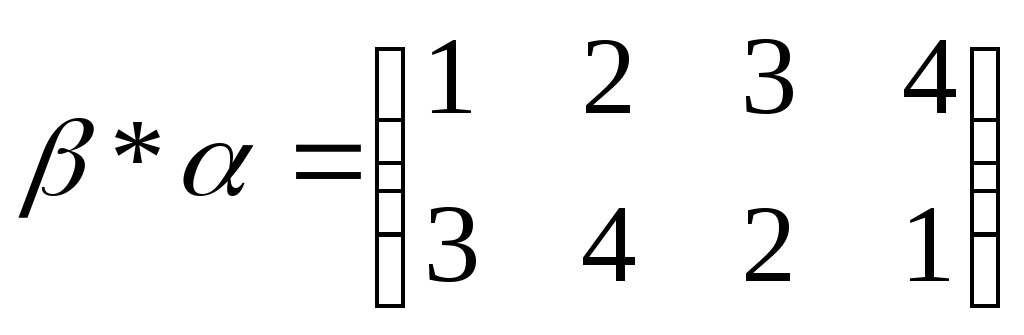
Свойства:
1. 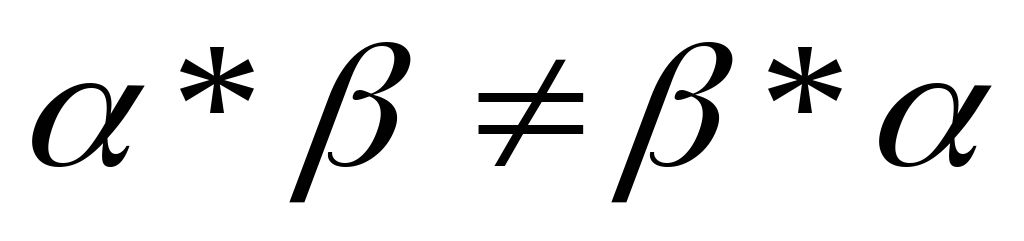 — произведение подстановок не коммутативно;
— произведение подстановок не коммутативно;
2. 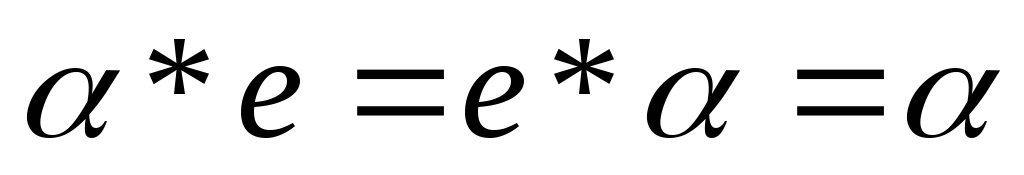
3. 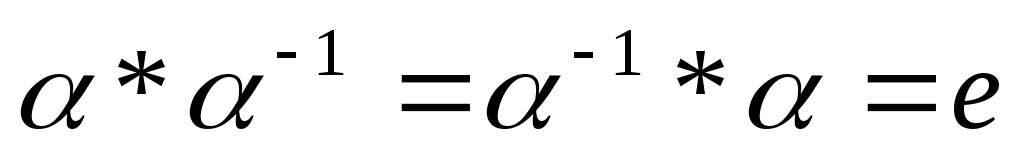
Подстановка называется четной, если общее число инверсий в ее строках, есть число четное, в противном случае подстановка называется нечетной.
Два числа образуют инверсию, если меньшее из них находиться правее большего.
Общее число инверсий определяют следующим образом:
определяем число инверсий для первой строки: для каждого числа подсчитываем количество чисел, меньше чем оно и стоящих правее его.
определяем число инверсий для второй строки: для каждого числа подсчитываем количество чисел, меньше чем оно и стоящих правее его.
складываем полученные значения.
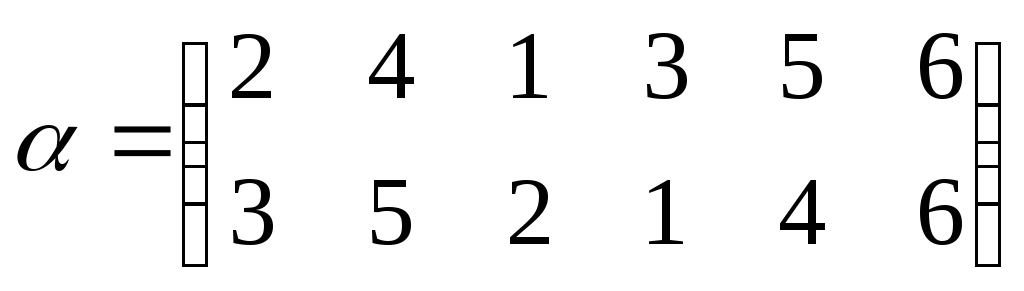
1. 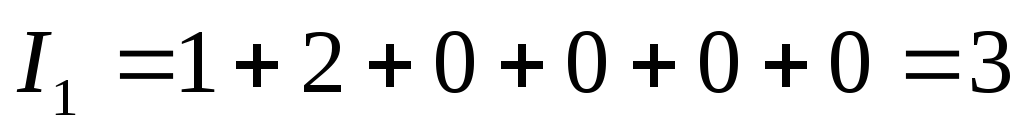
2. 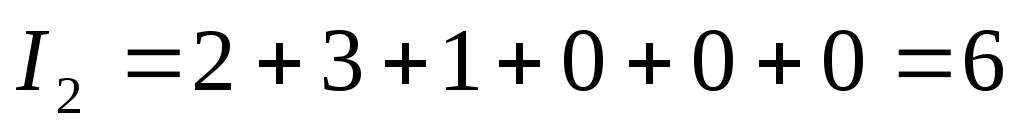
3. 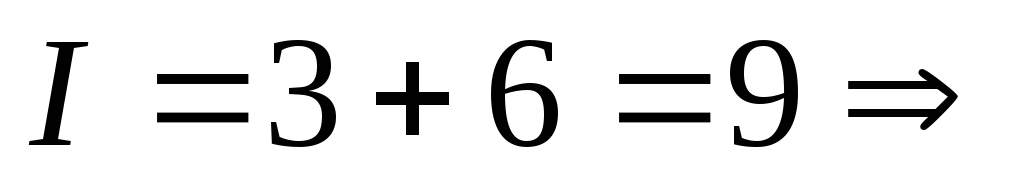 9
– нечетное, следовательно
9
– нечетное, следовательно – нечетная подстановка.
– нечетная подстановка.
Циклом
называется такая подстановка, каждый
элемент 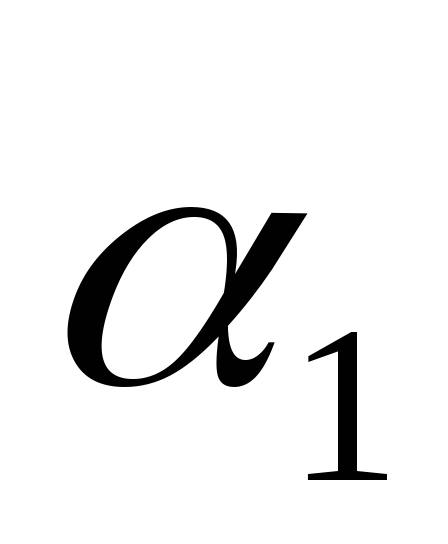 переходит
в элемент
переходит
в элемент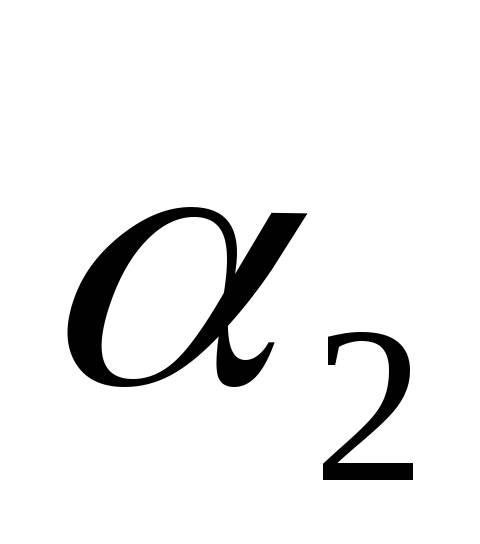 ,
,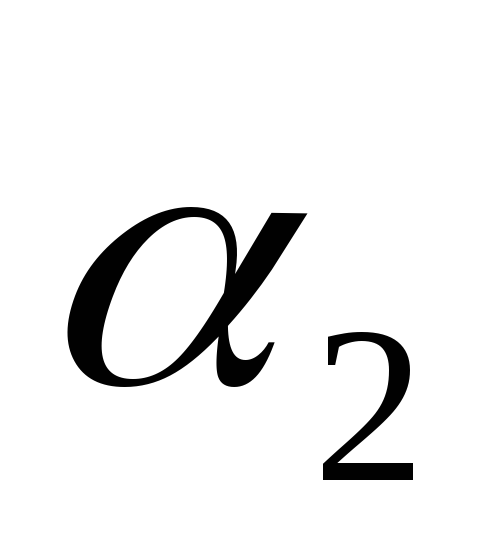 переходит
в элемент
переходит
в элемент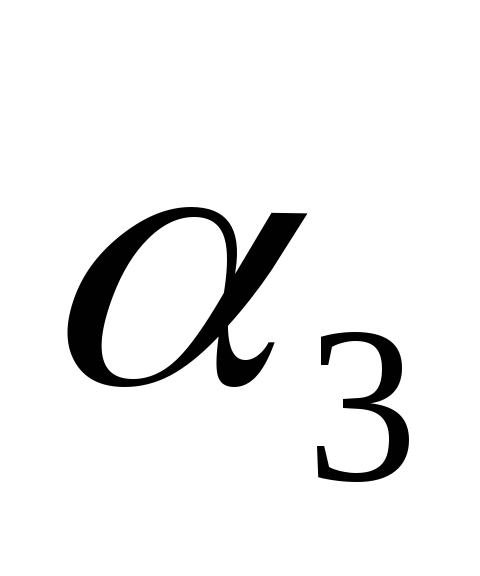 ,
…,
,
…,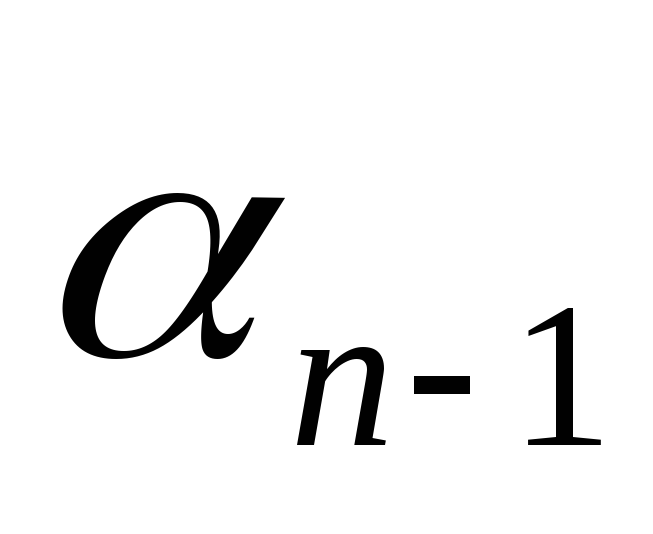 переходит
в элемент
переходит
в элемент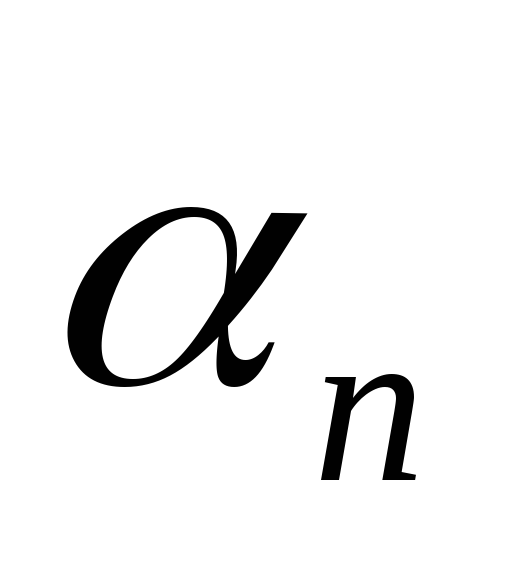 ,
,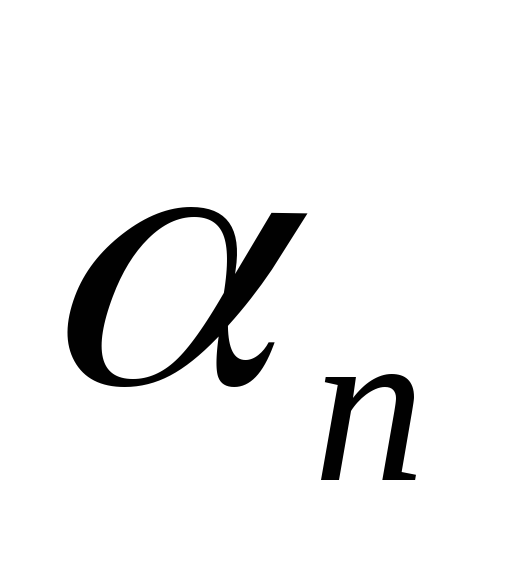 переходит
в элемент
переходит
в элемент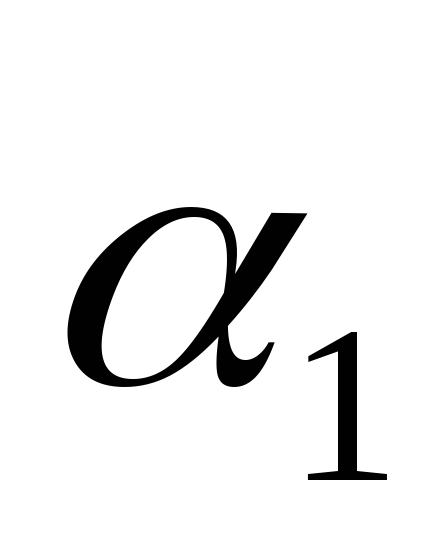
Цикл длины два называется транспозицией.
Любую подстановку можно представить в виде произведения независимых циклов.

Цикл длины один разрешается опускать в разложении подстановки в виде произведений.
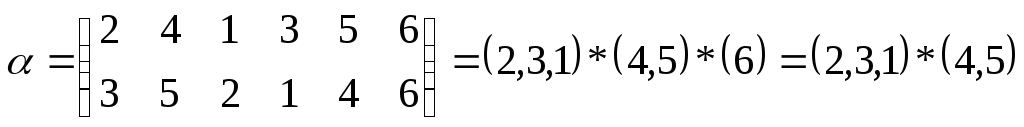
Обозначим m – число независимых циклов: m=3.
Декрементом (d) называется разность n – m, где n – степень подстановки, m – количество независимых циклов. Четность подстановки совпадает с четностью ее декремента:
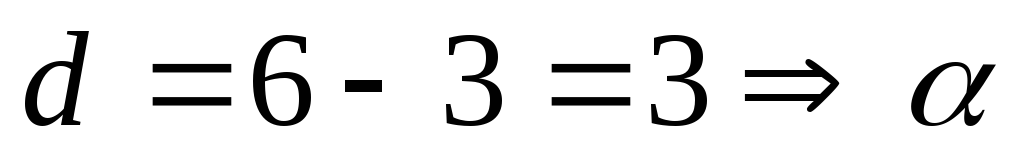 —
нечетная подстановка.
—
нечетная подстановка.
Методика решения уравнений с подстановками:
1. 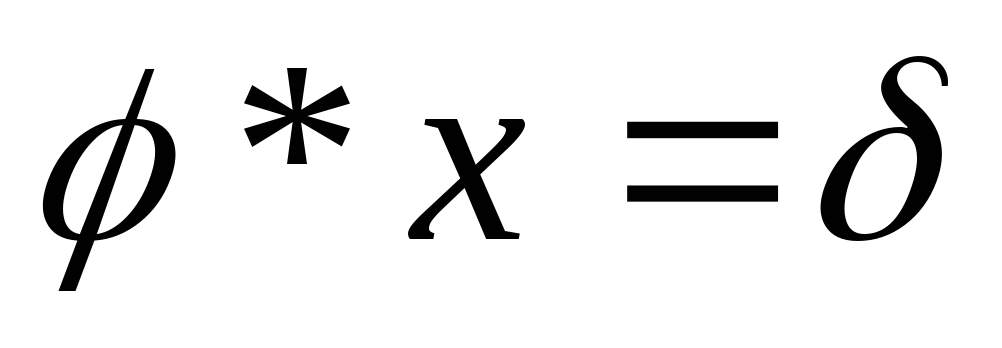 ,
где
,
где — известные подстановки,х – неизвестная подстановка.
— известные подстановки,х – неизвестная подстановка.
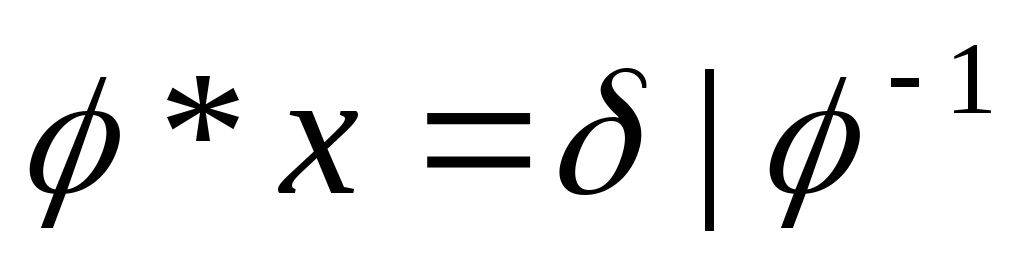
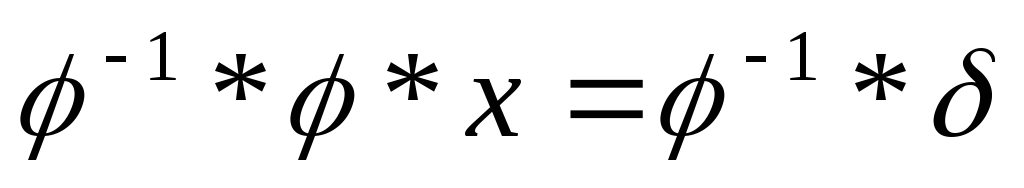
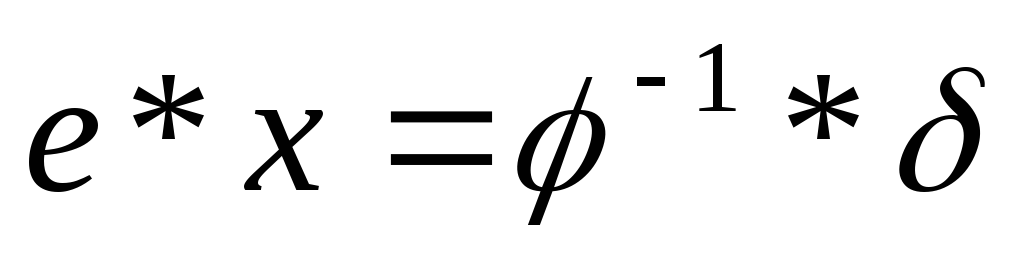
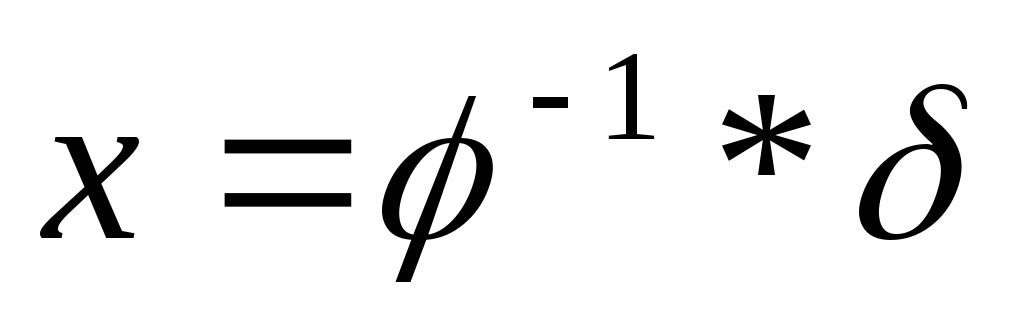
2. 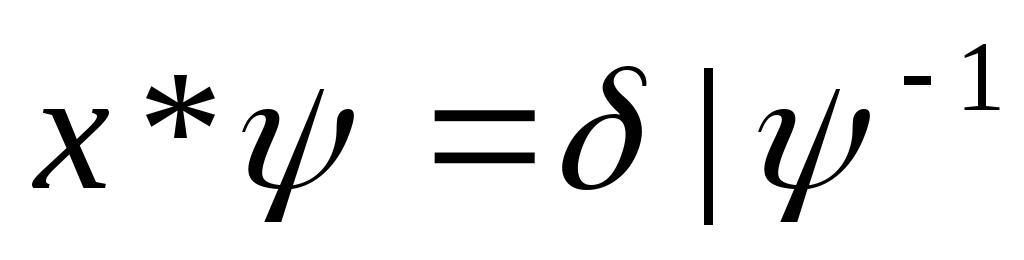 ,
где
,
где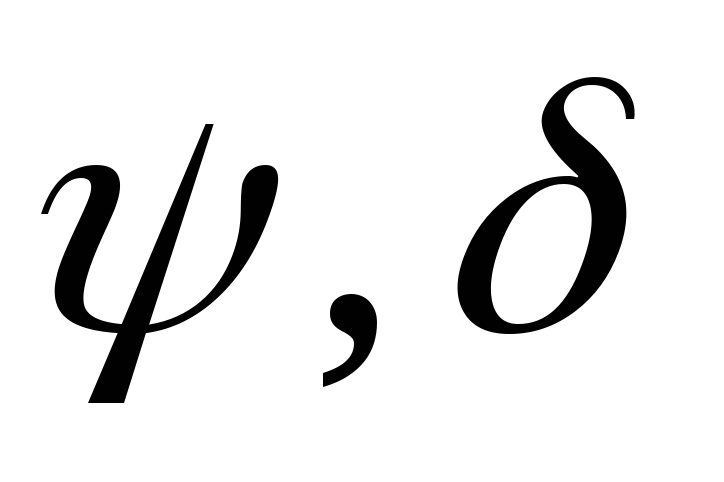 —
известные подстановки,х – неизвестная подстановка
—
известные подстановки,х – неизвестная подстановка
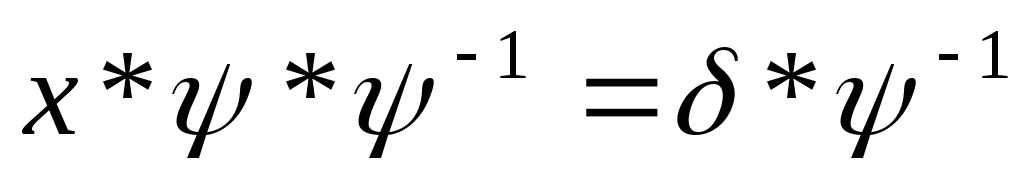
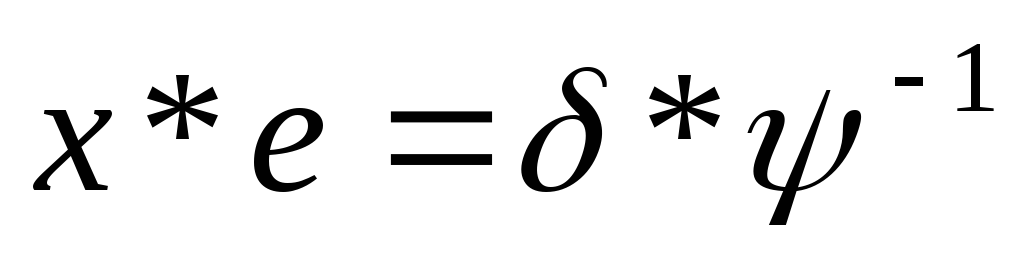
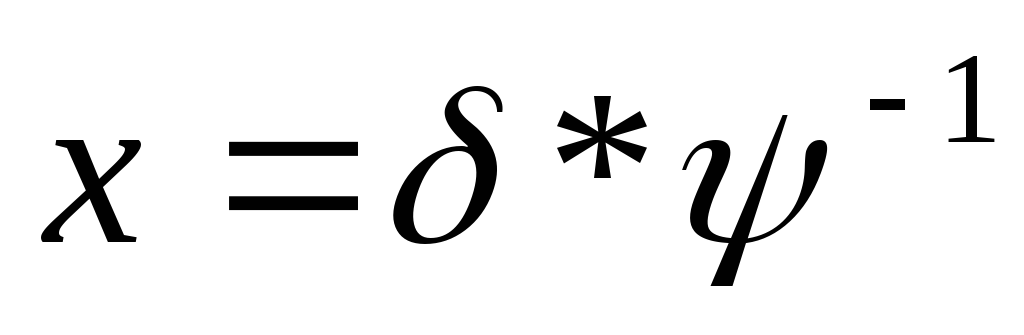
3. 

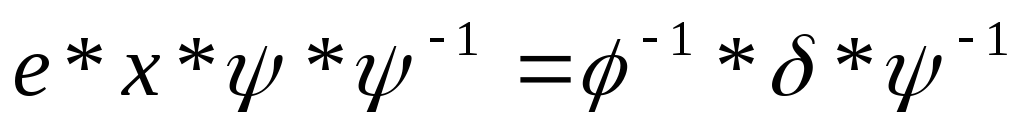
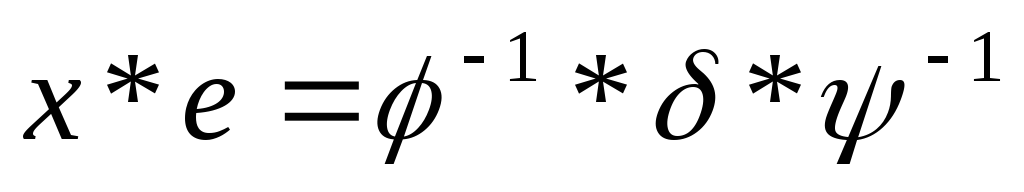

Знак подстановки
Говорят, что в данной строке элементы i и j составляют инверсию, если i > j, но i стоит в этой строке раньше.
(5 3 4 1 2) – число 5 образует 4 инверсии. Общее число инверсий в строке равно 8.
Знак подстановки
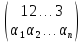
равен (-1)a, где а – число инверсий в строке (α1, α2, …, αn)
Пример 3.
Определить знак подстановки
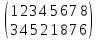
Решение.
Число инверсий в строке (3 4 5 2 1 8 7 6) равно 2+2+2+1+0+2+1=10
так как (-1)10=1, то данная подстановка является четной.
Знак подстановки можно определить и другим способом. Для этого надо разложить подстановку в произведение независимых циклов.
b = (k1-1)+(k2-1)+…+(kl-1)=k1+k2+…+kl-S, (5)
где k1 , k2 , …, kl – длины циклов.
Тогда знак равен (-1)b
Пусть дана подстановка n-й степени и пусть s есть число независимых циклов в её разложении плюс число символом, оставляемых ею на месте. Разность n – s называется декрементом этой подстановки. Декремент равен числу действительно перемещаемых символов, уменьшенному на число независимых циклов, входящих в разложение подстановки и равносилен b в формуле (5).
Замечание. Четность подстановки совпадает с четностью декремента этой подстановки.
Пример 4.
Определите знак подстановки
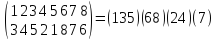
с помощью разложения подстановки в произведение независимых циклов.
Решение.
Данная подстановка раскладывается следующим образом в произведение независимых циклов.
b = 3+2+2+1–4 = 4
(-1)4 = 1
Это четная подстановка.
Умножение подстановок
Определение. Произведением первой подстановки на вторую называют последовательное выполнение двух подстановок n-й степени, приводящее к некоторой вполне определенной третьей подстановке n-й степени.
так, если даны подстановки четвертой степени
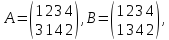
то
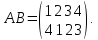
Действительно, при подстановке А символ 1 переходит в 3, но при В символ 3 переходит в 4, поэтому при АВ символ 1 переходит в 4, и т. д.
Можно перемножить лишь подстановки одинаковой степени. Умножение подстановки n-й степени при n ≥ 3некоммутативно. Действительно, для рассмотренных выше подстановок А и В произведение ВА имеет вид
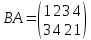
т. е. подстановка ВА отлична от подстановки АВ. Такие примеры можно подобрать для всех n при n ≥ 3, хотя для некоторых пар подстановок закон коммутативности случайно может выполняться.
Умножение подстановок ассоциативно, т. е. можно говорить о произведении любого конечного числа подстановок n-й степени, взятых (ввиду некоммутативности) в определенном порядке. В самом деле, пусть даны подстановки А, В и С и пусть символ i1, 1 ≤ i1 ≤ n, переходит при подстановке А в символ i2, i2 при подстановке В переходит в символ i3, а последний при подстановке С – в символ i4. Тогда при подстановке АВ символ i1 переходит в i3, при подстановке ВС символ i2 переходит в i4, а поэтому как при (АВ)С, так и при А(ВС) символ i1 ,будет переходить в символ i4.
Очевидно, что произведение любой подстановки А на тождественную подстановку Е, а также произведение Е на А, равно А:
АЕ=ЕА=А
Назовем, наконец, обратной для подстановки А такую подстановку А-1 той же степени, что
АА-1 = А-1А = Е
Легко видеть, что обратной подстановкой для подстановки
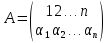
служит подстановка
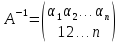
получающаяся из А переменой мест верхней и нижней строк.
Пример 5.
Найти подстановку, обратную данной
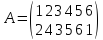
Решение.
Подстановка А-1, обратная подстановке А будет иметь вид
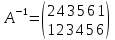
приведем её к каноническому виду.
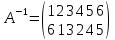
Пример 6.
Найти порядок указанного элемента в группе Sn, n=5
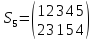
Решение:
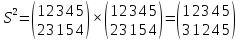
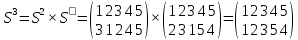
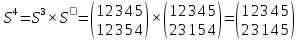
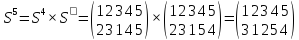
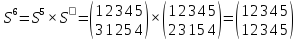
Наконец, получили тождественную подстановку Е
Ответ: 6
3.3. Перестановки, подстановки и их свойства
Рассмотрим теперь частный случай инъективных размещений, когда r = n, по‑прежнему полагая, что n‑X = ={1, 2, …, n}.
В этом случае мы можем считать, что имеет место биекция f: n‑X→ n‑X. Любая такая биективная функция именуется — подстановка. Результат ее применения к множеству n‑X называется перестановкой.
Подстановки обозначаются символами « f», «g», «h» или другими латинскими буквами.
Подстановка задается в виде биективной таблицы, где верхняя строка представляет исходный элемент, а нижняя — полученный из исходного, путем изменения порядка компонент элемента. Например, подстановка

1 2 3
f =
3 2 1
переводит элементы множества {1, 2, 3} так: 1 в 3, 2 в 2, а 3 в 1.
В другом примере, таблицы
 1 2 3
1 2 3 1 2 3
1 2 3
1 2 3 1 2 3
2 2 2 2 2 1 4 5 6
подстановками не являются: в первом и во втором примерах разные элементы переходят в один и тот же элемент, а в третьем появились значения, не принадлежащие X = {1, 2, 3}.
Задача получения множества всех подстановок на n‑X эквивалентна задаче получения всевозможных перестановок местами элементов соответствующего n‑X упорядоченного множества. Так из множества всех функций, полученных при решении задачи о размещениях при n = r = 3 имеем перестановки:
1, 2, 3 , 1, 3, 2, 2, 1, 3, 2, 3, 1, 3, 1, 2, 3, 2, 1.
Далее нам понадобится понятие факториала целого положительного числа n. Так именуется обозначение n!. (Символы «n! « читаются — «n‑факториал»).
Значение n! определяются следующим образом:
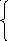
1, если n = 0,
n! =
12n, если n > 0.
Теорема 3.3 Число всех перестановок множества n‑X равно
Ann = n! (3.9)
Доказательство. Все перестановки множества n‑X определяются множеством всех подстановок из n‑X на n‑X. Поэтому полагая в формуле (3.7) n = r, получим
Ann = n(n — 1∙∙∙(n — (n — 1)) = n(n — 1)∙∙∙1 = n!,
что и требовалось.
Поскольку любая подстановка осуществляет биекцию из n‑X на n‑X, то это наводит на мысль, что можно записывать подстановки в виде одной строки, рассматривая соседние элементы, как подстановки из xi→ xi+1 →… . В связи с тем, что множество n‑X конечно, этот процесс должен закончиться на том же элементе, на котором начался, а затем повториться. Поэтому однострочные подстановки называют циклами. Одной подстановке может соответствовать некоторое множество циклов. Поясним это на примере.
 1
2 3 4 5 6 7 8
1
2 3 4 5 6 7 8
Пусть f =
4 5 6 7 8 3 2 1 .
Тогда 1→ 4, 4→ 7, 7→ 2 … и можно разложить подстановку в произведение двух циклов, области которых отмечены квадратными скобками.
f = [1 4 7 2 5 8 ][3 6]
Пусть дана подстановка f = [x1, x2, …, xn]. Пару (xi, xj) (i < j) будем называть инверсией подстановки f, если xi> xj. Подстановка называется четной, если число инверсий в ней четно и нечетной в противном случае.
Так подстановка [1 4 7 2 5 8 ] имеет следующие инверсии: (4 2), (7 2), (7 5), (8 1) и, следовательно, является четной.
Подстановка называется транспозицией, если она представляет цикл длины два.
Понятия инверсии и транспозиции используются, в частности, для упорядочения множеств.
Пусть элементы n‑X расположены в случайном порядке. Составим предикат: p(xi, xj) = 1 тогда и только тогда, когда имеет место инверсия xi, xj. Пусть также функция transp(xi, xj) осуществляет транспозицию элементов xi, xj, то есть переставляет их местами. Тогда алгоритм
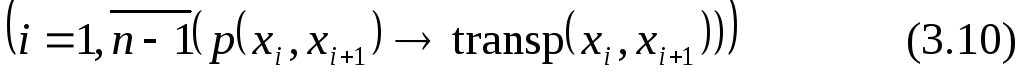
«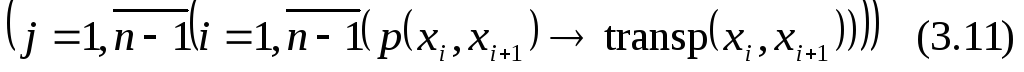 выталкивает»
наибольший элемент в конец списка
элементов множестваn‑X.
Решая эту же задачу повторно, для
элементов множеств (n — j)‑X,
(j = 1, n — 1) можно упорядочить все элементы n‑X по возрастанию. Алгоритм упорядочения
запишется так:
В программировании он
именуется как «пузырьковая сортировка».
выталкивает»
наибольший элемент в конец списка
элементов множестваn‑X.
Решая эту же задачу повторно, для
элементов множеств (n — j)‑X,
(j = 1, n — 1) можно упорядочить все элементы n‑X по возрастанию. Алгоритм упорядочения
запишется так:
В программировании он
именуется как «пузырьковая сортировка».
Множество всех подстановок n‑X множества обозначают Sn.
В алгебре этими же символами обозначают так называемую симметрическую группу. Рассмотрим, с чем связано применение понятия группы к перестановкам.
Произведением подстановок f и g называют подстановку, полученную последовательным применением вначале подстановки f, а затем — g и пишут gf. Например, если
 1
2 3 1 2 3
1
2 3 1 2 3
f = , g = ,
3 2 1 2 3 1
1 2 3
то gf = .
1 3 2
Непосредственно проверяется, что операция произведения подстановок свойствами коммутативности, вообще говоря, не обладает. Для того чтобы убедиться в этом, достаточно рассмотреть в предыдущем примере произведение fg. Применяя последовательно вначале g, а потом f, получим

1 2 3
fg =
2 1 3 .
Докажем, что операция произведения подстановок ассоциативна, то есть (hg)f = h(gf).
Пусть a — произвольная компонента элемента перестановки, которая применением f переходит в b. Запишем это так
a f b .
Пусть также имеем b g c и с h d .
Тогда последовательно применяя, вначале (hg)f, а затем h(gf), получим
a f b, b hg d a (hg)f d;
a gf c, c h d a h(gf) d,
что и требовалось.
Говорят, что множество G образует группу, если каждой паре элементов f, gG поставлен в соответствие элемент h = gf G так, что (hg)f = h(gf) и при этом для любого fG существует обратный элемент f -1G, такой что f -1f = е.
Нетрудно заметить, что в силу свойства биекции, данного по определению, для любой f Snоднозначно определена обратная подстановка, обозначаемая f-1, которая принадлежит G. Для того, чтобы ее получить, достаточно поменять строки в записи f. Если теперь обозначить е — тождественную подстановку, то есть подстановку, переводящую каждый элемент в себя, то становится видно, что для всех f G имеем f -1f = е.
Рассмотрим пример. Пусть



1 2 3 3 1 2 1 2 3
f = , тогда f-1 = и ff -1 =
3 1 2 1 2 3 1 2 3 .
Из перечисленных свойств множества Sn следует, что оно образует группу.
В настоящее время понятие группы широко применяется в различных математических построениях. Ниже мы используем групповые свойства перестановок для исследования структуры соединений.
 ,
таких что
,
таких что  выполняется что значения соответствовать
этим аргументам не будут совпадать
выполняется что значения соответствовать
этим аргументам не будут совпадать