| 1. | Значение функции | 1 вид — рецептивный | лёгкое | 3 Б. | Вычисление значения показательной функции f(x) по значению аргумента. Основание больше единицы. |
| 2. | Определение показательной функции | 1 вид — рецептивный | лёгкое | 1 Б. | Среди функций, заданных формулами, найти показательную функцию. |
| 3. | Свойства показательной функции (возрастание функции) | 1 вид — рецептивный | лёгкое | 1 Б. | Сравние двух чисел, используя свойство возрастания функции. |
| 4. | Значение аргумента | 1 вид — рецептивный | среднее | 1 Б. | По известному значению функции найти значение аргумента. |
| 5. | Преобразования графика показательной функции | 2 вид — интерпретация | среднее | 2 Б. | Построение графиков показательных функций вида y=f(x)+b и y=-f(x) |
| 6. | Область определения функции (показатель степени – дробь) | 2 вид — интерпретация | среднее | 2 Б. | Нахождение области определения показательной функции, показатель степени которой — дробь. |
| 7. | Свойства показательной функции (возрастание и убывание функции) | 2 вид — интерпретация | среднее | Определение по формуле возрастания и убывания показательной функции. | |
| 8. | График показательной функции, область определения и область значений функции | 2 вид — интерпретация | среднее | 3 Б. | Построение графика показательной функции, нахождение области определения, области значений функции и точек пересечения функции с осями координат. |
| 9. | Свойства показательной функции (убывание функции) | 1 вид — рецептивный | среднее | 2 Б. | Сравнение двух чисел, применяя свойство убывания показательной функции. |
| 10. | Вычисление значения функции | 1 вид — рецептивный | среднее | 3 Б. | Вычисление значения показательной функции y по значению аргумента. Основание больше нуля, но меньше единицы. |
| 11. | График показательной функции | 2 вид — интерпретация | среднее | 4 Б. | Выбор графика показательной функции вида y=f(x-a) или y=f(x)+b. |
| 12. | Область определения функции (показатель степени квадратный корень) | 2 вид — интерпретация | сложное | 5 Б. | |
| 13. | Свойства показательной функции (произведение степеней) | 2 вид — интерпретация | сложное | 3 Б. | Вычисление произведения степеней с одинаковыми основаниями, показатели которых — тригонометрические выражения. |
www.yaklass.ru
Показательная функция, её свойства и график
Если
каждому значению  из
некоторого множества действительных чисел поставлено в соответствие по
определённому правилу число
из
некоторого множества действительных чисел поставлено в соответствие по
определённому правилу число ,
то говорят, что на этом множестве определена функция.
,
то говорят, что на этом множестве определена функция.
При
этом 
 –
зависимой переменной или функцией.
–
зависимой переменной или функцией.Множество
значений ,
для которых определены значения
,
для которых определены значения  ,
называют областью определения функции.
,
называют областью определения функции.
Мы с вами уже говорили, что степень определена для любого положительного основания и любого действительного показателя.
Давайте вспомним основные свойства степени.
Пусть
 ,
,
 ,
,
 ,
,
 и
и
 —
любые действительные числа. Тогда верны следующие равенства:
—
любые действительные числа. Тогда верны следующие равенства:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ,
если
,
если  ,
,
 ;
;
 ,
если
,
если  ,
,
 ;
;
 ,
если
,
если  ,
,
 .
.
Понятие
степени с действительным показателем позволяет нам рассматривать функции вида  .
.
Итак,
пусть основание степени  .
Тогда каждому
.
Тогда каждому  соответствует
одно определённое число
соответствует
одно определённое число  .
То есть тем самым задана функция
.
То есть тем самым задана функция  .
.
В
случае если  ,
то функция
,
то функция  принимает
одно и то же значение
принимает
одно и то же значение  при
всех
при
всех  .
Этот случай нас интересовать не будет.
.
Этот случай нас интересовать не будет.
Запомните! Показательной
функцией называется функция вида  ,
где
,
где  —
заданное число,
—
заданное число,  ,
,
 .
.
Например,
функции  ‚
‚
 ‚
‚
 ,
,
 и
так далее – это показательные функции.
и
так далее – это показательные функции.
То
есть имеем дело с функциями вида  ,
где а — заданное положительное число, х — переменная. Такие
функции называют показательными. Это название объясняется тем, что
аргументом показательной функции является показатель степени, а основанием
степени — заданное число.
,
где а — заданное положительное число, х — переменная. Такие
функции называют показательными. Это название объясняется тем, что
аргументом показательной функции является показатель степени, а основанием
степени — заданное число.
Как же будет выглядеть график такой функции?
Итак,
давайте построим график функции  ,
например, при а = 2. Для этого, как обычно, найдём сначала координаты
некоторых точек графика и заполним таблицу значений функции.
,
например, при а = 2. Для этого, как обычно, найдём сначала координаты
некоторых точек графика и заполним таблицу значений функции.

Отметим эти точки на координатной плоскости и соединим.

Получившаяся
кривая является графиком функции  ,
аргумент которой может принимать любые действительные значения. Отметим, что
график функции
,
аргумент которой может принимать любые действительные значения. Отметим, что
график функции  проходит
через точку с координатами
проходит
через точку с координатами  ,
и расположен выше оси
,
и расположен выше оси  .
Если
.
Если  и
и
 увеличивается,
то график быстро приближается к оси
увеличивается,
то график быстро приближается к оси  ,
но не пересекает её. Таким образом, ось
,
но не пересекает её. Таким образом, ось  является
горизонтальной асимптотой графика функции
является
горизонтальной асимптотой графика функции  .
.
Если
 и
и
 увеличивается,
то график быстро поднимается вверх. Такой же вид имеет график любой функции
увеличивается,
то график быстро поднимается вверх. Такой же вид имеет график любой функции  ,
если
,
если  .
.
Если
же основание степени  ,
а точнее
,
а точнее  ,
то график функции будет симметричен относительно оси ординат.
,
то график функции будет симметричен относительно оси ординат.
Например,
нам нужно построить график функции  .
Поскольку
.
Поскольку  ,
то график функции
,
то график функции  мы
можем получить из графика функции
мы
можем получить из графика функции  с
помощью симметрии относительно оси ординат.
с
помощью симметрии относительно оси ординат.

Заметим,
что график этой функции также проходит через точку с координатами (0;1) и
расположен выше оси  .
Если
.
Если  и
и
 увеличивается,
то график быстро приближается к оси
увеличивается,
то график быстро приближается к оси  ,
не пересекает её. Таким образом, ось
,
не пересекает её. Таким образом, ось  является
горизонтальной асимптотой графика функции
является
горизонтальной асимптотой графика функции  .
Если
.
Если  и
и
 увеличивается,
то график быстро поднимается вверх. Такой же вид имеет график любой функции и
увеличивается,
то график быстро поднимается вверх. Такой же вид имеет график любой функции и ,
если
,
если  .
.
Рассматривая
эти графики, мы можем отметить несколько свойств, общих для всех функций вида  .
.
1.
Область определения показательной функции — множество  всех
действительных чисел.
всех
действительных чисел.
Это
свойство следует из того, что  ,
где
,
где  ,
определена для всех действительных
,
определена для всех действительных  .
.
2. Множество значений показательной функции — множество всех положительных чисел.
3.
Показательная функция  является
возрастающей на множестве всех действительных чисел, если
является
возрастающей на множестве всех действительных чисел, если  ,
и убывающей, если
,
и убывающей, если  .
.
А теперь давайте приступим к практической части нашего урока.
Задание.
Решите уравнение  .
.
Решение.
Введём вспомогательную переменную  .
.

Ответ:
 .
.
videouroki.net
| 1. | Значение функции | 1 вид — рецептивный | лёгкое | 3 Б. | Вычисление значения показательной функции f(x) по значению аргумента. Основание больше единицы. |
| 2. | Определение показательной функции | 1 вид — рецептивный | лёгкое | 1 Б. | Среди функций, заданных формулами, найти показательную функцию. |
| 3. | Свойства показательной функции (возрастание функции) | 1 вид — рецептивный | лёгкое | 1 Б. | Сравние двух чисел с использованием свойства возрастания функции. |
| 4. | Умножение степеней с одинаковым основанием | 1 вид — рецептивный | лёгкое | 1 Б. | Применение свойства умножения степеней с одинаковыми основаниями. |
| 5. | Деление степеней с одинаковыми основаниями | 1 вид — рецептивный | лёгкое | 2 Б. | Применение свойства «деление рациональных степеней с одинаковыми основаниями». |
| 6. | Возведение степени в степень | 1 вид — рецептивный | лёгкое | 2 Б. | Применение свойства: «Возведение рациональной степени в степень». |
| 7. | Значение аргумента | 1 вид — рецептивный | среднее | 1 Б. | По известному значению функции найти значение аргумента. |
| 8. | Преобразования графика показательной функции | 2 вид — интерпретация | среднее | 2 Б. | Построение графиков показательных функций вида y = f(x) + b и y = -f(x). |
| 9. | Область определения функции (показатель степени — дробь) | 2 вид — интерпретация | среднее | 2 Б. | Нахождение области определения показательной функции, показатель степени которой — дробь. |
| 10. | Свойства показательной функции (возрастание и убывание функции) | 2 вид — интерпретация | среднее | 2 Б. | Определение по формуле возрастания и убывания показательной функции. |
| 11. | Свойства степени с рациональным показателем (деление) | 2 вид — интерпретация | среднее | 3 Б. | Найти значение выражения, использовав свойства степени с рациональным показателем. |
| 12. | Свойства степени с рациональным показателем (умножение) | 2 вид — интерпретация | среднее | 5 Б. | Найти значение выражения, использовав свойства степени с рациональным показателем. |
| 13. | График показательной функции, область определения и область значений функции | 2 вид — интерпретация | среднее | 3 Б. | Построение графика показательной функции, нахождение области определения, области значений функции и точек пересечения функции с осями координат. |
| 14. | Решение уравнения графически | 2 вид — интерпретация | сложное | 4 Б. | Решение уравнения графически. В одной части уравнения — квадратичная, в другой — показательная функции. |
| 15. | Свойства показательной функции (произведение степеней) | 2 вид — интерпретация | сложное | 3 Б. | Вычисление произведения степеней с одинаковыми основаниями, показатели которых — тригонометрические выражения. |
www.yaklass.ru
Показательная функция, 11-й класс
Некоторые наиболее часто встречающиеся виды функций, прежде всего показательные, открывают доступ ко многим исследованиям.
Л. Эйлер
Цели урока
Ход урока
- Объявление темы урока, его целей, вводная беседа (5-6 минут).
Ребята, занимаем свои места, приступаем к работе.
Вы знаете, недавно мне в руки попала сенсационная секретная информация. Это был репортаж о запуске космического корабля, не вышедший, к сожалению, в эфир. Послушайте запись этого репортажа.
Звучит магнитная запись (приложение 1).
“22 ноября 2003 года в 10 часов 20 минут по московскому времени с космодрома “Плесецк” стартовал космический корабль “Русь–2”. Цель экспедиции: установить причины отсутствия связи с космической станцией “Русь–1”, работающей на планете Кармен. После стыковки космонавты обнаружили погибший экипаж станции. Капитан корабля, летчик-космонавт Игнатьев решил исследовать биосферу планеты. Исследования показали, что в верхнем слое грунта наблюдается необычайно быстрый рост числа колоний живых организмов (бактерий), что поставило под угрозу жизнь экипажа и грозит катастрофой планете. Как нормализовать ситуацию и предотвратить катастрофу?”
Итак, первая экспедиция погибла от неизвестных бактерий.
Ученые установили, что рост числа бактерий происходил по такой зависимости:
, где – время размножения, – число колоний бактерий (приложение 2,сл №1).
Подсчитайте, как изменится число колоний бактерий за 2 секунды? (увеличится до ). За 3 секунды? (увеличится до ) (слайд №2). Т.е. каждому моменту времени соответствует свое определенное число бактерий.
Я предлагаю вам исследовать эту зависимость. А к проблеме экспедиции мы вернемся в конце урока.
Зависимость между двумя переменными такого типа была замечена не только в процессе роста числа микроорганизмов, но и, например, в спорте – зависимость длины прыжка спортсмена с трамплина от начальной скорости полета, в медицине – способность почек выводить из крови радиоактивные изотопы, в предвыборных кампаниях. В рамках предвыборной кампании каждый кандидат выбирает себе в помощники двух доверенных лиц (слайд №3). Каждый из доверенных лиц в течение следующего дня, проводя агитационную работу, привлекает в команду этого кандидата еще по одному человеку. На следующий день агитационная работа проводится уже командой в 4 человека. Что произойдет с командой кандидата, если эту работу продолжить по той же схеме? Если эту работу продолжить, то команда кандидата будет очень быстро расти.
Для данного вида зависимостей ученые составили следующую математическую модель: (слайд №4).
Что представляет из себя правая часть формулы? (Степень).
Чему равно основание степени? (Основание равно ).
А что такое х? (показатель степени)
Поэтому эту функцию назвали.… Как вы думаете, как? (Показательной функцией) А почему?
Именно потому, что аргумент находится в показателе степени, она носит название показательной функции.
Попробуйте сформулировать тему урока. (“Показательная функция”)
Эта функция обладает одним замечательным свойством: скорость роста пропорциональна значению самой функции. Она как костер, который, чем больше разгорается, тем больше в него надо подкладывать дров.
Изучением этой функции мы и займемся сегодня на уроке.
Что значит “Изучить функцию”? (Дать определение, сформулировать свойства и построить график)
Следовательно, целями урока являются…(сформулировать определение, рассмотреть свойства и построить график показательной функции). А поможет нам в достижении целей – составление опорного конспекта (см. приложение 3), который лежит перед вами на столах (слайд №5).
Запишите тему урока в опорном конспекте.
Прежде чем говорить о показательной функции и ее свойствах, вспомните план исследования любой функции.
План исследования функции.
- Область определения функции.
- Четность (нечетность).
- Периодичность.
- Точки пересечения с осями координат, промежутки знакопостоянства.
- Производная и критические точки.
- Монотонность и экстремумы.
- График функции.
- Множество значений функции (слайд №6).
Сегодня на уроке мы рассмотрим только некоторые из свойств.
Посмотрите на экран, здесь изображены графики двух функций, для каждой из которых необходимо найти:
а) область определения функции;
б) множество значений функции;
в) точки пересечения графиков с осями координат;
г) промежутки монотонности;
д) наибольшее и наименьшее значения функции.
Ребята, работаем с графиком функции (слайд №7).
а) ; б) ; в) ;
г) возрастает на , убывает на и ; д) .
Рассматриваем график функции :
а) ; б) ; в) ;
г) возрастает на ; д) и нет.
- Изучение нового материала (18 – 20 минут).
Ребята, вернемся к изучаемой нами сегодня функции (слайд №8).
Какое значение может принимать основание ? ( и ).
Найдите значение (–7)1/2 (не имеет смысла), значит, договариваемся, что берем только положительное, т.е. .
А если ? ()
А ? (не имеет смысла.), т.е. .
Если взять , то…(получаем всегда 1). Рассматривать это значение в данном случае не будем, т.е. .
Итак, при каких же значениях будем рассматривать функцию? ( и ).
Теперь попробуйте сами сформулировать определение показательной функции (Функция вида , где , называется показательной функцией с основанием ) (слайд №9).
Учитель сам проговаривает еще раз.
Запишите определение в опорном конспекте.
Приведите примеры показательных функций: (слайд №10).
Изучили вы много функций:
Квадратичную и линейную,
Степенную и тригонометрические,
А теперь слушайте внимательно:
И тогда признаете обязательно,
Что одна из важнейших – показательная!
Т.к. по определению показательной функции, основание и , то, каким двум промежуткам должно принадлежать значение? ( или .)(слайд №11)
Выбрав из каждого промежутка, например, (из первого промежутка) и (из второго), рассмотрим две показательные функции и .
Построим графики этих функций.
Что нужно сделать для того, чтобы построить график функции?
Найти значения функций в некоторых точках.
Верно, найдем значения функций при .
Первый вариант делает расчеты для функции , а второй вариант – для , а потом проверим.
Зафиксируйте все найденные значения в опорных конспектах. В это время на экране появляются таблицы (слайд №12).
Давайте построим графики этих функций, вы выполняете это задание у себя в конспектах (первый вариант строит график функции , второй вариант – график функции ), а по одному представителю от каждого варианта предлагаю выйти к доске и продемонстрировать построение графиков.
Т.к. (по определению), то функция принимает только положительные значения.
Итак, мы с вами сформулировали определение показательной функции, построили график, исходя из графика, сформулируем свойства функции, и все наши рассуждения зафиксируем в таблице (слайд №13).
| 1. Область определения |
||
| 2. Множество значений |
||
| 3. Пересечение с осью OY |
при x = 0, y = 1 |
при x = 0, y = 1 |
| 4. Монотонность | Функция убывает на всей числовой прямой, т.е. если , то |
Функция возрастает на всей числовой прямой, т.е. если , то |
| 5. Наибольшее и наименьшее значения функции |
Не существует |
Не существует |
- Какова область определения функции? (Вся числовая прямая, т.е. )
- Найдите множество значений функции (все положительные числа, т.е. ).
- Назовите точки пересечения графика с осями координат(с осью Ох точек пересечения нет, с осью Оу точка, т.е. при х=0, у=1).
- Найдите промежутки монотонности функции (Функция убывает на всей числовой прямой, т.е. большему значению аргумента из ее области определения соответствует меньшее значение функции, или если , то . Функция возрастает на всей числовой прямой, т.е. если , то ).
- Назовите наибольшее и наименьшее значения функции (нет).
Значит, если основание , то показательная функция монотонно убывает на всей области определения, а, если , то монотонно возрастает.
Хоть нет названья линии ее,
И нет, как у параболы ветвей,
Но – положительна! И это всем вам видно
И жмется к оси Ох одним концом безобидно,
Вторым концом стремится ввысь!
А, ну-ка, степенная, попробуй, доберись!
Ребята, посмотрите на экран, здесь схематически изображен график показательной функции. (Характерным свойством является то, что график показательной функции с любым основанием проходит через точку (0; 1)) (слайд №14).
Есть точка нуль и единица.
И хоть график функции быстро вверх (вниз) стремится,
В любом он случае через эту точку проходит –
Она все графики в пучок единый сводит!
А свойство монотонности показательной функции используется при решении многих задач.
Например: 1) Сравнить числа, и .
Рассмотрим функцию , т.к. основание , а , то она монотонно убывает, сравниваем показатели: – 2 < 2, значит, .
2) Сравнить числа и .
Т.к. функция возрастает (основание больше единицы) и –2 < 2, то < .
Я предлагаю вам выполнить несколько заданий, чтобы проверить, как вы усвоили новый материал.
- Обучающая самостоятельная работа (4 минуты).
На листочках заранее написаны задания самостоятельной работы (см. приложение 4), необходимо только указать ответ, время для работы 4 минуты.
По истечении указанного времени:
Ребята, обменяйтесь листочками, проверьте правильность выполнения работы с помощью слайда, учитывая критерии, оцените работу товарища (правильные ответы проецируются на экран) (слайд №15).
После взаимопроверки, ученики возвращают свои работы. Кто получил сегодня “5”, “4”, “3”? Итак, “5” получили… человек, “4” – …, “3” – … Молодцы!!!
Я проанализирую ваши решения, и на следующем уроке объявлю вам результаты.
Что нового вы сегодня узнали на уроке? (дали определение, сформулировали свойства и построили график показательной функции.)
Достигли ли мы поставленных целей (слайд №15)?
Ребята, вернемс
urok.1sept.ru
Конспект урока 10 класс Показательная функция, ее свойства и график
Конспект урока по алгебре и началам математического анализа в 10 классе.
Широковой В.Г.
Тема: “Показательная функция, ее свойства и график”
Цель урока:
Ученик должен знать:
-Понятие показательной функции
-Свойства степени
-Область определения, множество значений показательной функции
-Алгоритм решения уравнений и строить график.
Ученик должен уметь:
-Уметь построить график функции
— Уметь решать уравнения.
Задачи урока:
Образовательные: увеличить знания по теме “Показательная функция, ее свойства и график”. Формировать умение использовать знания полученные ранее.
Развивающие: формировать устойчивость внимания. Совершенствовать вычислительные навыки и словестно-логическое мышление у учащихся. Развивать память.
Воспитательные: воспитывать интерес к данному предмету.
Тип урока: комбинированный.
Структура урока.
Организационный момент. (1мин.)
Проверка выполнения домашнего задания. (9мин.)
* Мини-тест
3. Объяснение нового материала. (15мин.)
4. Закрепление изученного материала. (15 мин.)
5. Подведение итогов урока. Выставление оценок и отметок. (4 мин).
6. Домашнее задание
Ход урока.
Организационный момент. (1мин.)
Проверка выполнения домашнего задания. (9мин.)
1 вариант.
Решите уравнение:

6 b) -6 c) -14 d) 14
Решите уравнение:

20 b) -20 c) -10 d) 10
Найти функцию, обратную к функции

 b)
b)  c)
c)  d)
d) 
Сравните числа
 и
и 
а)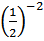 =
=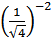 b)
b) 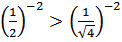 c)
c) 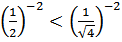
2 вариант.
Решите уравнение:

6 b) -6 c) -8 d) 8
Решите уравнение:

11 b) -11 c) -4 d) 4
Найти функцию, обратную к функции

 b)
b)  c)
c)  d)
d) 
Сравните числа
 и
и 
а)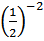 =
=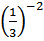 b)
b) 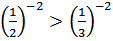 c)
c) 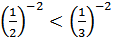
3. Объяснение нового материала. (15 мин.)
Напомним основные свойства степени






 , если
, если 
 , если
, если 
 , если
, если 
Показательной функцией называется функция вида 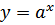 , где
, где 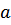 – заданное число,
– заданное число, 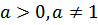 .
.
Примеры: 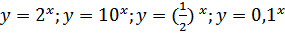
Свойства показательной функции.
Область определения показательной функции – множество R всех действительных чисел (
 )
)Множество значений показательной функций множество всех положительных чисел.
Показательная функция
 является возрастающей на множестве всех действительных чисел, если
является возрастающей на множестве всех действительных чисел, если  , и убывающей, если
, и убывающей, если  .
.
Это следует из свойств степени (8) и (9).
Пример 1. Построить графики функции 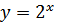 и
и 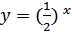
1* 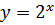
X
-2
-1
0
1
2
Y


1
2
4
График функции проходит через точку (0,1) и расположен выше оси 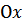 .
.
Если 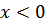 и
и 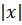 увеличивается, то график функции быстро приближается у оси
увеличивается, то график функции быстро приближается у оси 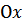 .
.
Если 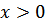 и
и 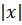 увеличивается, то график поднимается вверх.
увеличивается, то график поднимается вверх.
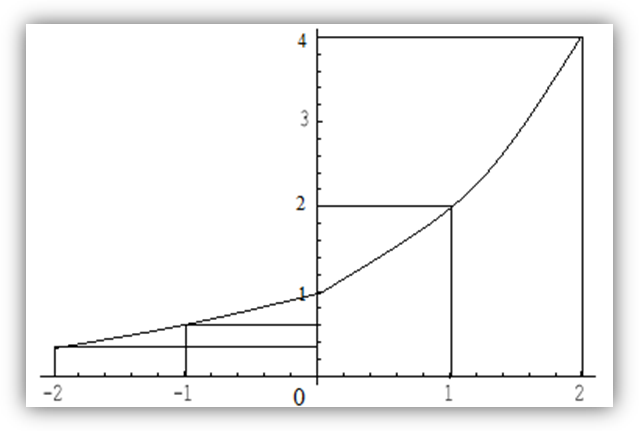
2* 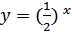
X
-2
-1
0
1
2
Y
4
2
1


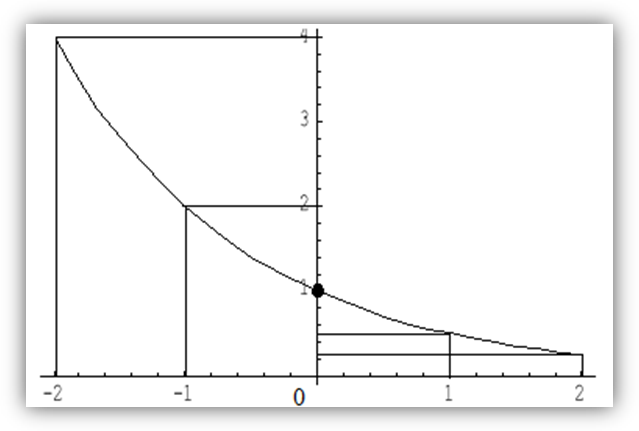
График функции проходит через точку (0,1) и расположен выше оси 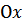 .
.
Если 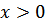 и
и 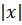 увеличивается, то график функции быстро приближается у оси
увеличивается, то график функции быстро приближается у оси 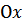 .
.
Если 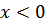 и
и 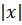 увеличивается, то график поднимается вверх.
увеличивается, то график поднимается вверх.
Пример 2. Решить уравнение 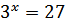 .
.
По свойству (2) показательной функции данное уравнение имеет корень, так как 27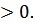
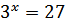
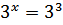
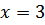
Ответ: 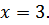 Других корней нет, так как функция
Других корней нет, так как функция 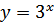 возрастает на всей числовой прямой.
возрастает на всей числовой прямой.
Закрепление изученного материала. (15 мин.)
№ 195 с. 75 (Устно) Используя свойство возрастания или убывания показательной функции, сравнить числа.
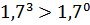
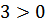
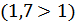
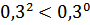
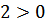
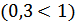
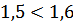
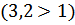
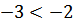
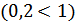
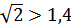
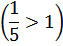
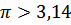
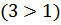
№ 197 с.76. Найти координаты точки пересечения графиков функции:
 и
и 
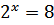
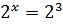
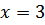
Ответ: (3;8) точка пересечения графиков функции
 и
и 
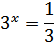
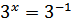
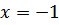
Ответ: (-1; ) точка пересечения графиков функции
) точка пересечения графиков функции
 и
и 
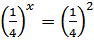
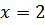
Ответ: (2; ) точка пересечения графиков функции
) точка пересечения графиков функции
 и
и 
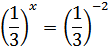
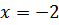
Ответ: (-2;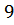 ) точка пересечения графиков функции.
) точка пересечения графиков функции.
№ 199 с.76 (Устно). Выяснить, является ли возрастающей или убывающей функция.
 значит, данная функция является возрастающей.
значит, данная функция является возрастающей. , значит данная функция является возрастающей.
, значит данная функция является возрастающей. значит, данная функция является возрастающей.
значит, данная функция является возрастающей.
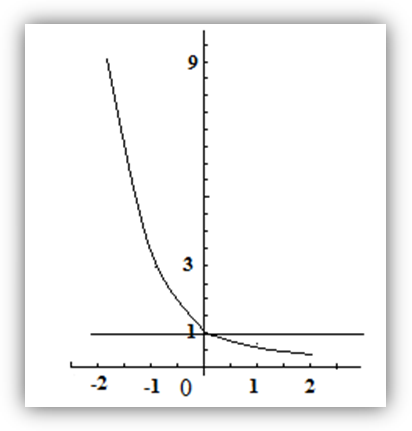
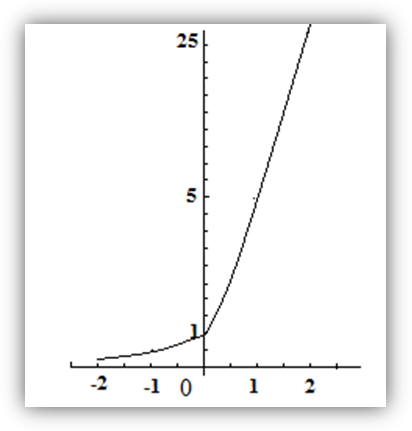
№200 с.76 (1,3) Решить графически неравенство.
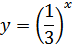
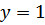
X
-2
-1
0
1
2
Y
9
3
1


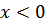
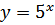
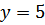
X
-2
-1
0
1
2
Y


1
5
25
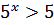
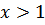
Подведение итогов урока. Выставление оценок и отметок (4 мин).
— Что такое показательная функция?
Ответ: Показательной функцией называется функция вида 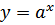 , где
, где 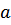 – заданное число,
– заданное число, 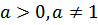 .
.
— Свойства показательной функции
Ответ: а) ООФ множество R (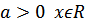 )
)
б) Множество значений показательной функции – множество всех положительных чисел
в) Показательная функция 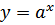 является возрастающей на множестве всех действительных чисел, если
является возрастающей на множестве всех действительных чисел, если 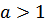 , и убывающей, если
, и убывающей, если 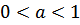 .
.
— Примеры показательной функции.
Ответ: (примерный) 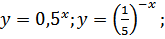
Задание на дом №192, №196, №200(2,4)
Литература: Ш.А. Алимов, Ю.М. Колягин 10-11 класс Алгебра и начала математического анализа.
infourok.ru
Показательная функция, ее свойства и график
Показательной функцией называется функция вида  , где
, где 
На этом интерактивном чертеже вы можете исследовать зависимость свойств функции  от значение
от значение  . Подвигайте ползунок и посмотрите, как меняются свойства показательной функции:
. Подвигайте ползунок и посмотрите, как меняются свойства показательной функции:
Обратите внимание:
- при
 функция не определена;
функция не определена; - при
 получаем функцию
получаем функцию  , определенную при
, определенную при  ;
; - при
 получаем функцию
получаем функцию  , определенную при
, определенную при  ;
; - график показательной функции всегда проходит через точку с координатами

Итак, при  график функции
график функции  имеет такой вид:
имеет такой вид:

При  график функции
график функции  выглядит так:
выглядит так:

Свойства показательной функции:
1.Область определения:  — нет ограничений на ОДЗ.
— нет ограничений на ОДЗ.
2. Множество значений:  — принимает только положительные значения.
— принимает только положительные значения.
3. При  функция
функция  убывает, то есть большему значению аргумента соответствует меньшее значение функции:
убывает, то есть большему значению аргумента соответствует меньшее значение функции:
если  , то
, то  .
.
4. При  функция
функция  возрастает, то есть большему значению аргумента соответствует большее значение функции:
возрастает, то есть большему значению аргумента соответствует большее значение функции:
если  , то
, то  .
.
5. График показательной функции всегда проходит через точку с координатами 
6. Поведение на бесконечности:
При  :
:
 при
при 
При  :
:
 при
при 
То есть график функции  имеет горизонтальную асимптоту
имеет горизонтальную асимптоту  .
.
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Показательная функция
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Тип урока: урок изучения нового материала.
Цель урока:обеспечить усвоение учащимися знаний о показательной функции, её свойствах, создать условия для развития умений получать знания посредством проведения исследовательской деятельности и анализа ситуации.
Развивающие задачи:
- развитие памяти учащихся;
- развитие умений сравнивать, обобщать, правильно формулировать задачи и излагать мысли;
- развитие логического мышления, внимания и умения работать в проблемной ситуации.
Воспитательные задачи:
- воспитание умения работать в коллективе, взаимопомощи, культуры общения.
- развитие познавательного интереса учащихся;
- развитие любознательности учащихся;
- развитие умений преодолевать трудности при решении математических задач; воспитание таких качеств характера, как настойчивость в достижении цели;
Средства обучения:компьютер, классная доска, слайдовая презентация, интерактивная доска, учебник «Алгебра и начала анализа10-11» под редакцией А.Г.Мордковича, чертёжные инструменты, карточки.
План урока
- Орг. момент 1 мин
- Повторение пройденного материала в форме игры 3-4мин
- Новая тема 13-15мин
- Закрепление изученного материала. 21-23мин
- Подведение итогов и домашнее задание 2 мин
Ход урока
1. Орг. момент.
2. Игра «Самый умный на уроке»
Эта игра проводится с целью актуализации знаний учащихся на уроке изучения нового материала по теме «Показательная функция и ее график».
Учащемуся предлагается в течение 60 секунд отвечать на вопросы. (листочки розданы заранее)
Звание «самого умного на уроке» присваивается тому, кто ответил на большее количество вопросов. (итог в конце урока — можно приготовить мини-призы)
Вопросы:
- Независимая переменная (х)
- Наглядный способ задания функции (графический)
- График четной функции симметричен относительно чего (Оу)
- График квадратичной функции называется (парабола)
- Что обозначают буквой D (область определения)
- Способ задания функции с помощью формулы (аналитический)
- График какой функции — прямая (линейной)
- О какой функции речь? Чем больше х, тем больше у. (возрастающая)
- Свойство функции f(-x) = f(x ) (четность)
- Множество значений, принимаемых независимой переменной (область определения)
- Что обозначают буквой Е ? (область значений)
- График нечетной функции симметричен относительно чего (начала координат)
- О чем речь? Чем меньше х, тем больше у. (убывание)
- Множество целых чисел — какая буква? (Z)
- Точки пересечения графики функции с осью Ох (нули функции)
- Множество действительных чисел — какая буква? (R)
- Свойство функции f(-x) = — f(x) (нечетность)
Проверка ответов слайд№3
3. Изучение новой темы.
а) определение
Вам предстоит сегодня много рассуждать, делать выводы, спорить.
В жизни мы часто сталкиваемся с зависимостями между величин. Оценка по контрольной работе зависит от количества и правильности выполненных заданий, стоимость покупки от количества купленного товара и цен. Одни зависимости носят случайный характер, другие постоянны.
Давайте рассмотрим следующие законы. Слайд 4-6
Рост древесины происходит по закону A=A0*akt
A — изменение количества древесины во времени;
A0 — начальное количество древесины;
t — время, к, а — некоторые постоянные.
Давление воздуха убывает с высотой по закону: P=P0*a-kh
P — давление на высоте h,
P0 — давление на уровне моря,
а — некоторая постоянная.
Изменение количества бактерий N=5t
N-число колоний бактерий в момент времени t
t- время размножения
— Что общее объединяет эти процессы? Слайд №7 — схожесть вида формулы, задающей закон у=с·акх
Тема нашего урока показательная функция. Слайд №8 (запись в тетрадях)
— Положим в этих формулах с=1,к=1, какую функцию получим? — у=ах
- постройте график Слайд№9
- что это за функция?
б) практическая работа. Слайд№10
— построить графики функций на отрезк е[-2;3] с шагом 1.
- 1 вариант у=2х,
- 2 вариант у=(1/2)х
Проверим правильность ваших построений Слайд №11
Давайте сравним графики функций у=2х , у=(3/2)х , у=(5/2)х
— Какие выводы мы можем сделать? — Чем больше основание ,тем более пологий график.
А теперь сравним графики функций у=(1/2)х , у=(4/6)х, у=(1/3)х и сделаем соответствующие выводы. — Чем больше основание, тем более пологий график.
Такие функции называются показательными.
И сегодня на уроке, мы должны дать определение показательной функции, рассмотреть некоторые свойства и научится применять эти свойства при выполнении заданий, определенного вида.
Итак, попробуйте сформулировать определение показательной функции.
(учащиеся отвечают, учитель, если нужно корректирует определение).
(На слайде №12 появляется определение, учащиеся записывают его в тетрадь)
По предложенной схеме исследовать функцию. Слайд №13
Каждый вариант исследует свою функцию
1. Область определения функции.
2. Область значений функции.
3. Точки пересечения с осями координат.
4. Промежутки возрастания и убывания.
в) проверка результатов практической работы.
Слайды №14,15
На экране появляются графики функций, учащиеся называют свойства, которые демонстрируются. Ученики делают записи в тетрадях.
4. Закрепление изученного.
Я предлагаю вам выполнить некоторые задания по теме нашего урока.
а) Устно.(учащиеся выбирают верный ответ, обосновывая выбор )
1.»Выбери показательную функцию«.
а) Функции заранее записаны на доске
; ; ; ; ; ; ; ; ; .
б). Из предложенного списка функций, выбрать ту функцию, которая является показательной: (На слайде16 )
Укажите множество значений функции:
1.
2.
3.
4.
Последняя функция — решение в тетрадь Слайд№17
3. Дана функция: у =аx + b. Вывести правило, по которому можно, не выполняя построение графика данной функции, найти область значения функции. Слайд №18-19 (правило записать в тетрадь)
Вывод:
Если у = а х+ b, то Е (у) = (b; +?)
Если у = ах -b, то Е (у) = (-b; +?)
4. Укажите возрастающую функцию. Слайд №20
5. Укажите убывающую функцию.
б) Письменно.
Используя свойства убывания или возрастания показательной функции, сравнить с единицей следующие числа: № 1322
Слайд №21
г) Самостоятельная работа (если необходимо с помощью учителя).
Приложение 1. Дидактический материал к уроку по теме «Показательная функция»
5. Домашнее задание. (на слайде №22)
6. Подведение итогов. Выставление оценок. (на слайде №23)
Фрагменты этого урока можно также использовать при повторении пройденного материала, при подготовке к экзамену.
Цветными геометрическими фигурами на слайдах показаны гиперссылки. (слайд №11,16)
В ходе подготовки данной работы использовались материалы из опыта работы: Морина С.А. — учитель математики МОУ СОШ №5 г.Железноводска.
urok.1sept.ru
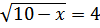
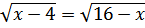
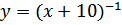
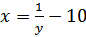 b)
b) 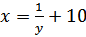 c)
c) 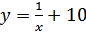 d)
d) 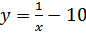
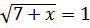
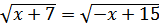
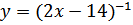
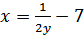 b)
b) 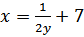 c)
c) 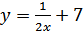 d)
d) 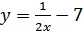
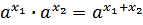
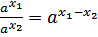
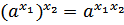
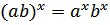
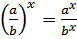
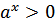
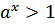 , если
, если 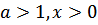
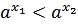 , если
, если 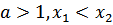
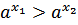 , если
, если 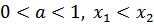
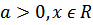 )
)

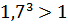
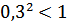
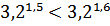
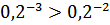
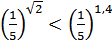
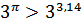
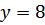
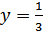
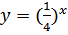 и
и 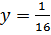
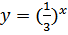 и
и 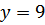
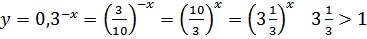 значит, данная функция является возрастающей.
значит, данная функция является возрастающей.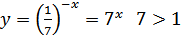 , значит данная функция является возрастающей.
, значит данная функция является возрастающей.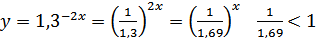 значит, данная функция является возрастающей.
значит, данная функция является возрастающей.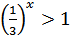


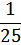

 функция не определена;
функция не определена; получаем функцию
получаем функцию  ;
; получаем функцию
получаем функцию  , определенную при
, определенную при  ;
;