Как построить график линейной функции
Как построить график линейной функции?
Графиком линейной функции является прямая. Для построения прямой достаточно знать две её точки. Следовательно, чтобы построить график линейной функции, нужно найти две любые точки, через которые он проходит.
Абсциссу, то есть координату x, для каждой точки выбираем сами. Удобно брать первой x=0. Следующую абсциссу желательно брать на расстоянии, не меньшем 2 единиц, например, x=2, или x=-2. Чем дальше друг от друга расположены точки, тем точнее получится график.
Если k и b — дроби, следует (по возможности) подбирать x таким образом, чтобы обе координаты (x;y) являлись целыми числами.
Примеры.
Построить график функции:
1) y=2x-5.
Это — линейная функция. Её графиком является прямая. Для построения прямой нужно взять две точки.
Если x=0, то y=2∙0-5= -5.
Если x=6, то y=2∙6-7=5.
Полученные точки (0;-5) и (6;7) отмечаем на координатной плоскости и проводим через них прямую.
2) y=6-0,8x
Если x=0, y=6-0,8∙0=6.
Если x=5, то y=6-0,8∙5=2.
Точки (0;6) и (5;2) отмечаем на координатной плоскости и проводим через них прямую.
Точки (0;3) и (-7;-2) отмечаем на координатной плоскости и проводим через них прямую.
Смешанное число переводим в неправильную дробь:
Точки (0;-7) и (-6;3) отмечаем на координатной плоскости и проводим через них прямую.
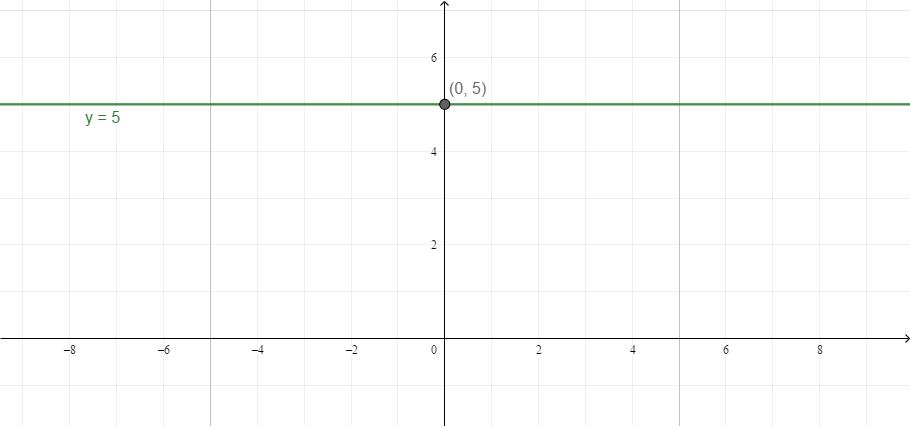
5) y=4
Это — частный случай линейной функции. Графиком является прямая, параллельная оси Ox. На оси Oy отмечаем точку (0;4) (можно отметить любую другую точку с ординатой y=4) и проводим через неё параллельно оси Ox прямую.
Другой частный случай линейной функции — прямую пропорциональность y=kx — рассмотрим отдельно.
www.algebraclass.ru
Как построить график линейной функции. Примеры :: SYL.ru
Для того, чтобы разобраться, как построить график линейной функции, важно понять саму суть функции. Функция — модель зависимости изменений одного параметра от другого.
Тема функциональных зависимостей по традиции открывается линейной функциональной зависимостью. Линейная — это самая простая зависимость. График линейной функции — прямая.
Жизнь и функции
В жизни линейные зависимости обычно встречаются в идеальных искусственных процессах, изменения в которых принимаются за постоянные. Например, когда человек едет куда-то с постоянной скоростью.
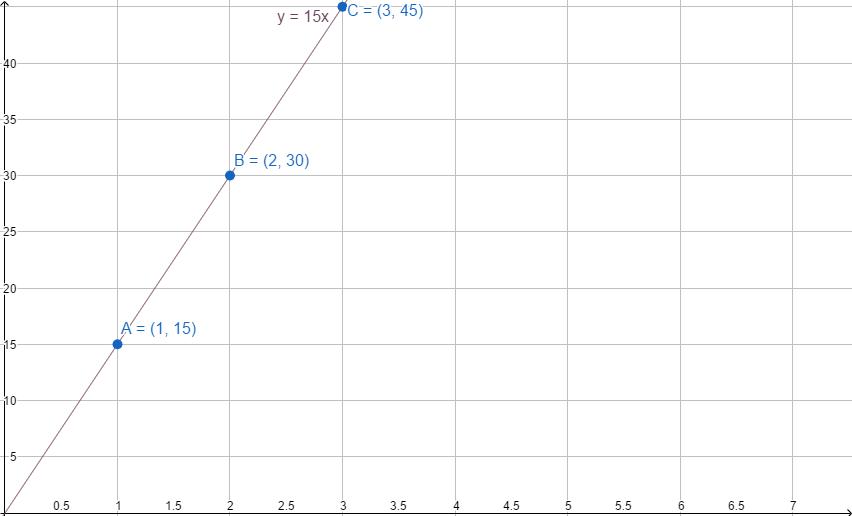
Расстояние, которое человек проедет на велосипеде, будет изменяться линейно в зависимости от количества часов, которые он едет. Если 15 километров он проезжает за час (точка А), то за два часа он проедет 30 километров (точка В), за три часа — 45 (точка С).
Зависимость описывается уравнением y = 15x. Как построить график линейной функции в этом случае?
- найти координаты точек, которые являются решением уравнения;
- построить их на координатной плоскости;
- соединить эти точки в линию.
Описание алгоритма
Поиск координат точек, которые являются решением уравнения, сводится к нахождению двух точек, однозначно определяющих прямую. Хотя достаточно выбрать два различных значения х и найти соответствующие им значения y, для самопроверки можно находить три пары значений. Это позволит быстро выявить возможную ошибку в вычислениях. Зачастую первое значение х выбирают равным нулю.
| y = 15x | (0, 0) | (1, 15) |
| x = 0 | x = 1 | |
| y = 15 × 0 | y = 15 × 1 | |
| y = 0 | y = 15 |
Второе значение х при большом k лучше подбирать рядом с первым. Иначе получится сильный разброс в значениях y и x, например, при x = 4 в рассмотренном уравнении y = 60. В любом случае, до того, как построить график линейной функции по найденным точкам, подбирают масштаб.
| у = 25 x | (0, 0) | (1, 25) |
| x = 0 | x = 1 | |
| y = 25 × 0 | y = 25 × 1 | |
| y = 0 | y = 25 |
Коэффициент при х
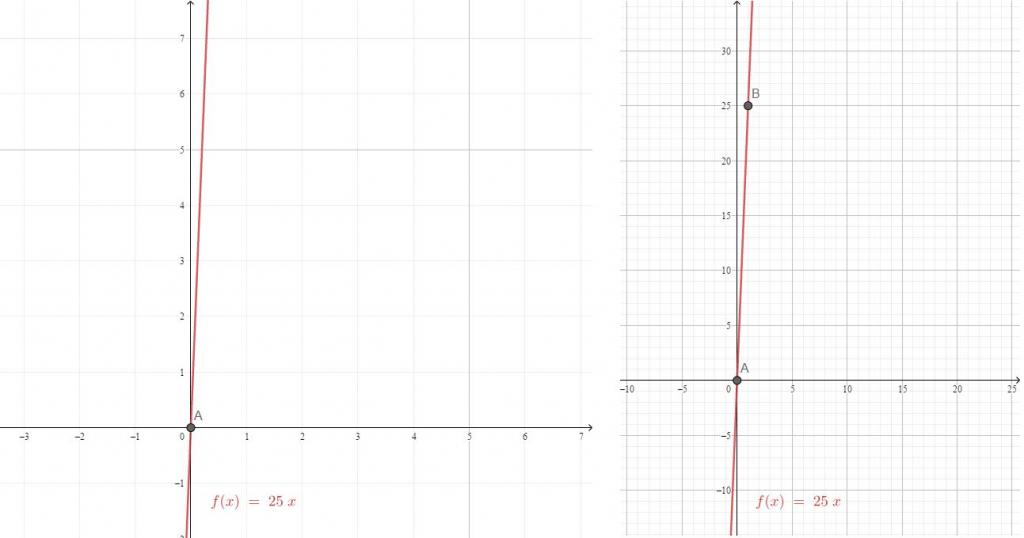
Уравнение линейной функции имеет вид y = kx + b. В зависимости от изменения коэффициента при неизвестном меняется и характер графика линейной функции y = kx.
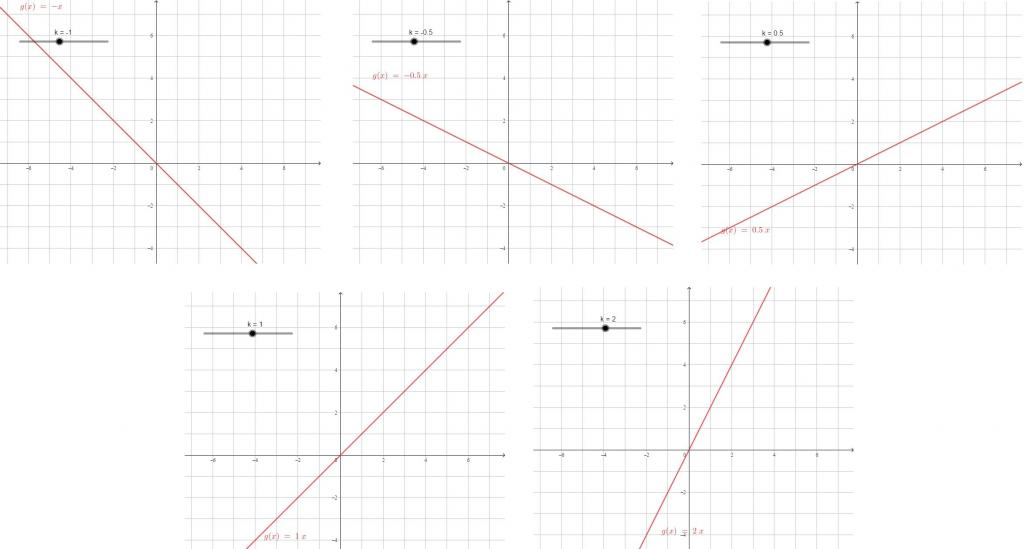
Чем больше по модулю коэффициент, тем большей крутизной обладает прямая, тем сильнее за одно и то же изменение значений х меняются значения y. Коэффициент при х выступает коэффициентом пропорциональности.
Свободный коэффициент
Свободный коэффициент — постоянная, которая не зависит от изменений значения x. Он показывает, где прямая пересекает OY.
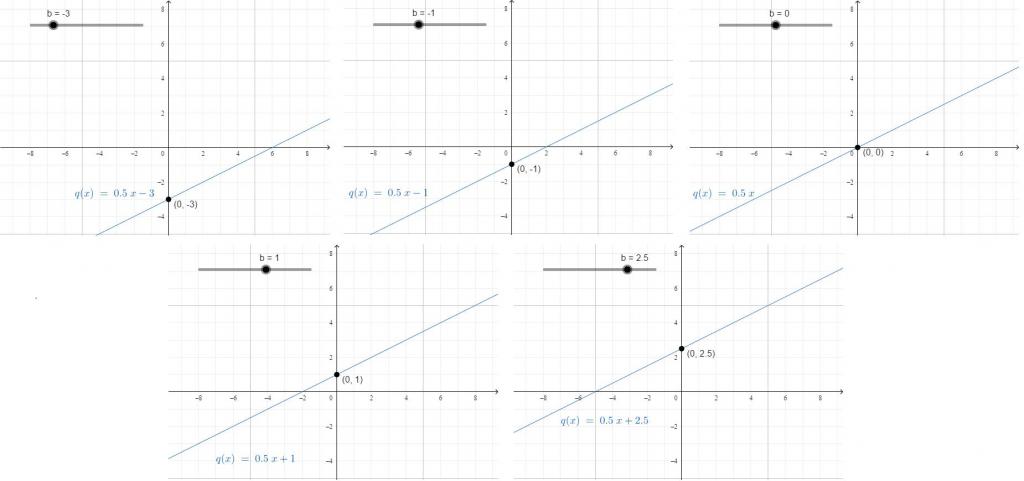
Например, человек с утра до 12 часов дня прошел 10 километров, а потом три часа ехал на велосипеде. Тогда расстояние, которое он преодолел за день: y = 15 × 3 + 10. Если же вы хотите вывести формулу для подсчета расстояния в конце каждого часа из трех, которые он проехал на велосипеде, можно воспользоваться: y = 15x + 10. В час дня он проехал 15 × 1 и еще прошел 10, в два часа он проехал 15 × 2, но прошел все те же 10.
График линейной функции y = kx + b описывает прямую, которая имеет угол наклона k и пересекает OY в точке с координатами (0, b). Анализ уравнения часто позволяет решать задачи, не строя график. Но для того, чтобы работать в уме, действия должны быть хорошо закреплены на визуальном материале.
Например, задача: найти точки пересечения y = — x2 и y = 0,5x + 5. Первая функция убывающая, вторая возрастающая, первая находится ниже второй, т. к. ветки параболы направлены вниз, и ее вершина находится в начале координат. Линейная функция должна была бы иметь гораздо больший угол наклона, чтобы быть более крутой и пересечь одну из веток параболы. Поэтому можно однозначно определить, что точек пересечения нет, не строя график и не производя подстановок.
Частные случаи
- Когда нет свободного коэффициента, он (на самом деле) равен нулю, а значит, прямая пересекает OY в нуле.
- Когда нет неизвестной х или y, y и x независимы друг от друга. Например, y = 5. Независимо от того, какое значение примет х, y всегда будет равен 5. Графически это можно представить в виде прямой линии, параллельной OX.

- То же самое справедливо для случая, когда переменная x равна числу: переменная х имеет постоянное значение.
Благодаря анализу уравнения еще до того, как построить график линейной функции, можно узнать ее примерное расположение на OY и угол наклона, а значит, и крутизну. Это помогает не только подобрать правильный масштаб и построить график, но и решить некоторые задачи в уме.
www.syl.ru
Конспект урока «Построение графика линейной функции»
Построение графика линейной функции
Тип урока: урок по изучению и первичному закреплению новых знаний и способов деятельности.
Формы работы: индивидуальная,групповая работа, самостоятельная практическая работа, фронтальный, индивидуальный опрос.
Требования к уровню подготовки:
Научить строить график линейной функции
изучить виды взаимного расположения графиков линейных функций;
познакомить с понятием угловой коэффициент, выяснить его геометрический смысл;
формировать умение определять взаимное расположение графиков линейных функций по их угловому коэффициенту.
Формирование УУД:
Познавательные: организовать деятельность учащихся на: восприятие, осмысление и первичное закрепление знаний, умений, а также опыта самостоятельной деятельности по теме «Взаимное расположение графиков линейной функций»
Регулятивные: способствовать формированию умения использовать приемы: обобщения, сравнения, выделения главного переноса знаний в новую ситуацию, развитие математического кругозора, мышления и речи, внимания и памяти.
Коммуникативные: содействовать воспитанию интереса к математике, активности, организованности, умению общаться; создать условия для организации частично-поисковой деятельности в процессе проведения лабораторно-практической работы, воспитание ответственного отношения к выполняемой работе через организацию групповой работы, развитие мышления, навыков публичного выступления
Личностные: установить связь между учебной деятельностью и мотивом.
Структура урока:
Организационный момент
Актуализация опорных знаний
Введение в тему, постановка учебных задач
Изучение нового материала в ходе выполнения практической работы
Первичное осмысление и закрепление учебного материала
Рефлексия
Запись и обсуждение домашнего задания
Ход урока.
Организационный момент.
Проверка домашнего задания
Математический диктант Раздать задания
Как называется функция у = – 3х + 2 [у = – 2х – 3]?
Для линейной функции у = 2 – 7х [у = – 7 + 2х] запишите, чему равны k и b.
3)Линейная функция задана формулой
Слайд1
Нет ни одной отрасли человеческих знаний, куда бы не входили понятия функции и ее графического изображения. (Лебединцев Константин Феофанович -математик ,методист)
1) Какую функцию называют линейной?
Что является графиком линейной функции?
(Линейной функцией называется функция вида у=кх+b, где к-угловой коэффициент( число), b— свободное число, х- аргумент, у- функция).
2) Какую переменную называют аргументом?
(Аргумент- это независимая переменная х)
Какая из двух переменных зависимая переменная ?
(функция – это зависимая переменная у)
Слайд2
Введение в тему, постановка учебных задач
Как можно задать математическую модель ?
Как можно задать функцию? (словесно, формулой, при помощи таблицы).
Действительно, чаще всего функции задаются формулой.
А еще как можно задать функцию?
(Графически)
4)Целеполагание
Какова цель нашего урока?
Цель нашего урока научиться строить график линейной функции
Хором
Запишем Число . Классная работа
Итак ,тема нашего урока
Слайд3
Построение графика линейной функции
Постановка учебных задач
Задача 1
Построить график функции
У= 3Х + 1
Слайд4
Что является графиком функции?
Друг другу
Про себя)
А сколько достаточно точек для построения прямой?
А почему?
Слайд5
Задача 2
Построить график функции
У= — 2Х + 1
Слайд6
(Строят на местах и на заготовленном листе)
Сформулируйте теорему о графике линейной функции
Слайд7
(Проговариваем вслух
Друг другу
Про себя)
А каков алгоритм построения графика функции?
Слайд7
(Проговариваем вслух
Друг другу
Про себя)
Физкультурная минутка
Практическая работа
Задания группам – лабораториям.
Отчет Лабораторий
Лаборатория №1.
Роль знака углового коэффициента.Выяснить, как влияет значение углового коэффициента на расположение графиков линейных функций относительно положительного направления оси абсцисс.
Постройте графики функций
у=2х-3 (k>0) у=-2х-3, (k<0) , у= -5 (k=0)
Сделайте выводы:
Если k>0, то угол наклона, то есть угол,образованный графиком линейной функции с положительным направлением оси абсцисс … Слайд8
(Проговариваем вслух
Друг другу
Про себя)
Если k<0, то угол наклона , то есть угол,образованный графиком линейной функции с положительным направлением оси абсцисс … Слайд9
(Проговариваем вслух
Друг другу
Про себя)
Если k=0, то …
Слайд10
(Проговариваем вслух
Друг другу
Про себя)
Лаборатория №2. Угловые коэффициенты функций равны.
Выяснить, как расположены графики линейных функций, если их угловые коэффициенты равны.
В одной системе координат постройте графики функции:
у= — х+3, у= — х- 5, у= — х.
Сделайте вывод:
Если угловые коэффициенты линейных функций равны, то их графики расположены … .
Слайд11
Слайд12
(Проговариваем вслух
Друг другу
Про себя)
Лаборатория №3. Свободные члены линейных функций равны.
Выяснить, как расположены графики линейных функций, если равны их свободные члены.
В одной системе координат постройте графики функции:
у= — 3 х + 4, у = х+ 4, у= 2 х + 4.
Сделайте вывод:
Если свободные члены линейных функций равны, то их графики …
(Проговариваем вслух
Друг другу
Про себя)
Слайд13
Слайд14
Лаборатория №4. Общий случай.
Выяснить, как расположены графики линейных функций, если их угловые коэффициенты положительны и по значению увеличиваются
В одной системе координат постройте графики функции:
у= 0,5 х + 2, у=4 х+2 , у=х+2.
Сделайте вывод: Если k>0 и возрастает, то угол наклона, то есть угол,образованный графиком линейной функции с положительным направлением оси абсцисс …
Слайд15
Слайд16
Домашнее задание
Слайд17
«3» — п.8, №8.6, 8.14 (а, б),8.19(а, б)
«4», «5» — п.8, №8.51(а, б), 8.52(а, б),8.22 (а)
Творческие проекты
1 «Использование и построение графиков линейной функции в медицине»
2«Использование и построение графиков линейной функции в физике»
3«Линейная функция в рисунках»
Домашнее задание
Слайд17
«3» — п.8, №8.6, 8.14 (а, б),8.19(а, б)
«4», «5» — п.8, №8.51(а, б), 8.52(а, б),8.22 (а)
Творческие проекты
1 «Использование и построение графиков линейной функции в медицине»
2«Использование и построение графиков линейной функции в физике»
3«Линейная функция в рисунках»
Творческое название проекта
1. «Использование и построение графиков линейной функции в медицине»
2.Построение графиков линейной функции
3. Творческое название проекта «Линейная функция в рисунках»
Предмет, класс
Краткая аннотация проекта
Вопросы, направляющие проект
Основополагающий вопрос
Проблемные вопросы
План проведения проекта
• Обсуждение вопросов проекта с учащимися;
• Разделение на группы, для работы над проектом;
• Дается список рекомендуемой литературы;
• Обсуждается тематика соблюдения авторских прав;
• Обсуждение планов и целей проекта с учащимися;
• Выполнение заданий по теме проекта.
• Письменный опрос для сбора текущих знаний по теме проекта;
• Конференция по теме проекта;
• Подготовка к защите проекта;
• Защита проектов, ответ защищающихся на вопросы других групп;
• Рефлексия работы над проектом: размышление о плюсах и минусах проектов, возможных доработках, обсуждение будущих проектов.
Визитная карточка проекта
Пример продукта проектной деятельности учащихся
Работа учеников
Материалы по формирующему и итоговому оцениванию
Материалы по сопровождению и поддержке проектной деятельности
Творческое название проекта «Использование и построение графиков линейной функции в физике»
Построение графиков линейной функции
Авторы проекта
Предмет, класс
Краткая аннотация проекта
Вопросы, направляющие проект
Основополагающий вопрос
Проблемные вопросы
План проведения проекта
• Обсуждение вопросов проекта с учащимися;
• Разделение на группы по для групповой работы над проектом;
• Дается список рекомендуемой литературы;
• Обсуждается тематика соблюдения авторских прав;
• Обсуждение планов и целей проекта с учащимися;
• Выполнение заданий по теме проекта.
• Письменный опрос для сбора текущих знаний по теме проекта;
• Конференция по теме проекта;
• Подготовка к защите проекта;
• Защита проектов, ответ защищающихся на вопросы других групп;
• Рефлексия работы над проектом: размышление о плюсах и минусах проектов, возможных доработках, обсуждение будущих проектов.
Визитная карточка проекта
Пример продукта проектной деятельности учащихся
Работа учеников
Материалы по формирующему и итоговому оцениванию
Материалы по сопровождению и поддержке проектной деятельности
Творческое название проекта «Линейная функция в рисунках»
Авторы проекта
Предмет, класс
Краткая аннотация проекта
Вопросы, направляющие проект
Основополагающий вопрос
Проблемные вопросы
План проведения проекта
• Обсуждение вопросов проекта с учащимися;
• Разделение на группы для групповой работы над проектом;
• Дается список рекомендуемой литературы;
• Обсуждается тематика соблюдения авторских прав;
• Обсуждение планов и целей проекта с учащимися;
• Выполнение заданий по теме проекта.
• Письменный опрос для сбора текущих знаний по теме проекта;
• Конференция по теме проекта;
• Подготовка к защите проекта;
• Защита проектов, ответ защищающихся на вопросы других групп;
• Рефлексия работы над проектом: размышление о плюсах и минусах проектов, возможных доработках, обсуждение будущих проектов.
Визитная карточка проекта
Визитка
Пример продукта проектной деятельности учащихся
Работа учеников
Материалы по формирующему и итоговому оцениванию
Анкета формирующего оценивания
Самооценка проекта учащегося
Материалы по сопровождению и поддержке проектной деятельности
Журнал наблюдений
Критерии самооценки работы в группе
Правила ведения дискуссии
infourok.ru
Урок по алгебре «Исследование графика линейной функции» (7 кл)
№
Деятельность учителя
Деятельность учащегося
Демонстрация
на доске
1
— приветствует учащихся
— приветствуют
учителя

2
Давайте вспомним тему прошлого урока и ответим на некоторые вопросы
Проговаривают тему (Построение графиков линейной функции)

3
Актуализация знаний Задание №1
Найдите значение функции
у = 3х + 4, если
•х = 2 , то у =
•х = -3, то у =
•х = 0 , то у =
•х = 0,5 , то у =
у = — 2х – 3,
•х= 2, то у =
•х = 0, то у =
•х = -1 , то у =
отвечают
4
-Какие частные случаи линейной функции вам известны?
-Первый случай, когда число b равно 0. Второй случай, когда число k равно 0

5
Выберите из предложенных формул линейной функции те, которые проходят через начало координат
Называют формулы

6
Назовите коэффициент к и ординату точки пересечения графика с осью ординат
Выбирают правильные ответы
7
Телеграмма: формула линейной функции – коэффициенты( сидящим за первыми партами выдаются карточки с формулой линейной функции, они выписывают на пустую карточку к=…, в=… и передают ее сидящему позади себя, он по данным к и в восстанавливает формулу линейной функции и т.д.
Работают самостоятельно, заполняя карточки и передавая их сидящему позади себя

8
Теперь ответьте на следующие вопросы:
(задания из ГИА)
Достаточно ли вам полученных знаний для того, чтобы ответить на вопросы?
Что для этого нужно сделать?
Отвечают



9
Теперь ответьте на следующие вопросы:
(задания из ГИА)
Достаточно ли вам полученных знаний для того, чтобы ответить на вопросы?
Что для этого нужно сделать?
Знаний не достаточно,
Формул линейных функций нет, необходимо знать как зависит график функции от к и в

10
Попробуйте сформулировать тему урока
Формулируют тему урока («Исследование графика линейной функции»
11
Давайте найдем как можно больше решений данной проблемы
Предлагаются все возможные способы и пути решения стоящей проблемы
12
Есть ли хорошие решения? (Выбираются из множества предложенных решений хорошие, эффективные.)
А теперь выберем единственное решение. (Выбирается самое сильное решение проблемы.)
Любопытно, а как это будет выглядеть на практике?
(Планируется работа по претворению выбранного решения в жизнь)
Предлагают способы решения данной проблемы, анализируют
13
В одной координатной плоскости построить графики функций: 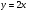 ;
; 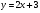 ;
;  .
.
Ответить на вопросы: 1) Графики функций представляют собой… 2) Что общего в формулах этих функций?
3) В каких координатных четвертях проходят графики?
4) Каково значение коэффициента по знаку?
5) Опишите, каков угол наклона графиков функций к оси Ох.
6) Чему равна ордината точки пересечения графиков с осью Оу?
Все строят графики в тетрадях, один у доски, отвечают на вопросы
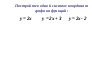
14
В одной координатной плоскости построить графики функций: 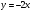 ;
; 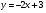 ;
; 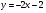 .
.
Ответить на вопросы:
1) Графики функций представляют собой…
2) Что общего в формулах этих функций?
3) В каких координатных четвертях расположены графики?
4) Каково значение коэффициента по знаку?
5) Опишите, каков угол наклона графиков функций к оси Ох.
6) Чему равна рдината точки пересечения графиков с осью Оу?
Все строят графики в тетрадях, один у доски, отвечают на вопросы
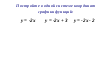
15
В одной координатной плоскости построить графики функций: 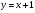 ;
; 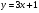 ;
; 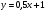 .
.
Ответьте на вопросы:
1) Графики функций представляют собой…
2) В какой точке пересекаются графики функций?
3) Каково значение коэффициента по знаку?
4) Какой угол наклона каждого графика к оси Ох? 5) Каково соотношение между значениями коэффициента k и величинами углов наклона графиков к оси Ох?
Все строят графики в тетрадях, один у доски, отвечают на вопросы

16
Теперь сделайте вывод, как от к и в зависит построение графика линейной функции?
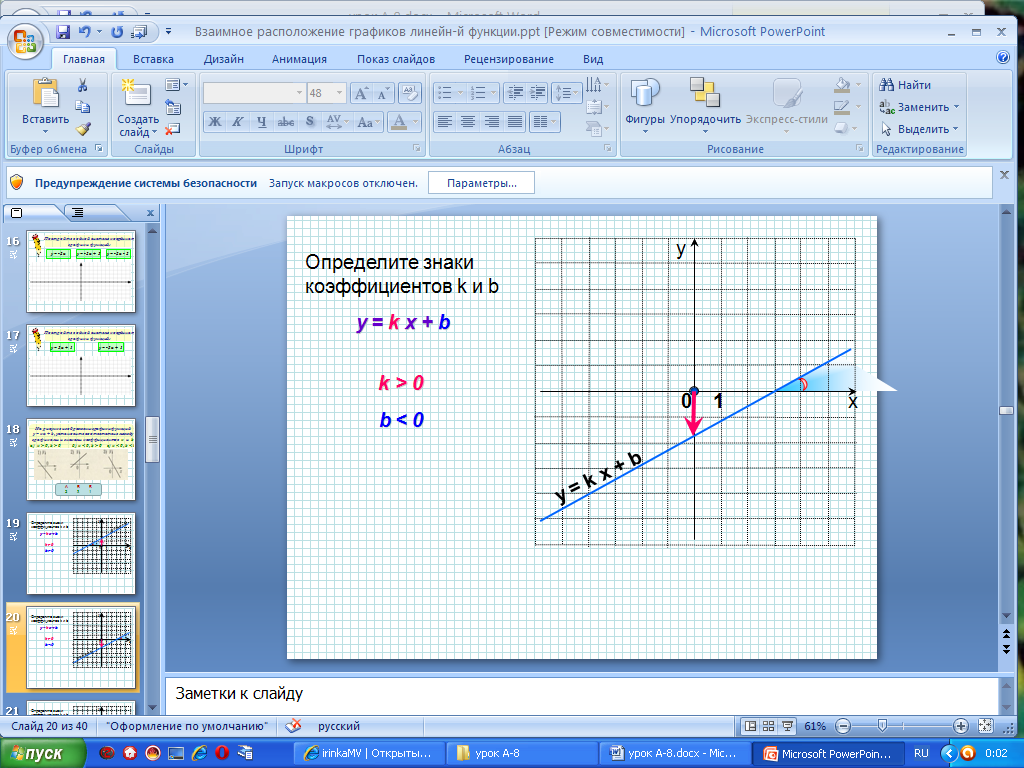
1.Если коэффициенты у функций одинаковые, то графики функций – параллельны.
2.Если коэффициенты различны, то графики функций – пересекаются.
3.Ордината точки пересечения графика функции с осью Оу равна b.
4.Если коэффициент k > 0, то графики расположены в I и III координатных четвертях, углы наклона графиков функции к оси Ох – острые.
5.Если коэффициент k < 0, то графики расположены во II и IV координатных четвертях, а углы наклона графиков функции к оси Ох – тупые.
6.Чем больше значение k, тем больше угол наклона графика функции к оси Ох.
17
Вернемся к заданию, которое вызвало у вас затруднение.
Попробуйте теперь ответить на вопрос
18
А можно ли, применив эти знания по другому ответить на вопрос предыдущих заданий?
19
Закрепление материала
(задания на доске с вариантами ответов.
Ответы записывают в тетрадях, обмениваются с соседом по парте, сверяют с ответами на доске, оценивают и поднимают сигнальные карточки


20
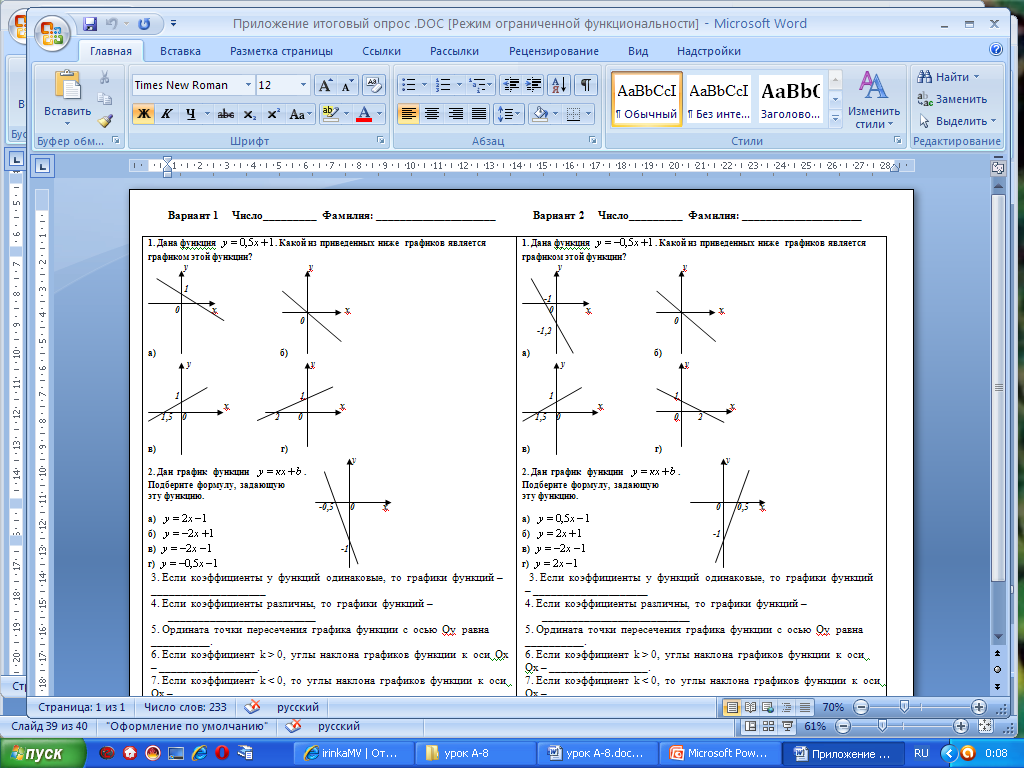
Проверим как вы усвоили материал сегодняшнего урока (выдается тест по вариантам)
Решают тест
21
Домашнее задание: «Создай паспорт”
Прием для систематизации, обобщения полученных знаний; для выделения существенных и несущественных признаков изучаемого явления; создания краткой характеристики изучаемого понятия,.Это универсальный прием составления обобщенной характеристики изучаемого явления по определенному плану
— Создайте паспорт по теме: «Линейная функция» в. В дальнейшем его можете использовать как опорный конспект
22
Предлагаю вам заполнить «Лист самоконтроля»
infourok.ru