Прямоугольная система координат в пространстве. Координаты вектора

В  классе мы с вами обсуждали прямоугольную систему координат. Тогда речь шла о плоскости: у нас были две перпендикулярные оси, и каждую точку плоскости мы задавали с помощью так называемых координат, то есть величин, которые требовалось «пройти» до данной точки от начала координат. (См. Рис. 1.)

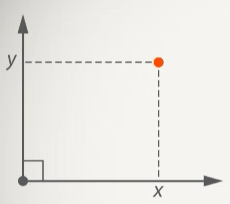
Рис. 1. Система координат на плоскости

С помощью координат было удобно решать разные задачи, но мы применяем их и в жизни. Например, в кинотеатре мы ищем свое кресло сначала по ряду, а затем по номеру в ряду. (См. Рис. 2.)

Рис. 2. Место в кинотеатре – модель координатной плоскости

Но мы живем не в двухмерном пространстве, а в трехмерном. Поэтому имеет смысл поговорить об аналоге уже привычной нам системы координат, перенеся ее в пространство.

Рассмотрим такую ситуацию. Предположим, что мы пошли не в кино, а на балет. У нас есть билет, на котором написаны ряд и место. Можем ли мы легко найти свое кресло? Да, если речь о партере. Но ведь мы можем сидеть и выше: в амфитеатре или на любом из ярусов. Поэтому в данном случае мы прибегаем к трем измерениям: сначала по высоте (ярус, амфитеатр или партер), затем уже ряд, а затем место. (См. Рис. 3.)

Рис. 3. Расположение мест в театре как пример трехмерной системы координат

Мы пользуемся координатами и тогда, когда выбираем товары в гипермаркете самообслуживания. Например, мы хотим купить стол и нам дается инструкция, что он находится в  ряду, на 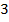 полке снизу, место номер 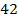. Мы сначала ищем ряд (первая координата), затем – место (вторая), потом – полку (третья). Можно, разумеется, сначала найти полку, а потом место. Так или иначе, речь идет о трех координатах.

Рассмотрим произвольную точку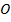

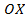 пространства. Проведем через нее три попарно перпендикулярные прямые. На каждой из них обозначим направление. Это и будут оси координат – теперь их стало три. Обратите внимание, что ось направлена к нам, ось  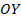вправо, а  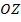– вверх. Порядок здесь важен, так как такие направления образуют так называемую правую тройку. (См. Рис. 4.)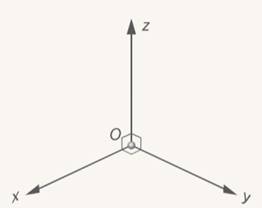

Рис. 4. Оси координат трехмерного пространства

Эту картинку можно поворачивать так, как нам удобно. Например, если мы ее повернем на 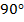 против часовой стрелки в плоскости 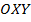, то получим следующую картинку: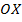

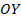 вправо,  – вглубь,  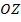– вверх. (См. Рис. 5.)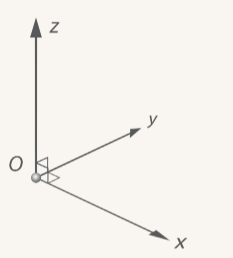

Рис. 5. Поворот «тройки» на 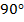 против часовой стрелки в плоскости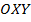

Все это допустимые картинки, выбирайте любую из них. Некоторым удобна последняя, ведь она получается естественным образом из плоскостной. (См. Рис. 6.)

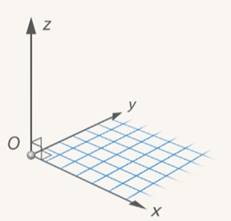
Рис. 6. К системе координат на плоскости добавили ось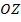

Рассмотрим тройку векторов ,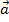

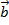
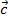, , отложенных от одной точки 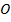. Эта тройка векторов называется правой, если векторы располагаются так, как расположены соответственно большой, указательный и средний пальцы правой руки. В противном случае тройка называется левой.

На рисунке (См. Рис. 7.) справа изображена правая тройка векторов, а слева – левая. Это также полностью соответствует правилам правой и левой руки из физики.

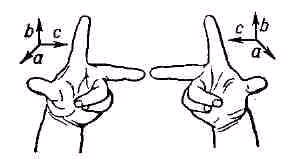
Рис. 7. Левая и правая тройки

Оси обозначаются 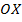 (ось абсцисс),  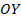(ось ординат) и  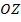(ось аппликат). (См. Рис. 8.)

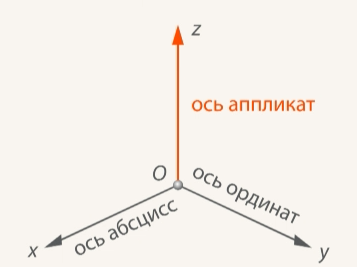
Рис. 8. Названия координатных осей

Соответствующие плоскости – 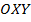, , 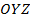 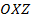– координатные плоскости. (См. Рис. 9.) Как и на плоскости, у каждой оси в пространстве есть положительное направление и отрицательное.

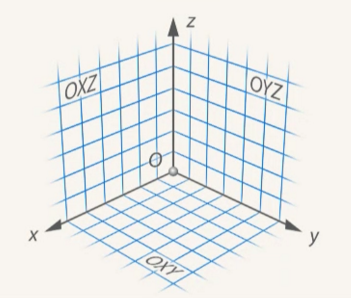
Рис. 9. Координатные плоскости

Координаты точки в пространстве определяются аналогично плоскостным. Рассмотрим произвольную точку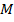

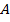 и проведем через нее плоскости, параллельные координатным. Эти плоскости пересекут наши оси в точках  (точка пересечения параллельной плоскости с осью 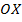),  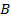(точка пересечения параллельной плоскости с осью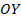 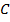) и  (точка пересечения параллельной плоскости с осью 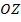). (См. Рис. 10.)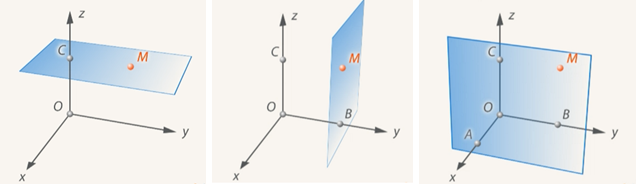

Рис. 10. Точки пересечения параллельных плоскостей с осями координат

Тогда абсцисса точки 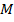 – это 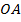 (в случае если  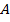лежит на положительной полуоси) и 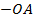, если  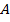– на отрицательной. (См. Рис. 11.)

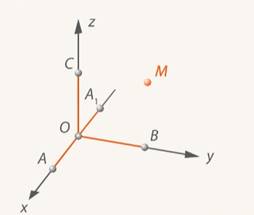
Рис. 11. Абсцисса точки 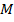 в зависимости от расположения точки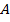

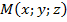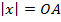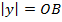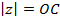Аналогично определяются ордината и аппликата. Записывают координаты в круглых скобках через точку с запятой: , где , ,  (либо 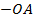, , 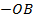 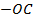– в зависимости от расположения на осях координат). Не пишите координаты точки через запятую, чтобы не спутать с десятичными дробями.

У точки могут быть и нулевые координаты, если она лежит в координатной плоскости. Например, если взять точку в плоскости 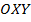, то ее координаты имеют вид 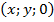. А точка на оси  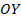имеет координаты 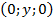. Начало же координат – точка  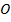– имеет координаты 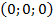. (См. Рис. 12.)

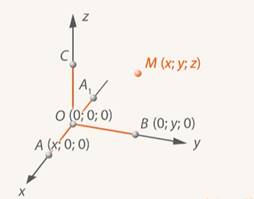
Рис. 12. Точки с нулевыми координатами

Как и на плоскости, отложим на каждой оси от начала координат в положительном направлении по вектору, длины которых будут равны 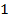. Эти векторы называют единичными, или ортами. Обозначают их соответственно 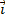, , 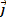 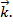(См. Рис. 13.)

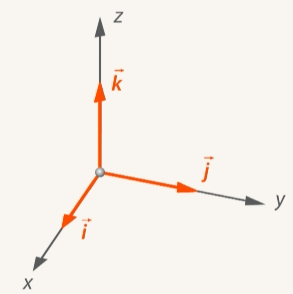
Рис. 13. Орты , ,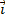

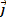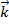
Эти векторы не компланарны, то есть не лежат в одной плоскости, а значит, каждый вектор пространства можно единственным образом разложить по векторам 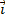, , 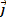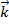: 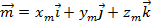. Такие коэффициенты 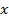; ; 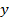 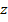называют координатами вектора и пишут:  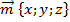– в фигурных скобках. (См. Рис. 14.)

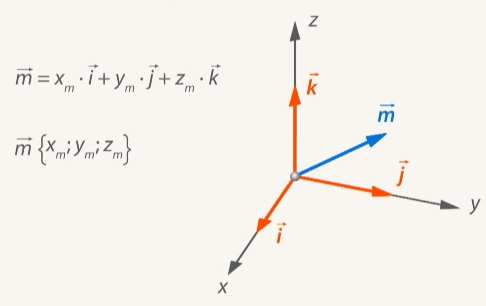
Рис. 14. Координаты вектора через орты

Так, например, вектор .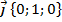

На этом уроке мы познакомились с понятием «система координат в пространстве» и выяснили, как задаются координаты точки и координаты вектора.

 

Список литературы

1. Атанасян Л.С. и др. Геометрия. Учебник для 10–11 классов. – 18-е изд. – М.: Просвещение, 2009. – 255 с.
2. А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002
3. В.Ф. Бутузов, Ю.А. Глазков. Рабочая тетрадь по геометрии 11 класс, 2013

 

Дополнительные рекомендованные ссылки на ресурсы Интернет

1. Yaklass.ru (Источник).
2. Cleverstudents.ru (Источник).
3. Alwebra.com.ua (Источник).

 

Домашнее задание

1. На каких расстояниях от координатных плоскостей находится точка
2. Определите, лежит ли данная точка на координатной оси. Если да, то укажите эту ось. , , , ,
3. Определите, принадлежит ли данная точка координатной плоскости. Если да, то назовите ее. , , , , .

Векторы на координатной плоскости

Теорема

В прямоугольной системе координат расстояние между точками \(P(x_1; y_1)\) и \(Q(x_2; y_2)\) выражается формулой \(\rho(P, Q) = \sqrt{(x_1 — x_2)^2 + (y_1 — y_2)^2}\).

 

Доказательство

Если \(PQ\parallel Ox\), то он лежит на некоторой прямой \(y = C\), тогда \(y_1 = y_2 = C\), следовательно, \(\sqrt{(x_1 — x_2)^2 + (y_1 — y_2)^2} = |x_1 — x_2|\), что равно его длине.

 

Если \(PQ\parallel Oy\), то он лежит на некоторой прямой \(x = C\), тогда \(x_1 = x_2 = C\), следовательно, \(\sqrt{(x_1 — x_2)^2 + (y_1 — y_2)^2} = |y_1 — y_2|\), что равно его длине.

 

Если \(PQ\) не параллелен осям, то рассмотрим прямоугольный треугольник \(PQM\), в котором \(PM\parallel Ox\), \(QM\parallel Oy\). По теореме Пифагора \(PQ^2 = PM^2 + QM^2\). Так как \(PM\parallel Ox\), то \(PM\) лежит на некоторой прямой \(y = C\), откуда \(PM = |x_1 — x_2|\), аналогично \(QM = |y_1 — y_2|\), тогда \(PQ^2 = (x_1 — x_2)^2 + (y_1 — y_2)^2\), откуда получаем требуемое равенство.

 

Утверждение

Если в прямоугольной системе координат точка \(M\) – середина отрезка \(PQ\), где \(P(x_1;y_1), \ Q(x_2;y_2)\), то

\[M\left(\dfrac{x_1 + x_2}{2}; \dfrac{y_1 + y_2}{2}\right)\]

Доказательство

Пусть \(M(a;b)\).

 

1) Пусть \(PQ\parallel Oy \Rightarrow x_1=x_2=a\). Значит, \(a=\dfrac{x_1+x_2}2=\dfrac{a+a}2\) – верно.

 

Т.к. \(PM=MQ\), следовательно, \(|y_2-b|=|y_1-b| \Rightarrow y_2-b=y_1-b\) или \(y_2-b=b-y_1\), что равносильно \(y_2=y_1\) или \(b=\dfrac{y_1+y_2}2\). Первое равенство невозможно (т.к. тогда точки \(P\) и \(Q\) совпадают).

 

2) Случай \(PQ\parallel Ox \Rightarrow y_1=y_2=b\) доказывается аналогично.

 

3) \(x_1\ne x_2, y_1\ne y_2\).

 

Тогда \(Ma=b\) – средняя линия трапеции \(x_1PQx_2\), следовательно, равна полусумме оснований, то есть \(b=\dfrac{y_1+y_2}2\).

 

Аналогично \(a=\dfrac{x_1+x_2}2\).  

\[{\Large{\text{Векторы на координатной плоскости}}}\]

Лемма

Если векторы \(\overrightarrow a\) и \(\overrightarrow b\) коллинеарны, то существует такое число \(\lambda\ne 0\), что \(\overrightarrow a=\lambda\overrightarrow b\).

 

Доказательство

1) Если \(\overrightarrow a\uparrow \uparrow \overrightarrow b\).

 

Рассмотрим вектор \(\dfrac1{|\overrightarrow a|}\overrightarrow a\). Данный вектор сонавправлен с \(\overrightarrow a\), а его длина равна \(1\). Тогда вектор \(\dfrac{|\overrightarrow b|}{|\overrightarrow a|}\overrightarrow a\) также сонаправлен с \(\overrightarrow a\), но его длина равна \(|\overrightarrow b|\). То есть равен вектору \(\overrightarrow b\).

 

2) Если \(\overrightarrow a\uparrow \downarrow \overrightarrow b\).

 

Аналогично доказывается, что \(\overrightarrow b=-\dfrac{|\overrightarrow b|}{|\overrightarrow a|}\overrightarrow a\).

 

Определение

Если вектор \(\overrightarrow p\) представлен как линейная комбинация двух векторов: \(\overrightarrow p=\alpha\overrightarrow a+\beta \overrightarrow b\), то говорят, что вектор \(\overrightarrow p\) разложен по векторам \(\overrightarrow a\) и \(\overrightarrow b\).

 

\(\alpha, \beta\) – коэффициенты разложения.  

Пусть векторы \(\overrightarrow i\), \(\overrightarrow j\) – векторы, длины которых равны \(1\), а направление совпадает с направлением осей \(Ox\) и \(Oy\) соответственно. Такие векторы называются единичными векторами.

 

Тогда если \(\overrightarrow p=a\overrightarrow i+b\overrightarrow j\), то \(\{a;b\}\) – координаты вектора \(\overrightarrow p\).

 

Свойства координат вектора

1. Равные векторы имеют равные координаты.

 

2. Координаты суммы векторов равны сумме координат каждого вектора: если \(\overrightarrow a\{x_1;y_1\}, \ \overrightarrow b\{x_2;y_2\}\), то \(\overrightarrow a+\overrightarrow b=\{x_1+x_2;y_1+y_2\}\).

 

3. Каждая координата произведения вектора на число равна произведению соответствующей координаты данного вектора на это число: \(\overrightarrow a\{x;y\}, \ \lambda \) – число, то \(\lambda\overrightarrow a\{\lambda x;\lambda y\}\).

 

Теорема

Если точки \(A(x_1;y_1), \ B(x_2;y_2)\), то \(\overrightarrow {AB}\{x_2-x_1;y_2-y_1\}\).
То есть каждая координата вектора равна разности соответствующих координат его конца и начала.

 

Следствие

Если \(\overrightarrow a\{x;y\}\), то длина \(|\overrightarrow a|=\sqrt{x^2+y^2}\).  

\[{\Large{\text{Скалярное произведение векторов}}}\]

Определение

Пусть от одной точки отложены два вектора \(\overrightarrow {AB}\) и \(\overrightarrow {AC}\). Тогда угол между этими векторами – это угол \(\angle BAC\), не превышающий развернутого угла.

 

Скалярное произведение векторов \(\overrightarrow a\) и \(\overrightarrow b\) – это число, равное произведению длин этих векторов на косинус угла между ними.
Обозначение: \(\overrightarrow a\cdot \overrightarrow b\) или \((\overrightarrow a, \overrightarrow b)\). \[(\overrightarrow a, \overrightarrow b)=|\overrightarrow a|\cdot |\overrightarrow b|\cdot \cos\widehat{(\overrightarrow a, \overrightarrow b)}\]

Следствия

1. Если ненулевые векторы взаимно перпендикулярны, то косинус угла между ними равен нулю, следовательно, и их скалярное произведение равно нулю.

 

2. Если угол между ненулевыми векторами острый, то скалярное произведение положительно.

 

3. Если угол между ненулевыми векторами тупой, то скалярное произведение отрицательно.

 

4.Скалярное произведение вектора на себя равно квадрату его длины: \(\overrightarrow a\cdot \overrightarrow a=|\overrightarrow a|^2\).

 

Теорема

В прямоугольной системе координат скалярное произведение векторов \(\overrightarrow a\{x_1;y_1\}\) и \(\overrightarrow b\{x_2;y_2\}\) выражается формулой:

\[\overrightarrow a\cdot \overrightarrow b=x_1x_2+y_1y_2\]

Доказательство

Рассмотрим вектор \(\overrightarrow c\):

 

Т.к. \(\overrightarrow a+\overrightarrow c=\overrightarrow b \Rightarrow \overrightarrow c=\overrightarrow b-\overrightarrow a \Rightarrow \overrightarrow c \{x_2-x_1; y_2-y_1\}\).

 

По теореме косинусов: \(|c|^2=|a|^2+|b|^2-2|a||b|\cos\alpha\), но \(|a||b|\cos \alpha=\overrightarrow a\cdot \overrightarrow b\), значит: \[\overrightarrow a\cdot \overrightarrow b=\dfrac12\left(|a|^2+|b|^2-|c|^2\right) =\dfrac12\left(x_1^2+y_1^2+x_2^2+y_2^2-(x_2-x_1)^2-(y_2-y_1)^2\right)=x_1x_2+y_1y_2\]

Свойства скалярного произведения

Для любых векторов \(\overrightarrow a, \overrightarrow b, \overrightarrow c\) и любого числа \(\lambda\) справедливо:

 

1. Скалярное произведение вектора на себя всегда неотрицательно, причем равно нулю оно тогда и только тогда, когда вектор нулевой: \(\overrightarrow a^2\geqslant 0, \quad \overrightarrow a^2=0 \Leftrightarrow |\overrightarrow a|=0\).

 

2. Переместительный закон: \(\overrightarrow a\cdot \overrightarrow b=\overrightarrow b\cdot \overrightarrow a\).

 

3. Распределительный закон: \(\overrightarrow a \cdot (\overrightarrow b+\overrightarrow c)=\overrightarrow a\cdot \overrightarrow b+\overrightarrow a\cdot \overrightarrow c\).

 

4. Сочетательный закон: \((\lambda\overrightarrow a)\cdot \overrightarrow b=\lambda (\overrightarrow a\cdot \overrightarrow b)\).

Трехмерное пространство: векторы, координаты :: SYL.ru

Еще из школьного курса алгебры и геометрии мы знаем о понятии трехмерного пространства. Если разобраться, сам термин «трехмерное пространство» определяется как система координат с тремя измерениями (это знают все). По сути, описать любой объемный объект можно при помощи длины, ширины и высоты в классическом понимании. Однако давайте, как говорится, копнем несколько глубже.

Что такое трехмерное пространство

Как уже стало ясно, понимание трехмерного пространства и объектов, способных существовать внутри него, определяется тремя основными понятиями. Правда, в случае с точкой это именно три значения, а в случае с прямыми, кривыми, ломаными линиями или объемными объектами соответствующих координат может быть больше.

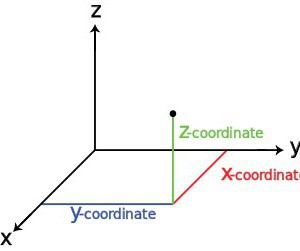
В данном случае все зависит именно от типа объекта и применяемой системы координат. Сегодня наиболее распространенной (классической) считается Декартова система, которую иногда еще называют прямоугольной. Она и некоторые другие разновидности будут рассмотрены несколько позже.

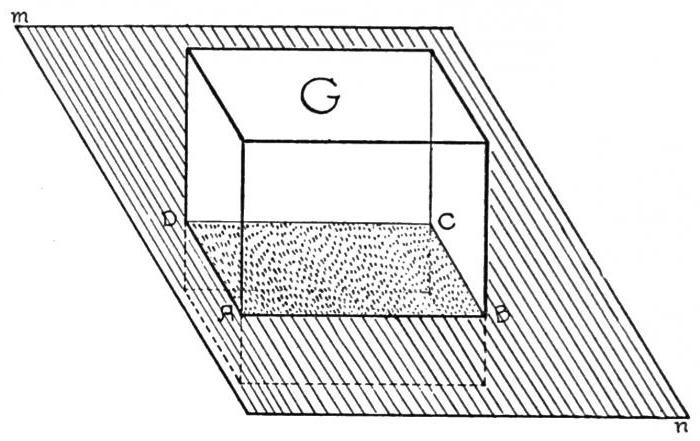
Кроме всего прочего, здесь нужно разграничивать абстрактные понятия (если можно так сказать, бесформенные) вроде точек, прямых или плоскостей и фигуры, обладающие конечными размерами или даже объемом. Для каждого из таких определений существуют и свои уравнения, описывающие их возможное положение в трехмерном пространстве. Но сейчас не об этом.

Понятие точки в трехмерном пространстве

Для начала определимся, что представляет собой точка в трехмерном пространстве. В общем-то, ее можно назвать некой основной единицей, определяющей любую плоскую или объемную фигуру, прямую, отрезок, вектор, плоскость и т. д.

Сама же точка характеризуется тремя основными координатами. Для них в прямоугольной системе применяются специальные направляющие, называемые осями X, Y и Z, причем первые две оси служат для выражения горизонтального положения объекта, а третья относится к вертикальному заданию координат. Естественно, для удобства выражения положения объекта относительно нулевых координат в системе приняты положительные и отрицательные значения. Однако же сегодня можно найти и другие системы.

Разновидности систем координат

Как уже говорилось, прямоугольная система координат, созданная Декартом, сегодня является основной. Тем не менее в некоторых методиках задания местоположения объекта в трехмерном пространстве применяются и некоторые другие разновидности.

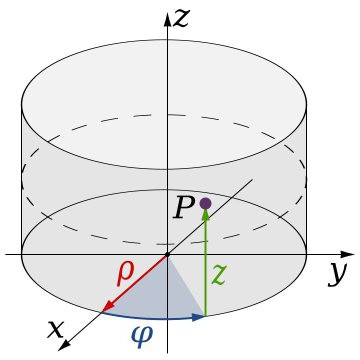
Наиболее известными считаются цилиндрическая и сферическая системы. Отличие от классической состоит в том, что при задании тех же трех величин, определяющих местоположение точки в трехмерном пространстве, одно из значений является угловым. Иными словами, в таких системах используется окружность, соответствующая углу в 360 градусов. Отсюда и специфичное задание координат, включающее такие элементы, как радиус, угол и образующая. Координаты в трехмерном пространстве (системе) такого типа подчиняются несколько другим закономерностям. Их задание в данном случае контролируется правилом правой руки: если совместить большой и указательный палец с осями X и Y, соответственно, остальные пальцы в изогнутом положении укажут на направление оси Z.

Понятие прямой в трехмерном пространстве

Теперь несколько слов о том, что представляет собой прямая в трехмерном пространстве. Исходя из основного понятия прямой, это некая бесконечная линия, проведенная через точку или две, не считая множества точек, расположенных в последовательности, не изменяющей прямое прохождение линии через них.

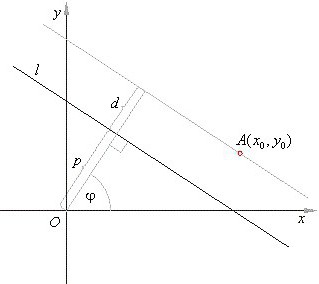
Если посмотреть на прямую, проведенную через две точки в трехмерном пространстве, придется учитывать по три координаты обеих точек. То же самое относится к отрезкам и векторам. Последние определяют базис трехмерного пространства и его размерность.

Определение векторов и базиса трехмерного пространства

Как принято считать, в трехмерной системе координат может существовать три основных вектора, которые определяют базис. При этом базисов с соответствующими независимыми тремя векторами может быть бесчисленное множество.

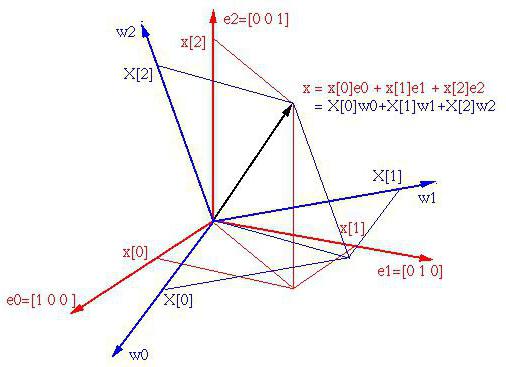
Заметьте, это могут быть только три вектора, но вот троек векторов можно определить сколько угодно. Размерность пространства определяется количеством линейно-независимых векторов (в нашем случае – три). И пространство, в котором имеется конечное число таких векторов, называется конечномерным.

Зависимые и независимые векторы

Что касается определения зависимых и независимых векторов, линейно-независимыми принято считать векторы, являющиеся проекциями (например, векторы оси X, спроецированные на ось Y).

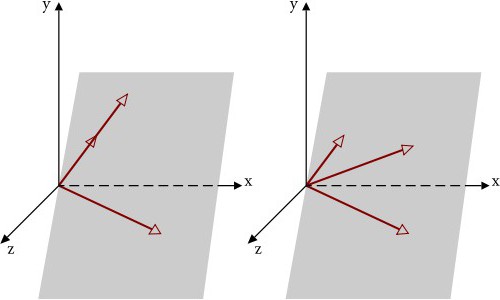
Как уже понятно, любой четвертый вектор является зависимым (теория линейных пространств). А вот три независимых вектора в трехмерном пространстве в обязательном порядке не должны лежать в одной плоскости. Кроме того, если определять независимые векторы в трехмерном пространстве, они не могут являться, так сказать, один продолжением другого. Как уже понятно, в рассматриваемом нами случае с тремя измерениями, согласно общей теории, можно построить исключительно только тройки линейно-независимых векторов в определенной системе координат (без разницы, какого типа).

Плоскость в трехмерном пространстве

Если рассматривать понятие плоскости, не вдаваясь в математические определения, для более простого понимания этого термина, такой объект можно рассматривать исключительно как двумерный. Иными словами, это бесконечная совокупность точек, у которых одна из координат является постоянной (константой).

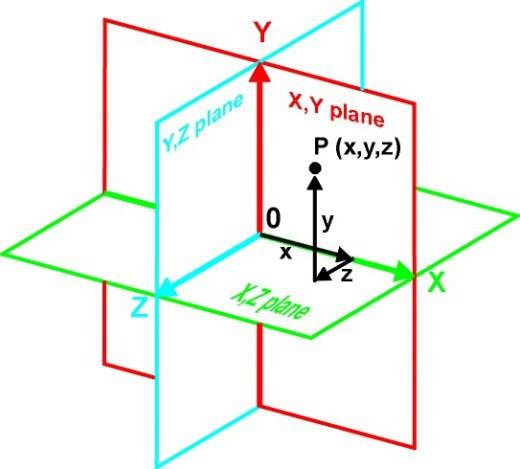
К примеру, плоскостью можно назвать любое количество точек с разными координатами по осям X и Y, но одинаковыми координатами по оси Z. В любом случае одна из трехмерных координат остается неизменной. Однако это, так сказать, общий случай. В некоторых ситуациях трехмерное пространство может пересекаться плоскостью по всем осям.

Существует ли более трех измерений

Вопрос о том, сколько может существовать измерений, достаточно интересен. Как считается, мы живем не в трехмерном с классической точки зрения пространстве, а в четырехмерном. Кроме известных всем длины, ширины и высоты, такое пространство включает в себя еще и время существования объекта, причем время и пространство между собой взаимосвязаны достаточно сильно. Это доказал еще Эйнштейн в своей теории относительности, хотя это больше относится к физике, нежели к алгебре и геометрии.

Интересен и тот факт, что сегодня ученые уже доказали существование как минимум двенадцати измерений. Конечно, понять, что они собой представляют, сможет далеко не каждый, поскольку это относится скорее к некой абстрактной области, которая находится вне человеческого восприятия мира. Тем не менее факт остается фактом. И не зря же многие антропологи и историки утверждают, что наши пращуры могли иметь некие специфичные развитые органы чувств вроде третьего глаза, которые помогали воспринимать многомерную действительность, а не исключительно трехмерное пространство.

Кстати сказать, сегодня существует достаточно много мнений по поводу того, что экстрасенсорика тоже является одним из проявлений восприятия многомерного мира, и тому можно найти достаточно много подтверждений.

Заметьте, что современными базовыми уравнениями и теоремами описать многомерные пространства, отличающиеся от нашего четырехмерного мира, тоже не всегда представляется возможным. Да и наука в этой области относится скорее к области теорий и предположений, нежели к тому, что можно явно ощутить или, так сказать, потрогать или увидеть воочию. Тем не менее косвенные доказательства существования многомерных миров, в которых может существовать четыре и более измерений, сегодня ни у кого не вызывают сомнений.

Заключение

В целом же, мы очень кратко рассмотрели основные понятия, относящиеся к трехмерному пространству и базовым определениям. Естественно, существует множество частных случаев, связанных с разными системами координат. К тому же мы постарались особо не лезть в математические дебри для объяснения основных терминов только для того, чтобы вопрос, связанный с ними, был понятен любому школьнику (так сказать, объяснение «на пальцах»).

Тем не менее, думается, даже из таких простых трактовок можно сделать вывод о математическом аспекте всех составляющих, входящих в базовый школьный курс алгебры и геометрии.

Как построить вектор?

Вектором принято называть отрезок, который имеет заданное направление. Как начало, так и конец вектора имеют фиксированную позицию, с помощью которых и определяется направление вектора. Рассмотрим подробнее, как построить вектор по заданным координатам.

1. Начертить систему координат (x, y, z) в пространстве, отметить на осях единичные отрезки.
2. Отложить на двух осях нужные координаты, провести от них пунктиром линии, параллельные осям, до пересечения. Поучится точка пересечения, которую нужно соединить пунктиром с началом координат.
3. Провести вектор из начала координат до полученной точки.
4. Отложить на третьей оси нужное число, через данную точку провести пунктирную линию, которая будет параллельна построенному вектору.
5. Из конца вектора провести пунктиром линию, параллельную третьей оси до пересечения с линией из прошлого пункта.
6. В завершении соединить начало координат и полученную точку.

Иногда требуется построить вектор, который будет результатом сложения или вычитания других векторов. Поэтому сейчас мы рассмотрим операции с векторами, узнаем, как их складывать и вычитать. 

Операции над вектором

Геометрические векторы можно складывать несколькими способами. Так, например, наиболее распространенным способом сложения векторов является правило треугольника. Чтобы сложить два вектора по этому правилу, необходимо расположить векторы параллельно друг другу таким образом, чтобы начало первого вектора совпадало с концом второго, при этом третья сторона полученного треугольника будет являться вектором суммы.

Также можно рассчитать сумму векторов по правилу параллелограмма. Векторы должны начинаться из одной точки, параллельно каждому вектору нужно начертить линию так, чтобы в итоге получился параллелограмм. Диагональ построенного параллелограмма будет являться суммой этих векторов.

Для вычитания двух векторов нужно сложить первый вектор и вектор, который будет противоположным второму. Для этого также используется правило треугольника, которое имеет следующую формулировку: разность векторов, которые перенесены таким образом, что их начала совпадают, является вектором, начало которого совпадает с концом вычитаемого вектора, а также с концом уменьшаемого вектора.
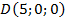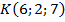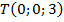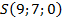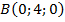
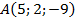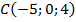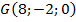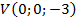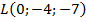