2.Квадратичная функция y=x² — Функции и их графики
В уравнении квадратичной функции:
a – старший коэффициент
b – второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:
Точки, обозначенные зелеными кружками – это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:
Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.
График функции имеет вид:
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.
Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .
В случае квадратичной функции нужно решить квадратное уравнение .
В процессе решения квадратного уравнения находим дискриминант: , который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:
2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ.
3. Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:
,
Если ,то график функции выглядит примерно так:
Следующий важный параметр графика квадратичной функции – координаты вершины параболы:
Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии паработы.
И еще один параметр, полезный при построении графика функции – точка пересечения параболы с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Функции y=x2 и y=x3 и их графики
Вопросы занятия:
· рассмотреть функцию y = x2, её свойства и график;
·
рассмотреть функцию y
= х3, её свойства и график.
Материал урока
На одном из предыдущих уроков мы с вами познакомились с линейной функцией, которую можно задать формулой вида:
Также вспомним, что графиком линейной функции является прямая.
На этом уроке мы рассмотрим функции:
А точнее, мы научимся строить графики этих функций и выясним некоторые их свойства.
Начнём с того, что выразим формулой зависимость площади квадрата от длины его стороны.Таким образом, зависимость площади квадрата от его стороны является примером функции.
Давайте построим график этой функции.
Составим таблицу значений x, y.
Далее полученные точки изобразим на координатной плоскости и проведём через них плавную линию.
Обратите внимание, что этот график неограниченно продолжается вверх справа и слева от оси игрек.
Теперь
выясним некоторые свойства функции y
= x2.
Из последнего свойства графика следует, что точки графика, имеющие противоположные абсциссы, симметричны относительно оси игрек.
Теперь давайте выразим формулой зависимость объёма куба от длины его ребра.
Если мы будем менять длину ребра, то и его объём будет меняться.
Зависимость объёма куба от длины его ребра является примером функции.
Построим график этой функции. Для этого придадим несколько значений аргументу икс и вычислим соответствующие значения функции.
Изобразим точки с полученными координатами на координатной плоскости и проведём через них плавную линию.
Обратите внимание, что этот график можно неограниченно продолжать справа от оси игрек вверх и слева от оси игрек вниз.
Поговорим о свойствах функции игрек равняется икс в кубе.
Следовательно,
точки графика, которые имеют противоположные абсциссы, расположены симметрично
относительно начала координат.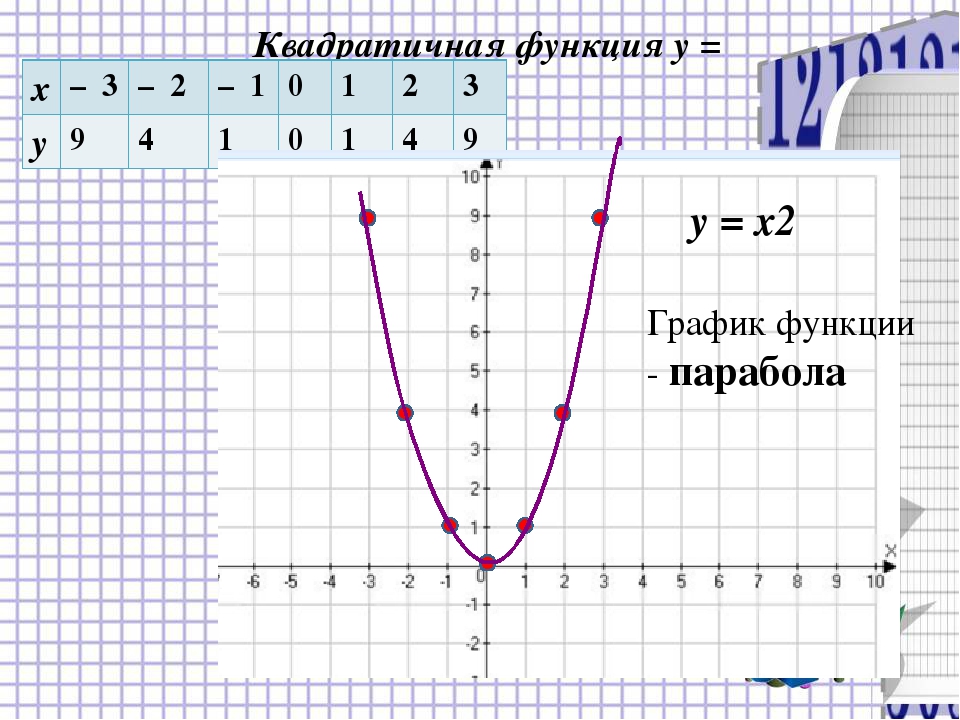
В повседневной жизни представление о параболе дают нам, например, траектории прыжков животных, радуга. Тросы висячего моста напоминают нам параболы.
Также параболу часто можно встретить в архитектуре.
Построение и решение графиков Функций
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Чтобы ребенок разобрался в теории и чувствовал себя увереннее на школьных контрольных, запишите его на современные уроки математики в онлайн-школу Skysmart.
Интерактивные задания, математические комиксы и карта прогресса в личном кабинете — математика еще никогда не была таким увлекательным приключением!
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x).
Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая.
На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки
— точки, в которых производная функции f(x) равна нулю.Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве.
Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции.
Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Как решаем:
Упростим формулу функции:
Задача 2.
Построим график функции
Как решаем:
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Как решаем:
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины
Ветви вверх, следовательно, a > 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 4. Построить графики функций:
а) y = 3x — 1
б) y = -x + 2
в) y = 2x
г) y = -1
Как решаем:
Воспользуемся методом построения линейных функций «по точкам».
а) y = 3x — 1
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
б) y = -x + 2
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
в) y = 2x
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
г) y = -1
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5.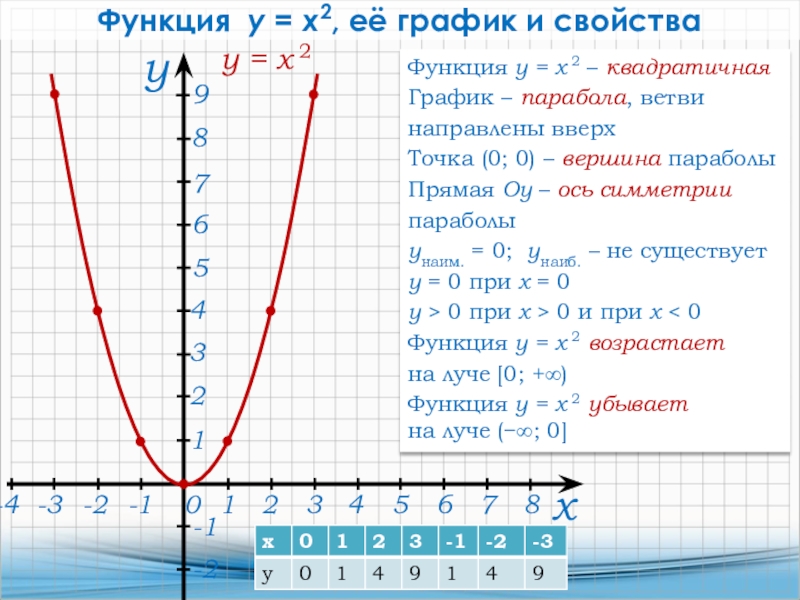
Построить график функции
Как решаем:
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
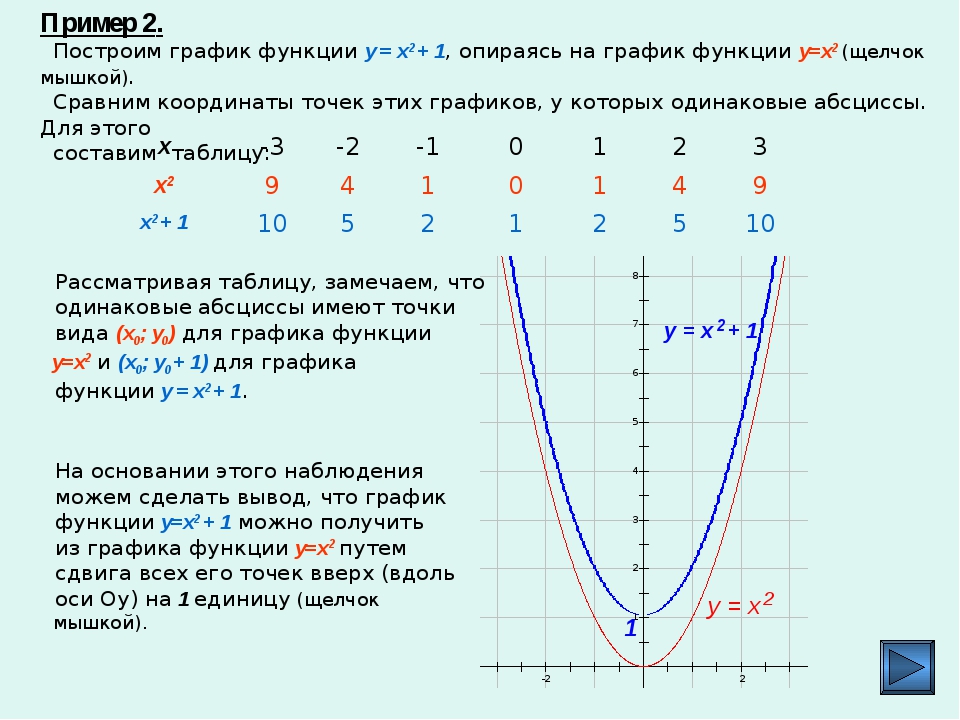
а) y = x² + 1
б)
в) y = (x — 1)² + 2
г)
д)
Как решаем:
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
y = x²
Сдвигаем график вверх на 1:
y = x² + 1
б)
Преобразование в одно действие типа f(x — a).
y = √x
Сдвигаем график вправо на 1:
y = √x — 1
в) y = (x — 1)² + 2
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
y = x²
Сдвигаем график вправо на 1:
y = (x — 1)²
Сдвигаем график вверх на 2:
y = (x — 1)² + 2
г)
Преобразование в одно действие типа
y = cos(x)
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
В детской школе Skysmart учиники чертят графики на специальной онлайн-доске. Учитель видит, как размышляет ученик и может вовремя его направить в нужную сторону.
Запишитесь на бесплатный вводный урок математики и занимайтесь в современном формате и с поддержкой заботливых учителей.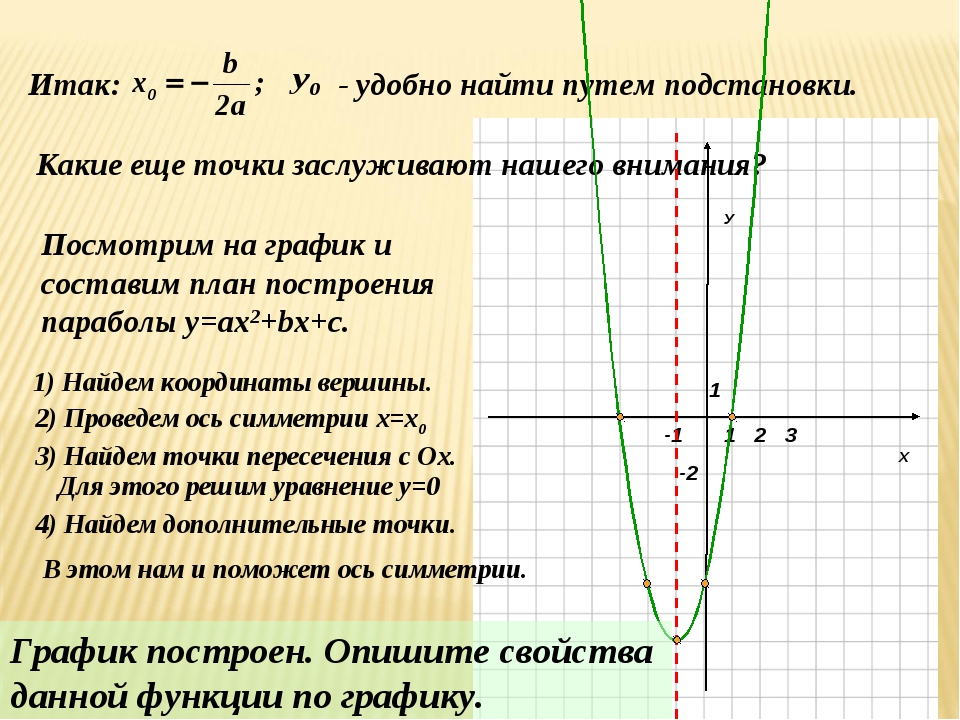
2 — 2x — 3′)
plt.ylabel(‘Ось y’)
plt.xlabel(‘Ось x’)
plt.grid()
plt.axis([-10, 16, -10, 10])
plt.scatter(x1, y1, s = 1, c = ‘b’)
plt.scatter(x1, -y1, s = 1, c= ‘b’)
plt.plot(x2, y2, ‘r—‘)
plt.plot(x2, -y2, ‘r—‘)
plt.show()
Вывод:
Надеюсь, из кода всё понятно, но немного поясню.
Поскольку |y| может быть только больше нуля, нам нужно выделить значения функции, которые >= 0 и нарисовать в основной части графика только их. Для этого мы делаем булевую маску для всех значений f(x) (в моём коде это значение обозначено как y, но мой y это не y из вашей формулы).
ind = y >= 0
Более понятно можно записать так:
ind = (y >= 0)
В ind у нас теперь булева маска, содержащая True на тех позициях, где y >= 0 и False, где y < 0.
Далее, мы отбираем по этой маске значения из наших массивов x и y:
x1 = x[ind]
y1 = y[ind]
А также мы отбираем остальные значения x и y, для чего инвертируем маску с помощью булевой операции инверсии ~ (где было True станет False и наоборот:
x2 = x[~ind]
y2 = y[~ind]
После этого мы рисуем основной график, причём два раза — один раз используя f(x), а другой раз -f(x) (по формуле |y| = f(x) получается, что у нас есть два графика: y = f(x) и y = -f(x)).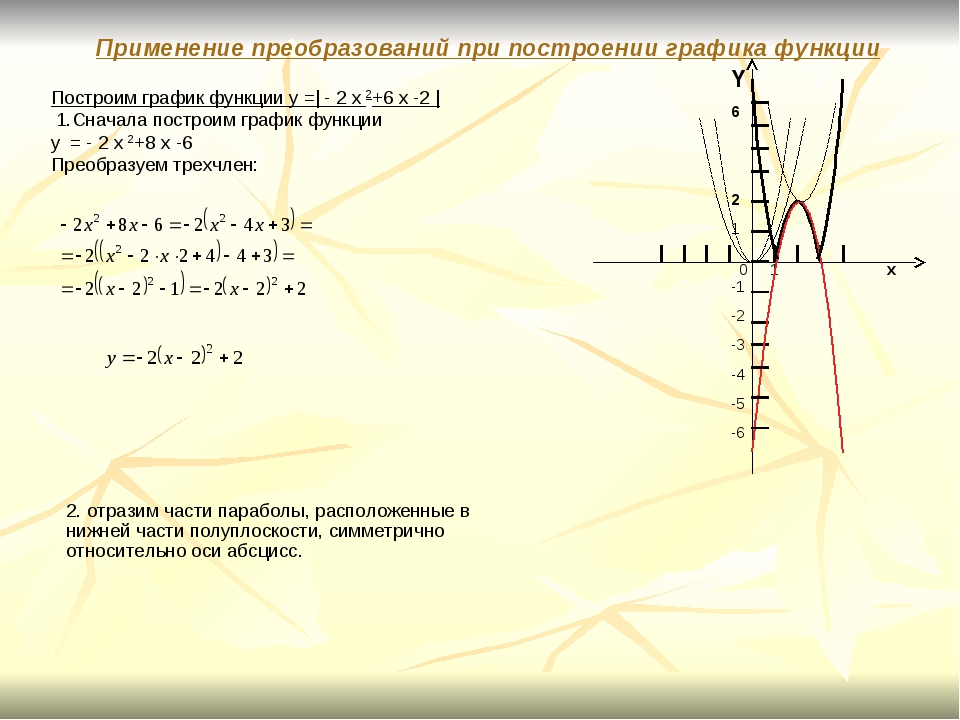
И затем рисуем псевдо-график там, где функция f(x) могла бы продолжаться, но из-за условия равенства модулю |y| она в этом месте прерывается.
y x2 2
Вы искали y x2 2? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как построить график функции y 2 x, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «y x2 2».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает.
Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как y x2 2,как построить график функции y 2 x,как построить график функции y 2 x 2,как построить график функции y 2x 2,как построить график функции y x в квадрате,парабола график функции у х2,у х 2 x 2. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и y x2 2. Просто введите задачу в окошко и нажмите
«решить» здесь (например, как построить график функции y 2 x 2).
Где можно решить любую задачу по математике, а так же y x2 2 Онлайн?
Решить задачу y x2 2 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе.
2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3 называется кубической функцией. Графиком кубической функции называется кубическая парабола. Общий вид параболы представлен на рисунке ниже.
Если график квадратичной функции был симметричен оси Оу, то график кубической параболы симметричен относительно начала координат, то есть точки (0;0).
Свойства кубической функции
Перечислим основные свойства кубической функции
- При х =0, у=0. у>0 при х>0 и y
- У кубической функции не существует не максимального ни минимального значения.
- Кубическая функция возрастает на всей числовой оси (-∞;+∞).
- Противоположным значениям х, соответствуют противоположные значения y.
Нужна помощь в учебе?
Предыдущая тема: Умножение одночленов и возведение одночлена в степень + примеры
Следующая тема:   Абсолютная погрешность: понятие, как вычислить + примеры
функция y=x² и её график, свойства, примеры
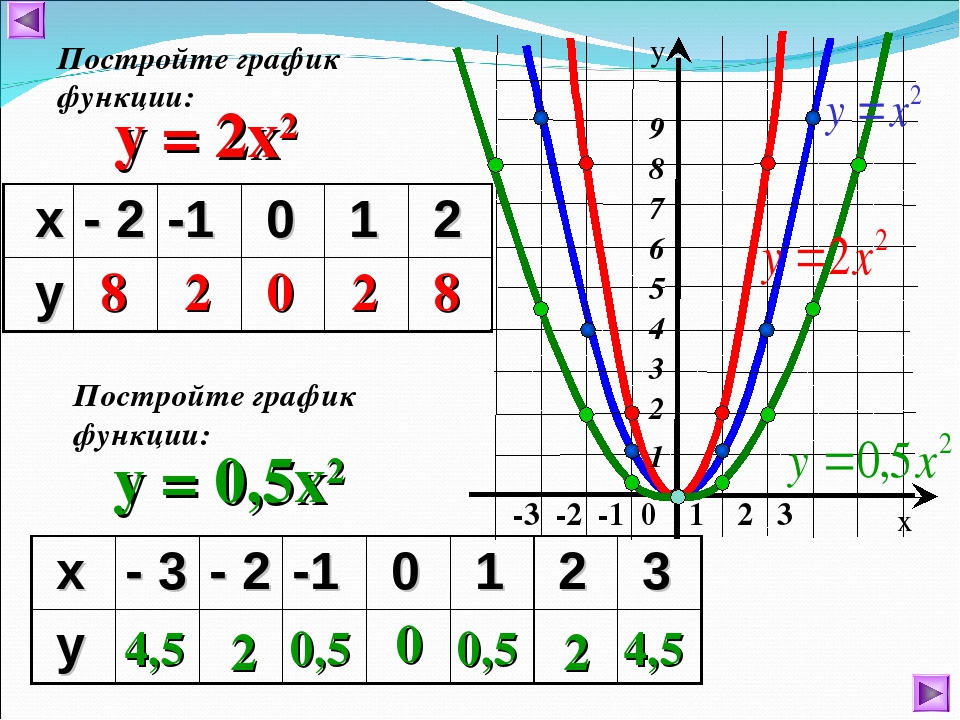
График функции y=x²
Составим таблицу для расчёта значений функции $y = x^2$:
x | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
$ y = x^2$ | 9 | 6,25 | 4 | 2,25 | 1 | 0,25 | 0 | 0,25 | 1 | 2,25 | 4 | 6,25 | 9 |
Отметим полученные точки на координатной плоскости и соединим их кривой:
Полученный график называют параболой.
2$, кроме двух точек с $ x \neq \pm 1 $.
РЕШЕНИЕ: 2) Для функции y = x2 — 4x — 5 выполните следующие задачи: a) Представьте функцию в форме y = a (x
РЕШЕНИЕ: 2) Для функции y = x2 — 4x — 5, выполнять следующие задачи: а) Представьте функцию в виде y = a (x — h) 2 + k. Отвечать: Показать работы в этой области б) Что такое т Алгебра -> Квадратичные уравнения и параболы -> РЕШЕНИЕ: 2) Для функции y = x2 — 4x — 5 выполните следующие задачи: а) Представьте функцию в виде y = a (x — h) 2 + k.Отвечать: Показать работы в этой области б) Что такое т Войти в систему
|
2 Графические квадратные уравнения с использованием оси симметрии
Квадратное уравнение это многочлен уравнение степень 2 . Стандартная форма квадратного уравнения:
0 знак равно а Икс 2 + б Икс + c
где а , б а также c все реальные числа и а ≠ 0 .
Если мы заменим 0 с участием у , то получаем квадратичная функция
у знак равно а Икс 2 + б Икс + c
чей график будет
парабола
.
Осью симметрии этой параболы будет линия Икс знак равно — б 2 а . Ось симметрии проходит через вершину, поэтому Икс -координата вершины — б 2 а .Заменять Икс знак равно — б 2 а в уравнении, чтобы найти у -координата вершины. Заменить еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -значения и нанесите точки. Присоединяйтесь к ним и вытяните параболу.
Пример 1:
Постройте параболу у знак равно Икс 2 — 7 Икс + 2 .
Сравните уравнение с
у
знак равно
а
Икс
2
+
б
Икс
+
c
найти значения
а
,
б
, а также
c
.
Здесь, а знак равно 1 , б знак равно — 7 а также c знак равно 2 .
Используйте значения коэффициентов, чтобы написать уравнение ось симметрии .
График квадратного уравнения в виде у знак равно а Икс 2 + б Икс + c осью симметрии является линия Икс знак равно — б 2 а . Итак, уравнение оси симметрии данной параболы имеет вид Икс знак равно — ( — 7 ) 2 ( 1 ) или же Икс знак равно 7 2 .
Заменять
Икс
знак равно
7
2
в уравнении, чтобы найти
у
-координата вершины.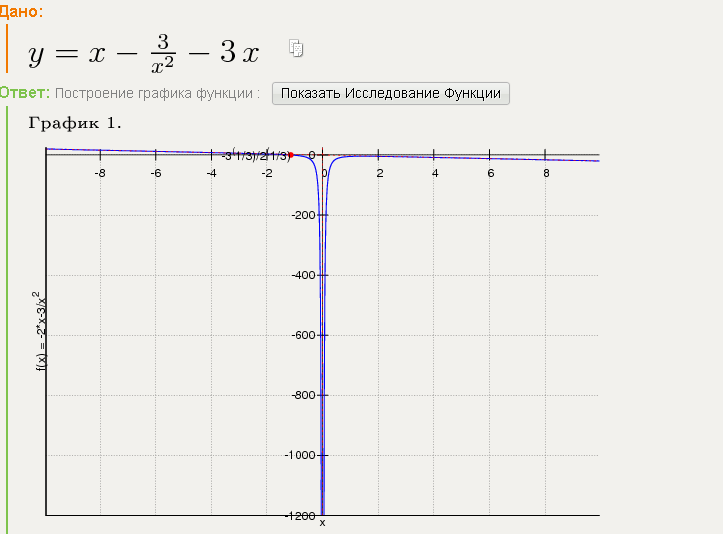
у знак равно ( 7 2 ) 2 — 7 ( 7 2 ) + 2 знак равно 49 4 — 49 2 + 2 знак равно 49 — 98 + 8 4 знак равно — 41 год 4
Следовательно, координаты вершины равны
(
7
2
,
—
41 год
4
)
.
А теперь замените еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -значения.
| Икс | у знак равно Икс 2 — 7 Икс + 2 |
| 0 | 2 |
| 1 | — 4 |
| 2 | — 8 |
| 3 | — 10 |
| 5 | — 8 |
| 7 | 2 |
Постройте точки и соедините их, чтобы получить параболу.
Пример 2:
Постройте параболу у знак равно — 2 Икс 2 + 5 Икс — 1 .
Сравните уравнение с у знак равно а Икс 2 + б Икс + c найти значения а , б , а также c .
Здесь, а знак равно — 2 , б знак равно 5 а также c знак равно — 1 .
Используйте значения коэффициентов, чтобы написать уравнение оси симметрии.
График квадратного уравнения в виде
у
знак равно
а
Икс
2
+
б
Икс
+
c
осью симметрии является линия
Икс
знак равно
—
б
2
а
.
Итак, уравнение оси симметрии данной параболы имеет вид
Икс
знак равно
—
(
5
)
2
(
—
2
)
или же
Икс
знак равно
5
4
.
Заменять Икс знак равно 5 4 в уравнении, чтобы найти у -координата вершины.
у знак равно — 2 ( 5 4 ) 2 + 5 ( 5 4 ) — 1 знак равно — 50 16 + 25 4 — 1 знак равно — 50 + 100 — 16 16 знак равно 34 16 знак равно 17 8
Следовательно, координаты вершины равны
(
5
4
,
17
8
)
.
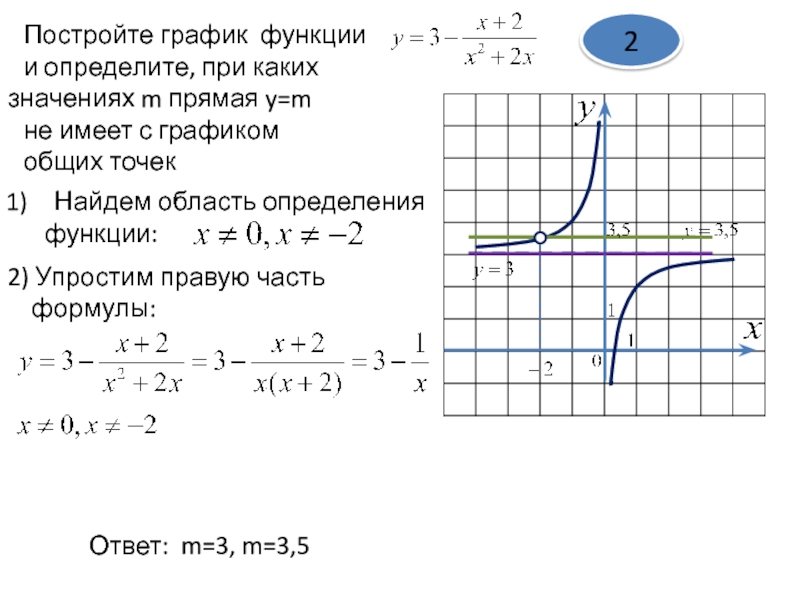
А теперь замените еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -значения.
| Икс | у знак равно — 2 Икс 2 + 5 Икс — 1 |
| — 1 | — 8 |
| 0 | — 1 |
| 1 | 2 |
| 2 | 1 |
| 3 | — 4 |
Постройте точки и соедините их, чтобы получить параболу.
Пример 3:
Постройте параболу Икс знак равно у 2 + 4 у + 2 .
Здесь, Икс является функцией у . Парабола открывается «вбок», а ось симметрии параболы горизонтальна. Стандартная форма уравнения горизонтальной параболы: Икс знак равно а у 2 + б у + c где а , б , а также c все реальные числа и а ≠ 0 а уравнение оси симметрии имеет вид у знак равно — б 2 а .
Сравните уравнение с
Икс
знак равно
а
у
2
+
б
у
+
c
найти значения
а
,
б
, а также
c
.
Здесь, а знак равно 1 , б знак равно 4 а также c знак равно 2 .
Используйте значения коэффициентов, чтобы написать уравнение оси симметрии.
График квадратного уравнения в виде Икс знак равно а у 2 + б у + c осью симметрии является линия у знак равно — б 2 а . Итак, уравнение оси симметрии данной параболы имеет вид у знак равно — 4 2 ( 1 ) или же у знак равно — 2 .
Заменять
у
знак равно
—
2
в уравнении, чтобы найти
Икс
-координата вершины.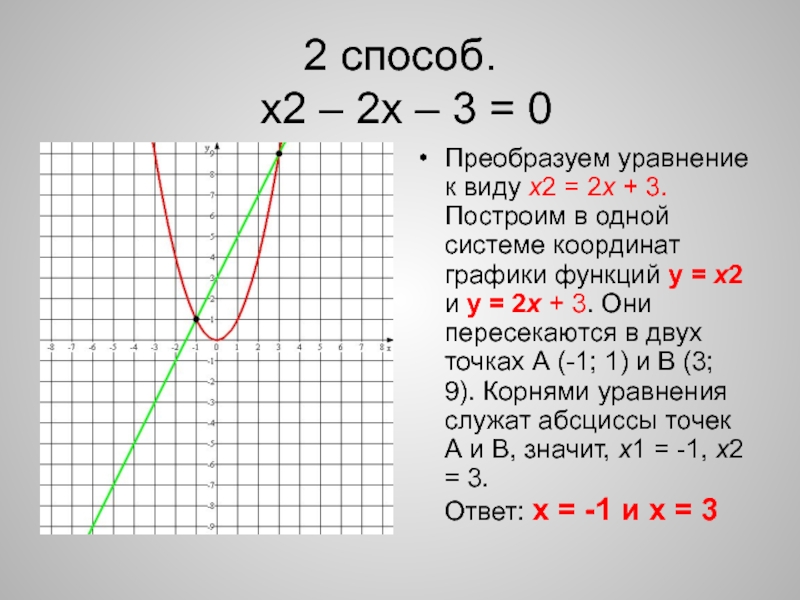
Икс знак равно ( — 2 ) 2 + 4 ( — 2 ) + 2 знак равно 4 — 8 + 2 знак равно — 2
Следовательно, координаты вершины равны ( — 2 , — 2 ) .
А теперь замените еще несколько у -значения в уравнении, чтобы получить соответствующие Икс -значения.
| у | Икс знак равно у 2 + 4 у + 2 |
| — 5 | 7 |
| — 4 | 2 |
| — 3 | — 1 |
| — 1 | — 1 |
| 0 | 2 |
| 1 | 7 |
Постройте точки и соедините их, чтобы получить параболу.
Графические уравнения, система уравнений с программой «Пошаговое решение математических задач»
Описание
Команда plot генерирует график практически любой функции или отношения, обнаруживаемого в математике средней школы и колледжа. Он будет отображать функции, заданные в форме y = f (x), например y = x 2 или y = 3x + 1, а также отношения вида f (x, y) = g (x, y) , например x 2 + y 2 = 4.
Чтобы использовать команду построения графика, просто перейдите к основному
страницу графика, введите свое уравнение (в терминах x и y), введите набор
значения x и y, для которых должен быть построен график, и нажмите «График»
кнопка.Ваше уравнение будет автоматически построено, и будет показан ответ.
в вашем браузере в течение нескольких секунд. Если вы хотите больше контроля над
процесс построения, продвинутый
страница графика позволяет отображать несколько графиков на одной диаграмме, а также
для точной настройки внешнего вида графиков с помощью ряда опций.
2 от x = 0 до x = 2, y = 0 до y = 3, показывающий линии сетки, но без галочки.2 = 1 от x = -2 до x = 2, y = -1,8 до y = 1,8
Параметры (только расширенная страница)
Деления Значения: отмечен или не отмечен
По умолчанию: установлен
Если установлен флажок Отметки, оси графика будут отображать отметки и числовые шкалы.
Линии сетки
Значения: установлен или не установлен
По умолчанию: не установлен
Если установлен флажок Линии сетки, на график будет наложена синяя сетка.
Оси
Значения: Нет или Автоматическая исходная точка или Исходная точка в (#, #)
По умолчанию: Автоматическая исходная точка
Параметр «Оси» управляет внешним видом и расположением осей на графике. Если отмечено «Нет», оси не будут отображаться вообще. Когда отмечено Автоматическое начало координат, оси будут отображаться. Две оси обычно пересекаются в точке (0,0), но иногда эта точка пересечения может быть расположена в другом месте.
Когда установлен флажок «Исходная точка в (#, #)» и вводится точка, оси будут отображаться, и их точка пересечения будет принудительно находиться в указанной точке.
Соотношение сторон
Значения: Один к одному или Золотое сечение или #: #
По умолчанию: Один к одному
Параметр Соотношение сторон управляет соотношением высоты графика к его ширине. Когда установлен флажок «Один к одному», соотношение составляет 1: 1, и масштабы на двух осях будут идентичными. Это гарантирует, что круги, например, действительно будут отображаться на экране круглыми. Когда выбрано золотое сечение, соотношение сторон составляет 1: 1 / г, где g — золотое сечение (приблизительно 1.6180). Это якобы дает соотношение высоты к ширине, которое особенно «приятно» для глаз. Когда выбрано #: # и введены два значения, будет применяться указанное соотношение сторон. Это полезно, если сюжет сильно сжат в одном или другом направлении и его нужно «растянуть», чтобы сделать его более четким.
{2} + k [/ latex]
где [latex] \ left (h, \ text {} k \ right) [/ latex] — вершина.2 [/ латекс]
Величина [латекса] а [/ латекса] указывает на растяжение графика. Если [latex] | a |> 1 [/ latex], точка, связанная с определенным значением [latex] x [/ latex], смещается дальше от оси [latex] x [/ latex] –, поэтому график кажется, становится уже, и появляется вертикальная растяжка. Но если [latex] | a | <1 [/ latex], точка, связанная с определенным значением [latex] x [/ latex], смещается ближе к оси [latex] x [/ latex] –, поэтому график кажется шире, но на самом деле есть вертикальное сжатие.{2}} {4a} \ end {align} [/ latex]
На практике, однако, обычно легче запомнить, что [latex] h [/ latex] является выходным значением функции, когда входным значением является [latex] h [/ latex], поэтому [latex] f \ left (h \ right) = f \ left (- \ dfrac {b} {2a} \ right) = k [/ latex].
Попробуй
Сетка координат наложена на квадратную траекторию баскетбольного мяча на рисунке ниже.
{2} +7 [/ латекс].Чтобы сделать снимок, [latex] h \ left (-7,5 \ right) [/ latex] должно быть около 4, но [latex] h \ left (-7,5 \ right) \ приблизительно 1,64 [/ latex]; он не выживает.
Внесите свой вклад!
У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.
Улучшить эту страницуПодробнее
Задача 5
Задача 55. Ничья график y = f ( x ) = x 2 + 2 x — 8.
- а) Что такое перехват и ?
- б) Каковы корни?
- в) Каковы координаты вершины?
- г) Запишите уравнение в стандарте или вершине форма.
- e) Решить относительно x
x 2 + 2 x -8 > 0
Прежде чем рисовать график, нужно ответить на вопросы а), б), и в).
а) Что такое перехват и ?
Пересечение y — это точка на графике, координата которой x равна 0.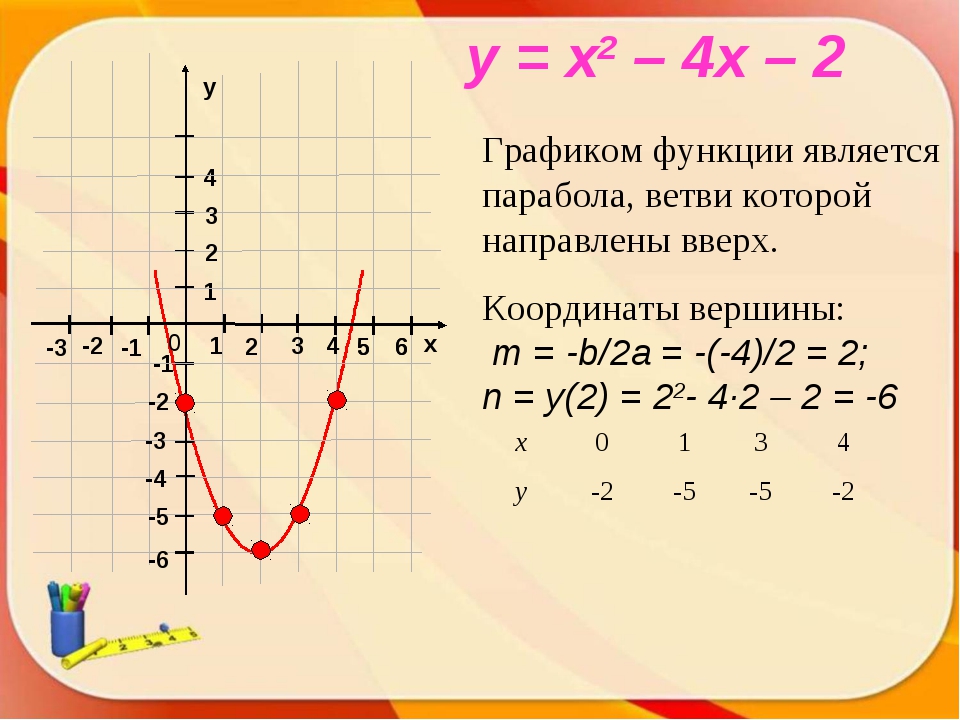
Итак, пусть x = 0 в уравнении, и мы получим
Это показывает, что пересечение y всегда является постоянным членом в полиноме.
верх
б) Какие корни?
Корни — это еще одно название для перехватчиков x . Они точек на графике, координаты которых y равны 0. Итак, пусть y = 0 в уравнение и получаем
0 = x 2 + 2 x — 8Это дает нам квадратное уравнение в x .& mbsp; Нам повезло чтобы на одной стороне уже был 0, так что мы готовы к факторизации.
0 = ( x -2) ( x + 4)Установите коэффициенты = 0.
x — 2 = 0 или x + 4 = 0Решить относительно x
x = 2 или x = -4верх
в) Каковы координаты вершины?
Если мы воспользуемся формулой для координаты x вершины, то
получаем
или
х = -1Теперь, когда у нас есть координата x- вершины, мы запускаем это число через функцию, чтобы найти координату y-
y = f (-1) = (-1) 2 + 2 (-1) — 8 = 1-2-8 = -9Итак, вершина находится в (-1, -9)
верх
Рекомендуется получить всю эту информацию перед построением графика.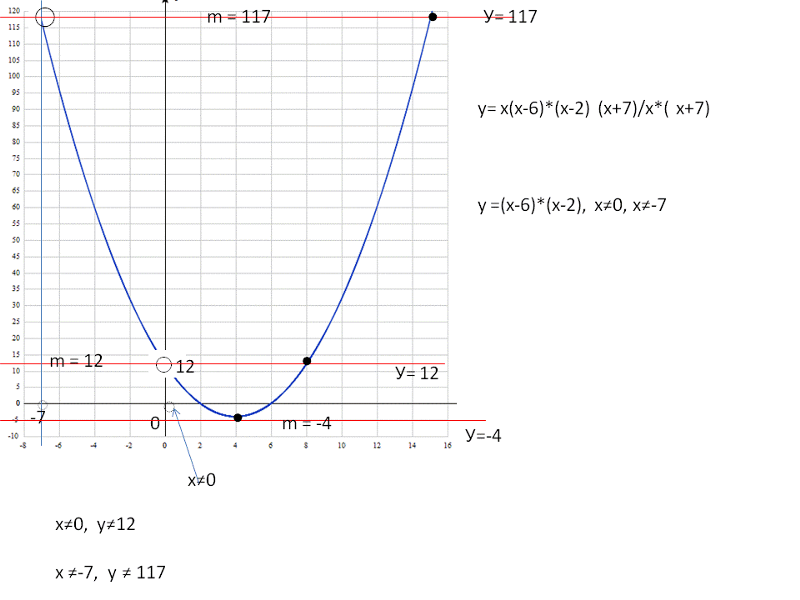
точки, чтобы нарисовать график.Когда мы наносим точки, поскольку теперь мы знаем, что
координата x вершины равна -1, мы хотим, чтобы -1 находился в
середина x , которые мы рисуем. Нам также понадобятся корни, x = -4
и 2, чтобы быть в интервале, содержащем x , которые мы строим, и в
хотя бы одна точка по другую сторону корней от вершины.
Когда мы строим эти точки, мы получаем
верх
г) Запишите уравнение в виде вершины.
Уравнение составляет
y = x 2 + 2 x — 8Половина линейного коэффициента равна 1, а квадрат 1 равен 1, поэтому складываем и вычитаем 1
y = x 2 + 2 x + 1-1-8Это упрощается до
y = ( x + 1) 2 — 9и мы видим координаты вершины в уравнении.
верх
e) Решите относительно x
x 2 + 2 x -8 ≥ 0 В процессе построения графика мы обнаружили
что корни были в -4 и 2.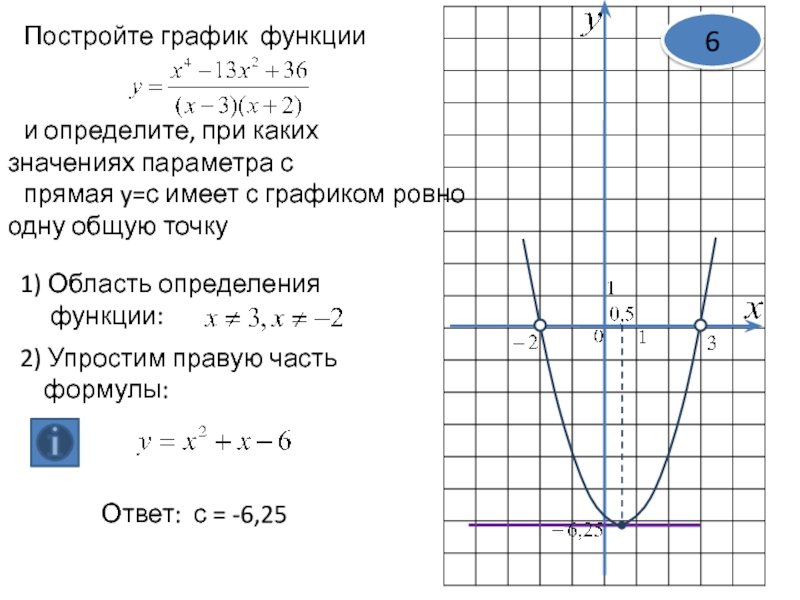
Когда мы делим вещественное число на прямую
в промежутки между корнями, и проверьте x в каждом
интервал.
Поскольку равенство разрешено, конечные точки интервалов, корни, являющиеся x , которые дадут ответы, равные 0 при подстановке в формулу будут решениями.Итак, рисуем квадратные скобки вокруг конечных точек.
Набор решений — это набор x , которые удовлетворяют
x ≤ -4 или x ≥ 2
В обозначении интервалов это получается
(-∞, -4] ∪ [2, ∞)
верх
Вернуться к тесту
Графики Квадратичные функции: примеры (стр. 3 из 4) Разделы: Введение, Значение ведущего коэффициента / Вершина, Примеры
Это та же квадратичная как в последнем примере. Я уже нашел вершину, когда работал над проблема выше. На этот раз мне также нужно найти точки пересечения, прежде чем я сделаю свой график. Чтобы найти перехват y , Я устанавливаю x равным нулю и решаю: Тогда y -перехват это точка (0, –2). Чтобы найти перехват x , Я устанавливаю y равным нулю и решаю: Тогда x -перехват находятся в точках (–1, 0) и ( 2 / 3 , 0).
Чтобы найти перехват y , Я устанавливаю x равным 0 и решаю: Чтобы найти перехват x , Я устанавливаю y равным 0 и решаю: 0 = x 2 — x — 12 0 = ( x — 4) ( x + 3) x = 4 или x = –3 Чтобы найти вершину, я посмотрите на коэффициенты: a = 1 и b = –1.Включение в формула, я получаю: Найти k , I заглушка h = 1 / 2 дюйма для x внутри y = x 2 — x — 12, и упростить: Когда у меня есть вершина, ось симметрии легко записать: x = 0,5. Сейчас Я найду несколько дополнительных точек графика, чтобы заполнить график: Для моего удобства, Я выбрал значения x которые были сосредоточены вокруг координаты x вершины.Теперь я могу построить параболу: Авторские права © Элизабет Стапель 2002-2011 Все права защищены. Вершина
в точке (0,5, –12,25), << Предыдущий Вверх | 1 | 2 | 3 | 4 | Вернуться к указателю Далее >>
|
3.1 Некоторые U-образные графики | G’Day Math
Руководство по содержаниюдля учителей PDF
РАЗДАЧИ СТУДЕНТОВ
Dexter_Course on Quadratics
Один из первых — обычно первый — непрямолинейный график, с которым сталкиваются в школе, — это график квадратного уравнения.2 \) когда-нибудь вертикально?
(Все ответы на практические вопросы приведены в конце РУКОВОДСТВА ДЛЯ УЧИТЕЛЯ по этому опыту.)
Я буду продолжать использовать фразу U-образная кривая или U-образная кривая , даже если это технически неверно. 2 \) (ну, фактически, вращаем его) против часовой стрелки относительно начала координат просто \ (0.01 \) градусов. Перехватывает ли ось \ (y \) этот наклонный график при некотором большом ненулевом значении?
Опять же, решения всех этих практических проблем можно найти в РУКОВОДСТВЕ ДЛЯ УЧИТЕЛЯ. Но позвольте мне помочь вам с этим вопросом прямо сейчас, поскольку на него чрезвычайно сложно ответить.
Математики тоже люди и тоже боятся вопросов и математических задач. Но один прием, который они часто используют, когда сталкиваются с вопросом, на который сначала не знают, как ответить, — это изменить вопрос!
Что самое страшное в этом вопросе? Это наклоняет U-образный график.Как на самом деле это сделать? Я лично не знаю! Итак, давайте вместо этого наклоним что-нибудь другое. Что, если мы сохраним график и вместо этого наклоним вертикальную ось на \ (0,01 \) градуса по часовой стрелке? Эта наклонная линия пересекает U-образный график?
Ой! Подожди! Это эквивалентно ответу на исходную проблему?
Вот самый большой сюрприз из всех этих U-образных графиков. Многие люди упускают из виду этот шок, когда впервые изучают квадратные уравнения.2 \) представляет собой симметричную U-образную кривую. С другой стороны, график \ (y = 2x \) — нет! Это прямая линия, проходящая через начало координат с антисимметрией, если хотите — график данных поднимается вправо, а уменьшается влево.
Теперь о странном вопросе: какая картина была бы получена, если бы мы «сложили» эти два графика?
Что мы могли под этим подразумевать?
Давайте посмотрим на каждое значение \ (x \) и сложим соответствующие им значения \ (y \).2 \), а линейное выражение \ (y = bx + c \) обязательно даст выражение, график которого представляет собой тот же симметричный U-образный график, возможно, сглаженный или немного скрученный, и, возможно, смещенный в новое положение на плоскости. .
Это просто поразительно!
Эта U-образная форма удивительно прочна, и нельзя не восхищаться ее надежностью.
Конечно, можно объяснить, почему это явление построения графиков имеет место, анализируя алгебру квадратных уравнений.Но, надеюсь, вы были столь же шокированы этим явлением, когда впервые начали учиться квадратичному графу.
Комментарий: Если вы ищете обзор квадратиков, их алгебры и их графиков, полный всех сюрпризов и потрясений, посетите www.gdaymath.com/courses.
Теперь о проблеме, которую мы рассмотрим в этих заметках.
Насколько распространены эти U-образные кривые квадратиков?
Являются ли U-образные кривые, которые мы видим во всевозможных контекстах, в основном одной и той же U-образной (возможно, как я уже сказал, они просто стали немного круче или сглажены и переместились или даже перевернулись)? Являются ли эти кривые настолько устойчивыми, чтобы иметь универсальный характер?
Например, школьная физика говорит нам, что путь брошенного объекта следует по дуге квадратичного графа.Это правда? Откуда нам знать?
Известный итальянский математик и физик Галилео Галилей (1564–1642) задался вопросом о форме цепи, висящей между двумя полюсами. (Мы видим эту форму в свисающих линиях электропередач, в форме веревок, которые окружают скульптуры в художественных музеях и т. Д.). Это та же самая квадратная U-образная форма? Откуда мы могли знать?
Греческие ученые древности использовали геометрию для описания всевозможных особых кривых. Они назвали одну из своих кривых параболой , и она тоже имеет U-образную форму.
Алгебра не была изобретена еще около 800 лет, поэтому эти ученые не задавались вопросом: Дана ли эта кривая квадратным уравнением? Но мы можем! Итак, это так? Откуда мы могли знать?
Знаменитая арка ворот Сент-Луиса в штате Миссури, США, имеет форму квадратичной кривой?
Является ли график уравнения, в котором записано мое прозвище, JIM, квадратичным? Эта кривая проходит через точки
\ (x = 1 \), \ (y = 10 \) и 1 -я буква моего имени — это 10 -я буква алфавита, J;
\ (x = 2 \), \ (y = 9 \) и 2 -я буква моего имени — это 9 -я буква алфавита, I;
\ (x = 3 \), \ (y = 13 \) и 3 -я буква моего имени — это 13 -я буква алфавита, М.