Общая схема исследования графика функции
Схема исследования функции
- Найти область значений E(f) и область определения D(f) функции;
- Определить четность или нечетность функции, периодичность функции;
- Найти точки пересечения графика функции с осями координат;
- Нахождение вертикальной, горизонтальной и наклонной асимптоты;
- Определение критических точек, экстремумов функции, наибольшее и наименьшее значение, интервалы монотонности функции — возрастания и убывания функции;
- Определение интервалов вогнутости, выпуклости, точек разрыва и перегиба функции;
- Построить график исходной функции (построить график, касательную и её производную онлайн).
Пример
Исследовать функцию и построить график функции
$y = \frac{{{x^2}}}{{x — 2}}$
Решение
1.
D(f)=(−∞;2)∪(2;+∞)
E(f)=(−∞;0)∪(8;+∞)
2.
Функция ни четная и ни нечётная, непериодическая
${\rm{f}}\left( { — {\rm{x}}} \right) = \frac{{{{( — x)}^2}}}{{ — x — 2}} = \frac{{{x^2}}}{{ — x — 2}}$
3.
Ox: ${\rm{y}} = \frac{{{x^2}}}{{x — 2}} = 0$, x=0 точка (0;0)
Oy: x=0, y=0 точка (0;0)
4.
Так как
$\mathop {{\rm{lim}}}\limits_{x \to + 2} \frac{{{x^2}}}{{x — 2}} = + \infty $
$\mathop {{\rm{lim}}}\limits_{x \to — 2} \frac{{{x^2}}}{{x — 2}} = — \infty $
следовательно
x = 2 — вертикальная асимптота
Уравнение наклонной асимптоты (как определить её, пример см. здесь)
y=x+2
5.
Вычисляем первую производную функции: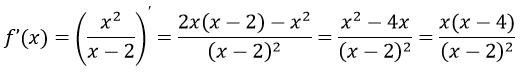
Находим критические точки:
$\frac{{x\left( {x — 4} \right)}}{{{{\left( {x — 2} \right)}^2}}} = 0$
отсюда получаем корни уравнения
x=2, x=4, x=0
Исследуем знак производной на интервалах
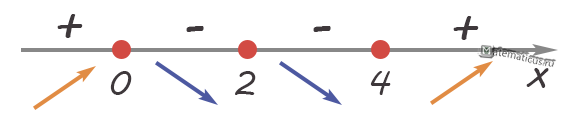
Функция возрастает при
$x∈\left( { — \infty ;0} \right)\mathop \cup \nolimits \left( {4; + \infty } \right)$
Функция убывает при
$x∈\left( {0;2} \right)\mathop \cup \nolimits \left( {2;4} \right)$
Функция имеет максимум при f(0)=0
Функция имеет минимум при
$f(4) = \frac{{{4^2}}}{{(4 — 2)}} = 8$
6.
Вычисляем вторую производную
${\rm{f}}\left( {\rm{x}} \right) = \left( {\frac{{{x^2} — 4x}}{{{{\left( {x — 2} \right)}^2}}}} \right){\rm{}} = \frac{{\left( {2x — 4} \right){{\left( {x — 2} \right)}^2} — \left( {{x^2} — 4x} \right)\left( {2x — 4} \right)}}{{{{\left( {x — 2} \right)}^4}}} = \frac{{4\left( {2x — 4} \right)}}{{{{\left( {x — 2} \right)}^4}}}$
Приравниваем к нулю и находим критические точки:
$\frac{{4\left( {2x — 4} \right)}}{{{{\left( {x — 2} \right)}^4}}} = 0$
x=2 точка разрыва функции
Функция выпукла вверх при x∈(−∞;2)
Функция выпукла вниз при x∈(2;+∞)
Точки перегиба нет.
7.
Строим график функции
Онлайн график можно построить здесь.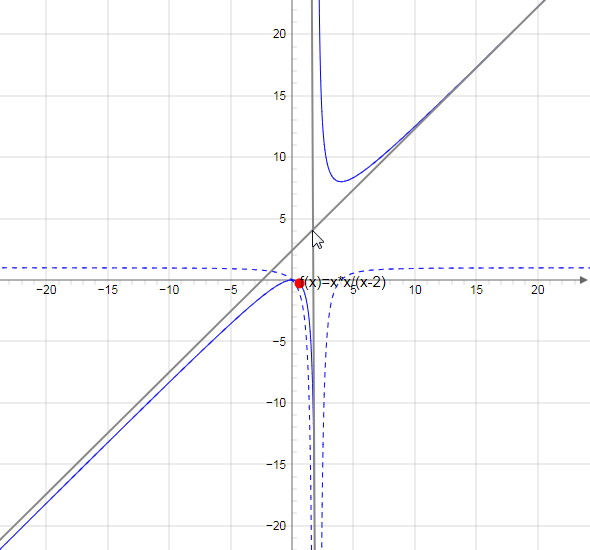
Пунктирной линией показана производная функции.
Общая схема исследования функции и построения графиков (Лекция №11)
- Найти ОДЗ и точки разрыва функции.
- Найти точки пересечения графика функции с осями координат.
- Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.
- Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.
- Найти асимптоты графика функции: а) вертикальные, b) наклонные.
- На основании проведенного исследования построить график функции.
Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной.
Вспомним, что функция называется четной, если при изменении знака аргумента значение функции не меняется: f(-x) = f(x) и функция называется нечетной, если f(-x) = -f(x).
В этом случае достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих ОДЗ. При отрицательных значениях аргумента график достраивается на том основании, что для четной функции он симметричен относительно оси Oy, а для нечетной относительно начала координат.
Примеры. Исследовать функции и построить их графики.
- .
1. Область определения функции D(у)= (–∞; +∞). Точек разрыва нет.
Пересечение с осью Ox: x = 0,у=
0.Функция нечетная, следовательно, можно исследовать ее только на промежутке [0, +∞).
2. . Критические точки: x1 = 1; x2= –1. 3. 4. а) Вертикальных асимптот нетб) . Асимптота – y = 0.
- .
- D(y)=(–∞; +∞). Точек
разрыва нет.
Пересечение с осью Ox: .
- .
- а) Вертикальных асимптот нет
б).
Наклонных асимптот нет.
- D(y)=(–∞; +∞). Точек
разрыва нет.
- .
- D(y)=(0; +∞). Функция
непрерывна на области определения.
Пересечение с осью :
- а) .
Вертикальная асимптота x = 0.
б).Наклонная асимптота
- D(y)=(0; +∞). Функция
непрерывна на области определения.
- .
- D(y)=(
–∞;0)È(0;1)È(1;+∞).
Функция имеет две точки разрыва x= 0 и x= 1.
Точек пересечения с осями координат нет.
- при любых действительных значениях x. Поэтому функция возрастает на всей числовой прямой.
-
а)
Вертикальные асимптоты x = 0, x = 1.
б)
Наклонная асимптота y = x + 1.
- D(y)=(
–∞;0)È(0;1)È(1;+∞).
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
Во многих приложениях математического анализа встречаются комбинации показательных функций. Эти комбинации рассматриваются как новые функции и обозначаются:
– гиперболический синус.
– гиперболический косинус.
С помощью этих функций можно определить еще две функции.
– гиперболический тангенс.
– гиперболический котангенс.
Функции sh x, ch x, th x определены, очевидно, для всех значений x, т.е. их область определения (–∞; +∞). Функция же cthx определена всюду за исключением точки x = 0.
Между гиперболическими функциями существуют следующие соотношения, аналогичные соответствующим соотношениям между тригонометрическими функциями.
Найдем: .
Т.е. .
.
Итак, .
Следовательно, .
Найдем производные гиперболических функций
.
Аналогично можно показать .
.
Т.е. и .
Графики гиперболических функций. Для того чтобы изобразить графики функций
shx и chx нужно вспомнить графики функций y = ex и y = e—x
Проведем исследования функции y = th x
- D(f) = (–∞; +∞), точек разрыва нет.
- Точка пересечения с осями координат .
-
, функция возрастает на (–∞; +∞).
- Вертикальной асимптоты нет.
.
y = cth x
- D. Точка разрыва x = 0 cth x = 0 – нет
-
убывает на .
- При x → +∞
Общая схема исследования функции и построение ее графика. — Студопедия
Изучение заданной функции и построение ее графика целесообразно проводить в следующем порядке:
1. Найти область определения функции.
2. Исследовать функцию на четность – нечетность.
3. Исследовать функцию на периодичность.
4. Найти точки пересечения с осями координат.
5. Найти экстремумы и интервалы монотонности функции.
6. Найти интервалы выпуклости и вогнутости и точки перегиба.
7. Найти асимптоты графика функции.
8. При необходимости найти некоторые дополнительные точки, уточняющие график функции.
9. Построить график на основе проведенного исследования.
Пример 12.2. Исследовать функцию 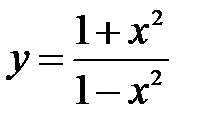 и построить ее график.
и построить ее график.
Решение:
1. Найдем область определения функции.
Данная функция имеет смысл, если знаменатель отличен от нуля:
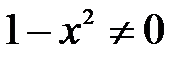 ;
; 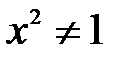 ;
; 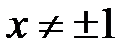 .
.
Таким образом, областью определения функции является множество всех действительных чисел, кроме 
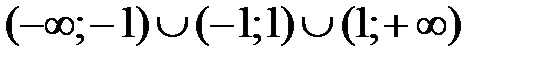 .
.2. Исследуем функцию на четность – нечетность.
Поскольку  , то функция четная, а ее график симметричен относительно оси ординат.
, то функция четная, а ее график симметричен относительно оси ординат.
3. Исследуем функцию на периодичность.
Данная функция не является периодической.
4. Найдем точки пересечения с осями координат.
Точка пересечения с осью ординат–  :
: 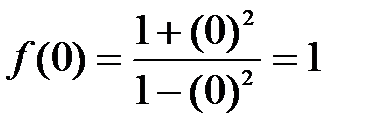 .
.
Точка пересечения с осью абсцисс– 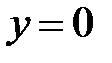 :
: 
5. Найдем экстремумы и интервалы монотонности функции.
· Найдем производную заданной функции:
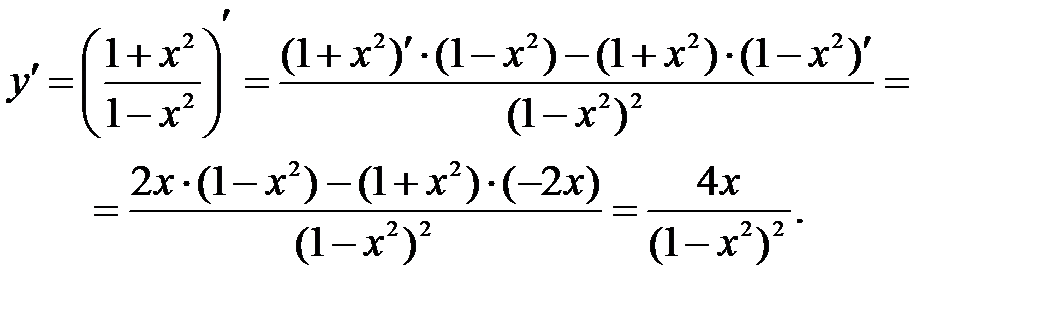
· Найдем точки, в которых
производная равна нулю –  =0:
=0: 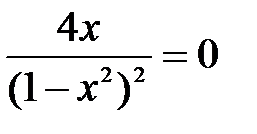 при
при 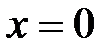 ;
;
производная не существует:  при
при 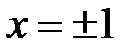
Однако критической является только точка  , так как значения
, так как значения 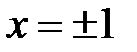 не входят в область определения функции.
не входят в область определения функции.
· Исследуем изменение знака производной при переходе через критическую точку:
при 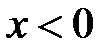
 ,при
,при 
 .
.
Таким образом,  – точка минимума, а
– точка минимума, а 
 и
и 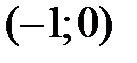 функция убывает, на интервалах
функция убывает, на интервалах 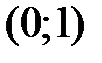 и
и  функция возрастает.
функция возрастает.6. Найдем интервалы выпуклости и вогнутости и точки перегиба.
· Найдем вторую производную заданной функции:
 .
.
· Найдем точки, в которых
вторая производная равна нулю – 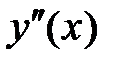 =0:
=0: 
вторая производная не существует: 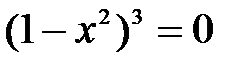 при
при  .
.
Критических точек на перегиб нет, так как значения 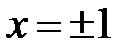 не входят в область определения функции.
не входят в область определения функции.
· Исследуем изменение знака второй производной:
на интервалах  и
и 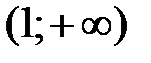
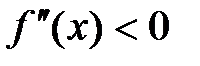 ,на интервале
,на интервале 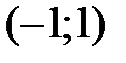
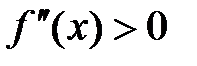 .
.
Таким образом, точек перегиба нет; на интервалах  и
и 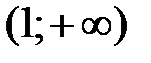 график функции выпуклый, а на интервале
график функции выпуклый, а на интервале 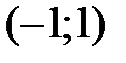 – вогнутый.
– вогнутый.
7. Найдем асимптоты.
· Исследуем поведение функции вблизи точек разрыва  :
:
 , следовательно, прямая
, следовательно, прямая 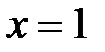 есть вертикальная асимптота. В силу симметричности графика функции
есть вертикальная асимптота. В силу симметричности графика функции  также вертикальная асимптота.
также вертикальная асимптота.
· Выясним поведение функции на бесконечности:
 .
.
Таким образом, прямая 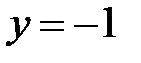 – горизонтальная асимптота.
– горизонтальная асимптота.
· Найдем наклонную асимптоту.
 .
.
Таким образом, наклонных асимптот нет.
9. График функции изображен на рисунке 12.1.
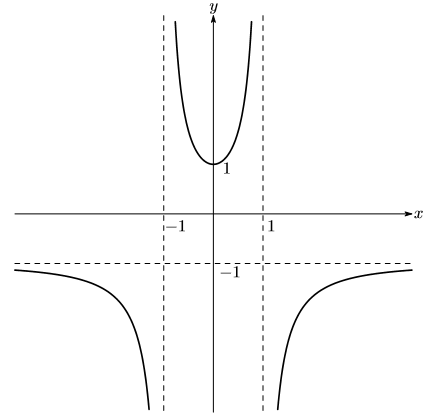
Рис. 12.1.График функции 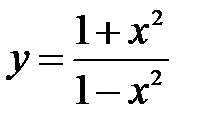 .
.
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Схема исследования поведения функций, применяемая для построения графиков функций
Для построения графика функции y = f (x) желательно сначала провести исследование поведения функции y = f (x) по следующей схеме.
Найти область определения D ( f ).
Выяснить, является ли функция y = f (x) четной или нечетной.
Выяснить, является ли функция y = f (x) периодической.
Найти асимптоты графика функции.
Вычислить производную функции f ‘ (x) .
Найти критические точки функции y = f (x) .
Найти интервалы возрастания и убывания функции y = f (x) .
Найти экстремумы функции y = f (x) .
Найти точки пересечения графика функции y = f (x) с осями координат.
Если не удается точно найти нули функции, то есть точки, в которых график функции пересекает ось абсцисс Ox, то нужно попытаться найти интервалы, на которых нули функции располагаются. Часто эти интервалы удается найти, зная точки максимума и минимума функции.
Вычислить вторую производную функции f » (x) .
Найти интервалы, на которых функция y = f (x) выпукла вверх, а также интервалы, на которых функция y = f (x) выпукла вниз.
Найти точки перегиба графика функции y = f (x) .
Замечание. Желательно рисовать схему поведения функции параллельно с проведением исследования свойств функции по описанному выше плану.
Примеры построения графиков функций
Пример 1. Построить график функции
| y = x3 + 8x2 + 16x + 128 | (1) |
Решение. Областью определения функции (1) является вся числовая прямая .
.
Функция (1) не является ни четной, ни нечетной.
Функция (1) не является периодической.
Вертикальных асимптот у графика функции (1) нет, так как для любого числа x0
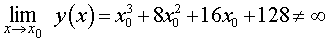
Проверим, есть ли у графика функции (1) наклонные асимптоты. Поскольку


то делаем вывод, что наклонных асимптот у графика функции (1) нет.
Теперь вычислим производную функции (1):
y’ (x) = 3x2 + 16x + 16 .
Поскольку y’ (x) существует для всех  , то все критические точки функции являются ее стационарными точками, то есть точками, в которых
, то все критические точки функции являются ее стационарными точками, то есть точками, в которых
y’ (x) = 0 .
Найдем стационарные точки функции (1), интервалы, на которых y’ (x) сохраняет знак, а также экстремумы функции. Для этого решим квадратное уравнение
3x2 + 16x + 16 = 0.
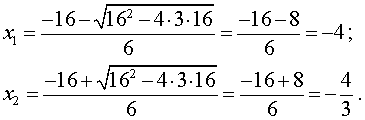
Изобразим на рисунке 1 диаграмму знаков производной y’ (x)
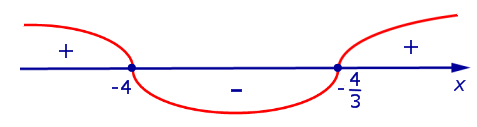

Рис.1
На интервалах  и
и  производная y’ (x) положительна, значит, функция (1) возрастает. На интервале
производная y’ (x) положительна, значит, функция (1) возрастает. На интервале  производная y’ (x) отрицательна, значит, функция (1) убывает. Схематически поведение функции (1) изображено на рисунке 2.
производная y’ (x) отрицательна, значит, функция (1) убывает. Схематически поведение функции (1) изображено на рисунке 2.


Рис.2
При переходе через точку x = – 4 производная функции y’ (x) меняет знак с «+» на «–» . Следовательно, точка x = – 4 является точкой максимума функции (1). При переходе через точку 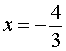 производная функции y’ (x) меняет знак с «–» на «+» . Следовательно, точка
производная функции y’ (x) меняет знак с «–» на «+» . Следовательно, точка 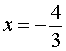 является точкой минимума функции (1).
является точкой минимума функции (1).
Найдем значения функции (1) в стационарных точках:
y (–4) = 256 ,

Теперь вычислим вторую производную функции (1):
y» (x) = (y’ (x))‘ = (3x2 + 16x + 16)‘ = 6x + 16 .
y» (x) = (y’ (x))‘ =
= (3x2 + 16x + 16)‘ =
= 6x + 16 .
Вторая производная y» (x) обращается в нуль при 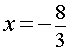 . Изобразим на рисунке 3 диаграмму знаков второй производной y» (x)
. Изобразим на рисунке 3 диаграмму знаков второй производной y» (x)
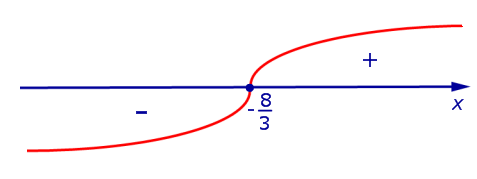
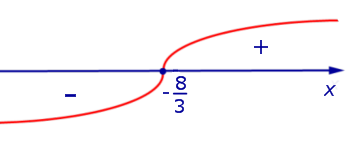
Рис.3
При переходе через точку 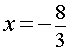 вторая производная функции y» (x) меняет знак с «–» на «+» . Следовательно,
вторая производная функции y» (x) меняет знак с «–» на «+» . Следовательно, 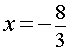 – точка перегиба графика функции (1). При
– точка перегиба графика функции (1). При  функция (1) выпукла вверх, при
функция (1) выпукла вверх, при 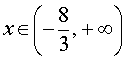 функция (1) выпукла вниз.
функция (1) выпукла вниз.
Дополним схему поведения функции, представленную на рисунке 2, новыми данными о направлении выпуклости функции (рис. 4).
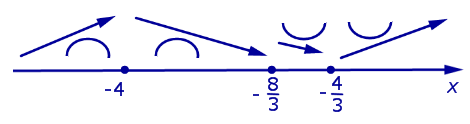

Рис.4
Для того, чтобы найти точки пересечения функции (1) с осью Ox , решим уравнение
x3 + 8x2 + 16x + 128 = 0 ,
x2 (x + 8) + 16 (x + 8) = 0 ,
(x + 8) (x2 + 16) = 0 .
Таким образом, точка (– 8; 0) является единственной точкой пересечения графика функции (1) с осью Ox . Точкой пересечения графика функции (1) с осью Oy будет точка (0; 128) .
На схеме поведения функции, представленной на рисунке 4, добавим информацию о знаках функции (1) (рис. 5).

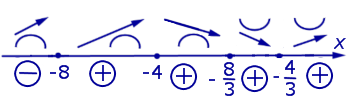
Рис.5
Принимая во внимание результаты исследования поведения функции (1) (большая часть данных компактно представлена на рисунке 5), мы можем построить график функции (1) (рис.6):
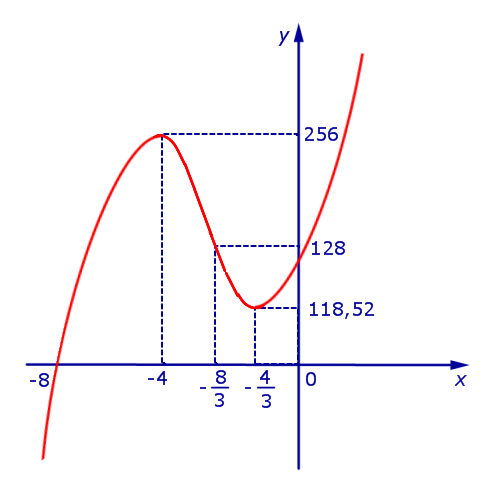
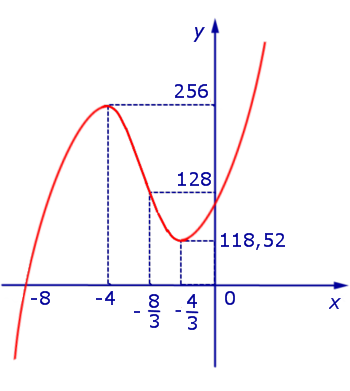
Рис.6
Пример 2. Построить график функции
 | (2) |
Решение. Областью определения функции (2) является вся числовая прямая, за исключением точки x = 0 , то есть 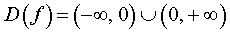 .
.
Функция (2) не является ни четной, ни нечетной.
Функция (2) не является периодической.
Прямая x = 0 является вертикальной асимптотой графика функции (2), так как
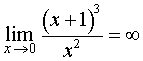
Для того, чтобы выяснить, имеются ли у графика функции (2) наклонные асимптоты, представим правую часть формулы (2) в другом виде:
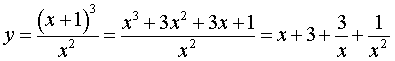 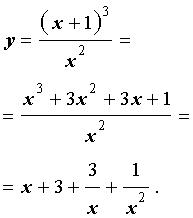 | (3) |
Из формулы (3) получаем равенство
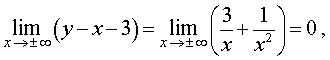
откуда вытекает, что прямая
y = x + 3
является наклонной асимптотой графика функции (2), как при 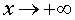 , так и при
, так и при 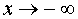 .
.
Теперь вычислим производную функции (2). Проще всего это сделать, воспользовавшись формулой (3):
 | (4) |
Для того, чтобы найти стационарные точки функции (2), преобразуем правую часть формулы (4):
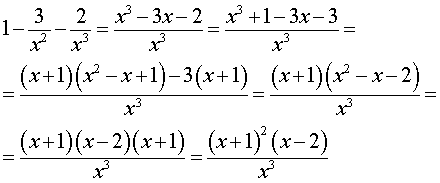

Следовательно,
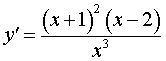 | (5) |
и стационарными точками функции (2) являются точки x = – 1 и x = 2 . Поскольку y’ (x) не существует при x = 0 , то критическими точками функции (2) являются точки
x = – 1 , x = 0, x = 2 .
Изобразим на рисунке 7 диаграмму знаков производной y’ (x)
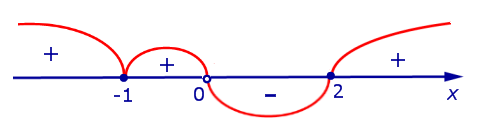

Рис.7
На интервалах  ,
,  и
и  производная y’ (x) положительна, значит, функция (2) возрастает на этих интервалах. На интервале (0, 2) производная y’ (x) отрицательна, значит, функция (2) убывает на этом интервале. Схематически поведение функции (2) изображено на рисунке 8.
производная y’ (x) положительна, значит, функция (2) возрастает на этих интервалах. На интервале (0, 2) производная y’ (x) отрицательна, значит, функция (2) убывает на этом интервале. Схематически поведение функции (2) изображено на рисунке 8.
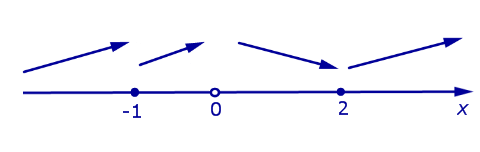
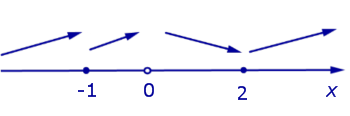
Рис.8
При переходе через точку x = – 1 производная функции y’ (x) знак не меняет, значит, в этой точке экстремума нет. При переходе через точку x = 2 производная функции y’ (x) меняет знак с «–» на «+» . Следовательно, точка x = 2 является точкой минимума функции (2).
Найдем значения функции (1) в стационарных точках:
y (–1) = 0 ,

Теперь перейдем к вычислению второй производной функции (2). Проще всего это сделать, воспользовавшись формулой (4):
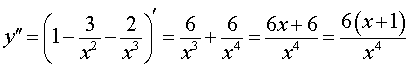
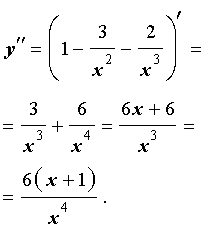
Вторая производная y» (x) обращается в нуль при x = – 1 . Изобразим на рисунке 9 диаграмму знаков второй производной y» (x)
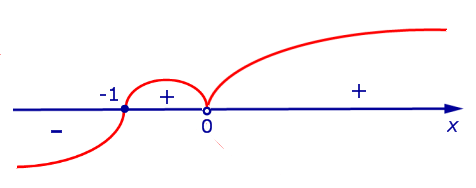

Рис.9
При переходе через точку x = – 1 вторая производная функции y» (x) меняет знак с «–» на «+» . Следовательно, x = – 1 – точка перегиба графика функции (2). При x < – 1 функция (2) выпукла вверх, при x > – 1 функция (2) выпукла вниз.
Дополним схему поведения функции, представленную на рисунке 8, данными о направлении выпуклости функции (рис. 10).
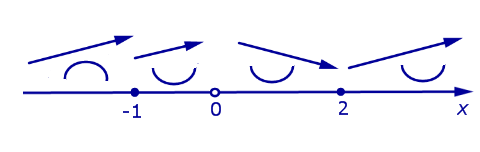
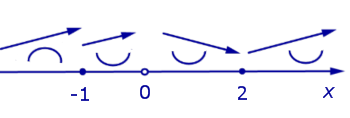
Рис.10
Найдем точки пересечения функции (2) с осями координат: точка (– 1; 0) является единственной точкой пересечения графика функции (2) с осью Ox , а точек пересечения графика функции (2) с осью Oy нет, поскольку x = 0 не входит в область определения функции (2).
На схеме поведения функции, представленной на рисунке 10, добавим информацию о знаках функции (2) (рис. 11).
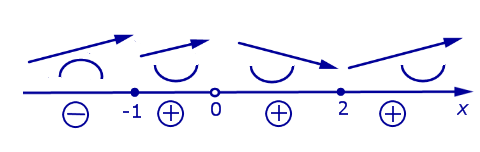

Рис.11
Принимая во внимание результаты исследования поведения функции (2) (большая часть данных компактно представлена на схеме рисунка 11), мы можем построить график функции (2) (рис.12):
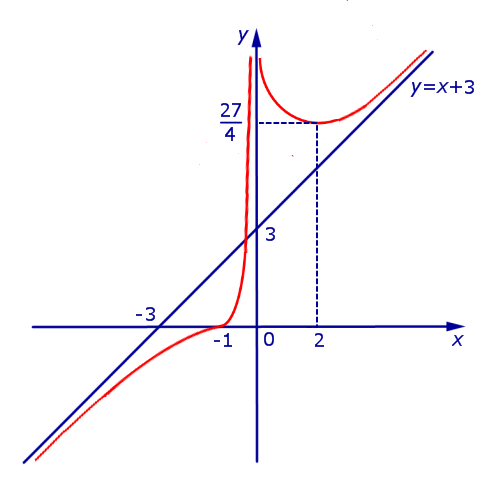

Рис.12

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
4.17. Общая схема исследования функции
Пусть – некоторая заданная функция. Требуется провести ее всестороннее (полное) исследование и построить ее график. Указанное полное исследование функции можно провести по следующей схеме.
1. Находим область определения функции. Заодно устанавливаем интервалы ее непрерывности и точки разрыва.
2. Исследуем функцию на четность-нечетность и тем самым устанавливаем возможную симметрию графика функции (относительно оси Oy или относительно начала координат). Для этого записываем выражение и сравниваем его с :
А) Если , то функция – четная. Ее график симметричен относительно оси Оу (рис. 4.16 (а)).
Б) Если , то функция – нечетная. Ее график симметричен относительно начала координат (рис. 4.16 (б)).
В) Если не имеет место ни вариант (а) ни вариант (б), то функция – общего вида (ее график симметрией (а) и (б) не обладает).
3. Исследуем функцию на периодичность (на повторяемость ее графика). Из элементарных функций это имеет смысл делать лишь для тригонометрических функций, ибо прочие функции заведомо не периодичны.
4. Исследуем поведение функции возле найденных в пункте 1 точек ее разрыва, а также возле границ области ее определения, учитывая при этом информацию, полученную в пунктах 2 и 3. Заодно устанавливаем (определяем) вертикальные и невертикальные асимптоты графика функции (см. § 3 главы 3).
5. Находим интервалы возрастания и убывания функции и точки ее экстремума (с помощью первой производной ). Заодно находим вершины и впадины графика функции и устанавливаем их тип (округлые; острые).
6. Находим интервалы выпуклости и интервалы вогнутости функции и точки ее перегиба (с помощью второй производной ). Заодно находим точки перегиба графика функции.
7. Находим точки пересечения графика функции с осями координат.
8. Строим график функции.
Пример 4. Провести полное исследование функции и построить ее график.
Решение. Реализуем изложенную выше схему.
1. Область определения функции – любые X, кроме . То есть функция определена (а следовательно, и непрерывна) на всей числовой оси Ох, кроме точки , которая, таким образом, является единственной точкой разрыва функции.
2. Исследуем функцию на четность-нечетность. Имеем: ; тогда . Как видим, . Значит, наша функция – нечетная, ее график симметричен относительно начала координат. А значит, в дальнейшем достаточно исследовать функцию лишь для , ибо для можно будет учесть указанную выше симметрию.
3. Функция – алгебраическая (не тригонометрическая), а следовательно, не периодична.
4. Исследуем поведение функции возле точки ее разрыва (справа, при ), а также при (на правой границе области ее определения):
А) При функция
То есть
( при ).
А это значит, что вертикальная прямая с уравнением (ось Оу) является вертикальной асимптотой графика функции. К ней справа (при ) неограниченно приближается график функции, устремляясь при этом вверх (рис. 4.17 (А)):
Б) При функция стремится, очевидно, к , ибо
.
При этом, очевидно, при функция стремится к эквивалентно функции , так как при . А это значит, что график нашей функции при стремится к прямой . То есть прямая – асимптота (наклонная асимптота) графика нашей функции. Причем график функции при стремится к прямой Сверху, ибо для всех (рис. 4.17 (Б)).
5. Найдем интервалы возрастания и убывания и точки экстремума функции (схема исследования изложена выше).
а) Находим производную :
;
Б) Найдем точки (значения X), подозрительные на экстремум:
.
не существует .
Точку исследовать не будем, так как она не входит в область определения функции. Не будем исследовать и отрицательную точку (см. пункт 2).
В) Нанесем оставшуюся подозрительную на экстремум точку на область определения функции (на ось Ох). При этом ограничимся рассмотрением лишь положительной полуоси :
В обоих получившихся интервалах найдем знак производной и отметим его. Тем самым устанавливаем интервал возрастания и интервал убывания функции. Заодно устанавливаем, что – точка минимума функции.
Г) Найдем значение функции в точке минимума и тем самым определим впадину графика функции:
; точка – впадина графика функции (округлая, т. к. ).
6. Найдем интервалы выпуклости и интервалы вогнутости функции, а также точки перегиба функции и ее графика (схема исследования изложена выше).
А) Найдем :
;
Б) Найдем точки (значения X), подозрительные на перегиб:
таких X нет.
не существует .
Но учитывать точку не будем, так как она не входит в область определения функции. Итак, рассматриваемая функция не имеет подозрительных на перегиб точек, а значит, точек перегиба у неё нет. И так как для , то для всех функция наша вогнутая.
7. Найдем точки пересечения графика функции с осями координат.
А) С осью Ох:
таких X нет.
Б) С осью Оу:
– не сущ.
Таким образом, ни с осью Ох, ни с осью Оу график нашей функции не пересекается.
8. Строим график функции – сначала для , а затем, по симметрии относительно начала координат, и для (рис. 4.18).
Упражнения
1. Провести полное исследование и построить графики функций:
А) ; б) ; в) .
Ответ:
| < Предыдущая | Следующая > |
|---|
Общая схема исследования функции — Студопедия
1) Найти область определения функции;
2) исследовать функцию на четность и периодичность;
3) выяснить существование асимптот;
4) определить, если это не вызовет особых затруднений, точки пересечения графика функции с координатными осями;
5) найти решение уравнения 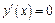 и точки, где
и точки, где 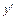 не существует; точки «подозрительные» на экстремум, исследовать с помощью достаточного условия экстремума, определить вид экстремума; вычислить значение функции в точках экстремума; найти интервалы монотонности функции;
не существует; точки «подозрительные» на экстремум, исследовать с помощью достаточного условия экстремума, определить вид экстремума; вычислить значение функции в точках экстремума; найти интервалы монотонности функции;
6) найти решения уравнений 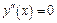 и точки, где
и точки, где 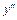 не существует; точки «подозрительные» на перегиб, исследовать с помощью достаточного условия; вычислить значения функции в точках перегиба; найти интервалы выпуклости и вогнутости графика функции;
не существует; точки «подозрительные» на перегиб, исследовать с помощью достаточного условия; вычислить значения функции в точках перегиба; найти интервалы выпуклости и вогнутости графика функции;
7) построить график функции.
Если исследование проведено без ошибок, то результаты всех этапов должны согласовываться друг с другом. Если же согласование отсутствует, необходимо проверить правильность результатов отдельных этапов и исправить найденные ошибки.
Пример 1. Найти производную от функции 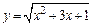 .
.
Решение. Введем вспомогательную функцию u=x2+3x+1, тогда можно записать 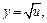 где u=x2+3x+1.
где u=x2+3x+1.
По формуле (1) имеем 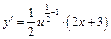 , или, заменив u на его значение:
, или, заменив u на его значение:
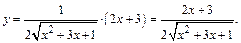
К такой подробной записи прибегают только на начальной стадии освоения правил дифференцирования, а обычно вспомогательную функцию вводят только мысленно и выполняют указанные действия.
Пример 2. Найти 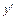 , если
, если 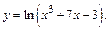
Решение. Мысленно за u принимаем выражение x 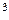 +7x–3 и получаем
+7x–3 и получаем
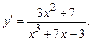
Пример 3.Найти 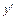 , если
, если 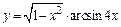 .
.
Решение. По правилу дифференцирования произведения записываем:

При вычислении 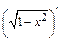 принимаем u=1
принимаем u=1  x2, тогда
x2, тогда
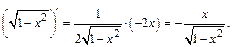
Таким образом,
 .
.
Пример 4.Найти 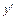 если
если 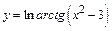 .
.
Решение.Принимаем 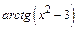 за вспомогательную функцию u и получим
за вспомогательную функцию u и получим 
При вычислении производной от 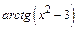 за вспомогательную функцию примем
за вспомогательную функцию примем  :
:
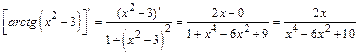 .
.
Подставим найденное значение в выражение для 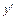 , окончательно получим:
, окончательно получим: 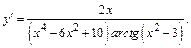
При наработке навыков вычисления производных запись можно проводить более компактно, покажем это на следующем примере.
Пример 5. Найти 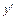 , если
, если 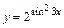 .
.
Решение.Сначала за вспомогательную функцию примем 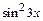 , затем функцию
, затем функцию 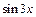 , после этого роль вспомогательной будет играть функция 3x и, наконец, к ней применяем одно из основных правил дифференцирования:
, после этого роль вспомогательной будет играть функция 3x и, наконец, к ней применяем одно из основных правил дифференцирования:
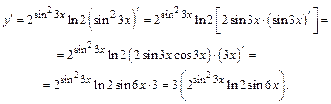
Пример 6. Дана функция 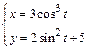 . Найти
. Найти 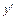 .
.
Решение. Дифференцируем исходные равенства по t:
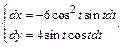
По формуле (2) получим
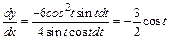
Пример 7. Используя правило Лопиталя, вычислить предел функции:
1) 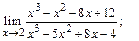 2)
2) 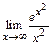 .
.
Решение. 1) Подстановка предельного значения аргумента x=2 приводит к неопределенности вида 0/0. Раскроем ее с помощью правила Лопиталя (3):
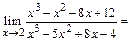
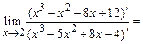

Однократное применение правила Лопиталя не приводит к раскрытию неопределенности (по прежнему получаем  ), поэтому применим его еще раз:
), поэтому применим его еще раз:
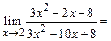
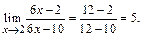
Таким образом, в результате двукратного применения правила Лопиталя находим, что искомый предел равен 5.
2) Убедившись, что имеет место неопределенность вида 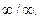 применим правило Лопиталя:
применим правило Лопиталя:
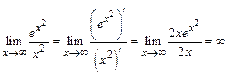 .
.
Пример 8.Исследовать функцию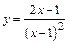 и построить ее график.
и построить ее график.
Решение. Проведем исследование по общей схеме, приведенной в п.
1. Функция определена при всех значениях аргумента x, кроме x=1.
2. Для установления четности или нечетности функции проверим выполнимость равенств 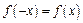 (тогда
(тогда 
 четная функция) или
четная функция) или  (для нечетной функции) для любых
(для нечетной функции) для любых  и
и  из области определения функции:
из области определения функции:
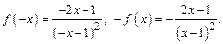
Следовательно 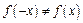 и
и 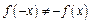 то есть данная функция не является ни четной ни нечетной. Также не является периодической.
то есть данная функция не является ни четной ни нечетной. Также не является периодической.
3. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т.е. на интервалах 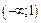 и
и 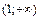 . В точке x=1 функция терпит разрыв второго рода.
. В точке x=1 функция терпит разрыв второго рода.
Так как x=1  точка разрыва функции, причем
точка разрыва функции, причем 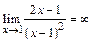 . Поэтому прямая x=1 является вертикальной асимптотой графика.
. Поэтому прямая x=1 является вертикальной асимптотой графика.
Для определения уравнения наклонной асимптоты 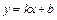 воспользуемся формулами:
воспользуемся формулами:
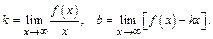
Тогда
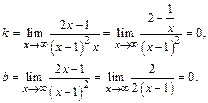
При вычислении последнего предела использовалось правило Лопиталя.
Значит прямая  есть горизонтальная асимптота графика исследуемой функции.
есть горизонтальная асимптота графика исследуемой функции.
4. Точки пересечения с осями координат: если 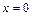 , то
, то 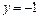 ; если
; если  , то
, то 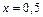 .
.
5. Для исследования функции на экстремум найдем ее первую производную:
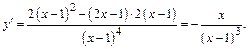
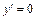 при
при 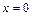 и
и 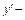 не существует при
не существует при 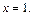 Тем самым имеем две критические точки:
Тем самым имеем две критические точки: 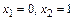 . Но точка
. Но точка 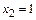 не принадлежит области определения функции, экстремума в ней быть не может.
не принадлежит области определения функции, экстремума в ней быть не может.
Для наглядности результаты представим в виде таблицы изменения знака 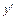 :
:
Табл.1.
В первом и третьем интервалах первая производная отрицательна, следовательно, здесь функция убывает, во втором интервале–положительна и данная функция возрастает. При переходе через точку x=0 первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум:  . Значит
. Значит 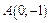
 точка минимума.
точка минимума.
6. Для определения точек перегиба графика функции и интервалов выпуклости и вогнутости кривой найдем вторую производную:

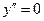 при
при 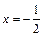 и
и  не существует при
не существует при  . Для наглядности результаты представим в виде таблицы изменения знака
. Для наглядности результаты представим в виде таблицы изменения знака 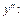
Табл.2.
На первом интервале вторая производная 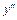 отрицательна и дуга исследуемой кривой выпукла; на втором и третьем интервалах
отрицательна и дуга исследуемой кривой выпукла; на втором и третьем интервалах 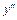 >0, тем самым график является вогнутым. При переходе через точку
>0, тем самым график является вогнутым. При переходе через точку 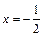
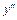 меняет свой знак, поэтому
меняет свой знак, поэтому 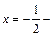 абсцисса точки перегиба. Следовательно,
абсцисса точки перегиба. Следовательно, 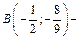 точка перегиба графика функции.
точка перегиба графика функции.
7. Учитывая полученные результаты, строим график функции (рис.10).

Рис. 10
Схема исследования функции с помощью производной — Студопедия
При исследовании функций и построении их графиков рекомендуется использовать следующую схему:
1. Найти область определения функции.
2. Исследовать функцию на четность – нечетность.
3. Найти вертикальные асимптоты.
4. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.
5. Найти экстремумы и интервалы монотонности функции.
6. Найти интервалы выпуклости функции и точки перегиба.
7. Найти точки пересечения графика с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
Пример 1. Исследовать функцию  и построить ее график.
и построить ее график.
Решение.
1. Область определения 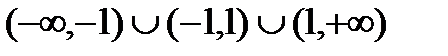 , т.е.
, т.е.  .
.
2. Функция четная, так как 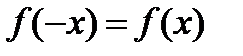 , и ее график симметричен относительно оси ординат.
, и ее график симметричен относительно оси ординат.
3. Вертикальные асимптоты могут пересекать ось абсцисс в точках 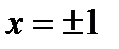 . Так как пределы функции при
. Так как пределы функции при  (слева) и при
(слева) и при 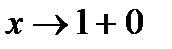 (справа) бесконечны, т.е.
(справа) бесконечны, т.е.
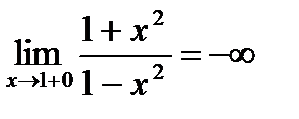 и
и 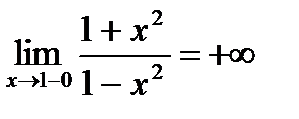 , то прямая х = 1 естьвертикальная асимптота. В силу симметрии графикаf(х) х= –1 также вертикальная асимптота.
, то прямая х = 1 естьвертикальная асимптота. В силу симметрии графикаf(х) х= –1 также вертикальная асимптота.
4. Поведение функции в бесконечности. Вычислим  .
.
В силу четности имеем также 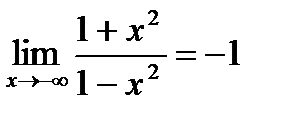 , т.е. прямаяу = – 1 – горизонтальная асимптота.
, т.е. прямаяу = – 1 – горизонтальная асимптота.
5. Экстремумы и интервалы монотонности.
Найдем 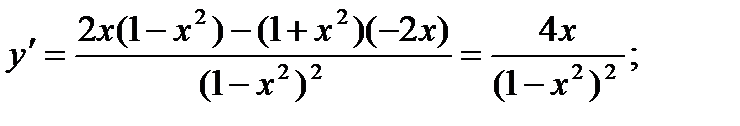
 при х = 0 и
при х = 0 и  не существует при
не существует при 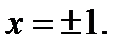
Однако критической является только точка х1 = 0 (так как
значения  не входят в область определения функции). Поскольку при х<0
не входят в область определения функции). Поскольку при х<0 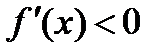 , а при х> 0
, а при х> 0 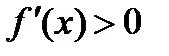 (рис. 11), то x= 0 – точка минимума и
(рис. 11), то x= 0 – точка минимума и  – минимум функции.
– минимум функции.
На интервалах  функция убывает, на интервалах
функция убывает, на интервалах 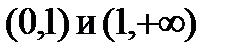 – возрастает.
– возрастает.
6. Интервалы выпуклости и точки перегиба.
Найдем

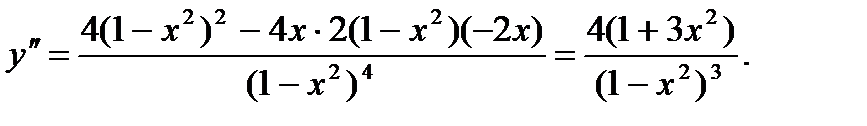
Очевидно, что 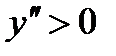 на интервале (–1, 1) и функция выпукла вниз на этом интервале.
на интервале (–1, 1) и функция выпукла вниз на этом интервале. 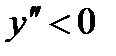 на интервале
на интервале  , и на этих интервалах функция выпукла вверх. Точек перегиба нет.
, и на этих интервалах функция выпукла вверх. Точек перегиба нет.
7. Точки пересечения с осями.
f(0) = 1, т.е. точка пересечения с осью ординат (0, 1).
Уравнение f(х) = 0 решений не имеет, следовательно, график функции не пересекает ось абсцисс.
График функции изображен на рисунок 12.
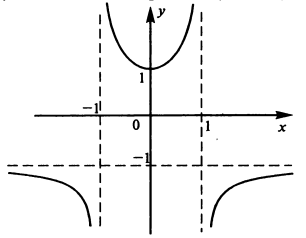
Рисунок 12 – График функции
Задания для самоконтроля
1.Вычислить производную функции:
2.
а) Дана функция 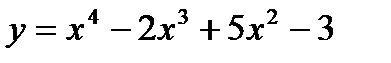 . Найти
. Найти 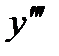
б) Дана функция 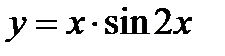 . Найти
. Найти 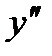
3. Составить уравнение касательной к графику функции 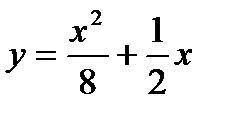 , проходящей через точку х0=2.
, проходящей через точку х0=2.
4.Исследовать функцию 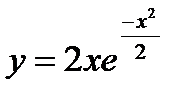 и построить ее график.
и построить ее график.
Исследование короткого замыкания
— Скачать бесплатно PDF
Скачать исследование короткого замыкания …
Электрическая распределительная системаИнженерная надежная защита Инженерная надежная защита — Часть I «Простой подход к расчетам короткого замыкания» Оглавление Стр. Основные соображения по расчетам короткого замыкания устройства без учета ………………… …………………………… ………………………………………………… 3… 3 — Почему короткое замыкание? Расчеты итогового значения …………… ………………………………… ………………………………………………………………… 3 ………………… 3 — Общие Общие Комментарии Комментарии к расчетам КЗ КЗ ………………………………………………………………………………………… 3… 3 — Асимметричные асимметричные калибровочные компоненты Компоненты ……………………………………………… ………………………………………………………………… …… ……………………… 3 3 — Отключающая способность, отключающая способность, мощность, короткое замыкание и токи короткого замыкания ……………………………… 4 …………… ………………… 4 3Ø Короткое замыкание, короткое замыкание и ток Расчеты, расчеты, процедуры Процедуры и методы Методы …………………………………… 5 ……………………… …………… 5 — Омический метод ………… …………………………………… …………………………………………………………………………………… 6 ……… …………………………… 6 — Метод ИТ-метода на единицу на единицу ………… …………………… …………………………………………… ………………… ………………… …………………… ………………… 1 ……… 11 1 — Процедура компьютерного программного обеспечения TRON® ………………… ………………………… ………………………………………………………… 16 …………… 16 — Point-to-Po Point-to-Point int Метод Метод ……………………………………………… …………………………………………………………………… ……… ………………… 17 …… 17 — Сравнение Сравнение результатов Результаты …………………………………………… ……………………………………… …………………………… ………………………… 19 …… 19 1Ø Расчет короткого замыкания на трансформаторе 1 Ø Система, система, процедуры, процедуры и методы, методы ………… …… 20 — Метод измерения на единицу на единицу Метод — Отказ от линии к линии Неисправности линии ………………………………………………………………………… ……………………………………………………… 21 ………… 21 — Метод единицы на единицу — Неисправности между фазой и нейтралью …………………………… ……………… ………………………………………………………… 22 ………… 22 — Метод «точка-точка» — точка-точка. Междуфазные неисправности ………………………………………… ……………………………………………………… 23 ……… 23 — Точка Двухточечный метод — замыкания между фазой и нейтралью ………………………………………………………………………………………………… 24 …… 24 — Сравнение Сравнение результатов Результаты ……………………………………………… …………………………………………………………… ………… ………………………… 24… 24 Раздел данных ………………………………………………………………………………… ……… 25 — Таблица Таблица 1 — Данные импеданса трансформатора …………………………………………………………………………………………………… …… 25 …………… 25 — Таблица Таблица 2 — Данные о реактивном сопротивлении трансформатора тока ……………………………………………………………………………… …………… 25 ……… 25 — Таблица Таблица 3 — Данные о реактивном сопротивлении выключателя Disconnecti ng Switch Switch …………………………………………… …………………… ………………………… 25… 25 — Таблица 4 — Данные по реактивному сопротивлению автоматического выключателя …………………………………………… …………………… ……………………………………………………… 26 ………… 26 — Таблица 5 — Данные импеданса изолированных проводов Импеданс проводов …………………………………………… ……………………………………………… 26… 26 — Таблица 6 — Значения «C» для данных метода PTP …………………………………………… …………………………………………………… 27 …………… 27 — Таблица Таблица 7 — Сопротивление шинопровода Да ta Данные ………………………………………………… ……………………………………………………………… 28 ………… … 28 — Таблица Таблица 8 — Факторы асимметричной асимметрии …………………………………………… ……………………………………………………… ……… 29 …………………… 29 Выборочная выборочная координация — EDP II …………………………………………… ……………………………… ………………………………… ……………………… 29 29 Selective Selective Protectio Protection n — EDP III ……………………………………………… ………………………………………………………………… ………………………… 29… 29
2
Надежная инженерная защита для распределительной электросети Система
Бюллетень EDP-1 (2004-1)
Часть 1 Простой подход к расчетам короткого замыкания
Bussmann
Система распределения электроэнергии
Основные соображения при расчетах коротких замыканий Почему расчеты коротких замыканий Несколько разделов национальной Электрические нормы и правила касаются надлежащей защиты от сверхтоков.Безопасное и надежное применение устройств защиты от сверхтоков, основанное на этих разделах, требует проведения исследования короткого замыкания и выборочного исследования координации.
Источники тока короткого замыкания, которые обычно учитываются, включают: — Электроэнергетику — Местное производство — Синхронные двигатели и — Асинхронные двигатели
Эти разделы, среди прочего, включают: 110-9 Номинальное отключение 110-10 Защита компонентов 230-65 Оборудование входа для обслуживания Оборудование 240-1 Защита проводников 250-95 Оборудование Заземление Защита заземляющих проводов 517-17 Медицинские учреждения — Выборочная избирательная координация
Токами разряда конденсаторов обычно можно пренебречь из-за их короткой продолжительности.В некоторых публикациях IEEE (Института инженеров по электротехнике и электронике) подробно описано, как рассчитать эти токи, если они значительны.
Асимметричные компоненты Ток короткого замыкания обычно приобретает асимметричную характеристику в течение первых нескольких циклов продолжительности. То есть, он смещен относительно нулевой оси, как показано на рисунке 1.
Соответствие этим разделам кода может быть наилучшим образом достигнуто путем проведения исследования коротких цепей и исследования выборочной координации.Защита электрической системы должна быть не только безопасной при любых условиях эксплуатации, но и для обеспечения непрерывности работы ее также следует выборочно координировать. Скоординированная система — это система, в которой изолируется только неисправная цепь, не нарушая никаких других частей системы. Устройства защиты от сверхтоков должны также обеспечивать защиту от короткого замыкания и перегрузки для компонентов системы, таких как шина, провод, контроллеры двигателей и т. Д. Для получения надежной, согласованной работы и обеспечения защиты компонентов системы от повреждений необходимо сначала рассчитать доступный ток короткого замыкания в различных критических точках электрической системы.Как только уровни короткого замыкания определены, инженер может указать надлежащие требования к номинальным характеристикам прерывания, выборочно координировать систему и обеспечить защиту компонентов.
C U R R E N T
TIME
Рисунок 1 На рисунке 2 обратите внимание, что полный ток короткого замыкания I a является суммой двух составляющих — симметричного среднеквадратичного тока IS и составляющей постоянного тока I DC. Составляющая постоянного тока является функцией накопленной энергии в системе при возникновении короткого замыкания.Он спадает до нуля после нескольких циклов из-за потерь I 2R в системе, при этом ток короткого замыкания симметричен относительно нулевой оси. Среднеквадратичное значение симметричного компонента может быть определено с помощью L aw Ома. Чтобы определить асимметричный компонент, необходимо знать отношение X / R системы. Чтобы получить отношение X / R, необходимо определить полное сопротивление и полное реактивное сопротивление цепи до точки повреждения. Максимальные термические и механические нагрузки на оборудование возникают в течение этих первых нескольких циклов.Важно сконцентрироваться на том, что происходит в течение первой половины цикла после возникновения неисправности.
Общие комментарии по расчетам короткого замыкания Расчеты короткого замыкания должны выполняться во всех критических точках системы. К ним относятся: — Служебный вход — Панельные панели — Центры управления двигателями — Пускатели двигателей — Автоматические переключатели — Центры нагрузки Обычно исследования короткого замыкания включают расчет состояния трехфазного замыкания на болтах. Это можно охарактеризовать как все три фазы, «скрепленные» вместе, чтобы создать соединение с нулевым сопротивлением.Это устанавливает состояние «наихудшего случая», которое приводит к максимальному тепловому и механическому напряжению в системе. Из этого расчета можно получить другие типы неисправностей.
3
Система распределения электроэнергии
Основные соображения при расчетах короткого замыкания Номинальное значение отключения, отключающая способность и токи короткого замыкания Номинальное значение отключения можно определить как «максимальный ток короткого замыкания, который защитное устройство может безопасно отключить, очистить, сбросить». при определенных условиях испытаний.«Отключающая способность» может быть определена как «фактический ток короткого замыкания, на прерывание которого было испытано защитное устройство». Национальный электротехнический кодекс требует наличия адекватных отключающих характеристик в разделах 110-9 и 230-65.
Для этого изучите рисунок 2 и обратитесь к таблице 8. IP = 115,450A
Ia
Ia = 66,500A
IDC
Is = 50,000ACURRENT
TIME Is
Раздел 110-9 Прерывание Рейтинг. Оборудование, предназначенное для отключения тока на уровнях повреждения, должно иметь отключающую способность, достаточную для напряжения системы и тока, доступного на линейных выводах оборудования.
Ia — Асимметричный среднеквадратичный ток IDC — Компонент постоянного тока
Раздел 230-65. Доступный ток короткого замыкания. Сервисное оборудование должно выдерживать ток короткого замыкания на его клеммах питания.
Is — компонент симметричного среднеквадратичного значения IP — мгновенный пиковый ток
Рис. 2 Низковольтные предохранители имеют номинальные характеристики отключения, выраженные в единицах симметричной составляющей тока короткого замыкания, I S. Им дается среднеквадратичный симметричный отключающий рейтинг при определенном коэффициенте мощности.фактор. Это означает, что предохранитель может отключать любой асимметричный ток, связанный с этим номиналом. Таким образом, только симметричная составляющая короткого замыкания cur
.10.6: RC-схемы — Физика LibreTexts
При использовании камеры со вспышкой зарядка конденсатора, питающего вспышку, занимает несколько секунд. Световая вспышка разряжает конденсатор за крошечные доли секунды. Почему зарядка занимает больше времени, чем разрядка? Этот вопрос и несколько других явлений, связанных с зарядкой и разрядкой конденсаторов, обсуждаются в этом модуле.
Цепи сопротивления и емкости
Цепь RC — это цепь, содержащая сопротивление и емкость.Как показано в разделе «Емкость», конденсатор — это электрический компонент, который накапливает электрический заряд, накапливая энергию в электрическом поле.
На рисунке \ (\ PageIndex {1a} \) показана простая схема RC , в которой используется источник постоянного напряжения \ (ε \), резистор \ (R \), конденсатор \ (C \), и двухпозиционный переключатель. Схема позволяет конденсатору заряжаться или разряжаться в зависимости от положения переключателя. Когда переключатель перемещается в положение \ ( A \) , конденсатор заряжается, в результате получается схема, показанная на рисунке \ (\ PageIndex {1b} \).Когда переключатель перемещается в положение B , конденсатор разряжается через резистор.
Рисунок \ (\ PageIndex {1} \): (a) Схема RC с двухполюсным переключателем, который можно использовать для зарядки и разрядки конденсатора. (b) Когда переключатель перемещается в положение A , схема сводится к простому последовательному соединению источника напряжения, резистора, конденсатора и переключателя. (c) Когда переключатель перемещается в положение B , схема сводится к простому последовательному соединению резистора, конденсатора и переключателя.Источник напряжения снят с цепи.Зарядка конденсатора
Мы можем использовать правило петли Кирхгофа, чтобы понять заряд конденсатора. Это приводит к уравнению \ (\ epsilon — V_R — V_C = 0 \). Это уравнение можно использовать для моделирования заряда как функции времени при зарядке конденсатора. Емкость определяется как \ (C = q / V \), поэтому напряжение на конденсаторе равно \ (V_C = \ frac {q} {C} \). Согласно закону Ома падение потенциала на резисторе равно \ (V_R = IR \), а ток определяется как \ (I = dq / dt \).{- \ frac {t} {\ tau}} \ right). \]
График зависимости заряда конденсатора от времени показан на рисунке \ (\ PageIndex {2a} \). Во-первых, обратите внимание, что по мере приближения времени к бесконечности экспонента стремится к нулю, поэтому заряд приближается к максимальному заряду \ (Q = C \ epsilon \) и имеет единицы кулонов. Единицы измерения RC — секунды, единицы времени. Эта величина известна как постоянная времени :
.\ [\ tau = RC. \]
В момент времени \ (t = \ tau = RC \) заряд равен \ (1 — e ^ {- 1} = 1 — 0.368 = 0,632 \) максимального заряда \ (Q = C \ epsilon \). Обратите внимание, что изменение скорости заряда во времени представляет собой наклон в точке графика зависимости заряда от времени. Наклон графика большой в момент времени \ (t — 0,0 \, s \) и приближается к нулю с увеличением времени.
По мере увеличения заряда конденсатора ток через резистор уменьшается, как показано на рисунке \ (\ PageIndex {2b} \). Ток через резистор можно найти, взяв производную заряда по времени.
\ [\ begin {align *} I (t) & = \ frac {dq} {dt} \\ [4pt] & = \ frac {d} {dt} \ left [C \ epsilon \ left (1 — e ^ {- \ frac {t} {RC}} \ right) \ right], \\ [4pt] & = C \ epsilon \ left (\ frac {1} {RC} \ right) e ^ {- \ frac { t} {RC}} \\ [4pt] & = \ frac {\ epsilon} {R} e ^ {- \ frac {t} {TC}} \\ [4pt] & = I_0 e ^ {- \ frac { t} {RC}}, \ end {align *} \]
\ [I (t) = I_0 e ^ {- t / \ tau}.{-1} = 0,368 I_0 \).
Рисунок \ (\ PageIndex {2} \): (a) Заряд конденсатора в зависимости от времени по мере заряда конденсатора. (б) Ток через резистор в зависимости от времени. (c) Разность напряжений на конденсаторе. (d) Разность напряжений на резисторе.На рисунках \ (\ PageIndex {2c} \) и \ (\ PageIndex {2d} \) показаны разности напряжений на конденсаторе и резисторе соответственно. По мере увеличения заряда конденсатора ток уменьшается, как и разница напряжений на резисторе \ (V_R (t) = (I_0R) e ^ {- t / \ tau} = \ epsilon e ^ {- t / \ tau } \).{-t / \ tau}) \).
Разряд конденсатора
Когда переключатель на рисунке \ (\ PageIndex {3a} \) перемещается в положение B , схема сокращается до схемы в части (c), и заряженному конденсатору позволяют разрядиться через резистор. График зависимости заряда конденсатора от времени показан на рисунке \ (\ PageIndex {3a} \). Использование правила петли Кирхгофа для анализа цепи по мере разряда конденсатора приводит к уравнению \ (- V_R -V_C = 0 \), которое упрощается до \ (IR + \ frac {q} {C} = 0 \).{-t / \ tau}. \]
Отрицательный знак показывает, что ток течет в направлении, противоположном току, наблюдаемому при зарядке конденсатора. На рисунке \ (\ PageIndex {3b} \) показан пример графика зависимости заряда от времени и тока от времени. График зависимости разности напряжений на конденсаторе и разности напряжений на резисторе от времени показан на рисунках \ (\ PageIndex {3c} \) и \ (\ PageIndex {3d} \). Обратите внимание, что величины заряда, тока и напряжения экспоненциально уменьшаются, приближаясь к нулю с увеличением времени.
Рисунок \ (\ PageIndex {3} \): (a) Заряд конденсатора в зависимости от времени по мере разряда конденсатора. (б) Ток через резистор в зависимости от времени. (c) Разность напряжений на конденсаторе. (d) Разность напряжений на резисторе.Теперь мы можем объяснить, почему упомянутой в начале этого раздела вспышке камера требует намного больше времени для зарядки, чем для разрядки: сопротивление при зарядке значительно больше, чем при разрядке. Внутреннее сопротивление батареи составляет большую часть сопротивления во время зарядки.По мере старения аккумулятора возрастающее внутреннее сопротивление делает процесс зарядки еще медленнее.
Пример \ (\ PageIndex {2} \): Осциллятор релаксации
Одним из применений схемы RC является релаксационный генератор, как показано ниже. Релаксационный генератор состоит из источника напряжения, резистора, конденсатора и неоновой лампы. Неоновая лампа действует как разомкнутая цепь (бесконечное сопротивление), пока разность потенциалов на неоновой лампе не достигнет определенного напряжения.При таком напряжении лампа действует как короткое замыкание (нулевое сопротивление), и конденсатор разряжается через неоновую лампу и производит свет. В показанном релаксационном генераторе источник напряжения заряжает конденсатор до тех пор, пока напряжение на конденсаторе не станет 80 В. Когда это происходит, неон в лампе выходит из строя и позволяет конденсатору разряжаться через лампу, создавая яркую вспышку. После того, как конденсатор полностью разрядится через неоновую лампу, он снова начинает заряжаться, и процесс повторяется.{-t / \ tau}) = ln \ left (1 — \ frac {V_C (t)} {\ epsilon} \ right), \]
\ [t = — \ tau ln \ left (1 — \ frac {V_C (t)} {\ epsilon} \ right) = -5.05 \, s \ cdot ln \ left (1 — \ frac {80 \, V } {100 \, V} \ right) = 8.13 \, s. \]
Значение
Одним из применений генератора релаксации является управление световыми индикаторами, которые мигают с частотой, определяемой значениями для R и C . В этом примере неоновая лампа будет мигать каждые 8,13 секунды с частотой \ (f = \ frac {1} {T} = \ frac {1} {8.13 \, s} = 0,55 \, Гц \). Осциллятор релаксации имеет множество других практических применений. Он часто используется в электронных схемах, где неоновая лампа заменяется транзистором или устройством, известным как туннельный диод. Описание транзистора и туннельного диода выходит за рамки этой главы, но вы можете рассматривать их как переключатели, управляемые напряжением. Обычно это разомкнутые переключатели, но при подаче правильного напряжения переключатель замыкается и проводит ток. «Выключатель» можно использовать для включения другой цепи, включения света или запуска небольшого двигателя.Осциллятор релаксации может быть использован для того, чтобы заставить мигать поворотники вашего автомобиля или ваш мобильный телефон вибрировать.
Цепи RC находят множество применений. Их можно эффективно использовать в качестве таймеров для таких приложений, как стеклоочистители прерывистого действия, кардиостимуляторы и стробоскопы. В некоторых моделях стеклоочистителей прерывистого действия используется переменный резистор для регулировки интервала между движениями стеклоочистителя. Увеличение сопротивления увеличивает постоянную времени RC , что увеличивает время между срабатываниями дворников.
Еще одно приложение — кардиостимулятор . Частота сердечных сокращений обычно контролируется электрическими сигналами, которые заставляют мышцы сердца сокращаться и перекачивать кровь. Когда сердечный ритм ненормален (сердцебиение слишком высокое или слишком низкое), для коррекции этого нарушения можно использовать кардиостимуляторы. У кардиостимуляторов есть датчики, которые обнаруживают движение тела и дыхание, чтобы увеличить частоту сердечных сокращений во время физических нагрузок, таким образом удовлетворяя повышенную потребность в крови и кислороде, а схема синхронизации RC может использоваться для контроля времени между сигналами напряжения, подаваемыми на сердце.
Забегая вперед к изучению цепей переменного тока (цепей переменного тока), переменные напряжения изменяются как синусоидальные функции с определенными частотами. Ученые часто регистрируют периодические изменения напряжения или электрических сигналов. Эти сигналы напряжения могут исходить от музыки, записанной микрофоном, или атмосферных данных, собранных радаром. Иногда эти сигналы могут содержать нежелательные частоты, известные как «шум». RC фильтры могут использоваться для фильтрации нежелательных частот.
В области изучения электроники популярное устройство, известное как таймер 555, выдает синхронизированные импульсы напряжения. Время между импульсами контролируется схемой RC . Это лишь некоторые из бесчисленных применений схем RC .
Пример \ (\ PageIndex {2} \): прерывистые работы дворников
Осциллятор релаксации используется для управления парой дворников. Релаксационный генератор состоит из конденсатора емкостью 10,00 мФ и переменного резистора (10,00 кОм), известного как реостат.Ручка, подключенная к переменному резистору, позволяет регулировать сопротивление от \ (0.00 \, \ Omega \) до \ (10.00 \, k \ Omega \). Выход конденсатора используется для управления переключателем, управляемым напряжением. Переключатель нормально разомкнут, но когда выходное напряжение достигает 10,00 В, переключатель замыкается, запитывая электродвигатель и разряжая конденсатор. Двигатель заставляет дворники один раз подметать лобовое стекло, и конденсатор снова начинает заряжаться. На какое сопротивление следует регулировать реостат при периоде работы щеток стеклоочистителя 10.3 \, \ Omega) ln \ left (1 — \ frac {10 \, V} {12 \, V} \ right) = 179,18 \, s = 2,98 \, мин. \]
Схема RC имеет тысячи применений и очень важна для изучения. Его можно не только использовать для измерения времени в цепях, но и для фильтрации нежелательных частот в цепи и использовать в источниках питания, например в вашем компьютере, чтобы преобразовать переменное напряжение в постоянное.
Авторы и авторство
Сэмюэл Дж.Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
circuit function — это … Что такое функция схемы?
выключатель — выключатель н. (Elec.) Устройство, содержащееся в электрической цепи, предназначенное для прерывания цепи, когда ток превышает заданное значение; его иногда называют {выключателем контактов}. Его функция — предотвращать возгорание или повреждение…… Международный английский словарь
Сложность схемы — В теоретической информатике сложность схемы — это ветвь теории вычислительной сложности, в которой булевы функции классифицируются в соответствии с размером или глубиной логических схем, которые их вычисляют.Логическая схема с n входными битами… Wikipedia
Минимизация схемы — В булевой алгебре минимизация схемы — это проблема получения наименьшей логической схемы (булевой формулы), которая представляет заданную булеву функцию или таблицу истинности. Считается, что общая проблема минимизации схемы неразрешима, [1]…… Wikipedia
Схема (теория компьютеров) — Схема в теории компьютеров — это теоретическая структура, имитирующая электрические пути и пути передачи данных, в которой напряжение и двоичные значения входят в начало схемы, проходят через ворота, которые выполняют некоторые вычисления и выводят ответ .Важный…… Википедия
Функциональный генератор — [http://www.agilent.com/u2761a U2761A] Модульный функциональный генератор USB от Agilent Technologies] Функциональный генератор — это электронное испытательное оборудование или программное обеспечение, используемое для генерации электрических сигналов. Эти формы сигналов могут быть либо…… Wikipedia
Автоматический выключатель — Для использования в других целях, см. Автоматический выключатель (значения). Воздушный выключатель для распределительного устройства низкого напряжения (менее 1000 вольт)… Wikipedia
Проектирование схем — Процесс проектирования схем может охватывать системы, начиная от сложных электронных систем и заканчивая отдельными транзисторами внутри интегральной схемы.Для простых схем процесс проектирования часто может выполняться одним человеком без…… Wikipedia
Автоматический выключатель (трансформаторы) — Трансформаторы имя персонажа = автоматический выключатель заголовок = принадлежность автоматического выключателя = нет подгруппа = ранг = функция = партнер по борьбе с роботом = девиз = альтернативные режимы = нет серия = трансформаторы: генерация 1 voiceby = автоматический выключатель вымышленный…… Википедия
выключатель — 1. Электр. Также называется выключателем.устройство для прерывания электрической цепи для предотвращения чрезмерного тока, вызванного коротким замыканием, повреждения устройства в цепи или возникновения пожара. 2. любые льготы по налогу на имущество…… Универсалиум
кругооборот — / ˈsɜkət / (скажем serkuht) существительное 1. действие движения или передвижения. 2. любой круговой или обходной путь; вокруг. 3. любой гоночный трек, который ведет обратно к месту старта, так что участники могут постоянно перемещаться по нему.4. Периодическое издание…… Австралийский английский словарь
Задержка цепи — Когда время увеличивается от нуля на клеммах индуктора, напряжение достигает определенного значения на кривой синусоиды перед током. Напряжение достигает своего отрицательного пика ровно на 90 градусов до того, как ток достигнет своего…… Энергетические условия
Характеристики кривых срабатывания и координации автоматического выключателя

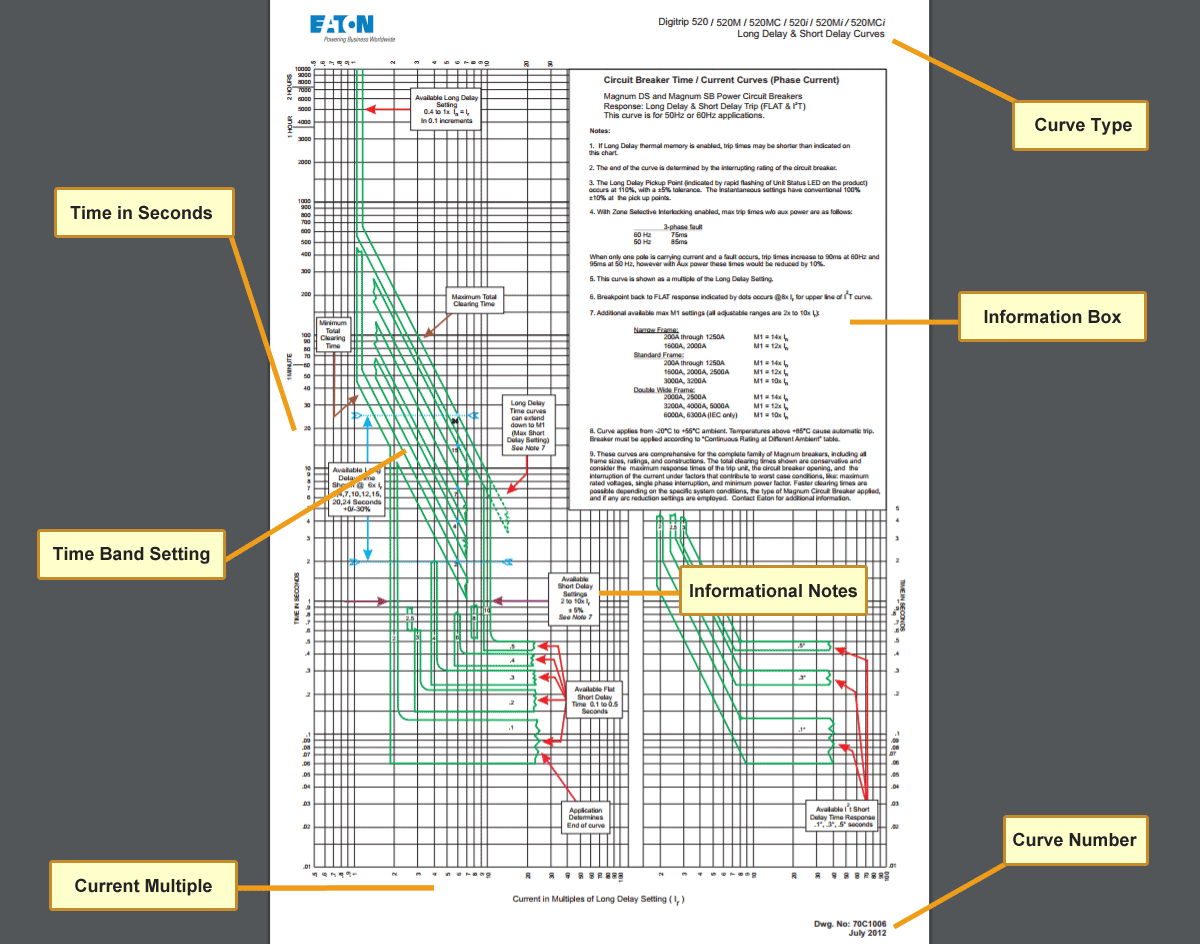
Рис. 1: Упрощенная временная кривая тока. Фото: TestGuy
Время-токовые кривые используются, чтобы показать количество времени, необходимое автоматическому выключателю для отключения при заданном уровне перегрузки по току.
Время-текущие кривые обычно отображаются в виде графика журнала. Цифры вдоль горизонтальной оси кривой представляют номинальный постоянный ток (In) для автоматического выключателя, цифры по вертикальной оси представляют время в секундах.
Чтобы определить, сколько времени потребуется выключателю для отключения: найдите текущее значение, кратное (In), внизу графика. Затем нарисуйте вертикальную линию до точки, где она пересекает кривую, а затем проведите горизонтальную линию с левой стороны графика, чтобы найти время поездки.
Общее время отключения автоматического выключателя — это сумма времени срабатывания выключателя, времени отключения, времени механической срабатывания и времени дуги.
Кривыеразработаны с использованием заранее определенных характеристик, таких как работа при температуре окружающей среды 40 ° C, поэтому имейте в виду, что фактические условия эксплуатации автоматического выключателя могут вызвать отклонения в его характеристиках.
У большинства кривых есть информационное окно, в котором будет указано, к какому выключателю применяется кривая. Это информационное окно может также содержать важные примечания от производителя, такие как допустимое отклонение от времени поездки.
Пример реальной кривой тока времени автоматического выключателя с основными моментами. Фото: TestGuy
Защита от перегрузки
Верхняя часть кривой время-ток показывает тепловую реакцию выключателя, изогнутая линия указывает номинальную производительность автоматического выключателя.
В термомагнитных выключателях тепловая перегрузка возникает, когда биметаллический провод внутри автоматического выключателя отклоняется после нагревания током нагрузки, освобождая рабочий механизм и размыкая контакты.
Чем больше перегрузка, тем быстрее биметаллическая полоса нагревается и отклоняется, чтобы устранить перегрузку. Это то, что известно как обратная временная кривая.
Долговременная функция
В электронных автоматических выключателях функция длительного действия (L) имитирует эффект термического биметаллического элемента.Номинальная точка срабатывания, в которой электронный расцепитель определяет перегрузку, составляет примерно 10% от выбранного номинального тока. После срабатывания автоматический выключатель сработает по истечении времени, заданного настройкой длительной задержки.
Защита от короткого замыкания
Нижняя часть кривой время-ток отображает реакцию автоматического выключателя на короткое замыкание. В термомагнитных выключателях место срабатывания при значительных сверхтоков приводит в действие магнитный якорь внутри автоматического выключателя, который отключает механизм.
Мгновенная функция
В электронных автоматических выключателях функция мгновенного действия (I) имитирует магнитную характеристику термомагнитного выключателя. Это достигается с помощью микропроцессора, который много раз в секунду берет выборки из формы волны переменного тока для вычисления истинного среднеквадратичного значения тока нагрузки. Мгновенное отключение происходит без преднамеренной задержки по времени.
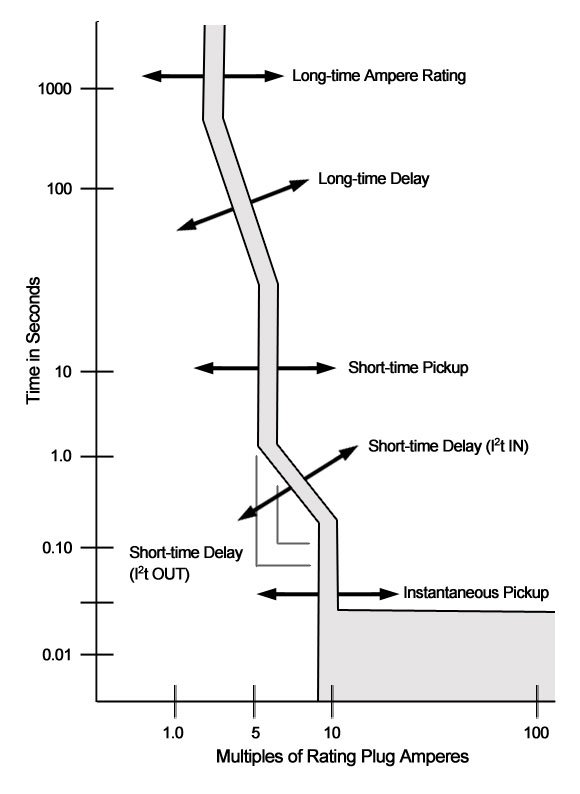
Рисунок 3: Комбинированная кривая LSIG. Фото: TestGuy.
Кратковременная функция
Некоторые электронные автоматические выключатели могут быть оснащены функцией короткого замыкания (S), которая дает автоматическому выключателю задержку перед срабатыванием при значительной перегрузке по току.Это позволяет осуществлять выборочную координацию между защитными устройствами, чтобы гарантировать, что только устройство, ближайшее к месту повреждения, отключается, не затрагивая другие цепи (см. Координацию автоматического выключателя ниже) .
I 2 t характеристика кратковременной функции определяет тип задержки. I 2 t IN приведет к обратнозависимой задержке, которая напоминает временные / токовые характеристики предохранителей. Это похоже на функцию долгого времени, за исключением гораздо более быстрой задержки.I 2 t OUT обеспечивает постоянную задержку, обычно 0,5 секунды или меньше, как указано на кривой время-ток.
Функция блокировки зоны
Автоматические выключатели, оборудованные блокировкой зон по короткой задержке без сигнала ограничения от нижестоящего устройства, будут иметь минимальный временной диапазон, применяемый независимо от настройки, это иногда называют максимальной неограниченной задержкой.
Когда мгновенная функция отключена, используется блокировка с кратковременной задержкой для мгновенного отключения автоматических выключателей в случае значительного короткого замыкания.Это называется кратковременной стойкостью и отображается на кривой срабатывания в виде абсолютного значения в амперах.
Связанные: Основные принципы селективной блокировки зон (ZSI)
Защита от замыканий на землю
Как и функция длительного действия, элемент защиты от замыкания на землю (G) состоит из установки срабатывания и задержки. Когда происходит замыкание фазы на землю, сумма фазных токов перестает быть равной, поскольку ток замыкания на землю возвращается через шину заземления.В 4-проводной системе четвертый трансформатор тока устанавливается на нейтральную шину для обнаружения этого дисбаланса.
Когда происходит дисбаланс тока, автоматический выключатель срабатывает, если величина превышает уставку срабатывания замыкания на землю. Если выключатель остается включенным в течение времени, заданного задержкой замыкания на землю, автоматический выключатель сработает. Защита от замыкания на землю иногда поставляется с функцией I 2 t, которая работает по тому же принципу, что и кратковременная задержка.
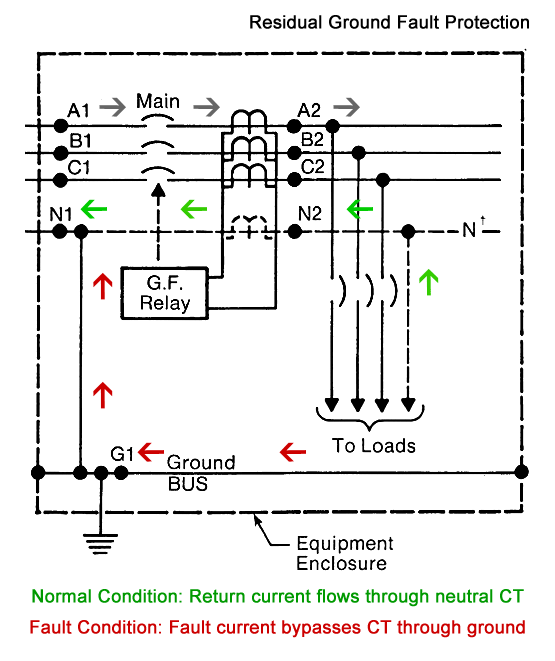
Пример 4-проводной системы защиты от замыканий на землю.Фото: TestGuy.
Защита от замыкания на землю требует наименьшего количества энергии для отключения автоматического выключателя, часто со значениями отключения, установленными значительно ниже уставки срабатывания длительного срабатывания. При проверке функции перегрузки или короткого замыкания автоматического выключателя защиту от замыкания на землю необходимо отключить или «убрать с дороги» для работы других функций.
Использование испытательного комплекта изготовителя или изменение проводки входа трансформатора тока нейтрали является предпочтительным методом испытания первичной инжекции на выключателе низкого напряжения с защитой от замыкания на землю, в противном случае два полюса могут быть соединены последовательно для обеспечения сбалансированных вторичных токов на расцепитель. .
Связано: Системы защиты от замыканий на землю: основы тестирования производительности
Координация автоматического выключателя
Время-токовые кривые необходимы для правильного согласования автоматических выключателей. В случае неисправности должен срабатывать только ближайший к неисправности автоматический выключатель, не затрагивая другие цепи.
В приведенном ниже примере три автоматических выключателя скоординированы таким образом, чтобы время отключения каждого выключателя было больше времени отключения выключателя (ей), расположенного ниже по цепи, независимо от величины повреждения.
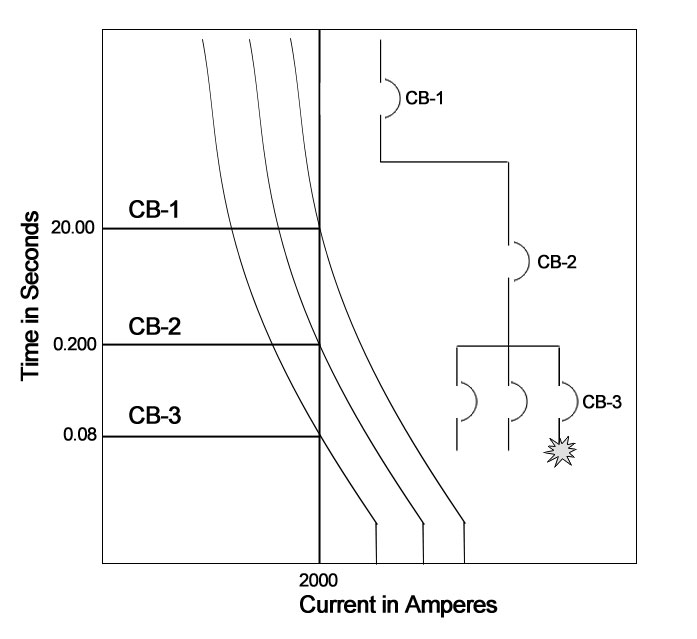
Упрощенный пример координации отключения выключателя. Фото: TestGuy.
Автоматический выключатель CB-3 настроен на отключение, если перегрузка 2000A или выше происходит в течение 0,080 секунд . Автоматический выключатель CB-2 сработает, если перегрузка сохраняется в течение 0,200 секунд, и автоматический выключатель CB-1 , если неисправность сохраняется в течение 20 секунд .
Если отказ происходит после выключателя CB-3 , он срабатывает первым и сбрасывает неисправность.Автоматические выключатели CB-2 и CB-1 будут продолжать обеспечивать питание цепи.
Каждая функция расцепителя должна быть скоординирована для предотвращения ложных срабатываний. Если автоматический выключатель питает часть оборудования, например, с большими пусковыми токами, значение мгновенного срабатывания должно быть выше, чем значение кратковременного срабатывания, чтобы предотвратить отключение, когда оборудование находится под напряжением.
Связано: Объяснение исследований координации электроэнергетической системы