4 у (x) = х4 — 2х2 + 3.
- Область определения: вся числовая прямая.
- Найдем производную функции:
у’ (x) = (х4 — 2х2 + 3)’ = 4x3 -4х.
у’ (x) = 0:
4x3 -4х = 0,
4х (х2 – 1) = 0,
4х (х – 1) (x + 1) = 0,
х1 = 0,
х2 = -1,
x3 = 1.
При х < -1, у’ (х) < 0, значит, функция убывает.
При -1 < х < 0, у’ (х) > 0, значит, функция возрастает.
При 0 < х < 1, у’ (х) < 0, значит, функция убывает.
При х > 1, у’ (х) > 0, значит, функция возрастает.
Точка х = 0 – точка максимума, y (0) = 3.
Точка х = -1 – точка минимума, y (-1) = 2.
Точка х = 1 – точка минимума, y (1) = 2.
- Найдем вторую производную:
у’’ (x) = (4x3 -4х)’ = 12x2 — 4.
у’’ (x) = 0:
12x2 — 4 = 0,
4 (3x2 – 1) = 0,
х = √3 /3, х = -√3 /3.
При х < -√3 /3, у’’ (х) > 0, значит, функция выпукла вниз (вогнута).
При -√3 /3 < х < √3 /3, у’’ (х) < 0, значит, функция выпукла вверх.
При х > √3 /3, у’’ (х) > 0, значит, функция выпукла вниз (вогнута)..
- Асимптот нет.
- Точек разрыва нет.
- у (-x) = х4 — 2х2 + 3 = у (х)
функция четная.
- График: http://bit.ly/2zfD1ey
у (x) = 2x3+3x2
- Область определения: вся числовая прямая.
- Найдем производную функции:
у’ (x) = (2x3+3x2)’ = 6x2 +6х.
у’ (x) = 0:
6x2 +6х = 0,
6х (х + 1) = 0,
х1 = 0,
х2 = -1.
При х < -1, у’ (х) > 0, значит, функция возрастает.
При -1 < х < 0, у’ (х) < 0, значит, функция убывает.
При х > 0, у’ (х) > 0, значит, функция возрастает.
Точка х = -1 – точка максимума, y (-1) = 1.
Точка х = 0 – точка минимума, y (0) = 0.
- Найдем вторую производную:
у’’ (x) = (6x2 +6х)’ = 12x + 6.
у’’ (x) = 0:
12x + 6= 0,
х = -1/2.
При х < -1/2, у’’ (х) < 0, значит, функция выпукла вверх.
При х > -1/2, у’’ (х) > 0, значит, функция выпукла вниз (вогнута).
- Асимптот нет.
- Точек разрыва нет.
- у (-x) = -2x3
функция общего вида.
- График: http://bit.ly/2hiMLKd
Контрольная по алгебре «Производные»
Вариант №1 | Вариант №2 | Вариант №3 | Вариант №4 |
y = x2 – 5x + 4
|
y = 5x2 + 15x – 1
|
y = -x2 + 8x – 7
|
y = x2 — 1
|
y = x3 – 3x2 + 2
y = — x3 + 3x – 2
Найти точки экстремума:
y = x2 – 8x + 19
y = x2 + 4x — 3
Найти промежутки монотонности:
y = x3 – 3x
Построить график:
y = x2 + 5
y = x3 + 3x2 – 4
Найти наибольшее и наименьшее значение функции на интервале:
y = x3 – 9x2 + 24x – 1; [-1;3]
y = 2 sin x; [-π/2; π]
Найти стационарные точки функции:
y = 2x2 – 9x + 7
y = 5x3 – 3x5
Найти точки экстремума:
y = 2x2 – 8x + 6
y = -3x2 + 6x – 10
Найти промежутки монотонности:
y = 60 + 45x – 3x2 – x3
Построить график:
y = 2x2 – 4
y = x4 – 2x2
Найти наибольшее и наименьшее значение функции на интервале:
y = x3 – 9x2 + 24x – 1; [3;6]
y = -2 cos x; [-2π; -π/2]
Найти стационарные точки функции:
y = 3x2 – 4x + 1
y = 2x2 – 10x + 4
Найти точки экстремума:
y = x3 – 3x – 10
y = 3x
Найти промежутки монотонности:
y = 2x3 – 3x2 – 36x + 40
Построить график:
y = 3x2 – 6
y = -x3 – 3x2 + 3
Найти наибольшее и наименьшее значение функции на интервале:
y = x3 – 9x2 + 24x – 1; [-2;3]
y = 6 cos x; [-π/2; 0]
Найти стационарные точки функции:
y = 5x2 – 10x + 1
y = -x3 +12x2 – 2
Найти точки экстремума:
y = x3 – 3x2 + 1
y = 3x2 – x + 2
Найти промежутки монотонности:
y = -x5 + 5x
Построить график:
y = 2x2 – 10
y = 8x3 – 3x4 – 7
Найти наибольшее и наименьшее значение функции на интервале:
y = x3 – 9x2 + 24x – 1; [3;5]
y = -0,5 sin x; [-π/2; π/2]
Ответы:
a) b)a) b)
a)
b)
5.
a) yнаим = yнаиб =
b) yнаим = yнаиб =
a) b)
a) b)
a)
b)
5. a) yнаим = yнаиб =
b) yнаим = yнаиб =
a) b)
a) b)
a)
b)
5. a) yнаим = yнаиб =
b) yнаим = yнаиб =
a) b)
a) b)
a)
b)
5. a) yнаим = yнаиб =
b) yнаим = yнаиб =
Вариант №5
Вариант №6
Вариант №7
Вариант №8
a) b)
a) b)
a)
b)
5.
2$
9
6,25
4
2,25
1
0,25
0
0,25
1
2,25
4
6,25
9
Отметим полученные точки на координатной плоскости и соединим их кривой:
Полученный график называют параболой. Точка (0;0) — это вершина параболы. Вершина делит график на левую и правую части, которые называют ветвями параболы.
Свойства параболы y=x²
1. Область определения $x \in (- \infty;+ \infty)$ — все действительные числа.
2. Область значений $y \in [0;+ \infty)$ — все неотрицательные действительные числа.
3. Функция убывает при $x \lt 0$, функция возрастает при $x \gt 0$.
4. Наименьшее значение функции y = 0 — в вершине параболы при x = 0. Вершина параболы совпадает с началом координат.
5. Все точки на ветвях параболы лежат выше оси абсцисс, для них $y \gt 0$.
2$, кроме двух точек с $ x \neq \pm 1 $.
Графические уравнения с программой «Пошаговое решение математических задач»
Введите уравнение, которое вы хотите построить, при необходимости установите зависимую переменную и нажмите кнопку «График».
Язык математики особенно эффективен для представления отношений между двумя или более переменными. В качестве примера рассмотрим пройденное расстояние через определенный промежуток времени автомобилем, движущимся с постоянной скоростью 40 миль в час. Мы можем представить эту взаимосвязь как
- 1.Словесное предложение:
Пройденное расстояние в милях равно сороккратному количеству пройденных часов. - 2. Уравнение:
d = 40r. - 3. Таблица значений.
- 4. График, показывающий зависимость между временем и расстоянием.
Мы уже использовали словесные предложения и уравнения для описания таких отношений;
в этой главе мы будем иметь дело с табличным и графическим представлениями.
7.1 РЕШЕНИЕ УРАВНЕНИЙ ОТ ДВУХ ПЕРЕМЕННЫХ
ЗАКАЗАННЫЕ ПАРЫ
Уравнение d = 40f объединяет расстояние d для каждого момента времени t.Например,
, если t = 1, то d = 40
, если t = 2, то d = 80
, если t = 3, то d = 120
и так далее.
Пара чисел 1 и 40, рассматриваемая вместе, называется решением уравнение d = 40r, потому что когда мы подставляем 1 вместо t и 40 вместо d в уравнении, мы получаем верное утверждение. Если мы согласны ссылаться на парные номера в указанном порядок, в котором первое число относится ко времени, а второе число относится к расстояния, мы можем сократить приведенные выше решения как (1, 40), (2, 80), (3, 120) и скоро.Мы называем такие пары чисел упорядоченными парами и ссылаемся на первую и вторые числа в парах как компоненты. При этом соглашении решения Уравнение d — 40t — это упорядоченные пары (t, d), компоненты которых удовлетворяют уравнению. Некоторые упорядоченные пары для t, равного 0, 1, 2, 3, 4 и 5, равны
(0,0), (1,40), (2,80), (3,120), (4,160) и (5,200)
Такие пары иногда отображаются в одной из следующих табличных форм.
В любом конкретном уравнении с двумя переменными, когда мы присваиваем значение одной переменных определяется значение другой переменной и, следовательно, зависит от первого.Удобно говорить о переменной, связанной с первый компонент упорядоченной пары как независимая переменная и переменная связанный со вторым компонентом упорядоченной пары как зависимая переменная. Если в уравнении используются переменные x и y, подразумевается, что заменить — элементы для x являются первыми компонентами и, следовательно, x — независимая переменная и замены y являются вторыми компонентами и, следовательно, y является зависимой переменной. Например, мы можем получить пары для уравнения
, подставив конкретное значение одной переменной в уравнение (1) и решив для другая переменная.
Пример 1
Найдите недостающий компонент, чтобы заказанная пара стала решением для
2х + у = 4
а. (0 ,?)
г. (1 ,?)
г. (2 ,?)
Решение
если x = 0, то 2 (0) + y = 4
y = 4
если x = 1, то 2 (1) + y = 4
y = 2
, если x = 2, то 2 (2) + y = 4
y = 0
Три пары теперь могут отображаться как три упорядоченные пары
(0,4), (1,2) и (2,0)
или в табличной форме
ЯВНО ВЫРАЖАЮЩИЙ ПЕРЕМЕННУЮ
Мы можем добавить -2x к обоим членам 2x + y = 4, чтобы получить
-2x + 2x + y = -2x + 4
y = -2x + 4
В уравнении (2), где y есть само по себе, мы говорим, что y явно выражается через
из х.
Часто бывает проще получить решения, если сначала выразить уравнения в такой форме
потому что зависимая переменная явно выражается через независимые
переменная.
Например, в уравнении (2) выше
, если x = 0, то y = -2 (0) + 4 = 4
, если x = 1, то y = -2 (1) + 4 = 2
, если x = 2, то y = -2 (2) + 4 = 0
Мы получаем те же пары, что и с помощью уравнения (1)
(0,4), (1,2) и (2,0)
Мы получили уравнение (2) добавлением одинаковой величины -2x к каждому члену уравнения (1), таким образом получая y отдельно.В общем, мы можем написать эквивалент уравнения с двумя переменными, используя свойства, которые мы ввели в главе 3, где мы решали уравнения первой степени с одной переменной.
Уравнения эквивалентны, если:
- Одно и то же количество прибавляется к равным количествам или вычитается из них.
- Равные количества умножаются или делятся на одинаковое ненулевое количество.
Пример 2
Решите 2y — 3x = 4 явно для y через x и получите решения для x = 0,
х = 1 и х = 2.
Решение
Во-первых, добавляя 3x к каждому члену, мы получаем
2y — 3x + 3x = 4 + 3x
2y = 4 + 3x (продолжение)
Теперь, разделив каждый член на 2, получаем
В этой форме мы получаем значения y для заданных значений x следующим образом:
В этом случае три решения: (0, 2), (1, 7/2) и (2, 5).
ОБОЗНАЧЕНИЕ ФУНКЦИЙ
Иногда мы используем специальные обозначения для наименования второго компонента упорядоченного пара, которая связана с указанным первым компонентом.Символ f (x), который часто используется для обозначения алгебраического выражения в переменной x, также может использоваться для обозначения значение выражения для конкретных значений x. Например, если
f (x) = -2x + 4
, где f (x) играет ту же роль, что и y в уравнении (2) на странице 285, тогда f (1) представляет значение выражения -2x + 4, когда x заменяется на 1
f (l) = -2 (1) + 4 = 2
Аналогично
f (0) = -2 (0) + 4 = 4
и
f (2) = -2 (2) + 4 = 0
Символ f (x) обычно называют обозначением функции.
Пример 3
Если f (x) = -3x + 2, найти f (-2) и f (2).
Решение
Замените x на -2, чтобы получить
f (-2) = -3 (-2) + 2 = 8
Замените x на 2, чтобы получить
f (2) = -3 (2) + 2 = -4
7.2 ГРАФИК ЗАКАЗАННЫХ ПАР
В разделе 1.1 мы увидели, что каждое число соответствует точке в строке. Simi- Как правило, каждая упорядоченная пара чисел (x, y) соответствует точке на плоскости. Чтобы граф упорядоченной пары чисел, мы начинаем с построения пары перпендикулярных числовые линии, называемые осями.Горизонтальная ось называется осью x, вертикальная ось называется осью Y, а их точка пересечения называется началом координат. Эти топоры разделите плоскость на четыре квадранта, как показано на рисунке 7.1.
Теперь мы можем присвоить упорядоченную пару чисел точке на плоскости, указав
на перпендикулярное расстояние точки от каждой из осей. Если первый
составляющая положительная, точка лежит правее вертикальной оси; если отрицательный, это
лежит слева.
Если второй компонент положительный, точка находится выше
Горизонтальная ось; если отрицательный, он находится внизу.
Пример 1
График (3, 2), (-3, 2), (-3, -2) и (3, -2) в прямоугольной системе координат.
Решение
График (3, 2) находится на 3 единицы правее
ось y и 2 единицы над осью x;
график (-3,2) лежит на 3 единицы слева от
ось y и на 2 единицы выше оси x;
график (-3, -2) лежит на 3 единицы слева от
ось y и на 2 единицы ниже оси x;
график (3, -2) лежит на 3 единицы правее
по оси Y и на 2 единицы ниже оси X.
Расстояние y, на котором точка расположена от оси x, называется ординатой. точки, а расстояние x, на котором точка расположена от оси y, называется абсцисса точки. Абсцисса и ордината вместе называются прямоугольником. Гулярные или декартовы координаты точки (см. рисунок 7.2).
7.3 ПОСТРОЕНИЕ УРАВНЕНИЙ ПЕРВОГО УРОВНЯ
В разделе 7.1 мы увидели, что решение уравнения с двумя переменными является упорядоченным
пара.
В разделе 7.2 мы видели, что компонентами упорядоченной пары являются
координаты точки на плоскости. Таким образом, чтобы построить график уравнения с двумя переменными, мы
Изобразите набор упорядоченных пар, которые являются решениями уравнения. Например, мы
может найти некоторые решения уравнения первой степени
у = х + 2
, положив x равным 0, -3, -2 и 3. Затем
для x = 0, y = 0 + 2 = 2
для x = 0, y = -3 + 2 = -1
для x = -2, y = -2 + 2-0
для x = 3, y = 3 + 2 = 5
и получаем решения
(0,2), (-3, -1), (-2,0) и (3,5)
, который может отображаться в табличной форме, как показано ниже.
Если мы изобразим точки, определенные этими упорядоченные пары и провести прямую через их, мы получаем график всех решений y = x + 2, как показано на рисунке 7.3. Это, каждое решение y = x + 2 лежит на прямой, и каждая точка на линии является решением у = х + 2.
Графики уравнений первой степени в двух
переменные всегда прямые; следовательно,
такие уравнения также называются линейными
уравнения.
В приведенном выше примере значения, которые мы использовали для x были выбраны случайным образом; мы могли бы использовать любые значения x, чтобы найти решения уравнения.Графики любых других упорядоченных пар, которые являются решениями уравнения, также будут быть на линии, показанной на рисунке 7.3. Фактически, каждое линейное уравнение с двумя переменными имеет бесконечное количество решений, график которых лежит на прямой. Однако мы только нужно найти два решения, потому что для определения прямая линия. Третий балл можно получить как проверку.
Чтобы построить уравнение первой степени:
- Постройте набор прямоугольных осей, показывающих масштаб, а переменная представляет отправляется каждой осью.
- Найдите две упорядоченные пары, которые являются решениями уравнения для построения графика присвоение любого удобного значения одной переменной и определение соответствующего значение другой переменной.
- Изобразите эти упорядоченные пары.
- Проведите прямую линию через точки.
- Проверьте, построив третью упорядоченную пару, которая является решением уравнения и убедитесь, что он лежит на линии.
Пример 1
Постройте уравнение y = 2x — 6.
Решение
Сначала мы выбираем любые два значения x, чтобы найти соответствующие значения y.
Мы будем использовать 1 и 4 для x.
Если x = 1, y = 2 (1) — 6 = -4
, если x = 4, y = 2 (4) — 6 = 2
Таким образом, два решения уравнения:
(1, -4) и (4, 2).
Затем мы строим график этих упорядоченных пар и проводим прямую линию через точки, как показано
на рисунке. Мы используем стрелки, чтобы показать, что
линия тянется бесконечно далеко в обоих направлениях.
Любая третья упорядоченная пара, удовлетворяющая
уравнение можно использовать в качестве проверки:
, если x = 5, y = 2 (5) -6 = 4
Затем отметим, что график (5, 4) также лежит на линии
. Чтобы найти решения уравнения, как мы уже отмечали, часто проще всего сначала решить
явно для y через x.
Пример 2
График x + 2y = 4.
Решение
Сначала решаем y через x, чтобы получить
Теперь мы выбираем любые два значения x, чтобы найти соответствующие значения y. Мы будем использовать 2 и 0 для x.
Таким образом, два решения уравнения: (2, 1) и (0, 2).
Затем мы графически отображаем эти упорядоченные пары и проведите прямую через точки, как показано на рисунке.
Любая третья упорядоченная пара, удовлетворяющая уравнение можно использовать как проверку:
Затем отметим, что график (-2, 3) также лежит на линии.
ОСОБЫЕ СЛУЧАИ ЛИНЕЙНЫХ УРАВНЕНИЙ
Уравнение y = 2 можно записать как
0x + y = 2
и может рассматриваться как линейное уравнение в двух переменные, у которых коэффициент при x равен 0. Некоторые решения 0x + y = 2 равны
(1,2), (-1,2) и (4,2)
Фактически, любая упорядоченная пара вида (x, 2) является
решение (1).
Графическое изображение решений
дает горизонтальную линию, как показано на рисунке
7.4.
Точно так же уравнение, такое как x = -3, может можно записать как
х + 0у = -3
и может рассматриваться как линейное уравнение в двух переменные, у которых коэффициент при y равен 0.
Некоторые решения x + 0y = -3 являются (-3, 5), (-3, 1) и (-3, -2). Фактически любой упорядоченная пара вида (-3, y) является решением из (2). Графическое изображение решений дает вертикальную линии, как показано на рисунке 7.5.
Пример 3
График
а. у = 3
б. х = 2
Решение
а. Мы можем записать y = 3 как Ox + y = 3.
Некоторые решения: (1, 3), (2,3) и (5, 3).
б. Мы можем записать x = 2 как x + Oy = 2.
Некоторые решения: (2, 4), (2, 1) и (2, -2).
7.4 МЕТОД ПЕРЕСЕЧЕНИЯ ГРАФИКА
В Разделе 7.3 мы присвоили значения x в уравнениях с двумя переменными, чтобы найти
соответствующие значения y.
Решения уравнения с двумя переменными, которые
обычно легче всего найти те, в которых первый или второй компонент
0. Например, если мы заменим 0 на x в уравнении
3x + 4y = 12
у нас
3 (0) + 4y = 12
y = 3
Таким образом, решением уравнения (1) является (0, 3).Мы также можем найти упорядоченные пары, которые решения уравнений с двумя переменными путем присвоения значений y и определения соответствующие значения x. В частности, если мы подставим 0 вместо y в уравнение (1), мы получите
3x + 4 (0) = 12
x = 4
и второе решение уравнения (4, 0). Теперь мы можем использовать упорядоченные пары (0, 3) и (4, 0) для построения графика уравнения (1). График представлен на рисунке 7.6. Уведомление что линия пересекает ось x в точке 4 и ось y в точке 3. По этой причине число 4 называется пересечением по оси x графа, а число 3 — точкой пересечения по оси y.
Такой способ построения графика линейного уравнения называется перехватом.
метод построения графиков. Обратите внимание, что когда мы используем этот метод построения графиков линейного
уравнение, нет никакого преимущества в том, чтобы сначала явно выразить y через x.
Пример 1
График 2x — y = 6 методом пересечения.
Решение
Мы находим точку пересечения с x, подставляя 0 вместо y в уравнение, чтобы получить
2x — (0) = 6
2x = 6
x = 3
Теперь мы находим точку пересечения по оси Y, подставляя для x в уравнении, чтобы получить
2 (0) — y = 6
-y = 6
y = -6
Упорядоченные пары (3, 0) и (0, -6) являются решениями 2x — y = 6.Графическое изображение этих
точки и соединив их прямой линией, получим график 2x — y = 6.
Если график пересекает оси в или около начала координат, метод перехвата не работает.
удовлетворительно. Затем мы должны построить график упорядоченной пары, которая является решением уравнения
и чей график не является началом координат или не слишком близок к началу координат.
Пример 2
График y = 3x.
Решение
Мы можем заменить 0 на x и найти
y = 3 (0) = 0
Аналогичным образом, заменив 0 на y, мы получим
0 = 3.x, x = 0
Таким образом, 0 является одновременно точкой пересечения по оси x и точкой пересечения с y.
Так как одной точки недостаточно для графического = 3x, мы прибегаем к методам, описанным в Раздел 7.3. Выбирая любое другое значение для x, скажем 2, мы получаем
у = 3 (2) = 6
Таким образом, (0, 0) и (2, 6) являются решениями уравнение. График y = 3x показан на правильно.
7,5 НАКЛОН ЛИНИИ
ФОРМУЛА НАКЛОНА
В этом разделе мы изучим важное свойство линии.Мы назначим число к линии, которую мы называем уклоном, что даст нам меру «крутизны» или «направление» линии.
Часто бывает удобно использовать специальные обозначения для различения прямоугольников.
Гулярные координаты двух разных точек. Мы можем обозначить одну пару координат
на (x 1 , y 1 (читается «x sub one, y sub one»), связанный с точкой P 1 , и второй
пара координат по (x 2 , y 2 ), связанная со второй точкой P 2 , как показано на рисунке
7.
7. Обратите внимание на рис. 7.7, что при переходе от P 1 к P 2 вертикальное изменение (или
расстояние по вертикали) между двумя точками составляет y 2 — y 1 , а изменение по горизонтали (или
расстояние по горизонтали) составляет x 2 — x 1 .
Отношение вертикального изменения к горизонтальному называется крутизной линия, содержащая точки P 1 и P 2 . Это соотношение обычно обозначают m. Таким образом,
Пример 1
Найдите наклон прямой, содержащей два точки с координатами (-4, 2) и (3, 5) как показано на рисунке справа. Решение
Обозначим (3, 5) как (x 2 , y 2 ) и (-4, 2)
как (x 1 , y 1 ). Подставляя в уравнение (1)
дает
Обратите внимание, что мы получим тот же результат, если подставим -4 и 2 вместо x 2 и y 2 и 3 и 5 для x 1 и y 1
Линии с различным уклоном показаны на Рисунке 7.
8 ниже. Наклоны линий, которые
вверх вправо положительны (рисунок 7.8а) и наклоны спускающихся вниз
справа отрицательны (рисунок 7.8b). Обратите внимание (рис. 7.8c), поскольку все
точки на горизонтальной линии имеют одинаковое значение y, y 2 — y 1 равно нулю для любых двух
точек, а наклон линии просто
Также обратите внимание (рисунок 7.8c), что, поскольку все точки на вертикали имеют одинаковое значение x, x 2 — x 1 равняется нулю для любых двух точек. Однако
не определено, поэтому вертикальная линия не имеет наклона.
ПАРАЛЛЕЛЬНЫЕ И ПЕРПЕНДИКУЛЯРНЫЕ ЛИНИИ
Рассмотрим линии, показанные на рисунке 7.9. Линия l 1 имеет наклон m 1 = 3, а линия l 2 имеет уклон м 2 = 3. В данном случае
Эти линии никогда не пересекаются и называются параллельными линиями. Теперь рассмотрим строки
показано на рисунке 7.10.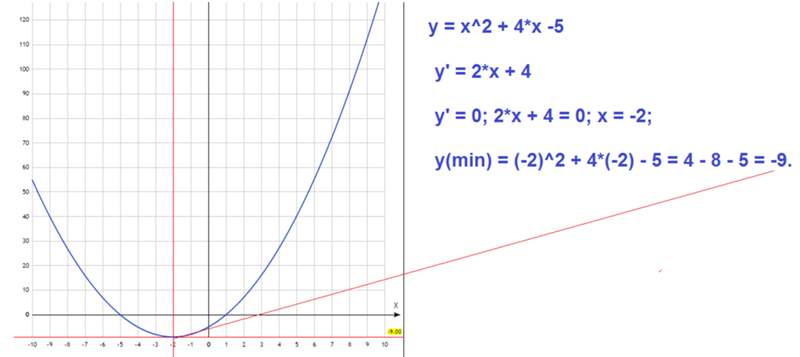
Линия l 1 имеет наклон m 1 = 1/2, а линия l 2 имеет наклон m 2 = -2.
В данном случае
Эти линии пересекаются, образуя прямой угол, и называются перпендикулярными линиями.
Как правило, если две линии имеют уклон и м2:
- а. Линии параллельны, если они имеют одинаковый наклон, то есть
если m 1 = m 2 .
г. Линии перпендикулярны, если произведение их уклонов равно -1, то есть если m 1 * m 2 = -1.
7.6 УРАВНЕНИЯ ПРЯМЫХ ЛИНИЙ
ФОРМА POINT-SLOPE
В разделе 7.5 мы нашли наклон прямой по формуле
Допустим, мы знаем, что линия проходит через точку (2, 3) и имеет наклон 2.Если мы обозначим любую другую точку на прямой как P (x, y) (см. Рис. 7.1а), наклоном формула
Таким образом, уравнение (1) — это уравнение прямой, проходящей через точку (2, 3), и имеет уклон 2.
В общем, допустим, мы знаем, что линия проходит через точку P 1 (x 1 , y 1 и имеет
уклон м.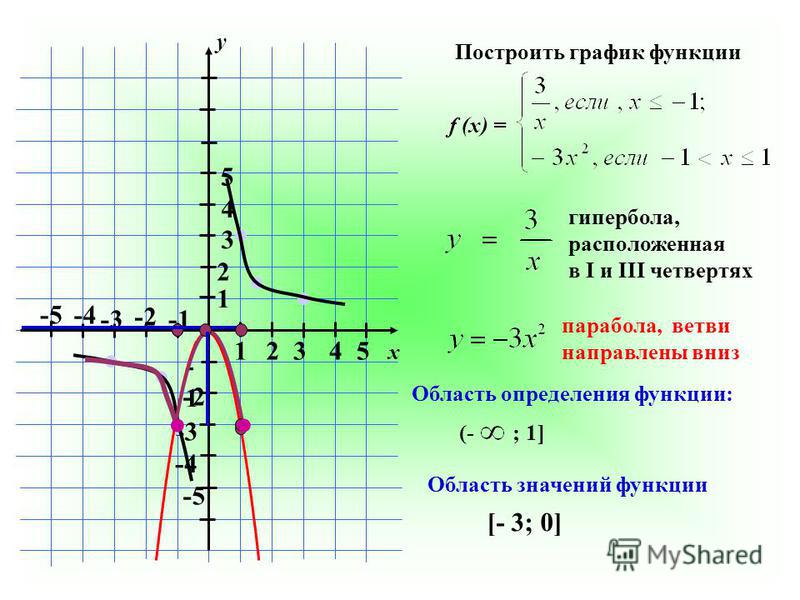
Если мы обозначим любую другую точку на прямой как P (x, y) (см. Рис. 7.11 b), то через
формула наклона
Уравнение (2) называется формой точечного уклона для линейного уравнения.В уравнении (2), m, x 1 и y 1 известны, а x и y — переменные, которые представляют координаты любая точка на линии. Таким образом, если нам известен наклон линии и точки на линии, мы можем найти уравнение линии, используя уравнение (2).
Пример 1
Линия имеет наклон -2 и проходит через точку (2, 4). Найдите уравнение прямой.
Решение
Замените -2 вместо m и (2, 4) вместо (x 1 , y 1 ) в уравнении (2)
Таким образом, прямая с наклоном -2, проходящая через точку (2, 4), имеет уравнение у = -2х + 8.Мы могли бы также записать уравнение в эквивалентной форме y + 2x = 8, 2x + y = 8 или 2x + y — 8 = 0.
ФОРМА НАКЛОНА
Теперь рассмотрим уравнение прямой с наклоном m и точкой пересечения оси y b, как показано на
Рисунок 7.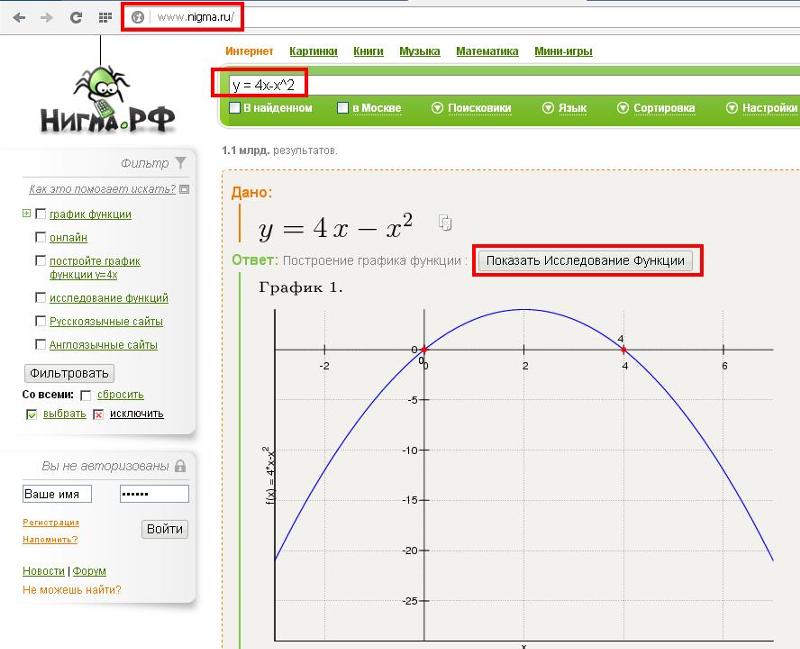
12. Подставив 0 вместо x 1 и b вместо y 1 в форме точечного наклона линейного
уравнение, имеем
y — b = m (x — 0)
y — b = mx
или
y = mx + b
Уравнение (3) называется формой пересечения наклона для линейного уравнения.Наклон и пересечение по оси Y можно получить непосредственно из уравнения в эта форма.
Пример 2 Если линия имеет уравнение
, то наклон линии должен быть -2, а точка пересечения оси Y — 8. Аналогично, график
г = -3x + 4
имеет наклон -3 и точку пересечения по оси Y 4; и график
имеет наклон 1/4 и точку пересечения по оси Y -2.
Если уравнение не записано в форме x = mx + b, и мы хотим знать наклон и / или точку пересечения по оси y, мы переписываем уравнение, решая для y через x.
Пример 3
Найдите наклон и точку пересечения оси Y 2x — 3y = 6.
Решение
Сначала мы решаем y в терминах x, добавляя -2x к каждому члену.
2x — 3y — 2x = 6 — 2x
— 3y = 6 — 2x
Теперь, разделив каждого члена на -3, мы получим
Сравнивая это уравнение с формой y = mx + b, отметим, что наклон m (величина коэффициент при x) равен 2/3, а точка пересечения оси y равна -2.
7.7 ПРЯМОЕ ИЗМЕНЕНИЕ
Частный случай уравнения первой степени с двумя переменными дается
y = kx (k — постоянная)
Такая связь называется прямой вариацией.Мы говорим, что переменная y изменяется прямо как x.
Пример 1
Мы знаем, что давление P в жидкости изменяется прямо пропорционально глубине d ниже поверхность жидкости. Мы можем обозначить это соотношение в символах как
P =
кДВ прямом варианте, если мы знаем набор условий для двух переменных, и если мы также знаем другое значение для одной из переменных, мы можем найти значение вторая переменная для этого нового набора условий.
В приведенном выше примере мы можем решить для константы k, чтобы получить
Поскольку отношение P / d является постоянным для каждого набора условий, мы можем использовать соотношение
для решения задач, связанных с прямым изменением.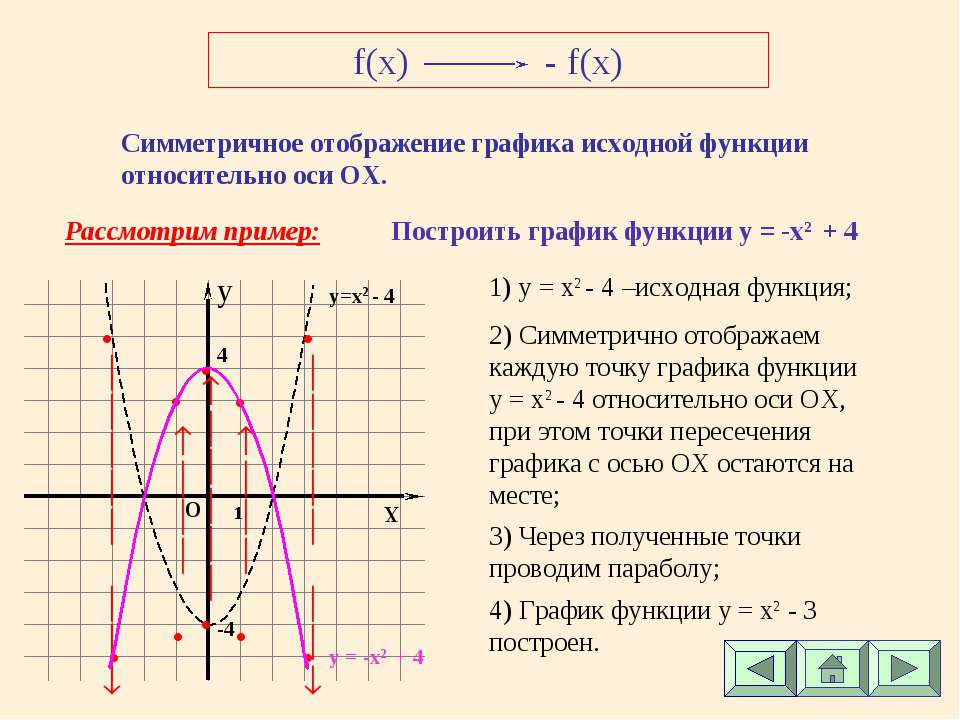
Пример 2
Если давление P изменяется прямо пропорционально глубине d и P = 40, когда d = 10, найдите P, когда d = 15.
Решение
Поскольку отношение P / d является постоянным, мы можем подставить значения для P и d и получить
пропорция
Таким образом, P = 60 при d = 15.
7.8 НЕРАВЕНСТВА В ДВУХ ПЕРЕМЕННЫХ
В разделах 7.3 и 7.4 мы построили уравнения с двумя переменными. В этом разделе мы построит график неравенств по двум переменным. Например, рассмотрим неравенство
у ≤ -x + 6
Решения — это упорядоченные пары чисел, которые «удовлетворяют» неравенству.Это, (a, b) является решением неравенства, если неравенство является истинным утверждением после того, как мы заменим a на x и b на y.
Пример 1
Определите, является ли данная упорядоченная пара решением y = -x + 6.
а. (1, 1)
б. (2, 5)
Решение
Упорядоченная пара (1, 1) является решением, потому что, когда 1 заменяется на x, а 1
подставляем вместо y, получаем
(1) = — (1) + 6, или 1 = 5
, что является правдой.
С другой стороны, (2, 5) не является решением, потому что когда
2 заменяется на x и 5 заменяется на y, мы получаем
(5) = — (2) + 6, или 5 = 4
, что является ложным заявлением.
Чтобы изобразить неравенство y = -x + 6, сначала построим уравнение y = -x + 6 показано на рисунке 7.13. Обратите внимание, что (3, 3), (3, 2), (3, 1), (3, 0) и т. Д., Связанные с точками, находящимися на линии или под ней, являются решениями неравенства y = -x + 6, тогда как (3,4), (3, 5) и (3,6), связанные с точками над линии не являются решениями неравенства. Фактически, все упорядоченные пары, связанные с точки на линии или ниже являются решениями y = — x + 6. Таким образом, каждая точка на или под чертой находится на графике.Мы представляем это, закрашивая область под линия (см. рисунок 7.14).
В общем, чтобы построить график неравенства первой степени с двумя переменными в виде
Ax + By = C или Ax + By = C, сначала строим график уравнения Ax + By = C и
затем определите, какая полуплоскость (область выше или ниже линии) содержит
решения.
Затем закрашиваем эту полуплоскость. Всегда можно определить, какая половина
плоскость заштриховать, выбрав точку (не на линии уравнения Ax + By = C)
и тестирование, чтобы увидеть, является ли упорядоченная пара, связанная с точкой, решением
учитывая неравенство.В таком случае закрашиваем полуплоскость, содержащую контрольную точку; в противном случае,
закрашиваем другую полуплоскость. Часто (0, 0) удобная контрольная точка.
Пример 2
График 2x + 3y = 6
Решение
Сначала построим линию 2x + 3y = 6 (см. График a). Используя начало координат как контрольную точку,
мы определяем, является ли (0, 0) решением 2x + 3y ≥ 6. Поскольку утверждение
2 (0) + 3 (0) = 6
ложно, (0, 0) не является решением и мы закрашиваем полуплоскость, не содержащую начало координат (см. график b).
Когда линия Ax + By = C проходит через начало координат, (0, 0) не является допустимым тестом точка, поскольку она находится на линии.
Пример 3
График y = 2x.
Решение
Начнем с построения линии y = 2x (см. График a). Поскольку линия проходит через
начало координат, мы должны выбрать другую точку не на линии в качестве нашей тестовой точки. Мы будем
используйте (0, 1). Поскольку выписка
(1) = 2 (0)
верно, (0, 1) — решение, и мы закрашиваем полуплоскость, содержащую (0, 1) (см. график б).
Если символ неравенства — ‘, точки на графике Ax + By = C не являются решениями неравенства. Затем мы используем пунктирную линию для графика Ax + By = C.
РЕЗЮМЕ ГЛАВЫ
Решение уравнения с двумя переменными — это упорядоченная пара чисел. в упорядоченная пара (x, y), x называется первым компонентом, а y называется вторым составная часть. Для уравнения с двумя переменными переменная, связанная с первой компонент решения называется независимой переменной, а переменная связанный со вторым компонентом, называется зависимой переменной.Обозначение функции f (x) используется для обозначения алгебраического выражения в x.
Когда х в
символ f (x) заменяется определенным значением, символ представляет значение
выражения для этого значения x.Пересечение двух перпендикулярных осей в системе координат называется происхождение системы, и каждая из четырех областей, на которые делится плоскость называется квадрантом. Компоненты упорядоченной пары (x, y), связанной с точки на плоскости называются координатами точки; x называется абсциссой точки, а y называется ординатой точки.
График уравнения первой степени с двумя переменными представляет собой прямую линию. То есть каждый упорядоченная пара, которая является решением уравнения, имеет график, лежащий на линии, и каждая точка в строке связана с упорядоченной парой, которая является решением уравнение.
Графики любых двух решений уравнения с двумя переменными могут быть использованы для получить график уравнения. Однако два решения уравнения в двух переменные, которые обычно легче всего найти, — это те, в которых либо первая, либо второй компонент равен 0.
Координата x точки, в которой линия пересекает ось x.
называется пересечением по оси x линии, а координата y точки, в которой линия
пересекает ось Y называется пересечением линии. Использование точек пересечения для построения графика
уравнение называется методом построения графика с пересечением.Наклон прямой, содержащей точки P 1 (x 1 , y 1 ) и P 2 (x 2 , y 2 ), определяется как
Две прямые параллельны, если они имеют одинаковый наклон (м 1 = м 2 ).
Две прямые перпендикулярны, если произведение их уклонов равно — l (m 1 * m 2 = -1).
Форма точки-наклона прямой с уклоном m, проходящей через точку (x 1 , y 1 ) это
y — y 1 — m (x — x 1 )
Угол пересечения линии с наклоном m и точкой пересечения по оси y равен
y = mx + b
Взаимосвязь, определяемая уравнением вида
y = kx (k постоянная)
называется прямой вариацией.
Решением неравенства с двумя переменными является упорядоченная пара чисел, которая, при подстановке в неравенство делает неравенство истинным утверждением. В График линейного неравенства от двух переменных представляет собой полуплоскость. Символы, представленные в этой главе, находятся на внутренней стороне передней обложки.
Когда х в
символ f (x) заменяется определенным значением, символ представляет значение
выражения для этого значения x.
Координата x точки, в которой линия пересекает ось x.
называется пересечением по оси x линии, а координата y точки, в которой линия
пересекает ось Y называется пересечением линии. Использование точек пересечения для построения графика
уравнение называется методом построения графика с пересечением.
Узнайте, как построить график правила функции, построить график входов (x) и выходов (y)
В этом видео мы узнаем, как построить график функции.Чтобы построить график функции, вы должны выбрать значения x и вставить их в уравнение. Как только вы подставите эти значения в уравнение, вы получите значение y . Ваши значения x и y составляют ваши координаты для одной точки. Продолжайте вводить значения x, чтобы получить координаты для построения большего количества точек на графике, и тогда вы увидите свою графическую функцию, как только точки будут соединены.
Обязательно пометьте свой график. После того, как вы закончите этот урок, просмотрите все наши уроки Алгебры 1 и попрактикуйтесь.
Пример построения графика функции-правила
Эти координаты будут выглядеть так:
и
Стенограмма видеоурока
Пример 1
Давайте выберем значения x, а затем решим соответствующие им значения y.
У нас есть значения x как.
Наша функция.
Итак, давайте заменим значения, чтобы получить значения.
А теперь нарисуем координаты.
Пример 2
Давайте выберем значения x, а затем решим соответствующие им значения y.
У нас есть значения x как.
Наша функция.
Итак, давайте заменим значения, чтобы получить значения.
А теперь нарисуем координаты.
Давайте рассмотрим график функции-правила.
Например:
Давайте выберем значения, а затем решим соответствующие им значения.
У нас есть значения as.
Наша функция.
Итак, давайте заменим значения, чтобы получить значения.
Если
, затем
так
Если
, затем
так
Если
, затем
так
Если
, затем
так
Если
, затем
так
Если
, затем
так
И, наконец, если
, затем
так
Давайте также напишем наши координаты и
Теперь давайте изобразим это.
После соединения точек важно поставить стрелки на обоих концах отрезка линии.
Потому что мы знаем, что эти точки являются точками функции. Но дело не только в этом.
Функция может перемещаться на обоих концах, обозначенных стрелками.
А затем пометьте график.
Построение линейного уравнения с помощью таблицы значений
Построение графика линейного уравнения
Линейное уравнение — это уравнение с двумя переменными, которое при построении графика дает прямую линию.
Вы, наверное, знаете, как читать график линейного уравнения, но как нам нарисовать линейное уравнение на координатной плоскости? Оказывается, на самом деле это не так уж и сложно! Первый шаг — научиться составлять таблицу значений.
Что такое таблица значений
Когда нам нужно построить линейное уравнение, вы начнете с создания таблицы значений. Таблица значений, как следует из названия, представляет собой графический способ определения значений, которые будут использоваться для создания вашего графика. Это место, где вы можете записать ответы, которые вы получите, когда найдете значения x и y. Вам нужно будет использовать как минимум 2 набора точек для построения линейного уравнения, но обычно вы делаете больше в таблице значений.
Таблица значений состоит из двух столбцов.В одном столбце перечислены значения x, а в одном столбце — соответствующие значения y. Давайте перейдем к выяснению того, как эту таблицу можно использовать для построения графиков линейных уравнений.
Построение линейных уравнений с использованием таблицы значений
Когда у вас есть пустая таблица значений и линейное уравнение, которое вы хотите построить графиком, вы можете взять любое значение x на оси x по вашему выбору, чтобы начать с таблицы. Допустим, вы берете число 3. Подставьте его в линейное уравнение, чтобы увидеть, что вы получите, когда решите относительно y по оси y.Представим, что у вас -5. Запишите оба этих числа в таблицу: 3 в столбце со значениями x и -5 в столбце для значений y.
Выберите другое значение x, с которым вы хотите работать, и снова решите относительно y. Повторите столько раз, сколько хотите, чтобы выработать наборы значений для включения в вашу таблицу. Когда у вас есть сумма, которая вас устраивает или которую требует ваш вопрос, вы можете затем взять эти значения x и y и нанести их в виде координат на график, чтобы отобразить точки на линейном уравнении!
Примеры задач
Вопрос 1:
График следующей функции с использованием таблицы значений
у = 3х — 1
Решение:
Сначала создайте таблицу значений для уравнения.
Используйте x, чтобы найти y. Вы можете использовать разные значения, но ваш график будет одинаковым независимо от того, какие значения вы используете.
Для x = -2
у = 3 (-2) — 1
г = -6 — 1
г = -7
Для x = -1
у = 3 (-1) — 1
г = -3 — 1
г = -4
Для x = 0
у = 3 (0) — 1
г = 0 — 1
г = -1
Для x = 1
у = 3 (1) — 1
г = 3 — 1
г = 2
Для x = 2
у = 3 (2) — 1
г = 6 — 1
г = 5
Теперь у нас есть полная таблица значений
Заполненная таблица значений x и yТеперь мы можем нанести упорядоченные пары на сетку
Построение данныхЗатем соедините точки прямой линией, и готово!
Связывание данных по прямойВопрос 2:
Изобразите следующую функцию, используя таблицу значений:
2x + 4y = 8
Решение:
Во-первых, мы хотим упростить уравнение
2x + 4y = 8
х + 2у = 4
2у = -x + 4
y = −12 \ frac {-1} {2} 2−1 x + 2
Теперь у нас есть уравнение в форме пересечения наклона.
Затем создайте таблицу значений для уравнения. Используйте x, чтобы найти y.
Таблица x решает относительно yДля x = -2
y = −12 \ frac {-1} {2} 2−1 (-2) + 2
г = 1 + 2
г = 3
Для x = -1
y = −12 \ frac {-1} {2} 2−1 (-1) + 2
г = 0,5 + 2
г = 2,5
Для x = 0
y = −12 \ frac {-1} {2} 2−1 (0) + 2
у = 0 + 2
г = 2
Для x = 1
y = −12 \ frac {-1} {2} 2−1 (1) + 2
у = -0.5 + 2
г = 1,5
Для x = 2
y = −12 \ frac {-1} {2} 2−1 (2) + 2
г = -1 + 2
г = 1
Теперь у нас есть полная таблица значений
Таблица заполненных данныхМы можем нанести упорядоченные пары на сетку.
Координаты, построенные с использованием таблицы данныхЗатем соедините точки прямой линией, и готово!
Свяжите данные вместе прямой линией Хотите проверить свой ответ, чтобы увидеть, насколько точен ваш график? Вот для справки онлайн-калькулятор.
Далее вы узнаете больше о таблице значений, как построить график линейных неравенств с двумя переменными и как построить график систем линейных неравенств. Вы также можете начать изучать введение в функции и способы их идентификации.
Линейные функции и их графики
Обзор линий графика
Напомним, что множество всех решений линейного уравнения может быть представлено на прямоугольной координатной плоскости с использованием прямой линии, проходящей по крайней мере через две точки; эта линия называется ее графиком.Например, чтобы построить график линейного уравнения 8x + 4y = 12, мы сначала решим относительно y .
8x + 4y = 12 Вычтем 8x с обеих сторон. 4y = −8x + 12 Разделим обе стороны на 4.y = −8x + 124 Упростим. Y = −8×4 + 124y = −2x + 3
Написано в этой форме, мы видим, что y зависит от x ; другими словами, x — это независимая переменная, которая определяет значения других переменных.
Обычно мы думаем о x -значении упорядоченной пары ( x , y ) как о независимой переменной.и y — зависимая переменная Переменная, значение которой определяется значением независимой переменной. Обычно мы думаем о y -значении упорядоченной пары ( x , y ) как о зависимой переменной. Выберите как минимум два x -значения и найдите соответствующие y -значения. Рекомендуется выбирать ноль, некоторые отрицательные числа, а также некоторые положительные числа. Здесь мы выберем пять значений x , определим соответствующие значения y , а затем сформируем репрезентативный набор упорядоченных парных решений.
x | y | y = −2x + 3 | Решения |
|---|---|---|---|
-2 | 7 | y = −2 (−2) + 3 = 4 + 3 = 7 | (-2, 7) |
-1 | 5 | y = −2 (−1) + 3 = 2 + 3 = 5 | (-1, 5) |
0 | 3 | y = −2 (0) + 3 = 0 + 3 = 3 | (0, 3) |
4 | −5 | y = −2 (4) + 3 = −8 + 3 = −5 | (4, −5) |
6 | −9 | y = −2 (6) + 3 = −12 + 3 = −9 | (6, −9) |
Постройте точки и проведите через них линию с помощью линейки.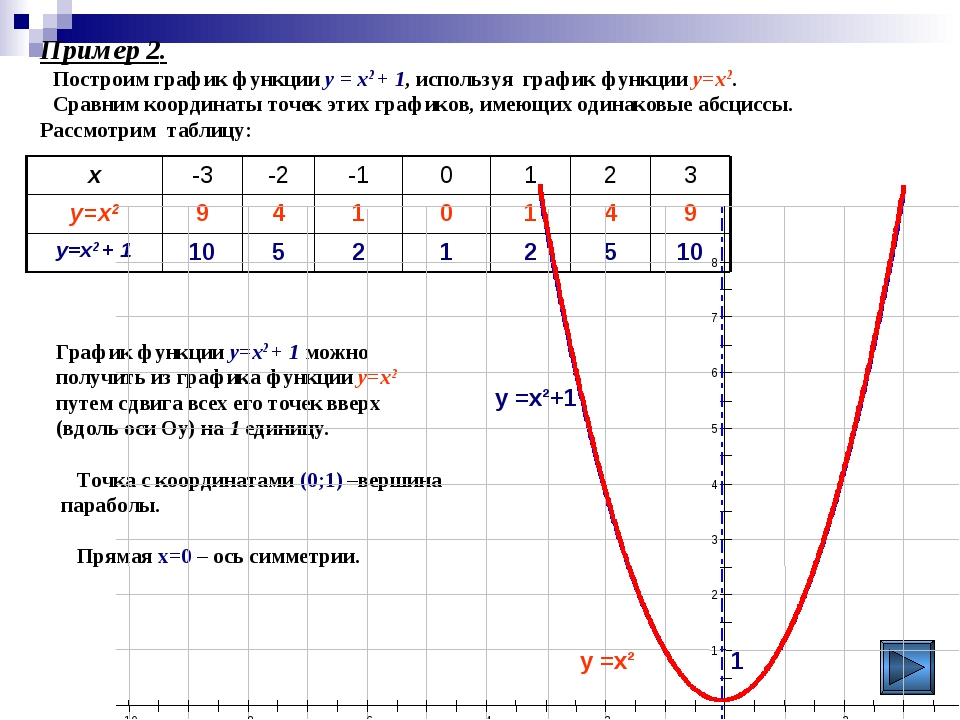
Обязательно добавьте стрелки на обоих концах, чтобы указать, что график неограничен.
Результирующая линия представляет все решения 8x + 4y = 12, которых бесконечно много. Вышеупомянутый процесс описывает метод построения графиков, известный как построение точек. Способ определения графика с использованием конечного числа типичных упорядоченных парных решений. Этот метод будет использоваться для построения графиков более сложных функций по мере продвижения в этом курсе.
Крутизну любого наклона можно измерить как отношение вертикального изменения к горизонтальному.Например, уклон 5% можно записать как 5100, что означает, что на каждые 100 футов вперед высота увеличивается на 5 футов.
В математике мы называем наклон линии наклоном Наклон линии, измеряемый как отношение вертикального изменения к горизонтальному изменению, часто называемый «подъем через пробег», обозначается буквой м .
Вертикальное изменение называется подъемом. Вертикальное изменение между любыми двумя точками на линии. Горизонтальное изменение называется пробегом. Горизонтальное изменение между любыми двумя точками на линии.. Для любых двух точек (x1, y1) и (x2, y2) мы можем получить подъем и пробег, вычитая соответствующие координаты.
Это приводит нас к формуле наклона. Наклон прямой, проходящей через точки (x1, y1) и (x2, y2), задается формулой m = y2 − y1x2 − x1 .. Для любых двух точек (x1, y1) и (x2, y2), наклон определяется по формуле:
Уклон m = riserun = y2 − y1x2 − x1 = ΔyΔx ← Изменение y ← Изменение x
Греческая буква дельта (Δ) часто используется для описания изменения количества.Поэтому наклон иногда описывают с помощью обозначения ΔyΔx, которое представляет изменение y , деленное на изменение x .
Пример 1
Найдите наклон прямой, проходящей через (−3, −5) и (2, 1).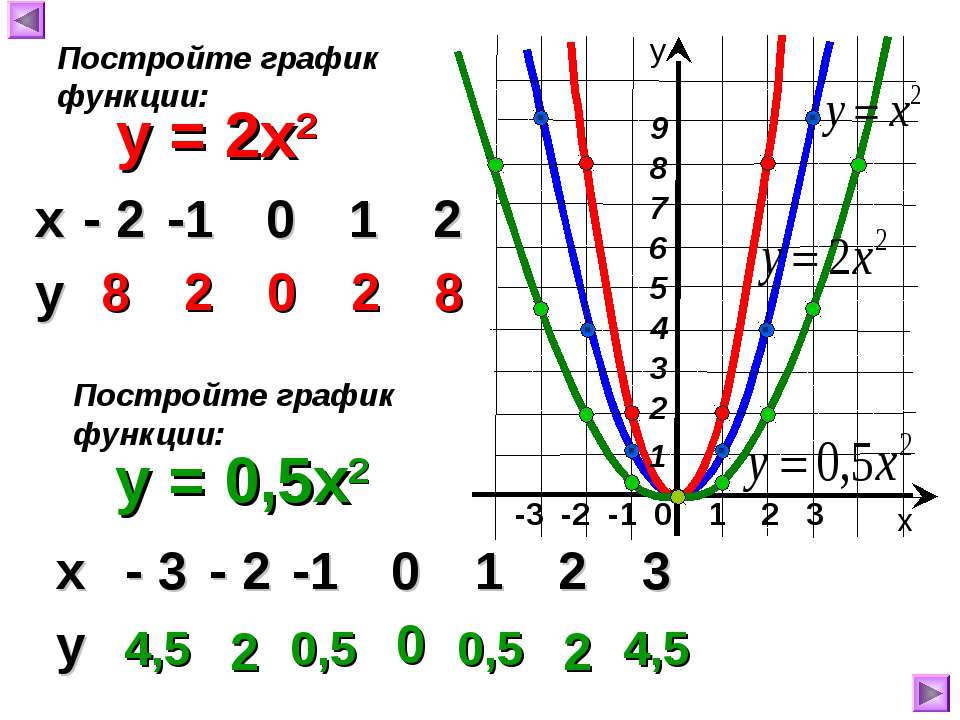
Решение:
Для заданных (−3, −5) и (2, 1) вычислите разницу значений y , деленную на разность значений x . Будьте последовательны при вычитании координат:
(x1, y1) (x2, y2) (- 3, −5) (2,1)
м = y2 − y1x2 − x1 = 1 — (- 5) 2 — (- 3) = 1 + 52 + 3 = 65
Неважно, какую точку вы считаете первой и второй.Однако, поскольку вычитание не является коммутативным, вы должны позаботиться о том, чтобы вычесть координаты первой точки из координат второй точки в том же порядке. Например, мы получим тот же результат, если применим формулу наклона с переключенными точками:
(x1, y1) (x2, y2) (2,1) (−3, −5)
м = y2 − y1x2 − x1 = −5−1−3−2 = −6−5 = 65
Ответ: m = 65
Убедитесь, что наклон равен 65, построив линию, описанную в предыдущем примере.
Конечно, график не является обязательным; Красота формулы наклона состоит в том, что по любым двум точкам мы можем получить наклон, используя только алгебру.
Пример 2
Найдите значение y , для которого наклон прямой, проходящей через (6, −3) и (−9, y), равен −23.
Решение:
Подставьте данную информацию в формулу наклона.
Наклон (x1, y1) (x2, y2) m = −23 (6, −3) (−9, y)
м = y2 − y1x2 − x1−23 = y — (- 3) −9−6−23 = y + 3 −15
После подстановки в данную информацию остается единственная переменная y .Решить.
−15 (−23) = — 15 (−y + 3 15) 10 = y + 37 = y
Ответ: y = 7
Есть четыре геометрических случая для значения наклона.
Если смотреть на график слева направо, линии с наклоном вверх имеют положительный наклон, а линии с наклоном вниз — отрицательный. В двух других случаях используются горизонтальные и вертикальные линии. Напомним, что если k — действительное число, мы имеем
y = k Горизонтальная линия x = k Вертикальная линия
Например, если мы построим график y = 2, мы получим горизонтальную линию, а если мы построим график x = −4, мы получим вертикальную линию.
По графикам мы можем определить две точки и рассчитать наклон по формуле наклона.
Горизонтальная линия | Вертикальная линия |
|---|---|
(x1, y1) (x2, y2) (- 3,2) (3, 2) м = y2 − y1x2 − x1 = 2− (2) 3 — (- 3) = 2−23 + 3 = 06 = 0 | (x1, y1) (x2, y2) (- 4, −1) (−4, 1) m = y2 − y1x2 − x1 = 1 — (- 1) −4 — (- 4) = 1 + 1−4 + 4 = 20 Не определено |
Обратите внимание, что точки на горизонтальной линии имеют одинаковые значения y .Следовательно, подъем равен нулю и, следовательно, наклон равен нулю. Точки на вертикальной линии имеют одинаковые значения x .
Следовательно, пробег равен нулю, что приводит к неопределенному уклону. В целом
Линейные функции
Для любого линейного уравнения в стандартной форме Любая невертикальная линия может быть записана в стандартной форме ax + by = c., Ax + by = c, мы можем решить для y , чтобы получить форму пересечения наклона Любая невертикальная линия может быть записана в сформируйте y = mx + b, где м — наклон, а (0, b ) — интервал y ., у = mx + b. Например,
3x − 4y = 8 ← Стандартная форма − 4y = −3x + 8y = −3x + 8−4y = −3x − 4 + 8−4y = 34x − 2 ← Форма пересечения наклона
Где x = 0, мы видим, что y = −2 и, следовательно, (0, −2) — решение для упорядоченной пары. Это точка, где график пересекает ось y и называется пересечением y Точка (или точки), где график пересекает ось y , выраженную в виде упорядоченной пары (0, y ) .
. Мы можем использовать эту точку и наклон как средство для быстрого построения линии.Например, чтобы построить график y = 34x − 2, начните с точки пересечения y (0, −2) и отметьте наклон, чтобы найти вторую точку. Затем используйте эти точки, чтобы построить линию следующим образом:
Тест с вертикальной линией показывает, что этот график представляет функцию. Кроме того, домен и диапазон состоят из всех действительных чисел.
В общем случае линейная функция Любая функция, которую можно записать в форме f (x) = mx + b, является функцией, которую можно записать в форме f (x) = mx + b Линейная функция где уклон м и b представляют любые действительные числа.Поскольку y = f (x), мы можем использовать y и f (x) как взаимозаменяемые, а упорядоченные парные решения на графе (x, y) можно записать в форме (x, f (x)).
(х, у) ⇔ (х, е (х))
Мы знаем, что любой интервал y будет иметь значение x , равное нулю.
Следовательно, перехват y может быть выражен как упорядоченная пара (0, f (0)). Для линейных функций
f (0) = m (0) + b = b
Следовательно, y -перехват любой линейной функции равен (0, b).Чтобы найти пересечение x Точка (или точки), в которой график пересекает ось x , выраженную в виде упорядоченной пары ( x , 0)., Точка, в которой функция пересекает ось x , находим x , где y = 0 или f (x) = 0.
Пример 3
Изобразите линейную функцию f (x) = — 53x + 6 и обозначьте точку пересечения x .
Решение:
Из функции мы видим, что f (0) = 6 (или b = 6) и, таким образом, y -перехват равен (0, 6).Также мы можем видеть, что наклон m = −53 = −53 = riserun. Начиная с точки пересечения и , отметьте вторую точку на 5 единиц ниже и на 3 единицы вправо. Проведите линейкой линию, проходящую через эти две точки.
Чтобы определить точку пересечения x , найдите значение x , при котором функция равна нулю. Другими словами, определить x , где f (x) = 0.
f (x) = — 53x + 60 = −53x + 653x = 6 (35) 53x = (35) 6x = 185 = 335
Следовательно, интервал x равен (185,0).Общее правило — помечать все важные моменты, которые нельзя четко прочитать на графике.
Ответ:
Пример 4
Определите линейную функцию, которая определяет данный график, и найдите точку пересечения x .
Решение:
Мы начинаем с чтения наклона графика. В этом случае начисляются два балла, и мы видим, что
м = стояк = −23
Кроме того, перехват y равен (0, 3) и, следовательно, b = 3.
Мы можем подставить в уравнение любую линейную функцию.
г (х) = mx + b ↓↓ g (x) = — 23x + 3
Чтобы найти точку пересечения x , мы устанавливаем g (x) = 0 и решаем относительно x .
г (x) = — 23x + 30 = −23x + 323x = 3 (32) 23x = (32) 3x = 92 = 412
Ответ: g (x) = — 23x + 3; x -перехват: (92,0)
Затем рассмотрите горизонтальные и вертикальные линии. Используйте тест вертикальной линии, чтобы убедиться, что любая горизонтальная линия представляет функцию, а вертикальная — нет.
Для любой горизонтальной линии тест вертикальной линии показывает, что каждое значение x в домене соответствует ровно одному значению y в диапазоне; это функция. Вертикальная линия, с другой стороны, не проходит тест вертикальной линии; это не функция. Вертикальная линия представляет собой набор упорядоченных пар, в которых все элементы в домене одинаковы.
Это нарушает требование о том, что функции должны связывать ровно один элемент в диапазоне с каждым элементом в домене.Резюмируем следующим образом:
Горизонтальная линия | Вертикальная линия | |
|---|---|---|
Уравнение: | у = 2 | х = −3 |
x-перехват: | Нет | (−3,0) |
Y-перехват: | (0,2) | Нет |
Домен: | (-∞, ∞) | {−3} |
Диапазон: | {2} | (-∞, ∞) |
Функция: | Есть | № |
Горизонтальную линию часто называют постоянной функцией .
Дано любое действительное число c ,
f (x) = c Константа функция
Пример 5
Постройте график постоянной функции g (x) = — 2 и укажите домен и диапазон.
Решение:
Здесь дана постоянная функция, эквивалентная y = −2. Это определяет горизонтальную линию через (0, −2).
Ответ: Домен: ℝ; диапазон: {−2}
Попробуй! График f (x) = 3x − 2 и обозначьте точку пересечения x .
Ответ:
Линейные уравнения и неравенства: графическая интерпретация
Мы можем использовать идеи этого раздела, чтобы развить геометрическое понимание того, что значит решать уравнения вида f (x) = g (x), где f и g — линейные функции. Используя алгебру, мы можем решить линейное уравнение 12x + 1 = 3 следующим образом:
12x + 1 = 312x = 2 (2) 12x = (2) 2x = 4
Решение этого уравнения: x = 4.
Геометрически это значение x пересечения двух графиков f (x) = 12x + 1 и g (x) = 3. Идея состоит в том, чтобы построить график линейных функций по обе стороны от уравнения и определить, где графики совпадают.
Пример 6
График f (x) = 12x + 1 и g (x) = 3 на одном и том же наборе осей и определяет, где f (x) = g (x).
Решение:
Здесь f — линейная функция с наклоном 12 и y -пересечение (0,1).Функция g является постоянной функцией и представляет собой горизонтальную линию. Изобразите обе эти функции на одном наборе осей.
Из графика видно, что f (x) = g (x), где x = 4. Другими словами, 12x + 1 = 3, где x = 4.
Ответ: x = 4
Мы можем немного расширить геометрическую интерпретацию для решения неравенств. Например, мы можем решить линейное неравенство 12x + 1≥3, используя алгебру, следующим образом:
12x + 1≥312x≥2 (2) 12x≥ (2) 2x≥4
Набор решений состоит из всех действительных чисел, больших или равных 4.
Геометрически это значения x , для которых график f (x) = 12x + 1 лежит над графиком g (x) = 3.
Пример 7
График f (x) = 12x + 1 и g (x) = 3 на одном и том же наборе осей и определить, где f (x) ≥g (x).
Решение:
На графике это заштриховано.
Из графика видно, что f (x) ≥g (x) или 12x + 1≥3, где x≥4.
Ответ: x -значения, решающие неравенство, в интервальной нотации: [4, ∞).
Основные выводы
- Мы можем построить линии, нанося точки. Выберите несколько значений для x , найдите соответствующие y -значения, а затем нанесите на график полученные решения для упорядоченных пар. Проведите линию через точки с помощью линейки, чтобы завершить график.
- Для любых двух точек на прямой мы можем вычислить наклон алгебраически, используя формулу наклона, m = riserun = y2 − y1x2 − x1 = ΔyΔx.
- Используйте форму пересечения наклона y = mx + b, чтобы быстро нарисовать график линии.От точки пересечения и (0, b) отметьте наклон, чтобы определить вторую точку. Поскольку две точки определяют линию, проведите линию через эти две точки линейкой, чтобы завершить график.
- Линейные функции имеют вид f (x) = mx + b, где наклон m и b — действительные числа. Чтобы найти точку пересечения x , если она существует, установите f (x) = 0 и решите относительно x .
- Поскольку y = f (x), мы можем использовать y, и f (x) как взаимозаменяемые.Любая точка на графике функции может быть выражена с помощью обозначения функции (x, f (x)).
Тематические упражнения
(-52,14) и (-12,54)
(−4, −3) и (−2, −3)
(12, -1) и (-1, -32)
м = 32; (6,10), (−4, у)
м = −13; (−6,4), (9, у)
м = −4; (−2,5), (−1, y)
м = 3; (1, −2), (−2, y)
м = 15; (1, у), (6,15)
м = −34; (−1, у), (−4,5)
Часть A: Графические линии по точкам построения
Найдите пять упорядоченных парных решений и график.
Найдите наклон прямой, проходящей через заданные точки.
Найдите значение y , для которого наклон прямой, проходящей через данные точки, имеет данный наклон.
По графику определите наклон.
Часть B: Линейные функции
Найдите точки пересечения x и y и используйте их для построения графика следующих функций.
Изобразите линейную функцию и обозначьте точку пересечения x .
Определите линейную функцию, которая определяет данный график, и найдите точку пересечения x .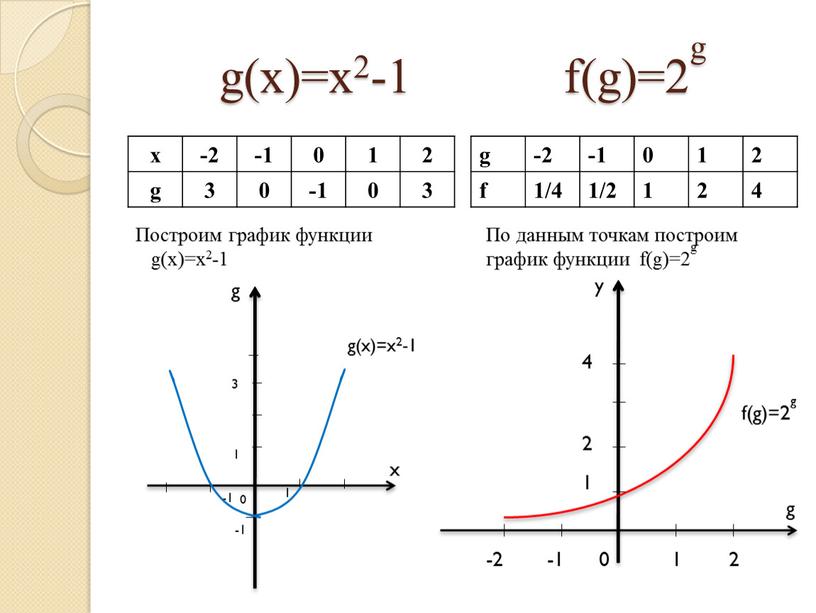
f (x) = 3x − 2, g (x) = — 2x + 3
f (x) = — 13x, g (x) = — 23x + 1
f (x) = 23x − 1, g (x) = — 43x − 3
f (x) = 32x + 3, g (x) = — 32x − 3
Часть C: Графическая интерпретация линейных уравнений и неравенств
Изобразите функции f и g на одном и том же наборе осей и определите, где f (x) = g (x).
Проверьте свой ответ алгебраически.
Постройте график функций f и g на одном и том же наборе осей и определите, где f (x) ≥g (x).
Проверьте свой ответ алгебраически.
Изобразите функции f и g на одном и том же наборе осей и определите, где f (x)
Все ли линейные функции имеют y -перехвата? У всех ли линейных функций есть x -перехват? Объясни.
Может ли функция иметь более одного перехвата y ? Объясни.
Как проверка вертикальной линии показывает, что вертикальная линия не является функцией?
Часть D: Обсуждение
ответов
ф (х) = х + 1; (−1,0)
f (x) = — 32x; (0,0)
Привет, Женева, Иногда, особенно после небольшого опыта, вы можете сказать по «форме» уравнения, какова «форма» графика.
Теперь я нанес эти точки на свой график. Теперь вы можете увидеть «форму» графика. Если вы нанесли эти точки точно и поместите линейку вдоль точек, вы увидите, что все они лежат на прямой линии. График y = 2x + 1 Если бы вы знали с самого начала, из «формы» уравнения, что график представляет собой прямую линию, вы могли бы построить график быстрее. В этом случае вам нужно только рассчитать и построить две точки, а линия, соединяющая эти две точки, является графиком. Надеюсь, это поможет, |
Если вы можете определить форму, это облегчит построение графика, но на данный момент давайте просто попробуем построить его, не зная заранее форму. Для этого я воспользуюсь таблицей значений. Я собираюсь выбрать несколько значений для переменной x, вычислить соответствующее значение y и затем записать свои результаты в таблицу. Так, например, когда x = 1, тогда y = 2 1 + 1 = 3, а когда x = 2, тогда y = y = 2 2 + 1 = 5. Вот моя таблица, включающая эти два значения x и еще несколько.
Нахождение точек пересечения по оси x и оси y | Колледж алгебры
Пересечения графика — это точки, в которых график пересекает оси. Пересечение x- — это точка, в которой график пересекает ось x- . В этот момент координата y- равна нулю.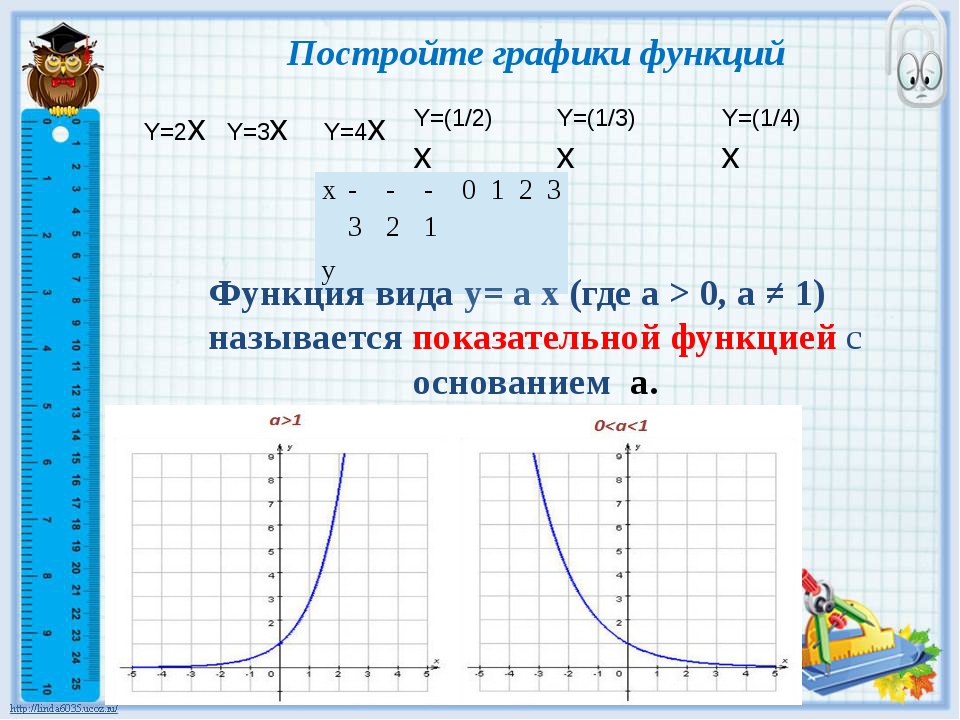
Пересечение y- — это точка, в которой график пересекает ось y- . В этот момент координата x- равна нулю.
Чтобы определить точку пересечения x- , мы устанавливаем y равным нулю и решаем относительно x . Аналогично, чтобы определить точку пересечения y- , мы устанавливаем x равным нулю и решаем относительно y . Например, найдем точки пересечения уравнения [латекс] y = 3x — 1 [/ latex].
Чтобы найти точку пересечения x- , установите [latex] y = 0 [/ latex].
[латекс] \ begin {array} {ll} y = 3x — 1 \ hfill & \ hfill \\ 0 = 3x — 1 \ hfill & \ hfill \\ 1 = 3x \ hfill & \ hfill \\ \ frac {1 } {3} = x \ hfill & \ hfill \\ \ left (\ frac {1} {3}, 0 \ right) \ hfill & x \ text {-intercept} \ hfill \ end {array} [/ latex]
Чтобы найти точку пересечения y- , установите [latex] x = 0 [/ latex].
[латекс] \ begin {array} {l} y = 3x — 1 \ hfill \\ y = 3 \ left (0 \ right) -1 \ hfill \\ y = -1 \ hfill \\ \ left (0, -1 \ right) y \ text {-intercept} \ hfill \ end {array} [/ latex]
Мы можем подтвердить, что наши результаты имеют смысл, наблюдая за графиком уравнения, показанным на рисунке 10.
Обратите внимание, что график пересекает оси там, где мы и предполагали.
Рисунок 12
Как: по уравнению найдите точки пересечения.
- Найдите точку пересечения x , задав [latex] y = 0 [/ latex] и решив для [latex] x [/ latex].
- Найдите точку пересечения y- , установив [latex] x = 0 [/ latex] и решив для [latex] y [/ latex].
Пример 4: Нахождение точек пересечения данного уравнения
Найдите точки пересечения уравнения [латекс] y = -3x — 4 [/ latex].Затем нарисуйте график, используя только точки пересечения.
Решение
Установите [latex] y = 0 [/ latex], чтобы найти точку пересечения x- .
[латекс] \ begin {array} {l} y = -3x — 4 \ hfill \\ 0 = -3x — 4 \ hfill \\ 4 = -3x \ hfill \\ — \ frac {4} {3} = x \ hfill \\ \ left (- \ frac {4} {3}, 0 \ right) x \ text {-intercept} \ hfill \ end {array} [/ latex]
Установите [latex] x = 0 [/ latex], чтобы найти точку пересечения y- .
[латекс] \ begin {array} {l} y = -3x — 4 \ hfill \\ y = -3 \ left (0 \ right) -4 \ hfill \\ y = -4 \ hfill \\ \ left ( 0, -4 \ right) y \ text {-intercept} \ hfill \ end {array} [/ latex]
Постройте обе точки и проведите через них линию, как показано на рисунке 11.
Рисунок 13
Попробуй 1
Найдите точки пересечения уравнения и нарисуйте график: [latex] y = — \ frac {3} {4} x + 3 [/ latex].
Решение
систем линейных уравнений
систем линейных уравненийЧасто приходится смотреть на несколько функций одного и того же независимого переменная. Рассмотрим предыдущий пример, где x — количество произведенных товаров. и продано, была независимой переменной в трех функциях: функции затрат, функция дохода и функция прибыли.
В целом там может быть:
n уравнений
v переменные
Решение систем уравнений
Есть четыре метода решения систем линейных уравнений:
а.
графическое решение
б. алгебраическое решение
c. метод исключения
d.метод замещения
Графическое решение
Пример 1
даны являются два следующих линейных уравнения:
f (x) = y = 1 + 0,5x
f (x) = y = 11 — 2x
Постройте график первого уравнения , найдя две точки данных. Установив сначала x, а затем y равны нулю, можно найти точку пересечения y на вертикальная ось и точка пересечения x на горизонтальной оси.
Если x = 0, тогда f (0) = 1 + .5 (0) = 1
Если y = 0, тогда f (x) = 0 = 1 + .5x
-,5x = 1
х = -2
Результирующий точки данных: (0,1) и (-2,0)
Постройте график второго уравнения , найдя две точки данных. От
установив сначала x, а затем y равными нулю, можно найти точку пересечения y
по вертикальной оси и точка пересечения x по горизонтальной оси.
Если x = 0, тогда f (0) = 11-2 (0) = 11
Если y = 0, тогда f (x) = 0 = 11 — 2x
2x = 11
х = 5,5
Результирующий точки данных: (0,11) и (5.5,0)
В точке пересечения двух уравнений x и y имеют одинаковые значения.
На графике эти значения можно прочитать как x = 4 и y = 3.
Пример 2
даны являются два следующих линейных уравнения:
f (x) = y = 15 — 5x
f (x) = y = 25 — 5x
Постройте график первого уравнения , найдя две точки данных. Установив сначала x, а затем y равны нулю, можно найти точку пересечения y на вертикальная ось и точка пересечения x на горизонтальной оси.
Если x = 0, тогда f (0) = 15-5 (0) = 15
Если y = 0, тогда f (x) = 0 = 15 — 5x
5x = 15
х = 3
Результирующий точки данных: (0,15) и (3,0)
Постройте график второго уравнения , найдя две точки данных.
От
установив сначала x, а затем y равными нулю, можно найти точку пересечения y
по вертикальной оси и точка пересечения x по горизонтальной оси.
Если x = 0, тогда f (0) = 25-5 (0) = 25
Если y = 0, тогда f (x) = 0 = 25 — 5x
5x = 25
х = 5
Результирующий точки данных: (0,25) и (5,0)
Из графика видно, что эти линии не пересекаются. Oни параллельны. У них одинаковый наклон.Нет однозначного решения.
Пример 3
даны являются два следующих линейных уравнения:
21x — 7y = 14
-15x + 5y = -10
Rewrite уравнения, поместив их в форму пересечения наклона.
Первый уравнение становится
7y = -14 + 21x
у = -2 + 3х
Второй уравнение становится
5лет = -10 + 15x
у = -2 + 3х
Изобразите любое уравнение, найдя две точки данных.Установив сначала
x, а затем y равный нулю, можно найти точку пересечения y по вертикали
ось и точку пересечения x на горизонтальной оси.
Если x = 0, тогда f (0) = -2 +3 (0) = -2
Если y = 0, тогда f (x) = 0 = -2 + 3x
3x = 2
х = 2/3
Результирующий точки данных: (0, -2) и (2 / 3,0)
Из графика видно, что эти уравнения эквивалентны.Там являются бесконечным числом решений.
Алгебраическое решение
Этот метод будет проиллюстрирован с помощью анализа спроса и предложения. Эта Тип анализа основан на работе великого английского экономиста Альфреда Маршалл.
Q = количество и P = цена
P (s) = функция предложения и P (d) = функция спроса
При построении графика цена располагается на вертикальной оси. Таким образом, цена — это
зависимая переменная.Было бы логичнее рассматривать количество как
зависимая переменная, и этот подход использовал великий французский экономист,
Леон Вальрас. Однако по соглашению экономисты продолжают строить графики, используя
Анализ Маршалла, который называют крестом Маршалла.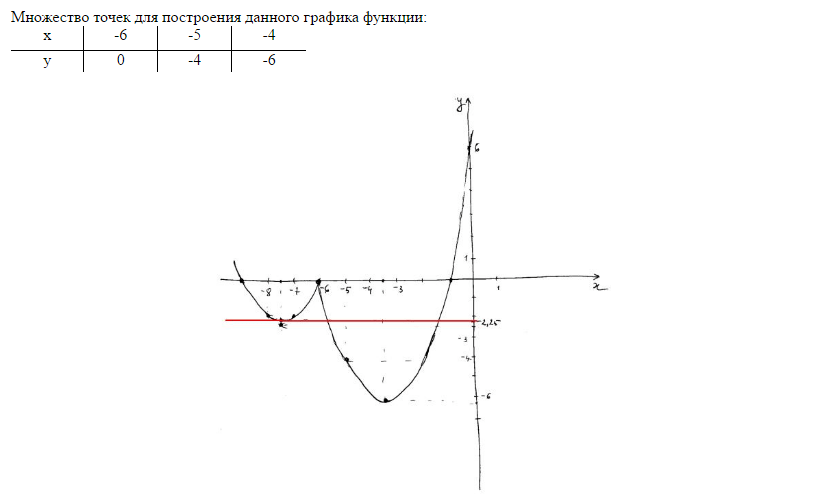
Цель состоит в том, чтобы найти равновесную цену и количество, т.е. решение где цена и количество будут иметь одинаковые значения в функции предложения и функция цены.
Q E = равновесная величина P E = равновесная цена
Для равновесия
предложение = спрос
или P (s) = P (d)
Учитывая следующие функции
П (т) = 3Q + 10 и P (d) = -1 / 2Q + 80
Приравняйте уравнения друг к другу и решите относительно Q.
P (т) = 3Q + 10 = -1 / 2Q + 80 = P (d)
3.5Q = 70
Q = 20 Равновесное количество 20.
Подставьте это значение вместо Q в любое уравнение и решите для P.
P (т) = 3 (20) + 10
П (т) = 70
П (г) = -1/2 (20) + 80
П (г) = 70 Цена равновесия — 70.
Метод исключения
Этот метод включает удаление переменных из уравнений. Переменные
удаляются последовательно, пока не останется только одна последняя переменная, т.
е.
пока не будет одно уравнение с одним неизвестным. Затем это уравнение решается
для одного неизвестного. Затем решение используется для нахождения второго
последняя переменная. Процедура повторяется путем добавления переменных в качестве их решений.
найдены.
Пример 1
2х + 3у = 5
-5x — 2y = 4
Порядок действий: удалить y.Коэффициенты при y не совпадают в два уравнения, но если бы они были, можно было бы сложить два уравнения и члены y будут сокращаться. Однако это возможно через умножение каждого уравнения, чтобы заставить члены y иметь одинаковые коэффициенты в каждом уравнении.
Шаг 1: Умножьте первое уравнение на 2, а второе уравнение умножьте на 3. Это дает
4х + 6у = 10
-15x — 6y = 12
Шаг 2: Сложите два уравнения.Это дает
-11x = 22
х = -2
Шаг 3: Решить относительно y в любом из исходных уравнений
2 (-2) + 3у = 5
3 года = 9
г = 3 или
-5 (-2) — 2y = 4
10–2y = 4
2y = 6
г = 3
Альтернативная процедура: удалить x.
Коэффициенты при x не совпадают
в двух уравнениях, но если бы они были, можно было бы добавить
два уравнения и члены y будут сокращаться. Однако возможно
путем умножения каждого уравнения, чтобы заставить члены x равняться
имеют одинаковые коэффициенты в каждом уравнении.
Шаг 1: Умножьте первое уравнение на 5, а второе уравнение умножьте на 2. Это дает
10x + 15y = 25
-10x — 4y = 8
Шаг 2: Сложите два уравнения.Это дает
11лет = 33
y = 3
Шаг 3: Решить относительно x в любом из исходных уравнений
2x + 3 (3) = 5
2x = -4
х = -2 или
-5x — 2 (3) = 4
— 5x = 10
х = -2
Пример 2
2x 1 + 5x 2 + 7x 3 = 2
4x 1 — 4x 2 — 3x 3 = 7
3x 1 — 3x 2 — 2x 3 = 5
В этом примере есть три переменные: x 1 , x 2 и
х 3 .
Одна из возможных процедур — удалить первый x 1 , , чтобы исключить следующие x 2 , а затем найти x 3 .
Значение, полученное для x 3 , используется для решения x 2 и
наконец, значения, полученные для x 3 и x 2 , используются для
решить относительно x 1 .
Процедура Часть A Сначала удалите x 1 .
Шаг 1 Умножение первое уравнение на 2 и вычтите второе уравнение из первого уравнение.Это дает
4x 1 + 10x 2 + 14x 3 = 4 первое уравнение
4x 1 — 4x 2 — 3x 3 = 7 второе уравнение
14x 2 + 17x 3 = -3 второе уравнение вычитается из первого
Шаг 2 Умножение первое уравнение на 3, третье уравнение умножьте на 2 и вычтите третье уравнение из первого уравнения.Это дает
6x 1 + 15x 2 + 21x 3 = 6 первое уравнение
6x 1 — 6x 2 — 4x 3 = 10 третье уравнение
21x 2 + 25x 3 = -4 третье уравнение вычитается из первого
Процедура, часть B Второе удаление x 2 .
Из Части А осталось два уравнения. Из этих двух уравнений исключить
х 2 .
14x 2 + 17x 3 = -3 первое уравнение
21x 2 + 25x 3 = -4 второе уравнение
Шаг 1 Умножение первое уравнение на 21, второе уравнение умножьте на 14. и вычтите второе уравнение из первого уравнения.Это дает
294x 2 + 357x 3 = -63 первое уравнение
294x 2 + 350x 3 = -56 второе уравнение
7x 3 = -7 второе уравнение вычитается из первого
x 3 = -1
Часть C Решите относительно x 2 , вставив значение, полученное для x 3 в любое уравнение из части B.
14x 2 + 17 (-1) = -3
1 4x 2 = 14
х 2 = 1 или
21x 2 + 25 (-1) = -4
21x 2 = 21
х 2 = 1
Часть D
Решите относительно x 1 , вставив полученные значения x 2 andx 3 в любом из трех исходных уравнений.
2x 1 + 5x 2 + 7x 3 = 2 первое исходное уравнение
2x 1 + 5 (1) + 7 (-1) = 2
2x 1 = 4
x 1 = 2 или
4x 1 — 4x 2 — 3x 3 = 7 секунд исходное уравнение
4x 1 — 4 (1) — 3 (-1) = 7
4x 1 = 8
х 1 = 2 или
3x 1 — 3x 2 — 2x 3 = 5 третье исходное уравнение
3x 1 — 3 (1) -2 (-1) = 5
3x 1 = 6
х 1 = 2
Метод замещения
Это включает в себя выражение одной переменной через другую, пока не будет
одно уравнение с одним неизвестным.Затем это уравнение решается для этого
один неизвестный. Затем результат используется для поиска переменной, которая была
выражается через переменную, решение которой было только что найдено.
Пример
12x — 7лет = 106 первое уравнение
8x + У = 82 второе уравнение
Решите второе уравнение для y, а затем подставьте полученное значение y в первое уравнение.
г = 82 — 8x второе уравнение, решенное относительно y
12x — 7 (82 — 8х) = 106 первое уравнение переписано в x
12x — 574 + 56x = 106
68x = 680
х = 10
Подставьте полученное значение x в любое из исходных эквивалентов.
12x — 7лет = 106 первое уравнение
12 (10) — 7лет = 106
7лет = 14
г = 2
8 (10) + У = 82 второе уравнение
г = 2
[индекс]
.
