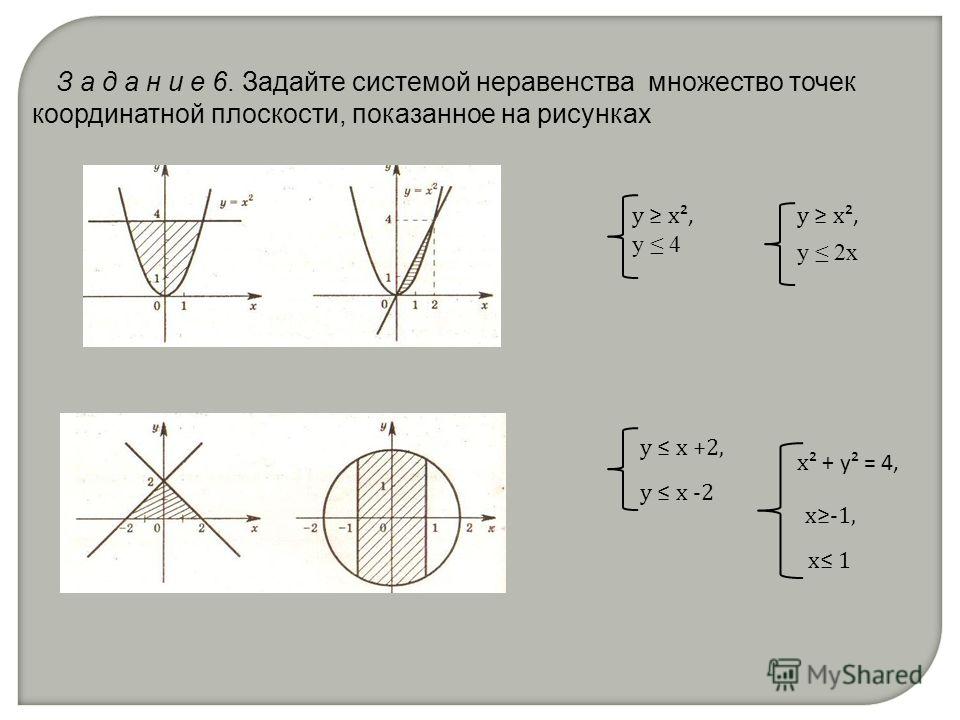
ГРАФИКА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Область допустимых планов. Оптимальный план и оптимум
Рассмотрим вопрос о решении задач линейного программирования. Подчеркнем, что на стадии решения задачи ее экономический смысл отступает на второй план. Можно даже вовсе не знать, из какой конкретной экономической ситуации возникла та или иная математическая модель. Решение задачи — это чисто математическая процедура. Однако, чтобы, получив результаты решения, воспользоваться ими, нужно, конечно, вернуться к экономическому содержанию задачи, сопоставить полученные результаты с конкретными экономическими условиями.
Рассмотрим сначала метод
решения относительно простых задач, задач
с двумя переменными. Как мы знаем, всякую
задачу линейного программирования можно
привести к стандартной форме.
Планы такой задачи — это пары чисел (x1, x2). Им соответствуют точки координатной плоскости (Рис. 2.1 ).
Рис. 2 .1. Ограниченная область допустимых планов
Область допустимых планов
Рассмотрим систему ограничений. Возьмем одно из неравенств системы,
Множество решений неравенства, то есть множество пар (x1, x2), компоненты которых удовлетворяют неравенству, геометрически представляет собой полуплоскость. Для того чтобы определить граничную прямую этой полуплоскости, следует заменить знак неравенства знаком равенства:
Множество решений полученного
уравнения представляет собой искомую
прямую.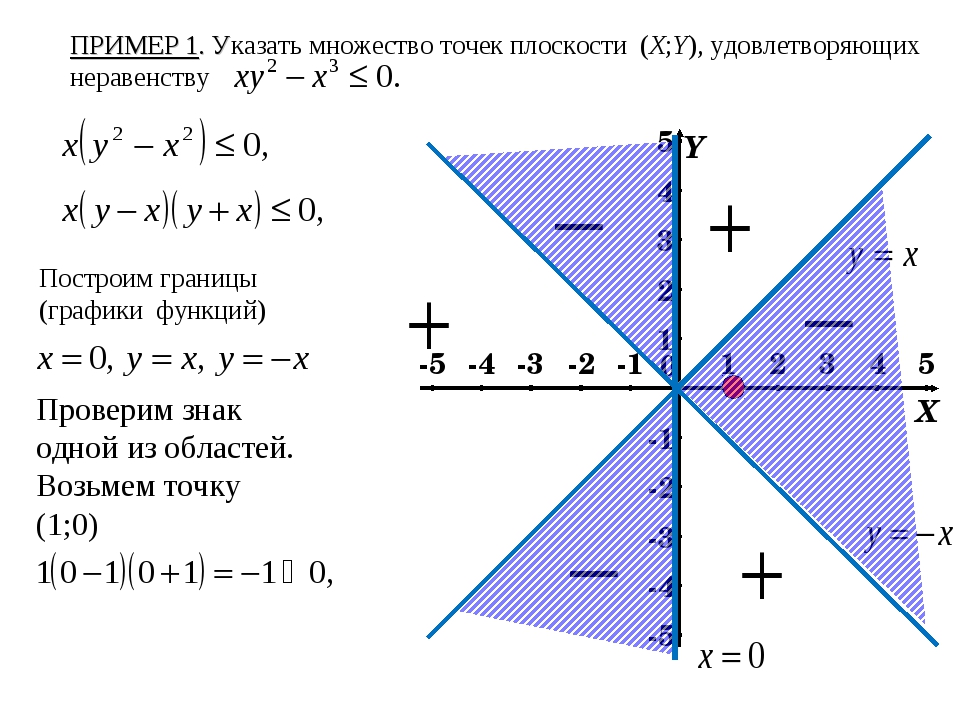 Таким образом, графическое
изображение решения неравенства, то есть
изображение полуплоскости, следует начать
с изображения граничной прямой.
Таким образом, графическое
изображение решения неравенства, то есть
изображение полуплоскости, следует начать
с изображения граничной прямой.
Для того, чтобы построить прямую, достаточно знать две ее точки. Построенная прямая разделит плоскость на две части, то есть определит две полуплоскости. Для того чтобы определить полуплоскость, соответствующую нашему неравенству, следует взять какую-нибудь точку в любой из полуплоскостей и проверить, удовлетворяют ли ее координаты нашему неравенству.
Если неравенство окажется
выполненным, то вся полуплоскость, в
которой лежит эта точка, является
множеством решений неравенства. Если
неравенство не выполнено, то множеством
решений является противоположная
полуплоскость. Отметим, что и в том, и в
другом случае граничная прямая относится к
множеству решений неравенства, так как
неравенство нестрогое и включает в себя
равенство.
Каждое из неравенств системы ограничений определит свою полуплоскость. Последние неравенства, требующие неотрицательности значений переменных, определяют правую и верхнюю полуплоскости, граничными прямыми которых являются координатные оси.
Множеством решений системы неравенств в целом является пересечение всех полуплоскостей, соответствующих отдельным неравенствам системы. Это пересечение и определяет множество допустимых планов. Это множество часто называют также областью допустимых планов (сокращенно ОДП). Оно представляет собой выпуклую многоугольную область.
В типичной, наиболее часто встречающейся ситуации, множество допустимых планов представляет собой ограниченную выпуклую многоугольную область — выпуклый многоугольник, расположенный в первой координатной четверти. Но возможны и другие варианты.
Оптимальный план и оптимум
Как найти оптимальный план?
Обратимся к целевой функции. Приравняем ее
какой-нибудь константе d
Приравняем ее
какой-нибудь константе d
.
Мы получили уравнение, определяющее некоторую прямую на координатной плоскости. Все точки этой прямой соответствуют одному и тому же значению целевой функции, равному d, одному и тому же уровню значений. Такая прямая называется линией уровня целевой функции.
При изменении величины d мы получим другую линию уровня, параллельную предыдущей. При увеличении d линия будет смещаться параллельно в одну сторону, при уменьшении — в другую.
Придавая величине d разные конкретные числовые значения, можно понять, какое направление смещения линии уровня соответствует увеличению значения целевой функции, а какое — уменьшению.
Однако, существует более
простой способ. А именно, изобразим в
координатной плоскости вектор, начало
которого находится в начале координат, а
конец которого упирается в точку с
координатами (c1, c2), где c1 и c2 — коэффициенты при
переменных в целевой функции. Это градиент
целевой функции. Этот вектор-градиент
перпендикулярен всем линиям уровня целевой
функции, а его направление указывает
направление роста значений функции.
Это градиент
целевой функции. Этот вектор-градиент
перпендикулярен всем линиям уровня целевой
функции, а его направление указывает
направление роста значений функции.
Для того чтобы найти
оптимальный план, нужно взять одну из линий
уровня, пересекающих область допустимых
планов. Затем следует параллельно смещать
эту линию в направлении градиента до ее . Крайним называется
положение линии уровня, удовлетворяющее
двум условиям: во-первых, в этом положении
линия уровня еще пересекает область
допустимых планов, во-вторых, при любом ее
дальнейшем смещении она перестает
пересекать эту область.
Точки области допустимых планов, лежащие на одной линии уровня, соответствуют одному и тому же допустимому значению целевой функции. Смещение линии уровня в направлении градиента соответствует росту значений целевой функции. Крайнее положение линии уровня соответствует максимальному допустимому значению целевой функции, то есть оптимуму. Все точки, находящиеся в пересечении области допустимых планов и линии уровня в ее крайнем положении, являются искомыми оптимальными планами.
На Рис. 2.1 множество оптимальных планов состоит из одной единственной точки — вершины многоугольника, обозначенной посредством X*max .
Заметим сразу, что если бы
требовалось решать задачу на минимум той же
самой целевой функции, то смещать линию
уровня следовало бы в направлении
уменьшения ее значений, то есть в
направлении, противоположном градиенту (или,
как иногда говорят, в направлении антиградиента). Линия уровня в новом крайнем положении
прошла бы через точку X*min (Рис.
2.1
).
Линия уровня в новом крайнем положении
прошла бы через точку X*min (Рис.
2.1
).
Если изменить знаки коэффициентов целевой функции c1 и c2 на противоположные, то градиент развернется на 180о, то есть совпадет с антиградиентом первоначальной целевой функции. Если отыскивать минимум этой новой целевой функции с измененными знаками, то следует смещать линию уровня в направлении антиградиента по отношению к новому градиенту, то есть в направлении прежнего градиента. Мы убеждается еще раз, что решение задачи на минимум для целевой функции с измененными знаками соответствует задаче на максимум исходной целевой функции.
Уравнения, неравенства с двумя переменными и их системы (17 ч) |
| ||||||||||
Дата: | ФИО учителя: | ||||||||||
Класс: 9 | Количество присутствующих: | Количество отсутствующих: | |||||||||
Тема урока | Системы
нелинейных неравенств с двумя переменными. (урок изучения новой темы). | ||||||||||
Цели обучения (ссылка на учебную программу) | Учащиеся будут: 9.2.2.4 решать системы нелинейных неравенств с двумя переменными; | ||||||||||
Цели урока | Решать системы нелинейных неравенств | ||||||||||
Критерии оценивания | — Строит график кривых (прямой,параболы, гиперболы, окружности), — Определяет границы кривых (входят или нет в заданную область), — Определяет область по знакам неравенств. | ||||||||||
Языковые цели
| Учащиеся будут: — использовать предметную лексику и терминологию раздела при решении задач; — комментировать геометрическую интерпретацию нелинейных неравенств; — обосновывать решение неравенств и их систем; —
комментировать ход решения задач. Предметная лексика и терминология — линейное/квадратное/дробное уравнение; — переменная/ось(и)/масштаб/кривая; — пересечение/точка пересечения; — таблица значений/множество точек; — заменить/преобразовать; — построить график/прямую/кривую; — нанести точки на график; — изобразить кривую; — уравнение окружности; — уравнение кривой; — заштрихованная область (площадь). Серия полезных фраз для диалога/письма — оси Оx и Оy представляют собой …. ; — точки на этой прямой/кривой… — таким образом, прямая представляет собой….; — оси координат x и y положительные или отрицательные; — координаты записываются в виде упорядоченных пар….; — корни уравнения являются точками пересечения…. | ||||||||||
Вид дифференциации | По форме обучения, по степени поддержки. | ||||||||||
Привитие ценностей | Академическая честность, открытость, сотрудничество, уважение, обучение на протяжении всей жизни. Привитие ценностей осуществляется посредством/через парную и групповую виды работ. | ||||||||||
Межпредметныя связь | Связь с жизнью | ||||||||||
Навыки использования ИКТ | https://www.geogebra.org/classic https://www.desmos.com/calculator https://bilimland.kz/ru/subject/algebra/9-klass/sistemy-nelinejnyx-neravenstv-s-dvumya-peremennymi | ||||||||||
Предварительные знания | Знание методов решения уравнения, систем уравнений и неравенств; владение навыками построения графиков | ||||||||||
Ход урока Начало урока | |||||||||||
Этапы урока | Запланированная деятельность на уроке | Ресурсы | |||||||||
1 урок | |||||||||||
Орг. 1 мин | Приветствие. Создание благоприятного психологического климата в классе. |
| |||||||||
Актуализация 4 мин | «Тинга – танга». Дети становятся в круг. Передают кубик, а учитель произносит без остановки «Тинга – танга». После остановки, учащийся у которого в руках остался кубик, отвечает на вопрос учителя по прошлой теме, в качестве актуализации. И так далее. — Что собой представляет графически равенство ? — Что собой представляет графически неравенство ? — Как называется кривая ? — При построении области ограниченной прямой сама прямая входит в решение? Ответ объяснить. — Что собой представляет графически неравенство ? — Верно ли, что уравнение проходит через начало координат? | карточки | |||||||||
Проблемная задача 3 мин |
Каким образом будет выглядеть математическая модель задачи? Каким способом можно решить задачу?
|
| |||||||||
Целеполагание 2 мин | Формулировка темы. Постановка целей урока и определение критериев к уроку самостоятельно учащимися. |
| |||||||||
Середина урока | |||||||||||
4 мин | Совместное
решение проблемного вопроса с разъяснениями. Напишите систему неравенств показывающую ежедневное количество производимых кастрюлей и изобразите графически.
Решение. 1) Примем за х – количество кастрюль из нержавеющей стали; за у количество медных кастрюль. Согласно условию задачи, можно написать следующую систему неравенств. 2) Решение неравенства изображает прямая и часть полуплоскости, расположенная ниже этой прямой. Решение неравенства изображает прямая и часть полуплоскости расположенной ниже этой прямой. 3) Решением системы является часть плоскости, закрашенная двумя цветами и охватывающая решения соответствующих обоих неравенств, включая граничные прямые. Эта задача на решение системы линейных неравенств. На уроке мы продолжим работать над нерением нелинейных неравенств.
Опрос: — Какие неравенства называются линейными? — Какие неравенства называются нелинейными? — Как решить графически неравенство? |
| |||||||||
4 мин | Для эффективной
работы необходимо провести объединетие в пары. Стратегия критического мышления «Соответствие». Учащимся нужно найти соответствие системы неравенств и её графического решения.
Проверка по ключу. | ПРИЛОЖЕНИЕ 4 | |||||||||
Изучение нового материала 7 мин | Стратегия «Класстер». Учащиеся произвольно объединяются в мини группы. Задача группы по заданию составить алгоритм решения системы нелинейных неравенств. Презентация алгаритмов решения группами. Обсуждение. Запись алгоритма решения в тетради.
Определение. Системой нелинейных неравенств с двумя переменными называется система неравенств, среди которых имеется нелинейное неравенство с двумя переменными. Например, системой нелинейных неравенств с двумя переменными являются следующие: , Решением системы нелинейных неравенств с двумя переменными
называется множество пар значений этих переменных, которая обращает все
неравенства системы в верные числовые неравенства. | карточка | |||||||||
2 мин | Просмотр видео. Разъяснение по решению. Акценты на сложных моментах. | https://bilimland.kz/ru/subject/algebra/9-klass/sistemy-nelinejnyx-neravenstv-s-dvumya-peremennymi
ПРИЛОЖЕНИЕ 1 | |||||||||
Практика 10 мин | Работа в тройках. Стратегия «совпадение». Учащиеся на группу или пару получают задание. Необходимо выполнить последовательно задания, не перепрыгивая, до совпадения ответов ответов в группе. Затем ответ на каждый пример группа отправляет в письменной форме учителю, для сверки. Если результаты рознятся, то происходит поиск ошибки в группах, до полного соответствия. Задание 1. Решить
уравнение . Дескриптор: — Верно строит график окружности и обозначает её границы, — Верно строит график прямой и обозначает её границы, — Верно определяет области решения неравенств.
Задание 2. Решить неравенство .
Дескриптор: — Верно строит график параболы и обозначает её границы, — Верно строит график гиперболы и обозначает её границы, — Верно определяет области решения неравенств.
Задание 3. Решить неравенство . Дескриптор: — Верно строит график гиперболы и обозначает её границы, — Верно строит график окружности и обозначает её границы, — Верно определяет области решения неравенств.
Проверка с программой geogebra.org/classic
Задание 1 Задание 2 Задание 3
Оценивание по критериям (составленным в
начале урока).
Обратная связь: — Хорошо ли вы усвоили алгоритм решения системы нелинейных неравенств? Насколько хорошо? — Какие проблемы возникают при решении? | ПРИЛОЖЕНИЕ 5
https://www.geogebra.org/classic
или
https://www.desmos.com/calculator
| |||||||||
Рефлексия 2 мин | Письменная обратная связь. Рефлексия «Сообщение учителю». Учащиеся отмечают, что узнали нового, что не получается, какие пункты нужно закрепить или повторить ещё раз. |
| |||||||||
Домашнее задание 1 мин | Дифференцированное домашнее задание. Обязательный уровень. Выполнить задания №1 и №2 рабочего листа.
Дополнительный уровень. Задания №3 и №4 карточки рабочего листа. Предлагаются учащимся для более глубокого понимания материала.
| Приложение 2, 3 | |||||||||
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? | Здоровье и соблюдение техники безопасности | |||||||||
| |||||||||||
Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? | Используйте данный раздел
для размышлений об уроке. | ||||||||||
| |||||||||||
Общая оценка Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1: 2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1: 2: Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?
| |||||||||||
Область определения функции двух переменных
Цели работы:
- повторить и систематизировать нахождение области определения функции, закрепить это понятие и наглядно представить в координатной плоскости и в пространстве;
- рассмотреть аналитические и геометрические
методы не изолированно друг от друга, а в тесной
взаимосвязи.
 Это позволит облегчить переход от
стандартных решений конкретных математических
задач к нестандартным;
Это позволит облегчить переход от
стандартных решений конкретных математических
задач к нестандартным; - воспитание интереса к математике и мультимедиа, активности, мобильности; восприятие компьютера, как инструмента обучения;
- использование компьютера для нахождения области определения и построения графиков с помощью графического редактора 3D Grapher 1.2, Copyright © 2000-2002 RomanLab Software и формирование информационной компетентности учащихся.
Определение функции двух переменных
Если каждой паре ( x;y) значений двух независимых друг от друга переменных величин х и у из некоторого множества D соответствует единственное значение величины, то говорят, что z есть функция двух независимых переменных x и y, определенная на множестве D.
Обозначается: z=f(x;y) или z=z(x;y).
Например, S=ab, S=S(a;b)- функции двух переменных; V=abc, V=V(a,b.c) – функция трех переменных;
A= – функция трех переменных.
Способы задания функций нескольких переменных
Чтобы задать функцию двух (трех) переменных, нужно указать способ, с помощью которого для каждой пары (тройки) значений аргументов можно найти соответствующее значение функции. Наиболее часто функция задается аналитически — это явное задание функции или неявное задание
Например, — это явно заданная функция двух переменных; уравнение задает неявно две функции двух переменных.
Область определения функции
Непрерывное множество пар значений независимых переменных , при которых функцияопределена, называется областью определения функции.
Область определения называется замкнутой
областью, если она включает в себя свою границу;
открытой областью, если она не включает в себя
свою границу; ограниченной областью, если может
быть помещена в круг конечного радиуса.
Геометрически изобразить область определения функции можно только для функций:
- одной переменной – на прямой ,
- двух переменных – на плоскости ,
- трех переменных– в пространстве .
Геометрическое изображение самой функции возможно только для функции двух переменных.
Графиком функции двух переменных является поверхность, проектирующаяся на плоскость в область D, которая является областью определения функции.
На рис. изображена поверхность графика функции и ее область определения.
В курсе учебного материала 9-го класса мы рассматриваем следующие задания на нахождение и построение области определения функции.
ПРИМЕРЫ
Найти область определения функции
Решение. Областью определения данной функции
является вся плоскость, т. к. нет ограничений на
переменные x и y.
к. нет ограничений на
переменные x и y.
2. Найти область определения функции .
Решение. Данная функция определена, когда xy > 0, т.е. в тех точках координатной плоскости, в которых знаки координат x и y - одинаковы. Это будут точки, лежащие в I и III координатных четвертях, т.е. множество точек, удовлетворяющих условиям:
и
3. Найти область определения функции .
Решение. Данная функция определена при условии, когда
т.е. . Это множество точек, лежащих внутри круга с центром в начале координат, радиус которого равен 2.Изобразить на координатной плоскости Оху область определения функции .
Решение. Подкоренное выражение должно быть
неотрицательно, т.е. следовательно, . Геометрическим
решением неравенства служит полуплоскость,
расположенная выше прямой и сама прямая.
5. Найти область определения функции и изобразить её графически.
.
Решение. Областью определения функции является множество точек плоскости, координаты которых удовлетворяют системе неравенств:
6. Изобразить на координатной плоскости Оху область определения функции
Решение. Эта функция определена, когда подкоренное выражение неотрицательно, т.е. Данным соотношениям удовлетворяют координаты всех точек, находящихся внутри кольца, образованного двумя окружностями с центрами в начале координат и радиусами R=3, R=4.
7. Изобразить на координатной плоскости Оху область определения функции
.
Решение. Учащиеся не могут найти область
определения данной функции аналитически, но с
помощью графического редактора 3D Grapher 1.2 это
выполняется легко.
В Приложении приведено ещё несколько примеров, с решениями, для учащихся девятых классов.
Для учащихся 10-11 классов мы предлагаем систему упражнений по нахождению и построению области определения функции двух переменных. При этом отрабатываются свойства логарифмических, тригонометрических и обратных тригонометрических функций. Данные упражнения можно использовать при изучении нового материала, при повторении, при решении уравнений и неравенств.
Найти и изобразить на плоскости область определения функции
Решение. Область определения функции есть
пересечение областей определения слагаемых
функции. Для первой функции подкоренное
выражение должно быть неотрицательным, т.е. Если
значение логарифмической функции
неотрицательно, то выражение, стоящее под знаком
логарифма, должно быть больше или равно единице,
т. е.
отсюда .
Это неравенство задает нам множество точек
плоскости, лежащих вне окружности с центром в
начале координат, радиуса 2, включая и точки
данной окружности. Вторая функция определена при
Следовательно, Имеем две параболы с вершиной в начале
координат . Поэтому полученное неравенство
задает нам часть плоскости, заключенную между
этими параболами, включая границы без начала
координат. Третья функция определена при
е.
отсюда .
Это неравенство задает нам множество точек
плоскости, лежащих вне окружности с центром в
начале координат, радиуса 2, включая и точки
данной окружности. Вторая функция определена при
Следовательно, Имеем две параболы с вершиной в начале
координат . Поэтому полученное неравенство
задает нам часть плоскости, заключенную между
этими параболами, включая границы без начала
координат. Третья функция определена при
Областью определения данной функции является общая часть найденных областей определения слагаемых.
Покажите на координатной плоскости xOy область определения функции
.
Решение. Ограничения для функции имеют вид:
3. Изобразить область определения функции
Решение. Эта функция определена при , т.е.
Областью определения является часть плоскости,
расположенная между двумя прямыми.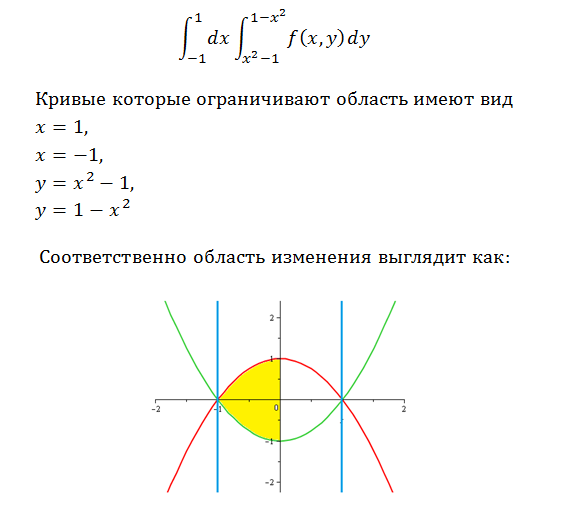
4. Найти область определения функции .
Решение. Областью определения функции является решение неравенства. Поэтому нужно решить неравенство
Решая данное неравенство, получим Это область, заключенная между двумя параболами и .
5. Построить область определения функции
Решение. Область определения данной функции определяется системой неравенств:
Первое неравенство определяет круг с центром в точке (-2;0) и радиусом равным 2 за исключением его границы:
Второе неравенство определяет I и III координатные четверти, за исключением осей.
В Приложении приведено ещё несколько примеров, с решениями, для учащихся десятых и одиннадцатых классов.
Рассмотрим задание С5, используя функцию двух переменных.
Найдите все значения параметра а, при
которых система , имеет ровно два решения.
Решение. Из второго уравнения находим y =. Первое уравнение принимает вид .
Пусть . В этом случае уравнение имеет единственное решение .
Запишем второе уравнение в виде = 0. Его дискриминант равен 4 , и он положителен, поскольку . Уравнение имеет два различных корня и Значит, в этом случае система имеет ровно два решения и .
Пусть теперь 1. В этом случае уравнение если и имеет корни, то только больше единицы Но тогда дискриминант уравнения = 0 отрицателен. Решений нет.
Ответ: .
С помощью графического редактора задаем функцию двух переменных , Находим значения а, при которых функция обращается в ноль.
На рисунке видно, что решением является интервал от 0 до 1.
При подготовке учащихся к итоговой аттестации
мы сталкиваемся с тем, что задания уровня С5
решаются тяжело и не сразу. А ведь это функция
двух переменных! Оперирование геометрическими
образами упрощает решение задач с параметрами, а
в некоторых случаях геометрический подход часто
является единственно возможным методом решения.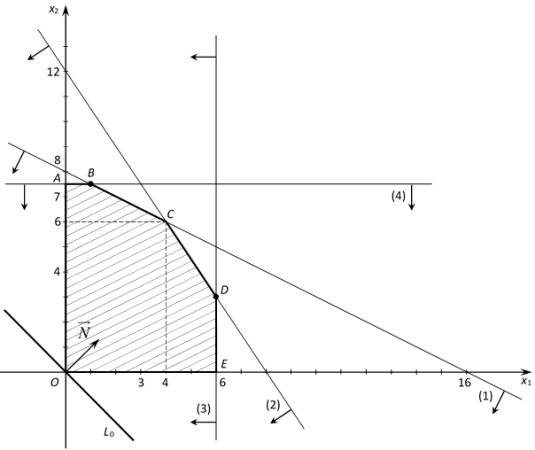 В сборнике ЕГЭ-2011 предложено задание.
В сборнике ЕГЭ-2011 предложено задание.
Найдите все значения а, такие, что для любого х выполняется неравенство.
Решение. Рассмотрим функцию
Если то убывает.
Если то возрастает.
Значит, наименьшее значение функции равно или , или . Поэтому решение задачи получаем из решения системы
Решений нет.Ответ: .
C помощью графического редактора мы построили график функции и определили значение параметра а при . График функции в системе координат выглядит следующим образом.
Приложение 1
Приложение 2
Приложение 3
Список источников и литературы.
- Математика (математический анализ):
учебно-методическое пособие для студентов
нематематических специальностей / О.Ю. Ватюкова,
Е.
 Е.Зайцева, Ю.В.Зайцева и др.; ВолГУ.-4-е изд.,
Волгоград: Волгоградское научное издательство,
2009. – 238с.
Е.Зайцева, Ю.В.Зайцева и др.; ВолГУ.-4-е изд.,
Волгоград: Волгоградское научное издательство,
2009. – 238с. - Дифференциальное исчисление функций нескольких переменных: типовой расчет по высшей математике / Сост.: А. В. Анкилов, Н. Я. Горячева, Т. Б. Распутько.- Ульяновск: УлГТУ, 2004.-32 с.
- ЕГЭ 2011. Математика. Типовые тестовые задания / И.Р. Высоцкий, Д.Д. Гущин, П.И.Захаров, В.С. Панферов, и др.; под ред. А.Л. Семенова, И.В. Ященко. -М.: Издательство “Экзамен”, 2011.-63с.
- Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010: Математика/авт.- сост. И.Р.Высоцкий, Д.Д. Гущин, П.И. Захаров и др.; под ред. А.Л. Семенова, И.В. Ященко. -М.: АСТ: Астрель, 2010.-93с.
- Мордкович А.Г. Алгебра . 9 класс. В 2 ч. Ч.1. Учебник
для учащихся общеобразовательных учреждений /
А.Г.Мордкович, П.В.Семенов .—11-е изд.
 , стер. -М.:
Мнемозина, 2009.-224 с.
, стер. -М.:
Мнемозина, 2009.-224 с. - Смирнова И.М. Геометрия. 10-11 кл.: Учеб. для общеобразоват. учреждений (гуманитарный профиль).- М.: Мнемозина,2004. -223с.
Системы линейных неравенств: особые случаи
Пурпурная математика
Область решения для предыдущего примера была ограниченным решением, потому что со всех сторон ее замыкали линии. Эта область решения представляла собой треугольник.
Но, поскольку границы областей решения образованы линиями, и поскольку линии не обязательно пересекаются друг с другом с пользой, существуют другие варианты, особые случаи для областей решения.Одним из особых случаев является система, в которой вы получаете решение, которое является «неограниченным»; то есть решение уходит навсегда в том или ином направлении.
MathHelp.
 com
comЧто является примером неограниченного решения?
- Решите следующую систему:
2 х − у > −3
4 х + у < 5
Как обычно, я сначала хочу решить эти неравенства для » y «.Я получаю следующую переставленную систему:
Каждое из них является строгим неравенством, поэтому мне нужно помнить, что мои границы должны быть пунктирными. Сами строки (представляющие случай «или равно», который здесь не применяется) не будут частью какого-либо решения этой системы.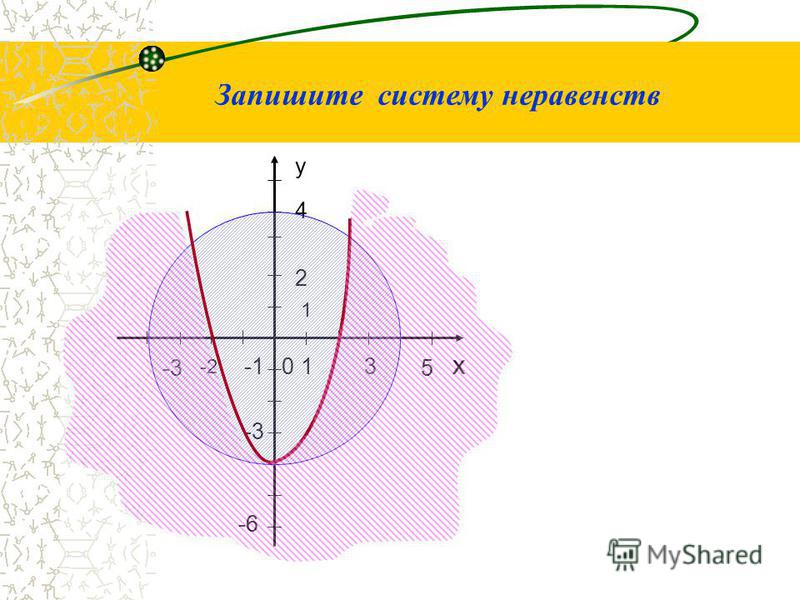
Построив первое неравенство, я получаю:
Из второго неравенства получаю:
Решение — это нижняя область, где два отдельных решения перекрываются.График, показывающий это перекрытие (вместе с четко пунктирными граничными линиями), и есть мой ответ:
.Тип решения, отображаемый в приведенном выше примере, называется «неограниченным», поскольку оно всегда продолжается по крайней мере в одном направлении (в данном случае всегда вниз).
Обратите внимание, как я нарисовал нижний край области решения. Я не провел резкой линии по низу своего рисунка; это подразумевало бы существование какой-то третьей линии, образующей дно области.Но дна нет. Поэтому я позволил моему затенению стать светлее по мере приближения к нижней части области графика.
Если у вас есть неограниченная область решения, убедитесь, что вы нарисовали ее так, чтобы она не выглядела ограниченной. Сделайте свой смысл ясным.
Конечно, всегда есть возможность вообще не получить решения.
Что является примером системы без решения?
- Решите следующую систему:
x − y ≤ −2
x − y ≥ 2
Сначала я решаю y и получаю эквивалентную систему:
Я отмечаю, что каждое из них представляет собой неравенство «или равное», поэтому область решения, если таковая имеется, будет включать линии.Поэтому я буду рисовать свои границы сплошными линиями.
Я рисую первое неравенство:
. ..и затем второй:
..и затем второй:
Но нет места, где бы отдельные решения пересекались. (Обратите внимание, что прямые y = x + 2 и y = x — 2 никогда не пересекаются, будучи параллельными прямыми с разными точками пересечения y .)
Поскольку области отдельных решений двух неравенств не пересекаются, то не может быть и решения системы неравенств. И поэтому мой ответ на упражнение:
Филиал
Если вы ответите, что решения нет, от вас, вероятно, ожидают, что вы сообщите об этом в письменном виде, как я сделал выше.В этом конкретном случае одного графика, вероятно, будет недостаточно; для полного кредита, четко укажите, что вы имеете в виду.
URL-адрес: https://www. purplemath.com/modules/syslneq2.htm
purplemath.com/modules/syslneq2.htm
Графическая система линейных неравенств
Ранее вы узнали, как построить график одного линейного неравенства на плоскости xy .В этом уроке мы будем иметь дело с системой линейных неравенств. Слово «система» подразумевает, что мы будем строить графики двух или более линейных неравенств одновременно. Решением системы будет область или область, где пересекаются графики всех линейных неравенств в системе.
ПРИМЕЧАНИЕ: Чтобы добиться успеха в построении графика линейных неравенств, вы должны знать, как построить линию на плоскости xy. В противном случае найдите время, чтобы просмотреть материал.
Шаги Как построить график системы линейных неравенств
Шаг 1: Отобразите каждое линейное неравенство в системе на одной и той же оси xy . Запомните ключевые шаги при построении графика линейного неравенства:
Запомните ключевые шаги при построении графика линейного неравенства:
- Изолируйте переменную « y » слева от неравенства.
- Если символы > и ≥, мы заштриховываем область над граничной линией, используя пунктирную и сплошную линии соответственно.
- С другой стороны, если символы < и ≤, мы заштриховываем область ниже граничной линии, используя пунктирную и сплошную линии соответственно.
Шаг 2: Закрасьте область, где пересекаются или перекрываются все области линейных неравенств. Если области пересечения нет, говорят, что система не имеет решения.
Давайте рассмотрим несколько примеров, чтобы проиллюстрировать процедуру.
Примеры построения системы линейных неравенств
Пример 1: Нарисуйте следующую систему линейных неравенств:
В данной задаче хорошо то, что все переменные y уже находятся в левой части символа неравенства.В этой форме мы можем легко определить, какую область заштриховать относительно линии границы.
- Нарисуйте первое неравенство y ≤ x − 1 . Поскольку у нас есть символ «меньше или равно», граница будет сплошной, и мы заштрихуем область под линией.
- Нарисуйте второе неравенство y < –2 x + 1 . Символ просто «меньше», поэтому линия границы будет пунктирной или пунктирной, и мы заштрихуем область под ней.
- Окончательным решением системы линейных неравенств будет область пересечения двух неравенств, как показано справа.
Мы называем эту область решения «неограниченной», потому что эта область на самом деле бесконечно расширяется в нисходящем направлении.
В следующем примере вы увидите пример «ограниченной» области.
Пример 2: Нарисуйте следующую систему линейных неравенств:
Система содержит три неравенства, значит, мы будем рисовать три из них.Обратите внимание, что все символы неравенства имеют компонент «равно». Это говорит нам о том, что все граничные линии будут сплошными.
Это говорит нам о том, что все граничные линии будут сплошными.
- Вот график первого неравенства, где граничная линия сплошная, а под ней находится заштрихованная область.
- Второе неравенство будет иметь сплошную граничную линию, а над ней находится заштрихованная область.
- Наконец, третье неравенство также будет иметь сплошную граничную линию и затенение области над ней.
- Как видите, заштрихованные области трех линейных неравенств перекрываются прямо в средней части.
Мы называем эту систему «ограниченной», потому что область, в которой лежат все решения, ограничена тремя сторонами, исходящими из граничных линий линейных неравенств.
Пример 3: Нарисуйте следующую систему линейных неравенств:
Когда я смотрю на три неравенства, включенные в систему, мне нужно учитывать три вещи:
- Перепишите первое неравенство x + 2 y < 2 так, чтобы переменная « y » была одна в левой части.
 Если вы правильно разработаете это, чтобы изолировать « y », это неравенство будет эквивалентно выражению .
Если вы правильно разработаете это, чтобы изолировать « y », это неравенство будет эквивалентно выражению . - Неравенство y > –1 будет иметь горизонтальную граничную линию.
- Неравенство x ≥ –3 будет иметь вертикальную граничную линию.
Если вам нужна помощь в построении графика вертикальных и горизонтальных линий, ознакомьтесь с этим отдельным уроком.
Теперь мы готовы построить график каждого из них.
- График будет представлять собой пунктирную граничную линию с заштрихованной областью, расположенной под ней.
- График y > –1 представляет собой пунктирную горизонтальную линию, проходящую через точку пересечения y в точке -1 с заштрихованной областью над ней.
- График x ≥ –3 представляет собой сплошную линию, проходящую через точку пересечения по оси x в точке -3 , с заштрихованной областью справа от нее.

- Решением этой системы является общая площадь пересечения всех трех неравенств.
Это также «ограниченная система», в которой область решения заключена в два отрезка пунктирной линии и один отрезок сплошной линии.
Пример 4: Нарисуйте следующую систему линейных неравенств:
Оба неравенства нужно переписать так, чтобы переменная « y » располагалась слева сама по себе.
Вот для первого. Обязательно меняйте направление символа неравенства всякий раз, когда вы делите неравенство на отрицательное число.
А вот и переписывание второго неравенства. На этот раз мы не делим неравенство на отрицательное число, поэтому ориентация или направление символа неравенства остается прежним.
Давайте нарисуем их на графике.
- График y > –2 x + 1 представляет собой пунктирную или «прерывистую» линию с заштрихованной областью над ней.

- График y ≤ –2 x − 3 представляет собой сплошную линию с заштрихованной областью под ней.
Поскольку две заштрихованные области не пересекаются и не перекрываются, это говорит нам о том, что данная система неравенств имеет НЕТ РЕШЕНИЯ .
Возможно, вы также заметили, что граничные линии имеют одинаковые наклоны, обе м = –2, что означает, что они параллельны и, следовательно, не пересекаются.
Вас также может заинтересовать:
Решение линейных неравенств
шага по построению графика линейных неравенств
Графические примеры линейных неравенств
Решение сложных неравенств
РЕШЕНО:Создать систему неравенств, образующую ограниченную область.
Стенограмма видео
Здравствуйте. Это проблема, где нам нужно создать свою собственную систему любых качеств, которая создает ограниченную область. Итак, что я здесь делаю, так это то, что я собираюсь использовать большинство точек com. Ах, отличный графический онлайн-калькулятор, бесплатный для молодежи. И я собираюсь начать с ввода некоторых уравнений здесь. Так почему же меньше, чем два X плюс один? Хорошо, и, как видите, по мере того, как вы что-то вводите, это становится слишком наглядным для нас. Итак, мы можем видеть прямо сейчас, что А, вот наша наша линия. Почему Y равно два х плюс один. И, конечно же, это меньше, чем равно. Так что это заштриховано ниже этой области. Хорошо, а потом я возьму другое уравнение и сделаю 2-е и 1-е отрицательными, чтобы оно пересекало эту линию.Итак, я собираюсь сказать, почему меньше или равно отрицательному? Скажем, три X, эм, и давайте плюс четыре, пока не будет второго уравнения. Хорошо. Итак, помните, что когда мы смотрим на эти два неравенства, то есть на решение любой системы неравенств, эти две области пересекаются. Итак, это происходит в этой области прямо здесь, верно? Но прямо сейчас у нас есть только одно очко.
Итак, что я здесь делаю, так это то, что я собираюсь использовать большинство точек com. Ах, отличный графический онлайн-калькулятор, бесплатный для молодежи. И я собираюсь начать с ввода некоторых уравнений здесь. Так почему же меньше, чем два X плюс один? Хорошо, и, как видите, по мере того, как вы что-то вводите, это становится слишком наглядным для нас. Итак, мы можем видеть прямо сейчас, что А, вот наша наша линия. Почему Y равно два х плюс один. И, конечно же, это меньше, чем равно. Так что это заштриховано ниже этой области. Хорошо, а потом я возьму другое уравнение и сделаю 2-е и 1-е отрицательными, чтобы оно пересекало эту линию.Итак, я собираюсь сказать, почему меньше или равно отрицательному? Скажем, три X, эм, и давайте плюс четыре, пока не будет второго уравнения. Хорошо. Итак, помните, что когда мы смотрим на эти два неравенства, то есть на решение любой системы неравенств, эти две области пересекаются. Итак, это происходит в этой области прямо здесь, верно? Но прямо сейчас у нас есть только одно очко. Гм, это действительно часть нашего возможного региона. Гм, Vergis легкость, потому что И это открытый конец, потому что, если бы мы прокрутили вниз, вы бы увидели, что это становится все больше и больше, и это будет продолжаться вечно.Таким образом, цель здесь состоит в том, чтобы получить область, которая является ограниченной областью. Итак, что я собираюсь сделать, так это просто провести линию, которая проходит горизонтально через эту темную заштрихованную область здесь, и, ах, горизонтальная линия будет «Почему равна чему-то?» Я скажу, что поставлю отрицательную тройку. Таким образом, вы можете видеть, что линия находится прямо там. И на самом деле, я должен сделать это больше или равным трем, чтобы он действительно затенялся вверх, и вы можете видеть, что теперь у нас есть возможная область. Э-э, это внутри этих трех вергисов, он, э-э, 0.62 точка два, минус, 23 и два. И 1/3 и минус три. И этот регион. А вот и наша допустимая область, и она теперь ограничена. Так что это одно из бесконечного множества решений этой проблемы, которые вы могли бы придумать, чтобы создать свою собственную возможную область.
Гм, это действительно часть нашего возможного региона. Гм, Vergis легкость, потому что И это открытый конец, потому что, если бы мы прокрутили вниз, вы бы увидели, что это становится все больше и больше, и это будет продолжаться вечно.Таким образом, цель здесь состоит в том, чтобы получить область, которая является ограниченной областью. Итак, что я собираюсь сделать, так это просто провести линию, которая проходит горизонтально через эту темную заштрихованную область здесь, и, ах, горизонтальная линия будет «Почему равна чему-то?» Я скажу, что поставлю отрицательную тройку. Таким образом, вы можете видеть, что линия находится прямо там. И на самом деле, я должен сделать это больше или равным трем, чтобы он действительно затенялся вверх, и вы можете видеть, что теперь у нас есть возможная область. Э-э, это внутри этих трех вергисов, он, э-э, 0.62 точка два, минус, 23 и два. И 1/3 и минус три. И этот регион. А вот и наша допустимая область, и она теперь ограничена. Так что это одно из бесконечного множества решений этой проблемы, которые вы могли бы придумать, чтобы создать свою собственную возможную область.
Графики квадратных неравенств
Квадратное неравенство вида
у > а Икс 2 + б Икс + с
(или заменить < , ≥ или ≤ за > ) представляет собой область плоскости, ограниченную парабола .
Чтобы построить квадратное неравенство, начните с построения параболы. Затем закрасьте область либо над ней, либо под ней, в зависимости от неравенства.
Если символ неравенства ≤ или ≥ , то область включает в себя параболу, поэтому ее следует изобразить сплошной линией.
В противном случае, если символ неравенства < или > , парабола должна быть нарисована пунктирной линией, чтобы указать, что область не включает свою границу.
Пример:
Нарисуйте квадратное неравенство.
у ≤ Икс 2 − Икс − 12
Соответствующее уравнение:
у знак равно Икс 2 − Икс − 12
Сначала мы замечаем, что а , коэффициент Икс 2 срок, равен 1 .С а положительно, парабола направлена вверх.
Правую часть можно представить как:
у знак равно ( Икс + 3 ) ( Икс − 4 )
Итак, парабола имеет Икс -перехватывает в − 3 и 4 . То вершина должно лежать посередине между ними, поэтому Икс -координата вершины 0.5 .
Подключение к этому Икс -значение, получаем:
у
знак равно
(
0,5
+
3
)
(
0,5
−
4
)
у
знак равно
(
3,5
)
(
−
3,5
)
у
знак равно
−
12. 25
25
Итак, вершина находится в ( 0,5 , − 12.25 ) .
Теперь у нас достаточно информации, чтобы нарисовать параболу. Не забудьте изобразить его сплошной линией, поскольку неравенство «меньше или равно».
Должны ли вы заштриховать область внутри или снаружи параболы? Лучший способ сказать это подключить точку выборки. ( 0 , 0 ) обычно проще всего:
0 ≤ ? 0 2 − 0 − 12 0 ≤ − 12
Итак, заштрихуйте область, которая нет включить точку ( 0 , 0 ) .
Введение в неравенства и обозначения интервалов
2.
 7 Введение в неравенства и обозначения интервалов
7 Введение в неравенства и обозначения интерваловЦели обучения
- Нанесите решения одного неравенства на числовую прямую и выразите решения, используя запись интервалов.
- Нанесите решения сложного неравенства на числовую прямую и выразите решения, используя запись интервалов.
Неограниченные интервалы
Алгебраическое неравенствоВыражения, связанные с символами ≤, <, ≥ и >., например x≥2, читается как « x больше или равно 2». Это неравенство имеет бесконечно много решений для x . Некоторые из решений 2, 3, 3,5, 5, 20 и 20,001. Поскольку невозможно перечислить все решения, необходима система, позволяющая четко передавать этот бесконечный набор. Два распространенных способа выражения решений неравенства — это графическое изображение их на числовой прямой. Решения алгебраического неравенства выражаются штриховкой решения на числовой прямой.и с использованием интервальной записи Текстовая система выражения решений алгебраического неравенства. .
.
Чтобы выразить решение графически, нарисуйте числовую линию и заштрихуйте все значения, являющиеся решениями неравенства. Обозначение интервала является текстовым и использует следующие специальные обозначения:
Определите обозначение интервала после построения графика набора решений на числовой прямой. Числа в интервальной записи следует записывать в том же порядке, в котором они появляются в числовой строке, причем меньшие числа в наборе появляются первыми.В данном примере имеет место инклюзивное неравенство. Неравенство, включающее граничную точку, обозначенную «или равной» частью символов ≤ и ≥ и закрытой точкой на числовой прямой, означает, что нижняя граница 2 входит в решение. Обозначьте это закрытой точкой на числовой прямой и квадратной скобкой в обозначении интервала. Символ (∞) читается как бесконечность. Символ (∞) указывает на то, что интервал не ограничен справа. и указывает, что набор неограничен справа на числовой прямой. Интервальное обозначение требует скобок для заключения бесконечности. Квадратная скобка указывает, что граница включена в решение. Скобки означают, что граница не включена. Бесконечность — это верхняя граница действительных чисел, но сама она не является действительным числом: она не может быть включена в набор решений.
Интервальное обозначение требует скобок для заключения бесконечности. Квадратная скобка указывает, что граница включена в решение. Скобки означают, что граница не включена. Бесконечность — это верхняя граница действительных чисел, но сама она не является действительным числом: она не может быть включена в набор решений.
Теперь сравните обозначение интервала в предыдущем примере со строгим, или неинклюзивным, неравенством, которое следует ниже:
Строгие неравенства Выражайте отношения порядка, используя символ < для «меньше чем» и > для «больше чем».” подразумевают, что решения могут быть очень близки к граничной точке, в данном случае 2, но на самом деле не включают ее. Обозначим эту идею открытой точкой на числовой прямой и круглой скобкой в записи интервала.
Пример 1: Постройте график и дайте эквивалент записи интервала: x<3.
Решение: Используйте открытую точку на 3 и заштрихуйте все действительные числа строго меньше 3. Используйте отрицательную бесконечность Символ (-∞) указывает на то, что интервал не ограничен слева.(−∞), чтобы указать, что набор решений не ограничен слева на числовой прямой.
Используйте отрицательную бесконечность Символ (-∞) указывает на то, что интервал не ограничен слева.(−∞), чтобы указать, что набор решений не ограничен слева на числовой прямой.
Ответ: Обозначение интервала: (−∞, 3)
Пример 2: Постройте график и задайте эквивалент записи интервала: x≤5.
Решение: Используйте закрытую точку и заштрихуйте все числа меньше 5 включительно.
Ответ: Обозначение интервала: (−∞, 5]
Важно понимать, что 5≥x равно x≤5.Оба требуют, чтобы значения x были меньше или равны 5. Во избежание путаницы рекомендуется переписать все неравенства с переменной слева. Кроме того, при использовании текста используйте «inf» как сокращенную форму бесконечности. Например, (−∞, 5] может быть выражено в текстовом виде как (−inf, 5].
Составное неравенствоДва неравенства в одном утверждении, соединенные словом «и» или словом «или». на самом деле два или более неравенства в одном утверждении, соединенные словом «и» или словом «или».Составные неравенства с логическим «или» требуют выполнения любого из условий. Следовательно, множество решений этого типа составного неравенства состоит из всех элементов множеств решений каждого неравенства. Когда мы соединяем эти отдельные наборы решений, это называется объединением. Набор, образованный путем соединения отдельных наборов решений, обозначенных логическим использованием слова «или» и обозначенных символом ∪., обозначаемым ∪. Например, решения сложного неравенства x<3 или x≥6 можно изобразить следующим образом:
на самом деле два или более неравенства в одном утверждении, соединенные словом «и» или словом «или».Составные неравенства с логическим «или» требуют выполнения любого из условий. Следовательно, множество решений этого типа составного неравенства состоит из всех элементов множеств решений каждого неравенства. Когда мы соединяем эти отдельные наборы решений, это называется объединением. Набор, образованный путем соединения отдельных наборов решений, обозначенных логическим использованием слова «или» и обозначенных символом ∪., обозначаемым ∪. Например, решения сложного неравенства x<3 или x≥6 можно изобразить следующим образом:
Иногда встречаются составные неравенства, в которых отдельные наборы решений перекрываются.В случае, когда составное неравенство содержит слово «или», мы объединяем все элементы обоих множеств, чтобы создать одно множество, содержащее все элементы каждого из них.
Пример 3: Постройте график и задайте эквивалент обозначения интервала: x≤−1 или x<3.
Решение: Объединить все решения обоих неравенств. Решения каждого неравенства нарисованы над числовой линией как средство определения объединения, которое изображено на числовой строке ниже.
Ответ: Обозначение интервала: (−∞, 3)
Любое действительное число меньше 3 в заштрихованной области числовой прямой удовлетворяет хотя бы одному из двух заданных неравенств.
Пример 4: Постройте график и задайте эквивалент обозначения интервала: x<3 или x≥−1.
Решение: Оба набора решений изображены над объединением, которое изображено ниже.
Ответ: Обозначение интервала: R = (−∞, ∞)
Когда вы объединяете оба набора решений и формируете объединение, вы можете видеть, что все действительные числа удовлетворяют исходному составному неравенству.
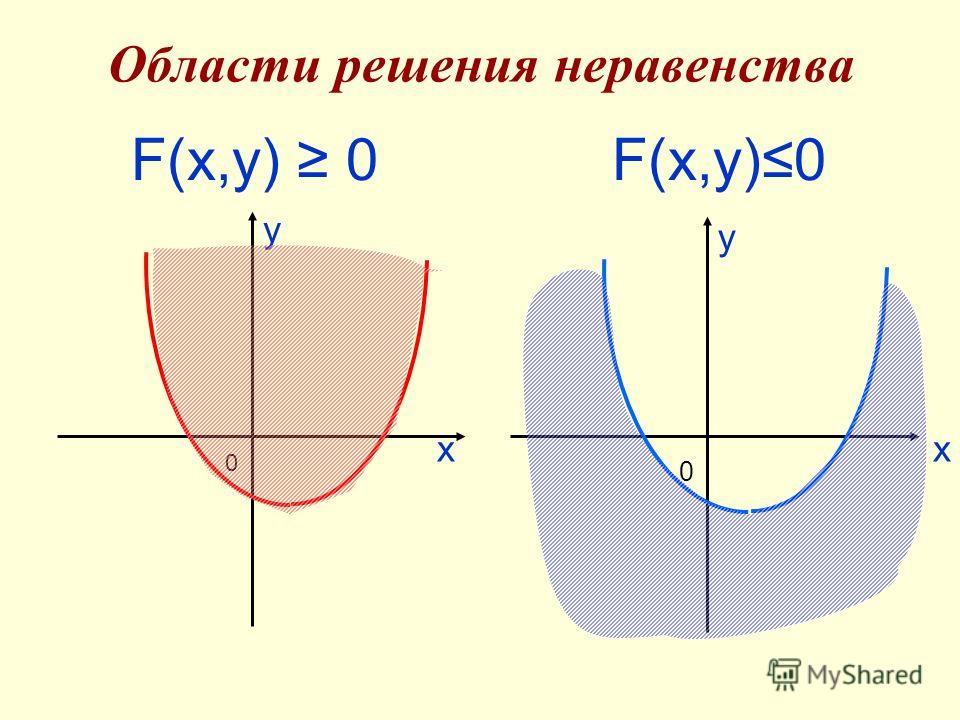
Подводя итог,
и
Ограниченные интервалы
Неравенство типа
гласит: «-1 единица меньше или равна x , а x меньше трех.Это составное неравенство, потому что его можно разложить следующим образом:
Логическое «и» требует, чтобы оба условия были истинными. Обоим неравенствам удовлетворяют все элементы пересечения. Множество, образованное общими значениями отдельных множеств решений, на что указывает логическое использование слова «и», обозначаемого символом ∩., обозначаемого ∩, множеств решений каждого.
Пример 5: Постройте график и задайте эквивалент обозначения интервала: x<3 и x≥−1.
Решение: Определите пересечение или перекрытие двух наборов решений. Решения каждого неравенства нарисованы над числовой линией как средство определения пересечения, которое изображено на числовой строке ниже.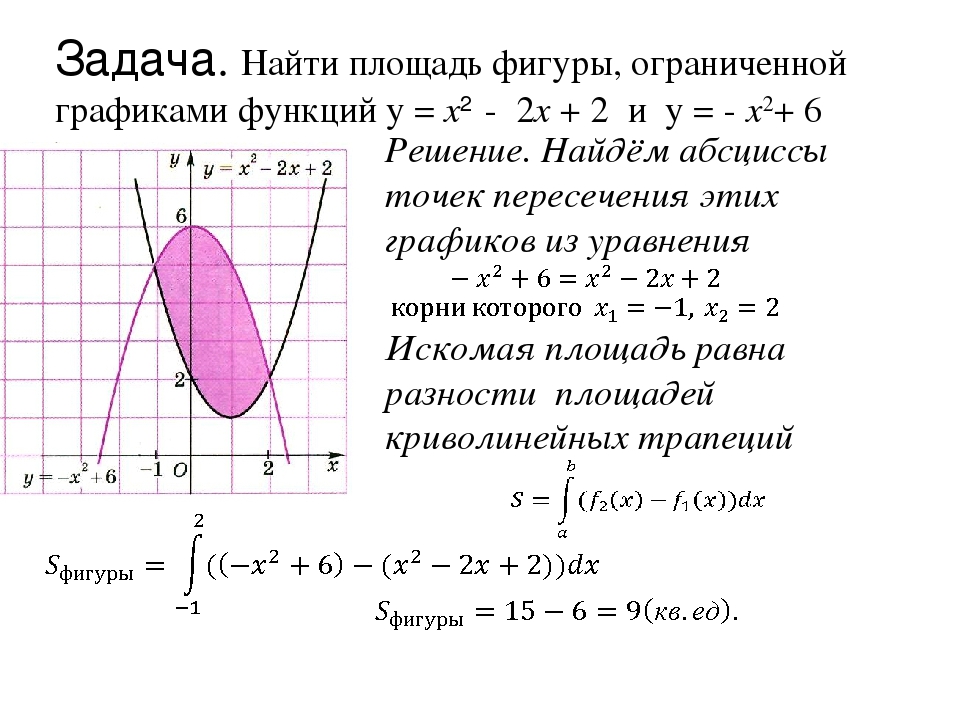
Здесь x=3 не является решением, так как решает только одно из неравенств.
Ответ: Обозначение интервала: [−1, 3)
В качестве альтернативы мы можем интерпретировать -1≤x<3 как все возможные значения для x между или ограниченными -1 и 3 на числовой прямой.Например, одним из таких решений является x=1. Обратите внимание, что 1 находится между -1 и 3 на числовой прямой или что -1 < 1 < 3. Точно так же мы можем видеть, что другие возможные решения - это -1, -0,99, 0, 0,0056, 1,8 и 2,99. Поскольку существует бесконечно много действительных чисел между -1 и 3, мы должны выразить решение графически и/или с помощью интервальной записи, в данном случае [-1, 3).
Пример 6: Постройте график и задайте эквивалент записи интервала: −32 Решение: Закрасьте все действительные числа, ограниченные или строго между -32=-112 и 2. Ответ: Обозначение интервала: (−32, 2) Пример 7: Постройте график и задайте эквивалент записи интервала: −5 Решение: Заштрихуйте все действительные числа от −5 до 15 и укажите, что верхняя граница, 15, включена в набор решений, используя закрытую точку. Ответ: Обозначение интервала: (−5, 15] В предыдущих двух примерах мы не разлагали неравенства; вместо этого мы решили думать обо всех действительных числах между двумя заданными границами. Подводя итог, В этом тексте мы используем интервальную запись. Однако в других ресурсах, с которыми вы, вероятно, столкнетесь, используется альтернативный метод описания наборов, называемый нотация построителя наборов. Система для описания наборов с использованием знакомой математической записи. Фигурные скобки группируют элементы набора, а многоточие указывает, что целые числа продолжаются вечно. В этом разделе мы хотим описать интервалы действительных чисел, например, действительные числа, большие или равные 2. Поскольку набор слишком велик для перечисления, нотация построителя набора позволяет нам описать его, используя знакомую математическую запись.Ниже приведен пример нотации конструктора наборов: Здесь x ∈ R описывает тип числа, где символ (∈) читается как «элемент». Это означает, что переменная x представляет собой действительное число. Вертикальная черта (|) читается как «такой, что». Наконец, утверждение x≥2 является условием, описывающим множество с помощью математических обозначений. На данном этапе нашего изучения алгебры предполагается, что все переменные представляют действительные числа. Чтобы описать сложные неравенства, такие как x<3 или x≥6, напишите {x|x<3 или x≥6}, что читается как «набор всех действительных чисел x , таких что x меньше 3 или x больше или равно 6». Запишите ограниченные интервалы, такие как −1≤x<3, как {x|−1≤x<3}, что читается как «множество всех действительных чисел x , таких что x больше или равно −1 и меньше 3. Часть A: Простые неравенства Нанесите все решения на числовую прямую и задайте соответствующее обозначение интервала. 1. х≤10 2. х>−5 3. х>0 4. х≤0 5. x≤−3 6. х≥−1 7. −4 8. 1≥x 9. х<−12 10. х≥−32 11. х≥−134 12. х<34 Часть B: Составные неравенства Нанесите графически все решения на числовую прямую и задайте соответствующее обозначение интервала. 13. −2 14. −5≤x≤−1 15. −5 16. 0≤x<15 17. 10 18. −40≤x<−10 19. 20. −30 21. −58 22. −34≤x≤12 23. −1≤x<112 24. −112 25.x<−3 или x>3 26. x<−2 или x≥4 27. x≤0 или x>10 28. x≤−20 или x≥−10 29. x<−23 или x>13 30. x≤−43 или x>−13 31. x>−5 или x<5 32. x<12 или x>−6 33. х<3 или х≥3 34. x≤0 или x>0 35. x<−7 или x<2 36.x≥−3 или x>0 37. х≥5 или х>0 38. x<15 или x≤10 39. x>−2 и x<3 40. x≥0 и x<5 41. x≥−5 и x≤−1 42. x<−4 и x>2 43. x≤3 и x>3 44. x≤5 и x≥5 45. 46. x<2 и x≤−1 47.x>0 и x≥−1 48. х<5 и х<2 Часть C: Обозначение интервала Определите неравенство, зная ответы, выраженные в виде интервалов. 49. (−∞, 7] 50. (−4, ∞) 51. [−12, ∞) 52. (−∞, −3) 53. (−8, 10] 54. (−20, 0] 55.(−14, −2) 56. [23, 43] 57. (−34, 12) 58. (−∞, −8) 59. (8, ∞) 60. (−∞, 4)∪[8, ∞) 61. (−∞, −2]∪[0, ∞) 62. (−∞, −5]∪(5, ∞) 63. (−∞, 0)∪(2, ∞) 64. (−∞, −15)∪(−5, ∞) Запишите эквивалентное неравенство. 65. Все действительные числа меньше 27. 66. Все действительные числа меньше или равные нулю. 67. Все действительные числа больше 5. 68. Все действительные числа, большие или равные −8. 69. Все действительные числа строго между −6 и 6. 70. Все действительные числа строго между −80 и 0. Часть D: Темы на доске обсуждений 71. Сравните нотацию интервала с нотацией построителя наборов.Поделитесь примером набора, описанного с использованием обеих систем. 72. Объясните, почему мы не используем скобки в обозначении интервала, когда бесконечность является конечной точкой. 73. Изучите и обсудите различные составные неравенства, особенно объединения и пересечения. 74. Исследуйте и обсуждайте историю бесконечности. 75. Исследуйте и обсудите вклад Георга Кантора. 76. Что такое диаграмма Венна? Объясни и выложи пример. 1: (−∞, 10] 3: (0, ∞) 5: (−∞, −3] 7: (−4, ∞) 9: (-∞, -12) 11: [−134, ∞) 13: (−2, 5) 15: (−5, 20] 17: (10, 40] 19: (0, 50] 21: (−58, 18) 23: [−1, 112) 25: (−∞, −3)∪(3, ∞) 27: (−∞, 0]∪(10, ∞) 29: (−∞, −23)∪(13, ∞) 31: Р 33: Р 35: (−∞, 2) 37: (0, ∞) 39: (−2, 3) 41: [−5, −1] 43: ∅ 45: {0} 47: (0, ∞) 49: х≤7 51: х≥−12 53: −8 55: −14 57: −34 59: х>8 61: x≤−2 или x≥0 63: x<0 или x>2 65: х<27 67: х>5 69: −6 В этом разделе вы: Комета Галлея ((Рисунок)) совершает оборот вокруг Солнца примерно раз в 75 лет. Его путь можно рассматривать как очень вытянутый эллипс. Другие кометы следуют аналогичным путям в космосе. Эти орбитальные траектории можно изучать с помощью систем уравнений. Эти системы, однако, отличаются от тех, которые мы рассмотрели в предыдущем разделе, потому что уравнения не являются линейными. В этом разделе мы рассмотрим пересечение параболы и прямой, окружности и прямой, окружности и эллипса. Методы решения систем нелинейных уравнений аналогичны методам решения линейных уравнений. Система нелинейных уравнений — это система двух или более уравнений с двумя или более переменными, содержащая хотя бы одно нелинейное уравнение. Существует три возможных типа решений системы нелинейных уравнений, включающих параболу и прямую. (рисунок) иллюстрирует возможные наборы решений для системы уравнений, включающей параболу и прямую. Дана система уравнений, содержащая прямую и параболу, найти решение. Решите систему уравнений. Решите данную систему уравнений подстановкой. и [/скрытый ответ] Как и в случае с параболой и прямой, при решении системы уравнений, представляющих окружность и прямую, возможны три исхода. (рисунок) иллюстрирует возможные наборы решений для системы уравнений, включающей окружность и прямую. Дана система уравнений, содержащая прямую и окружность, найти решение. Найдите пересечение заданного круга и заданной прямой подстановкой. Решите систему нелинейных уравнений. [/скрытый ответ] Мы видели, что подстановка часто является предпочтительным методом, когда система уравнений включает линейное уравнение и нелинейное уравнение. (рисунок) иллюстрирует возможные наборы решений для системы уравнений, включающей окружность и эллипс. Решите систему нелинейных уравнений. Найдите набор решений для данной системы нелинейных уравнений. [/скрытый ответ] Все уравнения в системах, с которыми мы сталкивались до сих пор, включали равенства, но мы также можем столкнуться с системами, включающими неравенства.Мы уже научились отображать линейные неравенства, изображая соответствующее уравнение, а затем заштриховывая область, представленную символом неравенства. Теперь мы выполним аналогичные шаги для построения графика нелинейного неравенства, чтобы научиться решать системы нелинейных неравенств. Напомним, что когда неравенство больше или меньше, график рисуется пунктирной линией.Когда неравенство больше или равно или меньше или равно, график рисуется сплошной линией. Графики создадут области на плоскости, и мы проверим каждую область в поисках решения. Если работает одна точка региона, работает весь регион. Это область, которую мы затеняем. См. (Рисунок). Для заданного неравенства, ограниченного параболой, нарисуйте график. Теперь, когда мы научились строить графики нелинейных неравенств, мы можем научиться строить графики систем нелинейных неравенств. Система нелинейных неравенств — это система двух или более неравенств с двумя или более переменными, содержащая хотя бы одно неравенство, которое не является линейным. Построение графика системы нелинейных неравенств аналогично построению графика системы линейных неравенств.Разница в том, что наш график может привести к большему количеству заштрихованных областей, представляющих решение, чем мы находим в системе линейных неравенств. Решением нелинейной системы неравенств является область графика, в которой перекрываются заштрихованные области графика каждого неравенства, или где области пересекаются, называемая допустимой областью. Дана система нелинейных неравенств, нарисуйте график. Постройте график данной системы неравенств. Постройте график данной системы неравенств. Закрасьте область, ограниченную двумя кривыми, над квадратичной и под линией. [/скрытый ответ] Объясните, может ли система двух нелинейных уравнений иметь ровно два решения.А если ровно три? Если нет, объясните почему. Если да, приведите пример такой системы в виде графика и объясните, почему ваш выбор дает два или три ответа. Нелинейная система может представлять собой две окружности, которые перекрываются и пересекаются в двух местах, следовательно, два решения. Нелинейная система может представлять собой параболу и окружность, где вершина параболы встречается с окружностью, а ветви также пересекают окружность, следовательно, есть три решения. [/скрытый ответ] При построении графика неравенства объясните, почему нам нужно проверить только одну точку, чтобы определить, является ли решением вся область? Когда вы рисуете систему неравенств, всегда ли будет допустимая область? Если да, объясните почему. №Там не должно быть допустимой области. Рассмотрим систему, ограниченную двумя параллельными прямыми. Одно неравенство представляет область выше верхней линии; другой представляет область ниже нижней линии. В этом случае в обеих областях нет точек на плоскости; следовательно, нет допустимой области. [/скрытый ответ] Если вы рисуете функцию доходов и затрат, объясните, как определить, в каких регионах есть прибыль. Если вы проводите анализ безубыточности и существует более одного решения, объясните, как вы будете определять, какие значения x являются прибыльными, а какие нет. Выберите любое число между каждым раствором и подключите к и Если тогда есть прибыль. [/скрытый ответ] Для следующих упражнений решите систему нелинейных уравнений с помощью подстановки. [/скрытый ответ] [/скрытый ответ] Для следующих упражнений решите систему нелинейных уравнений методом исключения. [/скрытый ответ] [/скрытый ответ] [/скрытый ответ] В следующих упражнениях используйте любой метод решения системы нелинейных уравнений. [/скрытый ответ] [/скрытый ответ] [/скрытый ответ] [/скрытый ответ] В следующих упражнениях используйте любой метод решения нелинейной системы. [/скрытый ответ] Решений не существует [/скрытый ответ] Решений не существует [/скрытый ответ] [/скрытый ответ] [/скрытый ответ] [/скрытый ответ] [/скрытый ответ] Для следующих упражнений постройте график неравенства. Для следующих упражнений найдите решения нелинейных уравнений с двумя переменными. [/скрытый ответ] Решение не существует [/скрытый ответ] Для следующих упражнений решите систему неравенств.Используйте калькулятор, чтобы построить график системы, чтобы подтвердить ответ. и [/скрытый ответ] Для следующих упражнений постройте систему нелинейных уравнений, описывающую заданное поведение, затем найдите требуемые решения. Два числа в сумме дают 300.Одно число в два раза больше квадрата другого числа. Какие числа? 12, 288 [/скрытый ответ] Квадраты двух чисел дают в сумме 360. Второе число равно половине значения квадрата первого числа. Какие числа? Компания по производству ноутбуков определила свои функции затрат и доходов на каждый день: и если они хотят получать прибыль, какой диапазон ноутбуков в день они должны производить? Округлите до ближайшего числа, которое принесет прибыль. 2–20 компьютеров [/скрытый ответ] Компания сотовой связи имеет следующие функции затрат и доходов: и какой ассортимент сотовых телефонов они должны производить каждый день, чтобы получить прибыль? Округлите до ближайшего числа, приносящего прибыль. Заштрихованная область на следующем рисунке может быть алгебраически описана как 𝐴∩𝐵∩𝐶, где 𝐴={𝑧∈ℂ∶( 𝑧)𝑎},𝐵={𝑧∈ℂ∶|𝑧|≤|𝑧−𝑧|},𝐶={𝑧∈ℂ∶|𝑧|≤|𝑧−𝑧|}.Im Найдите значения 𝑎, 𝑧,
и 𝑧, где 𝑎∈ℝ и 𝑧,𝑧∈ℂ. Область ограничена тремя линиями: 𝐿, 𝐿,
и 𝐿, как показано ниже. Первый из них, 𝐿, представлен
Im(𝑧)=2. Регион не содержит
граничные точки вдоль этой линии. Следовательно, 𝐴={𝑧∈ℂ∶(𝑧)2}Im. Теперь обратим внимание на
𝐿. Нам нужно описать эту прямую как серединный перпендикуляр к
отрезок линии между началом координат и другой точкой, которую мы обозначили
𝑃.Иногда, как в этом примере, это можно сделать с помощью
осмотр. Мы видим, что прямая проходит через две диагонально противоположные стороны.
вершины квадрата, определяемые точками (0,0), (3,0), (3,−3) и
(0,−3). Следовательно, это серединный перпендикуляр к отрезку.
между двумя другими диагонально противоположными вершинами. Следовательно, 𝐿 является
серединный перпендикуляр к отрезку между (0,0) и
𝑃(3,−3). Следовательно, 𝐵={𝑧∈ℂ∶|𝑧|≤|𝑧−(3−3𝑖)|}.Наконец, обращаем внимание на третью строку,
𝐿. Начнем с нахождения наклона 𝑚 линии 𝐿. Мы
можно вычислить по формуле
(−2,0), имеем 𝑚=−3−00−(−2)=−32. Таким образом, мы можем записать уравнение прямой как 𝑦=−32𝑥−3. Теперь найдем уравнение прямой, перпендикулярной этой, которая проходит через
источник. Напомним, что произведение наклонов двух перпендикулярных прямых равно
−1. Следовательно, наклон прямой, перпендикулярной
𝐿 равно 23. Следовательно, уравнение
перпендикулярная линия, проходящая через начало координат, определяется как 𝑦=23𝑥. Теперь нам нужно найти точку на этой прямой, расстояние которой до 𝐿 равно
равно расстоянию между 𝐿 и началом координат. Собирая наши 𝑥 члены в левой части, мы имеем
136𝑥=−3. Следовательно, 𝑥=−1813. Подставляя это обратно в одно из двух уравнений, мы находим соответствующее значение
из 𝑦 будет 𝑦=−1213. Мы можем представить это
как комплексное число 𝑤=−1813−1213𝑖. Мы бы хотели
эта точка должна лежать в середине 𝑃 и начала координат.Напомним, что
мы можем найти среднюю точку двух комплексных чисел, просто взяв их среднее значение. Следовательно,
так как 𝑤 является серединой отрезка между началом координат и
точка 𝑃, которую мы будем обозначать комплексным числом
𝑧, можно написать 𝑤=12(𝑧+0). Следовательно, 𝑧=2𝑤=2−1813−1213𝑖=−3613−2413𝑖. Следовательно, 𝐶=𝑧|⊤∈ 𝑧|≤|||𝑧−−3613−2413𝑖|||. Следовательно, мы можем представить область как 𝐴∩𝐵∩𝐶, где
𝐴={𝑧∈ℂ∶(𝑧)2},𝐵={𝑧∈ℂ∶|𝑧|≤|𝑧−(3−3𝑖)|},𝐶=𝑧∈ℂ∶|𝑧|≤|||𝑧 −−3613−2413𝑖|||.
Обозначение Set-Builder
 . Мы использовали набор обозначений для перечисления таких элементов, как целые числа
. Мы использовали набор обозначений для перечисления таких элементов, как целые числа По этой причине вы можете опустить «∈ R » и написать {x|x≥2}, что читается как «набор всех действительных чисел x таких, что x больше или равно 2. ”
По этой причине вы можете опустить «∈ R » и написать {x|x≥2}, что читается как «набор всех действительных чисел x таких, что x больше или равно 2. ” Ключевые выводы

Тематические упражнения
 0
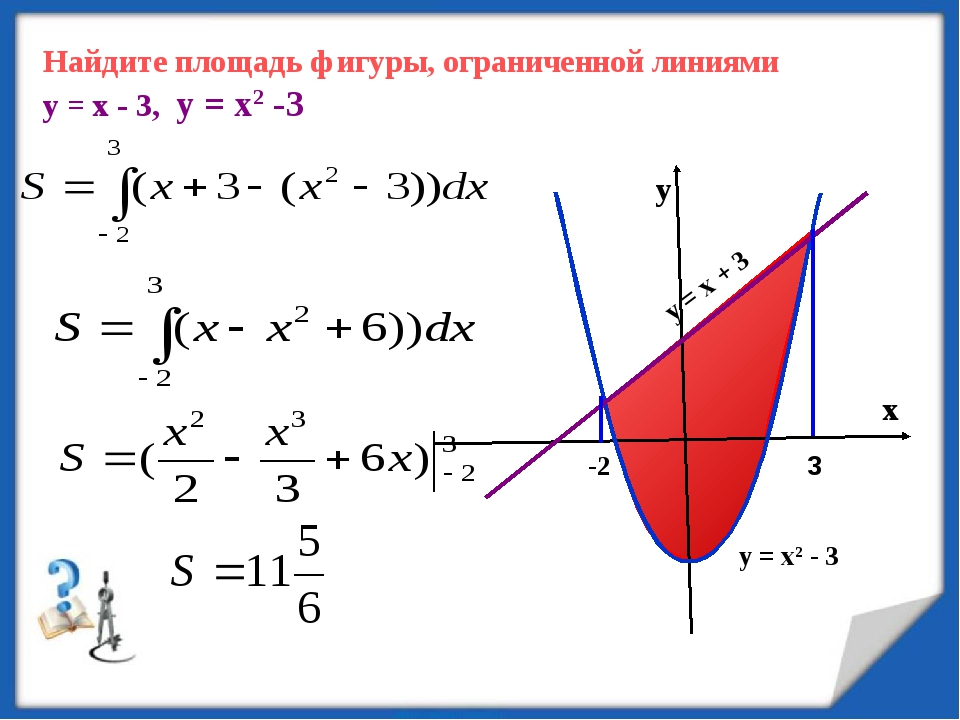
0 x≤0 и x≥0
x≤0 и x≥0
ответы
Две переменные — алгебра и тригонометрия
Цели обучения
Решение системы нелинейных уравнений с помощью подстановки
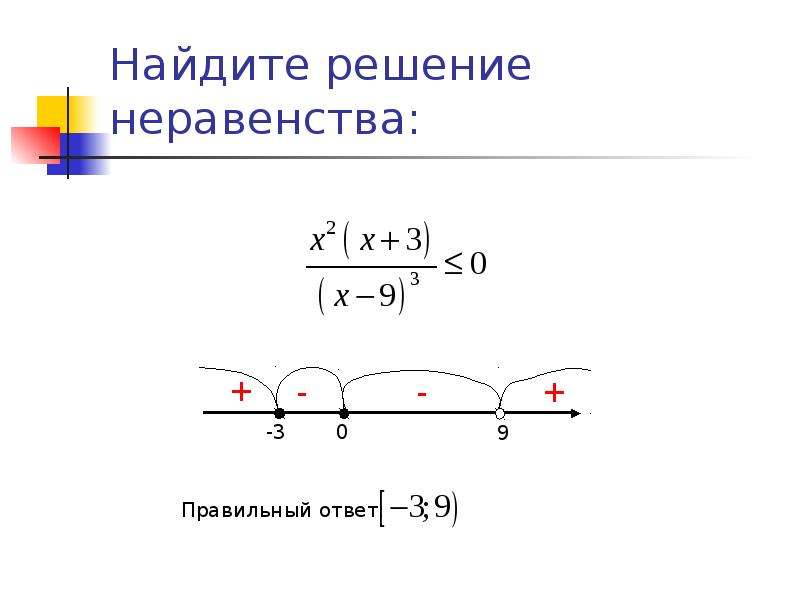
 Напомним, что линейное уравнение может иметь вид любого уравнения, которое нельзя записать в таком виде в нелинейном. Метод подстановки, который мы использовали для линейных систем, — это тот же метод, который мы будем использовать для нелинейных систем. Мы решаем одно уравнение для одной переменной, а затем подставляем результат во второе уравнение для решения другой переменной и так далее. Однако есть вариация возможных результатов.
Напомним, что линейное уравнение может иметь вид любого уравнения, которое нельзя записать в таком виде в нелинейном. Метод подстановки, который мы использовали для линейных систем, — это тот же метод, который мы будем использовать для нелинейных систем. Мы решаем одно уравнение для одной переменной, а затем подставляем результат во второе уравнение для решения другой переменной и так далее. Однако есть вариация возможных результатов. Пересечение параболы и прямой
Возможные типы решений для точек пересечения параболы и прямой
Рисунок 2. 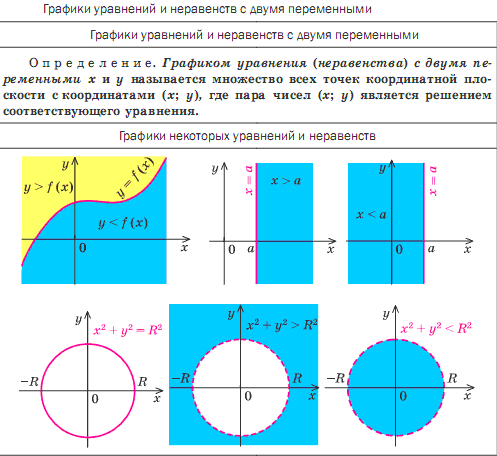
Решение системы нелинейных уравнений, представляющих параболу и прямую
Попробуйте
[скрытый ответ = ”fs-id1165135528358″] Пересечение окружности и линии
Возможные типы решений для точек пересечения окружности и прямой

Рисунок 4. Как
Нахождение пересечения окружности и прямой путем замены
Попробуйте
[скрытый ответ = ”fs-id1165135407492″] Решение системы нелинейных уравнений методом исключения
 Однако, когда оба уравнения в системе имеют одинаковые переменные второй степени, решить их методом исключения путем сложения часто проще, чем подстановкой. Как правило, исключение является гораздо более простым методом, когда система включает только два уравнения с двумя переменными (система два на два), а не система три на три, поскольку шагов меньше. В качестве примера исследуем возможные типы решений при решении системы уравнений, представляющих окружность и эллипс.
Однако, когда оба уравнения в системе имеют одинаковые переменные второй степени, решить их методом исключения путем сложения часто проще, чем подстановкой. Как правило, исключение является гораздо более простым методом, когда система включает только два уравнения с двумя переменными (система два на два), а не система три на три, поскольку шагов меньше. В качестве примера исследуем возможные типы решений при решении системы уравнений, представляющих окружность и эллипс. Возможные типы решений для точек пересечения окружности и эллипса
Рисунок 6.  Окружность и эллипс пересекаются в трех точках.
Окружность и эллипс пересекаются в трех точках. Решение системы нелинейных уравнений, представляющих окружность и эллипс
Попробуйте
[скрытый ответ = ”fs-id1165135245586″] График нелинейного неравенства
 Нелинейное неравенство — это неравенство, содержащее нелинейное выражение. График нелинейного неравенства очень похож на график линейного неравенства.
Нелинейное неравенство — это неравенство, содержащее нелинейное выражение. График нелинейного неравенства очень похож на график линейного неравенства. Как
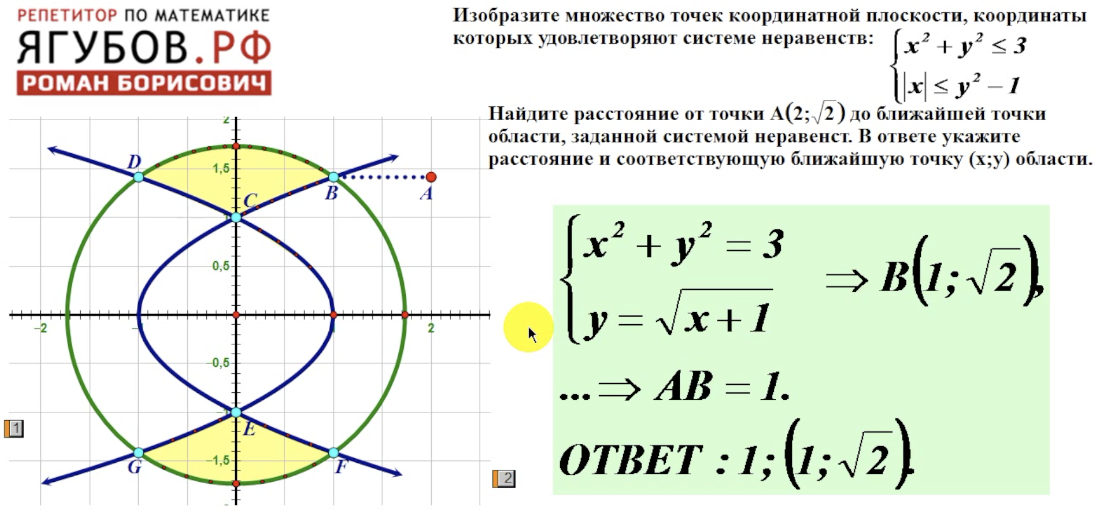 Если утверждение истинно, набор решений представляет собой область, включающую точку. Если утверждение неверно, набор решений представляет собой область по другую сторону линии границы.
Если утверждение истинно, набор решений представляет собой область, включающую точку. Если утверждение неверно, набор решений представляет собой область по другую сторону линии границы. Построение графика системы нелинейных неравенств

Как
График системы неравенств
Попробуйте
[скрытый ответ = ”fs-id1165132005102″] Ключевые понятия
 См. (Рисунок).
См. (Рисунок). См. (Рисунок).
См. (Рисунок). Секционные упражнения
Устный
[скрытый ответ = ”fs-id1165135359758″] Если нет, приведите пример графа неравенств, не имеющего допустимой области. Почему у него нет допустимой области?
Если нет, приведите пример графа неравенств, не имеющего допустимой области. Почему у него нет допустимой области?
[скрытый ответ = ”fs-id1165134188958″]
[скрытый ответ = ”fs-id1165137464254″]
Алгебраический
[скрытый ответ = ”fs-id1165137874937″]
[скрытый ответ = ”fs-id1165137665682″]
[скрытый ответ = ”fs-id11651353″]
[скрытый ответ = ”fs-id1165135582018″]
[скрытый ответ = ”fs-id1165133058925″]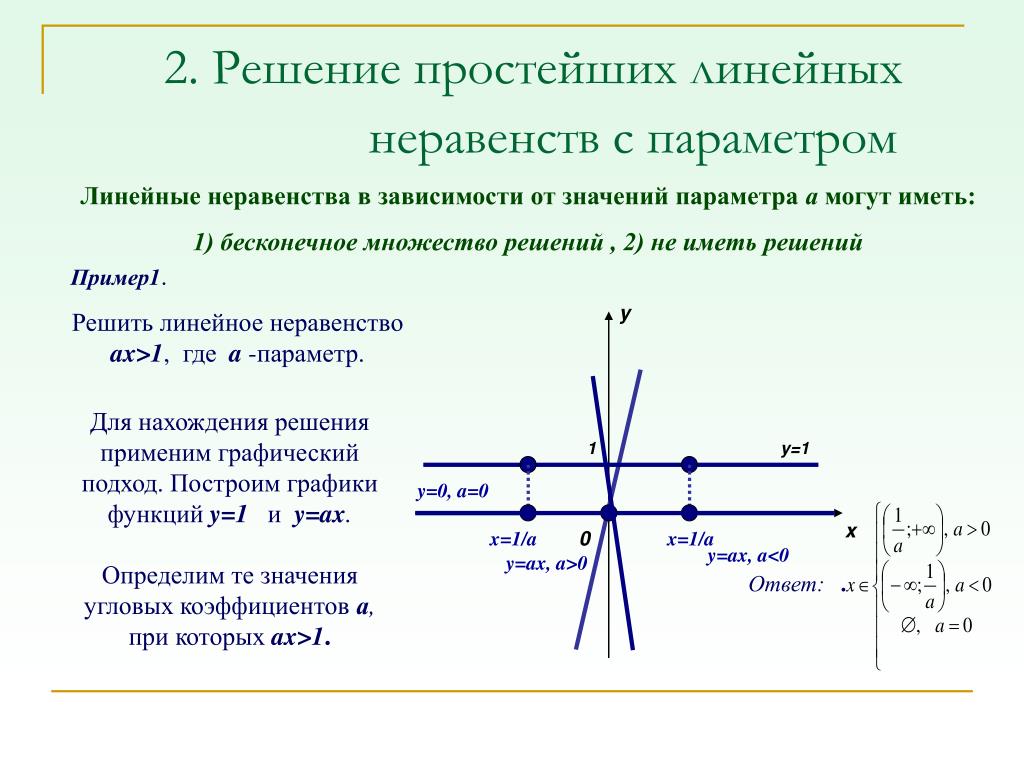
[скрытый ответ = ”fs-id1165133088775″]
[скрытый ответ = ”fs-id1165135621941″]
[скрытый ответ = ”fs-id1165133074890″]
[скрытый ответ = ”fs-id1165135616258″]
[скрытый ответ = ”fs-id1165135500985″]
[скрытый ответ = ”fs-id1165134294783″]
[скрытый ответ = ”fs-id1165133155738″]
[скрытый ответ = ”fs-id1165135258840″]
[скрытый ответ = ”fs-id1165134276573″]
[скрытый ответ = ”fs-id1165133210028″]
[скрытый ответ = ”fs-id1165135367599″] Расширения
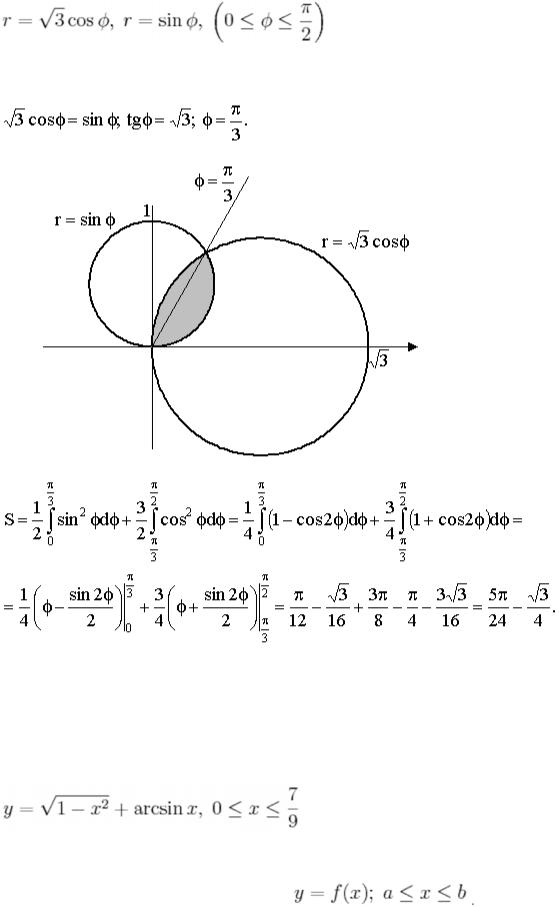
[скрытый ответ a=”fs-id1165135366840″][/скрытый ответ]
[скрытый ответ = ”fs-id1165134298420″]
[скрытый ответ = ”fs-id1165132213499″] Технология
[скрытый ответ = ”fs-id1165134557271″] Реальные приложения
[скрытый ответ = ”fs-id1165133007632″]
[скрытый ответ = ”fs-id1165135695980″]
Глоссарий
Объяснение урока: Области на комплексной плоскости
Пример 4: Описание составных областей на комплексной плоскости

Ответ
 Еще раз, нам нужно описать эту линию как перпендикуляр
биссектриса отрезка между началом координат и другой точкой, которую мы обозначили
𝑃. В этом случае сделать это путем осмотра сложнее. Поэтому мы продемонстрируем технику, которая легче обобщается.
Еще раз, нам нужно описать эту линию как перпендикуляр
биссектриса отрезка между началом координат и другой точкой, которую мы обозначили
𝑃. В этом случае сделать это путем осмотра сложнее. Поэтому мы продемонстрируем технику, которая легче обобщается. Для этого мы сначала
найти точку пересечения этих двух прямых. Приравняв два уравнения
строк, мы можем найти 𝑥 следующим образом: 23𝑥=−32𝑥−3.
Для этого мы сначала
найти точку пересечения этих двух прямых. Приравняв два уравнения
строк, мы можем найти 𝑥 следующим образом: 23𝑥=−32𝑥−3.



 момент
момент Если каждый из конвейеров работает на полную мощность, то ежедневно
производится не более 300 кастрюль. Так как потребность в кастрюлях из
нержавеющей стали больше, их ежедневно производят больше чем медных, но не
меньше 150 штук..
Если каждый из конвейеров работает на полную мощность, то ежедневно
производится не более 300 кастрюль. Так как потребность в кастрюлях из
нержавеющей стали больше, их ежедневно производят больше чем медных, но не
меньше 150 штук..





 Ответьте на самые важные вопросы о Вашем уроке из
левой колонки.
Ответьте на самые важные вопросы о Вашем уроке из
левой колонки.  Это позволит облегчить переход от
стандартных решений конкретных математических
задач к нестандартным;
Это позволит облегчить переход от
стандартных решений конкретных математических
задач к нестандартным; Е.Зайцева, Ю.В.Зайцева и др.; ВолГУ.-4-е изд.,
Волгоград: Волгоградское научное издательство,
2009. – 238с.
Е.Зайцева, Ю.В.Зайцева и др.; ВолГУ.-4-е изд.,
Волгоград: Волгоградское научное издательство,
2009. – 238с. , стер. -М.:
Мнемозина, 2009.-224 с.
, стер. -М.:
Мнемозина, 2009.-224 с. Если вы правильно разработаете это, чтобы изолировать « y », это неравенство будет эквивалентно выражению .
Если вы правильно разработаете это, чтобы изолировать « y », это неравенство будет эквивалентно выражению .
