Урок-мастерская по теме «Построение графика кусочной функции в табличном процессоре Excel по заданным параметрам»

Цели:

• Ознакомление учащихся с методом поиска подхода к решению задач и умелое применение данного метода в решении любых задач;
• Умение ставить вопросы, работать по алгоритму;
• Развитие математической речи учащихся в ходе комментирования, объяснения, аргументации смысла вопросов;
• Развитие навыков сотрудничества и взаимопомощи при работе в группе;
• Сформировать у учащихся понятие “точечная диаграмма”;
• Научить заполнять таблицу с учетом заданного интервала и шага.

План проведения мастерской:

1. Организационный момент.
2. Актуализация знаний.
3. Подготовительная работа.
4. Поиск подхода к решению задачи.
5. Работа в группах.
6. Обсуждение в мастерской.
7. Оценочно-рефлексивная деятельность.
8. Итог урока.

Оборудование урока: доска, экран, проектор, компьютер учителя, компьютеры для учащихся (кол-во 12), раздаточный материал. (Памятка 1 , памятка 2, конверт с заданием)

1. Организационный момент.

Учащиеся проходят в класс. Занимают свои места. Учителя приветствуют их.

2. Актуализация знаний.

На доске записано слово “Функция”. Учитель математики просит учащихся назвать ассоциации, связанные с этим словом.

3. Подготовительная работа.

Задание 1.

Учащимся предлагается 4 вида графиков и варианты функций. Соотнести графики функций с их алгебраической записью.

Графики и алгебраические записи размещены на маркерной доске.

Задание 2.

Учащимся предлагается 4 вида преобразования графиков. Необходимо объяснить, какой вид преобразования используется (данное задание учитель математики иллюстрирует, используя электронное сопровождение курса “Алгебра – 8” под редакцией А.Г.Мордковича).

4. Поиск подхода к решению задачи.

Каждый ученик получает карточку определённого цвета, на которой представлена часть того или иного графика. Учащиеся делятся на группы по цветам.

– Соедините части и скажите, что у Вас получилось? (График кусочной функции)

– Как построить график кусочной функции? Попробуйте вспомнить алгоритм.

Группа 1.

 

Группа 2.

Группа 3.

Группа 4.

5. Работа в группах.

Каждая группа получает конверты с заданиями. Учащиеся внутри группы сами определяют, кто и какую часть будет строить. Построив каждый кусочек функции на листе, учащийся выполняет построение на компьютере под руководством учителя информатики.

Необходимо построить таблицу значений “х” и “у”, заполнить для заданного интервала, самостоятельно выбрав шаг.

(Памятка 1.)

Для заполнения значений “у” необходимо правильно внести формулы в ячейку таблицы. (Памятка 2.)

Каждый ученик строит согласно своему заданию функцию и сохраняет работу на отдельном листе книги Excel, переименовав его согласно номеру задания.

Далее все части собираются на одном листе, а затем на компьютере. Если группы справились с заданием, то и на листе, и на компьютере графики одинаковы.

Раздаточный материал:

Конверт 1.

Конверт 2.

Конверт 3.

Конверт 4.

Приложение 1.

Приложение 2.

6. Обсуждение в мастерской.

Работы вывешиваются на доску. Учащиеся сравнивают полученный график с макетом, собранным ими в начале урока. Оценивают работы друг друга. Высказывают свои мнения.

Группа 1 получила после выполнения задания график вида:

Группа 2 получила после выполнения задания график вида:

Группа 3 получила после выполнения задания график вида:

Группа 4 получила после выполнения задания график вида:

7. Оценочно-рефлексивная деятельность.

Каждому ученику предлагается оценить свои чувства после выполнения работы. Для этого, на доске расположены 3 рисунка. Каждый ученик подходит к доске и прикрепляет к выбранному им рисунку клейкую бумагу. В конце подсчитывается количество прикреплённых бумажек к тому или иному рисунку. Обсуждается, почему выбрано то или иное настроение.

 

8. Итог урока.

В конце урока каждому ученику вручается сертификат и выполненная им работа.

Список используемой литературы:

1. Мордкович А.Г., Семенов П.В. методическое пособие для учителей “Алгебра и начало математического анализа 8 класс” М: “Мнемозина”, 2010 – 203 с.
2. Мордкович А.Г., Семенов П.В. “Алгебра. Задачник. Часть 2 8 класс” М: “Мнемозина”, 2011 – 272 с.
3. Семенов А.Л., Ященко И.В. “ГИА – 2013 ФИПИ “Математика: типовые экзаменационные варианты: 30 вариантов”” – М: “Национальное образование” , 2013 192 с. М: “Мнемозина”, 2010 – 203 с.
4. Мордкович А.Г., Семенов П.В. “Алгебра 8 класс. Электронное сопровождение курса” – М: “Мнемозина”, 2008.
5. Анеликова Л.А., Гусев О.Б. “ Информатика и информационно-коммуникационные технологии. Базовый уровень. 9 класс” – М: “Солон-пресс”, 2009–400с.
6. Крылов С.С., Чуркина Т.Е. “ГИА – 2013 ФИПИ “Информатика и ИКТ типовые экзаменационные варианты: 10 вариантов”” М: “Национальное образование” , 2013 – 144 с.
7. Угринович Н.Д. “информатика и ИКТ.9 класс” – М: БИНОМ лаборатория знаний, 2011 – 295c.
8. Горностаева А.М. “Информатика 8 класс. Поурочные планы по учебнику Угриновича Н.Д.” Волгоград: Учитель,2008 – 185 с.
9. Лапчик М.П. и др. “Методика преподавания информатики: Учебное пособие для студентов пед ВУЗов” – издательский центр “Академия”, 2001 – 624 с.

Электронные Образовательные Ресурсы

1. Федеральный институт педагогических измерений: http\\ www.fipi.ru
2. Методическая копилка учителя информатики: http \\ www.metod-kopilka.ru
3. Электронные учебники: http\\ www.agtu.ru
4. Единая коллекция цифровых образовательных ресурсов: http \\ school-collection.edu.ru
5. Информационный образовательный портал для учителей информатики и ИКТ: http \\ www.klyaksa.net
6. Сайт для учителей видео уроки: http\\ www.videouroki.net

urok.1sept.ru

Построение графика кусочно-заданной функции

Построение кусочно-линейной функции

Цикина Е.В., учитель математики МБОУ СОШ №4 г Шатура. МО

Построить график функции:

Будем строить график функции:

• При -3  х график функции совпадает с графиком функции у=х+2
• Построим график функции у=х+2
• «Вырежем кусочек» этого графика при -3  х
• При 1  х  4 график функции совпадает с графиком функции у=3
• Построим график функции у=3 (прямая параллельная оси Ох и проходящая через точку (0;3))
• « Вырежем кусочек» этого графика при 1  х  4
• Таким образом построили график данной функции

у

х

0

у

1

2

3

3

2

-3

0

х

-2

1

4

Постройте самостоятельно график функции:

videouroki.net

Графики кусочно-линейных функций — Математика

Графики кусочно – заданных функций

Мурзалиева Т.А. учитель математики МБОУ «Борская средняя общеобразовательная школа» Бокситогорский район Ленинградская область

Цель:

• освоить метод линейного сплайна для построения графиков, содержащих модуль;
• научиться применять его в простых ситуациях.

Под сплайном (от англ. spline — планка, рейка) обычно понимают кусочно-заданную функцию.

Такие функции были известны математикам давно, начиная еще с Эйлера (1707-1783г.,швейцарский, немецкий и российский математик), но их интенсивное изучение началось, фактически, только в середине XX века.

В 1946 году Исаак Шёнберг (1903- 1990г., румынский и американский математик) впервые употребил этот термин. С 1960 года с развитием вычислительной техники началось использование сплайнов в компьютерной графике и моделировании.

1 . Введение

2. Определение линейного сплайна

3. Определение модуля

4. Построение графиков

5. Практическая работа

Графики функций широко используются в различных областях инженерных знаний, поэтому умение строить, “читать”, прогнозировать их “поведение” имеют огромную роль в практической деятельности инженерных работников, метеорологов и людей других “математических” специальностей

Одно из основных назначений функций – описание реальных процессов, происходящих в природе.

Но издавна ученые – философы и естествоиспытатели выделяли два типа протекания процессов: постепенное ( непрерывное ) и скачкообразное.

При падении тела на землю сначала происходит непрерывное нарастание скорости движения , а в момент столкновения с поверхностью земли скорость изменяется скачкообразно , становясь равной нулю или меняя направление (знак) при «отскоке» тела от земли (например, если тело – мяч).

Но раз есть разрывные процессы, то необходимы средства их описаний. С этой целью вводятся в действие функции, имеющие разрывы .

a — формулой y = h(x), причем будем считать , что каждая из функций g(x) и h(x) определена для всех значений х и разрывов не имеет. Тогда , если g(a) = h(a), то функция f(x) имеет при х=а скачок; если же g(a) = h(a) = f(a), то «комбинированная» функция f разрывов не имеет. Если обе функции g и h элементарные, то f называется кусочно–элементарной. «

• Один из способов введения таких разрывов следующий:

Пусть функция y = f(x)

при x определена формулой y = g(x),

а при xa — формулой y = h(x), причем будем считать , что каждая из функций g(x) и h(x) определена для всех значений х и разрывов не имеет.

Тогда , если g(a) = h(a), то функция f(x) имеет при х=а скачок;

если же g(a) = h(a) = f(a), то «комбинированная» функция f разрывов не имеет. Если обе функции g и h элементарные, то f называется кусочно–элементарной.

Графики разрывных функций

Графики непрерывных функций

y=cos x

Построить график функции:

У=2-х

У= х

1

У = |X-1| + 1

0

1

Х=1 –точка смены формул

Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера».

Модулем числа а называется расстояние ( в единичных отрезках ) от начала координат до точки А ( а) .

Это определение раскрывает геометрический смысл модуля.

Модулем ( абсолютной величиной ) действительного числа а называется то самое число а ≥ 0, и противоположное число –а , если а

А

а

х

0

0 или х=0 у = -3х -2 при х «

у

У=-3х-2

У=3х-2

х

-1

у

-2

1

4

х

0

у

1

-2

1

1

1

х

0

-2

Построить график функции у = 3|х|-2.

По определению модуля, имеем: 3х – 2 при х0 или х=0

у =

-3х -2 при х

x n ) «

. Пусть заданы х 1 х 2 х n – точки смены формул в кусочно-элементарных функциях.

Функция f, определенная при всех х, называется кусочно-линейной, если она линейна на каждом интервале

и к тому же выполнены условия согласования, то есть в точках смены формул функция не терпит разрыв.

Непрерывная кусочно-линейная функция называется линейным сплайном . Её график есть ломаная с двумя бесконечными крайними звеньями – левым (отвечающим значениям x n ) и правым ( отвечающим значениям x x n )

Кусочно-элементарная функция может быть определена более чем двумя формулами

у

У =

1

0

х

1

-1

График – ломаная с двумя бесконечными крайними звеньями – левым (х1).

У=|x| — |x – 1|

Точки смены формул: х=0 и х=1.

У(0)=-1, у(1)=1.

График кусочно-линейной функции удобно строить, указывая на координатной плоскости вершины ломаной.

Кроме построения n вершин следует построить также две точки : одну левее вершины A 1 ( x 1;  y  ( x 1)), другую – правее вершины An  ( xn ;  y  ( xn )).

Заметим, что разрывную кусочно-линейную функцию нельзя представить в виде линейной комбинации модулей двучленов .

Построить график функции у = х+ |x -2| — |X|.

Непрерывная кусочно-линейная функция называется линейным сплайном

1.Точки смены формул: Х-2=0, Х=2 ; Х=0

у

2

2.Составим таблицу:

0

3

2

-1

х

1

0

2

1

у

0

х

2

У( 0 )= 0+|0-2|-|0|=0+2-0= 2 ;

у( 2 )=2+|2-2|-|2|=2+0-2= 0 ;

у (-1 )= -1+|-1-2| — |-1|= -1+3-1= 1 ;

у( 3 )=3+|3-2| — |3|=3+1-3= 1 .

Построить график функции у = |х+1| +|х| – |х -2|.

у

1 .Точки смены формул:

х+1=0, х=-1 ;

х=0 ; х-2=0, х=2.

2 . Составим таблицу:

1

3

x

0

2

-2

-1

-1

0

2

1

x

у

-1

-2

-1

5

6

y(-2)=|-2+1|+|-2|-|-2-2|=1+2-4=-1;

y(-1)=|-1+1|+|-1|-|-1-2|=0+1-3=-2;

y(0)=1+0-2=-1;

y(2)=|2+1|+|2|-|2-2|=3+2-0=5;

y(3)=|3+1|+|3|-|3-2|=4+3-1=6.

|x – 1| = |x + 3|

Решите уравнение:

Решение. Рассмотрим функцию y = |x -1| — |x +3|

Построим график функции /методом линейного сплайна/

• Точки смены формул:

х -1 = 0, х = 1; х + 3 =0, х = — 3.

y

2. Составим таблицу:

— 4

х

-3

2

1

1

— 4

4

4

у

— 4

0

x

1

y(- 4) =|- 4–1| — |- 4+3| =|- 5| — | -1| = 5-1=4;

y( -3 )=|- 3-1| — |-3+3|=|-4| = 4;

y( 1 )=|1-1| — |1+3| = — 4 ;

y(-1) = 0.

y(2)=|2-1| — |2+3|=1 – 5 = — 4.

Ответ: -1.

1. Построить графики кусочно-линейных функций методом линейного сплайна:

у = |x – 3| + |x|;

1). Точки смены формул:

у

2). Составим таблицу:

х

у

1

х

у( ) =

у( ) =

у( ) =

У( )=

2. Построить графики функций, используя УМК «Живая математика »

А) у = |2x – 4| + |x +1|

1) Точки смены формул:

2) y( ) =

y( ) =

y( ) =

у( ) =

Б) Постройте графики функций, установите закономерность :

a) у = |х – 4| б) y = |x| +1

y = |x + 3| y = |x| — 3

y = |x – 3| y = |x| — 5

y = |x + 4| y = |x| + 4

х

у

Используйте инструменты «Точка», «Отрезок», «Стрелка» на панели инструментов.

1. Меню «Графики».

2. Вкладка «Построить график».

.3. В окне «Калькулятор» задать формулу.

Постройте график функции:

1) У = 2х + 4

х

у

3) У =

х

у

2

4

1. Козина М.Е. Математика. 8-9 классы: сборник элективных курсов. – Волгоград: Учитель, 2006.

2. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 7 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение, 2011

3. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 8 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение , 2011

4. ВикипедиЯ свободная энциклопедия

http://ru.wikipedia.org/wiki/Spline

multiurok.ru

Лекция по теме «Как строить график кусочной функции»

Как построить график кусочной функции

Кусочные функции — это функции, заданные разными формулами на разных числовых промежутках. Например,

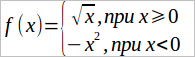
Такая запись обозначает, что значение функции вычисляется по формуле √x, когда x больше или равен нулю. Когда же x меньше нуля, то значение функции определяется по формуле –x². Например, если x = 4, то f(x) = 2, т. к. в данном случае используется формула извлечения корня. Если же x = –4, то f(x) = –16, т. к. в этом случае используется формула –x²(сначала возводим в квадрат, потом учитываем минус).

Чтобы построить график такой кусочной функции, сначала строятся графики двух разных функций не зависимо от значения x (т. е. на всей числовой прямой аргумента). После этого от полученных графиков берутся только те части, которые принадлежат соответствующим диапазонам x. Эти части графиков объединяются в один. Понятно, что в простых случаях чертить можно сразу части графиков, опустив предварительную прорисовку их «полных» вариантов.

Для приведенного выше примера для формулы y = √x получим такой график:

Здесь x в принципе не может принимать отрицательных значений (т. е. подкоренное выражение в данном случае не может быть отрицательным). Поэтому в график кусочной функции уйдет весь график уравнения y = √x.

Построим график функции f(x) = –x². Получим перевернутую параболу:

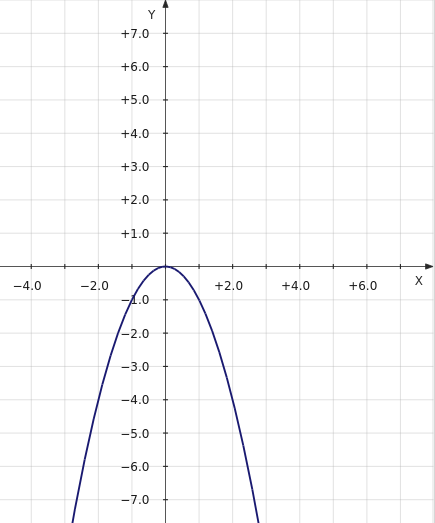
В данном случае в кусочную функции мы возьмем только ту часть параболы, для которой x принадлежит промежутку (–∞; 0). В результате получится такой график кусочной функции:

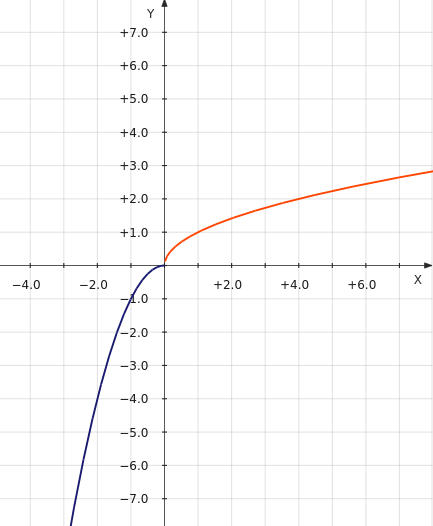
Рассмотрим другой пример:

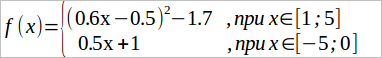
Графиком функции f(x) = (0.6x – 0.5)² – 1.7 будет видоизмененная парабола. Графиком f(x) = 0.5x + 1 является прямая:

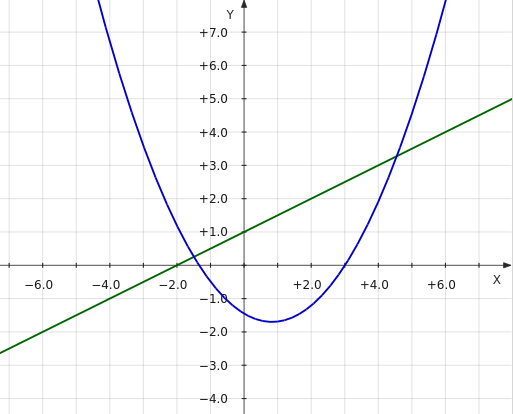
В кусочной функции x может принимать значения в ограниченных промежутках: от 1 до 5 и от –5 до 0. Ее график будет состоять из двух отдельных частей. Одну часть берем на промежутке [1; 5] от параболы, другую — на промежутке [–5; 0] от прямой:

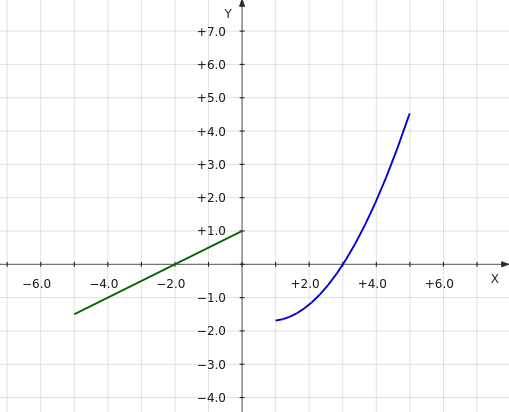
infourok.ru

Методическая разработка урока «Построение графиков кусочных функций»

Методическая разработка урока по математике и информатике , 9 класс.

Учителя Солуян Н.Н. и Пастух О.М.

Интегрированный урок по теме «Повторение. Построение графиков кусочных функций».

Цель урока: повторить, закрепить и обобщить умения обучающихся строить и читать графики кусочных функций, решать задания из ГИА.

Тип урока: урок обобщения и систематизации знаний.

Задачи:

Образовательные — обеспечить повторение, обобщение и систематизацию материала темы. Создать условия контроля (самоконтроля) усвоения знаний и умений.

Развивающие — способствовать формированию умения применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.

Воспитательные — содействовать воспитанию интереса к математике и информатике, активности, умения общаться, общей культуры.

Методы обучения: использование ИКТ, частично — поисковый. Работа по обобщающей схеме, создание презентаций, работа по решению экзаменационных заданий, системные обобщения, самопроверка, взаимопроверка.

Формы организации урока: фронтальная, индивидуальная, групповая.

Оборудование и материалы: интерактивная доска, мультимедийный проектор, компьютер, магнитная доска, указка.

ХОД УРОКА.

1. Организационный момент.

Построение графиков кусочных функций мы изучали еще в 7 классе, а в экзаменационных материалах содержатся задачи по данной теме. Поэтому сегодня на уроке мы будем повторять, обобщать, приводить в систему изученный материал, решать задания из ГИА.

Итак, проверим домашнее задание.

2. Проверка домашнего задания.

а)У доски: задание из ГИА: Для каждого графика укажи соответствующую ему формулу.

А					Б			1
								2
В					Г			3
								4
	А	Б	В	Г

б) заполни таблицу

№	Формула	Название графика	Схематические рисунки
1
2
3
4
5
6
7

Учитель: Вспомним, какие основные алгебраические функции мы изучали и что представляют графики этих функций?

/ Идет опрос класса по обобщающей схеме на интерактивной доске (слайд 2)/

Учитель: А теперь посмотрим, как справились с домашнем заданием.

/ Проверка таблицы и устного задания/

3.Построение графиков.

Учитель: В чем особенность графиков кусочных функций? Повторим как строить графики кусочных функций.

/ Идет работа по слайдам./

Задание 1: построить график функции (слайд 3,4)

Задание 2: построить график функции. Задать пошаговые команды компьютеру. (слайд 5,6)

Обычно на экзамене дают и какое- либо дополнительное задание. Например, определите при каких значениях К прямая у = К имеет с графиком функции только одну общую точку. (слайд 7)

Учитель: А теперь решим задание из ГИА.И.В. Ященко, вариант 9, №22.

Мы видим, что выполнение таких заданий достаточно трудоемко и требует много времени. Поэтому, следующее задание из сборника Е.А. Бунимович, вариант 6, № 21подготовили заранее в виде презентации под руководством учителя информатики Костюрина В. и Гончарова А. (слайд 8-19)

Учитель информатики: Почему при решении задачи по математике вы в своей работе ставите цель моделирования?

А на следующей презентации выполненной Бондаренко Д. и Трофименко А.рассмотрим построение еще одной кусочной функции. (слайд 20 — 24)

1. Построить график функции

2.Укажите промежуток, на котором функция возрастает.

Учитель информатики: Какую модель получили в результате решения задачи?

4 Блок информатики.

Учитель информатики: На уроках информатики мы с вами прошли тему «Моделирование», строили различные модели. Сейчас вы увидели еще примеры моделей в математике. Давайте вспомним некоторые определения из данной темы. Я предлагаю вам решить устно следующий тест … (слайд 25-30). Молодцы ребята. Теперь вы знаете что, решение любой задачи в математике сводится к построению модели на формальном языке.

5. Обучающая работа в группах.

Учитель Сегодня на уроке мы повторили как по формуле построить график, а бывает обратная задача: по графику определить формулу задающею функцию.

Задание: График функции состоит из двух лучей, исходящих из точек А и В и части параболы. Задайте эту функцию формулой.

Программу данного задания из ГИА приготовил заранее Фадеев А. (слайд 31 — 37)

Рассмотрим луч, исходящий из т. А.

— Каким уравнением можно задать этот луч?

у=кх + в

Значит, нам надо определить к и в. Для этого по графику выберем по две точки с координатами выраженными целыми числами.

Решить систему методом сложения.

Значит, уравнение первой части графика у = 5х + 7, при х -1.

Для определения остальных частей графика разобьемся на группы:

1 вариант определяют часть АВ,

2 вариант- луч исходящий из т.В.

Проверим правильность выбранных ответов.

6. Итог урока.

Итак, сегодня мы с вами повторили, как строить графики кусочных функций.

Какой алгоритм мы будем при этом применять?

7. Домашнее задание.

Ященко, вариант 10. №22, Бунимович, вариант3, № 22, вариант 2, №22.

А сейчас, я бы хотела, чтобы вы оценили при помощи смайликов свое отношение к уроку. (слайд 38)

multiurok.ru

Урок по алгебре в 7-м классе по теме «График кусочной функции, или График правильного питания»

Цели:

• повторение алгоритма построения графиков линейной функции, нахождение точек принадлежащих графику функции, введение алгоритма построения графика кусочной функции,
• развитие математических способностей, логического мышления,
• воспитание взаимоуважения друг к другу.

Тип: комбинированный.

Контроль: составление опорного конспекта, самостоятельная работа (интерактивные задания).

Форма: индивидуальная, групповая.

Оборудование: компьютеры, мультимедиа.

Метод: эвристический.

Ход урока

1 этап: Разминка

1) Устный счёт: №1. -18•(-3) – 134, -122•(-1/2)+ 53, 4•(-23)-134, -2•140+8, -48•1/8-345, 2•(-1/4)+536.

2) Теоретический:

– Какая функция называется линейной функцией? Запишите её.
– Как называется график линейной функции?
– Какая функция называется прямопропорциональной? Запишите её.
– Как называется k?

2 этап: Подготовительный

№2. Построить графики функций а) у=5х-3, б) у=-3х-4, в) у=-2х+1.

(У доски трое учащихся на построение графиков функций.)

№3. Найдите координаты точек (все выполняют в тетради).

3 этап: Построение

№4. Построить графики функций

1) у = 0,25х + 6,75 на отрезке [1;3],
2) у = 0,25х + 9,25 на отрезке [3;7],
3) у = 1/6х + 71/6 на отрезке [7;13],
4) у = 1/3х + 44/3 на отрезке [13;16]

Мы построили график кусочной функции

А также мы построили график правильного питания:

** завтрак – чай, хлеб с маслом и колбасой или сыром,
** школьный завтрак – горячее питание (суп, каша, ..),
** обед – из двух блюд,
** ужин – легкое питание.

№5. Постройте на графике правильного питания точки с координатами А (1;7), Р(7;11), С(7;13), В(16:20). Таким образом, вы должны понять, что в день вы должны получить все витамины.

Посмотрите таблицы содержания витаминов. [2], [3]

4 этап: самостоятельная работа (интерактивные задания)

Учащиеся по группам усаживаются за компьютер и выполняют задания. [1] Правильность выполнения проверяет учитель.

5 этап: домашнее задание

Составьте кусочную функцию и постройте её график.

6 этап: Заключительный

Подведение итогов.

– Что нового вы узнали из этого урока?
– Какие функции вы знаете?

Литература

:

1. Электронный учебник “Интерактивная математика 5–9 классы”.
2. Воробьёв Р.И. Питание и здоровье. М.: Медицина, 1998.
3. Мартынов С.М. Овощи плюс фрукты плюс ягоды получится здоровье: Беседы врача – педиатра о питании детей. Кн. для родителей. М: Просвещение 1999.

urok.1sept.ru

Построение графиков функций в Excel

Построение графиков функций — одна из возможностей  Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.

Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.

1) Рассмотрим пример построения графика линейной функции: y=5x-2

Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку

 

 

В нашем случае  y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.

В итоге мы получим табличку:

 

 

Теперь можно приступать к созданию графика.

Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)

 

 

Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ

 Выберем данные:  диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:

Нажимаем ОК. Перед нами график линейной функции.

2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x²-2

Параболу по двум точкам уже не построить, в отличии от прямой.

Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].

Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.

Заполняю столбец со значениями х, используя маркер автозаполнения  до значения х=5.

Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.

Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.

Получим:

Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.

Любые другие графики непрерывных функций строятся аналогично.

3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.

Рассмотрим это на примере функции у=1/х.

Функция определена на интервалах (- беск;0) и (0; +беск)

Создадим график функции на интервалах: [-4;0) и (0; 4].

Подготовим две таблички, где х изменяется с шагом 0,2:

Находим значения функции от каждого аргумента х аналогично примерам выше.

На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно

Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА  значениями из второй таблички

Получаем график функции y=1/x

В дополнение привожу видео — где показан порядок действий, описанный выше.

В следующей статье расскажу как создать 3-мерные графики в Excel.

Спасибо за внимание!

на Ваш сайт.

krivaksin.ru