Теорема, обратная теореме Пифагора. Видеоурок. Геометрия 8 Класс

На данном уроке мы поговорим об истории изучения свойств прямоугольных треугольников и о возникновении такого понятия, как пифагоровы тройки. Затем будет сформулирована и доказана теорема, обратная теореме Пифагора, и рассмотрены примеры на ее применение.

Сперва вспомним саму теорему Пифагора.

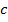Есть прямоугольный треугольник, угол  – прямой,  – гипотенуза,  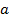и 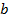 – катеты (см. Рис. 1).

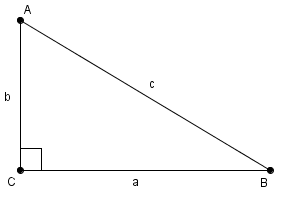
Рис. 1. Прямоугольный треугольник

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

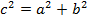
Угол 90 градусов – наибольший в данном треугольнике. Наибольшая сторона – .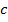

Квадрат длины наибольшей стороны равен сумме квадратов длин двух других сторон.

Перед нами иная ситуация. Мы не знаем, прямой угол  или нет. Но оказалось, что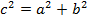

. Чему равен угол ? Что вообще мы можем сказать про такой треугольник?

Мы можем сказать, что сторона 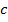 – наибольшая. , .

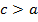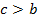Значит, угол  – наибольший. .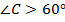

Если бы было иначе, то сумма всех углов была бы меньше 180 градусов. Но оказывается, угол

 в точности равен 90 градусам. В этом смысл теоремы, обратной теореме Пифагора.

Формулировка теоремы: если квадрат длины стороны треугольника равен сумме квадратов длин двух других сторон, то такой треугольник прямоугольный.

Докажем эту теорему.

Дано:.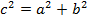

Доказать:.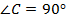

Доказательство

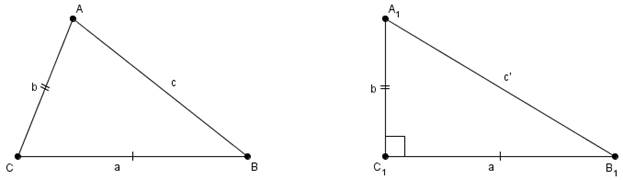
Рис. 2. Доказательство теоремы

Построим прямоугольный треугольник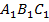

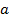 с катетами  и 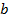. Угол  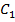– прямой (см. Рис. 2). ( ; ; ).

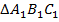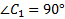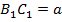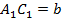
Такой треугольник существует. В этом прямоугольном треугольнике действует прямая теорема Пифагора, то есть: .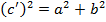

Но по условию: .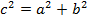

Отсюда следует, что 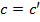. Значит, .

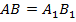Выясняется, что треугольники равны друг другу по трем сторонам: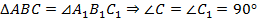

.

Теорема доказана.

Примечание: мы сконструировали треугольник 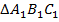, в котором искомое свойство присутствует, и доказали, что треугольники равны, а значит, углы .

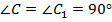Дано: стороны треугольника 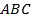 (см. Рис. 3).

Доказать: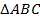 – прямоугольный.

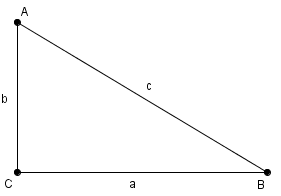
Рис. 3. Треугольник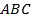

a) ; ;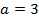

;

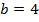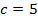
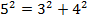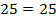
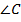 – прямой по обратной теореме Пифагора.

Это всем нам известный «египетский треугольник».

b) ; ;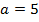

; ;

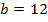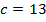
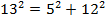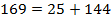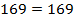
Данный треугольник также является прямоугольным.

Мы привели примеры так называемых «пифагоровых треугольников». Это такие прямоугольные треугольники, у которых длины сторон являются натуральными числами.

Проверьте, что следующие треугольники к ним относятся: 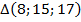;  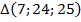– это частные примеры «пифагоровых треугольников».

А можно ли их описать в общем виде? Можно. Упомянем следующий факт:

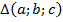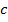,  – гипотенуза.

Пусть ,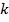

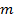
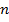,  – натуральные числа, где .

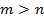По ним вычислили:

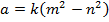
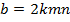
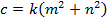
Как оказывается, треугольник с такими сторонами прямоугольный и он является «пифагоровым».

Приведем примеры.

1. 

; ;

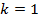
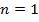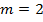
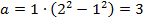
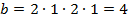
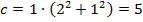
Получили известный нам «египетский треугольник»

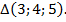
2. ; ;

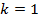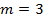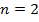
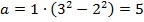
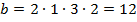
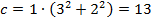
Получили тоже известный нам прямоугольный треугольник .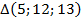

Прямую и обратную теорему Пифагора можно объединить в одну теорему. Она звучит так: треугольник является прямоугольным тогда и только тогда, когда квадрат длины одной стороны равен сумме квадратов длин двух других сторон (см. Рис. 4).

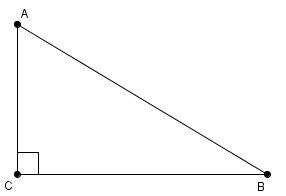
Рис. 4. Прямоугольный треугольник

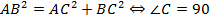
Далее перейдем к задачам.

Дано: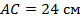; ; 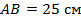 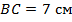(см. Рис. 5).

Доказать: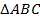 – прямоугольный.

Найти: его прямой угол.

Решение

Рис. 5. Иллюстрация к задаче 2

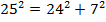
Урок 13. теорема пифагора. — Геометрия — 8 класс

Рассмотрим прямоугольный треугольник.
Соотношение между катетами и гипотенузой было известно еще в Древнем Египте и Вавилоне. Сегодня нам это соотношение известно как теорема Пифагора.
В современной формулировке теорема Пифагора звучит так: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Для доказательства теоремы Пифагора рассмотрим прямоугольный треугольник ABC с прямым углом C, катетами а, b и гипотенузой с

Достроим треугольник до квадрата со стороной a + b
S_{(большого квадрата)} = (a + b)²
S_{(большого квадрата)} = 4 ∙ S_ABC + c²
S_{(большого квадрата)} = 4 ∙ 1/2 ab + c²
(a + b)² = 4 ∙ 1/2 ab + c²
a² + 2ab + b² = 2ab + c², c² = a² + b²
Для теоремы Пифагора обратное утверждение также верно: если квадрат одной из сторон треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Для доказательства рассмотрим треугольник А₁В₁С₁, такой, что угол С₁ прямой, стороны A₁C₁ = АС, B₁C₁ = ВС.
По теореме Пифагора A₁B₁² = A₁C₁² + B₁C₁²
Из равенства сторон следует A₁B₁² = A₁C₁² + B₁C₁² = AC₂ + BC₂ = AB₂, поэтому
A₁B₁² = AB²
A₁B₁ = AB
Таким образом треугольники ABC и А₁B₁C₁ равны по трем сторонам, т.к. угол С₁ – прямой, то угол С также прямой. Треугольник ABC – прямоугольный.
Прямоугольные треугольники, длины сторон которых выражаются целыми числами, называют пифагоровыми треугольниками.

презентация на тему «Теорема Пифагора» (8 класс)

Урок по теме: «Теорема Пифагора»(8 класс)

Тип урока: урок изучения нового материала. ( по учебнику “Геометрия, 7–9”, учебник для общеобразовательных учреждений; Л.С. Атанасян и др.).

Цель:

познакомить учащихся с теоремой Пифагора и историческими сведениями, связанными с этой теоремой; развивать интерес к изучению математики, логическое мышление; внимание.

Ход урока:

1. Организационный момент.

СЛАЙД 1

Тема нашего урока «Теорема Пифагора». Сегодня на уроке мы познакомимся с биографией Пифагора, изучим одну из самых известных геометрических теорем древности, называемую теоремой Пифагора, одну из главных теорем планиметрии.

Многим известен сонет Шамиссо:

Пребудет вечной истина, как скоро

Ее познает слабый человек!

И ныне теорема Пифагора

Верна, как и в его далекий век.

Обильно было жертвоприношенье

Богам от Пифагора. Сто быков

Он отдал на закланье и сожженье

За света луч, пришедший с облаков.

Поэтому всегда с тех самых пор,

Чуть истина рождается на свет,

Быки ревут, ее почуя ,вслед.

Они не в силах свету помешать ,

А могут лишь закрыв глаза дрожать

От страха, что вселил в них Пифагор.

2. Актуализация знаний. (Подготовка к изучению нового материала, повторяется тот материал, который нужен будет при доказательстве теоремы)

СЛАЙД 2

1) Вопросы:

Какой четырехугольник называется квадратом?

Как найти площадь квадрата?

Какой треугольник называют прямоугольным?

Как называются стороны прямоугольного треугольника?

Как найти площадь прямоугольного треугольника?

СЛАЙД 3

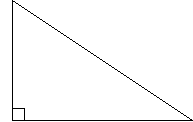
2) По данным на рисунке найдите площадь треугольника АВС, если 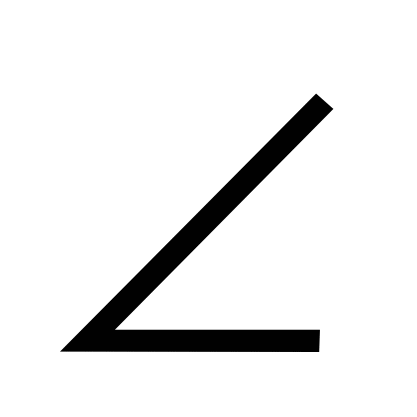А=60⁰, АВ = 14, ВС = 8.

А

В

С

СЛАЙД 4

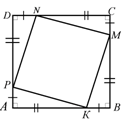
3) По данным рисунка докажите, что КLMN – квадрат.

L

B C

N

M

K

А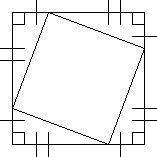 D

3. Изучение нового материала.

1) Историческая справка.

СЛАЙД 5

Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Как всякий отец, Мнесарх мечтал, что сын будет продолжать его дело — ремесло золотых дел мастера. Жизнь рассудила иначе. Будущий великий математик и философ уже в детстве обнаружил большие способности к наукам.

Пифагору приписывается изучение свойств целых чисел и пропорций, доказательство теоремы Пифагора и др. Пифагор — это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор — «убеждающий речью».)

СЛАЙД 6

Своими речами приобрёл 2000 учеников, которые вместе со своими семьями образовали школу-государство, где действовали законы и правила Пифагора. Школа Пифагора, или, как ее еще называют, пифагорейский союз, была одновременно и философской школой, и политической партией, и религиозным братством.

СЛАЙД 7

Излюбленной геометрической фигурой пифагорейцев была пентаграмма, называемая также пифагорейской звездой. Пифагорейцы пользовались этой фигурой, вычерчивая ее на песке, чтобы приветствовать и узнавать друг друга. Пентаграмма служила им паролем и была символом здоровья и счастья.

СЛАЙД 8

Несомненно, школа Пифагора сыграла большую роль в усовершенствовании научных методов разрешения математических проблем: в математику твердо вошло положение о необходимости строгих доказательств, что и придало ей значение особой науки.

Предание гласит, что когда Пифагор пришёл к теореме, носящей его имя, он принёс богам 100 быков. В пятисотых годах до нашей эры Пифагор был убит в уличной схватке во время народного восстания.

В настоящее время известно около 200 доказательств теоремы Пифагора.

Формулировки теоремы

СЛАЙД 9

У Евклида эта теорема гласит (дословный перевод):

«В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол».

В Geometria Culmonensis (около 1400 г.) в переводе теорема читается так :

«Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу».

В первом русском переводе евклидовых «Начал», сделанном Ф. И. Петрушевским, теорема

Пифагора изложена так:

«В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол».

2) Доказательство теоремы.

СЛАЙД 10

Достроим прямоугольник до квадрата со стороной a + b.

Ребята с помощью учителя по чертежу доказывают теорему, затем записывают доказательство в тетради, проводится проверка результатов с помощью компьютера.

СЛАЙД 11

Доказательство:

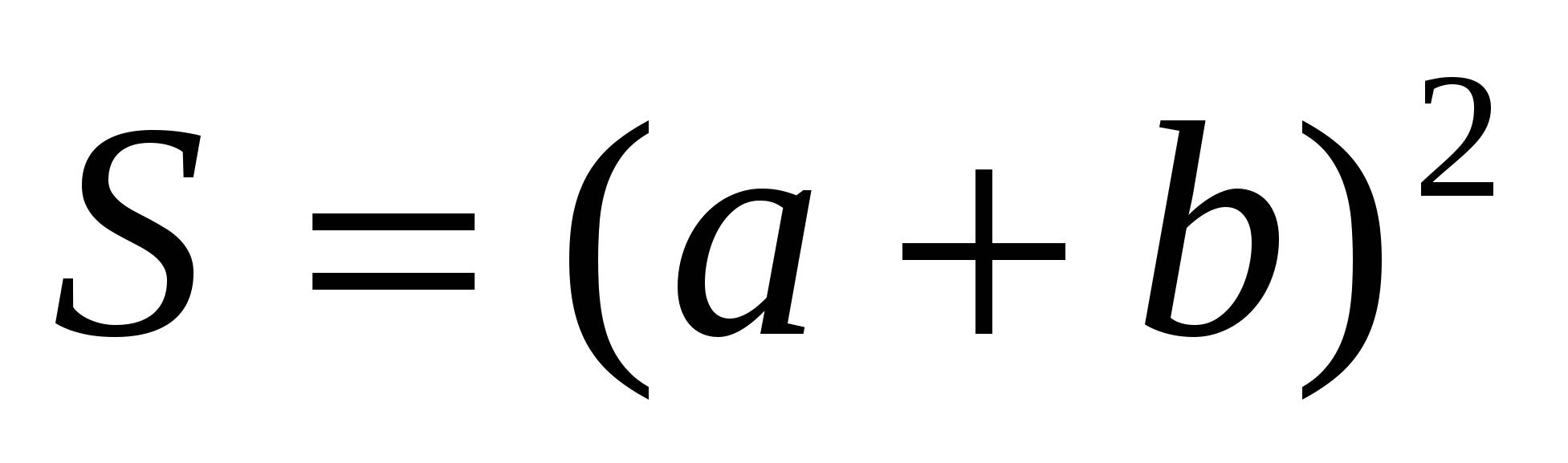— площадь квадрата

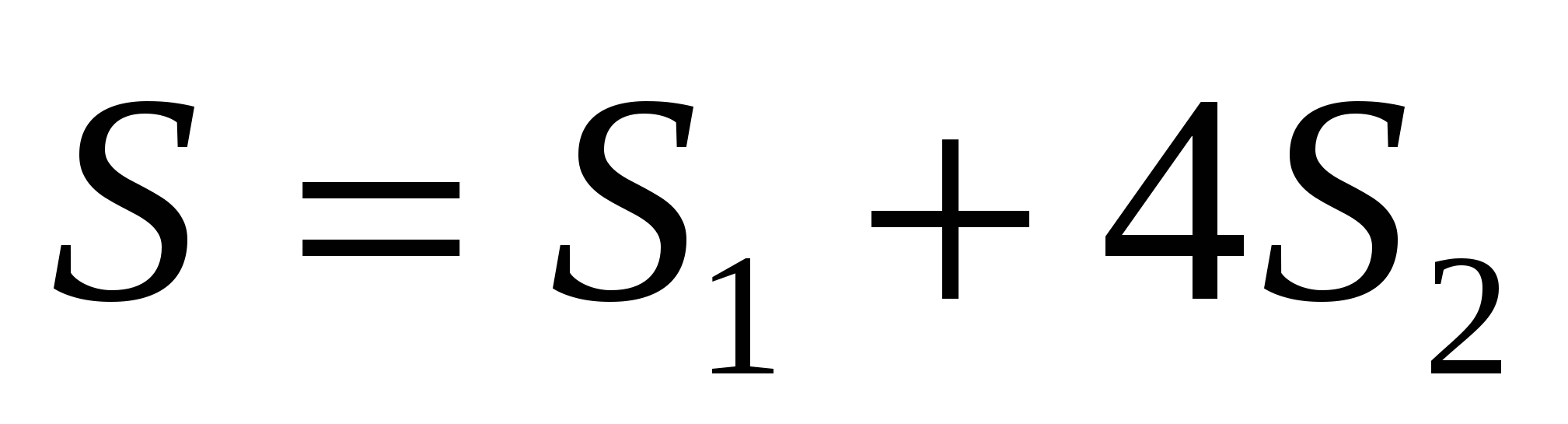
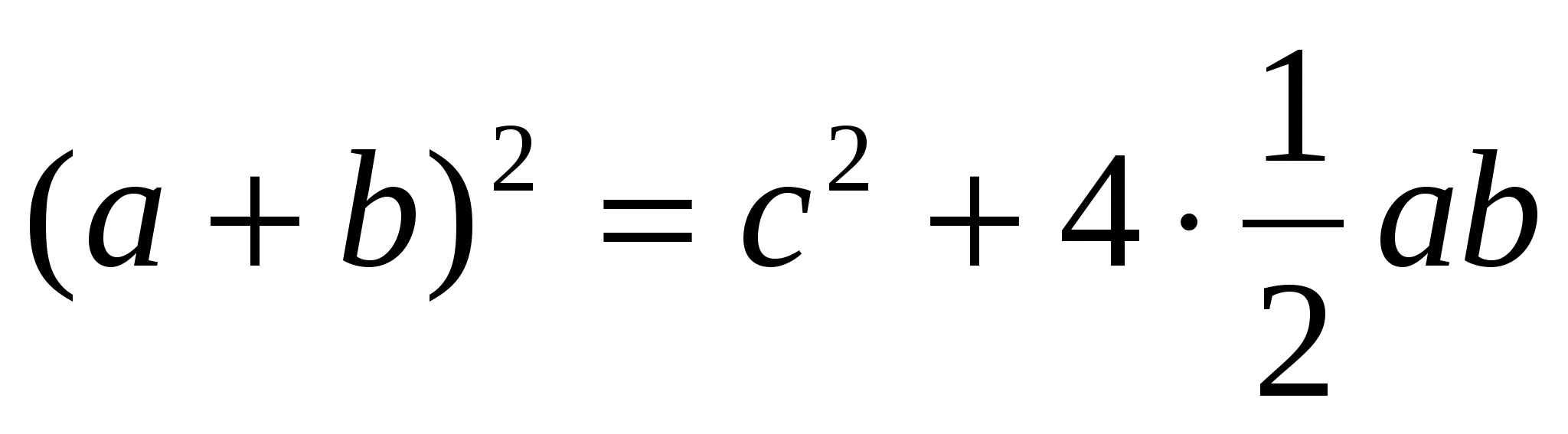
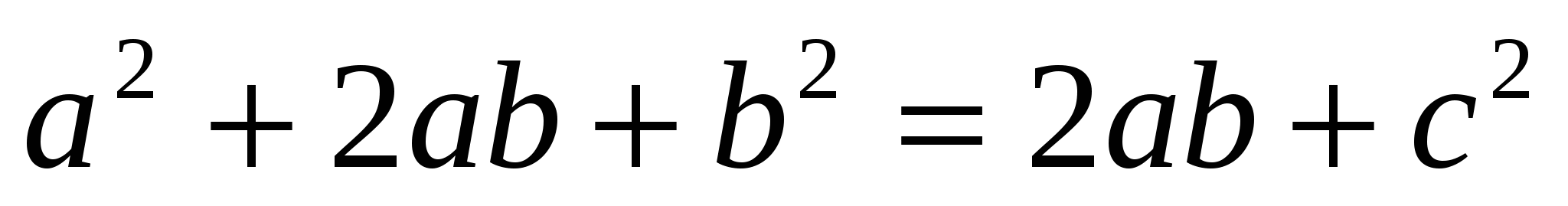
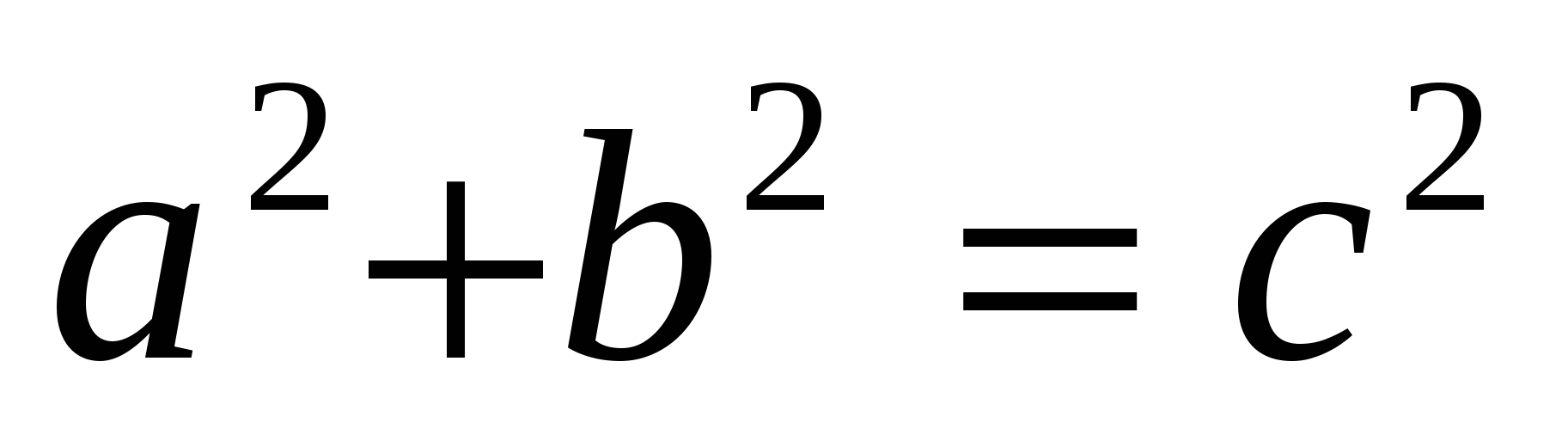— теорема доказана.

4. Первичное закрепление знаний.

Работа по учебнику (Применение теоремы Пифагора к решению задач).

Задачи решаются на доске и в тетрадях.

№ 483 (б),

№ 484 (а).

СЛАЙД 12

Вывод: с помощью теоремы Пифагора можно решать два вида задач:

1. Найти гипотенузу прямоугольного треугольника, если известны катеты.

2. Найти катет, если известна гипотенуза и другой катет.

.

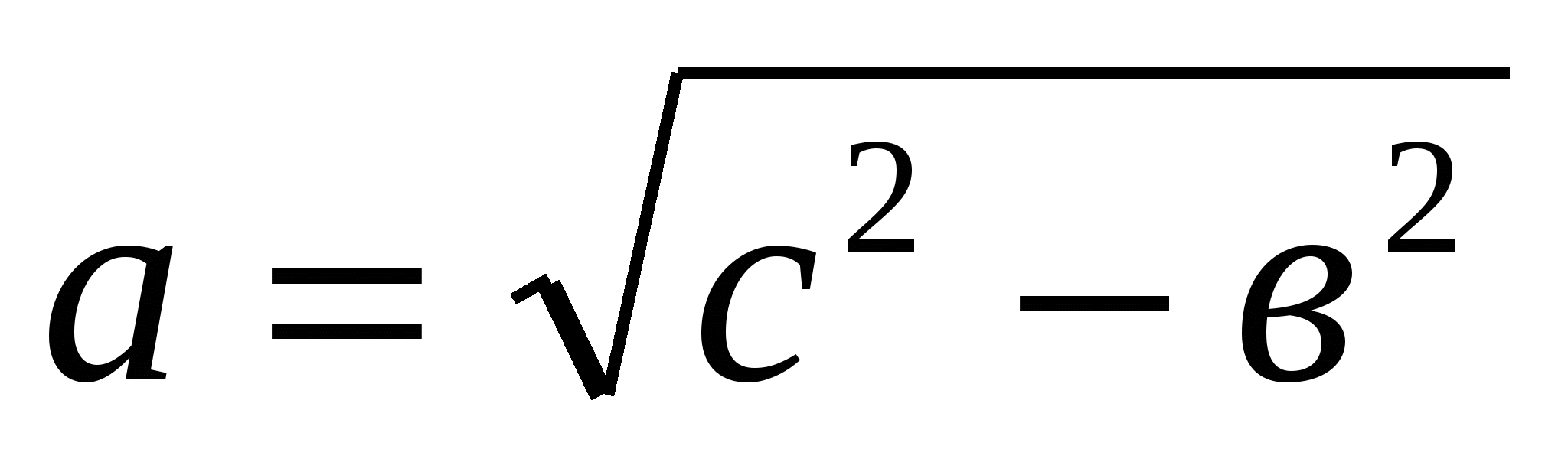
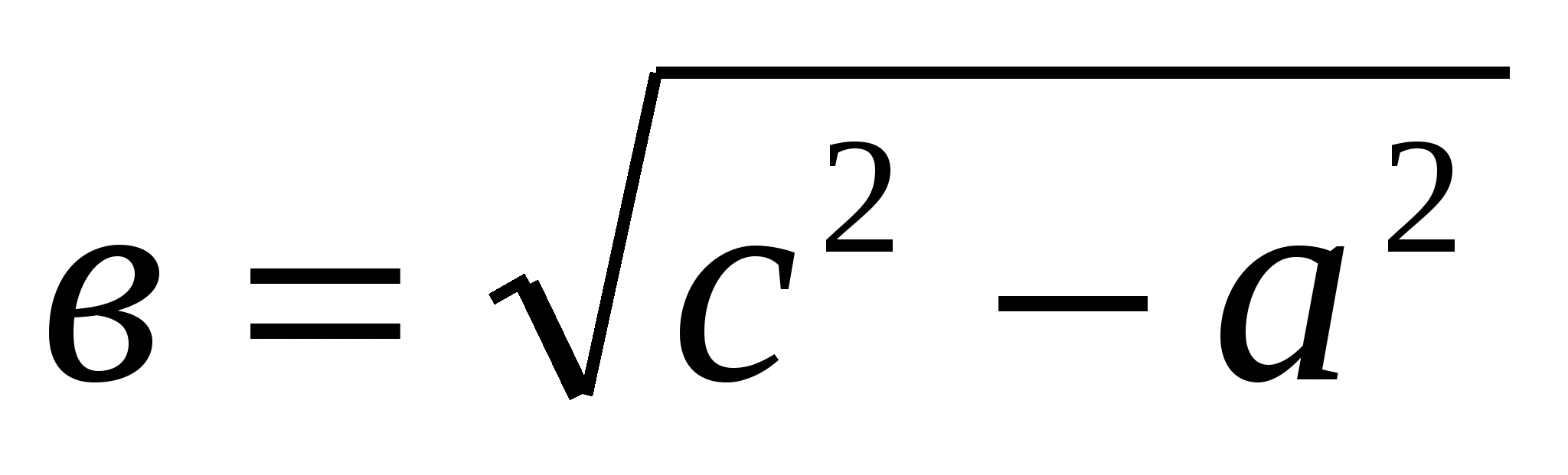5. Решение задач практического характера.

СЛАЙД 13

Мобильная связь

В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например радиусе R=200 км?, если известно. что радиус Земли равен 6380 км.)

Решение:

Пусть AB= x, BC=R=200 км, OC= r =6380 км.

OB = OA + AB

OB = r + x

Используя теорему Пифагора, получим ответ.

Ответ: 2,3 км.

СЛАЙД 14

6. Домашнее задание: П 54, № 483 (б), 484 (а). Можно предложить исследовательскую работу со следующей мотивирующей задачей: «Существуют ли другие доказательства теоремы?»

СЛАЙД 15

7. Итог урока.

Что нового вы узнали сегодня на уроке?

Для каких треугольников применяется теорема Пифагора?

В чём заключается теорема Пифагора?

СЛАЙД 16

Урок геометрии на тему «Теорема Пифагора» ( 8 класс)

Урок геометрии в 8-м классе по теме «Теорема Пифагора»

Разделы: Математика

Тип урока:

1-й час — урок ознакомления с новым материалом; 
2-й час — первичное закрепление изученного материала.

Учебное пособие: Л.С.Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина. Геометрия 7-9. Учебник для 7-9 классов средней школы. М.: Просвещение, 2004.

Цели и задачи урока:

1. Образовательные: познакомить учащихся с теоремой Пифагора, многообразием способов ее доказательства, применением при решении задач, повторить изученный ранее материал (площадь треугольника, ромба, прямоугольника, квадрата, параллелограмма), выработать умение применять теоретический материал для решения задач и доказательства теоремы.　 Закрепить полученные знания при решении практических задач.

2. Воспитательные: воспитывать познавательную активность, повышать интерес к изучению математики, показывая красоту математических доказательств, их стройность, логичность.

3. Развивающие: развивать умения обнаруживать способ доказательства нового математического утверждения и выполнять его, развивать мышление, память, навыки аргументированной речи, навыки доказательного воспроизведения в процессе деятельности.

Средства обучения (в том числе средства ИКТ): компьютер, мультимедийный проектор, презентация, выполненная при помощи программы PowerPoint (Приложение 1).

Методы и приемы: объяснительно-иллюстративный метод, вопросно-ответный метод, наглядный метод, словесный (рассказ, беседа, диалог), постановка проблемных вопросов, поисковый метод, эвристический метод, использование ИКТ, дифференцированный подход.

Формы организации деятельности учащихся: коллективная форма работы (фронтальный опрос, устная работа), индивидуальная работа (по карточке), письменная работа.

План урока:

1. Организационный момент.

2. Подготовительная работа по готовым чертежам:

3. Проверка домашнего задания.

4. Объяснение нового материала.

5. Различные способы доказательства теоремы Пифагора.

6. Постановка домашнего задания.

7. Первичное закрепление материала.

8. Решение задач.

9. Подведение итогов.

Ход урока

Объявление темы урока, постановка целей и задач перед учащимися: познакомиться с теоремой Пифагора, многообразием способов ее доказательства и ее применением при решении задач, а также повторить изученный ранее материал (площади треугольника, ромба, прямоугольника, квадрата, параллелограмма).

К доске с тетрадями вызываются 2 ученика для проверки на доске домашнего задания (выписывают на доске решения №480(б), №479 (б) – учебное пособие Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина. Геометрия 7-9. Учебник для 7-9 классов средней школы. М.: Просвещение, 2004.). В это время с классом проводится подготовительная работа – решение задач по готовым чертежам. Задачи транслируются учащимся посредством презентации (Приложение 1).

Проверка решений домашних задач:

№480 (б)

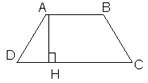
Дано: АВСD – трапеция, АВ и СD – основания. 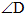= 30^о, АВ=2 см, СD = 10 см, DA = 8 см.

Найти S_АВСD

Решение: так как 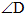 = 30^о, то АН = 0,5 AD = 4 см.

S_АВСD = 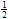(2 + 10)×4 = 24 см².

№479 (б)

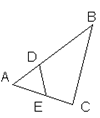
Дано: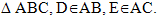 

АВ = 8 см, АС = 3 см, АЕ = 2 см. S_АВС = 10 см², S_АDE = 2 см².

Найти AD.

Решение:

Фронтальная работа с классом по готовым чертежам на слайдах (Приложение 1)

1. По данным рисунка найдите площадь четырехугольника АВСD.

2. Вычислить:

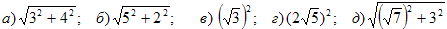
3. По данным рисунков найдите угол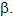 

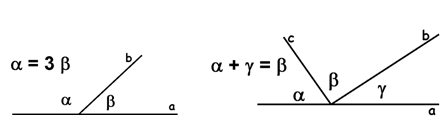
4. По данным рисунка докажите, что четырехугольник КМNР – квадрат (эта задача особенно важна, так как такая же фигура, как на рисунке, используется для доказательства теоремы).

Проверка домашнего задания, выписанного учеником на доске.

— Все согласны с решением задач? Какие есть замечания, дополнения?

— Дополнительный вопрос: какая теорема использовалась при решении задачи № 479, сформулируйте ее? (Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы).

Объяснение нового материала «Теорема Пифагора»

Учитель: Сегодня мы изучаем одну из самых известных геометрических теорем древности, называемую теоремой Пифагора. Ее и сейчас знают практически все, кто когда-либо изучал планиметрию. Теорема Пифагора одна из главных теорем планиметрии. Значение ее состоит в том, что с ее помощью можно доказать многие другие теоремы и решить множество задач.

(Учащиеся записывают в тетрадях тему урока – «Теорема Пифагора»).

Знаменитый греческий философ и математик Пифагор Самосский, именем которого названа теорема, жил около 2,5 тысяч лет тому назад. Он родился в 500 г до нашей эры и прожил 80 лет. Дошедшие до нас биографические сведения о Пифагоре отрывочны и далеко не достоверны. Пифагор – это не имя, а прозвище, данное　 ему за то, что он высказывал истину так же постоянно, как дельфийский оракул («Пифагор» значит «убеждающий речью»).

Знаменитая теорема Пифагора звучала так: Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов построенных на его катетах.

 

Про картинку, иллюстрирующую эту теорему, сложена шутливая поговорка: «Пифагоровы штаны на все стороны равны». Что имелось ввиду?

Теореме Пифагора можно дать эквивалентную формулировку, применив понятие равносоставленных фигур.

Попробуйте сформулировать теорему Пифагора по-другому.

— Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.

-Чтобы сформулировать теорему Пифагора в современном изложении, давайте вспомним, как найти площадь квадрата? (сторону квадрата возвести в квадрат). Тогда площадь квадрата, построенного на гипотенузе – это …? (квадрат гипотенузы), а площади квадратов, построенных на катетах – это …? (квадраты катетов). Попробуйте сами дать еще одну, современную формулировку теоремы Пифагора.

— В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

— Давайте в своих тетрадях начертим прямоугольный треугольник, обозначим катеты и гипотенузу буквами а, b, с и запишем формулу, которую нам дает теорема Пифагора (с² = а²+b²), перед формулой запишем слово «Доказать».

— Сейчас известно более трёхсот доказательств теоремы Пифагора. Не подлежит, однако, сомнению, что эту теорему знали за много лет до Пифагора. Так, за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным, и пользовались этим свойством (т.　е. теоремой, обратной теореме Пифагора) для построения прямых углов при планировке земельных участков и сооружений зданий. Это же самое проделывалось тысячи лет назад при строительстве великолепных храмов в Египте, Вавилоне, Китае, вероятно, и в Мексике. В самом древнем дошедшем до нас китайском математико-астрономическом сочинении, написанном примерно за 600 лет до Пифагора, среди других предложений, относящихся к прямоугольному треугольнику, содержится и теорема Пифагора. Еще раньше эта теорема была известна индусам. Таким образом, Пифагор не открыл это свойство прямоугольного треугольника, он, вероятно, первым сумел его обобщить и доказать, перевести тем самым из области практики в область науки. Сегодня мы с вами познакомимся с некоторыми из многочисленных доказательств теоремы Пифагора.

Различные способы доказательства теоремы Пифагора

Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы (для треугольника АВС квадрат, построенный на гипотенузе АС содержит 4 исходных треугольника, а квадраты, построенные на катетах – по 2 треугольника) Теорема доказана.

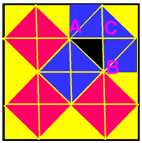
Еще одно наглядное доказательство теоремы Пифагора принадлежит индусам. Посмотрите внимательно на два квадрата, и вам всё станет ясно. Индусы к этому чертежу добавляли лишь одно слово: «СМОТРИ!»

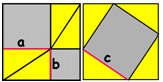
Кому стало ясно? Кто мне сможет объяснить, почему площадь серого квадрата, построенного на гипотенузе равна сумме площадей серых квадратов, построенных на катетах (Выслушать ответы учащихся. Из двух одинаковых квадратов вычитаем по 4 площади одинаковых треугольников).

— Двадцатый президент США Джеймс Гарфилд, который был избран президентом в 1880 году тоже смог привести свое доказательство теоремы Пифагора. Причём сделал он это доселе неизвестным способом. А узнать об этом широкие массы американцев смогли почти через 60 лет после его смерти. Правда, в изданной в 1940 году книге с доказательствами теоремы Пифагора доказательство Гарфилда затерялось, так как всего там было представлено 370 различных способов доказательства теоремы. Сейчас мы повторим путь доказательства Гарфилда и запишем его в тетрадь. Я вам подскажу только чертеж, с помощью которого Гарфилд доказал теорему Пифагора, а вы сейчас сами докажите теорему. При доказательстве используйте формулы для вычисления площади треугольника и площади трапеции. (В качестве повторения тем «Площадь треугольника» и «Площадь трапеции» учащимся будет полезно провести это доказательство письменно. Учитель добивается с помощью наводящих вопросов, чтобы дети сами провели рассуждения лучше, чтобы ученик или учитель записал доказательство на доске).

Доказательство Гарфилда:
На рисунке три прямоугольных треугольника составляют трапецию. Поэтому площадь этой фигуры можно находить по формуле площади прямоугольной трапеции, либо как сумму площадей трех треугольников. В первом случае эта площадь равна

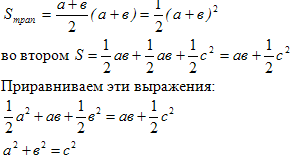
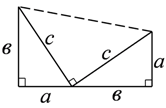
Рассмотрим еще одно доказательство теоремы Пифагора, которое приведено в вашем учебнике. Оно выполнено по следующему рисунку. Вам напоминает что-нибудь этот рисунок? Когда вы это видели? (Задача, решенная вначале урока)

(Учащимся сообщается лишь идея доказательства — достроить треугольник до квадрата со стороной (а + b) и выразить площадь квадрата возможными способами).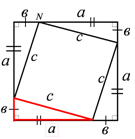

Доказательство (на уроке не проговаривается): S_кв. = (а + b)². С другой стороны квадрат составлен из четырех одинаковых треугольников с катетами а и в и квадрата со стороной с. Площади приравниваются:

Учащимся дается задание: дома самостоятельно провести это доказательство и записать полное доказательство в тетрадь, включая доказательства того факта, что внутри квадрат (в учебнике этот факт не доказывается). В классе выполняется только чертеж к доказательству теоремы)

Подводится промежуточный итог:

— Итак, сегодня вы познакомились с самой известной теоремой планиметрии – теоремой Пифагора. Кто сможет напомнить, как же формулируется теорема Пифагора? Кто запомнил? Как еще можно сформулировать?

Первичное закрепление материала.

1. Теорема Пифагора имеет большое практическое применение при решении задач. Она позволяет найти гипотенузу, зная катеты прямоугольного треугольника.

Выразите из формулы гипотенузу с. Почему взяли только положительное значение, ведь данное квадратное уравнение имеет два противоположных решения (речь идет о длине отрезка, который не может быть отрицательным) Выразите катет b; выразите катет а.

2. Дана таблица, в которой а и b катеты, с – гипотенуза.
Заполните пустые ячейки таблицы, произведя вычисления устно (таблица представлена на слайде,приложение 1).

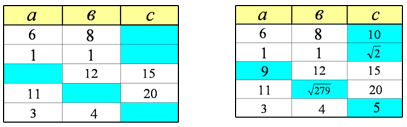
— Треугольник с катетами 3 и 4 и гипотенузой 5 называется египетским треугольником, так как он известен был еще древним египтянам, с помощью такого треугольника египтяне строили прямой угол.

3. Решение задач по готовым чертежам – самостоятельная работа в тетрадях по рядам. Каждый ряд имеет свой рисунок (чертежи заранее выполнены на доске): вычислить длину неизвестного отрезка х по данным рисунка. Затем, один отвечающий от каждого ряда комментирует вслух свое решение.

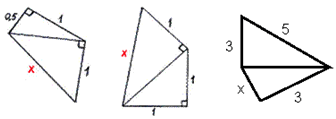
4. Постановка домашнего задания:

1. провести полное доказательство теоремы Пифагора путем достроения треугольника до квадрата со стороной (а + b).

2. индивидуальное задание сильным учащимся – найти и подготовить другие доказательства теоремы Пифагора.

3. Уметь доказывать теорему одним из способов.

4. Решить задачи: № 483 (а; б), № 484 (б, г), № 487.

5. дополнительное творческое задание (по желанию): придумайте сами чертеж к задаче, где для решения применялась бы теорема Пифагора (можно использовать комбинации различных фигур – прямоугольника, ромба, трапеции, прямоугольного треугольника). Предложите свою задачу классу.

5. Решение задач по учебнику с вызовом учеников к доске.

№ 493, № 494 – решение по вариантам самостоятельно с последующей проверкой– 1 вариант № 493, 2 вариант – № 494, по одному представителю от каждого варианта приглашаются к доске, они решают задачу на отворотах доски самостоятельно, не комментируя, а класс решает самостоятельно в тетрадях, затем крылья доски поворачиваются классу и проверяем ход решения задачи.

Решения:

№ 493

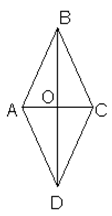
Дано: АВСD-ромб. АС = 10 см, BD = 24 см.

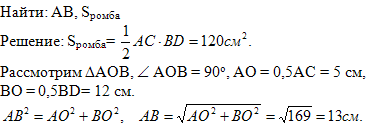
№ 494

Дано: АВСD-ромб. АВ = 10 см, АС = 12 см.

Найти BD, S_ромба

Решение:

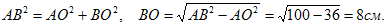
BD = 2ВО = 16 см.

Sромба= 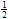 АС×BD= 96см²

№ 492

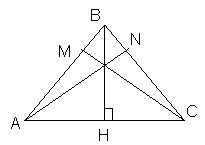
(Один ученик вызывается к доске и решает задачу с объяснением).

Дано: 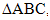 АВ = ВС = 10 см, АС = 12 см.

ВН, АN,СМ – высоты.

Найти: ВН, АN,СМ — ?

Решение: АН = 0,5 АС

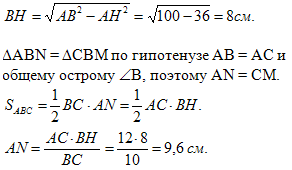
Подведение итогов:

• Что нового сегодня узнали?

• Как звучит теорема Пифагора?

• Понятны ли были способы доказательства теорем?

• Какую практическую пользу дает нам теорема Пифагора?

• Оценивание ответов учащихся, оглашение оценок за урок.

Теорема Пифагора (8 класс)

Теорема Пифагора

Урок изучения нового материала, учитель Демчук И.В., МБОУ СОШ №36 г. Томск

Цель и задачи урока

Образовательная:

• Обобщение и систематизация знаний по данной теме Развитие умений и навыков применения формул для решения задач
• Обобщение и систематизация знаний по данной теме
• Развитие умений и навыков применения формул для решения задач

Развивающая:

• Формирование и развитие умений анализировать условие задачи, составлять модель решения
• Формирование и развитие умений анализировать условие задачи, составлять модель решения

Воспитательная:

• Развитие творческих способностей учащихся
• Развитие творческих способностей учащихся

Задачи:

• Формирование прочных знаний, необходимых для продолжения образования Активизация познавательной деятельности учащихся через ИКТ – технологии
• Формирование прочных знаний, необходимых для продолжения образования
• Активизация познавательной деятельности учащихся через ИКТ – технологии

Устный опрос

• Какой треугольник называется прямоугольным?
• Как называются стороны прямоугольного треугольника?
• Как найти площадь прямоугольного треугольника?
• сторона квадрата равна aсм. Найдите его площадь
• Сторона квадрата равна a+b см. Найдите его площадь

Практическая работа

• Постройте прямоугольный треугольник по известным катетам : 1группа a=3, b=5; 2группа a=6,b=8; 3группа a=5,b=12
• Найдите длину гипотенузы
• Постройте на сторонах треугольника квадраты с данной стороной
• Найдите площади данных квадратов
• Сделайте вывод о соотношении данных площадей

Вывод

Площадь квадрата , построенного на гипотенузе, равна сумме площадей квадратов, построенных на его катетах

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы

Доказательство теоремы Пифагора

Достроим треугольник до квадрата

со стороной (a+b).

Площадь каждого треугольника ½ab

Площадь квадрата со стороной c равна с²

Площадь большого квадрата это

4*½ab+ c²

С другой стороны площадь большого квадрата (a+b)²=a²+2ab+b²

Таким образом, a²+2ab+b²=c²+2ab

Следовательно , a²+b²=c²

Различные доказательства знаменитой теоремы

Доказательство Эпштейна

Доказательство

Доказательство

Нильсена

Гутхейля

Доказательство

Перигаля

Немного о Пифагоре

Пифагор Самосский жил в vi веке до н.э. в

Древней Греции .В молодости он много

путешествовал по странам, побывал в Египте и Вавилоне, где изучал разные науки. Вернувшись на родину основал философскую школу закрытого типа- пифагорейский союз. Каждый вступавший в него отрекался от имущества и давал клятву хранить в тайне учение основателя. Пифагорейцы занимались математикой, философией, естественными науками. Ими были сделаны важнейшие открытия в арифметике и геометрии. Богатую историю имеет теорема, носящая имя Пифагора. Установлено, что она была известна еще за 1200 лет до Пифагора. Она была известна индусам, китайцам. Встречается и в вавилонских текстах. Пифагор не открыл, а обобщил и доказал свойство о соотношении между катетами и гипотенузой. В настоящее время известно более 200 доказательств теоремы.

Сто быков принес в жертву Пифагор …

Пребудет вечной истина , как скоро

Все познает слабый человек!

И ныне теорема Пифагора

Верна, как и в его далекий век.

Обильно было жертвоприношенье

Богам от Пифагора. Сто быков

Он отдал на закланье и сожженье

За свет луча , пришедший с облаков.

Поэтому всегда с тех самых пор,

Чуть истина рождается на свет,

Быки ревут её почуя , вслед.

Они не в силах свету помешать,

А могут лишь, закрыв глаза, дрожать,

От страха, Что вселил в них Пифагор

(А.Шамиссо)

Ослиный мост

Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда Pons Asinorum «ослиный мост» или elefuga — «бегство убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии. Слабые ученики, заучивавшие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста

Задание №1

Запишите теорему Пифагора для каждого из треугольников

Задание №2

В прямоугольном треугольнике a и b-катеты, c- гипотенуза.

• Выразить c через a и b
• Выразить a через b и c
• Выразить b через a и с

c

a

b

Задание №3

Вычислите , если возможно

• Сторону АС треугольника АВС
• Сторону MN треугольника MNK
• Диагональ KL прямоугольника KMLN
• Диагональ BD квадрата BCDF
• Сторону АВ ромба ABDE
• Сторону KP треугольника KPR

Проверочная работа

В прямоугольном треугольнике a и b катеты, c- гипотенуза. Заполните таблицу.

a

30

b

c

1

50

1

8

12

2

15

10

5

с

a

b

Проверим результаты

a

b

30

c

40

1

1

50

9

8

√ 2

12

6

15

2

10

√ 21

5

Ученические шаржи

• Шаржи из учебника XVI века

Ученический шарж XIX века

Теорема Пифагора

Если дан нам треугольник,

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим —

И таким простым путем

К результату мы придем.

Домашнее задание

Вычислите высоту CF

трапеции ABCD

Рефлексия

Деятельность на уроке

Оценка

Слушал объяснения

Принимал участие в обсуждении

Отвечал на вопросы учителя

Решал самостоятельно

Выполнил домашнее задание

Понял учебный материал

Статья по геометрии (8 класс) на тему: Теорема Пифагора и способы доказательства.

ТЕОРЕМА ПИФАГОРА И СПОСОБЫ ЕЕ ДОКАЗАТЕЛЬСТВА

          Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. В самом деле, теорема Пифагора проста, но не очевидна.  Эта  теорема  имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствуют о гигантском числе ее конкретных реализаций.

           Эта теорема была известна и в Древней Индии; об этом свидетельствуют следующие предложения,  содержащиеся в «Сутрах». В настоящее время известно более 150 доказательств теорема Пифагора.

 

           Сегодня теорема Пифагора применяется при решении задач и в строительстве. В школьной программе представлено простейшее доказательство этой теоремы, при этом бесследно исчезает первозданная геометрическая аура теоремы, теряется та нить Ариадны, которая вела древних мудрецов к истине.

            Пифагор – великий учёный. Родился около 570 г. до н. э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя матери неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.

«Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах».

Простейшее доказательство этой теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников ( рис.1), чтобы убедиться  в справедливости теоремы. Например для треугольника АВС : квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, содержат по два. Теорема доказана.

Древнекитайское доказательство.

Математические трактаты Древнего Китая дошли до нас в редакции II в. до н.э. Дело в том, что в 213 г. до н.э., китайский император Ши Хуан-ди, стремясь ликвидировать прежние традиции, приказал сжечь все древние книги. Во II в. до н.э. в Китае была изобретена бумага и одновременно начинается воссоздание древних книг. Так возникла «Тематика в девяти книгах» — главное из сохранившихся математико-астрономических сочинений в книге «Математики» помещён чертёж (рис.2а),доказывающий теорему Пифагора.

Ключ к этому доказательству (рис.2) подобрать нетрудно.  В самом деле, на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной а + b, а внутренний – квадрат со стороной с, построенный на гипотенузе (рис. 2б). если квадрат со стороной с вырезать и оставшиеся 4 затушёванных треугольника уложить в два прямоугольника (рис.2в), то ясно, что образовавшаяся пустота, с  одной стороны равна с2, а с другой – а2 +  b2 , т.е. с2  =  а2 +  b2

Теорема доказана.  Заметим, что при таком доказательстве построения внутри квадрата на гипотенузе, которые мы видим на древнекитайском чертеже (рис.2а), не используются.  По-видимому, древнекитайские математики имели другое доказательство. Именно, если в квадрате со стороной с два заштрихованных треугольника (рис.2б) отрезать и приложить гипотенузами к двум другим гипотенузам (рис.2г), то легко обнаружить, что полученная фигура, которую иногда называют «креслом невесты», состоит из двух квадратов со сторонами а и b, т.е. с2  =  а2 +  b2

Доказательство теоремы Пифагора.

Пусть Т – прямоугольный треугольник с катетами  а, b и гипотенузой с . Докажем, что

с2  =  а2 +  b2

 Построим квадрат  Е  со стороной а + b. На сторонах квадрата Е возьмём точки А,В,С,D так, чтобы отрезки АВ, ВС, СD, DА отсекали от квадрата Е прямоугольные треугольники Т1, Т2, Т3, Т4  с катетами а, b. Четырёхугольник АВСD обозначим буквой Р . Покажем , что Р – квадрат со стороной с. Все треугольники Т1, Т2, Т3, Т4  равны треугольнику Т ( по двум сторонам и углу между ними). Поэтому их гипотенузы равны гипотенузе  треугольника Т, т. е. отрезку с. Докажем, что все углы этого четырёхугольника прямые. Пусть  α и β — величины острых углов треугольника Т. Тогда, как вам известно, α + β = 90о. Угол  γ при вершине А четырёхугольника Р вместе с углами, равными α и β, составляет развёрнутый угол. Поэтому α + β + γ = 180о. И так как α + β = 90о , то γ = 90о. Точно так же доказывается, что и остальные углы четырёхугольника Р прямые. Следовательно, четырёхугольник Р – квадрат со стороной с. Квадрат Е со стороной а + b слагается из квадрата Р со стороной с и четырёх треугольников, равных треугольнику Т. Поэтому для их площадей выполняется равенство S(E) = S(Р) + 4S(Т).

Так как S(E) = (а + b)2  ; S(Р) = с2  и S(Т) = ½ (а b), то подставляя эти выражения в S(E) = S(Р) + 4S(Т) , получаем равенство (а + b)2  = с2 + 4 *(1/2) а b. Поскольку (а + b)2   = а2 +  b2+ +2 а b, то равенство (а + b)2  = с2 + 4 *(1/2) а b можно записать так : а2 +  b2 + 2 а b = с2 + 2аb

 Из равенства а2 +  b2 + 2 а b = с2 + 2аb следует , что с2  = а2 +  b2 , что и требовалось доказать.

                  В заключении хочется сказать о важности теоремы. Значение её состоит, прежде всего, в том, что из неё или с её помощью можно вывести большинство теорем геометрии. К сожалению, невозможно здесь привести все или даже самые красивые доказательства теоремы, однако, хочется надеяться, что приведённые примеры убедительно свидетельствуют об огромном интересе сегодня, да и вчера, проявляемом по отношению к ней.

Использованная литература:

1. А.П.Кисилев, Элементарная геометрия, М., « Просвещение», 1980г.
2. Энциклопедия для детей, Математика, т.11, М., «Аванта», 2002г.
3. Г.И.Глейзер, История математики в школе, М., «Просвещение», 1982г.
4. В.А.Гусев, А.Г.Мордкович, Математика, справочные материалы, М., «Просвещение», 1990г.

Методическая разработка по геометрии (8 класс) по теме: «Теорема Пифагора». Учебник Л.С.Атанасян «Геометрия 8 класс».

Урок по геометрии в 8 классе по теме: «Теорема Пифагора».

Учебник Л. С. Атанасян «Геометрия 7 – 9».

Подготовила  учитель математики МОУ- СОШ №3  Абросимова Г.Е

Тип: Урок изучения нового материала.

Цель: Знать, определения прямоугольного треугольника и его свойства,  формулу площадей прямоугольного треугольника, свойства площадей. Познакомить с теоремой Пифагора и ее доказательством. Научить решать задачи, используя теорему Пифагора. Cпособствовать развитию логического мышления и воспитанию графической культуры. Время урока – 45 минут.

Структура урока:

Устная работа. Повторение.

1.Дайте определение прямоугольного треугольника. Назовите катеты и гипотенузу.

2.Назовите формулы для вычисления площадей треугольника:

S = ah, a- основание, h- высота,  

S = ab, a- катет, b- катет.

3.Назовите свойства площадей фигур.

4.Назовите свойства и признаки прямоугольного треугольника.

      5. Задания записаны на доске.

Выполните следующие задания:

1. По данным рисунка найдите площадь четырехугольника ABCD (угол В – прямой).

2. По данным рисунка найдите угол β.

3. По данным рисунка докажите, что четырехугольник KMNP – квадрат.

   Итак, ребята, мы с вами вспомнили все зависимости       прямоугольного треугольника между сторонами и углами известные ранее нам.

Возникает проблема: Давайте посмотрим с вами, существует ли зависимость между гипотенузой и катетами в прямоугольном треугольнике и, если она существует, то, как она формулируется.

Поиск: Задание по рядам: построить прямоугольные треугольники, если катеты равны:  

1ряд   3 и 4 см

2ряд   12 и 5 см

3 ряд  6 и 8 см

Учитель  8 и 15 см

Таблица №1                                                                Таблица №2

а	3	12	6	8			9	144	36	64
в	4	5	8	15			16	25	64	225
с	5	13	10	17			25	169	100	289

     

   Различные гипотезы:

Если возьмем катеты a и b, как с получится?

        a +   = c , справедливо ли это и для каких случаев?

2. Возьмем b и с, как а получить?

           a =                              

Наши гипотезы справедливы не всегда, ребята, а что произойдет, если найдем зависимость квадратов значений сторон треугольника? (Заполняем таблицу №2)

 Теорема Пифагора.

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Дано: Δ ABC, C = 90°, AC = b, AB = c, BC = a.

Доказать:  = a2 + b2 

Доказательство:

1)Достроим треугольник до квадрата со стороной (а+b)

2)  = (

C другой стороны этот квадрат состоит из четырех равных прямоугольных треугольников.

 = ab, =  ,  = 4 +

Таким образом, ( 4*ab +

a2 + b2 = c2. Теорема доказана.

Просмотр презентации и чтение исторической справки

 Значение теоремы Пифагора.

Теорема Пифагора – одна из главных и, можно сказать, самая главная теорема геометрии. Значение ее состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии. Теорема Пифагора замечательна и тем, что сама по себе она вовсе не очевидна. Например, свойства равнобедренного треугольника можно видеть непосредственно на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что между его сторонами есть простое соотношение: c2 = a2 + b2.

Зато это соотношение между соответствующими площадями геометрических фигур становится очевидным из построения на рисунках:

На них мы видим два различных разбиения одного и того же квадрата со стороной а + b. На первом из них квадрат Q слагается из квадрата со стороной с и четырех треугольников; на втором – такой же квадрат слагается из квадратов со сторонами а и b и таких же четырех треугольников. Исключив на обоих рисунках треугольники, видим, что с2 = а2 + b2. В этом и состоит самый лучший математический стиль: посредством остроумного построения сделать не очевидное очевидным.

 Закрепление материала.

Тест №13 №1, 2, 4, 7

№4, 7  самостоятельное решение на доске, записать только решение. Работают сильные ученики по вариантам. В это время проверка и обсуждение №1, 2.

Итог урока

Домашнее задание: п.54, №483 (в), 484 (в, г, д)

Дополнительный материал к уроку (резерв):