График функции 2x 1: y=2x+1 Построить график функции — Школьные Знания.com — ЭкоДом: Дом своими руками
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Преобразование y = f (x + c), где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | Рисунок: |
Описание: В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | Рисунок: |
| Преобразование y = f (x) + c, где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | Рисунок: |
Описание: В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | Рисунок: |
| Преобразование y = – f (x |
Описание: График функции y = f (x) симметрично отражается относительно оси Ox. Рисунок: |
| Преобразование y = f ( – x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Oy. Рисунок: |
| Преобразование y = f (kx), где k – число |
Описание: В случае k > 1 происходит сжатие графика функции y = f (x) в k раз к оси Oy. Рисунок: |
Описание: В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в раз от оси Oy. Рисунок: |
Описание: В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в раз от оси Oy с последующим симметричным отражением графика относительно оси Oy.Рисунок: |
Описание: В случае k < – 1 происходит сжатие графика функции y = f (x) в | k | раз к оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: |
| Преобразование y = k f (x), где k – число |
Описание: В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. Рисунок: |
Описание: В случае 0 < k < 1 происходит сжатие графика функции y = f ( Рисунок: |
Описание: В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в раз к оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: |
Описание: В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: |
| Преобразование y = | f (x)| |
Описание: Часть графика функции y = f (x), расположенная в области , остаётся на месте. Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox. Рисунок: |
| Преобразование y = f (| x|) |
Описание: Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции y = f (x), расположенная в области остаётся на месте. Часть графика функции y = f (| x|), расположенная в области x < 0, получается из части графика, расположенной в области при помощи симметричного отражения относительно оси Oy. Рисунок: |
Функции и Графики — сайт по математике и не только!!! ЛИНЕЙНАЯ ФУНКЦИЯ Всё о Математических функциях и их графиках…
|
ЛИНЕЙНАЯ ФУНКЦИЯ
при k 0 R при k = 0 {b} если k 0, b 0, то функция ни четная и ни нечетная если k 0, b = 0, то функция нечетная если k = 0, b = 0, то функция четная если k = 0, b = 0, то функция равна нулю если k 0, то y = 0 при x = -b/k если k = 0, b 0, то нулей нет если k = 0, b = 0, то y = 0 при x R
если k = 0, b > 0, то функция возрастает при x R если k = 0, b x R если k = 0, b = 0, то функция постоянна при x R
Например: y = 2x + 2 Если x1 = 0, то y1 = 2; Через точки (0,2) и (-1;0) проведем прямую: Если коэффициент перед х дробный, удобно выбирать х1 и х2 так, чтобы у1 и у2 были целыми. y = — 1/3x + 2 Если x1 = 3, то y1 = 1; Если x1 = -3, то y2 = 3; Через точки (3;1) и (-3;3) провести прямую.
|
|
Сдвиги графиков функций
☰
Изменение значения k влияет на вид графика (степень крутизны в случае параболы), расположение ветвей в координатных четвертях и др. Однако точкой, через которую можно провести ось симметрии графиков, является точка O с координатами (0; 0).
Если же рассматривать функций, подобные перечисленным выше, у которых к переменной x или ко всей исходной функции прибавляется (или вычитается) какое-либо число, то графики этих функций остаются такими же как у исходных, однако смещаются относительно точки (0; 0).
Если обозначить исходные функции как y = f(x), то прибавление к x числа дает функции вида y = f(x+l), а прибавление ко всей исходной функции значения дает вид y = f(x) + m.
Например, если исходная функция y = 2x2, то примером первого типа будет функция y = 2(x+5)2, а второго — y = 2x2 + 5.
Для функций вида y = f(x+l) график смещается влево на l единиц, если l прибавляется. Если же l вычитается, то график смещается вправо. Действительно, представим параболу функции y = x2 и сравним ее с функцией y = (x+1)2. Когда x = 1, то для первой функции y = 1, а для второй — y = 4. Когда x = 0, для первой y = 0, для второй y = 1. Когда x = –1, для первой y = 1, для второй y = 0.
То есть график второй функции касается оси x в точке (–1; 0). Это значит, что график смещен влево по сравнению с исходным на 1.
Для функций вида y = f(x) + m график соответствующей функции y = f(x) смещается на m единиц, но уже по вертикальной оси (ось y). Здесь если m прибавляется, то график сдвигается вверх. Если m вычитается, то график сдвигается вниз.
Рассмотрим ту же параболу y = x2 и функцию y = x2 + 1. Когда x = 0, первая принимает значение 0, а у второй y = 1. Получить у второй функции значение y, которое равно 0, вообще невозможно. Это значит, что парабола имеет точку симметрии с координатами (0; 1), т. е. сдвинута от исходной вверх на 1.
Когда x = 0, первая принимает значение 0, а у второй y = 1. Получить у второй функции значение y, которое равно 0, вообще невозможно. Это значит, что парабола имеет точку симметрии с координатами (0; 1), т. е. сдвинута от исходной вверх на 1.
«Смешанные» функции вида y = f(x + l) + m сдвигаются вдоль оси x и y. Вдоль оси x они сдвигаются на l, а вдоль y — на значение m.
Построить график функции у=-x²+2x+8 (парабола) – решение и ответ
Формулировка задания: Построить график функции у = -x² + 2x + 8.
Решение:
Для построения графика параболы нужно построить таблицу значений x и y.
Для удобства начнем с точек, находящихся на осях Ox и Oy. Если точка лежит на оси Oy (x = 0), тогда:
x = 0 ⇒
y = -0² + 2 ⋅ 0 + 8 = 8
Если точка лежит на оси Ox (y = 0), нужно решить квадратное уравнение:
y = 0 ⇒
-x² + 2x + 8 = 0
a = -1, b = 2, c = 8
D = 2² – 4 ⋅ (-1) ⋅ 8 = 36
x1 = (-2 + 6) / (-2) = -2
x2 = (-2 – 6) / (-2) = 4
Таким образом, мы получили 3 точки пересечения с осями. Заполняем ими таблицу:
Заполняем ими таблицу:
Возьмем еще пару точек, которые будет просто посчитать, например, x = 1 и x = -1:
x = 1 ⇒
y = -1² + 2 ⋅ 1 + 8 = 9
x = -1
y = -(-1)² + 2 ⋅ (-1) + 8 = 5
Таблица значений теперь выглядит следующим образом:
Отметим полученные точки на координатной плоскости:
Координату x вершины параболы можно определить по любым 2 точкам параболы, у которых равно значение y: она лежит точно между ними. Например, найдем координату x вершины параболы по точкам (-2;0) и (4;0):
(4 – (-2)) / 2 = 6 / 2 = 3
xв = -2 + 3 = 1
Точка с таким значением x уже есть в таблице значений. Осталось построить график:
Поделитесь статьей с одноклассниками «Построить график функции у=-x²+2x+8 (парабола) – решение и ответ».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
Графики прямой, параболы, гиперболы, с модулем
Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
Для понимания друг друга введу немного «обзываний» системы координат:
Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.
Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1
Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:
А если теперь добавить модуль y = |2x − 1|.
Модуль — это всегда положительное значение, получается, что «y» должен быть всегда положительным.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).
Получается такая зеленая «галочка».
Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
Здесь отражаем относительно оси «y». Такая же галочка, только теперь через другую ось.
Смертельный номер: y = |2|x| − 1|.
Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.
В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!
А после этого отражаем относительно оси «y» то, что мы получили справа налево:
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.
Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x₁ = 1 и x₂ = -2.
Можно найти вершину у параболы и взять пару точек для точного построения.
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
А дальше что мелочиться: рассмотри сразу остальные графики с модулем!
Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
А теперь сразу комбо:
Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.
Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.
Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.
Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.
Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум, потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
А что будет, если мы добавим в знаменателе «−1»? График сдвинется вправо на единицу.
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!
Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.
Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.
Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:
Для параболы с одним модулем будет два кусочно-заданных графика:
C двумя модулями кусочно-заданных графиков будет четыре:
Таким способом, медленно и кропотливо можно построить любой график!
Выводы:
- Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
- Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
- Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль.
- Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
- Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
- Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
- Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.

- Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
Будь в курсе новых статеек, видео и легкого математического юмора.
Асимптоты графика функций: их виды, примеры решений
Будут и задачи для самостоятельного решения, к которым можно
посмотреть ответы.
Если предварительно построить асимптоты кривой, то многих случаях построение графика
функции облегчается.
Судьба асимптоты полна трагизма. Представьте себе, каково это: всю жизнь двигаться
по прямой к заветной цели, подойти к ней максимально близко, но так и не достигнуть её. Например, стремиться
соединить свой жизненный путь с путём желанного человека, в какой-то момент приблизиться к нему почти
вплотную, но даже не коснуться его. Или стремиться заработать миллиард, но до достижения этой цели
и записи в книгу рекордов Гиннеса для своего случая не достаёт сотых долей цента.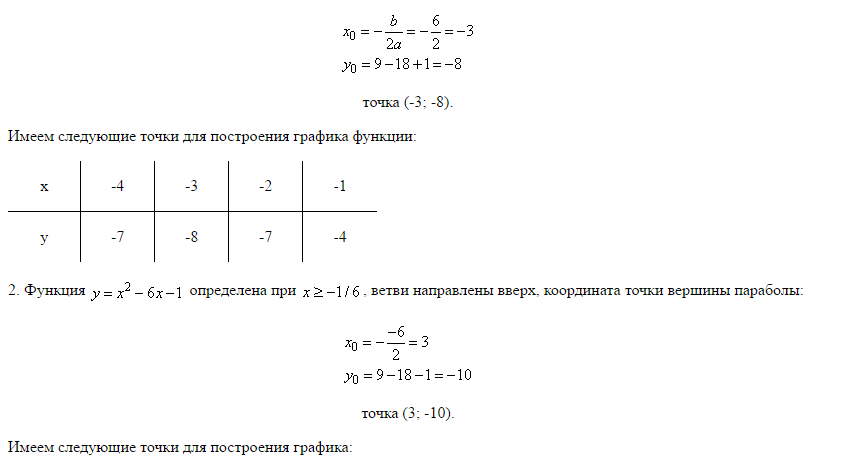 И тому подобное. Так
И тому подобное. Так
и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное
возможное расстояние, но так и не касается его.
Определение 1. Асимптотами называются такие прямые, к которым сколь угодно
близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус
бесконечности.
Определение 2. Прямая называется асимптотой графика функции, если расстояние
от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении
точки М от начала координат по какой-либо ветви графика функции.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Первое, что нужно узнать о вертикальных асимптотах: они параллельны
оси Oy.
Определение. Прямая x = a
Прямая x = a
является вертикальной асимптотой графика функции, если точка x = a
является точкой разрыва второго рода для этой функции.
Из определения следует, что прямая x = a
является вертикальной асимптотой графика функции f(x), если выполняется хотя бы одно
из условий:
-
(предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности) -
(предел функции при значении аргумента, стремящимся к некоторому значению a справа, равен плюс или минус бесконечности).
При этом функция f(x) может быть вообще не определена соответственно при
x ≥ a и
x ≤ a.
Замечание:
- символом
обозначается стремление x к a справа, причём x остаётся
больше a; - символом
обозначается стремление x к a слева, причём x остаётся меньше a.
Пример 1. График функции y=lnx
имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy) на границе
области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:
(рис. сверху).
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Пример 2.Найти асимптоты графика функции .
Пример 3. Найти асимптоты графика функции
Первое, что нужно узнать о горизонтальных асимптотах: они параллельны
оси Ox.
Если
(предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b),
то y = b – горизонтальная асимптота кривой y = f(x)
(правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности,
и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).
Пример 5. График функции
при a > 1 имеет левую горизонтальную
асимпототу y = 0 (т.е.
совпадающую с осью Ox), так как предел функции при стремлении «икса»
к минус бесконечности равен нулю:
Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении
«икса» к плюс бесконечности равен бесконечности:
Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны
осям координат, поэтому для их построения нам требовалось лишь определённое число — точка на оси
абсцисс или ординат, через которую проходит асимптота. Для наклонной асимптоты необходимо больше —
угловой коэффициент k, который показывает угол наклона прямой, и свободный член b, который показывает,
насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию,
Не успевшие забыть аналитическую геометрию,
а из неё — уравнения прямой, заметят, что для наклонной асимптоты находят уравнение
прямой с угловым коэффициентом. Существование наклонной асимптоты определяется следующей теоремой,
на основании которой и находят названные только что коэффициенты.
Теорема. Для того, чтобы кривая y = f(x) имела
асимптоту y = kx + b, необходимо и
достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции
при стремлении переменной x к плюс бесконечности и минус бесконечности:
(1)
и
(2)
Найденные таким образом числа k и b и являются коэффициентами
наклонной асимптоты.
В первом случае (при стремлении икса к плюс бесконечности) получается правая
наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.
Правая наклонная асимптота изображена на рис. снизу.
При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса
и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных,
эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только
один из них.
При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус
бесконечности прямая y = kx + b является двусторонней асимптотой кривой.
Если хотя бы один из пределов, определяющих асимптоту y = kx + b, не существует, то
график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота y = b
является частным случаем наклонной y = kx + b
при k = 0.
Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в
этом направлении нет наклонной, и наоборот.
Пример 6. Найти асимптоты графика функции
Решение. Функция определена на всей числовой прямой, кроме x = 0, т.е.
Поэтому в точке разрыва x = 0 кривая может иметь вертикальную
асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:
Следовательно, x = 0 – вертикальная асимптота
графика данной функции.
Горизонтальной асимптоты график данной функции не имеет, так как предел функции при
стремлении икса к плюс бесконечности равен плюс бесконечности:
Выясним наличие наклонной асимптоты:
Получили конечные пределы k = 2 и
b = 0.
Прямая y = 2x является двусторонней
наклонной асимптотой графика данной функции (рис. внутри примера).
внутри примера).
Пример 7. Найти асимптоты графика функции
Решение. Функция имеет одну точку разрыва x = −1.
Вычислим односторонние пределы и определим вид разрыва:
,
.
Заключение: x = −1 — точка разрыва второго рода,
поэтому прямая x = −1 является вертикальной асимптотой
графика данной функции.
Ищем наклонные асимптоты. Так как данная функция — дробно-рациональная, пределы при
и при
будут совпадать. Таким
образом, находим коэффициенты для подстановки в уравнение прямой — наклонной асимптоты:
Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем
уравнение наклонной асимптоты:
y = −3x + 5.
На рисунке график функции обозначен бордовым цветом, а асимптоты — чёрным.
Пример 8. Найти асимптоты графика функции
.
Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот.
Ищем наклонные асимптоты:
.
Таким образом, график данной функции имеет асимптоту y = 0 при
и не имеет асиптоты при
.
Пример 10. Найти асимптоты графика функции
Решение. Функция имеет область определения .
Так как вертикальная асимптота графика этой функции может быть только на границе области определения,
найдём односторонние пределы функции при :
,
.
Оба предела нашли, используя первый замечательный предел. Заключение: x = 0 — точка
устранимого разрыва, поэтому у графика функции нет вертикальных асимптот.
Ищем наклонные асимптоты:
Таким образом, при
наклонной асимптотой графика данной функции является прямая y = x.
Но при найденные пределы
не изменяются. Поэтому при
наклонной асимптотой графика данной функции также является y = x.
Пример 11. Найти асимптоты графика функции
.
Решение. Сначала найдём вертикальные асимптоты. Для этого найдём точки разрыва функции
и их виды. Знаменатель не может быть равным нулю, поэтому должно соблюдаться условие
.
Функция имеет две точки разрыва: ,
. Чтобы установить вид
разрыва, найдём односторонние пределы:
Так как все пределы равны бесконечности, обе точки разрыва — второго рода. Поэтому
график данной функции имеет две вертикальные асимптоты: x = 2 и
x = −2.
Ищем наклонные асимптоты. Так как данная функция является дробно-рациональной,
пределы при и при
совпадают. Поэтому,
определяя коэффициенты прямой, ищем просто пределы:
Подставляем найденные коэффициенты в уравнение прямой с угловым коэффициентом,
получаем уравнение наклонной асимптоты y = 2x.
Таким образом, график данной функции имеет три асимптоты: x = 2,
x = −2 и y = 2x.
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Поделиться с друзьями
Весь блок «Производная»
Как построить график функции
В этой статье разобран самый простой метод получения графика функции.
Суть метода: найти несколько точек принадлежащих графику, расставить их на координатной плоскости и соединить. Этот способ не лучший (лучший – построение графиков с помощью элементарных преобразований), но если вы все забыли или ничего не учили, то знайте, что у вас всегда есть план Б – возможность построить график по точкам.
Итак, алгоритм по шагам:
1. Представьте, как выглядит ваш график.
Строить гораздо легче, если вы понимаете, что примерно должны получить в итоге. Поэтому сначала посмотрите на функцию и представьте, как примерно должен выглядеть ее график. Все виды графиков элементарных функций вы можете найти здесь. Этот пункт желательный, но не обязательный.
Все виды графиков элементарных функций вы можете найти здесь. Этот пункт желательный, но не обязательный.
Пример: Построить график функции \(y=-\)\(\frac{2}{x}\)
Данная функция — гипербола с ветвями расположенными во второй и четвертой четверти. Её график выглядит как-то так:
2. Составьте таблицу точек, принадлежащих графику:
Теперь подставим разные значения «иксов» в функцию, и для каждого икса посчитаем значение «игрека».
Пример: \(y=-\)\(\frac{2}{x}\)
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
|
|
Результат вычислений удобно представлять в виде таблицы, примерно такой:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как вы могли догадаться, полученные пары «икс» и «игрек» — это точки, лежащие на нашем графике.
4. Постройте координатную плоскость и отметьте на ней точки из таблицы.
Пример:
5. Если нужно, найдите еще несколько точек и нанесите их на координатную плоскость.
Пример: Чтобы построить график мне не хватает нескольких точек из отрицательной части, а также рядом с осью игрек, поэтому я добавлю столбцы с \(x=-2\), \(x=-4\), \(x=\)\(\frac{1}{2}\) и \(x=-\)\(\frac{1}{2}\)
|
|
| |
|
|
| |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Постройте график
Постройте график
Теперь аккуратно и плавно соединяем точки.
Готово!
Скачать статью
Преобразования функций: сжатие и растяжение
Purplemath
Есть еще два преобразования, но их труднее «увидеть» с какой-либо степенью точности.
Первое из этих преобразований — умножение всей функции. Чтобы увидеть, как это выглядит, сравните графики 2 × f ( x ) = 2 x 2 , f ( x ) = x 2 и ½ × . f ( x ) = (½) x 2 , ниже:
график 2 × f ( x ) = 2 x 2 :
(Это более тонкий график, чем график обычной функции в поле ниже. )
MathHelp.com
график f ( x ) = x 2 :
(Это график обычной функции.)
график ½ × f ( x ) = (½) x 2 :
(Это толще, чем график обычной функции, который был показан в предыдущем поле. )
)
Первая парабола, парабола 2 x 2 , растет вдвое быстрее, чем x 2 (средний график), поэтому ее график получается высоким и тонким. С другой стороны, третья парабола, парабола для функции (½) x 2 , растет вдвое медленнее, чем x 2 , поэтому ее график короткий и толстый.
Грубо говоря, вы можете сказать, что первый график, будучи более тонким, умножается на что-то большее, чем 1, поэтому он растет быстрее, чем стандартный, и что третий график, будучи скватером, умножается на что-то меньшее, чем 1, поэтому он растет медленнее стандартного.Но, как правило, довольно сложно точно сказать, на что был умножен график, просто взглянув на картинку.
Например, можете ли вы сказать, что на графике ниже показано 1,4 × f ( x ) = 1,4 x 2 ?
Вряд ли.
Другой более сложный тип преобразования — это умножение аргумента функции. Часто это очень похоже на умножение всей функции. Например, рассмотрим графики f (2 x ) = (2 x ) 2 , f ( x ) = x 2 и f (½ x ) = (½ x) 2 , ниже:
Часто это очень похоже на умножение всей функции. Например, рассмотрим графики f (2 x ) = (2 x ) 2 , f ( x ) = x 2 и f (½ x ) = (½ x) 2 , ниже:
график f (2 x ) = (2 x ) 2 :
(Этот график растет вдвое быстрее, чем график обычной функции, показанный в следующем поле.)
график f ( x ) = x 2 :
(Это график обычной функции.)
график f (½ x ) = (½ x ) 2 :
(Этот график растет вдвое медленнее, чем график обычной функции, показанный в предыдущем поле.)
Как видите, умножение внутри функции (внутри аргумента функции) приводит к тому, что график становится тоньше или толще. Это очень похоже на другое преобразование умножения, но это преобразование — это умножение вне или на всей функции. И обычно это преобразование практически невозможно идентифицировать на графике или отличить от другого мультипликативного преобразования.
И обычно это преобразование практически невозможно идентифицировать на графике или отличить от другого мультипликативного преобразования.
Иногда, однако, полезно взглянуть на нули графика (если на нем более одного) или поворотные точки, поскольку они будут расширяться (если аргумент умножается на что-то большее, чем 1) или сгруппироваться в сторону ось y (если аргумент умножается на значение, меньшее 1).
Например, если посмотреть на y = x 2 -4, вы увидите, что умножение вне функции не меняет расположение нулей, но умножение внутри функции меняет:
график x 2 — 4:
(Это график f ( x ) с нулями при x = –2, 2)
график 2 × f ( x ) = 2 ( x 2 -4):
(Этот график выше, но нули соответствуют нулю исходной функции, показанной в предыдущем поле. )
график (2 x ) 2 — 4:
(Этот график не только стал выше, но и нули переместились внутрь, до x = –1, 1. )
)
Напомним, что преобразования «влево», «вправо», «вверх», «вниз», «переворот» и «зеркало» довольно просты, но преобразования «умножение», также называемые «растягиванием» и «сжатием» , может получиться немного беспорядочно.Просто надейтесь, что они от вас не часто требуются.
Типичные домашние задания по этой теме просят вас построить график преобразования функции с учетом исходной функции или же просят вас вычислить преобразование с учетом сравнительных графиков.
График f ( x ) = x 4 выглядит так:
Глядя на выражение для этого перевода, «+1» за пределами функции говорит мне, что график будет перемещен на вверх на на одну единицу. И «–2» внутри аргумента говорит мне, что график будет сдвинут на две единицы ВПРАВО. (Помните, что переключение влево-вправо происходит в обратном направлении от ожидаемого.)
Вообще лучше работать изнутри. Итак, я сначала сдвину график вправо на две единицы. Затем я подниму результат на одну единицу.
Затем я подниму результат на одну единицу.
Тогда мой переведенный график выглядит так:
Когда они заставляют вас строить график, перемещая другие графики, они не могут серьезно критиковать ваш рисунок, так как вы не должны делать Т-диаграмму и вычислять точные точки.Но постарайтесь, чтобы ваш график выглядел разумно.
Кстати, вы всегда можете «схитрить», особенно если у вас есть графический калькулятор, быстро построив график y = ( x — 2) 4 + 1 и убедившись, что он соответствует тому, что вы нарисовали. Но вам нужно знать, как выполнять преобразования функций, потому что есть способы задавать вопросы, которые не позволяют обмануть, как мы увидим в следующем разделе.
URL: https: // www.purplemath.com/modules/fcntrans3.htm
Функции — Алгебра — Математика A-Level Revision
В этом разделе рассматриваются функции в рамках более широкой темы алгебры.
Функцию можно рассматривать как правило, которое берет каждый элемент x набора и присваивает ему то же самое значение y , известное на его изображении.
x → Функция → y
Буква f, g или h часто используется для обозначения функции.Функция, которая возводит число в квадрат и добавляет 3, может быть записана как f (x) = x 2 + 5 . То же понятие можно использовать, чтобы показать, как функция влияет на определенные значения.
Пример
f (4) = 4 2 + 5 = 21, f (-10) = (-10) 2 +5 = 105 или альтернативно f : x → x 2 + 5 .
Фраза «y является функцией x» означает, что значение y зависит от значения x, поэтому:
- y можно записать через x (например,грамм. у = 3х).
- Если f (x) = 3x, а y является функцией x (т. Е. Y = f (x)), то значение y, когда x равно 4, равно f (4), которое находится путем замены x «s на 4. «с.
Пример
Если f (x) = 3x + 4, найти f (5) и f (x + 1).
f (5) = 3 (5) + 4 = 19
f (x + 1) = 3 (x + 1) + 4 = 3x + 7
Домен и диапазон
Область функции — это набор значений, которые вам разрешено вводить в функцию (то есть все значения, которые может принимать x).Диапазон функции — это набор всех значений, которые функция может принимать, другими словами, все возможные значения y, когда y = f (x). Итак, если y = x 2 , мы можем выбрать в качестве домена все действительные числа. Диапазон — это все действительные числа, большие (или равные) нулю, поскольку, если y = x 2 , y не может быть отрицательным.
Один к одному
Мы говорим, что функция является взаимно однозначной , если для каждой точки y в диапазоне функции существует только одно значение x такое, что y = f (x).f (x) = x 2 не один к одному, потому что, например, есть два значения x, такие что f (x) = 4 (а именно –2 и 2). На графике функция взаимно однозначна, если любая горизонтальная линия разрезает график только один раз.
На графике функция взаимно однозначна, если любая горизонтальная линия разрезает график только один раз.
Составные функции
fg означает выполнение функции g, затем функции f. Иногда fg записывается как fog
.
Пример
Если f (x) = x 2 и g (x) = x — 1, то
gf (x) = g (x 2 ) = x 2 — 1
fg (x) = f (x — 1) = (х — 1) 2
Как видите, fg не обязательно равно gf
Обратная функция
Обратной функцией функции является функция, которая обращает эффект исходной функции. Например, y = 2x, обратное y = ½ x.
Чтобы найти обратную функцию, поменяйте местами x «s и y» s и сделайте y объектом формулы.
Пример
Найдите обратное к f (x) = 2x + 1
Пусть y = f (x), поэтому y = 2x + 1
поменяет местами x «s и y» s:
x = 2y + 1
Сделайте y объектом формулы:
2y = x — 1, поэтому y = ½ (x — 1)
Следовательно, f -1 (x) = ½ (x — 1)
f -1 (x) — стандартное обозначение, обратное f (x). Говорят, что обратное существует тогда и только тогда, когда существует функция f -1 с ff -1 (x) = f -1 f (x) = x
Говорят, что обратное существует тогда и только тогда, когда существует функция f -1 с ff -1 (x) = f -1 f (x) = x
.
Обратите внимание, что график f -1 будет отражением f в линии y = x.
Это видео объясняет больше об обратной функции
Графики
Функции можно изобразить в виде графиков. Функция является непрерывной , если ее график не имеет разрывов. Примером прерывистого графа является y = 1 / x, поскольку граф нельзя нарисовать, не отрывая карандаш от бумаги:
Функция является периодической , если ее график повторяется через равные промежутки времени, этот интервал называется периодом.
Функция равна даже , если она не изменяется при замене x на -x. График такой функции будет симметричным по оси ординат. Даже функции, которые являются полиномами, имеют четные степени (например, y = x²).
Даже функции, которые являются полиномами, имеют четные степени (например, y = x²).
Функция является нечетной , если знак функции изменяется при замене x на -x. График функции будет иметь симметрию вращения относительно начала координат (например, y = x³).
Функция модуля
Модуль числа — это величина этого числа.Например, модуль -1 (| -1 |) равен 1. Модуль x, | x |, равен x для значений x, которые положительны, и -x для значений x, которые отрицательны. Итак, график y = | x | y = x для всех положительных значений x и y = -x для всех отрицательных значений x:
Преобразование графиков
Если y = f (x), график y = f (x) + c (где c — константа) будет графиком y = f (x), сдвинутым на c единиц вверх (в направлении y- ось).
Если y = f (x), график y = f (x + c) будет графиком y = f (x), сдвинутым на c единиц влево.
Если y = f (x), график y = f (x — c) будет графиком y = f (x), сдвинутым на c единиц вправо.
Если y = f (x), график y = af (x) представляет собой отрезок графика y = f (x), масштабный коэффициент (1 / a), параллельный оси x. [Масштабный коэффициент 1 / a означает, что «растяжение» фактически приводит к сжатию графика, если a — число больше 1]
Пример
График y = | x — 1 | будет таким же, как на приведенном выше графике, но со смещением на одну единицу вправо (так, чтобы точка V ударилась о ось x на 1, а не на 0).
Графики функций квадратного корня
Родительская функция функций формы
ж
Икс
знак равно
Икс
—
а
+
б
является
ж
Икс
знак равно
Икс
.
Обратите внимание, что
домен
из
ж
Икс
знак равно
Икс
является
Икс
≥
0
и
диапазон
является
y
≥
0
.
График
ж
Икс
знак равно
Икс
—
а
+
б
можно получить, переведя график
ж
Икс
знак равно
Икс
к
а
единиц вправо, а затем
б
единиц вверх.
Пример:
Нарисуйте график
y
знак равно
Икс
—
1
+
2
из родительского графа
y
знак равно
Икс
.
Решение:
Шаг 1. Нарисуйте график
y
знак равно
Икс
.
Шаг 2. Переместите график
y
знак равно
Икс
от
1
единицы справа, чтобы получить график
y
знак равно
Икс
—
1
.
Шаг 3. Переместите график
y
знак равно
Икс
—
1
от
2
единиц до получения графика
y
знак равно
Икс
—
1
+
2
.
Область определения функции
y
знак равно
Икс
—
1
+
2
является
Икс
≥
1
.
Диапазон функции
y
знак равно
Икс
—
1
+
2
является
y
≥
2
.
Линейные функции. Уравнение прямой
9
Набросок графика
Форма откоса-пересечения
Доказательство
МЫ НАЧИНАЕМ ИЗУЧЕНИЕ ГРАФИКОВ полиномиальных функций.
Мы обнаружим, что график каждой степени оставляет свою характерную подпись на плоскости x — y .
График полинома первой степени всегда представляет собой прямую линию. График многочлена второй степени — это кривая, известная как парабола. Полином третьей степени имеет вид, показанный справа. Навык координатной геометрии состоит в распознавании этой связи между уравнениями и их графиками. Следовательно, ученик должен знать, что график любого полинома первой степени y = ax + b является прямой линией, и, наоборот, любая прямая линия имеет в своем уравнении y = ax + б .
Рисование графика уравнения первой степени должно быть базовым навыком. См. Урок 33 алгебры.
Пример. Отметьте точки пересечения x и y и нарисуйте график
.
y = 2 x + 6.
Решение .
Перехват x — это корень. Это решение 2 x + 6 = 0. Перехват
x равен −3.
Перехват y — постоянный член, 6.
Итак, что означает утверждение, что y = 2 x + 6 является «уравнением» этой линии?
Это означает, что каждая пара координат ( x , y ), которая есть на графике, решает это уравнение. (Это означает, что координирующая пара находится на графике любого уравнения.) Каждая координированная пара ( x , y ) на этой линии равна
( x , 2 x + 6).
Таким образом, эта линия называется графиком уравнения y = 2 x + 6. А y = 2 x + 6 называется уравнением этой линии.
Каждое уравнение первой степени имеет график прямой. (Мы докажем это ниже.) По этой причине функции или уравнения первой степени, где 1 — старший показатель степени, называются линейными функциями или линейными уравнениями.
Проблема 1.Отметьте точки пересечения x и y и нарисуйте график
.
y = −3 x -3
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Перехват x — это решение для −3 x — 3 = 0. Это x = −1. Перехват y — постоянный член −3.
Задача 2. Нарисуйте график y = −4.
Уравнение вида y = Число, представляет собой горизонтальную линию.
См. Урок алгебры 33, раздел «Вертикальные и горизонтальные линии».
Форма откоса-пересечения
Эта линейная форма
y = ось + b
называется формой с пересечением наклона уравнения прямой.Потому что, как мы сейчас докажем, a — это наклон прямой (Тема 8), а b — постоянный член — это интервал y .
Эта форма первой степени
Топор + По + C = 0
, где A , B , C — целые числа, называется общей формой уравнения прямой.
Теорема. Уравнение
y = ось + b
— это уравнение прямой с наклоном a и y — пересечение b .
Для, прямая линия может быть указана с указанием ее наклона и
координаты одной точки на нем. (Теорема 8.3.)
Следовательно, пусть наклон прямой будет a , и пусть одна точка на ней будет ее пересечением y , (0, b ).
Тогда, если ( x , y ) являются координатами любой точки на этой линии, ее
уклон
| y — b x — 0 | = | y — b x | = a . |
На решение для y ,
y = ax + b .
Следовательно, поскольку переменные x и y являются координатами любой точки на этой прямой, это уравнение является уравнением прямой с наклоном a и y с интервалом b . Что мы и хотели доказать.
Что мы и хотели доказать.
Наклон прямой линии — это число — указывает скорость, с которой значение y изменяется по отношению к значению x .(Тема 8.)
Задача 3. Назовите наклон каждой линии и укажите значение каждого наклона.
а) y = 2 x + 6
Наклон равен 2. Это означает, что y увеличивается на 2 единицы на каждую 1 единицу x .
| Уклон — | 2 3 | .Это означает, что y уменьшается на 2 единицы на каждые |
| 3 шт. Размером x . | ||
c) y = x
Наклон равен 1. Это означает, что y увеличивает на 1 единицу на каждую 1 единицу x . Это функция идентичности.
См. Урок 5.
г) 3 x + 3 y = 1
Только тогда, когда y = ax + b , наклон будет a .Следовательно, при решении для y : y = — x + 1/3. Наклон равен -1. Это означает, что y уменьшается на 1 единицу за каждую единицу, которая увеличивается на x .
Наклон равен -1. Это означает, что y уменьшается на 1 единицу за каждую единицу, которая увеличивается на x .
Следующая тема: Квадраты: многочлены 2-й степени
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Как определить, является ли функция четной, нечетной или нет
Я подготовил восемь (8) рабочих примеров, чтобы проиллюстрировать процедуру или шаги, как выяснить, является ли данная функция четной, нечетной или ни одной из них. Математика, участвующая в расчетах, проста, если вы внимательно относитесь к каждому шагу своего решения.
Чтобы вникнуть в «суть» этой темы, изучите иллюстрацию ниже.
Как определить, является ли функция четной, нечетной или ни той, ни другой
Давайте поговорим о каждом случае.
ВАРИАНТ 1: Четная функция
Дана некоторая «стартовая» функция f \ left (x \ right):
- Если мы вычислим или заменим \ color {red} -x на f \ left (x \ right) и снова получим исходную или «начальную» функцию, это означает, что f \ left (x \ right) является четной функцией .
ВАРИАНТ 2: Нечетная функция
Дана некоторая «стартовая» функция f \ left (x \ right):
- Однако, если мы вычисляем или заменяем \ color {red} -x на f \ left (x \ right) и получаем отрицательное или противоположное значение «начальной» функции, это означает, что f \ left (x \ right) равно нечетная функция .
ВАРИАНТ 3: ни четная, ни нечетная функция
Дана некоторая «стартовая» функция f \ left (x \ right):
- Если мы вычислим или заменим \ color {red} -x на f \ left (x \ right) и мы не получим ни одного, ни второго случая, это означает, что f \ left (x \ right) равно ни даже ни нечетный .
 Другими словами, он не подпадает под классификацию четных или нечетных.
Другими словами, он не подпадает под классификацию четных или нечетных.
Примеры того, как алгебраически определить, является ли функция четной, нечетной или ни одной из них
Пример 1 : Определите алгебраически, является ли данная функция четной, нечетной или ни одной из них.2} — 3, вставьте значение \ color {red} -x и затем упростите. Что я получу? Давайте разберемся алгебраически.
Поскольку f \ left ({{\ color {red} — x}} \ right) = f \ left (x \ right), это означает, что f \ left (x \ right) является четной функцией !
График четной функции симметричен относительно оси y или вдоль вертикальной линии x = 0. Обратите внимание, что график функции равномерно срезан по оси y, и каждая половина является точным зеркалом другой. . Другой способ описания состоит в том, что каждая половина функции является отражением по оси y.3} + 2x, а затем упростить.
Как определить нечетную функцию
Важные советы, которые следует запомнить:
- Если вы когда-нибудь придете к другой функции после вычисления \ color {red} –x в заданном f \ left (x \ right), немедленно попробуйте вынести из него -1 и посмотреть, появляется ли исходная функция.
 Если это так, то у нас есть нечетная функция .
Если это так, то у нас есть нечетная функция .
- Эффект вычитания −1 приводит к изменению знаков членов внутри скобок.Это ключевой шаг для выявления нечетной функции.
Теперь, поскольку f \ left ({{\ color {red} — x}} \ right) = — f \ left (x \ right), это означает, что исходная функция f \ left (x \ right) является нечетная функция !
График нечетной функции имеет симметрию вращения относительно начала координат или в точке \ left ({0,0} \ right). 3} + 6x
В отличие от примера 3, где функция имеет четные степени, эта функция имеет нечетные степени, которые равны 7, 5, 3 и 1.К настоящему времени, я надеюсь, вы уже видите закономерность. Скорее всего, это странная функция, но мы проверим.
Подставляя \ color {red} -x в заданное f \ left (x \ right) и упрощая, получаем:
После вычитания −1 многочлен в скобках равен начальной функции. Он показывает, что это нечетная функция !
Пример 5 : Определить, является ли данная функция четной, нечетной или ни одной:
На этот раз я покажу вам пример функции, которая не является ни четной, ни нечетной. Вы готовы?
Вы готовы?
- Сначала проверьте, четный ли он. У нас есть случай f \ left ({\ color {red} {- x}} \ right) = f \ left (x \ right)?
Определенно не является четной функцией , поскольку f \ left ({\ color {red} {- x}} \ right) \ ne f \ left (x \ right).
- Во-вторых, проверьте, не является ли он нечетным, указав f \ left ({\ color {red} {- x}} \ right) = — f \ left (x \ right).
Даже после вычитания −1 я все еще не могу получить исходную функцию.
Это , не нечетная функция , так как f \ left ({\ color {red} {- x}} \ right) \ ne — f \ left (x \ right).
- Заключение: Поскольку мы достигли случая, когда f \ left ({\ color {red} {- x}} \ right) \ ne f \ left (x \ right) и f \ left ({\ color {red} { — x}} \ right) \ ne — f \ left (x \ right), эта функция не является ни четным, ни нечетным !
Пример 6 : Определите, является ли данная функция четной, нечетной или ни одной:
Решение:
Следовательно, функция g \ left (x \ right) является нечетной функцией !
Пример 7 : Определить, является ли данная функция четной, нечетной или ни одной:
Решение:
Следовательно, функция h \ left (x \ right) равна ни !
Пример 8 : Определить, является ли данная функция четной, нечетной или ни одной:
Решение:
Следовательно, функция k \ left (x \ right) является четной функцией !
Практика с рабочими листами
Нарисуйте график функции y = 1 + sin 2 x без использования калькулятора.

Построение линии на плоскости В упражнениях 35-42 нарисуйте график уравнения. x + 2y + 6 = 0
Исчисление: ранние трансцендентальные функции
Изобразите функцию вручную, не путем нанесения точек, а начав с графика одной из стандартных функций …
Исчисление: ранние трансцендентальные
Составные дроби Упростите составное дробное выражение. 66. x + yxy + xy
Precalculus: математика для расчетов (автономная книга)
Доходы и прибыль Доходы и прибыль Walt Disney Company за 2011 и 2013 годы показаны в таблице.(a …
Исчисление: прикладной подход (список курсов MindTap)
Преобразуйте каждое выражение в упражнениях 25-50 в его технологический эквивалент формулы, как в таблице в тексте. …
Конечная математика и прикладное исчисление (Список курсов MindTap)
Упростите выражения в упражнениях 97106. x3 / 2×5 / 2
Прикладное исчисление
Покажите, что последовательность, определенная как a1 = 2an + 1 = 13an, удовлетворяет 0 и 2 и убывает. Выведите, что последовательность …
Выведите, что последовательность …
Многопараметрическое исчисление
Исследователя интересуют привычки отправлять текстовые сообщения старшеклассникам в США.Исследователь …
Основы статистики для поведенческих наук (список курсов MindTap)
SOC Большой выборке респондентов была введена шкала для измерения предубеждений. Распределение sco …
Essentials Of Statistics
Найдите все точки на графике функции f (x) = 2sinx + sin2x, в которых касательная линия горизонтальна.
Исчисление (Список курсов MindTap)
Опишите разницу во внешнем виде между гистограммой и гистограммой и опишите обстоятельства, при которых…
Статистика для поведенческих наук (список курсов MindTap)
Используйте определение непрерывности и свойства пределов, чтобы показать, что функция непрерывна на …
Исчисление одной переменной
В упражнениях 47- 52, найдите и упростите f (a + h) f (a) h (h0) для каждой функции. 52. f (x) = x
Прикладное исчисление для управленческих, жизненных и социальных наук: краткий подход
Для задач 19–24 предоставьте следующую информацию. а) Каков уровень значимости? Укажите …
а) Каков уровень значимости? Укажите …
Понимание базовой статистики
Не существует хорошей формулы для стандартного нормального cdf (z), но было опубликовано несколько хороших приближений i …
Вероятность и статистика для инженерии и науки
Перерыв -Даже анализ OHaganBooks.com также получает доход через свою службу электронных книг oBooks. Гонорары авторов …
Конечная математика
Обратитесь к пирамидам упражнений 3 и 4.Какие из них обладают симметрией относительно линии?
Элементарная геометрия для студентов колледжа, 7e
Для задач 5-54 выполните следующие операции с действительными числами. Задачи 3-6 2.738.14
Intermediate Algebra
32. Напишите общее выражение для.
Математические приложения для управления, жизни и социальных наук
Выполните указанные операции и упростите: 536 + 1172 + 56
Элементарная техническая математика
ЭКСКУРСИИ Решите каждую из следующих головоломок. Примечание: авторы этого учебника не связаны …
Примечание: авторы этого учебника не связаны …
Математические экскурсии (список курсов MindTap)
Нарисуйте область и найдите ее область (если область конечна). 42. S = {(x, y) | x0,0yex}
Исчисление одной переменной: ранние трансцендентальные методы
Определение вогнутости В упражнениях 5-16 определите открытые интервалы, на которых строится график функции …
Вычисление одной переменной
Предположим, что алфавит состоит из букв от a до z в естественном порядке, за которыми следует пробел, а затем цифры от 0 до…
Элементы современной алгебры
Решите уравнение. При необходимости проверьте свои решения x + 42 = 43
Тригонометрия (список курсов MindTap)
Решите следующие задачи, используя 6,2%, до 117 000 долларов США, для налога на социальное обеспечение и 1,45%, без ограничения заработной платы, для …
Современная математика для бизнеса и потребителей
Верно ли:
Если f ′ (x) = g ′ (x), то f (x) = g (x).
Учебное пособие по исчислению одной переменной Стюарта: ранние трансцендентальные числа, 8-е
Площадь боковой поверхности В упражнениях 43 и 44 найдите площадь боковой поверхности над кривой C в xy-pla…
Исчисление: ранние трансцендентные функции (список курсов MindTap)
Полярное уравнение коники с эксцентриситетом 3 и директрисой x = −7 имеет следующий вид:
Учебное пособие по многомерному исчислению Стюарта, 8-е
Найдите такие условия a, b и d, что 22 верхняя треугольная матрица A = [ab0d] имеет обратную. Квадратная матрица i …
Конечная математика для управленческих, жизненных и социальных наук
В упражнениях с 1 по 4 используйте деление, чтобы написать уравнение в форме Ax + By = C, которое эквивалентно одному провайдеру…
Элементарная геометрия для студентов колледжа
Движение пружины В упражнении 55-58 сопоставьте дифференциальное уравнение с графиком конкретного решения. …
Многопараметрическое исчисление
Использование интегрирования по частям В упражнениях 11-14 найдите неопределенный интеграл, используя интегрирование по частям с …
Исчисление (список курсов MindTap)
Верно или неверно? В упражнениях 87–92 определите, истинно это утверждение или нет. Если это неверно, объясните, почему…
Если это неверно, объясните, почему…
Исчисление
Является ли следующая гипотеза проверяемой, опровергаемой и положительной? Поясните свой ответ. Гипотеза: Люди, которые молятся …
Методы исследования поведенческих наук (список курсов MindTap)
Снижают ли перерывы во время работы вашу продуктивность? По данным Калифорнийского университета Ирвайн …
Статистика для бизнеса и экономики, пересмотренная (Список курсов MindTap)
Открытие и написание Докажите, что уравнение линии с пересечением по оси x, 0 и пересечением по оси 0, б может быть…
Колледж по алгебре (Список курсов MindTap)
Выполните следующие упражнения для механического цеха. На показанной пластине нужно высверлить три круга. Диаметр 4.000 дюймов …
Математика для машинной технологии
Объясните общие преимущества и недостатки внутрипредметного дизайна по сравнению с межпредметным дизайном …
Методы исследования поведенческих наук (список курсов MindTap)
Выборка из 16 элементов дает стандартное отклонение выборки, равное 9. 5. Проверьте следующие гипотезы, используя = .05. W …
5. Проверьте следующие гипотезы, используя = .05. W …
СТАТИСТИКА F / БИЗНЕС + ЭКОНОМИКА-ТЕКСТ
Инженерно-строительная фирма в настоящее время работает над электростанциями на трех разных площадках. Определите события E …
Введение в статистику и анализ данных
Анализ удовлетворенности работой. Напомним, что в упражнении 50 директор по персоналу Electronics Associates разработал …
Основы статистики для бизнеса и экономики
Немногим ученикам удается завершить учебу, не пройдя стандартизированный вступительный тест, такой как Schol…
Математика: практическая одиссея
2. Десять человек приняли участие в вкусовом тесте с участием двух марок продукта. Примеры результатов показывают, что 7 предпочитают …
Современная бизнес-статистика с Microsoft Office Excel (с печатной картой доступа XLSTAT Education Edition) (Список курсов MindTap)
Нарисуйте картинку, чтобы проиллюстрировать лемму 10.1.1 (c): Если график G соединен и G содержит схему, затем ребро …
Дискретная математика с приложениями
Заполните квадрат для x2 + 8x и запишите результат в виде полного квадрата.
Функции и изменения: подход к моделированию алгебры колледжа (список курсов MindTap)
Средняя рабочая неделя для инженеров В начинающей компании считается около 60 часов. Недавно нанятый инженер …
Вводная статистика
В следующих упражнениях оцените интеграл с помощью формул площади. 83. 23 (3 | x |) dx
Calculus Volume 2
Верно или неверно? В упражнениях 91–93 определите, истинно это утверждение или нет. Обосновать ответ.Гип …
College Algebra
В задачах 39 и 40 используйте метод исключения Гаусса-Джордана, чтобы продемонстрировать, что данная система уравнений не имеет решения …
Первый курс по дифференциальным уравнениям с приложениями для моделирования (список курсов MindTap )
Для следующих упражнений каждый график имеет вид y = AsinBxory = AcosBx, где B> 0.
Квадратичная функция и ее график
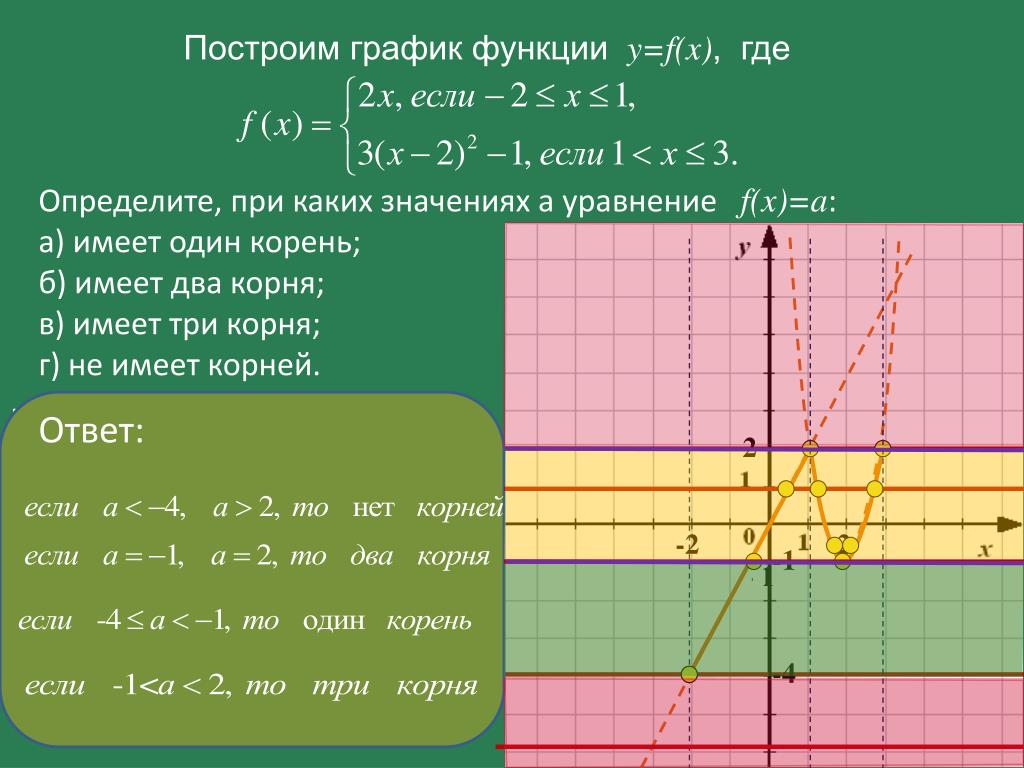
В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида , где называется квадратичной функцией.
В уравнении квадратичной функции:
a — старший коэффициент
b — второй коэффициент
с — свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:
Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:
Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.
График функции имеет вид:
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.
Итак, мы заметили:
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.
Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.
Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции — это точки пересечения графика функции с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .
В случае квадратичной функции нужно решить квадратное уравнение .
Теперь внимание!
В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:
Если ,то график функции выглядит как-то так:
2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:
3. Если ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:
,
Если ,то график функции выглядит примерно так:
Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный параметр графика квадратичной функции — координаты вершины параболы:
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой .
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции
1. Направление ветвей параболы.
Так как ,ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена
Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение:
,
3. Координаты вершины параболы:
4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:
Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции
Кррдинаты вершины параболы
Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:
Нанесем эти точки на координатную плоскость и соединим плавной линией:
2. Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболы
Уравнение квадратичной функции имеет вид — в этом уравнении — координаты вершины параболы
или в уравнении квадратичной функции , и второй коэффициент — четное число.
Построим для примера график функции .
Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно
- сначала построить график функции ,
- затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:
Теперь рассмотрим построение графика функции . В уравнении этой функции , и второй коэффициент — четное число.
Выделим в уравнении функции полный квадрат:
Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):
3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда
2. Координаты вершины параболы:
3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:
График квадратичной функции.
Перед вами график квадратичной функции вида .
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения ,
— сдвига графика функции вдоль оси от значения
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :
Скачать таблицу квадратичная функция
И.В. Фельдман, репетитор по математике.
Исследование функции онлайн y=f(x). Исследовать график функции.
Введите график функции
Исследуем график функции y=f(x), для этого задайте функцию f(x). 2*arctgh(x)*arcctgh(x)
2*arctgh(x)*arcctgh(x)
Что исследует?
Для периодических функций идет исследование графика функции только на промежутке периода
Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции
Что умеет находить этот калькулятор:
- Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
- Умеет определять точки пересечения графика функции с осями координат: Да
- Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
- Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
- Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
- Горизонтальные асимптоты графика функции: Да
- Наклонные асимптоты графика функции: Да
- Четность и нечетность функции: Да
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- Действительные числа
- вводить в виде 7.
 3
3 - — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Графические квадратные уравнения с использованием оси симметрии
Квадратное уравнение это многочлен уравнение степень 2 . Стандартная форма квадратного уравнения:
0 знак равно а Икс 2 + б Икс + c
где а , б и c все реальные числа и а ≠ 0 .
Если мы заменим 0 с участием у , то получаем квадратичная функция
у знак равно а Икс 2 + б Икс + c
чей граф будет
парабола
.
Осью симметрии этой параболы будет линия Икс знак равно — б 2 а . Ось симметрии проходит через вершину, поэтому Икс -координата вершины — б 2 а .Заменять Икс знак равно — б 2 а в уравнении, чтобы найти у -координата вершины. Заменить еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -значения и нанесите точки. Присоединяйтесь к ним и вытяните параболу.
Пример 1:
Постройте параболу у знак равно Икс 2 — 7 Икс + 2 .
Сравните уравнение с
у
знак равно
а
Икс
2
+
б
Икс
+
c
найти значения
а
,
б
, и
c
.
Здесь, а знак равно 1 , б знак равно — 7 и c знак равно 2 .
Используйте значения коэффициентов, чтобы написать уравнение ось симметрии .
График квадратного уравнения в виде у знак равно а Икс 2 + б Икс + c осью симметрии является линия Икс знак равно — б 2 а . Итак, уравнение оси симметрии данной параболы имеет вид Икс знак равно — ( — 7 ) 2 ( 1 ) или Икс знак равно 7 2 .
Заменять
Икс
знак равно
7
2
в уравнении, чтобы найти
у
-координата вершины.
у знак равно ( 7 2 ) 2 — 7 ( 7 2 ) + 2 знак равно 49 4 — 49 2 + 2 знак равно 49 — 98 + 8 4 знак равно — 41 год 4
Следовательно, координаты вершины равны
(
7
2
,
—
41 год
4
)
.
А теперь замените еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -ценности.
| Икс | у знак равно Икс 2 — 7 Икс + 2 |
| 0 | 2 |
| 1 | — 4 |
| 2 | — 8 |
| 3 | — 10 |
| 5 | — 8 |
| 7 | 2 |
Постройте точки и соедините их, чтобы получить параболу.
Пример 2:
Постройте параболу у знак равно — 2 Икс 2 + 5 Икс — 1 .
Сравните уравнение с у знак равно а Икс 2 + б Икс + c найти значения а , б , и c .
Здесь, а знак равно — 2 , б знак равно 5 и c знак равно — 1 .
Используйте значения коэффициентов, чтобы написать уравнение оси симметрии.
График квадратного уравнения в виде
у
знак равно
а
Икс
2
+
б
Икс
+
c
осью симметрии является линия
Икс
знак равно
—
б
2
а
. Итак, уравнение оси симметрии данной параболы имеет вид
Икс
знак равно
—
(
5
)
2
(
—
2
)
или
Икс
знак равно
5
4
.
Итак, уравнение оси симметрии данной параболы имеет вид
Икс
знак равно
—
(
5
)
2
(
—
2
)
или
Икс
знак равно
5
4
.
Заменять Икс знак равно 5 4 в уравнении, чтобы найти у -координата вершины.
у знак равно — 2 ( 5 4 ) 2 + 5 ( 5 4 ) — 1 знак равно — 50 16 + 25 4 — 1 знак равно — 50 + 100 — 16 16 знак равно 34 16 знак равно 17 8
Следовательно, координаты вершины равны
(
5
4
,
17
8
)
.
А теперь замените еще несколько Икс -значения в уравнении, чтобы получить соответствующие у -ценности.
| Икс | у знак равно — 2 Икс 2 + 5 Икс — 1 |
| — 1 | — 8 |
| 0 | — 1 |
| 1 | 2 |
| 2 | 1 |
| 3 | — 4 |
Постройте точки и соедините их, чтобы получить параболу.
Пример 3:
Постройте параболу Икс знак равно у 2 + 4 у + 2 .
Здесь, Икс является функцией у . Парабола открывается «вбок», а ось симметрии параболы горизонтальна. Стандартная форма уравнения горизонтальной параболы: Икс знак равно а у 2 + б у + c где а , б , и c все реальные числа и а ≠ 0 а уравнение оси симметрии имеет вид у знак равно — б 2 а .
Сравните уравнение с
Икс
знак равно
а
у
2
+
б
у
+
c
найти значения
а
,
б
, и
c
.
Здесь, а знак равно 1 , б знак равно 4 и c знак равно 2 .
Используйте значения коэффициентов, чтобы написать уравнение оси симметрии.
График квадратного уравнения в виде Икс знак равно а у 2 + б у + c осью симметрии является линия у знак равно — б 2 а . Итак, уравнение оси симметрии данной параболы имеет вид у знак равно — 4 2 ( 1 ) или у знак равно — 2 .
Заменять
у
знак равно
—
2
в уравнении, чтобы найти
Икс
-координата вершины.
Икс знак равно ( — 2 ) 2 + 4 ( — 2 ) + 2 знак равно 4 — 8 + 2 знак равно — 2
Следовательно, координаты вершины равны ( — 2 , — 2 ) .
А теперь замените еще несколько у -значения в уравнении, чтобы получить соответствующие Икс -ценности.
| у | Икс знак равно у 2 + 4 у + 2 |
| — 5 | 7 |
| — 4 | 2 |
| — 3 | — 1 |
| — 1 | — 1 |
| 0 | 2 |
| 1 | 7 |
Постройте точки и соедините их, чтобы получить параболу.
Графические квадратичные функции: больше примеров
Графики Квадратичные функции: примеры (стр. 4 из 4)
Разделы: Введение, Значение старшего коэффициента / Вершина, Примеры
- Найдите перехваты x и вершина y = x 2 4 x + 2.
Так как это так просто найти y -перехват (и в любом случае это будет точка на моей Т-диаграмме), они всего лишь просят x -перехватов в этот раз. Чтобы найти перехват x , Я поставил y равно 0 и решаем:
0 = x 2 4 х + 2
x 2 + 4 х 2 = 0
Для построения графиков
точки перехвата находятся примерно на (4. 4,
0) и (0,4,
0). (Когда я пишу
в ответ, я, конечно, буду использовать «точную» форму с
квадратные корни; десятичные приближения моего калькулятора предназначены только для
Помогая мне график.)
4,
0) и (0,4,
0). (Когда я пишу
в ответ, я, конечно, буду использовать «точную» форму с
квадратные корни; десятичные приближения моего калькулятора предназначены только для
Помогая мне график.)
Чтобы найти вершину, я посмотрите на коэффициенты: = 1 и b = 4. Тогда:
Найти к , Вилка х = 2 дюйма для x через у = х 2 4 x + 2, и упростить:
Сейчас найду дополнительные точек на графике, чтобы помочь мне заполнить график:
Обратите внимание, что я выбрал значения x которые были сосредоточены вокруг координаты x вершины.Теперь построю параболу:
.Вершина в (2, 6), и перехваты находятся на следующие точки:
(0, 2),, и
- Найдите x -перехваты
и вершина y = x 2 + 2 x 4.

Чтобы найти вершину, я посмотрите на коэффициенты: = 1 и b = 2. Тогда:
Найти к , Воткну х дюйм для x и упростить:
Вершина находится ниже x — ось, и, поскольку это отрицательная квадратичная величина, я знаю, что парабола равна будет перевернутым.Так может ли моя линия пересечь ось x ? Могут ли быть какие-нибудь перехваты x ? Конечно, нет! Поэтому я ожидаю получить «нет (настоящего) решения», когда Пытаюсь найти x -перехваты, но мне все равно нужно показать свою работу. Чтобы найти перехват x , Я поставил y равно 0 и решаем:
0 = x 2 + 2 х 4
x 2 2 х + 4 = 0
Как только получу отрицательный
внутри квадратного корня, я знаю, что не могу получить наглядное решение.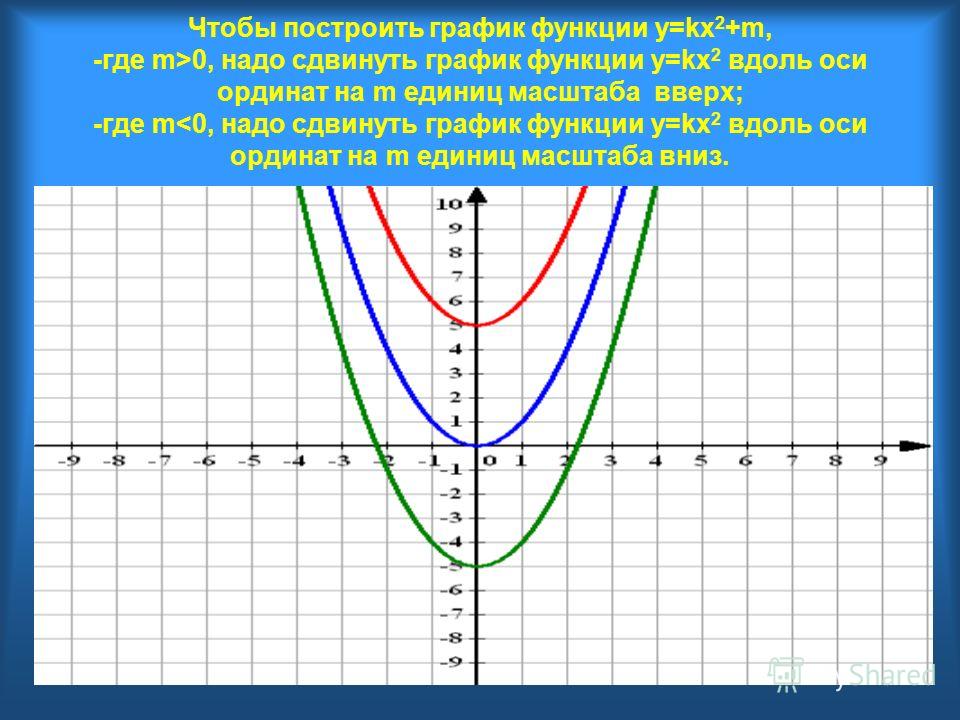 Итак, как и ожидалось, нет никаких перехватов x .
Теперь я найду несколько дополнительных точек на графике, чтобы заполнить свой график:
Итак, как и ожидалось, нет никаких перехватов x .
Теперь я найду несколько дополнительных точек на графике, чтобы заполнить свой график:
Обратите внимание, что я выбрал значения x которые были сосредоточены вокруг координаты x вершины. Теперь построю параболу: авторское право Элизабет Стапель 2002-2011 Все права защищены
Вершина в (1, 3), и единственный перехват находится в (0, 4).
Это последнее упражнение иллюстрирует
таким образом вы можете немного сократить свою работу. Если вы решите для вершины
сначала вы можете легко определить, нужно ли вам продолжить и искать x -перехват,
или если вы можете сразу перейти к нанесению некоторых точек и построению графика.
Если вершина ниже оси x (то есть, если y -значение
отрицательна), а квадратичная отрицательна (парабола открывается вниз),
тогда не будет х -перехватов. Аналогично, если вершина находится выше оси x (то есть, если y -значение
положительна), а квадратичная положительна (так что парабола открывается вверх),
тогда не будет х -перехватов.
Аналогично, если вершина находится выше оси x (то есть, если y -значение
положительна), а квадратичная положительна (так что парабола открывается вверх),
тогда не будет х -перехватов.
На большинстве графиков
Я сделал (правда, не первый), так уж получилось, что баллы
на Т-диаграмме были симметричны относительно вершины; то есть, что точки
«совпадают» по обе стороны от вершины.Пока парабола
всегда симметрично относительно вертикальной линии, проходящей через вершину (параболы
«ось»), точки Т-диаграммы могут быть несимметричными. Особенно,
точки Т-диаграммы не будут «совпадать», если координата x вершины не является целым числом или половинным числом
(например, «3,5»).
Предупреждение: не ждите, что сюжетные точки всегда будут «совпадать» на
обе стороны от вершины; в частности, не делайте половину баллов на
ваш T-график, а затем «заполните» остальную часть вашего T-графика,
предполагая симметрию, которая может не существовать.
Другие советы по построению графиков: Если парабола будет «тощей», то ожидайте, что вы получат очень большие значения на вашем Т-графике. Вы либо закончите с действительно высоким графиком или довольно коротким T-графиком. Если парабола будет «толстым», тогда ожидайте, что у вас, вероятно, будет для построения точек с дробями в качестве координат. В любом случае, когда вы иди, чтобы соединить точки, чтобы нарисовать параболу, это может тебе пригодиться повернуть бумагу на бок и сначала прорисовать действительно изогнутую часть вершину, убедившись, что она выглядит красивой и круглой.Затем переверните бумагу спиной правой стороной вверх и нарисуйте «стороны» параболы.
Предупреждение: нарисуйте свои графики
достаточно большой, чтобы его хорошо видел ваш инструктор. Если вы подходите больше
чем два или, может быть, три графика на одной стороне стандартного листа бумаги,
тогда вы рисуете свои графики слишком маленькими.
<< Предыдущая Вверх | 1 | 2 | 3 | 4 | Вернуться к индексу
Цитируйте эту статью как: | Стапель, Елизавета.«Графические квадратичные функции: примеры». Purplemath .
Доступно по номеру |
Проблема 5
Проблема 55. Ничья график y = f ( x ) = x 2 + 2 x — 8.
- а) Что такое перехват и ?
- б) Каковы корни?
- в) Каковы координаты вершины?
- г) Запишите уравнение в стандарте или вершине
форма.

- e) Решить относительно x
x 2 + 2 x -8 > 0
Прежде чем рисовать график, нужно ответить на вопросы а), б), и в).
а) Что такое перехват и ?
Пересечение y — это точка на графике, координата которой x равна 0. Итак, пусть x = 0 в уравнении, и мы получим
y = (0) 2 + 2 (0) — 8 = 0 + 0-8 = -8.Это показывает, что пересечение y всегда является постоянным членом в полиноме.
верх
б) Какие корни?
Корни — это еще одно название перехватов x . Они точек на графике, координаты которых y равны 0. Итак, пусть y = 0 в уравнение и получаем
0 = x 2 + 2 x — 8 Это дает нам квадратное уравнение в x .& mbsp; Нам повезло
чтобы на одной стороне уже был 0, поэтому мы готовы к факторизации.
Установите коэффициенты = 0.
x — 2 = 0 или x + 4 = 0Решить относительно x
x = 2 или x = -4верх
в) Какие координаты вершины?
Если мы воспользуемся формулой для координаты x вершины, то
получаем
или
х = -1Теперь, когда у нас есть координата x- вершины, мы запускаем это число через функцию, чтобы найти координату y-
y = f (-1) = (-1) 2 + 2 (-1) — 8 = 1-2-8 = -9Итак, вершина находится в (-1, -9)
верх
Перед построением графика рекомендуется получить всю эту информацию.
указывает, чтобы нарисовать график.Когда мы наносим точки, поскольку теперь мы знаем, что
координата x вершины равна -1, мы хотим, чтобы -1 находился в
середина x , которые мы рисуем. Нам также понадобятся корни, x = -4
и 2, чтобы быть в интервале, содержащем x , которые мы строим, и в
хотя бы одна точка по другую сторону корней от вершины.
Нам также понадобятся корни, x = -4
и 2, чтобы быть в интервале, содержащем x , которые мы строим, и в
хотя бы одна точка по другую сторону корней от вершины.
Когда мы строим эти точки, получаем
верх
г) Запишите уравнение в виде вершины.
Уравнение составляет
y = x 2 + 2 x — 8Половина линейного коэффициента равна 1, а квадрат 1 равен 1, поэтому складываем и вычитаем 1
y = x 2 + 2 x + 1-1-8Это упрощается до
y = ( x + 1) 2 — 9и мы видим координаты вершины в уравнении.
верх
e) Решите относительно x
x 2 + 2 x -8 ≥ 0 В процессе построения графика мы обнаружили
что корни были в -4 и 2. Когда мы делим действительное число на прямую
в промежутки между корнями, и проверьте x в каждом
интервал.
Так как равенство разрешено, конечные точки интервалов, корни, являющиеся x , которые дадут ответы, равные 0 при подстановке в формулу будут решения.Итак, рисуем квадратные скобки вокруг конечных точек.
Набор решений — это набор x , которые удовлетворяют
x ≤ -4 или x ≥ 2
В интервальной записи получается
.(-∞, -4] ∪ [2, ∞)
верх
Вернуться к тесту
Графические уравнения и системы уравнений с программой «Пошаговое решение математических задач»
ВВЕДЕНИЕ В КВАДРАТИКУ
Цели
В этом разделе вы будете складывать, вычитать, умножать и строить квадратичные диаграммы.
Словарь : Стандартный формат квадратного уравнения : y = ax 2 + bx + c ; a, b, c — постоянные; x — независимая переменная, а y — зависимая переменная. Квадраты также называются полиномами второй степени , потому что наивысший показатель степени равен 2. Уравнение пересечения наклона из второй главы y = mx + b называется полиномом первой степени , потому что наивысший показатель степени равен единице.
Квадраты также называются полиномами второй степени , потому что наивысший показатель степени равен 2. Уравнение пересечения наклона из второй главы y = mx + b называется полиномом первой степени , потому что наивысший показатель степени равен единице.
Зачем изучать квадратичность? Графики квадратных уравнений приводят к параболам (U-образные графики, открывающиеся вверх или вниз).Эта особенность квадратичности делает их хорошими моделями для описания пути объекта в воздухе или описания прибыли компании (примеры которых вы можете увидеть в конечной математике или в микроэкономике).
Пример 1. Мальчик, лежащий на спине, стреляет из пращи камнем прямо в воздух с начальной скоростью (силой, которую мальчик использует для выстрела камня) 64 фута в секунду. Квадратное уравнение, моделирующее высоту скалы, равно
.ч = -16т 2 + 64т.
а. Найдите высоту камня при t = 0.
В формуле h = -16t 2 + 64t, заменить t на 0.
ч = -16 (0) 2 +64 (0)
ч = 0
Камень находится на нулевом уровне в воздухе за 0 секунд. (Это точка прямо перед тем, как он стреляет камнем в воздух.)
г. Найдите высоту камня при t = 1.
В формуле h = -16t 2 + 64t, заменить t на 1.
Камень за одну секунду находится на высоте 48 футов в воздухе.
Объяснение : Возводится в квадрат только «1». -16 умножается на 1 2
г. Найдите высоту камня при t = 2.
В формуле h = -16t 2 + 64t, заменить t на 2.
Камень поднимается на 64 фута за 2 секунды.
Объяснение : Порядок операций требует, чтобы вы применяли экспоненты перед умножением.
г. Найдите высоту камня при t = 3.
В формуле h = -16t 2 + 64t заменить t на 3.
Камень составляет 48 футов в воздухе за 3 секунды.
e. Найдите высоту камня при t = 4.
В формуле h = -16t 2 + 64t, заменить t на 4.
Камень находится на нулевом уровне в воздухе за 4 секунды; то есть камень ударился о землю.
ф. Постройте график точек, полученных в частях от a до e.
Высота камня зависит от времени, поэтому h — зависимая переменная, а t — независимая переменная.Точки имеют вид (t, h).
Согласно графику, скала достигает максимальной высоты за 2 секунды. Максимальная высота 64 фута. Точка максимума или минимума квадратичной называется вершиной. Вы узнаете, как найти вершину в Разделе 4.3, Квадратичные приложения и графики.
Согласно графику, камень оказывается на земле в 0 секунд (прямо перед тем, как мальчик стреляет в него) и в 4 секунды (когда камень приземляется). Эти точки являются отсечками времени.Вы узнаете, как их найти, в следующем разделе 4.2, «Приложения квадратичной формулы».
Сложение и вычитание квадратичных:
Словарь : Чтобы добавить или вычесть квадратичные, объедините одинаковые термины. Подобные термины , первоначально представленные в Разделе 1.3, «Упрощение алгебраических выражений», имеют одинаковую переменную и одинаковый показатель степени. Например, 2x 2 и 5x 2 похожи на термины, а 3x 2 и 7x — нет.
Подобные термины , первоначально представленные в Разделе 1.3, «Упрощение алгебраических выражений», имеют одинаковую переменную и одинаковый показатель степени. Например, 2x 2 и 5x 2 похожи на термины, а 3x 2 и 7x — нет.
Коэффициент , первоначально представленный в разделе 1.3 «Упрощение алгебраических выражений», является числом, умножающим переменную. Например, коэффициент при 2x равен 2, а коэффициент при -x 2 равен -1.
Правило: Чтобы объединить одинаковые термины, сложите их коэффициенты
Напомним о распределительном свойстве : определение a (b + c) = ab + ac.
Не удалось объединить непохожие термины в скобках, поэтому мы использовали свойство распределения.После этого мы умножили 6x на 3, а затем -5 на 3.
Использовали свойство распределения и объединили аналогичные термины.
Пример 5. Уравнение прибыли: Прибыль = Выручка — Затраты
Если уравнение дохода для компании:
, а уравнение затрат:
найти уравнение прибыли для компании.
Подставил уравнения доходов и затрат в формулу прибыли. Необходимо использовать скобки.
Использовал свойство распределения и умножил уравнение доходов на 1, а уравнение затрат на -1.
Объединенные одинаковые термины.
Подставил уравнения доходов и затрат в формулу прибыли. Необходимо использовать круглые скобки. Использовал распределительное свойство. Умножил уравнение доходов на 1 и уравнение затрат на -1. Сочетание подобных терминов.
Умножение двух биномов.
Словарь : В биноме есть два члена (точно так же, как у велосипеда два колеса).
Правило: Чтобы умножить два бинома, умножьте каждый член первого члена на каждый член второго.
Пример 7. Умножаем (x + 2) (5x + 3).
Умножить x на 5x и 3 и умножить 2 на 5x и 3.
Объединить похожие термины.
FOIL — это простая мнемоника, чтобы запомнить, как умножить два бинома.
Пример 8. Умножаем (8x + 6) (x + 7).
Учебный совет: Напишите карточку с объяснением мнемонической ФОЛЬГИ. Часто просматривайте карту.
Резюме
Квадраты — важные уравнения в физике и микроэкономике.Техника сложения и вычитания квадратичных такая же, как мы практикуем весь семестр; то есть складывать или вычитать похожие термины. Для умножения используйте свойство распределения или FOIL. Вершина квадратичной будет объяснена более подробно в разделе «Графики квадратичных вычислений и приложения». Вершина — это точка максимума или минимума на квадратичном графике.
ПРИМЕНЕНИЕ КВАДРАТИЧЕСКОЙ ФОРМУЛЫ
Цель
В этом разделе показано, как решать квадратные уравнения.
Словарь : квадратное уравнение — это ax 2 + bx + c = 0. a, b и c — константы, а x — переменная.
Квадратичная формула ,, используется для решения квадратного уравнения.
Анализируем
Учебный совет: Напишите квадратное уравнение и квадратную формулу на карточках для заметок, чтобы вы могли ссылаться на них при выполнении домашнего задания.
Пример 1. Предположим, вы стоите на вершине утеса на высоте 375 футов над дном каньона и подбрасываете в воздух камень с начальной скоростью 82 фута в секунду.Уравнение, моделирующее высоту скалы над дном каньона:
ч = -16т 2 + 82т + 375.
Узнайте, сколько времени требуется камню, чтобы упасть на дно каньона.
Найдите t, когда h = 0.
Решите 0 = -16t 2 + 82t + 375.
Определите константы a, b и c.
Объяснение : Одна часть квадратного уравнения должна быть равна нулю.
а = -16, б = 82, с = 375
Пояснение :
a — коэффициент переменной, возведенный в квадрат.
b — коэффициент переменной в первой степени.
c — постоянная.
Используйте формулу корней квадратного уравнения
с a = -16, b = 82 и c = 375.
T = -2,916 — бессмысленный ответ, поскольку t — это время, за которое камень ударится о дно каньона, и время не может быть отрицательным.
T = 8,041 секунды — это время, за которое камень ударится о дно каньона.
Камень ударится о дно каньона за 8,041 секунды.
Пример 2. У владельца ранчо есть 500 ярдов ограждения, чтобы ограждать два соседних загона для свиней, которые упираются в сарай.Если площадь двух ручек должна составлять 20 700 квадратных ярдов, каковы должны быть размеры ручек?
L — длина обоих ручек.
а. Используйте таблицу, чтобы найти уравнение для площади ручек.
г. Упростите уравнение для площади.
г. Найдите W, когда A = 20 700.
Ширина 76,67 или 90 ярдов.
г. Найдите длину ручек.
Из таблицы в Части а, L = 500 — 3Вт.Подставляем W = 76,67 и W = 90 в уравнение для длины, L = 500 — 3w.
Размеры загонов для свиней, площадь которых составляет 20 700 квадратных ярдов, составляют 76,67 на 270 ярдов и 90 на 230 ярдов.
Пример 3. В ходе эксперимента необходимо контролировать температуру кислорода. Используя данные эксперимента, следующая квадратичная функция может смоделировать температуру кислорода,
Используя данные эксперимента, следующая квадратичная функция может смоделировать температуру кислорода,
T = 0,26 м 2 -4,1 м + 7,9
, где T измеряется в градусах Цельсия, а m представляет собой минуты, в течение которых был проведен эксперимент.Определите, когда температура кислорода составляет 0 градусов Цельсия.
Задача просит вас найти m при T = 0.
Температура кислорода составит 0 градусов Цельсия через 2,246 минуты 13,52 минуты.
Учебный совет: Ключевая идея, продемонстрированная в примере 3, заключается в том, как обрабатывать отрицательное b в квадратном уравнении.
Резюме
В этом разделе показано, как решить новый тип уравнения — квадратное уравнение. У них есть важные приложения во многих областях, таких как бизнес, физика и инженерия.Учиться разница между квадратным уравнением и квадратной формулой.
Квадратное уравнение: ax 2 + bx + c = 0.
- Одна часть уравнения должна быть равна нулю.

- a — коэффициент при x.
- b — коэффициент при x.
- c — постоянный член.
Квадратичная формула решает квадратное уравнение.
- Формула дает два решения.
- Калькулятор используется для поиска ответов.
- Первый шаг в вычислении формулы — это упростить извлечение квадратного корня.
КВАДРАТИЧЕСКИЕ ПРИЛОЖЕНИЯ И ГРАФИКИ
Цели
В этом разделе исследуются дополнительные ключевые точки квадратичного графика, вершины и пересечений. Эти моменты будут интерпретированы в приложениях.
Пример 1. Мальчик, лежащий на спине, стреляет из пращи камнем прямо в воздух с начальной скоростью (силой, которую мальчик использует, чтобы выстрелить в камень) 64 фута в секунду.Квадратное уравнение, моделирующее высоту скалы, равно
.ч = -16т 2 + 64т.
(Этот пример взят из Раздела 4.1 «Введение в квадратику», стр. 317.)
На странице 318 мы сгенерировали следующие значения:
Мы использовали точки, чтобы получить график ниже. Вершина и пересечения также отмечены на графике.
Вершина и пересечения также отмечены на графике.
Объяснение : Точка (0, 0) — это время и высота пересечения.
Вершина , (2,64) представляет максимальную высоту скалы. Скала достигает максимальной высоты 64 фута за 2 секунды.
Временные точки , (0, 0) и (4, 0) представляют, когда камень находится на земле. Камень оказывается на земле за 0 секунд до выстрела (это точка пересечения высоты ) и через 4 секунды, когда он возвращается на землю.
Чтобы построить квадратичную диаграмму, обозначенную уравнением y = ax 2 + bx + c, усвойте следующие термины:
Словарь : Вершина: Вершина — это максимальная или минимальная точка на графике.Чтобы найти вершину:
а. Найдите координату x:
b. Найдите координату y: подставьте значение x, полученное в части a, в формулу y = ax 2 + bx + c.
X intercept : установите y = 0 и решите 0 = ax 2 + bx + c, используя формулу корней квадратного уравнения,
Y-образная точка : установите x = 0 и найдите y.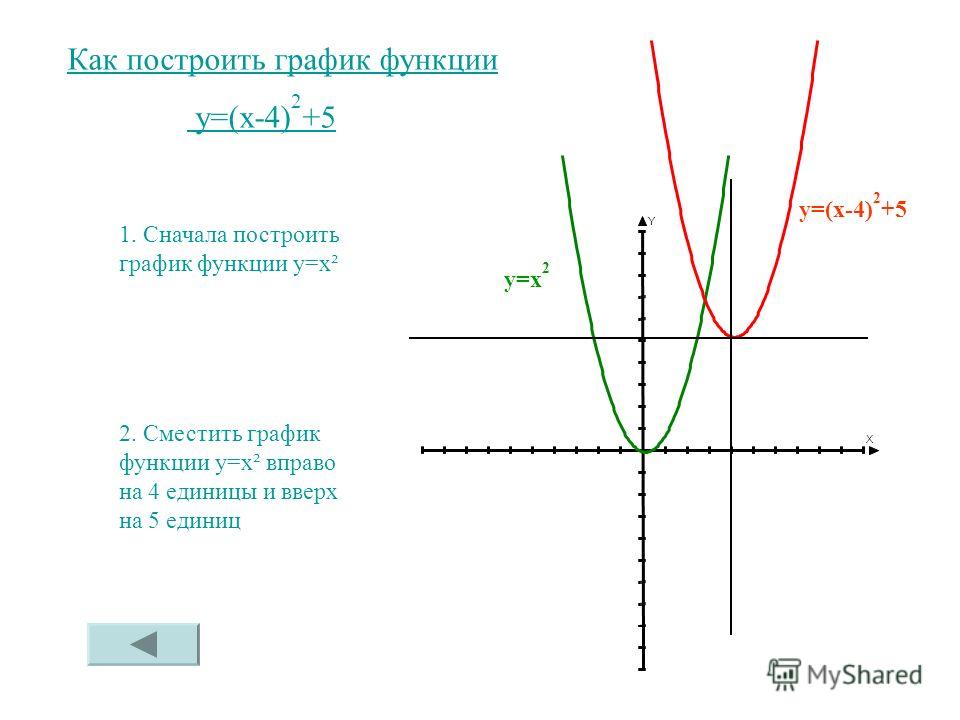 y всегда будет c, константой.
y всегда будет c, константой.
Учебный совет: Напишите процедуру и определения на трех карточках для удобного использования.
Пример 2. Компания D +++ производит компьютерные игры. Стоимость создания игр g в месяц составляет C = 0,4g 2 — 32g + 625. Выручка от продажи игр g в месяц составляет R = -0,6g 2 + 52g. Единицы измерения g — сотни, C и R — тысячи долларов.
а. Найдите уравнение прибыли.
г. Найдите вершину и объясните, что эта вершина означает с точки зрения создания компьютерных игр.
Формула для координаты g:
Из уравнения прибыли a = -1, b = 84.
Вершина — (42,1139). Если D +++ продаст 4200 игр, то они получат максимальную прибыль в размере 1 139 000 долларов.
г. Найдите g перехватывает и объясните, что они означают с точки зрения создания компьютерных игр.
Чтобы найти точку пересечения с g, установите P = 0.
Решить 0 = -g 2 + 84g — 625.
Используйте формулу корней квадратного уравнения, a = -1, b = 84, c = -625.
Перехваты g: (8.251, 0) и (75.75, 0).
Если они продадут 825 или 7 575 игр, они выйдут на уровень безубыточности.
г. Найдите перехватчики P и объясните, что они означают с точки зрения создания компьютерных игр.
Чтобы найти точку пересечения с P, установите g = 0.
P = -0 2 + 84 * 0-625
P = -625
Перехват по оси P равен (0, -625).
Стартовые затраты компании составляют 625 000 долларов.
e. Постройте график функции.
Постройте точки:
Вершина. (42, 1139).
Данный перехватывает. (8,251, 0) и (75,75, 0).
Перехват P. (0, -625).
Объяснение : Одно из объяснений того, что прибыль имеет две точки безубыточности, заключается в том, насколько эффективна компания в производстве продукта. Изготовление очень небольшого количества предметов обычно неэффективно. В какой-то момент фабрика становится очень эффективной в производстве продукта, но если фабрика пытается производить слишком много предметов, компания становится неэффективной в производстве своей продукции.
В какой-то момент фабрика становится очень эффективной в производстве продукта, но если фабрика пытается производить слишком много предметов, компания становится неэффективной в производстве своей продукции.
Помните, что единицы измерения g — сотни, а единицы P — тысячи.
Предположим, D +++ необходимо получать прибыль в размере 500 000 долларов (P = 500) в месяц. Нарисуйте эту линию на графике, полученном в Части b, и найдите, где линия пересекает график квадратичного. Напишите предложение, объясняющее, что означают ответы.
Эскиз P = 500 на предыдущем графике.
P = 500 — горизонтальная линия.
Если D +++ хочет получить прибыль в размере 500 000 долларов, им необходимо сделать и продать 1 672 или 6 728 игр.
Пояснение : График дает оценку того места, где пересекаются горизонтальная линия P = 500 и уравнение прибыли P = -g 2 + 84g-625. Алгебра дает точную точку их пересечения.
г. Используя график и ответы к Части c, определите, сколько компьютерных игр необходимо сделать и продать, чтобы гарантировать прибыль более 500 000 долларов.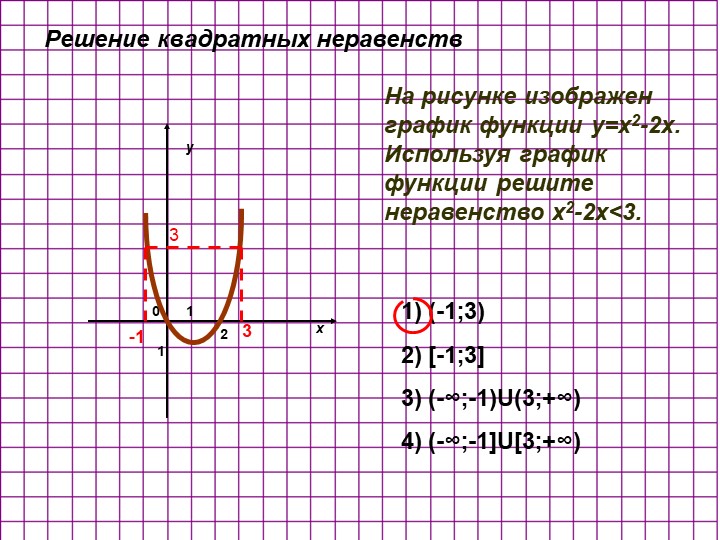
Компания получит прибыль более $ 500 000, если график прибыли будет выше горизонтальной линии P = 500.Эта проблема аналогична примеру 2d на стр. 203 в Разделе 2.9 «Приложения графиков».
Это происходит между точками g = 16,72 и g = 67,28 или
.16,72
Компания заработает более 500 000 долларов, если будет производить и продавать от 1 672 до 6 728 компьютерных игр.
Пример 3. Оператор питомника хочет поставить три соседние загоны для собак одинакового размера у стены. У него 96 метров забора.
а. Найдите формулу для площади.
Объяснение : Самая трудная часть таблицы — найти значение длины.Если фермер использует 10 метров для ширины загона, а есть 4 ширины, то он использовал 4 раза по 10, или 40 метров ограждения. Чтобы узнать, сколько ограждений осталось на эту длину, вычтите 40 из 96 — общего количества ограждений, доступных фермеру.
Формула площади загона для собак:
г. Найдите вершину и объясните, что это означает с точки зрения загонов для собак.
Формула для координаты W:
Из уравнения прибыли a = -4, b = 96.
Вершина равна (12, 576).
Вершина , (12, 576) представляет максимальную площадь трех загонов для собак. Когда W = 12, максимальная площадь будет 576. (Длина всех трех загонов будет 48 или длина одного загона для собак будет 16.) Будет три загона для собак размером 12 на 16 метров каждая.
г. Найдите W перехватывает и объясните, что они означают в терминах загонов для собак.
Чтобы найти точку пересечения с W, установите A = 0.
Решить 0 = -4W 2 + 96W.
Используйте формулу корней квадратного уравнения, a = -4, b = 96, c = 0.
W-точки перехвата: (0, 0) и (24, 0).
W-точки пересечения, (0, 0) и (24, 0) представляют ширину загона для собаки, которая даст нулевую площадь.
г. Найдите точку перехвата A и объясните, что это означает с точки зрения загонов для собак.
Чтобы найти точку пересечения A, установите W = 0.
Объяснение : Если ширина прямоугольника равна нулю, то площадь должна быть равна нулю.
Перехватчик A равен (0, 0).
Перехватчик A, (0, 0) — это область, когда W = 0.
e. Постройте уравнение
Постройте точки:
Вершина. (12, 576).
W перехватывает. (0, 0) и (24, 0).
Перехватчик A. (0, 0).
ф. Предположим, общая площадь должна быть 400 квадратных метров. На графике A = 400 найдите размеры загонов для собак.
Эскиз A = 400 на предыдущем графике.
A = 400 — горизонтальная линия.
Поскольку W, ширина, известна, длину L можно определить по формуле A = LW.
Решите относительно L, разделив обе части на W.
Размеры загона для собак, дающего площадь 400 квадратных метров, составляют 5,367 на 74,53 и 18,63 на 21,47.
Пример 4. В ходе эксперимента необходимо контролировать температуру кислорода. Используя данные эксперимента, следующая квадратичная функция может смоделировать температуру кислорода,
Используя данные эксперимента, следующая квадратичная функция может смоделировать температуру кислорода,
Т = 0.26 м 2 -4,1 м + 7,9
, где T измеряется в градусах Цельсия, а m представляет собой минуты, в течение которых был проведен эксперимент. Постройте уравнение, найдя вершину и точки пересечения. Обозначьте эти точки на графике и объясните, что означают вершина и пересечения с точки зрения модели.
Вернуться назад: Это та же модель, что использовалась в примере 3 на стр. 332. Этот пример работал при нулевой температуре.
Найдите вершину из T = 0.26 м 2 — 4,1 м + 7,9.
Формула для координаты m вершины:
Вершина равна (7,885, -8,263).
Найдите точки пересечения м T = 0,26 м 2 -4,1 м + 7,9
Чтобы найти m точек пересечения, установите T = 0.
Решить 0 = 0,26 м 2 -4,1 м + 7,9.
Используйте формулу корней квадратного уравнения, a = 0,26, b = -4,1, c = 7,9.
m точек пересечения (13.52, 0) и (2.246, 0).
Найдите точки пересечения T T = 0,26 м 2 — 4,1 м + 7,9
Чтобы найти точку пересечения с Т, установите m = 0.
Т-образная точка пересечения (0, 7.9).
Vertex: Минимальная температура составляет 7,885 минут. Минимальная температура составит -8,263 градуса по Цельсию.
м пересекает: Температура будет ноль градусов по Цельсию при 2.246 и 13.52 мин.
T intercept: Температура в начале эксперимента составляла 7,9 градусов Цельсия.
Учебные советы: Квадратичные диаграммы — это U-образные графики. В некоторых случаях они имеют U-образную форму, как в примере выше, или форму, как в примерах с 1 по 3. Если a в уравнении, y = ax 2 + bx + c, положительно, тогда график имеет U-образную форму, что есть, открываясь. Если a отрицательно, график имеет форму, то есть раскрывается вниз. Этот факт следует записать на карточке для заметок.
Этот факт следует записать на карточке для заметок.
Резюме
Графики квадратиков появляются по таким разнообразным предметам, как микроэкономика и физика. В этом разделе кратко излагаются основные идеи устройства.
Чтобы построить квадратичный график y = ax 2 + bx + c, вы должны найти:
- Вершина .
Формула для координаты x:
Чтобы найти координату y, подставьте свой ответ вместо координаты x в уравнение y = ax 2 + bx + c. - x перехватывает .Установите y = 0 и решите уравнение 0 = ax 2 + bx + c, используя формулу корней квадратного уравнения
- Перехватчик y .
Установите x = 0 в уравнении, y = ax 2 + bx + c, и найдите y. Обратите внимание, когда x = 0, y = c. - Если a отрицательное значение , обычно график выглядит следующим образом:
- Если a положительное значение , обычно график выглядит следующим образом:
ФАКТОРИНГ
Цели
Факторинг — это алгебраический метод, используемый для разделения выражения на составные части. Когда составные части перемножаются, результатом является исходное выражение. Иногда это можно использовать для решения квадратных уравнений. Факторинг — важный навык в MAT 100, Intermediate Algebra.
Когда составные части перемножаются, результатом является исходное выражение. Иногда это можно использовать для решения квадратных уравнений. Факторинг — важный навык в MAT 100, Intermediate Algebra.
Словарь : алгебраическое выражение учитывается, если последней операцией при вычислении выражения является умножение.
Пример 1. Какое выражение факторизуется , x 2 — 5x — 24 или (x — 8) (x + 3)?
Выберите значение x и подставьте его в выражение.
Пусть x = 3.
Поскольку последней операцией для (x — 8) (x + 3) было умножение, то факторизуется (x — 8) (x + 3).
Объяснение : Менее формально алгебраическое выражение факторизуется, если оно заключено в круглые скобки.
Словарь : Распределительное свойство — это a (b + c) = ab + ac. Левая часть подвергается факторизации, и a является общим множителем.
У вас должна быть возможность проверить с помощью свойства distributive.
Объяснение : Хотя 8x 3 + 4x равно как 2x (4x 2 + 2), так и 4 (2x 3 + x), ни один из них не считается полностью факторизованным, потому что в обоих случаях общее кратное 2, в 2x (4x 2 +2) и x в 4 (2x 3 + x) по-прежнему можно разложить на множители в скобках.
Факторинг трехчлена: (Трехчлен состоит из трех членов.) Чтобы разложить трехчлен на множители, вспомните аббревиатуру FOIL.
Учебный совет: Проверьте свои карточки для заметок на предмет определения слова «ФОЛЬГА».
Пример 4. Умножаем (x + 3) (x + 5).
(x + 3) (x + 5) факторизуется, а x 2 + 8x +15 — нет. Чтобы разложить на множители трехчлены, вам нужно знать, как были вычислены 8x и 15. 8x произошло от сложения 5x и 3x, а 15 — от умножения 5 и 3.
Пример 5. Множитель x 2 + 8x +15. (Это из Примера 4.)
Нам нужны два числа, которые при сложении равны 8, а при умножении равны 15. 3 и 5 в сумме дают 8, а при умножении — 15.
3 и 5 в сумме дают 8, а при умножении — 15.
Итак, x 2 + 8x +15 = (x + 3) (x + 5)
Пример 6. Фактор x 2 -4x- 12.
Нам нужны два числа, которые при сложении равны -4, а при умножении — -12. -6 и 2 в сумме дают -4, а при умножении -12.
Итак, x 2 -4x -12 = (x-6) (x + 2).
Пример 7. Коэффициент x 2 — 64.
Это не трехчлен, но он может стать одним, добавив 0x.
x 2 -64 = x 2 + 0x -64
Нам нужны два числа, которые при сложении равны 0, а при умножении равны -64.
-8 и 8 складываются в 0, а при умножении получается -64.
Итак, x 2 -64 = (x-8) (x + 8).
Этот пример называется факторизацией разности полных квадратов, и вы снова увидите это, если возьмете MAT 100, промежуточную алгебру.
Словарь : a 2 — b 2 — это разность полных квадратов .
Разность полных квадратов имеет специальную формулу факторизации: a 2 — b 2 = (a — b) (a + b)
Решение квадратных уравнений с помощью факторинга:
Если вы умножаете две величины и результат равен нулю, то вы знаете, что одна из величин должна быть равна нулю. В математической записи
В математической записи
, если a.b = 0, то a = 0 или b = 0.
Прежде чем вы подумаете, что разложение на множители для решения квадратичных уравнений намного проще, чем использование формулы квадратов, вы должны знать, что разложение на множители не всегда работает. Рассмотрите возможность изменения примера 8 всего на единицу до x 2 — 11x + 31 = 0. Вы не можете найти два целых числа, которые при сложении равны -11, а при умножении равны 31. Чтобы разложить на множитель x 2 — 11x + 31, вы должны использовать квадратичная формула. Вы узнаете, как разложить на множители любое квадратное уравнение в Precalculus I, MAT 161.
Резюме
В этом модуле представлены два метода факторинга. Первый — это общие факторы, использующие свойство распределения, ab + ac = a (b + c). Другой — факторизация трехчленов. Чтобы разложить на множители трехчлены, вам нужно знать, как работает FOIL. Если вы возьмете MAT 100, промежуточную алгебру, вы увидите больше факторинга.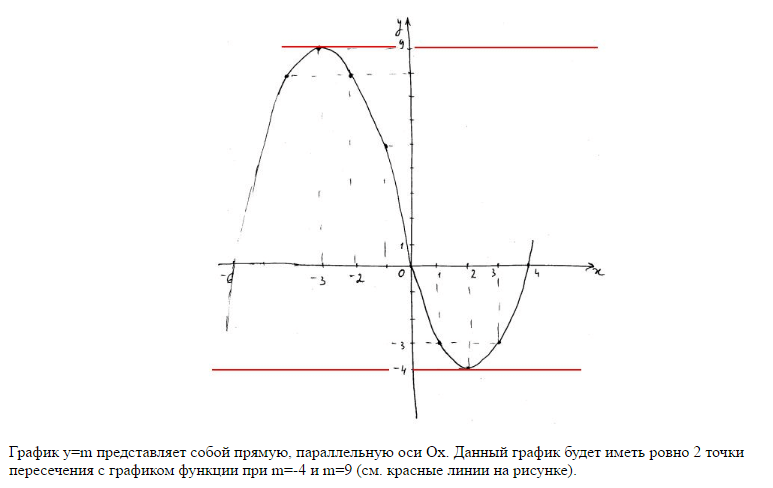
ОБЗОР ГЛАВЫ 4
Эта глава познакомила вас с квадратиками. Две основные темы — это квадратичная формула и квадратичные графики.Эти темы имеют множество приложений в бизнесе, физике и геометрии. Факторинг — важная тема в MAT 100, Intermediate Algebra.
Раздел 4.1: Введение в квадратичную науку
Раздел 4.2: Приложения квадратичной формулы
Определение: ax 2 + bx + c = 0 — квадратное уравнение.
Определение: квадратная формула.
Пример 4. Фермер хочет ограждать два соседних курятника напротив сарая.У него 125 футов забора. Какие должны быть размеры, если он хочет, чтобы общая площадь была 700 квадратных футов.
а. Заполните таблицу, чтобы найти уравнение для площади.
г. Найдите W, когда A = 700.
Размеры курятника, который даст площадь 700 квадратных футов, составляют 35 на 20 футов и 6,667 на 105 футов.
(Чтобы получить длину, разделите 700 на 6,667 и 35. )
)
Раздел 4.3: Квадратичные приложения и графики
Для построения квадратичного графика y = ax 2 + bx + c необходимо найти:
- Вершина:
Координата x вычисляется по формуле
Координата y вычисляется путем замены координаты x на y = ax 2 + bx + c. - Перехватчик x:
Установите y = 0 и решите 0 = ax 2 + bx + c, используя формулу корней квадратного уравнения. - Пересечение оси y:
Заменим x = 0 на y = ax 2 + bx + c. Обратите внимание, что когда x = 0, y = c.
Пример 5. Уравнение затрат на изготовление коробок для сока: C = 0,6B 2 — 24B + 36, а уравнение доходов — R = -0,4B 2 + 18B. B выражается в миллионах, а C и R — в тысячах долларов.
а. Найдите уравнение прибыли.
г. Изобразите уравнение прибыли и объясните, что точки пересечения B и P означают с точки зрения проблемы.
Вершина — (21, 405).
Найдите точку пересечения B. Установите P = 0.
точки пересечения B — это (0.875, 0) и (41.13, 0).
Найдите точку пересечения P. Установите B = 0.
Перехватчик P равен (0, -36).
г. Предположим, компании нужно заработать 200 000 долларов прибыли (P = 200).Изобразите линию P = 200 и найдите, сколько коробок из-под сока нужно сделать компании, чтобы заработать 200 000 долларов.
Чтобы получить прибыль в размере 200 000 долларов, компании необходимо произвести 6 682 или 35,32 миллиона ящиков для сока.
Вершина (21,405) представляет максимальную прибыль. Компания получит максимальную прибыль в размере 405 000 долларов, продав 21 миллион коробок для сока.
Перехватчики B (0,875, 0) и (41,13, 0) говорят нам, что компания сломается, даже если они продадут.875 или 41,13 миллиона ящиков сока.
Перехват P (0–36) представляет начальные затраты компании в размере 36 000 долларов.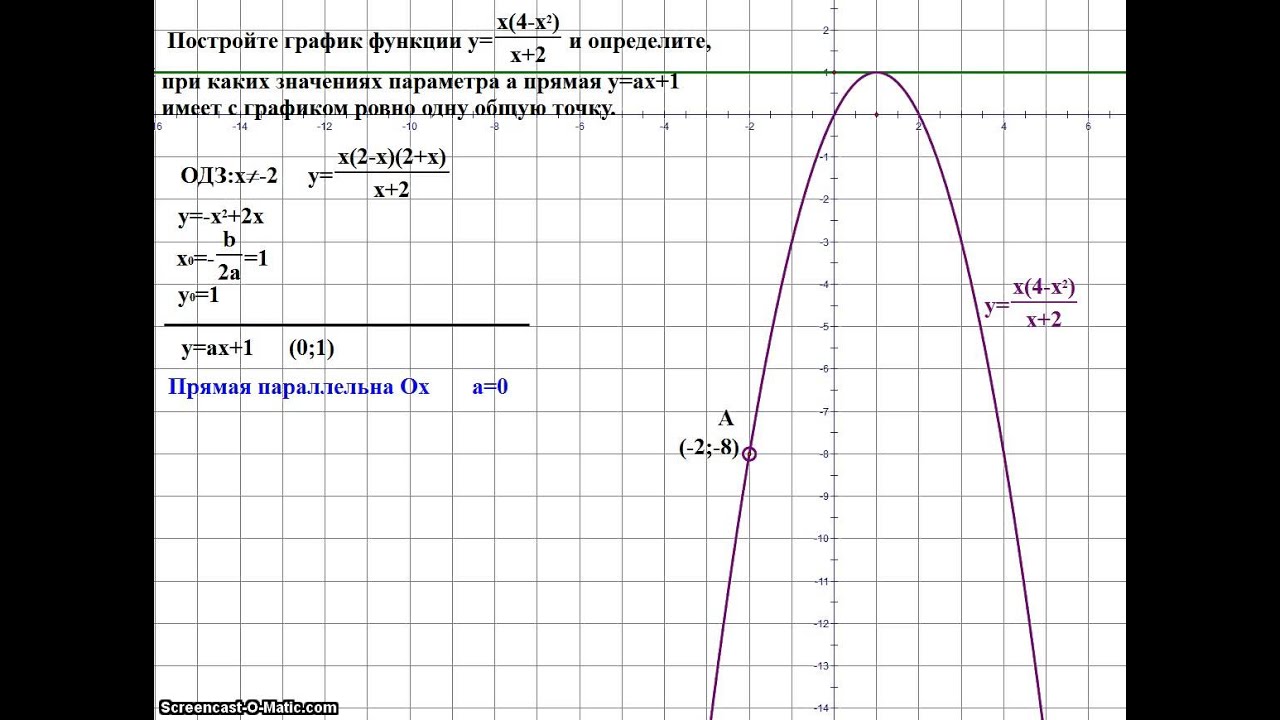
Раздел 4.4: Факторинг
Общие факторы:
Триномы:
Решение квадратных уравнений на множители.
Если a. b = 0, тогда a = 0 или b = 0
Советы по изучению:
- Практикуйте контрольный тест, начиная со следующей страницы, поместив себя в реалистичные условия экзамена.
- Найдите тихое место и используйте таймер, чтобы смоделировать продолжительность урока.
- Запишите свои ответы в домашнюю тетрадь или сделайте копию теста. После этого вы можете повторно сдать экзамен для дополнительной практики.
- Проверьте свои ответы.
- Дополнительный экзамен доступен на веб-странице MAT 011.
- НЕ ждите накануне вечером, чтобы заняться изучением.
Системы линейных и квадратных уравнений
| Линейное уравнение — это уравнение линии . | |
| Квадратное уравнение — это уравнение параболы , имеющее по крайней мере одну переменную в квадрате.  (например, x 2 ) (например, x 2 ) | |
| И вместе они образуют Систему линейного и квадратного уравнений |
A Система этих двух уравнений может быть решена (найти, где они пересекаются) либо:
- Графически (путем нанесения их обоих на график функций и увеличения)
- или используя Алгебра
Как решить с помощью алгебры
- Преобразуйте оба уравнения в формат «y =»
- Уравнять их друг с другом
- Упростить в формат «= 0» (как стандартное квадратное уравнение)
- Решите квадратное уравнение!
- Используйте линейное уравнение для вычисления совпадающих значений «y», чтобы получить (x, y) точек в качестве ответов
Поможет пример:
Пример: Решите эти два уравнения:
- y = x 2 — 5x + 7
- у = 2х + 1
Преобразуйте оба уравнения в формат y =:
Они оба в формате «y =», поэтому сразу переходите к следующему шагу
Уравнять их друг с другом
x 2 — 5x + 7 = 2x + 1
Упростить в формат «= 0» (как стандартное квадратное уравнение)
Вычтем 2x с обеих сторон: x 2 — 7x + 7 = 1
Вычтем 1 с обеих сторон: x 2 — 7x + 6 = 0
Решите квадратное уравнение!
(самая сложная часть для меня)
Вы можете прочитать, как решать квадратные уравнения, но здесь мы будем множить квадратное уравнение:
Начать с: x 2 — 7x + 6 = 0
Записать -7x как -x-6x: x 2 — x — 6x + 6 = 0
Тогда: x (x-1) — 6 (x-1) = 0
Тогда: (x-1) (x-6) = 0
Что дает нам решения x = 1 и x = 6
Используйте линейное уравнение для вычисления совпадающих значений «y», чтобы получить (x, y) точек в качестве ответов
Соответствующие значения y (см. Также график):
Также график):
- для x = 1 : y = 2x + 1 = 3
- для x = 6 : y = 2x + 1 = 13
Наше решение: две точки: (1,3) и (6,13)
Я рассматриваю это как три этапа:
Объедините в квадратное уравнение ⇒ Решите квадратичное уравнение ⇒ Вычислите точки
Решения
Возможны три случая:
- Нет реальное решение (случается, когда они никогда не пересекаются)
- Одно реальное решение (когда прямая только касается квадратичной)
- Два реальных решения (как в примере выше)
Время для другого примера!
Пример: Решите эти два уравнения:
- y — x 2 = 7 — 5x
- 4 года — 8x = -21
Преобразуйте оба уравнения в формат y =:
Первое уравнение: y — x 2 = 7 — 5x
Добавьте x 2 к обеим сторонам: y = x 2 + 7 — 5x
Второе уравнение: 4y — 8x = -21
Добавьте 8x к обеим сторонам: 4y = 8x — 21
Разделить все на 4: y = 2x — 5.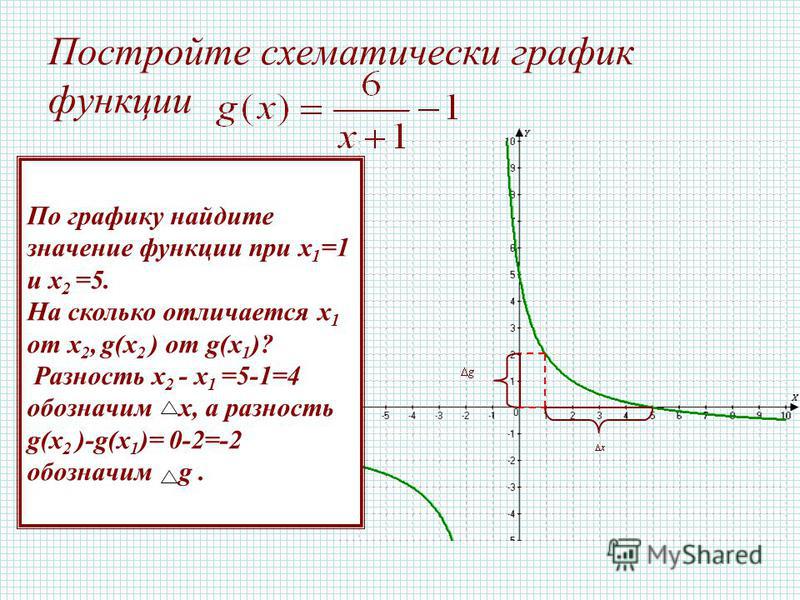 25
25
Уравнять их друг с другом
x 2 — 5x + 7 = 2x — 5,25
Упростить в формат «= 0» (как стандартное квадратное уравнение)
Вычтем 2x с обеих сторон: x 2 — 7x + 7 = -5,25
Добавьте 5,25 к обеим сторонам: x 2 — 7x + 12,25 = 0
Решите квадратное уравнение!
Использование квадратичной формулы из квадратных уравнений:
- x = [-b ± √ (b 2 -4ac)] / 2a
- x = [7 ± √ ((- 7) 2 -4 × 1 × 12.25)] / 2 × 1
- x = [7 ± √ (49 -49)] / 2
- x = [7 ± √0] / 2
- х = 3,5
Всего одно решение! («Дискриминант» равен 0)
Используйте линейное уравнение для вычисления совпадающих значений «y», чтобы получить (x, y) точек в качестве ответов
Соответствующее значение y:
- для x = 3,5 : y = 2x-5,25 = 1,75
Наше решение: (3. 5,1.75)
5,1.75)
Пример из реального мира
Кабум!
Ядро летит в воздухе по параболе: y = 2 + 0,12x — 0,002x 2
Земля наклонена вверх: y = 0,15x
Куда приземляется пушечное ядро?
Оба уравнения уже имеют формат «y =», поэтому приравняйте их друг к другу:
0,15x = 2 + 0,12x — 0,002x 2
Упростить в формат «= 0»:
Переместите все термины влево: 0.002x 2 + 0,15x — 0,12x — 2 = 0
Упростить: 0,002x 2 + 0,03x — 2 = 0
Умножить на 500: x 2 + 15x — 1000 = 0
Решите квадратное уравнение:
Разделить 15x на -25x + 40x: x 2 -25x + 40x — 1000 = 0
Тогда: x (x-25) + 40 (x-25) = 0
Тогда: (x + 40) (x-25) = 0
x = -40 или 25
Отрицательный ответ можно проигнорировать, поэтому x = 25
Используйте линейное уравнение для вычисления совпадающего значения «y»:
у = 0. 15 х 25 = 3,75
15 х 25 = 3,75
Итак, пушечное ядро попадает в склон под углом (25, 3,75)
.Вы также можете найти ответ графически, используя средство графического отображения функций:
.
Обе переменные в квадрате
Иногда можно возвести в квадрат ОБЕ члены квадратичной:
Пример: найти точки пересечения
Окружность x 2 + y 2 = 25
А прямая 3у — 2х = 6
Сначала введите строку в формате «y =»:
Переместите 2x вправо: 3y = 2x + 6
Разделить на 3: y = 2x / 3 + 2
СЕЙЧАС. Вместо преобразования круга в формат «y =» мы можем использовать замену на (заменить «y» в квадратичном выражении на линейное):
Положите y = 2x / 3 + 2 в уравнение круга: x 2 + (2x / 3 + 2) 2 = 25
Развернуть: x 2 + 4x 2 /9 + 2 (2x / 3) (2) + 2 2 = 25
Умножить все на 9: 9x 2 + 4x 2 + 2 (2x) (2) (3) + (9) (2 2 ) = (9) (25)
Упростить: 13x 2 + 24x + 36 = 225
Вычтем 225 с обеих сторон: 13x 2 + 24x — 189 = 0
Теперь он находится в стандартной квадратичной форме, давайте решим его:
13x 2 + 24x — 189 = 0
Разделить 24x на 63x-39x: 13x 2 + 63x — 39x — 189 = 0
Тогда: x (13x + 63) — 3 (13x + 63) = 0
Тогда: (x — 3) (13x + 63) = 0
Итак: x = 3 или -63/13
Теперь рассчитаем y-значения:
Подставляем x = 3 в линейное уравнение:- 3 года — 6 = 6
- 3y = 12
- г = 4
- Итак, одна точка (3, 4)
- 3 года + 126/13 = 6
- г + 42/13 = 2
- y = 2 — 42/13 = 26/13 — 42/13 = -16/13
- Итак, другая точка — (-63/13, -16/13)
Стандартная и вершинная форма уравнения параболы и ее связь с графиком параболы.
Уравнение параболы может быть выражено в стандартной или вершинной форме, как показано на рисунке ниже.
Вершинная форма уравнения
Вершинная форма уравнения параболы обычно выражается как: y = a (x-h) 2 + k
- (h, k) — это вершина , как вы можете видеть на картинке ниже
- Если a положительно, то парабола открывается вверх, как правильная буква «U».
- Если a отрицательно, то график открывается вниз, как вверх ногами «U».
Вершина и Уравнение формы направление-вершина
Часть I
Задача 1
Каков график следующей параболы y = (x – 1) ² + 1?
Покажи ответ Вершиной параболы является точка (1,1).
Задача 2
Каков график следующей параболы y = — (x – 1) ² + 1?
Покажи ответЗадача 3
Каков график следующей параболы y = (x + 2) ² –3?
Покажи ответОпределение вершины в форме вершины
Задача 4.
 1
1Какова вершина следующей параболы: y = (x + 3) ² + 4
Покажи ответВершиной является точка (-3,4)
Задача 4.2
Найдите вершину следующей параболы: y = (x — 3) ² + 4
Покажи ответЗадача 4.3
Какова вершина параболы, уравнение формы вершины которой имеет вид y = (x — 2) ² — 3
Покажи ответЧасть II
Задача 5.
 1
1 Какова вершина параболы со следующим уравнением:
у = 2 (х-3) 2 +4? Парабола открывается вверх или вниз?
Вершина — (3,4), и она открывается вверх, поскольку a положительно (это 2), она открывается вверх.
Задача 5.2
Если уравнение параболы имеет вид y = 3 (x + 3) 2 +4, какова его вершина? Куда он открывается?
Покажи ответ Vertex = (-3, 4), и открывается вверх, поскольку a положительно.
Задача 5.3
У параболы есть уравнение y = -22 (x — 9) 2 + 5. Какова ее вершина? В какую сторону открывается парабола?
Покажи ответVertex = (9, 5) и поскольку a отрицательно (это -22), открывается вниз.2 + bx + c {/ eq} — это , всегда , заданное как {eq} \ left (- \ dfrac {b} {2a}, f (- \ dfrac {b} {2a}) \ right) {/ экв}.
Шаг 2: Найдите {eq} x {/ eq} точки пересечения параболы (обратите внимание, что может быть 0, 1 или 2 {eq} x {/ eq} перехватывает!). Мы находим точки пересечения, решая {eq} y = f (x) = 0 {/ экв}.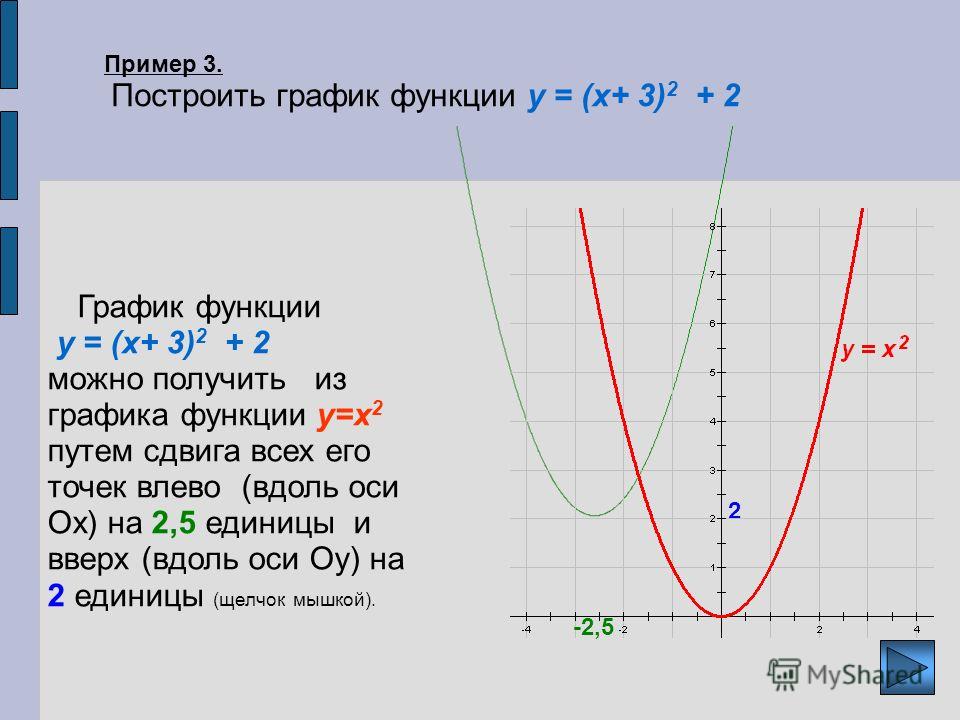
Шаг 3: Найдите {eq} y {/ eq} перехватить {eq} (0, f (0)) {/ eq}, которое квадратное уравнение всегда имеет !
Шаг 4: Теперь, когда у нас есть вершина, {eq} y {/ eq} перехватчик и, возможно, / {eq} x {/ eq} точки пересечения, мы можем нарисовать параболу, используя ось симметрии, если необходимо, чтобы помочь нам.2 + bx + c $$
Здесь мы рассматриваем квадратичные функции с {eq} a = 1 {/ экв}.
Парабола : график квадратичной функции. Параболы имеют характерную U-образную форму и открываются вверх, если {eq} a {/ eq} положительно, или вниз, если {eq} a {/ eq} отрицательно. Поскольку мы исследуем квадратичные функции, где {eq} a = 1 {/ eq}, все наши примеры откроются вверх. Обратитесь к приведенному ниже графику, чтобы увидеть типичную параболу.
Ось симметрии : Ось симметрии, находящаяся в вершине параболы, представляет собой вертикальную линию. График на одной стороне оси симметрии является зеркальным отображением графика на противоположной стороне оси. Обратитесь к изображению ниже, чтобы увидеть эффект «зеркального отображения» оси симметрии.
График на одной стороне оси симметрии является зеркальным отображением графика на противоположной стороне оси. Обратитесь к изображению ниже, чтобы увидеть эффект «зеркального отображения» оси симметрии.
Теперь давайте рассмотрим три примера, которые иллюстрируют, как построить параболу с учетом ее квадратичной функции! Наш первый пример начнем с уравнения графика, показанного выше. Воспроизведем график, исходя из его уравнения. Затем мы рассмотрим два других примера без визуальной ссылки, построив графики функций самостоятельно, решая ключевые точки по параболе.2 + 2x — 3 {/ экв}.
Шаг 1 : Сначала нам нужно найти вершину нашей параболы. Вершина задается точками {eq} \ left (- \ dfrac {b} {2a}, f (- \ dfrac {b} {2a}) \ right) {/ экв}.
Здесь {eq} a = 1 {/ eq} и {eq} b = 2 {/ eq}, поэтому:
$$ \ begin {align} — \ dfrac {b} {2a} & = — \ dfrac {2} {2 \ times 1} \\ & = -1 \ end {align} $$
Это {eq} x {/ eq} координата вершины. 2 + 2 (-1) — 3 \\ & = 1-2-3 \\ & = -4 \ end {align} $$
2 + 2 (-1) — 3 \\ & = 1-2-3 \\ & = -4 \ end {align} $$
Следовательно, вершина находится в {eq} (- 1, -4) {/ экв}.2 + 2х — 3 = (х-1) (х + 3) $$
Решая уравнение, получаем:
$$ (х-1) (х + 3) = 0 \\ \ begin {align} \\ & (x-1) = 0 \ \ text {или} & (x + 3) = 0 \\ & x = 1 & x = -3 \ end {align} $$
Это наши {eq} x {/ eq} перехватывает. Отметим эти точки на нашем развивающемся графике:
Шаг 3 : Хотя мы могли бы надежно нарисовать нашу параболу, используя предыдущие точки, давайте решим для {eq} y {/ eq} для практики и для дальнейшего повышения точности нашего эскиза.2 + 4 (-2) + 5 = 1 $$
Наша вершина появляется в {eq} (- 2,1) {/ eq}! Поскольку это будет самая низкая точка нашего графика, не может быть никаких {eq} x {/ eq} перехватывает, потому что {eq} (- 2,1) {/ eq} встречается над {eq} x Ось {/ eq}:
Если вы пытались решить для {eq} x {/ eq} перехватывает, вы обнаружите, что для них нет реальных решений. Таким образом, мы пропускаем шаг 2 и переходим сразу к шагу 3 .
Таким образом, мы пропускаем шаг 2 и переходим сразу к шагу 3 .
Шаг 3 : Найдите {eq} y {/ eq} перехват.2 + 4 (0) + 5 = 5 $$
Итак, точка пересечения находится в {eq} (0, 5) {/ eq}!
Шаг 4 : Теперь давайте воспользуемся осью симметрии, чтобы помочь нам найти третью точку, чтобы мы могли нарисовать график. Заметив, что ось симметрии находится в вершине, которую мы уже нашли, мы можем найти точку, противоположную {eq} y {/ eq} перехват. Считая более 2 единиц вправо и 4 единицы вверх, мы достигаем {eq} y {/ eq} пересечение с вершиной.2 — 6x & = 0 \\ х (х-6) & = 0 \ end {выровнять *} $$
Это означает, что {eq} x = 0 \ text {или} 6 {/ экв}. Итак, наш {eq} x {/ eq} точки перехвата находятся в {eq} (0, 0) {/ eq} и {eq} (6, 0) {/ eq}! Нанесите эти точки на свой график.
Шаг 3 : Найдите {eq} y {/ eq} перехватить, построив точку {eq} (0, f (0)) {/ экв}.

 k — угловой коэффициент k = tg a, b — ордината точки пересечения с осью
k — угловой коэффициент k = tg a, b — ордината точки пересечения с осью 
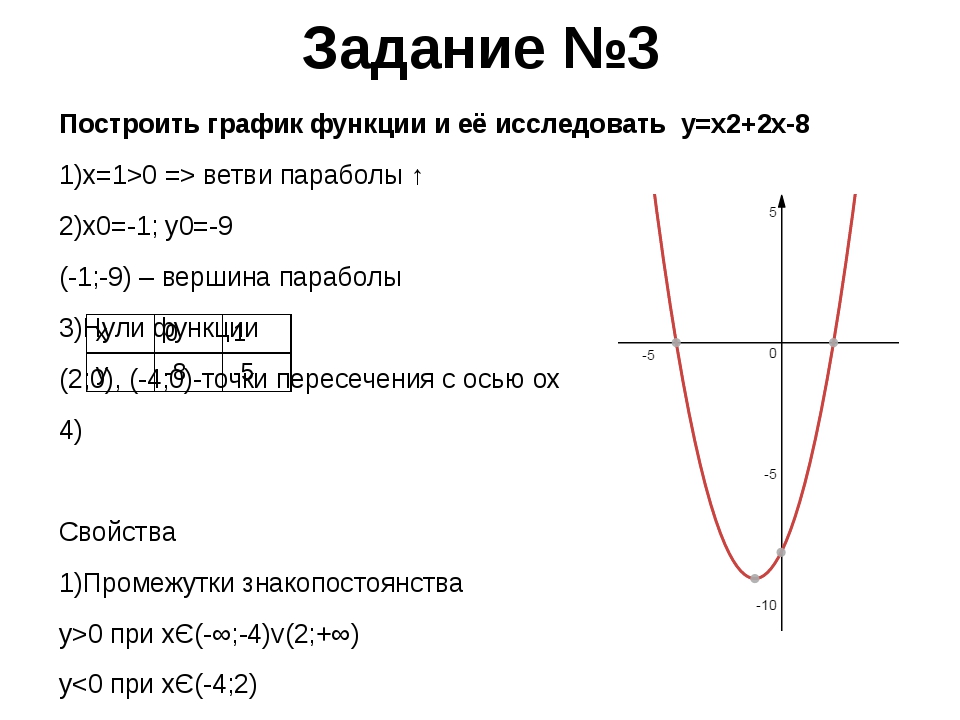 Построить график функции y = x
Построить график функции y = x
 Другими словами, он не подпадает под классификацию четных или нечетных.
Другими словами, он не подпадает под классификацию четных или нечетных. Если это так, то у нас есть нечетная функция .
Если это так, то у нас есть нечетная функция .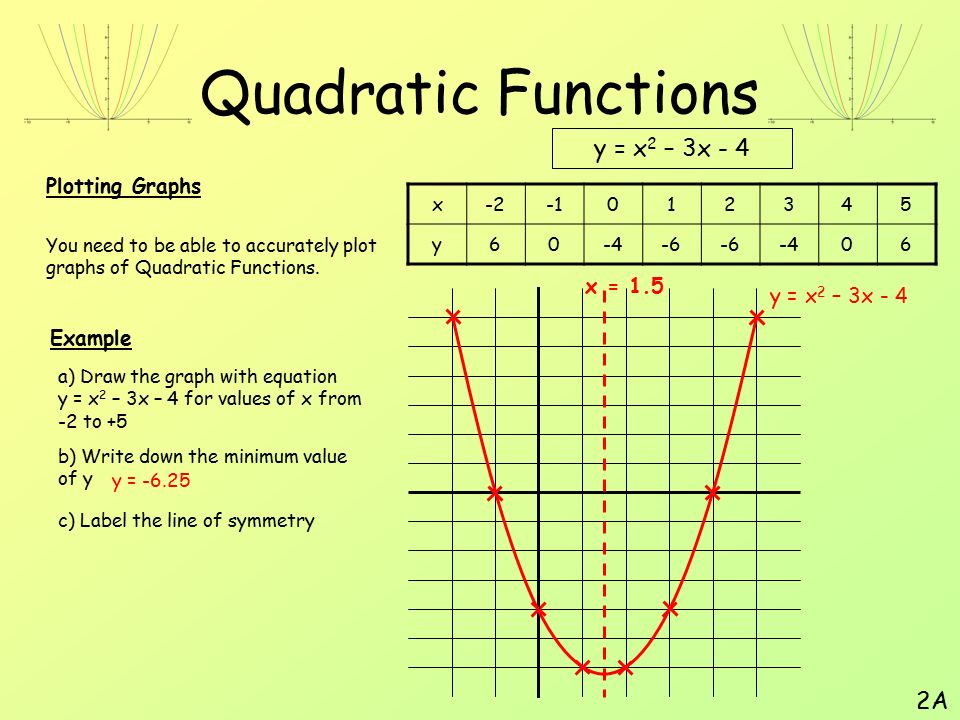 3
3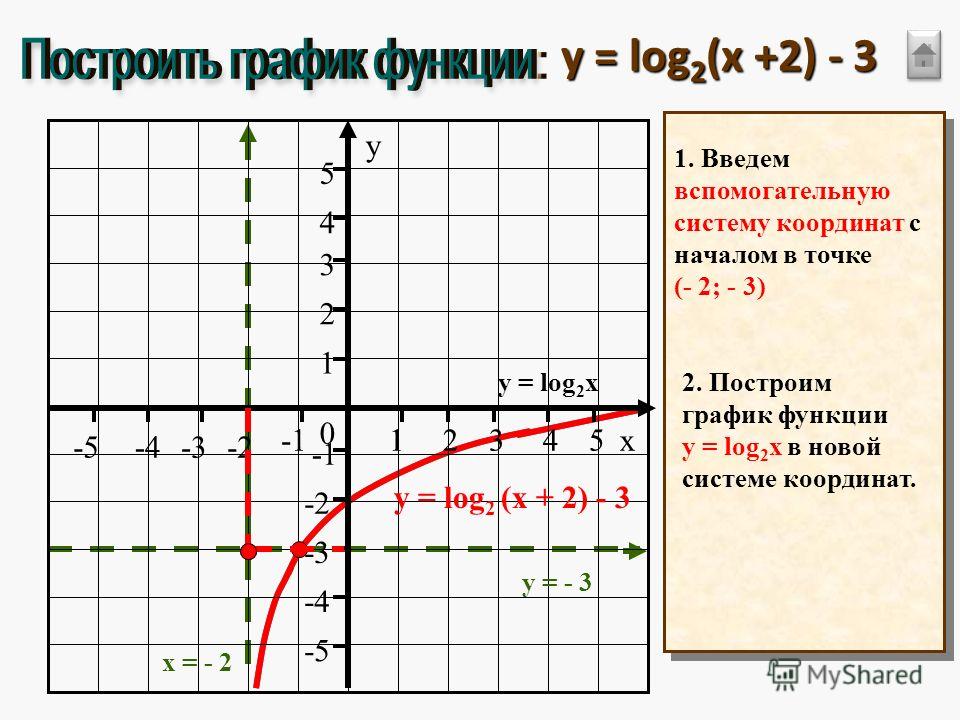 14159..
14159..