Поверхность пирамиды усеченной пирамиды – Конспект урока и презентация по геометрии на тему «Площадь поверхности пирамиды и усеченной пирамиды» (11 класс) — Детская игровая комната «Волшебный лес»

Posted on 12.10.202011.01.2020 by alexxlab

Содержание

Усечённая пирамида — Википедия

Материал из Википедии — свободной энциклопедии

Усеченная пирамида

Усечённая пирами́да — многогранник, образованный частью пирамиды отсечённой плоскостью параллельной её основанию.

Основание изначальной пирамиды а также параллельная ему грань называются основаниями усечённой пирамиды.
- Остальные грани называются боковыми.

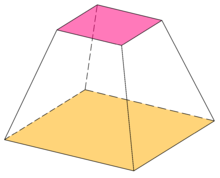Правильная усечённая пирамида

Если изначальная пирамида правильная то её усечённая пирамида также называется правильной.
- Высота боковой грани называется апофемой.

Боковые грани усечённой пирамиды представляют собой трапеции.

Объём пирамиды равен V=13⋅h(S1+S1⋅S2+S2){\displaystyle V={\tfrac {1}{3}}\cdot h(S_{1}+{\sqrt {S_{1}\cdot S_{2}}}+S_{2})}, где S1,S2{\displaystyle S_{1},S_{2}} — площади оснований, h{\displaystyle h} — высота усечённой пирамиды.

Правильная усечённая пирамида[править | править код]

Боковые рёбра правильной усечённой пирамиды, а также углы между ними и основанием пирамиды равны.
Боковые грани правильной усечённой пирамиды являются равнобедренными трапециями, равными между собой.
Равны двугранные углы между боковыми гранями, а также между каждой из граней и основанием пирамиды.
Площадь боковой поверхности равна полупроизведению суммы периметров её оснований и апофемы (высоты боковой грани): Sb=12(p1+p2)⋅l{\displaystyle S_{b}={\frac {1}{2}}(p_{1}+p_{2})\cdot l}, где p1{\displaystyle p_{1}} — периметр первого основания, p2{\displaystyle p_{2}} — периметр второго, а l{\displaystyle l} — апофема.
Площадь боковой поверхности равна Sb=|S1−S2|cos⁡φ{\displaystyle S_{b}={\frac {|S_{1}-S_{2}|}{\cos \varphi }}}, где S1,S2{\displaystyle S_{1},S_{2}} — площади оснований, а φ{\displaystyle \varphi } — двугранный угол при основании пирамиды.

ПОВЕРХНОСТЬ ПИРАМИДЫ И УСЕЧЕННОЙ ПИРАМИДЫ

Определение: Площадью полной поверхности пирамиды (усечённой пирамиды) называется сумма площадей всех её граней.

Определение: Площадью боковой поверхности пирамиды (усечённой пирамиды) называется сумма площадей её боковых граней.

Теорема: Площадь боковой поверхности правильной пирамиды равна половине произведения периметра её основания на апофему.

Дано:

SABC – правильная пирамида; ;

; – апофема;

Доказать: .

Теорема: Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров её оснований на апофему.

Дано:

– правильная усечённая пирамида;

; ;

; ;

– апофема;

Доказать:

.

Пример: В основании пирамиды лежит равнобедренный прямоугольный треугольник, катеты которого равны а. Боковые рёбра пирамиды наклонены к основанию под углом 60°. Найти площадь полной поверхности пирамиды.

Дано:

— пирамида;

; ; ;

;

Определить:

Решение:

; ; ; ;

; ; .

по стороне и прилежащим к ней углам:

1) SO — общая сторона;

2) , так как , , ;

3) .

Из равенства треугольников следует, что и .

Точка О одинаково удалена от вершин треугольника АВС, следовательно, она является центром окружности, описанной около этого треугольника. Центр окружности, описанной около прямоугольного треугольника, есть середина гипотенузы. Точка О — середина гипотенузы.

.

; .

; ; ; ; .

; , следовательно, .

— равносторонний треугольник, значит, .

; .

по трём сторонам, следовательно, .

;

; ;

;

.

.

Ответ: .

Замечание: Площадь боковой поверхности неправильнойусечённой пирамиды вычисляется по определению, каксумма площадей её боковых граней.

Упражнения:

Найти площадь полной поверхности пирамиды, основанием которой служит ромб с диагоналями 12 см и 16 см, а высота проходит через точку пересечения диагоналей ромба и равна 6,4 см.
Основанием пирамиды SABC является прямоугольный треугольник АВС с гипотенузой АВ = 25 см и катетом ВC = 7 см. Ребро SA перпендикулярно основанию и равно 18 см. Найти площадь полной поверхности пирамиды.

Найти площадь боковой поверхности правильной шестиугольной пирамиды, высота которой равна 4 дм, а боковое ребро равно 16 дм.
Найти площадь полной поверхности правильной четырёхугольной усечённой пирамиды, стороны оснований которой равны 18 см и 8 см, а высота равна 12 см.
Площадь боковой поверхности правильной четырёхугольной усечённой пирамиды вдвое меньше площади её полной поверхности. Стороны её оснований равны 12 дм и 6 дм. Найти высоту усечённой пирамиды.
Сторона нижнего основания правильной треугольной усечённой пирамиды равна 4 дм. Боковое ребро наклонено к плоскости основания под углом 60°. Найти площадь боковой поверхности усечённой пирамиды, если её высота равна 1 дм.
Площадь полной поверхности правильной четырёхугольной пирамиды равна 108 см². Двугранный угол при основании пирамиды равен 60°. Вычислить объём пирамиды.

Найти площадь полной поверхности правильной четырёхугольной усечённой пирамиды, стороны оснований которой равны 8 дм и 6 дм и боковая грань наклонена к большему основанию под углом 60°.
ОБЪЁМ ПИРАМИДЫ

Теорема: Объём пирамиды равен одной трети произведения площади основания пирамиды на её высоту.

Дано:

SABC — пирамида;

S(ABC)= S_осн.

SО ^ АВС; SО = h.

Доказать:

9. ОБЪЁМ УСЕЧЕННОЙ ПИРАМИДЫ

Дано:

ABCDA₁B₁C₁D₁ — усечённая пирамида;

S(ABCD) = S_н_.о_.; S (A₁B₁C₁D₁) = S_в_.о_.

h — высота усечённой пирамиды;

Определить: V_ус.пир.— ?

.

Упражнения:

Диагональ квадратного основания правильной пирамиды равна 6 см, высота пирамиды равна 15 см. Найти её объём.
Боковое ребро правильной шестиугольной пирамиды равно 14 дм, сторона её основания равна 2 дм. Найти объём пирамиды.
Основанием пирамиды является ромб со стороной 15 см. Боковые грани пирамиды наклонены к плоскости основания под углом 45°. Большая диагональ основания равна 24 см. Найти объём пирамиды.
Найти объём усечённой пирамиды, если площади её оснований равны 98 см² и 32 см², а высота соответствующей полной пирамиды равна 14 см.
В пирамиде через середину высоты проведена плоскость, параллельная её основанию. Определить объём образовавшейся усечённой пирамиды, если высота данной пирамиды равна 18 см, а площадь её основания равна 400 см².
Найти объём треугольной пирамиды, боковые рёбра которой попарно перпендикулярны и равны 10 см, 15 см, 9 см.
В треугольной усечённой пирамиде высота равна 10 см, стороны нижнего основания равны 27 м, 29 м, 52 м, а периметр верхнего основания равен 72 м. Найти объём усечённой пирамиды.
Стороны оснований правильной четырёхугольной усечённой пирамиды равны 40 см и 10 см. Площадь её полной поверхности равна 3400 см². Найти объём усечённой пирамиды.
ЦИЛИНДР. ПОВЕРХНОСТЬ И ОБЪЕМ ЦИЛИНДРА.

Определение: Геометрическое тело, полученное при вращении прямоугольника вокруг одной из его сторон, называется прямым круговым цилиндром.

Определение: Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.

AB – ось симметрии, высота цилиндра;AB = H;

AD– радиус основания цилиндра;AD = R.

Определение: Расстояние между плоскостями оснований является высотой прямого кругового цилиндра.

Радиусом цилиндра называется радиус его основания. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.

Два круга являются основаниями прямого кругового цилиндра. Отрезок, соединяющий точки окружностей оснований и перпендикулярный плоскостям оснований, называется образующей прямого кругового цилиндра.

Определение: Прямоугольник, одна сторона которого равна длине окружности основания цилиндра, а другая – его высоте, называется разверткой боковой поверхности цилиндра.

Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.

В дальнейшем мы будем рассматривать только прямой цилиндр, называя его для краткости просто цилиндром.

Определение: Цилиндр называется равносторонним, если его высота равна диаметру основания.

Сечения цилиндра.

Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник. Две его стороны − образующие цилиндра, а две другие − параллельные хорды оснований.

В частности, прямоугольником является осевое сечение. Осевое сечение — сечение цилиндра плоскостью, проходящей через его ось.

Сечение цилиндра плоскостью, параллельной основанию − круг.

Сечение цилиндра плоскостью не параллельной основанию и его оси – овал.

Теорема: Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту (S_бок.= 2πRH, где R − радиус основания цилиндра, Н − высота цилиндра).

Определение: Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.

S_осн.= πR² S_бок.= 2πRH S_полн.= 2πRH + 2πR².

Рассмотрим п-угольную прямую призму. При п→∞ периметр многоугольника, лежащего в основании призмы, будет стремиться к длине окружности основания цилиндра, площадь многоугольника, лежащего в основании призмы, будет стремиться к площади круга, являющегося основанием цилиндра. Объём п-угольной прямой призмы будет стремиться к объёму прямого кругового цилиндра.

Определение: Призма называется вписанной в цилиндр, если её основания вписаны в основания цилиндра.

Определение: Цилиндр называется вписанным в призму, если его основания вписаны в основания призмы.

Упражнения:

1. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующей цилиндра равен 60°. Найти: высоту, радиус основания, площадь основания цилиндра.

2. Площадь осевого сечения цилиндра равна 10 см², а площадь основания — 5 см². Найти высоту цилиндра.

3. Радиус основания цилиндра равен 4 см, а площадь его осевого сечения равна 72 см². Найти объём цилиндра.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
ПОВЕРХНОСТЬ ПИРАМИДЫ И УСЕЧЕННОЙ ПИРАМИДЫ — Студопедия.Нет
Определение: Площадью полной поверхности пирамиды (усечённой пирамиды) называется сумма площадей всех её граней.
Определение: Площадью боковой поверхности пирамиды (усечённой пирамиды) называется сумма площадей её боковых граней.
Теорема: Площадь боковой поверхности правильной пирамиды равна половине произведения периметра её основания на апофему.
Дано:
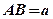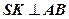SABC – правильная пирамида; ;
; – апофема;
.
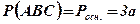Доказать: .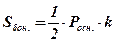
Теорема: Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров её оснований на апофему.

Дано:
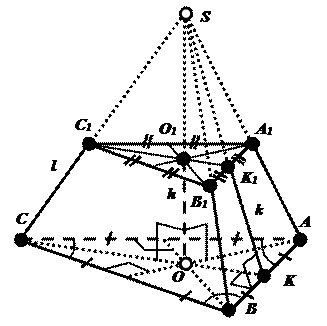
– правильная усечённая пирамида;
; ;
; ;
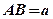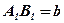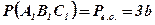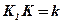– апофема;
Доказать:

.
Пример: В основании пирамиды лежит равнобедренный прямоугольный треугольник, катеты которого равны а. Боковые рёбра пирамиды наклонены к основанию под углом 60 °. Найти площадь полной поверхности пирамиды.
Дано:
— пирамида ;
; ;
;
;
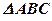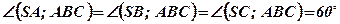Определить: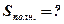
Решение:
; ; ; ;
;
; .
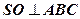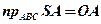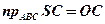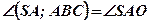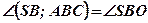
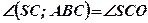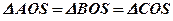по стороне и прилежащим к ней углам:
1) SO — общая сторона;
2) 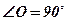, так как , , ;
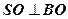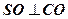3) .
Из равенства треугольников следует, что 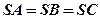  и .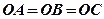
Точка О одинаково удалена от вершин треугольника АВС, следовательно, она является центром окружности, описанной около этого треугольника. Центр окружности, описанной около прямоугольного треугольника, есть середина гипотенузы. Точка О — середина гипотенузы.
.
; .
; ; ; ; .

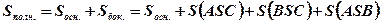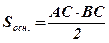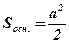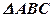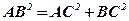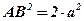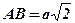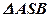; , следовательно, .
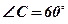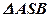— равносторонний треугольник, значит, .
; .
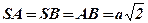по трём сторонам, следовательно, .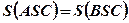
;
; ;
;
.
.
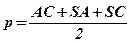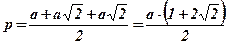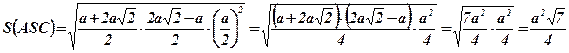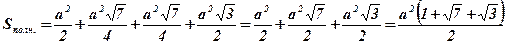Ответ: .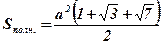
Замечание: Площадь боковой поверхности неправильнойусечённой пирамиды вычисляется по определению, каксумма площадей её боковых граней.
Упражнения:
Найти площадь полной поверхности пирамиды, основанием которой служит ромб с диагоналями 12 см и 16 см, а высота проходит через точку пересечения диагоналей ромба и равна 6,4 см.
Основанием пирамиды SABC является прямоугольный треугольник АВС с гипотенузой АВ = 25 см и катетом В C = 7 см. Ребро SA перпендикулярно основанию и равно 18 см. Найти площадь полной поверхности пирамиды.
Найти площадь боковой поверхности правильной шестиугольной пирамиды, высота которой равна 4 дм, а боковое ребро равно 16 дм.
Найти площадь полной поверхности правильной четырёхугольной усечённой пирамиды, стороны оснований которой равны 18 см и 8 см, а высота равна 12 см.
Площадь боковой поверхности правильной четырёхугольной усечённой пирамиды вдвое меньше площади её полной поверхности. Стороны её оснований равны 12 дм и 6 дм. Найти высоту усечённой пирамиды.
Сторона нижнего основания правильной треугольной усечённой пирамиды равна 4 дм. Боковое ребро наклонено к плоскости основания под углом 60 °. Найти площадь боковой поверхности усечённой пирамиды, если её высота равна 1 дм.
Площадь полной поверхности правильной четырёхугольной пирамиды равна 108 см². Двугранный угол при основании пирамиды равен 60 °. Вычислить объём пирамиды.
Найти площадь полной поверхности правильной четырёхугольной усечённой пирамиды, стороны оснований которой равны 8 дм и 6 дм и боковая грань наклонена к большему основанию под углом 60 °.
ОБЪЁМ ПИРАМИДЫ

Теорема: Объём пирамиды равен одной трети произведения площади основания пирамиды на её высоту.
Дано:
SABC — пирамида ;
S( ABC)= S_осн.
SО ^ АВС; SО = h.
Доказать: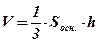
ОБЪЁМ УСЕЧЕННОЙ ПИРАМИДЫ
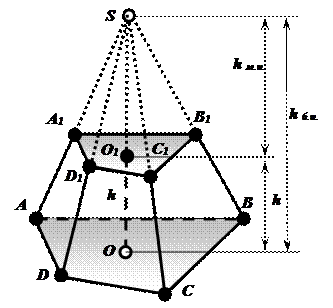Дано:
ABCDA₁ B₁ C₁ D₁ — усечённая пирамида;
S(ABCD) = S_н_.о_. ;   S (A₁B₁C₁D₁) = S_в_.о_.
h — высота усечённой пирамиды;
Определить:      V_ус.пир. — ?
.
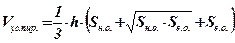Упражнения:
Диагональ квадратного основания правильной пирамиды равна 6 см, высота пирамиды равна 15 см. Найти её объём.
Боковое ребро правильной шестиугольной пирамиды равно 14 дм, сторона её основания равна 2 дм. Найти объём пирамиды.
Основанием пирамиды является ромб со стороной 15 см. Боковые грани пирамиды наклонены к плоскости основания под углом 45 °. Большая диагональ основания равна 24 см. Найти объём пирамиды.
Найти объём усечённой пирамиды, если площади её оснований равны 98 см² и 32 см², а высота соответствующей полной пирамиды равна 14 см.
В пирамиде через середину высоты проведена плоскость, параллельная её основанию. Определить объём образовавшейся усечённой пирамиды, если высота данной пирамиды равна 18 см, а площадь её основания равна 400 см².
Найти объём треугольной пирамиды, боковые рёбра которой попарно перпендикулярны и равны 10 см, 15 см, 9 см.
В треугольной усечённой пирамиде высота равна 10 см, стороны нижнего основания равны 27 м, 29 м, 52 м, а периметр верхнего основания равен 72 м. Найти объём усечённой пирамиды.
Стороны оснований правильной четырёхугольной усечённой пирамиды равны 40 см и 10 см. Площадь её полной поверхности равна 3400 см². Найти объём усечённой пирамиды.
ЦИЛИНДР. ПОВЕРХНОСТЬ И ОБЪЕМ ЦИЛИНДРА.
Определение: Геометрическое тело, полученное при вращении прямоугольника вокруг одной из его сторон, называется прямым круговым цилиндром.
Определение: Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
AB – ось симметрии, высота цилиндра;AB = H;
AD– радиус основания цилиндра;AD = R.
Определение: Расстояние между плоскостями оснований является высотой прямого кругового цилиндра.
Радиусом цилиндра называется радиус его основания. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.
Два круга являются основаниями прямого кругового цилиндра. Отрезок, соединяющий точки окружностей оснований и перпендикулярный плоскостям оснований, называется образующей прямого кругового цилиндра.
Определение: Прямоугольник, одна сторона которого равна длине окружности основания цилиндра, а другая – его высоте, называется разверткой боковой поверхности цилиндра.
Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.
В дальнейшем мы будем рассматривать только прямой цилиндр, называя его для краткости просто цилиндром.
Определение: Цилиндр называется равносторонним, если его высота равна диаметру основания.

Сечения цилиндра .
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник. Две его стороны − образующие цилиндра, а две другие − параллельные хорды оснований.
В частности, прямоугольником является осевое сечение. Осевое сечение — сечение цилиндра плоскостью, проходящей через его ось.
Сечение цилиндра плоскостью, параллельной основанию − круг.
Сечение цилиндра плоскостью не параллельной основанию и его оси – овал.

Теорема: Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту (S_бок.= 2πRH, где R − радиус основания цилиндра, Н − высота цилиндра).
Определение: Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.
S_осн.= πR²             S_бок.= 2πRH          S_полн.= 2πRH + 2πR².

Рассмотрим п-угольную прямую призму. При п→∞ периметр многоугольника, лежащего в основании призмы, будет стремиться к длине окружности основания цилиндра, площадь многоугольника, лежащего в основании призмы, будет стремиться к площади круга, являющегося основанием цилиндра. Объём п-угольной прямой призмы будет стремиться к объёму прямого кругового цилиндра.
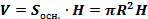
Определение: Призма называется вписанной в цилиндр, если её основания вписаны в основания цилиндра.
Определение: Цилиндр называется вписанным в призму, если его основания вписаны в основания призмы.
Упражнения:
1. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующей цилиндра равен 60 °. Найти: высоту, радиус основания, площадь основания цилиндра.
2. Площадь осевого сечения цилиндра равна 10 см², а площадь основания — 5 см². Найти высоту цилиндра.
3. Радиус основания цилиндра равен 4 см, а площадь его осевого сечения равна 72 см². Найти объём цилиндра.
Стальная болванка имеет форму правильной четырёхугольной призмы со стороной основания 0,40 м и высотой 1,00 м. Сколько метров проволоки можно изготовить из этой болванки вытягиванием?
Разработка урока «Пирамида. Усеченная пирамида»
Тема: «Пирамида. Усечённая пирамида. Площадь поверхности пирамиды, усеченной пирамиды»
Цель: Познакомить с понятиями пирамида, усеченная пирамида и научить вычислять площади поверхности пирамиды.
Задачи:
Образовательные:
изучить ещё один вид многогранников — пирамиду;
рассмотреть задачи, связанные с пирамидой и с усеченной пирамидой.
Развивающие:
развивать познавательный интерес через творческую активность;
развитие математического мышления, логической речи, вычислительных навыков, расширять кругозор обучающихся;
Воспитательные:
Методическая: применение ИКТ
Тип урока: комбинированный.
Форма проведения:групповая, индивидуальная.
Методы обучения:словесный,наглядно-иллюстративный; частично- поисковый; методы контроля и самоконтроля.
Межпредметные связи: история, черчение, литература.
Средства обучения: интерактивная доска (презентации и флипчарт), карточки с заданиями, оценочная таблица.
Ход занятия
1. Организационный момент:
Приветствие, проверка готовности к занятию.
Сообщение темы, цели и задач занятия.
2. Проверка знаний, умений и навыков по пройденному материалу:
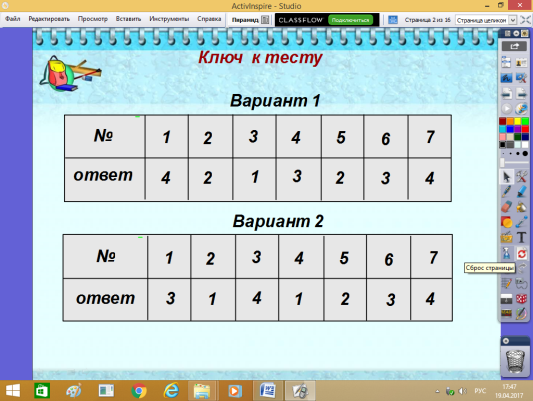
Взаимопроверка – решение теста (после решения обмениваются листочками с ответами, обучающиеся проверяют работу друг у друга.Готовый ключ высвечивается на доске)
Вариант 1
Какие из данных многогранников являются призмами?
1) а, б, в 2) б, в, г 3) а, в, г 4) а, б, г
Вершины многогранника обозначаются:
1) а, в, с, д … 2) А, В, С, Д …
3) ав, сд, ас, ад … 4) АВ, СВ, АД, СД …
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани называется:
1) диагональю 2) ребром
3) гранью 4) осью
Если боковые ребра призмы перпендикулярны основанию, то призма является:
1) наклонной 2) правильной
3) прямой 4) выпуклой
Если в основании призмы лежит параллелограмм, то она является:
1) правильной призмой 2) параллелепипедом
3) правильным многоугольником 4) пирамидой
Точка пересечения диагоналей параллелепипеда является его:
1) центром 2) линейным размером
3) центром симметрии 4) точкой сечения
Боковая поверхность прямой призмы равна:
1) произведению периметра на длину грани призмы
2) произведению длины грани призмы на основание
3) произведению длины грани призмы на высоту
4) произведению периметра основания на высоту призмы
Вариант 2
Какие из данных многогранников являются призмами?
1) а, б 2) б, в, г 3) а, г 4) а, б, г
Измерения прямоугольного параллелепипеда равны 8, 10, 4. Найдите диагональ параллелепипеда.
1) 14 2) 18+4 3) 58 4) 320
К многогранникам относятся:
1) параллелепипед 2) призма
3) пирамида 4) все ответы верны
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани называется:
1) диагональю 2) ребром
3) гранью 4) осью
Если в основании призмы лежит параллелограмм, то она является:
1) правильной призмой 2) параллелепипедом
3) правильным многоугольником 4) пирамидой
Площадь боковой поверхности прямоугольного параллелепипеда равна
1) сумма площадей боковых многоугольников
2) сумма площадей боковых ребер
3) сумма площадей боковых граней
4) сумма площадей оснований
Точка пересечения диагоналей параллелепипеда является его:
1) точкой сечения 2) центром
3) линейным размером 4) центром симметрии

Изложение нового материала:
Мы продолжаем с Вами изучать раздел геометрии «Многогранники».
Вспомним с Вами, Какие фигуры стереометрии мы уже изучили? (параллелепипед, призма).
— Выберите из представленных фигур известные модели, назовите их.
— Какие фигуры остались на столе? (тетраэдр и другие виды пирамиды). Как они называются? На что они похожи?
Сегодня на уроке познакомимся с понятием пирамида и ее элементами, научимся изображать пирамиду в тетради и распознавать ее среди других тел. Запишите в тетрадях число и тему занятия (тема записана на доске)
Определение пирамиды.
Виды пирамид.
Элементы пирамиды.
Свойства боковых рёбер и граней.
Усечённая пирамида.
Формулы для вычисления площади поверхности пирамиды, усеченной
пирамиды.
3.7 Историческая справка (презентация, подготовленная обучающимися)»
3. Формирование умений и навыков:
Решение задач:
«Дополнить запись» (на доске задана решенная задача, необходимо дописать пропущенную запись).
Задача:
Основание пирамиды – равнобедренный треугольник со сторонами 40 см, 25 см и 25 см. Ее высота проходит через вершину угла, противолежащего стороне 40 см, и равна 8 см. Найдите боковую поверхность пирамиды.
4.2Задание группам:(После решения задачи, представитель каждой группы должен показать свою работу на доске)
№1 Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности пирамиды.
(Ответ: 240)
№2 Основание пирамиды – прямоугольник со сторонами 6см и 8 см. Высота пирамиды равна 12 см и проходит через точку пересечения диагоналей основания. Найдите боковые ребра пирамиды. (Ответ: 13см.)
№3 Основание пирамиды – правильный треугольник со стороной 10см, одно из боковых ребер перпендикулярно плоскости основания и равно 5см. Вычислить площадь боковой поверхности пирамиды. (Ответ: 100см²)
4. Домашнее задание:
пп. 176-179
Решить задачи: стр.316 — №49, №62, №71, №77.
5. Подведение итогов занятия:
Анализ работы обучающихся.
Выставление и комментирование оценок.
Рефлексия: «Лестница успеха».
Площадь боковой поверхности усеченной пирамиды
Усеченная пирамида – это многогранник, который образуется основанием пирамиды и параллельным ему сечением. Можно сказать, что усеченная пирамида – это пирамиду со срезанной верхушкой. Эта фигура обладает множеством уникальных свойств: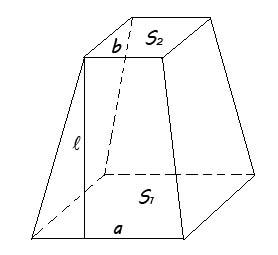
Боковые грани пирамиды являются трапециями;
Боковые ребра правильной усеченной пирамиды одинаковой длины и наклонены к основанию под одинаковым углом;
Основания являются подобными многоугольниками;
В правильной усеченной пирамиде, грани представляют собой одинаковые равнобедренные трапеции, площадь которых равна. Также они наклонены к основанию под одним углом.
Формула площади боковой поверхности усеченной пирамиды представляет собой сумму площадей ее сторон: ${S_b}=sum{i=1}{n}{S_i}$
Так как стороны усеченной пирамиды представляют собой трапеции, то для расчета параметров придется воспользоваться формулой площади трапеции. Для правильной усеченной пирамиды можно применить другую формулу расчета площади. Так как все ее стороны, грани, и углы при основании равны, то можно применить периметры основания и апофему, а также вывести площадь через угол при основании.
Если по условиям в правильной усеченной пирамиде даны апофема (высота боковой стороны) и длины сторон основания, то можно произвести расчет площади через полупроизведение суммы периметров оснований и апофемы:
$S={1/2}(P_1 + P_2) l$ $S={1/2}(P_1 + P_2) l$ Давайте рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная пятиугольная пирамида. Апофема l = 5 см, длина грани в большом основании равна a = 6 см, а грань в меньшем основании b = 4 см. Рассчитайте площадь усеченной пирамиды.
Для начала найдем периметры оснований. Так как нам дана пятиугольная пирамида, мы понимаем, что основания представляют собой пятиугольники. Значит, в основаниях лежит фигура с пятью одинаковыми сторонами. Найдем периметр большего основания:

Таким же образом находим периметр меньшего основания:

Теперь можем рассчитывать площадь правильной усеченной пирамиды. Подставляем данные в формулу: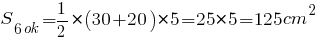
$S_{6ok}={1/2}*(30+20)*5=25*5=125 cm^2$
Таким образом, мы рассчитали площадь правильной усеченной пирамиды через периметры и апофему.
Еще один способ расчета площади боковой поверхности правильной пирамиды, это формула через углы у основания и площадь этих самых оснований.
$S_{6ok}={S_{1 OCH}-S_{2 OCH}}/{cos{beta}}$ $S={1/2}(P_1 + P_2) l$ Давайте рассмотрим пример расчета. Помним, что данная формула применяется только для правильной усеченной пирамиды.
Пусть дана правильная четырехугольная пирамида. Грань нижнего основания a = 6 см, а грань верхнего b = 4 см. Двухгранный угол при основании β = 60°. Найдите площадь боковой поверхности правильной усеченной пирамиды.
Для начала рассчитаем площадь оснований. Так как пирамида правильная, все грани оснований равны между собой. Учитывая, что в основании лежит четырехугольник, понимаем, что нужно будет рассчитать площадь квадрата. Она представляет собой произведение ширины на длину, но в квадрате эти значения совпадают. Найдем площадь большего основания:
$S_{1OCH}=6^2=36 cm^2$
$S_{2OCH}=4^2=16 cm^2$
Теперь используем найденные значения для расчета площади боковой поверхности.
$S_{6ok}= {36-16}/0.5 = 40 cm^2$
Зная несколько несложных формул, мы легко рассчитали площадь боковой трапеции усеченной пирамиды через различные значения.
Пирамида. Усеченная пирамида — Мегаобучалка

Пирамидой называется многогранник, одна из граней которого многоугольник (основание), а все остальные грани – треугольники с общей вершиной (боковые грани) (рис. 15). Пирамида называется правильной, если ее основанием является правильный многоугольник и вершина пирамиды проектируется в центр основания (рис. 16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром.

Рис. 15

Рис. 16

Боковым ребром пирамиды называется сторона боковой грани, не принадлежащая основанию Высотой пирамиды называется расстояние от ее вершины до плоскости основания. Все боковые ребра правильной пирамиды равны между собой, все боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой. Диагональным сечением называется сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Площадью боковой поверхности пирамиды называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех боковых граней и основания.
Теоремы
1. Если в пирамиде все боковые ребра равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности описанной около основания.
2. Если в пирамиде все боковые ребра имеют равные длины, то вершина пирамиды проектируется в центр окружности описанной около основания.
3. Если в пирамиде все грани равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности вписанной в основание.
Для вычисления объема произвольной пирамиды верна формула:
где V – объем;
S_осн – площадь основания;
H – высота пирамиды.

Для правильной пирамиды верны формулы:

где p – периметр основания;
h_а – апофема;
H – высота;
S_полн – площадь полной поверхности;
S_бок – площадь боковой поверхности;
S_осн – площадь основания;
V – объем правильной пирамиды.

Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды (рис. 17). Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды.

Основания усеченной пирамиды – подобные многоугольники. Боковые грани – трапеции. Высотой усеченной пирамиды называется расстояние между ее основаниями. Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Рис. 17

Для усеченной пирамиды справедливы формулы:

(4)
где S₁, S₂ – площади верхнего и нижнего оснований;
S_полн – площадь полной поверхности;
S_бок – площадь боковой поверхности;
H – высота;
V – объем усеченной пирамиды.
Для правильной усеченной пирамиды верна формула:
где p₁, p₂ – периметры оснований;
h_а – апофема правильной усеченной пирамиды.
Пример 1. В правильной треугольной пирамиде двугранный угол при основании равен 60º. Найти тангенс угла наклона бокового ребра к плоскости основания.
Решение. Сделаем рисунок (рис. 18).

Рис. 18

Пирамида правильная, значит в основании равносторонний треугольник и все боковые грани равные равнобедренные треугольники. Двугранный угол при основании – это угол наклона боковой грани пирамиды к плоскости основания. Линейным углом будет угол a между двумя перпендикулярами: и т.е. Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС). Угол наклона бокового ребра (например SB) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD. Чтобы найти тангенс необходимо знать катеты SO и OB. Пусть длина отрезка BD равна 3а. Точкой О отрезок BD делится на части: и Из находим SO: Из находим:
Ответ:
Пример 2. Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны см и см, а высота 4 см.
Решение. Для нахождения объема усеченной пирамиды воспользуемся формулой (4). Чтобы найти площади оснований необходимо найти стороны квадратов-оснований, зная их диагонали. Стороны оснований равны соответственно 2 см и 8 см. Значит площади оснований и Подставив все данные в формулу, вычислим объем усеченной пирамиды:
Ответ: 112 см³.
Пример 3. Найти площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой равны 10 см и 4 см, а высота пирамиды 2 см.
Решение. Сделаем рисунок (рис. 19).

Рис. 19

Боковая грань данной пирамиды является равнобокая трапеция. Для вычисления площади трапеции необходимо знать основания и высоту. Основания даны по условию, остается неизвестной только высота. Ее найдем из где А₁Е перпендикуляр из точки А₁ на плоскость нижнего основания, A₁D – перпендикуляр из А₁ на АС. А₁Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. так как (см. рис. 20) и С другой стороны ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:
MK = DE.
По теореме Пифагора из
Площадь боковой грани:

Рис. 20

Ответ:
Пример 4. В основании пирамиды лежит равнобокая трапеция, основания которой а и b (a > b). Каждая боковая грань образует с плоскостью основания пирамиды угол равный j. Найти площадь полной поверхности пирамиды.
Решение. Сделаем рисунок (рис. 21). Площадь полной поверхности пирамиды SABCD равна сумме площадей и площади трапеции ABCD.
Воспользуемся утверждением, что если все грани пирамиды равнонаклонены к плоскости основания, то вершина проектируется в центр вписанной в основание окружности. Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры получим:

Рис. 21

Аналогично и значит Таким образом задача свелась к нахождению площади трапеции АВСD. Изобразим трапецию ABCD отдельно (рис.22). Точка О – центр вписанной в трапецию окружности.

Рис. 22

Так как в трапецию можно вписать окружность, то или Из по теореме Пифагора имеем
Тогда
Площадь трапеции:
Значит,
Ответ:
Пример 5.Основание пирамиды – равносторонний треугольник со стороной а. Одна из боковых граней – равнобедренный прямоугольный треугольник, плоскость которого перпендикулярна плоскости основания. Найти площадь боковой поверхности пирамиды.
Решение. Сделаем рисунок (рис. 23).

Рис. 23

Площадь боковой поверхности данной пирамиды SABC состоит из суммы площадей ее боковых граней. Боковые грани – треугольники, один из которых прямоугольный и равнобедренный ( ), два других – равные треугольники Рассмотрим – по условию. Вычислим его площадь: Так как равнобедренный, то а так как то и следовательно в
Тогда
Рассмотрим SE найдем из По теореме Пифагора имеем Найдем DE. Для этого рассмотрим равносторонний треугольник основания (рис. 24). В отрезок DE является средней линией, значит, Находим SE:

Рис. 24
Теперь
Площадь боковой поверхности пирамиды равна:
Ответ:
Конспект урока и презентация по геометрии на тему «Площадь поверхности пирамиды и усеченной пирамиды» (11 класс)
Конспект
урока геометрии в 11 классе
по теме «Площадь поверхности пирамиды и усеченной пирамиды»
Цель: научиться вычислять площадь поверхности пирамиды и усеченной пирамиды.
Задачи урока:
Образовательные – Формирование устойчивых умений и навыков вычисления площади поверхности пирамиды и усеченной пирамиды.
Развивающие – Развитие математического мышления и логической речи учащихся, умения делать выводы, высказывать свои мысли и чувства, расширять кругозор учащихся.
Воспитательные – Воспитание интереса к предмету, уважительного отношения к одноклассникам; трудолюбия, прилежания, активности, внимания.
Тип урока: Урок закрепление.
Ресурсные материалы: Интерактивная доска, раздаточный материал.
Критерии успеха:
Я знаю – формулы вычисления площади поверхности пирамиды и усеченной пирамиды.
Я понимаю – как вычислять площадь поверхности пирамиды и усеченной пирамиды.
Я умею – вычислять площадь поверхности пирамиды и усеченной пирамиды.
Ожидаемые результаты:
1: определят цель урока, сформулируют знания о элементах и формулах площади поверхности пирамиды и усеченной пирамиды, примут участие в групповой работе;
2: научаться применять свои знания для вычисления площади поверхности пирамиды и усеченной пирамиды;
3: определят значимость изученной темы для себя, проявят лидерские качества, организуют работу групп.
фаза
Этапы урока
Деятельность учителя
Деятельность ученика
Форма, метод, прием, стратегия
Форма оценивания
Ресурсы
В

ы
з
о
в
а
1.Организационный момент.
2 мин.
Цель: Обеспечение благоприятного климата для работы на уроке и психологическая подготовка учащихся к предстоящему занятию.
Приветствие. Здравствуйте, ребята. Вот и настал наш урок. Я желаю нам сегодня хорошего урока.
Немного истории.
Заполнение электронного журнала.
Применяя прием критического мышления «Корзина идей» вместе с учащимися формулирую цели урока.
Психологический настрой на урок
Выступление ученика
Стратегия «Приветствие»
«корзина идей» прием КМ
Формативное
формативное устное поощрение учителя
Презентация
Электронный журнал.
Тема и цели урока на слайде.
2. Повторение основных понятий:
элементы и формулы площади поверхности пирамиды и усеченной пирамиды
Цель: Актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала.
Учитель предлагает ученикам с целью повторения основных понятий по теме «Пирамида и усеченная пирамида» устная работа тест «Проверь себя».
Тест проводится для повторения и создания ситуации успеха.
Правильные ответы на вопросы появляются после ответа ученика.
Ученики устно выполняют тест.
Фронтальная работа
формативное устное поощрение учителя
самопроверка
Презентация
3. Создание коллаборативной среды.
Цель: Создание условий, включающих каждого ученика в процесс обучения
Деление на группы:
Для создания атмосферы сотрудничества.
Учащимся раздаются цветные геометрические фигуры.
Ученики делятся на группы.
В группе распределение ролей.
Цветные геометрические фигуры.
О
с
м
ы
с
л
е
н
и
я
4.Работа в группах.
Цель: Создание ситуации успеха для каждого учащегося
Задание группам:
1 группа.
Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13.
Найдите площадь поверхности этой пирамиды.
2 группа
Дано:
МАВС – пирамида
АВ=12, АС=ВС=10,
АМ=ВМ=СМ=12
Найти: Sбок.
3 группа Дано:
МАВС – пирамида
АС=15, ВС=14, АВ=13.
Все двугранные углы
при ребрах основания равны 60⁰
Найти: Sп.п.
4 группа
Стороны оснований правильной треугольной усеченной пирамиды равны 4 см и 2 см, а боковое ребро равно 2 см.
Найдите:
1. апофему пирамиды;
2. площадь полной поверхности.
5 группа
Основанием пирамиды является прямоугольник, диагональ которого равна 8 см. Плоскости двух боковых граней перпендикулярны к плоскости основания, две другие образуют с основанием углы 30⁰ и 45⁰. Найдите площадь поверхности пирамиды
6 группа
Дано:
SАВС – пирамида
АВ=АС=ВС=1,
AD- высота ΔАВС
SA перпендикуляр ΔАВС
<SDA = 60⁰
Найти: Sбок.
Ученики используют основное свойство дроби, сокращают дроби.
По часовой стрелке в группе меняются и взаимооценивают друг друга..
Групповая работа
Формативное оценивание в группе друг друга.
Раздаточный материал.
5. Защита решений у доски
Цель: Умение обосновать правильность решения.
Учитель предлагает одному представителю от группы у доски защитить решение задачи.
Предоставляет возможность остальным учащимся задавать вопросы, предлагать свои решения задач, оценивать правильность решения и умение выступать перед аудиторией.
Представитель каждой группы у доски проводит защиту решения задачи.
Оценивают и корректируют работу других учащихся.
Индивидуальная, фронтальная
Взаимоценивание
Суммативное оценивание.
презентация
Р
е
ф
л
е
к
с
и
я
6.Рефлексия
Цель: Фиксирование допущенных ошибок. Выставление итоговых оценок
Подведение итога
Лист рефлексии
ФИ ученика_________
Сегодня я узнал новое…
На уроке мне пригодились знания…
Для меня было сложно…
На уроке мне понравилось…
Учитель просит ученика озвучить рефлексию (по желанию.
Заполняют листы рефлексии.
Один ученик озвучивает рефлексию (по желанию)
Листы рефлексии
7. Домашнее задание.
Тренажер по математике для подготовки к ЕНТ (стр.341)
№28, 35, 43, 48 (уровень В)
№2,19 (уровень А)
Любые три задачи на выбор.