правила, основные свойства и формулы

Логарифмы и правила действий с ними достаточно емкие и простые. Следовательно, разобраться в данной теме вам не составит труда. После того как вы узнаете все правила натуральных логарифмов, любая задача решится самостоятельно. Первое знакомство с этой темой может показаться скучным и бессмысленным, но именно при помощи логарифмов решились многие проблемы математиков XVI века. «О чем это?» — подумали вы. Прочтите статью до конца и узнаете, что этот раздел «царицы наук» может быть интересен не только математикам, ученым точных наук, но и простым ученикам средних школ.

Определение логарифма

Начнем с определения логарифма. Как гласят многие учебники: логарифмом числа b по основанию a (logab) является некое число с, для которого выполняется такое равенство: b=ac. То есть, говоря простыми словами, логарифм — определенная степень, в которую возводим основание, чтобы получить данное число. Но важно помнить, что логарифм вида logab имеет смысл только при: a>0; a — число, отличное от 1; b>0, следовательно, делаем вывод, что логарифм можно найти только у положительных чисел.

Классификация логарифмов по основанию

Логарифмы могут быть с любым положительным числом в основании. Но также существует два вида: натуральный и десятичный логарифмы.

• Натуральный логарифм — логарифм с основанием е (е — число Эйлера, численно приблизительно равняется 2,7, иррациональное число, которое ввели для показательной функции y = ex), обозначается как ln a = logea;
• Десятичный логарифм — логарифм с основанием 10, то есть log10a = lg a.

Основные правила логарифмов

Для начала нужно познакомиться с основным логарифмическим тождеством: alogab=b, далее следуют два таких основных правила:

• loga1 = 0 — так как любое число в нулевой степени равно 1;
• logaa = 1.

Благодаря открытию логарифма для нас не составит труда решить абсолютно любое показательно уравнение, ответ которого нельзя выразить натуральным числом, а только иррациональным. Например: 5х = 9, х = log59 (так как натурального х для данного уравнения не существует).

Действия с логарифмами

• loga(x · y) = logax+ logay — чтобы найти логарифм произведения, нужно сложить логарифмы сомножителей. Обратите внимание на то, что основания логарифмов одинаковы. Если записать это в обратном порядке, то получим правило сложения логарифмов.
• loga xy = logax — logay — чтобы найти логарифм частного, нужно найти разность логарифмов делимого и делителя. Обратите внимание: основания у логарифмов одинаковы. При записи в обратном порядке получаем правило вычитания логарифмов.

• logakxp = (p/k)*logax — таким образом, если в аргументе и основании логарифма стоят степени, то их можно выносить за знак логарифма.
• logax = logac xc — частный случай предыдущего правила, когда показатели степеней равны, их можно сократить.
• logax = (logbx)(logba) — так называемый модуль перехода, процедура приведения логарифма к другому основанию.
• logax = 1/logxa — частный случай перехода, смена мест основания и данного числа. Все выражение, образно говоря, переворачивается, и логарифм с новым основанием оказывается в знаменателе.

История возникновения логарифмов

В XVI веке возникла необходимость проведения многих приближенных вычислений для решения практических задач, главным образом, в астрономии (например, определение положения судна по Солнцу или звездам).

Эта потребность быстро росла и значительную трудность создавало умножение и деление многозначных чисел. И ученый-математик Непер при тригонометрических расчетах решил заменить трудоемкое умножение на обыкновенное сложение, сопоставив для этого некоторые прогрессии. Тогда деление, аналогично, заменяется на процедуру попроще и надежнее — вычитание, а дабы извлечь корень n-ой степени, нужно разделить логарифм подкоренного выражения на n. Решение такой нелегкой задачи в математике явно отображало цели Непера в науке. Вот как он писал об этом в начале своей книги «Рабдология»:

Я всегда старался, насколько позволяли мои силы и способности, освободить людей от трудности и скуки вычислений, докучливость которых обыкновенно отпугивает очень многих от изучения математики.

Название логарифма предложил сам Непер, он был получен путем совмещения греческих слов, которые в сочетании означали “число отношений”.

Основание логарифма ввел Спейдел. Его заимствовал Эйлер из теории о степенях и перенес в теорию логарифмов. Понятие логарифмирования стало известным благодаря Коппе в XIX веке. А использование натуральных и десятичных логарифмов, а также их обозначения появились благодаря Коши.

В 1614 году Джон Непер издал на латыни сочинение «Описание удивительной таблица логарифмов». Там было изложено краткое описание логарифмов, правил и их свойств. Так термин «логарифм» утвердился в точных науках.

Операцию логарифмирования и первое упоминание о ней появилось благодаря Валлису и Иоганну Бернулли, а окончательно установлена она была Эйлером в XVIII веке.

Именно заслуга Эйлера в распространении логарифмической функции вида y = logax на комплексную область. В первой половине XVIII века вышла его книга «Введение в анализ бесконечных», где были современные определения показательной и логарифмической функций.

Логарифмическая функция

Функция вида y = logах (имеет смысл, только если: а > 0, а ≠ 1).

• Логарифмическая функция определяется множеством всех положительных чисел, так как запись logах существует только при условии — х > 0;.
• Данная функция может принимать абсолютно все значения из множества R (действительных чисел). Так как у всякого действительного числа b есть положительное x, чтобы выполнялось равенство logaх = b, то есть, это уравнение имеет корень — х = аb (следует из того, что logaab= b).
• Функция возрастает на промежутке a>0, а убывает на промежутке 0
• Если а>0, то функция принимает положительные значения при х>1.

Следует помнить, что любые графики логарифмической функции у = logах имеют одну стационарную точку (1;0), так как logа 1 = 0. Это хорошо видно на иллюстрации графика ниже.

Как видим на изображениях, функция не имеет четности или нечетности, не имеет наибольших или наименьших значений, не ограничена сверху или снизу.

Логарифмическая функция y = logаx и показательная функция y = aх, где (а>0, а≠1), взаимно обратные. Это можно видеть на изображении их графиков.

Решение задач с логарифмами

Обычно решение задачи, содержащей логарифмы, основано на преобразовании их в стандартный вид или же направлено на упрощение выражений под знаком логарифма. Или же стоит переводить обычные натуральные числа в логарифмы с нужным основанием, проводить дальнейшие операции по упрощению выражения.

Есть некие тонкости, которые не стоит забывать:

• При решении неравенств, когда обе части стоят под логарифмами по правилу с одним основанием, не спешите «отбрасывать» знак логарифма. Помните о промежутках монотонности логарифмической функции. Так как, если основание больше 1 (случай, когда функция возрастает) — знак неравенства останется без изменений, но когда основание больше 0 и меньше 1 (случай, когда функция убывает) — знак неравенства изменится на противоположный;
• Не забывайте определения логарифма: logах = b, а>0, а≠1 и х>0, чтобы не потерять корней из-за неучтенной области допустимых значений. ОДЗ (область допустимых значений) существует практически для всех сложных функций.

При решении логарифмических уравнений рекомендуется пользоваться равносильными преобразованиями. Также, необходимо быть внимательным и учитывать возможные преобразования, которые способны привести к потере некоторых корней.

Это банальные, но масштабные ошибки, с которыми столкнулись многие на пути поиска верного ответа для задания. Правил решения логарифмов не так уж и много, поэтому эта тема проще, чем другие и последующие, но в ней стоит хорошо разобраться.

Вывод

Данная тема с первого взгляда может показаться сложной и громоздкой, но, исследуя ее глубже и глубже, начинаешь понимать, что тема просто заканчивается, а сложностей так ничего и не вызвало. Мы рассмотрели все свойства, правила и даже ошибки, касающиеся темы логарифмов. Успехов в обучении!

www.nastroy.net

Действия с логарифмами. Постигаем азы!

        На прошлом занятии мы познакомились с понятием логарифма и порешали несколько несложных примеров на определение и смысл логарифма. Для начального знакомства.)

        Теперь настал черёд более тесного знакомства с логарифмами и, соответственно, решения более серьёзных примеров. Начнём мы с ограничений в логарифмах.

 

Ограничения в логарифмах.

        Как и у любого математического понятия, у логарифма тоже есть свои свойства и фишки. Именно о них мы сейчас и будем разговаривать. И в первую очередь это ограничения в логарифмах. До сих пор мы с вами знали лишь два жёстких ограничения в математике:

        — нельзя делить на ноль;

        — нельзя извлекать корень чётной степени из отрицательного числа.

       

        С этого момента к этим двум добавляются дополнительные ограничения в логарифмах.

        Для начала запишем определение логарифма в самом общем виде. Через буквы.

        log_ab = c

        Напоминаю, что это равенство означает всего лишь решение показательного уравнения

        a^c = b.

        И всё.

        А теперь подумаем, любым ли числом может быть a? Пусть, к примеру, a = 1. Тогда получается забавная штука: единица в любой степени равна единице… И каким бы ни было число c, числа a и b останутся единичками. Та же самая история и с нулём. Не подходят эти числа в качестве основания…

        Отрицательные числа – очень вредные и капризные. В одну степень их можно возводить, а в другую – нельзя. Вот и поступили математики с ними, как со всеми капризными – вовсе исключили из рассмотрения.

        В результате у нас получилось такое ограничение на основание:

        a > 0,    a ≠ 1.

        А каким может быть число b? Давайте подумаем: если заведомо положительное основание a возвести любую степень c, то какое число мы в итоге получим? Верно, положительное число и получим!

        Отсюда ещё одно ограничение на аргумент логарифма:

        b > 0.

        Вот и все ограничения. Число c (значение логарифма) может быть совершенно любым.

        Конечно, при решении безобидных числовых примеров на логарифмы эти ограничения практически никак не сказываются. Зато когда столкнётесь с логарифмическими уравнениями и неравенствами, вы про эти ограничения ещё не раз вспомните! А если не вспомните, то я вам напомню. И буду напоминать при каждом удобном случае.) Ибо эти ограничения очень (!) важны при решении уравнений и неравенств. Про ОДЗ помните? Вот, то-то и оно…

 

Свойства логарифмов.

        Итак, с ограничениями на логарифмы разобрались. Пора переходить на следующий уровень и знакомиться со свойствами логарифмов. Вот они:

        

        Здесь всюду b>0 и c>0, а также a>0, a≠1.

        Вот такой вот джентльменский набор. Ни много ни мало.) Теперь кратенько пробежимся по каждому из этих свойств. Чтобы ясно было, откуда ноги растут, как говорится.)

        Начнём с первого свойства:

        

        Обычно это свойство именуют особо —

основным логарифмическим тождеством. Откуда же оно берётся? Запишем снова уже до боли знакомое нам равенство:

        log_ab = c

        Из самого определения логарифма мы с вами знаем, что, если число а (основание) возвести в степень c (показатель), то получим число b:

        a^c = b

        А теперь подумаем, чему же равно у нас число c? Да вот же оно:

        с = log_ab

        Подставим это выражение в предыдущее равенство и получим как раз то, что нам и требуется:

        

        «И зачем нам такая странная перетасовка?» — спросите вы. А затем, что многоэтажное выражение превращается в элементарное b! Полезная формула.) Это единственная формула, где логарифм стоит в показателе степени.

        Следующая группа формул (2-3):

        

        Думаю, тут комментарии излишни. Всё прямо из определения логарифма следует.) И даже примеры разбирались. В предыдущем материале. Кому всё-таки непонятно, применяем старый добрый способ — словесную расшифровку. Проверено, помогает.)

 

        Переходим к следующей группе формул (4-5):

        

        Коротко эти формулы называются логарифм произведения и логарифм частного (дроби).

        А вот с их доказательствами вопрос похитрее будет.) Эти два свойства проистекают из обычного умножения и деления степеней с одинаковым основанием. Как именно? Мы с седьмого класса помним, что при перемножении двух степеней с одинаковым основанием показатели степеней складываются, а при делении – вычитаются:

           

        Для доказательства, например, четвёртой формулы (логарифм произведения) придётся ввести вспомогательные обозначения:

        m = log_ab  

        и 

        n = log_ac.

        До конца доказывать эти две формулы я не буду. Как продолжить доказательство? Подставьте выражения для m и n в формулу умножения степеней и воспользуйтесь основным логарифмическим тождеством (формула №1). Попробуйте! Очень полезно.)

        Кстати, прошу обратить внимание: данные формулы справедливы только при одинаковых основаниях! Если основания разные, то, скорее всего, преобразования более мудрёные…

        Идём дальше. Следующая группа формул (6-7) – это формулы, позволяющие избавляться от степеней в аргументе или в основании логарифма:

        

        Смысл их тоже прост. Если аргумент логарифма возводится в степень, то показатель степени n можно вынести наружу и приписать перед логарифмом. То же самое происходит и тогда, когда в степень возводится

основание логарифма, только показатель степени переворачивается. Эти две полезные формулы избавляют нас от степеней в аргументе/основании. Если это мешает, конечно. Это понятно.)

        Осталась последняя формула №8:

        

        Это – так называемая формула перехода к новому основанию. Самая трудная для запоминания формула. Поэтому народ частенько и ленится её запоминать… А вы запомните. Не сочтите за труд.) Когда она применяется? А когда основания логарифмов – разные.) Скажем, в примере куча логарифмов по основанию 3 и затесался один логарифм по основанию 7. Его и менять надо. На тройку.) Мы с этой формулой крепко подружимся. И примеры тоже порешаем.) В соответствующем уроке.

        Вот такой вот перечень формул и свойств. Их вполне достаточно, чтобы уверенно решать примеры на логарифмы любого уровня сложности. Эти формулы нужно не просто помнить, но и уметь применять. Причём в обоих направлениях – как слева направо, так и справа налево.

        Ещё не помешало бы знать, что такое десятичный логарифм и что такое натуральный логарифм.

        Десятичный логарифм – это просто логарифм по основанию 10:

        log₁₀b = lg b

        В написании десятичного логарифма всего лишь пропадает буковка «о».

        Натуральный логарифм (хотя чего уж в нём такого натурального) – это логарифм по основанию e. Иррациональному числу «e».

        e = 2,71828182845…

        Что это за загадочное число, узнаете и поймёте, когда поступите в институт. В курсе матанализа.) В школьной математике это число практически не встречается, зато в высшей – сплошь и рядом.)

        Обозначается натуральный логарифм вот так:

        log

eb = ln b

        Логарифмы по этим основаниям хотя и имеют своё особое написание, но ни по определению, ни по свойствам ничем не отличаются от обычных логарифмов, скажем, по основанию два. Или три. И решаются точно так же.

        Итак, будем считать, что необходимая теоретическая база подготовлена. Переходим к практике.)

       

Начальный уровень. Немного формул. Немного дробей. Немного степеней.

        На этом уровне мы:

        — впрямую используем определение логарифма,

        — впрямую используем самые простые свойства логарифмов.

        Мыслей здесь особых не нужно. Главное – память и внимательность. Итак, читаем, смотрим, вникаем.

        Пример 1

        Вычислить:

        

        Решение примера вытекает непосредственно из определения и смысла логарифма. В какой степени 1/3 даёт 1/27? В кубе, конечно. То есть, в третьей степени.

        Ответ: 3.

 

        Следующий пример:

        Пример 2

        

        Всё то же самое, только дроби десятичные. Ну и что? Опять напрямую пользуемся определением логарифма: в какой степени 0,3 даст 0,09? В квадрате, разумеется! Или во второй степени.)

        Ответ: 2.

 

        И ещё один примерчик на дроби:

        Пример 3

        

        А вот тут некоторые могут и зависнуть. Почему? Потому что связь между 0,5 и 1/128 визуально просматривается плохо. Что делать?

        Что-что… Да к обычным дробям перейти! Вот вам и первый практический совет:

        Если в одном примере смешались в кучу разные типы дробей, то переходим к обыкновенным дробям.

         Этот приём, между прочим, работает не только в логарифмах, но и в других смежных темах – в показательных выражениях, в корнях.

        В нашем примере 0,5 = 5/10 = 1/2. Ну и как? Связь между 1/2 и 1/128 легче углядеть? Естественно! 1/128 – это 1/2 в седьмой степени.

        Ответ: 7

        Что? Забыли, что 128 – это 2 в седьмой степени? Срочно повторить степени!

 

        Следующий пример:

        Пример 4

        

        Прямое применение формулы разности логарифмов:

        

        И как вам? Оба логарифма по отдельности ровно не считаются, зато через формулу разности – отлично!

        Ответ: 1

       

        Ещё пример:

        Пример 5

        

        А вот здесь складывать по формуле нельзя: основания разные – тройка и двойка. А формула – штука жёсткая. Раз требуются одинаковые основания, значит, так и надо.

        Но тут ничего хитрого нет: оба логарифма считаются ровно.

        Ответ: 10.                     

        Не каждый, правда, догадается, что 243 – это 3 в пятой степени, а 32 – это 2 в пятой… Но тут дело уже не в логарифмах, дело в степенях!

        Вот вам и второй практический совет.

        Степени популярных чисел надо знать. В лицо!

        Конечно, возвести двойку в седьмую степень или тройку в пятую может каждый. Не в уме, так хотя бы на черновике. Но это умение слабо помогает в работе с логарифмами, да. А вот сообразить, какое число и в какой степени скрывается за числом 128 или 243 – это уже совсем другое дело. Почувствуйте разницу, что называется!

        Поскольку умение распознавать степени в лицо пригодится не только на этом уровне, но и на следующих, вот вам небольшое задание:

        Определить, какими степенями и каких чисел являются числа:

        4; 8; 16; 27; 32; 36; 49; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729; 1024.

        Ответы (вразброс, естественно):

        27²; 2¹⁰; 3⁶; 7²; 2⁶; 9²; 3⁴; 4³; 10²; 2⁵; 3⁵; 7³; 16²; 2⁷; 5³; 2⁸; 6²; 3³; 2⁹; 2⁴; 2²; 4⁵; 25²; 4⁴; 6³; 8²; 9³.

        Да-да! Не удивляйтесь, что ответов побольше, чем заданий. Например, 2⁸, 4⁴ и 16² – это всё 256.

        А теперь я настоятельно рекомендую взять любой учебник по школьной математике и порешать оттуда простейшие примеры на логарифмы. Порешали? Хоть что-то получилось? Тогда будем считать, что начальный уровень вы прошли. Переходим на следующий уровень.

 

Почти все формулы. Почти все степени. Поиск «братьев по степени».

        На этом уровне применяем почти все формулы работы с логарифмами. Кроме последней формулы перехода к новому основанию. А также закрепляем наши навыки работы со степенями.

        Поехали расширять наши возможности!

        Пример 6

        

        Вот тут прямое применение определения логарифма не годится: из четвёрки 128 простым возведением в степень никак не сделаешь. И формулы логарифмов непонятно как употреблять… Не беспокойтесь, сейчас всё получится.)  При маленьком условии, что вы узнали в лицо число 128. Да! Это 2 в седьмой степени! Так и запишем:

        log₄128 = log₄2⁷

        Вот и одна из формул (третья снизу) приходит на помощь. Та, где показатель степени ставится множителем перед логарифмом:

        log_axⁿ = n·log_ax

        Вот и выносим семёрку за наш логарифм. Пишем:

        log₄2⁷ = 7log₄2

        Что дальше? Дальше осталось вспомнить, что 4 = 2². Верно!

        7log₄2 = 7log₂²2

        Вот и ещё одна формулка в дело просится!) Вторая снизу, где в степень возводится основание логарифма. Только в этом случае при вынесении показателя наружу его надо перевернуть: 1/n.

        

        Записываем:

        

        Ответ: 3,5

        Вот так вот! А если бы мы не узнали в числе 128 степень двойки, то так и застряли бы на этом, в общем-то несложном примере…

                                           

        А теперь мы вплотную подошли к одному весьма и весьма полезному приёму в работе с логарифмическими и показательными выражениями. Приём этот называется «поиск братьев». Братьев по степени. И по разуму тоже.) Суть этого полезного приёма заключается в тщательном осмотре примера и распознавании одного и того же числа в разных степенях.

        Этот приём (шифровка одного и того же числа в разных степенях) – очень популярный приём в логарифмах! Да и в показательных уравнениях и неравенствах тоже. Например, числа 27 и 243 – родные братья! Да, 243 из 27 прямым возведением в натуральную степень никак не получить, но зато они – родня по тройке! Так как 27 = 3³, а 243 = 3⁵. В разобранном только что примере родственниками оказались 4 и 128. По числу 2. В общем, идея понятна, да?

        И зачем всё это нужно – распознавать степени и родственников? А затем, что примеры от этого проще становятся! И формулы свойств логарифмов сразу высвечиваются.) Особенно важно получить в примере одинаковые основания у логарифмов, ибо чем больше одинаковых значков в примере и меньше разных, тем лучше. И не нужно здесь применять формулу перехода к новому основанию: зачем же из пушки по воробьям палить.?)

 

        Следующий пример на братьев (или сестёр):

        Пример 7

        Вычислить:

        

        В примере стоит сумма логарифмов, но основания логарифмов разные – тройка и девятка. Стало быть, применять напролом формулу суммы логарифмов нельзя. Но! Первый логарифм уже считается ровно, получится просто тройка:

        log₃27 = log₃3³ = 3

        А со вторым логарифмом что? Из девятки 27 возведением в целую степень не получишь! Но зато 9 и 27 – родня! По тройке.) Самое время вспомнить, что:

        9 = 3²

        Что ж, поработаем отдельно со вторым логарифмом. Перейдём в основании от девятки к тройке. Поможет нам такое преобразование или нет – неизвестно. Но что-то делать всё-таки надо, правда? Итак, преобразовываем второй логарифм по второй (снизу) формуле – выносим степень из основания за логарифм:

        

        Осталось лишь сложить 3 (первый логарифм) и 3/2 (второй логарифм)

        Ответ: 4,5

 

        Так, с близкой роднёй разобрались. Идём дальше. Иногда пример может не соответствовать в точности формуле, а может быть лишь похожим на одну из формул. И наша задача – сначала преобразовать пример под ту или иную формулу. Как, например, этот:

        Пример 8

        

        Напоминаю, что запись lg означает просто логарифм по основанию 10. И всё.)

        Итак, основания логарифмов уже одинаковые – десятка. Ну прям напрашивается формула суммы логарифмов! А н-е-ет, не катит! Двойка во втором слагаемом всё портит. Коэффициент, понимаешь.) А формула применима только к чистым логарифмам, безо всяких коэффициентов. Но горевать рано! Мы эту двойку сейчас ликвидируем. Безопасно для примера.) Мы её внутрь логарифма загоним. Как? Всё по той же формуле логарифма от степени:

        log_axⁿ = n·log_ax

        Здесь как раз тот случай, когда формулу надо применять справа налево. Ни в одной другой теме школьной математики нельзя вот так красиво избавляться от мешающих коэффициентов, а в логарифмах – пожалуйста! Итак, избавляемся от двойки перед вторым логарифмом:

        2lg5 = lg5² = lg25

        Вот так. Осталось лишь сложить два логарифма по формуле логарифма произведения (опять же в применении справа налево). Вот и складываем:

        lg4 + lg25 = lg(4́·25) = lg100 = 2

        Напоминаю, что десятичные логарифмы формулу ничуть не портят, ибо они по своим свойствам ничем не отличаются от обычных!    

        Ответ: 2

        Вот вам и третий практический совет.

        Любую степень можно записать множителем перед логарифмом. И наоборот – любой числовой коэффициент можно спрятать внутрь логарифма. Если он мешает, конечно.

       Ну что, вот и состоялась наше более близкое знакомство с логарифмами! Осталось теперь с ними крепко подружиться. На следующем уровне и в следующем уроке.)

        Традиционные примеры для самостоятельного решения.

        Вычислить:

        

        

        

        

        Ответы (вразнобой): 0; 1; 2; 3; 

abudnikov.ru

правила, основные свойства и формулы :: SYL.ru

Логарифмы и правила действий с ними достаточно емкие и простые. Следовательно, разобраться в данной теме вам не составит труда. После того как вы узнаете все правила натуральных логарифмов, любая задача решится самостоятельно. Первое знакомство с этой темой может показаться скучным и бессмысленным, но именно при помощи логарифмов решились многие проблемы математиков XVI века. «О чем это?» — подумали вы. Прочтите статью до конца и узнаете, что этот раздел «царицы наук» может быть интересен не только математикам, ученым точных наук, но и простым ученикам средних школ.

Определение логарифма

Начнем с определения логарифма. Как гласят многие учебники: логарифмом числа b по основанию a (log_ab) является некое число с, для которого выполняется такое равенство: b=a^c. То есть, говоря простыми словами, логарифм — определенная степень, в которую возводим основание, чтобы получить данное число. Но важно помнить, что логарифм вида log_ab имеет смысл только при: a>0; a — число, отличное от 1; b>0, следовательно, делаем вывод, что логарифм можно найти только у положительных чисел.

Классификация логарифмов по основанию

Логарифмы могут быть с любым положительным числом в основании. Но также существует два вида: натуральный и десятичный логарифмы.

• Натуральный логарифм — логарифм с основанием е (е — число Эйлера, численно приблизительно равняется 2,7, иррациональное число, которое ввели для показательной функции y = e^x), обозначается как ln a = log_ea;
• Десятичный логарифм — логарифм с основанием 10, то есть log₁₀a = lg a.

Основные правила логарифмов

Для начала нужно познакомиться с основным логарифмическим тождеством: a^log_ab=b, далее следуют два таких основных правила:

• log_a1 = 0 — так как любое число в нулевой степени равно 1;
• log_aa = 1.

Благодаря открытию логарифма для нас не составит труда решить абсолютно любое показательно уравнение, ответ которого нельзя выразить натуральным числом, а только иррациональным. Например: 5^х = 9, х = log₅9 (так как натурального х для данного уравнения не существует).

Действия с логарифмами

• log_a(x · y) = log_ax+ log_ay — чтобы найти логарифм произведения, нужно сложить логарифмы сомножителей. Обратите внимание на то, что основания логарифмов одинаковы. Если записать это в обратном порядке, то получим правило сложения логарифмов.
• log_a xy = log_ax — log_ay — чтобы найти логарифм частного, нужно найти разность логарифмов делимого и делителя. Обратите внимание: основания у логарифмов одинаковы. При записи в обратном порядке получаем правило вычитания логарифмов.

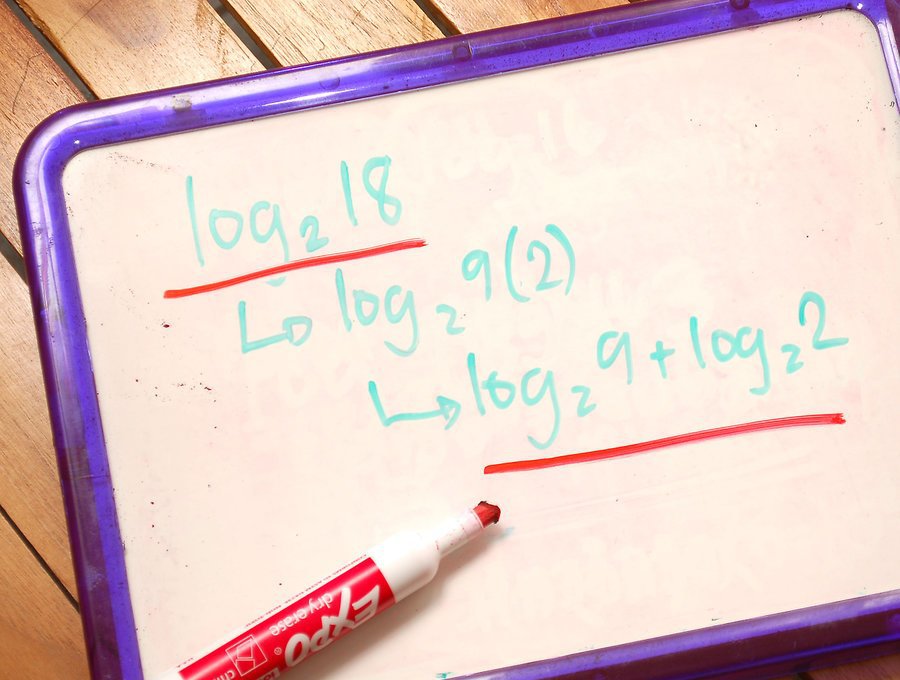
• log_a^kx^p = (p/k)*log_ax — таким образом, если в аргументе и основании логарифма стоят степени, то их можно выносить за знак логарифма.
• log_ax = log_a^c x^c — частный случай предыдущего правила, когда показатели степеней равны, их можно сократить.
• log_ax = (log_bx)\(log_ba) — так называемый модуль перехода, процедура приведения логарифма к другому основанию.
• log_ax = 1/log_xa — частный случай перехода, смена мест основания и данного числа. Все выражение, образно говоря, переворачивается, и логарифм с новым основанием оказывается в знаменателе.

История возникновения логарифмов

В XVI веке возникла необходимость проведения многих приближенных вычислений для решения практических задач, главным образом, в астрономии (например, определение положения судна по Солнцу или звездам).

Эта потребность быстро росла и значительную трудность создавало умножение и деление многозначных чисел. И ученый-математик Непер при тригонометрических расчетах решил заменить трудоемкое умножение на обыкновенное сложение, сопоставив для этого некоторые прогрессии. Тогда деление, аналогично, заменяется на процедуру попроще и надежнее — вычитание, а дабы извлечь корень n-ой степени, нужно разделить логарифм подкоренного выражения на n. Решение такой нелегкой задачи в математике явно отображало цели Непера в науке. Вот как он писал об этом в начале своей книги «Рабдология»:

Я всегда старался, насколько позволяли мои силы и способности, освободить людей от трудности и скуки вычислений, докучливость которых обыкновенно отпугивает очень многих от изучения математики.

Название логарифма предложил сам Непер, он был получен путем совмещения греческих слов, которые в сочетании означали “число отношений”.

Основание логарифма ввел Спейдел. Его заимствовал Эйлер из теории о степенях и перенес в теорию логарифмов. Понятие логарифмирования стало известным благодаря Коппе в XIX веке. А использование натуральных и десятичных логарифмов, а также их обозначения появились благодаря Коши.

В 1614 году Джон Непер издал на латыни сочинение «Описание удивительной таблица логарифмов». Там было изложено краткое описание логарифмов, правил и их свойств. Так термин «логарифм» утвердился в точных науках.

Операцию логарифмирования и первое упоминание о ней появилось благодаря Валлису и Иоганну Бернулли, а окончательно установлена она была Эйлером в XVIII веке.

Именно заслуга Эйлера в распространении логарифмической функции вида y = log_ax на комплексную область. В первой половине XVIII века вышла его книга «Введение в анализ бесконечных», где были современные определения показательной и логарифмической функций.

Логарифмическая функция

Функция вида y = log_ах (имеет смысл, только если: а > 0, а ≠ 1).

• Логарифмическая функция определяется множеством всех положительных чисел, так как запись log_ах существует только при условии — х > 0;.
• Данная функция может принимать абсолютно все значения из множества R (действительных чисел). Так как у всякого действительного числа b есть положительное x, чтобы выполнялось равенство log_aх = b, то есть, это уравнение имеет корень — х = а^b (следует из того, что log_aa^b= b).
• Функция возрастает на промежутке a>0, а убывает на промежутке 0<а<1.
• Если а>0, то функция принимает положительные значения при х>1.

Следует помнить, что любые графики логарифмической функции у = log_ах имеют одну стационарную точку (1;0), так как log_а 1 = 0. Это хорошо видно на иллюстрации графика ниже.

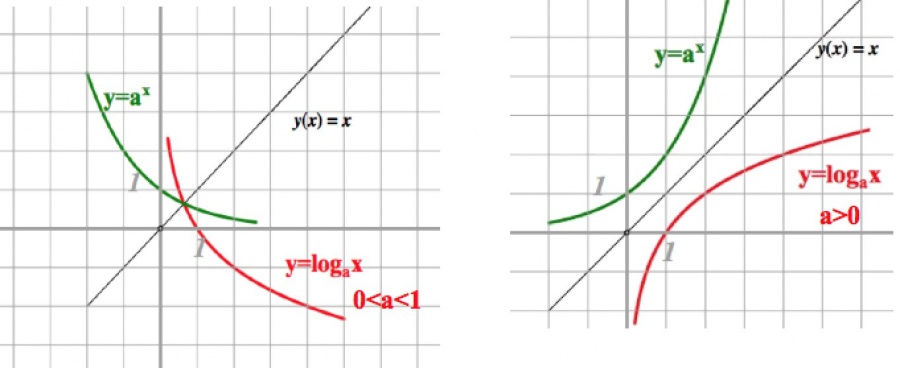
Как видим на изображениях, функция не имеет четности или нечетности, не имеет наибольших или наименьших значений, не ограничена сверху или снизу.

Логарифмическая функция y = log_аx и показательная функция y = a^х, где (а>0, а≠1), взаимно обратные. Это можно видеть на изображении их графиков.

Решение задач с логарифмами

Обычно решение задачи, содержащей логарифмы, основано на преобразовании их в стандартный вид или же направлено на упрощение выражений под знаком логарифма. Или же стоит переводить обычные натуральные числа в логарифмы с нужным основанием, проводить дальнейшие операции по упрощению выражения.

Есть некие тонкости, которые не стоит забывать:

• При решении неравенств, когда обе части стоят под логарифмами по правилу с одним основанием, не спешите «отбрасывать» знак логарифма. Помните о промежутках монотонности логарифмической функции. Так как, если основание больше 1 (случай, когда функция возрастает) — знак неравенства останется без изменений, но когда основание больше 0 и меньше 1 (случай, когда функция убывает) — знак неравенства изменится на противоположный;
• Не забывайте определения логарифма: log_ах = b, а>0, а≠1 и х>0, чтобы не потерять корней из-за неучтенной области допустимых значений. ОДЗ (область допустимых значений) существует практически для всех сложных функций.

При решении логарифмических уравнений рекомендуется пользоваться равносильными преобразованиями. Также, необходимо быть внимательным и учитывать возможные преобразования, которые способны привести к потере некоторых корней.

Это банальные, но масштабные ошибки, с которыми столкнулись многие на пути поиска верного ответа для задания. Правил решения логарифмов не так уж и много, поэтому эта тема проще, чем другие и последующие, но в ней стоит хорошо разобраться.

Вывод

Данная тема с первого взгляда может показаться сложной и громоздкой, но, исследуя ее глубже и глубже, начинаешь понимать, что тема просто заканчивается, а сложностей так ничего и не вызвало. Мы рассмотрели все свойства, правила и даже ошибки, касающиеся темы логарифмов. Успехов в обучении!

www.syl.ru

Пособие для обучающихся «Формулы и свойства логарифмов»

Государственное образовательное учреждение

среднего профессионального образования

Тульской области

«Алексинский машиностроительный техникум»

Формулы и свойства

логарифмов

Разработан

преподавателем

математики

Христофоровой М.Ю.

Определение

Логарифмом числа b по основанию α (loq_αb) называется такое число c, что b = α^c, то есть записи loq_αb = c и b = α^c  равносильны.

Логарифм числа b по основанию α  определяется как показатель степени, в которую надо возвести число α, чтобы получить число b.

Логарифм в переводе с греческого буквально означает «число, изменяющее отношение».

Обозначение логарифма: loq_αb

Произносится: «логарифм b по основанию α».

Логарифм имеет смысл, если α >0, α ≠1, b >0.

Правило о знаке логарифма:

— если основание α логарифма и число b расположены на числовой оси по одну сторону от 1, то loq_αb положителен.

— если основание α логарифма и число b расположены на числовой оси по разные стороны от 1, то loq_αb отрицателен.

Логарифм существует только у положительных чисел.

Вычисление логарифма называется логарифмированием.

Числа α , b чаще всего вещественные, но существует также теория комплексных логарифмов

Специальные обозначения:

1. Натуральный логарифм ln α — логарифм по основанию e, где e — число Эйлера.

2. Десятичный логарифм lq α  — логарифм по основанию 10.

Производная логарифмической функции равна:

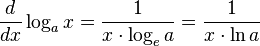
Интеграл от логарифма вычисляется интегрированием по частям:      

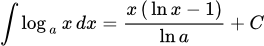
Свойства логарифмов:

1° 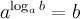    — основное логарифмическое тождество.

2°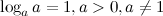    

3°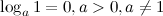    

Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю, т.к. из любого действительного числа можно получить 1 только возведя его в нулевую степень.

4° 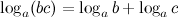    — логарифм произведения.

Логарифм произведения равен сумме логарифмов сомножителей.

5° 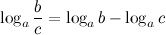    — логарифм частного.

Логарифм частного (дроби) равен разности логарифмов сомножителей.

6° 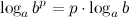    — логарифм степени.

Логарифм степени равен произведению показателя степени на логарифм ее основания.

7°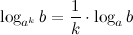    

8°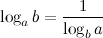    

9° 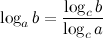    — переход к новому основанию.

Если выражения для основания логарифма и для логарифмируемого выражения содержат возведение в степень, для упрощения можно применить следующее тождество:

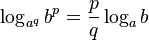
Это тождество сразу получается, если в логарифме слева заменить основание 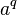 на 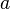 по вышеприведённой формуле замены основания. Следствия:

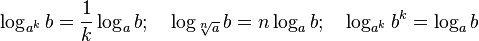
Ещё одно полезное тождество:

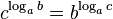
Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию .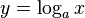

Она определена при .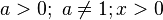

Область значений: .

Эта кривая часто называется логарифмикой.

Из формулы замены основания логарифма видно, что графики логарифмических функций с разными основаниями, бо́льшими единицы, отличаются один от другого только масштабом по оси ; графики для оснований, меньших единицы, являются их зеркальным отражением относительно горизонтальной оси.

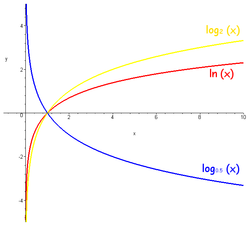
Функция является строго возрастающей при 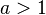  и строго убывающей при .

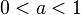График любой логарифмической функции проходит через точку 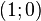. Функция непрерывна и неограниченно дифференцируема всюду в своей области определения.

Логарифм является монотонной функцией, поэтому экстремумов не имеет.

Ось ординат (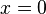) является левой вертикальной асимптотой

Из определения следует, что логарифмическая зависимость есть обратная функция для показательной функции , поэтому их графики симметричны относительно биссектрисы первого и третьего квадрантов (см. рисунок).

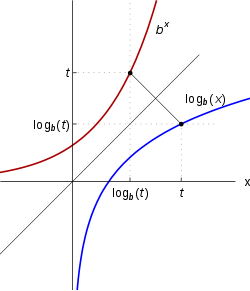
Как и показательная, логарифмическая функция относится к категории трансцендентных функций.

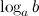
infourok.ru

Практическое применение логарифмов

Практическое применение логарифмов

Васильева  А.А. 1

---

1МАОУ Апрелевская СОШ №3 СУИОП

Королёва  О.Н. 1

---

1МАОУ Апрелевская СОШ №3 СУИОП

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Предмет исследования. Применение логарифма на практике, (тема) исторические примеры данного применения.

Актуальность. Регламентирующим принципом не только науки, но и жизни современного человека является поиск разумных объяснений, что значительно отличается от понятия выдвижения мнимых предсказаний. Наличие объяснительной теории в том или ином вопросе является критерием демаркации между научным и ненаучным подходом, к которому в свою очередь относятся различного рода мифы и легенды. Для такого подхода в науке имеются своего рода инструменты для выдвижения основательных гипотез. Логарифм – один из подобных приспособлений науки. О нем заходит речь в случаях беспрерывного изменения состояния изучаемого объекта с ходом времени, что в природе и технике является довольно часто встречающимся случаем.

Гипотеза. Логарифмы, как математический инструмент, позволяют делать основательные предсказания, основываясь на фундаментальной объяснительной теории, а так же позволяют значительно упрощать вычисления в области научных исследований.

Цель. Подтвердить гипотезу на ряде практических примеров.

Задачи.

Методологическое обоснование структуры изучаемого объекта.

Анализ проблемы.

Применение в различных математических вычислениях логарифм.

Создание программного кода для наглядного подтверждения или опровержения выдвинутой гипотезы.

Формулировка выводов проведенного исследования.

Методы исследования:

Восхождение от абстрактного к конкретному

Анализ

Метод визуализации данных

Метод динамического программирования

1. Понятие и свойства логарифмов

Для полного понимания концепции логарифмов и всего с ними связанного следует начать с элементарных основ. Два математических действия имеют по одному обратному. Речь идет о сложении и умножении. Обратное сложению – вычитание, это мы знаем с первого класса. Обратное умножению – деление. Это очень простые действия, с помощью которых математика в самом широком ее понимании не может справиться без дополнительных «инструментов». Возвышение в степень – пятое математическое действие. Оно имеет два обратных. Первое – извлечение корня, т.е. нахождение основания. Второе – логарифмирование, т.е. нахождение показателя, о котором и пойдет речь в работе.

Научное определение логарифма: «Логарифмом числа по основанию называется показатель степени , в которую нужно возвести , чтобы получить число «(М.Я.Выгодский Справочник по элементарной математике, с[274]). Нетрудно запутаться, но в целом понятно. Как и любой другой элемент элементарной математики, логарифмы имеют определенный ряд свойств. Не зная их, большая вероятность допустить ошибку или потратить порядком больше времени на вычисления. Логарифмы имеют следующие свойства:

Логарифм произведения равен сумме логарифмов сомножителей:

Логарифм частного равен логарифму делимого без логарифма делителя:

Логарифм степени равен произведению показателя степени на логарифм ее основания:

Логарифм корня равен частному от деления логарифма подкоренного выражения на показатель корня:

Последнее свойство является следствием предыдущего, т.к. .

В отдельные группы выделены логарифмы с основаниями 10 – десятичные и – натуральные. Их легко преобразовать друг в друга. Для представления десятичного логарифма в виде натурального необходимо разделить его на десятичный логарифм числа ( ).

2. Предшественники логарифма

На протяжении всего периода развития арифметики и счетной грамоты люди пытались находить различные способы упрощения и ускорения вычислительных работ. До того как логарифмы вошли в обиход их роль выполнял простой алгоритм вычислений, с помощью которого находили произведение двух чисел путем вычисления разности четвертей квадратов их суммы и равности. В виде формулы это выглядело так:

Это верно и можно проверить, является ли это выражение тождеством, выполнив раскрытие скобок и упрощение.

Этот алгоритм выполнялся быстро за счет того, что каждый математик имел составленную таблицу четвертей квадратов и все что нужно было сделать, это посчитать сами квадраты и вычесть их четверти. Однако раз уже был в ходу довольно удобный способ счета, сводивший умножение к вычитанию, зачем было придумывать такие сложные логарифмы? Все довольно просто. Мало какие важные вычисления обходятся перемножением только двух чисел. В жизни этот ряд может выглядеть нескончаемым. Это тождество удобно, если перемножать нужно только два числа. Точнее не столько удобно, сколько быстро выполнимо. Логарифмы позволяют не смотреть на количество множителей и одновременно упрощать и ускорять действия.

Что такого произошло в истории, что люди стали думать о новом способе счета? Потребность в этом была всегда, но настоятельная потребность возникла в 16 веке. Этот век славится обильным развитием судоходства, мореплавания на большие расстояния. Из этого факта вытекает следствие – сильное совершенствование астрономических расчетов, что в свою очередь и привело к появлению логарифмических расчетов. Попрошу читателя запомнить эту часть рассуждений. Мы к этому еще вернемся.

В конце столетия несколько ученых, независимо друг от друга приходят к выводу о том, что сложности сократятся, если заменить умножение и деление на порядок легче сложение и вычитание. Для этого необходимо было сопоставить геометрическую прогрессию с арифметической, при том, что геометрическая – исходная. Тогда упрощаются не только умножение и деление, но и извлечение корня определенной степени преобразуется в деление логарифма подкоренного выражения на имеющуюся степень.

Вся эта идея принадлежит Михаэлю Штифелю. Так считают, потому что он был первым, кто опубликовал ее в книге собственного написания.

Следующим этапом распространения логарифмов стал 1614 год. Выходит книга на латинском языке под названием «Описание удивительной таблицы логарифмов», автором которой является шотландец Джон Непер.

В одно время с Непером жил еще один математик – Бригг, который всю жизнь восхищался открытием своего современника и немало об этом говорил речей. Однажды он лично поехал в Шотландию только чтобы увидеть в глаза изобретателя столь гениальной вещи как логарифм. В течение своей жизни Бригг интересовался данной темой и даже прославился благодаря ей. Он сделал открытие десятичных логарифмов.

1703 год. Впервые выходят в свет таблицы на русском языке со значениями логарифмов, однако в каждой из них были допущены ошибки. Таблицы, заполненные правильными значениями, были изданы в 1857 году в Берлине.

Со временем логарифмы стали применяться практически во всех сферах жизни, где вычисление проводятся над многозначными числами или где необходима точность до 5-ого знака после запятой. На практике более точные результаты не используются. Логарифмы настолько уникальны, что способны описать практически любое физическое явление.

3. Логарифмическая линейка

Уже не раз говорилось о том, что логарифмы упрощают вычисления, делают их быстрее. Идею этого можно понять разве что на примере. Допустим, перед нами стоит задача найти произведение двух чисел: 10000 и 100. Можно начать их перемножать по всем установленным правилам, записать их в столбик и так далее. Однако согласитесь, более рационально посчитать, сложив количество нулей и приписав это количество в конечный результат. На основе чего этот метод имеет широкое распространение и неоспоримость итогового результата? На основе использования логарифмов. Представим это произведение таким образом: По всем правилам степеней результат будет равен . Однако чисел, которые можно так просто перемножать не так уж и много: 10, 100, 1000, 10000, 10000, 1000000 …

Этих чисел гораздо больше, если основание взять более близкое к 1. Стандартно для примера берут степени двойки. Хотелось бы посмотреть, как это работает, например с тройкой.

Составим таблицу.

Поставим задачу перемножить и . В таблице эти числа стоят под цифрами и соответственно. Складываем показатели степени и получаем . Под девяткой в таблице стоит число . Значит, Для деления справедлив алгоритм обратный данному. То есть если нам нужно разделить на , делаем следующее: под стоит , значит . Немного неясно, зачем это делать и знать, если всегда имеется при себе калькулятор. Чтобы понять смысл стоит задаться вопросом, а как калькулятор получает значение результата? Каждый калькулятор запрограммирован, код программы – те же вычисления, что мы только что провели, только написаны они на языке, понятном компьютеру. Суть этих действий одна как для человека, так и для машины.

Несмотря на то, что в таблице в нижней строке больше чисел, нежели когда мы брали числа с основанием 10, все же числа там далеко не все. Эта таблица не может нести практического значения. Однако, взяв за основание число гораздо более близкое к единице, эта проблема устраняется, и таблица становится очень полезным инструментом для вычислений.

На основе данного метода был создан уникальный инструмент для вычислений – логарифмическая линейка, которую изобрел английский ученый Гунтер. Ее можно отнести к логарифмическим диковинкам. Это такой же рядовой вычислительный прибор как калькулятор для школьника или счеты для греческого математика средневековья.

4. Логарифмы в различных сферах нашей жизни

На самом деле логарифмы применяются в любой науке, связанной с вычислениями, а иногда даже не имеющей к ним никакого отношения, как мы чуть позже убедимся. Чтобы рассмотреть каждую из них не хватит и месяца. Будут рассмотрены лишь некоторые из них.

1. Астрономия

«Изобретение логарифмов, сокращая вычисления нескольких месяцев в труд нескольких дней, словно удваивает жизнь астрономов». Знаменитая фраза великого ученого Лапласа о логарифмах упоминает астрономов. Астрономы не редко проводят сложные вычисления на основе данных, полученных в ходе долгих наблюдений. Какие же именно вычисления требуют применения логарифмов?

В астрономии логарифмы имеют очень обширное распространение. Это объясняется в первую очередь тем, что в этой науке задействованы очень большие масштабы. Для того чтобы просто представить себе Вселенную как объект или посмотреть на нее со стороны времени нужен соответствующий масштаб. Человеческое сознание не способно воспринимать такие вещи в реальном размере, а иногда даже не может воспринять в 10000000 раз уменьшенном виде. Для этого была создана логарифмическая шкала, которая используется не только в астрономии, но имеет в ней большое значение. Есть даже бумага, разлинованная в логарифмическом масштабе. Практически ее иногда используют для графиков степенных функций.

Практически каждая вторая формула в астрономии, астрофизике и других перекрестных науках не обходятся без логарифма. Примеры:

Расчет абсолютной визуальной звездной величины

Расчет относительной визуальной звездной величины

Расчет абсолютной болометрической звездной величины

Расчет относительной болометрической звездной величины

Теоретическая зависимость радиуса от массы для твердых планет

Расчет площади поверхности планеты

Разберем каждый случай по отдельности

Первые четыре пункта высчитывают различные звездные величины. Звездная величина – это классы, на которые разделены звезды по их блеску. Болометрическая звездная величина – это величина по всему спектру, включающая невидимое глазом излучение.

Соответствующие формулы для данных расчетов:

—

где относительная (наблюдаемая) визуальная звездная величина, – расстояние до звезды, – световой поток от звезды, – световой поток от Солнца: люмен. Все значения для практических измерений имеются для каждой изученной в полной мере звезды.

—

—

где – светимость звезды, – светимость Солнца: Вт, – относительная (наблюдаемая) болометрическая звездная величина.

—

— – теоретическая зависимость радиуса от массы для твердых планет, где радиус и масса планеты, – коэффициенты, зависящие от химического состава планеты.

На таблице представлены коэффициенты в формуле теоретической зависимости радиуса от массы для твердых планет.

По итогу изучения теоретического материала, представленного выше, была создана программа, позволяющая рассчитать абсолютную визуальную и абсолютную болометрическую звездные величины. Программа была написана на высокоуровневом языке общего назначения Python версии 3.4 (см. приложение 1 )

import math

#идет рассчет абсолютной визуальной звездной величны

F = int(input(‘Введите значение светового потока от рассматриваемой звезды\n’))

d_1 = F/3.4690000000000000000000000000000

d_2 = math.log10(d_1)

d_3 = 2.5 * d_2

d_4 = 4.82-d_3

print(‘Абсолюная визуальная звездная величина данной звезды ‘, d_4)

#рассчет абсолютной болометрической (по всему спектру, включая невидимое глазом излучение) звездной величины, для красивой работы лучше вводить запрашиваемые данные той же звезды

l1 = 3.842*10**26

l = int(input(‘Введите значение светимости звезды: ‘))

d1 = l/l1

d2 = math.log10(d1)

d3 = 2.5 * d2

d4 = 4.75 — d3

print(‘абсолютная болометрическая звездная величина данной звезды ‘, d4)

— – формула расчета площади поверхности планет, где , экваториальная полуось эллипсоида (для планет обе экваториальные полуоси равны, т.к. они представляют собой эллипсоиды вращения), полярная полуось (параллельная оси вращения).

В рамках практической части была проведена работа над созданием программ, высчитывающих площади поверхностей планет, также на высокоуровневом языке общего назначения Python версии 3.4 (см. приложение 2 ).

import math

a = float(input(‘Введите значение экваториальной полуоси эллипсоида \n’))

b = float(input(‘Введите значение полярной полуоси (параллельной оси вращения) \n’))

first = b/a

second = first**2

third = 1-second

e = math.sqrt(third)

d1 = 1+e

d2 = 1-e

d4 = math.log(d1/d2)

d5 = 1-e**2

d6 = 2*e

d7 = d5/d6

d8 = d7*d4

d9 = 1+d8

d10 = 2 * math.pi * a**2

d11 = d10*d9

print(‘площадь поверхности рассматриваемой планеты равна ‘, d11).

Правдивость данной расчетной программы была проверена на примере планеты Венеры путем ввода в программу ее данных. Программа показала высокую точность и верность вычислений (см. приложение 2 )

2. Навигация

Формулы помогают нам найти нужные значения, но для полного понимания сути существования логарифмов следует найти и изучить более наглядный материал. Навигация для этого самый лучший вариант.

Локсодромия – линия на сфере, которая пересекает под одинаковым углом меридианы. Другими словами это кривая, в каждой точке имеющая путевой угол

С использованием в навигации магнитных компасов стало зарождаться понятие локсодромии. Простой пример: самолет летит с постоянным курсом относительно меридиана, над которым пролетает, и если магнитное склонение нулевое и нет ветра, то самолет в этой ситуации осуществляет движение по линии локсодромии.

Уравнение локсодромии выглядит следующим образом: , где – постоянные для данной локсодромии величины. Для того чтобы найти долготу нужно подставить в правую часть равенства соответствующую ей широту . Локсодромия — не единственная область навигации, использующая логарифмы в своих вычислениях. Однако в данной работе будет рассмотрена только она.

По определению локсодромии можно понять, что она представляет собой логарифмическую спираль на сфере, которая асимптотически приближается к полюсам, но никогда не пересекает их.

Итогом была проведена практическая работа по построению логарифмической спирали различными способами. В приложении 3 показана спираль, построенная путем заложения в основу программы GeoGebra уравнения логарифмической спирали в полярных координатах ( ). В приложении 4 представлена логарифмическая спираль, построенная с помощью прямоугольников, стороны которых имеют определенное отношение. Длины их сторон представлены числовым рядом Фибоначчи. Такая же работа была проведена вручную.

3. Психология

Громкость звука измеряют в децибелах, которые пропорциональны логарифму мощности звука, воздействующего на ухо. Употребление логарифмических шкал продиктовано особенностями наших органов чувств: зрения, слуха и т.д. Человеческий мозг воспринимает раздражения от органов чувств не пропорционально силе раздражителя (как мы рассматривали мощность звука), а лишь пропорционально ее логарифму. Именно поэтому ухо одинаково способно слышать шорох листьев и не оглохнуть от громкого удара станка на заводе. А глаз может заметить, как блестит снег на свету и не ослепнуть, если посмотрит на Солнце, которое в миллиарды раз ярче.

Описанные выше сведения объединяются законом психофизики, установленным Фехнером, который говорит, что мера ощущения пропорциональная логарифму величины раздражения.

4. История

Тот факт, что логарифмическая шкала позволяет увидеть и осознать объекты большого масштаба позволяет применять понятие логарифма и в истории. Чтобы представить себе всю эволюцию нашего человечества нужно представить его историю в масштабе, который подвластен представлению. В этом на помощь приходит логарифмический масштаб (шкала). Такая система называется логарифмической шкалой времени.

Из этого следует, что логарифмы применимы в математическом моделировании развития мира, культуры, экономики и так далее.

5. Физика

То, какое значение логарифм имеет в физике, является отдельной темой для проекта по количеству материала, имеющегося по этому направлению. Здесь будет рассмотрена только одна формула – формула Циолковского.

Формула Циолковского значительно выделяется на фоне всех приведенных в этой работе расчетов. Это достижение было важным для истории тем, что открыло новую эпоху в сфере естествознания и космонавтики. Формула предназначена для того, чтобы рассчитывать характеристическую скорость летательного аппарата, т.е. скорость которую он приобретает под действием тяги двигателя, не имея воздействия со стороны других сил. Эта формула приобретает соответствующий вид в зависимости от вида самого рассматриваемого аппарата. Речь идет о количестве ступень ракеты. Для ракет с 2-мя, 3-мя ступенями действительная более сложная формула, которая не рассматривается в данной работе. Для ракет с 1-ой ступенью используется формула более простого вида: . Где – удельный импульс ракетного двигателя, – начальная масса РН (ракета-носителя), включающая в себя массу полезной нагрузки, самого аппарата и топлива на момент старта, – «сухая масса», т.е. масса полезной нагрузки и аппарата. На данный момент существует одна ракета подобного вида, разрабатываемая в России, обладающая одной ступенью. Она называется РН «Корона» и разрабатывается уже на протяжении 25 лет. Данные необходимые для подстановки были взяты из характеристик этого ракета-носителя и написана соответствующая программа. Результаты смотрите в приложении 5.

5. Незамысловатый фокус

Представьте, что в ваш город приехал фокусник, утверждающий, что может с легкостью вычислить корень высокой степени из многозначного числа. Перед представлением вы заготовили 31-ю степень какого-нибудь многозначного числа и в итоге получили пятизначное. Уверенные в том, что фокусник не сможет извлечь из него корень вы начинаете говорить «31-ая степень этого числа : пятизначное число …» и тут произошло чудо, этот волшебник уже написал вам ответ на доске, даже не услышав само число. Как так вышло?

На самом деле здесь нет ничего сложного. Есть только одно число, которое в 31-й степени дает пятизначное число. Однако даже если так, то откуда тот фокусник знал это и смог так быстро отыскать нужное число?

Для этого он заучил двузначные логарифмы для первых 15-20 чисел. Тем более эта задача сильно упрощается знанием того факта, что зная логарифмы 2,3 и 7, можно в уме легко найти логарифмы чисел первого десятка ( ).

Когда вы сказали фокуснику, что 31-ая степень числа дает пятизначное число, ему оставалось только выполнить следующее действие: . Значение этого выражения лежит где-то между 1,09 и 1,13. Этот интервал включает в себя только один логарифм от целого числа. Это 1,11 – логарифм числа 13. Конечно, чтобы такое проделать в уме нужна тренировка, но если видеть это все перед глазами, то все довольно просто.

Теперь уже перед вами стоит задача извлечь корень 64 степени из 20-значного числа. Получим: То есть значение лежит в интервале между или по-другому между 0,29 и 0,31. Такое значение только одно 0,3 – логарифм числа 2.

Заключение

Использование логарифмов дает людям преимущество в виде упрощения и ускорения сложных вычислительных операций. Бесспорно, будет нерационально использовать это при умножении 6 на 3, но при действиях с по-настоящему большими числами данное преимущество значительно упростит задачу.

Логарифмическая функция дает нам возможность по-другому взглянуть на масштабные процессы, происходящие в огромных пространствах и временных интервалах для понимания и осмысления общей картины.

В ходе работы поставленные задачи были выполнены, гипотеза подтверждена, проработана практическая часть и цель достигнута.

Список литературы

1. . Вильчек Ф. Красота физики: постигая устройство природы: пер. с англ. – 2-е изд. – М.: Альпина нон-фикшн, 2017.

2. Выгодский М.Я. Справочник по элементарной математике – Москва: Издательство: АСТ: 2017

3.Засов А.В., Постнов К.А. Общая астрофизика – Фрязино: Век 2: 2015

4 Перельман Я.И. Занимательная алгебра. – СПб.: СЗКЭО, 2017

5. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов – Москва: государственное издательство физико-математической литературы, 1963

6. Энциклопедия для детей: Т.8. Астрономия. – 2-е изд., глав.ред. М.Д.Аксенова – М.: Аванта+, 1999

7. https://ru.wikipedia.org – Википедия, Свободная Энциклопедия

Приложения

Приложение 1. Звездные величины. Расчет.

Приложение 2. Площадь планеты. Расчет и проверка.

(взято с википедии)

Приложение 3. Логарифмическая спираль

Приложение 4. Логарифмическая спираль

Приложение 5. Формула Циолковского. Расчет и проверка.

Просмотров работы: 7400

school-science.ru