Алгебра. Урок 8. Неравенства, системы неравенств.
Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
> больше,
≥ больше или равно,
< меньше,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
ax<bax≤bax>bax≥b
где a и b – любые числа, причем a≠0,x – переменная.
Примеры линейных неравенств:
3x<5x−2≥07−5x<1x≤0
Решить линейное неравенство – получить выражение вида:
x<cx≤cx>cx≥c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий >,<, точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥,≤, точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x<c |  | x∈(−∞;c) |
| x≤c |  | x∈(−∞;c] |
| x>c |  | x∈(c;+∞) |
| x≥c |  | x∈[c;+∞) |
- Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:
ax<bax≤bax>bax≥b
- Пусть получилось неравенство вида ax≤b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.
- Если a>0 то неравенство приобретает вид x≤ba.
- Если a<0, то знак неравенства меняется на противоположный, неравенство приобретает вид x≥ba.
- Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.
Примеры решения линейных неравенств:
№1. Решить неравенство 3(2−x)>18.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6−3x>18
−3x>18−6−3x>12|÷(−3)
Делим обе части неравенства на (-3) – коэффициент, который стоит перед x. Так как −3<0, знак неравенства поменяется на противоположный. x<12−3⇒x<−4 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x∈(−∞;−4)
№2. Решить неравество 6x+4≥3(x+1)−14.
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6x+4≥3x+3−14
6x−3x≥3−14−4
3x≥−15 | ÷3 Делим обе части неравенства на (3) – коэффициент, который стоит перед x. Так как 3>0, знак неравенства после деления меняться не будет.
x≥−153⇒x≥−5 Остается записать ответ (см. таблицу числовых промежутков).
Ответ: x∈[−5; +∞)
Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).
Примеры:
№1. Решить неравенство 6x−1≤2(3x−0,5).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
6x−1≤6x−1
6x−6x≤−1+1
0≤0
Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.
- x – любое число
- x∈(−∞;+∞)
- x∈ℝ
- Решить уравнение ax2+bx+c=0 и найти корни x1 и x2.
- Отметить на числовой прямой корни трехчлена.
- Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение ax2+bx+c вместо x.
- Выбрать подходящие интервалы (или интервал).
- Записать ответ.
- Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):
- Приравнять числитель дроби к нулю f(x)=0. Найти нули числителя.
- Приравнять знаменатель дроби к нулю g(x)=0. Найти нули знаменателя.
- Нанести нули числителя и нули знаменателя на ось x.
- Расставить знаки на интервалах.
- Выбрать подходящие интервалы и записать ответ.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f(x)g(x)>0.
- Приравниваем числитель к нулю f(x)=0.
- Приравниваем знаменатель к нулю g(x)=0.
- Наносим нули числителя и нули знаменателя на ось x.
- Расставляем знаки на интервалах.
- Выбираем подходящие интервалы и записываем ответ.
- Привести неравенство к виду f(x)g(x)≤0.
- Приравнять числитель к нулю f(x)=0.
- Приравнять знаменатель к нулю g(x)=0.
- Наносим нули числителя и нули знаменателя на ось x.
- Расставляем знаки на интервалах.
- Выбираем подходящие интервалы и записываем ответ.
- Первый шаг алгоритма уже выполнен. Неравенство приведено к виду f(x)g(x)>0.
- Приравнять числитель к нулю f(x)=0.
- Приравнять знаменатель к нулю g(x)=0.
- Наносим нули числителя и нули знаменателя на ось x.
- Расставляем знаки на интервалах.
- Выбираем подходящие интервалы и записываем ответ.
- Решить первое неравенство системы, изобразить его графически на оси x.
- Решить второе неравенство системы, изобразить его графически на оси x.
- Нанести решения первого и второго неравенств на ось x.
- Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
- Решаем первое неравенство системы.
- Решаем второе неравенство системы.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
- Решаем первое неравенство системы.
- Решаем второе неравенство системы.
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
- Решаем первое неравенство системы.
- Решаем второе неравенство системы
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
- Решаем первое неравенство системы.
- Решаем второе неравенство системы
- Наносим оба решения на ось x.
- Выбираем подходящие участки и записываем ответ.
- члены неравенства можно переносить из одной его части в другую с противоположным знаком;
- обе части неравенства можно умножать или делить на одно и то же положительное число;
- обе части неравенства можно умножать или делить на одно и то же отрицательное число и заменять при этом знак неравенства на противоположный.
- Если знак строгий (>, <), все точки выколотые (в круглые скобки).
- Если знак нестрогий (≥, ≤), корни числителя закрашенные, точки знаменателя выколотые [в квадратные скобки].
- Если корень является решением уравнения четное кол-во раз (2, 4, 6, 8), то в этой точке знак меняться не будет.
- Отдельная точка записывается {в фигурных скобках}.
№2. Решить неравенство x+3(2−3x)>−4(2x−12).
Решение:
Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.
x+6−9x>−8x+48
−8x+8x>48−6
0>42
Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.
Ответ: x∈∅
Квадратные неравенства
Квадратные неравенства – это неравенства вида: ax2+bx+c>0ax2+bx+c≥0ax2+bx+c<0ax2+bx+c≤0 где a, b, c — некоторые числа, причем a≠0,x — переменная.
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.
Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).
Алгоритм решения квадратного неравенства методом интервалов
Если знак неравенства строгий >,<, точки будут выколотые.

Если знак неравенства нестрогий ≥,≤, точки будут жирные (заштрихованный).

Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.
Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.
Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.
Примеры решения квадратных неравенств:
№1. Решить неравенство x2≥x+12.
Решение:
Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.
x2≥x+12
x2−x−12≥0
x2−x−12=0
a=1,b=−1,c=−12
D=b2−4ac=(−1)2−4⋅1⋅(−12)=1+48=49
D>0⇒ будет два различных действительных корня
x1,2=−b±D2a=−(−1)±492⋅1=1±72=[1+72=82=41−72=−62=−3
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:
x2−x−1=62−6−1=29>0
Это значит, что знак на интервале, в котором лежит точка 6 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪.
Точки -3 и 4 будут в квадратных скобках, так как они жирные.
Ответ: x∈(−∞;−3]∪[4;+∞)
№2. Решить неравенство −3x−2≥x2.
Решение:
Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.
−3x−2≥x2
−x2−3x−2≥0
−x2−3x−2=0
a=−1,b=−3,c=−2
D=b2−4ac=(−3)2−4⋅(−1)⋅(−2)=9−8=1
D>0⇒ будет два различных действительных корня
x1,2=−b±D2a=−(−3)±12⋅(−1)=3±1−2=[3+1−2=4−2=−23−1−2=2−2=−1
x1=−2,x2=−1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:
−x2−3x−2=−(0)2−3⋅0−2=−2<0
Это значит, что знак на интервале, в котором лежит точка 0 будет −.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Поскольку знак неравенства ≥, выбираем в ответ интервал со знаком +.
Точки -2 и -1 будут в квадратных скобках, так как они жирные.
Ответ: x∈[−2;−1]
№3. Решить неравенство 4<x2+3x.
Решение:
Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.
4<x2+3x
−x2−3x+4<0
−x2−3x+4=0
a=−1,b=−3,c=4
D=b2−4ac= (−3)2−4⋅(−1)⋅4=9+16=25
D>0⇒ будет два различных действительных корня
x1,2=−b±D2a=−(−3)±252⋅(−1)=3±5−2=[3+5−2=8−2=−43−5−2=−2−2=1
x1=−4,x2=1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:
−x2−3x+4=−(2)2−3⋅2+4=−6<0
Это значит, что знак на интервале, в котором лежит точка 2, будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Поскольку знак неравенства <, выбираем в ответ интервалы со знаком −.
Точки -4 и 1 будут в круглых скобках, так как они выколотые.
Ответ: x∈(−∞;−4)∪(1;+∞)
№4. Решить неравенство x2−5x<6.
Решение:
Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.
x2−5x<6
x2−5x−6<0
x2−5x−6=0
a=1,b=−5,c=−6
D=b2−4ac=(−5)2−4⋅1⋅(−6)=25+25=49
D>0⇒ будет два различных действительных корня
x1,2=−b±D2a=−(−5)±492⋅1=5±72=[5+72=122=65−72=−22=−1
x1=6,x2=−1
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:
x2−5x−6=102−5⋅10−6=100−50−6= 44>0
Это значит, что знак на интервале, в котором лежит точка 10 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Поскольку знак неравенства <, выбираем в ответ интервал со знаком -.
Точки -1 и 6 будут в круглых скобках, так как они выколотые
Ответ: x∈(−1;6)
№5. Решить неравенство x2<4.
Решение:
Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.
x2<4
x2−4<0
x2−4=0
(x−2)(x+2)=0⇔[x−2=0x+2=0 [x=2x=−2
x1=2,x2=−2
Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:
x2−4=32−4=9−4=5>0
Это значит, что знак на интервале, в котором лежит точка 3 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Поскольку знак неравенства <, выбираем в ответ интервал со знаком −.
Точки -2 и 2 будут в круглых скобках, так как они выколотые.
Ответ: x∈(−2;2)
№6. Решить неравенство x2+x≥0.
Решение:
Выносим общий множитель за скобку, находим корни уравнения x2+x=0.
x2+x≥0
x2+x=0
x(x+1)=0⇔[x=0x+1=0[x=0x=−1
x1=0,x2=−1
Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:
x2+x=12+1=2>0
Это значит, что знак на интервале, в котором лежит точка 1 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Поскольку знак неравенства ≥, выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.
Ответ: x∈(−∞;−1]∪[0;+∞)
Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.
Дробно рациональные неравенства
Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:
f(x)g(x)<0f(x)g(x)≤0f(x)g(x)>0f(x)g(x)≥0
Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).
Примеры дробно рациональных неравенств:
x−1x+3<03(x+8)≤5×2−1x>0x+20x≥x+3
Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.
Алгоритм решения дробно рациональных неравенств:
f(x)g(x)<0f(x)g(x)≤0f(x)g(x)>0f(x)g(x)≥0
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
Вне зависимости от знака неравенства
при нанесении на ось xнули знаменателя всегда выколотые.
Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.
Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.
Примеры решения дробно рациональных неравенств:
№1. Решить неравенство x−1x+3>0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
x−1=0
x=1 — это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
x+3=0
x=−3 — это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f(x)g(x):x−1x+3 = 2−12+3=15>0,
Это значит, что знак на интервале, в котором лежит точка 2 будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства >, выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.

Ответ: x∈(−∞;−3)∪(1;+∞)
№2. Решить неравенство 3(x+8)≤5.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
3(x+8)≤5
3(x+8)−5\x+8≤0
3x+8−5(x+8)x+8≤0
3−5(x+8)x+8≤0
3−5x−40x+8≤0
−5x−37x+8≤0
−5x−37=0
−5x=37
x=−375=−375=−7,4
x=−7,4 — ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
x+8=0
x=−8 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение f(x)g(x):
−5x−37x+8=−5⋅0−370+8=−378<0
Это значит, что знак на интервале, в котором лежит точка 0 будет -.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≤, выбираем в ответ интервалы со знаком -.
В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.

Ответ: x∈(−∞;−8)∪[−7,4;+∞)
№3. Решить неравенство x2−1x>0.
Решение:
Будем решать данное неравенство в соответствии с алгоритмом.
x2−1=0
(x−1)(x+1)=0⇒[x−1=0x+1=0[x=1x=−1
x1=1,x2=−1 — нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
x=0 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f(x)g(x):
x2−1x=22−12=4−12=32>0, Это значит, что знак на интервале, в котором лежит точка 2, будет +.
Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства >, выбираем в ответ интервалы со знаком +.
В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.

Ответ: x∈(−1;0)∪(1;+∞)
Системы неравенств
Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств — это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.
Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.
Пример системы неравенств:
{x+4>02x+3≤x2
Алгоритм решения системы неравенств
Примеры решений систем неравенств:
№1. Решить систему неравенств {2x−3≤57−3x≤1
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
2x−3≤5
2x≤8|÷2, поскольку 2>0, знак неравенства после деления сохраняется.
x≤4;
Графическая интерпретация:

Точка 4 на графике жирная, так как знак неравенства нестрогий.
7−3x≤1
−3x≤1−7
−3x≤−6|÷(−3), поскольку −3<0, знак неравенства после деления меняется на противоположный.
x≥2
Графическая интерпретация решения:

Точка 2 на графике жирная, так как знак неравенства нестрогий.

Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.
Ответ: x∈[2;4]
№2. Решить систему неравенств {2x−1≤51<−3x−2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
2x−1≤5
2x≤6|÷2, поскольку 2>0, знак неравенства после деления сохраняется.
x≤3
Графическая интерпретация:

Точка 3 на графике жирная, так как знак неравенства нестрогий.
1<−3x−2
3x<−1−2
3x<−3|÷3, поскольку 3>0, знак неравенства после деления сохраняется.
x<−1
Графическая интерпретация решения:

Точка -1 на графике выколотая, так как знак неравенства строгий.

Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.
Ответ: x∈(−∞;−1)
№3. Решить систему неравенств {3x+1≤2x−1x−7>5−x
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
3x+1≤2x−1
3x−2x≤−1−1
x≤−1
Графическая интерпретация решения:

x−7>5−x
x+x>5+7
2x>12| ÷2, поскольку 2>0, знак неравенства после деления сохраняется.
x>6
Графическая интерпретация решения:


Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.
Ответ: x∈∅
№4. Решить систему неравенств {x+4>02x+3≤x2
Решение:
Будем решать данную систему неравенств в соответствии с алгоритмом.
x+4>0
x>−4
Графическая интерпретация решения первого неравенства:

2x+3≤x2
−x2+2x+3≤0
Решаем методом интервалов.
−x2+2x+3=0
a=−1,b=2,c=3
D=b2−4ac=22−4⋅(−1)⋅3=4+12=16
D>0 — два различных действительных корня.
x1,2=−b±D2a=−2±162⋅(−1)=−2±4−2=[−2−4−2=−6−2=3−2+4−2=2−2=−1
Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.

Графическая интерпретация решения второго неравенства:


Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪.
Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.
Ответ: x∈(−4;−1]∪[3;+∞)
Скачать домашнее задание к уроку 8.
epmat.ru
Правила решения неравенств
☰
При решении числовых неравенств пользуются несколькими правилами, основанными на свойствах неравенств. Решить числовое неравенство с переменной — это значит, найти такие значения переменной (область значений), при которых данное неравенство становится верным. Обычно значения переменных выражаются пределами (множествами чисел, лучами, отрезками), которым они принадлежат.
Правила решения неравенств позволяют привести неравенство к виду, когда область значений становится очевидна. Например, x < b, где знак неравенства и число b могут быть любыми.
Перечислим эти правила.
Член неравенства можно перенести из одной его части в другую. При этом следует поменять знак этого члена на противоположный. Например:
3x + 4 < 10
3x < 10 – 4
Здесь положительное число 4 было перенесено из левой части неравенства в правую. При этом число стало отрицательным. Почему можно это делать? Одним из свойств числовых неравенств является следующее: если a < b, то a + c < b + c. Другими словами, если к обоим частям исходного неравенства прибавить одно и то же число, то получится равносильное неравенство.
Перенос члена неравенства из одной части в другую с противоположным знаком — это по-сути прибавление к обоим частям одного и того же числа. В приведенном выше примере к обоим частям неравенства было прибавлено число –4:
3x + 4 + (–4) < 10 + (–4)
3x < 10 – 4
Левую и правую части неравенства можно одновременно умножить или разделить на одно и тоже число. Если это число положительное, то знак неравенства не меняется. Если это число отрицательно, то знак неравенства меняется на противоположный.
Данное правило вытекает из свойства числовых неравенств. Если a < b и c > 0, то ac < bc; если же с < 0, то ac > bc. Это правило касается только умножения. Однако операцию деления можно представить, как умножение на 1/c (как дробь).
Например, неравенство 3x < 6 можно упростить, разделив обе его части на 3. Так как 3 — положительное число, то знак неравенства остается прежним. В результате получается неравенство вида x < 2, глядя на которое сразу можно сказать, что областью значения переменной x является числовой луч (–∞; 2). Именно при этих значениях переменной x исходное неравенство (которое было дано до упрощения) является верным.
Допустим, дано неравенство –0,5x ≥ 1. Здесь можно умножить обе части на –2 (чтобы получить 1x в левой части). Поскольку умножение выполняется на отрицательное число, то следует поменять знак неравенства на обратный. Получится x ≤ –2. Таким образом, неравенство –0,5x ≥ 1 верно при x ∈ (–∞; 2].
scienceland.info
Конспект «Решение неравенств первой степени»
Решение неравенств первой степени
Ключевые слова: основные понятия, неравенства первой степени, решение неравенств первой степени, примеры решения задач. Раздел ОГЭ по математике: 3.2.2. Неравенство с одной переменной. Решение неравенства.
Неравенства с одной переменной решают почти так же, как и уравнения. Значение переменной, при подстановке которой в неравенство получается верное числовое неравенство, называется решением неравенства. Решить неравенство – это значит найти все его решения или показать, что их нет.
Неравенства, у которых множества решений совпадают, называют равносильными. При решении неравенств пользуются следующими правилами, которые позволяют заменять одно неравенство другим, ему равносильным:
Рассмотрим, например, неравенство 3х(х+2) – 20 > 6х+7. Заменим его более простым равносильным ему неравенством:
3х2 + 6х – 20 > 6х + 7,
3х2 + 6х – 20 – 6х – 7 > 0,
3х2– 27 > 0,
х2– 9 > 0.
Сначала мы раскрыли скобки в левой части неравенства, затем из правой части в левую перенесли слагаемые с противоположными знаками, после приведения подобных разделили обе части неравенства на одно и то же положительное число 3. Получили квадратное неравенство (способ решения таких неравенств в следующем параграфе).
Решение неравенств первой степени
Неравенства первой степени – это неравенства вида ах + b > 0 или ах + b ≥ 0, ах + b < 0, ах + b ≤ 0, где а ≠ 0. Например, неравенства 2х – 3 > 0; 0,3x +1,2 > 0; 5 – 10x ≤ 0 являются неравенствами первой степени.
Решим, например, последнее из этих неравенств: 5 – 10x ≤ 0. Коэффициент при переменной х отрицательный, и всегда полезно сначала «избавиться» от отрицательного коэффициента при х. Для этого можно умножить обе части неравенства на –1 и не забыть заменить знак неравенства на противоположный. Получим: 10х – 5 ≥ 0. (Можно поступить и иначе – перенести –10х в правую часть с противоположным знаком: 5 ≤ 10х.) Далее: 10x ≥ 5, x ≥ 0,5. Последнее неравенство можно считать ответом, так как оно вполне ясно описывает множество всех значений x, являющихся его решениями. Можно также записать решение неравенства в виде числового промежутка: [0,5; +оо). На координатной прямой множество решений этого неравенства можно показать так:
Множеством решений неравенства первой степени всегда является числовой луч – или с принадлежащим ему началом, как в данном случае, или с непринадлежащим (в случае строгого неравенства).
Примеры решения задач
Пример 1. Определим, в каком случае на координатной прямой изображено множество решений неравенства 19 – 7x > 20 – 3(x – 5).
Самая правильная стратегия поиска ответа на вопрос состоит в том, чтобы просто решить неравенство.
19 – 7x > 20 – 3(x – 5),
19 – 7x > 20 – 3x +15,
–4x > 16,
4x < –16,
x < –4.
Ответ: 2.
Пример 2. Решим неравенство 
Сначала «избавимся» от дробей, умножив обе части неравенства на общий знаменатель дробей – число 6. При этом надо быть внимательным и не забыть умножить на 6 первое слагаемое в правой части:
После преобразований получим: х ≤ 2.
Ответ: х ≤ 2.
Пример 3. Решим неравенство 9(6 + 2x) < 4√5(6 + 2х).
Преобразуем неравенство следующим образом: 9(6 + 2х) – 4√5(6 + 2x) < 0 .
Теперь вынесем за скобки общий множитель 6 + 2x, получим: (6 + 2x)(9 – 4√5) < 0. Определим знак разности: 9 – 4√5. Так как 9 = √81, 4√5 = √80 и √81 > √80, то 9 – 4√5 > 0. Разделив обе части неравенства на положительное число 9 – 4√5, получаем неравенство 6 + 2x < 0. Отсюда x < –3.
Ответ: x < –3.
Это конспект по алгебре на тему «Решение неравенств первой степени». Выберите дальнейшие действия:
uchitel.pro
Метод интервалов, решение неравенств
 Решение неравенств
Решение неравенств
Метод интервалов
Перенос знаков
Выбор точек
Система и совокупность
Точка знакопостоянства
Что нельзя делать в неравенстве, даже под пытками:
1) Домножать на знаменатель.
2) Умножать/делить на отрицательное число, не меняя знак.
3) Убирать бездумно логарифм или основание.
Начнем с простого:
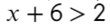
Линейные уравнения решаются обычным переносом. Икс в одной части оставим, а числа перенесем в другую:
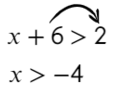
А само значение −4 нам подходит?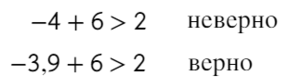
Нет, поэтому ставим круглые скобочки ()
Ответ: x ∈ ( −4; +oo).
Разберемся со скобками:
Когда мы включаем точку (корень числителя), или стоят знаки нестрогие (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>, <), скобки круглые «( )».
Если же возьмем пример, где придется делить или умножать на отрицательное число, то знак поменяется:
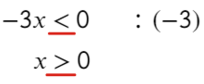 Ответ: x ∈ ( 0; +oo).
Ответ: x ∈ ( 0; +oo).
Следующий пример уже с дробью:

Приравняем числитель к нулю и скажем, что знаменатель не равен нулю:
к.ч. (корни числителя)
к.з. (корни знаменателя)

Расставляем корни числителя и знаменателя на одной прямой (сколько решаем неравенств, столько же чертим прямых). Попробуем подставить х = 0, чтобы определить знаки:
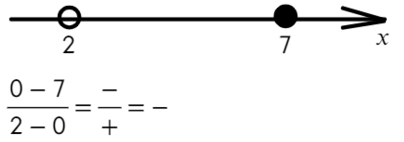
Там, где «0» (перед двойкой), ставим знак «−», а дальше знаки чередуем:
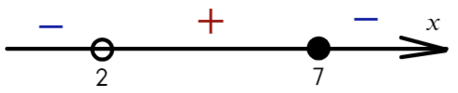
Из-за того, что знаком неравенства был «≥», нам подходят промежутки со знаком «+» и закрашенная точка:
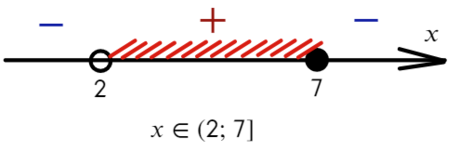
Когда мы включаем точку (корень числителя), или стоят знаки (≥, ≤), ставим «[ ]» — квадратные скобки. Если не включаем (корень знаменателя), или знак строгий (>, <), скобки круглые «( )».
Ответ: x ∈ (2; 7].
Данный пример можно решить по-другому. Подумаем, когда дробь больше нуля? Конечно, когда числитель и знаменатель — положительные значения или когда оба отрицательные. Поэтому данное неравенство можно разбить на две системы в совокупности:
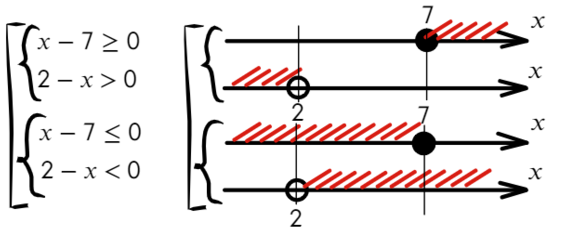
Отметим на прямой решение каждого неравенства.
Решением системы «{» является тот участок, который подходит обоим неравенствам.
Решением совокупности «[» является тот участок, который включен хотя бы в одно неравенство.
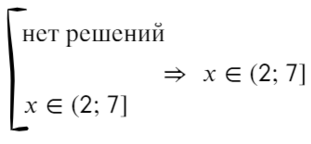
Мой любимый пример:
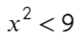
Покажу мастер-класс, как делать не надо. Дома не повторять!
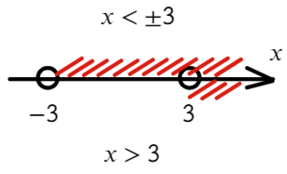
А теперь через метод интервалов разберемся, как сделать правильно:

Там, где ноль, ставим знак «−», рисуем прямую и отмечаем корни каждой скобки. А дальше чередуем:
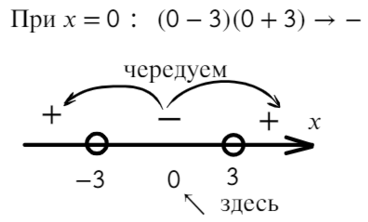
В данном неравенстве знак меньше, поэтому записываем в ответ промежуток, где знак «−».
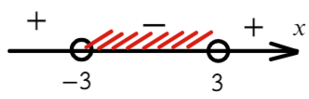
Ответ: x ∈ (−3; 3).
Перейдем к квадратному уравнению:
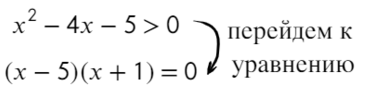
Разложим на множители и подставим x = 10, чтобы определить знак:
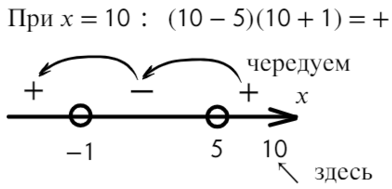
Нам требуются положительные значения:
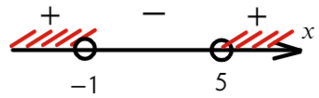
Второй способ разложить на множители:


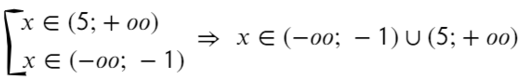
Ответ: x ∈ (−oo; −1) ∪ (5; +oo).
А теперь простой, но крайне показательный пример:
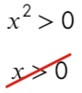
Убирать квадрат ни в коем случае нельзя. Простенький контрпример:
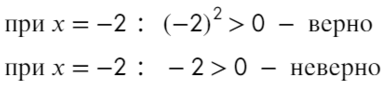
Надеюсь, убедил. Вместо знака больше поставим знак равно и попробуем решить методом интервалов:

Если корень повторяется четное количество раз, то в этой точке знак меняться не будет. Отмечать будем такую точку восклицательным знаком (а внутри него ±, чуть ниже объясню, зачем это).
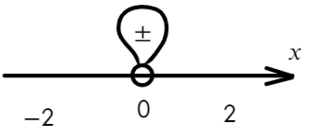
Проверим это:
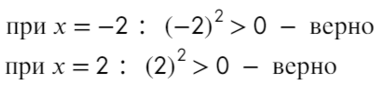
В данном неравенстве знак больше, тогда отметим те промежутки, где стоит знак «+».

Только точка «0» не подходит, 0 > 0 — неверно!
Ответ: x ∈ R \ {0} или x ∈ (−oo; 0) ∪ (0; +oo).
Переходим на новый уровень:
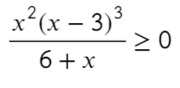
Все говорят, что домножать на знаменатель нельзя, а я говорю, что буду! (joke)
По методу координат найдем корни числителя и знаменателя:
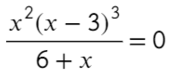
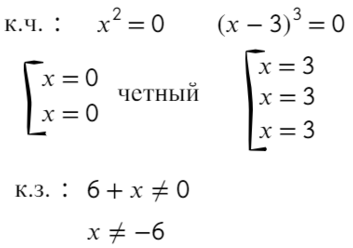
Отметим все корни на одной прямой (сколько неравенств, столько же и прямых). Ноль — корень четной кратности, над ним рисуем восклицательный знак! Если это корень числителя, то точка будет закрашена, если знаменателя — выколота (на ноль делить нельзя).

Требуется найти промежутки, где выражение больше или равно нулю. Нам подойдут все «промежутки», где знак плюс. Для этого подставим значение x = 1 и с промежутка [0; 3] начнем расставлять знаки. Там же находится единица.


Вот для чего ставят в восклицательном знаке ±: чтобы не потерять отдельные точки, в данном случае 0.
Ответ: (−oo; − 6) ∪ {0} ∪ [ 3; +oo).
Дальше интереснее:
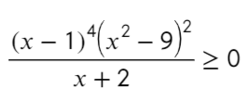
По той же схеме корни числителя и знаменателя:
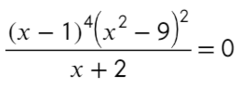
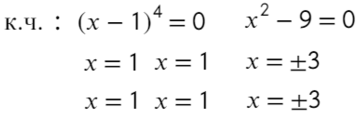


Определим знак при x = 10 и расставим знаки с промежутка, где присутствует 10:
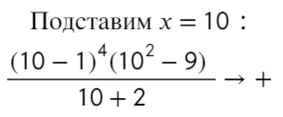
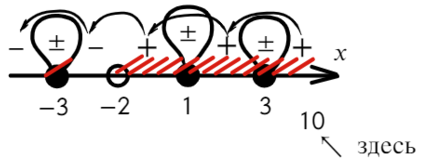
Все точки от − 2 закрашены, значит эти промежутки можно объединить в один.
Ответ: {−3} ∪ (−2; +oo).
Закрепляем последовательность:

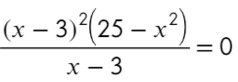
Точка x = 3 встречается 3 раза (2 раза в числителе и 1 раз в знаменателе), знак через нее меняться будет! А также эта точка будет выколота, проверь это, подставив в уравнение x = 3. На ноль же делить нельзя?
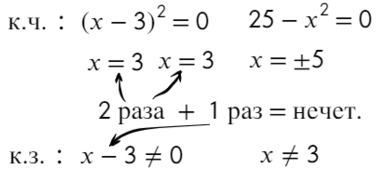
Подставим x = 10 и расставим знаки:

Ответ: [ −oo; −5) ∪ [ 3; 5).
Все скользкие моменты разобрали, стало понятнее?
Резюме:
Нашел ошибку/опечатку — напиши.
Группа с полезной информацией и легким математическим юмором.
ik-study.ru
Линейные и квадратные неравенства. Алгебра, 9 класс: уроки, тесты, задания.
| 1. |
Деление неравенства на отрицательное число
Сложность: лёгкое |
2 |
| 2. |
Число, которое является или не является решением неравенства с модулем
Сложность: лёгкое |
1 |
| 3. |
Линейное неравенство
Сложность: лёгкое |
3 |
| 4. |
Дробное неравенство, сводимое к линейному
Сложность: среднее |
4 |
| 5. |
Квадратное неравенство, сводимое к линейному (распределительный закон умножения)
Сложность: среднее |
3 |
| 6. |
Значения переменной, при которых выражение имеет смысл
Сложность: среднее |
4 |
| 7. |
Область определения корня из квадратного трёхчлена
Сложность: среднее |
5 |
| 8. |
Область определения корня из дроби
Сложность: среднее |
6 |
| 9. |
Значения переменной, при которых дробь имеет смысл (корень в знаменателе)
Сложность: среднее |
5 |
| 10. |
Целочисленные значения параметра
Сложность: сложное |
6 |
| 11. |
Натуральное значение параметра (целые числа из множества решений)
Сложность: сложное |
6 |
| 12. |
Натуральное значение параметра (натуральные числа из множества решений)
Сложность: сложное |
6 |
www.yaklass.ru
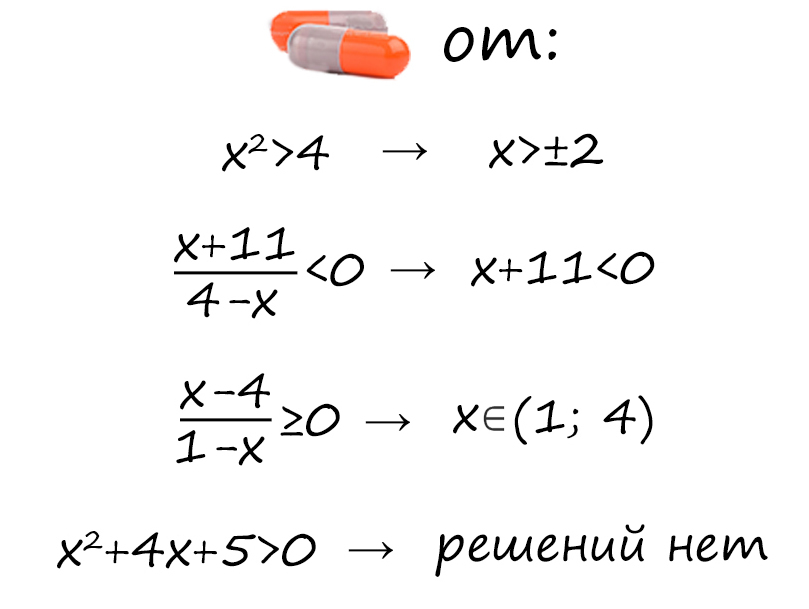 Решение неравенств
Решение неравенств