Решение задач с помощью составления уравнений

Нередко уравнения выручают нас при решении самых разнообразных задач – по математике, физике, механике, экономики и других областей.

Рассмотрим общий порядок решения задач с помощью уравнений.

1. Вводим переменные. Иными словами, буквами x, y, z мы обозначаем неизвестные нам величины, которые нам необходимо найти по условию задачи либо которые необходимы для отыскания искомых величин.

2. Составляем уравнение (систему уравнений) – при помощи введенных переменных и данных в условии задачи величин.

3. Решаем составленное уравнение (систему уравнений) и анализируем полученные данные (отбираем из решений те, которые подходят по смыслу задачи).

4. Если буквами x, y, z были обозначены не искомые величины, то при помощи полученных результатов находим ответ на вопрос задачи.

Применим полученные знания на практике и решим задачи.

Задача 1.

Для перевозки 60 т груза понадобилось некоторое количество машин. Из-за ремонта на дороге на каждую машину пришлось грузить на 0,5 т меньше, чем предполагалось, что привело к увеличению общего числа машин на 4 единицы. Какое количество машин было необходимо первоначально?

Решение.

1. Обозначим через х первоначальное количество машин. Тогда всего было использовано (х + 4) машин.

2. Предполагалось, что каждая машина равномерно празделит 60 т груза, т.е. на одну машину будет погружено 60/х т, но фактически на 1 машину было погружено 60/(х + 4) т, что на 0,5 меньше, чем планировалось.

3. На основе введенных переменных и выведенных выражений составим и решим уравнение:

60/х – 60/(х + 4) = 0,5

60/х – 60/(х + 4) = 0,5 ∙ 2х(х + 4)

120(х + 4) – 120х = х(х + 4)

120х + 480 – 120х = х² + 4х

х² + 4х – 480 = 0.

По теореме Виетта, х₁ + х₂ = -4, а х

1 ∙ х₂ = -480. Значит, х₁ = -24, х₂ = 20.

4. Анализируем полученные результаты. Число -24 не подходит по смыслу задачи (количество машин не может быть выражено отрицательным числом). Значит, наше решение – х₂ = 20, т.е. первоначально понадобилось 20 машин.

Ответ: 20.

Задача 2.

Моторная лодка, двигаясь со скоростью 20 км/ч, прошла расстояние между А и В по реке туда и обратно без остановок за 6 ч 15 мин. Расстояние между А и В составляет 60 км. Найти скорость течения реки.

Решение.

1. Примем за х скорость течения реки.

2. Т.к. по условию задачи лодка двигалась в обоих направлениях (туда и обратно), то по течению она шла со скоростью (20 + х) км/ч, против течения – со скоростью (20 – х) км/ч.

3. Чтобы найти время, нужно расстояние разделить на скорость, т.е. t = s/v. Иными словами, путь по течению займет у лодки 60/(20 + х) ч, а обратный путь – путь против течения займет 60/(20 – х) ч. По условию известно, что весь путь занял 6 ч 15 мин, т.е. 25/4 ч.

4. Используя вышеизложенные сведения, составим и решим уравнение:

60/(20 + х) + 60/(20 – х) = 25/4

60/(20 + х) + 60/(20 – х) = 25/4 ∙ 4(20 + х)(20 – х)

240(20 – х) + 240(20 + х) = 25(20 + х)(20 – х)

4800 – 240х + 4800 + 240х = 25(400 – х²)

9600 = 10000 – 25х²

25 х² = 10000 – 9600

25 х² = 400

х² = 16

х₁ = -4, х₂ = 4.

5. Анализируем полученные результаты. Число -4 не подходит по смыслу задачи (скорость течения не может быть выражена отрицательным числом). Значит, наше решение – х₂ = 4, т.е. скорость течения реки составляет 4 км/ч.

Ответ: 4.

Задача 3.

Есть кусок сплава меди с оловом массой 12 кг, содержащий 45% меди. Сколько чистого олова необходимо прибавить к этому куску , чтобы получившийся новый сплав содержал 40% меди?

Решение.

1. Примем за х массу добавленного олова. Тогда массу получившегося сплава мы обозначим как (12 + х) кг. Этот сплав содержит 40% меди, значит в новом сплаве меди будет 0,4(12 + х).

2. Исходный сплав массой 12 кг содержал 45% меди, значит, в нем было меди 0,45 ∙ 12 кг.

3. Т.к. масса меди в исходном и в новом сплаве одинакова, приходим к уравнению:

0,4(12 + х) = 0,45 ∙ 12

4,8 + 0,4х = 5,4

0,4х = 5,4 – 4,8

0,4х = 0,6

х = 0,6 : 0,4

х = 1,5.

Значит, к исходному сплаву необходимо добавить 1,5 кг олова.

Ответ: необходимо 1,5 кг олова.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Уравнения. Решение задач уравнением. 5-й класс

Цели:

• Образовательная

: систематизировать знания о способах решения уравнений; обобщить знания об алгоритме решения задачи при помощи уравнения; закрепить умения составлять уравнение по условию задачи

Воспитательная

: воспитывать аккуратность, уважение к окружающим, бережное отношение, настойчивость в достижении цели, культуру математической речи; рассмотреть меры профилактики сердечно-сосудистых заболеваний

Развивающая

: совершенствовать умения решать уравнения; закрепить навыки составления уравнения к условию задачи; развивать умения выделять главное, сравнивать, анализировать и делать выводы; развивать умения формулировать познавательные задачи; развивать креативные умений, учиться применять знания самостоятельно;

Тип урока: повторительно-обобщающий урок.

Вид урока: урок-соревнование.
Оборудование: доска ActivInspireт, карточки для ИКР, лист оценивания, учебник.

Приложение 2

Ход урока

1. Организационный момент

(Приложение 1) (стр. 1)

Долгожданный дан звонок,
Начинается урок.
Тут затеи и задачи,
Игры, шутки, –
Всё для вас
Пожелаю вам удачи-
За работу, в добрый час!

Давайте улыбнёмся друг другу и с хорошим настроением начнём наш урок (стр2)

Начать урок я хочу с вопроса к вам. Как вы думаете, что самое ценное на Земле? (выслушиваются варианты ответов учеников). Этот вопрос волновал человечество не одну тысячу лет. Вот какой ответ дал известный учёный Ал – Бируни: (стр3) «Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит». Пусть эти слова станут девизом нашего урока

2. Мотивация урока (стр4)

Разгадайте анаграмму и определите, какое слово лишнее. Что связывает оставшиеся слова между собой?

зачада
гукр
варунение
извененаяст

Ответ: задача, круг, уравнение, неизвестная. Лишнее слово – круг – геометрическая фигура, остальные слова не являются названиями геометрических фигур.

Какая связь между оставшимися словами? (условие задачи содержит неизвестную величину, значение которой нужно определить, уравнение тоже содержит неизвестную величину; многие задачи решают, составляя по условию уравнение)

На уроках математики вы действительно учитесь решать задачи, в том числе и при помощи составления уравнения. Уравнения у вас могут получиться самые разные, поэтому так важно умение решать любые уравнения. (стр5)

(Сообщение целей и задач, объяснение вида урока и правило оценивания по листу самооценки (

Приложение 5)

Загадка: (стр6)

Он есть у дерева, цветка,
Он есть у уравнений
И знак особый –
Связан с ним, конечно без сомнений.
Заданий многих он итог.
И с этим мы не спорим
Надеемся что каждый смог
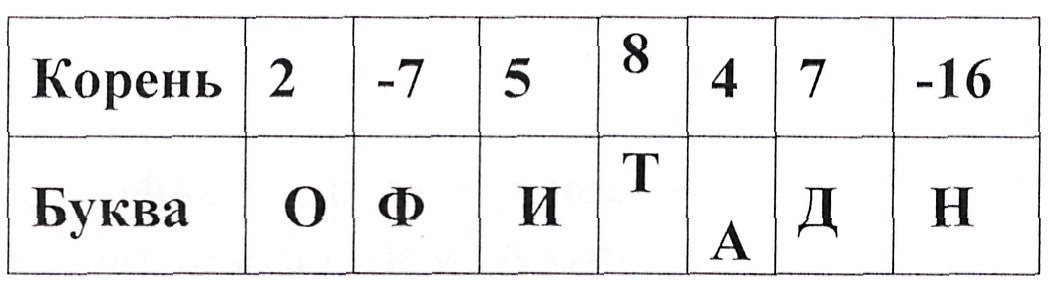
Ответить: это… (Корень)

3. Проверка домашнего задания (стр7)

138 – 5; 8 (взаимопроверка) У-5 Р-8 А-7 О-4 П-9
№126 – 7

4. Актуализация опорных знаний

Решить уравнения, повторяя правила нахождения неизвестного компонента

(стр8) (стр9)

а) х+15=40; б) у-10= 32;

в) 8-х=2; г) 70:у=7;

д) х:20=3; е) 25х=100

Что же такое уравнение? (Равенство, содержащее букву, значение которой нужно найти.)
Что такое корень уравнения? (Значение буквы, при котором из уравнения получается верное числовое равенство.)
Что значит решить уравнение? (Найти все его корни или убедиться в том, что корней нет.)

(Одновременно с устной работой ИКЗ индивидуально.) (Приложение 3), (Приложение 4)

5. Закрепление материала

А вот каким способом решения мы займемся сегодня – нам поможет узнать следующее задание: заполните таблицу буквами, соответствующими полученным ответам: (стр10)

3х-45=15	У -20
13х-23-5х=9	Р – 8
(х-12)*8=56	А – 19
51-3х=48	В – 1
13х-х=60	Н -5
(12х-5х)*4=252	Е – 9
(х+67):18=4	Н – 5
130-4х=70	И – 15
124:(х-5)=31	Е – 9

Ответ: УРВАНЕНИЕ (стр11)

29 сентября – всемирный день профилактики сердечно-сосудистых заболеваний. (стр12)

1. Масса человеческого сердца у взрослых составляет 250–300 грамм и зависит от величины тела и от физического развития и возраста человека.
2. Размер сердца соответствует в среднем сложенной в кулак кисти руки.
3. За одну минуту сердце взрослого человека, находящегося в покое, выталкивает в кровеносные сосуды 5–5,5 литров крови, при физической работе количество увеличивается до 15–20 литров. Всего за сутки сердце взрослого человека перекачивает до 10000 литров крови.
4. К 16 годам объём сердца у человека увеличивается в 3–3,5 раза.
5. В истории современной медицины известен случай, когда сердце человека остановилось и снова начало биться через 4 дня.
   Древние египтяне считали, что четвертый палец руки связан с сердцем специальным каналом. Именно из-за этого пошёл обычай носить обручальное кольцо на безымянном пальце.
6. Как считают специалисты, сердце обладает такой высокой надежностью и большим запаса прочности, которой вполне достаточно на жизнь в течении 150 лет

• Продукты полезные для сердца – Шпинат, Овёс, Орехи, Красная рыба (стр13–20)
• Калий –
главный внутриклеточный элемент, оказывающий многогранное воздействие на функционирование сердца. Мы часто “теряем” калий при стрессах, избыточном потреблении поваренной соли, алкоголя, сахара, кофе.
• Магний –
После кислорода, воды и пищи, магний, возможно, является самым важным для организма элементом. необходима для правильного функционирования организма
• Что противопоказано сердцу:
• Алкоголь –
Являясь клеточным ядом, алкоголь повреждает клетки сердечной мышцы и повышает давление, отравляя нервную и сердечно – сосудистую систему. Все 5–7 часов, пока выпитый алкоголь циркулирует в крови, сердце работает в неблагоприятном режиме. Пульс увеличивается до 100 ударов в минуту, в организме нарушается обмен веществ и питание сердечной мышцы Алкоголь нарушает кровообращение в кожных капиллярах, испытывает кислородное голодание.

Задача: Чтобы определить массу сердца взрослого человека, решите логический тест: (стр21)

Простые физические упражнения (Приложение 6)

1. Руки опущены вдоль туловища. Вдох. С напряжением поднять прямые руки через стороны вверх. Выдох. Вдох. Опустить руки через стороны вниз. Выдох. Вдох. Свести прямые руки перед собой, ладонями друг к другу. Выдох. Вдох. Развести руки в стороны ладонями назад. Выдох.
2. Руки согнуты в локтях. Ладони у груди. Вдох. Выбросить левую руку вперёд согнутой кистью, как бы отталкивая воздух. Выдох. Вдох. Вернуть руку к груди ладонью к себе. Выдох. Вдох. Выбросить правую руку вперёд. Выдох. Вдох. Вернуть руку к груди. Выдох. Вдох. Выбросить обе руки вперёд, ладонями от себя. Выдох. Вдох. Вернуться в исходное положение. Выдох.
3. Как бы косим косой траву. Вдох. Движение косой влево с одновременным выдохом. Вдох делается медленный, во время возврата в исходное положение. Сделав несколько движений влево, начинаем делать те же движения, но вправо.
4. Как бы вытряхиваем тяжелое одеяло, держа его за концы. Вдох. Резкое встряхивание. Выдох.

(стр22)

Задача 1: Бассейн вмещает 300 м³ воды и наполняется двумя трубами. Через первую трубу вода вливается со скоростью 20 м³/ч, а через вторую трубу – со скоростью 30 м³/ч. За сколько времени наполнится бассейн при одновременном включении двух труб? (Сколько м³ воды вольется в бассейн за 4 ч? Какой объем при этом останется незаполненным?)

Задача 2: Морковь дороже картофеля на 25т., за 3 кг картофеля и 4 кг моркови заплатили 520 тенге. Сколько стоит морковь, картофель?

Задача 3: Два поезда вышли одновременно навстречу друг другу из двух городов, расстояние между которыми 600 км. Скорость первого поезда 70 км/ч, а скорость второго 80 км/ч. Какое расстояние было между поездами через 3 ч после выхода?

х – расстояние между поездами через 3 ч после выхода
(70+80)*3+х=600
х = 150(км)

Задача 4: Пассажирский и товарный поезд вышли в одном направлении одновременно с двух станций, расстояние между которыми 512 км. Скорость пассажирского поезда была в 2 раза быстрее скорости товарного и через 8ч после выхода пассажирский поезд догнал товарный. С какими скоростями они шли?

2х*8-8х=512
х=64км/ч

Задача 5: В клетке находятся фазаны и кролики. Известно, что у них 35 голов и 94 ноги. Узнайте число фазанов и число кроликов.

Что мы можем взять за x в этой задаче – число фазанов или число кроликов?

Давайте возьмем за x сначала число фазанов, и решим задачу с помощью уравнения.

Решение:

1) Пусть x фазанов в клетке. Тогда кроликов в клетке 35-x. Всего у фазанов 2x ног, а у кроликов 4·(35-x) ног. Зная, что всего у них 94 ноги составим уравнение:

2x+ 4·(35-x) =94
2x+140-4x=94
2x=46,
х=23,
23 фазана в клетке

2) 35-23=12 (кроликов) в клетке,

Ответ: 23фазана и 12 кроликов в клетке

6. Физкультурная пауза (стр23)

Что-то мы засиделись! Надо бы нам размяться. Сейчас мы проведем с вами физкультминутку в виде эстафеты.

На доске примеры с пропущенными числами. Их нужно заполнить так, чтобы равенства были верными. Эстафетной палочкой будет кусок мела. По правилам нашей эстафеты можно: подсказывать своим товарищам, исправлять их ошибки, болеть за команду. Побеждает та команда, которая первая правильно заполнит все свободные клетки. Начинаем бегать по очереди под звуки музыки.

7	*	8	=
	:	4	=
	+	86	=
	:	4	=
	—	17	=
	*	12	=
	+	204	=

 

7	*	8	=	56
56	:	4	=	14
14	+	86	=	100
100	:	4	=	25
25	—	17	=	8
8	*	12	=	96
96	+	204	=	300

7. Контроль ЗУН (работа в группах) (стр24)

Решить задачу по карточке, работая в группе(всего 4 группы, задания устно проговариваются после его решения)

Задача 1 (уровень А)

Задача 2 (уровень А)

Туристы прошли пешком х км. И проехали на автомобиле3х км. Весь путь равен 124 км.

Вопрос: __________________________
Решение: _________________________

Задача 1 (уровень В)

Ученик задумал число. Умножил его на 2, к произведению прибавил 19 и получил сумму, равную 37. Какое число задумал ученик?
Отец старше сына на 20 чет, а сын моложе отца в 5 раз. Сколько лет отцу и сколько лет сыну?

8. Домашнее задание

(стр25)

Уровень А – №128, 125(2)
Уровень В – №112(3), 114(6)

9. Рефлексия

«Умение решать задачи – такое же практическое искусство, как умение плавать или бегать на лыжах. Ему можно научиться только путём подражания или упражнения» Пойа (стр26)

Что нового узнали? Ребята, сравните по вкусу мандарин и лимон. У кого настроение на этом уроке соответствует вкусу лимона? А вкусу мандарина? (стр27)

Поднимите руку, кто ответил на уроке хотя бы раз.
Поднимите руку, кто достиг желаемого.
Поаплодируйте себе.

10. Итог урока

Самооценка. Подведение итогов и выставление оценок

Спасибо за урок! (стр28)

Список литературы:

1. Математика 5, Т. Алдамуратова, Алматы «Атамүра», 2010.
2. Далингер В.А
. Обучение учащихся решению текстовых задач методом составления уравнений. – Омск, 19.
3. Колягин Ю.М
. Задачи в обучении математике: т.2. – М.: Просвещение, 1997.
4. Орехов Ф.А
. Решение задач методом составления уравнений. – М.: Просвещение, 1971.

urok.1sept.ru

Урок решения старинных задач по теме «Решение задач с уравнениями»

Цель урока:

1. Обобщить и углубить знания школьников по теме: Решение задач с помощью уравнений.
2. Способствовать развитию наблюдательности, умения анализировать, сравнивать, делать выводы.
3. Развивать творческие способности учеников путем решения старинных задач.

Ход урока

I. Вводная беседа учителя. Из истории уравнений.

Уже около 4000 лет назад вавилоняне и египтяне решали разные задачи землемерия, строительства и военного дела с помощью уравнений. Уравнение первой и второй степеней умели решать в древности также китайские и индийские ученые.

Задачи, решаемые с помощью уравнений, встречаются во многих текстах глубокой древности. В Московском папирусе, представляющем свиток, изготовленный из растений, на котором сделаны записи около 1850 г. до н.э., и в папирусе Ахмеса, например, содержащие задачи, в которых неизвестное имеет особый символ и название: “хау” или ”аха. Оно означает “количество”, ”куча”. Так называемое ”исчисление кучи”, или “вычисление хау”, приблизительно соответствует нашему решению задач с помощью уравнений.

II. Решение старинных задач.

1) Старинная русская задача (XVII век)

Один человек решил узнать, который теперь час. Ему ответили, что две пятых прошедших часов от полуночи до сего времени равны двум третям оставшегося времени до полудня. Смогли бы вы определить, сколько сейчас времени.

Решение:

Промежуток от полуночи до полудня составляет 12 часов. Если обозначить время от полуночи до искомого момента через t, то можно составить уравнение:

 часов.

Ответ: 7 часов 30 минут утра.

2) Задача 2. Пифагор Самосский (около 580-501 г. до н.э.)

Поликрит из баллады Шиллера тиран с острова Самос) однажды спросил на пиру Пифагора, сколько у того учеников. “Охотно скажу тебе, о Поликрит, – Отвечал Пифагор. – Половина моих учеников изучает прекрасную математику. Четверть исследует тайны вечной природы, седьмая часть молча укрепляет силу духа, храня в сердце учение. Добавь еще к ним трех юношей, из которых Теон превосходит прочих своими способностями. Столько учеников веду я к рождению вечной истины. ” Сколько учеников было Пифагора.

Решение:

Пусть x число учеников Пифагора. По условию задачи составим уравнение:

Ответ: 28 учеников.

3)Задача 3. Герон Александрийский (I до н.э.)

Из-под земли бьют четыре источника. Первый заполняет бассейн за 1 день, второй за 2 дня третий за 3 дня и четвертый за 4 дня. За сколько времени наполняют бассейны четыре источника вместе?

Решение:

Примем объем бассейна за 1. Пусть х – число дней, за которые источники вместе заполняют бассейн.

Следовательно, чтобы заполнить бассейн из четырех источников, требуется  дня, т.е. чуть меньше половины дня.

4) Задача 4. Евклид (III в. до н.э.)

Мул и осел под вьюком по дороге с мелкими шагами. Жалобно охал осёл, непосильно ношей придавлен. Это подметивший обратился к сопутчику с речью: “Что ж, старина, ты заныл и рыдаешь, будто девочка? Нёс бы вдвойне я, чем ты, если б отдал одну ты мне меру. Если ж ты у меня одну взял, то мы бы сровнялись”.

Сколько нес каждый из них?

Решение:

Если х – груз мула, то (х-1) – груз осла, увеличенный на единицу, а следовательно, первоначальный груз осла был (х-2). С другой стороны, (х+1) в 2 раза больше, чем груз осла, уменьшенный на 1 , т.е. (х-3). Таким образом,

x+1=2(x-3)

x=7

Груз мула равен 7, груз осла равен

х-2=5

Ответ: груз мула равен 7, груз осла равен 5.

5) Задача 5.

В 1881г. была найдена зарытой в земле близ Бахшали (северо-западная Индия) рукопись неизвестного автора, которая, как полагают, относится к VI-VIII вв. В этом памятнике, написанном на березовой коре и известным под названием ”Бахшалийской рукописи”, содержится такая задача:

“Из четырех жертвователей второй дал вдвое больше первого, третий – втрое больше второго, четвертый – вчетверо больше третьего, а все вместе дали 132. Сколько дал первый?”

Решение:

Пусть первый дал х то следующие дали 2х, 6х, 24х, все же вместе дали 132.

х+2х+6х+24х=132

33х=132

х=4

Следовательно, первый дал 4, второй 8, третий 24, четвертый 96.

6) Задача 6.

В своей «Всеобщей арифметике» Ньютон называет буквы, знаки действий, алгебраические выражения и уравнения языком алгебры. Чтобы решить задачу, пишет Ньютон, нужно лишь «перевести её с обыкновенного языка на язык символических выражений» язык алгебры. Перевод этот означает составление уравнения, решение которого ведёт к решению поставленной задачи.

Вот один из примеров, данных Ньютоном: Купец имел некоторую сумму денег. 100 фунтов из неё он затрачивал каждый год на содержание своей семьи, прибавляя к оставшейся сумме одну её треть. Через три года он обнаружил, что его состояние удвоилось. Сколько денег было у него вначале?»

Таким образом, заключает Ньютон, задача выражается уравнением:

решив которое находим х=1480.

III. Итог урока.

Ребята, с задачами каких стран вы познакомились, какие ученые создали эти старинные задачи.

Какая задача вам понравилась больше всего и почему.

IV. Домашнее задание.

Задача Бхаскара (Индия).

Некто сказал другу: «Дай мне 100 рупий, и я буду вдвое богаче тебя». Друг ответил: «Дай ты мне только 10, и я стану в 6 раз богаче тебя». Сколько было у каждого?

Решение:

170; 40. Вводя вспомогательное неизвестное, Бхаскара принимает, что первый имеет 2х – 10, тогда по условию задачи второй имеет х+100. Второе условие приводит к уравнению.

6(2х-100-10)=х+100+10, откуда х=70.

urok.1sept.ru

Решение задач с помощью уравнений

Тема урока: Решение задач с помощью уравнений

Цели урока:

1)образовательные: повторение и закрепление ЗУН учащихся по теме «Уравнения. Решение задач с помощью уравнений», навыков устных и письменных вычислений, упрощения алгебраических выражений;

2)развивающие: продолжить работу по развитию устной и письменной речи, изложению своих мыслей с применением математической терминологии, самостоятельного мышления, навыка самооценки и самопроверки;

3)воспитательные: содействовать формированию и развитию нравственных, трудовых, эстетических качеств личности учащихся.

Планируемые результаты:

Личностные:

• умение ясно, точно, грамотно излагать свои мысли, критичность и креативность мышления,

• активность при решении задач.

Предметные:

• умение применять изученные понятия, результаты и методы при решении уравнений и задач на составление уравнений.

• умение самостоятельно выбирать наиболее эффективные способы решения учебных задач, адекватно оценивать правильность или ошибочность выполнения учебной задачи,

Метапредметные:

• Умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;

• усиление прикладной направленности курса алгебры через решение различных текстовых задач.

Оборудование: компьютер, мультимедийный проектор, тематическое планирование, конспект урока.

Тип урока: комбинированный урок

Формы работы учащихся на уроке: индивидуальная, фронтальная, групповая.

Структура урока:

1. Организационный момент

2. Проверка домашнего задания

3. Актуализация опорных знаний.

4. Работа по карточкам

5. Историческая справка

6. Физкультминутка

7. Самостоятельная работа

8. Рефлексия

9. Домашнее задание

Ход урока

Организационный момент, вступительное слово учителя

Математику не зря называют «царицей наук», ей больше, чем какой-либо другой науке, свойственны красота, изящность и точность. Одно из замечательных качеств математики — любознательность. Постараемся доказать это на уроке. Мы изучили очень важную главу в курсе алгебры «УРАВНЕНИЯ». Вы знаете и умеете решать уравнения, приводимые к линейным, составлять различные уравнения по условию задачи. Знания не только надо иметь, но и надо уметь их показать, что вы и сделаете на сегодняшнем уроке, а я вам в этом помогу.

И начнем наш урок с проверки домашней работы

Проверка выполнения домашней работы

(двое учащихся заранее записывают решение на доске)

«В клетке находится неизвестное число фазанов и кроликов. Известно, что вся клетка содержит 35 голов и 94 ноги. Узнать число фазанов и число кроликов.»

Решение.

б) Пусть х кроликов в клетке, тогда (35 — х) фазанов в клетке, 4х ног у кроликов, 2(35 — х) ног у фазанов. Всего 94 ноги.

Составим и решим уравнение:

4х + 2(35 — х) = 94,

4х +70 — 2х =94,

2х = 24,

х = 12 кроликов в клетке,

35 — 12 = 23 фазана в клетке.

Ответ: 12 кроликов, 23 фазана.

г) Пусть х ног у кроликов, х /4 кроликов, тогда (94 — х) ног у фазанов, (94 — х) / 2 фазанов.

Всего 35 кроликов и фазанов.

Составим и решим уравнение:

х/4 + (94 — х)/2 = 35,

х + 188-2х=140,

-х = — 48,

х = 48 ног у кроликов,

1) 48 : 4 = 12 кроликов,

2) 35 — 12 =23 фазана.

Ответ: 12 кроликов, 23 фазана.

Учитель: Мы составили и решили 4 уравнения к одной задаче.

Несмотря на то, что уравнения а) и б) имели более простой вид

и решение, полезно рассматривать все случаи.

Актуализация опорных знаний.

(Устная работа с использованием мультимедийного проектора)

1) Решите уравнения: (Рис.1)

х + 23 = 50;

у-20 = -у.

Какое правило преобразования уравнений применяли при решении уравнений?

Какое число называется корнем уравнения?

Что значит решить уравнение?

Как называются уравнения вида:

4х = 60;

12 t = 96.

Какое правило преобразования уравнений применяли при решений этих уравнений?

2) Найдите ошибку (Рис.2)

Раскройте скобки:

9 — (8 -х) = 9 — 8 — х;

3 + (- х- 1) = 3 + х-1;

2(х — 5) = 2х -5.

3) Используя верное равенство 5*2 — 3=2*3 + 1, составьте уравнение, корень которого равен 2. (Рис 4)

Самостоятельная работа

Учитель: Итак, мы повторили правила преобразования уравнений, умеем раскрывать скобки, перед которыми стоят знаки «+» или «-«, приводить подобные слагаемые и, сейчас, каждому из вас предстоит выполнить самостоятельную работу по карточкам.Решите в тетради уравнения, внесите корень уравнения во второй столбик. Внизу есть таблица выбора ответов, запишите соответствующую букву в третий столбик и получите слово.Найдите корни каждого уравнения и впишите в третий столбец соответствующие им буквы.

1 вариант

Таблица выбора ответов:

2 вариант

Уравнение

Корень

Буква

6х + 10 = 28

— 5p = 16 -7p

-15 — 9у = 6у

6t — 26 = 2t + 2

16t — 5 = 15t — 10

7z + 40 = 3z

8х — 25 = 3х

Таблица выбора ответов:

Корень

-10

8

-1

3

-5

7

5

Буква

М

О

Р

X

3

Е

И

А знаете ли вы кто такие Диофант Александрийский и Мухаммед аль — Хорезми (демонстрируются портреты ученых на рисунках при помощи проектора)

Историческая справка (выступления учащихся)

Диофант Александрийский

Диофант — древнегреческий математик из Александрии.

Мы очень мало знаем о нем. Автор трактата Арифметика в 13 книгах (сохранились 6 книг) посвященного главным образом исследованию неопределенных уравнений (т.е. диофантовых уравнений). Одним из первых Диофант стал использовать при записи алгебраических рассуждений специальные знаки. Это был важный шаг в создании символического языка математики. На результаты, полученные Диофантом, впоследствии опирались Ферма, Эйлер, Гаусс и др. великие математики.

Мухаммед Аль — Хорезми

Мухаммад ибн Муса Хорезми — великий персидский математик, астроном и географ, основатель классической алгебры — жил на рубеже IX — X веков. Сведений о жизни ученого сохранилось крайне мало. Значительный период своей жизни он провел в Багдаде. Одно из главных сочинений аль — Хорезми называлось «Китаб аль-джебр вальмукабала», в переводе на русский: «Учение о переносах и сокращениях», то есть техника решения алгебраических уравнений. По-арабски это звучит « аль-джебр»; отсюда произошло название «алгебра».

Другое известное слово — «алгоритм», то есть четкое правило решения задач определенного типа — произошло от прозвания «аль-Хорезми». Третий известный термин, введенный в математику знаменитым согдийцем — это «синус».

Физкультминутка

Упражнения для головы, шейного и грудного отделов позвоночника «Имитации».

Для проведения физкультминутки используются упражнения для головы, шейного и грудного отделов позвоночника.

Упражнения:

1) «Черепаха»: наклоны головы вперед -назад.

2) «Маятник»: наклоны головы вправо-влево.

3) «Собачка»: вращение головы вокруг воображаемой оси, проходящей через нос и затылок.

4) «Сова»: поворот головы вправо-влево.

5) «Ёжик нахмурился» (плечи вперёд, подбородок к груди) —> «Ёжик весёлый» (плечи назад, голову назад).

6) «Весы»: левое плечо вверх, правое вниз. Поменять положение рук.

7) «Тянемся — потянемся»: руки вверх, вытягиваем позвоночник.

Решение задач.

1. В «геометрической алгебре» древних греков решение уравнений сводилось к построению отрезков, представляющих положительные корни уравнений. Зачатки новой, арифметической алгебры встречаются лишь у Диофанта. Рассмотрим задачу из «Арифметики» Диофанта.

Задача Диофанта

Если прибавить к 20 и отнять от 100 одно и то же число, то полученная сумма будет в 4 раза больше полученной разности. Найти неизвестное число.

Решение

Пусть х — неизвестное число,

по условию задачи составим уравнение:

х + 20 — (100 — х)*4,

х +20 = 400 — 4х;

х + 4х =400 — 20;

5х = 380; х = 380 : 5;

х =76 — неизвестное число.

Ответ. 76

2. Решить задачу по вариантам (Задача отображается на экране при помощи мультимедийного проектора)

«Турист за два дня прошёл 32 км, причём во второй день он прошёл

на 2 км меньше, чем в первый. Какое расстояние он прошёл в первый

день?»

Вариант 1

Решение:

Пусть х км прошел турист в первый день, тогда …

Вариант 2

Решение:

Пусть х км прошел турист во второй день, тогда …

Двое учеников решают задачу на доске

(Оба ученика верно составили уравнения. Но эти уравнения оказались разными:

1) х + (х-2) = 32;

2) х +(х + 2) = 32. Почему? (Закончить решение задачи дома)

Подведение итогов урока (учитель дает оценку работе обучаемых)

Рефлексия (ученикам раздаются карточки на которых они дописывают фразу)

1. Я научился (лась) …

2. Мне нравится …

3. Я умею …

4. Мне было интересно …

5. Я повторил (а) …

6. Я уверен (а), что …

Домашнее задание

№ 433(а, в), № 440, закончить задачу

infourok.ru

Алгоритмы решения задач с помощью систем уравнений

Объяснительная записка.

В курсе алгебры 9 класса отводится всего 4 часа на решение задач с помощью систем уравнений второй степени. Это задачи на движение, совместную работу и задачи с геометрическим содержанием. Мне захотелось расширить тематику задач, и на факультативе по алгебре я предложила учащимся задачи, которые не включены в учебник. Для каждого из рассматриваемых типов задач я предлагаю алгоритм решения. Уважаемые коллеги, быть может, это покажется интересным и вам.

Алгоритм решения задач на совместную работу.

1. Принимаем всю работу, которую необходимо выполнить за 1.
   Находим производительность труда каждого рабочего в отдельности, т.е. , где t – время, за которое этот рабочий может выполнить всю работу, работая отдельно.
2. Находим ту часть всей работы, которую выполняет каждый рабочий отдельно за то время, которое он работал.
3. Составляем уравнение, приравнивая объем всей работы к сумме слагаемых, каждое из которых есть часть всей работы, выполненная отдельно каждым из рабочих.

Задача №1

Один комбайнер может убрать урожай пшеницы с участка на 24 ч быстрее, чем другой. При совместной работе они закончат уборку урожая за 35 часов. Сколько времени потребуется каждому комбайнеру, чтобы одному убрать урожай?

1. Принимаем площадь участка, с которого необходимо собрать урожай, за 1.

2. Пусть х – время, необходимое первому комбайнеру для уборки всего урожая, у — время, необходимое второму
комбайнеру для уборки всего урожая. Тогда– производительность первого комбайнера, – производительность второго комбайнера.
3. 35 – часть участка, с которого может убрать урожай первый комбайнер за 35 часов работы, 35 – часть участка, с которого может убрать урожай второй комбайнер за 35 часов работы.

4.Составим систему уравнений:

у = 60, х = 84
Ответ: для уборки всего урожая первому комбайнеру потребуется 84 часа, второму – 60 часов.

Задача №2

Две бригады, работая совместно, могут выполнить некоторое задание за 3 ч 36 мин. Сколько времени затратит на выполнение этого задания каждая бригада, работая в отдельности, если известно, что первой бригаде требуется для этого на 3 часа больше времени, чем второй.

Задача №3

Мастер и ученик должны были выполнить некоторое задание. После четырех дней совместной работы ученик был переведен в другой цех, и, чтобы закончить выполнение задания, мастеру пришлось еще 2 дня работать одному. За сколько дней мог бы выполнить каждый из них это задание, если известно, что мастеру для этого требуется на 3 дня меньше, чем ученику?

Алгоритм решения задач, в которых используется формула двузначного числа.

1. Вводится обозначение:
   х – цифра десятков
   у – цифра единиц
2. Искомое двузначное число 10х + у
3. Составить систему уравнений

Задача №1.

Двузначное число в четыре раза больше суммы его цифр. Если к этому числу прибавить произведение его цифр, то получится 32. Найдите это двузначное число.

Х – цифра десятков. У – цифра единиц. 10х + у – искомое число.

2х² + 12х – 32 =0

х² +6х – 16 =0

х₁ =-8 (посторонний корень) х₂ =2, тогда у =4.

Ответ: 24.

Задача №2.
Двузначное число в трое больше суммы его цифр. Если из этого числа вычесть произведение его цифр, то получится 13. Найдите это двузначное число. (27).

Задача №3.
Двузначное число в шесть раз больше суммы его цифр. Если это число сложить с произведением его цифр, то получится 74. Найдите это число.(54).

Задача №4.
Сумма квадратов цифр двузначного числа равна 13. Если от этого числа отнять 9, то получим число, записанное теми же цифрами, но в обратном порядке. Найти число.(32).

Задача №5.
Произведение цифр двузначного числа в три раза меньше самого числа. Если к искомому числу прибавить 18, то получится число, написанное теми же цифрами, но в обратном порядке. Найти это число.

Алгоритм решения задач на смеси.

1. х – масса первого раствора, у – масса второго раствора, (х + у ) – масса полученной смеси.

2. Найти содержание растворенного вещества в растворах, т.е.
   а % от х, в % от у, с % от (х+у)

3. Составить систему уравнений.

Задача №1
Смешали 30% -ный раствор соляной кислоты с 10% -ным и получили 600г 15% -ого раствора. Сколько граммов каждого раствора было взято?

Введем обозначение. Пусть взяли х г первого раствора, у г – второго раствора, тогда масса третьего раствора – (х+у).

Определим количество растворенного вещества в первом, втором, третьем растворах, т.е. найдем 30% от х, 10% от у, 15% от 600.

Составим систему уравнений:


0,3х + 60 – 0,1х = 90
0,2х = 30
х = 30:0,2
х = 150, у = 600 – 150 = 450
Ответ: взяли 150 г первого раствора и 450 г второго раствора.

Задача №2
Имеется лом стали двух сортов с содержанием никеля 5% и 40%. Сколько нужно взять металла каждого их этих сортов, чтобы получить 140 т стали с содержанием 30% никеля?

Задача №3
Смешали 10% -ный и 25% -ный растворы соли и получили 3 кг 20% -ного раствора. Какое количество каждого раствора в килограммах было использовано?

Литература:

1. В.С. Крамор. Повторяем и систематизируем школьный курс алгебры и начал анализа. “ Просвещение”.
2. М.Б.Миндюк, Н.Г. Миндюк. Разноуровневые дидактические материалы по алгебре. 9 класс. “Генжер”.

3. М.И. Сканави. Сборник задач по математике для поступающих во втузы. “ Высшая школа”.

4. М.Л. Галицкий, А.М. Гольдман, Л.И. Звавич. Сборник задач по алгебре.

8 – 9. “ Просвещение”.

urok.1sept.ru

Ответы@Mail.Ru: Алгебра задачка помогите!!!!

Одна часть — х. Вторая часть х+0,2х х+х+0,2х=9,9 2,2х=9,9 х=4,5 м Одна часть 4,5 м, вторая часть 9,9-4,5=5,4м

Пусть х длина первой части, тогда 2-ая часть х+0.2*9.9, а в сумме 9.9 х + х+1.98=9.9 думаю дальше сам решишь! ))

если одна часть длиннее на 20 %, то она равна 1,2 х, где х — это первая часть. две части х + 1,2х = 9,9

х — меньшая часть 20% кабеля = 9.9 /100*20 = 1.98 след, х+ 1.98 — большая часть х+х+1.98 = 9.9 2х=7.92 х=3.96 — меньшая часть 3.96+1.98=5.94 — большая часть

пусть х м большая часть, тогда 0,2х м меньшая х+0,2х=9,9 1,2х=9,9 х=8,25м значит большая 8,25 м, а меньшая 9,9-8,25=1,65

touch.otvet.mail.ru

Урок алгебры в 8-м классе «Решение задач с помощью квадратных уравнений»

Цели и задачи урока:

• выработать умение применять квадратные уравнения для решения алгебраических и геометрических задач; продолжить формирование практических и теоретических умений и навыков по теме “Квадратные уравнения”;
• способствовать умению анализировать условие задач, развитию умения рассуждать, развитию познавательного интереса, умению видеть связь между математикой и окружающей жизнью;
• воспитывать внимательность и культуру мышления, самостоятельность и взаимопомощь.

Тип урока: формирование новых умений и знаний.

Комментарий к организации урока: содержание урока демонстрируется с помощью презентации, что экономит время урока. Приложение 1.

Оборудование урока: интерактивная доска, компьютер.

Ход урока.

1.Организационный момент. Постановка целей и задач урока.

2.Устная работа.

1). Назовите коэффициенты квадратного уравнения:

а) 2х²-х+3=0;
б) 4х+3х²-1=0;
в) -7х+х²-0,5=0;
г) 0,7-0,5х-х²=0;
д) х²+18+3х=0;
е) 5х²=7х+24;
ж) 12х=х²— 4;
з) 6х²+7х=0;
и) х²+5=0;
к) 7,2х²=4;
л) 2х²=0;
м) х(5-х)=0.

2). Укажите среди данных уравнений приведенные квадратные уравнения.

Проверка домашнего задания

Задача. Произведение двух последовательных натуральных чисел равно 552, а их сумма равна 47. Найдите эти числа. Найдите арифметический способ решения.

Решение. (Один из учащихся воспроизводит решение задачи на доске, объясняет) Разделим сумму чисел на два. 47 :2 = 23,5. Поставим точку с этой координатой на числовую прямую.              23    23,5    24                 Это число заключено между целыми натуральными числами 23 и 24. Их сумма равна 47. Проверим, действительно ли произведение их равно 552, 23 * 24 =552. Ответ: 23 и 24.

3. Контроль усвоения материала (письменный опрос с последующей взаимопроверкой).

Вариант 1.

1).Напишите формулу корней квадратного уравнения ах²+вх+с=0.

2).Заполните таблицу:

Уравнение	а	в	с	в2-4ас	х1	х2	х1+х2	х1*х2
х2-6х+9=0
	2	7	9
4х2=-7х

Вариант 2.

1). Напишите формулу корней квадратного уравнения ах²+2кх+с=0

2) Заполните таблицу:

Уравнение	а	в	с	в2-4ас	х1	х2	х1+х2	х1*х2
5х2-4х=0
	3	0	-27
-2х2=-5-3х

Творческая работа.

Составьте квадратное уравнение, используя следующие данные:

А) На гербе города Саратова изображена рыба. Посчитайте количество букв в названии и прибавьте к этому числу 1. Полученное число будет первым коэффициентом.
Ответ: Стерлядь, 8+1=9, а=9.

Б) В дате образования поселка Духовницкое сложите цифры и к сумме прибавьте 7. Полученное число будет вторым коэффициентом.
Ответ: 1778 г., 1+7+7+8=23, 23+7, в=30.

В) Наше село стоит на великой русской реке. Посчитайте количество букв в названии и возведите это число в квадрат. Полученное число будет третьим коэффициентом.
Ответ: Волга, 5, 5²=25, с=25.

Г) Все коэффициенты положительные числа. Составьте квадратное уравнение, решите его, найдите сумму и произведение корней этого уравнения. Ответ: 9у²+30у+25=0; D=0, у_1,2= -15/9; у₁ +у₂ = -15/9 + (-15/9)= -30/9= — 10/3; у*у = -15/9 * (-15/9)=225/81 =25/9.

4. Изучение нового материала (основные понятия).

(При рассмотрении решения задач опираюсь на знания учащихся, задаю наводящие вопросы, подвожу учащихся к самостоятельному решению).

Многие задачи алгебры, геометрии, физики, техники приводят к необходимости решения квадратных уравнений.

Мы с вами должны научиться проводить анализ задачи, вводить неизвестные величины, находить зависимость между данными задачи и неизвестными величинами.

Составим схему решения задач

1. Анализ условия
2. Выделение главных ситуаций
3. Введение неизвестных величин
4. Установление зависимости между данными задачи и неизвестными величинами
5. Составление уравнения
6. Решение уравнения
7. Запись ответа

Если в уравнении дискриминант положителен, решениями задачи могут быть оба корня уравнения. Иногда бывает, что по смыслу задачи ей удовлетворяет лишь один из корней квадратного уравнения.

Задача1. Произведение двух натуральных чисел равно 84. Одно из чисел на 5 больше другого. Найти эти числа.

Анализируем условие задачи, составляем и решаем уравнение.

Пусть меньшее из данных чисел равно х, тогда большее число равно х+5. По условию произведение этих чисел равно 84. Составим уравнение х(х+5)=84. Получили квадратное уравнение х²+5х-84=0. Решим это уравнение. D=5²-4*1*(-84)=25+336=361=19², х₁=(-5+19):2=7; х₂=(-5-19):2=-12. Второй корень по смыслу задачи не подходит, т.к. даны натуральные числа. Значит меньшее число равно 7, а большее число равно 7+5=12.
Ответ: 7 и 12.

Рассмотрим задачу с геометрическим содержанием, для решения которой, применяется формула площади треугольника.

Задача 2. Найдите катеты прямоугольного треугольника, если известно, что один из них на 7 см больше другого, а площадь этого треугольника равна 30 см².

Решение. Площадь прямоугольного треугольника равна половине произведения катетов. Длины катетов неизвестны. Площадь равна 30 см².

Пусть х см-длина одного катета, (х+7) см-длина второго катета . Используя формулу площади треугольника составим уравнение: х(х+7)/2=30 . Решим уравнение: х²+7х=60 , х²+7х-60=0, D=289, х₁=-12; х₂=5. Так как длина отрезка величина положительная, то только х=5 удовлетворяет условию задачи. Найдем длину второго катета: 5+7=12 см. Ответ: 5см и 12 см.

Задача3. Мяч брошен вертикально вверх с начальной скоростью 40 м/с. Через сколько секунд оно окажется на высоте 60 м?

Решение. Из курса физики известно, что если не учитывать сопротивление воздуха, то высота h(м), на которой брошенный вертикально вверх мяч окажется через t(c), может быть найдена по формуле h=V₀ t-gt²/2, где V_o(м/с)-начальная скорость, g-ускорение свободного падения, приближенно равное 10 м/с². Подставив значения h и V в формулу, получим 60=40t-5t². Получили квадратное уравнение, решим его. 5t²-40t+60=0, t²-8t+12=0, D=16, t₁=2; t₂=6. Рассмотрим график зависимости h от t, где h=40t-5t². Из графика видно, что мяч, брошенный вертикально вверх, в течении первых 4с поднимается вверх до высоты 80 м, а затем начинает падать. На высоте 60 м от земли оно оказывается дважды: через 2 с и через 6 с после бросания. Условию задачи удовлетворяют оба найденных корня.
Ответ: на высоте 60 м тело окажется через 2 с и через 6 с.

Рассмотрим старинную задачу, которая решается с помощью теоремы Пифагора, но полученное при решении уравнение после упрощения оказывается линейным.

Задача 4. (Задача Бхаскары, Индия, XIIв.)

Цветок лотоса возвышался над тихим озером на полфута. Когда порыв ветра отклонил цветок от прежнего места на 2 фута, цветок скрылся под водой. Определите глубину озера.

Решение. Пусть отрезки АВ и АС изображают лотос в двух положениях. Если АD = х – глубина озера, то ВD = 1/2, АС = х+1/2.

Составим уравнение х² + 2² = (х + 1/2)²,

Решим уравнение х² + 2² = х² +2*1/2х + (1/2)², х² + 4 — х² –х -1/4 =0, х=3 >¾. Ответ: глубина озера 3 3/4 фута.

5. Закрепление материала.

№559. (Один учащийся у доски самостоятельно решает, потом комментирует решение задачи, остальные решают на месте, проверяют решение)

Произведение двух натуральных чисел, одно из которых на 6 больше другого, равно 187. Найдите эти числа.

Решение.

Первое число	Второе число Произведение чисел
х	х + 6	187

Составим уравнение х(х+6)=187. Решим его: х²+6х-187=0. D=784, х=11, х=-17. Второй корень по смыслу задачи не подходит, т.к. даны натуральные числа. Значит меньшее число равно 11. Второе число равно 11+6=17. Ответ: 11 и 17.

№563. (Самостоятельная работа, с последующей проверкой)

Найдите катеты прямоугольного треугольника, если известно, что их сумма равна 23 см, а площадь данного треугольника равна 60 см². Решение. (х(23-х)):2=60. D=49, х₁=8, х₂=15. Ответ: 8 и 15.

6. Итоги урока. Мы рассмотрели задачи, которые решаются с помощью квадратного уравнения, учились видеть связь между математикой и окружающей жизнью, использовали в решении знания геометрии и физики.

7. Домашнее задание. П.23, № 560, 564,569(старинная задача). Дополнительные задания:№ 576, 557.

Индивидуальное задание: Брат и сестра собирали малину. Когда сестра собрала 2/3 своего двухлитрового бидона, трехлитровый бидон брата был почти полон. Ребята поменялись бидонами и через некоторое время одновременно закончили сбор ягод. Во сколько раз брат работал быстрее сестры?

Решение. Сначала сестра собрала 2/3 * 2 = 4/3л малины. Пусть брат собрал в k раз больше (k>1), то есть 4/3k л. Потом сестра собрала 3 – 4/3k, а брат в k раз больше: 3k – 4/3k², что составило 2 – 4/3 = 2/3 л. Составим уравнение

3k – 4/3k² = 2/3,

Откуда k = 2 (k = ¼ не удовлетворяет условию k >1). То есть брат работает быстрее сестры в 2 раза. Ответ: в 2 раза.

Результативность урока: материал к уроку подбирался с учетом лекций А.В. Шевкина “Текстовые задачи в школьном курсе математики”, использовались его рекомендации. Урок прошел с хорошей результативностью. При изучении нового материала учащиеся практически самостоятельно решали предложенные задачи. Наблюдался хороший темп урока. Задачи, связанные с окружающей жизнью разнообразили стандартные задачи из учебника.

urok.1sept.ru